Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-20T11:54:54.230Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological stability for homeomorphisms with global attractor

Part of: Topological dynamics Local and nonlocal bifurcation theory

Published online by Cambridge University Press:  29 November 2023

Carlos Arnoldo Morales Open the ORCID record for Carlos Arnoldo Morales [Opens in a new window]  and
Nguyen Thanh Nguyen
Carlos Arnoldo Morales*
Affiliation:
Instituto de Matemática, Universidade Federal do Rio de Janeiro, P. O. Box 68530, 21945-970 Rio de Janeiro, Brazil
Nguyen Thanh Nguyen
Affiliation:
Department of Mathematics, Chungnam National University, Daejeon 34134, Republic of Korea e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that every topologically stable homeomorphism with global attractor of 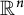$\mathbb {R}^n$ is topologically stable on its global attractor. The converse is not true. On the other hand, if a homeomorphism with global attractor of a locally compact metric space is expansive and has the shadowing property, then it is topologically stable. This extends the Walters stability theorem (Walters, On the pseudo-orbit tracing property and its relationship to stability. The structure of attractors in dynamical systems, 1978, pp. 231–244).

Keywords

Global attractorhomeomorphismtopological stability

MSC classification

Primary: 37B25: Lyapunov functions and stability; attractors, repellers
Secondary: 37G35: Attractors and their bifurcations
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 2 , June 2024 , pp. 493 - 503
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was partially supported by Basic Science Research Program through the NRF funded by the Ministry of Education (Grant No. 2022R1l1A3053628). C.A.M. was also partially supported by CNPq-Brazil (Grant No. 307776/2019-0).

References

Andromov, A. and Pontrjagin, L., Structurally stable systems . Dokl. Akad. Nauk URSS 14(1937), 247–251.Google Scholar
Artigue, A., Lipschitz perturbations of expansive systems . Discrete Contin. Dyn. Syst. 35(2015), 1829–1841.CrossRefGoogle Scholar
Bernardi, O., Florio, A., and Wiseman, J., The generalized recurrent set, explosions and Lyapunov functions . J. Dynam. Differential Equations 32(2020), no. 4, 1797–1817.CrossRefGoogle Scholar
Block, L. and Franke, J. E., The chain recurrent set, attractors, and explosions . Ergodic Theory Dynam. Systems 5(1985), no. 3, 321–327.CrossRefGoogle Scholar
Cousillas, G., Groisman, J., and Xavier, J., Topologically Anosov plane homeomorphisms . Topol. Methods Nonlinear Anal. 54(2019), 371–382.Google Scholar
Dydak, J. and Hoffland, C. S., An alternative definition of coarse structures . Topology Appl. 155(2008), 1013–1021.CrossRefGoogle Scholar
Gromov, M., Groups of polynomial growth and expanding maps . Inst. Hautes Études Sci. Publ. Math. 53(1981), 53–73.CrossRefGoogle Scholar
Hale, J., Asymptotic behavior of dissipative systems, Mathematical Surveys and Monographs, 25, American Mathematical Society, Providence, RI, 1988.Google Scholar
Hirsch, M., Differential topology, Graduate Text in Mathematics, 33, Springer, New York, 1976.CrossRefGoogle Scholar
Lee, J. and Nguyen, N., Topological stability of Chafee-Infante equations under Lipschitz perturbations of the domain and equation . J. Math. Anal. Appl. 517(2023), Article No. 126628, 28 pp.CrossRefGoogle Scholar
Lee, K., Nguyen, N.-T., and Yang, Y., Topological stability and spectral decomposition for homeomorphisms on noncompact spaces . Discrete Contin. Dyn. Syst. 38(2018), 2487–2503.CrossRefGoogle Scholar
Lee, J. and Rojas, A., A topological shadowing theorem . Proc. Indian Acad. Sci. Math. Sci. 132(2022), no. 1, Article No. 32, 9 pp.CrossRefGoogle Scholar
Nitecki, Z., On semi-stability for diffeomorphisms . Invent. Math. 14(1971), 83–122.CrossRefGoogle Scholar
Raugel, G., Global attractors in partial differential equations. In: B. Fiedler (ed.), Handbook of dynamical systems II, Freie Universität Berlin, Berlin, 2002, pp. 887–982.CrossRefGoogle Scholar
Robbin, J. W., Review of the article “on semi-stability for diffeomorphisms” (in Invent. Math. 14 (1971), 83–122, by Zbigniew Nitecki) . Mathematical Reviews/MathSciNet MR0293671.Google Scholar
Robinson, J. C., Infinite-dimensional dynamical systems. An introduction to dissipative parabolic PDEs and the theory of global attractors, Cambridge Texts in Applied Mathematics, Cambridge University Press, Cambridge, 2001.Google Scholar
Robinson, J. C. and Sánchez-Gabites, J. J., On finite-dimensional global attractors of homeomorphisms . Bull. Lond. Math. Soc. 48(2016), 483–498.CrossRefGoogle Scholar
Sears, M., Expansiveness of locally compact spaces . Math. Systems Theory 7(1974), 377–382.CrossRefGoogle Scholar
Shub, M. and Smale, S., Beyond hyperbolicity . Ann. of Math. (2) 96(1972), no. 3, 576–591.CrossRefGoogle Scholar
Smale, S., Differentiable dynamical systems . Bull. Amer. Math. Soc. 73(1967), 747–817.CrossRefGoogle Scholar
Utz, W. R., Unstable homeomorphisms . Proc. Amer. Math. Soc. 1(1950), 769–774.CrossRefGoogle Scholar
Walters, P., On the pseudo-orbit tracing property and its relationship to stability. The structure of attractors in dynamical systems . In Proc. Conf., North Dakota State Univ., Fargo, N.D., 1977, Lecture Notes in Mathematics, 668, Springer, Berlin, 1978, pp. 231–244.Google Scholar
Walters, P., Anosov diffeomorphisms are topologically stable . Topology 9(1970), 71–78.CrossRefGoogle Scholar
Weil, A., Sur les espaces a structure uniforme et Sur la topologie generale, Hermann, Paris, 1938.Google Scholar