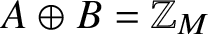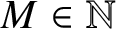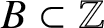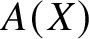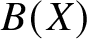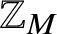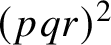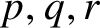1 Introduction
A set ![]() $A\subset \mathbb {Z}$ tiles the integers by translations if
$A\subset \mathbb {Z}$ tiles the integers by translations if ![]() $\mathbb {Z}$ can be covered by pairwise disjoint translates of A. Equivalently, there exists a set
$\mathbb {Z}$ can be covered by pairwise disjoint translates of A. Equivalently, there exists a set ![]() $T\subset \mathbb {Z}$ (the set of translations) such that every integer
$T\subset \mathbb {Z}$ (the set of translations) such that every integer ![]() $n\in \mathbb {Z}$ can be represented uniquely as
$n\in \mathbb {Z}$ can be represented uniquely as ![]() $n=a+t$ with
$n=a+t$ with ![]() $a\in A$ and
$a\in A$ and ![]() $t\in T$. Throughout this article, we assume that A is finite and nonempty, and call it a finite tile if it tiles the integers. Newman [Reference Newman34] proved that any tiling of
$t\in T$. Throughout this article, we assume that A is finite and nonempty, and call it a finite tile if it tiles the integers. Newman [Reference Newman34] proved that any tiling of ![]() $\mathbb {Z}$ by a finite set A must be periodic – that is,
$\mathbb {Z}$ by a finite set A must be periodic – that is, ![]() $T=B\oplus M\mathbb {Z}$ for some finite set
$T=B\oplus M\mathbb {Z}$ for some finite set ![]() $B\subset \mathbb {Z}$ such that
$B\subset \mathbb {Z}$ such that ![]() $\lvert A\rvert \lvert B\rvert =M$. Equivalently,
$\lvert A\rvert \lvert B\rvert =M$. Equivalently, ![]() $A\oplus B$ is a factorisation of the cyclic group
$A\oplus B$ is a factorisation of the cyclic group ![]() $\mathbb {Z}_M$, with B as the tiling complement.
$\mathbb {Z}_M$, with B as the tiling complement.
We are interested in investigating the properties of finite tiles. While this is a natural and attractive question, surprisingly little is known on this subject.
Newman’s proof provides a bound on the tiling period, ![]() $M\leq 2^{\max (A)-\min (A)}$. Thus, given a finite set
$M\leq 2^{\max (A)-\min (A)}$. Thus, given a finite set ![]() $A\subset \mathbb {Z}$, the question of whether A is a tile is at least in principle computationally decidable. However, Newman’s bound is exponential in diameter, and can therefore be very large even if A has only a few elements. A more effective bound was proved recently by Greenfeld and Tao [Reference Greenfeld and Tao13].
$A\subset \mathbb {Z}$, the question of whether A is a tile is at least in principle computationally decidable. However, Newman’s bound is exponential in diameter, and can therefore be very large even if A has only a few elements. A more effective bound was proved recently by Greenfeld and Tao [Reference Greenfeld and Tao13].
Further important reductions and observations were made by Sands [Reference Sands37], Tijdeman [Reference Tijdeman47] and Coven and Meyerowitz [Reference Coven and Meyerowitz2]. Sands’ theorem on replacement of factors [Reference Sands37] states that if ![]() $A\oplus B=\mathbb {Z}_M$ and M has at most two distinct prime divisors, then at least one of A and B must be contained in a proper subgroup of
$A\oplus B=\mathbb {Z}_M$ and M has at most two distinct prime divisors, then at least one of A and B must be contained in a proper subgroup of ![]() $\mathbb {Z}_M$. The proof of this is based on a characterisation of tiling pairs, also due to Sands, which we state here as Theorem 2.5. Tijdeman [Reference Tijdeman47] proved that if a finite set A tiles the integers, and if
$\mathbb {Z}_M$. The proof of this is based on a characterisation of tiling pairs, also due to Sands, which we state here as Theorem 2.5. Tijdeman [Reference Tijdeman47] proved that if a finite set A tiles the integers, and if ![]() $r\in \mathbb {N}$ is relatively prime to
$r\in \mathbb {N}$ is relatively prime to ![]() $\lvert A\rvert $, then
$\lvert A\rvert $, then ![]() $rA:=\{ra:a\in A\}$ also tiles
$rA:=\{ra:a\in A\}$ also tiles ![]() $\mathbb {Z}$ with the same tiling complement. Coven and Meyerowitz [Reference Coven and Meyerowitz2, Lemma 2.3] used this to prove that if a finite set A tiles the integers, then it also tiles
$\mathbb {Z}$ with the same tiling complement. Coven and Meyerowitz [Reference Coven and Meyerowitz2, Lemma 2.3] used this to prove that if a finite set A tiles the integers, then it also tiles ![]() $\mathbb {Z}_M$ for some M which has the same prime factors as
$\mathbb {Z}_M$ for some M which has the same prime factors as ![]() $\lvert A\rvert $.
$\lvert A\rvert $.
For the last two decades, the state-of-the-art work on the subject was due to Coven and Meyerowitz [Reference Coven and Meyerowitz2]. In order to describe their main result, we need to introduce some notation, which we will also use throughout this article. By translational invariance, we may assume that ![]() $A,B\subset \{0,1,\dotsc \}$ and that
$A,B\subset \{0,1,\dotsc \}$ and that ![]() $0\in A\cap B$. The characteristic polynomials (also known as mask polynomials) of A and B are
$0\in A\cap B$. The characteristic polynomials (also known as mask polynomials) of A and B are
 $$ \begin{align*} A(X)=\sum_{a\in A}X^a,\qquad B(X)=\sum_{b\in B}X^b. \end{align*} $$
$$ \begin{align*} A(X)=\sum_{a\in A}X^a,\qquad B(X)=\sum_{b\in B}X^b. \end{align*} $$Then ![]() $A\oplus B=\mathbb {Z}_M$ is equivalent to
$A\oplus B=\mathbb {Z}_M$ is equivalent to
 $$ \begin{align} A(X)B(X)=1+X+\dotsb+X^{M-1} \mod \left(X^M-1\right). \end{align} $$
$$ \begin{align} A(X)B(X)=1+X+\dotsb+X^{M-1} \mod \left(X^M-1\right). \end{align} $$ Let ![]() $\Phi _s(X)$ be the sth cyclotomic polynomial – that is, the unique monic, irreducible polynomial whose roots are the primitive sth roots of unity. Alternatively,
$\Phi _s(X)$ be the sth cyclotomic polynomial – that is, the unique monic, irreducible polynomial whose roots are the primitive sth roots of unity. Alternatively, ![]() $\Phi _s$ can be defined inductively via the identity
$\Phi _s$ can be defined inductively via the identity
 $$ \begin{align} X^n-1=\prod_{s\mid n}\Phi_s(X). \end{align} $$
$$ \begin{align} X^n-1=\prod_{s\mid n}\Phi_s(X). \end{align} $$In particular, equation (1.1) is equivalent to
Since ![]() $\Phi _s$ are irreducible, each
$\Phi _s$ are irreducible, each ![]() $\Phi _s(X)$ with
$\Phi _s(X)$ with ![]() $s\mid M$ must divide at least one of
$s\mid M$ must divide at least one of ![]() $A(X)$ and
$A(X)$ and ![]() $B(X)$.
$B(X)$.
Coven and Meyerowitz [Reference Coven and Meyerowitz2] proved the following theorem:
Theorem 1.1 [Reference Coven and Meyerowitz2]
Let ![]() $S_A$ be the set of prime powers
$S_A$ be the set of prime powers ![]() $p^\alpha $ such that
$p^\alpha $ such that ![]() $\Phi _{p^\alpha }(X)$ divides
$\Phi _{p^\alpha }(X)$ divides ![]() $A(X)$. Consider the following conditions:
$A(X)$. Consider the following conditions:
(T1)
 $A(1)=\prod _{s\in S_A}\Phi _s(1)$.
$A(1)=\prod _{s\in S_A}\Phi _s(1)$.(T2) If
 $s_1,\dotsc ,s_k\in S_A$ are powers of different primes, then
$s_1,\dotsc ,s_k\in S_A$ are powers of different primes, then  $\Phi _{s_1\dotsm s_k}(X)$ divides
$\Phi _{s_1\dotsm s_k}(X)$ divides  $A(X)$.
$A(X)$.
Then we have the following:
• If A satisfies (T1) and (T2), then A tiles
 $\mathbb {Z}$.
$\mathbb {Z}$.• If A tiles
 $\mathbb {Z}$, then (T1) holds.
$\mathbb {Z}$, then (T1) holds.• If A tiles
 $\mathbb {Z}$ and
$\mathbb {Z}$ and  $\lvert A\rvert $ has at most two distinct prime factors, then (T2) holds.
$\lvert A\rvert $ has at most two distinct prime factors, then (T2) holds.
Condition (T1) is, essentially, a counting condition, and is relatively easy to prove. For sets ![]() $A\subset \mathbb {Z}$ such that
$A\subset \mathbb {Z}$ such that ![]() $\lvert A\rvert $ is a prime power, (T1) is a necessary and sufficient condition for A to be a tile [Reference Newman34]. (In this case, (T2) is vacuous.)
$\lvert A\rvert $ is a prime power, (T1) is a necessary and sufficient condition for A to be a tile [Reference Newman34]. (In this case, (T2) is vacuous.)
Condition (T2) is much deeper. Coven and Meyerowitz [Reference Coven and Meyerowitz2] proved that if (T2) holds, then ![]() $A\oplus B^\flat =\mathbb {Z}_M$ is a tiling, where
$A\oplus B^\flat =\mathbb {Z}_M$ is a tiling, where ![]() $M=\mathrm {lcm}(S_A)$ and
$M=\mathrm {lcm}(S_A)$ and ![]() $B^\flat $ is an explicitly constructed and highly structured ‘standard’ tiling complement depending only on the prime-power cyclotomic divisors of
$B^\flat $ is an explicitly constructed and highly structured ‘standard’ tiling complement depending only on the prime-power cyclotomic divisors of ![]() $A(X)$. We prove in Section 3 that having a tiling complement of this type is in fact equivalent to (T2). While this equivalence was not stated explicitly in [Reference Coven and Meyerowitz2], it follows readily from the methods developed there.
$A(X)$. We prove in Section 3 that having a tiling complement of this type is in fact equivalent to (T2). While this equivalence was not stated explicitly in [Reference Coven and Meyerowitz2], it follows readily from the methods developed there.
The Coven–Meyerowitz proof of (T2) for all finite tiles with two distinct prime factors relies on the aforementioned structure and replacement theorems of Sands [Reference Sands37] and Tijdeman [Reference Tijdeman47]. In [Reference Coven and Meyerowitz2, Lemma 2.3], the authors deduce from Tijdeman’s theorem that if A tiles the integers and ![]() $\lvert A\rvert $ has at most two distinct prime factors, then A admits a tiling
$\lvert A\rvert $ has at most two distinct prime factors, then A admits a tiling ![]() $A\oplus B=\mathbb {Z}_M$, where M has at most two distinct prime factors. By Sands’ theorem, one of A and B must then be contained in a proper subgroup of
$A\oplus B=\mathbb {Z}_M$, where M has at most two distinct prime factors. By Sands’ theorem, one of A and B must then be contained in a proper subgroup of ![]() $\mathbb {Z}_M$. Coven and Meyerowitz use this to set up an inductive argument.
$\mathbb {Z}_M$. Coven and Meyerowitz use this to set up an inductive argument.
A closer analysis of the Coven–Meyerowitz argument yields the same result in the case when ![]() $M=p_1^{n_1} \dotsm p_K^{n_K}$, where
$M=p_1^{n_1} \dotsm p_K^{n_K}$, where ![]() $p_1,\dotsc ,p_K$ are distinct primes,
$p_1,\dotsc ,p_K$ are distinct primes, ![]() $n_1,\dotsc ,n_K\in \mathbb {N}$ are arbitrary and at most two of
$n_1,\dotsc ,n_K\in \mathbb {N}$ are arbitrary and at most two of ![]() $p_1,\dotsc ,p_K$ divide both
$p_1,\dotsc ,p_K$ divide both ![]() $\lvert A\rvert $ and
$\lvert A\rvert $ and ![]() $\lvert B\rvert $. Essentially, any such case can be reduced to the two-prime case via Tijdeman’s theorem and [Reference Coven and Meyerowitz2, Lemma 2.3], whereupon Theorem 1.1 may be applied. We provide the details in Corollary 6.2. (See also [Reference Dutkay and Kraus4, Reference Shi39, Reference Tao46].)
$\lvert B\rvert $. Essentially, any such case can be reduced to the two-prime case via Tijdeman’s theorem and [Reference Coven and Meyerowitz2, Lemma 2.3], whereupon Theorem 1.1 may be applied. We provide the details in Corollary 6.2. (See also [Reference Dutkay and Kraus4, Reference Shi39, Reference Tao46].)
The goal of the present article is to develop methods that can be used in the study of tilings ![]() $A\oplus B=\mathbb {Z}_M$, where M is permitted to have three or more prime factors dividing both
$A\oplus B=\mathbb {Z}_M$, where M is permitted to have three or more prime factors dividing both ![]() $\lvert A\rvert $ and
$\lvert A\rvert $ and ![]() $\lvert B\rvert $. Sands’ factorisation theorem does not hold in this case, with counterexamples in [Reference Lagarias and Szabó25, Reference Szabó43]. For the same reason, the Coven–Meyerowitz proof does not extend to such tilings. We emphasise that this is not just a technical issue. Tilings with three or more distinct prime factors dividing both
$\lvert B\rvert $. Sands’ factorisation theorem does not hold in this case, with counterexamples in [Reference Lagarias and Szabó25, Reference Szabó43]. For the same reason, the Coven–Meyerowitz proof does not extend to such tilings. We emphasise that this is not just a technical issue. Tilings with three or more distinct prime factors dividing both ![]() $\lvert A\rvert $ and
$\lvert A\rvert $ and ![]() $\lvert B\rvert $ are genuinely different, and any comprehensive analysis of them must account for new phenomena that have no counterparts for two prime factors, such as Szabó’s examples [Reference Szabó43].
$\lvert B\rvert $ are genuinely different, and any comprehensive analysis of them must account for new phenomena that have no counterparts for two prime factors, such as Szabó’s examples [Reference Szabó43].
The simplest tilings that cannot be reduced to the two-prime case using the methods of [Reference Coven and Meyerowitz2] are of the form ![]() $A\oplus B=\mathbb {Z}_M$, where
$A\oplus B=\mathbb {Z}_M$, where ![]() $\lvert A\rvert =\lvert B\rvert =p_1p_2p_3$ and
$\lvert A\rvert =\lvert B\rvert =p_1p_2p_3$ and ![]() $p_1,p_2,p_3$ are distinct primes. In our follow-up paper [Reference Łaba and Londner24], we use the methods developed here to resolve this case when
$p_1,p_2,p_3$ are distinct primes. In our follow-up paper [Reference Łaba and Londner24], we use the methods developed here to resolve this case when ![]() $p_1,p_2,p_3$ are odd.
$p_1,p_2,p_3$ are odd.
Theorem 1.2 [Reference Łaba and Londner24]
Let  $M=p_i^2p_j^2p_k^2$, where
$M=p_i^2p_j^2p_k^2$, where ![]() $p_i,p_j,p_k$ are distinct odd primes. Assume that
$p_i,p_j,p_k$ are distinct odd primes. Assume that ![]() $A\oplus B=\mathbb {Z}_M$, with
$A\oplus B=\mathbb {Z}_M$, with ![]() $\lvert A\rvert =\lvert B\rvert =p_ip_jp_k$. Then both A and B satisfy (T2).
$\lvert A\rvert =\lvert B\rvert =p_ip_jp_k$. Then both A and B satisfy (T2).
While our complete proof of Theorem 1.2 works only under the assumptions indicated, many of our tools, methods and intermediate results apply to general tilings ![]() $A\oplus B=\mathbb {Z}_M$, raising the possibility of further extensions and improvements. We therefore chose to present them here in more generality, deferring the actual proof of Theorem 1.2 to [Reference Łaba and Londner24], which is restricted to the three-prime setting.
$A\oplus B=\mathbb {Z}_M$, raising the possibility of further extensions and improvements. We therefore chose to present them here in more generality, deferring the actual proof of Theorem 1.2 to [Reference Łaba and Londner24], which is restricted to the three-prime setting.
We begin with the notation and preliminaries in Section 2. We identify  $\mathbb {Z}_M=\mathbb {Z}_{p_1^{n_1} \dotsm p_K^{n_K}}$ with
$\mathbb {Z}_M=\mathbb {Z}_{p_1^{n_1} \dotsm p_K^{n_K}}$ with  $\mathbb {Z}_{p_1^{n_1}}\oplus \dotsb \oplus \mathbb {Z}_{p_K^{n_K}}$, and use the induced coordinate system to identify the given tiling with a tiling of a multidimensional lattice. This allows a geometric viewpoint, whereby we can describe the tiling in terms of objects such as lines, planes or fibers (arithmetic progressions of maximal length on certain scales). We emphasise, however, that the problem under consideration is much more specific than the study of tilings of multidimensional lattices in general. It is important in our work that the different coordinate directions correspond to distinct primes.
$\mathbb {Z}_{p_1^{n_1}}\oplus \dotsb \oplus \mathbb {Z}_{p_K^{n_K}}$, and use the induced coordinate system to identify the given tiling with a tiling of a multidimensional lattice. This allows a geometric viewpoint, whereby we can describe the tiling in terms of objects such as lines, planes or fibers (arithmetic progressions of maximal length on certain scales). We emphasise, however, that the problem under consideration is much more specific than the study of tilings of multidimensional lattices in general. It is important in our work that the different coordinate directions correspond to distinct primes.
In Section 3, we present an alternative formulation of (T2) in terms of standard tiling complements. Roughly speaking, if ![]() $A\oplus B=\mathbb {Z}_M$ is a tiling, then B satisfies (T2) if and only if its tiling complement A can be replaced by a highly structured ‘standard set’
$A\oplus B=\mathbb {Z}_M$ is a tiling, then B satisfies (T2) if and only if its tiling complement A can be replaced by a highly structured ‘standard set’ ![]() $A^\flat $ with the same prime-power cyclotomic divisors as A. Such standard sets were already used in [Reference Coven and Meyerowitz2] to prove that (T1) and (T2) imply tiling. Here, we state the formal implication in the other direction. In this formulation, condition (T2) can be viewed as a distant cousin of questions on replacement of factors in factorisation of finite abelian groups (see [Reference Szabó44] for an overview).
$A^\flat $ with the same prime-power cyclotomic divisors as A. Such standard sets were already used in [Reference Coven and Meyerowitz2] to prove that (T1) and (T2) imply tiling. Here, we state the formal implication in the other direction. In this formulation, condition (T2) can be viewed as a distant cousin of questions on replacement of factors in factorisation of finite abelian groups (see [Reference Szabó44] for an overview).
In Section 4, we introduce one of our main tools, the box product. The idea comes from an unpublished paper [Reference Granville, Łaba and Wang11], and our main harmonic-analytic identity, Theorem 4.7, is in fact a reprise of [Reference Granville, Łaba and Wang11, Theorem 1] with relatively minor modifications. We are, however, able to use it much more effectively. (We caution the reader that, while [Reference Granville, Łaba and Wang11, Theorem 1] is correct, the proof of the main tiling result in [Reference Granville, Łaba and Wang11] contains an error that cannot be readily fixed with the methods of that paper.)
Our goal is to be able to start with an arbitrary tiling ![]() $A\oplus B=\mathbb {Z}_M$, and prove that either at least one of the sets A or B can be replaced directly by the corresponding standard tiling complement (which proves (T2), as already indicated) or else we can pass to tilings with a smaller period
$A\oplus B=\mathbb {Z}_M$, and prove that either at least one of the sets A or B can be replaced directly by the corresponding standard tiling complement (which proves (T2), as already indicated) or else we can pass to tilings with a smaller period ![]() $N\mid M$ and apply an inductive argument. The machinery to do this is developed in Sections 5–8, and includes the following main ingredients.
$N\mid M$ and apply an inductive argument. The machinery to do this is developed in Sections 5–8, and includes the following main ingredients.
Cuboids (Section 5) and fibering (Section 8) are our main tools in determining cyclotomic divisibility and proving structural properties. Cuboids have been used previously in the literature in the context of vanishing sums of roots of unity [Reference Steinberger42] and Fuglede’s spectral set conjecture [Reference Kiss, Malikiosis, Somlai and Vizer16]. We often have to use both cuboids and fibering at several scales at the same time. In particular, we introduce ‘multiscale’ cuboids that correspond to divisibility by combinations of several cyclotomic polynomials.
In Section 6, we discuss two reductions that allow us to pass to tilings with a smaller period, with the (T2) property preserved under the decomposition. We first review the subgroup reduction from [Reference Coven and Meyerowitz2]. Then we introduce a ‘slab reduction’, which we believe to be new and which covers many cases of interest that are not covered by the subgroup reduction. We also develop a criterion for this reduction to apply. A concrete example of this is provided in Corollary 6.8.
While the subgroup reduction is sufficient to prove Theorem 1.1, tilings with three or more distinct prime factors include cases where such inductive arguments do not appear to be easily applicable. One well-known obstruction to an inductive approach is provided by Szabó-type examples [Reference Szabó43]. However, Szabó’s examples are known to satisfy (T2). This was observed already by Coven and Meyerowitz [Reference Coven and Meyerowitz2]; see also [Reference Dutkay and Kraus4] for an explicit analysis of a class of examples based on Szabó’s idea.
We do not know whether Szabó-type constructions are the only obstacle to an inductive proof of (T2) for all finite tiles. In [Reference Łaba and Londner24], we prove that this is indeed true for classes of tilings that are broad enough to include all tilings of ![]() $\mathbb {Z}_M$ with
$\mathbb {Z}_M$ with ![]() $M=(p_1p_2p_3)^2$. The key new concept turns out to be saturating sets – subsets of A and B that saturate appropriately chosen box products (Section 7). Informally, if a tile A contains geometric configurations that indicate a lack of structure on a certain scale, we are able to use it to our advantage and locate highly structured configurations elsewhere in both A and B. In particular, the less structure we have in one of the tiles, the more structured the other one is expected to be. In the case
$M=(p_1p_2p_3)^2$. The key new concept turns out to be saturating sets – subsets of A and B that saturate appropriately chosen box products (Section 7). Informally, if a tile A contains geometric configurations that indicate a lack of structure on a certain scale, we are able to use it to our advantage and locate highly structured configurations elsewhere in both A and B. In particular, the less structure we have in one of the tiles, the more structured the other one is expected to be. In the case ![]() $M=(p_1p_2p_3)^2$, we use this to prove that all tilings with ‘unfibered grids’ (see [Reference Łaba and Londner24] for the definition) must in fact come from Szabó-type constructions. With this established, we can prove (T2) for such tilings by reduction to standard tiling complements. The full argument is carried out in [Reference Łaba and Londner24], but we also provide examples of this procedure here in Section 8.5.
$M=(p_1p_2p_3)^2$, we use this to prove that all tilings with ‘unfibered grids’ (see [Reference Łaba and Londner24] for the definition) must in fact come from Szabó-type constructions. With this established, we can prove (T2) for such tilings by reduction to standard tiling complements. The full argument is carried out in [Reference Łaba and Londner24], but we also provide examples of this procedure here in Section 8.5.
In addition to applications to proving structural conditions such as (T2), we are able to use saturating sets to identify sets ![]() $A\subset \mathbb {Z}_M$ that do not tile
$A\subset \mathbb {Z}_M$ that do not tile ![]() $\mathbb {Z}_M$ based on the presence of certain configurations. Results of this type include Lemma 7.10 and Proposition 7.11.
$\mathbb {Z}_M$ based on the presence of certain configurations. Results of this type include Lemma 7.10 and Proposition 7.11.
In Section 9 we discuss open questions and possible directions of study arising from our research so far.
Since the work of Coven and Meyerowitz, there has been essentially no progress in proving (T2), except for a few special cases of limited importance (such as [Reference Konyagin and Łaba22]) and cases covered by Corollary 6.2 [Reference Dutkay and Kraus4, Reference Shi39, Reference Tao46]. However, there have been significant recent developments on other questions related to tiling and cyclotomic divisibility. Notably, Bhattacharya [Reference Bhattacharya1] has established the periodic tiling conjecture in ![]() $\mathbb {Z}^2$, with a quantitative version due to Greenfeld and Tao [Reference Greenfeld and Tao13]. In a continuous setting, there has been recent work on tilings of the real line by a function [Reference Kolountzakis and Lev19].
$\mathbb {Z}^2$, with a quantitative version due to Greenfeld and Tao [Reference Greenfeld and Tao13]. In a continuous setting, there has been recent work on tilings of the real line by a function [Reference Kolountzakis and Lev19].
There is an important connection between the Coven–Meyerowitz tiling conditions and Fuglede’s spectral set conjecture [Reference Fuglede10]. The conjecture, dating back to the 1970s, states that a set ![]() $\Omega \subset \mathbb {R}^n$ of positive n-dimensional Lebesgue measure tiles
$\Omega \subset \mathbb {R}^n$ of positive n-dimensional Lebesgue measure tiles ![]() $\mathbb {R}^n$ by translations if and only if the space
$\mathbb {R}^n$ by translations if and only if the space ![]() $L^2(\Omega )$ admits an orthogonal basis of exponential functions. A set with the latter property is called a spectral set. While the question originated in functional analysis, it has intriguing connections to many other areas of mathematics, from convex geometry to wavelets, oscillatory integral estimates and number theory. The conjecture is now known to be false in dimensions
$L^2(\Omega )$ admits an orthogonal basis of exponential functions. A set with the latter property is called a spectral set. While the question originated in functional analysis, it has intriguing connections to many other areas of mathematics, from convex geometry to wavelets, oscillatory integral estimates and number theory. The conjecture is now known to be false in dimensions ![]() $3$ and higher [Reference Farkas, Matolcsi and Móra8, Reference Farkas and Révész9, Reference Kolountzakis and Matolcsi20, Reference Kolountzakis and Matolcsi21, Reference Matolcsi33, Reference Tao45]. Nonetheless, many important cases remain open and continue to attract attention. Iosevich, Katz and Tao [Reference Iosevich, Katz and Tao14] proved in 2003 that Fuglede’s conjecture holds for convex sets in
$3$ and higher [Reference Farkas, Matolcsi and Móra8, Reference Farkas and Révész9, Reference Kolountzakis and Matolcsi20, Reference Kolountzakis and Matolcsi21, Reference Matolcsi33, Reference Tao45]. Nonetheless, many important cases remain open and continue to attract attention. Iosevich, Katz and Tao [Reference Iosevich, Katz and Tao14] proved in 2003 that Fuglede’s conjecture holds for convex sets in ![]() $\mathbb {R}^2$; an analogous result in higher dimensions was proved only recently, by Greenfeld and Lev [Reference Greenfeld and Lev12] for
$\mathbb {R}^2$; an analogous result in higher dimensions was proved only recently, by Greenfeld and Lev [Reference Greenfeld and Lev12] for ![]() $n=3$ and by Lev and Matolcsi [Reference Lev and Matolcsi29] for general n. There has also been extensive work on the finite abelian group analogue of the conjecture [Reference Fallon, Mayeli and Villano7, Reference Fallon, Kiss and Somlai6, Reference Iosevich, Mayeli and Pakianathan15, Reference Kiss, Malikiosis, Somlai and Vizer16, Reference Kiss, Malikiosis, Somlai and Vizer17, Reference Kiss and Somlai18, Reference Malikiosis30, Reference Malikiosis and Kolountzakis31, Reference Shi39, Reference Shi40, Reference Somlai41, Reference Zhang48].
$n=3$ and by Lev and Matolcsi [Reference Lev and Matolcsi29] for general n. There has also been extensive work on the finite abelian group analogue of the conjecture [Reference Fallon, Mayeli and Villano7, Reference Fallon, Kiss and Somlai6, Reference Iosevich, Mayeli and Pakianathan15, Reference Kiss, Malikiosis, Somlai and Vizer16, Reference Kiss, Malikiosis, Somlai and Vizer17, Reference Kiss and Somlai18, Reference Malikiosis30, Reference Malikiosis and Kolountzakis31, Reference Shi39, Reference Shi40, Reference Somlai41, Reference Zhang48].
Combined with a sequence of results in [Reference Łaba23, Reference Lagarias and Wang26, Reference Lagarias and Wang27], proving (T2) for all finite integer tiles would resolve the ‘tiling implies spectrum’ part of Fuglede’s spectral set conjecture for all compact tiles of the real line in dimension ![]() $1$. Additionally, Dutkay and Lai [Reference Dutkay and Lai5] proved that if a similar property could be established for spectral sets, this would also resolve the converse part of the conjecture for compact sets in
$1$. Additionally, Dutkay and Lai [Reference Dutkay and Lai5] proved that if a similar property could be established for spectral sets, this would also resolve the converse part of the conjecture for compact sets in ![]() $\mathbb {R}$. While proving (T2) for a more narrow class of integer tiles does not have that implication, it still establishes one direction of Fuglede’s conjecture for that class of tiles in the finite group setting, as well as for sets
$\mathbb {R}$. While proving (T2) for a more narrow class of integer tiles does not have that implication, it still establishes one direction of Fuglede’s conjecture for that class of tiles in the finite group setting, as well as for sets ![]() $E=\bigcup _{a\in A} [a,a+1] \subset \mathbb {R}$, where
$E=\bigcup _{a\in A} [a,a+1] \subset \mathbb {R}$, where ![]() $A\subset \mathbb {Z}$ is an integer tile in the permitted class [Reference Łaba23].
$A\subset \mathbb {Z}$ is an integer tile in the permitted class [Reference Łaba23].
2 Notation and preliminaries
2.1 Multisets and mask polynomials
Let ![]() $M\geq 2$ be a fixed integer. Usually, we will work in either
$M\geq 2$ be a fixed integer. Usually, we will work in either ![]() $\mathbb {Z}_M$ or
$\mathbb {Z}_M$ or ![]() $\mathbb {Z}_N$ for some
$\mathbb {Z}_N$ for some ![]() $N\mid M$. In the context of the tiling problem, we reserve M for the tiling period and N for its divisors. We also reserve K for the number of the distinct prime divisors of M, and use
$N\mid M$. In the context of the tiling problem, we reserve M for the tiling period and N for its divisors. We also reserve K for the number of the distinct prime divisors of M, and use ![]() $p_1,\dotsc ,p_K$ to denote those divisors, so that
$p_1,\dotsc ,p_K$ to denote those divisors, so that
 $$ \begin{align*} M=\prod_{i=1}^K p_i^{n_i}, \end{align*} $$
$$ \begin{align*} M=\prod_{i=1}^K p_i^{n_i}, \end{align*} $$where ![]() $p_1,\dotsc ,p_K$ are distinct primes and
$p_1,\dotsc ,p_K$ are distinct primes and ![]() $n_1,\dotsc ,n_K\in \mathbb {N}$. We fix this notation and use it throughout the rest of the article. For a prime p, an integer m and a nonnegative integer
$n_1,\dotsc ,n_K\in \mathbb {N}$. We fix this notation and use it throughout the rest of the article. For a prime p, an integer m and a nonnegative integer ![]() $\alpha $, we will say that
$\alpha $, we will say that ![]() $p^\alpha \parallel m$ if
$p^\alpha \parallel m$ if ![]() $p^\alpha \mid m$ but
$p^\alpha \mid m$ but ![]() $p^{\alpha +1}\nmid m$.
$p^{\alpha +1}\nmid m$.
We use ![]() $A(X)$,
$A(X)$, ![]() $B(X)$, etc., to denote polynomials modulo
$B(X)$, etc., to denote polynomials modulo ![]() $X^M-1$ with integer coefficients. If
$X^M-1$ with integer coefficients. If ![]() $A(X)$ is such a polynomial, we define its weight function
$A(X)$ is such a polynomial, we define its weight function ![]() $w_A:\mathbb {Z}_M\to \mathbb {Z}$ so that
$w_A:\mathbb {Z}_M\to \mathbb {Z}$ so that ![]() $w_A(a)$ is the coefficient of
$w_A(a)$ is the coefficient of ![]() $X^a$ in
$X^a$ in ![]() $A(X)$. Thus
$A(X)$. Thus ![]() $A(X)=\sum _{a\in \mathbb {Z}_M} w_A(a) X^a$. If A has
$A(X)=\sum _{a\in \mathbb {Z}_M} w_A(a) X^a$. If A has ![]() $0$ or
$0$ or ![]() $1$ coefficients, then
$1$ coefficients, then ![]() $w_A$ is the characteristic function of a set
$w_A$ is the characteristic function of a set ![]() $A\subset \mathbb {Z}_M$. However, we will also consider polynomials with integer coefficients not necessarily equal to
$A\subset \mathbb {Z}_M$. However, we will also consider polynomials with integer coefficients not necessarily equal to ![]() $0$ or
$0$ or ![]() $1$. In that case,
$1$. In that case, ![]() $A(X)$ will correspond to a weighted multiset in
$A(X)$ will correspond to a weighted multiset in ![]() $\mathbb {Z}_M$, which we will also denote by A, with weights
$\mathbb {Z}_M$, which we will also denote by A, with weights ![]() $w_A(a)$ assigned to each
$w_A(a)$ assigned to each ![]() $a\in \mathbb {Z}_M$. We will use
$a\in \mathbb {Z}_M$. We will use ![]() $\mathcal {M}(\mathbb {Z}_M)$ to denote the family of all such weighted multisets in
$\mathcal {M}(\mathbb {Z}_M)$ to denote the family of all such weighted multisets in ![]() $\mathbb {Z}_M$, and reserve the notation
$\mathbb {Z}_M$, and reserve the notation ![]() $A\subset \mathbb {Z}_M$ for sets (with
$A\subset \mathbb {Z}_M$ for sets (with ![]() $0$ and
$0$ and ![]() $1$ weights). If
$1$ weights). If ![]() $A\in \mathcal {M}(\mathbb {Z}_M)$, the polynomial
$A\in \mathcal {M}(\mathbb {Z}_M)$, the polynomial ![]() $A(X)$ is sometimes called the mask polynomial of A. It will usually be clear from the context whether A refers to the weighted multiset or the corresponding polynomial; whenever there is any possibility of confusion, we will use A for the multiset and
$A(X)$ is sometimes called the mask polynomial of A. It will usually be clear from the context whether A refers to the weighted multiset or the corresponding polynomial; whenever there is any possibility of confusion, we will use A for the multiset and ![]() $A(X)$ for the polynomial.
$A(X)$ for the polynomial.
If ![]() $N\mid M$, then any
$N\mid M$, then any ![]() $A\in \mathcal {M}(\mathbb {Z}_M)$ induces a weighted multiset
$A\in \mathcal {M}(\mathbb {Z}_M)$ induces a weighted multiset ![]() $A \bmod N$ in
$A \bmod N$ in ![]() $\mathbb {Z}_N$, with the corresponding mask polynomial
$\mathbb {Z}_N$, with the corresponding mask polynomial ![]() $A(X) \bmod \left (X^N-1\right )$, and induced weights
$A(X) \bmod \left (X^N-1\right )$, and induced weights
 $$ \begin{align} w_A^N(x)= \sum_{x'\in\mathbb{Z}_M: x'\equiv x\bmod N} w_A(x'),\qquad x\in\mathbb{Z}_N. \end{align} $$
$$ \begin{align} w_A^N(x)= \sum_{x'\in\mathbb{Z}_M: x'\equiv x\bmod N} w_A(x'),\qquad x\in\mathbb{Z}_N. \end{align} $$For brevity, we will continue to write A and ![]() $A(X)$ for
$A(X)$ for ![]() $A \bmod N$ and
$A \bmod N$ and ![]() $A(X) \bmod \left (X^N-1\right )$, respectively, while working in
$A(X) \bmod \left (X^N-1\right )$, respectively, while working in ![]() $\mathbb {Z}_N$.
$\mathbb {Z}_N$.
If ![]() $A,B\in \mathcal {M}(\mathbb {Z}_M)$, we will use
$A,B\in \mathcal {M}(\mathbb {Z}_M)$, we will use ![]() $A+B$ to indicate the weighted multiset corresponding to the sum of mask polynomials, or, equivalently, the sum of weight functions:
$A+B$ to indicate the weighted multiset corresponding to the sum of mask polynomials, or, equivalently, the sum of weight functions:
We will use the convolution notation ![]() $A*B$ to denote the weighted sumset of A and B, so that
$A*B$ to denote the weighted sumset of A and B, so that ![]() $(A*B)(X)=A(X)B(X)$ and
$(A*B)(X)=A(X)B(X)$ and
 $$ \begin{align*} w_{A*B}(x)=(w_A*w_B)(x)=\sum_{y\in\mathbb{Z}_M} w_A(x-y)w_B(y). \end{align*} $$
$$ \begin{align*} w_{A*B}(x)=(w_A*w_B)(x)=\sum_{y\in\mathbb{Z}_M} w_A(x-y)w_B(y). \end{align*} $$If one of the sets is a singleton, say ![]() $A=\{x\}$, we will simplify the notation and write
$A=\{x\}$, we will simplify the notation and write ![]() $x*B=\{x\}*B$. The direct sum notation
$x*B=\{x\}*B$. The direct sum notation ![]() $A\oplus B$ is reserved for tilings – that is,
$A\oplus B$ is reserved for tilings – that is, ![]() $A\oplus B=\mathbb {Z}_M$ means that
$A\oplus B=\mathbb {Z}_M$ means that ![]() $A,B\subset \mathbb {Z}_M$ are both sets and
$A,B\subset \mathbb {Z}_M$ are both sets and  $A(X)B(X)=\frac {X^M-1}{X-1} \bmod \left (X^M-1\right )$.
$A(X)B(X)=\frac {X^M-1}{X-1} \bmod \left (X^M-1\right )$.
Since we will not need to use derivatives of polynomials in this article, we will use notation such as ![]() $A'$,
$A'$, ![]() $A''$, etc., to denote multisets and polynomials that need not have anything to do with the derivatives
$A''$, etc., to denote multisets and polynomials that need not have anything to do with the derivatives  $\frac {d}{dX}A(X)$,
$\frac {d}{dX}A(X)$,  $\frac {d^2}{dX^2}A(X)$ and so on.
$\frac {d^2}{dX^2}A(X)$ and so on.
2.2 Array coordinates
Suppose that  $M=\prod _{i=1}^K p_i^{n_i}$, where
$M=\prod _{i=1}^K p_i^{n_i}$, where ![]() $p_1,\dotsc ,p_K$ are distinct primes and
$p_1,\dotsc ,p_K$ are distinct primes and ![]() $n_i\in \mathbb {N}$. By the Chinese remainder theorem, we have
$n_i\in \mathbb {N}$. By the Chinese remainder theorem, we have
 $$ \begin{align*} \mathbb{Z}_M=\bigoplus_{i=1}^K \mathbb{Z}_{p_i^{n_i}}, \end{align*} $$
$$ \begin{align*} \mathbb{Z}_M=\bigoplus_{i=1}^K \mathbb{Z}_{p_i^{n_i}}, \end{align*} $$which we represent geometrically as a K-dimensional lattice. The tiling ![]() $A\oplus B=\mathbb {Z}_M$ can then be interpreted as a tiling of that lattice.
$A\oplus B=\mathbb {Z}_M$ can then be interpreted as a tiling of that lattice.
It will be useful to have an explicit coordinate system on ![]() $\mathbb {Z}_M$. We fix one as follows. Let
$\mathbb {Z}_M$. We fix one as follows. Let  $M_i = M/p_i^{n_i} = \prod _{j\neq i} p_j^{n_j}$; then each
$M_i = M/p_i^{n_i} = \prod _{j\neq i} p_j^{n_j}$; then each ![]() $x\in \mathbb {Z}_M$ can be written uniquely as
$x\in \mathbb {Z}_M$ can be written uniquely as
 $$ \begin{align*} x=\sum_{i=1}^K \pi_i(x) M_i,\quad \pi_i(x)\in \mathbb{Z}_{p_i^{n_i}}. \end{align*} $$
$$ \begin{align*} x=\sum_{i=1}^K \pi_i(x) M_i,\quad \pi_i(x)\in \mathbb{Z}_{p_i^{n_i}}. \end{align*} $$The mapping ![]() $x\to (\pi _1(x),\dotsc ,\pi _k(x))$ identifies x with an element of
$x\to (\pi _1(x),\dotsc ,\pi _k(x))$ identifies x with an element of  $\mathbb {Z}_{p_1^{n_1}}\times \dotsb \times \mathbb {Z}_{p_K^{n_K}}$. We will refer to the K-tuple
$\mathbb {Z}_{p_1^{n_1}}\times \dotsb \times \mathbb {Z}_{p_K^{n_K}}$. We will refer to the K-tuple ![]() $(\pi _1(x),\dotsc ,\pi _K(x))$ as the M-array coordinates of x.
$(\pi _1(x),\dotsc ,\pi _K(x))$ as the M-array coordinates of x.
We state a few easy properties for future reference.
(i)
 $x\equiv \pi _i(x)M_i \bmod p_i^{n_i}$.
$x\equiv \pi _i(x)M_i \bmod p_i^{n_i}$.(ii)
 $(x,M)=\prod _{i=1}^K p_i^{\gamma _i}$ if and only if
$(x,M)=\prod _{i=1}^K p_i^{\gamma _i}$ if and only if  $p_i^{\gamma _i} \parallel \pi _i(x)$ for each
$p_i^{\gamma _i} \parallel \pi _i(x)$ for each  $i=1,\dotsc ,K$.
$i=1,\dotsc ,K$.(iii) In particular,
 $x =0$ in
$x =0$ in  $\mathbb {Z}_M$ if and only if
$\mathbb {Z}_M$ if and only if  $\pi _i(x)=0$ for each
$\pi _i(x)=0$ for each  $i=1,\dotsc ,K$.
$i=1,\dotsc ,K$.(iv) If
 $x=\sum \pi _i(x)M_i$,
$x=\sum \pi _i(x)M_i$,  $y=\sum \pi _i(y)M_i$ and
$y=\sum \pi _i(y)M_i$ and  $x+y = z =\sum \pi _i(z)M_i$ are the respective coordinate representations, then
$x+y = z =\sum \pi _i(z)M_i$ are the respective coordinate representations, then  $\pi _i(z)\equiv \pi _i(x)+\pi _i(y) \bmod p_i^{n_i}$ for each
$\pi _i(z)\equiv \pi _i(x)+\pi _i(y) \bmod p_i^{n_i}$ for each  $i=1,\dotsc ,k$.
$i=1,\dotsc ,k$.
Each coordinate ![]() $\pi _i(x)$ of
$\pi _i(x)$ of ![]() $x\in \mathbb {Z}_M$ can be subdivided further into digits as follows. With
$x\in \mathbb {Z}_M$ can be subdivided further into digits as follows. With  $\mathbb {Z}_{p_i^{n_i}}$ represented as
$\mathbb {Z}_{p_i^{n_i}}$ represented as  $\left \{0,1,\dotsc , p_i^{n_i} -1\right \}$ with addition and multiplication modulo
$\left \{0,1,\dotsc , p_i^{n_i} -1\right \}$ with addition and multiplication modulo ![]() $p_i^{n_i}$, we can write uniquely
$p_i^{n_i}$, we can write uniquely
 $$ \begin{align*} \pi_i(x) = \sum_{j=0}^{n_i-1} \pi_{i,j}(x) p_i^{j},\quad \pi_{i,j}(x) \in\{0,1,\dotsc,p_i-1\}. \end{align*} $$
$$ \begin{align*} \pi_i(x) = \sum_{j=0}^{n_i-1} \pi_{i,j}(x) p_i^{j},\quad \pi_{i,j}(x) \in\{0,1,\dotsc,p_i-1\}. \end{align*} $$Observe that  $(x -x' ,M)=\prod _{j=1}^K p_i^{\gamma _i}$ if and only if for each
$(x -x' ,M)=\prod _{j=1}^K p_i^{\gamma _i}$ if and only if for each ![]() $i=1,\dotsc ,K$,
$i=1,\dotsc ,K$,
 $$ \begin{align} \gamma_i = \begin{cases} \min\left\{j: \pi_{i,j}(x)\neq \pi_{i,j}(x') \right\} &\text{if } \pi_i(x)\neq \pi_i(x'), \\ n_i &\text{if } \pi_i(x)=\pi_i(x'). \end{cases} \end{align} $$
$$ \begin{align} \gamma_i = \begin{cases} \min\left\{j: \pi_{i,j}(x)\neq \pi_{i,j}(x') \right\} &\text{if } \pi_i(x)\neq \pi_i(x'), \\ n_i &\text{if } \pi_i(x)=\pi_i(x'). \end{cases} \end{align} $$2.3 Grids, planes, lines, fibers
Definition 2.2. Let ![]() $D\mid M$. A D-grid in
$D\mid M$. A D-grid in ![]() $\mathbb {Z}_M$ is a set of the form
$\mathbb {Z}_M$ is a set of the form
for some ![]() $x\in \mathbb {Z}_M$.
$x\in \mathbb {Z}_M$.
An important case of interest is as follows. Let ![]() $N\mid M$. If
$N\mid M$. If ![]() $N=p_1^{\alpha _1} \dotsm p_K^{\alpha _K}$, with
$N=p_1^{\alpha _1} \dotsm p_K^{\alpha _K}$, with ![]() $\alpha _1,\dotsc ,\alpha _K\geq 0$, we define
$\alpha _1,\dotsc ,\alpha _K\geq 0$, we define
 $$ \begin{align*} D(N):= p_1^{\gamma_1} \dotsm p_K^{\gamma_K}, \end{align*} $$
$$ \begin{align*} D(N):= p_1^{\gamma_1} \dotsm p_K^{\gamma_K}, \end{align*} $$where ![]() $\gamma _i=\max (0,\alpha _i-1)$ for
$\gamma _i=\max (0,\alpha _i-1)$ for ![]() $i=1,\dotsc , K$. Then a
$i=1,\dotsc , K$. Then a ![]() $D(N)$-grid is a ‘top-level’ grid on the scale N, and a natural setting to work on that scale.
$D(N)$-grid is a ‘top-level’ grid on the scale N, and a natural setting to work on that scale.
While a grid ![]() $\Lambda $ is always an arithmetic progression in
$\Lambda $ is always an arithmetic progression in ![]() $\mathbb {Z}_M$, it is often helpful to represent
$\mathbb {Z}_M$, it is often helpful to represent ![]() $\mathbb {Z}_M$ by a K-dimensional coordinate array as in Section 2.2 and, accordingly, assign a geometric interpretation to
$\mathbb {Z}_M$ by a K-dimensional coordinate array as in Section 2.2 and, accordingly, assign a geometric interpretation to ![]() $\Lambda $. We point out several useful special cases.
$\Lambda $. We point out several useful special cases.
A line through ![]() $x\in \mathbb {Z}_M$ in the
$x\in \mathbb {Z}_M$ in the ![]() $p_i$ direction is the set
$p_i$ direction is the set
and a ![]() $(K-1)$-dimensional plane through
$(K-1)$-dimensional plane through ![]() $x\in \mathbb {Z}_M$ perpendicular to the
$x\in \mathbb {Z}_M$ perpendicular to the ![]() $p_i$ direction is a set of the form
$p_i$ direction is a set of the form
Note that formula (2.3) defines a plane on the scale ![]() $M_ip_i^{\alpha _i}$, which may be different from M.
$M_ip_i^{\alpha _i}$, which may be different from M.
An M-fiber in the ![]() $p_i$ direction is a set of the form
$p_i$ direction is a set of the form ![]() $x*F_i$, where
$x*F_i$, where ![]() $x\in \mathbb {Z}_M$ and
$x\in \mathbb {Z}_M$ and
Thus ![]() $x*F_i=\Lambda (x,M/p_i)$. (More complicated multiscale fiber chains will be defined later.) A set
$x*F_i=\Lambda (x,M/p_i)$. (More complicated multiscale fiber chains will be defined later.) A set ![]() $A\subset \mathbb {Z}_M$ is M-fibered in the
$A\subset \mathbb {Z}_M$ is M-fibered in the ![]() $p_i$ direction if there is a subset
$p_i$ direction if there is a subset ![]() $A'\subset A$ such that
$A'\subset A$ such that ![]() $A=A'*F_i$.
$A=A'*F_i$.
2.4 Cyclotomic polynomials and cyclotomic divisibility
We state a few basic facts about cyclotomic polynomials for future reference. By equation (1.2), we have
 $$ \begin{align} 1+X+X^2+\dotsb+X^{n-1}=\prod_{s\mid n,s\neq 1}\Phi_s(X). \end{align} $$
$$ \begin{align} 1+X+X^2+\dotsb+X^{n-1}=\prod_{s\mid n,s\neq 1}\Phi_s(X). \end{align} $$In particular, if p is a prime number, then ![]() $\Phi _p(X)=1+X+\dotsb +X^{p-1}$ and, more generally, by induction,
$\Phi _p(X)=1+X+\dotsb +X^{p-1}$ and, more generally, by induction,
 $$ \begin{align*} \Phi_{p^\alpha}(X)=\Phi_p\left(X^{p^{\alpha-1}}\right) = 1 + X^{p^{\alpha-1}} + X^{2p^{\alpha-1}} + \dotsb + X^{(p-1)p^{\alpha-1}}, \quad \alpha\geq 1. \end{align*} $$
$$ \begin{align*} \Phi_{p^\alpha}(X)=\Phi_p\left(X^{p^{\alpha-1}}\right) = 1 + X^{p^{\alpha-1}} + X^{2p^{\alpha-1}} + \dotsb + X^{(p-1)p^{\alpha-1}}, \quad \alpha\geq 1. \end{align*} $$Thus ![]() $\Phi _{p^\alpha }(1)=p$, and this together with equation (2.5) implies that
$\Phi _{p^\alpha }(1)=p$, and this together with equation (2.5) implies that ![]() $\Phi _s(1)=1$ for all s that are not prime powers.
$\Phi _s(1)=1$ for all s that are not prime powers.
Suppose that ![]() $A\oplus B=\mathbb {Z}_M$, with
$A\oplus B=\mathbb {Z}_M$, with  $M=\prod _{i=1}^K p_i^{n_i}$ as before. By equation (1.1), we have
$M=\prod _{i=1}^K p_i^{n_i}$ as before. By equation (1.1), we have ![]() $A(X)B(X)=1+X+\dotsb +X^{M-1} \bmod \left (X^M-1\right )$. For every prime power
$A(X)B(X)=1+X+\dotsb +X^{M-1} \bmod \left (X^M-1\right )$. For every prime power ![]() $s=p^\alpha \mid M$, we must have
$s=p^\alpha \mid M$, we must have ![]() $\Phi _s(X)\mid A(X)B(X)$, so that
$\Phi _s(X)\mid A(X)B(X)$, so that
 $$ \begin{align*} M= \prod_{i=1}^K \prod_{\alpha_i=1}^{n_i} \Phi_{p_i^{\alpha_i}}(1) \mid A(1)B(1)=\lvert A\rvert\lvert B\rvert=M. \end{align*} $$
$$ \begin{align*} M= \prod_{i=1}^K \prod_{\alpha_i=1}^{n_i} \Phi_{p_i^{\alpha_i}}(1) \mid A(1)B(1)=\lvert A\rvert\lvert B\rvert=M. \end{align*} $$It follows that
 $$ \begin{align*} \lvert A\vert= \prod_{s\in S_A} \Phi_s(1) \end{align*} $$
$$ \begin{align*} \lvert A\vert= \prod_{s\in S_A} \Phi_s(1) \end{align*} $$and similarly for B, with ![]() $S_A$,
$S_A$, ![]() $S_B$ defined as in Theorem 1.1; this is the proof of the tiling condition (T1) given in [Reference Coven and Meyerowitz2]. Moreover, for any prime power
$S_B$ defined as in Theorem 1.1; this is the proof of the tiling condition (T1) given in [Reference Coven and Meyerowitz2]. Moreover, for any prime power ![]() $s=p^{\alpha _i}\mid M$, we have that
$s=p^{\alpha _i}\mid M$, we have that ![]() $\Phi _s(X)$ divides exactly one of
$\Phi _s(X)$ divides exactly one of ![]() $A(X)$ and
$A(X)$ and ![]() $B(X)$. (This is not true for
$B(X)$. (This is not true for ![]() $s\mid M$ with two or more distinct prime factors. For such s, the corresponding cyclotomic polynomial
$s\mid M$ with two or more distinct prime factors. For such s, the corresponding cyclotomic polynomial ![]() $\Phi _s(X)$ may divide either one or both of
$\Phi _s(X)$ may divide either one or both of ![]() $A(X)$ and
$A(X)$ and ![]() $B(X)$.)
$B(X)$.)
Divisibility by prime-power cyclotomics has the following combinatorial interpretation. For ![]() $A\subset \mathbb {Z}_M$, the condition
$A\subset \mathbb {Z}_M$, the condition ![]() $\Phi _{p_i}\mid A$ means that the elements of A are uniformly distributed modulo
$\Phi _{p_i}\mid A$ means that the elements of A are uniformly distributed modulo ![]() $p_i$, so that
$p_i$, so that
More generally, for ![]() $1\leq \alpha \leq n_i$, we have
$1\leq \alpha \leq n_i$, we have ![]() $\Phi _{p_i^\alpha }(X)\mid A(X)$ if and only if
$\Phi _{p_i^\alpha }(X)\mid A(X)$ if and only if
 $$ \begin{align} \left\lvert A\cap \Pi\left(x,p_i^\alpha\right)\right\rvert=\frac{1}{p_i} \left\lvert A\cap \Pi\left(x,p_i^{\alpha-1}\right)\right\rvert \quad \forall x\in\mathbb{Z}_M, \end{align} $$
$$ \begin{align} \left\lvert A\cap \Pi\left(x,p_i^\alpha\right)\right\rvert=\frac{1}{p_i} \left\lvert A\cap \Pi\left(x,p_i^{\alpha-1}\right)\right\rvert \quad \forall x\in\mathbb{Z}_M, \end{align} $$so that the elements of A are uniformly distributed mod ![]() $p_i^\alpha $ within each residue class mod
$p_i^\alpha $ within each residue class mod  $p_i^{\alpha -1}$. In particular, this implies the following bound on the number of points of a tile in a plane on a scale
$p_i^{\alpha -1}$. In particular, this implies the following bound on the number of points of a tile in a plane on a scale ![]() $M_ip_i^{n_i-\alpha _i}$ or, equivalently, in an arithmetic progression of step
$M_ip_i^{n_i-\alpha _i}$ or, equivalently, in an arithmetic progression of step ![]() $p_i^{n_i-\alpha _i}$:
$p_i^{n_i-\alpha _i}$:
Lemma 2.3 Plane bound
Let ![]() $A\oplus B=\mathbb {Z}_M$, where
$A\oplus B=\mathbb {Z}_M$, where  $M=\prod _j p_j^{n_j}$ and
$M=\prod _j p_j^{n_j}$ and  $\lvert A\rvert =\prod _j p_j^{\beta _j}$. Then for every
$\lvert A\rvert =\prod _j p_j^{\beta _j}$. Then for every ![]() $x\in \mathbb {Z}_M$ and
$x\in \mathbb {Z}_M$ and ![]() $0\leq \alpha _i\leq n_i$ we have
$0\leq \alpha _i\leq n_i$ we have
 $$ \begin{align} \left\lvert A\cap\Pi\left(x,p_i^{n_i-\alpha_i}\right)\right\rvert\leq p_i^{\alpha_i}\prod_{\nu\neq i}p_\nu^{\beta_\nu}. \end{align} $$
$$ \begin{align} \left\lvert A\cap\Pi\left(x,p_i^{n_i-\alpha_i}\right)\right\rvert\leq p_i^{\alpha_i}\prod_{\nu\neq i}p_\nu^{\beta_\nu}. \end{align} $$ This bound is, in general, sharp. For example, if  $A\subset p_i^{n_i-1}\mathbb {Z}_M$ and
$A\subset p_i^{n_i-1}\mathbb {Z}_M$ and  $\Phi _{p_i^{n_i}}\mid A$, then
$\Phi _{p_i^{n_i}}\mid A$, then  $\left \lvert A\cap \Pi \left (x,p_i^{n_i}\right )\right \rvert =\lvert A\rvert /p_i$, so that estimate (2.7) holds with equality for
$\left \lvert A\cap \Pi \left (x,p_i^{n_i}\right )\right \rvert =\lvert A\rvert /p_i$, so that estimate (2.7) holds with equality for ![]() $\alpha _i=0$. Examples of sets
$\alpha _i=0$. Examples of sets ![]() $A\subset \mathbb {Z}_M$ with the foregoing properties are easy to construct using the standard tiling sets defined in Section 3.
$A\subset \mathbb {Z}_M$ with the foregoing properties are easy to construct using the standard tiling sets defined in Section 3.
We also note the following. Let ![]() $N\mid M$. Then the condition
$N\mid M$. Then the condition
means that ![]() $1+X+\dotsb +X^{N-1}$ divides
$1+X+\dotsb +X^{N-1}$ divides ![]() $A(X)$ or, equivalently, that the elements of A are uniformly distributed mod N. For example, let
$A(X)$ or, equivalently, that the elements of A are uniformly distributed mod N. For example, let ![]() $N= p_1p_2\dotsm p_K$. Suppose that
$N= p_1p_2\dotsm p_K$. Suppose that ![]() $\lvert A\rvert =N$ and that
$\lvert A\rvert =N$ and that ![]() $\Phi _{p_i}\mid A$ for all
$\Phi _{p_i}\mid A$ for all ![]() $i=1,\dotsc ,K$. Then A satisfies (T2) if and only if
$i=1,\dotsc ,K$. Then A satisfies (T2) if and only if ![]() $\Phi _s\mid A$ for all
$\Phi _s\mid A$ for all ![]() $s\mid N$ with
$s\mid N$ with ![]() $s\neq 1$ or, equivalently, if and only if each residue class mod N contains exactly one element of A.
$s\neq 1$ or, equivalently, if and only if each residue class mod N contains exactly one element of A.
2.5 Divisor set and divisor exclusion
Definition 2.4 Divisor set
For a set ![]() $A\subset \mathbb {Z}_M$, define
$A\subset \mathbb {Z}_M$, define
Informally, we will refer to the elements of ![]() $\mathrm {Div}(A)$ as the divisors of A or differences in A. We also define
$\mathrm {Div}(A)$ as the divisors of A or differences in A. We also define
for ![]() $A\subset \mathbb {Z}_M$ and
$A\subset \mathbb {Z}_M$ and ![]() $N\mid M$.
$N\mid M$.
Divisor sets will be a key concept in our analysis, thanks to the following theorem due to Sands [Reference Sands37]:
Theorem 2.5 Divisor exclusion [Reference Sands37]
If ![]() $A,B\subset \mathbb {Z}_M$ are sets, then
$A,B\subset \mathbb {Z}_M$ are sets, then ![]() $A\oplus B=\mathbb {Z}_M$ if and only if
$A\oplus B=\mathbb {Z}_M$ if and only if ![]() $\lvert A\rvert \lvert B\rvert =M$ and
$\lvert A\rvert \lvert B\rvert =M$ and
An alternative proof of Sands’ theorem, based on Theorem 4.7 and due to [Reference Granville, Łaba and Wang11], is included in Remark 4.10.
3 A reformulation of (T2)
3.1 Standard tiling complements
We continue to assume that  $M=\prod _{i=1}^K p_i^{n_i}$, where
$M=\prod _{i=1}^K p_i^{n_i}$, where ![]() $p_1,\dotsc ,p_K$ are distinct primes and
$p_1,\dotsc ,p_K$ are distinct primes and ![]() $n_i>0$. We equip
$n_i>0$. We equip ![]() $\mathbb {Z}_M$ with the array coordinate system from Section 2.2 and use the notation of that section. Recall also that the divisor set
$\mathbb {Z}_M$ with the array coordinate system from Section 2.2 and use the notation of that section. Recall also that the divisor set ![]() ${\mathrm {Div}}(A)$ for a set
${\mathrm {Div}}(A)$ for a set ![]() $A\subset \mathbb {Z}_M$ was defined in definition (2.8) which is a little bit circular.
$A\subset \mathbb {Z}_M$ was defined in definition (2.8) which is a little bit circular.
Definition 3.1. Let ![]() $A,B$ be sets in
$A,B$ be sets in ![]() $\mathbb {Z}_M$ such that
$\mathbb {Z}_M$ such that ![]() $A\oplus B=\mathbb {Z}_M$. Let
$A\oplus B=\mathbb {Z}_M$. Let
 $$ \begin{align*} \mathfrak{A}_i(A) =\left\{\alpha_i \in \{1,2,\dotsc,n_i\}: \Phi_{p_i^{\alpha_i}}(X) \mid A(X) \right\}. \end{align*} $$
$$ \begin{align*} \mathfrak{A}_i(A) =\left\{\alpha_i \in \{1,2,\dotsc,n_i\}: \Phi_{p_i^{\alpha_i}}(X) \mid A(X) \right\}. \end{align*} $$The standard tiling set ![]() $A^\flat $ is defined via its mask polynomial
$A^\flat $ is defined via its mask polynomial
 $$ \begin{align} A^\flat(X) &= \prod_{i=1}^{K} \prod_{\alpha_i\in \mathfrak{A}_i(A)} \Phi_{p_i}\left(X^{M_ip_i^{\alpha_i-1}}\right) \nonumber\\ &= \prod_{i=1}^{K} \prod_{\alpha_i\in \mathfrak{A}_i(A)} \left(1+ X^{M_ip_i^{\alpha_i-1}} + \dotsb + X^{\left(p_i-1\right)M_ip_i^{\alpha_i-1}} \right). \end{align} $$
$$ \begin{align} A^\flat(X) &= \prod_{i=1}^{K} \prod_{\alpha_i\in \mathfrak{A}_i(A)} \Phi_{p_i}\left(X^{M_ip_i^{\alpha_i-1}}\right) \nonumber\\ &= \prod_{i=1}^{K} \prod_{\alpha_i\in \mathfrak{A}_i(A)} \left(1+ X^{M_ip_i^{\alpha_i-1}} + \dotsb + X^{\left(p_i-1\right)M_ip_i^{\alpha_i-1}} \right). \end{align} $$
Figure 1 The standard sets  $A^\flat ,B^\flat \subset \mathbb {Z}_{p_i^2p_j^2}$ with
$A^\flat ,B^\flat \subset \mathbb {Z}_{p_i^2p_j^2}$ with ![]() $p_i=3, p_j=5$ and
$p_i=3, p_j=5$ and  $\Phi _{p_i^2}\Phi _{p_j^2}\mid A,\Phi _{p_i}\Phi _{p_j}\mid B$.
$\Phi _{p_i^2}\Phi _{p_j^2}\mid A,\Phi _{p_i}\Phi _{p_j}\mid B$.
Lemma 3.2. Define ![]() $A^\flat $ as before. Then
$A^\flat $ as before. Then ![]() $A^\flat (X)$ satisfies (T2) and has the same prime-power cyclotomic divisors as
$A^\flat (X)$ satisfies (T2) and has the same prime-power cyclotomic divisors as ![]() $A(X)$.
$A(X)$.
Proof. Set ![]() $\alpha \in \{1,2,\dotsc ,n_i\}$. Then
$\alpha \in \{1,2,\dotsc ,n_i\}$. Then  $\Phi _{p_i^{\alpha }}(X) \mid A^\flat (X)$ if and only if it divides one of the factors
$\Phi _{p_i^{\alpha }}(X) \mid A^\flat (X)$ if and only if it divides one of the factors  $\Phi _{p_i} (X^{M_ip_i^{\alpha _i-1}} )$ with
$\Phi _{p_i} (X^{M_ip_i^{\alpha _i-1}} )$ with ![]() $\alpha _i \in \mathfrak {A}_i(A)$. By Lemma 3.3, this happens if and only if
$\alpha _i \in \mathfrak {A}_i(A)$. By Lemma 3.3, this happens if and only if ![]() $\alpha =\alpha _i$. Furthermore, in that case we also have
$\alpha =\alpha _i$. Furthermore, in that case we also have  $\Phi _{d p_i^{\alpha _i}}(X) \mid A^\flat (X)$ for all
$\Phi _{d p_i^{\alpha _i}}(X) \mid A^\flat (X)$ for all ![]() $d\mid M_i$, so that in particular (T2) holds for
$d\mid M_i$, so that in particular (T2) holds for ![]() $A^\flat $.
$A^\flat $.
Lemma 3.3. Let
 $$ \begin{align*} \Psi(X)=1+X^{Np^{\alpha-1}} + X^{2Np^{\alpha-1}} + \dotsb + X^{(p-1)Np^{\alpha-1}} = \Phi_{p}\left(X^{Np^{\alpha-1}}\right), \end{align*} $$
$$ \begin{align*} \Psi(X)=1+X^{Np^{\alpha-1}} + X^{2Np^{\alpha-1}} + \dotsb + X^{(p-1)Np^{\alpha-1}} = \Phi_{p}\left(X^{Np^{\alpha-1}}\right), \end{align*} $$where ![]() $(N,p)=1$. Then
$(N,p)=1$. Then ![]() $\Phi _s(X)\mid \Psi (X)$ if and only if
$\Phi _s(X)\mid \Psi (X)$ if and only if ![]() $s=dp^\alpha $ for some
$s=dp^\alpha $ for some ![]() $d\mid N$.
$d\mid N$.
Proof. We have ![]() $\Phi _s(X)\mid \Psi (X)$ if and only if
$\Phi _s(X)\mid \Psi (X)$ if and only if  $\Psi \left (e^{2\pi i /s}\right )=0$ – that is,
$\Psi \left (e^{2\pi i /s}\right )=0$ – that is,  $\left (e^{2\pi i /s}\right )^{Np^{\alpha -1}}$ is a root of
$\left (e^{2\pi i /s}\right )^{Np^{\alpha -1}}$ is a root of ![]() $\Phi _p$. This happens if and only if
$\Phi _p$. This happens if and only if ![]() $\left (Np^{\alpha -1}\right )/s = k/p$ for some integer k such that
$\left (Np^{\alpha -1}\right )/s = k/p$ for some integer k such that ![]() $(k,p)=1$. Equivalently,
$(k,p)=1$. Equivalently, ![]() $Np^\alpha =ks$ with
$Np^\alpha =ks$ with ![]() $(k,p)=1$. This means that
$(k,p)=1$. This means that ![]() $k\mid N$ and
$k\mid N$ and  $s=\frac {N}{k}p^\alpha = d p^\alpha $, where
$s=\frac {N}{k}p^\alpha = d p^\alpha $, where ![]() $d=N/k$ is a divisor of N.
$d=N/k$ is a divisor of N.
Observe that the standard set ![]() $A^\flat $, while not necessarily a grid, is highly structured. In terms of array coordinates, we have
$A^\flat $, while not necessarily a grid, is highly structured. In terms of array coordinates, we have
 $$ \begin{align} A^\flat &= \left\{ x\in\mathbb{Z}_M: \pi_i(x)=\sum_{\alpha_i\in \mathfrak{A}_i(A)} \pi_{i,\alpha_i-1}(x)p_i^{\alpha_i-1}, \quad \pi_{i,\alpha_i-1}(x) \in\{ 0,1,\dotsc, p_i-1 \} \right\} \nonumber\\ &= \left\{x\in \mathbb{Z}_M:\ \pi_{i,\alpha_i-1}(x) =0 \text{ for all }i,\alpha_i \text{ such that }\alpha_i\notin \mathfrak{A}_i(A)\right\}. \end{align} $$
$$ \begin{align} A^\flat &= \left\{ x\in\mathbb{Z}_M: \pi_i(x)=\sum_{\alpha_i\in \mathfrak{A}_i(A)} \pi_{i,\alpha_i-1}(x)p_i^{\alpha_i-1}, \quad \pi_{i,\alpha_i-1}(x) \in\{ 0,1,\dotsc, p_i-1 \} \right\} \nonumber\\ &= \left\{x\in \mathbb{Z}_M:\ \pi_{i,\alpha_i-1}(x) =0 \text{ for all }i,\alpha_i \text{ such that }\alpha_i\notin \mathfrak{A}_i(A)\right\}. \end{align} $$The standard divisor set for A is
 $$ \begin{align} \mathrm{Div} \left(A^\flat \right) = \left\{ \prod_{i=1}^K p_i^{\alpha_i-1}: \alpha_i\in \mathfrak{A}_i(A)\cup\{n_i+1\},\quad i=1,\dotsc,K \right\}. \end{align} $$
$$ \begin{align} \mathrm{Div} \left(A^\flat \right) = \left\{ \prod_{i=1}^K p_i^{\alpha_i-1}: \alpha_i\in \mathfrak{A}_i(A)\cup\{n_i+1\},\quad i=1,\dotsc,K \right\}. \end{align} $$We will refer to the elements of ![]() $\mathrm {Div} (A^\flat )$ as standard divisors of A. The set
$\mathrm {Div} (A^\flat )$ as standard divisors of A. The set ![]() $B^\flat $ is defined similarly.
$B^\flat $ is defined similarly.
With these definitions, we have the following alternative formulations of (T2):
Proposition 3.4. Suppose that ![]() $A\oplus B=\mathbb {Z}_M$. Then the following are equivalent:
$A\oplus B=\mathbb {Z}_M$. Then the following are equivalent:
(i)
 $\mathrm {Div}(A^\flat ) \cap {\mathrm {Div}}(B)= \{M\}$.
$\mathrm {Div}(A^\flat ) \cap {\mathrm {Div}}(B)= \{M\}$.(ii)
 $A^\flat \oplus B= \mathbb {Z}_M$.
$A^\flat \oplus B= \mathbb {Z}_M$.(iii) B satisfies (T2).
(iv)
 $\left \lvert B\cap (x*A^\flat )\right \rvert =1$ for every
$\left \lvert B\cap (x*A^\flat )\right \rvert =1$ for every  $x\in \mathbb {Z}_M$.
$x\in \mathbb {Z}_M$.
Proof. The equivalence between (i) and (ii) is a special case of Theorem 2.5. The implication (iii) ![]() $\Rightarrow $ (ii) follows from the construction in the proof of [Reference Coven and Meyerowitz2, Theorem A]; the converse implication (ii)
$\Rightarrow $ (ii) follows from the construction in the proof of [Reference Coven and Meyerowitz2, Theorem A]; the converse implication (ii) ![]() $\Rightarrow $ (iii) was not pointed out there, but it also follows from the same construction. Specifically, by Lemma 3.3,
$\Rightarrow $ (iii) was not pointed out there, but it also follows from the same construction. Specifically, by Lemma 3.3, ![]() $A^\flat (X)$ is divisible by every cyclotomic polynomial
$A^\flat (X)$ is divisible by every cyclotomic polynomial ![]() $\Phi _s$ such that
$\Phi _s$ such that ![]() $p_i^\alpha \parallel s$ for some
$p_i^\alpha \parallel s$ for some ![]() $i\in \{1,\dotsc ,K\}$ and
$i\in \{1,\dotsc ,K\}$ and ![]() $\alpha \geq 1$ such that
$\alpha \geq 1$ such that ![]() $\Phi _{p_i^\alpha }\mid A$. In other words, the only s such that
$\Phi _{p_i^\alpha }\mid A$. In other words, the only s such that ![]() $s\mid M$ but
$s\mid M$ but ![]() $\Phi _s$ does not divide
$\Phi _s$ does not divide ![]() $A(X)$ are those with
$A(X)$ are those with  $s=\prod _{i=1}^k p_i^{\beta _i}$, where for each i we have either
$s=\prod _{i=1}^k p_i^{\beta _i}$, where for each i we have either ![]() $\beta _i=0$ or
$\beta _i=0$ or  $\Phi _{p_i^{\beta _i}}(X)\mid B(X)$. Let
$\Phi _{p_i^{\beta _i}}(X)\mid B(X)$. Let ![]() $\mathcal {S}_B$ be the set of such s.
$\mathcal {S}_B$ be the set of such s.
If B satisfies (T2), then all ![]() $\Phi _s$ with
$\Phi _s$ with ![]() $s\in \mathcal {S}_B$ divide
$s\in \mathcal {S}_B$ divide ![]() $B(X)$, which implies (ii). Conversely, suppose that (ii) holds. Then each
$B(X)$, which implies (ii). Conversely, suppose that (ii) holds. Then each ![]() $\Phi _s$ with
$\Phi _s$ with ![]() $s\mid M$ has to divide
$s\mid M$ has to divide ![]() $A(X)B(X)$. By Lemma 3.3 again, if
$A(X)B(X)$. By Lemma 3.3 again, if ![]() $s\in \mathcal {S}_B$, then
$s\in \mathcal {S}_B$, then ![]() $\Phi _s$ does not divide
$\Phi _s$ does not divide ![]() $A(X)$, so it must divide
$A(X)$, so it must divide ![]() $B(X)$. Therefore (T2) holds for B.
$B(X)$. Therefore (T2) holds for B.
For (iv), we shall prove that (ii) implies (iv) and (iv) implies (i). Suppose that (ii) holds. We first claim that
 $$ \begin{align} \left\lvert B\cap\left(x*A^\flat\right)\right\rvert\leq 1\quad \forall x\in\mathbb{Z}_M. \end{align} $$
$$ \begin{align} \left\lvert B\cap\left(x*A^\flat\right)\right\rvert\leq 1\quad \forall x\in\mathbb{Z}_M. \end{align} $$Indeed, if ![]() $b,b'\in B\cap (x*A^\flat )$, then
$b,b'\in B\cap (x*A^\flat )$, then ![]() $b=x+a$ and
$b=x+a$ and ![]() $b'=x+a'$ for some
$b'=x+a'$ for some ![]() $a,a'\in A^\flat $, so that
$a,a'\in A^\flat $, so that ![]() $b-a=b'-a'$, contradicting (ii) unless
$b-a=b'-a'$, contradicting (ii) unless ![]() $b=b'$ and
$b=b'$ and ![]() $a=a'$.
$a=a'$.
It remains to prove that ![]() $(x_0*A^\flat )\cap B\neq \emptyset $ for each
$(x_0*A^\flat )\cap B\neq \emptyset $ for each ![]() $x_0\in \mathbb {Z}_M$. Set
$x_0\in \mathbb {Z}_M$. Set ![]() $x_0\in \mathbb {Z}_M$. Since
$x_0\in \mathbb {Z}_M$. Since ![]() $\mathrm {Div}(B)=\mathrm {Div}(-B)$, we have
$\mathrm {Div}(B)=\mathrm {Div}(-B)$, we have ![]() $A^\flat \oplus (-B)=\mathbb {Z}_M$ by Theorem 2.5. It follows that there must exist
$A^\flat \oplus (-B)=\mathbb {Z}_M$ by Theorem 2.5. It follows that there must exist ![]() $a_0\in A^\flat$ and
$a_0\in A^\flat$ and ![]() $-b_0\in (-B)$ such that
$-b_0\in (-B)$ such that ![]() $a_0-b_0=-x_0$. The latter means
$a_0-b_0=-x_0$. The latter means ![]() $a_0+x_0=b_0$, implying
$a_0+x_0=b_0$, implying ![]() $(x_0*A^\flat )\cap B\neq \emptyset $, as claimed. Hence (iv) follows.
$(x_0*A^\flat )\cap B\neq \emptyset $, as claimed. Hence (iv) follows.
Finally, suppose that (i) fails. Then there exist ![]() $b,b'\in B$ and
$b,b'\in B$ and ![]() $m\in \mathrm {Div} (A^\flat )\setminus \{M\}$ such that
$m\in \mathrm {Div} (A^\flat )\setminus \{M\}$ such that ![]() $(b-b',M)=m$. But then
$(b-b',M)=m$. But then ![]() $b,b'\in B\cap (b*A^\flat )$ with
$b,b'\in B\cap (b*A^\flat )$ with ![]() $b\neq b'$, contradicting (iv).
$b\neq b'$, contradicting (iv).
Remark 3.5. If ![]() $A\oplus B$ tiles
$A\oplus B$ tiles ![]() $\mathbb {Z}_M$, where
$\mathbb {Z}_M$, where ![]() $M=p^n$ is a prime power, then (T2) holds vacuously for both sets. Hence we have both
$M=p^n$ is a prime power, then (T2) holds vacuously for both sets. Hence we have both ![]() $A\oplus B^\flat =\mathbb {Z}_M$ and
$A\oplus B^\flat =\mathbb {Z}_M$ and ![]() $A^\flat \oplus B=\mathbb {Z}_M$.
$A^\flat \oplus B=\mathbb {Z}_M$.
It is tempting to try to prove that if ![]() $A\oplus B=\mathbb {Z}_M$, then we should have
$A\oplus B=\mathbb {Z}_M$, then we should have ![]() $\mathrm {Div} (A^\flat )\subseteq {\mathrm {Div}}(A)$. By Proposition 3.4, this would imply that B satisfies (T2). However, the following example shows that
$\mathrm {Div} (A^\flat )\subseteq {\mathrm {Div}}(A)$. By Proposition 3.4, this would imply that B satisfies (T2). However, the following example shows that ![]() $\mathrm {Div}(A)$ does not in fact have to contain
$\mathrm {Div}(A)$ does not in fact have to contain ![]() $\mathrm {Div}(A^\flat )$:
$\mathrm {Div}(A^\flat )$:
Example 3.6. Let ![]() $M=p^2q$, where
$M=p^2q$, where ![]() $p,q$ are distinct primes with
$p,q$ are distinct primes with ![]() $p>q$, and let A be the set of numbers whose array coordinates in
$p>q$, and let A be the set of numbers whose array coordinates in ![]() $\mathbb {Z}_M$ are
$\mathbb {Z}_M$ are ![]() $(i+jp,i)$,
$(i+jp,i)$, ![]() $i=0,1,\dotsc ,q-1$,
$i=0,1,\dotsc ,q-1$, ![]() $j=0,1,\dotsc ,p-1$. Then
$j=0,1,\dotsc ,p-1$. Then ![]() $A\oplus B=\mathbb {Z}_M$ with
$A\oplus B=\mathbb {Z}_M$ with ![]() $B=\{(j,0): j=0,1,\dotsc ,p-1\}$, and both sets satisfy (T2). Since
$B=\{(j,0): j=0,1,\dotsc ,p-1\}$, and both sets satisfy (T2). Since ![]() $\Phi _{p^2}$ and
$\Phi _{p^2}$ and ![]() $\Phi _q$ divide
$\Phi _q$ divide ![]() $A(X)$, we have
$A(X)$, we have ![]() $A^\flat = \{(jp,i): i=0,1,\dotsc ,q-1, j=0,1,\dots ,p-1\}$, and in particular
$A^\flat = \{(jp,i): i=0,1,\dotsc ,q-1, j=0,1,\dots ,p-1\}$, and in particular ![]() $p\in \mathrm {Div}(A^\flat )$. However,
$p\in \mathrm {Div}(A^\flat )$. However, ![]() $p\notin \mathrm {Div}(A)$. To see this, consider
$p\notin \mathrm {Div}(A)$. To see this, consider ![]() $a,a'\in A$ with coordinates
$a,a'\in A$ with coordinates ![]() $(i+jp,i)$ and
$(i+jp,i)$ and ![]() $(i'+j'p,i')$. If
$(i'+j'p,i')$. If ![]() $i\neq i'$, then
$i\neq i'$, then ![]() $(a-a',M)=1$. If, on the other hand,
$(a-a',M)=1$. If, on the other hand, ![]() $i=i'$ but
$i=i'$ but ![]() $a\neq a'$, then
$a\neq a'$, then ![]() $(a-a',M)=pq$.
$(a-a',M)=pq$.
This shows that the condition ![]() $\mathrm {Div}(A^\flat )\subseteq {\mathrm {Div}}(A)$ is not necessary for a tiling, nor is it simply a consequence of
$\mathrm {Div}(A^\flat )\subseteq {\mathrm {Div}}(A)$ is not necessary for a tiling, nor is it simply a consequence of ![]() $A(X)$ having the requisite prime-power cyclotomic divisors. Note, however, that in this example we still have
$A(X)$ having the requisite prime-power cyclotomic divisors. Note, however, that in this example we still have ![]() $p\notin {\mathrm {Div}}(B)$.
$p\notin {\mathrm {Div}}(B)$.
3.2 (T2)-equivalence
Definition 3.7. We say that the tilings ![]() $A\oplus B=\mathbb {Z}_M$ and
$A\oplus B=\mathbb {Z}_M$ and ![]() $A'\oplus B=\mathbb {Z}_M$ are (T2)-equivalent if
$A'\oplus B=\mathbb {Z}_M$ are (T2)-equivalent if
Since the sets A and ![]() $A'$ tile the same group
$A'$ tile the same group ![]() $\mathbb {Z}_M$ with the same tiling complement B, they must have the same cardinality and the same prime-power cyclotomic divisors, as discussed in Section 2.4. For brevity, we will sometimes say simply that A is (T2)-equivalent to
$\mathbb {Z}_M$ with the same tiling complement B, they must have the same cardinality and the same prime-power cyclotomic divisors, as discussed in Section 2.4. For brevity, we will sometimes say simply that A is (T2)-equivalent to ![]() $A'$ if both M and B are clear from context.
$A'$ if both M and B are clear from context.
In practice, ![]() $A'$ will be a set obtained from A using certain permitted manipulations such as fiber shifts. We will use (T2)-equivalence to reduce proving (T2) for the initial tiling to proving (T2) for related tilings that are increasingly more structured. In particular, the following reduction is sufficient to prove (T2) for both sets in the given tiling:
$A'$ will be a set obtained from A using certain permitted manipulations such as fiber shifts. We will use (T2)-equivalence to reduce proving (T2) for the initial tiling to proving (T2) for related tilings that are increasingly more structured. In particular, the following reduction is sufficient to prove (T2) for both sets in the given tiling:
Corollary 3.8. Suppose that the tiling ![]() $A\oplus B=\mathbb {Z}_M$ is (T2)-equivalent to the tiling
$A\oplus B=\mathbb {Z}_M$ is (T2)-equivalent to the tiling ![]() $A^\flat \oplus B=\mathbb {Z}_M$. Then A and B satisfy (T2).
$A^\flat \oplus B=\mathbb {Z}_M$. Then A and B satisfy (T2).
4 Box product
4.1 Box-product characterisation of tiling
We continue to assume that  $M=\prod _{i=1}^K p_i^{n_i}$, where
$M=\prod _{i=1}^K p_i^{n_i}$, where ![]() $p_1,\dotsc ,p_K$ are distinct primes. We will use
$p_1,\dotsc ,p_K$ are distinct primes. We will use ![]() $\phi $ and
$\phi $ and ![]() $\mu $ to denote, respectively, the Euler totient function and the Möbius function: if
$\mu $ to denote, respectively, the Euler totient function and the Möbius function: if  $n=\prod _{j=1}^L q_j^{r_j}$, where
$n=\prod _{j=1}^L q_j^{r_j}$, where ![]() $q_1,\dotsc ,q_L$ are distinct primes, then
$q_1,\dotsc ,q_L$ are distinct primes, then
 $$ \begin{align*} \phi(n)&=n \prod_{j=1}^L \frac{q_j-1}{q_j} = \prod_{j=1}^L \left(q_j-1\right)q_j^{r_j-1},\\ \mu(n)&=\begin{cases} (-1)^L & \text{if }r_1=r_2=\dotsb=r_L=1, \\ 0 & \text{if } \exists j\in\{1,\dotsc,L\} \text{ such that }r_j\geq 2. \end{cases} \end{align*} $$
$$ \begin{align*} \phi(n)&=n \prod_{j=1}^L \frac{q_j-1}{q_j} = \prod_{j=1}^L \left(q_j-1\right)q_j^{r_j-1},\\ \mu(n)&=\begin{cases} (-1)^L & \text{if }r_1=r_2=\dotsb=r_L=1, \\ 0 & \text{if } \exists j\in\{1,\dotsc,L\} \text{ such that }r_j\geq 2. \end{cases} \end{align*} $$ Let ![]() $N\mid M$. Reordering the primes if necessary, we may assume that
$N\mid M$. Reordering the primes if necessary, we may assume that ![]() $N=p_1^{\alpha _1} \dotsm p_k^{\alpha _k}$, with
$N=p_1^{\alpha _1} \dotsm p_k^{\alpha _k}$, with ![]() $1\leq k\leq K$ and
$1\leq k\leq K$ and ![]() $\alpha _1,\dotsc ,\alpha _k\geq 1$.
$\alpha _1,\dotsc ,\alpha _k\geq 1$.
Definition 4.1 N-boxes
An N-box is a k-dimensional matrix
 $$ \begin{align*} \mathbb{A}=\left( \mathbb{A}_{\left(\gamma_1,\dotsc,\gamma_k\right)} \right) _{0\leq \gamma_j\leq \alpha_j, j=1,\dotsc,k} \end{align*} $$
$$ \begin{align*} \mathbb{A}=\left( \mathbb{A}_{\left(\gamma_1,\dotsc,\gamma_k\right)} \right) _{0\leq \gamma_j\leq \alpha_j, j=1,\dotsc,k} \end{align*} $$of size ![]() $(\alpha _1+1)\times \dotsm \times (\alpha _k+1)$, with entries
$(\alpha _1+1)\times \dotsm \times (\alpha _k+1)$, with entries ![]() $\mathbb {A}_{\left (\gamma _1,\dotsc ,\gamma _k\right )}\in \mathbb {R}$. Since each multi-index
$\mathbb {A}_{\left (\gamma _1,\dotsc ,\gamma _k\right )}\in \mathbb {R}$. Since each multi-index ![]() $(\gamma _1,\dotsc ,\gamma _k)$ with
$(\gamma _1,\dotsc ,\gamma _k)$ with ![]() $0\leq \gamma _j\leq \alpha _j$ can be uniquely associated with a divisor m of N given by
$0\leq \gamma _j\leq \alpha _j$ can be uniquely associated with a divisor m of N given by  $m=p_1^{\gamma _1}\dotsm p_k^{\gamma _k}$, we will use such divisors to index the entries of
$m=p_1^{\gamma _1}\dotsm p_k^{\gamma _k}$, we will use such divisors to index the entries of ![]() $\mathbb {A}$, so that
$\mathbb {A}$, so that
 $$ \begin{align*} \mathbb{A} = ( \mathbb{A}_m )_{m\mid N}, \quad \mathbb{A}_m = \mathbb{A}_{\left(\gamma_1,\dotsc,\gamma_k\right)} \text{ for } m=p_1^{\gamma_1}\dotsm p_k^{\gamma_k}. \end{align*} $$
$$ \begin{align*} \mathbb{A} = ( \mathbb{A}_m )_{m\mid N}, \quad \mathbb{A}_m = \mathbb{A}_{\left(\gamma_1,\dotsc,\gamma_k\right)} \text{ for } m=p_1^{\gamma_1}\dotsm p_k^{\gamma_k}. \end{align*} $$ For any ![]() $N\mid M$, N-boxes form a vector space over
$N\mid M$, N-boxes form a vector space over ![]() $\mathbb {R}$, with addition of boxes and multiplication of a box by a scalar defined in the obvious way. We also equip this space with an inner product structure as follows:
$\mathbb {R}$, with addition of boxes and multiplication of a box by a scalar defined in the obvious way. We also equip this space with an inner product structure as follows:
Definition 4.2 Box product
If ![]() $\mathbb {A}$ and
$\mathbb {A}$ and ![]() $\mathbb {B}$ are N-boxes, define
$\mathbb {B}$ are N-boxes, define
 $$ \begin{align} \langle \mathbb{A}, \mathbb{B} \rangle = \sum_{m\mid N} \frac{1}{\phi(N/m)} \mathbb{A}_m \mathbb{B}_m. \end{align} $$
$$ \begin{align} \langle \mathbb{A}, \mathbb{B} \rangle = \sum_{m\mid N} \frac{1}{\phi(N/m)} \mathbb{A}_m \mathbb{B}_m. \end{align} $$ Of course, this equation depends on N, but since N is determined by the fact of ![]() $\mathbb {A}$ and
$\mathbb {A}$ and ![]() $\mathbb {B}$ being N-boxes, we will not use additional subscripts or superscripts to indicate that.
$\mathbb {B}$ being N-boxes, we will not use additional subscripts or superscripts to indicate that.
The N-boxes associated with multisets in ![]() $\mathbb {Z}_N$ are as follows:
$\mathbb {Z}_N$ are as follows:
Definition 4.3 Boxes associated with multisets
Set ![]() $A\in \mathcal {M}(\mathbb {Z}_M)$ and let
$A\in \mathcal {M}(\mathbb {Z}_M)$ and let ![]() $N\mid M$. Consider the induced multiset
$N\mid M$. Consider the induced multiset ![]() $A\in \mathcal {M}(\mathbb {Z}_N)$, with the weight function mod N defined in equation (2.1). For
$A\in \mathcal {M}(\mathbb {Z}_N)$, with the weight function mod N defined in equation (2.1). For ![]() $x\in \mathbb {Z}_N$, define
$x\in \mathbb {Z}_N$, define  $\mathbb {A}^N[x] = \left (\mathbb {A}^N_m[x]\right )_{m\mid N}$, where
$\mathbb {A}^N[x] = \left (\mathbb {A}^N_m[x]\right )_{m\mid N}$, where
 $$ \begin{align*} \mathbb{A}^N_m[x] = \sum_{a\in \mathbb{Z}_N: (x-a,N)=m} w^N_A(a). \end{align*} $$
$$ \begin{align*} \mathbb{A}^N_m[x] = \sum_{a\in \mathbb{Z}_N: (x-a,N)=m} w^N_A(a). \end{align*} $$In particular, if ![]() $A\subset \mathbb {Z}_N$ is a set, we have
$A\subset \mathbb {Z}_N$ is a set, we have
If ![]() $N=M$, we will skip the superscript and write
$N=M$, we will skip the superscript and write ![]() $\mathbb {A}_m[x]=\mathbb {A}^M_m[x]$ whenever there is no possibility of confusion.
$\mathbb {A}_m[x]=\mathbb {A}^M_m[x]$ whenever there is no possibility of confusion.
Theorem 4.4 explains the reason for Definition 4.2. The theorem is based on [Reference Granville, Łaba and Wang11, Theorem 1] (see Sections 4.2 and 4.3 for details). The equivalence between ![]() $A\oplus B=\mathbb {Z}_M$ and the condition in (ii) provides an alternative proof of Theorem 2.5; however, Sands’ proof is easier and does not require Theorem 4.4. The point of Theorem 4.4 is that tiling also implies the formally stronger condition (4.2) for all
$A\oplus B=\mathbb {Z}_M$ and the condition in (ii) provides an alternative proof of Theorem 2.5; however, Sands’ proof is easier and does not require Theorem 4.4. The point of Theorem 4.4 is that tiling also implies the formally stronger condition (4.2) for all ![]() $N\mid M$ and
$N\mid M$ and ![]() $x,y\in \mathbb {Z}_M$.
$x,y\in \mathbb {Z}_M$.
Theorem 4.4 Box-product characterisation of tiling
(i) Suppose that
 $A\oplus B=\mathbb {Z}_M$ is a tiling. Then for any
$A\oplus B=\mathbb {Z}_M$ is a tiling. Then for any  $N\mid M$ and any
$N\mid M$ and any  $x,y\in \mathbb {Z}_M$, we have (4.2)In particular,
$x,y\in \mathbb {Z}_M$, we have (4.2)In particular, $$ \begin{align} \left\langle \mathbb{A}^N[x], \mathbb{B}^N[y] \right\rangle =\frac{\lvert A\rvert\lvert B\rvert}{N}= \frac{M}{N}. \end{align} $$(4.3)
$$ \begin{align} \left\langle \mathbb{A}^N[x], \mathbb{B}^N[y] \right\rangle =\frac{\lvert A\rvert\lvert B\rvert}{N}= \frac{M}{N}. \end{align} $$(4.3) $$ \begin{align} \left\langle \mathbb{A}^M[x], \mathbb{B}^M[y] \right\rangle =1\quad \forall x,y\in\mathbb{Z}_M. \end{align} $$
$$ \begin{align} \left\langle \mathbb{A}^M[x], \mathbb{B}^M[y] \right\rangle =1\quad \forall x,y\in\mathbb{Z}_M. \end{align} $$(ii) Conversely, suppose that
 $A,B\subset \mathbb {Z}_M$ are sets such that
$A,B\subset \mathbb {Z}_M$ are sets such that  $\lvert A\rvert \lvert B\rvert =M$ and
$\lvert A\rvert \lvert B\rvert =M$ and  $\left \langle \mathbb {A}^M[a], \mathbb {B}^M[b] \right \rangle =1$ for all
$\left \langle \mathbb {A}^M[a], \mathbb {B}^M[b] \right \rangle =1$ for all  $a\in A$ and
$a\in A$ and  $b\in B$. Then
$b\in B$. Then  $A\oplus B=\mathbb {Z}_M$.
$A\oplus B=\mathbb {Z}_M$.
Corollary 4.5. Under the assumptions of Theorem 4.4, let ![]() $\mathcal {L}^N(A)$ be the linear space spanned by the boxes
$\mathcal {L}^N(A)$ be the linear space spanned by the boxes ![]() $\mathbb {A}^N[x]$ – that is,
$\mathbb {A}^N[x]$ – that is,
 $$ \begin{align*} \mathcal{L}^N(A)=\left\{ \sum_{x\in\mathbb{Z}_N} c_x \mathbb{A}^N[x]: c_x\in\mathbb{R}\right\}, \end{align*} $$
$$ \begin{align*} \mathcal{L}^N(A)=\left\{ \sum_{x\in\mathbb{Z}_N} c_x \mathbb{A}^N[x]: c_x\in\mathbb{R}\right\}, \end{align*} $$and similarly for B. Then for any N-boxes ![]() $\mathbb {A}\in \mathcal {L}^N(A)$ and
$\mathbb {A}\in \mathcal {L}^N(A)$ and ![]() $\mathbb {B}\in \mathcal {L}^N(B)$, we have
$\mathbb {B}\in \mathcal {L}^N(B)$, we have
 $$ \begin{align} \langle \mathbb{A}, \mathbb{B} \rangle = \frac{1}{N}\Sigma(\mathbb{A}) \Sigma(\mathbb{B}), \end{align} $$
$$ \begin{align} \langle \mathbb{A}, \mathbb{B} \rangle = \frac{1}{N}\Sigma(\mathbb{A}) \Sigma(\mathbb{B}), \end{align} $$where ![]() $\Sigma (\mathbb {A})=\sum _{m\mid N} \mathbb {A}_m$.
$\Sigma (\mathbb {A})=\sum _{m\mid N} \mathbb {A}_m$.
N-boxes ![]() $\mathbb {A}^N[x]$,
$\mathbb {A}^N[x]$, ![]() $x\in \mathbb {Z}_M$, are a convenient way of encoding structural information about A. Theorem 4.4 provides a tiling criterion for
$x\in \mathbb {Z}_M$, are a convenient way of encoding structural information about A. Theorem 4.4 provides a tiling criterion for ![]() $A\oplus B=\mathbb {Z}_M$ in terms of the box product, and it is also possible to express cyclotomic divisibility in terms of N-boxes. However, this convenience comes with some loss of information. In [Reference Łaba and Londner24], we have to work with the actual sets A and B, not just with the N-boxes representing them. We do not know whether it is possible to give a proof of properties such as (T2) purely in terms of the N-boxes associated with the sets.
$A\oplus B=\mathbb {Z}_M$ in terms of the box product, and it is also possible to express cyclotomic divisibility in terms of N-boxes. However, this convenience comes with some loss of information. In [Reference Łaba and Londner24], we have to work with the actual sets A and B, not just with the N-boxes representing them. We do not know whether it is possible to give a proof of properties such as (T2) purely in terms of the N-boxes associated with the sets.
Remark 4.6. The equivalence between Proposition 3.4(iii) and (iv) can be stated in terms of M-boxes. Suppose that ![]() $A\oplus B=\mathbb {Z}_M$ is a tiling. Then the following are equivalent:
$A\oplus B=\mathbb {Z}_M$ is a tiling. Then the following are equivalent:
(i) B satisfies (T2).
(ii)
 $\sum _{m\in \mathrm {Div}\left (A^\flat \right )} \mathbb {B}_m[y]=1$ for all
$\sum _{m\in \mathrm {Div}\left (A^\flat \right )} \mathbb {B}_m[y]=1$ for all  $y\in \mathbb {Z}_M$.
$y\in \mathbb {Z}_M$.
Indeed, Proposition 3.4(iv) can be rewritten as follows: For any ![]() $y\in \mathbb {Z}_M$, there exist unique
$y\in \mathbb {Z}_M$, there exist unique ![]() $b\in B$ and
$b\in B$ and ![]() $a\in A^\flat $ such that
$a\in A^\flat $ such that ![]() $b=y+a$, or equivalently,
$b=y+a$, or equivalently, ![]() $y-b=-a$. Since
$y-b=-a$. Since ![]() $\{a\in \mathbb {Z}_M: (-a,M)\in \mathrm {Div} (A^\flat ) \}=A^\flat $, this implies the claim.
$\{a\in \mathbb {Z}_M: (-a,M)\in \mathrm {Div} (A^\flat ) \}=A^\flat $, this implies the claim.
4.2 A Fourier-analytic identity
Fix ![]() $N=p_1^{\alpha _1} \dotsm p_k^{\alpha _k}$, where
$N=p_1^{\alpha _1} \dotsm p_k^{\alpha _k}$, where ![]() $p_1,\dotsc ,p_k$ are distinct primes and
$p_1,\dotsc ,p_k$ are distinct primes and ![]() $\alpha _1,\dotsc ,\alpha _k\in \mathbb {N}$. Set
$\alpha _1,\dotsc ,\alpha _k\in \mathbb {N}$. Set ![]() $A,B,C,D\in \mathcal {M}(\mathbb {Z}_N)$. For
$A,B,C,D\in \mathcal {M}(\mathbb {Z}_N)$. For ![]() $m\mid N$, we define
$m\mid N$, we define
 $$ \begin{align*} \mathbb{A}_m^N [C] :=\sum_{c\in C}\mathbb{A}^N_m[c] w_C(c) =\sum_{a,c\in\mathbb{Z}_N} w_A(a) w_C(c) \mathbf{1}_{(a-c,N)=m}. \end{align*} $$
$$ \begin{align*} \mathbb{A}_m^N [C] :=\sum_{c\in C}\mathbb{A}^N_m[c] w_C(c) =\sum_{a,c\in\mathbb{Z}_N} w_A(a) w_C(c) \mathbf{1}_{(a-c,N)=m}. \end{align*} $$In particular, if ![]() $A(X)$ is a polynomial with
$A(X)$ is a polynomial with ![]() $0$ or
$0$ or ![]() $1$ coefficients corresponding to a set
$1$ coefficients corresponding to a set ![]() $A\subset \mathbb {Z}_N$, then
$A\subset \mathbb {Z}_N$, then
This defines N-boxes in the sense of Definition 4.3, and in particular we may consider the box product
 $$ \begin{align*} \left\langle \mathbb{A}^N[C], \mathbb{B}^N[D] \right\rangle = \sum_{m|N} \frac{1}{\phi(N/m)} \mathbb{A}_m^N[C] \mathbb{B}_m^N[D]. \end{align*} $$
$$ \begin{align*} \left\langle \mathbb{A}^N[C], \mathbb{B}^N[D] \right\rangle = \sum_{m|N} \frac{1}{\phi(N/m)} \mathbb{A}_m^N[C] \mathbb{B}_m^N[D]. \end{align*} $$ The following theorem is a slight generalisation of the main identity from [Reference Granville, Łaba and Wang11]. Specifically, [Reference Granville, Łaba and Wang11, Theorem 1] states that equation (4.6) holds when ![]() $A(X)$ and
$A(X)$ and ![]() $B(X)$ are polynomials corresponding to multisets
$B(X)$ are polynomials corresponding to multisets ![]() $A,B\subset \mathbb {Z}_N$. We will need an extension of it to four polynomials, not necessarily with nonnegative coefficients. The proof is essentially the same, but since [Reference Granville, Łaba and Wang11] remains unpublished, we include it here for completeness.
$A,B\subset \mathbb {Z}_N$. We will need an extension of it to four polynomials, not necessarily with nonnegative coefficients. The proof is essentially the same, but since [Reference Granville, Łaba and Wang11] remains unpublished, we include it here for completeness.
Theorem 4.7. Let ![]() $A(X),B(X),C(X),D(X)$ be polynomials modulo
$A(X),B(X),C(X),D(X)$ be polynomials modulo ![]() $X^N-1$ with integer coefficients. Then
$X^N-1$ with integer coefficients. Then
 $$ \begin{align} \left\langle \mathbb{A}^N[C], \mathbb{B}^N[D] \right\rangle=\sum_{d\mid N} \frac{1}{N\phi(d) } \left[ \sum_{\zeta:\Phi_d(\zeta)=0} A(\zeta)\overline{C(\zeta)} \right] \left[ \sum_{\zeta:\Phi_d(\zeta)=0} B(\zeta)\overline{D(\zeta)} \right]. \end{align} $$
$$ \begin{align} \left\langle \mathbb{A}^N[C], \mathbb{B}^N[D] \right\rangle=\sum_{d\mid N} \frac{1}{N\phi(d) } \left[ \sum_{\zeta:\Phi_d(\zeta)=0} A(\zeta)\overline{C(\zeta)} \right] \left[ \sum_{\zeta:\Phi_d(\zeta)=0} B(\zeta)\overline{D(\zeta)} \right]. \end{align} $$In particular,
 $$ \begin{align} \left\langle \mathbb{A}^N[A], \mathbb{B}^N[B] \right\rangle =\sum_{d\mid N} \frac{1}{N\phi(d) } \mathcal{E}_d(A) \mathcal{E}_d(B), \end{align} $$
$$ \begin{align} \left\langle \mathbb{A}^N[A], \mathbb{B}^N[B] \right\rangle =\sum_{d\mid N} \frac{1}{N\phi(d) } \mathcal{E}_d(A) \mathcal{E}_d(B), \end{align} $$where
 $$ \begin{align*} \mathcal{E}_d(A)=\sum_{\zeta:\Phi_d(\zeta)=0} \lvert A(\zeta)\rvert^2. \end{align*} $$
$$ \begin{align*} \mathcal{E}_d(A)=\sum_{\zeta:\Phi_d(\zeta)=0} \lvert A(\zeta)\rvert^2. \end{align*} $$ The rest of this section is devoted to the proof of Theorem 4.7. We will use the discrete Fourier transform in ![]() $\mathbb {Z}_N$: If
$\mathbb {Z}_N$: If ![]() $f:\mathbb {Z}_N\to \mathbb {C}$ is a function, then
$f:\mathbb {Z}_N\to \mathbb {C}$ is a function, then
 $$ \begin{align*} \widehat{f}(\xi)= \sum_{x\in\mathbb{Z}_N} f(x) e^{2\pi i x\xi/N},\quad \xi\in\mathbb{Z}_N. \end{align*} $$
$$ \begin{align*} \widehat{f}(\xi)= \sum_{x\in\mathbb{Z}_N} f(x) e^{2\pi i x\xi/N},\quad \xi\in\mathbb{Z}_N. \end{align*} $$Lemma 4.8. Define
 $$ \begin{align*} \Lambda_m &:=\{x\in\mathbb{Z}_N: m\mid x\}, \\ H_m &:= \{x\in\mathbb{Z}_N: (x,N)=m\} = \Lambda_m \setminus \bigcup_{m': m\mid m'\mid N,m'\neq m} \Lambda_{m'}. \end{align*} $$
$$ \begin{align*} \Lambda_m &:=\{x\in\mathbb{Z}_N: m\mid x\}, \\ H_m &:= \{x\in\mathbb{Z}_N: (x,N)=m\} = \Lambda_m \setminus \bigcup_{m': m\mid m'\mid N,m'\neq m} \Lambda_{m'}. \end{align*} $$Then  $\widehat {\mathbf {1}_{H_m}}(\xi )=G_\xi (N/m)$, where
$\widehat {\mathbf {1}_{H_m}}(\xi )=G_\xi (N/m)$, where
 $$ \begin{align} G_\xi(v)=\sum_{d\mid(v,\xi)} \mu(v/d) d. \end{align} $$
$$ \begin{align} G_\xi(v)=\sum_{d\mid(v,\xi)} \mu(v/d) d. \end{align} $$Proof. Using the fact that
 $$ \begin{align*} \widehat{\mathbf{1}_{\Lambda_m}} (\xi)= \frac{N}{m} \mathbf{1}_{\Lambda_{N/m}}(\xi), \end{align*} $$
$$ \begin{align*} \widehat{\mathbf{1}_{\Lambda_m}} (\xi)= \frac{N}{m} \mathbf{1}_{\Lambda_{N/m}}(\xi), \end{align*} $$we get by inclusion-exclusion
 $$ \begin{align*} \widehat{\mathbf{1}_{H_m}}(\xi) &= \sum_{d\mid\frac{N}{m}} \mu(d) \widehat{\mathbf{1}_{\Lambda_{md}}}(\xi) \\ &= \sum_{d\mid\frac{N}{m}} \mu(d) \frac{N}{md} \mathbf{1}_{\Lambda_{N/md}}(\xi) \\ &= \sum_{d'\mid\frac{N}{m} } \mu\left( \frac{N}{md'} \right) d' \mathbf{1}_{\Lambda_{d}}(\xi) \\ &= \sum_{d'\mid \left(\frac{N}{m},\xi\right) } \mu\left( \frac{N}{md'} \right) d' \\ &= G_\xi(N/m). \end{align*} $$
$$ \begin{align*} \widehat{\mathbf{1}_{H_m}}(\xi) &= \sum_{d\mid\frac{N}{m}} \mu(d) \widehat{\mathbf{1}_{\Lambda_{md}}}(\xi) \\ &= \sum_{d\mid\frac{N}{m}} \mu(d) \frac{N}{md} \mathbf{1}_{\Lambda_{N/md}}(\xi) \\ &= \sum_{d'\mid\frac{N}{m} } \mu\left( \frac{N}{md'} \right) d' \mathbf{1}_{\Lambda_{d}}(\xi) \\ &= \sum_{d'\mid \left(\frac{N}{m},\xi\right) } \mu\left( \frac{N}{md'} \right) d' \\ &= G_\xi(N/m). \end{align*} $$Proposition 4.9. We have
 $$ \begin{align} \sum_{v\mid N} \frac{1}{\phi(v)} G_\xi(v) G_{\xi'}(v) = \begin{cases} \frac{N}{\phi(N/d)} & \text{if } (\xi,N)=(\xi',N)=d, \\ 0 & \text{if } (\xi,N)\neq (\xi',N). \end{cases} \end{align} $$
$$ \begin{align} \sum_{v\mid N} \frac{1}{\phi(v)} G_\xi(v) G_{\xi'}(v) = \begin{cases} \frac{N}{\phi(N/d)} & \text{if } (\xi,N)=(\xi',N)=d, \\ 0 & \text{if } (\xi,N)\neq (\xi',N). \end{cases} \end{align} $$Proof. We first claim that for every ![]() $\xi $, the function
$\xi $, the function ![]() $G_\xi (v)$ is multiplicative in v. Indeed, let
$G_\xi (v)$ is multiplicative in v. Indeed, let ![]() $(x,y)=1$,
$(x,y)=1$, ![]() $(x,\xi )=t$ and
$(x,\xi )=t$ and ![]() $(y,\xi )=s$. Then
$(y,\xi )=s$. Then ![]() $(t,s)=1$ and
$(t,s)=1$ and ![]() $(xy,\xi )=ts$. Writing
$(xy,\xi )=ts$. Writing ![]() $u=u^\prime \cdot u^{\prime \prime }$,
$u=u^\prime \cdot u^{\prime \prime }$, ![]() $u^\prime \mid x$ and
$u^\prime \mid x$ and ![]() $u^{\prime \prime }\mid y$, we get
$u^{\prime \prime }\mid y$, we get
 $$ \begin{align*} G_\xi(xy)=\sum_{u\mid(xy,\xi)} \mu\left(\frac{xy}{u}\right) u=\sum_{u^\prime\mid(x,\xi),u^{\prime\prime}\mid(y,\xi)} \mu\left(\frac{x}{u^\prime}\right) \mu\left(\frac{y}{u^{\prime\prime}}\right) u^\prime u^{\prime\prime}=G_\xi(x)G_\xi(y). \end{align*} $$
$$ \begin{align*} G_\xi(xy)=\sum_{u\mid(xy,\xi)} \mu\left(\frac{xy}{u}\right) u=\sum_{u^\prime\mid(x,\xi),u^{\prime\prime}\mid(y,\xi)} \mu\left(\frac{x}{u^\prime}\right) \mu\left(\frac{y}{u^{\prime\prime}}\right) u^\prime u^{\prime\prime}=G_\xi(x)G_\xi(y). \end{align*} $$Therefore, ![]() $G_\xi (v)$ is entirely determined by its values
$G_\xi (v)$ is entirely determined by its values ![]() $G_\xi (v)$ on prime powers
$G_\xi (v)$ on prime powers ![]() $p_i^j$,
$p_i^j$, ![]() $j=0,1,\dotsc ,\alpha _i$,
$j=0,1,\dotsc ,\alpha _i$, ![]() $i=1,\dotsc ,k$. Let
$i=1,\dotsc ,k$. Let ![]() $\xi =p_1^{\nu _1}\dotsm p_k^{\nu _k}$. Then
$\xi =p_1^{\nu _1}\dotsm p_k^{\nu _k}$. Then  $p_i^\kappa \parallel \left (p_i^j,\xi \right )$ for
$p_i^\kappa \parallel \left (p_i^j,\xi \right )$ for ![]() $\kappa =\min (j,\nu _i)$. If
$\kappa =\min (j,\nu _i)$. If ![]() $j=0$, we have
$j=0$, we have ![]() $\kappa =0$ and
$\kappa =0$ and  $G_\xi \left (p_i^0\right )=G_\xi (1)=1$. If
$G_\xi \left (p_i^0\right )=G_\xi (1)=1$. If ![]() $j\geq 1$, we have
$j\geq 1$, we have
 $$ \begin{align*} G_\xi\left(p_i^j\right)=\sum_{u\mid p_i^\kappa}\mu\left(\frac{p_i^j}{u}\right) u= \begin{cases} p_i^j -p_i^{j-1} & \text{if } \kappa=j,\\ -p_i^{j-1} & \text{if } \kappa=j-1,\\ 0 & \text{if } \kappa <j, \end{cases} \end{align*} $$
$$ \begin{align*} G_\xi\left(p_i^j\right)=\sum_{u\mid p_i^\kappa}\mu\left(\frac{p_i^j}{u}\right) u= \begin{cases} p_i^j -p_i^{j-1} & \text{if } \kappa=j,\\ -p_i^{j-1} & \text{if } \kappa=j-1,\\ 0 & \text{if } \kappa <j, \end{cases} \end{align*} $$which is equivalent to
 $$ \begin{align} G_\xi\left(p_i^j\right)= \begin{cases} p_i^j -p_i^{j-1}=\phi\left(p_i^j\right) & \text{if } j\leq \nu_i,\\ -p_i^{\nu_i} & \text{if } j=\nu_i+1,\\ 0 & \text{if } j>\nu_i+1. \end{cases} \end{align} $$
$$ \begin{align} G_\xi\left(p_i^j\right)= \begin{cases} p_i^j -p_i^{j-1}=\phi\left(p_i^j\right) & \text{if } j\leq \nu_i,\\ -p_i^{\nu_i} & \text{if } j=\nu_i+1,\\ 0 & \text{if } j>\nu_i+1. \end{cases} \end{align} $$Next, if F is a multiplicative function, then
 $$ \begin{align*} \sum_{v\mid N}F(v) =\sum_{0\leq j_1\leq \alpha_1, \dotsc, 0\leq j_k\leq \alpha_k} F\left(p_{1}^{j_1}\dotsm p_{k}^{j_k}\right) =\prod_{i=1}^k \left(\sum_{j_i=0}^{\alpha_i}F\left(p_i^{j_i}\right)\right). \end{align*} $$
$$ \begin{align*} \sum_{v\mid N}F(v) =\sum_{0\leq j_1\leq \alpha_1, \dotsc, 0\leq j_k\leq \alpha_k} F\left(p_{1}^{j_1}\dotsm p_{k}^{j_k}\right) =\prod_{i=1}^k \left(\sum_{j_i=0}^{\alpha_i}F\left(p_i^{j_i}\right)\right). \end{align*} $$Applying this with ![]() $F(v)=G_\xi (v)G_{\xi '}(v)$ for fixed
$F(v)=G_\xi (v)G_{\xi '}(v)$ for fixed ![]() $\xi ,\xi '$, we get
$\xi ,\xi '$, we get
 $$ \begin{align} \sum_{v\mid N} \frac{1}{\phi(v)} G_\xi (v) G_{\xi^\prime} (v) =\prod_{i=1}^k \left( \sum_{j_i=0}^{\alpha_i} \frac{1}{\phi\left(p_i^{j_i}\right)}G_\xi \left(p_i^{j_i}\right)G_{\xi^\prime} \left(p_i^{j_i}\right) \right). \end{align} $$
$$ \begin{align} \sum_{v\mid N} \frac{1}{\phi(v)} G_\xi (v) G_{\xi^\prime} (v) =\prod_{i=1}^k \left( \sum_{j_i=0}^{\alpha_i} \frac{1}{\phi\left(p_i^{j_i}\right)}G_\xi \left(p_i^{j_i}\right)G_{\xi^\prime} \left(p_i^{j_i}\right) \right). \end{align} $$ Fix a prime divisor ![]() $p_i\mid N$, and consider the corresponding factor in equation (4.10). Suppose that
$p_i\mid N$, and consider the corresponding factor in equation (4.10). Suppose that ![]() $0\leq \nu ,\nu ' \leq \alpha _i$ are such that
$0\leq \nu ,\nu ' \leq \alpha _i$ are such that  $p_i^\nu \parallel \xi , p_i^{\nu '} \parallel \xi ^\prime $. Without loss of generality, we may assume that
$p_i^\nu \parallel \xi , p_i^{\nu '} \parallel \xi ^\prime $. Without loss of generality, we may assume that ![]() $\nu \leq \nu '$. In accordance with equation (4.9), we have three cases.
$\nu \leq \nu '$. In accordance with equation (4.9), we have three cases.
• If
 $\nu <\nu '\leq \alpha _i$, then
$\nu <\nu '\leq \alpha _i$, then  $\nu +1\leq \alpha _i$ and
$\nu +1\leq \alpha _i$ and  $$ \begin{align*} \sum_{j=0}^{\alpha_i} \frac{1}{\phi\left(p_i^j\right)} G_\xi\left(p_i^j\right) G_{\xi^\prime}\left(p_i^j\right) & =1+\sum_{j=1}^{\nu} \frac{1}{\phi\left(p_i^j\right)} \phi\left(p_i^j\right) \left(p_i^j -p_i^{j-1}\right) +\frac{1}{\phi\left(p_i^{\nu+1}\right)} \phi\left(p_i^{\nu+1}\right) \left(-p_i^n\right)\\ & = 1+\sum_{j=1}^{\nu} \left(p_i^j -p_i^{j-1}\right) -p^\nu=0. \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{\alpha_i} \frac{1}{\phi\left(p_i^j\right)} G_\xi\left(p_i^j\right) G_{\xi^\prime}\left(p_i^j\right) & =1+\sum_{j=1}^{\nu} \frac{1}{\phi\left(p_i^j\right)} \phi\left(p_i^j\right) \left(p_i^j -p_i^{j-1}\right) +\frac{1}{\phi\left(p_i^{\nu+1}\right)} \phi\left(p_i^{\nu+1}\right) \left(-p_i^n\right)\\ & = 1+\sum_{j=1}^{\nu} \left(p_i^j -p_i^{j-1}\right) -p^\nu=0. \end{align*} $$• If
 $\nu =\nu ' < \alpha _i$, then
$\nu =\nu ' < \alpha _i$, then  $\nu +1=\nu ' +1 \leq \alpha _i$ and
$\nu +1=\nu ' +1 \leq \alpha _i$ and  $$ \begin{align*} \sum_{j=0}^{\alpha_i} \frac{1}{\phi\left(p_i^j\right)} G_\xi\left(p_i^j\right) G_{\xi^\prime}\left(p_i^j\right) =1+\sum_{j=1}^{\nu} \left(p_i^j-p_i^{j-1}\right)+\frac{1}{p_i^{\nu+1}-p_i^\nu} \left(-p_i^\nu\right)^2=\frac{p_i^{\nu+1}}{p_i-1}. \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{\alpha_i} \frac{1}{\phi\left(p_i^j\right)} G_\xi\left(p_i^j\right) G_{\xi^\prime}\left(p_i^j\right) =1+\sum_{j=1}^{\nu} \left(p_i^j-p_i^{j-1}\right)+\frac{1}{p_i^{\nu+1}-p_i^\nu} \left(-p_i^\nu\right)^2=\frac{p_i^{\nu+1}}{p_i-1}. \end{align*} $$• If
 $\nu =\nu '=\alpha _i$, then
$\nu =\nu '=\alpha _i$, then  $$ \begin{align*} \sum_{j=0}^{\alpha_i} \frac{1}{\phi\left(p_i^j\right)} G_\xi\left(p_i^j\right) G_{\xi^\prime}\left(p_i^j\right) =1+\sum_{j=1}^{\alpha_i} \left(p_i^j-p_i^{j-1}\right)=p_i^{\alpha_i}. \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{\alpha_i} \frac{1}{\phi\left(p_i^j\right)} G_\xi\left(p_i^j\right) G_{\xi^\prime}\left(p_i^j\right) =1+\sum_{j=1}^{\alpha_i} \left(p_i^j-p_i^{j-1}\right)=p_i^{\alpha_i}. \end{align*} $$
Since
 $$ \begin{align*} \frac{p_i^{\alpha_i}}{\phi\left(p_i^{\alpha_i-\nu}\right)}= \begin{cases} p^{\alpha_i} & \text{if }\nu=\alpha_i, \\ \frac{p^{\alpha_i}}{\left(p_i-1\right)p_i^{\alpha_i-\nu-1}} = \frac{p_i^{\nu+1}}{p_i-1} & \text{if } \nu<\alpha_i, \end{cases} \end{align*} $$
$$ \begin{align*} \frac{p_i^{\alpha_i}}{\phi\left(p_i^{\alpha_i-\nu}\right)}= \begin{cases} p^{\alpha_i} & \text{if }\nu=\alpha_i, \\ \frac{p^{\alpha_i}}{\left(p_i-1\right)p_i^{\alpha_i-\nu-1}} = \frac{p_i^{\nu+1}}{p_i-1} & \text{if } \nu<\alpha_i, \end{cases} \end{align*} $$we conclude that
 $$ \begin{align*} \sum_{j=0}^{\alpha_i} \frac{1}{\phi\left(p_i^j\right)} G_\xi\left(p_i^j\right) G_{\xi^\prime}\left(p_i^j\right)= \begin{cases} 0 & \text{if }\nu\neq\nu',\\ \frac{p_i^{\alpha_i}}{\phi\left(p_i^{\alpha_i-\nu}\right)} & \text{if } \nu=\nu'.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{\alpha_i} \frac{1}{\phi\left(p_i^j\right)} G_\xi\left(p_i^j\right) G_{\xi^\prime}\left(p_i^j\right)= \begin{cases} 0 & \text{if }\nu\neq\nu',\\ \frac{p_i^{\alpha_i}}{\phi\left(p_i^{\alpha_i-\nu}\right)} & \text{if } \nu=\nu'.\\ \end{cases} \end{align*} $$We now plug this into equation (4.10), and since ![]() $p_i$ is no longer fixed, we write
$p_i$ is no longer fixed, we write ![]() $\nu _i$ and
$\nu _i$ and ![]() $\nu ^{\prime }_i$ instead of
$\nu ^{\prime }_i$ instead of ![]() $\nu $ and
$\nu $ and ![]() $\nu '$. If
$\nu '$. If ![]() $(\xi ,N)\neq (\xi ^\prime ,N)$, then
$(\xi ,N)\neq (\xi ^\prime ,N)$, then ![]() $\nu _i\neq \nu ^{\prime }_i$ for at least one
$\nu _i\neq \nu ^{\prime }_i$ for at least one ![]() $p_i$, so that
$p_i$, so that
 $$ \begin{align*} \sum_{v\mid N} \frac{1}{\phi(v)} G_\xi (v) G_{\xi^\prime} (v)=0. \end{align*} $$
$$ \begin{align*} \sum_{v\mid N} \frac{1}{\phi(v)} G_\xi (v) G_{\xi^\prime} (v)=0. \end{align*} $$If, on the other hand, ![]() $(\xi ,N)=(\xi ^\prime ,N)$, we get
$(\xi ,N)=(\xi ^\prime ,N)$, we get
 $$ \begin{align*} \sum_{v\mid N} \frac{1}{\phi(v)} G_\xi (v) G_{\xi^\prime} (v) =\prod_{i=1}^k \frac{p_i^{\alpha_i} }{\phi\left(p_i^{\alpha_i-\nu_i}\right)} =\frac{N}{\phi(N/(\xi,N))}, \end{align*} $$
$$ \begin{align*} \sum_{v\mid N} \frac{1}{\phi(v)} G_\xi (v) G_{\xi^\prime} (v) =\prod_{i=1}^k \frac{p_i^{\alpha_i} }{\phi\left(p_i^{\alpha_i-\nu_i}\right)} =\frac{N}{\phi(N/(\xi,N))}, \end{align*} $$which proves the proposition.
In order to finish the proof of Theorem 4.7, we write
 $$ \begin{align*} \begin{split} \mathbb{A}^N_m[C] & =\sum_{x,y,z\in\mathbb{Z}_N} w_A(x)w_C(y)\mathbf{1}_{H_m}(z)\mathbf{1}_{x-y=z} \\ & =\frac{1}{N}\sum_{x,y,z\in\mathbb{Z}_N} w_A(x)w_C(y)\mathbf{1}_{H_m}(z) \sum_{\xi \in \mathbb{Z}_N} e^{-2\pi i \xi (x-y+z)/N} \\ & = \frac{1}{N} \sum_{\xi \in \mathbb{Z}_N} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } \widehat{\mathbf{1}_{H_m}}(\xi) \\ & = \frac{1}{N} \sum_{\xi \in \mathbb{Z}_N} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } G_\xi (N/m). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \mathbb{A}^N_m[C] & =\sum_{x,y,z\in\mathbb{Z}_N} w_A(x)w_C(y)\mathbf{1}_{H_m}(z)\mathbf{1}_{x-y=z} \\ & =\frac{1}{N}\sum_{x,y,z\in\mathbb{Z}_N} w_A(x)w_C(y)\mathbf{1}_{H_m}(z) \sum_{\xi \in \mathbb{Z}_N} e^{-2\pi i \xi (x-y+z)/N} \\ & = \frac{1}{N} \sum_{\xi \in \mathbb{Z}_N} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } \widehat{\mathbf{1}_{H_m}}(\xi) \\ & = \frac{1}{N} \sum_{\xi \in \mathbb{Z}_N} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } G_\xi (N/m). \end{split} \end{align*} $$Therefore
 $$ \begin{align*} \left\langle \mathbb{A}^N[C], \mathbb{B}^N[D] \right\rangle & =\frac{1}{N^2} \sum_{v\mid N} \frac{1}{\phi(v)} \left(\sum_{\xi \in \mathbb{Z}_N} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } G_\xi (v)\right)\left(\sum_{\xi^\prime \in \mathbb{Z}_N} \widehat{w_B}(\xi') \overline{ \widehat{w_D}(\xi') } G_{\xi^\prime} (v)\right) \\ & = \frac{1}{N^2} \sum_{\xi, \xi^\prime \in \mathbb{Z}_N} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } \widehat{w_B}(\xi') \overline{ \widehat{w_D}(\xi') } \left[\sum_{v\mid N} \frac{1}{\phi(v)} G_\xi (v) G_{\xi^\prime} (v)\right]. \end{align*} $$
$$ \begin{align*} \left\langle \mathbb{A}^N[C], \mathbb{B}^N[D] \right\rangle & =\frac{1}{N^2} \sum_{v\mid N} \frac{1}{\phi(v)} \left(\sum_{\xi \in \mathbb{Z}_N} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } G_\xi (v)\right)\left(\sum_{\xi^\prime \in \mathbb{Z}_N} \widehat{w_B}(\xi') \overline{ \widehat{w_D}(\xi') } G_{\xi^\prime} (v)\right) \\ & = \frac{1}{N^2} \sum_{\xi, \xi^\prime \in \mathbb{Z}_N} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } \widehat{w_B}(\xi') \overline{ \widehat{w_D}(\xi') } \left[\sum_{v\mid N} \frac{1}{\phi(v)} G_\xi (v) G_{\xi^\prime} (v)\right]. \end{align*} $$By Proposition 4.9,
 $$ \begin{align*} \left\langle \mathbb{A}^N[C], \mathbb{B}^N[D] \right\rangle & =\frac{1}{N^2} \sum_{d\mid N} \frac{N}{\phi(N/d)} \left(\sum_{\xi: \left(\xi,N\right)=d} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } \right) \left(\sum_{\xi^\prime: \left(\xi^\prime,N\right)=d} \widehat{w_B}(\xi') \overline{ \widehat{w_D}(\xi') } \right), \end{align*} $$
$$ \begin{align*} \left\langle \mathbb{A}^N[C], \mathbb{B}^N[D] \right\rangle & =\frac{1}{N^2} \sum_{d\mid N} \frac{N}{\phi(N/d)} \left(\sum_{\xi: \left(\xi,N\right)=d} \widehat{w_A}(\xi) \overline{ \widehat{w_C}(\xi) } \right) \left(\sum_{\xi^\prime: \left(\xi^\prime,N\right)=d} \widehat{w_B}(\xi') \overline{ \widehat{w_D}(\xi') } \right), \end{align*} $$which is equation (4.6), since  $ \widehat {w_A}(\xi ) = A\left (e^{-2\pi i \xi /N}\right )$ and
$ \widehat {w_A}(\xi ) = A\left (e^{-2\pi i \xi /N}\right )$ and ![]() $\zeta = e^{-2\pi i \xi /N}$ is a root of
$\zeta = e^{-2\pi i \xi /N}$ is a root of ![]() $\Phi _d(X)$ if and only if
$\Phi _d(X)$ if and only if ![]() $(\xi ,N)=N/d$.
$(\xi ,N)=N/d$.
4.3 Proof of Theorem 4.4
(i) Assume that
 $A\oplus B=\mathbb {Z}_M$. Let
$A\oplus B=\mathbb {Z}_M$. Let  $N\mid M$, and let
$N\mid M$, and let  $C=\{x\}$ and
$C=\{x\}$ and  $D=\{y\}$ for
$D=\{y\}$ for  $x,y\in \mathbb {Z}_N$. By equation (4.5), we have If
$x,y\in \mathbb {Z}_N$. By equation (4.5), we have If $$ \begin{align*} \left\langle \mathbb{A}^N[x], \mathbb{B}^N[y] \right\rangle =\sum_{d\mid N} \frac{1}{N \phi(d) } \left[ \sum_{\zeta:\Phi_d(\zeta)=0} A(\zeta)\overline{C(\zeta)} \right] \left[ \sum_{\zeta:\Phi_d(\zeta)=0} B(\zeta)\overline{D(\zeta)} \right]. \end{align*} $$
$$ \begin{align*} \left\langle \mathbb{A}^N[x], \mathbb{B}^N[y] \right\rangle =\sum_{d\mid N} \frac{1}{N \phi(d) } \left[ \sum_{\zeta:\Phi_d(\zeta)=0} A(\zeta)\overline{C(\zeta)} \right] \left[ \sum_{\zeta:\Phi_d(\zeta)=0} B(\zeta)\overline{D(\zeta)} \right]. \end{align*} $$ $d\neq 1$, then
$d\neq 1$, then  $\Phi _d(X)$ divides at least one of
$\Phi _d(X)$ divides at least one of  $A(X)$ and
$A(X)$ and  $B(X)$. Hence the only nonzero contribution is from
$B(X)$. Hence the only nonzero contribution is from  $d=1$, which yields This proves equation (4.2).
$d=1$, which yields This proves equation (4.2). $$ \begin{align*} \left\langle \mathbb{A}^N[x], \mathbb{B}^N[y] \right\rangle = \frac{1}{N} A(1)C(1)B(1)D(1) = \frac{\lvert A\rvert \lvert B\rvert}{N}. \end{align*} $$
$$ \begin{align*} \left\langle \mathbb{A}^N[x], \mathbb{B}^N[y] \right\rangle = \frac{1}{N} A(1)C(1)B(1)D(1) = \frac{\lvert A\rvert \lvert B\rvert}{N}. \end{align*} $$(ii) Suppose that
 $A,B\subset \mathbb {Z}_M$ satisfy
$A,B\subset \mathbb {Z}_M$ satisfy  $\left \langle \mathbb {A}^M[a], \mathbb {B}^M[b] \right \rangle =1$ for all
$\left \langle \mathbb {A}^M[a], \mathbb {B}^M[b] \right \rangle =1$ for all  $a\in A,b\in B$. Then By equation (4.6), this implies that
$a\in A,b\in B$. Then By equation (4.6), this implies that $$ \begin{align*} \left\langle \mathbb{A}^M[A], \mathbb{B}^M[B] \right\rangle &= \sum_{a\in A,b\in B} \left\langle \mathbb{A}^M[a], \mathbb{B}^M[b] \right\rangle\\ &= \sum_{a\in A,b\in B} 1 = \lvert A\rvert \lvert B\rvert=M. \end{align*} $$However, we are also assuming that
$$ \begin{align*} \left\langle \mathbb{A}^M[A], \mathbb{B}^M[B] \right\rangle &= \sum_{a\in A,b\in B} \left\langle \mathbb{A}^M[a], \mathbb{B}^M[b] \right\rangle\\ &= \sum_{a\in A,b\in B} 1 = \lvert A\rvert \lvert B\rvert=M. \end{align*} $$However, we are also assuming that $$ \begin{align*} \sum_{d\mid M} \frac{1}{\phi(d) } \mathcal{E}_d(A) \mathcal{E}_d(B) = M^2. \end{align*} $$
$$ \begin{align*} \sum_{d\mid M} \frac{1}{\phi(d) } \mathcal{E}_d(A) \mathcal{E}_d(B) = M^2. \end{align*} $$ $\mathcal {E}_1(A) \mathcal {E}_1(B)= \lvert A\rvert ^2 \lvert B\rvert ^2 = M^2$. Hence
$\mathcal {E}_1(A) \mathcal {E}_1(B)= \lvert A\rvert ^2 \lvert B\rvert ^2 = M^2$. Hence  $\mathcal {E}_d(A) \mathcal {E}_d(B)=0$ for all
$\mathcal {E}_d(A) \mathcal {E}_d(B)=0$ for all  $d\mid M$,
$d\mid M$,  $d\neq 1$, so that
$d\neq 1$, so that  $A\oplus B=\mathbb {Z}_M$ as claimed.
$A\oplus B=\mathbb {Z}_M$ as claimed.
Remark 4.10. We indicate a proof of Theorem 2.5 based on equation (4.6). Suppose that ![]() $A\oplus B=\mathbb {Z}_M$ is a tiling, and apply equation (4.6) with
$A\oplus B=\mathbb {Z}_M$ is a tiling, and apply equation (4.6) with ![]() $N=M$. Since
$N=M$. Since ![]() $\Phi _d(X)\mid A(X)B(X)$ for all
$\Phi _d(X)\mid A(X)B(X)$ for all ![]() $d\mid M$,
$d\mid M$, ![]() $d\neq 1$, we get
$d\neq 1$, we get
 $$ \begin{align*} \sum_{m\mid M}\frac{1}{\phi(M/m)} \mathbb{A}^M_m[A]\mathbb{B}^M_m[B] = \frac{\lvert A(1)\rvert^2 \lvert B(1)\rvert^2}{M}=M. \end{align*} $$
$$ \begin{align*} \sum_{m\mid M}\frac{1}{\phi(M/m)} \mathbb{A}^M_m[A]\mathbb{B}^M_m[B] = \frac{\lvert A(1)\rvert^2 \lvert B(1)\rvert^2}{M}=M. \end{align*} $$But we also have ![]() $\mathbb {A}^M_M[A]\mathbb {B}^M_M[B]=\lvert A\rvert \lvert B\rvert =M$. Hence all other terms
$\mathbb {A}^M_M[A]\mathbb {B}^M_M[B]=\lvert A\rvert \lvert B\rvert =M$. Hence all other terms ![]() $\mathbb {A}^M_m[A]\mathbb {B}^M_m[B]$ with
$\mathbb {A}^M_m[A]\mathbb {B}^M_m[B]$ with ![]() $m\neq M$ must vanish. This proves Theorem 2.5.
$m\neq M$ must vanish. This proves Theorem 2.5.
5 Cuboids
5.1 Definitions
Definition 5.1. Let  $M=\prod _{i=1}^K p_i^{n_i}$.
$M=\prod _{i=1}^K p_i^{n_i}$.
(i) A cuboid type
 $\mathcal {T}$ on
$\mathcal {T}$ on  $\mathbb {Z}_N$ is an ordered triple
$\mathbb {Z}_N$ is an ordered triple  $\mathcal {T}= (N,\vec {\delta }, T)$, where
$\mathcal {T}= (N,\vec {\delta }, T)$, where•
 $N=\prod _{i=1}^K p_i^{n_i-\alpha _i}$ is a divisor of M, with
$N=\prod _{i=1}^K p_i^{n_i-\alpha _i}$ is a divisor of M, with  $0\leq \alpha _i\leq n_i$ for each
$0\leq \alpha _i\leq n_i$ for each  $i=1,\dotsc ,K$;
$i=1,\dotsc ,K$;•
 $\vec {\delta }=(\delta _1,\dotsc ,\delta _K)$, with
$\vec {\delta }=(\delta _1,\dotsc ,\delta _K)$, with  $0\leq \delta _i\leq n_i-\alpha _i$ for
$0\leq \delta _i\leq n_i-\alpha _i$ for  $i=1,\dotsc ,K$;
$i=1,\dotsc ,K$;•
 $T\subset \mathbb {Z}_N$ is a nonempty set.
$T\subset \mathbb {Z}_N$ is a nonempty set.
We will refer to N as the scale of
 $\mathcal {T}$, and to T as its template. We also define
$\mathcal {T}$, and to T as its template. We also define  $\mathfrak {J} =\mathfrak {J}_{\vec \delta } := \{j: \delta _j\neq 0\}$.
$\mathfrak {J} =\mathfrak {J}_{\vec \delta } := \{j: \delta _j\neq 0\}$.(ii) Let
 $\mathcal {T} =(N,\vec {\delta }, T)$ be a cuboid type as described. A cuboid
$\mathcal {T} =(N,\vec {\delta }, T)$ be a cuboid type as described. A cuboid  $\Delta $ of type
$\Delta $ of type  $\mathcal {T}$ is a weighted multiset corresponding to a mask polynomial of the form (5.1)
$\mathcal {T}$ is a weighted multiset corresponding to a mask polynomial of the form (5.1) $$ \begin{align} \Delta(X)= X^c\prod_{j\in \mathfrak{J}} \left(1-X^{d_j}\right), \end{align} $$
$$ \begin{align} \Delta(X)= X^c\prod_{j\in \mathfrak{J}} \left(1-X^{d_j}\right), \end{align} $$where
 $c,d_j$ are elements of
$c,d_j$ are elements of  $\mathbb {Z}_M$ such that
$\mathbb {Z}_M$ such that  $\left (d_j,N\right )=N/p_j^{\delta _j}$. The vertices of
$\left (d_j,N\right )=N/p_j^{\delta _j}$. The vertices of  $\Delta $ are the points (5.2)
$\Delta $ are the points (5.2) $$ \begin{align} x_{\vec\epsilon}=c+\sum_{j\in \mathfrak{J}} \epsilon_jd_j: \vec{\epsilon} = \left(\epsilon_j\right)_{j\in \mathfrak{J}} \in\{0,1\}^{\lvert\mathfrak{J}\rvert}, \end{align} $$
$$ \begin{align} x_{\vec\epsilon}=c+\sum_{j\in \mathfrak{J}} \epsilon_jd_j: \vec{\epsilon} = \left(\epsilon_j\right)_{j\in \mathfrak{J}} \in\{0,1\}^{\lvert\mathfrak{J}\rvert}, \end{align} $$with weights
 $w_\Delta \left (x_{\vec \epsilon }\right )=(-1)^{\sum _{j\in \mathfrak {J}}\epsilon _j}$.
$w_\Delta \left (x_{\vec \epsilon }\right )=(-1)^{\sum _{j\in \mathfrak {J}}\epsilon _j}$.(iii) Set
 $A\in \mathcal {M}(\mathbb {Z}_N)$, and let
$A\in \mathcal {M}(\mathbb {Z}_N)$, and let  $\Delta $ be a cuboid of type
$\Delta $ be a cuboid of type  $\mathcal {T}$. Then the
$\mathcal {T}$. Then the  $(\Delta ,T)$-evaluation of A is where we recall that
$(\Delta ,T)$-evaluation of A is where we recall that $$ \begin{align*} \mathbb{A}^{\mathcal{T}} [\Delta] = \mathbb{A}^N_N[\Delta*T]= \sum_{ \vec\epsilon\in\{0,1\}^k} w_\Delta\left(x_{\vec\epsilon}\right) \mathbb{A}^N_N\left[x_{\vec\epsilon}*T\right], \end{align*} $$
$$ \begin{align*} \mathbb{A}^{\mathcal{T}} [\Delta] = \mathbb{A}^N_N[\Delta*T]= \sum_{ \vec\epsilon\in\{0,1\}^k} w_\Delta\left(x_{\vec\epsilon}\right) \mathbb{A}^N_N\left[x_{\vec\epsilon}*T\right], \end{align*} $$ $x*T=\{x+t: \ t\in T\}$, so that
$x*T=\{x+t: \ t\in T\}$, so that  $$ \begin{align*} \mathbb{A}^N_N\left[x_{\vec\epsilon}*T\right]:= \sum_{t\in T} \mathbb{A}^N_N\left[x_{\vec\epsilon}+t\right]. \end{align*} $$
$$ \begin{align*} \mathbb{A}^N_N\left[x_{\vec\epsilon}*T\right]:= \sum_{t\in T} \mathbb{A}^N_N\left[x_{\vec\epsilon}+t\right]. \end{align*} $$
For consistency, we will also write
 $$ \begin{align*} \mathbb{A}^{\mathcal{T}} [x] = \mathbb{A}^N_N[x*T],\quad x\in\mathbb{Z}_M. \end{align*} $$
$$ \begin{align*} \mathbb{A}^{\mathcal{T}} [x] = \mathbb{A}^N_N[x*T],\quad x\in\mathbb{Z}_M. \end{align*} $$In some situations, it will be easier to write out ![]() $\Delta $ in its polynomial form. We will then identify the polynomial
$\Delta $ in its polynomial form. We will then identify the polynomial ![]() $\Delta (X)$ with the corresponding weighted multiset
$\Delta (X)$ with the corresponding weighted multiset ![]() $\Delta $, and write
$\Delta $, and write ![]() $\mathbb {A}^{\mathcal {T}} [\Delta (X)]$ instead of
$\mathbb {A}^{\mathcal {T}} [\Delta (X)]$ instead of ![]() $\mathbb {A}^{\mathcal {T}} [\Delta ]$.
$\mathbb {A}^{\mathcal {T}} [\Delta ]$.
Definition 5.2. Set ![]() $A\in \mathcal {M}(\mathbb {Z}_M)$, and let
$A\in \mathcal {M}(\mathbb {Z}_M)$, and let  $\mathcal {T} = (N,\vec \delta ,T)$ be a cuboid type as before. We will say that A is
$\mathcal {T} = (N,\vec \delta ,T)$ be a cuboid type as before. We will say that A is ![]() $\mathcal {T}$-null if for every cuboid
$\mathcal {T}$-null if for every cuboid ![]() $\Delta $ of type
$\Delta $ of type ![]() $\mathcal {T}$,
$\mathcal {T}$,

Figure 2 An N-cuboid with N having three prime factors.
Lemma 5.3. Set ![]() $A\in \mathcal {M}(\mathbb {Z}_M)$, and let
$A\in \mathcal {M}(\mathbb {Z}_M)$, and let  $\mathcal {T} = (N,\vec \delta ,T)$ be a cuboid type. Suppose that for all
$\mathcal {T} = (N,\vec \delta ,T)$ be a cuboid type. Suppose that for all ![]() $m\mid N$, the cyclotomic polynomial
$m\mid N$, the cyclotomic polynomial ![]() $\Phi _m(X)$ divides at least one of
$\Phi _m(X)$ divides at least one of ![]() $A(X)$,
$A(X)$, ![]() $T(X)$, or
$T(X)$, or  $1-X^{N/p_j^{\delta _j}}$ for some
$1-X^{N/p_j^{\delta _j}}$ for some  $j\in \mathfrak {J}(\vec \delta )$. Then A is
$j\in \mathfrak {J}(\vec \delta )$. Then A is ![]() $\mathcal {T}$-null.
$\mathcal {T}$-null.
Proof. This follows, for example, from Theorem 4.7 applied to ![]() $A(X)$ and
$A(X)$ and ![]() $C(X)=\Delta (X)T(X)$, with
$C(X)=\Delta (X)T(X)$, with ![]() $B=D=\{0\}$.
$B=D=\{0\}$.
5.2 Classic cuboids
Definition 5.4. An N-cuboid is a cuboid of type  $\mathcal {T}=(N,\vec {\delta },T)$, where
$\mathcal {T}=(N,\vec {\delta },T)$, where ![]() $N\mid M$,
$N\mid M$, ![]() $T(X)=1$ and
$T(X)=1$ and ![]() $\delta _j=1$ for all j such that
$\delta _j=1$ for all j such that ![]() $p_j\mid N$. Thus, N-cuboids have the form
$p_j\mid N$. Thus, N-cuboids have the form
 $$ \begin{align*} \Delta(X)= X^c\prod_{p_j\mid N} \left(1-X^{\rho_jN/p_j}\right) \end{align*} $$
$$ \begin{align*} \Delta(X)= X^c\prod_{p_j\mid N} \left(1-X^{\rho_jN/p_j}\right) \end{align*} $$with ![]() $ (\rho _j,p_j)=1$ for all j, and the associated
$ (\rho _j,p_j)=1$ for all j, and the associated ![]() $\Delta $-evaluation of a multiset
$\Delta $-evaluation of a multiset ![]() $A\in \mathcal {M}(\mathbb {Z}_N)$ is
$A\in \mathcal {M}(\mathbb {Z}_N)$ is
 $$ \begin{align*} \mathbb{A}^N_N[\Delta] = \sum_{ \vec\epsilon\in\{0,1\}^{\lvert\mathfrak{J}\rvert}} w_\Delta\left(x_{\vec\epsilon}\right) \mathbb{A}^N_N\left[x_{\vec\epsilon}\right], \end{align*} $$
$$ \begin{align*} \mathbb{A}^N_N[\Delta] = \sum_{ \vec\epsilon\in\{0,1\}^{\lvert\mathfrak{J}\rvert}} w_\Delta\left(x_{\vec\epsilon}\right) \mathbb{A}^N_N\left[x_{\vec\epsilon}\right], \end{align*} $$where ![]() $\mathfrak {J}= \{j: p_j\mid N \}$ and the cuboid vertices
$\mathfrak {J}= \{j: p_j\mid N \}$ and the cuboid vertices ![]() $x_{\vec \epsilon }$ are defined in equation (5.2). If
$x_{\vec \epsilon }$ are defined in equation (5.2). If ![]() $\mathcal {T}$ is as before and
$\mathcal {T}$ is as before and ![]() $A\in \mathcal {M}(\mathbb {Z}_N)$ is
$A\in \mathcal {M}(\mathbb {Z}_N)$ is ![]() $\mathcal {T}$-null, we will also say for short that A is N-null.
$\mathcal {T}$-null, we will also say for short that A is N-null.
The geometric interpretation of N-cuboids ![]() $\Delta $ is as follows. With notation as in Definition 5.4, recall that
$\Delta $ is as follows. With notation as in Definition 5.4, recall that ![]() $D(N)=N/\prod _{j\in \mathfrak {J}}p_j$. Then the vertices
$D(N)=N/\prod _{j\in \mathfrak {J}}p_j$. Then the vertices ![]() $x_{\vec \epsilon }$ of
$x_{\vec \epsilon }$ of ![]() $\Delta $ form a full-dimensional rectangular box in the grid
$\Delta $ form a full-dimensional rectangular box in the grid ![]() $\Lambda (c,D(N))$, with one vertex at c and alternating
$\Lambda (c,D(N))$, with one vertex at c and alternating ![]() $\pm 1$ weights. We reserve the term ‘N-cuboid’, without cuboid type explicitly indicated, to refer to cuboids as in Definition 5.4; for cuboids of any other type, we will always specify
$\pm 1$ weights. We reserve the term ‘N-cuboid’, without cuboid type explicitly indicated, to refer to cuboids as in Definition 5.4; for cuboids of any other type, we will always specify ![]() $\mathcal {T}$.
$\mathcal {T}$.
The following cyclotomic divisibility test has been known and used previously in the literature (see, for example, [Reference Steinberger42, Section 3] in the context of vanishing sums of roots of unity, or [Reference Kiss, Malikiosis, Somlai and Vizer16, Section 3] and [Reference Kiss, Malikiosis, Somlai and Vizer17] with applications to the ‘spectral implies tiling’ direction of Fuglede’s conjecture.
Proposition 5.5. Set ![]() $A\in \mathcal {M}(\mathbb {Z}_N)$. Then the following are equivalent:
$A\in \mathcal {M}(\mathbb {Z}_N)$. Then the following are equivalent:
(i)
 $\Phi _N(X)|A(X)$.
$\Phi _N(X)|A(X)$.(ii) For all N-cuboids
 $\Delta $, we have (5.4)
$\Delta $, we have (5.4) $$ \begin{align} \mathbb{A}^N_N[\Delta]=0. \end{align} $$
$$ \begin{align} \mathbb{A}^N_N[\Delta]=0. \end{align} $$
Proof. Let ![]() $m\mid N$ satisfy
$m\mid N$ satisfy ![]() $m\neq N$. Then
$m\neq N$. Then ![]() $m\mid (N/p_i)$ for some i such that
$m\mid (N/p_i)$ for some i such that ![]() $p_i\mid N$, so that
$p_i\mid N$, so that ![]() $\Phi _m\mid (1-X^{N/p_i})$. The implication (i)
$\Phi _m\mid (1-X^{N/p_i})$. The implication (i) ![]() $\Rightarrow $ (ii) now follows from Lemma 5.3.
$\Rightarrow $ (ii) now follows from Lemma 5.3.
An alternative proof that (i) implies (ii) (without using Theorem 4.7; compare [Reference Kiss, Malikiosis, Somlai and Vizer16, Reference Steinberger42]) is as follows. By classic results on vanishing sums of roots of unity [Reference de Bruijn3, Reference Lam and Leung28, Reference Mann32, Reference Rédei35, Reference Rédei36, Reference Schoenberg38], ![]() $\Phi _N(X)\mid A(X)$ if and only if
$\Phi _N(X)\mid A(X)$ if and only if ![]() $A(X)$ is a linear combination of the polynomials
$A(X)$ is a linear combination of the polynomials  $\Phi _p(X^{N/p})$, where p runs over all prime divisors of N, with integer (but not necessarily nonnegative) coefficients. Equivalently,
$\Phi _p(X^{N/p})$, where p runs over all prime divisors of N, with integer (but not necessarily nonnegative) coefficients. Equivalently, ![]() $\Phi _N(X)\mid A(X)$ if and only if A can be represented as a linear combination of N-fibers. It is very easy to see that equation (5.4) holds for all N-cuboids
$\Phi _N(X)\mid A(X)$ if and only if A can be represented as a linear combination of N-fibers. It is very easy to see that equation (5.4) holds for all N-cuboids ![]() $\Delta $ if
$\Delta $ if ![]() $A \bmod N$ is an N-fiber; therefore it also holds if
$A \bmod N$ is an N-fiber; therefore it also holds if ![]() $A \bmod N$ is a linear combination of such fibers.
$A \bmod N$ is a linear combination of such fibers.
The proof that (ii) implies (i) is by induction on the number of prime divisors of N (this argument was also known previously in the literature; see, for example, [Reference Steinberger42, Proposition 2.4]). We present it here for completeness.
If ![]() $N=p^\alpha $ is a prime power, the claim follows from equation (2.6). Suppose that the claim is true for all
$N=p^\alpha $ is a prime power, the claim follows from equation (2.6). Suppose that the claim is true for all ![]() $N'$ with at most k prime divisors. Suppose that N has
$N'$ with at most k prime divisors. Suppose that N has ![]() $k+1$ prime divisors, and that
$k+1$ prime divisors, and that ![]() $A\in \mathcal {M}(\mathbb {Z}_N)$ obeys equation (5.4) for all N-cuboids
$A\in \mathcal {M}(\mathbb {Z}_N)$ obeys equation (5.4) for all N-cuboids ![]() $\Delta $ in
$\Delta $ in ![]() $\mathbb {Z}_N$. Let p be a prime divisor of N, and let
$\mathbb {Z}_N$. Let p be a prime divisor of N, and let ![]() $N'=N/p^\alpha $, where
$N'=N/p^\alpha $, where ![]() $(N',p)=1$.
$(N',p)=1$.
Assume first that
 $$ \begin{align} A\in\mathcal{M}\left( p^{\alpha-1}\mathbb{Z}_N\right). \end{align} $$
$$ \begin{align} A\in\mathcal{M}\left( p^{\alpha-1}\mathbb{Z}_N\right). \end{align} $$Write  $A(X)=\sum _{j=0}^{p-1} X^{jN/p } A_j(X)$, where
$A(X)=\sum _{j=0}^{p-1} X^{jN/p } A_j(X)$, where ![]() $A_j\in \mathcal {M}(p^{\alpha }\mathbb {Z}_N)$. Each ‘layer’
$A_j\in \mathcal {M}(p^{\alpha }\mathbb {Z}_N)$. Each ‘layer’ ![]() $A_j$ can be identified in the obvious manner with a multiset in
$A_j$ can be identified in the obvious manner with a multiset in ![]() $\mathbb {Z}_{N'}$.
$\mathbb {Z}_{N'}$.
For ![]() $j=0,1,\dotsc ,p-1$, let
$j=0,1,\dotsc ,p-1$, let ![]() $A_{j,0}$ be the weighted multiset defined via
$A_{j,0}$ be the weighted multiset defined via ![]() ${A}_{j,0}(X)= {A}_j(X)-{A}_0(X)$. The condition (5.4) implies that, with the obvious notation,
${A}_{j,0}(X)= {A}_j(X)-{A}_0(X)$. The condition (5.4) implies that, with the obvious notation,
 $$ \begin{align*} \left(\mathbb{A}_{j,0}\right)^{N'} [\Delta'] =0 \end{align*} $$
$$ \begin{align*} \left(\mathbb{A}_{j,0}\right)^{N'} [\Delta'] =0 \end{align*} $$for every full-dimensional cuboid ![]() $\Delta '$ in
$\Delta '$ in ![]() $\mathbb {Z}_{N'}$. By the inductive assumption,
$\mathbb {Z}_{N'}$. By the inductive assumption, ![]() $\Phi _{N'}(X)\mid A_{j,0}(X)$. By the structure theorem for vanishing sums of roots of unity,
$\Phi _{N'}(X)\mid A_{j,0}(X)$. By the structure theorem for vanishing sums of roots of unity, ![]() ${A}_{j,0}$ is a linear combination of
${A}_{j,0}$ is a linear combination of ![]() $N'$-fibers in
$N'$-fibers in ![]() $\mathbb {Z}_{N'}$. Returning to
$\mathbb {Z}_{N'}$. Returning to ![]() $\mathbb {Z}_N$ now, and summing in j, we get that
$\mathbb {Z}_N$ now, and summing in j, we get that ![]() $A(X) = A'(X)+A''(X)$, where the following are true:
$A(X) = A'(X)+A''(X)$, where the following are true:
•
 $A'(X)=\sum _{j=0}^{p-1} X^{jN/p } A_{j,0}(X)$. By the foregoing argument,
$A'(X)=\sum _{j=0}^{p-1} X^{jN/p } A_{j,0}(X)$. By the foregoing argument,  ${A}'$ is a linear combination of fibers in directions perpendicular to p.
${A}'$ is a linear combination of fibers in directions perpendicular to p.•
 ${A}''=\sum _{j=0}^{p-1} X^{jN/p} A_0(X)$. This is a linear combination of fibers in the p direction.
${A}''=\sum _{j=0}^{p-1} X^{jN/p} A_0(X)$. This is a linear combination of fibers in the p direction.
Thus ![]() ${A}$ is a linear combination of fibers, and therefore
${A}$ is a linear combination of fibers, and therefore ![]() $\Phi _N(X)\mid A(X)$.
$\Phi _N(X)\mid A(X)$.
Finally, in the general case without assumption (5.5), we can write A as a union of multisets ![]() $A^{(i)}$,
$A^{(i)}$, ![]() $i=0,1,\dotsc , p^{\alpha -1} -1$, where each
$i=0,1,\dotsc , p^{\alpha -1} -1$, where each ![]() $A^{(i)}$ is a translate of a multiset satisfying assumption (5.5). If equation (5.4) holds for A, then it also holds for each
$A^{(i)}$ is a translate of a multiset satisfying assumption (5.5). If equation (5.4) holds for A, then it also holds for each ![]() $A^{(i)}$. By the previous argument, we get that
$A^{(i)}$. By the previous argument, we get that ![]() $\Phi _N(X)\mid A^{(i)}(X)$ for each i, and therefore it divides
$\Phi _N(X)\mid A^{(i)}(X)$ for each i, and therefore it divides ![]() $A(X)$. This completes the proof that (ii) implies (i).
$A(X)$. This completes the proof that (ii) implies (i).
Remark 5.6. Proposition 5.5 implies in particular that for any ![]() $N\mid M$,
$N\mid M$, ![]() $\Phi _N$ divides A if and only if it divides the mask polynomial of
$\Phi _N$ divides A if and only if it divides the mask polynomial of ![]() $A\cap \Lambda (x,D(N))$ for every
$A\cap \Lambda (x,D(N))$ for every ![]() $x\in \mathbb {Z}_M$. Indeed, the vertices of any N-cuboid
$x\in \mathbb {Z}_M$. Indeed, the vertices of any N-cuboid ![]() $\Delta $ are all contained in the same
$\Delta $ are all contained in the same ![]() $D(N)$-grid. Hence the divisibility of A by
$D(N)$-grid. Hence the divisibility of A by ![]() $\Phi _M$ is associated with the structure of A on such grids.
$\Phi _M$ is associated with the structure of A on such grids.
5.3 Multiscale cuboids
In many situations, we need to work with cuboids on several scales simultaneously. This happens, for example, when we investigate the divisibility of a polynomial ![]() $A(X)$ by combinations of cyclotomic polynomials, or when we try to reduce a tiling of
$A(X)$ by combinations of cyclotomic polynomials, or when we try to reduce a tiling of ![]() $\mathbb {Z}_M$ to tilings of cosets of a subgroup. We will use cuboids with nontrivial templates to facilitate such multiscale cuboid analysis.
$\mathbb {Z}_M$ to tilings of cosets of a subgroup. We will use cuboids with nontrivial templates to facilitate such multiscale cuboid analysis.
Definition 5.7 Folding templates
Let  $M=\prod _{i=1}^K p_i^{n_i}$ and
$M=\prod _{i=1}^K p_i^{n_i}$ and  $N=\prod _{i=1}^K p_i^{n_i-\alpha _i}$, with
$N=\prod _{i=1}^K p_i^{n_i-\alpha _i}$, with ![]() $0\leq \alpha _i\leq n_i$ for
$0\leq \alpha _i\leq n_i$ for ![]() $i=1,\dotsc ,K$. The folding template
$i=1,\dotsc ,K$. The folding template  $T^M_N$ is given by
$T^M_N$ is given by
 $$ \begin{align*} T^M_N(X) = \prod_{i:p_i\mid\frac{M}{N}} \prod_{\nu_i=1}^{\alpha_i} \Psi_{M/p_i^{\nu_i}}(X) \equiv \frac{X^M-1}{X^N-1} \bmod \left(X^M-1\right), \end{align*} $$
$$ \begin{align*} T^M_N(X) = \prod_{i:p_i\mid\frac{M}{N}} \prod_{\nu_i=1}^{\alpha_i} \Psi_{M/p_i^{\nu_i}}(X) \equiv \frac{X^M-1}{X^N-1} \bmod \left(X^M-1\right), \end{align*} $$where
 $$ \begin{align} \Psi_{M/p_i^\delta}(X)= \Phi_{p_i}\left(X^{M/p_i^\delta}\right) = 1+X^{M/p_i^{\delta}}+ X^{2M/p_i^{\delta}} + \dotsb + X^{(p_i-1) M/p_i^{\delta}}. \end{align} $$
$$ \begin{align} \Psi_{M/p_i^\delta}(X)= \Phi_{p_i}\left(X^{M/p_i^\delta}\right) = 1+X^{M/p_i^{\delta}}+ X^{2M/p_i^{\delta}} + \dotsb + X^{(p_i-1) M/p_i^{\delta}}. \end{align} $$When M is fixed, we will sometimes write ![]() $T_N$ instead of
$T_N$ instead of  $T^M_N$, for simplicity.
$T^M_N$, for simplicity.
Strictly speaking,  $\Psi _{M/p_i^\delta }$ depends on both M and
$\Psi _{M/p_i^\delta }$ depends on both M and ![]() $p_i^\delta $, not just on their quotient; however, both numbers will always be clear from the context. We also note that
$p_i^\delta $, not just on their quotient; however, both numbers will always be clear from the context. We also note that ![]() $\Psi _{M/p_i}=F_i$.
$\Psi _{M/p_i}=F_i$.
Definition 5.7 allow us to consider N-cuboids as cuboids with templates in ![]() $\mathbb {Z}_M$. Specifically, let
$\mathbb {Z}_M$. Specifically, let ![]() $N\mid M$ be as in Definition 5.7. Then for any
$N\mid M$ be as in Definition 5.7. Then for any ![]() $A\in \mathcal {M}(\mathbb {Z}_M)$ and
$A\in \mathcal {M}(\mathbb {Z}_M)$ and ![]() $x\in \mathbb {Z}_M$,
$x\in \mathbb {Z}_M$,
 $$ \begin{align} \mathbb{A}^N_N[x]= \mathbb{A}^M_M\left[x*T^M_N\right]. \end{align} $$
$$ \begin{align} \mathbb{A}^N_N[x]= \mathbb{A}^M_M\left[x*T^M_N\right]. \end{align} $$Consequently, we have the following:
Lemma 5.8. With M and N as in Definition 5.7, let  $\mathcal {T}= (M,\vec {\delta },T^M_N)$, where
$\mathcal {T}= (M,\vec {\delta },T^M_N)$, where
 $$ \begin{align} \delta_i= \begin{cases} \alpha_i+1 & \text{if }\alpha_i<n_i, \\ 0 &\text{if } \alpha_i=n_i, \end{cases} \quad i\in\{1,\dotsc,K\}. \end{align} $$
$$ \begin{align} \delta_i= \begin{cases} \alpha_i+1 & \text{if }\alpha_i<n_i, \\ 0 &\text{if } \alpha_i=n_i, \end{cases} \quad i\in\{1,\dotsc,K\}. \end{align} $$We will sometimes write  $\vec {\delta }=\vec {\delta }^M_N$ to indicate the dependence on M and N. Let
$\vec {\delta }=\vec {\delta }^M_N$ to indicate the dependence on M and N. Let ![]() $A\in \mathcal {M}(\mathbb {Z}_M)$ be a multiset. Then the following are equivalent:
$A\in \mathcal {M}(\mathbb {Z}_M)$ be a multiset. Then the following are equivalent:
•
 $\Phi _N\mid A$;
$\Phi _N\mid A$;• A is
 $\mathcal {T}$-null in
$\mathcal {T}$-null in  $\mathbb {Z}_M$;
$\mathbb {Z}_M$;• the multiset induced by A in
 $\mathbb {Z}_N$ is N-null (see Definition 5.4).
$\mathbb {Z}_N$ is N-null (see Definition 5.4).
Let
 $$ \begin{align} \Delta=X^c\prod_{i:p_i\mid N} \left(1-X^{d_i}\right), \quad c\in\mathbb{Z}_M,\quad (M,d_i)=M/p_i^{\alpha_i+1}, \end{align} $$
$$ \begin{align} \Delta=X^c\prod_{i:p_i\mid N} \left(1-X^{d_i}\right), \quad c\in\mathbb{Z}_M,\quad (M,d_i)=M/p_i^{\alpha_i+1}, \end{align} $$be a cuboid of type ![]() $\mathcal {T}$ as in Lemma 5.8. Then the cuboid
$\mathcal {T}$ as in Lemma 5.8. Then the cuboid ![]() $\Delta \bmod N$, induced by
$\Delta \bmod N$, induced by ![]() $\Delta $ in
$\Delta $ in ![]() $\mathbb {Z}_N$, is an N-cuboid. Conversely, any N-cuboid
$\mathbb {Z}_N$, is an N-cuboid. Conversely, any N-cuboid ![]() $\Delta '$ in
$\Delta '$ in ![]() $\mathbb {Z}_N$ can be written (not necessarily uniquely) as
$\mathbb {Z}_N$ can be written (not necessarily uniquely) as ![]() $\Delta \pmod N$, where
$\Delta \pmod N$, where ![]() $\Delta $ is a cuboid of the form (5.9) in
$\Delta $ is a cuboid of the form (5.9) in ![]() $\mathbb {Z}_M$. Therefore, whenever working on scales N and M simultaneously, we will represent N-cuboids as cuboids of the form (5.9) in
$\mathbb {Z}_M$. Therefore, whenever working on scales N and M simultaneously, we will represent N-cuboids as cuboids of the form (5.9) in ![]() $\mathbb {Z}_M$. In this notation, a multiset
$\mathbb {Z}_M$. In this notation, a multiset ![]() $A\in \mathcal {M}(\mathbb {Z}_M)$ satisfies any one (therefore all) of the conditions in Lemma 5.8 if and only if
$A\in \mathcal {M}(\mathbb {Z}_M)$ satisfies any one (therefore all) of the conditions in Lemma 5.8 if and only if
 $$ \begin{align*} \mathbb{A}^N_N[\Delta]= \mathbb{A}^{\mathcal{T}}[\Delta]= \mathbb{A}^M_M\left[\Delta*T^M_N\right]=0 \end{align*} $$
$$ \begin{align*} \mathbb{A}^N_N[\Delta]= \mathbb{A}^{\mathcal{T}}[\Delta]= \mathbb{A}^M_M\left[\Delta*T^M_N\right]=0 \end{align*} $$for all ![]() $\Delta $ as in equation (5.9). Transitions between several intermediate scales
$\Delta $ as in equation (5.9). Transitions between several intermediate scales ![]() $N_1,N_2,\dotsc \mid M$ will be handled similarly, with
$N_1,N_2,\dotsc \mid M$ will be handled similarly, with ![]() $\mathbb {Z}_M$ as the default ambient space.
$\mathbb {Z}_M$ as the default ambient space.

Figure 3 A classic M-cuboid (green) vs. a multiscale cuboid (red) corresponding to the product ![]() $\Phi _M\Phi _{M/p_i}$.
$\Phi _M\Phi _{M/p_i}$.
Cuboids with more general templates can be used to indicate divisibility by combinations of several cyclotomic polynomials. We will be particularly interested in implications of the form ‘if ![]() $\Phi _{s_1},\dotsc ,\Phi _{s_l}$ divide
$\Phi _{s_1},\dotsc ,\Phi _{s_l}$ divide ![]() $A(X)$, then A is
$A(X)$, then A is ![]() $\mathcal {T}$-null for a given cuboid type
$\mathcal {T}$-null for a given cuboid type ![]() $\mathcal {T}$’. It will not be necessary to aim for ‘if and only if’ conditions such as those in Lemma 5.8.
$\mathcal {T}$’. It will not be necessary to aim for ‘if and only if’ conditions such as those in Lemma 5.8.
Example 5.9. Let  $M=\prod _{i=1}^K p_i^{n_i}$.
$M=\prod _{i=1}^K p_i^{n_i}$.
(1) Assume that
 $n_i\geq 2$ for some
$n_i\geq 2$ for some  $i\in \{1,\dotsc ,K\}$. Let
$i\in \{1,\dotsc ,K\}$. Let  $\mathcal {T}=(M, \vec {\delta }, 1)$ and
$\mathcal {T}=(M, \vec {\delta }, 1)$ and  $\mathcal {T}'=(M, \vec {\delta }, T^M_{M/p_i})$, with
$\mathcal {T}'=(M, \vec {\delta }, T^M_{M/p_i})$, with  $\delta _i=2$ and
$\delta _i=2$ and  $\delta _j=1$ for
$\delta _j=1$ for  $j\neq i$. Then The first equivalence follows from Lemma 5.8. The second one is easy to check directly. Specifically, if
$j\neq i$. Then The first equivalence follows from Lemma 5.8. The second one is easy to check directly. Specifically, if $$ \begin{align*} \Phi_{M/p_i}\mid A & \Leftrightarrow A \text{ is }\mathcal{T}'\text{-null},\\ \Phi_M \Phi_{M/p_i}\mid A & \Leftrightarrow A \text{ is }\mathcal{T}\text{-null}. \end{align*} $$
$$ \begin{align*} \Phi_{M/p_i}\mid A & \Leftrightarrow A \text{ is }\mathcal{T}'\text{-null},\\ \Phi_M \Phi_{M/p_i}\mid A & \Leftrightarrow A \text{ is }\mathcal{T}\text{-null}. \end{align*} $$ $\Delta $ is a cuboid of type
$\Delta $ is a cuboid of type  $\mathcal {T}$, then
$\mathcal {T}$, then  $\Phi _m\mid \Delta $ for all
$\Phi _m\mid \Delta $ for all  $m\mid M$ except for
$m\mid M$ except for  $m\in \{M/p_i,M\}$; conversely, both M-cuboids and
$m\in \{M/p_i,M\}$; conversely, both M-cuboids and  $M/p_i$-cuboids can be expressed as linear combinations of cuboids of type
$M/p_i$-cuboids can be expressed as linear combinations of cuboids of type  $\mathcal {T}$. (A similar result appears in [Reference Kiss, Malikiosis, Somlai and Vizer17, Lemma 2.13], where it is stated in terms of ‘n-dimensional cube rules’ and applied to Fuglede’s conjecture on cyclic groups.)
$\mathcal {T}$. (A similar result appears in [Reference Kiss, Malikiosis, Somlai and Vizer17, Lemma 2.13], where it is stated in terms of ‘n-dimensional cube rules’ and applied to Fuglede’s conjecture on cyclic groups.)(2) Set
 $2\leq \alpha \leq n_i$. Then if and only if A is
$2\leq \alpha \leq n_i$. Then if and only if A is $$ \begin{align*} \Phi_M \Phi_{M/p_i}\dotsm \Phi_{M/p_i^{\alpha}}\mid A \end{align*} $$
$$ \begin{align*} \Phi_M \Phi_{M/p_i}\dotsm \Phi_{M/p_i^{\alpha}}\mid A \end{align*} $$ $\mathcal {T}_\alpha $-null, where
$\mathcal {T}_\alpha $-null, where  $\mathcal {T}_\alpha =(M, \vec {\delta }, 1)$,
$\mathcal {T}_\alpha =(M, \vec {\delta }, 1)$,  $\delta _i=\alpha +1$ if
$\delta _i=\alpha +1$ if  $\alpha _i<n_i$,
$\alpha _i<n_i$,  $\delta _i=0$ if
$\delta _i=0$ if  $\alpha _i=n_i$ and
$\alpha _i=n_i$ and  $\delta _j=1$ for
$\delta _j=1$ for  $j\neq i$. This can be proved in the same way as in the previous example.
$j\neq i$. This can be proved in the same way as in the previous example.(3) Assume that
 $n_i\geq 2$ for some
$n_i\geq 2$ for some  $i\in \{1,\dotsc ,K\}$. Let
$i\in \{1,\dotsc ,K\}$. Let  $\mathcal {T}=(M, \vec {\delta }, T)$, where
$\mathcal {T}=(M, \vec {\delta }, T)$, where  $\delta _i=3$ if
$\delta _i=3$ if  $n_i\geq 3$,
$n_i\geq 3$,  $\delta _i=0$ if
$\delta _i=0$ if  $n_i=2$,
$n_i=2$,  $\delta _j=1$ for
$\delta _j=1$ for  $j\neq i$ and We claim that if
$j\neq i$ and We claim that if $$ \begin{align*} T(X)=\frac{X^{M/p_i}-1}{X^{M/p_i^2}-1} = 1+X^{M/p_i^2}+\dotsb+X^{(p_i-1)M/p_i^2}. \end{align*} $$
$$ \begin{align*} T(X)=\frac{X^{M/p_i}-1}{X^{M/p_i^2}-1} = 1+X^{M/p_i^2}+\dotsb+X^{(p_i-1)M/p_i^2}. \end{align*} $$ $\Phi _M\Phi _{M/p_i^2}\mid A$, then A is
$\Phi _M\Phi _{M/p_i^2}\mid A$, then A is  $\mathcal {T}$-null. Indeed, if
$\mathcal {T}$-null. Indeed, if  $n_i\geq 3$, cuboids of type
$n_i\geq 3$, cuboids of type  $\mathcal {T}$ have the formwhere
$\mathcal {T}$ have the formwhere $$ \begin{align*} \Delta(X)=X^c\left(1-X^{\mu_iM/p_i^3}\right)\prod_{j\neq i}\left(1-X^{\mu_jM/p_j}\right), \end{align*} $$
$$ \begin{align*} \Delta(X)=X^c\left(1-X^{\mu_iM/p_i^3}\right)\prod_{j\neq i}\left(1-X^{\mu_jM/p_j}\right), \end{align*} $$ $(\mu _i,M)=(\mu _j,M)=1$. It follows that
$(\mu _i,M)=(\mu _j,M)=1$. It follows that  $\Delta (X)T(X)$ is divisible by all cyclotomic polynomials
$\Delta (X)T(X)$ is divisible by all cyclotomic polynomials  $\Phi _m(X)$,
$\Phi _m(X)$,  $m\mid M$, except for
$m\mid M$, except for  $\Phi _{M/p_i^2}$ and
$\Phi _{M/p_i^2}$ and  $\Phi _M$. If
$\Phi _M$. If  $n_i=2$, the same argument applies, except that there is no factor
$n_i=2$, the same argument applies, except that there is no factor  $1-X^{\mu _iM/p_i^3}$ in
$1-X^{\mu _iM/p_i^3}$ in  $\Delta (X)$.
$\Delta (X)$.
6 Tiling reductions
6.1 Subgroup reduction
In this section, we discuss two ways in which the question of proving (T2) for a tiling ![]() $A\oplus B=\mathbb {Z}_M$ (and, more generally, investigating the structure of such tilings) may be reduced to the analogous question for tilings
$A\oplus B=\mathbb {Z}_M$ (and, more generally, investigating the structure of such tilings) may be reduced to the analogous question for tilings ![]() $A'\oplus B'=\mathbb {Z}_{N}$, where
$A'\oplus B'=\mathbb {Z}_{N}$, where ![]() $N\mid M$ and
$N\mid M$ and ![]() $N\neq M$. We start with a recap, in a slightly more general setting, of the reduction that Coven and Meyerowitz used in [Reference Coven and Meyerowitz2] to prove Theorem 1.1.
$N\neq M$. We start with a recap, in a slightly more general setting, of the reduction that Coven and Meyerowitz used in [Reference Coven and Meyerowitz2] to prove Theorem 1.1.
Theorem 6.1 Subgroup reduction [Reference Coven and Meyerowitz2, Lemma 2.5]; see also [Reference Dutkay and Kraus4, Theorem 4.4]
Assume that ![]() $ A\oplus B=\mathbb {Z}_M $, where
$ A\oplus B=\mathbb {Z}_M $, where  $M=\prod _{i=1}^K p_i^{n_i}$, and that:
$M=\prod _{i=1}^K p_i^{n_i}$, and that:
(i) there exists an
 $i\in \{1,\dotsc ,K\}$ such that
$i\in \{1,\dotsc ,K\}$ such that  $A\subset p_i\mathbb {Z}_M$ and
$A\subset p_i\mathbb {Z}_M$ and(ii) (T2) holds for both
 $A'$ and
$A'$ and  $B'$ in any tiling
$B'$ in any tiling  $A'\oplus B'=\mathbb {Z}_{N_i} $, where
$A'\oplus B'=\mathbb {Z}_{N_i} $, where  $N_i=M/p_i$,
$N_i=M/p_i$,  $\lvert A'\rvert =\lvert A\rvert $ and
$\lvert A'\rvert =\lvert A\rvert $ and  $\lvert B'\rvert =\lvert B\rvert /p_i$.
$\lvert B'\rvert =\lvert B\rvert /p_i$.
Then ![]() $ A $ and
$ A $ and ![]() $ B $ satisfy (T2).
$ B $ satisfy (T2).
Proof. We have ![]() $A(X)=A'(X^{p_i})$ for some
$A(X)=A'(X^{p_i})$ for some ![]() $A'\subset \mathbb {Z}_{N_i}$. Write also
$A'\subset \mathbb {Z}_{N_i}$. Write also
 $$ \begin{align*} B(X)\equiv \sum_{\nu=0}^{p_i-1} X^{\nu M/p_i^{n_i-1}} B_\nu( X^{p_i})\mbox{ mod }X^M-1, \end{align*} $$
$$ \begin{align*} B(X)\equiv \sum_{\nu=0}^{p_i-1} X^{\nu M/p_i^{n_i-1}} B_\nu( X^{p_i})\mbox{ mod }X^M-1, \end{align*} $$where ![]() $B_\nu \subset \mathbb {Z}_{N_i}$ for
$B_\nu \subset \mathbb {Z}_{N_i}$ for ![]() $\nu =0,1,\dotsc ,p_i-1$. If
$\nu =0,1,\dotsc ,p_i-1$. If ![]() $b\in B$ and
$b\in B$ and ![]() $b\equiv r \bmod p_i$, then
$b\equiv r \bmod p_i$, then ![]() $a+b\equiv r \bmod p_i$ for all
$a+b\equiv r \bmod p_i$ for all ![]() $a\in A$; in other words, the tiling breaks down into separate tilings of residue classes mod
$a\in A$; in other words, the tiling breaks down into separate tilings of residue classes mod ![]() $p_i$, with
$p_i$, with ![]() $A'\oplus B_\nu =\mathbb {Z}_{N_i}$ for each
$A'\oplus B_\nu =\mathbb {Z}_{N_i}$ for each ![]() $\nu $.
$\nu $.
By assumption (ii), ![]() $A'$ and
$A'$ and ![]() $B_\nu $ satisfy (T2) for all
$B_\nu $ satisfy (T2) for all ![]() $\nu $. We need to check that this is still true for A and B. We first claim that for any polynomial
$\nu $. We need to check that this is still true for A and B. We first claim that for any polynomial ![]() $F(X)$ and any
$F(X)$ and any ![]() $s\in \mathbb {N}$,
$s\in \mathbb {N}$,
where
 $$ \begin{align*} \tau(s)=\begin{cases} s &\text{if }p_i\nmid s,\\ p_is &\text{if }p_i\mid s. \end{cases} \end{align*} $$
$$ \begin{align*} \tau(s)=\begin{cases} s &\text{if }p_i\nmid s,\\ p_is &\text{if }p_i\mid s. \end{cases} \end{align*} $$Indeed, we have ![]() $\Phi _{\tau (s)}(X)\mid F(X^{p_i})$ if and only if
$\Phi _{\tau (s)}(X)\mid F(X^{p_i})$ if and only if ![]() $F(e^{2\pi i p_i/\tau (s)})=0$. This means that
$F(e^{2\pi i p_i/\tau (s)})=0$. This means that ![]() $F(e^{2\pi i /s})=0$ if
$F(e^{2\pi i /s})=0$ if ![]() $p_i\mid s$, and
$p_i\mid s$, and ![]() $F(e^{2\pi i p_i/s})=0$ if
$F(e^{2\pi i p_i/s})=0$ if ![]() $p_i\nmid s$. In both cases, this is equivalent to
$p_i\nmid s$. In both cases, this is equivalent to ![]() $\Phi _s\mid F$.
$\Phi _s\mid F$.
Observe first that, by equation (2.6), we must have
Suppose that ![]() $s_1,\dotsc ,s_k$ are powers of distinct primes such that
$s_1,\dotsc ,s_k$ are powers of distinct primes such that ![]() $\Phi _{s_1}\dotsm \Phi _{s_k}\mid A$. As already noted, we cannot have
$\Phi _{s_1}\dotsm \Phi _{s_k}\mid A$. As already noted, we cannot have ![]() $s_j=p_i$ for any j. Let
$s_j=p_i$ for any j. Let  $s^{\prime }_j=s_j/p_i$ if
$s^{\prime }_j=s_j/p_i$ if ![]() $s_j$ is a power of
$s_j$ is a power of ![]() $p_i$, and
$p_i$, and  $s^{\prime }_j=s_j$ otherwise. Then
$s^{\prime }_j=s_j$ otherwise. Then ![]() $s^{\prime }_j$ are prime powers, and
$s^{\prime }_j$ are prime powers, and  $s_j=\tau (s^{\prime }_j)$. By equivalence (6.1),
$s_j=\tau (s^{\prime }_j)$. By equivalence (6.1), ![]() $\Phi _{s^{\prime }_1}\dotsm \Phi _{s^{\prime }_k}\mid A'$, and since (T2) holds for
$\Phi _{s^{\prime }_1}\dotsm \Phi _{s^{\prime }_k}\mid A'$, and since (T2) holds for ![]() $A'$, we have
$A'$, we have ![]() $\Phi _{s^{\prime }_1\dotsm s^{\prime }_k}\mid A'$. Since
$\Phi _{s^{\prime }_1\dotsm s^{\prime }_k}\mid A'$. Since ![]() $\tau (s^{\prime }_1\dotsm s^{\prime }_k)=s_1\dotsm s_k$, we get that
$\tau (s^{\prime }_1\dotsm s^{\prime }_k)=s_1\dotsm s_k$, we get that ![]() $\Phi _{s_1\dotsm s_k}\mid A$.
$\Phi _{s_1\dotsm s_k}\mid A$.
Suppose now that ![]() $s_1,\dotsc ,s_k$ are powers of distinct primes such that
$s_1,\dotsc ,s_k$ are powers of distinct primes such that ![]() $\Phi _{s_1}\dotsm \Phi _{s_k}\mid B$ and
$\Phi _{s_1}\dotsm \Phi _{s_k}\mid B$ and ![]() $s_1,\dotsc ,s_k\neq p_i$, and define
$s_1,\dotsc ,s_k\neq p_i$, and define ![]() $s^{\prime }_1,\dotsc ,s^{\prime }_k$ as before. Then for
$s^{\prime }_1,\dotsc ,s^{\prime }_k$ as before. Then for ![]() $j=1,\dotsc ,k$ we have
$j=1,\dotsc ,k$ we have ![]() $\Phi _{s_j}\nmid A$, and therefore
$\Phi _{s_j}\nmid A$, and therefore  $\Phi _{s^{\prime }_j}\nmid A'$ and, since
$\Phi _{s^{\prime }_j}\nmid A'$ and, since ![]() $A'\oplus B_\nu =\mathbb {Z}_{N_i}$ is a tiling,
$A'\oplus B_\nu =\mathbb {Z}_{N_i}$ is a tiling,  $\Phi _{s^{\prime }_j}\mid B_\nu $ for each
$\Phi _{s^{\prime }_j}\mid B_\nu $ for each ![]() $\nu $. Since
$\nu $. Since ![]() $B_\nu $ satisfies (T2), we have
$B_\nu $ satisfies (T2), we have ![]() $\Phi _{s^{\prime }_1\dotsm s^{\prime }_k}\mid B_\nu $. It follows that
$\Phi _{s^{\prime }_1\dotsm s^{\prime }_k}\mid B_\nu $. It follows that ![]() $\Phi _{s_1\dotsm s_k}\mid B_\nu (X^{p_i})$ for each
$\Phi _{s_1\dotsm s_k}\mid B_\nu (X^{p_i})$ for each ![]() $\nu $, and therefore
$\nu $, and therefore ![]() $\Phi _{s_1\dotsm s_k}\mid B$.
$\Phi _{s_1\dotsm s_k}\mid B$.
Finally, suppose that ![]() $s_1,\dotsc ,s_k$ are powers of distinct primes such that
$s_1,\dotsc ,s_k$ are powers of distinct primes such that ![]() $\Phi _{s_1}\dotsm \Phi _{s_k}\mid B$ and
$\Phi _{s_1}\dotsm \Phi _{s_k}\mid B$ and ![]() $s_1,\dotsc ,s_k$ are not powers of
$s_1,\dotsc ,s_k$ are not powers of ![]() $p_i$, and consider
$p_i$, and consider ![]() $\Phi _{p_is}$ with
$\Phi _{p_is}$ with ![]() $s=s_1\dotsm s_k$. We have
$s=s_1\dotsm s_k$. We have
 $$ \begin{align*} B \left(e^{2\pi i/p_is}\right)= \sum_{\nu=0}^{p_i-1} e^{2\pi i \nu M/sp_i^{n_i}} B_\nu\left( e^{2\pi is}\right)=0, \end{align*} $$
$$ \begin{align*} B \left(e^{2\pi i/p_is}\right)= \sum_{\nu=0}^{p_i-1} e^{2\pi i \nu M/sp_i^{n_i}} B_\nu\left( e^{2\pi is}\right)=0, \end{align*} $$by (T2), for each ![]() $B_\nu $.
$B_\nu $.
Corollary 6.2. Let ![]() $ A\oplus B=\mathbb {Z}_M $, where
$ A\oplus B=\mathbb {Z}_M $, where  $M=p_1^{n_1}p_2^{n_2}p_3^{n_3} \dotsm p_K^{n_K}$. Assume that for each
$M=p_1^{n_1}p_2^{n_2}p_3^{n_3} \dotsm p_K^{n_K}$. Assume that for each ![]() $i\geq 3$, the prime factor
$i\geq 3$, the prime factor ![]() $p_i$ divides at most one of
$p_i$ divides at most one of ![]() $\lvert A \rvert $ and
$\lvert A \rvert $ and ![]() $\lvert B \rvert $. (This happens, for example, if
$\lvert B \rvert $. (This happens, for example, if ![]() $n_i=1$ for
$n_i=1$ for ![]() $i\not \in \{1,2\}$). Then both A and B satisfy (T2).
$i\not \in \{1,2\}$). Then both A and B satisfy (T2).
Proof. This is not stated explicitly in [Reference Coven and Meyerowitz2], but it follows by a very similar argument. (See also [[Reference Dutkay and Kraus4], Reference Shi39, Reference Tao46].) We proceed by induction in the number of prime factors. If ![]() $K=2$ and
$K=2$ and ![]() $M=p_1^{n_1}p_2^{n_2}$, this is Theorem 1.1. Suppose that
$M=p_1^{n_1}p_2^{n_2}$, this is Theorem 1.1. Suppose that ![]() $K\geq 3$ and that (T2) holds for both
$K\geq 3$ and that (T2) holds for both ![]() $A'$ and
$A'$ and ![]() $B'$ in any tiling
$B'$ in any tiling ![]() $ A'\oplus B'=\mathbb {Z}_{M/p_K}$. By the assumption of the lemma, at least one of
$ A'\oplus B'=\mathbb {Z}_{M/p_K}$. By the assumption of the lemma, at least one of ![]() $\lvert A \rvert $ and
$\lvert A \rvert $ and ![]() $\lvert B \rvert $ is not divisible by
$\lvert B \rvert $ is not divisible by ![]() $p_K$. Assume without loss of generality that
$p_K$. Assume without loss of generality that ![]() $p_K\nmid \lvert A\rvert $. By Tijdeman’s theorem [Reference Tijdeman47, Theorem 1] (see also [Reference Coven and Meyerowitz2, Lemma 2.2]),
$p_K\nmid \lvert A\rvert $. By Tijdeman’s theorem [Reference Tijdeman47, Theorem 1] (see also [Reference Coven and Meyerowitz2, Lemma 2.2]), ![]() $\tilde A\oplus B=\mathbb {Z}_M$ is again a tiling, where
$\tilde A\oplus B=\mathbb {Z}_M$ is again a tiling, where ![]() $\tilde A(X)=A(X^{p_K})$. We have
$\tilde A(X)=A(X^{p_K})$. We have ![]() $\tilde A\subset p_K\mathbb {Z}_M$, so that we may apply Theorem 6.1 to conclude that
$\tilde A\subset p_K\mathbb {Z}_M$, so that we may apply Theorem 6.1 to conclude that ![]() $\tilde A$ and B satisfy (T2). By equivalence (6.1), this also means that A satisfies (T2), since the (T2) condition for A involves only cyclotomic polynomials
$\tilde A$ and B satisfy (T2). By equivalence (6.1), this also means that A satisfies (T2), since the (T2) condition for A involves only cyclotomic polynomials ![]() $\Phi _s$ with
$\Phi _s$ with ![]() $(s,p_K)=1$.
$(s,p_K)=1$.
6.2 Slab reduction
Our second tiling reduction also involves passing from a tiling ![]() $A\oplus B=\mathbb {Z}_M$ to a tiling of a smaller cyclic group. However, instead of restricting to residue classes and thus constructing a family of tilings of a subgroup
$A\oplus B=\mathbb {Z}_M$ to a tiling of a smaller cyclic group. However, instead of restricting to residue classes and thus constructing a family of tilings of a subgroup ![]() $p_i\mathbb {Z}_M$, we will use periodicity. Recall that M-fibers
$p_i\mathbb {Z}_M$, we will use periodicity. Recall that M-fibers ![]() $F_i$ and M-fibered sets were defined in Section 2.3 (see formula (2.4)). Let
$F_i$ and M-fibered sets were defined in Section 2.3 (see formula (2.4)). Let  $M=\prod _{i=1}^K p_i^{n_i}$, and define
$M=\prod _{i=1}^K p_i^{n_i}$, and define
 $$ \begin{align} A_{p_i}=\left\{a\in A: 0\leq\pi_i(a)\leq p_i^{n_i-1}-1\right\}, \end{align} $$
$$ \begin{align} A_{p_i}=\left\{a\in A: 0\leq\pi_i(a)\leq p_i^{n_i-1}-1\right\}, \end{align} $$where ![]() $\pi _i$ is the array coordinate defined in Section 2.2. Suppose that we have
$\pi _i$ is the array coordinate defined in Section 2.2. Suppose that we have ![]() $S\oplus B=\mathbb {Z}_M$, where S is the
$S\oplus B=\mathbb {Z}_M$, where S is the ![]() $M/p_i$-periodic extension of
$M/p_i$-periodic extension of ![]() $A_{p_i}$ to
$A_{p_i}$ to ![]() $\mathbb {Z}_M$:
$\mathbb {Z}_M$:
Then we may reduce the period of the tiling and write ![]() $A_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$, where
$A_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$, where ![]() $A_{p_i}$ and B are now considered mod
$A_{p_i}$ and B are now considered mod ![]() $M/p_i$.
$M/p_i$.
As a motivating example, suppose that ![]() $A\oplus B=\mathbb {Z}_M$, with M as before, and that A is M-fibered in the
$A\oplus B=\mathbb {Z}_M$, with M as before, and that A is M-fibered in the ![]() $p_i$ direction. Let
$p_i$ direction. Let ![]() $A'$ be a set obtained from A by choosing one point from each fiber, so that
$A'$ be a set obtained from A by choosing one point from each fiber, so that ![]() $\lvert A'\rvert =\lvert A\rvert /p_i$ and
$\lvert A'\rvert =\lvert A\rvert /p_i$ and ![]() $A=A'*F_i$. Then A is the periodic extension of
$A=A'*F_i$. Then A is the periodic extension of ![]() $A'$, and we have
$A'$, and we have ![]() $A'\oplus B=\mathbb {Z}_{M/p_i}$.
$A'\oplus B=\mathbb {Z}_{M/p_i}$.
Our main results in this section are Theorem 6.5 and Corollary 6.7, where we develop a criterion for ![]() $A_{p_i}$ to admit periodic tilings as described, and prove that passing to such tilings preserves the (T2) property.
$A_{p_i}$ to admit periodic tilings as described, and prove that passing to such tilings preserves the (T2) property.
Lemma 6.3. Set ![]() $ A\in \mathcal {M}(\mathbb {Z}_{M}) $, with M as before. Assume that
$ A\in \mathcal {M}(\mathbb {Z}_{M}) $, with M as before. Assume that ![]() $\Phi _d\mid A$ for some d such that
$\Phi _d\mid A$ for some d such that ![]() $p_i^{n_i}\mid d\mid M$. Then for every
$p_i^{n_i}\mid d\mid M$. Then for every ![]() $1\leq \alpha _i\leq n_i $,
$1\leq \alpha _i\leq n_i $,
 $$ \begin{align*} \Phi_{d/p_i^{\alpha_i}}\mid A \Rightarrow \Phi_{d/p_i^{\alpha_i}}\mid A_{p_i}. \end{align*} $$
$$ \begin{align*} \Phi_{d/p_i^{\alpha_i}}\mid A \Rightarrow \Phi_{d/p_i^{\alpha_i}}\mid A_{p_i}. \end{align*} $$Proof. Let  $d = M/\prod _{j\neq i} p_j^{\alpha _j}$ and
$d = M/\prod _{j\neq i} p_j^{\alpha _j}$ and ![]() $d'=d/p_i^{\alpha _i}$. Assume that
$d'=d/p_i^{\alpha _i}$. Assume that ![]() $\Phi _d\Phi _{d'}\mid A$. We would like to show that
$\Phi _d\Phi _{d'}\mid A$. We would like to show that ![]() $\Phi _{d'}\mid A_{p_i}$. To this end, we define cuboid types
$\Phi _{d'}\mid A_{p_i}$. To this end, we define cuboid types  $\mathcal {T}=(M,\vec \delta ,T_d)$ and
$\mathcal {T}=(M,\vec \delta ,T_d)$ and  $\mathcal {T}'=(M,\vec \delta ',T_{d'})$, where
$\mathcal {T}'=(M,\vec \delta ',T_{d'})$, where  $T_d=T^M_d$,
$T_d=T^M_d$,  $T_{d'}=T^M_{d'}$ are the folding templates from Definition 5.7 and
$T_{d'}=T^M_{d'}$ are the folding templates from Definition 5.7 and  $\vec {\delta }=\vec {\delta }^M_d$,
$\vec {\delta }=\vec {\delta }^M_d$,  $\vec {\delta }'=\vec {\delta }^M_{d'}$ are defined as in equation (5.8), with
$\vec {\delta }'=\vec {\delta }^M_{d'}$ are defined as in equation (5.8), with ![]() $N=d$ and
$N=d$ and ![]() $N=d'$, respectively.
$N=d'$, respectively.
Let S be the periodic extension of ![]() $A_{p_i}$ to
$A_{p_i}$ to ![]() $\mathbb {Z}_M$ defined in equation (6.3). We have
$\mathbb {Z}_M$ defined in equation (6.3). We have ![]() $\Phi _d\mid F_i$ but
$\Phi _d\mid F_i$ but ![]() $\Phi _{d'}\nmid F_i$, so that
$\Phi _{d'}\nmid F_i$, so that ![]() $\Phi _{d'}\mid S$ if and only if
$\Phi _{d'}\mid S$ if and only if ![]() $\Phi _{d'}\mid A_{p_i}$. We need to prove that
$\Phi _{d'}\mid A_{p_i}$. We need to prove that
 $$ \begin{align*} \mathbb{S}^{d'}_{d'}[\Delta]=0 \end{align*} $$
$$ \begin{align*} \mathbb{S}^{d'}_{d'}[\Delta]=0 \end{align*} $$for all cuboids ![]() $\Delta $ of type
$\Delta $ of type ![]() $\mathcal {T}'$. Fix such a cuboid
$\mathcal {T}'$. Fix such a cuboid
 $$ \begin{align*} \Delta(X)=X^y\cdot\prod_j \left(1-X^{d_j}\right), \quad y\in\mathbb{Z}_M, \left(d_j,M\right)=M/p_{j}^{\delta^{\prime}_j}. \end{align*} $$
$$ \begin{align*} \Delta(X)=X^y\cdot\prod_j \left(1-X^{d_j}\right), \quad y\in\mathbb{Z}_M, \left(d_j,M\right)=M/p_{j}^{\delta^{\prime}_j}. \end{align*} $$Let
 $$ \begin{align*} \Delta_i(X)=X^y\cdot\prod_{j\neq i} \left(1-X^{d_j}\right) \end{align*} $$
$$ \begin{align*} \Delta_i(X)=X^y\cdot\prod_{j\neq i} \left(1-X^{d_j}\right) \end{align*} $$so that
 $$ \begin{align*} \Delta(X)=\begin{cases} \left(1-X^{d_i}\right)\Delta_i(X)&\text{if }\alpha_i<n_i,\\ \Delta_i(X)&\text{if }\alpha_i=n_i. \end{cases} \end{align*} $$
$$ \begin{align*} \Delta(X)=\begin{cases} \left(1-X^{d_i}\right)\Delta_i(X)&\text{if }\alpha_i<n_i,\\ \Delta_i(X)&\text{if }\alpha_i=n_i. \end{cases} \end{align*} $$ Observe that if ![]() $\rho _i\in \mathbb {Z}_M$ satisfies
$\rho _i\in \mathbb {Z}_M$ satisfies ![]() $(\rho _i,M)=M/p_i$, then
$(\rho _i,M)=M/p_i$, then ![]() $(1-X^{\rho _i})\Delta _i(X)$ is a cuboid of type
$(1-X^{\rho _i})\Delta _i(X)$ is a cuboid of type ![]() $\mathcal {T}$. Since A is
$\mathcal {T}$. Since A is ![]() $\mathcal {T}$-null, we have
$\mathcal {T}$-null, we have  $\mathbb {A}^d_d [\left (1-X^{\rho _i}\right )\Delta _i(X)]=0$, so that
$\mathbb {A}^d_d [\left (1-X^{\rho _i}\right )\Delta _i(X)]=0$, so that
 $$ \begin{align*} \mathbb{A}^d_d[\Delta_i]=\mathbb{A}^d_d[\rho_i*\Delta_i]. \end{align*} $$
$$ \begin{align*} \mathbb{A}^d_d[\Delta_i]=\mathbb{A}^d_d[\rho_i*\Delta_i]. \end{align*} $$Averaging the last equality over all ![]() $\rho _i\in \{M/p_i,2M/p_i,\dotsc ,(p_i-1)M/p_i\}$, we get
$\rho _i\in \{M/p_i,2M/p_i,\dotsc ,(p_i-1)M/p_i\}$, we get
 $$ \begin{align*} \mathbb{A}^d_d[\Delta_i]=\frac{1}{\phi(p_i)}\mathbb{A}^d_d[\Delta_i*(F_i-1)]. \end{align*} $$
$$ \begin{align*} \mathbb{A}^d_d[\Delta_i]=\frac{1}{\phi(p_i)}\mathbb{A}^d_d[\Delta_i*(F_i-1)]. \end{align*} $$Clearly we may take linear combinations of the latter – that is, for any set ![]() $V\subset \mathbb {Z}_M$,
$V\subset \mathbb {Z}_M$,
 $$ \begin{align} \mathbb{A}^d_d[\Delta_i*V]=\frac{1}{\phi(p_i)}\mathbb{A}^d_d[\Delta_i*(F_i-1)*V]. \end{align} $$
$$ \begin{align} \mathbb{A}^d_d[\Delta_i*V]=\frac{1}{\phi(p_i)}\mathbb{A}^d_d[\Delta_i*(F_i-1)*V]. \end{align} $$ Let ![]() $\Psi \subset \mathbb {Z}_M$ be a set such that
$\Psi \subset \mathbb {Z}_M$ be a set such that  $\Psi (X)\equiv \prod _{\nu =2}^{\alpha _i}\Psi _{M/p_i^\nu }(X) \bmod X^{M/p_i}-1$, and
$\Psi (X)\equiv \prod _{\nu =2}^{\alpha _i}\Psi _{M/p_i^\nu }(X) \bmod X^{M/p_i}-1$, and
 $$ \begin{align} 0\leq\pi_i(y+z) \leq p_i^{n_i-1}-1\quad \forall z\in \Psi. \end{align} $$
$$ \begin{align} 0\leq\pi_i(y+z) \leq p_i^{n_i-1}-1\quad \forall z\in \Psi. \end{align} $$Then
 $$ \begin{align*} T_{d'}(X)&= T_d(X)F_i(X)\Psi(X)\\[3pt] &= T_d(X)\Psi(X) +(F_i-1)T_d(X)\Psi(X) , \end{align*} $$
$$ \begin{align*} T_{d'}(X)&= T_d(X)F_i(X)\Psi(X)\\[3pt] &= T_d(X)\Psi(X) +(F_i-1)T_d(X)\Psi(X) , \end{align*} $$so that
 $$ \begin{align*} \mathbb{A}^{d'}_{d'}[\Delta_i]&= \mathbb{A}^M_M\left[\Delta_i*T_{d'}\right]\\[3pt] &=\mathbb{A}^M_M[\Delta_i*T_d*\Psi ] +\mathbb{A}^M_M[\Delta_i*(F_i-1)*T_d*\Psi]\\[3pt] &=\mathbb{A}^d_d[\Delta_i*\Psi]+\mathbb{A}^d_d[\Delta_i*(F_i-1)*\Psi]. \end{align*} $$
$$ \begin{align*} \mathbb{A}^{d'}_{d'}[\Delta_i]&= \mathbb{A}^M_M\left[\Delta_i*T_{d'}\right]\\[3pt] &=\mathbb{A}^M_M[\Delta_i*T_d*\Psi ] +\mathbb{A}^M_M[\Delta_i*(F_i-1)*T_d*\Psi]\\[3pt] &=\mathbb{A}^d_d[\Delta_i*\Psi]+\mathbb{A}^d_d[\Delta_i*(F_i-1)*\Psi]. \end{align*} $$By equation (6.4) with ![]() $V=\Psi $, we get
$V=\Psi $, we get
 $$ \begin{align} \mathbb{A}^{d'}_{d'}[\Delta_i]=\frac{p_i}{\phi(p_i)}\mathbb{A}^d_d[\Delta_i*\Psi]. \end{align} $$
$$ \begin{align} \mathbb{A}^{d'}_{d'}[\Delta_i]=\frac{p_i}{\phi(p_i)}\mathbb{A}^d_d[\Delta_i*\Psi]. \end{align} $$ The proof of equation (6.6) used only the fact that ![]() $\Phi _d\mid A$. Since S has the same property, it follows that
$\Phi _d\mid A$. Since S has the same property, it follows that
 $$ \begin{align*} \mathbb{S}^{d'}_{d'}[\Delta_i]=\frac{p_i}{\phi(p_i)}\mathbb{S}^d_d[\Delta_i*\Psi], \end{align*} $$
$$ \begin{align*} \mathbb{S}^{d'}_{d'}[\Delta_i]=\frac{p_i}{\phi(p_i)}\mathbb{S}^d_d[\Delta_i*\Psi], \end{align*} $$By inequality (6.5), we also have
 $$ \begin{align*} \mathbb{A}^d_d[\Delta_i*\Psi]=\mathbb{S}^d_d[\Delta_i*\Psi]. \end{align*} $$
$$ \begin{align*} \mathbb{A}^d_d[\Delta_i*\Psi]=\mathbb{S}^d_d[\Delta_i*\Psi]. \end{align*} $$ Assume first that ![]() $\alpha _i<n_i$, and note that all of the foregoing arguments apply with
$\alpha _i<n_i$, and note that all of the foregoing arguments apply with ![]() $\Delta _i$ replaced by
$\Delta _i$ replaced by ![]() $d_i*\Delta _i$, yielding the same conclusions with
$d_i*\Delta _i$, yielding the same conclusions with ![]() $\Psi $ replaced by
$\Psi $ replaced by ![]() $\Psi '$, such that inequality (6.5) holds with y replaced by
$\Psi '$, such that inequality (6.5) holds with y replaced by ![]() $y+d_i$. Recall that A is
$y+d_i$. Recall that A is ![]() $\mathcal {T}'$-null, so that
$\mathcal {T}'$-null, so that
 $$ \begin{align*} 0&=\mathbb{A}^{d'}_{d'}[\Delta]\\[3pt] &= \mathbb{A}^{d'}_{d'}[\Delta_i]-\mathbb{A}^{d'}_{d'}[{d_i}*\Delta_i]\\[3pt] &= \frac{p_i}{\phi(p_i)}\left(\mathbb{A}^d_d[\Delta_i*\Psi]-\mathbb{A}^d_d[{d_i}*\Delta_i*\Psi']\right)\\[3pt] &=\frac{p_i}{\phi(p_i)}\left(\mathbb{S}^d_d[\Delta_i*\Psi]-\mathbb{S}^d_d[{d_i}*\Delta_i*\Psi']\right). \end{align*} $$
$$ \begin{align*} 0&=\mathbb{A}^{d'}_{d'}[\Delta]\\[3pt] &= \mathbb{A}^{d'}_{d'}[\Delta_i]-\mathbb{A}^{d'}_{d'}[{d_i}*\Delta_i]\\[3pt] &= \frac{p_i}{\phi(p_i)}\left(\mathbb{A}^d_d[\Delta_i*\Psi]-\mathbb{A}^d_d[{d_i}*\Delta_i*\Psi']\right)\\[3pt] &=\frac{p_i}{\phi(p_i)}\left(\mathbb{S}^d_d[\Delta_i*\Psi]-\mathbb{S}^d_d[{d_i}*\Delta_i*\Psi']\right). \end{align*} $$Taking the convolution with ![]() $\Psi _{M/p_i}$, and using the fact that
$\Psi _{M/p_i}$, and using the fact that ![]() $\Psi (X)\Psi _{M/p_i}(X)\equiv \Psi '(X)\Psi _{M/p_i}(X) \bmod (X^M-1)$, we conclude that
$\Psi (X)\Psi _{M/p_i}(X)\equiv \Psi '(X)\Psi _{M/p_i}(X) \bmod (X^M-1)$, we conclude that
 $$ \begin{align*} 0 &= \mathbb{S}^d_d\left[\Delta*\Psi* \Psi_{M/p_i}\right]\\[3pt] &= \mathbb{S}^{d'}_{d'}[\Delta]. \end{align*} $$
$$ \begin{align*} 0 &= \mathbb{S}^d_d\left[\Delta*\Psi* \Psi_{M/p_i}\right]\\[3pt] &= \mathbb{S}^{d'}_{d'}[\Delta]. \end{align*} $$It follows that S is ![]() $\mathcal {T}'$-null, as required.
$\mathcal {T}'$-null, as required.
If ![]() $\alpha _i=n_i$, the proof is the same except that then
$\alpha _i=n_i$, the proof is the same except that then ![]() $\Delta =\Delta _i$, and so the terms with
$\Delta =\Delta _i$, and so the terms with ![]() $d_i*\Delta _i$ do not appear in the calculation.
$d_i*\Delta _i$ do not appear in the calculation.
Lemma 6.4. Set ![]() $ A\in \mathcal {M}(\mathbb {Z}_{M}) $, with M as before, and let
$ A\in \mathcal {M}(\mathbb {Z}_{M}) $, with M as before, and let ![]() $p_i^{n_i}\mid d\mid M$ and
$p_i^{n_i}\mid d\mid M$ and ![]() $ 1\leq \alpha _i\leq n_i $. Assume that
$ 1\leq \alpha _i\leq n_i $. Assume that  $\Phi _{d/p_i^{\alpha _i}}\mid A^{\prime }_{p_i}$ for all translates
$\Phi _{d/p_i^{\alpha _i}}\mid A^{\prime }_{p_i}$ for all translates ![]() $A'$ of A. Then
$A'$ of A. Then  $\Phi _d\Phi _{d/p_i^{\alpha _i}}\mid A$.
$\Phi _d\Phi _{d/p_i^{\alpha _i}}\mid A$.
Proof. Let  $d = M/\prod _{j\neq i} p_j^{\alpha _j}$ and
$d = M/\prod _{j\neq i} p_j^{\alpha _j}$ and ![]() $d'=d/p_i^{\alpha _i}$. Define the cuboid types
$d'=d/p_i^{\alpha _i}$. Define the cuboid types  $\mathcal {T}=(M,\vec \delta ,T_d)$ and
$\mathcal {T}=(M,\vec \delta ,T_d)$ and  $\mathcal {T}'=(M,\vec \delta ',T_{d'})$ as in the proof of Lemma 6.3.
$\mathcal {T}'=(M,\vec \delta ',T_{d'})$ as in the proof of Lemma 6.3.
In order to prove that ![]() $\Phi _{d'}\mid A$, it suffices to show
$\Phi _{d'}\mid A$, it suffices to show  $ \mathbb {A}^{d'}_{d'}[\Delta ]=0$ for all cuboids of the form
$ \mathbb {A}^{d'}_{d'}[\Delta ]=0$ for all cuboids of the form
 $$ \begin{align} \Delta'(X)=X^y\cdot\prod_j \left(1-X^{d_j}\right), \quad y\in\mathbb{Z}_M, \left(d_j,M\right)=M/p_{j}^{\delta^{\prime}_j}. \end{align} $$
$$ \begin{align} \Delta'(X)=X^y\cdot\prod_j \left(1-X^{d_j}\right), \quad y\in\mathbb{Z}_M, \left(d_j,M\right)=M/p_{j}^{\delta^{\prime}_j}. \end{align} $$We write  $ A(X)=\sum _{\nu =0}^{p_i-1} A_{\nu }(X) $, where
$ A(X)=\sum _{\nu =0}^{p_i-1} A_{\nu }(X) $, where
 $$ \begin{align} A_{\nu}=\left\{a\in A\mid 0\leq\pi_i(a)-\nu p_i^{n_i-1}\leq p_i^{n_i-1}-1\right\},\quad\nu=0,1,\dotsc, p_i-1. \end{align} $$
$$ \begin{align} A_{\nu}=\left\{a\in A\mid 0\leq\pi_i(a)-\nu p_i^{n_i-1}\leq p_i^{n_i-1}-1\right\},\quad\nu=0,1,\dotsc, p_i-1. \end{align} $$Then
 $$ \begin{align*} \mathbb{A}^{d'}_{d'}[\Delta']=\sum_{\nu=0}^{p_i-1}(\mathbb{A}_\nu)^{d'}_{d'}[\Delta'] =0 \end{align*} $$
$$ \begin{align*} \mathbb{A}^{d'}_{d'}[\Delta']=\sum_{\nu=0}^{p_i-1}(\mathbb{A}_\nu)^{d'}_{d'}[\Delta'] =0 \end{align*} $$using the assumption that ![]() $A_\nu $ are
$A_\nu $ are ![]() $\mathcal {T}'$-null for all
$\mathcal {T}'$-null for all ![]() $\nu $.
$\nu $.
We now prove that ![]() $ \Phi _d\mid A $. It suffices to show
$ \Phi _d\mid A $. It suffices to show  $\mathbb {A}^d_d[\Delta ]=0$ for any cuboid of the form
$\mathbb {A}^d_d[\Delta ]=0$ for any cuboid of the form
 $$ \begin{align} \Delta(X)=\left(1-X^{M/p_i}\right)\Delta_i(X), \end{align} $$
$$ \begin{align} \Delta(X)=\left(1-X^{M/p_i}\right)\Delta_i(X), \end{align} $$where ![]() $y\in \mathbb {Z}_N$, and
$y\in \mathbb {Z}_N$, and
 $$ \begin{align*} \Delta_i(X)=X^y\cdot\prod_{j\neq i} \left(1-X^{d_j}\right), \quad y\in\mathbb{Z}_M, \left(d_j,M\right)=M/p_{j}^{\delta_j}. \end{align*} $$
$$ \begin{align*} \Delta_i(X)=X^y\cdot\prod_{j\neq i} \left(1-X^{d_j}\right), \quad y\in\mathbb{Z}_M, \left(d_j,M\right)=M/p_{j}^{\delta_j}. \end{align*} $$Indeed, any cuboid of type ![]() $\mathcal {T}$ can be written as a linear combination of cuboids as in equation (6.9).
$\mathcal {T}$ can be written as a linear combination of cuboids as in equation (6.9).
Let  $\Psi (X)= \prod _{\nu =2}^{\alpha _i}\Psi _{M/p_i^\nu }(X)$, and
$\Psi (X)= \prod _{\nu =2}^{\alpha _i}\Psi _{M/p_i^\nu }(X)$, and
 $$ \begin{align*} \Delta''(X)=\begin{cases} \left(1-X^{M/p_i^{\alpha_i+1}}\right)\Delta_i(X)&\text{if }\alpha_i<n_i,\\ \Delta_i(X)&\text{if }\alpha_i=n_i. \end{cases} \end{align*} $$
$$ \begin{align*} \Delta''(X)=\begin{cases} \left(1-X^{M/p_i^{\alpha_i+1}}\right)\Delta_i(X)&\text{if }\alpha_i<n_i,\\ \Delta_i(X)&\text{if }\alpha_i=n_i. \end{cases} \end{align*} $$Define also
 $$ \begin{align*} A^{\prime}_i&=\left\{a\in A: 0\leq\pi_i(a-y)\leq p_i^{n_i-1}-1\right\},\\[4pt] A^{\prime\prime}_i&=\left\{a\in A: 1\leq\pi_i(a-y)\leq p_i^{n_i-1}\right\}. \end{align*} $$
$$ \begin{align*} A^{\prime}_i&=\left\{a\in A: 0\leq\pi_i(a-y)\leq p_i^{n_i-1}-1\right\},\\[4pt] A^{\prime\prime}_i&=\left\{a\in A: 1\leq\pi_i(a-y)\leq p_i^{n_i-1}\right\}. \end{align*} $$By our assumption on A, ![]() $ \Phi _{d'} $ divides both
$ \Phi _{d'} $ divides both ![]() $A^{\prime }_i$ and
$A^{\prime }_i$ and ![]() $A^{\prime \prime }_i$. Suppose first that
$A^{\prime \prime }_i$. Suppose first that ![]() $\alpha _i<n_i$. Then
$\alpha _i<n_i$. Then
 $$ \begin{align*} 0&= \left(\mathbb{A}^{\prime}_i\right)^{d'}_{d'}[\Delta''] = \mathbb{A}^{d}_{d}[\Delta_i*\Psi] - \mathbb{A}^{d}_{d}\left[\left(M/p_i^{\alpha_i+1}\right)*\Delta_i*\Psi\right], \\[4pt] 0&= \left(\mathbb{A}^{\prime\prime}_i\right)^{d'}_{d'}[\Delta''] = \mathbb{A}^{d}_{d}[\Delta_i*\Psi'] - \mathbb{A}^{d}_{d}\left[\left(M/p_i^{\alpha_i+1}\right)*\Delta_i*\Psi\right], \end{align*} $$
$$ \begin{align*} 0&= \left(\mathbb{A}^{\prime}_i\right)^{d'}_{d'}[\Delta''] = \mathbb{A}^{d}_{d}[\Delta_i*\Psi] - \mathbb{A}^{d}_{d}\left[\left(M/p_i^{\alpha_i+1}\right)*\Delta_i*\Psi\right], \\[4pt] 0&= \left(\mathbb{A}^{\prime\prime}_i\right)^{d'}_{d'}[\Delta''] = \mathbb{A}^{d}_{d}[\Delta_i*\Psi'] - \mathbb{A}^{d}_{d}\left[\left(M/p_i^{\alpha_i+1}\right)*\Delta_i*\Psi\right], \end{align*} $$where ![]() $\Psi '(X)=\Psi -1+X^{M/p_i}$. Taking the difference, we get
$\Psi '(X)=\Psi -1+X^{M/p_i}$. Taking the difference, we get
 $$ \begin{align*} 0&=\left(\mathbb{A}^{\prime}_i\right)^{d'}_{d'}[\Delta''] - \left(\mathbb{A}^{\prime\prime}_i\right)^{d'}_{d'}[\Delta''] \\[4pt] &= \mathbb{A}^{d}_{d}[\Delta_i*\Psi] - \mathbb{A}^{d}_{d}[\Delta_i*\Psi'] \\[4pt] & = \mathbb{A}^{d}_{d}[\Delta], \end{align*} $$
$$ \begin{align*} 0&=\left(\mathbb{A}^{\prime}_i\right)^{d'}_{d'}[\Delta''] - \left(\mathbb{A}^{\prime\prime}_i\right)^{d'}_{d'}[\Delta''] \\[4pt] &= \mathbb{A}^{d}_{d}[\Delta_i*\Psi] - \mathbb{A}^{d}_{d}[\Delta_i*\Psi'] \\[4pt] & = \mathbb{A}^{d}_{d}[\Delta], \end{align*} $$which proves the claim.
If ![]() $\alpha _i=n_i$, the proof is the same, except that the terms with
$\alpha _i=n_i$, the proof is the same, except that the terms with  $(M/p_i^{\alpha _i+1})*\Delta _i$ are replaced by
$(M/p_i^{\alpha _i+1})*\Delta _i$ are replaced by ![]() $0$ in the calculation.
$0$ in the calculation.
Theorem 6.5. Assume that ![]() $A\oplus B=\mathbb {Z}_M$ and
$A\oplus B=\mathbb {Z}_M$ and  $\Phi _{p_i^{n_i}}\mid A$. Then the following are equivalent:
$\Phi _{p_i^{n_i}}\mid A$. Then the following are equivalent:
(i) For any translate
 $ A' $ of
$ A' $ of  $ A $, we have
$ A $, we have  $A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$.
$A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$.(ii) For every d such that
 $p_i^{n_i}\mid d\mid M$, at least one of the following holds: (6.10)
$p_i^{n_i}\mid d\mid M$, at least one of the following holds: (6.10) $$ \begin{align} \Phi_d\mid A, \end{align} $$(6.11)
$$ \begin{align} \Phi_d\mid A, \end{align} $$(6.11) $$ \begin{align} \Phi_{d/p_i}\Phi_{d/p_i^2}\dotsm \Phi_{d/p_i^{n_i}}\mid B. \end{align} $$
$$ \begin{align} \Phi_{d/p_i}\Phi_{d/p_i^2}\dotsm \Phi_{d/p_i^{n_i}}\mid B. \end{align} $$(iii) For every
 $p_i^{n_i}\mid m\mid M$, (6.12)
$p_i^{n_i}\mid m\mid M$, (6.12) $$ \begin{align} m\in \mathrm{Div}(A) \Rightarrow m/p_i\notin \mathrm{Div}(B). \end{align} $$
$$ \begin{align} m\in \mathrm{Div}(A) \Rightarrow m/p_i\notin \mathrm{Div}(B). \end{align} $$
Proof. Let ![]() $N_i=M/p_i$. The assumption that
$N_i=M/p_i$. The assumption that  $\Phi _{p_i^{n_i}}\mid A$ implies that for any translate
$\Phi _{p_i^{n_i}}\mid A$ implies that for any translate ![]() $A'$ of A, we have
$A'$ of A, we have  $\left \lvert A^{\prime }_{p_i}\right \rvert =\lvert A\rvert /p_i$, so that
$\left \lvert A^{\prime }_{p_i}\right \rvert =\lvert A\rvert /p_i$, so that
 $$ \begin{align} \left\lvert A^{\prime}_{p_i}\right\rvert\lvert B\rvert=N_i. \end{align} $$
$$ \begin{align} \left\lvert A^{\prime}_{p_i}\right\rvert\lvert B\rvert=N_i. \end{align} $$ (i) ![]() $\Rightarrow $ (ii): Assume that (i) holds, and suppose that condition (6.11) fails for some
$\Rightarrow $ (ii): Assume that (i) holds, and suppose that condition (6.11) fails for some ![]() $p_i^{n_i}\mid d\mid M$. Then there is an
$p_i^{n_i}\mid d\mid M$. Then there is an ![]() $\alpha _i$ such that
$\alpha _i$ such that ![]() $ 1\leq \alpha _i\leq n_i$ and
$ 1\leq \alpha _i\leq n_i$ and  $\Phi _{d/p_i^{\alpha _i}}\nmid B$. Then
$\Phi _{d/p_i^{\alpha _i}}\nmid B$. Then  $\Phi _{d/p_i^{\alpha _i}}\mid A^{\prime }_{p_i}$ for any translate
$\Phi _{d/p_i^{\alpha _i}}\mid A^{\prime }_{p_i}$ for any translate ![]() $ A' $ of
$ A' $ of ![]() $ A $. By Lemma 6.4, condition (6.10) must hold.
$ A $. By Lemma 6.4, condition (6.10) must hold.
(ii) ![]() $\Rightarrow $ (i): Assume that (ii) holds. With equation (6.13) in place, it suffices to prove that for every
$\Rightarrow $ (i): Assume that (ii) holds. With equation (6.13) in place, it suffices to prove that for every ![]() $ d'\mid N_i$,
$ d'\mid N_i$, ![]() $d'>1 $,
$d'>1 $, ![]() $ \Phi _{d'}$ divides at least one of
$ \Phi _{d'}$ divides at least one of ![]() $A^{\prime }_{p_i}(X)$ and
$A^{\prime }_{p_i}(X)$ and ![]() $B(X)$. Let
$B(X)$. Let ![]() $d'\mid N_i$,
$d'\mid N_i$, ![]() $d'>1$, and suppose that
$d'>1$, and suppose that ![]() $\Phi _{d'}\nmid B$. Then
$\Phi _{d'}\nmid B$. Then ![]() $d'=d/p_i^{\alpha _i}$ for some
$d'=d/p_i^{\alpha _i}$ for some ![]() $ p_i^{n_i}\mid d\mid M$ and
$ p_i^{n_i}\mid d\mid M$ and ![]() $ 1\leq \alpha _i\leq n_i$. By (ii), we must have
$ 1\leq \alpha _i\leq n_i$. By (ii), we must have ![]() $\Phi _d\mid A$. Since
$\Phi _d\mid A$. Since ![]() $A\oplus B=\mathbb {Z}_M$ is a tiling, we must also have
$A\oplus B=\mathbb {Z}_M$ is a tiling, we must also have ![]() $\Phi _{d'}\mid A$. By Lemma 6.3, we must have
$\Phi _{d'}\mid A$. By Lemma 6.3, we must have ![]() $\Phi _{d'}\mid A^{\prime }_{p_i}$ as claimed.
$\Phi _{d'}\mid A^{\prime }_{p_i}$ as claimed.
(i) ![]() $\Rightarrow $ (iii): Assume that (i) holds. This implies in particular that
$\Rightarrow $ (iii): Assume that (i) holds. This implies in particular that ![]() $A^{\prime }_{p_i}$ and
$A^{\prime }_{p_i}$ and ![]() $B \bmod \mathbb {Z}_{N_i}$ are sets, so that
$B \bmod \mathbb {Z}_{N_i}$ are sets, so that ![]() $N_i\not \in \mathrm {Div}(B)$ and condition (6.12) holds for
$N_i\not \in \mathrm {Div}(B)$ and condition (6.12) holds for ![]() $m=M$.
$m=M$.
Next, Theorem 2.5 applied to the tiling ![]() $A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{N_i}$ implies that
$A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{N_i}$ implies that
Suppose that condition (6.12) fails for some ![]() $m\neq M$ such that
$m\neq M$ such that ![]() $p_i^{n_i}\mid m\mid M$, so that
$p_i^{n_i}\mid m\mid M$, so that ![]() $m\in \mathrm {Div}(A)$ and
$m\in \mathrm {Div}(A)$ and ![]() $m/p_i\in \mathrm {Div}(B)$. Then
$m/p_i\in \mathrm {Div}(B)$. Then ![]() $m/p_i \neq N_i$ and
$m/p_i \neq N_i$ and ![]() $m/p_i\in \mathrm {Div}_{N_i}(A) \cap \mathrm {Div}_{N_i}(B)$. But this contradicts equation (6.14).
$m/p_i\in \mathrm {Div}_{N_i}(A) \cap \mathrm {Div}_{N_i}(B)$. But this contradicts equation (6.14).
(iii) ![]() $\Rightarrow $ (i): Assume that (iii) holds. By Theorem 2.5, it suffices to prove that
$\Rightarrow $ (i): Assume that (iii) holds. By Theorem 2.5, it suffices to prove that ![]() $A^{\prime }_{p_i}, B \bmod \mathbb {Z}_{N_i}$ are sets such that equation (6.14) holds.
$A^{\prime }_{p_i}, B \bmod \mathbb {Z}_{N_i}$ are sets such that equation (6.14) holds.
We first verify that ![]() $A^{\prime }_{p_i}, B \bmod \mathbb {Z}_{N_i}$ are sets. Indeed, if
$A^{\prime }_{p_i}, B \bmod \mathbb {Z}_{N_i}$ are sets. Indeed, if ![]() $a,a'\in A^{\prime }_{p_i}$ and
$a,a'\in A^{\prime }_{p_i}$ and ![]() $a\equiv a' \bmod N_i$, then
$a\equiv a' \bmod N_i$, then ![]() $a=a'$ by the definition of
$a=a'$ by the definition of ![]() $A^{\prime }_{p_i}$. On the other hand,
$A^{\prime }_{p_i}$. On the other hand, ![]() $M\in \mathrm {Div}(A)$ trivially, and by formula (6.12) it follows that
$M\in \mathrm {Div}(A)$ trivially, and by formula (6.12) it follows that ![]() $N_i\not \in \mathrm {Div}(B)$, so that
$N_i\not \in \mathrm {Div}(B)$, so that ![]() $B \bmod N_i$ is also a set.
$B \bmod N_i$ is also a set.
Suppose now that equation (6.14) fails, with ![]() $m_1\in (\mathrm {Div}_{N_i}(A) \cap \mathrm {Div}_{N_i}(B))\setminus \{N_i\}$. Since
$m_1\in (\mathrm {Div}_{N_i}(A) \cap \mathrm {Div}_{N_i}(B))\setminus \{N_i\}$. Since ![]() $\mathrm {Div}(A)\cap \mathrm {Div}(B)=\{M\}$, we must have
$\mathrm {Div}(A)\cap \mathrm {Div}(B)=\{M\}$, we must have ![]() $m_1=m_2/p_i$ for some
$m_1=m_2/p_i$ for some ![]() $m_2$ with
$m_2$ with ![]() $p_i^{n_i}\mid m_2\mid M$, so that
$p_i^{n_i}\mid m_2\mid M$, so that
 $$ \begin{align*} m_{j}\in\mathrm{Div}(A^{\prime}_{p_i}),\quad m_{k}\in\mathrm{Div}(B) \end{align*} $$
$$ \begin{align*} m_{j}\in\mathrm{Div}(A^{\prime}_{p_i}),\quad m_{k}\in\mathrm{Div}(B) \end{align*} $$for some permutation ![]() $(j,k)$ of
$(j,k)$ of ![]() $(1,2)$. By the definition of
$(1,2)$. By the definition of ![]() $A^{\prime }_{p_i}$, we cannot have
$A^{\prime }_{p_i}$, we cannot have  $p_i^{n_i-1}\parallel s$ for
$p_i^{n_i-1}\parallel s$ for ![]() $s\in \mathrm {Div}(A^{\prime }_{p_i})$, so that
$s\in \mathrm {Div}(A^{\prime }_{p_i})$, so that ![]() $j=2$,
$j=2$, ![]() $k=1$. But this contradicts condition (6.12).
$k=1$. But this contradicts condition (6.12).
Remark 6.6. In the special case when A is M-fibered in the ![]() $ p_i$ direction, the condition (6.11) of Theorem 6.5 is satisfied, since then
$ p_i$ direction, the condition (6.11) of Theorem 6.5 is satisfied, since then ![]() $ \Phi _d\mid A$ for all
$ \Phi _d\mid A$ for all ![]() $p_i^{n_i}\mid d\mid M$. It is also easy to verify directly that condition (6.12) holds in this case.
$p_i^{n_i}\mid d\mid M$. It is also easy to verify directly that condition (6.12) holds in this case.
Corollary 6.7 Slab reduction
Assume that ![]() $ A\oplus B=\mathbb {Z}_M $, where
$ A\oplus B=\mathbb {Z}_M $, where  $M=\prod _{i=1}^K p_i^{n_i}$, and that the following are true:
$M=\prod _{i=1}^K p_i^{n_i}$, and that the following are true:
• (T2) holds for both
 $A'$ and
$A'$ and  $B'$ in any tiling
$B'$ in any tiling  $ A'\oplus B'=\mathbb {Z}_{N_i} $, where
$ A'\oplus B'=\mathbb {Z}_{N_i} $, where  $N_i=M/p_i$,
$N_i=M/p_i$,  $\lvert A'\rvert =\lvert A\rvert /p_i$ and
$\lvert A'\rvert =\lvert A\rvert /p_i$ and  $\lvert B'\rvert =\lvert B\rvert $;
$\lvert B'\rvert =\lvert B\rvert $;• there exists an
 $i\in \{1,\dotsc ,K\}$ such that
$i\in \{1,\dotsc ,K\}$ such that  $\Phi _{p_i^{n_i}}\mid A$ and
$\Phi _{p_i^{n_i}}\mid A$ and  $A,B$ obey one (therefore all) of Theorem 6.5(i)–(iii).
$A,B$ obey one (therefore all) of Theorem 6.5(i)–(iii).
Then ![]() $ A $ and
$ A $ and ![]() $ B $ satisfy (T2).
$ B $ satisfy (T2).
Proof. We are assuming that ![]() $A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$ for any translate
$A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$ for any translate ![]() $ A'$ of
$ A'$ of ![]() $ A $. By the inductive part of the assumption,
$ A $. By the inductive part of the assumption, ![]() $A^{\prime }_{p_i}$ and B satisfy (T2). It remains to prove (T2) for
$A^{\prime }_{p_i}$ and B satisfy (T2). It remains to prove (T2) for ![]() $ A $. Suppose that
$ A $. Suppose that  $d=\prod _{j\in J} p_j^{\alpha _j}$, where
$d=\prod _{j\in J} p_j^{\alpha _j}$, where ![]() $J\subset \{1,\dotsc ,K\}$,
$J\subset \{1,\dotsc ,K\}$, ![]() $1\leq \alpha _j\leq n_j$ for all
$1\leq \alpha _j\leq n_j$ for all ![]() $j\in J$, and
$j\in J$, and  $\Phi _{p_j^{\alpha _j}}(X)\mid A(X)$ for all
$\Phi _{p_j^{\alpha _j}}(X)\mid A(X)$ for all ![]() $j\in J$. For each prime power
$j\in J$. For each prime power  $p_j^{\alpha _j}$ with
$p_j^{\alpha _j}$ with ![]() $\alpha _j\neq 0$, the polynomial
$\alpha _j\neq 0$, the polynomial  $\Phi _{p_j^{\alpha _j}}(X)$ can divide only one of A and B in the tiling
$\Phi _{p_j^{\alpha _j}}(X)$ can divide only one of A and B in the tiling ![]() $A\oplus B=\mathbb {Z}_M$, hence
$A\oplus B=\mathbb {Z}_M$, hence
 $$ \begin{align} \Phi_{p_j^{\alpha_j}}\nmid B \quad \forall j\in J. \end{align} $$
$$ \begin{align} \Phi_{p_j^{\alpha_j}}\nmid B \quad \forall j\in J. \end{align} $$ Write  $ A(X)=\sum _{\nu =0}^{p_i-1} A_{\nu }(X) $, where
$ A(X)=\sum _{\nu =0}^{p_i-1} A_{\nu }(X) $, where ![]() $A_\nu $ are as in formula (6.8), so that
$A_\nu $ are as in formula (6.8), so that ![]() $A_\nu \oplus B=\mathbb {Z}_{N_i}$ for each
$A_\nu \oplus B=\mathbb {Z}_{N_i}$ for each ![]() $\nu $. We consider two cases:
$\nu $. We consider two cases:
• Assume that either
 $i\not \in J$, or
$i\not \in J$, or  $i\in J$ but
$i\in J$ but  $\alpha _i\neq n_i$. By formula (6.15), we have
$\alpha _i\neq n_i$. By formula (6.15), we have  $\Phi _{p_j^{\alpha _j}}\mid A_\nu $ for all
$\Phi _{p_j^{\alpha _j}}\mid A_\nu $ for all  $j\in J$ and
$j\in J$ and  $\nu =0,1,\dotsc ,p_i-1$. We are assuming that (T2) holds for
$\nu =0,1,\dotsc ,p_i-1$. We are assuming that (T2) holds for  $A_\nu $, so that
$A_\nu $, so that  $\Phi _d\mid A_\nu $. Summing over
$\Phi _d\mid A_\nu $. Summing over  $\nu $, we get that
$\nu $, we get that  $\Phi _d\mid A$.
$\Phi _d\mid A$.• Assume now that
 $i\in J$ and
$i\in J$ and  $\alpha _i=n_i$, and let
$\alpha _i=n_i$, and let  $d'=d/p_i^{n_i}$. Then
$d'=d/p_i^{n_i}$. Then  $\Phi _{d'}\mid A^{\prime }_{p_i}$ for any translate
$\Phi _{d'}\mid A^{\prime }_{p_i}$ for any translate  $A'$ of A, by the argument in the first case applied to
$A'$ of A, by the argument in the first case applied to  $A'$ instead of A. By Lemma 6.4, it follows that
$A'$ instead of A. By Lemma 6.4, it follows that  $\Phi _d\mid A$.
$\Phi _d\mid A$.
We note the following special case:
Corollary 6.8. Assume that ![]() $ A\oplus B=\mathbb {Z}_M $, where
$ A\oplus B=\mathbb {Z}_M $, where  $M=p_1^{n_1}p_2^{n_2}p_3^{n_3}$ and
$M=p_1^{n_1}p_2^{n_2}p_3^{n_3}$ and ![]() $p_1,p_2,p_3$ are distinct primes. Moreover, assume that there is a permutation
$p_1,p_2,p_3$ are distinct primes. Moreover, assume that there is a permutation ![]() $(i,j,k)$ of
$(i,j,k)$ of ![]() $(1,2,3)$ such that
$(1,2,3)$ such that  $\lvert A\rvert =p_i p_j^{\alpha _j} p_k^{\alpha _k}$ for some
$\lvert A\rvert =p_i p_j^{\alpha _j} p_k^{\alpha _k}$ for some ![]() $0\leq \alpha _j\leq n_j$,
$0\leq \alpha _j\leq n_j$, ![]() $0\leq \alpha _k\leq n_k$, and that A is M-fibered in the
$0\leq \alpha _k\leq n_k$, and that A is M-fibered in the ![]() $p_i$ direction. Then
$p_i$ direction. Then ![]() $ A $ and
$ A $ and ![]() $ B $ satisfy (T2).
$ B $ satisfy (T2).
7 Saturating sets
7.1 Preliminaries
Definition 7.1 Restricted N-boxes
Set ![]() $A,X\subseteq \mathbb {Z}_M$, and
$A,X\subseteq \mathbb {Z}_M$, and ![]() $x\in \mathbb {Z}_M$. The restriction of
$x\in \mathbb {Z}_M$. The restriction of ![]() $\mathbb {A}^N[x]$ to X is the N-box
$\mathbb {A}^N[x]$ to X is the N-box ![]() $\mathbb {A}^N[x\mid X]$ with entries
$\mathbb {A}^N[x\mid X]$ with entries
 $$ \begin{align*} \mathbb{A}^N_m[x\mid X] = \sum_{a\in X: (x-a,N)=m} w^N_A(a), \quad m\mid N. \end{align*} $$
$$ \begin{align*} \mathbb{A}^N_m[x\mid X] = \sum_{a\in X: (x-a,N)=m} w^N_A(a), \quad m\mid N. \end{align*} $$In particular,
The next definition is the key to our analysis of unfibered tilings in [Reference Łaba and Londner24]. While it could be extended in an obvious way to N-boxes with ![]() $N\mid M$, our current arguments only use the M-box version here.
$N\mid M$, our current arguments only use the M-box version here.
Definition 7.2 Saturating sets
Set ![]() $A,B\subseteq \mathbb {Z}_M$, and
$A,B\subseteq \mathbb {Z}_M$, and ![]() $x,y\in \mathbb {Z}_M$. Define
$x,y\in \mathbb {Z}_M$. Define
 $$ \begin{gather*} A_{x,y}:=\{a\in A: (x-a,M)=(y-b,M) \text{ for some }b\in B\}, \\ A_{x}:=\bigcup_{b\in B} A_{x,b}. \end{gather*} $$
$$ \begin{gather*} A_{x,y}:=\{a\in A: (x-a,M)=(y-b,M) \text{ for some }b\in B\}, \\ A_{x}:=\bigcup_{b\in B} A_{x,b}. \end{gather*} $$Equivalently,
We will refer to ![]() $A_x$ as the saturating set for x. The sets
$A_x$ as the saturating set for x. The sets ![]() $B_{y,x}$ and
$B_{y,x}$ and ![]() $B_y$ are defined similarly, with A and B interchanged.
$B_y$ are defined similarly, with A and B interchanged.
With this notation, ![]() $A_{x,y}$ is the minimal set that saturates (the A-side of) the product
$A_{x,y}$ is the minimal set that saturates (the A-side of) the product  $\left \langle \mathbb {A}^M[x], \mathbb {B}^M[y]\right \rangle $, in the sense that
$\left \langle \mathbb {A}^M[x], \mathbb {B}^M[y]\right \rangle $, in the sense that
 $$ \begin{align} \left\langle \mathbb{A}^M[x\mid X], \mathbb{B}^M[y]\right\rangle = \left\langle \mathbb{A}^M[x], \mathbb{B}^M[y]\right\rangle \end{align} $$
$$ \begin{align} \left\langle \mathbb{A}^M[x\mid X], \mathbb{B}^M[y]\right\rangle = \left\langle \mathbb{A}^M[x], \mathbb{B}^M[y]\right\rangle \end{align} $$holds for ![]() $X=A_{x,y}$, and if
$X=A_{x,y}$, and if ![]() $X\subset \mathbb {Z}_M$ is any other set for it holds, then
$X\subset \mathbb {Z}_M$ is any other set for it holds, then ![]() $A_{x,y}\subset X$. The set
$A_{x,y}\subset X$. The set ![]() $A_x$ is the minimal set such that
$A_x$ is the minimal set such that
 $$ \begin{align} \left\langle \mathbb{A}^M[x\mid A_x], \mathbb{B}^M[b]\right\rangle =\left\langle \mathbb{A}^M[x], \mathbb{B}^M[b]\right\rangle \quad \forall b\in B. \end{align} $$
$$ \begin{align} \left\langle \mathbb{A}^M[x\mid A_x], \mathbb{B}^M[b]\right\rangle =\left\langle \mathbb{A}^M[x], \mathbb{B}^M[b]\right\rangle \quad \forall b\in B. \end{align} $$ While Definition 7.2 makes sense for general sets ![]() $A,B\subseteq \mathbb {Z}_M$, our intended application is to the tiling situation
$A,B\subseteq \mathbb {Z}_M$, our intended application is to the tiling situation ![]() $A\oplus B= \mathbb {Z}_M$. In that case, by Theorem 4.4, the box products on the right side of equations (7.2) and (7.3) evaluate to
$A\oplus B= \mathbb {Z}_M$. In that case, by Theorem 4.4, the box products on the right side of equations (7.2) and (7.3) evaluate to ![]() $1$. Hence
$1$. Hence ![]() $A_{x,y}$ is the smallest set such that
$A_{x,y}$ is the smallest set such that
 $$ \begin{align} \left\langle \mathbb{A}^M\left[x\mid A_{x,y}\right], \mathbb{B}^M[y]\right\rangle = 1, \end{align} $$
$$ \begin{align} \left\langle \mathbb{A}^M\left[x\mid A_{x,y}\right], \mathbb{B}^M[y]\right\rangle = 1, \end{align} $$and ![]() $A_x$ is the smallest set such that
$A_x$ is the smallest set such that
 $$ \begin{align} \left\langle \mathbb{A}^M[x\mid A_x], \mathbb{B}^M[b]\right\rangle =1 \quad \forall b\in B. \end{align} $$
$$ \begin{align} \left\langle \mathbb{A}^M[x\mid A_x], \mathbb{B}^M[b]\right\rangle =1 \quad \forall b\in B. \end{align} $$Observe in particular that a saturating set for any ![]() $x\in \mathbb {Z}_M$ must be nonempty, and that by Theorem 2.5,
$x\in \mathbb {Z}_M$ must be nonempty, and that by Theorem 2.5,
In the next few definitions and lemmas, we will work toward geometric descriptions of saturating sets. Assume that ![]() $A\oplus B= \mathbb {Z}_M$. Set
$A\oplus B= \mathbb {Z}_M$. Set ![]() $x\in \mathbb {Z}_M\setminus A$, and suppose that
$x\in \mathbb {Z}_M\setminus A$, and suppose that ![]() $a\in A_x$. By equation (7.1) and divisor exclusion, we must have
$a\in A_x$. By equation (7.1) and divisor exclusion, we must have ![]() $(x-a,M)\not \in \mathrm {Div}(A)$, and in particular
$(x-a,M)\not \in \mathrm {Div}(A)$, and in particular ![]() $(x-a,M)\neq (a'-a,M)$ for all
$(x-a,M)\neq (a'-a,M)$ for all ![]() $a'\in A$. This motivates the following definition:
$a'\in A$. This motivates the following definition:
Definition 7.3. Let ![]() $M=p_1^{n_1}\dotsm p_K^{n_K}$, where
$M=p_1^{n_1}\dotsm p_K^{n_K}$, where ![]() $p_1,\dotsc ,p_K$ are distinct primes, and set
$p_1,\dotsc ,p_K$ are distinct primes, and set ![]() $x,x'\in \mathbb {Z}_M$,
$x,x'\in \mathbb {Z}_M$, ![]() $x\neq x'$. Suppose that
$x\neq x'$. Suppose that ![]() $(x-x',M)=p_1^{\alpha _1}\dotsm p_K^{\alpha _K}$, with
$(x-x',M)=p_1^{\alpha _1}\dotsm p_K^{\alpha _K}$, with ![]() $0\leq \alpha _j\leq n_j$ for
$0\leq \alpha _j\leq n_j$ for ![]() $j=1,\dotsc ,K$.
$j=1,\dotsc ,K$.
Define
 $$ \begin{align} \mathrm{Span}(x,x')&=\bigcup_{i: \alpha_i<n_i} \Pi\left(x,p_i^{\alpha_i+1}\right), \nonumber\\ \mathrm{Bispan}(x,x')&= \mathrm{Span}(x,x')\cup \mathrm{Span}(x',x). \end{align} $$
$$ \begin{align} \mathrm{Span}(x,x')&=\bigcup_{i: \alpha_i<n_i} \Pi\left(x,p_i^{\alpha_i+1}\right), \nonumber\\ \mathrm{Bispan}(x,x')&= \mathrm{Span}(x,x')\cup \mathrm{Span}(x',x). \end{align} $$Example 7.4. Let  $M=p_1^{n_1}p_2^{n_2}p_3^{n_3}$, where
$M=p_1^{n_1}p_2^{n_2}p_3^{n_3}$, where ![]() $p_1,p_2,p_3$ are distinct primes and
$p_1,p_2,p_3$ are distinct primes and ![]() $n_1,n_2,n_3\geq 2$. Set
$n_1,n_2,n_3\geq 2$. Set ![]() $x,x'\in \mathbb {Z}_M$, and let
$x,x'\in \mathbb {Z}_M$, and let ![]() $m=(x-x',M)$.
$m=(x-x',M)$.
• Suppose that
 $m=M/p_1p_2p_3$, so that
$m=M/p_1p_2p_3$, so that  $\alpha _i=n_i-1$ for
$\alpha _i=n_i-1$ for  $i=1,2,3$, and represent
$i=1,2,3$, and represent  $\mathbb {Z}_M$ as a
$\mathbb {Z}_M$ as a  $3$-dimensional M-array. Then
$3$-dimensional M-array. Then  $\mathrm {Span}(x,x')$ is the union of the
$\mathrm {Span}(x,x')$ is the union of the  $2$-dimensional planes
$2$-dimensional planes  $\Pi (x,p_i^{n_i})$ with
$\Pi (x,p_i^{n_i})$ with  $i=1,2,3$, all passing through x, and similarly for
$i=1,2,3$, all passing through x, and similarly for  $\mathrm {Span}(x',x)$, with x and
$\mathrm {Span}(x',x)$, with x and  $x'$ interchanged. Geometrically,
$x'$ interchanged. Geometrically,  $\mathrm {Bispan}(x,x')$ is the union of those
$\mathrm {Bispan}(x,x')$ is the union of those  $2$-dimensional planes at the top scale that contain at least one
$2$-dimensional planes at the top scale that contain at least one  $2$-dimensional face of the
$2$-dimensional face of the  $3$-dimensional rectangular box ‘spanned’ by x and
$3$-dimensional rectangular box ‘spanned’ by x and  $x'$.
$x'$.• Suppose now that
 $m=M/p_i$ for some
$m=M/p_i$ for some  $i\in \{1,2,3\}$. Then
$i\in \{1,2,3\}$. Then  $\mathrm {Span}(x,x')=\Pi (x,p_i^{n_i})$ is a single plane passing through x and perpendicular to the
$\mathrm {Span}(x,x')=\Pi (x,p_i^{n_i})$ is a single plane passing through x and perpendicular to the  $p_i$ direction, and similarly for
$p_i$ direction, and similarly for  $\mathrm {Span}(x',x)=\Pi (x',p_i^{n_i})$.
$\mathrm {Span}(x',x)=\Pi (x',p_i^{n_i})$.• If
 $m=M/p_ip_j$ for some
$m=M/p_ip_j$ for some  $i\neq j$, then
$i\neq j$, then  $\mathrm {Span}(x,x')=\Pi (x,p_i^{n_i})\cup \Pi (x,p_j^{n_j})$ is a union of two planes.
$\mathrm {Span}(x,x')=\Pi (x,p_i^{n_i})\cup \Pi (x,p_j^{n_j})$ is a union of two planes.
The higher-dimensional case has a similar interpretation. As should be clear from the foregoing example, the definition is not symmetric with respect to ![]() $x,x'$, so that
$x,x'$, so that ![]() $\mathrm {Span}(x,x')\neq \mathrm {Span}(x',x)$. However, we have the following:
$\mathrm {Span}(x,x')\neq \mathrm {Span}(x',x)$. However, we have the following:
Lemma 7.5. Set ![]() $x,x'\in \mathbb {Z}_M$. Then
$x,x'\in \mathbb {Z}_M$. Then
Proof. We have ![]() $x'\in \mathrm {Span}(x,z)$ if and only if there exist
$x'\in \mathrm {Span}(x,z)$ if and only if there exist ![]() $i\in \{1,\dotsc ,K\}$ and
$i\in \{1,\dotsc ,K\}$ and ![]() $0\leq \alpha _i<n_i$ such that
$0\leq \alpha _i<n_i$ such that ![]() $p_i^{\alpha _i}\parallel x-z$,
$p_i^{\alpha _i}\parallel x-z$, ![]() $p_i^{\alpha _i} \parallel x'-z$ and
$p_i^{\alpha _i} \parallel x'-z$ and  $p_i^{\alpha _i+1}\mid x-x'$. These conditions are clearly symmetric with respect to x and
$p_i^{\alpha _i+1}\mid x-x'$. These conditions are clearly symmetric with respect to x and ![]() $x'$.
$x'$.
Lemma 7.6. If ![]() $(x-x',M)=(x-x'',M)=m$, then
$(x-x',M)=(x-x'',M)=m$, then ![]() $\mathrm {Span}(x,x')=\mathrm {Span}(x,x'')$.
$\mathrm {Span}(x,x')=\mathrm {Span}(x,x'')$.
Proof. This follows directly from the definition.
Lemma 7.7. Set ![]() $A,B\subset \mathbb {Z}_M$,
$A,B\subset \mathbb {Z}_M$, ![]() $x,x'\in \mathbb {Z}_M$ and
$x,x'\in \mathbb {Z}_M$ and ![]() $a\in A$. If
$a\in A$. If ![]() $(x-a,M) \neq (x'-a,M)$, then
$(x-a,M) \neq (x'-a,M)$, then ![]() $a\in \mathrm {Bispan}(x,x')$.
$a\in \mathrm {Bispan}(x,x')$.
Proof. Suppose that ![]() $(x-a,M)\neq (x'-a,M)$. It follows that
$(x-a,M)\neq (x'-a,M)$. It follows that ![]() $(x-a,p_i^{n_i})\neq (x'-a,p_i^{n_i})$ for some
$(x-a,p_i^{n_i})\neq (x'-a,p_i^{n_i})$ for some ![]() $i\in \{1,\dotsc ,K\}$. Interchanging x and
$i\in \{1,\dotsc ,K\}$. Interchanging x and ![]() $x'$ if necessary, we may assume that
$x'$ if necessary, we may assume that ![]() $p_i^{\alpha _i}\parallel x-a$ and
$p_i^{\alpha _i}\parallel x-a$ and  $p_i^{\alpha _i+1}\mid x'-a$ for some
$p_i^{\alpha _i+1}\mid x'-a$ for some ![]() $\alpha _i\in \{0,1,\dotsc , n_i-1\}$. Hence
$\alpha _i\in \{0,1,\dotsc , n_i-1\}$. Hence ![]() $p_i^{\alpha _i}\parallel x-x'$, and
$p_i^{\alpha _i}\parallel x-x'$, and ![]() $a\in \mathrm {Span} (x',x)$.
$a\in \mathrm {Span} (x',x)$.
Lemma 7.8. Let ![]() $A,B\subset \mathbb {Z}_M$ be fixed. Then the following are true:
$A,B\subset \mathbb {Z}_M$ be fixed. Then the following are true:
(i) For any
 $x,x',y\in \mathbb {Z}_M$, we have (7.8)
$x,x',y\in \mathbb {Z}_M$, we have (7.8) $$ \begin{align} A_{x',y}\subset A_{x,y}\cup\mathrm{Bispan}(x,x'). \end{align} $$
$$ \begin{align} A_{x',y}\subset A_{x,y}\cup\mathrm{Bispan}(x,x'). \end{align} $$(ii) Suppose that
 $A\oplus B=\mathbb {Z}_M$. Then for any
$A\oplus B=\mathbb {Z}_M$. Then for any  $x\in \mathbb {Z}_M$, (7.9)
$x\in \mathbb {Z}_M$, (7.9) $$ \begin{align} A_x \subset \bigcap_{a\in A} \mathrm{Bispan} (x,a). \end{align} $$
$$ \begin{align} A_x \subset \bigcap_{a\in A} \mathrm{Bispan} (x,a). \end{align} $$
Proof. To prove (i), suppose that ![]() $a\in A_{x',y}$. Then
$a\in A_{x',y}$. Then ![]() $(x'-a,M)=(y-b,M)$ for some
$(x'-a,M)=(y-b,M)$ for some ![]() $b\in B$. If
$b\in B$. If ![]() $(x-a,M)=(x'-a,M)$, it follows that
$(x-a,M)=(x'-a,M)$, it follows that ![]() $a\in A_{x,y}$. If, on the other hand,
$a\in A_{x,y}$. If, on the other hand, ![]() $(x-a,M)\neq (x'-a,M)$, then by Lemma 7.7 we must have
$(x-a,M)\neq (x'-a,M)$, then by Lemma 7.7 we must have ![]() $a\in \mathrm {Bispan}(x,x')$. This proves inclusion (7.8). Part (ii) follows from (i) and equation (7.6), since
$a\in \mathrm {Bispan}(x,x')$. This proves inclusion (7.8). Part (ii) follows from (i) and equation (7.6), since ![]() $a\in \mathrm {Span}(a,x)$.
$a\in \mathrm {Span}(a,x)$.
We note a lemma which will be useful in the evaluation of saturating sets:
Lemma 7.9 Enhanced divisor exclusion
Let ![]() $A\oplus B=\mathbb {Z}_M$, with
$A\oplus B=\mathbb {Z}_M$, with  $M=\prod _{i=1}^K p_i^{n_i}$. Let
$M=\prod _{i=1}^K p_i^{n_i}$. Let  $m=\prod _{i=1}^K p_i^{\alpha _i}$ and
$m=\prod _{i=1}^K p_i^{\alpha _i}$ and  $m'=\prod _{i=1}^K p_i^{\alpha ^{\prime }_i}$, with
$m'=\prod _{i=1}^K p_i^{\alpha ^{\prime }_i}$, with ![]() $0\leq \alpha _i,\alpha ^{\prime }_i\leq n_i$. Assume that at least one of
$0\leq \alpha _i,\alpha ^{\prime }_i\leq n_i$. Assume that at least one of ![]() $m,m'$ is different from M, and that for every
$m,m'$ is different from M, and that for every ![]() $i=1,\dotsc ,K$ we have either
$i=1,\dotsc ,K$ we have either ![]() $\alpha _i\neq \alpha ^{\prime }_i$ or
$\alpha _i\neq \alpha ^{\prime }_i$ or ![]() $\alpha _i =\alpha ^{\prime }_i=n_i$. Then for all
$\alpha _i =\alpha ^{\prime }_i=n_i$. Then for all ![]() $x,y\in \mathbb {Z}_M$ we have
$x,y\in \mathbb {Z}_M$ we have
 $$ \begin{align*} \mathbb{A}^M_m[x] \mathbb{A}^M_{m'}[x] \mathbb{B}^M_m[y] \mathbb{B}^M_{m'}[y] =0. \end{align*} $$
$$ \begin{align*} \mathbb{A}^M_m[x] \mathbb{A}^M_{m'}[x] \mathbb{B}^M_m[y] \mathbb{B}^M_{m'}[y] =0. \end{align*} $$In other words, there are no configurations ![]() $(a,a',b,b')\in A\times A\times B\times B$ such that
$(a,a',b,b')\in A\times A\times B\times B$ such that
Proof. If we did have a configuration as in equation (7.10), then under the assumptions of the lemma we would have
 $$ \begin{align*} (a-a',M)=(b-b',M)=\prod_{i=1}^K p_i^{\min\left(\alpha_i,\alpha^{\prime}_i\right)}, \end{align*} $$
$$ \begin{align*} (a-a',M)=(b-b',M)=\prod_{i=1}^K p_i^{\min\left(\alpha_i,\alpha^{\prime}_i\right)}, \end{align*} $$with the right side different from M. But that is prohibited by Theorem 2.5.
7.2 Examples and applications
We first provide examples of using Lemma 7.8 to derive geometric constraints on saturating sets. For simplicity, in these examples we return to the three-prime case with  $M=p_1^{n_1}p_2^{n_2}p_3^{n_3}$, where
$M=p_1^{n_1}p_2^{n_2}p_3^{n_3}$, where ![]() $p_1,p_2,p_3$ are distinct primes and
$p_1,p_2,p_3$ are distinct primes and ![]() $n_1,n_2,n_3\geq 2$. Assume that
$n_1,n_2,n_3\geq 2$. Assume that ![]() $A\oplus B=\mathbb {Z}_M$ is a tiling, and set
$A\oplus B=\mathbb {Z}_M$ is a tiling, and set ![]() $x\in \mathbb {Z}_M$.
$x\in \mathbb {Z}_M$.
• Suppose that
 $(x-a,M)=M/p_i$ for some
$(x-a,M)=M/p_i$ for some  $a\in A$ and
$a\in A$ and  $i\in \{1,2,3\}$. Then
$i\in \{1,2,3\}$. Then  $$ \begin{align*} A_x\subset \mathrm{Bispan}(x,a)=\Pi\left(x,p_i^{n_i}\right) \cup\Pi\left(a,p_i^{n_i}\right). \end{align*} $$
$$ \begin{align*} A_x\subset \mathrm{Bispan}(x,a)=\Pi\left(x,p_i^{n_i}\right) \cup\Pi\left(a,p_i^{n_i}\right). \end{align*} $$
• Suppose that there are two distinct elements
 $a,a'\in A$ such that
$a,a'\in A$ such that  $(x-a,M)=(x-a',M)=M/p_i$. Then
$(x-a,M)=(x-a',M)=M/p_i$. Then  $$ \begin{align*} A_x\subset \mathrm{Bispan}(x,a)\cap\mathrm{Bispan}(x,a')=\Pi\left(x,p_i^{n_i}\right). \end{align*} $$
$$ \begin{align*} A_x\subset \mathrm{Bispan}(x,a)\cap\mathrm{Bispan}(x,a')=\Pi\left(x,p_i^{n_i}\right). \end{align*} $$
• Suppose that there are two elements
 $a_i,a_j\in A$ such that
$a_i,a_j\in A$ such that  $(x-a_i,M)=M/p_i$ and
$(x-a_i,M)=M/p_i$ and  $(x-a_j,M)=M/p_j$, with
$(x-a_j,M)=M/p_j$, with  $i,j\in \{1,2,3\}$ distinct. Then where
$i,j\in \{1,2,3\}$ distinct. Then where $$ \begin{align*} A_x\subset \mathrm{Bispan}(x,a_i)\cap\mathrm{Bispan}(x,a_j)=\ell_k(x)\cup\ell_k(a_i)\cup\ell_k\left(a_j\right)\cup\ell_k\left(x_{ij}\right), \end{align*} $$
$$ \begin{align*} A_x\subset \mathrm{Bispan}(x,a_i)\cap\mathrm{Bispan}(x,a_j)=\ell_k(x)\cup\ell_k(a_i)\cup\ell_k\left(a_j\right)\cup\ell_k\left(x_{ij}\right), \end{align*} $$ $\{1,2,3\}\setminus \{i,j\}=\{k\}$, and
$\{1,2,3\}\setminus \{i,j\}=\{k\}$, and  $x_{ij}\in \mathbb {Z}_M$ is the unique point such that
$x_{ij}\in \mathbb {Z}_M$ is the unique point such that  $(x_{ij}-a_i,M)=M/p_j$ and
$(x_{ij}-a_i,M)=M/p_j$ and  $(x_{ij}-a_j,M)=M/p_i$.
$(x_{ij}-a_j,M)=M/p_i$.• Suppose that
 $(x-a,M)=M/p_ip_j$ for some
$(x-a,M)=M/p_ip_j$ for some  $a\in A$ and
$a\in A$ and  $i,j\in \{1,2,3\}$ distinct. Then
$i,j\in \{1,2,3\}$ distinct. Then  $$ \begin{align*} A_x\subset \Pi\left(x,p_i^{n_i}\right) \cup\Pi\left(a,p_i^{n_i}\right)\cup \Pi\left(x,p_i^{n_j}\right) \cup\Pi\left(a,p_i^{n_j}\right). \end{align*} $$
$$ \begin{align*} A_x\subset \Pi\left(x,p_i^{n_i}\right) \cup\Pi\left(a,p_i^{n_i}\right)\cup \Pi\left(x,p_i^{n_j}\right) \cup\Pi\left(a,p_i^{n_j}\right). \end{align*} $$• We leave it as an easy exercise for the reader to verify that if there are
 $a,a',a''\in A$ such that
$a,a',a''\in A$ such that  $(z-z',M)=M/p_ip_j$ for all pairs of distinct elements
$(z-z',M)=M/p_ip_j$ for all pairs of distinct elements  $z,z'\in \{x,a,a',a''\}$, then
$z,z'\in \{x,a,a',a''\}$, then  $$ \begin{align*} A_x\subset \Pi\left(x,p_i^{n_i}\right) \cup \Pi\left(x,p_i^{n_j}\right). \end{align*} $$
$$ \begin{align*} A_x\subset \Pi\left(x,p_i^{n_i}\right) \cup \Pi\left(x,p_i^{n_j}\right). \end{align*} $$• Suppose that
 $x\in \mathbb {Z}_M\setminus A$ and
$x\in \mathbb {Z}_M\setminus A$ and  $y\in \mathbb {Z}_M\setminus B$ with (7.11)We claim that
$y\in \mathbb {Z}_M\setminus B$ with (7.11)We claim that $$ \begin{align} (x-a,M)=(y-b,M)=M/p_i \text{ for some } a\in A,b\in B. \end{align} $$(7.12)One way to prove this is as follows. Let
$$ \begin{align} (x-a,M)=(y-b,M)=M/p_i \text{ for some } a\in A,b\in B. \end{align} $$(7.12)One way to prove this is as follows. Let $$ \begin{align} A_{x,y}\subset\Pi\left(x,p_i^{n_i-1}\right),\qquad B_{y,x}\subset\Pi\left(y,p_i^{n_i-1}\right). \end{align} $$
$$ \begin{align} A_{x,y}\subset\Pi\left(x,p_i^{n_i-1}\right),\qquad B_{y,x}\subset\Pi\left(y,p_i^{n_i-1}\right). \end{align} $$ $a\in A$ and
$a\in A$ and  $b\in B$ be as in equation (7.11). As in the first example here, we have
$b\in B$ be as in equation (7.11). As in the first example here, we have  $A_{x,b}\subset \mathrm {Bispan}(x,a)\subset \Pi (x,p_i^{n_i-1})$. Hence
$A_{x,b}\subset \mathrm {Bispan}(x,a)\subset \Pi (x,p_i^{n_i-1})$. Hence  $B_{b,x} \subset \Pi (b,p_i^{n_i-1})=\Pi (y,p_i^{n_i-1})$. Applying inclusion (7.8) to B, and using the fact that
$B_{b,x} \subset \Pi (b,p_i^{n_i-1})=\Pi (y,p_i^{n_i-1})$. Applying inclusion (7.8) to B, and using the fact that  $\mathrm {Bispan}(y,b)\subset \Pi (y,p_i^{n_i-1})$, we get that
$\mathrm {Bispan}(y,b)\subset \Pi (y,p_i^{n_i-1})$, we get that  $B_{y,x} \subset \Pi (y,p_i^{n_i-1})$ as claimed. This also implies the first half of claim (7.12). Alternatively, claim (7.12) can also be deduced from Lemma 7.9.
$B_{y,x} \subset \Pi (y,p_i^{n_i-1})$ as claimed. This also implies the first half of claim (7.12). Alternatively, claim (7.12) can also be deduced from Lemma 7.9.
Saturating sets are very useful in identifying configurations that cannot occur in tiling complements. For example, we have the following easy but important lemma:
Lemma 7.10 No missing joints
Let ![]() $A\oplus B=\mathbb {Z}_M$, where
$A\oplus B=\mathbb {Z}_M$, where ![]() $M=p_1^{n_1}\dotsm p_K^{n_K}$. Suppose that
$M=p_1^{n_1}\dotsm p_K^{n_K}$. Suppose that
and that for some ![]() $x\in \mathbb {Z}_M$ there exist
$x\in \mathbb {Z}_M$ there exist ![]() $a_1,\dotsc , a_K\in A$ such that
$a_1,\dotsc , a_K\in A$ such that
Then ![]() $x\in A$.
$x\in A$.
Proof. Suppose that ![]() $x\not \in A$, and let
$x\not \in A$, and let ![]() $\Delta $ be the M-cuboid with vertices
$\Delta $ be the M-cuboid with vertices ![]() $x,a_1,\dotsc ,a_K$. By formulas (7.14) and (7.9), the saturating set
$x,a_1,\dotsc ,a_K$. By formulas (7.14) and (7.9), the saturating set ![]() $A_x$ is contained in the vertex set of
$A_x$ is contained in the vertex set of ![]() $\Delta $. But that is impossible by disjointness condition (7.13).
$\Delta $. But that is impossible by disjointness condition (7.13).
As an application, we prove the following restriction on fibered grids that can be a part of a tiling set:
Proposition 7.11. Let ![]() $M=p_1^{n_1}p_2^{n_3}p_2^{n_3}$. Assume that
$M=p_1^{n_1}p_2^{n_3}p_2^{n_3}$. Assume that ![]() $A\oplus B=\mathbb {Z}_M$ is a tiling, and that there exists a
$A\oplus B=\mathbb {Z}_M$ is a tiling, and that there exists a ![]() $D(M)$-grid
$D(M)$-grid ![]() $\Lambda $ such that
$\Lambda $ such that ![]() $A\cap \Lambda $ is a nonempty union of disjoint M-fibers. Then there is a subset
$A\cap \Lambda $ is a nonempty union of disjoint M-fibers. Then there is a subset ![]() $\{\nu _1,\nu _2\}\subset \{1,2,3\}$ of cardinality
$\{\nu _1,\nu _2\}\subset \{1,2,3\}$ of cardinality ![]() $2$ such that
$2$ such that ![]() $A\cap \Lambda $ is a union of disjoint M-fibers in the
$A\cap \Lambda $ is a union of disjoint M-fibers in the ![]() $p_{\nu _1}$ and
$p_{\nu _1}$ and ![]() $p_{\nu _2}$ directions.
$p_{\nu _2}$ directions.
Proof. Fix A and ![]() $\Lambda $ as in the statement of the proposition. We will say that
$\Lambda $ as in the statement of the proposition. We will say that ![]() $\kappa :A\cap \Lambda \to \{1,2,3\}$ is an assignment function if
$\kappa :A\cap \Lambda \to \{1,2,3\}$ is an assignment function if ![]() $A\cap \Lambda $ can be written as
$A\cap \Lambda $ can be written as
 $$ \begin{align*} A\cap\Lambda=\bigcup_{a\in A\cap\Lambda} \left(a*F_{\kappa(a)}\right), \end{align*} $$
$$ \begin{align*} A\cap\Lambda=\bigcup_{a\in A\cap\Lambda} \left(a*F_{\kappa(a)}\right), \end{align*} $$where for any ![]() $a,a'\in A\cap \Lambda $, the fibers
$a,a'\in A\cap \Lambda $, the fibers ![]() $a*F_{\kappa (a)}$ and
$a*F_{\kappa (a)}$ and ![]() $a'*F_{\kappa (a')}$ are either identical or disjoint. Thus if
$a'*F_{\kappa (a')}$ are either identical or disjoint. Thus if ![]() $a'\in a*F_{\kappa (a)}$, then
$a'\in a*F_{\kappa (a)}$, then ![]() $\kappa (a')=\kappa (a)$. Note that
$\kappa (a')=\kappa (a)$. Note that ![]() $\kappa $ is not necessarily unique, since there exist sets that can be split into nonintersecting fibers in more than one way. We will use
$\kappa $ is not necessarily unique, since there exist sets that can be split into nonintersecting fibers in more than one way. We will use ![]() $\Xi $ to denote the set of all assignment functions for
$\Xi $ to denote the set of all assignment functions for ![]() $A\cap \Lambda $.
$A\cap \Lambda $.
It suffices to prove that any assignment function ![]() $\kappa \in \Xi $ may take at most two values. To prove this, assume for contradiction that there exists
$\kappa \in \Xi $ may take at most two values. To prove this, assume for contradiction that there exists ![]() $\kappa \in \Xi $ such that
$\kappa \in \Xi $ such that ![]() $\kappa (a_1)=1, \kappa (a_2)=2, \kappa (a_3)=3$ for some
$\kappa (a_1)=1, \kappa (a_2)=2, \kappa (a_3)=3$ for some ![]() $a_1,a_2,a_3\in A\cap \Lambda $. Then the fibers
$a_1,a_2,a_3\in A\cap \Lambda $. Then the fibers ![]() $a_1*F_1$,
$a_1*F_1$, ![]() $a_2*F_2$,
$a_2*F_2$, ![]() $a_3*F_3$ are contained in A and pairwise disjoint.
$a_3*F_3$ are contained in A and pairwise disjoint.
Let ![]() $x\in \Lambda $ be the point such that
$x\in \Lambda $ be the point such that
 $$ \begin{align*} \Pi\left(a_1,p_2^{n_2}\right)\cap \Pi\left(a_2,p_3^{n_3}\right)\cap \Pi\left(a_3,p_1^{n_1}\right) = \{x\}. \end{align*} $$
$$ \begin{align*} \Pi\left(a_1,p_2^{n_2}\right)\cap \Pi\left(a_2,p_3^{n_3}\right)\cap \Pi\left(a_3,p_1^{n_1}\right) = \{x\}. \end{align*} $$Then there are points ![]() $a^{\prime }_1\in a_1*F_1, a^{\prime }_2\in a_2*F_2, a^{\prime }_3\in a_3*F_3$ such that
$a^{\prime }_1\in a_1*F_1, a^{\prime }_2\in a_2*F_2, a^{\prime }_3\in a_3*F_3$ such that
Moreover, ![]() $\{D(M)\mid m\mid M\}\subset \mathrm {Div}(A\cap \Lambda )$, and hence disjointness condition (7.13) holds. By Lemma 7.10, we must have
$\{D(M)\mid m\mid M\}\subset \mathrm {Div}(A\cap \Lambda )$, and hence disjointness condition (7.13) holds. By Lemma 7.10, we must have ![]() $x\in A$. However, there is no permitted value for
$x\in A$. However, there is no permitted value for ![]() $\kappa (x)$, since
$\kappa (x)$, since ![]() $x*F_1$ intersects
$x*F_1$ intersects ![]() $a_2*F_2$,
$a_2*F_2$, ![]() $x*F_2$ intersects
$x*F_2$ intersects ![]() $a_3*F_3$ and
$a_3*F_3$ and ![]() $x*F_3$ intersects
$x*F_3$ intersects ![]() $a_1*F_1$. This contradicts the definition of
$a_1*F_1$. This contradicts the definition of ![]() $\kappa $.
$\kappa $.
For example, under the assumptions of Proposition 7.11, if ![]() $A\oplus B=\mathbb {Z}_M$ is a tiling, then
$A\oplus B=\mathbb {Z}_M$ is a tiling, then ![]() $A\cap \Lambda $ cannot consist of three nonintersecting fibers in different directions.
$A\cap \Lambda $ cannot consist of three nonintersecting fibers in different directions.

Figure 4 A ![]() $D(M)$-grid with disjoint M-fibers in all three directions.
$D(M)$-grid with disjoint M-fibers in all three directions.
Remark 7.12. Suppose that ![]() $\Phi _M\mid A$, where
$\Phi _M\mid A$, where  $M=p_1^{n_1}p_2^{n_2}p_3^{n_3}$. Let
$M=p_1^{n_1}p_2^{n_2}p_3^{n_3}$. Let ![]() $\Lambda $ be a
$\Lambda $ be a ![]() $D(M)$-grid such that
$D(M)$-grid such that ![]() $A\cap \Lambda \neq \emptyset $. As discussed in Section 5.2,
$A\cap \Lambda \neq \emptyset $. As discussed in Section 5.2, ![]() $A\cap \Lambda (X)$ can be written as
$A\cap \Lambda (X)$ can be written as
 $$ \begin{align} (A\cap\Lambda)(X)=\sum_{\nu\in\{1,2,3\}} Q_\nu(X) F_\nu(X), \end{align} $$
$$ \begin{align} (A\cap\Lambda)(X)=\sum_{\nu\in\{1,2,3\}} Q_\nu(X) F_\nu(X), \end{align} $$where ![]() $Q_1,Q_2,Q_3$ are polynomials with integer coefficients depending on both A and
$Q_1,Q_2,Q_3$ are polynomials with integer coefficients depending on both A and ![]() $\Lambda $. If, in addition,
$\Lambda $. If, in addition, ![]() $Q_1,Q_2,Q_3$ are polynomials with nonnegative coefficients, then
$Q_1,Q_2,Q_3$ are polynomials with nonnegative coefficients, then ![]() $A\cap \Lambda $ is a nonempty union of disjoint M-fibers. By Proposition 7.11, if
$A\cap \Lambda $ is a nonempty union of disjoint M-fibers. By Proposition 7.11, if ![]() $A\oplus B=\mathbb {Z}_M$ is a tiling, then
$A\oplus B=\mathbb {Z}_M$ is a tiling, then ![]() $A\cap \Lambda $ can be written in the form of equation (7.15) with at least one of
$A\cap \Lambda $ can be written in the form of equation (7.15) with at least one of ![]() $Q_1,Q_2,Q_3$ equal to
$Q_1,Q_2,Q_3$ equal to ![]() $0$.
$0$.
It is likely that some consistency conditions of this type occur more broadly in tiling sets. For example, in [Reference Łaba and Londner24, Theorem 9.1(IIa)], we prove a much more difficult and technical result of this type on a lower scale.
8 Fibers and cofibers
8.1 Fibers and fiber chains
Definition 8.1. Let ![]() $N\mid M$, and assume that
$N\mid M$, and assume that  $p_i^\delta \mid N$ for some
$p_i^\delta \mid N$ for some ![]() $\delta \geq 1$. Define
$\delta \geq 1$. Define
 $$ \begin{align} \Psi_{N/p_i^\delta}(X):= \Phi_{p_i}\left(X^{N/p_i^\delta}\right) = 1+X^{N/p_i^{\delta}}+ X^{2N/p_i^{\delta}} + \dotsb + X^{(p_i-1) N/p_i^{\delta}}. \end{align} $$
$$ \begin{align} \Psi_{N/p_i^\delta}(X):= \Phi_{p_i}\left(X^{N/p_i^\delta}\right) = 1+X^{N/p_i^{\delta}}+ X^{2N/p_i^{\delta}} + \dotsb + X^{(p_i-1) N/p_i^{\delta}}. \end{align} $$This is the same notation as in formula (5.6), but here we are using it for a different purpose. Specifically, we will use polynomials of the form (8.1) as building blocks for multiscale fibers and fiber chains. While  $\Psi _{N/p_i^\delta }$ depends on both
$\Psi _{N/p_i^\delta }$ depends on both  ${N/p_i^\delta }$ and
${N/p_i^\delta }$ and ![]() $p_i$, both numbers will always be clear from the context. We will also use the fact that
$p_i$, both numbers will always be clear from the context. We will also use the fact that
 $$ \begin{align} \Psi_{N/p_i^\delta}(X)= \frac{ X^{N/p_i^{\delta-1}}-1}{X^{N/p_i^{\delta}}-1} =\prod_{s\mid M: s\neq 1, p_i^{\nu-\delta+1}\parallel s} \Phi_s(X), \end{align} $$
$$ \begin{align} \Psi_{N/p_i^\delta}(X)= \frac{ X^{N/p_i^{\delta-1}}-1}{X^{N/p_i^{\delta}}-1} =\prod_{s\mid M: s\neq 1, p_i^{\nu-\delta+1}\parallel s} \Phi_s(X), \end{align} $$where ![]() $\nu \geq 1$ is the exponent such that
$\nu \geq 1$ is the exponent such that ![]() $p_i^\nu \parallel N$.
$p_i^\nu \parallel N$.
Definition 8.2 Fibers and fiber chains
Let ![]() $N\mid M$, and assume that
$N\mid M$, and assume that ![]() $p_i\mid N$.
$p_i\mid N$.
(i) A set
 $F_0\subset \mathbb {Z}_M$ is an N-fiber in the
$F_0\subset \mathbb {Z}_M$ is an N-fiber in the  $p_i$ direction if
$p_i$ direction if  $F_0 \bmod N$ has the mask polynomial (8.3)with fixed
$F_0 \bmod N$ has the mask polynomial (8.3)with fixed $$ \begin{align} F_0(X)\equiv c X^a \Psi_{N/p_i}(X) \bmod X^N-1, \end{align} $$
$$ \begin{align} F_0(X)\equiv c X^a \Psi_{N/p_i}(X) \bmod X^N-1, \end{align} $$ $c\in \mathbb {N}$ and
$c\in \mathbb {N}$ and  $a\in \mathbb {Z}_N$. Equivalently,
$a\in \mathbb {Z}_N$. Equivalently,  $F_0 \bmod N$ is a multiset in
$F_0 \bmod N$ is a multiset in  $\mathbb {Z}_N$ with weights If a fiber
$\mathbb {Z}_N$ with weights If a fiber $$ \begin{align*} w_{F_0}^N(x) = \begin{cases} c & \text{if }x\in \{ a, a+N/p_i, a+2N/p_i,\dotsc,a+(p_i-1) N/p_i\}, \\ 0 & \text{otherwise.}\\ \end{cases} \end{align*} $$
$$ \begin{align*} w_{F_0}^N(x) = \begin{cases} c & \text{if }x\in \{ a, a+N/p_i, a+2N/p_i,\dotsc,a+(p_i-1) N/p_i\}, \\ 0 & \text{otherwise.}\\ \end{cases} \end{align*} $$ $F_0$ has the form (8.3), we will refer to c as its multiplicity, and will say that the fiber is rooted at a or passes through a.
$F_0$ has the form (8.3), we will refer to c as its multiplicity, and will say that the fiber is rooted at a or passes through a.(ii) A set
 $A\subset \mathbb {Z}_M$ is N-fibered in the
$A\subset \mathbb {Z}_M$ is N-fibered in the  $p_i$ direction if it can be written as a union of disjoint N-fibers in the
$p_i$ direction if it can be written as a union of disjoint N-fibers in the  $p_i$ direction, all with the same multiplicity.
$p_i$ direction, all with the same multiplicity.(iii) Let
 $\mathcal {P}\subset \{1,2, \dotsc ,n_i\}$ be nonempty, where
$\mathcal {P}\subset \{1,2, \dotsc ,n_i\}$ be nonempty, where  $p_i^{n_i}\parallel M$. A set
$p_i^{n_i}\parallel M$. A set  $F\subset \mathbb {Z}_M$ is a
$F\subset \mathbb {Z}_M$ is a  $\mathcal {P}$-fiber chain in the
$\mathcal {P}$-fiber chain in the  $p_i$ direction if
$p_i$ direction if  $\lvert F\rvert = p_i^{\lvert \mathcal {P}\rvert }$ and F is N-fibered in the
$\lvert F\rvert = p_i^{\lvert \mathcal {P}\rvert }$ and F is N-fibered in the  $p_i$ direction for each
$p_i$ direction for each  $N=M/p_i^{\alpha -1}$, where
$N=M/p_i^{\alpha -1}$, where  $\alpha \in \mathcal {P}$. We will also use the convention that if
$\alpha \in \mathcal {P}$. We will also use the convention that if  $\mathcal {P}=\emptyset $, then a
$\mathcal {P}=\emptyset $, then a  $\mathcal {P}$-fiber chain in any direction is any singleton set
$\mathcal {P}$-fiber chain in any direction is any singleton set  $\{x\}$ with
$\{x\}$ with  $x\in \mathbb {Z}_M$.
$x\in \mathbb {Z}_M$.(iv) A set
 $A\subset \mathbb {Z}_M$ is
$A\subset \mathbb {Z}_M$ is  $\mathcal {P}$-fibered in the
$\mathcal {P}$-fibered in the  $p_i$ direction if it can be written as a union of disjoint
$p_i$ direction if it can be written as a union of disjoint  $\mathcal {P}$-fiber chains in the
$\mathcal {P}$-fiber chains in the  $p_i$ direction.
$p_i$ direction.
We list a few examples. Observe that although we will not use ![]() $\mathcal {P}$-fiber chains with multiplicities greater than
$\mathcal {P}$-fiber chains with multiplicities greater than ![]() $1$, Definition 8.2(iii) does require the concept of N-fibers with multiplicity.
$1$, Definition 8.2(iii) does require the concept of N-fibers with multiplicity.
• A
 $\{1\}$-fiber chain in the
$\{1\}$-fiber chain in the  $p_i$ direction is simply an M-fiber in that direction, and a
$p_i$ direction is simply an M-fiber in that direction, and a  $\{1\}$-fibered set in the
$\{1\}$-fibered set in the  $p_i$ direction with multiplicity
$p_i$ direction with multiplicity  $1$ is M-fibered in that direction, as defined in Section 2.3.
$1$ is M-fibered in that direction, as defined in Section 2.3.• A
 $\{2\}$-fiber chain in the
$\{2\}$-fiber chain in the  $p_i$ direction is a set
$p_i$ direction is a set  $F\subset \mathbb {Z}_M$ such that for some
$F\subset \mathbb {Z}_M$ such that for some  $a\in \mathbb {Z}_M$ we have
$a\in \mathbb {Z}_M$ we have  $F(x)\equiv X^a(1+X^{M/p_i^2}+X^{2M/p_i^2}+ \dotsb +X^{(p_i-1)M/p_i^2}) \bmod (X^{M/p_i}-1)$. Note that
$F(x)\equiv X^a(1+X^{M/p_i^2}+X^{2M/p_i^2}+ \dotsb +X^{(p_i-1)M/p_i^2}) \bmod (X^{M/p_i}-1)$. Note that  $\lvert F\rvert =p_i$.
$\lvert F\rvert =p_i$.• A
 $\{1,2\}$-fiber chain in the
$\{1,2\}$-fiber chain in the  $p_i$ direction is a set
$p_i$ direction is a set  $F\subset \mathbb {Z}_M$ such that for some
$F\subset \mathbb {Z}_M$ such that for some  $a\in \mathbb {Z}_M$ we have
$a\in \mathbb {Z}_M$ we have  $F(x)\equiv X^a(1+X^{M/p_i^2}+X^{2M/p_i^2}+ \dotsb +X^{\left (p_i^2-1\right )M/p_i^2}) \bmod (X^{M}-1)$. Note that
$F(x)\equiv X^a(1+X^{M/p_i^2}+X^{2M/p_i^2}+ \dotsb +X^{\left (p_i^2-1\right )M/p_i^2}) \bmod (X^{M}-1)$. Note that  $\lvert F\rvert =p_i^2$, F is M-fibered in the
$\lvert F\rvert =p_i^2$, F is M-fibered in the  $p_i$ direction with multiplicity
$p_i$ direction with multiplicity  $1$ and
$1$ and  $M/p_i$-fibered in the
$M/p_i$-fibered in the  $p_i$ direction with multiplicity
$p_i$ direction with multiplicity  $p_i$.
$p_i$.
Lemma 8.3 Properties of fibered sets
Assume that ![]() $A\subset \mathbb {Z}_M$ is
$A\subset \mathbb {Z}_M$ is ![]() $\mathcal {P}$-fibered in the
$\mathcal {P}$-fibered in the ![]() $p_i$ direction for some
$p_i$ direction for some ![]() $\mathcal {P}\subset \{1,2,\dotsc ,n_i\}$. Then the following hold:
$\mathcal {P}\subset \{1,2,\dotsc ,n_i\}$. Then the following hold:
(i) We have
(8.4)In particular, $$ \begin{align} \prod_{\alpha\in \mathcal{P}} \Psi_{M/p_i^{\alpha}}(X)\mid A(X). \end{align} $$
$$ \begin{align} \prod_{\alpha\in \mathcal{P}} \Psi_{M/p_i^{\alpha}}(X)\mid A(X). \end{align} $$ $\Phi _s(X)\mid A(X)$ for all
$\Phi _s(X)\mid A(X)$ for all  $s\mid M$,
$s\mid M$,  $s\neq 1$, such that
$s\neq 1$, such that  $s=p_i^{n_i-\alpha +1}s'$, where
$s=p_i^{n_i-\alpha +1}s'$, where  $\alpha \in \mathcal {P}$ and
$\alpha \in \mathcal {P}$ and  $(s',p_i)=1$.
$(s',p_i)=1$.(ii) We have
 $p_i^{\lvert \mathcal {P}\rvert } \mid \lvert A\rvert $. In particular, a
$p_i^{\lvert \mathcal {P}\rvert } \mid \lvert A\rvert $. In particular, a  $\mathcal {P}$-fiber chain F as in Definition 8.2(iii) is a minimal set that is
$\mathcal {P}$-fiber chain F as in Definition 8.2(iii) is a minimal set that is  $\mathcal {P}$-fibered in the
$\mathcal {P}$-fibered in the  $p_i$ direction.
$p_i$ direction.(iii)
 $\{M/p_i^{\alpha }: \alpha \in \mathcal {P} \}\subset \mathrm {Div}(A)$.
$\{M/p_i^{\alpha }: \alpha \in \mathcal {P} \}\subset \mathrm {Div}(A)$.(iv) Let
 $F\subset \mathbb {Z}_M$ be a
$F\subset \mathbb {Z}_M$ be a  $\mathcal {P}$-fiber chain with multiplicity
$\mathcal {P}$-fiber chain with multiplicity  $1$ in the
$1$ in the  $p_i$ direction. Translating F if necessary, we may assume that
$p_i$ direction. Translating F if necessary, we may assume that  $0\in F$. Let
$0\in F$. Let  $\gamma =\max \mathcal {P}$. Then
$\gamma =\max \mathcal {P}$. Then  $F\subset (M/p_i^\gamma )\mathbb {Z}_M\subset \ell _i(0)$, and F tiles
$F\subset (M/p_i^\gamma )\mathbb {Z}_M\subset \ell _i(0)$, and F tiles  $(M/p_i^\gamma )\mathbb {Z}_M\simeq \mathbb {Z}_{p_i^\gamma }$ with the standard tiling complement G, where (We use the convention that an empty product is equal to
$(M/p_i^\gamma )\mathbb {Z}_M\simeq \mathbb {Z}_{p_i^\gamma }$ with the standard tiling complement G, where (We use the convention that an empty product is equal to $$ \begin{align*} G(X)=\prod_{\tau: 1\leq\tau<\gamma, \tau\notin\mathcal{P}} \Psi_{M/p_i^{\tau}}(X). \end{align*} $$
$$ \begin{align*} G(X)=\prod_{\tau: 1\leq\tau<\gamma, \tau\notin\mathcal{P}} \Psi_{M/p_i^{\tau}}(X). \end{align*} $$ $1$.)
$1$.)
Proof. Part (i) follows directly from the definition, and (ii) follows from (i) since ![]() $\Phi _{M/p_i^\alpha }(1)=p_i$. For (iii), set
$\Phi _{M/p_i^\alpha }(1)=p_i$. For (iii), set ![]() $\alpha \in \mathcal {P}$, and let
$\alpha \in \mathcal {P}$, and let ![]() $a,a'\in A$ be elements that belong to the same
$a,a'\in A$ be elements that belong to the same  $M/p_i^{\alpha -1}$-fiber in the
$M/p_i^{\alpha -1}$-fiber in the ![]() $p_i$ direction, but not to the same
$p_i$ direction, but not to the same  $M/p_i^\beta $-fiber in the
$M/p_i^\beta $-fiber in the ![]() $p_i$ direction for any
$p_i$ direction for any ![]() $\beta <\alpha -1$. Then
$\beta <\alpha -1$. Then ![]() $(a-a',M)=M/p_i^\alpha $, as claimed.
$(a-a',M)=M/p_i^\alpha $, as claimed.
We now prove (iv). Assume that ![]() $0\in F$. Since
$0\in F$. Since  $\Psi _{M/p_i^\alpha }(X)=\Phi _{p_i^{\gamma -\alpha +1}}(X^{M/p_i^\gamma })$ for
$\Psi _{M/p_i^\alpha }(X)=\Phi _{p_i^{\gamma -\alpha +1}}(X^{M/p_i^\gamma })$ for ![]() $\alpha \leq \gamma $, by (i) we have
$\alpha \leq \gamma $, by (i) we have  $F(X)\equiv Q(X)\Psi (X^{M/p_i^\gamma }) \bmod (X^M-1)$, where
$F(X)\equiv Q(X)\Psi (X^{M/p_i^\gamma }) \bmod (X^M-1)$, where
 $$ \begin{align*} \Psi(X)=\prod_{\alpha\in \mathcal{P}} \Phi_{p_i^{\gamma-\alpha+1}}(X). \end{align*} $$
$$ \begin{align*} \Psi(X)=\prod_{\alpha\in \mathcal{P}} \Phi_{p_i^{\gamma-\alpha+1}}(X). \end{align*} $$Since ![]() $\Psi (1)=\prod _{\alpha \in \mathcal {P}}p_i = \lvert F\rvert $, we have
$\Psi (1)=\prod _{\alpha \in \mathcal {P}}p_i = \lvert F\rvert $, we have ![]() $Q(1)=1$. Splitting up the weighted multiset corresponding to
$Q(1)=1$. Splitting up the weighted multiset corresponding to ![]() $Q(X)$ into residue classes mod
$Q(X)$ into residue classes mod  $M/p_i^\gamma $, and using the fact that F is a set, we see that
$M/p_i^\gamma $, and using the fact that F is a set, we see that  $Q\in \mathcal {M}(\left (M/p_i^\gamma \right )\mathbb {Z}_M)$. Hence
$Q\in \mathcal {M}(\left (M/p_i^\gamma \right )\mathbb {Z}_M)$. Hence  $F\subset (M/p_i^\gamma )\mathbb {Z}_M$.
$F\subset (M/p_i^\gamma )\mathbb {Z}_M$.
Let  $F'=\{\frac {x}{M/p_i^\gamma }: x\in F\}$, so that
$F'=\{\frac {x}{M/p_i^\gamma }: x\in F\}$, so that  $F' \subset \mathbb {Z}_{p_i^\gamma }$ and
$F' \subset \mathbb {Z}_{p_i^\gamma }$ and ![]() $\Psi (X)\mid F'(X),$ with
$\Psi (X)\mid F'(X),$ with ![]() $\Psi (1)= \lvert p_i\rvert ^{\lvert \mathcal {P}\rvert } = \lvert F'\rvert $. This is the (T1) tiling condition for
$\Psi (1)= \lvert p_i\rvert ^{\lvert \mathcal {P}\rvert } = \lvert F'\rvert $. This is the (T1) tiling condition for ![]() $F'$. Hence
$F'$. Hence ![]() $F'$ tiles
$F'$ tiles  $\mathbb {Z}_{p_i^\gamma }$ with the standard tiling complement (see Remark 3.5). Rescaling back to
$\mathbb {Z}_{p_i^\gamma }$ with the standard tiling complement (see Remark 3.5). Rescaling back to ![]() $F\subset \mathbb {Z}_M$, we get (iv).
$F\subset \mathbb {Z}_M$, we get (iv).
8.2 Cofibers and cofibered structures
Given a tiling ![]() $A\oplus B=\mathbb {Z}_M$, we will be interested in the occurrences of ‘complementary’ fiber chains in A and B, in the following sense:
$A\oplus B=\mathbb {Z}_M$, we will be interested in the occurrences of ‘complementary’ fiber chains in A and B, in the following sense:
Definition 8.4 Cofibers
Set ![]() $A, B\subset \mathbb {Z}_M$, and fix
$A, B\subset \mathbb {Z}_M$, and fix ![]() $1\leq \gamma \leq n_i$. Let
$1\leq \gamma \leq n_i$. Let ![]() $\mathcal {P}_A, \mathcal {P}_B$ be two disjoint sets such that
$\mathcal {P}_A, \mathcal {P}_B$ be two disjoint sets such that
We say that ![]() $F\subset A,G\subset B$ are
$F\subset A,G\subset B$ are ![]() $(\mathcal {P}_A, \mathcal {P}_B)$-cofibers in the
$(\mathcal {P}_A, \mathcal {P}_B)$-cofibers in the ![]() $p_i$ direction if:
$p_i$ direction if:
• F is a
 $\mathcal {P}_A$-fiber chain in the
$\mathcal {P}_A$-fiber chain in the  $p_i$ direction and
$p_i$ direction and• G is a
 $\mathcal {P}_B$-fiber chain in the
$\mathcal {P}_B$-fiber chain in the  $p_i$ direction.
$p_i$ direction.
We will also refer to ![]() $(F,G)$ as a
$(F,G)$ as a ![]() $(\mathcal {P}_A, \mathcal {P}_B)$-cofiber pair.
$(\mathcal {P}_A, \mathcal {P}_B)$-cofiber pair.
Note that if ![]() $\gamma =1$, then one of the sets
$\gamma =1$, then one of the sets ![]() $\mathcal {P}_A$ and
$\mathcal {P}_A$ and ![]() $\mathcal {P}_B$ must be empty. If
$\mathcal {P}_B$ must be empty. If ![]() $\gamma =1$ and
$\gamma =1$ and ![]() $\mathcal {P}_A=\emptyset $, then F is a singleton and G is an M-fiber in the
$\mathcal {P}_A=\emptyset $, then F is a singleton and G is an M-fiber in the ![]() $p_i$ direction.
$p_i$ direction.
Our goal will be to find global cofibered structures, as we will describe. If ![]() $A\oplus B=\mathbb {Z}_M$ is a tiling pair, having a cofibered structure will often allow us to reduce proving (T2) for
$A\oplus B=\mathbb {Z}_M$ is a tiling pair, having a cofibered structure will often allow us to reduce proving (T2) for ![]() $(A,B)$ to proving it to an equivalent but simpler tiling pair. In order to allow for intermediate steps involving sets that are only partially fibered, we state the definition for arbitrary sets
$(A,B)$ to proving it to an equivalent but simpler tiling pair. In order to allow for intermediate steps involving sets that are only partially fibered, we state the definition for arbitrary sets ![]() $A,B\subset \mathbb {Z}_M$:
$A,B\subset \mathbb {Z}_M$:
Definition 8.5 Cofibered structure and cofibered sets
Set ![]() $A, B\subset \mathbb {Z}_M$, and fix
$A, B\subset \mathbb {Z}_M$, and fix ![]() $1\leq \gamma \leq n_i$. Let
$1\leq \gamma \leq n_i$. Let ![]() $\mathcal {P}_A, \mathcal {P}_B$ be two disjoint sets obeying condition (8.5).
$\mathcal {P}_A, \mathcal {P}_B$ be two disjoint sets obeying condition (8.5).
(i) We say that the pair
 $(A,B)$ has a
$(A,B)$ has a  $(\mathcal {P}_A, \mathcal {P}_B)$-cofibered structure in the
$(\mathcal {P}_A, \mathcal {P}_B)$-cofibered structure in the  $p_i$ direction if:
$p_i$ direction if:• B is
 $\mathcal {P}_B$-fibered in the
$\mathcal {P}_B$-fibered in the  $p_i$ direction and
$p_i$ direction and• A contains at least one ‘complementary’
 $\mathcal {P}_A$-fiber chain
$\mathcal {P}_A$-fiber chain  $F\subset A$ in the
$F\subset A$ in the  $p_i$ direction, which we will call a cofiber for this structure. We will say that F is rooted at
$p_i$ direction, which we will call a cofiber for this structure. We will say that F is rooted at  $a\in A$ if
$a\in A$ if  $a\in F$.
$a\in F$.
(ii) We say that the pair
 $(A,B)$ is
$(A,B)$ is  $(\mathcal {P}_A, \mathcal {P}_B)$-cofibered in the
$(\mathcal {P}_A, \mathcal {P}_B)$-cofibered in the  $p_i$ direction if:
$p_i$ direction if:• A is
 $\mathcal {P}_A$-fibered in the
$\mathcal {P}_A$-fibered in the  $p_i$ direction and
$p_i$ direction and• B is
 $\mathcal {P}_B$-fibered in the
$\mathcal {P}_B$-fibered in the  $p_i$ direction.
$p_i$ direction.
We emphasise that part (i) of the definition is not symmetric with respect to A and B. Our convention is that the second set in the pair must be fibered in its entirety. While a cofibered structure may have more than one cofiber in A, we do not require that the entire pair ![]() $(A,B)$ be cofibered. We will refer to the number
$(A,B)$ be cofibered. We will refer to the number ![]() $\gamma $ in Definitions 8.4 and 8.5 as the depth of, respectively, the cofiber pair or the cofibered structure.
$\gamma $ in Definitions 8.4 and 8.5 as the depth of, respectively, the cofiber pair or the cofibered structure.
If A and B satisfy Definition 8.5(i), then by Lemma 8.3,
 $$ \begin{align} \left\{M/p_i^{\alpha}: \alpha \in \mathcal{P}_A\right\}\subseteq\mathrm{Div}(A),\qquad \left\{M/p_i^{\beta}: \beta \in \mathcal{P}_B\right\}\subseteq \mathrm{Div}(B), \end{align} $$
$$ \begin{align} \left\{M/p_i^{\alpha}: \alpha \in \mathcal{P}_A\right\}\subseteq\mathrm{Div}(A),\qquad \left\{M/p_i^{\beta}: \beta \in \mathcal{P}_B\right\}\subseteq \mathrm{Div}(B), \end{align} $$ $$ \begin{align} \prod_{\beta\in\mathcal{P}_B} \Psi_{M/p_i^{\beta}}(X)\mid B(X), \end{align} $$
$$ \begin{align} \prod_{\beta\in\mathcal{P}_B} \Psi_{M/p_i^{\beta}}(X)\mid B(X), \end{align} $$and if a cofiber F is rooted at some ![]() $a\in A$, then
$a\in A$, then
 $$ \begin{align} X^a\prod_{\alpha\in \mathcal{P}_A} \Psi_{M/p_i^{\alpha}}(X) \mid F(X). \end{align} $$
$$ \begin{align} X^a\prod_{\alpha\in \mathcal{P}_A} \Psi_{M/p_i^{\alpha}}(X) \mid F(X). \end{align} $$Remark 8.6. Assume that ![]() $A, B\subset \mathbb {Z}_M$ satisfy
$A, B\subset \mathbb {Z}_M$ satisfy ![]() $\mathrm {Div}(A)\cap \mathrm {Div}(B)=\{M\}$, and fix
$\mathrm {Div}(A)\cap \mathrm {Div}(B)=\{M\}$, and fix ![]() $1\leq \gamma \leq n_i$. Let
$1\leq \gamma \leq n_i$. Let ![]() $\mathcal {P}_A, \mathcal {P}_B$ be two disjoint sets obeying condition (8.5). Assume that
$\mathcal {P}_A, \mathcal {P}_B$ be two disjoint sets obeying condition (8.5). Assume that
 $$ \begin{align} \left\{M/p_i^{\alpha}: \alpha \in \mathcal{P}_A\right\}\cap\mathrm{Div}(B)=\emptyset. \end{align} $$
$$ \begin{align} \left\{M/p_i^{\alpha}: \alpha \in \mathcal{P}_A\right\}\cap\mathrm{Div}(B)=\emptyset. \end{align} $$(In particular, if ![]() $A\oplus B=\mathbb {Z}_M$ and A contains a
$A\oplus B=\mathbb {Z}_M$ and A contains a ![]() $\mathcal {P}_A$-fiber chain in the
$\mathcal {P}_A$-fiber chain in the ![]() $p_i$ direction, then this equation holds by Lemma 8.3(iii) and divisor exclusion.) Then, in order to prove that B is
$p_i$ direction, then this equation holds by Lemma 8.3(iii) and divisor exclusion.) Then, in order to prove that B is ![]() $\mathcal {P}_B$-fibered in the
$\mathcal {P}_B$-fibered in the ![]() $p_i$ direction, it suffices to verify that every
$p_i$ direction, it suffices to verify that every ![]() $b\in B$ belongs to a
$b\in B$ belongs to a ![]() $\mathcal {P}_B$-fiber chain
$\mathcal {P}_B$-fiber chain ![]() $F(b)$ in the
$F(b)$ in the ![]() $p_i$ direction. Indeed, by Lemma 8.3 (iv), every
$p_i$ direction. Indeed, by Lemma 8.3 (iv), every ![]() $F(b)$ is a maximal subset of
$F(b)$ is a maximal subset of  $b*(M/p_i^\gamma )\mathbb {Z}_M$ such that
$b*(M/p_i^\gamma )\mathbb {Z}_M$ such that ![]() $\mathrm {Div}(F(b))\cap \{M/p_i^{\alpha }: \alpha \in \mathcal {P}_A\}=\emptyset $. Hence, under the given assumptions, any two fiber chains
$\mathrm {Div}(F(b))\cap \{M/p_i^{\alpha }: \alpha \in \mathcal {P}_A\}=\emptyset $. Hence, under the given assumptions, any two fiber chains ![]() $F(b)$ and
$F(b)$ and ![]() $F(b')$ with
$F(b')$ with ![]() $b,b'\in B$ must be either identical or disjoint.
$b,b'\in B$ must be either identical or disjoint.
8.3 Fiber shifting
Cofibered structures are important for two reasons. On one hand, they arise naturally from ![]() $1$-dimensional saturating spaces (see Lemma 8.10). On the other hand, with a cofibered structure in place, Lemma 8.7 allows us to shift the cofibers in A as indicated while maintaining both the tiling property and the (T2) status of A. Applying such shifts repeatedly, we are able to reduce many cases to simpler tilings where (T2) is easy to verify.
$1$-dimensional saturating spaces (see Lemma 8.10). On the other hand, with a cofibered structure in place, Lemma 8.7 allows us to shift the cofibers in A as indicated while maintaining both the tiling property and the (T2) status of A. Applying such shifts repeatedly, we are able to reduce many cases to simpler tilings where (T2) is easy to verify.
Lemma 8.7 Fiber-shifting lemma
Let ![]() $A\oplus B=\mathbb {Z}_M$. Assume that the pair
$A\oplus B=\mathbb {Z}_M$. Assume that the pair ![]() $(A,B)$ has a
$(A,B)$ has a ![]() $(\mathcal {P}_A, \mathcal {P}_B)$-cofibered structure, with a cofiber
$(\mathcal {P}_A, \mathcal {P}_B)$-cofibered structure, with a cofiber ![]() $F\subset A$. Let
$F\subset A$. Let ![]() $A'$ be the set obtained from A by shifting F by
$A'$ be the set obtained from A by shifting F by  $M/p_i^{\beta }$ for any
$M/p_i^{\beta }$ for any ![]() $\beta \in \mathcal {P}_B$. Then
$\beta \in \mathcal {P}_B$. Then ![]() $A'\oplus B=\mathbb {Z}_M$, and A is (T2)-equivalent to
$A'\oplus B=\mathbb {Z}_M$, and A is (T2)-equivalent to ![]() $A'$.
$A'$.
Proof. We have
 $$ \begin{align*} A'(X)=A(X)+(X^{kM/p_i^{\beta}}-1)F(X) \end{align*} $$
$$ \begin{align*} A'(X)=A(X)+(X^{kM/p_i^{\beta}}-1)F(X) \end{align*} $$for some k with ![]() $(k,p_i)=1$.
$(k,p_i)=1$.
We must prove that ![]() $\Phi _s(X)\mid A'(X)B(X)$ for all
$\Phi _s(X)\mid A'(X)B(X)$ for all ![]() $s\mid M, s\neq 1$. Fix such s, and write it as
$s\mid M, s\neq 1$. Fix such s, and write it as  $s=p_i^{n_i-\gamma }s'$, where
$s=p_i^{n_i-\gamma }s'$, where ![]() $(s,p_i)=1$. Consider three cases:
$(s,p_i)=1$. Consider three cases:
• If
 $\gamma \geq \beta $, then
$\gamma \geq \beta $, then  $\Phi _s(X)\mid (X^{kM/p_i^{\beta }}-1)$, and therefore it divides A if and only if it divides
$\Phi _s(X)\mid (X^{kM/p_i^{\beta }}-1)$, and therefore it divides A if and only if it divides  $A'$.
$A'$.• If
 $\gamma < \beta $ and
$\gamma < \beta $ and  $\gamma \in \mathcal {P}_B$, then
$\gamma \in \mathcal {P}_B$, then  $\Phi _s(X)\mid \Psi _{M/p_i^{\gamma }}(X) \mid B(X)$.
$\Phi _s(X)\mid \Psi _{M/p_i^{\gamma }}(X) \mid B(X)$.• If
 $\gamma < \beta $ and
$\gamma < \beta $ and  $\gamma \in \mathcal {P}_A$, then
$\gamma \in \mathcal {P}_A$, then  $\Phi _s(X)\mid \Psi _{M/p_i^{\gamma }}(X) \mid F(X)$, therefore
$\Phi _s(X)\mid \Psi _{M/p_i^{\gamma }}(X) \mid F(X)$, therefore  $\Phi _s$ divides A if and only if it divides
$\Phi _s$ divides A if and only if it divides  $A'$.
$A'$.
This implies the first part of the lemma.
Suppose furthermore that ![]() $\Phi _s$ is a (T2) cyclotomic polynomial of A, in the sense that
$\Phi _s$ is a (T2) cyclotomic polynomial of A, in the sense that ![]() $s=s_1\dotsm s_\tau $, where
$s=s_1\dotsm s_\tau $, where ![]() $s_1,\dotsc ,s_\tau $ are powers of distinct primes such that
$s_1,\dotsc ,s_\tau $ are powers of distinct primes such that ![]() $\Phi _{s_1}\dotsm \Phi _{s_\tau }\mid A$. In particular, we must have
$\Phi _{s_1}\dotsm \Phi _{s_\tau }\mid A$. In particular, we must have  $\Phi _{p_i^{n_i-\gamma }}\mid A$, and therefore
$\Phi _{p_i^{n_i-\gamma }}\mid A$, and therefore  $\Phi _{p_i^{n_i-\gamma }}\nmid B$. By the foregoing analysis applied to
$\Phi _{p_i^{n_i-\gamma }}\nmid B$. By the foregoing analysis applied to  $p_i^{n_i-\gamma }$ instead of s, we must have either
$p_i^{n_i-\gamma }$ instead of s, we must have either ![]() $\gamma \geq \beta $ or
$\gamma \geq \beta $ or ![]() $\gamma \in \mathcal {P}_A$. In both cases, we get that
$\gamma \in \mathcal {P}_A$. In both cases, we get that ![]() $\Phi _s$ divides A if and only if it divides
$\Phi _s$ divides A if and only if it divides ![]() $A'$, so that the (T2) property is preserved when we pass from A to
$A'$, so that the (T2) property is preserved when we pass from A to ![]() $A'$.
$A'$.
8.4 Fibers and  $1$-dimensional saturating spaces
$1$-dimensional saturating spaces
We now prove that ![]() $1$-dimensional saturating sets imply cofibered structures.
$1$-dimensional saturating sets imply cofibered structures.
Lemma 8.8. Assume that ![]() $A\oplus B=\mathbb {Z}_M$, and let
$A\oplus B=\mathbb {Z}_M$, and let ![]() $x,y\in \mathbb {Z}_M$.
$x,y\in \mathbb {Z}_M$.
(i) Let
 $1\leq \alpha ,\alpha '\leq n_i$, with
$1\leq \alpha ,\alpha '\leq n_i$, with  $\alpha \neq \alpha '$. Then In particular, if
$\alpha \neq \alpha '$. Then In particular, if $$ \begin{align*} \mathbb{A}_{M/p_i^{\alpha}} [x] \mathbb{B}_{M/p_i^{\alpha}} [y] \mathbb{A}_{M/p_i^{\alpha'}} [x] \mathbb{B}_{M/p_i^{\alpha'}} [y] =0. \end{align*} $$
$$ \begin{align*} \mathbb{A}_{M/p_i^{\alpha}} [x] \mathbb{B}_{M/p_i^{\alpha}} [y] \mathbb{A}_{M/p_i^{\alpha'}} [x] \mathbb{B}_{M/p_i^{\alpha'}} [y] =0. \end{align*} $$ $A_{x,y}\subset \ell _i(x)$, then the product
$A_{x,y}\subset \ell _i(x)$, then the product  $\langle \mathbb {A}[x],\mathbb {B}[y]\rangle $ is saturated by a single divisor.
$\langle \mathbb {A}[x],\mathbb {B}[y]\rangle $ is saturated by a single divisor.(ii) Suppose that
 $A_x\subset \ell _i(x)$. Then there exists an
$A_x\subset \ell _i(x)$. Then there exists an  $\alpha $ with
$\alpha $ with  $0\leq \alpha \leq n_i$ such that
$0\leq \alpha \leq n_i$ such that  $$ \begin{align*} \mathbb{A}_{M/p_i^{\alpha}} [x] \mathbb{B}_{M/p_i^{\alpha}} [b] = \phi\left(p_i^\alpha\right)\text{ for all }b\in B. \end{align*} $$
$$ \begin{align*} \mathbb{A}_{M/p_i^{\alpha}} [x] \mathbb{B}_{M/p_i^{\alpha}} [b] = \phi\left(p_i^\alpha\right)\text{ for all }b\in B. \end{align*} $$
Definition 8.9. Set ![]() $\mathcal {P}\subset \{1,2,\dotsc ,n_i\}$, and let
$\mathcal {P}\subset \{1,2,\dotsc ,n_i\}$, and let ![]() $F\subset \mathbb {Z}_M$ be a
$F\subset \mathbb {Z}_M$ be a ![]() $\mathcal {P}$-fiber chain in the
$\mathcal {P}$-fiber chain in the ![]() $p_i$ direction.
$p_i$ direction.
(i) An element
 $x\in \mathbb {Z}_M$ is at distance m from F if
$x\in \mathbb {Z}_M$ is at distance m from F if  $m\mid M$ is the maximal divisor such that
$m\mid M$ is the maximal divisor such that  $(z-x,M)=m$ for some
$(z-x,M)=m$ for some  $z\in F$.
$z\in F$.(ii) If
 $1\leq \delta \leq n_i$, we will write
$1\leq \delta \leq n_i$, we will write  $\mathcal {P}[\delta ]= \mathcal {P}\cap \{1,2,\dotsc ,\delta \}$.
$\mathcal {P}[\delta ]= \mathcal {P}\cap \{1,2,\dotsc ,\delta \}$.
If ![]() $x\in \mathbb {Z}_M$ and
$x\in \mathbb {Z}_M$ and ![]() $F\subset \mathbb {Z}_M$ is a
$F\subset \mathbb {Z}_M$ is a ![]() $\mathcal {P}$-fiber chain in the
$\mathcal {P}$-fiber chain in the ![]() $p_i$ direction, then for all
$p_i$ direction, then for all ![]() $z\in F$ we have
$z\in F$ we have  $(z-x,M)=m'p_i^{\alpha (z)}$, where
$(z-x,M)=m'p_i^{\alpha (z)}$, where ![]() $m'\mid (M/p_i^{n_i})$ is the same for all
$m'\mid (M/p_i^{n_i})$ is the same for all ![]() $z\in F$. In particular, the distance from x to F is well defined and is equal to
$z\in F$. In particular, the distance from x to F is well defined and is equal to  $m'p_i^{\max _{z\in F}\alpha (z)}$.
$m'p_i^{\max _{z\in F}\alpha (z)}$.
Lemma 8.10 The structure of  $1$-dimensional saturating spaces
$1$-dimensional saturating spaces
Assume that ![]() $A\oplus B =\mathbb {Z}_M$ is a tiling.
$A\oplus B =\mathbb {Z}_M$ is a tiling.
(i) Suppose that
 $ x, y\in \mathbb {Z}_M $ satisfy
$ x, y\in \mathbb {Z}_M $ satisfy  $x\notin A$ and (8.10)for some
$x\notin A$ and (8.10)for some $$ \begin{align} \mathbb{A}^M_{M/p_i^\gamma}[x]\mathbb{B}^M_{M/p_i^\gamma}[y]=\phi\left(p_i^\gamma\right) \end{align} $$
$$ \begin{align} \mathbb{A}^M_{M/p_i^\gamma}[x]\mathbb{B}^M_{M/p_i^\gamma}[y]=\phi\left(p_i^\gamma\right) \end{align} $$ $ 0<\gamma \leq n_i $. Then there exist two disjoint sets
$ 0<\gamma \leq n_i $. Then there exist two disjoint sets  $\mathcal {P}_A,\mathcal {P}_B $ with (8.11)
$\mathcal {P}_A,\mathcal {P}_B $ with (8.11) $$ \begin{align} \mathcal{P}_A\cup\mathcal{P}_B = \{1,\dotsc,\gamma-1\}, \end{align} $$(8.12)such that the following holds. Let
$$ \begin{align} \mathcal{P}_A\cup\mathcal{P}_B = \{1,\dotsc,\gamma-1\}, \end{align} $$(8.12)such that the following holds. Let $$ \begin{align} \left\{M/p_i^{\alpha}: \alpha \in \mathcal{P}_A\right\}\subseteq\mathrm{Div}(A),\qquad \left\{M/p_i^{\beta}: \beta \in \mathcal{P}_B\right\}\subseteq \mathrm{Div}(B), \end{align} $$
$$ \begin{align} \left\{M/p_i^{\alpha}: \alpha \in \mathcal{P}_A\right\}\subseteq\mathrm{Div}(A),\qquad \left\{M/p_i^{\beta}: \beta \in \mathcal{P}_B\right\}\subseteq \mathrm{Div}(B), \end{align} $$ $A_0\subset A_{x,y}$ be a maximal subset such that for all
$A_0\subset A_{x,y}$ be a maximal subset such that for all  $a,a'\in A_0$ with
$a,a'\in A_0$ with  $a\neq a'$ we have
$a\neq a'$ we have  $(a-a',M)=M/p_i^{\gamma }$, and let
$(a-a',M)=M/p_i^{\gamma }$, and let  $B_0$ be a similar subset of
$B_0$ be a similar subset of  $B_{y,x}$. Then one of the sets
$B_{y,x}$. Then one of the sets  $A_0$ and
$A_0$ and  $B_0$ has cardinality
$B_0$ has cardinality  $1$, the other has cardinality
$1$, the other has cardinality  $p_i-1$, and furthermore (8.13)where
$p_i-1$, and furthermore (8.13)where $$ \begin{align} A_{x,y}=\bigcup_{a\in A_0}F(a),\qquad B_{y,x}= \bigcup_{b\in B_0}G(b), \end{align} $$
$$ \begin{align} A_{x,y}=\bigcup_{a\in A_0}F(a),\qquad B_{y,x}= \bigcup_{b\in B_0}G(b), \end{align} $$ $F(a)$ is a
$F(a)$ is a  $\mathcal {P}_A$-fiber chain in the
$\mathcal {P}_A$-fiber chain in the  $p_i$ direction rooted at a and
$p_i$ direction rooted at a and  $G(b)$ is a
$G(b)$ is a  $\mathcal {P}_B$-fiber chain in the
$\mathcal {P}_B$-fiber chain in the  $p_i$ direction rooted at b.
$p_i$ direction rooted at b.(ii) Suppose that
 $x\in \mathbb {Z}_M\setminus A$ and
$x\in \mathbb {Z}_M\setminus A$ and  $A_x\subset \ell _i(x)$, with (8.14)where
$A_x\subset \ell _i(x)$, with (8.14)where $$ \begin{align} \mathbb{A}^M_{M/p_i^\gamma}[x]\mathbb{B}^M_{M/p_i^\gamma}[b]=\phi\left(p_i^\gamma\right) \text{ for all }b\in B, \end{align} $$
$$ \begin{align} \mathbb{A}^M_{M/p_i^\gamma}[x]\mathbb{B}^M_{M/p_i^\gamma}[b]=\phi\left(p_i^\gamma\right) \text{ for all }b\in B, \end{align} $$ $ 0<\gamma \leq n_i $ (as follows from Lemma 8.8(ii)). Then the pair
$ 0<\gamma \leq n_i $ (as follows from Lemma 8.8(ii)). Then the pair  $(A,B)$ has a
$(A,B)$ has a  $(\mathcal {P}_A,\mathcal {P}_B\cup \{\gamma \})$-cofibered structure, with
$(\mathcal {P}_A,\mathcal {P}_B\cup \{\gamma \})$-cofibered structure, with  $A_{x}$ as a
$A_{x}$ as a  $\mathcal {P}_A$-cofiber at a distance
$\mathcal {P}_A$-cofiber at a distance  $M/p_i^\gamma $ from x.
$M/p_i^\gamma $ from x.
Proof. We first prove (i). Define ![]() $A_0$ and
$A_0$ and ![]() $B_0$ as before. Since
$B_0$ as before. Since  $A_0\subset x*(M/p_i^{\gamma })\mathbb {Z}_M$ and each element of
$A_0\subset x*(M/p_i^{\gamma })\mathbb {Z}_M$ and each element of ![]() $A_0\cup \{x\}$ is contained in a different residue class mod
$A_0\cup \{x\}$ is contained in a different residue class mod  $M/p_i^{\gamma }$, we have
$M/p_i^{\gamma }$, we have ![]() $\lvert A_0\rvert \leq p_i-1$, and similarly for
$\lvert A_0\rvert \leq p_i-1$, and similarly for ![]() $B_0$. By divisor exclusion, at most one of these sets has cardinality greater than
$B_0$. By divisor exclusion, at most one of these sets has cardinality greater than ![]() $1$.
$1$.
Next, let  $A_1\subset x*(M/p_i^{\gamma })\mathbb {Z}_M$ be a maximal subset of
$A_1\subset x*(M/p_i^{\gamma })\mathbb {Z}_M$ be a maximal subset of ![]() $A_{x,y}$ such that
$A_{x,y}$ such that
 $$ \begin{align*} \forall a,a'\in A_1 \text{ with } a\neq a', \text{ we have }(a-a',M)=M/p_i^{\gamma-1}, \end{align*} $$
$$ \begin{align*} \forall a,a'\in A_1 \text{ with } a\neq a', \text{ we have }(a-a',M)=M/p_i^{\gamma-1}, \end{align*} $$and define ![]() $B_1$ similarly. Then
$B_1$ similarly. Then ![]() $\lvert A_1\rvert \leq p_i\lvert A_0\rvert $, since for each
$\lvert A_1\rvert \leq p_i\lvert A_0\rvert $, since for each ![]() $a\in A_1$ there must be a ‘parent’
$a\in A_1$ there must be a ‘parent’ ![]() $a_0\in A_0$ with
$a_0\in A_0$ with  $M/p_i^{\gamma -1}\mid a-a_0$, and each
$M/p_i^{\gamma -1}\mid a-a_0$, and each ![]() $a_0$ can have at most
$a_0$ can have at most ![]() $p_i$ such ‘children’
$p_i$ such ‘children’ ![]() $a\in A_1$ (we allow
$a\in A_1$ (we allow ![]() $a=a_0$, so that
$a=a_0$, so that ![]() $A_0\subset A_1$). Similarly,
$A_0\subset A_1$). Similarly, ![]() $\lvert B_1\rvert \leq p_i\lvert B_0\rvert $. Moreover, if
$\lvert B_1\rvert \leq p_i\lvert B_0\rvert $. Moreover, if ![]() $\lvert A_1\rvert>\lvert A_0\rvert $, then we must have
$\lvert A_1\rvert>\lvert A_0\rvert $, then we must have  $M/p_i^{\gamma -1}\in \mathrm {Div}(A)$, and similarly for B, so that at least one of
$M/p_i^{\gamma -1}\in \mathrm {Div}(A)$, and similarly for B, so that at least one of ![]() $\lvert A_1\rvert =\lvert A_0\rvert $ and
$\lvert A_1\rvert =\lvert A_0\rvert $ and ![]() $\lvert B_1\rvert =\lvert B_0\rvert $ must hold. If
$\lvert B_1\rvert =\lvert B_0\rvert $ must hold. If ![]() $\lvert A_1\rvert>\lvert A_0\rvert $, we place
$\lvert A_1\rvert>\lvert A_0\rvert $, we place ![]() $\gamma -1$ in
$\gamma -1$ in ![]() $\mathcal {P}_A$; otherwise we place it in
$\mathcal {P}_A$; otherwise we place it in ![]() $\mathcal {P}_B$.
$\mathcal {P}_B$.
We continue by induction, constructing a sequence of sets
and two disjoint sets ![]() $\mathcal {P}_A,\mathcal {P}_B $ obeying condition (8.11), so that for each
$\mathcal {P}_A,\mathcal {P}_B $ obeying condition (8.11), so that for each ![]() $l=1,2,\dotsc , \gamma -1$:
$l=1,2,\dotsc , \gamma -1$:
• if
 $l\in \mathcal {P}_A$, then
$l\in \mathcal {P}_A$, then  $\left \lvert A_{\gamma -l+1}\right \rvert \leq p_i\left \lvert A_{\gamma -l}\right \rvert $,
$\left \lvert A_{\gamma -l+1}\right \rvert \leq p_i\left \lvert A_{\gamma -l}\right \rvert $,  $\left \lvert B_{\gamma -l+1}\right \rvert =\left \lvert B_{\gamma -l}\right \rvert $ and
$\left \lvert B_{\gamma -l+1}\right \rvert =\left \lvert B_{\gamma -l}\right \rvert $ and  $M/p_i^{\gamma -l}\not \in \mathrm {Div}(B)$; and
$M/p_i^{\gamma -l}\not \in \mathrm {Div}(B)$; and• if
 $l\in \mathcal {P}_B$, then the same holds with A and B interchanged.
$l\in \mathcal {P}_B$, then the same holds with A and B interchanged.
It follows that
 $$ \begin{align*} \mathbb{A}^M_{M/p_i^\gamma}[x]\mathbb{B}^M_{M/p_i^\gamma}[y] \leq \lvert A_0\rvert\lvert B_0\rvert p_i^{\lvert\mathcal{P}_A\rvert} p_i^{\lvert\mathcal{P}_B\rvert} \leq (p_i-1) p_i^{\gamma -1} = \phi\left(p_i^\gamma\right). \end{align*} $$
$$ \begin{align*} \mathbb{A}^M_{M/p_i^\gamma}[x]\mathbb{B}^M_{M/p_i^\gamma}[y] \leq \lvert A_0\rvert\lvert B_0\rvert p_i^{\lvert\mathcal{P}_A\rvert} p_i^{\lvert\mathcal{P}_B\rvert} \leq (p_i-1) p_i^{\gamma -1} = \phi\left(p_i^\gamma\right). \end{align*} $$Furthermore, for the equality to hold, one of the sets ![]() $A_0,B_0$ must have cardinality
$A_0,B_0$ must have cardinality ![]() $p_i-1$; for each
$p_i-1$; for each ![]() $a\in A_0$, the set
$a\in A_0$, the set  $F(a):=\{a\in A_{x,y}: M/p_i^{\gamma -1}\mid a-a_0\}$ must be a full
$F(a):=\{a\in A_{x,y}: M/p_i^{\gamma -1}\mid a-a_0\}$ must be a full ![]() $\mathcal {P}_A$-fiber chain in the
$\mathcal {P}_A$-fiber chain in the ![]() $p_i$ direction rooted at a; and a similar statement must hold for B. This yields the structure described in part (i).
$p_i$ direction rooted at a; and a similar statement must hold for B. This yields the structure described in part (i).
For part (ii), assume that condition (8.14) holds, and let ![]() $B_0(b)$ be the set from formula (8.12) with
$B_0(b)$ be the set from formula (8.12) with ![]() $y=b$ for each
$y=b$ for each ![]() $b\in B$. Since
$b\in B$. Since  $M/p_i^\gamma \in \mathrm {Div}(B)$, we must have
$M/p_i^\gamma \in \mathrm {Div}(B)$, we must have ![]() $\lvert A_0\rvert =1$ and
$\lvert A_0\rvert =1$ and ![]() $\lvert B_0(b)\rvert =p_i-1$. Fix
$\lvert B_0(b)\rvert =p_i-1$. Fix ![]() $b\in B$, so that
$b\in B$, so that
 $$ \begin{align*} B_{b,x}= \bigcup_{b'\in B_0(b)}G(b'). \end{align*} $$
$$ \begin{align*} B_{b,x}= \bigcup_{b'\in B_0(b)}G(b'). \end{align*} $$Set ![]() $b'\in B_0(b)$, and apply part (i) of the lemma with
$b'\in B_0(b)$, and apply part (i) of the lemma with ![]() $y=b'$. Since
$y=b'$. Since ![]() $b\in B_{b',x}$, there is a
$b\in B_{b',x}$, there is a ![]() $\mathcal {P}_B$-fiber chain
$\mathcal {P}_B$-fiber chain ![]() $G(b)\subset B$ rooted at b, so that
$G(b)\subset B$ rooted at b, so that
 $$ \begin{align*} B_{b',x}= G(b)\cup \bigcup_{b''\in B_0(b),b''\neq b'}G(b''). \end{align*} $$
$$ \begin{align*} B_{b',x}= G(b)\cup \bigcup_{b''\in B_0(b),b''\neq b'}G(b''). \end{align*} $$Thus ![]() $\bigcup _{b''\in B_0(b)\cup \{b\}}G(b'')$ is a
$\bigcup _{b''\in B_0(b)\cup \{b\}}G(b'')$ is a ![]() $(\mathcal {P}_B\cup \{\gamma \})$-fiber chain in B, rooted at b. Applying this argument to all
$(\mathcal {P}_B\cup \{\gamma \})$-fiber chain in B, rooted at b. Applying this argument to all ![]() $b\in B$, and using Remark 8.6, we get the cofibered structure as indicated.
$b\in B$, and using Remark 8.6, we get the cofibered structure as indicated.
The following special case will be used frequently in [Reference Łaba and Londner24]:
Corollary 8.11. Assume that ![]() $A\oplus B =\mathbb {Z}_M$ is a tiling. Suppose that
$A\oplus B =\mathbb {Z}_M$ is a tiling. Suppose that ![]() $x\in \mathbb {Z}_M\setminus A$,
$x\in \mathbb {Z}_M\setminus A$, ![]() $b\in B$,
$b\in B$, ![]() $M/p_i\in \mathrm {Div}(A)$ and
$M/p_i\in \mathrm {Div}(A)$ and
 $$ \begin{align} \mathbb{A}^M_{M/p_i^2}[x]\mathbb{B}^M_{M/p_i^2}[b]=\phi\left(p_i^2\right). \end{align} $$
$$ \begin{align} \mathbb{A}^M_{M/p_i^2}[x]\mathbb{B}^M_{M/p_i^2}[b]=\phi\left(p_i^2\right). \end{align} $$Then there exists a ![]() $(\{1\},\{2\})$-cofiber pair
$(\{1\},\{2\})$-cofiber pair ![]() $(F,G)$ such that
$(F,G)$ such that ![]() $F\subset A$ is at distance
$F\subset A$ is at distance  $M/p_i^2$ from x,
$M/p_i^2$ from x, ![]() $G\subset B$ is rooted at b and
$G\subset B$ is rooted at b and
 $$ \begin{align} \mathbb{A}^M_{M/p_i^2}[x\mid F]\mathbb{B}^M_{M/p_i^2}[b \mid G]=\phi\left(p_i^2\right). \end{align} $$
$$ \begin{align} \mathbb{A}^M_{M/p_i^2}[x\mid F]\mathbb{B}^M_{M/p_i^2}[b \mid G]=\phi\left(p_i^2\right). \end{align} $$In particular, if ![]() $M/p_i\in \mathrm {Div}(A)$ and
$M/p_i\in \mathrm {Div}(A)$ and ![]() $A_x\subset \ell _i(x)$ with
$A_x\subset \ell _i(x)$ with  $M/p_i^2$ as the contributing divisor (compare Lemma 8.8(ii)), then the pair
$M/p_i^2$ as the contributing divisor (compare Lemma 8.8(ii)), then the pair ![]() $(A,B)$ has a
$(A,B)$ has a ![]() $(\{1\},\{2\})$-cofibered structure.
$(\{1\},\{2\})$-cofibered structure.
For simplicity, when M is fixed, we will write ‘![]() $(1,2)$-cofiber pair’ instead of ‘
$(1,2)$-cofiber pair’ instead of ‘![]() $(\{1\},\{2\})$-cofiber pair’, and similarly for cofibered structures.
$(\{1\},\{2\})$-cofiber pair’, and similarly for cofibered structures.
8.5 Examples and applications
Let ![]() $M=p_1^{n_1}\dotsm p_K^{n_K}$ with
$M=p_1^{n_1}\dotsm p_K^{n_K}$ with ![]() $K\geq 3$ and
$K\geq 3$ and ![]() $p_1,\dotsc ,p_K\geq 3$. Assume that
$p_1,\dotsc ,p_K\geq 3$. Assume that ![]() $A\oplus B=\mathbb {Z}_M$ and
$A\oplus B=\mathbb {Z}_M$ and ![]() $\lvert A\rvert =p_1\dotsm p_K$. Let also
$\lvert A\rvert =p_1\dotsm p_K$. Let also ![]() $\Lambda $ be a fixed
$\Lambda $ be a fixed ![]() $D(M)$-grid, and assume that
$D(M)$-grid, and assume that ![]() $0\in A\cap \Lambda $.
$0\in A\cap \Lambda $.
Example 8.12. By Lemma 7.10, we cannot have ![]() $\Lambda \setminus A=\{x\}$ for a single point
$\Lambda \setminus A=\{x\}$ for a single point ![]() $x\in \Lambda $. Similarly, we cannot have
$x\in \Lambda $. Similarly, we cannot have ![]() $A\cap \Lambda =A_0$ if
$A\cap \Lambda =A_0$ if ![]() $A_0$ is obtained from
$A_0$ is obtained from ![]() $\Lambda $ by deleting a few more points in an ‘unstructured’ way so that the assumptions of Lemma 7.10 still apply.
$\Lambda $ by deleting a few more points in an ‘unstructured’ way so that the assumptions of Lemma 7.10 still apply.
Suppose, however, that ![]() $A_0=\Lambda \setminus (x*F_i)$ for some
$A_0=\Lambda \setminus (x*F_i)$ for some ![]() $x\in \Lambda $ and
$x\in \Lambda $ and ![]() $i\in \{1,\dotsc ,K\}$. Then Lemma 7.10 is no longer applicable, and indeed, it is possible to have
$i\in \{1,\dotsc ,K\}$. Then Lemma 7.10 is no longer applicable, and indeed, it is possible to have ![]() $A\cap \Lambda =A_0$. However, as we now show, this determines the structure of the entire set A, and in particular, both A and B satisfy (T2).
$A\cap \Lambda =A_0$. However, as we now show, this determines the structure of the entire set A, and in particular, both A and B satisfy (T2).
Indeed, we have ![]() $\mathbb {A}_{M/p_j}[x]\geq 2$ for all
$\mathbb {A}_{M/p_j}[x]\geq 2$ for all ![]() $j\neq i$. It follows by inclusion (7.9) that
$j\neq i$. It follows by inclusion (7.9) that ![]() $A_x\subset \ell _i(x)$. By Proposition 8.10, the pair
$A_x\subset \ell _i(x)$. By Proposition 8.10, the pair ![]() $(A,B)$ has a
$(A,B)$ has a ![]() $(\mathcal {P}_A,\mathcal {P}_B)$-cofibered structure of depth
$(\mathcal {P}_A,\mathcal {P}_B)$-cofibered structure of depth ![]() $\gamma \geq 2$, with
$\gamma \geq 2$, with ![]() $1\in \mathcal {P}_A$ since
$1\in \mathcal {P}_A$ since ![]() $M/p_i\in \mathrm {Div}(A)$. In particular, A must contain an M-fiber in the
$M/p_i\in \mathrm {Div}(A)$. In particular, A must contain an M-fiber in the ![]() $p_i$ direction at distance
$p_i$ direction at distance  $M/p_i^\gamma $ from x. By Lemma 8.7, we can shift that fiber to x, proving that A is (T2)-equivalent to
$M/p_i^\gamma $ from x. By Lemma 8.7, we can shift that fiber to x, proving that A is (T2)-equivalent to ![]() $\Lambda $. Thus
$\Lambda $. Thus ![]() $A^\flat =\Lambda $, and Corollary 3.8 implies (T2) for both A and B.
$A^\flat =\Lambda $, and Corollary 3.8 implies (T2) for both A and B.
We note that the same argument still applies if ![]() $A\cap \Lambda $ has several fibers missing (possibly in different directions). This is the case in, for example, Szabó-type examples in [Reference Lagarias and Szabó25, Reference Szabó43].
$A\cap \Lambda $ has several fibers missing (possibly in different directions). This is the case in, for example, Szabó-type examples in [Reference Lagarias and Szabó25, Reference Szabó43].
Example 8.13. We now consider a more difficult example where saturating sets are not as obvious. Let  $M=p_i^{2}p_j^{2}p_k^{2}$ with
$M=p_i^{2}p_j^{2}p_k^{2}$ with ![]() $p_i,p_j,p_k\geq 3$, and assume that
$p_i,p_j,p_k\geq 3$, and assume that ![]() $\lvert A\rvert =p_ip_jp_k$ tiles
$\lvert A\rvert =p_ip_jp_k$ tiles ![]() $\mathbb {Z}_M$. Suppose that there exists an element
$\mathbb {Z}_M$. Suppose that there exists an element ![]() $x\in \Lambda \setminus A$ such that
$x\in \Lambda \setminus A$ such that
 $$ \begin{align} \mathbb{A}_{M/p_i}[x]=\phi(p_i), \qquad \mathbb{A}_{M/p_jp_k}[x]=\phi\left(p_jp_k\right) \end{align} $$
$$ \begin{align} \mathbb{A}_{M/p_i}[x]=\phi(p_i), \qquad \mathbb{A}_{M/p_jp_k}[x]=\phi\left(p_jp_k\right) \end{align} $$and ![]() $\mathbb {A}_m[x]=0$ for all
$\mathbb {A}_m[x]=0$ for all ![]() $m\in \{D(M)\mid m\mid M\}\setminus \{M/p_i,M/p_jp_k\} $. In the terminology of [Reference Łaba and Londner24], this is a
$m\in \{D(M)\mid m\mid M\}\setminus \{M/p_i,M/p_jp_k\} $. In the terminology of [Reference Łaba and Londner24], this is a ![]() $p_i$-full plane structure. We prove in [Reference Łaba and Londner24, Section 7] that for a broader class of tilings including this situation, we have
$p_i$-full plane structure. We prove in [Reference Łaba and Londner24, Section 7] that for a broader class of tilings including this situation, we have ![]() $A^\flat =\Lambda $ and the tiling
$A^\flat =\Lambda $ and the tiling ![]() $A\oplus B=\mathbb {Z}_M$ is (T2)-equivalent to
$A\oplus B=\mathbb {Z}_M$ is (T2)-equivalent to ![]() $\Lambda \oplus B=\mathbb {Z}_M$ via fiber shifts. By Corollary 3.8, both A and B satisfy (T2). For expository purposes, we restrict our attention here to this specific structure.
$\Lambda \oplus B=\mathbb {Z}_M$ via fiber shifts. By Corollary 3.8, both A and B satisfy (T2). For expository purposes, we restrict our attention here to this specific structure.
Consider the saturating set ![]() $A_x$, with x as before. This time, geometric restrictions alone are not sufficient to confine
$A_x$, with x as before. This time, geometric restrictions alone are not sufficient to confine ![]() $A_x$ to a single line through x. Nonetheless, with an additional argument we have the following lemma:
$A_x$ to a single line through x. Nonetheless, with an additional argument we have the following lemma:
Lemma 8.14. Under the assumptions of Example 8.13, we have either ![]() $A_x\subset \ell _j(x)$ or
$A_x\subset \ell _j(x)$ or ![]() $A_x\subset \ell _k(x)$.
$A_x\subset \ell _k(x)$.
Proof. By inclusion (7.9), we have
Set ![]() $b\in B$. Suppose that
$b\in B$. Suppose that ![]() $A_{x,b}\cap \ell _j(x)$ is nonempty. Since
$A_{x,b}\cap \ell _j(x)$ is nonempty. Since ![]() $M/p_j\in \mathrm {Div}(A)$, we must have
$M/p_j\in \mathrm {Div}(A)$, we must have
 $$ \begin{align} \mathbb{A}_{M/p_j^2}[x]\mathbb{B}_{M/p_j^2}[b]>0. \end{align} $$
$$ \begin{align} \mathbb{A}_{M/p_j^2}[x]\mathbb{B}_{M/p_j^2}[b]>0. \end{align} $$If we also had ![]() $A_{x,b}\cap \ell _k(x)\neq \emptyset $ for the same b, that would imply that
$A_{x,b}\cap \ell _k(x)\neq \emptyset $ for the same b, that would imply that
 $$ \begin{align} \mathbb{A}_{M/p_k^2}[x]\mathbb{B}_{M/p_k^2}[b]>0; \end{align} $$
$$ \begin{align} \mathbb{A}_{M/p_k^2}[x]\mathbb{B}_{M/p_k^2}[b]>0; \end{align} $$however, having inequalities (8.19) and (8.20) at the same time would contradict Lemma 7.9. Therefore we must have either ![]() $A_{x,b}\subset \ell _j(x)$ or
$A_{x,b}\subset \ell _j(x)$ or ![]() $A_{x,b}\subset \ell _k(x)$. Notice that in the former case we have
$A_{x,b}\subset \ell _k(x)$. Notice that in the former case we have
 $$ \begin{align} \mathbb{A}_{M/p_j^2}[x]\mathbb{B}_{M/p_j^2}[b]=\phi(p_j^2). \end{align} $$
$$ \begin{align} \mathbb{A}_{M/p_j^2}[x]\mathbb{B}_{M/p_j^2}[b]=\phi(p_j^2). \end{align} $$Since ![]() $M/p_j\in \mathrm {Div}(A)$, this can only happen if
$M/p_j\in \mathrm {Div}(A)$, this can only happen if
 $$ \begin{align} \mathbb{A}_{M/p_j^2}[x]=p_j \text{ and } \mathbb{B}_{M/p_j^2}[b]=\phi(p_j). \end{align} $$
$$ \begin{align} \mathbb{A}_{M/p_j^2}[x]=p_j \text{ and } \mathbb{B}_{M/p_j^2}[b]=\phi(p_j). \end{align} $$In other words, the pair ![]() $(A\cap \ell _j(x), B\cap \ell _j(b))$ contains a
$(A\cap \ell _j(x), B\cap \ell _j(b))$ contains a ![]() $(1,2)$-cofiber pair in the
$(1,2)$-cofiber pair in the ![]() $p_j$ direction. If
$p_j$ direction. If ![]() $A_{x,b}\subset \ell _k(x)$, equations (8.21) and (8.22) hold with j replaced by k.
$A_{x,b}\subset \ell _k(x)$, equations (8.21) and (8.22) hold with j replaced by k.

Figure 5 A ![]() $p_i$-full plane structure on a
$p_i$-full plane structure on a ![]() $D(M)$-grid.
$D(M)$-grid.
We claim that either ![]() $A_x\subset \ell _j(x)$ or
$A_x\subset \ell _j(x)$ or ![]() $A_x\subset \ell _k(x)$. Indeed, assume for contradiction that there exist
$A_x\subset \ell _k(x)$. Indeed, assume for contradiction that there exist ![]() $b_j,b_k\in B$ such that
$b_j,b_k\in B$ such that ![]() $A_{x,b_j}\subset \ell _j(x)$ and
$A_{x,b_j}\subset \ell _j(x)$ and ![]() $A_{x,b}\subset \ell _k(x)$. It follows from equation (8.22) that
$A_{x,b}\subset \ell _k(x)$. It follows from equation (8.22) that
 $$ \begin{align*} \left\lvert A\cap\Pi\left(x,p_i^{n_i}\right)\right\rvert&\geq \mathbb{A}_{M/p_j^2}[x]+\mathbb{A}_{M/p_k^2}[x]+\mathbb{A}_{M/p_jp_k}[x] \\ &=p_j+p_k+\left(p_j-1\right)(p_k-1)\\ &=p_jp_k+1. \end{align*} $$
$$ \begin{align*} \left\lvert A\cap\Pi\left(x,p_i^{n_i}\right)\right\rvert&\geq \mathbb{A}_{M/p_j^2}[x]+\mathbb{A}_{M/p_k^2}[x]+\mathbb{A}_{M/p_jp_k}[x] \\ &=p_j+p_k+\left(p_j-1\right)(p_k-1)\\ &=p_jp_k+1. \end{align*} $$This, however, contradicts Lemma 2.3.
Assume, without loss of generality, that ![]() $A_x\subset \ell _j(x)$. By Corollary 8.11, the pair
$A_x\subset \ell _j(x)$. By Corollary 8.11, the pair ![]() $(A,B)$ has a
$(A,B)$ has a ![]() $(1,2)$-cofibered structure in the
$(1,2)$-cofibered structure in the ![]() $p_j$ direction, with a cofiber in A at distance
$p_j$ direction, with a cofiber in A at distance  $M/p_j^2$ from x. By Lemma 8.7, we may shift the cofiber to x. Let
$M/p_j^2$ from x. By Lemma 8.7, we may shift the cofiber to x. Let ![]() $A'$ be the set thus obtained, so that
$A'$ be the set thus obtained, so that ![]() $A'\cap \Lambda $ contains all points of
$A'\cap \Lambda $ contains all points of ![]() $A\cap \Lambda $ plus, additionally, the fiber
$A\cap \Lambda $ plus, additionally, the fiber ![]() $x*F_j\subset A'$. Moreover,
$x*F_j\subset A'$. Moreover, ![]() $A'$ is (T2)-equivalent to A, and
$A'$ is (T2)-equivalent to A, and ![]() $A'\oplus B=\mathbb {Z}_M$.
$A'\oplus B=\mathbb {Z}_M$.
In this example, we do not get (T2)-equivalence to a standard set right away. Instead, the new set ![]() $A'$ contains a structure we call a
$A'$ contains a structure we call a ![]() $p_j$-corner [Reference Łaba and Londner24], consisting of two nonintersecting M-fibers in the
$p_j$-corner [Reference Łaba and Londner24], consisting of two nonintersecting M-fibers in the ![]() $p_i$ and
$p_i$ and ![]() $p_k$ directions in
$p_k$ directions in ![]() $\Lambda $. We then have to work further with that structure to prove that, ultimately,
$\Lambda $. We then have to work further with that structure to prove that, ultimately, ![]() $A'$ (therefore A) is (T2)-equivalent to
$A'$ (therefore A) is (T2)-equivalent to ![]() $\Lambda $.
$\Lambda $.
9 Conjectures and open questions
9.1 Tiling reductions
We first consider the question of whether proving properties such as (T2) or, more generally, proving structure and classification results for tilings, could be accomplished by inductive arguments involving reduction to tilings of smaller groups.
Let ![]() $A\oplus B=\mathbb {Z}_M$ be a tiling, and assume for convenience that
$A\oplus B=\mathbb {Z}_M$ be a tiling, and assume for convenience that ![]() $0\in A\cap B$. If M has at most two distinct prime factors, then Sands’ theorem [Reference Sands37] states that at least one of A, B must be contained in
$0\in A\cap B$. If M has at most two distinct prime factors, then Sands’ theorem [Reference Sands37] states that at least one of A, B must be contained in ![]() $p\mathbb {Z}_M$ for some prime
$p\mathbb {Z}_M$ for some prime ![]() $p\mid M$. Thus we can always use Theorem 6.1 to decompose such a tiling into tilings of residue classes, with at least one of the sets A and B tiling
$p\mid M$. Thus we can always use Theorem 6.1 to decompose such a tiling into tilings of residue classes, with at least one of the sets A and B tiling ![]() $p\mathbb {Z}_M$. This was the route taken in [Reference Coven and Meyerowitz2].
$p\mathbb {Z}_M$. This was the route taken in [Reference Coven and Meyerowitz2].
Suppose now that  $M=\prod _{i=1}^K p_i^{n_i}$, where
$M=\prod _{i=1}^K p_i^{n_i}$, where ![]() $p_i$ are distinct primes and
$p_i$ are distinct primes and ![]() $K\geq 3$. Sands’ theorem no longer holds in that setting, with counterexamples given by Szabó [Reference Szabó43] (see also [Reference Lagarias and Szabó25]). However, it is conceivable that other inductive arguments, not based on Theorem 6.1, may still apply. For example, the following question is open:
$K\geq 3$. Sands’ theorem no longer holds in that setting, with counterexamples given by Szabó [Reference Szabó43] (see also [Reference Lagarias and Szabó25]). However, it is conceivable that other inductive arguments, not based on Theorem 6.1, may still apply. For example, the following question is open:
Question 1. Let ![]() $A\oplus B=\mathbb {Z}_M$ with
$A\oplus B=\mathbb {Z}_M$ with  $M=\prod _{i=1}^K p_i^{n_i}$.
$M=\prod _{i=1}^K p_i^{n_i}$.
(i) (Strong version) Suppose that
 $\Phi _{p_i^{n_i}}\mid A$ for some
$\Phi _{p_i^{n_i}}\mid A$ for some  $i\in \{1,2,\dotsc ,K\}$. Is it always true that, in the notation of Theorem 6.5, we have
$i\in \{1,2,\dotsc ,K\}$. Is it always true that, in the notation of Theorem 6.5, we have  $A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$ for every translate
$A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$ for every translate  $A'$ of A?
$A'$ of A?(ii) (Weak version) Must there always exist some
 $i\in \{1,2,\dotsc ,K\}$ such that either
$i\in \{1,2,\dotsc ,K\}$ such that either  $A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$ for every translate
$A^{\prime }_{p_i}\oplus B=\mathbb {Z}_{M/p_i}$ for every translate  $A'$ of A, or
$A'$ of A, or  $A\oplus B^{\prime }_{p_i}=\mathbb {Z}_{M/p_i}$ for every translate
$A\oplus B^{\prime }_{p_i}=\mathbb {Z}_{M/p_i}$ for every translate  $B'$ of B?
$B'$ of B?
We do not know of any counterexamples to this. Szabó’s examples [Reference Szabó43] satisfy the conditions of Theorem 6.5, as do all tilings of period  $M=p_1^2p_2^2p_3^2$, where
$M=p_1^2p_2^2p_3^2$, where ![]() $p_1,p_2,p_3$ are all odd [Reference Łaba and Londner24].
$p_1,p_2,p_3$ are all odd [Reference Łaba and Londner24].
Assume that  $\Phi _{p_i^{n_i}}\mid A$ for some
$\Phi _{p_i^{n_i}}\mid A$ for some ![]() $i\in \{1,2,\dotsc ,K\}$. By Proposition 3.4, property (T2) for B is equivalent to
$i\in \{1,2,\dotsc ,K\}$. By Proposition 3.4, property (T2) for B is equivalent to ![]() $A^\flat \oplus B=\mathbb {Z}_M$, where
$A^\flat \oplus B=\mathbb {Z}_M$, where ![]() $A^\flat $ is the corresponding standard tiling complement. Heuristically, the slab reduction could be thought of as going part of the way in that direction, with the original tile A replaced by a new tile S which keeps some of the structure of A but, additionally, is periodic in the
$A^\flat $ is the corresponding standard tiling complement. Heuristically, the slab reduction could be thought of as going part of the way in that direction, with the original tile A replaced by a new tile S which keeps some of the structure of A but, additionally, is periodic in the ![]() $p_i$ direction. On the other hand, even if we assume a priori that both A and B satisfy (T2), this does not appear to imply the slab reduction in any obvious formal way. We do not know whether it is always possible to start with the original tiling and reach
$p_i$ direction. On the other hand, even if we assume a priori that both A and B satisfy (T2), this does not appear to imply the slab reduction in any obvious formal way. We do not know whether it is always possible to start with the original tiling and reach ![]() $A^\flat \oplus B=\mathbb {Z}_M$ via a sequence of slab reductions or other similar steps. While it does follow from [Reference Łaba and Londner24] that all tilings of odd period
$A^\flat \oplus B=\mathbb {Z}_M$ via a sequence of slab reductions or other similar steps. While it does follow from [Reference Łaba and Londner24] that all tilings of odd period  $M=p_1^2p_2^2p_3^2$ satisfy the conditions of Theorem 6.5, this is obtained a posteriori as a consequence of our classification of all such tilings, with (T2) and the classification results obtained by other means in some cases.
$M=p_1^2p_2^2p_3^2$ satisfy the conditions of Theorem 6.5, this is obtained a posteriori as a consequence of our classification of all such tilings, with (T2) and the classification results obtained by other means in some cases.
It is worthwhile to describe Szabó-type examples in more detail. (For the purpose of this paper, we use a modification of Szabó’s original construction in [Reference Szabó43], which was set in a different abelian group but was nonetheless based on the same idea. See also the examples in [Reference Lagarias and Szabó25] and [Reference Dutkay and Kraus4].) We start with the standard tiling ![]() $A^\flat \oplus B^\flat =\mathbb {Z}_M$, where
$A^\flat \oplus B^\flat =\mathbb {Z}_M$, where  $M=p_1^2p_2^2p_3^2$,
$M=p_1^2p_2^2p_3^2$, ![]() $A^\flat $ is the standard tiling set with
$A^\flat $ is the standard tiling set with  $\Phi _{p_i^2}\mid A$ for all
$\Phi _{p_i^2}\mid A$ for all ![]() $i\in \{1,2,3\}$ and
$i\in \{1,2,3\}$ and ![]() $B^\flat $ is the standard tiling set with
$B^\flat $ is the standard tiling set with ![]() $\Phi _{p_i}\mid B$ for all
$\Phi _{p_i}\mid B$ for all ![]() $i\in \{1,2,3\}$. We then use fiber shifts (Lemma 8.7) to modify
$i\in \{1,2,3\}$. We then use fiber shifts (Lemma 8.7) to modify ![]() $A^\flat $ so that for each i, one M-fiber in
$A^\flat $ so that for each i, one M-fiber in ![]() $A^\flat $ in the
$A^\flat $ in the ![]() $p_i$ direction is shifted by a distance
$p_i$ direction is shifted by a distance  $M/p_i^2$. For
$M/p_i^2$. For ![]() $K=3$, the M-fibers in all three directions can be selected so that all three shifts can be performed independently without destroying the tiling property. This produces a new tiling
$K=3$, the M-fibers in all three directions can be selected so that all three shifts can be performed independently without destroying the tiling property. This produces a new tiling ![]() $A \oplus B^\flat =\mathbb {Z}_M$ in which neither A nor
$A \oplus B^\flat =\mathbb {Z}_M$ in which neither A nor ![]() $B^\flat $ is contained in a proper subgroup of
$B^\flat $ is contained in a proper subgroup of ![]() $\mathbb {Z}_M$.
$\mathbb {Z}_M$.
Noting that the pair ![]() $(A,B^\flat )$ in this construction has a
$(A,B^\flat )$ in this construction has a ![]() $(1,2)$-cofibered structure in all three directions, one might ask whether one of A or B must in fact be contained in a proper subgroup if no such obstructions are present. This motivates the following question:
$(1,2)$-cofibered structure in all three directions, one might ask whether one of A or B must in fact be contained in a proper subgroup if no such obstructions are present. This motivates the following question:
Question 2. Let ![]() $A\oplus B=\mathbb {Z}_M$ with
$A\oplus B=\mathbb {Z}_M$ with  $M=\prod _{i=1}^K p_i^{n_i}$. Suppose that
$M=\prod _{i=1}^K p_i^{n_i}$. Suppose that  $\Phi _{p_i^{n_i}}\mid A$ for some
$\Phi _{p_i^{n_i}}\mid A$ for some ![]() $i\in \{1,2,\dotsc ,K\}$. Is it always true that at least one of the following must hold?
$i\in \{1,2,\dotsc ,K\}$. Is it always true that at least one of the following must hold?
(i) (Subgroup tiling)
 $A\subset \mathbb {Z}_{M/p_i}$.
$A\subset \mathbb {Z}_{M/p_i}$.(ii) (Obstruction) There exists an element
 $x\in \mathbb {Z}_M\setminus A$ such that
$x\in \mathbb {Z}_M\setminus A$ such that  $A_x\subset \ell _i(x)$. Furthermore, the pair
$A_x\subset \ell _i(x)$. Furthermore, the pair  $(A,B)$ has a
$(A,B)$ has a  $(\mathcal {P}_A,\mathcal {P}_B)$-cofibered structure of depth at least
$(\mathcal {P}_A,\mathcal {P}_B)$-cofibered structure of depth at least  $2$, with
$2$, with  $1\in \mathcal {P}_A$.
$1\in \mathcal {P}_A$.
It is possible that, at least for ![]() $K\geq 4$, more complicated obstructions may occur that cannot be reduced to
$K\geq 4$, more complicated obstructions may occur that cannot be reduced to ![]() $1$-dimensional saturating spaces. However, the results of [Reference Łaba and Londner24] show that the answer is affirmative if
$1$-dimensional saturating spaces. However, the results of [Reference Łaba and Londner24] show that the answer is affirmative if  $M=p_1^2p_2^2p_3^2$. It seems reasonable to conjecture the following:
$M=p_1^2p_2^2p_3^2$. It seems reasonable to conjecture the following:
Conjecture 9.1. The answers to Questions 1 (both versions) and 2 are affirmative when M has at most three distinct prime factors.
Proposition 3.4 also relates the (T2) property to divisor sets, in the sense that B satisfies (T2) if and only if its divisor set ![]() $\mathrm {Div}(B)$ is disjoint from
$\mathrm {Div}(B)$ is disjoint from ![]() $\mathrm {Div}(A^\flat )$. The equivalence between Theorem 6.5(ii) and (iii) establishes a more granular result in this direction, by connecting a smaller family of differences in A to the corresponding family of cyclotomic polynomials. Specifically, if we write
$\mathrm {Div}(A^\flat )$. The equivalence between Theorem 6.5(ii) and (iii) establishes a more granular result in this direction, by connecting a smaller family of differences in A to the corresponding family of cyclotomic polynomials. Specifically, if we write ![]() $S_i:=\{m:p_i^{n_i}\mid m\mid M\}$ for a fixed
$S_i:=\{m:p_i^{n_i}\mid m\mid M\}$ for a fixed ![]() $i\in \{1,\dotsc ,K\}$, then Theorem 6.5 establishes a fundamental connection between the set of differences
$i\in \{1,\dotsc ,K\}$, then Theorem 6.5 establishes a fundamental connection between the set of differences ![]() $m\in \mathrm {Div}(A)\cap S_i$ and the collection of all cyclotomic polynomials
$m\in \mathrm {Div}(A)\cap S_i$ and the collection of all cyclotomic polynomials ![]() $\Phi _d$ dividing A, for
$\Phi _d$ dividing A, for ![]() $d\in S_i$. It would be interesting to know whether such relationships exist on the level of individual differences and cyclotomic polynomials. As an extreme example of a hypothetical result of this type, we state the following:
$d\in S_i$. It would be interesting to know whether such relationships exist on the level of individual differences and cyclotomic polynomials. As an extreme example of a hypothetical result of this type, we state the following:
Conjecture 9.2. If  $\Phi _{p_i^{n_i}}\mid A$, then
$\Phi _{p_i^{n_i}}\mid A$, then ![]() $M/p_i\notin \mathrm {Div}(B)$.
$M/p_i\notin \mathrm {Div}(B)$.
This conjecture can be stated purely in terms of differences, since  $\Phi _{p_i^{n_i}}\mid A$ if and only if
$\Phi _{p_i^{n_i}}\mid A$ if and only if ![]() $M/p_i\in \mathrm {Div}(A^\flat )$. It is obviously necessary in order for (T2) to hold, though not sufficient. Absent a proof of (T2) in its full generality, this might be an interesting direction to explore.
$M/p_i\in \mathrm {Div}(A^\flat )$. It is obviously necessary in order for (T2) to hold, though not sufficient. Absent a proof of (T2) in its full generality, this might be an interesting direction to explore.
Our saturating-set techniques provide partial support for the conjecture, as follows. Suppose that ![]() $M/p_i\in \mathrm {Div}(B)$, with
$M/p_i\in \mathrm {Div}(B)$, with ![]() $(b-b',M)=M/p_i$ for some
$(b-b',M)=M/p_i$ for some ![]() $b,b'\in B$. Suppose further that Conjecture 9.2 is true. Then
$b,b'\in B$. Suppose further that Conjecture 9.2 is true. Then  $\Phi _{p_i^{n_i}}\nmid A$, so that
$\Phi _{p_i^{n_i}}\nmid A$, so that  $\Phi _{p_i^{n_i}}\mid B$. In particular,
$\Phi _{p_i^{n_i}}\mid B$. In particular,
 $$ \begin{align*} \left\lvert B\cap \Pi\left(y,p_i^{n_i}\right)\right\rvert= \frac{1}{p_i} \left\lvert B\cap \Pi\left(b,p_i^{n_i-1}\right)\right\rvert \end{align*} $$
$$ \begin{align*} \left\lvert B\cap \Pi\left(y,p_i^{n_i}\right)\right\rvert= \frac{1}{p_i} \left\lvert B\cap \Pi\left(b,p_i^{n_i-1}\right)\right\rvert \end{align*} $$for every ![]() $y\in \mathbb {Z}_M$ with
$y\in \mathbb {Z}_M$ with ![]() $(y-b,M)=M/p_i$. We do not know how to prove this, but we can prove the weaker statement that
$(y-b,M)=M/p_i$. We do not know how to prove this, but we can prove the weaker statement that ![]() $B\cap \Pi (y,p_i^{n_i})\neq \emptyset $ for each such y. Indeed, if
$B\cap \Pi (y,p_i^{n_i})\neq \emptyset $ for each such y. Indeed, if ![]() $y\in B$, this is obvious. If, on the other hand,
$y\in B$, this is obvious. If, on the other hand, ![]() $y\not \in B$, then by inclusion (7.9) we have
$y\not \in B$, then by inclusion (7.9) we have ![]() $B_y\subset \Pi (y,p_i^{n_i})$, and in particular
$B_y\subset \Pi (y,p_i^{n_i})$, and in particular ![]() $B\cap \Pi (y,p_i^{n_i})$ is nonempty.
$B\cap \Pi (y,p_i^{n_i})$ is nonempty.
We note that fibering plays a significant role in all our tiling arguments. For instance, if A is M-fibered in some direction, this is sufficient to apply slab reduction (see Remark 6.6). At the other extreme, if ![]() $\Phi _M\mid A$ but A fails to be M-fibered on some
$\Phi _M\mid A$ but A fails to be M-fibered on some ![]() $D(M)$-grid, our strategy in [Reference Łaba and Londner24] is to identify and use cofibered structures, which in particular implies fibering in B on a lower scale. Motivated by this, we conjecture the following:
$D(M)$-grid, our strategy in [Reference Łaba and Londner24] is to identify and use cofibered structures, which in particular implies fibering in B on a lower scale. Motivated by this, we conjecture the following:
Conjecture 9.3. For every i there exists ![]() $1\leq \alpha _i < n_i$ such that either A or B is
$1\leq \alpha _i < n_i$ such that either A or B is ![]() $M/p_i^{\alpha _i}$-fibered in the
$M/p_i^{\alpha _i}$-fibered in the ![]() $p_i$ direction. In particular, if M has three prime factors,
$p_i$ direction. In particular, if M has three prime factors, ![]() $\Phi _M\mid A$ and there exists a
$\Phi _M\mid A$ and there exists a ![]() $D(M)$-grid
$D(M)$-grid ![]() $\Lambda $ such that
$\Lambda $ such that ![]() $A\cap \Lambda $ is not fibered in any direction, then B is fibered in all directions on some scale. (This happens, for example, in Szabó’s examples.)
$A\cap \Lambda $ is not fibered in any direction, then B is fibered in all directions on some scale. (This happens, for example, in Szabó’s examples.)
9.2 Saturating sets
We have seen in Lemma 8.10 and Corollary 8.11 that if ![]() $A_x\subset \ell _i(x)$ for some
$A_x\subset \ell _i(x)$ for some ![]() $i\in \{1,\dotsc ,K\}$ and
$i\in \{1,\dotsc ,K\}$ and ![]() $x\in \mathbb {Z}\setminus A$, this implies a cofibered structure in
$x\in \mathbb {Z}\setminus A$, this implies a cofibered structure in ![]() $(A,B)$. By Lemma 8.7, this allows us to shift M-fibers in A in the given direction. We use this in [Reference Łaba and Londner24] to reduce
$(A,B)$. By Lemma 8.7, this allows us to shift M-fibers in A in the given direction. We use this in [Reference Łaba and Londner24] to reduce ![]() $A\oplus B=\mathbb {Z}_M$ to (T2)-equivalent tilings
$A\oplus B=\mathbb {Z}_M$ to (T2)-equivalent tilings ![]() $A'\oplus B=\mathbb {Z}_M$, where
$A'\oplus B=\mathbb {Z}_M$, where ![]() $A'$ has additional regularity properties. It would therefore be interesting to either find a structure theorem (an analogue of Lemma 8.10) for saturating sets contained in higher-dimensional subspaces or, alternatively, to find a systematic way of adding geometric constraints on saturating sets until we find a cofibered structure.
$A'$ has additional regularity properties. It would therefore be interesting to either find a structure theorem (an analogue of Lemma 8.10) for saturating sets contained in higher-dimensional subspaces or, alternatively, to find a systematic way of adding geometric constraints on saturating sets until we find a cofibered structure.
In all examples where we have been able to determine saturating sets, we found that they enjoy pleasant ‘splitting’ properties. For example, suppose that ![]() $(x-a,M)=M/p_i$ for some
$(x-a,M)=M/p_i$ for some ![]() $a\in A$ and
$a\in A$ and ![]() $i\in \{1,\dotsc ,K\}$. By inclusion (7.9), we have
$i\in \{1,\dotsc ,K\}$. By inclusion (7.9), we have
However, what actually tends to happen is that either ![]() $A_x\subset \Pi (x,p_i^{n_i})$ or
$A_x\subset \Pi (x,p_i^{n_i})$ or ![]() $A_x\subset \Pi (a,p_i^{n_i})$. For instance, if
$A_x\subset \Pi (a,p_i^{n_i})$. For instance, if ![]() $\mathbb {A}_{M/p_i}[a]>0$, then
$\mathbb {A}_{M/p_i}[a]>0$, then ![]() $\mathbb {A}_{M/p_i}[x]\geq 2$ and
$\mathbb {A}_{M/p_i}[x]\geq 2$ and
If, however, ![]() $\mathbb {B}_{M/p_i}[b]>0$, then
$\mathbb {B}_{M/p_i}[b]>0$, then
For an example of a less-obvious situation where this happens, see, for example, [Reference Łaba and Londner24, Lemma 9.18].
Similarly, suppose that ![]() $K=3$ and set
$K=3$ and set ![]() $x\in \mathbb {Z}_M$. Assume that there are two elements
$x\in \mathbb {Z}_M$. Assume that there are two elements ![]() $a_i,a_j\in A$ such that
$a_i,a_j\in A$ such that ![]() $(x-a_i,M)=M/p_i$ and
$(x-a_i,M)=M/p_i$ and ![]() $(x-a_j,M)=M/p_j$, with
$(x-a_j,M)=M/p_j$, with ![]() $i,j\in \{1,2,3\}$ distinct. Then, by formula (7.9) again,
$i,j\in \{1,2,3\}$ distinct. Then, by formula (7.9) again,
where ![]() $x_{ij}\in \mathbb {Z}_M$ is the unique point such that
$x_{ij}\in \mathbb {Z}_M$ is the unique point such that ![]() $(x_{ij}-a_i,M)=M/p_j$ and
$(x_{ij}-a_i,M)=M/p_j$ and ![]() $(x_{ij}-a_j,M)=M/p_i$. However, in all tiling examples that we have worked out,
$(x_{ij}-a_j,M)=M/p_i$. However, in all tiling examples that we have worked out, ![]() $A_x$ is in fact contained in just one of these lines. An example of this type of situation is provided by [Reference Łaba and Londner24, Lemma 4.6]. See also Lemma 8.14 for a different example where the initial geometric constraints restrict the saturating set to a union of two lines (inclusion 8.18), but then additional arguments show that only one of these lines may participate.
$A_x$ is in fact contained in just one of these lines. An example of this type of situation is provided by [Reference Łaba and Londner24, Lemma 4.6]. See also Lemma 8.14 for a different example where the initial geometric constraints restrict the saturating set to a union of two lines (inclusion 8.18), but then additional arguments show that only one of these lines may participate.
Returning to the ‘two planes’ situation as in inclusion (9.1), we can in fact say a little bit more. By inclusion (9.1), we have for any ![]() $b\in B$,
$b\in B$,
 $$ \begin{align*} 1=\sum_{p_i^{n_i}\mid m}\frac{1}{\phi(M/m)}\left(\mathbb{A}_m[x]\mathbb{B}_m[b]+\mathbb{A}_{m/p_i}[x]\mathbb{B}_{m/p_i}[b]\right). \end{align*} $$
$$ \begin{align*} 1=\sum_{p_i^{n_i}\mid m}\frac{1}{\phi(M/m)}\left(\mathbb{A}_m[x]\mathbb{B}_m[b]+\mathbb{A}_{m/p_i}[x]\mathbb{B}_{m/p_i}[b]\right). \end{align*} $$Suppose that ![]() $\mathbb {B}_m[b]$ and
$\mathbb {B}_m[b]$ and ![]() $\mathbb {B}_{m/p_i}[b]$ are both nonzero for some m with
$\mathbb {B}_{m/p_i}[b]$ are both nonzero for some m with ![]() $p_i^{n_i}\mid m\mid M$. If there were an
$p_i^{n_i}\mid m\mid M$. If there were an ![]() $a'\in A$ with
$a'\in A$ with ![]() $(x-a',M)\in \{m,m/p_i\}$, then we would also have
$(x-a',M)\in \{m,m/p_i\}$, then we would also have ![]() $(a-a',M)\in \{m,m/p_i\}$, contradicting divisor exclusion. Moreover, if
$(a-a',M)\in \{m,m/p_i\}$, contradicting divisor exclusion. Moreover, if ![]() $\mathbb {B}_{m/p_i}[b]\neq 0$, then any
$\mathbb {B}_{m/p_i}[b]\neq 0$, then any ![]() $a'\in A$ with
$a'\in A$ with ![]() $(x-a',M)\in \{m,m/p_i\}$ must lie in the plane
$(x-a',M)\in \{m,m/p_i\}$ must lie in the plane ![]() $\Pi (a,p_i^{n_i})$. Hence
$\Pi (a,p_i^{n_i})$. Hence
 $$ \begin{align} 1=\sum_{p_i^{n_i}\mid m}\frac{1}{\phi(M/m)}\left(\delta_m\mathbb{A}_m[x]\mathbb{B}_m[b] +(1-\delta_m)\mathbb{A}_{m}[a]\mathbb{B}_{m/p_i}[b]\right), \end{align} $$
$$ \begin{align} 1=\sum_{p_i^{n_i}\mid m}\frac{1}{\phi(M/m)}\left(\delta_m\mathbb{A}_m[x]\mathbb{B}_m[b] +(1-\delta_m)\mathbb{A}_{m}[a]\mathbb{B}_{m/p_i}[b]\right), \end{align} $$where ![]() $\delta _m\in \{0,1\}$ for all
$\delta _m\in \{0,1\}$ for all ![]() $p_i^{n_i}\mid m$.
$p_i^{n_i}\mid m$.
It appears reasonable to conjecture the following:
Conjecture 9.4. Let ![]() $A\oplus B=\mathbb {Z}_M$ be a tiling, and assume that
$A\oplus B=\mathbb {Z}_M$ be a tiling, and assume that ![]() $(x-a,M)=M/p_i$ for some
$(x-a,M)=M/p_i$ for some ![]() $a\in A$,
$a\in A$, ![]() $x\in \mathbb {Z}_M\setminus A$ and
$x\in \mathbb {Z}_M\setminus A$ and ![]() $i\in \{1,\dotsc ,K\}$. Then either
$i\in \{1,\dotsc ,K\}$. Then either ![]() $A_x\subset \Pi (x,p_i^{n_i})$ or
$A_x\subset \Pi (x,p_i^{n_i})$ or ![]() $A_x\subset \Pi (a,p_i^{n_i})$. Furthermore, either
$A_x\subset \Pi (a,p_i^{n_i})$. Furthermore, either ![]() $\delta _m=1$ for all m or
$\delta _m=1$ for all m or ![]() $\delta _m=0$ for all m, depending only on the choice of
$\delta _m=0$ for all m, depending only on the choice of ![]() $a\in A$ and
$a\in A$ and ![]() $b\in B$.
$b\in B$.
A similar reasoning, with only slightly more effort, applies to ![]() $A_{x,y}$ and
$A_{x,y}$ and ![]() $B_{y,x}$ as in formula (7.12) with
$B_{y,x}$ as in formula (7.12) with ![]() $x\in \mathbb {Z}_M\setminus A$ and
$x\in \mathbb {Z}_M\setminus A$ and ![]() $y\in \mathbb {Z}_M\setminus B$.
$y\in \mathbb {Z}_M\setminus B$.
9.3 Subspace bounds
The special case of Lemma 2.3 with ![]() $K=3$ and
$K=3$ and ![]() $\alpha _i=0$ is a simple but very effective tool in [Reference Łaba and Londner24]. It would be useful to have similar bounds for lower-dimensional subspaces, for example lines in the three-prime case. In this regard, we formulate the following modest conjecture:
$\alpha _i=0$ is a simple but very effective tool in [Reference Łaba and Londner24]. It would be useful to have similar bounds for lower-dimensional subspaces, for example lines in the three-prime case. In this regard, we formulate the following modest conjecture:
Conjecture 9.5. Suppose that ![]() $p_i^{\alpha _i}\parallel \lvert A\rvert $ with
$p_i^{\alpha _i}\parallel \lvert A\rvert $ with ![]() $\alpha _i<n_i$. Then for all
$\alpha _i<n_i$. Then for all ![]() $x\in \mathbb {Z}_{M}$,
$x\in \mathbb {Z}_{M}$,
This is clearly true when:
•
 $p_i^{n_i}$ exceeds the plane bounds
$p_i^{n_i}$ exceeds the plane bounds  $\left \lvert A\cap \Pi (x,p_j^{n_j})\right \rvert $ for
$\left \lvert A\cap \Pi (x,p_j^{n_j})\right \rvert $ for  $j\neq i$ and
$j\neq i$ and• A satisfies (T2) (in this case,
 $A\oplus B^\flat =\mathbb {Z}_M$ and there exists
$A\oplus B^\flat =\mathbb {Z}_M$ and there exists  $\beta _i$ so that
$\beta _i$ so that  $M/p_i^{\beta _i}\notin \mathrm {Div}(A)$).
$M/p_i^{\beta _i}\notin \mathrm {Div}(A)$).
Acknowledgements
This research was supported by the Natural Sciences and Engineering Research Council of Canada (Discovery Grant 22R80520)
Conflicts of Interest:
None.