Conceptual Framework

Production theory is the basis of the estimation of a stochastic frontier and input-output relationships in the present study. It is assumed that farms are offered a certain technology set that describes the relationship between inputs and outputs. The farmer can allocate inputs to generate outputs within the technology. Some inputs, such as land, could be exogenous in the short run, while others are endogenous. We assume that the farmer can choose inputs to optimize a cost-minimization objective function. Eventually optimizing behavior makes all input and output choices endogenous (Kumbhakar, Asche, and Tveteras Reference Kumbhakar, Asche and Tveteras2013). Endogenous decision variables imply the possibility of farms with inefficient production, which could then be measured by the DF approach. Furthermore, the setting of multioutput multi-input DFs allows to account for marginal interactive and substitutional relationships between inputs and outputs through elasticities. Elasticities are estimated with respect to each input and output. A marginal shadow value for wheat seeds is derived through an economic evaluation of the marginal effects between the input (seed) and the output (wheat). This value is then used to evaluate the economic impact of marginal yield-increasing wheat seeds, which constitutes the main aim of the study. The MSV differs from market price because it evaluates the importance of the innovation within the production technology in monetary units while considering substitutional input relationships. Yield-increasing seeds are viewed as an embodied innovation, thereby implying that it is under the farmer's control to introduce the innovation and potentially extend her/his seed expenditures. The MSV indicates the maximum price premium for marginal yield-increasing seed innovations paid by the average farmer.

In the model used in the study, input markets are seen as perfectly competitive. This implies that the size of a single farm relative to the size of the market is so small such that the farm has no influence on input prices.

This section involves the introduction of the theoretical framework of the DF upon which we base our marginal shadow value calculation. The production technology set at time t, (S ^t) represents an input vector $x^t = \lpar x_1^t\comma \; \ldots\comma \; x_N^t \rpar \in R_ + ^N {\rm \; } $ that produces an output vector $y^t = \lpar y_1^t\comma \; \ldots\comma \; y_M^t \rpar \in R_ + ^M $, which is formally expressed as follows:

(1)$$S^t = \lcub \lpar x^t\comma \; \; y^t\rpar \colon \; x^t\; {\rm can}\; {\rm produce}\; y^t\rcub $$

(Newman and Matthews Reference Newman and Matthews2006).

S^t denotes all feasible input–output vectors, and all inputs are assumed as freely disposable.

We apply an input-oriented DF, developed by Shephard (Reference Shephard1970), to represent multi-output and multi-input technologies. Given a technically feasible set (S ^t), the input-oriented DF measures for each observation the largest radial contraction of an input vector (x ^t), given outputs (y ^t) (Färe and Primont Reference Färe and Primont1995). The mathematical representation of the optimization function is as follows:

(2)$$D_{\rm I}^t (x^t,y^t) = \mathop {\max} \limits_{ {\rm \rho}} \{ { {\rm \rho}} \gt 0:(x^t/{ {\rm \rho}} )\; \in S^t)\}.$$

This functional form measures the maximum scalar (denote as ρ), such that x ^t/ρ remains in the feasible production technology set. The DF assumes values lesser than or equal to 1. That is $D_{\rm I}^t \lpar x^t\comma \; y^t\rpar \le 1\quad {\rm if}\; x^t \in S^t$.

The DF value for a given observation corresponds to 1 if and only if the observation is part of the frontier of the production technology set S ^t. Values between 0 and 1 indicate production with a distance to the production frontier and, thus, technical inefficiency (Coelli and Fleming Reference Coelli and Fleming2004). Increasing efficiency of a farm corresponds to a larger ρ value, which implies that the farm is closer to the stochastic frontier. By definition $D_{\rm I}^t \lpar x^t\comma \; y^t\rpar $ is a non-decreasing, positively linearly homogenous and concave in x ^t and nonincreasing in y ^t (Coelli and Fleming Reference Coelli and Fleming2004, Sauer, Frohberg, and Hockmann Reference Sauer, Frohberg and Hockmann2006).

Multi-output Multi-input Stochastic Input-distance Function Approach

For the analysis in the study, an input-oriented DF was selected as we focus on marginal input effects. We estimate a multi-output multi-input distance DF in a flexible translog form, allowing for all possible input-output interactions and including dummy variables for year (denoted as (Y)), country (denoted as (C)) and economic size (denoted as (E)):

(3)$$\eqalign{{\rm ln}D_{\rm I}^t \lpar x\comma \; y\comma \; t\rpar &= { {\rm \alpha}} _0 + \mathop \sum \limits_{m = 1}^M { {\rm \beta}} _m{\rm ln}y_m^t + \displaystyle{1 \over 2}\mathop \sum \limits_{m = 1}^M \mathop \sum \limits_{n = 1}^N { {\rm \beta}} _{mn}{\rm ln}y_m^t {\rm ln}y_n^t + \mathop \sum \limits_{k = 1}^K { {\rm \alpha}} _k{\rm ln}x_k^t \cr & \quad+ \displaystyle{1 \over 2}\mathop \sum \limits_{k = 1}^K \mathop \sum \limits_{l = 1}^L { {\rm \alpha}} _{kl}{\rm ln}x_k^t {\rm ln}x_l^t + \mathop \sum \limits_{k = 1}^K \mathop \sum \limits_{m = 1}^M { {\rm \delta}} _{km}{\rm ln}x_k^t {\rm ln}y_m^t \cr &\quad+ { {\rm \omega}} _0t + \displaystyle{1 \over 2}{ {\rm \omega}} _{00}t^2 + \mathop \sum \limits_{m = 1}^M { {\rm \zeta}} _{mt}{\rm ln}y_m^t t + \mathop \sum \limits_{k = 1}^K {\rm \eta} _{kt}{\rm ln}x_k^t t \cr &\quad+ \mathop \sum \limits_{\,p = 1}^P { {\vartheta}} _pY_p + \mathop \sum \limits_{q = 1}^Q { {\rm \iota}} _qC_q + \mathop \sum \limits_{r = 1}^R {\rm \kappa} _rE_r} $$

$D_{\rm I}^t $ denotes the measured input distance function (IDF), where y and x correspond to vectors of outputs and inputs, respectively. The subscripts m and n denote farm output, and the subscripts k and l denote farm inputs. All inputs and outputs include a time trend (t). Furthermore, α,β, δ, ω, ζ, η, ${\vartheta} $, ${\rm \iota} $, and κ denote parameters to be estimated.

An input variable (in this case, seeds, as denoted by $x_1^t $) is used to normalize the stochastic IDF. This imposes linear homogeneity with respect to the inputs $\left({\sum\nolimits_{k = 1}^K {a_k} = 1} \right)$ (Coelli and Perelman Reference Coelli and Perelman1999). Additionally, for symmetry purposes the restriction α_kl = α_lk, (k, l = 1, 2, …, L) and β_mn = β_nm (m, n = 1, 2, …, M) is fulfilled (Coelli and Perelman Reference Coelli and Perelman1999). Therefore, the DF can be rewritten to enable its econometric estimation as follows:

(4)$$\eqalign{{\rm ln}\left( {\displaystyle{{D_{\rm I}^t } \over {x_1^t }}} \right) &= {\rm \alpha} _0 + \mathop \sum \limits_{m = 1}^M {\rm \beta} _m{\rm ln}y_m^t + \displaystyle{1 \over 2}\mathop \sum \limits_{m = 1}^M \mathop \sum \limits_{n = 1}^N {\rm \beta} _{mn}{\rm ln}y_m^t {\rm ln}y_n^t + \mathop \sum \limits_{k = 2}^K {\rm \alpha} _k{\rm ln}\left( {\displaystyle{{x_k^t } \over {x_1^t }}} \right) \cr & \quad+ \displaystyle{1 \over 2}\mathop \sum \limits_{k = 2}^K \mathop \sum \limits_{l = 2}^L {\rm \alpha} _{kl}{\rm ln}\left( {\displaystyle{{x_k^t } \over {x_1^t }}} \right){\rm ln}\left( {\displaystyle{{x_l^t } \over {x_1^t }}} \right) + \mathop \sum \limits_{k = 2}^K \mathop \sum \limits_{m = 1}^M {\rm \delta} _{km}{\rm ln}\left( {\displaystyle{{x_k^t } \over {x_1^t }}} \right){\rm ln}y_m^t \cr &\quad+ {\rm \omega} _0t + \displaystyle{1 \over 2}{\rm \omega} _{00}t^2 + \mathop \sum \limits_{m = 1}^M {\rm \zeta} _{mt}{\rm ln}y_m^t t + \mathop \sum \limits_{k = 2}^K {\rm \eta} _{kt}{\rm ln}\left( {\displaystyle{{x_k^t } \over {x_1^t }}} \right)t \cr &\quad+ \mathop \sum \limits_{\,p = 1}^P {\vartheta} _pY_p + \mathop \sum \limits_{q = 1}^Q {\rm \iota} _qC + \mathop \sum \limits_{r = 1}^R {\rm \kappa} _rE_r = {\rm TL}\left( {y_m^t ,\left( {\displaystyle{{x_k^t } \over {x_1^t }}} \right),t} \right) \cr &\quad+ \mathop \sum \limits_{\,p = 1}^P {\vartheta} _pY_p + \mathop \sum \limits_{q = 1}^Q {\rm \iota} _qC_q + \mathop \sum \limits_{r = 1}^R {\rm \kappa} _rE_r} $$

where TL denotes translog. The equation can be rearranged as follows:

(5)$${\rm ln}D_{\rm I}^t - {\rm ln}x_1^t = {\rm TL}\big({y_m^t\comma \; \Big({\displaystyle{{x_k^t} \over {x_1^t}}} \Big)\comma \; t} \big)+ \mathop \sum \limits_{\,p = 1}^P {\vartheta} _pY_p + \mathop \sum \limits_{q = 1}^Q {\rm \iota} _qC_q + \mathop \sum \limits_{r = 1}^R {\rm \kappa} _rE_r$$

(6)$$- {\rm ln}x_1^t = {\rm TL}\big({y_m^t\comma \; \Big({\displaystyle{{x_k^t} \over {x_1^t}}} \Big)\comma \; t} \big)+ \mathop \sum \limits_{\,p = 1}^P {\vartheta} _pY_p + \mathop \sum \limits_{q = 1}^Q {\rm \iota} _qC_q + \mathop \sum \limits_{R = 1}^R {\rm \kappa} _rE_r - {\rm ln}D_I^t {\rm \; } $$

By setting $ - {\rm ln}D_{0i}^t = - u_i^t $ and including a symmetric error $\lpar v_i^t \rpar $ that reflects random factors such as measurement errors, stochastic shocks, or unobserved inputs, the stochastic input DF (Coelli and Perelman Reference Coelli and Perelman1996) is obtained as follows:

(7)$$- {\rm ln}x_1^t = {\rm TL}\big( {y_m^t, \Big( {\displaystyle{{x_k^t} \over {x_1^t}}} \Big),t} \big) + \mathop \sum \limits_{\,p = 1}^P {\vartheta} _pY_p + \mathop \sum \limits_{q = 1}^Q {\rm \iota} _qC_q + \mathop \sum \limits_{r = 1}^R {\rm \kappa} _rE_r - u^t + v^t$$

where $v_i^t $ denotes a random error term, which is assumed to be independent and identically distributed (i.i.d.) with $N\lpar 0\comma \; {\rm \sigma} _v^2 \rpar $ and independent of $u_i^t $, and intended to capture events beyond the farmer's control. The term u _i corresponds to a non-negative random error term, which is assumed to be i.i.d. with $N\lpar {\rm \mu}\comma \; {\rm \sigma} _u^2 \rpar $ and to follow the specification $u_i^t = u_i\; {\rm exp}\lpar - \; {\rm \eta} \lpar t - T\rpar \rpar $, that is intended to capture time-varying technical inefficiency effects in inputs (Battese and Coelli Reference Battese and Coelli1992).

The first-order partial derivatives of equation 7 measure the partial elasticities for inputs x _k (${\rm \varepsilon} _{x_1\comma x_k}$) and the partial elasticity for outputs y _m (${\rm \varepsilon} _{x_1\comma y_m}$) relative to x ₁. The value for ${\rm \varepsilon} _{x_1\comma y_m} \left({ - {\rm \varepsilon} _{D^{\rm I}\comma y_m} = - \displaystyle{{\partial {\rm ln}D_i} \over {\partial {\rm ln}y_m}} = \displaystyle{{\partial {\rm ln}x_1} \over {\partial {\rm ln}y_m}} = {\rm \varepsilon} _{x_1\comma y_m}} \right)$ estimates the required percentage change in x ₁ from a 1 percent change in y _m, holding all output ratios constant (Paul and Nehring Reference Paul and Nehring2005). The mean of the negative sums of the partial elasticities of y _m (${\rm \varepsilon} _{x_1\comma y_m}$) represents scale economies at the sample mean $\left({{\rm SE} = - \sum\nolimits_{m = 1}^M {{\rm \varepsilon} _{x_1\comma y_m}}} \right)$ (Paul and Nehring Reference Paul and Nehring2005). Thus, it reflects the extent to which overall input use must increase to support a 1 percent increase in all outputs by holding all input ratios constant. The elasticities of inputs $\lpar {\rm \varepsilon} _{x_{\rm 1}\comma x_k}\rpar $ contain information on the slope of the production possibility frontier and represent the output contribution of x _k relative to x ₁.

Further, for each subsample, technical change (TC), as the first-order partial derivative with respect to time (t) and technical efficiency (TE), are determined for each subsample. Given this, it is possible to differentiate various European production systems. The individual technical efficiency for the ith firm is then estimated as follows:

(8)$${\rm T}{\rm E}_i\lpar u\comma \; x\comma \; t\rpar = \exp \lpar - u_i\rpar = \displaystyle{{x_i^t} \over {x_i^{t{^\ast}}}} $$

where TE_i measures the deviation of particular observations from the estimated frontier (Paul and Nehring Reference Paul and Nehring2005).

Marginal Shadow Value

The estimation of shadow prices is based upon the IDF's dual relationship with the cost function (Färe and Primont Reference Färe and Primont2006). The partial elasticities, as mentioned previously, contain information on marginal products (MP) which are used to derive MSVs. In this study we are interested in the marginal shadow value for seeds as wheat output increases. Thus, we predominantly focus on the partial elasticity relationship ${\rm \varepsilon} _{x_1\comma y_m}$ with x ₁ = x _seeds and y _m = y _wheat:

(9)$${\rm \varepsilon} _{x_1\comma \; y_m} = \displaystyle{{\partial {\rm ln}x_1} \over {\partial {\rm ln}y_m}}.$$

From the partial elasticity for output (or ‘input share’ of y _m [relative to x ₁]) ${\rm \varepsilon} _{x_1\comma y_m}$, we can calculate the marginal product (∂x ₁/∂y _m) of y _m on x ₁, as follows:

(10)$${\rm \varepsilon} _{x_1\comma y_m} = \displaystyle{{\partial {\rm ln}x_1} \over {\partial {\rm ln}y_m}} = \displaystyle{{\partial x_1} \over {\partial y_m}}\displaystyle{{y_m} \over {x_1}}$$

(11)$${\rm M}{\rm P}_{x_1\comma y_m} = \displaystyle{{\partial x_1} \over {\partial y_m}} = \displaystyle{{{\rm \varepsilon} _{x_1\comma y_m}{^\ast}x_1} \over {y_m}}$$

In order to derive the MSV per ha, ${\rm M}{\rm P}_{x_1.y_m}$ is multiplied with the average total expenditures on seeds/ha $\lpar E_{{\rm seeds}}*{\rm h}{\rm a}^{ - 1}\rpar $ as given below:

(12)$${\rm MS}{\rm V}_{x_{{\rm seeds}}.y_m} = {\rm M}{\rm P}_{x_{{\rm seeds}}.y_m}(E_{{\rm seeds}}{^\ast}{\rm h}{\rm a}^{ - 1}).$$

With respect to the model structure, the study follows Kumbhakar, Wang, and Horncastle (Reference Kumbhakar, Wang and Horncastle2015), assuming a half-normal distribution of the inefficiency term (u ^t). Estimates of the parameters for the above-outlined model were obtained using maximum likelihood procedures based on a STATA 13 routine.

Data and Estimation

Annual FADN data with 302,041 observations in 23 European countries (Belgium (BEL), Czech Republic (CZE), Denmark (DEN), Germany (DEU), Greece (ELL), Spain (ESP), Estonia (EST), France (FRA), Hungary (HUN), Ireland (IRE), Italy (ITA), Lithuania (LTU), Luxembourg (LUX), Latvia (LVA), Netherlands (NED), Austria (OST), Poland (POL), Portugal (POR), Finland (SUO), Sweden (SVE), Slovenia (SVN), Slovakia (SVK), and the United Kingdom (UKI)), from 2005 to 2012, are used for the analysis. The FADN data set consists of annual accountancy data from a sample of commercial agricultural holdings in the EU. The data were collected by the Member States of the EU by following a harmonized bookkeeping principle (Commission Reference Commission2016).

Within the countries of the EU, the Common Agricultural Policy (CAP) sets common farming regulations, e.g., with respect to environmental standards and subsidy payments (decoupled direct payments). Nevertheless, crop production systems differ due to farm structures, traditional differences, and especially due to agroclimatic conditions. To account for these differences, four subsamples (Table 1) were formed based on agroclimatic zones proposed by Bouma (Reference Bouma2005). The subsamples North, East, South and West include the following different countries:

Table 1. Subsamples’ Composition

The farms in the samples produce a variety of outputs (i.e., crops, dairy, livestock) for which they rely on a variety of inputs. This study focuses on the characteristics of specialized crop-producing farms because these are most likely to engage in wheat production. Therefore, the farms selected from the sample include farms that generate at least 60 percent of their annual revenue by crop production in every year of observation. This results in an unbalanced panel based on a total of 73,719 observations after removing outliers from the sample. The farms remaining in the sample operated on an annual average area of 1,733,293 ha, which is approximately equal to 1.6 percent of European crop land (EUROSTAT 2016a). The average farm size in the sample is 186.5 ha, of which 70 ha on average were cultivated with wheat. The largest farms in the sample are in the Eastern region, where the average farm size is 230 ha.

The model estimation included specifying inputs and outputs based upon the production process of wheat farms. Two output variables are selected, namely total production of common wheat ($y_1^t $) and total production of other field crops ($y_2^t $), which account for all produced crops except wheat. Furthermore, five input variables were included, namely seed and plants ($x_1^t $), fertilizers ($x_2^t $), crop protection ($x_3^t $), machinery ($x_4^t $), labor ($x_4^t $), and total crop area ($x_5^t $). The variables measured in monetary terms (€) refer to total production value ($y_1^t\comma \; \; y_2^t $) and input expenditures ($x_1^t\comma \; \; x_2^t $, $x_3^t $). All data measured in EUR were deflated using real agricultural price indices with the base year 2005 provided by the Eurostat database (EUROSTAT 2016b).

The analysis is conducted the entire sample as well as separately for the four subsamples (production regions North, East, South and West). The descriptive statistics for the entire sample are reported in Table 2.

Table 2. Descriptive Statistics of the Sample Variables (Aggregated Sample)

Note: All monetary values are adjusted for inflation using the price indices for agricultural outputs and inputs with base year 2005 (EUROSTAT 2016b).

From 2005 to 2012, the average total crops area per year in the sample remains almost constant in the range of 183–197 ha, and the average yearly wheat cultivation area ranges between 66 ha and 73 ha. Simultaneously, the total output of wheat varies between 571 €/ha and 1,256 €/ha and indicates an upward trend over time. Expenditures for seeds and plants increased from 64 €/ha to 85 €/ha, while labor, on average, remained constant between 6,290 h and 6,991 h. The included dummy variables to account for year (Y), country (C), and economic size (E) are defined according to the FADN. It is assumed that C picks up country differences in production systems, subsidy payments, and environmental conditions within a country. With respect to E, the FADN defines 14 different classes according to the standard output of farms (Commission Reference Commission2016).

Different observations in the data set show 0 values for individual variables, which cannot be handled by the logarithmic functional specification. We follow the procedure outlines by Rasmussen (Reference Rasmussen2010) and deleted those observations (a total of 2,287 observations were deleted). Only 3 percent of the sample was affected by this, and thus a significant bias is not expected with respect to the results.

In the empirical application of production or distance functions on agricultural holdings endogeneity is a general concern as discussed by, e.g., Kumbhakar (Reference Kumbhakar2001), Kumbhakar (Reference Kumbhakar2011), Brümmer, Glauben, and Thijssen (Reference Brümmer, Glauben and Thijssen2002), Sauer and Latacz-Lohmann (Reference Sauer and Latacz-Lohmann2015), and Solís, Bravo-Ureta, and Quiroga (Reference Solís, Bravo-Ureta and Quiroga2009). Endogeneity problems occur in an IDF if outputs are not exogenously given. This problem occurs in agricultural crop production to a certain extent, because they are partly the result of exogenous climate factors and endogenous farming decisions. The endogeneity impact of outputs on the next season's inputs is less problematic in developed countries compared to developing countries where a bad harvest strongly influences the possibility to invest in next season's inputs. Farms in developed countries mostly follow a standard cultivation pattern that is far less influenced by the previous harvest outcome. Compared to multi-output production functions, DFs are superior in avoiding such endogeneity problems, although they fail avoiding them completely (Kumbhakar Reference Kumbhakar2011). Because the inputs on the right-hand side of equation 4 appear as ratios, they are likely to suffer less from endogeneity (Brümmer, Glauben, and Thijssen Reference Brümmer, Glauben and Thijssen2002). Additionally, outputs are assumed to be exogenous to the farm's input choice to the extent that farms are cost minimizers, and panel data estimators control for farmers’ input adjustment due to unobserved time-invariant conditions (Sauer and Wossink Reference Sauer and Wossink2013).

Empirical Results and Discussion

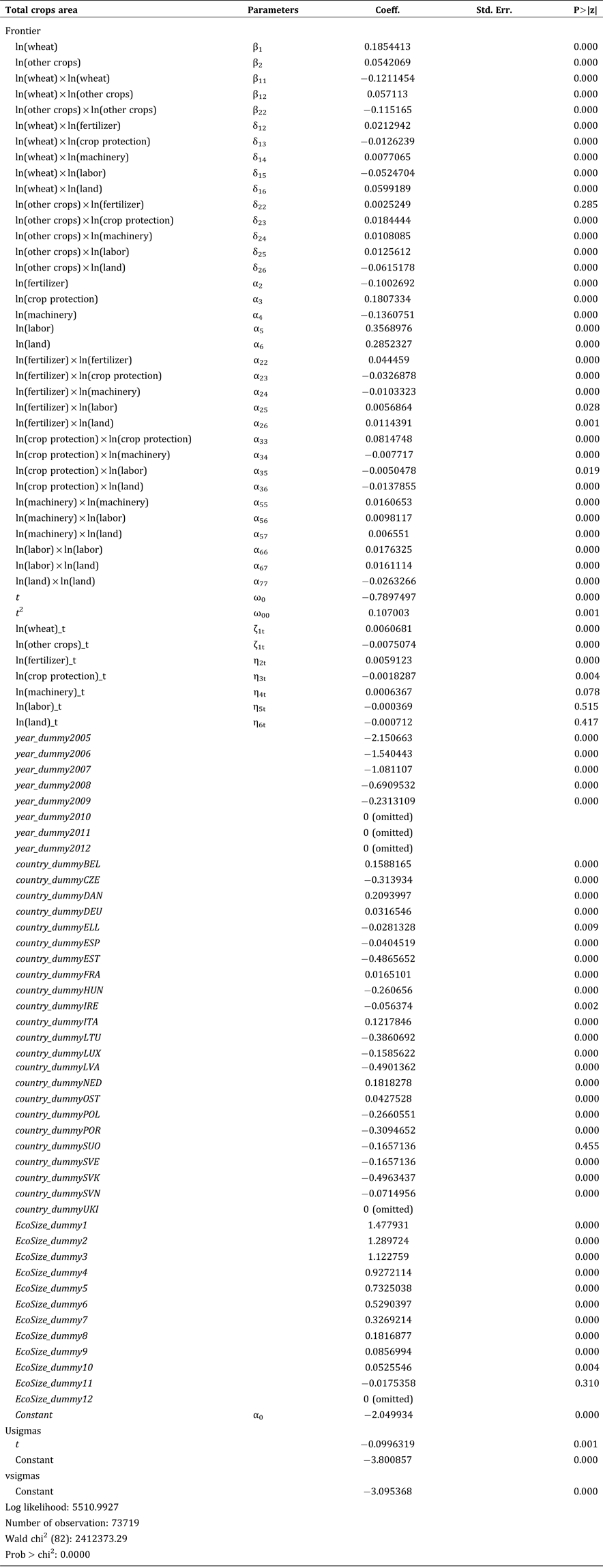
This section presents the results for first-order elasticities, marginal shadow values, scale economies, technical efficiency, and technical change. Detailed estimates for the parameters of the IDF based on aggregated data for 23 European countries are presented in Table A1 (Appendix). In the estimation for the entire sample, we find more than 90 percent of the parameters to be statistically significant different from zero at least at the 5 percent level. Particularly, first-order coefficients and the dummy variables Y, C, and E are mostly significant. A number of coefficients for the interaction variables (second order terms) are also significantly different from zero. This indicates non-linearities in the production structure and therefore supports the application of a flexible translog specification (Rahman Reference Rahman2009).

Applying the delta method, we derive the partial first-order elasticities of the translog function at the sample means for the entire EU region and the four subsamples as reported in Table 3. Furthermore, Table 3 reports the estimate of the MSV, SE, TE, and TC evaluated at the sample means.

Table 3. Elasticities MSV, SE, TE and TC (with delta method evaluated at the sample means)

Note: Marginal shadow value (MSV), scale economies (SE), technical efficiency (TE), technical change (TC).

The first-order derivatives or partial elasticities reflect input substitutability with respect to seeds $\lpar {\rm \varepsilon} _{x_1\comma x_k}\rpar $ and marginal output contributions $\lpar {\rm \varepsilon} _{x_1\comma y_m}\rpar $. As the dependent variable in equation 7 is − lnx ₁, these estimates show negative signs for partial derivatives with respect to outputs and positive signs for partial derivatives with respect to inputs. The positive signs of all elasticities for the inputs imply their substitutability with total seed expenditures (∂lnx₁/∂lnx_k <0). The negative signs of all elasticities for the outputs imply that a reduction in total seed expenditures (x ₁) is positively associated with a reduction in outputs (∂lnx₁/∂lny_m >0) (Rahman Reference Rahman2009). Thus, the estimations confirm the monotonicity conditions for the specified stochastic input-oriented distance frontier at the sample means (Rasmussen Reference Rasmussen2010). The (input) elasticities for outputs $\lpar {\rm \varepsilon} _{x_1\comma y_m}\rpar $ represent the percentage in x ₁ associated with a 1 percent change in y _m, holding all input ratios (ln(x _k/x ₁)) constant. Because x ₁ corresponds to the relative measure for the inputs, all other inputs need to change similar to x ₁ in order to hold the input ratios constant. Thus, ${\rm \varepsilon} _{x_1\comma y_m}$ summarizes the (total) input expansion required for a 1 percent increase in y _m and can be considered an input share of y _m (relative to x ₁) (Paul and Nehring Reference Paul and Nehring2005). For example, the elasticity of −0.24430 for wheat output $\lpar {\rm \varepsilon} _{x_1\comma y_1}\rpar $ implies that a 1 percent increase in wheat production is associated with a 0.24430 percent increase in (all) inputs, measured at the sample mean and holding all input ratios constant.

In a manner similar to ${\rm \varepsilon} _{x_1\comma y_m}$, the elasticities for the inputs $\lpar {\rm \varepsilon} _{x_1.x_k} \rpar $ represent the percentage change of x ₁ associated with a 1 percent change in x _k. However, in an IDF (equation 7) x _k is measured relative to x ₁. For example, the elasticity value of 0.30212 for the input land $\lpar {\rm \varepsilon} _{x_1\comma x_6}\rpar \; $ implies that a 1 percent decrease in the ratio of land (x ₆) to seeds (x ₁), due to a change in x ₆, could be substituted by 0.30212 percent increase in all inputs. Again, this change, which would keep production constant, is measured at the sample means.

For every subsample, ${\rm \varepsilon} _{x_1\comma y_2}$ is found to exceed ${\rm \varepsilon} _{x_1\comma y_1}$, which confirms that the production of y ₂ (crops other than wheat) requires a higher input share for farms at the sample means. The estimates for the partial elasticities of inputs (${\rm \varepsilon} _{x_1.x_k}$) represent their proportional marginal productivity. The variables land (${\rm \varepsilon} _{x_1.x_5}$) and labor (${\rm \varepsilon} _{x_1.x_6}$) show the largest magnitudes, and this suggests that these are the inputs with the highest contribution to outputs within the estimated models.

Technical Efficiency and Technical Change

The results indicated that technical efficiency (TE) remains fairly constant over time and varies between 0.896 and 0.925 at the aggregated EU level. The estimates exceed that in a previous study of the TE of European crop farmers by Rasmussen (Reference Rasmussen2010), where a value of 0.82 was determined based on data from 1985 to 2006. However, Paul and Nehring (Reference Paul and Nehring2005) determined a higher TE of crop farms in the U.S. corn belt of 0.94 from 1996 to 2000. It is important to note that TE is only measured within each subsample and only comparable to a limited extent between different subsamples.

The rate of technical change (TC) can be calculated using the derivative of the DF (in logs) with respect to t ${\rm \lpar }{\rm \varepsilon} _{D_i\comma \; t} = \partial {\rm ln}D_i/\partial t{\rm \rpar }$ (Kumbhakar, Asche, and Tveteras Reference Kumbhakar, Asche and Tveteras2013). We determine an average annual TC of −0.291 percent, thereby implying a negative technical change over time, albeit at a relatively low rate. In contrast, Sauer and Latacz-Lohmann (Reference Sauer and Latacz-Lohmann2015) analyzed German dairy farms from 1996–2010 and found a positive average annual technical change of 1.5 percent.

Scale Economies

The negative sum of elasticities of outputs (${\rm \varepsilon} _{x_1\comma y_m}$) represents scale economies (SE) at the sample means. Thus, it reflects the extent to which overall input use must increase to support a 1 percent increase in all outputs (Paul and Nehring Reference Paul and Nehring2005). Values below 1 imply that the production possibility frontier expands more than proportionally with an increase in resources, which indicates increasing returns to scale. Accordingly, an SE value of 0.5203 (Table 3) indicates that a 0.5203 percent increase in all inputs is required to sustain a 1 percent increase in outputs. Thus, on average, European crop farmers are likely to benefit from economies of scale. Figure 1 shows increasing SE with increasing economic size, which indicates that farms in higher economic classes are closer to the optimal farm size. We derive low SE values at the sample mean similar to previous European farms studies including Paul and Nehring (Reference Paul and Nehring2005) (SE value of 0.654) and Fleming and Lien (Reference Fleming and Lien2009) (SE value of 0.700).

Figure 1. Average MSV and SE relative to Economic Class.

The analysis provides detailed insight into the European crop production system. However, due to data aggregation and availability, it is not possible to check specifically for farm individual aspects, such as soil quality or farmers’ characteristics. For example, Sauer and Latacz-Lohmann (Reference Sauer and Latacz-Lohmann2015) show in their DF model that the farmers’ age and education level affect efficiency and investment in innovations.

Marginal Shadow Value

We estimate an average MSV for yield-increasing seed material of 18.87 €/ha for the average European crop farm. Depending on the region, this value varies between 15.60 €/ha and 31.85 €/ha (Table 3). The reason for these differences is not easy to identify but can rather be considered a result of complex differences in regional crop production systems and technologies influenced by factors such as climate conditions, farm structure, and land and labor availability. Further, because the MSV measures a percentage increase of absolute terms, one can expect a region with generally lower revenue/ha—e.g., the North and East regions—to show a lower MSV/ha. Within the total sample, we identify increasing average MSVs with an increase in economic class (Figure 1). Consequently, farmers in a higher economic class could pay a higher price for yield-increasing seeds.

Incremental revenue from a 1 percent yield increase in wheat are, on average, 92.9 €/ha for EU crop farms. The MSV for the input seed is 20.3 percent of this value. The result is consistent with production theory because the incremental use of different substitutable inputs could lead to a yield increase. Elasticities indicate the marginal output effect for individual inputs. Thus, the MSV for one specific input must always be smaller than the incremental revenue due to substitutability.

Robustness

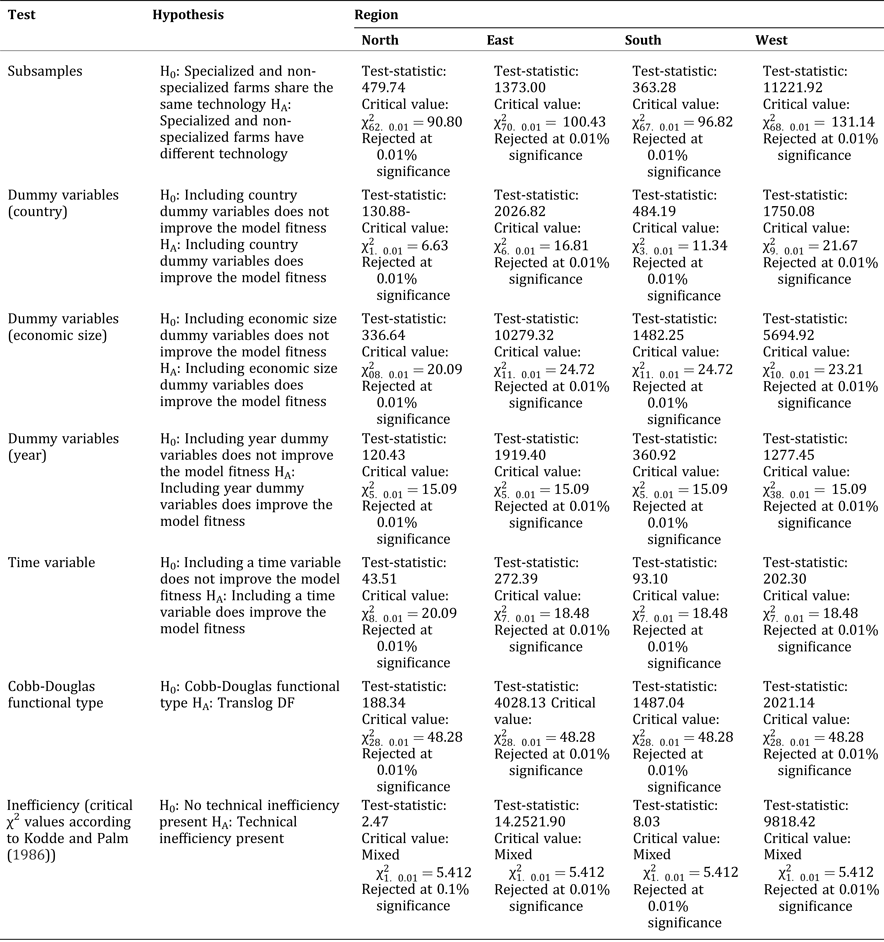
Various specifications of the model were compared based on likelihood ratio tests, for which the results are presented in Table A2 (Appendix). We tested for systematic differences between the model with different subgroups (specialized crop farms and general farms), with and without dummy variables (year, country, and economics size), and with and without a time variable to include technical change. The test results support the sampling decision at statistically significant levels. Further, we find the chosen translog functional form superior to a Cobb-Douglas functional form. The hypothesis of no inefficiencies in the model was rejected at least at a 10 percent level for all four subgroups.