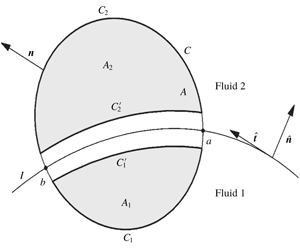
Brøns et al. (Reference Brøns, Thompson, Leweke and Hourigan2014) have analysed the vorticity generation from two-dimensional interfaces as well as the vorticity flux across such interfaces. In the expressions (2.18) for the vorticity source at the interface and (2.19) for the rate of change of circulation  $\text{d}\unicode[STIX]{x1D6E4}/\text{d}t$ of a material volume
$\text{d}\unicode[STIX]{x1D6E4}/\text{d}t$ of a material volume  $A$ which includes both fluids, a term
$A$ which includes both fluids, a term
 $$\begin{eqnarray}\int _{a}^{b}\unicode[STIX]{x1D705}\unicode[STIX]{x27E6}(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}})(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}})\unicode[STIX]{x27E7}\,\text{d}s\end{eqnarray}$$
$$\begin{eqnarray}\int _{a}^{b}\unicode[STIX]{x1D705}\unicode[STIX]{x27E6}(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}})(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}})\unicode[STIX]{x27E7}\,\text{d}s\end{eqnarray}$$ occurs. The integral is taken along the part of the interface which is inside  $A$,
$A$,  $\unicode[STIX]{x1D705}$ is the curvature of the interface,
$\unicode[STIX]{x1D705}$ is the curvature of the interface,  $\boldsymbol{u}$ is the fluid velocity,
$\boldsymbol{u}$ is the fluid velocity,  $\hat{\boldsymbol{n}}$ and
$\hat{\boldsymbol{n}}$ and  $\hat{\boldsymbol{t}}$ are the normal and tangential vectors of the interface, respectively, and
$\hat{\boldsymbol{t}}$ are the normal and tangential vectors of the interface, respectively, and  $\unicode[STIX]{x27E6}q\unicode[STIX]{x27E7}=q_{2}-q_{1}$ denotes the jump of a quantity
$\unicode[STIX]{x27E6}q\unicode[STIX]{x27E7}=q_{2}-q_{1}$ denotes the jump of a quantity  $q$ across the interface.
$q$ across the interface.
In the derivation it is implicitly assumed that
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\int _{a}^{b}\unicode[STIX]{x1D6FE}\,\text{d}s=\int _{a}^{b}\frac{\text{d}\unicode[STIX]{x1D6FE}}{\text{d}t}\,\text{d}s,\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}\int _{a}^{b}\unicode[STIX]{x1D6FE}\,\text{d}s=\int _{a}^{b}\frac{\text{d}\unicode[STIX]{x1D6FE}}{\text{d}t}\,\text{d}s,\end{eqnarray}$$ where  $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x27E6}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}}\unicode[STIX]{x27E7}$ is the strength of the vortex sheet at the interface. Terrington, Hourigan & Thompson (Reference Terrington, Hourigan and Thompson2020) point out that this is valid only if the interface is stationary, and in that case (1) is zero. An expression for
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x27E6}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}}\unicode[STIX]{x27E7}$ is the strength of the vortex sheet at the interface. Terrington, Hourigan & Thompson (Reference Terrington, Hourigan and Thompson2020) point out that this is valid only if the interface is stationary, and in that case (1) is zero. An expression for  $\text{d}\unicode[STIX]{x1D6E4}/\text{d}t$ which is valid for arbitrary unsteady interfaces is derived by Terrington et al. (Reference Terrington, Hourigan and Thompson2020), equation (2.22), and no term like (1) occurs there. Hence, the conclusion drawn by Brøns et al. (Reference Brøns, Thompson, Leweke and Hourigan2014), that normal motion of a curved interface is a source of vorticity given by (1), is not correct. In § 3 of Brøns et al. (Reference Brøns, Thompson, Leweke and Hourigan2014), several examples are considered. Except for one, all have a stationary interface, and here the assumption (2) leads to correct results. For the case of a solid cylinder with time-varying radius
$\text{d}\unicode[STIX]{x1D6E4}/\text{d}t$ which is valid for arbitrary unsteady interfaces is derived by Terrington et al. (Reference Terrington, Hourigan and Thompson2020), equation (2.22), and no term like (1) occurs there. Hence, the conclusion drawn by Brøns et al. (Reference Brøns, Thompson, Leweke and Hourigan2014), that normal motion of a curved interface is a source of vorticity given by (1), is not correct. In § 3 of Brøns et al. (Reference Brøns, Thompson, Leweke and Hourigan2014), several examples are considered. Except for one, all have a stationary interface, and here the assumption (2) leads to correct results. For the case of a solid cylinder with time-varying radius  $R$ and angular velocity
$R$ and angular velocity  $\unicode[STIX]{x1D6FA}$ discussed in § 3.2.1 the analysis is also correct, as (2) is not used. To compute the vorticity flux
$\unicode[STIX]{x1D6FA}$ discussed in § 3.2.1 the analysis is also correct, as (2) is not used. To compute the vorticity flux  $\unicode[STIX]{x1D70E}_{1}$ into the fluid, the general expression valid for a no-slip boundary, equation (2.24), is employed:
$\unicode[STIX]{x1D70E}_{1}$ into the fluid, the general expression valid for a no-slip boundary, equation (2.24), is employed:
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}=\frac{\text{d}}{\text{d}t}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{t}})+\frac{1}{\unicode[STIX]{x1D70C}_{1}}\frac{\unicode[STIX]{x2202}p_{1}}{\unicode[STIX]{x2202}s}+\unicode[STIX]{x1D705}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{n}})(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{t}})-\frac{1}{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{n}})^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}=\frac{\text{d}}{\text{d}t}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{t}})+\frac{1}{\unicode[STIX]{x1D70C}_{1}}\frac{\unicode[STIX]{x2202}p_{1}}{\unicode[STIX]{x2202}s}+\unicode[STIX]{x1D705}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{n}})(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{t}})-\frac{1}{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{n}})^{2}.\end{eqnarray}$$For the expanding cylinder
 $$\begin{eqnarray}\frac{\text{d}}{\text{d}t}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{t}})=-\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R),\quad \unicode[STIX]{x1D705}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{n}})(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{t}})=-\frac{1}{R}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R)\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}}{\text{d}t}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{t}})=-\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R),\quad \unicode[STIX]{x1D705}(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{n}})(\boldsymbol{U}\boldsymbol{\cdot }\hat{\boldsymbol{t}})=-\frac{1}{R}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R)\end{eqnarray}$$are both in general non-zero, which after a simplification yields (3.6) in Brøns et al. (Reference Brøns, Thompson, Leweke and Hourigan2014),
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}=-\frac{1}{R}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}_{1}=-\frac{1}{R}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R^{2}).\end{eqnarray}$$The total flux of vorticity into the fluid is
 $$\begin{eqnarray}\int _{0}^{2\unicode[STIX]{x03C0}R}\unicode[STIX]{x1D70E}_{1}\,\text{d}s=-2\unicode[STIX]{x03C0}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\int _{0}^{2\unicode[STIX]{x03C0}R}\unicode[STIX]{x1D70E}_{1}\,\text{d}s=-2\unicode[STIX]{x03C0}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R^{2}).\end{eqnarray}$$This is balanced by the rate of change of circulation of the solid cylinder,
 $$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D6E4}}{\text{d}t}=\frac{\text{d}}{\text{d}t}\int _{cylinder}\unicode[STIX]{x1D714}\,\text{d}A=2\unicode[STIX]{x03C0}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{d}\unicode[STIX]{x1D6E4}}{\text{d}t}=\frac{\text{d}}{\text{d}t}\int _{cylinder}\unicode[STIX]{x1D714}\,\text{d}A=2\unicode[STIX]{x03C0}\frac{\text{d}}{\text{d}t}(\unicode[STIX]{x1D6FA}R^{2}).\end{eqnarray}$$Hence, the normal motion of the curved interface is not a source of vorticity as the total circulation is constant. However, it contributes to the flux of vorticity between the solid cylinder and the fluid.
Finally, we note that a term  $\unicode[STIX]{x1D705}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}$ has inadvertently been omitted by Brøns et al. (Reference Brøns, Thompson, Leweke and Hourigan2014) in the discussion of the role of the pressure boundary condition at fluid interfaces. This is pointed out by Terrington et al. (Reference Terrington, Hourigan and Thompson2020). Corrected expressions are for (2.15)
$\unicode[STIX]{x1D705}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}$ has inadvertently been omitted by Brøns et al. (Reference Brøns, Thompson, Leweke and Hourigan2014) in the discussion of the role of the pressure boundary condition at fluid interfaces. This is pointed out by Terrington et al. (Reference Terrington, Hourigan and Thompson2020). Corrected expressions are for (2.15)
 $$\begin{eqnarray}\unicode[STIX]{x27E6}p\unicode[STIX]{x27E7}=-2\left.\unicode[STIX]{x27E6}\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}})+\unicode[STIX]{x1D705}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}\right)\right.\unicode[STIX]{x27E7}-T\unicode[STIX]{x1D705}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x27E6}p\unicode[STIX]{x27E7}=-2\left.\unicode[STIX]{x27E6}\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}})+\unicode[STIX]{x1D705}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}}\right)\right.\unicode[STIX]{x27E7}-T\unicode[STIX]{x1D705}\end{eqnarray}$$– which is identical to equation (2.29) in Terrington et al. (Reference Terrington, Hourigan and Thompson2020) – for (2.17)
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left.\unicode[STIX]{x27E6}\frac{p}{\unicode[STIX]{x1D70C}}\right.\unicode[STIX]{x27E7}=-\frac{2}{\unicode[STIX]{x1D70C}_{2}}\left.\unicode[STIX]{x27E6}\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}s^{2}}(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(\unicode[STIX]{x1D705}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}})\right)\right.\unicode[STIX]{x27E7}-\frac{1}{\unicode[STIX]{x1D70C}_{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(T\unicode[STIX]{x1D705})+\left.\unicode[STIX]{x27E6}\frac{1}{\unicode[STIX]{x1D70C}}\right.\unicode[STIX]{x27E7}\frac{\unicode[STIX]{x2202}p_{1}}{\unicode[STIX]{x2202}s}\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left.\unicode[STIX]{x27E6}\frac{p}{\unicode[STIX]{x1D70C}}\right.\unicode[STIX]{x27E7}=-\frac{2}{\unicode[STIX]{x1D70C}_{2}}\left.\unicode[STIX]{x27E6}\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}s^{2}}(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(\unicode[STIX]{x1D705}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}})\right)\right.\unicode[STIX]{x27E7}-\frac{1}{\unicode[STIX]{x1D70C}_{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(T\unicode[STIX]{x1D705})+\left.\unicode[STIX]{x27E6}\frac{1}{\unicode[STIX]{x1D70C}}\right.\unicode[STIX]{x27E7}\frac{\unicode[STIX]{x2202}p_{1}}{\unicode[STIX]{x2202}s}\end{eqnarray}$$and for (2.22)
 $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left.\unicode[STIX]{x27E6}\frac{p}{\unicode[STIX]{x1D70C}}\right.\unicode[STIX]{x27E7}=-2\frac{\unicode[STIX]{x27E6}\unicode[STIX]{x1D707}\unicode[STIX]{x27E7}}{\unicode[STIX]{x1D70C}_{2}}\left(\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}s^{2}}(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(\unicode[STIX]{x1D705}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}})\right)-\frac{1}{\unicode[STIX]{x1D70C}_{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(T\unicode[STIX]{x1D705})+\left.\unicode[STIX]{x27E6}\frac{1}{\unicode[STIX]{x1D70C}}\right.\unicode[STIX]{x27E7}\frac{\unicode[STIX]{x2202}p_{1}}{\unicode[STIX]{x2202}s}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}\left.\unicode[STIX]{x27E6}\frac{p}{\unicode[STIX]{x1D70C}}\right.\unicode[STIX]{x27E7}=-2\frac{\unicode[STIX]{x27E6}\unicode[STIX]{x1D707}\unicode[STIX]{x27E7}}{\unicode[STIX]{x1D70C}_{2}}\left(\frac{\unicode[STIX]{x2202}^{2}}{\unicode[STIX]{x2202}s^{2}}(\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{t}})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(\unicode[STIX]{x1D705}\boldsymbol{u}\boldsymbol{\cdot }\hat{\boldsymbol{n}})\right)-\frac{1}{\unicode[STIX]{x1D70C}_{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}s}(T\unicode[STIX]{x1D705})+\left.\unicode[STIX]{x27E6}\frac{1}{\unicode[STIX]{x1D70C}}\right.\unicode[STIX]{x27E7}\frac{\unicode[STIX]{x2202}p_{1}}{\unicode[STIX]{x2202}s}.\end{eqnarray}$$The latter is identical to (2.31) in Terrington et al. (Reference Terrington, Hourigan and Thompson2020).
Acknowledgements
Fruitful discussions with S. J. Terrington are gratefully acknowledged.