1. Introduction
We are concerned with analysing the existence of analytic first integrals at the origin of the $\mathbb {Z}_2\otimes \mathbb {Z}_2$![]() -symmetric analytic systems, i.e. invariant to $(x,\,y,\,z)\leftrightarrow (-x,\,-y,\,-z)$
-symmetric analytic systems, i.e. invariant to $(x,\,y,\,z)\leftrightarrow (-x,\,-y,\,-z)$![]() and whose origin is a Hopf-zero singularity,
and whose origin is a Hopf-zero singularity,

with $i,\,j,\,k\ge 0,\,\ i+j+k\ge 3$![]() and $i+j+k$
and $i+j+k$![]() odd. Under the conditions of $\mathbb {Z}_2\otimes \mathbb {Z}_2$
odd. Under the conditions of $\mathbb {Z}_2\otimes \mathbb {Z}_2$![]() -symmetry, performing a change of variables $(x,\,y,\,z)=(x+p_3(x,\,y,\,z),\,y+q_3(x,\,y,\,z),\,z+r_3(x,\,y,\,z))$
-symmetry, performing a change of variables $(x,\,y,\,z)=(x+p_3(x,\,y,\,z),\,y+q_3(x,\,y,\,z),\,z+r_3(x,\,y,\,z))$![]() with $p_3,\,q_3,\,r_3$
with $p_3,\,q_3,\,r_3$![]() homogeneous cubic polynomials, we obtain an orbital normal form up to order $3$
homogeneous cubic polynomials, we obtain an orbital normal form up to order $3$![]() of the system (1.1)
of the system (1.1)

with

see [Reference Algaba, Freire and Gamero1, Reference Chen, Wang and Yang12, Reference Chen, Wang and Yang13, Reference Gazor and Mokhtari15, Reference Guckenheimer and Holmes17, Reference Yu and Yuan23]. This normal form is the simplest orbital normal form up to order 3 of the system (1.1). Therefore, if $(a_1,\,a_2,\,b_1,\,b_2)$![]() is non-zero, system (1.1) is not orbitally equivalent to $(-y,\,x,\,0)^{T}$
is non-zero, system (1.1) is not orbitally equivalent to $(-y,\,x,\,0)^{T}$![]() , i.e. it is not linearizable.
, i.e. it is not linearizable.
Recall that a first integral at the origin of a system $\dot {{{\mathbf {x}}}}={{\mathbf {F}}}({{\mathbf {x}}}),$![]() is a scalar function $I$
is a scalar function $I$![]() that is constant on a neighbourhood $\mathcal {U}$
that is constant on a neighbourhood $\mathcal {U}$![]() along of any solution of the system and $I({{\mathbf 0}})=0.$
along of any solution of the system and $I({{\mathbf 0}})=0.$![]() If $I$
If $I$![]() is a $\mathcal {C}^{1}$
is a $\mathcal {C}^{1}$![]() function, using the chain rule, it means that $F(I):=\nabla I \cdot {{\mathbf {F}}}=0$
function, using the chain rule, it means that $F(I):=\nabla I \cdot {{\mathbf {F}}}=0$![]() on $\mathcal {U}$
on $\mathcal {U}$![]() , where $F$
, where $F$![]() denotes the differential operator associated to the system. We say that system (1.1) is completely analytically integrable if it admits two functionally independent local analytic first integrals. García [Reference García14] has proved that a Hopf-zero singularity is completely analytically integrable if, and only if, it is orbitally equivalent to its linear part $(-y,\,x,\,0)^{T}.$
denotes the differential operator associated to the system. We say that system (1.1) is completely analytically integrable if it admits two functionally independent local analytic first integrals. García [Reference García14] has proved that a Hopf-zero singularity is completely analytically integrable if, and only if, it is orbitally equivalent to its linear part $(-y,\,x,\,0)^{T}.$![]() He also proved that both integrability problem and centre problem (that consists of determining whether there is a neighbourhood of the singularity foliated by period orbits, including a curve of equilibria) are equivalent for system (1.1). So, as a direct consequence of [Reference García14], system (1.1) with $(a_1,\,a_2,\,b_1,\,b_2)$
He also proved that both integrability problem and centre problem (that consists of determining whether there is a neighbourhood of the singularity foliated by period orbits, including a curve of equilibria) are equivalent for system (1.1). So, as a direct consequence of [Reference García14], system (1.1) with $(a_1,\,a_2,\,b_1,\,b_2)$![]() non-zero does not have two functionally independent analytic first integral since it is not linearizable. In other words, the $\mathbb {Z}_2\otimes \mathbb {Z}_2$
non-zero does not have two functionally independent analytic first integral since it is not linearizable. In other words, the $\mathbb {Z}_2\otimes \mathbb {Z}_2$![]() -symmetric Hopf-zero singularity we are considering is not completely integrable and our analysis will be focused on detecting the existence of one functionally independent analytic first integral for such a singularity.
-symmetric Hopf-zero singularity we are considering is not completely integrable and our analysis will be focused on detecting the existence of one functionally independent analytic first integral for such a singularity.
This is a difficult problem and there are few known satisfactory methods to solve it. In the present paper, we use the orbital normal form obtained in [Reference Algaba, Freire and Gamero1] to establish necessary conditions for the existence of analytic first integrals and formal inverse Jacobi multipliers.
The first result provides an orbital normal form for the systems (1.1) having one, and only one, functionally independent analytic first integral.
Theorem 1.1 Consider the analytic system (1.1) with $a_1^{2}+b_1^{2}\ne 0$![]() and $a_2^{2}+b_2^{2}\ne 0$
and $a_2^{2}+b_2^{2}\ne 0$![]() where $(a_1,\,a_2,\,b_1,\,b_2)$
where $(a_1,\,a_2,\,b_1,\,b_2)$![]() is given in (1.3). System (1.1) has one, and only one, functionally independent analytic first integral if, and only if, it is orbitally equivalent to the system
is given in (1.3). System (1.1) has one, and only one, functionally independent analytic first integral if, and only if, it is orbitally equivalent to the system

where $\Psi$![]() is a formal function with $\Psi (0,\,0)=0$
is a formal function with $\Psi (0,\,0)=0$![]() and $(a_1,\,a_2,\,b_1,\,b_2)$
and $(a_1,\,a_2,\,b_1,\,b_2)$![]() satisfying one of the following two conditions:
satisfying one of the following two conditions:
(a) $a_1=a_2=0$
 (or $b_1=b_2=0).$
(or $b_1=b_2=0).$ Moreover, in this case, an analytic first integral is of the form $x^{2}+y^{2}+\cdots$
Moreover, in this case, an analytic first integral is of the form $x^{2}+y^{2}+\cdots$ (or $z^{2}+\cdots$
(or $z^{2}+\cdots$ ).
).(b) there exists a rational $m$
 such that $p:=b_2(b_1-a_1)m,\,\ q:=a_1(a_2-b_2)m$
such that $p:=b_2(b_1-a_1)m,\,\ q:=a_1(a_2-b_2)m$ and $s:=(a_1b_2-a_2b_1)m$
and $s:=(a_1b_2-a_2b_1)m$ are natural numbers and $\mbox {gcd}(p,\,q,\,s)=1.$
are natural numbers and $\mbox {gcd}(p,\,q,\,s)=1.$ Moreover, in this case, an analytic first integral is of the form $(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}+\cdots.$
Moreover, in this case, an analytic first integral is of the form $(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}+\cdots.$
Remark 1.2 The assumptions $a_1^{2}+b_1^{2}\ne 0$![]() and $a_2^{2}+b_2^{2}\ne 0$
and $a_2^{2}+b_2^{2}\ne 0$![]() in theorem 1.1 are necessary. System
in theorem 1.1 are necessary. System

satisfies $a_1=b_1=0$![]() and $a_2=-2,\,\ b_2=1.$
and $a_2=-2,\,\ b_2=1.$![]() On the one hand, $(x^{2}+y^{2})z^{2}(z^{2}-(x^{2}+y^{2})^{2})$
On the one hand, $(x^{2}+y^{2})z^{2}(z^{2}-(x^{2}+y^{2})^{2})$![]() is a polynomial first integral of (1.5). As $(a_1,\,a_2,\,b_1,\,b_2)$
is a polynomial first integral of (1.5). As $(a_1,\,a_2,\,b_1,\,b_2)$![]() is non-zero, it has one and only one functionally independent analytic first integral. On the other hand, system (1.5) in cylindrical coordinates is
is non-zero, it has one and only one functionally independent analytic first integral. On the other hand, system (1.5) in cylindrical coordinates is
By [Reference Algaba, Freire and Gamero1], system (1.5) is an orbital normal form and it is unique, therefore the terms $r^{5}\partial _r$![]() and $-3r^{4}z\partial _z$
and $-3r^{4}z\partial _z$![]() can not be removed. So, it is not orbitally equivalent to system (1.4).
can not be removed. So, it is not orbitally equivalent to system (1.4).
We conclude that if $(a_1,\,a_2,\,b_1,\,b_2)$![]() is non-zero but $a_1=b_1=0$
is non-zero but $a_1=b_1=0$![]() or $a_2=b_2=0,$
or $a_2=b_2=0,$![]() there are systems (1.1) not orbitally equivalent to systems (1.4) with one analytic first integral. Thus, in this case, the analytic partial integrability problem is an open problem.
there are systems (1.1) not orbitally equivalent to systems (1.4) with one analytic first integral. Thus, in this case, the analytic partial integrability problem is an open problem.
An inverse Jacobi multiplier for a system $\dot {{{\mathbf {x}}}}={{\mathbf {F}}}({{\mathbf {x}}}),\,\ {{\mathbf {x}}}\in \mathbb {R}^{n},$![]() is a smooth function $J$
is a smooth function $J$![]() which satisfies $F(J)=\mbox {div}({{\mathbf {F}}})J$
which satisfies $F(J)=\mbox {div}({{\mathbf {F}}})J$![]() in a neighbourhood of the origin. When $J$
in a neighbourhood of the origin. When $J$![]() does not vanish in an open set, then the above equality becomes $\mbox {div}(\frac {{{\mathbf {F}}}}{J})=0.$
does not vanish in an open set, then the above equality becomes $\mbox {div}(\frac {{{\mathbf {F}}}}{J})=0.$![]() For planar systems, the inverse Jacobi multipliers are usually referred as inverse integrating factors, see [Reference Berrone and Giacomini7].
For planar systems, the inverse Jacobi multipliers are usually referred as inverse integrating factors, see [Reference Berrone and Giacomini7].
The inverse Jacobi multiplier is a useful tool in the study of vector fields. So, for example, the existence of a class of inverse Jacobi multipliers (or inverse integrating factors) has been used for the study of the Hopf bifurcation and centre problem, see [Reference Buică, García and Maza9–Reference Buică, García and Maza11, Reference Giné and Peralta-Salas16, Reference Zhang24], and for the integrability problem in general, see [Reference Algaba, Fuentes, Gamero and García2, Reference Buică and García8, Reference Weng and Zhang21].
Here, we solve the analytic partial-integrability problem for systems (1.1) through the existence of an inverse Jacobi multiplier.
Theorem 1.3 Consider the analytic system (1.1) with $a_1^{2}+b_1^{2}\ne 0$![]() and $a_2^{2}+b_2^{2}\ne 0$
and $a_2^{2}+b_2^{2}\ne 0$![]() where $(a_1,\,a_2,\,b_1,\,b_2)$
where $(a_1,\,a_2,\,b_1,\,b_2)$![]() is given in (1.3). System (1.1) has one, and only one, functionally independent analytic first integral if, and only if, it has a formal inverse Jacobi multiplier of the form
is given in (1.3). System (1.1) has one, and only one, functionally independent analytic first integral if, and only if, it has a formal inverse Jacobi multiplier of the form
with $(a_1,\,a_2,\,b_1,\,b_2)$![]() satisfying one of the following two conditions:
satisfying one of the following two conditions:
(a) $a_1=a_2=0$
 (or $b_1=b_2=0),$
(or $b_1=b_2=0),$
(b) $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$
 and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$ are rational numbers different from zero with the same sign.
are rational numbers different from zero with the same sign.
This theorem is proved in § 3.
We note that the degree of the lowest-degree term of the analytic first integral is two or $2(p+q+s)$![]() while the degree of the lowest-degree of the inverse Jacobi multiplier is five.
while the degree of the lowest-degree of the inverse Jacobi multiplier is five.
2. Computation of necessary conditions of analytic partial integrability of system (1.2)
In this section, we give a result that provides an efficient method for obtaining necessary conditions of existence of one analytic first integral of system (1.2) (orbital normal forms up to order 3 of systems whose origin is a symmetric Hopf-zero singularity). Here, we denote by $\mathscr {P}_j$![]() the vector space of the homogeneous polynomials of degree $j$
the vector space of the homogeneous polynomials of degree $j$![]() with three variables. First, we present the following result.
with three variables. First, we present the following result.
Proposition 2.1 The following statements are satisfied:
(i) Consider system (1.2) with $a_1=a_2=0$
 and $b_1b_2\ne 0.$
and $b_1b_2\ne 0.$ Then, there exists a scalar function $I=x^{2}+y^{2}+\sum _{k\ge 2}I_{2k},$
Then, there exists a scalar function $I=x^{2}+y^{2}+\sum _{k\ge 2}I_{2k},$ with $I_{2k}\in \mathscr {P}_{2k}$
with $I_{2k}\in \mathscr {P}_{2k}$ unique module $(x^{2}+y^{2})^{k},$
unique module $(x^{2}+y^{2})^{k},$ for all $k,$
for all $k,$ that verifies
(2.1)\begin{equation} F(I)=\sum_{k\ge 2}\left(\eta_k(x^{2}+y^{2})^{k}+\nu_kz^{2k}\right). \end{equation}
that verifies
(2.1)\begin{equation} F(I)=\sum_{k\ge 2}\left(\eta_k(x^{2}+y^{2})^{k}+\nu_kz^{2k}\right). \end{equation}
(ii) Consider system (1.2) with $b_1=b_2=0$
 and $a_1a_2\ne 0.$
and $a_1a_2\ne 0.$ Then, there exists a scalar function $I=z^{2}+\sum _{k\ge 2}I_{2k}$
Then, there exists a scalar function $I=z^{2}+\sum _{k\ge 2}I_{2k}$ with $I_{2k}\in \mathscr {P}_{2k}$
with $I_{2k}\in \mathscr {P}_{2k}$ unique module $z^{2k}$
unique module $z^{2k}$ for all $k,$
for all $k,$ that verifies
(2.2)\begin{equation} F(I)=\sum_{k\ge 2}\left(\eta_k(x^{2}+y^{2})^{k}+\nu_kz^{2k}\right). \end{equation}
that verifies
(2.2)\begin{equation} F(I)=\sum_{k\ge 2}\left(\eta_k(x^{2}+y^{2})^{k}+\nu_kz^{2k}\right). \end{equation}
(iii) Consider system (1.2) where $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$
 and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$ are rational numbers different from zero with the same sign. Let $p:=b_2(b_1-a_1)m,\,\ q:=a_1(a_2-b_2)m$
are rational numbers different from zero with the same sign. Let $p:=b_2(b_1-a_1)m,\,\ q:=a_1(a_2-b_2)m$ and $s:=(a_1b_2-a_2b_1)m$
and $s:=(a_1b_2-a_2b_1)m$ with $m$
with $m$ a rational number such that $p,\,q$
a rational number such that $p,\,q$ and $s$
and $s$ are natural numbers and $\mbox {gcd}(p,\,q,\,s)=1.$
are natural numbers and $\mbox {gcd}(p,\,q,\,s)=1.$ Then, there exists a scalar function $I=I_{2M}+\sum _{k>M}I_{2k},$
Then, there exists a scalar function $I=I_{2M}+\sum _{k>M}I_{2k},$ with $I_{2M}=(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s},$
with $I_{2M}=(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s},$ (i.e. $M=p+q+s$
(i.e. $M=p+q+s$ ) with $I_{2k}$
) with $I_{2k}$ unique if $k\not \equiv 0(\mbox {mod}\, M),$
unique if $k\not \equiv 0(\mbox {mod}\, M),$ and $I_{2Mk}$
and $I_{2Mk}$ unique module $I_{2M}^{k},$
unique module $I_{2M}^{k},$ for all $k,$
for all $k,$ that verifies
(2.3)\begin{align} F(I)& =\sum_{{\scriptsize q(k-1)\not\equiv 0(\mbox{mod}\, M)}}\nu_kz^{2k}+\sum_{{\scriptsize q(k-1)\equiv 0(\mbox{mod}\, M)}\atop{\scriptsize p(k-1)\not\equiv 0(\mbox{mod}\, M)}}\eta_k(x^{2}+y^{2})^{k}\\ & \quad+\sum_{{\scriptsize k-1\equiv 0(\mbox{mod}\,M)}}\left(\nu_kz^{2k}+\eta_{k}(x^{2}+y^{2})^{k}\right). \nonumber \end{align}
that verifies
(2.3)\begin{align} F(I)& =\sum_{{\scriptsize q(k-1)\not\equiv 0(\mbox{mod}\, M)}}\nu_kz^{2k}+\sum_{{\scriptsize q(k-1)\equiv 0(\mbox{mod}\, M)}\atop{\scriptsize p(k-1)\not\equiv 0(\mbox{mod}\, M)}}\eta_k(x^{2}+y^{2})^{k}\\ & \quad+\sum_{{\scriptsize k-1\equiv 0(\mbox{mod}\,M)}}\left(\nu_kz^{2k}+\eta_{k}(x^{2}+y^{2})^{k}\right). \nonumber \end{align}
Proof. Taylor expansion of the associated vector field of system (1.2) is ${{\mathbf {F}}}={{\mathbf {F}}}_1+{{\mathbf {F}}}_3+\sum _{j\ge 2}{{\mathbf {F}}}_{2j+1},$![]() with ${{\mathbf {F}}}_1=(-y,\,x,\,0)^{T}$
with ${{\mathbf {F}}}_1=(-y,\,x,\,0)^{T}$![]() and ${{\mathbf {F}}}_3=(-y+x(a_1(x^{2}+y^{2})+a_2z^{2}),$
and ${{\mathbf {F}}}_3=(-y+x(a_1(x^{2}+y^{2})+a_2z^{2}),$![]() $x+y(a_1(x^{2}+y^{2})+a_2z^{2}),\,z(b_1(x^{2}+y^{2})+b_2z^{2}))^{T}.$
$x+y(a_1(x^{2}+y^{2})+a_2z^{2}),\,z(b_1(x^{2}+y^{2})+b_2z^{2}))^{T}.$![]() If $I=I_2+\sum _{k\ge 2}I_{2k}$
If $I=I_2+\sum _{k\ge 2}I_{2k}$![]() with $I_{2k}\in \mathscr {P}_{2k},$
with $I_{2k}\in \mathscr {P}_{2k},$![]() then $F(I)$
then $F(I)$![]() has only even-degree homogeneous terms. The equation $F(I)=0$
has only even-degree homogeneous terms. The equation $F(I)=0$![]() to degree two is satisfied. The $2k$
to degree two is satisfied. The $2k$![]() -degree term of $F(I),\,\ k\ge 2$
-degree term of $F(I),\,\ k\ge 2$![]() is
is
where $R_{2k}=\sum _{j=1}^{k-2}F_{2k-2j+1}(I_{2j}).$![]()
The procedure for obtaining the scalar function $I$![]() will have the following scheme: For each order $k$
will have the following scheme: For each order $k$![]() , we first compute $I_{2k}$
, we first compute $I_{2k}$![]() to get an expression more reduced of $R_{2k}$
to get an expression more reduced of $R_{2k}$![]() . Let us note that the term $I_{2k}$
. Let us note that the term $I_{2k}$![]() , in general, is not unique. Later on, in the following step, we will use the no-uniqueness of $I_{2k-2}$
, in general, is not unique. Later on, in the following step, we will use the no-uniqueness of $I_{2k-2}$![]() for obtaining the simplest expression of $F(I)_{2k}.$
for obtaining the simplest expression of $F(I)_{2k}.$![]()
The above scheme suggests us to consider the following linear operators. The operator
It is easy to prove that $\mbox {Ker}({{\ell }^{(3)}}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k},\,(x^{2}+y^{2})^{k-1}z^{2},\,\cdots,\, z^{2k}\}.$![]() Moreover, $\mathscr {P}_{2k}=\mbox {Range}({{\ell }^{(3)}}_{2k})\bigoplus \mbox {Ker}({{\ell }^{(3)}}_{2k}).$
Moreover, $\mathscr {P}_{2k}=\mbox {Range}({{\ell }^{(3)}}_{2k})\bigoplus \mbox {Ker}({{\ell }^{(3)}}_{2k}).$![]() Therefore, for all $k\ge 2,$
Therefore, for all $k\ge 2,$![]() we can choose $\mbox {Cor}({{\ell }^{(3)}}_{2k})=\mbox {Ker}({{\ell }^{(3)}}_{2k}),$
we can choose $\mbox {Cor}({{\ell }^{(3)}}_{2k})=\mbox {Ker}({{\ell }^{(3)}}_{2k}),$![]() a complementary subspace to $\mbox {Range}({{\ell }^{(3)}}_{2k}).$
a complementary subspace to $\mbox {Range}({{\ell }^{(3)}}_{2k}).$![]()
We also consider the linear operator:
The transformed by $\tilde {{\ell }}^{(3)}_{2k}$![]() of an element of the basis of $\mbox {Ker}({{\ell }^{(3)}}_{2k-2}),\,\ (x^{2}+y^{2})^{k_0}z^{2j_0}$
of an element of the basis of $\mbox {Ker}({{\ell }^{(3)}}_{2k-2}),\,\ (x^{2}+y^{2})^{k_0}z^{2j_0}$![]() with $0\le k_0,\, j_0\le k-1,\,\ k_0+j_0= k-1,$
with $0\le k_0,\, j_0\le k-1,\,\ k_0+j_0= k-1,$![]() is
is
where $A_{j_0,k_0}=b_1j_0+a_1k_0$![]() and $B_{j_0,k_0}=b_2j_0+a_2k_0.$
and $B_{j_0,k_0}=b_2j_0+a_2k_0.$![]()
Therefore, the operator $\tilde {{\ell }}^{(3)}_{2k}$![]() is well-defined.
is well-defined.
We analyse each case:
Consider system (1.2) with $a_1=a_2=0$![]() and $b_1b_2\ne 0.$
and $b_1b_2\ne 0.$![]() The proof consists on the computation, degree to degree, of the homogeneous terms of $I=I_2+I_4+\cdots,$
The proof consists on the computation, degree to degree, of the homogeneous terms of $I=I_2+I_4+\cdots,$![]() with $I_2=x^{2}+y^{2},$
with $I_2=x^{2}+y^{2},$![]() satisfying (2.1).
satisfying (2.1).
The transformed by $\tilde {{\ell }}^{(3)}_{2k}$![]() of an element of the basis of $\mbox {Ker}({{\ell }^{(3)}}_{2k-2})$
of an element of the basis of $\mbox {Ker}({{\ell }^{(3)}}_{2k-2})$![]() is
is
Therefore, $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k-1}\}$![]() and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k},\,z^{2k}\}.$
and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k},\,z^{2k}\}.$![]()
We write $I_{2k-2}=I_{2k-2}^{a}+I_{2k-2}^{b}$![]() with $I_{2k-2}^{b}$
with $I_{2k-2}^{b}$![]() fixed in the previous step and $I_{2k-2}^{a}\in \mbox {Ker}({{\ell }^{(3)}}_{2k-2})$
fixed in the previous step and $I_{2k-2}^{a}\in \mbox {Ker}({{\ell }^{(3)}}_{2k-2})$![]() . So, for $k\ge 2,$
. So, for $k\ge 2,$![]()
We now write $\tilde {R}_{2k}=F_3(I_{2k-2}^{b})+R_{2k}=\tilde {R}_{2k}^{(r)}+\tilde {R}_{2k}^{(c)}$![]() with $\tilde {R}_{2k}^{(r)}\in \mbox {Range}({{\ell }^{(3)}}_{2k})$
with $\tilde {R}_{2k}^{(r)}\in \mbox {Range}({{\ell }^{(3)}}_{2k})$![]() and $\tilde {R}_{2k}^{(c)}\in \mbox {Cor}({{\ell }^{(3)}}_{2k}).$
and $\tilde {R}_{2k}^{(c)}\in \mbox {Cor}({{\ell }^{(3)}}_{2k}).$![]()
Reasoning as in the classical Normal Form Theory, we choose $I_{2k}$![]() such that ${{\ell }^{(3)}}_{2k}(I_{2k})=-\tilde {R}_{2k}^{(r)}$
such that ${{\ell }^{(3)}}_{2k}(I_{2k})=-\tilde {R}_{2k}^{(r)}$![]() and choose $I_{2k-2}^{a}$
and choose $I_{2k-2}^{a}$![]() in order to annihilate the part of $\tilde {R}_{2k}^{(c)}$
in order to annihilate the part of $\tilde {R}_{2k}^{(c)}$![]() belonging to the range of the operator $\tilde {{\ell }}^{(3)}_{2k}.$
belonging to the range of the operator $\tilde {{\ell }}^{(3)}_{2k}.$![]() So, we have that $F(I)_{2k}=\eta _k(x^{2}+y^{2})^{k}+\nu _kz^{2k}\in \mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k}),$
So, we have that $F(I)_{2k}=\eta _k(x^{2}+y^{2})^{k}+\nu _kz^{2k}\in \mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k}),$![]() with $\eta _k$
with $\eta _k$![]() and $\nu _k$
and $\nu _k$![]() real numbers.
real numbers.
Last on, we note that the solutions of the equation (2.1) are $I_{2k}+\lambda _k(x^{2}+y^{2})^{k},$![]() where $I_{2k}$
where $I_{2k}$![]() is the unique solution chosen following the recursive procedure and $\lambda _k$
is the unique solution chosen following the recursive procedure and $\lambda _k$![]() real, that is, $I_{2k}$
real, that is, $I_{2k}$![]() is unique module $(x^{2}+y^{2})^{k}.$
is unique module $(x^{2}+y^{2})^{k}.$![]()
Consider system (1.2) with $b_1=b_2=0$![]() and $a_1a_2\ne 0.$
and $a_1a_2\ne 0.$![]() In this case, we derive, degree to degree, the homogeneous terms of $I=I_2+I_4+\cdots,$
In this case, we derive, degree to degree, the homogeneous terms of $I=I_2+I_4+\cdots,$![]() with $I_2=z^{2},$
with $I_2=z^{2},$![]() satisfying the equation (2.2).
satisfying the equation (2.2).
It has that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{z^{2(k-1)}\}$![]() and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k},\,z^{2k}\}.$
and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k},\,z^{2k}\}.$![]() Reasoning as before, we obtain the result.
Reasoning as before, we obtain the result.
For systems (1.2) where $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$![]() and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$![]() are rational numbers different from zero with the same sign, we compute the homogeneous terms of $I=I_{2M}+\sum _{k>M}I_{2k},$
are rational numbers different from zero with the same sign, we compute the homogeneous terms of $I=I_{2M}+\sum _{k>M}I_{2k},$![]() with $I_{2M}=(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s},$
with $I_{2M}=(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s},$![]() satisfying the equation (2.3). It has that $\tilde {{\ell }}^{(3)}_{2k}((x^{2}+y^{2})^{k_0}z^{2j_0})$
satisfying the equation (2.3). It has that $\tilde {{\ell }}^{(3)}_{2k}((x^{2}+y^{2})^{k_0}z^{2j_0})$![]() is given by (2.6) where
is given by (2.6) where
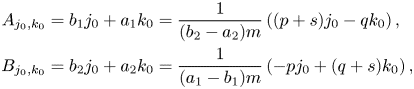
with $0\le k_0,\, j_0\le k-1,\,\ k_0+j_0= k-1.$![]() Note that $(p+s)j_0-qk_0=Mj_0-q(k-1),$
Note that $(p+s)j_0-qk_0=Mj_0-q(k-1),$![]() i.e. $\{A_{j_0,k_0}\},\,\ j_0=0,\,\dots,\, k-1,$
i.e. $\{A_{j_0,k_0}\},\,\ j_0=0,\,\dots,\, k-1,$![]() is an arithmetic progression whose difference is $M\ne 0$
is an arithmetic progression whose difference is $M\ne 0$![]() , and $-pj_0+(q+s)k_0=Mk_0-p(k-1),\,$
, and $-pj_0+(q+s)k_0=Mk_0-p(k-1),\,$![]() i.e. $\{B_{j_0,k_0}\},\,\ k_0=0,\,\dots,\, k-1,$
i.e. $\{B_{j_0,k_0}\},\,\ k_0=0,\,\dots,\, k-1,$![]() is an arithmetic progression whose difference is $M$
is an arithmetic progression whose difference is $M$![]() . Therefore, the numbers $A_{j_0,k_0}$
. Therefore, the numbers $A_{j_0,k_0}$![]() with $0\le k_0,\, j_0\le k-1,\,\ k_0+j_0= k-1,$
with $0\le k_0,\, j_0\le k-1,\,\ k_0+j_0= k-1,$![]() are different and the numbers $B_{j_0,k_0}$
are different and the numbers $B_{j_0,k_0}$![]() also are different. Fixed $k$
also are different. Fixed $k$![]() , this fact allows us to distinguish the following cases:
, this fact allows us to distinguish the following cases:
If $A_{j_0,k_0}\ne 0$![]() for all $0\le k_0,\, j_0\le k-1,$
for all $0\le k_0,\, j_0\le k-1,$![]() with $k_0+j_0= k-1,$
with $k_0+j_0= k-1,$![]() (i.e. $q(k-1)\not \equiv 0(\mbox {mod}\, M)$
(i.e. $q(k-1)\not \equiv 0(\mbox {mod}\, M)$![]() ), it has that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k})=\{ 0\}$
), it has that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k})=\{ 0\}$![]() and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{z^{2k}\}.$
and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{z^{2k}\}.$![]()
If there exists $j_1$![]() with $0< j_1< k-1$
with $0< j_1< k-1$![]() such that $A_{j_1,k_1}=0,$
such that $A_{j_1,k_1}=0,$![]() that is $Mj_1=q(k-1),$
that is $Mj_1=q(k-1),$![]() and $B_{j_0,k_0}\ne 0$
and $B_{j_0,k_0}\ne 0$![]() for all $0\le k_0,\, j_0\le k-1,$
for all $0\le k_0,\, j_0\le k-1,$![]() it has that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k})=\{ 0\}$
it has that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k})=\{ 0\}$![]() and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k}\}.$
and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k}\}.$![]()
Otherwise, there exist $(j_1,\,k_1),\, (j_2,\,k_2)$![]() such that $A_{j_1,k_1}=0$
such that $A_{j_1,k_1}=0$![]() and $B_{j_2,k_2}=0.$
and $B_{j_2,k_2}=0.$![]() We are going to prove that $k-1$
We are going to prove that $k-1$![]() is a multiple of $M$
is a multiple of $M$![]() . Indeed, we have that $k-1=\frac {j_1}{q}M=\frac {k_1}{p+s}M=\frac {j_2}{q+s}M=\frac {k_2}{p}M,$
. Indeed, we have that $k-1=\frac {j_1}{q}M=\frac {k_1}{p+s}M=\frac {j_2}{q+s}M=\frac {k_2}{p}M,$![]() i.e. $\frac {p(k-1)}{M},\, = \frac {q(k-1)}{M}$
i.e. $\frac {p(k-1)}{M},\, = \frac {q(k-1)}{M}$![]() and $\frac {s(k-1)}{M}$
and $\frac {s(k-1)}{M}$![]() are natural numbers. Thus, $\frac {(n_1p+n_2q+n_3s)(k-1)}{M}$
are natural numbers. Thus, $\frac {(n_1p+n_2q+n_3s)(k-1)}{M}$![]() is an integer number, for all $n_1,\,n_2,\,n_3\in \mathbb {Z}.$
is an integer number, for all $n_1,\,n_2,\,n_3\in \mathbb {Z}.$![]() On the other hand, from Bezout identity, there exist $m_1,\,m_2,\,m_3\in \mathbb {Z}$
On the other hand, from Bezout identity, there exist $m_1,\,m_2,\,m_3\in \mathbb {Z}$![]() such that $m_1p+m_2q+m_3s=1$
such that $m_1p+m_2q+m_3s=1$![]() since $\mbox {gcd}(p,\,q,\,s)=1.$
since $\mbox {gcd}(p,\,q,\,s)=1.$![]() Therefore, $\frac {k-1}{M}$
Therefore, $\frac {k-1}{M}$![]() is a natural number. So, $k-1$
is a natural number. So, $k-1$![]() is a multiple of $M$
is a multiple of $M$![]() .
.
If we write $k=1+\hat {k}M,$![]() it has that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{I_{2M}^{\hat {k}}\}$
it has that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{I_{2M}^{\hat {k}}\}$![]() . Moreover, $j_1=\frac {q}{q+s}j_2$
. Moreover, $j_1=\frac {q}{q+s}j_2$![]() . Thus $j_1< j_2$
. Thus $j_1< j_2$![]() and we can choose as a complementary subspace of the range of the operator $\tilde {{\ell }}^{(3)}_{2k}$
and we can choose as a complementary subspace of the range of the operator $\tilde {{\ell }}^{(3)}_{2k}$![]() to $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k},\,z^{2k}\}.$
to $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k})=\mbox {Span}\{(x^{2}+y^{2})^{k},\,z^{2k}\}.$![]() Reasoning as before, we obtain the result.
Reasoning as before, we obtain the result.
The following result characterizes the analytic integrability of system (1.2). An algorithm for obtaining necessary conditions of existence of a first integral can be derived following the scheme of the proof of proposition 2.1.
Theorem 2.2 Consider system (1.2) with $(a_1,\,a_2,\,b_1,\,b_2)$![]() satisfying one of the following two conditions:
satisfying one of the following two conditions:
(a) $a_1=a_2=0$
 and $b_1b_2\ne 0$
and $b_1b_2\ne 0$ (or $b_1=b_2=0$
(or $b_1=b_2=0$ and $a_1a_2\ne 0$
and $a_1a_2\ne 0$ ).
).(b) $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$
 and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$ are rational numbers different from zero with the same sign.
are rational numbers different from zero with the same sign.
Then, system (1.2) has one, and only one, functionally independent analytic first integral if, and only if, the equations (2.1), (2.2) and (2.3) , introduced in proposition 2.1, satisfy $\eta _k=0$![]() and $\nu _k=0$
and $\nu _k=0$![]() for all $k.$
for all $k.$![]()
Proof. Consider the function $I$![]() introduced in proposition 2.1. The sufficient condition is trivial. If $\eta _k=\nu _k=0,$
introduced in proposition 2.1. The sufficient condition is trivial. If $\eta _k=\nu _k=0,$![]() for all $k,$
for all $k,$![]() then the function $I$
then the function $I$![]() is a formal first integral since $F(I)=0.$
is a formal first integral since $F(I)=0.$![]() From lemma 3.1, system (1.2) admits an analytic first integral. Moreover, from García [Reference García14] it is not completely analytically integrable because it is not linearizable. Therefore, system (1.2) has a unique functionally independent first integral.
From lemma 3.1, system (1.2) admits an analytic first integral. Moreover, from García [Reference García14] it is not completely analytically integrable because it is not linearizable. Therefore, system (1.2) has a unique functionally independent first integral.
Let us prove the necessary condition. If system (1.2) has an analytic first integral then, from theorem 1.1, according to each case, it admits an analytic first integral $\tilde {I}$![]() of the form $x^{2}+y^{2}+\cdots,\,\ z^{2}+\cdots$
of the form $x^{2}+y^{2}+\cdots,\,\ z^{2}+\cdots$![]() or $(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}+\cdots,$
or $(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}+\cdots,$![]() having only even-degree homogeneous terms. Then, $I_p=\tilde {I}-\sum _{k\ge 2}\beta _k\tilde {I}^{k}$
having only even-degree homogeneous terms. Then, $I_p=\tilde {I}-\sum _{k\ge 2}\beta _k\tilde {I}^{k}$![]() is also a formal first integral, i.e. $F(I_p)=0.$
is also a formal first integral, i.e. $F(I_p)=0.$![]() To complete the proof it is enough to choose $\beta _k$
To complete the proof it is enough to choose $\beta _k$![]() such that $I_p$
such that $I_p$![]() is the unique scalar function given by proposition 2.1. Thus, by the uniqueness of $I_p$
is the unique scalar function given by proposition 2.1. Thus, by the uniqueness of $I_p$![]() , $\eta _k=\nu _k=0,$
, $\eta _k=\nu _k=0,$![]() for all $k.$
for all $k.$![]()
We can also provide an integrability criterium based on the existence of an inverse Jacobi multiplier of system (1.2). First, we give an auxiliary result.
Proposition 2.3 The following statements are satisfied:
(i) Consider system (1.2) with $a_1=a_2=0$
 and $b_1b_2\ne 0.$
and $b_1b_2\ne 0.$ Then, there exists a scalar function
\[ J=J_5+\displaystyle\sum_{k\ge 3}J_{2k+1} \]with $J_5=(x^{2}+y^{2})z(b_1(x^{2}+y^{2})+b_2z^{2})$
Then, there exists a scalar function
\[ J=J_5+\displaystyle\sum_{k\ge 3}J_{2k+1} \]with $J_5=(x^{2}+y^{2})z(b_1(x^{2}+y^{2})+b_2z^{2})$
 and $J_{2k+1}\in \mathscr {P}_{2k+1}$
and $J_{2k+1}\in \mathscr {P}_{2k+1}$ unique module $(x^{2}+y^{2})^{k-1}z(b_1(x^{2}+y^{2})+b_2z^{2})$
unique module $(x^{2}+y^{2})^{k-1}z(b_1(x^{2}+y^{2})+b_2z^{2})$ for all $k$
for all $k$ , that verifies
(2.7)\begin{equation} F(J)-J\mbox{div}({{\mathbf{F}}})=\sum_{k\ge 3}\left(\eta_kz(x^{2}+y^{2})^{k}+\nu_kz^{2k+1}\right). \end{equation}
, that verifies
(2.7)\begin{equation} F(J)-J\mbox{div}({{\mathbf{F}}})=\sum_{k\ge 3}\left(\eta_kz(x^{2}+y^{2})^{k}+\nu_kz^{2k+1}\right). \end{equation}
(ii) Consider system (1.2) with $b_1=b_2=0$
 and $a_1a_2\ne 0.$
and $a_1a_2\ne 0.$ Then, there exists a scalar function
\[ J=J_5+\displaystyle\sum_{k\ge 3}J_{2k+1} \]with $J_5=(x^{2}+y^{2})z(a_1(x^{2}+y^{2})+a_2z^{2})$
Then, there exists a scalar function
\[ J=J_5+\displaystyle\sum_{k\ge 3}J_{2k+1} \]with $J_5=(x^{2}+y^{2})z(a_1(x^{2}+y^{2})+a_2z^{2})$
 and $J_{2k+1}\in \mathscr {P}_{2k+1}$
and $J_{2k+1}\in \mathscr {P}_{2k+1}$ unique module $(x^{2}+y^{2})z^{2k-3}(a_1(x^{2}+y^{2})+a_2z^{2})$
unique module $(x^{2}+y^{2})z^{2k-3}(a_1(x^{2}+y^{2})+a_2z^{2})$ for all $k$
for all $k$ , that verifies
(2.8)\begin{equation} F(J)-J\mbox{div}({{\mathbf{F}}})=\sum_{k\ge 3}\left(\eta_kz(x^{2}+y^{2})^{k}+\nu_kz^{2k+1}\right). \end{equation}
, that verifies
(2.8)\begin{equation} F(J)-J\mbox{div}({{\mathbf{F}}})=\sum_{k\ge 3}\left(\eta_kz(x^{2}+y^{2})^{k}+\nu_kz^{2k+1}\right). \end{equation}
(iii) Consider system (1.2) where $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$
 and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$ are rational numbers different from zero with the same sign. Let $p:=b_2(b_1-a_1)m,\,\ q:=a_1(a_2-b_2)m$
are rational numbers different from zero with the same sign. Let $p:=b_2(b_1-a_1)m,\,\ q:=a_1(a_2-b_2)m$ and $s:=(a_1b_2-a_2b_1)m$
and $s:=(a_1b_2-a_2b_1)m$ where $m$
where $m$ is a rational such that $p,\,q$
is a rational such that $p,\,q$ and $s$
and $s$ are natural numbers with $\mbox {gcd}(p,\,q,\,s)=1$
are natural numbers with $\mbox {gcd}(p,\,q,\,s)=1$ . Then, there exists a scalar function
\[ J=J_5+\displaystyle\sum_{k\ge 3}J_{2k+1} \]with $J_5=(x^{2}+y^{2})z((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2}),$
. Then, there exists a scalar function
\[ J=J_5+\displaystyle\sum_{k\ge 3}J_{2k+1} \]with $J_5=(x^{2}+y^{2})z((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2}),$
 $J_{2k+1}$
$J_{2k+1}$ unique if $k\not \equiv 3 (\mbox {mod}\, M)$
unique if $k\not \equiv 3 (\mbox {mod}\, M)$ being $M=p+q+s$
being $M=p+q+s$ and $J_{2kM+5}$
and $J_{2kM+5}$ unique module $(x^{2}+y^{2})^{pk+1}z^{2qk+1}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{sk+1}$
unique module $(x^{2}+y^{2})^{pk+1}z^{2qk+1}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{sk+1}$ for all $k$
for all $k$ , that verifies
(2.9)\begin{align} F(J)-J\mbox{div}({{\mathbf{F}}})& =\sum_{{\scriptsize q(k-3)\not\equiv 0(\mbox{mod}\, M)}}\nu_kz^{2k+1}+ \sum_{{\scriptsize q(k-3)\equiv 0(\mbox{mod}\, M)}\atop{\scriptsize p(k-3)\not\equiv 0( \mbox{mod}\,M)}}\eta_k(x^{2}+y^{2})^{k}z \\ & \quad+ \sum_{{\scriptsize k-3\equiv 0(\mbox{mod}\,M)}}\left(\nu_kz^{2k+1}+\eta_{k}(x^{2}+y^{2})^{k}z\right). \nonumber \end{align}
, that verifies
(2.9)\begin{align} F(J)-J\mbox{div}({{\mathbf{F}}})& =\sum_{{\scriptsize q(k-3)\not\equiv 0(\mbox{mod}\, M)}}\nu_kz^{2k+1}+ \sum_{{\scriptsize q(k-3)\equiv 0(\mbox{mod}\, M)}\atop{\scriptsize p(k-3)\not\equiv 0( \mbox{mod}\,M)}}\eta_k(x^{2}+y^{2})^{k}z \\ & \quad+ \sum_{{\scriptsize k-3\equiv 0(\mbox{mod}\,M)}}\left(\nu_kz^{2k+1}+\eta_{k}(x^{2}+y^{2})^{k}z\right). \nonumber \end{align}
Proof. Taylor expansion of the associated vector field of system (1.2) is ${{\mathbf {F}}}={{\mathbf {F}}}_1+{{\mathbf {F}}}_3+\sum _{k\ge 2}{{\mathbf {F}}}_{2k+1},$![]() with ${{\mathbf {F}}}_1=(-y,\,x,\,0)^{T}$
with ${{\mathbf {F}}}_1=(-y,\,x,\,0)^{T}$![]() and ${{\mathbf {F}}}_3=(-y+x(a_1(x^{2}+y^{2})+a_2z^{2}),$
and ${{\mathbf {F}}}_3=(-y+x(a_1(x^{2}+y^{2})+a_2z^{2}),$![]() $x+y(a_1(x^{2}+y^{2})+a_2z^{2}),\,z(b_1(x^{2}+y^{2})+b_2z^{2}))^{T}.$
$x+y(a_1(x^{2}+y^{2})+a_2z^{2}),\,z(b_1(x^{2}+y^{2})+b_2z^{2}))^{T}.$![]() Thus $F(J)-J\mbox {div}({{\mathbf {F}}})$
Thus $F(J)-J\mbox {div}({{\mathbf {F}}})$![]() has only odd-degree homogeneous terms. The term of degree five of $F(J)-J\mbox {div}({{\mathbf {F}}})$
has only odd-degree homogeneous terms. The term of degree five of $F(J)-J\mbox {div}({{\mathbf {F}}})$![]() is zero. The $2k+1$
is zero. The $2k+1$![]() -degree term of $F(J)-J\mbox {div}({{\mathbf {F}}}),\,\ k\ge 3$
-degree term of $F(J)-J\mbox {div}({{\mathbf {F}}}),\,\ k\ge 3$![]() is
is
where $R_{2k+1}=\sum _{j=1}^{k-2}F_{2k-2j+1}(J_{2j+1})-J_{2j+1}\mbox {div}({{\mathbf {F}}}_{2k-2j+1}).$![]()
Applying Euler Theorem for homogeneous function, it has that $F_3(J_{2k-1})-J_{2k-1}\mbox {div}({{\mathbf {F}}}_3)=(F_3-\frac {1}{2k-1}\mbox {div}({{\mathbf {F}}}_3)(x,\,y,\,z)^{T})(J_{2k-1})$![]()
The above expression suggests us to consider the following linear operators. The operator
It is easy to prove that $\mbox {Ker}({{\ell }^{(3)}}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k}z,\,(x^{2}+y^{2})^{k-1}z^{3},\,\cdots, z^{2k+1}\}.$![]() Moreover, we can choose $\mbox {Cor}({{\ell }^{(3)}}_{2k+1})=\mbox {Ker}({{\ell }^{(3)}}_{2k+1}).$
Moreover, we can choose $\mbox {Cor}({{\ell }^{(3)}}_{2k+1})=\mbox {Ker}({{\ell }^{(3)}}_{2k+1}).$![]()
We also consider the linear operator:
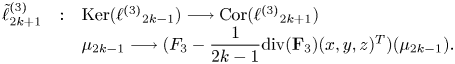
The transformed by $\tilde {{\ell }}^{(3)}_{2k+1}$![]() of an element of the basis of $\mbox {Ker}({{\ell }^{(3)}}_{2k-1}),\, (x^{2}+y^{2})^{k_0}z^{2j_0+1}$
of an element of the basis of $\mbox {Ker}({{\ell }^{(3)}}_{2k-1}),\, (x^{2}+y^{2})^{k_0}z^{2j_0+1}$![]() with $0\le k_0,\, j_0\le k-1,\,\ k_0+j_0= k-1,$
with $0\le k_0,\, j_0\le k-1,\,\ k_0+j_0= k-1,$![]() is
is
where $A_{j_0,k_0}=b_1j_0+a_1(k_0-2)$![]() and $B_{j_0,k_0}=b_2(j_0-1)+a_2(k_0-1).$
and $B_{j_0,k_0}=b_2(j_0-1)+a_2(k_0-1).$![]() Therefore, the operator $\tilde {{\ell }}^{(3)}_{2k+1}$
Therefore, the operator $\tilde {{\ell }}^{(3)}_{2k+1}$![]() is well-defined.
is well-defined.
If we write $J_{2k-1}=J_{2k-1}^{a}+J_{2k-1}^{b}$![]() with $J_{2k-1}^{b}$
with $J_{2k-1}^{b}$![]() chosen in the previous step and $J_{2k-1}^{a}\in \mbox {Ker}({{\ell }^{(3)}}_{2k-1}),$
chosen in the previous step and $J_{2k-1}^{a}\in \mbox {Ker}({{\ell }^{(3)}}_{2k-1}),$![]() the expression (2.10), for $k\ge 3$
the expression (2.10), for $k\ge 3$![]() , becomes
, becomes
where $\tilde {R}_{2k+1}=F_3(J_{2k-1}^{b})-J_{2k-1}^{b}\mbox {div}({{\mathbf {F}}}_3)+R_{2k+1}.$![]()
We now write $\tilde {R}_{2k+1}=\tilde {R}_{2k+1}^{(r)}+\tilde {R}_{2k+1}^{(c)}$![]() with $\tilde {R}_{2k+1}^{(r)}\in \mbox {Range}({{\ell }^{(3)}}_{2k+1})$
with $\tilde {R}_{2k+1}^{(r)}\in \mbox {Range}({{\ell }^{(3)}}_{2k+1})$![]() and $\tilde {R}_{2k+1}^{(c)}\in \mbox {Cor}({{\ell }^{(3)}}_{2k+1}).$
and $\tilde {R}_{2k+1}^{(c)}\in \mbox {Cor}({{\ell }^{(3)}}_{2k+1}).$![]() We now choose $J_{2k+1}$
We now choose $J_{2k+1}$![]() such that ${{\ell }^{(3)}}_{2k+1}(J_{2k+1})=-\tilde {R}_{2k+1}^{(r)}$
such that ${{\ell }^{(3)}}_{2k+1}(J_{2k+1})=-\tilde {R}_{2k+1}^{(r)}$![]() and choose $J_{2k-1}^{a}$
and choose $J_{2k-1}^{a}$![]() in order to annihilate the part of $\tilde {R}_{2k+1}^{(c)}$
in order to annihilate the part of $\tilde {R}_{2k+1}^{(c)}$![]() belonging to the range of the operator $\tilde {{\ell }}^{(3)}_{2k+1}.$
belonging to the range of the operator $\tilde {{\ell }}^{(3)}_{2k+1}.$![]()
Last on, we note that the solution of the equation (2.1) is $J_{2k+1}+J_{2k+1}^{b},$![]() for any $J_{2k+1}^{b}\in \mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+2})$
for any $J_{2k+1}^{b}\in \mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+2})$![]() real and $J_{2k+1}$
real and $J_{2k+1}$![]() is unique module $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})$
is unique module $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})$![]() .
.
We finish the proof, obtaining the expression of $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})$![]() and $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})$
and $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})$![]() for each case:
for each case:
Consider system (1.2) with $a_1=a_2=0$![]() and $b_1b_2\ne 0.$
and $b_1b_2\ne 0.$![]() It has that $A_{j_0,k_0}=b_1j_0,\, B_{j_0,k_0}=b_2(j_0-1).$
It has that $A_{j_0,k_0}=b_1j_0,\, B_{j_0,k_0}=b_2(j_0-1).$![]() So, $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k-2}z(b_1(x^{2}+y^{2})+b_2z^{2})\}$
So, $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k-2}z(b_1(x^{2}+y^{2})+b_2z^{2})\}$![]() and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k}z,\,z^{2k+1}\}.$
and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k}z,\,z^{2k+1}\}.$![]()
Consider system (1.2) with $b_1=b_2=0$![]() and $a_1a_2\ne 0.$
and $a_1a_2\ne 0.$![]() It has that $A_{j_0,k_0}=a_1(k_0-2),\, B_{j_0,k_0}=a_2(k_0-1).$
It has that $A_{j_0,k_0}=a_1(k_0-2),\, B_{j_0,k_0}=a_2(k_0-1).$![]() So, $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})z^{2(k-2)}(a_1(x^{2}+y^{2})+a_2z^{2})\}$
So, $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})z^{2(k-2)}(a_1(x^{2}+y^{2})+a_2z^{2})\}$![]() and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k}z,\,z^{2k+1}\}.$
and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k}z,\,z^{2k+1}\}.$![]()
For the systems (1.2) with $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$![]() and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$![]() are rational numbers different from zero with the same sign, it has that $\tilde {{\ell }}^{(3)}_{2k}((x^{2}+y^{2})^{k_0}z^{2j_0+1})$
are rational numbers different from zero with the same sign, it has that $\tilde {{\ell }}^{(3)}_{2k}((x^{2}+y^{2})^{k_0}z^{2j_0+1})$![]() is given by (2.13) where
is given by (2.13) where
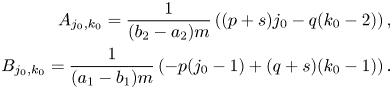
Note that $(p+s)j_0-q(k_0-2)=Mj_0-q(k-3)$![]() i.e. $\{A_{j_0,k_0}\},\,\ j_0=0,\,\dots,\, k-1,$
i.e. $\{A_{j_0,k_0}\},\,\ j_0=0,\,\dots,\, k-1,$![]() is an arithmetic progression whose difference is $M\ne 0$
is an arithmetic progression whose difference is $M\ne 0$![]() , and $-p(j_0-1)+(q+s)(k_0-1)=M(k_0-1)-p(k-3),$
, and $-p(j_0-1)+(q+s)(k_0-1)=M(k_0-1)-p(k-3),$![]() i.e. $\{B_{j_0,k_0}\},\,\ k_0=0,\,\dots,\, k-1,$
i.e. $\{B_{j_0,k_0}\},\,\ k_0=0,\,\dots,\, k-1,$![]() is an arithmetic progression whose difference is $M$
is an arithmetic progression whose difference is $M$![]() .
.
Therefore, the numbers $A_{j_0,k_0}$![]() with $0\le k_0,\, j_0\le k-1,\,\ k_0+j_0= k-1,$
with $0\le k_0,\, j_0\le k-1,\,\ k_0+j_0= k-1,$![]() are different and the numbers $B_{j_0,k_0}$
are different and the numbers $B_{j_0,k_0}$![]() also are different. Fixed $k$
also are different. Fixed $k$![]() , this fact allows us to distinguish the following cases:
, this fact allows us to distinguish the following cases:
If $A_{j_0,k_0}\ne 0$![]() for all $0\le k_0,\, j_0\le k-1,$
for all $0\le k_0,\, j_0\le k-1,$![]() with $k_0+j_0= k-1,$
with $k_0+j_0= k-1,$![]() then $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\{ 0\}$
then $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\{ 0\}$![]() and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{z^{2k+1}\}.$
and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{z^{2k+1}\}.$![]()
If there exists $j_1$![]() with $0< j_1< k-1$
with $0< j_1< k-1$![]() such that $A_{j_1,k_1}=0,$
such that $A_{j_1,k_1}=0,$![]() that is $Mj_1=q(k-3),$
that is $Mj_1=q(k-3),$![]() and $B_{j_0,k_0}\ne 0$
and $B_{j_0,k_0}\ne 0$![]() for all $0\le k_0,\, j_0\le k-1,$
for all $0\le k_0,\, j_0\le k-1,$![]() it has that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\{ 0\}$
it has that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\{ 0\}$![]() and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k}z\}.$
and we can choose $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k}z\}.$![]()
Otherwise, there exist $(j_1,\,k_1),\, (j_2,\,k_2)$![]() such that $A_{j_1,k_1}=0$
such that $A_{j_1,k_1}=0$![]() and $B_{j_2,k_2}=0.$
and $B_{j_2,k_2}=0.$![]() Reasoning as in the proof of proposition 2.1, we have that $k-3$
Reasoning as in the proof of proposition 2.1, we have that $k-3$![]() is a multiple of $M$
is a multiple of $M$![]() .
.
If we write $k=3+\hat {k}M,$![]() it is easy to check that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{J_5I_{2M}^{\hat {k}}\}$
it is easy to check that $\mbox {Ker}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{J_5I_{2M}^{\hat {k}}\}$![]() where $I_{2M}=(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}$
where $I_{2M}=(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}$![]() and we can choose as a complementary subspace of the range of the operator $\tilde {{\ell }}^{(3)}_{2k+1}$
and we can choose as a complementary subspace of the range of the operator $\tilde {{\ell }}^{(3)}_{2k+1}$![]() to $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k}z,\,z^{2k+1}\}.$
to $\mbox {Cor}(\tilde {{\ell }}^{(3)}_{2k+1})=\mbox {Span}\{(x^{2}+y^{2})^{k}z,\,z^{2k+1}\}.$![]()
The following result characterizes the analytic integrability of system (1.2). An algorithm for obtaining of necessary conditions of existence of an inverse Jacobi multiplier can be derived following the scheme of the proof of proposition 2.3.
Theorem 2.4 Consider system (1.2) with $(a_1,\,a_2,\,b_1,\,b_2)$![]() satisfying one of the following two conditions:
satisfying one of the following two conditions:
(a) $a_1=a_2=0$
 and $b_1b_2\ne 0$
and $b_1b_2\ne 0$ (or $b_1=b_2=0$
(or $b_1=b_2=0$ and $a_1a_2\ne 0$
and $a_1a_2\ne 0$ ).
).(b) $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$
 and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$ are rational numbers different from zero with the same sign.
are rational numbers different from zero with the same sign.
Then, system (1.2) has one, and only one, functionally independent analytic first integral if, and only if, the equations (2.7), (2.8) and (2.9) , introduced in proposition 2.3, satisfy $\eta _k=0$![]() and $\nu _k=0$
and $\nu _k=0$![]() for all $k.$
for all $k.$![]()
Proof. Its proof is similar to the one of theorem 2.2.
3. Proofs of the main results
In the proof of theorem 1.1, we will use the following result that is a direct consequence of [Reference Mattei and Moussu20, theorem A]. It states that the analysis of the integrability for analytic systems can be reduced to the formal context.
Lemma 3.1 Consider the analytic system $\dot {{{\mathbf {x}}}}={{\mathbf {F}}}({{\mathbf {x}}}),\,\ {{\mathbf {x}}}\in \mathbb {R}^{n}$![]() and denote the formal system $\dot {\tilde {{{\mathbf {x}}}}}=\tilde {{{\mathbf {F}}}}(\tilde {{{\mathbf {x}}}}),$
and denote the formal system $\dot {\tilde {{{\mathbf {x}}}}}=\tilde {{{\mathbf {F}}}}(\tilde {{{\mathbf {x}}}}),$![]() transformed of ${{\mathbf {F}}}$
transformed of ${{\mathbf {F}}}$![]() by the change ${{\mathbf {x}}}=\phi (\tilde {{{\mathbf {x}}}})$
by the change ${{\mathbf {x}}}=\phi (\tilde {{{\mathbf {x}}}})$![]() where $\phi$
where $\phi$![]() is a formal diffeomorphism. Then, for each $\tilde {I}$
is a formal diffeomorphism. Then, for each $\tilde {I}$![]() a formal first integral of $\dot {\tilde {{{\mathbf {x}}}}}=\tilde {{{\mathbf {F}}}}(\tilde {{{\mathbf {x}}}}),$
a formal first integral of $\dot {\tilde {{{\mathbf {x}}}}}=\tilde {{{\mathbf {F}}}}(\tilde {{{\mathbf {x}}}}),$![]() there exists a formal scalar function $\hat {l}$
there exists a formal scalar function $\hat {l}$![]() with $\hat {l}(0)=0,\,\ \hat {l}'(0)=1,$
with $\hat {l}(0)=0,\,\ \hat {l}'(0)=1,$![]() such that $\hat {l}\circ \tilde {I}\circ \phi ^{-1}$
such that $\hat {l}\circ \tilde {I}\circ \phi ^{-1}$![]() is an analytic first integral of $\dot {{{\mathbf {x}}}}={{\mathbf {F}}}({{\mathbf {x}}}).$
is an analytic first integral of $\dot {{{\mathbf {x}}}}={{\mathbf {F}}}({{\mathbf {x}}}).$![]()
Proof of theorem 1.1. As, by hypothesis $(a_1,\,a_2,\,b_1,\,b_2)$![]() is non-zero, the system (1.1) is not orbitally equivalent to $(-y,\,x,\,0)^{T}.$
is non-zero, the system (1.1) is not orbitally equivalent to $(-y,\,x,\,0)^{T}.$![]() From García [Reference García14], the system (1.1) is not completely analytically integrable, it has at most one functionally independent analytic first integral.
From García [Reference García14], the system (1.1) is not completely analytically integrable, it has at most one functionally independent analytic first integral.
We prove the sufficient condition. We see that system (1.4), satisfying one of the series of conditions (a) or (b), it has a polynomial first integral. In fact, we distinguish the cases separately:
(a) System (1.4) with $a_1=a_2=0,$
 has the first integral $x^{2}+y^{2}.$
has the first integral $x^{2}+y^{2}.$ And system (1.4) with $b_1=b_2=0,$
And system (1.4) with $b_1=b_2=0,$ has the first integral $z.$
has the first integral $z.$
(b) Assume that there is a rational number $m$
 such that $p:=b_2(b_1-a_1)m,\,\ q:=a_1(a_2-b_2)m$
such that $p:=b_2(b_1-a_1)m,\,\ q:=a_1(a_2-b_2)m$ and $s:=(a_1b_2-a_2b_1)m$
and $s:=(a_1b_2-a_2b_1)m$ are natural numbers. The polynomial $(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}$
are natural numbers. The polynomial $(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}$ is a first integral of system (1.4).
is a first integral of system (1.4).
Assume that system (1.1) is orbitally equivalent to system (1.4), i.e. there exists a change of variables $\phi$![]() and a reparameterization of the time-variable such that the first one becomes the second one. Let $\tilde {I}$
and a reparameterization of the time-variable such that the first one becomes the second one. Let $\tilde {I}$![]() a polynomial first integral of system (1.4). Undoing the change of variables, system (1.1) is formally integrable and by applying lemma 3.1, there exists a scalar function $\hat {l}$
a polynomial first integral of system (1.4). Undoing the change of variables, system (1.1) is formally integrable and by applying lemma 3.1, there exists a scalar function $\hat {l}$![]() such that $I=\hat {l}\circ \tilde {I}\circ \phi ^{-1}$
such that $I=\hat {l}\circ \tilde {I}\circ \phi ^{-1}$![]() with $I({{\mathbf 0}})=0$
with $I({{\mathbf 0}})=0$![]() is an analytic first integral of the system (1.1).
is an analytic first integral of the system (1.1).
We see the necessary condition. We assume that the analytic system (1.1) has one functionally independent analytic first integral and $(a_1,\,a_2,\,b_1,\,b_2)$![]() is non-zero, performing a formal change of variables and a re-parameterization of the time-variable, system (1.1) can be transformed into
is non-zero, performing a formal change of variables and a re-parameterization of the time-variable, system (1.1) can be transformed into
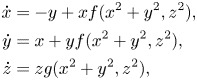
where $f,\,g$![]() are formal functions with $f(x^{2}+y^{2},\,z^{2})=a_1(x^{2}+y^{2})+a_2z^{2}+\mbox {h.o.t.}$
are formal functions with $f(x^{2}+y^{2},\,z^{2})=a_1(x^{2}+y^{2})+a_2z^{2}+\mbox {h.o.t.}$![]() and $g(x^{2}+y^{2},\,z^{2})=b_1(x^{2}+y^{2})+b_2z^{2}+\mbox {h.o.t.},$
and $g(x^{2}+y^{2},\,z^{2})=b_1(x^{2}+y^{2})+b_2z^{2}+\mbox {h.o.t.},$![]() see [Reference Algaba, Freire and Gamero1, Reference Guckenheimer and Holmes17].
see [Reference Algaba, Freire and Gamero1, Reference Guckenheimer and Holmes17].
This system is a Poincaré–Dulac normal form, by [Reference Yamanaka22] a formal first integral of system (3.5) is a first integral of its linear part, i.e. $I(x,\,y,\,z)=I(x^{2}+y^{2},\,z^{2}).$![]()
By using cylindrical coordinates, the system is
Doing the change $R=r^{2},\, Z=z^{2},\, \Theta =2\theta$![]() and $\tau =2t,$
and $\tau =2t,$![]() system (3.2) is transformed into
system (3.2) is transformed into
and if the system (3.3) admits some first integral, then it is of the form $I=I(R,\,Z),$![]() i.e. it is invariant under rotations.
i.e. it is invariant under rotations.
Removing the azimuthal component, we obtain the planar system
with $\hat {f},\,\hat {g}$![]() having terms of degree greater than or equals to two in $R,\,Z,$
having terms of degree greater than or equals to two in $R,\,Z,$![]() that is $R=0$
that is $R=0$![]() and $Z=0$
and $Z=0$![]() invariant curves of the system.
invariant curves of the system.
Hence, the analysis of the integrability problem for system (3.3) (or for system (1.2)) is equivalent to the corresponding one for planar system (3.4).
In summary, the system (1.2) with $a_1^{2}+b_1^{2}\ne 0$![]() and $a_2^{2}+b_2^{2}\ne 0,$
and $a_2^{2}+b_2^{2}\ne 0,$![]() admits some formal first integral if, and only if, system (3.4) is formally integrable. The integrability problem of these systems is studied in § 4.
admits some formal first integral if, and only if, system (3.4) is formally integrable. The integrability problem of these systems is studied in § 4.
From proposition 4.1, if system (3.4) is formally integrable, then one of the following conditions is satisfied:
(a) $a_1=a_2=0$
 (or $b_1=b_2=0).$
(or $b_1=b_2=0).$
We study the first case $a_1=a_2=0$
 and $b_1b_2\ne 0$
and $b_1b_2\ne 0$ (the other case is analogous changing $R$
(the other case is analogous changing $R$ by $Z$
by $Z$ ).
).From theorem 4.2, if system (3.4) is formally integrable, then there exist a change of variables and a reparameterization of the time such that system (3.4) is transformed into
\[ R'=0,\qquad Z'=Z(b_1R+b_2Z), \]i.e., the three-dimensional system (3.3) is transformed into a system of the form (3.5)\begin{equation} (R',Z',\Theta')^{T}:=(0,Z(b_1R+b_2Z),1+\Psi(R,Z))^{T} \end{equation}where $\Psi$
(3.5)\begin{equation} (R',Z',\Theta')^{T}:=(0,Z(b_1R+b_2Z),1+\Psi(R,Z))^{T} \end{equation}where $\Psi$
 is a formal function and $\Psi (0,\,0)=0.$
is a formal function and $\Psi (0,\,0)=0.$
Undoing the change, $(x,\,y,\,z,\,t)=(\sqrt {R}cos(\Theta /2),\,\sqrt {R}sin(\Theta /2),\,\sqrt {Z},\,\tau /2),$
 we obtain system (1.4). These changes transform the first integral $R$
we obtain system (1.4). These changes transform the first integral $R$ of (3.3) into a first integral of system (1.1) which has the expression $I=I(x^{2}+y^{2},\,z^{2})=x^{2}+y^{2}+\cdots$
of (3.3) into a first integral of system (1.1) which has the expression $I=I(x^{2}+y^{2},\,z^{2})=x^{2}+y^{2}+\cdots$
(b) Assume that $p:=b_2(b_1-a_1)m,\,\ q:=a_1(a_2-b_2)m$
 and $s:=(a_1b_2-a_2b_1)m$
and $s:=(a_1b_2-a_2b_1)m$ are natural numbers and $\mbox {gcd}(p,\,q,\,s)=1.$
are natural numbers and $\mbox {gcd}(p,\,q,\,s)=1.$ By theorem 4.3, if system (3.4) is formally integrable at the origin then it is orbitally equivalent to
\[ R'=R(a_1R+a_2Z),\quad Z'=Z(b_1R+b_2Z), \]or equivalently, system (1.1) is is orbitally equivalent to system (1.4). Moreover, in such a case, it has an analytic first integral of the form $(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}+\cdots$
By theorem 4.3, if system (3.4) is formally integrable at the origin then it is orbitally equivalent to
\[ R'=R(a_1R+a_2Z),\quad Z'=Z(b_1R+b_2Z), \]or equivalently, system (1.1) is is orbitally equivalent to system (1.4). Moreover, in such a case, it has an analytic first integral of the form $(x^{2}+y^{2})^{p}z^{2q}((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2})^{s}+\cdots$

We give the following result we will use in the proof of theorem 1.3. It states the well-known relationship among inverse Jacobi multipliers of formally orbital equivalent vector fields.
Lemma 3.2 Let $\Phi$![]() be a diffeomorphism and $\eta$
be a diffeomorphism and $\eta$![]() a function on $U\subset \mathbf {C}^{n}$
a function on $U\subset \mathbf {C}^{n}$![]() such that $\mbox {det} D\Phi$
such that $\mbox {det} D\Phi$![]() has no zero on $U$
has no zero on $U$![]() and $\eta (\mathbf {0})\ne 0$
and $\eta (\mathbf {0})\ne 0$![]() . If $J\in \mathbb {C}[[x_1,\,\dots,\,x_n]]$
. If $J\in \mathbb {C}[[x_1,\,\dots,\,x_n]]$![]() is an inverse Jacobi multiplier of $\dot {{{\mathbf {x}}}}={{\mathbf {F}}}({{\mathbf {x}}}),$
is an inverse Jacobi multiplier of $\dot {{{\mathbf {x}}}}={{\mathbf {F}}}({{\mathbf {x}}}),$![]() then $\eta (\mathbf {y})(\mbox {det}(D\Phi (\mathbf {y}))^{-1}J(\Phi (\mathbf {y}))$
then $\eta (\mathbf {y})(\mbox {det}(D\Phi (\mathbf {y}))^{-1}J(\Phi (\mathbf {y}))$![]() is an inverse Jacobi multiplier of $\dot {\mathbf {y}}=\Phi _*(\eta {{\mathbf {F}}})(\mathbf {y}):=D\Phi (\mathbf {y})^{-1}\eta (\mathbf {y}){{\mathbf {F}}}(\Phi (\mathbf {y}))$
is an inverse Jacobi multiplier of $\dot {\mathbf {y}}=\Phi _*(\eta {{\mathbf {F}}})(\mathbf {y}):=D\Phi (\mathbf {y})^{-1}\eta (\mathbf {y}){{\mathbf {F}}}(\Phi (\mathbf {y}))$![]() .
.
Proof of theorem 1.3. We assume that $a_1^{2}+b_1^{2}\ne 0$![]() and $a_2^{2}+b_2^{2}\ne 0.$
and $a_2^{2}+b_2^{2}\ne 0.$![]() From García [Reference García14], the system (1.1) is not completely analytically integrable, it has at most one analytic first integral.
From García [Reference García14], the system (1.1) is not completely analytically integrable, it has at most one analytic first integral.
We see the necessary condition. We assume that system (1.1) has one, and only one, functionally independent analytic first integral. From theorem 1.1, it is orbitally equivalent to system (1.4) satisfying one of the series of conditions (a) or (b). It is easy to check that system (1.4) has the polynomial inverse Jacobi multiplier $J_5=(x^{2}+y^{2})z((b_1-a_1)(x^{2}+y^{2})+(b_2-a_2)z^{2}).$![]() From lemma 3.2, system (1.1) has an inverse Jacobi multiplier of the form $J=J_5+\cdots$
From lemma 3.2, system (1.1) has an inverse Jacobi multiplier of the form $J=J_5+\cdots$![]()
We prove the sufficient condition. We assume that the analytic system (1.1) has an inverse Jacobi multiplier of the form $J=J_5+\cdots$![]() and $(a_1,\,a_2,\,b_1,\,b_2)$
and $(a_1,\,a_2,\,b_1,\,b_2)$![]() satisfies one of the series of conditions (a) or (b).
satisfies one of the series of conditions (a) or (b).
Reasoning as in proof of theorem 1.1 and applying lemma 3.2, system (1.1) has an inverse Jacobi multiplier of the form $J=J_5+\cdots$![]() if system (3.4) has an inverse integrating factor of the form $\hat {J}=\hat {J}_3+\cdots$
if system (3.4) has an inverse integrating factor of the form $\hat {J}=\hat {J}_3+\cdots$![]() with $\hat {J}_3=RZ((b_1-a_1)R+(b_2-a_2)Z).$
with $\hat {J}_3=RZ((b_1-a_1)R+(b_2-a_2)Z).$![]()
We notice that $\hat {J}_3=RZ(b_1R+b_2Z)-RZ(a_1R+a_2Z).$![]() Thus, applying theorem 4.4, we have the result.
Thus, applying theorem 4.4, we have the result.
4. Auxiliary results: analytic integrability of the systems (3.4)
The following result provides necessary conditions of formal integrability of system (3.4).
Proposition 4.1 Assume that system (3.4) with $a_1^{2}+b_1^{2}\ne 0$![]() and $a_2^{2}+b_2^{2}\ne 0,$
and $a_2^{2}+b_2^{2}\ne 0,$![]() has a formal first integral in a neighbourhood of the origin. Then, one of the following conditions is satisfied:
has a formal first integral in a neighbourhood of the origin. Then, one of the following conditions is satisfied:
(a) $a_1=a_2=0$
 (or $b_1=b_2=0).$
(or $b_1=b_2=0).$
(b) $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$
 and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$ are rational numbers different from zero with the same sign.
are rational numbers different from zero with the same sign.
Proof. Let $I=I_M+\mbox {h.o.t.}$![]() a formal first integral of system (3.4) and let ${{\mathbf {F}}}={{\mathbf {F}}}_2+\cdots$
a formal first integral of system (3.4) and let ${{\mathbf {F}}}={{\mathbf {F}}}_2+\cdots$![]() be the associated vector field to system (3.4). Equation $F(I)=0$
be the associated vector field to system (3.4). Equation $F(I)=0$![]() for degree $M+1$
for degree $M+1$![]() is $F_2(I_M)=0,$
is $F_2(I_M)=0,$![]() i.e. ${{\mathbf {F}}}_2(R,\,Z)=(R(a_1R+a_2Z),\,Z(b_1R+b_2Z))^{T}$
i.e. ${{\mathbf {F}}}_2(R,\,Z)=(R(a_1R+a_2Z),\,Z(b_1R+b_2Z))^{T}$![]() is polynomially integrable and $I_M$
is polynomially integrable and $I_M$![]() is a first integral of ${{\mathbf {F}}}_2.$
is a first integral of ${{\mathbf {F}}}_2.$![]() So, if ${{\mathbf {F}}}$
So, if ${{\mathbf {F}}}$![]() is formally integrable then ${{\mathbf {F}}}_2$
is formally integrable then ${{\mathbf {F}}}_2$![]() is polynomially integrable.
is polynomially integrable.
We study the polynomial integrability of ${{\mathbf {F}}}_2$![]() (necessary condition of formal integrability). We distinguish the following cases separately:
(necessary condition of formal integrability). We distinguish the following cases separately:
• Assume $a_1=a_2=0$
 (or $b_1=b_2=0).$
(or $b_1=b_2=0).$ In such a case, $I=R$
In such a case, $I=R$ (or $I=Z$
(or $I=Z$ ) is a polynomial first integral of ${{\mathbf {F}}}_2$
) is a polynomial first integral of ${{\mathbf {F}}}_2$ .
.• Assume $a_1= b_1\ne 0.$
 If $a_2\ne b_2,$
If $a_2\ne b_2,$ the origin of ${{\mathbf {F}}}_2$
the origin of ${{\mathbf {F}}}_2$ is an isolated singular point and $(R,\,Z)^{T}\wedge {{\mathbf {F}}}_2$
is an isolated singular point and $(R,\,Z)^{T}\wedge {{\mathbf {F}}}_2$ has multiple factors, thus ${{\mathbf {F}}}_2$
has multiple factors, thus ${{\mathbf {F}}}_2$ is not polynomially integrable, by [Reference Algaba, García and Reyes6, theorem 3.1].
is not polynomially integrable, by [Reference Algaba, García and Reyes6, theorem 3.1].Otherwise, $a_1=b_1\ne 0$
 and $a_2=b_2\ne 0,$
and $a_2=b_2\ne 0,$ the vector field ${{\mathbf {F}}}_2$
the vector field ${{\mathbf {F}}}_2$ is of the form $(a_1R+a_2Z)(R,\,Z)^{T}$
is of the form $(a_1R+a_2Z)(R,\,Z)^{T}$ which is not polynomially integrable.
which is not polynomially integrable.• Assume $a_2= b_2\ne 0.$
 In this case, the result follows by changing $R$
In this case, the result follows by changing $R$ by $Z$
by $Z$ .
.• Assume $a_1\ne b_1$
 and $a_2\ne b_2.$
and $a_2\ne b_2.$ From [Reference Algaba, García and Reyes3, proposition 1.7], as the factors of $(R,\,Z)^{T}\wedge {{\mathbf {F}}}_2$
From [Reference Algaba, García and Reyes3, proposition 1.7], as the factors of $(R,\,Z)^{T}\wedge {{\mathbf {F}}}_2$ are $R,\, Z$
are $R,\, Z$ and $(b_1-a_1)R+(b_2-a_2)Z,$
and $(b_1-a_1)R+(b_2-a_2)Z,$ if it exists a polynomial first integral of ${{\mathbf {F}}}_2$
if it exists a polynomial first integral of ${{\mathbf {F}}}_2$ , then it has the expression $I_M=R^{p}Z^{q}((b_1-a_1)R+(b_2-a_2)Z)^{s}$
, then it has the expression $I_M=R^{p}Z^{q}((b_1-a_1)R+(b_2-a_2)Z)^{s}$ with $p,\,q,\,s$
with $p,\,q,\,s$ natural numbers. By imposing $F_2(I_M)=0,$
natural numbers. By imposing $F_2(I_M)=0,$ we have that
\[ a_1(p+s)+b_1q=0,\quad a_2p+b_2(q+s)=0. \]Thus, $a_1,\,a_2,\,b_1$
we have that
\[ a_1(p+s)+b_1q=0,\quad a_2p+b_2(q+s)=0. \]Thus, $a_1,\,a_2,\,b_1$
 and $b_2$
and $b_2$ are different from zero. The natural exponents of the invariant curves in the expression of the first integral $I_M$
are different from zero. The natural exponents of the invariant curves in the expression of the first integral $I_M$ are of the form
\[ p=b_2(b_1-a_1)m,\quad q=a_1(a_2-b_2)m,\quad s=(a_1b_2-a_2b_1)m \]with $m$
are of the form
\[ p=b_2(b_1-a_1)m,\quad q=a_1(a_2-b_2)m,\quad s=(a_1b_2-a_2b_1)m \]with $m$
 a rational number. So, $I_M$
a rational number. So, $I_M$ is polynomial if $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$
is polynomial if $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$ and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$ are rational numbers with same sign.
are rational numbers with same sign.
We now provide necessary and sufficient conditions of formal integrability of the system (3.4) with $a_1^{2}+b_1^{2}\ne 0$![]() and $a_2^{2}+b_2^{2}\ne 0.$
and $a_2^{2}+b_2^{2}\ne 0.$![]()
By proposition 4.1, we only study the system (3.4) satisfying the series of conditions (a) or (b). For the formal integrability of the systems 3.4 case (a), we have the following result.
Theorem 4.2 System (3.4) with $a_1=a_2=0$![]() and $b_1b_2\ne 0$
and $b_1b_2\ne 0$![]() (or, $b_1=b_2=0$
(or, $b_1=b_2=0$![]() and $a_1a_2\ne 0$
and $a_1a_2\ne 0$![]() ) is formally integrable if, and only if, it is formally orbitally equivalent to system $(\dot {R},\,\dot {Z})^{T}=(0,\,Z(b_1R+b_2Z))^{T}$
) is formally integrable if, and only if, it is formally orbitally equivalent to system $(\dot {R},\,\dot {Z})^{T}=(0,\,Z(b_1R+b_2Z))^{T}$![]() (or, $(\dot {R},\,\dot {Z})^{T}=(R(a_1R+a_2Z),\,0)^{T}$
(or, $(\dot {R},\,\dot {Z})^{T}=(R(a_1R+a_2Z),\,0)^{T}$![]() ), i.e. it is orbital equivalent to its lowest-degree homogeneous component.
), i.e. it is orbital equivalent to its lowest-degree homogeneous component.
Proof. We consider the system 3.4 with $a_1=a_2=0$![]() and $b_1b_2\ne 0$
and $b_1b_2\ne 0$![]() . The other case is analogous, it is enough to change $R$
. The other case is analogous, it is enough to change $R$![]() by $Z$
by $Z$![]() .
.
The sufficient condition is trivial because $R$![]() is a polynomial first integral of system $(\dot {R},\,\dot {Z})^{T}=(0,\,Z(b_1R+b_2Z))^{T}$
is a polynomial first integral of system $(\dot {R},\,\dot {Z})^{T}=(0,\,Z(b_1R+b_2Z))^{T}$![]() . Undoing the change of variables system (3.4) is formally integrable.
. Undoing the change of variables system (3.4) is formally integrable.
We see now the necessary condition. Assume that system (3.4) with $a_1=a_2=0$![]() and $b_1,\,b_2\ne 0$
and $b_1,\,b_2\ne 0$![]() , is formally integrable. By theorem A.2, system (3.4) is orbitally equivalent to $\tilde {{{\mathbf {G}}}}={{\mathbf {G}}}_2+\cdots$
, is formally integrable. By theorem A.2, system (3.4) is orbitally equivalent to $\tilde {{{\mathbf {G}}}}={{\mathbf {G}}}_2+\cdots$![]() given in (A.3) which is also formally integrable. We assume that there exists $k_0:=\mathrm {min}\{k\in \mathbb {N},\, k\ge 2 : \alpha _{k}^{2}+\beta _k^{2}\neq 0\}.$
given in (A.3) which is also formally integrable. We assume that there exists $k_0:=\mathrm {min}\{k\in \mathbb {N},\, k\ge 2 : \alpha _{k}^{2}+\beta _k^{2}\neq 0\}.$![]() We study two cases separately:
We study two cases separately:
• If $\frac {\alpha _k}{b_1}=\frac {\beta _k}{b_2}=\lambda \ne 0,$
 for all $k\geq k_0$
for all $k\geq k_0$ then $\tilde {{{\mathbf {G}}}}=(b_1R+b_2Z)\bar {{{\mathbf {G}}}}$
then $\tilde {{{\mathbf {G}}}}=(b_1R+b_2Z)\bar {{{\mathbf {G}}}}$ with $\bar {{{\mathbf {G}}}}=(\lambda R^{k_0}+\cdots ),\, Z(1+\lambda R^{k_0-1}+\cdots )^{T}.$
with $\bar {{{\mathbf {G}}}}=(\lambda R^{k_0}+\cdots ),\, Z(1+\lambda R^{k_0-1}+\cdots )^{T}.$ The origin of $\bar {{{\mathbf {G}}}}$
The origin of $\bar {{{\mathbf {G}}}}$ is an isolated saddle node point (the linear part evaluated at origin only has one eigenvalue zero). From [Reference Li, Llibre and Zhang18, Reference Li, Llibre and Zhang19], $\bar {{{\mathbf {G}}}}$
is an isolated saddle node point (the linear part evaluated at origin only has one eigenvalue zero). From [Reference Li, Llibre and Zhang18, Reference Li, Llibre and Zhang19], $\bar {{{\mathbf {G}}}}$ is not analytically integrable. Therefore, $\tilde {{{\mathbf {G}}}}$
is not analytically integrable. Therefore, $\tilde {{{\mathbf {G}}}}$ is not analytically integrable.
is not analytically integrable.• Otherwise, If $\frac {\alpha _k}{b_1}\ne \frac {\beta _k}{b_2}$
 for some $k\geq k_0$
for some $k\geq k_0$ then $b_1R+b_2Z=0$
then $b_1R+b_2Z=0$ is an invariant curve of $\tilde {{{\mathbf {G}}}}$
is an invariant curve of $\tilde {{{\mathbf {G}}}}$ which pass by the origin and whose cofactor is $b_2Z+\sum _{k\geq k_0}(\alpha _k R^{k}+\beta _kR^{k-1}Z)$
which pass by the origin and whose cofactor is $b_2Z+\sum _{k\geq k_0}(\alpha _k R^{k}+\beta _kR^{k-1}Z)$ . Therefore $b_1R+b_2Z$
. Therefore $b_1R+b_2Z$ is a factor of any analytic first integral at the origin $I$
is a factor of any analytic first integral at the origin $I$ of $\tilde {{{\mathbf {G}}}}$
of $\tilde {{{\mathbf {G}}}}$ . On the other hand, if $I=I_M+\cdots$
. On the other hand, if $I=I_M+\cdots$ is a first integral of $\tilde {{{\mathbf {G}}}}$
is a first integral of $\tilde {{{\mathbf {G}}}}$ then $I_M$
then $I_M$ is a polynomial first integral of ${{\mathbf {G}}}_2$
is a polynomial first integral of ${{\mathbf {G}}}_2$ first homogeneous component of $\tilde {{{\mathbf {G}}}}$
first homogeneous component of $\tilde {{{\mathbf {G}}}}$ . This fact is a contradiction since $I_M=R.$
. This fact is a contradiction since $I_M=R.$
For the case (b), we have a similar result.
Theorem 4.3 Consider system (3.4) such that $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$![]() and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$![]() are rational numbers different from zero with the same sign. This system is formally integrable if, and only if, it is formally orbital equivalent to system $(\dot {R},\,\dot {Z})^{T}=(R(a_1R+a_2Z),\,Z(b_1R+b_2Z))^{T},$
are rational numbers different from zero with the same sign. This system is formally integrable if, and only if, it is formally orbital equivalent to system $(\dot {R},\,\dot {Z})^{T}=(R(a_1R+a_2Z),\,Z(b_1R+b_2Z))^{T},$![]() (that is it is orbital equivalent to its lowest-degree homogeneous component).
(that is it is orbital equivalent to its lowest-degree homogeneous component).
Proof. Let $m$![]() be an integer number such that $p=b_2(b_1-a_1)m,\,\quad q=a_1(a_2-b_2)m$
be an integer number such that $p=b_2(b_1-a_1)m,\,\quad q=a_1(a_2-b_2)m$![]() and $s=(a_1b_2-a_2b_1)m$
and $s=(a_1b_2-a_2b_1)m$![]() are natural numbers with $\mbox {gcd}(p,\,q,\,s)=1.$
are natural numbers with $\mbox {gcd}(p,\,q,\,s)=1.$![]()
Performing the scaled-change $(R,\,Z,\,\tau )\rightarrow (-pa_1R,\,-qb_2Z,\,pq\tau ),$![]() system (3.4) turns into
system (3.4) turns into
The formal integrability of system (4.1) has been studied in [Reference Algaba, García and Reyes3]. By [Reference Algaba, García and Reyes3, theorem 2.11], if system (4.1) is formally integrable at the origin then it is linearizable (orbitally equivalent to its leading homogeneous term).
The following result characterizes the formal integrability of system (3.4) through the existence of a formal inverse integrating factor of this system.
Theorem 4.4 Consider system (3.4) with $a_1^{2}+b_1^{2}\ne 0$![]() or $a_2^{2}+b_2^{2}\ne 0,$
or $a_2^{2}+b_2^{2}\ne 0,$![]() satisfying one of the following series of conditions:
satisfying one of the following series of conditions:
(a) $a_1=a_2=0$
 (or $b_1=b_2=0).$
(or $b_1=b_2=0).$
(b) $b_2(b_1-a_1),\,\ a_1(a_2-b_2)$
 and $a_1b_2-a_2b_1$
and $a_1b_2-a_2b_1$ are rational numbers different from zero with the same sign.
are rational numbers different from zero with the same sign.Then, system (3.4) is formally integrable if, and only if, it has a formal inverse integrating factor of the form $V=RZ((b_1-a_1)R+(b_2-a_2)Z)+\cdots$
 .
.
Proof. System (3.4) is of the form $(R',\,Z')^{T}=(P_2+\cdots,\,Q_2+\cdots )^{T}$![]() , a perturbation of a quadratic system, where $P_2=R(a_1R+a_2Z),\,\ Q_2=Z(b_1R+b_2Z).$
, a perturbation of a quadratic system, where $P_2=R(a_1R+a_2Z),\,\ Q_2=Z(b_1R+b_2Z).$![]()
The polynomial $xQ_2-yP_2=RZ[(b_1-a_1)R+(b_2-a_2)Z]$![]() under the series of condition (a) or (b) has only simple factors on $\mathbb {C}[x,\,y]$
under the series of condition (a) or (b) has only simple factors on $\mathbb {C}[x,\,y]$![]() . From Algaba et al. [Reference Algaba, García and Reyes4, theorem 6], system (3.4) has a formal inverse integrating factor $(xQ_2-yP_2)+\mbox {h.o.t.}$
. From Algaba et al. [Reference Algaba, García and Reyes4, theorem 6], system (3.4) has a formal inverse integrating factor $(xQ_2-yP_2)+\mbox {h.o.t.}$![]() if, and only if, it is orbitally equivalent to $(P_2,\,Q_2)^{T}$
if, and only if, it is orbitally equivalent to $(P_2,\,Q_2)^{T}$![]() . From theorems 4.2 and 4.3, the result follows.
. From theorems 4.2 and 4.3, the result follows.
5. Applications
We consider the family of differential systems
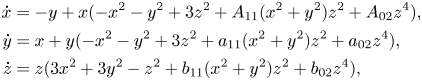
with $A_{11},\,A_{02},\,a_{11},\,a_{02},\,b_{11},\,b_{02}$![]() real numbers. The following result gives the systems of the family with one functionally independent analytic first integral.
real numbers. The following result gives the systems of the family with one functionally independent analytic first integral.
Theorem 5.1 System (5.1) has one, and only one, independent analytic first integral if, and only if, it satisfies at least one of the following conditions:
(i) $A_{02}-a_{02}=A_{11}-a_{11}=b_{11}+3b_{02}=A_{02}+2b_{02}+a_{11}=0,$

(ii) $A_{02}-a_{02}=A_{11}-a_{11}=b_{11}+a_{11}=A_{02}+5b_{02}=0.$

Proof. System (5.1) is a perturbation of system (1.2) with $a_1=-1,\,a_2=3,\, b_1=3,\, b_2=-1.$![]() Therefore, it has at most one functionally independent first integral. We prove the necessary condition. For that, we apply Theorem 2.4. System (5.1) satisfies condition $(b)$
Therefore, it has at most one functionally independent first integral. We prove the necessary condition. For that, we apply Theorem 2.4. System (5.1) satisfies condition $(b)$![]() of theorem 2.4 since $b_2(b_1-a_1)=-4,\,\ a_1(a_2-b_2)=-4$
of theorem 2.4 since $b_2(b_1-a_1)=-4,\,\ a_1(a_2-b_2)=-4$![]() and $a_1b_2-a_2b_1=-8$
and $a_1b_2-a_2b_1=-8$![]() are rational numbers different from zero with the same sign.
are rational numbers different from zero with the same sign.
We impose the existence of a formal function $J=J_5+\cdots$![]() with $J_5=(x^{2}+y^{2})z(x^{2}+y^{2}-z^{2})$
with $J_5=(x^{2}+y^{2})z(x^{2}+y^{2}-z^{2})$![]() introduced in proposition 2.3 satisfying (2.9) with $p=q=1,\,s=2$
introduced in proposition 2.3 satisfying (2.9) with $p=q=1,\,s=2$![]() that is $M=4.$
that is $M=4.$![]() Equation (2.9) to degree 19 is
Equation (2.9) to degree 19 is
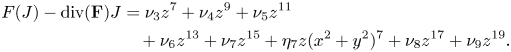
Following the procedure given in proof of proposition 2.3, we compute the coefficients of $F(J)-\mbox {div}({{\mathbf {F}}})J$![]() and the proof consists on the vanishing of its terms:
and the proof consists on the vanishing of its terms:
The coefficient $\nu _3$![]() is null and $\nu _4=A_{02}+10b_{02}+A_{11}+a_{02}+a_{11}+2b_{11}.$
is null and $\nu _4=A_{02}+10b_{02}+A_{11}+a_{02}+a_{11}+2b_{11}.$![]() Solving the equation $\nu _4=0$
Solving the equation $\nu _4=0$![]() , we have $A_{02}=-10b_{02}-A_{11}-a_{02}-a_{11}-2b_{11}.$
, we have $A_{02}=-10b_{02}-A_{11}-a_{02}-a_{11}-2b_{11}.$![]() For order 11, we have $\nu _5= (b_{11}+3b_{02})(2b_{11}+A_{11}+a_{11}).$
For order 11, we have $\nu _5= (b_{11}+3b_{02})(2b_{11}+A_{11}+a_{11}).$![]() Imposing $\nu _5=0$
Imposing $\nu _5=0$![]() , we distinguish two cases: Case 1. $b_{11}=-3b_{02}.$
, we distinguish two cases: Case 1. $b_{11}=-3b_{02}.$![]() In this case, $\nu _6=\eta _7=0$
In this case, $\nu _6=\eta _7=0$![]() and $\nu _7= (A_{11}+a_{02}+2b_{02})(A_{11}+2a_{02}+a_{11}+4b_{02}).$
and $\nu _7= (A_{11}+a_{02}+2b_{02})(A_{11}+2a_{02}+a_{11}+4b_{02}).$![]()
Case 1.1. $A_{11}=-a_{02}-2b_{02}.$![]() To order 17, we have $\nu _8= (a_{02}+a_{11}+2b_{02})^{2}(a_{02}-a_{11}+4b_{02}).$
To order 17, we have $\nu _8= (a_{02}+a_{11}+2b_{02})^{2}(a_{02}-a_{11}+4b_{02}).$![]() If $a_{02}=-a_{11}-2b_{02},$
If $a_{02}=-a_{11}-2b_{02},$![]() we arrive to case (i). Otherwise, $a_{02}=a_{11}-4b_{02},$
we arrive to case (i). Otherwise, $a_{02}=a_{11}-4b_{02},$![]() we have $\nu _9= (a_{11}-b_{02})^{2}.$
we have $\nu _9= (a_{11}-b_{02})^{2}.$![]() Therefore $a_{11}=b_{02},$
Therefore $a_{11}=b_{02},$![]() i.e. case (i).
i.e. case (i).
Case 1.2. $A_{11}=-2a_{02}-a_{11}-4b_{02},$![]() we have $\nu _8= (a_{02}+a_{11}+2b_{02})^{2}(a_{02}+3b_{02}).$
we have $\nu _8= (a_{02}+a_{11}+2b_{02})^{2}(a_{02}+3b_{02}).$![]() If $a_{02}=-a_{11}-2b_{02},$
If $a_{02}=-a_{11}-2b_{02},$![]() we arrive to case (i). Otherwise, $a_{02}=-3b_{02},$
we arrive to case (i). Otherwise, $a_{02}=-3b_{02},$![]() we have $\nu _9=(a_{11}-b_{02})^{2}$
we have $\nu _9=(a_{11}-b_{02})^{2}$![]() . Imposing $\nu _9=0$
. Imposing $\nu _9=0$![]() , we have $a_{11}=b_{02},$
, we have $a_{11}=b_{02},$![]() i.e. case (i).
i.e. case (i).
Case 2. $b_{11}=-\frac {1}{2}(A_{11}+a_{11}).$![]() In this case, $\nu _6=\eta _{7}=0$
In this case, $\nu _6=\eta _{7}=0$![]() and $\nu _7= (a_{02}+5b_{02})(2a_{02}+A_{11}-a_{11}+10b_{02}).$
and $\nu _7= (a_{02}+5b_{02})(2a_{02}+A_{11}-a_{11}+10b_{02}).$![]() Imposing the vanishing of $\nu _7$
Imposing the vanishing of $\nu _7$![]() , we have:
, we have:
Case 2.1. $a_{02}=-5b_{02}.$![]() To order 17, $\nu _8= (A_{11}-a_{11})^{2}(A_{11}+a_{11}+6b_{02}).$
To order 17, $\nu _8= (A_{11}-a_{11})^{2}(A_{11}+a_{11}+6b_{02}).$![]() If $A_{11}=a_{11},$
If $A_{11}=a_{11},$![]() we are in the case (ii). Otherwise, $A_{11}=-a_{11}-6b_{02},$
we are in the case (ii). Otherwise, $A_{11}=-a_{11}-6b_{02},$![]() we have $\nu _9=(5b_{02}^{2}+96)(3b_{02}+a_{11})^{2}.$
we have $\nu _9=(5b_{02}^{2}+96)(3b_{02}+a_{11})^{2}.$![]() Thus, $\nu _{9}=0$
Thus, $\nu _{9}=0$![]() if $a_{11}=-3b_{02},$
if $a_{11}=-3b_{02},$![]() i.e. case (ii).
i.e. case (ii).
Case 2.2. $a_{02}=\frac {1}{2}(-A_{11}+a_{11}-10b_{02}).$![]() To order 17, we have $\nu _8= (A_{11}-a_{11})^{2}(3A_{11}+3a_{11}-32b_{02}).$
To order 17, we have $\nu _8= (A_{11}-a_{11})^{2}(3A_{11}+3a_{11}-32b_{02}).$![]() For $A_{11}=a_{11},$
For $A_{11}=a_{11},$![]() we have the case (ii). Otherwise, $A_{11}=-a_{11}+\frac {32}{3}b_{02},$
we have the case (ii). Otherwise, $A_{11}=-a_{11}+\frac {32}{3}b_{02},$![]() we have $\nu _9=(1152+115b_{02}^{2})(16b_{02}-3a_{11})^{2}$
we have $\nu _9=(1152+115b_{02}^{2})(16b_{02}-3a_{11})^{2}$![]() . So, $a_{11}=\frac {16}{3}b_{02},$
. So, $a_{11}=\frac {16}{3}b_{02},$![]() i.e. case (ii).
i.e. case (ii).
We prove the sufficient condition. It is easy to check that $(x^{2}+y^{2})z(x^{2}+y^{2}-z^{2})(1-b_{02}z^{2})$![]() is an inverse Jacobi multiplier of system (5.1) case (i) and $(x^{2}+y^{2})z(3x^{2}+3y^{2}-3z^{2}-a_{11}(x^{2}+y^{2})z^{2}+3b_{02}z^{4})$
is an inverse Jacobi multiplier of system (5.1) case (i) and $(x^{2}+y^{2})z(3x^{2}+3y^{2}-3z^{2}-a_{11}(x^{2}+y^{2})z^{2}+3b_{02}z^{4})$![]() is an inverse Jacobi multiplier of system (5.1) case (ii). Thus, both are of the form $J_5+\cdots$
is an inverse Jacobi multiplier of system (5.1) case (ii). Thus, both are of the form $J_5+\cdots$![]() . The result follows applying theorem 1.3.
. The result follows applying theorem 1.3.
We consider the family of differential systems
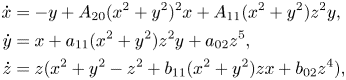
with $A_{20},\,A_{11},\,a_{11},\,a_{02},\,b_{11},\,b_{02}$![]() real numbers. The following result gives the systems of the family with one functionally independent analytic first integral.
real numbers. The following result gives the systems of the family with one functionally independent analytic first integral.
Theorem 5.2 System (5.2) has one, and only one, independent analytic first integral if, and only if, $A_{20}=A_{11}=a_{11}=a_{02}=0.$![]()
Proof. System (5.2) belongs to the family of systems (1.2) with $a_1=a_2=0$![]() and $b_1=1,\, b_2=-1.$
and $b_1=1,\, b_2=-1.$![]() Therefore, it has at most one functionally independent first integral.
Therefore, it has at most one functionally independent first integral.
We prove the necessary condition. For that, we apply theorem 2.2. We impose the existence of a formal function $I=(x^{2}+y^{2})+\cdots$![]() introduced in proposition 2.1 satisfying (2.1). Following the procedure given in proof of proposition 2.1, we compute the coefficients of $F(I)$
introduced in proposition 2.1 satisfying (2.1). Following the procedure given in proof of proposition 2.1, we compute the coefficients of $F(I)$![]() and we obtain $\eta =0,\,\ \nu _2=0$
and we obtain $\eta =0,\,\ \nu _2=0$![]() and to degree 6, it has that $\eta _3=A_{20}$
and to degree 6, it has that $\eta _3=A_{20}$![]() and $\nu _3=a_{11}.$
and $\nu _3=a_{11}.$![]() Thus, we impose that $A_{20}=a_{11}=0.$
Thus, we impose that $A_{20}=a_{11}=0.$![]() In this case, the equation $F(I)=0$
In this case, the equation $F(I)=0$![]() to order 8 is zero and to order 10 and 12, we have $\eta _5=0,\,\ \nu _5= 5a_{02}b_{11}$
to order 8 is zero and to order 10 and 12, we have $\eta _5=0,\,\ \nu _5= 5a_{02}b_{11}$![]() and $\eta _6=0,\, \nu _6=-10a_{02}b_{02}b_{11}-10a_{02}^{2}-\frac {1}{4}A_{11}^{2}.$
and $\eta _6=0,\, \nu _6=-10a_{02}b_{02}b_{11}-10a_{02}^{2}-\frac {1}{4}A_{11}^{2}.$![]()
On the one hand, if $a_{02}=0,$![]() it has that $\nu _6$
it has that $\nu _6$![]() is zero if $A_{11}$
is zero if $A_{11}$![]() is zero. On the other hand, if $b_{11}=0$
is zero. On the other hand, if $b_{11}=0$![]() , then $\nu _6=-10a_{02}^{2}-\frac {1}{4}A_{11}^{2}$
, then $\nu _6=-10a_{02}^{2}-\frac {1}{4}A_{11}^{2}$![]() . So, if $\nu _6=0$
. So, if $\nu _6=0$![]() , we have that $A_{20}=A_{11}=a_{11}=a_{02}=0.$
, we have that $A_{20}=A_{11}=a_{11}=a_{02}=0.$![]()
The sufficiency is trivial since $x^{2}+y^{2}$![]() is a first integral of system (5.2) with $A_{20}=A_{11}=a_{11}=a_{02}=0.$
is a first integral of system (5.2) with $A_{20}=A_{11}=a_{11}=a_{02}=0.$![]()
Acknowledgements
This work has been partially supported by Ministerio de Economia y Competitividad, Plan Nacional I+D+I co-financed with FEDER funds, in the frame of the project PGC2018-096265-B-I00, and by Consejería de Educación y Ciencia de la Junta de Andalucía (FQM-276, P12-FQM-1658 and UHU126150).
Appendix A. An orbital normal form for systems (3.4) with $a_1=a_2=0.$
In this section, we give an orbitally equivalent normal form for a general two-dimensional vector field ${{\mathbf {F}}}={{\mathbf {F}}}_n+\cdots$![]() , where ${{\mathbf {F}}}_n$
, where ${{\mathbf {F}}}_n$![]() , the leading term of ${{\mathbf {F}}}$
, the leading term of ${{\mathbf {F}}}$![]() , is a homogeneous polynomial of degree $n.$
, is a homogeneous polynomial of degree $n.$![]()
For that, we need to define the following linear operators (in this section, $\mathscr {P}_j$![]() denotes the vector space of homogeneous polynomials of degree $j$
denotes the vector space of homogeneous polynomials of degree $j$![]() with two variables):
with two variables):
(Lie operator of the leading term of ${{\mathbf {F}}}$![]() ) and
) and
${{\ell }}_{n+k}^{{{\mathrm {c}}}} : \Delta _{k+1} \longrightarrow \Delta _{n+k}$![]() defined by
defined by
where the subspaces $\Delta _{k+1}$![]() and $\Delta _{n+k}$
and $\Delta _{n+k}$![]() satisfy that $\mathscr {P}_{k+1}=\Delta _{k+1}\bigoplus h \mathscr {P}_{k-n}$
satisfy that $\mathscr {P}_{k+1}=\Delta _{k+1}\bigoplus h \mathscr {P}_{k-n}$![]() and $\mathscr {P}_{n+k}=\Delta _{n+k}\bigoplus h \mathscr {P}_{k-1},$
and $\mathscr {P}_{n+k}=\Delta _{n+k}\bigoplus h \mathscr {P}_{k-1},$![]() respectively (such subspaces must be considered as fixed), being $h=\frac {1}{n+1}(x,\,y)^{T}\wedge {{\mathbf {F}}}_n$
respectively (such subspaces must be considered as fixed), being $h=\frac {1}{n+1}(x,\,y)^{T}\wedge {{\mathbf {F}}}_n$![]() a homogeneous polynomial non-zero of degree $n+1.$
a homogeneous polynomial non-zero of degree $n+1.$![]()
Next result is [Reference Algaba, García and Reyes5, theorem A.32]. It provides an expression of an orbital normal form for the vector fields ${{\mathbf {F}}}$![]() with leading term non-conservative.
with leading term non-conservative.
Proposition A.1 Let ${{\mathbf {F}}}={{\mathbf {F}}}_n+\mbox {h.o.t.}$![]() with ${{\mathbf {F}}}_n$
with ${{\mathbf {F}}}_n$![]() homogeneous polynomial vector field of degree $n$
homogeneous polynomial vector field of degree $n$![]() . If ${{\mathrm {Ker}}}\left ( {{{\ell }}_{n+k}^{{{\mathrm {c}}}}} \right )=\left \{ {0} \right \}$
. If ${{\mathrm {Ker}}}\left ( {{{\ell }}_{n+k}^{{{\mathrm {c}}}}} \right )=\left \{ {0} \right \}$![]() for all $k\in \mathbb {N}$
for all $k\in \mathbb {N}$![]() then ${{\mathbf {F}}}$
then ${{\mathbf {F}}}$![]() is orbitally equivalent to
is orbitally equivalent to
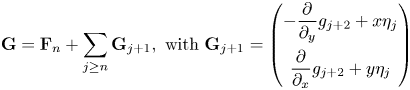
where $g_{j+2}\in {{\mathrm {Cor}}}\left ( {{{\ell }}^{c}_{j+2}} \right )$![]() (a complementary subspace to $\mbox {Range}({{\ell }}^{c}_{j+2})$
(a complementary subspace to $\mbox {Range}({{\ell }}^{c}_{j+2})$![]() ) and $\eta _{j}\in {{\mathrm {Cor}}}\left ( {{{\ell }}_{j}} \right )$
) and $\eta _{j}\in {{\mathrm {Cor}}}\left ( {{{\ell }}_{j}} \right )$![]() (a complementary subspace to $\mbox {Range}({{\ell }}_{j})$
(a complementary subspace to $\mbox {Range}({{\ell }}_{j})$![]() ).
).
We apply proposition A.1 for obtaining an orbital normal form of system (3.4) with $a_1=a_2=0$![]() and $b_1,\,b_2\ne 0.$
and $b_1,\,b_2\ne 0.$![]()
Theorem A.2 A formal orbital normal form for the system (3.4) with $a_1=a_2=0$![]() and $b_1b_2\ne 0$
and $b_1b_2\ne 0$![]() is
is
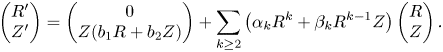
where $\alpha _{k},\,\beta _{k}\in \mathbb {R}$![]() .
.
Proof. We first prove that the hypothesis of proposition A.1 are satisfied, i.e. ${{\mathrm {Ker}}}\left ( {{{\ell }}_{k+2}^{{{\mathrm {c}}}}} \right )=\left \{ {0} \right \}$![]() for all $k\in \mathbb {N}.$
for all $k\in \mathbb {N}.$![]()
In this case, ${{\mathbf {F}}}_2=(0,\,Z(b_1R+b_2Z))^{T}.$![]() Therefore, $h=\frac {1}{3}(b_1R+b_2Z)RZ$
Therefore, $h=\frac {1}{3}(b_1R+b_2Z)RZ$![]() and $\mbox {div}({{\mathbf {F}}}_2)=b_1R+2b_2Z.$
and $\mbox {div}({{\mathbf {F}}}_2)=b_1R+2b_2Z.$![]()
We denote ${{\mathbf {F}}}_2^{(k)}={{\mathbf {F}}}_2-\frac {1}{k+2}\mbox {div}({{\mathbf {F}}}_2)(R,\,Z)^{T}= \frac {1}{k+2}\left (\!\!\begin {smallmatrix} -R(b_1R+2b_2Z)\\ Z((k+1)b_1R+kb_2Z)\end {smallmatrix}\!\!\right ).$![]() Consider the following bases for departure and arrival spaces of the operator $\ell _{k+2}^{c}$
Consider the following bases for departure and arrival spaces of the operator $\ell _{k+2}^{c}$![]() :
:
Taking into account that $3R^{i}Z^{j}h=b_1R^{i+2}Z^{j+1}+b_2R^{i+1}Z^{j+2}$![]() , we have that
, we have that
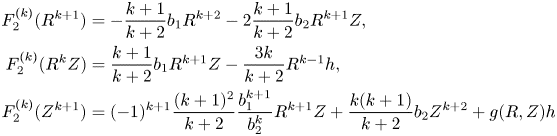
The matrix associated to the operator $\ell _{k+2}^{(c)}$![]() respect to the basis given is
respect to the basis given is
with $A=(-1)^{k+1}{\textstyle {\frac {(k+1)^{2}}{k+2}}}{\textstyle {\frac {b_1^{k+1}}{b_2^{k}}}}.$![]() The determinant of the matrix is not zero, therefore ${{\mathrm {Ker}}}(\ell _{k+2}^{(c)})=\left \{ {0} \right \}$
The determinant of the matrix is not zero, therefore ${{\mathrm {Ker}}}(\ell _{k+2}^{(c)})=\left \{ {0} \right \}$![]() . Moreover, ${{\mathrm {Cor}}}(\ell _{k+2}^{(c)})=\left \{ {0} \right \}$
. Moreover, ${{\mathrm {Cor}}}(\ell _{k+2}^{(c)})=\left \{ {0} \right \}$![]() since $\ell _{k+2}^{(c)}$
since $\ell _{k+2}^{(c)}$![]() is full range.
is full range.
On the other hand, the linear operator $\ell _{k+1},\, k\ge 1,$![]() is $\ell _{k+1}(p)=Z(b_1R+b_2Z)\frac {\partial }{\partial _Z}p,$
is $\ell _{k+1}(p)=Z(b_1R+b_2Z)\frac {\partial }{\partial _Z}p,$![]() with $p\in \mathscr {P}_{k}.$
with $p\in \mathscr {P}_{k}.$![]() So, the range of $\ell _{k+1}$
So, the range of $\ell _{k+1}$![]() has dimension $k$
has dimension $k$![]() and thus the dimension of any complementary subspace of ${{\mathrm {Range}}}(\ell _{k+1})$
and thus the dimension of any complementary subspace of ${{\mathrm {Range}}}(\ell _{k+1})$![]() is $2$
is $2$![]() . To finish the proof of our result, it is enough to check that the subspace ${{\mathrm {Span}}}\left \{ {R^{k+1},\,R^{k}Z} \right \}$
. To finish the proof of our result, it is enough to check that the subspace ${{\mathrm {Span}}}\left \{ {R^{k+1},\,R^{k}Z} \right \}$![]() is a complementary subspace of ${{\mathrm {Range}}}(\ell _{k+1}).$
is a complementary subspace of ${{\mathrm {Range}}}(\ell _{k+1}).$![]()





