1. Introduction
Hurd and Johnsons Glaciers are located on Livingston Island (LI), the second largest island in the South Shetland Islands (SSI) archipelago, which lies nearly parallel to the northern tip of the Antarctic Peninsula (AP), known as Trinity Peninsula (Fig. 1). The AP regional climate has warmed by as much as +0.53°C(10a)−1 for the period 1951–2006 (Reference TurnerTurner and others, 2009), four times larger than the worldwide average of +0.13°C (10 a)−1 for the same period (Reference SolomonSolomon and others, 2007). In contrast, warming has been relatively modest over West Antarctica, and statistically significant trends of warming or cooling have not been observed over most of East Antarctica (Reference TurnerTurner and others, 2005a, Reference Turner2009; Reference Steig, Schneider, Rutherford, Mann, Comiso and ShindellSteig and others, 2009). The AP recent surface temperature warming together with higher ocean temperatures have helped drive the disintegration of some ice shelves on the northeastern coast of the AP (Reference MacAyeal, Scambos, Hulbe and FahnestockMacAyeal and others, 2003; Reference Shepherd, Wingham, Payne and SkvarcaShepherd and others, 2003; Reference Van den BroekeVan den Broeke, 2005; Reference Cook and VaughanCook and Vaughan, 2010), with subsequent acceleration of the inland glaciers feeding the ice shelves (Reference Rott, Skvarca and NaglerRott and others, 1996; Reference Rignot, Casassa, Gogineni, Krabill, Rivera and ThomasRignot and others, 2004; Reference Scambos, Bohlander, Shuman and SkvarcaScambos and others, 2004). The current rate of basal melting under the AP ice shelves has been quantified by Reference Pritchard, Ligtenberg, Fricker, Vaughan, Van den Broeke and PadmanPritchard and others (2012). Higher atmospheric and oceanic temperatures have also contributed to the retreat during the past half-century of marine glacier fronts along the western coast of the AP, north of ∼70°S (Reference Cook, Fox, Vaughan and FerrignoCook and others, 2005). An overall trend of retreating ice fronts has also been observed in studies analysing both marine- and land-terminating glaciers in the region (Reference RauRau and others, 2004), though the latter has shown a range of different glacier variations throughout the study area over the period analysed (1986–2002), including stationary ice fronts on the northwestern coast of the AP. A widespread acceleration trend of glaciers on the AP west coast has been observed from repeated flow rate measurements during 1992–2005 and attributed to a dynamic response to frontal thinning (Reference Pritchard and VaughanPritchard and Vaughan, 2007).

Fig. 1. Location and surface elevation map of Hurd and Johnsons Glaciers, Hurd Peninsula, Livingston Island. The dashed line indicates the divide between Hurd and Johnsons Glaciers, while the dotted line indicates the divide between MacGregor and its neighbouring unnamed tongue. The arrows indicate the approximate flow directions on the basins not included in our study. Elevations and outline are based on a survey during summer 1998/99 and 2000/01. Positions of the mass-balance stakes at the end of the 2009/10 season are indicated with red dots. The positions of the automatic weather stations (AWSs) at Juan Carlos I station (JCI) and Johnsons Glacier (JG) are also shown
However, an overall mass loss cannot be inferred directly from either front retreat or flow acceleration (or both), since these losses could be balanced by an increased accumulation rate. In fact, much evidence points to such an increase: an increasing trend in winter accumulation in the northwestern AP observed in ERA-40 reanalysis data (Reference Miles, Marshall, McConnell and AristarainMiles and others, 2008), an increase in the annual total of precipitation days at Faraday/Vernadsky station (Reference Turner, Lachlan-Cope, Colwell and MarshallTurner and others, 2005b), accumulation increases inferred from shallow ice cores (Reference Aristarain, Delmas and StievenardAristarain and others, 2004; Reference Frey, Bales and McConnellFrey and others, 2006; Reference Miles, Marshall, McConnell and AristarainMiles and others, 2008) and assessments of accumulation distribution based on regional climate models (Reference Van de Berg, Van den Broeke, Reijmer and Van MeijgaardVan de Berg and others, 2006; Reference Van den Broeke, Van de Berg and Van MeijgaardVan den Broeke and others, 2006).
Consequently, basin-wide mass-balance estimates are required to quantify the actual mass losses. For large basins, the most effective tools at our disposal are remote-sensing tools, such as repeated altimetry or gravimetry, or the inputminus-output (IOM) method combining interferometric synthetic aperture radar (InSAR) velocities with modelled snow accumulation. Most of the studies using these tools have shown an overall mass loss of the ice covering the AP, though the discrepancies in the estimates are often large due to the limitations inherent in each technique. Discrepancies are particularly due to a large impact of the glacial isostatic adjustment (GIA) model selected for the Gravity Recovery and Climate Experiment (GRACE)-based results and, to a much lesser extent, to the altimetry results (Reference Wingham, Shepherd, Muir and MarshallWingham and others, 2006; Reference RignotRignot and others, 2008; Reference Chen, Wilson, Blankenship and TapleyChen and others, 2009; Reference WuWu and others, 2010; Reference Ivins, Watkins, Yuan, Dietrich, Casassa and RülkeIvins and others, 2011; Reference Rignot, Velicogna, Van den Broeke, Monaghan and LenaertsRignot and others, 2011; Reference Zwally and GiovinettoZwally and Giovinetto, 2011; Reference Jacob, Wahr, Pfeffer and SwensonJacob and others, 2012; Reference Whitehouse, Bentley, Milne, King and ThomasWhitehouse and others, 2012a,Reference Whitehouse, Bentley and Le Brocqb).
The above-mentioned wide-scale measurements, however, are not sufficient if we aim to study the interannual variability of mass balance or its link with climate drivers. Most of the above methods provide geodetic average mass balances for periods usually comprising several years (of the satellite-based methods, only GRACE can provide monthly estimates, at scales of a few hundred kilometres and larger). Classical direct measurements of surface mass balance (SMB) (e.g. Reference Østrem and BrugmanØstrem and Brugman, 1991) are therefore still important, not only because of their finer time resolution, but also as ground-truthing for the remote-sensing measurements, all of which involve important uncertainties. Among such uncertainties we could highlight those related to GIA for gravity change measurements, firn compaction for altimetry changes, or ice thickness at flux gates for InSAR. Moreover, if the direct measurements are conducted twice per year, at the beginning and end of the melting season, the classical method allows separation of summer and winter balances and thus can shed light on the physical mechanisms contributing to any observed mass-balance trend (e.g. whether increased melting is partly balanced by increased precipitation).
In spite of its importance, there is currently very little ongoing glacier mass-balance monitoring in the AP region. Aside from Hurd and Johnsons Glaciers, only one AP glacier appears in the World Glacier Monitoring Service (WGMS) database (http://www.geo.uzh.ch/microsite/wgms) as being monitored: Glaciar Bahía del Diablo located on Vega Island (Fig. 1) at the northeastern tip of the AP, which has been monitored continuously since 2000 (Reference Skvarca, De Angelis and ErmolinSkvarca and others, 2004). However, this glacier is measured just once per year, implying that only annual mass balance can be determined, without separation of summer and winter balances. Some other AP glaciers appear in the WGMS database, but only for discontinued and usually very short monitoring programmes. Among those earlier efforts to monitor mass balance in the AP region, the most remarkable is that of Spartan Glacier, for which a complete mass-balance programme was carried out during 1971–74 (Reference Jamieson and WagerJamieson and Wager, 1983; Reference Wager and JamiesonWager and Jamieson, 1983). Measurements during a 6 year period (1969–74 of which only 1969–71 were reported to the WGMS) were undertaken on glacier G1 on Deception Island in the SSI (Reference Orheim and GovorukhaOrheim and Govorukha, 1982), but this is a minute glacier, <0.5 km2 in area, in a location with extremely high geothermal heat flow associated with volcanic activity. All other AP glaciers recorded in the WGMS database are limited to a single year of measurements (Reference Dyurgerov and MeierDyurgerov and Meier, 2005). A compendium of additional in situ mass-balance measurements in the AP region, previous to 2002, can be found in the analysis by Reference Turner, Lachlan-Cope, Marshal, Morris, Mulvaney and WinterTurner and others (2002) of the spatial variability of the mass balance of the AP. However, these are just point measurements at stakes, stake arrays, shallow ice cores or snow pits and do not represent mass balances for complete basins. Mass-balance studies at locations close to our study site include: (1) the work involving mass-balance stakes, snow pits and shallow ice cores on the Rotch Ice Dome in the western part of LI from 1971/72 to 1973/74 (Reference Orheim and GovorukhaOrheim and Govorukha, 1982); (2) the work on Nelson Island ice cap from 1986/86 to 1988/89, with shallow ice cores sampling the period 1970–88 (Reference Qin, Zielinski, Germani, Ren, Wang and WangQin and others, 1994; Reference RenRen and others, 1995); and (3) the work on King George Island ice cap during 1969/70 and 1970/71 (Reference Orheim and GovorukhaOrheim and Govorukha, 1982) and from 1985 to 1992, with emphasis on 1991/92, and including shallow ice cores sampling the period 1971–92 (Reference Wen, Kang, Han, Xie, Liu and WangWen and others, 1998). To the above we could add average mass-balance estimates during 1970–2006 on Bowles Plateau icefield on LI, based on dated radar-detected tephra layers (Reference MacheretMacheret and others, 2009). However, none of these studies estimates the mass balance of any glacier at a basin-wide scale.
Basin-scale mass-balance measurements on AP glaciers are also of interest to the studies quantifying the mass losses from the mountain glaciers and ice caps peripheral to the ice sheets and their contribution to sea-level rise (e.g. Reference Hock, De Woul and RadićHock and others, 2009; Reference Radić and HockRadić and Hock, 2010, Reference Radić and Hock2011) because, in the case of Antarctica, the vast majority of such glaciers are concentrated on the AP and surrounding islands.
Reference Van den Broeke, Van de Berg and Van MeijgaardVan den Broeke and others (2006) pointed out that to improve our understanding of Antarctic mass (im)balance and associated changes in global sea level, new observations from high-accumulation zones, especially from coastal West Antarctica and the western AP, are urgently needed. In similar terms, Reference RignotRignot and others (2008) stressed that few reliable in situ coastal accumulation data exist for comparison. This paper contributes to relieving the remarkable scarcity of SMB data from this Antarctic region, which has been revealed to be so sensitive to recent climate change.
We present a new 10 year SMB record of Hurd and Johnsons Glaciers, with detail of summer and winter balances, and analyse them with regard to earlier local or regional mass-balance estimates and local and regional meteorological conditions and trends. The earlier local mass-balance studies include our average geodetic mass-balance (GMB) estimates during 1957–2000 for Hurd and Johnsons Glaciers (Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others, 2007) and earlier mass-balance measurements by the glaciological method on Johnsons Glacier during 1995–99 (Reference XimenisXimenis, 2001). The latter, however, only include mass-balance estimates for particular stake locations and not for the entire glacier due to the limited coverage of the net of mass-balance stakes on Johnsons Glacier prior to the study period. An additional interest in the mass-balance dataset presented in this paper is that it corresponds to two glaciers that, though located next to each other, have very different dynamic behaviours since Johnsons is a tidewater glacier while Hurd Glacier terminates on land.
2. Geographical Setting
Hurd Peninsula ice cap (62°39′–62°42′ S, 60°19′–60°25′ W; Fig. 1) covers an area of ∼13.5 km2 and spans an altitude range from sea level to ∼370 m a.s.l. It consists of two main glaciers, Hurd and Johnsons, plus three unnamed tongues flowing eastwards and southwards, which are heavily crevassed icefalls with typical slopes of 30°, but locally up to 45° or higher. We shall refer to the tongue flowing southwards as MacGregor Glacier. The local ice divide separating Johnsons and Hurd Glaciers has altitudes between 250 and 330 m a.s.l. Johnsons (5.36 km2) is a tidewater glacier that terminates in an ice cliff ∼50ma.s.l. extending 570 m along the coast. Typical surface slopes for Johnsons Glacier range between 10° in its northern areas and 6° in the southern ones. Hurd Glacier (4.03 km2) embraces three main tongues, Argentina (flowing northwestwards), Las Palmas (flowing westwards) and Sally Rocks (flowing southwestwards), all terminating on land and with ice thickness tapering to zero at their snouts. Sally Rocks tongue has typical surface slopes of ∼3°, while Argentina and Las Palmas tongues are much steeper (∼13°). Our mass-balance study focuses on Hurd and Johnsons Glaciers and excludes the basins flowing eastwards and southwards.
The average ice thickness in 1999–2001 for the ensemble Hurd –Johnsons determined from seismic and ground-penetrating radar data (Reference Benjumea, YuYa, Navarro and TeixidóBenjumea and others, 2003; Reference Navarro, YuYa and BenjumeaNavarro and others, 2005, Reference Navarro2009) was 93.6 ± 2.5 m. The maximum values, ∼200 m, correspond to the accumulation zone of Hurd Glacier; the maximum ice thickness of Johnsons Glacier is only ∼160 m. Johnsons Glacier bed is rather regular, with altitudes decreasing towards the ice front, where glacier bed elevation is slightly below sea level (typically –5 m). Hurd Glacier, however, is more irregular, with a clear over-deepening in the area of thickest ice close to the head of the Argentina side lobe and another overdeepening, though less pronounced, near the head of the Las Palmas side lobe.
The ice surface velocities of Johnsons Glacier increase downstream of the ice divide, reaching values up to 65 m a−1 at the fastest part of the calving front (Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others, 2010), while the largest ice velocities for Hurd Glacier are typically ∼5 m a−1 (Reference OteroOtero, 2008).
Hurd Peninsula ice cap is a polythermal ice mass showing an upper layer of cold ice several tens of metres thick in the ablation zone. In the snouts of Hurd Glacier (in the Sally Rocks area) and its side lobes Argentina and Las Palmas, where the glacier thickness tapers to zero, the cold ice layer extends down to bedrock so the glacier is frozen to the bed in these terminal areas, implying a compressional stress regime. In contrast, the area close to Johnsons calving front shows the extensional stress regime characteristic of the terminus of tidewater glaciers (Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others, 2007; Reference NavarroNavarro and others, 2009; Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others, 2010).
3. Data and Methods
The Spanish Antarctic station Juan Carlos I (JCI), located on Hurd Peninsula and very close to Hurd and Johnsons Glaciers (Fig. 1), provided the logistic support to the mass-balance measurements presented in this paper. It is open only during the austral summer (approximately from late November to early March), which controls the fieldwork schedule. Fortunately, we are able to nearly capture the start and end of each melting season, thus allowing us to separate the summer and winter mass balances. Since 1988, meteorological measurements have been maintained all year round by an automatic weather station (AWS) at JCI. During the summer, this is complemented by manual meteorological observations. Since December 2006, another AWS, including a snow-depth sonic sensor, has operated on the upper ablation zone of Johnsons Glacier (Fig. 1) at 166 m a.s.l. at installation time. On-glacier data records are often lost during the coldest and darkest part of the winter because of either battery malfunction or power shortage, since the solar panel is unable to recharge the battery during darkness.
3.1. Climatological conditions
Hurd Peninsula ice cap is subjected to the maritime climate pattern characteristic of the western AP region, with some peculiarities due to local conditions. The highest temperatures in Antarctica are found in the AP region, where there is a prevailing northwesterly wind. The geometry and orograpahy of LI, however, condition the wind regime, protecting Hurd Peninsula from the regionally prevailing wind, so that the prevailing winds are from the northeast, mostly katabatic from the higher elevations to the northeast and east of Hurd Peninsula, and from the southwest, where Hurd Peninsula faces the open ocean. The AWS at JCI shows predominant wind directions from the north-northeast, followed by south-southwest, with strongest winds from the east-northeast. The average wind speed is 4 m s−1,though gusts above 28 ms−1 are frequent and peak values up to 44 m s−1have been reached. In the case of the AWS at Johnsons Glacier, the predominant wind directions are from the southwest, followed by north-northeast and east-northeast, with strongest winds from the east-northeast. The average wind speed is 4 ms−1, also with frequent gusts above 28 ms−1 and with peak values up to 46 ms−1. The strongest winds are associated with deep low-pressure systems to the north of LI. The temperatures in the western AP can rise to several degrees above freezing during the summer, and monthly means are positive for several months of the year. On LI, the annual average temperature at JCI during our entire mass-balance measurement period of 2002–11 was −1.1°C, with average summer (December, January, February (DJF)) and winter (June, July, August (JJA)) temperatures of 2.8°C and −4.4°C, respectively, and extremes of 10.9°C and −22.6°C. Annual averages from the glacier AWS are not representative because of the data gaps during winter, but temperatures are usually 2–3°C lower than those recorded at JCI. The summer average at Johnsons Glacier is 0.3°C. The cloudiness (measured at JCI and assumed similar at both AWSs) is high, with an average of 6/8 of covered sky, and, consequently, the ratio of global radiation at the surface to top-of-atmosphere radiation is small. On average, 2 hours d−1 during summer and spring are cloud-free. However, high fluxes of global radiation are measured on cloud-free days during such seasons, with daily average values of up to 347 W m−2. The relative humidity is very high, with average values above 80% at JCI and 90% on the glacier.
On Hurd and Johnsons Glaciers, mass gain is dominated by direct snowfall and wind redistribution of snow, without any contribution from snow avalanches. The glacier ice hardly receives any debris from the surrounding mountains, except at the lowest elevations of its outlets. Tephra layers from the recent eruptions of neighbouring Deception Island, however, are a common feature on these glaciers (Reference Pallàs, Smellie, Casas and CalvetPallàs and others, 2001).
3.2. SMB measurements and computations
Throughout this paper we use the mass-balance terminology, symbols and units recommended by Reference CogleyCogley and others (2011). In particular, b and B are used to denote mass balance, with the lower-case symbol referring to its value at a point on the glacier surface or the column beneath such a point, and the upper-case symbol referring to the glacier-wide quantity; and the subscripts w, s and a are used to represent winter, summer and annual values, respectively.
Previous glaciological studies of Hurd Peninsula ice cap include mass balance and ice dynamics from stake measurements at an earlier net of stakes limited to Johnsons Glacier, much sparser than used in the present study and mostly focused on the ablation zone (Reference Ximenis, Calvet, Enrique, Corbera, Gamboa and FurdadaXimenis and others, 1999; Reference XimenisXimenis, 2001). These authors did not attempt to make an integrated mass-balance computation for the whole of Johnsons Glacier but just provided point mass-balance values at individual stakes, corresponding approximately to the hydrological years 1995–99. Unless otherwise stated, mass-balance years used throughout this paper are hydrological years for the Southern Hemisphere as defined by the WGMS, so 2011 starts on 1 April 2010 and ends on 31 March 2011. Therefore, whenever we refer to the mass-balance observation period 2002–11 we mean the period from 1 April 2001 to 31 March 2011.
We extended the existing net of Johnsons Glacier to obtain better sampling over the accumulation zone. We also extended the net to neighbouring Hurd Glacier, resulting in the net of stakes shown in Figure 1. The stakes are wooden poles of melis pine (southern yellow pine, Pinus taeda), 3.65 m in length and 0.045 m in diameter, which are maintained (extended or re-drilled as needed) at the end of each melting season or whenever necessary. A seasonal average of 45 stakes, ranging from 36 to 51, was surveyed during the summer field seasons of 2001/02 to 2010/11 in order to calculate the mass balances for the hydrological years 2002–11. As shown in Figure 1, four stakes lie on the head of MacGregor Glacier, outside the boundary of the area considered in our mass-balance calculations. Such stakes are measured and used for mass-balance contour interpolation purposes, but this area is excluded from the computations of mass balance for Hurd Glacier. In addition to mass-balance measurements, Hurd and Johnsons stakes are also positioned by differential GPS (DGPS) several times during each season to estimate glacier surface velocities.
Winter (b w) and summer (b s) point SMBs were obtained using the direct glaciological method (e.g. Reference Østrem and BrugmanØstrem and Brugman, 1991).
Winter accumulation was obtained from snow probing at the locations of the stakes and additionally from snow pits in the accumulation zone that were excavated to the depth of the last summer layer (at present, snow depth is additionally surveyed at ∼50 points different from the stake locations). These activities were undertaken in late November or early December, as soon as possible after the opening of the JCI research station.
Measurements of the height of the surface on the stakes were conducted two to four times during the melt seasons. The date of the last measurement of the season was limited by the closing time of JCI, normally in late February or early March. Melting on the glaciers later in the season is normal and thus not captured in the seasonal surface lowering. This post-field-season melting was quantified as the discrepancy between the snow depth of the subsequent year and the difference in stake height from the last measurement of the season to the first subsequent year. In the event that no postfield-season melting occurred the discrepancy will be zero, i.e. all the change in stake height is due to snow accumulation. In the event that a stake was lost during the winter or if for any other reason no measurement was available in the subsequent year, linear interpolations between elevations obtained at the remaining stakes would be used to quantify the post-seasonal melt. An example of the effect of this postfield-season melting correction is shown in Figure 2.

Fig. 2. Ablation measured at Hurd and Johnsons stakes during the field season 2008/09 (crosses) and estimated ablation during the entire melting season 2008/09 (in field season + post-field season) (diamonds).
Snow accumulation and surface lowering were converted to water equivalents (w.e.) by applying a density versus depth function constructed from a combination of density measurements from snow pits undertaken with a vertical spacing of 10–20cm. Until the 2003/04 season, densities were measured in shallow snow pits (up to 1 m) at various locations at the beginning of the season. Starting from the 2004/05 season, snow pits were excavated down to the previous summer layer at the beginning and end of each season.
At stakes where snow remained at the end of the melt season, the mass loss was calculated as the mass of the snowpack at the beginning of the season minus the mass of the remaining snow at the end of the season using a density versus depth function based on the beginning- and end-season snow-pit densities, respectively. For seasons prior to 2004/05, for which no end-of-season densities are available, the average seasonal densification of 13% was used. At stakes where seasonal surface lowering exceeded snow accumulation depth, the excess was considered to be melting of ice with a density of 900 kg m–3. In cases in which snow depth exceeded maximum pit depth, the density corresponding to maximum snow-pit depth was used.
Densities are expected to have a spatial variation, which cannot be captured by the limited number of snow pits. However, the variation with depth and seasons can serve as an indication of the errors caused by real variation and measurement error. The relative standard deviation of beginning-of-season measurements was 12% and for endof-season measurements was 13%. Lumping snow-pit densities from the 2004/05 season and later in 10 cm depth intervals enables calculation of the relative standard deviation within an interval, which is typically below <10% (maximum 12%) for both beginning- and end-of-season values. We therefore estimate the error in the total balances due to uncertainties in determination of density to be a maximum of 10% for the integrated mass balances, but occasionally higher for individual stake values.
A few winter accumulation readings from the 2004/05 and 2005/06 seasons were suspected to have been exaggerated. They showed much higher accumulation than neighbouring stakes, creating an unusual (compared with other years) and unlikely (compared with the pattern that could be expected on a relatively flat surface) pattern of accumulation. Consequently, they were corrected using the mean snow accumulation pattern determined from the other 8 years of readings. First a correction factor was obtained describing the deviation from the spatial mean for the specific season to the mean over the other 8 years. Thereafter a specific factor for each of the suspicious stakes, describing their typical spatial offset from the spatial mean, was obtained and applied. We present the more conservative (lower) corrected value in the results but give an additional error provoked by the uncertainty raised.
The obtained point values of b w and b s were interpolated over the glacier surface into a 25 m resolution grid using a kriging routine that utilizes best linear fit of the variogram. The balances of the two individual glaciers were obtained by applying separate blanking masks. An annual balance grid, b a, was calculated as b w+b s for each gridcell. Balances were calculated in elevation bands of 20 m and for the full integrated extent of the glaciers. The resulting glacier-wide SMBs are denoted by B a, B w and B s, respectively. Elevation data were provided by a digital elevation model (DEM) of corresponding grid size, obtained from interpolation of 852 survey points measured during the field seasons of 1998/99 (Johnsons Glacier, using a total station) and 2000/01 (Hurd Glacier, using DGPS). The DEM used for the mass-balance computations of all years is the same one, with corresponding planar areas (projected onto a horizontal plane) for Hurd and Johnsons Glaciers of 4.03 and 5.36 km2, respectively. This is justified by the small surface elevation changes and almost negligible area changes during the observation period (the front positions of Argentina, Las Palmas and Hurd–Sally Rocks are measured yearly and have changed little; the Johnsons Glacier calving-front position is measured every few years and has remained nearly unchanged). Note that the planar areas reported here are 15% (Hurd) and 4% (Johnsons) smaller than those reported by Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others (2007), 4.73 and 5.61 km2, respectively. This is due to a more careful delineation of the boundaries of the glacier basins (particularly at the ice divides) in the present study, using an improved topography and assuming that topographic divides coincide with flow divides. The larger difference for Hurd Glacier is due to the fact that Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others (2007) included in the area of Hurd Glacier the portion of the head of MacGregor Glacier, which we have intentionally excluded from our estimates because it belongs to a different drainage basin.
Accumulation–area ratio (AAR) is defined as the ratio of 25 m gridcells with b a exceeding zero to the total number of cells. Equilibrium-line altitude (ELA) was, in elevation bands of 5 m, calculated as the band with b a closest to zero.
3.3. Comparing surface and geodetic mass balances
One of our aims is to compare the climatic mass balance (here approximated by the SMB) for the period 2002–11 with the GMB for the period 1957–2000. The latter was estimated by Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others (2007) for the Hurd– Johnsons ensemble. We present here the GMBs for each glacier computed separately. Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others (2007) estimated the GMB from the DEMs of the glacier surface for 1957 (constructed from aerial photogrammetry) and 1999/2000 (obtained from surface-based geodetic measurements). We note that in Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others (2007) the measurement period is stated as 1956–2000 due to an error in the dating of the original photos, which actually correspond to 1957. The GMB was calculated as the volume of the difference between the DEMs, multiplied by the ratio of ice density (900 kg m−3) to water density (1000 kg m−3) and divided by the average glacier area during 1957–2000 and the number of years in the period. Johnsons Glacier calving-front positions did not pose a problem because the calving front has remained at a nearly constant position at least from 1957 to the present. Using the density of ice assumes that Sorge’s law (Reference BaderBader, 1954) holds, i.e. that all volume changes are of glacier ice and, therefore, that there are no changes in firn thickness or density. This is a reasonable assumption in the case of Hurd and Johnsons Glaciers, since most of the volume changes occur at lower elevations below the ELA (Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others, 2007) and thus involve ice rather than firn. The error in the GMB was estimated using the technique described by Reference Huss, Bauder and FunkHuss and others (2009), assuming an error in ice density of 50 kg m–3 and the DEM errors given by Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others (2007).
For Hurd Glacier, which terminates on land, surface and geodetic balances can be compared directly. However, since Johnsons is a tidewater glacier, it is necessary to add the calving flux to the SMB before comparing it with the GMB.
3.4. Volumetric calving flux
We computed the volumetric calving flux using measured ice thickness and modelled velocities at the calving front. We employed a full-Stokes three-dimensional dynamical model incorporating a crevasse-penetration depth calving law (Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others, 2010) tuned to fit the observed glacier surface velocities measured at a net of ∼20 stakes (some of them close to the calving front), averaged over a 3 year period (2004/05 to 2007/08) within the mass-balance observation interval. The calving-front position has remained nearly unchanged during the entire 10 year mass-balance measurement period 2002–11 (also nearly coincident with its position in 1957), and the ice-velocity changes during this period have been small (Navarro and others, unpublished data). The thickness at the calving front is accurately known from combined geodetic measurements of the emerged part and bathymetric measurements close to the calving front. The maximum ice thickness at the calving front is 83 m.
The calving front is divided into N adjacent trapezia with parallel sides in the vertical direction. At the centre of each trapezium the vertically averaged horizontal velocity is computed from the model velocities by numerical integration of the equation

where ui is the component of the horizontal velocity perpendicular to the calving front and Hi is the ice thickness at the calving front for trapezium i. The volumetric calving flux 4) (dimensions L3T−1) is then computed as
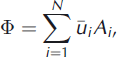
where Ai , i = 1, …, N, are the areas of each trapezium.
To obtain an estimate of the error in calving flux we applied standard error propagation techniques (e.g. Reference Bevington and RobinsonBevington and Robinson, 2002) under the assumption that the variables involved were uncorrelated. For the error in average velocity at the calving front, we used the 5.4 m a–1 misfit between modelled and observed velocities at the Johnsons Glacier net of stakes computed by Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others (2010). We approximated the error in calving-front area as the product of the length of the calving front (573.8 m) times the 3.1 m of surface elevation error in the 2000 DEM estimated by Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others (2007).
4. Results
The winter, summer and annual SMB results are shown in Table 1. On Hurd Glacier 6 of the 10 years yielded negative annual balances compared with 4 years on Johnsons Glacier. Mean B a was −0. 15 ± 0. 10 m w.e. for Hurd Glacier and 0.05 ± 0.10 m w.e. for Johnsons Glacier.
Table 1. Winter (B w), summer (B s) and annual (B a) surface mass balances (m w.e.), ELA (m a.s.l.) and AAR (%) for Hurd and Johnsons Glaciers during the hydrological years (Southern Hemisphere) 2002–11. The error in the annual mass balance (not shown in table for brevity) is assumed to be 0.10 m w.e. (Reference JanssonJansson, 1999)

The difference in average B a between the two glaciers is primarily an effect of the 23% higher average B w and secondly of the 8% less negative average B s on Johnsons Glacier compared with Hurd Glacier. Maximum difference between the glaciers in B w for an individual year was 0.29 m w.e. and that for B s was 0.24 m w.e.; both occurred for the hydrological year 2006. It is also noteworthy that the B a for Hurd Glacier for 2006 is much more negative than for 2007, which had the same ELA and similar AAR. As is apparent from Figure 3, there is a strong correlation between the annual B s of both glaciers (coefficient of determination r 2 = 0.95), while it is less pronounced for B w (r 2 = 0.64). For both glaciers the variability in B a is mainly driven by B s, but from the 10 years of measurements no significant trend is detectable in either winter, summer or annual SMB (Fig. 4), as revealed by the poor coefficients of determination (r 2 = 0.10–0.27) of the linear fits of all winter, summer and annual SMBs versus time. There is a strong correlation between ELA and AAR for both glaciers (r 2 = 0.97 for Hurd and r 2 = 0.95 for Johnsons) and also a good correlation between B a and ELA, best for Johnsons (r 2 = 0.82 for Hurd and r 2 = 0.94 for Johnsons), which implies that for these glaciers ELA is a good proxy for annual SMB.

Fig. 3. (a) Winter mass balance (B w, m w.e.) on Hurd versus Johnsons Glaciers for the mass-balance years 2001/02 to 2010/11. (b) As for (a) but for summer mass balance (B s).

Fig. 4. Surface mass-balance series of (a) Hurd and (b) Johnsons Glaciers (white bar B w; grey bar B s; red/blue B a, red if negative, blue if positive). Grey and black dashed lines represent the 10 year average B w and B s, respectively. Years shown are Southern Hemisphere hydrological years.
Accumulation on Johnsons Glacier is concentrated in the elevation interval 150–300m a.s.l., where b w is significantly higher compared with Hurd Glacier, while b s of Hurd Glacier dominates at the lowest elevations partly because of its larger share of area below 150 m a.s.l., where ablation rates are highest (Figs 5 and 6)

Fig. 5. (a) Relative altitude–area distribution. (b) Absolute cumulative accumulation as a share of the total absolute accumulation for the specific glacier 2001/02 to 2010/11. (c) Same as (b) but for surface ablation. (d) Absolute cumulative SMB 2001/02 to 2010/11. Each bar represents a 20 m altitude band.

Fig. 6. Mean b w, b s and b a 2001/02 to 2010/11 versus altitude in 20 m elevation intervals. The curves for Johnsons Glacier start at 50 m because this is the approximate height of its calving front. Though Johnsons Glacier has some area below 50 m, its share of the total area is negligible and moreover it is not sampled by any stake, so introducing it in this figure would just cause extrapolation artefacts..
Figure 7 shows the spatial distribution of the 10 year averages of the balances b w, b s and b a.

Fig. 7. Spatial distribution of the average b w, b s and b a (m w.e.) 2001/02 to 2010/11. The dashed line indicates the ice divide between Hurd and Johnsons Glaciers.
Higher ablation and lower accumulation rates result in lower AAR and higher ELA for Hurd Glacier. Based on the cumulative b a grid, calculations of mean ELA for Hurd yielded 228 m a.s.l. and AAR of 44%; corresponding values for Johnsons Glacier were 187 m a.s.l. and 61%, respectively, but large interannual variations in both ELA and AAR are present (Table 1). ELA for Johnsons Glacier is lower than that for Hurd Glacier, which is characteristic of tidewater versus land-terminating glaciers under similar climatic settings.
As shown in Figure 8 and Table 2, B s is correlated with the mean summer (DJF) temperatures from the nearby JCI record, as well as with the temperature of Bellingshausen station on King George Island and with the surface temperature of the gridpoint closest to Hurd Peninsula (61.9°S, 60.0°W) in the US National Centers for Environmental Prediction/US National Center for Atmospheric Research (NCEP/NCAR) reanalysis data. The latter is included to give the general temperature fluctuations in the area.

Fig. 8. (a) B s (m w.e.) for Hurd and Johnsons Glaciers. (b) Summer (DJF) temperatures (°C) at JCI, Bellingshausen, King George Island (BAS, 2011) and the gridpoint closest to Hurd Peninsula in the surface level NCEP/NCAR temperature dataset.
Table 2. Coefficients of determination (r 2) showing the degrees of correlation between the average summer mass balances for Hurd and Johnsons Glaciers and the average summer temperatures T s at Juan Carlos I and Bellingshausen stations, as well as the corresponding temperature from NCEP/NCAR reanalysis data

The results for the comparison between the average total mass balances (including SMB and calving losses, where appropriate) during the periods 2002–11 and 1957–2000 are shown in Table 3. Since Hurd is a land-terminating glacier, the GMB can be compared directly with the SMB (taken here as an approximation of the climatic mass balance). However, since Johnsons is a tidewater glacier, to obtain the equivalent GMB for 2002–11 we added to the average SMB the volumetric calving flux obtained using the technique described in Section 2, (8.23 ± 1.89) × 105 m3 a−1, normalized by Johnsons Glacier area and multiplied by the ratio of ice density to water density. We see that the total mass balance of both Hurd and Johnsons Glaciers has nearly halved from 1957–2000 to 2002–11, subject to the limitations implied by the small magnitudes of the mass-balance values involved and their comparatively large uncertainties.
Table 3. Average GMB during 1957–2000 and average SMB, volumetric calving flux divided by glacier area and equivalent GMB during 2002–11 for Hurd and Johnsons Glaciers. All quantities are m w.e.a−1. The error in the quotient between volumetric calving flux and Johnsons Glacier area was computed, using standard error propagation (Reference Bevington and RobinsonBevington and Robinson, 2002), from the error in calving flux given in the text and the error in Johnsons Glacier area given by Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others (2007)

5. Discussion
5.1. Interannual variability of SMB
During the hydrological years 2002–11, the more negative annual SMBs for Hurd and Johnsons Glaciers tend to occur during the early to middle years, while the more positive annual SMBs appear during the later years (Fig. 4). The large interannual variability of the SMB, together with the shortness of the time series, does not allow us to infer any significant trend. Least-squares linear fits to the changes in mass balance versus time result in poor fits for the annual mass balance (r 2 = 0.21 for both glaciers) and even poorer for the summer and winter balances (r 2 = 0.10–0.12) except for the winter balance of Hurd Glacier (r 2 = 0.27). The annual SMB of Hurd Glacier shows a larger interannual variability compared with Johnsons Glacier, as manifested by the standard deviations of 44 versus 30 m w.e., respectively (Table 1). The winter balance shows a smaller interannual variability than the summer balance, the difference being larger for Hurd Glacier. The larger interannual variability for the summer balance is a consequence of the large interannual variability of the temperature record and the good correlation between annual average summer temperature at JCI and B s shown in Figure 8 and Table 2 (coefficients of determination r 2 = 0.57–0.58). The latter also supports the strong correlation between annual B s for both glaciers (r 2 = 0.95).
5.2. Understanding the variability
Figure 4 shows that the more positive annual balances are generally associated with larger winter accumulation (2011 data provide the clearest example), but also with reduced summer melting (2010 data illustrate this). The important contribution of the reduced summer melting in producing positive annual balances is reinforced by the fact that, for both glaciers, all the years with positive annual mass balance have summer balance less negative than average, while not all winter accumulations are above the average (for Johnsons Glacier, 2004 and 2010 show winter balances slightly below the average).
The average SMBs over the 10 year observation period are −0.15 ± 0.10 m w.e. for Hurd Glacier and 0.05 ± 0.10 m w.e. for Johnsons Glacier. The difference between the glaciers results from a combination of higher accumulation rates and lower ablation rates for Johnsons Glacier compared with Hurd Glacier. The higher accumulation is attributed to the snow redistribution by wind, since the predominant wind directions measured at the AWS on Johnsons Glacier are from the southwest (coming from Hurd) followed by north-northeast and east-northeast (coming from the unnamed glacier to the north), and Johnsons surface has a concave shape compared with the more convex shape of Hurd and the unnamed glacier to the north of Johnsons. The hypsometry of Hurd Glacier (Fig. 5a), with a much larger share of area at the lowermost altitudes (<100 m) compared with Johnsons Glacier, contributes to larger melt rates.
5.3. Deceleration of the mass losses
A striking result from our mass-balance data is the deceleration of the mass loss of both glaciers from 1957–2000 to 2002–11 in a region that has shown a sustained climate warming during recent decades. Comparing the average GMB for the period 1957–2000 with the equivalent GMB for the period 2002–11 given in Table 3, we see that the annual mass loss has nearly halved for both glaciers, subject to the uncertainties given. This result is less striking when we note that, although the SSI have experienced a noticeable warming, this has focused on the winter and autumn, while the summer and spring trends are nearly negligible, as shown in Table 4. In fact, the average summer temperatures at Bellingshausen for the periods 1957–2000 and 2002–11 are nearly equal, 1.1 ± 0.5°C and 1.2 ± 0.5°C, respectively (the uncertainties given are the standard deviations). At a wider regional level, on the western side of the AP the greatest warming over the past 50 years has occurred in winter and spring (Reference TurnerTurner and others, 2005a, Reference Turner2009), as it has in continental West Antarctica (Reference Steig, Schneider, Rutherford, Mann, Comiso and ShindellSteig and others, 2009). Only in the eastern margin of the AP are the summer temperature trends large. These excursions with opposite signs on either side of the AP are a feature of the Antarctic dipole, an interannual standing-wave pattern that results in opposite temperature and sea-ice anomalies between the Weddell Sea and the Amundsen and Bellingshausen Seas (Reference YuanYuan, 2004), which has also been observed on millennial timescales (Reference MulvaneyMulvaney and others, 2012).
Table 4. Temperature trends at Bellingshausen station (62°12′ S, 58°56′ W) (BAS, 2011)

Other evidence of the recent deceleration of the annual mass losses is provided by the comparison between the SMB values reported in this paper and those reported by Reference XimenisXimenis (2001) for Johnsons Glacier, which span the hydrological years 1995–99. During this period, the net of stakes was limited to Johnsons Glacier and was much sparser than that reported in this paper. The number of stakes measured per year ranged from 7 to 16, with an average of 13. Ten of the stakes were distributed along two particular flowlines (of 3 and 7 stakes), but overall most of the stakes sampled the ablation zone (with many of them concentrated in a narrow zone at low altitude) and only 3–5 stakes, depending on the year, sampled the accumulation zone. As a result of this non-uniform distribution, Reference XimenisXimenis (2001) did not compute basin-wide balances, but only SMBs at particular stakes. Neither is a mass-balance versus elevation average curve presented. The closest element for comparison is figure 4.14 of Reference XimenisXimenis (2001), which shows the average SMB for each stake over the observation period as a function of its average elevation (note that point SMBs are not weighted by areas of elevation bins). In the period 1995–99, with the exception of a single stake, all measured stakes with positive mass balance are above 270 m (and the ELA is reported at ∼250m a.s.l.), while our average ELA for Johnsons Glacier during 2002–11 is 187137m. If we distribute stakes from Reference XimenisXimenis (2001) in 50 m elevation bins, the comparison with our SMB values for the uppermost two or three bins (200/250 to 350 m) shows values that are not so different. However, as we move to the lower bins the differences become very marked, with typical mass balances more negative during the period 1995–99 compared with 2002–11 by amounts of ∼0.5, 1.0 and 2.5 m w.e. for the three lowermost bins (50–200 m). We note that 1995–2000 has been the longest period of sustained high summer average temperatures (close to 2°C) within the Bellingshausen/Deception Island temperature record, spanning from 1944 to the present (with a gap during 1946) (BAS, 2011).
Modelling of melting by Reference Jonsell, Navarro, Bañón, Lapazaran and OteroJonsell and others (2012), combining mass-balance and on-glacier AWS data, suggests that Hurd and Johnsons Glaciers are very sensitive to air temperature changes: a 0.5°C temperature increase (decrease) implies a 56% (44%) increase (decrease) in melt rate. The main reason for this high sensitivity is that the summer air temperatures are close to zero almost everywhere on the glacier. The average summer temperature for the AWS on Johnsons Glacier (∼165 m a.s.l.) over the period December 2006–December 2011 is 0.3°C. Taking into account the lapse rate and the limited altitude range of Hurd and Johnsons Glaciers reveals that most of the glacier has summer temperatures near zero. Consequently, years with temperatures only slightly above (below) the average can show much higher (lower) melt rates. Figure 8 and Table 2 illustrate the good correlation between B s at Hurd and Johnsons Glaciers and the average summer temperatures at JCI and Bellingshausen (r 2 = 0.57–0.58 and 0.50–0.55, respectively), as well as the NCEP/NCAR grid value for the cell including Hurd Peninsula (r 2 = 0.79). Note that JCI shows enhanced temperature fluctuations compared with those at Bellingshausen. The last decade has shown, on average, lower summer surface temperatures at both Bellingshausen and JCI compared with those of the second half of the 1990s, which was the warmest period in the region over the past 50 years. The last decade has shown two particularly cold summers, 2003/04 and 2009/10 (Fig. 8), which had a clear influence on reduced summer melting, especially important in 2009/10 (Figs 4 and 8). Such temperature changes are within the ranges of the natural variability in the region (Reference King, Turner, Marshall, Connolley, Lachlan-Cope, Domack, Burnett, Leventer, Conley, Kirby and BindschadlerKing and others, 2003; Reference StastnaStastna, 2010; BAS, 2011).
5.4. Explaining the deceleration of the mass losses
We attribute the decrease in mass loss from 1957–2000 to 2002–11 to a combination of increased accumulation in the region, as a result of the recent deepening of the circumpolar pressure trough, and occasional decreased melt due to episodic lower summer temperatures during the past decade.
Several independent observational and modelling results support increased accumulation rates on the west coast of the AP during recent decades. Among them: (1) the annual total of precipitation days at Faraday/Vernadsky station (65°15′ S, 64°16′ W) has been increasing at a rate of + 12.4 days (10a)−1 since the early 1950s (Reference Turner, Lachlan-Cope, Colwell and MarshallTurner and others, 2005b) to reach a total number of 270–290 precipitation days per year during the last decade analysed; (2) ice cores from the southern part of the AP (Reference Frey, Bales and McConnellFrey and others, 2006) and near the northern tip of the AP (Reference Aristarain, Delmas and StievenardAristarain and others, 2004) show accumulation increases over the second half of the 20th century; (3) an increasing trend in winter (JJA) accumulation in the northwestern AP has been observed in ERA-40 reanalysis data (Reference Miles, Marshall, McConnell and AristarainMiles and others, 2008); and (4) regional climate modelling by Reference Van den Broeke, Van de Berg and Van MeijgaardVan den Broeke and others (2006), forced with ERA-40 reanalysis data, shows an accumulation increase by 96% (1992–2003 versus 1980–2004) for the western AP, though these results must be treated with care because accumulation on the narrow spine of the AP may be sensitive to snowdrift (Reference Turner, Lachlan-Cope, Marshal, Morris, Mulvaney and WinterTurner and others, 2002; Reference Van Lipzig, King, Lachlan-Cope and Van den BroekeVan Lipzig and others, 2004). Reference Turner, Lachlan-Cope, Colwell and MarshallTurner and others (2005b) have attributed the positive trends in precipitation on the western side of the AP to a deepening of the circumpolar pressure trough, which has enhanced the ascent of air masses and precipitation in the region.
We mention above the strong sensitivity of Hurd and Johnsons Glaciers to air temperature changes pointed out by Reference Jonsell, Navarro, Bañón, Lapazaran and OteroJonsell and others (2012) and explain how the episodes of lower local temperatures during the summers of 2003/04 and 2009/10 had an impact on reduced melting. Additionally, Reference Jonsell, Navarro, Bañón, Lapazaran and OteroJonsell and others (2012) showed that surface melting is also sensitive to the fraction of top-of-atmosphere radiation that reaches the ground: an increase (decrease) in this fraction by half a standard deviation of its daily mean leads to an increase (decrease) of melt by 15%. However, Reference Jonsell, Navarro, Bañón, Lapazaran and OteroJonsell and others (2012) noted that the air temperature and the fraction of top-of-atmosphere radiation that reaches the ground are anticorrelated in the Johnsons Glacier AWS record, meaning that under present climate conditions a temperature increase is in general associated with a cloudier sky. Extrapolating this to a temperature increase driven by climate change implies that increased melt due to higher temperature will to some extent be balanced by reduced direct radiation. In the light of the modelling by Reference Jonsell, Navarro, Bañón, Lapazaran and OteroJonsell and others (2012), we can also hypothesize that the lower temperatures during the past decade might have reduced the fluxes of turbulent energy (latent and sensible), therefore reducing the number or amplitude of the episodes of extreme melting described by Reference Jonsell, Navarro, Bañón, Lapazaran and OteroJonsell and others (2012). We finally note, following Reference Jonsell, Navarro, Bañón, Lapazaran and OteroJonsell and others (2012), that climate change at these latitudes will probably be driven mainly by the associated changes in cyclonic activity and pathways, hence changes will neither be static nor solely impact a single meteorological variable and consequently melt model sensitivity experiments provide only a first level of understanding of the response of glaciers to climate change.
5.5. Comparison with other regional observations
There are other regional observations of decelerated mass losses during the past decade. Reference Davies, Carrivick, Glasser, Hambrey and SmellieDavies and others (2012), based on a study of 194 glaciers on Trinity Peninsula, Vega Island and James Ross Island, have pointed out several results showing decelerated recession from 1988–2001 to 2001–09. (1) During 1988–2001, 90% of glaciers receded, while during 2001–09 only 79% receded; glaciers on the western side of Trinity Peninsula retreated relatively little. (2) The total glacierized area in the northern AP has declined at an average of 30.4 ± 0.99 km2 a−1since 2001, with total losses of glacierized area of 11.1% during 1988–2001 and 3.3% during 2001–09. (3) Tidewater glaciers on the drier, cooler eastern Trinity Peninsula experienced fastest recession from 1988 to 2001, with limited frontal retreat after 2001. (4) Land-terminating glaciers on James Ross Island also retreated fastest in the period 1988–2001. Reference Davies, Carrivick, Glasser, Hambrey and SmellieDavies and others (2012) noted that the east–west difference is largely a result of temperature and precipitation gradients across the AP.
Unfortunately, a comparison with the various mass-balance studies in the AP region reported in Section 1, even with those in the neighbouring islands of the SSI archipelago, is not possible because such studies correspond to periods that do not overlap with that covered by the present study (2002–11). Though they overlap with the period analysed by Reference Molina, Navarro, Calver, Garcı’a-Sellés and LapazaranMolina and others (2007), the latter gives an average value only for the entire period 1957–2000, while the other reported studies span periods of just a few years, often corresponding to very distant locations. Neither can a proper time evolution be analysed, since the short measurement periods in the various studies do not form a proper time series, as they often correspond to locations very distant from each other and the time gaps are large and irregular. Moreover, almost none of these studies (with the very few exceptions of glaciers reported in the WGMS database) provide basin-scale SMB values. The only meaningful comparison that we have extracted from these studies is that referred to the ELA, discussed in Section 5.6.
The only glacier in the AP region with a SMB record comparable with those of Hurd and Johnsons Glaciers is Glaciar Bahia del Diablo (63°49′ S, 57°26′ W) on Vega Island to the northeast of the tip of the AP (Fig. 1). It is a land-terminating glacier of ∼14.3 km2, spanning an altitude range of 75–630 m and facing northeast/east (Reference Skvarca, De Angelis and ErmolinSkvarca and others, 2004; WGMS database). The annual mass balances for Hurd and Johnsons Glaciers and Glaciar Bahia del Diablo are shown in Figure 9. The main similarity is that for all three glaciers the negative SMBs tend to be concentrated in the early to middle years, while the positive SMBs occur in the late years. Glaciar Bahia del Diablo can be more easily compared with Hurd Glacier, as both are land-terminating. Hurd Glacier usually has more extreme negative mass balances, which we attribute to its lower altitude range, but there are clear exceptions to this, the most remarkable being those of 2002 and 2008. The lack of a clear correlation (r 2 = 0.30 for Glaciar Bahia del Diablo and Hurd Glacier and r 2 = 0.36 for Glaciar Bahía del Diablo and Johnsons Glacier) is not surprising, considering the different climatic settings of the glaciers, with Hurd and Johnsons Glaciers influenced by the warmer and wetter maritime climate of the western AP and Glaciar Bahía del Diablo dominated by the colder and drier climate of the eastern AP. Moreover, the fact that Glacier Bahía del Diablo is surveyed only once per year, near the end of the melting season, implies that it is not possible to separate the winter and summer balances, making it difficult to understand the main drivers of the changes in the observed annual balances, while our records for Hurd and Johnsons Glaciers allow for a more complete analysis.

Fig. 9. Annual SMBs of Hurd and Johnsons Glaciers and Glaciar Bahía del Diablo. Years shown are Southern Hemisphere hydrological years.
5.6. Analysis of changes in ELA
The good correlation between B a and ELA for Hurd and Johnsons Glaciers pointed out earlier (r 2 = 0.82 for Hurd and r 2 = 0.94 for Johnsons) implies that for these glaciers the ELA is a good proxy for annual SMB. Consequently, a look at the ELA of glaciers on LI or other neighbouring islands of the SSI archipelago is of interest.
Mass-balance studies conducted by Reference Orheim and GovorukhaOrheim and Govorukha (1982) on Rotch Dome (western part of LI) during the period 1971–74 suggest an ELA at 150m a.s.l. Reference Ximenis, Calvet, Enrique, Corbera, Gamboa and FurdadaXimenis and others (1999) report a rising trend of the ELA of Johnsons Glacier between 1965 and 1997 from a mean value of 200 m in 1965–93 to 235 m in 1992/93 to 250 m during 1995–97, coincident with the period of the highest regional summer temperatures (second half of the 1990s). This is consistent with Reference Rückamp, Braun, Suckro and BlindowRückamp and others (2011) noting a rise in the ELA for Bellingshausen Dome, on neighbouring King George Island, from 140 m in 1967 to 200 m in 1999 (Reference Orheim and GovorukhaOrheim and Govorukha, 1982; Reference Wen, Kang, Han, Xie, Liu and WangWen and others, 1998; Reference Braun, Rau, Saurer and GoβmannBraun and others, 2000). However, our average ELA for Johnsons Glacier for 2002–11 is 187 ± 37 m, much lower than all those reported by Reference Ximenis, Calvet, Enrique, Corbera, Gamboa and FurdadaXimenis and others (1999), while our average ELA for Hurd Glacier for 2002–11 is 228 ± 57m. Such a large variability of the ELA of these glaciers implies that any apparent trend based on limited observations should be taken with great caution.
6. Conclusions
The main conclusions resulting from our analysis are:
-
1. The average annual SMBs over the 10 year observation period 2002–11 are −0.15 ± 0.10 m w.e. for Hurd Glacier and 0.05 ± 0.10 m w.e. for Johnsons Glacier. The average ELAs and AAR for these glaciers are 228 ± 157 m and 44 ± 24% (Hurd) and 187 ± 37m and 61 ± 21% (Johnsons). The quoted uncertainties for ELA and AAR are their standard deviations.
-
2. The current volumetric calving flux of Johnsons Glacier is estimated to be (8.23 ± 1.89) × 105m3a−1 . Adding these calving losses (normalized by glacier area) to the SMB gives an average total annual mass balance of −0.09 ± 0.11 m w.e. for Johnsons Glacier during 2002–11.
-
3. There has been a deceleration of the mass losses of these glaciers from their average values during the period 1957–2000 to those for the decade 2002–11. Subject to the uncertainties given, the mass losses have almost halved, from −0.27 ± 0.09 to −0.15 ± 0.10 m w.e.a−1 for Hurd Glacier and from −0.16 ± 0.09 to −0.09 ± 0.11 m w.e.a−1for Johnsons Glacier.
-
4. We attribute this decrease in mass loss from 1957–2000 to 2002–11 to a combination of increased accumulation in the region, as a result of the recent deepening of the circumpolar pressure trough, and decreased melt associated with episodic years of lower summer temperatures during the past decade which are within the ranges of the natural variability in the region.
-
5. Given the strong sensitivity of these glaciers to air temperature changes (Reference Jonsell, Navarro, Bañón, Lapazaran and OteroJonsell and others, 2012), a return to regional warmer summer conditions would likely imply an immediate return to increased melt.
Acknowledgements
We thank the mountain technicians of JCI station, as well as the technician in charge of the GPS base station at JCI, for continuous support of our fieldwork activities. We also thank the Met Office (AEMET) personnel for support of the on-glacier AWS maintenance, and in particular Manuel Bañón for support in meteorological data analysis. Massbalance calculations were made using a slightly modified version of a MatlabTM script developed by Rickard Pettersson, Uppsala University, Sweden. The paper was greatly improved by the comments and suggestions of Nick Barrand, an anonymous reviewer and Al Rasmussen, who also did a complete revision of the English writing style. This research was funded by subsequent grants from the Spanish National Plan of R&D, the most recent one CTM2008-05878/ANT.















