Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T15:14:48.075Z Has data issue: false hasContentIssue false
  • English
  • Français

The structure and budget of turbulent kinetic energy in front of a wall-mounted cylinder – CORRIGENDUM

Published online by Cambridge University Press:  29 May 2018

Wolfgang Schanderl ,
Ulrich Jenssen ,
Claudia Strobl  and
Michael Manhart
Rights & Permissions [Opens in a new window]

Abstract

An abstract is not available for this content. As you have access to this content, full HTML content is provided on this page. A PDF of this content is also available in through the ‘Save PDF’ action button.
Type
Corrigendum
Information
Journal of Fluid Mechanics , Volume 847 , 25 July 2018 , pp. 907 - 911
Check for updates
Copyright
© 2018 Cambridge University Press 

In Schanderl et al. (Reference Schanderl, Jenssen, Strobl and Manhart2017), incorrect particle image velocimetry (PIV) results were presented owing to mistaken use of the wrong calibration file in the processing of the data. None of the conclusions are affected by this unfortunate error, but the quantitative PIV results need updating with table 2 and figures 7, 8, 11, 12, 15 and 18 replaced with the following.

The spatial resolution was $0.00295D$ (instead of $0.0038D$ as given in the original article) which corresponds to 339 data points per cylinder diameter, which affected both the spatial position and the amplitudes of the measured flow quantities. While in the results published in the original article the measured position of the horseshoe vortex was by $0.03D$ more upstream, it turned out that with the correct calibration, it is by $0.03D$ more downstream of the simulated horseshoe vortex centre. The positions of the other critical points in the symmetry plane, as given in table 2, have changed as well. The magnitudes of the velocity and its statistics are reduced. For example, it was reported that the measured peak value of the in-plane turbulent kinetic energy was 30 % larger than the in-plane turbulent kinetic energy simulated by large eddy simulation (LES). With the correct calibration, those peak values coincide with $k_{ip,peak}\approx 0.07u_{b}^{2}$ .

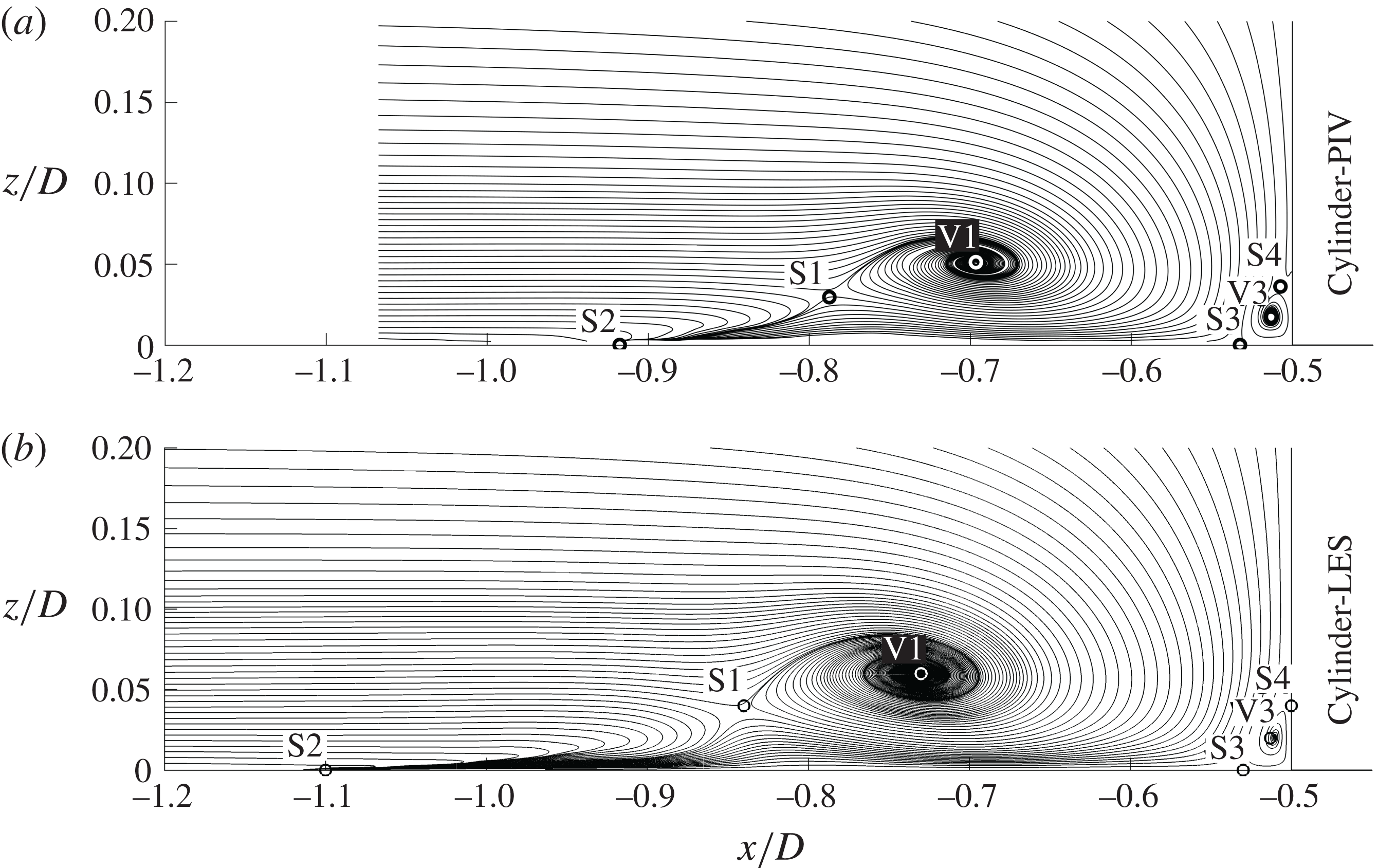
Figure 7. Streamlines of the time-averaged flow field in the symmetry plane in front of the cylinder for (a) PIV and (b) LES.

Table 2. Positions of critical points. If no $z_{Si}$ is given, the corresponding stagnation point is located at the bottom plate.

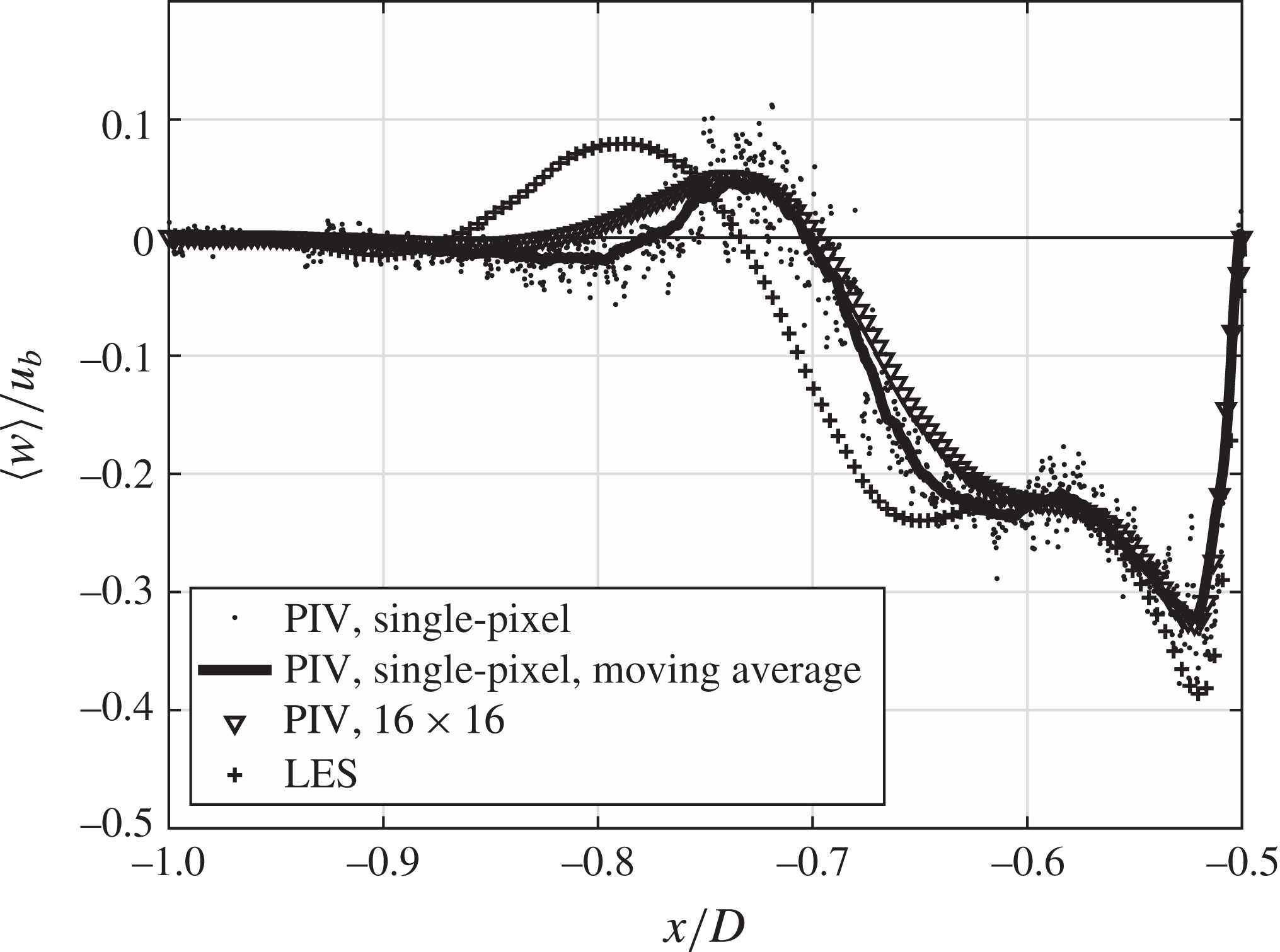
Figure 8. Profiles of the wall-normal velocity component $\langle w\rangle$ in the symmetry plane in front of the cylinder at a wall distances of $z_{V1}=0.06D$ .

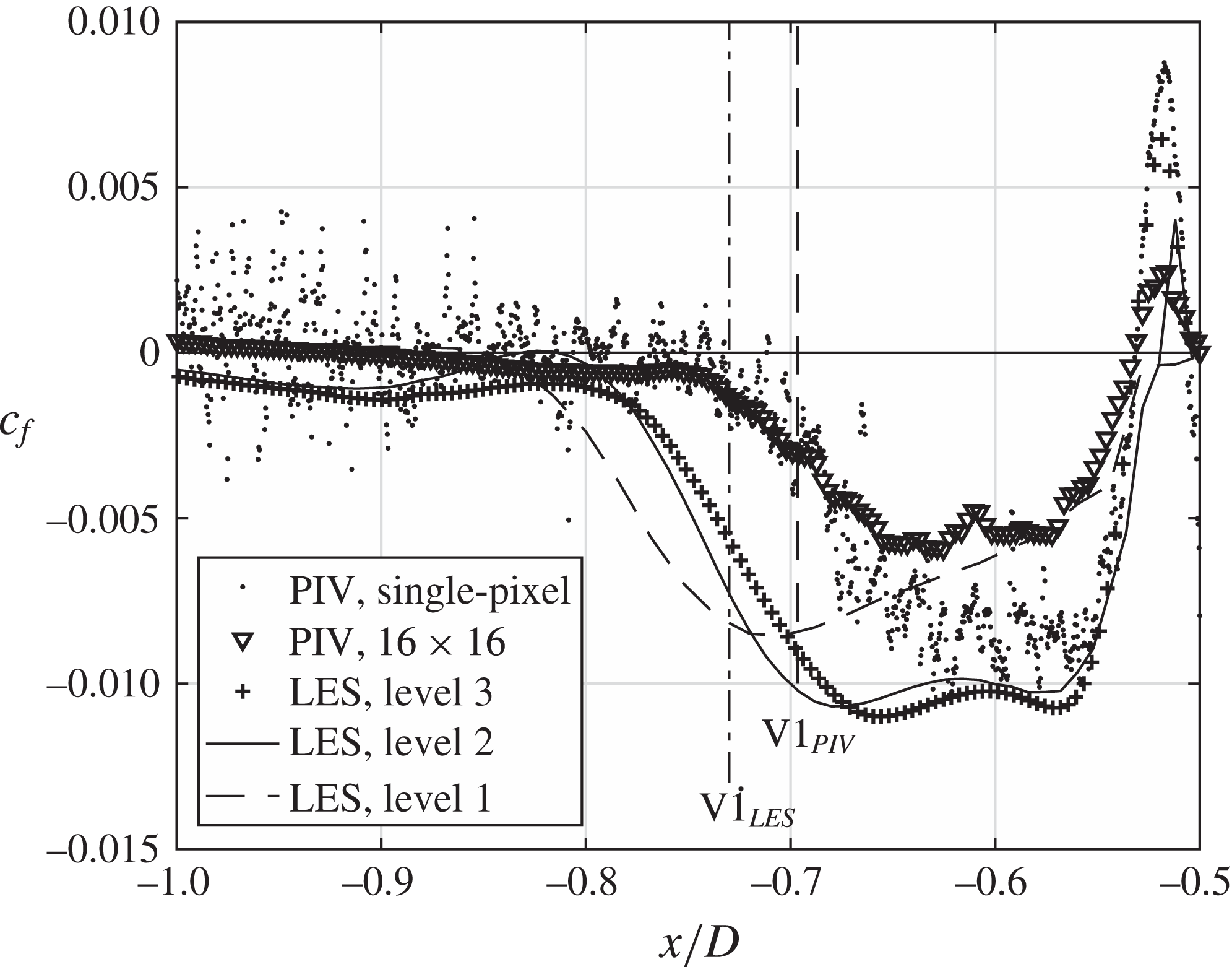
Figure 11. Distribution of the friction coefficient $c_{f}=\langle \unicode[STIX]{x1D70F}_{w}\rangle /(\unicode[STIX]{x1D70C}/2u_{b}^{2})$ over $x/D$ in the symmetry plane in front of the cylinder.

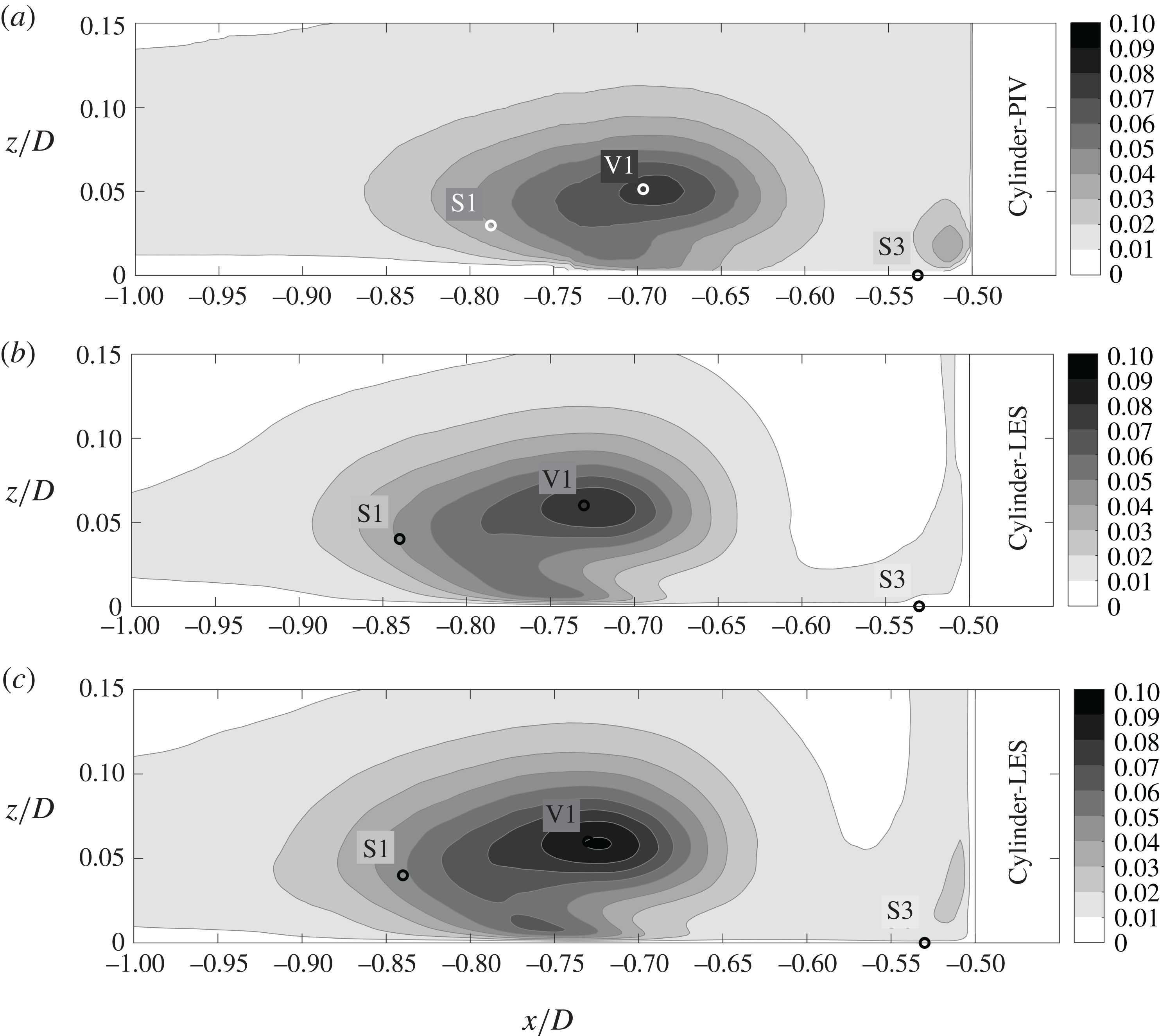
Figure 12. Turbulent kinetic energy in the symmetry plane in front of the cylinder. In-plane turbulent kinetic energy $k_{ip}/u_{b}^{2}$ measured by PIV (a) and simulated by LES (b). Full turbulent kinetic energy $k/u_{b}^{2}$ simulated by LES (c).

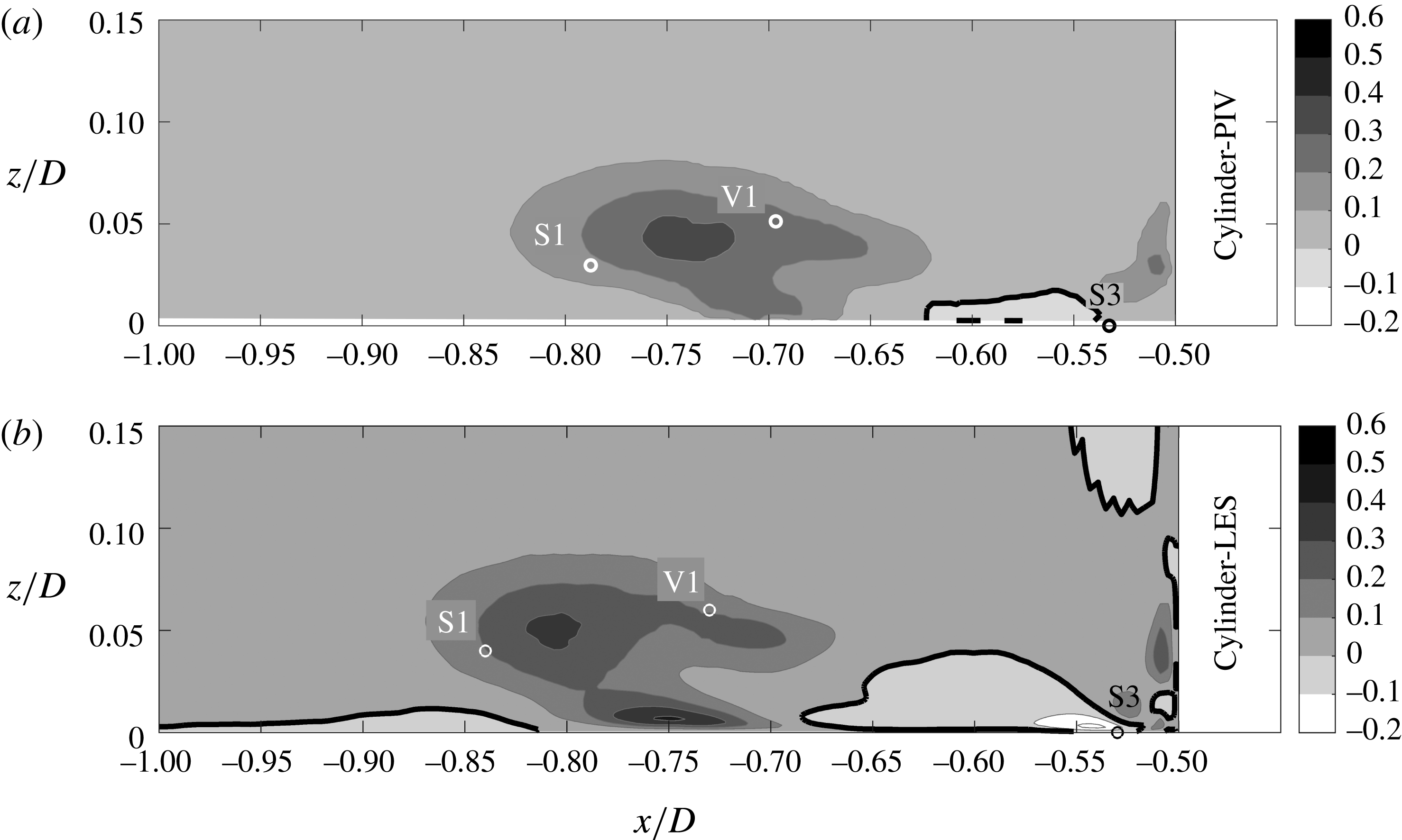
Figure 15. Production of turbulent kinetic energy in the symmetry plane in front of the cylinder. In-plane production from PIV (a) and total production from LES (b). The isoline marks $PD/u_{b}^{3}=0$ .

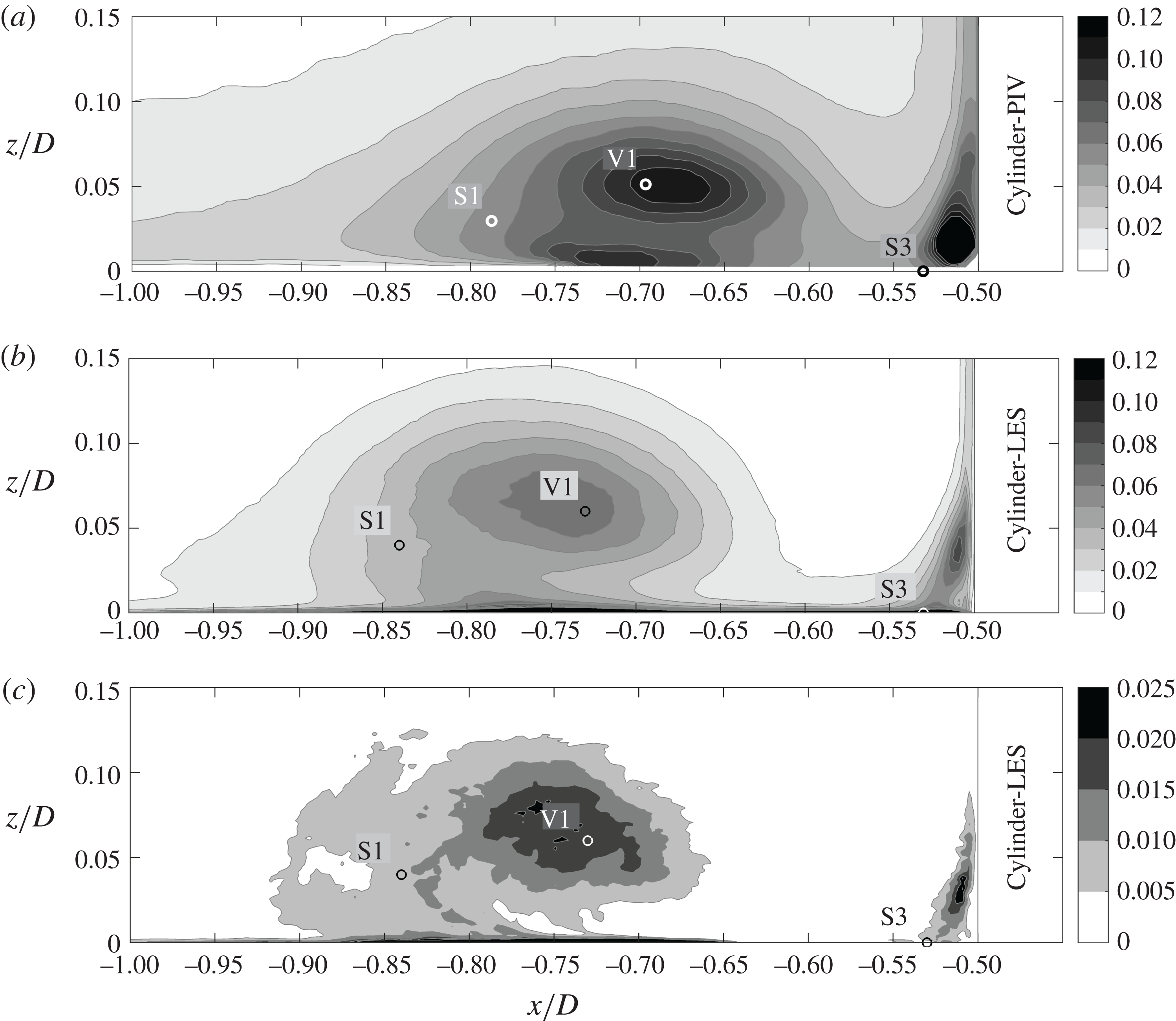
Figure 18. Total dissipation of turbulent kinetic energy $\unicode[STIX]{x1D716}D/u_{b}^{3}$ taken from PIV (a) and LES (b) and modelled dissipation $\unicode[STIX]{x1D716}_{SGS}D/u_{b}^{3}$ taken from the LES (c) in the symmetry plane in front of the cylinder. Note the different amplitudes of the colour bars.

References

Schanderl, W., Jenssen, U., Strobl, C. & Manhart, M. 2017 The structure and budget of turbulent kinetic energy in front of a wall-mounted cylinder. J. Fluid Mech. 827, 285–321.Google Scholar
Figure 0

Figure 7. Streamlines of the time-averaged flow field in the symmetry plane in front of the cylinder for (a) PIV and (b) LES.

Figure 1

Table 2. Positions of critical points. If no $z_{Si}$ is given, the corresponding stagnation point is located at the bottom plate.

Figure 2

Figure 8. Profiles of the wall-normal velocity component $\langle w\rangle$ in the symmetry plane in front of the cylinder at a wall distances of $z_{V1}=0.06D$.

Figure 3

Figure 11. Distribution of the friction coefficient $c_{f}=\langle \unicode[STIX]{x1D70F}_{w}\rangle /(\unicode[STIX]{x1D70C}/2u_{b}^{2})$ over $x/D$ in the symmetry plane in front of the cylinder.

Figure 4

Figure 12. Turbulent kinetic energy in the symmetry plane in front of the cylinder. In-plane turbulent kinetic energy $k_{ip}/u_{b}^{2}$ measured by PIV (a) and simulated by LES (b). Full turbulent kinetic energy $k/u_{b}^{2}$ simulated by LES (c).

Figure 5

Figure 15. Production of turbulent kinetic energy in the symmetry plane in front of the cylinder. In-plane production from PIV (a) and total production from LES (b). The isoline marks $PD/u_{b}^{3}=0$.

Figure 6

Figure 18. Total dissipation of turbulent kinetic energy $\unicode[STIX]{x1D716}D/u_{b}^{3}$ taken from PIV (a) and LES (b) and modelled dissipation $\unicode[STIX]{x1D716}_{SGS}D/u_{b}^{3}$ taken from the LES (c) in the symmetry plane in front of the cylinder. Note the different amplitudes of the colour bars.