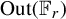1 Introduction
The purpose of this paper is to introduce and examine two piecewise Riemannian metrics, called the entropy metric and the pressure metric, on the Culler–Vogtmann outer space
![]() $CV(\mathbb {F}_r)$
. The Culler–Vogtmann outer space is the moduli space of unit-volume marked metric graphs and as such it is often viewed as the analog of the Teichmüller space of an orientable surface
$CV(\mathbb {F}_r)$
. The Culler–Vogtmann outer space is the moduli space of unit-volume marked metric graphs and as such it is often viewed as the analog of the Teichmüller space of an orientable surface
![]() $S_g$
. Both the Culler–Vogtmann outer space and the Teichmüller space admit a natural properly discontinuous action by a group. For the Culler–Vogtmann outer space, the group is the outer automorphism group of a free group
$S_g$
. Both the Culler–Vogtmann outer space and the Teichmüller space admit a natural properly discontinuous action by a group. For the Culler–Vogtmann outer space, the group is the outer automorphism group of a free group
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r) = \operatorname {\mathrm {Aut}}(\mathbb {F}_r)/\operatorname {\mathrm {Inn}}(\mathbb {F}_r)$
. For the Teichmüller space, the group is the mapping class group of the surface
$\operatorname {\mathrm {Out}}(\mathbb {F}_r) = \operatorname {\mathrm {Aut}}(\mathbb {F}_r)/\operatorname {\mathrm {Inn}}(\mathbb {F}_r)$
. For the Teichmüller space, the group is the mapping class group of the surface
![]() $\operatorname {\mathrm {MCG}}(S_g) = \pi _0 (\operatorname {\mathrm {Homeo}}^+(S_g))$
. Strengthening the connection between these spaces and groups are the facts that (i)
$\operatorname {\mathrm {MCG}}(S_g) = \pi _0 (\operatorname {\mathrm {Homeo}}^+(S_g))$
. Strengthening the connection between these spaces and groups are the facts that (i)
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
is isomorphic to the group of homotopy equivalences of a graph whose fundamental group is isomorphic to
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
is isomorphic to the group of homotopy equivalences of a graph whose fundamental group is isomorphic to
![]() $\mathbb {F}_r$
, that is,
$\mathbb {F}_r$
, that is,
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
can be thought of as the mapping class group of a graph, and (ii) the Dehn–Nielsen–Baer theorem which states that the extended mapping class group
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
can be thought of as the mapping class group of a graph, and (ii) the Dehn–Nielsen–Baer theorem which states that the extended mapping class group
![]() $\operatorname {\mathrm {MCG}}^\pm (S_g)$
(which also includes isotopy classes of orientation-reversing homeomorphisms) is isomorphic to
$\operatorname {\mathrm {MCG}}^\pm (S_g)$
(which also includes isotopy classes of orientation-reversing homeomorphisms) is isomorphic to
![]() $\operatorname {\mathrm {Out}}(\pi _1(S_g))$
[Reference Dehn17]. This analogy has led to much fruitful research on the outer automorphism group of a free group
$\operatorname {\mathrm {Out}}(\pi _1(S_g))$
[Reference Dehn17]. This analogy has led to much fruitful research on the outer automorphism group of a free group
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
.
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
.
The metrics on the Culler–Vogtmann outer space we consider in this paper are analogs to the classical Weil–Petersson metric on the Teichmüller space of an orientable surface. The Weil–Petersson metric has been studied extensively from the point of view of both geometric analysis and geometric group theory. On the one hand, it enjoys many important analytic properties which can be expressed naturally in terms of hyperbolic geometry on
![]() $S_g$
. Its utility in geometric group theory then stems from the fact that every isometry of the Weil–Petersson metric is induced by a mapping class [Reference Masur and Wolf25]. Thus, the action of
$S_g$
. Its utility in geometric group theory then stems from the fact that every isometry of the Weil–Petersson metric is induced by a mapping class [Reference Masur and Wolf25]. Thus, the action of
![]() $\operatorname {\mathrm {MCG}}(S_g)$
on the Teichmüller space equipped with the Weil–Petersson metric encodes information about useful invariants for mapping classes.
$\operatorname {\mathrm {MCG}}(S_g)$
on the Teichmüller space equipped with the Weil–Petersson metric encodes information about useful invariants for mapping classes.
As the piecewise Riemannian metrics on the Culler–Vogtmann outer space that we study in this paper are motivated by the classical Weil–Petersson metric on the Teichmüller space of a closed surface, it is natural to ask to what extent they are true analogs of the Weil–Petersson metric. A major takeaway from the work in this paper is that they should be seen as natural analogs from the geometric analysis point of view, but not from the geometric group theory perspective. Specifically, while we highlight some similarities between these metrics and the Weil–Petersson metric as seen from the analytic point of view (Theorems 1.1 and 1.2) the main result (Theorem 1.3) of this paper shows that from the geometric group-theoretic perspective, these metrics are not useful (except possibly when
![]() $r=3$
). The content of this theorem is summarized as follows: the action of
$r=3$
). The content of this theorem is summarized as follows: the action of
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the metric completion of the Culler–Vogtmann outer space has a fixed point for
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the metric completion of the Culler–Vogtmann outer space has a fixed point for
![]() $r \geq 4$
. The remainder of this introduction discusses these metrics more thoroughly and provides context for the main results.
$r \geq 4$
. The remainder of this introduction discusses these metrics more thoroughly and provides context for the main results.
1.1 Metrics on outer space
The topology of
![]() $CV(\mathbb {F}_r)$
has been well studied; see, for instance, the survey papers of Bestvina [Reference Bestvina and Li5] and Vogtmann [Reference Vogtmann35]. The metric theory of
$CV(\mathbb {F}_r)$
has been well studied; see, for instance, the survey papers of Bestvina [Reference Bestvina and Li5] and Vogtmann [Reference Vogtmann35]. The metric theory of
![]() $CV(\mathbb {F}_r)$
has been steadily developing over the past decade. What is desired is a theory that reflects the dynamical properties of the natural action by
$CV(\mathbb {F}_r)$
has been steadily developing over the past decade. What is desired is a theory that reflects the dynamical properties of the natural action by
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
, that further elucidates the connection between
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
, that further elucidates the connection between
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
and
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
and
![]() $\operatorname {\mathrm {MCG}}(S)$
, and that leads to useful new discoveries.
$\operatorname {\mathrm {MCG}}(S)$
, and that leads to useful new discoveries.
The metric that has received the most attention to date is the Lipschitz metric. Points in the Culler–Vogtmann outer space are represented by triples
![]() $(G,\rho ,\ell )$
where G is a finite connected graph,
$(G,\rho ,\ell )$
where G is a finite connected graph,
![]() $\rho \colon \thinspace \mathcal {R}_r \to G$
is a homotopy equivalence where
$\rho \colon \thinspace \mathcal {R}_r \to G$
is a homotopy equivalence where
![]() $\mathcal {R}_r$
is the r-rose, and
$\mathcal {R}_r$
is the r-rose, and
![]() $\ell $
is a function from the edges of G to
$\ell $
is a function from the edges of G to
![]() $(0,\infty )$
for which the sum of
$(0,\infty )$
for which the sum of
![]() $\ell (e)$
over all edges of G is equal to
$\ell (e)$
over all edges of G is equal to
![]() $1$
. (See §2.2 for complete details.) We think of the function
$1$
. (See §2.2 for complete details.) We think of the function
![]() $\ell $
as specifying the length of each edge and as such
$\ell $
as specifying the length of each edge and as such
![]() $\ell $
determines a metric on G where the interior of each edge e is locally isometric to the interval
$\ell $
determines a metric on G where the interior of each edge e is locally isometric to the interval
![]() $(0,\ell (e))$
. The Lipschitz distance between two unit-volume marked metric graphs
$(0,\ell (e))$
. The Lipschitz distance between two unit-volume marked metric graphs
![]() $(G_1,\rho _1,\ell _1)$
and
$(G_1,\rho _1,\ell _1)$
and
![]() $(G_2,\rho _2,\ell _2)$
in
$(G_2,\rho _2,\ell _2)$
in
![]() $CV(\mathbb {F}_r)$
is defined by
$CV(\mathbb {F}_r)$
is defined by
where
![]() $\operatorname {\mathrm {Lip}}(f)$
is the Lipschitz constant of the function
$\operatorname {\mathrm {Lip}}(f)$
is the Lipschitz constant of the function
![]() $f \colon \thinspace G_1 \to G_2$
using the metrics induced by
$f \colon \thinspace G_1 \to G_2$
using the metrics induced by
![]() $\ell _1$
and
$\ell _1$
and
![]() $\ell _2$
. respectively. In general the function
$\ell _2$
. respectively. In general the function
![]() $d_{\operatorname {\mathrm {Lip}}}$
is not symmetric. As such,
$d_{\operatorname {\mathrm {Lip}}}$
is not symmetric. As such,
![]() is not a true metric, but an asymmetric metric. See [Reference Algom-Kfir1, Reference Algom-Kfir and Bestvina2, Reference Francaviglia and Martino20] for more on the asymmetric aspects of the Lipschitz metric.
is not a true metric, but an asymmetric metric. See [Reference Algom-Kfir1, Reference Algom-Kfir and Bestvina2, Reference Francaviglia and Martino20] for more on the asymmetric aspects of the Lipschitz metric.
Regardless, the Lipschitz metric has been essential in several recent developments for
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
. This is in part due to the fact that the Lipschitz metric connects the dynamical properties of an outer automorphism of
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
. This is in part due to the fact that the Lipschitz metric connects the dynamical properties of an outer automorphism of
![]() $\mathbb {F}_r$
acting on
$\mathbb {F}_r$
acting on
![]() $CV(\mathbb {F}_r)$
to its action on conjugacy classes—of elements and of free factors—in
$CV(\mathbb {F}_r)$
to its action on conjugacy classes—of elements and of free factors—in
![]() $\mathbb {F}_r$
. Notable are the ‘Bers-like proof’ of the existence of train-tracks by Bestvina [Reference Bestvina6], the proof of hyperbolicity of the free factor complex by Bestvina and Feighn [Reference Bestvina and Feighn8], and the proof of hyperbolicity of certain free group extensions by Dowdall and Taylor [Reference Dowdall and Taylor18].
$\mathbb {F}_r$
. Notable are the ‘Bers-like proof’ of the existence of train-tracks by Bestvina [Reference Bestvina6], the proof of hyperbolicity of the free factor complex by Bestvina and Feighn [Reference Bestvina and Feighn8], and the proof of hyperbolicity of certain free group extensions by Dowdall and Taylor [Reference Dowdall and Taylor18].
In this way, the Lipschitz metric is akin to the Teichmüller metric on Teichmüller space which was used to prove the corresponding statements for the mapping class group [Reference Bers4, Reference Farb and Mosher19, Reference Masur and Minsky26]. One can also define the Lipschitz metric on Teichmüller space using the same idea as in (1.1), and in this setting it is oftentimes called Thurston’s asymmetric metric [Reference Thurston34]. This metric has seen renewed attention lately, in part due to the usefulness of the Lipschitz metric on
![]() $CV(\mathbb {F}_r)$
.
$CV(\mathbb {F}_r)$
.
As a result of McMullen’s interpretation of the Weil–Petersson metric on Teichmüller space via tools from the thermodynamic formalism applied to the geodesic flow on the hyperbolic surface [Reference McMullen27, Theorem 1.12], there exists a natural candidate for the Weil–Petersson metric on the Culler–Vogtmann outer space. This idea was originally pursued by Pollicott and Sharp [Reference Pollicott and Sharp31].
1.2 Thermodynamic metrics
The metrics we consider in this paper arise from the tools of the thermodynamic formalism as developed by Bowen [Reference Bowen9], Parry and Pollicott [Reference Parry and Pollicott29], Ruelle [Reference Ruelle32] and others. The central objects involved are the notions of entropy and pressure. For a graph G, these notions define functions
where n is the number of (geometric) edges in G and
![]() $\mathcal {M}(G) = \mathbb {R}_{>0}^n$
—this space parametrizes the length functions on G. The entropy and pressure functions are real analytic, strictly convex and are related by
$\mathcal {M}(G) = \mathbb {R}_{>0}^n$
—this space parametrizes the length functions on G. The entropy and pressure functions are real analytic, strictly convex and are related by
![]() $\mathfrak {h}_G(\ell ) = 1$
if and only if
$\mathfrak {h}_G(\ell ) = 1$
if and only if
![]() $\mathfrak {P}_G(-\ell ) = 0$
(see Theorem 3.7). As these functions are smooth and strictly convex, their Hessians induce an inner product on the tangent space of the unit-entropy subspace
$\mathfrak {P}_G(-\ell ) = 0$
(see Theorem 3.7). As these functions are smooth and strictly convex, their Hessians induce an inner product on the tangent space of the unit-entropy subspace
![]() $\mathcal {M}^1(G) = \{ \ell \in \mathcal {M}(G) \mid \mathfrak {h}_G(\ell ) = 1 \}$
at a length function (see Definition 3.10). Hence the notions of entropy and pressure induce Riemannian metrics on
$\mathcal {M}^1(G) = \{ \ell \in \mathcal {M}(G) \mid \mathfrak {h}_G(\ell ) = 1 \}$
at a length function (see Definition 3.10). Hence the notions of entropy and pressure induce Riemannian metrics on
![]() $\mathcal {M}^1(G)$
which we call the entropy metric and pressure metric, respectively. By
$\mathcal {M}^1(G)$
which we call the entropy metric and pressure metric, respectively. By
![]() $d_{\mathfrak {h},G}$
and
$d_{\mathfrak {h},G}$
and
![]() $d_{\mathfrak {P},G}$
we denote the induced distance functions on
$d_{\mathfrak {P},G}$
we denote the induced distance functions on
![]() $\mathcal {M}^1(G)$
. We caution the reader that these metrics have been considered by others with conflicting terminology. Throughout this introduction, we will use the above terminology even when referencing the work of others. See Remark 3.11 for a further discussion.
$\mathcal {M}^1(G)$
. We caution the reader that these metrics have been considered by others with conflicting terminology. Throughout this introduction, we will use the above terminology even when referencing the work of others. See Remark 3.11 for a further discussion.
Pollicott and Sharp initiated the study of the thermodynamic metrics when they first defined the pressure metric on
![]() $\mathcal {M}^1(G)$
[Reference Pollicott and Sharp31]. They proved that the pressure metric is not complete for the 2-rose
$\mathcal {M}^1(G)$
[Reference Pollicott and Sharp31]. They proved that the pressure metric is not complete for the 2-rose
![]() $\mathcal {R}_2$
and they derived formulas for the sectional curvature for the theta graph
$\mathcal {R}_2$
and they derived formulas for the sectional curvature for the theta graph
![]() $\Theta _2$
and barbell graph
$\Theta _2$
and barbell graph
![]() $\mathcal {B}_2$
(see Figure 2 for these graphs). Additionally, Pollicott and Sharp produce a dynamical characterization of the entropy metric in terms of generic geodesics similar to Wolpert’s result for the Weil–Petersson metric [Reference Wolpert37] (see Remark 3.11). Kao furthered these results by showing that the pressure metric is incomplete for
$\mathcal {B}_2$
(see Figure 2 for these graphs). Additionally, Pollicott and Sharp produce a dynamical characterization of the entropy metric in terms of generic geodesics similar to Wolpert’s result for the Weil–Petersson metric [Reference Wolpert37] (see Remark 3.11). Kao furthered these results by showing that the pressure metric is incomplete for
![]() $\Theta _2$
,
$\Theta _2$
,
![]() $\mathcal {B}_2$
and the 3-rose
$\mathcal {B}_2$
and the 3-rose
![]() $\mathcal {R}_3$
, and by showing that the entropy metric is complete for
$\mathcal {R}_3$
, and by showing that the entropy metric is complete for
![]() $\mathcal {R}_2$
[Reference Kao22]. Additionally, he derives formulas for the sectional curvature with respect to both the entropy and the pressure metric for
$\mathcal {R}_2$
[Reference Kao22]. Additionally, he derives formulas for the sectional curvature with respect to both the entropy and the pressure metric for
![]() $\Theta _2$
,
$\Theta _2$
,
![]() $\mathcal {B}_2$
and
$\mathcal {B}_2$
and
![]() $\mathcal {R}_3$
. Xu shows that for certain graphs, the moduli space
$\mathcal {R}_3$
. Xu shows that for certain graphs, the moduli space
![]() $\mathcal {M}^1(G)$
equipped with the entropy metric arises in the completion of the Teichmüller space of a surface with boundary using the pressure metric [Reference Xu39].
$\mathcal {M}^1(G)$
equipped with the entropy metric arises in the completion of the Teichmüller space of a surface with boundary using the pressure metric [Reference Xu39].
In this paper we will investigate the entropy metric not only on the moduli space of a single graph, but on the full moduli space of all marked graphs. Let
![]() $\mathcal {X}(\mathbb {F}_r)$
be the space of marked metric graphs so that contained in
$\mathcal {X}(\mathbb {F}_r)$
be the space of marked metric graphs so that contained in
![]() $\mathcal {X}(\mathbb {F}_r)$
is the Culler–Vogtmann outer space
$\mathcal {X}(\mathbb {F}_r)$
is the Culler–Vogtmann outer space
![]() $CV(\mathbb {F}_r)$
. The notion of entropy extends to
$CV(\mathbb {F}_r)$
. The notion of entropy extends to
![]() $\mathcal {X}(\mathbb {F}_r)$
by
$\mathcal {X}(\mathbb {F}_r)$
by
![]() $\mathfrak {h}([(G,\rho ,\ell )]) = \mathfrak {h}_G(\ell )$
and we set
$\mathfrak {h}([(G,\rho ,\ell )]) = \mathfrak {h}_G(\ell )$
and we set
There is a homeomorphism between
![]() $CV(\mathbb {F}_r)$
and
$CV(\mathbb {F}_r)$
and
![]() $\mathcal {X}^1(\mathbb {F}_r)$
defined by scaling the length function (see §3.1). Fixing a graph G and a marking
$\mathcal {X}^1(\mathbb {F}_r)$
defined by scaling the length function (see §3.1). Fixing a graph G and a marking
![]() $\rho \colon \thinspace \mathcal {R}_r \to G$
, the map
$\rho \colon \thinspace \mathcal {R}_r \to G$
, the map
![]() $\mathcal {M}^1(G) \to \mathcal {X}^1(\mathbb {F}_r)$
that sends a length function
$\mathcal {M}^1(G) \to \mathcal {X}^1(\mathbb {F}_r)$
that sends a length function
![]() $\ell $
in
$\ell $
in
![]() $\mathcal {M}^1(G)$
to the point determined by
$\mathcal {M}^1(G)$
to the point determined by
![]() $(G,\rho ,\ell )$
in
$(G,\rho ,\ell )$
in
![]() $\mathcal {X}^1(\mathbb {F}_r)$
is an embedding whose image we denote by
$\mathcal {X}^1(\mathbb {F}_r)$
is an embedding whose image we denote by
![]() $\mathcal {X}^1(G,\rho )$
. Considering all marked graphs individually, this induces a piecewise Riemannian metric on
$\mathcal {X}^1(G,\rho )$
. Considering all marked graphs individually, this induces a piecewise Riemannian metric on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
. See §3.3 for complete details. We denote the induced distance function on
$\mathcal {X}^1(\mathbb {F}_r)$
. See §3.3 for complete details. We denote the induced distance function on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
by
$\mathcal {X}^1(\mathbb {F}_r)$
by
![]() $d_{\mathfrak {h}}$
.
$d_{\mathfrak {h}}$
.
For a closed orientable surface
![]() $S_g$
, one can repeat the above discussion using the moduli space of marked Riemannian metrics with constant curvature
$S_g$
, one can repeat the above discussion using the moduli space of marked Riemannian metrics with constant curvature
![]() $\mathcal {X}(S_g)$
. In this case, the entropy and the area of the Riemann surface are directly related. In particular, the unit-entropy, constant-curvature metrics correspond to the hyperbolic metrics, that is, those with constant curvature equal to
$\mathcal {X}(S_g)$
. In this case, the entropy and the area of the Riemann surface are directly related. In particular, the unit-entropy, constant-curvature metrics correspond to the hyperbolic metrics, that is, those with constant curvature equal to
![]() $-1$
, and hence to those with area equal to
$-1$
, and hence to those with area equal to
![]() $2\pi (2g - 2)$
. In other words, the entropy and area normalizations on
$2\pi (2g - 2)$
. In other words, the entropy and area normalizations on
![]() $\mathcal {X}(S_g)$
result in the same subspace, the Teichmüller space of the surface. McMullen proved that the ensuing entropy metric on the Teichmüller space is proportional to the Weil–Petersson metric [Reference McMullen27, Theorem 1.12].
$\mathcal {X}(S_g)$
result in the same subspace, the Teichmüller space of the surface. McMullen proved that the ensuing entropy metric on the Teichmüller space is proportional to the Weil–Petersson metric [Reference McMullen27, Theorem 1.12].
It is this connection between the entropy metric and the Weil–Petersson metric that drives the research in this paper. After introducing the framework for both the entropy and the pressure metrics in §3, we specialize the discussion to the entropy metric because of this connection to the Weil–Petersson metric. All of the main results of this paper have analogous statements for the pressure metric and the proofs are similar, and in most cases substantially easier. The statements for the pressure metric are given in §1.6.
It is not necessary for this paper, but we mention that building on work of McMullen, Bridgeman [Reference Bridgeman10] and Bridgeman et al [Reference Bridgeman, Canary, Labourie and Samborino11] used these same ideas to define a metric on the space of conjugacy classes of regular irreducible representations of a hyperbolic group into a special linear group.
In the next three subsections, we explain our main results on the entropy metric on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
and their relation to the Weil–Petersson metric on Teichmüller space.
$\mathcal {X}^1(\mathbb {F}_r)$
and their relation to the Weil–Petersson metric on Teichmüller space.
1.3 Incompletion of the metric
Our first main result concerns the completion of the entropy metric on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
. Wolpert showed that the Weil–Petersson metric on Teichmüller space is not complete [Reference Wolpert36]. Our first theorem shows that when
$\mathcal {X}^1(\mathbb {F}_r)$
. Wolpert showed that the Weil–Petersson metric on Teichmüller space is not complete [Reference Wolpert36]. Our first theorem shows that when
![]() $r \geq 3$
, the same holds for the entropy metric on
$r \geq 3$
, the same holds for the entropy metric on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
.
$\mathcal {X}^1(\mathbb {F}_r)$
.
Theorem 1.1. The metric space
![]() $(\mathcal {X}^{1}(\mathbb {F}_r),d_{\mathfrak {h}})$
is complete if
$(\mathcal {X}^{1}(\mathbb {F}_r),d_{\mathfrak {h}})$
is complete if
![]() $r = 2$
and incomplete if
$r = 2$
and incomplete if
![]() $r \,{\geq}\, 3$
.
$r \,{\geq}\, 3$
.
For
![]() $r \geq 3$
, this theorem is proved by exhibiting a finite-length path in
$r \geq 3$
, this theorem is proved by exhibiting a finite-length path in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
that exits every compact subset. This path is defined by sending the length of one edge in
$\mathcal {M}^1(\mathcal {R}_r)$
that exits every compact subset. This path is defined by sending the length of one edge in
![]() $\mathcal {R}_r$
to infinity, while shrinking the others to maintain unit entropy (Proposition 7.8). This strategy—also used by Pollicott and Sharp [Reference Pollicott and Sharp31] and Kao [Reference Kao22]—shows that
$\mathcal {R}_r$
to infinity, while shrinking the others to maintain unit entropy (Proposition 7.8). This strategy—also used by Pollicott and Sharp [Reference Pollicott and Sharp31] and Kao [Reference Kao22]—shows that
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is incomplete. We further show in §8 that this path also exits every compact set in
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is incomplete. We further show in §8 that this path also exits every compact set in
![]() $\mathcal {X}^1(\mathbb {F}_r)$
. As
$\mathcal {X}^1(\mathbb {F}_r)$
. As
![]() $d_{\mathfrak {h},\mathcal {R}_r}$
is an upper bound to
$d_{\mathfrak {h},\mathcal {R}_r}$
is an upper bound to
![]() $d_{\mathfrak {h}}$
(when defined), this path still has finite length when considered in
$d_{\mathfrak {h}}$
(when defined), this path still has finite length when considered in
![]() $\mathcal {X}^1(\mathbb {F}_r)$
and thus Theorem 1.1 follows.
$\mathcal {X}^1(\mathbb {F}_r)$
and thus Theorem 1.1 follows.
The path described above illustrates a general method for producing paths that exit every compact subset and that have finite length in the entropy metric: deform the metric by sending the length of some collection of edges to infinity while shrinking the others to maintain unit entropy. So long as the complement of the collection supports a unit-entropy metric, this path will have finite length. This explains why
![]() $(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete: any metric on a graph where every component has rank at most 1 has entropy equal to zero. In §6 we demonstrate the calculations required to prove that
$(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete: any metric on a graph where every component has rank at most 1 has entropy equal to zero. In §6 we demonstrate the calculations required to prove that
![]() $(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete.
$(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete.
This is completely analogous to the setting of the Weil–Petersson metric on Teichmüller space. In that setting, deforming a hyperbolic metric on
![]() $S_g$
by pinching a simple closed curve results in a path with finite length that exits every compact set. Moreover, the geometric analysis agrees. For the path in
$S_g$
by pinching a simple closed curve results in a path with finite length that exits every compact set. Moreover, the geometric analysis agrees. For the path in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
described above, if we parametrize the long edge by
$\mathcal {M}^1(\mathcal {R}_r)$
described above, if we parametrize the long edge by
![]() $-\log (t)$
as
$-\log (t)$
as
![]() $t \to 0$
, then the entropy norm along this path is
$t \to 0$
, then the entropy norm along this path is
![]() $O(t^{-1/2})$
, as shown in Proposition 7.8. For the path in the Teichmüller space of
$O(t^{-1/2})$
, as shown in Proposition 7.8. For the path in the Teichmüller space of
![]() $S_g$
, if we parametrize the curve which is being pinched by t as
$S_g$
, if we parametrize the curve which is being pinched by t as
![]() $t \to 0$
, then the Weil–Petersson norm along this path is
$t \to 0$
, then the Weil–Petersson norm along this path is
![]() $O(t^{-1/2})$
[Reference Wolpert and Papadopoulos38, §7]. Note that in this case, the length of the shortest curve that intersects the pinched one has length approximately
$O(t^{-1/2})$
[Reference Wolpert and Papadopoulos38, §7]. Note that in this case, the length of the shortest curve that intersects the pinched one has length approximately
![]() $-\log (t)$
.
$-\log (t)$
.
1.4 The moduli space of the r-rose
Our second main result is concerned with the entropy metric on the moduli space of the r-rose
![]() $\mathcal {R}_r$
.
$\mathcal {R}_r$
.
Theorem 1.2. The completion of
![]() $(\mathcal {M}^{1}(\mathcal {R}_{r}),d_{\mathfrak {h},\mathcal {R}_r})$
is homeomorphic to the complement of the vertices of an
$(\mathcal {M}^{1}(\mathcal {R}_{r}),d_{\mathfrak {h},\mathcal {R}_r})$
is homeomorphic to the complement of the vertices of an
![]() $(r-1)$
-simplex.
$(r-1)$
-simplex.
The space
![]() $\mathcal {M}^1(\mathcal {R}_r)$
is homeomorphic to the interior of an
$\mathcal {M}^1(\mathcal {R}_r)$
is homeomorphic to the interior of an
![]() $(r-1)$
-simplex. The faces added in the completion for
$(r-1)$
-simplex. The faces added in the completion for
![]() $d_{\mathfrak {h},\mathcal {R}_r}$
correspond to unit-entropy metrics on subroses. Such a metric is obtained as the limit of a sequence of length functions on
$d_{\mathfrak {h},\mathcal {R}_r}$
correspond to unit-entropy metrics on subroses. Such a metric is obtained as the limit of a sequence of length functions on
![]() $\mathcal {R}_r$
by sending the length of a collection of edges to infinity and scaling the others to maintain unit entropy. Specifically, a
$\mathcal {R}_r$
by sending the length of a collection of edges to infinity and scaling the others to maintain unit entropy. Specifically, a
![]() $(k-1)$
-dimensional face of the completion corresponds to the moduli space of unit-entropy metrics on a sub-k-rose. As before, intuitively, the vertices of the
$(k-1)$
-dimensional face of the completion corresponds to the moduli space of unit-entropy metrics on a sub-k-rose. As before, intuitively, the vertices of the
![]() ${(r-1)}$
-simplex are missing in the completion as there does not exist a unit-entropy metric on
${(r-1)}$
-simplex are missing in the completion as there does not exist a unit-entropy metric on
![]() $\mathcal {R}_1$
.
$\mathcal {R}_1$
.
That unit-entropy metrics on subroses arise as points in the completion follows from the calculations provided for the proof of incompleteness in Theorem 1.1 and some continuity arguments. This is shown in §9.1. The difficult part of the proof of Theorem 1.2 is showing that any path in
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
that sends the length of one edge to 0 (and hence the lengths of the other edges to infinity) necessarily has infinite length. This argument appears in Lemma 7.10 and Proposition 7.14. In §9.2 we combine these two facts to complete the proof of Theorem 1.2.
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
that sends the length of one edge to 0 (and hence the lengths of the other edges to infinity) necessarily has infinite length. This argument appears in Lemma 7.10 and Proposition 7.14. In §9.2 we combine these two facts to complete the proof of Theorem 1.2.
In Example 9.7 we compare the completion of
![]() $(\mathcal {M}^1(\mathcal {R}_3),d_{\mathfrak {h},\mathcal {R}_3})$
to the closure of the unit-volume metrics on
$(\mathcal {M}^1(\mathcal {R}_3),d_{\mathfrak {h},\mathcal {R}_3})$
to the closure of the unit-volume metrics on
![]() $\mathcal {R}_3$
in the axes topology on
$\mathcal {R}_3$
in the axes topology on
![]() $CV(\mathbb {F}_3)$
(see §2.2 for definitions). By Theorem 1.2, the completion in the entropy metric is a
$CV(\mathbb {F}_3)$
(see §2.2 for definitions). By Theorem 1.2, the completion in the entropy metric is a
![]() $2$
-simplex without vertices, whereas the closure in the axes topology is a
$2$
-simplex without vertices, whereas the closure in the axes topology is a
![]() $2$
-simplex. More interestingly, the newly added edges and vertices are dual: edges in the entropy completion correspond to vertices in the axes closure and the missing vertices in the entropy completion correspond to the edges in the axes closure. This is explained in detail in Example 9.7 and illustrated in Figure 6.
$2$
-simplex. More interestingly, the newly added edges and vertices are dual: edges in the entropy completion correspond to vertices in the axes closure and the missing vertices in the entropy completion correspond to the edges in the axes closure. This is explained in detail in Example 9.7 and illustrated in Figure 6.
While it is not necessary for Theorem 1.2, we mention that in §9.3 we prove that the diameter of a cross-section of the
![]() $(r-1)$
-simplex goes to 0 as the length of one of the edges goes to 0, that is, as the cross-section moves out toward one of the missing vertices. In other words, the completion of
$(r-1)$
-simplex goes to 0 as the length of one of the edges goes to 0, that is, as the cross-section moves out toward one of the missing vertices. In other words, the completion of
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is geometrically akin to an ideal hyperbolic
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is geometrically akin to an ideal hyperbolic
![]() $(r-1)$
-simplex; see Lemma 9.9.
$(r-1)$
-simplex; see Lemma 9.9.
1.5 A fixed point in the completion
Whereas the first two main results demonstrate the similarity between the geometric analysis for the Weil–Petersson metric on the Teichmüller space and the entropy metric on the Culler–Vogtmann outer space, our final main result provides a stark contrast between these two metrics with respect to geometric group theory.
Theorem 1.3. The subspace
![]() $(\mathcal {X}^1(\mathcal {R}_{r},{\textrm {id}}) \cdot \operatorname {\mathrm {Out}}(\mathbb {F}_r),d_{\mathfrak {h}}) \subset (\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is bounded if
$(\mathcal {X}^1(\mathcal {R}_{r},{\textrm {id}}) \cdot \operatorname {\mathrm {Out}}(\mathbb {F}_r),d_{\mathfrak {h}}) \subset (\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is bounded if
![]() $r \geq 4$
. Moreover, the action of
$r \geq 4$
. Moreover, the action of
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the completion of
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the completion of
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has a fixed point.
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has a fixed point.
This subspace consists of the unit-entropy metrics on every marked r-rose. To illustrate the difference with respect to the setting of the Weil–Petersson metric on Teichmüller space, we mention the fact due to Daskalopoulos and Wentworth that pseudo-Anosov mapping classes have positive translation length in their action on the Teichmüller space [Reference Daskalopoulos and Wentworth16]. In particular, the action of the mapping class group does not have a fixed point in the completion of Teichmüller space with the Weil–Petersson metric.
The first step in the proof of Theorem 1.3 is to show that the image of the inclusion map
![]() $\mathcal {M}^1(\mathcal {R}_r) \to \mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \subset \mathcal {X}^1(\mathbb {F}_r)$
has bounded diameter for
$\mathcal {M}^1(\mathcal {R}_r) \to \mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \subset \mathcal {X}^1(\mathbb {F}_r)$
has bounded diameter for
![]() $r \geq 4$
. This result is particularly striking in contrast to Theorem 1.2, since implicit in that theorem is that the space
$r \geq 4$
. This result is particularly striking in contrast to Theorem 1.2, since implicit in that theorem is that the space
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter. Boundedness of the image of
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter. Boundedness of the image of
![]() $\mathcal {M}^1(\mathcal {R}_r)$
is achieved by showing that the map induced via Theorem 1.2,
$\mathcal {M}^1(\mathcal {R}_r)$
is achieved by showing that the map induced via Theorem 1.2,
![]() $\Phi \colon \thinspace \Delta ^{r-1} - V \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
, extends to
$\Phi \colon \thinspace \Delta ^{r-1} - V \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
, extends to
![]() $\Delta ^{r-1}$
, where
$\Delta ^{r-1}$
, where
![]() $\Delta ^{r-1}$
is an
$\Delta ^{r-1}$
is an
![]() $(r-1)$
-simplex,
$(r-1)$
-simplex,
![]() $V \subset \Delta ^{r-1}$
is the set of vertices, and
$V \subset \Delta ^{r-1}$
is the set of vertices, and
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
is the completion of
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
is the completion of
![]() $\mathcal {X}^1(\mathbb {F}_r)$
for
$\mathcal {X}^1(\mathbb {F}_r)$
for
![]() $d_{\mathfrak {h}}$
. The existence of this extension shows that
$d_{\mathfrak {h}}$
. The existence of this extension shows that
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
lies in a compact set and hence is bounded.
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
lies in a compact set and hence is bounded.
In order to show that
![]() $\Phi \colon \thinspace \Delta ^{r-1} - V \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
extends to the set V, we show that
$\Phi \colon \thinspace \Delta ^{r-1} - V \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
extends to the set V, we show that
![]() $\Phi $
maps every
$\Phi $
maps every
![]() $(k-1)$
-dimensional face of
$(k-1)$
-dimensional face of
![]() $\Delta ^{r-1} - V$
to a single point when
$\Delta ^{r-1} - V$
to a single point when
![]() $1 < k < r-1$
. This is shown in §11. This fact, together with the previously mentioned fact about the diameter of the cross-sections going to 0, gives that
$1 < k < r-1$
. This is shown in §11. This fact, together with the previously mentioned fact about the diameter of the cross-sections going to 0, gives that
![]() $\Phi $
extends to the set V and that the entire
$\Phi $
extends to the set V and that the entire
![]() $(r-3)$
-skeleton of
$(r-3)$
-skeleton of
![]() $\Delta ^{r-1}$
is mapped to a single point in
$\Delta ^{r-1}$
is mapped to a single point in
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. The collapse of a
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. The collapse of a
![]() $(k-1)$
-dimensional face of
$(k-1)$
-dimensional face of
![]() $\Delta ^{r-1} - V$
for
$\Delta ^{r-1} - V$
for
![]() $1 < k < r-1$
arises from paths in
$1 < k < r-1$
arises from paths in
![]() $\mathcal {X}^1(\mathbb {F}_r)$
connecting points in
$\mathcal {X}^1(\mathbb {F}_r)$
connecting points in
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
whose length is much shorter than paths in
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
whose length is much shorter than paths in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
connecting the same points. In other words, there are shortcuts present in
$\mathcal {M}^1(\mathcal {R}_r)$
connecting the same points. In other words, there are shortcuts present in
![]() $\mathcal {X}^1(\mathbb {F}_r)$
that are not present in
$\mathcal {X}^1(\mathbb {F}_r)$
that are not present in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
.
$\mathcal {M}^1(\mathcal {R}_r)$
.
These shortcuts are most easily understood in terms of unit-entropy metrics on marked subgraphs, that is, points in the completion of
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
. Pathologies arise when the subgraph is not connected. In this case, the entropy of the metric on the subgraph is the maximum of the entropy—in the previous sense—on a component of the subgraph. Hence, by holding the length function constant on a component of the subgraph with unit entropy, we are free to modify the length function on the other components at will, so long as the entropy is never greater than 1 on any of these components. In Proposition 3.12 we show that the entropy and pressure metrics can be computed using the second derivatives of the lengths of edges along a path. Hence the length of a path that changes the length of the edges in a component with entropy less than 1 linearly has zero length in either of these metrics.
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
. Pathologies arise when the subgraph is not connected. In this case, the entropy of the metric on the subgraph is the maximum of the entropy—in the previous sense—on a component of the subgraph. Hence, by holding the length function constant on a component of the subgraph with unit entropy, we are free to modify the length function on the other components at will, so long as the entropy is never greater than 1 on any of these components. In Proposition 3.12 we show that the entropy and pressure metrics can be computed using the second derivatives of the lengths of edges along a path. Hence the length of a path that changes the length of the edges in a component with entropy less than 1 linearly has zero length in either of these metrics.
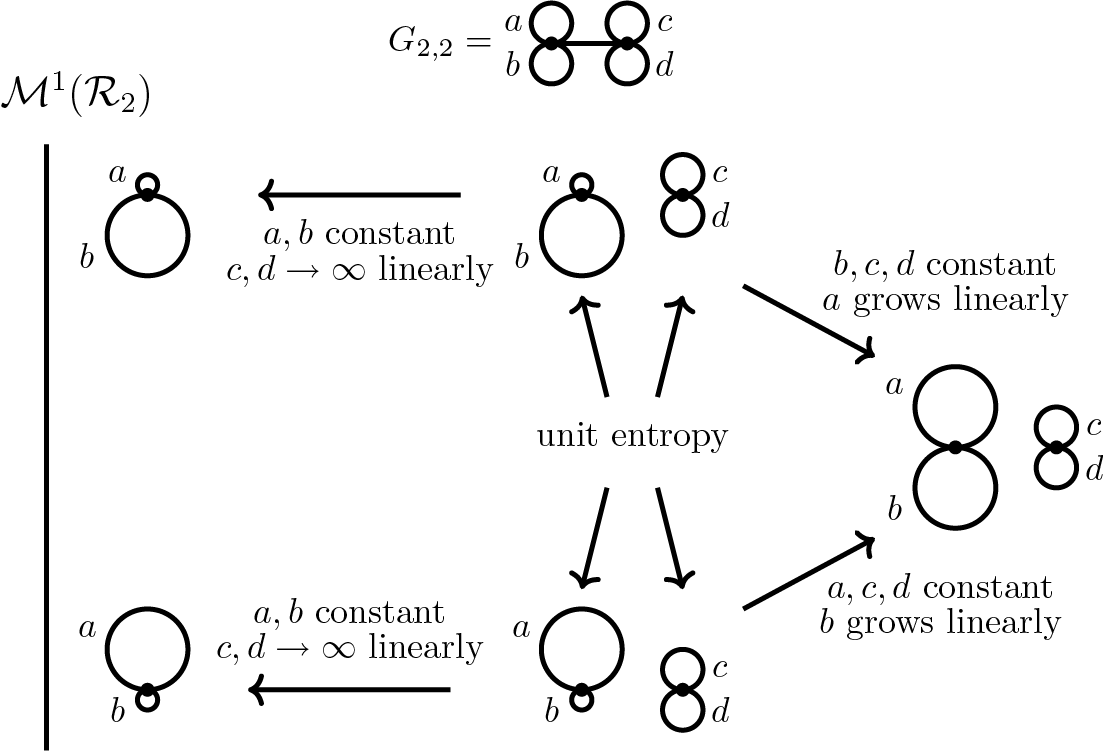
Figure 1 Illustration of a path with length 0 in the completion of
![]() $(\mathcal {M}^1(G_{2,2}),d_{\mathfrak {h},G_{2,2}})$
.
$(\mathcal {M}^1(G_{2,2}),d_{\mathfrak {h},G_{2,2}})$
.
Figure 1 illustrates the central idea that is exploited in §10 to show that many paths have zero length. This figure is taking place in the completion of
![]() $\mathcal {M}^1(G_{2,2})$
using the metric
$\mathcal {M}^1(G_{2,2})$
using the metric
![]() $d_{\mathfrak {h},G_{2,2}}$
. This space has
$d_{\mathfrak {h},G_{2,2}}$
. This space has
![]() $\mathcal {M}^1(\mathcal {R}_4)$
as a face in
$\mathcal {M}^1(\mathcal {R}_4)$
as a face in
![]() $\mathcal {X}^1(\mathbb {F}_4)$
corresponding to the collapse of the separating edge. The completion of
$\mathcal {X}^1(\mathbb {F}_4)$
corresponding to the collapse of the separating edge. The completion of
![]() $\mathcal {M}^1(\mathcal {R}_4)$
has an edge corresponding to unit-entropy metrics on two of the edges (denoted a and b in Figure 1). This edge also corresponds to a subset in the completion of
$\mathcal {M}^1(\mathcal {R}_4)$
has an edge corresponding to unit-entropy metrics on two of the edges (denoted a and b in Figure 1). This edge also corresponds to a subset in the completion of
![]() $\mathcal {M}^1(G_{2,2})$
. Illustrated in Figure 1 is a path through unit-entropy length functions on subgraphs of
$\mathcal {M}^1(G_{2,2})$
. Illustrated in Figure 1 is a path through unit-entropy length functions on subgraphs of
![]() $G_{2,2}$
, that is, points in the completion. As all edge lengths are changing linearly, this path has length 0 and hence all of these length functions correspond to the same point in the completion.
$G_{2,2}$
, that is, points in the completion. As all edge lengths are changing linearly, this path has length 0 and hence all of these length functions correspond to the same point in the completion.
This shows that the edge corresponding to
![]() $\mathcal {M}^1(\mathcal {R}_2)$
is mapped by
$\mathcal {M}^1(\mathcal {R}_2)$
is mapped by
![]() $\Phi $
to a point. The same idea works for any sub-k-rose of
$\Phi $
to a point. The same idea works for any sub-k-rose of
![]() $\mathcal {R}_r$
so long as
$\mathcal {R}_r$
so long as
![]() $1 < k < r-1$
: it is necessary to separate two subroses, each of which supports a unit-entropy metric. This is the reason why we require
$1 < k < r-1$
: it is necessary to separate two subroses, each of which supports a unit-entropy metric. This is the reason why we require
![]() $r \geq 4$
in Theorem 1.3.
$r \geq 4$
in Theorem 1.3.
Once we know that the entire
![]() $(r-3)$
-skeleton of
$(r-3)$
-skeleton of
![]() $\Delta ^{r-1}$
is mapped by
$\Delta ^{r-1}$
is mapped by
![]() $\Phi $
to a point in
$\Phi $
to a point in
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
, we utilize the structure of the Culler–Vogtmann outer space to conclude in §12 that this point is independent of the marking
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
, we utilize the structure of the Culler–Vogtmann outer space to conclude in §12 that this point is independent of the marking
![]() $\rho \colon \thinspace \mathcal {R}_r \to \mathcal {R}_r$
used to define the inclusion
$\rho \colon \thinspace \mathcal {R}_r \to \mathcal {R}_r$
used to define the inclusion
![]() $\mathcal {M}^1(\mathcal {R}_r) \to \mathcal {X}^1(\mathbb {F}_r)$
. This completes the proof of Theorem 1.3.
$\mathcal {M}^1(\mathcal {R}_r) \to \mathcal {X}^1(\mathbb {F}_r)$
. This completes the proof of Theorem 1.3.
1.6 Analogous statements for pressure metric
For the pressure metric on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
we have the following analogs of Theorems 1.1–1.3. By
$\mathcal {X}^1(\mathbb {F}_r)$
we have the following analogs of Theorems 1.1–1.3. By
![]() $d_{\mathfrak {P}}$
we denote the induced distance function.
$d_{\mathfrak {P}}$
we denote the induced distance function.
-
(1) The space
 $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {P}})$
is incomplete for
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {P}})$
is incomplete for
 $r \geq 2$
.
$r \geq 2$
. -
(2) The completion of
 $(\mathcal {M}^{1}(\mathcal {R}_{r}),d_{\mathfrak {P},\mathcal {R}_r})$
is homeomorphic to an
$(\mathcal {M}^{1}(\mathcal {R}_{r}),d_{\mathfrak {P},\mathcal {R}_r})$
is homeomorphic to an
 $(r-1)$
-simplex.
$(r-1)$
-simplex. -
(3) The space
 $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {P}})$
is bounded if
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {P}})$
is bounded if
 $r \geq 2$
; moreover, the action of
$r \geq 2$
; moreover, the action of
 $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the completion of
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the completion of
 $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {P}})$
has a fixed point.
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {P}})$
has a fixed point.
These can be shown using techniques similar—and simpler—to those in this paper. The key source of the distinction between the entropy and pressure metrics is that the length function that assigns 0 to the unique edge on
![]() $\mathcal {R}_1$
has pressure equal to 0 even through the entropy is not defined. Hence the path in
$\mathcal {R}_1$
has pressure equal to 0 even through the entropy is not defined. Hence the path in
![]() $\mathcal {M}^1(\mathcal {R}_2)$
that sends the length of one edge to infinity while shrinking the length of the other (necessarily to 0) to maintain unit entropy has finite length in the pressure metric, whereas the length in the entropy metric is infinite.
$\mathcal {M}^1(\mathcal {R}_2)$
that sends the length of one edge to infinity while shrinking the length of the other (necessarily to 0) to maintain unit entropy has finite length in the pressure metric, whereas the length in the entropy metric is infinite.
1.7 Further discussion and questions
This work raises a number of questions.
Our proof that the action of
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the completion of
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the completion of
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has a fixed point relies heavily on the assumption that
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has a fixed point relies heavily on the assumption that
![]() $r \geq 4$
: the key construction uses an edge that separates a given graph into two subgraphs, each with rank at least
$r \geq 4$
: the key construction uses an edge that separates a given graph into two subgraphs, each with rank at least
![]() $2$
. This leaves the door open to a negative answer for the following question, which would allow for interesting applications specifically for
$2$
. This leaves the door open to a negative answer for the following question, which would allow for interesting applications specifically for
![]() $\mathbb {F}_3$
.
$\mathbb {F}_3$
.
Question 1.4. Does
![]() $(\mathcal {X}^1(\mathbb {F}_3),d_{\mathfrak {h}})$
admit an
$(\mathcal {X}^1(\mathbb {F}_3),d_{\mathfrak {h}})$
admit an
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_3)$
-invariant bounded subcomplex?
$\operatorname {\mathrm {Out}}(\mathbb {F}_3)$
-invariant bounded subcomplex?
Theorem 1.3 demonstrates the existence of an
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
orbit in
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
orbit in
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
with bounded diameter but we do not yet know that the entire space has bounded diameter. We therefore ask the following question.
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
with bounded diameter but we do not yet know that the entire space has bounded diameter. We therefore ask the following question.
Question 1.5. Is
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
bounded for
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
bounded for
![]() $r \geq 4$
?
$r \geq 4$
?
We believe the answer to this question is yes. Indeed, the only way
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
could fail to be bounded is if the subspace
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
could fail to be bounded is if the subspace
![]() $(\mathcal {X}^1(G,\rho ),d_{\mathfrak {h}})$
has infinite diameter for some marked graph
$(\mathcal {X}^1(G,\rho ),d_{\mathfrak {h}})$
has infinite diameter for some marked graph
![]() $\rho \colon \thinspace \mathcal {R}_r \to G$
. As the diameter of
$\rho \colon \thinspace \mathcal {R}_r \to G$
. As the diameter of
![]() $(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \cdot \operatorname {\mathrm {Out}}(\mathbb {F}_r),d_{\mathfrak {h}})$
is bounded, to answer the question in the affirmative, it would suffice to find a bound (in terms of r) on the distance from any point
$(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \cdot \operatorname {\mathrm {Out}}(\mathbb {F}_r),d_{\mathfrak {h}})$
is bounded, to answer the question in the affirmative, it would suffice to find a bound (in terms of r) on the distance from any point
![]() $\mathcal {X}^1(\mathbb {F}_r)$
to a point in
$\mathcal {X}^1(\mathbb {F}_r)$
to a point in
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \cdot \phi $
for some
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \cdot \phi $
for some
![]() $\phi \in \operatorname {\mathrm {Out}}(\mathbb {F}_r)$
. Another approach to answer Question 1.5 in the affirmative would be to show the existence of a bound (in terms of r) on distance from any point in
$\phi \in \operatorname {\mathrm {Out}}(\mathbb {F}_r)$
. Another approach to answer Question 1.5 in the affirmative would be to show the existence of a bound (in terms of r) on distance from any point in
![]() $\mathcal {X}^1(G, \rho )$
to a completion point represented by a unit-entropy metric on a proper subgraph (with the goal of getting to a point in the completion of a marked rose via induction). This led us to the following question, which is of independent interest and we pose here as a conjecture.
$\mathcal {X}^1(G, \rho )$
to a completion point represented by a unit-entropy metric on a proper subgraph (with the goal of getting to a point in the completion of a marked rose via induction). This led us to the following question, which is of independent interest and we pose here as a conjecture.
Conjecture 1.6. For any
![]() $r \geq 3$
there exists
$r \geq 3$
there exists
![]() $C> 0$
so that any metric graph of rank r with unit entropy contains a proper subgraph with entropy at least C.
$C> 0$
so that any metric graph of rank r with unit entropy contains a proper subgraph with entropy at least C.
It suffices to show the conjecture for a fixed topological type of graph since, for a given rank r, there are only finitely many topological types of graph of rank r.
One can also define the notion of the entropy metric on the Teichmüller space of a surface with boundary. In [Reference Xu39], Xu shows that this metric is incomplete. As mentioned previously, McMullen proved that for closed surfaces, the entropy metric is a constant multiple of the Weil–Petersson metric. However, by partially characterizing the completion of the entropy metric in the bordered setting, Xu is able to show that this is not true in the presence of boundary. Concretely, Xu identifies certain graphs G so that, in the notation of this paper,
![]() $(\mathcal {M}^{1}(G),d_{\mathfrak {h}})$
isometrically embeds in the completion of the Teichmüller space of the surface equipped with the entropy metric. We therefore ask if the work in this paper can be used to fully understand the completion of the Teichmüller space of a bordered surface equipped with the entropy metric.
$(\mathcal {M}^{1}(G),d_{\mathfrak {h}})$
isometrically embeds in the completion of the Teichmüller space of the surface equipped with the entropy metric. We therefore ask if the work in this paper can be used to fully understand the completion of the Teichmüller space of a bordered surface equipped with the entropy metric.
Problem 1.7. Fully characterize the completion of
![]() $(\mathcal {M}^{1}(G), d_{\mathfrak {h},G})$
for an arbitrary graph G and use this to study the completion of the Teichmüller space of a bordered surface, equipped with the entropy metric.
$(\mathcal {M}^{1}(G), d_{\mathfrak {h},G})$
for an arbitrary graph G and use this to study the completion of the Teichmüller space of a bordered surface, equipped with the entropy metric.
The pathology exhibited by Theorem 1.3 relies on the existence of a sequence of unit-entropy length functions whose limiting metric is supported on a subgraph with multiple components where the metric on some component need not have entropy equal to 1. This behavior does not occur in the Teichmüller space of a closed surface since a unit-entropy metric on a constant-curvature surface is a hyperbolic metric and vice versa, and thus for the subsurface supporting the limit of a sequence of unit-entropy metrics, the metric on each component also has entropy equal to 1. One can also consider an entropy function defined over the moduli space of singular flat metrics on a closed surface. This setting appears more similar to the situation of Theorem 1.3 in that the unit-entropy condition is not encoded by the local geometry. It appears likely that some version of Theorem 1.3 holds for singular flat metrics, and so we therefore ask our final question of this introduction.
Question 1.8. Can the techniques used in this paper in the setting of metric graphs apply to the study of an entropy metric on the moduli space of singular flat metrics on a closed surface?
2 Graphs and outer space
In this section we introduce some concepts that are necessary for the sequel. First, we set some notation for dealing with graphs. Then we define the Culler–Vogtmann outer space—including its topology—and the
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
action on this space.
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
action on this space.
2.1 Graphs
We use Serre’s convention for graphs [Reference Serre33]. That is, an (undirected) graph is a tuple
![]() $G = (V,E,o,\tau ,\bar {\phantom {e}})$
where:
$G = (V,E,o,\tau ,\bar {\phantom {e}})$
where:
-
(1) V and E are sets, called the vertices and the directed edges (we think of E as containing two copies, with opposite orientations, of each undirected edge);
-
(2)
 $o,\tau \colon \thinspace E \to V$
are functions that specify the originating and terminating vertices of an edge;
$o,\tau \colon \thinspace E \to V$
are functions that specify the originating and terminating vertices of an edge; -
(3)
 $\bar {\phantom {e}} \colon \thinspace E \to E$
is a fixed point free involution such that
$\bar {\phantom {e}} \colon \thinspace E \to E$
is a fixed point free involution such that
 $o(e) = \tau (\bar {e})$
(
$o(e) = \tau (\bar {e})$
(
 $\bar {\phantom {e}}$
flips edges).
$\bar {\phantom {e}}$
flips edges).
We fix an orientation on G, that is, a subset
![]() $E_{+} \subset E$
that contains exactly one edge from each pair
$E_{+} \subset E$
that contains exactly one edge from each pair
![]() $\{e,\bar {e}\}$
. Since we consider the pair
$\{e,\bar {e}\}$
. Since we consider the pair
![]() $\{e,\bar {e}\}$
to be a single edge, the number of edges of G is
$\{e,\bar {e}\}$
to be a single edge, the number of edges of G is
![]() $|E_{+}| = |E|/2$
. The valance of a vertex v is the number of edges from
$|E_{+}| = |E|/2$
. The valance of a vertex v is the number of edges from
![]() $e \in E_+$
with
$e \in E_+$
with
![]() $o(e)=v$
plus the number of edges from
$o(e)=v$
plus the number of edges from
![]() $e \in E_+$
with
$e \in E_+$
with
![]() $\tau (e)=v$
(an edge e for which
$\tau (e)=v$
(an edge e for which
![]() $o(e) = \tau (e) =v$
contributes
$o(e) = \tau (e) =v$
contributes
![]() $2$
to the valance). Oftentimes when defining a graph we only specify the edges in
$2$
to the valance). Oftentimes when defining a graph we only specify the edges in
![]() $E_+$
(together with the restrictions of o and
$E_+$
(together with the restrictions of o and
![]() $\tau $
to
$\tau $
to
![]() $E_+$
). The complete set of edges is then defined as
$E_+$
). The complete set of edges is then defined as
![]() $E = E_+ \cup \overline {E}_+$
, where
$E = E_+ \cup \overline {E}_+$
, where
![]() $\overline {E}_+$
is a copy of
$\overline {E}_+$
is a copy of
![]() $E_+$
, and
$E_+$
, and
![]() $o,\tau $
, and
$o,\tau $
, and
![]() $\bar {\phantom {e}}$
are defined in the obvious way. We blur the distinction between the tuple
$\bar {\phantom {e}}$
are defined in the obvious way. We blur the distinction between the tuple
![]() $(V,E,o,\tau ,\bar {\phantom {e}})$
and the corresponding one-dimensional CW-complex with
$(V,E,o,\tau ,\bar {\phantom {e}})$
and the corresponding one-dimensional CW-complex with
![]() $0$
-cells V and
$0$
-cells V and
![]() $1$
-cells
$1$
-cells
![]() $E_+$
.
$E_+$
.
The space of length functions on G is the open convex cone
We consider this set as a subset of
![]() $\mathbb {R}^{\lvert {E_+} \rvert }$
. A length function
$\mathbb {R}^{\lvert {E_+} \rvert }$
. A length function
![]() $\ell \colon \thinspace E_{+} \to \mathbb {R}_{>0}$
extends to a function
$\ell \colon \thinspace E_{+} \to \mathbb {R}_{>0}$
extends to a function
![]() $\ell \colon \thinspace E \to \mathbb {R}_{>0}$
by
$\ell \colon \thinspace E \to \mathbb {R}_{>0}$
by
![]() $\ell (e) = \ell (\bar {e})$
if
$\ell (e) = \ell (\bar {e})$
if
![]() $e \notin E_{+}$
. By
$e \notin E_{+}$
. By
![]() $\mathbf {1} \in \mathcal {M}(G)$
we denote the constant function with value 1.
$\mathbf {1} \in \mathcal {M}(G)$
we denote the constant function with value 1.
An edge path is a sequence of edges
![]() $(e_{1},\ldots ,e_{n})$
in E such that
$(e_{1},\ldots ,e_{n})$
in E such that
![]() $\tau (e_{i}) = o(e_{i+1})$
for
$\tau (e_{i}) = o(e_{i+1})$
for
![]() $i = 1,\ldots , n-1$
. A function
$i = 1,\ldots , n-1$
. A function
![]() $f \colon \thinspace E \to \mathbb {R}$
(in particular, a length function) extends to a function on edge paths
$f \colon \thinspace E \to \mathbb {R}$
(in particular, a length function) extends to a function on edge paths
![]() $\gamma = (e_{1},\ldots ,e_{n})$
by
$\gamma = (e_{1},\ldots ,e_{n})$
by
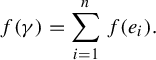 $$ \begin{align} f(\gamma) = \sum_{i=1}^{n} f(e_{i}). \end{align} $$
$$ \begin{align} f(\gamma) = \sum_{i=1}^{n} f(e_{i}). \end{align} $$
2.2 Outer space
We will introduce some definitions and notation for the Culler– Vogtmann outer space. This space was originally defined by Culler and Vogtmann [Reference Culler and Vogtmann14]. For more information, see for example the survey papers by Vogtmann [Reference Vogtmann35] or Bestvina [Reference Bestvina and Li5].
Let
![]() $\mathcal {R}_r$
be the r-rose. That is,
$\mathcal {R}_r$
be the r-rose. That is,
![]() $\mathcal {R}_r$
the graph with a unique vertex v and r edges. Fix an isomorphism
$\mathcal {R}_r$
the graph with a unique vertex v and r edges. Fix an isomorphism
![]() $\mathbb {F}_r \cong \pi _1(\mathcal {R}_r,v)$
. A marked metric graph (of rank r) is a triple
$\mathbb {F}_r \cong \pi _1(\mathcal {R}_r,v)$
. A marked metric graph (of rank r) is a triple
![]() $(G,\rho ,\ell )$
where:
$(G,\rho ,\ell )$
where:
-
(1) G is a finite connected graph without vertices of valence
 $1$
or
$1$
or
 $2$
;
$2$
; -
(2)
 $\rho \colon \thinspace \mathcal {R}_r \to G$
is a homotopy equivalence; and
$\rho \colon \thinspace \mathcal {R}_r \to G$
is a homotopy equivalence; and -
(3)
 $\ell $
is a length function on G.
$\ell $
is a length function on G.
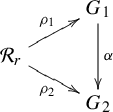
There is an equivalence relation on the set of marked metric graphs defined by
![]() $(G_1,\rho _1,\ell _1) \sim (G_2,\rho _2,\ell _2)$
if there exists a graph automorphism
$(G_1,\rho _1,\ell _1) \sim (G_2,\rho _2,\ell _2)$
if there exists a graph automorphism
![]() $\alpha \colon \thinspace G_1 \to G_2$
such that
$\alpha \colon \thinspace G_1 \to G_2$
such that
![]() $\ell _1 = \ell _2 \circ \alpha $
and such that the following diagram commutes up to homotopy:
$\ell _1 = \ell _2 \circ \alpha $
and such that the following diagram commutes up to homotopy:
We let
![]() $\mathcal {X}(\mathbb {F}_r)$
denote the set of equivalence classes of marked metric graphs of rank r. The group
$\mathcal {X}(\mathbb {F}_r)$
denote the set of equivalence classes of marked metric graphs of rank r. The group
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
acts on
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
acts on
![]() $\mathcal {X}(\mathbb {F}_r)$
on the right by precomposing the marking. Specifically, for any outer automorphism
$\mathcal {X}(\mathbb {F}_r)$
on the right by precomposing the marking. Specifically, for any outer automorphism
![]() $\phi \in \operatorname {\mathrm {Out}}(\mathbb {F}_r)$
, there is a homotopy equivalence
$\phi \in \operatorname {\mathrm {Out}}(\mathbb {F}_r)$
, there is a homotopy equivalence
![]() $g_\phi \colon \thinspace \mathcal {R}_r \to \mathcal {R}_r$
that induces
$g_\phi \colon \thinspace \mathcal {R}_r \to \mathcal {R}_r$
that induces
![]() $\phi $
on
$\phi $
on
![]() $\pi _1(\mathcal {R}_r)$
via the aforementioned fixed isomorphism
$\pi _1(\mathcal {R}_r)$
via the aforementioned fixed isomorphism
![]() $\mathbb {F}_r \cong \pi _1(\mathcal {R}_r,*)$
. Moreover, this homotopy equivalence is unique up to homotopy. With this, we define
$\mathbb {F}_r \cong \pi _1(\mathcal {R}_r,*)$
. Moreover, this homotopy equivalence is unique up to homotopy. With this, we define
This action respects the equivalence relation on marked metric graphs and so defines an action on
![]() $\mathcal {X}(\mathbb {F}_r)$
as claimed.
$\mathcal {X}(\mathbb {F}_r)$
as claimed.
Let
![]() $\mathcal {G}_r$
denote the set of finite connected graphs without vertices of valence
$\mathcal {G}_r$
denote the set of finite connected graphs without vertices of valence
![]() $1$
or
$1$
or
![]() $2$
whose fundamental group has rank r. We observe that this is a finite set. Given a graph
$2$
whose fundamental group has rank r. We observe that this is a finite set. Given a graph
![]() $G \in \mathcal {G}_r$
and homotopy equivalence
$G \in \mathcal {G}_r$
and homotopy equivalence
![]() $\rho \colon \thinspace \mathcal {R}_r \to G$
, we set
$\rho \colon \thinspace \mathcal {R}_r \to G$
, we set
There is a bijection
![]() $\mathcal {X}(G,\rho ) \to \mathcal {M}(G)$
defined by
$\mathcal {X}(G,\rho ) \to \mathcal {M}(G)$
defined by
![]() $[(G_0,\rho _0,\ell _0)] \mapsto \ell _0$
. These sets partition the set
$[(G_0,\rho _0,\ell _0)] \mapsto \ell _0$
. These sets partition the set
![]() $\mathcal {X}(\mathbb {F}_r)$
and are permuted under the action by
$\mathcal {X}(\mathbb {F}_r)$
and are permuted under the action by
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
. Specifically, for each
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
. Specifically, for each
![]() $G \in \mathcal {G}_r$
we fix a marking
$G \in \mathcal {G}_r$
we fix a marking
![]() $\rho _G \colon \thinspace \mathcal {R}_r \to G$
. Then
$\rho _G \colon \thinspace \mathcal {R}_r \to G$
. Then
There is a topology on
![]() $\mathcal {X}(\mathbb {F}_r)$
that is often defined in three different ways. We will need to use the first two and for completeness we explain all three here.
$\mathcal {X}(\mathbb {F}_r)$
that is often defined in three different ways. We will need to use the first two and for completeness we explain all three here.
The weak topology. The notion of a collapse induces a partial order on the set of marked graphs. Specifically, for two graphs G and
![]() $G_0$
, we say that G collapses to
$G_0$
, we say that G collapses to
![]() $G_0$
if there is a surjection
$G_0$
if there is a surjection
![]() $c \colon \thinspace G \to G_0$
such that the image of any edge in G is either a vertex or an edge of
$c \colon \thinspace G \to G_0$
such that the image of any edge in G is either a vertex or an edge of
![]() $G_0$
and such that
$G_0$
and such that
![]() $c^{-1}(x)$
is a contractible subgraph of G for each point x of
$c^{-1}(x)$
is a contractible subgraph of G for each point x of
![]() $G_0$
. The map c is a called a collapse. Observe that if the map
$G_0$
. The map c is a called a collapse. Observe that if the map
![]() $c \colon \thinspace G \to G_0$
is a collapse, then a length function
$c \colon \thinspace G \to G_0$
is a collapse, then a length function
![]() $\ell \in \mathcal {M}(G_0)$
can be considered as a degenerate length function
$\ell \in \mathcal {M}(G_0)$
can be considered as a degenerate length function
![]() $\ell _{G_0}$
on G by
$\ell _{G_0}$
on G by
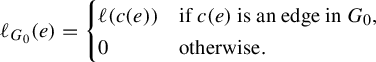 $$ \begin{align} \ell_{G_0}(e) = \begin{cases} \ell(c(e)) & \mbox{if}\ c(e)\ \mbox{is an edge in}\ G_0, \\ 0 & \mbox{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \ell_{G_0}(e) = \begin{cases} \ell(c(e)) & \mbox{if}\ c(e)\ \mbox{is an edge in}\ G_0, \\ 0 & \mbox{otherwise}. \end{cases} \end{align} $$
This defines a map
![]() $c^* \colon \thinspace \mathcal {M}(G_0) \to \mathbb {R}_{\geq 0}^{\lvert {E_+} \rvert }$
by
$c^* \colon \thinspace \mathcal {M}(G_0) \to \mathbb {R}_{\geq 0}^{\lvert {E_+} \rvert }$
by
![]() $c^*(\ell ) = \ell _{G_0}$
. We now define the following subset of
$c^*(\ell ) = \ell _{G_0}$
. We now define the following subset of
![]() $\mathbb {R}_{\geq 0}^{\lvert {E_+} \rvert }$
:
$\mathbb {R}_{\geq 0}^{\lvert {E_+} \rvert }$
:
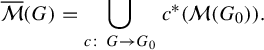 $$ \begin{align} \overline{\mathcal{M}}(G) = \bigcup_{c \colon\thinspace G \to G_0} c^*(\mathcal{M}(G_0)). \end{align} $$
$$ \begin{align} \overline{\mathcal{M}}(G) = \bigcup_{c \colon\thinspace G \to G_0} c^*(\mathcal{M}(G_0)). \end{align} $$
We note the
![]() $\mathcal {M}(G)$
is a subset of
$\mathcal {M}(G)$
is a subset of
![]() $\overline {\mathcal {M}}(G)$
as the identity map
$\overline {\mathcal {M}}(G)$
as the identity map
![]() ${\textrm {id}} \colon \thinspace G \to G$
is a collapse.
${\textrm {id}} \colon \thinspace G \to G$
is a collapse.
Next, given two marked graphs
![]() $\rho \colon \thinspace \mathcal {R}_r \to G$
and
$\rho \colon \thinspace \mathcal {R}_r \to G$
and
![]() $\rho _0 \colon \thinspace \mathcal {R}_r \to G_0$
, we say that
$\rho _0 \colon \thinspace \mathcal {R}_r \to G_0$
, we say that
![]() $(G,\rho )$
collapses to
$(G,\rho )$
collapses to
![]() $(G_0,\rho _0)$
if there is a collapse
$(G_0,\rho _0)$
if there is a collapse
![]() $c \colon \thinspace G \to G_0$
such that
$c \colon \thinspace G \to G_0$
such that
![]() $\rho _0 \simeq c \circ \rho $
. In this case we write
$\rho _0 \simeq c \circ \rho $
. In this case we write
![]() $(G_0,\rho _0) \leq (G_,\rho )$
. We now define the following subset of
$(G_0,\rho _0) \leq (G_,\rho )$
. We now define the following subset of
![]() $\mathcal {X}(\mathbb {F}_r)$
:
$\mathcal {X}(\mathbb {F}_r)$
:
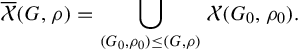 $$ \begin{align} \overline{\mathcal{X}}(G,\rho) = \bigcup_{(G_0,\rho_0) \leq (G,\rho)} \mathcal{X}(G_0,\rho_0). \end{align} $$
$$ \begin{align} \overline{\mathcal{X}}(G,\rho) = \bigcup_{(G_0,\rho_0) \leq (G,\rho)} \mathcal{X}(G_0,\rho_0). \end{align} $$
The bijection
![]() $\mathcal {X}(G,\rho ) \to \mathcal {M}(G)$
extends in a natural way to a bijection
$\mathcal {X}(G,\rho ) \to \mathcal {M}(G)$
extends in a natural way to a bijection
![]() $\overline {\mathcal {X}}(G,\rho ) \to \overline {\mathcal {M}}(G)$
and allows us to consider
$\overline {\mathcal {X}}(G,\rho ) \to \overline {\mathcal {M}}(G)$
and allows us to consider
![]() $\overline {\mathcal {X}}(G,\rho )$
as a subset of
$\overline {\mathcal {X}}(G,\rho )$
as a subset of
![]() $\mathbb {R}_{\geq 0}^{\lvert {E_+} \rvert }$
.
$\mathbb {R}_{\geq 0}^{\lvert {E_+} \rvert }$
.
The weak topology is defined using this collection of subsets. Specifically, a set
![]() $U \subseteq \mathcal {X}(\mathbb {F}_r)$
is open if
$U \subseteq \mathcal {X}(\mathbb {F}_r)$
is open if
![]() $U \cap \overline {\mathcal {X}}(G,\rho )$
is open as a subset of
$U \cap \overline {\mathcal {X}}(G,\rho )$
is open as a subset of
![]() $\mathbb {R}_{\geq 0}^{\lvert {E_+} \rvert }$
for all marked graphs
$\mathbb {R}_{\geq 0}^{\lvert {E_+} \rvert }$
for all marked graphs
![]() $(G,\rho )$
.
$(G,\rho )$
.
The axes topology. Given a marked metric graph
![]() $(G,\rho ,\ell )$
and an element
$(G,\rho ,\ell )$
and an element
![]() $g \in \mathbb {F}_r$
, we denoted by
$g \in \mathbb {F}_r$
, we denoted by
![]() $\ell ([g])$
the
$\ell ([g])$
the
![]() $\ell $
-length of the shortest loop in G representing the conjugacy class
$\ell $
-length of the shortest loop in G representing the conjugacy class
![]() $[\rho (g)]$
. This induces a function
$[\rho (g)]$
. This induces a function
![]() ${\textrm {Len}} \colon \thinspace \mathcal {X}(\mathbb {F}_r) \to \mathbb {R}_{\geq 0}^{\mathbb {F}_r}$
where
${\textrm {Len}} \colon \thinspace \mathcal {X}(\mathbb {F}_r) \to \mathbb {R}_{\geq 0}^{\mathbb {F}_r}$
where
![]() ${\textrm {Len}}([(G,\rho ,\ell )]) \colon \thinspace \mathbb {F}_r \to \mathbb {R}_{\geq 0}$
is the function defined by
${\textrm {Len}}([(G,\rho ,\ell )]) \colon \thinspace \mathbb {F}_r \to \mathbb {R}_{\geq 0}$
is the function defined by
Culler and Morgan proved that the map
![]() ${\textrm {Len}}$
is injective [Reference Culler and Morgan13, 3.7 Theorem]. The resulting subspace topology on
${\textrm {Len}}$
is injective [Reference Culler and Morgan13, 3.7 Theorem]. The resulting subspace topology on
![]() ${\textrm {Len}}(\mathcal {X}(\mathbb {F}_r)) \subset \mathbb {R}_{\geq 0}^{\mathbb {F}_r}$
is called the axes topology. It is known that this topology agrees with the weak topology. (See [Reference Culler and Vogtmann14, §1.1] or [Reference Guirardel and Levitt21, Proposition 5.4].)
${\textrm {Len}}(\mathcal {X}(\mathbb {F}_r)) \subset \mathbb {R}_{\geq 0}^{\mathbb {F}_r}$
is called the axes topology. It is known that this topology agrees with the weak topology. (See [Reference Culler and Vogtmann14, §1.1] or [Reference Guirardel and Levitt21, Proposition 5.4].)
The equivariant Gromov–Hausdorff topology. We will not need this definition, and we only remark that Paulin showed that it is equivalent to the axes topology [Reference Paulin30, Main Theorem].
There is an action of
![]() $\mathbb {R}_{>0}$
on
$\mathbb {R}_{>0}$
on
![]() $\mathcal {X}(\mathbb {F}_r)$
given by scaling the length function. Specifically,
$\mathcal {X}(\mathbb {F}_r)$
given by scaling the length function. Specifically,
![]() $a \cdot (G,\rho ,\ell ) = (G,\rho ,a\cdot \ell )$
. The quotient of
$a \cdot (G,\rho ,\ell ) = (G,\rho ,a\cdot \ell )$
. The quotient of
![]() $\mathcal {X}(\mathbb {F}_r)$
is denoted
$\mathcal {X}(\mathbb {F}_r)$
is denoted
![]() $\mathbb {P}\mathcal {X}(\mathbb {F}_r)$
.
$\mathbb {P}\mathcal {X}(\mathbb {F}_r)$
.
There are many continuous sections of the quotient map
![]() $\mathcal {X}(\mathbb {F}_r) \to \mathbb {P}\mathcal {X}(\mathbb {F}_r)$
. An often used choice uses the notion of the volume of a length function,
$\mathcal {X}(\mathbb {F}_r) \to \mathbb {P}\mathcal {X}(\mathbb {F}_r)$
. An often used choice uses the notion of the volume of a length function,
![]() $\operatorname {\mathrm {vol}}(\ell )$
, that we define now. For a length function
$\operatorname {\mathrm {vol}}(\ell )$
, that we define now. For a length function
![]() $\ell \in \mathcal {M}(G)$
, we define the volume of
$\ell \in \mathcal {M}(G)$
, we define the volume of
![]() $\ell $
by
$\ell $
by
![]() $\operatorname {\mathrm {vol}}(\ell ) = \sum _{e \in E_+}\ell (e)$
. There is a section
$\operatorname {\mathrm {vol}}(\ell ) = \sum _{e \in E_+}\ell (e)$
. There is a section
![]() $\mathcal {V} \colon \thinspace \mathbb {P}\mathcal {X}(\mathbb {F}_r) \to \mathcal {X}(\mathbb {F}_r)$
defined by
$\mathcal {V} \colon \thinspace \mathbb {P}\mathcal {X}(\mathbb {F}_r) \to \mathcal {X}(\mathbb {F}_r)$
defined by
 $$ \begin{align*} \mathcal{V}([ [(G,\rho,\ell)]]) = \bigg[\bigg(G,\rho,\frac{1}{\operatorname{\mathrm{vol}}(\ell)}\ell\bigg)\bigg]. \end{align*} $$
$$ \begin{align*} \mathcal{V}([ [(G,\rho,\ell)]]) = \bigg[\bigg(G,\rho,\frac{1}{\operatorname{\mathrm{vol}}(\ell)}\ell\bigg)\bigg]. \end{align*} $$
We denote the image of this section by
![]() $CV(\mathbb {F}_r)$
; it is known as the Culler–Vogtmann outer space. Further, given a marked graph
$CV(\mathbb {F}_r)$
; it is known as the Culler–Vogtmann outer space. Further, given a marked graph
![]() $\rho \colon \thinspace \mathcal {R}_r \to G$
, we set
$\rho \colon \thinspace \mathcal {R}_r \to G$
, we set
![]() $CV(G,\rho ) = \mathcal {X}(G,\rho ) \cap CV(\mathbb {F}_r)$
. This set is homeomorphic to an open simplex of dimension
$CV(G,\rho ) = \mathcal {X}(G,\rho ) \cap CV(\mathbb {F}_r)$
. This set is homeomorphic to an open simplex of dimension
![]() $\lvert {E_+} \rvert - 1$
.
$\lvert {E_+} \rvert - 1$
.
Example 2.1. There are three graphs in
![]() $\mathcal {G}_2$
: the
$\mathcal {G}_2$
: the
![]() $2$
-rose
$2$
-rose
![]() $\mathcal {R}_2$
, the theta graph
$\mathcal {R}_2$
, the theta graph
![]() $\Theta _2$
and the barbell graph
$\Theta _2$
and the barbell graph
![]() $\mathcal {B}_2$
; see Figure 2. Figure 3 shows a portion of
$\mathcal {B}_2$
; see Figure 2. Figure 3 shows a portion of
![]() $CV(\mathbb {F}_2)$
and how these simplices piece together. The homotopy equivalences used for Figure 3 are as follows:
$CV(\mathbb {F}_2)$
and how these simplices piece together. The homotopy equivalences used for Figure 3 are as follows:
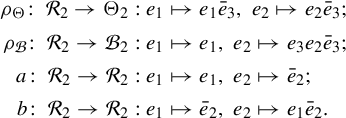 $$ \begin{align*} \rho_\Theta \colon\thinspace \mathcal{R}_2 \to \Theta_2 & : e_1 \mapsto e_1\bar{e}_3, \, e_2 \mapsto e_2\bar{e}_3; \\ \rho_{\mathcal{B}} \colon\thinspace \mathcal{R}_2 \to \mathcal{B}_2 & : e_1 \mapsto e_1, \, e_2 \mapsto e_3e_2\bar{e}_3; \\ a \colon\thinspace \mathcal{R}_2 \to \mathcal{R}_2 & : e_1 \mapsto e_1, \, e_2 \mapsto \bar{e}_2; \\ b \colon\thinspace \mathcal{R}_2 \to \mathcal{R}_2 & : e_1 \mapsto \bar{e}_2, \, e_2 \mapsto e_1\bar{e}_2. \end{align*} $$
$$ \begin{align*} \rho_\Theta \colon\thinspace \mathcal{R}_2 \to \Theta_2 & : e_1 \mapsto e_1\bar{e}_3, \, e_2 \mapsto e_2\bar{e}_3; \\ \rho_{\mathcal{B}} \colon\thinspace \mathcal{R}_2 \to \mathcal{B}_2 & : e_1 \mapsto e_1, \, e_2 \mapsto e_3e_2\bar{e}_3; \\ a \colon\thinspace \mathcal{R}_2 \to \mathcal{R}_2 & : e_1 \mapsto e_1, \, e_2 \mapsto \bar{e}_2; \\ b \colon\thinspace \mathcal{R}_2 \to \mathcal{R}_2 & : e_1 \mapsto \bar{e}_2, \, e_2 \mapsto e_1\bar{e}_2. \end{align*} $$
Notice that
![]() $\rho _\Theta $
is the homotopy inverse to the map
$\rho _\Theta $
is the homotopy inverse to the map
![]() $\Theta _2 \to \mathcal {R}_2$
that collapses the edge
$\Theta _2 \to \mathcal {R}_2$
that collapses the edge
![]() $e_3$
. Likewise
$e_3$
. Likewise
![]() $\rho _\Theta \circ b$
is the homotopy inverse to the collapse of
$\rho _\Theta \circ b$
is the homotopy inverse to the collapse of
![]() $e_2$
and
$e_2$
and
![]() $\rho _\Theta \circ b^2$
is the homotopy inverse to the collapse of
$\rho _\Theta \circ b^2$
is the homotopy inverse to the collapse of
![]() $e_1$
. Similarly,
$e_1$
. Similarly,
![]() $\rho _{\mathcal {B}}$
is the homotopy inverse to the map
$\rho _{\mathcal {B}}$
is the homotopy inverse to the map
![]() $\mathcal {B}_2 \to \mathcal {R}_2$
that collapses
$\mathcal {B}_2 \to \mathcal {R}_2$
that collapses
![]() $e_3$
.
$e_3$
.
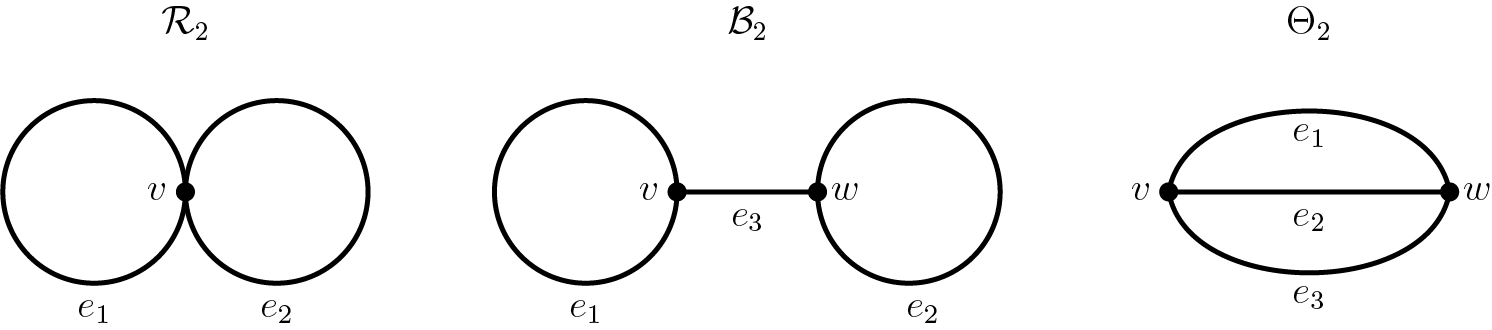
Figure 2 The three homeomorphism types of graphs in
![]() $\mathcal {G}_2$
.
$\mathcal {G}_2$
.
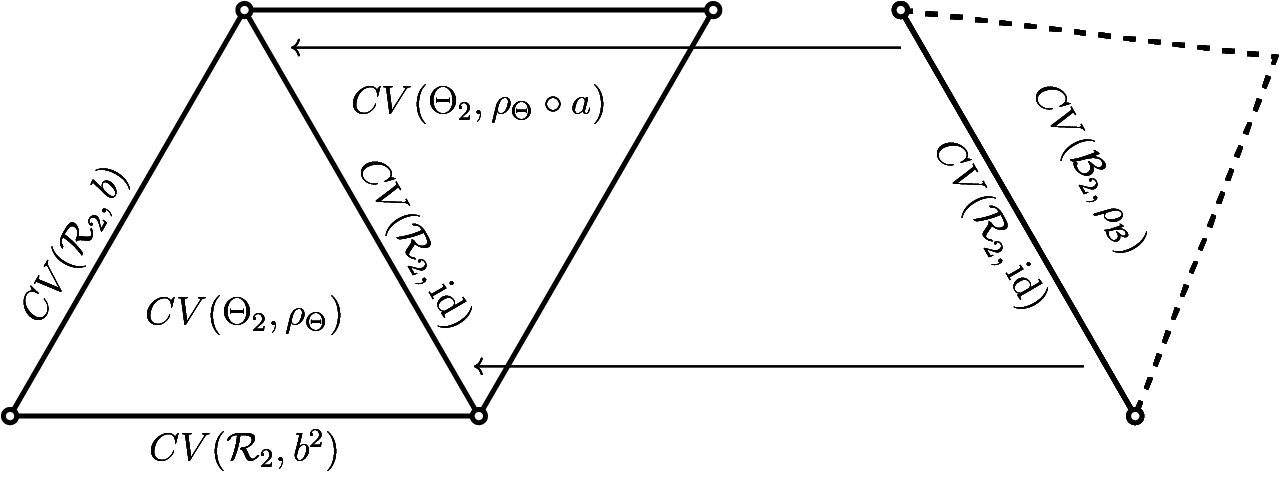
Figure 3 A portion of the Culler–Vogtmann outer space
![]() $CV(\mathbb {F}_2)$
.
$CV(\mathbb {F}_2)$
.
One of the goals of this paper is to investigate a different continuous section of the quotient map. This uses the notion of entropy,
![]() $\mathfrak {h}_G(\ell )$
, defined in §3.1. Using this notion, there is a section
$\mathfrak {h}_G(\ell )$
, defined in §3.1. Using this notion, there is a section
![]() $\mathcal {H} \colon \thinspace \mathbb {P}\mathcal {X}(\mathbb {F}_r) \to \mathcal {X}(\mathbb {F}_r)$
defined by
$\mathcal {H} \colon \thinspace \mathbb {P}\mathcal {X}(\mathbb {F}_r) \to \mathcal {X}(\mathbb {F}_r)$
defined by
We will denote the image of this section by
![]() $\mathcal {X}^1(\mathbb {F}_r)$
.
$\mathcal {X}^1(\mathbb {F}_r)$
.
3 Thermodynamic metrics
In this section we introduce the entropy and pressure of a length function in
![]() $\mathcal {M}(G)$
, for a graph G as in §2.1. By normalizing the entropy to be equal to 1, we realize
$\mathcal {M}(G)$
, for a graph G as in §2.1. By normalizing the entropy to be equal to 1, we realize
![]() $\mathcal {X}^1(\mathbb {F}_r)$
(as defined in §2.2) as a section of
$\mathcal {X}^1(\mathbb {F}_r)$
(as defined in §2.2) as a section of
![]() $\mathcal {X}(\mathbb {F}_r) \to \mathbb {P}\mathcal {X}(\mathbb {F}_r)$
; it will follow that
$\mathcal {X}(\mathbb {F}_r) \to \mathbb {P}\mathcal {X}(\mathbb {F}_r)$
; it will follow that
![]() $\mathcal {X}^1(\mathbb {F}_r)$
is homeomorphic to
$\mathcal {X}^1(\mathbb {F}_r)$
is homeomorphic to
![]() $CV(\mathbb {F}_r)$
(see Theorem 3.5). We use entropy and pressure to construct piecewise Riemannian metrics on
$CV(\mathbb {F}_r)$
(see Theorem 3.5). We use entropy and pressure to construct piecewise Riemannian metrics on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
, which we call the thermodynamic metrics. Pollicott and Sharp were the first to consider one of these metrics [Reference Pollicott and Sharp31]. Kao [Reference Kao22] and Xu [Reference Xu39] have also investigated these metrics. In these papers, the metric is only considered for a single marked graph and never on the entire outer space, as we will do here.
$\mathcal {X}^1(\mathbb {F}_r)$
, which we call the thermodynamic metrics. Pollicott and Sharp were the first to consider one of these metrics [Reference Pollicott and Sharp31]. Kao [Reference Kao22] and Xu [Reference Xu39] have also investigated these metrics. In these papers, the metric is only considered for a single marked graph and never on the entire outer space, as we will do here.
3.1 Entropy
Fix a finite connected graph
![]() $G = (V,E,o,\tau ,\bar {\phantom {e}})$
. An edge path
$G = (V,E,o,\tau ,\bar {\phantom {e}})$
. An edge path
![]() $(e_1,\ldots ,e_n)$
in a graph G is reduced if
$(e_1,\ldots ,e_n)$
in a graph G is reduced if
![]() $e_{i} \neq \bar {e}_{i+1}$
for
$e_{i} \neq \bar {e}_{i+1}$
for
![]() $i = 1,\ldots ,n-1$
. A reduced edge path
$i = 1,\ldots ,n-1$
. A reduced edge path
![]() $(e_1,\ldots ,e_n)$
is a based circuit if
$(e_1,\ldots ,e_n)$
is a based circuit if
![]() $\tau (e_{n}) = o(e_{1})$
and
$\tau (e_{n}) = o(e_{1})$
and
![]() $e_{n} \neq \bar {e}_{1}$
. The set of all based circuits in G is denoted by
$e_{n} \neq \bar {e}_{1}$
. The set of all based circuits in G is denoted by
![]() $\mathcal {C}(G)$
. For a length function
$\mathcal {C}(G)$
. For a length function
![]() $\ell \in \mathcal {M}(G)$
and a real number
$\ell \in \mathcal {M}(G)$
and a real number
![]() $t \geq 0$
, define
$t \geq 0$
, define
Definition 3.1. The entropy of a length function
![]() $\ell \in \mathcal {M}(G)$
is
$\ell \in \mathcal {M}(G)$
is
Remark 3.2. We defined entropy as the growth rate of the number of reduced based circuits. In the literature, there exist many equivalent definitions of entropy. In particular, one can count the growth of reduced edge paths in G starting at a particular vertex and the adjective ‘based’ can be removed from the count of circuits [Reference Kapovich and Rivin24, Proposition 2.3]. This shows that
![]() $\mathfrak {h}_G(\ell )$
equals the volume entropy of
$\mathfrak {h}_G(\ell )$
equals the volume entropy of
![]() $(G,\ell )$
. The volume entropy is defined as the exponential growth rate of the volume of balls in
$(G,\ell )$
. The volume entropy is defined as the exponential growth rate of the volume of balls in
![]() $({\widetilde G}, g_\ell )$
, where
$({\widetilde G}, g_\ell )$
, where
![]() ${\widetilde G}$
is the universal cover of G and
${\widetilde G}$
is the universal cover of G and
![]() $g_\ell $
is the piecewise Riemannian metric obtained by pulling back the length function
$g_\ell $
is the piecewise Riemannian metric obtained by pulling back the length function
![]() $\ell $
. That is,
$\ell $
. That is,
where
![]() $B(x,t)$
is the ball of radius t centered at
$B(x,t)$
is the ball of radius t centered at
![]() $x \in {\widetilde G}$
, which is an arbitrary basepoint.
$x \in {\widetilde G}$
, which is an arbitrary basepoint.
Example 3.3. The number of reduced edge paths in
![]() $\mathcal {R}_{r}$
with
$\mathcal {R}_{r}$
with
![]() $\mathbf {1}$
-length equal to n is exactly
$\mathbf {1}$
-length equal to n is exactly
![]() $2r(2r-1)^{n-1}$
. Thus for any vertex
$2r(2r-1)^{n-1}$
. Thus for any vertex
![]() $v \in \widetilde {\mathcal {R}}_r$
we have
$v \in \widetilde {\mathcal {R}}_r$
we have
Hence
![]() $\mathfrak {h}_{\mathcal {R}_r}(\mathbf {1}) = \log (2r-1)$
.
$\mathfrak {h}_{\mathcal {R}_r}(\mathbf {1}) = \log (2r-1)$
.
The next lemma shows that entropy is homogeneous of degree
![]() $-1$
and thus any length function
$-1$
and thus any length function
![]() $\ell \in \mathcal {M}(G)$
can be scaled to have unit entropy. Specifically,
$\ell \in \mathcal {M}(G)$
can be scaled to have unit entropy. Specifically,
![]() $\mathfrak {h}_G(a \cdot \ell ) = 1$
if and only if
$\mathfrak {h}_G(a \cdot \ell ) = 1$
if and only if
![]() $a = \mathfrak {h}_G(\ell )$
.
$a = \mathfrak {h}_G(\ell )$
.
Lemma 3.4. Let G be a finite connected graph and fix
![]() $\ell \in \mathcal {M}(G)$
. If
$\ell \in \mathcal {M}(G)$
. If
![]() $a \in \mathbb {R}_{>0}$
, then
$a \in \mathbb {R}_{>0}$
, then
Proof. We reparametrize the limit defining entropy by setting
![]() $s = a t$
. Then
$s = a t$
. Then
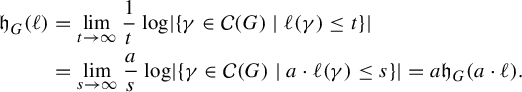 $$ \begin{align*} \mathfrak{h}_G(\ell) & = \lim_{t \to \infty} \frac{1}{t} \log \lvert {\{\gamma \in \mathcal{C}(G) \mid \ell(\gamma) \leq t\}} \rvert \\ & = \lim_{s \to \infty} \frac{a}{s} \log \lvert {\{\gamma \in \mathcal{C}(G) \mid a \cdot \ell(\gamma) \leq s\}} \rvert = a\mathfrak{h}_G(a \cdot \ell).\\[-40pt] \end{align*} $$
$$ \begin{align*} \mathfrak{h}_G(\ell) & = \lim_{t \to \infty} \frac{1}{t} \log \lvert {\{\gamma \in \mathcal{C}(G) \mid \ell(\gamma) \leq t\}} \rvert \\ & = \lim_{s \to \infty} \frac{a}{s} \log \lvert {\{\gamma \in \mathcal{C}(G) \mid a \cdot \ell(\gamma) \leq s\}} \rvert = a\mathfrak{h}_G(a \cdot \ell).\\[-40pt] \end{align*} $$
Entropy defines an
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
-invariant function on
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
-invariant function on
![]() $\mathcal {X}(\mathbb {F}_r)$
by
$\mathcal {X}(\mathbb {F}_r)$
by
![]() $\mathfrak {h}([(G,\rho ,\ell )]) = \mathfrak {h}_G(\ell )$
. This function was investigated by Kapovich and Nagnibeda, who showed the following theorem.
$\mathfrak {h}([(G,\rho ,\ell )]) = \mathfrak {h}_G(\ell )$
. This function was investigated by Kapovich and Nagnibeda, who showed the following theorem.
Theorem 3.5. [Reference Kapovich and Nagnibeda23, Theorem A]
The entropy function
![]() $\mathfrak {h} \colon \thinspace \mathcal {X}(\mathbb {F}_r) \to \mathbb {R}$
is continuous.
$\mathfrak {h} \colon \thinspace \mathcal {X}(\mathbb {F}_r) \to \mathbb {R}$
is continuous.
In particular, the map
![]() $\mathcal {H} \colon \thinspace \mathbb {P}\mathcal {X}(\mathbb {F}_r) \to \mathcal {X}(\mathbb {F}_r)$
defined by normalizing to have unit entropy,
$\mathcal {H} \colon \thinspace \mathbb {P}\mathcal {X}(\mathbb {F}_r) \to \mathcal {X}(\mathbb {F}_r)$
defined by normalizing to have unit entropy,
is a section. Hence the image
![]() $\mathcal {X}^1(\mathbb {F}_r) = \{[(G,\rho ,\ell )] \in \mathcal {X}(\mathbb {F}_r) \mid \mathfrak {h}_G(\ell ) = 1 \}$
is homeomorphic to
$\mathcal {X}^1(\mathbb {F}_r) = \{[(G,\rho ,\ell )] \in \mathcal {X}(\mathbb {F}_r) \mid \mathfrak {h}_G(\ell ) = 1 \}$
is homeomorphic to
![]() $CV(\mathbb {F}_r)$
.
$CV(\mathbb {F}_r)$
.
3.2 Pressure
Fix a finite connected graph
![]() $G = (V,E,o,\tau ,\bar {\phantom {e}})$
. We assume throughout this subsection and the next that
$G = (V,E,o,\tau ,\bar {\phantom {e}})$
. We assume throughout this subsection and the next that
![]() $\chi (G) < 0$
(where
$\chi (G) < 0$
(where
![]() $\chi (G) = \lvert {V} \rvert - \tfrac 12\lvert {E} \rvert $
is the Euler characteristic of G—note the
$\chi (G) = \lvert {V} \rvert - \tfrac 12\lvert {E} \rvert $
is the Euler characteristic of G—note the
![]() $\tfrac 12$
factor is present as E includes edges with both orientations) and that G has no vertices with valence equal to
$\tfrac 12$
factor is present as E includes edges with both orientations) and that G has no vertices with valence equal to
![]() $1$
or
$1$
or
![]() $2$
.
$2$
.
Define
![]() $A_{G} \in \operatorname {\mathrm {Mat}}_{\lvert {E} \rvert }(\mathbb {R})$
by
$A_{G} \in \operatorname {\mathrm {Mat}}_{\lvert {E} \rvert }(\mathbb {R})$
by
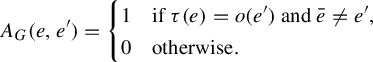 $$ \begin{align} A_{G}(e,e') = \begin{cases} 1 & \mbox{if } \tau(e) = o(e') \mbox{ and } \bar{e} \neq e', \\ 0 & \mbox{otherwise. } \end{cases} \end{align} $$
$$ \begin{align} A_{G}(e,e') = \begin{cases} 1 & \mbox{if } \tau(e) = o(e') \mbox{ and } \bar{e} \neq e', \\ 0 & \mbox{otherwise. } \end{cases} \end{align} $$
It follows that the entry
![]() $A_{G}^{n}(e,e')$
is the number of reduced edge paths of the form
$A_{G}^{n}(e,e')$
is the number of reduced edge paths of the form
![]() $(e_{1},\ldots , e_{n})$
where
$(e_{1},\ldots , e_{n})$
where
![]() $e_1 = e$
,
$e_1 = e$
,
![]() $\tau (e_{n}) = o(e')$
and
$\tau (e_{n}) = o(e')$
and
![]() $\bar {e}_n \neq e'$
. In particular,
$\bar {e}_n \neq e'$
. In particular,
![]() $\operatorname {\mathrm {tr}}(A_{G}^{n})$
is the number of based edge circuits with
$\operatorname {\mathrm {tr}}(A_{G}^{n})$
is the number of based edge circuits with
![]() $\mathbf {1}$
-length equal to n. Denoting the spectral radius of a matrix by
$\mathbf {1}$
-length equal to n. Denoting the spectral radius of a matrix by
![]() , we get, from the definition of entropy, that
, we get, from the definition of entropy, that
We remark that the above assumptions on G ensure that
![]() $A_G$
is irreducible.
$A_G$
is irreducible.
In order to get a matrix that incorporates the metric and is related to entropy, we scale the rows of
![]() $A_G$
as follows: given a function
$A_G$
as follows: given a function
![]() $f \colon \thinspace E \to \mathbb {R}$
, we define
$f \colon \thinspace E \to \mathbb {R}$
, we define
![]() $A_{G,f} \in \operatorname {\mathrm {Mat}}_{\lvert {E} \rvert }(\mathbb {R})$
by
$A_{G,f} \in \operatorname {\mathrm {Mat}}_{\lvert {E} \rvert }(\mathbb {R})$
by
As for
![]() $A_{G}$
, it follows that
$A_{G}$
, it follows that
![]() $A_{G,f}^{n}(e,e')$
is the sum of
$A_{G,f}^{n}(e,e')$
is the sum of
![]() $\exp (-f(\gamma ))$
over all edge paths of the form
$\exp (-f(\gamma ))$
over all edge paths of the form
![]() $\gamma = (e_{1},\ldots , e_{n})$
where
$\gamma = (e_{1},\ldots , e_{n})$
where
![]() $e_1 = e$
,
$e_1 = e$
,
![]() $\tau (e_{n}) = o(e')$
and
$\tau (e_{n}) = o(e')$
and
![]() $\bar {e}_n \neq e'$
.
$\bar {e}_n \neq e'$
.
Definition 3.6. The pressure of a function
![]() $f \colon \thinspace E \to \mathbb {R}$
is defined as
$f \colon \thinspace E \to \mathbb {R}$
is defined as
![]() $\mathfrak {P}_G(f) = \log \operatorname {\mathrm {spec}} (A_{G,-f})$
.
$\mathfrak {P}_G(f) = \log \operatorname {\mathrm {spec}} (A_{G,-f})$
.
By equation (3.2) we have that
![]() $\mathfrak {P}_G(\mathbf {0}) = \mathfrak {h}_G(\mathbf {1})$
as
$\mathfrak {P}_G(\mathbf {0}) = \mathfrak {h}_G(\mathbf {1})$
as
![]() $A_{G,-\mathbf {0}} = A_G$
, where
$A_{G,-\mathbf {0}} = A_G$
, where
![]() $\mathbf {0}$
is the zero function.
$\mathbf {0}$
is the zero function.
The connection between entropy and pressure is given by the following theorem.
Theorem 3.7. Suppose that
![]() $G = (V,E,o,\tau ,\bar {\phantom {e}})$
is a finite connected graph. Then the following statements hold.
$G = (V,E,o,\tau ,\bar {\phantom {e}})$
is a finite connected graph. Then the following statements hold.
-
(1) For any length function
 $\ell \in \mathcal {M}(G)$
,
$\ell \in \mathcal {M}(G)$
,
 $\mathfrak {P}_G(-\ell ) = 0$
if and only if
$\mathfrak {P}_G(-\ell ) = 0$
if and only if
 $\mathfrak {h}_G(\ell ) = 1$
.
$\mathfrak {h}_G(\ell ) = 1$
. -
(2) The pressure function
 $\mathfrak {P}_G \colon \thinspace \mathbb {R}^{\lvert {E_{+}} \rvert } \to \mathbb {R}$
is real analytic and convex.
$\mathfrak {P}_G \colon \thinspace \mathbb {R}^{\lvert {E_{+}} \rvert } \to \mathbb {R}$
is real analytic and convex. -
(3) The entropy function
 $\mathfrak {h}_G \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
is real analytic and strictly convex.
$\mathfrak {h}_G \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
is real analytic and strictly convex.
Proof. The first item appears in the work of Pollicott and Sharp [Reference Pollicott and Sharp31, Lemma 3.1(2)].
The properties of pressure stated in the second item can be found in the work of Parry and Pollicott [Reference Parry and Pollicott29, Propositions 4.7 and 4.12].
The properties of entropy stated in the third item can be found in the work of McMullen [Reference McMullen28, Proposition A.4]. Kapovich and Nagnibeda gave an alternative proof of the real analyticity of
![]() $\mathfrak {h}_G$
[Reference Kapovich and Nagnibeda23].
$\mathfrak {h}_G$
[Reference Kapovich and Nagnibeda23].
Let
![]() $\mathcal {M}^1(G) = \{ \ell \in \mathcal {M}(G) \mid \mathfrak {h}_G(\ell ) = 1 \}$
. By the first item above, we have that alternatively
$\mathcal {M}^1(G) = \{ \ell \in \mathcal {M}(G) \mid \mathfrak {h}_G(\ell ) = 1 \}$
. By the first item above, we have that alternatively
![]() $\mathcal {M}^{1}(G) = \{ \ell \in \mathcal {M}(G) \mid \mathfrak {P}_G(-\ell ) = 0 \}$
. To see that
$\mathcal {M}^{1}(G) = \{ \ell \in \mathcal {M}(G) \mid \mathfrak {P}_G(-\ell ) = 0 \}$
. To see that
![]() $\mathcal {M}^1(G)$
is a codimension-
$\mathcal {M}^1(G)$
is a codimension-
![]() $1$
submanifold of
$1$
submanifold of
![]() $\mathbb {R}^{\lvert {E_{+}} \rvert }$
we need to argue that
$\mathbb {R}^{\lvert {E_{+}} \rvert }$
we need to argue that
![]() $1$
is a regular value of
$1$
is a regular value of
![]() $\mathfrak {h}_G$
. This follows from the following lemma. We denote the standard Euclidean inner product on
$\mathfrak {h}_G$
. This follows from the following lemma. We denote the standard Euclidean inner product on
![]() $\mathbb {R}^n$
by
$\mathbb {R}^n$
by
![]() .
.
Lemma 3.8. Let G be a finite connected graph and fix
![]() $\ell \in \mathcal {M}(G)$
. Then
$\ell \in \mathcal {M}(G)$
. Then
![]() $\langle \ell ,\nabla \mathfrak {h}_G(\ell ) \rangle = -\mathfrak {h}_G(\ell )$
.
$\langle \ell ,\nabla \mathfrak {h}_G(\ell ) \rangle = -\mathfrak {h}_G(\ell )$
.
Proof. This follows from the homogeneity of the entropy function (Lemma 3.4). Indeed,
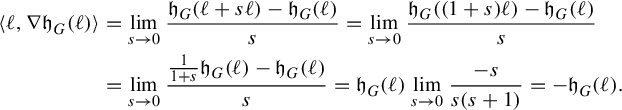 $$ \begin{align*} \langle \ell,\nabla \mathfrak{h}_G(\ell) \rangle &= \lim_{s \to 0} \frac{\mathfrak{h}_G(\ell + s\ell) - \mathfrak{h}_G(\ell)}{s} = \lim_{s \to 0} \frac{\mathfrak{h}_G((1+s)\ell) - \mathfrak{h}_G(\ell)}{s} \\ &= \lim_{s \to 0} \frac{\frac{1}{1+s}\mathfrak{h}_G(\ell) - \mathfrak{h}_G(\ell)}{s} = \mathfrak{h}_G(\ell) \lim_{s \to 0} \frac{-s}{s(s+1)} = -\mathfrak{h}_G(\ell).\\[-46pt] \end{align*} $$
$$ \begin{align*} \langle \ell,\nabla \mathfrak{h}_G(\ell) \rangle &= \lim_{s \to 0} \frac{\mathfrak{h}_G(\ell + s\ell) - \mathfrak{h}_G(\ell)}{s} = \lim_{s \to 0} \frac{\mathfrak{h}_G((1+s)\ell) - \mathfrak{h}_G(\ell)}{s} \\ &= \lim_{s \to 0} \frac{\frac{1}{1+s}\mathfrak{h}_G(\ell) - \mathfrak{h}_G(\ell)}{s} = \mathfrak{h}_G(\ell) \lim_{s \to 0} \frac{-s}{s(s+1)} = -\mathfrak{h}_G(\ell).\\[-46pt] \end{align*} $$
We record the following properties of the partial derivatives and the gradient of the pressure function. Given a function
![]() $f \colon \thinspace \mathbb {R}^{\lvert {E_+} \rvert } \to \mathbb {R}$
and an edge
$f \colon \thinspace \mathbb {R}^{\lvert {E_+} \rvert } \to \mathbb {R}$
and an edge
![]() $e \in E_+$
, we denote the partial derivative of f with respect to the eth coordinate by
$e \in E_+$
, we denote the partial derivative of f with respect to the eth coordinate by
![]() $\partial _{e} f$
. Let
$\partial _{e} f$
. Let
![]() denote the usual
denote the usual
![]() $L^{1}$
-norm on vectors in
$L^{1}$
-norm on vectors in
![]() $\mathbb {R}^{n}$
.
$\mathbb {R}^{n}$
.
Lemma 3.9. Let
![]() $G = (V,E,o,\tau ,\bar {\phantom {e}})$
be a finite connected graph and fix
$G = (V,E,o,\tau ,\bar {\phantom {e}})$
be a finite connected graph and fix
![]() $\ell \in \mathcal {M}(G)$
. Then the following statements hold.
$\ell \in \mathcal {M}(G)$
. Then the following statements hold.
-
(1)
 $\partial _{e} \mathfrak {P}_G(\ell )> 0$
for any
$\partial _{e} \mathfrak {P}_G(\ell )> 0$
for any
 $e \in E_+$
.
$e \in E_+$
. -
(2)
 $\| {\nabla \mathfrak {P}_G(\ell )} \|_1 = 1$
.
$\| {\nabla \mathfrak {P}_G(\ell )} \|_1 = 1$
.
Proof. By the Perron–Frobenius theorem, the spectral radius of
![]() $A_{G,\ell }$
is realized by a positive, real, simple eigenvalue
$A_{G,\ell }$
is realized by a positive, real, simple eigenvalue
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $\mathbf {v} \in \mathbb {R}^{\lvert {E} \rvert }$
be a corresponding positive left eigenvector so that
$\mathbf {v} \in \mathbb {R}^{\lvert {E} \rvert }$
be a corresponding positive left eigenvector so that
![]() $\mathbf {v} A_{G,\ell } = \lambda \mathbf {v}$
. Consider the matrix
$\mathbf {v} A_{G,\ell } = \lambda \mathbf {v}$
. Consider the matrix
![]() $Q_{G,\ell } \in \operatorname {\mathrm {Mat}}_{\lvert {E} \rvert }(\mathbb {R})$
defined by
$Q_{G,\ell } \in \operatorname {\mathrm {Mat}}_{\lvert {E} \rvert }(\mathbb {R})$
defined by
![]() $Q_{G,\ell }(e,e') = ({\mathbf {v}(e)}/{\lambda \mathbf {v}(e')})A_{G,\ell }(e,e')$
. Again, by the Perron–Frobenius theorem, as this matrix is column stochastic, there is a positive vector
$Q_{G,\ell }(e,e') = ({\mathbf {v}(e)}/{\lambda \mathbf {v}(e')})A_{G,\ell }(e,e')$
. Again, by the Perron–Frobenius theorem, as this matrix is column stochastic, there is a positive vector
![]() $\mathbf {p} \in \mathbb {R}^{\lvert {E} \rvert }$
with
$\mathbf {p} \in \mathbb {R}^{\lvert {E} \rvert }$
with
![]() $Q_{G,\ell }\mathbf {p} = \mathbf {p}$
and
$Q_{G,\ell }\mathbf {p} = \mathbf {p}$
and
![]() $\| {\mathbf {p}} \|_1 = 1$
. As explained by Parry and Pollicott, we have that
$\| {\mathbf {p}} \|_1 = 1$
. As explained by Parry and Pollicott, we have that
![]() $\partial _{e} \mathfrak {P}_G(\ell ) = \mathbf {p}(e) + \mathbf {p}(\bar {e})$
[Reference Parry and Pollicott29, Ch. 2, Remark 1 and Proposition 4.10]. Items (3.9) and (3.9) readily follow.
$\partial _{e} \mathfrak {P}_G(\ell ) = \mathbf {p}(e) + \mathbf {p}(\bar {e})$
[Reference Parry and Pollicott29, Ch. 2, Remark 1 and Proposition 4.10]. Items (3.9) and (3.9) readily follow.
3.3 Thermodynamic metrics
Fix a finite connected graph
![]() $G = (V,E,o,\tau ,\bar {\phantom {e}})$
. As in the previous section, we assume that
$G = (V,E,o,\tau ,\bar {\phantom {e}})$
. As in the previous section, we assume that
![]() $\chi (G) < 0$
and that G has no vertices with valence equal to
$\chi (G) < 0$
and that G has no vertices with valence equal to
![]() $1$
or
$1$
or
![]() $2$
. The tangent space
$2$
. The tangent space
![]() $T_{\ell }\mathcal {M}^{1}(G)$
at the length function
$T_{\ell }\mathcal {M}^{1}(G)$
at the length function
![]() $\ell \in \mathcal {M}^{1}(G)$
is the space of vectors
$\ell \in \mathcal {M}^{1}(G)$
is the space of vectors
![]() $\mathbf {v} \in \mathbb {R}^{\lvert {E_{+}} \rvert }$
such that
$\mathbf {v} \in \mathbb {R}^{\lvert {E_{+}} \rvert }$
such that
![]() $\langle \mathbf {v},\nabla \mathfrak {h}_G(\ell ) \rangle = 0$
. The tangent bundle
$\langle \mathbf {v},\nabla \mathfrak {h}_G(\ell ) \rangle = 0$
. The tangent bundle
![]() $T\mathcal {M}^{1}(G)$
is the subspace of
$T\mathcal {M}^{1}(G)$
is the subspace of
![]() $\mathcal {M}^1(G) \times \mathbb {R}^{\lvert {E_{+}} \rvert }$
consisting of pairs
$\mathcal {M}^1(G) \times \mathbb {R}^{\lvert {E_{+}} \rvert }$
consisting of pairs
![]() $(\ell ,\mathbf {v})$
where
$(\ell ,\mathbf {v})$
where
![]() $\mathbf {v} \in T_{\ell }\mathcal {M}^{1}(G)$
.
$\mathbf {v} \in T_{\ell }\mathcal {M}^{1}(G)$
.
We now define two Riemannian metrics on
![]() $\mathcal {M}^{1}(G)$
. We denote the Hessian (that is, the matrix of second derivatives) of a smooth function
$\mathcal {M}^{1}(G)$
. We denote the Hessian (that is, the matrix of second derivatives) of a smooth function
![]() $f \colon \thinspace \mathbb {R}^{n} \to \mathbb {R}$
by
$f \colon \thinspace \mathbb {R}^{n} \to \mathbb {R}$
by
![]() $\mathbf {H}[f(x)]$
.
$\mathbf {H}[f(x)]$
.
Definition 3.10. Given a length function
![]() $\ell \in \mathcal {M}^{1}(G)$
and tangent vectors
$\ell \in \mathcal {M}^{1}(G)$
and tangent vectors
![]() $\mathbf {v}_{1},\mathbf {v}_{2} \in T_{\ell } \mathcal {M}^{1}(G)$
we define the entropy metric by
$\mathbf {v}_{1},\mathbf {v}_{2} \in T_{\ell } \mathcal {M}^{1}(G)$
we define the entropy metric by
and the pressure metric by
The associated norms on the tangent bundle
![]() $T\mathcal {M}^{1}(G)$
are denoted by
$T\mathcal {M}^{1}(G)$
are denoted by
By Theorem 3.7(3) we have that
![]() is positive definite. Positive definiteness of
is positive definite. Positive definiteness of
![]() on
on
![]() $T_\ell \mathcal {M}^1(G)$
has been noted by others, but also follows from the positive definiteness of
$T_\ell \mathcal {M}^1(G)$
has been noted by others, but also follows from the positive definiteness of
![]() by Proposition 3.12.
by Proposition 3.12.
Remark 3.11. Other authors have considered these metrics with different and conflicting terminology. We discuss this now using the notation introduced above. Pollicott and Sharp defined
![]() , calling it the Weil–Petersson metric [Reference Pollicott and Sharp31]. Kao defined
, calling it the Weil–Petersson metric [Reference Pollicott and Sharp31]. Kao defined
![]() , calling it the Weil–Petersson metric, and also studied
, calling it the Weil–Petersson metric, and also studied
![]() , calling it the pressure metric [Reference Kao22]. Xu considered
, calling it the pressure metric [Reference Kao22]. Xu considered
![]() , calling it the pressure metric [Reference Xu39]. We use the terminology as stated in Definition 3.10 as it accurately reflects the functions on which the metrics are based. The definitions of these metrics in the literature are not those as given in Definition 3.10, but are equivalent as can be seen by Proposition 3.12.
, calling it the pressure metric [Reference Xu39]. We use the terminology as stated in Definition 3.10 as it accurately reflects the functions on which the metrics are based. The definitions of these metrics in the literature are not those as given in Definition 3.10, but are equivalent as can be seen by Proposition 3.12.
We note that Theorem 3 in the paper by Pollicott and Sharp [Reference Pollicott and Sharp31] holds for the metric
![]() and not for
and not for
![]() as claimed.
as claimed.
The following proposition shows that these metrics lie in the same conformal class and that they can be calculated using the second derivative along a path. This feature is essential particularly for the material in §10.
Proposition 3.12. Let G be a finite connected graph. If
![]() $\ell _{t} \colon \thinspace (-1,1) \to \mathcal {M}^{1}(G)$
is a smooth path, then
$\ell _{t} \colon \thinspace (-1,1) \to \mathcal {M}^{1}(G)$
is a smooth path, then
Additionally, given a length function
![]() $\ell \in \mathcal {M}^{1}(G)$
and tangent vectors
$\ell \in \mathcal {M}^{1}(G)$
and tangent vectors
![]() $\mathbf {v}_{1},\mathbf {v}_{2} \in T_{\ell } \mathcal {M}^{1}(G)$
, we have
$\mathbf {v}_{1},\mathbf {v}_{2} \in T_{\ell } \mathcal {M}^{1}(G)$
, we have
Proof. Differentiating the equation
![]() $\mathfrak {P}_G(-\ell _{t}) = 0$
with respect to t, we have
$\mathfrak {P}_G(-\ell _{t}) = 0$
with respect to t, we have
![]() $\langle \dot \ell _{t}, \nabla \mathfrak {P}_G(-\ell _{t}) \rangle = 0$
. Differentiating again, we find that
$\langle \dot \ell _{t}, \nabla \mathfrak {P}_G(-\ell _{t}) \rangle = 0$
. Differentiating again, we find that
Hence
![]() $\| {(\ell _{t},\dot \ell _{t})} \|_{\mathfrak {P}}^{2} = \langle \dot \ell _{t},\mathbf {H} [\mathfrak {P}(-\ell _{t})]\dot \ell _{t} \rangle = \langle \ddot \ell _{t},\nabla \mathfrak {P}(-\ell _{t}) \rangle $
as claimed.
$\| {(\ell _{t},\dot \ell _{t})} \|_{\mathfrak {P}}^{2} = \langle \dot \ell _{t},\mathbf {H} [\mathfrak {P}(-\ell _{t})]\dot \ell _{t} \rangle = \langle \ddot \ell _{t},\nabla \mathfrak {P}(-\ell _{t}) \rangle $
as claimed.
The proof of the analogous statement for the entropy norm is similar, observing that
![]() $\mathfrak {h}_G(\ell _t) = 1$
.
$\mathfrak {h}_G(\ell _t) = 1$
.
By Lemma 3.8, we have that
![]() $\langle \ell ,\nabla \mathfrak {h}_G(\ell ) \rangle = -1$
for any
$\langle \ell ,\nabla \mathfrak {h}_G(\ell ) \rangle = -1$
for any
![]() $\ell \in \mathcal {M}^{1}(G)$
. Further, we have that
$\ell \in \mathcal {M}^{1}(G)$
. Further, we have that
![]() $\nabla \mathfrak {P}_G(-\ell )$
is non-zero by Lemma 3.9 and hence is parallel to
$\nabla \mathfrak {P}_G(-\ell )$
is non-zero by Lemma 3.9 and hence is parallel to
![]() $\nabla \mathfrak {h}_G(\ell )$
by Theorem 3.7(1). Hence we find that
$\nabla \mathfrak {h}_G(\ell )$
by Theorem 3.7(1). Hence we find that
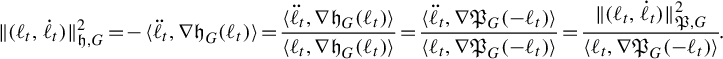 $$ \begin{align*} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{h},G}^{2} \kern1.2pt{=}\kern1.2pt{-}\kern1.2pt\langle \ddot\ell_{t},\kern-1pt\nabla\mathfrak{h}_G(\ell_{t}) \rangle \kern1.2pt{=}\kern1.2pt \frac{\langle \ddot\ell_{t},\kern-1pt\nabla\mathfrak{h}_G(\ell_{t}) \rangle}{\langle \ell_{t},\kern-1pt\nabla \mathfrak{h}_G(\ell_{t}) \rangle} \kern1.2pt{=}\kern1.2pt \frac{\langle \ddot\ell_{t},\kern-1pt\nabla\mathfrak{P}_G(-\ell_{t}) \rangle}{\langle \ell_{t},\kern-1pt\nabla \mathfrak{P}_G(-\ell_{t}) \rangle} \kern1.2pt{=}\kern1.2pt \frac{\| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{P},G}^{2}}{\langle \ell_{t},\kern-1pt\nabla \mathfrak{P}_G(-\ell_{t}) \rangle}\kern-1pt. \end{align*} $$
$$ \begin{align*} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{h},G}^{2} \kern1.2pt{=}\kern1.2pt{-}\kern1.2pt\langle \ddot\ell_{t},\kern-1pt\nabla\mathfrak{h}_G(\ell_{t}) \rangle \kern1.2pt{=}\kern1.2pt \frac{\langle \ddot\ell_{t},\kern-1pt\nabla\mathfrak{h}_G(\ell_{t}) \rangle}{\langle \ell_{t},\kern-1pt\nabla \mathfrak{h}_G(\ell_{t}) \rangle} \kern1.2pt{=}\kern1.2pt \frac{\langle \ddot\ell_{t},\kern-1pt\nabla\mathfrak{P}_G(-\ell_{t}) \rangle}{\langle \ell_{t},\kern-1pt\nabla \mathfrak{P}_G(-\ell_{t}) \rangle} \kern1.2pt{=}\kern1.2pt \frac{\| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{P},G}^{2}}{\langle \ell_{t},\kern-1pt\nabla \mathfrak{P}_G(-\ell_{t}) \rangle}\kern-1pt. \end{align*} $$
By polarization, the norm determines the inner product and so the claim follows.
Positive definiteness of the Hessians follows from strict convexity of
![]() $\mathfrak {h}_G$
and
$\mathfrak {h}_G$
and
![]() $\mathfrak {P}_G$
on
$\mathfrak {P}_G$
on
![]() $\mathcal {M}(G)$
and
$\mathcal {M}(G)$
and
![]() $\mathbb {R}^{\lvert {E_{+}} \rvert }$
, respectively (Theorem 3.7).
$\mathbb {R}^{\lvert {E_{+}} \rvert }$
, respectively (Theorem 3.7).
Using these norms, we can define the entropy or pressure length of a piecewise smooth path
![]() $\ell _{t} \colon \thinspace [t_0,t_1] \to \mathcal {M}^{1}(G)$
by
$\ell _{t} \colon \thinspace [t_0,t_1] \to \mathcal {M}^{1}(G)$
by
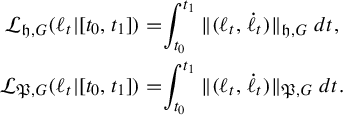 $$ \begin{align*} \mathcal{L}_{\mathfrak{h},G}(\ell_{t}|[t_0,t_1])&=\! \int_{t_0}^{t_1} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{h},G} \, dt,\\ \mathcal{L}_{\mathfrak{P},G}(\ell_{t}|[t_0,t_1])&=\! \int_{t_0}^{t_1} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{P},G} \, dt. \end{align*} $$
$$ \begin{align*} \mathcal{L}_{\mathfrak{h},G}(\ell_{t}|[t_0,t_1])&=\! \int_{t_0}^{t_1} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{h},G} \, dt,\\ \mathcal{L}_{\mathfrak{P},G}(\ell_{t}|[t_0,t_1])&=\! \int_{t_0}^{t_1} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{P},G} \, dt. \end{align*} $$
These induce the entropy and pressure distance functions on
![]() $\mathcal {M}^1(G)$
by
$\mathcal {M}^1(G)$
by
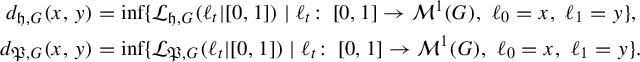 $$ \begin{align*} d_{\mathfrak{h},G}(x,y) &= \inf\{ \mathcal{L}_{\mathfrak{h},G}(\ell_{t}|[0,1]) \mid \ell_{t} \colon\thinspace [0,1] \to \mathcal{M}^{1}(G), \, \ell_{0} = x, \, \ell_{1} = y \},\\ d_{\mathfrak{P},G}(x,y) &= \inf\{ \mathcal{L}_{\mathfrak{P},G}(\ell_{t}|[0,1]) \mid \ell_{t} \colon\thinspace [0,1] \to \mathcal{M}^{1}(G), \, \ell_{0} = x, \, \ell_{1} = y \}. \end{align*} $$
$$ \begin{align*} d_{\mathfrak{h},G}(x,y) &= \inf\{ \mathcal{L}_{\mathfrak{h},G}(\ell_{t}|[0,1]) \mid \ell_{t} \colon\thinspace [0,1] \to \mathcal{M}^{1}(G), \, \ell_{0} = x, \, \ell_{1} = y \},\\ d_{\mathfrak{P},G}(x,y) &= \inf\{ \mathcal{L}_{\mathfrak{P},G}(\ell_{t}|[0,1]) \mid \ell_{t} \colon\thinspace [0,1] \to \mathcal{M}^{1}(G), \, \ell_{0} = x, \, \ell_{1} = y \}. \end{align*} $$
Given a marked graph
![]() $(G,\rho )$
, we set
$(G,\rho )$
, we set
![]() $\mathcal {X}^1(G,\rho ) = \mathcal {X}(G,\rho ) \cap \mathcal {X}^1(\mathbb {F}_r)$
. Using the natural bijection
$\mathcal {X}^1(G,\rho ) = \mathcal {X}(G,\rho ) \cap \mathcal {X}^1(\mathbb {F}_r)$
. Using the natural bijection
![]() $\mathcal {X}^1(G,\rho ) \leftrightarrow \mathcal {M}^1(G)$
, we get metrics and distance functions on
$\mathcal {X}^1(G,\rho ) \leftrightarrow \mathcal {M}^1(G)$
, we get metrics and distance functions on
![]() $\mathcal {X}^1(G,\rho )$
that we denote using the same notation as above.
$\mathcal {X}^1(G,\rho )$
that we denote using the same notation as above.
Next, we explain how these fit together to get distance functions on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
. Suppose
$\mathcal {X}^1(\mathbb {F}_r)$
. Suppose
![]() $\alpha _t \colon \thinspace [0,1] \to \mathcal {X}^1(\mathbb {F}_r)$
is a piecewise smooth path and that there is a partition
$\alpha _t \colon \thinspace [0,1] \to \mathcal {X}^1(\mathbb {F}_r)$
is a piecewise smooth path and that there is a partition
![]() $t_1 = 0 < t_2 < \cdots < t_{n+1} = 1$
and marked graphs
$t_1 = 0 < t_2 < \cdots < t_{n+1} = 1$
and marked graphs
![]() $(G_k,\rho _k)$
for
$(G_k,\rho _k)$
for
![]() $k = 1,\ldots ,n$
such that
$k = 1,\ldots ,n$
such that
![]() $\alpha _t \in \mathcal {X}^1(G_k,\rho _k)$
for
$\alpha _t \in \mathcal {X}^1(G_k,\rho _k)$
for
![]() $t \in (t_k,t_{k+1})$
. We set
$t \in (t_k,t_{k+1})$
. We set
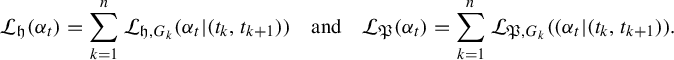 $$ \begin{align*} \mathcal{L}_{\mathfrak{h}}(\alpha_t) & = \sum_{k=1}^n \mathcal{L}_{\mathfrak{h},G_k}(\alpha_t | (t_k,t_{k+1})) \quad \mbox{and} \quad \mathcal{L}_{\mathfrak{P}}(\alpha_t) = \sum_{k=1}^n \mathcal{L}_{\mathfrak{P},G_k}((\alpha_t | (t_k,t_{k+1})). \end{align*} $$
$$ \begin{align*} \mathcal{L}_{\mathfrak{h}}(\alpha_t) & = \sum_{k=1}^n \mathcal{L}_{\mathfrak{h},G_k}(\alpha_t | (t_k,t_{k+1})) \quad \mbox{and} \quad \mathcal{L}_{\mathfrak{P}}(\alpha_t) = \sum_{k=1}^n \mathcal{L}_{\mathfrak{P},G_k}((\alpha_t | (t_k,t_{k+1})). \end{align*} $$
These define distance functions on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
as usual—by taking the infimum of the lengths of paths—that we denote by
$\mathcal {X}^1(\mathbb {F}_r)$
as usual—by taking the infimum of the lengths of paths—that we denote by
![]() $d_{\mathfrak {h}}$
and
$d_{\mathfrak {h}}$
and
![]() $d_{\mathfrak {P}}$
. It is obvious that the proposed distance functions are symmetric and satisfy the triangle inequality; positive definiteness of the Hessians implies non-degeneracy. However, it is not obvious that the distances they define are finite: a priori it may be possible that the length of a path that collapses an edge is infinite. This will be addressed in §5.
$d_{\mathfrak {P}}$
. It is obvious that the proposed distance functions are symmetric and satisfy the triangle inequality; positive definiteness of the Hessians implies non-degeneracy. However, it is not obvious that the distances they define are finite: a priori it may be possible that the length of a path that collapses an edge is infinite. This will be addressed in §5.
Remark 3.13. For the remainder of the paper we will mainly be concerned with the entropy metric. As stated in §1.6, the main results of this paper also hold for the pressure metric with slightly altered hypotheses.
4 A determinant-defining equation for
 $\mathcal {M}^{1}(G)$
$\mathcal {M}^{1}(G)$
The purpose of this section is to derive formulas to assist in computing the metrics introduced in the previous section. The first of these appears in §4.1, specifically Proposition 4.6, where it is shown that these metrics can be computed using finite sums of exponential functions on
![]() $\mathcal {M}^1(G)$
. Next, in §4.2, we present a simplification for certain graphs that is useful in the sequel.
$\mathcal {M}^1(G)$
. Next, in §4.2, we present a simplification for certain graphs that is useful in the sequel.
4.1 Determinant equation
Fix a finite connected graph
![]() $G = (V,E,o,\tau ,\bar {\phantom {e}})$
. We always assume that
$G = (V,E,o,\tau ,\bar {\phantom {e}})$
. We always assume that
![]() $\chi (G) < 0$
and G has no vertices of valence
$\chi (G) < 0$
and G has no vertices of valence
![]() $1$
or
$1$
or
![]() $2$
.
$2$
.
Let
![]() $D_{G}$
be the directed graph with adjacency matrix
$D_{G}$
be the directed graph with adjacency matrix
![]() $A_{G}$
. Thus the vertex set for
$A_{G}$
. Thus the vertex set for
![]() $D_G$
is the set E (recall our notation
$D_G$
is the set E (recall our notation
![]() $E = E_+ \cup \overline {E}_+$
) and there is an edge from e to
$E = E_+ \cup \overline {E}_+$
) and there is an edge from e to
![]() $e'$
if
$e'$
if
![]() $A_G(e,e') = 1$
, that is, if
$A_G(e,e') = 1$
, that is, if
![]() $\tau (e) = o(e')$
and
$\tau (e) = o(e')$
and
![]() $\bar {e} \neq e'$
. The cycle complex of
$\bar {e} \neq e'$
. The cycle complex of
![]() $D_{G}$
, denoted by
$D_{G}$
, denoted by
![]() $C_{G}$
, is the abstract simplicial complex with an n-simplex for each collection
$C_{G}$
, is the abstract simplicial complex with an n-simplex for each collection
![]() $\Delta = \{ z_{1},\ldots ,z_{n+1}\}$
of pairwise disjoint simple cycles, that is, embedded loops, in
$\Delta = \{ z_{1},\ldots ,z_{n+1}\}$
of pairwise disjoint simple cycles, that is, embedded loops, in
![]() $D_{G}$
.
$D_{G}$
.
Example 4.1. Suppose that G is the barbell graph as shown below:
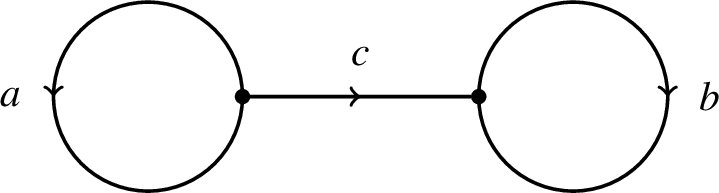
Order the edges of G by a,
![]() $\bar {a}$
, b,
$\bar {a}$
, b,
![]() $\bar {b}$
, c,
$\bar {b}$
, c,
![]() $\bar {c}$
. The matrix
$\bar {c}$
. The matrix
![]() $A_{G}$
and directed graph
$A_{G}$
and directed graph
![]() $D_{G}$
are as presented below:
$D_{G}$
are as presented below:
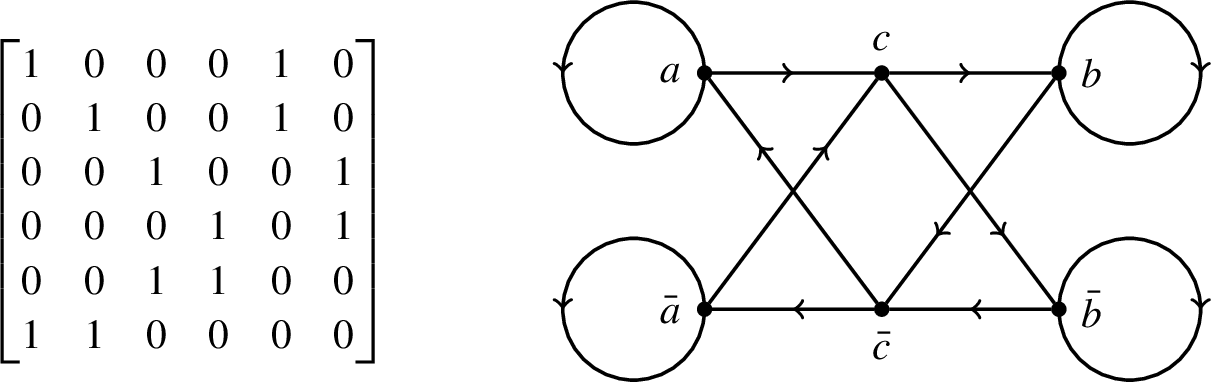
There are eight simple cycles in
![]() $D_G$
:
$D_G$
:
![]() $\gamma _{a} = (a)$
,
$\gamma _{a} = (a)$
,
![]() $\gamma _{\bar {a}} = (\bar {a})$
,
$\gamma _{\bar {a}} = (\bar {a})$
,
![]() $\gamma _{b} = (b)$
,
$\gamma _{b} = (b)$
,
![]() $\gamma _{\bar {b}} = (\bar {b})$
,
$\gamma _{\bar {b}} = (\bar {b})$
,
![]() $\gamma _{ab} = (a,c,b,\bar {c})$
,
$\gamma _{ab} = (a,c,b,\bar {c})$
,
![]() $\gamma _{a\bar {b}} = (a,c,\bar {b},\bar {c})$
,
$\gamma _{a\bar {b}} = (a,c,\bar {b},\bar {c})$
,
![]() $\gamma _{\bar {a}b} = (\bar {a},c,b,\bar {c})$
and
$\gamma _{\bar {a}b} = (\bar {a},c,b,\bar {c})$
and
![]() $\gamma _{\bar {a}\bar {b}} = (\bar {a},c,\bar {b},\bar {c})$
. The cycle complex
$\gamma _{\bar {a}\bar {b}} = (\bar {a},c,\bar {b},\bar {c})$
. The cycle complex
![]() $C_{G}$
is the flag complex whose 1-skeleton is shown in Figure 4.
$C_{G}$
is the flag complex whose 1-skeleton is shown in Figure 4.
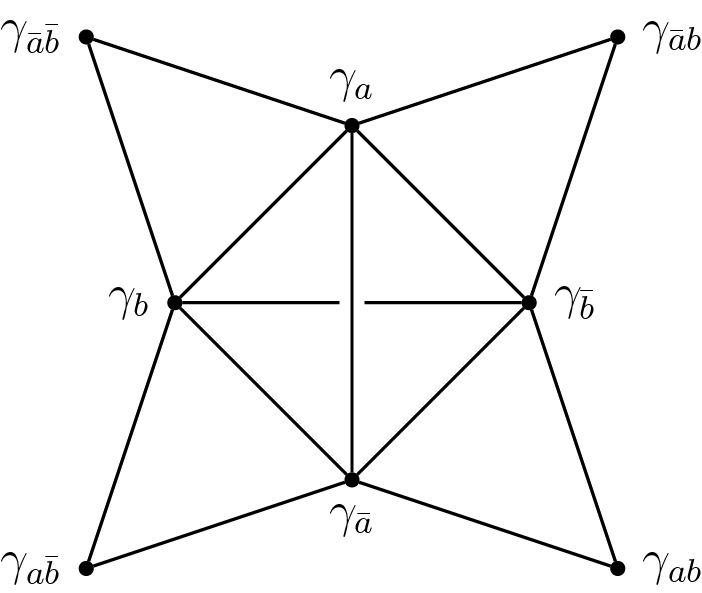
Figure 4 The 1-skeleton of the cycle complex
![]() $C_G$
in Example 4.1.
$C_G$
in Example 4.1.
Given a function
![]() $f \colon \thinspace E \to \mathbb {R}$
(in particular, a length function) and a simple cycle z in
$f \colon \thinspace E \to \mathbb {R}$
(in particular, a length function) and a simple cycle z in
![]() $D_G$
, we set
$D_G$
, we set
![]() $f(z) = \sum _{i=1}^n f(e_i)$
where
$f(z) = \sum _{i=1}^n f(e_i)$
where
![]() $e_1,\ldots ,e_n$
are the vertices in
$e_1,\ldots ,e_n$
are the vertices in
![]() $D_G$
traversed by z (each corresponding to an oriented edge in G). Likewise, for a simplex
$D_G$
traversed by z (each corresponding to an oriented edge in G). Likewise, for a simplex
![]() $\Delta = \{ z_{1},\ldots ,z_{n}\}$
in
$\Delta = \{ z_{1},\ldots ,z_{n}\}$
in
![]() $C_G$
we set
$C_G$
we set
![]() $f(\Delta ) = \sum _{k=1}^{n} f(z_{k})$
. We consider the empty set as a simplex and define
$f(\Delta ) = \sum _{k=1}^{n} f(z_{k})$
. We consider the empty set as a simplex and define
![]() $f(\emptyset ) = 0$
for any function
$f(\emptyset ) = 0$
for any function
![]() $f \colon \thinspace E \to \mathbb {R}$
. Lastly, for a simplex
$f \colon \thinspace E \to \mathbb {R}$
. Lastly, for a simplex
![]() $\Delta = \{z_1,\ldots ,z_n\}$
we set
$\Delta = \{z_1,\ldots ,z_n\}$
we set
![]() $\lvert {\Delta } \rvert = n$
.
$\lvert {\Delta } \rvert = n$
.
Recall that given a length function
![]() $\ell \in \mathcal {M}(G)$
, the matrix
$\ell \in \mathcal {M}(G)$
, the matrix
![]() $A_{G,\ell }$
is defined by
$A_{G,\ell }$
is defined by
![]() $A_{G,\ell }(e,e') = \exp (-\ell (e))A_G(e,e')$
. We consider the function
$A_{G,\ell }(e,e') = \exp (-\ell (e))A_G(e,e')$
. We consider the function
![]() $F_{G} \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
given by
$F_{G} \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
given by
This function can be expressed using the cycle complex
![]() $C_G$
as follows.
$C_G$
as follows.
Theorem 4.2. Let G be a finite connected graph and fix
![]() $\ell \in \mathcal {M}(G)$
. Then
$\ell \in \mathcal {M}(G)$
. Then
 $$ \begin{align*} F_{G}(\ell) = \sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta)). \end{align*} $$
$$ \begin{align*} F_{G}(\ell) = \sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta)). \end{align*} $$
Proof. This follows from the coefficient theorem for digraphs. See, for instance, [Reference Cvetković and Rowlinson15] and [Reference Algom-Kfir, Hironaka and Rafi3, Theorems 2.5 and 2.14].
Example 4.3. We apply Theorem 4.2 to the case when G is the barbell graph as in Example 4.1. Using the change of variables
![]() $x = \exp (-\ell (a))$
,
$x = \exp (-\ell (a))$
,
![]() $y = \exp (-\ell (b))$
and
$y = \exp (-\ell (b))$
and
![]() $z = \exp (-\ell (c))$
, we find that
$z = \exp (-\ell (c))$
, we find that
 $$ \begin{align*} F_{G}(\ell) &= \, 1 - (2x + 2y + 4xyz^{2}) + (x^{2} + y^{2} + 4xy + 4x^{2}yz^{2} + 4xy^{2}z^{2} ) \\ &\quad -(2x^{2}y + 2xy^{2} + 4x^{2}y^{2}z^{2}) + x^{2}y^{2}. \end{align*} $$
$$ \begin{align*} F_{G}(\ell) &= \, 1 - (2x + 2y + 4xyz^{2}) + (x^{2} + y^{2} + 4xy + 4x^{2}yz^{2} + 4xy^{2}z^{2} ) \\ &\quad -(2x^{2}y + 2xy^{2} + 4x^{2}y^{2}z^{2}) + x^{2}y^{2}. \end{align*} $$
The following statements show how the function
![]() $F_{G}$
is related to
$F_{G}$
is related to
![]() $\mathcal {M}^{1}(G)$
.
$\mathcal {M}^{1}(G)$
.
Lemma 4.4. For
![]() $\ell \in \mathcal {M}^{1}(G)$
we have:
$\ell \in \mathcal {M}^{1}(G)$
we have:
-
(1)
 $F_{G}(\ell ) = 0$
;
$F_{G}(\ell ) = 0$
; -
(2)
 $\nabla F_{G}(\ell ) \neq 0$
; and moreover,
$\nabla F_{G}(\ell ) \neq 0$
; and moreover, -
(3)
 $\partial _{e} F_G(\ell )> 0$
for any
$\partial _{e} F_G(\ell )> 0$
for any
 $e \in E_+$
.
$e \in E_+$
.
Proof. Since
![]() $\ell $
lies in
$\ell $
lies in
![]() $\mathcal {M}^{1}(G)$
, Theorem 3.7(1) and the definition of pressure imply that
$\mathcal {M}^{1}(G)$
, Theorem 3.7(1) and the definition of pressure imply that
![]() $\operatorname {\mathrm {spec}}(A_{G,\ell }) = 1$
. Above we remarked that the assumptions on G imply that
$\operatorname {\mathrm {spec}}(A_{G,\ell }) = 1$
. Above we remarked that the assumptions on G imply that
![]() $A_G$
is irreducible; hence so is
$A_G$
is irreducible; hence so is
![]() $A_{G,\ell }$
. By the Perron–Frobenius theorem the spectral radius of
$A_{G,\ell }$
. By the Perron–Frobenius theorem the spectral radius of
![]() $A_{G,\ell }$
is realized by a positive, real, simple eigenvalue; (1) follows.
$A_{G,\ell }$
is realized by a positive, real, simple eigenvalue; (1) follows.
Now consider the function
![]() $p \colon \thinspace \mathbb {R} \to \mathbb {R}$
defined by
$p \colon \thinspace \mathbb {R} \to \mathbb {R}$
defined by
![]() $p(t) = \det (I - tA_{G,\ell })$
. Let
$p(t) = \det (I - tA_{G,\ell })$
. Let
![]() $1 = \lambda _{1}, \ldots , \lambda _{\lvert {E} \rvert }$
be the roots of the characteristic polynomial of
$1 = \lambda _{1}, \ldots , \lambda _{\lvert {E} \rvert }$
be the roots of the characteristic polynomial of
![]() $A_{G,\ell }$
. Then we can write
$A_{G,\ell }$
. Then we can write
 $$ \begin{align*} p(t) = (1-t)\prod_{i=2}^{\lvert {E} \rvert} (1-t\lambda_{i}). \end{align*} $$
$$ \begin{align*} p(t) = (1-t)\prod_{i=2}^{\lvert {E} \rvert} (1-t\lambda_{i}). \end{align*} $$
Therefore, taking the derivative, we find that
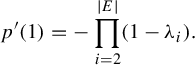 $$ \begin{align*} p'(1) = -\prod_{i=2}^{\lvert {E} \rvert} (1-\lambda_{i}).\end{align*} $$
$$ \begin{align*} p'(1) = -\prod_{i=2}^{\lvert {E} \rvert} (1-\lambda_{i}).\end{align*} $$
For
![]() $i = 2,\ldots , \lvert {E} \rvert $
we have that
$i = 2,\ldots , \lvert {E} \rvert $
we have that
![]() $|\lambda _i| \leq 1$
and
$|\lambda _i| \leq 1$
and
![]() $\lambda _i \neq 1$
. Combining these observations with the fact that complex eigenvalues come in conjugate pairs, it follows that
$\lambda _i \neq 1$
. Combining these observations with the fact that complex eigenvalues come in conjugate pairs, it follows that
![]() $p'(1) < 0$
. Observe that
$p'(1) < 0$
. Observe that
![]() $F_{G}(\ell + s \cdot \mathbf {1}) = \det (I - \exp (-s)A_{G,\ell }) = p(\exp (-s))$
. Therefore we have that
$F_{G}(\ell + s \cdot \mathbf {1}) = \det (I - \exp (-s)A_{G,\ell }) = p(\exp (-s))$
. Therefore we have that
![]() $\langle \mathbf {1},\nabla F_{G}(\ell ) \rangle = -p'(1)\exp (0)> 0$
, giving (2).
$\langle \mathbf {1},\nabla F_{G}(\ell ) \rangle = -p'(1)\exp (0)> 0$
, giving (2).
We claim that
![]() $\nabla F_G(\ell )$
is parallel to
$\nabla F_G(\ell )$
is parallel to
![]() $\nabla \mathfrak {P}_G(\ell )$
for
$\nabla \mathfrak {P}_G(\ell )$
for
![]() $\ell \in \mathcal {M}^1(G)$
. Indeed, this follows as (1), (2) and Theorem 3.7 imply that
$\ell \in \mathcal {M}^1(G)$
. Indeed, this follows as (1), (2) and Theorem 3.7 imply that
![]() $\mathfrak {P}_G^{-1}(0) = \mathcal {M}^1(G)$
is a connected component of
$\mathfrak {P}_G^{-1}(0) = \mathcal {M}^1(G)$
is a connected component of
![]() $F_G^{-1}(0)$
. By (2) and Lemma 3.9(2) the gradients of
$F_G^{-1}(0)$
. By (2) and Lemma 3.9(2) the gradients of
![]() $F_G$
and
$F_G$
and
![]() $\mathfrak {P}_G$
are non-zero for this subset. As gradients are always orthogonal to level sets, the claim follows. Hence by Lemma 3.9(1), we have that either
$\mathfrak {P}_G$
are non-zero for this subset. As gradients are always orthogonal to level sets, the claim follows. Hence by Lemma 3.9(1), we have that either
![]() $\partial _{e} F_G(\ell )> 0$
or
$\partial _{e} F_G(\ell )> 0$
or
![]() $\partial _{e} F_G(\ell ) < 0$
for all
$\partial _{e} F_G(\ell ) < 0$
for all
![]() $e \in E_+$
and
$e \in E_+$
and
![]() $\ell \in \mathcal {M}^1(G)$
. Since
$\ell \in \mathcal {M}^1(G)$
. Since
![]() $\langle \mathbf {1},\nabla F_G(\ell ) \rangle>0$
, we must have the former, whence (3).
$\langle \mathbf {1},\nabla F_G(\ell ) \rangle>0$
, we must have the former, whence (3).
As a remarked in the proof of Lemma 4.4, we have the following corollary.
Corollary 4.5. The unit-entropy moduli space
![]() $\mathcal {M}^{1}(G)$
is a connected component of the level set
$\mathcal {M}^{1}(G)$
is a connected component of the level set
![]() $\{ \ell \in \mathcal {M}(G) \mid F_{G}(\ell ) = 0 \}$
.
$\{ \ell \in \mathcal {M}(G) \mid F_{G}(\ell ) = 0 \}$
.
Using these observations, we can compute the entropy and pressure norms using the function
![]() $F_{G}$
.
$F_{G}$
.
Proposition 4.6. If
![]() $\ell _{t} \colon \thinspace (-1,1) \to \mathcal {M}^{1}(G)$
is a smooth path, then
$\ell _{t} \colon \thinspace (-1,1) \to \mathcal {M}^{1}(G)$
is a smooth path, then
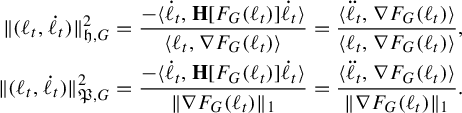 $$ \begin{align*} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{h},G}^{2} &= \frac{-\langle \dot\ell_{t},\mathbf{H} [F_{G}(\ell_{t})]\dot\ell_{t} \rangle}{\langle \ell_{t},\nabla F_{G}(\ell_{t}) \rangle}= \frac{\langle \ddot\ell_{t},\nabla F_{G}(\ell_{t}) \rangle}{\langle \ell_{t},\nabla F_{G}(\ell_{t}) \rangle}, \\ \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{P},G}^{2} &= \frac{-\langle \dot\ell_{t},\mathbf{H} [F_{G}(\ell_{t})]\dot\ell_{t} \rangle}{\| {\nabla F_{G}(\ell_{t})} \|_{1}}= \frac{\langle \ddot\ell_{t},\nabla F_{G}(\ell_{t}) \rangle}{\| {\nabla F_{G}(\ell_{t})} \|_{1}}. \end{align*} $$
$$ \begin{align*} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{h},G}^{2} &= \frac{-\langle \dot\ell_{t},\mathbf{H} [F_{G}(\ell_{t})]\dot\ell_{t} \rangle}{\langle \ell_{t},\nabla F_{G}(\ell_{t}) \rangle}= \frac{\langle \ddot\ell_{t},\nabla F_{G}(\ell_{t}) \rangle}{\langle \ell_{t},\nabla F_{G}(\ell_{t}) \rangle}, \\ \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{P},G}^{2} &= \frac{-\langle \dot\ell_{t},\mathbf{H} [F_{G}(\ell_{t})]\dot\ell_{t} \rangle}{\| {\nabla F_{G}(\ell_{t})} \|_{1}}= \frac{\langle \ddot\ell_{t},\nabla F_{G}(\ell_{t}) \rangle}{\| {\nabla F_{G}(\ell_{t})} \|_{1}}. \end{align*} $$
Proof. The proof of the formula for the entropy norm is similar to that of Proposition 3.12 and left to the reader.
The proof of the formula for the pressure norm is again similar, noting that
![]() ${\| {\nabla \mathfrak {P}(\ell )} \|_{1} = 1}$
as stated in Lemma 3.9(2).
${\| {\nabla \mathfrak {P}(\ell )} \|_{1} = 1}$
as stated in Lemma 3.9(2).
Using Theorem 4.2, we can compute the partial derivatives of
![]() $F_G$
. We find for any edges
$F_G$
. We find for any edges
![]() $e,e' \in E_+$
that
$e,e' \in E_+$
that
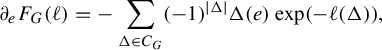 $$ \begin{align} \hspace{-8pt}\partial_{e} F_{G}(\ell) &= -\sum_{\Delta \in C_G} (-1)^{\lvert {\Delta} \rvert}\Delta(e)\exp(-\ell(\Delta)), \end{align} $$
$$ \begin{align} \hspace{-8pt}\partial_{e} F_{G}(\ell) &= -\sum_{\Delta \in C_G} (-1)^{\lvert {\Delta} \rvert}\Delta(e)\exp(-\ell(\Delta)), \end{align} $$
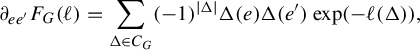 $$ \begin{align} \partial_{e e'} F_{G}(\ell) &= \sum_{\Delta \in C_G} (-1)^{\lvert {\Delta} \rvert}\Delta(e)\Delta(e')\exp(-\ell(\Delta)), \end{align} $$
$$ \begin{align} \partial_{e e'} F_{G}(\ell) &= \sum_{\Delta \in C_G} (-1)^{\lvert {\Delta} \rvert}\Delta(e)\Delta(e')\exp(-\ell(\Delta)), \end{align} $$
where
![]() $\Delta (e) \in \{0,1,2\}$
denotes the cardinality of the intersection
$\Delta (e) \in \{0,1,2\}$
denotes the cardinality of the intersection
![]() $\{e,\bar {e}\} \cap \Delta $
. Using this notation, we remark that
$\{e,\bar {e}\} \cap \Delta $
. Using this notation, we remark that
![]() $\ell (\Delta ) = \sum _{e \in E_+} \Delta (e)\ell (e)$
for a length function
$\ell (\Delta ) = \sum _{e \in E_+} \Delta (e)\ell (e)$
for a length function
![]() $\ell \in \mathcal {M}(G)$
and simplex
$\ell \in \mathcal {M}(G)$
and simplex
![]() $\Delta \in C_G$
. Given a vector
$\Delta \in C_G$
. Given a vector
![]() $\mathbf {v} \in \mathbb {R}^{\lvert {E_+} \rvert }$
and a simplex
$\mathbf {v} \in \mathbb {R}^{\lvert {E_+} \rvert }$
and a simplex
![]() $\Delta \in C_G$
, we set
$\Delta \in C_G$
, we set
![]() $\mathbf {v}(\Delta ) = \sum _{e \in E_+} \Delta (e)\mathbf {v}(e)$
. Using these expressions, we can rewrite the dot products appearing in the formulas for the metrics in Proposition 4.6 as sums over simplices in
$\mathbf {v}(\Delta ) = \sum _{e \in E_+} \Delta (e)\mathbf {v}(e)$
. Using these expressions, we can rewrite the dot products appearing in the formulas for the metrics in Proposition 4.6 as sums over simplices in
![]() $C_{G}$
rather than over the edges of G as follows.
$C_{G}$
rather than over the edges of G as follows.
Lemma 4.7. For
![]() $\ell \in \mathcal {M}(G)$
, we have
$\ell \in \mathcal {M}(G)$
, we have
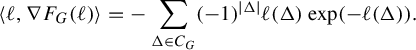 $$ \begin{align*} \langle \ell, \nabla F_{G}(\ell) \rangle = -\sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert}\ell(\Delta)\exp(-\ell(\Delta)). \end{align*} $$
$$ \begin{align*} \langle \ell, \nabla F_{G}(\ell) \rangle = -\sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert}\ell(\Delta)\exp(-\ell(\Delta)). \end{align*} $$
Proof. We compute:
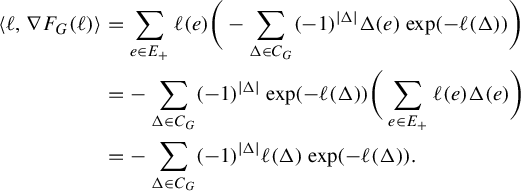 $$ \begin{align*} \langle \ell, \nabla F_{G}(\ell) \rangle & = \sum_{e \in E_{+}} \ell(e) \bigg(-\sum_{\Delta \in {C_{G}}}(-1)^{\lvert {\Delta} \rvert}\Delta(e)\exp(-\ell(\Delta))\bigg) \\ & = -\sum_{\Delta \in {C_{G}}} (-1)^{\lvert {\Delta} \rvert}\exp(-\ell(\Delta)) \bigg(\sum_{e \in E_{+}} \ell(e)\Delta(e)\bigg) \\ & = -\sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert}\ell(\Delta)\exp(-\ell(\Delta)).\\[-47pt] \end{align*} $$
$$ \begin{align*} \langle \ell, \nabla F_{G}(\ell) \rangle & = \sum_{e \in E_{+}} \ell(e) \bigg(-\sum_{\Delta \in {C_{G}}}(-1)^{\lvert {\Delta} \rvert}\Delta(e)\exp(-\ell(\Delta))\bigg) \\ & = -\sum_{\Delta \in {C_{G}}} (-1)^{\lvert {\Delta} \rvert}\exp(-\ell(\Delta)) \bigg(\sum_{e \in E_{+}} \ell(e)\Delta(e)\bigg) \\ & = -\sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert}\ell(\Delta)\exp(-\ell(\Delta)).\\[-47pt] \end{align*} $$
Lemma 4.8. Let G be a finite connected graph. If
![]() $(\ell , \mathbf {v}) \in T\mathcal {M}^{1}(G)$
, then
$(\ell , \mathbf {v}) \in T\mathcal {M}^{1}(G)$
, then
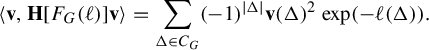 $$ \begin{align*} \langle \mathbf{v}, \mathbf{H}[F_{G}(\ell)]\mathbf{v} \rangle = \sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert}\mathbf{v}(\Delta)^{2}\exp(-\ell(\Delta)). \end{align*} $$
$$ \begin{align*} \langle \mathbf{v}, \mathbf{H}[F_{G}(\ell)]\mathbf{v} \rangle = \sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert}\mathbf{v}(\Delta)^{2}\exp(-\ell(\Delta)). \end{align*} $$
Proof. This is similar to Lemma 4.7. The eth component of
![]() $\mathbf {H}[F_{G}(\ell )]\mathbf {v}$
is
$\mathbf {H}[F_{G}(\ell )]\mathbf {v}$
is
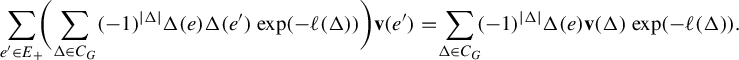 $$ \begin{align*}\sum_{e' \in E_{+}}\! \!\bigg(\! \sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert} \Delta(e)\Delta(e')\exp(-\ell(\Delta))\bigg) \mathbf{v}(e') =\! \sum_{\Delta \in C_{G}}\! (-1)^{\lvert {\Delta} \rvert} \Delta(e)\mathbf{v}(\Delta)\exp(-\ell(\Delta)). \end{align*} $$
$$ \begin{align*}\sum_{e' \in E_{+}}\! \!\bigg(\! \sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert} \Delta(e)\Delta(e')\exp(-\ell(\Delta))\bigg) \mathbf{v}(e') =\! \sum_{\Delta \in C_{G}}\! (-1)^{\lvert {\Delta} \rvert} \Delta(e)\mathbf{v}(\Delta)\exp(-\ell(\Delta)). \end{align*} $$
Hence
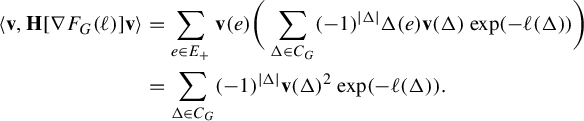 $$ \begin{align*} \langle \mathbf{v}, \mathbf{H}[\nabla F_{G}(\ell)]\mathbf{v} \rangle & = \sum_{e \in E_{+}} \mathbf{v}(e) \bigg(\sum_{\Delta \in {C_{G}}}(-1)^{\lvert {\Delta} \rvert}\Delta(e)\mathbf{v}(\Delta)\exp(-\ell(\Delta))\bigg) \\ &= \sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert}\mathbf{v}(\Delta)^{2}\exp(-\ell(\Delta)).\\[-46pt] \end{align*} $$
$$ \begin{align*} \langle \mathbf{v}, \mathbf{H}[\nabla F_{G}(\ell)]\mathbf{v} \rangle & = \sum_{e \in E_{+}} \mathbf{v}(e) \bigg(\sum_{\Delta \in {C_{G}}}(-1)^{\lvert {\Delta} \rvert}\Delta(e)\mathbf{v}(\Delta)\exp(-\ell(\Delta))\bigg) \\ &= \sum_{\Delta \in C_{G}} (-1)^{\lvert {\Delta} \rvert}\mathbf{v}(\Delta)^{2}\exp(-\ell(\Delta)).\\[-46pt] \end{align*} $$
By Lemma 4.4, if
![]() $\mathfrak {h}_G(\ell ) = 1$
then
$\mathfrak {h}_G(\ell ) = 1$
then
![]() $F_{G}(\ell ) = 0$
. The next lemma gives a partial converse.
$F_{G}(\ell ) = 0$
. The next lemma gives a partial converse.
Lemma 4.9. If
![]() $\mathfrak {h}_G(\ell ) < 1$
, then
$\mathfrak {h}_G(\ell ) < 1$
, then
![]() $F_G(\ell )> 0$
.
$F_G(\ell )> 0$
.
Proof. We begin by showing that if
![]() $\mathfrak {h}_G(\ell ) < 1$
, then
$\mathfrak {h}_G(\ell ) < 1$
, then
![]() $F_G(\ell ) \neq 0$
. To begin, we observe that if
$F_G(\ell ) \neq 0$
. To begin, we observe that if
![]() $\mathfrak {h}_G(\ell ) < 1$
, then
$\mathfrak {h}_G(\ell ) < 1$
, then
![]() $\mathfrak {P}_G(-\ell ) < 0$
. Indeed, let
$\mathfrak {P}_G(-\ell ) < 0$
. Indeed, let
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}(G)$
be the path defined by
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}(G)$
be the path defined by
We have that
![]() $\langle \nabla \mathfrak {P}_G(-\ell _t), - \dot \ell _t \rangle> 0$
as each component of
$\langle \nabla \mathfrak {P}_G(-\ell _t), - \dot \ell _t \rangle> 0$
as each component of
![]() $\nabla \mathfrak {P}_G(-\ell _t)$
is positive by Lemma 3.9(1) and each component of
$\nabla \mathfrak {P}_G(-\ell _t)$
is positive by Lemma 3.9(1) and each component of
![]() $-\dot \ell _t$
is positive by construction. Notice that
$-\dot \ell _t$
is positive by construction. Notice that
![]() $\mathfrak {P}_G(-\ell _1) = 0$
by Theorem 3.7(1) since
$\mathfrak {P}_G(-\ell _1) = 0$
by Theorem 3.7(1) since
![]() $\mathfrak {h}_G(\ell _1) = 1$
. Therefore, we find that
$\mathfrak {h}_G(\ell _1) = 1$
. Therefore, we find that
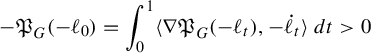 $$ \begin{align*} -\mathfrak{P}_G(-\ell_0) = \int_0^1 \langle \nabla \mathfrak{P}_G(-\ell_t),-\dot \ell_t \rangle \, dt> 0 \end{align*} $$
$$ \begin{align*} -\mathfrak{P}_G(-\ell_0) = \int_0^1 \langle \nabla \mathfrak{P}_G(-\ell_t),-\dot \ell_t \rangle \, dt> 0 \end{align*} $$
and hence
![]() $\mathfrak {P}_G(-\ell ) = \mathfrak {P}_G(-\ell _0)$
is negative as claimed. Therefore we have that
$\mathfrak {P}_G(-\ell ) = \mathfrak {P}_G(-\ell _0)$
is negative as claimed. Therefore we have that
![]() $\operatorname {\mathrm {spec}} (A_{G,\ell }) < 1$
and, in particular,
$\operatorname {\mathrm {spec}} (A_{G,\ell }) < 1$
and, in particular,
![]() $1$
is not an eigenvalue of
$1$
is not an eigenvalue of
![]() $A_{G,\ell }$
. Hence
$A_{G,\ell }$
. Hence
![]() $F_G(\ell ) \neq 0$
. This completes the claim that
$F_G(\ell ) \neq 0$
. This completes the claim that
![]() $F_G(\ell ) \neq 0$
for any
$F_G(\ell ) \neq 0$
for any
![]() $\ell \in \mathcal {M}(G)$
where
$\ell \in \mathcal {M}(G)$
where
![]() $\mathfrak {h}_G(\ell ) < 1$
.
$\mathfrak {h}_G(\ell ) < 1$
.
We now complete the proof of the lemma. Suppose that
![]() $\mathfrak {h}_G(\ell ) < 1$
and consider the continuous function
$\mathfrak {h}_G(\ell ) < 1$
and consider the continuous function
![]() $p \colon \thinspace [0,\infty ) \to \mathbb {R}$
defined by
$p \colon \thinspace [0,\infty ) \to \mathbb {R}$
defined by
![]() $p(t) = F_G(\ell + t \cdot \mathbf {1})$
. As
$p(t) = F_G(\ell + t \cdot \mathbf {1})$
. As
![]() $\mathfrak {h}_G(\ell + t \cdot \mathbf {1}) < 1$
for all
$\mathfrak {h}_G(\ell + t \cdot \mathbf {1}) < 1$
for all
![]() $t \in [0,\infty )$
, by the above claim we have that
$t \in [0,\infty )$
, by the above claim we have that
![]() $p(t) \neq 0$
. Since
$p(t) \neq 0$
. Since
![]() ${p(t) \to 1}$
as
${p(t) \to 1}$
as
![]() $t \to \infty $
, we have that
$t \to \infty $
, we have that
![]() $p(t)> 0$
for all
$p(t)> 0$
for all
![]() $t \in [0,\infty )$
. In particular, we have that
$t \in [0,\infty )$
. In particular, we have that
![]() $F_G(\ell ) = p(0)> 0$
.
$F_G(\ell ) = p(0)> 0$
.
4.2 A simplification
The function
![]() $F_{G}$
factors non-trivially in special cases as a result of certain aspects of the graph G. In such a case, we can replace
$F_{G}$
factors non-trivially in special cases as a result of certain aspects of the graph G. In such a case, we can replace
![]() $F_G$
with one of these factors and simplify the expressions for the entropy and pressure norm from Proposition 4.6.
$F_G$
with one of these factors and simplify the expressions for the entropy and pressure norm from Proposition 4.6.
For instance, one factorization occurs if e is a loop edge. When
![]() $\ell (e) = 0$
the vector
$\ell (e) = 0$
the vector
![]() $\mathbf {v} \in \mathbb {R}^{\lvert {E} \rvert }$
, where
$\mathbf {v} \in \mathbb {R}^{\lvert {E} \rvert }$
, where
![]() $\mathbf {v}(e) = 1$
,
$\mathbf {v}(e) = 1$
,
![]() $\mathbf {v}(\bar {e}) = -1$
, and the rest of the entries are equal to 0, is an eigenvector of
$\mathbf {v}(\bar {e}) = -1$
, and the rest of the entries are equal to 0, is an eigenvector of
![]() $A_{G,\ell }$
with eigenvalue 1. This means
$A_{G,\ell }$
with eigenvalue 1. This means
![]() $1-\exp (-\ell (e))$
is a factor of
$1-\exp (-\ell (e))$
is a factor of
![]() $F_{G}$
.
$F_{G}$
.
Example 4.10. Using the notation from Example 4.3, we have that both
![]() $1-x$
and
$1-x$
and
![]() $1-y$
are factors of
$1-y$
are factors of
![]() $F_{G}$
. Factoring, we have
$F_{G}$
. Factoring, we have
Another case where there is a factorization of
![]() $F_{G}$
is when the edge involution
$F_{G}$
is when the edge involution
![]() $e \leftrightarrow \bar {e}$
is a graph automorphism of G. There are only two types of graphs for which such an automorphism exists:
$e \leftrightarrow \bar {e}$
is a graph automorphism of G. There are only two types of graphs for which such an automorphism exists:
-
(1) the r-rose,
 $\mathcal {R}_{r}$
;
$\mathcal {R}_{r}$
; -
(2) the graph
 $\Theta _{r}$
with vertices, v and w, and edges
$\Theta _{r}$
with vertices, v and w, and edges
 $e_1, \ldots ,e_{r+1}$
where
$e_1, \ldots ,e_{r+1}$
where
 $o(e_i) = v$
and
$o(e_i) = v$
and
 $\tau (e_i) = w$
for
$\tau (e_i) = w$
for
 $i = 1,\ldots ,r+1$
.
$i = 1,\ldots ,r+1$
.
In this case ordering the edges in
![]() $E_+$
first and then ordering the edges in
$E_+$
first and then ordering the edges in
![]() $E - E_+$
accordingly, we have that
$E - E_+$
accordingly, we have that
 $$ \begin{align*} A_G = \begin{bmatrix} B_G & B^{\prime}_G \\ B^{\prime}_G & B_G \end{bmatrix} \end{align*} $$
$$ \begin{align*} A_G = \begin{bmatrix} B_G & B^{\prime}_G \\ B^{\prime}_G & B_G \end{bmatrix} \end{align*} $$
for two matrices
![]() $B_G,B^{\prime }_G \in \operatorname {\mathrm {Mat}}_{\lvert {E_+} \rvert }(\mathbb {R})$
. Thus
$B_G,B^{\prime }_G \in \operatorname {\mathrm {Mat}}_{\lvert {E_+} \rvert }(\mathbb {R})$
. Thus
 $$ \begin{align*} F_G(\ell) &= \det(I - A_{G,\ell}) = \det \begin{bmatrix} I - B_{G,\ell} & -B^{\prime}_{G,\ell} \\ -B^{\prime}_{G,\ell} & I - B_{G,\ell} \end{bmatrix} \\ & = \det(I - B_{G,\ell} - B^{\prime}_{G,\ell})\det(I - B_{G,\ell} + B^{\prime}_{G,\ell}). \end{align*} $$
$$ \begin{align*} F_G(\ell) &= \det(I - A_{G,\ell}) = \det \begin{bmatrix} I - B_{G,\ell} & -B^{\prime}_{G,\ell} \\ -B^{\prime}_{G,\ell} & I - B_{G,\ell} \end{bmatrix} \\ & = \det(I - B_{G,\ell} - B^{\prime}_{G,\ell})\det(I - B_{G,\ell} + B^{\prime}_{G,\ell}). \end{align*} $$
Since each row of
![]() $B_G$
or
$B_G$
or
![]() $B^{\prime }_G$
corresponds to an edge
$B^{\prime }_G$
corresponds to an edge
![]() $e \in E_+$
the notation
$e \in E_+$
the notation
![]() $B_{G,\ell }$
and
$B_{G,\ell }$
and
![]() $B^{\prime }_{G,\ell }$
still makes sense.
$B^{\prime }_{G,\ell }$
still makes sense.
For
![]() $\mathcal {R}_r$
, we have that
$\mathcal {R}_r$
, we have that
![]() $B_{\mathcal {R}_r}$
is the
$B_{\mathcal {R}_r}$
is the
![]() $r \times r$
matrix consisting of all
$r \times r$
matrix consisting of all
![]() $1$
s and
$1$
s and
![]() $B^{\prime }_{\mathcal {R}_r} = B_{\mathcal {R}_r} - I$
. In this case
$B^{\prime }_{\mathcal {R}_r} = B_{\mathcal {R}_r} - I$
. In this case
These are precisely the factors which were observed above for loop edges.
For
![]() $\Theta _{r}$
, we have that
$\Theta _{r}$
, we have that
![]() $B_{\Theta _r}$
is the
$B_{\Theta _r}$
is the
![]() $(r+1) \times (r+1)$
matrix consisting of all
$(r+1) \times (r+1)$
matrix consisting of all
![]() $0$
s and
$0$
s and
![]() $B^{\prime }_{\Theta _r}$
is the
$B^{\prime }_{\Theta _r}$
is the
![]() $(r + 1) \times (r+1)$
matrix where all diagonal entries are
$(r + 1) \times (r+1)$
matrix where all diagonal entries are
![]() $0$
and all non-diagonal entries are
$0$
and all non-diagonal entries are
![]() $1$
. In this case we have
$1$
. In this case we have
In general, we now construct a graph quotient
![]() $D_{G} \to \overline {D}_{G}$
that identifies certain edge pairs
$D_{G} \to \overline {D}_{G}$
that identifies certain edge pairs
![]() $\{e,\bar {e}\}$
resulting in a new matrix
$\{e,\bar {e}\}$
resulting in a new matrix
![]() $\overline {A}_{G}$
, which selects the appropriate factor. In this new matrix, every row corresponds to either an edge
$\overline {A}_{G}$
, which selects the appropriate factor. In this new matrix, every row corresponds to either an edge
![]() $e \in E$
or an edge pair
$e \in E$
or an edge pair
![]() $\{ e,\bar {e}\}$
, and so we can still make sense of
$\{ e,\bar {e}\}$
, and so we can still make sense of
![]() $\overline {A}_{G,f}$
for a function
$\overline {A}_{G,f}$
for a function
![]() $f \colon \thinspace E_+ \to \mathbb {R}$
.
$f \colon \thinspace E_+ \to \mathbb {R}$
.
When G is
![]() $\mathcal {R}_r$
or
$\mathcal {R}_r$
or
![]() $\Theta _{r}$
, we take
$\Theta _{r}$
, we take
![]() $\overline {D}_{\Theta _{r}}$
to be the quotient of
$\overline {D}_{\Theta _{r}}$
to be the quotient of
![]() $D_{\Theta _{r}}$
by the orientation-reversing automorphism
$D_{\Theta _{r}}$
by the orientation-reversing automorphism
![]() $e \mapsto \bar {e}$
. In this case
$e \mapsto \bar {e}$
. In this case
![]() $\overline {A}_{G,\ell } = B_{G,\ell } + B^{\prime }_{G,\ell }$
.
$\overline {A}_{G,\ell } = B_{G,\ell } + B^{\prime }_{G,\ell }$
.
Otherwise, for each pair
![]() $\{e,\bar {e}\}$
that is a loop edge of G, we identify the vertices of
$\{e,\bar {e}\}$
that is a loop edge of G, we identify the vertices of
![]() $D_{G}$
corresponding to e and
$D_{G}$
corresponding to e and
![]() $\bar {e}$
, now denoted
$\bar {e}$
, now denoted
![]() $e\bar {e}$
, keep the incoming edges and identify the outgoing edges that have the same terminal vertex. We call the resulting graph
$e\bar {e}$
, keep the incoming edges and identify the outgoing edges that have the same terminal vertex. We call the resulting graph
![]() $\overline {D}_{G}$
. Algebraically, we add together the columns corresponding to e and
$\overline {D}_{G}$
. Algebraically, we add together the columns corresponding to e and
![]() $\bar {e}$
and delete one of the rows corresponding to e and
$\bar {e}$
and delete one of the rows corresponding to e and
![]() $\bar {e}$
.
$\bar {e}$
.
We define
![]() $\overline {F}_{G} \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
by
$\overline {F}_{G} \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
by
The formula in Theorem 4.2, the formulas for the partial derivatives in (4.2) and (4.3), and the inner products in Lemmas 4.7 and 4.8 hold for
![]() $\overline {F}_{G}$
using the complex
$\overline {F}_{G}$
using the complex
![]() $\overline {C}_G$
, which is the cycle complex of the directed graph
$\overline {C}_G$
, which is the cycle complex of the directed graph
![]() $\overline {D}_G$
.
$\overline {D}_G$
.
Example 4.11. For G equal to the barbell graph as in Example 4.1 we have
![]() $\overline {A}_{G}$
and
$\overline {A}_{G}$
and
![]() $\overline {D}_{G}$
as shown below (columns of the matrix are ordered as
$\overline {D}_{G}$
as shown below (columns of the matrix are ordered as
![]() $a\bar {a}$
,
$a\bar {a}$
,
![]() $b\bar {b}$
, c,
$b\bar {b}$
, c,
![]() $\bar {c}$
):
$\bar {c}$
):
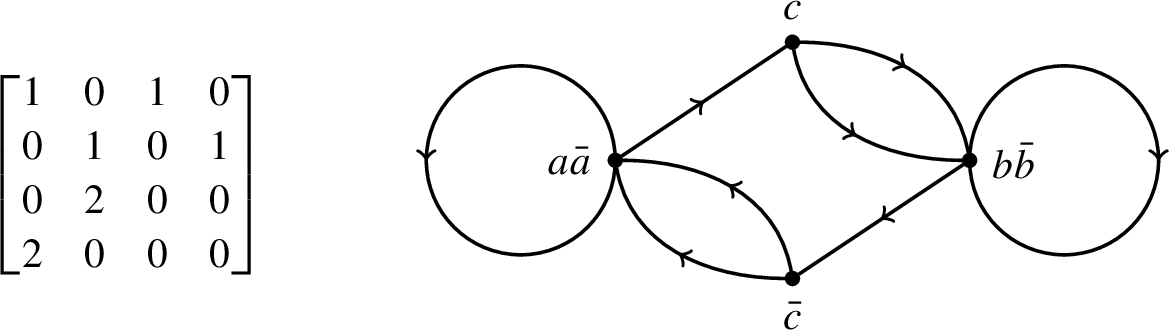
The two directed edges from
![]() $\bar {c}$
to
$\bar {c}$
to
![]() $a\bar {a}$
are identified with the set
$a\bar {a}$
are identified with the set
![]() $\{a ,\bar {a}\}$
so that we think of the sequence
$\{a ,\bar {a}\}$
so that we think of the sequence
![]() $c,a$
or
$c,a$
or
![]() $c,\bar {a}$
as specifying which of the two edges between
$c,\bar {a}$
as specifying which of the two edges between
![]() $\bar {c}$
and
$\bar {c}$
and
![]() $a\bar {a}$
to traverse in a cycle. There are six simple cycles:
$a\bar {a}$
to traverse in a cycle. There are six simple cycles:
![]() $\gamma _{a\bar {a}} = (a\bar {a})$
,
$\gamma _{a\bar {a}} = (a\bar {a})$
,
![]() $\gamma _{b\bar {b}} = (b\bar {b})$
,
$\gamma _{b\bar {b}} = (b\bar {b})$
,
![]() $\gamma _{ab} = (a,c,b,\bar {c})$
,
$\gamma _{ab} = (a,c,b,\bar {c})$
,
![]() $\gamma _{a\bar {b}} = (a,c,\bar {b},\bar {c})$
,
$\gamma _{a\bar {b}} = (a,c,\bar {b},\bar {c})$
,
![]() $\gamma _{\bar {a}b} = (\bar {a},c,b,\bar {c})$
and
$\gamma _{\bar {a}b} = (\bar {a},c,b,\bar {c})$
and
![]() $\gamma _{\bar {a}\bar {b}} = (\bar {a},c,\bar {b},\bar {c})$
. The cycle complex
$\gamma _{\bar {a}\bar {b}} = (\bar {a},c,\bar {b},\bar {c})$
. The cycle complex
![]() $\overline {C}_{G}$
is shown below:
$\overline {C}_{G}$
is shown below:
Using Theorem 4.2, we find (with
![]() $x = \exp (-\ell (a))$
,
$x = \exp (-\ell (a))$
,
![]() $y = \exp (-\ell (b))$
and
$y = \exp (-\ell (b))$
and
![]() $z = \exp (-\ell (c))$
) that
$z = \exp (-\ell (c))$
) that
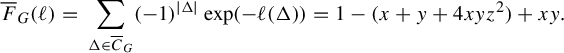 $$ \begin{align*} \overline{F}_{G}(\ell) =& \, \sum_{\Delta \in \overline{C}_{G}} (-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta)) = 1 - (x + y + 4xyz^{2}) + xy. \end{align*} $$
$$ \begin{align*} \overline{F}_{G}(\ell) =& \, \sum_{\Delta \in \overline{C}_{G}} (-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta)) = 1 - (x + y + 4xyz^{2}) + xy. \end{align*} $$
The astute reader will notice the comparison with Example 4.10.
Lemma 4.12. With the above setup,
![]() $\operatorname {\mathrm {spec}}(\overline {A}_{G,\ell }) = \operatorname {\mathrm {spec}}(A_{G,\ell })$
.
$\operatorname {\mathrm {spec}}(\overline {A}_{G,\ell }) = \operatorname {\mathrm {spec}}(A_{G,\ell })$
.
Proof. Each circuit in
![]() $\overline {D}_{G}$
lifts to at most two circuits of the same length in
$\overline {D}_{G}$
lifts to at most two circuits of the same length in
![]() $D_{G}$
. Thus
$D_{G}$
. Thus
![]() $\operatorname {\mathrm {tr}}(\overline {A}_{G,\ell }^{n}) \leq \operatorname {\mathrm {tr}}(A_{G,\ell }^{n}) \leq 2\operatorname {\mathrm {tr}}(\overline {A}_{G,\ell }^{n})$
for all
$\operatorname {\mathrm {tr}}(\overline {A}_{G,\ell }^{n}) \leq \operatorname {\mathrm {tr}}(A_{G,\ell }^{n}) \leq 2\operatorname {\mathrm {tr}}(\overline {A}_{G,\ell }^{n})$
for all
![]() $n \in \mathbb {N}$
and so the lemma follows.
$n \in \mathbb {N}$
and so the lemma follows.
In particular, we have that
![]() $\mathfrak {P}_G(-\ell ) = \log \operatorname {\mathrm {spec}}(\overline {A}_{G,\ell })$
. As in Corollary 4.5, we have the following statement. This follows for the same reasons as in Lemma 4.4 as
$\mathfrak {P}_G(-\ell ) = \log \operatorname {\mathrm {spec}}(\overline {A}_{G,\ell })$
. As in Corollary 4.5, we have the following statement. This follows for the same reasons as in Lemma 4.4 as
![]() $\overline {F}_G(\ell ) = 0$
and
$\overline {F}_G(\ell ) = 0$
and
![]() $\nabla \overline {F}_G(\ell ) \neq 0$
for
$\nabla \overline {F}_G(\ell ) \neq 0$
for
![]() $\ell \in \mathcal {M}^1(G)$
.
$\ell \in \mathcal {M}^1(G)$
.
Proposition 4.13. The unit-entropy moduli space
![]() $\mathcal {M}^{1}(G)$
is a connected component of the level set
$\mathcal {M}^{1}(G)$
is a connected component of the level set
![]() $\{ \ell \in \mathcal {M}(G) \mid \overline {F}_{G}(\ell ) = 0 \}$
.
$\{ \ell \in \mathcal {M}(G) \mid \overline {F}_{G}(\ell ) = 0 \}$
.
We also observe that the formulas for the metrics in Proposition 4.6 hold for
![]() $\overline {F}_G$
.
$\overline {F}_G$
.
Proposition 4.14. If
![]() $\ell _{t} \colon \thinspace (-1,1) \to \mathcal {M}^{1}(G)$
is a smooth path, then
$\ell _{t} \colon \thinspace (-1,1) \to \mathcal {M}^{1}(G)$
is a smooth path, then
 $$ \begin{align*} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{h},G}^{2} &= \frac{-\langle \dot\ell_{t},\mathbf{H} [\overline{F}_{G}(\ell_{t})]\dot\ell_{t} \rangle}{\langle \ell_{t},\nabla \overline{F}_{G}(\ell_{t}) \rangle}= \frac{\langle \ddot\ell_{t},\nabla \overline{F}_{G}(\ell_{t}) \rangle}{\langle \ell_{t},\nabla \overline{F}_{G}(\ell_{t}) \rangle}, \\ \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{P},G}^{2} &= \frac{-\langle \dot\ell_{t},\mathbf{H} [\overline{F}_{G}(\ell_{t})]\dot\ell_{t} \rangle}{\| {\nabla \overline{F}_{G}(\ell_{t})} \|_{1}}= \frac{\langle \ddot\ell_{t},\nabla \overline{F}_{G}(\ell_{t}) \rangle}{\| {\nabla \overline{F}_{G}(\ell_{t})} \|_{1}}. \end{align*} $$
$$ \begin{align*} \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{h},G}^{2} &= \frac{-\langle \dot\ell_{t},\mathbf{H} [\overline{F}_{G}(\ell_{t})]\dot\ell_{t} \rangle}{\langle \ell_{t},\nabla \overline{F}_{G}(\ell_{t}) \rangle}= \frac{\langle \ddot\ell_{t},\nabla \overline{F}_{G}(\ell_{t}) \rangle}{\langle \ell_{t},\nabla \overline{F}_{G}(\ell_{t}) \rangle}, \\ \| {(\ell_{t},\dot\ell_{t})} \|_{\mathfrak{P},G}^{2} &= \frac{-\langle \dot\ell_{t},\mathbf{H} [\overline{F}_{G}(\ell_{t})]\dot\ell_{t} \rangle}{\| {\nabla \overline{F}_{G}(\ell_{t})} \|_{1}}= \frac{\langle \ddot\ell_{t},\nabla \overline{F}_{G}(\ell_{t}) \rangle}{\| {\nabla \overline{F}_{G}(\ell_{t})} \|_{1}}. \end{align*} $$
5 The topology induced by the entropy metric
The purpose of this section is to show that the metric topology induced by
![]() $d_{\mathfrak {h}}$
on
$d_{\mathfrak {h}}$
on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
is the same as the weak topology on
$\mathcal {X}^1(\mathbb {F}_r)$
is the same as the weak topology on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
. We do so using the formulas for the entropy metric derived in §4 and seeing that they behave as one might anticipate with regards to collapses. We refer the reader back to §2.2 for the notation used in this section.
$\mathcal {X}^1(\mathbb {F}_r)$
. We do so using the formulas for the entropy metric derived in §4 and seeing that they behave as one might anticipate with regards to collapses. We refer the reader back to §2.2 for the notation used in this section.
By Theorem 3.5 we have that
![]() $\mathfrak {h}_G \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
extends to a continuous function on
$\mathfrak {h}_G \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
extends to a continuous function on
![]() $\overline {\mathcal {M}}(G)$
. Indeed, if
$\overline {\mathcal {M}}(G)$
. Indeed, if
![]() $c\colon \thinspace G \to G_0$
is a collapse, then for
$c\colon \thinspace G \to G_0$
is a collapse, then for
![]() $\ell \in \mathcal {M}(G_0)$
we have
$\ell \in \mathcal {M}(G_0)$
we have
![]() $\mathfrak {h}_G(c^*(\ell )) = \mathfrak {h}_{G_0}(\ell )$
. We set
$\mathfrak {h}_G(c^*(\ell )) = \mathfrak {h}_{G_0}(\ell )$
. We set
![]() $\overline {\mathcal {M}}^1(G) = \{ \ell \in \overline {\mathcal {M}}(G) \mid \mathfrak {h}_G(\ell ) = 1 \}$
and observe that we have
$\overline {\mathcal {M}}^1(G) = \{ \ell \in \overline {\mathcal {M}}(G) \mid \mathfrak {h}_G(\ell ) = 1 \}$
and observe that we have
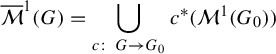 $$ \begin{align*} \overline{\mathcal{M}}^1(G) = \bigcup_{c \colon\thinspace G \to G_0} c^*(\mathcal{M}^1(G_0)) \end{align*} $$
$$ \begin{align*} \overline{\mathcal{M}}^1(G) = \bigcup_{c \colon\thinspace G \to G_0} c^*(\mathcal{M}^1(G_0)) \end{align*} $$
as well. This set is homeomorphic to the closure of
![]() $CV(G,\rho )$
in
$CV(G,\rho )$
in
![]() $CV(\mathbb {F}_r)$
for any marking
$CV(\mathbb {F}_r)$
for any marking
![]() $\rho \colon \thinspace \mathcal {R}_r \to G$
. Given a graph G, we observe that
$\rho \colon \thinspace \mathcal {R}_r \to G$
. Given a graph G, we observe that
![]() $F_G:\mathcal {M}(G) \to \mathbb {R}$
admits an extension (still denoted
$F_G:\mathcal {M}(G) \to \mathbb {R}$
admits an extension (still denoted
![]() $F_G$
) to
$F_G$
) to
![]() $\mathbb {R}^{\lvert {E_+} \rvert }$
. In particular,
$\mathbb {R}^{\lvert {E_+} \rvert }$
. In particular,
![]() $F_G$
is defined on
$F_G$
is defined on
![]() $\overline {\mathcal {M}}(G) \subset \mathbb {R}^{\lvert {E_+} \rvert }$
. The next result shows that this function behaves as expected with respect to collapses.
$\overline {\mathcal {M}}(G) \subset \mathbb {R}^{\lvert {E_+} \rvert }$
. The next result shows that this function behaves as expected with respect to collapses.
Lemma 5.1. If
![]() $c \colon \thinspace G \to G_0$
is a collapse, then
$c \colon \thinspace G \to G_0$
is a collapse, then
![]() $F_G \circ c^* = F_{G_0}$
.
$F_G \circ c^* = F_{G_0}$
.
Proof. It suffices to consider the case when
![]() $c \colon \thinspace G \to G_0$
is the collapse of a single edge
$c \colon \thinspace G \to G_0$
is the collapse of a single edge
![]() $e \in E_{+}$
. Order the edges in E starting with e and
$e \in E_{+}$
. Order the edges in E starting with e and
![]() $\bar {e}$
. Since e can be collapsed, it is not a loop and so we have that
$\bar {e}$
. Since e can be collapsed, it is not a loop and so we have that
![]() $A_{G}(e,e) = A_{G}(\bar {e},\bar {e}) = 0$
. By definition,
$A_{G}(e,e) = A_{G}(\bar {e},\bar {e}) = 0$
. By definition,
![]() $A_{G}(e,\bar {e}) = A_{G}(\bar {e},e) = 0$
. Thus the top-leftmost
$A_{G}(e,\bar {e}) = A_{G}(\bar {e},e) = 0$
. Thus the top-leftmost
![]() $2 \times 2$
block of the matrix
$2 \times 2$
block of the matrix
![]() $I - A_{G}$
is the
$I - A_{G}$
is the
![]() $2 \times 2$
identity matrix.
$2 \times 2$
identity matrix.
Let
![]() $\ell \in \mathcal {M}(G_0)$
. For an edge
$\ell \in \mathcal {M}(G_0)$
. For an edge
![]() $e' \notin \{e,\bar {e}\}$
, the entry
$e' \notin \{e,\bar {e}\}$
, the entry
![]() $[I - A_{G,c^*(\ell )}](e,e')$
is either
$[I - A_{G,c^*(\ell )}](e,e')$
is either
![]() $-1$
or
$-1$
or
![]() $0$
depending on whether or not
$0$
depending on whether or not
![]() $e'$
can follow e. Likewise for
$e'$
can follow e. Likewise for
![]() $[I - A_{G,c^*(\ell )}](\bar {e},e')$
. Again, as e is not a loop, for any edge
$[I - A_{G,c^*(\ell )}](\bar {e},e')$
. Again, as e is not a loop, for any edge
![]() $e' \notin \{e,\bar {e}\}$
, at most one of these entries is non-zero.
$e' \notin \{e,\bar {e}\}$
, at most one of these entries is non-zero.
For each edge
![]() $e' \notin \{e, \bar {e}\}$
, where
$e' \notin \{e, \bar {e}\}$
, where
![]() $[I - A_{G,c^*(\ell )}](e,e') = -1$
, we consider the column operation that adds the column for e to the column for
$[I - A_{G,c^*(\ell )}](e,e') = -1$
, we consider the column operation that adds the column for e to the column for
![]() $e'$
. This zeros the
$e'$
. This zeros the
![]() $(e,e')$
entry. The
$(e,e')$
entry. The
![]() $(\bar {e},e')$
entry was previously 0 and is unaffected by this operation. We next see what effect this has on the remaining rows. In the row for
$(\bar {e},e')$
entry was previously 0 and is unaffected by this operation. We next see what effect this has on the remaining rows. In the row for
![]() $e'' \notin \{e,\bar {e}\}$
, this adds
$e'' \notin \{e,\bar {e}\}$
, this adds
![]() $-\exp (-\ell (e''))$
to
$-\exp (-\ell (e''))$
to
![]() $A_{G,c^*(\ell )}(e'',e')$
if e can follow
$A_{G,c^*(\ell )}(e'',e')$
if e can follow
![]() $e''$
and 0 otherwise. In the former case, the previous entry was either 0 (
$e''$
and 0 otherwise. In the former case, the previous entry was either 0 (
![]() $e' \neq e''$
) or 1 (
$e' \neq e''$
) or 1 (
![]() $e' = e''$
) as e is not a loop edge. In other words, this adds
$e' = e''$
) as e is not a loop edge. In other words, this adds
![]() $-\exp (-\ell (e''))$
whenever
$-\exp (-\ell (e''))$
whenever
![]() $e'$
can follow
$e'$
can follow
![]() $e''$
in
$e''$
in
![]() $G_0$
. Therefore, the remaining entries in the column for
$G_0$
. Therefore, the remaining entries in the column for
![]() $e'$
agree with the corresponding entries in the column of
$e'$
agree with the corresponding entries in the column of
![]() $I - A_{G_0,\ell }$
for
$I - A_{G_0,\ell }$
for
![]() $e'$
.
$e'$
.
Hence, after performing column operations to
![]() $I - A_{G,c^*(\ell )}$
with the column for e to clear out the rest of the row for e and column operations with the column for
$I - A_{G,c^*(\ell )}$
with the column for e to clear out the rest of the row for e and column operations with the column for
![]() $\bar {e}$
to clear out the rest of the row for
$\bar {e}$
to clear out the rest of the row for
![]() $\bar {e}$
, the resulting matrix has lower block triangular form. The top-leftmost
$\bar {e}$
, the resulting matrix has lower block triangular form. The top-leftmost
![]() $2 \times 2$
block is still the
$2 \times 2$
block is still the
![]() $2 \times 2$
identity matrix and the bottom-rightmost
$2 \times 2$
identity matrix and the bottom-rightmost
![]() ${(\lvert {E} \rvert - 2)} \times (\lvert {E} \rvert - 2)$
block is
${(\lvert {E} \rvert - 2)} \times (\lvert {E} \rvert - 2)$
block is
![]() $I - A_{G_0,\ell }$
.
$I - A_{G_0,\ell }$
.
As these column operations do not change the determinant, we have for
![]() $\ell \in \mathcal {M}(G_0)$
that
$\ell \in \mathcal {M}(G_0)$
that
As a consequence of Lemma 5.1 we deduce the following result. If
![]() $c \colon \thinspace G \to G_0$
is a collapse and
$c \colon \thinspace G \to G_0$
is a collapse and
![]() $e \in E_+$
is an edge such that
$e \in E_+$
is an edge such that
![]() $c(e)$
is not a vertex, then
$c(e)$
is not a vertex, then
![]() $\partial _{c(e)} F_{G_0}(\ell ) = \partial _{e} F_G(c^*(\ell ))$
for all
$\partial _{c(e)} F_{G_0}(\ell ) = \partial _{e} F_G(c^*(\ell ))$
for all
![]() $\ell \in \mathcal {M}(G_0)$
. Similarly, in this same setting, if additionally
$\ell \in \mathcal {M}(G_0)$
. Similarly, in this same setting, if additionally
![]() $c(e')$
is not a vertex for an edge
$c(e')$
is not a vertex for an edge
![]() $e' \in E_+$
, then
$e' \in E_+$
, then
![]() $\partial _{c(e) c(e')} F_{G_0}(\ell ) = \partial _{e e'} F_G(c^*(\ell ))$
.
$\partial _{c(e) c(e')} F_{G_0}(\ell ) = \partial _{e e'} F_G(c^*(\ell ))$
.
The tangent bundle
![]() $T\overline {\mathcal {M}}^1(G)$
is the subspace of
$T\overline {\mathcal {M}}^1(G)$
is the subspace of
![]() $(\ell ,\mathbf {v}) \in \mathbb {R}^{\lvert {E_+} \rvert } \times \mathbb {R}^{\lvert {E_+} \rvert }$
such that
$(\ell ,\mathbf {v}) \in \mathbb {R}^{\lvert {E_+} \rvert } \times \mathbb {R}^{\lvert {E_+} \rvert }$
such that
![]() $\ell \in \overline {\mathcal {M}}^1(G)$
and
$\ell \in \overline {\mathcal {M}}^1(G)$
and
![]() $\langle \mathbf {v},\nabla F_G(\ell ) \rangle = 0$
. Given a collapse, we let
$\langle \mathbf {v},\nabla F_G(\ell ) \rangle = 0$
. Given a collapse, we let
![]() $\mathbf {c}^* \colon \thinspace \mathbb {R}^{\lvert {(E_0)_+} \rvert } \to \mathbb {R}^{\lvert {E_+} \rvert }$
be the derivative of the map
$\mathbf {c}^* \colon \thinspace \mathbb {R}^{\lvert {(E_0)_+} \rvert } \to \mathbb {R}^{\lvert {E_+} \rvert }$
be the derivative of the map
![]() $c^* \colon \thinspace \mathcal {M}(G_0) \to \mathcal {M}(G)$
and
$c^* \colon \thinspace \mathcal {M}(G_0) \to \mathcal {M}(G)$
and
![]() $Tc^* \colon \thinspace T\mathcal {M}^1(G_0) \to T\overline {\mathcal {M}}^1(G)$
be the map given by
$Tc^* \colon \thinspace T\mathcal {M}^1(G_0) \to T\overline {\mathcal {M}}^1(G)$
be the map given by
![]() $Tc^*(\ell ,\mathbf {v}) = (c^*(\ell ),\mathbf {c}^*(\mathbf {v}))$
.
$Tc^*(\ell ,\mathbf {v}) = (c^*(\ell ),\mathbf {c}^*(\mathbf {v}))$
.
Using this notation, we see that
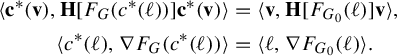 $$ \begin{align*} \langle \mathbf{c}^*(\mathbf{v}),\mathbf{H}[F_{G}(c^*(\ell))]\mathbf{c}^*(\mathbf{v}) \rangle &= \langle \mathbf{v}, \mathbf{H}[F_{G_0}(\ell)]\mathbf{v} \rangle, \\ \langle c^*(\ell),\nabla F_G(c^*(\ell)) \rangle &= \langle \ell,\nabla F_{G_0}(\ell) \rangle. \end{align*} $$
$$ \begin{align*} \langle \mathbf{c}^*(\mathbf{v}),\mathbf{H}[F_{G}(c^*(\ell))]\mathbf{c}^*(\mathbf{v}) \rangle &= \langle \mathbf{v}, \mathbf{H}[F_{G_0}(\ell)]\mathbf{v} \rangle, \\ \langle c^*(\ell),\nabla F_G(c^*(\ell)) \rangle &= \langle \ell,\nabla F_{G_0}(\ell) \rangle. \end{align*} $$
Hence, by Proposition 4.6, we get the following proposition.
Proposition 5.2. Let G be a finite connected graph. The entropy norm
![]() extends to a continuous semi-norm
extends to a continuous semi-norm
![]() . Specifically, if
. Specifically, if
![]() $c \colon \thinspace G \to G_0$
is a collapse and
$c \colon \thinspace G \to G_0$
is a collapse and
![]() $(\ell ,\mathbf {v}) = Tc^*(\ell _0,\mathbf {v}_0)$
, then the extension satisfies
$(\ell ,\mathbf {v}) = Tc^*(\ell _0,\mathbf {v}_0)$
, then the extension satisfies
Consequently, we see that the distance function
![]() $d_{\mathfrak {h},G}$
extends to a distance function on
$d_{\mathfrak {h},G}$
extends to a distance function on
![]() $\overline {\mathcal {M}}^1(G)$
and that the induced topology is the same as the subspace topology. As
$\overline {\mathcal {M}}^1(G)$
and that the induced topology is the same as the subspace topology. As
![]() $\mathcal {X}^1(\mathbb {F}_r)$
is locally finite, the metric topology agrees with the weak topology, as we now show.
$\mathcal {X}^1(\mathbb {F}_r)$
is locally finite, the metric topology agrees with the weak topology, as we now show.
Theorem 5.3. The metric topology on
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is the same as the weak topology on
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is the same as the weak topology on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
.
$\mathcal {X}^1(\mathbb {F}_r)$
.
Proof. Let
![]() $U \subseteq \mathcal {X}^1(\mathbb {F}_r)$
be an open set in the weak topology and fix a marked metric graph
$U \subseteq \mathcal {X}^1(\mathbb {F}_r)$
be an open set in the weak topology and fix a marked metric graph
![]() $x = [(G,\rho ,\ell )] \in U$
. There are finitely many marked graphs
$x = [(G,\rho ,\ell )] \in U$
. There are finitely many marked graphs
![]() $(G_1,\rho _1), \ldots , (G_n,\rho _n)$
such that
$(G_1,\rho _1), \ldots , (G_n,\rho _n)$
such that
![]() $(G,\rho ) \leq (G_i,\rho _i)$
. By definition of the weak topology, the set
$(G,\rho ) \leq (G_i,\rho _i)$
. By definition of the weak topology, the set
![]() $U \cap \overline {\mathcal {X}}^1(G_i,\rho _i)$
is open in
$U \cap \overline {\mathcal {X}}^1(G_i,\rho _i)$
is open in
![]() $\overline {\mathcal {X}}^1(G_i,\rho _i)$
in the subspace topology inherited from
$\overline {\mathcal {X}}^1(G_i,\rho _i)$
in the subspace topology inherited from
![]() $\mathbb {R}_{\geq 0}^{\lvert {(E_i)_+} \rvert }$
, where
$\mathbb {R}_{\geq 0}^{\lvert {(E_i)_+} \rvert }$
, where
![]() $E_i$
is the set of edges for
$E_i$
is the set of edges for
![]() $G_i$
. As remarked above after Proposition 5.2, this set is also open in the metric topology induced by
$G_i$
. As remarked above after Proposition 5.2, this set is also open in the metric topology induced by
![]() $d_{\mathfrak {h},G_i}$
. Hence there is an
$d_{\mathfrak {h},G_i}$
. Hence there is an
![]() $\epsilon _i> 0$
such that
$\epsilon _i> 0$
such that
Let
![]() $\epsilon = \min \{ \epsilon _i \mid 1 \leq i \leq n \}$
. As
$\epsilon = \min \{ \epsilon _i \mid 1 \leq i \leq n \}$
. As
![]() $d_{\mathfrak {h}}(x,y) \leq d_{\mathfrak {h},G_i}(x,y)$
for any
$d_{\mathfrak {h}}(x,y) \leq d_{\mathfrak {h},G_i}(x,y)$
for any
![]() $y \in \overline {\mathcal {X}}^1(G_i,\rho _i)$
we have
$y \in \overline {\mathcal {X}}^1(G_i,\rho _i)$
we have
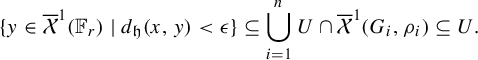 $$ \begin{align*} \{ y \in \overline{\mathcal{X}}^1(\mathbb{F}_r) \mid d_{\mathfrak{h}}(x,y) < \epsilon \} \subseteq \bigcup_{i=1}^n U \cap \overline{\mathcal{X}}^1(G_i,\rho_i) \subseteq U.\end{align*} $$
$$ \begin{align*} \{ y \in \overline{\mathcal{X}}^1(\mathbb{F}_r) \mid d_{\mathfrak{h}}(x,y) < \epsilon \} \subseteq \bigcup_{i=1}^n U \cap \overline{\mathcal{X}}^1(G_i,\rho_i) \subseteq U.\end{align*} $$
Hence the metric topology is finer than the subspace topology.
Next, fix a marked metric graph
![]() $x = [(G,\rho ,\ell )] \in \mathcal {X}^1(\mathbb {F}_r)$
and let
$x = [(G,\rho ,\ell )] \in \mathcal {X}^1(\mathbb {F}_r)$
and let
![]() $\epsilon> 0$
. Enumerate the finitely many marked graphs
$\epsilon> 0$
. Enumerate the finitely many marked graphs
![]() $(G_1,\rho _1), \ldots , (G_n,\rho _n)$
such that
$(G_1,\rho _1), \ldots , (G_n,\rho _n)$
such that
![]() $(G,\rho ) \leq (G_i,\rho _i$
) and such that
$(G,\rho ) \leq (G_i,\rho _i$
) and such that
![]() $G_i$
is trivalent. In other words,
$G_i$
is trivalent. In other words,
![]() $(G_i,\rho _i)$
are maximal elements in the partial order on marked graphs. As the norm varies continuously by Proposition 5.2, there is an L and an open neighborhood
$(G_i,\rho _i)$
are maximal elements in the partial order on marked graphs. As the norm varies continuously by Proposition 5.2, there is an L and an open neighborhood
![]() $V \subseteq \bigcup _{i=1}^n \overline {\mathcal {X}}^1(G_i,\rho _i)$
of x in the weak topology such that
$V \subseteq \bigcup _{i=1}^n \overline {\mathcal {X}}^1(G_i,\rho _i)$
of x in the weak topology such that
![]() $\| {(y,\mathbf {v})} \|_{\mathfrak {h},G_i} \leq L$
whenever
$\| {(y,\mathbf {v})} \|_{\mathfrak {h},G_i} \leq L$
whenever
![]() $y \in \overline {\mathcal {X}}^1(G_i) \cap V$
and
$y \in \overline {\mathcal {X}}^1(G_i) \cap V$
and
![]() $\langle \mathbf {v},\mathbf {v} \rangle = 1$
. Therefore, there is an open neighborhood U of x in the weak topology such that
$\langle \mathbf {v},\mathbf {v} \rangle = 1$
. Therefore, there is an open neighborhood U of x in the weak topology such that
Hence the subspace topology is finer than the metric topology.
6 The entropy metric on
 $\mathcal {X}^1(\mathbb {F}_2)$
$\mathcal {X}^1(\mathbb {F}_2)$
The goal of this section is to show that
![]() $(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete. This appears as Proposition 6.8 in §6.4. The results in this section are not necessary for the remainder of the paper and can safely be skipped by a reader primarily interested in Theorems 1.2 and 1.3. However, the calculations can serve as a good introduction to estimating lengths with the entropy metric. In particular, the main strategy in each of Lemmas 6.1, 6.3 and 6.5 is very similar to the main strategy of Lemma 7.10 in §7.3 which is the key tool used to show that
$(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete. This appears as Proposition 6.8 in §6.4. The results in this section are not necessary for the remainder of the paper and can safely be skipped by a reader primarily interested in Theorems 1.2 and 1.3. However, the calculations can serve as a good introduction to estimating lengths with the entropy metric. In particular, the main strategy in each of Lemmas 6.1, 6.3 and 6.5 is very similar to the main strategy of Lemma 7.10 in §7.3 which is the key tool used to show that
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter.
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter.
To begin, we analyze the metric for each of the three topological types of graphs that appear in rank
![]() $2$
: the 2-rose
$2$
: the 2-rose
![]() $\mathcal {R}_2$
, the barbell graph
$\mathcal {R}_2$
, the barbell graph
![]() $\mathcal {B}_2$
and the theta graph
$\mathcal {B}_2$
and the theta graph
![]() $\Theta _2$
. We refer the reader back to Figure 2 for these graphs. To this end, we define a continuous function
$\Theta _2$
. We refer the reader back to Figure 2 for these graphs. To this end, we define a continuous function
![]() $\textsf {m} \colon \thinspace \mathcal {X}^1(\mathbb {F}_2) \to \mathbb {R}$
which is a slight variation of the volume function in that it counts separating edges twice. In particular, it does not depend on the marking. The exact definition appears in §6.4. The strategy is to show that for any path
$\textsf {m} \colon \thinspace \mathcal {X}^1(\mathbb {F}_2) \to \mathbb {R}$
which is a slight variation of the volume function in that it counts separating edges twice. In particular, it does not depend on the marking. The exact definition appears in §6.4. The strategy is to show that for any path
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(G)$
for
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(G)$
for
![]() $G \in \{\mathcal {R}_2,\mathcal {B}_2,\Theta _2\}$
, if
$G \in \{\mathcal {R}_2,\mathcal {B}_2,\Theta _2\}$
, if
![]() $\textsf {m}(\ell _0)$
and
$\textsf {m}(\ell _0)$
and
![]() $\textsf {m}(\ell _1)$
are large enough, then the length of
$\textsf {m}(\ell _1)$
are large enough, then the length of
![]() $\ell _t$
is bounded below by
$\ell _t$
is bounded below by
These calculations appear in the next three sections (Propositions 6.2, 6.4, and 6.6).
Using these estimates, it is not too hard to see that if
![]() $(x_n)_{n \in \mathbb {N}} \subset \mathcal {X}^1(\mathbb {F}_2)$
is Cauchy, then there is an L such that
$(x_n)_{n \in \mathbb {N}} \subset \mathcal {X}^1(\mathbb {F}_2)$
is Cauchy, then there is an L such that
![]() $\textsf {m}(x_n) \leq L$
for all n (Lemma 6.7). From here, using local finiteness of
$\textsf {m}(x_n) \leq L$
for all n (Lemma 6.7). From here, using local finiteness of
![]() $\mathcal {X}^1(\mathbb {F}_2)$
and a compactness argument, the completeness of
$\mathcal {X}^1(\mathbb {F}_2)$
and a compactness argument, the completeness of
![]() $(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
follows. In the calculations, we make use of Lemmas 4.7 and 4.8.
$(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
follows. In the calculations, we make use of Lemmas 4.7 and 4.8.
6.1 The 2-rose
Denote the edges of
![]() $\mathcal {R}_2$
by
$\mathcal {R}_2$
by
![]() $e_1$
and
$e_1$
and
![]() $e_2$
. To make the calculations in this subsection easier to read, given a length function
$e_2$
. To make the calculations in this subsection easier to read, given a length function
![]() $\ell \in \mathcal {M}(\mathcal {R}_2)$
, we set
$\ell \in \mathcal {M}(\mathcal {R}_2)$
, we set
![]() $a = \ell (e_1)$
,
$a = \ell (e_1)$
,
![]() $b = \ell (e_2)$
and
$b = \ell (e_2)$
and
![]() $m = \ell (e_1) + \ell (e_2)$
. Applying the definition of
$m = \ell (e_1) + \ell (e_2)$
. Applying the definition of
![]() $\overline {F}_G$
from §4.2 to
$\overline {F}_G$
from §4.2 to
![]() $\mathcal {R}_2$
, we find the formula
$\mathcal {R}_2$
, we find the formula
Lemma 6.1. Suppose
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^{1}(\mathcal {R}_{2})$
is a smooth path such that for all
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^{1}(\mathcal {R}_{2})$
is a smooth path such that for all
![]() $t \in [0,1]$
we have
$t \in [0,1]$
we have
![]() $\dot m_t> 0$
. If
$\dot m_t> 0$
. If
![]() $m_0 \geq 4$
, then
$m_0 \geq 4$
, then
Proof. Suppose that
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {R}_2)$
is a path where
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {R}_2)$
is a path where
![]() $\dot m_t> 0$
as in the statement of the lemma and assume that
$\dot m_t> 0$
as in the statement of the lemma and assume that
![]() $m_0 \geq 4$
. We reparametrize the path
$m_0 \geq 4$
. We reparametrize the path
![]() $\ell _t$
so that
$\ell _t$
so that
![]() $m_t = t$
.
$m_t = t$
.
Let
![]() $n_t = \min \{a_t,b_t\}$
. As
$n_t = \min \{a_t,b_t\}$
. As
![]() $\overline {F}_{\mathcal {R}_2}(\ell _t) = 0$
, we have
$\overline {F}_{\mathcal {R}_2}(\ell _t) = 0$
, we have
In particular,
![]() $2\exp (-n_t) \geq 1 - 3\exp (-t) \geq 2\exp (-1)$
as
$2\exp (-n_t) \geq 1 - 3\exp (-t) \geq 2\exp (-1)$
as
![]() $t \geq 4$
and so
$t \geq 4$
and so
![]() $n_t < 1$
for all t.
$n_t < 1$
for all t.
Setting
![]() $p_t = \max \{a_t,b_t\}$
, we find that
$p_t = \max \{a_t,b_t\}$
, we find that
![]() $p_t = t - n_t \geq t-1$
. Therefore, as
$p_t = t - n_t \geq t-1$
. Therefore, as
![]() $t - 1 \geq 1$
for
$t - 1 \geq 1$
for
![]() $t \geq 4$
, the edge that realizes the minimum of
$t \geq 4$
, the edge that realizes the minimum of
![]() $\{a_t,b_t\}$
does not depend on t and hence we may assume that
$\{a_t,b_t\}$
does not depend on t and hence we may assume that
![]() $b_t = n_t$
and that
$b_t = n_t$
and that
![]() $a_t = p_t \geq t-1$
. This gives us that
$a_t = p_t \geq t-1$
. This gives us that
![]() $\exp (-a_t) \leq \exp (-t + 1)$
. Hence, again as
$\exp (-a_t) \leq \exp (-t + 1)$
. Hence, again as
![]() $\overline {F}_{\mathcal {R}_2}(\ell _t) = 0$
, we have
$\overline {F}_{\mathcal {R}_2}(\ell _t) = 0$
, we have
This enables us to give an upper bound on the denominator in the expression for the entropy norm. Specifically, using the fact that
![]() $x\exp (-x) \leq 1 - \exp (-x)$
for
$x\exp (-x) \leq 1 - \exp (-x)$
for
![]() $x \geq 0$
, we have
$x \geq 0$
, we have
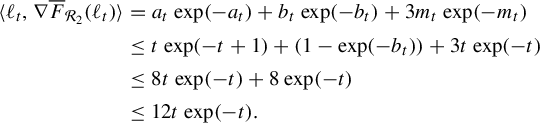 $$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{\mathcal{R}_2}(\ell_t) \rangle & = a_t\exp(-a_t) + b_t\exp(-b_t) +3m_t\exp(-m_t) \\ & \leq t\exp(-t+1) + (1 - \exp(-b_t)) +3t\exp(-t) \\ & \leq 8t\exp(-t) + 8\exp(-t) \\ & \leq 12t\exp(-t). \end{align*} $$
$$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{\mathcal{R}_2}(\ell_t) \rangle & = a_t\exp(-a_t) + b_t\exp(-b_t) +3m_t\exp(-m_t) \\ & \leq t\exp(-t+1) + (1 - \exp(-b_t)) +3t\exp(-t) \\ & \leq 8t\exp(-t) + 8\exp(-t) \\ & \leq 12t\exp(-t). \end{align*} $$
In the final inequality we used that fact that
![]() $t \geq 4$
. The expression for
$t \geq 4$
. The expression for
![]() $\langle \ell _t,\nabla \overline {F}_{\mathcal {R}_2}(\ell _t) \rangle $
can be computed either directly from (6.1) or via Lemma 4.7.
$\langle \ell _t,\nabla \overline {F}_{\mathcal {R}_2}(\ell _t) \rangle $
can be computed either directly from (6.1) or via Lemma 4.7.
Next, we get an upper bound on the numerator in the expression for the entropy norm by just using
![]() $m_t$
. Specifically,
$m_t$
. Specifically,
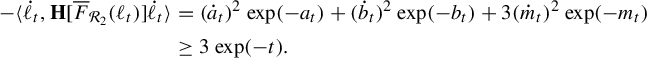 $$ \begin{align*} -\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\mathcal{R}_2}(\ell_t)]\dot \ell_t \rangle & = (\dot a_t)^2\exp(-a_t) + (\dot b_t)^2\exp(-b_t) + 3(\dot m_t)^2\exp(-m_t) \\ & \geq 3\exp(-t). \end{align*} $$
$$ \begin{align*} -\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\mathcal{R}_2}(\ell_t)]\dot \ell_t \rangle & = (\dot a_t)^2\exp(-a_t) + (\dot b_t)^2\exp(-b_t) + 3(\dot m_t)^2\exp(-m_t) \\ & \geq 3\exp(-t). \end{align*} $$
As above, the expression for
![]() $-\langle \dot \ell _t,\mathbf {H}[\overline {F}_{\mathcal {R}_2}(\ell _t)]\dot \ell _t \rangle $
can be computed either directly from (6.1) or via Lemma 4.8.
$-\langle \dot \ell _t,\mathbf {H}[\overline {F}_{\mathcal {R}_2}(\ell _t)]\dot \ell _t \rangle $
can be computed either directly from (6.1) or via Lemma 4.8.
Hence we find that the entropy norm along this path is bounded below by
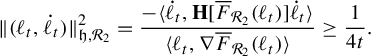 $$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{R}_2} = \frac{-\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\mathcal{R}_2}(\ell_t)]\dot \ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_{\mathcal{R}_2}(\ell_t) \rangle}\geq \frac{1}{4t}. \end{align*} $$
$$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{R}_2} = \frac{-\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\mathcal{R}_2}(\ell_t)]\dot \ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_{\mathcal{R}_2}(\ell_t) \rangle}\geq \frac{1}{4t}. \end{align*} $$
Therefore the length of this path in the entropy metric is at least
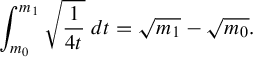 $$ \begin{align*} \int_{m_0}^{m_1} \sqrt{\frac{1}{4t}} \, dt &= \sqrt{m_1} - \sqrt{m_0}. \\[-42pt]\end{align*} $$
$$ \begin{align*} \int_{m_0}^{m_1} \sqrt{\frac{1}{4t}} \, dt &= \sqrt{m_1} - \sqrt{m_0}. \\[-42pt]\end{align*} $$
Using this lemma, we can get a lower bound on the distance between length functions in
![]() $\mathcal {M}^1(\mathcal {R}_2)$
in terms of the sum of the lengths of edges, so long as they are sufficiently large.
$\mathcal {M}^1(\mathcal {R}_2)$
in terms of the sum of the lengths of edges, so long as they are sufficiently large.
Proposition 6.2. Suppose
![]() $\ell $
and
$\ell $
and
![]() $\ell '$
are length functions in
$\ell '$
are length functions in
![]() $\mathcal {M}^1(\mathcal {R}_2)$
where
$\mathcal {M}^1(\mathcal {R}_2)$
where
![]() $m = \ell (e_1) + \ell (e_2)$
and
$m = \ell (e_1) + \ell (e_2)$
and
![]() $m' = \ell '(e_1) + \ell '(e_2)$
are at least
$m' = \ell '(e_1) + \ell '(e_2)$
are at least
![]() $4$
. Then
$4$
. Then
Proof. Let
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {R}_2)$
be a piecewise smooth path such that
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {R}_2)$
be a piecewise smooth path such that
![]() $\ell _0 = \ell $
and
$\ell _0 = \ell $
and
![]() $\ell _1 = \ell '$
. Let
$\ell _1 = \ell '$
. Let
![]() $\delta \in [0,1]$
be the minimal value such that
$\delta \in [0,1]$
be the minimal value such that
![]() $m_t \geq 4$
for
$m_t \geq 4$
for
![]() $t \in [\delta ,1]$
. In particular,
$t \in [\delta ,1]$
. In particular,
![]() ${m_\delta \leq m}$
.
${m_\delta \leq m}$
.
By only considering the smooth subpaths of
![]() $\ell _t|[\delta ,1]$
for which
$\ell _t|[\delta ,1]$
for which
![]() $\dot m_t> 0$
, by Lemma 6.1, we find that
$\dot m_t> 0$
, by Lemma 6.1, we find that
This also provides a lower bound on
![]() $\mathcal {L}_{\mathfrak {h},\mathcal {R}_2}(\ell _t|[0,1])$
. Since the path was arbitrary this also is a lower bound on the distance between
$\mathcal {L}_{\mathfrak {h},\mathcal {R}_2}(\ell _t|[0,1])$
. Since the path was arbitrary this also is a lower bound on the distance between
![]() $\ell $
and
$\ell $
and
![]() $\ell '$
.
$\ell '$
.
6.2 The barbell graph
Let
![]() $\mathcal {B}_2$
denote the graph with vertices v and w, and edges
$\mathcal {B}_2$
denote the graph with vertices v and w, and edges
![]() $e_1$
,
$e_1$
,
![]() $e_2$
and
$e_2$
and
![]() $e_3$
where
$e_3$
where
![]() $o(e_1) = \tau (e_1) = v$
,
$o(e_1) = \tau (e_1) = v$
,
![]() $o(e_2) = \tau (e_2) = w$
, and
$o(e_2) = \tau (e_2) = w$
, and
![]() $o(e_3) = v$
and
$o(e_3) = v$
and
![]() $\tau (e_3) = w$
. To make the calculations in this section easier to read, given a length function
$\tau (e_3) = w$
. To make the calculations in this section easier to read, given a length function
![]() $\ell \in \mathcal {M}(\mathcal {B}_2)$
, we set
$\ell \in \mathcal {M}(\mathcal {B}_2)$
, we set
![]() $a = \ell (e_1)$
,
$a = \ell (e_1)$
,
![]() $b = \ell (e_2)$
and
$b = \ell (e_2)$
and
![]() $m = \ell (e_1) + \ell (e_2) + 2\ell (e_3)$
. Applying the definition of
$m = \ell (e_1) + \ell (e_2) + 2\ell (e_3)$
. Applying the definition of
![]() $\overline {F}_G$
from §4.2 to
$\overline {F}_G$
from §4.2 to
![]() $\mathcal {B}_2$
, we find the formula
$\mathcal {B}_2$
, we find the formula
Lemma 6.3. Suppose
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^{1}(\mathcal {B}_{2})$
is a smooth path such that for all
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^{1}(\mathcal {B}_{2})$
is a smooth path such that for all
![]() $t \in [0,1]$
we have
$t \in [0,1]$
we have
![]() $\dot m_t> 0$
. If
$\dot m_t> 0$
. If
![]() $m_0 \geq 4$
, then
$m_0 \geq 4$
, then
Proof. Suppose that
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {B}_2)$
is a path where
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {B}_2)$
is a path where
![]() $\dot m_t> 0$
as in the statement of the lemma and assume that
$\dot m_t> 0$
as in the statement of the lemma and assume that
![]() $m_0 \geq 4$
. We reparametrize the path
$m_0 \geq 4$
. We reparametrize the path
![]() $\ell _t$
so that
$\ell _t$
so that
![]() $m_t = t$
.
$m_t = t$
.
As
![]() $\overline {F}_{\mathcal {B}_2}(\ell _t) = 0$
, we have
$\overline {F}_{\mathcal {B}_2}(\ell _t) = 0$
, we have
This enables us to give an upper bound on the denominator in the expression for the entropy norm. Specifically, using the fact that
![]() $x\exp (-x) \leq 1 - \exp (-x)$
for
$x\exp (-x) \leq 1 - \exp (-x)$
for
![]() $x \geq 0$
, we have
$x \geq 0$
, we have
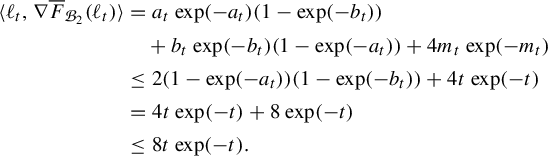 $$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{\mathcal{B}_2}(\ell_t) \rangle & = a_t\exp(-a_t)(1 - \exp(-b_t))\\ &\quad+ b_t\exp(-b_t)(1 - \exp(-a_t)) + 4m_t\exp(-m_t) \\ & \leq 2(1-\exp(-a_t))(1-\exp(-b_t)) + 4t\exp(-t) \\ & = 4t\exp(-t) + 8\exp(-t) \\ & \leq 8t\exp(-t). \end{align*} $$
$$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{\mathcal{B}_2}(\ell_t) \rangle & = a_t\exp(-a_t)(1 - \exp(-b_t))\\ &\quad+ b_t\exp(-b_t)(1 - \exp(-a_t)) + 4m_t\exp(-m_t) \\ & \leq 2(1-\exp(-a_t))(1-\exp(-b_t)) + 4t\exp(-t) \\ & = 4t\exp(-t) + 8\exp(-t) \\ & \leq 8t\exp(-t). \end{align*} $$
The penultimate line follows from (6.2), and in the final inequality we use the fact that
![]() $t \geq 4$
.
$t \geq 4$
.
Next, we get a lower bound on the numerator in the expression for the entropy norm. We claim that
![]() $-\langle \dot \ell _t,\mathbf {H}[\overline {F}_{\mathcal {B}_2}(\ell _t)]\dot \ell _t \rangle \geq (\dot m_t)^2\exp (-m_t)$
. We have that
$-\langle \dot \ell _t,\mathbf {H}[\overline {F}_{\mathcal {B}_2}(\ell _t)]\dot \ell _t \rangle \geq (\dot m_t)^2\exp (-m_t)$
. We have that
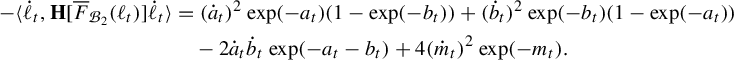 $$ \begin{align*} -\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\mathcal{B}_2}(\ell_t)]\dot \ell_t \rangle & = (\dot a_t)^2\exp(-a_t)(1 - \exp(-b_t)) + (\dot b_t)^2\exp(-b_t)(1 - \exp(-a_t)) \\ & \quad - 2\dot a_t \dot b_t\exp(-a_t - b_t) + 4(\dot m_t)^2\exp(-m_t). \end{align*} $$
$$ \begin{align*} -\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\mathcal{B}_2}(\ell_t)]\dot \ell_t \rangle & = (\dot a_t)^2\exp(-a_t)(1 - \exp(-b_t)) + (\dot b_t)^2\exp(-b_t)(1 - \exp(-a_t)) \\ & \quad - 2\dot a_t \dot b_t\exp(-a_t - b_t) + 4(\dot m_t)^2\exp(-m_t). \end{align*} $$
Therefore if
![]() $\dot a_t \dot b_t < 0$
then each term is positive and so the claim holds. Therefore, we assume that
$\dot a_t \dot b_t < 0$
then each term is positive and so the claim holds. Therefore, we assume that
![]() $\dot a_t$
and
$\dot a_t$
and
![]() $\dot b_t$
have the same sign. As
$\dot b_t$
have the same sign. As
![]() $\langle \dot \ell _t , \nabla \overline {F}_{\mathcal {B}_2}(\ell _t) \rangle = 0$
, we have that
$\langle \dot \ell _t , \nabla \overline {F}_{\mathcal {B}_2}(\ell _t) \rangle = 0$
, we have that
We write this equation as
![]() $w = u + v$
. As
$w = u + v$
. As
![]() $\overline {F}_{\mathcal {B}_2}(\ell _t) = 0$
, we find that
$\overline {F}_{\mathcal {B}_2}(\ell _t) = 0$
, we find that
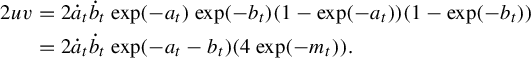 $$ \begin{align*} 2uv & = 2\dot a_t \dot b_t\exp(-a_t)\exp(-b_t)(1 - \exp(-a_t))(1 - \exp(-b_t))\\ &= 2\dot a_t \dot b_t\exp(-a_t-b_t)(4\exp(-m_t)). \end{align*} $$
$$ \begin{align*} 2uv & = 2\dot a_t \dot b_t\exp(-a_t)\exp(-b_t)(1 - \exp(-a_t))(1 - \exp(-b_t))\\ &= 2\dot a_t \dot b_t\exp(-a_t-b_t)(4\exp(-m_t)). \end{align*} $$
As
![]() $2xy \leq \tfrac 34(x+y)^2$
for all x and y, we find that
$2xy \leq \tfrac 34(x+y)^2$
for all x and y, we find that
Therefore
![]() $2\dot a_t \dot b_t\exp (-a_t-b_t) \leq 3(\dot m_t)^2\exp (-m_t)$
. From this the claim now follows, and furthermore that
$2\dot a_t \dot b_t\exp (-a_t-b_t) \leq 3(\dot m_t)^2\exp (-m_t)$
. From this the claim now follows, and furthermore that
Hence we find that the entropy norm along this path is bounded below by
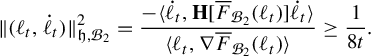 $$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{B}_2} = \frac{-\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\mathcal{B}_2}(\ell_t)]\dot \ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_{\mathcal{B}_2}(\ell_t) \rangle}\geq \frac{1}{8t}. \end{align*} $$
$$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{B}_2} = \frac{-\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\mathcal{B}_2}(\ell_t)]\dot \ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_{\mathcal{B}_2}(\ell_t) \rangle}\geq \frac{1}{8t}. \end{align*} $$
Therefore the length of this path in the entropy metric is at least
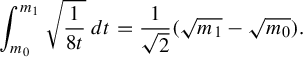 $$ \begin{align*} \int_{m_0}^{m_1} \sqrt{\frac{1}{8t}} \, dt &= \frac{1}{\sqrt{2}} (\sqrt{m_1} - \sqrt{m_0}).\\[-42pt] \end{align*} $$
$$ \begin{align*} \int_{m_0}^{m_1} \sqrt{\frac{1}{8t}} \, dt &= \frac{1}{\sqrt{2}} (\sqrt{m_1} - \sqrt{m_0}).\\[-42pt] \end{align*} $$
As for the 2-rose, we obtain the following proposition.
Proposition 6.4. Suppose
![]() $\ell $
and
$\ell $
and
![]() $\ell '$
are length functions in
$\ell '$
are length functions in
![]() $\mathcal {M}^1(\mathcal {B}_2)$
where
$\mathcal {M}^1(\mathcal {B}_2)$
where
![]() $m = \ell (e_1) + \ell (e_2) + 2\ell (e_3)$
and
$m = \ell (e_1) + \ell (e_2) + 2\ell (e_3)$
and
![]() $m' = \ell '(e_1) + \ell '(e_2) + 2\ell '(e_3)$
are at least
$m' = \ell '(e_1) + \ell '(e_2) + 2\ell '(e_3)$
are at least
![]() $4$
. Then
$4$
. Then
6.3 The theta graph
Let
![]() $\Theta _2$
denote the graph with vertices v and w, and edges
$\Theta _2$
denote the graph with vertices v and w, and edges
![]() $e_1$
,
$e_1$
,
![]() $e_2$
and
$e_2$
and
![]() $e_3$
where
$e_3$
where
![]() $o(e_i) = v$
and
$o(e_i) = v$
and
![]() $\tau (e_i) = w$
for
$\tau (e_i) = w$
for
![]() $i \in \{1,2,3\}$
. To make the calculations in this section easier to read, given a length function
$i \in \{1,2,3\}$
. To make the calculations in this section easier to read, given a length function
![]() $\ell \in \mathcal {M}(\Theta _2)$
, we set
$\ell \in \mathcal {M}(\Theta _2)$
, we set
![]() $a = \ell (e_1) + \ell (e_2)$
,
$a = \ell (e_1) + \ell (e_2)$
,
![]() $b = \ell (e_2) + \ell (e_3)$
,
$b = \ell (e_2) + \ell (e_3)$
,
![]() $c = \ell (e_3) + \ell (e_1)$
and
$c = \ell (e_3) + \ell (e_1)$
and
![]() $m = \ell (e_1) + \ell (e_2) + \ell (e_3)$
. Applying the definition of
$m = \ell (e_1) + \ell (e_2) + \ell (e_3)$
. Applying the definition of
![]() $\overline {F}_G$
from §4.2 to
$\overline {F}_G$
from §4.2 to
![]() $\Theta _2$
, we find the formula
$\Theta _2$
, we find the formula
Lemma 6.5. Suppose
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^{1}(\Theta _{2})$
is a smooth path such that for all
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^{1}(\Theta _{2})$
is a smooth path such that for all
![]() $t \in [0,1]$
we have
$t \in [0,1]$
we have
![]() $\dot m_t> 0$
. If
$\dot m_t> 0$
. If
![]() $m_0 \geq 4$
, then
$m_0 \geq 4$
, then
Proof. Suppose that
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\Theta _2)$
is a path where
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\Theta _2)$
is a path where
![]() $\dot m_t> 0$
as in the statement of the lemma and assume that
$\dot m_t> 0$
as in the statement of the lemma and assume that
![]() $m_0 \geq 4$
. We reparametrize the path
$m_0 \geq 4$
. We reparametrize the path
![]() $\ell _t$
so that
$\ell _t$
so that
![]() $m_t = t$
.
$m_t = t$
.
Let
![]() $n_t = \min \{a_t,b_t,c_t\}$
. As
$n_t = \min \{a_t,b_t,c_t\}$
. As
![]() $\overline {F}_{\Theta _2}(\ell _t) = 0$
, we have
$\overline {F}_{\Theta _2}(\ell _t) = 0$
, we have
In particular,
![]() $3\exp (-n_t) \geq 1- 2\exp (-t)> 3\exp (-2)$
as
$3\exp (-n_t) \geq 1- 2\exp (-t)> 3\exp (-2)$
as
![]() $t \geq 4$
and thus
$t \geq 4$
and thus
![]() $n_t < 2$
for all t.
$n_t < 2$
for all t.
Setting
![]() $p_t = \max \{a_t,b_t,c_t\}$
and
$p_t = \max \{a_t,b_t,c_t\}$
and
![]() $q_t = a_t + b_t + c_t - p_t - n_t$
so that
$q_t = a_t + b_t + c_t - p_t - n_t$
so that
![]() $\{ p_t,q_t,n_t \} = \{ a_t,b_t,c_t \}$
for all t, we find that
$\{ p_t,q_t,n_t \} = \{ a_t,b_t,c_t \}$
for all t, we find that
![]() $p_t,q_t \geq t-2$
as
$p_t,q_t \geq t-2$
as
![]() $p_t + q_t = 2t - n_t \geq 2t - 2$
and
$p_t + q_t = 2t - n_t \geq 2t - 2$
and
![]() ${p_t,q_t \leq t}$
. Therefore, as
${p_t,q_t \leq t}$
. Therefore, as
![]() $t - 2 \geq 2$
for
$t - 2 \geq 2$
for
![]() $t \geq 4$
, the cycle that realizes the minimum of
$t \geq 4$
, the cycle that realizes the minimum of
![]() $\{a_t,b_t\,c_t\}$
does not depend on t and therefore we may assume that
$\{a_t,b_t\,c_t\}$
does not depend on t and therefore we may assume that
![]() $c_t = \min \{a_t,b_t,c_t\}$
and thus
$c_t = \min \{a_t,b_t,c_t\}$
and thus
![]() $a_t,b_t \geq t-2$
. Therefore
$a_t,b_t \geq t-2$
. Therefore
![]() $\exp (-a_t),\exp (-b_t) \leq \exp (-t+2)$
. Hence, again as
$\exp (-a_t),\exp (-b_t) \leq \exp (-t+2)$
. Hence, again as
![]() $\overline {F}_{\Theta _2}(\ell _t) = 0$
, we have
$\overline {F}_{\Theta _2}(\ell _t) = 0$
, we have
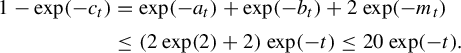 $$ \begin{align*} 1 - \exp(-c_t) &= \exp(-a_t) + \exp(-b_t) + 2\exp(-m_t)\\ &\leq (2\exp(2) + 2)\exp(-t) \leq 20\exp(-t). \end{align*} $$
$$ \begin{align*} 1 - \exp(-c_t) &= \exp(-a_t) + \exp(-b_t) + 2\exp(-m_t)\\ &\leq (2\exp(2) + 2)\exp(-t) \leq 20\exp(-t). \end{align*} $$
This enables us to give an upper bound on the denominator in the expression for the entropy norm. Specifically, using the fact that
![]() $x\exp (-x) \leq 1 - \exp (-x)$
for
$x\exp (-x) \leq 1 - \exp (-x)$
for
![]() $x \geq 0$
, we have
$x \geq 0$
, we have
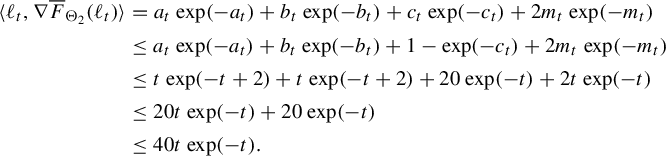 $$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{\Theta_2}(\ell_t) \rangle & = a_t\exp(-a_t) + b_t\exp(-b_t) + c_t\exp(-c_t)+ 2m_t\exp(-m_t) \\ & \leq a_t\exp(-a_t) + b_t\exp(-b_t) + 1 - \exp(-c_t)+ 2m_t\exp(-m_t) \\ & \leq t\exp(-t+2) + t\exp(-t+2) + 20\exp(-t) + 2t\exp(-t) \\ & \leq 20t\exp(-t) + 20\exp(-t) \\ & \leq 40t\exp(-t). \end{align*} $$
$$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{\Theta_2}(\ell_t) \rangle & = a_t\exp(-a_t) + b_t\exp(-b_t) + c_t\exp(-c_t)+ 2m_t\exp(-m_t) \\ & \leq a_t\exp(-a_t) + b_t\exp(-b_t) + 1 - \exp(-c_t)+ 2m_t\exp(-m_t) \\ & \leq t\exp(-t+2) + t\exp(-t+2) + 20\exp(-t) + 2t\exp(-t) \\ & \leq 20t\exp(-t) + 20\exp(-t) \\ & \leq 40t\exp(-t). \end{align*} $$
In the final inequality we used the fact that
![]() $t \geq 4$
.
$t \geq 4$
.
Next, we get a lower bound on the numerator in the expression for the entropy norm by just using
![]() $m_t$
. Specifically,
$m_t$
. Specifically,
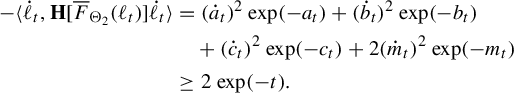 $$ \begin{align*} -\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\Theta_2}(\ell_t)]\dot \ell_t \rangle & = (\dot a_t)^2\exp(-a_t) + (\dot b_t)^2\exp(-b_t)\\ &\quad+ (\dot c_t)^2\exp(-c_t) + 2(\dot m_t)^2\exp(-m_t) \\ & \geq 2\exp(-t). \end{align*} $$
$$ \begin{align*} -\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\Theta_2}(\ell_t)]\dot \ell_t \rangle & = (\dot a_t)^2\exp(-a_t) + (\dot b_t)^2\exp(-b_t)\\ &\quad+ (\dot c_t)^2\exp(-c_t) + 2(\dot m_t)^2\exp(-m_t) \\ & \geq 2\exp(-t). \end{align*} $$
Hence we find that the entropy norm along this path is bounded below by
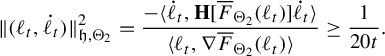 $$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\Theta_2} = \frac{-\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\Theta_2}(\ell_t)]\dot \ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_{\Theta_2}(\ell_t) \rangle}\geq \frac{1}{20t}. \end{align*} $$
$$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\Theta_2} = \frac{-\langle \dot \ell_t,\mathbf{H}[\overline{F}_{\Theta_2}(\ell_t)]\dot \ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_{\Theta_2}(\ell_t) \rangle}\geq \frac{1}{20t}. \end{align*} $$
Therefore the length of this path in the entropy metric is at least
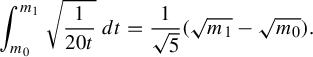 $$ \begin{align*} \int_{m_0}^{m_1} \sqrt{\frac{1}{20t}} \, dt &= \frac{1}{\sqrt{5}} (\sqrt{m_1} - \sqrt{m_0}).\\[-42pt] \end{align*} $$
$$ \begin{align*} \int_{m_0}^{m_1} \sqrt{\frac{1}{20t}} \, dt &= \frac{1}{\sqrt{5}} (\sqrt{m_1} - \sqrt{m_0}).\\[-42pt] \end{align*} $$
Again, as for the 2-rose, we obtain the following proposition.
Proposition 6.6. Suppose
![]() $\ell $
and
$\ell $
and
![]() $\ell '$
are length functions in
$\ell '$
are length functions in
![]() $\mathcal {M}^1(\Theta _2)$
where
$\mathcal {M}^1(\Theta _2)$
where
![]() $m = \ell (e_1) + \ell (e_2) + \ell (e_3)$
and
$m = \ell (e_1) + \ell (e_2) + \ell (e_3)$
and
![]() $m' = \ell '(e_1) + \ell '(e_2) + \ell '(e_3)$
are at least
$m' = \ell '(e_1) + \ell '(e_2) + \ell '(e_3)$
are at least
![]() $4$
. Then
$4$
. Then
6.4
 $(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete
$(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete
We can now prove the main result of this section that the entropy metric on
![]() $\mathcal {X}^1(\mathbb {F}_2)$
is complete. Given a marked metric graph
$\mathcal {X}^1(\mathbb {F}_2)$
is complete. Given a marked metric graph
![]() $x = [(G,\rho ,\ell )]$
in
$x = [(G,\rho ,\ell )]$
in
![]() $\mathcal {X}^1(\mathbb {F}_2)$
, we let
$\mathcal {X}^1(\mathbb {F}_2)$
, we let
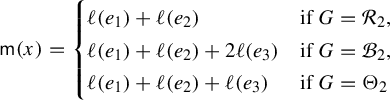 $$ \begin{align*}\textsf{m}(x) = \begin{cases} \ell(e_1) + \ell(e_2) & \mbox{if } G = \mathcal{R}_2, \\ \ell(e_1) + \ell(e_2) + 2\ell(e_3) & \mbox{if } G = \mathcal{B}_2, \\ \ell(e_1) + \ell(e_2) + \ell(e_3) & \mbox{if } G = \Theta_2 \\ \end{cases}\end{align*} $$
$$ \begin{align*}\textsf{m}(x) = \begin{cases} \ell(e_1) + \ell(e_2) & \mbox{if } G = \mathcal{R}_2, \\ \ell(e_1) + \ell(e_2) + 2\ell(e_3) & \mbox{if } G = \mathcal{B}_2, \\ \ell(e_1) + \ell(e_2) + \ell(e_3) & \mbox{if } G = \Theta_2 \\ \end{cases}\end{align*} $$
We remark that
![]() $\textsf {m} \colon \thinspace \mathcal {X}^1(\mathbb {F}_2) \to \mathbb {R}$
is an
$\textsf {m} \colon \thinspace \mathcal {X}^1(\mathbb {F}_2) \to \mathbb {R}$
is an
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_2)$
-invariant continuous function.
$\operatorname {\mathrm {Out}}(\mathbb {F}_2)$
-invariant continuous function.
Lemma 6.7. Let
![]() $(x_n)_{n \in \mathbb {N}}$
be a Cauchy sequence in
$(x_n)_{n \in \mathbb {N}}$
be a Cauchy sequence in
![]() $(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
. Then there is an L such that
$(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
. Then there is an L such that
![]() $\textsf {m}(x_n) \leq L$
for all n.
$\textsf {m}(x_n) \leq L$
for all n.
Proof. Suppose that
![]() $(x_n)_{n \in \mathbb {N}}$
is a sequence in
$(x_n)_{n \in \mathbb {N}}$
is a sequence in
![]() $\mathcal {X}^1(\mathbb {F}_2)$
such that
$\mathcal {X}^1(\mathbb {F}_2)$
such that
![]() $\textsf {m}(x_n) \to \infty $
. We will show that
$\textsf {m}(x_n) \to \infty $
. We will show that
![]() $(x_n)_{n \in \mathbb {N}}$
is not Cauchy by showing that
$(x_n)_{n \in \mathbb {N}}$
is not Cauchy by showing that
![]() $\limsup d_{\mathfrak {h}}(x_1,x_n) = \infty $
.
$\limsup d_{\mathfrak {h}}(x_1,x_n) = \infty $
.
Let
![]() $m = \max \{\textsf {m}(x_1),4\}$
. Given
$m = \max \{\textsf {m}(x_1),4\}$
. Given
![]() $N \geq 0$
, we let n be such that
$N \geq 0$
, we let n be such that
![]() $\sqrt {\textsf {m}(x_n)} \geq \sqrt {5}N + \sqrt {m}$
. Consider a path
$\sqrt {\textsf {m}(x_n)} \geq \sqrt {5}N + \sqrt {m}$
. Consider a path
![]() $\alpha _t \colon \thinspace [0,1] \to \mathcal {X}^1(\mathbb {F}_2)$
such that
$\alpha _t \colon \thinspace [0,1] \to \mathcal {X}^1(\mathbb {F}_2)$
such that
![]() $\alpha _0 = x_1$
and
$\alpha _0 = x_1$
and
![]() $\alpha _1 = x_n$
. Let
$\alpha _1 = x_n$
. Let
![]() $\delta \in [0,1]$
be the minimal value such that
$\delta \in [0,1]$
be the minimal value such that
![]() $\textsf {m}(\alpha _t) \geq 4$
for all
$\textsf {m}(\alpha _t) \geq 4$
for all
![]() $t \in [\delta ,1]$
. In particular,
$t \in [\delta ,1]$
. In particular,
![]() $\textsf {m}(\alpha _\delta ) \leq m$
.
$\textsf {m}(\alpha _\delta ) \leq m$
.
Combining Propositions 6.2, 6.4 and 6.6, we find that
This also provides a lower bound on
![]() $\mathcal {L}_{\mathfrak {h}}(\alpha _t|[0,1])$
. Since the path was arbitrary, this also is a lower bound on
$\mathcal {L}_{\mathfrak {h}}(\alpha _t|[0,1])$
. Since the path was arbitrary, this also is a lower bound on
![]() $d_{\mathfrak {h}}(x_1,x_n)$
.
$d_{\mathfrak {h}}(x_1,x_n)$
.
Therefore
![]() $d_{\mathfrak {h}}(x_1,x_n) \geq N$
, showing that
$d_{\mathfrak {h}}(x_1,x_n) \geq N$
, showing that
![]() $\limsup d_{\mathfrak {h}}(x_1,x_n) = \infty $
as claimed.
$\limsup d_{\mathfrak {h}}(x_1,x_n) = \infty $
as claimed.
Given
![]() $L \geq 0$
, we set
$L \geq 0$
, we set
![]() $\mathcal {X}^1_L(\mathbb {F}_2) = \{ x \in \mathcal {X}^1(\mathbb {F}_2) \mid \textsf {m}(x) \leq L \}$
, and additionally, given a marked graph
$\mathcal {X}^1_L(\mathbb {F}_2) = \{ x \in \mathcal {X}^1(\mathbb {F}_2) \mid \textsf {m}(x) \leq L \}$
, and additionally, given a marked graph
![]() $\rho \colon \thinspace \mathcal {R}_2 \to G$
, we set
$\rho \colon \thinspace \mathcal {R}_2 \to G$
, we set
![]() $\mathcal {X}^1_L(G,\rho ) = \mathcal {X}^1(G,\rho ) \cap \mathcal {X}^1_L(\mathbb {F}_2)$
. We remark that the closure of
$\mathcal {X}^1_L(G,\rho ) = \mathcal {X}^1(G,\rho ) \cap \mathcal {X}^1_L(\mathbb {F}_2)$
. We remark that the closure of
![]() $\mathcal {X}^1_L(G,\rho )$
is compact. As
$\mathcal {X}^1_L(G,\rho )$
is compact. As
![]() $\mathcal {X}^1(\mathbb {F}_2)$
is locally finite and there are only finitely many topological types of graphs, the following statement holds. For all
$\mathcal {X}^1(\mathbb {F}_2)$
is locally finite and there are only finitely many topological types of graphs, the following statement holds. For all
![]() $L, D \geq 0$
, there is an N such that if
$L, D \geq 0$
, there is an N such that if
![]() $x \in \mathcal {X}^1_L(\mathbb {F}_2)$
then there is a collection of marked graphs
$x \in \mathcal {X}^1_L(\mathbb {F}_2)$
then there is a collection of marked graphs
![]() $(G_1,\rho _1),\ldots ,(G_N,\rho _N)$
such that
$(G_1,\rho _1),\ldots ,(G_N,\rho _N)$
such that
 $$ \begin{align*} \{x' \in \mathcal{X}^1_L(\mathbb{F}_2) \mid d_{\mathfrak{h}}(x,x') \leq D \} \subseteq \bigcup_{k=1}^N \mathcal{X}^1_L(G_k,\rho_k).\end{align*} $$
$$ \begin{align*} \{x' \in \mathcal{X}^1_L(\mathbb{F}_2) \mid d_{\mathfrak{h}}(x,x') \leq D \} \subseteq \bigcup_{k=1}^N \mathcal{X}^1_L(G_k,\rho_k).\end{align*} $$
Proposition 6.8. The metric space
![]() $(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete.
$(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete.
Proof. Let
![]() $(x_n)_{n \in \mathbb {N}}$
be a Cauchy sequence in
$(x_n)_{n \in \mathbb {N}}$
be a Cauchy sequence in
![]() $(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
. By Lemma 6.7, there is an L such that
$(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
. By Lemma 6.7, there is an L such that
![]() $(x_n) \subset \mathcal {X}^1_L(\mathbb {F}_2)$
. Let
$(x_n) \subset \mathcal {X}^1_L(\mathbb {F}_2)$
. Let
![]() $n_0$
be such that
$n_0$
be such that
![]() $d_{\mathfrak {h}}(x_n,x_m) \leq 1$
if
$d_{\mathfrak {h}}(x_n,x_m) \leq 1$
if
![]() $n,m \geq n_0$
. By the above remark, there are finitely marked graphs
$n,m \geq n_0$
. By the above remark, there are finitely marked graphs
![]() $(G_1,\rho _1), \ldots , (G_N,\rho _N)$
such that
$(G_1,\rho _1), \ldots , (G_N,\rho _N)$
such that
 $$ \begin{align*} \{ x_n | n \geq n_0 \} \subset \{ x' \in \mathcal{X}^1_L(\mathbb{F}_2) \mid d_{\mathfrak{h}}(x_{n_0},x') \leq 1 \} \subseteq \bigcup_{k=1}^N \mathcal{X}^1_L(G_k,\rho_k). \end{align*} $$
$$ \begin{align*} \{ x_n | n \geq n_0 \} \subset \{ x' \in \mathcal{X}^1_L(\mathbb{F}_2) \mid d_{\mathfrak{h}}(x_{n_0},x') \leq 1 \} \subseteq \bigcup_{k=1}^N \mathcal{X}^1_L(G_k,\rho_k). \end{align*} $$
As the closure of this set in
![]() $\mathcal {X}^1(\mathbb {F}_2)$
is compact, the sequence
$\mathcal {X}^1(\mathbb {F}_2)$
is compact, the sequence
![]() $(x_n)_{n \in \mathbb {N}}$
converges.
$(x_n)_{n \in \mathbb {N}}$
converges.
7 The moduli space of the rose
The purpose of this section is to examine the entropy metric on the moduli space of an r-rose
![]() $\mathcal {M}^1(\mathcal {R}_r)$
. We begin in §7.1 by computing the function
$\mathcal {M}^1(\mathcal {R}_r)$
. We begin in §7.1 by computing the function
![]() $\overline {F}_{\mathcal {R}_r}$
introduced in §4.2. For the r-rose, we can strengthen Proposition 4.13 and conclude that
$\overline {F}_{\mathcal {R}_r}$
introduced in §4.2. For the r-rose, we can strengthen Proposition 4.13 and conclude that
![]() $\mathcal {M}^1(\mathcal {R}_r)$
equals the set of length functions
$\mathcal {M}^1(\mathcal {R}_r)$
equals the set of length functions
![]() $\ell $
for which
$\ell $
for which
![]() $\overline {F}_{\mathcal {R}_r}(\ell ) = 0$
. Next, in §7.2 we show that
$\overline {F}_{\mathcal {R}_r}(\ell ) = 0$
. Next, in §7.2 we show that
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
for
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
for
![]() $r \geq 3$
is not complete by producing paths that have finite length yet no accumulation point. Lastly, in §7.3 we show that
$r \geq 3$
is not complete by producing paths that have finite length yet no accumulation point. Lastly, in §7.3 we show that
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter. Specifically, a path that shrinks the length of an edge to zero necessarily has infinite length.
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter. Specifically, a path that shrinks the length of an edge to zero necessarily has infinite length.
7.1
 $\mathcal {M}^1(\mathcal {R}_r)$
as a zero locus
$\mathcal {M}^1(\mathcal {R}_r)$
as a zero locus
In this section we compute the function
![]() $\overline {F}_{\mathcal {R}_r}$
. This appears as Proposition 7.3. In Proposition 7.5 we prove that
$\overline {F}_{\mathcal {R}_r}$
. This appears as Proposition 7.3. In Proposition 7.5 we prove that
![]() $\mathcal {M}^1(\mathcal {R}_r) = \{\ell \in \mathcal {M}(\mathcal {R}_r) \mid \overline {F}_{\mathcal {R}_r}(\ell ) = 0 \}$
; this strengthens Proposition 4.13 in this setting.
$\mathcal {M}^1(\mathcal {R}_r) = \{\ell \in \mathcal {M}(\mathcal {R}_r) \mid \overline {F}_{\mathcal {R}_r}(\ell ) = 0 \}$
; this strengthens Proposition 4.13 in this setting.
First we set some notation for working with the graph
![]() $\mathcal {R}_r$
. We identify the unoriented edges of
$\mathcal {R}_r$
. We identify the unoriented edges of
![]() $\mathcal {R}_{r}$
with the set
$\mathcal {R}_{r}$
with the set
![]() $[r] = \{1,2,\ldots ,r\}$
. To simplify the expressions, we will use r as the identifying subscript rather than
$[r] = \{1,2,\ldots ,r\}$
. To simplify the expressions, we will use r as the identifying subscript rather than
![]() $\mathcal {R}_{r}$
and we will use variables
$\mathcal {R}_{r}$
and we will use variables
![]() $\ell = (\ell ^1,\ldots , \ell ^r)$
to denote the length of the unoriented edges. The matrix
$\ell = (\ell ^1,\ldots , \ell ^r)$
to denote the length of the unoriented edges. The matrix
![]() $\overline {A}_{r,\ell } \in \operatorname {\mathrm {Mat}}_{r}(\mathbb {R})$
has rows and columns indexed by
$\overline {A}_{r,\ell } \in \operatorname {\mathrm {Mat}}_{r}(\mathbb {R})$
has rows and columns indexed by
![]() $[r]$
, and we have
$[r]$
, and we have
where
![]() is the Kronecker delta function.
is the Kronecker delta function.
For the calculations in this section, we need the following combinatorial identities.
Lemma 7.1. For any
![]() $r \geq 1$
and any
$r \geq 1$
and any
![]() $x \in \mathbb {R}$
, the following equations hold:
$x \in \mathbb {R}$
, the following equations hold:
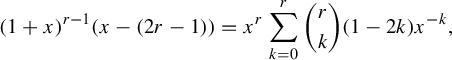 $$ \begin{align} (1 + x)^{r-1}(x - (2r-1)) &= x^r\sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} (1-2k) x^{-k}, \end{align} $$
$$ \begin{align} (1 + x)^{r-1}(x - (2r-1)) &= x^r\sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} (1-2k) x^{-k}, \end{align} $$
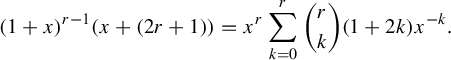 $$ \begin{align} (1 + x)^{r-1}(x + (2r+1)) &= x^r\sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} (1+2k) x^{-k}. \end{align} $$
$$ \begin{align} (1 + x)^{r-1}(x + (2r+1)) &= x^r\sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} (1+2k) x^{-k}. \end{align} $$
Proof. Differentiate the equation
![]() $(1+x)^{r} = \sum _{k=0}^{r}\genfrac {(}{)}{0pt}{1}{r}{k} x^{r-k}$
and multiply it by x to obtain the equality
$(1+x)^{r} = \sum _{k=0}^{r}\genfrac {(}{)}{0pt}{1}{r}{k} x^{r-k}$
and multiply it by x to obtain the equality
![]() $rx(1+x)^{r-1} = \sum _{k=0}^{r} (r-k) \genfrac {(}{)}{0pt}{1}{r}{k} x^{r-k}$
. Therefore
$rx(1+x)^{r-1} = \sum _{k=0}^{r} (r-k) \genfrac {(}{)}{0pt}{1}{r}{k} x^{r-k}$
. Therefore
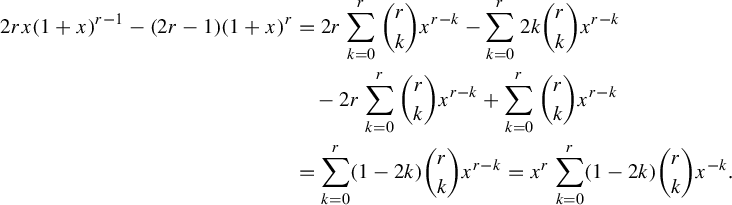 $$ \begin{align*} 2rx(1+x)^{r-1} - (2r-1)(1+x)^{r} &= 2r\sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} x^{r-k} - \sum_{k=0}^{r} 2k \genfrac{(}{)}{0pt}{0}{r}{k} x^{r-k} \\ & \quad - 2r\sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} x^{r-k} + \sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} x^{r-k} \\ & = \sum_{k=0}^{r} (1 - 2k) \genfrac{(}{)}{0pt}{0}{r}{k}x^{r-k} = x^{r}\sum_{k=0}^{r}(1-2k)\genfrac{(}{)}{0pt}{0}{r}{k} x^{-k}. \end{align*} $$
$$ \begin{align*} 2rx(1+x)^{r-1} - (2r-1)(1+x)^{r} &= 2r\sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} x^{r-k} - \sum_{k=0}^{r} 2k \genfrac{(}{)}{0pt}{0}{r}{k} x^{r-k} \\ & \quad - 2r\sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} x^{r-k} + \sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} x^{r-k} \\ & = \sum_{k=0}^{r} (1 - 2k) \genfrac{(}{)}{0pt}{0}{r}{k}x^{r-k} = x^{r}\sum_{k=0}^{r}(1-2k)\genfrac{(}{)}{0pt}{0}{r}{k} x^{-k}. \end{align*} $$
The left-hand side in the above equation simplifies to
![]() $(1 + x)^{r-1}(x - (2r-1))$
. This shows (7.2). In a similar manner one can derive (7.3).
$(1 + x)^{r-1}(x - (2r-1))$
. This shows (7.2). In a similar manner one can derive (7.3).
Corollary 7.2. For any
![]() $r \geq 1$
,
$r \geq 1$
,
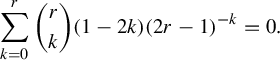 $$ \begin{align} \sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} (1-2k)(2r-1)^{-k} = 0. \end{align} $$
$$ \begin{align} \sum_{k=0}^{r} \genfrac{(}{)}{0pt}{0}{r}{k} (1-2k)(2r-1)^{-k} = 0. \end{align} $$
Proof. Evaluate equation (7.2) with
![]() $x = 2r-1$
. The left-hand side becomes
$x = 2r-1$
. The left-hand side becomes
![]() $0$
. Dividing the resulting equation by
$0$
. Dividing the resulting equation by
![]() $(2r-1)^{r}$
, we obtain (7.4).
$(2r-1)^{r}$
, we obtain (7.4).
Given a length function
![]() $\ell = (\ell ^1,\ldots ,\ell ^n) \in \mathcal {M}(\mathcal {R}_r)$
and a subset
$\ell = (\ell ^1,\ldots ,\ell ^n) \in \mathcal {M}(\mathcal {R}_r)$
and a subset
![]() $S \subseteq [r]$
, we define
$S \subseteq [r]$
, we define
![]() $\ell ^S = \sum _{k \in S} \ell ^k$
. In particular, we have
$\ell ^S = \sum _{k \in S} \ell ^k$
. In particular, we have
![]() $\ell ^\emptyset = 0$
.
$\ell ^\emptyset = 0$
.
Proposition 7.3. For any
![]() $r \geq 2$
and any length function
$r \geq 2$
and any length function
![]() $\ell \in \mathcal {M}(\mathcal {R}_r)$
,
$\ell \in \mathcal {M}(\mathcal {R}_r)$
,
Proof. Using the expansion of the determinant via permutations of
![]() $[r]$
, we can express
$[r]$
, we can express
![]() $\overline {F}_{r}(\ell ) = \det (I - \overline {A}_{r,\ell })$
as
$\overline {F}_{r}(\ell ) = \det (I - \overline {A}_{r,\ell })$
as
for some coefficients
![]() $c_{S,r} \in \mathbb {R}$
depending on the subset
$c_{S,r} \in \mathbb {R}$
depending on the subset
![]() $S \subseteq [r]$
and the rank r. Further, it is apparent that the coefficient
$S \subseteq [r]$
and the rank r. Further, it is apparent that the coefficient
![]() $c_{S,r}$
only depends on the cardinality of S. It remains to determine these coefficients. We will do so by induction.
$c_{S,r}$
only depends on the cardinality of S. It remains to determine these coefficients. We will do so by induction.
For
![]() $r=2$
, we compute
$r=2$
, we compute
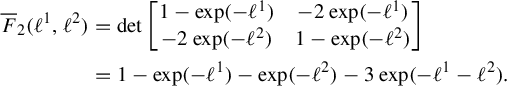 $$ \begin{align*} \overline{F}_{2}(\ell^{1},\ell^{2}) &= \det\left[\begin{matrix} 1 - \exp(-\ell^{1}) & -2\exp(-\ell^{1}) \\ -2\exp(-\ell^{2}) & 1 - \exp(-\ell^{2}) \end{matrix}\right] \\ & = 1 - \exp(-\ell^{1}) - \exp(-\ell^{2}) - 3\exp(-\ell^{1} - \ell^{2}). \end{align*} $$
$$ \begin{align*} \overline{F}_{2}(\ell^{1},\ell^{2}) &= \det\left[\begin{matrix} 1 - \exp(-\ell^{1}) & -2\exp(-\ell^{1}) \\ -2\exp(-\ell^{2}) & 1 - \exp(-\ell^{2}) \end{matrix}\right] \\ & = 1 - \exp(-\ell^{1}) - \exp(-\ell^{2}) - 3\exp(-\ell^{1} - \ell^{2}). \end{align*} $$
This shows the proposition for
![]() $r = 2$
.
$r = 2$
.
Suppose
![]() $r \geq 3$
and that the proposition holds for
$r \geq 3$
and that the proposition holds for
![]() $r-1$
. That is, we assume that
$r-1$
. That is, we assume that
![]() $c_{S,r-1} = 1-2\lvert {S} \rvert $
for any
$c_{S,r-1} = 1-2\lvert {S} \rvert $
for any
![]() $S \subseteq [r-1]$
. Since
$S \subseteq [r-1]$
. Since
![]() $c_{S,r}$
only depends on the cardinality of S, this implies that
$c_{S,r}$
only depends on the cardinality of S, this implies that
![]() $c_{S,r} = 1 - 2\lvert {S} \rvert $
for any
$c_{S,r} = 1 - 2\lvert {S} \rvert $
for any
![]() $S \subseteq [r]$
where
$S \subseteq [r]$
where
![]() $\lvert {S} \rvert < r$
as well. Hence it only remains to compute
$\lvert {S} \rvert < r$
as well. Hence it only remains to compute
![]() $c_{[r],r}$
.
$c_{[r],r}$
.
To compute
![]() $c_{[r],r}$
, we make use of Corollary 7.2. Indeed, by Example 3.3, we have
$c_{[r],r}$
, we make use of Corollary 7.2. Indeed, by Example 3.3, we have
![]() $\mathfrak {h}_r(\log (2r-1) \cdot \mathbf {1}) {{\kern-1pt}={\kern-1pt}} 1$
. Therefore, by Proposition 4.13, we obtain
$\mathfrak {h}_r(\log (2r-1) \cdot \mathbf {1}) {{\kern-1pt}={\kern-1pt}} 1$
. Therefore, by Proposition 4.13, we obtain
![]() ${\overline {F}_{r}(\log (2r-1) \cdot \mathbf {1}) {{\kern-1pt}={\kern-1pt}} 0}$
. Hence
${\overline {F}_{r}(\log (2r-1) \cdot \mathbf {1}) {{\kern-1pt}={\kern-1pt}} 0}$
. Hence
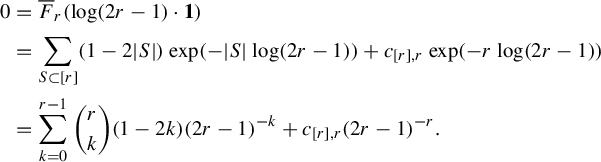 $$ \begin{align*} 0 & = \overline{F}_{r}(\log(2r-1) \cdot \mathbf{1}) \\ & = \sum_{S \subset [r]} (1 - 2\lvert {S} \rvert) \exp(-\lvert {S} \rvert\log(2r-1)) + c_{[r],r}\exp(-r\log(2r-1)) \\ & = \sum_{k=0}^{r-1} \genfrac{(}{)}{0pt}{0}{r}{k} (1-2k)(2r-1)^{-k} + c_{[r],r}(2r-1)^{-r}. \end{align*} $$
$$ \begin{align*} 0 & = \overline{F}_{r}(\log(2r-1) \cdot \mathbf{1}) \\ & = \sum_{S \subset [r]} (1 - 2\lvert {S} \rvert) \exp(-\lvert {S} \rvert\log(2r-1)) + c_{[r],r}\exp(-r\log(2r-1)) \\ & = \sum_{k=0}^{r-1} \genfrac{(}{)}{0pt}{0}{r}{k} (1-2k)(2r-1)^{-k} + c_{[r],r}(2r-1)^{-r}. \end{align*} $$
By Corollary 7.2, we find that
![]() $c_{[r],r} = 1-2r$
as desired.
$c_{[r],r} = 1-2r$
as desired.
Example 7.4. For
![]() $r = 2$
and
$r = 2$
and
![]() $r = 3$
, using the coordinates
$r = 3$
, using the coordinates
![]() $x = \exp (-\ell ^{1})$
,
$x = \exp (-\ell ^{1})$
,
![]() $y = \exp (-\ell ^{2})$
and
$y = \exp (-\ell ^{2})$
and
![]() $z = \exp (-\ell ^{3})$
, we find
$z = \exp (-\ell ^{3})$
, we find
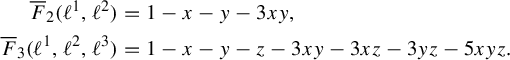 $$ \begin{align*} \overline{F}_{2}(\ell^{1},\ell^{2}) &= 1 - x - y - 3xy,\\ \overline{F}_{3}(\ell^{1},\ell^{2},\ell^{3}) &= 1 - x - y - z - 3xy - 3xz - 3yz - 5xyz. \end{align*} $$
$$ \begin{align*} \overline{F}_{2}(\ell^{1},\ell^{2}) &= 1 - x - y - 3xy,\\ \overline{F}_{3}(\ell^{1},\ell^{2},\ell^{3}) &= 1 - x - y - z - 3xy - 3xz - 3yz - 5xyz. \end{align*} $$
Figure 5 shows
![]() $\mathcal {M}^{1}(\mathcal {R}_{r})$
as a subset of
$\mathcal {M}^{1}(\mathcal {R}_{r})$
as a subset of
![]() $\mathcal {M}(\mathcal {R}_r)$
for
$\mathcal {M}(\mathcal {R}_r)$
for
![]() $r = 2$
and
$r = 2$
and
![]() $r = 3$
.
$r = 3$
.
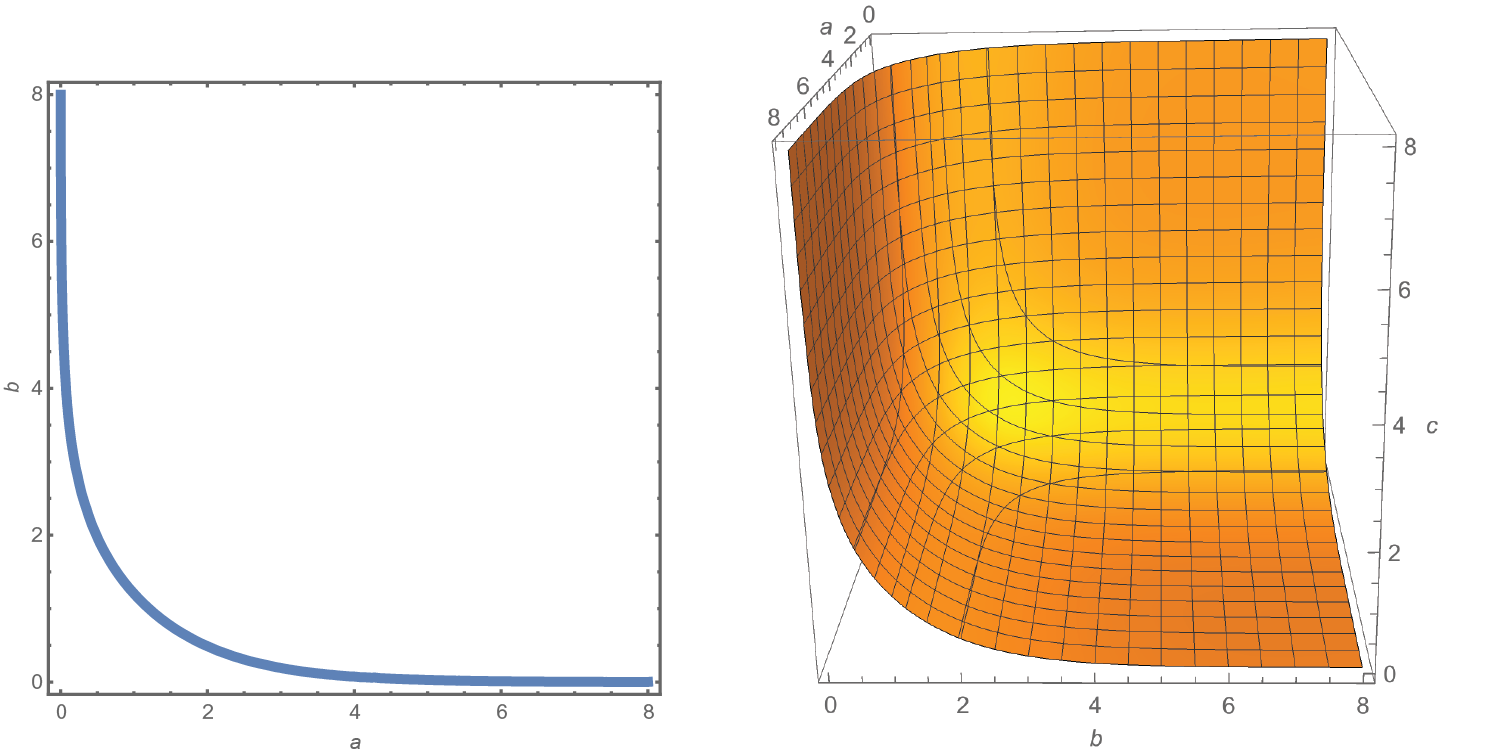
Figure 5 The hypersurfaces
![]() $\mathcal {M}^{1}(\mathcal {R}_{r})$
for the roses with 2 and 3 petals.
$\mathcal {M}^{1}(\mathcal {R}_{r})$
for the roses with 2 and 3 petals.
Using Proposition 7.3, we can provide a strengthening of Proposition 4.13 for the r-rose.
Proposition 7.5. For any
![]() $r \geq 2$
, the unit-entropy moduli space
$r \geq 2$
, the unit-entropy moduli space
![]() $\mathcal {M}^{1}(\mathcal {R}_{r}) $
equals the level set
$\mathcal {M}^{1}(\mathcal {R}_{r}) $
equals the level set
![]() $\{\ell \in \mathcal {M}(\mathcal {R}_r) \mid \overline {F}_{r}(\ell ) = 0 \}$
.
$\{\ell \in \mathcal {M}(\mathcal {R}_r) \mid \overline {F}_{r}(\ell ) = 0 \}$
.
Proof. By Proposition 4.13, we have that
![]() $\mathcal {M}^{1}(\mathcal {R}_{r}) \subseteq \{\ell \in \mathcal {M}(\mathcal {R}_r) \mid \overline {F}_{r}(\ell ) = 0 \}$
. Suppose that
$\mathcal {M}^{1}(\mathcal {R}_{r}) \subseteq \{\ell \in \mathcal {M}(\mathcal {R}_r) \mid \overline {F}_{r}(\ell ) = 0 \}$
. Suppose that
![]() $\overline {F}_{r}(\ell ) = 0$
for some
$\overline {F}_{r}(\ell ) = 0$
for some
![]() $\ell \in \mathcal {M}(\mathcal {R}_r)$
. Set
$\ell \in \mathcal {M}(\mathcal {R}_r)$
. Set
![]() $h = \mathfrak {h}_r(\ell )$
. We need to show that
$h = \mathfrak {h}_r(\ell )$
. We need to show that
![]() $h = 1$
.
$h = 1$
.
Consider the function
![]() $p \colon \thinspace \mathbb {R}_{>0} \to \mathbb {R}$
defined by
$p \colon \thinspace \mathbb {R}_{>0} \to \mathbb {R}$
defined by
![]() $p(t) = \overline {F}_{r}(t \cdot \ell )$
. We have
$p(t) = \overline {F}_{r}(t \cdot \ell )$
. We have
![]() $p(1) = \overline {F}_{r}(\ell ) = 0$
. As
$p(1) = \overline {F}_{r}(\ell ) = 0$
. As
![]() $\mathfrak {h}_r(h \cdot \ell ) = 1$
, we have
$\mathfrak {h}_r(h \cdot \ell ) = 1$
, we have
![]() $p(h) = \overline {F}_{r}(h \cdot \ell ) = 0$
as well by Proposition 4.13.
$p(h) = \overline {F}_{r}(h \cdot \ell ) = 0$
as well by Proposition 4.13.
Using the expression for
![]() $\overline {F}_r(\ell )$
derived in Proposition 7.3, we compute that
$\overline {F}_r(\ell )$
derived in Proposition 7.3, we compute that
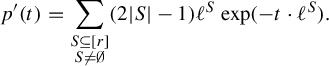 $$ \begin{align*} p'(t) = \sum_{\substack{S \subseteq [r] \\ S \neq \emptyset}} (2\lvert {S} \rvert - 1)\ell^{S}\exp(-t \cdot \ell^{S}). \end{align*} $$
$$ \begin{align*} p'(t) = \sum_{\substack{S \subseteq [r] \\ S \neq \emptyset}} (2\lvert {S} \rvert - 1)\ell^{S}\exp(-t \cdot \ell^{S}). \end{align*} $$
Therefore
![]() $p'(t)> 0$
for all
$p'(t)> 0$
for all
![]() $t \in \mathbb {R}_{>0}$
. As
$t \in \mathbb {R}_{>0}$
. As
![]() $p(h \cdot \ell ) = 0 = p(\ell )$
, we must have that
$p(h \cdot \ell ) = 0 = p(\ell )$
, we must have that
![]() $h \cdot \ell = \ell $
and hence
$h \cdot \ell = \ell $
and hence
![]() $h = 1$
.
$h = 1$
.
7.2 Finite-length paths in
 $\mathcal {M}^1(\mathcal {R}_r)$
for
$\mathcal {M}^1(\mathcal {R}_r)$
for
 $r \geq 3$
$r \geq 3$
Using the computation of
![]() $\overline {F}_r$
, in Proposition 7.8 we will compute the length of the path in
$\overline {F}_r$
, in Proposition 7.8 we will compute the length of the path in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
starting at
$\mathcal {M}^1(\mathcal {R}_r)$
starting at
![]() $\log (2r-1) \cdot \mathbf {1}$
that blows up the length of one edge while shrinking the lengths of the others at the same rate. As we will show, when r is at least
$\log (2r-1) \cdot \mathbf {1}$
that blows up the length of one edge while shrinking the lengths of the others at the same rate. As we will show, when r is at least
![]() $3$
, this path has finite length and thus the moduli space
$3$
, this path has finite length and thus the moduli space
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is not complete for
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is not complete for
![]() $r \geq 3$
.
$r \geq 3$
.
Before we begin, it is useful to introduce the following functions
![]() $X_{i}, Y_{i} \colon \thinspace \mathcal {M}(\mathcal {R}_r) \to \mathbb {R}$
for each
$X_{i}, Y_{i} \colon \thinspace \mathcal {M}(\mathcal {R}_r) \to \mathbb {R}$
for each
![]() $i \in [r]$
:
$i \in [r]$
:
Both
![]() $X_{i}$
and
$X_{i}$
and
![]() $Y_{i}$
are constant with respect to
$Y_{i}$
are constant with respect to
![]() $\ell ^{i}$
. Using these functions, we can isolate the terms in
$\ell ^{i}$
. Using these functions, we can isolate the terms in
![]() $\overline {F}_r(\ell )$
in which
$\overline {F}_r(\ell )$
in which
![]() $\ell ^i$
appears and write
$\ell ^i$
appears and write
Hence for
![]() $\ell \in \mathcal {M}^{1}(\mathcal {R}_{r})$
, as
$\ell \in \mathcal {M}^{1}(\mathcal {R}_{r})$
, as
![]() $\overline {F}_r(\ell ) = 0$
we can solve for
$\overline {F}_r(\ell ) = 0$
we can solve for
![]() $\ell ^i$
and write
$\ell ^i$
and write
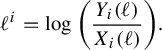 $$ \begin{align} \ell^{i} = \log\bigg(\frac{Y_{i}(\ell)}{X_{i}(\ell)}\bigg). \end{align} $$
$$ \begin{align} \ell^{i} = \log\bigg(\frac{Y_{i}(\ell)}{X_{i}(\ell)}\bigg). \end{align} $$
Further, we find the following expression for the partial derivative of
![]() $\overline {F}_r(\ell )$
with respect to
$\overline {F}_r(\ell )$
with respect to
![]() $\ell ^i$
:
$\ell ^i$
:
We observe the following inequalities for any
![]() $\ell \in \mathcal {M}^{1}(\mathcal {R}_{r})$
.
$\ell \in \mathcal {M}^{1}(\mathcal {R}_{r})$
.
Lemma 7.6. Let
![]() $r \geq 2$
and let
$r \geq 2$
and let
![]() $\ell \in \mathcal {M}^1(\mathcal {R}_r)$
. Then
$\ell \in \mathcal {M}^1(\mathcal {R}_r)$
. Then
Proof. For (7.11), we first note that
![]() $X_i(\ell ) = \exp (-\ell ^i)Y_i(\ell )$
for all
$X_i(\ell ) = \exp (-\ell ^i)Y_i(\ell )$
for all
![]() $\ell \in \mathcal {M}^1(\mathcal {R}_r)$
by Proposition 4.13 and (7.8). Since every term in
$\ell \in \mathcal {M}^1(\mathcal {R}_r)$
by Proposition 4.13 and (7.8). Since every term in
![]() $Y_i(\ell )$
has a positive coefficient, we find that
$Y_i(\ell )$
has a positive coefficient, we find that
![]() $0 < X_i(\ell )$
. As the term in
$0 < X_i(\ell )$
. As the term in
![]() $X_i(\ell )$
corresponding to
$X_i(\ell )$
corresponding to
![]() $S = \emptyset $
is
$S = \emptyset $
is
![]() $1$
and all other terms have negative coefficients, we find
$1$
and all other terms have negative coefficients, we find
![]() $X_i(\ell ) < 1$
.
$X_i(\ell ) < 1$
.
For (7.12), we have that the term in
![]() $Y_i(\ell )$
corresponding to
$Y_i(\ell )$
corresponding to
![]() $S = \emptyset $
is
$S = \emptyset $
is
![]() $1$
and all other terms have positive coefficients, thus
$1$
and all other terms have positive coefficients, thus
![]() $1 < Y_i(\ell )$
. The terms in
$1 < Y_i(\ell )$
. The terms in
![]() $1 - X_i(\ell )$
and
$1 - X_i(\ell )$
and
![]() $Y_i(\ell ) - 1$
correspond to the non-empty subsets
$Y_i(\ell ) - 1$
correspond to the non-empty subsets
![]() $S \subseteq [r] - \{i\}$
. The coefficient for the term corresponding to S in
$S \subseteq [r] - \{i\}$
. The coefficient for the term corresponding to S in
![]() $1 - X_i(\ell )$
is
$1 - X_i(\ell )$
is
times the coefficient for the same term in
![]() $Y_i(\ell ) - 1$
. As this ratio is bounded by
$Y_i(\ell ) - 1$
. As this ratio is bounded by
![]() $3$
, we find that
$3$
, we find that
![]() $Y_i(\ell ) - 1 \leq 3(1 - X_i(\ell ))$
. Hence, as
$Y_i(\ell ) - 1 \leq 3(1 - X_i(\ell ))$
. Hence, as
![]() $1 - X_i(\ell ) < 1$
by (7.11), we have
$1 - X_i(\ell ) < 1$
by (7.11), we have
![]() $Y_i(\ell ) - 1 < 3$
and so
$Y_i(\ell ) - 1 < 3$
and so
![]() $Y_i(\ell ) < 4$
.
$Y_i(\ell ) < 4$
.
We record the following calculation.
Lemma 7.7. Let
![]() $r \geq 2$
, and let
$r \geq 2$
, and let
![]() $\ell \in \mathcal {M}^1(\mathcal {R}_r)$
be such that
$\ell \in \mathcal {M}^1(\mathcal {R}_r)$
be such that
![]() $\ell ^i = \log (L)$
for
$\ell ^i = \log (L)$
for
![]() $i \in [r-1]$
for some
$i \in [r-1]$
for some
![]() $L> 2r - 3$
. Then
$L> 2r - 3$
. Then
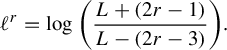 $$ \begin{align} \ell^r = \log\bigg(\frac{L + (2r-1)}{L - (2r - 3)}\bigg). \end{align} $$
$$ \begin{align} \ell^r = \log\bigg(\frac{L + (2r-1)}{L - (2r - 3)}\bigg). \end{align} $$
Proof. For any
![]() $S \subseteq [r-1]$
we have
$S \subseteq [r-1]$
we have
![]() $\exp (-\ell ^S) = \exp (-\lvert {S} \rvert \log L) = L^{-\lvert {S} \rvert }$
. Hence, by Lemma 7.1, we have that
$\exp (-\ell ^S) = \exp (-\lvert {S} \rvert \log L) = L^{-\lvert {S} \rvert }$
. Hence, by Lemma 7.1, we have that
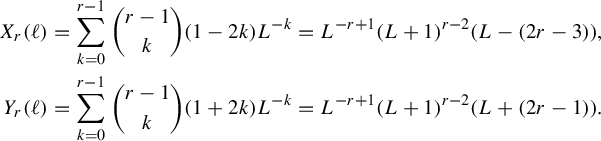 $$ \begin{align*} X_r(\ell) &= \sum_{k=0}^{r-1} \genfrac{(}{)}{0pt}{0}{r-1}{k}(1-2k)L^{-k} = L^{-r+1}(L+1)^{r-2}(L - (2r - 3)), \\ Y_r(\ell) &= \sum_{k=0}^{r-1} \genfrac{(}{)}{0pt}{0}{r-1}{k} (1+2k)L^{-k} = L^{-r+1}(L+1)^{r-2}(L + (2r - 1)). \end{align*} $$
$$ \begin{align*} X_r(\ell) &= \sum_{k=0}^{r-1} \genfrac{(}{)}{0pt}{0}{r-1}{k}(1-2k)L^{-k} = L^{-r+1}(L+1)^{r-2}(L - (2r - 3)), \\ Y_r(\ell) &= \sum_{k=0}^{r-1} \genfrac{(}{)}{0pt}{0}{r-1}{k} (1+2k)L^{-k} = L^{-r+1}(L+1)^{r-2}(L + (2r - 1)). \end{align*} $$
Therefore, by (7.9), we find that
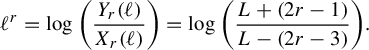 $$ \begin{align*} \ell^{r} = \log\bigg(\frac{Y_r(\ell)}{X_r(\ell)}\bigg) = \log \bigg(\frac{L + (2r - 1)}{L - (2r - 3)}\bigg).\\[-42pt] \end{align*} $$
$$ \begin{align*} \ell^{r} = \log\bigg(\frac{Y_r(\ell)}{X_r(\ell)}\bigg) = \log \bigg(\frac{L + (2r - 1)}{L - (2r - 3)}\bigg).\\[-42pt] \end{align*} $$
For any
![]() $r \geq 3$
, we will construct a path
$r \geq 3$
, we will construct a path
![]() $\ell _t \colon \thinspace [0,1) \to \mathcal {M}^1(\mathcal {R}_{r})$
that has finite length and the property that
$\ell _t \colon \thinspace [0,1) \to \mathcal {M}^1(\mathcal {R}_{r})$
that has finite length and the property that
![]() $\ell ^r_t \to \infty $
as
$\ell ^r_t \to \infty $
as
![]() $t \to 1^-$
.
$t \to 1^-$
.
Proposition 7.8. Fix
![]() $r \geq 3$
and let
$r \geq 3$
and let
![]() $N_{t} = 2(r-t)-1$
. Let
$N_{t} = 2(r-t)-1$
. Let
![]() $\ell _t \colon \thinspace [0,1) \to \mathcal {M}^1(\mathcal {R}_{r})$
be the smooth path where
$\ell _t \colon \thinspace [0,1) \to \mathcal {M}^1(\mathcal {R}_{r})$
be the smooth path where
![]() $\ell ^i_t = \log (N_{t})$
for
$\ell ^i_t = \log (N_{t})$
for
![]() $i \in [r-1]$
. Then
$i \in [r-1]$
. Then
![]() $\mathcal {L}_{\mathfrak {h},r}(\ell _t|[0,1))$
is finite and
$\mathcal {L}_{\mathfrak {h},r}(\ell _t|[0,1))$
is finite and
![]() $\ell ^r_t \to \infty $
as
$\ell ^r_t \to \infty $
as
![]() $t \to 1^-$
.
$t \to 1^-$
.
Proof. Let
![]() $\ell _t \colon \thinspace [0,1) \to \mathcal {M}^1(\mathcal {R}_{r})$
be as in the statement. Using Lemma 7.7, we find that
$\ell _t \colon \thinspace [0,1) \to \mathcal {M}^1(\mathcal {R}_{r})$
be as in the statement. Using Lemma 7.7, we find that
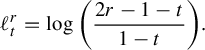 $$ \begin{align*} \ell^{r}_t = \log \bigg(\frac{2r - 1 -t}{1-t}\bigg). \end{align*} $$
$$ \begin{align*} \ell^{r}_t = \log \bigg(\frac{2r - 1 -t}{1-t}\bigg). \end{align*} $$
In particular, we have
![]() $\ell ^r_t \to \infty $
when
$\ell ^r_t \to \infty $
when
![]() $t \to 1^-$
as claimed.
$t \to 1^-$
as claimed.
We first provide a lower bound on
![]() $\langle \ell _t,\nabla \overline {F}_r(\ell _t) \rangle $
. This is the denominator of the expression for the entropy norm in Proposition 4.14. Using the expressions for the partial derivatives for
$\langle \ell _t,\nabla \overline {F}_r(\ell _t) \rangle $
. This is the denominator of the expression for the entropy norm in Proposition 4.14. Using the expressions for the partial derivatives for
![]() $\overline {F}_r(\ell _t)$
in (7.10), the fact that
$\overline {F}_r(\ell _t)$
in (7.10), the fact that
![]() $1 < Y_i(\ell _t)$
from (7.12) and that
$1 < Y_i(\ell _t)$
from (7.12) and that
![]() $\ell ^r_t \exp (-\ell ^r_t)Y_r(\ell _t)> 0$
, we have that
$\ell ^r_t \exp (-\ell ^r_t)Y_r(\ell _t)> 0$
, we have that
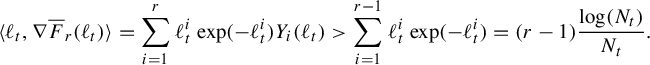 $$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{r}(\ell_t) \rangle = \sum_{i=1}^{r} \ell^{i}_t\exp(-\ell^{i}_t)Y_{i}(\ell_t)> \sum_{i=1}^{r-1} \ell^{i}_t\exp(-\ell^{i}_t) = (r-1)\frac{\log(N_{t})}{N_{t}}. \end{align*} $$
$$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{r}(\ell_t) \rangle = \sum_{i=1}^{r} \ell^{i}_t\exp(-\ell^{i}_t)Y_{i}(\ell_t)> \sum_{i=1}^{r-1} \ell^{i}_t\exp(-\ell^{i}_t) = (r-1)\frac{\log(N_{t})}{N_{t}}. \end{align*} $$
As
![]() $\log (N_t) \geq \log (N_1)$
and
$\log (N_t) \geq \log (N_1)$
and
![]() $N_t \leq N_0$
for all
$N_t \leq N_0$
for all
![]() $t \in [0,1]$
, we conclude that
$t \in [0,1]$
, we conclude that
Next, we provide an upper bound on
![]() $\langle \ddot \ell _t, \nabla \overline {F}_r(\ell _t) \rangle $
. This is the numerator of the expression for the entropy norm in Proposition 4.14. To do so, we compute that
$\langle \ddot \ell _t, \nabla \overline {F}_r(\ell _t) \rangle $
. This is the numerator of the expression for the entropy norm in Proposition 4.14. To do so, we compute that
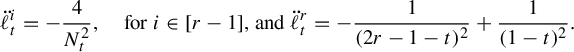 $$ \begin{align*} \ddot \ell^i_{t} = -\frac{4}{N_{t}^{2}}, \quad\mbox{for } i \in [r-1], \mbox{and } \ddot \ell^r_{t} = -\frac{1}{(2r - 1 -t)^{2}} + \frac{1}{(1-t)^{2}}. \end{align*} $$
$$ \begin{align*} \ddot \ell^i_{t} = -\frac{4}{N_{t}^{2}}, \quad\mbox{for } i \in [r-1], \mbox{and } \ddot \ell^r_{t} = -\frac{1}{(2r - 1 -t)^{2}} + \frac{1}{(1-t)^{2}}. \end{align*} $$
In particular,
![]() $\ddot \ell ^{i}_t \exp (-\ell ^{i}_t)Y_{i}(\ell _t) < 0$
for
$\ddot \ell ^{i}_t \exp (-\ell ^{i}_t)Y_{i}(\ell _t) < 0$
for
![]() $i \in [r-1]$
and
$i \in [r-1]$
and
![]() $\ddot \ell _t^r < {1}/{(1-t)^2}$
. Combining these with the expressions for the partial derivatives for
$\ddot \ell _t^r < {1}/{(1-t)^2}$
. Combining these with the expressions for the partial derivatives for
![]() $\overline {F}_r(\ell _t)$
in (7.10) and the fact that
$\overline {F}_r(\ell _t)$
in (7.10) and the fact that
![]() ${Y_i(\ell _t) < 4}$
(7.12), we have that
${Y_i(\ell _t) < 4}$
(7.12), we have that
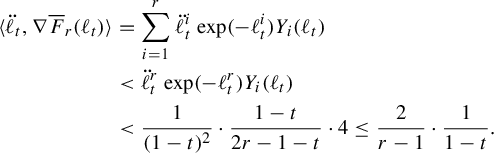 $$ \begin{align} \langle \ddot \ell_t, \nabla \overline{F}_{r}(\ell_t) \rangle &= \sum_{i=1}^{r} \ddot \ell^i_t\exp(-\ell^i_{t})Y_{i}(\ell_t) \notag \\ & < \ddot \ell^r_{t} \exp(-\ell^r_{t})Y_{i}(\ell_t) \notag \\ & < \frac{1}{(1-t)^{2}} \cdot \frac{1-t}{2r - 1 -t} \cdot 4 \leq \frac{2}{r-1} \cdot \frac{1}{1-t}. \end{align} $$
$$ \begin{align} \langle \ddot \ell_t, \nabla \overline{F}_{r}(\ell_t) \rangle &= \sum_{i=1}^{r} \ddot \ell^i_t\exp(-\ell^i_{t})Y_{i}(\ell_t) \notag \\ & < \ddot \ell^r_{t} \exp(-\ell^r_{t})Y_{i}(\ell_t) \notag \\ & < \frac{1}{(1-t)^{2}} \cdot \frac{1-t}{2r - 1 -t} \cdot 4 \leq \frac{2}{r-1} \cdot \frac{1}{1-t}. \end{align} $$
Proposition 4.14, together with the bounds appearing in (7.14) and (7.15), implies that
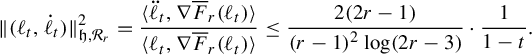 $$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{R}_r} = \frac{\langle \ddot \ell_t, \nabla \overline{F}_{r}(\ell_t) \rangle}{\langle \ell_t,\nabla \overline{F}_{r}(\ell_t) \rangle} \leq \frac{2(2r-1)}{(r-1)^2\log(2r - 3)} \cdot \frac{1}{1-t}. \end{align*} $$
$$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{R}_r} = \frac{\langle \ddot \ell_t, \nabla \overline{F}_{r}(\ell_t) \rangle}{\langle \ell_t,\nabla \overline{F}_{r}(\ell_t) \rangle} \leq \frac{2(2r-1)}{(r-1)^2\log(2r - 3)} \cdot \frac{1}{1-t}. \end{align*} $$
Therefore, the entropy length of the path
![]() $\ell _t \colon \thinspace [0,1) \to \mathcal {M}^{1}(\mathcal {R}_{r})$
is finite as claimed.
$\ell _t \colon \thinspace [0,1) \to \mathcal {M}^{1}(\mathcal {R}_{r})$
is finite as claimed.
As a consequence, we obtain that
![]() $\mathcal {M}^1(\mathcal {R}_r)$
is not complete when
$\mathcal {M}^1(\mathcal {R}_r)$
is not complete when
![]() $r \geq 3$
.
$r \geq 3$
.
Proposition 7.9. For any
![]() $r \geq 3$
, the moduli space
$r \geq 3$
, the moduli space
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is not complete.
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is not complete.
In §8 we will use Proposition 7.8 to show that
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is not complete as well when
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is not complete as well when
![]() $r \geq 3$
.
$r \geq 3$
.
7.3 The diameter of
 $\mathcal {M}^1(\mathcal {R}_r)$
is infinite
$\mathcal {M}^1(\mathcal {R}_r)$
is infinite
In this subsection we show that
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter by showing that any path that shrinks an edge to
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter by showing that any path that shrinks an edge to
![]() $0$
has infinite length. Before we begin, it is useful to introduce the following functions. For distinct
$0$
has infinite length. Before we begin, it is useful to introduce the following functions. For distinct
![]() $i, j \in [r]$
, we define
$i, j \in [r]$
, we define
 $$ \begin{align} X_{ij}(\ell) &= \sum_{S \subseteq [r] - \{i,j\}} (1 + 2\lvert {S} \rvert) \exp(-\ell^{S}), \end{align} $$
$$ \begin{align} X_{ij}(\ell) &= \sum_{S \subseteq [r] - \{i,j\}} (1 + 2\lvert {S} \rvert) \exp(-\ell^{S}), \end{align} $$
 $$ \begin{align} Y_{ij}(\ell) &= \sum_{S \subseteq [r] - \{i,j\}} (3 + 2\lvert {S} \rvert) \exp(-\ell^{S}). \end{align} $$
$$ \begin{align} Y_{ij}(\ell) &= \sum_{S \subseteq [r] - \{i,j\}} (3 + 2\lvert {S} \rvert) \exp(-\ell^{S}). \end{align} $$
As in Lemma 7.6, we observe that, for any
![]() $\ell \in \mathcal {M}^1(\mathcal {R}_r)$
, we have
$\ell \in \mathcal {M}^1(\mathcal {R}_r)$
, we have
Notice that both
![]() $X_{ij}$
and
$X_{ij}$
and
![]() $Y_{ij}$
are constant with respect to both
$Y_{ij}$
are constant with respect to both
![]() $\ell ^{i}$
and
$\ell ^{i}$
and
![]() $\ell ^{j}$
. For any distinct
$\ell ^{j}$
. For any distinct
![]() $i,j \in [r]$
, these functions allow us to write
$i,j \in [r]$
, these functions allow us to write
Using (7.19) plus the expressions for the partial derivatives for
![]() $\overline {F}_r(\ell )$
in (7.10), we find the following expressions for the second partial derivatives of
$\overline {F}_r(\ell )$
in (7.10), we find the following expressions for the second partial derivatives of
![]() $\overline {F}_r(\ell )$
:
$\overline {F}_r(\ell )$
:
The following technical lemma is the main tool for estimating length. Intuitively, it says that when one of the edge lengths—
![]() $\ell ^r$
in the statement—is short, the length of a path is bounded below by the difference in the square roots of the lengths of second shortest edge—
$\ell ^r$
in the statement—is short, the length of a path is bounded below by the difference in the square roots of the lengths of second shortest edge—
![]() $\ell ^1$
in the statement—at the endpoints of the path. In the statement below, shortness of
$\ell ^1$
in the statement—at the endpoints of the path. In the statement below, shortness of
![]() $\ell ^r$
is guaranteed by taking
$\ell ^r$
is guaranteed by taking
![]() $\ell ^1$
large enough.
$\ell ^1$
large enough.
Lemma 7.10. Let
![]() $r \geq 2$
. There is an
$r \geq 2$
. There is an
![]() $L_r$
with the following property. Suppose
$L_r$
with the following property. Suppose
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^{1}(\mathcal {R}_{r})$
is a piecewise smooth path such that, for all
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^{1}(\mathcal {R}_{r})$
is a piecewise smooth path such that, for all
![]() $t \in [0,1]$
:
$t \in [0,1]$
:
-
(1)
 $\ell ^1_t = \min \{ \ell ^i_t \mid i \in [r - 1] \}$
;
$\ell ^1_t = \min \{ \ell ^i_t \mid i \in [r - 1] \}$
; -
(2)
 $\ell ^1_0 \geq L_r$
; and
$\ell ^1_0 \geq L_r$
; and -
(3)
 $\dot \ell ^1_t> 0$
.
$\dot \ell ^1_t> 0$
.
Then
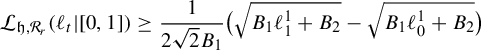 $$ \begin{align*} \mathcal{L}_{\mathfrak{h},\mathcal{R}_r}(\ell_t|[0,1]) \geq \frac{1}{2\sqrt{2}B_{1}} \big(\sqrt{B_{1}\ell^1_1 + B_{2}} - \sqrt{B_{1}\ell^1_0 + B_{2}}\big) \end{align*} $$
$$ \begin{align*} \mathcal{L}_{\mathfrak{h},\mathcal{R}_r}(\ell_t|[0,1]) \geq \frac{1}{2\sqrt{2}B_{1}} \big(\sqrt{B_{1}\ell^1_1 + B_{2}} - \sqrt{B_{1}\ell^1_0 + B_{2}}\big) \end{align*} $$
where
![]() $B_1 = 4(r-1)$
and
$B_1 = 4(r-1)$
and
![]() $B_2 = 2^{r+3}(2r-1)$
.
$B_2 = 2^{r+3}(2r-1)$
.
Proof. Let
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {R}_r)$
be as in the statement. By (3) we may reparametrize the path so that
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {R}_r)$
be as in the statement. By (3) we may reparametrize the path so that
![]() $\ell ^1_t = t$
. Let
$\ell ^1_t = t$
. Let
![]() $L_r$
be large enough so that
$L_r$
be large enough so that
The method of proof is similar to the calculations performed in §6. Specifically, using the expression
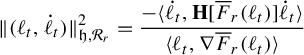 $$ \begin{align} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{R}_r} = \frac{-\langle \dot \ell_t, \mathbf{H}[\overline{F}_{r}(\ell_t)]\dot\ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_r(\ell_t) \rangle} \end{align} $$
$$ \begin{align} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{R}_r} = \frac{-\langle \dot \ell_t, \mathbf{H}[\overline{F}_{r}(\ell_t)]\dot\ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_r(\ell_t) \rangle} \end{align} $$
from Proposition 4.14, we show that the square of the entropy norm along this path is bounded from below by
![]() $1/2(B_1 t + B_2)$
. This is done by showing that the denominator is bounded from above by
$1/2(B_1 t + B_2)$
. This is done by showing that the denominator is bounded from above by
![]() $\exp (-t)(B_1t + B_2)$
in (7.27), and that the numerator is bounded from below by
$\exp (-t)(B_1t + B_2)$
in (7.27), and that the numerator is bounded from below by
![]() $\tfrac 12\exp (-t)$
in (7.33).
$\tfrac 12\exp (-t)$
in (7.33).
We first provide the upper bound on
![]() $\langle \ell _t,\nabla \overline {F}_r(\ell _t) \rangle $
.
$\langle \ell _t,\nabla \overline {F}_r(\ell _t) \rangle $
.
As
![]() $\ell ^i_t \geq \ell ^1_t = t$
for all
$\ell ^i_t \geq \ell ^1_t = t$
for all
![]() $i \in [r-1]$
, we have that
$i \in [r-1]$
, we have that
![]() $\exp (-\ell ^S_t) \leq \exp (-t)$
for all non-empty subsets
$\exp (-\ell ^S_t) \leq \exp (-t)$
for all non-empty subsets
![]() $S \subseteq [r-1]$
. Since
$S \subseteq [r-1]$
. Since
![]() $1 - 2\lvert {S} \rvert \geq -(2r-3)$
for any non-empty subset
$1 - 2\lvert {S} \rvert \geq -(2r-3)$
for any non-empty subset
![]() $S \subseteq [r-1]$
, using the definition of
$S \subseteq [r-1]$
, using the definition of
![]() $X_i(\ell _t)$
in (7.6) we have that
$X_i(\ell _t)$
in (7.6) we have that
Therefore
As
![]() $t \geq L_r$
we additionally find that
$t \geq L_r$
we additionally find that
As
![]() $0 < X_r(\ell _t) < 1$
by (7.11) and
$0 < X_r(\ell _t) < 1$
by (7.11) and
![]() $-\log (1-x) \leq {x}/({1-x})$
for all
$-\log (1-x) \leq {x}/({1-x})$
for all
![]() $0 < x < 1$
, using (7.24) and (7.25), we find that
$0 < x < 1$
, using (7.24) and (7.25), we find that
Similarly, as
![]() $1 < Y_r(\ell _t)$
by (7.12) and
$1 < Y_r(\ell _t)$
by (7.12) and
![]() $\log (x) \leq x - 1$
for all
$\log (x) \leq x - 1$
for all
![]() $x \geq 1$
, using the definition of
$x \geq 1$
, using the definition of
![]() $Y_i(\ell _t)$
from (7.7), we have that
$Y_i(\ell _t)$
from (7.7), we have that
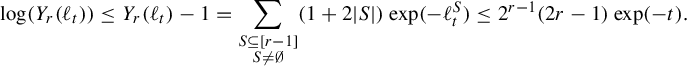 $$ \begin{align*} \log(Y_r(\ell_t)) \leq Y_r(\ell_t) - 1 = \sum_{\substack{S \subseteq [r-1] \\ S \neq \emptyset}} (1 + 2\lvert {S} \rvert)\exp(-\ell^S_t) \leq 2^{r-1}(2r-1)\exp(-t). \end{align*} $$
$$ \begin{align*} \log(Y_r(\ell_t)) \leq Y_r(\ell_t) - 1 = \sum_{\substack{S \subseteq [r-1] \\ S \neq \emptyset}} (1 + 2\lvert {S} \rvert)\exp(-\ell^S_t) \leq 2^{r-1}(2r-1)\exp(-t). \end{align*} $$
Thus by (7.9), we find
As
![]() $x\exp (-x)$
is decreasing for
$x\exp (-x)$
is decreasing for
![]() $x> 1$
, we have that
$x> 1$
, we have that
![]() $\ell ^i_{t}\exp (-\ell ^i_{t}) \leq \ell ^1_{t}\exp (-\ell ^1_t) = t\exp (-t)$
for
$\ell ^i_{t}\exp (-\ell ^i_{t}) \leq \ell ^1_{t}\exp (-\ell ^1_t) = t\exp (-t)$
for
![]() $i \in [r-1]$
. Using the expressions for the partial derivatives of
$i \in [r-1]$
. Using the expressions for the partial derivatives of
![]() $\overline {F}_r(\ell _t)$
in (7.10) and the fact that
$\overline {F}_r(\ell _t)$
in (7.10) and the fact that
![]() $Y_i(\ell _t) < 4$
from (7.12), we have that
$Y_i(\ell _t) < 4$
from (7.12), we have that
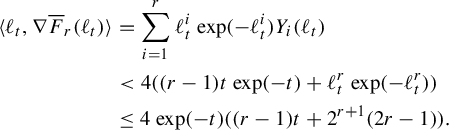 $$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{r}(\ell_t) \rangle &= \sum_{i=1}^{r} \ell^i_{t}\exp(-\ell^i_{t})Y_{i}(\ell_t)\notag \\ & < 4((r-1)t\exp(-t) + \ell^r_{t}\exp(-\ell^r_{t}) ) \\ & \leq 4\exp(-t)((r-1)t + 2^{r+1}(2r-1)).\notag \end{align*} $$
$$ \begin{align*} \langle \ell_t,\nabla \overline{F}_{r}(\ell_t) \rangle &= \sum_{i=1}^{r} \ell^i_{t}\exp(-\ell^i_{t})Y_{i}(\ell_t)\notag \\ & < 4((r-1)t\exp(-t) + \ell^r_{t}\exp(-\ell^r_{t}) ) \\ & \leq 4\exp(-t)((r-1)t + 2^{r+1}(2r-1)).\notag \end{align*} $$
As defined above, we have that
![]() $B_{1} = 4(r-1)$
and
$B_{1} = 4(r-1)$
and
![]() $B_{2} = 2^{r+3}(2r-1)$
. Hence
$B_{2} = 2^{r+3}(2r-1)$
. Hence
Next we provide a lower bound on
![]() $-\langle \dot \ell _t,\mathbf {H}[\overline {F}_r(\ell _t)]\dot \ell _t \rangle $
. Using the expressions for the second partial derivatives of
$-\langle \dot \ell _t,\mathbf {H}[\overline {F}_r(\ell _t)]\dot \ell _t \rangle $
. Using the expressions for the second partial derivatives of
![]() $\overline {F}_r(\ell _t)$
in (7.20) and (7.21), we have that
$\overline {F}_r(\ell _t)$
in (7.20) and (7.21), we have that
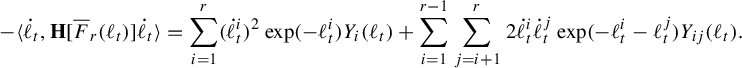 $$ \begin{align} -\langle \dot\ell_t,\mathbf{H}[\overline{F}_{r}(\ell_t)]\dot\ell_t \rangle = \sum_{i=1}^{r} (\dot \ell^i_{t})^{2}\exp(-\ell^i_{t})Y_{i}(\ell_t) + \sum_{i=1}^{r-1} \sum_{j = i+1}^{r} 2\dot \ell^i_{t} \dot \ell^j_{t} \exp(-\ell^i_{t}-\ell^j_{t})Y_{ij}(\ell_t). \end{align} $$
$$ \begin{align} -\langle \dot\ell_t,\mathbf{H}[\overline{F}_{r}(\ell_t)]\dot\ell_t \rangle = \sum_{i=1}^{r} (\dot \ell^i_{t})^{2}\exp(-\ell^i_{t})Y_{i}(\ell_t) + \sum_{i=1}^{r-1} \sum_{j = i+1}^{r} 2\dot \ell^i_{t} \dot \ell^j_{t} \exp(-\ell^i_{t}-\ell^j_{t})Y_{ij}(\ell_t). \end{align} $$
The following claim says that the diagonal terms in
![]() $\mathbf {H}[\overline {F}_r(\ell _t)]$
dominate in the current setting, that is, when one of the edge lengths is small.
$\mathbf {H}[\overline {F}_r(\ell _t)]$
dominate in the current setting, that is, when one of the edge lengths is small.
Claim 7.11.
![]() $\displaystyle \tfrac 12\langle (\dot \ell _t)^{2},\nabla \overline {F}_{r}(\ell _t) \rangle \leq -\langle \dot \ell _t,\mathbf {H}[\overline {F}_{r}(\ell _t)]\dot \ell _t \rangle \leq \tfrac 32\langle (\dot \ell _t)^{2},\nabla \overline {F}_{r}(\ell _t) \rangle .$
$\displaystyle \tfrac 12\langle (\dot \ell _t)^{2},\nabla \overline {F}_{r}(\ell _t) \rangle \leq -\langle \dot \ell _t,\mathbf {H}[\overline {F}_{r}(\ell _t)]\dot \ell _t \rangle \leq \tfrac 32\langle (\dot \ell _t)^{2},\nabla \overline {F}_{r}(\ell _t) \rangle .$
Proof of Claim 7.11
We observe that the first summand in (7.28) is exactly
![]() $\langle (\dot \ell _t)^2,\nabla \overline {F}_r(\ell ) \rangle $
. The claim is thus proved by showing that the second summand has absolute value bounded above by
$\langle (\dot \ell _t)^2,\nabla \overline {F}_r(\ell ) \rangle $
. The claim is thus proved by showing that the second summand has absolute value bounded above by
![]() $\tfrac 12\langle (\dot \ell _t)^2,\nabla \overline {F}_r(\ell _t) \rangle $
. We accomplish this by breaking this summand into various pieces.
$\tfrac 12\langle (\dot \ell _t)^2,\nabla \overline {F}_r(\ell _t) \rangle $
. We accomplish this by breaking this summand into various pieces.
To begin, we focus on the terms in this summand where
![]() $j = r$
.
$j = r$
.
Let
![]() $K_{r} \subseteq [r - 1]$
be the set of indices where
$K_{r} \subseteq [r - 1]$
be the set of indices where
![]() $\lvert {2\dot \ell ^i_{t} \exp (-\ell ^i_{t})Y_{ir}(\ell _t)} \rvert \leq ({1}/{2r})\lvert {\dot \ell ^r_{t}Y_{r}(\ell _t)} \rvert $
. Summing over the elements in
$\lvert {2\dot \ell ^i_{t} \exp (-\ell ^i_{t})Y_{ir}(\ell _t)} \rvert \leq ({1}/{2r})\lvert {\dot \ell ^r_{t}Y_{r}(\ell _t)} \rvert $
. Summing over the elements in
![]() $K_r$
, we find that
$K_r$
, we find that
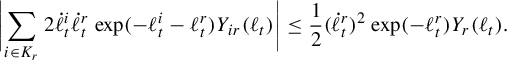 $$ \begin{align} \bigg\lvert {\sum_{i \in K_{r}} 2\dot \ell^i_{t} \dot \ell^r_{t}\exp(-\ell^i_{t} - \ell^r_{t})Y_{ir}(\ell_t)} \bigg\rvert \leq \frac{1}{2}(\dot \ell^r_{t})^{2}\exp(-\ell^r_{t})Y_r(\ell_t). \end{align} $$
$$ \begin{align} \bigg\lvert {\sum_{i \in K_{r}} 2\dot \ell^i_{t} \dot \ell^r_{t}\exp(-\ell^i_{t} - \ell^r_{t})Y_{ir}(\ell_t)} \bigg\rvert \leq \frac{1}{2}(\dot \ell^r_{t})^{2}\exp(-\ell^r_{t})Y_r(\ell_t). \end{align} $$
From the definition of
![]() $L_r$
we have
$L_r$
we have
![]() $24r\exp (-L_r) \leq 1/12$
. Thus if
$24r\exp (-L_r) \leq 1/12$
. Thus if
![]() $i < r$
and
$i < r$
and
![]() $i \notin K_r$
as
$i \notin K_r$
as
![]() $\ell ^i_t \geq L_r$
and
$\ell ^i_t \geq L_r$
and
![]() $Y_{ir}(\ell _t) < 3\max \{Y_i(\ell _t), Y_r(\ell _t)\}$
from (7.18), we have that
$Y_{ir}(\ell _t) < 3\max \{Y_i(\ell _t), Y_r(\ell _t)\}$
from (7.18), we have that
Thus for
![]() $i < r$
and
$i < r$
and
![]() $i \notin K_r$
we have that
$i \notin K_r$
we have that
Next we turn our attention to the terms where
![]() $j < r$
.
$j < r$
.
For
![]() $i \in [r - 1]$
we let
$i \in [r - 1]$
we let
![]() $K_{i} \subseteq [r - 1]$
be the set of indices where
$K_{i} \subseteq [r - 1]$
be the set of indices where
![]() $\lvert {\dot \ell ^i_{t}} \rvert> \lvert {\dot \ell ^j_{t}} \rvert $
or where
$\lvert {\dot \ell ^i_{t}} \rvert> \lvert {\dot \ell ^j_{t}} \rvert $
or where
![]() $\lvert {\dot \ell ^i_{t}} \rvert = \lvert {\dot \ell ^j_{t}} \rvert $
and
$\lvert {\dot \ell ^i_{t}} \rvert = \lvert {\dot \ell ^j_{t}} \rvert $
and
![]() $j> i$
. We observe that for any distinct pair of indices
$j> i$
. We observe that for any distinct pair of indices
![]() $i,j \in [r-1]$
either
$i,j \in [r-1]$
either
![]() $j \in K_i$
and
$j \in K_i$
and
![]() $i \notin K_j$
or
$i \notin K_j$
or
![]() $i \in K_j$
and
$i \in K_j$
and
![]() $j \notin K_i$
. From the definition of
$j \notin K_i$
. From the definition of
![]() $L_r$
we have
$L_r$
we have
![]() $2\exp (-L_r) \leq 1/12r$
. Hence as
$2\exp (-L_r) \leq 1/12r$
. Hence as
![]() $Y_{ij}(\ell _t) < 3Y_i(\ell _t)$
from (7.18), we find that
$Y_{ij}(\ell _t) < 3Y_i(\ell _t)$
from (7.18), we find that
![]() $2\exp (-\ell ^j_{t})Y_{ij}(\ell _t) \leq {({1}/{4r})}Y_{i}(\ell _t)$
for
$2\exp (-\ell ^j_{t})Y_{ij}(\ell _t) \leq {({1}/{4r})}Y_{i}(\ell _t)$
for
![]() $j \in [r-1]$
. Therefore, summing over the indices in
$j \in [r-1]$
. Therefore, summing over the indices in
![]() $K_i$
we find that
$K_i$
we find that
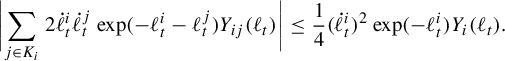 $$ \begin{align} \bigg\lvert {\sum_{j \in K_{i}} 2\dot \ell^i_{t} \dot \ell^j_{t}\exp(-\ell^i_{t} - \ell^j_{t})Y_{ij}(\ell_t) } \bigg\rvert \leq \frac{1}{4}(\dot \ell^i_{t})^{2}\exp(-\ell^i_{t})Y_{i}(\ell_t). \end{align} $$
$$ \begin{align} \bigg\lvert {\sum_{j \in K_{i}} 2\dot \ell^i_{t} \dot \ell^j_{t}\exp(-\ell^i_{t} - \ell^j_{t})Y_{ij}(\ell_t) } \bigg\rvert \leq \frac{1}{4}(\dot \ell^i_{t})^{2}\exp(-\ell^i_{t})Y_{i}(\ell_t). \end{align} $$
Rearranging the terms and using (7.29), (7.31) and (7.32), we find that
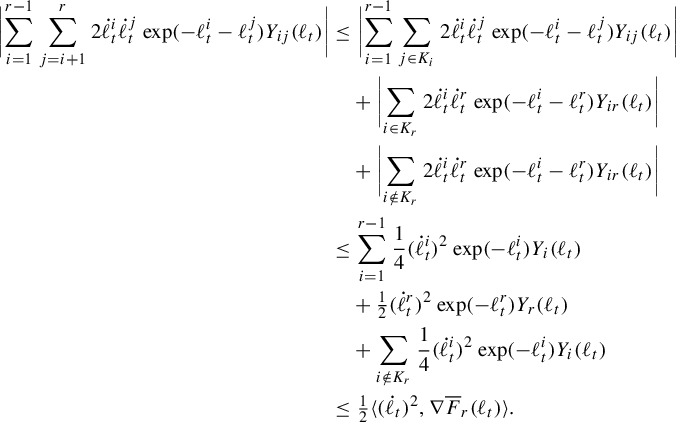 $$ \begin{align*} \bigg\lvert {\sum_{i=1}^{r-1}\sum_{j=i+1}^{r}2\dot \ell^i_{t} \dot \ell^j_{t} \exp(-\ell^i_{t} - \ell^j_{t})Y_{ij}(\ell_t)} \bigg\rvert &\leq \bigg\lvert {\sum_{i=1}^{r-1} \sum_{j \in K_{i}}2\dot \ell^i_{t} \dot \ell^j_{t} \exp(-\ell^i_{t} - \ell^j_{t})Y_{ij}(\ell_t)} \bigg\rvert \\ &\quad+ \bigg\lvert {\sum_{i \in K_{r}}2\dot \ell^i_{t} \dot \ell^r_{t} \exp(-\ell^i_{t} - \ell^r_{t})Y_{ir}(\ell_t)} \bigg\rvert \\ &\quad+ \bigg\lvert {\sum_{i \notin K_{r}}2\dot \ell^i_{t} \dot \ell^r_{t} \exp(-\ell^i_{t} - \ell^r_{t})Y_{ir}(\ell_t)} \bigg\rvert \\ &\leq \sum_{i=1}^{r-1}\frac{1}{4}(\dot \ell^i_{t})^{2}\exp(-\ell^i_{t})Y_{i}(\ell_t) \\ &\quad + \tfrac{1}{2}(\dot \ell^r_{t})^{2}\exp(-\ell^r_{t})Y_{r}(\ell_t) \\ &\quad + \sum_{i \notin K_r} \frac{1}{4}(\dot \ell^i_{t})^{2}\exp(-\ell^i_{t})Y_{i}(\ell_t) \\ &\leq \tfrac{1}{2}\langle (\dot\ell_t)^{2},\nabla \overline{F}_{r}(\ell_t) \rangle. \end{align*} $$
$$ \begin{align*} \bigg\lvert {\sum_{i=1}^{r-1}\sum_{j=i+1}^{r}2\dot \ell^i_{t} \dot \ell^j_{t} \exp(-\ell^i_{t} - \ell^j_{t})Y_{ij}(\ell_t)} \bigg\rvert &\leq \bigg\lvert {\sum_{i=1}^{r-1} \sum_{j \in K_{i}}2\dot \ell^i_{t} \dot \ell^j_{t} \exp(-\ell^i_{t} - \ell^j_{t})Y_{ij}(\ell_t)} \bigg\rvert \\ &\quad+ \bigg\lvert {\sum_{i \in K_{r}}2\dot \ell^i_{t} \dot \ell^r_{t} \exp(-\ell^i_{t} - \ell^r_{t})Y_{ir}(\ell_t)} \bigg\rvert \\ &\quad+ \bigg\lvert {\sum_{i \notin K_{r}}2\dot \ell^i_{t} \dot \ell^r_{t} \exp(-\ell^i_{t} - \ell^r_{t})Y_{ir}(\ell_t)} \bigg\rvert \\ &\leq \sum_{i=1}^{r-1}\frac{1}{4}(\dot \ell^i_{t})^{2}\exp(-\ell^i_{t})Y_{i}(\ell_t) \\ &\quad + \tfrac{1}{2}(\dot \ell^r_{t})^{2}\exp(-\ell^r_{t})Y_{r}(\ell_t) \\ &\quad + \sum_{i \notin K_r} \frac{1}{4}(\dot \ell^i_{t})^{2}\exp(-\ell^i_{t})Y_{i}(\ell_t) \\ &\leq \tfrac{1}{2}\langle (\dot\ell_t)^{2},\nabla \overline{F}_{r}(\ell_t) \rangle. \end{align*} $$
As explained above, the claim now follows.
Thus, applying Claim 7.11 and by focusing on the term in
![]() $\langle (\dot \ell _t)^2,\nabla \overline {F}_r(\ell _t) \rangle $
corresponding to
$\langle (\dot \ell _t)^2,\nabla \overline {F}_r(\ell _t) \rangle $
corresponding to
![]() $\ell ^1_t$
and tossing out the rest—which are all non-negative—we get our desired bound:
$\ell ^1_t$
and tossing out the rest—which are all non-negative—we get our desired bound:
For the last inequality, recall from (7.12) that
![]() $1 < Y_1(\ell _t)$
. Combining (7.33) with our previous bound on
$1 < Y_1(\ell _t)$
. Combining (7.33) with our previous bound on
![]() $\langle \ell _t,\nabla \overline {F}_r(\ell _t) \rangle $
from (7.27), we see that
$\langle \ell _t,\nabla \overline {F}_r(\ell _t) \rangle $
from (7.27), we see that
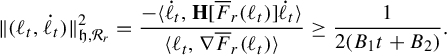 $$ \begin{align*} \| {(\ell_t,\dot\ell_t)} \|_{\mathfrak{h},\mathcal{R}_r}^{2} = \frac{-\langle \dot\ell_t,\mathbf{H}[\overline{F}_{r}(\ell_t)]\dot\ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_r(\ell_t) \rangle} \geq \frac{1}{2(B_{1}t + B_{2})}. \end{align*} $$
$$ \begin{align*} \| {(\ell_t,\dot\ell_t)} \|_{\mathfrak{h},\mathcal{R}_r}^{2} = \frac{-\langle \dot\ell_t,\mathbf{H}[\overline{F}_{r}(\ell_t)]\dot\ell_t \rangle}{\langle \ell_t,\nabla \overline{F}_r(\ell_t) \rangle} \geq \frac{1}{2(B_{1}t + B_{2})}. \end{align*} $$
Hence the length of this path in the entropy metric is at least
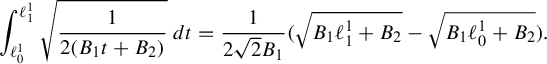 $$ \begin{align*} \int_{\ell^1_0}^{\ell^1_1} \sqrt{\frac{1}{2(B_{1}t + B_{2})}} \, dt &= \frac{1}{2\sqrt{2}B_{1}} (\sqrt{B_{1}\ell^1_1 + B_{2}} - \sqrt{B_{1}\ell^1_0 + B_{2}}).\end{align*} $$
$$ \begin{align*} \int_{\ell^1_0}^{\ell^1_1} \sqrt{\frac{1}{2(B_{1}t + B_{2})}} \, dt &= \frac{1}{2\sqrt{2}B_{1}} (\sqrt{B_{1}\ell^1_1 + B_{2}} - \sqrt{B_{1}\ell^1_0 + B_{2}}).\end{align*} $$
Before we can apply Lemma 7.10 to show that
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter, we require two more estimates. The first states that for a length function in
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter, we require two more estimates. The first states that for a length function in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
when
$\mathcal {M}^1(\mathcal {R}_r)$
when
![]() $\ell ^r$
is bounded from below, there is an upper bound on the length of the shortest edge that is not r.
$\ell ^r$
is bounded from below, there is an upper bound on the length of the shortest edge that is not r.
Lemma 7.12. Let
![]() $r \geq 2$
. If
$r \geq 2$
. If
![]() $\ell \in \mathcal {M}^1(\mathcal {R}_r)$
where
$\ell \in \mathcal {M}^1(\mathcal {R}_r)$
where
![]() $\ell ^r \geq \log (3)$
, then
$\ell ^r \geq \log (3)$
, then
![]() $\min \{\ell ^i \mid i \in [r-1]\} \leq \log (4r - 5)$
.
$\min \{\ell ^i \mid i \in [r-1]\} \leq \log (4r - 5)$
.
Proof. We first prove the lemma under the additional assumption that
![]() $\ell ^i = \ell ^1$
for any
$\ell ^i = \ell ^1$
for any
![]() $i \in [r-1]$
. In this case, we have that
$i \in [r-1]$
. In this case, we have that
![]() $\ell ^i = \log (L)$
for
$\ell ^i = \log (L)$
for
![]() $i \in [r - 1]$
and some
$i \in [r - 1]$
and some
![]() $L> 2r - 3$
. By Lemma 7.7, we have
$L> 2r - 3$
. By Lemma 7.7, we have
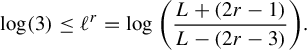 $$ \begin{align*} \log(3) \leq \ell^r = \log\bigg(\frac{L + (2r - 1)}{L - (2r - 3)}\bigg). \end{align*} $$
$$ \begin{align*} \log(3) \leq \ell^r = \log\bigg(\frac{L + (2r - 1)}{L - (2r - 3)}\bigg). \end{align*} $$
Hence we have that
![]() $3(L - (2r - 3)) \leq L + (2r-1)$
, which implies that
$3(L - (2r - 3)) \leq L + (2r-1)$
, which implies that
![]() $L \leq 4r - 5$
.
$L \leq 4r - 5$
.
Next we prove the general case. Let
![]() $\ell \in \mathcal {M}^1(\mathcal {R}_r)$
be such that
$\ell \in \mathcal {M}^1(\mathcal {R}_r)$
be such that
![]() $\ell ^r \geq \log (3)$
. Without loss of generality, we assume that
$\ell ^r \geq \log (3)$
. Without loss of generality, we assume that
![]() $\ell ^1 = \min \{\ell ^i \mid i \in [r-1]\}$
.
$\ell ^1 = \min \{\ell ^i \mid i \in [r-1]\}$
.
If
![]() $\ell ^1 \leq \log (2r - 3)$
, then we are done.
$\ell ^1 \leq \log (2r - 3)$
, then we are done.
Otherwise, we may decrease the lengths
![]() $\ell ^2,\ldots ,\ell ^{r-1}$
to be equal to
$\ell ^2,\ldots ,\ell ^{r-1}$
to be equal to
![]() $\ell ^1$
while increasing
$\ell ^1$
while increasing
![]() $\ell ^r$
to maintain the fact that the metric has unit entropy. The assumption that
$\ell ^r$
to maintain the fact that the metric has unit entropy. The assumption that
![]() ${\ell ^1> \log (2r-3)}$
ensures that
${\ell ^1> \log (2r-3)}$
ensures that
![]() $\ell ^r$
is finite. Denote the resulting metric by
$\ell ^r$
is finite. Denote the resulting metric by
![]() $\hat \ell $
. Observe that
$\hat \ell $
. Observe that
![]() $\hat \ell ^r \geq \ell ^r \geq \log (3)$
. By the special case considered above,
$\hat \ell ^r \geq \ell ^r \geq \log (3)$
. By the special case considered above,
![]() $\hat \ell ^i \leq \log (4r - 5)$
for each
$\hat \ell ^i \leq \log (4r - 5)$
for each
![]() $i \in [r-1]$
. As
$i \in [r-1]$
. As
![]() $\ell ^1 = \hat \ell ^1$
, this completes the proof of the lemma.
$\ell ^1 = \hat \ell ^1$
, this completes the proof of the lemma.
The second estimate shows that when the length of an edge is small for a length function in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
, the lengths of the other edges must be very large.
$\mathcal {M}^1(\mathcal {R}_r)$
, the lengths of the other edges must be very large.
Lemma 7.13. Let
![]() $r \geq 2$
and let
$r \geq 2$
and let
![]() $\ell \in \mathcal {M}^1(\mathcal {R}_r)$
. For any
$\ell \in \mathcal {M}^1(\mathcal {R}_r)$
. For any
![]() $\epsilon> 0$
, if
$\epsilon> 0$
, if
![]() $\ell ^i \leq \epsilon $
for some
$\ell ^i \leq \epsilon $
for some
![]() $i \in [r]$
, then for any
$i \in [r]$
, then for any
![]() $j \in [r] - \{i\}$
we have
$j \in [r] - \{i\}$
we have
![]() $\ell ^j> -\log (\exp (\epsilon ) - 1)$
.
$\ell ^j> -\log (\exp (\epsilon ) - 1)$
.
Proof. The subrose consisting of the edges i and j has entropy less than or equal to
![]() $1$
(strictly less than
$1$
(strictly less than
![]() $1$
when
$1$
when
![]() $r \geq 3$
). By Lemma 7.7, this implies that
$r \geq 3$
). By Lemma 7.7, this implies that
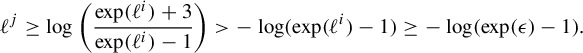 $$ \begin{align*} \ell^j \geq \log \bigg(\frac{\exp(\ell^i) + 3}{\exp(\ell^i) - 1}\bigg)> -\log(\exp(\ell^i) - 1 ) \geq -\log (\exp(\epsilon) - 1).\\[-42pt] \end{align*} $$
$$ \begin{align*} \ell^j \geq \log \bigg(\frac{\exp(\ell^i) + 3}{\exp(\ell^i) - 1}\bigg)> -\log(\exp(\ell^i) - 1 ) \geq -\log (\exp(\epsilon) - 1).\\[-42pt] \end{align*} $$
We can now prove the main inequality in this section that shows that any path that shrinks the length of an edge to zero must have infinite length.
Proposition 7.14. Let
![]() $r \geq 2$
. For any
$r \geq 2$
. For any
![]() $D> 0$
, there is an
$D> 0$
, there is an
![]() $\epsilon> 0$
such that for any
$\epsilon> 0$
such that for any
![]() $\ell \in \mathcal {M}^1(\mathcal {R}_r)$
with
$\ell \in \mathcal {M}^1(\mathcal {R}_r)$
with
![]() $\min \{\ell ^i \mid i \in [r]\} \leq \epsilon $
we have
$\min \{\ell ^i \mid i \in [r]\} \leq \epsilon $
we have
![]() $d_{\mathfrak {h},\mathcal {R}_r}(\log (2r-1) \cdot \mathbf {1},\ell ) \geq D$
.
$d_{\mathfrak {h},\mathcal {R}_r}(\log (2r-1) \cdot \mathbf {1},\ell ) \geq D$
.
Proof. Let
![]() $L_0 = \max \{\log (4r - 5), L_r\}$
, where
$L_0 = \max \{\log (4r - 5), L_r\}$
, where
![]() $L_r$
is the constant from Lemma 7.10. Fix an
$L_r$
is the constant from Lemma 7.10. Fix an
![]() $\epsilon> 0$
such that
$\epsilon> 0$
such that
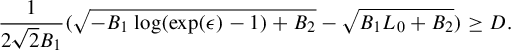 $$ \begin{align*} \frac{1}{2\sqrt{2}B_1}(\sqrt{-B_1 \log(\exp(\epsilon)-1) + B_2} - \sqrt{B_1 L_0 + B_2}) \geq D. \end{align*} $$
$$ \begin{align*} \frac{1}{2\sqrt{2}B_1}(\sqrt{-B_1 \log(\exp(\epsilon)-1) + B_2} - \sqrt{B_1 L_0 + B_2}) \geq D. \end{align*} $$
Since
![]() $-\log (x - 1) \to \infty $
as
$-\log (x - 1) \to \infty $
as
![]() $x \to 1^+$
, such an
$x \to 1^+$
, such an
![]() $\epsilon $
exists. Observe that for this
$\epsilon $
exists. Observe that for this
![]() $\epsilon $
we have that
$\epsilon $
we have that
![]() $-\log (\exp (\epsilon ) - 1) \geq L_0$
.
$-\log (\exp (\epsilon ) - 1) \geq L_0$
.
Let
![]() $\ell \in \mathcal {M}^1(\mathcal {R}_r)$
be such that
$\ell \in \mathcal {M}^1(\mathcal {R}_r)$
be such that
![]() $\min \{\ell ^i \mid i \in [r]\} \leq \epsilon $
and let
$\min \{\ell ^i \mid i \in [r]\} \leq \epsilon $
and let
![]() $\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {R}_r)$
be a piecewise smooth path where
$\ell _t \colon \thinspace [0,1] \to \mathcal {M}^1(\mathcal {R}_r)$
be a piecewise smooth path where
![]() $\ell _0 = \log (2r-1) \cdot \mathbf {1}$
and
$\ell _0 = \log (2r-1) \cdot \mathbf {1}$
and
![]() $\ell _1 = \ell $
. We will show that the entropy length of this path is at least D. As the path is arbitrary, this shows that
$\ell _1 = \ell $
. We will show that the entropy length of this path is at least D. As the path is arbitrary, this shows that
![]() $d_{\mathfrak {h},\mathcal {R}_r}(\log (2r-1) \cdot \mathbf {1},\ell ) \geq D$
as desired.
$d_{\mathfrak {h},\mathcal {R}_r}(\log (2r-1) \cdot \mathbf {1},\ell ) \geq D$
as desired.
Without loss of generality, assume that
![]() $\ell ^r = \min \{\ell ^i \mid i \in [r]\}$
. Let
$\ell ^r = \min \{\ell ^i \mid i \in [r]\}$
. Let
![]() $\delta _0 \in [0,1]$
be the minimal value so that
$\delta _0 \in [0,1]$
be the minimal value so that
![]() $\ell ^r_t = \min \{\ell ^i_t \mid i \in [r], t \in [\delta _0,1]\}$
. We observe that
$\ell ^r_t = \min \{\ell ^i_t \mid i \in [r], t \in [\delta _0,1]\}$
. We observe that
![]() $\ell ^r_{\delta _0} \geq \log (3)$
. Indeed, there is another index
$\ell ^r_{\delta _0} \geq \log (3)$
. Indeed, there is another index
![]() $i \in [r-1]$
such that
$i \in [r-1]$
such that
![]() $\ell ^i_{\delta _0} = \ell ^r_{\delta _0}$
. If
$\ell ^i_{\delta _0} = \ell ^r_{\delta _0}$
. If
![]() $\ell ^r_{\delta _0} < \log (3)$
, then the entropy of the subgraph consisting of the ith and rth edges is greater than
$\ell ^r_{\delta _0} < \log (3)$
, then the entropy of the subgraph consisting of the ith and rth edges is greater than
![]() $1$
. This contradicts the fact that the entropy of
$1$
. This contradicts the fact that the entropy of
![]() $\ell _{\delta _0}$
is equal to
$\ell _{\delta _0}$
is equal to
![]() $1$
.
$1$
.
As there is an automorphism of the r-rose permuting any two edges, by redefining
![]() $\ell _t$
if necessary, we may assume that
$\ell _t$
if necessary, we may assume that
![]() $\ell ^1_t = \min \{\ell ^i_t \mid i \in [r - 1]\}$
for each
$\ell ^1_t = \min \{\ell ^i_t \mid i \in [r - 1]\}$
for each
![]() $t \in [\delta _0,1]$
. By Lemma 7.12, as
$t \in [\delta _0,1]$
. By Lemma 7.12, as
![]() $\ell ^r_{\delta _0} \geq \log (3)$
, we have that
$\ell ^r_{\delta _0} \geq \log (3)$
, we have that
![]() $\ell ^1_{\delta _0} \leq \log (4r-5) \leq L_0$
. By Lemma 7.13, as
$\ell ^1_{\delta _0} \leq \log (4r-5) \leq L_0$
. By Lemma 7.13, as
![]() $\ell ^r_1 \leq \epsilon $
, we have that
$\ell ^r_1 \leq \epsilon $
, we have that
![]() $\ell ^1_1> -\log (\exp (\epsilon ) - 1) \geq L_0$
.
$\ell ^1_1> -\log (\exp (\epsilon ) - 1) \geq L_0$
.
Let
![]() $\delta _1 \in [\delta _0,1]$
be the minimal value so that
$\delta _1 \in [\delta _0,1]$
be the minimal value so that
![]() $\ell ^1_t \geq L_0$
for all
$\ell ^1_t \geq L_0$
for all
![]() $t \in [\delta _1,1]$
. As
$t \in [\delta _1,1]$
. As
![]() $\mathcal {L}_{\mathfrak {h},\mathcal {R}_r}(\ell _t|[0,1]) \geq \mathcal {L}_{\mathfrak {h},\mathcal {R}_r}(\ell _t|[\delta _1,1])$
, it suffices to show that the latter is bounded below by D.
$\mathcal {L}_{\mathfrak {h},\mathcal {R}_r}(\ell _t|[0,1]) \geq \mathcal {L}_{\mathfrak {h},\mathcal {R}_r}(\ell _t|[\delta _1,1])$
, it suffices to show that the latter is bounded below by D.
By only considering the portion of
![]() $\ell _t$
along the subintervals of
$\ell _t$
along the subintervals of
![]() $[\delta _1,1]$
with
$[\delta _1,1]$
with
![]() $\dot \ell ^1_t> 0$
, we find by Lemma 7.10 that
$\dot \ell ^1_t> 0$
, we find by Lemma 7.10 that
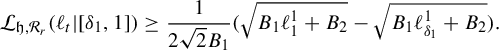 $$ \begin{align*} \mathcal{L}_{\mathfrak{h},\mathcal{R}_r}(\ell_t|[\delta_1,1]) \geq \frac{1}{2\sqrt{2}B_1}(\sqrt{B_1\ell^1_1 + B_2} - \sqrt{B_1\ell^1_{\delta_1} + B_2}). \end{align*} $$
$$ \begin{align*} \mathcal{L}_{\mathfrak{h},\mathcal{R}_r}(\ell_t|[\delta_1,1]) \geq \frac{1}{2\sqrt{2}B_1}(\sqrt{B_1\ell^1_1 + B_2} - \sqrt{B_1\ell^1_{\delta_1} + B_2}). \end{align*} $$
As
![]() $\ell ^r_1 \leq \epsilon $
, we have
$\ell ^r_1 \leq \epsilon $
, we have
![]() $\ell ^1_1 \geq -\log (\exp (\epsilon ) - 1)$
by Lemma 7.13. By definition
$\ell ^1_1 \geq -\log (\exp (\epsilon ) - 1)$
by Lemma 7.13. By definition
![]() $\ell ^1_{\delta _1} = L_0$
. Therefore
$\ell ^1_{\delta _1} = L_0$
. Therefore
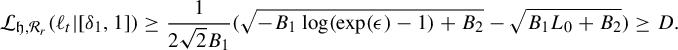 $$ \begin{align*} \hspace{-12pt}\mathcal{L}_{\mathfrak{h},\mathcal{R}_r}(\ell_t|[\delta_1,1]) \geq \frac{1}{2\sqrt{2}B_1}(\sqrt{-B_1\log(\exp(\epsilon)-1) + B_2} - \sqrt{B_1 L_0 + B_2}) \geq D.\\[-44pt] \end{align*} $$
$$ \begin{align*} \hspace{-12pt}\mathcal{L}_{\mathfrak{h},\mathcal{R}_r}(\ell_t|[\delta_1,1]) \geq \frac{1}{2\sqrt{2}B_1}(\sqrt{-B_1\log(\exp(\epsilon)-1) + B_2} - \sqrt{B_1 L_0 + B_2}) \geq D.\\[-44pt] \end{align*} $$
8 Proof of Theorem 1.1
In this section we give the proof of the first main result of this paper. Theorem 1.1 states that
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is complete when
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is complete when
![]() $r = 2$
and not complete if
$r = 2$
and not complete if
![]() $r \geq 3$
.
$r \geq 3$
.
Proof of Theorem 1.1
In §6 we showed that
![]() $(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete (Proposition 6.8), and so it remains to show that
$(\mathcal {X}^1(\mathbb {F}_2),d_{\mathfrak {h}})$
is complete (Proposition 6.8), and so it remains to show that
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is not complete when
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
is not complete when
![]() $r \geq 3$
. This is a simple consequence of Proposition 7.8, as we now explain.
$r \geq 3$
. This is a simple consequence of Proposition 7.8, as we now explain.
Let
![]() $r \geq 3$
and let
$r \geq 3$
and let
![]() $\ell _t \colon \thinspace [0,1) \to \mathcal {M}^1(\mathcal {R}_r)$
be the path described in Proposition 7.8. Using the natural homeomorphism
$\ell _t \colon \thinspace [0,1) \to \mathcal {M}^1(\mathcal {R}_r)$
be the path described in Proposition 7.8. Using the natural homeomorphism
![]() $\mathcal {M}^1(\mathcal {R}_r) \leftrightarrow \mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
, we can consider
$\mathcal {M}^1(\mathcal {R}_r) \leftrightarrow \mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
, we can consider
![]() $\ell _t$
as a path in
$\ell _t$
as a path in
![]() $\mathcal {X}^1(\mathbb {F}_r)$
.
$\mathcal {X}^1(\mathbb {F}_r)$
.
The sequence of length functions
![]() $(\ell _{1-1/n})_{n \in \mathbb {N}}$
is a Cauchy sequence in
$(\ell _{1-1/n})_{n \in \mathbb {N}}$
is a Cauchy sequence in
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
as the entropy distance on
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
as the entropy distance on
![]() $\mathcal {M}^1(\mathcal {R}_r)$
is an upper bound on the entropy distance on
$\mathcal {M}^1(\mathcal {R}_r)$
is an upper bound on the entropy distance on
![]() $\mathcal {X}^1(\mathbb {F}_r)$
.
$\mathcal {X}^1(\mathbb {F}_r)$
.
We claim that this sequence does not have a limit. Indeed, any length function
![]() $\ell $
that does not lie in
$\ell $
that does not lie in
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
has an open neighborhood in the weak topology that does not intersect
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
has an open neighborhood in the weak topology that does not intersect
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
. As the metric topology and the weak topology agree, any possible limit of this sequence must lie in
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
. As the metric topology and the weak topology agree, any possible limit of this sequence must lie in
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
. However, as
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
. However, as
![]() $\ell _{1-1/n}^r \to \infty $
as
$\ell _{1-1/n}^r \to \infty $
as
![]() $n \to \infty $
, we see that for any
$n \to \infty $
, we see that for any
![]() $\ell \in \mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
, there is an open neighborhood of
$\ell \in \mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
, there is an open neighborhood of
![]() $\ell $
in the weak topology
$\ell $
in the weak topology
![]() $U \subset \mathcal {X}^1(\mathbb {F}_r)$
such that
$U \subset \mathcal {X}^1(\mathbb {F}_r)$
such that
![]() $\ell _{1-1/n} \in U$
for only finitely many n. Hence, again as the metric topology and the weak topology agree, we see that this sequence does not have a limit in
$\ell _{1-1/n} \in U$
for only finitely many n. Hence, again as the metric topology and the weak topology agree, we see that this sequence does not have a limit in
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
.
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
.
9 The completion of
 $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
The goal of this section is to prove Theorem 1.2 which states that the completion of
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is homeomorphic to the complement of the vertices in an
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is homeomorphic to the complement of the vertices in an
![]() ${(r-1)}$
-simplex. Intuitively, the newly added completion points correspond to unit-entropy metrics on the subroses of
${(r-1)}$
-simplex. Intuitively, the newly added completion points correspond to unit-entropy metrics on the subroses of
![]() $\mathcal {R}_r$
consisting of at least two edges. Specifically, a face of dimension
$\mathcal {R}_r$
consisting of at least two edges. Specifically, a face of dimension
![]() $k-1$
corresponds to unit-entropy metrics on a sub-k-rose. We observe that
$k-1$
corresponds to unit-entropy metrics on a sub-k-rose. We observe that
![]() $\mathcal {R}_1$
does not possess a metric with unit entropy. This accounts for the missing vertices in the completion.
$\mathcal {R}_1$
does not possess a metric with unit entropy. This accounts for the missing vertices in the completion.
There are two steps to the proof. First, in §9.1 we introduce a model space
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
for the completion of
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
for the completion of
![]() $\mathcal {M}^1(\mathcal {R}_r)$
with respect to the entropy metric. This model considers
$\mathcal {M}^1(\mathcal {R}_r)$
with respect to the entropy metric. This model considers
![]() $\mathcal {M}(\mathcal {R}_r)$
as a subset of
$\mathcal {M}(\mathcal {R}_r)$
as a subset of
![]() $[0,\infty ]^r$
and adds the faces where at most
$[0,\infty ]^r$
and adds the faces where at most
![]() $r-2$
of the coordinates are equal to
$r-2$
of the coordinates are equal to
![]() $\infty $
. It is apparent from the construction that
$\infty $
. It is apparent from the construction that
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is homeomorphic to the complement of the vertices in an
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is homeomorphic to the complement of the vertices in an
![]() $(r-1)$
-simplex. Proposition 9.6 shows that the distance function
$(r-1)$
-simplex. Proposition 9.6 shows that the distance function
![]() $d_{\mathfrak {h},\mathcal {R}_r}$
on
$d_{\mathfrak {h},\mathcal {R}_r}$
on
![]() $\mathcal {M}^1(\mathcal {R}_r)$
extends to a distance function on
$\mathcal {M}^1(\mathcal {R}_r)$
extends to a distance function on
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
. It is clear that
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
. It is clear that
![]() $\mathcal {M}^1(\mathcal {R}_r)$
is dense in
$\mathcal {M}^1(\mathcal {R}_r)$
is dense in
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
. In §9.2 we complete the proof of Theorem 1.2 by showing that
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
. In §9.2 we complete the proof of Theorem 1.2 by showing that
![]() $(\widehat {\mathcal {M}}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is complete. Example 9.7 illustrates
$(\widehat {\mathcal {M}}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is complete. Example 9.7 illustrates
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_3)$
and contrasts this with the closure of
$\widehat {\mathcal {M}}^1(\mathcal {R}_3)$
and contrasts this with the closure of
![]() $CV(\mathcal {R}_3,{\textrm {id}})$
considered as a subset of
$CV(\mathcal {R}_3,{\textrm {id}})$
considered as a subset of
![]() $\mathbb {R}^{\mathbb {F}_3}$
in the axis topology.
$\mathbb {R}^{\mathbb {F}_3}$
in the axis topology.
Finally, in §9.3 we show that the diameter of cross-section of
![]() $\mathcal {M}^1(\mathcal {R}_r)$
consisting of length functions with
$\mathcal {M}^1(\mathcal {R}_r)$
consisting of length functions with
![]() $\ell ^i = \epsilon $
for some fixed
$\ell ^i = \epsilon $
for some fixed
![]() $i \in [r]$
and
$i \in [r]$
and
![]() $\epsilon> 0$
goes to zero as
$\epsilon> 0$
goes to zero as
![]() $\epsilon \to 0^+$
. This is important for §11 where we show that
$\epsilon \to 0^+$
. This is important for §11 where we show that
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
is a bounded subset of
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
is a bounded subset of
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
.
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
.
9.1 The model space
 $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
In this section we introduce a model for the completion of
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
. As mentioned above, we add the faces to
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
. As mentioned above, we add the faces to
![]() $\mathcal {M}^1(\mathcal {R}_r)$
corresponding to subroses consisting of at least two edges where the rest of the edge lengths are infinite.
$\mathcal {M}^1(\mathcal {R}_r)$
corresponding to subroses consisting of at least two edges where the rest of the edge lengths are infinite.
Topologize
![]() $[0,\infty ]$
as a closed interval. The natural inclusion
$[0,\infty ]$
as a closed interval. The natural inclusion
![]() $\mathcal {M}^{1}(\mathcal {R}_{r}) \subset (0,\infty )^{r} \subset [0,\infty ]^{r}$
is an embedding. By setting
$\mathcal {M}^{1}(\mathcal {R}_{r}) \subset (0,\infty )^{r} \subset [0,\infty ]^{r}$
is an embedding. By setting
![]() $x + \infty = \infty $
and
$x + \infty = \infty $
and
![]() $\exp {(-\infty )} = 0$
we get that the functions
$\exp {(-\infty )} = 0$
we get that the functions
![]() $\overline {F}_{r}$
from (7.5),
$\overline {F}_{r}$
from (7.5),
![]() $X_{i}$
from (7.2),
$X_{i}$
from (7.2),
![]() $Y_{i}$
from (7.7),
$Y_{i}$
from (7.7),
![]() $X_{ij}$
from (7.16) and
$X_{ij}$
from (7.16) and
![]() $Y_{ij}$
from (7.17) extend to continuous functions on
$Y_{ij}$
from (7.17) extend to continuous functions on
![]() $[0,\infty ]^{r}$
, and the entropy function
$[0,\infty ]^{r}$
, and the entropy function
![]() $\mathfrak {h}_r(\ell )$
extends to
$\mathfrak {h}_r(\ell )$
extends to
![]() $(0,\infty ]^{r}$
.
$(0,\infty ]^{r}$
.
Given a subset
![]() $S \subseteq [r]$
, we identify the subsets
$S \subseteq [r]$
, we identify the subsets
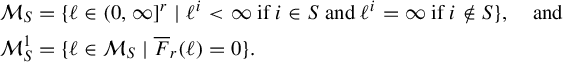 $$ \begin{align*} \mathcal{M}_{S} &= \{ \ell \in (0,\infty]^{r} \mid \ell^i < \infty \text{ if } i \in S \text{ and } \ell^i = \infty \text{ if } i \notin S \},\quad \mbox{and} \\ \mathcal{M}^{1}_{S} &= \{ \ell \in \mathcal{M}_{S} \mid \overline{F}_{r}(\ell) = 0 \}. \end{align*} $$
$$ \begin{align*} \mathcal{M}_{S} &= \{ \ell \in (0,\infty]^{r} \mid \ell^i < \infty \text{ if } i \in S \text{ and } \ell^i = \infty \text{ if } i \notin S \},\quad \mbox{and} \\ \mathcal{M}^{1}_{S} &= \{ \ell \in \mathcal{M}_{S} \mid \overline{F}_{r}(\ell) = 0 \}. \end{align*} $$
Notice that
![]() $\mathcal {M}_{[r]} = \mathcal {M}(\mathcal {R}_{r})$
and that
$\mathcal {M}_{[r]} = \mathcal {M}(\mathcal {R}_{r})$
and that
![]() $\mathcal {M}_{S} \cap \mathcal {M}_{S'} = \emptyset $
if
$\mathcal {M}_{S} \cap \mathcal {M}_{S'} = \emptyset $
if
![]() $S \neq S'$
. We further observe that
$S \neq S'$
. We further observe that
![]() $\mathcal {M}^1_\emptyset = \emptyset $
and
$\mathcal {M}^1_\emptyset = \emptyset $
and
![]() $\mathcal {M}^1_{\{i\}} = \emptyset $
for any
$\mathcal {M}^1_{\{i\}} = \emptyset $
for any
![]() $i \in [r]$
. For the latter, note that
$i \in [r]$
. For the latter, note that
![]() $X_i(\ell ) = 1$
and
$X_i(\ell ) = 1$
and
![]() $Y_i(\ell ) = 1$
for any
$Y_i(\ell ) = 1$
for any
![]() $\ell \in \mathcal {M}_{\{i\}}$
. Thus for
$\ell \in \mathcal {M}_{\{i\}}$
. Thus for
![]() $\ell \in \mathcal {M}_{\{i\}}$
we have that
$\ell \in \mathcal {M}_{\{i\}}$
we have that
![]() $\overline {F}_r(\ell ) = 1 - \exp (-\ell ^i)> 0$
.
$\overline {F}_r(\ell ) = 1 - \exp (-\ell ^i)> 0$
.
Fix
![]() $S \subseteq [r]$
with
$S \subseteq [r]$
with
![]() $\lvert {S} \rvert> 1$
and let
$\lvert {S} \rvert> 1$
and let
![]() $\iota _{S} \colon \thinspace S \to \{1,2,\ldots , \lvert {S} \rvert \}$
be the order-preserving bijection and let
$\iota _{S} \colon \thinspace S \to \{1,2,\ldots , \lvert {S} \rvert \}$
be the order-preserving bijection and let
![]() $\varepsilon _{S} \colon \thinspace [0,\infty ]^{\lvert {S} \rvert } \to [0,\infty ]^{r}$
be the embedding defined by
$\varepsilon _{S} \colon \thinspace [0,\infty ]^{\lvert {S} \rvert } \to [0,\infty ]^{r}$
be the embedding defined by
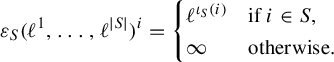 $$ \begin{align*} \varepsilon_{S}(\ell^{1},\ldots,\ell^{\lvert {S} \rvert})^i = \begin{cases} \ell^{\iota_{S}(i)} & \mbox{if } i \in S, \\ \infty & \mbox{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \varepsilon_{S}(\ell^{1},\ldots,\ell^{\lvert {S} \rvert})^i = \begin{cases} \ell^{\iota_{S}(i)} & \mbox{if } i \in S, \\ \infty & \mbox{otherwise}. \end{cases} \end{align*} $$
The function
![]() $\varepsilon _S$
allows us to consider a length function on
$\varepsilon _S$
allows us to consider a length function on
![]() $\mathcal {R}_{\lvert {S} \rvert }$
as a length function on
$\mathcal {R}_{\lvert {S} \rvert }$
as a length function on
![]() $\mathcal {R}_r$
where the edges not in S have infinite length. Indeed, with these definitions we have
$\mathcal {R}_r$
where the edges not in S have infinite length. Indeed, with these definitions we have
![]() $\varepsilon _{S}(\mathcal {M}(\mathcal {R}_{\lvert {S} \rvert })) = \mathcal {M}_{S}$
. The following lemma is immediate from Proposition 7.3 and the definitions.
$\varepsilon _{S}(\mathcal {M}(\mathcal {R}_{\lvert {S} \rvert })) = \mathcal {M}_{S}$
. The following lemma is immediate from Proposition 7.3 and the definitions.
Lemma 9.1. Let
![]() $r \geq 2$
and let
$r \geq 2$
and let
![]() $S \subseteq [r]$
have
$S \subseteq [r]$
have
![]() $\lvert {S} \rvert> 1$
. Then the following statements are true.
$\lvert {S} \rvert> 1$
. Then the following statements are true.
-
(1)
 $\overline {F}_{r} \circ \varepsilon _{S} = \overline {F}_{\lvert {S} \rvert }$
.
$\overline {F}_{r} \circ \varepsilon _{S} = \overline {F}_{\lvert {S} \rvert }$
. -
(2) For
 $\ell \in \mathcal {M}(\mathcal {R}_{\lvert {S} \rvert })$
, we have
$\ell \in \mathcal {M}(\mathcal {R}_{\lvert {S} \rvert })$
, we have
 $\mathfrak {h}_r(\varepsilon _{S}(\ell )) = \mathfrak {h}_{\lvert {S} \rvert }(\ell )$
.
$\mathfrak {h}_r(\varepsilon _{S}(\ell )) = \mathfrak {h}_{\lvert {S} \rvert }(\ell )$
. -
(3)
 $\varepsilon _{S}$
restricts to a homeomorphism
$\varepsilon _{S}$
restricts to a homeomorphism
 $\mathcal {M}^{1}(\mathcal {R}_{\lvert {S} \rvert }) \to \mathcal {M}^{1}_{S}$
.
$\mathcal {M}^{1}(\mathcal {R}_{\lvert {S} \rvert }) \to \mathcal {M}^{1}_{S}$
.
Next we define the sets
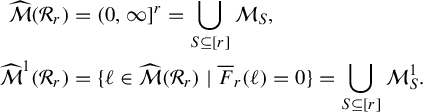 $$ \begin{align*} \widehat{\mathcal{M}}(\mathcal{R}_{r}) &= (0,\infty]^r = \bigcup_{S \subseteq [r]} \mathcal{M}_{S}, \\ \widehat{\mathcal{M}}^{1}(\mathcal{R}_{r}) &= \{ \ell \in \widehat{\mathcal{M}}(\mathcal{R}_{r}) \mid \overline{F}_{r}(\ell) = 0 \} = \bigcup_{S \subseteq [r]} \mathcal{M}^1_S. \end{align*} $$
$$ \begin{align*} \widehat{\mathcal{M}}(\mathcal{R}_{r}) &= (0,\infty]^r = \bigcup_{S \subseteq [r]} \mathcal{M}_{S}, \\ \widehat{\mathcal{M}}^{1}(\mathcal{R}_{r}) &= \{ \ell \in \widehat{\mathcal{M}}(\mathcal{R}_{r}) \mid \overline{F}_{r}(\ell) = 0 \} = \bigcup_{S \subseteq [r]} \mathcal{M}^1_S. \end{align*} $$
The set
![]() $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
is homeomorphic to the complement of the set of vertices in an
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
is homeomorphic to the complement of the set of vertices in an
![]() ${(r-1)}$
-simplex. Applying Proposition 7.5, Lemma 9.1, and the above definitions, we get the following result.
${(r-1)}$
-simplex. Applying Proposition 7.5, Lemma 9.1, and the above definitions, we get the following result.
Proposition 9.2. Let
![]() $r \geq 2$
. A length function
$r \geq 2$
. A length function
![]() $\ell \in \widehat {\mathcal {M}}(\mathcal {R}_r)$
lies in
$\ell \in \widehat {\mathcal {M}}(\mathcal {R}_r)$
lies in
![]() $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
if and only if it has entropy equal to
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
if and only if it has entropy equal to
![]() $1$
.
$1$
.
As
![]() $Y_i(\ell )$
and
$Y_i(\ell )$
and
![]() $Y_{ij}(\ell )$
extend to continuous functions on
$Y_{ij}(\ell )$
extend to continuous functions on
![]() $\widehat {\mathcal {M}}(\mathcal {R}_r)$
, using the expressions for the partial derivatives of
$\widehat {\mathcal {M}}(\mathcal {R}_r)$
, using the expressions for the partial derivatives of
![]() $\overline {F}_r(\ell )$
in (7.10), (7.20) and (7.21), we see that
$\overline {F}_r(\ell )$
in (7.10), (7.20) and (7.21), we see that
![]() $\partial _{i} \overline {F}_r(\ell )$
,
$\partial _{i} \overline {F}_r(\ell )$
,
![]() $\partial _{i i} \overline {F}_r(\ell )$
and
$\partial _{i i} \overline {F}_r(\ell )$
and
![]() $\partial _{i j} \overline {F}_r(\ell )$
extend to continuous functions on
$\partial _{i j} \overline {F}_r(\ell )$
extend to continuous functions on
![]() $\widehat {\mathcal {M}}(\mathcal {R}_r)$
. Using these formulas, we see that extensions satisfy the following properties.
$\widehat {\mathcal {M}}(\mathcal {R}_r)$
. Using these formulas, we see that extensions satisfy the following properties.
Lemma 9.3. Let
![]() $r \geq 2$
, let
$r \geq 2$
, let
![]() $S \subseteq [r]$
have
$S \subseteq [r]$
have
![]() $\lvert {S} \rvert> 1$
and fix
$\lvert {S} \rvert> 1$
and fix
![]() $\ell \in \mathcal {M}(\mathcal {R}_{\lvert {S} \rvert })$
. Then for
$\ell \in \mathcal {M}(\mathcal {R}_{\lvert {S} \rvert })$
. Then for
![]() $i,j \in [r]$
the following hold:
$i,j \in [r]$
the following hold:
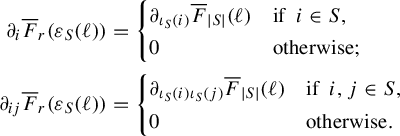 $$ \begin{align*} \partial_{i} \overline{F}_r(\varepsilon_S(\ell)) &= \begin{cases} \partial_{\iota_S(i)} \overline{F}_{\lvert {S} \rvert}(\ell) & \text{if }\ i \in S, \\ 0 & \text{otherwise; } \end{cases}\\ \partial_{i j} \overline{F}_r(\varepsilon_S(\ell)) &= \begin{cases} \partial_{\iota_S(i) \iota_S(j)} \overline{F}_{\lvert {S} \rvert}(\ell) & \text{if }\ i, j \in S, \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \partial_{i} \overline{F}_r(\varepsilon_S(\ell)) &= \begin{cases} \partial_{\iota_S(i)} \overline{F}_{\lvert {S} \rvert}(\ell) & \text{if }\ i \in S, \\ 0 & \text{otherwise; } \end{cases}\\ \partial_{i j} \overline{F}_r(\varepsilon_S(\ell)) &= \begin{cases} \partial_{\iota_S(i) \iota_S(j)} \overline{F}_{\lvert {S} \rvert}(\ell) & \text{if }\ i, j \in S, \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
Hence both
![]() $\nabla \overline {F}_{r}(\ell )$
and
$\nabla \overline {F}_{r}(\ell )$
and
![]() $\mathbf {H}[\overline {F}_{r}(\ell )]$
are well defined for
$\mathbf {H}[\overline {F}_{r}(\ell )]$
are well defined for
![]() $\ell \in \widehat {\mathcal {M}}(\mathcal {R}_r)$
. Additionally, the inner product
$\ell \in \widehat {\mathcal {M}}(\mathcal {R}_r)$
. Additionally, the inner product
![]() $\langle \ell ,\nabla \overline {F}_r(\ell ) \rangle $
extends continuously as we next show.
$\langle \ell ,\nabla \overline {F}_r(\ell ) \rangle $
extends continuously as we next show.
Lemma 9.4. Let
![]() $r \geq 2$
. The function
$r \geq 2$
. The function
![]() $\ell \mapsto \langle \ell ,\nabla \overline {F}_{r}(\ell ) \rangle $
has a continuous extension to
$\ell \mapsto \langle \ell ,\nabla \overline {F}_{r}(\ell ) \rangle $
has a continuous extension to
![]() $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
. Moreover, if
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
. Moreover, if
![]() $S \subseteq [r]$
has
$S \subseteq [r]$
has
![]() $\lvert {S} \rvert> 1$
and
$\lvert {S} \rvert> 1$
and
![]() $\ell \in \mathcal {M}_{\lvert {S} \rvert }$
, then
$\ell \in \mathcal {M}_{\lvert {S} \rvert }$
, then
Proof. Both of these statements follow from the expressions for the partial derivatives of
![]() $\overline {F}_r(\ell )$
in (7.10) as
$\overline {F}_r(\ell )$
in (7.10) as
![]() $x\exp (-x) \to 0$
when
$x\exp (-x) \to 0$
when
![]() $x \to \infty $
.
$x \to \infty $
.
We define the tangent bundle
![]() $T\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
as the subspace of
$T\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
as the subspace of
![]() $(\ell ,\mathbf {v}) \in \widehat {\mathcal {M}}^1(\mathcal {R}_r) \times \mathbb {R}^{r}$
where
$(\ell ,\mathbf {v}) \in \widehat {\mathcal {M}}^1(\mathcal {R}_r) \times \mathbb {R}^{r}$
where
![]() $\langle \mathbf {v},\nabla \overline {F}_{r}(\ell ) \rangle = 0$
. The subset of
$\langle \mathbf {v},\nabla \overline {F}_{r}(\ell ) \rangle = 0$
. The subset of
![]() $(\ell ,\mathbf {v}) \in T\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
where
$(\ell ,\mathbf {v}) \in T\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
where
![]() $\ell \in \mathcal {M}^{1}_{S}$
is denoted by
$\ell \in \mathcal {M}^{1}_{S}$
is denoted by
![]() $T\mathcal {M}^{1}_{S}$
. For consistency, we denote
$T\mathcal {M}^{1}_{S}$
. For consistency, we denote
![]() $T\mathcal {M}_{[r]}^{1}$
by
$T\mathcal {M}_{[r]}^{1}$
by
![]() $T\mathcal {M}^{1}(\mathcal {R}_{r})$
. There is an embedding
$T\mathcal {M}^{1}(\mathcal {R}_{r})$
. There is an embedding
![]() $\boldsymbol {\varepsilon _S} \colon \thinspace \mathbb {R}^{\lvert {S} \rvert } \to \mathbb {R}^r$
defined by
$\boldsymbol {\varepsilon _S} \colon \thinspace \mathbb {R}^{\lvert {S} \rvert } \to \mathbb {R}^r$
defined by
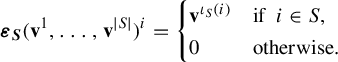 $$ \begin{align*} \boldsymbol{\varepsilon_S}(\mathbf{v}^{1},\ldots,\mathbf{v}^{\lvert {S} \rvert})^i = \begin{cases} \mathbf{v}^{\iota_{S}(i)} & \mbox{if }\ i \in S, \\ 0 & \mbox{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \boldsymbol{\varepsilon_S}(\mathbf{v}^{1},\ldots,\mathbf{v}^{\lvert {S} \rvert})^i = \begin{cases} \mathbf{v}^{\iota_{S}(i)} & \mbox{if }\ i \in S, \\ 0 & \mbox{otherwise}. \end{cases} \end{align*} $$
This allows us to define an embedding
![]() $T_{S} \colon \thinspace T\mathcal {M}^{1}(\mathcal {R}_{\lvert {S} \rvert }) \to T\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
whose image is contained in
$T_{S} \colon \thinspace T\mathcal {M}^{1}(\mathcal {R}_{\lvert {S} \rvert }) \to T\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
whose image is contained in
![]() $T\mathcal {M}^1_S$
by
$T\mathcal {M}^1_S$
by
![]() $T_S(\ell ,\mathbf {v}) = (\varepsilon _S(\ell ),\boldsymbol {\varepsilon _S}(\mathbf {v}))$
. Proposition 4.14, together with Lemmas 9.3 and 9.4, has the following implication.
$T_S(\ell ,\mathbf {v}) = (\varepsilon _S(\ell ),\boldsymbol {\varepsilon _S}(\mathbf {v}))$
. Proposition 4.14, together with Lemmas 9.3 and 9.4, has the following implication.
Proposition 9.5. Let
![]() $r \ge 2$
. The entropy norm
$r \ge 2$
. The entropy norm
![]() extends to a continuous semi-norm
extends to a continuous semi-norm
![]() . Moreover, the embedding maps
. Moreover, the embedding maps
![]() $T_S \colon \thinspace T\mathcal {M}^1(\mathcal {R}_{\lvert {S} \rvert }) \to T\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
are norm-preserving. Specifically, if
$T_S \colon \thinspace T\mathcal {M}^1(\mathcal {R}_{\lvert {S} \rvert }) \to T\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
are norm-preserving. Specifically, if
![]() $S \subseteq [r]$
has
$S \subseteq [r]$
has
![]() $\lvert {S} \rvert> 1$
, and
$\lvert {S} \rvert> 1$
, and
![]() $(\ell ,\mathbf {v}) = T_{S}(\ell _{S},\mathbf {v}_S)$
, then the extension satisfies
$(\ell ,\mathbf {v}) = T_{S}(\ell _{S},\mathbf {v}_S)$
, then the extension satisfies
The reason why the extension fails to be a norm is as follows. If
![]() $(\ell ,\mathbf {v}) \in \mathcal {M}^1_S \times \mathbb {R}^r$
and
$(\ell ,\mathbf {v}) \in \mathcal {M}^1_S \times \mathbb {R}^r$
and
![]() $\mathbf {v}^i \kern-.5pt =\kern-.5pt 0$
for
$\mathbf {v}^i \kern-.5pt =\kern-.5pt 0$
for
![]() $i \kern-.5pt \in\kern-.5pt S$
, then
$i \kern-.5pt \in\kern-.5pt S$
, then
![]() $(\ell ,\mathbf {v}) \kern-.5pt\in\kern-.5pt T\mathcal {M}^1_S$
as
$(\ell ,\mathbf {v}) \kern-.5pt\in\kern-.5pt T\mathcal {M}^1_S$
as
![]() $\partial _{i} \overline {F}_r(\ell )\kern-.5pt = 0$
whenever
$\partial _{i} \overline {F}_r(\ell )\kern-.5pt = 0$
whenever
![]() $i \kern-.5pt\notin\kern-.5pt S$
. Further,
$i \kern-.5pt\notin\kern-.5pt S$
. Further,
![]() $\partial _{i j} \overline {F}_r(\ell )\kern-.5pt = 0$
whenever
$\partial _{i j} \overline {F}_r(\ell )\kern-.5pt = 0$
whenever
![]() $i \notin S$
or
$i \notin S$
or
![]() $j \notin S$
. Thus
$j \notin S$
. Thus
![]() $-\langle \mathbf {v},\mathbf {H}[\overline {F}_r](\ell )\mathbf {v} \rangle = 0$
and hence
$-\langle \mathbf {v},\mathbf {H}[\overline {F}_r](\ell )\mathbf {v} \rangle = 0$
and hence
![]() $\| {(\ell ,\mathbf {v})} \|_{\mathfrak {h},\mathcal {R}_r} = 0$
for such points.
$\| {(\ell ,\mathbf {v})} \|_{\mathfrak {h},\mathcal {R}_r} = 0$
for such points.
The following proposition is the main result of this section. It shows that
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is contained in the completion of
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is contained in the completion of
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_{r}})$
.
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_{r}})$
.
Proposition 9.6. Let
![]() $r \geq 2$
. The following statements hold.
$r \geq 2$
. The following statements hold.
-
(1) The extension of the entropy norm defines a distance function
 $d_{\mathfrak {h},\mathcal {R}_r}$
on
$d_{\mathfrak {h},\mathcal {R}_r}$
on
 $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
.
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
. -
(2) The inclusion
 $(\mathcal {M}^{1}(\mathcal {R}_{r}),d_{\mathfrak {h},\mathcal {R}_r}) \to (\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r}),d_{\mathfrak {h},\mathcal {R}_r})$
is an isometric embedding.
$(\mathcal {M}^{1}(\mathcal {R}_{r}),d_{\mathfrak {h},\mathcal {R}_r}) \to (\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r}),d_{\mathfrak {h},\mathcal {R}_r})$
is an isometric embedding. -
(3) The topology induced by
 $d_{\mathfrak {h},\mathcal {R}_r}$
equals the subspace topology
$d_{\mathfrak {h},\mathcal {R}_r}$
equals the subspace topology
 $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r}) \subseteq [0,\infty ]^{r}$
.
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r}) \subseteq [0,\infty ]^{r}$
.
Proof. By definition
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_{2}) = \mathcal {M}^1(\mathcal {R}_{2})$
. Hence the proposition is obvious for
$\widehat {\mathcal {M}}^1(\mathcal {R}_{2}) = \mathcal {M}^1(\mathcal {R}_{2})$
. Hence the proposition is obvious for
![]() $r = 2$
. We assume from now on that
$r = 2$
. We assume from now on that
![]() $r \geq 3$
.
$r \geq 3$
.
First we need to show that for each
![]() $\ell ,\ell ' \in \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
there is a path
$\ell ,\ell ' \in \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
there is a path
![]() $\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
with
$\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
with
![]() $\ell _0 = \ell $
and
$\ell _0 = \ell $
and
![]() $\ell _1 = \ell '$
that has finite length so that
$\ell _1 = \ell '$
that has finite length so that
![]() $d_{\mathfrak {h},\mathcal {R}_r}(\ell ,\ell ')$
is defined. Notice that by Proposition 9.5 for each
$d_{\mathfrak {h},\mathcal {R}_r}(\ell ,\ell ')$
is defined. Notice that by Proposition 9.5 for each
![]() $S \subseteq [r]$
with
$S \subseteq [r]$
with
![]() $\lvert {S} \rvert> 1$
, any two points in
$\lvert {S} \rvert> 1$
, any two points in
![]() $\mathcal {M}^1_S$
can be joined by a path of finite length. Hence it suffices to show that, for any
$\mathcal {M}^1_S$
can be joined by a path of finite length. Hence it suffices to show that, for any
![]() $S \subseteq [r]$
with
$S \subseteq [r]$
with
![]() $\lvert {S} \rvert> 1$
, there is a path of finite length joining
$\lvert {S} \rvert> 1$
, there is a path of finite length joining
![]() $\log (2r-1) \cdot \mathbf {1} \in \mathcal {M}^1(\mathcal {R}_r)$
to
$\log (2r-1) \cdot \mathbf {1} \in \mathcal {M}^1(\mathcal {R}_r)$
to
![]() $\varepsilon _S(\log (2\lvert {S} \rvert - 1) \cdot \mathbf {1}) \in \mathcal {M}^1_S$
.
$\varepsilon _S(\log (2\lvert {S} \rvert - 1) \cdot \mathbf {1}) \in \mathcal {M}^1_S$
.
Recall that in Proposition 7.8 we showed that there is a path
![]() $\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_{r})$
where
$\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_{r})$
where
![]() $\ell _0 = \log (2r-1) \cdot \mathbf {1}$
and
$\ell _0 = \log (2r-1) \cdot \mathbf {1}$
and
![]() $\ell _1 = \varepsilon _{[r-1]}(\log (2r-3) \cdot \mathbf {1}) \in \mathcal {M}_{[r-1]}^1$
that has finite length.
$\ell _1 = \varepsilon _{[r-1]}(\log (2r-3) \cdot \mathbf {1}) \in \mathcal {M}_{[r-1]}^1$
that has finite length.
Now, given
![]() $S \subseteq [r]$
with
$S \subseteq [r]$
with
![]() $\lvert {S} \rvert> 1$
, we inductively define subsets
$\lvert {S} \rvert> 1$
, we inductively define subsets
![]() $S_i$
for
$S_i$
for
![]() $i = 0,\ldots , r-\lvert {S} \rvert $
by
$i = 0,\ldots , r-\lvert {S} \rvert $
by
![]() $S_0 = [r]$
, and
$S_0 = [r]$
, and
![]() $S_{i+1} = S_i - \{\max (S_i - S)\}$
so that
$S_{i+1} = S_i - \{\max (S_i - S)\}$
so that
![]() $S_{r - \lvert {S} \rvert } = S$
. The calculation in Proposition 7.8 shows that there is a finite-length path
$S_{r - \lvert {S} \rvert } = S$
. The calculation in Proposition 7.8 shows that there is a finite-length path
![]() $(\ell _i)_t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
with
$(\ell _i)_t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
with
![]() $(\ell _i)_0 = \varepsilon _{S_i}(\log (2(r-i) - 1) \cdot \mathbf {1}) \in \mathcal {M}^1_{S_i}$
and
$(\ell _i)_0 = \varepsilon _{S_i}(\log (2(r-i) - 1) \cdot \mathbf {1}) \in \mathcal {M}^1_{S_i}$
and
![]() $(\ell _i)_1 = \varepsilon _{S_{i+1}}(\log (2(r - (i+1)) - 1) \cdot \mathbf {1}) \in \mathcal {M}^1_{S_{i+1}}$
. The concatenation of these paths is a path with finite length from
$(\ell _i)_1 = \varepsilon _{S_{i+1}}(\log (2(r - (i+1)) - 1) \cdot \mathbf {1}) \in \mathcal {M}^1_{S_{i+1}}$
. The concatenation of these paths is a path with finite length from
![]() $\log (2r - 1)\cdot \mathbf {1} \in \mathcal {M}^1(\mathcal {R}_r)$
to
$\log (2r - 1)\cdot \mathbf {1} \in \mathcal {M}^1(\mathcal {R}_r)$
to
![]() $\varepsilon _S(\log (2\lvert {S} \rvert - 1) \cdot \mathbf {1}) \in \mathcal {M}^1_S$
. Therefore
$\varepsilon _S(\log (2\lvert {S} \rvert - 1) \cdot \mathbf {1}) \in \mathcal {M}^1_S$
. Therefore
![]() $d_{\mathfrak {h},\mathcal {R}_r}(\ell ,\ell ')$
is defined for all
$d_{\mathfrak {h},\mathcal {R}_r}(\ell ,\ell ')$
is defined for all
![]() $\ell ,\ell ' \in \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
.
$\ell ,\ell ' \in \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
.
Next, we show that
![]() $d_{\mathfrak {h},\mathcal {R}_r}$
defines a distance function on
$d_{\mathfrak {h},\mathcal {R}_r}$
defines a distance function on
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
. Symmetry and the triangle inequality obviously hold. What needs to be checked is that if
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
. Symmetry and the triangle inequality obviously hold. What needs to be checked is that if
![]() $\ell $
and
$\ell $
and
![]() $\ell '$
are distinct points in
$\ell '$
are distinct points in
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
, then there is an
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
, then there is an
![]() $\epsilon $
such that any path from
$\epsilon $
such that any path from
![]() $\ell $
to
$\ell $
to
![]() $\ell '$
has length at least
$\ell '$
has length at least
![]() $\epsilon $
.
$\epsilon $
.
This is clear if at least one of
![]() $\ell $
and
$\ell $
and
![]() $\ell '$
lie in
$\ell '$
lie in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
. Indeed, say
$\mathcal {M}^1(\mathcal {R}_r)$
. Indeed, say
![]() $\ell $
lies in
$\ell $
lies in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
. Then there is an open set
$\mathcal {M}^1(\mathcal {R}_r)$
. Then there is an open set
![]() $U \subset \mathcal {M}^1(\mathcal {R}_r)$
containing
$U \subset \mathcal {M}^1(\mathcal {R}_r)$
containing
![]() $\ell $
with compact closure
$\ell $
with compact closure
![]() $\overline {U}$
such that
$\overline {U}$
such that
![]() $\ell ' \notin \overline {U}$
. Further, there is an
$\ell ' \notin \overline {U}$
. Further, there is an
![]() $\epsilon> 0$
such that if
$\epsilon> 0$
such that if
![]() $d_{\mathfrak {h},\mathcal {R}_r}(\ell ,\ell '') < \epsilon $
then
$d_{\mathfrak {h},\mathcal {R}_r}(\ell ,\ell '') < \epsilon $
then
![]() $\ell '' \in U$
. Hence any path from
$\ell '' \in U$
. Hence any path from
![]() $\ell $
to
$\ell $
to
![]() $\ell '$
must have length at least
$\ell '$
must have length at least
![]() $\epsilon $
and therefore
$\epsilon $
and therefore
![]() $d_{\mathfrak {h},\mathcal {R}_r}(\ell ,\ell ') \geq \epsilon> 0$
.
$d_{\mathfrak {h},\mathcal {R}_r}(\ell ,\ell ') \geq \epsilon> 0$
.
It remains to consider the case where neither
![]() $\ell $
nor
$\ell $
nor
![]() $\ell '$
lies in
$\ell '$
lies in
![]() $\mathcal {M}^1(\mathcal {R}_r)$
. Suppose that there is a sequence of paths
$\mathcal {M}^1(\mathcal {R}_r)$
. Suppose that there is a sequence of paths
![]() $(\ell _n)_t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
from
$(\ell _n)_t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
from
![]() $\ell ,\ell ' \in \widehat {\mathcal {M}}^1(\mathcal {R}_r) - \mathcal {M}^1(\mathcal {R}_r)$
where
$\ell ,\ell ' \in \widehat {\mathcal {M}}^1(\mathcal {R}_r) - \mathcal {M}^1(\mathcal {R}_r)$
where
![]() $\mathcal {L}_{\mathfrak {h},\mathcal {R}_r}((\ell _n)_t | [0,1]) \to 0$
. As the lengths of the paths
$\mathcal {L}_{\mathfrak {h},\mathcal {R}_r}((\ell _n)_t | [0,1]) \to 0$
. As the lengths of the paths
![]() $(\ell _n)_t$
go to
$(\ell _n)_t$
go to
![]() $0$
, by Proposition 7.14, there is an
$0$
, by Proposition 7.14, there is an
![]() $\epsilon> 0$
such that
$\epsilon> 0$
such that
![]() $((\ell _n)_t)^i \geq \epsilon $
for all
$((\ell _n)_t)^i \geq \epsilon $
for all
![]() $t \in [0,1]$
and all n. Hence the images of the paths lie in a compact set of
$t \in [0,1]$
and all n. Hence the images of the paths lie in a compact set of
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
and, by the Arzelà–Ascoli theorem, there is a path
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
and, by the Arzelà–Ascoli theorem, there is a path
![]() $\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
from
$\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
from
![]() $\ell $
to
$\ell $
to
![]() $\ell '$
with length
$\ell '$
with length
![]() $0$
.
$0$
.
The image of such a path must be contained in
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r) - \mathcal {M}^1(\mathcal {R}_r)$
. As
$\widehat {\mathcal {M}}^1(\mathcal {R}_r) - \mathcal {M}^1(\mathcal {R}_r)$
. As
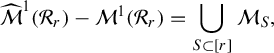 $$ \begin{align*} \widehat{\mathcal{M}}^1(\mathcal{R}_r) - \mathcal{M}^1(\mathcal{R}_r) = \bigcup_{S \subset [r]} \mathcal{M}_S, \end{align*} $$
$$ \begin{align*} \widehat{\mathcal{M}}^1(\mathcal{R}_r) - \mathcal{M}^1(\mathcal{R}_r) = \bigcup_{S \subset [r]} \mathcal{M}_S, \end{align*} $$
we must have that
![]() $\dot \ell _t = 0$
since the semi-norm is non-degenerate on any
$\dot \ell _t = 0$
since the semi-norm is non-degenerate on any
![]() $T\mathcal {M}^1_S$
by Proposition 9.5 and hence
$T\mathcal {M}^1_S$
by Proposition 9.5 and hence
![]() $\ell = \ell '$
.
$\ell = \ell '$
.
This shows (1).
Item (2) follows as any path in
![]() $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
with endpoints in
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
with endpoints in
![]() $\mathcal {M}^{1}(\mathcal {R}_{r})$
is close to a path entirely contained in
$\mathcal {M}^{1}(\mathcal {R}_{r})$
is close to a path entirely contained in
![]() $\mathcal {M}^{1}(\mathcal {R}_{r})$
by continuity of the semi-norm.
$\mathcal {M}^{1}(\mathcal {R}_{r})$
by continuity of the semi-norm.
Item (3) now follows by continuity of the semi-norm.
9.2 Proof of Theorem 1.2
We can now complete the proof of Theorem 1.2 which states that the completion of
![]() $\mathcal {M}^1(\mathcal {R}_{r})$
with respect to the entropy metric is homeomorphic to the complement of the vertices of an
$\mathcal {M}^1(\mathcal {R}_{r})$
with respect to the entropy metric is homeomorphic to the complement of the vertices of an
![]() $(r-1)$
-simplex. We accomplish this by showing that
$(r-1)$
-simplex. We accomplish this by showing that
![]() $(\widehat {\mathcal {M}}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is the completion as we have already observed that this space is homeomorphic to the complement of the vertices of an
$(\widehat {\mathcal {M}}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is the completion as we have already observed that this space is homeomorphic to the complement of the vertices of an
![]() $(r-1)$
-simplex.
$(r-1)$
-simplex.
Proof of Theorem 1.2
As the inclusion map
![]() $(\mathcal {M}^{1}(\mathcal {R}_{r}), d_{\mathfrak {h},\mathcal {R}_r}) \to (\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r}), d_{\mathfrak {h},\mathcal {R}_r})$
is an isometric embedding by Proposition 9.6(2) and the image is clearly dense, it remains to show that
$(\mathcal {M}^{1}(\mathcal {R}_{r}), d_{\mathfrak {h},\mathcal {R}_r}) \to (\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r}), d_{\mathfrak {h},\mathcal {R}_r})$
is an isometric embedding by Proposition 9.6(2) and the image is clearly dense, it remains to show that
![]() $(\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r}), d_{\mathfrak {h},\mathcal {R}_r})$
is complete.
$(\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r}), d_{\mathfrak {h},\mathcal {R}_r})$
is complete.
To this end, let
![]() $(\ell _n )_{n \in \mathbb {N}} \subset \widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
be a Cauchy sequence. Then for each
$(\ell _n )_{n \in \mathbb {N}} \subset \widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
be a Cauchy sequence. Then for each
![]() $1 \leq i \leq r$
, we have that
$1 \leq i \leq r$
, we have that
![]() $(\ell ^i)_{n}$
limits to some
$(\ell ^i)_{n}$
limits to some
![]() $\ell _\infty ^i \in [0,\infty ]^{r}$
where
$\ell _\infty ^i \in [0,\infty ]^{r}$
where
![]() $\overline {F}_{r}(\ell ^1_\infty ,\ldots ,\ell ^r_{\infty }) = 0$
. What remains to be shown is that such a limiting length function
$\overline {F}_{r}(\ell ^1_\infty ,\ldots ,\ell ^r_{\infty }) = 0$
. What remains to be shown is that such a limiting length function
![]() $\ell _\infty $
belongs to
$\ell _\infty $
belongs to
![]() $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
.
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{r})$
.
Let
![]() $S = \{ i \in [r] \mid \ell ^i_\infty \neq \infty \}$
. If
$S = \{ i \in [r] \mid \ell ^i_\infty \neq \infty \}$
. If
![]() $\ell ^i \neq 0$
for all
$\ell ^i \neq 0$
for all
![]() $i \in [r]$
, then
$i \in [r]$
, then
![]() $\ell \in \mathcal {M}^1_S \subset \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
and we are done. This is indeed always the case as by Proposition 7.14, the limiting length
$\ell \in \mathcal {M}^1_S \subset \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
and we are done. This is indeed always the case as by Proposition 7.14, the limiting length
![]() $\ell ^i_\infty $
is bounded away from zero for all i since the sequence is Cauchy.
$\ell ^i_\infty $
is bounded away from zero for all i since the sequence is Cauchy.
Example 9.7. In this example, we compare the completion
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_3)$
with the closure of
$\widehat {\mathcal {M}}^1(\mathcal {R}_3)$
with the closure of
![]() $CV(\mathcal {R}_3,{\textrm {id}})$
considered as a subset of
$CV(\mathcal {R}_3,{\textrm {id}})$
considered as a subset of
![]() $\mathbb {R}^{\mathbb {F}_3}$
. Recall that
$\mathbb {R}^{\mathbb {F}_3}$
. Recall that
![]() $CV(\mathcal {R}_3,{\textrm {id}}) \subset CV(\mathbb {F}_3)$
is the space of length functions on
$CV(\mathcal {R}_3,{\textrm {id}}) \subset CV(\mathbb {F}_3)$
is the space of length functions on
![]() $\mathcal {R}_3$
with unit volume, that is, the sum of the lengths of the edges is equal to 1. For the current discussion, the marking is irrelevant. For more information about the closure of
$\mathcal {R}_3$
with unit volume, that is, the sum of the lengths of the edges is equal to 1. For the current discussion, the marking is irrelevant. For more information about the closure of
![]() $CV(\mathbb {F}_r)$
in
$CV(\mathbb {F}_r)$
in
![]() $\mathbb {R}^{\mathbb {F}_r}$
we refer the reader to the papers by Bestvina and Feighn [Reference Bestvina and Feighn7] and Cohen and Lustig [Reference Cohen and Lustig12].
$\mathbb {R}^{\mathbb {F}_r}$
we refer the reader to the papers by Bestvina and Feighn [Reference Bestvina and Feighn7] and Cohen and Lustig [Reference Cohen and Lustig12].
We again consider Figure 5 in §7.1, which shows
![]() $\mathcal {M}^{1}(\mathcal {R}_{r})$
for
$\mathcal {M}^{1}(\mathcal {R}_{r})$
for
![]() $r = 2$
and
$r = 2$
and
![]() $r = 3$
. These images suggest that as the length of one of the edges goes to infinity, the moduli space
$r = 3$
. These images suggest that as the length of one of the edges goes to infinity, the moduli space
![]() $\mathcal {M}^{1}(\mathcal {R}_{3})$
limits to the moduli space
$\mathcal {M}^{1}(\mathcal {R}_{3})$
limits to the moduli space
![]() $\mathcal {M}^{1}(\mathcal {R}_{2})$
for the subgraph consisting of the other two edges. There are three such
$\mathcal {M}^{1}(\mathcal {R}_{2})$
for the subgraph consisting of the other two edges. There are three such
![]() $\mathcal {R}_{2}$
subgraphs in
$\mathcal {R}_{2}$
subgraphs in
![]() $\mathcal {R}_{3}$
, each contributing a one-dimensional face to
$\mathcal {R}_{3}$
, each contributing a one-dimensional face to
![]() $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
. Figure 6 shows a schematic of
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
. Figure 6 shows a schematic of
![]() $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
contrasted with
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
contrasted with
![]() $\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
, the closure of
$\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
, the closure of
![]() $CV(\mathcal {R}_3,{\textrm {id}})$
considered as a subset of
$CV(\mathcal {R}_3,{\textrm {id}})$
considered as a subset of
![]() $\mathbb {R}^{\mathbb {F}_3}$
. The spaces are not homeomorphic;
$\mathbb {R}^{\mathbb {F}_3}$
. The spaces are not homeomorphic;
![]() $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
is a 2-simplex without vertices, whereas
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
is a 2-simplex without vertices, whereas
![]() $\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
is a 2-simplex. A more striking difference comes from the duality between the newly added edges and vertices.
$\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
is a 2-simplex. A more striking difference comes from the duality between the newly added edges and vertices.
-
• In
 $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
, as
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
, as
 $c \to \infty $
we obtain a copy of
$c \to \infty $
we obtain a copy of
 $\mathcal {M}^{1}(\mathcal {R}_{2})$
for the subgraph on a and b. In
$\mathcal {M}^{1}(\mathcal {R}_{2})$
for the subgraph on a and b. In
 $\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
, the corresponding sequence would send
$\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
, the corresponding sequence would send
 $a,b \to 0$
,
$a,b \to 0$
,
 $c \to 1$
and the result is a single point corresponding to the graph of groups decomposition of
$c \to 1$
and the result is a single point corresponding to the graph of groups decomposition of
 $\langle a,b,c \rangle $
with underlying graph
$\langle a,b,c \rangle $
with underlying graph
 $\mathcal {R}_1$
where
$\mathcal {R}_1$
where
 $\langle a,b \rangle $
is the vertex group and the edge group is trivial.
$\langle a,b \rangle $
is the vertex group and the edge group is trivial. -
• In
 $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
, as
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
, as
 $b,c \to \infty $
there is no limit. This is a missing vertex of the 2-simplex; this stems from the fact that
$b,c \to \infty $
there is no limit. This is a missing vertex of the 2-simplex; this stems from the fact that
 $\mathcal {R}_1$
cannot be scaled to have unit entropy. In
$\mathcal {R}_1$
cannot be scaled to have unit entropy. In
 $\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
, the corresponding sequence would send
$\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
, the corresponding sequence would send
 $a \to 0$
and we obtain a one-dimensional face in the closure corresponding to unit-volume length functions on the graph of groups decomposition of
$a \to 0$
and we obtain a one-dimensional face in the closure corresponding to unit-volume length functions on the graph of groups decomposition of
 $\langle a,b,c \rangle $
with underlying graph
$\langle a,b,c \rangle $
with underlying graph
 $\mathcal {R}_{2}$
where
$\mathcal {R}_{2}$
where
 $\langle a \rangle $
is the vertex group and both edge groups are trivial.
$\langle a \rangle $
is the vertex group and both edge groups are trivial.
Figure 6 The completion of entropy normalization
 $\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
contrasted with the closure of the volume normalization
$\widehat {\mathcal {M}}^{1}(\mathcal {R}_{3})$
contrasted with the closure of the volume normalization
 $\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
in
$\overline {CV(\mathcal {R}_{3},{\textrm {id}})}$
in
 $\mathbb {R}^{\mathbb {F}_3}$
.
$\mathbb {R}^{\mathbb {F}_3}$
.
9.3 The thin part of
 $\mathcal {M}^1(\mathcal {R}_r)$
$\mathcal {M}^1(\mathcal {R}_r)$
For
![]() $\epsilon> 0$
and
$\epsilon> 0$
and
![]() $i \in [r]$
, we define
$i \in [r]$
, we define
We use the letter ‘S’ as we think of this subset as a slice of the moduli space. The goal of this section is to prove the following proposition.
Proposition 9.8. Let
![]() $r \geq 2$
and let
$r \geq 2$
and let
![]() $i \in [r]$
. Then
$i \in [r]$
. Then
Topologically, we have seen that
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is homeomorphic to a simplex with its vertices removed. Proposition 9.8 shows that geometrically
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is homeomorphic to a simplex with its vertices removed. Proposition 9.8 shows that geometrically
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is similar to an ideal hyperbolic simplex, with cross-sections whose diameter shrinks to zero as we move toward an ideal vertex.
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is similar to an ideal hyperbolic simplex, with cross-sections whose diameter shrinks to zero as we move toward an ideal vertex.
Given distinct
![]() $i,j \in [r]$
and
$i,j \in [r]$
and
![]() $\epsilon> 0$
, we let
$\epsilon> 0$
, we let
![]() $\ell _{i,j}(\epsilon )$
denote the length function in
$\ell _{i,j}(\epsilon )$
denote the length function in
![]() $\mathcal {M}^1_{\{i,j\}}$
where
$\mathcal {M}^1_{\{i,j\}}$
where
![]() $(\ell _{i,j}(\epsilon ))^i = \epsilon $
. As a result, we get that
$(\ell _{i,j}(\epsilon ))^i = \epsilon $
. As a result, we get that
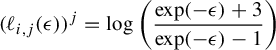 $$ \begin{align} (\ell_{i,j}(\epsilon))^j = \log\bigg(\frac{\exp(-\epsilon) + 3}{\exp(-\epsilon) - 1}\bigg) \end{align} $$
$$ \begin{align} (\ell_{i,j}(\epsilon))^j = \log\bigg(\frac{\exp(-\epsilon) + 3}{\exp(-\epsilon) - 1}\bigg) \end{align} $$
by Lemma 7.7.
We begin with a technical lemma that bounds the length of a path in
![]() $\mathcal {S}_\epsilon ^i$
to such a point.
$\mathcal {S}_\epsilon ^i$
to such a point.
Lemma 9.9. Let
![]() $r \geq 2$
. There is a constant D with the following property. Let
$r \geq 2$
. There is a constant D with the following property. Let
![]() $0 < \epsilon < \log (2)$
and let
$0 < \epsilon < \log (2)$
and let
![]() $i \in [r]$
. Suppose
$i \in [r]$
. Suppose
![]() $\ell \in \mathcal {S}_\epsilon ^i$
and that
$\ell \in \mathcal {S}_\epsilon ^i$
and that
![]() $j \in [r] - \{i\}$
is such that
$j \in [r] - \{i\}$
is such that
![]() $\ell ^j = \min \{\ell ^k \mid k \in [r] - \{i\}\}$
. Then
$\ell ^j = \min \{\ell ^k \mid k \in [r] - \{i\}\}$
. Then
Proof. Using the notation of the lemma, we consider the path
![]() $\ell _t \colon \thinspace [0, \infty ) \rightarrow \mathcal {S}^{i}_{\epsilon }$
defined by
$\ell _t \colon \thinspace [0, \infty ) \rightarrow \mathcal {S}^{i}_{\epsilon }$
defined by
Note that
![]() $\ell ^j_t$
is not specified; its value is determined by the constraint that
$\ell ^j_t$
is not specified; its value is determined by the constraint that
![]() $\mathfrak {h}_r(\ell _t) = 1$
. Notice that
$\mathfrak {h}_r(\ell _t) = 1$
. Notice that
![]() $\ell _t$
extends to a path
$\ell _t$
extends to a path
![]() $\ell _t \colon \thinspace [0,\infty ] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
and
$\ell _t \colon \thinspace [0,\infty ] \to \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
and
![]() $\ell _\infty = \ell _{i,j}(\epsilon ) \in \mathcal {M}^1_{\{i,j\}}$
. We observe that since the length of
$\ell _\infty = \ell _{i,j}(\epsilon ) \in \mathcal {M}^1_{\{i,j\}}$
. We observe that since the length of
![]() $\ell ^k_t$
is increasing for
$\ell ^k_t$
is increasing for
![]() $k \neq i,j$
and as
$k \neq i,j$
and as
![]() $\ell ^i_t$
is constant, we have
$\ell ^i_t$
is constant, we have
![]() $\ell ^j_t \leq \ell ^j$
for all t.
$\ell ^j_t \leq \ell ^j$
for all t.
Given a subset
![]() $S \subseteq [r]$
, let
$S \subseteq [r]$
, let
![]() $\lvert {S} \rvert _i = \lvert {S} \rvert - 1$
if
$\lvert {S} \rvert _i = \lvert {S} \rvert - 1$
if
![]() $i \in S$
and let
$i \in S$
and let
![]() $\lvert {S} \rvert _i = \lvert {S} \rvert $
otherwise. With this definition, for a subset
$\lvert {S} \rvert _i = \lvert {S} \rvert $
otherwise. With this definition, for a subset
![]() $S \subseteq [r] - \{j\}$
we have that
$S \subseteq [r] - \{j\}$
we have that
![]() $\ell ^S_t = \ell ^S + \lvert {S} \rvert _i t$
. Therefore, using the definition of
$\ell ^S_t = \ell ^S + \lvert {S} \rvert _i t$
. Therefore, using the definition of
![]() $X_j(\ell _t)$
from (7.6) and
$X_j(\ell _t)$
from (7.6) and
![]() $Y_j(\ell _t)$
from (7.7), we find that
$Y_j(\ell _t)$
from (7.7), we find that
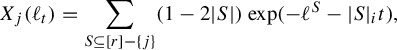 $$ \begin{align} X_j(\ell_t) & = \sum_{S \subseteq [r] - \{j\}} (1 - 2\lvert {S} \rvert) \exp(-\ell^S - \lvert {S} \rvert_i t), \end{align} $$
$$ \begin{align} X_j(\ell_t) & = \sum_{S \subseteq [r] - \{j\}} (1 - 2\lvert {S} \rvert) \exp(-\ell^S - \lvert {S} \rvert_i t), \end{align} $$
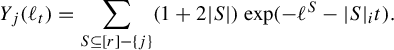 $$ \begin{align} Y_j(\ell_t) & = \sum_{S \subseteq [r] - \{j\}} (1 + 2\lvert {S} \rvert) \exp(-\ell^S - \lvert {S} \rvert_i t). \end{align} $$
$$ \begin{align} Y_j(\ell_t) & = \sum_{S \subseteq [r] - \{j\}} (1 + 2\lvert {S} \rvert) \exp(-\ell^S - \lvert {S} \rvert_i t). \end{align} $$
Let
![]() $p(t) = \log (Y_j(\ell _t))$
and
$p(t) = \log (Y_j(\ell _t))$
and
![]() $q(t) = -\log (X_j(\ell _t))$
, and so
$q(t) = -\log (X_j(\ell _t))$
, and so
![]() $\ell ^j(t) = p(t) + q(t)$
by (7.9). The next two claims establish bounds on the second derivatives of
$\ell ^j(t) = p(t) + q(t)$
by (7.9). The next two claims establish bounds on the second derivatives of
![]() $p(t)$
and
$p(t)$
and
![]() $q(t)$
.
$q(t)$
.
Claim 9.10. There is a constant
![]() $C_1$
such that
$C_1$
such that
![]() $\lvert {\ddot p(t)} \rvert \leq C_1 \exp (-t)$
.
$\lvert {\ddot p(t)} \rvert \leq C_1 \exp (-t)$
.
Proof of Claim 9.10
Using that fact that
![]() $1 < Y_j(\ell _t)$
from (7.12), we have
$1 < Y_j(\ell _t)$
from (7.12), we have
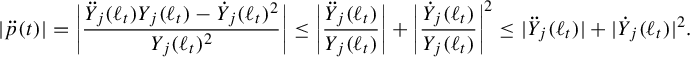 $$ \begin{align*} \lvert {\ddot p(t)} \rvert &= \bigg\lvert {\frac{\ddot Y_j(\ell_t) Y_j(\ell_t) - \dot Y_j(\ell_t)^2}{Y_j(\ell_t)^2}} \bigg\rvert \leq \bigg\lvert {\frac{\ddot Y_j(\ell_t)}{Y_j(\ell_t)}} \bigg\rvert + \bigg\lvert {\frac{\dot Y_j(\ell_t)}{Y_j(\ell_t)}} \bigg\rvert^2 \leq \lvert {\ddot Y_j(\ell_t)} \rvert + \lvert {\dot Y_j(\ell_t)} \rvert^2. \end{align*} $$
$$ \begin{align*} \lvert {\ddot p(t)} \rvert &= \bigg\lvert {\frac{\ddot Y_j(\ell_t) Y_j(\ell_t) - \dot Y_j(\ell_t)^2}{Y_j(\ell_t)^2}} \bigg\rvert \leq \bigg\lvert {\frac{\ddot Y_j(\ell_t)}{Y_j(\ell_t)}} \bigg\rvert + \bigg\lvert {\frac{\dot Y_j(\ell_t)}{Y_j(\ell_t)}} \bigg\rvert^2 \leq \lvert {\ddot Y_j(\ell_t)} \rvert + \lvert {\dot Y_j(\ell_t)} \rvert^2. \end{align*} $$
The summands in
![]() $\lvert {\ddot Y_j(\ell _t)} \rvert $
have the form
$\lvert {\ddot Y_j(\ell _t)} \rvert $
have the form
The summands in
![]() $\lvert {\dot Y_j(\ell _t)} \rvert ^2$
have the form
$\lvert {\dot Y_j(\ell _t)} \rvert ^2$
have the form
Each non-zero term in (9.6) and (9.7) has the form
![]() $A\exp (-B - Ct)$
where
$A\exp (-B - Ct)$
where
![]() $A, B \geq 0$
and
$A, B \geq 0$
and
![]() $C \geq 1$
. Hence each term is bounded by
$C \geq 1$
. Hence each term is bounded by
![]() $A\exp (-t)$
for some
$A\exp (-t)$
for some
![]() $A \geq 0$
. The existence of
$A \geq 0$
. The existence of
![]() $C_1$
is now clear.
$C_1$
is now clear.
Claim 9.11. There is a constant
![]() $C_2$
such that
$C_2$
such that
![]() $\lvert {\ddot q(t)} \rvert \leq C_2 \exp (-t)$
.
$\lvert {\ddot q(t)} \rvert \leq C_2 \exp (-t)$
.
Proof of Claim 9.11
Using the facts that
![]() $1 < Y_j(\ell _t)$
from (7.12) and
$1 < Y_j(\ell _t)$
from (7.12) and
![]() $\exp (-\ell ^j_t)Y_j(\ell _t) = X_j(\ell _t)$
from (7.8), we find that
$\exp (-\ell ^j_t)Y_j(\ell _t) = X_j(\ell _t)$
from (7.8), we find that
![]() $\exp (-\ell ^j_t) \leq \exp (-\ell ^j_t)Y_j(\ell _t) = X_j(\ell _t)$
. Hence
$\exp (-\ell ^j_t) \leq \exp (-\ell ^j_t)Y_j(\ell _t) = X_j(\ell _t)$
. Hence
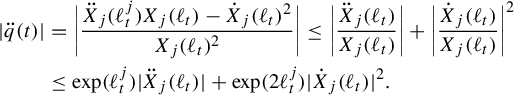 $$ \begin{align*} \lvert {\ddot q(t)} \rvert &= \bigg\lvert {\frac{\ddot X_j(\ell_t^j) X_j(\ell_t) - \dot X_j(\ell_t)^2}{X_j(\ell_t)^2}} \bigg\rvert \leq \bigg\lvert {\frac{\ddot X_j(\ell_t)}{X_j(\ell_t)}} \bigg\rvert + \bigg\lvert {\frac{\dot X_j(\ell_t)}{X_j(\ell_t)}} \bigg\rvert^2\\ &\leq \exp(\ell^j_t)\lvert {\ddot X_j(\ell_t)} \rvert + \exp(2\ell^j_t)\lvert {\dot X_j(\ell_t)} \rvert^2. \end{align*} $$
$$ \begin{align*} \lvert {\ddot q(t)} \rvert &= \bigg\lvert {\frac{\ddot X_j(\ell_t^j) X_j(\ell_t) - \dot X_j(\ell_t)^2}{X_j(\ell_t)^2}} \bigg\rvert \leq \bigg\lvert {\frac{\ddot X_j(\ell_t)}{X_j(\ell_t)}} \bigg\rvert + \bigg\lvert {\frac{\dot X_j(\ell_t)}{X_j(\ell_t)}} \bigg\rvert^2\\ &\leq \exp(\ell^j_t)\lvert {\ddot X_j(\ell_t)} \rvert + \exp(2\ell^j_t)\lvert {\dot X_j(\ell_t)} \rvert^2. \end{align*} $$
The summands in
![]() $\exp (\ell ^j_t)\lvert {\ddot X_j(\ell _t)} \rvert $
have the form
$\exp (\ell ^j_t)\lvert {\ddot X_j(\ell _t)} \rvert $
have the form
The summands in
![]() $\exp (2\ell ^j_t)\lvert {\dot X_j(\ell _t)} \rvert ^2$
have the form
$\exp (2\ell ^j_t)\lvert {\dot X_j(\ell _t)} \rvert ^2$
have the form
As
![]() $\ell ^j_t \leq \min \{\ell ^k \mid k \in [r] - \{i\}\}$
, we find that
$\ell ^j_t \leq \min \{\ell ^k \mid k \in [r] - \{i\}\}$
, we find that
![]() $\ell ^j_t - \ell ^S \leq 0$
for all
$\ell ^j_t - \ell ^S \leq 0$
for all
![]() $S \subseteq [r] - \{j\}$
when
$S \subseteq [r] - \{j\}$
when
![]() $\lvert {S} \rvert _i \neq 0$
. Hence, as above, each non-zero term in (9.8) and (9.9) has the form
$\lvert {S} \rvert _i \neq 0$
. Hence, as above, each non-zero term in (9.8) and (9.9) has the form
![]() $A\exp (-B - Ct)$
where
$A\exp (-B - Ct)$
where
![]() $A,B \geq 0$
and
$A,B \geq 0$
and
![]() $C \geq 1$
. The existence of
$C \geq 1$
. The existence of
![]() $C_2$
is now clear.
$C_2$
is now clear.
We can now bound the entropy norm of
![]() $(\ell _t, \dot \ell _t)$
using Proposition 4.14. As
$(\ell _t, \dot \ell _t)$
using Proposition 4.14. As
![]() $\ddot \ell ^k_t = 0$
for
$\ddot \ell ^k_t = 0$
for
![]() $k \neq j$
and
$k \neq j$
and
![]() $\ell ^k_t\partial _{k} \overline {F}_r(\ell _t) = \ell ^k_t\exp (-\ell ^k_t)Y_k(\ell _t)> 0$
for all k from (7.10), we find that
$\ell ^k_t\partial _{k} \overline {F}_r(\ell _t) = \ell ^k_t\exp (-\ell ^k_t)Y_k(\ell _t)> 0$
for all k from (7.10), we find that
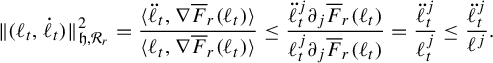 $$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{R}_r} = \frac{\langle \ddot \ell_t,\nabla \overline{F}_r(\ell_t) \rangle}{\langle \ell_t,\nabla \overline{F}_r(\ell_t) \rangle} \leq \frac{\ddot \ell^j_t \partial_{j} \overline{F}_r(\ell_t)}{\ell^j_t\partial_{j} \overline{F}_r(\ell_t)} = \frac{\ddot \ell^j_t}{\ell^j_t} \leq \frac{\ddot \ell^j_t}{\ell^j}. \end{align*} $$
$$ \begin{align*} \| {(\ell_t,\dot \ell_t)} \|^2_{\mathfrak{h},\mathcal{R}_r} = \frac{\langle \ddot \ell_t,\nabla \overline{F}_r(\ell_t) \rangle}{\langle \ell_t,\nabla \overline{F}_r(\ell_t) \rangle} \leq \frac{\ddot \ell^j_t \partial_{j} \overline{F}_r(\ell_t)}{\ell^j_t\partial_{j} \overline{F}_r(\ell_t)} = \frac{\ddot \ell^j_t}{\ell^j_t} \leq \frac{\ddot \ell^j_t}{\ell^j}. \end{align*} $$
Thus we can bound the length of the path
![]() $\ell _t$
by
$\ell _t$
by
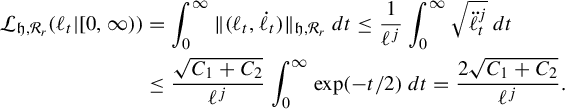 $$ \begin{align*} \mathcal{L}_{\mathfrak{h},\mathcal{R}_r}(\ell_t|[0,\infty)) & = \int_0^\infty \| {(\ell_t,\dot \ell_t)} \|_{\mathfrak{h},\mathcal{R}_r} \, dt \leq \frac{1}{\ell^j}\int_0^\infty \sqrt{\ddot \ell^j_t} \, dt \\ & \leq \frac{\sqrt{C_1 + C_2}}{\ell^j} \int_0^\infty \exp(-t/2) \, dt = \frac{2\sqrt{C_1 + C_2}}{\ell^j}. \end{align*} $$
$$ \begin{align*} \mathcal{L}_{\mathfrak{h},\mathcal{R}_r}(\ell_t|[0,\infty)) & = \int_0^\infty \| {(\ell_t,\dot \ell_t)} \|_{\mathfrak{h},\mathcal{R}_r} \, dt \leq \frac{1}{\ell^j}\int_0^\infty \sqrt{\ddot \ell^j_t} \, dt \\ & \leq \frac{\sqrt{C_1 + C_2}}{\ell^j} \int_0^\infty \exp(-t/2) \, dt = \frac{2\sqrt{C_1 + C_2}}{\ell^j}. \end{align*} $$
As
![]() $\ell _j \geq -\log (\exp (\epsilon )-1)$
(9.2), setting
$\ell _j \geq -\log (\exp (\epsilon )-1)$
(9.2), setting
![]() $D = 2\sqrt {C_1 + C_2}$
we complete the proof of the lemma.
$D = 2\sqrt {C_1 + C_2}$
we complete the proof of the lemma.
Proof of Proposition 9.8
Let
![]() $r \geq 2$
and let D be the constant from Lemma 9.9. Fix
$r \geq 2$
and let D be the constant from Lemma 9.9. Fix
![]() $i \in [r]$
and let
$i \in [r]$
and let
![]() $\ell _\epsilon \in \mathcal {S}_\epsilon ^i$
, defined by
$\ell _\epsilon \in \mathcal {S}_\epsilon ^i$
, defined by
![]() $\ell ^i_\epsilon = \epsilon $
and such that all other
$\ell ^i_\epsilon = \epsilon $
and such that all other
![]() $\ell ^j_\epsilon $
are equal. By Lemma 9.9, we have that
$\ell ^j_\epsilon $
are equal. By Lemma 9.9, we have that
for all
![]() $j \in [r] - \{i\}$
. In particular, the set
$j \in [r] - \{i\}$
. In particular, the set
![]() $\{\ell _{i,j}(\epsilon ) \mid j \in [r] - \{i\}\}$
has diameter at most
$\{\ell _{i,j}(\epsilon ) \mid j \in [r] - \{i\}\}$
has diameter at most
![]() ${2D}/({-\log (\exp (\epsilon ) - 1)})$
.
${2D}/({-\log (\exp (\epsilon ) - 1)})$
.
Again, by Lemma 9.9, each
![]() $\ell \in \mathcal {S}_\epsilon ^i$
has distance at most
$\ell \in \mathcal {S}_\epsilon ^i$
has distance at most
![]() ${D}/({-\log (\exp (\epsilon )-1)})$
from some point in
${D}/({-\log (\exp (\epsilon )-1)})$
from some point in
![]() $\{\ell _{i,j}(\epsilon ) \mid j \in [r] - \{i\}\}$
. Hence
$\{\ell _{i,j}(\epsilon ) \mid j \in [r] - \{i\}\}$
. Hence
As
![]() $-\log (\exp (\epsilon ) - 1) \to \infty $
as
$-\log (\exp (\epsilon ) - 1) \to \infty $
as
![]() $\epsilon \to 0^+$
, the proof of the proposition is complete.
$\epsilon \to 0^+$
, the proof of the proposition is complete.
10 The moduli space of a graph with a separating edge
The purpose of this section is to introduce tools to analyze the entropy metric on the moduli space of a graph with a separating edge. Throughout this section, let
![]() $G = (V,E,o,\tau ,\bar {\phantom {e}})$
be a finite connected graph which consists of two disjoint connected subgraphs
$G = (V,E,o,\tau ,\bar {\phantom {e}})$
be a finite connected graph which consists of two disjoint connected subgraphs
![]() $G_1$
, with edges
$G_1$
, with edges
![]() $e^1_1,\ldots ,e^1_{n_1}$
, and
$e^1_1,\ldots ,e^1_{n_1}$
, and
![]() $G_2$
, with edges
$G_2$
, with edges
![]() $e^2_1,\ldots , e^2_{n_2}$
connected by an edge
$e^2_1,\ldots , e^2_{n_2}$
connected by an edge
![]() $e_0$
. We assume that both
$e_0$
. We assume that both
![]() $G_1$
and
$G_1$
and
![]() $G_2$
have rank at least
$G_2$
have rank at least
![]() $2$
. We begin our analysis in §10.1 by showing that there exist paths of finite length limiting to any unit-entropy metric on either
$2$
. We begin our analysis in §10.1 by showing that there exist paths of finite length limiting to any unit-entropy metric on either
![]() $G_1$
or
$G_1$
or
![]() $G_2$
. Using this, in §10.2 we construct a space
$G_2$
. Using this, in §10.2 we construct a space
![]() $\widehat {\mathcal {M}}^1(G)$
that is similar to the construction of
$\widehat {\mathcal {M}}^1(G)$
that is similar to the construction of
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
from §9. The main difference is that in this section, we do not bother to construct the entire completion of
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
from §9. The main difference is that in this section, we do not bother to construct the entire completion of
![]() $(\mathcal {M}^1(G),d_{\mathfrak {h},G})$
, rather we just add the points that correspond to a length function of entropy
$(\mathcal {M}^1(G),d_{\mathfrak {h},G})$
, rather we just add the points that correspond to a length function of entropy
![]() $1$
on
$1$
on
![]() $G_1 \cup e_0$
or
$G_1 \cup e_0$
or
![]() $G_2 \cup e_0$
or
$G_2 \cup e_0$
or
![]() $G_1 \cup G_2$
. This is sufficient for our purposes. Proposition 10.6 is the culmination of this analysis where we show that there is a map from
$G_1 \cup G_2$
. This is sufficient for our purposes. Proposition 10.6 is the culmination of this analysis where we show that there is a map from
![]() $\widehat {\mathcal {M}}^1(G)$
to the completion of
$\widehat {\mathcal {M}}^1(G)$
to the completion of
![]() $(\mathcal {M}^1(G),d_{\mathfrak {h},G})$
that collapses these newly added length functions to a single point.
$(\mathcal {M}^1(G),d_{\mathfrak {h},G})$
that collapses these newly added length functions to a single point.
10.1 Finite-length paths in
 $\mathcal {M}^1(G)$
$\mathcal {M}^1(G)$
We seek to show that there is a finite-length path in
![]() $(\mathcal {M}^1(G),d_{\mathfrak {h},G})$
that limits onto an arbitrary unit-entropy metric on either
$(\mathcal {M}^1(G),d_{\mathfrak {h},G})$
that limits onto an arbitrary unit-entropy metric on either
![]() $G_1$
or
$G_1$
or
![]() $G_2$
. This calculation appears in Proposition 10.2. Given a length function
$G_2$
. This calculation appears in Proposition 10.2. Given a length function
![]() $\ell \in \mathcal {M}(G)$
we denote
$\ell \in \mathcal {M}(G)$
we denote
![]() $\ell ^{0} = \ell (e_0)$
,
$\ell ^{0} = \ell (e_0)$
,
![]() $\ell ^1 = (\ell (e^1_1),\ldots ,\ell (e^1_{n_1}))$
and
$\ell ^1 = (\ell (e^1_1),\ldots ,\ell (e^1_{n_1}))$
and
![]() $\ell ^2 = (\ell (e^2_1),\ldots ,\ell (e^2_{n_2}))$
.
$\ell ^2 = (\ell (e^2_1),\ldots ,\ell (e^2_{n_2}))$
.
Given a simplex
![]() $\Delta \in C_G$
and an edge
$\Delta \in C_G$
and an edge
![]() $e \in E$
of G, we recall that
$e \in E$
of G, we recall that
![]() $\Delta (e)$
denotes the number of times e or
$\Delta (e)$
denotes the number of times e or
![]() $\bar e$
appears as a vertex in a simple cycle contained in
$\bar e$
appears as a vertex in a simple cycle contained in
![]() $\Delta $
. By the construction of
$\Delta $
. By the construction of
![]() $C_G$
we have that
$C_G$
we have that
![]() $\Delta (e) \in \{0,1,2\}$
for any edge. Further,
$\Delta (e) \in \{0,1,2\}$
for any edge. Further,
![]() $\Delta (e_0) \in \{0,2\}$
as
$\Delta (e_0) \in \{0,2\}$
as
![]() $e_0$
is separating.
$e_0$
is separating.
Analogous to the functions
![]() $Y_i$
defined in §7.2 that allowed us to isolate the variable
$Y_i$
defined in §7.2 that allowed us to isolate the variable
![]() $\ell ^i$
for the r-rose, we define a function
$\ell ^i$
for the r-rose, we define a function
![]() $Y \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
by
$Y \colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
by
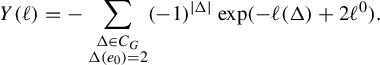 $$ \begin{align*} Y(\ell) = -\sum_{\substack{\Delta \in C_{G} \\ \Delta(e_0) = 2}}(-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta) + 2\ell^0). \end{align*} $$
$$ \begin{align*} Y(\ell) = -\sum_{\substack{\Delta \in C_{G} \\ \Delta(e_0) = 2}}(-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta) + 2\ell^0). \end{align*} $$
Notice that this function is constant with respect to
![]() $\ell ^0$
as we may write
$\ell ^0$
as we may write
Hence if
![]() $\Delta (e_0) = 2$
, then
$\Delta (e_0) = 2$
, then
![]() $\ell (\Delta ) - 2\ell ^0$
has no dependence on
$\ell (\Delta ) - 2\ell ^0$
has no dependence on
![]() $\ell ^0$
. Also we remark that the function
$\ell ^0$
. Also we remark that the function
![]() $Y\colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
has a continuous extension to
$Y\colon \thinspace \mathcal {M}(G) \to \mathbb {R}$
has a continuous extension to
![]() $[0,\infty ]^{\lvert {E_+} \rvert }$
and is bounded on
$[0,\infty ]^{\lvert {E_+} \rvert }$
and is bounded on
![]() $[0,\infty ]^{\lvert {E_+} \rvert }$
. With this notation we have the following expression for
$[0,\infty ]^{\lvert {E_+} \rvert }$
. With this notation we have the following expression for
![]() $F_G$
.
$F_G$
.
Lemma 10.1. Let
![]() $\ell \in \mathcal {M}(G)$
. Then
$\ell \in \mathcal {M}(G)$
. Then
![]() $F_{G}(\ell ) = F_{G_1}(\ell ^1)F_{G_2}(\ell ^2) - \exp (-2\ell ^0)Y(\ell )$
.
$F_{G}(\ell ) = F_{G_1}(\ell ^1)F_{G_2}(\ell ^2) - \exp (-2\ell ^0)Y(\ell )$
.
Proof. Let
![]() $\Delta $
be a simplex in
$\Delta $
be a simplex in
![]() $C_G$
. If
$C_G$
. If
![]() $\Delta (e_0) = 0$
, then
$\Delta (e_0) = 0$
, then
![]() $\Delta $
is the join of two (possibly empty) simplices
$\Delta $
is the join of two (possibly empty) simplices
![]() $\Delta _1 \in C_{G_1}$
and
$\Delta _1 \in C_{G_1}$
and
![]() $\Delta _2 \in C_{G_2}$
. Indeed, if
$\Delta _2 \in C_{G_2}$
. Indeed, if
![]() $\Delta = \{\gamma ^1_1,\ldots ,\gamma ^1_{m_1},\gamma ^2_1,\ldots , \gamma ^2_{m_2} \}$
, then
$\Delta = \{\gamma ^1_1,\ldots ,\gamma ^1_{m_1},\gamma ^2_1,\ldots , \gamma ^2_{m_2} \}$
, then
![]() $\Delta = \Delta _1 \ast \Delta _2$
where
$\Delta = \Delta _1 \ast \Delta _2$
where
![]() $\Delta _i = \{\gamma ^i_1,\ldots ,\gamma ^i_{m_i}\}$
for
$\Delta _i = \{\gamma ^i_1,\ldots ,\gamma ^i_{m_i}\}$
for
![]() $i = 1$
,
$i = 1$
,
![]() $2$
. We have
$2$
. We have
![]() $\lvert {\Delta } \rvert = m_1 + m_2 = \lvert {\Delta _1} \rvert + \lvert {\Delta _2} \rvert $
and thus
$\lvert {\Delta } \rvert = m_1 + m_2 = \lvert {\Delta _1} \rvert + \lvert {\Delta _2} \rvert $
and thus
Therefore, by Theorem 4.2, we find that
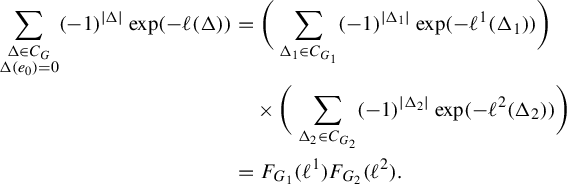 $$ \begin{align*} \sum_{\substack{\Delta \in C_{G} \\ \Delta(e_0) = 0}}(-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta)) &= \bigg(\sum_{\Delta_1 \in C_{G_1}}(-1)^{\lvert {\Delta_1} \rvert}\exp(-\ell^1(\Delta_1))\bigg)\\&\quad\times\bigg( \sum_{\Delta_2 \in C_{G_2}}(-1)^{\lvert {\Delta_2} \rvert} \exp(-\ell^2(\Delta_2))\bigg) \\ &= F_{G_1}(\ell^1) F_{G_2}(\ell^2). \end{align*} $$
$$ \begin{align*} \sum_{\substack{\Delta \in C_{G} \\ \Delta(e_0) = 0}}(-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta)) &= \bigg(\sum_{\Delta_1 \in C_{G_1}}(-1)^{\lvert {\Delta_1} \rvert}\exp(-\ell^1(\Delta_1))\bigg)\\&\quad\times\bigg( \sum_{\Delta_2 \in C_{G_2}}(-1)^{\lvert {\Delta_2} \rvert} \exp(-\ell^2(\Delta_2))\bigg) \\ &= F_{G_1}(\ell^1) F_{G_2}(\ell^2). \end{align*} $$
If
![]() $\Delta (e_0) = 2$
, then
$\Delta (e_0) = 2$
, then
Hence, by the definition of
![]() $Y(\ell )$
, we have
$Y(\ell )$
, we have
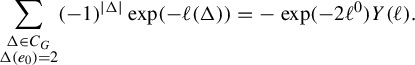 $$ \begin{align*} \sum_{\substack{\Delta \in C_{G} \\ \Delta(e_0) = 2}}(-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta)) = -\exp(-2\ell^0)Y(\ell). \end{align*} $$
$$ \begin{align*} \sum_{\substack{\Delta \in C_{G} \\ \Delta(e_0) = 2}}(-1)^{\lvert {\Delta} \rvert} \exp(-\ell(\Delta)) = -\exp(-2\ell^0)Y(\ell). \end{align*} $$
As
![]() $e_0$
is separating, there are no simplices in
$e_0$
is separating, there are no simplices in
![]() $C_G$
for which
$C_G$
for which
![]() $\Delta (e_0) = 1$
. By Theorem 4.2 again, the lemma follows.
$\Delta (e_0) = 1$
. By Theorem 4.2 again, the lemma follows.
In particular, for
![]() $\ell \in \mathcal {M}^1(G)$
we have
$\ell \in \mathcal {M}^1(G)$
we have
![]() $F_G(\ell ) = 0$
by Lemma 4.4, and thus
$F_G(\ell ) = 0$
by Lemma 4.4, and thus
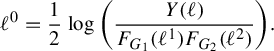 $$ \begin{align} \ell^0 = \frac{1}{2}\log\bigg(\frac{Y(\ell)}{F_{G_1}(\ell^1)F_{G_2}(\ell^2)} \bigg). \end{align} $$
$$ \begin{align} \ell^0 = \frac{1}{2}\log\bigg(\frac{Y(\ell)}{F_{G_1}(\ell^1)F_{G_2}(\ell^2)} \bigg). \end{align} $$
Using the above expression for
![]() $F_G$
and
$F_G$
and
![]() $\ell ^0$
, we will give a method of a finite-length path in G for which
$\ell ^0$
, we will give a method of a finite-length path in G for which
![]() $\ell ^0 \to \infty $
.
$\ell ^0 \to \infty $
.
Proposition 10.2. Fix a length function
![]() $\ell ' \in \mathcal {M}^1(G_1)$
and let
$\ell ' \in \mathcal {M}^1(G_1)$
and let
![]() ${1 < x_1,\ldots ,x_{n_1} < \infty}$
be such that
${1 < x_1,\ldots ,x_{n_1} < \infty}$
be such that
![]() $\ell '(e^1_i) = \log (x_i)$
for
$\ell '(e^1_i) = \log (x_i)$
for
![]() $1 \leq i \leq n_1$
. Let
$1 \leq i \leq n_1$
. Let
![]() $\ell \in \mathcal {M}^1(G)$
be such that
$\ell \in \mathcal {M}^1(G)$
be such that
![]() ${\ell (e^1_i) = \log (x_i + 1)}$
for
${\ell (e^1_i) = \log (x_i + 1)}$
for
![]() $1 \leq i \leq n_1$
and let
$1 \leq i \leq n_1$
and let
![]() $\ell _t \colon \thinspace [0,1) \to \widehat {\mathcal {M}}^1(G)$
be the path defined by
$\ell _t \colon \thinspace [0,1) \to \widehat {\mathcal {M}}^1(G)$
be the path defined by
![]() $\ell _t(e^1_i) = \log (x_i + 1 - t)$
,
$\ell _t(e^1_i) = \log (x_i + 1 - t)$
,
![]() $\ell _t^2 = \ell ^2$
and
$\ell _t^2 = \ell ^2$
and
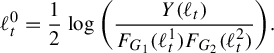 $$ \begin{align} \ell_t^0 = \frac{1}{2} \log\bigg(\frac{Y(\ell_t)}{F_{G_1}(\ell_t^1)F_{G_2}(\ell_t^2)}\bigg). \end{align} $$
$$ \begin{align} \ell_t^0 = \frac{1}{2} \log\bigg(\frac{Y(\ell_t)}{F_{G_1}(\ell_t^1)F_{G_2}(\ell_t^2)}\bigg). \end{align} $$
Then
![]() $\mathcal {L}_{\mathfrak {h},G}(\ell _t|[0,1))$
is finite and
$\mathcal {L}_{\mathfrak {h},G}(\ell _t|[0,1))$
is finite and
![]() $\ell _t^0 \to \infty $
as
$\ell _t^0 \to \infty $
as
![]() $t \to 1^-$
.
$t \to 1^-$
.
Proof. We will use the notation as in the statement of the proposition. As
![]() $\mathfrak {h}_{G_1}(\ell ') = 1$
, we must have that
$\mathfrak {h}_{G_1}(\ell ') = 1$
, we must have that
![]() $\ell _t^0 \to \infty $
at
$\ell _t^0 \to \infty $
at
![]() $t \to 1^-$
. Indeed, if not then the limiting length function has unit entropy, and with this length function the subgraph
$t \to 1^-$
. Indeed, if not then the limiting length function has unit entropy, and with this length function the subgraph
![]() $G_1$
also has unit entropy.
$G_1$
also has unit entropy.
Notice that since
![]() $\ell _t(e)\partial _{e} F_G(\ell _t)> 0$
for all
$\ell _t(e)\partial _{e} F_G(\ell _t)> 0$
for all
![]() $e \in E_+$
by Lemma 4.4(3), we have that
$e \in E_+$
by Lemma 4.4(3), we have that
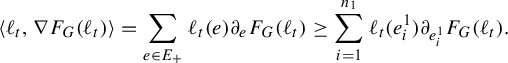 $$ \begin{align} \langle \ell_t,\nabla F_G(\ell_t) \rangle = \sum_{e \in E_+} \ell_t(e)\partial_{e} F_G(\ell_t) \geq \sum_{i=1}^{n_1} \ell_t(e^1_i)\partial_{e^1_i} F_G(\ell_t). \end{align} $$
$$ \begin{align} \langle \ell_t,\nabla F_G(\ell_t) \rangle = \sum_{e \in E_+} \ell_t(e)\partial_{e} F_G(\ell_t) \geq \sum_{i=1}^{n_1} \ell_t(e^1_i)\partial_{e^1_i} F_G(\ell_t). \end{align} $$
By Lemma 10.1, we compute that
Thus since
![]() $\partial _{e^1_i} Y(\ell )$
is bounded on
$\partial _{e^1_i} Y(\ell )$
is bounded on
![]() $\mathcal {M}(G)$
, we see that
$\mathcal {M}(G)$
, we see that
![]() $\langle \ell _t,\nabla F_G(\ell _t) \rangle $
has a limit, as
$\langle \ell _t,\nabla F_G(\ell _t) \rangle $
has a limit, as
![]() ${t \to 1^-}$
, that is bounded below by
${t \to 1^-}$
, that is bounded below by
![]() $F_{G_2}(\ell ^2)\langle \ell ',\nabla F_{G_1}(\ell ') \rangle $
, which is positive by Lemma 4.4(3) and Lemma 4.9. (We will see in Lemma 10.4(2) that the limit is in fact exactly equal to
$F_{G_2}(\ell ^2)\langle \ell ',\nabla F_{G_1}(\ell ') \rangle $
, which is positive by Lemma 4.4(3) and Lemma 4.9. (We will see in Lemma 10.4(2) that the limit is in fact exactly equal to
![]() $F_{G_2}(\ell ^2)\langle \ell ',\nabla F_{G_1}(\ell ') \rangle $
.) Hence there is an
$F_{G_2}(\ell ^2)\langle \ell ',\nabla F_{G_1}(\ell ') \rangle $
.) Hence there is an
![]() $\epsilon> 0$
such that
$\epsilon> 0$
such that
for all
![]() $t \in [0,1)$
.
$t \in [0,1)$
.
We compute that
![]() $\ddot \ell _t(e^1_i) = ({-1})/({x_i + 1 - t}) < 0$
, hence
$\ddot \ell _t(e^1_i) = ({-1})/({x_i + 1 - t}) < 0$
, hence
![]() $\ddot \ell _t(e^1_i) \partial _{e^1_i} F_G(\ell _t) < 0$
for all
$\ddot \ell _t(e^1_i) \partial _{e^1_i} F_G(\ell _t) < 0$
for all
![]() $0 < t < 1$
and
$0 < t < 1$
and
![]() $1 \leq i \leq n_1$
. Clearly
$1 \leq i \leq n_1$
. Clearly
![]() $\ddot \ell _t(e^2_i) \partial _{e^2_i} F_G(\ell _t) = 0$
for all
$\ddot \ell _t(e^2_i) \partial _{e^2_i} F_G(\ell _t) = 0$
for all
![]() $1 \leq i \leq n_2$
and
$1 \leq i \leq n_2$
and
![]() $0 < t < 1$
. Thus
$0 < t < 1$
. Thus
To deal with this term, we need the following claim.
Claim 10.3. There are polynomials
![]() $p,q \in \mathbb {R}[t]$
where
$p,q \in \mathbb {R}[t]$
where
![]() $p(t), q(t) \neq 0$
for
$p(t), q(t) \neq 0$
for
![]() $t \in [0,1]$
such that
$t \in [0,1]$
such that
Proof of Claim 10.3
As
![]() $F_{G}(\ell _t) = 0$
, we have that
$F_{G}(\ell _t) = 0$
, we have that
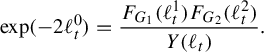 $$ \begin{align*} \exp(-2\ell_t^0) = \frac{F_{G_1}(\ell_t^1)F_{G_2}(\ell_t^2)}{Y(\ell_t)}. \end{align*} $$
$$ \begin{align*} \exp(-2\ell_t^0) = \frac{F_{G_1}(\ell_t^1)F_{G_2}(\ell_t^2)}{Y(\ell_t)}. \end{align*} $$
Let
![]() $\ell (E_i) = \sum _{j = 1}^{n_i} \ell (e^i_j)$
for
$\ell (E_i) = \sum _{j = 1}^{n_i} \ell (e^i_j)$
for
![]() $i = 1$
,
$i = 1$
,
![]() $2$
. Notice that we can write
$2$
. Notice that we can write
![]() $F_{G_1}(\ell _t^1)$
as
$F_{G_1}(\ell _t^1)$
as
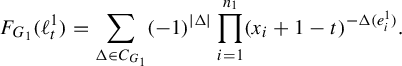 $$ \begin{align*} F_{G_1}(\ell_t^1) = \sum_{\Delta \in C_{G_1}} (-1)^{\lvert {\Delta} \rvert}\prod_{i=1}^{n_1} (x_i +1 -t)^{-\Delta(e^1_i)}. \end{align*} $$
$$ \begin{align*} F_{G_1}(\ell_t^1) = \sum_{\Delta \in C_{G_1}} (-1)^{\lvert {\Delta} \rvert}\prod_{i=1}^{n_1} (x_i +1 -t)^{-\Delta(e^1_i)}. \end{align*} $$
Hence
![]() $\exp (2\ell _t(E_1))F_{G_1}(\ell _t^1)$
is a polynomial in t with real coefficients. Also, we observe that
$\exp (2\ell _t(E_1))F_{G_1}(\ell _t^1)$
is a polynomial in t with real coefficients. Also, we observe that
![]() $\exp (2\ell _t(E_2))F_{G_2}(\ell _t^2)$
is a non-zero constant with respect to t. By the definition of
$\exp (2\ell _t(E_2))F_{G_2}(\ell _t^2)$
is a non-zero constant with respect to t. By the definition of
![]() $\ell _t$
we have that
$\ell _t$
we have that
![]() $F_{G_1}(\ell _1^1) = 0$
. Hence we can write
$F_{G_1}(\ell _1^1) = 0$
. Hence we can write
where
![]() $p(t) \in \mathbb {R}[t]$
. As the left-hand side of this equation does not vanish for
$p(t) \in \mathbb {R}[t]$
. As the left-hand side of this equation does not vanish for
![]() $t \in [0,1)$
by Lemma 4.9, we see that
$t \in [0,1)$
by Lemma 4.9, we see that
![]() $p(t) \neq 0$
for
$p(t) \neq 0$
for
![]() $t \in [0,1)$
. To show that
$t \in [0,1)$
. To show that
![]() $p(1) \neq 0$
, we see that
$p(1) \neq 0$
, we see that
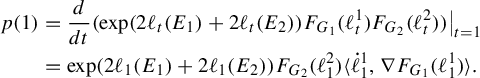 $$ \begin{align*} p(1) & = \frac{d}{dt}(\exp(2\ell_t(E_1)+2\ell_t(E_2))F_{G_1}(\ell_t^1)F_{G_2}(\ell_t^2)) \big|_{t=1} \\ & = \exp(2\ell_1(E_1) + 2\ell_1(E_2))F_{G_2}(\ell_1^2)\langle \dot \ell_1^1,\nabla F_{G_1}(\ell_1^1) \rangle. \end{align*} $$
$$ \begin{align*} p(1) & = \frac{d}{dt}(\exp(2\ell_t(E_1)+2\ell_t(E_2))F_{G_1}(\ell_t^1)F_{G_2}(\ell_t^2)) \big|_{t=1} \\ & = \exp(2\ell_1(E_1) + 2\ell_1(E_2))F_{G_2}(\ell_1^2)\langle \dot \ell_1^1,\nabla F_{G_1}(\ell_1^1) \rangle. \end{align*} $$
As
![]() $\ell _1^1 \in \mathcal {M}^1(G_1)$
, we have that
$\ell _1^1 \in \mathcal {M}^1(G_1)$
, we have that
![]() $\nabla F_{G_1}(\ell _1^1)$
is non-zero and parallel to
$\nabla F_{G_1}(\ell _1^1)$
is non-zero and parallel to
![]() $\nabla \mathfrak {h}_{G_1}(\ell _1^1)$
by Lemma 4.4. Since
$\nabla \mathfrak {h}_{G_1}(\ell _1^1)$
by Lemma 4.4. Since
![]() $\mathfrak {h}_{G_1}(\ell _t^1)$
is increasing with respect to t as every edge length is decreasing (past
$\mathfrak {h}_{G_1}(\ell _t^1)$
is increasing with respect to t as every edge length is decreasing (past
![]() $t = 1$
as well), we have that
$t = 1$
as well), we have that
![]() $\langle \dot \ell _1^1,\nabla \mathfrak {h}_{G_1}(\ell _1^1) \rangle \neq 0$
. Hence
$\langle \dot \ell _1^1,\nabla \mathfrak {h}_{G_1}(\ell _1^1) \rangle \neq 0$
. Hence
![]() $p(1) \neq 0$
as well.
$p(1) \neq 0$
as well.
In a similar way, we observe that we can write
for some
![]() $q(t) \in \mathbb {R}[t]$
. As
$q(t) \in \mathbb {R}[t]$
. As
![]() $Y(\ell _t) = \exp (2\ell ^0)F_{G_1}(\ell _t^1)F_{G_2}(\ell _t^2)$
by Lemma 10.1, we see that
$Y(\ell _t) = \exp (2\ell ^0)F_{G_1}(\ell _t^1)F_{G_2}(\ell _t^2)$
by Lemma 10.1, we see that
![]() $Y(\ell _t) \neq 0$
for
$Y(\ell _t) \neq 0$
for
![]() $t \in [0,1)$
by Lemma 4.9 and hence
$t \in [0,1)$
by Lemma 4.9 and hence
![]() $q(t) \neq 0$
for
$q(t) \neq 0$
for
![]() $t \in [0,1)$
as well. As
$t \in [0,1)$
as well. As
![]() $t \to 1^-$
, we have that
$t \to 1^-$
, we have that
![]() $\ell _t^0 \to \infty $
and thus
$\ell _t^0 \to \infty $
and thus
![]() ${(1-t)p(t)}/{q(t)} \to 0$
as
${(1-t)p(t)}/{q(t)} \to 0$
as
![]() $t \to 1^-$
. As
$t \to 1^-$
. As
![]() $p(1) \neq 0$
, we must have that
$p(1) \neq 0$
, we must have that
![]() $q(1) \neq 0$
as well.
$q(1) \neq 0$
as well.
By Claim 10.3, we compute that
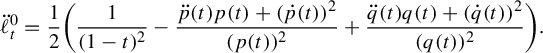 $$ \begin{align*} \ddot \ell_t^0 &= \frac{1}{2}\bigg(\frac{1}{(1-t)^2} - \frac{\ddot p(t) p(t) + (\dot p(t))^2}{(p(t))^2} + \frac{\ddot q(t) q(t) + (\dot q(t))^2}{(q(t))^2} \bigg). \end{align*} $$
$$ \begin{align*} \ddot \ell_t^0 &= \frac{1}{2}\bigg(\frac{1}{(1-t)^2} - \frac{\ddot p(t) p(t) + (\dot p(t))^2}{(p(t))^2} + \frac{\ddot q(t) q(t) + (\dot q(t))^2}{(q(t))^2} \bigg). \end{align*} $$
Using Lemma 10.1 and Claim 10.3, we find that
Hence we see that there exists a constant
![]() $C> 0$
such that
$C> 0$
such that
Therefore, by combining Proposition 4.6 with (10.5), (10.6) and (10.7), we have that
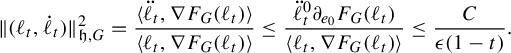 $$ \begin{align*} \| {(\ell_t, \dot \ell_t)} \|^2_{\mathfrak{h},G} = \frac{\langle \ddot \ell_t,\nabla F_G(\ell_t) \rangle}{\langle \ell_t,\nabla F_G(\ell_t) \rangle} \leq \frac{\ddot \ell_t^0 \partial_{e_0} F_G(\ell_t)}{\langle \ell_t,\nabla F_G(\ell_t) \rangle} \leq \frac{C}{\epsilon(1-t)}. \end{align*} $$
$$ \begin{align*} \| {(\ell_t, \dot \ell_t)} \|^2_{\mathfrak{h},G} = \frac{\langle \ddot \ell_t,\nabla F_G(\ell_t) \rangle}{\langle \ell_t,\nabla F_G(\ell_t) \rangle} \leq \frac{\ddot \ell_t^0 \partial_{e_0} F_G(\ell_t)}{\langle \ell_t,\nabla F_G(\ell_t) \rangle} \leq \frac{C}{\epsilon(1-t)}. \end{align*} $$
Hence the length of
![]() $\ell _t$
is finite.
$\ell _t$
is finite.
10.2 The model space
 $\widehat {\mathcal {M}}^1(G)$
$\widehat {\mathcal {M}}^1(G)$
The previous example shows that we should expect some points in the completion of
![]() $(\mathcal {M}^1(G),d_{\mathfrak {h},G})$
to correspond to unit-entropy metrics on
$(\mathcal {M}^1(G),d_{\mathfrak {h},G})$
to correspond to unit-entropy metrics on
![]() $G_1$
or
$G_1$
or
![]() $G_2$
. For the model, we add these points to
$G_2$
. For the model, we add these points to
![]() $\mathcal {M}^1(G)$
as well as points that correspond to unit-entropy metrics on
$\mathcal {M}^1(G)$
as well as points that correspond to unit-entropy metrics on
![]() $G_1 \cup G_2$
. To this end, we set
$G_1 \cup G_2$
. To this end, we set
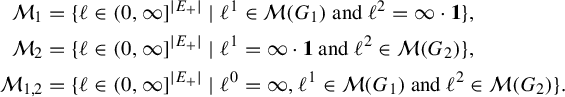 $$ \begin{align*} \mathcal{M}_1 & = \{ \ell \in (0,\infty]^{\lvert {E_+} \rvert} \mid \ell^1 \in \mathcal{M}(G_1) \mbox{ and } \ell^2 = \infty \cdot \mathbf{1} \}, \\ \mathcal{M}_2 & = \{ \ell \in (0,\infty]^{\lvert {E_+} \rvert} \mid \ell^1 = \infty \cdot \mathbf{1} \mbox{ and } \ell^2 \in \mathcal{M}(G_2) \}, \\ \mathcal{M}_{1,2} & = \{ \ell \in (0,\infty]^{\lvert {E_+} \rvert} \mid \ell^0 = \infty, \ell^1 \in \mathcal{M}(G_1) \mbox{ and } \ell^2 \in \mathcal{M}(G_2) \}. \end{align*} $$
$$ \begin{align*} \mathcal{M}_1 & = \{ \ell \in (0,\infty]^{\lvert {E_+} \rvert} \mid \ell^1 \in \mathcal{M}(G_1) \mbox{ and } \ell^2 = \infty \cdot \mathbf{1} \}, \\ \mathcal{M}_2 & = \{ \ell \in (0,\infty]^{\lvert {E_+} \rvert} \mid \ell^1 = \infty \cdot \mathbf{1} \mbox{ and } \ell^2 \in \mathcal{M}(G_2) \}, \\ \mathcal{M}_{1,2} & = \{ \ell \in (0,\infty]^{\lvert {E_+} \rvert} \mid \ell^0 = \infty, \ell^1 \in \mathcal{M}(G_1) \mbox{ and } \ell^2 \in \mathcal{M}(G_2) \}. \end{align*} $$
We consider their union
![]() $\widehat {\mathcal {M}}(G) = \mathcal {M}(G) \cup \mathcal {M}_1 \cup \mathcal {M}_2 \cup \mathcal {M}_{1,2}$
as a subset of
$\widehat {\mathcal {M}}(G) = \mathcal {M}(G) \cup \mathcal {M}_1 \cup \mathcal {M}_2 \cup \mathcal {M}_{1,2}$
as a subset of
![]() $(0,\infty ]^{\lvert {E_+} \rvert }$
, endowed with the subspace topology as in §9. There are obvious embeddings
$(0,\infty ]^{\lvert {E_+} \rvert }$
, endowed with the subspace topology as in §9. There are obvious embeddings
![]() $\varepsilon _i \colon \thinspace \mathcal {M}(G_i) \to \mathcal {M}_i$
for
$\varepsilon _i \colon \thinspace \mathcal {M}(G_i) \to \mathcal {M}_i$
for
![]() $i = 1$
,
$i = 1$
,
![]() $2$
where we set
$2$
where we set
![]() $\varepsilon _i(\ell )^0 = \infty $
, and an obvious embedding
$\varepsilon _i(\ell )^0 = \infty $
, and an obvious embedding
![]() $\varepsilon _{1,2} \colon \thinspace \mathcal {M}(G_1) \times \mathcal {M}(G_2) \to \mathcal {M}_{1,2}$
as well. Next, we define
$\varepsilon _{1,2} \colon \thinspace \mathcal {M}(G_1) \times \mathcal {M}(G_2) \to \mathcal {M}_{1,2}$
as well. Next, we define
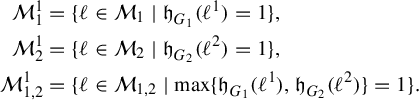 $$ \begin{align*} \mathcal{M}^1_1 & = \{ \ell \in \mathcal{M}_1 \mid \mathfrak{h}_{G_1}(\ell^1) = 1\}, \\ \mathcal{M}^1_2 & = \{ \ell \in \mathcal{M}_2 \mid \mathfrak{h}_{G_2}(\ell^2) = 1\}, \\ \mathcal{M}^1_{1,2} & = \{ \ell \in \mathcal{M}_{1,2} \mid \max\{\mathfrak{h}_{G_1}(\ell^1),\mathfrak{h}_{G_2}(\ell^2)\} = 1 \}. \end{align*} $$
$$ \begin{align*} \mathcal{M}^1_1 & = \{ \ell \in \mathcal{M}_1 \mid \mathfrak{h}_{G_1}(\ell^1) = 1\}, \\ \mathcal{M}^1_2 & = \{ \ell \in \mathcal{M}_2 \mid \mathfrak{h}_{G_2}(\ell^2) = 1\}, \\ \mathcal{M}^1_{1,2} & = \{ \ell \in \mathcal{M}_{1,2} \mid \max\{\mathfrak{h}_{G_1}(\ell^1),\mathfrak{h}_{G_2}(\ell^2)\} = 1 \}. \end{align*} $$
Our model space is the union of these sets. Specifically, we define
Using (4.2), we see that each partial derivative of
![]() $F_G$
extends to a bounded continuous function on
$F_G$
extends to a bounded continuous function on
![]() $\widehat {\mathcal {M}}(G)$
. The naturality of these extensions is the same as in Lemma 9.3. Even more, the inner product
$\widehat {\mathcal {M}}(G)$
. The naturality of these extensions is the same as in Lemma 9.3. Even more, the inner product
![]() $\langle \ell ,\nabla F_G(\ell ) \rangle $
has a continuous extension as was the case in Lemma 9.4.
$\langle \ell ,\nabla F_G(\ell ) \rangle $
has a continuous extension as was the case in Lemma 9.4.
Lemma 10.4. The function
![]() $\ell \mapsto \langle \ell ,\nabla F_G(\ell ) \rangle $
has a continuous extension to
$\ell \mapsto \langle \ell ,\nabla F_G(\ell ) \rangle $
has a continuous extension to
![]() $\widehat {\mathcal {M}}(G)$
. This extension is such that the following statements hold.
$\widehat {\mathcal {M}}(G)$
. This extension is such that the following statements hold.
-
(1) If
 $i \in \{1,2\}$
and
$i \in \{1,2\}$
and
 $\ell \in \mathcal {M}_i$
, then
$\ell \in \mathcal {M}_i$
, then  $$ \begin{align*}\langle \ell,\nabla F_{G}(\ell) \rangle = \langle \ell^i,\nabla F_{G_i}(\ell^i) \rangle. \end{align*} $$
$$ \begin{align*}\langle \ell,\nabla F_{G}(\ell) \rangle = \langle \ell^i,\nabla F_{G_i}(\ell^i) \rangle. \end{align*} $$
-
(2) If
 $\ell \in \mathcal {M}_{1,2}$
, then
$\ell \in \mathcal {M}_{1,2}$
, then  $$ \begin{align*}\langle \ell,\nabla F_{G}(\ell) \rangle = F_{G_2}(\ell^2)\langle \ell^1,\nabla F_{G_1}(\ell^1) \rangle + F_{G_1}(\ell^1)\langle \ell^2,\nabla F_{G_2}(\ell^2) \rangle. \end{align*} $$
$$ \begin{align*}\langle \ell,\nabla F_{G}(\ell) \rangle = F_{G_2}(\ell^2)\langle \ell^1,\nabla F_{G_1}(\ell^1) \rangle + F_{G_1}(\ell^1)\langle \ell^2,\nabla F_{G_2}(\ell^2) \rangle. \end{align*} $$
-
(3) For all
 $\ell \in \widehat {\mathcal {M}}(G)$
, we have
$\ell \in \widehat {\mathcal {M}}(G)$
, we have
 $\langle \ell ,\nabla F_G(\ell ) \rangle \geq 0$
with equality if and only if
$\langle \ell ,\nabla F_G(\ell ) \rangle \geq 0$
with equality if and only if
 $\mathfrak {h}_{G_1}(\ell ^1) = \mathfrak {h}_{G_2}(\ell ^2) = 1$
.
$\mathfrak {h}_{G_1}(\ell ^1) = \mathfrak {h}_{G_2}(\ell ^2) = 1$
.
Proof. From Lemma 4.4(3) and the expression for
![]() $\partial _{e} F_G(\ell )$
in (4.2), we see that there is a constant
$\partial _{e} F_G(\ell )$
in (4.2), we see that there is a constant
![]() $A> 0$
such that
$A> 0$
such that
![]() $0 < \partial _{e} F_G(\ell ) \leq A\exp (-\ell (e))$
for any edge
$0 < \partial _{e} F_G(\ell ) \leq A\exp (-\ell (e))$
for any edge
![]() $e \in E_+$
. The existence of the continuous extension now follows for the same reason as for Lemma 9.4.
$e \in E_+$
. The existence of the continuous extension now follows for the same reason as for Lemma 9.4.
If
![]() $\ell ^1 = \infty \cdot \mathbf {1}$
, then
$\ell ^1 = \infty \cdot \mathbf {1}$
, then
![]() $Y(\ell ) = 0$
. Indeed, this follows as every simple cycle in G that contains
$Y(\ell ) = 0$
. Indeed, this follows as every simple cycle in G that contains
![]() $e_0$
must also contain an edge in
$e_0$
must also contain an edge in
![]() $G_1$
as
$G_1$
as
![]() $e_0$
is separating. Likewise, if
$e_0$
is separating. Likewise, if
![]() $\ell ^2 = \infty \cdot \mathbf {1}$
, then
$\ell ^2 = \infty \cdot \mathbf {1}$
, then
![]() $Y(\ell ) = 0$
as well. Hence
$Y(\ell ) = 0$
as well. Hence
![]() $\partial _{e_0} F_G(\ell ) = 2\exp (-2\ell ^0)Y(\ell ) = 0$
for
$\partial _{e_0} F_G(\ell ) = 2\exp (-2\ell ^0)Y(\ell ) = 0$
for
![]() $\ell \in \mathcal {M}_i$
when
$\ell \in \mathcal {M}_i$
when
![]() $i = 1$
,
$i = 1$
,
![]() $2$
. This, together with the paragraph above, shows (1).
$2$
. This, together with the paragraph above, shows (1).
Using Lemma 10.1, we compute the following expression for
![]() $\langle \ell ,\nabla F_G(\ell ) \rangle $
:
$\langle \ell ,\nabla F_G(\ell ) \rangle $
:
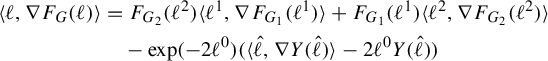 $$ \begin{align*} \langle \ell,\nabla F_{G}(\ell) \rangle &= F_{G_2}(\ell^2)\langle \ell^1,\nabla F_{G_1}(\ell^1) \rangle + F_{G_1}(\ell^1)\langle \ell^2,\nabla F_{G_2}(\ell^2) \rangle \\ &\quad- \exp(-2\ell^0)(\langle \hat{\ell},\nabla Y(\hat\ell) \rangle - 2\ell^0 Y(\hat\ell)) \end{align*} $$
$$ \begin{align*} \langle \ell,\nabla F_{G}(\ell) \rangle &= F_{G_2}(\ell^2)\langle \ell^1,\nabla F_{G_1}(\ell^1) \rangle + F_{G_1}(\ell^1)\langle \ell^2,\nabla F_{G_2}(\ell^2) \rangle \\ &\quad- \exp(-2\ell^0)(\langle \hat{\ell},\nabla Y(\hat\ell) \rangle - 2\ell^0 Y(\hat\ell)) \end{align*} $$
From this (2) is apparent.
As
![]() $\langle \ell ,\nabla F_G(\ell ) \rangle> 0$
for all
$\langle \ell ,\nabla F_G(\ell ) \rangle> 0$
for all
![]() $\ell \in \mathcal {M}^1(G)$
by Lemma 4.4(3), the extension is clearly non-negative. Statement (3) now follows from (1) and (2) as
$\ell \in \mathcal {M}^1(G)$
by Lemma 4.4(3), the extension is clearly non-negative. Statement (3) now follows from (1) and (2) as
![]() $\langle \ell ,\nabla F_{G_i}(\ell ) \rangle> 0$
for any
$\langle \ell ,\nabla F_{G_i}(\ell ) \rangle> 0$
for any
![]() $\ell \in \mathcal {M}^1(G_i)$
again by Lemma 4.4(3) and
$\ell \in \mathcal {M}^1(G_i)$
again by Lemma 4.4(3) and
![]() $F_{G_i}(\ell )> 0$
for any
$F_{G_i}(\ell )> 0$
for any
![]() $\ell \in \mathcal {M}^1(G_i)$
if
$\ell \in \mathcal {M}^1(G_i)$
if
![]() $\mathfrak {h}(G_i)(\ell ) < 1$
by Lemma 4.9.
$\mathfrak {h}(G_i)(\ell ) < 1$
by Lemma 4.9.
Next we partition
![]() $\widehat {\mathcal {M}}^1(G)$
into two subsets that we call the singular points and regular points, respectively:
$\widehat {\mathcal {M}}^1(G)$
into two subsets that we call the singular points and regular points, respectively:
 $$ \begin{align*} \widehat{\mathcal{M}}^1(G)_{\textrm{sing}} & = \{ \ell \in \widehat{\mathcal{M}}^1(G) \mid \mathfrak{h}_{G_1}(\ell^1) = \mathfrak{h}_{G_2}(\ell^2) = 1 \}, \\ \widehat{\mathcal{M}}^1(G)_{\textrm{reg}} & = \widehat{\mathcal{M}}^1(G) - \widehat{\mathcal{M}}^1(G)_{\textrm{sing}}. \end{align*} $$
$$ \begin{align*} \widehat{\mathcal{M}}^1(G)_{\textrm{sing}} & = \{ \ell \in \widehat{\mathcal{M}}^1(G) \mid \mathfrak{h}_{G_1}(\ell^1) = \mathfrak{h}_{G_2}(\ell^2) = 1 \}, \\ \widehat{\mathcal{M}}^1(G)_{\textrm{reg}} & = \widehat{\mathcal{M}}^1(G) - \widehat{\mathcal{M}}^1(G)_{\textrm{sing}}. \end{align*} $$
Notice that
![]() $\widehat {\mathcal {M}}^1(G)_{\textrm {sing}}$
is a subset of
$\widehat {\mathcal {M}}^1(G)_{\textrm {sing}}$
is a subset of
![]() $\mathcal {M}^1_{1,2}$
.
$\mathcal {M}^1_{1,2}$
.
As in §9.1, we also define the tangent bundle
![]() $T\widehat {\mathcal {M}}^1(G)$
to be the subspace of
$T\widehat {\mathcal {M}}^1(G)$
to be the subspace of
![]() $(\ell ,\mathbf {v}) \in \widehat {\mathcal {M}}^1(G) \times \mathbb {R}^{\lvert {E_+} \rvert }$
where
$(\ell ,\mathbf {v}) \in \widehat {\mathcal {M}}^1(G) \times \mathbb {R}^{\lvert {E_+} \rvert }$
where
![]() $\langle \mathbf {v},\nabla F_G(\ell ) \rangle = 0$
. There are obvious embeddings
$\langle \mathbf {v},\nabla F_G(\ell ) \rangle = 0$
. There are obvious embeddings
![]() $T\varepsilon _i \colon \thinspace T\mathcal {M}^1(G_i) \to T\widehat {\mathcal {M}}^1(G)$
for
$T\varepsilon _i \colon \thinspace T\mathcal {M}^1(G_i) \to T\widehat {\mathcal {M}}^1(G)$
for
![]() $i = 1$
,
$i = 1$
,
![]() $2$
defined using
$2$
defined using
![]() $\varepsilon _i \colon \thinspace \mathcal {M}^1(G_i) \to \mathcal {M}_i$
as in §9.1. We define
$\varepsilon _i \colon \thinspace \mathcal {M}^1(G_i) \to \mathcal {M}_i$
as in §9.1. We define
![]() $T\widehat {\mathcal {M}}^1_{\textrm {reg}}(G)$
to be the subset of
$T\widehat {\mathcal {M}}^1_{\textrm {reg}}(G)$
to be the subset of
![]() $(\ell ,\mathbf {v}) \in T\widehat {\mathcal {M}}^1(G)$
where
$(\ell ,\mathbf {v}) \in T\widehat {\mathcal {M}}^1(G)$
where
![]() $\ell \in \widehat {\mathcal {M}}^1(G)_{\textrm {reg}}$
. Proposition 4.6 together with Lemma 10.4 implies the following proposition.
$\ell \in \widehat {\mathcal {M}}^1(G)_{\textrm {reg}}$
. Proposition 4.6 together with Lemma 10.4 implies the following proposition.
Proposition 10.5. The entropy norm
![]() extends to a continuous semi-norm
extends to a continuous semi-norm
![]() . Moreover, the embedding maps
. Moreover, the embedding maps
![]() $T\varepsilon _i \colon \thinspace T\mathcal {M}^1(G_i) \kern1.2pt{\to} T\widehat {\mathcal {M}}^1(G)$
are norm-preserving.
$T\varepsilon _i \colon \thinspace T\mathcal {M}^1(G_i) \kern1.2pt{\to} T\widehat {\mathcal {M}}^1(G)$
are norm-preserving.
As in §9.1, we have the following proposition that shows us that there is a map from
![]() $\widehat {\mathcal {M}}^1(G)$
to the completion of
$\widehat {\mathcal {M}}^1(G)$
to the completion of
![]() $\mathcal {M}^1(G)$
with respect to the entropy metric.
$\mathcal {M}^1(G)$
with respect to the entropy metric.
Proposition 10.6. The following statements hold.
-
(1) The entropy norm defines a pseudo-metric
 $d_{\mathfrak {h},G}$
on
$d_{\mathfrak {h},G}$
on
 $\widehat {\mathcal {M}}^{1}(G)$
.
$\widehat {\mathcal {M}}^{1}(G)$
. -
(2) We have
 $\operatorname {\mathrm {diam}}(\mathcal {M}^1_1 \cup \mathcal {M}^1_2 \cup \mathcal {M}^1_{1,2}) = 0$
.
$\operatorname {\mathrm {diam}}(\mathcal {M}^1_1 \cup \mathcal {M}^1_2 \cup \mathcal {M}^1_{1,2}) = 0$
. -
(3) The inclusion
 $(\mathcal {M}^{1}(G),d_{\mathfrak {h},G}) \to (\widehat {\mathcal {M}}^{1}(G),d_{\mathfrak {h},G})$
is an isometric embedding.
$(\mathcal {M}^{1}(G),d_{\mathfrak {h},G}) \to (\widehat {\mathcal {M}}^{1}(G),d_{\mathfrak {h},G})$
is an isometric embedding.
Proof. As in Proposition 9.6, we need to show that for any
![]() $\ell , \ell ' \in \widehat {\mathcal {M}}^1(G)$
there is a path
$\ell , \ell ' \in \widehat {\mathcal {M}}^1(G)$
there is a path
![]() $\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}(G)$
with
$\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}(G)$
with
![]() $\ell _0 = \ell $
and
$\ell _0 = \ell $
and
![]() $\ell _1 = \ell '$
that has finite length.
$\ell _1 = \ell '$
that has finite length.
To this end, fix a point
![]() $\ell \in \mathcal {M}^1(G)$
. There are several cases depending on whether
$\ell \in \mathcal {M}^1(G)$
. There are several cases depending on whether
![]() $\ell ' \in \mathcal {M}^1_1$
,
$\ell ' \in \mathcal {M}^1_1$
,
![]() $\ell ' \in \mathcal {M}^1_2$
or
$\ell ' \in \mathcal {M}^1_2$
or
![]() $\ell ' \in \mathcal {M}^1_{1,2}$
.
$\ell ' \in \mathcal {M}^1_{1,2}$
.
We first deal with the case that
![]() $\ell ' \in \mathcal {M}^1_{1,2}$
. Without loss of generality we assume that
$\ell ' \in \mathcal {M}^1_{1,2}$
. Without loss of generality we assume that
![]() $\mathfrak {h}_{G_1}((\ell ')^1) = 1$
. In Proposition 10.2 we produced a path
$\mathfrak {h}_{G_1}((\ell ')^1) = 1$
. In Proposition 10.2 we produced a path
![]() $\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(G)$
where
$\ell _t \colon \thinspace [0,1] \to \widehat {\mathcal {M}}^1(G)$
where
![]() $\ell _0 \in \mathcal {M}^1(G)$
and
$\ell _0 \in \mathcal {M}^1(G)$
and
![]() $\ell _1 \in \mathcal {M}_{1,2}$
is such that
$\ell _1 \in \mathcal {M}_{1,2}$
is such that
![]() $\ell _1^1 = (\ell ')^1$
. We can concatenate the path
$\ell _1^1 = (\ell ')^1$
. We can concatenate the path
![]() $\ell _t$
with a path
$\ell _t$
with a path
![]() $\tilde \ell _t \colon \thinspace [0,1] \to \mathcal {M}^1_{1,2}$
from
$\tilde \ell _t \colon \thinspace [0,1] \to \mathcal {M}^1_{1,2}$
from
![]() $\ell _1$
to
$\ell _1$
to
![]() $\ell '$
in
$\ell '$
in
![]() $\mathcal {M}^1_{1,2}$
as follows. We define the path by
$\mathcal {M}^1_{1,2}$
as follows. We define the path by
and we observe that
![]() $\tilde \ell _0 = \ell _1$
to
$\tilde \ell _0 = \ell _1$
to
![]() $\tilde \ell _1 = \ell '$
. Note that by the convexity of entropy we have that
$\tilde \ell _1 = \ell '$
. Note that by the convexity of entropy we have that
with equality only possible at the endpoints. Hence the interior of the path
![]() $\tilde \ell _t$
lies in
$\tilde \ell _t$
lies in
![]() $\widehat {\mathcal {M}}^1(G)_{\textrm {reg}}$
. Further,
$\widehat {\mathcal {M}}^1(G)_{\textrm {reg}}$
. Further,
as the length of edges in
![]() $G_2$
is changing linearly. Hence there is a path of finite length from a length function in
$G_2$
is changing linearly. Hence there is a path of finite length from a length function in
![]() $\mathcal {M}^1(G)$
to any length function in
$\mathcal {M}^1(G)$
to any length function in
![]() $\mathcal {M}^1_{1,2}$
.
$\mathcal {M}^1_{1,2}$
.
Next, we deal with the case that
![]() $\ell ' \in \mathcal {M}_1$
; the case of
$\ell ' \in \mathcal {M}_1$
; the case of
![]() $\ell ' \in \mathcal {M}_2$
is symmetric. We will show that we can connect
$\ell ' \in \mathcal {M}_2$
is symmetric. We will show that we can connect
![]() $\ell '$
to a length function in
$\ell '$
to a length function in
![]() $\mathcal {M}_{1,2}$
with a concatenation of two paths that have finite length—in fact each has length
$\mathcal {M}_{1,2}$
with a concatenation of two paths that have finite length—in fact each has length
![]() $0$
. Let
$0$
. Let
![]() $\ell '' \in \mathcal {M}(G_2)$
have entropy less than
$\ell '' \in \mathcal {M}(G_2)$
have entropy less than
![]() $1$
. The paths
$1$
. The paths
![]() $(\ell _1)_t$
and
$(\ell _1)_t$
and
![]() $(\ell _2)_t$
are as follows:
$(\ell _2)_t$
are as follows:
 $$ \begin{align*} (\ell_1)_t & \colon\thinspace [0,\infty] \to \widehat{\mathcal{M}}^1(G) \quad (\ell_1)_t = ((\ell')^0 + t,(\ell')^1,\infty \cdot \mathbf{1}), \\ (\ell_2)_t & \colon\thinspace [0,\infty] \to \widehat{\mathcal{M}}^1(G) \quad (\ell_2)_t = (\infty,(\ell')^1,(\ell')^2 + t \cdot \mathbf{1}). \end{align*} $$
$$ \begin{align*} (\ell_1)_t & \colon\thinspace [0,\infty] \to \widehat{\mathcal{M}}^1(G) \quad (\ell_1)_t = ((\ell')^0 + t,(\ell')^1,\infty \cdot \mathbf{1}), \\ (\ell_2)_t & \colon\thinspace [0,\infty] \to \widehat{\mathcal{M}}^1(G) \quad (\ell_2)_t = (\infty,(\ell')^1,(\ell')^2 + t \cdot \mathbf{1}). \end{align*} $$
The concatenation of
![]() $(\ell _1)_t|[0,\infty ]$
and
$(\ell _1)_t|[0,\infty ]$
and
![]() $(\ell _2)_t|[\infty ,0]$
is a path from
$(\ell _2)_t|[\infty ,0]$
is a path from
![]() $\ell '$
to
$\ell '$
to
![]() $\ell ''$
. We observe that
$\ell ''$
. We observe that
![]() $(\ddot \ell _1)_t = 0$
and
$(\ddot \ell _1)_t = 0$
and
![]() $(\ddot \ell _2)_t = 0$
as edge lengths are changing linearly. Also, we observe that the interiors of these paths lie in
$(\ddot \ell _2)_t = 0$
as edge lengths are changing linearly. Also, we observe that the interiors of these paths lie in
![]() $\widehat {\mathcal {M}}^1(G)_{\textrm {reg}}$
. Hence
$\widehat {\mathcal {M}}^1(G)_{\textrm {reg}}$
. Hence
![]() $\| {((\ell _k)_t,(\dot \ell _k)_t)} \|_{\mathfrak {h},G} = 0$
for
$\| {((\ell _k)_t,(\dot \ell _k)_t)} \|_{\mathfrak {h},G} = 0$
for
![]() $k = 1$
,
$k = 1$
,
![]() $2$
showing that the paths have finite—in fact zero—length.
$2$
showing that the paths have finite—in fact zero—length.
This shows (10.6).
The previous argument shows that for any
![]() $\ell \in \mathcal {M}^1_1$
, there is an
$\ell \in \mathcal {M}^1_1$
, there is an
![]() $\ell ' \in \mathcal {M}^1_{1,2}$
such that
$\ell ' \in \mathcal {M}^1_{1,2}$
such that
![]() $d_{\mathfrak {h},G}(\ell ,\ell ') = 0$
. Likewise the analogous statement holds for
$d_{\mathfrak {h},G}(\ell ,\ell ') = 0$
. Likewise the analogous statement holds for
![]() $\ell \in \mathcal {M}^1_2$
. Given,
$\ell \in \mathcal {M}^1_2$
. Given,
![]() $\ell , \ell ' \in \mathcal {M}_{1,2}$
, we will show that
$\ell , \ell ' \in \mathcal {M}_{1,2}$
, we will show that
![]() $d_{\mathfrak {h},G}(\ell ,\ell ') = 0$
, completing the proof of (10.6). There are four cases depending on the entropies of the length functions
$d_{\mathfrak {h},G}(\ell ,\ell ') = 0$
, completing the proof of (10.6). There are four cases depending on the entropies of the length functions
![]() $\ell ^1$
,
$\ell ^1$
,
![]() $\ell ^2$
,
$\ell ^2$
,
![]() $(\ell ')^1$
and
$(\ell ')^1$
and
![]() $(\ell ')^2$
.
$(\ell ')^2$
.
The first case we consider is when
![]() $\mathfrak {h}_{G_1}(\ell ^1) = 1$
and
$\mathfrak {h}_{G_1}(\ell ^1) = 1$
and
![]() $\mathfrak {h}_{G_2}((\ell ')^2) = 1$
. In this case we consider the concatenation of the two paths
$\mathfrak {h}_{G_2}((\ell ')^2) = 1$
. In this case we consider the concatenation of the two paths
![]() $(\ell _1)_t$
and
$(\ell _1)_t$
and
![]() $(\ell _2)_t$
that are defined as follows:
$(\ell _2)_t$
that are defined as follows:
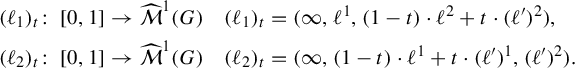 $$ \begin{align*} (\ell_1)_t & \colon\thinspace [0,1] \to \widehat{\mathcal{M}}^1(G) \quad (\ell_1)_t = (\infty,\ell^1,(1-t) \cdot \ell^2 + t\cdot (\ell')^2), \\ (\ell_2)_t & \colon\thinspace [0,1] \to \widehat{\mathcal{M}}^1(G) \quad (\ell_2)_t = (\infty,(1-t) \cdot \ell^1 + t \cdot (\ell')^1,(\ell')^2). \end{align*} $$
$$ \begin{align*} (\ell_1)_t & \colon\thinspace [0,1] \to \widehat{\mathcal{M}}^1(G) \quad (\ell_1)_t = (\infty,\ell^1,(1-t) \cdot \ell^2 + t\cdot (\ell')^2), \\ (\ell_2)_t & \colon\thinspace [0,1] \to \widehat{\mathcal{M}}^1(G) \quad (\ell_2)_t = (\infty,(1-t) \cdot \ell^1 + t \cdot (\ell')^1,(\ell')^2). \end{align*} $$
As above, the interiors of these paths lie in
![]() $\widehat {\mathcal {M}}^1(G)_{\textrm {reg}}$
and they have length
$\widehat {\mathcal {M}}^1(G)_{\textrm {reg}}$
and they have length
![]() $0$
since the lengths of edges are changing linearly. This completes this case.
$0$
since the lengths of edges are changing linearly. This completes this case.
The case where
![]() $\mathfrak {h}_{G_2}(\ell ^2) = 1$
and
$\mathfrak {h}_{G_2}(\ell ^2) = 1$
and
![]() $\mathfrak {h}_{G_1}((\ell ')^1) = 1$
is similar.
$\mathfrak {h}_{G_1}((\ell ')^1) = 1$
is similar.
Next we consider the case where
![]() $\mathfrak {h}_{G_1}(\ell ^1) = 1$
and
$\mathfrak {h}_{G_1}(\ell ^1) = 1$
and
![]() $\mathfrak {h}_{G_1}((\ell ')^1) = 1$
. Fix a length function
$\mathfrak {h}_{G_1}((\ell ')^1) = 1$
. Fix a length function
![]() $\ell '' \in \mathcal {M}^1_{1,2}$
with
$\ell '' \in \mathcal {M}^1_{1,2}$
with
![]() $\mathfrak {h}_{G_2}((\ell '')^2) = 1$
. By the first argument, we can connect both
$\mathfrak {h}_{G_2}((\ell '')^2) = 1$
. By the first argument, we can connect both
![]() $\ell $
and
$\ell $
and
![]() $\ell '$
to
$\ell '$
to
![]() $\ell ''$
with paths of length
$\ell ''$
with paths of length
![]() $0$
. Concatenating these two paths shows that this case holds as well.
$0$
. Concatenating these two paths shows that this case holds as well.
The case where
![]() $\mathfrak {h}_{G_2}(\ell ^2) = 1$
and
$\mathfrak {h}_{G_2}(\ell ^2) = 1$
and
![]() $\mathfrak {h}_{G_2}((\ell ')^2) = 1$
is similar.
$\mathfrak {h}_{G_2}((\ell ')^2) = 1$
is similar.
This completes the proof of (10.6).
We observe that any path in
![]() $\widehat {\mathcal {M}}^1(G)$
is close to a path in
$\widehat {\mathcal {M}}^1(G)$
is close to a path in
![]() $\mathcal {M}^1(G)$
. Thus by Proposition 10.5, we have that the inclusion
$\mathcal {M}^1(G)$
. Thus by Proposition 10.5, we have that the inclusion
![]() $(\mathcal {M}^1(G),d_{\mathfrak {h},G}) \to (\widehat {\mathcal {M}}^1(G),d_{\mathfrak {h},G})$
is an isometric embedding, hence (10.6) holds.
$(\mathcal {M}^1(G),d_{\mathfrak {h},G}) \to (\widehat {\mathcal {M}}^1(G),d_{\mathfrak {h},G})$
is an isometric embedding, hence (10.6) holds.
11
 $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
has bounded diameter in
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
has bounded diameter in
 $\mathcal {X}^1(\mathbb {F}_r)$
$\mathcal {X}^1(\mathbb {F}_r)$
In this section we make use of the collapsing phenomena witnessed in the previous section to show that even though
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter (Proposition 7.14), the subspace
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
has infinite diameter (Proposition 7.14), the subspace
![]() $(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}),d_{\mathfrak {h}}) \subset (\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has bounded diameter. The idea is as follows. Using the natural bijection
$(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}),d_{\mathfrak {h}}) \subset (\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has bounded diameter. The idea is as follows. Using the natural bijection
![]() $\mathcal {M}^1(\mathcal {R}_r) \leftrightarrow \mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
, since
$\mathcal {M}^1(\mathcal {R}_r) \leftrightarrow \mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
, since
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is the completion of
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is the completion of
![]() $(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
(§9) there is a map
$(\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
(§9) there is a map
![]() $\Phi \colon \thinspace \widehat {\mathcal {M}}^1(\mathcal {R}_r) \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
where
$\Phi \colon \thinspace \widehat {\mathcal {M}}^1(\mathcal {R}_r) \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
where
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
is the completion of
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
is the completion of
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
. Indeed, if a sequence
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
. Indeed, if a sequence
![]() $(\ell _n) \subset (\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is Cauchy, then so is its image under
$(\ell _n) \subset (\mathcal {M}^1(\mathcal {R}_r),d_{\mathfrak {h},\mathcal {R}_r})$
is Cauchy, then so is its image under
![]() $\Phi $
in
$\Phi $
in
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
as
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
as
![]() $\Phi $
is
$\Phi $
is
![]() $1$
-Lipschitz. As
$1$
-Lipschitz. As
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is homeomorphic to the complement of the vertices of an
$\widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is homeomorphic to the complement of the vertices of an
![]() $(r-1)$
-simplex, we can consider
$(r-1)$
-simplex, we can consider
![]() $\Phi $
as the map
$\Phi $
as the map
![]() $\Phi \colon \thinspace \Delta ^{r-1} - V \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
where
$\Phi \colon \thinspace \Delta ^{r-1} - V \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
where
![]() $\Delta ^{r-1}$
is the standard
$\Delta ^{r-1}$
is the standard
![]() $(r-1)$
-dimensional simplex and
$(r-1)$
-dimensional simplex and
![]() $V \subset \Delta ^{r-1}$
is the set of vertices. We will show that the map
$V \subset \Delta ^{r-1}$
is the set of vertices. We will show that the map
![]() $\Phi $
extends to the vertex set V. Since the image
$\Phi $
extends to the vertex set V. Since the image
![]() $\Phi (\Delta ^{r-1})$
is compact and contains
$\Phi (\Delta ^{r-1})$
is compact and contains
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
, it follows that
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
, it follows that
![]() $(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}),d_{\mathfrak {h}})$
has bounded diameter.
$(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}),d_{\mathfrak {h}})$
has bounded diameter.
This is accomplished by considering
![]() $\mathcal {M}^1(\mathcal {R}_r)$
as the face of
$\mathcal {M}^1(\mathcal {R}_r)$
as the face of
![]() $\mathcal {M}^1(G)$
for a particular graph G that has a separating edge and using the tools developed in §10. Lemma 11.1 establishes that the subset
$\mathcal {M}^1(G)$
for a particular graph G that has a separating edge and using the tools developed in §10. Lemma 11.1 establishes that the subset
![]() $\bigcup \{\mathcal {M}_S \mid 1 < \lvert {S} \rvert < r-1 \} \subset \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is collapsed to a single point in the completion of
$\bigcup \{\mathcal {M}_S \mid 1 < \lvert {S} \rvert < r-1 \} \subset \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is collapsed to a single point in the completion of
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
. We recall that
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
. We recall that
![]() $\mathcal {M}^1_S \subset \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is the subset of unit-entropy length functions on the subrose
$\mathcal {M}^1_S \subset \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
is the subset of unit-entropy length functions on the subrose
![]() $\mathcal {R}_{\lvert {S} \rvert } \subseteq \mathcal {R}_r$
utilizing the edges in
$\mathcal {R}_{\lvert {S} \rvert } \subseteq \mathcal {R}_r$
utilizing the edges in
![]() $S \subseteq [r]$
; the length of an edge in
$S \subseteq [r]$
; the length of an edge in
![]() $[r] - S$
is
$[r] - S$
is
![]() $\infty $
. The subset
$\infty $
. The subset
![]() $\mathcal {M}^1_S$
corresponds to an
$\mathcal {M}^1_S$
corresponds to an
![]() $(\lvert {S} \rvert -1)$
-dimensional face of
$(\lvert {S} \rvert -1)$
-dimensional face of
![]() $\Delta ^{r-1}$
. Thus Lemma 11.1 shows that the entire
$\Delta ^{r-1}$
. Thus Lemma 11.1 shows that the entire
![]() $(r-3)$
-skeleton of
$(r-3)$
-skeleton of
![]() $\Delta ^{r-1}$
is collapsed to a point by
$\Delta ^{r-1}$
is collapsed to a point by
![]() $\Phi $
in
$\Phi $
in
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
.
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
.
Lemma 11.1. For
![]() $r \geq 4$
,
$r \geq 4$
,
![]() $\Phi $
maps the subset
$\Phi $
maps the subset
![]() $\bigcup \{\mathcal {M}_S \mid 1 < \lvert {S} \rvert < r-1 \} \subset \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
to a single point in
$\bigcup \{\mathcal {M}_S \mid 1 < \lvert {S} \rvert < r-1 \} \subset \widehat {\mathcal {M}}^1(\mathcal {R}_r)$
to a single point in
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
.
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
.
Proof. Fix
![]() $r \geq 4$
and let S be a subset of
$r \geq 4$
and let S be a subset of
![]() $[r]$
with
$[r]$
with
![]() $1 < \lvert {S} \rvert < r - 1$
. To begin, we claim that the image of
$1 < \lvert {S} \rvert < r - 1$
. To begin, we claim that the image of
![]() $\mathcal {M}^1_S$
is a single point in
$\mathcal {M}^1_S$
is a single point in
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. To this end, we set
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. To this end, we set
![]() $n_1 = \lvert {S} \rvert $
and
$n_1 = \lvert {S} \rvert $
and
![]() $n_2 = r - \lvert {S} \rvert $
. Notice that
$n_2 = r - \lvert {S} \rvert $
. Notice that
![]() $n_1,n_2 \geq 2$
. Let
$n_1,n_2 \geq 2$
. Let
![]() $G_{n_1,n_2}$
be the graph that consists of two vertices
$G_{n_1,n_2}$
be the graph that consists of two vertices
![]() $v_1$
and
$v_1$
and
![]() $v_2$
, and edges
$v_2$
, and edges
![]() $e_0$
,
$e_0$
,
![]() $e^1_1,\ldots ,e^1_{n_1}$
and
$e^1_1,\ldots ,e^1_{n_1}$
and
![]() $e^2_1,\ldots ,e^2_{n_2}$
. The edges are attached via the following table.
$e^2_1,\ldots ,e^2_{n_2}$
. The edges are attached via the following table.

See Figure 7. We adopt the notation introduced in §10 for
![]() $G_{n_1,n_2}$
.
$G_{n_1,n_2}$
.
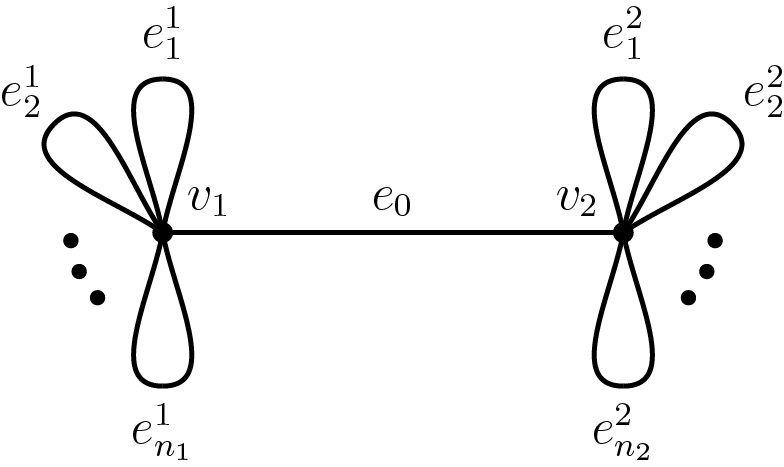
Figure 7 The graph
![]() $G_{n_1,n_2}$
: there are
$G_{n_1,n_2}$
: there are
![]() $n_1$
loop edges attached to
$n_1$
loop edges attached to
![]() $v_1$
and
$v_1$
and
![]() $n_2$
loop edges attached to
$n_2$
loop edges attached to
![]() $v_2$
.
$v_2$
.
Let
![]() $c \colon \thinspace G_{n_1,n_2} \to \mathcal {R}_r$
be the map induced by collapsing the edge
$c \colon \thinspace G_{n_1,n_2} \to \mathcal {R}_r$
be the map induced by collapsing the edge
![]() $e_0$
and let
$e_0$
and let
![]() $\rho \colon \thinspace \mathcal {R}_r \to G_{n_1,n_2}$
be a map so that
$\rho \colon \thinspace \mathcal {R}_r \to G_{n_1,n_2}$
be a map so that
![]() $c \circ \rho $
is homotopic to
$c \circ \rho $
is homotopic to
![]() ${\textrm {id}} \colon \thinspace \mathcal {R}_r \to \mathcal {R}_r$
. Thus
${\textrm {id}} \colon \thinspace \mathcal {R}_r \to \mathcal {R}_r$
. Thus
Specifically, viewing
![]() $\overline {\mathcal {X}}^1(G_{n_1,n_2},\rho )$
as a subset of
$\overline {\mathcal {X}}^1(G_{n_1,n_2},\rho )$
as a subset of
![]() $[0,\infty )^{1 + n_1 + n_2}$
, we see that
$[0,\infty )^{1 + n_1 + n_2}$
, we see that
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
is the image of the embedding
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}})$
is the image of the embedding
![]() $\varepsilon \colon \thinspace \mathcal {M}^1(\mathcal {R}_r) \to [0,\infty )^{1 + n_1 + n_2}$
where
$\varepsilon \colon \thinspace \mathcal {M}^1(\mathcal {R}_r) \to [0,\infty )^{1 + n_1 + n_2}$
where
![]() $\varepsilon (\ell )^0 = 0$
.
$\varepsilon (\ell )^0 = 0$
.
Moreover,
![]() $\varepsilon $
extends to an embedding
$\varepsilon $
extends to an embedding
![]() $\widehat {\mathcal {M}}^1(\mathcal {R}_r) \to [0,\infty ]^{1 + n_1 + n_2}$
in the same way. Under this embedding,
$\widehat {\mathcal {M}}^1(\mathcal {R}_r) \to [0,\infty ]^{1 + n_1 + n_2}$
in the same way. Under this embedding,
![]() $\varepsilon (\mathcal {M}^1_S)$
is the face of
$\varepsilon (\mathcal {M}^1_S)$
is the face of
![]() $\mathcal {M}^1_1 \subset \widehat {\mathcal {M}}^1(G_{n_1,n_2}) \subset [0,\infty ]^{1 + n_1 + n_2}$
. Indeed, the set
$\mathcal {M}^1_1 \subset \widehat {\mathcal {M}}^1(G_{n_1,n_2}) \subset [0,\infty ]^{1 + n_1 + n_2}$
. Indeed, the set
![]() $\mathcal {M}^1_1$
is homeomorphic to
$\mathcal {M}^1_1$
is homeomorphic to
![]() $(0,\infty ] \times \mathcal {M}^1_S$
. By Proposition 10.6(2), the set
$(0,\infty ] \times \mathcal {M}^1_S$
. By Proposition 10.6(2), the set
![]() $\mathcal {M}^1_1$
maps to a single point in
$\mathcal {M}^1_1$
maps to a single point in
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. Hence so does
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. Hence so does
![]() $\mathcal {M}^1_S$
, completing the proof of our claim.
$\mathcal {M}^1_S$
, completing the proof of our claim.
As the diameter of the thin part goes to zero as the short edge goes to zero (Proposition 9.8), the point that
![]() $\mathcal {M}^1_S$
is sent to is independent of S.
$\mathcal {M}^1_S$
is sent to is independent of S.
The main result of this section now follows easily.
Proposition 11.2. For
![]() $r \geq 4$
, the subspace
$r \geq 4$
, the subspace
![]() $(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}),d_{\mathfrak {h}}) \subset (\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has bounded diameter.
$(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}),d_{\mathfrak {h}}) \subset (\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has bounded diameter.
Proof. As explained above in the introduction to this section, by Theorem 1.2, there is a map
![]() $\Phi \colon \thinspace \Delta ^{r-1} - V \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. By Lemma 11.1, the map
$\Phi \colon \thinspace \Delta ^{r-1} - V \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. By Lemma 11.1, the map
![]() $\Phi $
extends to V and the entire
$\Phi $
extends to V and the entire
![]() $(r-3)$
-skeleton of
$(r-3)$
-skeleton of
![]() $\Delta ^{r-1}$
is mapped to a single point. As
$\Delta ^{r-1}$
is mapped to a single point. As
![]() $\Delta ^{r-1}$
is compact,
$\Delta ^{r-1}$
is compact,
![]() $\Phi (\Delta ^{r-1})$
is compact and hence has bounded diameter. Thus
$\Phi (\Delta ^{r-1})$
is compact and hence has bounded diameter. Thus
![]() $\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \subset \Phi (\Delta ^{r-1}) \subset \mathcal {X}^1(\mathbb {F})$
has bounded diameter too.
$\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \subset \Phi (\Delta ^{r-1}) \subset \mathcal {X}^1(\mathbb {F})$
has bounded diameter too.
12 Proof of Theorem 1.3
The goal of this final section is the proof of the last of the main results. Theorem 1.3 states that the
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
-invariant subcomplex
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
-invariant subcomplex
![]() $(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \cdot \operatorname {\mathrm {Out}}(\mathbb {F}_r),d_{\mathfrak {h}})$
has bounded diameter and, moreover, that the action of
$(\mathcal {X}^1(\mathcal {R}_r,{\textrm {id}}) \cdot \operatorname {\mathrm {Out}}(\mathbb {F}_r),d_{\mathfrak {h}})$
has bounded diameter and, moreover, that the action of
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the completion of
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on the completion of
![]() $(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has a global fixed point. This point is the image of
$(\mathcal {X}^1(\mathbb {F}_r),d_{\mathfrak {h}})$
has a global fixed point. This point is the image of
![]() $\bigcup \{\mathcal {M}_S \mid 1 < \lvert {S} \rvert < r-1 \}$
for any marking of the rose. We show that the image of this point in the completion is independent of the marking. This is done by showing that it is independent for markings that differ by a single simple move—we call such markings Nielsen adjacent. This is accomplished again by making use of a graph with a separating edge and the analysis in §10. This simple move suffices to connect any two markings and the theorem easily follows.
$\bigcup \{\mathcal {M}_S \mid 1 < \lvert {S} \rvert < r-1 \}$
for any marking of the rose. We show that the image of this point in the completion is independent of the marking. This is done by showing that it is independent for markings that differ by a single simple move—we call such markings Nielsen adjacent. This is accomplished again by making use of a graph with a separating edge and the analysis in §10. This simple move suffices to connect any two markings and the theorem easily follows.
Proof of Theorem 1.3
Given a marked rose
![]() $(\mathcal {R}_r,\rho )$
, there is an embedding
$(\mathcal {R}_r,\rho )$
, there is an embedding
![]() $\Phi _\rho \colon \mathcal {M}^1(\mathcal {R}_r) \kern0.5pt{\to} \mathcal {X}^1(\mathbb {F}_r)$
whose image is
$\Phi _\rho \colon \mathcal {M}^1(\mathcal {R}_r) \kern0.5pt{\to} \mathcal {X}^1(\mathbb {F}_r)$
whose image is
![]() $\mathcal {X}^1(\mathcal {R}_r,\rho )$
. As in §11, this map extends to
$\mathcal {X}^1(\mathcal {R}_r,\rho )$
. As in §11, this map extends to
![]() $\Phi _\rho \colon \thinspace \widehat {\mathcal {M}}^1(\mathcal {R}_r) \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
where
$\Phi _\rho \colon \thinspace \widehat {\mathcal {M}}^1(\mathcal {R}_r) \to \widehat {\mathcal {X}}^1(\mathbb {F}_r)$
where
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
is the completion of
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
is the completion of
![]() $\mathcal {X}^1(\mathbb {F}_r)$
with the entropy metric. By Lemma 11.1,
$\mathcal {X}^1(\mathbb {F}_r)$
with the entropy metric. By Lemma 11.1,
![]() $\Phi _\rho $
maps
$\Phi _\rho $
maps
![]() $\bigcup \{ \mathcal {M}^1_S \mid 1 < \lvert {S} \rvert < r - 1 \}$
to a single point in
$\bigcup \{ \mathcal {M}^1_S \mid 1 < \lvert {S} \rvert < r - 1 \}$
to a single point in
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. Let
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
. Let
![]() $x_{\rho }$
denote this point in
$x_{\rho }$
denote this point in
![]() $\overline {\mathcal {X}}(\mathbb {F})$
.
$\overline {\mathcal {X}}(\mathbb {F})$
.
Given an integer
![]() $r> 2$
, we define a graph
$r> 2$
, we define a graph
![]() $\Gamma _{r}$
that has two vertices v and w, and edges
$\Gamma _{r}$
that has two vertices v and w, and edges
![]() $e^1_1,\ldots ,e^1_{r-2}$
and
$e^1_1,\ldots ,e^1_{r-2}$
and
![]() $e^2_0,e^2_1,e^2_{3}$
. The edges are attached via the following table.
$e^2_0,e^2_1,e^2_{3}$
. The edges are attached via the following table.

See Figure 8. We call such a graph a rose-theta graph.
Figure 8 The graphs
![]() $\Gamma _r$
and
$\Gamma _r$
and
![]() $\widehat \Gamma _r$
. In
$\widehat \Gamma _r$
. In
![]() $\Gamma _{r}$
there are
$\Gamma _{r}$
there are
![]() $r-2$
loop edges attached to v and three edges connecting v to w. In
$r-2$
loop edges attached to v and three edges connecting v to w. In
![]() $\widehat \Gamma _{r}$
, there are
$\widehat \Gamma _{r}$
, there are
![]() $r-2$
loop edges attached to
$r-2$
loop edges attached to
![]() $v_1$
, three edges connecting
$v_1$
, three edges connecting
![]() $v_2$
to w and a separating edge connecting
$v_2$
to w and a separating edge connecting
![]() $v_1$
to
$v_1$
to
![]() $v_2$
.
$v_2$
.
Given
![]() $i \in \{0,1,2\}$
, collapsing the edge
$i \in \{0,1,2\}$
, collapsing the edge
![]() $e^2_i$
induces a map
$e^2_i$
induces a map
![]() $c_i \colon \thinspace \Gamma _r \to \mathcal {R}_{r}$
. We say two marked roses
$c_i \colon \thinspace \Gamma _r \to \mathcal {R}_{r}$
. We say two marked roses
![]() $(\mathcal {R}_r,\rho _1)$
and
$(\mathcal {R}_r,\rho _1)$
and
![]() $(\mathcal {R}_r,\rho _2)$
are Nielsen adjacent if there is a marked rose-theta graph
$(\mathcal {R}_r,\rho _2)$
are Nielsen adjacent if there is a marked rose-theta graph
![]() $(\Gamma _r,\rho )$
such that
$(\Gamma _r,\rho )$
such that
![]() $\rho _i \simeq c_i \circ \rho $
for
$\rho _i \simeq c_i \circ \rho $
for
![]() $i = 1$
,
$i = 1$
,
![]() $2$
for some collapses
$2$
for some collapses
![]() $c_i \colon \thinspace \Gamma _r \to \mathcal {R}_r$
. Given any two marked roses,
$c_i \colon \thinspace \Gamma _r \to \mathcal {R}_r$
. Given any two marked roses,
![]() $(\mathcal {R}_r,\rho )$
and
$(\mathcal {R}_r,\rho )$
and
![]() $(\mathcal {R}_r,\rho ')$
, it is well known that there is a sequence of markings
$(\mathcal {R}_r,\rho ')$
, it is well known that there is a sequence of markings
![]() $\rho = \rho _1,\ldots ,\rho _n = \rho '$
such that
$\rho = \rho _1,\ldots ,\rho _n = \rho '$
such that
![]() $(\mathcal {R}_r, \rho _{i-1})$
and
$(\mathcal {R}_r, \rho _{i-1})$
and
![]() $(\mathcal {R}_r,\rho _i)$
are Nielsen adjacent for
$(\mathcal {R}_r,\rho _i)$
are Nielsen adjacent for
![]() $i = 2,\ldots ,n$
. For instance, see [Reference Culler and Vogtmann14].
$i = 2,\ldots ,n$
. For instance, see [Reference Culler and Vogtmann14].
We will prove the theorem by showing that if
![]() $(\mathcal {R}_r,\rho _1)$
and
$(\mathcal {R}_r,\rho _1)$
and
![]() $(\mathcal {R}_r,\rho _2)$
are Nielsen adjacent, then
$(\mathcal {R}_r,\rho _2)$
are Nielsen adjacent, then
![]() $x_{\rho _1} = x_{\rho _2}$
. Notice that the collection
$x_{\rho _1} = x_{\rho _2}$
. Notice that the collection
![]() $\{x_{{\textrm {id}} \cdot \phi }\}$
is invariant under the action by
$\{x_{{\textrm {id}} \cdot \phi }\}$
is invariant under the action by
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
. Hence this also shows that the action of
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
. Hence this also shows that the action of
![]() $\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on
$\operatorname {\mathrm {Out}}(\mathbb {F}_r)$
on
![]() $\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
has a global fixed point.
$\widehat {\mathcal {X}}^1(\mathbb {F}_r)$
has a global fixed point.
To this end, let
![]() $(\Gamma _r,\rho )$
be the marked rose-theta graph such that
$(\Gamma _r,\rho )$
be the marked rose-theta graph such that
![]() $\rho _i \simeq c_i \circ \rho $
. We need to introduce a separating edge to take advantage of the shortcuts utilized in §10. Let
$\rho _i \simeq c_i \circ \rho $
. We need to introduce a separating edge to take advantage of the shortcuts utilized in §10. Let
![]() $\widehat \Gamma _{r}$
be the graph obtained from blowing up the vertex v in
$\widehat \Gamma _{r}$
be the graph obtained from blowing up the vertex v in
![]() $\Gamma _r$
. Specifically, in
$\Gamma _r$
. Specifically, in
![]() $\widehat {\Gamma }_r$
there are three vertices
$\widehat {\Gamma }_r$
there are three vertices
![]() $v_1$
,
$v_1$
,
![]() $v_2$
and w, and edges
$v_2$
and w, and edges
![]() $e_0$
,
$e_0$
,
![]() $e^1_1,\ldots ,e^1_{r-2}$
and
$e^1_1,\ldots ,e^1_{r-2}$
and
![]() $e^2_0,e^2_1,e^2_{3}$
. The edges are attached via the following table.
$e^2_0,e^2_1,e^2_{3}$
. The edges are attached via the following table.

See Figure 8. We adopt the notation from §10 for
![]() $\widehat \Gamma _r$
.
$\widehat \Gamma _r$
.
Let
![]() $c \colon \thinspace \widehat \Gamma _r \to \Gamma _r$
be the map that collapses the edge
$c \colon \thinspace \widehat \Gamma _r \to \Gamma _r$
be the map that collapses the edge
![]() $e_0$
. There is a marking
$e_0$
. There is a marking
![]() $\hat \rho \colon \thinspace \mathcal {R}_r \to \widehat \Gamma _r$
such that
$\hat \rho \colon \thinspace \mathcal {R}_r \to \widehat \Gamma _r$
such that
![]() $c \circ \hat \rho \simeq \rho $
. Viewing
$c \circ \hat \rho \simeq \rho $
. Viewing
![]() $\overline {\mathcal {X}}^1(\widehat {\Gamma }_r,\hat \rho )$
as a subset of
$\overline {\mathcal {X}}^1(\widehat {\Gamma }_r,\hat \rho )$
as a subset of
![]() $[0,\infty ]^{r+2}$
, there are two embeddings corresponding to
$[0,\infty ]^{r+2}$
, there are two embeddings corresponding to
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
denoted
$\rho _2$
denoted
![]() $\varepsilon _1, \varepsilon _2 \colon \thinspace \widehat {\mathcal {M}}^1(\mathcal {R}_r) \to [0,\infty ]^{r+2}$
where
$\varepsilon _1, \varepsilon _2 \colon \thinspace \widehat {\mathcal {M}}^1(\mathcal {R}_r) \to [0,\infty ]^{r+2}$
where
![]() $\varepsilon _i(\ell )^0 = \varepsilon _i(\ell )(e^2_i) = 0$
for
$\varepsilon _i(\ell )^0 = \varepsilon _i(\ell )(e^2_i) = 0$
for
![]() $i = 1$
,
$i = 1$
,
![]() $2$
.
$2$
.
Let
![]() $S \subset [r]$
denote the set of edges
$S \subset [r]$
denote the set of edges
![]() $\{c_i(e^1_1),\ldots , c_i(e^1_{r-2})\}$
in
$\{c_i(e^1_1),\ldots , c_i(e^1_{r-2})\}$
in
![]() $\mathcal {R}_r$
. Notice that this set is independent of i. Both
$\mathcal {R}_r$
. Notice that this set is independent of i. Both
![]() $\varepsilon _1(\mathcal {M}^1_S)$
and
$\varepsilon _1(\mathcal {M}^1_S)$
and
![]() $\varepsilon _2(\mathcal {M}^1_S)$
are faces of
$\varepsilon _2(\mathcal {M}^1_S)$
are faces of
![]() $\mathcal {M}^1_{1,2} \subset \widehat {\mathcal {M}}^1(\widehat {\Gamma }_r)$
. Hence by Proposition 10.6(2), we have that
$\mathcal {M}^1_{1,2} \subset \widehat {\mathcal {M}}^1(\widehat {\Gamma }_r)$
. Hence by Proposition 10.6(2), we have that
![]() $x_{\rho _1} = x_{\rho _2}$
.
$x_{\rho _1} = x_{\rho _2}$
.
Acknowledgements
The authors thank the Institute for Computational and Experimental Research in Mathematics (ICERM) for hosting the workshop Effective and Algorithmic Methods in Hyperbolic Geometry and Free Groups, at which work on this project began. We also thank Jing Tao for suggesting Question 1.8 and the referee for a careful reading and for helpful comments. The first author is supported by NSF grant DMS-1807319. The second author is supported by Simons Foundation Grant No. 316383. The third author is supported by Simons Foundation Grant No. 637880.