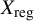Introduction
Introducing the main problem
Einstein metrics are a central object in differential geometry. A Kähler–Einstein metric on a complex manifold is a Kähler metric whose Ricci curvature is proportional to the metric tensor. A foundational result of Yau [Reference YauYau78] allows one to construct many examples of these fundamental objects.
In connection with the minimal model program, singular Kähler–Einstein metrics on mildly singular Kähler varieties X have been constructed in [Reference Eyssidieux, Guedj and ZeriahiEGZ09, Reference Berman and GuenanciaBG14, Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBE+19] and further studied by many authors (see [Reference Guedj and ZeriahiGZ17, Reference BoucksomBou18, Reference DonaldsonDon18, Reference LiLi22] and the references therein). These are Kähler forms
![]() $\omega _{\mathrm {KE}}=\omega +dd^c \varphi _{\mathrm {KE}}$
on the regular part
$\omega _{\mathrm {KE}}=\omega +dd^c \varphi _{\mathrm {KE}}$
on the regular part
![]() $X_{\mathrm {reg}}$
of X, where
$X_{\mathrm {reg}}$
of X, where
![]() $c_1(X)=\lambda [\omega ]$
is proportional to a reference Kähler class
$c_1(X)=\lambda [\omega ]$
is proportional to a reference Kähler class
![]() $[\omega ]$
, such that
$[\omega ]$
, such that
and which admit bounded (or mildly unbounded) local potential near the singularities
![]() $X_{\mathrm {sing}}$
. In particular,
$X_{\mathrm {sing}}$
. In particular,
![]() $\omega _{\mathrm {KE}}$
uniquely extends as a positive closed current to X.
$\omega _{\mathrm {KE}}$
uniquely extends as a positive closed current to X.
One constructs
![]() $\omega _{\mathrm {KE}}=\omega +dd^c \varphi _{\mathrm {KE}}$
by solving a complex Monge–Ampère equation
$\omega _{\mathrm {KE}}=\omega +dd^c \varphi _{\mathrm {KE}}$
by solving a complex Monge–Ampère equation
where
![]() $n=\dim _{{\mathbb {C}}} X$
and
$n=\dim _{{\mathbb {C}}} X$
and
![]() $\mu _X$
is an appropriate volume form.
$\mu _X$
is an appropriate volume form.
Due to the presence of singularities, the geometry of these Kähler–Einstein currents is quite mysterious despite recent important progress [Reference Donaldson and SunDS14, Reference Hein and SunHS17]. Understanding the asymptotic behavior of
![]() $\varphi _{\mathrm {KE}}$
near
$\varphi _{\mathrm {KE}}$
near
![]() $X_{\mathrm {sing}}$
is a major open problem.
$X_{\mathrm {sing}}$
is a major open problem.
In this note, we partially address the following basic question:
Main Question. Is the Kähler–Einstein metric
![]() $\omega _{\mathrm {KE}}$
solving Equation (KE) a Kähler current, that is, does
$\omega _{\mathrm {KE}}$
solving Equation (KE) a Kähler current, that is, does
![]() $\omega _{\mathrm {KE}}$
dominate a Kähler form?
$\omega _{\mathrm {KE}}$
dominate a Kähler form?
Note that, unless X is smooth,
![]() $\omega _{\mathrm {KE}}$
is never dominated by a Kähler form, cf Corollary 1.9.
$\omega _{\mathrm {KE}}$
is never dominated by a Kähler form, cf Corollary 1.9.
Known cases. Although the question sounds much easier than asking for asymptotics of
![]() $\omega _{\mathrm {KE}}$
, it has not yet been addressed in full generality and only a handful of particular cases seem to be understood, which we briefly survey below.
$\omega _{\mathrm {KE}}$
, it has not yet been addressed in full generality and only a handful of particular cases seem to be understood, which we briefly survey below.
![]() $\bullet $
Orbifold singularities. If X has only finite quotient singularities (i.e., X is an orbifold), then
$\bullet $
Orbifold singularities. If X has only finite quotient singularities (i.e., X is an orbifold), then
![]() $\omega _{\mathrm {KE}}$
is a smooth orbifold Kähler metric (i.e., it is a Kähler metric in the local smooth uniformizing charts). In particular,
$\omega _{\mathrm {KE}}$
is a smooth orbifold Kähler metric (i.e., it is a Kähler metric in the local smooth uniformizing charts). In particular,
![]() $\omega _{\mathrm {KE}}$
is a Kähler current. Since two-dimensional log terminal singularities are quotient singularities, it follows that the main question admits a positive answer in dimension two for log terminal singularities. More generally,
$\omega _{\mathrm {KE}}$
is a Kähler current. Since two-dimensional log terminal singularities are quotient singularities, it follows that the main question admits a positive answer in dimension two for log terminal singularities. More generally,
![]() $\omega _{\mathrm {KE}}$
is orbifold-smooth near any quotient singularity of X at least when X is projective [Reference Li and TianLT19]; in particular, it is a Kähler current on the orbifold locus of X.
$\omega _{\mathrm {KE}}$
is orbifold-smooth near any quotient singularity of X at least when X is projective [Reference Li and TianLT19]; in particular, it is a Kähler current on the orbifold locus of X.
![]() $\bullet $
Limits of smooth spaces. Other examples include when X admits a crepant resolution or when X can be suitably obtained as limit of smooth Kähler–Einstein manifolds [Reference Ruan and ZhangRZ11b, Reference Donaldson and SunDS14, Reference Hein and SunHS17]. The common thread in the situations appearing in loc. cit. is that one can embed
$\bullet $
Limits of smooth spaces. Other examples include when X admits a crepant resolution or when X can be suitably obtained as limit of smooth Kähler–Einstein manifolds [Reference Ruan and ZhangRZ11b, Reference Donaldson and SunDS14, Reference Hein and SunHS17]. The common thread in the situations appearing in loc. cit. is that one can embed
![]() $\iota : X\hookrightarrow \mathbb P^N$
with
$\iota : X\hookrightarrow \mathbb P^N$
with
![]() $\omega _{\mathrm {KE}}=\omega _{\mathrm {FS}}|_X+dd^c \varphi $
and approximate
$\omega _{\mathrm {KE}}=\omega _{\mathrm {FS}}|_X+dd^c \varphi $
and approximate
![]() $(X, \omega _{\mathrm {KE}})$
by a sequence of compact Kähler manifolds
$(X, \omega _{\mathrm {KE}})$
by a sequence of compact Kähler manifolds
![]() $(X_k, \omega _k)$
such that there are
$(X_k, \omega _k)$
such that there are
-
- embeddings
 $\iota _k:X_k \hookrightarrow \mathbb P^N$
with
$\iota _k:X_k \hookrightarrow \mathbb P^N$
with
 $\omega _k=\omega _{\mathrm {FS}}|_{\iota _k(X_k)}+dd^c \varphi _k$
and
$\omega _k=\omega _{\mathrm {FS}}|_{\iota _k(X_k)}+dd^c \varphi _k$
and
 $ \|\varphi _k\|_{L^{\infty }(X_k)} \leqslant C$
,
$ \|\varphi _k\|_{L^{\infty }(X_k)} \leqslant C$
, -
- uniform Ricci lower bounds
 $\mathrm {Ric} \, \omega _k \geqslant -C \omega _k$
$\mathrm {Ric} \, \omega _k \geqslant -C \omega _k$
for some uniform constant
![]() $C>0$
. From these estimates, an easy application of Chern–Lu formula yields
$C>0$
. From these estimates, an easy application of Chern–Lu formula yields
![]() $\omega _k\geqslant C^{-1} \omega _{\mathrm {FS}}|_{\iota _k(X_k)}$
from which the strict positivity of
$\omega _k\geqslant C^{-1} \omega _{\mathrm {FS}}|_{\iota _k(X_k)}$
from which the strict positivity of
![]() $\omega _{\mathrm {KE}}$
follows.
$\omega _{\mathrm {KE}}$
follows.
In summary, the ideas above allow to treat the case of singular Kähler–Einstein varieties that are degenerations of smooth Kähler manifolds with uniform lower Ricci bound and uniform
![]() $L^{\infty }$
bound for its potential.
$L^{\infty }$
bound for its potential.
Unfortunately, general singular Kähler–Einstein metrics
![]() $\omega _{\mathrm {KE}}$
on a singular space X arise by construction as limits of smooth Kähler metrics
$\omega _{\mathrm {KE}}$
on a singular space X arise by construction as limits of smooth Kähler metrics
![]() $\omega _\varepsilon $
on a desingularization
$\omega _\varepsilon $
on a desingularization
![]() $\pi :\widehat X\to X$
such that
$\pi :\widehat X\to X$
such that
![]() $\mathrm {Ric}_{\omega _\varepsilon } \to -\infty $
along any divisor
$\mathrm {Ric}_{\omega _\varepsilon } \to -\infty $
along any divisor
![]() $E\subset \widehat X$
with positive discrepancy. Moreover, a general singular variety cannot be obtained as a degeneration of smooth varieties since there might be (even local and topological) obstructions to smoothability. This prevents one from directly applying the above ideas to a general singular Kähler–Einstein space. This paper grew out of an attempt to find the largest possible field of application of the general technique recalled above. More precisely, the goal of the present paper is threefold:
$E\subset \widehat X$
with positive discrepancy. Moreover, a general singular variety cannot be obtained as a degeneration of smooth varieties since there might be (even local and topological) obstructions to smoothability. This prevents one from directly applying the above ideas to a general singular Kähler–Einstein space. This paper grew out of an attempt to find the largest possible field of application of the general technique recalled above. More precisely, the goal of the present paper is threefold:
-
A. Formulate a general framework where the above global strategy applies mutatis mutandis, including nonprojective Kähler spaces as well as singular pairs.
-
B. Provide a local version of the approach that enables to treat isolated smoothable singularities.
-
C. Develop a systematic use of the technique in order to enlarge the class of singularities (beyond the smoothable or crepant ones) for which one can answer positively the main question above, using a several step degeneration process.
So far, most (general) results about singular Kähler–Einstein metrics have been derived by establishing uniform a priori estimates on smooth approximants (space and metric). The novelty of our approach is that, given a singular space/metric
![]() $(X,\omega _{\mathrm {KE}})$
, we are able to answer the main question positively for
$(X,\omega _{\mathrm {KE}})$
, we are able to answer the main question positively for
![]() $(X,\omega _{\mathrm {KE}})$
as soon as one can suitably approximate our space/metric by a possibly singular space/metric on which we can qualitatively answer the main question, as long as we have a lower bound on the Ricci curvature and a uniform bound on a suitable potential. We refer to the last paragraph of this introduction or § 5 for an explicit application of this principle.
$(X,\omega _{\mathrm {KE}})$
as soon as one can suitably approximate our space/metric by a possibly singular space/metric on which we can qualitatively answer the main question, as long as we have a lower bound on the Ricci curvature and a uniform bound on a suitable potential. We refer to the last paragraph of this introduction or § 5 for an explicit application of this principle.
Statement of the results
Let us now get a bit more explicit and expand what we mean by the above-stated goals. Our first main result is as follows:
Theorem A. Let X be a normal compact Kähler space with log terminal singularities such that
![]() $K_X\sim _{{\mathbb {Q}}}\mathcal O_X$
, and let
$K_X\sim _{{\mathbb {Q}}}\mathcal O_X$
, and let
![]() $\alpha $
be a Kähler class. If X is smoothable, then the unique singular Ricci-flat metric
$\alpha $
be a Kähler class. If X is smoothable, then the unique singular Ricci-flat metric
![]() $\omega _{\mathrm {KE}} \in \alpha $
dominates a Kähler form.
$\omega _{\mathrm {KE}} \in \alpha $
dominates a Kähler form.
This strict positivity result actually holds in more general contexts [canonically polarized varieties,
![]() ${\mathbb {Q}}$
-Fano varieties, Kawamata log terminal (klt) pairs] as we explain in Theorem 2.8. The existence of a global smoothing is a rather restrictive assumption, although it holds, for example, at the boundary of the moduli space of positively curved Kähler–Einstein metrics. The latter has a natural compactification arising from the Gromov–Hausdorff topology, and the geometric meaning of the boundary points was elucidated in [Reference Donaldson and SunDS14, Reference Spotti, Sun and YaoSSY16].
${\mathbb {Q}}$
-Fano varieties, Kawamata log terminal (klt) pairs] as we explain in Theorem 2.8. The existence of a global smoothing is a rather restrictive assumption, although it holds, for example, at the boundary of the moduli space of positively curved Kähler–Einstein metrics. The latter has a natural compactification arising from the Gromov–Hausdorff topology, and the geometric meaning of the boundary points was elucidated in [Reference Donaldson and SunDS14, Reference Spotti, Sun and YaoSSY16].
An isolated singularity is more likely to admit a local smoothing. Shifting perspective, we use the local singular theory developed in [Reference Guedj, Guenancia and ZeriahiGGZ23] to establish a positivity result of solutions to local Monge–Ampère equations at isolated smoothable singularities. As a consequence, we obtain our second main result.
Theorem B. Let X be a normal compact Kähler space with log terminal singularities such that
![]() $K_X\sim _{{\mathbb {Q}}}\mathcal O_X$
, and let
$K_X\sim _{{\mathbb {Q}}}\mathcal O_X$
, and let
![]() $\alpha $
be a Kähler class. The unique singular Ricci-flat metric
$\alpha $
be a Kähler class. The unique singular Ricci-flat metric
![]() $\omega _{\mathrm {KE}} \in \alpha $
dominates a Kähler form near any smoothable isolated singularity.
$\omega _{\mathrm {KE}} \in \alpha $
dominates a Kähler form near any smoothable isolated singularity.
The result is more general, and we refer the reader to Theorem 4.1 and Corollary 4.6 for more precise results, including the case of klt pairs with isolated singularities.
As recalled earlier, the basic idea is not new. Deforming X in a smooth Kähler approximant
![]() $X_t$
, we would like to use Chern–Lu formula [Reference ChernChe68, Reference LuLu68] and establish a uniform lower bound for smooth approximants
$X_t$
, we would like to use Chern–Lu formula [Reference ChernChe68, Reference LuLu68] and establish a uniform lower bound for smooth approximants
![]() $\omega _{\mathrm {KE},t} \geqslant C^{-1} \omega _t$
on nearby smooth fibers. This requires to establish uniform a priori bounds for families of degenerate complex Monge–Ampère potentials, a theme which has known important progress in the last decade (see [Reference Rong and ZhangRZ11a, Reference Spotti, Sun and YaoSSY16, Reference Di Nezza, Guedj and GuenanciaDNGG23]), but which still requires further understanding in order to extend Theorem B to the positively curved setting.
$\omega _{\mathrm {KE},t} \geqslant C^{-1} \omega _t$
on nearby smooth fibers. This requires to establish uniform a priori bounds for families of degenerate complex Monge–Ampère potentials, a theme which has known important progress in the last decade (see [Reference Rong and ZhangRZ11a, Reference Spotti, Sun and YaoSSY16, Reference Di Nezza, Guedj and GuenanciaDNGG23]), but which still requires further understanding in order to extend Theorem B to the positively curved setting.
Our last result answers the main question positively in dimension three, in nonpositive curvature, unconditionally to any smoothability assumptions on the singularities.
Theorem C. Let X be a normal compact Kähler space of dimension three with log terminal singularities such that
![]() $K_X\sim _{{\mathbb {Q}}}\mathcal O_X$
, and let
$K_X\sim _{{\mathbb {Q}}}\mathcal O_X$
, and let
![]() $\alpha $
be a Kähler class. The unique singular Ricci-flat metric
$\alpha $
be a Kähler class. The unique singular Ricci-flat metric
![]() $\omega _{\mathrm {KE}} \in \alpha $
dominates a Kähler form.
$\omega _{\mathrm {KE}} \in \alpha $
dominates a Kähler form.
Here again, there is a version of this statement in negative curvature, cf Theorem 5.3, which surprisingly requires significantly more work than the Calabi–Yau case, cf below. The general idea behind the proof of Theorem C is that one can reduce the situation to the smooth case via a two-step degeneration. More precisely it goes as follows.
Step 1. One can reduce to the case where X has canonical singularities, up to passing to the index one cover.
Step 2. The first degeneration amounts to considering a terminalization
![]() $\pi : \widehat X\to X$
. Since X is canonical,
$\pi : \widehat X\to X$
. Since X is canonical,
![]() $\pi $
is crepant, that is,
$\pi $
is crepant, that is,
![]() $K_{\widehat X}=\pi ^*K_X$
is trivial. Now, one can realize
$K_{\widehat X}=\pi ^*K_X$
is trivial. Now, one can realize
![]() $\pi ^*\omega _{\mathrm {KE}}$
as limit of singular Ricci flat metrics
$\pi ^*\omega _{\mathrm {KE}}$
as limit of singular Ricci flat metrics
![]() $\omega _\varepsilon \in \pi ^*\alpha +\varepsilon \beta $
, where
$\omega _\varepsilon \in \pi ^*\alpha +\varepsilon \beta $
, where
![]() $\beta $
is a Kähler class on
$\beta $
is a Kähler class on
![]() $\widehat X$
.
$\widehat X$
.
Step 3. Now,
![]() $\widehat X$
has terminal singularities of index one, hence these are (locally) smoothable by a classification result of Reid and we can apply Theorem B to
$\widehat X$
has terminal singularities of index one, hence these are (locally) smoothable by a classification result of Reid and we can apply Theorem B to
![]() $(\widehat X, \omega _\varepsilon )$
and use Chern–Lu inequality on the singular space
$(\widehat X, \omega _\varepsilon )$
and use Chern–Lu inequality on the singular space
![]() $\widehat X$
to conclude.
$\widehat X$
to conclude.
In the case where
![]() $K_X$
is ample, the terminalization map is not crepant anymore. Instead, a boundary divisor
$K_X$
is ample, the terminalization map is not crepant anymore. Instead, a boundary divisor
![]() $\widehat \Delta $
arises on
$\widehat \Delta $
arises on
![]() $\widehat X$
so that
$\widehat X$
so that
![]() $K_{\widehat X}+\widehat \Delta =\pi ^*K_X$
and we are then required to generalize Theorem B to the case of klt pairs. This is not as innocuous as it may sound since, even though
$K_{\widehat X}+\widehat \Delta =\pi ^*K_X$
and we are then required to generalize Theorem B to the case of klt pairs. This is not as innocuous as it may sound since, even though
![]() $\widehat X$
has only isolated singularities, it is not the case for the pair
$\widehat X$
has only isolated singularities, it is not the case for the pair
![]() $(\widehat X, \widehat \Delta )$
anymore! Taking care of this difficulty involves an additional (third) degeneration process (cf. Theorem 4.5), highlighting the guiding principle of this article.
$(\widehat X, \widehat \Delta )$
anymore! Taking care of this difficulty involves an additional (third) degeneration process (cf. Theorem 4.5), highlighting the guiding principle of this article.
Contents
We recall basic facts from analysis on complex spaces in Section 1. We prove Theorem A in Section 2, using uniform a priori estimates from [Reference Spotti, Sun and YaoSSY16, Reference Di Nezza, Guedj and GuenanciaDNGG23]. We study holomorphic families of Dirichlet problems for the complex Monge–Ampère equation in Section 3, using a priori estimates from [Reference Guan and LiGL10, Reference Guedj, Guenancia and ZeriahiGGZ23], and prove Theorem B in Section 4. We use the previous techniques, together with some classical facts from the Minimal Model Program in dimension three, to establish Theorem C in Section 5.
1 The Monge–Ampère operator on complex spaces
In this section, we let X be a reduced complex analytic space of pure dimension
![]() $n \geqslant 1$
. We will denote by
$n \geqslant 1$
. We will denote by
![]() $X_{\mathrm {reg}}$
the complex manifold of regular points of X. The set
$X_{\mathrm {reg}}$
the complex manifold of regular points of X. The set
of singular points is an analytic subset of X of complex codimension
![]() $\geqslant 1$
.
$\geqslant 1$
.
1.1 Plurisubharmonic functions
By definition, for each point
![]() $x_0 \in X$
there exists a neighborhood U of
$x_0 \in X$
there exists a neighborhood U of
![]() $x_0$
and a local embedding
$x_0$
and a local embedding
![]() $j: U \hookrightarrow \mathbb C^N$
onto an analytic subset of
$j: U \hookrightarrow \mathbb C^N$
onto an analytic subset of
![]() $\mathbb C^N$
for some
$\mathbb C^N$
for some
![]() $N \geqslant 1$
.
$N \geqslant 1$
.
Using these local embeddings, it is possible to define the spaces of smooth forms of given degree on X. The notion of currents on X is then defined by duality by their action on compactly supported smooth forms on X. The operators
![]() $\partial $
and
$\partial $
and
![]() $\bar {\partial }$
, d,
$\bar {\partial }$
, d,
![]() $d^c$
and
$d^c$
and
![]() $dd^c$
are then well defined by duality (see [Reference DemaillyDem85] for a careful treatment).
$dd^c$
are then well defined by duality (see [Reference DemaillyDem85] for a careful treatment).
In the same way, one can define the analytic notions of holomorphic and plurisubharmonic functions. There are essentially two different notions:
Definition 1.1. Let
![]() $u : X \longrightarrow \mathbb R \cup \{-\infty \}$
be a given function.
$u : X \longrightarrow \mathbb R \cup \{-\infty \}$
be a given function.
1. We say that u is plurisubharmonic on X if it is locally the restriction of a plurisubharmonic function on a local embedding of X onto an analytic subset of
![]() $\mathbb C^N$
.
$\mathbb C^N$
.
2. We say that u is weakly plurisubharmonic on X if u is locally bounded from above on X and its restriction to the complex manifold
![]() $X_{\mathrm {reg}}$
is plurisubharmonic.
$X_{\mathrm {reg}}$
is plurisubharmonic.
Fornaess and Narasimhan proved in [Reference Fornæss and NarasimhanFN80] that u is plurisubarmonic on X if and only if for any analytic disc
![]() $h : \mathbb D \longrightarrow X$
, the restriction
$h : \mathbb D \longrightarrow X$
, the restriction
![]() $u \circ h$
is subharmonic on
$u \circ h$
is subharmonic on
![]() $\mathbb D$
or identically
$\mathbb D$
or identically
![]() $- \infty $
.
$- \infty $
.
If u is weakly plurisubharmonic on X, u is plurisubharmonic on
![]() $X_{\mathrm {reg}}$
, hence upper semicontinuous on
$X_{\mathrm {reg}}$
, hence upper semicontinuous on
![]() $X_{\mathrm {reg}}$
. Since no assumption is made on u at singular points, it is natural to extend u to X by the following formula:
$X_{\mathrm {reg}}$
. Since no assumption is made on u at singular points, it is natural to extend u to X by the following formula:
The function
![]() $u^*$
is upper semicontinuous, locally integrable on X and satisfies
$u^*$
is upper semicontinuous, locally integrable on X and satisfies
![]() $dd^c u^* \geqslant 0$
in the sense of currents on X. By Demailly [Reference DemaillyDem85], the two notions are equivalent when X is locally irreducible. More precisely, we will need the following result:
$dd^c u^* \geqslant 0$
in the sense of currents on X. By Demailly [Reference DemaillyDem85], the two notions are equivalent when X is locally irreducible. More precisely, we will need the following result:
Theorem 1.2. [Reference DemaillyDem85]
Assume that X is a locally irreducible analytic space and
![]() $u : X \longrightarrow \mathbb R \cup \{-\infty \}$
is a weakly plurisubharmonic function on X, then the function
$u : X \longrightarrow \mathbb R \cup \{-\infty \}$
is a weakly plurisubharmonic function on X, then the function
![]() $u^*$
defined by (1.1) is plurisubharmonic on X.
$u^*$
defined by (1.1) is plurisubharmonic on X.
Observe that since u is plurisubharmonic on
![]() $X_{\mathrm {reg}}$
, we have
$X_{\mathrm {reg}}$
, we have
![]() $u^* = u$
on
$u^* = u$
on
![]() $X_{\mathrm {reg}}$
. Hence,
$X_{\mathrm {reg}}$
. Hence,
![]() $u^*$
is the upper semicontinuous extension of
$u^*$
is the upper semicontinuous extension of
![]() $u|_{X_{\mathrm {reg}}}$
to X.
$u|_{X_{\mathrm {reg}}}$
to X.
Following [Reference Fornæss and NarasimhanFN80], we say that X is Stein if it admits a
![]() ${\mathcal C}^2$
-smooth strongly plurisubharmonic exhaustion. We will use the following definition:
${\mathcal C}^2$
-smooth strongly plurisubharmonic exhaustion. We will use the following definition:
Definition 1.3. A domain
![]() $\Omega \Subset X$
is strongly pseudoconvex if it admits a negative
$\Omega \Subset X$
is strongly pseudoconvex if it admits a negative
![]() ${\mathcal C}^2$
-smooth strongly plurisubharmonic exhaustion, that is, a function
${\mathcal C}^2$
-smooth strongly plurisubharmonic exhaustion, that is, a function
![]() $\rho $
strongly plurisubharmonic in a neighborhood
$\rho $
strongly plurisubharmonic in a neighborhood
![]() $\Omega '$
of
$\Omega '$
of
![]() $\overline {\Omega }$
such that
$\overline {\Omega }$
such that
![]() $\Omega := \{ x \in \Omega ' \,; \, \rho (x) < 0\}$
and
$\Omega := \{ x \in \Omega ' \,; \, \rho (x) < 0\}$
and
is relatively compact for any
![]() $c < 0$
.
$c < 0$
.
Our complex spaces will be assumed to be reduced, locally irreducible of dimension
![]() $n \geqslant 1$
. We denote by
$n \geqslant 1$
. We denote by
![]() $\mathrm {PSH}(X)$
the set of plurisubharmonic functions on X.
$\mathrm {PSH}(X)$
the set of plurisubharmonic functions on X.
1.2 Dirichlet problem on singular complex spaces
The complex Monge–Ampère measure
![]() $(dd^c u)^n$
of a smooth psh function in a domain of
$(dd^c u)^n$
of a smooth psh function in a domain of
![]() ${\mathbb {C}}^n$
is the radon measure
${\mathbb {C}}^n$
is the radon measure
 $$ \begin{align*}(dd^c u)^n=c \det \left( \frac{\partial^2 u}{\partial z_i \partial \overline{z}_j} \right) dV_{\mathrm{eucl}}, \end{align*} $$
$$ \begin{align*}(dd^c u)^n=c \det \left( \frac{\partial^2 u}{\partial z_i \partial \overline{z}_j} \right) dV_{\mathrm{eucl}}, \end{align*} $$
where
![]() $c>0$
is a normalizing constant. The definition has been extended to any bounded psh function by Bedford–Taylor, who laid down the foundations of pluripotential theory in [Reference Bedford and TaylorBT76, Reference Bedford and TaylorBT82].
$c>0$
is a normalizing constant. The definition has been extended to any bounded psh function by Bedford–Taylor, who laid down the foundations of pluripotential theory in [Reference Bedford and TaylorBT76, Reference Bedford and TaylorBT82].
The Dirichlet problem for the complex Monge–Ampère operator has been studied extensively by many authors (see [Reference Guedj and ZeriahiGZ17] and the references therein).
The complex Monge–Ampère operator has been defined and studied on complex spaces by Bedford in [Reference BedfordBed82] and Demailly in [Reference DemaillyDem85]. It turns out that if
![]() $u \in \mathrm {PSH}(X) \cap L^{\infty }_{\mathrm {loc}} (X)$
, the Monge–Ampère measure
$u \in \mathrm {PSH}(X) \cap L^{\infty }_{\mathrm {loc}} (X)$
, the Monge–Ampère measure
![]() $(dd^c u)^n$
is well defined on
$(dd^c u)^n$
is well defined on
![]() $X_{\mathrm {reg}}$
and can be extended to X as a Borel measure with zero mass on
$X_{\mathrm {reg}}$
and can be extended to X as a Borel measure with zero mass on
![]() $X_{\mathrm {sing}}$
. Thus, all standard properties of the complex Monge–Ampère operator acting on
$X_{\mathrm {sing}}$
. Thus, all standard properties of the complex Monge–Ampère operator acting on
![]() $ \mathrm {PSH}(X) \cap L^{\infty }_{\mathrm {loc}} (X)$
extend to this setting (see [Reference BedfordBed82, Reference DemaillyDem85]).
$ \mathrm {PSH}(X) \cap L^{\infty }_{\mathrm {loc}} (X)$
extend to this setting (see [Reference BedfordBed82, Reference DemaillyDem85]).
The Dirichlet problem has been studied only recently in that context. We recall the following which is a combination of [Reference Guedj, Guenancia and ZeriahiGGZ23] and [Reference Datar, Fu and SongDFS23, Reference FuFu23].
Theorem 1.4. Let X be a Stein space of dimension
![]() $n \geqslant 1$
, reduced and locally irreducible, with an isolated log terminal singularity
$n \geqslant 1$
, reduced and locally irreducible, with an isolated log terminal singularity
![]() $X_{\mathrm {sing}}=\{p\}$
. Let
$X_{\mathrm {sing}}=\{p\}$
. Let
![]() $\Omega \subset X$
be a bounded strongly pseudoconvex domain with smooth boundary. Fix a smooth volume form
$\Omega \subset X$
be a bounded strongly pseudoconvex domain with smooth boundary. Fix a smooth volume form
![]() $dV$
on X,
$dV$
on X,
![]() $\phi \in {\mathcal C}^{\infty }(\partial \Omega )$
and
$\phi \in {\mathcal C}^{\infty }(\partial \Omega )$
and
![]() $0 <f \in {\mathcal C}^{\infty }(\overline {\Omega } \setminus \{p\})$
with
$0 <f \in {\mathcal C}^{\infty }(\overline {\Omega } \setminus \{p\})$
with
![]() $f \in L^p(\Omega ,dV)$
for some
$f \in L^p(\Omega ,dV)$
for some
![]() $p>1$
. Fix
$p>1$
. Fix
![]() $\lambda \in {\mathbb {R}}^+$
. Then there exists a unique plurisubharmonic function u in
$\lambda \in {\mathbb {R}}^+$
. Then there exists a unique plurisubharmonic function u in
![]() $\Omega $
which satisfies the following:
$\Omega $
which satisfies the following:
-
○ u is continuous on
 $\overline {\Omega }$
with
$\overline {\Omega }$
with
 $u_{|\partial \Omega }=\phi $
;
$u_{|\partial \Omega }=\phi $
; -
○ u is smooth in
 ${\Omega } \setminus \{p\}$
${\Omega } \setminus \{p\}$
-
○ u satisfies
 $(dd^c u)^n=e^{\lambda u}f dV$
.
$(dd^c u)^n=e^{\lambda u}f dV$
.
As shown further in [Reference Guedj, Guenancia and ZeriahiGGZ23], one has a uniform a priori bound on
![]() $\|u\|_{L^{\infty }(\Omega )}$
which depends on n,
$\|u\|_{L^{\infty }(\Omega )}$
which depends on n,
![]() $p>1$
and
$p>1$
and
![]() $\|f\|_{L^p(\Omega )}$
. This bound only weakly depends on the geometry of
$\|f\|_{L^p(\Omega )}$
. This bound only weakly depends on the geometry of
![]() $\Omega \hookrightarrow X$
, as we indicate in Theorem 3.6 so as to establish a uniform family version of this estimate.
$\Omega \hookrightarrow X$
, as we indicate in Theorem 3.6 so as to establish a uniform family version of this estimate.
1.3 Canonical measure of a
 ${\mathbb {Q}}$
-Gorenstein germ
${\mathbb {Q}}$
-Gorenstein germ
Let
![]() $(X,x)$
be a germ of normal complex space of dimension n such that
$(X,x)$
be a germ of normal complex space of dimension n such that
![]() $mK_X$
is Cartier for some integer
$mK_X$
is Cartier for some integer
![]() $m\geqslant 1$
. If
$m\geqslant 1$
. If
![]() $\sigma $
is a trivialization of
$\sigma $
is a trivialization of
![]() $mK_X$
over
$mK_X$
over
![]() $X_{\mathrm {reg}}$
, then the expression
$X_{\mathrm {reg}}$
, then the expression
defines a positive measure
![]() $\mu _{X,\sigma }$
on
$\mu _{X,\sigma }$
on
![]() $X_{\mathrm {reg}}$
; we still denote by
$X_{\mathrm {reg}}$
; we still denote by
![]() $\mu _{X,\sigma }$
its trivial extension to X. If
$\mu _{X,\sigma }$
its trivial extension to X. If
![]() $\tau $
is a trivialization of
$\tau $
is a trivialization of
![]() $m'K_X$
, then there exists
$m'K_X$
, then there exists
![]() $g\in \mathcal O_X(X)^*$
such that
$g\in \mathcal O_X(X)^*$
such that
![]() $\mu _{X,\tau }=|g|^2\mu _{X, \sigma }$
so that the qualitative behavior of the measure on the singular germ does not depend on the choice of
$\mu _{X,\tau }=|g|^2\mu _{X, \sigma }$
so that the qualitative behavior of the measure on the singular germ does not depend on the choice of
![]() $\sigma $
. In the following, one will just write
$\sigma $
. In the following, one will just write
![]() $\mu _X$
for
$\mu _X$
for
![]() $\mu _{X,\sigma }$
.
$\mu _{X,\sigma }$
.
Let
![]() $\omega $
be a smooth Hermitian form on X, restriction of a smooth Hermitian form under an embedding
$\omega $
be a smooth Hermitian form on X, restriction of a smooth Hermitian form under an embedding
![]() $(X,x)\hookrightarrow \mathbb C^N$
. We denote by f the density of
$(X,x)\hookrightarrow \mathbb C^N$
. We denote by f the density of
![]() $\mu _X$
with respect to
$\mu _X$
with respect to
![]() $\omega ^n$
, that is,
$\omega ^n$
, that is,
![]() $\mu _X=f\omega ^n$
. In the following, the
$\mu _X=f\omega ^n$
. In the following, the
![]() $L^p$
spaces are considered with respect to
$L^p$
spaces are considered with respect to
![]() $\omega ^n$
.
$\omega ^n$
.
We will see below (cf proof of Lemma 1.6) that
![]() $-\log f$
is quasi-psh; in particular,
$-\log f$
is quasi-psh; in particular,
![]() $\log f \in L^1$
. As a consequence, one can make the following definition
$\log f \in L^1$
. As a consequence, one can make the following definition
Definition 1.5. Let
![]() $X,\mu _X, \omega , f$
be as above. The Ricci curvature current of
$X,\mu _X, \omega , f$
be as above. The Ricci curvature current of
![]() $\omega $
is defined as
$\omega $
is defined as
This expression yields a
![]() $(1,1)$
current with potentials which is independent of the trivialization
$(1,1)$
current with potentials which is independent of the trivialization
![]() $\sigma $
. On
$\sigma $
. On
![]() $X_{\mathrm {reg}}$
, it coincides with the usual Ricci curvature of the Kähler metric
$X_{\mathrm {reg}}$
, it coincides with the usual Ricci curvature of the Kähler metric
![]() $\omega $
, but we will see in the lemma below that
$\omega $
, but we will see in the lemma below that
![]() $\mathrm {Ric} \, \omega $
is not a smooth form unless X is smooth.
$\mathrm {Ric} \, \omega $
is not a smooth form unless X is smooth.
One can extend the definition of Ricci curvature for currents that are not necessarily smooth. More precisely, let
![]() $T=dd^c \varphi $
be a positive
$T=dd^c \varphi $
be a positive
![]() $(1,1)$
current with potential
$(1,1)$
current with potential
![]() $\varphi \in L^{\infty }(X)$
. Assume that
$\varphi \in L^{\infty }(X)$
. Assume that
![]() $T^n=g\omega ^n$
has a density g satisfying
$T^n=g\omega ^n$
has a density g satisfying
![]() $\log g\in L^1$
. One defines
$\log g\in L^1$
. One defines
![]() $\mathrm {Ric} \, T:=\mathrm {Ric} \, \omega - dd^c \log g$
which yields a
$\mathrm {Ric} \, T:=\mathrm {Ric} \, \omega - dd^c \log g$
which yields a
![]() $(1,1)$
current with potentials depending only on T (and not on
$(1,1)$
current with potentials depending only on T (and not on
![]() $\omega $
or
$\omega $
or
![]() $\varphi $
). In particular, the construction can be globalized to positive
$\varphi $
). In particular, the construction can be globalized to positive
![]() $(1,1)$
currents with local potentials on a normal complex space with
$(1,1)$
currents with local potentials on a normal complex space with
![]() ${\mathbb {Q}}$
-Gorenstein singularities.
${\mathbb {Q}}$
-Gorenstein singularities.
Recall that
![]() $(X,x)$
has log terminal singularities if and only if
$(X,x)$
has log terminal singularities if and only if
![]() $\mu _X$
has finite mass, that is,
$\mu _X$
has finite mass, that is,
![]() $f\in L^1$
. It is standard to see that the latter condition is actually equivalent to having
$f\in L^1$
. It is standard to see that the latter condition is actually equivalent to having
![]() $f\in L^p$
for some
$f\in L^p$
for some
![]() $p>1$
, cf, for example, [Reference Eyssidieux, Guedj and ZeriahiEGZ09, Lemma 6.4].
$p>1$
, cf, for example, [Reference Eyssidieux, Guedj and ZeriahiEGZ09, Lemma 6.4].
The following result shows that the measure
![]() $\mu _X$
has a singular density with respect to a smooth volume form unless
$\mu _X$
has a singular density with respect to a smooth volume form unless
![]() $(X,x)$
is smooth, compare [Reference LiLi23].
$(X,x)$
is smooth, compare [Reference LiLi23].
Lemma 1.6. Let
![]() $(X,x)$
be a germ of normal complex space of dimension n such that
$(X,x)$
be a germ of normal complex space of dimension n such that
![]() $mK_X$
is Cartier, and let
$mK_X$
is Cartier, and let
![]() $\omega $
be a smooth Kähler metric. Let f be the density of
$\omega $
be a smooth Kähler metric. Let f be the density of
![]() $\mu _X$
with respect to
$\mu _X$
with respect to
![]() $\omega ^n$
, that is,
$\omega ^n$
, that is,
![]() $\mu _X=f\omega ^n$
. We have
$\mu _X=f\omega ^n$
. We have
Moreover, the latter condition is equivalent to the existence of
![]() $k\in {\mathbb {R}}_+$
such that
$k\in {\mathbb {R}}_+$
such that
Proof. In order to lighten the notation, we will assume that
![]() $m=1$
. The proof of the general case is essentially identical. One direction of the lemma is obvious, so we need to show that boundedness of the density implies smoothness of the germ.
$m=1$
. The proof of the general case is essentially identical. One direction of the lemma is obvious, so we need to show that boundedness of the density implies smoothness of the germ.
We can assume that we have an embedding
![]() $X\hookrightarrow \mathbb C^N$
such that for all n-tuple
$X\hookrightarrow \mathbb C^N$
such that for all n-tuple
![]() $I\subset \{1, \ldots , N\}$
, the linear projections
$I\subset \{1, \ldots , N\}$
, the linear projections
![]() $p_I:X\to \mathbb C^n$
are finite maps. It is not difficult to check that there exists a smooth function G on X such that
$p_I:X\to \mathbb C^n$
are finite maps. It is not difficult to check that there exists a smooth function G on X such that
![]() $\omega ^n=e^G\omega _{\mathbb C^N}^n|_X$
.
$\omega ^n=e^G\omega _{\mathbb C^N}^n|_X$
.
Given any I, there exists a holomorphic function
![]() $\zeta _I$
on
$\zeta _I$
on
![]() $X_{\mathrm {reg}}$
such that
$X_{\mathrm {reg}}$
such that
![]() $dz_I|_{X_{\mathrm {reg}}} = \zeta _I \sigma $
. By normality of X,
$dz_I|_{X_{\mathrm {reg}}} = \zeta _I \sigma $
. By normality of X,
![]() $\zeta _I$
extends to a holomorphic function on X. This shows that
$\zeta _I$
extends to a holomorphic function on X. This shows that
![]() $f=(e^G\sum _I |\zeta _I|^2)^{-1}$
up to some positive constant. In particular,
$f=(e^G\sum _I |\zeta _I|^2)^{-1}$
up to some positive constant. In particular,
![]() $-\log f$
is quasi-psh.
$-\log f$
is quasi-psh.
Next, if f is bounded on X, then there exists I such that
![]() $\zeta _I(x)\neq 0$
. In particular,
$\zeta _I(x)\neq 0$
. In particular,
![]() $\zeta _I$
is nonvanishing on the germ
$\zeta _I$
is nonvanishing on the germ
![]() $(X,x)$
, and
$(X,x)$
, and
![]() $dz_I|_{X_{\mathrm {reg}}}$
is a trivialization of
$dz_I|_{X_{\mathrm {reg}}}$
is a trivialization of
![]() $K_{X_{\mathrm {reg}}}$
. In other words, the map
$K_{X_{\mathrm {reg}}}$
. In other words, the map
![]() $p_I: X\to \mathbb C^n$
is étale on
$p_I: X\to \mathbb C^n$
is étale on
![]() $X_{\mathrm {reg}}$
, hence everywhere by purity of the branch locus. This shows that
$X_{\mathrm {reg}}$
, hence everywhere by purity of the branch locus. This shows that
![]() $(X,x)$
is smooth.
$(X,x)$
is smooth.
As for the last claim, assume that
![]() $(X,x)$
is singular. Then
$(X,x)$
is singular. Then
![]() $\psi :=\log (\sum _I |\zeta _I|^2)$
is psh with analytic singularities and satisfies
$\psi :=\log (\sum _I |\zeta _I|^2)$
is psh with analytic singularities and satisfies
![]() $\psi (x)=-\infty $
and by definition, we have
$\psi (x)=-\infty $
and by definition, we have
![]() $\mathrm {Ric} \, \omega = -dd^c(\psi +G)$
. If the Ricci curvature of
$\mathrm {Ric} \, \omega = -dd^c(\psi +G)$
. If the Ricci curvature of
![]() $\omega $
were bounded from below, there would exist
$\omega $
were bounded from below, there would exist
![]() $A>0$
such that
$A>0$
such that
![]() $dd^c(A\|z\|^2-\psi )\geqslant 0$
. In particular,
$dd^c(A\|z\|^2-\psi )\geqslant 0$
. In particular,
![]() $A\|z\|^2-\psi $
would be psh on
$A\|z\|^2-\psi $
would be psh on
![]() $X_{\mathrm {reg}}$
, hence bounded above near x, which is absurd.
$X_{\mathrm {reg}}$
, hence bounded above near x, which is absurd.
Remark 1.7. The Ricci curvature of
![]() $\omega $
is, however, always bounded from above. This follows from the fact that curvature decreases when passing to holomorphic submanifolds.
$\omega $
is, however, always bounded from above. This follows from the fact that curvature decreases when passing to holomorphic submanifolds.
Remark 1.8. The first statement in Lemma 1.6 extends immediately to the setting of log pairs
![]() $(X,D)$
. Indeed, if
$(X,D)$
. Indeed, if
![]() $D\neq \emptyset $
, let us write
$D\neq \emptyset $
, let us write
![]() $D=\sum a_iD_i$
with
$D=\sum a_iD_i$
with
![]() $a_i\neq 0$
and work at a general point
$a_i\neq 0$
and work at a general point
![]() $y\in D_i$
where both X and D are smooth so that
$y\in D_i$
where both X and D are smooth so that
![]() $D_i=(g_i=0)$
for some holomorphic function
$D_i=(g_i=0)$
for some holomorphic function
![]() $g_i$
defined near y. In a neighborhood of y, the density of
$g_i$
defined near y. In a neighborhood of y, the density of
![]() $\mu _{(X, D)}$
looks like
$\mu _{(X, D)}$
looks like
![]() $|g_i|^{-2a_i}$
hence it is not bounded.
$|g_i|^{-2a_i}$
hence it is not bounded.
Corollary 1.9. Let
![]() $(X,\omega )$
be a Stein or compact Kähler space with log terminal singularities admitting a Kähler–Einstein metric
$(X,\omega )$
be a Stein or compact Kähler space with log terminal singularities admitting a Kähler–Einstein metric
![]() $\omega _{\mathrm {KE}}$
in the sense of [Reference Guedj, Guenancia and ZeriahiGGZ23] or [Reference Eyssidieux, Guedj and ZeriahiEGZ09], respectively. Assume that there exists
$\omega _{\mathrm {KE}}$
in the sense of [Reference Guedj, Guenancia and ZeriahiGGZ23] or [Reference Eyssidieux, Guedj and ZeriahiEGZ09], respectively. Assume that there exists
![]() $C>0$
such that
$C>0$
such that
Then X is smooth.
Proof. Pick
![]() $x\in X$
and choose a neighborhood U of x bearing a trivialization
$x\in X$
and choose a neighborhood U of x bearing a trivialization
![]() $\sigma $
of
$\sigma $
of
![]() $mK_{U_{\mathrm {reg}}}$
and write
$mK_{U_{\mathrm {reg}}}$
and write
![]() $\mu _U:=i^{n^2} (\sigma \wedge \bar \sigma )^{\frac 1m}$
. Next, one can ensure that there exists
$\mu _U:=i^{n^2} (\sigma \wedge \bar \sigma )^{\frac 1m}$
. Next, one can ensure that there exists
![]() $\varphi \in \mathrm {PSH}(U)\cap L^{\infty }(U)$
such that
$\varphi \in \mathrm {PSH}(U)\cap L^{\infty }(U)$
such that
![]() $\omega _{\mathrm {KE}}|_{U}=dd^c \varphi $
. There exist
$\omega _{\mathrm {KE}}|_{U}=dd^c \varphi $
. There exist
![]() $\lambda \in {\mathbb {R}}$
and a pluriharmonic (hence smooth) function h on U such that
$\lambda \in {\mathbb {R}}$
and a pluriharmonic (hence smooth) function h on U such that
In particular, the domination
![]() $\omega _{\mathrm {KE}} \leqslant C\omega $
implies that the density of
$\omega _{\mathrm {KE}} \leqslant C\omega $
implies that the density of
![]() $\mu _U$
with respect to
$\mu _U$
with respect to
![]() $\omega ^n$
is bounded. The conclusion now follows from Lemma 1.6.
$\omega ^n$
is bounded. The conclusion now follows from Lemma 1.6.
2 Global smoothing
In this section, we show that singular Kähler–Einstein metrics are Kähler currents when the variety X admits a global smoothing.
2.1 Kähler–Einstein currents
Let X be a Kähler normal compact space. The study of complex Monge–Ampère equations in this context has been initiated in [Reference Eyssidieux, Guedj and ZeriahiEGZ09], providing a way of constructing singular Kähler–Einstein metrics and extending Yau’s fundamental solution to the Calabi conjecture [Reference YauYau78]. More precisely, it is proven there that given a Kähler metric
![]() $\omega $
on X, a nonnegative number
$\omega $
on X, a nonnegative number
![]() $\lambda \in \{0,1\}$
and a nonnegative function
$\lambda \in \{0,1\}$
and a nonnegative function
![]() $f\in L^p(X)$
for some
$f\in L^p(X)$
for some
![]() $p>1$
(satisfying
$p>1$
(satisfying
![]() $\int _X f\omega ^n = \int _X \omega ^n$
if
$\int _X f\omega ^n = \int _X \omega ^n$
if
![]() $\lambda =0$
), then the equation
$\lambda =0$
), then the equation
has a unique solution
![]() $\varphi \in \mathrm {PSH}(X,\omega ) \cap L^{\infty }(X)$
(with the additional normalization
$\varphi \in \mathrm {PSH}(X,\omega ) \cap L^{\infty }(X)$
(with the additional normalization
![]() $\sup _X \varphi =0$
if
$\sup _X \varphi =0$
if
![]() $\lambda =0$
).
$\lambda =0$
).
Let us now explain the relation between Equation (2.1) above and the existence of singular Kähler–Einstein metrics.
We choose a pair
![]() $(X,D)$
consisting of an n-dimensional compact Kähler variety X and a divisor
$(X,D)$
consisting of an n-dimensional compact Kähler variety X and a divisor
![]() $D=\sum a_i D_i$
with
$D=\sum a_i D_i$
with
![]() $a_i \in [0,1] \cap \mathbb Q$
. We assume that there exists an integer
$a_i \in [0,1] \cap \mathbb Q$
. We assume that there exists an integer
![]() $m\geqslant 1$
such that
$m\geqslant 1$
such that
![]() $m(K_X+D)$
is a line bundle. More precisely, we mean by this that the reflexive hull of the coherent sheaf
$m(K_X+D)$
is a line bundle. More precisely, we mean by this that the reflexive hull of the coherent sheaf
![]() $\left (\det (\Omega _X^1)\otimes \mathcal O_X(D)\right )^{\otimes m}$
is locally free.
$\left (\det (\Omega _X^1)\otimes \mathcal O_X(D)\right )^{\otimes m}$
is locally free.
Given a Hermitian metric h on
![]() $K_X+D$
and the singular metric
$K_X+D$
and the singular metric
![]() $e^{-\phi _D}$
on
$e^{-\phi _D}$
on
![]() $X_{\mathrm {reg}}$
(unique up to a positive multiple), one can construct a measure
$X_{\mathrm {reg}}$
(unique up to a positive multiple), one can construct a measure
![]() $\mu _{(X,D),h}$
on X as follows. If U is any open set where
$\mu _{(X,D),h}$
on X as follows. If U is any open set where
![]() $m(K_X+D)$
admits a trivialization
$m(K_X+D)$
admits a trivialization
![]() $\sigma $
on
$\sigma $
on
![]() $U_{\mathrm {reg}}$
, then the expression
$U_{\mathrm {reg}}$
, then the expression
 $$ \begin{align*}\frac{(\sigma \wedge \bar \sigma)^{\frac 1m}}{|\sigma|_{h^{\otimes m}}^{\frac 2m}}e^{-\phi_D}\end{align*} $$
$$ \begin{align*}\frac{(\sigma \wedge \bar \sigma)^{\frac 1m}}{|\sigma|_{h^{\otimes m}}^{\frac 2m}}e^{-\phi_D}\end{align*} $$
defines a measure on
![]() $U_{\mathrm {reg}}$
which is independent of m as well as the choice of
$U_{\mathrm {reg}}$
which is independent of m as well as the choice of
![]() $\sigma $
and can thus be patched to a measure on
$\sigma $
and can thus be patched to a measure on
![]() $X_{\mathrm {reg}}$
. Its extension by
$X_{\mathrm {reg}}$
. Its extension by
![]() $0$
on
$0$
on
![]() $X_{\mathrm {sing}}$
is by definition
$X_{\mathrm {sing}}$
is by definition
![]() $\mu _{(X,D),h}$
. We recall the following properties satisfied by the measure
$\mu _{(X,D),h}$
. We recall the following properties satisfied by the measure
![]() $\mu :=\mu _{(X,D),h}$
, cf [Reference Eyssidieux, Guedj and ZeriahiEGZ09, Lemma 6.4].
$\mu :=\mu _{(X,D),h}$
, cf [Reference Eyssidieux, Guedj and ZeriahiEGZ09, Lemma 6.4].
-
○ The Ricci curvature of
 $\mu $
on
$\mu $
on
 $X_{\mathrm {reg}}$
is equal to
$X_{\mathrm {reg}}$
is equal to
 $-i\Theta (h)+[D]$
.
$-i\Theta (h)+[D]$
. -
○ The mass
 $\int _X d\mu $
is finite if and only if
$\int _X d\mu $
is finite if and only if
 $(X,D)$
has klt singularities.
$(X,D)$
has klt singularities. -
○ If
 $\mu $
has finite mass, then the density f of
$\mu $
has finite mass, then the density f of
 $\mu $
wrt
$\mu $
wrt
 $\omega ^n$
(i.e.,
$\omega ^n$
(i.e.,
 $\mu =f\cdot \omega ^n$
) satisfies
$\mu =f\cdot \omega ^n$
) satisfies
 $f\in L^p(X)$
for some
$f\in L^p(X)$
for some
 $p>1$
.
$p>1$
.
From now on, we work in the following
Setup 2.1. Let
![]() $(X,D)$
be a pair where X is a compact normal Kähler space and D is an effective
$(X,D)$
be a pair where X is a compact normal Kähler space and D is an effective
![]() $\mathbb Q$
-divisor. Assume that
$\mathbb Q$
-divisor. Assume that
![]() $(X,D)$
has klt singularities, pick a Kähler metric
$(X,D)$
has klt singularities, pick a Kähler metric
![]() $\omega $
and a Hermitian metric h on
$\omega $
and a Hermitian metric h on
![]() $K_X+D$
, normalized so that
$K_X+D$
, normalized so that
![]() $\int _X d\mu _{(X,D),h}=\int _X\omega ^n$
. We assume either
$\int _X d\mu _{(X,D),h}=\int _X\omega ^n$
. We assume either
-
○
 $K_X+D$
is ample and
$K_X+D$
is ample and
 $\omega = i\Theta (h)$
, or
$\omega = i\Theta (h)$
, or -
○
 $K_X+D \equiv 0$
and h satisfies
$K_X+D \equiv 0$
and h satisfies
 $i\Theta (h)=0$
, or else
$i\Theta (h)=0$
, or else -
○
 $K_X+D$
is antiample and
$K_X+D$
is antiample and
 $\omega = -i\Theta (h)$
.
$\omega = -i\Theta (h)$
.
Definition 2.2. In the Setting 2.1 above, a Kähler–Einstein metric
![]() $\omega _{\mathrm {KE}}:=\omega +dd^c \varphi _{\mathrm {KE}}$
is a solution of the Monge–Ampère equation
$\omega _{\mathrm {KE}}:=\omega +dd^c \varphi _{\mathrm {KE}}$
is a solution of the Monge–Ampère equation
where
![]() $\lambda = 1,0$
or
$\lambda = 1,0$
or
![]() $-1$
according to whether we are in the first, second or third case. It satisfies
$-1$
according to whether we are in the first, second or third case. It satisfies
in the weak sense.
By the results [Reference Eyssidieux, Guedj and ZeriahiEGZ09] recalled above, Equation (2.2) admits a unique solution
![]() $\omega _{\mathrm {KE}}$
whenever
$\omega _{\mathrm {KE}}$
whenever
![]() $\lambda \in \{0,1\}$
. Its potential
$\lambda \in \{0,1\}$
. Its potential
![]() $\varphi _{\mathrm {KE}}$
is globally bounded on X and
$\varphi _{\mathrm {KE}}$
is globally bounded on X and
![]() $\omega _{\mathrm {KE}}$
is a honest Kähler–Einstein metric on
$\omega _{\mathrm {KE}}$
is a honest Kähler–Einstein metric on
![]() $X_{\mathrm {reg}} \setminus \mathrm {Supp}(D)$
, and it has cone singularities along D generically [Reference GuenanciaGue13]. For
$X_{\mathrm {reg}} \setminus \mathrm {Supp}(D)$
, and it has cone singularities along D generically [Reference GuenanciaGue13]. For
![]() $\lambda =-1$
, we refer the reader to [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBE+19, Reference BoucksomBou18].
$\lambda =-1$
, we refer the reader to [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBE+19, Reference BoucksomBou18].
Kähler–Einstein theory in positive curvature is notoriously more complicated than in nonpositive curvature. For that reason, we will make additional assumptions when working in the log Fano case and introduce the following
Setup 2.3. In the Setup 2.1 and in the case where
![]() $-(K_X+D)$
is ample, we assume additionally that
$-(K_X+D)$
is ample, we assume additionally that
-
○ There exists a Kähler–Einstein metric
 $\omega _{\mathrm {KE}}$
,
$\omega _{\mathrm {KE}}$
, -
○
 $\mathrm {Aut}^\circ (X,D)=0$
.
$\mathrm {Aut}^\circ (X,D)=0$
.
The assumption on the automorphism group is to ensure uniqueness of the KE metric. Actually, assuming existence of a Kähler-Einstein (KE) metric, its uniqueness is equivalent to the discreteness of
![]() $\mathrm {Aut}(X,D)$
.
$\mathrm {Aut}(X,D)$
.
In summary, in Setup 2.3 above, there exists in each three cases a unique Kähler–Einstein metric
![]() $\omega _{\mathrm {KE}}\in [\omega ]$
. This is by [Reference Eyssidieux, Guedj and ZeriahiEGZ09] if
$\omega _{\mathrm {KE}}\in [\omega ]$
. This is by [Reference Eyssidieux, Guedj and ZeriahiEGZ09] if
![]() $K_X+D \geqslant 0$
and by [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBE+19, Theorem 5.1] if
$K_X+D \geqslant 0$
and by [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBE+19, Theorem 5.1] if
![]() $K_X+D<0$
.
$K_X+D<0$
.
2.2 Kähler currents
Let us start by recalling the following terminology.
Definition 2.4. Let
![]() $(X,\omega )$
be a compact Kähler space, and let T be a closed, positive
$(X,\omega )$
be a compact Kähler space, and let T be a closed, positive
![]() $(1,1)$
-current. We say that T is a Kähler current if there exists
$(1,1)$
-current. We say that T is a Kähler current if there exists
![]() $\varepsilon>0$
such that the inequality
$\varepsilon>0$
such that the inequality
![]() $T\geqslant \varepsilon \omega $
holds globally on X in the sense of currents.
$T\geqslant \varepsilon \omega $
holds globally on X in the sense of currents.
In our main case of interest, T will have local potentials, that is, there exist a finite open covering
![]() $X=\cup _{\alpha \in I} U_\alpha $
and functions
$X=\cup _{\alpha \in I} U_\alpha $
and functions
![]() $u_\alpha \in \mathrm {PSH}(U_\alpha )$
such that
$u_\alpha \in \mathrm {PSH}(U_\alpha )$
such that
![]() $T|_{U_\alpha }=dd^c u_\alpha $
. Up to refining the cover, one can assume that
$T|_{U_\alpha }=dd^c u_\alpha $
. Up to refining the cover, one can assume that
![]() $\omega |_{U_\alpha }=dd^c \varphi _\alpha $
for some strictly psh functions
$\omega |_{U_\alpha }=dd^c \varphi _\alpha $
for some strictly psh functions
![]() $\varphi _\alpha $
on
$\varphi _\alpha $
on
![]() $U_\alpha $
. Then T is a Kähler current if and only if there exists
$U_\alpha $
. Then T is a Kähler current if and only if there exists
![]() $\varepsilon>0$
such that for all
$\varepsilon>0$
such that for all
![]() $\alpha \in I$
, one has
$\alpha \in I$
, one has
![]() $u_\alpha -\varepsilon \varphi _\alpha \in \mathrm {PSH}(U_\alpha )$
.
$u_\alpha -\varepsilon \varphi _\alpha \in \mathrm {PSH}(U_\alpha )$
.
In the following, we will repeatedly use the following classical result:
Lemma 2.5. Let X be a normal complex space, and let T be a closed
![]() $(1,1)$
- current on X admitting locally bounded potentials. Assume that there exists a closed analytic set
$(1,1)$
- current on X admitting locally bounded potentials. Assume that there exists a closed analytic set
![]() $Z\subsetneq X$
such that
$Z\subsetneq X$
such that
![]() $T|_{X\setminus Z}\geqslant 0$
. Then,
$T|_{X\setminus Z}\geqslant 0$
. Then,
![]() $T\geqslant 0$
everywhere on X.
$T\geqslant 0$
everywhere on X.
Proof. The claim is an immediate application of Chern–Levine–Nirenberg inequality that ensures that T puts no mass on pluripolar sets. Alternatively, fix an open neighborhood U of a point
![]() $x\in Z$
such that
$x\in Z$
such that
![]() $T|_U=dd^c\varphi $
. One can choose
$T|_U=dd^c\varphi $
. One can choose
![]() $\varphi $
such that
$\varphi $
such that
![]() $\varphi |_{U\setminus Z}$
is psh and locally bounded near Z, hence it extends to a psh function
$\varphi |_{U\setminus Z}$
is psh and locally bounded near Z, hence it extends to a psh function
![]() $\psi $
on U. Since
$\psi $
on U. Since
![]() $\varphi =\psi $
almost everywhere on U, we have
$\varphi =\psi $
almost everywhere on U, we have
![]() $T|_U=dd^c\psi \geqslant 0$
.
$T|_U=dd^c\psi \geqslant 0$
.
The purpose of this section is to study when
![]() $\omega _{\mathrm {KE}}$
is a Kähler current, by using a smoothability assumption. Our results are inspired by a result due to Ruan and Zhang [Reference Ruan and ZhangRZ11b, Lemma 5.2], and the main tool throughout the paper will be Chern–Lu inequality, which we recall below as it can be found in, for example, [Reference RubinsteinRub14, Proposition 7.2]
$\omega _{\mathrm {KE}}$
is a Kähler current, by using a smoothability assumption. Our results are inspired by a result due to Ruan and Zhang [Reference Ruan and ZhangRZ11b, Lemma 5.2], and the main tool throughout the paper will be Chern–Lu inequality, which we recall below as it can be found in, for example, [Reference RubinsteinRub14, Proposition 7.2]
Proposition 2.6 (Chern–Lu inequality)
Let X be a complex manifold endowed with two Kähler metrics
![]() $\omega , \widehat \omega $
. Assume that there are constants
$\omega , \widehat \omega $
. Assume that there are constants
![]() $C_1, C_2, C_3 \in \mathbb R$
such that
$C_1, C_2, C_3 \in \mathbb R$
such that
Then, we have the following inequality on X
Next, we introduce the following definition
Definition 2.7. Let
![]() $(X,D)$
be a klt pair with X compact, and let
$(X,D)$
be a klt pair with X compact, and let
![]() $\omega $
be a Kähler metric. We say that
$\omega $
be a Kähler metric. We say that
![]() $(X,D,[\omega ])$
admits a
$(X,D,[\omega ])$
admits a
![]() $\mathbb Q$
-Gorenstein smoothing if there exists a triplet
$\mathbb Q$
-Gorenstein smoothing if there exists a triplet
![]() $(\mathcal X, \mathcal D, [\omega _{\mathcal X}])$
consisting of a normal complex space
$(\mathcal X, \mathcal D, [\omega _{\mathcal X}])$
consisting of a normal complex space
![]() $\mathcal X$
, an effective
$\mathcal X$
, an effective
![]() $\mathbb Q$
-divisor
$\mathbb Q$
-divisor
![]() $\mathcal D$
, and a smooth,
$\mathcal D$
, and a smooth,
![]() $(1,1)$
-form
$(1,1)$
-form
![]() $\omega _{\mathcal X}$
on
$\omega _{\mathcal X}$
on
![]() $\mathcal X$
admitting a proper, surjective holomorphic map
$\mathcal X$
admitting a proper, surjective holomorphic map
![]() $\pi :\mathcal X \to \mathbb D$
satisfying:
$\pi :\mathcal X \to \mathbb D$
satisfying:
-
1.
 $K_{\mathcal X/\mathbb D}+\mathcal D$
is a
$K_{\mathcal X/\mathbb D}+\mathcal D$
is a
 $\mathbb Q$
-line bundle.
$\mathbb Q$
-line bundle. -
2. Every irreducible component of
 $\mathcal D$
surjects onto
$\mathcal D$
surjects onto
 $\mathbb D$
.
$\mathbb D$
. -
3.
 $(\mathcal X, \mathcal D)|_{\pi ^{-1}(0)} \simeq (X,D)$
.
$(\mathcal X, \mathcal D)|_{\pi ^{-1}(0)} \simeq (X,D)$
. -
4. For
 $t\neq 0$
,
$t\neq 0$
,
 $(X_t, D_t)=(\mathcal X, \mathcal D)|_{\pi ^{-1}(t)}$
is log smooth.
$(X_t, D_t)=(\mathcal X, \mathcal D)|_{\pi ^{-1}(t)}$
is log smooth. -
5. For
 $t\in \mathbb D$
,
$t\in \mathbb D$
,
 $\omega _t:=\omega _{\mathcal X}|_{X_t}$
is Kähler and
$\omega _t:=\omega _{\mathcal X}|_{X_t}$
is Kähler and
 $[\omega _0]=[\omega ]$
.
$[\omega _0]=[\omega ]$
.
Let us make few remarks:
-
1. If
 $K_X+D$
is ample or antiample, then so is
$K_X+D$
is ample or antiample, then so is
 $K_{X_t}+D_t$
for t small. Then, the last condition in the definition above is automatic if
$K_{X_t}+D_t$
for t small. Then, the last condition in the definition above is automatic if
 $\omega \in \pm c_1(K_X+D)$
, by using an embedding of
$\omega \in \pm c_1(K_X+D)$
, by using an embedding of
 $\mathcal X$
into
$\mathcal X$
into
 $\mathbb P^N\times \mathbb D$
via sections of
$\mathbb P^N\times \mathbb D$
via sections of
 $\pm m(K_{X_t}+D_t)$
for m large.
$\pm m(K_{X_t}+D_t)$
for m large. -
2. If
 $K_X+D$
is numerically trivial, then so is
$K_X+D$
is numerically trivial, then so is
 $K_{X_t}+D_t$
for t small, cf, for example, [Reference Druel and GuenanciaDG18, Lemma 2.12].
$K_{X_t}+D_t$
for t small, cf, for example, [Reference Druel and GuenanciaDG18, Lemma 2.12]. -
3. The pair
 $(X_t, D_t)$
is automatically klt for any
$(X_t, D_t)$
is automatically klt for any
 $t\in \mathbb D$
.
$t\in \mathbb D$
.
Theorem 2.8. Let
![]() $(X,D,[\omega ])$
as in Setup 2.3, and assume that
$(X,D,[\omega ])$
as in Setup 2.3, and assume that
![]() $(X,D,[\omega ])$
admits a
$(X,D,[\omega ])$
admits a
![]() $\mathbb Q$
-Gorenstein smoothing. Then, the Kähler–Einstein metric
$\mathbb Q$
-Gorenstein smoothing. Then, the Kähler–Einstein metric
![]() $\omega _{\mathrm {KE}}$
is a Kähler current. That is, there exists
$\omega _{\mathrm {KE}}$
is a Kähler current. That is, there exists
![]() $C>0$
such that
$C>0$
such that
Remark 2.9. Along the same lines, one can obtain the result above assuming instead that
![]() $(X,D)$
admits a crepant resolution, that is, a proper bimeromorphic map
$(X,D)$
admits a crepant resolution, that is, a proper bimeromorphic map
![]() $p:\widetilde X\to X$
such that
$p:\widetilde X\to X$
such that
![]() $K_{\widetilde X}+\widetilde D=p^*(K_X+D)$
, where
$K_{\widetilde X}+\widetilde D=p^*(K_X+D)$
, where
![]() $\widetilde D$
is the proper transform of D.
$\widetilde D$
is the proper transform of D.
Proof. We consider the smoothing
![]() $\pi :(\mathcal X,\mathcal D)\to \mathbb D$
. Up to shrinking
$\pi :(\mathcal X,\mathcal D)\to \mathbb D$
. Up to shrinking
![]() $\mathbb D$
slightly and adding
$\mathbb D$
slightly and adding
![]() $\pi ^*dd^c |t|^2$
to
$\pi ^*dd^c |t|^2$
to
![]() $\omega _{\mathcal X}$
, one can assume that the later form is strictly positive. Since
$\omega _{\mathcal X}$
, one can assume that the later form is strictly positive. Since
![]() $\omega _{\mathcal X}$
is the restriction of a smooth positive
$\omega _{\mathcal X}$
is the restriction of a smooth positive
![]() $(1,1)$
-form under local embedding
$(1,1)$
-form under local embedding
![]() $\mathcal X \underset {\mathrm {loc}}{\hookrightarrow } \mathbb C^N$
, one can assume that the bisectional curvature of
$\mathcal X \underset {\mathrm {loc}}{\hookrightarrow } \mathbb C^N$
, one can assume that the bisectional curvature of
![]() $\omega _{\mathcal X}|_{\mathcal X^{\mathrm {reg}}}$
is bounded above by a given constant
$\omega _{\mathcal X}|_{\mathcal X^{\mathrm {reg}}}$
is bounded above by a given constant
![]() $C_1$
, maybe up to shrinking
$C_1$
, maybe up to shrinking
![]() $\mathbb D$
just a little more. This is because the bisectional curvature decreases when passing to holomorphic submanifolds. By the same argument, we see the bisectional curvature of
$\mathbb D$
just a little more. This is because the bisectional curvature decreases when passing to holomorphic submanifolds. By the same argument, we see the bisectional curvature of
![]() $\omega _t=\omega _{\mathcal X}|_{X_t}$
is bounded above by
$\omega _t=\omega _{\mathcal X}|_{X_t}$
is bounded above by
![]() $C_1$
, for any
$C_1$
, for any
![]() $t\in \mathbb D$
.
$t\in \mathbb D$
.
For
![]() $t\in \mathbb D$
, we consider
$t\in \mathbb D$
, we consider
![]() $\widetilde {\omega }_{t}=\omega _t+dd^c \varphi _t$
the unique Kähler–Einstein metric of the pair
$\widetilde {\omega }_{t}=\omega _t+dd^c \varphi _t$
the unique Kähler–Einstein metric of the pair
![]() $(X_t, D_t)$
. For
$(X_t, D_t)$
. For
![]() $t\neq 0$
, existence and uniqueness of
$t\neq 0$
, existence and uniqueness of
![]() $\widetilde {\omega }_{t}$
is due to [Reference KołodziejKoł98] when
$\widetilde {\omega }_{t}$
is due to [Reference KołodziejKoł98] when
![]() $\lambda \geqslant 0$
and to [Reference Spotti, Sun and YaoSSY16, Reference Li, Wang and XuLWX19], cf also [Reference Pan and TrusianiPT23] when
$\lambda \geqslant 0$
and to [Reference Spotti, Sun and YaoSSY16, Reference Li, Wang and XuLWX19], cf also [Reference Pan and TrusianiPT23] when
![]() $\lambda <0$
. In the latter case, we need t to be small enough. The Kähler–Einstein metric solves
$\lambda <0$
. In the latter case, we need t to be small enough. The Kähler–Einstein metric solves
for some nonnegative function
![]() $f_t$
on
$f_t$
on
![]() $X_t$
satisfying
$X_t$
satisfying
![]() $\int _{X_t} f_t^p \omega _t^n\leqslant C(p,\omega )$
for some
$\int _{X_t} f_t^p \omega _t^n\leqslant C(p,\omega )$
for some
![]() $p>1$
and some constant
$p>1$
and some constant
![]() $C(p,\omega )$
independent of
$C(p,\omega )$
independent of
![]() $t\in \mathbb D$
. This is proved in [Reference Di Nezza, Guedj and GuenanciaDNGG23, Lemma 4.4] assuming additionally
$t\in \mathbb D$
. This is proved in [Reference Di Nezza, Guedj and GuenanciaDNGG23, Lemma 4.4] assuming additionally
![]() $X_0$
has canonical singularities, but the klt case can be proved with minimal changes, cf also Equation (3.6) in the next section.
$X_0$
has canonical singularities, but the klt case can be proved with minimal changes, cf also Equation (3.6) in the next section.
If
![]() $\lambda =0$
, we normalize
$\lambda =0$
, we normalize
![]() $\varphi _t$
by
$\varphi _t$
by
![]() $\sup _{X_t} \varphi _t =0$
. We claim that up to shrinking
$\sup _{X_t} \varphi _t =0$
. We claim that up to shrinking
![]() $\mathbb D$
, there exists a constant
$\mathbb D$
, there exists a constant
![]() $C_2>0$
such that
$C_2>0$
such that
for any
![]() $t\in \mathbb D$
.
$t\in \mathbb D$
.
If
![]() $\lambda>0$
, this is a consequence of [Reference Di Nezza, Guedj and GuenanciaDNGG23, Theorem E]. If
$\lambda>0$
, this is a consequence of [Reference Di Nezza, Guedj and GuenanciaDNGG23, Theorem E]. If
![]() $\lambda =0$
, this is a consequence of the proof of [Reference Di Nezza, Guedj and GuenanciaDNGG23, Theorem 6.1]. Indeed, in loc. cit. the fibers are assumed to be canonical but this is a mostly cosmetic assumption since going from canonical to klt singularities leaves the proof resting on [Reference Di Nezza, Guedj and GuenanciaDNGG23, Lemma 4.4] unchanged, as explained above. Finally, if
$\lambda =0$
, this is a consequence of the proof of [Reference Di Nezza, Guedj and GuenanciaDNGG23, Theorem 6.1]. Indeed, in loc. cit. the fibers are assumed to be canonical but this is a mostly cosmetic assumption since going from canonical to klt singularities leaves the proof resting on [Reference Di Nezza, Guedj and GuenanciaDNGG23, Lemma 4.4] unchanged, as explained above. Finally, if
![]() $\lambda <0$
, the estimate (2.5) is proved in [Reference Spotti, Sun and YaoSSY16, Proposition 2.23], [Reference Li, Wang and XuLWX19, Theorem 1.2 (iii)] when
$\lambda <0$
, the estimate (2.5) is proved in [Reference Spotti, Sun and YaoSSY16, Proposition 2.23], [Reference Li, Wang and XuLWX19, Theorem 1.2 (iii)] when
![]() $\mathcal D$
is plurianticanonical and in [Reference Pan and TrusianiPT23, Theorem 5.10] in general.
$\mathcal D$
is plurianticanonical and in [Reference Pan and TrusianiPT23, Theorem 5.10] in general.
Set
![]() $E:=\mathrm {Supp}(\mathcal D)$
. We choose a smooth Hermitian metric h on
$E:=\mathrm {Supp}(\mathcal D)$
. We choose a smooth Hermitian metric h on
![]() $\mathcal O_{\mathcal X}(E)$
, a section s of that line bundle cutting out E, and we introduce the function
$\mathcal O_{\mathcal X}(E)$
, a section s of that line bundle cutting out E, and we introduce the function
![]() $\psi :=\log |s|^2_{h}$
. It satisfies
$\psi :=\log |s|^2_{h}$
. It satisfies
![]() $dd^c \psi =-i\Theta _h( E)$
on
$dd^c \psi =-i\Theta _h( E)$
on
![]() $\mathcal X \setminus E$
, hence there exists a constant
$\mathcal X \setminus E$
, hence there exists a constant
![]() $C_3>0$
such that
$C_3>0$
such that
We introduce a number
![]() $\varepsilon>0$
(meant to go to zero), and we assume wlog that
$\varepsilon>0$
(meant to go to zero), and we assume wlog that
![]() $\varepsilon C_3 \leqslant 1$
. We also define
$\varepsilon C_3 \leqslant 1$
. We also define
![]() $v_t:=\log \mathrm {tr}_{\widetilde {\omega }_{t}} \omega _t$
, which is smooth on
$v_t:=\log \mathrm {tr}_{\widetilde {\omega }_{t}} \omega _t$
, which is smooth on
![]() $X_t \setminus E$
and globally bounded (for
$X_t \setminus E$
and globally bounded (for
![]() $t\neq 0$
). We want to quantify that bound.
$t\neq 0$
). We want to quantify that bound.
On
![]() $X_t\setminus E$
, we have
$X_t\setminus E$
, we have
![]() $\mathrm {Ric} \, \widetilde {\omega }_{t} \geqslant -\widetilde {\omega }_{t}$
and
$\mathrm {Ric} \, \widetilde {\omega }_{t} \geqslant -\widetilde {\omega }_{t}$
and
![]() $\mathrm {Bisec}(X_t,\omega _t) \leqslant C_1$
. By Chern–Lu inequality, that is, Proposition 2.6, we get
$\mathrm {Bisec}(X_t,\omega _t) \leqslant C_1$
. By Chern–Lu inequality, that is, Proposition 2.6, we get
Using the identity
![]() $\widetilde {\omega }_{t}=\omega _t+dd^c \varphi _t$
and the inequality (2.6), we get
$\widetilde {\omega }_{t}=\omega _t+dd^c \varphi _t$
and the inequality (2.6), we get
where
![]() $A=2(C_1+1)$
and
$A=2(C_1+1)$
and
![]() $C_4=An+1$
. The maximum of the term inside the Laplacian is attained on
$C_4=An+1$
. The maximum of the term inside the Laplacian is attained on
![]() $X_t\setminus E$
, and an easy application of the maximum principle shows
$X_t\setminus E$
, and an easy application of the maximum principle shows
for any
![]() $x\in X_t \setminus E$
and
$x\in X_t \setminus E$
and
![]() $\varepsilon>0$
, and where
$\varepsilon>0$
, and where
![]() $C_5=\log C_4+2AC_2+1$
. Passing to the limit when
$C_5=\log C_4+2AC_2+1$
. Passing to the limit when
![]() $\varepsilon \to 0$
, we find
$\varepsilon \to 0$
, we find
Next, we choose a continuous family of smooth maps
![]() $F_t:X_{\mathrm {reg}} \to X_t$
inducing a diffeomorphism onto their image and such that
$F_t:X_{\mathrm {reg}} \to X_t$
inducing a diffeomorphism onto their image and such that
![]() $F_0=\mathrm {Id}_{X_{\mathrm {reg}}}$
. We claim that
$F_0=\mathrm {Id}_{X_{\mathrm {reg}}}$
. We claim that
![]() $F_t^*\widetilde {\omega }_{t}$
converges locally smoothly to
$F_t^*\widetilde {\omega }_{t}$
converges locally smoothly to
![]() $\omega _{\mathrm {KE}}$
on
$\omega _{\mathrm {KE}}$
on
![]() $X_{\mathrm {reg}}\setminus E$
when
$X_{\mathrm {reg}}\setminus E$
when
![]() $t\to 0$
. Thanks to Equation (2.7), this would imply that
$t\to 0$
. Thanks to Equation (2.7), this would imply that
hence everywhere on X by Lemma 2.5.
Set
![]() $X^\circ :=X_{\mathrm {reg}} \setminus E$
. In order to show the convergence, we claim successively:
$X^\circ :=X_{\mathrm {reg}} \setminus E$
. In order to show the convergence, we claim successively:
-
○ The family of functions
 $F_t^*\varphi _t$
is precompact in the
$F_t^*\varphi _t$
is precompact in the
 $\mathcal C^2_{\mathrm {loc}}(X^\circ )$
-topology.
$\mathcal C^2_{\mathrm {loc}}(X^\circ )$
-topology. -
○ Each cluster value
 $\omega _{\infty }=\omega +dd^c \varphi _{\infty }$
of
$\omega _{\infty }=\omega +dd^c \varphi _{\infty }$
of
 $F_t^*\widetilde {\omega }_{t}$
solves the Monge–Ampère equation
$F_t^*\widetilde {\omega }_{t}$
solves the Monge–Ampère equation  $$\begin{align*}(\omega+dd^c \varphi_{\infty})^n=e^{\lambda \varphi_{\infty} }f_0\omega^n \quad \mbox{on } X^\circ.\end{align*}$$
$$\begin{align*}(\omega+dd^c \varphi_{\infty})^n=e^{\lambda \varphi_{\infty} }f_0\omega^n \quad \mbox{on } X^\circ.\end{align*}$$
-
○ Each cluster value
 $\varphi _{\infty }$
is globally bounded on
$\varphi _{\infty }$
is globally bounded on
 $X^\circ $
, hence its unique
$X^\circ $
, hence its unique
 $\omega $
-psh extension to X solves the equation above on X.
$\omega $
-psh extension to X solves the equation above on X.
By uniqueness of the Kähler–Einstein metric, it would then follow that
![]() $\omega _{\infty }=\omega _{\mathrm {KE}}$
, concluding the proof of the convergence. Let us briefly justify each of the items above.
$\omega _{\infty }=\omega _{\mathrm {KE}}$
, concluding the proof of the convergence. Let us briefly justify each of the items above.
The first point follows from the local Laplacian estimate on
![]() $X^\circ $
obtained from Equation (2.7). Indeed, once the Laplacian estimates are obtained, one can invoke Evans–Krylov and Schauder estimates since
$X^\circ $
obtained from Equation (2.7). Indeed, once the Laplacian estimates are obtained, one can invoke Evans–Krylov and Schauder estimates since
![]() $F_t^*\omega _t$
(resp.
$F_t^*\omega _t$
(resp.
![]() $F_t^*J_t, F_t^*f_t$
) converges locally smoothly on
$F_t^*J_t, F_t^*f_t$
) converges locally smoothly on
![]() $X^\circ $
to
$X^\circ $
to
![]() $\omega $
(resp
$\omega $
(resp
![]() $J, f_0$
) when
$J, f_0$
) when
![]() $t\to 0$
.
$t\to 0$
.
The second item is an immediate consequence of the first one. As for the last one, it is a consequence of Equation (2.5).
3 Isolated singularities
3.1 Families of Monge–Ampère equations in a local setting
Throughout this section, we will work in the following geometric context.
Setup 3.1. Let
![]() ${\mathcal {X}} \Subset \mathbb C^N$
be a bounded normal Stein space of dimension
${\mathcal {X}} \Subset \mathbb C^N$
be a bounded normal Stein space of dimension
![]() $n+1$
endowed with a surjective holomorphic map
$n+1$
endowed with a surjective holomorphic map
![]() $\pi : {\mathcal {X}}\to \mathbb D$
such that
$\pi : {\mathcal {X}}\to \mathbb D$
such that
-
1.
 ${\mathcal {X}}$
is
${\mathcal {X}}$
is
 ${\mathbb {Q}}$
-Gorenstein and
${\mathbb {Q}}$
-Gorenstein and
 $K_{{\mathcal {X}}/\mathbb D} \sim _{\mathbb Q} \mathcal O_{{\mathcal {X}}}$
.
$K_{{\mathcal {X}}/\mathbb D} \sim _{\mathbb Q} \mathcal O_{{\mathcal {X}}}$
. -
2. For every
 $t\in \mathbb D$
, the schematic fiber
$t\in \mathbb D$
, the schematic fiber
 $X_t=\pi ^{-1}(t)$
is irreducible and reduced.
$X_t=\pi ^{-1}(t)$
is irreducible and reduced. -
3.
 $X_0$
has klt singularities.
$X_0$
has klt singularities.
In the following, we fix a basepoint
![]() $0\in X_0$
.
$0\in X_0$
.
The first item means that there exists an integer
![]() $m\geqslant 1$
such that the reflexive hull of
$m\geqslant 1$
such that the reflexive hull of
![]() $K_{{\mathcal {X}}}^{\otimes m}$
is trivial. Once and for all, we pick a trivialization
$K_{{\mathcal {X}}}^{\otimes m}$
is trivial. Once and for all, we pick a trivialization
![]() $\Omega \in H^0({\mathcal {X}}, mK_{{\mathcal {X}}})$
, that is,
$\Omega \in H^0({\mathcal {X}}, mK_{{\mathcal {X}}})$
, that is,
![]() $\Omega |_{{\mathcal {X}}_{\mathrm {reg}}}$
is nonvanishing. We set
$\Omega |_{{\mathcal {X}}_{\mathrm {reg}}}$
is nonvanishing. We set
![]() $\Omega _t:=\frac {\Omega }{(d\pi )^{\otimes m}}\big |_{X_t}\in H^0(X_t, mK_{X_t})$
; this induces a trivialization of
$\Omega _t:=\frac {\Omega }{(d\pi )^{\otimes m}}\big |_{X_t}\in H^0(X_t, mK_{X_t})$
; this induces a trivialization of
![]() $mK_{X_t}$
, and we define the measure
$mK_{X_t}$
, and we define the measure
cf § 1.3. Recall that
![]() $X_t$
has klt singularities if and only if
$X_t$
has klt singularities if and only if
![]() $\mu _{X_t}$
has finite mass on each compact subset of
$\mu _{X_t}$
has finite mass on each compact subset of
![]() $X_t$
. Since
$X_t$
. Since
![]() $X_0$
is klt, inversion of adjunction [Reference Kollár and MoriKM98, Theorem 5.50] (cf also § 3.2.1) shows that
$X_0$
is klt, inversion of adjunction [Reference Kollár and MoriKM98, Theorem 5.50] (cf also § 3.2.1) shows that
![]() ${\mathcal {X}}$
is klt in the neighborhood of
${\mathcal {X}}$
is klt in the neighborhood of
![]() $X_0$
, hence for any
$X_0$
, hence for any
![]() ${\mathcal {X}}'\Subset {\mathcal {X}}$
there exists
${\mathcal {X}}'\Subset {\mathcal {X}}$
there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() ${\mathcal {X}}'\cap X_t$
is klt for
${\mathcal {X}}'\cap X_t$
is klt for
![]() $|t|<\delta $
. We will therefore shrink
$|t|<\delta $
. We will therefore shrink
![]() ${\mathcal {X}}$
so that each
${\mathcal {X}}$
so that each
![]() $X_t$
is relatively compact in a klt space for
$X_t$
is relatively compact in a klt space for
![]() $|t|$
small enough.
$|t|$
small enough.
Definition 3.2. We will use the following terminology.
-
1. A holomorphic map
 $\pi :{\mathcal {X}}\to \mathbb D$
as in Setup 3.1 is a smoothing of
$\pi :{\mathcal {X}}\to \mathbb D$
as in Setup 3.1 is a smoothing of
 $X_0$
if
$X_0$
if
 $\pi $
is smooth over
$\pi $
is smooth over
 $\mathbb D^*$
.
$\mathbb D^*$
. -
2. A normal Stein space X is smoothable if there exists a family
 $\pi :{\mathcal {X}}\to \mathbb D$
as in Setup 3.1 such that
$\pi :{\mathcal {X}}\to \mathbb D$
as in Setup 3.1 such that
 $X\simeq X_0=\pi ^{-1}(0)$
and
$X\simeq X_0=\pi ^{-1}(0)$
and
 ${\mathcal {X}}\to \mathbb D$
is a smoothing of
${\mathcal {X}}\to \mathbb D$
is a smoothing of
 $X_0$
.
$X_0$
.
In the geometric context provided by Setup 3.1, one can consider a natural family of Monge–Ampère equations which we now describe and whose analysis will take up most of this section. We pick a smooth, strictly psh nonpositive function
![]() $\rho $
on
$\rho $
on
![]() ${\mathcal {X}}$
such that
${\mathcal {X}}$
such that
![]() $\partial {\mathcal {X}}= \{\rho =0\}$
and set
$\partial {\mathcal {X}}= \{\rho =0\}$
and set
![]() $\omega = dd^c \rho $
. The restriction
$\omega = dd^c \rho $
. The restriction
![]() $\omega |_{X_t}$
of
$\omega |_{X_t}$
of
![]() $\omega $
to the fiber
$\omega $
to the fiber
![]() $X_t$
will be denoted by
$X_t$
will be denoted by
![]() $\omega _t$
. Next, we extend F (resp. h) to a smooth function on
$\omega _t$
. Next, we extend F (resp. h) to a smooth function on
![]() $\overline {\mathcal {X}})$
(resp.
$\overline {\mathcal {X}})$
(resp.
![]() $\partial {\mathcal {X}}$
) which we still denote by F (resp. h). We also choose a (small) neighborhood V of
$\partial {\mathcal {X}}$
) which we still denote by F (resp. h). We also choose a (small) neighborhood V of
![]() $\partial {\mathcal {X}}$
and set
$\partial {\mathcal {X}}$
and set
![]() $V_t=V \cap X_t$
. We are interested in the Dirichlet problem, that is, finding a plurisubharmonic function
$V_t=V \cap X_t$
. We are interested in the Dirichlet problem, that is, finding a plurisubharmonic function
![]() $u_t \in \mathrm {PSH}(X_t)\cap \mathcal C^0(\overline {X_t})$
solution of
$u_t \in \mathrm {PSH}(X_t)\cap \mathcal C^0(\overline {X_t})$
solution of
 $$\begin{align} \begin{cases} (dd^c u_t)^n = e^{\lambda u_t+F_t} \mu_{X_t} & \mbox{on } X_t\\ u_t|_{\partial X_t}=h_t \end{cases}. \end{align}$$
$$\begin{align} \begin{cases} (dd^c u_t)^n = e^{\lambda u_t+F_t} \mu_{X_t} & \mbox{on } X_t\\ u_t|_{\partial X_t}=h_t \end{cases}. \end{align}$$
with
![]() $\lambda \in \{0,1\}$
. If
$\lambda \in \{0,1\}$
. If
![]() $X_t$
is smooth, then the existence and uniqueness of
$X_t$
is smooth, then the existence and uniqueness of
![]() $u_t$
is classical and provides a solution which is smooth in
$u_t$
is classical and provides a solution which is smooth in
![]() $\overline {X_t}$
(see [Reference Caffarelli, Kohn, Nirenberg and SpruckCKNS85, Reference Guan and LiGL10]). In this more general setting, the existence and uniqueness of
$\overline {X_t}$
(see [Reference Caffarelli, Kohn, Nirenberg and SpruckCKNS85, Reference Guan and LiGL10]). In this more general setting, the existence and uniqueness of
![]() $u_t$
is provided by [Reference Guedj, Guenancia and ZeriahiGGZ23, Theorem A] for
$u_t$
is provided by [Reference Guedj, Guenancia and ZeriahiGGZ23, Theorem A] for
![]() $\lambda =0$
since
$\lambda =0$
since
![]() $X_t$
is klt up to the boundary so that the density of
$X_t$
is klt up to the boundary so that the density of
![]() $\mu _{X_t}$
with respect to
$\mu _{X_t}$
with respect to
![]() $\omega _t^n$
belongs to
$\omega _t^n$
belongs to
![]() $L^p(X_t, \omega _t^n)$
for some
$L^p(X_t, \omega _t^n)$
for some
![]() $p>1$
. The case
$p>1$
. The case
![]() $\lambda =1$
can be treated along very similar lines.
$\lambda =1$
can be treated along very similar lines.
The main technical contribution of this section is summarized in the following result.
Proposition 3.3. Let
![]() $\pi : {\mathcal {X}}\to \mathbb D$
be a family as in Setup 3.1, and let
$\pi : {\mathcal {X}}\to \mathbb D$
be a family as in Setup 3.1, and let
![]() $u_t$
be the solution of the Monge–Ampère equation (
MAt
). We have the following.
$u_t$
be the solution of the Monge–Ampère equation (
MAt
). We have the following.
-
1. There exist constants
 $ \delta , C>0$
such that for any
$ \delta , C>0$
such that for any
 $|t|<\delta $
, we have
$|t|<\delta $
, we have
 $\|u_t\|_{L^{\infty }(X_t)} \leqslant C$
.
$\|u_t\|_{L^{\infty }(X_t)} \leqslant C$
. -
2. If
 $\pi $
is smooth outside the basepoint
$\pi $
is smooth outside the basepoint
 $0\in X_0$
, then for any
$0\in X_0$
, then for any
 $t\neq 0$
Equation (
MAt
) admits a smooth subsolution
$t\neq 0$
Equation (
MAt
) admits a smooth subsolution
 $\underline {u}_t$
such that for any
$\underline {u}_t$
such that for any $$\begin{align*}dd^c \underline{u}_t \geqslant \varepsilon \omega_t \,\, \mbox{on} \, X_t, \quad \mbox{and} \quad \|\underline {u}_t\|_{\mathcal C^k(\bar V_t)} \leqslant C(k)\end{align*}$$
$$\begin{align*}dd^c \underline{u}_t \geqslant \varepsilon \omega_t \,\, \mbox{on} \, X_t, \quad \mbox{and} \quad \|\underline {u}_t\|_{\mathcal C^k(\bar V_t)} \leqslant C(k)\end{align*}$$
 $k\in \mathbb N$
, where
$k\in \mathbb N$
, where
 $\varepsilon , C=C(k)>0$
are constant that do not depend on t.
$\varepsilon , C=C(k)>0$
are constant that do not depend on t.
The proof of Proposition 3.3 is quite lengthy and will be provided in § 3.2 below.
Building upon Proposition 3.3, one can prove the following local version of Theorem 2.8, which will also be useful for understanding global problems further along in the paper.
Theorem 3.4. Let
![]() $X'\Subset \mathbb C^N$
be a normal, connected n-dimensional Stein space with an isolated klt singularity at the origin. Let
$X'\Subset \mathbb C^N$
be a normal, connected n-dimensional Stein space with an isolated klt singularity at the origin. Let
![]() $X\Subset X'$
be a strongly pseudoconvex domain containing the origin and such that
$X\Subset X'$
be a strongly pseudoconvex domain containing the origin and such that
![]() $K_{X}\sim _{\mathbb Q}\mathcal O_{X}$
. Consider the solution
$K_{X}\sim _{\mathbb Q}\mathcal O_{X}$
. Consider the solution
![]() $u\in \mathrm {PSH}(X)\cap L^{\infty }(X)$
of
$u\in \mathrm {PSH}(X)\cap L^{\infty }(X)$
of
 $$ \begin{align} \begin{cases} (dd^c u)^n = e^{\lambda u+F} \mu_X & \mbox{on } X\\ u|_{\partial X}=h, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} (dd^c u)^n = e^{\lambda u+F} \mu_X & \mbox{on } X\\ u|_{\partial X}=h, \end{cases} \end{align} $$
where
![]() $F\in \mathcal C^{\infty }(\overline X)$
,
$F\in \mathcal C^{\infty }(\overline X)$
,
![]() $h\in \mathcal C^{\infty }(\partial X)$
and
$h\in \mathcal C^{\infty }(\partial X)$
and
![]() $\lambda \in \{0,1\}$
.
$\lambda \in \{0,1\}$
.
If X is smoothable, then
![]() $dd^cu$
is a Kähler current. More precisely, there exists
$dd^cu$
is a Kähler current. More precisely, there exists
![]() $C>0$
such that
$C>0$
such that
![]() $dd^cu \geqslant C^{-1} \omega _{\mathbb C^N}|_X$
.
$dd^cu \geqslant C^{-1} \omega _{\mathbb C^N}|_X$
.
The proof of Theorem 3.4 is provided in § 3.3. Its flavor is very similar to the proof of its global counterpart, but the a priori estimates in the local setting require significantly more work. The latter are quite classical on a fixed manifold, and one only needs to check that the arguments can be made to work in families, which we have chosen to do carefully in the appendix of the preprint version of this text.
3.2 Proof of Proposition 3.3
The proof involves a careful analysis of the behavior of the measure
![]() $\mu _{X_t}$
which is achieved using the semistable reduction theorem following the lines of [Reference Di Nezza, Guedj and GuenanciaDNGG23, § 4]. The two items in the theorem are then proved separately.
$\mu _{X_t}$
which is achieved using the semistable reduction theorem following the lines of [Reference Di Nezza, Guedj and GuenanciaDNGG23, § 4]. The two items in the theorem are then proved separately.
3.2.1 Semistable model
By [Reference Kempf, Knudsen, Mumford and Saint-DonatKKMSD73], one can find a semistable model of
![]() $\pi $
. More precisely, up to shrinking
$\pi $
. More precisely, up to shrinking
![]() ${\mathbb {D}}$
, there exists a finite cover
${\mathbb {D}}$
, there exists a finite cover
![]() $\varphi :t\mapsto t^k$
of the disk for some integer
$\varphi :t\mapsto t^k$
of the disk for some integer
![]() $k\geqslant 1$
and a proper, surjective birational morphism
$k\geqslant 1$
and a proper, surjective birational morphism
![]() $g:=\mathcal Y \to {\mathcal {X}}':=({\mathcal {X}}\times _{\varphi }{\mathbb {D}})^{\nu }$
from a smooth manifold
$g:=\mathcal Y \to {\mathcal {X}}':=({\mathcal {X}}\times _{\varphi }{\mathbb {D}})^{\nu }$
from a smooth manifold
![]() ${\mathcal {Y}}$
, where
${\mathcal {Y}}$
, where
![]() $\nu $
stands for the normalization, as below
$\nu $
stands for the normalization, as below

such that around any point
![]() $y\in p^{-1}(0)$
, there exists an integer
$y\in p^{-1}(0)$
, there exists an integer
![]() $\ell \leqslant n+1$
and a system of coordinates
$\ell \leqslant n+1$
and a system of coordinates
![]() $(z_0, \ldots , z_n)$
centered at y and such that
$(z_0, \ldots , z_n)$
centered at y and such that
![]() $p(z_0, \ldots , z_n)=z_0\cdots z_\ell $
. Moreover,
$p(z_0, \ldots , z_n)=z_0\cdots z_\ell $
. Moreover,
![]() $\pi '$
is smooth (resp. g is étale) away from
$\pi '$
is smooth (resp. g is étale) away from
![]() $h^{-1}(\mathrm {Sing}(\pi ))$
, and that set has
$h^{-1}(\mathrm {Sing}(\pi ))$
, and that set has
![]() $\pi '$
-relative codimension at least two.
$\pi '$
-relative codimension at least two.
Thanks to the generic smoothness theorem, one can shrink
![]() ${\mathbb {D}}$
so that p is smooth away from
${\mathbb {D}}$
so that p is smooth away from
![]() $0$
. In particular, the induced morphism
$0$
. In particular, the induced morphism
![]() $f|_{Y_t}:Y_t\to X_{\varphi (t)}$
is a resolution of singularities for any
$f|_{Y_t}:Y_t\to X_{\varphi (t)}$
is a resolution of singularities for any
![]() $t\neq 0$
, where
$t\neq 0$
, where
![]() $Y_t=p^{-1}(t)$
. We want to understand the behavior of the measures (or volume forms)
$Y_t=p^{-1}(t)$
. We want to understand the behavior of the measures (or volume forms)
![]() $\mu _{X_t}$
when
$\mu _{X_t}$
when
![]() $t\to 0$
. This can be achieved quite explicitly on
$t\to 0$
. This can be achieved quite explicitly on
![]() ${\mathcal {Y}}$
via pull back by f as we now explain.
${\mathcal {Y}}$
via pull back by f as we now explain.
As we mentioned above,
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
are smooth in codimension one (even in codimension two); this implies that
$\pi '$
are smooth in codimension one (even in codimension two); this implies that
![]() ${\mathcal {X}}'\to {\mathcal {X}}\times _{\varphi }{\mathbb {D}}$
is isomorphic in codimension one, hence
${\mathcal {X}}'\to {\mathcal {X}}\times _{\varphi }{\mathbb {D}}$
is isomorphic in codimension one, hence
![]() $X_0'\to ({\mathcal {X}}\times _{\varphi }{\mathbb {D}})_0$
is finite and generically
$X_0'\to ({\mathcal {X}}\times _{\varphi }{\mathbb {D}})_0$
is finite and generically
![]() $1-1$
. Next,
$1-1$
. Next,
![]() $({\mathcal {X}}\times _{\varphi }{\mathbb {D}})_0\to X_0$
is finite and
$({\mathcal {X}}\times _{\varphi }{\mathbb {D}})_0\to X_0$
is finite and
![]() $1-1$
on points. Therefore,
$1-1$
on points. Therefore,
![]() $X_0'\to X_0$
is finite and generically
$X_0'\to X_0$
is finite and generically
![]() $1-1$
, hence it is isomorphic since
$1-1$
, hence it is isomorphic since
![]() $X_0$
is normal. In particular,
$X_0$
is normal. In particular,
![]() $X_0'$
is irreducible and has klt singularities.
$X_0'$
is irreducible and has klt singularities.
Next, we write
where the
![]() $E_i$
’s are g-exceptional divisors and
$E_i$
’s are g-exceptional divisors and
![]() $Y_0$
is the strict transform of
$Y_0$
is the strict transform of
![]() $X_0'$
; it is irreducible. One should observe that some of the divisors
$X_0'$
; it is irreducible. One should observe that some of the divisors
![]() $E_i$
’s may be irreducible components of
$E_i$
’s may be irreducible components of
![]() $p^{-1}(0)$
so that the inclusion
$p^{-1}(0)$
so that the inclusion
![]() $Y_0 \subsetneq p^{-1}(0)$
is strict in general. The divisors
$Y_0 \subsetneq p^{-1}(0)$
is strict in general. The divisors
![]() $E_i$
not included in the fiber
$E_i$
not included in the fiber
![]() $p^{-1}(0)$
surject onto
$p^{-1}(0)$
surject onto
![]() ${\mathbb {D}}$
since we have assumed that
${\mathbb {D}}$
since we have assumed that
![]() $p^{-1}(t)$
is irreducible for
$p^{-1}(t)$
is irreducible for
![]() $t\neq 0$
. In other words, we have
$t\neq 0$
. In other words, we have
The divisor
![]() $E:=\sum _{i\in I} E_i$
is the exceptional locus of g and
$E:=\sum _{i\in I} E_i$
is the exceptional locus of g and
![]() $E+Y_0$
has simple normal crossing support. Now, restrict Equation (3.2) to each irreducible component of
$E+Y_0$
has simple normal crossing support. Now, restrict Equation (3.2) to each irreducible component of
![]() $Y_0$
and use adjunction to obtain
$Y_0$
and use adjunction to obtain
Since
![]() $E+Y_0$
is SNC,
$E+Y_0$
is SNC,
![]() $g|_{Y_0}: Y_0\to X_0'$
is a log resolution of
$g|_{Y_0}: Y_0\to X_0'$
is a log resolution of
![]() $X_0'$
and we find that
$X_0'$
and we find that
Indeed, since
![]() $X_0'$
is klt, the inequality above holds for for any i such that
$X_0'$
is klt, the inequality above holds for for any i such that
![]() $E_i \cap Y_0 \neq \emptyset $
. And that set of indices i coincides with the full set I thanks to Equation (3.3) and the connectedness of the fibers of g.
$E_i \cap Y_0 \neq \emptyset $
. And that set of indices i coincides with the full set I thanks to Equation (3.3) and the connectedness of the fibers of g.
3.2.2 Analysis of
 $\mu _t$
$\mu _t$
Let
![]() $\omega $
be a fixed Kähler metric on
$\omega $
be a fixed Kähler metric on
![]() ${\mathcal {X}}$
, and let us define the function
${\mathcal {X}}$
, and let us define the function
![]() $\gamma $
on
$\gamma $
on
![]() ${\mathcal {X}}_{\mathrm {reg}}= {\mathcal {X}} \setminus \mathrm {Sing}(\pi )$
by
${\mathcal {X}}_{\mathrm {reg}}= {\mathcal {X}} \setminus \mathrm {Sing}(\pi )$
by
The main result in this section is the following:
Lemma 3.5. Up to shrinking
![]() ${\mathbb {D}}$
, there exists
${\mathbb {D}}$
, there exists
![]() $p>1$
and a constant
$p>1$
and a constant
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $t\in {\mathbb {D}}$
, one has
$t\in {\mathbb {D}}$
, one has
 $$ \begin{align} \int_{X_t} e^{-p\gamma}\omega_t^n \leqslant C. \end{align} $$
$$ \begin{align} \int_{X_t} e^{-p\gamma}\omega_t^n \leqslant C. \end{align} $$
Proof of Lemma 3.5
Equation (3.2) can be reformulated by saying that the form
![]() $f^*(\frac 1 {\pi ^m} \Omega )$
is a holomorphic section of
$f^*(\frac 1 {\pi ^m} \Omega )$
is a holomorphic section of
![]() $mK_{{\mathcal {Y}}}$
on
$mK_{{\mathcal {Y}}}$
on
![]() ${\mathcal {Y}}\setminus p^{-1}(0)$
with a (possibly negative) vanishing order
${\mathcal {Y}}\setminus p^{-1}(0)$
with a (possibly negative) vanishing order
![]() $ma_i$
along
$ma_i$
along
![]() $E_i$
and a pole or order m along
$E_i$
and a pole or order m along
![]() $Y_0$
. Given
$Y_0$
. Given
![]() $y\in Y_0$
, pick a coordinate chart
$y\in Y_0$
, pick a coordinate chart
![]() $(U,\underline z)$
centered at y such that
$(U,\underline z)$
centered at y such that
![]() $p(z_0, \ldots , z_n)=z_0\cdots z_\ell $
for some
$p(z_0, \ldots , z_n)=z_0\cdots z_\ell $
for some
![]() $\ell \leqslant n+1$
. We can relabel the coordinates so that
$\ell \leqslant n+1$
. We can relabel the coordinates so that
![]() $(z_1, \ldots , z_n)$
are a system of coordinates on
$(z_1, \ldots , z_n)$
are a system of coordinates on
![]() $Y_0$
and
$Y_0$
and
![]() $U\cap Y_0=(z_0=0)$
. Note that
$U\cap Y_0=(z_0=0)$
. Note that
![]() $(z_1, \ldots , z_n)$
remains a system of coordinates on
$(z_1, \ldots , z_n)$
remains a system of coordinates on
![]() $Y_t$
for
$Y_t$
for
![]() $|t|$
small. One can choose an injection
$|t|$
small. One can choose an injection
![]() $\{1, \ldots , \ell \}\to I$
such that
$\{1, \ldots , \ell \}\to I$
such that
![]() $U\cap E_i=(z_i=0)$
for
$U\cap E_i=(z_i=0)$
for
![]() $1\leqslant i\leqslant \ell $
and
$1\leqslant i\leqslant \ell $
and
![]() $E_i\cap U=\emptyset $
for the other indices
$E_i\cap U=\emptyset $
for the other indices
![]() $i\in I$
.
$i\in I$
.
On
![]() $U\setminus p^{-1}(0)$
, one can write
$U\setminus p^{-1}(0)$
, one can write
 $$ \begin{align} f^*\left(\frac 1 {\pi^m} \Omega\right)= a(z_0, \ldots, z_n) \left( \frac{dz_0}{z_0}\wedge dz_1 \wedge \cdots \wedge dz_n\right)^{\otimes m} \end{align} $$
$$ \begin{align} f^*\left(\frac 1 {\pi^m} \Omega\right)= a(z_0, \ldots, z_n) \left( \frac{dz_0}{z_0}\wedge dz_1 \wedge \cdots \wedge dz_n\right)^{\otimes m} \end{align} $$
for some holomorphic function a on
![]() $U\setminus E$
such that
$U\setminus E$
such that
![]() $b(z):=z_1^{ma_1^-}\cdots z_\ell ^{ma_\ell ^-} a(z)$
extends holomorphically across E, where one defines
$b(z):=z_1^{ma_1^-}\cdots z_\ell ^{ma_\ell ^-} a(z)$
extends holomorphically across E, where one defines
![]() $x^-:=-\min \{0,x\}$
for any
$x^-:=-\min \{0,x\}$
for any
![]() $x\in {\mathbb {R}}$
. Since
$x\in {\mathbb {R}}$
. Since
![]() $ma_i>-m$
from Equation (3.5), we get
$ma_i>-m$
from Equation (3.5), we get
![]() $0\leqslant ma_i^-<m$
.
$0\leqslant ma_i^-<m$
.
We have
 $$\begin{align*}f^*\frac{\Omega}{(d\pi)^{\otimes m}}= \frac{f^*\Omega}{(dp)^{\otimes m}}=\frac{f^*(\frac 1 {\pi^m} \Omega)}{(\frac{dp}p)^{\otimes m}}\end{align*}$$
$$\begin{align*}f^*\frac{\Omega}{(d\pi)^{\otimes m}}= \frac{f^*\Omega}{(dp)^{\otimes m}}=\frac{f^*(\frac 1 {\pi^m} \Omega)}{(\frac{dp}p)^{\otimes m}}\end{align*}$$
as well as
![]() $\frac {dz_0}{z_0}\wedge dz_1 \wedge \cdots \wedge dz_n= \frac {dp}{p}\wedge dz_1 \wedge \cdots \wedge dz_n$
on U. Combining those two identities with Equation (3.7) and recalling that we defined
$\frac {dz_0}{z_0}\wedge dz_1 \wedge \cdots \wedge dz_n= \frac {dp}{p}\wedge dz_1 \wedge \cdots \wedge dz_n$
on U. Combining those two identities with Equation (3.7) and recalling that we defined
![]() $\Omega _t=\frac {\Omega }{(d\pi )^{\otimes m}}|_{X_t}$
, we get on
$\Omega _t=\frac {\Omega }{(d\pi )^{\otimes m}}|_{X_t}$
, we get on
![]() $U\cap Y_t$
:
$U\cap Y_t$
:
and therefore there exists
![]() $C>0$
such that
$C>0$
such that
 $$ \begin{align} f^*\mu_{X_t} \leqslant C \, \frac{idz_1\wedge d\bar z_1 \wedge \cdots \wedge idz_n\wedge d\bar z_n }{\prod_{i=1}^\ell |z_i|^{2a_i^-}}. \end{align} $$
$$ \begin{align} f^*\mu_{X_t} \leqslant C \, \frac{idz_1\wedge d\bar z_1 \wedge \cdots \wedge idz_n\wedge d\bar z_n }{\prod_{i=1}^\ell |z_i|^{2a_i^-}}. \end{align} $$
Arguing as in the proof of [Reference Rong and ZhangRZ11a, Thm. B.1(i)], we can shrink
![]() ${\mathcal {X}}$
further so that there exist bounded holomorphic functions
${\mathcal {X}}$
further so that there exist bounded holomorphic functions
![]() $(\sigma _1, \cdots , \sigma _r)$
on
$(\sigma _1, \cdots , \sigma _r)$
on
![]() ${\mathcal {X}}$
satisfying
${\mathcal {X}}$
satisfying
![]() $V(\sigma _1, \ldots , \sigma _r)\subset {\mathcal {X}}_{\mathrm {sing}}$
and
$V(\sigma _1, \ldots , \sigma _r)\subset {\mathcal {X}}_{\mathrm {sing}}$
and
It follows from Equation (3.9) that there exists a constant
![]() $A>0$
such that
$A>0$
such that
![]() $f^*\gamma \geqslant A \log |s_E|^2$
, where
$f^*\gamma \geqslant A \log |s_E|^2$
, where
![]() $s_E\in H^0({\mathcal {X}},{\mathcal {O}}_{{\mathcal {X}}}(E))$
cuts out the exceptional divisor E and
$s_E\in H^0({\mathcal {X}},{\mathcal {O}}_{{\mathcal {X}}}(E))$
cuts out the exceptional divisor E and
![]() $|\cdot |$
is a smooth Hermitian metric on
$|\cdot |$
is a smooth Hermitian metric on
![]() ${\mathcal {O}}_{{\mathcal {X}}}(E)$
. Next, since
${\mathcal {O}}_{{\mathcal {X}}}(E)$
. Next, since
![]() $f:Y_t\to X_t$
is generically finite (with degree bounded independently of t), we get for any
$f:Y_t\to X_t$
is generically finite (with degree bounded independently of t), we get for any
![]() $p=1+\delta $
:
$p=1+\delta $
:
 $$ \begin{align*}\int_{X_t}e^{-p\gamma}\omega_t^n \leqslant \int_{Y_t}e^{-\delta f^*\gamma}f^*(i^{n^2}\Omega_t\wedge \overline \Omega_t)^{\frac 1m} \leqslant \int_{Y_t}|s_E|^{-2\delta A} d\mu_{X_t}. \end{align*} $$
$$ \begin{align*}\int_{X_t}e^{-p\gamma}\omega_t^n \leqslant \int_{Y_t}e^{-\delta f^*\gamma}f^*(i^{n^2}\Omega_t\wedge \overline \Omega_t)^{\frac 1m} \leqslant \int_{Y_t}|s_E|^{-2\delta A} d\mu_{X_t}. \end{align*} $$
Now, one can cover
![]() $Y_t$
by finitely many open sets
$Y_t$
by finitely many open sets
![]() $U_t=U\cap Y_t$
as above. On U, the system of coordinates
$U_t=U\cap Y_t$
as above. On U, the system of coordinates
![]() $(z_0, \ldots , z_n)$
induces a system of coordinates
$(z_0, \ldots , z_n)$
induces a system of coordinates
![]() $(z_1, \ldots , z_n)$
on
$(z_1, \ldots , z_n)$
on
![]() $U_t$
such that we have
$U_t$
such that we have
 $$ \begin{align*}|s_E|^{-2\delta A} \mu_{X_t} \leqslant C \prod_{i=1}^\ell |z_i|^{-2(\delta A+a_i^-)} idz_1\wedge d\bar z_1 \wedge \cdots \wedge idz_n\wedge d\bar z_n \end{align*} $$
$$ \begin{align*}|s_E|^{-2\delta A} \mu_{X_t} \leqslant C \prod_{i=1}^\ell |z_i|^{-2(\delta A+a_i^-)} idz_1\wedge d\bar z_1 \wedge \cdots \wedge idz_n\wedge d\bar z_n \end{align*} $$
for some uniform constant C thanks to Equation (3.8). Since
![]() $U\Subset \mathbb C^{n+1}$
, the
$U\Subset \mathbb C^{n+1}$
, the
![]() $U_t$
live in a fixed compact subset of
$U_t$
live in a fixed compact subset of
![]() $\mathbb C^n$
and the lemma follows by taking
$\mathbb C^n$
and the lemma follows by taking
![]() $\delta <\frac {1-\max a_i^-}{A}$
.
$\delta <\frac {1-\max a_i^-}{A}$
.
3.2.3 Proof of the uniform estimate
The first item of Proposition 3.3 is a consequence of Equation (3.6) and the following more general statement.
Theorem 3.6. Let
![]() $\pi : {\mathcal {X}}\to \mathbb D$
be a family as in Setup 3.1. Fix
$\pi : {\mathcal {X}}\to \mathbb D$
be a family as in Setup 3.1. Fix
![]() $p>1$
,
$p>1$
,
![]() $\lambda \in {\mathbb {R}}^+$
,
$\lambda \in {\mathbb {R}}^+$
,
![]() $h \in {\mathcal C}^{\infty }(\partial {\mathcal X})$
and
$h \in {\mathcal C}^{\infty }(\partial {\mathcal X})$
and
![]() $f_t \in L^p(X_t)$
. There exists a unique plurisubharmonic function
$f_t \in L^p(X_t)$
. There exists a unique plurisubharmonic function
![]() $u_t \in \mathrm {PSH}(X_t)\cap \mathcal C^0(\overline {X_t})$
solution of
$u_t \in \mathrm {PSH}(X_t)\cap \mathcal C^0(\overline {X_t})$
solution of
 $$ \begin{align*} \begin{cases} (dd^c u_t)^n = f_te^{\lambda u_t} \omega_t^n & \mbox{on } X_t\\ u_t|_{\partial X_t}=h_t. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} (dd^c u_t)^n = f_te^{\lambda u_t} \omega_t^n & \mbox{on } X_t\\ u_t|_{\partial X_t}=h_t. \end{cases} \end{align*} $$
Moreover,
![]() $\|u_t\|_{L^{\infty }(X_t)} \leqslant C \|f_t\|_{L^p(X_t)}^{1/n}$
, where C only depends on
$\|u_t\|_{L^{\infty }(X_t)} \leqslant C \|f_t\|_{L^p(X_t)}^{1/n}$
, where C only depends on
![]() $p,n$
and
$p,n$
and
![]() $\|h_t\|_{L^{\infty }(\partial X_t)}$
.
$\|h_t\|_{L^{\infty }(\partial X_t)}$
.
Proof. The existence and uniqueness of
![]() $u_t$
is proved in [Reference Guedj, Guenancia and ZeriahiGGZ23, Theorem A] when
$u_t$
is proved in [Reference Guedj, Guenancia and ZeriahiGGZ23, Theorem A] when
![]() $\lambda =0$
; the case
$\lambda =0$
; the case
![]() $\lambda>0$
can be treated similarly.
$\lambda>0$
can be treated similarly.
The key point here is to show that the solutions
![]() $u_t$
are uniformly bounded on
$u_t$
are uniformly bounded on
![]() $X_t$
when
$X_t$
when
![]() $t\in \mathbb D$
varies, as soon as the densities
$t\in \mathbb D$
varies, as soon as the densities
![]() $f_t$
are uniformly bounded in
$f_t$
are uniformly bounded in
![]() $L^p$
. This follows from the analysis developed in [Reference Guedj, Guenancia and ZeriahiGGZ23], which is an extension of Kolodziej’s technique [Reference KołodziejKoł98]. Indeed, [Reference Guedj, Guenancia and ZeriahiGGZ23, Proposition 1.8] (applied with
$L^p$
. This follows from the analysis developed in [Reference Guedj, Guenancia and ZeriahiGGZ23], which is an extension of Kolodziej’s technique [Reference KołodziejKoł98]. Indeed, [Reference Guedj, Guenancia and ZeriahiGGZ23, Proposition 1.8] (applied with
![]() $v=0$
) shows that
$v=0$
) shows that
![]() $u_t$
is globally bounded on
$u_t$
is globally bounded on
![]() $X_t$
, while the uniform bound (3.6) allows one to show that this bound is also independent of t. We provide a sketch of the proof as a courtesy to the reader.
$X_t$
, while the uniform bound (3.6) allows one to show that this bound is also independent of t. We provide a sketch of the proof as a courtesy to the reader.
Step 1. We claim that there exists
![]() $m_1,C_1 \geqslant 1$
such that
$m_1,C_1 \geqslant 1$
such that
 $$ \begin{align} \int_{X_t} \exp(-2^{-m_1}v_t) \omega_t^n \leqslant C_1, \end{align} $$
$$ \begin{align} \int_{X_t} \exp(-2^{-m_1}v_t) \omega_t^n \leqslant C_1, \end{align} $$
for all
![]() $t \in \mathbb D$
and for all
$t \in \mathbb D$
and for all
![]() $v_t \in {\mathcal F}_t$
, where
$v_t \in {\mathcal F}_t$
, where
 $$ \begin{align*}{\mathcal F}_t:=\left\{ w \in \mathrm{PSH}(X_t) \cap L^{\infty}(X_t), \; w_{| \partial X_t}=0 \text{ and } \int_{X_t} (dd^c w)^n \leqslant 1 \right\}. \end{align*} $$
$$ \begin{align*}{\mathcal F}_t:=\left\{ w \in \mathrm{PSH}(X_t) \cap L^{\infty}(X_t), \; w_{| \partial X_t}=0 \text{ and } \int_{X_t} (dd^c w)^n \leqslant 1 \right\}. \end{align*} $$
Indeed, the family
![]() ${\mathcal F}_t$
is relatively compact, and any function w in
${\mathcal F}_t$
is relatively compact, and any function w in
![]() $\overline {{\mathcal F}_t}$
belongs to the domain of definition of the complex Monge–Ampère operator, with zero boundary values and Monge–Ampère mass less than
$\overline {{\mathcal F}_t}$
belongs to the domain of definition of the complex Monge–Ampère operator, with zero boundary values and Monge–Ampère mass less than
![]() $1$
. It follows from Demailly’s comparison theorem that the Lelong number
$1$
. It follows from Demailly’s comparison theorem that the Lelong number
![]() $\nu (w,x)$
is less than
$\nu (w,x)$
is less than
![]() $1$
at a smooth point and less than
$1$
at a smooth point and less than
![]() $\mathrm {mult}(X_t,x)^{-1/n}$
if x is singular.
$\mathrm {mult}(X_t,x)^{-1/n}$
if x is singular.
If
![]() $p_t:\widetilde {X_t} \rightarrow X_t$
is the blow up of a (single) smooth subvariety, then
$p_t:\widetilde {X_t} \rightarrow X_t$
is the blow up of a (single) smooth subvariety, then
![]() $\nu (w,p_t(y)) \leqslant \nu (w \circ p_t,y) \leqslant 2 \nu (w,p_t(y))$
if y belongs to the exceptional set
$\nu (w,p_t(y)) \leqslant \nu (w \circ p_t,y) \leqslant 2 \nu (w,p_t(y))$
if y belongs to the exceptional set
![]() $E_t$
of
$E_t$
of
![]() $p_t$
, while
$p_t$
, while
![]() $\nu (w \circ p_t,y)=\nu (w,p_t(y))$
otherwise. This can be checked by embedding
$\nu (w \circ p_t,y)=\nu (w,p_t(y))$
otherwise. This can be checked by embedding
![]() $X_t$
locally in
$X_t$
locally in
![]() $\mathbb C^N$
and using the explicit expression of the blow up of a smooth subvariety in the Euclidean space. We infer that there exists
$\mathbb C^N$
and using the explicit expression of the blow up of a smooth subvariety in the Euclidean space. We infer that there exists
![]() $m_1 \in {\mathbb {N}}$
such that
$m_1 \in {\mathbb {N}}$
such that
![]() $\nu (w \circ f,y) \leqslant 2^{m_1} \nu (w,f(y)) \leqslant 2^{m_1}$
for all
$\nu (w \circ f,y) \leqslant 2^{m_1} \nu (w,f(y)) \leqslant 2^{m_1}$
for all
![]() $y \in Y_t$
.
$y \in Y_t$
.
We thus have a uniform control of the Lelong numbers of the compact family
![]() $f^* \overline {{\mathcal F}_t}$
. Using the subextension trick [Reference Guedj, Guenancia and ZeriahiGGZ23, Lemma 1.7], we further reduce to controlling
$f^* \overline {{\mathcal F}_t}$
. Using the subextension trick [Reference Guedj, Guenancia and ZeriahiGGZ23, Lemma 1.7], we further reduce to controlling
 $$ \begin{align*}\int_{X^{\prime}_t} \exp(-2^{-m_1}v_t) \omega_t^n = \int_{Y^{\prime}_t} \exp(-2^{-m_1}v_t \circ f) \omega_t^n \end{align*} $$
$$ \begin{align*}\int_{X^{\prime}_t} \exp(-2^{-m_1}v_t) \omega_t^n = \int_{Y^{\prime}_t} \exp(-2^{-m_1}v_t \circ f) \omega_t^n \end{align*} $$
on a relatively compact subset
![]() $X^{\prime }_t \Subset X_t$
. We finally invoke Skoda’s uniform integrability theorem which holds for holomorphic families; see [Reference Di Nezza, Guedj and GuenanciaDNGG23, Theorem 2.9].
$X^{\prime }_t \Subset X_t$
. We finally invoke Skoda’s uniform integrability theorem which holds for holomorphic families; see [Reference Di Nezza, Guedj and GuenanciaDNGG23, Theorem 2.9].
Step 2. We claim that for all compact subsets
![]() $K \subset X_t$
,
$K \subset X_t$
,
 $$ \begin{align} \mathrm{Vol}_{\omega_t}(K) \leqslant C_1 \exp \left( -\frac{1}{2^{m_1}\mathrm{Cap}(K,X_t)^{1/n}} \right), \end{align} $$
$$ \begin{align} \mathrm{Vol}_{\omega_t}(K) \leqslant C_1 \exp \left( -\frac{1}{2^{m_1}\mathrm{Cap}(K,X_t)^{1/n}} \right), \end{align} $$
where
![]() $\mathrm {Cap}(K,X_t):=\sup \{ \int _K (dd^c w)^n, \, w \in \mathrm {PSH}(X_t) \text { with } 0 \leqslant w \leqslant 1 \}$
denotes the Monge–Ampère capacity.
$\mathrm {Cap}(K,X_t):=\sup \{ \int _K (dd^c w)^n, \, w \in \mathrm {PSH}(X_t) \text { with } 0 \leqslant w \leqslant 1 \}$
denotes the Monge–Ampère capacity.
Indeed, set
![]() $\lambda =\mathrm {Cap}(K,X_t)^{-1/n}$
and
$\lambda =\mathrm {Cap}(K,X_t)^{-1/n}$
and
![]() $v_t=\lambda h_{K,X_t}^*$
, where
$v_t=\lambda h_{K,X_t}^*$
, where
![]() $h_{K,X_t}^*$
denotes the relative extremal function of the compact set K (see [Reference Guedj and ZeriahiGZ17, Definition 4.30]). It follows from [Reference Guedj and ZeriahiGZ17, Theorem 4.34] that
$h_{K,X_t}^*$
denotes the relative extremal function of the compact set K (see [Reference Guedj and ZeriahiGZ17, Definition 4.30]). It follows from [Reference Guedj and ZeriahiGZ17, Theorem 4.34] that
![]() $\int _{X_t} (dd^c v_t)^n=1$
and
$\int _{X_t} (dd^c v_t)^n=1$
and
![]() $v_t+\lambda =0$
a.e. on K, hence
$v_t+\lambda =0$
a.e. on K, hence
 $$ \begin{align*} \mathrm{Vol}_{\omega_t}(K) &= \int_K \exp \left( -2^{-m} [\lambda+v_t] \right) \omega_t^n \\ &\leqslant \exp ( -2^{-m}\lambda) \int_{X_t} \exp \left( -2^{-m} v_t \right) \omega_t^n \\ &\leqslant C_1 \exp \left( -\frac{1}{2^{m_1}\mathrm{Cap}(K,X_t)^{1/n}} \right), \end{align*} $$
$$ \begin{align*} \mathrm{Vol}_{\omega_t}(K) &= \int_K \exp \left( -2^{-m} [\lambda+v_t] \right) \omega_t^n \\ &\leqslant \exp ( -2^{-m}\lambda) \int_{X_t} \exp \left( -2^{-m} v_t \right) \omega_t^n \\ &\leqslant C_1 \exp \left( -\frac{1}{2^{m_1}\mathrm{Cap}(K,X_t)^{1/n}} \right), \end{align*} $$
where the last inequality follows from Equation (3.10).
Step 3. Let
![]() $\Phi $
denotes the maximal psh extension of h to
$\Phi $
denotes the maximal psh extension of h to
![]() ${\mathcal X}$
: This is the largest psh function in
${\mathcal X}$
: This is the largest psh function in
![]() ${\mathcal X}$
which lies below h at the boundary. It is uniformly bounded in
${\mathcal X}$
which lies below h at the boundary. It is uniformly bounded in
![]() ${\mathcal X}$
, satisfies
${\mathcal X}$
, satisfies
![]() $u_t \leqslant \Phi _t$
and coincides with h at the boundary. We claim that for all
$u_t \leqslant \Phi _t$
and coincides with h at the boundary. We claim that for all
![]() $s,\delta>0$
$s,\delta>0$
where
![]() $1/p+1/q=1$
. It follows indeed from [Reference Guedj, Kolodziej and ZeriahiGKZ08, Lemma 1.3] that
$1/p+1/q=1$
. It follows indeed from [Reference Guedj, Kolodziej and ZeriahiGKZ08, Lemma 1.3] that
 $$ \begin{align*}\delta^n \mathrm{Cap}\{u_t-\Phi_t<-s-\delta-1\} \leqslant \int_{\{u_t-\Phi_t<-s-1\}} (dd^c u_t)^n. \end{align*} $$
$$ \begin{align*}\delta^n \mathrm{Cap}\{u_t-\Phi_t<-s-\delta-1\} \leqslant \int_{\{u_t-\Phi_t<-s-1\}} (dd^c u_t)^n. \end{align*} $$
Since
![]() $(dd^c u_t)^n=f_t \omega _t^n$
, we can apply Hölder inequality, together with Equation (3.11) and the elementary inequality
$(dd^c u_t)^n=f_t \omega _t^n$
, we can apply Hölder inequality, together with Equation (3.11) and the elementary inequality
![]() $\exp (-x^{-1/n}) \leqslant c_{n,p} x^{2q}$
, valid for all
$\exp (-x^{-1/n}) \leqslant c_{n,p} x^{2q}$
, valid for all
![]() $x>0$
, to conclude.
$x>0$
, to conclude.
Conclusion. It follows from Equation (3.12) that the function
![]() $g(s):=\mathrm {Cap}\{u_t-\Phi _t<-s-1\}^{1/n}$
satisfies
$g(s):=\mathrm {Cap}\{u_t-\Phi _t<-s-1\}^{1/n}$
satisfies
![]() $\delta g(s+\delta ) \leqslant B g(s)^2$
for all
$\delta g(s+\delta ) \leqslant B g(s)^2$
for all
![]() $s,\delta>0$
, with
$s,\delta>0$
, with
![]() $B=c_{n,p}^{1/n} \|f_t\|^{1/n}_{L^p(X_t)}2^{-m_1q/n}$
. We can invoke DeGiorgi’s lemma (see [Reference Guedj, Kolodziej and ZeriahiGKZ08, Lemma 1.5] with
$B=c_{n,p}^{1/n} \|f_t\|^{1/n}_{L^p(X_t)}2^{-m_1q/n}$
. We can invoke DeGiorgi’s lemma (see [Reference Guedj, Kolodziej and ZeriahiGKZ08, Lemma 1.5] with
![]() $\tau =1$
) to conclude that
$\tau =1$
) to conclude that
![]() $g(s)=0$
for
$g(s)=0$
for
![]() $s \geqslant 4Bg(0)$
. Thus,
$s \geqslant 4Bg(0)$
. Thus,
![]() $u_t \geqslant \Phi _t-4Bg(0)-1$
, which yields a uniform lower bound on
$u_t \geqslant \Phi _t-4Bg(0)-1$
, which yields a uniform lower bound on
![]() $u_t$
if we can uniformly bound
$u_t$
if we can uniformly bound
![]() $g(0)$
from above.
$g(0)$
from above.
To estimate
![]() $g(0)=\mathrm {Cap}\{u_t-\Phi _t<-1\}^{1/n}$
, we let
$g(0)=\mathrm {Cap}\{u_t-\Phi _t<-1\}^{1/n}$
, we let
![]() $w_t$
denote the extremal function of the set
$w_t$
denote the extremal function of the set
![]() $\{u_t-\Phi _t<-1\}$
. Recall that
$\{u_t-\Phi _t<-1\}$
. Recall that
![]() $-1 \leqslant w_t \leqslant 0$
, hence
$-1 \leqslant w_t \leqslant 0$
, hence
Using Stokes theorem n times, we thus obtain, following [Reference BłockiBło93],
 $$ \begin{align*} \mathrm{Cap}\{u_t-\Phi_t<-1\} &\leqslant \int_{X_t} (\Phi_t-u_t)^n (dd^c w_t)^n \\ &\leqslant n! \int_{X_t} (dd^c u_t)^n \leqslant n! \|f_t\|_{L^p(X_t)} \mathrm{Vol}_{\omega_t}(X_t)^{1/q}, \end{align*} $$
$$ \begin{align*} \mathrm{Cap}\{u_t-\Phi_t<-1\} &\leqslant \int_{X_t} (\Phi_t-u_t)^n (dd^c w_t)^n \\ &\leqslant n! \int_{X_t} (dd^c u_t)^n \leqslant n! \|f_t\|_{L^p(X_t)} \mathrm{Vol}_{\omega_t}(X_t)^{1/q}, \end{align*} $$
which shows that
![]() $g(0)$
is uniformly bounded from above by
$g(0)$
is uniformly bounded from above by
![]() $c^{\prime }_n \|f_t\|_{L^p(X_t)}^{1/n}$
.
$c^{\prime }_n \|f_t\|_{L^p(X_t)}^{1/n}$
.
3.2.4 Existence of a suitable subsolution
The exceptional divisor E of g satisfies that there exist positive rational numbers
![]() $(b_i)_{i\in I}$
such that
$(b_i)_{i\in I}$
such that
![]() $-\sum _{i\in I} b_i E_i$
is g-ample, hence f-ample as well. On each
$-\sum _{i\in I} b_i E_i$
is g-ample, hence f-ample as well. On each
![]() $\mathcal O_{{\mathcal {Y}}}(E_i)$
, one can pick a section
$\mathcal O_{{\mathcal {Y}}}(E_i)$
, one can pick a section
![]() $s_i$
cutting out
$s_i$
cutting out
![]() $E_i$
as well as a smooth Hermitian metric
$E_i$
as well as a smooth Hermitian metric
![]() $h_i$
such that
$h_i$
such that
![]() $\rho ':=f^*(A\rho )+\sum _{i\in i} b_i \log |s_i|^2_{h_i}$
is strictly psh on
$\rho ':=f^*(A\rho )+\sum _{i\in i} b_i \log |s_i|^2_{h_i}$
is strictly psh on
![]() ${\mathcal {Y}}$
for
${\mathcal {Y}}$
for
![]() $A\gg 1$
.
$A\gg 1$
.
From now on, we assume that
![]() $\pi $
is smooth away from our distinguished point
$\pi $
is smooth away from our distinguished point
![]() $0\in X_0 \subset {\mathcal {X}}$
. This ensures for all
$0\in X_0 \subset {\mathcal {X}}$
. This ensures for all
![]() $t\neq 0$
,
$t\neq 0$
,
![]() $\rho '$
is bounded on
$\rho '$
is bounded on
![]() $Y_t\simeq X_{\varphi (t)}$
and that
$Y_t\simeq X_{\varphi (t)}$
and that
![]() $\rho '$
is smooth on
$\rho '$
is smooth on
![]() $\partial Y\simeq \partial X$
.
$\partial Y\simeq \partial X$
.
Next, one defines for
![]() $\delta>0$
small enough (to be determined later) the function
$\delta>0$
small enough (to be determined later) the function
Up to scaling the metrics
![]() $h_i$
, we find that v is strictly psh. More precisely, we can cover
$h_i$
, we find that v is strictly psh. More precisely, we can cover
![]() ${\mathcal {Y}}$
with finitely many coordinate charts
${\mathcal {Y}}$
with finitely many coordinate charts
![]() $(U_\alpha )_{\alpha }$
such that
$(U_\alpha )_{\alpha }$
such that
![]() $U_\alpha \cap E=(z_1\cdots z_{\ell _\alpha }=0)$
for some number
$U_\alpha \cap E=(z_1\cdots z_{\ell _\alpha }=0)$
for some number
![]() $ \ell _\alpha \leqslant n$
and in these charts we have
$ \ell _\alpha \leqslant n$
and in these charts we have
 $$ \begin{align} dd^c v|_{U_\alpha} \geqslant c \left[ \omega_{{\mathcal{Y}}}|_{U_\alpha}+\sum_{k=1}^{\ell_\alpha} \frac{idz_k\wedge d\bar z_k}{|z_k|^{2(1-\delta)}}\right] \end{align} $$
$$ \begin{align} dd^c v|_{U_\alpha} \geqslant c \left[ \omega_{{\mathcal{Y}}}|_{U_\alpha}+\sum_{k=1}^{\ell_\alpha} \frac{idz_k\wedge d\bar z_k}{|z_k|^{2(1-\delta)}}\right] \end{align} $$
for some
![]() $c>0$
and some fixed Kähler metric
$c>0$
and some fixed Kähler metric
![]() $\omega _{{\mathcal {Y}}}$
on
$\omega _{{\mathcal {Y}}}$
on
![]() ${\mathcal {Y}}$
. In particular, it follows from Equation (3.13) above and Equation (3.8) that
${\mathcal {Y}}$
. In particular, it follows from Equation (3.13) above and Equation (3.8) that
for some uniform
![]() $c'>0$
. Since v is uniformly bounded above on
$c'>0$
. Since v is uniformly bounded above on
![]() ${\mathcal {Y}}$
and F is bounded on
${\mathcal {Y}}$
and F is bounded on
![]() ${\mathcal {X}}$
, we can scale up v so that
${\mathcal {X}}$
, we can scale up v so that
Given
![]() $t\in \mathbb D^*$
, there exists s such that
$t\in \mathbb D^*$
, there exists s such that
![]() $\varphi (s)=t$
, and we denote by
$\varphi (s)=t$
, and we denote by
![]() $v_t$
the function on
$v_t$
the function on
![]() $X_t$
defined by
$X_t$
defined by
![]() $v|_{Y_s}$
under the identification
$v|_{Y_s}$
under the identification
![]() $Y_s \simeq X_t$
via f. Clearly,
$Y_s \simeq X_t$
via f. Clearly,
![]() $v_t$
satisfies
$v_t$
satisfies
At this point,
![]() $v_t$
is not a subsolution of Equation (MAt) because the boundary condition is not satisfied. So we pick a cut-off function
$v_t$
is not a subsolution of Equation (MAt) because the boundary condition is not satisfied. So we pick a cut-off function
![]() $\chi $
compactly supported on
$\chi $
compactly supported on
![]() ${\mathcal {X}}$
and satisfying
${\mathcal {X}}$
and satisfying
![]() $\chi \equiv 1$
near
$\chi \equiv 1$
near
![]() $0$
. Next, we still denote by h an arbitrary smooth extension of h from
$0$
. Next, we still denote by h an arbitrary smooth extension of h from
![]() $\partial {\mathcal {X}}$
to
$\partial {\mathcal {X}}$
to
![]() ${\mathcal {X}}$
. Finally, we set
${\mathcal {X}}$
. Finally, we set
One can easily see that for B large enough,
![]() $\underline {u}_t$
is a subsolution of Equation (MAt). Moreover, it is obvious on the shape of
$\underline {u}_t$
is a subsolution of Equation (MAt). Moreover, it is obvious on the shape of
![]() $\underline {u}_t$
that the estimates claimed in the second item of Proposition 3.3 are satisfied.
$\underline {u}_t$
that the estimates claimed in the second item of Proposition 3.3 are satisfied.
3.3 Proof of Theorem 3.4
In this final subsection, we borrow the notation of Setup 3.1 and assume that
![]() $\pi $
is smooth outside of
$\pi $
is smooth outside of
![]() $0\in X_0$
. We consider the solution
$0\in X_0$
. We consider the solution
![]() $u_t$
of Equation (MAt).
$u_t$
of Equation (MAt).
First, we are going to derive higher-order estimates near
![]() $\partial X_t$
of
$\partial X_t$
of
![]() $u_t$
of Equation (MAt). We will then conclude the proof of Theorem 3.4 by using Chern–Lu inequality as in the proof of Theorem 2.8.
$u_t$
of Equation (MAt). We will then conclude the proof of Theorem 3.4 by using Chern–Lu inequality as in the proof of Theorem 2.8.
Lemma 3.7. There exists
![]() $C_1>0$
such that for all
$C_1>0$
such that for all
![]() $t\neq 0$
,
$t\neq 0$
,
![]() $\|u_t\|_{{\mathcal C}^1(\partial X_t)} \leqslant C_1$
.
$\|u_t\|_{{\mathcal C}^1(\partial X_t)} \leqslant C_1$
.
Proof. Let H be an arbitrary smooth extension of h to
![]() ${\mathcal X}$
. For A large enough, the function
${\mathcal X}$
. For A large enough, the function
![]() $v:=A\rho -H$
is a smooth psh function near
$v:=A\rho -H$
is a smooth psh function near
![]() $\overline {{\mathcal X}}$
such that
$\overline {{\mathcal X}}$
such that
![]() $v_t=-h_t$
on
$v_t=-h_t$
on
![]() $\partial X_t$
. Thus,
$\partial X_t$
. Thus,
![]() $u_t+v_t$
is psh in
$u_t+v_t$
is psh in
![]() $X_t$
with zero boundary values. It follow from the maximum principle that
$X_t$
with zero boundary values. It follow from the maximum principle that
![]() $u_t+v_t \leqslant 0$
in
$u_t+v_t \leqslant 0$
in
![]() $X_t$
. Using the subsolution constructed in the previous subsection, we obtain a two-sided bound
$X_t$
. Using the subsolution constructed in the previous subsection, we obtain a two-sided bound
with
![]() $\underline {u}_t=u_t=-v_t=h_t$
on
$\underline {u}_t=u_t=-v_t=h_t$
on
![]() $\partial X_t$
. The desired uniform
$\partial X_t$
. The desired uniform
![]() ${\mathcal C}^1$
-bound on
${\mathcal C}^1$
-bound on
![]() $\partial X_t$
follows.
$\partial X_t$
follows.
Once
![]() $\|u_t\|_{{\mathcal C}^1(\partial X_t)}$
is under control, one can obtain a global control of
$\|u_t\|_{{\mathcal C}^1(\partial X_t)}$
is under control, one can obtain a global control of
![]() $\|u_t\|_{{\mathcal C}^1(V_t)} $
in a neighborhood
$\|u_t\|_{{\mathcal C}^1(V_t)} $
in a neighborhood
![]() $V_t$
of
$V_t$
of
![]() $\partial X_t$
that avoids the singular point. The proof of the following proposition is given in the appendix of the preprint version as Proposition 6.1.
$\partial X_t$
that avoids the singular point. The proof of the following proposition is given in the appendix of the preprint version as Proposition 6.1.
Proposition 3.8. There exists
![]() $C_1'>0$
such that for all
$C_1'>0$
such that for all
![]() $t\neq 0$
,
$t\neq 0$
,
![]() $\|u_t\|_{{\mathcal C}^1(V_t)} \leqslant C_1'$
.
$\|u_t\|_{{\mathcal C}^1(V_t)} \leqslant C_1'$
.
In the appendix of the preprint version, we explain how to derive Laplacian estimates near the boundary from lower order ones, cf. Theorem 6.3 there, as a combination of the main results of [Reference Caffarelli, Kohn, Nirenberg and SpruckCKNS85, Reference Guan and LiGL10] in the setting of holomorphic families. It is then straightforward to obtain the following
Proposition 3.9. There exists
![]() $C_2>0$
such that for all
$C_2>0$
such that for all
![]() $t\neq 0$
, we have
$t\neq 0$
, we have
Proof. It follows from Proposition 3.3 and Lemma 3.7 that the assumptions of Theorem 6.3 in the preprint version are met and that we have uniform upper bounds on
![]() $\|u_t\|_{{\mathcal C}^1(\overline {V_t})}$
,
$\|u_t\|_{{\mathcal C}^1(\overline {V_t})}$
,
![]() $\|v_t\|_{{\mathcal C}^2(\overline {V_t})}$
,
$\|v_t\|_{{\mathcal C}^2(\overline {V_t})}$
,
![]() $\|f_t\|_{{\mathcal C}^1(\overline {V_t})}$
,
$\|f_t\|_{{\mathcal C}^1(\overline {V_t})}$
,
![]() $\|h\|_{{\mathcal C}^4(\partial X_t)}$
,
$\|h\|_{{\mathcal C}^4(\partial X_t)}$
,
![]() $\varepsilon ^{-1},\delta ^{-1}$
. The proposition follows.
$\varepsilon ^{-1},\delta ^{-1}$
. The proposition follows.
End of the proof of Theorem 3.4
Pick a Kähler metric
![]() $\widehat \omega $
on
$\widehat \omega $
on
![]() $\mathcal X$
, and set
$\mathcal X$
, and set
![]() $\widehat \omega _t:=\widehat \omega |_{X_t}$
. Since
$\widehat \omega _t:=\widehat \omega |_{X_t}$
. Since
![]() $(dd^c u_t)^n$
is uniformly comparable to
$(dd^c u_t)^n$
is uniformly comparable to
![]() $\widehat \omega _t^n$
in a small neighborhood of
$\widehat \omega _t^n$
in a small neighborhood of
![]() $\partial X_t$
, the uniform bound
$\partial X_t$
, the uniform bound
![]() $\|\Delta u_t\|_{L^{\infty }(\partial X_t)} \leqslant C_2$
actually yields a uniform constant
$\|\Delta u_t\|_{L^{\infty }(\partial X_t)} \leqslant C_2$
actually yields a uniform constant
![]() $c_2>0$
such that
$c_2>0$
such that
Indeed, let
![]() $\sigma :=\inf _{t} \inf _{p\in \partial X_t} \liminf _{z\to p, z\in \partial X_t} \frac {\theta _t^n(z)}{\widehat \omega _t^n(z)}$
; we have
$\sigma :=\inf _{t} \inf _{p\in \partial X_t} \liminf _{z\to p, z\in \partial X_t} \frac {\theta _t^n(z)}{\widehat \omega _t^n(z)}$
; we have
![]() $\sigma>0$
since
$\sigma>0$
since
![]() $\pi $
is smooth along
$\pi $
is smooth along
![]() $\partial {\mathcal {X}}$
and
$\partial {\mathcal {X}}$
and
![]() $\|u_t\|_{L^{\infty }(X_t)}$
is uniformly bounded below by Theorem 3.6. Given
$\|u_t\|_{L^{\infty }(X_t)}$
is uniformly bounded below by Theorem 3.6. Given
![]() $p\in \partial X_t$
, we have
$p\in \partial X_t$
, we have
![]() $\limsup _{z\to p, z\in X_t} \mathrm {tr}_{\widehat \omega _t}\theta _t(z) \leqslant C$
by our boundary Laplacian estimate, hence
$\limsup _{z\to p, z\in X_t} \mathrm {tr}_{\widehat \omega _t}\theta _t(z) \leqslant C$
by our boundary Laplacian estimate, hence
and Equation (3.14) follows.
Arguing as in the proof of Theorem 2.8, we consider
![]() $v_t=\log \mathrm {tr}_{{\theta _t}}(\widehat \omega _t)$
, where
$v_t=\log \mathrm {tr}_{{\theta _t}}(\widehat \omega _t)$
, where
![]() $\theta _t=dd^c u_t$
and deduce from the Chern–Lu formula that
$\theta _t=dd^c u_t$
and deduce from the Chern–Lu formula that
for uniform constants
![]() $A,C_3>0$
. We infer that
$A,C_3>0$
. We infer that
![]() $v_t \leqslant C_4$
is uniformly bounded from above. Indeed, either the maximum of the function
$v_t \leqslant C_4$
is uniformly bounded from above. Indeed, either the maximum of the function
![]() $v_t-A u_t$
is reached in
$v_t-A u_t$
is reached in
![]() $X_t$
, and the bound follows from Equation (3.15) and the uniform bound on
$X_t$
, and the bound follows from Equation (3.15) and the uniform bound on
![]() $u_t$
or the maximum of
$u_t$
or the maximum of
![]() $v_t-A u_t$
is reached on
$v_t-A u_t$
is reached on
![]() $\partial X_t$
and we conclude from Equation (3.14).
$\partial X_t$
and we conclude from Equation (3.14).
Therefore,
![]() $dd^c u_t \geqslant C_4^{-1}\widehat \omega _t$
in
$dd^c u_t \geqslant C_4^{-1}\widehat \omega _t$
in
![]() $X_t$
for all
$X_t$
for all
![]() $t \neq 0$
. Similarly to what we have done at the end of the proof of Theorem 2.8, we conclude by letting
$t \neq 0$
. Similarly to what we have done at the end of the proof of Theorem 2.8, we conclude by letting
![]() $t \rightarrow 0$
that
$t \rightarrow 0$
that
![]() $dd^c u_0 \geqslant C_4^{-1} \widehat \omega _0$
, hence
$dd^c u_0 \geqslant C_4^{-1} \widehat \omega _0$
, hence
![]() $\omega _{\mathrm {KE}} =dd^c u_0$
is a Kähler current. The proof of Theorem 3.4 is complete.
$\omega _{\mathrm {KE}} =dd^c u_0$
is a Kähler current. The proof of Theorem 3.4 is complete.
4 Kähler–Einstein currents near isolated smoothable singularities
We now use the previous analysis to establish the strict positivity of singular Kähler–Einstein metrics of nonpositive curvature near smoothable isolated singularities.
4.1 The case of klt spaces X
Theorem 4.1. Let X be a compact Kähler normal space with klt singularities such that either
![]() $K_X$
is ample or
$K_X$
is ample or
![]() $K_X \sim _{{\mathbb {Q}}} \mathcal O_X$
. Then a Kähler–Einstein metric
$K_X \sim _{{\mathbb {Q}}} \mathcal O_X$
. Then a Kähler–Einstein metric
![]() $\omega _{\mathrm {KE}}$
in the sense of Definition 2.2 is a Kähler current near an isolated smoothable singularity of X.
$\omega _{\mathrm {KE}}$
in the sense of Definition 2.2 is a Kähler current near an isolated smoothable singularity of X.
Remark 4.2. In the case where X is a
![]() ${\mathbb {Q}}$
-Fano Kähler–Einstein variety (i.e.,
${\mathbb {Q}}$
-Fano Kähler–Einstein variety (i.e.,
![]() $-K_X$
is ample), we expect a similar result to hold as well, but this requires a better understanding of local families of Kähler–Einstein metrics of positive curvature.
$-K_X$
is ample), we expect a similar result to hold as well, but this requires a better understanding of local families of Kähler–Einstein metrics of positive curvature.
Proof. We work near an isolated singular point a. We let B denote a small strictly pseudoconvex neighborhood of a in X, isomorphic to the trace of a ball in some local embedding in
![]() ${\mathbb {C}}^N$
, and let
${\mathbb {C}}^N$
, and let
![]() $\rho $
denote a local smooth potential for
$\rho $
denote a local smooth potential for
![]() $\omega =dd^c \rho $
in B.
$\omega =dd^c \rho $
in B.
Recall from [Reference Eyssidieux, Guedj and ZeriahiEGZ09, Reference PăunPău08] that the Kähler–Einstein potential
![]() $\varphi _{\mathrm {KE}}$
is smooth in
$\varphi _{\mathrm {KE}}$
is smooth in
![]() $B \setminus \{a\}$
. Define
$B \setminus \{a\}$
. Define
![]() $\lambda =1$
if
$\lambda =1$
if
![]() $K_X$
is ample, and
$K_X$
is ample, and
![]() $\lambda =0$
if
$\lambda =0$
if
![]() $K_X \equiv 0$
, and set
$K_X \equiv 0$
, and set
![]() $F=\lambda \rho $
. The local theory recalled in Section 1.2 shows that
$F=\lambda \rho $
. The local theory recalled in Section 1.2 shows that
![]() $\psi =\rho +\varphi _{\mathrm {KE}}$
is the unique solution of the Dirichlet problem
$\psi =\rho +\varphi _{\mathrm {KE}}$
is the unique solution of the Dirichlet problem
We assume that
![]() $(X,a)$
is a smoothable singularity in the sense of Definition 3.2, and we let
$(X,a)$
is a smoothable singularity in the sense of Definition 3.2, and we let
![]() $\pi : {\mathcal X} \rightarrow \mathbb D$
denote a smoothing so that
$\pi : {\mathcal X} \rightarrow \mathbb D$
denote a smoothing so that
![]() $B=\pi ^{-1}(0)$
and
$B=\pi ^{-1}(0)$
and
![]() $X_t=\pi ^{-1}(t)$
is smooth for all
$X_t=\pi ^{-1}(t)$
is smooth for all
![]() $t \neq 0$
. We let h denote a smooth extension of
$t \neq 0$
. We let h denote a smooth extension of
![]() $(\rho +\varphi _{\mathrm {KE}})_{| \partial B}$
to
$(\rho +\varphi _{\mathrm {KE}})_{| \partial B}$
to
![]() $\partial {\mathcal X}$
and still denote by F a smooth extension of F to
$\partial {\mathcal X}$
and still denote by F a smooth extension of F to
![]() ${\mathcal X}$
. It follows from Proposition 3.3 that there exists a unique function
${\mathcal X}$
. It follows from Proposition 3.3 that there exists a unique function
![]() $u_t \in \mathrm {PSH}(X_t) \cap {\mathcal C}^0(\overline {X_t})$
such that
$u_t \in \mathrm {PSH}(X_t) \cap {\mathcal C}^0(\overline {X_t})$
such that
 $$ \begin{align} \begin{cases} (dd^c u_t)^n = e^{\lambda u_t+F_t} \mu_t & \mbox{on } X_t\\ u_t|_{\partial X_t}=h_t \end{cases}. \end{align} $$
$$ \begin{align} \begin{cases} (dd^c u_t)^n = e^{\lambda u_t+F_t} \mu_t & \mbox{on } X_t\\ u_t|_{\partial X_t}=h_t \end{cases}. \end{align} $$
together with a uniform bound
![]() $\|u_t\|_{L^{\infty }(X_t)} \leqslant C_0$
. We can thus apply Theorem 3.4 and conclude that
$\|u_t\|_{L^{\infty }(X_t)} \leqslant C_0$
. We can thus apply Theorem 3.4 and conclude that
![]() $dd^c u_0=dd^c \psi =\omega _{KE}$
is a Kähler current near a.
$dd^c u_0=dd^c \psi =\omega _{KE}$
is a Kähler current near a.
4.2 The case of klt pairs
 $(X,\Delta )$
$(X,\Delta )$
We would now like to investigate the strict positivity of Kähler–Einstein currents
![]() $\omega _{\mathrm {KE}}$
associated to compact klt pairs
$\omega _{\mathrm {KE}}$
associated to compact klt pairs
![]() $(X, \Delta )$
near a smoothable isolated singularity
$(X, \Delta )$
near a smoothable isolated singularity
![]() $x\in X$
. There are two possibilities.
$x\in X$
. There are two possibilities.
Case 1. If
![]() $x\notin \mathrm {Supp}(\Delta )$
, then one can find a neighborhood U of x such that
$x\notin \mathrm {Supp}(\Delta )$
, then one can find a neighborhood U of x such that
![]() $\partial U \cap \mathrm {Supp}(\Delta )=\emptyset $
so that
$\partial U \cap \mathrm {Supp}(\Delta )=\emptyset $
so that
![]() $\omega _{\mathrm {KE}}$
is smooth on
$\omega _{\mathrm {KE}}$
is smooth on
![]() $\partial U$
, and the same arguments used in the proof of Theorem 4.1 will carry over mutatis mutandis to show that
$\partial U$
, and the same arguments used in the proof of Theorem 4.1 will carry over mutatis mutandis to show that
![]() $\omega _{\mathrm {KE}}$
is a Kähler current near x.
$\omega _{\mathrm {KE}}$
is a Kähler current near x.
Case 2. If
![]() $x\in \mathrm {Supp}(\Delta )$
, then as a singularity of the pair
$x\in \mathrm {Supp}(\Delta )$
, then as a singularity of the pair
![]() $(X,\Delta )$
, it is not isolated anymore. This reflects on the metric side as well since on the boundary
$(X,\Delta )$
, it is not isolated anymore. This reflects on the metric side as well since on the boundary
![]() $\partial U$
of a small neighborhood of x,
$\partial U$
of a small neighborhood of x,
![]() $\omega _{\mathrm {KE}}$
is not smooth anymore. More precisely,
$\omega _{\mathrm {KE}}$
is not smooth anymore. More precisely,
![]() $\omega _{\mathrm {KE}}$
has conic singularities, to be understood in a generalized sense since
$\omega _{\mathrm {KE}}$
has conic singularities, to be understood in a generalized sense since
![]() $\Delta $
may not have simple normal crossings (snc) support near
$\Delta $
may not have simple normal crossings (snc) support near
![]() $\partial U$
. Even if
$\partial U$
. Even if
![]() $\Delta $
were smooth (or snc) away from x, the local analysis developed so far could not be applied directly and one would have to derive boundary Laplacian estimate in this singular conic setting which probably requires a lot of work. Instead, we can regularize the conic singularities globally to avoid boundary problems when applying Chern–Lu inequality. This will require us to assume that each component
$\Delta $
were smooth (or snc) away from x, the local analysis developed so far could not be applied directly and one would have to derive boundary Laplacian estimate in this singular conic setting which probably requires a lot of work. Instead, we can regularize the conic singularities globally to avoid boundary problems when applying Chern–Lu inequality. This will require us to assume that each component
![]() $\Delta _i$
of
$\Delta _i$
of
![]() $\Delta $
is
$\Delta $
is
![]() ${\mathbb {Q}}$
-Cartier and that any singularity of X is isolated and smoothable.
${\mathbb {Q}}$
-Cartier and that any singularity of X is isolated and smoothable.
We will state the main result of this section with a slightly weaker assumption than local smoothability, which will be useful later when we work with threefolds.
Definition 4.3. We say that a germ of normal complex space
![]() $(X,x)$
is
$(X,x)$
is
![]() ${\mathbb {Q}}$
-smoothable if there exists a finite Galois quasi-étale cover
${\mathbb {Q}}$
-smoothable if there exists a finite Galois quasi-étale cover
![]() $p:Y\to X$
with Y normal and connected such that for all
$p:Y\to X$
with Y normal and connected such that for all
![]() $y\in p^{-1}(x)$
,
$y\in p^{-1}(x)$
,
![]() $(Y,y)$
is smoothable in the sense of Definition 3.2.
$(Y,y)$
is smoothable in the sense of Definition 3.2.
In the definition above, one can always shrink Y and assume that
![]() $p^{-1}(x)$
is a singleton.
$p^{-1}(x)$
is a singleton.
It will be convenient to introduce the following setup.
Setup 4.4. Let
![]() $(X,\omega _X)$
be an n-dimensional compact Kähler space endowed with an effective
$(X,\omega _X)$
be an n-dimensional compact Kähler space endowed with an effective
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $\Delta =\sum a_i \Delta _i$
such that
$\Delta =\sum a_i \Delta _i$
such that
![]() $(X,\Delta )$
has klt singularities. We assume that each component
$(X,\Delta )$
has klt singularities. We assume that each component
![]() $\Delta _i$
of
$\Delta _i$
of
![]() $\Delta $
is a
$\Delta $
is a
![]() ${\mathbb {Q}}$
-Cartier divisor and that X has only
${\mathbb {Q}}$
-Cartier divisor and that X has only
![]() ${\mathbb {Q}}$
-smoothable, isolated singularities.
${\mathbb {Q}}$
-smoothable, isolated singularities.
We are now ready to state the main result.
Theorem 4.5. Let
![]() $(X,\Delta )$
be as in Setup 4.4, and consider the unique (normalized) solution
$(X,\Delta )$
be as in Setup 4.4, and consider the unique (normalized) solution
![]() $\varphi \in \mathrm {PSH}(X,\omega _X)\cap L^{\infty }(X)$
of the Monge–Ampère equation
$\varphi \in \mathrm {PSH}(X,\omega _X)\cap L^{\infty }(X)$
of the Monge–Ampère equation
where
![]() $F\in \mathcal C^{\infty }(X)$
, h is a smooth Hermitian metric on the
$F\in \mathcal C^{\infty }(X)$
, h is a smooth Hermitian metric on the
![]() ${\mathbb {Q}}$
-line bundle
${\mathbb {Q}}$
-line bundle
![]() $K_X+\Delta $
and
$K_X+\Delta $
and
![]() $\lambda \in \{0,1\}$
.
$\lambda \in \{0,1\}$
.
Then, the current
![]() $\omega _\varphi =\omega _X+dd^c \varphi $
is a Kähler current.
$\omega _\varphi =\omega _X+dd^c \varphi $
is a Kähler current.
As an immediate consequence of the theorem above, we get:
Corollary 4.6. Let
![]() $(X,\Delta )$
be as in Setup 4.4 such that
$(X,\Delta )$
be as in Setup 4.4 such that
![]() $K_X+\Delta $
is ample (resp.
$K_X+\Delta $
is ample (resp.
![]() $K_X+\Delta \sim _{{\mathbb {Q}}} \mathcal O_X$
). Then the unique Kähler–Einstein metric
$K_X+\Delta \sim _{{\mathbb {Q}}} \mathcal O_X$
). Then the unique Kähler–Einstein metric
![]() $\omega _{\mathrm {KE}}$
(resp.
$\omega _{\mathrm {KE}}$
(resp.
![]() $\omega _{\mathrm {KE}}\in \{\omega _X\}$
) solving
$\omega _{\mathrm {KE}}\in \{\omega _X\}$
) solving
is a Kähler current.
Remark 4.7. We would like to add two comments on the result above
-
- It is conceivable that one could remove the assumption on the components
 $\Delta _i$
of
$\Delta _i$
of
 $\Delta $
being
$\Delta $
being
 ${\mathbb {Q}}$
-Cartier by considering a
${\mathbb {Q}}$
-Cartier by considering a
 ${\mathbb {Q}}$
-factorialization
${\mathbb {Q}}$
-factorialization
 $Y\to X$
of X, but it is not completely clear how the smoothability assumption would lift to Y.
$Y\to X$
of X, but it is not completely clear how the smoothability assumption would lift to Y. -
- There is a noticeable difference between the assumptions of Theorem 4.1 and Corollary 4.6, as in the latter one we need to assume that all singularities are isolated. It has to do with the fact that we deal with isolated singular points that may not be isolated as singularity of the pair
 $(X,\Delta )$
as explained in the beginning of § 4.2, and this requires a subtle combination of local and global methods. If one is only interested in isolated singular points in
$(X,\Delta )$
as explained in the beginning of § 4.2, and this requires a subtle combination of local and global methods. If one is only interested in isolated singular points in
 $X\setminus \mathrm {Supp}(\Delta )$
, then we would not need any global assumptions on the singularities of X elsewhere, cf ibid.
$X\setminus \mathrm {Supp}(\Delta )$
, then we would not need any global assumptions on the singularities of X elsewhere, cf ibid.
Proof of Theorem 4.5
By assumption, one can find an integer
![]() $m>0$
and sections
$m>0$
and sections
![]() $s_i\in H^0(X,\mathcal O_X(m\Delta _i))$
such that
$s_i\in H^0(X,\mathcal O_X(m\Delta _i))$
such that
![]() $\mathrm {div}(s_i)=m\Delta _i$
. We pick Hermitian metrics
$\mathrm {div}(s_i)=m\Delta _i$
. We pick Hermitian metrics
![]() $h_i$
on the
$h_i$
on the
![]() ${\mathbb {Q}}$
-line bundle
${\mathbb {Q}}$
-line bundle
![]() $O_X(\Delta _i)$
and define
$O_X(\Delta _i)$
and define
![]() $|s_i|^2:=|s_i|^2_{h_i^{\otimes m}}$
. Since
$|s_i|^2:=|s_i|^2_{h_i^{\otimes m}}$
. Since
![]() $K_X$
is
$K_X$
is
![]() ${\mathbb {Q}}$
-Cartier (as a difference
${\mathbb {Q}}$
-Cartier (as a difference
![]() $K_X=(K_X+\Delta )-\Delta )$
of
$K_X=(K_X+\Delta )-\Delta )$
of
![]() ${\mathbb {Q}}$
-Cartier divisors), one can find a metric
${\mathbb {Q}}$
-Cartier divisors), one can find a metric
![]() $h_X$
on
$h_X$
on
![]() $K_X$
such that
$K_X$
such that
![]() $h=h_X\otimes \bigotimes _i h_i^{\otimes a_i}$
. Setting
$h=h_X\otimes \bigotimes _i h_i^{\otimes a_i}$
. Setting
![]() $b_i:=\frac {a_i} m$
, one can rewrite the Monge-Ampère equation solved by
$b_i:=\frac {a_i} m$
, one can rewrite the Monge-Ampère equation solved by
![]() $\varphi $
as
$\varphi $
as
We consider the unique (normalized) solution
![]() $\varphi _\varepsilon $
of the regularized equation
$\varphi _\varepsilon $
of the regularized equation
and we set
![]() $\omega _\varepsilon :=\omega _X+dd^c \varphi _\varepsilon $
. It follows from [Reference Eyssidieux, Guedj and ZeriahiEGZ09, Reference PăunPău08] that
$\omega _\varepsilon :=\omega _X+dd^c \varphi _\varepsilon $
. It follows from [Reference Eyssidieux, Guedj and ZeriahiEGZ09, Reference PăunPău08] that
![]() $\omega _\varepsilon $
is a Kähler form on
$\omega _\varepsilon $
is a Kähler form on
![]() $X_{\mathrm {reg}}$
for any
$X_{\mathrm {reg}}$
for any
![]() $\varepsilon>0$
, and moreover there is a uniform constant
$\varepsilon>0$
, and moreover there is a uniform constant
![]() $C_0>0$
such that
$C_0>0$
such that
thanks to [Reference Guedj and ZeriahiGZ12, Theorem C] applied to a desingularization of X. Therefore, we can reduce the proof of the theorem to showing that there exists a constant
![]() $C>0$
independent of
$C>0$
independent of
![]() $\varepsilon $
such that
$\varepsilon $
such that
Claim 4.8. The uniform inequality (4.3) holds if for any
![]() $\varepsilon>0$
, one has the qualitative inequality
$\varepsilon>0$
, one has the qualitative inequality
where
![]() $C_\varepsilon>0$
is a positive constant that may depend on
$C_\varepsilon>0$
is a positive constant that may depend on
![]() $\varepsilon $
.
$\varepsilon $
.
Proof of Claim 4.8
Here again, the key tool is Chern–Lu inequality, Proposition 2.6. The bisectional curvature of
![]() $\omega _X$
is bounded above since
$\omega _X$
is bounded above since
![]() $\omega _X$
can be extended to a Kähler metric in local embeddings in
$\omega _X$
can be extended to a Kähler metric in local embeddings in
![]() $\mathbb C^N$
, and we need to bound
$\mathbb C^N$
, and we need to bound
![]() $\mathrm {Ric} \, \omega _\varepsilon $
from below.
$\mathrm {Ric} \, \omega _\varepsilon $
from below.
A classical computation shows that if s is a holomorphic section cutting out a divisor D and if
![]() $h_D$
is a smooth Hermitian metric on
$h_D$
is a smooth Hermitian metric on
![]() $L:=\mathcal O_X(D)$
, then
$L:=\mathcal O_X(D)$
, then
 $$\begin{align*}\Theta_{h_D}(L)+dd^c \log(|s|^2_{h_D}+\varepsilon^2) = \frac{\varepsilon^2}{(|s|_{h_D}^2+\varepsilon^2)^2} \cdot |D's\wedge \overline{D's}|^2_{h_D}-\frac{\varepsilon^2}{|s|_{h_D}^2+\varepsilon^2} \cdot \Theta_{h_D}(L).\end{align*}$$
$$\begin{align*}\Theta_{h_D}(L)+dd^c \log(|s|^2_{h_D}+\varepsilon^2) = \frac{\varepsilon^2}{(|s|_{h_D}^2+\varepsilon^2)^2} \cdot |D's\wedge \overline{D's}|^2_{h_D}-\frac{\varepsilon^2}{|s|_{h_D}^2+\varepsilon^2} \cdot \Theta_{h_D}(L).\end{align*}$$
In particular, if one choses a constant
![]() $C_D>0$
such that
$C_D>0$
such that
![]() $\Theta _{h_D}(L)\leqslant C_D\omega _X$
, then
$\Theta _{h_D}(L)\leqslant C_D\omega _X$
, then
Since
and F is smooth (so that its Hessian is bounded with respect to
![]() $\omega _X$
), inequality (4.5) ensures that one can find
$\omega _X$
), inequality (4.5) ensures that one can find
![]() $C_1>0$
such that
$C_1>0$
such that
Finally, let
![]() $\psi \in \mathrm {PSH}(X,\omega _X)$
be such that
$\psi \in \mathrm {PSH}(X,\omega _X)$
be such that
![]() $(\psi =-\infty )=X_{\mathrm {sing}}$
and
$(\psi =-\infty )=X_{\mathrm {sing}}$
and
![]() $\psi |_{X_{\mathrm {reg}}}\in \mathcal C^{\infty }(X_{\mathrm {reg}})$
. For any
$\psi |_{X_{\mathrm {reg}}}\in \mathcal C^{\infty }(X_{\mathrm {reg}})$
. For any
![]() $\delta>0$
, the smooth quantity
$\delta>0$
, the smooth quantity
on
![]() $X_{\mathrm {reg}}$
tends to
$X_{\mathrm {reg}}$
tends to
![]() $-\infty $
near
$-\infty $
near
![]() $X_{\mathrm {sing}}$
thanks to our assumption (4.4). In particular, the quantity above achieves its maximum on
$X_{\mathrm {sing}}$
thanks to our assumption (4.4). In particular, the quantity above achieves its maximum on
![]() $X_{\mathrm {reg}}$
. Moreover, our curvature estimates coupled with Proposition 2.6 yield a constant
$X_{\mathrm {reg}}$
. Moreover, our curvature estimates coupled with Proposition 2.6 yield a constant
![]() $C_2>0$
such that
$C_2>0$
such that
on
![]() $X_{\mathrm {reg}}$
. Since
$X_{\mathrm {reg}}$
. Since
![]() $-\Delta _{\omega _\varepsilon } \varphi _\varepsilon \geqslant -n+\mathrm {tr}_{\omega _\varepsilon }\omega _X$
, we infer that
$-\Delta _{\omega _\varepsilon } \varphi _\varepsilon \geqslant -n+\mathrm {tr}_{\omega _\varepsilon }\omega _X$
, we infer that
where
![]() $C_3=-1+n(C_2+1)$
. A classical application of the maximum principle shows that
$C_3=-1+n(C_2+1)$
. A classical application of the maximum principle shows that
with
![]() $C_4=C_3e^{2C_0(C_2+1)}$
. Passing to the limit when
$C_4=C_3e^{2C_0(C_2+1)}$
. Passing to the limit when
![]() $\delta \to 0$
, we get
$\delta \to 0$
, we get
hence everywhere on X by Lemma 2.5. The claim follows.
In order to prove the theorem, we are left to establishing the qualitative estimate (4.4). In order to achieve that, we use a local deformation argument. From now on,
![]() $\varepsilon>0$
is fixed and all subsequent constants are allowed to depend on
$\varepsilon>0$
is fixed and all subsequent constants are allowed to depend on
![]() $\varepsilon $
. Since
$\varepsilon $
. Since
![]() $\omega _\varepsilon $
is smooth on
$\omega _\varepsilon $
is smooth on
![]() $X_{\mathrm {reg}}$
, it is enough to work in small neighborhoods of the finitely many singular points in X. From now on, we pick a small Stein neighborhood
$X_{\mathrm {reg}}$
, it is enough to work in small neighborhoods of the finitely many singular points in X. From now on, we pick a small Stein neighborhood
![]() $U'$
of x admitting a quasi-étale cover
$U'$
of x admitting a quasi-étale cover
![]() $p:V'\to U'$
such that
$p:V'\to U'$
such that
![]() $p^{-1}(x)=\{y\}$
is a singleton and
$p^{-1}(x)=\{y\}$
is a singleton and
![]() $(V',y)$
admits a smoothing
$(V',y)$
admits a smoothing
![]() $\mathcal V\to \mathbb D$
whose fibers
$\mathcal V\to \mathbb D$
whose fibers
![]() $V_t$
satisfy
$V_t$
satisfy
![]() $V_0\simeq V'$
.
$V_0\simeq V'$
.
One can assume that
![]() $U'$
is small enough so that
$U'$
is small enough so that
![]() $\omega _X|_{U'}=dd^c \rho $
for some smooth strictly psh function
$\omega _X|_{U'}=dd^c \rho $
for some smooth strictly psh function
![]() $\rho $
on
$\rho $
on
![]() $U'$
. Next, since p is quasi-étale, we have
$U'$
. Next, since p is quasi-étale, we have
![]() $K_{V'}=p^*K_{U'}$
and the smooth Hermitian metric
$K_{V'}=p^*K_{U'}$
and the smooth Hermitian metric
![]() $h_{U'}:=h_X|_{U'}$
on
$h_{U'}:=h_X|_{U'}$
on
![]() $K_{U'}$
pulls back to a smooth Hermitian metric
$K_{U'}$
pulls back to a smooth Hermitian metric
![]() $h_{V'}$
on
$h_{V'}$
on
![]() $K_{V'}$
satisfying
$K_{V'}$
satisfying
![]() $p^*\left (d\mu _{U',h_X}\right )=d\mu _{V',h_{V'}}$
.
$p^*\left (d\mu _{U',h_X}\right )=d\mu _{V',h_{V'}}$
.
Next, we fix
![]() $U\Subset U'$
strongly pseudoconvex and set
$U\Subset U'$
strongly pseudoconvex and set
![]() $V:=p^{-1}(U)$
. The function
$V:=p^{-1}(U)$
. The function
![]() $v_\varepsilon :=p^*(\rho +\varphi _\varepsilon )$
satisfies
$v_\varepsilon :=p^*(\rho +\varphi _\varepsilon )$
satisfies
 $$\begin{align*}\begin{cases} (dd^c v_\varepsilon)^n = e^{\lambda v_\varepsilon+p^*(F-\lambda \rho)} \frac{d\mu_{V,h_V}}{\prod_i (|p^*s_i|^2+\varepsilon^2)^{b_i}} & \mbox{on } V\\ v_\varepsilon|_{\partial V}=p^*((\rho+\varphi_\varepsilon)|_{\partial U}), \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} (dd^c v_\varepsilon)^n = e^{\lambda v_\varepsilon+p^*(F-\lambda \rho)} \frac{d\mu_{V,h_V}}{\prod_i (|p^*s_i|^2+\varepsilon^2)^{b_i}} & \mbox{on } V\\ v_\varepsilon|_{\partial V}=p^*((\rho+\varphi_\varepsilon)|_{\partial U}), \end{cases} \end{align*}$$
hence by Theorem 3.4 the current
![]() $dd^cv_\varepsilon $
is a Kähler current. In particular, it dominates a multiple of
$dd^cv_\varepsilon $
is a Kähler current. In particular, it dominates a multiple of
![]() $p^*(\omega _X)|_U$
. Pushing forward, we get that in restriction to U, we have
$p^*(\omega _X)|_U$
. Pushing forward, we get that in restriction to U, we have
![]() $\omega _\varepsilon \geqslant C_{\varepsilon }^{-1} \omega _X$
and the theorem is proved.
$\omega _\varepsilon \geqslant C_{\varepsilon }^{-1} \omega _X$
and the theorem is proved.
5 Kähler–Einstein currents on threefolds
In this final section, we provide two results in dimension three (zero and negative curvature) ensuring that Kähler–Einstein metrics on a compact klt space are Kähler currents without any extra assumption on the singularities. Although the proofs of the two results follow the same lines, we have chosen to write them separately to highlight the nontrivial simplifications occurring in the zero curvature case (or dually to insist on the consequential additional difficulties popping up in the negative curvature case).
The crucial input specific to dimension three is Reid’s classification of terminal singularities:
Theorem 5.1. ([Reference ReidRei80]) Let
![]() $(X,x)$
be an (isolated) terminal singularity of dimension three such that
$(X,x)$
be an (isolated) terminal singularity of dimension three such that
![]() $K_X\sim _{{\mathbb {Z}}} \mathcal O_X$
. Then
$K_X\sim _{{\mathbb {Z}}} \mathcal O_X$
. Then
![]() $(X,x)$
is a compound du Val singularity. In particular, any terminal singularity of dimension three is
$(X,x)$
is a compound du Val singularity. In particular, any terminal singularity of dimension three is
![]() ${\mathbb {Q}}$
-smoothable.
${\mathbb {Q}}$
-smoothable.
Recall that a compound du Val singularity is a hypersurface singularity isomorphic to
![]() $(f+tg=0)\subset \mathbb C^3\times {\mathbb {C}},$
where
$(f+tg=0)\subset \mathbb C^3\times {\mathbb {C}},$
where
![]() $f,g\in {\mathbb {C}}[x,y,z]$
are such that
$f,g\in {\mathbb {C}}[x,y,z]$
are such that
![]() $(f=0)\subset {\mathbb {C}}^3$
is a du Val surface singularity, cf, for example, [Reference Kollár and MoriKM98, § 4.2 & Definition 5.32]. Such a singularity can be smoothed out, for example, by
$(f=0)\subset {\mathbb {C}}^3$
is a du Val surface singularity, cf, for example, [Reference Kollár and MoriKM98, § 4.2 & Definition 5.32]. Such a singularity can be smoothed out, for example, by
![]() $(f+tg+s=0)\subset \mathbb C^3\times {\mathbb {C}}\times {\mathbb {C}}$
, where the total space is a smooth hypersurface of
$(f+tg+s=0)\subset \mathbb C^3\times {\mathbb {C}}\times {\mathbb {C}}$
, where the total space is a smooth hypersurface of
![]() ${\mathbb {C}}^5$
.
${\mathbb {C}}^5$
.
The second statement follows from the first after considering the quasi-étale index one cover
![]() $Y\to X$
making
$Y\to X$
making
![]() $K_Y$
Cartier [Reference Kollár and MoriKM98, Definition 5.19].
$K_Y$
Cartier [Reference Kollár and MoriKM98, Definition 5.19].
5.1 Calabi–Yau threefolds with klt singularities
Theorem 5.2. Let
![]() $(X,\omega _X)$
be a normal compact Kähler space of dimension three with klt singularities such that
$(X,\omega _X)$
be a normal compact Kähler space of dimension three with klt singularities such that
![]() $K_X\sim _{{\mathbb {Q}}} \mathcal O_X$
. Then the Kähler–Einstein metric
$K_X\sim _{{\mathbb {Q}}} \mathcal O_X$
. Then the Kähler–Einstein metric
![]() $\omega _{\mathrm {KE}}\in [\omega _X]$
is a Kähler current.
$\omega _{\mathrm {KE}}\in [\omega _X]$
is a Kähler current.
Proof. Let
![]() $p:Y\to X$
be the quasi-étale index one cover of X. Clearly,
$p:Y\to X$
be the quasi-étale index one cover of X. Clearly,
![]() $p^*\omega _{\mathrm {KE}}$
is the Kähler–Einstein metric in the Kähler class
$p^*\omega _{\mathrm {KE}}$
is the Kähler–Einstein metric in the Kähler class
![]() $p^*[\omega _X]$
so that if we prove the statement for Y, it will follow for X by push-forward (since any Kähler form on Y dominates a multiple of
$p^*[\omega _X]$
so that if we prove the statement for Y, it will follow for X by push-forward (since any Kähler form on Y dominates a multiple of
![]() $p^*\omega _X$
).
$p^*\omega _X$
).
From now on, one can assume that
![]() $K_X\sim _{{\mathbb {Z}}} \mathcal O_X$
and, in particular, X has canonical singularities. Let us consider a terminalization
$K_X\sim _{{\mathbb {Z}}} \mathcal O_X$
and, in particular, X has canonical singularities. Let us consider a terminalization
![]() $\pi : \widehat X \to X$
of X, cf [Reference Kollár and MoriKM98, Theorem 6.23]. The complex space
$\pi : \widehat X \to X$
of X, cf [Reference Kollár and MoriKM98, Theorem 6.23]. The complex space
![]() $\widehat X$
is Kähler, and it has terminal singularities, hence isolated singularities. Moreover, one has
$\widehat X$
is Kähler, and it has terminal singularities, hence isolated singularities. Moreover, one has
![]() $K_{\widehat X}=\pi ^*K_X$
, that is,
$K_{\widehat X}=\pi ^*K_X$
, that is,
![]() $\pi $
is crepant (but in general, the exceptional locus of
$\pi $
is crepant (but in general, the exceptional locus of
![]() $\pi $
might have codimension one components). This implies that
$\pi $
might have codimension one components). This implies that
![]() $K_{\widehat X}\sim _{{\mathbb {Z}}} \mathcal O_{\widehat X}$
so that
$K_{\widehat X}\sim _{{\mathbb {Z}}} \mathcal O_{\widehat X}$
so that
![]() $\widehat X$
has smoothable singularities by Theorem 5.1. Moreover, since
$\widehat X$
has smoothable singularities by Theorem 5.1. Moreover, since
![]() $\pi $
is crepant, it is automatically isomorphic over
$\pi $
is crepant, it is automatically isomorphic over
![]() $X_{\mathrm {reg}}$
.
$X_{\mathrm {reg}}$
.
We choose
![]() $\widehat \omega $
a Kähler metric on
$\widehat \omega $
a Kähler metric on
![]() $\widehat X$
, and one considers the singular Ricci flat metric
$\widehat X$
, and one considers the singular Ricci flat metric
![]() $\omega _\varepsilon \in [\pi ^*\omega _X+\varepsilon \widehat \omega ]$
. One can write
$\omega _\varepsilon \in [\pi ^*\omega _X+\varepsilon \widehat \omega ]$
. One can write
![]() $\omega _\varepsilon = \pi ^*\omega _X+\varepsilon \widehat \omega +dd^c \varphi _\varepsilon $
with
$\omega _\varepsilon = \pi ^*\omega _X+\varepsilon \widehat \omega +dd^c \varphi _\varepsilon $
with
![]() $\sup _{\widehat X}\varphi _\varepsilon =0$
, where
$\sup _{\widehat X}\varphi _\varepsilon =0$
, where
![]() $\varphi _{\varepsilon }$
is a solution of
$\varphi _{\varepsilon }$
is a solution of
![]() $(\pi ^*\omega _X+\varepsilon \widehat \omega +dd^c \varphi _{\varepsilon })^n=c_{\varepsilon } \mu _{\hat {X}}=c_{\varepsilon } \hat {f} \widehat \omega ^n$
, where
$(\pi ^*\omega _X+\varepsilon \widehat \omega +dd^c \varphi _{\varepsilon })^n=c_{\varepsilon } \mu _{\hat {X}}=c_{\varepsilon } \hat {f} \widehat \omega ^n$
, where
![]() $c_\varepsilon =\frac {[\pi ^*\omega _X+\varepsilon \widehat \omega ]^n}{ \mu _{\widehat X}(\widehat X)}$
and
$c_\varepsilon =\frac {[\pi ^*\omega _X+\varepsilon \widehat \omega ]^n}{ \mu _{\widehat X}(\widehat X)}$
and
![]() $\hat {f} \in L^{1+\delta }(\widehat X,\widehat \omega ^n)$
with
$\hat {f} \in L^{1+\delta }(\widehat X,\widehat \omega ^n)$
with
![]() $\delta>0$
since
$\delta>0$
since
![]() $\hat {X}$
has terminal singularities. It follows from the techniques in [Reference Eyssidieux, Guedj and ZeriahiEGZ08, Reference Demailly and PaliDP10] that
$\hat {X}$
has terminal singularities. It follows from the techniques in [Reference Eyssidieux, Guedj and ZeriahiEGZ08, Reference Demailly and PaliDP10] that
where
![]() $C_0>0$
is independent of
$C_0>0$
is independent of
![]() $\varepsilon $
. The discerning reader will have noticed that the situation is slightly different from the one in loc. cit. since X is singular. To patch this little gap, one could, for example, appeal to [Reference Di Nezza, Guedj and GuenanciaDNGG23, Theorem A] applied to a desingularization of
$\varepsilon $
. The discerning reader will have noticed that the situation is slightly different from the one in loc. cit. since X is singular. To patch this little gap, one could, for example, appeal to [Reference Di Nezza, Guedj and GuenanciaDNGG23, Theorem A] applied to a desingularization of
![]() $\widetilde X\to \widehat X$
with reference form the pull-back of
$\widetilde X\to \widehat X$
with reference form the pull-back of
![]() $\pi ^*\omega _X+\varepsilon \widehat \omega $
to
$\pi ^*\omega _X+\varepsilon \widehat \omega $
to
![]() $\widetilde X$
, and this would yield the uniform estimate. As for the stability statement, it is a classical consequence of the uniform estimate: One first gets higher-order estimates locally on
$\widetilde X$
, and this would yield the uniform estimate. As for the stability statement, it is a classical consequence of the uniform estimate: One first gets higher-order estimates locally on
![]() $X_{\mathrm {reg}}$
using Tsuji’s trick and then one uses uniqueness of the Kähler–Einstein metric to conclude that the relatively compact family
$X_{\mathrm {reg}}$
using Tsuji’s trick and then one uses uniqueness of the Kähler–Einstein metric to conclude that the relatively compact family
![]() $(\varphi _\varepsilon )_{\varepsilon>0}$
has a single cluster value in
$(\varphi _\varepsilon )_{\varepsilon>0}$
has a single cluster value in
![]() $L^1(\widehat X)$
which is nothing but
$L^1(\widehat X)$
which is nothing but
![]() $\varphi _0$
.
$\varphi _0$
.
The main point to establish is that there is a constant
![]() $C>0$
independent of
$C>0$
independent of
![]() $\varepsilon $
such that
$\varepsilon $
such that
Indeed, passing to the limit when
![]() $\varepsilon \to 0$
would then imply that
$\varepsilon \to 0$
would then imply that
![]() $\pi ^*\omega _{\mathrm {KE}}\geqslant C^{-1} \pi ^*\omega _X$
and the theorem would follow by pushing forward by
$\pi ^*\omega _{\mathrm {KE}}\geqslant C^{-1} \pi ^*\omega _X$
and the theorem would follow by pushing forward by
![]() $\pi $
.
$\pi $
.
Now, we know that inequality (5.2) holds for any
![]() $\varepsilon>0$
with a constant
$\varepsilon>0$
with a constant
![]() $C=C_\varepsilon $
depending a priori from
$C=C_\varepsilon $
depending a priori from
![]() $\varepsilon $
, as this is the content of Theorem 4.1. As before, we will use Chern–Lu inequality to make this qualitative control quantitative.
$\varepsilon $
, as this is the content of Theorem 4.1. As before, we will use Chern–Lu inequality to make this qualitative control quantitative.
Choose a function
![]() $\psi \in \mathrm {PSH}(X,\omega _X)$
be such that
$\psi \in \mathrm {PSH}(X,\omega _X)$
be such that
![]() $(\psi =-\infty )=X_{\mathrm {sing}}$
and
$(\psi =-\infty )=X_{\mathrm {sing}}$
and
![]() $\psi |_{X_{\mathrm {reg}}}\in \mathcal C^{\infty }(X_{\mathrm {reg}})$
. For any
$\psi |_{X_{\mathrm {reg}}}\in \mathcal C^{\infty }(X_{\mathrm {reg}})$
. For any
![]() $\delta>0$
, the smooth quantity
$\delta>0$
, the smooth quantity
on
![]() $\pi ^{-1}(X_{\mathrm {reg}}) \subset \widehat X \setminus \mathrm {Exc}(\pi )$
tends to
$\pi ^{-1}(X_{\mathrm {reg}}) \subset \widehat X \setminus \mathrm {Exc}(\pi )$
tends to
![]() $-\infty $
near
$-\infty $
near
![]() $\pi ^{-1}(X_{\mathrm {sing}})$
since
$\pi ^{-1}(X_{\mathrm {sing}})$
since
![]() $\omega _\varepsilon $
is a Kähler form. In particular, the quantity above achieves its maximum on
$\omega _\varepsilon $
is a Kähler form. In particular, the quantity above achieves its maximum on
![]() $X_{\mathrm {reg}}$
.
$X_{\mathrm {reg}}$
.
Next, the bisectional curvature of
![]() $\pi ^*\omega _X$
is well defined and bounded above uniformly on
$\pi ^*\omega _X$
is well defined and bounded above uniformly on
![]() $\pi ^{-1}(X_{\mathrm {reg}})$
, while
$\pi ^{-1}(X_{\mathrm {reg}})$
, while
![]() $\mathrm {Ric} \,\omega _\varepsilon = 0$
. By Chern–Lu inequality (Proposition 2.6), we find a constant
$\mathrm {Ric} \,\omega _\varepsilon = 0$
. By Chern–Lu inequality (Proposition 2.6), we find a constant
![]() $C_2>0$
such that
$C_2>0$
such that
on
![]() $\pi ^{-1}(X_{\mathrm {reg}})$
. Since
$\pi ^{-1}(X_{\mathrm {reg}})$
. Since
![]() $-dd^c \varphi _\varepsilon =-\omega _\varepsilon +\pi ^{*}\omega _X+\varepsilon \widehat \omega $
, we have
$-dd^c \varphi _\varepsilon =-\omega _\varepsilon +\pi ^{*}\omega _X+\varepsilon \widehat \omega $
, we have
hence
where
![]() $C_3=-1+n(C_2+1)$
. Using Equation (5.1), we obtain in the end
$C_3=-1+n(C_2+1)$
. Using Equation (5.1), we obtain in the end
with
![]() $C_4=C_3e^{C_0(C_2+1)}$
, holding on
$C_4=C_3e^{C_0(C_2+1)}$
, holding on
![]() $\pi ^{-1}(X_{\mathrm {reg}})$
for any
$\pi ^{-1}(X_{\mathrm {reg}})$
for any
![]() $\delta>0$
. Equivalently, we have
$\delta>0$
. Equivalently, we have
![]() $\omega _\varepsilon \geqslant C_4 e^{-\delta (\sup _X \psi - \psi )}\, \pi ^*\omega _X$
. After passing to the limit when
$\omega _\varepsilon \geqslant C_4 e^{-\delta (\sup _X \psi - \psi )}\, \pi ^*\omega _X$
. After passing to the limit when
![]() $\delta \to 0$
, one can appeal to Lemma 2.5 to obtain Equation (5.2), hence the theorem.
$\delta \to 0$
, one can appeal to Lemma 2.5 to obtain Equation (5.2), hence the theorem.
5.2 Canonically polarized threefolds with klt singularities
Theorem 5.3. Let X be a normal projective variety of dimension three with klt singularities such that
![]() $K_X$
is ample. Then the Kähler–Einstein metric
$K_X$
is ample. Then the Kähler–Einstein metric
![]() $\omega _{\mathrm {KE}}$
is a Kähler current.
$\omega _{\mathrm {KE}}$
is a Kähler current.
Proof. The reduction to the terminal case is a bit more involved here. More precisely, we cannot easily assume that X has canonical singularities without resorting to a local argument which would collapse since the singularities of X are not isolated. Instead, we use a
![]() ${\mathbb {Q}}$
-factorial terminalization
${\mathbb {Q}}$
-factorial terminalization
![]() $\pi :\widehat X\to X$
whose existence (in any dimension) is guaranteed by [Reference Birkar, Cascini, Hacon and McKernanBCHM10, Corollary 1.4.3]. The map
$\pi :\widehat X\to X$
whose existence (in any dimension) is guaranteed by [Reference Birkar, Cascini, Hacon and McKernanBCHM10, Corollary 1.4.3]. The map
![]() $\pi $
is such that there exists an effective divisor
$\pi $
is such that there exists an effective divisor
![]() $\widehat \Delta $
on
$\widehat \Delta $
on
![]() $\widehat X$
such that
$\widehat X$
such that
![]() $K_{\widehat X}+\widehat \Delta =\pi ^*K_X$
and
$K_{\widehat X}+\widehat \Delta =\pi ^*K_X$
and
![]() $(\widehat X, \widehat \Delta )$
is a terminal pair, hence
$(\widehat X, \widehat \Delta )$
is a terminal pair, hence
![]() $\widehat X$
has isolated
$\widehat X$
has isolated
![]() ${\mathbb {Q}}$
-smoothable singularities by Theorem 5.1. Moreover,
${\mathbb {Q}}$
-smoothable singularities by Theorem 5.1. Moreover,
![]() $\widehat X$
is
$\widehat X$
is
![]() ${\mathbb {Q}}$
-factorial.
${\mathbb {Q}}$
-factorial.
Next, let
![]() $\widehat \omega $
be a Kähler metric on
$\widehat \omega $
be a Kähler metric on
![]() $\widehat X$
and let us consider the twisted Kähler–Einstein metric
$\widehat X$
and let us consider the twisted Kähler–Einstein metric
![]() $\omega _\varepsilon \in c_1(\pi ^*K_X)+\varepsilon [\widehat \omega ]$
, that is, the solution of
$\omega _\varepsilon \in c_1(\pi ^*K_X)+\varepsilon [\widehat \omega ]$
, that is, the solution of
If
![]() $\omega _X\in c_1(K_X)$
is a Kähler metric, say the curvature of an Hermitian metric h on
$\omega _X\in c_1(K_X)$
is a Kähler metric, say the curvature of an Hermitian metric h on
![]() $K_X$
, one can write
$K_X$
, one can write
![]() $\omega _\varepsilon = \pi ^*\omega _X+\varepsilon \widehat \omega +dd^c \varphi _\varepsilon $
, where
$\omega _\varepsilon = \pi ^*\omega _X+\varepsilon \widehat \omega +dd^c \varphi _\varepsilon $
, where
![]() $\varphi _{\varepsilon }$
is a solution of
$\varphi _{\varepsilon }$
is a solution of
with
![]() $\hat {f} \in L^{1+\delta }(\widehat X,\widehat \omega ^n)$
with
$\hat {f} \in L^{1+\delta }(\widehat X,\widehat \omega ^n)$
with
![]() $\delta>0$
since
$\delta>0$
since
![]() $\hat {X}$
has terminal singularities. As in the Calabi–Yau case, one has
$\hat {X}$
has terminal singularities. As in the Calabi–Yau case, one has
where
![]() $C>0$
is independent of
$C>0$
is independent of
![]() $\varepsilon $
. The only difference with the Calabi–Yau case is that we first need to show that there exists
$\varepsilon $
. The only difference with the Calabi–Yau case is that we first need to show that there exists
![]() $C>0 $
independent of
$C>0 $
independent of
![]() $\varepsilon $
such that
$\varepsilon $
such that
This is certainly classical, but we recall the argument for the reader’s convenience. First, one can assume without loss of generality that
![]() $\mu :=\mu _{(\hat {X},\widehat \Delta ), \pi ^*h}$
is a probability measure. By Jensen’s inequality, we infer that
$\mu :=\mu _{(\hat {X},\widehat \Delta ), \pi ^*h}$
is a probability measure. By Jensen’s inequality, we infer that
for some
![]() $C_{1}>0$
independent of
$C_{1}>0$
independent of
![]() $\varepsilon $
. Let
$\varepsilon $
. Let
![]() $p:\widetilde X\to \widehat X$
be a resolution of singularities, and let
$p:\widetilde X\to \widehat X$
be a resolution of singularities, and let
![]() $\omega _{\widetilde X}$
be a Kähler metric on
$\omega _{\widetilde X}$
be a Kähler metric on
![]() $\widetilde X$
. Up to scaling the latter metric, one can assume that
$\widetilde X$
. Up to scaling the latter metric, one can assume that
![]() $p^*(\pi ^*\omega _X+\varepsilon \widehat \omega )\leqslant \omega _{\widetilde X}$
and
$p^*(\pi ^*\omega _X+\varepsilon \widehat \omega )\leqslant \omega _{\widetilde X}$
and
![]() $p^*\mu \leqslant \omega _{\widetilde X}^n$
, where the latter follows since
$p^*\mu \leqslant \omega _{\widetilde X}^n$
, where the latter follows since
![]() $\widehat X$
has terminal (hence canonical) singularities. By the usual compactness properties of
$\widehat X$
has terminal (hence canonical) singularities. By the usual compactness properties of
![]() $\omega _{\widetilde X}$
-psh functions, we find a constant
$\omega _{\widetilde X}$
-psh functions, we find a constant
![]() $C_{2}$
such that
$C_{2}$
such that
 $$\begin{align*}\int_{\widetilde X}(\sup_{\widetilde X}\psi-\psi)\omega_{\widetilde X}^n \leqslant C_{2}\end{align*}$$
$$\begin{align*}\int_{\widetilde X}(\sup_{\widetilde X}\psi-\psi)\omega_{\widetilde X}^n \leqslant C_{2}\end{align*}$$
for any
![]() $\psi \in \mathrm {PSH}(\widetilde X, \omega _{\widetilde X})$
. Now,
$\psi \in \mathrm {PSH}(\widetilde X, \omega _{\widetilde X})$
. Now,
 $$ \begin{align*} \sup_{\widehat X} \varphi_\varepsilon &= \int_{\widehat X}(\sup_{\widehat X} \varphi_\varepsilon-\varphi_\varepsilon)d\mu+\int_{\widehat X} \varphi_\varepsilon d\mu\\ & \leqslant \int_{\widehat X}(\sup_{\widetilde X} p^*\varphi_\varepsilon-p^*\varphi_\varepsilon)\omega_{\widetilde X}^n+C_1\\ & \leqslant C_1+C_2 \end{align*} $$
$$ \begin{align*} \sup_{\widehat X} \varphi_\varepsilon &= \int_{\widehat X}(\sup_{\widehat X} \varphi_\varepsilon-\varphi_\varepsilon)d\mu+\int_{\widehat X} \varphi_\varepsilon d\mu\\ & \leqslant \int_{\widehat X}(\sup_{\widetilde X} p^*\varphi_\varepsilon-p^*\varphi_\varepsilon)\omega_{\widetilde X}^n+C_1\\ & \leqslant C_1+C_2 \end{align*} $$
since
![]() $p^*\varphi _\varepsilon \in \mathrm {PSH}(\widetilde X, \omega _{\widetilde X})$
. Hence, Equation (5.4) follows.
$p^*\varphi _\varepsilon \in \mathrm {PSH}(\widetilde X, \omega _{\widetilde X})$
. Hence, Equation (5.4) follows.
Coming back to proof of the main result, the remaining point to establish is that there is a constant
![]() $C>0$
independent of
$C>0$
independent of
![]() $\varepsilon $
such that
$\varepsilon $
such that
Thanks to Theorem 4.5, inequality (5.5) holds for any
![]() $\varepsilon>0$
with a constant
$\varepsilon>0$
with a constant
![]() $C=C_\varepsilon $
depending a priori from
$C=C_\varepsilon $
depending a priori from
![]() $\varepsilon $
. In order to make this bound quantitative, the exact same strategy as in the Calabi–Yau case applies.
$\varepsilon $
. In order to make this bound quantitative, the exact same strategy as in the Calabi–Yau case applies.
Competing interest
The authors have no competing interest to declare.
Funding statement
The authors are partially supported by the research project Hermetic (ANR-11-LABX-0040) and the ANR projects Paraplui (ANR-20-CE40-0019) and Karmapolis (ANR-21-CE40-0010).