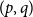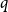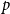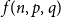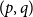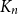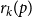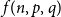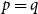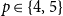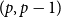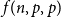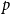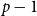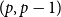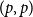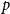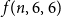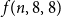1. Introduction
Let
![]() $p$
and
$p$
and
![]() $q$
be positive integers such that
$q$
be positive integers such that
![]() $1 \leq q \leq \binom{p}{2}$
. We say that an edge-colouring of a graph
$1 \leq q \leq \binom{p}{2}$
. We say that an edge-colouring of a graph
![]() $G$
is a
$G$
is a
![]() $(p,q)$
-colouring if any
$(p,q)$
-colouring if any
![]() $p$
-clique of
$p$
-clique of
![]() $G$
contains edges of at least
$G$
contains edges of at least
![]() $q$
distinct colours. In 1975, Erdős and Shelah [Reference Erdős5] posed the question of determining
$q$
distinct colours. In 1975, Erdős and Shelah [Reference Erdős5] posed the question of determining
![]() $f(n,p,q)$
, the minimum number of colours needed to give a
$f(n,p,q)$
, the minimum number of colours needed to give a
![]() $(p,q)$
-colouring of the complete graph on
$(p,q)$
-colouring of the complete graph on
![]() $n$
vertices,
$n$
vertices,
![]() $K_n$
.
$K_n$
.
This function
![]() $f(n,p,q)$
is known as the Erdős-Gyárfás function after the authors of the first paper [Reference Erdős and Gyárfás6] to systematically study
$f(n,p,q)$
is known as the Erdős-Gyárfás function after the authors of the first paper [Reference Erdős and Gyárfás6] to systematically study
![]() $(p,q)$
-colourings. The majority of their work focused on understanding the asymptotic behaviour of this function as
$(p,q)$
-colourings. The majority of their work focused on understanding the asymptotic behaviour of this function as
![]() $n \rightarrow \infty$
for fixed values of
$n \rightarrow \infty$
for fixed values of
![]() $p$
and
$p$
and
![]() $q$
. One of their primary results was a general upper bound of
$q$
. One of their primary results was a general upper bound of
 \begin{align*} f(n,p,q) = O\left (n^{\frac{p-2}{\binom{p}{2}-q+1}}\right ) \end{align*}
\begin{align*} f(n,p,q) = O\left (n^{\frac{p-2}{\binom{p}{2}-q+1}}\right ) \end{align*}
obtained using the Lovász Local Lemma, while one of the main problems they left open was the determination of
![]() $q$
, given a fixed value of
$q$
, given a fixed value of
![]() $p$
, for which
$p$
, for which
![]() $f(n,p,q) = \Omega (n^{\varepsilon })$
for some constant
$f(n,p,q) = \Omega (n^{\varepsilon })$
for some constant
![]() $\varepsilon$
, but
$\varepsilon$
, but
![]() $f(n,p,q-1)=n^{o(1)}$
. Towards this end, they found that
$f(n,p,q-1)=n^{o(1)}$
. Towards this end, they found that
where the lower bound is given by a simple induction argument and the upper bound is a special case of their general upper bound. However, they did not determine whether
![]() $f(n,p,p-1)=n^{o(1)}$
.
$f(n,p,p-1)=n^{o(1)}$
.
In 2015, Conlon, Fox, Lee, and Sudakov [Reference Conlon, Fox, Lee and Sudakov3], building on work done on small cases by Mubayi and Eichhorn [Reference Eichhorn and Mubayi4, Reference Mubayi7], showed that
![]() $f(n,p,p-1)=n^{o(1)}$
by constructing an explicit
$f(n,p,p-1)=n^{o(1)}$
by constructing an explicit
![]() $(p,p-1)$
-colouring using very few colours. In [Reference Cameron and Heath2], we slightly modified their colouring, which we call the CFLS colouring, and paired it with an ‘algebraic’ construction to show
$(p,p-1)$
-colouring using very few colours. In [Reference Cameron and Heath2], we slightly modified their colouring, which we call the CFLS colouring, and paired it with an ‘algebraic’ construction to show
![]() $f(n,5,5) \leq n^{1/3+o(1)}$
. This improves on the general upper bound found by Erdős and Gyárfás and comes close to matching their lower bound in terms of order of growth. Our construction built on the ideas of Mubayi in [Reference Mubayi8], where he gave an explicit construction showing
$f(n,5,5) \leq n^{1/3+o(1)}$
. This improves on the general upper bound found by Erdős and Gyárfás and comes close to matching their lower bound in terms of order of growth. Our construction built on the ideas of Mubayi in [Reference Mubayi8], where he gave an explicit construction showing
![]() $f(n,4,4) \leq n^{1/2+o(1)}$
.
$f(n,4,4) \leq n^{1/2+o(1)}$
.
In this paper, we push these ideas further. In Section 2, we prove the following result.
Theorem 1.1.
For any
![]() $p \geq 3$
, there is a
$p \geq 3$
, there is a
![]() $(p,p-1)$
-colouring of
$(p,p-1)$
-colouring of
![]() $K_n$
using
$K_n$
using
![]() $n^{o(1)}$
colours such that the only
$n^{o(1)}$
colours such that the only
![]() $p$
-cliques that contain exactly
$p$
-cliques that contain exactly
![]() $p-1$
distinct edge colours are isomorphic (as edge-coloured graphs) to one of the edge-coloured
$p-1$
distinct edge colours are isomorphic (as edge-coloured graphs) to one of the edge-coloured
![]() $p$
-cliques given in the definition below.
$p$
-cliques given in the definition below.
Definition 1.1. Given an edge-colouring
![]() $f\;:\;E(K_n) \rightarrow C$
, we say that a subset
$f\;:\;E(K_n) \rightarrow C$
, we say that a subset
![]() $S \subseteq V(K_n)$
has a leftover structure under
$S \subseteq V(K_n)$
has a leftover structure under
![]() $f$
if either
$f$
if either
![]() $|S|=1$
or there exists a bipartition (which we will call the initial bipartition) of
$|S|=1$
or there exists a bipartition (which we will call the initial bipartition) of
![]() $S$
into nonempty sets
$S$
into nonempty sets
![]() $A$
and
$A$
and
![]() $B$
for which
$B$
for which
-
 $A$
and
$A$
and
 $B$
each have a leftover structure under
$B$
each have a leftover structure under
 $f$
;
$f$
; -
 $f(A) \cap f(B) = \emptyset$
; and
$f(A) \cap f(B) = \emptyset$
; and -
there is a fixed colour
 $\alpha \in C$
such that
$\alpha \in C$
such that
 $f(a,b)=\alpha$
for all
$f(a,b)=\alpha$
for all
 $a \in A$
and all
$a \in A$
and all
 $b \in B$
and
$b \in B$
and
 $\alpha \not \in f(A)$
and
$\alpha \not \in f(A)$
and
 $\alpha \not \in f(B)$
.
$\alpha \not \in f(B)$
.
See Figure 1 for an example of a leftover structure. Alternatively, a more constructive definition is to say that a
![]() $p$
-clique
$p$
-clique
![]() $S$
is leftover if either
$S$
is leftover if either
![]() $p=1$
or if it can be formed from a leftover
$p=1$
or if it can be formed from a leftover
![]() $(p-1)$
-clique by taking one of its vertices
$(p-1)$
-clique by taking one of its vertices
![]() $x$
, making a copy
$x$
, making a copy
![]() $x'$
, colouring
$x'$
, colouring
![]() $xx'$
with a new colour, and colouring
$xx'$
with a new colour, and colouring
![]() $x'y$
with the same colour as
$x'y$
with the same colour as
![]() $xy$
for each
$xy$
for each
![]() $y \in S$
for which
$y \in S$
for which
![]() $y \neq x$
. Note that it is easy to see by induction that these
$y \neq x$
. Note that it is easy to see by induction that these
![]() $p$
-cliques always contain exactly
$p$
-cliques always contain exactly
![]() $p-1$
colours.
$p-1$
colours.

Figure 1. An example of a
![]() $p$
-clique with a leftover structure.
$p$
-clique with a leftover structure.
One of the general difficulties in producing explicit
![]() $(p,q)$
-colourings is dealing with the large number of possible non-isomorphic ways to colour the edges of a
$(p,q)$
-colourings is dealing with the large number of possible non-isomorphic ways to colour the edges of a
![]() $p$
-clique with fewer than
$p$
-clique with fewer than
![]() $q$
colours in order to demonstrate that a construction avoids them. By identifying the ‘bad’ structures that are leftover after using only
$q$
colours in order to demonstrate that a construction avoids them. By identifying the ‘bad’ structures that are leftover after using only
![]() $n^{o(1)}$
colours, we are able to greatly reduce the amount of case-checking required in identifying
$n^{o(1)}$
colours, we are able to greatly reduce the amount of case-checking required in identifying
![]() $(p,p)$
-colourings, which would otherwise make this problem intractable for large
$(p,p)$
-colourings, which would otherwise make this problem intractable for large
![]() $p$
.
$p$
.
More precisely, one of the nice properties of these leftover structures is that any subset of vertices of a leftover clique induces a clique that is itself leftover. Therefore, any edge-colouring of
![]() $K_n$
that eliminates leftover
$K_n$
that eliminates leftover
![]() $p$
-cliques also eliminates all leftover
$p$
-cliques also eliminates all leftover
![]() $P$
-cliques for any
$P$
-cliques for any
![]() $P \geq p$
. Moreover, by Theorem 1.1, if this colouring uses
$P \geq p$
. Moreover, by Theorem 1.1, if this colouring uses
![]() $n^{\varepsilon +o(1)}$
colours, then
$n^{\varepsilon +o(1)}$
colours, then
![]() $f(n,P,P) \leq n^{\varepsilon +o(1)}$
, as the product of this colouring with the one guaranteed in Theorem 1.1 will avoid any
$f(n,P,P) \leq n^{\varepsilon +o(1)}$
, as the product of this colouring with the one guaranteed in Theorem 1.1 will avoid any
![]() $P$
-clique with fewer than
$P$
-clique with fewer than
![]() $P$
colours for each
$P$
colours for each
![]() $P \geq p$
.
$P \geq p$
.
As a specific example, in [Reference Cameron and Heath2] we gave a
![]() $(5,5)$
-colouring of
$(5,5)$
-colouring of
![]() $K_n$
that used
$K_n$
that used
![]() $n^{1/3+o(1)}$
colours. Since this colouring avoids leftover 5-cliques, then it also avoids leftover
$n^{1/3+o(1)}$
colours. Since this colouring avoids leftover 5-cliques, then it also avoids leftover
![]() $P$
-cliques for all
$P$
-cliques for all
![]() $P \geq 5$
. Therefore, if we take the product of this colouring with the appropriate one developed in Section 2 that eliminates all
$P \geq 5$
. Therefore, if we take the product of this colouring with the appropriate one developed in Section 2 that eliminates all
![]() $6$
-cliques with 5 or fewer colours other than leftover
$6$
-cliques with 5 or fewer colours other than leftover
![]() $6$
-cliques, then we have a
$6$
-cliques, then we have a
![]() $(6,6)$
-colouring that uses only
$(6,6)$
-colouring that uses only
![]() $n^{1/3+o(1)}$
colours, improving the best-known upper bound given above,
$n^{1/3+o(1)}$
colours, improving the best-known upper bound given above,
![]() $O(n^{2/5})$
.
$O(n^{2/5})$
.
In Section 3, we generalize the algebraic portion of our colouring in [Reference Cameron and Heath2], the ‘Modified Dot Product’ colouring, to a version that eliminates leftover
![]() $6$
-cliques with
$6$
-cliques with
![]() $O(n^{1/3})$
colours (making the above example redundant) and eliminates leftover
$O(n^{1/3})$
colours (making the above example redundant) and eliminates leftover
![]() $8$
-cliques with
$8$
-cliques with
![]() $O(n^{1/4})$
colours. By taking the product of these colourings with the appropriate ones developed in Section 2, this gives us the following theorem.
$O(n^{1/4})$
colours. By taking the product of these colourings with the appropriate ones developed in Section 2, this gives us the following theorem.
Theorem 1.2. We have the following upper bounds:
This improves the best-known upper bound
![]() $f(n,8,8) = O(n^{2/7})$
as well.
$f(n,8,8) = O(n^{2/7})$
as well.
2. Modified CFLS colouring
In this section, we define an edge-colouring
![]() $\psi _p$
of the complete graph with vertex set
$\psi _p$
of the complete graph with vertex set
![]() $\{0,1\}^{\alpha }$
for some positive integer
$\{0,1\}^{\alpha }$
for some positive integer
![]() $\alpha$
. This construction is the product of two colourings,
$\alpha$
. This construction is the product of two colourings,
![]() $\psi _p = c_p \times \Delta _p$
, where
$\psi _p = c_p \times \Delta _p$
, where
![]() $c_p$
is the
$c_p$
is the
![]() $(p+3,p+2)$
-colouring defined in [Reference Conlon, Fox, Lee and Sudakov3]. In many places, this section tracks parts of the proof given in [Reference Conlon, Fox, Lee and Sudakov3], and we have attempted to keep the notation consistent with that paper to make cross-referencing easier.
$(p+3,p+2)$
-colouring defined in [Reference Conlon, Fox, Lee and Sudakov3]. In many places, this section tracks parts of the proof given in [Reference Conlon, Fox, Lee and Sudakov3], and we have attempted to keep the notation consistent with that paper to make cross-referencing easier.
We will prove the following lemma about the colouring
![]() $c_p$
.
$c_p$
.
Lemma 2.1.
Let
![]() $p$
be a fixed positive integer. Any subset
$p$
be a fixed positive integer. Any subset
![]() $S \subseteq \{0,1\}^{\alpha }$
with
$S \subseteq \{0,1\}^{\alpha }$
with
![]() $|S| \leq p+3$
vertices that contains exactly
$|S| \leq p+3$
vertices that contains exactly
![]() $|S|-1$
distinct colours under the edge-colouring
$|S|-1$
distinct colours under the edge-colouring
![]() $c_p$
either has a leftover structure under
$c_p$
either has a leftover structure under
![]() $c_p$
or contains a striped
$c_p$
or contains a striped
![]() $K_4$
under
$K_4$
under
![]() $c_p$
.
$c_p$
.
A striped
![]() $K_4$
, as described by the following definition, was first defined in [Reference Mubayi8].
$K_4$
, as described by the following definition, was first defined in [Reference Mubayi8].
Definition 2.1. Let
![]() $f\;:\;E(G) \rightarrow C$
be an edge-colouring of a graph
$f\;:\;E(G) \rightarrow C$
be an edge-colouring of a graph
![]() $G$
. We call any 4-clique of
$G$
. We call any 4-clique of
![]() $G$
,
$G$
,
![]() $\{a,b,c,d\} \subseteq V(G)$
, for which
$\{a,b,c,d\} \subseteq V(G)$
, for which
![]() $f(ab)=f(cd)$
,
$f(ab)=f(cd)$
,
![]() $f(ac)=f(bd)$
,
$f(ac)=f(bd)$
,
![]() $f(ad)=f(bc)$
,
$f(ad)=f(bc)$
,
![]() $f(ab) \neq f(ac)$
,
$f(ab) \neq f(ac)$
,
![]() $f(ab) \neq f(ad)$
, and
$f(ab) \neq f(ad)$
, and
![]() $f(ac) \neq f(ad)$
a striped
$f(ac) \neq f(ad)$
a striped
![]() $K_4$
.
$K_4$
.
We will also prove the following result about the colouring
![]() $\psi _p$
.
$\psi _p$
.
Lemma 2.2.
There is no striped
![]() $K_4$
under the edge-colouring
$K_4$
under the edge-colouring
![]() $\psi _p$
.
$\psi _p$
.
These two lemmas are enough to conclude that
![]() $\psi _p$
is a
$\psi _p$
is a
![]() $(p+3,p+2)$
-colouring for which any clique
$(p+3,p+2)$
-colouring for which any clique
![]() $S$
with
$S$
with
![]() $|S| \leq p+3$
that contains exactly
$|S| \leq p+3$
that contains exactly
![]() $|S|-1$
colours must have a leftover structure.
$|S|-1$
colours must have a leftover structure.
2.1 The construction
For some positive integer
![]() $p$
, let
$p$
, let
be fixed positive integers such that
![]() $r_d | r_{d+1}$
for each
$r_d | r_{d+1}$
for each
![]() $d=1,\ldots,p-1$
. These
$d=1,\ldots,p-1$
. These
![]() $r_i$
will be called the parameters of our edge-colouring.
$r_i$
will be called the parameters of our edge-colouring.
For any
![]() $\alpha \geq r_p$
, let
$\alpha \geq r_p$
, let
![]() $n=2^{\alpha }$
, and associate each vertex of the complete graph
$n=2^{\alpha }$
, and associate each vertex of the complete graph
![]() $K_n$
with its own unique binary string of length
$K_n$
with its own unique binary string of length
![]() $\alpha$
. For each
$\alpha$
. For each
![]() $d=1,\ldots,p$
, let
$d=1,\ldots,p$
, let
![]() $\alpha = a_dr_d+b_d$
for positive integers
$\alpha = a_dr_d+b_d$
for positive integers
![]() $a_d,b_d$
such that
$a_d,b_d$
such that
![]() $1 \leq b_d \leq r_d$
. For each string
$1 \leq b_d \leq r_d$
. For each string
![]() $x \in \{0,1\}^{\alpha }$
, we let
$x \in \{0,1\}^{\alpha }$
, we let
where
![]() $x_i^{(d)}$
denotes a binary string in
$x_i^{(d)}$
denotes a binary string in
![]() $\{0,1\}^{r_d}$
for each
$\{0,1\}^{r_d}$
for each
![]() $i=1,\ldots,a_d$
and
$i=1,\ldots,a_d$
and
![]() $x_{a_d+1}^{(d)}$
denotes a binary string from
$x_{a_d+1}^{(d)}$
denotes a binary string from
![]() $\{0,1\}^{b_d}$
. We will call these substrings
$\{0,1\}^{b_d}$
. We will call these substrings
![]() $r_d$
-blocks of
$r_d$
-blocks of
![]() $x$
, including the final one which may or may not actually have length equal to
$x$
, including the final one which may or may not actually have length equal to
![]() $r_d$
.
$r_d$
.
In the following definitions, we let
![]() $r_0=1$
and
$r_0=1$
and
![]() $r_{p+1}=\alpha$
. First, we define a function
$r_{p+1}=\alpha$
. First, we define a function
![]() $\eta _d$
for any
$\eta _d$
for any
![]() $d=0,\ldots,p$
on domain
$d=0,\ldots,p$
on domain
![]() $\{0,1\}^{\beta } \times \{0,1\}^{\beta }$
where
$\{0,1\}^{\beta } \times \{0,1\}^{\beta }$
where
![]() $\beta$
is any positive integer as
$\beta$
is any positive integer as
 \begin{align*} \eta _d(x,y) = \left \{ \begin{array}{ll} \left (i,\{x_i^{(d)},y_i^{(d)}\}\right ) & \quad x \neq y\\ 0 & \quad x=y \end{array} \right . \end{align*}
\begin{align*} \eta _d(x,y) = \left \{ \begin{array}{ll} \left (i,\{x_i^{(d)},y_i^{(d)}\}\right ) & \quad x \neq y\\ 0 & \quad x=y \end{array} \right . \end{align*}
where
![]() $i$
denotes the minimum index for which
$i$
denotes the minimum index for which
![]() $x_i^{(d)} \neq y_i^{(d)}$
.
$x_i^{(d)} \neq y_i^{(d)}$
.
For
![]() $x,y \in \{0,1\}^{\alpha }$
and
$x,y \in \{0,1\}^{\alpha }$
and
![]() $0 \leq d \leq p$
, let
$0 \leq d \leq p$
, let
And let
Next, we assume that the binary strings of
![]() $\{0,1\}^{\beta }$
are lexicographically ordered for every positive integer
$\{0,1\}^{\beta }$
are lexicographically ordered for every positive integer
![]() $\beta$
. For
$\beta$
. For
![]() $1 \leq i \leq a_p+1$
and binary strings
$1 \leq i \leq a_p+1$
and binary strings
![]() $x\lt y$
, define
$x\lt y$
, define
 \begin{align*} \delta _{p,i}(x,y) = \left \{ \begin{array}{ll} +1 & \quad \text{if }\; x_i^{(p)} \leq y_i^{(p)}\\ -1 & \quad \text{if }\; x_i^{(p)} \gt y_i^{(p)}. \end{array} \right . \end{align*}
\begin{align*} \delta _{p,i}(x,y) = \left \{ \begin{array}{ll} +1 & \quad \text{if }\; x_i^{(p)} \leq y_i^{(p)}\\ -1 & \quad \text{if }\; x_i^{(p)} \gt y_i^{(p)}. \end{array} \right . \end{align*}
Let
Finally, let
2.2 Number of colours
For any positive integer
![]() $n$
, let
$n$
, let
![]() $\beta$
be the positive integer for which
$\beta$
be the positive integer for which
For each
![]() $d=1,\ldots,p+1$
, let
$d=1,\ldots,p+1$
, let
![]() $r_d=\beta ^d$
in the construction of
$r_d=\beta ^d$
in the construction of
![]() $\psi _p$
. Specifically, this means we are constructing the colouring on the complete graph with vertex set
$\psi _p$
. Specifically, this means we are constructing the colouring on the complete graph with vertex set
![]() $\{0,1\}^{\alpha }$
where
$\{0,1\}^{\alpha }$
where
![]() $\alpha =\beta ^{p+1}$
. We can apply this colouring to
$\alpha =\beta ^{p+1}$
. We can apply this colouring to
![]() $K_n$
by arbitrarily associating each vertex of
$K_n$
by arbitrarily associating each vertex of
![]() $K_n$
with a unique binary string from
$K_n$
with a unique binary string from
![]() $\{0,1\}^{\alpha }$
and taking the induced colouring.
$\{0,1\}^{\alpha }$
and taking the induced colouring.
As shown in [Reference Conlon, Fox, Lee and Sudakov3], for these choices of parameters
![]() $r_d$
, the colouring
$r_d$
, the colouring
![]() $c_p$
uses at most
$c_p$
uses at most
![]() $2^{4(p+1)\beta ^p\log _2 \beta }$
colours. On the other hand,
$2^{4(p+1)\beta ^p\log _2 \beta }$
colours. On the other hand,
![]() $\Delta _p$
uses
$\Delta _p$
uses
colours. So all together,
![]() $\psi _p$
uses at most
$\psi _p$
uses at most
![]() $2^{4(p+1)\beta ^p\log _2 \beta +\beta }$
colours, where
$2^{4(p+1)\beta ^p\log _2 \beta +\beta }$
colours, where
Thus, for any fixed
![]() $p$
,
$p$
,
![]() $\psi _p$
uses a total of
$\psi _p$
uses a total of
![]() $n^{o(1)}$
colours.
$n^{o(1)}$
colours.
2.3 Refinement of functions
Before we prove Lemma 2.1, it will be helpful to give the following definition and results about refinement of functions. The definition and Lemma 2.3 are paraphrased from [Reference Conlon, Fox, Lee and Sudakov3].
Definition 2.2. Let
![]() $f\;:\;A \rightarrow B$
and
$f\;:\;A \rightarrow B$
and
![]() $g\;:\;A \rightarrow C$
. We say that
$g\;:\;A \rightarrow C$
. We say that
![]() $f$
refines
$f$
refines
![]() $g$
if
$g$
if
![]() $f(a_1)=f(a_2)$
implies that
$f(a_1)=f(a_2)$
implies that
![]() $g(a_1)=g(a_2)$
for all
$g(a_1)=g(a_2)$
for all
![]() $a_1,a_2 \in A$
.
$a_1,a_2 \in A$
.
Lemma 2.3 (Lemma 4.1(vi) from [Reference Conlon, Fox, Lee and Sudakov3]). Let
![]() $f,g$
be functions on domain
$f,g$
be functions on domain
![]() $A$
. If
$A$
. If
![]() $f$
refines
$f$
refines
![]() $g$
, then for all
$g$
, then for all
![]() $A' \subseteq A$
, we have
$A' \subseteq A$
, we have
![]() $|f(A')| \geq |g(A')|$
.
$|f(A')| \geq |g(A')|$
.
Lemma 2.4.
Let
![]() $f,g$
be functions on domain
$f,g$
be functions on domain
![]() $A$
. If
$A$
. If
![]() $f$
refines
$f$
refines
![]() $g$
and
$g$
and
![]() $S \subseteq A$
is a finite subset for which
$S \subseteq A$
is a finite subset for which
![]() $|f(S)|=|g(S)|$
, then
$|f(S)|=|g(S)|$
, then
for all
![]() $s_1,s_2 \in S$
.
$s_1,s_2 \in S$
.
Proof. The forward direction follows from the definition of
![]() $f$
refining
$f$
refining
![]() $g$
. Conversely, if we have
$g$
. Conversely, if we have
![]() $g(s_1)=g(s_2)$
but
$g(s_1)=g(s_2)$
but
![]() $f(s_1) \neq f(s_2)$
for some
$f(s_1) \neq f(s_2)$
for some
![]() $s_1,s_2 \in S$
, then
$s_1,s_2 \in S$
, then
![]() $|f(S)| \geq |g(S)|+1$
, a contradiction.
$|f(S)| \geq |g(S)|+1$
, a contradiction.![]()
In particular, Lemma 2.4 implies that if some edge-colouring of a clique
![]() $S$
is refined by another edge-colouring, but
$S$
is refined by another edge-colouring, but
![]() $S$
contains the same number of colours under each, then the edge-colourings must be isomorphic.
$S$
contains the same number of colours under each, then the edge-colourings must be isomorphic.
2.4 Proof of Lemma 2.1
Let
![]() $S \subseteq \{0,1\}^{\alpha }$
be a set of
$S \subseteq \{0,1\}^{\alpha }$
be a set of
![]() $|S| \leq p+3$
vertices which contains exactly
$|S| \leq p+3$
vertices which contains exactly
![]() $|S|-1$
distinct edge colours under
$|S|-1$
distinct edge colours under
![]() $c_p$
. We will prove that
$c_p$
. We will prove that
![]() $S$
either has a leftover structure or contains a striped
$S$
either has a leftover structure or contains a striped
![]() $K_4$
by induction on
$K_4$
by induction on
![]() $\alpha$
, similar to the proof of Theorem 2.2 from [Reference Conlon, Fox, Lee and Sudakov3].
$\alpha$
, similar to the proof of Theorem 2.2 from [Reference Conlon, Fox, Lee and Sudakov3].
For the base case, consider
![]() $\alpha \leq r_p$
. Then for any
$\alpha \leq r_p$
. Then for any
![]() $x,y \in S$
, the first component of
$x,y \in S$
, the first component of
![]() $c_p(x,y)$
is
$c_p(x,y)$
is
Therefore, all of the edges of
![]() $S$
receive distinct colours. So it must be that
$S$
receive distinct colours. So it must be that
![]() $|S|-1=\binom{|S|}{2}$
, which happens only when
$|S|-1=\binom{|S|}{2}$
, which happens only when
![]() $|S|=1,2$
. In either case,
$|S|=1,2$
. In either case,
![]() $S$
trivially has a leftover structure.
$S$
trivially has a leftover structure.
Now assume that
![]() $\alpha \gt r_p$
and that the statement is true for shorter binary strings. For each
$\alpha \gt r_p$
and that the statement is true for shorter binary strings. For each
![]() $d=1,\ldots,p$
, let
$d=1,\ldots,p$
, let
![]() $\alpha _d$
be the largest integer strictly less than
$\alpha _d$
be the largest integer strictly less than
![]() $\alpha$
that is divisible by
$\alpha$
that is divisible by
![]() $r_d$
. For any
$r_d$
. For any
![]() $x \in S$
, let
$x \in S$
, let
![]() $x=(x'_{\!\!d},x''_{\!\!\!d})$
for
$x=(x'_{\!\!d},x''_{\!\!\!d})$
for
![]() $x'_{\!\!d} \in \{0,1\}^{\alpha _d}$
and
$x'_{\!\!d} \in \{0,1\}^{\alpha _d}$
and
![]() $x''_{\!\!\!d} \in \{0,1\}^{\alpha -\alpha _d}$
.
$x''_{\!\!\!d} \in \{0,1\}^{\alpha -\alpha _d}$
.
Let
![]() $S_d$
denote the set of
$S_d$
denote the set of
![]() $\alpha _d$
-prefixes of
$\alpha _d$
-prefixes of
![]() $S$
,
$S$
,
For each
![]() $x'_{\!\!d} \in S_d$
, let
$x'_{\!\!d} \in S_d$
, let
Let
![]() $\Lambda _I^{(d)}$
be the set of colours contained in
$\Lambda _I^{(d)}$
be the set of colours contained in
![]() $S$
found on edges that go between vertices from two distinct
$S$
found on edges that go between vertices from two distinct
![]() $T$
-sets,
$T$
-sets,
Similarly, let
![]() $\Lambda _E^{(d)}$
denote the set of colours contained in
$\Lambda _E^{(d)}$
denote the set of colours contained in
![]() $S$
found on edges between vertices from the same
$S$
found on edges between vertices from the same
![]() $T$
-set,
$T$
-set,
Note that these sets of colours,
![]() $\Lambda _I^{(d)}$
and
$\Lambda _I^{(d)}$
and
![]() $\Lambda _E^{(d)}$
, partition all of the colours contained in
$\Lambda _E^{(d)}$
, partition all of the colours contained in
![]() $S$
. Therefore,
$S$
. Therefore,
Next, define
 \begin{align*} C_I^{(d)} &= \left \{(c_p(x'_{\!\!d},y'_{\!\!d}),\eta _{d-1}(x''_{\!\!\!d},y''_{\!\!\!d}))|x,y \in S;\; x'_{\!\!d} \neq y'_{\!\!d}\right \}\\ C_E^{(d)} &= \left \{\{x''_{\!\!\!d},y''_{\!\!\!d}\}|x,y \in S;\; x \neq y;\; x'_{\!\!d} = y'_{\!\!d}\right \}.\\ \end{align*}
\begin{align*} C_I^{(d)} &= \left \{(c_p(x'_{\!\!d},y'_{\!\!d}),\eta _{d-1}(x''_{\!\!\!d},y''_{\!\!\!d}))|x,y \in S;\; x'_{\!\!d} \neq y'_{\!\!d}\right \}\\ C_E^{(d)} &= \left \{\{x''_{\!\!\!d},y''_{\!\!\!d}\}|x,y \in S;\; x \neq y;\; x'_{\!\!d} = y'_{\!\!d}\right \}.\\ \end{align*}
It is shown in [Reference Conlon, Fox, Lee and Sudakov3] that
![]() $|\Lambda _I^{(d)}| \geq |C_I^{(d)}|$
and that
$|\Lambda _I^{(d)}| \geq |C_I^{(d)}|$
and that
![]() $|\Lambda _E^{(d)}| \geq |C_E^{(d)}|$
. The second inequality is easier to see since any distinct
$|\Lambda _E^{(d)}| \geq |C_E^{(d)}|$
. The second inequality is easier to see since any distinct
![]() $x,y \in S$
for which
$x,y \in S$
for which
![]() $x'_{\!\!d} = y'_{\!\!d}$
give
$x'_{\!\!d} = y'_{\!\!d}$
give
![]() $\xi _d=\left (0,\ldots,0,(i,\{x''_{\!\!\!d},y''_{\!\!\!d}\})\right )$
as the appropriate component of
$\xi _d=\left (0,\ldots,0,(i,\{x''_{\!\!\!d},y''_{\!\!\!d}\})\right )$
as the appropriate component of
![]() $c_p(x,y)$
. Although the first inequality seems intuitively true, its proof is a bit more subtle. The following fact (proved in [Reference Conlon, Fox, Lee and Sudakov3]) together with Lemma 2.3 gives us the desired inequality.
$c_p(x,y)$
. Although the first inequality seems intuitively true, its proof is a bit more subtle. The following fact (proved in [Reference Conlon, Fox, Lee and Sudakov3]) together with Lemma 2.3 gives us the desired inequality.
Fact 2.1 (Lemma 4.3 from [Reference Conlon, Fox, Lee and Sudakov3]). For
![]() $x,y \in \{0,1\}^{\alpha }$
, let
$x,y \in \{0,1\}^{\alpha }$
, let
Then
![]() $c_p$
refines
$c_p$
refines
![]() $\gamma _d$
as functions on domain
$\gamma _d$
as functions on domain
![]() $\{0,1\}^{\alpha } \times \{0,1\}^{\alpha }$
.
$\{0,1\}^{\alpha } \times \{0,1\}^{\alpha }$
.
We will also use the following fact which is proven in [Reference Conlon, Fox, Lee and Sudakov3], although not stated as a claim or lemma that can be easily cited. (See the final sentence of the second-to-final paragraph on page 11.)
Fact 2.2 (proved in [Reference Conlon, Fox, Lee and Sudakov3]). There exists an integer
![]() $1 \leq d \leq p$
for which
$1 \leq d \leq p$
for which
Therefore,
which implies that
Let
 \begin{align*} \tilde{c}_p(x,y) = \left \{ \begin{array}{ll} (c_p(x'_{\!\!d},y'_{\!\!d}),\eta _{d-1}(x''_{\!\!\!d},y''_{\!\!\!d})) & \quad \text{if }\; x'_{\!\!d} \neq y'_{\!\!d}\\ \{x''_{\!\!\!d},y''_{\!\!\!d}\} & \quad \text{otherwise}. \end{array} \right . \end{align*}
\begin{align*} \tilde{c}_p(x,y) = \left \{ \begin{array}{ll} (c_p(x'_{\!\!d},y'_{\!\!d}),\eta _{d-1}(x''_{\!\!\!d},y''_{\!\!\!d})) & \quad \text{if }\; x'_{\!\!d} \neq y'_{\!\!d}\\ \{x''_{\!\!\!d},y''_{\!\!\!d}\} & \quad \text{otherwise}. \end{array} \right . \end{align*}
Then by Fact 2.1, we know that
![]() $\tilde{c}_p$
refines
$\tilde{c}_p$
refines
![]() $c_p$
. And since
$c_p$
. And since
![]() $|\Lambda _I^{(d)}|+|\Lambda _E^{(d)}| = |C_I^{(d)}|+|C_E^{(d)}|$
, then by Lemma 2.4, we know that the structure of
$|\Lambda _I^{(d)}|+|\Lambda _E^{(d)}| = |C_I^{(d)}|+|C_E^{(d)}|$
, then by Lemma 2.4, we know that the structure of
![]() $S$
under
$S$
under
![]() $\tilde{c}_p$
must be the same as the structure of
$\tilde{c}_p$
must be the same as the structure of
![]() $S$
under
$S$
under
![]() $c_p$
. Therefore, we need only show that
$c_p$
. Therefore, we need only show that
![]() $S$
either has a leftover structure or contains a striped
$S$
either has a leftover structure or contains a striped
![]() $K_4$
under
$K_4$
under
![]() $\tilde{c}_p$
to complete the proof. We consider two cases: either there exists some
$\tilde{c}_p$
to complete the proof. We consider two cases: either there exists some
![]() $\omega \in C_E^{(d)}$
that appears more than once in
$\omega \in C_E^{(d)}$
that appears more than once in
![]() $S$
under
$S$
under
![]() $\tilde{c}_p$
or each
$\tilde{c}_p$
or each
![]() $\omega \in C_E^{(d)}$
appears exactly once in
$\omega \in C_E^{(d)}$
appears exactly once in
![]() $S$
under
$S$
under
![]() $\tilde{c}_p$
.
$\tilde{c}_p$
.
Case 1: Let
![]() $\omega \in C_E^{(d)}$
appear on at least two edges in
$\omega \in C_E^{(d)}$
appear on at least two edges in
![]() $S$
. This implies that
$S$
. This implies that
![]() $\omega =\{x''_{\!\!\!d},y''_{\!\!\!d}\}$
and so there must exist
$\omega =\{x''_{\!\!\!d},y''_{\!\!\!d}\}$
and so there must exist
![]() $a,b,c,e \in S$
such that
$a,b,c,e \in S$
such that
![]() $a=(x'_{\!\!d},x''_{\!\!\!d})$
,
$a=(x'_{\!\!d},x''_{\!\!\!d})$
,
![]() $b=(x'_{\!\!d},y''_{\!\!\!d})$
,
$b=(x'_{\!\!d},y''_{\!\!\!d})$
,
![]() $c=(y'_{\!\!d},x''_{\!\!\!d})$
, and
$c=(y'_{\!\!d},x''_{\!\!\!d})$
, and
![]() $e=(y'_{\!\!d},y''_{\!\!\!d})$
for some
$e=(y'_{\!\!d},y''_{\!\!\!d})$
for some
![]() $x'_{\!\!d} \neq y'_{\!\!d}$
. Therefore,
$x'_{\!\!d} \neq y'_{\!\!d}$
. Therefore,
 \begin{align*} \tilde{c}_p(a,b)=\tilde{c}_p(c,e)&=\{x''_{\!\!\!d},y''_{\!\!\!d}\}\\ \tilde{c}_p(a,c)=\tilde{c}_p(b,e)&=(c_p(x'_{\!\!d},y'_{\!\!d}),0)\\ \tilde{c}_p(a,e)=\tilde{c}_p(b,c)&=(c_p(x'_{\!\!d},y'_{\!\!d}),\eta _{d-1}(x''_{\!\!\!d},y''_{\!\!\!d})), \end{align*}
\begin{align*} \tilde{c}_p(a,b)=\tilde{c}_p(c,e)&=\{x''_{\!\!\!d},y''_{\!\!\!d}\}\\ \tilde{c}_p(a,c)=\tilde{c}_p(b,e)&=(c_p(x'_{\!\!d},y'_{\!\!d}),0)\\ \tilde{c}_p(a,e)=\tilde{c}_p(b,c)&=(c_p(x'_{\!\!d},y'_{\!\!d}),\eta _{d-1}(x''_{\!\!\!d},y''_{\!\!\!d})), \end{align*}
and all three colours are distinct. Hence,
![]() $S$
contains a striped
$S$
contains a striped
![]() $K_4$
under
$K_4$
under
![]() $\tilde{c}_p$
.
$\tilde{c}_p$
.
Case 2: If each
![]() $\omega \in C_E^{(d)}$
appears exactly once in
$\omega \in C_E^{(d)}$
appears exactly once in
![]() $S$
under
$S$
under
![]() $\tilde{c}_p$
, then we know that
$\tilde{c}_p$
, then we know that
 \begin{align*} |C_E^{(d)}| = \sum _{x'_{\!\!d} \in S_d}\binom{|T_{x'_{\!\!d}}|}{2} \end{align*}
\begin{align*} |C_E^{(d)}| = \sum _{x'_{\!\!d} \in S_d}\binom{|T_{x'_{\!\!d}}|}{2} \end{align*}
since each edge within a given
![]() $T$
-set receives a unique colour. Moreover, if we let
$T$
-set receives a unique colour. Moreover, if we let
then we know that
Therefore,
 \begin{align*} |S_d|-1+\sum _{x'_{\!\!d} \in S_d}\binom{|T_{x'_{\!\!d}}|}{2} &\leq |S|-1\\[4pt] \sum _{x'_{\!\!d} \in S_d}\binom{|T_{x'_{\!\!d}}|}{2} &\leq |S|-|S_d|\\[4pt] \sum _{x'_{\!\!d} \in S_d}\binom{|T_{x'_{\!\!d}}|}{2} &\leq \sum _{x'_{\!\!d} \in S_d} (|T_{x'_{\!\!d}}|-1)\\[4pt] \sum _{x'_{\!\!d} \in S_d}(|T_{x'_{\!\!d}}|-1)(|T_{x'_{\!\!d}}|-2) &\leq 0. \end{align*}
\begin{align*} |S_d|-1+\sum _{x'_{\!\!d} \in S_d}\binom{|T_{x'_{\!\!d}}|}{2} &\leq |S|-1\\[4pt] \sum _{x'_{\!\!d} \in S_d}\binom{|T_{x'_{\!\!d}}|}{2} &\leq |S|-|S_d|\\[4pt] \sum _{x'_{\!\!d} \in S_d}\binom{|T_{x'_{\!\!d}}|}{2} &\leq \sum _{x'_{\!\!d} \in S_d} (|T_{x'_{\!\!d}}|-1)\\[4pt] \sum _{x'_{\!\!d} \in S_d}(|T_{x'_{\!\!d}}|-1)(|T_{x'_{\!\!d}}|-2) &\leq 0. \end{align*}
Hence, we have
![]() $|T_{x'_{\!\!d}}|=1,2$
for each
$|T_{x'_{\!\!d}}|=1,2$
for each
![]() $x'_{\!\!d} \in S_d$
. This implies that
$x'_{\!\!d} \in S_d$
. This implies that
![]() $|C_E^{(d)}|=\sum _{x'_{\!\!d} \in S_d} (|T_{x'_{\!\!d}}|-1)$
and
$|C_E^{(d)}|=\sum _{x'_{\!\!d} \in S_d} (|T_{x'_{\!\!d}}|-1)$
and
![]() $|C_I^{(d)}|=|C_B^{(d)}|=|S_d|-1$
. So by induction,
$|C_I^{(d)}|=|C_B^{(d)}|=|S_d|-1$
. So by induction,
![]() $S_d$
either has a leftover structure or contains a striped
$S_d$
either has a leftover structure or contains a striped
![]() $K_4$
under
$K_4$
under
![]() $c_p$
. Furthermore, the colouring defined by
$c_p$
. Furthermore, the colouring defined by
 \begin{align*} c'_{\!\!p}(x,y) = \left \{ \begin{array}{ll} c_p(x'_{\!\!d},y'_{\!\!d}) & \quad \text{if }\; x'_{\!\!d} \neq y'_{\!\!d}\\ \{x''_{\!\!\!d},y''_{\!\!\!d}\} & \quad \text{otherwise} \end{array} \right . \end{align*}
\begin{align*} c'_{\!\!p}(x,y) = \left \{ \begin{array}{ll} c_p(x'_{\!\!d},y'_{\!\!d}) & \quad \text{if }\; x'_{\!\!d} \neq y'_{\!\!d}\\ \{x''_{\!\!\!d},y''_{\!\!\!d}\} & \quad \text{otherwise} \end{array} \right . \end{align*}
is refined by
![]() $\tilde{c}_p$
, and
$\tilde{c}_p$
, and
![]() $S$
contains exactly
$S$
contains exactly
![]() $|S|-1$
colours under both
$|S|-1$
colours under both
![]() $c'_{\!\!p}$
and
$c'_{\!\!p}$
and
![]() $\tilde{c}_p$
. So by Lemma 2.4, the edge-colouring of
$\tilde{c}_p$
. So by Lemma 2.4, the edge-colouring of
![]() $S$
under
$S$
under
![]() $\tilde{c}_p$
is isomorphic to the one under
$\tilde{c}_p$
is isomorphic to the one under
![]() $c'_{\!\!p}$
, and hence it is sufficient to show that
$c'_{\!\!p}$
, and hence it is sufficient to show that
![]() $S$
has either a leftover structure or contains a striped
$S$
has either a leftover structure or contains a striped
![]() $K_4$
under
$K_4$
under
![]() $c'_{\!\!p}$
.
$c'_{\!\!p}$
.
If
![]() $S_d$
has a leftover structure under
$S_d$
has a leftover structure under
![]() $c_p$
, then we see that
$c_p$
, then we see that
![]() $S$
also has a leftover structure under
$S$
also has a leftover structure under
![]() $c'_{\!\!p}$
since we can form
$c'_{\!\!p}$
since we can form
![]() $S$
under
$S$
under
![]() $c'_{\!\!p}$
from
$c'_{\!\!p}$
from
![]() $S_d$
under
$S_d$
under
![]() $c_p$
by a sequence of splits as described in the definition of a leftover structure. That is, for each
$c_p$
by a sequence of splits as described in the definition of a leftover structure. That is, for each
![]() $x'_{\!\!d} \in S_d$
for which
$x'_{\!\!d} \in S_d$
for which
![]() $|T_{x'_{\!\!d}}| = 2$
, we replace
$|T_{x'_{\!\!d}}| = 2$
, we replace
![]() $x'_{\!\!d}$
with two vertices with a new edge colour between them, and the same edge colours that
$x'_{\!\!d}$
with two vertices with a new edge colour between them, and the same edge colours that
![]() $x'_{\!\!d}$
already had to the rest of the vertices.
$x'_{\!\!d}$
already had to the rest of the vertices.
On the other hand, if
![]() $S_d$
contains a striped
$S_d$
contains a striped
![]() $K_4$
under
$K_4$
under
![]() $c_p$
, then
$c_p$
, then
![]() $S$
must contain a striped
$S$
must contain a striped
![]() $K_4$
under
$K_4$
under
![]() $c'_{\!\!p}$
with colours entirely from
$c'_{\!\!p}$
with colours entirely from
![]() $C_B^{(d)}$
. This concludes the proof.
$C_B^{(d)}$
. This concludes the proof.
2.5 Proof of Lemma 2.2
Let
![]() $a,b,c,d \in \{0,1\}^{\alpha }$
be four distinct vertices, and assume towards a contradiction that they form a striped
$a,b,c,d \in \{0,1\}^{\alpha }$
be four distinct vertices, and assume towards a contradiction that they form a striped
![]() $K_4$
under
$K_4$
under
![]() $\psi _p$
. Specifically, assume that
$\psi _p$
. Specifically, assume that
![]() $\psi _p(a,b)=\psi _p(c,d)$
,
$\psi _p(a,b)=\psi _p(c,d)$
,
![]() $\psi _p(a,c)=\psi _p(b,d)$
, and
$\psi _p(a,c)=\psi _p(b,d)$
, and
![]() $\psi _p(a,d)=\psi _p(b,c)$
.
$\psi _p(a,d)=\psi _p(b,c)$
.
Without loss of generality, we may assume the following: that
![]() $a$
is the minimum element of the four under the lexicographic ordering of
$a$
is the minimum element of the four under the lexicographic ordering of
![]() $\{0,1\}^{\alpha }$
; that for some
$\{0,1\}^{\alpha }$
; that for some
![]() $i \leq j,k$
,
$i \leq j,k$
,
 \begin{align*} \eta _p(a,b) = \eta _p(c,d) &= (i,\{x,y\})\\ \eta _p(a,c) = \eta _p(b,d) &= (j,\{z,w\})\\ \eta _p(a,d) = \eta _p(b,c) &= (k,\{s,t\}); \end{align*}
\begin{align*} \eta _p(a,b) = \eta _p(c,d) &= (i,\{x,y\})\\ \eta _p(a,c) = \eta _p(b,d) &= (j,\{z,w\})\\ \eta _p(a,d) = \eta _p(b,c) &= (k,\{s,t\}); \end{align*}
and that
![]() $a_i^{(p)}=c_i^{(p)}=x$
while
$a_i^{(p)}=c_i^{(p)}=x$
while
![]() $b_i^{(p)}=d_i^{(p)}=y$
. It follows from the ordering that
$b_i^{(p)}=d_i^{(p)}=y$
. It follows from the ordering that
![]() $x \lt y$
and that
$x \lt y$
and that
![]() $a\lt c\lt b,d$
. Furthermore, we have
$a\lt c\lt b,d$
. Furthermore, we have
![]() $i\lt j$
since
$i\lt j$
since
![]() $a$
and
$a$
and
![]() $c$
do not differ in the
$c$
do not differ in the
![]() $i^{th}$
block. Similarly, we see that
$i^{th}$
block. Similarly, we see that
![]() $(k,\{s,t\})=(i,\{x,y\})$
. Without loss of generality, we may assume
$(k,\{s,t\})=(i,\{x,y\})$
. Without loss of generality, we may assume
![]() $a_j^{(p)}=b_j^{(p)}=z$
and
$a_j^{(p)}=b_j^{(p)}=z$
and
![]() $c_j^{(p)}=d_j^{(p)}=w$
. Therefore,
$c_j^{(p)}=d_j^{(p)}=w$
. Therefore,
![]() $z\lt w$
and
$z\lt w$
and
![]() $a\lt c\lt b\lt d$
.
$a\lt c\lt b\lt d$
.
Now, it follows that
![]() $\delta _j(a,d) = +1$
and that
$\delta _j(a,d) = +1$
and that
![]() $\delta _j(c,b)=-1$
, contradicting our assumption that
$\delta _j(c,b)=-1$
, contradicting our assumption that
![]() $\psi _p(a,d)=\psi _p(c,b)$
.
$\psi _p(a,d)=\psi _p(c,b)$
.
3. Modified Dot Product colouring
Fix an odd prime power
![]() $q$
and a positive integer
$q$
and a positive integer
![]() $d$
. In this section, we prove Theorem 1.2 by giving an edge-colouring
$d$
. In this section, we prove Theorem 1.2 by giving an edge-colouring
![]() $\varphi _d$
for the complete graph on
$\varphi _d$
for the complete graph on
![]() $n=(q-1)^d$
vertices that uses
$n=(q-1)^d$
vertices that uses
![]() $(3d+1)q-1$
colours and contains no leftover 6-cliques when
$(3d+1)q-1$
colours and contains no leftover 6-cliques when
![]() $d=3$
and no leftover 8-cliques when
$d=3$
and no leftover 8-cliques when
![]() $d=4$
.
$d=4$
.
In what follows, we make use of several standard concepts and results from linear algebra without providing explicit definitions or proofs. We highly recommend Linear Algebra Methods in Combinatorics by László Babai and Péter Frankl [Reference Babai and Frankl1] for a detailed treatment of these ideas. In particular, Chapter 2 covers all of the necessary background for our argument.
3.1 The construction
Let
![]() ${\mathbb{F}}_q^*$
denote the nonzero elements of the finite field with
${\mathbb{F}}_q^*$
denote the nonzero elements of the finite field with
![]() $q$
elements, and let
$q$
elements, and let
![]() $({\mathbb{F}}_q^*)^d$
denote the set of ordered
$({\mathbb{F}}_q^*)^d$
denote the set of ordered
![]() $d$
-tuples of elements from
$d$
-tuples of elements from
![]() ${\mathbb{F}}_q^*$
. In other words,
${\mathbb{F}}_q^*$
. In other words,
![]() $({\mathbb{F}}_q^*)^d$
is the set of
$({\mathbb{F}}_q^*)^d$
is the set of
![]() $d$
-dimensional vectors over the field
$d$
-dimensional vectors over the field
![]() ${\mathbb{F}}_q$
without zero components. In what follows, we will assume that the set
${\mathbb{F}}_q$
without zero components. In what follows, we will assume that the set
![]() ${\mathbb{F}}_q^*$
is endowed with a linear order which can be arbitrarily chosen. We then order the set
${\mathbb{F}}_q^*$
is endowed with a linear order which can be arbitrarily chosen. We then order the set
![]() $({\mathbb{F}}_q^*)^d$
with lexicographic ordering based on the order applied to
$({\mathbb{F}}_q^*)^d$
with lexicographic ordering based on the order applied to
![]() ${\mathbb{F}}_q^*$
.
${\mathbb{F}}_q^*$
.
Define a set of colours
![]() $C_d$
as the disjoint union
$C_d$
as the disjoint union
where
![]() $\text{DOT}={\mathbb{F}}_q^*$
, and ZERO, UP, and DOWN are each copies of the set
$\text{DOT}={\mathbb{F}}_q^*$
, and ZERO, UP, and DOWN are each copies of the set
![]() $\{1,\ldots,d\} \times{\mathbb{F}}_q$
. Let
$\{1,\ldots,d\} \times{\mathbb{F}}_q$
. Let
be a colouring function of pairs of distinct vectors,
![]() $x\lt y$
, defined by
$x\lt y$
, defined by
 \begin{align*} \varphi _d\left (x,y\right ) = \left \{ \begin{array}{ll} (i,x_i+y_i)_{\text{ZERO}} & \quad \text{if }\; x \cdot y=0\\ (i,x_i+y_i)_{\text{UP}} & \quad \text{if }\; x \cdot y \neq 0 \text{ and } x \cdot y = x \cdot x\\ (i,x_i+y_i)_{\text{DOWN}} & \quad \text{if }\; x \cdot y \not \in \{0,x \cdot x\} \text{ and } x \cdot y = y \cdot y\\ x \cdot y & \quad \text{otherwise}\\ \end{array} \right . \end{align*}
\begin{align*} \varphi _d\left (x,y\right ) = \left \{ \begin{array}{ll} (i,x_i+y_i)_{\text{ZERO}} & \quad \text{if }\; x \cdot y=0\\ (i,x_i+y_i)_{\text{UP}} & \quad \text{if }\; x \cdot y \neq 0 \text{ and } x \cdot y = x \cdot x\\ (i,x_i+y_i)_{\text{DOWN}} & \quad \text{if }\; x \cdot y \not \in \{0,x \cdot x\} \text{ and } x \cdot y = y \cdot y\\ x \cdot y & \quad \text{otherwise}\\ \end{array} \right . \end{align*}
where
![]() $i$
is the first coordinate for which
$i$
is the first coordinate for which
![]() $x=(x_1,\ldots,x_d)$
differs from
$x=(x_1,\ldots,x_d)$
differs from
![]() $y=(y_1,\ldots,y_d)$
and
$y=(y_1,\ldots,y_d)$
and
![]() $x \cdot y$
denotes the standard inner product (dot product).
$x \cdot y$
denotes the standard inner product (dot product).
3.2 Number of colours
Let
![]() $n$
be a positive integer. Let
$n$
be a positive integer. Let
![]() $q$
be the smallest odd prime power for which
$q$
be the smallest odd prime power for which
![]() $n \leq (q-1)^d$
. Then we can colour the edges of
$n \leq (q-1)^d$
. Then we can colour the edges of
![]() $K_n$
by arbitrarily associating each vertex with a unique vector from
$K_n$
by arbitrarily associating each vertex with a unique vector from
![]() $({\mathbb{F}}_q^*)^d$
and taking the colouring induced by
$({\mathbb{F}}_q^*)^d$
and taking the colouring induced by
![]() $\varphi _d$
. By Bertrand’s Postulate,
$\varphi _d$
. By Bertrand’s Postulate,
![]() $q \leq 2(n^{1/d}+1)$
. Therefore, the number of colours used by
$q \leq 2(n^{1/d}+1)$
. Therefore, the number of colours used by
![]() $\varphi _d$
on
$\varphi _d$
on
![]() $K_n$
is at most
$K_n$
is at most
3.3 Proof of Theorem 1.2
Definition 3.1. Given a subset of vectors
![]() $S \subseteq{\mathbb{F}}^d$
, let
$S \subseteq{\mathbb{F}}^d$
, let
![]() $\text{rk}(S)$
denote the rank of the subset, the dimension of the linear subspace spanned by the vectors of
$\text{rk}(S)$
denote the rank of the subset, the dimension of the linear subspace spanned by the vectors of
![]() $S$
. Let
$S$
. Let
![]() ${\textrm{af}}(S)$
denote the affine dimension of
${\textrm{af}}(S)$
denote the affine dimension of
![]() $S$
, the dimension of the affine subspace (also known as the affine hull) spanned by
$S$
, the dimension of the affine subspace (also known as the affine hull) spanned by
![]() $S$
.
$S$
.
Definition 3.2. A colour
![]() $\alpha \in C_d$
has the dot property if
$\alpha \in C_d$
has the dot property if
![]() $\alpha \in \text{DOT} \cup \text{ZERO}$
. Note that if
$\alpha \in \text{DOT} \cup \text{ZERO}$
. Note that if
![]() $\alpha$
has the dot property, then
$\alpha$
has the dot property, then
![]() $\varphi _d\left (a,b\right ) = \varphi _d\left (e,f\right )=\alpha$
implies that
$\varphi _d\left (a,b\right ) = \varphi _d\left (e,f\right )=\alpha$
implies that
![]() $a \cdot b = e \cdot f$
for any
$a \cdot b = e \cdot f$
for any
![]() $a,b,e,f\in ({\mathbb{F}}_q^*)^d$
.
$a,b,e,f\in ({\mathbb{F}}_q^*)^d$
.
Lemma 3.1.
Let
![]() $\{s_1,\ldots,s_t\} \subseteq ({\mathbb{F}}_q^*)^d$
be a set of linearly independent vectors and let
$\{s_1,\ldots,s_t\} \subseteq ({\mathbb{F}}_q^*)^d$
be a set of linearly independent vectors and let
![]() $a,b \in ({\mathbb{F}}_q^*)^d$
such that
$a,b \in ({\mathbb{F}}_q^*)^d$
such that
for some
![]() $\alpha,\beta \in C_d$
and for each
$\alpha,\beta \in C_d$
and for each
![]() $1\leq i \leq t$
. Then
$1\leq i \leq t$
. Then
![]() $s_1,\ldots, s_{t},b$
are linearly independent.
$s_1,\ldots, s_{t},b$
are linearly independent.
Proof. Assume towards a contradiction that
![]() $b=\sum _{j=1}^{t} \lambda _j s_j$
for some scalars
$b=\sum _{j=1}^{t} \lambda _j s_j$
for some scalars
![]() $\lambda _1,\ldots,\lambda _{t} \in{\mathbb{F}}_q$
. We will first show that
$\lambda _1,\ldots,\lambda _{t} \in{\mathbb{F}}_q$
. We will first show that
![]() $\sum _{j=1}^{t}\lambda _j=1$
.
$\sum _{j=1}^{t}\lambda _j=1$
.
If
![]() $\alpha \in$
DOT, then
$\alpha \in$
DOT, then
![]() $b=\sum _{j=1}^{t}\lambda _j s_j$
implies that
$b=\sum _{j=1}^{t}\lambda _j s_j$
implies that
 \begin{align*} \alpha =a \cdot b = \sum _{j=1}^{t}\lambda _j(a\cdot s_j)=\sum _{j=1}^{t}\lambda _j\alpha . \end{align*}
\begin{align*} \alpha =a \cdot b = \sum _{j=1}^{t}\lambda _j(a\cdot s_j)=\sum _{j=1}^{t}\lambda _j\alpha . \end{align*}
Therefore,
![]() $\sum _{j=1}^{t}\lambda _j=1$
since
$\sum _{j=1}^{t}\lambda _j=1$
since
![]() $\alpha \notin$
ZERO.
$\alpha \notin$
ZERO.
If
![]() $\alpha \notin$
DOT, then
$\alpha \notin$
DOT, then
where
![]() $i$
is the first index of difference between
$i$
is the first index of difference between
![]() $a$
and
$a$
and
![]() $b$
. Thus,
$b$
. Thus,
![]() $s_{j,i}=b_i$
for all
$s_{j,i}=b_i$
for all
![]() $1\leq j\leq t$
. But then
$1\leq j\leq t$
. But then
![]() $b=\sum _{j=1}^{t}\lambda _j s_j$
implies that
$b=\sum _{j=1}^{t}\lambda _j s_j$
implies that
 \begin{align*} b_i=\sum _{j=1}^{t}\lambda _j s_{j,i}=\sum _{j=1}^{t}\lambda _j b_i. \end{align*}
\begin{align*} b_i=\sum _{j=1}^{t}\lambda _j s_{j,i}=\sum _{j=1}^{t}\lambda _j b_i. \end{align*}
Hence,
![]() $\sum _{j=1}^{t}\lambda _j=1$
since
$\sum _{j=1}^{t}\lambda _j=1$
since
![]() $b_i \neq 0$
. Therefore, for any
$b_i \neq 0$
. Therefore, for any
![]() $\alpha \in C_d$
we have
$\alpha \in C_d$
we have
![]() $\sum _{j=1}^{t} \lambda _j=1$
.
$\sum _{j=1}^{t} \lambda _j=1$
.
Now, if
![]() $\beta$
has the dot property, then let
$\beta$
has the dot property, then let
![]() $\beta '$
denote
$\beta '$
denote
![]() $b \cdot s_j$
for all
$b \cdot s_j$
for all
![]() $j=1,\ldots,t$
. We have
$j=1,\ldots,t$
. We have
 \begin{align*} b \cdot b =\sum _{j=1}^{t}\lambda _j(b\cdot s_j)=\sum _{j=1}^{t}\lambda _j\beta '=\beta '. \end{align*}
\begin{align*} b \cdot b =\sum _{j=1}^{t}\lambda _j(b\cdot s_j)=\sum _{j=1}^{t}\lambda _j\beta '=\beta '. \end{align*}
But this implies that
![]() $\beta \in \text{UP} \cup \text{DOWN}$
, contradicting that
$\beta \in \text{UP} \cup \text{DOWN}$
, contradicting that
![]() $\beta$
has the dot property.
$\beta$
has the dot property.
So we must assume that
![]() $\beta$
does not have the dot property. It follows that
$\beta$
does not have the dot property. It follows that
where
![]() $k$
is the first index of difference between
$k$
is the first index of difference between
![]() $b$
and
$b$
and
![]() $s_1$
. Therefore,
$s_1$
. Therefore,
![]() $s_{1,k}=\cdots =s_{t,k}$
, and so
$s_{1,k}=\cdots =s_{t,k}$
, and so
 \begin{align*} b_k = \sum _{j=1}^t \lambda _j s_{j,k} = \sum _{j=1}^t \lambda _j s_{1,k} = s_{1,k}, \end{align*}
\begin{align*} b_k = \sum _{j=1}^t \lambda _j s_{j,k} = \sum _{j=1}^t \lambda _j s_{1,k} = s_{1,k}, \end{align*}
contradicting our choice of
![]() $k$
.
$k$
.
Since we reach a contradiction for all colours
![]() $\beta$
, it must be the case that
$\beta$
, it must be the case that
![]() $s_1,\ldots, s_{t},b$
are linearly independent vectors, as desired.
$s_1,\ldots, s_{t},b$
are linearly independent vectors, as desired.![]()
We now define a particular instance of leftover structure that will be useful in our arguments.
Definition 3.3. We call the set of vectors
![]() $S=\{s_1,\ldots,s_t\} \subseteq ({\mathbb{F}}_q^*)^d$
a
$S=\{s_1,\ldots,s_t\} \subseteq ({\mathbb{F}}_q^*)^d$
a
![]() $t$
-falling star under the colouring
$t$
-falling star under the colouring
![]() $\varphi _d$
if
$\varphi _d$
if
![]() $\varphi _d\left (s_i,s_j\right )=\alpha _i$
for all
$\varphi _d\left (s_i,s_j\right )=\alpha _i$
for all
![]() $1\leq j \lt i\leq t$
, as shown in Figure 2. For any set of vectors
$1\leq j \lt i\leq t$
, as shown in Figure 2. For any set of vectors
![]() $T \subseteq ({\mathbb{F}}_q^*)^d$
under
$T \subseteq ({\mathbb{F}}_q^*)^d$
under
![]() $\varphi _d$
, let
$\varphi _d$
, let
![]() $FS(T)$
denote the maximum
$FS(T)$
denote the maximum
![]() $t$
such that
$t$
such that
![]() $T$
contains a
$T$
contains a
![]() $t$
-falling star.
$t$
-falling star.

Figure 2. A
![]() $t$
-falling star.
$t$
-falling star.
The following result about these falling stars is an easy consequence of Lemma 3.1 which can be shown by induction on the number of vectors.
Corollary 3.2.
Let
![]() $S=\{s_1,\ldots,s_t\} \subseteq ({\mathbb{F}}_q^*)^d$
be a
$S=\{s_1,\ldots,s_t\} \subseteq ({\mathbb{F}}_q^*)^d$
be a
![]() $t$
-falling star under
$t$
-falling star under
![]() $\varphi _d$
. Then the vectors
$\varphi _d$
. Then the vectors
![]() $s_1, \ldots, s_{t-1}$
are linearly independent. Consequently, for any subset
$s_1, \ldots, s_{t-1}$
are linearly independent. Consequently, for any subset
![]() $T \subseteq ({\mathbb{F}}_q^*)^d$
,
$T \subseteq ({\mathbb{F}}_q^*)^d$
,
Moreover, if
![]() $T$
is contained within a monochromatic neighbourhood of some other vector, then
$T$
is contained within a monochromatic neighbourhood of some other vector, then
Definition 3.4. Let
![]() $A,B \subseteq{\mathbb{F}}_q^d$
be disjoint sets of vectors. We say that
$A,B \subseteq{\mathbb{F}}_q^d$
be disjoint sets of vectors. We say that
![]() $A$
confines
$A$
confines
![]() $B$
if for each
$B$
if for each
![]() $a \in A$
,
$a \in A$
,
![]() $a \cdot x = a \cdot y$
for every
$a \cdot x = a \cdot y$
for every
![]() $x,y \in B$
.
$x,y \in B$
.
Lemma 3.3.
Let
![]() $A,B \subseteq{\mathbb{F}}_q^d$
be disjoint sets of vectors such that
$A,B \subseteq{\mathbb{F}}_q^d$
be disjoint sets of vectors such that
![]() $A$
confines
$A$
confines
![]() $B$
. Then
$B$
. Then
Proof. Let
![]() $t={\textrm{rk}}(A)$
, and let
$t={\textrm{rk}}(A)$
, and let
![]() $a_1,\ldots, a_t$
be linearly independent vectors from
$a_1,\ldots, a_t$
be linearly independent vectors from
![]() $A$
. Since
$A$
. Since
![]() $A$
confines
$A$
confines
![]() $B$
, then for each
$B$
, then for each
![]() $a_i$
, there exists an
$a_i$
, there exists an
![]() $\alpha _i \in{\mathbb{F}}_q$
such that
$\alpha _i \in{\mathbb{F}}_q$
such that
![]() $a_i \cdot b = \alpha _i$
for all
$a_i \cdot b = \alpha _i$
for all
![]() $b \in B$
. Therefore,
$b \in B$
. Therefore,
![]() $B$
is a subset of the solution space for the matrix equation,
$B$
is a subset of the solution space for the matrix equation,
 \begin{align*} \left (\begin{array}{c} - a_1 - \\ \vdots \\ - a_t - \end{array}\right ) \left (\begin{array}{c} \mid \\ x \\ \mid \end{array}\right ) = \left (\begin{array}{c} \alpha _1\\ \vdots \\ \alpha _t\end{array}\right ). \end{align*}
\begin{align*} \left (\begin{array}{c} - a_1 - \\ \vdots \\ - a_t - \end{array}\right ) \left (\begin{array}{c} \mid \\ x \\ \mid \end{array}\right ) = \left (\begin{array}{c} \alpha _1\\ \vdots \\ \alpha _t\end{array}\right ). \end{align*}
Since
![]() $a_1,\ldots, a_t$
are linearly independent, the matrix of these
$a_1,\ldots, a_t$
are linearly independent, the matrix of these
![]() $t$
vectors has full rank, and hence, the solution set is an affine space of dimension
$t$
vectors has full rank, and hence, the solution set is an affine space of dimension
![]() $d-t$
, as desired.
$d-t$
, as desired.![]()
Lemma 3.4.
Let
![]() $A,B \subseteq ({\mathbb{F}}_q^*)^d$
be disjoint sets of vectors and
$A,B \subseteq ({\mathbb{F}}_q^*)^d$
be disjoint sets of vectors and
![]() $\alpha \in C_d$
such that
$\alpha \in C_d$
such that
![]() $\varphi _d(a,b)=\alpha$
for all
$\varphi _d(a,b)=\alpha$
for all
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
. Then either
$b \in B$
. Then either
![]() $A$
confines
$A$
confines
![]() $B$
or
$B$
or
![]() $B$
confines
$B$
confines
![]() $A$
(or both).
$A$
(or both).
Proof. If
![]() $\alpha$
has the dot property, then it is trivial that
$\alpha$
has the dot property, then it is trivial that
![]() $A$
and
$A$
and
![]() $B$
confine one another. So assume that
$B$
confine one another. So assume that
![]() $\alpha \in \text{UP} \cup \text{DOWN}$
. It follows that the first position of difference
$\alpha \in \text{UP} \cup \text{DOWN}$
. It follows that the first position of difference
![]() $i$
is the same between any
$i$
is the same between any
![]() $a \in A$
and any
$a \in A$
and any
![]() $b \in B$
. Moreover, every vector of
$b \in B$
. Moreover, every vector of
![]() $A$
has the same
$A$
has the same
![]() $i^{th}$
component, every vector of
$i^{th}$
component, every vector of
![]() $B$
has the same
$B$
has the same
![]() $i^{th}$
component, and every vector of
$i^{th}$
component, and every vector of
![]() $A \cup B$
has the same
$A \cup B$
has the same
![]() $j^{th}$
component for each
$j^{th}$
component for each
![]() $1 \leq j \lt i$
if
$1 \leq j \lt i$
if
![]() $i\gt 1$
. Since the vectors are ordered lexicographically based on an underlying linear order of
$i\gt 1$
. Since the vectors are ordered lexicographically based on an underlying linear order of
![]() ${\mathbb{F}}_q^*$
, it follows that either
${\mathbb{F}}_q^*$
, it follows that either
![]() $a\lt b$
for all
$a\lt b$
for all
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
, or
$b \in B$
, or
![]() $b\lt a$
for all
$b\lt a$
for all
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
.
$b \in B$
.
Without loss of generality, assume that
![]() $a\lt b$
for all
$a\lt b$
for all
![]() $a \in A$
and
$a \in A$
and
![]() $b \in B$
. If
$b \in B$
. If
![]() $\alpha \in \text{UP}$
, then for any particular
$\alpha \in \text{UP}$
, then for any particular
![]() $a \in A$
,
$a \in A$
,
![]() $a \cdot b = a \cdot a$
for every
$a \cdot b = a \cdot a$
for every
![]() $b \in B$
. Therefore,
$b \in B$
. Therefore,
![]() $A$
confines
$A$
confines
![]() $B$
. Similarly, if
$B$
. Similarly, if
![]() $\alpha \in \text{DOWN}$
, then for any particular
$\alpha \in \text{DOWN}$
, then for any particular
![]() $b \in B$
,
$b \in B$
,
![]() $b \cdot a = b \cdot b$
for every
$b \cdot a = b \cdot b$
for every
![]() $a \in A$
, so
$a \in A$
, so
![]() $B$
confines
$B$
confines
![]() $A$
.
$A$
.![]()
Lemma 3.5.
Let
![]() $t \geq 2$
be an integer. An affine subspace of
$t \geq 2$
be an integer. An affine subspace of
![]() ${\mathbb{F}}_q^d$
of dimension
${\mathbb{F}}_q^d$
of dimension
![]() $t-2$
will contain no
$t-2$
will contain no
![]() $t$
-falling stars of
$t$
-falling stars of
![]() $({\mathbb{F}}_q^*)^d$
under
$({\mathbb{F}}_q^*)^d$
under
![]() $\varphi _d$
. Therefore,
$\varphi _d$
. Therefore,
for any subset of vectors
![]() $S \subseteq ({\mathbb{F}}_q^*)^d$
.
$S \subseteq ({\mathbb{F}}_q^*)^d$
.
Proof. We will proceed by induction on
![]() $t$
. The base case
$t$
. The base case
![]() $t=2$
is trivial since an affine subspace of dimension 0 is just one vector while a
$t=2$
is trivial since an affine subspace of dimension 0 is just one vector while a
![]() $2$
-falling star contains two distinct vectors.
$2$
-falling star contains two distinct vectors.
So assume that
![]() $t \geq 3$
and that the statement is true for
$t \geq 3$
and that the statement is true for
![]() $t-1$
. Let
$t-1$
. Let
![]() $s_1,\ldots,s_t$
be
$s_1,\ldots,s_t$
be
![]() $t$
distinct vectors that form a
$t$
distinct vectors that form a
![]() $t$
-falling star. That is, let
$t$
-falling star. That is, let
![]() $\alpha _1,\ldots,\alpha _{t-1} \in C_d$
and let
$\alpha _1,\ldots,\alpha _{t-1} \in C_d$
and let
![]() $\varphi _d\left (s_i,s_j\right ) = \alpha _i$
when
$\varphi _d\left (s_i,s_j\right ) = \alpha _i$
when
![]() $1 \leq i \lt j \leq t$
. Assume towards a contradiction that these vectors are contained inside an affine subspace of dimension
$1 \leq i \lt j \leq t$
. Assume towards a contradiction that these vectors are contained inside an affine subspace of dimension
![]() $t-2$
. Then there exist scalars
$t-2$
. Then there exist scalars
![]() $\lambda _1,\ldots,\lambda _{t-1} \in{\mathbb{F}}_q$
such that
$\lambda _1,\ldots,\lambda _{t-1} \in{\mathbb{F}}_q$
such that
![]() $s_t=\sum _{j=1}^{t-1} \lambda _j s_j$
and
$s_t=\sum _{j=1}^{t-1} \lambda _j s_j$
and
![]() $\sum _{j=1}^{t-1} \lambda _j=1$
.
$\sum _{j=1}^{t-1} \lambda _j=1$
.
First, note that if
![]() $\lambda _1=0$
, then the vectors
$\lambda _1=0$
, then the vectors
![]() $s_2,\ldots,s_t$
form a
$s_2,\ldots,s_t$
form a
![]() $(t-1)$
-falling star and are contained in an affine subspace of dimension
$(t-1)$
-falling star and are contained in an affine subspace of dimension
![]() $t-3$
, a contradiction of the inductive hypothesis. So we must assume in what follows that
$t-3$
, a contradiction of the inductive hypothesis. So we must assume in what follows that
![]() $\lambda _1 \neq 0$
.
$\lambda _1 \neq 0$
.
Now, we consider two cases: either
![]() $\alpha _1 \in \text{DOT}$
or
$\alpha _1 \in \text{DOT}$
or
![]() $\alpha _1 \not \in \text{DOT}$
. If
$\alpha _1 \not \in \text{DOT}$
. If
![]() $\alpha _1 \in \text{DOT}$
, then
$\alpha _1 \in \text{DOT}$
, then
 \begin{align*} \alpha _1=s_1 \cdot s_t = s_1 \cdot \sum _{j=1}^{t-1} \lambda _j s_j = \lambda _1(s_1 \cdot s_1)+\alpha _1 \sum _{j=2}^{t-1} \lambda _j = \lambda _1(s_1 \cdot s_1)+\alpha _1(1-\lambda _1). \end{align*}
\begin{align*} \alpha _1=s_1 \cdot s_t = s_1 \cdot \sum _{j=1}^{t-1} \lambda _j s_j = \lambda _1(s_1 \cdot s_1)+\alpha _1 \sum _{j=2}^{t-1} \lambda _j = \lambda _1(s_1 \cdot s_1)+\alpha _1(1-\lambda _1). \end{align*}
Therefore,
![]() $\lambda _1(s_1 \cdot s_1 - \alpha _1)=0$
. Since
$\lambda _1(s_1 \cdot s_1 - \alpha _1)=0$
. Since
![]() $\lambda _1 \neq 0$
, it follows that
$\lambda _1 \neq 0$
, it follows that
which that implies
![]() $\alpha _1 \not \in \text{DOT}$
, a contradiction.
$\alpha _1 \not \in \text{DOT}$
, a contradiction.
So assume that
![]() $\alpha _1 \not \in \text{DOT}$
, and let
$\alpha _1 \not \in \text{DOT}$
, and let
![]() $i$
denote the index of the first component where
$i$
denote the index of the first component where
![]() $s_1$
differs from the other vectors. In this case,
$s_1$
differs from the other vectors. In this case,
and hence
![]() $s_{2,i}=\cdots =s_{t,i}$
. Therefore,
$s_{2,i}=\cdots =s_{t,i}$
. Therefore,
 \begin{align*} s_{t,i}=\sum _{j=1}^{t-1}\lambda _j s_{j,i} = \lambda _1 s_{1,i} + s_{t,i} \sum _{j=2}^{t-1} \lambda _j = \lambda _1 s_{1,i}+s_{t,i}(1-\lambda _1). \end{align*}
\begin{align*} s_{t,i}=\sum _{j=1}^{t-1}\lambda _j s_{j,i} = \lambda _1 s_{1,i} + s_{t,i} \sum _{j=2}^{t-1} \lambda _j = \lambda _1 s_{1,i}+s_{t,i}(1-\lambda _1). \end{align*}
So
![]() $\lambda _1(s_{1,i}-s_{t,i})=0$
. Since
$\lambda _1(s_{1,i}-s_{t,i})=0$
. Since
![]() $\lambda _1 \neq 0$
, we have
$\lambda _1 \neq 0$
, we have
![]() $s_{1,i}=s_{t,i}$
, a contradiction of our choice of
$s_{1,i}=s_{t,i}$
, a contradiction of our choice of
![]() $i$
.
$i$
.![]()
Lemma 3.6.
Let
![]() $S \subseteq ({\mathbb{F}}_q^*)^d$
be a set of
$S \subseteq ({\mathbb{F}}_q^*)^d$
be a set of
![]() $p \geq 1$
vectors with a leftover structure under the colouring
$p \geq 1$
vectors with a leftover structure under the colouring
![]() $\varphi _d$
. Then
$\varphi _d$
. Then
Proof. We will prove this by induction on
![]() $p$
. The base case when
$p$
. The base case when
![]() $p=1$
is trivial, so assume that
$p=1$
is trivial, so assume that
![]() $S$
has
$S$
has
![]() $p \geq 2$
vectors. Then
$p \geq 2$
vectors. Then
![]() $S$
has an initial bipartition,
$S$
has an initial bipartition,
![]() $S=A \cup B$
, and we note that
$S=A \cup B$
, and we note that
Since
![]() $|A|,|B|\lt p$
, then by induction
$|A|,|B|\lt p$
, then by induction
![]() $FS(T) \geq \left \lceil \log _2(|T|) \right \rceil + 1$
for
$FS(T) \geq \left \lceil \log _2(|T|) \right \rceil + 1$
for
![]() $T=A,B$
. Thus, we have
$T=A,B$
. Thus, we have
and since
![]() $\max (|A|,|B|) \geq \left \lceil \frac{p}{2} \right \rceil$
, then
$\max (|A|,|B|) \geq \left \lceil \frac{p}{2} \right \rceil$
, then
Lemma 3.7.
Let
![]() $p\geq 2$
and
$p\geq 2$
and
![]() $T\geq 0$
be integers. Let
$T\geq 0$
be integers. Let
![]() $S \subseteq ({\mathbb{F}}_q^*)^d$
be a subset of
$S \subseteq ({\mathbb{F}}_q^*)^d$
be a subset of
![]() $p$
vectors with a leftover structure under
$p$
vectors with a leftover structure under
![]() $\varphi _d$
. If
$\varphi _d$
. If
![]() $T \geq 1$
, let
$T \geq 1$
, let
![]() $a_1,\ldots,a_T \in ({\mathbb{F}}_q^*)^d$
and
$a_1,\ldots,a_T \in ({\mathbb{F}}_q^*)^d$
and
![]() $\alpha _1,\ldots,\alpha _T \in C_d$
such that
$\alpha _1,\ldots,\alpha _T \in C_d$
such that
![]() $\varphi _d\left (a_i,a_j\right )=\alpha _i$
for all
$\varphi _d\left (a_i,a_j\right )=\alpha _i$
for all
![]() $1\leq i\lt j\leq T$
and
$1\leq i\lt j\leq T$
and
![]() $\varphi _d\left (a_i,s\right )=\alpha _i$
for all
$\varphi _d\left (a_i,s\right )=\alpha _i$
for all
![]() $1\leq i \leq T$
and all
$1\leq i \leq T$
and all
![]() $s \in S$
.
$s \in S$
.
Then there exists a sequence of positive integers,
![]() $x_1,\ldots,x_t$
such that
$x_1,\ldots,x_t$
such that
![]() $\sum _{i=1}^t x_i=p-1$
and for each
$\sum _{i=1}^t x_i=p-1$
and for each
![]() $i=1,\ldots,t$
, the following three conditions hold:
$i=1,\ldots,t$
, the following three conditions hold:
-
(1)
 $1 \leq x_i \leq \left \lfloor \frac{p-s_i}{2} \right \rfloor$
;
$1 \leq x_i \leq \left \lfloor \frac{p-s_i}{2} \right \rfloor$
; -
(2)
 $\left \lceil \log _2(x_i) \right \rceil + \left \lceil \log _2(p-s_i-x_i) \right \rceil \leq d-1$
;
$\left \lceil \log _2(x_i) \right \rceil + \left \lceil \log _2(p-s_i-x_i) \right \rceil \leq d-1$
; -
(3)
 $\left \lceil \log _2(p-s_i-x_i) \right \rceil \leq d-i-T$
,
$\left \lceil \log _2(p-s_i-x_i) \right \rceil \leq d-i-T$
,
where
![]() $s_i=0$
if
$s_i=0$
if
![]() $i=1$
and
$i=1$
and
![]() $s_i=\sum _{j=1}^{i-1}x_j$
otherwise.
$s_i=\sum _{j=1}^{i-1}x_j$
otherwise.
Proof. We will prove this by induction on
![]() $p$
. For the base case, let
$p$
. For the base case, let
![]() $p=2$
. Let
$p=2$
. Let
![]() $x_1=1$
be the entire sequence. Then the first two conditions hold trivially since the sum of the sequence is 1, and since
$x_1=1$
be the entire sequence. Then the first two conditions hold trivially since the sum of the sequence is 1, and since
for any
![]() $d \geq 1$
. For the third condition, since
$d \geq 1$
. For the third condition, since
![]() $\left \lceil \log _2(1) \right \rceil = 0$
, it suffices to show that
$\left \lceil \log _2(1) \right \rceil = 0$
, it suffices to show that
![]() $T+1 \leq d$
. This follows from Corollary 3.2, since
$T+1 \leq d$
. This follows from Corollary 3.2, since
![]() $S \cup \{a_1,\ldots,a_T\}$
forms a
$S \cup \{a_1,\ldots,a_T\}$
forms a
![]() $(T+2)$
-falling star, and hence
$(T+2)$
-falling star, and hence
![]() $d \geq{\textrm{rk}}\left (S \cup \{a_1,\ldots,a_T\}\right ) \geq T+1$
.
$d \geq{\textrm{rk}}\left (S \cup \{a_1,\ldots,a_T\}\right ) \geq T+1$
.
So assume that
![]() $S$
is a set of
$S$
is a set of
![]() $p$
vertices for
$p$
vertices for
![]() $p \geq 3$
and that the statement is true for smaller sets. Let the initial bipartition of
$p \geq 3$
and that the statement is true for smaller sets. Let the initial bipartition of
![]() $S$
be
$S$
be
![]() $S=A \cup B$
. By Lemma 3.4, we may assume without loss of generality that
$S=A \cup B$
. By Lemma 3.4, we may assume without loss of generality that
![]() $A$
confines
$A$
confines
![]() $B$
. Therefore,
$B$
. Therefore,
![]() ${\textrm{af}}(B) \leq d-{\textrm{rk}}(A)$
by Lemma 3.3. By Corollary 3.2, we know that
${\textrm{af}}(B) \leq d-{\textrm{rk}}(A)$
by Lemma 3.3. By Corollary 3.2, we know that
![]() ${\textrm{rk}}(A) \geq FS(A)$
since
${\textrm{rk}}(A) \geq FS(A)$
since
![]() $A$
is in a monochromatic neighbourhood of any vector from
$A$
is in a monochromatic neighbourhood of any vector from
![]() $B$
. And by Lemma 3.5, we know that
$B$
. And by Lemma 3.5, we know that
![]() ${\textrm{af}}(B) \geq FS(B)-1$
. Thus,
${\textrm{af}}(B) \geq FS(B)-1$
. Thus,
![]() $FS(A)+FS(B)-1 \leq d$
. So by Lemma 3.6, we can conclude that
$FS(A)+FS(B)-1 \leq d$
. So by Lemma 3.6, we can conclude that
Therefore, setting
![]() $x_1=\min \{|A|,|B|\}$
guarantees that
$x_1=\min \{|A|,|B|\}$
guarantees that
![]() $1 \leq x_1 \leq \left \lfloor \frac{p}{2} \right \rfloor$
and that
$1 \leq x_1 \leq \left \lfloor \frac{p}{2} \right \rfloor$
and that
This gives us a positive integer
![]() $x_1$
which satisfies the first two conditions. Moreover, by Corollary 3.2 and Lemma 3.6,
$x_1$
which satisfies the first two conditions. Moreover, by Corollary 3.2 and Lemma 3.6,
 \begin{align*} d \geq{\textrm{rk}}\left (S \cup \{a_1,\ldots,a_T\}\right ) &\geq FS(S\cup \{a_1,\ldots, a_T\})-1\\ & \geq (T+1+\max\!\left (FS(A),FS(B)\right ))-1\\ &\geq T + \left \lceil \log _2(p-x_1) \right \rceil +1. \end{align*}
\begin{align*} d \geq{\textrm{rk}}\left (S \cup \{a_1,\ldots,a_T\}\right ) &\geq FS(S\cup \{a_1,\ldots, a_T\})-1\\ & \geq (T+1+\max\!\left (FS(A),FS(B)\right ))-1\\ &\geq T + \left \lceil \log _2(p-x_1) \right \rceil +1. \end{align*}
Thus,
![]() $x_1$
also satisfies the third condition.
$x_1$
also satisfies the third condition.
Let
![]() $S'$
denote the larger of the two parts
$S'$
denote the larger of the two parts
![]() $A$
and
$A$
and
![]() $B$
, and let
$B$
, and let
![]() $a_{T+1}$
denote an arbitrary vector from
$a_{T+1}$
denote an arbitrary vector from
![]() $S \setminus S'$
. Then
$S \setminus S'$
. Then
![]() $S'$
contains
$S'$
contains
![]() $p-x_1\lt p$
vectors and has a leftover structure under
$p-x_1\lt p$
vectors and has a leftover structure under
![]() $\varphi _d$
. Moreover,
$\varphi _d$
. Moreover,
![]() $S'$
and
$S'$
and
![]() $a_1,\ldots,a_{T},a_{T+1}$
satisfy the monochromatic neighbourhood conditions of the hypothesis. Hence, by induction there exists a sequence of positive integers
$a_1,\ldots,a_{T},a_{T+1}$
satisfy the monochromatic neighbourhood conditions of the hypothesis. Hence, by induction there exists a sequence of positive integers
![]() $x_1',\ldots,x'_{\!\!t^{\prime}}$
such that
$x_1',\ldots,x'_{\!\!t^{\prime}}$
such that
![]() $\sum _{i=1}^{t'}x'_{\!\!i}=p-x_1-1$
and for each
$\sum _{i=1}^{t'}x'_{\!\!i}=p-x_1-1$
and for each
![]() $i=1,\ldots,t'$
, the following three conditions hold:
$i=1,\ldots,t'$
, the following three conditions hold:
-
(1)
 $1 \leq x'_{\!\!i} \leq \left \lfloor \frac{p-x_1-s'_{\!\!i}}{2} \right \rfloor$
;
$1 \leq x'_{\!\!i} \leq \left \lfloor \frac{p-x_1-s'_{\!\!i}}{2} \right \rfloor$
; -
(2)
 $\left \lceil \log _2(x'_{\!\!i}) \right \rceil + \left \lceil \log _2(p-x_1-s'_{\!\!i}-x'_{\!\!i}) \right \rceil \leq d-1$
;
$\left \lceil \log _2(x'_{\!\!i}) \right \rceil + \left \lceil \log _2(p-x_1-s'_{\!\!i}-x'_{\!\!i}) \right \rceil \leq d-1$
; -
(3)
 $\left \lceil \log _2(p-x_1-s'_{\!\!i}-x'_{\!\!i}) \right \rceil \leq d-i-(T+1)$
,
$\left \lceil \log _2(p-x_1-s'_{\!\!i}-x'_{\!\!i}) \right \rceil \leq d-i-(T+1)$
,
where
![]() $s'_{\!\!i}=0$
if
$s'_{\!\!i}=0$
if
![]() $i=1$
and
$i=1$
and
![]() $s'_{\!\!i}=\sum _{j=1}^{i-1}x'_{\!\!j}$
otherwise.
$s'_{\!\!i}=\sum _{j=1}^{i-1}x'_{\!\!j}$
otherwise.
Let
![]() $x_i=x'_{i-1}$
for
$x_i=x'_{i-1}$
for
![]() $2\leq i \leq t'+1$
and let
$2\leq i \leq t'+1$
and let
![]() $t=t'+1$
to get a sequence
$t=t'+1$
to get a sequence
![]() $x_1,\ldots,x_t$
for which
$x_1,\ldots,x_t$
for which
 \begin{align*} \sum _{i=1}^t x_i=x_1+\sum _{i=1}^{t'}x_i'=x_1+p-x_1-1=p-1. \end{align*}
\begin{align*} \sum _{i=1}^t x_i=x_1+\sum _{i=1}^{t'}x_i'=x_1+p-x_1-1=p-1. \end{align*}
For each
![]() $i=2,\ldots,t$
, the first two conditions are satisfied since
$i=2,\ldots,t$
, the first two conditions are satisfied since
![]() $x_1+s'_{\!\!i}=s_{i+1}$
, and the third condition is satisfied since
$x_1+s'_{\!\!i}=s_{i+1}$
, and the third condition is satisfied since
![]() $d-i-(T+1)=d-(i+1)-T$
.
$d-i-(T+1)=d-(i+1)-T$
.![]()
Corollary 3.8.
Let
![]() $S \subseteq ({\mathbb{F}}_q^*)^3$
be a set of 6 vectors. Then
$S \subseteq ({\mathbb{F}}_q^*)^3$
be a set of 6 vectors. Then
![]() $S$
cannot have a leftover structure under the colouring
$S$
cannot have a leftover structure under the colouring
![]() $\varphi _3$
.
$\varphi _3$
.
Proof. If such a set exists, then by Lemma 3.7 with
![]() $T=0$
, a positive integer
$T=0$
, a positive integer
![]() $x_1$
exists such that
$x_1$
exists such that
![]() $1 \leq x_1 \leq 3$
and
$1 \leq x_1 \leq 3$
and
It is simple to check that no such integer exists.![]()
Corollary 3.9.
Let
![]() $S \subseteq ({\mathbb{F}}_q^*)^4$
be a set of 8 vectors. Then
$S \subseteq ({\mathbb{F}}_q^*)^4$
be a set of 8 vectors. Then
![]() $S$
cannot have a leftover structure under the colouring
$S$
cannot have a leftover structure under the colouring
![]() $\varphi _4$
.
$\varphi _4$
.
Proof. If such a set exists, then by Lemma 3.7 with
![]() $T=0$
, we must be able to find a sequence of positive integers
$T=0$
, we must be able to find a sequence of positive integers
![]() $x_1,x_2,\ldots,x_t$
that satisfy the conditions given in the Lemma. In particular,
$x_1,x_2,\ldots,x_t$
that satisfy the conditions given in the Lemma. In particular,
![]() $1 \leq x_1 \leq 4$
and
$1 \leq x_1 \leq 4$
and
We can check and find that
![]() $x_1=1$
is the only possibility. Therefore,
$x_1=1$
is the only possibility. Therefore,
![]() $1 \leq x_2 \leq 3$
such that
$1 \leq x_2 \leq 3$
such that
A quick check reveals that no such integer exists.![]()
Theorem 1.2 follows from Theorem 1.1 and Corollaries 3.8 and 3.9.
4. Conclusion
The proof of Lemma 3.7 actually shows which leftover
![]() $p$
-cliques can appear under
$p$
-cliques can appear under
![]() $\varphi _d$
for a particular
$\varphi _d$
for a particular
![]() $d$
. For example, this proof implies that the only leftover
$d$
. For example, this proof implies that the only leftover
![]() $5$
-clique that can appear under
$5$
-clique that can appear under
![]() $\varphi _3$
is a monochromatic
$\varphi _3$
is a monochromatic
![]() $C_4$
contained inside a monochromatic neighbourhood of one vertex (that is, an initial
$C_4$
contained inside a monochromatic neighbourhood of one vertex (that is, an initial
![]() $(1,4)$
-bipartition with a
$(1,4)$
-bipartition with a
![]() $(2,2)$
-bipartition inside the part with four vertices). In [Reference Cameron and Heath2], we handled this specific leftover structure by splitting each colour class of
$(2,2)$
-bipartition inside the part with four vertices). In [Reference Cameron and Heath2], we handled this specific leftover structure by splitting each colour class of
![]() $\varphi _3$
into four new colours determined by certain relations between vectors. While the current paper can be viewed as our attempt to fully generalize the colouring techniques used in [Reference Cameron and Heath2] and [Reference Mubayi8], it does not generalize the splitting that was crucial for handling the final leftover
$\varphi _3$
into four new colours determined by certain relations between vectors. While the current paper can be viewed as our attempt to fully generalize the colouring techniques used in [Reference Cameron and Heath2] and [Reference Mubayi8], it does not generalize the splitting that was crucial for handling the final leftover
![]() $5$
-clique. Perhaps such a generalized splitting would be enough to give
$5$
-clique. Perhaps such a generalized splitting would be enough to give
![]() $f(n,p,p) \leq n^{1/(p-2) +o(1)}$
for
$f(n,p,p) \leq n^{1/(p-2) +o(1)}$
for
![]() $p \geq 6$
or at least improve the best-known upper bounds for values of
$p \geq 6$
or at least improve the best-known upper bounds for values of
![]() $p$
other than the two addressed in this paper.
$p$
other than the two addressed in this paper.
Acknowledgements
This research was partially supported by NSF RTG Grant DMS-1937241 and NSF RTG Grant DMS-1839918.