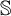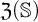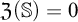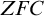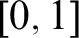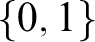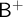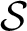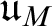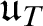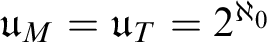Research Article
INDEPENDENCE PROOFS IN NON-CLASSICAL SET THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2021, pp. 979-1010
-
- Article
- Export citation
THE ZHOU ORDINAL OF LABELLED MARKOV PROCESSES OVER SEPARABLE SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 27 February 2023, pp. 1011-1032
-
- Article
- Export citation
FRACTIONAL-VALUED MODAL LOGIC
- Part of:
-
- Published online by Cambridge University Press:
- 31 August 2021, pp. 1033-1052
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TOWARDS THE INEVITABILITY OF NON-CLASSICAL PROBABILITY
- Part of:
-
- Published online by Cambridge University Press:
- 21 February 2022, pp. 1053-1079
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERPRETATION, LOGIC AND PHILOSOPHY: JEAN NICOD’S GEOMETRY IN THE SENSIBLE WORLD
- Part of:
-
- Published online by Cambridge University Press:
- 02 July 2021, pp. 1080-1109
-
- Article
- Export citation
ON ZARDINI’S RULES FOR MULTIPLICATIVE QUANTIFICATION AS THE SOURCE OF CONTRA(DI)CTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 19 July 2022, pp. 1110-1119
-
- Article
- Export citation
COLLECTION FRAMES FOR DISTRIBUTIVE SUBSTRUCTURAL LOGICS
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2022, pp. 1120-1157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HUME’S PRINCIPLE, BAD COMPANY, AND THE AXIOM OF CHOICE
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2022, pp. 1158-1176
-
- Article
- Export citation
A SUBSTRUCTURAL GENTZEN CALCULUS FOR ORTHOMODULAR QUANTUM LOGIC
- Part of:
-
- Published online by Cambridge University Press:
- 27 January 2022, pp. 1177-1198
-
- Article
- Export citation
TWO-SORTED FREGE ARITHMETIC IS NOT CONSERVATIVE
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2022, pp. 1199-1232
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SET THEORY AND A MODEL OF THE MIND IN PSYCHOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1233-1259
-
- Article
- Export citation
PROOF SYSTEMS FOR EXACT ENTAILMENT
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2022, pp. 1260-1295
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A SIMPLE SEQUENT SYSTEM FOR MINIMALLY INCONSISTENT LP
- Part of:
-
- Published online by Cambridge University Press:
- 23 February 2022, pp. 1296-1311
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
RSL volume 16 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 December 2023, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
RSL volume 16 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 December 2023, pp. b1-b2
-
- Article
-
- You have access
- Export citation