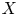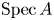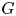Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barthel, Tobias
Castellana, Natàlia
Heard, Drew
and
Sanders, Beren
2024.
On surjectivity in tensor triangular geometry.
Mathematische Zeitschrift,
Vol. 308,
Issue. 4,
Benson, David John
Iyengar, Srikanth B.
Krause, Henning
and
Pevtsova, Julia
2024.
Fibrewise stratification of group representations.
Annals of Representation Theory,
Vol. 1,
Issue. 1,
p.
97.
Barthel, Tobias
Castellana, Natàlia
Heard, Drew
Naumann, Niko
and
Pol, Luca
2025.
Quillen stratification in equivariant homotopy theory.
Inventiones mathematicae,
Vol. 239,
Issue. 1,
p.
219.