I. INTRODUCTION
Magnesium alloys have high potential for application as structural materials, since they are the lightest, and have the highest natural abundance, among all the conventional structural alloys. The need for magnesium alloys with an improved suite of mechanical properties, including e.g., strength, toughness and fatigue resistance, is driven by reliability and safety requirements, and two strategies in alloy design are being widely considered to address these. Specifically, grain refinementReference Armstrong, Codd, Douthwaite and Petch1–Reference Barnett4 and the addition of solute elementsReference Agnew, Yoo and Tome5–Reference Butt, Ghauri, Qamar, Hashmi and Feltham10 are both active topics in the magnesium research field.
Although much research emphasizes the properties noted above, it is important to recognize that there are secondary properties that may also be affected by grain refinement and alloying additions, and these can also be critical for many applications. Rate dependence and high-rate mechanical properties fall into this category. In many loading situations of practical relevance for structural materials, the local strain-rates are quite high, especially for automotive and transportation applications involving high-rate impacts, or for localized regions of geometries nominally under low loading rates. For example, the strain-rate in the crack-tip region during fracture has been reported to be at least 100 times higher than the global rate.Reference Somekawa, Inoue, Singh and Mukai11
The mechanical properties and deformation behaviors of magnesium and magnesium alloys are unique compared with those of more conventional metallic materials, because of their hexagonal close packed (hcp) structure. The major slip system in single crystalline and coarse-grained magnesium alloys at room temperature lies on the basal plane, and deformation twins form to compensate for the lack of slip systems during plastic deformation. The orientation distribution of basal planes, i.e., texture, also tends to affect mechanical properties such as strength and ductility. Conventional wrought magnesium alloys, with basal planes generally parallel to the processing direction, show asymmetry in the yield strength; yield strength in tension is higher than that in compression.12 As a result, when tensile force is applied along the c-axis, deformation twins, i.e., ![]() type twins, are formed at quite a low applied stress.Reference Koike13 When the basal plane is oriented at 45° to the applied stress direction and basal dislocations are easily activated, ductility can be high. The elongation-to-failure in magnesium alloys produced by equal channel angular extrusion (ECAE) and tested along the extrusion axis is reported to be three or four times higher than that in the conventional wrought processed magnesium alloys, because the basal planes in this alloy are textured such that they preferentially lie close to the preferred angle, 45°, with the applied stress direction.Reference Mukai, Yamanoi, Watanabe and Higashi14
type twins, are formed at quite a low applied stress.Reference Koike13 When the basal plane is oriented at 45° to the applied stress direction and basal dislocations are easily activated, ductility can be high. The elongation-to-failure in magnesium alloys produced by equal channel angular extrusion (ECAE) and tested along the extrusion axis is reported to be three or four times higher than that in the conventional wrought processed magnesium alloys, because the basal planes in this alloy are textured such that they preferentially lie close to the preferred angle, 45°, with the applied stress direction.Reference Mukai, Yamanoi, Watanabe and Higashi14
The deformation response of magnesium and its alloys under high-strain-rate loading has also been investigated.Reference Li, Joshi, Azevedo, Ma, Ramesh, Figueiredo and Langdon15–Reference Mukai, Yamanoi and Higashi22 Some papers show the effect of texture on the high-rate mechanical properties; the stress-strain response is anisotropic due to the formation of twins, similarly to the situation in the quasistatic strain-rate regime as described above. Watanabe and Ishikawa investigated the deformation mechanism at elevated temperature up to 673 K.Reference Watanabe and Ishikawa16, Reference Ishikawa, Watanabe and Mukai21 They reported that both dislocation glide and twins contributed to plasticity in the high-strain-rate regime in a coarse-grained alloy. On the other hand, the formation of deformation twins is apparently suppressed by grain refinement.Reference Meyers, Vohringer and Lubarda23, Reference Lahaie, Embury, Chadwick and Gray24 Mukai et al.Reference Mukai, Yamanoi, Watanabe, Ishikawa and Higashi20 suggested that the dominant deformation behavior even in the high-strain-rate regime is dislocation slip for fine-grained magnesium alloys. Li et al.Reference Li, Joshi, Azevedo, Ma, Ramesh, Figueiredo and Langdon15 also reported that the overall role of twins is fairly minor at high strain-rates in ECAE-processed magnesium alloys with an average grain size of 0.8 μm.
Most of these works have used uniaxial macroscopic testing, such as the split Hopkinson bar technique, and thus the deformation resistance is studied on macroscopic scales, averaging over many microstructural length scales and features. On the other hand, recently, nanoindentation has been widely used for the investigation of mechanical properties and deformation behavior in small volumes of material, i.e., at scales smaller than each individual grain in the material. High-strain-rate indentation methods have also been developed and examined in metallic materialsReference Constantinides, Tweedie, Holbrook, Barragan, Smith and Van Vliet25–Reference Tirupataiah and Sundararajan27 and polymers.Reference Constantinides, Tweedie, Savva, Smith and Van Vliet28, Reference Kalcioglu, Qu, Strawhecker, Shazly, Edelman, VanLandingham, Smith and Van Vliet29 However, even though fine-grained magnesium alloys exhibit unusual behavior at high rates, the use of high-strain-rate indentation to explore some of these behaviors has not yet been reported. Therefore, the present study is focused on the high-strain-rate nanoindentation response of fine-grained magnesium alloys. We systematically explore the effect of both elevated temperature and alloying elements on the dynamic hardness in the high-strain-rate regime. We also explore the dominant deformation mechanism based on postmortem microstructural observations around the indentations.
II. EXPERIMENTAL PROCEDURE
Four kinds of Mg-0.3at.%X (X = Al, Li, Y and Zn) binary alloys as well as 99.95 wt.% pure magnesium were used in this study. The binary alloys were produced by casting, followed by solution treatment at 773 K for 7.2 ks. The solutionized binary alloys and pure magnesium samples were extruded at temperatures in the range 373 ∼ 623 K with a reduction ratio of 18. The initial microstructures of all the extruded alloys comprised an average grain size of 2 ∼ 3 μm, and no second-phase precipitates (as expected since all of these alloys are within the solubility limit). Details on the initial microstructures are reported elsewhere.Reference Somekawa and Schuh30
Instrumented high-strain-rate indentation testing was carried out using a Micro Materials Nanotest 600 (Birmingham, UK), configured for single impact dynamic hardness measurements, and equipped with a cube-corner tip. The indenter was mounted to a pendulum and accelerated into the sample surface by the high kinetic and potential energy of the pendulum, which is actuated to apply load via electromagnetic interaction. The displacement was tracked during the impact and rebound of the tip, measured though a capacitive transducer mounted on the opposite end of the pendulum. More details on the apparatus are available in Refs. Reference Trelewicz and Schuh26 and Reference Constantinides, Tweedie, Savva, Smith and Van Vliet28. It is important to note that the scale of the tests here is large compared with that of the microstructure: the width of a typical indentation is of the order of ∼ 10 μm, which means that the plastic zone spans many dozens of grains (average grain size of 2 ∼ 3 μm). The tests may be regarded as essentially “macroscopic” with respect to the microstructure. At these large scales, the tip geometry is also essentially perfect and apex blunting may be neglected.
For every sample and test condition explored at room temperature, at least 50 nominally identical indentations were performed near the middle of the extrusion-transverse direction (ED-TD) plane to minimize the effect of texture, i.e., basal plane distribution. The nanoindentation samples with dimensions of about 10 × 10 mm2 and thickness of 3.5 mm were prepared by mechanical polishing with colloidal silica slurry, followed by a final polishing with bare cloth under water for around 5 min to remove any remaining residual strain.
The high rate indentation behavior at elevated temperature was also investigated using the same equipment, although only for three of the extruded materials: Mg-Li and Mg-Y alloys, as well as pure magnesium. The testing temperatures were 323, 348 and 373 K respectively, where the initial microstructure remained stable over the timescales relevant for the experiments, i.e., negligible grain growth and second-phase precipitation. Both the tip and the sample were heated to the testing temperature to within ± 0.1 K. In addition, both force and displacement were independently calibrated in every testing condition. For the series of measurements at elevated temperatures a minimum of 40 identical indentations was performed for each tested condition and sample.
The deformed microstructures beneath some selected indentations were observed using a JEOL 2000FX-II (Tokyo, Japan) transmission electron microscope (TEM) with an accelerating voltage of 200 kV. TEM samples were prepared by the focused ion beam (FIB) technique in a dual-beam FEI Helios 600 (Hillsboro, OR), which allows the preparation of site-specific microsamples for microstructural observation. A typical indented surface observed by scanning electron microscopy is shown in Fig. 1(a). A platinum layer with a thickness of several μm was deposited on the specific area containing the indented surface to protect the surface from damage during the subsequent FIB trenching process, as shown in Fig. 1(b). Next, deep trenches were dug around the platinum coating layer, as shown in Fig. 1(c). The side and bottom parts of the specimen were cut by tilting forward by 52°, after mounting the specimen to a micromanipulator arm. The microsample specimen was finally mounted on a copper mesh as shown in Fig. 1(d). Both planar sidewalls of the specimen were milled by a gallium ion beam to produce an electron transparent thin film for TEM observation; the final thickness was around 70 nm.

FIG. 1. Micrographs showing the sequence of sample preparation steps for the microsampling method by FIB, which was used to prepare site-specific TEM samples beneath the indentations.
III. ANALYSIS OF HIGH-STRAIN-RATE INDENTATIONS
Typical examples of the measured response during high rate indentation of pure magnesium are shown in Fig. 2: (a) displacement and (b) corresponding velocity [calculated as the first derivative of (a)] as a function of time. These traces begin at a time when the tip is out of contact with the sample and accelerating through the air. The point of initial contact is identified by the onset of tip deceleration, as indicated by the dotted arrows, and is defined as h = 0; the initial contact velocity is denoted as v in. The subsequent portions of the traces in Fig. 2 follow the initial deep indentation formed as the tip slows to a velocity of zero, followed by the rebound of the tip from the sample (negative velocity). In fact, several subsequent lower-velocity impacts between tip and sample are tracked after the first rebound; none of these involves the same velocity or depth attained on the first, plastic indentation cycle. In the analysis, the first indentation is therefore the main focus.

FIG. 2. A typical example of raw output data from the high strain-rate hardness tests: (a) displacement and (b) corresponding velocity as a function of time in pure magnesium.
The indentation strain-rate, ![]() , is a function of depth; however, an average quantity characteristic of the entire first impression can be roughly approximated as:
, is a function of depth; however, an average quantity characteristic of the entire first impression can be roughly approximated as:
where h max is the maximum penetration depth. Since a typical initial contact velocity is 1.2 mm/s and a typical indentation depth is 7 ∼ 8 μm as shown in Fig. 2, the strain-rate is about ∼ 150/s for all our tests.
The hardness at high strain-rate, H dyn, quantifies the energy per unit volume dissipated as plastic work during impact-induced deformation. The change in kinetic energy of the indenter due to plastic work during impact isReference Johnson31:
where m is the effective mass of the pendulum and tip (= 0.21 kg, calibrated against quartz glass), P is the indentation load, vout is the outgoing velocity at the point where the tip detaches from the sample on the first rebound, and h res is the residual plastic depth at the point of detachment.
Although the point of initial contact between tip and sample is a clearly identifiable signal in the curves of Fig. 2, the identification of the point of detachment is less obvious. Accordingly, the values of vout and h res are best obtained with insight obtained by inspecting the second impact event, as shown in Fig. 2. Following the initial rebound, the indenter tip slows and again accelerates back towards the sample, and the tip recontacts the surface within the residual impression created by the preceding (first) impact. Taking the point of contact on the second impact to be equal to the residual depth of the first impact, the point of initial deceleration of the second impact vsi, defines the residual plastic depth, h res, and the velocity at the corresponding point on the initial rebound curve is identified as the outgoing velocity of vout.
The hardness, H dyn, is defined as the ratio of load to projected contact area, A c, where for a self-similar indenter geometry, A c = c·h 2 with the constant c = 2.59 for the cube-corner tip. The hardness is taken to be a material constant, and thus it can be substituted into Eq. (2) for P, yielding an effective dynamic hardness, H dyn:
As a validation check on Eq. (3), for each indentation the maximum load of the indentation, P, and the projected contact area of the impression, A c, can also be measured and used to calculate hardness following the traditional definition:
The maximum load can be read directly from the data acquired during testing, while the contact area can be measured from a microscopic observation after the test. Using Eqs. (3) and (4), average hardnesses of H dyn and H area in pure magnesium are calculated to be about ∼ 750 and ∼ 700 MPa, respectively, which sets the error bar on Eq. (3) to be ∼ 8% for the present dataset.
IV. RESULTS
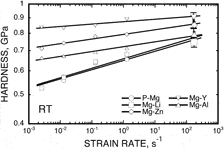
The dynamic hardness measurements from the present alloys [obtained by use of Eq. (3)] at room temperature are shown in Fig. 3. This figure includes a series of quasistatic nanoindentation data from the same set of experimental materials, which is reported in our previous work.Reference Somekawa and Schuh30 When the measurements of H dyn are supplemented into Fig. 3 at the approximate strain-rate of 150 ∼ 170 s–1, they align well with the quasistatic data to within measurement and extrapolation errors in spite of the difference in testing methods. The dynamic hardness of the Mg-Y alloys is the highest and that of pure magnesium is the lowest, which is the same trend seen in the quasistatic strain-rate regime. Since the alloys all have similar grain sizes of 2 ∼ 3 μm and no precipitate particles, the difference in hardness must be related to other factors. The strain-rate sensitivity in the Mg-Li alloy and pure magnesium are higher compared with that in the Mg-Y alloy.

FIG. 3. The variation in hardness as a function of strain-rate at room temperature in the magnesium and magnesium alloys with an average grain size of 2–3 μm. This figure also reproduces quasistatic nanoindentation data from the same set of experimental materials, using the open small symbols, from Ref. Reference Somekawa and Schuh30.
The variation in hardness, H dyn, as a function of temperature in the high strain-rate regime is shown in Fig. 4. The hardness decreases with temperature, as expected, although the degree of hardness reduction is influenced by the alloying elements. The hardness in pure magnesium drops by half even at the relatively low temperature of 373 K, whereas the hardness in the Mg-Y alloy decreases only 20 % over the same range. For comparison, this figure also includes the reported tensile test results of Ref. Reference Watanabe, Owashi, Uesugi, Takigawa and Higashi8 for pure magnesium with a grain size of 1 μm at a low strain-rate of 3 × 10−5 s-1, converted approximately into hardness using the Tabor relation (= 3.3σReference Sellars and McTegart32). In spite of the difference in testing methods, the temperature dependence of the hardness/stress at low strain-rates is apparently about the same as that in the high strain-rate regime in pure magnesium.

FIG. 4. Hardness as a function of temperature in the high strain-rate regime. This figure also includes literature data based on uniaxial testing, which was converted into hardness using the Tabor equation (= 3.3 × σ), for pure magnesium with a grain size of 1 μm, tested at a strain-rate of 3 × 10−5 s-1 (Ref. Reference Watanabe, Owashi, Uesugi, Takigawa and Higashi8).
The deformed microstructure beneath indentations is shown in the TEM micrographs of Fig. 5, for indentations for pure magnesium at (a) room temperature and (b) 373 K and (c) for the Mg-Y alloy at room temperature. The selected-area electron diffraction (SAED) patterns are also inset in each figure. In spite of the severe deformation evident in the bright-field images, the SAED patterns provide no evidence for the existence of deformation twins at either testing temperature, for either of the two materials. Although micrographs are not shown here, TEM observations for the other alloys were all qualitatively similar; no formation of twins is apparent in these fine grain structures. Instead of twins, beneath each indentation we always observe a copious amount of dislocation debris. The dominant deformation mechanism of the fine-grained magnesium alloys at high strain-rate is apparently not twinning, but dislocation slip.

FIG. 5. Typical TEM images in the region beneath high strain-rate indentations: (a) indented pure magnesium at room temperature, (b) indented pure magnesium at 373 K and (c) indented Mg-Y alloy at room temperature. Some oxidation can be observed in Fig. (b) due to handling of the sample in air.
V. DISCUSSION
In magnesium, as in many other metals, when the strain-rate is high or the temperature is low, the deformation mechanism is likely to lie in the power-law breakdown regime. And for the conditions of the present tests, we expect that this regime is the one sampled here as well. We may therefore analyze the deformation mechanism of our fine-grained alloys in the high-strain-rate regime with reference to a common constitutive equation for the breakdown regime such asReference Tabor33, Reference Frost and Ashby34:
where A is a constant, α (= 0.022 for magnesium alloysReference Song, Horton, Kim and Nieh35) is a constant, n (= 1/m; m is the power-law creep strain-rate sensitivity) is the stress exponent, D0 is a pre-exponential factor, Q is the activation energy, R is the gas constant and T is temperature. For low applied stresses, this expression reduces to a creep power-law:
for which the n-value is that of dislocation climb (= 4 ∼ 10 for magnesiumReference Frost and Ashby34) and G is the shear modulus. If the raw data are naïvely analyzed in the context of a power-law of the form of Eq. (6), then an “effective” n-value much greater than n = 4 can result, owing to the hyperbolic sine term in Eq. (5). This is shown in Fig. 3, where the effective n-value is given by the slope in double-logarithmic plot, and is found to be more than around 20. This apparent n-value is very high, and characteristic of the power-law breakdown regime, which is usually associated with dislocation glide as the kinetically rate-limiting process underlying deformation.Reference Frost and Ashby34 This is reasonable given the high rates of our experiments in Fig. 2, where creep mechanisms are less likely to participate in deformation. On the other hand, at slower rates, as in recent nanoindentation creep studies, pure magnesium can exhibit a low n-value of ∼ 4Reference Wang, Mukai and Nieh36 and an even lower n-value of 2.5 near grain boundaries even at room temperature.Reference Somekawa and Mukai37
Using the above models as a guide, we may also estimate the activation energies for deformation from our data. There n-values in the power-law creep and power-law breakdown regimes are reported to be in the range of about 4 ∼ 10 for magnesium and 4 ∼ 10 for metallic materials.Reference Frost and Ashby34 Typical examples showing the relationship between [sinh(ασ)]n and reciprocal temperature at a fixed strain-rate of 150 s-1 are illustrated in Fig. 6, using representative n-values of 5 and 10. The activation energies, which can be calculated from the slope of the line in this figure, are obtained to be 152 ∼ 302, 113 ∼ 225 and 84 ∼ 169 kJ/mol for pure magnesium, Mg-Li alloy and Mg-Y alloy, respectively. The activation energy in the power-law creep and power-law breakdown regimes is reported to be about 230 kJ/mol,Reference Frost and Ashby34 which is the range of the present results. Thus, the present data appear generally consistent with power-law breakdown as a dominant deformation mechanism, i.e., the rate controlling process is likely associated with dislocation motion.

FIG. 6. Typical plots of the relationship between sinh [ασ]n and reciprocal temperature at a fixed strain-rate of 150 s–1, where the n-value used is 5 (right y-axis) or 10 (left y-axis) in this analysis.
The above discussion suggests that dislocation activity, not twinning, is the dominant deformation mechanism, which aligns with the microscopic observations in Fig. 5. The activation energy for deformation twinning in magnesium is unknown, but it is interesting to note that in another hcp metal (Ti-V), when deformation twins contributed to deformation, the activation energy has been reported to be much lower than for competing mechanisms ∼ 40 kJ/mol.Reference Oberson and Ankem38
Next, we consider possible reasons why no twins are formed in these materials, either at low or high rates. In magnesium, deformation twins are generally nucleated at grain boundaries, and thus the critical stress to form them, σtwin, closely relates to grain size. In fact, the twinning stress is taken to follow a Hall-Petch scaling.Reference Meyers, Vohringer and Lubarda23, Reference Lahaie, Embury, Chadwick and Gray24
where σ0 and k are constants and d is the grain size. Barnett et al.Reference Barnett, Keshavarz, Beer and Atwell39 obtained the values of σ0 and k in magnesium alloys as 40 MPa and 9.4 MPa mm1/2. Those authors also reported a critical grain size, d cri, where the dominant deformation mechanism transitions from twinning to dislocation slip, which they estimated as follows:
where the Z-parameter is (= ![]() × exp(Q/RT)). Here the apparent activation energy, Q, is that for the lattice diffusion in magnesium.Reference Frost and Ashby34 When the grain size is finer than the critical grain size, the deformation mechanism is dislocation slip, i.e., the stress required for twinning becomes too high [Eq. (7)] and dislocation activity therefore prevails.
× exp(Q/RT)). Here the apparent activation energy, Q, is that for the lattice diffusion in magnesium.Reference Frost and Ashby34 When the grain size is finer than the critical grain size, the deformation mechanism is dislocation slip, i.e., the stress required for twinning becomes too high [Eq. (7)] and dislocation activity therefore prevails.
The critical grain sizes in this study at room temperature and 373 K are calculated as ∼ 4 and ∼ 20 μm, respectively, using Eq. (8). Since the grain size of the present alloys is below the critical grain size, the expected deformation mechanism is dislocation slip. Using Eq. (7), we also confirm that the hardness level expected for twinning is of order ∼ 250 MPa, which is quite close to the measured values for our alloys (227 ∼ 272 MPa, obtained from the hardness values of 750 ∼ 900 MPa in Fig. 3). The estimated stress is near the crossover point, which would also suggest that, in the present experimental conditions, twinning begins to be suppressed and dislocation activity emerges as the dominant mechanism. While there are several uncertainties in the present calculations (e.g., Hall-Petch parameters, Tabor parameter), they both align qualitatively quite well with the microstructural observations in Fig. 5.
Finally, it is worth quickly mentioning the reason for the difference in dynamic hardness among the present alloys. Our previous paper on deformation in the quasistatic range showedReference Somekawa and Schuh30 that the solid solution strengthening estimated using a first-principles model from Ref. Reference Yasi, Erctor and Trinkle40 explained the relative strengthening efficacy of the various alloying elements; Y > Zn > Al > Li. Although the strain-rate in the present study is higher than that in our previous work, the same basic conclusions apply here, with the same ranking of solutes. It is interesting, though, that at a sufficiently high strain-rate, the extrapolation of the trends in Fig. 3 suggests a possible crossover in the ranking; it is not clear that this is expected on the basis of existing solid solution strengthening models, and may point to an interesting direction for future modeling work.
VI. SUMMARY
Deformation behavior in the high-strain-rate regime, ∼ 150/s, was investigated in fine-grained magnesium dilute binary alloys and pure magnesium, by a method of instrumented high-rate nanoindentation. Both ambient and elevated temperatures up to 373 K were studied. The following results were obtained:
1) The dynamic hardness could be obtained by measuring the energy per unit volume dissipated as plastic work during impact-induced deformation; this method conformed to a more traditional approach of measuring the applied load and cross-sectional area. The hardness of fine-grained magnesium and its alloys in the high-strain-rate regime aligned well with existing quasistatic data to within measurement and extrapolation uncertainties.
2) Site-specific TEM observations made beneath the indentations showed no evidence for twinning even at high strain-rates, for any of the various alloys.
3) By analyzing the activation energy of deformation, which was around 152 ∼ 302, 113 ∼ 225 and 84 ∼ 169 kJ/mol for pure magnesium, Mg-Li alloy and Mg-Y alloy, respectively, we concluded that the data are consistent with a dislocation-based deformation mechanism, i.e., power-law breakdown, in all the present alloys.
ACKNOWLEDGMENTS
The authors are grateful to Dr. A. F. Schwartzman (Massachusetts Institute of Technology) and Dr. A. Singh (National Institute for Materials Science) for their help with the indentation method and TEM observation, respectively. This work was supported at MIT by the US Army Research Office under grant W911QX-09-P-0009, by the Institute for Soldier Nanotechnologies and by the JSPS Grant-in-Aid for Young Scientists (B) No. 21760564.