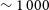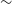1. Introduction
In 2017, the Advanced Laser Interferometer Gravitational-Wave Observatory and Virgo Interferometer (aLIGO/Virgo; Aasi et al. Reference Aasi2015; Acernese et al. Reference Acernese2014) detected gravitational waves (GWs) from a binary neutron star (BNS) merger, GW170817 (Abbott et al. Reference Abbott2017a), followed by the detection of gamma rays 1.7![]() $\,\textrm{s}$ later (GRB 170817A; Abbott et al. Reference Abbott2017b). It was the first joint detection of GWs and electromagnetic radiation from the same source. However, the delay in issuing the alert and large error region prevented most telescopes from searching for any prompt transient event microseconds around the merger.
$\,\textrm{s}$ later (GRB 170817A; Abbott et al. Reference Abbott2017b). It was the first joint detection of GWs and electromagnetic radiation from the same source. However, the delay in issuing the alert and large error region prevented most telescopes from searching for any prompt transient event microseconds around the merger.
Many models (including some that predate the discovery of fast radio bursts (FRBs; Lorimer et al. Reference Lorimer, Bailes, McLaughlin, Narkevic and Crawford2007; Thornton et al. Reference Thornton2013; Cordes & Chatterjee Reference Cordes and Chatterjee2019)) predict prompt radio emission associated with compact object mergers. This emission could be generated by the magnetic field interactions during the inspiral (Hansen & Lyutikov Reference Hansen and Lyutikov2001; Lai Reference Lai2012; Totani Reference Totani2013; Metzger & Zivancev Reference Metzger and Zivancev2016; Wang et al. Reference Wang, Yang, Wu, Dai and Wang2016, Reference Wang, Peng, Wu and Dai2018), interaction between a relativistic jet and interstellar medium (Pshirkov & Postnov Reference Pshirkov and Postnov2010), or the collapse of a supramassive neutron star remnant into a black hole (Ravi & Lasky Reference Ravi and Lasky2014; Falcke & Rezzolla Reference Falcke and Rezzolla2014). In particular, prompt emission may be in the form of short coherent radio pulses like FRBs. While some estimates suggested that neutron star mergers could not be the sole progenitors of FRBs because the volumetric rate of FRBs is significantly higher than that of BNS mergers, ![]() $\gtrsim$
$\gtrsim$ ![]() $10^4\,{\rm Gpc}^{-3}\,{\rm yr}^{-1}$ (Ravi Reference Ravi2019; Cao, Yu & Zhou Reference Cao, Yu and Zhou2018) versus
$10^4\,{\rm Gpc}^{-3}\,{\rm yr}^{-1}$ (Ravi Reference Ravi2019; Cao, Yu & Zhou Reference Cao, Yu and Zhou2018) versus ![]() $1540_{-1220}^{+3200}\,{\rm Gpc}^{-3}\,{\rm yr}^{-1}$ (Abbott et al. Reference Abbott2017b, also see Callister, Kanner, & Weinstein Reference Callister, Kanner and Weinstein2016), other estimates of the FRB rate have found better agreement (Lu & Piro Reference Lu and Piro2019). However, the detection of repeating FRBs (e.g., FRB121102 Spitler et al. Reference Spitler2016) clearly demonstrates that not all FRBs originate from BNS mergers. Further complications have come from recent observations, when the Galactic magnetar SGR 1935+2154 had X-ray outbursts (Mereghetti et al. Reference Mereghetti2020a, 2020b; Ridnaia et al. Reference Ridnaia2020a, Reference Ridnaia2020b ; Zhang et al. Reference Zhang2020) accompanied by simultaneous radio bursts (Scholz & Chime/Frb Collaboration 2020) of a brightness consistent with faint extragalactic FRBs (Bochenek et al. Reference Bochenek, Ravi, Belov, Hallinan, Kocz, Kulkarni and McKenna2020; Margalit et al. Reference Margalit, Beniamini, Sridhar and Metzger2020). James et al. (Reference James, Anderson, Wen, Bosveld, Chu, Kovalam, Slaven-Blair and Williams2019b), Macquart & Ekers (Reference Macquart and Ekers2018), and James et al. (Reference James, Ekers, Macquart, Bannister and Shannon2019a) also note that the FRB distribution we have got so far may be different by taking statistical and systemic effects into account. As it stands, the fraction of non-repeating FRBs potentially caused by BNS mergers is unclear, but a single discovery would change that. Furthermore, the detection of prompt emission from a BNS merger would be a useful tool to measure the interstellar medium and magnetic environment (Lu, Kumar, & Narayan Reference Lu, Kumar and Narayan2019) near the merger and locate the progenitor quickly, going from the 10–1 000 deg
$1540_{-1220}^{+3200}\,{\rm Gpc}^{-3}\,{\rm yr}^{-1}$ (Abbott et al. Reference Abbott2017b, also see Callister, Kanner, & Weinstein Reference Callister, Kanner and Weinstein2016), other estimates of the FRB rate have found better agreement (Lu & Piro Reference Lu and Piro2019). However, the detection of repeating FRBs (e.g., FRB121102 Spitler et al. Reference Spitler2016) clearly demonstrates that not all FRBs originate from BNS mergers. Further complications have come from recent observations, when the Galactic magnetar SGR 1935+2154 had X-ray outbursts (Mereghetti et al. Reference Mereghetti2020a, 2020b; Ridnaia et al. Reference Ridnaia2020a, Reference Ridnaia2020b ; Zhang et al. Reference Zhang2020) accompanied by simultaneous radio bursts (Scholz & Chime/Frb Collaboration 2020) of a brightness consistent with faint extragalactic FRBs (Bochenek et al. Reference Bochenek, Ravi, Belov, Hallinan, Kocz, Kulkarni and McKenna2020; Margalit et al. Reference Margalit, Beniamini, Sridhar and Metzger2020). James et al. (Reference James, Anderson, Wen, Bosveld, Chu, Kovalam, Slaven-Blair and Williams2019b), Macquart & Ekers (Reference Macquart and Ekers2018), and James et al. (Reference James, Ekers, Macquart, Bannister and Shannon2019a) also note that the FRB distribution we have got so far may be different by taking statistical and systemic effects into account. As it stands, the fraction of non-repeating FRBs potentially caused by BNS mergers is unclear, but a single discovery would change that. Furthermore, the detection of prompt emission from a BNS merger would be a useful tool to measure the interstellar medium and magnetic environment (Lu, Kumar, & Narayan Reference Lu, Kumar and Narayan2019) near the merger and locate the progenitor quickly, going from the 10–1 000 deg![]() $^2$ localisation from GW alone (Singer et al. Reference Singer2014; Abbott et al. Reference Abbott2020) to
$^2$ localisation from GW alone (Singer et al. Reference Singer2014; Abbott et al. Reference Abbott2020) to ![]() $\sim$arcmin (Bannister et al. Reference Bannister2017) for FRBs localised by the Australian Square Kilometre Array Pathfinder (ASKAP; Johnston et al. Reference Johnston2008). Combining this localisation with distance constraints from GW pipelines may be sufficient to uniquely identify a host galaxy, even in the absence of sub-arcsecond localisation.
$\sim$arcmin (Bannister et al. Reference Bannister2017) for FRBs localised by the Australian Square Kilometre Array Pathfinder (ASKAP; Johnston et al. Reference Johnston2008). Combining this localisation with distance constraints from GW pipelines may be sufficient to uniquely identify a host galaxy, even in the absence of sub-arcsecond localisation.
The timing of radio emission relative to the merger varies between different models. Totani (Reference Totani2013) predicts that FRBs produced by the magnetic field interactions could occur milliseconds before the BNS merger, while Falcke & Rezzolla (Reference Falcke and Rezzolla2014) predict an FRB due to the collapse of the supramassive neutron star produced 10–10 000![]() $\,\textrm{s}$ after the merger. Hence to detect or put limits on this prompt emission, we need to cover the GW error region as quickly as possible, ideally before the merger occurs, and then continue observing for minutes to hours after.
$\,\textrm{s}$ after the merger. Hence to detect or put limits on this prompt emission, we need to cover the GW error region as quickly as possible, ideally before the merger occurs, and then continue observing for minutes to hours after.
In late 2021, a four-detector GW network with the two aLIGO instruments, aLIGO Hanford (H) and aLIGO Livingston (L) combined with Phase 1 of Advanced Virgo (V) and the Kamioka Gravitational Wave Detector (KAGRA, or K; Somiya Reference Somiya2012; Aso et al. Reference Aso, Michimura, Somiya, Ando, Miyakawa, Sekiguchi, Tatsumi and Yamamoto2013) will be online for the fourth GW observing run (O4; Abbott et al. Reference Abbott2018), with BNS detectability ranges from 160–190 Mpc (L, H) to 90–120 Mpc (V) to 25–130 Mpc (K). During O4, the network is expected to detect between 3 and 110 BNS mergers using the estimated BNS event rate of 110–3 840 Gpc–3 yr–1 scaled from the observation of GW170817 (Abbott et al. Reference Abbott2019).
In contrast to O3 and earlier, where GW alerts were released only after the mergers with latencies of minutes to hours, in the O4 observing period it is expected that at least one negative-latency pipeline will be operating on the LHVK network. Negative-latency pipelines use matched filters to detect GW signals in the inspiral phase, which enables an alert to be released before the BNS merger occurs (Cannon et al. Reference Cannon2012; Chu et al. Reference Chu, Howell, Rowlinson and Gao2016). James et al. (Reference James, Anderson, Wen, Bosveld, Chu, Kovalam, Slaven-Blair and Williams2019b) illustrated that summed parallel infinite impulse response (SPIIR; Hooper et al. Reference Hooper, Chung, Luan, Blair, Chen and Wen2012a, Reference Hooper2012b) can detect GW170817-like events about 30![]() $\,\textrm{s}$ before the merger with detection signal-to-noise ratio (SNR) of
$\,\textrm{s}$ before the merger with detection signal-to-noise ratio (SNR) of ![]() $\sim$10. Chu et al. (Reference Chu, Howell, Rowlinson and Gao2016) found that the median localisation error areas can be better than 500 deg
$\sim$10. Chu et al. (Reference Chu, Howell, Rowlinson and Gao2016) found that the median localisation error areas can be better than 500 deg![]() $^2$ with a four-detector network 40
$^2$ with a four-detector network 40![]() $\,\textrm{s}$ before the coalescence.
$\,\textrm{s}$ before the coalescence.
There have been several unsuccessful attempts to search for prompt radio emission from compact binary coalescence at low radio frequencies. Callister et al. (Reference Callister2019) used the Owens Valley Radio Observatory Long Wavelength Array (OVRO-LWA, observing at 27–85 MHz)Footnote a to search for the prompt emission from the binary black hole merger GW170104, while Anderson et al. (Reference Anderson2018) used the OVRO-LWA to search for prompt emission from the cosmological short gamma-ray burst 170112A. Similarly, Rowlinson & Anderson (Reference Rowlinson and Anderson2019) examined data (Kaplan et al. Reference Kaplan2015) from the Murchison Widefield Array (MWA; Tingay et al. Reference Tingay2013, observing at 70–300 MHz) from the short gamma-ray burst 150424A. However, these events are well beyond the BNS detection sensitivity distance in O4 (![]() $z\sim 0.05$). More broadly, Kaplan et al. (Reference Kaplan, Murphy, Rowlinson, Croft, Wayth and Trott2016) investigated strategies to observe prompt emission from GW events with the MWA (also see James et al. Reference James, Anderson, Wen, Bosveld, Chu, Kovalam, Slaven-Blair and Williams2019b).
$z\sim 0.05$). More broadly, Kaplan et al. (Reference Kaplan, Murphy, Rowlinson, Croft, Wayth and Trott2016) investigated strategies to observe prompt emission from GW events with the MWA (also see James et al. Reference James, Anderson, Wen, Bosveld, Chu, Kovalam, Slaven-Blair and Williams2019b).
The Australian Square Kilometer Array Pathfinder (ASKAP; Johnston et al. Reference Johnston2008) is a ![]() $36 \times 12$-m antenna radio telescope located in Western Australia, operating over the frequency range 700 MHz to 1.8 GHz. In 2019, we conducted follow-up observations of several GW events with ASKAP in its standard imaging mode (e.g., Dobie et al. Reference Dobie2019b). In parallel, the Commensal Real-time ASKAP Fast Transients (CRAFT) survey Macquart et al. Reference Macquart2010) has developed high time resolution (1 ms) capabilities on ASKAP, which has resulted in the discovery of at least 32 FRBs (e.g., Shannon et al. Reference Shannon2018; Bannister et al. Reference Bannister2017; Reference Bannister2019). The localisation precision for ASKAP can be
$36 \times 12$-m antenna radio telescope located in Western Australia, operating over the frequency range 700 MHz to 1.8 GHz. In 2019, we conducted follow-up observations of several GW events with ASKAP in its standard imaging mode (e.g., Dobie et al. Reference Dobie2019b). In parallel, the Commensal Real-time ASKAP Fast Transients (CRAFT) survey Macquart et al. Reference Macquart2010) has developed high time resolution (1 ms) capabilities on ASKAP, which has resulted in the discovery of at least 32 FRBs (e.g., Shannon et al. Reference Shannon2018; Bannister et al. Reference Bannister2017; Reference Bannister2019). The localisation precision for ASKAP can be ![]() $\sim$arcminute with probabilistic localisation techniques (e.g., Bannister et al. Reference Bannister2017), going to
$\sim$arcminute with probabilistic localisation techniques (e.g., Bannister et al. Reference Bannister2017), going to ![]() $\sim$arcsecond using standard interferometry techniques (e.g., Bannister et al. Reference Bannister2019). ASKAP covers sky regions of a higher detection sensitivity for the GW detector network than some other radio telescopes (we show the corresponding sensitivity map in Figure 1). This enables ASKAP to detect GW signals earlier. However, the differences will be smaller in the future with more detectors joining the network.
$\sim$arcsecond using standard interferometry techniques (e.g., Bannister et al. Reference Bannister2019). ASKAP covers sky regions of a higher detection sensitivity for the GW detector network than some other radio telescopes (we show the corresponding sensitivity map in Figure 1). This enables ASKAP to detect GW signals earlier. However, the differences will be smaller in the future with more detectors joining the network.

Figure 1. Sensitivity map of the gravitational wave detector network in O4 (HLVK). The colour is proportional to the relative signal-to-noise ratio. The red line shows the ASKAP horizon (15![]() $^\circ$ in elevation angle) and the red star is where ASKAP is located.
$^\circ$ in elevation angle) and the red star is where ASKAP is located.
In this paper, we discuss the capabilities of ASKAP for detecting prompt emission from GW events.
2. Negative-latency pipelines
There are a number of pipelines running on aLIGO/Virgo that are designed to rapidly identify compact binary merger events. The key pipelines are GstLAL (Messick et al. Reference Messick2017; Sachdev et al. Reference Sachdev2019), multi-band template analysis (MBTA; Adams et al. Reference Adams2016), PyCBC Live (Dal Canton & Harry Reference Dal Canton and Harry2017; Nitz et al. Reference Nitz, Dal Canton, Davis and Reyes2018), and SPIIR (Hooper et al. Reference Hooper, Chung, Luan, Blair, Chen and Wen2012a, Reference Hooper2012b).
Each pipeline sends an alert to the Gravitational-Wave Candidate Event Database (GraceDB)Footnote b if the detection statistic (e.g., SNR) of the candidate passes a predetermined threshold. In order to collect the information about a single physical event in one place and issue a single alert per physical event, GraceDB gathers individual alerts into a ‘superevent’ data model.Footnote c Pipelines which send out superevents quickly will facilitate searches for prompt emission from BNSs.
Bayesian triangulation and rapid localisation (BAYESTAR; Singer & Price Reference Singer and Price2016) algorithms can offer observers a rapid parameter estimation for the GW events including the event localisation (e.g., Figure 2 for GW170817), distance, and component masses estimates. In general, increasing from a two-detector network to a three-detector network (O3) and to a four-detector network operating in O4 will improve localisation (e.g., Chu et al. Reference Chu, Howell, Rowlinson and Gao2016; Abbott et al. Reference Abbott2017b).

Figure 2. Sky localisation maps for GW170817 (Abbott et al. Reference Abbott2017b; left) and the initial map for GW190814 (https://gracedb.ligo.org/apiweb/superevents/S190814bv/files/bayestar.fits.gz.) (Abbott et al. Reference Abbott2020; right). The colour is proportional to the log![]() $_{10}$ of the probability. Maps are plotted in equatorial coordinates using the Mollweide projection. The 90% credible regions are shown by the white lines. The optimised tilings of ASKAP (Dobie et al. Reference Dobie, Murphy, Kaplan, Ghosh, Bannister and Hunstead2019a) to cover 90% credible region are shown in the red squares. Each square is 6
$_{10}$ of the probability. Maps are plotted in equatorial coordinates using the Mollweide projection. The 90% credible regions are shown by the white lines. The optimised tilings of ASKAP (Dobie et al. Reference Dobie, Murphy, Kaplan, Ghosh, Bannister and Hunstead2019a) to cover 90% credible region are shown in the red squares. Each square is 6![]() $\times$6 deg
$\times$6 deg![]() $^2$ FoV of ASKAP. The number of ASKAP tilings for GW170817 is 3, while that for GW190814 is 35. The cyan star shows the position with the maximum posterior probability for both events and the pink star shows where GW170817 actually was. Zoomed regions show the insets around the maximum posterior probability positions. The sizes for zoomed regions are 30
$^2$ FoV of ASKAP. The number of ASKAP tilings for GW170817 is 3, while that for GW190814 is 35. The cyan star shows the position with the maximum posterior probability for both events and the pink star shows where GW170817 actually was. Zoomed regions show the insets around the maximum posterior probability positions. The sizes for zoomed regions are 30![]() $\times$30 deg
$\times$30 deg![]() $^2$ (left) and 20
$^2$ (left) and 20![]() $\times$20 deg
$\times$20 deg![]() $^2$ (right), respectively.
$^2$ (right), respectively.
However, moving to a negative-latency search will reduce the SNR at detection and hence increase the location uncertainty. In general, the earlier the detection is, the lower SNR the pipeline will determine and the worse the localisation the pipeline will produce (Chu et al. Reference Chu, Howell, Rowlinson and Gao2016). James et al. (Reference James, Anderson, Wen, Bosveld, Chu, Kovalam, Slaven-Blair and Williams2019b) shows that the SNR of the GW170817 signal at ![]() $t_0- 30\,$ (i.e., 30
$t_0- 30\,$ (i.e., 30![]() $\,\textrm{s}$ before the merger at
$\,\textrm{s}$ before the merger at ![]() $t_0$) is one-third of that at the time of the merger. Cannon et al. (Reference Cannon2012) and Chu et al. (Reference Chu, Howell, Rowlinson and Gao2016) show that the localisation can be thousands of square degrees at
$t_0$) is one-third of that at the time of the merger. Cannon et al. (Reference Cannon2012) and Chu et al. (Reference Chu, Howell, Rowlinson and Gao2016) show that the localisation can be thousands of square degrees at ![]() $t_0-30\,$s, even if it is less than 30 deg
$t_0-30\,$s, even if it is less than 30 deg![]() $^2$ at
$^2$ at ![]() $t_0$. Chu et al. (Reference Chu, Howell, Rowlinson and Gao2016) used simulated data to calculate the median 90% credible regions at different times prior to merger for different detector networks. The 90% credible region will improve from about 2 200 deg
$t_0$. Chu et al. (Reference Chu, Howell, Rowlinson and Gao2016) used simulated data to calculate the median 90% credible regions at different times prior to merger for different detector networks. The 90% credible region will improve from about 2 200 deg![]() $^2$ to 1 600 deg
$^2$ to 1 600 deg![]() $^2$ at
$^2$ at ![]() $t_0-40\,$s from O3 with the LHV network to O4 with the LHVK network.
$t_0-40\,$s from O3 with the LHV network to O4 with the LHVK network.
3. ASKAP capabilities
ASKAP consists of 36 antennas which can point along their altitude and azimuth axes separately, with operating characteristics in Table 1. The telescope can slew at a rate of 3 and 1 deg sec–1 in azimuth and altitude, respectively. The rotation range for the azimuth axis is from ![]() $-270^{\circ}$ to
$-270^{\circ}$ to ![]() $270^{\circ}$ to allow for cable wraps. When reaching one of these limits, the antennas may need to unwrap by
$270^{\circ}$ to allow for cable wraps. When reaching one of these limits, the antennas may need to unwrap by ![]() $\pm360^{\circ}$ even if the target position is very close to the starting position, adding an additional overhead of
$\pm360^{\circ}$ even if the target position is very close to the starting position, adding an additional overhead of ![]() $\sim$120
$\sim$120![]() $\,\textrm{s}$. ASKAP has an additional rotation axis where the dish rotates around the optical axis. In a typical fast-slew strategy, we would choose not to change the dish rotation in order to minimise the total settling time.
$\,\textrm{s}$. ASKAP has an additional rotation axis where the dish rotates around the optical axis. In a typical fast-slew strategy, we would choose not to change the dish rotation in order to minimise the total settling time.
Table 1. ASKAP antenna mount operating characteristicsa.

a From Australia Telescope National Facility (ATNF): https://www.atnf.csiro.au/projects/askap/ASKAP_Antenna_public_specification_Nov08_v0.0.pdf.
There are two operational modes for ASKAP to look for FRB-like emissionFootnote d: collimated incoherent mode and fly’s eye mode (Bannister et al. Reference Bannister2017, and see Table 2). In the collimated incoherent mode, all the antennas point in the same direction, and the total power detected at each antenna is combined incoherently. In the fly’s eye mode, each antenna points in a different direction and we can achieve a total field of view (FoV) N![]() $\times$30 deg
$\times$30 deg![]() $^2$ with N antennas, albeit with reduced sensitivity.
$^2$ with N antennas, albeit with reduced sensitivity.
Table 2. Sensitivity, field-of-view (FoV), and angular resolution for different ASKAP of sub-arrays.

aThis assumes that we can use all 36 antennas and all antennas operate in the same configuration but different sub-array points to different positions.
bWith integration time of 1 ms, bandwidth of 336 MHz.
There is also a mode between the collimated incoherent mode and fly’s eye mode where one can use the 36 antennas in separate incoherent sub-arrays. For example, 36 antennas can be operated simultaneously as 6 separate 6-antenna arrays, with each sub-array producing a separate data stream. Fly’s eye mode is equivalent to 1-antenna sub-arrays, while full collimated incoherent mode is corresponding to 36-antenna sub-array.
The detection uncertainty, ![]() $\sigma_{\rm det}$, for a single ASKAP antenna is
$\sigma_{\rm det}$, for a single ASKAP antenna is
where SEFD is the system equivalent flux density (![]() $\sim$2 000 Jy for ASKAP)Footnote e,
$\sim$2 000 Jy for ASKAP)Footnote e, ![]() $\Delta\nu=336\,$MHz is the bandwidth, t is the integration time, and
$\Delta\nu=336\,$MHz is the bandwidth, t is the integration time, and ![]() $N_{\rm pol}=2$ is the number of the polarisations. Typical FRB searches use
$N_{\rm pol}=2$ is the number of the polarisations. Typical FRB searches use ![]() $t=1\,$ms. Using the equation above, the noise for a single ASKAP dish for an FRB search is roughly 2.4 Jy. When combining multiple antennas incoherently the noise decreases as
$t=1\,$ms. Using the equation above, the noise for a single ASKAP dish for an FRB search is roughly 2.4 Jy. When combining multiple antennas incoherently the noise decreases as ![]() $1/\sqrt{N_{\rm ant}}$, with
$1/\sqrt{N_{\rm ant}}$, with ![]() $N_{\rm ant}$ the number of antennas. Therefore, the noise can reach
$N_{\rm ant}$ the number of antennas. Therefore, the noise can reach ![]() $\sim 0.4$ Jy for the collimated incoherent mode when using all 36 antennas.
$\sim 0.4$ Jy for the collimated incoherent mode when using all 36 antennas.
4. Slewing simulations
Most models predict that prompt emission (if present) would occur within a few seconds of the merger (e.g., Hansen & Lyutikov Reference Hansen and Lyutikov2001). The chance of detecting this prompt emission will depend on both the latency of the pipelines and the slew time of the antennas. If the latency plus the slew time is smaller than the delay before radio emission, it may be possible to detect prompt emission.
Given initial and final positions of each antenna, we can use Table 1 to calculate the slew time for both axes (including acceleration and deceleration) and take the maximum of the two axis times as the slew time of each antenna. However, since we consider observation modes where all of the antennas end up pointing in different positions, we take the maximum of the slew times of all antennas as the slew time for the event.
We test this with two limiting cases: (1) a small event region where all of the antennas point to the same location (credible region ![]() $\lesssim$ ASKAP FoV) and (2) a large event region where we use the fly’s eye mode to tile as much as we can. Since the starting positions are unknown, we simulate this with randomised starting positions but two concrete sky maps: GW170817 (Abbott et al. Reference Abbott2017b) as a small region (
$\lesssim$ ASKAP FoV) and (2) a large event region where we use the fly’s eye mode to tile as much as we can. Since the starting positions are unknown, we simulate this with randomised starting positions but two concrete sky maps: GW170817 (Abbott et al. Reference Abbott2017b) as a small region (![]() $\sim$
$\sim$![]() $30\,{\rm deg}^2$), and GW190814 as a large region (
$30\,{\rm deg}^2$), and GW190814 as a large region (![]() $\sim$
$\sim$![]() $772\,{\rm deg}^2$), as illustrated in Figure 2. We use the initial bayestar skymap for GW190814 (LIGO Scientific Collaboration and Virgo Collaboration et al. 2019) as an example of a poor early-time localisation (although we note that the final LALInference skymap had a smaller 90% localisation of
$772\,{\rm deg}^2$), as illustrated in Figure 2. We use the initial bayestar skymap for GW190814 (LIGO Scientific Collaboration and Virgo Collaboration et al. 2019) as an example of a poor early-time localisation (although we note that the final LALInference skymap had a smaller 90% localisation of ![]() $\sim$
$\sim$![]() $30\,{\rm deg}^2$ which was similar to that for GW170817). The 90% localisation in Figure 2 is significantly larger than the ASKAP FoV and is elongated (like most GW localisations) and therefore it serves as a useful illustration.
$30\,{\rm deg}^2$ which was similar to that for GW170817). The 90% localisation in Figure 2 is significantly larger than the ASKAP FoV and is elongated (like most GW localisations) and therefore it serves as a useful illustration.
The starting conditions were randomised with equal probability for all azimuths and uniform in cosine of the elevation angle (equal probability per sky area) between ![]() $15^{\circ}$ and
$15^{\circ}$ and ![]() $89^{\circ}$.
$89^{\circ}$.
For the small region, GW170817 (![]() $\sim$
$\sim$![]() $30\,{\rm deg}^2$), we can cover the 90% credible region with three FoVs (shown in Figures 2 and 3). Figure 3 shows the spatial distribution of slewing time for GW170817. The median slewing time to get on-source is 40.3 s, with a range of 15.5–59.3
$30\,{\rm deg}^2$), we can cover the 90% credible region with three FoVs (shown in Figures 2 and 3). Figure 3 shows the spatial distribution of slewing time for GW170817. The median slewing time to get on-source is 40.3 s, with a range of 15.5–59.3![]() $\,\textrm{s}$ for the 10th and 90th percentiles, respectively, as shown in Figure 4.
$\,\textrm{s}$ for the 10th and 90th percentiles, respectively, as shown in Figure 4.

Figure 3. Slew time (indicated by the grey scale) for different starting positions for GW170817 as a function of starting azimuth and altitude. The red rectangles show the tiling for the bayestar skymap from the HLV network. The blue star shows the point where GW170817 is and the green star shows the maximum probability position of the skymap. The figure is in the azimuth/altitude coordinates and is modified to cover azimuths from ![]() $-270^{\circ}$ to
$-270^{\circ}$ to ![]() $270^{\circ}$, allowing for antenna motion over that range.
$270^{\circ}$, allowing for antenna motion over that range.

Figure 4. Cumulative histogram of slew times for GW170817 (blue) and GW190814 (orange) for different initial positions. The y-axis shows the fraction of the events whose slew time is smaller than the value on the x-axis.
For the large region, we used the strategy in Dobie et al. (Reference Dobie, Murphy, Kaplan, Ghosh, Bannister and Hunstead2019a) to optimise the ASKAP pointing. For simplicity, we called the coverage of a single antenna tiling. This strategy optimises the tiling centre position to tile as much of the 90% credible region as ASKAP can. If more than the maximum 36 antennas are needed to tile the 90% credible region, then less area will be covered. However, if we can cover the 90% region with fewer than 36 antennas, then more than one antenna is pointed towards the highest probability region. We used the GW190814 bayestar localisation to perform our simulation for the large region. We need all 36 antennas to cover the 90% credible region. As is shown in Figure 3, the 50th and 90th percentiles slewing times to get on-source are 65.2 and 102.0![]() $\,\textrm{s}$.
$\,\textrm{s}$.
5. Discussion
There could be as many as tens of BNS mergers detected by the HLVK GW detector network in the O4 run (Abbott et al. Reference Abbott2018). It may be impossible to follow up every event, especially including false alarms that increased during the low-latency portions of O3 and might increase further with negative latencies.
Only high signal-to-noise GW events will be amenable to negative-latency detections, such that the reduced signal-to-noise ratio will still pass the detection threshold. Overall, higher SNR detections lead to smaller localisations, with ![]() $A \propto \left(\rho \sigma_f\right)^{-2}$ where
$A \propto \left(\rho \sigma_f\right)^{-2}$ where ![]() $\rho$ is the SNR and
$\rho$ is the SNR and ![]() $\sigma_f$ is the effective bandwidth of the source in the detector (Fairhurst Reference Fairhurst2009). While high-
$\sigma_f$ is the effective bandwidth of the source in the detector (Fairhurst Reference Fairhurst2009). While high-![]() $\rho$ events will have well-localised detections eventually, moving to negative latency will reduce the instantaneous
$\rho$ events will have well-localised detections eventually, moving to negative latency will reduce the instantaneous ![]() $\rho$ and
$\rho$ and ![]() $\sigma_f$ and therefore increase the sky area accordingly. At the threshold where
$\sigma_f$ and therefore increase the sky area accordingly. At the threshold where ![]() $\rho\geq 8$ at
$\rho\geq 8$ at ![]() $t_0-30\,$s, the first localisation map would have an area of
$t_0-30\,$s, the first localisation map would have an area of ![]() $\sim \mathrm{few}\times 10^3\,{\rm deg}^2$, decreasing to a few
$\sim \mathrm{few}\times 10^3\,{\rm deg}^2$, decreasing to a few ![]() ${\rm deg}^2$ for the final detection with
${\rm deg}^2$ for the final detection with ![]() $\rho\sim 25$ (Cannon et al. Reference Cannon2012).
$\rho\sim 25$ (Cannon et al. Reference Cannon2012).
We now examine how a likely scenario could play out for a prompt ASKAP search. The typical time for downloading the skymap and calculating the pointings is of the order of 1![]() $\,\textrm{s}$. We examine a nominal event occuring at a distance of
$\,\textrm{s}$. We examine a nominal event occuring at a distance of ![]() $\sim$
$\sim$![]() $130\,$Mpc, with an early-warning
$130\,$Mpc, with an early-warning ![]() $\rho=8$ at
$\rho=8$ at ![]() $t_0-30\,$s and a 90% localisation of
$t_0-30\,$s and a 90% localisation of ![]() $\sim5\,000\,{\rm deg}^2$. This would imply a slew time of 60–90
$\sim5\,000\,{\rm deg}^2$. This would imply a slew time of 60–90![]() $\,\textrm{s}$, similar to the GW190814 case in Section 4. The dispersion measure, induced by the intergalactic medium, of events at this distance is
$\,\textrm{s}$, similar to the GW190814 case in Section 4. The dispersion measure, induced by the intergalactic medium, of events at this distance is ![]() $363\,{\rm pc}\,{\rm cm}^{-3}$ (James et al. Reference James, Anderson, Wen, Bosveld, Chu, Kovalam, Slaven-Blair and Williams2019b) and therefore a time delay to an ASKAP frequency of 900 MHz of only 1.9
$363\,{\rm pc}\,{\rm cm}^{-3}$ (James et al. Reference James, Anderson, Wen, Bosveld, Chu, Kovalam, Slaven-Blair and Williams2019b) and therefore a time delay to an ASKAP frequency of 900 MHz of only 1.9![]() $\,\textrm{s}$. The time delay due to the intergalactic medium is relatively small compared to the slewing time, and in this case the time delay can be considered negligible ASKAP will therefore miss this event by
$\,\textrm{s}$. The time delay due to the intergalactic medium is relatively small compared to the slewing time, and in this case the time delay can be considered negligible ASKAP will therefore miss this event by ![]() $\gtrsim$1 min. However, we note that based on Figure 4, there are about 10% of events where the slew time will be
$\gtrsim$1 min. However, we note that based on Figure 4, there are about 10% of events where the slew time will be ![]() $\sim 50\,$s, in which case we may be able to conduct a search for pre-merger prompt emission.
$\sim 50\,$s, in which case we may be able to conduct a search for pre-merger prompt emission.
An ideal event for our search would have an early-warning sky area which is only a single ASKAP FoV (comparable to our simulation of the GW170817 skymap in Figures 2 and 4). Such an event would have a final ![]() $\rho\gtrsim 60$ (at the time of the merger), corresponding to sources closer than
$\rho\gtrsim 60$ (at the time of the merger), corresponding to sources closer than ![]() $\sim$
$\sim$![]() $24\,{\rm Mpc}$ (Cannon et al. Reference Cannon2012), or a rate of
$24\,{\rm Mpc}$ (Cannon et al. Reference Cannon2012), or a rate of ![]() $0.1^{+0.2}_{-0.1}\,{\rm yr}^{-1}$ based on the BNS rate in Abbott et al. (Reference Abbott2017b). Therefore, the prospects of seeing such an event during a year-long observing campaign are
$0.1^{+0.2}_{-0.1}\,{\rm yr}^{-1}$ based on the BNS rate in Abbott et al. (Reference Abbott2017b). Therefore, the prospects of seeing such an event during a year-long observing campaign are ![]() $\sim$
$\sim$![]() $0.1$. For any realistic scenario, we will of course lose 60% of events to those detected below the ASKAP horizon, as well as
$0.1$. For any realistic scenario, we will of course lose 60% of events to those detected below the ASKAP horizon, as well as ![]() $\sim$30% (assuming the alert for the event with small early-warning skymap is released 30s before the merger) of the remaining events to those where the slew time is unacceptably long, meaning that we may only trigger on 12% of these very bright events. So we expect that ASKAP may be able to observe
$\sim$30% (assuming the alert for the event with small early-warning skymap is released 30s before the merger) of the remaining events to those where the slew time is unacceptably long, meaning that we may only trigger on 12% of these very bright events. So we expect that ASKAP may be able to observe ![]() $\sim$
$\sim$![]() $0.012$ events during O4. At least at radio wavelengths, we are not sensitive to weather and significantly less sensitive to day/night distinctions.
$0.012$ events during O4. At least at radio wavelengths, we are not sensitive to weather and significantly less sensitive to day/night distinctions.
The discussion above focused on whether ASKAP could observe prompt emission but did not consider whether or not it could detect it. For that, we need to understand the flux density predictions of different models. Some models (e.g., Pshirkov & Postnov Reference Pshirkov and Postnov2010; Hansen & Lyutikov Reference Hansen and Lyutikov2001) predict that BNS mergers can produce FRB-like emission at low radio frequencies, ![]() $\lesssim$
$\lesssim$![]() $100\,$MHz, but this is too low for ASKAP, and some of them have a hard cut-off at the high frequency end (e.g., Wang et al. Reference Wang, Peng, Wu and Dai2018). Moreover, no FRBs have been detected at those frequencies (e.g., Rowlinson et al. Reference Rowlinson2016; Chawla et al. Reference Chawla2017; Tingay et al. Reference Tingay2015; Sokolowski et al. Reference Sokolowski2018, although new detections are coming closer, Pilia et al. Reference Pilia2020; Chawla et al. Reference Chawla2020), which may influence the BNS/FRB rate comparison (e.g., Callister et al. Reference Callister, Kanner and Weinstein2016). Wang et al. (Reference Wang, Yang, Wu, Dai and Wang2016), Ravi & Lasky (Reference Ravi and Lasky2014) and Lyutikov (Reference Lyutikov2013) predict the total power that can be emitted by BNS mergers. However, the flux density at a given frequency is not clear. Instead, we parameterise this as
$100\,$MHz, but this is too low for ASKAP, and some of them have a hard cut-off at the high frequency end (e.g., Wang et al. Reference Wang, Peng, Wu and Dai2018). Moreover, no FRBs have been detected at those frequencies (e.g., Rowlinson et al. Reference Rowlinson2016; Chawla et al. Reference Chawla2017; Tingay et al. Reference Tingay2015; Sokolowski et al. Reference Sokolowski2018, although new detections are coming closer, Pilia et al. Reference Pilia2020; Chawla et al. Reference Chawla2020), which may influence the BNS/FRB rate comparison (e.g., Callister et al. Reference Callister, Kanner and Weinstein2016). Wang et al. (Reference Wang, Yang, Wu, Dai and Wang2016), Ravi & Lasky (Reference Ravi and Lasky2014) and Lyutikov (Reference Lyutikov2013) predict the total power that can be emitted by BNS mergers. However, the flux density at a given frequency is not clear. Instead, we parameterise this as ![]() $4\pi d^2 \nu S_\nu = x L$, where x depends on the spectrum of the emission and the upper and lower frequency limits. In Totani (Reference Totani2013), the signal is predicted to be
$4\pi d^2 \nu S_\nu = x L$, where x depends on the spectrum of the emission and the upper and lower frequency limits. In Totani (Reference Totani2013), the signal is predicted to be ![]() $\sim$
$\sim$![]() $10^3\,{\rm Jy}$ at
$10^3\,{\rm Jy}$ at ![]() $24\,{\rm Mpc}$, at a frequency of
$24\,{\rm Mpc}$, at a frequency of ![]() $888\,{\rm MHz}$ (assuming a radio emission efficiency of
$888\,{\rm MHz}$ (assuming a radio emission efficiency of ![]() $\epsilon\sim 10^{-3}$, magnetic field strength of
$\epsilon\sim 10^{-3}$, magnetic field strength of ![]() $B\sim 10^{12.5}\,{\rm G}$, neutron star radius of
$B\sim 10^{12.5}\,{\rm G}$, neutron star radius of ![]() $R\sim 10\,{\rm km}$, and rotation periods of
$R\sim 10\,{\rm km}$, and rotation periods of ![]() $P\sim 0.5\,{\rm ms}$). According to Table 2, if the merger follows the mechanism shown in Totani (Reference Totani2013), even with fly’s eye mode ASKAP can detect the signal if covering the burst region. As mentioned above, BNSs within 24 Mpc are estimated to occur infrequently, at a rate of
$P\sim 0.5\,{\rm ms}$). According to Table 2, if the merger follows the mechanism shown in Totani (Reference Totani2013), even with fly’s eye mode ASKAP can detect the signal if covering the burst region. As mentioned above, BNSs within 24 Mpc are estimated to occur infrequently, at a rate of ![]() $0.1^{+0.2}_{-0.1}\,{\rm yr}^{-1}$. Though the expected flux density is high, the rate for such a bright event is low, which makes it harder to detect any prompt emission. For the other models, we could detect them if
$0.1^{+0.2}_{-0.1}\,{\rm yr}^{-1}$. Though the expected flux density is high, the rate for such a bright event is low, which makes it harder to detect any prompt emission. For the other models, we could detect them if ![]() $x>3\times10^{-6}$ (assuming a radio luminosity of
$x>3\times10^{-6}$ (assuming a radio luminosity of ![]() $L\sim10^{40}\,{\rm erg}\,{\rm s}^{-1}$ as in Wang et al. Reference Wang, Yang, Wu, Dai and Wang2016, an event distance of
$L\sim10^{40}\,{\rm erg}\,{\rm s}^{-1}$ as in Wang et al. Reference Wang, Yang, Wu, Dai and Wang2016, an event distance of ![]() $d\sim24\,{\rm Mpc}$, and on observing frequency of 888 MHz).
$d\sim24\,{\rm Mpc}$, and on observing frequency of 888 MHz).
In this paper, we have mainly focused on BNS mergers, although one of our sky maps in Figure 2 was actually from a neutron-star black-hole (NSBH) merger. We generally consider BNS mergers as more favourable to production of electromagnetic (EM) counterparts in general and FRB-like emission in particular, although Mingarelli, Levin & Lazio (Reference Mingarelli, Levin and Lazio2015) hypothesises that NSBH mergers could also produce FRBs. However, NSBH mergers will generally contain only a single magnetosphere and in many cases the NS will be swallowed by the BH without disruption (Mingarelli et al. Reference Mingarelli, Levin and Lazio2015; Chatterjee et al. Reference Chatterjee, Ghosh, Brady, Kapadia, Miller, Nissanke and Pannarale2020), so many models for prompt emission will fail. Separately, NSBH mergers will generally be more distant (e.g., Abbott et al. Reference Abbott2019), leading to fainter EM emission, and the poorly constrained merger rate (Abbott et al. Reference Abbott2020) makes predictions difficult. Regardless, ASKAP still can and will search for the prompt emission from a well-localised NSBH merger, because the basic detection scenarios in terms of localisation will be similar to that for BNS mergers.
6. Conclusion
The detection of prompt emission from BNS mergers requires a radio instrument of sufficient sensitivity that is capable of being on-target before the arrival of a burst. In this paper, we estimated the probability for ASKAP to capture the prompt emission with negative-latency alerts from aLIGO/Virgo using two observational modes suitable for FRB-like emission. Fly’s eye mode can achieve higher sky coverage but less sensitivity, while the collimated incoherent mode gains sensitivity at the expense of sky area. Given that faint, poorly localised events will also have minimal advance warning and so will not allow for sufficient slew times, it may be nearly impossible to capture any prompt emission from those events. However, brighter events will have both better advance warning and smaller localisations areas enabling more sensitive observations and more confident coverage of the whole localisation area: we can achieve better sensitivity (down to 3.2 Jy using all antennas incoherently with an 8![]() $\sigma$ detection threshold). If FRB-like emission can be detected from these events, we can get a more accurate localisation for the event (as small as 3
$\sigma$ detection threshold). If FRB-like emission can be detected from these events, we can get a more accurate localisation for the event (as small as 3![]() $^{\prime\prime}\times 3^{\prime\prime}$ with more than three antennas with the same pointing), which can enable follow-up across the electromagnetic spectrum. While expected to be rare (
$^{\prime\prime}\times 3^{\prime\prime}$ with more than three antennas with the same pointing), which can enable follow-up across the electromagnetic spectrum. While expected to be rare (![]() $\sim$
$\sim$![]() $0.012\,{\rm yr}^{-1}$), ASKAP observations of negative-latency triggers have the potential to discover prompt emission from BNS mergers or at least constrain their origin.
$0.012\,{\rm yr}^{-1}$), ASKAP observations of negative-latency triggers have the potential to discover prompt emission from BNS mergers or at least constrain their origin.
Acknowledgements
We thank Prof. Jolien Creighton and Dr. Deep Chatterjee for helpful discussions. We thank the referee for his/her thorough review and highly appreciate the comments and suggestions, which significantly contributed to improving the quality of the publication. TM acknowledges the support of the Australian Research Council through grant DP190100561. DD is supported by an Australian Government Research Training Program Scholarship. DK is supported by NSF grant AST-1816492. Parts of this research were conducted by the Australian Research Council Centre of Excellence for Gravitational Wave Discovery (OzGrav), project number CE170100004. The Australian SKA Pathfinder is part of the Australia Telescope National Facility which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. The Murchison Radio-astronomy Observatory is managed by the CSIRO, who also provide operational support to ASKAP. We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site. This research has made use of NASA’s Astrophysics Data System Bibliographic Services.