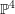Introduction
Let
![]() $X$
be a smooth complex projective variety that is rational, that is, admits a birational map
$X$
be a smooth complex projective variety that is rational, that is, admits a birational map
![]() $\unicode[STIX]{x1D71A}:\mathbb{P}^{r}{\dashrightarrow}X$
where
$\unicode[STIX]{x1D71A}:\mathbb{P}^{r}{\dashrightarrow}X$
where
![]() $r=\dim (X)$
. The map
$r=\dim (X)$
. The map
![]() $\unicode[STIX]{x1D71A}$
blows up various subvarieties of
$\unicode[STIX]{x1D71A}$
blows up various subvarieties of
![]() $\mathbb{P}^{r}$
– to what extent are these determined by
$\mathbb{P}^{r}$
– to what extent are these determined by
![]() $X$
? We can always precompose
$X$
? We can always precompose
![]() $\unicode[STIX]{x1D71A}$
by a birational automorphism of
$\unicode[STIX]{x1D71A}$
by a birational automorphism of
![]() $\mathbb{P}^{r}$
(i.e., a Cremona transformation) so we must take this into account.
$\mathbb{P}^{r}$
(i.e., a Cremona transformation) so we must take this into account.
For small dimensions these subvarieties are determined by
![]() $X$
. When
$X$
. When
![]() $r=1$
,
$r=1$
,
![]() $\unicode[STIX]{x1D71A}$
extends to an isomorphism; if
$\unicode[STIX]{x1D71A}$
extends to an isomorphism; if
![]() $r=2$
,
$r=2$
,
![]() $\unicode[STIX]{x1D71A}$
is resolved by blowing up points in
$\unicode[STIX]{x1D71A}$
is resolved by blowing up points in
![]() $\mathbb{P}^{2}$
. The case of
$\mathbb{P}^{2}$
. The case of
![]() $3$
-folds was analyzed by Clemens and Griffiths [Reference Clemens and GriffithsCG72]. We may assume that
$3$
-folds was analyzed by Clemens and Griffiths [Reference Clemens and GriffithsCG72]. We may assume that
![]() $\unicode[STIX]{x1D71A}$
(respectively,
$\unicode[STIX]{x1D71A}$
(respectively,
![]() $\unicode[STIX]{x1D71A}^{-1}$
) is resolved by blowing up a finite number of points and non-singular irreducible curves; let
$\unicode[STIX]{x1D71A}^{-1}$
) is resolved by blowing up a finite number of points and non-singular irreducible curves; let
![]() $C_{1},\ldots ,C_{k}$
(respectively,
$C_{1},\ldots ,C_{k}$
(respectively,
![]() $D_{1},\ldots ,D_{l}$
) denote those of positive genus. Comparing the Hodge structures on middle cohomology groups using the blow-up formula, we obtain an isomorphism of principally polarized abelian varieties:
$D_{1},\ldots ,D_{l}$
) denote those of positive genus. Comparing the Hodge structures on middle cohomology groups using the blow-up formula, we obtain an isomorphism of principally polarized abelian varieties:
The factors are Jacobians of curves and the intermediate Jacobian of
![]() $X$
. Principally polarized abelian varieties admit unique decompositions into irreducible factors and the Jacobian of a curve is irreducible with respect to the natural polarization. It follows that
$X$
. Principally polarized abelian varieties admit unique decompositions into irreducible factors and the Jacobian of a curve is irreducible with respect to the natural polarization. It follows that
![]() $J(X)$
can be expressed as a product of Jacobians of curves
$J(X)$
can be expressed as a product of Jacobians of curves
![]() $C_{i_{1}},\ldots ,C_{i_{t}}$
,
$C_{i_{1}},\ldots ,C_{i_{t}}$
,
![]() $\{i_{1},\ldots ,i_{t}\}\subset \{1,\ldots ,k\}$
, and these curves are determined up to isomorphism by the Torelli theorem.
$\{i_{1},\ldots ,i_{t}\}\subset \{1,\ldots ,k\}$
, and these curves are determined up to isomorphism by the Torelli theorem.
Therefore, we focus on
![]() $4$
-folds and their middle cohomology. Suppose that a smooth projective surface
$4$
-folds and their middle cohomology. Suppose that a smooth projective surface
![]() $\unicode[STIX]{x1D6F4}$
is contained in the base locus of
$\unicode[STIX]{x1D6F4}$
is contained in the base locus of
![]() $\unicode[STIX]{x1D71A}$
. The blow-up formula gives a homomorphism of Hodge structures
$\unicode[STIX]{x1D71A}$
. The blow-up formula gives a homomorphism of Hodge structures
can we recover
![]() $\unicode[STIX]{x1D6F4}$
from its image? Keeping track of divisor classes of
$\unicode[STIX]{x1D6F4}$
from its image? Keeping track of divisor classes of
![]() $\unicode[STIX]{x1D6F4}$
is complicated, as they might disappear under subsequent blow-downs. Thus all we can expect to recover is the transcendental cohomology
$\unicode[STIX]{x1D6F4}$
is complicated, as they might disappear under subsequent blow-downs. Thus all we can expect to recover is the transcendental cohomology
![]() $T(\unicode[STIX]{x1D6F4})\subset H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Z})$
.
$T(\unicode[STIX]{x1D6F4})\subset H^{2}(\unicode[STIX]{x1D6F4},\mathbb{Z})$
.
Mukai and Orlov [Reference Orlov.Orl97] have shown that K3 surfaces offer many examples of non-birational surfaces
![]() $R$
and
$R$
and
![]() $\hat{R}$
with
$\hat{R}$
with
![]() $T(R)\simeq T(\hat{R})$
as integral Hodge structures. These are explained through the notion of derived equivalence. There are cubic
$T(R)\simeq T(\hat{R})$
as integral Hodge structures. These are explained through the notion of derived equivalence. There are cubic
![]() $4$
-folds [Reference HassettHas16] whose Hodge structures show the trace of several derived equivalent K3 surfaces. However, these are not known to be rational. Nevertheless, this raises the following question.
$4$
-folds [Reference HassettHas16] whose Hodge structures show the trace of several derived equivalent K3 surfaces. However, these are not known to be rational. Nevertheless, this raises the following question.
Question 0.1. Let
![]() $R$
and
$R$
and
![]() $\hat{R}$
be derived equivalent K3 surfaces. Do there exist smooth projective
$\hat{R}$
be derived equivalent K3 surfaces. Do there exist smooth projective
![]() $4$
-folds
$4$
-folds
![]() $X$
,
$X$
,
![]() $P$
, and
$P$
, and
![]() $\hat{P}$
and birational maps
$\hat{P}$
and birational maps
such that
![]() $R$
and
$R$
and
![]() $\hat{R}$
are birational to components of the base loci of
$\hat{R}$
are birational to components of the base loci of
![]() $\unicode[STIX]{x1D71A}$
and
$\unicode[STIX]{x1D71A}$
and
![]() $\hat{\unicode[STIX]{x1D71A}}$
respectively, and the induced
$\hat{\unicode[STIX]{x1D71A}}$
respectively, and the induced
induce an isomorphism
![]() $T(R)\simeq T(\hat{R})$
?
$T(R)\simeq T(\hat{R})$
?
In other words, are derived equivalences of K3 surfaces induced by birational maps? It makes sense to start with the case where
![]() $P\simeq \hat{P}\simeq \mathbb{P}^{4}$
. Are derived equivalences of K3 surfaces induced by Cremona transformations?
$P\simeq \hat{P}\simeq \mathbb{P}^{4}$
. Are derived equivalences of K3 surfaces induced by Cremona transformations?
This last question may be too ambitious, as the base loci of Cremona transformations are highly constrained. According to Crauder and Katz [Reference Crauder and KatzCK89], the Cremona transformation of
![]() $\mathbb{P}^{4}$
which can be resolved by blowing up along a smooth and irreducible surface
$\mathbb{P}^{4}$
which can be resolved by blowing up along a smooth and irreducible surface
![]() $S\subset \mathbb{P}^{4}$
occurs as one of the following two cases:
$S\subset \mathbb{P}^{4}$
occurs as one of the following two cases:
(1)
 $S$
is a quintic elliptic scroll
$S$
is a quintic elliptic scroll
 $S=\mathbb{P}_{C}(E)$
, where
$S=\mathbb{P}_{C}(E)$
, where
 $C$
is an elliptic curve and
$C$
is an elliptic curve and
 $E$
is a rank-two vector bundle with
$E$
is a rank-two vector bundle with
 $e=-\text{deg}(\bigwedge ^{2}E)=-1$
;
$e=-\text{deg}(\bigwedge ^{2}E)=-1$
;(2)
 $S$
is a degree-10 determinantal surface given by the vanishing of the
$S$
is a degree-10 determinantal surface given by the vanishing of the
 $4\times 4$
minors of a
$4\times 4$
minors of a
 $4\times 5$
matrix of linear forms.
$4\times 5$
matrix of linear forms.
Here we present an example where derived equivalences of K3 surfaces are explained through Cremona transformations, and offer further evidence that such examples are quite rare. We can explain derived equivalences among degree-
![]() $12$
K3 surfaces in this way; however, we do not know how to realize derived equivalences of higher-degree K3 surfaces.
$12$
K3 surfaces in this way; however, we do not know how to realize derived equivalences of higher-degree K3 surfaces.
Our construction gives new examples of zero-divisors in the Grothendieck ring of complex algebraic varieties. The difference of each derived equivalent pair is non-vanishing in the ring and annihilated by the class of the affine line. The first example in this direction is given by the Pfaffian–Grassmannian Calabi–Yau
![]() $3$
-folds [Reference BorisovBor15, Reference MartinMar16]. Other examples include Calabi–Yau
$3$
-folds [Reference BorisovBor15, Reference MartinMar16]. Other examples include Calabi–Yau
![]() $3$
-folds from Grassmannians of type
$3$
-folds from Grassmannians of type
![]() $G_{2}$
[Reference Ito, Miura, Okawa and UedaIMOU16a, Reference KuznetsovKuz16]. Kuznetsov and Shinder [Reference Kuznetsov and ShinderKS17] have formulated general conjectures relating derived equivalence to zero-divisors in the Grothendieck ring; our example is an instance of [Reference Kuznetsov and ShinderKS17, Conjecture 1.6]. The relationship between zero-divisors in the Grothendieck ring and approaches to the rationality of cubic
$G_{2}$
[Reference Ito, Miura, Okawa and UedaIMOU16a, Reference KuznetsovKuz16]. Kuznetsov and Shinder [Reference Kuznetsov and ShinderKS17] have formulated general conjectures relating derived equivalence to zero-divisors in the Grothendieck ring; our example is an instance of [Reference Kuznetsov and ShinderKS17, Conjecture 1.6]. The relationship between zero-divisors in the Grothendieck ring and approaches to the rationality of cubic
![]() $4$
-folds is discussed in [Reference Galkin and ShinderGS14].
$4$
-folds is discussed in [Reference Galkin and ShinderGS14].
Section 1 presents preliminary results on Cremona transformations with singular base loci. The construction of our rational map is in § 2 and we verify the non-trivial derived equivalence in § 3. We apply the results to study the Grothendieck ring in § 4. Section 5 shows these constructions do not admit obvious extensions through a generalization of the classification of Crauder and Katz; the underlying computations are also used to analyze the maps defined in § 2.
1 Cremona transformation with singular base locus
1.1 Terminology and notation
A Cremona transformation of
![]() $\mathbb{P}^{n}$
is a birational map
$\mathbb{P}^{n}$
is a birational map
![]() $f:\mathbb{P}^{n}{\dashrightarrow}\mathbb{P}^{n}$
. Its base locus
$f:\mathbb{P}^{n}{\dashrightarrow}\mathbb{P}^{n}$
. Its base locus
![]() $\text{Bs}(f)$
is the subscheme where
$\text{Bs}(f)$
is the subscheme where
![]() $f$
is undefined.
$f$
is undefined.
Throughout this paper, we consider the Cremona transformation
![]() $f:\mathbb{P}^{4}{\dashrightarrow}\mathbb{P}^{4}$
with base locus resolved by blowing up an irreducible surface
$f:\mathbb{P}^{4}{\dashrightarrow}\mathbb{P}^{4}$
with base locus resolved by blowing up an irreducible surface
![]() $S$
, with singular locus consisting of transverse double points, which means a point where the surface has two smooth branches meeting transversally.
$S$
, with singular locus consisting of transverse double points, which means a point where the surface has two smooth branches meeting transversally.
Suppose
![]() $S$
has
$S$
has
![]() $\unicode[STIX]{x1D6FF}$
transverse double points which form a subset
$\unicode[STIX]{x1D6FF}$
transverse double points which form a subset
![]() $\unicode[STIX]{x1D6E5}\subset \mathbb{P}^{4}$
. The blow-up of
$\unicode[STIX]{x1D6E5}\subset \mathbb{P}^{4}$
. The blow-up of
![]() $\mathbb{P}^{4}$
along
$\mathbb{P}^{4}$
along
![]() $S$
can be factored as follows.
$S$
can be factored as follows.
(1) Blow up
 $\mathbb{P}^{4}$
along
$\mathbb{P}^{4}$
along
 $\unicode[STIX]{x1D6E5}$
, introducing
$\unicode[STIX]{x1D6E5}$
, introducing
 $\unicode[STIX]{x1D6FF}$
exceptional divisors
$\unicode[STIX]{x1D6FF}$
exceptional divisors
 $E_{1},\ldots ,E_{\unicode[STIX]{x1D6FF}}$
isomorphic to
$E_{1},\ldots ,E_{\unicode[STIX]{x1D6FF}}$
isomorphic to
 $\mathbb{P}^{3}$
. Let
$\mathbb{P}^{3}$
. Let
 $P$
denote the resulting
$P$
denote the resulting
 $4$
-fold and
$4$
-fold and
 $S^{\prime }$
the proper transform of
$S^{\prime }$
the proper transform of
 $S$
, which is now smooth.
$S$
, which is now smooth.(2) Blow up
 $P$
along
$P$
along
 $S^{\prime }$
to obtain
$S^{\prime }$
to obtain
 $P^{\prime }$
. Let
$P^{\prime }$
. Let
 $E$
denote the resulting exceptional divisor and
$E$
denote the resulting exceptional divisor and
 $E_{1}^{\prime },\ldots ,E_{\unicode[STIX]{x1D6FF}}^{\prime }$
the proper transforms of the first group of exceptional divisors. Each
$E_{1}^{\prime },\ldots ,E_{\unicode[STIX]{x1D6FF}}^{\prime }$
the proper transforms of the first group of exceptional divisors. Each
 $E_{i}^{\prime }$
is isomorphic to
$E_{i}^{\prime }$
is isomorphic to
 $E_{i}\simeq \mathbb{P}^{3}$
blown up along two skew lines
$E_{i}\simeq \mathbb{P}^{3}$
blown up along two skew lines
 $Q_{i}^{\prime },Q_{i}^{\prime \prime }\subset E_{i}$
.
$Q_{i}^{\prime },Q_{i}^{\prime \prime }\subset E_{i}$
.(3) Each
 $E_{i}^{\prime }$
is a
$E_{i}^{\prime }$
is a
 $\mathbb{P}^{1}$
-bundle over
$\mathbb{P}^{1}$
-bundle over
 $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Indeed, through each
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. Indeed, through each
 $p\in E_{i}$
not on
$p\in E_{i}$
not on
 $Q_{i}^{\prime }$
and
$Q_{i}^{\prime }$
and
 $Q_{i}^{\prime \prime }$
passes a unique line
$Q_{i}^{\prime \prime }$
passes a unique line
 $l$
intersecting
$l$
intersecting
 $Q_{i}^{\prime }$
and
$Q_{i}^{\prime }$
and
 $Q_{i}^{\prime \prime }$
. The bundle map is given by
$Q_{i}^{\prime \prime }$
. The bundle map is given by
 $p\mapsto (l\cap Q_{i}^{\prime },l\,\cap \,Q_{i}^{\prime \prime })\in Q_{i}^{\prime }\times Q_{i}^{\prime \prime }$
. Blow down each
$p\mapsto (l\cap Q_{i}^{\prime },l\,\cap \,Q_{i}^{\prime \prime })\in Q_{i}^{\prime }\times Q_{i}^{\prime \prime }$
. Blow down each
 $E_{i}^{\prime }$
to
$E_{i}^{\prime }$
to
 $\mathbb{P}^{1}\times \mathbb{P}^{1}$
. The resulting
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
. The resulting
 $X$
is isomorphic to
$X$
is isomorphic to
 $\text{Bl}_{S}\mathbb{P}^{4}$
.
$\text{Bl}_{S}\mathbb{P}^{4}$
.
Remark . The blow-up
![]() $X\rightarrow \mathbb{P}^{4}$
has a quadric surface
$X\rightarrow \mathbb{P}^{4}$
has a quadric surface
![]() $Q_{i}$
,
$Q_{i}$
,
![]() $i=1,\ldots ,\unicode[STIX]{x1D6FF}$
, over each transverse double point of
$i=1,\ldots ,\unicode[STIX]{x1D6FF}$
, over each transverse double point of
![]() $S$
. Then
$S$
. Then
![]() $P^{\prime }$
is obtained as the blow-up of
$P^{\prime }$
is obtained as the blow-up of
![]() $X$
along these quadrics.
$X$
along these quadrics.
Let
![]() $\unicode[STIX]{x1D70B}_{1}:X\rightarrow \mathbb{P}^{4}$
be the blow-up along
$\unicode[STIX]{x1D70B}_{1}:X\rightarrow \mathbb{P}^{4}$
be the blow-up along
![]() $S$
and
$S$
and
![]() $\unicode[STIX]{x1D70B}_{2}:X\rightarrow \mathbb{P}^{4}$
the resolution of
$\unicode[STIX]{x1D70B}_{2}:X\rightarrow \mathbb{P}^{4}$
the resolution of
![]() $f$
so that
$f$
so that
![]() $\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}_{1}\circ f$
. We organize these maps into a diagram:
$\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}_{1}\circ f$
. We organize these maps into a diagram:

Note that, by the definition of blow-up,
![]() $X$
is exactly the graph of
$X$
is exactly the graph of
![]() $f$
. Let
$f$
. Let
![]() $L$
(respectively,
$L$
(respectively,
![]() $M$
) denote the divisor of the hyperplane class of the left (respectively, right)
$M$
) denote the divisor of the hyperplane class of the left (respectively, right)
![]() $\mathbb{P}^{4}$
. We also use
$\mathbb{P}^{4}$
. We also use
![]() $L$
(respectively,
$L$
(respectively,
![]() $M$
) to denote its pullbacks to
$M$
) to denote its pullbacks to
![]() $X$
,
$X$
,
![]() $P$
and
$P$
and
![]() $P^{\prime }$
(respectively,
$P^{\prime }$
(respectively,
![]() $X$
and
$X$
and
![]() $P^{\prime }$
).
$P^{\prime }$
).
It’s clear that
![]() $L^{4}=1$
. We have
$L^{4}=1$
. We have
on
![]() $X$
as
$X$
as
![]() $f$
is birational. We define
$f$
is birational. We define
![]() $n$
by
$n$
by
and
![]() $\unicode[STIX]{x1D709}$
by
$\unicode[STIX]{x1D709}$
by
We may interpret
![]() $n$
and
$n$
and
![]() $\unicode[STIX]{x1D709}$
as the degrees of the homogeneous forms inducing
$\unicode[STIX]{x1D709}$
as the degrees of the homogeneous forms inducing
![]() $f$
and
$f$
and
![]() $f^{-1}$
, respectively. Define
$f^{-1}$
, respectively. Define
![]() $m$
as the multiplicity of
$m$
as the multiplicity of
![]() $S$
in the base locus. It is clear that
$S$
in the base locus. It is clear that
Since a non-degenerate subvariety in projective space has degree greater than one, the linear system in
![]() $|M|$
inducing
$|M|$
inducing
![]() $P^{\prime }\rightarrow \mathbb{P}^{4}$
must be complete. Thus we have
$P^{\prime }\rightarrow \mathbb{P}^{4}$
must be complete. Thus we have
We use these equations in our classification of Cremona transformations below.
1.2 Computing the intersection numbers
Let
![]() $\unicode[STIX]{x1D6F4}$
denote the normalization of
$\unicode[STIX]{x1D6F4}$
denote the normalization of
![]() $S$
and let
$S$
and let
![]() $K_{\unicode[STIX]{x1D6F4}}$
be its canonical class. Then the blow-up of
$K_{\unicode[STIX]{x1D6F4}}$
be its canonical class. Then the blow-up of
![]() $\unicode[STIX]{x1D6F4}$
along the preimage of the transverse double points is isomorphic to
$\unicode[STIX]{x1D6F4}$
along the preimage of the transverse double points is isomorphic to
![]() $S^{\prime }$
. We denote by
$S^{\prime }$
. We denote by
![]() $C$
a general sectional curve of
$C$
a general sectional curve of
![]() $S$
and also its preimages in
$S$
and also its preimages in
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $S^{\prime }$
. Let
$S^{\prime }$
. Let
![]() $d=C^{2}=\deg S$
. Note that
$d=C^{2}=\deg S$
. Note that
![]() $E_{i}\cap S^{\prime }=Q_{i}^{\prime }\cup Q_{i}^{\prime \prime }$
are exactly the exceptional curves on
$E_{i}\cap S^{\prime }=Q_{i}^{\prime }\cup Q_{i}^{\prime \prime }$
are exactly the exceptional curves on
![]() $S^{\prime }$
over the
$S^{\prime }$
over the
![]() $i$
th double point.
$i$
th double point.
Lemma 1.1. We have
![]() $LE_{i}^{\prime }=0$
. We also have
$LE_{i}^{\prime }=0$
. We also have
![]() $E^{3}E_{i}^{\prime }=-4$
,
$E^{3}E_{i}^{\prime }=-4$
,
![]() $E^{2}E_{i}^{\prime 2}=2$
,
$E^{2}E_{i}^{\prime 2}=2$
,
![]() $EE_{i}^{\prime 3}=0$
and
$EE_{i}^{\prime 3}=0$
and
![]() $E_{i}^{\prime 4}=-1$
.
$E_{i}^{\prime 4}=-1$
.
Proof. First,
![]() $LE_{i}^{\prime }=0$
since their intersection is empty.
$LE_{i}^{\prime }=0$
since their intersection is empty.
Recall that
![]() $E_{i}^{\prime }$
is isomorphic to
$E_{i}^{\prime }$
is isomorphic to
![]() $E_{i}\simeq \mathbb{P}^{3}$
blown up at skew lines
$E_{i}\simeq \mathbb{P}^{3}$
blown up at skew lines
![]() $Q_{i}^{\prime }$
and
$Q_{i}^{\prime }$
and
![]() $Q_{i}^{\prime \prime }$
. Write
$Q_{i}^{\prime \prime }$
. Write
![]() $\text{Pic}(E_{i}^{\prime })=\langle H,\widetilde{Q}^{\prime },\widetilde{Q}^{\prime \prime }\rangle$
where
$\text{Pic}(E_{i}^{\prime })=\langle H,\widetilde{Q}^{\prime },\widetilde{Q}^{\prime \prime }\rangle$
where
![]() $H$
is the polarization from
$H$
is the polarization from
![]() $\mathbb{P}^{3}$
, while
$\mathbb{P}^{3}$
, while
![]() $\widetilde{Q}^{\prime }$
and
$\widetilde{Q}^{\prime }$
and
![]() $\widetilde{Q}^{\prime \prime }$
are the exceptional divisors over the lines. We clearly have
$\widetilde{Q}^{\prime \prime }$
are the exceptional divisors over the lines. We clearly have
![]() $\widetilde{Q}^{\prime }\widetilde{Q}^{\prime \prime }=0$
and
$\widetilde{Q}^{\prime }\widetilde{Q}^{\prime \prime }=0$
and
![]() $\widetilde{Q}^{\prime }H^{2}=\widetilde{Q}^{\prime \prime }H^{2}=0$
. Since
$\widetilde{Q}^{\prime }H^{2}=\widetilde{Q}^{\prime \prime }H^{2}=0$
. Since
![]() $N_{Q_{i}^{\prime }/\mathbb{P}^{3}}={\mathcal{O}}_{Q_{i}^{\prime }}(1)\oplus {\mathcal{O}}_{Q_{i}^{\prime }}(1)$
, writing
$N_{Q_{i}^{\prime }/\mathbb{P}^{3}}={\mathcal{O}}_{Q_{i}^{\prime }}(1)\oplus {\mathcal{O}}_{Q_{i}^{\prime }}(1)$
, writing
![]() $\unicode[STIX]{x1D701}=c_{1}({\mathcal{O}}_{\mathbb{P}(N_{Q_{i}^{\prime }/\mathbb{P}^{3}})}(1))$
, we obtain
$\unicode[STIX]{x1D701}=c_{1}({\mathcal{O}}_{\mathbb{P}(N_{Q_{i}^{\prime }/\mathbb{P}^{3}})}(1))$
, we obtain
![]() $\unicode[STIX]{x1D701}^{2}+2H\unicode[STIX]{x1D701}=0$
in the Chow group of
$\unicode[STIX]{x1D701}^{2}+2H\unicode[STIX]{x1D701}=0$
in the Chow group of
![]() $\widetilde{Q}^{\prime }=\mathbb{P}(N_{Q_{i}^{\prime }/\mathbb{P}^{3}})$
. We have
$\widetilde{Q}^{\prime }=\mathbb{P}(N_{Q_{i}^{\prime }/\mathbb{P}^{3}})$
. We have
![]() $\widetilde{Q}^{\prime }|_{\widetilde{Q}^{\prime }}=-\unicode[STIX]{x1D701}$
, so that
$\widetilde{Q}^{\prime }|_{\widetilde{Q}^{\prime }}=-\unicode[STIX]{x1D701}$
, so that
We have
![]() $N_{E_{i}^{\prime }/P^{\prime }}={\mathcal{O}}(-H)$
and
$N_{E_{i}^{\prime }/P^{\prime }}={\mathcal{O}}(-H)$
and
![]() $E|_{E_{i}^{\prime }}=\widetilde{Q}^{\prime }+\widetilde{Q}^{\prime \prime }$
. Thus we obtain
$E|_{E_{i}^{\prime }}=\widetilde{Q}^{\prime }+\widetilde{Q}^{\prime \prime }$
. Thus we obtain
 $$\begin{eqnarray}\displaystyle E^{3}E_{i}^{\prime } & = & \displaystyle (\widetilde{Q}^{\prime }+\widetilde{Q}^{\prime \prime })^{3}=\widetilde{Q}^{\prime 3}+\widetilde{Q}^{\prime \prime 3}=-4,\nonumber\\ \displaystyle E^{2}E_{i}^{\prime 2} & = & \displaystyle (\widetilde{Q}^{\prime }+\widetilde{Q}^{\prime \prime })^{2}(-H)=2,\nonumber\\ \displaystyle EE_{i}^{\prime 3} & = & \displaystyle (\widetilde{Q}^{\prime }+\widetilde{Q}^{\prime \prime })(-H)^{2}=0,\nonumber\\ \displaystyle E_{i}^{\prime 4} & = & \displaystyle (-H)^{3}=-1.\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E^{3}E_{i}^{\prime } & = & \displaystyle (\widetilde{Q}^{\prime }+\widetilde{Q}^{\prime \prime })^{3}=\widetilde{Q}^{\prime 3}+\widetilde{Q}^{\prime \prime 3}=-4,\nonumber\\ \displaystyle E^{2}E_{i}^{\prime 2} & = & \displaystyle (\widetilde{Q}^{\prime }+\widetilde{Q}^{\prime \prime })^{2}(-H)=2,\nonumber\\ \displaystyle EE_{i}^{\prime 3} & = & \displaystyle (\widetilde{Q}^{\prime }+\widetilde{Q}^{\prime \prime })(-H)^{2}=0,\nonumber\\ \displaystyle E_{i}^{\prime 4} & = & \displaystyle (-H)^{3}=-1.\square\nonumber\end{eqnarray}$$
Lemma 1.2. The intersection numbers involving
![]() $L$
and
$L$
and
![]() $E$
are:
$E$
are:
(1)
 $L^{3}E=0$
and
$L^{3}E=0$
and
 $L^{2}E^{2}=-d$
;
$L^{2}E^{2}=-d$
;(2)
 $LE^{3}=-5d-K_{\unicode[STIX]{x1D6F4}}C$
;
$LE^{3}=-5d-K_{\unicode[STIX]{x1D6F4}}C$
;(3)
 $E^{4}=-15d-5K_{\unicode[STIX]{x1D6F4}}C-c_{2}(\unicode[STIX]{x1D6F4})+6\unicode[STIX]{x1D6FF}$
;
$E^{4}=-15d-5K_{\unicode[STIX]{x1D6F4}}C-c_{2}(\unicode[STIX]{x1D6F4})+6\unicode[STIX]{x1D6FF}$
;
(3’)
 $E^{4}=d^{2}-25d-10K_{\unicode[STIX]{x1D6F4}}C-{K_{\unicode[STIX]{x1D6F4}}}^{2}+4\unicode[STIX]{x1D6FF}$
.
$E^{4}=d^{2}-25d-10K_{\unicode[STIX]{x1D6F4}}C-{K_{\unicode[STIX]{x1D6F4}}}^{2}+4\unicode[STIX]{x1D6FF}$
.
Proof.
![]() $L^{3}E=0$
since a general line does not intersect
$L^{3}E=0$
since a general line does not intersect
![]() $S$
. We have
$S$
. We have
![]() $L^{2}E^{2}=-\text{deg}S^{\prime }=-d$
.
$L^{2}E^{2}=-\text{deg}S^{\prime }=-d$
.
Assume that
![]() $C=S\cap L$
for some hyperplane
$C=S\cap L$
for some hyperplane
![]() $L\simeq \mathbb{P}^{3}$
. Then
$L\simeq \mathbb{P}^{3}$
. Then
![]() $LE^{3}=s(C,L)_{0}$
, the zeroth Segre class of
$LE^{3}=s(C,L)_{0}$
, the zeroth Segre class of
![]() $C$
in
$C$
in
![]() $L$
, which equals
$L$
, which equals
![]() $[c(N_{C/L})^{-1}]_{0}=[c(C)c(\unicode[STIX]{x1D704}^{\ast }T_{\mathbb{P}^{3}})^{-1}]_{0}=[([C]-K_{\unicode[STIX]{x1D6F4}}C-C^{2})([C]-4d)]_{0}=-5d-K_{\unicode[STIX]{x1D6F4}}C$
.
$[c(N_{C/L})^{-1}]_{0}=[c(C)c(\unicode[STIX]{x1D704}^{\ast }T_{\mathbb{P}^{3}})^{-1}]_{0}=[([C]-K_{\unicode[STIX]{x1D6F4}}C-C^{2})([C]-4d)]_{0}=-5d-K_{\unicode[STIX]{x1D6F4}}C$
.
We have
![]() $E^{4}=-s(S^{\prime },P)_{0}=-[c(N_{S^{\prime }/P})^{-1}]_{0}=-[c(S^{\prime })c(P)|_{S^{\prime }}^{-1}]_{0}$
. Let
$E^{4}=-s(S^{\prime },P)_{0}=-[c(N_{S^{\prime }/P})^{-1}]_{0}=-[c(S^{\prime })c(P)|_{S^{\prime }}^{-1}]_{0}$
. Let
![]() $\unicode[STIX]{x1D716}:P\rightarrow \mathbb{P}^{4}$
be the blow-up. The blow-up formula for Chern classes gives
$\unicode[STIX]{x1D716}:P\rightarrow \mathbb{P}^{4}$
be the blow-up. The blow-up formula for Chern classes gives
Thus we have
and also
Let
![]() $\unicode[STIX]{x1D70F}:S^{\prime }\rightarrow \unicode[STIX]{x1D6F4}$
be the blow-up. Then we have
$\unicode[STIX]{x1D70F}:S^{\prime }\rightarrow \unicode[STIX]{x1D6F4}$
be the blow-up. Then we have
Multiply the results to get
![]() $E^{4}=-15d-5K_{\unicode[STIX]{x1D6F4}}C-c_{2}(\unicode[STIX]{x1D6F4})+6\unicode[STIX]{x1D6FF}$
.
$E^{4}=-15d-5K_{\unicode[STIX]{x1D6F4}}C-c_{2}(\unicode[STIX]{x1D6F4})+6\unicode[STIX]{x1D6FF}$
.
Another expression for
![]() $E^{4}$
is derived from
$E^{4}$
is derived from
We have
![]() $c_{2}(N_{S^{\prime }/P})=d^{2}-4\unicode[STIX]{x1D6FF}$
. On the other hand,
$c_{2}(N_{S^{\prime }/P})=d^{2}-4\unicode[STIX]{x1D6FF}$
. On the other hand,
 $$\begin{eqnarray}\begin{array}{@{}ccl@{}}c_{1}(N_{S^{\prime }/P})\,\, & =\,\, & c_{1}(T_{P})|_{S^{\prime }}-c_{1}(T_{S^{\prime }})\\ \,\, & =\,\, & -(-5L+3\unicode[STIX]{x1D6F4}_{i}E_{i})|_{S^{\prime }}-(-K_{S^{\prime }})\\ \,\, & =\,\, & 5C+\unicode[STIX]{x1D70F}^{\ast }K_{\unicode[STIX]{x1D6F4}}-2\unicode[STIX]{x1D6F4}_{i}(Q_{i}^{\prime }+Q_{i}^{\prime \prime }),\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccl@{}}c_{1}(N_{S^{\prime }/P})\,\, & =\,\, & c_{1}(T_{P})|_{S^{\prime }}-c_{1}(T_{S^{\prime }})\\ \,\, & =\,\, & -(-5L+3\unicode[STIX]{x1D6F4}_{i}E_{i})|_{S^{\prime }}-(-K_{S^{\prime }})\\ \,\, & =\,\, & 5C+\unicode[STIX]{x1D70F}^{\ast }K_{\unicode[STIX]{x1D6F4}}-2\unicode[STIX]{x1D6F4}_{i}(Q_{i}^{\prime }+Q_{i}^{\prime \prime }),\end{array}\end{eqnarray}$$
hence we deduce
and also
2 Construction of our example
In this section, we use Mukai’s construction [Reference MukaiMuk88] to produce an explicit example of a degree-12 K3 surface
![]() $R\subset \mathbb{P}^{7}$
together with three points
$R\subset \mathbb{P}^{7}$
together with three points
![]() $p_{1},p_{2},p_{3}\in R$
. This example helps us prove the following theorem.
$p_{1},p_{2},p_{3}\in R$
. This example helps us prove the following theorem.
Theorem 2.1. Let
![]() $R\subset \mathbb{P}^{7}$
be a generic K3 surface of degree
$R\subset \mathbb{P}^{7}$
be a generic K3 surface of degree
![]() $12$
and
$12$
and
![]() $\unicode[STIX]{x1D6F1}:=\{p_{1},p_{2},p_{3}\}\subset R$
a generic triple of points.
$\unicode[STIX]{x1D6F1}:=\{p_{1},p_{2},p_{3}\}\subset R$
a generic triple of points.
(1) Projection from
 $\unicode[STIX]{x1D6F1}$
maps
$\unicode[STIX]{x1D6F1}$
maps
 $R$
to a surface
$R$
to a surface
 $S\subset \mathbb{P}^{4}$
with three transverse double points.
$S\subset \mathbb{P}^{4}$
with three transverse double points.(2) The complete linear system
 $M$
of quartics vanishing along
$M$
of quartics vanishing along
 $S$
cuts out
$S$
cuts out
 $S$
scheme-theoretically.
$S$
scheme-theoretically.(3)
 $M$
induces a birational map
$M$
induces a birational map
 $f:\mathbb{P}^{4}{\dashrightarrow}\mathbb{P}^{4}$
.
$f:\mathbb{P}^{4}{\dashrightarrow}\mathbb{P}^{4}$
.(4) The base locus of the inverse
 $f^{-1}$
is also a projection of a degree-
$f^{-1}$
is also a projection of a degree-
 $12$
K3 surface from three points.
$12$
K3 surface from three points.
2.1 Orthogonal Grassmannian
Let
![]() $V$
be a 10-dimensional vector space equipped with a non-degenerate quadratic form
$V$
be a 10-dimensional vector space equipped with a non-degenerate quadratic form
![]() $q$
. The five-dimensional subspaces of
$q$
. The five-dimensional subspaces of
![]() $V$
isotropic with respect to
$V$
isotropic with respect to
![]() $q$
form a subvariety
$q$
form a subvariety
![]() ${\mathcal{S}}$
of the Grassmannian G
${\mathcal{S}}$
of the Grassmannian G
![]() $(5,V)$
. It has two components
$(5,V)$
. It has two components
![]() ${\mathcal{S}}^{+}$
and
${\mathcal{S}}^{+}$
and
![]() ${\mathcal{S}}^{-}$
which are isomorphic to each other. They are called orthogonal Grassmannians and are denoted by OG
${\mathcal{S}}^{-}$
which are isomorphic to each other. They are called orthogonal Grassmannians and are denoted by OG
![]() $(5,V)$
.
$(5,V)$
.
Fix a 5-subspace
![]() $W\in \text{OG}(5,V)$
and let
$W\in \text{OG}(5,V)$
and let
![]() $W^{\ast }$
be its orthogonal complement with respect to
$W^{\ast }$
be its orthogonal complement with respect to
![]() $q$
. Then OG
$q$
. Then OG
![]() $(5,V)$
can be identified scheme-theoretically as the zero locus in
$(5,V)$
can be identified scheme-theoretically as the zero locus in
of the quadratic form [Reference Iliev and MarkushevichIM04, §2]
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}}\displaystyle \det W\oplus \bigwedge ^{2}W\oplus W^{\ast }\,\, & \longrightarrow \,\, & \displaystyle \bigwedge ^{4}W\oplus W\\ (x,\unicode[STIX]{x1D6FA},v)\,\, & \longmapsto \,\, & (x(v)+\frac{1}{2}\unicode[STIX]{x1D6FA}\wedge \unicode[STIX]{x1D6FA},\,\unicode[STIX]{x1D6FA}(v)).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}\displaystyle \det W\oplus \bigwedge ^{2}W\oplus W^{\ast }\,\, & \longrightarrow \,\, & \displaystyle \bigwedge ^{4}W\oplus W\\ (x,\unicode[STIX]{x1D6FA},v)\,\, & \longmapsto \,\, & (x(v)+\frac{1}{2}\unicode[STIX]{x1D6FA}\wedge \unicode[STIX]{x1D6FA},\,\unicode[STIX]{x1D6FA}(v)).\end{array}\end{eqnarray}$$
Here we choose an isomorphism
![]() $\mathbb{C}\simeq \det W$
. This induces an isomorphism
$\mathbb{C}\simeq \det W$
. This induces an isomorphism
![]() $\bigwedge ^{4}W\simeq W^{\ast }$
.
$\bigwedge ^{4}W\simeq W^{\ast }$
.
Let
![]() $\mathbf{x}=(x_{0},\ldots ,x_{15})$
be the homogeneous coordinate for
$\mathbf{x}=(x_{0},\ldots ,x_{15})$
be the homogeneous coordinate for
![]() $\mathbb{P}^{15}$
. Then (2.1) can be explicitly written down as ten quadrics:
$\mathbb{P}^{15}$
. Then (2.1) can be explicitly written down as ten quadrics:

2.2 An explicit example
Mukai [Reference MukaiMuk88, §3] proves that a generic K3 surface of degree 12 appears as a linear section of OG
![]() $(5,V)$
and vice versa.
$(5,V)$
and vice versa.
For example, the
![]() $\mathbb{P}^{7}\subset \mathbb{P}^{15}$
spanned by the rows of the
$\mathbb{P}^{7}\subset \mathbb{P}^{15}$
spanned by the rows of the
![]() $8\times 16$
matrix
$8\times 16$
matrix
 $$\begin{eqnarray}\mathbf{H}=\left(\begin{array}{@{}rrrrrrrrrrrrrrrr@{}}-1 & 3 & 2 & 0 & 2 & -3 & -1 & 0 & 3 & 1 & 0 & 3 & 0 & 2 & 0 & -3\\ 1 & 0 & -3 & 0 & -2 & 1 & 1 & 0 & -2 & -1 & -1 & -1 & 0 & 4 & 0 & 2\\ -1 & -3 & -2 & 0 & -3 & 0 & 3 & 2 & -1 & -3 & -1 & 2 & -1 & 2 & 0 & 3\\ 3 & 0 & 0 & 2 & 2 & 3 & 0 & 1 & 2 & -1 & 0 & 2 & -1 & -2 & 2 & 3\\ 0 & -1 & 1 & -1 & 0 & 1 & -3 & 3 & 2 & 2 & 1 & 3 & 0 & -3 & 0 & -3\\ 1 & 0 & 0 & 0 & 0 & -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 2 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 3 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{H}=\left(\begin{array}{@{}rrrrrrrrrrrrrrrr@{}}-1 & 3 & 2 & 0 & 2 & -3 & -1 & 0 & 3 & 1 & 0 & 3 & 0 & 2 & 0 & -3\\ 1 & 0 & -3 & 0 & -2 & 1 & 1 & 0 & -2 & -1 & -1 & -1 & 0 & 4 & 0 & 2\\ -1 & -3 & -2 & 0 & -3 & 0 & 3 & 2 & -1 & -3 & -1 & 2 & -1 & 2 & 0 & 3\\ 3 & 0 & 0 & 2 & 2 & 3 & 0 & 1 & 2 & -1 & 0 & 2 & -1 & -2 & 2 & 3\\ 0 & -1 & 1 & -1 & 0 & 1 & -3 & 3 & 2 & 2 & 1 & 3 & 0 & -3 & 0 & -3\\ 1 & 0 & 0 & 0 & 0 & -1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 2 & 1 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 3 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{array}\right)\end{eqnarray}$$
cuts out a degree-12 K3 surface R on OG
![]() $(5,V)$
. More explicitly, let
$(5,V)$
. More explicitly, let
![]() $\mathbf{z}=(z_{0},\ldots ,z_{7})$
be homogeneous coordinates for
$\mathbf{z}=(z_{0},\ldots ,z_{7})$
be homogeneous coordinates for
![]() $\mathbb{P}^{7}$
. We define the inclusion
$\mathbb{P}^{7}$
. We define the inclusion
![]() $\unicode[STIX]{x1D704}:\mathbb{P}^{7}{\hookrightarrow}\mathbb{P}^{15}$
by
$\unicode[STIX]{x1D704}:\mathbb{P}^{7}{\hookrightarrow}\mathbb{P}^{15}$
by
Then we get
![]() $R=\unicode[STIX]{x1D704}^{-1}(\text{OG}(5,V))$
.
$R=\unicode[STIX]{x1D704}^{-1}(\text{OG}(5,V))$
.
The last three rows of
![]() $\mathbf{H}$
are chosen as solutions of (2.2) so that they form a triple of points
$\mathbf{H}$
are chosen as solutions of (2.2) so that they form a triple of points
![]() $\unicode[STIX]{x1D6F1}=\{p_{1},p_{2},p_{3}\}\subset R$
. With this choice the projection from
$\unicode[STIX]{x1D6F1}=\{p_{1},p_{2},p_{3}\}\subset R$
. With this choice the projection from
![]() $\unicode[STIX]{x1D6F1}$
is exactly the map
$\unicode[STIX]{x1D6F1}$
is exactly the map
which takes
![]() $R$
to
$R$
to
![]() $S=\unicode[STIX]{x1D70B}(R)$
.
$S=\unicode[STIX]{x1D70B}(R)$
.
We manipulate this example in a computer algebra systemFootnote
1
over the finite field
![]() $\mathbb{F}_{7}$
. We compute that
$\mathbb{F}_{7}$
. We compute that
![]() $S$
is singular along three transverse double points
$S$
is singular along three transverse double points
![]() $\{a_{1},a_{2},a_{3}\}$
and is the base locus of a Cremona transformation
$\{a_{1},a_{2},a_{3}\}$
and is the base locus of a Cremona transformation
Moreover, the base locus of the inverse
![]() $(\overline{f})^{-1}$
is again a surface
$(\overline{f})^{-1}$
is again a surface
![]() $\overline{T}$
singular along three transverse double points
$\overline{T}$
singular along three transverse double points
![]() $\{b_{1},b_{2},b_{3}\}$
. The matrix
$\{b_{1},b_{2},b_{3}\}$
. The matrix
![]() $\mathbf{H}$
is chosen such that the preimage of
$\mathbf{H}$
is chosen such that the preimage of
![]() $\{a_{1},a_{2},a_{3}\}$
on
$\{a_{1},a_{2},a_{3}\}$
on
![]() $R$
and the preimage of
$R$
and the preimage of
![]() $\{b_{1},b_{2},b_{3}\}$
on the normalization of
$\{b_{1},b_{2},b_{3}\}$
on the normalization of
![]() $\overline{T}$
are
$\overline{T}$
are
![]() $\mathbb{F}_{7}$
-rational points. This is the smallest field where our computer could quickly find such an
$\mathbb{F}_{7}$
-rational points. This is the smallest field where our computer could quickly find such an
![]() $\mathbf{H}$
.
$\mathbf{H}$
.
2.3 Proof of Theorem 2.1
We prove Theorem 2.1 for our example first.
We confirm the following properties by computer over
![]() $\mathbb{F}_{7}$
.
$\mathbb{F}_{7}$
.
(1)
 $S$
is singular along three points. The preimage of each singular point on
$S$
is singular along three points. The preimage of each singular point on
 $R$
has two points outside
$R$
has two points outside
 $\unicode[STIX]{x1D6F1}$
. So they are transverse double points.
$\unicode[STIX]{x1D6F1}$
. So they are transverse double points.(2) The ideal of
 $S$
is generated by five quartics
$S$
is generated by five quartics
 $\overline{f}_{0},\ldots ,\overline{f}_{4}$
.
$\overline{f}_{0},\ldots ,\overline{f}_{4}$
.
The double-point formula [Reference FultonFul98, Theorem 9.3] indicates that the three transverse double points of (1) exist over characteristic zero. Indeed, let
![]() $\unicode[STIX]{x1D716}:\unicode[STIX]{x1D6F4}\rightarrow S$
be the normalization. Then
$\unicode[STIX]{x1D716}:\unicode[STIX]{x1D6F4}\rightarrow S$
be the normalization. Then
![]() $\unicode[STIX]{x1D6F4}$
is isomorphic to
$\unicode[STIX]{x1D6F4}$
is isomorphic to
![]() $R$
blown up at three points. The double-point class
$R$
blown up at three points. The double-point class
![]() $\mathbb{D}(\unicode[STIX]{x1D716})\in \text{CH}_{0}(\unicode[STIX]{x1D6F4})$
is given by the formula
$\mathbb{D}(\unicode[STIX]{x1D716})\in \text{CH}_{0}(\unicode[STIX]{x1D6F4})$
is given by the formula
It is easy to verify that
![]() $\mathbb{D}(\unicode[STIX]{x1D716})=6$
. The quantity
$\mathbb{D}(\unicode[STIX]{x1D716})=6$
. The quantity
![]() $\frac{1}{2}\mathbb{D}(\unicode[STIX]{x1D716})=3$
counts the number of singularities on
$\frac{1}{2}\mathbb{D}(\unicode[STIX]{x1D716})=3$
counts the number of singularities on
![]() $S$
with multiplicity if the singular locus is a finite set. Therefore (1) implies that the singular locus of
$S$
with multiplicity if the singular locus is a finite set. Therefore (1) implies that the singular locus of
![]() $S$
consists of three transverse double points. This proves Theorem 2.1(1).
$S$
consists of three transverse double points. This proves Theorem 2.1(1).
The five quartics
![]() $\overline{f}_{0},\ldots ,\overline{f}_{4}$
lift to a basis
$\overline{f}_{0},\ldots ,\overline{f}_{4}$
lift to a basis
![]() $f_{0},\ldots ,f_{4}$
for the ideal of
$f_{0},\ldots ,f_{4}$
for the ideal of
![]() $S$
over characteristic zero. In particular, Theorem 2.1(2) holds. The forms
$S$
over characteristic zero. In particular, Theorem 2.1(2) holds. The forms
![]() $f_{0},\ldots ,f_{4}$
define a rational map
$f_{0},\ldots ,f_{4}$
define a rational map
which reduces to
over
![]() $\mathbb{F}_{7}$
. The degree of
$\mathbb{F}_{7}$
. The degree of
![]() $f$
is computed by the self-intersection
$f$
is computed by the self-intersection
![]() $M^{4}$
, which can be expanded as the right-hand side of equation (5.2). It is easy to check that our example satisfies
$M^{4}$
, which can be expanded as the right-hand side of equation (5.2). It is easy to check that our example satisfies
Inserting these data into (5.2), we get
![]() $M^{4}=1$
, that is, the map
$M^{4}=1$
, that is, the map
![]() $f$
is birational. Thus Theorem 2.1(3) holds.
$f$
is birational. Thus Theorem 2.1(3) holds.
The inverse
![]() $(\overline{f})^{-1}$
can be calculated by computer. It consists of five quartics also and the base locus is a surface
$(\overline{f})^{-1}$
can be calculated by computer. It consists of five quartics also and the base locus is a surface
![]() $\overline{T}$
singular along three points. These are transverse double points since each point has two preimage points on the normalization. By the same reasons as above, the base locus of
$\overline{T}$
singular along three points. These are transverse double points since each point has two preimage points on the normalization. By the same reasons as above, the base locus of
![]() $f^{-1}$
is again a surface cut by five quartics and singular along three transverse double points. Then Theorem 2.1(4) follows from Theorem 5.1.
$f^{-1}$
is again a surface cut by five quartics and singular along three transverse double points. Then Theorem 2.1(4) follows from Theorem 5.1.
Next, we prove Theorem 2.1 in the generic case.
It is clear that (1), (2), and (3) of the theorem are open conditions, so they hold for a generic example. As a consequence of Theorem 5.1, property (4) holds once Bs(
![]() $f^{-1}$
) is a surface cut out by five quartics and singular along three transverse double points. These are open conditions again, so Theorem 2.1 holds for a generic example.
$f^{-1}$
) is a surface cut out by five quartics and singular along three transverse double points. These are open conditions again, so Theorem 2.1 holds for a generic example.
2.4 Some geometry of the construction
Let
![]() $f$
be a Cremona transformation of Theorem 2.1. It has a resolution
$f$
be a Cremona transformation of Theorem 2.1. It has a resolution

Let
![]() $S_{L}$
and
$S_{L}$
and
![]() $S_{M}$
be the base locus of
$S_{M}$
be the base locus of
![]() $f$
and its inverse
$f$
and its inverse
![]() $f^{-1}$
, respectively. Then
$f^{-1}$
, respectively. Then
![]() $\unicode[STIX]{x1D70B}_{1}$
is the blow-up along
$\unicode[STIX]{x1D70B}_{1}$
is the blow-up along
![]() $S_{L}$
. Recall that
$S_{L}$
. Recall that
![]() $X$
coincides with the graph of
$X$
coincides with the graph of
![]() $f$
as well as
$f$
as well as
![]() $f^{-1}$
. Therefore,
$f^{-1}$
. Therefore,
![]() $\unicode[STIX]{x1D70B}_{2}$
is the blow-up along
$\unicode[STIX]{x1D70B}_{2}$
is the blow-up along
![]() $S_{M}$
.
$S_{M}$
.
This example has
![]() $d=9$
,
$d=9$
,
![]() $K_{\unicode[STIX]{x1D6F4}}C=3$
,
$K_{\unicode[STIX]{x1D6F4}}C=3$
,
![]() $c_{2}(\unicode[STIX]{x1D6F4})=27$
,
$c_{2}(\unicode[STIX]{x1D6F4})=27$
,
![]() $\unicode[STIX]{x1D6FF}=3$
, and
$\unicode[STIX]{x1D6FF}=3$
, and
Evaluating Lemmas 1.1 and 1.2 with this data yields the following corollary.
Corollary 2.2. We have
(1)
 $LE_{i}^{\prime }=0$
,
$LE_{i}^{\prime }=0$
,
 $E^{3}E_{i}^{\prime }=-4$
,
$E^{3}E_{i}^{\prime }=-4$
,
 $E^{2}E_{i}^{\prime 2}=2$
,
$E^{2}E_{i}^{\prime 2}=2$
,
 $EE_{i}^{\prime 3}=0$
,
$EE_{i}^{\prime 3}=0$
,
 $E_{i}^{\prime 4}=-1$
;
$E_{i}^{\prime 4}=-1$
;(2)
 $L^{3}E=0$
,
$L^{3}E=0$
,
 $L^{2}E^{2}=-9$
,
$L^{2}E^{2}=-9$
,
 $LE^{3}=-48$
,
$LE^{3}=-48$
,
 $E^{4}=-159$
.
$E^{4}=-159$
.
Thus consequently,
(3)
 $L^{3}M=4$
,
$L^{3}M=4$
,
 $L^{2}M^{2}=7$
,
$L^{2}M^{2}=7$
,
 $LM^{3}=4$
,
$LM^{3}=4$
,
 $M^{4}=1$
.
$M^{4}=1$
.
Let
![]() $X_{0},\ldots ,X_{4}$
be the homogeneous coordinates for
$X_{0},\ldots ,X_{4}$
be the homogeneous coordinates for
![]() $\mathbb{P}^{4}$
. The Cremona transformation
$\mathbb{P}^{4}$
. The Cremona transformation
![]() $f$
is ramified along the locus
$f$
is ramified along the locus
![]() $\unicode[STIX]{x1D6E9}$
where the Jacobian matrix
$\unicode[STIX]{x1D6E9}$
where the Jacobian matrix
is degenerate. So
![]() $\unicode[STIX]{x1D6E9}$
is a degree-15 hypersurface in
$\unicode[STIX]{x1D6E9}$
is a degree-15 hypersurface in
![]() $\mathbb{P}^{4}$
defined by
$\mathbb{P}^{4}$
defined by
This locus is called the P-locus, which is classically defined as the image of the exceptional divisor of the blow-up
![]() $\unicode[STIX]{x1D70B}_{2}$
[Reference DolgachevDol12, §7.1.4]. In particular,
$\unicode[STIX]{x1D70B}_{2}$
[Reference DolgachevDol12, §7.1.4]. In particular,
![]() $\unicode[STIX]{x1D6E9}$
is irreducible. It also follows that
$\unicode[STIX]{x1D6E9}$
is irreducible. It also follows that
![]() $\unicode[STIX]{x1D6E9}$
is the locus contracted by
$\unicode[STIX]{x1D6E9}$
is the locus contracted by
![]() $f$
and its image is the base locus
$f$
and its image is the base locus
![]() $S_{M}$
.
$S_{M}$
.
Proposition 2.3. The locus
![]() $\unicode[STIX]{x1D6E9}\subset \mathbb{P}^{4}$
contracted by
$\unicode[STIX]{x1D6E9}\subset \mathbb{P}^{4}$
contracted by
![]() $f$
is an irreducible hypersurface of degree
$f$
is an irreducible hypersurface of degree
![]() $15$
. It has multiplicity four along
$15$
. It has multiplicity four along
![]() $S_{L}$
. Moreover, it equals the union of all of the
$S_{L}$
. Moreover, it equals the union of all of the
![]() $4$
-secant lines to
$4$
-secant lines to
![]() $S_{L}$
. The analogous statement holds for the inverse
$S_{L}$
. The analogous statement holds for the inverse
![]() $f^{-1}$
by symmetry.
$f^{-1}$
by symmetry.
Proof. Let
![]() $m$
be the multiplicity of
$m$
be the multiplicity of
![]() $\unicode[STIX]{x1D6E9}$
along
$\unicode[STIX]{x1D6E9}$
along
![]() $S_{L}$
. Then the divisor class of its pullback to
$S_{L}$
. Then the divisor class of its pullback to
![]() $X$
equals
$X$
equals
Here we use
![]() $E_{X}$
to denote the exceptional divisor of the blow-up
$E_{X}$
to denote the exceptional divisor of the blow-up
![]() $\unicode[STIX]{x1D70B}_{1}$
. Because
$\unicode[STIX]{x1D70B}_{1}$
. Because
![]() $\unicode[STIX]{x1D6E9}$
is contracted onto a surface, we have
$\unicode[STIX]{x1D6E9}$
is contracted onto a surface, we have
By definition,
![]() $E_{X}$
is mapped onto the
$E_{X}$
is mapped onto the
![]() $P$
-locus of the inverse map
$P$
-locus of the inverse map
![]() $f^{-1}$
. In particular, it is again a degree-15 hypersurfaces in
$f^{-1}$
. In particular, it is again a degree-15 hypersurfaces in
![]() $\mathbb{P}^{4}$
by symmetry. So
$\mathbb{P}^{4}$
by symmetry. So
![]() $M^{3}E_{X}=15$
, which implies
$M^{3}E_{X}=15$
, which implies
![]() $m=4$
.
$m=4$
.
Let
![]() $F_{X}$
be the exceptional locus of the blow-up
$F_{X}$
be the exceptional locus of the blow-up
![]() $\unicode[STIX]{x1D70B}_{2}$
. We have
$\unicode[STIX]{x1D70B}_{2}$
. We have
![]() $L=4M-F_{X}$
by symmetry, hence
$L=4M-F_{X}$
by symmetry, hence
(Note that this equals
![]() $15L-4E_{X}=\unicode[STIX]{x1D6E9}_{X}$
.) The fiber of the map
$15L-4E_{X}=\unicode[STIX]{x1D6E9}_{X}$
.) The fiber of the map
![]() $F_{X}\rightarrow S_{M}$
over a smooth point is represented by the class
$F_{X}\rightarrow S_{M}$
over a smooth point is represented by the class
The image
![]() $l=\unicode[STIX]{x1D70B}_{1}(l_{X})$
is a rational curve of degree
$l=\unicode[STIX]{x1D70B}_{1}(l_{X})$
is a rational curve of degree
The intersection number between
![]() $l$
and
$l$
and
![]() $S_{L}$
can be computed by
$S_{L}$
can be computed by
Hence the fibers of
![]() $F_{X}\rightarrow S_{M}$
away from the double points is mapped by
$F_{X}\rightarrow S_{M}$
away from the double points is mapped by
![]() $\unicode[STIX]{x1D70B}_{1}$
to 4-secant lines to
$\unicode[STIX]{x1D70B}_{1}$
to 4-secant lines to
![]() $S_{L}$
. In other words,
$S_{L}$
. In other words,
![]() $S_{L}$
admits a family of 4-secant lines parametrized by the smooth locus of
$S_{L}$
admits a family of 4-secant lines parametrized by the smooth locus of
![]() $S_{M}$
.
$S_{M}$
.
Conversely, every 4-secant line
![]() $l$
to
$l$
to
![]() $S_{L}$
satisfies
$S_{L}$
satisfies
So
![]() $l$
is contracted to a point by
$l$
is contracted to a point by
![]() $f$
. Hence the union of the 4-secant lines to
$f$
. Hence the union of the 4-secant lines to
![]() $S_{L}$
forms a 3-fold contained in
$S_{L}$
forms a 3-fold contained in
![]() $\unicode[STIX]{x1D6E9}$
and thus coincides with
$\unicode[STIX]{x1D6E9}$
and thus coincides with
![]() $\unicode[STIX]{x1D6E9}$
.◻
$\unicode[STIX]{x1D6E9}$
.◻
3 Derived equivalences of K3 surfaces
Let us retain the notation of § 2.4. By Theorem 2.1, there exists two degree-12 K3 surfaces
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
projected onto the base loci
$R_{M}$
projected onto the base loci
![]() $S_{L}$
and
$S_{L}$
and
![]() $S_{M}$
, respectively. This section is devoted to the following results.
$S_{M}$
, respectively. This section is devoted to the following results.
Theorem 3.1. The two K3 surfaces
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
are derived equivalent. They are non-isomorphic if they have Picard number one.
$R_{M}$
are derived equivalent. They are non-isomorphic if they have Picard number one.
Corollary 3.2. There is a birational map
![]() $\unicode[STIX]{x1D70E}:R_{L}^{[3]}{\dashrightarrow}R_{M}^{[3]}$
between the Hilbert schemes of length three subschemes.
$\unicode[STIX]{x1D70E}:R_{L}^{[3]}{\dashrightarrow}R_{M}^{[3]}$
between the Hilbert schemes of length three subschemes.
3.1 Derived equivalences and general strategy
Let
![]() $R$
and
$R$
and
![]() $\hat{R}$
denote K3 surfaces and
$\hat{R}$
denote K3 surfaces and
![]() $T(R)$
and
$T(R)$
and
![]() $T(\hat{R})$
the corresponding transcendental lattices. Recall that
$T(\hat{R})$
the corresponding transcendental lattices. Recall that
![]() $R$
and
$R$
and
![]() $\hat{R}$
are derived equivalent if and only if
$\hat{R}$
are derived equivalent if and only if
![]() $T(R)$
and
$T(R)$
and
![]() $T(\hat{R})$
are Hodge isometric [Reference Orlov.Orl97]. Suppose that
$T(\hat{R})$
are Hodge isometric [Reference Orlov.Orl97]. Suppose that
![]() $R$
has Picard rank one and degree
$R$
has Picard rank one and degree
![]() $2n$
. Let
$2n$
. Let
![]() $\unicode[STIX]{x1D70F}(n)$
be the number of prime factors of
$\unicode[STIX]{x1D70F}(n)$
be the number of prime factors of
![]() $n$
. Then the number of isomorphism classes of K3 surfaces derived equivalent to
$n$
. Then the number of isomorphism classes of K3 surfaces derived equivalent to
![]() $R$
is equal to
$R$
is equal to
![]() $2^{\unicode[STIX]{x1D70F}(n)-1}$
[Reference Hosono, Lian, Oguiso and YauHLOY03]. Thus a general degree-
$2^{\unicode[STIX]{x1D70F}(n)-1}$
[Reference Hosono, Lian, Oguiso and YauHLOY03]. Thus a general degree-
![]() $12$
K3 surface admits a unique such partner.
$12$
K3 surface admits a unique such partner.
Our general approach is to prove that
![]() $T(R_{L})$
is isometric to
$T(R_{L})$
is isometric to
![]() $T(R_{M})$
by showing that both of them can be identified as the transcendental sublattice of
$T(R_{M})$
by showing that both of them can be identified as the transcendental sublattice of
![]() $H^{4}(X,\mathbb{Z})$
. Then we show that the induced isomorphism on the discriminant groups is non-trivial, which implies that
$H^{4}(X,\mathbb{Z})$
. Then we show that the induced isomorphism on the discriminant groups is non-trivial, which implies that
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
are not isomorphic to each other.
$R_{M}$
are not isomorphic to each other.
3.2 The middle cohomology of
 $X$
$X$
Retain the notation of § 1. Let
![]() $H_{L}$
be the polarization of
$H_{L}$
be the polarization of
![]() $R_{L}$
. Let
$R_{L}$
. Let
![]() $F_{1}$
,
$F_{1}$
,
![]() $F_{2}$
, and
$F_{2}$
, and
![]() $F_{3}$
be the exceptional curves from the projection
$F_{3}$
be the exceptional curves from the projection
![]() $R_{L}{\dashrightarrow}S_{L}$
. We consider
$R_{L}{\dashrightarrow}S_{L}$
. We consider
![]() $H_{L}$
,
$H_{L}$
,
![]() $F_{1}$
,
$F_{1}$
,
![]() $F_{2}$
, and
$F_{2}$
, and
![]() $F_{3}$
as curves on
$F_{3}$
as curves on
![]() $S_{L}$
. Their strict transforms
$S_{L}$
. Their strict transforms
![]() $\widetilde{H}_{L}$
,
$\widetilde{H}_{L}$
,
![]() $\widetilde{F}_{1}$
,
$\widetilde{F}_{1}$
,
![]() $\widetilde{F}_{2}$
,
$\widetilde{F}_{2}$
,
![]() $\widetilde{F}_{3}$
on
$\widetilde{F}_{3}$
on
![]() $X$
together with
$X$
together with
![]() $L^{2}$
and the quadrics
$L^{2}$
and the quadrics
![]() $Q_{1}$
,
$Q_{1}$
,
![]() $Q_{2}$
,
$Q_{2}$
,
![]() $Q_{3}$
form a rank-eight sublattice
$Q_{3}$
form a rank-eight sublattice
![]() $A_{L}(X)\subset H^{4}(X,\mathbb{Z})$
. We have
$A_{L}(X)\subset H^{4}(X,\mathbb{Z})$
. We have
where
![]() $i=1,2,3$
. These classes are mutually disjoint, so the intersection matrix for
$i=1,2,3$
. These classes are mutually disjoint, so the intersection matrix for
![]() $A_{L}(X)$
is
$A_{L}(X)$
is

where
![]() $I_{3\times 3}$
is the identity matrix of rank 3.
$I_{3\times 3}$
is the identity matrix of rank 3.
Lemma 3.3. There is a decomposition
where
![]() $H^{4}(X,\mathbb{Z})_{\text{alg}}$
is the sublattice spanned by algebraic classes. We have
$H^{4}(X,\mathbb{Z})_{\text{alg}}$
is the sublattice spanned by algebraic classes. We have
when
![]() $R_{L}$
has Picard number one. Here we use
$R_{L}$
has Picard number one. Here we use
![]() $\unicode[STIX]{x1D6EC}(-1)$
to denote a lattice
$\unicode[STIX]{x1D6EC}(-1)$
to denote a lattice
![]() $\unicode[STIX]{x1D6EC}$
equipped with the negative of its original product.
$\unicode[STIX]{x1D6EC}$
equipped with the negative of its original product.
Proof. We apply the blow-up formula for cohomology to the composition
![]() $P^{\prime }\rightarrow P\rightarrow \mathbb{P}^{4}$
and the map
$P^{\prime }\rightarrow P\rightarrow \mathbb{P}^{4}$
and the map
![]() $P^{\prime }\rightarrow X$
to obtain two decompositions for
$P^{\prime }\rightarrow X$
to obtain two decompositions for
![]() $H^{4}(P^{\prime },\mathbb{Z})$
. Then we compare them to get our result.
$H^{4}(P^{\prime },\mathbb{Z})$
. Then we compare them to get our result.
Let
![]() $S_{L}^{\prime }\subset P$
be the strict transform of
$S_{L}^{\prime }\subset P$
be the strict transform of
![]() $S_{L}$
. Recall that
$S_{L}$
. Recall that
![]() $S_{L}^{\prime }$
is isomorphic to
$S_{L}^{\prime }$
is isomorphic to
![]() $R_{L}$
blown up at
$R_{L}$
blown up at
![]() $3+6=9$
points, where three are from the projection
$3+6=9$
points, where three are from the projection
![]() $R_{L}{\dashrightarrow}S_{L}$
while six are from the resolution
$R_{L}{\dashrightarrow}S_{L}$
while six are from the resolution
![]() $S_{L}^{\prime }\rightarrow S_{L}$
. Thus we have
$S_{L}^{\prime }\rightarrow S_{L}$
. Thus we have
Let
![]() $\widetilde{Q}_{i}^{\prime }$
and
$\widetilde{Q}_{i}^{\prime }$
and
![]() $\widetilde{Q}_{i}^{\prime \prime }$
be the strict transforms of
$\widetilde{Q}_{i}^{\prime \prime }$
be the strict transforms of
![]() $Q_{i}^{\prime }$
and
$Q_{i}^{\prime }$
and
![]() $Q_{i}^{\prime \prime }$
on
$Q_{i}^{\prime \prime }$
on
![]() $P^{\prime }$
. Since
$P^{\prime }$
. Since
![]() $P^{\prime }\rightarrow P$
is the blow-up along
$P^{\prime }\rightarrow P$
is the blow-up along
![]() $S_{L}^{\prime }$
, we have
$S_{L}^{\prime }$
, we have
For every
![]() $i$
, we have
$i$
, we have
and
![]() $E_{i}^{\prime 4}=-1$
. With these it is straightforward to prove the isometry
$E_{i}^{\prime 4}=-1$
. With these it is straightforward to prove the isometry
whence (3.2) equals
By the description of the map
![]() $E_{i}{\dashrightarrow}Q_{i}$
, the two fiber classes on
$E_{i}{\dashrightarrow}Q_{i}$
, the two fiber classes on
![]() $Q_{i}\simeq \mathbb{P}^{1}\times \mathbb{P}^{1}$
pull back to hyperplanes in
$Q_{i}\simeq \mathbb{P}^{1}\times \mathbb{P}^{1}$
pull back to hyperplanes in
![]() $E_{i}$
containing either
$E_{i}$
containing either
![]() $Q_{i}^{\prime }$
or
$Q_{i}^{\prime }$
or
![]() $Q_{i}^{\prime \prime }$
, which correspond to the classes
$Q_{i}^{\prime \prime }$
, which correspond to the classes
![]() $-E_{i}^{\prime 2}-\widetilde{Q}_{i}^{\prime }$
or
$-E_{i}^{\prime 2}-\widetilde{Q}_{i}^{\prime }$
or
![]() $-E_{i}^{\prime 2}-\widetilde{Q}_{i}^{\prime \prime }$
on
$-E_{i}^{\prime 2}-\widetilde{Q}_{i}^{\prime \prime }$
on
![]() $P^{\prime }$
, respectively. The map
$P^{\prime }$
, respectively. The map
![]() $P^{\prime }\rightarrow X$
is the blow-up along
$P^{\prime }\rightarrow X$
is the blow-up along
![]() $Q_{i}$
,
$Q_{i}$
,
![]() $i=1,2,3$
, so
$i=1,2,3$
, so
Combining (3.3) and (3.4), we get
Both
![]() $Q_{i}$
and
$Q_{i}$
and
![]() $E_{i}^{\prime 2}+\widetilde{Q}_{i}^{\prime }+\widetilde{Q}_{i}^{\prime \prime }$
are orthogonal to
$E_{i}^{\prime 2}+\widetilde{Q}_{i}^{\prime }+\widetilde{Q}_{i}^{\prime \prime }$
are orthogonal to
![]() $L^{2}$
,
$L^{2}$
,
![]() $\widetilde{F}_{i=1,2,3}$
and
$\widetilde{F}_{i=1,2,3}$
and
![]() $H^{2}(R_{L},\mathbb{Z})$
, and
$H^{2}(R_{L},\mathbb{Z})$
, and
![]() $Q_{i}^{2}=(E_{i}^{\prime 2}+\widetilde{Q}_{i}^{\prime }+\widetilde{Q}_{i}^{\prime \prime })^{2}=1$
, so
$Q_{i}^{2}=(E_{i}^{\prime 2}+\widetilde{Q}_{i}^{\prime }+\widetilde{Q}_{i}^{\prime \prime })^{2}=1$
, so
![]() $Q_{i}=\pm (E_{i}^{\prime 2}+\widetilde{Q}_{i}^{\prime }+\widetilde{Q}_{i}^{\prime \prime })$
. Therefore
$Q_{i}=\pm (E_{i}^{\prime 2}+\widetilde{Q}_{i}^{\prime }+\widetilde{Q}_{i}^{\prime \prime })$
. Therefore
 $$\begin{eqnarray}\displaystyle H^{4}(X,\mathbb{Z}) & \simeq & \displaystyle \langle Q_{i},\;L^{2},\;\widetilde{F}_{i}\rangle _{i=1,2,3}\oplus H^{2}(R_{L},\mathbb{Z})(-1)\nonumber\\ \displaystyle & \simeq & \displaystyle \langle Q_{i},\;L^{2},\;\widetilde{F}_{i}\rangle _{i=1,2,3}\oplus NS(R_{L})(-1)\oplus _{\bot }T(R_{L})(-1)\nonumber\\ \displaystyle & \simeq & \displaystyle H^{4}{(X,\mathbb{Z})_{\text{alg}}\oplus }_{\bot }T(R_{L})(-1),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{4}(X,\mathbb{Z}) & \simeq & \displaystyle \langle Q_{i},\;L^{2},\;\widetilde{F}_{i}\rangle _{i=1,2,3}\oplus H^{2}(R_{L},\mathbb{Z})(-1)\nonumber\\ \displaystyle & \simeq & \displaystyle \langle Q_{i},\;L^{2},\;\widetilde{F}_{i}\rangle _{i=1,2,3}\oplus NS(R_{L})(-1)\oplus _{\bot }T(R_{L})(-1)\nonumber\\ \displaystyle & \simeq & \displaystyle H^{4}{(X,\mathbb{Z})_{\text{alg}}\oplus }_{\bot }T(R_{L})(-1),\nonumber\end{eqnarray}$$
where
![]() $NS(R_{L})$
is the Néron–Severi lattice of
$NS(R_{L})$
is the Néron–Severi lattice of
![]() $R_{L}$
.
$R_{L}$
.
When
![]() $R_{L}$
has Picard number one, we have
$R_{L}$
has Picard number one, we have
![]() $NS(R_{L})(-1)\simeq \langle \widetilde{H}_{L}\rangle$
. In this case
$NS(R_{L})(-1)\simeq \langle \widetilde{H}_{L}\rangle$
. In this case
Lemma 3.3 also proves the decomposition
from the side of
![]() $f^{-1}$
. So there is an isometry
$f^{-1}$
. So there is an isometry
which allows us to conclude the following proposition.
Proposition 3.4.
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
are derived equivalent.
$R_{M}$
are derived equivalent.
3.3 The discriminant groups
For an arbitrary lattice
![]() $\unicode[STIX]{x1D6EC}$
with dual lattice
$\unicode[STIX]{x1D6EC}$
with dual lattice
![]() $\unicode[STIX]{x1D6EC}^{\ast }:=\text{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})$
, we denote by
$\unicode[STIX]{x1D6EC}^{\ast }:=\text{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})$
, we denote by
![]() $d\unicode[STIX]{x1D6EC}:=\unicode[STIX]{x1D6EC}^{\ast }/\unicode[STIX]{x1D6EC}$
its discriminant group.
$d\unicode[STIX]{x1D6EC}:=\unicode[STIX]{x1D6EC}^{\ast }/\unicode[STIX]{x1D6EC}$
its discriminant group.
Let
![]() $A_{M}(X)$
be the lattice constructed in the same way as
$A_{M}(X)$
be the lattice constructed in the same way as
![]() $A_{L}(X)$
from the side of
$A_{L}(X)$
from the side of
![]() $f^{-1}$
. Assume
$f^{-1}$
. Assume
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
have Picard number one. Then Lemma 3.3 implies that there is an isometry
$R_{M}$
have Picard number one. Then Lemma 3.3 implies that there is an isometry
such that
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{A}\oplus \unicode[STIX]{x1D711}_{T}$
with respect to the decompositions. It induces the commutative diagram
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{A}\oplus \unicode[STIX]{x1D711}_{T}$
with respect to the decompositions. It induces the commutative diagram

These groups are all isomorphic to
![]() $\mathbb{Z}/12\mathbb{Z}$
. From the intersection matrix (3.1) we know that
$\mathbb{Z}/12\mathbb{Z}$
. From the intersection matrix (3.1) we know that
![]() $dA_{L}(X)$
is generated by
$dA_{L}(X)$
is generated by
![]() $-\widetilde{H}_{L}/12$
. Similarly,
$-\widetilde{H}_{L}/12$
. Similarly,
![]() $dA_{M}(X)$
is generated by
$dA_{M}(X)$
is generated by
![]() $-\widetilde{H}_{M}/12$
, where
$-\widetilde{H}_{M}/12$
, where
![]() $H_{M}$
is the polarization of
$H_{M}$
is the polarization of
![]() $R_{M}$
and
$R_{M}$
and
![]() $\widetilde{H}_{M}$
is the strict transform on
$\widetilde{H}_{M}$
is the strict transform on
![]() $X$
.
$X$
.
Lemma 3.5. We have the following equations in
![]() $H^{4}(X,\mathbb{Z})$
:
$H^{4}(X,\mathbb{Z})$
:
(1)
 $M^{2}=7L^{2}-3\widetilde{H}_{L}+4(\widetilde{F}_{1}+\widetilde{F}_{2}+\widetilde{F}_{3})+2(Q_{1}+Q_{2}+Q_{3})$
;
$M^{2}=7L^{2}-3\widetilde{H}_{L}+4(\widetilde{F}_{1}+\widetilde{F}_{2}+\widetilde{F}_{3})+2(Q_{1}+Q_{2}+Q_{3})$
;(2)
 $\widetilde{H}_{M}=36L^{2}-17\widetilde{H}_{L}+24(\widetilde{F}_{1}+\widetilde{F}_{2}+\widetilde{F}_{3})+12(Q_{1}+Q_{2}+Q_{3})$
.
$\widetilde{H}_{M}=36L^{2}-17\widetilde{H}_{L}+24(\widetilde{F}_{1}+\widetilde{F}_{2}+\widetilde{F}_{3})+12(Q_{1}+Q_{2}+Q_{3})$
.
Proof. The following computation is based on Corollary 2.2. Assume that
Then
![]() $a=L^{2}M^{2}=7$
. For
$a=L^{2}M^{2}=7$
. For
![]() $i=1,2,3$
, we have
$i=1,2,3$
, we have
 $$\begin{eqnarray}\displaystyle g_{i} & = & \displaystyle M^{2}Q_{i}=-M^{2}E_{i}^{\prime 2}\nonumber\\ \displaystyle & = & \displaystyle -(4L-E-2\unicode[STIX]{x1D6F4}_{j}E_{j}^{\prime })^{2}E_{i}^{\prime 2}=-(-E-2\unicode[STIX]{x1D6F4}_{j}E_{j}^{\prime })^{2}E_{i}^{\prime 2}\nonumber\\ \displaystyle & = & \displaystyle -E^{2}E_{i}^{\prime 2}-4EE_{i}^{\prime 3}-4E_{i}^{\prime 4}=-2-0+4=2.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{i} & = & \displaystyle M^{2}Q_{i}=-M^{2}E_{i}^{\prime 2}\nonumber\\ \displaystyle & = & \displaystyle -(4L-E-2\unicode[STIX]{x1D6F4}_{j}E_{j}^{\prime })^{2}E_{i}^{\prime 2}=-(-E-2\unicode[STIX]{x1D6F4}_{j}E_{j}^{\prime })^{2}E_{i}^{\prime 2}\nonumber\\ \displaystyle & = & \displaystyle -E^{2}E_{i}^{\prime 2}-4EE_{i}^{\prime 3}-4E_{i}^{\prime 4}=-2-0+4=2.\nonumber\end{eqnarray}$$
Let
![]() $\widetilde{C}$
be the strict transform of the sectional curve
$\widetilde{C}$
be the strict transform of the sectional curve
![]() $C$
on
$C$
on
![]() $P^{\prime }$
. Note that
$P^{\prime }$
. Note that
so we find
 $$\begin{eqnarray}\displaystyle 4 & = & \displaystyle LM^{3}=(LM)M^{2}\nonumber\\ \displaystyle & = & \displaystyle (4L^{2}-\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}\widetilde{F}_{i})(7L^{2}+b\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}f_{j}\widetilde{F}_{j}+2\unicode[STIX]{x1D6F4}_{k}Q_{k})\nonumber\\ \displaystyle & = & \displaystyle 28+12b+f_{1}+f_{2}+f_{3},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 4 & = & \displaystyle LM^{3}=(LM)M^{2}\nonumber\\ \displaystyle & = & \displaystyle (4L^{2}-\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}\widetilde{F}_{i})(7L^{2}+b\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}f_{j}\widetilde{F}_{j}+2\unicode[STIX]{x1D6F4}_{k}Q_{k})\nonumber\\ \displaystyle & = & \displaystyle 28+12b+f_{1}+f_{2}+f_{3},\nonumber\end{eqnarray}$$
and thus
We also have
which is equivalent to
By the Cauchy–Schwarz inequality,
Applying (3.5) and (3.6), we get
![]() $(-12b-24)^{2}\leqslant 3(12b^{2}-60)$
, that is,
$(-12b-24)^{2}\leqslant 3(12b^{2}-60)$
, that is,
The only integer solution is
![]() $b=-3$
. Because (3.7) becomes an equality in this case, we have
$b=-3$
. Because (3.7) becomes an equality in this case, we have
![]() $(f_{1},f_{2},f_{3})=f(1,1,1)$
for some integer
$(f_{1},f_{2},f_{3})=f(1,1,1)$
for some integer
![]() $f$
. We obtain
$f$
. We obtain
![]() $f=4$
by setting
$f=4$
by setting
![]() $b=-3$
in (3.5). As a result, we find
$b=-3$
in (3.5). As a result, we find
Next, assume that
By symmetry,
![]() $\widetilde{H}_{L}L^{n}M^{2-n}=\widetilde{H}_{M}M^{n}L^{2-n}$
for
$\widetilde{H}_{L}L^{n}M^{2-n}=\widetilde{H}_{M}M^{n}L^{2-n}$
for
![]() $n=0,1,2$
. In particular,
$n=0,1,2$
. In particular,
We have
 $$\begin{eqnarray}\displaystyle 12 & = & \displaystyle \widetilde{H}_{L}(4L^{2}-\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}\widetilde{F}_{i})=\widetilde{H}_{L}(LM)=\widetilde{H}_{M}(ML)\nonumber\\ \displaystyle & = & \displaystyle (36L^{2}+b\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}f_{i}\widetilde{F}_{i}+\unicode[STIX]{x1D6F4}_{j}g_{j}Q_{j})(4L^{2}-\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}\widetilde{F}_{i})\nonumber\\ \displaystyle & = & \displaystyle 144+12b+f_{1}+f_{2}+f_{3}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 12 & = & \displaystyle \widetilde{H}_{L}(4L^{2}-\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}\widetilde{F}_{i})=\widetilde{H}_{L}(LM)=\widetilde{H}_{M}(ML)\nonumber\\ \displaystyle & = & \displaystyle (36L^{2}+b\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}f_{i}\widetilde{F}_{i}+\unicode[STIX]{x1D6F4}_{j}g_{j}Q_{j})(4L^{2}-\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}\widetilde{F}_{i})\nonumber\\ \displaystyle & = & \displaystyle 144+12b+f_{1}+f_{2}+f_{3}.\nonumber\end{eqnarray}$$
Rearrange to obtain
Applying the symmetry again, we get
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \widetilde{H}_{L}L^{2}=\widetilde{H}_{M}M^{2}\nonumber\\ \displaystyle & = & \displaystyle (36L^{2}+b\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}f_{i}\widetilde{F}_{i}+\unicode[STIX]{x1D6F4}_{j}g_{j}Q_{j})(7L^{2}-3\widetilde{H}_{L}+4\unicode[STIX]{x1D6F4}_{i}\widetilde{F}_{i}+2\unicode[STIX]{x1D6F4}_{j}Q_{j})\nonumber\\ \displaystyle & = & \displaystyle 252+36b+4(f_{1}+f_{2}+f_{3})+2(g_{1}+g_{2}+g_{3}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \widetilde{H}_{L}L^{2}=\widetilde{H}_{M}M^{2}\nonumber\\ \displaystyle & = & \displaystyle (36L^{2}+b\widetilde{H}_{L}+\unicode[STIX]{x1D6F4}_{i}f_{i}\widetilde{F}_{i}+\unicode[STIX]{x1D6F4}_{j}g_{j}Q_{j})(7L^{2}-3\widetilde{H}_{L}+4\unicode[STIX]{x1D6F4}_{i}\widetilde{F}_{i}+2\unicode[STIX]{x1D6F4}_{j}Q_{j})\nonumber\\ \displaystyle & = & \displaystyle 252+36b+4(f_{1}+f_{2}+f_{3})+2(g_{1}+g_{2}+g_{3}),\nonumber\end{eqnarray}$$
whence
and combining with (3.8) gives
We also have
from which we obtain
By the Cauchy–Schwarz inequality,
and
Add the two inequalities and then apply (3.10) to get
which can be arranged as
The only integer solution is
![]() $b=-17$
which makes (3.13) an equality. This forces (3.11) and (3.12) to be equalities also. Therefore
$b=-17$
which makes (3.13) an equality. This forces (3.11) and (3.12) to be equalities also. Therefore
![]() $(f_{1},f_{2},f_{3})=f(1,1,1)$
and
$(f_{1},f_{2},f_{3})=f(1,1,1)$
and
![]() $(g_{1},g_{2},g_{3})=g(1,1,1)$
for some integers
$(g_{1},g_{2},g_{3})=g(1,1,1)$
for some integers
![]() $f$
and
$f$
and
![]() $g$
. We get
$g$
. We get
![]() $f=24$
from (3.8) and
$f=24$
from (3.8) and
![]() $g=12$
from (3.9). As a consequence,
$g=12$
from (3.9). As a consequence,
Proposition 3.6. The isomorphism
![]() ${\unicode[STIX]{x1D711}_{A}}_{\ast }:dA_{M}(X)\xrightarrow[{}]{{\sim}}dA_{L}(X)$
equals multiplication by
${\unicode[STIX]{x1D711}_{A}}_{\ast }:dA_{M}(X)\xrightarrow[{}]{{\sim}}dA_{L}(X)$
equals multiplication by
![]() $7$
on
$7$
on
![]() $\mathbb{Z}/12\mathbb{Z}$
.
$\mathbb{Z}/12\mathbb{Z}$
.
Proof. Recall that
![]() $\unicode[STIX]{x1D711}_{A}$
acts as the identity map on
$\unicode[STIX]{x1D711}_{A}$
acts as the identity map on
![]() $H^{4}(X,\mathbb{Z})_{\text{alg}}$
, thus
$H^{4}(X,\mathbb{Z})_{\text{alg}}$
, thus
![]() $\unicode[STIX]{x1D711}_{A}(\widetilde{H}_{M})=\widetilde{H}_{M}$
. By Lemma 3.5 we have
$\unicode[STIX]{x1D711}_{A}(\widetilde{H}_{M})=\widetilde{H}_{M}$
. By Lemma 3.5 we have
as a map from
![]() $A_{M}(X)$
to
$A_{M}(X)$
to
![]() $A_{L}(X)$
. Therefore
$A_{L}(X)$
. Therefore
 $$\begin{eqnarray}\displaystyle {\unicode[STIX]{x1D711}_{A}}_{\ast }(-{\textstyle \frac{1}{12}}\widetilde{H}_{M}) & = & \displaystyle -3L^{2}+{\textstyle \frac{17}{12}}\widetilde{H}_{L}-2(\widetilde{F}_{1}+\widetilde{F}_{2}+\widetilde{F}_{3})-(Q_{1}+Q_{2}+Q_{3})\nonumber\\ \displaystyle & = & \displaystyle -17\cdot (-{\textstyle \frac{1}{12}}\widetilde{H}_{L})\quad \text{mod}\;A_{L}(X)\nonumber\\ \displaystyle & = & \displaystyle 7\cdot (-{\textstyle \frac{1}{12}}\widetilde{H}_{L})\quad \text{mod}\;A_{L}(X).\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\unicode[STIX]{x1D711}_{A}}_{\ast }(-{\textstyle \frac{1}{12}}\widetilde{H}_{M}) & = & \displaystyle -3L^{2}+{\textstyle \frac{17}{12}}\widetilde{H}_{L}-2(\widetilde{F}_{1}+\widetilde{F}_{2}+\widetilde{F}_{3})-(Q_{1}+Q_{2}+Q_{3})\nonumber\\ \displaystyle & = & \displaystyle -17\cdot (-{\textstyle \frac{1}{12}}\widetilde{H}_{L})\quad \text{mod}\;A_{L}(X)\nonumber\\ \displaystyle & = & \displaystyle 7\cdot (-{\textstyle \frac{1}{12}}\widetilde{H}_{L})\quad \text{mod}\;A_{L}(X).\square\nonumber\end{eqnarray}$$
Remark . By the symmetry of the Cremona transformation
![]() $f$
, the rank-eight lattice
$f$
, the rank-eight lattice
![]() $H^{4}(X,\mathbb{Z})_{\text{alg}}$
is also spanned by the classes
$H^{4}(X,\mathbb{Z})_{\text{alg}}$
is also spanned by the classes
constructed in a similar way from the right-hand side. Here
![]() $\widetilde{G}_{1},\widetilde{G}_{2},\widetilde{G}_{3}$
are from the exceptional curves and
$\widetilde{G}_{1},\widetilde{G}_{2},\widetilde{G}_{3}$
are from the exceptional curves and
![]() $K_{1},K_{2},K_{3}$
are from the transverse double points. The full transformation between the two set of bases is
$K_{1},K_{2},K_{3}$
are from the transverse double points. The full transformation between the two set of bases is
 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}M^{2}\\ \widetilde{H}_{M}\\ \widetilde{G}_{1}\\ \widetilde{G}_{2}\\ \widetilde{G}_{3}\\ K_{1}\\ K_{2}\\ K_{3}\end{array}\right)=\left(\begin{array}{@{}cccccccc@{}}7 & -3 & 4 & 4 & 4 & 2 & 2 & 2\\ 36 & -17 & 24 & 24 & 24 & 12 & 12 & 12\\ 4 & -2 & 3 & 3 & 3 & 2 & 1 & 1\\ 4 & -2 & 3 & 3 & 3 & 1 & 2 & 1\\ 4 & -2 & 3 & 3 & 3 & 1 & 1 & 2\\ 2 & -1 & 2 & 1 & 1 & 1 & 1 & 1\\ 2 & -1 & 1 & 2 & 1 & 1 & 1 & 1\\ 2 & -1 & 1 & 1 & 2 & 1 & 1 & 1\end{array}\right)\cdot \left(\begin{array}{@{}c@{}}L^{2}\\ \widetilde{H}_{L}\\ \widetilde{F}_{1}\\ \widetilde{F}_{2}\\ \widetilde{F}_{3}\\ Q_{1}\\ Q_{2}\\ Q_{3}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}M^{2}\\ \widetilde{H}_{M}\\ \widetilde{G}_{1}\\ \widetilde{G}_{2}\\ \widetilde{G}_{3}\\ K_{1}\\ K_{2}\\ K_{3}\end{array}\right)=\left(\begin{array}{@{}cccccccc@{}}7 & -3 & 4 & 4 & 4 & 2 & 2 & 2\\ 36 & -17 & 24 & 24 & 24 & 12 & 12 & 12\\ 4 & -2 & 3 & 3 & 3 & 2 & 1 & 1\\ 4 & -2 & 3 & 3 & 3 & 1 & 2 & 1\\ 4 & -2 & 3 & 3 & 3 & 1 & 1 & 2\\ 2 & -1 & 2 & 1 & 1 & 1 & 1 & 1\\ 2 & -1 & 1 & 2 & 1 & 1 & 1 & 1\\ 2 & -1 & 1 & 1 & 2 & 1 & 1 & 1\end{array}\right)\cdot \left(\begin{array}{@{}c@{}}L^{2}\\ \widetilde{H}_{L}\\ \widetilde{F}_{1}\\ \widetilde{F}_{2}\\ \widetilde{F}_{3}\\ Q_{1}\\ Q_{2}\\ Q_{3}\end{array}\right).\end{eqnarray}$$
This expression is unique up to the ordering of the exceptional curves and the transverse double points on each side. The top two rows are computed by Lemma 3.5. The other rows can be computed in a similar way.
3.4 Proofs of Theorem 3.1 and its Corollary
We first prove the theorem.
The derived equivalence follows from Proposition 3.4. Note that this implies that the Picard numbers of
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
are the same.
$R_{M}$
are the same.
Assume
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
have Picard number one. Suppose they are isomorphic. Then there is an isometry
$R_{M}$
have Picard number one. Suppose they are isomorphic. Then there is an isometry
which induces the isomorphism
 $$\begin{eqnarray}\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D703}_{\ast }: & dT(R_{L}) & \tilde{\,\rightarrow } & dT(R_{M})\\ & -{\displaystyle \frac{\widetilde{H}_{L}}{12}} & \mapsto & -{\displaystyle \frac{\widetilde{H}_{M}}{12}}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D703}_{\ast }: & dT(R_{L}) & \tilde{\,\rightarrow } & dT(R_{M})\\ & -{\displaystyle \frac{\widetilde{H}_{L}}{12}} & \mapsto & -{\displaystyle \frac{\widetilde{H}_{M}}{12}}\end{array}\end{eqnarray}$$
under the identifications
![]() $dT(R_{L})\simeq dA_{L}(X)$
and
$dT(R_{L})\simeq dA_{L}(X)$
and
![]() $dT(R_{M})\simeq dA_{M}(X)$
.
$dT(R_{M})\simeq dA_{M}(X)$
.
By Proposition 3.6, the composition
![]() $\unicode[STIX]{x1D711}_{A}\circ \unicode[STIX]{x1D703}$
is an automorphism on
$\unicode[STIX]{x1D711}_{A}\circ \unicode[STIX]{x1D703}$
is an automorphism on
![]() $T(R_{L})$
acting as multiplication by 7 on
$T(R_{L})$
acting as multiplication by 7 on
![]() $dT(R_{L})$
. This contradicts the fact that the only automorphism on
$dT(R_{L})$
. This contradicts the fact that the only automorphism on
![]() $T(R_{L})$
is the identity [Reference OguisoOgu02]. Hence
$T(R_{L})$
is the identity [Reference OguisoOgu02]. Hence
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
cannot be isomorphic to each other.
$R_{M}$
cannot be isomorphic to each other.
Next we prove the corollary.
The corollary is trivial if
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
are isomorphic, so we assume that they are non-isomorphic.
$R_{M}$
are isomorphic, so we assume that they are non-isomorphic.
Given a generic triple of points
![]() $\unicode[STIX]{x1D6F1}_{L}\in R_{L}^{[3]}$
, we determine a degree-12 K3 surface
$\unicode[STIX]{x1D6F1}_{L}\in R_{L}^{[3]}$
, we determine a degree-12 K3 surface
![]() $R_{M}$
and a triple of points
$R_{M}$
and a triple of points
![]() $\unicode[STIX]{x1D6F1}_{M}\in R_{M}^{[3]}$
through the following steps.
$\unicode[STIX]{x1D6F1}_{M}\in R_{M}^{[3]}$
through the following steps.
(1) Project
 $R_{L}$
from
$R_{L}$
from
 $\unicode[STIX]{x1D6F1}_{L}$
to obtain
$\unicode[STIX]{x1D6F1}_{L}$
to obtain
 $S_{L}\subset \mathbb{P}^{4}$
, whose ideal defines a Cremona transformation
$S_{L}\subset \mathbb{P}^{4}$
, whose ideal defines a Cremona transformation
 $f:\mathbb{P}^{4}{\dashrightarrow}\mathbb{P}^{4}$
.
$f:\mathbb{P}^{4}{\dashrightarrow}\mathbb{P}^{4}$
.(2) The base locus of
 $f^{-1}$
is a surface
$f^{-1}$
is a surface
 $S_{M}$
singular along three transverse double points. Normalize
$S_{M}$
singular along three transverse double points. Normalize
 $S_{M}$
to get
$S_{M}$
to get
 $\unicode[STIX]{x1D6F4}_{M}$
.
$\unicode[STIX]{x1D6F4}_{M}$
.(3)
 $\unicode[STIX]{x1D6F4}_{M}$
is the blow-up of a degree-12 K3 surface
$\unicode[STIX]{x1D6F4}_{M}$
is the blow-up of a degree-12 K3 surface
 $R_{M}$
along three points. The three exceptional curves on
$R_{M}$
along three points. The three exceptional curves on
 $\unicode[STIX]{x1D6F4}_{M}$
are contracted to
$\unicode[STIX]{x1D6F4}_{M}$
are contracted to
 $\unicode[STIX]{x1D6F1}_{M}\in R_{M}^{[3]}$
.
$\unicode[STIX]{x1D6F1}_{M}\in R_{M}^{[3]}$
.
Recall that two derived equivalent K3 surfaces of degree 12 uniquely determine each other up to isomorphism. So
![]() $R_{M}$
is independent of the choice of
$R_{M}$
is independent of the choice of
![]() $\unicode[STIX]{x1D6F1}_{L}\in R_{L}^{[3]}$
by Theorem 3.1. Hence there is a rational map
$\unicode[STIX]{x1D6F1}_{L}\in R_{L}^{[3]}$
by Theorem 3.1. Hence there is a rational map
It is birational because
![]() $\unicode[STIX]{x1D6F1}_{L}$
is uniquely determined by
$\unicode[STIX]{x1D6F1}_{L}$
is uniquely determined by
![]() $\unicode[STIX]{x1D6F1}_{M}$
through the same process as above.
$\unicode[STIX]{x1D6F1}_{M}$
through the same process as above.
3.5 Connections between our construction and other approaches
The derived equivalence and geometric connections between the degree-12 K3 surfaces
![]() $(R_{L},H_{L})$
and
$(R_{L},H_{L})$
and
![]() $(R_{M},H_{M})$
admit several interpretations.
$(R_{M},H_{M})$
admit several interpretations.
3.5.1 Mukai lattices
For a K3 surface
![]() $R$
, the Mukai lattice
$R$
, the Mukai lattice
equipped with a weight-two Hodge structure, that is, the standard Hodge structure on the middle summand and the outer summands taken as
![]() $(1,1)$
classes. This is polarized by
$(1,1)$
classes. This is polarized by
Each coherent sheaf
![]() $E$
yields a Mukai vector
$E$
yields a Mukai vector
where
![]() $r(E)$
is the rank and
$r(E)$
is the rank and
![]() $r(E)+s(E)=\unicode[STIX]{x1D712}(E)$
. Mukai [Reference MukaiMuk87] has shown that the second cohomology of a moduli space
$r(E)+s(E)=\unicode[STIX]{x1D712}(E)$
. Mukai [Reference MukaiMuk87] has shown that the second cohomology of a moduli space
![]() $M_{v}(R)$
may be expressed as
$M_{v}(R)$
may be expressed as
provided
![]() $v$
is primitive and satisfies certain technical conditions. A derived equivalence between
$v$
is primitive and satisfies certain technical conditions. A derived equivalence between
![]() $R$
and
$R$
and
![]() $\hat{R}$
induces an isomorphism of Hodge structures
$\hat{R}$
induces an isomorphism of Hodge structures
which may be chosen so that
![]() $\hat{R}=M_{v}(R)$
with
$\hat{R}=M_{v}(R)$
with
![]() $\unicode[STIX]{x1D6F7}(v)=(0,0,1)$
.
$\unicode[STIX]{x1D6F7}(v)=(0,0,1)$
.
We return to our degree-12 K3 surfaces
![]() $R_{M}$
and
$R_{M}$
and
![]() $R_{L}$
. We may interpret
$R_{L}$
. We may interpret
![]() $R_{M}$
as a moduli space of vector bundles on
$R_{M}$
as a moduli space of vector bundles on
![]() $R_{L}$
and vice versa [Reference MukaiMuk99]. Let
$R_{L}$
and vice versa [Reference MukaiMuk99]. Let
![]() $M_{(2,H_{L},3)}(R_{L})$
denote the moduli space of rank-two stable bundles
$M_{(2,H_{L},3)}(R_{L})$
denote the moduli space of rank-two stable bundles
![]() $E$
with
$E$
with
![]() $c_{1}(E)=H_{L}$
and
$c_{1}(E)=H_{L}$
and
![]() $\unicode[STIX]{x1D712}(R_{L},E)=5$
, which is isomorphic to
$\unicode[STIX]{x1D712}(R_{L},E)=5$
, which is isomorphic to
![]() $R_{M}$
. The universal bundle
$R_{M}$
. The universal bundle
![]() ${\mathcal{E}}\rightarrow R_{L}\times R_{M}$
induces a Hodge isometry
${\mathcal{E}}\rightarrow R_{L}\times R_{M}$
induces a Hodge isometry
described above. We have
and
![]() $\unicode[STIX]{x1D6F7}$
restricts to the isogeny on transcendental cohomology mentioned in §3.1. It follows formally that
$\unicode[STIX]{x1D6F7}$
restricts to the isogeny on transcendental cohomology mentioned in §3.1. It follows formally that
thus after a shift the Mukai vector of ideal sheaves of length-three subschemes of
![]() $R_{L}$
goes to the Mukai vector of length-three subschemes of
$R_{L}$
goes to the Mukai vector of length-three subschemes of
![]() $R_{M}$
. We obtain an isomorphism
$R_{M}$
. We obtain an isomorphism
of Hodge structures arising from Mukai lattices. Thus the Torelli theorem [Reference MarkmanMar11, Corollary 9.9] yields a birational equivalence
Corollary 3.2 is quite natural from this perspective.
Remark . We also have
![]() $\unicode[STIX]{x1D6F7}(1,0,-1)=(1,H_{M},5)$
. Elements of
$\unicode[STIX]{x1D6F7}(1,0,-1)=(1,H_{M},5)$
. Elements of
![]() $M_{(1,H_{M},5)}(R_{M})$
may be interpreted as
$M_{(1,H_{M},5)}(R_{M})$
may be interpreted as
![]() $I_{Z}(H_{M})$
where
$I_{Z}(H_{M})$
where
![]() $Z\subset R_{M}$
has length two. Similar reasoning gives
$Z\subset R_{M}$
has length two. Similar reasoning gives
3.5.2 Homological projective duality
Mukai [Reference MukaiMuk99, Example 1.3] proposed an interpretation of the derived equivalence via linear algebra, which was explored in detail by Iliev and Markushevich [Reference Iliev and MarkushevichIM04]. The key observation is that the components
![]() ${\mathcal{S}}^{+}$
and
${\mathcal{S}}^{+}$
and
![]() ${\mathcal{S}}^{-}$
described in § 2.1 are naturally embedded in dual projective spaces
${\mathcal{S}}^{-}$
described in § 2.1 are naturally embedded in dual projective spaces
Codimension-
![]() $r$
subspaces
$r$
subspaces
![]() $\mathbb{P}\subset \mathbb{P}^{15}$
correspond to codimension-
$\mathbb{P}\subset \mathbb{P}^{15}$
correspond to codimension-
![]() $(16-r)$
subspaces
$(16-r)$
subspaces
![]() $\mathbb{P}^{\bot }\subset \check{\mathbb{P}}^{15}$
. When
$\mathbb{P}^{\bot }\subset \check{\mathbb{P}}^{15}$
. When
![]() $r=8$
, the K3 surfaces
$r=8$
, the K3 surfaces
![]() $R={\mathcal{S}}^{+}\cap \mathbb{P}$
and
$R={\mathcal{S}}^{+}\cap \mathbb{P}$
and
![]() ${\check{R}}={\mathcal{S}}^{-}\cap \mathbb{P}^{\bot }$
are dual. These are derived equivalent and generally non-isomorphic. Kuznetsov [Reference KuznetsovKuz06, §6.2] has interpreted this derived equivalence via homological projective duality.
${\check{R}}={\mathcal{S}}^{-}\cap \mathbb{P}^{\bot }$
are dual. These are derived equivalent and generally non-isomorphic. Kuznetsov [Reference KuznetsovKuz06, §6.2] has interpreted this derived equivalence via homological projective duality.
It would be interesting to construct the Cremona transformation through this mechanism, by introducing the data of the three points on the K3 surface into the duality construction.
4 Zero-divisors in the Grothendieck ring
Let
![]() $K_{0}(\text{Var}/\mathbb{C})$
denote the Grothendieck ring of complex algebraic varieties. It is the abelian group generated by isomorphism classes of complex algebraic varieties subject to the relation
$K_{0}(\text{Var}/\mathbb{C})$
denote the Grothendieck ring of complex algebraic varieties. It is the abelian group generated by isomorphism classes of complex algebraic varieties subject to the relation
where
![]() $U$
is an open subvariety of
$U$
is an open subvariety of
![]() $Z$
. The multiplication is induced by the Cartesian product
$Z$
. The multiplication is induced by the Cartesian product
which is associative and commutative with unit
![]() $1=[\operatorname{Spec}\mathbb{C}]$
. More generally, if
$1=[\operatorname{Spec}\mathbb{C}]$
. More generally, if
![]() $Z\rightarrow X$
is a Zariski locally trivial bundle with fibers isomorphic to
$Z\rightarrow X$
is a Zariski locally trivial bundle with fibers isomorphic to
![]() $Y$
, by stratifying the base it is easy to prove that
$Y$
, by stratifying the base it is easy to prove that
Let
![]() $\mathbb{L}=[\mathbb{A}^{1}]$
be the class of the affine line in
$\mathbb{L}=[\mathbb{A}^{1}]$
be the class of the affine line in
![]() $K_{0}(\text{Var}/\mathbb{C})$
. Consider a pair of non-isomorphic smooth projective varieties
$K_{0}(\text{Var}/\mathbb{C})$
. Consider a pair of non-isomorphic smooth projective varieties
![]() $X$
and
$X$
and
![]() $Y$
which are derived equivalent. It is interesting to know if there exists
$Y$
which are derived equivalent. It is interesting to know if there exists
![]() $k\geqslant 0$
satisfying
$k\geqslant 0$
satisfying
and what the minimal
![]() $k$
is if it exists [Reference Kuznetsov and ShinderKS17].
$k$
is if it exists [Reference Kuznetsov and ShinderKS17].
When
![]() $X$
is a generic K3 surface of degree 12, Ito et al. [Reference Ito, Miura, Okawa and UedaIMOU16b] prove that there exists
$X$
is a generic K3 surface of degree 12, Ito et al. [Reference Ito, Miura, Okawa and UedaIMOU16b] prove that there exists
![]() $Y$
non-trivially derived equivalent to
$Y$
non-trivially derived equivalent to
![]() $X$
such that (4.1) holds for
$X$
such that (4.1) holds for
![]() $k=3$
. Actually, this can be improved to
$k=3$
. Actually, this can be improved to
![]() $k=1$
straightforwardly from the point of view of the Cremona transformation.
$k=1$
straightforwardly from the point of view of the Cremona transformation.
Theorem 4.1. Let
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
be a generic pair of K3 surfaces associated with our Cremona transformation. Then we have
$R_{M}$
be a generic pair of K3 surfaces associated with our Cremona transformation. Then we have
in
![]() $K_{0}(\text{Var}/\mathbb{C})$
. The relation is minimal in the sense that
$K_{0}(\text{Var}/\mathbb{C})$
. The relation is minimal in the sense that
![]() $[R_{L}]-[R_{M}]\neq 0$
.
$[R_{L}]-[R_{M}]\neq 0$
.
Proof. Recall that
![]() $\unicode[STIX]{x1D6F4}_{L}$
is the normalization of
$\unicode[STIX]{x1D6F4}_{L}$
is the normalization of
![]() $S_{L}$
as well as the blow-up of
$S_{L}$
as well as the blow-up of
![]() $R_{L}$
at three points. Hence we have
$R_{L}$
at three points. Hence we have
From the blow-up
![]() $\unicode[STIX]{x1D70B}_{1}:X\rightarrow \mathbb{P}^{4}$
we obtain
$\unicode[STIX]{x1D70B}_{1}:X\rightarrow \mathbb{P}^{4}$
we obtain
 $$\begin{eqnarray}\displaystyle [X] & = & \displaystyle ([\mathbb{P}^{4}]-[S_{L}])+[\unicode[STIX]{x1D70B}_{1}^{-1}(S_{L})]\nonumber\\ \displaystyle & = & \displaystyle ([\mathbb{P}^{4}]-[S_{L}])+(([S_{L}]-3)[\mathbb{P}^{1}]+[Q_{1}]+[Q_{2}]+[Q_{3}])\nonumber\\ \displaystyle & = & \displaystyle ([\mathbb{P}^{4}]-[S_{L}])+(([S_{L}]-3)[\mathbb{P}^{1}]+3[\mathbb{P}^{1}]^{2})\nonumber\\ \displaystyle & = & \displaystyle [\mathbb{P}^{4}]+3[\mathbb{P}^{1}]([\mathbb{P}^{1}]-1)+[S_{L}]([\mathbb{P}^{1}]-1)\nonumber\\ \displaystyle & = & \displaystyle [\mathbb{P}^{4}]+3[\mathbb{P}^{1}]\mathbb{L}+[S_{L}]\mathbb{L}\nonumber\\ \displaystyle & = & \displaystyle [\mathbb{P}^{4}]+3[\mathbb{P}^{1}]\mathbb{L}+[R_{L}]\mathbb{L}+3\mathbb{L}^{2}-3\mathbb{L}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [X] & = & \displaystyle ([\mathbb{P}^{4}]-[S_{L}])+[\unicode[STIX]{x1D70B}_{1}^{-1}(S_{L})]\nonumber\\ \displaystyle & = & \displaystyle ([\mathbb{P}^{4}]-[S_{L}])+(([S_{L}]-3)[\mathbb{P}^{1}]+[Q_{1}]+[Q_{2}]+[Q_{3}])\nonumber\\ \displaystyle & = & \displaystyle ([\mathbb{P}^{4}]-[S_{L}])+(([S_{L}]-3)[\mathbb{P}^{1}]+3[\mathbb{P}^{1}]^{2})\nonumber\\ \displaystyle & = & \displaystyle [\mathbb{P}^{4}]+3[\mathbb{P}^{1}]([\mathbb{P}^{1}]-1)+[S_{L}]([\mathbb{P}^{1}]-1)\nonumber\\ \displaystyle & = & \displaystyle [\mathbb{P}^{4}]+3[\mathbb{P}^{1}]\mathbb{L}+[S_{L}]\mathbb{L}\nonumber\\ \displaystyle & = & \displaystyle [\mathbb{P}^{4}]+3[\mathbb{P}^{1}]\mathbb{L}+[R_{L}]\mathbb{L}+3\mathbb{L}^{2}-3\mathbb{L}.\end{eqnarray}$$
By symmetry, we also have
Subtracting (4.3) from (4.2), we get
Next we show that
![]() $[R_{L}]\neq [R_{M}]$
, and it is sufficient to show that
$[R_{L}]\neq [R_{M}]$
, and it is sufficient to show that
![]() $[R_{L}]\neq [R_{M}]$
modulo
$[R_{L}]\neq [R_{M}]$
modulo
![]() $\mathbb{L}$
. According to [Reference Larsen and LuntsLL03],
$\mathbb{L}$
. According to [Reference Larsen and LuntsLL03],
![]() $[R_{L}]=[R_{M}]\,\text{mod}\,\mathbb{L}$
if and only if
$[R_{L}]=[R_{M}]\,\text{mod}\,\mathbb{L}$
if and only if
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
are stably birational. Because a K3 surface is not rationally connected, this implies that
$R_{M}$
are stably birational. Because a K3 surface is not rationally connected, this implies that
![]() $R_{L}$
and
$R_{L}$
and
![]() $R_{M}$
are birational and thus isomorphic, contradicting Theorem 3.1.◻
$R_{M}$
are birational and thus isomorphic, contradicting Theorem 3.1.◻
5 Exclusion of alternative constructions
This section shows that there exists just one class of Cremona transformations of
![]() $\mathbb{P}^{4}$
that can be resolved by blowing up an irreducible surface
$\mathbb{P}^{4}$
that can be resolved by blowing up an irreducible surface
![]() $S$
with transverse double points: the class constructed in § 2. Recall that [Reference Crauder and KatzCK89] classified the case where
$S$
with transverse double points: the class constructed in § 2. Recall that [Reference Crauder and KatzCK89] classified the case where
![]() $S$
is smooth.
$S$
is smooth.
Theorem 5.1. Let
![]() $S\subset \mathbb{P}^{4}$
be an irreducible surface of degree
$S\subset \mathbb{P}^{4}$
be an irreducible surface of degree
![]() $d$
with
$d$
with
![]() $\unicode[STIX]{x1D6FF}>0$
transverse double points. Assume there exists a Cremona transformation
$\unicode[STIX]{x1D6FF}>0$
transverse double points. Assume there exists a Cremona transformation
resolved by blowing up
![]() $S$
. Let
$S$
. Let
![]() $n$
and
$n$
and
![]() $\unicode[STIX]{x1D709}$
denote the degrees of the homogeneous forms inducing
$\unicode[STIX]{x1D709}$
denote the degrees of the homogeneous forms inducing
![]() $f$
and
$f$
and
![]() $f^{-1}$
respectively, and
$f^{-1}$
respectively, and
![]() $m$
the multiplicity of
$m$
the multiplicity of
![]() $S$
in the base locus. Then we have
$S$
in the base locus. Then we have
and
![]() $S$
is obtained by projecting a degree-
$S$
is obtained by projecting a degree-
![]() $12$
K3 surface from three points.
$12$
K3 surface from three points.
The remainder of this section is devoted to the proof of Theorem 5.1.
5.1 Extracting Diophantine equations
By Lemmas 1.1 and 1.2, equation (1.3) can be expressed as
Similarly, equation (1.1) can be expressed as
and equivalently as
The two formulas follow from the two expressions Lemma 1.2(3) and (3
′
) for
![]() $E^{4}$
, respectively. The right-hand sides of these equations are arranged as polynomials in
$E^{4}$
, respectively. The right-hand sides of these equations are arranged as polynomials in
![]() $n$
and
$n$
and
![]() $m$
. Note that only the coefficients of
$m$
. Note that only the coefficients of
![]() $m^{4}$
reflect the appearance of transverse double points.
$m^{4}$
reflect the appearance of transverse double points.
5.2 Enumeration of combinatorial cases
Lemma 5.2. Only the following
![]() $(n,m,\unicode[STIX]{x1D709})$
can occur:
$(n,m,\unicode[STIX]{x1D709})$
can occur:

Proof. In the smooth case, the same list [Reference Crauder and KatzCK89, Theorem 1.6] is obtained by using [Reference Crauder and KatzCK89, Lemma 0.2] and [Reference Crauder and KatzCK89, Formulae 0.3]. The proof of the former proceeds unchanged even with the transverse double points. The latter can be derived from (5.1) and (5.2) and only the terms with power of
![]() $m$
up to two matter, so transverse double points do not change the result. Therefore the same elimination process works and we obtain the same list.◻
$m$
up to two matter, so transverse double points do not change the result. Therefore the same elimination process works and we obtain the same list.◻
5.3 Exclusion of cases
Here we show that only case (b) can occur.
Lemma 5.3. Cases (c) and (e) do not occur.
Proof. The proof is similar to the smooth case [Reference Crauder and KatzCK89, Lemma 3.2].
Assume case (c) holds. Then (5.1) reduces to
and (5.2) reduces to
This is odd on the left and even on the right, a contradiction.
Assume case (e) holds. Now (5.1) reduces to
so
![]() $d$
is divisible by 5. On the other hand, (5.2) becomes
$d$
is divisible by 5. On the other hand, (5.2) becomes
Note that 5 divides the right but not the left, a contradiction.◻
Lemma 5.4. Cases (d), (f) and (g) do not occur.
Proof. Let
![]() $I_{S}$
be the ideal sheaf of
$I_{S}$
be the ideal sheaf of
![]() $S\subset \mathbb{P}^{4}$
. Generally, the global sections of
$S\subset \mathbb{P}^{4}$
. Generally, the global sections of
![]() $I_{S}^{m}(n)$
and
$I_{S}^{m}(n)$
and
![]() ${\mathcal{O}}_{P^{\prime }}(M)$
are bijective canonically. So we have
${\mathcal{O}}_{P^{\prime }}(M)$
are bijective canonically. So we have
by equation (1.4).
We prove the lemma case by case. In each case, we prove by contradiction in the following situations
Assume case (d) holds. Suppose
![]() $h^{0}(\mathbb{P}^{4},I_{S}(4))=0$
. Consider the surjective map
$h^{0}(\mathbb{P}^{4},I_{S}(4))=0$
. Consider the surjective map
By hypothesis,
![]() $h^{0}(\mathbb{P}^{4},I_{S}(k))=0$
for all
$h^{0}(\mathbb{P}^{4},I_{S}(k))=0$
for all
![]() $k\leqslant 4$
. Since
$k\leqslant 4$
. Since
![]() $k_{1}+k_{2}=9$
implies
$k_{1}+k_{2}=9$
implies
![]() $k_{1}\leqslant 4$
or
$k_{1}\leqslant 4$
or
![]() $k_{2}\leqslant 4$
, the left-hand side of (5.4) vanishes. Thus
$k_{2}\leqslant 4$
, the left-hand side of (5.4) vanishes. Thus
![]() $h^{0}(\mathbb{P}^{4},I_{S}^{2}(9))=0$
, contradicting (5.3).
$h^{0}(\mathbb{P}^{4},I_{S}^{2}(9))=0$
, contradicting (5.3).
Let
![]() $X_{0},\ldots ,X_{4}$
be a basis of degree-one forms on
$X_{0},\ldots ,X_{4}$
be a basis of degree-one forms on
![]() $\mathbb{P}^{4}$
in what follows.
$\mathbb{P}^{4}$
in what follows.
Suppose
![]() $h^{0}(\mathbb{P}^{4},I_{S}(4))\,=\,1$
. Let
$h^{0}(\mathbb{P}^{4},I_{S}(4))\,=\,1$
. Let
![]() $A\,\in \,H^{0}(\mathbb{P}^{4},I_{S}(4))$
be a generator. This forces
$A\,\in \,H^{0}(\mathbb{P}^{4},I_{S}(4))$
be a generator. This forces
![]() $h^{0}(\mathbb{P}^{4},I_{S}(k))\,=\,0$
for all
$h^{0}(\mathbb{P}^{4},I_{S}(k))\,=\,0$
for all
![]() $k\leqslant 3$
. It follows that
$k\leqslant 3$
. It follows that
![]() $H^{0}(\mathbb{P}^{4},I_{S}^{2}(8))$
is generated by
$H^{0}(\mathbb{P}^{4},I_{S}^{2}(8))$
is generated by
![]() $A^{2}$
. Then (5.3) indicates that
$A^{2}$
. Then (5.3) indicates that
![]() $A^{2}X_{0},\ldots ,A^{2}X_{4}$
form a basis for
$A^{2}X_{0},\ldots ,A^{2}X_{4}$
form a basis for
![]() $H^{0}(\mathbb{P}^{4},I_{S}^{2}(9))$
. As a result, the linear system
$H^{0}(\mathbb{P}^{4},I_{S}^{2}(9))$
. As a result, the linear system
![]() $|I_{S}^{2}(9)|$
defines an automorphism of
$|I_{S}^{2}(9)|$
defines an automorphism of
![]() $\mathbb{P}^{4}$
instead of a Cremona transformation.
$\mathbb{P}^{4}$
instead of a Cremona transformation.
Suppose
![]() $h^{0}(\mathbb{P}^{4},I_{S}(4))\geqslant 2$
. Let
$h^{0}(\mathbb{P}^{4},I_{S}(4))\geqslant 2$
. Let
![]() $A,B\in H^{0}(\mathbb{P}^{4},I_{S}(4))$
be independent. Then
$A,B\in H^{0}(\mathbb{P}^{4},I_{S}(4))$
be independent. Then
![]() $A^{2}$
and
$A^{2}$
and
![]() $AB$
are independent in
$AB$
are independent in
![]() $H^{0}(\mathbb{P}^{4},I_{S}^{2}(8))$
. We claim that there exists an
$H^{0}(\mathbb{P}^{4},I_{S}^{2}(8))$
. We claim that there exists an
![]() $i$
such that
$i$
such that
![]() $A^{2}X_{i}$
is not a linear combination of
$A^{2}X_{i}$
is not a linear combination of
![]() $ABX_{j}$
,
$ABX_{j}$
,
![]() $j=0,\ldots ,4$
. Suppose not, that is,
$j=0,\ldots ,4$
. Suppose not, that is,
![]() $A^{2}X_{i}=ABL_{i}$
for some linear form
$A^{2}X_{i}=ABL_{i}$
for some linear form
![]() $L_{i}$
,
$L_{i}$
,
![]() $i=0,\ldots ,4$
. Then we have
$i=0,\ldots ,4$
. Then we have
![]() $A/B=L_{0}/X_{0}=L_{1}/X_{1}$
, which implies that
$A/B=L_{0}/X_{0}=L_{1}/X_{1}$
, which implies that
![]() $L_{0}=X_{0}L_{1}/X_{1}$
, so
$L_{0}=X_{0}L_{1}/X_{1}$
, so
![]() $X_{1}$
divides
$X_{1}$
divides
![]() $L_{1}$
. Therefore
$L_{1}$
. Therefore
![]() $A/B=L_{1}/X_{1}$
is a scalar, thus
$A/B=L_{1}/X_{1}$
is a scalar, thus
![]() $A$
and
$A$
and
![]() $B$
are dependent, a contradiction. As a result, there exists an
$B$
are dependent, a contradiction. As a result, there exists an
![]() $i$
such that
$i$
such that
![]() $A^{2}X_{i}$
and
$A^{2}X_{i}$
and
![]() $ABX_{0},\ldots ,ABX_{4}$
form an independent subset of
$ABX_{0},\ldots ,ABX_{4}$
form an independent subset of
![]() $H^{0}(\mathbb{P}^{4},I_{S}^{2}(9))$
. Thus
$H^{0}(\mathbb{P}^{4},I_{S}^{2}(9))$
. Thus
![]() $h^{0}(\mathbb{P}^{4},I_{S}^{2}(9))\geqslant 6>5$
, a contradiction.
$h^{0}(\mathbb{P}^{4},I_{S}^{2}(9))\geqslant 6>5$
, a contradiction.
Assume case (f) holds. Suppose
![]() $h^{0}(\mathbb{P}^{4},I_{S}(4))=0$
. Then
$h^{0}(\mathbb{P}^{4},I_{S}(4))=0$
. Then
![]() $h^{0}(\mathbb{P}^{4},I_{S}(k))=0$
for all
$h^{0}(\mathbb{P}^{4},I_{S}(k))=0$
for all
![]() $k\leqslant 4$
. Now we consider the map
$k\leqslant 4$
. Now we consider the map
At least one
![]() $k_{i}\leqslant 4$
,
$k_{i}\leqslant 4$
,
![]() $i=1,\ldots ,5$
, if their sum equals 24. Hence the left-hand side of (5.5) vanishes. Thus
$i=1,\ldots ,5$
, if their sum equals 24. Hence the left-hand side of (5.5) vanishes. Thus
![]() $h^{0}(\mathbb{P}^{4},I_{S}^{2}(24))=0\neq 5$
.
$h^{0}(\mathbb{P}^{4},I_{S}^{2}(24))=0\neq 5$
.
Suppose
![]() $h^{0}(\mathbb{P}^{4},I_{S}(4))\geqslant 1$
. Let
$h^{0}(\mathbb{P}^{4},I_{S}(4))\geqslant 1$
. Let
![]() $A\in H^{0}(\mathbb{P}^{4},I_{S}(4))$
be a non-zero element. Then
$A\in H^{0}(\mathbb{P}^{4},I_{S}(4))$
be a non-zero element. Then
![]() $A^{5}\in H^{0}(\mathbb{P}^{4},I_{S}^{5}(20))$
. Multiplication by
$A^{5}\in H^{0}(\mathbb{P}^{4},I_{S}^{5}(20))$
. Multiplication by
![]() $A^{5}$
defines an injection
$A^{5}$
defines an injection
Thus
![]() $h^{0}(\mathbb{P}^{4},I_{S}^{5}(24))\geqslant \binom{8}{4}=70>5$
, a contradiction.
$h^{0}(\mathbb{P}^{4},I_{S}^{5}(24))\geqslant \binom{8}{4}=70>5$
, a contradiction.
The elimination of case (g) is similar to that of case (f). In case (g), we use the surjection
to rule out the situation
![]() $h^{0}(\mathbb{P}^{4},I_{S}(4))=0$
. If
$h^{0}(\mathbb{P}^{4},I_{S}(4))=0$
. If
![]() $H^{0}(\mathbb{P}^{4},I_{S}(4))$
contains
$H^{0}(\mathbb{P}^{4},I_{S}(4))$
contains
![]() $A\neq 0$
, then multiplication of
$A\neq 0$
, then multiplication of
![]() $A^{10}$
with 9-forms produces
$A^{10}$
with 9-forms produces
![]() $\binom{13}{4}=715$
independent elements in
$\binom{13}{4}=715$
independent elements in
![]() $H^{0}(\mathbb{P}^{4},I_{S}^{10}(49))$
, which is not allowed.◻
$H^{0}(\mathbb{P}^{4},I_{S}^{10}(49))$
, which is not allowed.◻
Lemma 5.5. In cases (a) and (b) we have:

The invariants
![]() $d$
and
$d$
and
![]() $\unicode[STIX]{x1D6FF}$
satisfy
$\unicode[STIX]{x1D6FF}$
satisfy
![]() $(d-5)^{2}=2\unicode[STIX]{x1D6FF}$
in case (a) and
$(d-5)^{2}=2\unicode[STIX]{x1D6FF}$
in case (a) and
![]() $(d-10)(d-15)=2\unicode[STIX]{x1D6FF}$
in case (b).
$(d-10)(d-15)=2\unicode[STIX]{x1D6FF}$
in case (b).
Proof. In order to compute the invariants in the list, we first use (5.1) to express
![]() $K_{\unicode[STIX]{x1D6F4}}C$
in
$K_{\unicode[STIX]{x1D6F4}}C$
in
![]() $d$
with given
$d$
with given
![]() $n$
,
$n$
,
![]() $m$
, and
$m$
, and
![]() $\unicode[STIX]{x1D709}$
. Then (5.2) (respectively, (5.2
′
)) allows us to express
$\unicode[STIX]{x1D709}$
. Then (5.2) (respectively, (5.2
′
)) allows us to express
![]() $c_{2}(\unicode[STIX]{x1D6F4})$
(respectively,
$c_{2}(\unicode[STIX]{x1D6F4})$
(respectively,
![]() $K_{\unicode[STIX]{x1D6F4}}^{2}$
) in
$K_{\unicode[STIX]{x1D6F4}}^{2}$
) in
![]() $d$
and
$d$
and
![]() $\unicode[STIX]{x1D6FF}$
. We compute
$\unicode[STIX]{x1D6FF}$
. We compute
![]() $12\unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})$
and
$12\unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})$
and
![]() $g(C)$
by Noether’s formula and the genus formula, respectively. The upper bound for
$g(C)$
by Noether’s formula and the genus formula, respectively. The upper bound for
![]() $d$
comes from the inequality
$d$
comes from the inequality
![]() $d<(n/m)^{2}$
which holds generally [Reference Crauder and KatzCK89, Formulae 0.3(v)].
$d<(n/m)^{2}$
which holds generally [Reference Crauder and KatzCK89, Formulae 0.3(v)].
We have
![]() $h^{0}(\mathbb{P}^{4},I_{S}(n))=h^{0}(P^{\prime },M)=5$
by (1.4). On the other hand,
$h^{0}(\mathbb{P}^{4},I_{S}(n))=h^{0}(P^{\prime },M)=5$
by (1.4). On the other hand,
![]() $h^{1}(\mathbb{P}^{4},I_{S}(n))=0$
by [Reference DolgachevDol12, Proposition 7.1.4]. Hence
$h^{1}(\mathbb{P}^{4},I_{S}(n))=0$
by [Reference DolgachevDol12, Proposition 7.1.4]. Hence
where the second equality follows from the functoriality of the Euler characteristic. The short exact sequence
implies that
![]() $\unicode[STIX]{x1D712}(P,nL-2\unicode[STIX]{x1D6F4}_{i}E_{i})$
counts the dimension of the space of degree-
$\unicode[STIX]{x1D712}(P,nL-2\unicode[STIX]{x1D6F4}_{i}E_{i})$
counts the dimension of the space of degree-
![]() $n$
polynomials singular along
$n$
polynomials singular along
![]() $\unicode[STIX]{x1D6E5}$
, so
$\unicode[STIX]{x1D6E5}$
, so
By the previous computations and the Riemann–Roch formula, we have
whence
Then the two equations are obtained by setting
![]() $\unicode[STIX]{x1D712}(P,I_{S^{\prime }}(n))=5$
.◻
$\unicode[STIX]{x1D712}(P,I_{S^{\prime }}(n))=5$
.◻
Lemma 5.6. Case (a) does not occur.
Proof. Assume (a) is satisfied. Then the same argument as in [Reference Crauder and KatzCK89, Theorem 3.3] implies that
![]() $d=5$
. By Lemma 5.5 we have
$d=5$
. By Lemma 5.5 we have
![]() $\unicode[STIX]{x1D6FF}=0$
.◻
$\unicode[STIX]{x1D6FF}=0$
.◻
5.4 Geometric analysis of the remaining case
To complete the proof of Theorem 5.1, it remains to analyze the last possible case.
Lemma 5.7. We have
![]() $(d,\unicode[STIX]{x1D6FF})=(8,7)$
or
$(d,\unicode[STIX]{x1D6FF})=(8,7)$
or
![]() $(9,3)$
. The invariants in these cases are:
$(9,3)$
. The invariants in these cases are:

Proof. By the previous part only case (b) is allowed.
By Lemma 5.5, we have
![]() $d\leqslant 15$
and
$d\leqslant 15$
and
![]() $g(C)=4d-29\geqslant 0$
. Hence
$g(C)=4d-29\geqslant 0$
. Hence
![]() $8\leqslant d\leqslant 15$
. Then
$8\leqslant d\leqslant 15$
. Then
![]() $(d-10)(d-15)=2\unicode[STIX]{x1D6FF}$
and our hypothesis
$(d-10)(d-15)=2\unicode[STIX]{x1D6FF}$
and our hypothesis
![]() $\unicode[STIX]{x1D6FF}>0$
force
$\unicode[STIX]{x1D6FF}>0$
force
![]() $d=8$
or
$d=8$
or
![]() $9$
, which implies that
$9$
, which implies that
![]() $\unicode[STIX]{x1D6FF}=7$
or
$\unicode[STIX]{x1D6FF}=7$
or
![]() $3$
, respectively.
$3$
, respectively.
The invariants are computed directly by using Lemma 5.5.◻
Consider the linear system
![]() $|K_{\unicode[STIX]{x1D6F4}}+C|$
for both cases of Lemma 5.7. We have
$|K_{\unicode[STIX]{x1D6F4}}+C|$
for both cases of Lemma 5.7. We have
![]() $h^{1}(K_{\unicode[STIX]{x1D6F4}}+C)=0$
by Kodaira vanishing and
$h^{1}(K_{\unicode[STIX]{x1D6F4}}+C)=0$
by Kodaira vanishing and
![]() $h^{2}(K_{\unicode[STIX]{x1D6F4}}+C)=h^{0}(-C)=0$
by Serre duality.
$h^{2}(K_{\unicode[STIX]{x1D6F4}}+C)=h^{0}(-C)=0$
by Serre duality.
Lemma 5.8. The case
![]() $(d,\unicode[STIX]{x1D6FF})=(8,7)$
is not allowed.
$(d,\unicode[STIX]{x1D6FF})=(8,7)$
is not allowed.
Proof. By the Riemann–Roch formula,
 $$\begin{eqnarray}\begin{array}{@{}ccl@{}}h^{0}(K_{\unicode[STIX]{x1D6F4}}+C)\,\, & =\,\, & \unicode[STIX]{x1D712}(K_{\unicode[STIX]{x1D6F4}}+C)\\ \,\, & =\,\, & \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})+\frac{1}{2}(K_{\unicode[STIX]{x1D6F4}}+C)C\\ \,\, & =\,\, & 0+\frac{1}{2}(-4+8)=2.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccl@{}}h^{0}(K_{\unicode[STIX]{x1D6F4}}+C)\,\, & =\,\, & \unicode[STIX]{x1D712}(K_{\unicode[STIX]{x1D6F4}}+C)\\ \,\, & =\,\, & \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})+\frac{1}{2}(K_{\unicode[STIX]{x1D6F4}}+C)C\\ \,\, & =\,\, & 0+\frac{1}{2}(-4+8)=2.\end{array}\end{eqnarray}$$
Because
![]() $c_{2}(\unicode[STIX]{x1D6F4})=5$
,
$c_{2}(\unicode[STIX]{x1D6F4})=5$
,
![]() $\unicode[STIX]{x1D6F4}$
cannot be
$\unicode[STIX]{x1D6F4}$
cannot be
![]() $\mathbb{P}^{2}$
,
$\mathbb{P}^{2}$
,
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, or a minimal ruled surface. This implies that
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, or a minimal ruled surface. This implies that
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}(K_{\unicode[STIX]{x1D6F4}}+C)$
is generated by global sections [Reference SommeseSom81, Proposition 2.2]. Hence the system
${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}(K_{\unicode[STIX]{x1D6F4}}+C)$
is generated by global sections [Reference SommeseSom81, Proposition 2.2]. Hence the system
![]() $|K_{\unicode[STIX]{x1D6F4}}+C|$
defines a morphism
$|K_{\unicode[STIX]{x1D6F4}}+C|$
defines a morphism
the adjunction mapping.
Consider the Stein factorization

where
![]() $r$
is a proper morphism with connected fibers and
$r$
is a proper morphism with connected fibers and
![]() $s$
is a finite morphism. By [Reference SommeseSom81, (2.3)], this leads to two possible situations.
$s$
is a finite morphism. By [Reference SommeseSom81, (2.3)], this leads to two possible situations.
(1)
 $\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=0$
. Here we have
$\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=0$
. Here we have
 $g(C)=1$
, a contradiction.
$g(C)=1$
, a contradiction.(2)
 $\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=1$
. Then there exists a
$\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=1$
. Then there exists a
 $\mathbb{P}^{1}$
-bundle
$\mathbb{P}^{1}$
-bundle
 $\unicode[STIX]{x1D70B}:R\rightarrow \unicode[STIX]{x1D6F4}^{\prime }$
such that
$\unicode[STIX]{x1D70B}:R\rightarrow \unicode[STIX]{x1D6F4}^{\prime }$
such that
 $r$
factors aswhere
$r$
factors aswhere
 $\unicode[STIX]{x1D6F4}$
is the blow-up of
$\unicode[STIX]{x1D6F4}$
is the blow-up of
 $R$
in at most one point of each fiber blown up, and
$R$
in at most one point of each fiber blown up, and
 $C$
meets the generic fiber with degree two. Furthermore, the map
$C$
meets the generic fiber with degree two. Furthermore, the map
 $s$
is an isomorphism except possibly if
$s$
is an isomorphism except possibly if
 $g(C)=3$
and
$g(C)=3$
and
 $h^{1,0}(\unicode[STIX]{x1D6F4})=1$
.
$h^{1,0}(\unicode[STIX]{x1D6F4})=1$
.
Let us analyze situation (2): the map
![]() $s$
cannot be an isomorphism. Otherwise,
$s$
cannot be an isomorphism. Otherwise,
![]() $R$
is a Hirzebruch surface and
$R$
is a Hirzebruch surface and
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})=\unicode[STIX]{x1D712}({\mathcal{O}}_{R})=1$
, a contradiction. Hence we obtain
$\unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})=\unicode[STIX]{x1D712}({\mathcal{O}}_{R})=1$
, a contradiction. Hence we obtain
Then
![]() $\unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})=0$
and
$\unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})=0$
and
![]() $c_{2}(\unicode[STIX]{x1D6F4})=5$
implies that
$c_{2}(\unicode[STIX]{x1D6F4})=5$
implies that
![]() $\unicode[STIX]{x1D6F4}$
has Hodge diamond
$\unicode[STIX]{x1D6F4}$
has Hodge diamond
 $$\begin{eqnarray}\begin{array}{@{}ccccc@{}} & & 1 & & \\ & 1 & & 1 & \\ 0 & & 7 & & 0.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccccc@{}} & & 1 & & \\ & 1 & & 1 & \\ 0 & & 7 & & 0.\end{array}\end{eqnarray}$$
Since the Néron–Severi group of
![]() $R$
has rank two, we conclude that
$R$
has rank two, we conclude that
![]() $\unicode[STIX]{x1D6F4}$
is the blow-up of
$\unicode[STIX]{x1D6F4}$
is the blow-up of
![]() $R$
along five points on distinct fibers, and
$R$
along five points on distinct fibers, and
![]() $R$
is ruled over the elliptic curve
$R$
is ruled over the elliptic curve
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
.
$\unicode[STIX]{x1D6F4}^{\prime }$
.
Let
![]() $h$
be the class of a section on
$h$
be the class of a section on
![]() $R$
and
$R$
and
![]() $f$
be the class of a fiber so that
$f$
be the class of a fiber so that
for some integer
![]() $m$
. According to the description of (2), the image of
$m$
. According to the description of (2), the image of
![]() $C$
in
$C$
in
![]() $R$
gives a class
$R$
gives a class
![]() $H=2h+bf$
for some integer
$H=2h+bf$
for some integer
![]() $b$
and
$b$
and
![]() $C=\unicode[STIX]{x1D716}^{\ast }H-\sum _{i=1}^{5}F_{i}$
where
$C=\unicode[STIX]{x1D716}^{\ast }H-\sum _{i=1}^{5}F_{i}$
where
![]() $F_{1},\ldots ,F_{5}$
are the exceptional curves on
$F_{1},\ldots ,F_{5}$
are the exceptional curves on
![]() $\unicode[STIX]{x1D6F4}$
. Note that
$\unicode[STIX]{x1D6F4}$
. Note that
![]() $K_{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D716}^{\ast }K_{R}+\sum _{i=1}^{5}F_{i}$
. Thus we have
$K_{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D716}^{\ast }K_{R}+\sum _{i=1}^{5}F_{i}$
. Thus we have
and consequently,
On the other hand, we can use the exact sequence
to get
![]() $\unicode[STIX]{x1D712}(h)=m$
, and then use
$\unicode[STIX]{x1D712}(h)=m$
, and then use
to obtain
![]() $\unicode[STIX]{x1D712}(2h)=3m$
. Then an induction on
$\unicode[STIX]{x1D712}(2h)=3m$
. Then an induction on
![]() $n$
with the sequence
$n$
with the sequence
implies that
![]() $\unicode[STIX]{x1D712}(H)=\unicode[STIX]{x1D712}(2h+bf)=3m+3b$
. But this implies
$\unicode[STIX]{x1D712}(H)=\unicode[STIX]{x1D712}(2h+bf)=3m+3b$
. But this implies
![]() $11=\unicode[STIX]{x1D712}(H)$
is divisible by
$11=\unicode[STIX]{x1D712}(H)$
is divisible by
![]() $3$
, a contradiction.◻
$3$
, a contradiction.◻
Proposition 5.9. If
![]() $S$
has a transverse double point, then it can only be the image of a K3 surface
$S$
has a transverse double point, then it can only be the image of a K3 surface
![]() $R\subset \mathbb{P}^{7}$
of degree
$R\subset \mathbb{P}^{7}$
of degree
![]() $12$
projected from three points on
$12$
projected from three points on
![]() $R$
, and the number of transverse double points must be
$R$
, and the number of transverse double points must be
![]() $\unicode[STIX]{x1D6FF}=3$
.
$\unicode[STIX]{x1D6FF}=3$
.
Proof. By the Riemann–Roch formula,
 $$\begin{eqnarray}\begin{array}{@{}ccl@{}}h^{0}(K_{\unicode[STIX]{x1D6F4}}+C)\,\, & =\,\, & \unicode[STIX]{x1D712}(K_{\unicode[STIX]{x1D6F4}}+C)\\ \,\, & =\,\, & \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})+\frac{1}{2}(K_{\unicode[STIX]{x1D6F4}}+C)C\\ \,\, & =\,\, & 2+\frac{1}{2}(3+9)=8.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccl@{}}h^{0}(K_{\unicode[STIX]{x1D6F4}}+C)\,\, & =\,\, & \unicode[STIX]{x1D712}(K_{\unicode[STIX]{x1D6F4}}+C)\\ \,\, & =\,\, & \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})+\frac{1}{2}(K_{\unicode[STIX]{x1D6F4}}+C)C\\ \,\, & =\,\, & 2+\frac{1}{2}(3+9)=8.\end{array}\end{eqnarray}$$
Because
![]() $c_{2}(\unicode[STIX]{x1D6F4})=27$
,
$c_{2}(\unicode[STIX]{x1D6F4})=27$
,
![]() $\unicode[STIX]{x1D6F4}$
cannot be
$\unicode[STIX]{x1D6F4}$
cannot be
![]() $\mathbb{P}^{2}$
,
$\mathbb{P}^{2}$
,
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
, or a minimal ruled surface. It follows that
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
, or a minimal ruled surface. It follows that
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}(K_{\unicode[STIX]{x1D6F4}}+C)$
is generated by global sections [Reference SommeseSom81, Proposition 2.2]. Hence
${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}(K_{\unicode[STIX]{x1D6F4}}+C)$
is generated by global sections [Reference SommeseSom81, Proposition 2.2]. Hence
![]() $|K_{\unicode[STIX]{x1D6F4}}+C|$
defines an adjunction morphism with Stein factorization
$|K_{\unicode[STIX]{x1D6F4}}+C|$
defines an adjunction morphism with Stein factorization

There are three possible situations [Reference SommeseSom81, (2.3)].
(1)
 $\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=0$
. We have
$\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=0$
. We have
 $g(C)=1$
, a contradiction.
$g(C)=1$
, a contradiction.(2)
 $\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=1$
. Then
$\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=1$
. Then
 $r:\unicode[STIX]{x1D6F4}\rightarrow \unicode[STIX]{x1D6F4}^{\prime }$
is again obtained by blowing up a
$r:\unicode[STIX]{x1D6F4}\rightarrow \unicode[STIX]{x1D6F4}^{\prime }$
is again obtained by blowing up a
 $\mathbb{P}^{1}$
-bundle, with no more than one point in a fiber blown up. In particular,
$\mathbb{P}^{1}$
-bundle, with no more than one point in a fiber blown up. In particular,
 $1\geqslant \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})=2$
, a contradiction.
$1\geqslant \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}})=2$
, a contradiction.(3)
 $\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=2$
. Then
$\dim \unicode[STIX]{x1D719}(\unicode[STIX]{x1D6F4})=2$
. Then
 $r:\unicode[STIX]{x1D6F4}\rightarrow \unicode[STIX]{x1D6F4}^{\prime }$
expresses
$r:\unicode[STIX]{x1D6F4}\rightarrow \unicode[STIX]{x1D6F4}^{\prime }$
expresses
 $\unicode[STIX]{x1D6F4}$
as the blow-up of a smooth surface
$\unicode[STIX]{x1D6F4}$
as the blow-up of a smooth surface
 $\unicode[STIX]{x1D6F4}^{\prime }$
along a finite set with
$\unicode[STIX]{x1D6F4}^{\prime }$
along a finite set with
 $F\cdot C=1$
for any positive-dimensional fiber
$F\cdot C=1$
for any positive-dimensional fiber
 $F$
of
$F$
of
 $r$
. Moreover,
$r$
. Moreover,
 $s:\unicode[STIX]{x1D6F4}^{\prime }\rightarrow \mathbb{P}^{7}$
is an embedding.
$s:\unicode[STIX]{x1D6F4}^{\prime }\rightarrow \mathbb{P}^{7}$
is an embedding.
Now we are in situation (3). Let
![]() $F_{1},\ldots ,F_{k}$
be the exceptional curves on
$F_{1},\ldots ,F_{k}$
be the exceptional curves on
![]() $\unicode[STIX]{x1D6F4}$
relative to
$\unicode[STIX]{x1D6F4}$
relative to
![]() $r$
and let
$r$
and let
![]() $H$
be the very ample divisor on
$H$
be the very ample divisor on
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
which defines
$\unicode[STIX]{x1D6F4}^{\prime }$
which defines
![]() $s$
. Then
$s$
. Then
and it follows that
 $$\begin{eqnarray}\displaystyle 9 & = & \displaystyle C^{2}=H^{2}-k,\nonumber\\ \displaystyle 3 & = & \displaystyle K_{\unicode[STIX]{x1D6F4}}C=K_{\unicode[STIX]{x1D6F4}^{\prime }}H+k,\nonumber\\ \displaystyle -3 & = & \displaystyle K_{\unicode[STIX]{x1D6F4}}^{2}=K_{\unicode[STIX]{x1D6F4}^{\prime }}^{2}-k.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 9 & = & \displaystyle C^{2}=H^{2}-k,\nonumber\\ \displaystyle 3 & = & \displaystyle K_{\unicode[STIX]{x1D6F4}}C=K_{\unicode[STIX]{x1D6F4}^{\prime }}H+k,\nonumber\\ \displaystyle -3 & = & \displaystyle K_{\unicode[STIX]{x1D6F4}}^{2}=K_{\unicode[STIX]{x1D6F4}^{\prime }}^{2}-k.\nonumber\end{eqnarray}$$
By the Riemann–Roch formula,
 $$\begin{eqnarray}\begin{array}{@{}ccl@{}}8=\unicode[STIX]{x1D712}(H)\,\, & =\,\, & \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}^{\prime }})+\frac{1}{2}H(H-K_{\unicode[STIX]{x1D6F4}^{\prime }})\\ \,\, & =\,\, & 2+\frac{1}{2}((9+k)-(3-k))\\ \,\, & =\,\, & 5+k,\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccl@{}}8=\unicode[STIX]{x1D712}(H)\,\, & =\,\, & \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}^{\prime }})+\frac{1}{2}H(H-K_{\unicode[STIX]{x1D6F4}^{\prime }})\\ \,\, & =\,\, & 2+\frac{1}{2}((9+k)-(3-k))\\ \,\, & =\,\, & 5+k,\end{array}\end{eqnarray}$$
which implies that
![]() $k=3$
. Hence
$k=3$
. Hence
![]() $\unicode[STIX]{x1D6F4}$
is obtained by blowing up
$\unicode[STIX]{x1D6F4}$
is obtained by blowing up
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
along three distinct points, and
$\unicode[STIX]{x1D6F4}^{\prime }$
along three distinct points, and
![]() $\unicode[STIX]{x1D6F4}^{\prime }\subset \mathbb{P}^{7}$
has
$\unicode[STIX]{x1D6F4}^{\prime }\subset \mathbb{P}^{7}$
has
We claim that
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
is a K3 surface. Indeed, its Kodaira dimension
$\unicode[STIX]{x1D6F4}^{\prime }$
is a K3 surface. Indeed, its Kodaira dimension
![]() $\unicode[STIX]{x1D705}\neq 2$
since
$\unicode[STIX]{x1D705}\neq 2$
since
![]() $K_{\unicode[STIX]{x1D6F4}^{\prime }}H=0$
. If
$K_{\unicode[STIX]{x1D6F4}^{\prime }}H=0$
. If
![]() $\unicode[STIX]{x1D705}=1$
, then
$\unicode[STIX]{x1D705}=1$
, then
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
has minimal model
$\unicode[STIX]{x1D6F4}^{\prime }$
has minimal model
![]() $R$
an elliptic surface, such that
$R$
an elliptic surface, such that
![]() $nK_{R}$
is numerically equivalent to a positive linear combination of some fiber classes if
$nK_{R}$
is numerically equivalent to a positive linear combination of some fiber classes if
![]() $n$
is large enough [Reference BeauvilleBea96, Proposition IX.3]. This implies that
$n$
is large enough [Reference BeauvilleBea96, Proposition IX.3]. This implies that
![]() $K_{\unicode[STIX]{x1D6F4}^{\prime }}$
is numerically effective, which contradicts the fact that
$K_{\unicode[STIX]{x1D6F4}^{\prime }}$
is numerically effective, which contradicts the fact that
![]() $K_{\unicode[STIX]{x1D6F4}^{\prime }}H=0$
. If
$K_{\unicode[STIX]{x1D6F4}^{\prime }}H=0$
. If
![]() $\unicode[STIX]{x1D705}=-\infty$
, then
$\unicode[STIX]{x1D705}=-\infty$
, then
![]() $h^{1,0}(\unicode[STIX]{x1D6F4}^{\prime })=0$
and thus
$h^{1,0}(\unicode[STIX]{x1D6F4}^{\prime })=0$
and thus
![]() $1\geqslant \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}^{\prime }})=2$
, a contradiction. As a result,
$1\geqslant \unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6F4}^{\prime }})=2$
, a contradiction. As a result,
![]() $\unicode[STIX]{x1D6F4}^{\prime }$
has
$\unicode[STIX]{x1D6F4}^{\prime }$
has
![]() $\unicode[STIX]{x1D705}=0$
and thus is a K3 surface.
$\unicode[STIX]{x1D705}=0$
and thus is a K3 surface.
Besides, the birational map
![]() $R{\dashrightarrow}\unicode[STIX]{x1D6F4}\rightarrow S$
can be realized as the projection from three points on
$R{\dashrightarrow}\unicode[STIX]{x1D6F4}\rightarrow S$
can be realized as the projection from three points on
![]() $R$
. Furthermore, the fact that
$R$
. Furthermore, the fact that
![]() $\unicode[STIX]{x1D6FF}=3$
can also be verified directly by the double-point formula as in § 2.3.◻
$\unicode[STIX]{x1D6FF}=3$
can also be verified directly by the double-point formula as in § 2.3.◻
Acknowledgements
We are grateful for conversations with Lev Borisov that inspired this work. The manuscript benefited from correspondence with Alexander Kuznetsov. The authors are grateful for the support of the National Science Foundation through grant DMS-1551514.