Introduction
As well as direct intuitive insight, experimental studies of the internal flow structure of snow avalanches provide a basis for understanding internal dissipative processes. Unfortunately, in real-scale avalanches, direct internal measurements are difficult to obtain: avalanche events can hardly be predicted and their extent and initial and boundary conditions cannot be controlled. However, these problems can be partly resolved by artificially releasing avalanches in designated field sites equipped with measurement devices (Reference Dent, Burrell, Schmidt, Louge, Adams and JazbutisDent and others, 1998; Reference IsslerIssler, 1999, Reference Issler, Hutter and Kirchner2003; Reference Lied, Moe, Kristensen, Issler, Naaim and Naaim-BouvetLied and others, 2004). Optical velocity sensors mounted on pylons in the avalanche track comprise part of the integral measurement concepts of such sites. Note that, except for frequency-modulated continuous-wave (FM-CW) radars, non-intrusive measurement techniques fail to capture the internal flow behaviour of dense avalanches.
Optical velocity measurements are constrained by the fact that this measurement technique is essentially intrusive and requires large technical efforts to minimize the flow distortion by the sensors and their carrier structures. Although an optical velocity measurement system has been operational at the Swiss field site Vallée de la Sionne (VdlS) since 2002, undistorted and uninterrupted velocity records during the entire avalanche event (which allow study of the evolution of the internal velocity) are extremely rare. The flow may detach from the sensors due to shock-wave-like effects, sensors may be covered by ice or lumped snow or dilute flow may produce sensor signals that are difficult to interpret. Furthermore, processing optical velocity measurement data is a delicate matter (Reference McElwaine and TiefenbacherMcElwaine and Tiefenbacher, 2003) because the underlying correlation analysis is very sensitive to electronic noise in the measurement set-up. This may lead to false interpretation of the data (Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009).
Here we present data from the dense part of a medium-sized avalanche at the VdlS field site, recorded on 26 March 2008. The data quality is extraordinarily high. For the first time, the internal flow velocity could be recorded continuously at various heights at the measurement mast for all parts of the avalanche, allowing a detailed description of the evolution of the internal velocity structure of the avalanche over time. After a short introduction to the field site and the velocity measurement set-up, we characterize the medium-sized and mixed wet-dry avalanche on 26 March 2008 using the recorded velocity time series. In particular, we provide evidence for velocity profile inversions at the transition from the avalanche front to the avalanche body. We propose a simplistic empirical description of this effect in terms of reverse eddies travelling with the flow, and briefly discuss our observations.
Measurement Set-Up
The Vallée de la Sionne field site
At the real-scale test site in the VdlS, Canton Valais, Switzerland, natural and artficially released avalanches which run on a ∼2700 m long avalanche track with a vertical drop of approximately 1300 m are investigated.
Among other measurement devices, a 20 m high mast at the start of the run-out zone of the track is equipped with measurement devices for impact pressure, flow velocity, density, flow height and air pressure in the suspension layer of avalanches. A shelter on the counterslope houses the data acquisition system and Doppler radars to track the avalanche (front) velocity. Detailed descriptions of the VdlS test site and its various measurement set-ups can be found in Reference IsslerIssler (1999, Reference Issler, Hutter and Kirchner2003), Reference Sovilla, Burlando and BarteltSovilla and others (2006), Reference Gauer, Kern, Kristensen, Lied, Rammer and SchreiberGauer and others (2007), Reference Rammer, Kern, Gruber and TiefenbacherRammer and others (2007) and Reference Sovilla, Schaer, Kern and BarteltSovilla and others (2008a,Reference Sovilla, Schaer and Rammerb). The site was upgraded with a new and powerful data acquisition system in autumn 2007, which allows multiple dynamic measures with a very high spatiotemporal resolution to be recorded.
Optical velocity measurement
At the hillside face of the measurement mast, nine optical velocity sensors were placed between 1 and 2 m and at 3, 4 and 5 m above the ground (Fig. 1). In order to minimize flow disturbances and to avoid detachment of the passing flow, the sensors are mounted flush with the side walls of wedges (Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009).

Fig. 1. Optical velocity sensor mounted in flow wedges on the mast at the VdlS test site. Streamwise spacing of the two reflectivity sensors, d, is 0.03 m. The flow direction is from right to left along the line between the two sensors. Sensors are mounted at a vertical distance of 125 mm.
The principle of optical velocity measurements is based on recording the reflectivity of the passing flow at two points A and B with a flow-wise spacing d = 0.03 m which, using the Taylor hypothesis, results in two similar time series A(t) and B(t + τ) with a local time lag τ(ts) at ts. Accordingly, the velocity u(ts) of the passing flow is estimated to be u(t s) = d/τ (t s). The time lag τ(ts) is determined by a correlation analysis of the sensor signals A(t) and B(t). At the VdlS test site, each optical velocity sensor consists of two reflectivity sensors placed along a flow-parallel line (Fig. 1). Optical velocity measurements in snow avalanches were introduced by Reference Nishimura, Maeno, Sandersen, Kristensen, Norem and LiedNishimura and others (1993); Reference Nishimura and ItoNishimura and Ito (1997) and Reference Dent, Burrell, Schmidt, Louge, Adams and JazbutisDent and others (1998). More recent studies have been performed by Reference Kern, Tiefenbacher and McElwaineKern and others (2004) and Reference Tiefenbacher and KernTiefenbacher and Kern (2004). For discussions of fundamental constraints of the measurement technique and error analysis, see Reference McElwaine and TiefenbacherMcElwaine and Tiefenbacher (2003) and Reference Kern, Bartelt, Sovilla and BuserKern and others (2009). Reflectivity data were sampled at 20 kHz and were processed into velocity time series with a time resolution of 0.01 s (excluding unphysically high accelerations). Finally, the time series were smoothed using a running mean over 0.5 s. For technical details of data acquisition and analysis procedures, see Reference Kern, Bartelt, Sovilla and BuserKern and others (2009).
Avalanche on 26 March 2008
On 21 March 2008, a significant snowfall had accumulated about 0.8 m of new snow in the release zone of the avalanche track. This was followed by some mi nor snow accumulations, the most important in the late evening of 24 March which added 0.2 m of new snow. The week before the artificial release on 26 March, the temperature had been about –10°C in the release zone (subject to diurnal fluctuations) and the speed of the westerly wind had been moderate, not exceeding 9 m s∼1. At the time of artificial release (1347 h), the temperature in the release area was about -3 °C after a significant temperature rise from -12°C in the morning. The weather was sunny and there were weak easterly winds with speeds below 2 m s–1. The ∼400 m long fracture was about 1 m high and was composed of two subsequent 0.5 m high fractures. For obvious reasons the snow height at the mast, which is situated in the avalanche track at ∼1640 ma.s.l., could not be measured on site. Using data from the nearby observation station Montana (VS), we estimate the total snow height at the mast before the event to be 0.8 ± 0.3 m which is consistent with estimates from photographs of the mast area taken from the bunker at the counterslope.
The measurement mast was hit approximately 4s after the central avalanche front had passed the mast on the orographic leftside, i.e. the measurement mast did not match the centre line of the flow. Accordingly, the time series represents the flow field at a streamline that was laterally shifted against the flow centre line by about 25% of the avalanche width.
Figure 2 shows the time series of flow velocities at different heights above the ground. Since even the lowest sensors show non-zero velocities, the basal sliding surface or the basal interface must have been situated between the ground and a height of z = 1 m. We use the term ‘sliding surface’ if there is slip at the transition surface between stationary and moving snow. If there is no slip, we term the transition surface ‘basal interface’. From in situ observations of the sliding surface after the event, its position was estimated to be ∼0.4–0.5 m above the ground. Except for the dilute front, no meaningful signals were recorded by the sensor at z = 3 m (Fig. 2a), which suggests that the surface of the dense flow was situated between z = 2 m and z = 3 m. This is consistent with the dense-flow surface locations determined by switches which are only triggered by dense-flow parts.
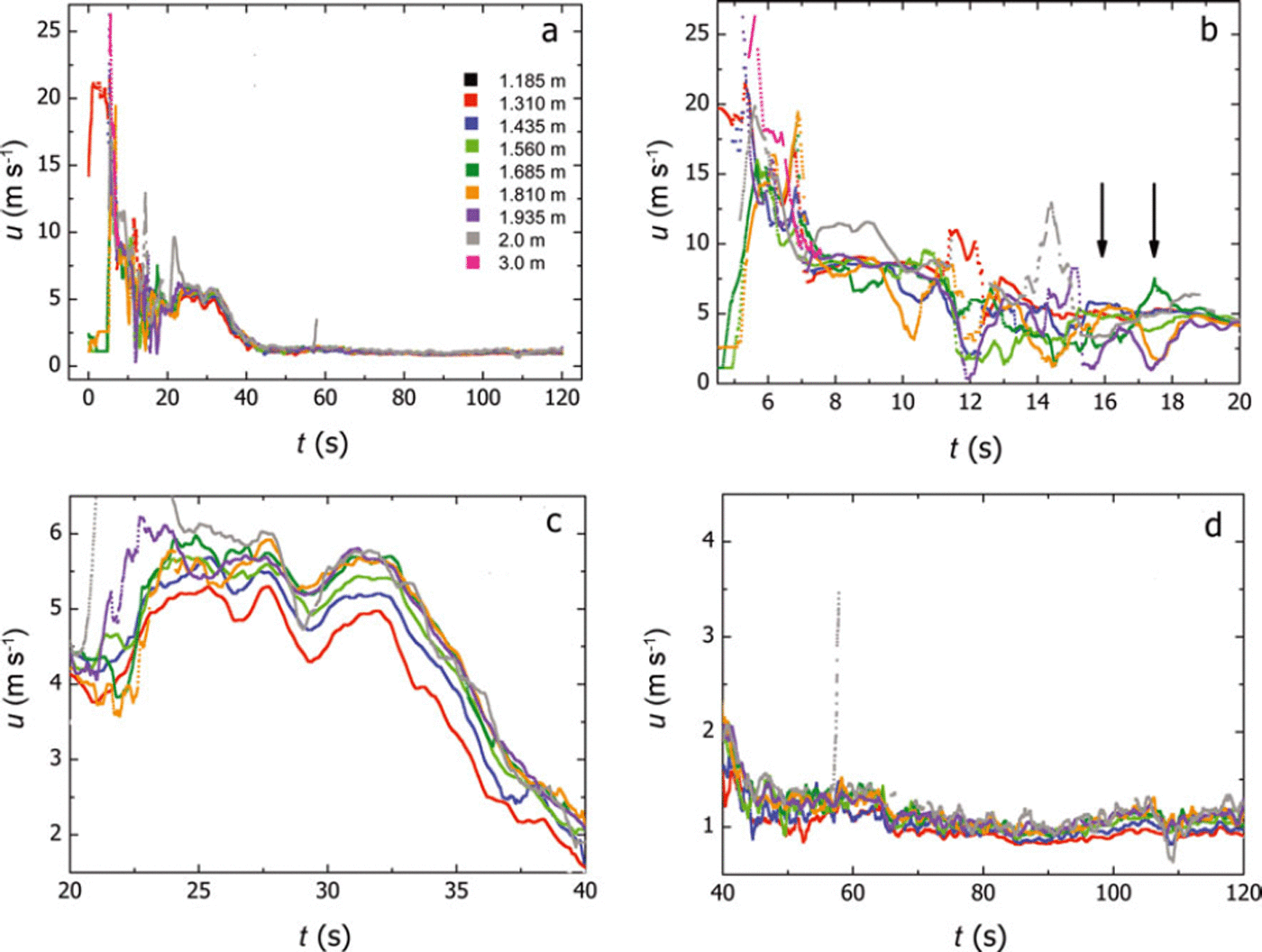
Fig. 2. Time series of velocity sensors at 1–3 m above the ground: (a) overview of total duration of the event; (b) head of the avalanche; (c) avalanche body; and (d) avalanche tail exhibiting plug-flow behaviour. Arrows in (b) indicate velocity profile inversions at the transition between head and tail.
In the time-series plots of Figure 2, we can identify five consecutive flow phases:
-
1. t < 15 s (Fig. 2b): avalanche front. After the impact of the front at t = 5.25 s, the flow rapidly decelerates. The velocities at different heights are strongly fluctuating and weakly correlated due to the dilute-flow characteristics of the front, except the comparatively smooth plateau for t ∈ [7 s, 9.5 s].
-
2. 15s ≤ 20s (Fig. 2b): transition from front to body. We observe two extended velocity profile inversions for t ∈ [15 s, 18 s], where the second is much more pronounced (see arrows in Fig. 2). At this time, the dilute-front part of the avalanche has already passed and the flow characteristics change towards a shear-flow state. In the following, we restrict ourselves to considering the latter pronounced velocity inversion.
-
3. 20s ≤ t < 33 s (Fig. 2c): avalanche body. Until t = 30s, a dense shear flow with an overriding low-shear zone (that almost exhibits plug-flow behaviour) forms and then decelerates for t > 33 s. Assuming simple steady shear flow
 and a sliding surface at z = 0.5 m above the ground, we estimate the mean shear rate
and a sliding surface at z = 0.5 m above the ground, we estimate the mean shear rate  at t = 31 s to be about 3.8 s–1. For the top low-shear layer (1.685m ≤ z ≤ 2.0m), we find
at t = 31 s to be about 3.8 s–1. For the top low-shear layer (1.685m ≤ z ≤ 2.0m), we find  . For the intermediate layer, 1.185 m < z < 1.685 m and
. For the intermediate layer, 1.185 m < z < 1.685 m and  . Finally, for 0.5 m ≤ z ≤ 1.185 m we have
. Finally, for 0.5 m ≤ z ≤ 1.185 m we have  . The shear rate decreases with height above the basal interface or sliding surface.
. The shear rate decreases with height above the basal interface or sliding surface. -
4. 33s ≤ t < 40s (Fig. 2c): transition from body to tail. Despite overall deceleration, the general shear structure with a low-shear layer overriding a high-shear layer is preserved until the flow characteristics gradually turn into plug-like behaviour for t > 35 s.
-
5. t > 40s (Fig. 2d): avalanche tail. Except for a velocity drop at t ∼ 66s, the flow moves slowly at almost constant velocity, modulated by surge-like variations. Although some shear is present, the shear rate over the entire captured flow depth hardly exceeds 0.3 s–1. We therefore conclude that the tail of the avalanche is dominated by plug-like flow behaviour in the uppermost 1 m thick layer and that the shear must be concentrated somewhere below in the 0.5 m thick basal layer.
Velocity Profile Inversions
Referring to Figure 2b, we observe velocity profile inversions (marked by arrows) close to the transition from the partly dilute avalanche head to the avalanche body. The first of the inversions is distorted; the second is rather pronounced and clear. As the velocity time series at different heights only provides a two-dimensional (2-D) cut through the avalanche flow, direct conclusions on the generating mechanism of the profile inversions cannot be drawn.
We judge that a distortion due to the mast is unlikely to be the generation mechanism. Other (i.e. later) parts of the avalanche do not show similar behaviour and we note that the profile inversion may be empirically described by a reverse eddy travelling with the mean velocity ūx of the flow. In fluid dynamics, the swirling of a fluid that occurs when two flows collide is referred to as an eddy. Accordingly, we adopt the fluid dynamics picture for our avalanche flow and propose that three-dimensional (3-D) spreading effects inside the avalanche flow are involved in this effect. Intrusion of faster neighbouring flow parts during spreading towards the sides is likely to have caused the inversions (recall that the pylon was not hit by the centre of the avalanche).
We now aim to reproduce the observed velocity profile inversion in the framework of a simplistic description for a 2-D elliptical eddy (Fig. 3). We analyse the influence of a superimposed eddy on the downstream velocity ux =u(z)êx, where x denotes the downslope flow direction and z is the direction normal to flow. The measurement mast can be considered as fixed at the origin of the x–z coordinate system. Furthermore, we denote the location of the eddy centre by r c and assume that it is travelling at a constant height z c with mean downslope velocity ūx, i.e. r c = (x c(t = 0) + ūxt, z c).
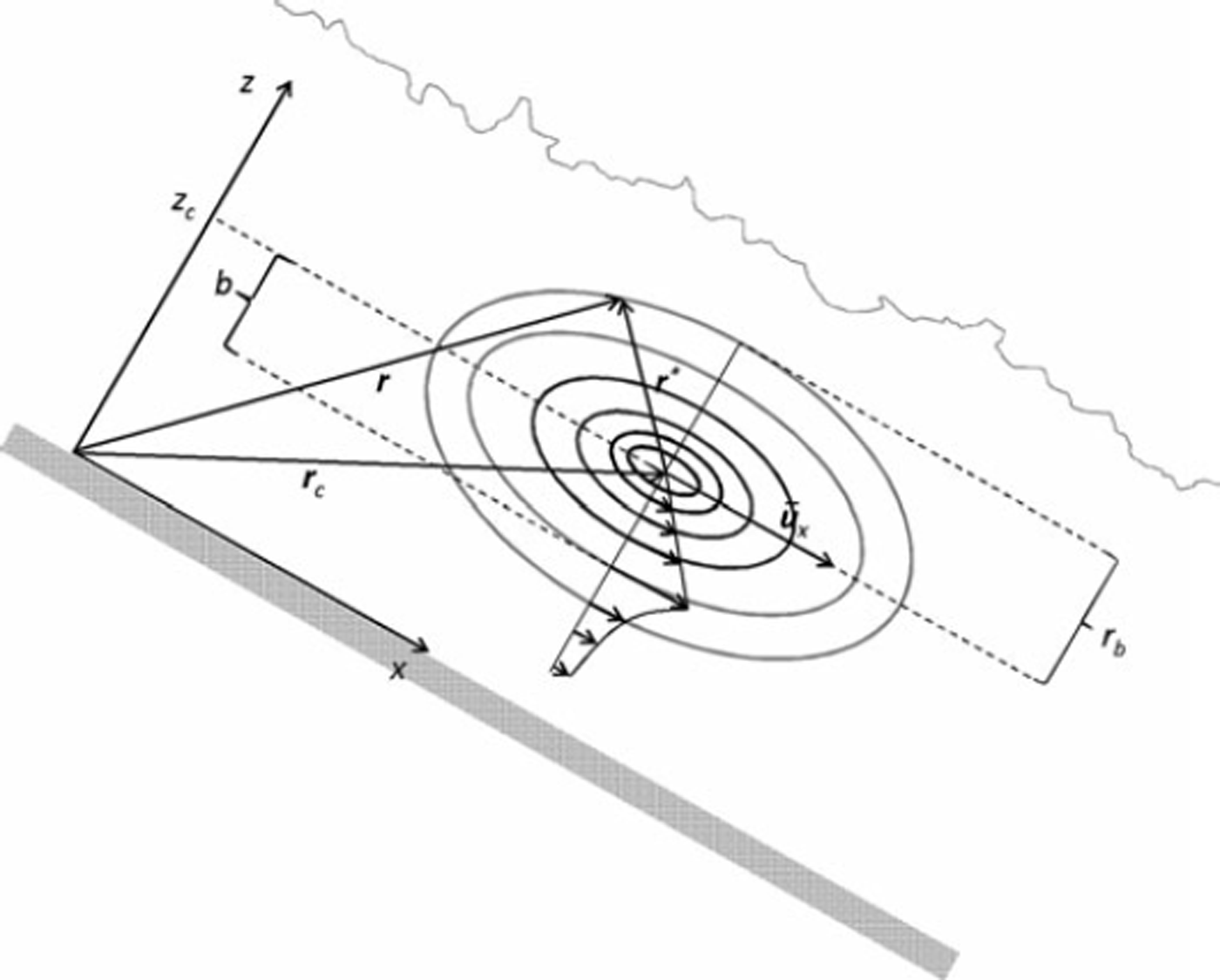
Fig. 3. Sketch of a reverse elliptical eddy travelling with the flow.
For the description of the velocity field of the eddy, we choose the eddy centre as a reference and obtain the eddy coordinates (see Fig. 3) as
We employ a simplistic velocity field for a stationary elliptical eddy centred at r c. Any point on an elliptical streamline in the eddy coordinate system can be written as
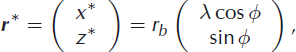
where λ is the eccentricity and rb is the small radius of the ellipse (in the z direction), related to the eddy coordinates (x*, z*) by the ellipse equation
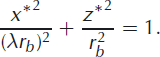
If the point moves along an ˙ elliptical streamline with a constant angular velocity co = φ, we have
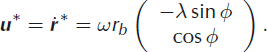
A very simple eddy velocity field can be constructed by demanding that for rb ≤ b, the velocity should linearly increase with rb and decrease as r b −1 for rb > b. We obtain
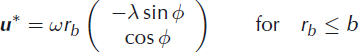
and
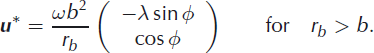
Note that this eddy is a simplistic ad hoc construction and by no means a consequence of any equations of motion. Using the definitions of r* and rc (Equation (1)), we finally have
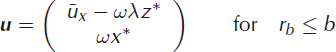
and
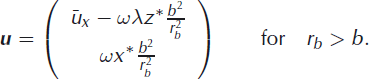
The downstream velocity ux(x*,z*) is therefore given by the x-components of Equations (3) and (4):
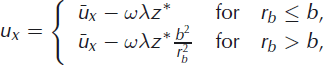
where rb = rb(x*,z*) is given by Equation (2).
We now compute the time evolution of ux(z, t) for z = 1.685 m, z = 1.81 m and z = 1.935 m. These correspond to the heights of the velocity sensors which encountered the velocity profile inversion, assuming the trajectory of the eddy centre to be ![]() with xc(t = 0) = 87.8 m upstream of the mast, zc = 1.75 m and
with xc(t = 0) = 87.8 m upstream of the mast, zc = 1.75 m and ![]() . For the eddy geometry we choose b = 0.3m and A = 4. Figure 4 shows a comparison of the measured velocity time series against the synthetic eddy velocity time series in the time interval [15 s, 18s].
. For the eddy geometry we choose b = 0.3m and A = 4. Figure 4 shows a comparison of the measured velocity time series against the synthetic eddy velocity time series in the time interval [15 s, 18s].
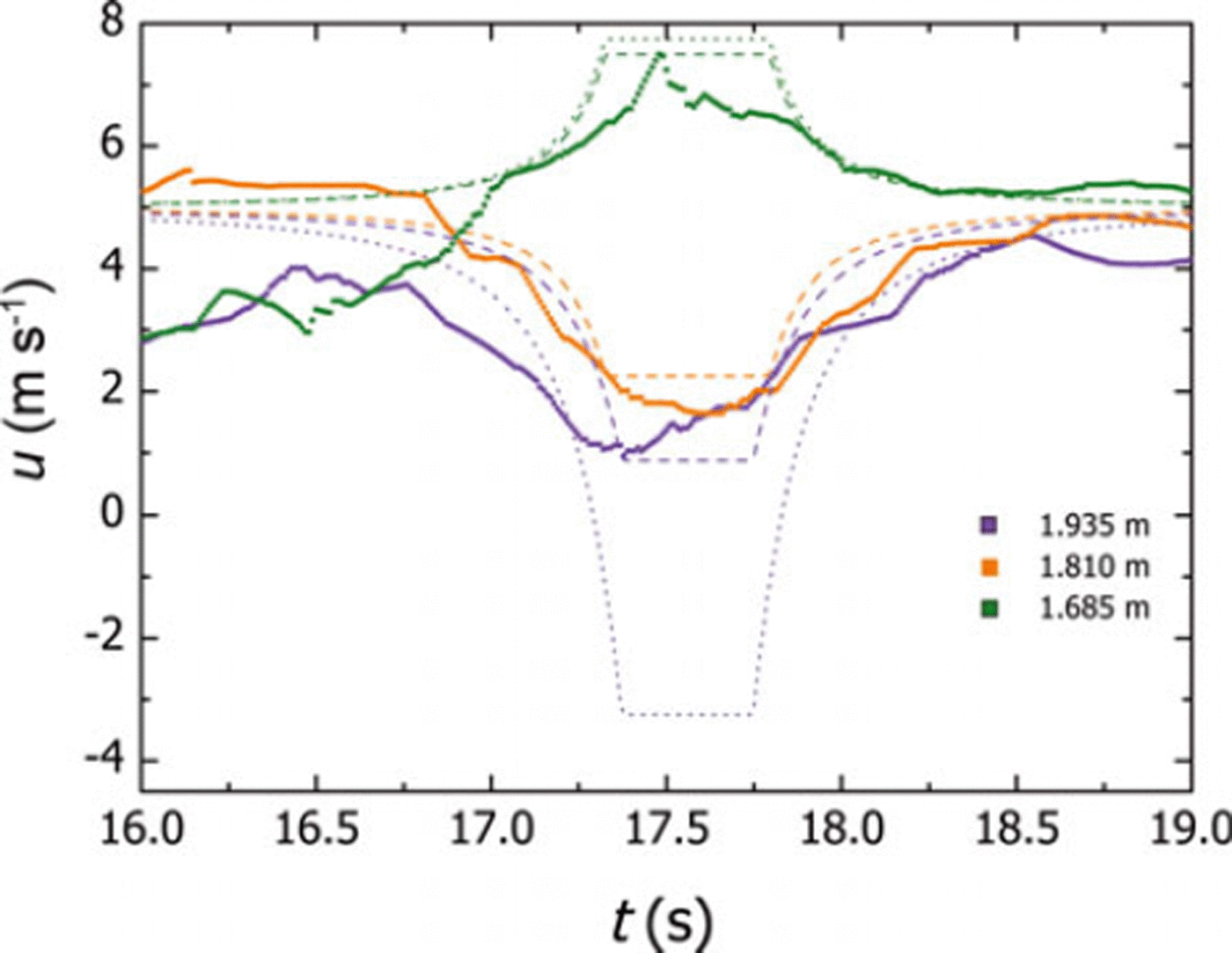
Fig. 4. Velocity profile inversions. Thick lines: measurement data; dashed lines: velocities computed with superimposed reverse eddy (![]() , zc = 1.75 m, b = 0.3 m, A = 4.0, ω(z = 1.685) = 10s–1 , ω(z = 1.81) = 13s–1 and ω(z = 1.935) = 5.5s–1); dotted lines: velocities computed with superimposed reverse eddy with uniform ω = 1 3 s–1.
, zc = 1.75 m, b = 0.3 m, A = 4.0, ω(z = 1.685) = 10s–1 , ω(z = 1.81) = 13s–1 and ω(z = 1.935) = 5.5s–1); dotted lines: velocities computed with superimposed reverse eddy with uniform ω = 1 3 s–1.
The eddy velocities match the measured velocities well (Fig. 4). Note, however, that to obtain this satisfactory matching, we had to accept angular velocities ω that vary considerably with height (note the bad matching with uniform ω indicated in Fig. 4). Note that the displayed eddy velocities are fits with respect to ω, yielding ω(z = 1.685 m) = 10s–1 , ω(z = 1.81 m) = 13s–1 and ω(z = 1.935 m) = 5.5 s–1. This is certainly due to the fact that our simplistic empirical eddy picture does not capture the full complexity of the real flow structure. Technically speaking, there is a structural error in the simplistic model (Reference RougierRougier, 2007). It is therefore important to state that the interpretation in terms of an eddy is not meant as the construction of a model, but rather an illustration of what might be taking place.
Discussion
As the time evolution of (regular) shear profiles in the VdlS avalanches has been extensively discussed elsewhere (Reference Bartelt and BuserBartelt and Buser, 2009; Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009), we confine ourselves to a few general remarks on the orders of magnitude of the observed shear rates. We also give a tentative interpretation of the observed velocity profile inversion.
At the ‘revolving door’ area of small avalanches, Reference Dent, Burrell, Schmidt, Louge, Adams and JazbutisDent and others (1998) observed a narrow (i.e. ∼1cm thick) high-shear layer ![]() underneath a low-shear layer. As these avalanches were small, they are comparable to the chute-flow experiments performed by Reference Tiefenbacher and KernTiefenbacher and Kern (2004) that resulted in a similar shear structure. In our real-scale avalanche, the basal interface/sliding surface was not captured. We therefore have no experimental evidence that would allow direct comparison to the ‘revolving door’ experiments with respect to the existence of a narrow high-shear layer (see also Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009).
underneath a low-shear layer. As these avalanches were small, they are comparable to the chute-flow experiments performed by Reference Tiefenbacher and KernTiefenbacher and Kern (2004) that resulted in a similar shear structure. In our real-scale avalanche, the basal interface/sliding surface was not captured. We therefore have no experimental evidence that would allow direct comparison to the ‘revolving door’ experiments with respect to the existence of a narrow high-shear layer (see also Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009).
The VdlS avalanche reported here has a considerably larger flow height (about 2 m) where the shear zone is extended over 0.5 m. These orders of magnitude are comparable to those of an avalanche measured at the Ryggfon site in Norway by Reference Nishimura, Maeno, Sandersen, Kristensen, Norem and LiedNishimura and others (1993), who estimated the shear rate to be ![]() . Note that, for their estimate, Reference Nishimura, Maeno, Sandersen, Kristensen, Norem and LiedNishimura and others (1993) used two optical velocity sensors with 1 m vertical spacing, which does not allow statements on the shear profile. However, the obtained estimate of the overall shear rate is compatible with the shear rates of the avalanche considered here and of other avalanches measured at the VdlS site (Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009).
. Note that, for their estimate, Reference Nishimura, Maeno, Sandersen, Kristensen, Norem and LiedNishimura and others (1993) used two optical velocity sensors with 1 m vertical spacing, which does not allow statements on the shear profile. However, the obtained estimate of the overall shear rate is compatible with the shear rates of the avalanche considered here and of other avalanches measured at the VdlS site (Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009).
The key feature of the VdlS avalanche recorded with the new high-resolution set-up is the occurence of velocity profile inversions. Note that the inversion extends to about 0.25 m in height; this is less than the spatial resolution of 0.4 m of the old optical velocity measurement set-up, before the spatial resolution at the mast was refined to 0.125 m.
Recent experimental observations on scaled dilute avalanche flows (Reference KoeglKoegl, 2009) indicate that velocity profile inversions are a characteristic feature of the dilute front part of avalanches. These observations are consistent with theoretical considerations modelling the dilute avalanche front in terms of a rotational gravity flow (Reference McElwaineMcElwaine, 2005). Our observations, however, refer to the dense flow part of the avalanche well behind the front. Note that in dilute flow, accurate measurements such as those presented are not possible for technical reasons (Reference Kern, Bartelt, Sovilla and BuserKern and others, 2009). Furthermore, the small scale of the locally observed inversion rules out generic behaviour of rotational gravity flow as a possible source – the inversion would have to extend over the scale of the avalanche front.
It is therefore unlikely that the observed velocity inversions represent typical behaviour of the dilute avalanche front. The generation mechanism of the effect remains unclear: to date, direct experimental observation of the 3-D flow behaviour is lacking. As indicated above, we can only speculate that the velocity inversion might be caused by 3-D spreading effects such as faster flow parts laterally intruding into slower flow layers that are more distant from the flow centre line. This tentative explanation is motivated by the fact that the velocities were recorded at the mast location that was laterally displaced from the centre line of the flow.
Conclusions
The avalanche event of 26 March 2008 allowed high-resolution velocity profiles over all parts of the avalanche to be collected. In terms of absence of disjoint structures and electronic distortion, the data quality achieved with the new velocity measurement and data acquisition set-up has not been reached before. The dataset allows detailed spatial analysis of the flow structure. At the transition from the avalanche front to the avalanche body, the flow exhibits profile inversions that can be modelled by reverse 2-D eddies travelling with the flow. The avalanche shows a typical shear structure also observed in earlier measurements. However, the profile inversions are a feature that is only visible with the new set-up with refined spatial resolution.
We suggest that these inversions are produced by 3-D flow structures due to lateral spreading effects. Velocity profile inversions are also present at the front of rotational gravity currents. As the presented small-scale velocity inversions were observed well behind the front where the dilute, gravity-current-like part of the flow had already passed, this explanation is unlikely. However, the interpretation of the eddies as a secondary effect of lateral spreading is also a speculation which cannot yet be directly supported by experimental evidence; this is consequently open to discussion. Envisioned high-resolution radar measurements of the 3-D velocity field in the dilute flow part might help to identify gravity flow features near the avalanche front and to provide additional evidence to distinguish them from the dense-flow features reported in this contribution.
Acknowledgements
This work was partly funded by a R’Equip grant of the Swiss National Science Foundation. We thank M. Hiller and the staff of Mettler & Fuchs for designing and setting up the new data acquisition system, F. Dufour for organizing the field test, C. Wuilloud and the Canton Valais for generous financial support. Many thanks are due to all colleagues who participated in the field campaign.






