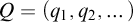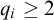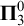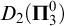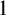1 Introduction
1.1 Review of definability notions
In any topological space X, the collection of Borel sets
![]() $\mathcal {B}(X)$
is the smallest
$\mathcal {B}(X)$
is the smallest
![]() $\sigma $
-algebra containing the open sets. They are stratified into levels, the Borel hierarchy, by defining
$\sigma $
-algebra containing the open sets. They are stratified into levels, the Borel hierarchy, by defining
![]() $\boldsymbol {\Sigma }^0_1=$
the open sets,
$\boldsymbol {\Sigma }^0_1=$
the open sets,
![]() $\boldsymbol {\Pi }^0_1= \neg \boldsymbol {\Sigma }^0_1= \{ X-A\colon A \in \boldsymbol {\Sigma }^0_1\}=$
the closed sets, and for
$\boldsymbol {\Pi }^0_1= \neg \boldsymbol {\Sigma }^0_1= \{ X-A\colon A \in \boldsymbol {\Sigma }^0_1\}=$
the closed sets, and for
![]() $\alpha <\omega _1$
we let
$\alpha <\omega _1$
we let
![]() $\boldsymbol {\Sigma }^0_\alpha $
be the collection of countable unions
$\boldsymbol {\Sigma }^0_\alpha $
be the collection of countable unions
![]() $A=\bigcup _n A_n$
where each
$A=\bigcup _n A_n$
where each
![]() $A_n \in \boldsymbol {\Pi }^0_{\alpha _n}$
for some
$A_n \in \boldsymbol {\Pi }^0_{\alpha _n}$
for some
![]() $\alpha _n<\alpha $
. We also let
$\alpha _n<\alpha $
. We also let
![]() $\boldsymbol {\Pi }^0_\alpha =\neg \boldsymbol {\Sigma }^0_\alpha $
. Alternatively,
$\boldsymbol {\Pi }^0_\alpha =\neg \boldsymbol {\Sigma }^0_\alpha $
. Alternatively,
![]() $A\in \boldsymbol {\Pi }^0_\alpha $
if
$A\in \boldsymbol {\Pi }^0_\alpha $
if
![]() $A=\bigcap _n A_n$
where
$A=\bigcap _n A_n$
where
![]() $A_n\in \boldsymbol {\Sigma }^0_{\alpha _n}$
where each
$A_n\in \boldsymbol {\Sigma }^0_{\alpha _n}$
where each
![]() $\alpha _n<\alpha $
. We also set
$\alpha _n<\alpha $
. We also set
![]() $\boldsymbol {\Delta }^0_\alpha = \boldsymbol {\Sigma }^0_\alpha \cap \boldsymbol {\Pi }^0_\alpha $
, in particular
$\boldsymbol {\Delta }^0_\alpha = \boldsymbol {\Sigma }^0_\alpha \cap \boldsymbol {\Pi }^0_\alpha $
, in particular
![]() $\boldsymbol {\Delta }^0_1$
is the collection of clopen sets. For any topological space,
$\boldsymbol {\Delta }^0_1$
is the collection of clopen sets. For any topological space,
![]() $\mathcal {B}(X)=\bigcup _{\alpha <\omega _1} \boldsymbol {\Sigma }^0_\alpha = \bigcup _{\alpha <\omega _1}\boldsymbol {\Pi }^0_\alpha $
. All of the collections
$\mathcal {B}(X)=\bigcup _{\alpha <\omega _1} \boldsymbol {\Sigma }^0_\alpha = \bigcup _{\alpha <\omega _1}\boldsymbol {\Pi }^0_\alpha $
. All of the collections
![]() $\boldsymbol {\Delta }^0_\alpha $
,
$\boldsymbol {\Delta }^0_\alpha $
,
![]() $\boldsymbol {\Sigma }^0_\alpha $
,
$\boldsymbol {\Sigma }^0_\alpha $
,
![]() $\boldsymbol {\Pi }^0_\alpha $
are pointclasses, that is, they are closed under inverse images of continuous functions. A basic fact (see [Reference Kechris12]) is that for any uncountable Polish space X, there is no collapse in the levels of the Borel hierarchy, that is, all the various pointclasses
$\boldsymbol {\Pi }^0_\alpha $
are pointclasses, that is, they are closed under inverse images of continuous functions. A basic fact (see [Reference Kechris12]) is that for any uncountable Polish space X, there is no collapse in the levels of the Borel hierarchy, that is, all the various pointclasses
![]() $\boldsymbol {\Delta }^0_\alpha $
,
$\boldsymbol {\Delta }^0_\alpha $
,
![]() $\boldsymbol {\Sigma }^0_\alpha $
,
$\boldsymbol {\Sigma }^0_\alpha $
,
![]() $\boldsymbol {\Pi }^0_\alpha $
, for
$\boldsymbol {\Pi }^0_\alpha $
, for
![]() $\alpha <\omega _1$
, are all distinct. Thus, these levels of the Borel hierarchy can be used to calibrate the descriptive complexity of a set. We say a set
$\alpha <\omega _1$
, are all distinct. Thus, these levels of the Borel hierarchy can be used to calibrate the descriptive complexity of a set. We say a set
![]() $A\subseteq X$
is
$A\subseteq X$
is
![]() $\boldsymbol {\Sigma }^0_\alpha $
(resp.
$\boldsymbol {\Sigma }^0_\alpha $
(resp.
![]() $\boldsymbol {\Pi }^0_\alpha $
) hard if
$\boldsymbol {\Pi }^0_\alpha $
) hard if
![]() $A \notin \boldsymbol {\Pi }^0_\alpha $
(resp.
$A \notin \boldsymbol {\Pi }^0_\alpha $
(resp.
![]() $A\notin \boldsymbol {\Sigma }^0_\alpha $
). This says A is “no simpler” than a
$A\notin \boldsymbol {\Sigma }^0_\alpha $
). This says A is “no simpler” than a
![]() $\boldsymbol {\Sigma }^0_\alpha $
set. We say A is
$\boldsymbol {\Sigma }^0_\alpha $
set. We say A is
![]() $\boldsymbol {\Sigma }^0_\alpha $
-complete if
$\boldsymbol {\Sigma }^0_\alpha $
-complete if
![]() $A\in \boldsymbol {\Sigma }^0_\alpha \setminus \boldsymbol {\Pi }^0_\alpha $
, that is,
$A\in \boldsymbol {\Sigma }^0_\alpha \setminus \boldsymbol {\Pi }^0_\alpha $
, that is,
![]() $A \in \boldsymbol {\Sigma }^0_\alpha $
and A is
$A \in \boldsymbol {\Sigma }^0_\alpha $
and A is
![]() $\boldsymbol {\Sigma }^0_\alpha $
hard. This says A is exactly at the complexity level
$\boldsymbol {\Sigma }^0_\alpha $
hard. This says A is exactly at the complexity level
![]() $\boldsymbol {\Sigma }^0_\alpha $
. Likewise, A is
$\boldsymbol {\Sigma }^0_\alpha $
. Likewise, A is
![]() $\boldsymbol {\Pi }^0_\alpha $
-complete if
$\boldsymbol {\Pi }^0_\alpha $
-complete if
![]() $A\in \boldsymbol {\Pi }^0_\alpha \setminus \boldsymbol {\Sigma }^0_\alpha $
.
$A\in \boldsymbol {\Pi }^0_\alpha \setminus \boldsymbol {\Sigma }^0_\alpha $
.
A set
![]() $D\subseteq X$
is in the class
$D\subseteq X$
is in the class
![]() $D_2(\boldsymbol {\Pi }^0_3)$
if
$D_2(\boldsymbol {\Pi }^0_3)$
if
![]() $D=A\setminus B$
where
$D=A\setminus B$
where
![]() $A, B\in \boldsymbol {\Pi }^0_3$
. A set D is
$A, B\in \boldsymbol {\Pi }^0_3$
. A set D is
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-hard if
$D_2(\boldsymbol {\Pi }^0_3)$
-hard if
![]() $X\setminus D \notin D_2(\boldsymbol {\Pi }^0_3)$
, and D is
$X\setminus D \notin D_2(\boldsymbol {\Pi }^0_3)$
, and D is
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-complete if it is in
$D_2(\boldsymbol {\Pi }^0_3)$
-complete if it is in
![]() $D_2(\boldsymbol {\Pi }^0_3)$
and is
$D_2(\boldsymbol {\Pi }^0_3)$
and is
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-hard. As with the classes
$D_2(\boldsymbol {\Pi }^0_3)$
-hard. As with the classes
![]() $\boldsymbol {\Sigma }^0_\alpha $
,
$\boldsymbol {\Sigma }^0_\alpha $
,
![]() $\boldsymbol {\Pi }^0_\alpha $
, the class
$\boldsymbol {\Pi }^0_\alpha $
, the class
![]() $D_2(\boldsymbol {\Pi }^0_3)$
has a universal set and so is non-selfdual, that is, it is not closed under complements (we will define a particular complete set for
$D_2(\boldsymbol {\Pi }^0_3)$
has a universal set and so is non-selfdual, that is, it is not closed under complements (we will define a particular complete set for
![]() $D_2(\boldsymbol {\Pi }^0_3)$
in Section 3.2).
$D_2(\boldsymbol {\Pi }^0_3)$
in Section 3.2).
Ki and Linton [Reference Ki and Linton13] proved that the set
![]() $\mathcal {N}(b)$
of base-b normal numbers (Definition 1.1 below) is
$\mathcal {N}(b)$
of base-b normal numbers (Definition 1.1 below) is
![]() $\boldsymbol {\Pi }^0_3(\mathbb {R})$
-complete. Further work was done by Becher, Heiber, and Slaman [Reference Becher, Heiber and Slaman5] who settled a conjecture of Kechris by showing that the set of absolutely normal numbers is
$\boldsymbol {\Pi }^0_3(\mathbb {R})$
-complete. Further work was done by Becher, Heiber, and Slaman [Reference Becher, Heiber and Slaman5] who settled a conjecture of Kechris by showing that the set of absolutely normal numbers is
![]() $\boldsymbol {\Pi }^0_3(\mathbb {R})$
-complete. Furthermore, Becher and Slaman [Reference Becher and Slaman6] proved that the set of numbers normal in at least one base is
$\boldsymbol {\Pi }^0_3(\mathbb {R})$
-complete. Furthermore, Becher and Slaman [Reference Becher and Slaman6] proved that the set of numbers normal in at least one base is
![]() $\boldsymbol {\Sigma }^0_4(\mathbb {R})$
-complete. In another direction, Airey et al. [Reference Airey, Jackson, Kwietniak and Mance1, Reference Airey, Jackson, Kwietniak and Mance2] showed that for any dynamical system with a weak form of the specification property, the set of generic points for the system is
$\boldsymbol {\Sigma }^0_4(\mathbb {R})$
-complete. In another direction, Airey et al. [Reference Airey, Jackson, Kwietniak and Mance1, Reference Airey, Jackson, Kwietniak and Mance2] showed that for any dynamical system with a weak form of the specification property, the set of generic points for the system is
![]() $\boldsymbol {\Pi }^0_3$
-complete. This result generalizes the Ki–Linton result to many numeration systems other than the standard base b one.
$\boldsymbol {\Pi }^0_3$
-complete. This result generalizes the Ki–Linton result to many numeration systems other than the standard base b one.
1.2 Normal numbers
We recall the definition of a normal number.
Definition 1.1. A real number x is normal of order k in base b if all blocks of digits of length k in base b occur with relative frequency
![]() $b^{-k}$
in the b-ary expansion of x. We denote this set by
$b^{-k}$
in the b-ary expansion of x. We denote this set by
![]() $\mathscr {N}_{k}( b )$
. Moreover, x is normal in base b if it is normal of order k in base b for all natural numbers k. We denote the set of normal numbers in base b by
$\mathscr {N}_{k}( b )$
. Moreover, x is normal in base b if it is normal of order k in base b for all natural numbers k. We denote the set of normal numbers in base b by
We also wish to mention one of the most fundamental and important results relating to normal numbers in base b. The following is due to Wall in his Ph.D. dissertation [Reference Wall23].
Theorem 1.2 (Wall).
A real number x is normal in base b if and only if the sequence
![]() $(b^nx)$
is uniformly distributed mod
$(b^nx)$
is uniformly distributed mod
![]() $1$
.
$1$
.
While it is not difficult to prove Theorem 1.2, its importance in the theory of normal numbers cannot be understated. Large portions of the theory of normal numbers in base b make use of Theorem 1.2. We provide an example of a theorem that provides motivation for the main problem studied in this paper.
Theorem 1.3 (Wall).
Footnote
1
For all rational numbers
![]() $q$
(for the second inclusion we assume also
$q$
(for the second inclusion we assume also
![]() $q \neq 0$
) and integers
$q \neq 0$
) and integers
![]() $b \geq 2$
, we have
$b \geq 2$
, we have
 $$ \begin{align*} q+\mathscr{N}(b) &\subseteq \mathscr{N}(b);\\ q\mathscr{N}(b) &\subseteq \mathscr{N}(b). \end{align*} $$
$$ \begin{align*} q+\mathscr{N}(b) &\subseteq \mathscr{N}(b);\\ q\mathscr{N}(b) &\subseteq \mathscr{N}(b). \end{align*} $$
That is, normality in base b is preserved by rational addition and multiplication.
Moreover, Theorem 1.2 suggests a dynamical interpretation of normality which allows the definition of normality to be extended to other expansions such as the regular continued fraction expansion, the Lüroth series expansion, and the
![]() $\beta $
-expansions. See [Reference Dajani and Kraaikamp8] for a basic treatment and introduction to this idea.
$\beta $
-expansions. See [Reference Dajani and Kraaikamp8] for a basic treatment and introduction to this idea.
In this paper, we are interested in a class of expansions known as the Q-Cantor series expansions that includes the b-ary expansions as a special case, but do not admit an extension of Theorem 1.2. The study of normal numbers and other statistical properties of real numbers with respect to large classes of Cantor series expansions was first done by Erdős and Rényi in [Reference Erdős and Rényi9, Reference Erdős and Rényi10], by Rényi in [Reference Rényi18–Reference Rényi20], and by Turán in [Reference Šalát22].
The Q-Cantor series expansions, first studied by Cantor in [Reference Cantor7], are a natural generalization of the b-ary expansions. Cantor’s motivation to study the Cantor series expansions was to extend the well-known proof of the irrationality of the number
![]() $e=\sum 1/n!$
to a larger class of numbers. Results along these lines may be found in the monograph of Galambos [Reference Galambos11]. If
$e=\sum 1/n!$
to a larger class of numbers. Results along these lines may be found in the monograph of Galambos [Reference Galambos11]. If
![]() $Q=(q_i)_{i=1}^{\infty }$
is a sequence of integers with each
$Q=(q_i)_{i=1}^{\infty }$
is a sequence of integers with each
![]() $q_i\geq 2$
, then we say that Q is a basic sequence. Given a basic sequence
$q_i\geq 2$
, then we say that Q is a basic sequence. Given a basic sequence
![]() $Q=(q_i)_{i=1}^{\infty }$
, the Q-Cantor series expansion of a real number x is the (unique)Footnote
2
expansion of the form
$Q=(q_i)_{i=1}^{\infty }$
, the Q-Cantor series expansion of a real number x is the (unique)Footnote
2
expansion of the form
 $$ \begin{align} x=a_0+\sum_{i=1}^{\infty} \frac {a_i} {q_1 q_2 \cdots q_i}, \end{align} $$
$$ \begin{align} x=a_0+\sum_{i=1}^{\infty} \frac {a_i} {q_1 q_2 \cdots q_i}, \end{align} $$
where
![]() $a_0=\left \lfloor x \right \rfloor $
and
$a_0=\left \lfloor x \right \rfloor $
and
![]() $a_i$
is in
$a_i$
is in
![]() $\{0,1,\ldots ,q_i-1\}$
for
$\{0,1,\ldots ,q_i-1\}$
for
![]() $i\geq 1$
with
$i\geq 1$
with
![]() $a_i \neq q_i-1$
infinitely often. We abbreviate (1) with the notation
$a_i \neq q_i-1$
infinitely often. We abbreviate (1) with the notation
![]() $x=a_0.a_1a_2a_3\ldots $
w.r.t. Q. If
$x=a_0.a_1a_2a_3\ldots $
w.r.t. Q. If
![]() $I=[i,j]$
is an interval in
$I=[i,j]$
is an interval in
![]() $\mathbb {N}$
and the basic sequence Q is understood, we let, with a slight abuse of notation,
$\mathbb {N}$
and the basic sequence Q is understood, we let, with a slight abuse of notation,
![]() $x \restriction I$
denote the sequence of digits
$x \restriction I$
denote the sequence of digits
![]() $a_i,\dots , a_j$
.
$a_i,\dots , a_j$
.
For a basic sequence
![]() $Q=(q_i)$
, a block
$Q=(q_i)$
, a block
![]() $B=(e_1, e_2, \ldots , e_k)\in \omega ^{<\omega }$
, and a natural number j, define
$B=(e_1, e_2, \ldots , e_k)\in \omega ^{<\omega }$
, and a natural number j, define
 $$ \begin{align*}\mathcal{I}_{Q,j}(B) = \begin{cases} 1 &\text{ if } e_1 < q_j, e_2 < q_{j+1}, \ldots, e_k < q_{j+k-1}, \\ 0 &\text{ otherwise}, \end{cases} \end{align*} $$
$$ \begin{align*}\mathcal{I}_{Q,j}(B) = \begin{cases} 1 &\text{ if } e_1 < q_j, e_2 < q_{j+1}, \ldots, e_k < q_{j+k-1}, \\ 0 &\text{ otherwise}, \end{cases} \end{align*} $$
and let
 $$ \begin{align} Q_n(B)=\sum_{j=1}^n \frac {\mathcal{I}_{Q,j}(B)} {q_j q_{j+1} \cdots q_{j+k-1}}. \end{align} $$
$$ \begin{align} Q_n(B)=\sum_{j=1}^n \frac {\mathcal{I}_{Q,j}(B)} {q_j q_{j+1} \cdots q_{j+k-1}}. \end{align} $$
Let
 $$ \begin{align*}Q_n^{(k)}:=\sum_{j=1}^n \frac {1} {q_j q_{j+1} \cdots q_{j+k-1}} \mbox{ and } T_{Q,n}(x):=\left(\prod_{j=1}^n q_j\right) x \bmod{1}. \end{align*} $$
$$ \begin{align*}Q_n^{(k)}:=\sum_{j=1}^n \frac {1} {q_j q_{j+1} \cdots q_{j+k-1}} \mbox{ and } T_{Q,n}(x):=\left(\prod_{j=1}^n q_j\right) x \bmod{1}. \end{align*} $$
![]() $Q_n(B)$
gives the expected number of occurrences of the block B in the Cantor series expansion of x with a starting position in
$Q_n(B)$
gives the expected number of occurrences of the block B in the Cantor series expansion of x with a starting position in
![]() $[1,n]$
. We say B has infinite expectation if
$[1,n]$
. We say B has infinite expectation if
![]() $\lim _{n \to \infty } Q_n(B)=\infty $
.
$\lim _{n \to \infty } Q_n(B)=\infty $
.
![]() $Q_n^{(k)}$
is the expected number of occurrences of
$Q_n^{(k)}$
is the expected number of occurrences of
![]() $0_k$
(the length k block of
$0_k$
(the length k block of
![]() $0$
s) with a start in
$0$
s) with a start in
![]() $[1,n]$
(which is also the expected number of occurrences of
$[1,n]$
(which is also the expected number of occurrences of
![]() $1_k$
). We also let
$1_k$
). We also let
![]() $Q_{m,n}(B)=\sum _{j=m}^n \frac {\mathcal {I}_{Q,j}(B)} {q_j q_{j+1} \cdots q_{j+k-1}}$
, which is expected number of occurrences of B with a start in
$Q_{m,n}(B)=\sum _{j=m}^n \frac {\mathcal {I}_{Q,j}(B)} {q_j q_{j+1} \cdots q_{j+k-1}}$
, which is expected number of occurrences of B with a start in
![]() $[m,n]$
.
$[m,n]$
.
A basic sequence Q is k-divergent if
![]() $\lim _{n \rightarrow \infty } Q_n^{(k)}=\infty $
, fully divergent if Q is k-divergent for all k, and k-convergent if it is not k-divergent. A basic sequence Q is infinite in limit if
$\lim _{n \rightarrow \infty } Q_n^{(k)}=\infty $
, fully divergent if Q is k-divergent for all k, and k-convergent if it is not k-divergent. A basic sequence Q is infinite in limit if
![]() $q_i \rightarrow \infty $
.
$q_i \rightarrow \infty $
.
For a block
![]() $B=(e_1,\dots ,e_k)$
as above we let
$B=(e_1,\dots ,e_k)$
as above we let
![]() $|B|=k$
denote the length of B, and let
$|B|=k$
denote the length of B, and let
![]() $\| B\|=(e_1+1)+\cdots +(e_k+1)$
. For
$\| B\|=(e_1+1)+\cdots +(e_k+1)$
. For
![]() $1 \leq t \leq k$
we let
$1 \leq t \leq k$
we let
![]() $B(t)=e_t$
denote the tth element of the block B.
$B(t)=e_t$
denote the tth element of the block B.
For x a real with Q-Cantor series expansion
![]() $a_0.a_1a_2\cdots $
, we let
$a_0.a_1a_2\cdots $
, we let
![]() $N^Q_n(B,x)$
be the number of i with
$N^Q_n(B,x)$
be the number of i with
![]() $1\leq i \leq n$
such that
$1\leq i \leq n$
such that
![]() $x\restriction [i, i+|B|-1]=B$
. We let
$x\restriction [i, i+|B|-1]=B$
. We let
![]() $N^Q_{m,n}(B,x)$
be the number of
$N^Q_{m,n}(B,x)$
be the number of
![]() $i \in [m, n]$
with
$i \in [m, n]$
with
![]() $x\restriction [i,i+|B|-1]=B$
. This counts the number of occurrences of the block B with a start in the interval
$x\restriction [i,i+|B|-1]=B$
. This counts the number of occurrences of the block B with a start in the interval
![]() $[m,n]$
.
$[m,n]$
.
Motivated by Theorem 1.2, we make the following definitions of normality for Cantor series expansions.
Definition 1.4. A real number x is Q-normal of order k if for all blocks B of length k such that
![]() $\lim _{n \to \infty } Q_n(B) = \infty $
,
$\lim _{n \to \infty } Q_n(B) = \infty $
,
 $$ \begin{align} \lim_{n \rightarrow \infty} \frac {N_n^Q (B,x)} {Q_n(B)}=1. \end{align} $$
$$ \begin{align} \lim_{n \rightarrow \infty} \frac {N_n^Q (B,x)} {Q_n(B)}=1. \end{align} $$
We let
![]() $\mathscr {N}_{k}( Q )$
be the set of numbers that are Q-normal of order k. The real number x is Q-normal if
$\mathscr {N}_{k}( Q )$
be the set of numbers that are Q-normal of order k. The real number x is Q-normal if
![]() $x \in \mathscr {N}(Q) := \bigcap _{k=1}^{\infty } \mathscr {N}_{k}( Q ).$
$x \in \mathscr {N}(Q) := \bigcap _{k=1}^{\infty } \mathscr {N}_{k}( Q ).$
Definition 1.5. A real number x is Q-ratio normal of order k (here we write
![]() $x \in \mathscr {RN}_{k}( Q )$
) if for all blocks
$x \in \mathscr {RN}_{k}( Q )$
) if for all blocks
![]() $B_1$
and
$B_1$
and
![]() $B_2$
of length k such that
$B_2$
of length k such that
![]() $\lim _{n \to \infty } \min (Q_n(B_1),Q_n(B_2)) = \infty $
, we have
$\lim _{n \to \infty } \min (Q_n(B_1),Q_n(B_2)) = \infty $
, we have
 $$ \begin{align} \lim_{n \to \infty} \frac {N_n^Q (B_1,x)/Q_n(B_1)} {N_n^Q (B_2,x)/Q_n(B_2)}=1. \end{align} $$
$$ \begin{align} \lim_{n \to \infty} \frac {N_n^Q (B_1,x)/Q_n(B_1)} {N_n^Q (B_2,x)/Q_n(B_2)}=1. \end{align} $$
We say that x is Q-ratio normal if
![]() $x \in \mathscr {RN}(Q) := \bigcap _{k=1}^{\infty } \mathscr {RN}_{k}( Q ).$
$x \in \mathscr {RN}(Q) := \bigcap _{k=1}^{\infty } \mathscr {RN}_{k}( Q ).$
Definition 1.6. A real number x is Q-distribution normal if the sequence
![]() $(T_{Q,n}(x))_{n=0}^\infty $
is uniformly distributed mod
$(T_{Q,n}(x))_{n=0}^\infty $
is uniformly distributed mod
![]() $1$
. Let
$1$
. Let
![]() $\mathscr {DN}(Q)$
be the set of Q-distribution normal numbers.
$\mathscr {DN}(Q)$
be the set of Q-distribution normal numbers.
We note that by Theorem 1.2, the analogous versions of the above definitions are equivalent for the b-ary expansions. The situation is far more interesting in the case that Q is infinite in limit and fully divergent.
It was proved in [Reference Mance16] that the directed graph in Figure 1 gives the complete containment relationships between these notions when Q is infinite in limit and fully divergent. The vertices are labeled with all possible intersections of one, two, or three choices of the sets
![]() $\mathscr {N}(Q)$
,
$\mathscr {N}(Q)$
,
![]() $\mathscr {RN}(Q)$
, and
$\mathscr {RN}(Q)$
, and
![]() $\mathscr {DN}(Q)$
, where we know that
$\mathscr {DN}(Q)$
, where we know that
![]() $\mathscr {N}(Q)=\mathscr {N}(Q) \cap \mathscr {RN}(Q)$
and
$\mathscr {N}(Q)=\mathscr {N}(Q) \cap \mathscr {RN}(Q)$
and
![]() $\mathscr {N}(Q) \cap \mathscr {DN}(Q)=\mathscr {N}(Q) \cap \mathscr {DN}(Q) \cap \mathscr {RN}(Q)$
. The set labeled on vertex A is a subset of the set labeled on vertex B if and only if there is a directed path from A to B. For example,
$\mathscr {N}(Q) \cap \mathscr {DN}(Q)=\mathscr {N}(Q) \cap \mathscr {DN}(Q) \cap \mathscr {RN}(Q)$
. The set labeled on vertex A is a subset of the set labeled on vertex B if and only if there is a directed path from A to B. For example,
![]() $\mathscr {N}(Q) \cap \mathscr {DN}(Q) \subseteq \mathscr {RN}(Q)$
, so all numbers that are Q-normal and Q-distribution normal are also Q-ratio normal.
$\mathscr {N}(Q) \cap \mathscr {DN}(Q) \subseteq \mathscr {RN}(Q)$
, so all numbers that are Q-normal and Q-distribution normal are also Q-ratio normal.

Figure 1 Relations between the different notions of normality.
We remark that all inclusions suggested from Figure 1 are either easily proved (
![]() $\mathscr {N}(Q) \subseteq \mathscr {RN}(Q)$
) or are trivial. The difficulty comes in showing a lack of inclusion. The most challenging of these is to prove that there is a basic sequence Q where
$\mathscr {N}(Q) \subseteq \mathscr {RN}(Q)$
) or are trivial. The difficulty comes in showing a lack of inclusion. The most challenging of these is to prove that there is a basic sequence Q where
![]() $\mathscr {RN}(Q) \cap \mathscr {DN}(Q) \backslash \mathscr {N}(Q)\neq \emptyset $
.
$\mathscr {RN}(Q) \cap \mathscr {DN}(Q) \backslash \mathscr {N}(Q)\neq \emptyset $
.
As the equivalence of these definitions is so key to the study of normality in base b, it is natural to ask how “independent” these sets are. There have been two approaches to measure this. First, it is natural to ask if, for example, there is a simple condition
![]() $P(x)$
where if x is Q-normal and
$P(x)$
where if x is Q-normal and
![]() $P(x)$
also holds, we will have the x is Q-distribution normal (or any other permutation of definitions of normality). One example of such an attempt to find a condition
$P(x)$
also holds, we will have the x is Q-distribution normal (or any other permutation of definitions of normality). One example of such an attempt to find a condition
![]() $P(x)$
is motivated by Theorem 1.3. This theorem strongly fails when Q is infinite in limit and fully divergent: Q-distribution normality is preserved only by non-zero integer multiplication while Q-normality and Q-ratio normality aren’t even preserved by integer multiplication. In fact, the easiest way to construct members of
$P(x)$
is motivated by Theorem 1.3. This theorem strongly fails when Q is infinite in limit and fully divergent: Q-distribution normality is preserved only by non-zero integer multiplication while Q-normality and Q-ratio normality aren’t even preserved by integer multiplication. In fact, the easiest way to construct members of
![]() $\mathscr {N}(Q) \backslash \mathscr {DN}(Q)$
is to use the techniques presented in [Reference Mance16] to construct members of the (surprisingly) non-empty set
$\mathscr {N}(Q) \backslash \mathscr {DN}(Q)$
is to use the techniques presented in [Reference Mance16] to construct members of the (surprisingly) non-empty set
This motivated Samuel Roth to ask the third author if it is true that
![]() $nx \in \mathscr {N}(Q)$
for all natural numbers n implies that
$nx \in \mathscr {N}(Q)$
for all natural numbers n implies that
![]() $x \in \mathscr {DN}(Q)$
at the 2012 RTG conference: Logic, Dynamics, and Their Interactions, with a Celebration of the Work of Dan Mauldin in Denton, Texas. This question was later strongly shown to be false in [Reference Airey, Mance and Vandehey4] as it was shown that there exist basic sequences Q such that
$x \in \mathscr {DN}(Q)$
at the 2012 RTG conference: Logic, Dynamics, and Their Interactions, with a Celebration of the Work of Dan Mauldin in Denton, Texas. This question was later strongly shown to be false in [Reference Airey, Mance and Vandehey4] as it was shown that there exist basic sequences Q such that
Any other attempt to find such an additional condition that would allow one to get from one form of normality to another has thus far failed.
The second method has been to attempt to find the “size” of the difference sets suggested by Figure 1. All of these difference sets are meager and have zero measure. The Hausdorff dimension of most of these difference sets has been calculated in [Reference Airey and Mance3]. In particular, when Q is infinite in limit and fully divergent, all non-empty difference sets except for
![]() $\mathscr {N}(Q) \backslash \mathscr {DN}(Q)$
are known to have full Hausdorff dimension. The Hausdorff dimension of
$\mathscr {N}(Q) \backslash \mathscr {DN}(Q)$
are known to have full Hausdorff dimension. The Hausdorff dimension of
![]() $\mathscr {N}(Q) \backslash \mathscr {DN}(Q)$
is known to have full Hausdorff dimension only for a small class of infinite in limit and fully divergent basic sequences Q.
$\mathscr {N}(Q) \backslash \mathscr {DN}(Q)$
is known to have full Hausdorff dimension only for a small class of infinite in limit and fully divergent basic sequences Q.
Another approach to measuring the difference sets is to determine the exact descriptive complexity of these sets. If we show that for two of these classes (for a given Q) the difference set is
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-complete, then the difference has maximum logical complexity. One of the main results of this paper, Theorem 1.15, is to establish this fact for the five non-trivial difference sets. As we mention in some examples below, this can be used to rule out potential theorems connecting the different classes.
$D_2(\boldsymbol {\Pi }^0_3)$
-complete, then the difference has maximum logical complexity. One of the main results of this paper, Theorem 1.15, is to establish this fact for the five non-trivial difference sets. As we mention in some examples below, this can be used to rule out potential theorems connecting the different classes.
Remark 1.7. When Q is infinite in limit and k-divergent, conditions (3) and (4) can be replaced by
 $$ \begin{align*}\lim_{n \rightarrow \infty} \frac {N_n^Q (B,x)} {Q_n^{(k)}}=1 \mbox{ and } \lim_{n \to \infty} \frac {N_n^Q (B_1,x)} {N_n^Q (B_2,x)}=1, \end{align*} $$
$$ \begin{align*}\lim_{n \rightarrow \infty} \frac {N_n^Q (B,x)} {Q_n^{(k)}}=1 \mbox{ and } \lim_{n \to \infty} \frac {N_n^Q (B_1,x)} {N_n^Q (B_2,x)}=1, \end{align*} $$
respectively. This class of expansions will be important for us throughout this paper. Moreover,
![]() $\mathscr {N}_{k}( Q )=\mathscr {RN}_{k}( Q )=\mathbb {R}$
if and only if Q is k-convergent.
$\mathscr {N}_{k}( Q )=\mathscr {RN}_{k}( Q )=\mathbb {R}$
if and only if Q is k-convergent.
Remark 1.8. Assuming
![]() $Q=(q_i)$
is infinite in limit, we have the following easy facts about distribution normality. A real x with Q-Cantor series expansion
$Q=(q_i)$
is infinite in limit, we have the following easy facts about distribution normality. A real x with Q-Cantor series expansion
![]() $a_0.a_1a_2\cdots $
is in
$a_0.a_1a_2\cdots $
is in
![]() $\mathscr {DN}(Q)$
iff the sequence
$\mathscr {DN}(Q)$
iff the sequence
![]() $(\frac {a_i}{q_i})$
is uniformly distributed mod 1. If
$(\frac {a_i}{q_i})$
is uniformly distributed mod 1. If
![]() $y=b_0.b_1b_2\cdots $
and
$y=b_0.b_1b_2\cdots $
and
![]() $\lim _{i \to \infty } \frac {a_i-b_i}{q_i} =0$
, then
$\lim _{i \to \infty } \frac {a_i-b_i}{q_i} =0$
, then
![]() $x \in \mathscr {DN}(Q)$
iff
$x \in \mathscr {DN}(Q)$
iff
![]() $y \in \mathscr {DN}(Q)$
. Also, if
$y \in \mathscr {DN}(Q)$
. Also, if
![]() $\{ i \colon a_i \neq b_i\}$
has density
$\{ i \colon a_i \neq b_i\}$
has density
![]() $0$
, then
$0$
, then
![]() $x \in \mathscr {DN}(Q)$
iff
$x \in \mathscr {DN}(Q)$
iff
![]() $y \in \mathscr {DN}(Q)$
.
$y \in \mathscr {DN}(Q)$
.
We will need the following theorem of [Reference Mance15].
Theorem 1.9. The sets
![]() $\mathscr {N}(Q), \mathscr {RN}(Q)$
, and
$\mathscr {N}(Q), \mathscr {RN}(Q)$
, and
![]() $\mathscr {DN}(Q)$
are sets of full measure for all basic sequences Q.Footnote
3
$\mathscr {DN}(Q)$
are sets of full measure for all basic sequences Q.Footnote
3
1.3 Statement of results
We will prove the following theorems. First we address the complexity of the various normality classes themselves. Theorems 1.10 and 1.11 can be seen as generalizations of the Ki–Linton result as
![]() $\mathscr {N}(Q)$
,
$\mathscr {N}(Q)$
,
![]() $\mathscr {RN}(Q)$
, and
$\mathscr {RN}(Q)$
, and
![]() $\mathscr {DN}(Q)$
all coincide when Q is the constant b sequence. The proofs, particularly that of Theorem 1.11, have, however, significant extra complications.
$\mathscr {DN}(Q)$
all coincide when Q is the constant b sequence. The proofs, particularly that of Theorem 1.11, have, however, significant extra complications.
Theorem 1.10. For all basic sequences Q, the set
![]() $\mathscr {DN}(Q)$
is
$\mathscr {DN}(Q)$
is
![]() $\boldsymbol {\Pi }^0_3$
-complete.
$\boldsymbol {\Pi }^0_3$
-complete.
Theorem 1.11. The sets
![]() $\mathscr {N}(Q)$
and
$\mathscr {N}(Q)$
and
![]() $\mathscr {RN}(Q)$
are
$\mathscr {RN}(Q)$
are
![]() $\boldsymbol {\Pi }^0_3$
-complete if Q is
$\boldsymbol {\Pi }^0_3$
-complete if Q is
![]() $1$
-divergent, and clopen if Q is
$1$
-divergent, and clopen if Q is
![]() $1$
-convergent. Moreover,
$1$
-convergent. Moreover,
![]() $\mathscr {N}_k(Q)$
and
$\mathscr {N}_k(Q)$
and
![]() $\mathscr {RN}_k(Q)$
are
$\mathscr {RN}_k(Q)$
are
![]() $\boldsymbol {\Pi }^0_3$
-complete if Q is k-divergent and clopen if Q is k-convergent.
$\boldsymbol {\Pi }^0_3$
-complete if Q is k-divergent and clopen if Q is k-convergent.
We can extend Theorem 1.11 to show the following.
Theorem 1.12. Let
![]() $\mathscr {C}$
be a collection of blocks. Then the set
$\mathscr {C}$
be a collection of blocks. Then the set
 $$ \begin{align*}\mathscr{N}_{\mathscr{C}}(Q)=\left\{x \in {\mathbb{R}} \colon \lim_{n \to \infty} \frac {N_n^Q(B,x)} {Q_n(B)} =1\ \forall B\in {\mathscr{C}} \text{ such that } \lim_{n \to \infty} Q_n(B) = \infty \right\} \end{align*} $$
$$ \begin{align*}\mathscr{N}_{\mathscr{C}}(Q)=\left\{x \in {\mathbb{R}} \colon \lim_{n \to \infty} \frac {N_n^Q(B,x)} {Q_n(B)} =1\ \forall B\in {\mathscr{C}} \text{ such that } \lim_{n \to \infty} Q_n(B) = \infty \right\} \end{align*} $$
is
![]() $\boldsymbol {\Pi }^0_3$
-complete if there exists
$\boldsymbol {\Pi }^0_3$
-complete if there exists
![]() $B \in {\mathscr {C}}$
such that
$B \in {\mathscr {C}}$
such that
![]() $\lim _{n \to \infty } Q_n(B) = \infty $
and clopen otherwise. Similarly, the set
$\lim _{n \to \infty } Q_n(B) = \infty $
and clopen otherwise. Similarly, the set
 $$ \begin{align*} \mathscr{RN}_{\mathscr{C}}(Q)=& \left\{ x \in \mathbb{R} \colon \lim_{n \to \infty} \frac {N_n^Q(B_1,x)/Q_n(B_1)} {N_n^Q(B_2,x)/Q_n(B_2)}=1 \ \forall B_1,B_2\in \mathscr{C} \text{ such that } \right. \\ & \qquad |B_1|=|B_2| \text{ and } \left. \lim_{n \to \infty} \min(Q_n(B_1),Q_n(B_2)) = \vphantom{\frac {N_n^Q(B_1,x)/Q_n(B_1)} {N_n^Q(B_2,x)/Q_n(B_2)}} \infty \right\} \end{align*} $$
$$ \begin{align*} \mathscr{RN}_{\mathscr{C}}(Q)=& \left\{ x \in \mathbb{R} \colon \lim_{n \to \infty} \frac {N_n^Q(B_1,x)/Q_n(B_1)} {N_n^Q(B_2,x)/Q_n(B_2)}=1 \ \forall B_1,B_2\in \mathscr{C} \text{ such that } \right. \\ & \qquad |B_1|=|B_2| \text{ and } \left. \lim_{n \to \infty} \min(Q_n(B_1),Q_n(B_2)) = \vphantom{\frac {N_n^Q(B_1,x)/Q_n(B_1)} {N_n^Q(B_2,x)/Q_n(B_2)}} \infty \right\} \end{align*} $$
is
![]() $\boldsymbol {\Pi }^0_3$
-complete if there exist
$\boldsymbol {\Pi }^0_3$
-complete if there exist
![]() $B_1, B_2 \in \mathscr {C}$
such that
$B_1, B_2 \in \mathscr {C}$
such that
![]() $\lim _{n \to \infty } \min (Q_n(B_1),Q_n(B_2)) = \infty $
and
$\lim _{n \to \infty } \min (Q_n(B_1),Q_n(B_2)) = \infty $
and
![]() $\mathscr {C}$
satisfies the following hypothesis
$\mathscr {C}$
satisfies the following hypothesis
![]() $:$
$:$
![]() $(\star ).$
For every
$(\star ).$
For every
![]() $B\in \mathscr {C}$
with infinite expectation there is a block
$B\in \mathscr {C}$
with infinite expectation there is a block
![]() $B' \in \mathscr {C}$
of infinite expectation with
$B' \in \mathscr {C}$
of infinite expectation with
![]() $|B'|=|B|$
and an integer
$|B'|=|B|$
and an integer
![]() $1 \leq t \leq |B|$
such that
$1 \leq t \leq |B|$
such that
![]() $|B(t)-B'(t')|>1$
for all
$|B(t)-B'(t')|>1$
for all
![]() $1 \leq t' \leq |B'|$
.
$1 \leq t' \leq |B'|$
.
If there do not exist
![]() $B_1, B_2 \in \mathscr {C}$
such that
$B_1, B_2 \in \mathscr {C}$
such that
![]() $\lim _{n \to \infty } \min (Q_n(B_1),Q_n(B_2)) = \infty $
, then
$\lim _{n \to \infty } \min (Q_n(B_1),Q_n(B_2)) = \infty $
, then
![]() $\mathscr {RN}_{\mathscr {C}}(Q)$
is clopen.
$\mathscr {RN}_{\mathscr {C}}(Q)$
is clopen.
Remark 1.13. The
![]() $\boldsymbol {\Pi }^0_3$
-completeness of
$\boldsymbol {\Pi }^0_3$
-completeness of
![]() $\mathscr {N}_{\mathscr {C}}$
holds for general
$\mathscr {N}_{\mathscr {C}}$
holds for general
![]() $\mathscr {C}$
(and all Q), but the
$\mathscr {C}$
(and all Q), but the
![]() $\boldsymbol {\Pi }^0_3$
-completeness of
$\boldsymbol {\Pi }^0_3$
-completeness of
![]() $\mathscr {RN}_{\mathscr {C}}$
requires the extra hypothesis
$\mathscr {RN}_{\mathscr {C}}$
requires the extra hypothesis
![]() $(\star )$
on
$(\star )$
on
![]() $\mathscr {C}$
. We do not know if this extra hypothesis is necessary. For base b expansions, normality and ratio normality coincide so the extra assumption is not needed, but we do not know for general Q.
$\mathscr {C}$
. We do not know if this extra hypothesis is necessary. For base b expansions, normality and ratio normality coincide so the extra assumption is not needed, but we do not know for general Q.
Remark 1.14. The proof of Theorem 1.12 will also show the
![]() $\boldsymbol {\Pi }^0_3$
-completeness for a variation of ratio normality which we call strong ratio normality. Here we remove the restriction that
$\boldsymbol {\Pi }^0_3$
-completeness for a variation of ratio normality which we call strong ratio normality. Here we remove the restriction that
![]() $|B_1|=|B_2|$
in the above definition of
$|B_1|=|B_2|$
in the above definition of
![]() $\mathscr {RN}_{\mathscr {C}}(Q)$
. We can accordingly relax the
$\mathscr {RN}_{\mathscr {C}}(Q)$
. We can accordingly relax the
![]() $(\star )$
assumption by removing the requirement that
$(\star )$
assumption by removing the requirement that
![]() $|B'|=|B|$
.
$|B'|=|B|$
.
The next theorem addresses the complexity of the difference sets. We note that the hypotheses on Q are necessary as the various normality classes coincide for base b expansions (where Q is not infinite in limit) and when Q is not
![]() $1$
-divergent then
$1$
-divergent then
![]() $\mathscr {N}(Q)$
and
$\mathscr {N}(Q)$
and
![]() $\mathscr {RN}(Q)$
are clopen.
$\mathscr {RN}(Q)$
are clopen.
Theorem 1.15. Assume that Q is infinite in limit and
![]() $1$
-divergent. Then the sets
$1$
-divergent. Then the sets
![]() $\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
,
$\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
,
![]() $\mathscr {DN}(Q)\setminus \mathscr {RN}(Q)$
,
$\mathscr {DN}(Q)\setminus \mathscr {RN}(Q)$
,
![]() $\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
,
$\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
,
![]() $\mathscr {RN}(Q)\setminus \mathscr {DN}(Q)$
, and
$\mathscr {RN}(Q)\setminus \mathscr {DN}(Q)$
, and
![]() $\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
are all
$\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
are all
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-complete.
$D_2(\boldsymbol {\Pi }^0_3)$
-complete.
Theorem 1.15 imposes limitations on the relationships between the classes
![]() $\mathscr {N}(Q)$
,
$\mathscr {N}(Q)$
,
![]() $\mathscr {RN}(Q)$
, and
$\mathscr {RN}(Q)$
, and
![]() $\mathscr {DN}(Q)$
. For example, consider the sets
$\mathscr {DN}(Q)$
. For example, consider the sets
![]() $\mathscr {N}(Q)$
and
$\mathscr {N}(Q)$
and
![]() $\mathscr {RN}(Q)$
. Since
$\mathscr {RN}(Q)$
. Since
![]() $\mathscr {RN}(Q) \setminus \mathscr {N}(Q)$
is
$\mathscr {RN}(Q) \setminus \mathscr {N}(Q)$
is
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-complete, there cannot be a
$D_2(\boldsymbol {\Pi }^0_3)$
-complete, there cannot be a
![]() $\boldsymbol {\Sigma }^0_3$
set A such that
$\boldsymbol {\Sigma }^0_3$
set A such that
![]() $A\cap \mathscr {RN}(Q)=\mathscr {N}(Q)$
(as otherwise we would have
$A\cap \mathscr {RN}(Q)=\mathscr {N}(Q)$
(as otherwise we would have
![]() $\mathscr {RN}(Q)\setminus \mathscr {N}(Q)=\mathscr {RN}(Q)\setminus A \in \boldsymbol {\Pi }^0_3$
, a contradiction). Thus, no
$\mathscr {RN}(Q)\setminus \mathscr {N}(Q)=\mathscr {RN}(Q)\setminus A \in \boldsymbol {\Pi }^0_3$
, a contradiction). Thus, no
![]() $\boldsymbol {\Sigma }^0_3$
condition can be added to the assumption of ratio normality to give the set of normal numbers. Equivalently, anytime a
$\boldsymbol {\Sigma }^0_3$
condition can be added to the assumption of ratio normality to give the set of normal numbers. Equivalently, anytime a
![]() $\boldsymbol {\Sigma }^0_3$
set contains
$\boldsymbol {\Sigma }^0_3$
set contains
![]() $\mathscr {N}(Q)$
(or
$\mathscr {N}(Q)$
(or
![]() $\mathscr {DN}(Q)$
), then it must contain elements of
$\mathscr {DN}(Q)$
), then it must contain elements of
![]() $\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
and
$\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
and
![]() $\mathscr {DN}(Q) \setminus \mathscr {N}(Q)$
(resp.
$\mathscr {DN}(Q) \setminus \mathscr {N}(Q)$
(resp.
![]() $\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
, and so
$\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
, and so
![]() $\mathscr {RN}(Q)\setminus \mathscr {DN}(Q)$
). For example, though
$\mathscr {RN}(Q)\setminus \mathscr {DN}(Q)$
). For example, though
![]() $\mathscr {N}(Q)$
has Lebesgue measure one, any
$\mathscr {N}(Q)$
has Lebesgue measure one, any
![]() $\boldsymbol {\Pi }^0_2$
set of measure one which contains
$\boldsymbol {\Pi }^0_2$
set of measure one which contains
![]() $\mathscr {N}(Q)$
must contain an element of
$\mathscr {N}(Q)$
must contain an element of
![]() $\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
, as well as
$\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
, as well as
![]() $\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
. Many naturally occurring sets of reals A are defined by conditions which result in them being
$\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
. Many naturally occurring sets of reals A are defined by conditions which result in them being
![]() $\boldsymbol {\Sigma }^0_3$
sets. Examples include countable sets, co-countable sets, the class BA of badly approximable numbers (which is a
$\boldsymbol {\Sigma }^0_3$
sets. Examples include countable sets, co-countable sets, the class BA of badly approximable numbers (which is a
![]() $\boldsymbol {\Sigma }^0_2$
set), the Liouville numbers (which is a
$\boldsymbol {\Sigma }^0_2$
set), the Liouville numbers (which is a
![]() $\boldsymbol {\Pi }^0_2$
set), and the set of
$\boldsymbol {\Pi }^0_2$
set), and the set of
![]() $x\in [0,1]$
where a particular continuous function
$x\in [0,1]$
where a particular continuous function
![]() $f\colon [0,1]\to \mathbb {R}$
is not differentiable. In all these cases the theorem implies that the set either omits some normal number, or else contains a number which is ratio normal but not normal (and likewise for
$f\colon [0,1]\to \mathbb {R}$
is not differentiable. In all these cases the theorem implies that the set either omits some normal number, or else contains a number which is ratio normal but not normal (and likewise for
![]() $\mathscr {DN}(Q)$
). Of course, many of these statements are easy to see directly, but the point is that they all follow immediately from the general complexity result, Theorem 1.15.
$\mathscr {DN}(Q)$
). Of course, many of these statements are easy to see directly, but the point is that they all follow immediately from the general complexity result, Theorem 1.15.
Previous work of Mance [Reference Mance14] had shown that all of the non-trivial difference sets (all except
![]() $\mathscr {N}(Q)\setminus \mathscr {RN}(Q)$
, which is trivially empty) are non-empty assuming Q is infinite in limit k-divergent for all k. Thus, Theorem 1.15 strengthens this in two ways: we relax the hypothesis to Q being
$\mathscr {N}(Q)\setminus \mathscr {RN}(Q)$
, which is trivially empty) are non-empty assuming Q is infinite in limit k-divergent for all k. Thus, Theorem 1.15 strengthens this in two ways: we relax the hypothesis to Q being
![]() $1$
-divergent, and we show the difference sets are actually
$1$
-divergent, and we show the difference sets are actually
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-complete.
$D_2(\boldsymbol {\Pi }^0_3)$
-complete.
To mention another application of Theorem 1.15, consider (relative to a fixed basic sequence Q which is infinite in limit and
![]() $1$
-divergent) the following weakening of distribution normality. Say a real x is
$1$
-divergent) the following weakening of distribution normality. Say a real x is
![]() $\epsilon $
-weakly distribution normal (for
$\epsilon $
-weakly distribution normal (for
![]() $\epsilon>0$
) if there is an
$\epsilon>0$
) if there is an
![]() $\ell $
such that for all
$\ell $
such that for all
![]() $N\geq \ell $
and all intervals
$N\geq \ell $
and all intervals
![]() $(a,b) \subseteq (0,1)$
$(a,b) \subseteq (0,1)$
 $$ \begin{align*} \left| \frac{1}{N} \# \{ n <N\colon q_0 \cdots q_{n-1} x\ \mod 1 \in [a,b]\} -(b-a)\right| \leq \epsilon. \end{align*} $$
$$ \begin{align*} \left| \frac{1}{N} \# \{ n <N\colon q_0 \cdots q_{n-1} x\ \mod 1 \in [a,b]\} -(b-a)\right| \leq \epsilon. \end{align*} $$
The set
![]() $\mathscr {WDN}(Q)_\epsilon $
of
$\mathscr {WDN}(Q)_\epsilon $
of
![]() $\epsilon $
-weakly distributional normal numbers is easily a
$\epsilon $
-weakly distributional normal numbers is easily a
![]() $\boldsymbol {\Sigma }^0_2$
set. It therefore follows from Theorem 1.15 that
$\boldsymbol {\Sigma }^0_2$
set. It therefore follows from Theorem 1.15 that
![]() $\mathscr {N}(Q)\cap \mathscr {WDN}(Q)_\epsilon \setminus \mathscr {DN}(Q)$
is non-empty.
$\mathscr {N}(Q)\cap \mathscr {WDN}(Q)_\epsilon \setminus \mathscr {DN}(Q)$
is non-empty.
For one more example, let
![]() $\mathscr {R}(Q)$
denote the set of rich numbers. These are the x such that every block
$\mathscr {R}(Q)$
denote the set of rich numbers. These are the x such that every block
![]() $B \in \omega ^{<\omega }$
occurs in the Q-ary expansion of x. The set
$B \in \omega ^{<\omega }$
occurs in the Q-ary expansion of x. The set
![]() $\mathscr {R}(Q)$
is easily a
$\mathscr {R}(Q)$
is easily a
![]() $\boldsymbol {\Pi }^0_2$
set, and contains the ratio normal numbers (and so also the normal numbers). From Theorem 1.15 it therefore follows that
$\boldsymbol {\Pi }^0_2$
set, and contains the ratio normal numbers (and so also the normal numbers). From Theorem 1.15 it therefore follows that
![]() $\mathscr {DN}(Q)\cap \mathscr {R}(Q) \setminus \mathscr {N}(Q)$
is non-empty. In other words, distribution normal and rich does not imply normal (if this failed, then
$\mathscr {DN}(Q)\cap \mathscr {R}(Q) \setminus \mathscr {N}(Q)$
is non-empty. In other words, distribution normal and rich does not imply normal (if this failed, then
![]() $\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
would be equal to
$\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
would be equal to
![]() $\mathscr {DN}(Q)\setminus \mathscr {R}(Q)$
which a
$\mathscr {DN}(Q)\setminus \mathscr {R}(Q)$
which a
![]() $\boldsymbol {\Pi }^0_3$
set, contradicting Theorem 1.15).
$\boldsymbol {\Pi }^0_3$
set, contradicting Theorem 1.15).
2
 $\boldsymbol {\Pi }^0_3$
-completeness of the normality classes
$\boldsymbol {\Pi }^0_3$
-completeness of the normality classes
Throughout,
![]() ${Q}=(q_i)_{i=1}^\infty $
will denote a basic sequence, that is, a sequence of integers
${Q}=(q_i)_{i=1}^\infty $
will denote a basic sequence, that is, a sequence of integers
![]() $q_i$
with
$q_i$
with
![]() $q_i \geq 2$
for all i.
$q_i \geq 2$
for all i.
Note that the
![]() $\boldsymbol {\Pi }^0_3$
-completeness of the set
$\boldsymbol {\Pi }^0_3$
-completeness of the set
![]() $\mathscr {N}(Q) \cap [0,1]$
(and likewise for
$\mathscr {N}(Q) \cap [0,1]$
(and likewise for
![]() $\mathscr {RN}(Q)\cap [0,1]$
and
$\mathscr {RN}(Q)\cap [0,1]$
and
![]() $\mathscr {DN}(Q) \cap [0,1]$
) immediately implies the
$\mathscr {DN}(Q) \cap [0,1]$
) immediately implies the
![]() $\boldsymbol {\Pi }^0_3$
-completeness of
$\boldsymbol {\Pi }^0_3$
-completeness of
![]() $\mathscr {N}(Q)$
, since if
$\mathscr {N}(Q)$
, since if
![]() $\mathscr {N}(Q)$
were in
$\mathscr {N}(Q)$
were in
![]() $\boldsymbol {\Sigma }^0_3$
, then so would be
$\boldsymbol {\Sigma }^0_3$
, then so would be
![]() $\mathscr {N}(Q)\cap [0,1]$
. Similarly, the
$\mathscr {N}(Q)\cap [0,1]$
. Similarly, the
![]() $\boldsymbol {\Pi }^0_3$
-completeness of the difference sets restricted to
$\boldsymbol {\Pi }^0_3$
-completeness of the difference sets restricted to
![]() $[0,1]$
(for example
$[0,1]$
(for example
![]() $\mathscr {RN}(Q) \setminus \mathscr {N}(Q) \cap [0,1]$
) implies the
$\mathscr {RN}(Q) \setminus \mathscr {N}(Q) \cap [0,1]$
) implies the
![]() $\boldsymbol {\Pi }^0_3$
-completeness of the difference set (e.g.,
$\boldsymbol {\Pi }^0_3$
-completeness of the difference set (e.g.,
![]() $\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
). So, for the rest of the paper we will restrict our attention to reals in
$\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
). So, for the rest of the paper we will restrict our attention to reals in
![]() $[0,1]$
, that is, when we write
$[0,1]$
, that is, when we write
![]() $\mathscr {N}(Q)$
etc., we will henceforth mean
$\mathscr {N}(Q)$
etc., we will henceforth mean
![]() $\mathscr {N}(Q)\cap [0,1]$
.
$\mathscr {N}(Q)\cap [0,1]$
.
The basic sequence Q forms the set of bases for the expansion of an real
![]() $x \in [0,1]$
into a Cantor series
$x \in [0,1]$
into a Cantor series
 $$ \begin{align*} x= \sum_{i=1}^\infty \frac{a_i}{q_1 \cdots q_i}, \end{align*} $$
$$ \begin{align*} x= \sum_{i=1}^\infty \frac{a_i}{q_1 \cdots q_i}, \end{align*} $$
where
![]() $0 \leq a_i < q_i$
. Recall we abbreviate the above equation by writing
$0 \leq a_i < q_i$
. Recall we abbreviate the above equation by writing
![]() $x=.a_1 a_2\cdots $
when Q is understood. Let
$x=.a_1 a_2\cdots $
when Q is understood. Let
![]() $X_{Q}$
be the set of all sequences
$X_{Q}$
be the set of all sequences
![]() $(a_i)_{i=1}^{\infty }$
with
$(a_i)_{i=1}^{\infty }$
with
![]() $0 \leq a_i <q_i$
.
$0 \leq a_i <q_i$
.
![]() $X_{Q}$
is a compact Polish space with the product of the discrete topologies on the sets
$X_{Q}$
is a compact Polish space with the product of the discrete topologies on the sets
![]() $\{ 0,1,\dots ,q_i-1\}$
. We let
$\{ 0,1,\dots ,q_i-1\}$
. We let
![]() $\varphi _2 \colon X_Q \to [0,1]$
be the map
$\varphi _2 \colon X_Q \to [0,1]$
be the map
![]() $\varphi _2((a_i))=.a_1a_2\dots $
. Our reduction maps will always be of the form
$\varphi _2((a_i))=.a_1a_2\dots $
. Our reduction maps will always be of the form
![]() $\varphi (x)=\varphi _2\circ \varphi _1$
, where
$\varphi (x)=\varphi _2\circ \varphi _1$
, where
![]() $\varphi _1\colon \omega ^\omega \to X_Q$
will vary from proof to proof.
$\varphi _1\colon \omega ^\omega \to X_Q$
will vary from proof to proof.
We first prove the completeness result for distribution normality, Theorem 1.10.
Proof of Theorem 1.10. Let
![]() $P=\{ x \in \omega ^\omega \colon \lim _n x(n)=\infty \}$
. It is well-known that P is
$P=\{ x \in \omega ^\omega \colon \lim _n x(n)=\infty \}$
. It is well-known that P is
![]() $\boldsymbol {\Pi }^0_3$
-complete. We define a continuous
$\boldsymbol {\Pi }^0_3$
-complete. We define a continuous
![]() $\varphi \colon \omega ^\omega \to [0,1]$
which will be a reduction of P to
$\varphi \colon \omega ^\omega \to [0,1]$
which will be a reduction of P to
![]() $\mathscr {DN}(Q)$
, that is, such that
$\mathscr {DN}(Q)$
, that is, such that
![]() $P= \varphi ^{-1}(\mathscr {DN}(Q))$
. This suffices to show that
$P= \varphi ^{-1}(\mathscr {DN}(Q))$
. This suffices to show that
![]() $\mathscr {DN}(Q)$
is
$\mathscr {DN}(Q)$
is
![]() $\boldsymbol {\Pi }^0_3$
-complete. Again,
$\boldsymbol {\Pi }^0_3$
-complete. Again,
![]() $\varphi $
will be of the form
$\varphi $
will be of the form
![]() $\varphi =\varphi _2\circ \varphi _1$
where
$\varphi =\varphi _2\circ \varphi _1$
where
![]() $\varphi _2$
is as above.
$\varphi _2$
is as above.
Let
![]() $0=b_0<b_1<b_2<\cdots $
be a sufficiently fast-growing sequence from
$0=b_0<b_1<b_2<\cdots $
be a sufficiently fast-growing sequence from
![]() $\mathbb {N}$
, so that in particular
$\mathbb {N}$
, so that in particular
![]() $\lim _n \frac {b_0+\cdots +b_{n-1}}{b_n}=0$
. Let
$\lim _n \frac {b_0+\cdots +b_{n-1}}{b_n}=0$
. Let
![]() $I_n=[b_{n-1},b_n)$
, which we call the nth block of
$I_n=[b_{n-1},b_n)$
, which we call the nth block of
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Fix a
![]() $z=(z_i)_{i=1}^\infty \in X_Q$
such that
$z=(z_i)_{i=1}^\infty \in X_Q$
such that
![]() $\varphi _2(z)=.z_1 z_2\cdots \in \mathscr {DN}(Q)$
. We will use z as a “reference point” from which we make certain modifications depending on the point
$\varphi _2(z)=.z_1 z_2\cdots \in \mathscr {DN}(Q)$
. We will use z as a “reference point” from which we make certain modifications depending on the point
![]() $x \in \omega ^\omega $
.
$x \in \omega ^\omega $
.
Fix
![]() $x \in \omega ^\omega $
and we describe the construction for
$x \in \omega ^\omega $
and we describe the construction for
![]() $\varphi _1(x)$
. Let
$\varphi _1(x)$
. Let
![]() $x'(n)=\min \{ x(n),n\}$
. Clearly
$x'(n)=\min \{ x(n),n\}$
. Clearly
![]() $x \in P$
iff
$x \in P$
iff
![]() $x'\in P$
. Consider the nth block
$x'\in P$
. Consider the nth block
![]() $I_n$
. We may assume the
$I_n$
. We may assume the
![]() $b_n$
grow fast enough so that for all n and all
$b_n$
grow fast enough so that for all n and all
![]() $k \leq n+2$
, for all
$k \leq n+2$
, for all
![]() $b \geq b_{n-1}$
we have that
$b \geq b_{n-1}$
we have that
 $$ \begin{align} \left| \frac{1}{b} \# \left\{ i <b \colon T_{Q,i}\left( z \right) \in \left[0,\frac{1}{k}\right) \right\} -\frac{1}{k}\right| < \frac{1}{2n}. \end{align} $$
$$ \begin{align} \left| \frac{1}{b} \# \left\{ i <b \colon T_{Q,i}\left( z \right) \in \left[0,\frac{1}{k}\right) \right\} -\frac{1}{k}\right| < \frac{1}{2n}. \end{align} $$
For
![]() $i \in I_n$
we define
$i \in I_n$
we define
![]() $a_i= (\varphi _1(x))(i)$
as follows. For
$a_i= (\varphi _1(x))(i)$
as follows. For
![]() $i \in I_n$
, if
$i \in I_n$
, if
![]() $T_{Q,i}\left ( z \right ) \notin [0, \frac {1}{x'(n)+2})$
, then we set
$T_{Q,i}\left ( z \right ) \notin [0, \frac {1}{x'(n)+2})$
, then we set
![]() $a_i=z_i$
. If
$a_i=z_i$
. If
![]() $T_{Q,i}\left ( z \right ) \in [0, \frac {1}{x'(n)+2})$
, then we set
$T_{Q,i}\left ( z \right ) \in [0, \frac {1}{x'(n)+2})$
, then we set
![]() $a_i$
to be the least integer in
$a_i$
to be the least integer in
![]() $[z_i, q_i)$
such that
$[z_i, q_i)$
such that
![]() $\frac {a_i}{q_i}> \frac {1}{x'(n)+2}$
.
$\frac {a_i}{q_i}> \frac {1}{x'(n)+2}$
.
This defines the map
![]() $\varphi _1$
, and it is clear that
$\varphi _1$
, and it is clear that
![]() $\varphi _1$
, and thus
$\varphi _1$
, and thus
![]() $\varphi $
, is continuous. We show
$\varphi $
, is continuous. We show
![]() $\varphi $
is a reduction of P to
$\varphi $
is a reduction of P to
![]() $\mathscr {DN}(Q)$
.
$\mathscr {DN}(Q)$
.
First suppose that
![]() $x \notin P$
. Then there is an
$x \notin P$
. Then there is an
![]() $i_0$
such that for infinitely many n we have
$i_0$
such that for infinitely many n we have
![]() $x'(n)=i_0$
. For such n we have that for all
$x'(n)=i_0$
. For such n we have that for all
![]() $i \in I_n$
that
$i \in I_n$
that
![]() $T_{Q,i}\left ( \varphi (x) \right ) \notin [0,\frac {1}{x'(n)+2})$
, and thus
$T_{Q,i}\left ( \varphi (x) \right ) \notin [0,\frac {1}{x'(n)+2})$
, and thus
![]() $T_{Q,i}\left ( \varphi (x) \right ) \notin [0,\frac {1}{i_0+2})$
. This follows from the facts that
$T_{Q,i}\left ( \varphi (x) \right ) \notin [0,\frac {1}{i_0+2})$
. This follows from the facts that
and if
![]() $T_{Q,i}\left ( z \right )\in [0,\frac {1}{x'(n)+2})$
then by definition of
$T_{Q,i}\left ( z \right )\in [0,\frac {1}{x'(n)+2})$
then by definition of
![]() $a_i$
we have that
$a_i$
we have that
![]() $T_{Q,i}\left ( \varphi (x) \right ) \geq \frac {a_i}{q_i}> \frac {1}{x'(n)+2}$
. Since
$T_{Q,i}\left ( \varphi (x) \right ) \geq \frac {a_i}{q_i}> \frac {1}{x'(n)+2}$
. Since
![]() $\frac {b_0+\cdots +b_{n-1}}{b_n}$
tends to
$\frac {b_0+\cdots +b_{n-1}}{b_n}$
tends to
![]() $0$
, it follows that
$0$
, it follows that
![]() $\varphi (x)\notin \mathscr {DN}(Q)$
.
$\varphi (x)\notin \mathscr {DN}(Q)$
.
Assume now
![]() $x \in P$
, and we show that
$x \in P$
, and we show that
![]() $\varphi (x) \in \mathscr {DN}(Q)$
. From Remark 1.8 it suffices to show that
$\varphi (x) \in \mathscr {DN}(Q)$
. From Remark 1.8 it suffices to show that
![]() $\{ i \colon a_i \neq z_i\}$
has density
$\{ i \colon a_i \neq z_i\}$
has density
![]() $0$
. Fix
$0$
. Fix
![]() $\epsilon>0$
. Since
$\epsilon>0$
. Since
![]() $x \in P$
,
$x \in P$
,
![]() $\lim _{n \to \infty } x'(n)=\infty $
. Fix
$\lim _{n \to \infty } x'(n)=\infty $
. Fix
![]() $n_0$
large enough so that
$n_0$
large enough so that
![]() $\frac {1}{x'(n)+2} <\frac {\epsilon }{2}$
for all
$\frac {1}{x'(n)+2} <\frac {\epsilon }{2}$
for all
![]() $n \geq n_0$
. If
$n \geq n_0$
. If
![]() $n \geq n_0$
, then for all
$n \geq n_0$
, then for all
![]() $k \in I_n$
we have that
$k \in I_n$
we have that
 $$ \begin{align} \left|\frac{1}{k} \# \left\{ i <k \colon T_{Q,i}\left( z \right) \in \left[0, \frac{1}{x'(n_0)+2}\right) \right\} -\frac{1}{x'(n_0)+2} \right| < \frac{1}{2n} \leq \frac{1}{x'(n_0)+2}<\frac{\epsilon}{2}. \end{align} $$
$$ \begin{align} \left|\frac{1}{k} \# \left\{ i <k \colon T_{Q,i}\left( z \right) \in \left[0, \frac{1}{x'(n_0)+2}\right) \right\} -\frac{1}{x'(n_0)+2} \right| < \frac{1}{2n} \leq \frac{1}{x'(n_0)+2}<\frac{\epsilon}{2}. \end{align} $$
For
![]() $n \geq n_0$
, the
$n \geq n_0$
, the
![]() $i \in I_n$
for which
$i \in I_n$
for which
![]() $a_i \neq z_i$
are the i for which
$a_i \neq z_i$
are the i for which
![]() $T_{Q,i}\left ( z \right ) \in [0, \frac {1}{x'(n)+2})$
, which is a subset of the
$T_{Q,i}\left ( z \right ) \in [0, \frac {1}{x'(n)+2})$
, which is a subset of the
![]() $i \in I_n$
for which
$i \in I_n$
for which
![]() $T_{Q,i}\left ( z \right ) \in [0, \frac {1}{x'(n_0)+2})$
, for n large enough. From Equation (6) it follows that for all large enough n and
$T_{Q,i}\left ( z \right ) \in [0, \frac {1}{x'(n_0)+2})$
, for n large enough. From Equation (6) it follows that for all large enough n and
![]() $k>b_n$
that
$k>b_n$
that
Thus,
![]() $\{ i \colon a_i \neq z_i\}$
has density
$\{ i \colon a_i \neq z_i\}$
has density
![]() $0$
.⊣
$0$
.⊣
We next prove the completeness result, Theorem 1.11, for the classes
![]() $\mathscr {N}(Q)$
and
$\mathscr {N}(Q)$
and
![]() $\mathscr {RN}(Q)$
.
$\mathscr {RN}(Q)$
.
Proof of Theorem 1.11. Suppose
![]() ${Q}$
is
${Q}$
is
![]() $1$
-divergent and we first show that
$1$
-divergent and we first show that
![]() $\mathscr {N}(Q)$
and
$\mathscr {N}(Q)$
and
![]() $\mathscr {RN}(Q)$
are
$\mathscr {RN}(Q)$
are
![]() $\boldsymbol {\Pi }^0_3$
-complete. Let
$\boldsymbol {\Pi }^0_3$
-complete. Let
![]() $P\subseteq \omega ^\omega $
be the
$P\subseteq \omega ^\omega $
be the
![]() $\boldsymbol {\Pi }^0_3$
-complete set as before. Fix
$\boldsymbol {\Pi }^0_3$
-complete set as before. Fix
![]() $z =(z_i)_{i=1}^\infty \in X_Q$
such that
$z =(z_i)_{i=1}^\infty \in X_Q$
such that
![]() $\varphi _2(z)=.z_1z_2,\dots \in \mathscr {N}(Q)$
.
$\varphi _2(z)=.z_1z_2,\dots \in \mathscr {N}(Q)$
.
We say a block
![]() $B \in \omega ^k$
is good if
$B \in \omega ^k$
is good if
![]() $\lim _{n} Q_n(B)=\infty $
, that is, the block B has an infinite expectation. Recall that if
$\lim _{n} Q_n(B)=\infty $
, that is, the block B has an infinite expectation. Recall that if
![]() $B=(e_1,\dots ,e_k)$
, then
$B=(e_1,\dots ,e_k)$
, then
![]() $\|B\|=\sum _{1\leq i \leq k } (e_i+1)$
.
$\|B\|=\sum _{1\leq i \leq k } (e_i+1)$
.
We let
![]() $0=b_0<b_1<\cdots $
be a sufficiently fast-growing sequence so that the following hold:
$0=b_0<b_1<\cdots $
be a sufficiently fast-growing sequence so that the following hold:
-
(1)
 $b_n-b_{n-1}> 2^n b_{n-1}$
.
$b_n-b_{n-1}> 2^n b_{n-1}$
. -
(2)
 $\frac {1}{Q_m(B)} |N^Q_{m}(B,z)-Q_m(B)|<\frac {1}{n}$
for any good B with
$\frac {1}{Q_m(B)} |N^Q_{m}(B,z)-Q_m(B)|<\frac {1}{n}$
for any good B with
 $\|B\|\leq n$
, and any
$\|B\|\leq n$
, and any
 $m \geq b_{n-1}$
.
$m \geq b_{n-1}$
. -
(3)
 $\frac {b_{n-1}}{Q_{b_n}(B)} < \frac {1}{4^n}$
for any good B with
$\frac {b_{n-1}}{Q_{b_n}(B)} < \frac {1}{4^n}$
for any good B with
 $\|B\|\leq n$
.
$\|B\|\leq n$
.
We define the map
![]() $\varphi _1 \colon \omega ^\omega \to X_Q$
, and our final reduction map will be
$\varphi _1 \colon \omega ^\omega \to X_Q$
, and our final reduction map will be
![]() $\varphi =\varphi _2\circ \varphi _1$
where
$\varphi =\varphi _2\circ \varphi _1$
where
![]() $\varphi _2$
is as in the proof of Theorem 1.10. Let
$\varphi _2$
is as in the proof of Theorem 1.10. Let
![]() $I_n=[b_{n-1},b_n)$
. For
$I_n=[b_{n-1},b_n)$
. For
![]() $x \in \omega ^\omega $
, let
$x \in \omega ^\omega $
, let
![]() $x'(n)=\max \{ 27, \min \{ x(n),n\} \}$
. We define
$x'(n)=\max \{ 27, \min \{ x(n),n\} \}$
. We define
![]() $\varphi _1(x)\restriction I_n$
as follows.
$\varphi _1(x)\restriction I_n$
as follows.
Let
![]() $B_0,B_1,\dots , B_p$
enumerate the good blocks which occur among the first
$B_0,B_1,\dots , B_p$
enumerate the good blocks which occur among the first
![]() $\lfloor \sqrt [6]{x'(n)} \rfloor $
many blocks, where we order the blocks first by
$\lfloor \sqrt [6]{x'(n)} \rfloor $
many blocks, where we order the blocks first by
![]() $\| B\|$
and then lexicographically. Note that this ordering of the blocks has order-type
$\| B\|$
and then lexicographically. Note that this ordering of the blocks has order-type
![]() $\omega $
and the ith block in this ordering has length
$\omega $
and the ith block in this ordering has length
![]() $\leq i$
. So, for
$\leq i$
. So, for
![]() $j \leq p$
we have
$j \leq p$
we have
![]() $|B_j| \leq \sqrt [6]{x'(n)} \leq \sqrt [6]{n}$
.
$|B_j| \leq \sqrt [6]{x'(n)} \leq \sqrt [6]{n}$
.
For each
![]() $0\leq i \leq p$
let
$0\leq i \leq p$
let
![]() $m(i) \in [b_{n-1},b_n)$
be the least m so that
$m(i) \in [b_{n-1},b_n)$
be the least m so that
![]() $N_{m,b_n}(B_i,z) \leq \frac {2}{\sqrt [3]{x'(n)}} Q_{b_n}(B_i)$
. Note that
$N_{m,b_n}(B_i,z) \leq \frac {2}{\sqrt [3]{x'(n)}} Q_{b_n}(B_i)$
. Note that
![]() $N_{m(i),b_n}(B_i,z)\geq \frac {3}{2 \sqrt [3]{x'(n)}} Q_{b_n}(B_i)$
. Let
$N_{m(i),b_n}(B_i,z)\geq \frac {3}{2 \sqrt [3]{x'(n)}} Q_{b_n}(B_i)$
. Let
![]() $m=\max \{ m(i)\colon 0 \leq i \leq p\}$
. Let
$m=\max \{ m(i)\colon 0 \leq i \leq p\}$
. Let
![]() $i_0$
be such that
$i_0$
be such that
![]() $m(i_0)=m$
. We note that
$m(i_0)=m$
. We note that
![]() $i_0=i_0(n)$
depends on n, but as n is fixed for the rest of the definition of
$i_0=i_0(n)$
depends on n, but as n is fixed for the rest of the definition of
![]() $\varphi _1(x)\restriction I_n$
, we will just write
$\varphi _1(x)\restriction I_n$
, we will just write
![]() $i_0$
.
$i_0$
.
Consider the block
![]() $B_{i_0}$
. We say a block
$B_{i_0}$
. We say a block
![]() $B_j$
is sparse relative to
$B_j$
is sparse relative to
![]() $B_{i_0}$
if
$B_{i_0}$
if
![]() $Q_{b_n}(B_j)< \frac {1}{4 |B_j|4^{|B_j|} \sqrt {x'(n)}} Q_{b_n}(B_{i_0})$
. Let
$Q_{b_n}(B_j)< \frac {1}{4 |B_j|4^{|B_j|} \sqrt {x'(n)}} Q_{b_n}(B_{i_0})$
. Let
![]() $A\subseteq I_n$
be the set of
$A\subseteq I_n$
be the set of
![]() $i \in [m,b_n]$
such that
$i \in [m,b_n]$
such that
![]() $z\restriction [i, i+|B_{i_0}|-1]=B_{i_0}$
. Let r be the digit altering function defined as follows. If
$z\restriction [i, i+|B_{i_0}|-1]=B_{i_0}$
. Let r be the digit altering function defined as follows. If
![]() $B_{i_0}(1)=0$
, then r maps
$B_{i_0}(1)=0$
, then r maps
![]() $0$
to
$0$
to
![]() $1$
and leaves all other values fixed. If
$1$
and leaves all other values fixed. If
![]() $B_{i_0}(1)\neq 0$
then r maps
$B_{i_0}(1)\neq 0$
then r maps
![]() $B_{i_0}(1)$
to
$B_{i_0}(1)$
to
![]() $B_{i_0}(1)-1$
and leaves all other values fixed. Since the block
$B_{i_0}(1)-1$
and leaves all other values fixed. Since the block
![]() $B_{i_0}$
is fixed for the rest of the definition, the function r is also. Note that r applied to a valid Q expansion results in a valid Q expansion. Also, r is at most
$B_{i_0}$
is fixed for the rest of the definition, the function r is also. Note that r applied to a valid Q expansion results in a valid Q expansion. Also, r is at most
![]() $2$
-to-
$2$
-to-
![]() $1$
, so each block B has most
$1$
, so each block B has most
![]() $2^{|B|}$
many preimages under r (we apply r to a block by applying it to each digit).
$2^{|B|}$
many preimages under r (we apply r to a block by applying it to each digit).
Let
![]() $A' \subseteq A$
be those
$A' \subseteq A$
be those
![]() $i \in A$
such that for all
$i \in A$
such that for all
![]() $j<p$
such that
$j<p$
such that
![]() $B_j$
is sparse relative to
$B_j$
is sparse relative to
![]() $B_{i_0}$
, and all
$B_{i_0}$
, and all
![]() $q<|B_j|$
,
$q<|B_j|$
,
![]() $z \restriction [ i-q,\dots ,i-q+|B_j|-1]\neq B_j$
and
$z \restriction [ i-q,\dots ,i-q+|B_j|-1]\neq B_j$
and
![]() $z \restriction [ i-q,\dots ,i-q+|B_j|-1]\notin B^S_j$
, where
$z \restriction [ i-q,\dots ,i-q+|B_j|-1]\notin B^S_j$
, where
![]() $S\subseteq |B_j|$
and
$S\subseteq |B_j|$
and
![]() $B^S_j$
is the set of blocks B such that
$B^S_j$
is the set of blocks B such that
![]() $r(B)=B_j$
(here
$r(B)=B_j$
(here
![]() $r(B)$
means apply r to all of the digits of B).
$r(B)$
means apply r to all of the digits of B).
Note that if
![]() $z'$
is obtained by applying r to the digits
$z'$
is obtained by applying r to the digits
![]() $z_i$
for i in a subset of
$z_i$
for i in a subset of
![]() $A'$
, then
$A'$
, then
![]() $z\restriction I_n$
and
$z\restriction I_n$
and
![]() $z'\restriction I_n$
have the same number of occurrences of the block
$z'\restriction I_n$
have the same number of occurrences of the block
![]() $B_j$
for
$B_j$
for
![]() $j=1,\dots ,p$
.
$j=1,\dots ,p$
.
Note that
 $$ \begin{align*} |A'|\geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) -\sum_{j<p} \sum_{S\subseteq |B_j|} \sum_{r_S(B)=B_j} |B_j| N^Q_{m,b_n}(B,z), \end{align*} $$
$$ \begin{align*} |A'|\geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) -\sum_{j<p} \sum_{S\subseteq |B_j|} \sum_{r_S(B)=B_j} |B_j| N^Q_{m,b_n}(B,z), \end{align*} $$
where the first sum ranges over the j such that
![]() $B_j$
is sparse relative to
$B_j$
is sparse relative to
![]() $B_{i_0}$
, and the third sum ranges over blocks B with
$B_{i_0}$
, and the third sum ranges over blocks B with
![]() $r_S(B)=B_j$
, where
$r_S(B)=B_j$
, where
![]() $r_S$
applies r to the digits in the set S. Since r either lowers a digit or changes a
$r_S$
applies r to the digits in the set S. Since r either lowers a digit or changes a
![]() $0$
to a
$0$
to a
![]() $1$
, it follows that if
$1$
, it follows that if
![]() $r_S(B)=B_j$
then
$r_S(B)=B_j$
then
![]() $Q_k(B)\leq Q_k(B_j)$
for any k.
$Q_k(B)\leq Q_k(B_j)$
for any k.
Thus,
 $$ \begin{align*} |A^{\prime}_n|& \geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - \sum_{j<p} |B_j| 4^{|B_j|} N^Q_{b_n}(B_j) \\ & \geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - (1+\frac{1}{n})\sum_{j<p} |B_j| 4^{|B_j|} Q_{b_n}(B_j) \\ & \geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - (1+\frac{1}{n})\sum_{j<p} |B_j| 4^{|B_j|} \left(\frac{1}{4 |B_j|4^{|B_j|} \sqrt{x'(n)}} Q_{b_n}(B_{i_0})\right) \\ & \geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - \frac{1}{2} \frac{\sqrt[6]{x'(n)}}{\sqrt{x'(n)}} Q_{b_n}(B_{i_0}) \\ & = \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - \frac{1}{2 \sqrt[3]{x'(n)}} Q_{b_n}(B_{i_0}) \\ & \geq \frac{1}{\sqrt[3]{x'(n)}} Q_{b_n}(B_{i_0}) \end{align*} $$
$$ \begin{align*} |A^{\prime}_n|& \geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - \sum_{j<p} |B_j| 4^{|B_j|} N^Q_{b_n}(B_j) \\ & \geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - (1+\frac{1}{n})\sum_{j<p} |B_j| 4^{|B_j|} Q_{b_n}(B_j) \\ & \geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - (1+\frac{1}{n})\sum_{j<p} |B_j| 4^{|B_j|} \left(\frac{1}{4 |B_j|4^{|B_j|} \sqrt{x'(n)}} Q_{b_n}(B_{i_0})\right) \\ & \geq \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - \frac{1}{2} \frac{\sqrt[6]{x'(n)}}{\sqrt{x'(n)}} Q_{b_n}(B_{i_0}) \\ & = \frac{3}{2\sqrt[3] {x'(n)}}Q_{b_n}(B_{i_0}) - \frac{1}{2 \sqrt[3]{x'(n)}} Q_{b_n}(B_{i_0}) \\ & \geq \frac{1}{\sqrt[3]{x'(n)}} Q_{b_n}(B_{i_0}) \end{align*} $$
for all large enough n. Let
![]() $A"$
be the last
$A"$
be the last
![]() $\frac {1}{x'(n)} Q_{b_n}(B_{i_0})$
elements of
$\frac {1}{x'(n)} Q_{b_n}(B_{i_0})$
elements of
![]() $A'$
.
$A'$
.
For
![]() $i \in I_n$
, let
$i \in I_n$
, let
 $$ \begin{align*} \varphi_1(x)(i)=\begin{cases} r(z_i) &\text{if } i \in A",\\ z_i &\text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \varphi_1(x)(i)=\begin{cases} r(z_i) &\text{if } i \in A",\\ z_i &\text{otherwise.} \end{cases} \end{align*} $$
Note that
![]() $\varphi _1(x)\restriction I_n$
is obtained from
$\varphi _1(x)\restriction I_n$
is obtained from
![]() $z \restriction I_n$
by changing certain digits, the number of such changes being
$z \restriction I_n$
by changing certain digits, the number of such changes being
![]() $|A"|=\frac {1}{x'(n)} Q_{b_n}(B_{i_0})$
. Note that the least element i of
$|A"|=\frac {1}{x'(n)} Q_{b_n}(B_{i_0})$
. Note that the least element i of
![]() $A"$
is at least the number m from above (since
$A"$
is at least the number m from above (since
![]() $A" \subseteq A \subseteq [m,b_n]$
) and
$A" \subseteq A \subseteq [m,b_n]$
) and
 $$ \begin{align*} N_m(B_{i_0},z) & \geq N_{b_n}(B_{i_0},z)-N_{m,b_n}(B_{i_0},z) \\ & \geq N_{b_n}(B_{i_0},z)-\frac{2}{\sqrt[3]{x'(n)}} Q_{b_n}(B_{i_0}) \\ & \geq \left((1-\frac{1}{n})-\frac{2}{\sqrt[3]{x'(n)}}\right) Q_{b_n}(B_{i_0}), \end{align*} $$
$$ \begin{align*} N_m(B_{i_0},z) & \geq N_{b_n}(B_{i_0},z)-N_{m,b_n}(B_{i_0},z) \\ & \geq N_{b_n}(B_{i_0},z)-\frac{2}{\sqrt[3]{x'(n)}} Q_{b_n}(B_{i_0}) \\ & \geq \left((1-\frac{1}{n})-\frac{2}{\sqrt[3]{x'(n)}}\right) Q_{b_n}(B_{i_0}), \end{align*} $$
since
![]() $m=m(i_0)$
and using the definition of
$m=m(i_0)$
and using the definition of
![]() $m(i_0)$
. Since
$m(i_0)$
. Since
![]() $x'(n)\geq 27$
,
$x'(n)\geq 27$
,
![]() $N_m(B_{i_0},z)\geq \frac {1}{3} Q_{b_n}(B_{i_0})$
and in particular
$N_m(B_{i_0},z)\geq \frac {1}{3} Q_{b_n}(B_{i_0})$
and in particular
![]() $m \geq \frac {1}{3} Q_{b_n}(B_{i_0})$
. From property (3) of the
$m \geq \frac {1}{3} Q_{b_n}(B_{i_0})$
. From property (3) of the
![]() $b_n$
it follows that the first element of
$b_n$
it follows that the first element of
![]() $A"$
is at least
$A"$
is at least
![]() $\frac {4^n}{3} b_{n-1}>2^{n-1} b_{n-1}$
, for all large enough n.
$\frac {4^n}{3} b_{n-1}>2^{n-1} b_{n-1}$
, for all large enough n.
Suppose first that
![]() $x \notin P$
. There is a least
$x \notin P$
. There is a least
![]() $\ell $
, which we call
$\ell $
, which we call
![]() $\ell _0$
, such that for infinitely many n we have that
$\ell _0$
, such that for infinitely many n we have that
![]() $x'(n)=\ell _0$
. At such a stage n in the construction, we consider the first
$x'(n)=\ell _0$
. At such a stage n in the construction, we consider the first
![]() $\sqrt [6]{\ell _0}$
many blocks. So, for infinitely many such n we may assume that the block
$\sqrt [6]{\ell _0}$
many blocks. So, for infinitely many such n we may assume that the block
![]() $B_{i_0}$
is fixed, that is, the value of
$B_{i_0}$
is fixed, that is, the value of
![]() $i_0$
does not depend on n along this subsequence. Then for large enough such n we have:
$i_0$
does not depend on n along this subsequence. Then for large enough such n we have:
 $$ \begin{align} N^Q_{b_n}(B_{i_0},\varphi_1(x)) & \leq b_{n-1}+ N^Q_{b_n}(B_{i_0},z) -\frac{1}{\ell_0} Q_{b_n}(B_{i_0})\nonumber\\ & \leq b_{n-1}+ Q_{b_n}(B_{i_0})\left(1+\frac{1}{n}\right) - \frac{1}{\ell_0} Q_{b_n}(B_{i_0}) \nonumber\\ & \leq \left(\frac{1}{4^n}+1+\frac{1}{n} -\frac{1}{\ell_0}\right) Q_{b_n}(B_{i_0})\nonumber\\ & \leq \left(1-\frac{1}{2\ell_0}\right) Q_{b_n}(B_{i_0}). \end{align} $$
$$ \begin{align} N^Q_{b_n}(B_{i_0},\varphi_1(x)) & \leq b_{n-1}+ N^Q_{b_n}(B_{i_0},z) -\frac{1}{\ell_0} Q_{b_n}(B_{i_0})\nonumber\\ & \leq b_{n-1}+ Q_{b_n}(B_{i_0})\left(1+\frac{1}{n}\right) - \frac{1}{\ell_0} Q_{b_n}(B_{i_0}) \nonumber\\ & \leq \left(\frac{1}{4^n}+1+\frac{1}{n} -\frac{1}{\ell_0}\right) Q_{b_n}(B_{i_0})\nonumber\\ & \leq \left(1-\frac{1}{2\ell_0}\right) Q_{b_n}(B_{i_0}). \end{align} $$
This shows
![]() $\varphi (x)\notin \mathscr {N}(Q)$
when
$\varphi (x)\notin \mathscr {N}(Q)$
when
![]() $x \notin P$
. Consider the block
$x \notin P$
. Consider the block
![]() $B_{i_0}$
which is fixed along the subsequence. If
$B_{i_0}$
which is fixed along the subsequence. If
![]() $B_{i_0}(1) \geq 1$
, then we obtain
$B_{i_0}(1) \geq 1$
, then we obtain
![]() $\varphi _1(x)\restriction I_n$
from
$\varphi _1(x)\restriction I_n$
from
![]() $z \restriction I_n$
by lowering certain occurrences of the digit
$z \restriction I_n$
by lowering certain occurrences of the digit
![]() $B_{i_0}(1)$
to
$B_{i_0}(1)$
to
![]() $B_{i_0}(1)-1$
. This will not decrease the number of occurrences of the block
$B_{i_0}(1)-1$
. This will not decrease the number of occurrences of the block
![]() $0_k$
, where
$0_k$
, where
![]() $k=|B_{i_0}|$
. So,
$k=|B_{i_0}|$
. So,
![]() $N^Q_{b_n}(0_k,\varphi _1(x))\geq N^Q_{b_n}(0_k,z)\geq Q_{b_n}(0_k)(1-\epsilon )$
, for small
$N^Q_{b_n}(0_k,\varphi _1(x))\geq N^Q_{b_n}(0_k,z)\geq Q_{b_n}(0_k)(1-\epsilon )$
, for small
![]() $\epsilon $
(say
$\epsilon $
(say
![]() $\epsilon < \frac {1}{3\ell _0}$
) and all large enough n. This, along with Equation (7), shows
$\epsilon < \frac {1}{3\ell _0}$
) and all large enough n. This, along with Equation (7), shows
![]() $\varphi _1(x)\notin \mathscr {RN}(Q)$
. If
$\varphi _1(x)\notin \mathscr {RN}(Q)$
. If
![]() $B_{i_0}(1)=0$
, then r maps
$B_{i_0}(1)=0$
, then r maps
![]() $0$
to
$0$
to
![]() $1$
and leaves all other digits unchanged. This cannot decrease the number of occurrences of the block
$1$
and leaves all other digits unchanged. This cannot decrease the number of occurrences of the block
![]() $1_k$
. So,
$1_k$
. So,
![]() $N^Q_{b_n}(1_k,\varphi _1(x))\geq N^Q_{b_n}(1_k,z)\geq Q_{b_n}(1_k)(1-\epsilon )$
which again shows
$N^Q_{b_n}(1_k,\varphi _1(x))\geq N^Q_{b_n}(1_k,z)\geq Q_{b_n}(1_k)(1-\epsilon )$
which again shows
![]() $\varphi _1(x)\notin \mathscr {RN}(Q)$
.
$\varphi _1(x)\notin \mathscr {RN}(Q)$
.
Suppose now that
![]() $x \in P$
so that
$x \in P$
so that
![]() $\lim _n x'(n)=\infty $
. Let B be a good block, and fix
$\lim _n x'(n)=\infty $
. Let B be a good block, and fix
![]() $\epsilon>0$
. Let
$\epsilon>0$
. Let
![]() $n_0>|B|$
be such that for all
$n_0>|B|$
be such that for all
![]() $n \geq n_0$
,
$n \geq n_0$
,
![]() $x'(n)$
is large enough that B is one of the first
$x'(n)$
is large enough that B is one of the first
![]() $\sqrt [6]{x'(n)}$
many blocks. Consider now
$\sqrt [6]{x'(n)}$
many blocks. Consider now
![]() $n \geq n_0$
and corresponding interval
$n \geq n_0$
and corresponding interval
![]() $I_n$
. Let
$I_n$
. Let
![]() $\delta>0$
and assume n is sufficiently large and inductively that we have shown
$\delta>0$
and assume n is sufficiently large and inductively that we have shown
![]() $|N^Q_{b_{n-1}}(B,z)-N^Q_{b_{n-1}}(B,\varphi _1(x))| \leq \delta Q_{b_{n-1}}(B)$
.
$|N^Q_{b_{n-1}}(B,z)-N^Q_{b_{n-1}}(B,\varphi _1(x))| \leq \delta Q_{b_{n-1}}(B)$
.
Consider first the case B is sparse at stage n relative to
![]() $B_{i_0}$
. Let p be as before, so
$B_{i_0}$
. Let p be as before, so
![]() $p \leq \sqrt [6]{x'(n)}$
. Then
$p \leq \sqrt [6]{x'(n)}$
. Then
![]() $B=B_j$
for some
$B=B_j$
for some
![]() $j \leq p$
. So, for any
$j \leq p$
. So, for any
![]() $i \in I_n$
we have that if
$i \in I_n$
we have that if
![]() $z \restriction [ i, i+|B|-1]=B$
or
$z \restriction [ i, i+|B|-1]=B$
or
![]() $\varphi _1(x) \restriction [ i, i+|B|-1]=B$
then
$\varphi _1(x) \restriction [ i, i+|B|-1]=B$
then
![]() $[i,i+|B|-1]\cap A^{\prime }_n=\emptyset $
. Since
$[i,i+|B|-1]\cap A^{\prime }_n=\emptyset $
. Since
![]() $x \restriction I_n$
is obtained from
$x \restriction I_n$
is obtained from
![]() $z \restriction I_n$
by changing the value only at points of
$z \restriction I_n$
by changing the value only at points of
![]() $A^{\prime \prime }_n \subseteq A^{\prime }_n$
, it follows that for any
$A^{\prime \prime }_n \subseteq A^{\prime }_n$
, it follows that for any
![]() $k \in [b_{n-1},b_n]$
that
$k \in [b_{n-1},b_n]$
that
![]() $|N^Q_{k}(B,z)-N^Q_{k}(B,\varphi _1(x))|= |N^Q_{b_{n-1}}(B,z)-N^Q_{b_{n-1}}(B,\varphi _1(x))|$
. So we have for
$|N^Q_{k}(B,z)-N^Q_{k}(B,\varphi _1(x))|= |N^Q_{b_{n-1}}(B,z)-N^Q_{b_{n-1}}(B,\varphi _1(x))|$
. So we have for
![]() $k\in [b_{n-1},b_n]$
and large enough n:
$k\in [b_{n-1},b_n]$
and large enough n:
 $$ \begin{align} |N^Q_k(B,\varphi_1(x))-Q_k(B)|& \leq |N^Q_k(B,z)-Q_k(B)|+|N^Q_{b_{n-1}}(B,\varphi_1(x)) -N^Q_{b_{n-1}}(B,z)| \nonumber\\ & \leq |N^Q_k(B,z)-Q_k(B)|+ \delta Q_{b_{n-1}}(B) \nonumber\\ & \leq \frac{1}{2^n}Q_k(B)+ \delta Q_{k}(B) \nonumber\\ & \leq Q_k(B) \left(\frac{1}{2^n}+\delta \right), \end{align} $$
$$ \begin{align} |N^Q_k(B,\varphi_1(x))-Q_k(B)|& \leq |N^Q_k(B,z)-Q_k(B)|+|N^Q_{b_{n-1}}(B,\varphi_1(x)) -N^Q_{b_{n-1}}(B,z)| \nonumber\\ & \leq |N^Q_k(B,z)-Q_k(B)|+ \delta Q_{b_{n-1}}(B) \nonumber\\ & \leq \frac{1}{2^n}Q_k(B)+ \delta Q_{k}(B) \nonumber\\ & \leq Q_k(B) \left(\frac{1}{2^n}+\delta \right), \end{align} $$
which verifies normality for the block B. Since
![]() $|N^Q_{b_n}(B,z)-N^Q_{b_n}(B,\varphi _1(x))|= |N^Q_{b_{n-1}}(B,z)-N^Q_{b_{n-1}}(B,\varphi _1(x))|$
, the inductive hypothesis at
$|N^Q_{b_n}(B,z)-N^Q_{b_n}(B,\varphi _1(x))|= |N^Q_{b_{n-1}}(B,z)-N^Q_{b_{n-1}}(B,\varphi _1(x))|$
, the inductive hypothesis at
![]() $b_n$
follows immediately.
$b_n$
follows immediately.
Consider next the case that
![]() $B=B_j$
is not sparse at stage n relative to
$B=B_j$
is not sparse at stage n relative to
![]() $B_{i_0}$
. From the definition of
$B_{i_0}$
. From the definition of
![]() $i_0$
and m we have that
$i_0$
and m we have that
 $$ \begin{align} Q_m(B) \geq Q_{m_j}(B_j)\geq \left(1-\frac{2}{\sqrt[3]{x'(n)}}\right) Q_{b_n}(B_j). \end{align} $$
$$ \begin{align} Q_m(B) \geq Q_{m_j}(B_j)\geq \left(1-\frac{2}{\sqrt[3]{x'(n)}}\right) Q_{b_n}(B_j). \end{align} $$
From the definition of being sparse relative to
![]() $B_{i_0}$
we have that
$B_{i_0}$
we have that
 $$ \begin{align} Q_{b_n}(B) \geq \frac{1}{4 |B| 4^{|B|} \sqrt{x'(n)}} Q_{b_n}(B_{i_0}). \end{align} $$
$$ \begin{align} Q_{b_n}(B) \geq \frac{1}{4 |B| 4^{|B|} \sqrt{x'(n)}} Q_{b_n}(B_{i_0}). \end{align} $$
Recall that
![]() $\varphi _1(x) \restriction I_n$
and
$\varphi _1(x) \restriction I_n$
and
![]() $z\restriction I_n$
only differ on
$z\restriction I_n$
only differ on
![]() $A"$
, and
$A"$
, and
![]() $\min (A")\geq m$
.
$\min (A")\geq m$
.
Now let
![]() $k \in [b_{n-1},b_n]$
, and we estimate
$k \in [b_{n-1},b_n]$
, and we estimate
![]() $|N^Q_k(B,\varphi _1(x))-Q_k(B)|$
. If
$|N^Q_k(B,\varphi _1(x))-Q_k(B)|$
. If
![]() $k<m$
then
$k<m$
then
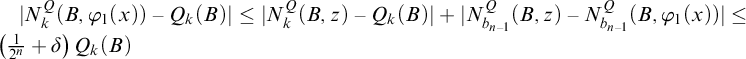 $|N^Q_k(B,\varphi _1(x))-Q_k(B)|\leq |N^Q_k(B,z)-Q_k(B)|+ |N^Q_{b_{n-1}}(B,z)-N^Q_{b_{n-1}}(B,\varphi _1(x))| \leq \left ( \frac {1}{2^n}+\delta \right ) Q_k(B)$
, which verifies normality for B.
$|N^Q_k(B,\varphi _1(x))-Q_k(B)|\leq |N^Q_k(B,z)-Q_k(B)|+ |N^Q_{b_{n-1}}(B,z)-N^Q_{b_{n-1}}(B,\varphi _1(x))| \leq \left ( \frac {1}{2^n}+\delta \right ) Q_k(B)$
, which verifies normality for B.
So, assume
![]() $k \geq m$
. We have
$k \geq m$
. We have
 $$ \begin{align*} |N^Q_k(B,\varphi_1(x))-Q_k(B)| & \leq b_{n-1}+ \frac{1}{x'(n)} Q_{b_n}(B_{i_0}) + |N^Q_{k}(B,z)-Q_k(B)| \\ & \leq \frac{1}{2^n} Q_{b_n}(B)+ \frac{1}{x'(n)} Q_{b_n}(B_{i_0})+ \frac{1}{2^n} Q_k(B) \\ & \leq \frac{1}{2^n} \frac{1}{1- \frac{2}{\sqrt[3]{x'(n)}}} Q_m(B) +\frac{1}{x'(n)} Q_{b_n}(B_{i_0})+ \frac{1}{2^n} Q_k(B) \\ & \leq \frac{1}{2^{n-2}}Q_m(B)+ \frac{1}{x'(n)} Q_{b_n}(B_{i_0})+ \frac{1}{2^n} Q_k(B) \\ & \leq \frac{1}{2^{n-3}}Q_k(B)+ \frac{1}{x'(n)} 4|B|4^{|B|} \sqrt{x'(n)} Q_{b_n}(B) \\ & \leq \frac{1}{2^{n-3}}Q_k(B)+ \frac{1}{x'(n)} 4|B|4^{|B|} \sqrt{x'(n)} \frac{1}{1- \frac{2}{\sqrt[3]{x'(n)}}} Q_m(B) \\ & \leq \frac{1}{2^{n-3}}Q_k(B)+ \frac{12|B|4^{|B|}}{\sqrt{x'(n)}} Q_k(B). \end{align*} $$
$$ \begin{align*} |N^Q_k(B,\varphi_1(x))-Q_k(B)| & \leq b_{n-1}+ \frac{1}{x'(n)} Q_{b_n}(B_{i_0}) + |N^Q_{k}(B,z)-Q_k(B)| \\ & \leq \frac{1}{2^n} Q_{b_n}(B)+ \frac{1}{x'(n)} Q_{b_n}(B_{i_0})+ \frac{1}{2^n} Q_k(B) \\ & \leq \frac{1}{2^n} \frac{1}{1- \frac{2}{\sqrt[3]{x'(n)}}} Q_m(B) +\frac{1}{x'(n)} Q_{b_n}(B_{i_0})+ \frac{1}{2^n} Q_k(B) \\ & \leq \frac{1}{2^{n-2}}Q_m(B)+ \frac{1}{x'(n)} Q_{b_n}(B_{i_0})+ \frac{1}{2^n} Q_k(B) \\ & \leq \frac{1}{2^{n-3}}Q_k(B)+ \frac{1}{x'(n)} 4|B|4^{|B|} \sqrt{x'(n)} Q_{b_n}(B) \\ & \leq \frac{1}{2^{n-3}}Q_k(B)+ \frac{1}{x'(n)} 4|B|4^{|B|} \sqrt{x'(n)} \frac{1}{1- \frac{2}{\sqrt[3]{x'(n)}}} Q_m(B) \\ & \leq \frac{1}{2^{n-3}}Q_k(B)+ \frac{12|B|4^{|B|}}{\sqrt{x'(n)}} Q_k(B). \end{align*} $$
Since
![]() $x'(n)\to \infty $
, this shows normality for the block B. Similarly, letting
$x'(n)\to \infty $
, this shows normality for the block B. Similarly, letting
![]() $k=b_n$
we have
$k=b_n$
we have
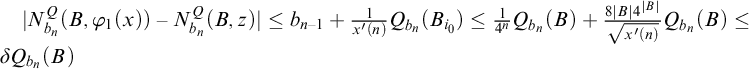 $|N^Q_{b_n}(B,\varphi _1(x))-N^Q_{b_n}(B,z)|\leq b_{n-1}+\frac {1}{x'(n)} Q_{b_n}(B_{i_0}) \leq \frac {1}{4^n} Q_{b_n}(B)+ \frac {8|B|4^{|B|}}{\sqrt {x'(n)}} Q_{b_n}(B) \leq \delta Q_{b_n}(B)$
, which verifies the inductive hypothesis at
$|N^Q_{b_n}(B,\varphi _1(x))-N^Q_{b_n}(B,z)|\leq b_{n-1}+\frac {1}{x'(n)} Q_{b_n}(B_{i_0}) \leq \frac {1}{4^n} Q_{b_n}(B)+ \frac {8|B|4^{|B|}}{\sqrt {x'(n)}} Q_{b_n}(B) \leq \delta Q_{b_n}(B)$
, which verifies the inductive hypothesis at
![]() $b_n$
.
$b_n$
.
This completes the proof that
![]() $\mathscr {N}(Q)$
and
$\mathscr {N}(Q)$
and
![]() $\mathscr {RN}(Q)$
are
$\mathscr {RN}(Q)$
are
![]() $\boldsymbol {\Pi }^0_3$
-complete assuming Q is
$\boldsymbol {\Pi }^0_3$
-complete assuming Q is
![]() $1$
-divergent. If Q is
$1$
-divergent. If Q is
![]() $1$
-convergent, then every x is in
$1$
-convergent, then every x is in
![]() $\mathscr {N}(Q)$
and
$\mathscr {N}(Q)$
and
![]() $\mathscr {RN}(Q)$
, so the conclusion of Theorem 1.11 holds trivially.⊣
$\mathscr {RN}(Q)$
, so the conclusion of Theorem 1.11 holds trivially.⊣
The second part of Theorem 1.11 concerning
![]() $\mathscr {N}_k(Q)$
and
$\mathscr {N}_k(Q)$
and
![]() $\mathscr {RN}_k(Q)$
and the proof of Theorem 1.12 are slight generalizations of the proof of Theorem 1.11 given above. Since the proofs are similar we just sketch the differences.
$\mathscr {RN}_k(Q)$
and the proof of Theorem 1.12 are slight generalizations of the proof of Theorem 1.11 given above. Since the proofs are similar we just sketch the differences.
Proof of Theorem 1.12. We use the notation and terminology of the proof of Theorem 1.11. We may assume that all of the blocks
![]() $B\in \mathscr {C}$
have infinite expectation, that is,
$B\in \mathscr {C}$
have infinite expectation, that is,
![]() $\displaystyle \lim _{n \to \infty } Q_n(B)=\infty $
. At stage n of the construction we again let
$\displaystyle \lim _{n \to \infty } Q_n(B)=\infty $
. At stage n of the construction we again let
![]() $p=\lfloor \sqrt [6]{x'(n)} \rfloor $
, and let
$p=\lfloor \sqrt [6]{x'(n)} \rfloor $
, and let
![]() $B_1,\dots ,B_p$
enumerate the first p many blocks of
$B_1,\dots ,B_p$
enumerate the first p many blocks of
![]() $\mathscr {C}$
. We define the block
$\mathscr {C}$
. We define the block
![]() $B_{i_0}$
as before, maximizing the value of
$B_{i_0}$
as before, maximizing the value of
![]() $m(i)$
for
$m(i)$
for
![]() $1 \leq i \leq p$
. For the first part of Theorem 1.12 we may use the same digit changing function r as in the proof of Theorem 1.11. If
$1 \leq i \leq p$
. For the first part of Theorem 1.12 we may use the same digit changing function r as in the proof of Theorem 1.11. If
![]() $x\in P$
, then the proof of Theorem 1.11 shows that
$x\in P$
, then the proof of Theorem 1.11 shows that
![]() $\varphi (x)\in \mathscr {N}_{\mathscr {C}}(Q)$
. If
$\varphi (x)\in \mathscr {N}_{\mathscr {C}}(Q)$
. If
![]() $x \notin P$
, then for infinitely many n the value of
$x \notin P$
, then for infinitely many n the value of
![]() $i_0$
will be constant, and
$i_0$
will be constant, and
![]() $B_{i_0}$
is a block in
$B_{i_0}$
is a block in
![]() $\mathscr {C}$
. As in Equation (7), this gives an
$\mathscr {C}$
. As in Equation (7), this gives an
![]() $\epsilon>0$
such that for infinitely many n we have
$\epsilon>0$
such that for infinitely many n we have
![]() $|N^Q_{b_n}(B_{i_0},\varphi _1(x))-Q_{b_n}(B_{i_0})|>\epsilon Q_{b_n}(B_{i_0})$
. Thus,
$|N^Q_{b_n}(B_{i_0},\varphi _1(x))-Q_{b_n}(B_{i_0})|>\epsilon Q_{b_n}(B_{i_0})$
. Thus,
![]() $\varphi (x)\notin \mathscr {N}_{\mathscr {C}}(Q)$
. For the second statement of Theorem 1.12 we modify the argument as the blocks
$\varphi (x)\notin \mathscr {N}_{\mathscr {C}}(Q)$
. For the second statement of Theorem 1.12 we modify the argument as the blocks
![]() $0_k$
and
$0_k$
and
![]() $1_k$
used in the proof of Theorem 1.11 may not be in
$1_k$
used in the proof of Theorem 1.11 may not be in
![]() $\mathscr {C}$
. The additional hypothesis of Theorem 1.12, however, guarantees the existence of a block
$\mathscr {C}$
. The additional hypothesis of Theorem 1.12, however, guarantees the existence of a block
![]() $B_j\in \mathscr {C}$
and an integer t such that
$B_j\in \mathscr {C}$
and an integer t such that
![]() $|B_{i_0}(t)-B_j(t')|>1$
for all
$|B_{i_0}(t)-B_j(t')|>1$
for all
![]() $t'$
. As in the argument after Equation (7), we modify the definition of
$t'$
. As in the argument after Equation (7), we modify the definition of
![]() $\varphi _1(x)\restriction I_n$
to change by
$\varphi _1(x)\restriction I_n$
to change by
![]() $1$
all occurrences of
$1$
all occurrences of
![]() $B_{i_0}(t)$
in
$B_{i_0}(t)$
in
![]() $z \restriction I_n$
which correspond to a possible occurrence of
$z \restriction I_n$
which correspond to a possible occurrence of
![]() $B_{i_0}$
(that is, the integers
$B_{i_0}$
(that is, the integers
![]() $i \in I_n$
where
$i \in I_n$
where
![]() $z\restriction [i-t+1,i+|B_{i_0}|]=B_{i_0}$
). This will not affect the number of occurrences of the block
$z\restriction [i-t+1,i+|B_{i_0}|]=B_{i_0}$
). This will not affect the number of occurrences of the block
![]() $B_j$
in
$B_j$
in
![]() $I_n$
. This gives that
$I_n$
. This gives that
![]() $\varphi (x)\notin \mathscr {RN}_{\mathscr {C}}(Q)$
.⊣
$\varphi (x)\notin \mathscr {RN}_{\mathscr {C}}(Q)$
.⊣
3 Proof of Theorem 1.15
We will show the
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-completeness of the non-trivial combinations of the form
$D_2(\boldsymbol {\Pi }^0_3)$
-completeness of the non-trivial combinations of the form
![]() $A\setminus B$
where
$A\setminus B$
where
![]() $A,B$
are one of
$A,B$
are one of
![]() $\mathscr {N}(Q)$
,
$\mathscr {N}(Q)$
,
![]() $\mathscr {DN}(Q)$
, and
$\mathscr {DN}(Q)$
, and
![]() $\mathscr {RN}(Q)$
. There are five non-trivial combinations, as
$\mathscr {RN}(Q)$
. There are five non-trivial combinations, as
![]() $\mathscr {N}(Q)\subseteq \mathscr {RN}(Q)$
. Section 3.1 handles four of these cases, which are essentially done by the same proof. The fifth case,
$\mathscr {N}(Q)\subseteq \mathscr {RN}(Q)$
. Section 3.1 handles four of these cases, which are essentially done by the same proof. The fifth case,
![]() $\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
, is more complicated and will be handled in Section 3.2. We note that the
$\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
, is more complicated and will be handled in Section 3.2. We note that the
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-completeness of the sets
$D_2(\boldsymbol {\Pi }^0_3)$
-completeness of the sets
![]() $A\setminus B$
implies that the sets of the form
$A\setminus B$
implies that the sets of the form
![]() $A\cap B$
or of the form
$A\cap B$
or of the form
![]() $A\cup B$
(for
$A\cup B$
(for
![]() $A,B \in \mathscr {N}(Q), \mathscr {DN}(Q), \mathscr {RN}(Q)$
) are
$A,B \in \mathscr {N}(Q), \mathscr {DN}(Q), \mathscr {RN}(Q)$
) are
![]() $\boldsymbol {\Pi }^0_3$
-complete by the following simple lemma.
$\boldsymbol {\Pi }^0_3$
-complete by the following simple lemma.
Lemma 3.1. If
![]() $A,B$
are
$A,B$
are
![]() $\boldsymbol {\Pi }^0_3$
and
$\boldsymbol {\Pi }^0_3$
and
![]() $A\setminus B$
is
$A\setminus B$
is
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-complete, then
$D_2(\boldsymbol {\Pi }^0_3)$
-complete, then
![]() $A\cup B$
and
$A\cup B$
and
![]() $A\cap B$
are
$A\cap B$
are
![]() $\boldsymbol {\Pi }^0_3$
-complete.
$\boldsymbol {\Pi }^0_3$
-complete.
Proof. Suppose that
![]() $A\cup B$
were
$A\cup B$
were
![]() $\boldsymbol {\Sigma }^0_3$
. Then
$\boldsymbol {\Sigma }^0_3$
. Then
![]() $A\setminus B= (A\cup B)\setminus B$
would be
$A\setminus B= (A\cup B)\setminus B$
would be
![]() $\boldsymbol {\Sigma }^0_3$
, a contradiction. Likewise, if
$\boldsymbol {\Sigma }^0_3$
, a contradiction. Likewise, if
![]() $A\cap B$
were
$A\cap B$
were
![]() $\boldsymbol {\Sigma }^0_3$
then
$\boldsymbol {\Sigma }^0_3$
then
![]() $A\setminus B=A\setminus (A\cap B)$
would be
$A\setminus B=A\setminus (A\cap B)$
would be
![]() $\boldsymbol {\Pi }^0_3$
, a contradiction.⊣
$\boldsymbol {\Pi }^0_3$
, a contradiction.⊣
Lastly, we note that since
![]() $\mathscr {N}(Q), \mathscr {RN}(Q)$
, and
$\mathscr {N}(Q), \mathscr {RN}(Q)$
, and
![]() $\mathscr {DN}(Q)$
are sets of full measure by Theorem 1.9, their intersections are nonempty. We will freely use this fact without mentioning it.
$\mathscr {DN}(Q)$
are sets of full measure by Theorem 1.9, their intersections are nonempty. We will freely use this fact without mentioning it.
3.1 Completeness of
 $\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
,
$\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
,
 $\mathscr {DN}(Q)\setminus \mathscr {RN}(Q)$
,
$\mathscr {DN}(Q)\setminus \mathscr {RN}(Q)$
,
 $\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
, and
$\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
, and
 $\mathscr {RN}(Q)\setminus \mathscr {DN}(Q)$
$\mathscr {RN}(Q)\setminus \mathscr {DN}(Q)$
Theorem 3.2. Let Q be infinite in limit and
![]() $1$
-divergent. Then the sets
$1$
-divergent. Then the sets
![]() $\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
,
$\mathscr {DN}(Q)\setminus \mathscr {N}(Q)$
,
![]() $\mathscr {DN}(Q)\setminus \mathscr {RN}(Q)$
,
$\mathscr {DN}(Q)\setminus \mathscr {RN}(Q)$
,
![]() $\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
, and
$\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
, and
![]() $\mathscr {RN}(Q)\setminus \mathscr {DN}(Q)$
are all
$\mathscr {RN}(Q)\setminus \mathscr {DN}(Q)$
are all
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-complete.
$D_2(\boldsymbol {\Pi }^0_3)$
-complete.
Proof. Let
![]() $C=\{ x \in \omega ^\omega \colon x(2n) \to \infty \}$
and
$C=\{ x \in \omega ^\omega \colon x(2n) \to \infty \}$
and
![]() $D=\{ x \in \omega ^\omega \colon x(2n+1)\to \infty \}$
. It is easy to see that
$D=\{ x \in \omega ^\omega \colon x(2n+1)\to \infty \}$
. It is easy to see that
![]() $C\setminus D$
is
$C\setminus D$
is
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-complete.
$D_2(\boldsymbol {\Pi }^0_3)$
-complete.
Fix a fast growing sequence
![]() $\{ b_n\}$
, so in particular
$\{ b_n\}$
, so in particular
![]() $(2^n\sum _{i<n}b_i)/b_n \to 0$
. Recall
$(2^n\sum _{i<n}b_i)/b_n \to 0$
. Recall
![]() $0_k$
denotes the sequence of length k consisting of all
$0_k$
denotes the sequence of length k consisting of all
![]() $0$
s. We introduce two basic operations which can be performed on an interval
$0$
s. We introduce two basic operations which can be performed on an interval
![]() $I\in \mathbb {N}^{[a,b]}$
of digits:
$I\in \mathbb {N}^{[a,b]}$
of digits:
![]() $\Theta _{k,\ell }$
: Let
$\Theta _{k,\ell }$
: Let
![]() $A\subseteq [a,b]$
be the set of j which start an occurrence of
$A\subseteq [a,b]$
be the set of j which start an occurrence of
![]() $0_k$
, that is,
$0_k$
, that is,
![]() $(I(j),\dots ,I(j+k-1))=0_k$
. Let
$(I(j),\dots ,I(j+k-1))=0_k$
. Let
![]() $A'\subseteq A$
be the last
$A'\subseteq A$
be the last
![]() $\lfloor \frac {|A|}{\ell } \rfloor $
many elements of A. For each
$\lfloor \frac {|A|}{\ell } \rfloor $
many elements of A. For each
![]() $j \in A'$
, change the digit
$j \in A'$
, change the digit
![]() $I(j)$
from a
$I(j)$
from a
![]() $0$
to a
$0$
to a
![]() $1$
.
$1$
.
![]() $\Xi _k$
: For every
$\Xi _k$
: For every
![]() $j\in [a,b]$
with
$j\in [a,b]$
with
![]() $I(j)\in [\frac {k}{k+1} q_j, q_j]$
, change the digit from
$I(j)\in [\frac {k}{k+1} q_j, q_j]$
, change the digit from
![]() $I(j)$
to
$I(j)$
to
![]() $q_j-1$
.
$q_j-1$
.
For the difference hierarchy results we will use both operations, exploiting the fact that, roughly speaking, they allow us to modify normality/ratio normality and distribution normality independently.
Let
![]() $z\in \mathscr {DN}(Q) \cap \mathscr {RN}(Q)$
, and let
$z\in \mathscr {DN}(Q) \cap \mathscr {RN}(Q)$
, and let
![]() $(z_i)_{i=1}^\infty \in X_Q$
be the digits of the Q-Cantor series expansion of z.
$(z_i)_{i=1}^\infty \in X_Q$
be the digits of the Q-Cantor series expansion of z.
We suppose the
![]() $b_n$
are chosen so that for all
$b_n$
are chosen so that for all
![]() $k \leq 2n$
such that Q is k-divergent we have
$k \leq 2n$
such that Q is k-divergent we have
![]() $Q^{(k)}_{{b_n}}> 2^n b_{n-1}$
and
$Q^{(k)}_{{b_n}}> 2^n b_{n-1}$
and
![]() $\forall m \geq b_{n}\ |N^Q_m(0_k,z)-Q^{(k)}_{m}|< \frac {1}{2^n} Q^{(k)}_{m}$
.
$\forall m \geq b_{n}\ |N^Q_m(0_k,z)-Q^{(k)}_{m}|< \frac {1}{2^n} Q^{(k)}_{m}$
.
Suppose first that
![]() $\lim _n Q^{(k)}_{n}=\infty $
for all k, that is, Q is fully divergent. Given
$\lim _n Q^{(k)}_{n}=\infty $
for all k, that is, Q is fully divergent. Given
![]() $x \in \omega ^\omega $
, we define
$x \in \omega ^\omega $
, we define
![]() $\varphi _1(x)\in X_Q$
as follows. Let
$\varphi _1(x)\in X_Q$
as follows. Let
![]() $x'(n)=\max \{ 2, \min \{ x(n),n\}\}$
. Consider the interval of digits
$x'(n)=\max \{ 2, \min \{ x(n),n\}\}$
. Consider the interval of digits
![]() $z\restriction I_n$
, where
$z\restriction I_n$
, where
![]() $I_n= [b_{n-1},b_n)$
. We let
$I_n= [b_{n-1},b_n)$
. We let
![]() $\varphi _1(x)\restriction [b_{n-1}, b_n)$
be given by starting with
$\varphi _1(x)\restriction [b_{n-1}, b_n)$
be given by starting with
![]() $z\restriction I_n$
and applying the operation
$z\restriction I_n$
and applying the operation
![]() $\Theta _{x'(2n),x'(2n)}$
and then the operation
$\Theta _{x'(2n),x'(2n)}$
and then the operation
![]() $\Xi _{x'(2n+1)}$
to it.
$\Xi _{x'(2n+1)}$
to it.
Recall
![]() $\varphi _2\colon X_Q\to [0,1]$
is the continuous map
$\varphi _2\colon X_Q\to [0,1]$
is the continuous map
 $$ \begin{align*} \varphi_2(d_1, d_2\dots)= \sum_{i=1}^\infty \frac{d_i}{q_1\cdots q_i}. \end{align*} $$
$$ \begin{align*} \varphi_2(d_1, d_2\dots)= \sum_{i=1}^\infty \frac{d_i}{q_1\cdots q_i}. \end{align*} $$
We show that
![]() $\varphi =\varphi _2 \circ \varphi _1$
is a reduction from
$\varphi =\varphi _2 \circ \varphi _1$
is a reduction from
![]() $C\setminus D$
to
$C\setminus D$
to
![]() $\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
. In fact, we show that
$\mathscr {N}(Q)\setminus \mathscr {DN}(Q)$
. In fact, we show that
![]() $x \in C$
iff
$x \in C$
iff
![]() $\varphi (x) \in \mathscr {N}(Q)$
and
$\varphi (x) \in \mathscr {N}(Q)$
and
![]() $x \in D$
iff
$x \in D$
iff
![]() $\varphi (x)\in \mathscr {DN}(Q)$
.
$\varphi (x)\in \mathscr {DN}(Q)$
.
Since
![]() $q_i\to \infty $
, the
$q_i\to \infty $
, the
![]() $\Theta $
operation does not affect distribution normality as it involves changing each digit in the Q Cantor series expansion by at most
$\Theta $
operation does not affect distribution normality as it involves changing each digit in the Q Cantor series expansion by at most
![]() $1$
(see Remark 1.8). Also, as
$1$
(see Remark 1.8). Also, as
![]() $q_i\to \infty $
we have that the
$q_i\to \infty $
we have that the
![]() $\Xi $
operation does not effect normality, since for any block of digits B we have that
$\Xi $
operation does not effect normality, since for any block of digits B we have that
![]() $|N^Q_n(B,z)-N^Q_n(B,y)|$
is bounded with n (regardless of x), where y is the result of applying the
$|N^Q_n(B,z)-N^Q_n(B,y)|$
is bounded with n (regardless of x), where y is the result of applying the
![]() $\Xi $
operation in all of the
$\Xi $
operation in all of the
![]() $I_n$
.
$I_n$
.
First suppose
![]() $x\in C$
, so
$x\in C$
, so
![]() $x(2n)\to \infty $
. Let w be the result of applying just the first operation
$x(2n)\to \infty $
. Let w be the result of applying just the first operation
![]() $\Theta _{x'(2n),x'(2n)}$
to z in each of the intervals
$\Theta _{x'(2n),x'(2n)}$
to z in each of the intervals
![]() $I_n$
. We claim that
$I_n$
. We claim that
![]() $w \in \mathscr {N}(Q)$
. Consider a block B of digits, and let
$w \in \mathscr {N}(Q)$
. Consider a block B of digits, and let
![]() $k=|B|$
denote its length. First note that for any
$k=|B|$
denote its length. First note that for any
![]() $\epsilon>0$
and all large enough n we have
$\epsilon>0$
and all large enough n we have
 $$ \begin{align*} | N^Q_{b_n}(B,w)-N^Q_{b_n}(B,z)|& \leq b_{n-1}+ \frac{2|B| }{x'(2n)} N^Q_{b_n}(0_{x'(2n)},z) \\ & \leq b_{n-1}+ \frac{2|B| }{x'(2n)} \left(1+\frac{1}{2^n}\right) Q_{b_n}(0_{x'(2n)}) \\ & \leq b_{n-1}+ \frac{2|B| }{x'(2n)} 2 Q_{b_n}(B) \\ & \leq \epsilon Q_{b_n}(B). \end{align*} $$
$$ \begin{align*} | N^Q_{b_n}(B,w)-N^Q_{b_n}(B,z)|& \leq b_{n-1}+ \frac{2|B| }{x'(2n)} N^Q_{b_n}(0_{x'(2n)},z) \\ & \leq b_{n-1}+ \frac{2|B| }{x'(2n)} \left(1+\frac{1}{2^n}\right) Q_{b_n}(0_{x'(2n)}) \\ & \leq b_{n-1}+ \frac{2|B| }{x'(2n)} 2 Q_{b_n}(B) \\ & \leq \epsilon Q_{b_n}(B). \end{align*} $$
Since
![]() $z \in \mathscr {N}(Q)$
, for large enough n we have
$z \in \mathscr {N}(Q)$
, for large enough n we have
![]() $| N^Q_{b_n}(B,w)- Q_{b_n}(B)|<2 \epsilon Q_{b_n}(B)$
. Fix
$| N^Q_{b_n}(B,w)- Q_{b_n}(B)|<2 \epsilon Q_{b_n}(B)$
. Fix
![]() $\epsilon>0$
, and consider now n large enough and
$\epsilon>0$
, and consider now n large enough and
![]() $k \in [b_{n-1},b_n)$
. Let m be the first element of
$k \in [b_{n-1},b_n)$
. Let m be the first element of
![]() $A'$
in
$A'$
in
![]() $I_n$
. Note that
$I_n$
. Note that
![]() $|A| \geq 2^n b_{n-1}$
, and so
$|A| \geq 2^n b_{n-1}$
, and so
![]() $m \geq 2^{n-1}b_{n-1}$
as
$m \geq 2^{n-1}b_{n-1}$
as
![]() $x'(2n)\geq 2$
. If
$x'(2n)\geq 2$
. If
![]() $k <m$
then we have
$k <m$
then we have
 $$ \begin{align*} | N^Q_k(B,w)-Q_k(B)| & \leq |N^Q_{b_{n-1}}(B,w)-Q_{b_{n-1}}(B)| + |N^Q_{b_{n-1},k}(B,w)-Q_{b_{n-1},k}(B)| \\ & \leq 2\epsilon Q_{b_{n-1}}(B)+ |N^Q_{b_{n-1},k}(B,z)-Q_{b_{n-1},k}(B)| \\ & \leq 2\epsilon Q_{b_{n-1}}(B)+ |N^Q_k(B,z)-Q_k(B)|+ |N^Q_{b_{n-1}}(B,z)-Q_{b_{n-1}}(B)| \\ & \leq \left(2\epsilon +\frac{2}{2^n}\right) Q_k(B). \end{align*} $$
$$ \begin{align*} | N^Q_k(B,w)-Q_k(B)| & \leq |N^Q_{b_{n-1}}(B,w)-Q_{b_{n-1}}(B)| + |N^Q_{b_{n-1},k}(B,w)-Q_{b_{n-1},k}(B)| \\ & \leq 2\epsilon Q_{b_{n-1}}(B)+ |N^Q_{b_{n-1},k}(B,z)-Q_{b_{n-1},k}(B)| \\ & \leq 2\epsilon Q_{b_{n-1}}(B)+ |N^Q_k(B,z)-Q_k(B)|+ |N^Q_{b_{n-1}}(B,z)-Q_{b_{n-1}}(B)| \\ & \leq \left(2\epsilon +\frac{2}{2^n}\right) Q_k(B). \end{align*} $$
If
![]() $k\geq m$
, then for large enough n first note that we have
$k\geq m$
, then for large enough n first note that we have
 $$ \begin{align*} Q_k(B) & \geq Q_k(0_{x'(2n)}) \geq (1-\frac{1}{2^n}) N^Q_k(0_{x'(2n)},z) \\ & \geq (1-\frac{1}{2^n}) (1-\frac{1}{x'(2n)})N^Q_{b_n}(0_{x'(2n)},z) \\ & \geq (1-\frac{1}{2^n})^2 (1-\frac{1}{x'(2n)}) Q_{b_n}(0_{x'(2n)}) \\ & \geq \frac{1}{2} Q_{b_n}(0_{x'(2n)}) \\ & \geq 2^{n-1} b_{n-1}. \end{align*} $$
$$ \begin{align*} Q_k(B) & \geq Q_k(0_{x'(2n)}) \geq (1-\frac{1}{2^n}) N^Q_k(0_{x'(2n)},z) \\ & \geq (1-\frac{1}{2^n}) (1-\frac{1}{x'(2n)})N^Q_{b_n}(0_{x'(2n)},z) \\ & \geq (1-\frac{1}{2^n})^2 (1-\frac{1}{x'(2n)}) Q_{b_n}(0_{x'(2n)}) \\ & \geq \frac{1}{2} Q_{b_n}(0_{x'(2n)}) \\ & \geq 2^{n-1} b_{n-1}. \end{align*} $$
So we have
 $$ \begin{align} | N^Q_k(B,w)-Q_k(B)| & \leq b_{n-1}+ \frac{2|B| }{x'(2n)} N^Q_{k}(0_{x'(2n)},z)+ |N^Q_k(B,z)-Q_k(B)| \nonumber\\& \leq \frac{2}{2^n}Q_k(B)+ \frac{2|B| }{x'(2n)} N^Q_{k}(0_{|B|},z) +\frac{1}{2^n}Q_k(B) \nonumber\\ & \leq \frac{3}{2^n}Q_k(B)+ \frac{3 |B| }{x'(2n)} Q_{k}(B) \nonumber\\ & \leq \epsilon Q_k(B). \end{align} $$
$$ \begin{align} | N^Q_k(B,w)-Q_k(B)| & \leq b_{n-1}+ \frac{2|B| }{x'(2n)} N^Q_{k}(0_{x'(2n)},z)+ |N^Q_k(B,z)-Q_k(B)| \nonumber\\& \leq \frac{2}{2^n}Q_k(B)+ \frac{2|B| }{x'(2n)} N^Q_{k}(0_{|B|},z) +\frac{1}{2^n}Q_k(B) \nonumber\\ & \leq \frac{3}{2^n}Q_k(B)+ \frac{3 |B| }{x'(2n)} Q_{k}(B) \nonumber\\ & \leq \epsilon Q_k(B). \end{align} $$
This shows that
![]() $w \in \mathscr {N}(Q)$
.
$w \in \mathscr {N}(Q)$
.
If
![]() $x \notin C$
, say
$x \notin C$
, say
![]() $x(2n)= c$
for infinitely many n, then for infinitely many n we have
$x(2n)= c$
for infinitely many n, then for infinitely many n we have
 $$ \begin{align} N^Q_{b_n}(0_c,w) & \leq N^Q_{b_n}(0_c,z) + b_{n-1}-\frac{1}{c} N^Q_{b_{n-1},b_n}(0_c,z) \nonumber\\ & \leq \left(1+\frac{1}{2^n}\right) Q_{b_n}(0_c) +2 b_{n-1} - \frac{1}{c} N^Q_{b_n}(0_c,z) \nonumber\\ & \leq \left(1+\frac{3}{2^n}\right) Q_{b_n}(0_c) - \frac{1}{c} \left(1-\frac{1}{2^n}\right) Q_{b_n}(0_c) \nonumber\\ & \leq \left(1-\frac{1}{2c}\right) Q_{b_n}(0_c). \end{align} $$
$$ \begin{align} N^Q_{b_n}(0_c,w) & \leq N^Q_{b_n}(0_c,z) + b_{n-1}-\frac{1}{c} N^Q_{b_{n-1},b_n}(0_c,z) \nonumber\\ & \leq \left(1+\frac{1}{2^n}\right) Q_{b_n}(0_c) +2 b_{n-1} - \frac{1}{c} N^Q_{b_n}(0_c,z) \nonumber\\ & \leq \left(1+\frac{3}{2^n}\right) Q_{b_n}(0_c) - \frac{1}{c} \left(1-\frac{1}{2^n}\right) Q_{b_n}(0_c) \nonumber\\ & \leq \left(1-\frac{1}{2c}\right) Q_{b_n}(0_c). \end{align} $$
On the other hand, the block
![]() $1_c$
occurs in
$1_c$
occurs in
![]() $w \restriction [0,b_n)$
at least as many times as it does in
$w \restriction [0,b_n)$
at least as many times as it does in
![]() $z\restriction [0,b_n)$
. So,
$z\restriction [0,b_n)$
. So,
![]() $N^Q_{b_n}(1_c,w) \geq N^Q_{b_n}(1_c,z) \geq (1-\frac {1}{2^n}) Q_{b_n}(1_c)$
. Since
$N^Q_{b_n}(1_c,w) \geq N^Q_{b_n}(1_c,z) \geq (1-\frac {1}{2^n}) Q_{b_n}(1_c)$
. Since
![]() $Q_{b_n}(0_c)=Q_{b_n}(1_c)$
, it follows that
$Q_{b_n}(0_c)=Q_{b_n}(1_c)$
, it follows that
![]() $w \notin \mathscr {RN}(Q)$
(and also
$w \notin \mathscr {RN}(Q)$
(and also
![]() $w \notin \mathscr {N}(Q)$
).
$w \notin \mathscr {N}(Q)$
).
If
![]() $x \in D$
, so
$x \in D$
, so
![]() $x(2n+1)\to \infty $
, then
$x(2n+1)\to \infty $
, then
![]() $\varphi (x) \in \mathscr {DN}(Q)$
. We use the fact that if
$\varphi (x) \in \mathscr {DN}(Q)$
. We use the fact that if
![]() $u=.u_1u_2\dots \in \mathscr {DN}(Q)$
and
$u=.u_1u_2\dots \in \mathscr {DN}(Q)$
and
![]() $v=.v_1v_2\dots $
is such that
$v=.v_1v_2\dots $
is such that
![]() $|(u_i-v_i)/q_i|\to 0$
, then
$|(u_i-v_i)/q_i|\to 0$
, then
![]() $v \in \mathscr {DN}(Q)$
(see Remark 1.8). If
$v \in \mathscr {DN}(Q)$
(see Remark 1.8). If
![]() $x \notin D$
, then
$x \notin D$
, then
![]() $\varphi (x) \notin \mathscr {DN}(Q)$
since for infinitely many intervals
$\varphi (x) \notin \mathscr {DN}(Q)$
since for infinitely many intervals
![]() $[b_{n-1},b_n)$
we have that
$[b_{n-1},b_n)$
we have that
![]() $(\varphi _1(x))(i)/q_i \notin [1-\epsilon ,1-\frac {\epsilon }{2}]$
, where
$(\varphi _1(x))(i)/q_i \notin [1-\epsilon ,1-\frac {\epsilon }{2}]$
, where
![]() $\epsilon = \frac {1}{c+1}$
and
$\epsilon = \frac {1}{c+1}$
and
![]() $x(2n+1)=c$
for infinitely many n.
$x(2n+1)=c$
for infinitely many n.
So we have that if
![]() $x \in C$
then
$x \in C$
then
![]() $\varphi (x)\in \mathscr {N}(Q)$
, and if
$\varphi (x)\in \mathscr {N}(Q)$
, and if
![]() $x \notin C$
then
$x \notin C$
then
![]() $\varphi (x)\notin \mathscr {RN}(Q)$
. Also,
$\varphi (x)\notin \mathscr {RN}(Q)$
. Also,
![]() $x \in D$
iff
$x \in D$
iff
![]() $\varphi (x) \in \mathscr {DN}(Q)$
. Thus, in the last two cases of the theorem,
$\varphi (x) \in \mathscr {DN}(Q)$
. Thus, in the last two cases of the theorem,
![]() $\varphi $
is a reduction of
$\varphi $
is a reduction of
![]() $C\setminus D$
to the desired difference set. For the first two cases of the theorem,
$C\setminus D$
to the desired difference set. For the first two cases of the theorem,
![]() $\varphi $
is a reduction of
$\varphi $
is a reduction of
![]() $D\setminus C$
to the desired difference set. This completes the proof of Theorem 3.2 in the case where Q is fully divergent.
$D\setminus C$
to the desired difference set. This completes the proof of Theorem 3.2 in the case where Q is fully divergent.
Assume now that there is a largest integer
![]() $k_0$
such that Q is
$k_0$
such that Q is
![]() $k_0$
-divergent. We again obtain
$k_0$
-divergent. We again obtain
![]() $\varphi _1(x)\restriction [b_{n-1},b_{n})$
by applying two operations. One of these is
$\varphi _1(x)\restriction [b_{n-1},b_{n})$
by applying two operations. One of these is
![]() $\Xi _{x'(2n+1)}$
, where the operation
$\Xi _{x'(2n+1)}$
, where the operation
![]() $\Xi $
is as before. For the other, we use operation
$\Xi $
is as before. For the other, we use operation
![]() $\Theta _{k_0, x'(2n)}$
.
$\Theta _{k_0, x'(2n)}$
.
If
![]() $x \notin C$
, then
$x \notin C$
, then
![]() $\varphi (x)\notin \mathscr {RN}(Q)$
as before. If
$\varphi (x)\notin \mathscr {RN}(Q)$
as before. If
![]() $x \in C$
, that is,
$x \in C$
, that is,
![]() $x(2n)\to \infty $
, then the argument of Equation (11) shows that
$x(2n)\to \infty $
, then the argument of Equation (11) shows that
![]() $\lim _k \frac {|N^Q_k(B,w)-Q_k(B)|}{Q_k(B)}=0$
for any block B of length
$\lim _k \frac {|N^Q_k(B,w)-Q_k(B)|}{Q_k(B)}=0$
for any block B of length
![]() $\leq k_0$
. Since this accounts for all of the blocks of infinite expectation, we have that
$\leq k_0$
. Since this accounts for all of the blocks of infinite expectation, we have that
![]() $w \in \mathscr {N}(Q)$
. Since the second operation does not affect normality, it follows that
$w \in \mathscr {N}(Q)$
. Since the second operation does not affect normality, it follows that
![]() $\varphi (x)\in \mathscr {N}(Q)$
.
$\varphi (x)\in \mathscr {N}(Q)$
.
As before, we have that
![]() $x\in D$
iff
$x\in D$
iff
![]() $\varphi (x)\in \mathscr {DN}(Q)$
. So we again have that
$\varphi (x)\in \mathscr {DN}(Q)$
. So we again have that
![]() $x \in C$
implies
$x \in C$
implies
![]() $\varphi (x)\in \mathscr {N}(Q)$
,
$\varphi (x)\in \mathscr {N}(Q)$
,
![]() $x \notin C$
implies
$x \notin C$
implies
![]() $\varphi (x)\notin \mathscr {RN}(Q)$
, and
$\varphi (x)\notin \mathscr {RN}(Q)$
, and
![]() $x \in D$
iff
$x \in D$
iff
![]() $\varphi (x)\in \mathscr {DN}(Q)$
. Thus, as in the previous case
$\varphi (x)\in \mathscr {DN}(Q)$
. Thus, as in the previous case
![]() $\varphi $
gives the desired reductions.⊣
$\varphi $
gives the desired reductions.⊣
3.2 Completeness of
 $\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
$\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
We will need to define a class of functions
![]() $\psi _{P,Q}$
in order to prove the last case of Theorem 1.15. Let
$\psi _{P,Q}$
in order to prove the last case of Theorem 1.15. Let
![]() $P=(p_i)$
and
$P=(p_i)$
and
![]() $Q=(q_i)$
be basic sequences. If
$Q=(q_i)$
be basic sequences. If
![]() $x=a_0.a_1a_2 \cdots $
w.r.t. P, then put
$x=a_0.a_1a_2 \cdots $
w.r.t. P, then put
 $$ \begin{align*}\psi_{P,Q}(x)=\sum_{i=1}^\infty \frac {\min(a_i,q_i-1)} {q_1 \cdots q_i}. \end{align*} $$
$$ \begin{align*}\psi_{P,Q}(x)=\sum_{i=1}^\infty \frac {\min(a_i,q_i-1)} {q_1 \cdots q_i}. \end{align*} $$
We will need the following theorem of [Reference Mance16].
Theorem 3.3. Suppose that P and Q are basic sequences which are infinite in limit. If
![]() $x=a_0.a_1a_2\cdots $
w.r.t. P satisfies
$x=a_0.a_1a_2\cdots $
w.r.t. P satisfies
![]() $a_i< q_{i}-1$
for infinitely many i, then for every block B
$a_i< q_{i}-1$
for infinitely many i, then for every block B
While Theorem 3.3 is not difficult to prove, it has been an essential tool in proving some of the more difficult theorems about Q-normal numbers.
Recall that for a basic sequence Q and block
![]() $B, Q_n(B)$
(see Equation (2)) denotes the expected number of occurrences of B with a starting position in
$B, Q_n(B)$
(see Equation (2)) denotes the expected number of occurrences of B with a starting position in
![]() $[1,n]$
with respect to the basic sequence Q. Since we will be dealing with several basic sequences in this section, we extend this notation in a natural manner. Namely, if P (or R) are basic sequences, then we let
$[1,n]$
with respect to the basic sequence Q. Since we will be dealing with several basic sequences in this section, we extend this notation in a natural manner. Namely, if P (or R) are basic sequences, then we let
![]() $P_n(B)$
(or
$P_n(B)$
(or
![]() $R_n(B)$
) denote the expected number of occurrences of B with a starting position in
$R_n(B)$
) denote the expected number of occurrences of B with a starting position in
![]() $[1,n]$
with respect to P (or R). We similarly use the notation
$[1,n]$
with respect to P (or R). We similarly use the notation
![]() $N^P_n(B,z)$
to denote the number of occurrences of B in the P-Cantor series for z with starting position in
$N^P_n(B,z)$
to denote the number of occurrences of B in the P-Cantor series for z with starting position in
![]() $[1,n]$
.
$[1,n]$
.
We will use the following lemma about concatenating intervals of normal sequences for different basic sequences.
Lemma 3.4. Let P, Q be basic sequences which are infinite in limit and assume that
![]() $\limsup _i \frac {p_i}{q_i}$
is finite. Let
$\limsup _i \frac {p_i}{q_i}$
is finite. Let
![]() $u \in \mathscr {N}(P)$
, and
$u \in \mathscr {N}(P)$
, and
![]() $v \in \mathscr {N}(Q)$
. Let
$v \in \mathscr {N}(Q)$
. Let
![]() $B \in \omega ^{<\omega }$
have infinite expectation with respect to P and Q, and let
$B \in \omega ^{<\omega }$
have infinite expectation with respect to P and Q, and let
![]() $\epsilon>0$
. Then there is an
$\epsilon>0$
. Then there is an
![]() $i_0$
such that if
$i_0$
such that if
![]() $i'>i\geq i_0$
then
$i'>i\geq i_0$
then
![]() $|N^R_{i'}(B,w)-R_{i'}(B)|<\epsilon R_{i'}(B)$
where
$|N^R_{i'}(B,w)-R_{i'}(B)|<\epsilon R_{i'}(B)$
where
![]() $w\restriction [0,i)=u$
,
$w\restriction [0,i)=u$
,
![]() $w \restriction [i,\infty )=v$
,
$w \restriction [i,\infty )=v$
,
![]() $R\restriction [0,i)=P$
, and
$R\restriction [0,i)=P$
, and
![]() $R\restriction [i,\infty )=Q$
.
$R\restriction [i,\infty )=Q$
.
Proof. Fix C such that
![]() $\frac {p_i}{q_i}\leq C$
for all i. Since
$\frac {p_i}{q_i}\leq C$
for all i. Since
![]() $\frac {p_i}{q_i}\leq C$
, and B has infinite expectation with respect to P and Q, for large enough i we have that
$\frac {p_i}{q_i}\leq C$
, and B has infinite expectation with respect to P and Q, for large enough i we have that
![]() $Q_i(B)\leq 2C^{|B|} P_i(B)$
. Let
$Q_i(B)\leq 2C^{|B|} P_i(B)$
. Let
![]() $i_0$
be such that for all
$i_0$
be such that for all
![]() $i \geq i_0$
we have that
$i \geq i_0$
we have that
![]() $|N^Q_i(B,v)-Q_i(B)|<\epsilon ' Q_i(B)$
and
$|N^Q_i(B,v)-Q_i(B)|<\epsilon ' Q_i(B)$
and
![]() $|N^P_i(B,u)-P_i(B)|<\epsilon ' P_i(B)$
where
$|N^P_i(B,u)-P_i(B)|<\epsilon ' P_i(B)$
where
![]() $\epsilon '=\frac {\epsilon }{3+4C^{|B|}}$
. Let
$\epsilon '=\frac {\epsilon }{3+4C^{|B|}}$
. Let
![]() $i'>i \geq i_0$
. We then have
$i'>i \geq i_0$
. We then have
 $$ \begin{align*} |N^R_{i'}(B,w)-R_{i'}(B)|& \leq |N^P_i(B,u)-P_i(B)|+|N^Q_{i,i'}(B,v)-Q_{i,i'}(B)| \\ & \leq \epsilon' P_i(B)+ |N^Q_{i}(B,v)-Q_{i}(B)|+| N^Q_{i'}(B,v)-Q_{i'}(B)| \\ & \leq \epsilon' P_i(B)+ \epsilon' Q_i(B)+ \epsilon' Q_{i'}(B) \\ & \leq \epsilon' R_i(B)+ 2\epsilon' Q_{i'}(B) \\ & \leq \epsilon' R_i(B)+ 2\epsilon' (Q_i(B)+ Q_{i,i'}(B)) \\ & \leq \epsilon' R_i(B)+ 2\epsilon' (2C^{|B|} P_i(B) +Q_{i,i'}(B)) \\ & \leq \epsilon' R_i(B)+ 2\epsilon' (1+2C^{|B|})R_{i'}(B) \\ & \leq \epsilon' (3+4C^{|B|}) R_{i'}(B) \leq \epsilon R_{i'}(B).\\[-32pt] \end{align*} $$
$$ \begin{align*} |N^R_{i'}(B,w)-R_{i'}(B)|& \leq |N^P_i(B,u)-P_i(B)|+|N^Q_{i,i'}(B,v)-Q_{i,i'}(B)| \\ & \leq \epsilon' P_i(B)+ |N^Q_{i}(B,v)-Q_{i}(B)|+| N^Q_{i'}(B,v)-Q_{i'}(B)| \\ & \leq \epsilon' P_i(B)+ \epsilon' Q_i(B)+ \epsilon' Q_{i'}(B) \\ & \leq \epsilon' R_i(B)+ 2\epsilon' Q_{i'}(B) \\ & \leq \epsilon' R_i(B)+ 2\epsilon' (Q_i(B)+ Q_{i,i'}(B)) \\ & \leq \epsilon' R_i(B)+ 2\epsilon' (2C^{|B|} P_i(B) +Q_{i,i'}(B)) \\ & \leq \epsilon' R_i(B)+ 2\epsilon' (1+2C^{|B|})R_{i'}(B) \\ & \leq \epsilon' (3+4C^{|B|}) R_{i'}(B) \leq \epsilon R_{i'}(B).\\[-32pt] \end{align*} $$
⊣
We now prove the following theorem which gives the last case of Theorem 1.15.
Theorem 3.5. Let Q be a basic sequence which is infinite in limit and
![]() $1$
-divergent. Then the set
$1$
-divergent. Then the set
![]() $\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
is
$\mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
is
![]() $D_2(\boldsymbol {\Pi }^0_3)$
-complete.
$D_2(\boldsymbol {\Pi }^0_3)$
-complete.
Proof. Let
![]() $C, D\subseteq \omega ^\omega $
be as in Section 3.1. For
$C, D\subseteq \omega ^\omega $
be as in Section 3.1. For
![]() $k, n\in \mathbb {N}$
, recall that
$k, n\in \mathbb {N}$
, recall that
![]() $Q^{(k)}_{n}$
denotes the sum
$Q^{(k)}_{n}$
denotes the sum
![]() $Q^{(k)}_{n}= \sum _{i=1}^n \frac {1}{q_i q_{i+1}\cdots q_{i+k-1}}$
.
$Q^{(k)}_{n}= \sum _{i=1}^n \frac {1}{q_i q_{i+1}\cdots q_{i+k-1}}$
.
For each m, let
![]() $P_m=( \max (2,\lfloor \frac {m+1}{m+2} q_i \rfloor ))_{i=1}^\infty $
. Recall
$P_m=( \max (2,\lfloor \frac {m+1}{m+2} q_i \rfloor ))_{i=1}^\infty $
. Recall
![]() $(P_m)_i(B)$
denotes the expectation of B in the first i digits of
$(P_m)_i(B)$
denotes the expectation of B in the first i digits of
![]() $P_m$
, as in Equation (2), and
$P_m$
, as in Equation (2), and
![]() $(P_m)_i^{(k)}$
denotes the expectation of
$(P_m)_i^{(k)}$
denotes the expectation of
![]() $0_k$
in the first i digits of
$0_k$
in the first i digits of
![]() $P_m$
. We fix for the rest of the proof
$P_m$
. We fix for the rest of the proof
![]() $w_m\in \mathscr {N}(P_m)$
, which we identify with a
$w_m\in \mathscr {N}(P_m)$
, which we identify with a
![]() $P_m$
-Cantor series expansion.
$P_m$
-Cantor series expansion.
Given a strictly increasing sequence
![]() $\{ b_n\}$
(which we will choose below) and an
$\{ b_n\}$
(which we will choose below) and an
![]() $x \in \omega ^\omega $
we define a new basic sequence
$x \in \omega ^\omega $
we define a new basic sequence
![]() $P_x=P(x, \{ b_n\},Q)=(p^x_i)$
as follows. Let
$P_x=P(x, \{ b_n\},Q)=(p^x_i)$
as follows. Let
![]() $x'(n)=\min \{ x(n),n\}$
. Let
$x'(n)=\min \{ x(n),n\}$
. Let
![]() $p^x_i=P_{x'(2n+1)}(i)=\max (2,\lfloor \frac {x'(2n+1)+1}{x'(2n+1)+2} q_i \rfloor ) $
for
$p^x_i=P_{x'(2n+1)}(i)=\max (2,\lfloor \frac {x'(2n+1)+1}{x'(2n+1)+2} q_i \rfloor ) $
for
![]() $i \in [b_{n-1},b_{n})$
. Note that
$i \in [b_{n-1},b_{n})$
. Note that
![]() $p_i \leq q_i$
for all i, and if
$p_i \leq q_i$
for all i, and if
![]() $x(2n+1)\to \infty $
then
$x(2n+1)\to \infty $
then
![]() $\lim _i \frac {p^x_i}{q_i}=1$
. Also
$\lim _i \frac {p^x_i}{q_i}=1$
. Also
![]() $Q^{(k)}_{n} \leq (P_x)^{(k)}_{n}$
for all
$Q^{(k)}_{n} \leq (P_x)^{(k)}_{n}$
for all
![]() $k, n$
.
$k, n$
.
Claim 3.6. Suppose Q is k-divergent. If
![]() $x(2n+1)\to \infty $
then
$x(2n+1)\to \infty $
then
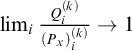 $\lim _i \frac {Q^{(k)}_{i}}{(P_x)^{(k)}_{i}} \to 1$
. If
$\lim _i \frac {Q^{(k)}_{i}}{(P_x)^{(k)}_{i}} \to 1$
. If
![]() $x(2n+1)$
does not tend to
$x(2n+1)$
does not tend to
![]() $\infty $
and
$\infty $
and
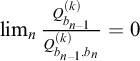 $\lim _n \frac {Q^{(k)}_{{b_{n-1}}}}{Q^{(k)}_{{b_{n-1}},b_{n}}}=0$
, there is a subsequence of
$\lim _n \frac {Q^{(k)}_{{b_{n-1}}}}{Q^{(k)}_{{b_{n-1}},b_{n}}}=0$
, there is a subsequence of
![]() $\frac {Q^{(k)}_{i}}{(P_x)^{(k)}_{i}}$
which is bounded away from
$\frac {Q^{(k)}_{i}}{(P_x)^{(k)}_{i}}$
which is bounded away from
![]() $1$
.⊣
$1$
.⊣
Proof. If
![]() $x(2n+1)\to \infty $
, then
$x(2n+1)\to \infty $
, then
![]() $\ell _n=\frac {x(2n+1)+1}{x(2n+1)+2} \to 1$
and so
$\ell _n=\frac {x(2n+1)+1}{x(2n+1)+2} \to 1$
and so
![]() $p^x_i/q_i$
tends to
$p^x_i/q_i$
tends to
![]() $1$
. Note that
$1$
. Note that
![]() $\left ( \frac {1}{q_jq_{j+1}\cdots q_{j+k-1}}\right ) / \left ( \frac {1}{p_jp_{j+1}\cdots p_{j+k-1}}\right ) =(\ell _n)^k$
for all
$\left ( \frac {1}{q_jq_{j+1}\cdots q_{j+k-1}}\right ) / \left ( \frac {1}{p_jp_{j+1}\cdots p_{j+k-1}}\right ) =(\ell _n)^k$
for all
![]() $j \in [b_n,b_{n+1})$
. We then have that for all k that
$j \in [b_n,b_{n+1})$
. We then have that for all k that
![]() $Q^{(k)}_{i}/ (P_x)^{(k)}_{i}\to 1$
using the simple fact that if
$Q^{(k)}_{i}/ (P_x)^{(k)}_{i}\to 1$
using the simple fact that if
![]() $c_j,d_j \geq 0$
,
$c_j,d_j \geq 0$
,
![]() $\sum _j c_j=\infty $
,
$\sum _j c_j=\infty $
,
![]() $\sum _j d_j=\infty $
, and
$\sum _j d_j=\infty $
, and
![]() $c_j/d_j \to 1$
, then
$c_j/d_j \to 1$
, then
![]() $\left ( \sum _{j=1}^i c_j \right ) / \left ( \sum _{j=1}^i d_j \right ) \to 1$
.
$\left ( \sum _{j=1}^i c_j \right ) / \left ( \sum _{j=1}^i d_j \right ) \to 1$
.
If
![]() $x(2n+1)$
does not tend to
$x(2n+1)$
does not tend to
![]() $\infty $
, then
$\infty $
, then
![]() $\exists u <1$
such that
$\exists u <1$
such that
![]() $\ell _n \leq u$
for infinitely many n. So, for infinitely many n we have that
$\ell _n \leq u$
for infinitely many n. So, for infinitely many n we have that
![]() $Q^{(k)}_{b_{n-1}, b_{n}} \leq u^k (P_x)^{(k)}_{b_{n-1}, b_{n}}$
. Thus, for infinitely many n
$Q^{(k)}_{b_{n-1}, b_{n}} \leq u^k (P_x)^{(k)}_{b_{n-1}, b_{n}}$
. Thus, for infinitely many n
 $$ \begin{align*} \frac{Q^{(k)}_{b_{n}}}{(P_x)^{(k)}_{b_{n}}}& = \frac{Q^{(k)}_{b_{n-1}}+ Q^{(k)}_{b_{n-1}, b_{n}}} {(P_x)^{(k)}_{b_{n-1}}+ (P_x)^{(k)}_{b_{n-1}, b_{n}}} \leq \frac{Q^{(k)}_{b_{n-1}}+ Q^{(k)}_{b_{n-1}, b_{n}}} {Q^{(k)}_{b_{n-1}}+ (P_x)^{(k)}_{b_{n-1}, b_{n}}} \leq \frac{Q^{(k)}_{b_{n-1}}+ Q^{(k)}_{b_{n-1}, b_{n}}} {Q^{(k)}_{b_{n-1}}+ (\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} \\ & \leq \frac{Q^{(k)}_{b_{n-1}}+ (\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}+(1-\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} {Q^{(k)}_{b_{n-1}}+ (\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} \\ & = 1- \left( \frac{1}{u^k} -1\right) \frac{ Q^{(k)}_{b_{n-1}, b_{n}}}{Q^{(k)}_{b_{n-1}}+ (\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} \\ & \leq 1- \left( \frac{1}{u^k}-1 \right) \frac{ Q^{(k)}_{b_{n-1}, b_{n}}}{ (\frac{2}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} = 1- \left( \frac{1}{u^k} -1\right) \frac{u^k}{2} \\ & = 1- \frac{1}{2} (1-u^k).\\[-32pt] \end{align*} $$
$$ \begin{align*} \frac{Q^{(k)}_{b_{n}}}{(P_x)^{(k)}_{b_{n}}}& = \frac{Q^{(k)}_{b_{n-1}}+ Q^{(k)}_{b_{n-1}, b_{n}}} {(P_x)^{(k)}_{b_{n-1}}+ (P_x)^{(k)}_{b_{n-1}, b_{n}}} \leq \frac{Q^{(k)}_{b_{n-1}}+ Q^{(k)}_{b_{n-1}, b_{n}}} {Q^{(k)}_{b_{n-1}}+ (P_x)^{(k)}_{b_{n-1}, b_{n}}} \leq \frac{Q^{(k)}_{b_{n-1}}+ Q^{(k)}_{b_{n-1}, b_{n}}} {Q^{(k)}_{b_{n-1}}+ (\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} \\ & \leq \frac{Q^{(k)}_{b_{n-1}}+ (\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}+(1-\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} {Q^{(k)}_{b_{n-1}}+ (\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} \\ & = 1- \left( \frac{1}{u^k} -1\right) \frac{ Q^{(k)}_{b_{n-1}, b_{n}}}{Q^{(k)}_{b_{n-1}}+ (\frac{1}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} \\ & \leq 1- \left( \frac{1}{u^k}-1 \right) \frac{ Q^{(k)}_{b_{n-1}, b_{n}}}{ (\frac{2}{u^k}) Q^{(k)}_{b_{n-1}, b_{n}}} = 1- \left( \frac{1}{u^k} -1\right) \frac{u^k}{2} \\ & = 1- \frac{1}{2} (1-u^k).\\[-32pt] \end{align*} $$
⊣
First assume that Q is k-divergent for all k. Using Lemma 3.4 we then inductively pick the
![]() $b_n$
satisfying the following:
$b_n$
satisfying the following:
-
(1) For all
 $m_1,m_2 \leq n+1$
and all
$m_1,m_2 \leq n+1$
and all
 $i>b_{n-1}$
, let
$i>b_{n-1}$
, let
 $P=P(m_1,m_2,i)$
be defined by:
$P=P(m_1,m_2,i)$
be defined by:
 $P\restriction [0,b_{n-1})= P_{m_1} \restriction [0,b_{n-1})$
and
$P\restriction [0,b_{n-1})= P_{m_1} \restriction [0,b_{n-1})$
and
 $P\restriction [b_{n-1},i)= P_{m_2} \restriction [b_{n-1},i)$
. Let
$P\restriction [b_{n-1},i)= P_{m_2} \restriction [b_{n-1},i)$
. Let
 $w\restriction [0,b_{n-1})=w_{m_1}$
and
$w\restriction [0,b_{n-1})=w_{m_1}$
and
 $w \restriction [b_{n-1},i)=w_{m_2}\restriction [b_{n-1},i)$
. Then for any B with
$w \restriction [b_{n-1},i)=w_{m_2}\restriction [b_{n-1},i)$
. Then for any B with
 $\|B\|\leq n+1$
we have
$\|B\|\leq n+1$
we have
 $|N^P_i(B, w)-P_i(B)|<\frac {1}{2^n} P_i(B)$
.
$|N^P_i(B, w)-P_i(B)|<\frac {1}{2^n} P_i(B)$
. -
(2)
 $(P_m)_{b_{n-1},b_n}(0_{2n})> 2^n b_{n-1}$
for all
$(P_m)_{b_{n-1},b_n}(0_{2n})> 2^n b_{n-1}$
for all
 $m \leq n$
.
$m \leq n$
.
Given
![]() $x \in \omega ^\omega $
, we define
$x \in \omega ^\omega $
, we define
![]() $\varphi _1(x)$
as follows. Suppose
$\varphi _1(x)$
as follows. Suppose
![]() $\varphi _1(x)\restriction b_{n-1}$
has been defined. Let
$\varphi _1(x)\restriction b_{n-1}$
has been defined. Let
![]() $y \restriction [b_{n-1},b_{n})= w_{x(2n+1)}\restriction [b_{n-1},b_{n})$
. Then we perform the operation
$y \restriction [b_{n-1},b_{n})= w_{x(2n+1)}\restriction [b_{n-1},b_{n})$
. Then we perform the operation
![]() $\Theta _{x'(2n),x'(2n)}$
of Section 3.1 on
$\Theta _{x'(2n),x'(2n)}$
of Section 3.1 on
![]() $y \restriction [b_{n-1},b_{n})$
to produce
$y \restriction [b_{n-1},b_{n})$
to produce
![]() $\varphi _1(x) \restriction [b_{n-1},b_{n})$
. This defines
$\varphi _1(x) \restriction [b_{n-1},b_{n})$
. This defines
![]() $\varphi _1(x)\restriction [b_{n-1},b_{n})$
. Doing this for all blocks
$\varphi _1(x)\restriction [b_{n-1},b_{n})$
. Doing this for all blocks
![]() $[b_{n-1},b_{n})$
produces
$[b_{n-1},b_{n})$
produces
![]() $\varphi _1(x)$
.
$\varphi _1(x)$
.
If
![]() $x \notin C$
, that is
$x \notin C$
, that is
![]() $x(2n)$
does not tend to
$x(2n)$
does not tend to
![]() $\infty $
, then
$\infty $
, then
![]() $\varphi (x) \notin \mathscr {RN}(Q)$
. This is because if
$\varphi (x) \notin \mathscr {RN}(Q)$
. This is because if
![]() $k=\liminf x(2n)$
, then there will be infinitely many n for which
$k=\liminf x(2n)$
, then there will be infinitely many n for which
![]() $0_k$
occurs in
$0_k$
occurs in
![]() $[0,b_{n})$
at most
$[0,b_{n})$
at most
 $$\begin{align}N^{P_{x'(2n+1)}}_{b_n}(0_k,w_{x'(2n+1)})\left(1-\frac{1}{k}\right)+b_{n-1} & \leq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{k}\right)\left(1+\frac{1}{2^n}\right)+b_{n-1} \nonumber\\ & \leq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{k}+\frac{1}{2^{n-1}}\right) \nonumber\\& \leq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{2k}\right) \end{align} $$
$$\begin{align}N^{P_{x'(2n+1)}}_{b_n}(0_k,w_{x'(2n+1)})\left(1-\frac{1}{k}\right)+b_{n-1} & \leq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{k}\right)\left(1+\frac{1}{2^n}\right)+b_{n-1} \nonumber\\ & \leq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{k}+\frac{1}{2^{n-1}}\right) \nonumber\\& \leq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{2k}\right) \end{align} $$
many times while
![]() $1_k$
occurs at least
$1_k$
occurs at least
 $$ \begin{align} \begin{aligned} N^{P_{x'(2n+1)}}_{b_{n}}(1_k,w_{x'(2n+1)}) -b_{n-1}& \geq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{2^n}\right)-b_{n-1} \\ & \geq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{2^{n-1}}\right) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} N^{P_{x'(2n+1)}}_{b_{n}}(1_k,w_{x'(2n+1)}) -b_{n-1}& \geq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{2^n}\right)-b_{n-1} \\ & \geq (P_{x'(2n+1)})^{(k)}_{b_{n}} \left(1-\frac{1}{2^{n-1}}\right) \end{aligned} \end{align} $$
many times.
If
![]() $x(2n)\to \infty $
but
$x(2n)\to \infty $
but
![]() $x(2n+1)$
does not tend to infinity, then
$x(2n+1)$
does not tend to infinity, then
![]() $\varphi (x)\in \mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
. To see this, first note that the point y as above is in
$\varphi (x)\in \mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
. To see this, first note that the point y as above is in
![]() $\mathscr {RN}(Q)$
. Recall
$\mathscr {RN}(Q)$
. Recall
![]() $P_x$
is defined by
$P_x$
is defined by
![]() $P_x \restriction [b_{n-1},b_{n})=P_{x(2n+1)}\restriction [b_{n-1},b_{n})$
. We show that
$P_x \restriction [b_{n-1},b_{n})=P_{x(2n+1)}\restriction [b_{n-1},b_{n})$
. We show that
![]() $y \in \mathscr {N}(P_x)$
, which implies
$y \in \mathscr {N}(P_x)$
, which implies
![]() $y \in \mathscr {RN}(Q)$
. For any B, for large enough n, and for any
$y \in \mathscr {RN}(Q)$
. For any B, for large enough n, and for any
![]() $b_{n-1} \leq i <b_{n}$
we have from property (1) of the
$b_{n-1} \leq i <b_{n}$
we have from property (1) of the
![]() $b_n$
:
$b_n$
:
where
![]() $y'$
and
$y'$
and
![]() $P'$
are defined by:
$P'$
are defined by:
 $$ \begin{align*} \begin{aligned} y'\restriction[0,b_{n-1})&=w_{x(2n-1)} \restriction [0,b_{n-1}), \\ y' \restriction [b_{n-1},i)&=w_{x(2n+1)}\restriction i, \\ P' \restriction [0,b_{n-1})&=P_{x(2n-1)}, \\ P'\restriction [b_{n-1},i)&= P_{x(2n+1)}\restriction [b_{n-1},i). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} y'\restriction[0,b_{n-1})&=w_{x(2n-1)} \restriction [0,b_{n-1}), \\ y' \restriction [b_{n-1},i)&=w_{x(2n+1)}\restriction i, \\ P' \restriction [0,b_{n-1})&=P_{x(2n-1)}, \\ P'\restriction [b_{n-1},i)&= P_{x(2n+1)}\restriction [b_{n-1},i). \end{aligned} \end{align*} $$
Also, from property (2) of the
![]() $b_n$
we have:
$b_n$
we have:
Finally,
From Equations 15–17 we have
![]() $|N^{P_x}_i(B,y)-(P_x)_i(B)|\leq \frac {4}{2^{n}} (P_x)_i(B)$
. This shows that
$|N^{P_x}_i(B,y)-(P_x)_i(B)|\leq \frac {4}{2^{n}} (P_x)_i(B)$
. This shows that
![]() $y \in \mathscr {RN}(Q)$
. Since
$y \in \mathscr {RN}(Q)$
. Since
![]() $x(2n+1)$
does not tend to infinity, then from Claim 3.6 there is a subsequence on which
$x(2n+1)$
does not tend to infinity, then from Claim 3.6 there is a subsequence on which
![]() $\frac {Q^{(k)}_{i}}{(P_x)^{(k)}_{i}}$
is bounded away from
$\frac {Q^{(k)}_{i}}{(P_x)^{(k)}_{i}}$
is bounded away from
![]() $1$
. Since y is
$1$
. Since y is
![]() $P_x$
-normal, we have that y is not Q-normal.
$P_x$
-normal, we have that y is not Q-normal.
The operation applied to y to produce
![]() $\varphi _1(x)$
does not affect normality or ratio normality if
$\varphi _1(x)$
does not affect normality or ratio normality if
![]() $x(2n) \to \infty $
(this is just as in Section 3.1). So,
$x(2n) \to \infty $
(this is just as in Section 3.1). So,
![]() $\varphi (x) \in \mathscr {RN}(Q) \setminus \mathscr {N}(Q)$
.
$\varphi (x) \in \mathscr {RN}(Q) \setminus \mathscr {N}(Q)$
.
Finally, if
![]() $x(n)\to \infty $
, then as above
$x(n)\to \infty $
, then as above
![]() $y \in \mathscr {N}(P_x)$
. As
$y \in \mathscr {N}(P_x)$
. As
![]() $x(2n+1)\to \infty $
, we have from Claim 3.6 that
$x(2n+1)\to \infty $
, we have from Claim 3.6 that
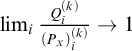 $\lim _i \frac {Q^{(k)}_{i}}{(P_x)^{(k)}_{i}} \to 1$
and it follows that
$\lim _i \frac {Q^{(k)}_{i}}{(P_x)^{(k)}_{i}} \to 1$
and it follows that
![]() $y \in \mathscr {N}(Q)$
. Since
$y \in \mathscr {N}(Q)$
. Since
![]() $x(2n)\to \infty $
as well, from the argument in Section 3.1 we also have that
$x(2n)\to \infty $
as well, from the argument in Section 3.1 we also have that
![]() $y=\varphi (x)\in \mathscr {N}(Q)$
.
$y=\varphi (x)\in \mathscr {N}(Q)$
.
So, in all cases we have that
![]() $x \in C\setminus D$
iff
$x \in C\setminus D$
iff
![]() $\varphi (x) \in \mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
.
$\varphi (x) \in \mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
.
Suppose now that there is a largest integer
![]() $k_0$
such that Q is
$k_0$
such that Q is
![]() $k_0$
-divergent. The proof is essentially identical to that above. We let
$k_0$
-divergent. The proof is essentially identical to that above. We let
![]() $P_m$
be as before, and now let
$P_m$
be as before, and now let
![]() $w_m$
be
$w_m$
be
![]() $\leq k_0$
normal with respect to
$\leq k_0$
normal with respect to
![]() $P_m$
, that is, for all B of length
$P_m$
, that is, for all B of length
![]() $\leq k_0$
we have
$\leq k_0$
we have
![]() $\lim _i \frac {N_i(B,w_m)}{(P_m)_i(B)}=1$
. We define
$\lim _i \frac {N_i(B,w_m)}{(P_m)_i(B)}=1$
. We define
![]() $\varphi _1(x)$
by first defining y exactly as before (using the values
$\varphi _1(x)$
by first defining y exactly as before (using the values
![]() $x(2n+1)$
). We then modify y to
$x(2n+1)$
). We then modify y to
![]() $\varphi _1(x)$
, (using
$\varphi _1(x)$
, (using
![]() $x(2n)$
) but in a slightly different manner. Namely, we get
$x(2n)$
) but in a slightly different manner. Namely, we get
![]() $\varphi _1(x)\restriction [b_{n-1},b_{n})$
from
$\varphi _1(x)\restriction [b_{n-1},b_{n})$
from
![]() $y \restriction [b_{n-1},b_{n})$
as follows. Let
$y \restriction [b_{n-1},b_{n})$
as follows. Let
![]() $A\subseteq [b_{n-1},b_n)$
be the integers i in this interval such that
$A\subseteq [b_{n-1},b_n)$
be the integers i in this interval such that
![]() $y \restriction [i,i+k_0-1)= 0_{k_0}$
. Let
$y \restriction [i,i+k_0-1)= 0_{k_0}$
. Let
![]() $A' \subseteq A$
be the last
$A' \subseteq A$
be the last
![]() $\lfloor \frac {|A|}{x(2n)}\rfloor $
many elements of A. For each
$\lfloor \frac {|A|}{x(2n)}\rfloor $
many elements of A. For each
![]() $i \in A'$
we change
$i \in A'$
we change
![]() $y(i)$
from a
$y(i)$
from a
![]() $0$
to a
$0$
to a
![]() $1$
, and for all other i in this interval we set
$1$
, and for all other i in this interval we set
![]() $\varphi _1(x)(i)=y(i)$
.
$\varphi _1(x)(i)=y(i)$
.
If
![]() $x(2n)$
does not tend to infinity, then easily
$x(2n)$
does not tend to infinity, then easily
![]() $\varphi (x) \notin \mathscr {RN}(Q)$
as
$\varphi (x) \notin \mathscr {RN}(Q)$
as
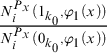 $\frac {N^{P_x}_i(1_{k_0},\varphi _1(x))}{N^{P_x}_i(0_{k_0},\varphi _1(x))}$
does not tend to
$\frac {N^{P_x}_i(1_{k_0},\varphi _1(x))}{N^{P_x}_i(0_{k_0},\varphi _1(x))}$
does not tend to
![]() $1$
. If
$1$
. If
![]() $x(2n)$
tends to infinity, then we easily have that
$x(2n)$
tends to infinity, then we easily have that
![]() $\varphi (x)$
is in
$\varphi (x)$
is in
![]() $\mathscr {N}(Q)$
(or
$\mathscr {N}(Q)$
(or
![]() $\mathscr {RN}(Q)$
) iff y is in
$\mathscr {RN}(Q)$
) iff y is in
![]() $\mathscr {N}(Q)$
(resp.
$\mathscr {N}(Q)$
(resp.
![]() $\mathscr {RN}(Q)$
). In this case, as above, we have that if
$\mathscr {RN}(Q)$
). In this case, as above, we have that if
![]() $x(2n+1)\to \infty $
then
$x(2n+1)\to \infty $
then
![]() $y\in \mathscr {N}(Q)$
, and if
$y\in \mathscr {N}(Q)$
, and if
![]() $x(2n+1)$
does not tend to infinity then
$x(2n+1)$
does not tend to infinity then
![]() $y \in \mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
. So, in all cases we have
$y \in \mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
. So, in all cases we have
![]() $x \in C\setminus D$
iff
$x \in C\setminus D$
iff
![]() $\varphi (x)\in \mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
.⊣
$\varphi (x)\in \mathscr {RN}(Q)\setminus \mathscr {N}(Q)$
.⊣
3.3 Further discussion
Theorem 3.2 can be extended further. First, the hypothesis that
![]() $Q=(q_i)$
in infinite in limit can be weakened to the following condition studied by Šalát [Reference Turán21]:
$Q=(q_i)$
in infinite in limit can be weakened to the following condition studied by Šalát [Reference Turán21]:
![]() $\lim _{N\to \infty } \frac {1}{N} \sum _{i=1}^N \frac {1}{q_i}=0$
. This condition is equivalent to saying that there is a set
$\lim _{N\to \infty } \frac {1}{N} \sum _{i=1}^N \frac {1}{q_i}=0$
. This condition is equivalent to saying that there is a set
![]() $D\subseteq \mathbb {N}$
of density
$D\subseteq \mathbb {N}$
of density
![]() $0$
such that
$0$
such that
![]() $(q_i)_{i \notin D}$
tends to infinity (see Theorem 1.20 of [Reference Walters24]). Since changing a sequence on a set of density
$(q_i)_{i \notin D}$
tends to infinity (see Theorem 1.20 of [Reference Walters24]). Since changing a sequence on a set of density
![]() $0$
may affect normality and ratio normality, we must now use the argument of Theorem 1.11. At stage n of the construction of
$0$
may affect normality and ratio normality, we must now use the argument of Theorem 1.11. At stage n of the construction of
![]() $\varphi _1(x)\restriction I_n$
, we again use two operations
$\varphi _1(x)\restriction I_n$
, we again use two operations
![]() $\Theta ^{\prime }_{x'(2n)}$
and
$\Theta ^{\prime }_{x'(2n)}$
and
![]() $\Xi ^{\prime }_{x'(2n+1)}$
. The first operation
$\Xi ^{\prime }_{x'(2n+1)}$
. The first operation
![]() $\Theta ^{\prime }_{x'(2n)}$
is the operation implicitly described in the proof of Theorem 1.11. That is, we define the block
$\Theta ^{\prime }_{x'(2n)}$
is the operation implicitly described in the proof of Theorem 1.11. That is, we define the block
![]() $B_{i_0}$
exactly as in that proof, and define the sets
$B_{i_0}$
exactly as in that proof, and define the sets
![]() $A, A',A"\subseteq I_n$
as in that proof. We then eliminate the occurrences of the block
$A, A',A"\subseteq I_n$
as in that proof. We then eliminate the occurrences of the block
![]() $B_{i_0}$
at the points of
$B_{i_0}$
at the points of
![]() $A"$
by applying the digit changing function r as in Theorem 1.11. Let w be the result of applying this first operation to z (so w is the
$A"$
by applying the digit changing function r as in Theorem 1.11. Let w be the result of applying this first operation to z (so w is the
![]() $\varphi _1(x)$
of Theorem 1.11). The proof of Theorem 1.11 did not require that Q be infinite in limit, and so we have that
$\varphi _1(x)$
of Theorem 1.11). The proof of Theorem 1.11 did not require that Q be infinite in limit, and so we have that
![]() $x(2n)\to \infty $
implies
$x(2n)\to \infty $
implies
![]() $w \in \mathscr {N}(Q)$
and
$w \in \mathscr {N}(Q)$
and
![]() $x(2n) \nrightarrow \infty $
implies
$x(2n) \nrightarrow \infty $
implies
![]() $w \notin \mathscr {RN}(Q)$
. The function r changes digits by at most
$w \notin \mathscr {RN}(Q)$
. The function r changes digits by at most
![]() $1$
, and does not affect distribution normality using Remark 1.8 and the fact that D has density
$1$
, and does not affect distribution normality using Remark 1.8 and the fact that D has density
![]() $0$
(changing a sequence on a set of density
$0$
(changing a sequence on a set of density
![]() $0$
does not affect distribution normality). So,
$0$
does not affect distribution normality). So,
![]() $w \in \mathscr {DN}(Q)$
. The second operation
$w \in \mathscr {DN}(Q)$
. The second operation
![]() $\Xi ^{\prime }_{x'(2n+1)}$
is the operation
$\Xi ^{\prime }_{x'(2n+1)}$
is the operation
![]() $\Xi _{x'(2n+1)}$
of Theorem 3.2 except we only apply the operation to digits not in D. We let
$\Xi _{x'(2n+1)}$
of Theorem 3.2 except we only apply the operation to digits not in D. We let
![]() $\varphi _1(x)$
be the result of applying these operations to w. The operations
$\varphi _1(x)$
be the result of applying these operations to w. The operations
![]() $\Xi ^{\prime }_{x'(2n+1)}$
do not affect normality or distribution normality as
$\Xi ^{\prime }_{x'(2n+1)}$
do not affect normality or distribution normality as
![]() $q_i\to \infty $
off of D, and so for every block B,
$q_i\to \infty $
off of D, and so for every block B,
![]() $|N^Q_m(B,\varphi _1(x))-N^Q_m(B,w)|$
is bounded with m. As in Theorem 3.2 we have that
$|N^Q_m(B,\varphi _1(x))-N^Q_m(B,w)|$
is bounded with m. As in Theorem 3.2 we have that
![]() $\varphi _1(x)\in \mathscr {DN}(Q)$
iff
$\varphi _1(x)\in \mathscr {DN}(Q)$
iff
![]() $x(2n+1)\to \infty $
. So,
$x(2n+1)\to \infty $
. So,
![]() $\varphi =\varphi _2\circ \varphi _1$
is a reduction of
$\varphi =\varphi _2\circ \varphi _1$
is a reduction of
![]() $C\setminus D$
(or
$C\setminus D$
(or
![]() $D\setminus C$
depending on the case) to the desired set.
$D\setminus C$
depending on the case) to the desired set.
Second, we can prove the version of Theorem 3.2 with
![]() $\mathscr {N}(Q)$
and
$\mathscr {N}(Q)$
and
![]() $\mathscr {RN}(Q)$
replaced with
$\mathscr {RN}(Q)$
replaced with
![]() $\mathscr {N}_k(Q)$
and
$\mathscr {N}_k(Q)$
and
![]() $\mathscr {RN}_k(Q)$
, provided we assume that Q is k-divergent (and infinite in limit, or more generally
$\mathscr {RN}_k(Q)$
, provided we assume that Q is k-divergent (and infinite in limit, or more generally
![]() $\lim _{N\to \infty } \frac {1}{N} \sum _{i=1}^N \frac {1}{q_i}=0$
). We proceed as above except in defining the block
$\lim _{N\to \infty } \frac {1}{N} \sum _{i=1}^N \frac {1}{q_i}=0$
). We proceed as above except in defining the block
![]() $B_{i_0}$
used in the first operation, and we only consider the first
$B_{i_0}$
used in the first operation, and we only consider the first
![]() $\sqrt [6]{x'(2n)}$
many good blocks
$\sqrt [6]{x'(2n)}$
many good blocks
![]() $B_1,\dots ,B_p$
of length k. This makes sense since there is some block of length k, namely
$B_1,\dots ,B_p$
of length k. This makes sense since there is some block of length k, namely
![]() $0_k$
, which has infinite expectation. If w again denotes the result of applying the first operation in all of the
$0_k$
, which has infinite expectation. If w again denotes the result of applying the first operation in all of the
![]() $I_n$
, then the proof of Theorem 1.11 shows that if
$I_n$
, then the proof of Theorem 1.11 shows that if
![]() $x(2n)\to \infty $
then
$x(2n)\to \infty $
then
![]() $|N^Q_m(B,w)-N^Q_m(B,z)|/Q_m(B)\to 0$
for all blocks B of length k. It follows that if
$|N^Q_m(B,w)-N^Q_m(B,z)|/Q_m(B)\to 0$
for all blocks B of length k. It follows that if
![]() $x(2n)\to \infty $
then
$x(2n)\to \infty $
then
![]() $w \in \mathscr {N}_k(Q)$
and if
$w \in \mathscr {N}_k(Q)$
and if
![]() $x(2n) \nrightarrow \infty $
then
$x(2n) \nrightarrow \infty $
then
![]() $w \notin \mathscr {RN}_k(Q)$
. Also,
$w \notin \mathscr {RN}_k(Q)$
. Also,
![]() $w \in \mathscr {DN}(Q)$
as above. The second operation works exactly as in the above argument, so
$w \in \mathscr {DN}(Q)$
as above. The second operation works exactly as in the above argument, so
![]() $\varphi _1(x) \in \mathscr {DN}(Q)$
iff
$\varphi _1(x) \in \mathscr {DN}(Q)$
iff
![]() $x(2n+1)\to \infty $
. So,
$x(2n+1)\to \infty $
. So,
![]() $\varphi =\varphi _2\circ \varphi _1$
again gives the desired reduction.
$\varphi =\varphi _2\circ \varphi _1$
again gives the desired reduction.
Acknowledgments
The second author was supported by NSF grant DMS-1800323. The third author was supported by grant 2019/34/E/ST1/00082 for the project “Set theoretic methods in dynamics and number theory,” NCN (The National Science Centre of Poland).