A laboratory for mathematics

The MACSYMA system was built and maintained under the auspices of Project MAC, and later the Laboratory of Computer Science at MIT, beginning in the 1960s and into the 1980s, at which time the system was privatized, amid some controversy,Footnote ²⁷ and licensed to Symbolics Inc.Footnote ²⁸ The MACSYMA development team, called the ‘Mathlab group’, was constituted primarily of mathematics and electrical-engineering faculty and doctoral students who had an interest in computing and in the automation of mathematical knowledge in particular. MACSYMA differed from most earlier computer systems for mathematical problem solving insofar as it was not merely for numerical calculating. It was not just for solving differential equations, performing Fourier transforms or calculating series; it was for manipulating non-numeric, symbolic mathematical systems. MACSYMA allowed users to represent, simplify, substitute, transform and infer with algebraic expressions and logical propositions and, in so doing, free up its human users to pursue what they believed were more important and ‘properly human’ cognitive tasks like ‘interpretation, analysis, planning and conjecture’.Footnote ²⁹

In this regard, MACSYMA was a part of a large-scale transformation that unfolded during the 1960s across the United States in which computers went from being treated as larger and more powerful versions of the electric calculating machines and human computers that preceded them, to symbolic machines that could manipulate formal systems whether they referred to numbers or not. The first reprogrammable digital computers in the United States were both functionally intended and conceptually understood as numerical data processors. Numbers were input to the computer, instructions were given for the functional and arithmetic manipulation and storage of numbers, and numeric values were also the output. The developers of MACYSYMA, alongside artificial-intelligence and automated-reasoning researchers, as well as those who sought to establish ‘computer science’ as an academic discipline, instead subscribed to a vision of computers as symbol-processing machines, capable of manipulating any formal system whatever. This vision gained traction during the 1960s and 1970s, as evidenced by the creation of several conferences and journals focused on symbolic, non-numeric and algebraic computing during that time, many serving as platforms for the circulation of research on and with the MACSYMA system.Footnote ³⁰

The Mathlab group that oversaw its development at MIT was named after an earlier algebraic computing system that informed the project. MATHLAB was first introduced at the Fall Joint Computer Conference in 1965 by Carl Engelman, who held an MS in mathematics from MIT and who spent the majority of his career at the MITRE Corporation. Around the same time, two doctoral dissertations were under way at MIT that also sought to automate elements of non-numeric mathematical practice. William Martin completed his PhD in electrical engineering in 1967 by developing the ‘Symbolic Mathematical Laboratory’, which offered tools for the automated manipulation of mathematical expressions.Footnote ³¹ Moses, who received his PhD in mathematics in 1967, developed two programs – SIN (Symbolic INtegrator) and SOLDIER (SOLution of Ordinary Differential Equations Routine) – for automated integration.Footnote ³² Martin and Moses were both hired as faculty immediately following their receipt of doctoral degrees (this was not uncommon in computing at MIT at the time), and continued their research in the automation of non-numeric mathematics, a field that was gaining popularity throughout the growing computing research community in the US. MACSYMA was first devised in 1969 when Martin decided that MIT should launch a larger-scale effort to combine his systems with Moses's SIN and SOLDIER, and Engelman's MATHLAB, and grow from there. Bob Fano, then director of Project MAC, supported the idea, and in May of 1968 submitted the inaugural application for ARPA and Office of Naval Research funding, proposing that symbolic manipulation systems

The application was successful and, by the end of the year, MACSYMA development was under way.

The system grew quickly. By 1971 it consisted of 60,000 words of code (a word being a standardized chunk of computer memory in which instructions were stored) and no less than twenty subroutines that could perform mathematical operations at the user's behest.Footnote ³⁴ By the mid-1970s, MACSYMA had become so popular and lucrative that it no longer needed ARPA funding, and instead a User Consortium was developed for support.Footnote ³⁵ The community which had learned to use the system, integrated it into their problem-solving practice, and in some cases contributed to its capacities, would now pay dues for the privilege. The original members of the consortium were the Department of Energy; NASA; the US Navy; Schlumberger, an oil and gas exploration company that invested heavily in expert-systems research in the 1970s and 1980s; and several universities (though some were exempted from dues).Footnote ³⁶ The consortium revealed the suite of institutions that had access – all of which were connected to the ARPANET, and with it, the PDP-10 computer that housed the MACSYMA system. Access and use were infrastructural and institutional, as well as intellectual, feats.

The US Navy made a survey between 1977 and 1979 of the various ways MACSYMA was being used in their research centres across the country. Everything, from ‘analysis of circuits of the Sidewinder missile control systems’ at the Naval Weapons Center, to ‘finding intensity statistics for a multiple-scatter model of wave propagation through a random medium’ at the Naval Research Laboratory, to the ‘generation of graphs for presentation and inclusion in reports’ at the Naval Ship Research and Development Center, was among the hundreds of reported uses.Footnote ³⁷ Elsewhere, users were finding applications of MACSYMA's capabilities for everything from the solution of theoretical-physics problems, to the optimization of databases, to the study of medical devices, to the generation of examples and counterexamples for number-theoretic conjectures. The users of MACSYMA cut across disciplinary boundaries and included mathematicians, doctors, engineers, physicists and others. They were a community of primarily ARPA-funded mathematical scientists at powerful institutions in the military–industrial–academic complex who may not have had other reasons to interact. By the late 1970s, MACSYMA had, in many ways, outgrown even the formidable infrastructure of MIT and it became, in 1981–3, one of the earliest government-funded computer systems to be privatized, at which point the hard-won MACSYMA community became a market and the automated knowledge at work in the system was commodified. Once it had been extracted, packaged, operationalized and centralized, mathematical knowledge could now conveniently be put up for sale.

Plans and situated thinking

MACSYMA was designed to assist in problem solving by performing operations like algebraic simplification, differentiation, symbolic integration, matrix multiplication and so on, in an automated way. The central insight was that many complex mathematical problems can be broken down into series of these various operations. The MACSYMA user's job was to break a problem down into sub-problems, each of which is known to be solvable by the MACSYMA system. This was called ‘planning’ and it was picked out as one of the uniquely human abilities for which automated tools were to free the human mind.Footnote ³⁸ Planning is an industrial term, as Grier, Penn, and Kennedy have shown, entering the world of computing by way of inter- and post-war industrial culture.

According to Genesereth, who completed a PhD in applied mathematics at Harvard University, and worked on the MACSYMA system during the 1970s, a ‘typical’ (read, ‘ideal’) MACSYMA user should proceed analytically: ‘in solving his problem the user acts in accordance with a standard, high level planning algorithm’.Footnote ³⁹ Depending on the complexity of the problem, sub-problems themselves may need to be broken down into further sub-problems executable by MACSYMA, and so on ‘until a level is reached containing only MACSYMA commands’.Footnote ⁴⁰ That is, the user takes the problem she wants to solve and codes an algorithmic path through MACSYMA's capabilities that would hopefully culminate in a solution. Genesereth represented planning algorithms as a ‘state and transition augmented network (called SATAN)’ (see Figure 1).Footnote ⁴¹ MACSYMA users disciplined their problem-solving practice in order to follow SATAN through the dark mills of automated mathematics.

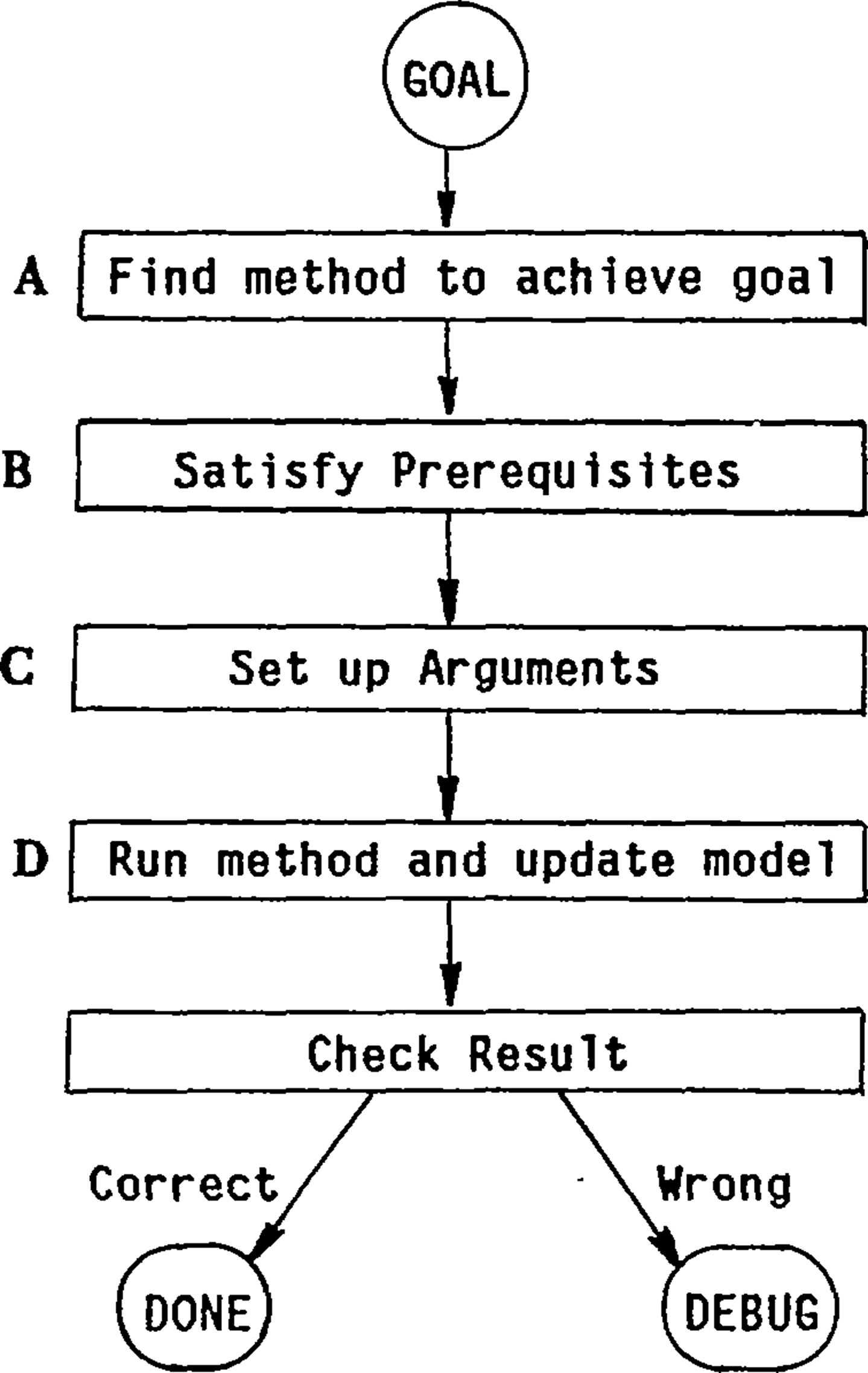
Figure 1. Diagram of the SATAN planning strategy. The original caption reads ‘A flowchart for the “typical” user's planning strategy’. Michael Genesereth, ‘The difficulties of using MACSYMA and the function of user aids’, Proceedings of the 1977 MACSYMA Users’ Conference, NASA, 1977, pp. 291–308, 297.

The practice of breaking down mathematical problems into constituent sub-problems long precedes the modern digital computer. For example, throughout the nineteenth century, machines were manufactured that could perform only addition. Adding machines could solve any problem that could be reduced to a series of additions.Footnote ⁴² Multiplication is such a problem. In order to multiply two numbers together, you just need to be able to add and count (add 1) each time you've added. MACSYMA could do a lot more than just add but the principle was similar. MACSYMA also allowed people to call on operations that were more difficult by hand or that they may not have the mathematical knowledge to execute on their own.

For example, one may wish to minimize a convex function (a bowl-shaped curve) f(x) – that is, find the input to that function that outputs the lowest number on the curve (that input is called the ‘minimizer’ of the function). This task can be broken down into steps that MACSYMA can execute. Thanks to the fact that f(x) is convex, a point x is known to be a minimizer of f if, and only if, the derivative of f is equal to zero at x. In order to solve this problem, one can first take the derivative of f(x) and then solve for any value x where the derivative f′(x) is equal to 0. Once any point x has been found such that f′(x) = 0, this point will be a minimizer of f and the problem is solved. Here, the two sub-problems are (1) taking the derivative and (2) solving the equations. This process can be solved on paper, but it can be tedious. MACSYMA could do derivatives and solve specific equations, and so a solution to this problem can also be produced by translating this plan into the appropriate executable MACSYMA commands, beginning with

$${\rm DIFF}\lpar {{\rm EXP}\lpar {{\rm F}\lpar {\rm X} \rpar \comma \;{\rm X}\comma \;1} \rpar } \rpar \semicolon \;$$

The function ‘DIFF(exp, v1, n1, v2, n2, …) differentiates [the] exp[ression] with respect to each vi, ni times’. Next, a user could call the SOLVE command in order to get MACSYMA to solve f(x) wherever f′(x) = 0.Footnote ⁴³ Here, the drudgery of executing these steps was replaced by the drudgery of planning the sub-problem sequence and programming MACSYMA to execute it, in hopes that time is spared in the end. ‘In using automatic, recursive rule application, the user is sacrificing the effort necessary to control MACSYMA to eliminate the drudgery of applying the rules himself’.Footnote ⁴⁴ Planning – coming up with a series of MACSYMA operations that would solve a given problem – and programming – translating that series into the requisite commands – were the primary tasks of the MACSYMA user, and its utility corresponded to one's ability to encode problem solving this way.

However, there was no algorithm for coming up with a problem-solving algorithm. One of the ‘Maxims for the MACSYMA user’ found in the Primer was ‘The user should anticipate a certain amount of trial-and-error in many calculations in order to determine a good sequence of operations for obtaining the solution.’Footnote ⁴⁵ The Manual explained each particular capability of the system and how to call it so users could plan problem-solving paths. The Manual is also peppered throughout with suggestions about the effects of ordering and combining certain operations. For example, some of MACSYMA's ‘most powerful and versatile commands’ were those for the evaluation and simplification of algebraic expressions. Calling EV(exp, arg1, …, argn), for example, ‘evaluates the expression exp in the environment specified by the argi’. However, for certain problems, it may make sense to simplify an expression before evaluating it, or to ‘resimplify’ it without ‘reevaluating’. As such, NOEVAL – a function that ‘suppresses the evaluation phase of EV’ – the Manual states, ‘is useful in conjunction with the other [argument specifications] in causing exp to be resimplified without being reevaluated’.Footnote ⁴⁶ Or, another example, the function XTHRU(exp) ‘combines all terms’ of an expression over a common denominator. ‘It can be better’, the Manual notes, to use XTHRU before calling another function RATSIMP(exp) (which ‘rationally simplifies’ a given expression) ‘in order to cause explicit factors of the gcd of the numerator and denominator to be canceled thus simplifying the expression to be RATSIMPed’.Footnote ⁴⁷ That is, XTHRU does one particular part of the simplification that makes the next part more effective and efficient. These operations were specified in relation to others, to signal the importance of sequential thinking – of planning, especially where resource consumption was concerned.

The system included many hundreds of operations and variations like these and, as such, charting possible and optimal paths and combinations could be difficult:

The goal was not simply to learn to use MACSYMA; it was to see mathematical problem solving through the lens of the system's capabilities such that one could be a better planner, recognize dimensions in a problem one might not have been looking for before, and develop a sense of what sequences of MACSYMA operations were effective in different problem domains.

Each MACSYMA operation was meant to be an encoding of existing mathematical practice, the system imagined as a collective repository of the things mathematicians know how to do. MACSYMA thus embodied a theory of knowledge – specifically that it can be made both explicit and procedural for the purposes of automation.Footnote ⁴⁹ Martin and Fateman, the two primary drivers of MACSYMA's development, mused in 1971, ‘Our rough hypothesis is that a mathematician knows perhaps 10 000 mathematical facts. For example, if a student learned four facts an hour, four hours a day, five days a week, nine months a year for forty years, he would learn some 12 000 facts.’Footnote ⁵⁰ Most of those facts, they believed, took the form of operations, of ‘how-tos’: mathematicians know how to integrate, they know how to simplify algebraic expressions, they know how to take the limit of a function. In general, expert-systems practitioners theorized knowledge as procedural in this way, believing it could be translated into commands of the kind that can be given to a computer. But herein lay one of the core difficulties for making use of the system.

Genesereth proposed that MACSYMA was grounded in a ‘conception of mathematical knowledge as a body of programming rules’.Footnote ⁵¹ In trying to explain why many users struggled with the system, he suggested that ‘a user may define his operators by the identities they satisfy, but MACSYMA insists on function definitions and unidirectional replacement rules’. That is, mathematicians may define their objects by the properties they have or the constraints they satisfy, but MACSYMA requires instead a procedure for creating that object or for recognizing instances where it can be replaced with some equivalent. As a simple example, one definition of an even number might be, ‘n is even if, and only if, there exists a number m such that n = 2m’. All even numbers will satisfy this property, but this definition doesn't offer an explicit procedure for creating even numbers or establishing whether a given number is even. One such procedure might be ‘divide n by 2. If there is no remainder, then n is even’. This is a trivial example, because the transition from a property-based definition to a procedural one is somewhat obvious. However, these translations were often quite difficult, and in some cases impossible. Mathematical knowledge could only be ‘implemented in MACSYMA as variable values, function definitions, and TELLSIMP rules, etc., rather than as a set of mathematical definitions and constraints’.Footnote ⁵² MACSYMA development involved the translation of mathematical knowledge and practice into programming rules, and that required users to learn to think in these terms as well. Planning meant not only translating a given problem into MACSYMA-executable sub-problems and commands, but also thinking of the objects and relations at stake in a given problem procedurally in the first place. This was part of how MACSYMA users learned to think like developers, like planners, like programmers. And ideally they would be able to contribute their own knowledge to the system, in the requisite, procedural, operationalized form.

Users were encouraged to encode and operationalize their own knowledge, and attach it to the system in the so-called ‘SHARE directory’:

Users were not only meant to think like developers, but ideally to become them, able to translate their own knowledge and needs into the system. One function of the ever-updating Reference Manual was to catalogue the collective code contributed by those users and make it available to others. Each SHARE directory module was introduced by the command a user would type to call it forth. For example, ‘INTSCE LISP contains a routine, written by Richard Bogen, for integrating products of sines, cosines and exponentials of the form EX(A*X+B)*COS(C*X)^N*SIN(C*X)^M. The call is INTSCE(expr,var).’Footnote ⁵⁴ Little information was given for each contribution besides the author's name, the call command and a couple of examples. The directory tracked how successfully users’ knowledge and needs had been shoehorned into the affordances of the system, packaged for automation. It was a repository of shared codes.

Economizing mathematics

The ‘ideal user’ of the MACSYMA system adopted as much as possible the perspective of a developer. The previous section focused on the translation of mathematical knowledge and practice into MACSYMA-executable operations. This section turns to the awareness of resources that users were also meant to share with developers, who must understand and accommodate the limitations of the system. The training materials aimed to instill a sense that computing resources were both scarce and shared, and thus everyone had to adopt a certain etiquette of consumption.Footnote ⁵⁵ Throughout the user aids, economic language was used to describe the project of problem solving with MACSYMA – computing operations were ‘jobs’ and resource-reducing plans ‘paid’. Part of thinking like a developer was thinking economically in this way.

Ellen Golden highlighted many of MACSYMA's limitations in An Introduction to ITS for the MACSYMA User. For example, the system ‘will permit you to have up to eight jobs at one time, but since the system can only accommodate about 120 jobs for all users (including the systems jobs), it is not recommended to have more than two or three’.Footnote ⁵⁶ She continues:

Paying attention to a job's impact on the system as a whole – how many cycles, how much memory it consumed, was a shared code of conduct. Speaking of his experience using MACSYMA at Harvard University in the 1980s, number theorist Fernando Gouvea indicated that ‘the hardest part is that we were all using shared computers with not that much capability which meant that you could easily do things that would get you in trouble, that would get the systems administrator screaming at you – “you shouldn't be using all our cycles!”’Footnote ⁵⁸ Whereas most end users of today's computing systems can operate in relative isolation and ignorance of what others are doing, or of the overall systems and networks in which they are consuming resources, MACSYMA users were made aware that they operated in an ecosystem of shared and limited resources, and had to behave accordingly.

In addition to situating one's ‘jobs’ within the MACSYMA economy, users were also trained to recognize and anticipate excessively consumptive dimensions of their algorithmic planning. For example, two ‘Maxims for the MACSYMA user’ in the Primer referred to the exponential growth of certain computations: ‘A common tendency for a beginning user is to needlessly generalize a problem and thus cause inevitable exponential growth … The user should be aware of the types of calculations which in the general case have exponential growth.’Footnote ⁵⁹ This is to say that it might be possible to easily execute a particular simplification or evaluation of an expression, matrix or Taylor series. However, a user who wanted to evaluate more than one case might ‘consider obtaining the determinant of the general case’ and this could lead to an explosion of data that would quickly exhaust the available memory. In planning a problem-solving course through the system, some ‘intermediate swell’ was usually inevitable, but good planning involved cost-cutting decisions all the way through: ‘it always pays to think before one tries a powerful method’, ‘it pays to reduce the number of variables in a problem as much possible’, ‘it pays if one can reduce the degrees of the variables’, ‘it sometimes pays to convert all expressions to the internal rational function form’, and so on.Footnote ⁶⁰ Many of the ‘Maxims for MACSYMA users’ evidenced the economic and industrial thinking that users should bring to bear on their problem-solving plans. Even though MACSYMA was meant to offer automated versions of known techniques, the system could pursue them to quite inhuman lengths, exceeding what users would have experienced with pencil and paper. As such, they had to develop intuitions for the behaviour of the inhuman execution of familiar techniques and economize accordingly.

MACSYMA users had to adopt the economic thinking required of developers, both to situate their own goals within the economy of jobs, and to develop the most economical plans they could for solving a given problem. In this way, too, users had to translate their problem-solving needs to accommodate the limitations of the system and one another.

The difficulty with simplicity

One of the most notorious economical concerns in MACSYMA's history related to representation. The question of algebraic simplification epitomizes the tension between users’ needs and developers’ needs. Simplification is all about representation – there are uncountably many different ways to represent mathematical expressions, and mathematicians choose to work with the symbolic and formal systems that they find most amenable to their problem-solving needs. A primary activity of mathematical scientists is to transform algebraic expressions into amenable forms, to perform substitutions and transformations. For example, ‘Many symbolic calculations take the following form: One starts with some equations such as y = g(h), z = h(x), f = x ² + y ² + z ², and expressions such as $E\colon \sum_{i=0}^5 c_i x^i$. Later one substitutes such questions and expressions into another expression such as $[(\partial f / \partial x)^2 + 2E^2]/f^3$. Then one attempts to simplify the resulting expression.’Footnote ⁶¹ This was precisely a set of practices that MACSYMA was designed to help with. In manipulating, substituting and simplifying expressions in this way, mathematicians might seek to understand expressions better, to see how they behave, to understand relationships. However, at the heart of this practice are sets of assumptions about what simplicity is, and this turned out to be a controversial subject.

In ‘Simplification: a guide for the perplexed’, Moses explained why MACSYMA was designed as it was, and how users needed to think differently about simplicity in order to make sense of, and make use of, the system:

These two desires can be in tension. Designers have to consider the affordances of their machines – specific economies of computer memory and processing time – that are quite foreign to those whose practice was grounded in paper and pencil. Users were expecting to find automated versions of their paper-based practices, and instead they found computer-oriented versions that were unfamiliar and unruly.

For example, expression [1] sin(4θ) and expression [2]

$4 \frac{1 - \cos^2(\pi/2 - \theta) / \cos^2(\theta)}{1 + \cos^2(\pi/2 - \theta)/\cos^2(\theta)} \cos(\theta) \cos(\pi/2 - \theta)$

are equivalent. They return the same result no matter what value θ has. We might prefer to work with [1] because it is smaller, easier to read, more intuitive, easier to calculate. However, MACSYMA designers might prefer [2]. In implementing a large-scale system like MACSYMA, it could be more economical to implement only one function, or operation, when possible. For example, it might be more economical to do all trigonometric calculations in terms of cosine, rather than implementing cosine, sine, tangent, cotangent and so on. (This is possible because sin(x) = cos(x − π/2), and other trigonometric functions can be represented in terms of one another as well). While [2] is not the simplest representation of [1] in terms of cosine, it could be more amenable to the built-in trigonometric manipulations that MACSYMA can do.

For MACSYMA designers, simplicity was a function of implementation, not visual conciseness or ease of use. But these design features made the system hard to use: ‘One of the most common complaints of users of algebraic manipulation systems is that the expressions obtained as results of a calculation are incomprehensible and therefore essentially useless.’Footnote ⁶³ MACSYMA designers worked continuously to accommodate users and to produce modules that could translate between the forms of expressions that the computer could most easily work and those that users would most like to see on a screen. But ‘simplification for the sake of comprehension’ was, for the developer, just one form of simplification among many. MACSYMA's power derived in part from design choices that adhered to other definitions of simplicity, forms that economized for resources other than those used in paper-and-pencil-based practice. Breaking a problem down into MACSYMA-executable sub-problems was, among other things, a literal act of translation in which ‘the user must translate his problems into MACSYMA's terms’.Footnote ⁶⁴

A designer had to decide ‘how he will represent expressions, what changes of representation his system will perform automatically, which of these automatic transformations he will let the user override and modify, and what additional facilities for simplifying expressions his system will have’.Footnote ⁶⁵ There were inherent trade-offs in these decisions concerning how many forms of representation a system can handle, and how much freedom users have in choosing their own forms of representation. Not all problems translated easily into MACSYMA's terms, and some could not be translated.

Genesereth included the friction between users’ representational choices and MACSYMA's in his taxonomy of ‘Difficulties with the MACSYMA system’. He called them ‘communication difficulties’, the ‘result of the difference between the primitive objects, actions, and relations in the user's problem and those provided by the system.’Footnote ⁶⁶ Often a user simply did not know how to reformalize their problem into MACSYMA's terms. Other times, however, there was no ‘mapping between the primitives of the user's problem and their representation in MACSYMA’. In the language of expert systems, MACSYMA lacked the ‘necessary expertise’ to solve such problems. MACSYMA users, therefore, had to develop familiarity not just with the capabilities of the system, but with the representational structures required or permitted by its various operations. Designers and users of the system had to think in terms of new economies, develop different intuitions for problem solving, and learn new representational forms in order for MACSYMA to be a useful system. These, too, were shared codes of conduct that triangulated between users, developers and the machine.

‘Finally, there are still people!’

Ironically, in spite of the rejection of tacit knowledge implied by the project of fully automating mathematical knowledge, the MACSYMA community depended on human interaction and informal communication for the transfer of technical skill. In addition to the thousands of pages of training materials that circulated, users still struggled to think like programmers, to plan, to break down problems through the lens of MACSYMA capabilities, and to work with the forms of representation the system demanded. There were likely many obstacles to this transition – background, interest, exposure to computing technology, access to community and infrastructure, and more beyond what I can explore here. As such, people supplemented paper in the making of this community in many ways, or, as Ellen Lewis put it at the end of her report on the various aids for MACSYMA users, ‘Finally, there are still people!’Footnote ⁶⁷

Harry Collins and Diana Forsythe each observed that artificial intelligence sought to remove knowledge from its social context.Footnote ⁶⁸ Artificial-intelligence and expert-systems researchers theorized knowledge as something that could be elicited, formalized, automated, and as such something that did not inhere in a body or community or context. However, this position is undone in practice, where ‘the social’ is not erased by automation at all but rather rearranged around it, mediated, obscured and encoded within it.

First of all, as was common in early time-sharing systems, there was no privacy in MACSYMA. Any online user could request a list of everyone who was online at a given time and could even observe the jobs they had under way. The MIT development team would often observe users and offer assistance if they appeared to be having trouble. Genesereth wrote that these human consultants ‘proved to be its most effective user aid’.Footnote ⁶⁹ Lewis too emphasized,

While the development team was overwhelmingly male, Lewis herself played a huge role in maintaining the MACSYMA system, handling incoming and outgoing correspondence, writing, typesetting, editing and distributing the documentation, and in this way articulating and documenting the roles of ‘user’ and ‘developer’ as they took shape. She was (as indicated here) also sometimes the one offering online help. There are still people, but their roles and genders and labour were so easily hidden in these encoded relationships.

There were also multiple commands that users could call to connect with other users. One command, added after the system was made available outside the MIT community, was :SEND(“message”); with which users could ask for help from any other users who were logged in. Another, less generous, command permitted users to request help mid-programming: ‘If you feel you are hopelessly “lost” there is a program called LUSER which will send a message requesting help for you. All you have to do is type :LUSER (followed by a carriage return, of course).’Footnote ⁷¹ The pejorative command signals the often cruel culture of competence signalling that served (and still serves) to police the borders of technical communities.

MACSYMA-mediated community communication and the mountains of paper-based training materials, however, ultimately did not substitute for the face-to-face development of shared codes of conduct. Some members of the Mathlab group toured user institutions, like the US Navy, to offer in-person courses on MACSYMA use. The MACSYMA User's Conference was inaugurated in 1977 to bring users and developers together. Many of the training documents discussed here, like Lewis's ‘User aids for MACSYMA’ and Genesereth's ‘The difficulties of using MACSYMA and the function of user aids’, were first presented at the Users’ Conference. The importance of informal human communication and face-to-face communication in developing the MACSYMA community is perhaps ironic given that the belief that knowledge could be extracted from social context, community and embodiment was at the very heart of the project. The social, however, was not erased by their efforts. It was recoded.

MACSYMA codes of conduct were developed to accommodate and coordinate the needs of users, the priorities of developers and the limitations of machines. These codes were both technical and social, ranging from the translation of mathematical problem solving into algorithmic planning to the norms of resource sharing and online communication. Users had to think as much as possible like developers, and all had to accommodate the obtuse limitations of the underlying computing machinery. The reams of paper that constituted MACSYMA user aids enshrined these codes, revealed their changes over time, and sought to carry them across distances, institutions and disciplines. Throughout, the power of this paper-based training regime and its online counterparts was undermined by the comparative efficacy of human help.

Never to be deterred in their ambitions to automate, however, there were computerized versions of the ‘help’ commands with which users could query the system itself rather than another person. The :HELP( ); command was designed to answer ‘How do I <do something>’ and ‘What are the <arguments, switches> for <command>’ questions.Footnote ⁷² MACSYMA would return best-guess answers based on a rudimentary natural-language processor. The :OPTIONS( ); command activated an ‘Options Interpreter’ that took the name of some MACSYMA command as an input and output a list of things you might do with it.Footnote ⁷³ The :DESCRIBE( ); command offered more specific information about other commands, including the inputs and arguments they required. Finally, the :EXAMPLE( ) command and the DEMO directory, in keeping with the print materials’ orientation to teaching by example, would output example calls of given commands.

Further, Genesereth lamented,

Lewis as well, in describing the automated assistance available in 1977, wrote, ‘This HELPer is the beginning of the ADVISOR subsystems which will ultimately take the place of the communication with human advisors for most questions.’Footnote ⁷⁵ Needless to say, the Advisor was never completed in accordance with this vision. Neither did MACSYMA ever become a consolidated body of all mathematical knowledge, formalized as programming rules, though efforts in this direction continue today. The rejection of tacit knowledge that underlay the development of this system undid itself as the paper-training regime failed to fully and easily induct mathematicians into the MACSYMA user community. Instead, far more interesting and complicated social and technical relationships developed, and these constituted the system itself and its users.

Although MACSYMA did not live up to its developers’ ambitious visions, it was nonetheless an incredible success. Thousands of people learned to think in new ways, to become planners, to develop economic intuitions – communities spanning navy research facilities, oil and gas companies, universities and hospitals – and more disciplined themselves according to codes shared with each other and with the machine in order to automate their mathematical problem-solving practice. But this recoding was born out of formidable acts of discipline and of reformalization in which the objects and practices of mathematics were conceived in the terms of the system.

So much debate, then and now, orbits the question of what machines can and cannot do, what they will and will not make possible. However, the MACSYMA story highlights the degree to which this question is somewhat beside the point. The real question is, what are people willing to do for their machines? And for the people who build, use and profit from them? What new technical and social codes of conduct take shape as people accommodate the machine and encounter each other through it? The user's manuals and printed aids are our best remaining map of what the negotiation of those new codes looked like in the MACSYMA case and how they took shape at the intersection of mathematics and programming, of people and machines, and of users and developers.