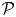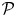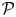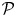What makes an informal proof acceptable to mathematicians? Of the various criteria proposed over the long lifespan of this question, two interesting suggestions have recently emerged. These are transferability and fixability.
To a first approximation, a proof ${\cal P}$![]() of a theorem T is transferable when a typical expert can become convinced of T solely on the basis of their prior knowledge and the information contained in ${\cal P}$
of a theorem T is transferable when a typical expert can become convinced of T solely on the basis of their prior knowledge and the information contained in ${\cal P}$![]() . Easwaran (Reference Easwaran2009) argues that transferability is a constraint on acceptable proof.Footnote 1
. Easwaran (Reference Easwaran2009) argues that transferability is a constraint on acceptable proof.Footnote 1
Meanwhile, a proof ${\cal P}$![]() is fixable when it's possible for other experts to correct any mistakes ${\cal P}$
is fixable when it's possible for other experts to correct any mistakes ${\cal P}$![]() contains without having to devise significant new mathematics. Habgood-Coote and Tanswell (Reference Habgood-Coote and Tanswell2023) observe that some acceptable proofs are both fixable and in need of fixing, in the sense that they contain non-trivial mistakes.Footnote 2
contains without having to devise significant new mathematics. Habgood-Coote and Tanswell (Reference Habgood-Coote and Tanswell2023) observe that some acceptable proofs are both fixable and in need of fixing, in the sense that they contain non-trivial mistakes.Footnote 2
The claim that acceptable proofs must be transferable seems quite plausible. The claim that some acceptable proofs need fixing seems plausible too. Unfortunately, these attractive suggestions stand in tension with one another.
Before explaining why, let me introduce some terminology. Say that an error in a proof is substantive if its fix wouldn't be routine and immediately obvious to a typical expert.Footnote 3 And say that an error is fatal if it renders the argument as stated incorrect. Finally, call a proof broken if it contains at least one error that's both substantive and fatal.
Non-substantive errors aren't very interesting even if they're fatal (because they're trivial to fix), and non-fatal errors aren't very interesting even if they're substantive (because they pose no threat to the argument). I want to ignore such uninteresting mistakes here. So let me define a BF proof to be one that's both broken and fixable. In other words, a BF proof contains at least one error that's both substantive and fatal, but current experts could correct all its (fatal) errors without having to develop significant new mathematics.Footnote 4
More precisely, then, what I want to argue is the following: the claim that all acceptable proofs are transferable is in tension with the claim that some BF proofs are acceptable.
As should be clear from the above discussion, I use the term “proof” throughout the paper to denote a proof attempt or “simil-proof” (De Toffoli Reference De Toffoli2021, Reference De Toffoli, Silva and Oliveira2022).Footnote 5 A proof in this sense may contain errors, whether fixable or not. While this usage is common in mathematics, some authors prefer to set “proof” aside as a success term. Since many of my examples will be arguments whose success is precisely what's at issue, I adopt the broader meaning in order to minimize distracting hedges and distinctions.
Like Easwaran, my main concern is with the descriptive question of which proofs mathematicians actually accept in practice, rather than the normative question of which proofs one ought to accept. I briefly discuss the normative issue in section 3. The goal there is to show that my proposed constraint on acceptable proofs plausibly has better epistemic consequences than a more demanding alternative.
In any case, the answers to the descriptive and normative questions aren't unrelated. As Easwaran writes, “the success of mathematics suggests that the norm of acceptability that is implicit in the practice probably has some strong connection to the objective epistemic norms. Thus, the project of understanding this norm of acceptability…can itself be seen as part of understanding the epistemology of mathematics” (342).
1. The tension
I alluded above to a tension between a certain Transferability Thesis and a certain fixability thesis. The tension, briefly stated, is this. According to the ideal of transferability, everything a suitably well-informed mathematician needs to become convinced of a theorem T is contained in its proof ${\cal P}$![]() . But this isn't the case with broken proofs. Since broken proofs contain substantive errors, a reader will have to do some work of her own – perhaps a considerable amount – in order to identify the mistakes and devise the necessary repairs. Since some of these substantive errors are fatal, the proof won't go through unless the repairs are made. So broken proofs aren't transferable. Hence BF proofs aren't transferable either. This reasoning leads to a dilemma: either transferability isn't a genuine constraint on acceptability, or else BF proofs are never acceptable.
. But this isn't the case with broken proofs. Since broken proofs contain substantive errors, a reader will have to do some work of her own – perhaps a considerable amount – in order to identify the mistakes and devise the necessary repairs. Since some of these substantive errors are fatal, the proof won't go through unless the repairs are made. So broken proofs aren't transferable. Hence BF proofs aren't transferable either. This reasoning leads to a dilemma: either transferability isn't a genuine constraint on acceptability, or else BF proofs are never acceptable.
Below I'll discuss several responses to this argument. To that end, it will be convenient to recast the argument as a reductio ad absurdum, the task then being to identify the false premise or premises:
1. BF Thesis: Some BF proofs are acceptable.
2. Let ${\cal P}$
 be an acceptable BF proof. Then, since ${\cal P}$
be an acceptable BF proof. Then, since ${\cal P}$ is broken, ${\cal P}$
is broken, ${\cal P}$ contains fatal errors that require non-trivial work to identify and fix.
contains fatal errors that require non-trivial work to identify and fix.3. If a proof contains fatal errors that require non-trivial work to identify and fix, that proof isn't transferable. So ${\cal P}$
 isn't transferable.
isn't transferable.4. Transferability Thesis: All acceptable proofs are transferable.
5. By premises 2 and 4, ${\cal P}$
 is transferable. Contradiction.
is transferable. Contradiction.
2. Possible responses
The above argument is valid, and premise 2 essentially states a definition. Yet the conclusion is contradictory. We therefore have four main options. The first option is to reject the very notion of BF proof and insist that brokenness and fixability are incompatible. The second is to deny BF Thesis and insist that no BF proofs are acceptable. The third is to deny premise 3 and insist that all BF proofs are transferable. The last is to deny Transferability Thesis and insist that some acceptable proofs are non-transferable. I consider these options in turn. In the end I'll argue that Transferability Thesis is the problem, and that acceptable proofs need to only satisfy a weaker constraint I call “corrigibility.”
2.1. BF proofs don't exist
One might suspect that the above argument rests on a conceptual mistake: the notion that brokenness and fixability are compatible, and the dependent claim that some BF proofs exist.
The basic issue is this. A broken proof, by definition, takes substantial work to repair. But if a proof is too flawed, then repairing it will exceed experts' capabilities, and hence the proof will no longer count as fixable. It's perhaps unclear that one can have it both ways at once. A skeptic might make an argument like the following: “Fixing a broken proof requires creativity and original thinking. But creatively generating a novel piece of a proof is tantamount to devising significant new mathematics, and a proof whose errors require new mathematics is unfixable by definition. So fixability and brokenness aren't compatible.”
But this argument doesn't work, and the conclusion is mistaken. The argument fails because it wrongly equates one kind of inventiveness – namely, the insight needed to see how to fix a problem using existing techniques – with a distinct kind – namely, the creation of novel mathematics. A broken proof can easily require the former without requiring the latter.
The original proof of Jordan's curve theorem is a plausible historical example of a BF proof. (The curve theorem is the fact that every non-self-intersecting closed curve in ℝ2 divides the plane into exactly two connected components.) It's generally agreed that Jordan's own attempted proof, given in his Cours d'Analyse, wasn't completely correct. For some time Jordan's proof was thought to be hopeless, and the first widely accepted proof due to Veblen used entirely different methods. But subsequent reevaluation of Jordan's proof has yielded a more positive assessment. Many mathematicians now consider its flaws modest and repairable. According to Michael Reeken, for instance, “Jordan's proof does not present the details in a satisfactory way. But the idea is right and with some polishing the proof would be impeccable” (quoted in Hales [Reference Hales2007]: 46). Hales himself presents a modernized version of Jordan's proof, with the aim of “preserv[ing] all of Jordan's major ideas, while avoiding [the original proof's] minor shortcomings” (46). The current consensus seems to be, then, that Jordan's proof was flawed but basically sound, and that fixing its errors requires no substantial innovations.
A second historical case is Perelman's proof of the Poincaré conjecture. It's well known that Perelman was awarded (and refused) both a Fields Medal and a Clay Institute Millennium Prize for proving Poincaré's 1904 statement about 3-manifolds homeomorphic to the 3-sphere. What's less widely known is that Perelman's papers presented a proof sketch rather than a complete argument. In the years since the appearance of the papers in 2003–4, several groups of mathematicians have scrutinized and retooled parts of Perelman's work in order to turn his ideas into a fully articulated proof. In addition to the gaps in need of filling, this process has uncovered a number of mistakes in Perelman's arguments. But it's generally agreed that these errors are all fixable. As the authors of one set of notes write: “Regarding the proofs, [Perelman's 2003 and 2004 papers] contain some incorrect statements and incomplete arguments, which we have attempted to point out to the reader…We did not find any serious problems, meaning problems that cannot be corrected using the methods introduced by Perelman” (Kleiner and Lott Reference Kleiner and Lott2008: 2588). Similarly, the authors of a detailed 2006 presentation of Perelman's proof conclude that, in spite of the need for repairs, “full credit [for] proving Poincaré's conjecture goes to Hamilton and Perelman” (Cao and Zhu Reference Cao and Zhu2006: 4).Footnote 6
These cases show that BF proofs exist in practice and not just in theory. They also suggest that Habgood-Coote and Tanswell's notion of fixability tracks mathematicians' judgments about acceptability: what determines whether a proof contains “serious problems,” and whether its author deserves credit for the result, is in part whether the errors in the proof can be repaired using existing techniques. This gives some reassurance that the fixability standard captures a genuine element of mathematical practice.
2.2. BF proofs aren't acceptable
The second option, and perhaps the most immediately appealing, is to deny that any BF proofs are ever (knowingly) accepted by the mathematical community.
Before discussing this option, let me clarify the notion of acceptance at issue here. To say that ${\cal P}$![]() is accepted as a proof of T is to say that the relevant experts consider ${\cal P}$
is accepted as a proof of T is to say that the relevant experts consider ${\cal P}$![]() adequate to establish T. As the Jordan and Poincaré cases suggest, some telling symptoms of ${\cal P}$
adequate to establish T. As the Jordan and Poincaré cases suggest, some telling symptoms of ${\cal P}$![]() 's acceptance are as follows:
's acceptance are as follows:
• ${\cal P}$
 is published (or deemed publishable) in a mainstream mathematics journal.
is published (or deemed publishable) in a mainstream mathematics journal.• The discoverer of ${\cal P}$
 is credited with having proved T.
is credited with having proved T.• ${\cal P}$
 is cited or used by other mathematicians as a proof of T.
is cited or used by other mathematicians as a proof of T.
If T is regarded by the community as a proven theorem, it follows that at least one proof of T has been accepted.Footnote 7
It's easy to see why BF proofs might seem unacceptable. After all, BF proofs fail to give complete and correct arguments for their conclusions. And surely an acceptable proof has to do that, whatever else it does.
This line of thought may be intuitively plausible, but in fact it doesn't accurately reflect mathematical practice. Mathematicians are often happy enough to accept incomplete or flawed proofs, provided that the problems aren't too serious and that someone knows (or could figure out) how to fix them. The operative standard for proof acceptance is often closer to “believed to be correct in outline” than to “confirmed accurate in every detail.”
One way to see this is by considering the refereeing process for mathematics journals. Reviewers aren't generally expected to check every line of a submitted proof, and most don't do so. As the number theorist Melvyn Nathanson writes: “Many (I think most) papers in most refereed journals are not refereed. There is a presumptive referee who looks at the paper, reads the introduction and the statements of the results, glances at the proofs, and, if everything seems okay, recommends publication. Some referees do check proofs line-by-line, but many do not” (Nathanson Reference Nathanson2008: 773).
Data obtained from mathematics journal editors and referees largely corroborate this picture. In a survey of editors, “estimating the novelty of results” was rated a more important task for referees than “checking the correctness of results,” and about half the editors surveyed said that referees should check some but not necessarily all of a paper's arguments in detail (Geist et al. Reference Geist, Löwe, Van Kerkhove, Löwe and Müller2010). Similarly, in her interviews with seven mathematicians about their refereeing practices, Line Andersen found them to be focused on overall believability rather than local accuracy. Andersen summarizes her findings as follows:
The interviews suggest that when a referee checks a proof for correctness, she usually does not check every step of the proof…She begins by holding the proof, considered in broad outline, up against the landscape of what she knows. She checks whether each subresult of the proof seems reasonable in light of what she knows and, at least for most of the subresults, whether it seems reasonable that this type of result can be proved in this type of way, with this type of tools. If so, she will usually not go on to check the subproof line by line…She then turns her focus to the parts that stand out as surprising or suspicious. These are the parts she typically checks line by line. (Andersen Reference Andersen2017: 185–86)
Unsurprisingly given these methods, Andersen concludes that “[p]ublished proofs often contain minor errors, but it appears that they rarely contain critical or unrepairable errors” (185).
If BF proofs were deemed generally unacceptable, this is surely not the attitude toward mistakes one would expect from mathematicians and their acceptance-signaling institutions. The fact that the discipline shows a great deal of tolerance for fixable errors in published proofs is strong evidence that such mistakes are no bar to acceptability.
For a concrete example of a broadly accepted proof containing many mistakes (some subsequently fixed, others as yet unfixed, still others presumably unknown), I refer readers to Habgood-Coote and Tanswell's (Reference Habgood-Coote and Tanswell2023) discussion of the classification of finite simple groups. As Habgood-Coote and Tanswell show, mathematicians' positive appraisal of the proof of the classification theorem is based largely on optimism about its repairability – an optimism seemingly untroubled by the complex, decades-long process of identifying problems and making the necessary repairs, which is still far from complete. If broken proofs were always unacceptable, no mathematician could reasonably call the classification theorem a proven result. And yet group theorists do so. I conclude that BF Thesis is true.
2.3. BF proofs are transferable
According to the third strategy I want to consider, BF proofs are transferable after all, and hence premise 3 of the above argument is false.
Perhaps the most promising way to make this case is by comparing mistakes to gaps. Everyone agrees that acceptable informal proofs are often gappy, in the sense that they omit premises or pieces of reasoning that are necessary for their arguments to work. But the presence of gaps (of the right kind) need not conflict with transferability. As Easwaran says, “a proof sketch can in many cases be sufficient for the reader to convince herself of the result” (355), and so a gappy proof will be transferable as long as the gaps are “ones that relevant experts can see and still be convinced” (355, fn. 14). In practice, these are precisely the kinds of omissions typically found in published proofs: mathematicians leave out details which are tedious to state and which would be easily reconstructable by fellow experts (Andersen Reference Andersen2020; Fallis Reference Fallis2003). Say that a proof has benign gaps if it omits details of this kind.
Is a proof containing fixable mistakes really so different from one containing benign gaps? It might seem not. Both mistakes and gaps represent respects in which a proof is incomplete as stated. Both may require the reader to exert some effort in order to arrive at full conviction and understanding. And a sufficiently well-informed reader should be able to succeed at this if the mistakes are truly fixable or the gaps are truly benign. It's tempting to conclude from these similarities that BF proofs must be transferable if gappy proofs are.
There's something to this argument, but I don't think it refutes premise 3 in anything like full generality. To see why the comparison fails, recall that a proof is transferable only if the information contained in the proof is sufficient to convince a well-informed reader of its conclusion. Benignly gappy proofs satisfy this condition because their omissions are chosen to complement experts' background knowledge. A typical reader can therefore follow the proof without having to do any significant extracurricular work.
This isn't to say that every benign gap can be easily and thoughtlessly filled by any expert. Some amount of cognitive effort, or even a considerable amount, may be required. But this is also true of proofs whose steps are fully specified. It isn't always trivial to see that T follows from P, Q, R, and S, even if all the relevant propositions and inferential relations are spelled out: reasoning is hard, after all, and human capabilities are limited. So the distinguishing feature of benign gaps isn't ease, but rather straightforwardness. In a benignly gappy proof, it's clear which pieces are missing, and a knowledgeable reader will need minimal creativity to fill them in.
The same isn't true for BF proofs, at least not in general. Perhaps some BF proofs will count as transferable, if their mistakes are minor and the fixes simple. But not all BF proofs are like this. In typical cases, identifying and fixing the errors in a BF proof will require resources beyond the information contained in the proof and the background knowledge it presupposes.
To start with, the reader will have to notice the fatal errors and appreciate their significance. This might itself be a highly non-trivial task – if the proof's author could overlook the problems after thinking through the argument many times, it will be easy for the average reader to do the same. And assuming the mistakes are recognized, the reader will have to perform a substantial, open-ended search for a suitable problem-solving strategy, often with no guarantee of success. (Even if the theorem is known to be true on the basis of some alternative proof, this attempt might turn out to be hopeless.)
In general, none of this will be straightforward in the sense required for transferability: while a fixable proof requires no new mathematics to repair, it may well require creative and non-obvious uses of existing mathematics. And when a proof makes such demands, a typical expert will need more than the proof and their prior knowledge to become convinced of the result.
One might wonder whether a proposal of Habgood-Coote and Tanswell's can vindicate the claim that BF proofs are transferable. On the proposal in question, we have reason to prefer a collectivized or social notion of transferability over Easwaran's individualist notion. A proof counts as transferable in the social sense if “a relevant expert community would become convinced of the truth of the theorem just by consideration of each of the steps in the proof” (23).
The motivation for this proposal derives from cases like that of the classification theorem. As Habgood-Coote and Tanswell point out, the current proof of the theorem is too long and complex for any single human mathematician to review, and the proof is therefore not transferable in a practical sense: no actual person can become convinced by a proof which no actual person can competently read through. Even if a single mathematician has never studied each part of the proof and deemed them all acceptable, though, it's plausible that the group theory community as a whole has done so. Each step has been reviewed and approved by some group theorist at some point, and these verdicts are common knowledge. By pooling its members' attitudes toward the parts of the proof, it seems, the community has become convinced of the truth of the theorem.
This case seems to show that unsurveyability Footnote 8 is compatible with transferability in the social sense. Is the same true of brokenness? That is, will a BF proof typically be transferable with respect to a relevant expert community, even if it fails to be transferable with respect to individual community members? If so, this would provide a way to reject premise 3. We'd only have to follow Habgood-Coote and Tanswell in adopting the social notion of transferability.
I don't believe this strategy can be used to show that BF proofs are transferable.Footnote 9 Brokenness differs from unsurveyability in a crucial respect. The latter is primarily a problem of individual cognitive limitations: what's too complex for a single person may be tractable for many mathematicians working together. But brokenness is primarily an intrinsic property of a proof: the existence and severity of a set of mistakes doesn't depend on the number of mathematicians reviewing the argument. So a broken proof that's untransferable for one will be untransferable for many.
Of course it's true that, by putting its members' heads together, a community may be able to fix a broken proof more efficiently than a single expert could. But we can't infer much from this. As argued above, the barrier to transferability posed by broken proofs has to do with straightforwardness rather than ease and effort. The issue is whether the information contained in the proof (together with standard background knowledge) suffices for conviction, or whether significant and open-ended additional work is required. If this sort of work is required – as it often is with BF proofs – it's required of a community no less than of a single mathematician.
Perhaps there are rare cases in which it makes a difference to adopt the social viewpoint. For instance, some proofs may contain errors that are barely complex enough to count as substantive for any individual mathematician, but which, by combining its members' knowledge, the community as a whole could repair immediately with minimal creativity. This would be a case of a proof that's broken and hence untransferable in the individual sense, but non-broken and transferable in the social sense. Even if this sort of case is possible in principle, though, it requires special conditions that are surely uncommon in practice. There's no reason to expect most errors to pose precisely the sort of difficulty that's trivial for the expert community but non-trivial for any single expert.
I conclude that premise 3 is true, at least for typical choices of ${\cal P}$![]() . BF proofs are often not transferable.
. BF proofs are often not transferable.
2.4. Some acceptable proofs are non-transferable
The fourth possibility is that some acceptable proofs are non-transferable, and hence that Transferability Thesis is false. Having ruled out the other options, this last one had better be correct – and I think it is.
In view of the above discussion, the problem with Transferability Thesis is evidently as follows. An acceptable proof is not necessarily one that a typical expert would find convincing as is, but rather one that an expert would judge to be correct in outline and fixable where broken (by the relevant mathematical community using the methods at their disposal, not necessarily by the reader herself). So acceptable proofs need not be transferable, but merely corrigible.
I take corrigibility to be closely related but not identical to Habgood-Coote and Tanswell's notion of fixability. The requirement that corrigible proofs be basically correct, or correct in outline, is one difference.
Some motivation for this requirement: consider Alice, a poorly prepared calculus student who's asked to prove the intermediate value theorem on an exam. Having reviewed her notes for a few minutes before class, she vaguely remembers some important steps of the proof – let c be the supremum of something, show that c can't be either smaller or bigger than something. She manages to produce a few patchy and confused lines with a passing resemblance to the textbook proof.
Is Alice's proof fixable, in Habgood-Coote and Tanswell's sense? Apparently it is, since any calculus teacher could fix its mistakes without having to invent new mathematics. But the proof surely isn't acceptable. (It couldn't be published in a decent journal, for instance, even if no other proof existed yet.) The reason, I take it, is that an acceptable proof has to be correct in spirit – it has to know what it's trying to do, and it has to have a clear and workable plan for getting there, even if it fails to finesse certain details. This strikes me as an importantly stronger constraint than what's required by fixability, and one that better captures the precise type of error-tolerance displayed by mathematicians.Footnote 10
The claim that acceptable proofs need only be corrigible points to a complex and underappreciated social dimension of acceptability. A lone mathematician can determine that a mistake-free proof is acceptable – all analyses agree about this. Similarly, there's no problem if a reader notices mistakes which she knows how to fix herself. The most interesting case is when a proof is known or suspected to contain errors which the reader doesn't trust herself to catch, or isn't sure how to fix, but which she reasonably believes to be detectable and repairable by the community if necessary.
I've tried to show that this last case is common on the frontiers of research, where mathematicians are often expected to make determinations of acceptability without being able to personally verify every step of a purported proof. So it's important for a theory of acceptability to get this case right. If the arguments I've given are correct, then most standard accounts (including Easwaran's) have failed here. Contrary to received wisdom, a proof that's known or suspected to be broken can nevertheless be acceptable – and in fact many such proofs are accepted all the time.Footnote 11
This conclusion also seems to conflict with De Toffoli's suggestion that a proof is acceptable only if it's transferable, and transferable just in case it's a priori verifiable (De Toffoli Reference De Toffoli2021). Assuming that “verifiable” entails “correct as stated,” BF proofs seem not to be verifiable at all.
These problems notwithstanding, though, it's hard to believe that Transferability Thesis is entirely misguided. There's surely something to Easwaran's observation that mathematicians reject probabilistic proofs because some of their steps are uncheckable black boxes. And nothing in the above dialectic challenges this insight. Probabilistic proofs fail to be transferable in a completely different way than BF proofs, so the acceptability of the latter implies nothing about the former.
So it may be fruitful to think of Easwaran's notion of transferability as comprising two distinct properties, only one of which is truly required for acceptability. The first such property is that of all the steps in a proof being independently checkable in principle by any competent reader. Call this feature evaluability.Footnote 12 The second such property is that of a proof containing all the information necessary to be recognized as correct by a typical expert with appropriate background knowledge. Call this feature impeccability. Easwaran makes a convincing case that acceptable proofs must be evaluable. But I've argued that acceptable proofs need not be impeccable – corrigibility will do instead.
3. The normative question
My focus here has been on the standard governing acceptability in current mathematical practice. But it's also worth asking what this standard achieves, and whether it's epistemically justifiable. Why should mathematicians aim at corrigibility rather than some other target?
It might seem at first that a stricter policy would yield better results. If journal referees spent much more time checking for mistakes, editors tried much harder to print only impeccable mathematics, and the mathematical community withheld credit from authors of erroneous proofs, then the rate of accepted proofs with defects might decrease substantially. Wouldn't this be a good thing for the state of mathematical knowledge?
Not necessarily. There are at least two reasons why not.
The first has to do with the tradeoffs involved in adopting a stricter standard. Mathematical peer review is notoriously slow and onerous even in its current form. As of 2020, the median time from submission to acceptance was over 1.5 years at highly regarded journals like Acta Mathematica, Annals of Mathematics, Inventiones Mathematicae, and the Journal of the AMS (Notices of the AMS 2021). If editors only solicited reports from referees known to be maximally diligent and knowledgeable, and those referees were expected to spend, say, twice as long verifying the correctness of submitted papers, the already-protracted review process might risk breaking down altogether. (Presumably, few junior mathematicians can afford to wait three, four, or five years for an acceptance decision, and many would opt out of publishing in journals with this model. And with editors competing over a smaller pool of overburdened referees, fewer journals might be able to exist at all.)
The tradeoff in question, then, seems to be roughly as follows. On the one hand, imposing stricter standards on acceptance would decrease the number of accepted-but-broken proofs. (It might also reduce the number of outright false published results, but these are probably rare as it is, so this benefit would be small.) On the other hand, the production of new community-approved mathematics would slow down significantly. And the already-vexed peer review system would be subjected to great and perhaps unmanageable stress. It's doubtful that this is an epistemically advantageous trade.Footnote 13
The second fact favoring current standards is that the proofs of most genuinely important results are reviewed, rewritten, adapted, and improved a number of times after they first appear. If the original version of a proof contained mistakes, these will eventually be discovered and corrected if possible. Meanwhile, mistakes in less important work might go forever unnoticed. But precisely because these results aren't widely known and used, the epistemic damage will remain localized. In a sense, then, it's an inefficiency to build extreme caution into the standards for initial acceptance. If a proof turns out to matter to the larger project of mathematics, it will naturally receive high levels of scrutiny over time, and if not, then whatever errors it contains won't do much harm.
From an epistemic-consequentialist standpoint, therefore, something like the standard of corrigibility is well motivated. A much looser criterion for acceptability would let in too much bad mathematics. But a much stricter criterion would impose heavy burdens on the community, slow down the growth of knowledge, and fail to improve on the long-run performance of the current standard in the cases that matter most.Footnote 14