I. INTRODUCTION
According to informal and formal listening tests, the vast majority of listeners prefer a clean band-limited version of audio over a heavily distorted full-band one. In perceptual audio coding, commonly only the low-frequency (LF) components are reproduced. For super wideband (SWB) audio signals, which have a bandwidth of 50 Hz–14 kHz, often only wideband (WB) audio signals with the frequencies below 7 kHz are coded in the existing telecommunication network to facilitate transmission efficiency [Reference Cantzos, Mouchtaris and Kyriakakis1]. The resulting lack of frequency components above 7 kHz degrades the naturalness and expressiveness of audio signals. As a result, an important issue in mobile audio communications is how to make the existing WB audio systems achieve the auditory quality of SWB audio signals at minimum cost. This motivates the use of bandwidth extension (BWE) of audio signals. By analyzing the time–frequency characteristics of WB audio signals, high-frequency (HF) components above 7 kHz can be artificially restored at the decoder to improve auditory quality [Reference Vary and Martin2].
The popular BWE methods used in audio coding standards are non-blind, such as spectral band replication of MPEG4 [Reference Ekstrand3], the noise-filling (NF) technique of the International Telecommunication Union – Telecommunication Standardization Sector (ITU-T) G.722.1 WB audio codec [4], and the spectral folding technique of ITU-T G.719 full-band audio codec [5]. In these methods, first the time–frequency energy of the audio signals is extracted at the encoder. Then, the proper method of spectral patching for each subband is determined according to the correlation between HF and LF spectra. Finally, the time–frequency energy and the control parameters of spectral patching are quantized and transmitted to the decoder as side information. If an appropriate decoder is used, the side information is utilized to reconstruct the discarded high frequencies and the subjective quality can be near transparent from the original SWB signals [Reference Larsen and Aarts6]. But the drawback is that the additional bit-rates of 1–5 kb/s should be provided for the non-blind BWE module [Reference Tobias and Schuller7,Reference Ragot8]. Most communication systems over existing mobile networks do not specifically allocate additional bits for BWE module and the decoder that cannot use the side information only decodes the LF information [Reference Larsen and Aarts6]. Unlike non-blind BWE methods, blind BWE methods can extend the bandwidth only using the statistical properties of the LF audio spectrum, without any auxiliary information regarding the discarded HF components. Independent of the sending side of the transmission link and of existing source coding and network infrastructure, the SWB audio signals can be artificially reproduced via blind BWE methods in the terminal device at the receiving end to enhance the auditory quality of the bandwidth-limited audio signals [Reference Marin, Heute and Antweiler9]. This motivates the focus on blind BWE methods in this paper.
Conventional blind BWE methods can be split into two subtasks: the extension of the spectral envelope and the extension of the fine spectrum. The spectral envelope can be estimated from some a priori information about the nature of correlation between WB audio and the HF signals using codebook mapping [Reference Jax10,Reference Werner and Schuller11], Gaussian mixture models (GMM) [Reference Nilsson, Gustafsson, Andersen and Kleijn12–Reference Nour-Eldin and Kabal14], hidden Markov models (HMM) [Reference Jax and Vary15–Reference Song and Martynovich17], and neural network [Reference Pulakka and Alku18]. The commonly used methods for generating HF fine spectrum of audio signals are based on a “harmonic + noise” model [Reference Vary and Martin2,Reference Ragot8,Reference Iser, Minker and Schmidt19]. For most BWE schemes, spectral folding [Reference Pulakka and Alku18,Reference Laaksonen, Myllylä and Niemistö20] and spectral translation (ST) [Reference Tsujino and Kikuiri21,Reference Berisha and Spanias22] are applied and have shown high effectiveness. The fine spectrum of the low frequencies is directly folded or translated into the HF bands; however, the harmonic relations of the audio signal may be destroyed by spectral shifting within the boundary region between HF and LF spectra, which can lead to undesired auditory roughness [Reference Nagel and Disch23]. In the G.722.1C audio codec [24], the noise is generated frame-wise and is filled into the fine spectrum in the HF bands, which are not quantized and coded. Alternatively, a harmonic bandwidth extension method (HBE) [Reference Nagel and Disch23] can be applied as a blind BWE method combined with the estimation of spectral envelope based on a GMM [Reference Liu, Bao, Jia and Sha25]. Spectral stretching is utilized to extend the LF components between 3.5 and 7 kHz to the higher octave in order to restore partial HF harmonics. In addition, non-linear processing in the time domain (TDNP) [Reference Larsen, Aarts and Danessis26] can reproduce new HF harmonic components using non-linear filtering methods, such as power function and rectification. However, there are an unlimited number of possible non-linear filtering functions, and it is quite difficult to find that particular function that yields the best results in the BWE application. Besides, the effects of the non-linear function for different types of audio signals are very difficult to predict, and this significantly affects the auditory quality of the extended signals [Reference Larsen and Aarts6].
The aforementioned methods of fine spectrum estimation are all derived from the “harmonic + noise” model. They emphasize the restoration of the HF harmonics for tonal signals and maintain the random-like structure for noise signals [Reference Berisha and Spanias22]. However, audio signals generated from different instruments exhibit various spectral characteristics. The HF components generated by percussion instruments are nearly independent of the fundamental frequency. For stringed instruments, the vibration of strings gives rise to a series of strong harmonics. Wind instruments can shape a steady air current and produce resonances with specific frequencies. Meanwhile, for all the types of audio signals, the resonance and radiation of sound in diverse resonators determine audio spectra and weaken the overtone structure with the increasing of frequencies. Furthermore, if diverse instruments perform at the same time, the HF spectrum of audio signals cannot maintain identical tonality with the LF spectrum. Accordingly, the resulting spectra display non-linear characteristics, but cannot be simply described by adding the noise to the harmonics. Inspired by these facts, we introduced the non-linear prediction theory into BWE and proved that audio spectrum has remarkable non-linearity in the previous studies [Reference Sha, Bao, Jia and Liu27–Reference Liu, Bao, Zhang, Zhang, Bao and Bu29]. This paper presents a new method of non-linear prediction to implement audio bandwidth extension from WB to SWB in the frequency domain. Firstly, the LF fine spectrum which is separated from WB audio is converted into a multi-dimensional space using a state-space reconstruction (SSR). According to the dynamical system theory, the trajectory in the reconstructed state space is completely equivalent to the original audio system in terms of diffeomorphism, and the point in state space shares the similar evolving behaviors with its nearest neighbors. Inspired by these, a non-linear prediction based on nearest-neighbor mapping (NNM) is employed to restore the fine spectrum of the high frequencies. The nearest neighbor of the given state point is selected from the state points of the LF components, and the evolving trajectory of the nearest neighbor is used to substitute the evolution of the given point for further predicting the unknown HF fine spectrum. Moreover, an HMM is applied in the spectral envelope extension of the high frequencies. By exploiting the state transition process of HMM, the temporal correlation between adjacent frames can be captured to make the spectral envelope of the extended audio signals smoother over time and better-matched to the original ones. This is beneficial to the auditory quality of the extended audio signals. Then, a minimum mean square error (MMSE) estimator based on HMM is utilized to estimate the spectral envelope of the HF components. Finally, the HF components are regenerated by appropriately shaping a recovered fine spectrum and are combined with the original WB audio to form a SWB audio signal with a bandwidth of 14 kHz.
In the next section, the new BWE method is described in detail, and then the application of the proposed BWE method in the G.722.1 WB audio codec is briefly discussed. In Section III, the proposed method and the reference BWE methods are evaluated in terms of objective quality measurements and subjective listening tests. Then, analysis of computational complexity is further presented for the proposed method. Finally, conclusions are drawn in Section IV.
II. BANDWIDTH EXTENSION METHOD
The proposed BWE method extends the audio bandwidth of WB audio by generating the frequency components in the band 7–14 kHz without any auxiliary information and can therefore be done at the decoder in the terminal device. A block diagram of the proposed BWE method is shown in Fig. 1.

Fig. 1. Block diagram of the proposed BWE method.
The input signal is a WB audio signal sampled at 16 kHz and the bandwidth is 7 kHz. By up-sampling and low-pass filtering, the resulting signal with a sampling rate of 32 kHz is divided into frames with 20 ms length and a window with 50% overlap is used between frames. Then, the windowed signal is transformed into the frequency domain by a modulated lapped transform (MLT), which is also used in the G.722.1 codec as time–frequency transform [24]. The MLT coefficients below 7 kHz, C mlt (i), i = 0 − 279, are uniformly divided into 14 sub-bands and the root-mean square (RMS) of each sub-band, E rms (r), r = 0, …, 13, is computed to roughly present the spectral envelope of LF spectrum as follows:
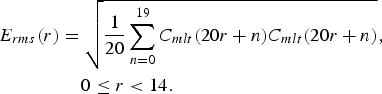 $$\eqalign{{E_{rms}}\lpar r\rpar & = \sqrt {\displaystyle{1 \over {20}}\sum\limits_{n = 0}^{19} {{C_{mlt}}} \lpar 20r + n\rpar {C_{mlt}}\lpar 20r + n\rpar } \comma \; \cr & \, \quad 0 \le r < 14.}$$
$$\eqalign{{E_{rms}}\lpar r\rpar & = \sqrt {\displaystyle{1 \over {20}}\sum\limits_{n = 0}^{19} {{C_{mlt}}} \lpar 20r + n\rpar {C_{mlt}}\lpar 20r + n\rpar } \comma \; \cr & \, \quad 0 \le r < 14.}$$
Here, the normalized MLT coefficients C norm_mlt (i) are adopted to represent fine spectrum of audio signals as follows:
The one-dimensional fine spectrum can be converted into a multi-dimensional space via SSR [Reference Holger30,Reference Small31]. A non-linear prediction model is built up to recover the HF fine spectrum from the vectors in the multi-dimensional space representing the LF fine spectrum. The recovered HF fine spectrum needs to be further normalized to ensure that its spectral flatness is consistent with the LF fine spectrum.
In addition, the normalized MLT coefficients in the HF bands are also uniformly divided into 14 sub-bands. The RMS of HF sub-bands indicating the HF spectral envelope is estimated by an HMM-based Bayesian estimator according to a set of time-domain and frequency-domain features extracted frame by frame from the WB audio [Reference Liu, Bao, Zhang, Zhang, Bao and Bu29]. Then, the spectral shape of the predicted fine spectrum is adjusted by using the estimated energy of HF sub-bands. Finally, the artificially generated HF components are combined with the original LF components to reproduce the bandwidth-extended audio signals by using inverse MLT (IMLT). The remainder of this section will describe the details of the proposed blind BWE method.
A) State-space reconstruction
In our earlier works [Reference Sha, Bao, Jia and Liu27,Reference Liu, Bao, Jia and Sha28], the statistical analysis based on the maximum Lyapunov exponent has been made on the audio spectrum. The results show that for various types of audio signals there is significantly non-linear correlation between spectral coefficients. Inspired by these facts, a non-linear prediction model is built up to simulate the relationship between spectral coefficients.
A normalized MLT coefficients C norm_mlt (i), is represented by a non-linear function of the adjacent MLT coefficients, C norm_mlt (i − 1), C norm_mlt (i − 2), C norm_mlt (i − 3), …, using the formula
where F[.] denotes a non-linear function and i is the frequency index of the normalized MLT coefficients.
1) SELECTION OF EMBEDDING DELAY
In order to reduce correlation redundancy between adjacent MLT coefficients, only some MLT coefficients are selected to predict C norm_mlt (i) and Formula (3) needs to be revised into a sparse form via a delay reconstruction method [Reference Holger30,Reference Packard, Crutchfield, Farmer and Shaw32] as follows:
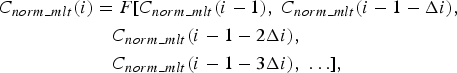 $$\eqalign{C_{norm\_mlt} \lpar i\rpar & =F\lsqb C_{norm\_mlt} \lpar i - 1\rpar \comma \; C_{norm\_mlt} \lpar i - 1 - \Delta i\rpar \comma \; \cr & \quad C_{norm\_mlt} \lpar i - 1 - 2 \Delta i\rpar \comma \; \cr & \quad C_{norm\_mlt} \lpar i - 1 - 3 \Delta i\rpar \comma \; \ldots\rsqb \comma \; }$$
$$\eqalign{C_{norm\_mlt} \lpar i\rpar & =F\lsqb C_{norm\_mlt} \lpar i - 1\rpar \comma \; C_{norm\_mlt} \lpar i - 1 - \Delta i\rpar \comma \; \cr & \quad C_{norm\_mlt} \lpar i - 1 - 2 \Delta i\rpar \comma \; \cr & \quad C_{norm\_mlt} \lpar i - 1 - 3 \Delta i\rpar \comma \; \ldots\rsqb \comma \; }$$
where Δ i is defined as the embedding delay, and any two adjacent MLT coefficients stand Δ i frequency indices apart. The value of Δ i determines the sparseness of non-linear prediction model. A quite small Δ i will lead to a strong correlation between the spectral coefficients used for prediction and reduces the generalization performance of the prediction model. If Δ i is quite large, then the spectral coefficients may be mutually independent and the error of prediction model is increased. Therefore, an autocorrelation-based selection method of embedding delay [Reference Holger30] is adopted in this paper to improve the sparseness of the non-linear prediction model. The autocorrelation function of the normalized MLT coefficients C norm_mlt (i) at lag i′ is defined as
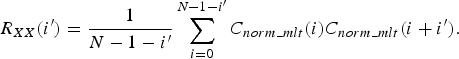 $$R_{XX} \lpar i^\prime\rpar ={\displaystyle{1} \over {N - 1 - i^\prime}}\sum_{i=0}^{N-1-i^\prime} C_{norm\_mlt}\lpar i\rpar C_{norm\_mlt} \lpar i+i^\prime\rpar .$$
$$R_{XX} \lpar i^\prime\rpar ={\displaystyle{1} \over {N - 1 - i^\prime}}\sum_{i=0}^{N-1-i^\prime} C_{norm\_mlt}\lpar i\rpar C_{norm\_mlt} \lpar i+i^\prime\rpar .$$
According to the experimental results, when the autocorrelation value of f(i) is initially down to the empirical threshold, (1 − 1/e) of R XX (0), the lag of frequency indices i′ is set to the optimal embedding delay Δ i. The fine spectrum for a frame of violin signals and the autocorrelation function of MLT coefficients are shown in Figs 2 and 3, respectively. For this example, the appropriate embedding delay Δ i is chosen as 1.

Fig. 2. Fine spectrum for a frame of violin signals.
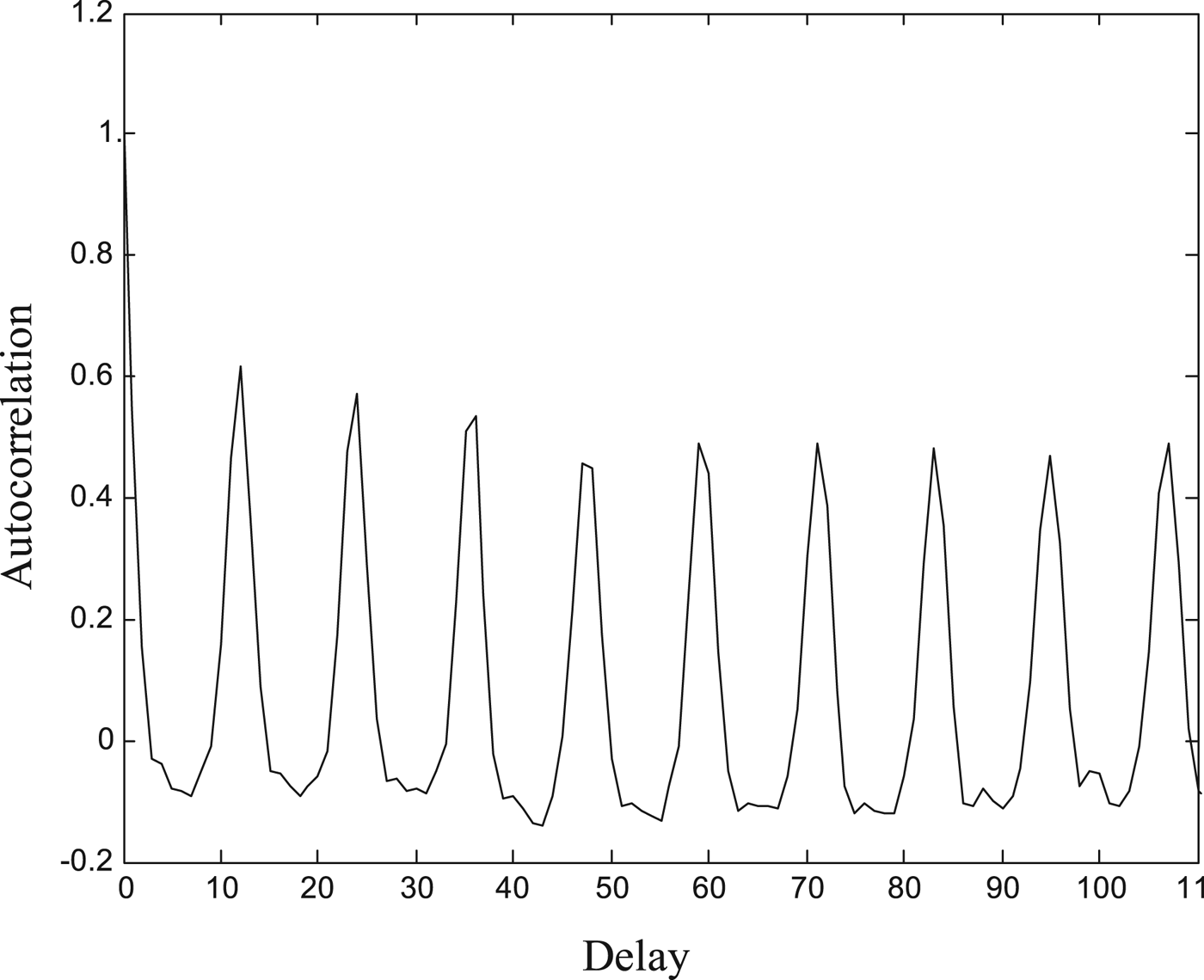
Fig. 3. Example of autocorrelation function for fine spectrum of violin signals.
2) SELECTION OF EMBEDDING DIMENSION
The delay reconstruction method also restricts the number of the input coefficients for the prediction model due to the weak correlation between two coefficients, which are far apart from each other. The finite-order model of non-linear prediction is implemented as follows:
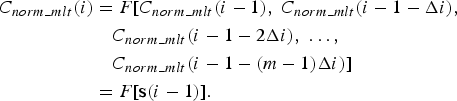 $$\eqalign{C_{norm\_mlt} \lpar i\rpar & = F\lsqb C_{norm\_mlt} \lpar i - 1\rpar \comma \; C_{norm\_mlt} \lpar i - 1 - \Delta i\rpar \comma \; \cr &\quad C_{norm\_mlt} \lpar i - 1 - 2 \Delta i\rpar \comma \; \ldots\comma \; \cr & \quad C_{norm\_mlt} \lpar i - 1 - \lpar m - 1\rpar \Delta i\rpar \rsqb \cr & = F\lsqb {\bf s}\lpar i - 1\rpar \rsqb .} $$
$$\eqalign{C_{norm\_mlt} \lpar i\rpar & = F\lsqb C_{norm\_mlt} \lpar i - 1\rpar \comma \; C_{norm\_mlt} \lpar i - 1 - \Delta i\rpar \comma \; \cr &\quad C_{norm\_mlt} \lpar i - 1 - 2 \Delta i\rpar \comma \; \ldots\comma \; \cr & \quad C_{norm\_mlt} \lpar i - 1 - \lpar m - 1\rpar \Delta i\rpar \rsqb \cr & = F\lsqb {\bf s}\lpar i - 1\rpar \rsqb .} $$
Here, the input coefficients of the non-linear function F[.] can be represented by a state vector s(i) which describes the local structure of audio spectrum. The variable i corresponds to the frequency index of the normalized MLT coefficients. The variable m is defined as the embedding dimension of state vector s(i). According to Embedding theorem [Reference Takens33], m should be large enough to ensure that a state vector can preserve the sufficient information to describe the output MLT coefficients in most cases. In practice, if m is much larger, the reliability of the prediction is also affected. Therefore, the false nearest-neighbor (FNN) method [Reference Rhodes and Morar34,Reference Hegger and Kantz35] is utilized to select a proper embedding dimension m.
Based on the theory of non-linear dynamics [Reference Holger30], the set of state vectors s(i) is defined as a multi-dimensional state space S,
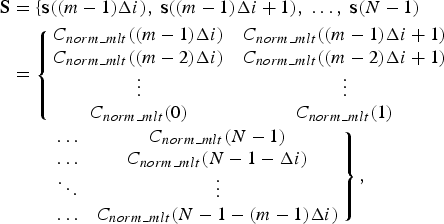 $$\eqalign{{\bf S} &= \lcub {\bf s} \lpar \lpar m - 1\rpar \Delta i\rpar \comma \; {\bf s} \lpar \lpar m - 1\rpar \Delta i + 1\rpar \comma \; \ldots\comma \; {\bf s} \lpar N - 1\rpar \cr & = \left\{{\matrix{ {{C_{norm\_mlt}}\lpar \lpar m - 1\rpar \Delta i\rpar } \hfill & {{C_{norm\_mlt}}\lpar \lpar m - 1\rpar \Delta i + 1\rpar } \cr {{C_{norm\_mlt}}\lpar \lpar m - 2\rpar \Delta i\rpar } \hfill & {{C_{norm\_mlt}}\lpar \lpar m - 2\rpar \Delta i + 1\rpar } \cr \hfill \vdots \hfill & \vdots \cr \hfill {{C_{norm\_mlt}}\lpar 0\rpar } \hfill & {{C_{norm\_mlt}}\lpar 1\rpar } \cr}} \right. \cr & \quad \quad \left. {\matrix{\ldots \hfill & {{C_{norm\_mlt}}\lpar N - 1\rpar } \cr \hfill \ldots \hfill & {{C_{norm\_mlt}}\lpar N - 1 - \Delta i\rpar } \cr \hfill \ddots \hfill & \vdots \cr \hfill \ldots \hfill & {{C_{norm\_mlt}}\lpar N - 1 - \lpar m - 1\rpar \Delta i\rpar } \cr}} \right\}\comma \; }$$
$$\eqalign{{\bf S} &= \lcub {\bf s} \lpar \lpar m - 1\rpar \Delta i\rpar \comma \; {\bf s} \lpar \lpar m - 1\rpar \Delta i + 1\rpar \comma \; \ldots\comma \; {\bf s} \lpar N - 1\rpar \cr & = \left\{{\matrix{ {{C_{norm\_mlt}}\lpar \lpar m - 1\rpar \Delta i\rpar } \hfill & {{C_{norm\_mlt}}\lpar \lpar m - 1\rpar \Delta i + 1\rpar } \cr {{C_{norm\_mlt}}\lpar \lpar m - 2\rpar \Delta i\rpar } \hfill & {{C_{norm\_mlt}}\lpar \lpar m - 2\rpar \Delta i + 1\rpar } \cr \hfill \vdots \hfill & \vdots \cr \hfill {{C_{norm\_mlt}}\lpar 0\rpar } \hfill & {{C_{norm\_mlt}}\lpar 1\rpar } \cr}} \right. \cr & \quad \quad \left. {\matrix{\ldots \hfill & {{C_{norm\_mlt}}\lpar N - 1\rpar } \cr \hfill \ldots \hfill & {{C_{norm\_mlt}}\lpar N - 1 - \Delta i\rpar } \cr \hfill \ddots \hfill & \vdots \cr \hfill \ldots \hfill & {{C_{norm\_mlt}}\lpar N - 1 - \lpar m - 1\rpar \Delta i\rpar } \cr}} \right\}\comma \; }$$
where N − 1 = 279 corresponds to the cut-off frequency of the WB audio. Any two state vectors whose distance is the minimum in the state space are defined as a pair of nearest neighbors. In an appropriate embedding dimension, some neighbors in the state space with a low embedding dimension will no longer be neighbors. This type of nearest neighbors in the low-dimensional space is defined as FNN. With the increase of embedding dimension, FNNs will gradually disappear. So the main idea of FNN method is to examine how the number of FNNs changes as a function of dimension. If the ratio of FNN to all the state vectors does not decrease with the increase of dimension, an appropriate embedding dimension can be determined. The detection method of FNN is detailed in [Reference Rhodes and Morar34]. For an example of the frame of violin signals shown in Fig. 2, the ratio of FNN to all the state vectors as a function of dimension is shown in Fig. 4. If the dimension is larger than 20, the ratio of FNN is not obviously decreasing. The fine spectrum of audio signals is reliably embedded into the state space with the embedding dimension of 20.
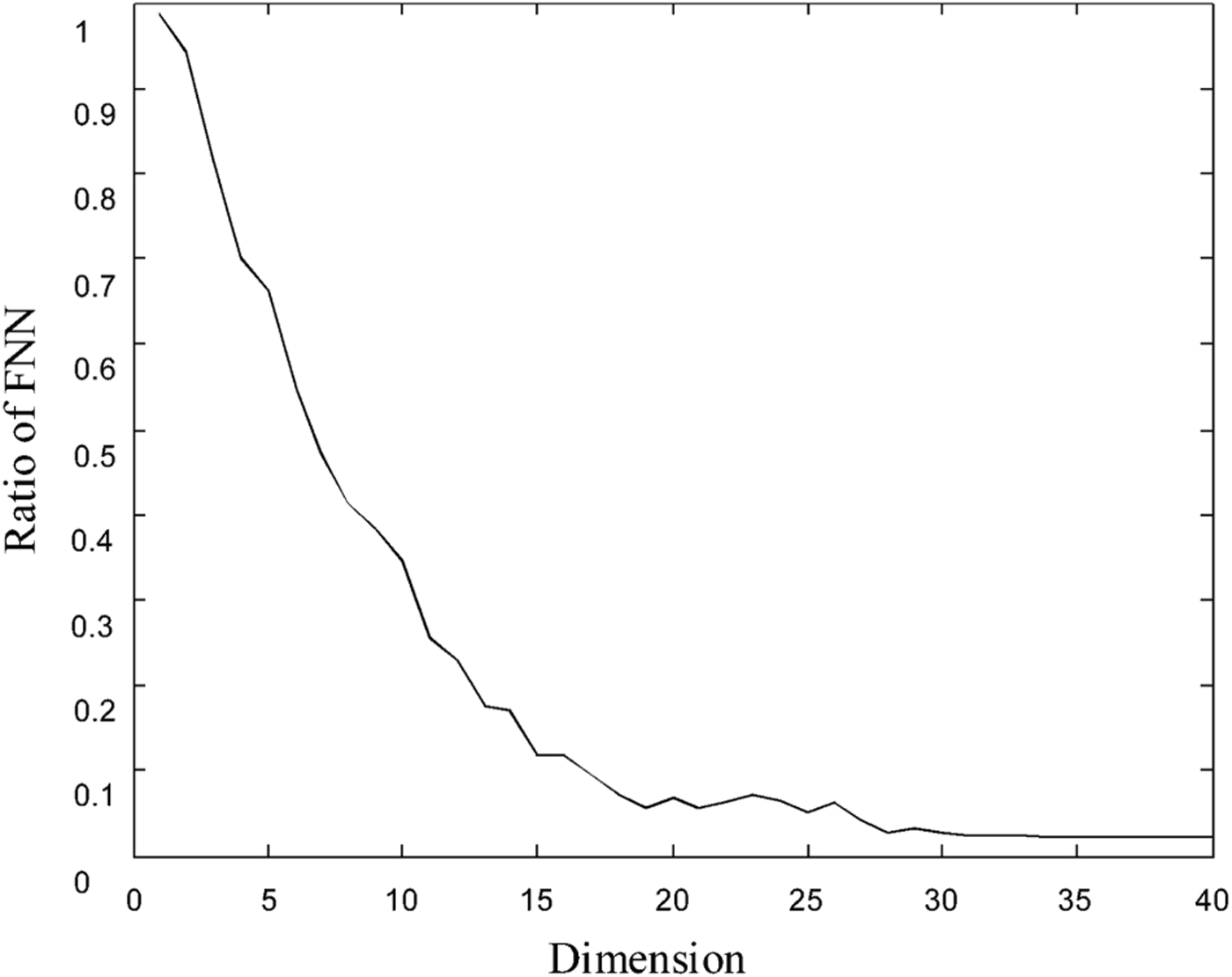
Fig. 4. The relationship between ratio of FNN to all the state vectors and state-space dimension.
3) ANALYSIS OF STATE TRAJECTORY
Once the embedding delay Δ i and the embedding dimension m are determined, a state space can be reconstructed from the fine spectrum of audio signals via the delay reconstruction method derived from Formula (7). Here, by mapping the multi-dimensional space into a three-dimensional space, the change of state vectors with the increase of the frequency index i, which are called the state trajectory, can be visualized and guide us in the analysis of audio characteristics. As a visualized example, we select a SWB audio signal of a violin to reconstruct the state space and analyze the state trajectory. The violin signal comes from the sound quality assessment material (SQAM) recordings for subjective tests of audio signals by the European Broadcasting Union [Reference Waters36]. The semitone of violin segment is D4, and the pitch is about 296 Hz. Embedding delay Δ i and embedding dimension m are set to 1 and 3, respectively. Audio signals with the frame length of 20 ms are transformed by MLT. The fine spectrum of audio signals is represented by the normalized MLT coefficients and the state space is reconstructed. The state trajectories of the fine spectra for LF and HF signals are demonstrated in Figs 5 and 6, respectively. It is manifest that the state trajectories turn dispersed with increasing frequency, but nearly all the state vectors for both the HF and LF signals are localized in a certain range to form a hyper-ellipsoidal structure which cannot be predicted by a multivariate linear model. For other orchestral instruments, symphony and pop music from SQAM, the analysis results of state trajectory are similar. It indicates that the state trajectories of audio spectrum are characterized by regular structure and the state vectors are predictable once the state space is properly reconstructed. Moreover, the audio spectra of some percussion music and live background sound are also analyzed in a three-dimensional space. Although the state vectors are scattered in a disorderly way over a certain area, the trajectories of both LF and HF fine spectra show the similar characteristics of randomness.

Fig. 5. Example of state trajectory for LF fine spectrum of audio signal.

Fig. 6. Example of state trajectory for HF fine spectrum of audio signal.
The aforementioned results about state trajectory analysis show that the audio spectrum has significant non-linearity and the state trajectories can be predictable for different audio signals. Once two state vectors are a pair of neighbors in the state space, they will share the similar change processes with the increase of frequency. Inspired by the facts, a prediction model based on NNM is built up in this paper to recover the fine spectrum of high frequencies from that of low frequencies.
B) Non-linear prediction based on NNM
For the fine spectrum of audio signals, a regular structure is represented in an appropriate state space. The straightforward idea [Reference Sha, Bao, Jia and Liu27] is to adopt a non-linear function for describing the relationship between the unknown MLT coefficients and the given state vector using Formula (6). The output MLT coefficients of the non-linear function will be used to generate a new state vector which becomes the input vector for the next iteration of non-linear prediction. Due to no information transmitted about the error between the predictive value and the true value, the accumulative error cannot be controlled and the output coefficients go to a constant value after multi-step predictions.
In this paper, a new non-linear prediction is adopted according to NNM. Instead of parameterizing a non-linear function, the NNM method considers the unknown MLT coefficients and the given state vector as a pair of one-to-one mapping for describing the change processes of audio spectrum in the state space. Each given state vector is compared with each vector in the state space constructed by the LF fine spectrum. Once the nearest neighbor is exactly determined, the output of prediction model will be estimated by the output MLT coefficient corresponding to the neighbor vector. It is beneficial because the stability of prediction model is ensured without using the output coefficients of the prediction model to re-generate the state vectors for searching neighbors.
A block diagram of the prediction model for the fine spectrum of high frequencies is shown in Fig. 7. After removing the spectral envelope of the WB audio, the normalized MLT coefficients C norm_mlt (i), i = 0, …, 279 represents the LF fine spectrum below 7 kHz. The amplitude values of fine spectrum |C norm_mlt (i)|, i = 0, …, 279 are used as the input coefficients and the amplitude values of HF fine spectrum | C norm_mlt (i)|, i = 280, …, 559 are restored via the non-linear prediction module. Finally, combining with the estimated envelope of the HF spectrum and the sign of MLT coefficients, the MLT coefficients in the range of 7–1 kHz are reproduced. The detailed algorithm is described as follows.

Fig. 7. Block diagram of non-linear prediction for fine spectrum using NNM.
1) ESTABLISHING SHAPE SET OF LF FINE SPECTRUM
Using the normalized MLT coefficients in the LF bands C norm_mlt (i), i = 0, …, 279, the state vector describing the LF fine spectrum s p (i) can be represented as
The embedding delay Δ i and the embedding dimension m are computed via the autocorrelation method and the FNN method, respectively, and are used to reconstruct the state space S p = {s p (i)| i = (m − 1)Δ i, (m − 1)Δ i + 1, …, 279}. Each vector of S p can describe the local spectral structure of the LF components. Accordingly, the state space S p is also defined as the shape set of the LF fine spectrum and provide sufficient information for the dynamic structure of the LF fine spectrum with increasing frequency. It is established every frame with different characteristics of audio spectrum and is not updated by using the predicted MLT coefficients.
2) SEARCHING NEAREST NEIGHBORS
By using the FNN method, the FNNs are eliminated by appropriately increasing the embedding dimension. So the change processes of a given state vector can be estimated by the change of the neighbors. The detailed procedure of searching the nearest neighbors is as follows:
-
• Pitch detection: The pitch t 0 of the band-limited SWB audio signals is computed in the time domain by a normalized cross correlation method. The frequency index i f of MLT coefficient whose frequency corresponds to the pitch t 0 can be used for a coarse search of nearest neighbors and is derived as,
(9)where ⌊·⌋ represents the rounding function. $$i_f =\left\lfloor \displaystyle{1280} \over {t_0}\right\rfloor\comma \;$$
$$i_f =\left\lfloor \displaystyle{1280} \over {t_0}\right\rfloor\comma \;$$
-
• Coarse searching: The last state vector in the LF components s p (i), i = 279, is determined as the estimated state vector. And coarse searching will be performed. The state vectors {s p (i − i f ), s p (i − 2i {f}), s p (i − 3i f ),… } are firstly chosen as the initial candidate nearest neighbors of s p(i). Then, the distance between s p(i) and each initial candidate nearest neighbor is computed. If the distance is larger than a given threshold, the corresponding candidate nearest neighbor is considered outside the neighborhood of s p(i) and is discarded. Otherwise, it is determined as a candidate nearest neighbor s ′ p(j) through coarse searching.
-
• Fine searching: The inner product between s p(i) and each candidate nearest neighbor {s ′ p(j)} are computed one by one. Here, the inner product is adopted instead of the distance measurement due to taking more angle information of state space into consideration. The state vector s p(i NN ) which maximizes the modulus of the inner product is selected as the nearest neighbor of s p(i).i NN is the index of state vector with the maximal modulus of inner product and defined as,
(10) $$i_{NN} ={\mathop{\arg\max }\limits_j}\left\{\vert \langle {\bf s}_{\bf p}^{\prime} \lpar j\rpar \comma \; {\bf s}_{\bf p} \lpar i\rpar \rangle\vert \right\}.$$
$$i_{NN} ={\mathop{\arg\max }\limits_j}\left\{\vert \langle {\bf s}_{\bf p}^{\prime} \lpar j\rpar \comma \; {\bf s}_{\bf p} \lpar i\rpar \rangle\vert \right\}.$$
3) NEAREST NEIGHBOR MAPPING
By maximizing the inner product, the true neighbor of the estimated state vector s p (i) is determined. The relationship between the neighbor s p (i NN ) and the amplitude of the normalized MLT coefficients | C norm_mlt (i NN + 1)| is presented by a mapping function F[.] as,
Likewise, for the estimated state vector s p (i), i = 279, the amplitude of the normalized MLT coefficients |C norm_mlt (i + 1)| is predicted by the similar mapping function as follows:
Because the nearest neighbors are very close in the state space, the distance between s p (i) and s p (i NN ) is considered to be small. With the same mapping function, |C norm_mlt (i + 1)| can be approximately estimated by using the output MLT coefficients fed by s p (i NN ) as follows:
Finally, we should decide whether the frequency corresponding to |Ĉ norm_mlt (i + 1)| rises to the cut-off frequency of 14 kHz. If so, the iterations will be stopped. Otherwise, let i = i + 1, and repeat the steps of searching nearest neighbors and NNM.
4) PRELIMINARY DISCUSSION
As an example, a segment of audio signal from a violin is preliminarily used to evaluate the proposed prediction method about the fine spectrum of high frequencies. The audio signal has a length of 12 s. The fine spectra of SWB audio signal, WB audio signal, and the predicted audio signal are given in Fig. 8. Analysis result shows that the harmonic structure of the predicted audio signals is improved, and the HF components of the audio signal are well restored. Good results are also achieved in the amplitude prediction of fine spectrum for percussion music and live background sound because the state trajectories of both their HF and LF components share a similar characteristic. However, a challenge appears for some particular audio signals whose LF components have large differences from the HF ones. Take a very high-pitched voice to the accompaniment of bass drums as an example. The noise-like sound produced by drums blurs the harmonic structure in the LF components. If the harmonic structure has emerged from the noisy spectrum in the LF region, the predicted HF components may present characteristics similar to the original ones. Otherwise, the proposed NNM method cannot work well to recover the voice in the HF components. The similar situation may also appear for the audio signals which have individual tonal components in HF regions.
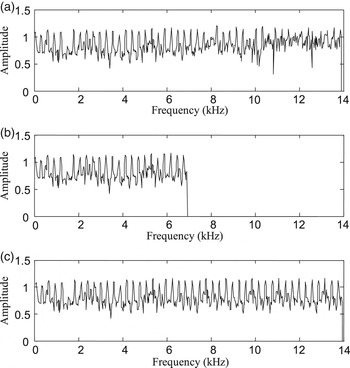
Fig. 8. The comparison of fine spectrum for audio signals from violin. (a) Original spectrum; (b) truncated spectrum; (c) extended spectrum.
In addition, normalized mean-square error is adopted to analyze the influence of embedding delay and embedding dimension over the extension performance of the proposed method and further evaluate the prediction accuracy of HF fine spectrum compared with different BWE methods. The original fine spectrum of HF components is referred to as C norm_mlt(i), i = 280,281,…,559 and its estimated values is Ĉnorm_mlt(i), i = 280,281,…,559. Then, the normalized mean-square error ε NMSE is defined as,
 $$\varepsilon _{NMSE} ={{1 \over 280}{\sum\limits_{i=280}^{559}} {\lpar C_{norm\_mlt} \lpar i\rpar -\hat {C}_{norm\_mlt} \lpar i\rpar \rpar ^2} \over {\sigma _m ^2}}\comma \;$$
$$\varepsilon _{NMSE} ={{1 \over 280}{\sum\limits_{i=280}^{559}} {\lpar C_{norm\_mlt} \lpar i\rpar -\hat {C}_{norm\_mlt} \lpar i\rpar \rpar ^2} \over {\sigma _m ^2}}\comma \;$$
where σ m 2 is the variance of C norm_mlt (i). If ε NMSE is quite large, then the spectral distance induced by BWE is large.
In the proposed BWE method, the autocorrelation method is used to select a proper embedding delay. We experimented with different thresholds and selected an empirical value according to the extension performance of the proposed method. Figure 9 shows little difference of extension performance with different thresholds in autocorrelation method. Therefore, the SSR-based prediction method is not sensitive to the parameter of delay and the traditional threshold (1 − 1/e)R XX (0) is used. Also, the threshold in the FNN method needs to be analyzed. We experimented with several values of ratio and empirically optimized the threshold under the extension performance. As shown in Fig. 10, the value of ε NMSE diminished with the decrease of ratio threshold of FNN. But in practice, a small threshold may cause an increase in the computational complexity. According to the preliminary experiments, when the threshold is down to 5%, the embedding dimension selected by the FNN method will be up to over 25. Due to the increase of embedding dimension, the complexity of the SSR module will increase to more than 6 weighted million operations per second (WMOPS) for the worst case, and is almost double the complexity when the threshold is selected to 10%. Therefore, a proper threshold should be selected which considers both extension performance and computational complexity. Here, it is set to 10%.
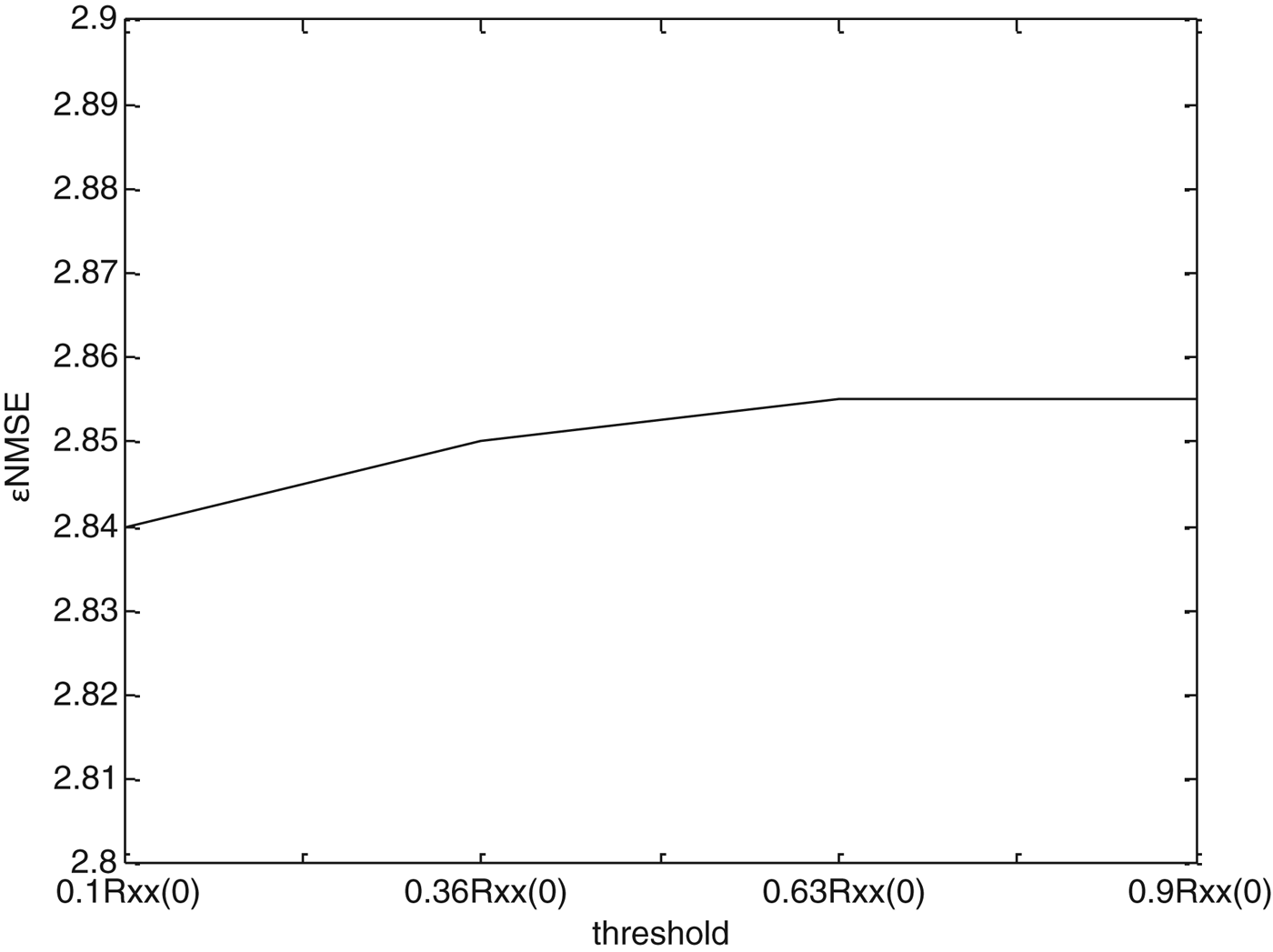
Fig. 9. ε NMSE of proposed BWE method with different thresholds in autocorrelation method.
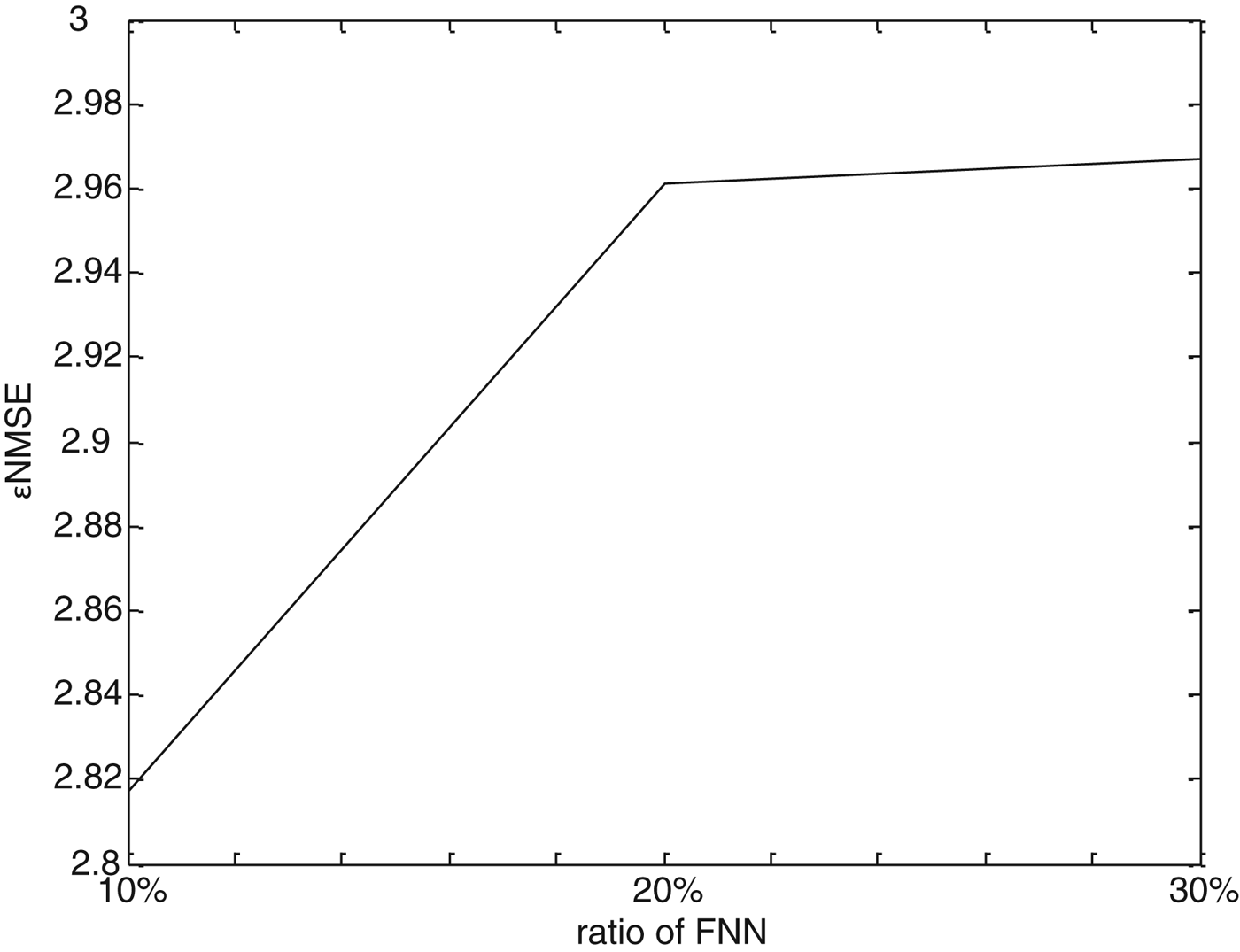
Fig. 10. ε NMSE of proposed BWE method with different ratio of FNN.
In addition, the prediction accuracy of HF fine spectrum is evaluated and compared with different BWE methods by ε NMSE . ε NMSE can guide us in measuring the distortion between the predicted fine spectrum and the original one. In our BWE method, the embedding delay and embedding dimension are adaptively determined by using the autocorrelation method and the FNN method. For the HBE method, the stretching factor is set to 2. And the square function is used as a non-linear function in the TDNP method. Thus, the normalized mean-square error values from four methods are listed in Table 1. It is shown that the prediction error of HBE is the largest because the odd harmonics are not completely reconstructed and the spectral shape of even harmonics is also changed. And the prediction errors from the ST method and TDNP method are in the range of 3.5–5. The TDNP method is suitable for harmonic signals with regards to auditory quality, but the frequency-mixing distortion generated by non-linear processing in time domain leads to a larger error. The ST method directly translates the LF fine spectrum into the HF region. This method reacts sensitively to the spectral characteristics of audio signals. For the violin signals, both the HF and LF components share the strong harmonic characteristics. The moderate distortion is mainly caused by spectral shifting between HF and LF spectra. For some pop music, the noise-like components below 2 kHz generated by accompanying instruments may directly translate into the HF components and lead to more perceptible distortion. In addition, the prediction error of the proposed method is only 2.86. As shown in Fig. 8(c), the HF harmonic structure predicted by the proposed NNM method is substantially consistent with that of the LF spectrum although some artifacts still exist in the HF region. Therefore, it indicates that the proposed BWE method has higher accuracy for spectral prediction compared with conventional BWE methods.
Table 1. Comparison of normalized mean square error for four BWE methods.

C) Estimation of spectral envelope based on HMM
The WB signals are up-sampled at 32 kHz and framed with the length of 20 ms. Time-domain and frequency-domain features F X are computed from the resulting signals and used to estimate the spectral envelope of the HF components F Y based on MMSE by a hidden Markov model [Reference Jax and Vary15,Reference Song and Martynovich17,Reference Liu, Bao, Zhang, Zhang, Bao and Bu29]. After the energy adjustment of the HF components, the HF spectrum from 7 to 14 kHz is restored and is combined with the original LF components to reproduce the SWB audio signals via an IMLT.
1) FEATURE SELECTION
The features extracted from the WB signals are selected for the purpose of differentiating between various audio signals with a different spectral envelope in the HF components. Considering computational complexity, correlation, and independence among data, a 26-dimensional time–frequency feature vector is extracted to describe the auditory perception of the WB audio signals, as shown in Table 2. The precise definition of these specific features of audio signals was given in Reference [Reference Liu, Bao, Jia and Sha25]. The zero-crossing rate F ZCR and the gradient index F g are adopted to distinguish the harmonic signal from the noise-like signal [Reference Vary and Martin2]. The sub-band RMS, F rms (i), i = 0, …, 13, and the flux of sub-band F flux are used to further represent the spectral envelope information of the WB audio signals. Besides, three MPEG-7 audio descriptors (audio spectrum centroid F ASC , audio spectrum spread F ASS and spectrum flatness measurement F SFM (i), i = 7, …, 13) are also employed to supplement the timbre features [Reference Deng, Simmermacher and Cranefield37,38]. F ASC describes the position of dominant spectral content in the power spectrum and roughly indicates the timbre of audio signals. F ASS describes the departure of audio spectrum from F ASC to depict the auditory brightness of audio signals. F SFM (i) are defined as the ratio of geometric mean value to algebraic mean value for MLT coefficients in each sub-band in the frequencies from 3.5 to 7 kHz. The values of F SFM (i) are fixed between 0 and 1. If F SFM (i) = 0, the signal is totally tonal, otherwise if F SFM (i) = 1 it is noise-like.
Table 2. Time-frequency features for describing WB audio signals.

In addition, the estimated spectral envelope of HF components F Y can be represented by RMS of sub-bands, F rms (i), i = 14, …, 27, in the frequencies from 7 to 14 kHz. In the training of a priori knowledge, the statistical distribution of joint feature vector F Z = {F X , F Y } is computed to guide us in estimating F Y under the given F X .
2) TRAINING OF A PRIORI KNOWLEDGE
The block diagram of a priori knowledge training based on HMM is shown in Fig. 11. Firstly, an LBG-based vector quantization method [Reference Lloyd39] is employed to divide the feature space of F Y into N s = 16 cells. Each cell is referred to as a model state S i . According to the state transition process, the actual state transition series {S i } can be obtained, and the distribution probability of each state P(S i ) and the one-step transition probability of actual state series P(S i | S j ) are computed, respectively. Next, for the joint feature vector F Z = {F X ,F Y }, an independent subset F Z|Si = {F X ,F Y |S i } is built for each model state. The joint probability density of each state p(F X,F Y |S i ) is modeled by a GMM with 32 mixtures and full covariance matrices, and the parameters of a GMM are trained by the standard expectation–maximization algorithm [Reference Dempster, Laird and Rubin40]. Thereby, P(S i ), P(S i |S j ), and p(F X , F Y | S i ) are used as a priori knowledge for training with an off-line approach.
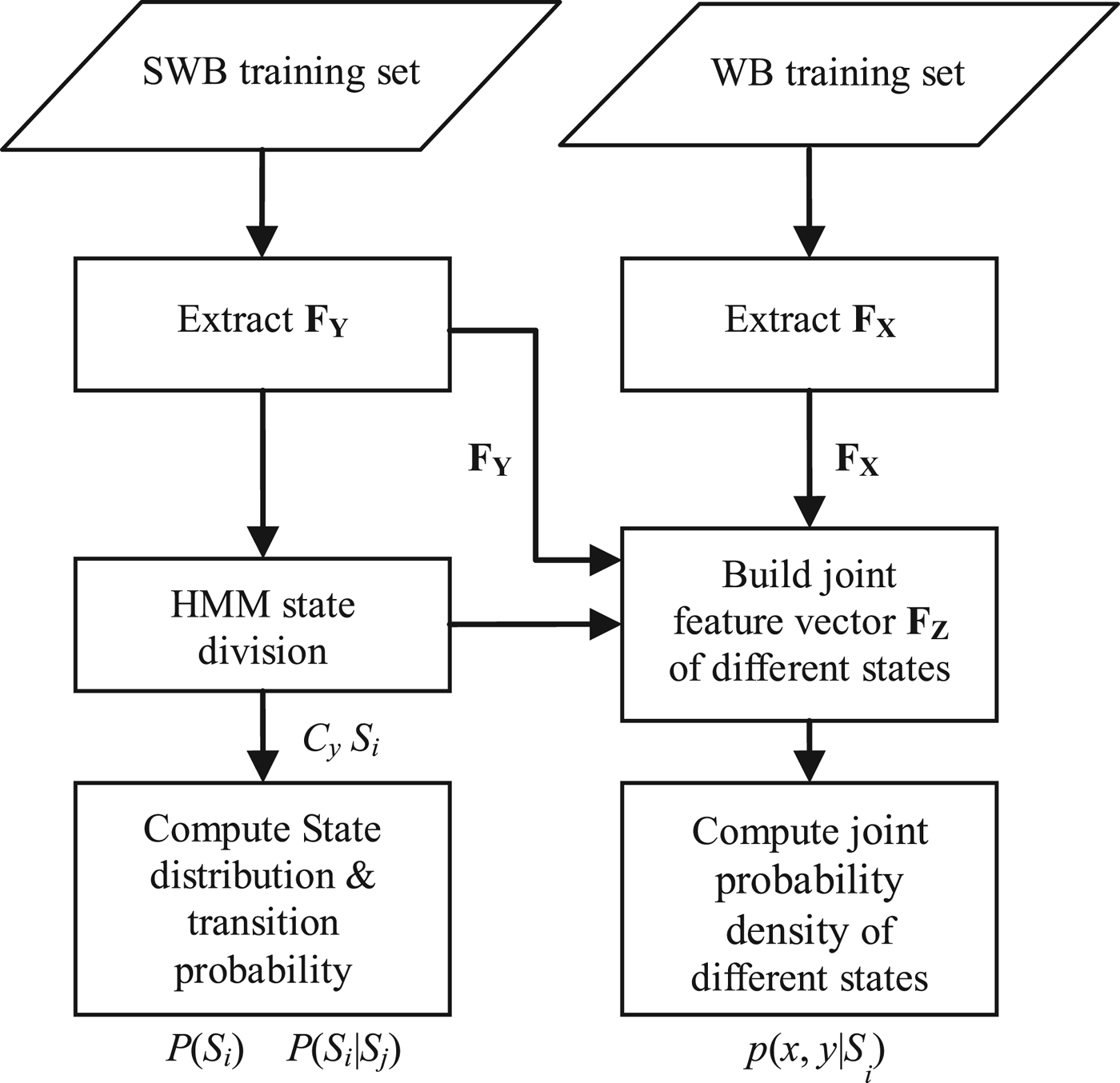
Fig. 11. Block diagram of a priori knowledge training.
3) ESTIMATION OF THE HF SPECTRAL ENVELOPE
For each state S i of the HMM model, an MMSE estimator is used to obtain the conditional expectation E{F Y |S i ,F X} of F Y given the WB features F X ,
which can be calculated from the joint probability distribution function p(F X ,F Y | S i ) [Reference Nilsson, Gustafsson, Andersen and Kleijn12].
If the WB feature vector of the m k th frame, F X (m k ) = {F X (m k − 1), F X } is known, a posterior probability of the ith state, P(S i | F X (m k )) can be computed in a recursive fashion [Reference Patrick and Fingscheidt41] as follows:
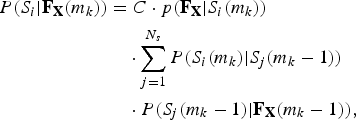 $$\eqalign{P\lpar S_i \vert {\bf F}_{\bf X} \lpar m_k\rpar \rpar &=C\cdot p\lpar {\bf F}_{\bf X} \vert S_i \lpar m_k\rpar \rpar \cr &\quad \cdot \sum\limits_{j=1}^{N_s} P\lpar S_i \lpar m_k \rpar \vert S_j \lpar m_k -1\rpar \rpar \cr & \quad \cdot P\lpar S_j \lpar m_k-1\rpar \vert {\bf F}_{\bf X} \lpar m_k -1\rpar \rpar \comma \; }$$
$$\eqalign{P\lpar S_i \vert {\bf F}_{\bf X} \lpar m_k\rpar \rpar &=C\cdot p\lpar {\bf F}_{\bf X} \vert S_i \lpar m_k\rpar \rpar \cr &\quad \cdot \sum\limits_{j=1}^{N_s} P\lpar S_i \lpar m_k \rpar \vert S_j \lpar m_k -1\rpar \rpar \cr & \quad \cdot P\lpar S_j \lpar m_k-1\rpar \vert {\bf F}_{\bf X} \lpar m_k -1\rpar \rpar \comma \; }$$
where the marginal probability density p(F X (m k )| S i (m k )) of F X , can be derived from the GMM corresponding to the ith state and C is the normalized factor, which keeps the sum of P(S i (m k )| F X (m k )) over all the states be equal to 1.
Taking the state transition process into consideration, the HHM-based MMSE estimator can be performed to obtain the optimal estimation of the HF spectral envelope
![]() $\hat{\bf F}_{\bf Y}$
and is expressed as,
$\hat{\bf F}_{\bf Y}$
and is expressed as,
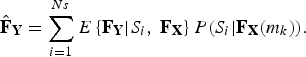 $$\hat{\bf F}_{\bf Y} =\sum\limits_{i=1}^{Ns} E \left\{{\bf F}_{\bf Y} \vert S_i \comma \; {\bf F}_{\bf X}\right\}P\lpar S_i \vert {\bf F}_{\bf X} \lpar m_k \rpar \rpar .$$
$$\hat{\bf F}_{\bf Y} =\sum\limits_{i=1}^{Ns} E \left\{{\bf F}_{\bf Y} \vert S_i \comma \; {\bf F}_{\bf X}\right\}P\lpar S_i \vert {\bf F}_{\bf X} \lpar m_k \rpar \rpar .$$
It is worth noting that each state defined by vector quantization is assumed to be stationary and represents the characteristics of one particular SWB audio. The state transition process described by a Markov chain can effectively describe the evolution among “attack, decay, sustain and release” part of a sound in the time domain. Accordingly, the dynamic performance of the BWE method can be improved by using an HMM-based estimator [Reference Song and Martynovich17]. Especially for the transition between different parts of audio, the sudden change of the HF energy caused by misestimating the spectral envelope is reduced.
D) Synthesis of HF components
The fine spectrum of HF components is reconstructed by using non-linear prediction based on NNM, but the sign information of MLT coefficients is not independently predicted. One alternative method is to fill the random sign into the HF coefficients. But informal listening tests show that if the random sign is filled into the HF coefficients, the sporadic noise will be included in the reproduced audio signals with BWE. Thereby, the sign information in the frequency range from 0 to 7 kHz is translated into the sign of HF coefficients for improving the continuity of HF tonal components in the time domain, and the HF components in the band 7–14 kHz are generated via the energy adjustment of the HF fine spectrum according to the estimated spectral envelope Ê rms (r) as follows:
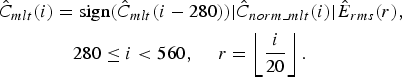 $$\eqalign{\hat{C}_{mlt} \lpar i\rpar &=\hbox{sign}\lpar \hat {C}_{mlt} \lpar i-280\rpar \rpar \vert \hat{C}_{norm\_mlt} \lpar i\rpar \vert \hat{E}_{rms} \lpar r\rpar \comma \; \cr &\quad 280\le i \lt 560\comma \; \quad r=\left\lfloor{i \over 20}\right\rfloor.}$$
$$\eqalign{\hat{C}_{mlt} \lpar i\rpar &=\hbox{sign}\lpar \hat {C}_{mlt} \lpar i-280\rpar \rpar \vert \hat{C}_{norm\_mlt} \lpar i\rpar \vert \hat{E}_{rms} \lpar r\rpar \comma \; \cr &\quad 280\le i \lt 560\comma \; \quad r=\left\lfloor{i \over 20}\right\rfloor.}$$
E) Application of blind bandwidth extension in audio codec
In order to verify the performance of bandwidth extension in practical audio codecs, the proposed method has been used on the audio signals decoded by ITU-T G.722.1 WB audio codec [4] at 24 kb/s to implement blind BWE. The audio signals decoded by ITU-T G.722.1C SWB audio codec [24] are used to compare the performance with the extended SWB audio signals. The encoding and decoding principles of G.722.1 and G.722.1C are described as follows.
1) G.722.1 AND G.722.1C CODEC
For the G.722.1 codec, the bandwidth of input signals is 7 kHz, and the sampling rate is 16 kHz. As shown in Fig. 12, an MLT is performed with the frame length of 20 ms and a 50% overlap is used between frames. The MLT coefficients below 7 kHz are uniformly divided into 14 sub-bands. The spectral envelope of each sub-band is scalar quantized and Huffman coded, and 4 bits of control bits are used to indicate the bit allocation and quantization strategy. At last, the Scalar Quantization and Vector Huffman coding (SQVH) of the normalized MLT coefficients is performed.
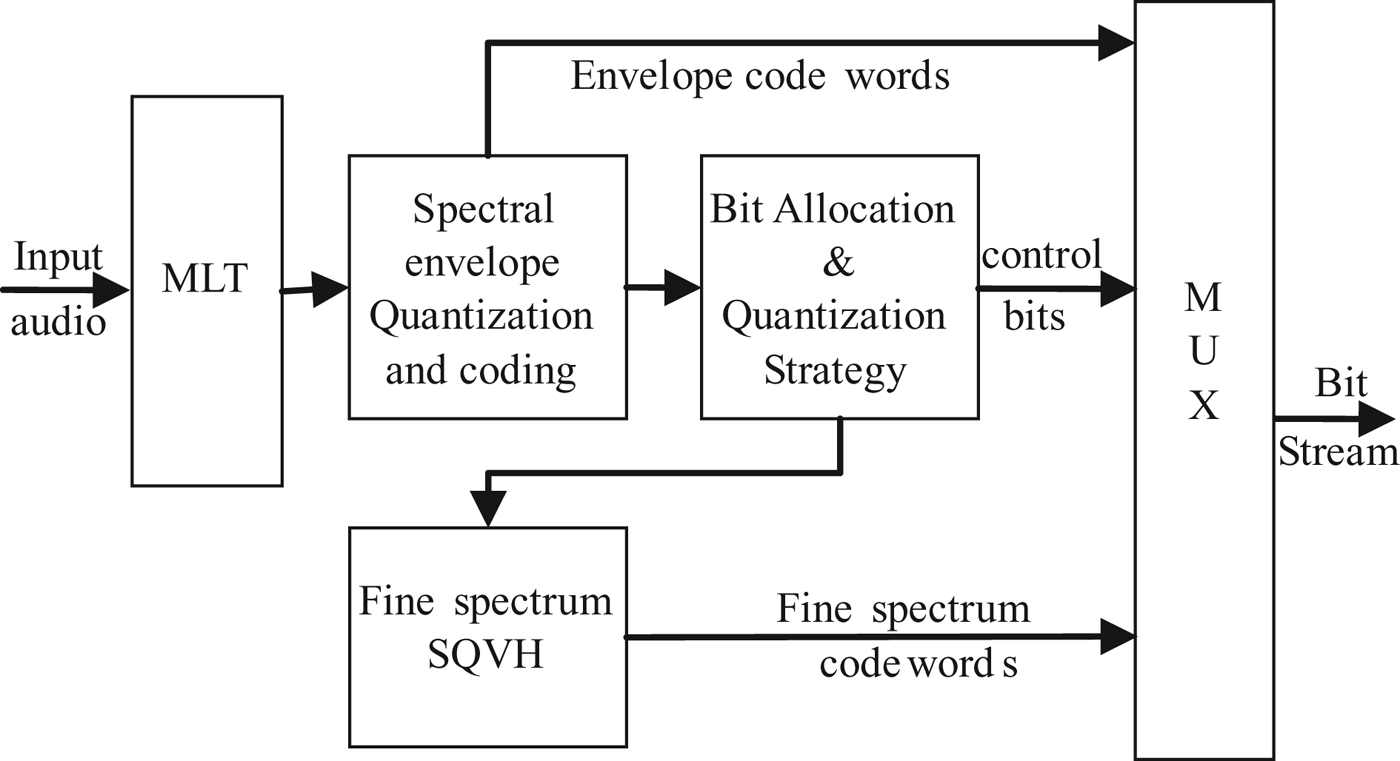
Fig. 12. Block diagram of G.722.1 encoder.
The inverse process of quantization and encoding is performed in the decoder to reproduce the WB audio signals. However, for some sub-bands with lower energy, no MLT coefficients are transmitted as the fine spectrum due to the limitation of coding bit-rates. To avoid audible artifacts, the decoder reproduces these MLT coefficients using NF for which these coefficients are replaced with values of random sign and amplitude proportional to the sub-band energy.
As an extended mode of G.722.1, the G.722.1C codec adopts the same framework as the G.722.1 main body and is designed to operate with an audio signal sampled at 32 kHz. Since the frequency information transmitted by G.722.1C is double that of G.722.1, G.722.1C must allocate more bits to the LF information in order to facilitate coding efficiency. For G.722.1C at 24 kb/s, only the sub-band energy of the HF components is transmitted to the decoder at about 2 kb/s, while the fine structure of the HF spectrum is almost reproduced by NF. With the increasing of bit-rate, more information describing the fine spectrum is encoded and the quality of the reproduced signals is further enhanced. G.722.1C can be referred to as a non-blind BWE method, which can improve the brightness of the reproduced audio signals at low bit rates. Therefore, it is selected as an important reference method to evaluate the performance of proposed blind BWE method.
2) APPLICATION FRAMEWORK OF THE PROPOSED BWE METHOD
In order to extend the bandwidth of audio signals decoded by G.722.1, the proposed BWE method is embedded into G.722.1 decoder as a separate module. The block diagram of the G.722.1 decoder with BWE is depicted in Fig. 13, and the algorithm is presented in Table 3.
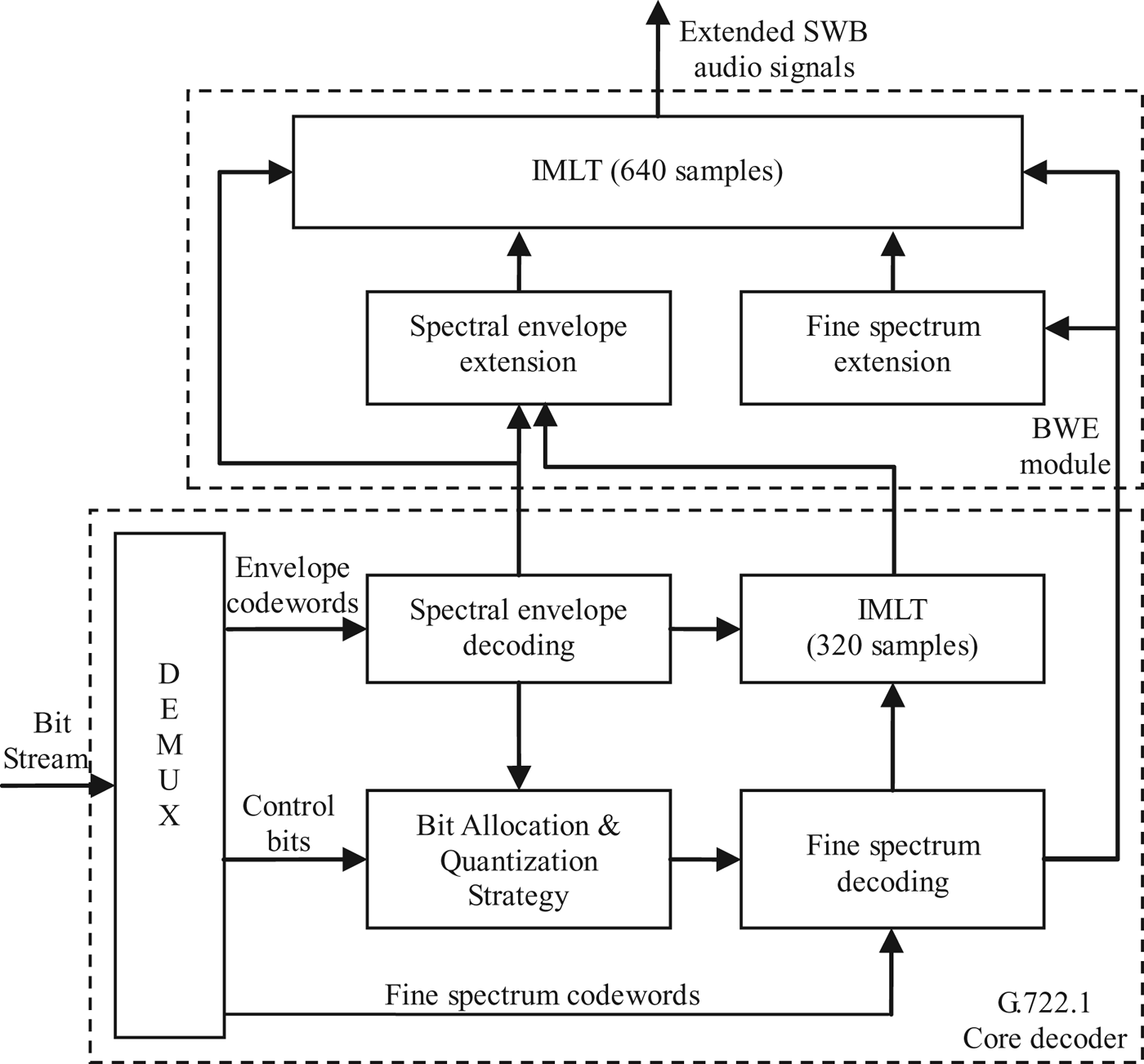
Fig. 13. Block diagram of G.722.1 decoder with BWE.
Table 3. Algorithm of G.722.1 decoder with the BWE function.

The normalized MLT coefficients decoded from the fine spectrum code words according to control bits are used to recover the HF fine spectrum by using the non-linear prediction based on NNM. In addition, a set of features computed from the decoded sub-band energy and the reproduced WB audio is fed into the HMM-based estimator. After the energy adjustment, the regenerated HF components are combined with the original WB audio to form a SWB audio signal via an IMLT. It is worth noting that, because the G.722.1 codec and the proposed BWE method adopt the same time–frequency transform, no additional complexity of time–frequency transform is required in the G.722.1 + BWE scheme.
III. EVALUATION AND TEST RESULTS
The goal of this work is to enhance the auditory quality of the WB audio, and to make the reproduced signal achieve a comparable performance with the SWB audio coding. This section will describe the subjective and objective evaluations of the proposed BWE method in comparison with the reference methods, as well as the WB audio decoded by G.722.1 and the SWB audio decoded by G.722.1C. Analysis of computational complexity is also presented.
A) Training
In the proposed method, statistical dependencies between the features computed from the WB audio and the HF spectral envelope are modeled as an HMM. The training data come from the lossless audio data of the 39th Annual American Music Awards recorded by the American Broadcasting Corporation. It contains different types of dialogues, music, singing, and live background sound. The audio signals were transcoded by high-quality equipment and digitally stored by using 16-bit PCM with the sampling frequency of 32 kHz and the bandwidth of 14 kHz. The length of training data was about 2 h and its level was normalized to −26 dBov. The parallel WB audio signals were generated after low-pass filtering and down-sampling. The time-domain and frequency-domain features extracted from the WB signals were used as the input features F X . The HF spectral envelope F Y was computed from the training samples in the parallel SWB database. The joint vector F Z = {F X ,F Y } were modeled by an HMM. By using a LBG algorithm, the feature space of F Y is divided into 16 states. Additionally, the state probability and transition probabilities are easily computed according to the hybrid-training approach proposed by Jax and Vary [Reference Jax and Vary15]. The joint probability density p(F X ,F Y | S i ) of each state can be approximated by a GMM trained using the standard expectation–maximization algorithm. The model has 32 mixtures and full covariance matrices. According to an informal listening test, no evident difference can be perceived with increase of the number of states and Gaussian mixtures.
B) Test data and reference methods
Eighteen audio signals were chosen for test from the standard audio quality assessment database of MPEG. None of these signals was included in the training data. Each audio signal had a length between 10 and 20 s and was sampled at 32 kHz with the bandwidth of 14 kHz. These test signals were clean and could be divided into three types: simple audio, complicated audio, and singing audio. Each type had six audio data. In the simple audio data, no more than three instruments were performing at the same time. But the complicated audio data contained more types of instruments performing simultaneously. Singing with accompaniment was classified as singing data. Moreover, the sound level of each test signal was also normalized to −26 dBov.
The test signals were down-sampled at 16 kHz and processed with the G.722.1 codec at 24 kb/s as WB references. SWB references were produced with the G.722.1C codec at 24 and 32 kb/s. Test items for BWE were obtained by applying the proposed method and reference methods to the G.722.1-coded WB signals. In summary, the eight processing types included in the evaluations are listed below.
-
• G.722.1: WB audio coded with the G.722.1 codec at 24 kb/s;
-
• G.722.1C-24: SWB audio coded with the G.722.1C codec at 24 kb/s;
-
• G.722.1C-32: SWB audio coded with the G.722.1C codec at 32 kb/s;
-
• NNM: G.722.1-coded WB audio processed with the proposed BWE method;
-
• ST: G.722.1-coded WB audio processed with the ST method;
-
• TDNP: G.722.1-coded WB audio processed with the TDNP method;
-
• HBE: G.722.1-coded WB audio processed with the HBE method;
-
• CP: G.722.1-coded WB audio processed with the chaotic prediction (CP) method [Reference Sha, Bao, Jia and Liu27].
For G.722.1C at 24 and 32 kb/s, the bit rate of about 2 kb/s is used for the sub-band energy in the HF components. The NF is used to reproduce the HF fine spectrum in the SWB codec at 24 kb/s, while additional code-words describing the HF fine spectrum are transmitted to decoder at 32 kb/s. The original methods of ST, TDNP, and HBE need the cost of small side information describing the spectral envelope of the original HF components. In order to compare with the blind BWE method, the same MMSE estimator based on HMM as the proposed method is used in these methods to reconstruct the RMS energy of sub-bands in the HF components. The ST and spectral stretching methods are processed in the frequency domain for the ST and HBE methods, respectively. The TDNP method adopts the non-linear processing based on a square function to reproduce the new HF harmonic components in the time domain. So the extended audio signals have to been translated into the frequency domain for adjusting the spectral envelope. In addition, the CP method reconstructs the HF fine spectrum by the joint prediction between linear and non-linear functions, and further adjusts the harmonics and spectral envelope without side information.
C) Objective evaluation
Audio signals generated using the proposed method, the reference methods (ST, TDNP, HBE, and CP), and G.722.1C, were objectively evaluated in terms of the log spectral distortion (LSD) [Reference Pulakka, Laaksonen, Vainio, Pohjalainen and Alku42] and the segmental signal-to-noise ratio (SNRseg) [Reference Richards43] in comparison with the original SWB audio. Before evaluation, the processed signals are aligned with the original signals in the time domain and resampled at 32 kHz.
1) LOG SPECTRAL DISTORTION
For 18 test signals, differences between the differently processed SWB signals and the original SWB signals were compared in terms of LSD measure, which is commonly used for the comparison of the audio spectra. LSD based on the fast Fourier transform power spectrum has been employed for the BWE evaluation in this paper, and its measurement is defined as,
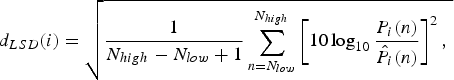 $$d_{LSD} \lpar i\rpar =\sqrt{{1 \over N_{high} -N_{low} +1} \sum\limits_{n=N_{low}}^{N_{high}}\left[10 \log _{10} {P_i \lpar n\rpar \over \hat {P}_i \lpar n\rpar }\right]^2\comma \; }$$
$$d_{LSD} \lpar i\rpar =\sqrt{{1 \over N_{high} -N_{low} +1} \sum\limits_{n=N_{low}}^{N_{high}}\left[10 \log _{10} {P_i \lpar n\rpar \over \hat {P}_i \lpar n\rpar }\right]^2\comma \; }$$
where d
LSD
(i) is the LSD value of the ith frame, P
i
and
![]() $\hat{P}_{i}$
are the power spectra of the original SWB audio signals and the audio signals processed with different methods, respectively. N
high
and N
low
are the indices corresponding to the upper and lower bound of the frequency band from 7 to 14 kHz. The analysis was performed using a discrete Fourier transformation (DFT) in 20-ms frames without overlapping. The frame-based LSD is averaged over all the frames for each test signal and the mean LSD is used as an objective quality measurement for BWE.
$\hat{P}_{i}$
are the power spectra of the original SWB audio signals and the audio signals processed with different methods, respectively. N
high
and N
low
are the indices corresponding to the upper and lower bound of the frequency band from 7 to 14 kHz. The analysis was performed using a discrete Fourier transformation (DFT) in 20-ms frames without overlapping. The frame-based LSD is averaged over all the frames for each test signal and the mean LSD is used as an objective quality measurement for BWE.
The results of LSD measurement are shown in Fig. 14. Through BWE, the LSD of complicated audio signals is much larger than other types of audio signals. Because various types of instruments are involved in the complicated audio signals, the energy in the HF spectrum is relatively high and not easy to estimate accurately. The distortion of simple audio signals is the smallest, on one hand, because the typical harmonic components in the solo of violin, orchestral instruments, and guitar are easy to recover. On the other hand, the energy attenuation of their HF components is obvious, thus it may lead to a low distortion.
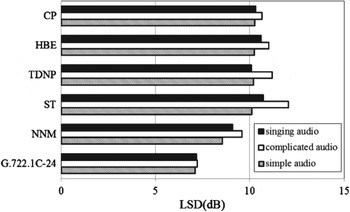
Fig. 14. LSD for different BWE methods.
As shown in Fig. 14, the SWB audio reproduced by G.722.1C can achieve the best objective quality for all the three types of audio. The spectral distortion induced by ST is the largest and the mean LSD of ST is about 11 dB. The LSD of ST seems to be different from the normalized mean-square error of ST in Section II. This is because LSD emphasizes the distortion induced by an estimated spectral envelope, instead of the fine spectrum of the extended signals. For the complicated audio with a high energy in the HF bands, some noisy components translated from the components below 2 kHz lead to a higher average distortion. Moreover, LSDs of the TDNP, HBE, and CP methods are similar, and the mean values are around 10.5 dB. NNM method shows a better extension performance than others and the mean LSD is close to 9 dB. Furthermore, the LSD of complicated audio is 1 dB higher than that of simple audio for both the NNM method and the HBE method. Thus, the fine spectrum prediction for complicated audio needs to be further optimized.
2) SEGMENTAL SIGNAL-TO-NOISE RATIO
Besides LSD, SNRseg is also used as an objective quality measurement to evaluate the differences between the reproduced signals and the original signals in the time domain. It is defined as,
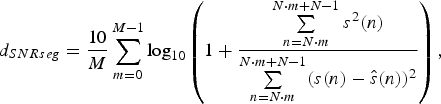 $$d_{SNRseg} ={10 \over M} \sum\limits_{m=0}^{M-1} \log_{10} \left(1+{\sum\limits_{n=N\cdot m}^{N\cdot m+N-1} s^2\lpar n\rpar \over \sum\limits_{n=N\cdot m}^{N\cdot m+N-1} \lpar s\lpar n\rpar -\hat {s}\lpar n\rpar \rpar ^2}\right)\comma \;$$
$$d_{SNRseg} ={10 \over M} \sum\limits_{m=0}^{M-1} \log_{10} \left(1+{\sum\limits_{n=N\cdot m}^{N\cdot m+N-1} s^2\lpar n\rpar \over \sum\limits_{n=N\cdot m}^{N\cdot m+N-1} \lpar s\lpar n\rpar -\hat {s}\lpar n\rpar \rpar ^2}\right)\comma \;$$
where s(n) and ŝ(n) are the original SWB audio signals and the reproduced audio signals, respectively. N = 640 is the frame length of audio signals and M represents the frame number of each test signal. The SNRseg values of different BWE methods are shown in Fig. 15.
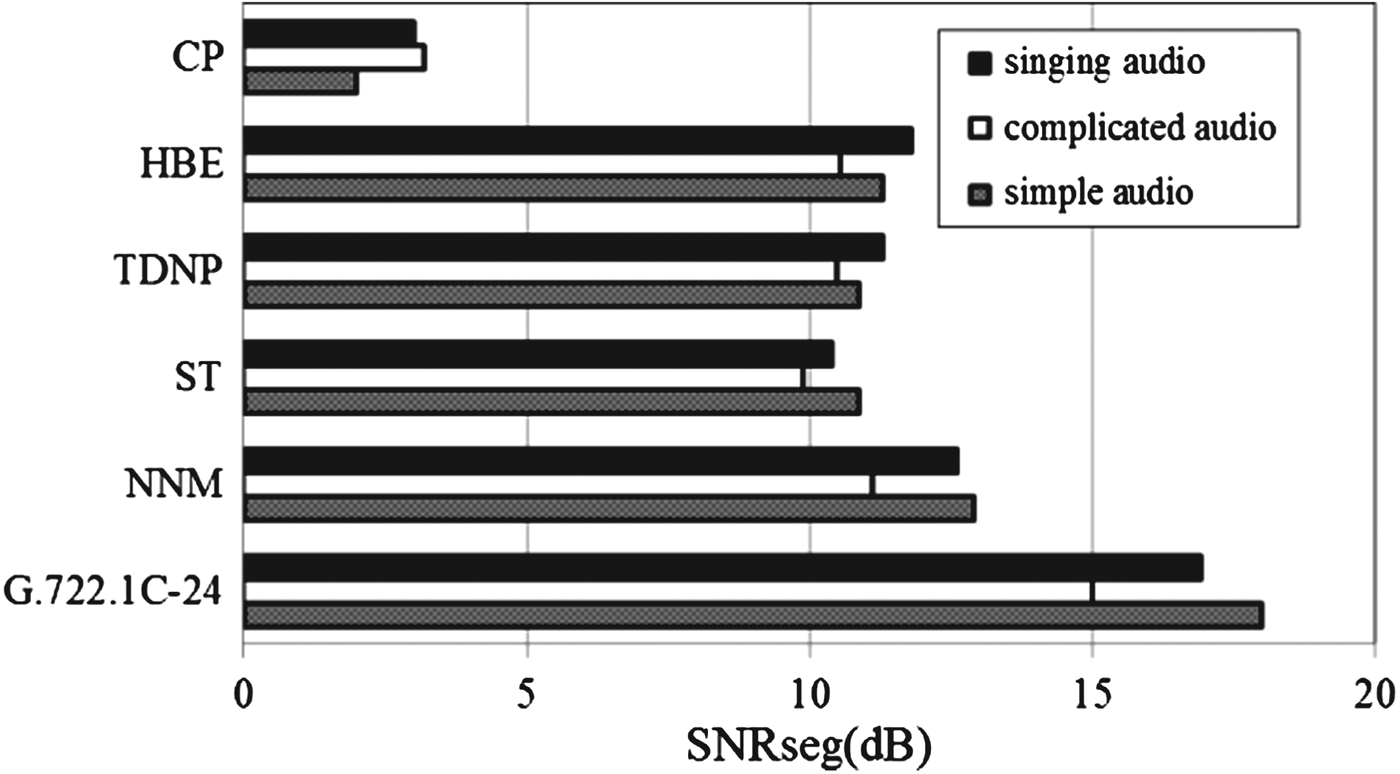
Fig. 15. SNRseg for different BWE methods.
As shown in Fig. 15, the mean SNRseg of complicated audio is the lowest for each method. The CP method does not specially amend the spectral envelope according to the dynamic properties of audio signals, so the SNRseg value is relatively low. The SNRseg values of ST, TDNP, HBE, and NNM show a similar performance, because the similar estimation method based on HMM is employed to shape the spectral envelope of the HF components. The proposed NNM method achieves more than 1 dB improvement over the reference methods, but is inferior to the G.722.1C SWB audio coding.
D) Subjective listening tests
MUltiple Stimuli with Hidden Reference and Anchor (MUSHRA) listening test and comparison category rating (CCR) listening test are presented in comparison with WB audio reproduced by G.722.1 and SWB audio reproduced by G.722.1C.
1) MUSHRA LISTENING TESTS
The listening test was conducted for subjective assessment using MUSHRA methodology recommended by ITU-R BS.1543-1 [44] and was mainly used to grade the degree of audio quality impairment for the BWE methods, SWB audio codec and WB audio codec. In each test case, the listener was presented with the labeled reference, a certain number of test signals, a hidden version of the reference and an anchor. The original SWB audio signal was included as a hidden reference and the low-pass filtered signal with bandwidth of 3.5 kHz as an anchor. The impairments of audio quality for G.722.1 codec at 24 k/s, G.722.1C codec at 24 k/s and 32 kb/s, ST method, HBE method, TDNP method, CP method and proposed NNM method were evaluated for the subjective listening test using the following a 100-point scale: 100–80, Excellent; 80–60, Good; 60–40, Fair; 40–20, Poor; and 20–0, Bad.
15 male and 5 female listeners took part in the test and the age range was from 22 to 30 years old. The test was arranged in the quiet room conforming to the specifications of the ITU-R recommendation BS.1116-1 [45] and only the test attendee was present in the room during the test. Five test signals including pop music, guitar, sax, and drums were selected from the MPEG database [46], and the level of the original test signals and the processed signals was normalized to −26 dB. They were played to both ears through AKG K271 MKII headphones. Each listener compared all the processing types of test signals. In each test case, the listeners could switch at will between the reference signal and any other differently processed signals under test. All the audio signals could be repeated any number of times, and no time limitation is required for giving the response. Before the formal test, another test signal was used for training in order to obtain reliable results. The training phase exposed the listeners to the full range and nature of impairments that would be experienced during the test. Moreover, the listeners were instructed to adjust the sound volume to a suitable level and knew well the test process. During each test case, listeners derived their grade for a given test signal by comparing it to the reference signal, as well as to the other signals, and recorded their assessment of the quality in a previously prepared form. After the test, the comments on the test signals for the listeners were collected and analyzed by the experimenters.
On the assumption that the individual scores meet normal distribution, the mean scores and 95% confidence interval are calculated according to the statistical analysis method mentioned in ITU-R BS.1543-1, and the result for each processing type are illustrated in Fig. 16. The G.722.1C codec at 32 kb/s was considered substantially better than the BWE methods and the WB codec. The performance of the G.722.1C codec at 24 kb/s was a little weaker because the fine spectra of both LF and HF are coarsely reproduced. Due to the same estimation method of HF spectral envelope, ST, HBE, TDNP, and NNM showed a similar performance for extending the audio bandwidth and outperformed the G.722.1 WB audio codec in terms of subjective auditory quality with statistical significance. The proposed NNM method gave marginally better performance than TDNP and performs better than other three BWE methods with statistical significance. But NNM showed slightly impairment compared to the G.722.1C codec at 24 kb/s. In addition, the CP method adopts a different architecture from other methods and also showed a moderate performance.
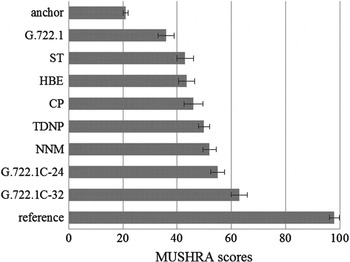
Fig. 16. Mean subjective scores with 95% confidence intervals for the MUSHRA listening test.
2) CCR LISTENING TESTS
Additionally, a CCR listening test which is similar to the subjective assessment method recommended by ITU-T P.800 [47] was used to pairwise evaluate the differences of audio quality for G.722.1C at 24 kb/s, TDNP, and NNM. In each test case, two differently processed versions of the same test signals were presented to the listeners. Listeners used the following seven-point comparison mean opinion scores (CMOS) to judge the quality of the second audio sample relative to that of the first: 3, much better; 2, better; 1, slightly better; 0, the same; −1, slightly worse; −2, worse; −3 much worse.
A total of 20 listeners who also participated in the CCR test were invited to take part in the test. The test was arranged in the quiet room and the differently processed types of the five MPEG testing signals were played to both ears through AKG K271 MKII headphones for listening tests. Each listener had a short practice before actual tests to adjust the volume setting to a suitable level, and was allowed to repeat each pair of testing data with no time limitation before giving their answers.
Three groups of tests were presented to each listener. They are the comparison between NNM method and TDNP method, the comparison between G.722.1C codec and TDNP method, and the comparison between NNM method and G.722.1C codec. The distributions of listener rating for each group of tests are shown in Fig. 17. The bars indicate the relative frequencies of the scores given in the comparisons between the two processing methods. Bars on the positive side show preference for the latter method. The mean score for each group of tests is also shown on the horizontal axis with the 95% confidence interval. The proposed NNM method and G.722.1C SWB audio codec showed an improved performance compared with the TDNP method. The SWB audio reproduced by NNM method had the similar quality as the audio signals decoded by G.722.1C. This means that the proposed NNM method is able to enhance the quality of audio signals decoded by G.722.1 and achieves better performance than the TDNP method on average.
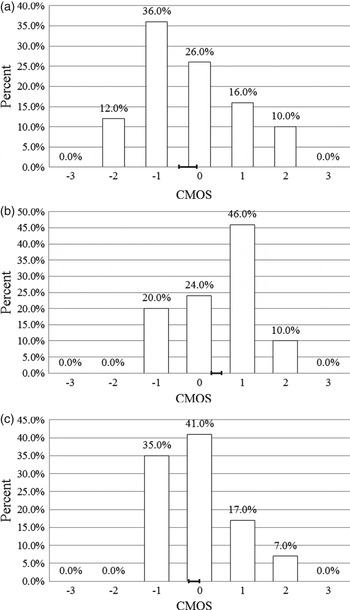
Fig. 17. Distributions of listener rating in CCR tests. (a) Comparison between NNM and TDNP. (b) Comparison between TDNP and G.722.1C. (c) Comparison between G.722.1C and NNM.
E) Algorithmic complexity
Table 4 lists the relevant complexity figures for the proposed BWE method. The algorithm complexity is measured in WMOPS for the worst case [48]. For memory requirements, the proposed method needs about 32 K bytes RAM and 47 K bytes ROM. The test signals from the MPEG database were used to evaluate the proposed method. Except the MLT and the IMLT, the major contributions come from the estimation of the HF spectral envelope and from the SSR. We additionally observe that the complexity of the modules for the SSR and the fine spectrum restoration is relevant to the values of two embedding parameters (Δ i and m). In order to reduce the increasing complexity, the fixed embedding parameters can be used instead of the adaptive selection methods mentioned in Section II and the space grid method can be employed to describe state space in order to implement fast searching for nearest neighbors. Using these fast algorithms, a suboptimal version is built up and the reduced complexity is about 3.2 WMOPS, while the LSD value of the revised version rises about 1 dB on average.
Table 4. Algorithm complexity of proposed BWE method.

F) Discussion
The proposed method adopts the framework of the frequency-domain processing methods as most modern audio codecs and is able to directly adjust the envelope and tonality on the audio spectrum of the reproduced signals. Taking the actual audio codecs into consideration, the frequency-domain blind BWE methods show more feasibility, because it can be appropriately revised and be easily applied into the actual SWB audio decoder to substitute for all or parts of the true HF reconstruction module [Reference Berisha and Spanias22,Reference Geiser, Hervé and Peter49] at the mode of low bit-rates. It helps reduce the quality variations between the audio signals with different bandwidth [Reference Larsen and Aarts6]. So the proposed method is also feasible to actual audio codec.
In comparison with the state-of-the-art time-domain method of TDNP, the subjective listening tests indicate that the proposed NNM method gives slightly better performance. For the TDNP method, the partial harmonic components in HF regions are exactly reproduced by non-linear filtering and the phase of restored HF signals is continuous. So this method shows particular advantages for signals with strong harmonics. For a common audio, the spectrum may switch from the harmonic-like one to the noise-like one with the increase of frequency. The additional tonal components reproduced by TDNP, which do not appear in the original HF regions, will introduce audible artifact. The proposed method trends to follow the evolution of spectral characteristics from LF to HF and preserves a proper level of residual noise in the HF regions. Especially for complicated audio and singing, this can improve the robustness of BWE methods when the HF spectrum shows a different characteristic from the LF one.
Additionally, it can be found from the observation on some stringed music during test that the audio signals reproduced by NNM may show some distortion because the estimation of pitch becomes unstable, when the fundamental frequency of audio signals varies rapidly. During coarse searching, the improper neighbors might be searched out and lead to some perceptible distortion. The pitch smoothing methods, such as median filtering, parabola interpolation, and dynamic programming, might solve this problem during a vibrato arises. By reducing the variation of HF overtone frequencies, the auditory quality of reproduced audio can be guaranteed to a certain extent.
IV. CONCLUSIONS
A new method for blind bandwidth extension from WB to SWB audio signals was presented in this paper. Our research was motivated by studies of the non-linear characteristics for the fine spectrum of audio signals. In state space, a non-linear prediction based on NNM was employed to restore the fine spectrum of high frequencies from the LF state vectors. In addition, the spectral envelope of HF components was estimated by HMM without any side information. The proposed BWE method was applied to extend the bandwidth of the audio signals coded by the G.722.1 codec at 24 kb/s. The results of the objective measurements indicate that the NNM method effectively restores the original HF components and performs better than the reference BWE methods. In terms of the subjective listening tests the NNM method is preferable over G.722.1 codec, ST method, CP method, and HBE method on an average. Moreover, NNM gives marginally better performance than TDNP method and shows a quality similar to the G.722.1C SWB audio codec at 24 kb/s.
ACKNOWLEDGEMENT
This work was supported by the National Natural Science Foundation of China under Grant number 61072089.
Xin Liu received the B.S. and M.S. degrees in Electronic Engineering from the Beijing University of Technology in 2009 and 2011, respectively. Now he is a Ph.D. candidate in the School of Electronic Information and Control Engineering, Beijing University of Technology, Beijing, China. His research interests are in the areas of coding and bandwidth extension for speech and audio signals.
Chang-chun Bao received the B.S. degree in Telecommunication Engineering from Chang Chun Institute of Posts and Telecommunications; M.S. and Ph.D. degrees in Communication and Electronic System from the Jilin University of Technology, Changchun, in 1987, 1992, and 1995, respectively. From August of 1992 to June of 1993, he was a visiting scholar in Tsinghua University. From December of 1995 to November of 1997, he was a Postdoctoral Research Fellow and an Associate Professor in Xidian University. He joined the Beijing University of Technology as an Associate Professor in 1997, and was promoted to a full Professor in 1999. From July to September in 1998, he was a senior researcher in the Digital System Technology Laboratory, Radio Products Research Group, Land Mobile Products Sector Motorola, Florida, USA. From March to August in 2004, he was a visiting professor in the University of Wollongong. His research interests are in the areas of speech & audio signal processing. Dr. Bao is a Senior Member of IEEE, a Board and Senior Member of Chinese Institute of Electronics (CIE), a Board member of the Acoustical Society of China (ASC), a Board Member of Signal Processing Academy of CIE, a member of International Speech Communication Association (ISCA), a member of Asia-Pacific Signal and Information Processing Association (APSIPA), and a Vice-Chairman of National Conference on Man–Machine Speech Communication-Standing Committee in China.























