NOMENCLATURE
- ADS-B
Automatic Dependent Surveillance – Broadcast
- AIRM
ATM Information Reference Model
- AIRMET
Airmen’s Meteorological Information
- AIXM
Aeronautical Information Exchange Model
- ATM
air traffic management
- DNOTAM
Digital NOTAM
- EDUU
ICAO code for the Rhine FIR in upper airspace
- EFB
Electrongic Flight Bag
- ePIB
(digitally) enhanced PIB/electronic PIB
- ETL
extraction, transformation, and load
- FAA
Federal Aviation Administration
- FIR
flight information region
- GML
Geography Markup Language
- ICAO
International Civil Aviation Organisation
- IWXXM
ICAO Meteorological Information Exchange Model
- LOVV
ICAO code of the Austrian FIR
- LOWW
ICAO code of Vienna International Airport
- LZBB
ICAO code of the Slovakian FIR
- LZIB
ICAO code of Bratislava Airport
- METAR
Meteorological Aerodrome Report
- NOTAM
notice to airman
- OLAP
Online analytical processing
- OWL
Web Ontology Language
- PIB
Pre-Flight Information Bulletin
- RDF
Resource Description Framework
- SIGMET
Significant Meteorological Information
- SPARQL
SPARQL Protocol and RDF Query Language
- SPECI
special meteorological report
- SWIM
System Wide Information Management
- TAF
Terminal Aerodrome Forecast
- UML
Unified Modelling Language
- XML
Extensible Markup Language
 $c, C, \mathcal{C}$
$c, C, \mathcal{C}$an individual semantic data container, a set of semantic data containers, and the universe of semantic data containers
-
 $\bar{C}_q$
$\bar{C}_q$ the base containers of cube q
 $d, D, \mathcal{D}$
$d, D, \mathcal{D}$an individual dimension, a set of dimensions, and the universe of dimensions
 $e, E, \mathcal{E}$
$e, E, \mathcal{E}$an individual dimension member, a set of dimension members, and the universe of dimension members
 $\hat{e}_d$
$\hat{e}_d$the top member of dimension d
- f
a generic function
 $G_q, G_k$
$G_q, G_k$the granularity space of cube q and metacube k, respectively
- g(p)
the granularity of point p
 $\bar{g}_c, \bar{g}_k$
$\bar{g}_c, \bar{g}_k$the base granularity of cube q and metacube k, respectively
 $H, H^+$
$H, H^+$a level hierarchy and its transitive closure
 $i, I, \mathcal{I}$
$i, I, \mathcal{I}$an individual data item, a set of data items, and the universe of data items
 $k, K, \mathcal{K}$
$k, K, \mathcal{K}$an individual metacube, a set of metacubes, and the universe of metacubes
 $l, L, \mathcal{L}$
$l, L, \mathcal{L}$an individual dimension level, a set of dimension levels, and the universe of dimension levels
 $l_d(e)$
$l_d(e)$the level of dimension member e in dimension d
 $\hat{l}_d$
$\hat{l}_d$the top level of dimension d
- p, P
a point and a set of points
 $\bar{P}_q, \bar{P}_k$
$\bar{P}_q, \bar{P}_k$the base space of cube q and metacube k, respectively
 $p_k(q)$
$p_k(q)$coordinates (point) of cube q in metacube k
 $p_q(c)$
$p_q(c)$coordinates (point) of container c in cube q
 $q, Q, \mathcal{Q}$
$q, Q, \mathcal{Q}$an individual cube, a set of cubes, and the universe of cubes
 $\bar{Q}_k$
$\bar{Q}_k$the base cubes of metacube k
 $R, R^+$
$R, R^+$a roll-up hierarchy of dimension members and its transitive closure
 $\alpha$
$\alpha$an abstraction operation
 $\mu$
$\mu$a merge operation
 $\chi$
$\chi$a drill-across operation
 $\preceq, \prec$
$\preceq, \prec$refexive/irreflexive partial order of dimension members, levels, or granularities
1.0 INTRODUCTION
A Pre-flight Information Bulletin (PIB) provides pilots with current Notices to Airmen(1)but may also include other types of messages relevant for a flight(2) e.g., meteorological information. A Notice to Airmen (NOTAM) notifies aviation personnel about temporary changes regarding flight conditions(3) e.g., closure of airports or unserviceable navigation aids. Among the meteorological information relevant for the PIB are routine meteorological reports, special meteorological reports, and meteorological forecasts concerning the weather at an aerodrome or within an airspace. A Meteorological Aerodrome Report (METAR) reports current weather conditions at an aerodrome, whereas a Terminal Aerodrome Forecast (TAF) provides a weather forecast for an aerodrome. A special weather report (SPECI) reports on significant changes in current weather conditions at an aerodrome. Similarly, Airmen’s Meteorological Information (AIRMETs) and Significant Meteorological Information (SIGMETs) report on weather conditions and significant weather events, respectively, within a wider area(4). PIBs are traditionally delivered on paper in textual form, with limited possibilities for structuring the data, overwhelming pilots with an abundance of information. In order to alleviate this problem, electronic or (digitally) enhanced PIBs have been introduced.
An electronic or (digitally) enhanced PIB (ePIB) provides the messages in digital form, typically stored in Extensible Markup Language (XML) format, which allows for improved representation and packaging of the relevant information for advanced use in applications(Reference Savulov5,Reference Pelchen-Medwed and Porosnicu6) . Digital NOTAMs (DNOTAMs) allow for automated filtering as well as classification of messages along different dimensions (or facets) e.g., importance, geographic area, flight phase, and event scenario, that can be employed to flexibly structure the ePIB to reduce information overload(Reference Steiner, Kovacic, Burgstaller, Schrefl, Friesacher and Gringinger7). Using the classification rules developed in the Semantic NOTAM (SemNOTAM) project(Reference Steiner, Kovacic, Burgstaller, Schrefl, Friesacher and Gringinger7), DNOTAMs can be packaged into semantic data containers (Reference Kovacic, Steiner, Schuetz, Neumayr, Burgstaller, Schrefl and Wilson8), each container comprising e.g., the DNOTAMs relevant for a certain flight on a particular date. Consider, for example, the semantic containers on the left-hand side of Fig. 1. For a fixed flight and date (not shown in the figure), these containers hold the relevant DNOTAMs for different segments in a flight information region (FIR), importance levels, and flight phases. The first container holds the relevent DNOTAMs for the EDUU-01 segment of the Rhine FIR in upper airspace (EDUU) classified as reports of an operational restriction for the cruise flight phase. The second container holds the DNOTAMs for the EDUU-02 segment of the EDUU FIR classified as flight critical for the descent flight phase, respectively. Rule-based approaches similar to SemNOTAM could also be devised for messages other than DNOTAMs, collecting METARs, Terminal Aerodrome Forecasts (TAFs), AIRMETs, etc. into semantic containers. Indeed, an Electronic Flight Bag (EFB) platform may display various kinds of relevant information for a flight(Reference Hiltunen, Chase, Kendra and Jo9). The challenge lies in the organisation of such information in a way that enables applications to flexibly select, combine, and rearrange the relevant information for a specific task.
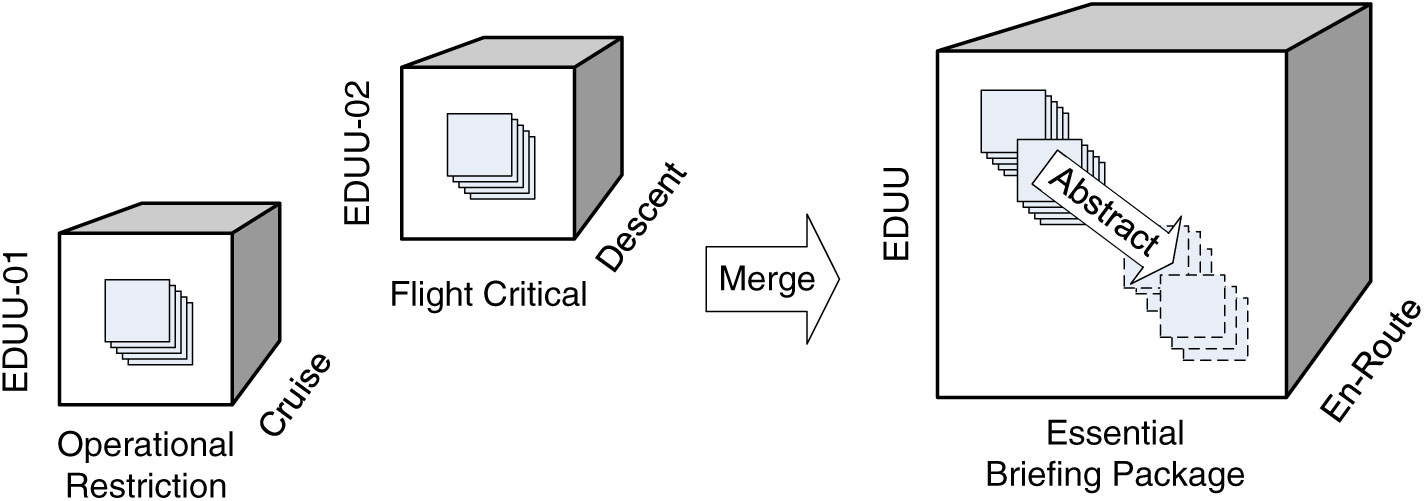
Figure 1. Illustration of the proposed theoretical framework for semantic container operations.
In this paper – an extension of a previous conference paper(Reference Schuetz, Neumayr, Schrefl, Gringinger and Wilson10) presented at the ICAS 2018 Congress – we propose a framework for the combination and summarisation of information for air traffic management (ATM) packaged into semantic containers. The framework employs merge and abstraction operations in order to provide management summaries of relevant information. To that end, we adapt the well-established concept of data cubes (or OLAP cubes) from data warehousing – i.e., multidimensional data structures for online analytical processing (OLAP)(Reference Vaisman and Zimányi11) (see Section 2.3) – as well as the corresponding OLAP query operations to work with ATM information. Hence, we propose the notion of the ATM information cube, which hierarchically organises semantic containers along different dimensions relating to the container content e.g., the geographic and temporal applicability, flight criticality, and flight phase that the container content is relevant for. In this regard, we assume the existence of appropriate rule-based filtering mechanisms to collect ATM information into the containers. The SemNOTAM classification rules(Reference Steiner, Kovacic, Burgstaller, Schrefl, Friesacher and Gringinger7), for example, provide a first reduction of the information overload in pilot briefings by packaging DNOTAMs into collections of containers, analogous to OLAP cubes. Leveraging the hierarchical organisation of containers, the individual containers can be merged along the dimension hierarchies in order to obtain more comprehensive containers of ATM information. For example, dimension hierarchies specify that the essential briefing package subsumes flight critical and operational restriction importances, the EDUU FIR subsumes the EDUU-01 and EDUU-02 segments, and the en-route phase subsumes the descent and cruise phases. A container with flight critical DNOTAMs for the EDUU-02 segment when the flight is in descent phase and a container with DNOTAMs about operational restrictions for the EDUU-01 segment when the flight is in cruise phase, respectively, may then be merged into a single container with DNOTAMs that comprises the essential briefing package for the EDUU FIR when the flight is in an en-route phase (Fig. 1). The dimension hierarchies serve to formulate the corresponding query. Subsequently, the messages themselves can be further summarised to obtain more abstract messages. For example, individual DNOTAMs concerning specific runway closures for landing aircraft are summarised by a single abstract DNOTAM indicating the existence of a runway closure for landing aircraft in a specific context, with only more general (abstract) information about obstructions, hazards, construction activity, etc. given different variants of the abstraction operation may be employed in practice.
The remainder of this paper is organised as follows. In Section 2, we present background information regarding semantic data containers, rule-based filtering and annotation of ATM information, and data warehousing; we also review related work. In Section 3, we define the notions of the ATM information cube and the metacube (or a cube of ATM information cubes). In Section 4, we define operations for flexibly combining semantic containers – the merge operation. In Section 5, we define operations for abstracting data items (messages) within semantic containers. In Section 6, we discuss implementation of the presented approach. We conclude with a summary and an outlook on future work. In the appendix, we present adapted excerpts of standard ATM information exchange models employed in the examples.
2.0 BACKGROUND
In this section, we present relevant background information on semantic data containers, rule-based filtering and annotation of ATM information as well as data warehousing and OLAP. We also review related work.
2.1 Semantic Data Containers
The semantic container approach as developed in the course of the BEST projectFootnote * is a flexible way of compartmentalising ATM information that complements the service-oriented architecture of SWIM (System Wide Information Management) with techniques for ontology-based data description and discovery(Reference Kovacic, Steiner, Schuetz, Neumayr, Burgstaller, Schrefl and Wilson8,Reference Neumayr, Gringinger, Schuetz, Schrefl, Wilson and Vennesland12) . A semantic data container is a data product that consists of content and description. The content is a set of data items of a specific type e.g., ATM messages such as DNOTAMs and METARs. The container description consists of administrative metadata i.e., information about provenance, data quality, etc., and a membership condition(Reference Kovacic, Steiner, Schuetz, Neumayr, Burgstaller, Schrefl and Wilson8). The data items that fulfil a container’s membership condition constitute that container’s content.
The membership condition describes multiple facets of the container’s content. In this regard, the membership condition may refer to geographic and temporal facets of container content, but also various other semantic facets. For example, a DNOTAM container may contain all the DNOTAMs with a specific spatial and temporal scope e.g., Vienna airport on 14 May 2018, and refer to a specific scenario e.g., taxiway closure. For each facet, a semantic container’s membership condition associates a concept from an ontology. An ontology is a ‘formal, explicit specification of a shared conceptualisation’(Reference Studer, Benjamins and Fensel13) of a real-world domain of interest and consists of multiple concepts that are hierarchically organised. For example, the LOWW concept represents Vienna airport and is under the LOVV concept, which represents the Austrian FIR. Various knowledge representation languages e.g., the Web Ontology Language (OWL), may serve to define these ontologies. From the hierarchy of ontology concepts that make up the faceted membership descriptions derives a hierarchy of semantic containers. For example, a semantic container with DNOTAMs for Vienna airport on 14 May 2018 is more specific than a container with DNOTAMs for the Austrian FIR in May 2018. The hierarchy of semantic containers then serves to discover existing semantic containers that most closely satisfy certain information needed by a specific end user or application.
2.2 Rule-Based Filtering and Annotation of ATM Information
Information processing and reasoning techniques at the instance level complement the metadata-centric semantic container approach – in order to fill the semantic containers with actual content. The SemNOTAM approach(Reference Steiner, Kovacic, Burgstaller, Schrefl, Friesacher and Gringinger7,Reference Burgstaller, Steiner, Neumayr, Schrefl and Gringinger14) , for example, employs a formal rule system to filter and annotate DNOTAMs with importance levels according to a user’s interest specification. In the SemNOTAM approach, the SemNOTAM engine receives a set of DNOTAMs as input and the user’s interest specification as argument. The SemNOTAM engine further translates the input into a representation that suits knowledge-based reasoning, and selects from the SemNOTAM knowledge base the relevant set of filtering and annotation rules which the knowledge-base reasoner executes against the input ATM information. The term ‘filtering’, in this context, refers to the disregarding of input DNOTAMs in the result set whereas ‘annotation’ refers to the assignment of importance levels e.g., flight critical, to DNOTAMs. In this regard, legal constraints demand that pilots receive all potentially relevant NOTAMs for a flight. The employed filter rules must hence guarantee a recall of one hundred percent. The result of the reasoning process – a filtered and enriched set of DNOTAMs – is provided to the user, who typically will be a pilot or air traffic controller. The filtered and enriched set of DNOTAMs could then become the content of a semantic container, with the argument interest specification constituting the membership condition.
2.3 Data Warehousing and OLAP
A data warehouse supports the decision-making process in enterprises, providing an integrated view on the available data with a focus on the subjects of the analysis(Reference Vaisman and Zimányi11) e.g., flight and airport operations performance, booking numbers. An extraction, transformation, and load (ETL) process serves to fill the data warehouse with data from various source systems(Reference Sherman15). The transformation phase converts the data in a format suitable for analysis and cleans the data. Analysts may then work with the data by running algorithms for statistical analysis (data mining, machine learning) or by interactively performing ad hoc queries using a declarative query language or graphical user interface, which is commonly referred to as OLAP.
The multidimensional model is the predominant data modelling paradigm in data warehousing and the fundamental of OLAP. The central data structure is the data cube (or OLAP cube), a multidimensional space spanned by multiple dimensions. Each point (or cell) in a data cube represents a fact of interest i.e., an occurrence of a business event e.g., flight or ground handling, which is quantified by measures e.g., fuel consumption, flight or turnaround time. The dimensions typically consist of hierarchically organised levels, which allow for the analysis of the measures at various levels of granularity. For example, a data cube captures the flight time per connection and date i.e., a data cube with flight time as measure, connection, and date as dimensions. The flight dimension has an origin level and a destination level, and the date dimension has a month level, meaning that each flight has a destination and each date belongs to a month.
Common OLAP operations are slice-and-dice, roll-up and drill-down, and drill-across. Slice-and-dice refers to the selection of a subset of data from a cube. For example, an analyst interested in flight performance selects only the cells of the cube about flights from a certain origin airport in a particular year. Roll-up refers to the aggregation of data along the dimension hierarchies, with drill-down being the inverse. For example, the flight dimension, having a destination level and a month level allows the analyst to obtain average flight times to destination airports for each month, rolling up the cube to destination-month granularity (vice versa for drill-down). Drill-across refers to the combination of data from different cubes with overlapping dimensions. For example, a drill-across may relate flight time from the flight performance cube with turnaround time from the ground handling cube, using the flight and date dimensions to relate those two cubes.
2.4 Related Work
Traditional OLAP systems work on multidimensional models with numeric measures(Reference Vaisman and Zimányi11). Going beyond numeric measures, InfoNetOLAP(Reference Chen, Zhu, Yan, Han, Yu and Ramakrishnan16), which is also known as Graph OLAP, associates weighted graphs with dimension attributes. Topological and informational roll-up are the basic kinds of operations, which are akin to the merge and abstraction operations presented in this paper. The focus of Graph OLAP, however, is weighted directed graphs with highly structured and homogeneous data not suited for schema-rich ATM information.
The concept of ATM information cubes builds on the ideas developed in our previous work(Reference Schütz, Neumayr, Schrefl, Salinesi, Norrie and Pastor17) the use of business model ontologies for the management and summarisation of complex information in OLAP cubes. The cells of such an OLAP cube are associated with business knowledge that is valid in a particular context as defined by the dimensions of the cube. The Resource Description Framework (RDF) provides the knowledge representation language for such business knowledge.
The research project AIRPORTS(Reference Martínez-Prieto, Bregon, García-Miranda, Álvarez Esteban, Díaz and Scarlatti18), a joint effort between Technology Europe and Boeing Research, developed a data architecture to merge Automatic Dependent Surveillance – Broadcast (ADS-B) messages with flight-related information using a data lake platform. In the course of this project, a conceptual data model was defined to give an overview of the available ATM business information. One major goal was to retrieve clean ADS-B messages by improving the data quality through a combination of information form several providers to obtain more accurate information. Another goal was to enrich the surveillance information with other available information about airports, aircraft and air traffic control. The proposed information processing pipeline includes acquisition, cleaning, transformation, and enrichment of the data, which are then delivered to ATM systems. Future work includes a data analytics framework based on the processing pipeline for improvement of the performance of ATM systems and of the decision-making processes. Similarly, ATM information cubes may be considered as a structured data lake approach towards managing ATM information.
3.0 ATM INFORMATION CUBES
A semantic data container is a flexible data structure for storing data items of various kinds (see Section 2.1); the concept is central to the notion of ATM information cubes. Note that we employ the terms ‘semantic data container’ and ‘semantic container’ synonymously. For the purposes of this paper, we formally define the concept of semantic data container as follows.
Definition 1 (Semantic data container). A semantic data container ![]() $c \in \mathcal{C}$, taken from the universe of semantic data containers
$c \in \mathcal{C}$, taken from the universe of semantic data containers ![]() $\mathcal{C}$, contains a set of data items
$\mathcal{C}$, contains a set of data items ![]() $I_c \subseteq \mathcal{I}$ taken from the universe of data items
$I_c \subseteq \mathcal{I}$ taken from the universe of data items ![]() $\mathcal{I}$.
$\mathcal{I}$.
We arrange semantic containers in ATM information cubes along multiple dimensions (or facets) of content description. For that arrangement of semantic containers, we borrow the data cube metaphor from data warehousing and OLAP (see Section 2.3). The dimensions of the ATM information cube span a multidimensional space where each point associates a set of ATM data items e.g., DNOTAMs or METARs, rather than numeric values as in traditional data cubes. Each semantic container then becomes associated with a point in a multidimensional space according to the container’s membership condition. Consider, for example, the three-dimensional ATM information cube in Fig. 2. Individual DNOTAMs are collected into semantic containers along geography, importance, and scenario dimensions. Each semantic container in that cube hence contains a set of DNOTAMs describing a specific scenario(19) for a specific geographic segment within a FIR with some importance e.g., operational restriction, or flight critical, for the flight and date that the cube has been defined for. Note that the flight and date are fixed for that cube, which constitutes additional context information necessary to correctly interpret that cube. In the following, we formally define the notions of dimensions and ATM information cubes.
Definition 2 (Dimension). A dimension ![]() $d \in \mathcal{D}$, taken from the universe of ATM information dimensions
$d \in \mathcal{D}$, taken from the universe of ATM information dimensions ![]() $\mathcal{D}$, is a 5-tuple
$\mathcal{D}$, is a 5-tuple ![]() ${(E_d, L_d, l_d, R_d, H_d)}$ where
${(E_d, L_d, l_d, R_d, H_d)}$ where ![]() $E_d$ is a set of members
$E_d$ is a set of members ![]() $E_d \subseteq \mathcal{E}$ from the universe of dimension members
$E_d \subseteq \mathcal{E}$ from the universe of dimension members ![]() $\mathcal{E}$, and
$\mathcal{E}$, and ![]() $L_d \in \mathcal{L}$ is a set of levels from the universe of levels
$L_d \in \mathcal{L}$ is a set of levels from the universe of levels ![]() $\mathcal{L}$. Surjective function
$\mathcal{L}$. Surjective function ![]() $l_d : E_d \rightarrow L_d$ maps dimension members to levels. Dimension members are arranged in a roll-up hierarchy, represented by the anti-symmetric relation
$l_d : E_d \rightarrow L_d$ maps dimension members to levels. Dimension members are arranged in a roll-up hierarchy, represented by the anti-symmetric relation ![]() $R_d \subseteq E_d \times E_d$. The roll-up hierarchy has a single top member
$R_d \subseteq E_d \times E_d$. The roll-up hierarchy has a single top member ![]() $\hat{e}_d \stackrel{\textrm{def}}{=} e \in E_d : (\mathord{\hbox{$\rlap\exists{\hbox{/}}$}} e' \in E_d : (e,e') \in R_d)$. We say e directly rolls up to e′ if
$\hat{e}_d \stackrel{\textrm{def}}{=} e \in E_d : (\mathord{\hbox{$\rlap\exists{\hbox{/}}$}} e' \in E_d : (e,e') \in R_d)$. We say e directly rolls up to e′ if ![]() ${(e,e') \in R_d}$; and e rolls up to e′ if
${(e,e') \in R_d}$; and e rolls up to e′ if ![]() ${(e,e') \in R_d^+}$, where
${(e,e') \in R_d^+}$, where ![]() $R_d^+$ is the transitive closure of
$R_d^+$ is the transitive closure of ![]() $R_d$; and e is the same as or rolls up to e′, denoted as
$R_d$; and e is the same as or rolls up to e′, denoted as ![]() $e \preceq e'$, if
$e \preceq e'$, if ![]() ${(e,e') \in R_d^+\, \vee \, e = e'}$. Dimension levels are arranged in a level hierarchy, represented by the anti-symmetric relation
${(e,e') \in R_d^+\, \vee \, e = e'}$. Dimension levels are arranged in a level hierarchy, represented by the anti-symmetric relation ![]() $H_d \subseteq L_d \times L_d$. The level hierarchy has a single top level
$H_d \subseteq L_d \times L_d$. The level hierarchy has a single top level ![]() $\hat{l}_d \stackrel{\textrm{def}}{=} l \in L_d : (\mathord{\hbox{$\rlap\exists{\hbox{/}}$}} l' \in L_d : (l,l') \in H_d)$ and a single bottom level
$\hat{l}_d \stackrel{\textrm{def}}{=} l \in L_d : (\mathord{\hbox{$\rlap\exists{\hbox{/}}$}} l' \in L_d : (l,l') \in H_d)$ and a single bottom level ![]() $\bar{l}_d \stackrel{\textrm{def}}{=} l \in L_d : (\mathord{\hbox{$\rlap\exists{\hbox{/}}$}} l' \in L_d : (l',l) \in H_d)$. We say l directly rolls up to l′ if
$\bar{l}_d \stackrel{\textrm{def}}{=} l \in L_d : (\mathord{\hbox{$\rlap\exists{\hbox{/}}$}} l' \in L_d : (l',l) \in H_d)$. We say l directly rolls up to l′ if ![]() ${(l,l') \in H_d}$; l rolls up to l′ if
${(l,l') \in H_d}$; l rolls up to l′ if ![]() ${(l,l') \in H_d^+}$, where
${(l,l') \in H_d^+}$, where ![]() $H_d^+$ is the transitive closure of
$H_d^+$ is the transitive closure of ![]() $H_d$; l is the same as or rolls up to l′, denoted as
$H_d$; l is the same as or rolls up to l′, denoted as ![]() $l \preceq l'$, if
$l \preceq l'$, if ![]() ${(l,l') \in H_d^+ \vee l = l'}$. The roll-up hierarchy corresponds to the level hierarchy i.e.,
${(l,l') \in H_d^+ \vee l = l'}$. The roll-up hierarchy corresponds to the level hierarchy i.e., ![]() ${(e,e') \in R_d \Rightarrow (l_d(e),l_d(e')) \in H_d}$. For each roll-up level of its dimension, a dimension member rolls up to exactly one member i.e.,
${(e,e') \in R_d \Rightarrow (l_d(e),l_d(e')) \in H_d}$. For each roll-up level of its dimension, a dimension member rolls up to exactly one member i.e., ![]() ${(l_d(e),l') \in H_d^+ \Rightarrow \exists! e' \in E_d : (e,e') \in R_d^+ \wedge l_d(e') = l'}$; alternative roll-up paths eventually converge. We further note that
${(l_d(e),l') \in H_d^+ \Rightarrow \exists! e' \in E_d : (e,e') \in R_d^+ \wedge l_d(e') = l'}$; alternative roll-up paths eventually converge. We further note that ![]() $a \prec b \stackrel{\textrm{def}}{=} a \preceq b \wedge a \neq b$.
$a \prec b \stackrel{\textrm{def}}{=} a \preceq b \wedge a \neq b$.
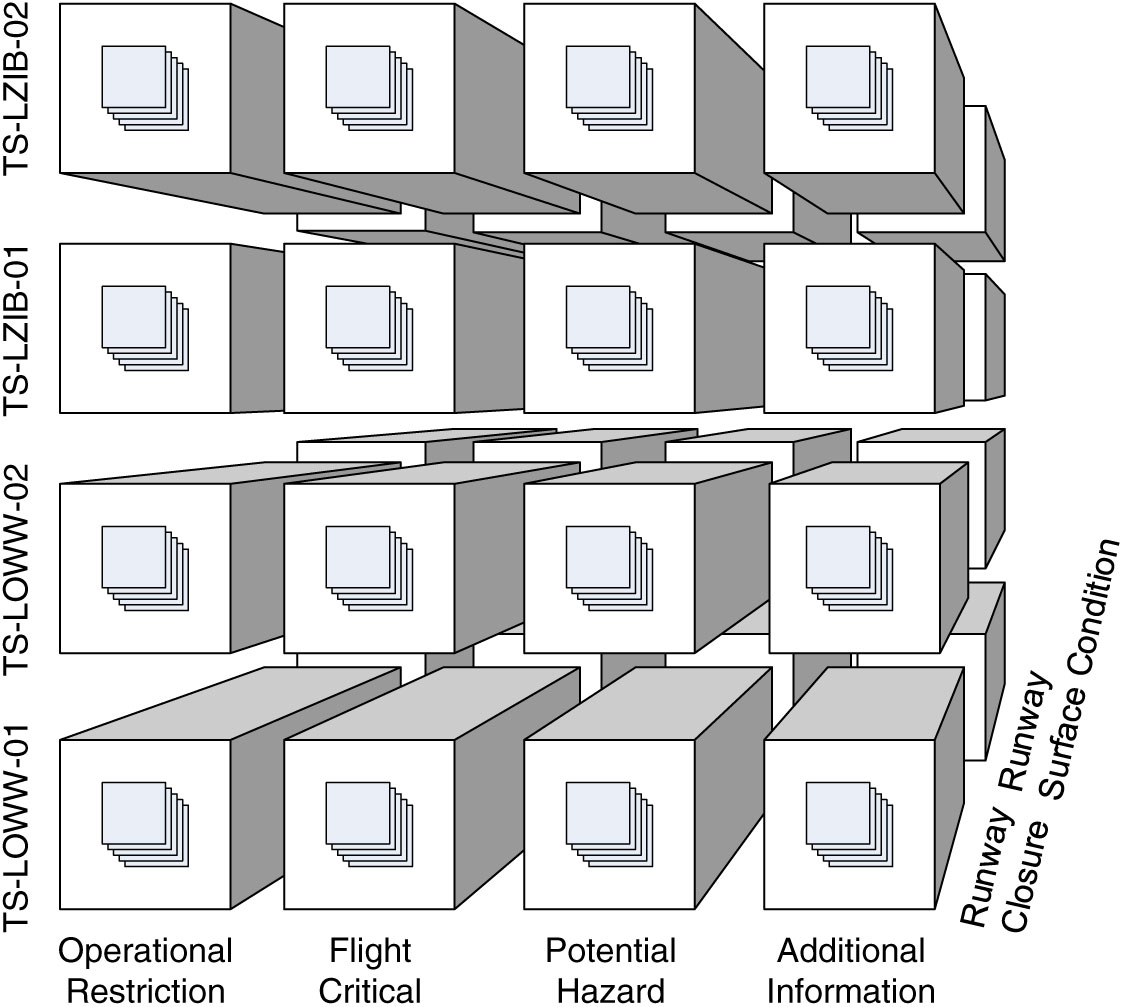
Figure 2. An example ATM information cube with geographic, importance, and scenario dimensions.
The dimensions characterise the ATM information cube, and their members identify points (or cells) in the cube. In order to allow for roll-up operations i.e., viewing the cube’s contents at different granularity levels (see Section 4), a cube employs hierarchically organised dimensions. Consider, for example, the dimension hierarchies in Fig. 3, which illustrates the dimension hierarchies for the cube from Fig. 2 with importance, geography, and scenario dimensions. The importance dimension hierarchy follows the importance classification system for DNOTAMs from the SemNOTAM project(Reference Steiner, Kovacic, Burgstaller, Schrefl, Friesacher and Gringinger7). The scenario dimension hierarchy follows the organisation of the specification of airport operation scenarios(19) defined by the Federal Aviation Administration (FAA) for DNOTAMs; for other types of messages, similar classifications may be conceived. The geography dimension hierarchy consists only of transition segments to airports, which are assigned to a FIR. Using the roll-up relationships of the dimension hierarchies, a pilot may view e.g., DNOTAMs per FIR rather than individual transition segments (see Section 4). We note that alternative roll-up relationships could be defined e.g., to support alternative geographic classifications. Based on the definition of dimensions, we formally define the notion of ATM information cube as follows.

Figure 3. Example dimension hierarchies of an ATM data cube: levels (in boldface) and level members.
Definition 3 (ATM information cube). A cube ![]() $q \in \mathcal{Q}$, taken from the universe of ATM information cubes
$q \in \mathcal{Q}$, taken from the universe of ATM information cubes ![]() $\mathcal{Q}$, is a 4-tuple
$\mathcal{Q}$, is a 4-tuple ![]() ${(C_q,D_q,p_q,\bar{g}_q)}$ where
${(C_q,D_q,p_q,\bar{g}_q)}$ where ![]() $C_q \subseteq \mathcal{C}$ are the cube’s semantic containers, and
$C_q \subseteq \mathcal{C}$ are the cube’s semantic containers, and ![]() $D_q = \{d_1, \dots, d_n\} \subseteq \mathcal{D}$ are the cube’s dimensions which span a multidimensional space
$D_q = \{d_1, \dots, d_n\} \subseteq \mathcal{D}$ are the cube’s dimensions which span a multidimensional space ![]() $P_q \stackrel{\textrm{def}}{=} E_{d_1} \times \dots \times E_{d_n}$. Injective function
$P_q \stackrel{\textrm{def}}{=} E_{d_1} \times \dots \times E_{d_n}$. Injective function ![]() $p_q: C_q \rightarrow P_q$ maps each container to a point in the multidimensional space. The cube’s dimensions further span a granularity space
$p_q: C_q \rightarrow P_q$ maps each container to a point in the multidimensional space. The cube’s dimensions further span a granularity space ![]() $G_q = L_{d_1} \times \dots \times L_{d_n}$. A point
$G_q = L_{d_1} \times \dots \times L_{d_n}$. A point ![]() $p = (e_1, \dots, e_n) \in P_q$ has granularity
$p = (e_1, \dots, e_n) \in P_q$ has granularity ![]() $g(p) \stackrel{\textrm{def}}{=} (l_{d_1}(e_1), \dots, l_{d_n}(e_n))$. A point
$g(p) \stackrel{\textrm{def}}{=} (l_{d_1}(e_1), \dots, l_{d_n}(e_n))$. A point ![]() $p = (e_1, \dots, e_n)$ is the same as or rolls up to
$p = (e_1, \dots, e_n)$ is the same as or rolls up to ![]() $p' = (e_1', \dots, e_n')$, denoted as
$p' = (e_1', \dots, e_n')$, denoted as ![]() $p \preceq p'$, if
$p \preceq p'$, if ![]() $e_1 \preceq e_1' \wedge \dots \wedge e_n \preceq e_n'$. A granularity
$e_1 \preceq e_1' \wedge \dots \wedge e_n \preceq e_n'$. A granularity ![]() $g = (l_1, \dots, l_n)$ is the same as or rolls up to another granularity
$g = (l_1, \dots, l_n)$ is the same as or rolls up to another granularity ![]() $g' = (l_1', \dots, l_n')$, denoted as
$g' = (l_1', \dots, l_n')$, denoted as ![]() $g \preceq g'$, if
$g \preceq g'$, if ![]() $l_1 \preceq l_1' \wedge \dots \wedge l_n \preceq l_n'$. The cube’s base granularity
$l_1 \preceq l_1' \wedge \dots \wedge l_n \preceq l_n'$. The cube’s base granularity ![]() $\bar{g}_q$ denotes the finest granularity that the cube may comprise semantic containers at i.e.,
$\bar{g}_q$ denotes the finest granularity that the cube may comprise semantic containers at i.e., ![]() $\forall c \in C_q : \bar{g}_q \preceq g(p_q(c))$. The cube’s base containers
$\forall c \in C_q : \bar{g}_q \preceq g(p_q(c))$. The cube’s base containers ![]() $\bar{C}_q \stackrel{\textrm{def}}{=} \{ c \in C_q \mid g(p_q(c)) = \bar{g}_q \}$ are containers at the base granularity. The base space
$\bar{C}_q \stackrel{\textrm{def}}{=} \{ c \in C_q \mid g(p_q(c)) = \bar{g}_q \}$ are containers at the base granularity. The base space ![]() $\bar{P}_q \stackrel{\textrm{def}}{=} \{p \in P_q \mid g(p) = \bar{g}_q\}$ consists of all points at the cube’s base granularity.
$\bar{P}_q \stackrel{\textrm{def}}{=} \{p \in P_q \mid g(p) = \bar{g}_q\}$ consists of all points at the cube’s base granularity.
The coordinates of a container correspond to a semantic description of the data items inside the container – the container’s membership condition. For example, the point identified by TS-LOWW-01, Flight Critical, and Runway Closure indicates that the associated semantic container comprises the DNOTAMs about runway closures that are flight critical for the TS-LOWW-01 transition segment. Now, the attentive reader will notice two things. First, nowhere in the model has the data item type been fixed to ‘DNOTAM’. Second, the importance of a DNOTAM depends on many things – first and foremost on the particular flight and date. Yet, the cube has no dimensions for indicating flight and date. In the example, the data item type, flight, and date are implicit constants that set the context for the cube. For each flight and date, a separate cube of DNOTAMs would exist. The pilot could dynamically select containers of DNOTAMs along the dimensions within that context only. Likewise, for other types of messages e.g., METARs, a separate ATM information cube would exist. Subsequently, a cube of ATM information cubes may organise multiple individual cubes and explicitly represent the otherwise tacit context information (see Section 3.2). A drill-across operation could then be used to combine the information from different cubes in such a cube of ATM information cubes (see Section 4.2).
The ATM information cube is potentially sparse i.e., not every cell at the base granularity has a semantic container attached. A common issue for business intelligence applications are Null values – i.e., missing, unknown, or invalid values – for dimension attributes(Reference Sherman15). Applications must handle Null values appropriately. Otherwise, Null values may result in ‘misleading or inaccurate results’(Reference Sherman15). A missing container at a particular granularity could hence be interpreted as indicating an unknown or missing value, whereas an empty semantic container indicates that there exist no messages specific to that particular context. Similarly, when collecting ATM messages into semantic containers e.g., along an importance dimension, in some cases, the messages may not be assigned to any one particular member e.g., importance class(Reference Steiner, Kovacic, Burgstaller, Schrefl, Friesacher and Gringinger7). On the one hand, there could be custom Null values in the dimensions e.g., an unknown importance. On the other hand, ATM messages could be directly added to a point of a coarser granularity. For example, a DNOTAM is known to be in the essential briefing package, although it is not known whether the DNOTAM is flight critical or denotes merely an operational restriction. To that end, in the following subsection, we introduce the notion of multigranular ATM information cubes.
3.1 Multigranular ATM Information Cubes
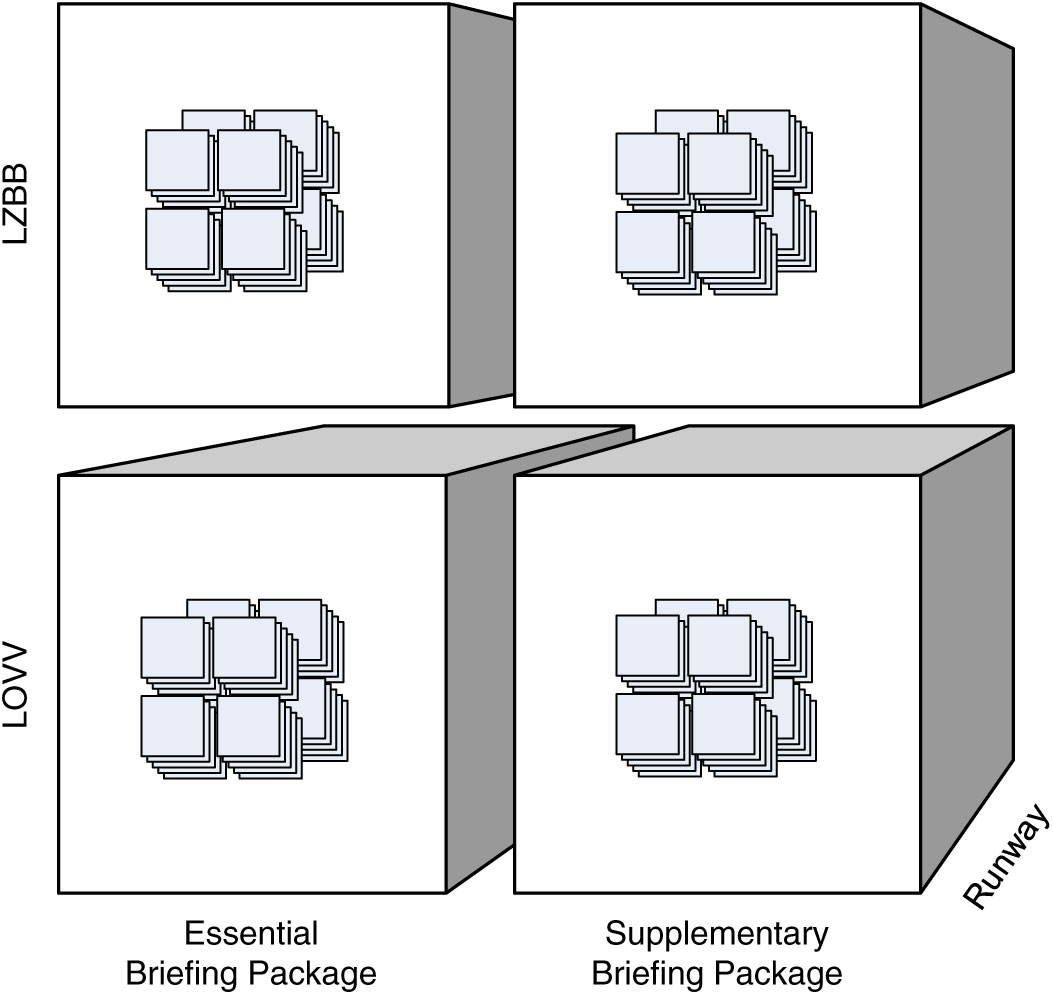
While the example cube in Fig. 2 shows an ATM information cube that associates semantic containers only with a single, base granularity, we may well contemplate the existence of a multigranular ATM information cube that also associates semantic containers with coarser levels of granularity. For example, in some cases, individual DNOTAMs may not fall unambiguously into a single importance category, such as flight critical or operational restriction. Consider then the ATM information cube in Fig. 4: a cube that associates data items explicitly with the coarser supplementary briefing package and the essential briefing package granularity levels rather than the more specific operational restriction and flight critical or potential hazard and additional information importance granularities, respectively.
The containers associated with coarser granularities are composite containers. For example, in Fig. 4, the cell identified by the point LOVV, Essential Briefing Package, and Runway (denoted by dotted lines) associates a composite container that consists of the eight component containers at the finer segment-importance-scenario granularity along with data items associated specifically with the coarser FIR-package-keyword granularity. Therefore, on the one hand, a semantic container at a coarser granularity also (transitively) comprises the data items packaged at finer granularities. For example, if some message is flight critical for a segment of the LOVV region then, all other things remaining unchanged, that message is also in the essential briefing package for the entire LOVV region. On the other hand, the component containers ‘inherit’ the data items that the composite container explicitly associates with the coarser granularity level: The data items propagate from the composite container to the component containers. For example, the data items generally classified as part of the essential briefing package should likewise be included in packages for operational restriction and flight critical, respectively. Similarly, the data items relevant for an entire FIR should also be included in the packages for individual transition segments within that FIR. Legal requirements also mandate that no relevant information is disregarded, necessitating a top-down data sharing mechanism along the level hierarchies. Formally, we define the notion of composite container and the data sharing mechanism as follows.

Figure 4. A multigranular ATM information cube.
Definition 4 (Composite container and shared data) A composite container ![]() $c \in \mathcal{C}$ is a semantic container, which, in addition to its own data items
$c \in \mathcal{C}$ is a semantic container, which, in addition to its own data items ![]() $I_c$, has a set of component containers
$I_c$, has a set of component containers ![]() $C_c$. Data items of the composite container are shared by component containers i.e.,
$C_c$. Data items of the composite container are shared by component containers i.e., ![]() $\forall c' \in C_c: i \in I_c \Rightarrow i \in I_{c'}$. A container c′ is a component of composite container c if its coordinates p(c′) roll up to c’s coordinates p(c) i.e.,
$\forall c' \in C_c: i \in I_c \Rightarrow i \in I_{c'}$. A container c′ is a component of composite container c if its coordinates p(c′) roll up to c’s coordinates p(c) i.e., ![]() $p(c') \prec p(c) \Rightarrow c' \in C_c$.
$p(c') \prec p(c) \Rightarrow c' \in C_c$.
As an alternative to multigranular cubes where composite containers indicate the shared data items of component containers at finer granularities, the shared data items may be redundantly associated with multiple containers. The drawback of that alternative representation lies in the reduced expressiveness of the model. A multigranular cube explicitly represents shared data items relevant for a broader context. For example, the collection of a DNOTAM into a semantic container for the LOVV FIR explicitly marks the DNOTAM as relevant for the entire Austrian airspace. Collecting that message into each semantic container for a segment in the LOVV FIR would hide the fact that the DNOTAM is relevant for the FIR as a whole. Furthermore, there is a subtle difference between collecting a DNOTAM into the containers for each segment in a FIR and collecting a DNOTAM into the container for the FIR. The former case could just be down to chance and only temporary; however, for now, each container has the particular DNOTAM but possible additions of containers may change that state.
Concerning the materialisation of data sharing and container composition within ATM information cubes, we note the following. In theory, each possible granularity level in a cube could have a composite container associated, having component containers from the more finely grained points underneath. A composite container, when selected, should return the data items specific to the composite container as well as the component containers’ data items. Materialisation of these composite sets of data items would speed up performance. In practice, however, the materialisation of composite containers at every possible granularity level may be infeasible due to combinatorial explosion. A common solution in data warehousing is the selection of beneficial aggregate views for materialisation(Reference Harinarayan, Rajaraman and Ullman20). Materialization of downward propagation, however, is unproblematic when the ATM information is predominantly available at the base granularity. The operators for semantic containers (see Section 4) are inherently related to the materialisation of data sharing and container composition. The merge-union operation is an explicit mechanism for materialising the data item sets of composite containers. The merge-intersect operation, on the other hand, facilitates the extraction of common data items from lower levels by materialising commonalities at coarser levels.
3.2 Cubes of ATM Information Cubes
We propose ATM information cubes being built for a certain operational context e.g., a specific flight on a particular date. In the previous sections, a cube’s operational context was not explicitly defined in the model but assumed to be implicit constants outside the model. Thus, in order to externalise that context, we propose to arrange the ATM information cubes themselves into multidimensional structures (Fig. 5).

Figure 5. A cube of ATM information cubes (metacube).
A cube of ATM information cubes – a metacube – consists of several cubes, the sets of dimensions of which will typically overlap but not necessarily be equal. For example, the metacube in Fig. 5 has ATM information cubes with different dimensionality depending on the data item type. Cubes of DNOTAMs have geography, importance, and scenario dimensions, whereas cubes of METARs have geography, importance, and currentness dimensions. The currentness, in this respect, refers to the precise time of the METAR’s underlying observation. While the dimensions can be manifold, we assume data item type, flight, and date/time as the typical candidates for dimensions. A point in such a metacube may contain e.g., a cube of DNOTAMs relevant for flight OS93 on 15 March 2018, or a cube of METARs relevant for flight OS93 on 16 March 2018.
Definition 5 (Metacube). A metacube ![]() $k \in \mathcal{K}$, taken from the universe of ATM information metacubes
$k \in \mathcal{K}$, taken from the universe of ATM information metacubes ![]() $\mathcal{K}$, is a 4-tuple
$\mathcal{K}$, is a 4-tuple ![]() ${(Q_k,D_k,p_k,\bar{g}_k)}$ where
${(Q_k,D_k,p_k,\bar{g}_k)}$ where ![]() $Q_k \subseteq \mathcal{Q}$ are the metacube’s cubes, and
$Q_k \subseteq \mathcal{Q}$ are the metacube’s cubes, and ![]() $D_k = \{d_1, \dots, d_n\} \subseteq \mathcal{D}$ are the metacube’s dimensions which span a multidimensional space
$D_k = \{d_1, \dots, d_n\} \subseteq \mathcal{D}$ are the metacube’s dimensions which span a multidimensional space ![]() $P_k \stackrel{\textrm{def}}{=} E_{d_1} \times \dots \times E_{d_n}$. Injective function
$P_k \stackrel{\textrm{def}}{=} E_{d_1} \times \dots \times E_{d_n}$. Injective function ![]() $p_k: Q_k \rightarrow P_k$ maps each cube to a point in the multidimensional space. The notion of granularity and the roll-up relationships between granularities is defined the same way as for ATM information cubes. The metacube’s base granularity
$p_k: Q_k \rightarrow P_k$ maps each cube to a point in the multidimensional space. The notion of granularity and the roll-up relationships between granularities is defined the same way as for ATM information cubes. The metacube’s base granularity ![]() $\bar{g}_k$ denotes the finest granularity that the metacube may comprise cubes at i.e.,
$\bar{g}_k$ denotes the finest granularity that the metacube may comprise cubes at i.e., ![]() $\forall q \in Q_k : \bar{g}_k \preceq g(p_k(q))$. The metacube’s base cubes
$\forall q \in Q_k : \bar{g}_k \preceq g(p_k(q))$. The metacube’s base cubes ![]() $\bar{Q}_k \stackrel{\textrm{def}}{=} \{ q \in Q_k \mid g(p_k(q)) = \bar{g}_k \}$ are cubes at the base granularity. The base space
$\bar{Q}_k \stackrel{\textrm{def}}{=} \{ q \in Q_k \mid g(p_k(q)) = \bar{g}_k \}$ are cubes at the base granularity. The base space ![]() $\bar{P}_k \stackrel{\textrm{def}}{=} \{p \in P_k \mid g(p) = \bar{g}_k\}$ consists of all points at the metacube’s base granularity.
$\bar{P}_k \stackrel{\textrm{def}}{=} \{p \in P_k \mid g(p) = \bar{g}_k\}$ consists of all points at the metacube’s base granularity.
A metacube serves as a kind of registry of the ATM information cubes that are built for specific contexts. Rather than building an all-purpose, comprehensive ATM information cube, the ATM information cubes themselves remain relatively small and focused on a specific context, which facilitates handling and ensures that the ATM information cubes can be easily replicated e.g., on aircraft. Depending on the task, using the dimensions of the metacube, a user may select multiple ATM information cubes and apply the drill-across operation (see Section 4.2) to obtain a more comprehensive ATM information cube required for the task.
4.0 OPERATIONS ON ATM INFORMATION CUBES
In this section, we present operations that allow for flexibly combining individual semantic containers that are organized in ATM information cubes. We first introduce merge operations, which combine semantic containers within a single ATM information cube. We then introduce the drill-across operation, which combines semantic containers from different cubes within a metacube. We do not focus on generic slice-and-dice operations for selection of subsets of the cube as these operations do not differ from their counterparts in traditional OLAP.
4.1 Merge of Semantic Containers
Individual semantic containers may be aggregated – merged – along the hierarchically ordered dimensions of an ATM information cube. In this respect, the essential operation is the merge-union operation, which takes an input cube and returns as output a cube with a specified coarser base granularity where the lower-level containers from the input cube are merged. The merge-union operation produces flat containers that comprise the data items from multiple individual semantic containers but, unlike composite containers, do not preserve component container structure.
Figure 6 illustrates the result of applying the merge-union operation on a three-dimensional input cube with segment-importance-scenario base granularity (Fig. 3). The resulting cube has a coarser base granularity than the input cube, namely FIR-package-keyword granularity. The containers in the output cube contain the same data items as in the input cube’s containers. For example, the semantic container for LZBB, Essential Briefing Package, and Runway in the output cube comprises the data items from eight base containers of the input cube, which roll up to the point identified by LZBB, Essential Briefing Package, and Runway. Hence, the semantic containers at the FIR-package-keyword granularity are hence flattened with respect to composite containers at the corresponding granularity in the input cube.
Another merge variant is the merge-intersect operation, which aims at analysing the information contained in multiple semantic containers by creating the intersection of the involved containers’ data items, leaving the base granularity of the cube unchanged. The merge-intersect operation serves to identify the common data items of a set of multiple semantic containers. For example, a merge-intersect operation on the cube from Fig. 2 with a FIR-package-keyword merge granularity, in order to obtain the data items for the container at the point identified by LZBB, Essential Briefing Package, and Runway, selects the intersection of data item sets from all semantic containers at points that roll up to that specific point. The containers at the coarser merge granularity, thus, receive additional data items from the containers underneath at finer granularities, whereas the base containers remain unchanged by that operation. Formally, we define the variants of the merge operation as follows.
Definition 6 (Merge operation). A merge operation
![]() $\mu^{\mathsf{met}}(q,g)$
takes as input the cube
$\mu^{\mathsf{met}}(q,g)$
takes as input the cube
![]() $q = (C_q, D_q, p_q, \bar{g}_{q})$
and granularity
$q = (C_q, D_q, p_q, \bar{g}_{q})$
and granularity
![]() $g = (l_1, \dots, l_n)$
, where
$g = (l_1, \dots, l_n)$
, where
![]() $\bar{g}_q \prec g$
, with
$\bar{g}_q \prec g$
, with
![]() $\mathsf{met} \in \{\cup,\cap\}$
, producing as output cube
$\mathsf{met} \in \{\cup,\cap\}$
, producing as output cube
![]() $q' = (C_{q'}, D_{q'}, p_{q'}, \bar{g}_{q'})$
with
$q' = (C_{q'}, D_{q'}, p_{q'}, \bar{g}_{q'})$
with
![]() $\bar{g}_{q'} = g$
as base granularity. The output cube’s dimensions are equal to the input cube’s dimensions i.e.,
$\bar{g}_{q'} = g$
as base granularity. The output cube’s dimensions are equal to the input cube’s dimensions i.e.,
![]() $D_{q'} = D_q$
. Function
$D_{q'} = D_q$
. Function
![]() $p_{q'}$
maps q′ ’s non-base containers as defined by
$p_{q'}$
maps q′ ’s non-base containers as defined by
![]() $p_q$
i.e.,
$p_q$
i.e.,
![]() $\forall c \in C_{q'} \setminus \bar{C}_{q'} : p_{q'}(c) = p_q(c)$
. The resulting set of containers is
$\forall c \in C_{q'} \setminus \bar{C}_{q'} : p_{q'}(c) = p_q(c)$
. The resulting set of containers is
![]() $C_{q'} = \bar{C}_{q'} \cup \{ c \in C_q \mid g \prec g(p_q(c)) \}$
, where the base containers
$C_{q'} = \bar{C}_{q'} \cup \{ c \in C_q \mid g \prec g(p_q(c)) \}$
, where the base containers
![]() $\bar{C}_{q'}$
and the mapping of base containers to points are defined as follows:
$\bar{C}_{q'}$
and the mapping of base containers to points are defined as follows:
Merge-union (
 $\mathsf{met} = \cup$
): For each point p in the new base space
$\mathsf{met} = \cup$
): For each point p in the new base space
 $\bar{P}_{q'}$
there is a container c′ with the union of data items of containers rolling up or equal to p if and only if there is at least one container in the input cube rolling up or equal to p i.e.,
$\bar{P}_{q'}$
there is a container c′ with the union of data items of containers rolling up or equal to p if and only if there is at least one container in the input cube rolling up or equal to p i.e.,
 $\forall p \in \bar{P}_{q'}: (\exists c \in C_q : p_q(c) \preceq p) \Leftrightarrow \exists c' \in \bar{C}_{q'}: p_{q'}(c') = p \wedge I_{c'} = \bigcup_{c \in C_q: p_{q}(c) \preceq p_{q'}(c')}(I_{c})$
.
$\forall p \in \bar{P}_{q'}: (\exists c \in C_q : p_q(c) \preceq p) \Leftrightarrow \exists c' \in \bar{C}_{q'}: p_{q'}(c') = p \wedge I_{c'} = \bigcup_{c \in C_q: p_{q}(c) \preceq p_{q'}(c')}(I_{c})$
.Merge-intersect (
 $\mathsf{met} = \cap$
): For each point p in the new base space
$\mathsf{met} = \cap$
): For each point p in the new base space
 $\bar{P}_{q'}$
there is a container c′ with the intersection of data items of containers rolling up or equal to p if and only if there is at least one container in the input cube rolling up or equal to p i.e.,
$\bar{P}_{q'}$
there is a container c′ with the intersection of data items of containers rolling up or equal to p if and only if there is at least one container in the input cube rolling up or equal to p i.e.,
 $\forall p \in \bar{P}_{q'}: (\exists c \in C_q : p_q(c) \preceq p) \Leftrightarrow \exists c' \in \bar{C}_{q'}: p_{q'}(c') = p \wedge I_{c'} = \bigcap_{c \in C_q: p_{q}(c) \preceq p_{q'}(c')}(I_{c})$
.
$\forall p \in \bar{P}_{q'}: (\exists c \in C_q : p_q(c) \preceq p) \Leftrightarrow \exists c' \in \bar{C}_{q'}: p_{q'}(c') = p \wedge I_{c'} = \bigcap_{c \in C_q: p_{q}(c) \preceq p_{q'}(c')}(I_{c})$
.
In traditional OLAP cubes, the ‘double-counting problem’(Reference Vaisman and Zimányi11) leads to summarisability issues(Reference Lenz and Shoshani21): counting the same numeric measure twice typically yields erroneous results. In the case of ATM information cubes and merge operations, the double-counting problem is not an issue. Consider, for example, the same DNOTAM being included in multiple semantic containers. Now imagine those containers being merged into a single semantic container. The merge-union operation would then simply ‘ignore’ the duplicate occurrences of data items when compiling the merged semantic container. The merge-intersect operation, on the other hand, specifically aims at identifying duplicates.
We further propose a split operation as the inverse of merge-union. That split operation would serve to divide existing semantic containers into multiple containers with a subset of the original container’s data items using specific features of the data items in the semantic container. For example, given a semantic container with a set of DNOTAMs with importance annotations, a split operation may create multiple semantic containers – one container for each different importance level. At this point, we omit the formal definition of split.
4.2 Drill Across the Metacube
The drill-across operation combines different cubes within a metacube along the dimension hierarchies of the metacube, using the cubes’ common dimensions to join the cubes. The drill-across operation takes an input metacube and returns an output metacube with a specified coarser base granularity, where the lower-level cubes from the input cube are joined over their common dimensions. Consider, for example, the metacube in Fig. 7, which shows the result of a drill-across operation on the three-dimensional metacube from Fig. 5. The drill-across operation, in this example, changes the metacube granularity such that the data item type dimension is rolled up to the dimension’s top (or all) level and hence effectively reduces the dimensionality of the metacube (although formally the dimension is still there). The DNOTAM cubes in the input metacube have Geography, Importance, and Scenario dimensions, whereas the METAR cubes have Geography, Importance, and Currentness dimensions. The cubes from the input metacube about DNOTAMs and METARs are joined over their common Geography and Importance dimensions. The drill-across operation first applies the merge-union operation on the DNOTAM and METAR cubes from the input metacube in order to obtain a common granularity by rolling up the Scenario and Currentness dimensions to the all level before obtaining cubes with both DNOTAMs and METARs.
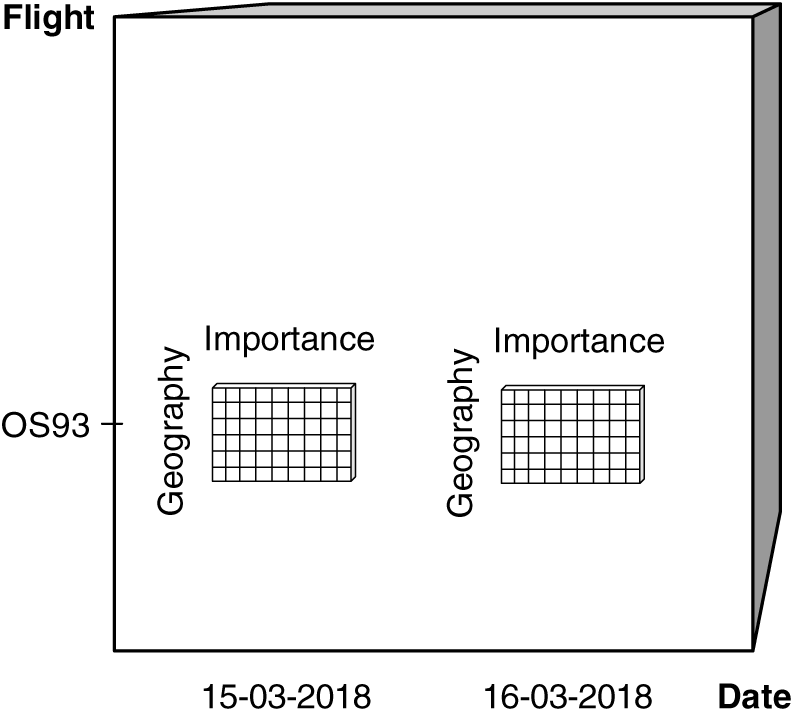
Figure 7. A drill across the metacube from Fig. 5 over the item type dimension.
Definition 7 (Drill-across operation). A drill-across operation
![]() $\chi(k,g)$
has as input the metacube
$\chi(k,g)$
has as input the metacube
![]() $k = (Q_k, D_k, p_k, \bar{g}_k)$
and granularity
$k = (Q_k, D_k, p_k, \bar{g}_k)$
and granularity
![]() $g = (l_1, \dots, l_n)$
, where
$g = (l_1, \dots, l_n)$
, where
![]() $\bar{g}_k \prec g$
, producing as output a metacube
$\bar{g}_k \prec g$
, producing as output a metacube
![]() $k' = (Q_{k'},D_{k'},p_{k'},\bar{g}_{k'})$
with g as k′ ’s base granularity
$k' = (Q_{k'},D_{k'},p_{k'},\bar{g}_{k'})$
with g as k′ ’s base granularity
![]() $\bar{g}_{k'}$
. The output metacube’s dimensions are equal to the input metacube’s dimensions i.e.,
$\bar{g}_{k'}$
. The output metacube’s dimensions are equal to the input metacube’s dimensions i.e.,
![]() $D_{k'} = D_k$
. Function
$D_{k'} = D_k$
. Function
![]() $p_{k'} : Q_{k'} \rightarrow P_{k'}$
maps k′ ’s non-base cubes to points as defined by
$p_{k'} : Q_{k'} \rightarrow P_{k'}$
maps k′ ’s non-base cubes to points as defined by
![]() $p_k$
i.e.,
$p_k$
i.e.,
![]() $\forall q \in Q_{k'} \setminus \bar{Q}_{k'} : p_{k'}(q) = p_k(q)$
. The resulting set of cubes is
$\forall q \in Q_{k'} \setminus \bar{Q}_{k'} : p_{k'}(q) = p_k(q)$
. The resulting set of cubes is
![]() $Q_{k'} = \bar{Q}_{k'} \cup \{ q \in Q_k \mid g \prec g(p_k(q)) \}$
, where the base cubes
$Q_{k'} = \bar{Q}_{k'} \cup \{ q \in Q_k \mid g \prec g(p_k(q)) \}$
, where the base cubes
![]() $\bar{Q}_{k'}$
and the mapping of base cubes to points are obtained as follows:
$\bar{Q}_{k'}$
and the mapping of base cubes to points are obtained as follows:
1. For each point
 $p \in P_k: g(p) = g$
in the input metacube k at the roll-up granularity, get the set of cubes
$p \in P_k: g(p) = g$
in the input metacube k at the roll-up granularity, get the set of cubes
 $Q_p$
associated with points that are the same as or roll up to the respective point p at the roll-up granularity i.e.,
$Q_p$
associated with points that are the same as or roll up to the respective point p at the roll-up granularity i.e.,
 $Q_p \stackrel{\textrm{def}}{=} \{q \in Q_k \mid p_k(q) \preceq p \}$
.
$Q_p \stackrel{\textrm{def}}{=} \{q \in Q_k \mid p_k(q) \preceq p \}$
.2. For each such set
 $Q_p$
, obtain a single cube
$Q_p$
, obtain a single cube
 $q_p$
, which becomes k′ ’s base cube for point p, as follows:
$q_p$
, which becomes k′ ’s base cube for point p, as follows:
a. The set
 $D_{q_p}$
of
$D_{q_p}$
of
 $q_p$
’s dimensions consists of the common dimensions of the cubes in
$q_p$
’s dimensions consists of the common dimensions of the cubes in
 $Q_p$
i.e.,
$Q_p$
i.e.,
 $D_{q_p} \stackrel{\textrm{def}}{=} \bigcap_{q' \in Q_p} D_{q'}$
.
$D_{q_p} \stackrel{\textrm{def}}{=} \bigcap_{q' \in Q_p} D_{q'}$
.b. The base granularity
 $\bar{g}_{q_p}$
of
$\bar{g}_{q_p}$
of
 $q_p$
is the finest common base granularity of the cubes in
$q_p$
is the finest common base granularity of the cubes in
 $Q_p$
over the dimensions
$Q_p$
over the dimensions
 $D_{q_p} = \{ d_1, \dots, d_n \}$
in the granularity space
$D_{q_p} = \{ d_1, \dots, d_n \}$
in the granularity space
 $G_{q_p} = L_{d_1} \times \dots \times L_{d_n}$
spanned by the levels of these dimensions. For each
$G_{q_p} = L_{d_1} \times \dots \times L_{d_n}$
spanned by the levels of these dimensions. For each
 $q' \in Q_p$
,
$q' \in Q_p$
,
 $\bar{g}'_{q'} \preceq \bar{g}_{q_p}$
holds, where
$\bar{g}'_{q'} \preceq \bar{g}_{q_p}$
holds, where
 $\bar{g}'_{q'}$
is the projection of q′ ’s base granularity
$\bar{g}'_{q'}$
is the projection of q′ ’s base granularity
 $\bar{g}_{q'}$
onto the granularity space
$\bar{g}_{q'}$
onto the granularity space
 $G_{q_p}$
, and there is no finer granularity that satisfies that condition.
$G_{q_p}$
, and there is no finer granularity that satisfies that condition.c. Obtain a set
 $Q'_p$
that consists of the cubes obtained by applying the merge-union operator to each cube
$Q'_p$
that consists of the cubes obtained by applying the merge-union operator to each cube
 $q' \in Q_p$
with a granularity g′ as argument, where each component of g′ corresponds to the respective component of
$q' \in Q_p$
with a granularity g′ as argument, where each component of g′ corresponds to the respective component of
 $\bar{g}_{q_p}$
for the dimensions in
$\bar{g}_{q_p}$
for the dimensions in
 $D_{q_p}$
, or
$D_{q_p}$
, or
 $\hat{l}_{d}$
for the dimensions
$\hat{l}_{d}$
for the dimensions
 $d \in D_{q'} \setminus D_{q_p}$
.
$d \in D_{q'} \setminus D_{q_p}$
.d. Each base point
 $\bar{p} \in \bar{P}_{q_p}$
is associated with a new container c′, with
$\bar{p} \in \bar{P}_{q_p}$
is associated with a new container c′, with
 $p_{q_p}(c') \stackrel{\textrm{def}}{=} \bar{p}$
, and c′ ’s set of data items
$p_{q_p}(c') \stackrel{\textrm{def}}{=} \bar{p}$
, and c′ ’s set of data items
 $I_{c'}$
consists of the union of the sets of data items from the containers at the equivalent points in the cubes in
$I_{c'}$
consists of the union of the sets of data items from the containers at the equivalent points in the cubes in
 $Q'_{p}$
. The point
$Q'_{p}$
. The point
 $\bar{p} \in \bar{P}_{q_p}$
is equivalent to a point
$\bar{p} \in \bar{P}_{q_p}$
is equivalent to a point
 $p' \in P_{q'}$
of some
$p' \in P_{q'}$
of some
 $q' \in Q'_{p}$
if, and only if, each component of p′ corresponds to the respective component of
$q' \in Q'_{p}$
if, and only if, each component of p′ corresponds to the respective component of
 $\bar{p}$
for the dimensions in
$\bar{p}$
for the dimensions in
 $D_{q_p}$
, or
$D_{q_p}$
, or
 $\hat{l}_{d}$
for the dimensions
$\hat{l}_{d}$
for the dimensions
 $d \in D_{q'} \setminus D_{q_p}$
.
$d \in D_{q'} \setminus D_{q_p}$
.
3. The obtained single cube
 $q_p$
for each set
$q_p$
for each set
 $Q_p$
becomes associated with the respective point p i.e.,
$Q_p$
becomes associated with the respective point p i.e.,
 $p_{k'}(q_p) \stackrel{\textrm{def}}{=} p$
.
$p_{k'}(q_p) \stackrel{\textrm{def}}{=} p$
.
The drill-across operation is the metacube counterpart of the merge-union operation. The drill-across operation changes a metacube’s base granularity and combines the contents associated with the merged points. In case of the drill-across operation the contents are ATM information cubes. In order to sensibly combine cubes from the different points, the cubes must be joined over common dimensions, with non-common dimensions rolled up to the implicit all level. The drill-across operation, just like the merge-union operation, preserves all data items from the cubes in the input metacube – only their organisation into ATM information cubes is different in the output cube.
We also propose a pivot operation to obtain a self-contained ATM information cube from a metacube by adding the metacube dimensions to the component cube. That ATM information cube explicitly contains the context information. For these added dimensions, the dimension member is fixed to the respective points from the metacube. For example, the DNOTAM cube for OS93 on 15 March 2018 associates containers only with points that have a value DNOTAM in the item type dimension; OS93 in the flight dimension, and 15 March 2018 in the date dimension. The inverse of pivot would be the unpivot operation, which essentially corresponds to a merge operation with a merge granularity on the all level. At this point, we omit the formal definition of pivot and unpivot operations.
5.0 OPERATIONS ON SEMANTIC CONTAINERS
The notion of abstraction serves as an umbrella term for a wide variety of different operations. Abstraction, as opposed to merge and drill-across, denotes operations that produce new data items and links between data items. Originally proposed for working with RDF data(Reference Schütz, Neumayr, Schrefl, Salinesi, Norrie and Pastor17), the principle of abstraction is independent from any concrete data or information model. In the following, we therefore provide a generic, formal definition of the abstraction operation.
Definition 8 (Abstraction operation). An abstraction operation
![]() $\alpha^{f}(c)$
has as input a container c, applies an argument function f, and returns a container c′ as output. The function f specifies how the input container’s set of data items translates into the output container’s set of data items; we refer to this function as abstraction function.
$\alpha^{f}(c)$
has as input a container c, applies an argument function f, and returns a container c′ as output. The function f specifies how the input container’s set of data items translates into the output container’s set of data items; we refer to this function as abstraction function.
We employ Unified Modelling Language (UML) object diagrams to illustrate the principle of the abstraction operation. Consider an object diagram (Fig. 8) that shows DNOTAMs according to the Aeronautical Information Exchange Model (AIXM) 5.1.1 information exchange model (see Section 8.1 in the appendix). In particular, the object diagram shows two DNOTAMs about the surface conditions of runways as well as two DNOTAMs about the closure of runway directions. The LOWW-16/34 runway has two layers of contaminants with an overall extent of 0.31m: dry snow (0.29m) and ice (0.02m). The LOWW-11/29 runway has a layer of ice with an extent of 0.01m. Both runways, however, have a specified length and width already cleared of contaminants, while the remainder of the runway has winter services going on, thus leading to the closure of one runway direction from each runway. The closures are due to snow and ice removal, respectively, and for each runway the closure affects only one runway direction whereas the other remains open.
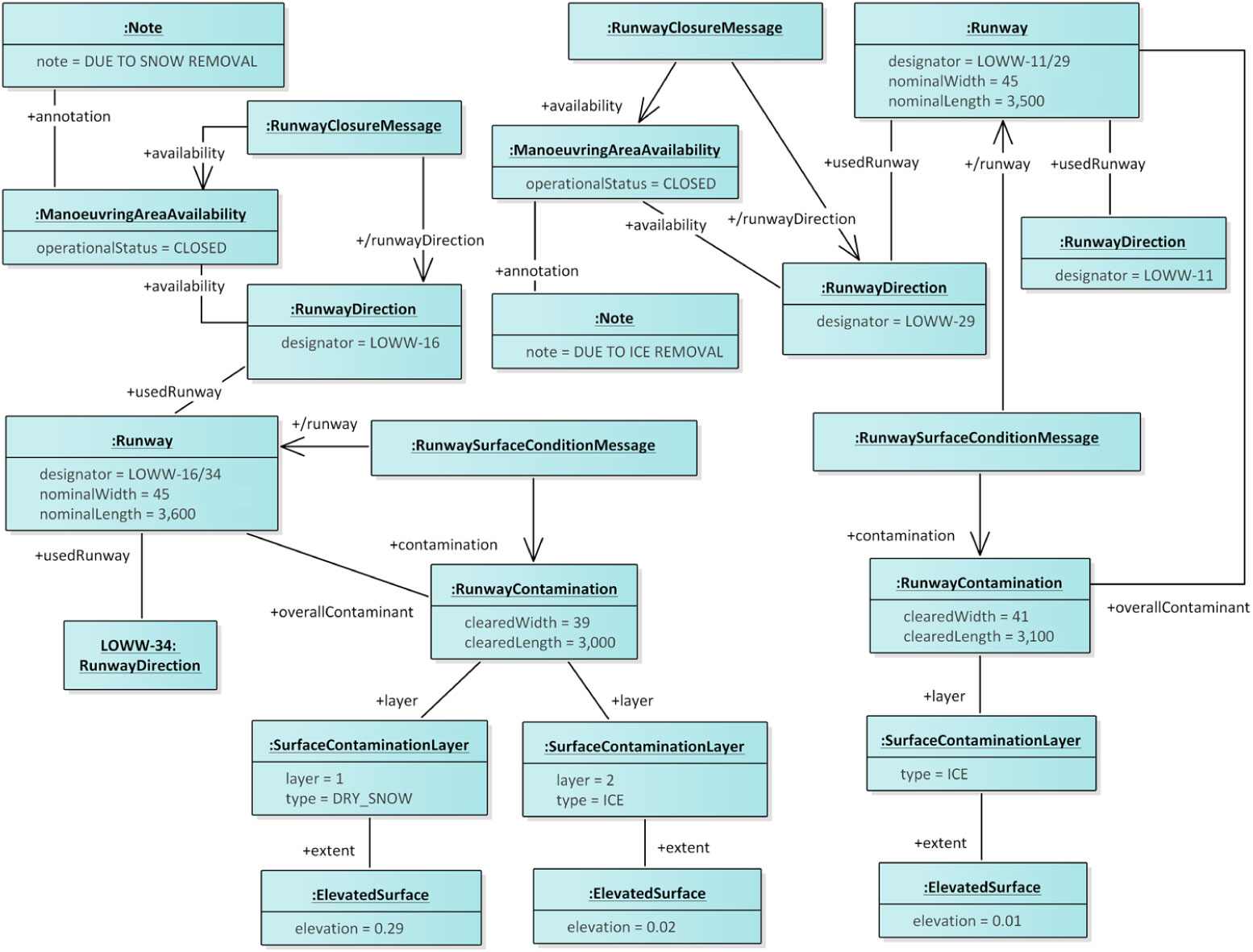
Figure 8. An object diagram illustratings DNOTAMs according to the AIXM 5.1.1 metamodel (see Section 8.1).
Assume the DNOTAMs in Fig. 8 concern the destination airport of a particular flight e.g., OS93 from Washington-Dulles to Vienna. At the beginning of a flight, detailed information about the destination is not interesting for the pilot preparing a flight. Rather, the pilot may prefer a management summary suitable for display during the preparation and early phases of that flight that might only show abstracted DNOTAMs alerting the pilot to wintry conditions at the destination airport with runway closures in place. The summary may also include average, minimum, and maximum of the contaminant’s extent in order to allow the pilot to get a grasp of the severity of the situation at a single glance. Legal requirements mandating that pilots receive all the relevant information are not violated by the abstraction operation – provided the filtering rules are correct (see Section 2.2): pilots receive the full set of relevant information and employ abstraction to get a high-level overview. We note, however, that user interfaces will have to address the possibility of pilots missing important information when relying solely on summaries.
Consider then the abstracted DNOTAM information in Fig. 9, which is the result of applying the abstraction operation with an abstraction function that combines DNOTAMs about surface contamination and runway closures, respectively. The application of such function to the DNOTAMs from Fig. 8 produces an AbstractedRunwayClosureMessage with abstracted information about the runway closures as well as an AbstractedRunwaySurfaceConditionMessage with abstracted information about runway contamination. The abstracted DNOTAMs reference a generic LOWW-Runway rather than specific runway directions. The abstracted DNOTAMs summarise the attributes, such as the cleared length and width of the contaminated runways and provides average, minimum, and maximum values for these numeric attributes. The objects’ count attributes preserve information about the size of the input model. For example, while the abstracted DNOTAM about surface condition has only one generic runway contamination, the count attribute documents the number of runway contaminations in the input model. The type of contamination is ‘SNOW_OR_ICE’, which subsumes the ‘SNOW’ and ‘ICE’ layers from the input DNOTAMs. Information about such subsumption relationships between attribute values could be derived from ontologies e.g., the NASA ATM Ontology(Reference Keller22); the attribute values would then be concepts from ontologies.
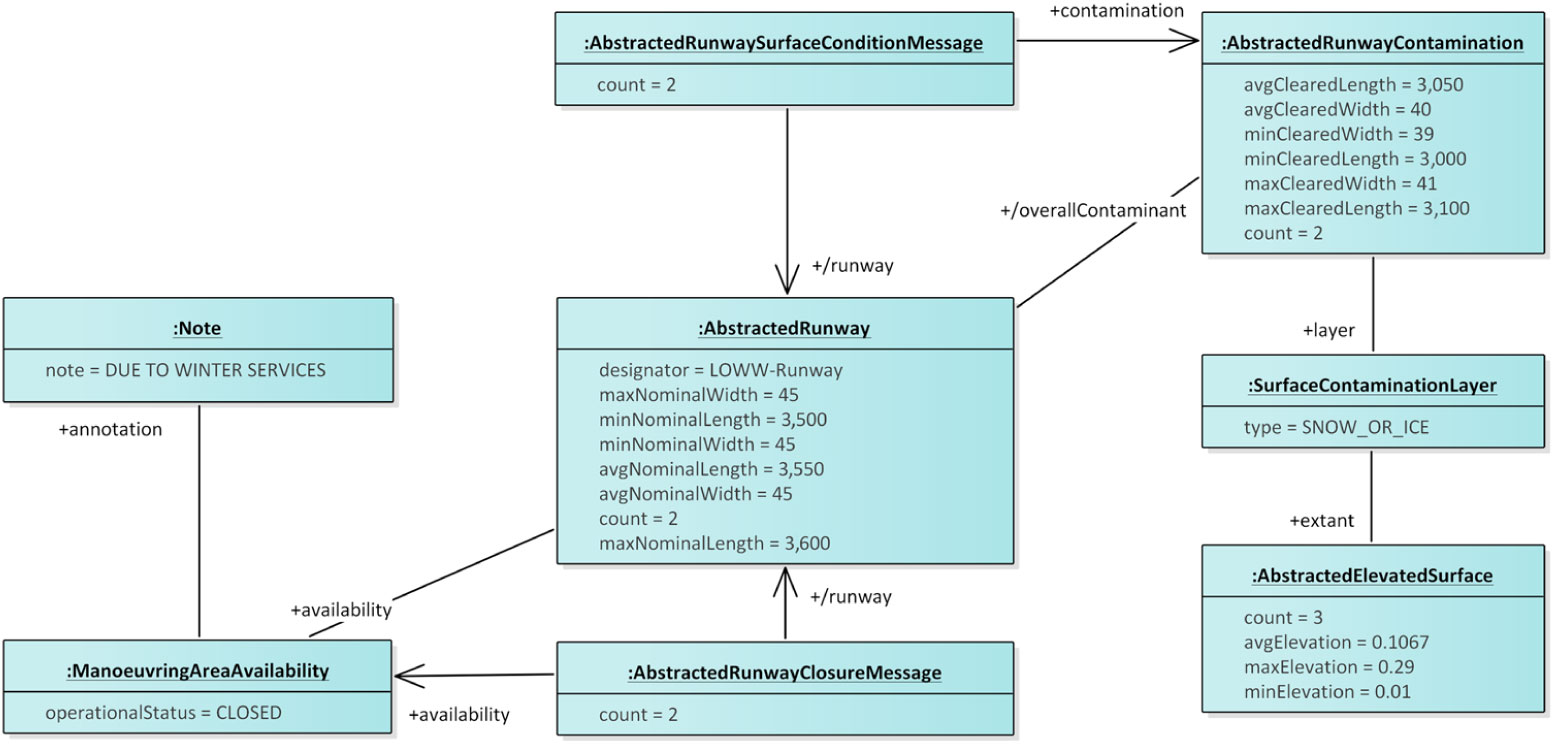
Figure 9. An example of abstracted DNOTAM information obtained from the DNOTAM information in Fig. 8.
The abstraction operation, with a different abstraction function, also applies to other types of data items e.g., METARs. Consider, for example, the METARs according to IWXMM 2.1.1 represented in Fig. 10. The three observations concern the Vienna airport and record air temperature and pressure (qnh) as well as wind speed and direction at specific points in time. Two of these observations state that cloud and visibility are not okay (cloudAndVisibilityOK = FALSE). Only these observations report on cloud layers and visual range. The first METAR reports on a single layer of broken fractus clouds (amount is ‘BKN’, cloudType is 7) at a base height of 1,600m. That same METAR also reports on a mean visual range of 4,500m with a past tendency of going down (pastTendency is ‘DOWN’) for the LOWW-11 runway direction as well as a mean visual range of 4,000m with a past tendency of going down for the LOWW-16 runway direction. The second METAR reports on a layer of broken fractus clouds (amount is ‘BKN’, cloudType is 8) at a base height of 1,400m as well as on an overcast layer of altocumulusd clouds (amount is ‘OVC’, cloudType is 7) at a base height of 2,800m. That same METAR also reports on a mean visual range of 3,000m with a past tendency of going down for the LOWW-11 runway direction as well as a mean visual range of 3,500m with a past tendency of going down for the LOWW-16 runway direction.
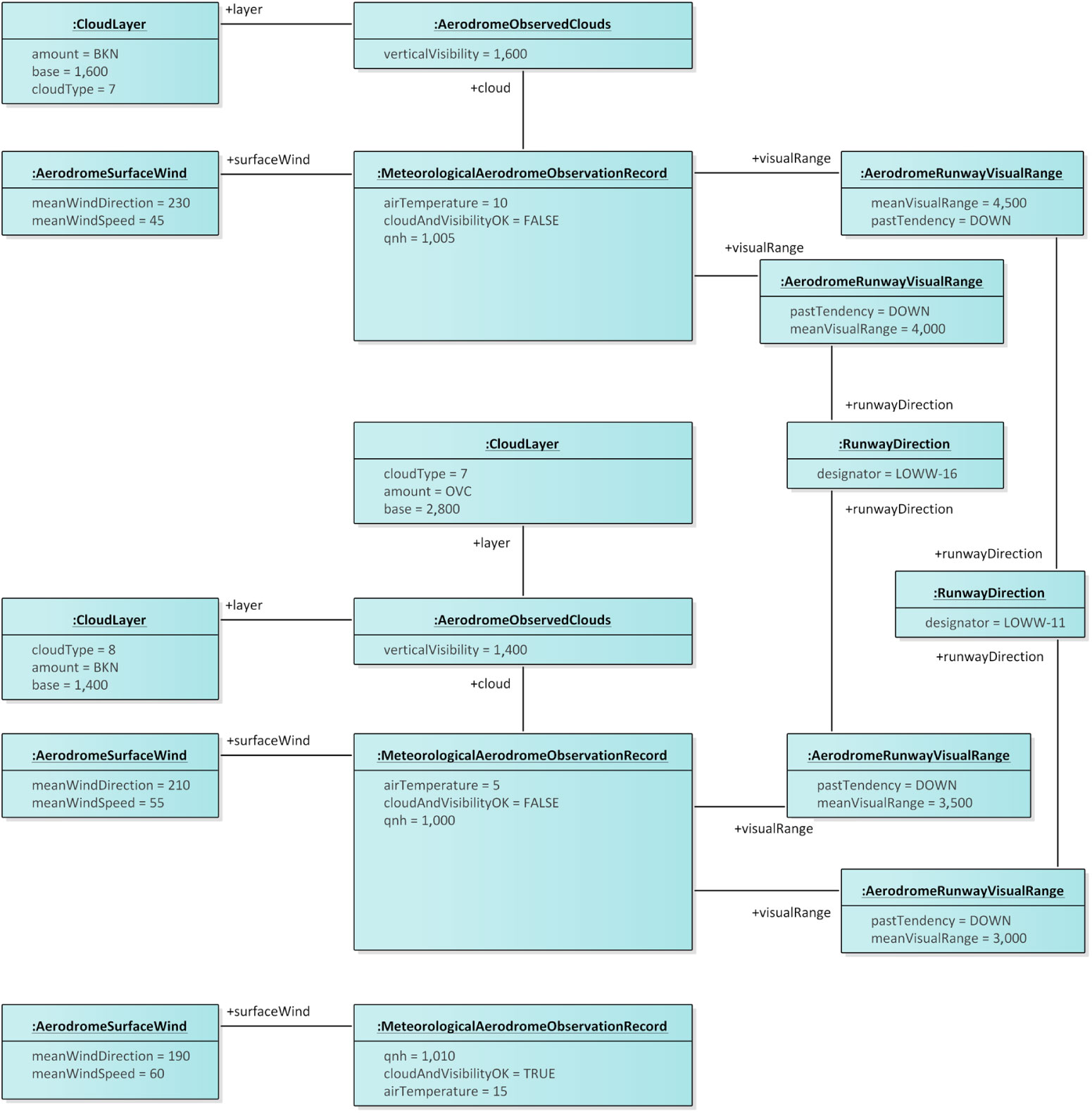
Figure 10. An object diagram illustratings METARs according to the IWXXM 2.1.1 metamodel (see Section 8.2).
Consider then the abstracted METAR information in Fig. 11 that is the result of applying the abstraction operation with an abstraction function that, on the one hand, collects into a single abstracted METAR the information about clouds and visual range from various METARs and, on the other hand, collects into another abstracted METAR the information about surface wind from various METARs. The first abstracted METAR object subsumes those METARs with cloud and visibility issues to report on. The second abstracted METAR object, on the other hand, subsumes all METARs from the original set. Note that, in this case, the double-counting problem(Reference Vaisman and Zimányi11) may become an issue. Looking at the count attribute values from the abstracted METARs, an observer may conclude that five METARs were in the original set, whereas the true number is three. Hence, a direct comparison of these abstracted METARs would yield misleading results from a statistics perspective. When the purpose of such abstraction is to provide a management summary of pilot briefings rather than conducting a statistical analysis, the double-counting problem is a minor concern since the goal of the abstraction is to provide pilots with a concise representation of the contents rather than a precise statistical analysis.
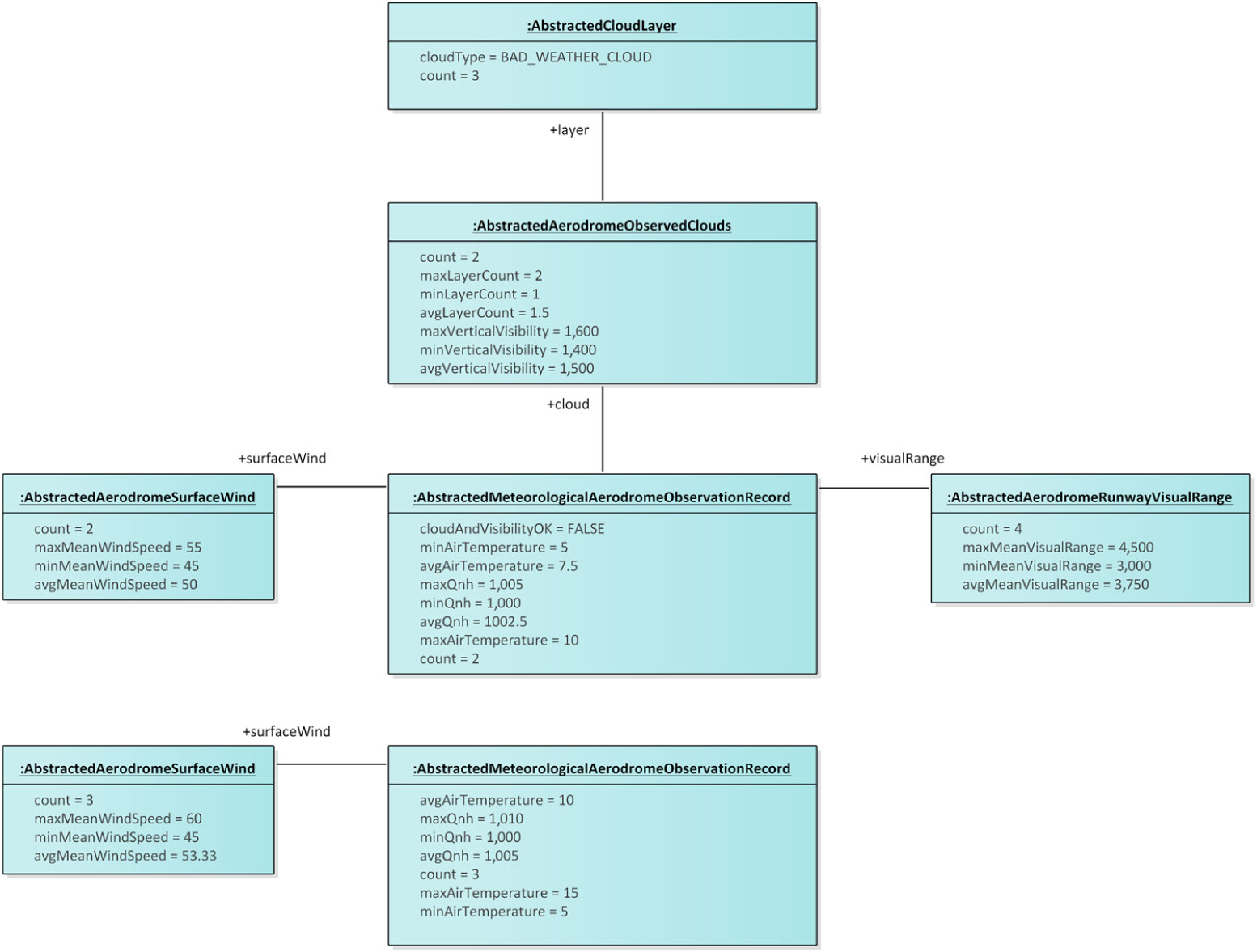
Figure 11. An example of abstracted METAR information obtained from the METAR information in Fig. 10.
The abstraction function that conducts the actual abstraction of data items is akin to the aggregation function in traditional OLAP. Just like there are different aggregation functions to summarise numeric values e.g., Sum, Min, Max, Count, there are different abstraction functions to summarise more complex data items e.g., DNOTAMs and METARs. There may exist different abstraction functions for different data item types e.g., DNOTAMs may be summarised differently than METARs. Other abstraction functions may apply to a variety of data item types. The identification and definition of an extensive catalog of abstraction functions merits further investigation and is left for future work.
6.0 IMPLEMENTATION
In the traditional data warehouse architecture(Reference Vaisman and Zimányi11), ETL processes extract data from various sources and transform these data before loading them into the data cubes. Similarly, the presented approach for ATM information cubes assumes the existence of ETL processes that populate the cells of ATM information cubes with actual data items. Rule-based approaches may serve to collect ATM data items into different semantic containers that are then arranged in ATM information cubes. The SemNOTAM project(Reference Steiner, Kovacic, Burgstaller, Schrefl, Friesacher and Gringinger7), for example, has investigated the possibility to filter DNOTAMs and create DNOTAM annotations that indicate importance of DNOTAMs for specific flights. The SemNOTAM engine(Reference Burgstaller, Steiner, Neumayr, Schrefl and Gringinger14) employs ObjectLogic(Reference Angele23) – an extension of F-Logic(Reference Kifer and Lausen24) – to implement rules for automatic filtering and annotation of DNOTAMs. In the course of the BEST project, we then studied the integration of the SemNOTAM engine into the semantic container approach(Reference Gringinger, Fabianek and Schuetz25). Specifically, we created a proof-of-concept prototype that employs the SemNOTAM engine to create semantic containers along with the appropriate semantic descriptions, which would allow to create BEST-enabled SWIM information services for filtering and annotating DNOTAMs. Such SWIM information services would serve to create the semantic containers for ATM information cubes in the course of an ETL process. Similar services could be developed for other kinds of ATM information e.g., METARs, provided the existence of an appropriate rule base for filtering and importance annotation. Thus, the development of the required ETL processes for creating ATM information cubes is generally feasible.
An implementation of the presented framework may employ the RDF for the representation of ATM information cubes, while the SPARQL query language may serve for the implementation of the merge and abstraction operations(Reference Schnepf26). This approach relies on a translation of ATM data items into a suitable RDF representation. For DNOTAMs according to the AIXM standard, an RDF representation is a natural fit since the AIXM standard builds on Geography Markup Language (GML), which was heavily influenced by RDF(Reference Lake, Burggraf, Trninić and Rae27). An advantage of the RDF representation is the seamless integration with existing ontologies e.g., the NASA ATM Ontology(Reference Keller22) or the ATM Information Reference Model (AIRM) Ontology(Reference Vennesland, Neumayr, Schuetz and Savulov28), which are typically serialised in RDF. Such ontologies could then be used for performing abstraction operations e.g., by providing the grouping properties for individuals referenced in the ATM data items. The implementation of abstraction itself relies on the graph structure of the RDF representation. Different variants of the abstraction operation have been implemented as SPARQL queries, which in general replace individual entities in the RDF graph with more abstract entities. As an alternative, XML may serve for the representation of ATM information cubes, while XQuery may serve for the implementation of the query operations.
Traditional data warehouse implementations often employ a star schema to represent an OLAP cube using a relational database management system (see Vaisman and Zimányi(Reference Vaisman and Zimányi11) for more information). As an alternative to the RDF-based implementation of ATM information cubes, a relational representation would employ an ensemble of relational star schema tables to represent the corresponding ATM information. ATM information, however, is typically semi-structured and quite heterogeneous – we refer to the description of DNOTAM airport operations scenarios as an example(19). In this regard, relational star schemas are too rigid for providing a flexible representation of diverse ATM information. ATM information cubes can be considered a structured data lake approach to managing ATM information. A data lake collects raw data for further analysis(Reference Russom29) and is more flexible regarding the rigidity of the schema than traditional relational implementations.
Performance experiments with a proof-of-concept RDF-based implementationFootnote † suggest feasibility of ATM information cubes for operational tasks e.g., providing pilots with a cube of DNOTAMs and METARs relevant for a specific flight on a certain date as part of the ePIB. In this case, the number of cells as well as the number of messages will remain rather limited and, consequently, performance is not an issue. The concept of ATM information cubes, however, also lends itself to post-operational analysis in Air Traffic Flow and Capacity Management, where a post-operations team analyses operational events in order to identify lessons learned for the benefit of future operations and to compile an overview of occurred incidents(Reference Niarchakou and Simón Selva30). Currently, a data warehouse provides the post-operations team with statistical data about flight operations(Reference Niarchakou and Simón Selva30). Complementary to that data warehouse, a data lake of ATM information cubes may serve the air traffic flow post-operations team to analyse past operations and provide a high-level overview of incidents. Accordingly, the number of cells as well as the number of messages will increase considerably compared to an ATM information cube for an individual flight. In that case, distributed storage and parallelisation of computation may alleviate potential performance issues(Reference Zaharia31).
7.0 CONCLUSION
In this paper, we introduced the concept of ATM information cube, an adaptation of the data cube metaphor, where instead of numeric measure values, each cell consists of a set of data items e.g., DNOTAMs or METARs. Dedicated query operations allow for the merge and abstraction of the data items organised in ATM information cubes in order to provide a condensed view – a management summary – of relevant ATM information. The presented framework is independent from any particular data format and may be applied to organise arbitrary data item types. Dependent on the type of data format and data item type, different abstraction functions are applicable. Future work will identify, describe, and implement a set of common abstraction functions for ATM information.
In this paper, we focused on the application of ATM information cubes in pilot briefings. We proposed building an ATM information cube per flight and date, thus keeping the expected number of cells and contained messages relatively small. Future work will investigate the applicability of the presented approach in other ATM activities e.g., Air Traffic Flow and Capacity Management, resulting in potentially larger ATM information cubes, venturing into the realm of ‘big data’. In this regard, future work will also investigate issues specific to big data processing as well as the possibility of positioning the ATM information cube framework as a structured data lake solution for big data processing in the ATM domain.
ACKNOWLEDGEMENTS
This work has received funding from the SESAR Joint Undertaking under grant agreement No 699298 under the European Union’s Horizon 2020 research and innovation program. The views expressed in this paper are those of the authors.
APPENDIX 8.0 ATM INFORMATION EXCHANGE MODELS
In this section, we briefly present UML diagrams describing those parts of the (adapted) AIXM and IWXXM standards relevant to the understanding of the examples in the main sections of this paper.
8.1 Aeronautical Information Exchange Model
The Aeronautical Information Exchange Model (AIXM) is a standard model for exchanging information about aeronautical features(32). Figure 12 shows an adapted excerpt of the AIXM 5.1.1 metamodel. The AIXMBasicMessage class represents the concept of DNOTAMs, which is central to AIXM. In contrast to the AIXM standard, the AIXMBasicMessage class has been specialised in order to account for different scenarios(19), namely runway closure and runway surface condition. For simplicity’s sake, we omit the AIXM temporality model(33) and assume that temporal information only serves to collect the DNOTAMs into different semantic data containers along a time dimension.
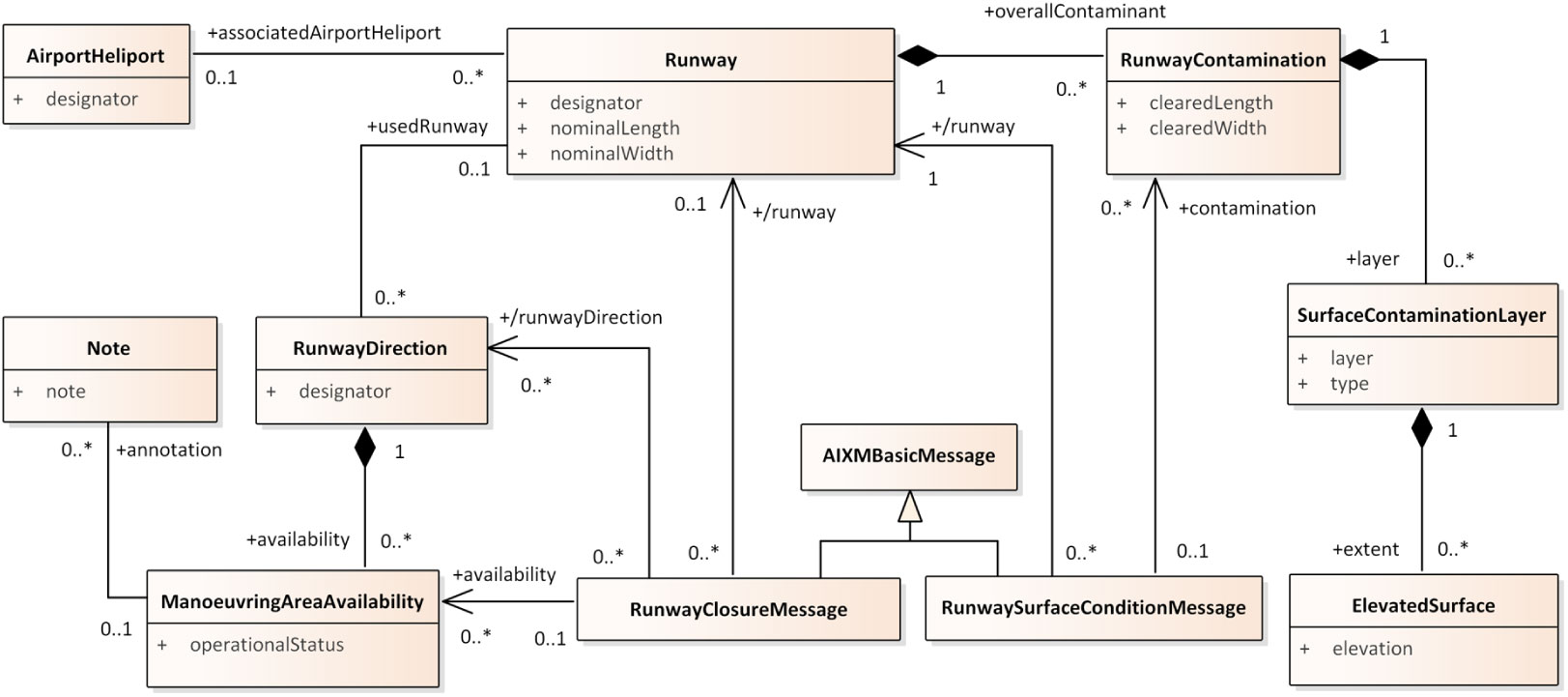
Figure 12. An adapted excerpt of the AIXM 5.1.1 metamodel, extended with messages for different scenarios.
The message classes have associations to the types of aeronautical features the changes of which the messages of the respective type announce. For example, the RunwayClosureMessage class represents messages according to the scenario of runway closure by runway direction(19); a runway closure message indicates availability of different runway directions. Hence, the RunwayClosureMessage has relationships to the ManoeuvringAreaAvailability, RunwayDirection, and Runway classes. The RunwaySurfaceCondition class, on the other hand, represents messages according to the scenario of a contaminant e.g., snow or ice present on a runway. The RunwaySurfaceCondition class, hence, has relationships to the Runway-Conamination and Runway classes.
The RunwayContamination class represents the presence of layers of contaminants e.g., snow, on a particular runway, as well as the length and width of the part of the runway cleared from the contaminant. The RunwayContamination class has a relationship to SurfaceContaminationLayer, which represents a layer of some type of contaminant. The relationship of RunwayContamination to ElevatedSurface represents the extent of each layer of contaminant. The extent of a layer may not be uniform over the entire course of a runway. The RunwayDirection class associates the ManoeuvringAreaAvailability class in order to indicate availability of runway directions. In particular, the ManoeuvringAreaAvailability class specifies an operational status e.g., closed. The associated Note class specifies the reason for closure e.g., due to snow removal.
8.2 ICAO Meteorological Information Exchange Model
The ICAO Meteorological Information Exchange Model (IWXXM) is a standard model for exchanging information about meteorological observations(34). Figure 13 shows an adapted excerpt of the IWXXM 2.1.1 metamodel. The MeteorologicalAerodromeObservationRecord class represents METARs – a central type of messages in IWXXM. Besides air temperature (attribute airTemperature), air pressure (qnh), and an indicator of visibility (cloudAndVisibilityOK), METARs may contain data about surface wind, clouds, and visual range. The MeteorologicalAerodromeObservationRecord class hence has relationships to the AerodromeSurfaceWind, AerodromeObservedClouds, and AerodromeRunwayVisualRange classes. The AerodromeSurfaceWind class represents mean direction and speed of surface winds at an aerodrome. The AerodromeRunwayVisualRange class indicates the mean visual range at a runway direction as well as the tendency (up or down, no change). The AerodromeObservedClouds class records the vertical visibility at an aerodrome as well as the different observed cloud layers, represented by the relationship to the CloudLayer class. The CloudLayer class represents the amount e.g., broken or overcast, the base height, and the cloud type.

Figure 13. An adapted excerpt of the IWXXM 2.1.1 metamodel.