Published online by Cambridge University Press: 23 August 2023
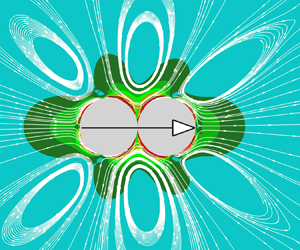
We investigate the hydrodynamics of a spherical and dumbbell-shaped swimmer in a viscoelastic fluid, modelled by the Giesekus constitutive equation. The ‘squirmer’, a model of a micro-swimmer with tangential surface waves at its boundaries, is simulated utilizing a direct-forcing fictitious domain method. We consider the competitive effects of the fluid inertia and elasticity on the locomotion of the swimmers. For the neutral squirmer, its speed increases monotonically with increasing Reynolds number in the Giesekus fluid, in contrast to holding a constant speed in a Newtonian one. Meanwhile, the speed of the finite inertial squirmer increases monotonically with fluid elasticity, as measured by the Weissenberg number. Regarding the dumbbell-shaped swimmers in the Giesekus fluid, we find the pusher–puller (the puller is in front of the pusher) dumbbell swimming to be significantly faster than other dumbbells, providing practical guidance in assembling the complex micro-swimming devices. We further consider the squirmer's (or the dumbbell-shaped squirmer's) energy expenditure and hydrodynamic efficiency, finding that swimming in viscoelastic fluids expends less energy than its Newtonian counterpart, and the neutral squirmer expends more energy than a pusher or puller. The energy expenditure and hydrodynamic efficiency are relevant to steady swimming speeds, in which a faster counterpart squirmer (dumbbell-shaped squirmer) expends less energy but has higher hydrodynamic efficiency.