Corrected odds ratio

Although TND has sometimes been referred to as a special case of the case–control design, there is a distinct feature in the sampling procedure of TND. It has been pointed out that the adjustment methods for misclassification bias developed for cohort studies do not apply to case–control studies because the sampling ratio in case–control studies (differential recruitment) varies between case and control groups [Reference Greenland12, Reference Kleinbaum, Kupper and Morgenstern13]. However, as we have shown in Section ‘Characterising bias in TND studies’, both cases (TD patients) and controls (ND patients) are sampled at the same ratio (q) in TND studies. This suggests that the existing bias correction formulas developed for a hypothetical setting [Reference Kleinbaum, Kupper and Morgenstern13] where the whole population is evenly sampled (which is unrealistic in traditional studies) may be applicable to TND studies.

By left-multiplying Equation (1) with the inverted matrix C ⁻¹, we can obtain the corrected odds ratio γ* as

(3)$$\gamma ^\ast\! = \,\displaystyle{{X_V-\lpar \lpar 1-\beta \rpar /\beta \rpar Y_V} \over {Y_V-\lpar \lpar 1-\alpha \rpar /\alpha \rpar X_V}}\cdot \displaystyle{{Y_U-\lpar \lpar 1-\alpha \rpar /\alpha \rpar X_U} \over {X_U-\lpar \lpar 1-\beta \rpar /\beta \rpar Y_U}}\comma \;$$

which adjusts for misclassification to give an asymptotically-unbiased estimate of γ. This result can also be derived by maximising the likelihood accounting for misclassification in the observed TND data (see the Supplementary Document).

All four components of (3) (two numerators and two denominators) are usually expected to be non-negative with moderate VE (less than 100%) because these components are considered to be proportional to reconstructed true case counts. However, in some (relatively rare) cases, one or more components may become negative due to random fluctuations in observation. Theoretically, negative values are not permitted as true case counts, and thus such negative quantities would need to be truncated to 0. As a result, the corrected odds ratio can be either 0 or infinity. It is unrealistic in clinical settings that vaccines have absolute 100% or −100% effectiveness. Uncertainty around such MLEs should be carefully considered; increasing sample size or redesigning the study might be recommended where possible. Alternatively, the Bayesian framework may be used to yield an interval estimate with the likelihood shown in section ‘Direct likelihood method for the logistic regression model’ adapted for a univariate model.

The confidence interval for VE can be obtained by assuming log-normality of the odds ratio γ, i.e.

$$\gamma = \gamma ^\ast \exp \lpar { \pm 1.96\sigma^\ast } \rpar \comma \;$$

where σ is the shape parameter of the log-normal distribution and is empirically given as

(4)$$\eqalign{\sigma ^\ast{} = &\,SD\lpar {\log \lpar {\gamma^\ast } \rpar } \rpar \cr = &\,c\sqrt {\matrix{{\displaystyle{{X_VY_V\lpar {X_V + Y_V} \rpar } \over {{[ {\alpha Y_V-\lpar {1-\alpha } \rpar X_V} ] }^2{[ {\beta X_V-\lpar {1-\beta } \rpar Y_V} ] }^2}}+}\cr{ \displaystyle{{X_UY_U\lpar {X_U + Y_U} \rpar } \over {{[ {\alpha Y_U-\lpar {1-\alpha } \rpar X_U} ] }^2{[ {\beta X_U-\lpar {1-\beta } \rpar Y_U} ] }^2}}}}} .} $$

See the Supplementary Document for details of the MLE and confidence intervals.

Simulation

To assess the performance of the corrected odds ratio given in Equation (3) and uncertainty around it, we used simulation studies. TND study datasets were drawn from Poisson distributions (see the Supplementary Document for model settings and the likelihood function) as it is a reasonable assumption when medically-attended cases are recruited over the study period. We parameterised the mean incidence in the dataset by the ‘baseline medical attendance’ λ _V = qm _V(r ₁μ + r ₀)n _V and λ _U = qm _U(r ₁μ + r ₀)n _U, so that λ _V and λ _U correspond to the mean number of vaccinated/unvaccinated patients when vaccine has no effect (i.e. γ = 1 and VE = 0). The mean total sample size (given as ((1 + γδ)/(1 + δ))λ _V + λ _U) was set to be 3000. Parameter values were chosen according to a range of scenarios shown in Table 2, and the true VE=1−γ was compared with the estimates obtained from the simulated data. For each scenario, simulation was repeated 500 times to yield the distribution of estimates. Reproducible codes (including those for simulations in later sections) are reposited on GitHub (https://github.com/akira-endo/TND-biascorrection/).

Table 2. Simulation settings

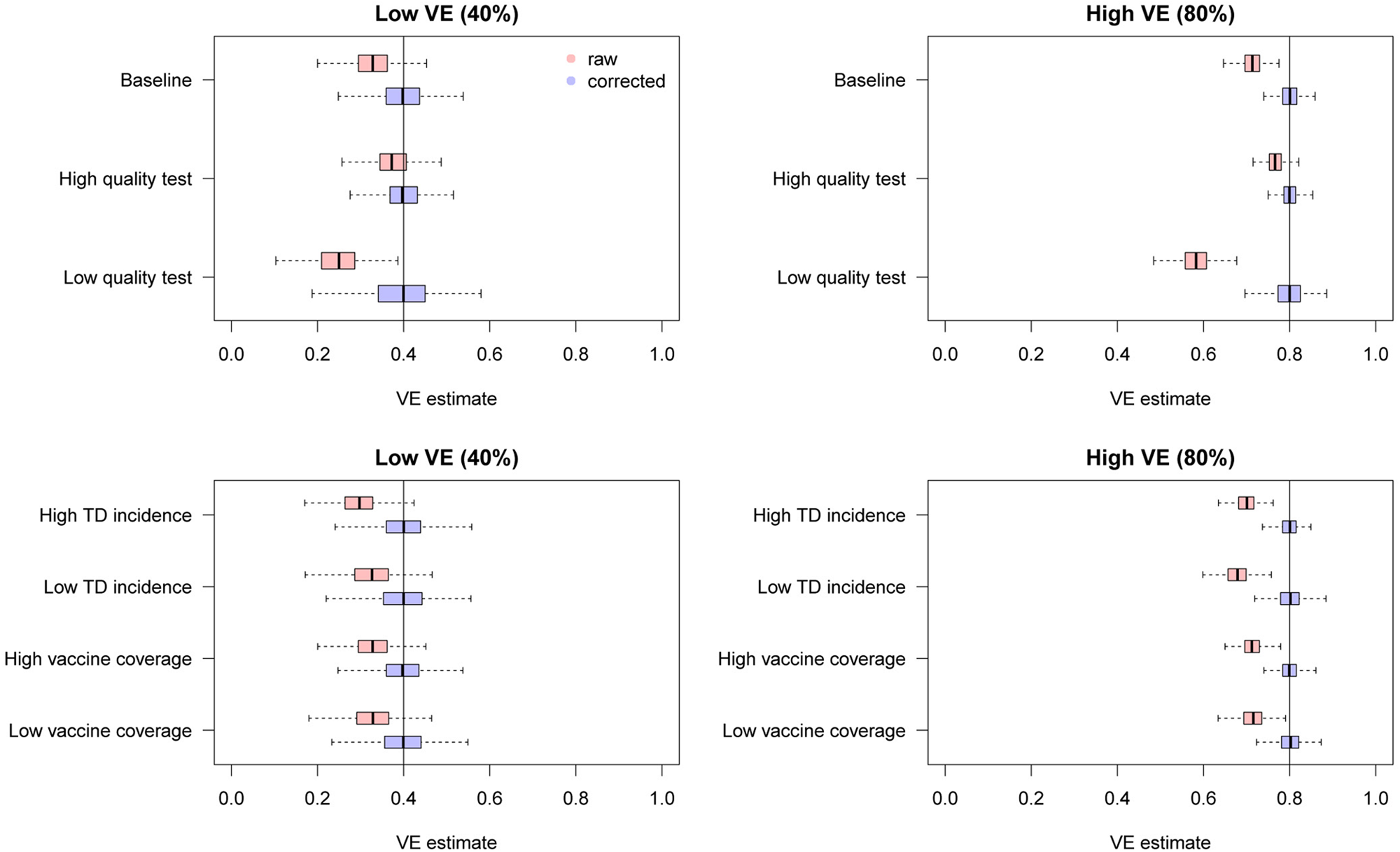
We found that the uncorrected estimates, directly obtained from the raw case counts that were potentially misclassified, exhibited substantial underestimation of VE for most parameter values (Fig. 3). On the other hand, our bias correction method was able to yield unbiased estimates in every setting, whose median almost correspond to the true VE. Although the corrected and uncorrected distributions were similar (with a difference in median ~5%) when VE is relatively low (40%) and the test has sufficiently high sensitivity and specificity (95% and 97%, respectively), they became distinguishable with a higher VE (80%). With lower test performances, the bias in the VE estimates can be up to 10–20%, which may be beyond the level of acceptance in VE studies.

Fig. 3. Bias correction for simulated data in the univariate setting. The distributions of bias-corrected VE estimates (boxplots in blue) are compared with those of raw VE estimates without correction (red). Five hundred independent datasets were randomly generated for each set of parameter values, and the corrected and uncorrected VE estimates are compared with the true value (black solid line). See Table 2 for parameter settings in each scenario.

Bias correction of VEs reported in previous studies

We have seen that the degree of bias for uncorrected VE estimates depends on parameter values. To explore the possible degree of bias in existing VE studies, we extracted the reported crude VEs (i.e. VEs unadjusted for potential confounders) from two systematic reviews [Reference Leung21, Reference Darvishian23]Footnote ⁵ and applied our bias correction method assuming different levels of test sensitivity and specificity. The case counts for each study summarised in the reviews were considered eligible for the analysis if the total sample size exceeded 200. Varying the assumed sensitivity and specificity, we investigated the possible discrepancy between the reported VE (or crude VE derived from the case counts if unreported in the reviews) and bias-corrected VE. We did not consider correcting adjusted VEs because it requires access to the original datasets.

Figure 4 displays the discrepancy between the reported VE and bias-corrected VE corresponding to a range of assumptions on the test performance. Many of the extracted studies employed PCR for the diagnostic test, which is expected to have a high performance. However, the true performance of PCR cannot be definitively measured as there is currently no other gold-standard test available. Figure 4 suggests that even a slight decline in the test performance can introduce a non-negligible bias in some parameter settings. Our bias correction methods may therefore also be useful in TND studies using PCR, which would enable a sensitivity analysis accounting for potential misdiagnosis by PCR tests. In this light, it is useful that the corrected odds ratio

$$\gamma ^\ast{ = } \displaystyle{{X_V-\lpar \lpar 1-\beta \rpar /\beta \rpar Y_V} \over {Y_V-\lpar \lpar 1-\alpha \rpar /\alpha \rpar X_V}}\cdot \displaystyle{{Y_U-\lpar \lpar 1-\alpha \rpar /\alpha \rpar X_U} \over {X_U-\lpar \lpar 1-\beta \rpar /\beta \rpar Y_U}}$$

is a monotonic function of both α and β (given that all the four components are positive). The possible range of VE in a sensitivity analysis is obtained by supplying γ* with the assumed upper/lower limits of sensitivity and specificity.

Fig. 4. Bias correction method applied to published VE estimates assuming various test sensitivity and specificity. Case count data were extracted from two systematic reviews [Reference Leung21, Reference Darvishian23]. Each connected set of dots show how (crude) VE estimates reported in the review varies when imperfect sensitivity and specificity are assumed. Black dots on the grey diagonal line denote the original VEs reported in the reviews. This should correspond to the true value if sensitivity = specificity = 1. Coloured dots show the bias-corrected VE considering potential misclassification.

Theoretical framework

TND studies often employ a multivariate regression framework to address potential confounding variables such as age. The most widespread approach is to use generalised linear models (e.g. logistic regression) and include vaccination history as well as other confounding variables as covariates. The estimated linear coefficient for vaccination history can then be converted VE (in the logistic regression model, the linear coefficient for vaccination history corresponds to log (1 − VE)). In this situation, the likelihood function now reflects a regression model and thus the bias-corrected estimate in the univariate analysis (Equation (3)) is no longer applicable. We therefore need to develop a separate multivariate TND study framework to correct for bias in multivariate analysis.

Suppose that covariates ξ = (ξ ¹, ξ ², …, ξ ⁿ) are included in the model, and that ξ ¹ corresponds to vaccination history (1: vaccinated, 0: unvaccinated). These covariates ξ _i, as well as outcome variable Z _i (i.e. test results) are available for each individual i included in the study. In TND studies, it is often convenient to model the binomial probability for the true outcome p ₁(ξ _i), i.e. the conditional probability that the true outcome is TD as opposed to ND given an individual has covariates ξ _i. Let us use parameter set θ to model the binomial probabilities p ₁ (and p ₀ = 1 − p ₁). Using the binomial probability $\pi _{Z_i}$ for observed (potentially misclassified) outcome Z _i, we can obtain the MLE for θ by maximising

(5)$$\eqalign{& {\cal L}\left( {\theta ; D} \right) = \mathop \prod \limits_S^{i = 1} \pi _{Z_i}\left( {\xi _i;\theta } \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathop \prod \limits_{i\in \left\{ + \right\}} \left[ {\alpha p_1\left( {\xi _i;\theta } \right) + \left( {1-\beta } \right)p_0\left( {\xi _i;\theta } \right)} \right] \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \mathop \prod \limits_{i\in \left\{ - \right\}} \left[ {\left( {1-\alpha } \right)p_1\left( {\xi _i;\theta } \right) + \beta p_0\left( {\xi _i;\theta } \right)} \right].} $$

With the estimate θ*, the VE estimate for an individual with covariates ξ ^2:n = (ξ ², ξ ³, …, ξ ⁿ) is given as (1−odds ratio):

(6)$${\rm VE}\lpar {\xi^{2\colon n}} \rpar = 1-\displaystyle{{\,p_1\lpar {\xi^1 = 1\comma \;\xi^{2\colon n}\semicolon \;\theta^\ast } \rpar } \over {\,p_0\lpar {\xi^1 = 1\comma \;\xi^{2\colon n}\semicolon \;\theta^\ast } \rpar }}{\rm /}\displaystyle{{\,p_1\lpar {\xi^1 = 0\comma \;\xi^{2\colon n}\semicolon \;\theta^\ast } \rpar } \over {\,p_0\lpar {\xi^1 = 0\comma \;\xi^{2\colon n}\semicolon \;\theta^\ast } \rpar }}.$$

See the Supplementary Document for further details.

Direct likelihood method for the logistic regression model

The logistic regression model is well-suited for modelling binomial probabilities p ₁ and p ₀. The log-odds ($\log \left({{{p_1} \over {p_0}}} \right)$) is characterised by a linear predictor as:

(7)$$\log \left({\displaystyle{{\,p_1\lpar {\xi \semicolon \;\theta } \rpar } \over {\,p_0\lpar {\xi \semicolon \;\theta } \rpar }}} \right) = \theta _0 + \theta _1\xi ^1 + \cdots + \theta _n\xi ^n.$$

In the logistic regression model where covariate ξ ₁ indicates vaccination history, the corresponding coefficient θ ₁ gives the VE estimate: VE = 1 − exp (θ ₁). Due to the assumed linearity, the estimated VE value is common across individuals regardless of covariates ξ ^2:n.

We can employ the direct likelihood method by combining Equations (5) and (7). The usual logistic regression optimises θ by assuming that the test results follow Bernoulli distributions Z _i ~ Bernoulli(p ₁(ξ _i;θ)) (Z _i = 1 for positive test results and 0 for negative). To correct the misclassification bias, we instead need to use the modified probabilities to construct the likelihood accounting for diagnostic error, i.e.

(8)$$Z_i\sim {\rm Bernoulli}\lpar {{\pi }_ + \lpar {\xi_i\semicolon \;\theta } \rpar } \rpar = {\rm Bernoulli}\lpar {\alpha p_1\lpar {\xi_i\semicolon \;\theta } \rpar + \lpar {1-\beta } \rpar p_0\lpar {\xi_i\semicolon \;\theta } \rpar } \rpar.$$

Parameter θ is estimated by directly maximising the probability of observing {Z _i} based on Equation (8)

Note that as long as the binomial probability is the modelling target, other type of models (e.g. machine learning classifiers) could also be employed under a similar framework.

Multiple overimputation combined with existing tools

The direct likelihood method presented in the previous section is the most rigorous MLE approach and would therefore be preferable whenever possible. However, it is often technically-demanding to implement such approaches as it involves re-defining the likelihood; if we wanted to use existing tools for logistic regression (or other models), for example, we would need to modify the internal algorithm of such tools. This is in particular complicated in tools for generalised linear models including logistic regression, whose standard algorithm is the iteratively reweighted least squares method [Reference Sidney Burrus24], which does not involve the explicit likelihood. To ensure that our correction methods can be employed without losing access to substantial existing software resources, we also propose another method, which employs a MO framework [Reference Blackwell, Honaker and King15] to account for misclassification. Whereas multiple imputation only considers missing values, MO is proposed as a more general concept which includes overwriting mismeasured values in the dataset by imputation. In our multivariate bias correction method, test results in the dataset (which are potentially misclassified) are randomly overimputed.

Let M be an existing estimation software tool whose likelihood specification cannot be reprogrammed. Given data d = {z _i, ξ _i}_i=1,2,…S, where z _i denotes the true disease state (z = 1 for TD and z = 0 for ND), M would be expected to return at least the following two elements: the point estimate of VE (ɛ _d) and the predicted binomial probability $\hat{p}_1\lpar {\xi_i} \rpar $ for each individual i. From the original observed dataset D, J copies of imputed datasets $\lcub {{\tilde{D}}^j} \rcub = \lcub {{\tilde{D}}^1\comma \;{\tilde{D}}^2\comma \;\ldots \comma \;{\tilde{D}}^J} \rcub $ are generated by the following procedure.

1. (1) For i = 1, 2, …, S, impute disease state $\tilde{z}_i^j $ based on the test result Z _i. Each $\tilde{z}_i^j $ is sampled from a Bernoulli distribution conditional to Z _i:

   (9)$$\tilde{z}_i^j \sim \left\{{\matrix{ {{\rm Bernoulli}\lpar {1-{\tilde{\varphi }}_{i + }} \rpar } \hfill & {\lpar {Z_i = 1} \rpar } \hfill \cr {{\rm Bernoulli}\lpar {{\tilde{\varphi }}_{i-}} \rpar } \hfill & {\lpar {Z_i = 0} \rpar } \hfill \cr } } \right..$$

2. (2) $\tilde{\varphi }_{i + }$ and $\tilde{\varphi }_{i-}$ are estimated probabilities that the test result for individual i is incorrect (i.e. z _i ≠ Z _i) given Z _i. The sampling procedure (9) is therefore interpreted as the test result Z _i being ‘flipped’ at a probability $\tilde{\varphi }_{i + }$ or $\tilde{\varphi }_{i-}$. Later we will discuss possible procedures to obtain these probabilities.

3. (3) Apply M to $\tilde{D}^j = \lcub {\tilde{z}_i^j \comma \;\xi_i} \rcub $ to yield a point estimate of VE (ɛ ^j).

4. (4) Repeat (1) and (2) for j = 1, 2, …, J to yield MO estimates {ɛ ^j}_j=1,…J.

Once MO estimates {ɛ ^j} are obtained, the pooled estimate and confidence intervals of VE are obtained by appropriate summary statistics, e.g. Rubin's rules [Reference Rubin25]. As long as the estimated ‘flipping’ probabilities $\tilde{\varphi }_{i \pm } = \lpar {{\tilde{\varphi }}_{i + }\comma \;{\tilde{\varphi }}_{i-}} \rpar $ are well chosen, this MO procedure should provide an unbiased estimate of VE with a sufficiently large number of iterations J.

As a method to estimate the flipping probability $\tilde{\varphi }_{i \pm }$, here we propose the parametric bootstrapping described as follows. Given the observed test result Z _i, $\tilde{\varphi }_{i \pm }$ is given as the Bayesian probability

(10)$$\eqalign{&{\cal P}\lpar z_i = Z_i\vert Z_i\rpar \cr &\!\!= \!\left\{\!\!\!\!{\matrix{ {\displaystyle{{\alpha {\cal P}\lpar z_i = 1\rpar } \over {\alpha {\cal P}\lpar z_i = 1\rpar + \lpar 1-\beta \rpar {\cal P}\lpar z_i = 0\rpar }} = \displaystyle{{\alpha p_1\lpar \xi_i\rpar } \over {\alpha p_1\lpar \xi_i\rpar + \lpar 1-\beta \rpar p_0\lpar \xi_i\rpar }}} & \!\!\!\!{\lpar Z_i = 1\rpar } \cr {\displaystyle{{\beta {\cal P}\lpar z_i = 0\rpar } \over {\lpar 1-a\rpar {\cal P}\lpar z_i = 1\rpar + \beta {\cal P}\lpar z_i = 0\rpar }} = \displaystyle{{\beta p_0\lpar \xi_i\rpar } \over {\lpar 1-\alpha \rpar p_1\lpar \xi_i\rpar + \beta p_0\lpar \xi_i\rpar }}} & \!\!\!\!\!{\lpar Z_i = 0\rpar } \cr } } \right.$$

Although the true binomial probabilities p ₀(ξ _i), p ₁(ξ _i) are unknown, their estimators are derived with the inverted classification matrix in the same manner as Equation (3). By substituting

$$\left[{\matrix{ {\,p_1\lpar {\xi_i} \rpar } \cr {\,p_0\lpar {\xi_i} \rpar } \cr } } \right]$$

with

$$C^{{-}1}\left[{\matrix{ {\pi_ + \lpar {\xi_i} \rpar } \cr {\pi_-\lpar {\xi_i} \rpar } \cr } } \right]\comma \;$$

we get

(11)$$\matrix{ {{\tilde{\varphi }}_{i + } = 1-{\cal P}\lpar {z_i = 1\vert Z_i = 1} \rpar = \displaystyle{{1-\beta } \over {\alpha + \beta -1}}} & {\left[{\alpha \cdot \displaystyle{{\pi_-\lpar {\xi_i} \rpar } \over {\pi_ + \lpar {\xi_i} \rpar }}-\lpar {1-\alpha } \rpar } \right]} \cr {{\tilde{\varphi }}_{i-} = 1-{\cal P}\lpar {z_i = 0\vert Z_i = 0} \rpar = \displaystyle{{1-\alpha } \over {\alpha + \beta -1}}} & {\left[{\beta \cdot \displaystyle{{\pi_ + \lpar {\xi_i} \rpar } \over {\pi_-\lpar {\xi_i} \rpar }}-\lpar {1-\beta } \rpar } \right]} \cr } $$

These probabilities can be computed provided the odds of the test results π ₊ (ξ _i)/π ₋(ξ _i). We approximate this odds by applying estimation tool M to the original data D; i.e. the predicted binomial probability $\hat{p}_1\lpar {\xi_i} \rpar $ obtained from D is used as a proxy of π ₊ (ξ _i). Generally it is not assured that true and observed probabilities p ₁(ξ _i) and π ₊ (ξ _i) have the same mechanistic structure captured by M; however, when our concern is limited to the use of model-predicted probabilities to smooth the data D, we may expect for M to provide a sufficiently good approximation. The above framework can be regarded as a variant of parametric bootstrapping methods as MO datasets are generated from data D assuming a parametric model M. The whole bias correction procedure is presented in pseudocode (Fig. 5); sample R code is also available on GitHub (https://github.com/akira-endo/TND-biascorrection/).

Fig. 5. Multiple imputation with parametric bootstrapping.

EM algorithm

Another possible approach to addressing misclassification is the use of the EM algorithm, which has been proposed for case–control studies in a previous study (where differential recruitment was not considered) [Reference Magder and Hughes26]. Because of its methodological similarity, the algorithm can also be applied to the TND. The original EM algorithm presented in [Reference Magder and Hughes26] would produce, if properly implemented, the result equivalent to the direct likelihood approach. However, the original EM algorithm requires that the model can handle non-integer sample weights (which may not always be assured). Moreover, computing confidence intervals in EM algorithm can be complicated. We therefore recommend parametric bootstrapping as the first choice of bias correction method when the direct likelihood approach is inconvenient.

Simulation of bias correction with parametric bootstrapping

To assess the performance of this method, we used the same simulation framework as in the univariate analysis (Table 2). In addition to vaccination history (denoted by ξ ¹), we consider one categorical and one continuous covariate. Let us assume that ξ ₂ represents the age group (categorical; 1: child, 0: adult) and ξ ₃ the pre-infection antibody titre against TD (continuous). Suppose that the population ratio between children and adults is 1:2, and that ξ ₃ is scaled so that it is standard normally distributed in the population. For simplicity, we assumed that all the covariates are mutually independent with regard to the distribution and effects (i.e. no association between covariates and no interaction effects). The relative risk of children was set to be 2 and 1.5 for TD and ND, respectively, and a unit increase in the antibody titre was assumed to halve the risk of TD (and not to affect the risk of ND). The mean total sample size λ was set to be 3000, and 500 sets of simulation data were generated for each scenario. VE estimates were corrected by the parametric bootstrapping approach (the number of iterations J = 100) and were compared with the raw (uncorrected) VE estimates.

Figure 6 shows the distributions of estimates with and without bias correction in the multivariate setting. Our bias correction (parametric bootstrapping) provided unbiased estimates for all the scenarios considered. Overall, biases in the uncorrected estimates were larger than those in the univariate setting. In some scenarios, the standard error of the bias-corrected estimates was extremely wide. This was primarily because of the uncertainty already introduced before misclassification rather than the failure of bias correction (as can be seen in the Supplementary Fig. S3). Larger sample size is required to yield accurate estimates in those settings, as the information loss due to misclassification will be added on top of the inherent uncertainty in the true data.

Fig. 6. Bias correction for simulated data in the multivariate setting. The distributions of bias-corrected (blue) and uncorrected (red) VE estimates from 500 simulations are compared. Dotted lines denote median and black solid lines denote the true VE. The parametric bootstrapping bias correction method was used for bias correction.

The number of confounding variables

We investigated how the bias in uncorrected VE estimates can be affected by the number of confounding variables. In addition to the vaccine history ξ ¹, we added a set of categorical/continuous confounding variables to the model and assessed the degree of bias caused by misclassification. The characteristics of the variables were inherited from those in section ‘Simulation of bias correction with parametric bootstrapping’: categorical variable ‘age’ and continuous variable ‘pre-infection antibody titre’. That is, individuals were assigned multiple covariates (e.g. ‘categorical variable A’, ‘categorical variable B’, …, ‘continuous variable A’, ‘continuous variable B’, …) whose distribution and effect were identical to ‘age’ (for categorical variables) and ‘antibody titre’ (for continuous variables) in section ‘Simulation of bias correction with parametric bootstrapping’. No interaction between covariates was assumed. The covariate set in section ‘Simulation of bias correction with parametric bootstrapping’ being baseline (the number of covariates: (vaccine, categorical, continuous) = (1, 1, 1)), we employed two more scenarios with a larger number of covariates: (1, 3, 3) and (1, 5, 5).

The simulation results are presented in Figure 7. Overall, additional confounding variables led to more severe bias in the uncorrected VE estimates towards underestimation. These results further highlight the importance of bias correction when heterogeneous disease risks are expected; VE estimates adjusted for many confounding variables can exhibit substantial misclassification bias.

Fig. 7. Bias in raw VE estimates from simulated data in the presence of different numbers of confounding variables. The distributions in red, purple and blue correspond to uncorrected VE estimates in the presence of 2, 6 and 10 confounding variables in addition to the vaccination history.