1. Introduction
Knowledge of glacier volume is important for assessing the cryospheric contribution to sea-level rise, glacier response to climate change (Reference Vaughan and StockerVaughan and others, 2013), and water resource management at the local to regional scale (Reference JonesJones, 1999; Reference Hock, Rees, Williams and RamirezHock and others, 2006). An estimate of ice volume and its spatial distribution is a prerequisite for glacier runoff projections. Whereas glacier areas in many mountain regions around the globe are well surveyed using optical satellite sensors, and data on glacier area are available in digital inventories (e.g. Reference Kargel, Leonard, Bishop, Kääb and RaupKargel and others, 2014; Reference PfefferPfeffer and others, 2014), measurements of ice thickness are sparse by comparison, and a global dataset does not exist. Due to lack of information on ice thickness, ice volume is often estimated using empirical or physical scaling relationships (e.g. Reference Van de Wal and WildVan de Wal and Wild, 2001; Reference Radić and HockRadić and Hock, 2010). Volume–area (V-A) scaling is a commonly used method as it requires only glacier area as input (Reference Chen and OhmuraChen and Ohmura, 1990), with just two adjustable parameters determined empirically from regression of glacier data (e.g. Reference Chen and OhmuraChen and Ohmura, 1990) or from theoretical analyses (Reference BahrBahr, 1997; Reference Bahr, Meier and PeckhamBahr and others, 1997). Several scaling relationships are proposed; some are regional and some are used globally (Reference GrinstedGrinsted, 2013). Estimations may have gross errors for individual glaciers, but the uncertainty is reduced for larger glacier samples (Reference MeierMeier and others, 2007). A minimum sample size of ∼100 glaciers is recommended (Reference BahrBahr, 2012; Reference Farinotti and HussFarinotti and Huss, 2013). Although more accurate scaling relations can be obtained through characterization of individual glacier shape, slope and size (Reference Adhikari and MarshallAdhikari and Marshall, 2012; Reference GrinstedGrinsted, 2013) and by local calibration, scaling approaches still have large uncertainties (Reference Haeberli and HoelzleHaeberli and Hoelzle, 1995; Reference Cogley, Henderson-Sellers and McGuffieCogley, 2012; Reference Farinotti and HussFarinotti and Huss, 2013). Scaling does not, for instance, account for individual glacier characteristics such as surface geometry or local climate, and does not provide information on the spatial distribution of ice thickness. Thus, alternative methods are needed to obtain glacier-specific ice volume and distributed ice thickness.
Recent studies have demonstrated that glacier ice thickness distribution can be estimated using physically based approaches based on a digital terrain model (DTM) and glacier outlines (e.g. Reference Clarke, Berthier, Schoof and JaroschClarke and others, 2009, Reference Clarke2013; Reference Farinotti, Huss, Bauder, Funk and TrufferFarinotti and others, 2009) or by using a DTM, glacier outlines and flowlines (Reference Paul and LinsbauerPaul and Linsbauer, 2012). Application of such approaches is possible at the global scale (Reference Huss and FarinottiHuss and Farinotti, 2012) but can also be calibrated for regional studies (Reference Linsbauer, Paul and HaeberliLinsbauer and others, 2012).
In a previous inventory of glaciers in northern Scandinavia, ice volume was estimated by simply assuming mean thickness per size class (Reference Østrem, Haakensen and MelanderØstrem and others, 1973). In the inventory of South Norway, measurements of Swedish valley glaciers were used to assess the relation between glacier area and volume and to calculate ice volume within river basins (Reference Østrem, Dale Selvig and TandbergØstrem and others, 1988). Since the 1980s, ice thickness measurements have been carried out by radio-echo sounding (RES) on many glaciers in Norway. Measurements were conducted on smaller mountain glaciers as well as on the largest ice caps. So far, however, a total ice volume estimate for Norway has not been derived from these data. Here we provide an overview of ice thickness measurements available for mainland Norway, use a distributed model (Reference Huss and FarinottiHuss and Farinotti, 2012) to interpolate data and to derive an ice volume estimate for all individual Norwegian glaciers, and compare measured ice volume with results from various V-A scaling relations.
2. Data
2.1. Ice thickness data
We used all ice thickness data that were available in digital format (Table 1; Fig. 1). The source of the data is the database of the Norwegian Water Resources and Energy Directorate (NVE), with a few additions from collaborators. Information on the data collection and processing is documented in individual reports and papers, where available (Table 1). Although there might be other thickness measurements in Norway of which we are not aware, or to which we do not have data access, we are confident that our thickness data compilation includes most measurements.
Table 1. Ice thickness measurements in Norway used in this study (see Fig. 1 for locations). Glaciers are sorted with the largest complexes first (NO 1–26), then measurements for other glaciers (ID 54–2743) arranged by size. Glacier complex codes, glacier IDs and area (A tot) are from the recent glacier inventory of Norway (Andreassen and others, 2012b). Max is measured maximum ice thickness. Vcalc is calculated glacier volume from the measurements. is uncertainty in interpolated volume (15–20 %). A int is area of interpolation; in cases where A int < A tot mean thickness, T, is calculated for A int. Type is data source (c: digitized bed contours; p: measured point data). Uncertainty refers to the point measurements. Units are number of units from the complex used for calibration of the distributed model and V-A coefficients
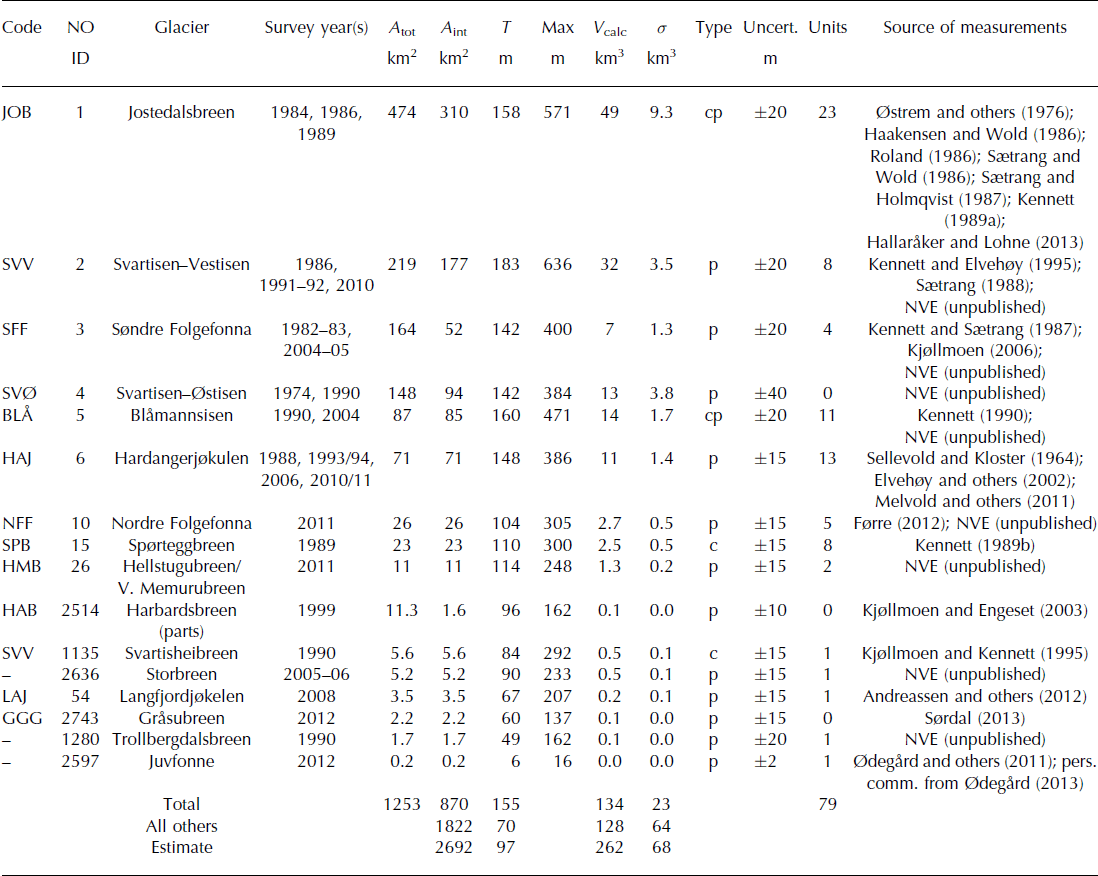

Fig. 1. Location map of glaciers with ice thickness measurements in Norway used in this study. Insets show southern Norway (1), Svartisen (2), Blåmannsisen (BLÅ) and Langfjordjøkelen (LAJ). Glaciers with ice thickness measurements are in blue, others in grey. Numbers refer to glacier ID and letters to glacier complex code (Table 1).
The first measurements of glacier thickness were carried out on Austerdalsbreen in the 1950s, using gravity measurements and hot-water drilling (Reference Bull and HardyBull and Hardy, 1957; Reference WardWard, 1961). Other investigations in the 1960s and 1970s used seismic soundings at Folgefonna and Hardangerjøkulen (NGU, 1964; Reference Sellevold and KlosterSellevold and Kloster, 1964) and hot-water drilling at Nigardsbreen (Reference Østrem, Liestøl and WoldØstrem and others, 1976), but measurements were sparse and only covered minor parts of the glaciers. In 1981, the Glacier Office at NVE (now Section for Glaciers, Ice and Snow) purchased a non-commercial RES instrument for ice thickness measurements (Reference Sverrisson, Johannesson and BjørnssonSverrisson and others, 1980). Measurements were conducted using this ground-based RES system on many glaciers including the largest ice caps, Jostedalsbreen, Svartisen, Folgefonna, Blåmannsisen and Hardangerjøkulen, from the early 1980s onwards. As it is difficult to access heavily crevassed outlets, helicopter-borne RES measurements have also been conducted (Reference Kennett, Laumann and LundKennett and others, 1993). Data were typically published in contract reports by NVE, and a few in peer-reviewed publications, while some investigations remained unpublished (e.g. investigations at Trollbergdalsbreen and Svartisen-Østisen; Table 1). Data reporting varies: some reports contain ice thickness maps and give the maximum thicknesses; others contain only surface and bedrock topography maps, since deriving the hydrological drainage divides was often the main purpose of the investigations. In recent years, new studies have been conducted, both in order to extend measurements on already surveyed glaciers (Reference Melvold, Laumann and NesjeMelvold and others, 2011) and to obtain data for unmeasured glaciers (Reference Andreassen, Kjøllmoen, Rasmussen, Melvold and NordliAndreassen and others, 2012a). The RES equipment, an impulse radar with antennas whose centre frequency is typically 10 MHz, has changed little since its introduction (Reference Sverrisson, Johannesson and BjørnssonSverrisson and others, 1980). Currently the receiver comprises a 12-bit analogue/ digital (A/D) converter at 100 Msamples s−1 with each stored trace stacked 8–16-fold (e.g. Reference Pettersson, Christoffersen, Dowdeswell, Pohjola and HubbardPettersson and others, 2011). Navigation has been improved using global navigation satellite systems (GNSS). In the first years of recording, post-processing was done manually. Gradually, digital procedures were introduced, and today all data processing is performed digitally. Some of the older data are therefore not available in digital format but as analogue maps. Data have also been collected by other parties (e.g. Reference Ødegård, Nesje, Isaksen and EikenØdegård and others, 2011; Reference FørreFørre, 2012).
The measured glaciers include the largest ice caps, with numerous outlets, such as Jostedalsbreen (474 km2) and Svartisen-Vestisen; smaller ice caps such as Langfjordjøkelen; valley and cirque glaciers such as Trollbergdalsbreen, Storbreen and Hellstugubreen; and the small ice patch Juvfonne (0.15 km2). On some glaciers, only a few measurements are available, while on others the dataset is dense and provides good spatial coverage (e.g. Fig. 2). Almost all RES measurements were carried out in spring (March–May) when the ice surface is covered by winter snow and a snowmobile is used to carry the equipment. A few RES measurements are also carried out in summer/early fall (e.g. Reference Hallaråker and LohneHallaråker and Lohne, 2013; Reference SørdalSørdal, 2013). Uncertainties in the measured and interpolated ice thickness data are discussed in Section 3.1.1.

Fig. 2. Examples of various ice thickness data: Vestisen (SVV), Blåmannsisen (BLÅ), Gråsubreen (2743), Storbreen (2636) and Nordre Folgefonna (NFF). See Figure 1 for locations. Vestisen has been measured in several campaigns, and bed contours are available for Svartisheibreen. Ice thickness of Blåmannsisen was derived from interpolated bed contours made from campaigns in 1989 covering large parts of the glacier and additional measurements of Rundvassbreen in 2004. At Gråsubreen, three profiles were collected in fall 2012. At Storbreen, point measurements were collected in 2005 and 2006. At Nordre Folgefonna, dense measurements were performed in 2012.
2.2. Glacier inventory data
Glacier outlines, area and other inventory parameters are sourced from the newest glacier inventory of Norway published by NVE in 2012 (Andreassen and others, 2012b; available at www.nve.no/glacier). The inventory was derived from Landsat imagery acquired during 1999–2006. Glacier outlines were mapped using the established band-ratio method following recent guidelines and recommendations (Reference PaulPaul and others, 2009; Reference Racoviteanu, Paul, Raup, Khalsa and ArmstrongRacoviteanu and others, 2009), and are available online from the Global Land Ice Measurements from Space (GLIMS) database (www.glims.org).
All automatically mapped snow and ice polygons from the band-ratio method (using bands red/SWIR (shortwave infrared)) were visually inspected using composites of satellite image bands, digital topographic maps and orthophotos where available. All polygons to be included in the inventory were assigned a unique ID. Glacier complexes were divided into glacier flow units using drainage divides defined by glacier surface topography (Fig. 3). Glacier complexes were assigned a glacier complex code to be able to differentiate between glacier complexes and single glaciers (Fig. 3).

Fig. 3. Illustration of glacier flow units and glacier complexes for (a) Langfjordjøkelen, northern Norway, and (b) a section in Jotunheimen, southern Norway. To create an inventory of individual glaciers the glacier complexes are divided into glacier units using flow divides. Langfjordjøkelen (LAJ) is a complex divided by flow divides into eight units with individual IDs 49–56 , and the Hellstugubreen/Vestre Memurubreen (HMB) complex consists of two units (IDs 2768 and 2772) and is surrounded by many single glaciers that are not part of complexes.
In total, 3143 glacier units were included in the new inventory. They are hereafter referred to as glaciers. The total glacier area is 2692 ± 81 km2; 1523 km2 (57%) is located in southern Norway, and 1169 km2 (43%) in northern Norway.
2.3. Digital terrain model
Topographic parameters for the ice thickness calculations were derived from the national DTM with 20 m resolution (DTM20), which covers all of Norway, provided by the Norwegian mapping authorities (Statens kartverk). The DTM was put together from contours and elevation points from the main map series of Norway 1 : 50 000 and is the same as used for the glacier inventory, with some updates. The reported vertical root-mean-square error (RMSE) of the DTM20 is 2–6 m, but the accuracy and the mapping data vary from region to region. Over recent years the maps providing the base of the DTM have gradually been updated with data from new aerial photos from the 2000s, but not all regions are yet updated. The DTM20 is thus based on glacier extent and surface topography from different years, and not necessarily close in time to the Landsat imagery used for compilation of the glacier inventory.
3. Methods
3.1. Interpolating ice thickness measurements
The ice thickness data were used to interpolate thickness maps for estimating total glacier volume and calibrating the distributed model. Data collected prior to 1989 were often available only as hand-drawn bed contour maps (e.g. for Svartisheibreen and Blåmannisen (Fig. 2), Spørteggbreen and Jostedalsbreen). For some of these glaciers newer point data were also available (Table 1). Whereas these bed contour maps are generally based on interpolation of measurements with good spatial coverage, the Jostedalsbreen bed contour map was hand-drawn for visual purposes and lacks measurements in many parts. Where no measurements were available, the bed map was drawn from best guess using surface topography and slope. Although we excluded glaciers from the ice cap that were lacking ice thickness measurements, the volume estimate is more uncertain when the original data are not available digitally.
For glaciers with bedrock maps, contours were digitized and point datasets of ice thickness were extracted using current surface topography, either from detailed DTMs based on laser scanning, where available, or from the DTM20. Newer data collected since 1990 were available in digital format as point datasets and used directly. Point datasets were then interpolated to ice thickness grids using the function ‘Topo to raster’ in ArcGIS, based on the ANUDEM program (e.g. Reference HutchinsonHutchinson, 1989), with glacier outlines used as boundary condition where ice thickness is zero. The ‘Topo to raster’ function was preferred as it works well with contour inputs and can combine both contour and point data (Reference Fischer and KuhnFischer and Kuhn, 2013).
Glaciers with available data used for interpolation and/or validation are summarized in Table 1. Our dataset includes nine glacier complexes with numerous outlet glaciers, four glaciers that are part of glacier complexes and three single glaciers (Storbreen, Trollbergdalsbreen and Juvfonne). The total area of all glaciers with ice thickness measurements is 1227 km2. However, as measurements were sparse for some parts of the glaciers and data coverage was not sufficient for interpolation, non-measured areas were masked out from the interpolated ice thickness maps. Hence, ice thickness was interpolated for 870 km2, accounting for 32% of Norway’s total glacier area (Table 1). From the dataset we selected 79 glaciers considered to have sufficient coverage for calculating mean thickness. The 79 units range in size from 0.15 km2 (Juvfonne) to 47.6 km2 (Tunsbergdalsbreen, JOB). The total area of these glaciers is 628 km2, 24% of Norway’s glacier area.
3.1.1. Uncertainties
Common uncertainties for all ice thickness measurements arise from the propagation velocity of electromagnetic waves in snow, firn and ice, inaccuracies when picking reflectors, and the resolution of the radar system. Only data collected in recent years have been analysed with two-dimensional migration methods to improve ice thickness and bedrock determination in steep terrain. The effect of not carrying out migration could significantly increase the error in estimated ice thickness on steep slopes (Reference Moran, Greenfield, Arcone and DelaneyMoran and others, 2000). However, as most of the older RES has been collected in easily accessible terrain (without steep slopes and crevasses) this effect is assumed to be small. Uncertainty in determining bedrock elevation is also affected by inaccurate positioning of radar traces, and uncertain surface elevations. Although methods have been basically the same for almost all RES data used in this study, the older data have more uncertainties in positioning and surface topography. The effect of each uncertainty component on the total error will vary depending on local conditions, reference data, position precision, etc. To assess the accuracy of the measurements, it is standard procedure to compare ice thickness at profile intersections where crossover points are available (e.g. Reference Kennett, Laumann and LundKennett and others, 1993; Petterson and others, 2011; Reference Andreassen, Kjøllmoen, Rasmussen, Melvold and NordliAndreassen and others, 2012a). The overall error in ice thickness points is typically estimated to be ±15 m when measured with 10 MHz RES (Reference Sætrang and WoldSætrang and Wold, 1986; Reference KennettKennett, 1990). Table 1 provides error estimates in the point measurements for each of the glaciers in our dataset.
For the interpolation from point measurements to mean thickness of glaciers or glacier complexes, the representativeness of the measured points is important (e.g. Reference FischerFischer, 2009; Reference Navarro, Eisen, Pellikka and ReeseNavarro and Eisen, 2010). For practical reasons, ice thickness measurements are typically acquired along profiles not equally distributed over the glacier. Thus, the accuracy of the ice thickness data points is not necessarily consistent with the accuracy of mean thickness (e.g. Reference FischerFischer, 2009). The uncertainty in interpolated ice thicknesses depends on distance to the nearest data point and local terrain. Measurements are biased towards more gently sloping parts of the glacier, whereas measurements in steeper regions are scarce. The effect of using the ‘Topo to raster’ interpolation compared to other automatic interpolation algorithms (e.g. kriging, inverse distance weighting or spline) was tested on Hardangerjøkulen, and the effect on mean ice thickness was small (±2 m). The representativeness of the point data is more important for the interpolated ice thickness than the interpolation method used. The ice thickness dataset also spans several decades, and the surface topography and inventory data refer to different years. We have eliminated some of the uncertainty by referring the ice thickness or bed topography data to ‘current’ topography to obtain ‘current’ ice thicknesses, wherever possible. Data are meant to be representative for the period 1999–2011. We estimated the error in mean interpolated ice thickness at 15–20 %. The best relative accuracy (15%) was expected for glaciers with dense spatial coverage and new digital data such as Hardangerjøkulen, Nordre Folgefonna and Hellstugubreen/Vestre Memurubreen.
3.2. Distributed ice thickness
3.2.1. Model description
To calculate the ice thickness distribution of glaciers in Norway we use the approach by Reference Huss and FarinottiHuss and Farinotti (2012) that has been applied to a global dataset and represents a further development of the model described by Reference Farinotti, Huss, Bauder, Funk and TrufferFarinotti and others (2009). The model estimates the surface mass-balance distribution, calculates the volumetric balance flux and converts it into thickness using the flow law for ice (Reference GlenGlen, 1955) with a digital glacier mask and a DTM as input. Mean ice thickness is calculated in elevation bins along a longitudinal profile, and the ice thickness is finally extrapolated by inverse-distance weighting, resulting in an ice thickness estimate for every gridcell of the glacier. Below we briefly describe the principles and discuss the adaptation and calibration of the model to Norwegian glaciers.
First, the DTM was intersected with the glacier outlines, providing area Si and mean slope αi for all glacier surface elevation bands i. We chose a vertical spacing of elevation bands dz =10 m. Width wi of each elevation band is obtained with wi = Si /li = Si tan(αi )/dz, where li is the horizontally projected length of the elevation band. The three-dimensional geometry is thus reduced to a simplified two-dimensional (2-D) shape of the glacier.
To conserve mass, surface mass balance b must be balanced by ice flux divergence and the surface elevation change ∂h/∂t. Following Reference Farinotti, Huss, Bauder, Funk and TrufferFarinotti and others (2009), b and ∂h/∂t are lumped into a new variable, the ‘apparent mass balance’, ![]() , defined as
, defined as
where ρ is the ice density. This allows direct calculation of the balancing ice volume flux, including for glaciers that do not have steady-state geometry. The apparent mass-balance distribution is calculated using a reference altitudinal gradient ![]() . As demonstrated by Reference Rasmussen and AndreassenRasmussen and Andreassen (2005), mass-balance gradients are remarkably linear in Norway and vary little from year to year. We therefore used a linear gradient and did not introduce a smaller gradient in the accumulation area, as did Reference Huss and FarinottiHuss and Farinotti (2012). For glaciers smaller than a critical area
. As demonstrated by Reference Rasmussen and AndreassenRasmussen and Andreassen (2005), mass-balance gradients are remarkably linear in Norway and vary little from year to year. We therefore used a linear gradient and did not introduce a smaller gradient in the accumulation area, as did Reference Huss and FarinottiHuss and Farinotti (2012). For glaciers smaller than a critical area ![]() is reduced linearly with glacier area. This reduction is carried out since flow dynamics are less important for a change in dh/dt on small glaciers (Reference Huss and FarinottiHuss and Farinotti, 2012). Gradients of annual balance in Norway are greatest (6.4–8.7 m w.e. km−1) at maritime glaciers, and lower (5.7–6.1 m w.e. km−1) for more continental glaciers (Reference Rasmussen and AndreassenRasmussen and Andreassen, 2005). We used a continentality index C to adjust the reference apparent surface mass-balance gradient
is reduced linearly with glacier area. This reduction is carried out since flow dynamics are less important for a change in dh/dt on small glaciers (Reference Huss and FarinottiHuss and Farinotti, 2012). Gradients of annual balance in Norway are greatest (6.4–8.7 m w.e. km−1) at maritime glaciers, and lower (5.7–6.1 m w.e. km−1) for more continental glaciers (Reference Rasmussen and AndreassenRasmussen and Andreassen, 2005). We used a continentality index C to adjust the reference apparent surface mass-balance gradient ![]() to local conditions. Values of C were calculated from the equilibrium-line altitude (ELA) of each glacier, derived from its median elevation, and a latitude-dependent reference ELA as described in Reference Huss and FarinottiHuss and Farinotti (2012), with a continentality index as a constant parameter f
cont = 2400 m. C is used to adapt the reference apparent surface mass-balance gradient db/dz
0 to local conditions.
to local conditions. Values of C were calculated from the equilibrium-line altitude (ELA) of each glacier, derived from its median elevation, and a latitude-dependent reference ELA as described in Reference Huss and FarinottiHuss and Farinotti (2012), with a continentality index as a constant parameter f
cont = 2400 m. C is used to adapt the reference apparent surface mass-balance gradient db/dz
0 to local conditions.

For each glacier, the apparent mass-balance distribution is computed using the gradient ![]() with the ELA that yields a balanced mass budget. Then the volumetric balance flux q for each elevation band i of the glacier is calculated by integration of b along the glacier.
with the ELA that yields a balanced mass budget. Then the volumetric balance flux q for each elevation band i of the glacier is calculated by integration of b along the glacier.
To obtain ice thickness using Glen’s (1955) flow law, we need to account for the fraction of flux attributed to sliding at the glacier base. Volumetric flux is therefore multiplied by (1 − f sl), a factor assumed to be constant along the glacier. f sl varies between 0 and 0.55 and is calculated from the area and continentality C for each glacier (see Reference Huss and FarinottiHuss and Farinotti, 2012, for details and parameters).
The ice thickness hi for every elevation band i is then computed as

with qi the ice flux normalized by glacier width, f sl the factor accounting for basal sliding, n = 3 the exponent of the flow law, the ice density, g the acceleration due to gravity, and F s,i =wi /(2hi + wi ) a valley shape factor (Reference NyeNye, 1965). The rate factor of the flow law, A f, is assumed to be 0.075 bar−3 a−1 for temperate glaciers (see, e.g., Reference GudmundssonGudmundsson, 1999). Glaciers in Norway are temperate with a few exceptions (Andreassen and others, 2012b). Hence, considering temperature effects on A f is not necessary (see also Reference ClarkeClarke and others, 2013).
Finally, the mean elevation band thickness hi is extrapolated from the simplified 2-D shape of the glacier to a regular grid by weighting the distance to the closest glacier boundary point and prescribing a weight proportional to (sin α) n /(n+2) based on Eqn (3) (see also Reference Farinotti, Huss, Bauder, Funk and TrufferFarinotti and others, 2009). The assumption that local thickness at the glacier boundary is zero is not applied at ice divides, where we directly assign the mean thickness of the respective elevation band. This extrapolation scheme conserves elevation band ice volume, and results in an estimate of ice thickness for each gridcell of every glacier (see Fig. 4).
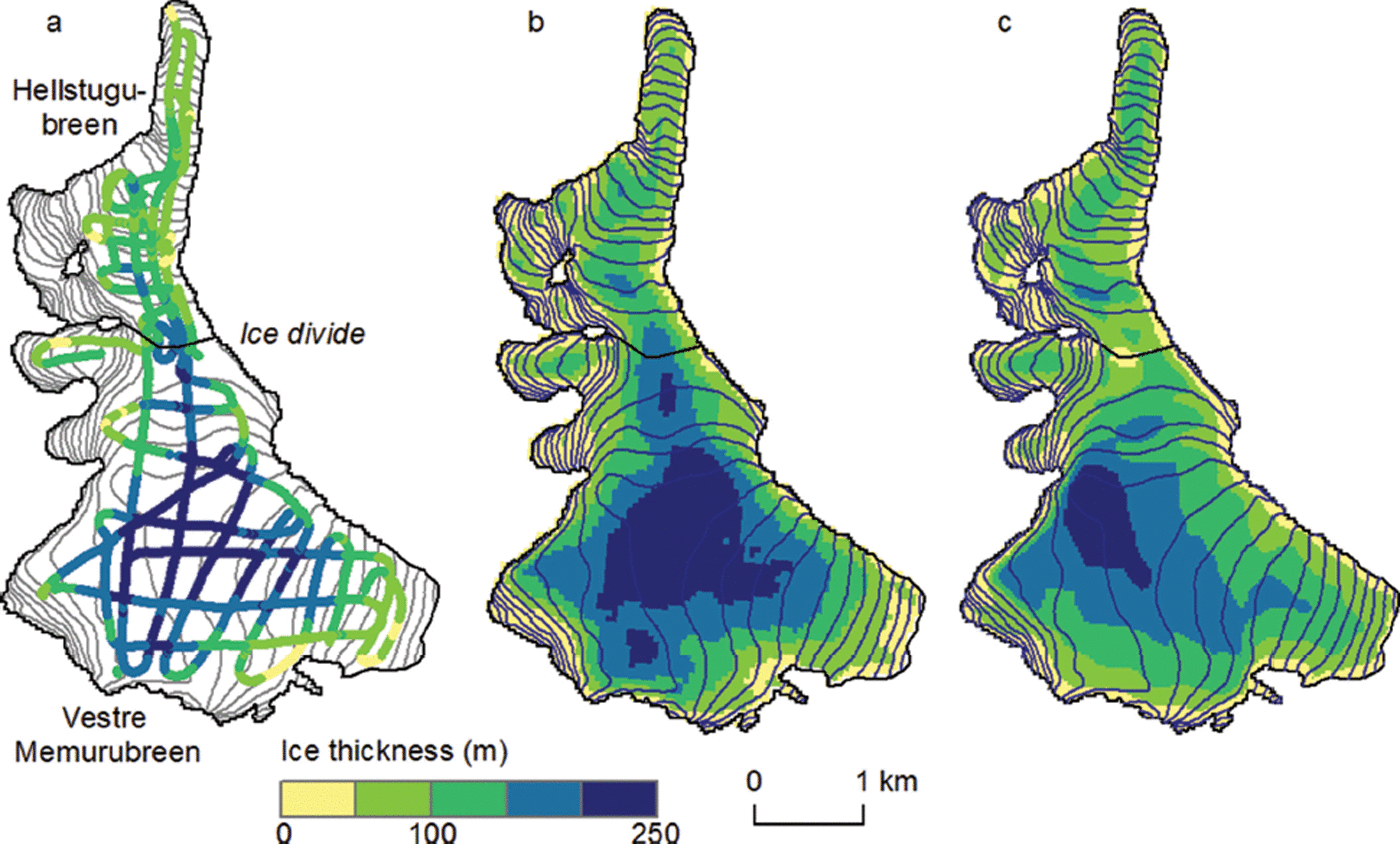
Fig. 4. Ice thickness of Hellstugubreen/Vestre Memurubreen with 50 m surface contours (glacier complex HMB; see Fig. 1 for location and Fig. 3 for reference). (a) Observed thickness points along profiles; (b) interpolated map from the measurements; and (c) ice thickness map computed from the distributed model.
3.2.2. Calibration, validation and uncertainty
To calibrate and test the performance of the model, calculated ice thicknesses were compared with point datasets of ice thickness and with average interpolated ice thicknesses for individual glaciers. Ice thickness point measurements of 32 glaciers in Norway were used in a first phase. The modelled ice thickness h
mod was compared with measured ice thickness h
meas on a point-by-point basis. All available point thickness observations and corresponding calculated thicknesses for the same locations were then arithmetically averaged, providing one mean value per glacier. The apparent mass-balance gradient ![]() and S
crit were varied among physically reasonable bounds to test the sensitivity of the results on the chosen parameters and to study model performance relative to measured point data. We also varied other model parameters to assess their impact on the results, but chose to keep the reference values used by Reference Huss and FarinottiHuss and Farinotti (2012). In a second phase, interpolated mean ice thickness from glaciers was compared with mean thickness calculated by the distributed model for the same glaciers. The model was calibrated by adjusting
and S
crit were varied among physically reasonable bounds to test the sensitivity of the results on the chosen parameters and to study model performance relative to measured point data. We also varied other model parameters to assess their impact on the results, but chose to keep the reference values used by Reference Huss and FarinottiHuss and Farinotti (2012). In a second phase, interpolated mean ice thickness from glaciers was compared with mean thickness calculated by the distributed model for the same glaciers. The model was calibrated by adjusting ![]() and S
crit to minimize the error in mean thickness of all glaciers and to fit the modelled volume of all 79 glaciers so it agreed with the volume interpolated from measurements.
and S
crit to minimize the error in mean thickness of all glaciers and to fit the modelled volume of all 79 glaciers so it agreed with the volume interpolated from measurements.
For ![]() and S
crit = 10 km2 the difference between the average of modelled and observed ice thickness (h
Δ = h
mod − h
meas) was 0m for mean thickness, and –10 m for the mean of point data of the 32 glaciers. Results further revealed a RMSE of 28 m (Fig. 5) of hΔ
for the interpolated mean ice thickness from the 79 glaciers. Although relatively large hΔ
were found for some glaciers, 52% (70%) of the units were in agreement within ±20 (30) m. This is within the uncertainty of the interpolated measurements.
and S
crit = 10 km2 the difference between the average of modelled and observed ice thickness (h
Δ = h
mod − h
meas) was 0m for mean thickness, and –10 m for the mean of point data of the 32 glaciers. Results further revealed a RMSE of 28 m (Fig. 5) of hΔ
for the interpolated mean ice thickness from the 79 glaciers. Although relatively large hΔ
were found for some glaciers, 52% (70%) of the units were in agreement within ±20 (30) m. This is within the uncertainty of the interpolated measurements.

Fig. 5. Comparison of mean thickness calculated from the distributed model and interpolated from the measurements for 79 glaciers in Norway.
To evaluate the model results, the thickness maps were also visually compared with interpolated maps. Modelled thickness distributions for the glacier complex Hellstugubreen/Vestre Memurubreen, which is densely covered by RES measurements, show a good qualitative agreement (Fig. 3). hΔ was −1 and 13 m, respectively. The modelled and interpolated volume based on measurements for the glacier complex are 1.19 and 1.27 km3, respectively. The model captures the general pattern of ice thickness distribution but disagrees with the observations for some regions of the glacier. This can be attributed to simplifications in the methodology, which does not use additional linear information such as manually assigned flowlines. Results from Hardangerjøkulen (Fig. 6) showed that, although hΔ varies among the glaciers from −26 m to +42 m, the agreement of total modelled volume (9.9 km3) and interpolated volume from measurements (10.0 km3) was good. It should be emphasized that the model was calibrated to fit the mean thickness for all 79 glaciers, and was not optimized on these two glacier complexes. Hellstugubreen/Vestre Memurubreen consists of two valley glaciers joined by an ice divide, whereas Hardangerjøkulen exhibits a stronger maritime influence and is representative for a typical Norwegian ice cap. Thus, the results for these two quite densely measured complexes show that the model is capable of estimating ice volume in agreement with interpolated observations and that it performs reasonably well for different glacier types and climate conditions. Considering that only glacier outlines and a DTM are needed as model input and that the model, although based on physical assumptions, uses a simplified approach, the overall agreement is satisfying. Nevertheless, the mismatch can be significant for some sites, and results must be interpreted with care for individual glaciers.
Fig. 6. Calculated ice thickness of Hardangerjøkulen (HAJ; see Fig. 1 for location). (a) Observed points along profiles and interpolated map from the measurements. (b) Ice thickness map computed from the distributed model for each flow unit.
Uncertainties in the model results stem from parameterizations in the model, as well as from uncertainties in the input data, namely the glacier area outlines and the DTM. Uncertainties in the glacier area are expected to be ±3% (Andreassen and others, 2012b). If the glacier boundary is shifted relative to the underlying DTM, this can cause errors evaluated in glacier hypsometry and thus calculated ice thickness. However, all outlines were checked against the DTM20 during inventory generation, and shifts were found to be minor.
Following Reference Huss and FarinottiHuss and Farinotti (2012), we calculate the overall uncertainty in calculated ice volume, σ v, as
where σ M, σ Area and σ DTM are the uncertainties inherent to the modelling approach, the glacier area (outlines) and the DTM, respectively. The three individual uncertainties are assumed to be mutually uncorrelated. Thus, assuming an uncertainty of σ M, σ Area and σ DTM of 11% (according to Reference Huss and FarinottiHuss and Farinotti, 2012), 3% and 3% respectively gives an uncertainty of the total ice volume of Norway of 12%.
3.3. Other ice thickness estimates
3.3.1. Simple size scaling
In the first inventory of north Scandinavia, few thickness data were available to estimate the ice volume, and a simple size scaling was used to estimate volume (Reference Østrem, Haakensen and MelanderØstrem and others, 1973): glaciers <1 km2 were assumed to have a mean thickness of 25 m, glaciers 1–5 km2 a mean thickness of 50 m, glaciers 5–20 km2 a mean thickness of 125 m, and glaciers >20 km2 a mean thickness of 200 m. We applied this simple size scaling to all 3143 glaciers in the 1999–2006 inventory.
3.3.2. Volume–area scaling
Glacier volume can be estimated from the surface area, A, using the scaling relationship
where c and γ are coefficients, usually derived from data, but values of γ = 1.375 for glaciers and γ = 1.25 for ice caps have also been inferred from theoretical considerations (Reference BahrBahr, 1997). To estimate ice volume for Norwegian glaciers we obtained specific parameters directly from our ice thickness dataset (Fig. 7), and compared these to previously published scaling coefficients (Table 2). We also derived scaling parameters for the ice volume calculated from the distributed model for all 3143 glaciers in Norway.
From the literature we selected laws that are used globally (Reference Radić and HockRadić and Hock, 2010; Reference BahrBahr, 2012; Reference GrinstedGrinsted, 2013) or for the European Alps (Reference Chen and OhmuraChen and Ohmura, 1990). We used the scaling laws for glaciers and applied them to all glaciers. In addition, where separate scaling laws for glaciers and ice caps were given, we also applied the laws for ice caps for the 169 glacier complexes and the laws for glaciers for the 2366 single glaciers and calculated the volume as the sum of these. We do not calculate scaling coefficients for ice caps from our own dataset due to the small number (9) and their limited area range.
Table 2. Results of different volume–area scaling relationships applied to all Norwegian glaciers. Volume V is estimated with Eqn (5). Vc+s is the calculated total volume for glacier complexes + single glaciers, and Vunits for all glaciers

Fig. 7. Thickness–area (a) and V-A scaling (b) relationship fitted to interpolated volume derived from ice thickness data for 79 glaciers.
4. Results
4.1. Ice thickness observations
Glaciers with available data are shown in Table 1. Measured maximum thicknesses range from 636 m at Svartisen-Vestisen (SVV) and 571 m at Jostedalsbreen to 16 m at the ice patch Juvfonne. Except for this small ice patch, all glaciers have measured maximum ice thicknesses >100 m. Even for the small Storbreen (5 km2), maximum ice thickness was found to exceed 230 m. Measurements on the six largest ice caps (Nos. 1–6 in Table 1) reveal ice thicknesses >380 m. The mean thickness interpolated from the measurements of the glaciers ranges from 6 m for Juvfonne to 279 m for Storglombreen (SVV). The estimated mean thickness of the ice caps ranges from 100 to 180 m; the six largest have mean thicknesses >140 m. As an ice cap will have outlet glaciers with different mean thicknesses, some outlets will be thicker than the mean thickness of the entire ice cap. For example, Austdalsbreen (10 km2), an outlet glacier from Jostedalsbreen, has a mean thickness of 189 m, whereas the mean thickness of the ice cap is estimated at 158 m. Engabreen (35.9 km2) and Storglombreen (41.2 km2), outlets from Svartisen-Vestisen, have mean thicknesses of 210 and 279 m, respectively, compared to the mean ice-cap thickness of 183 m.
Regarding the ice caps it should be emphasized that data coverage may vary, and only at Hardangerjøkulen and Hellstugubreen/Vestre Memurubreen was interpolation to all flow units possible. Nevertheless, the results indicate that mean ice thickness is similar for all larger ice caps and weakly correlates with their total area. For example, the data interpolated from Jostedalsbreen (474 km2), Hardangerjøkulen (71 km2) and Blåmannsisen (87 km2) all reveal mean ice thicknesses of ∼150 m (Table 1). The somewhat higher mean thickness of Svartisen-Vestisen (219 km2), 183 m, might be explained by the exclusion of smaller sub-basins due to insufficient data coverage.
Altogether, the area with ice thickness data available from direct interpolation of measurements accounts for 870 km2. The total volume is 134 ± 23 km3, and the mean thickness for these glaciers is 155 m. Ice thickness of the remaining parts can be expected to be smaller since measurements are biased towards the larger glaciers, with greater ice thicknesses. Assuming a mean ice thickness of all non-covered parts of 70 ± 35 m gives an additional volume of 128 ± 64 km3 and total ice volume estimate of 262 ± 68 km3. This crude approach likely overestimates the mean thickness of small glaciers and underestimates the larger ice caps and glaciers, but provides a first estimate of the total ice volume, without involving modelling.
4.2. Ice volume from distributed model
The total volume estimate based on the calibrated distributed model is 280 ± 34 km3. The 510 glaciers with an area >1 km2 contribute 93% to the total volume, and, averaged over their area, the mean thickness is 124 m. The mean thickness of the total glacier area in Norway is 104 m. The estimated volume for Norway when running the model using the original globally applied parameter values by Reference Huss and FarinottiHuss and Farinotti (2012) is ∼14% lower (240 km3). According to the model, the 15 largest glacier complexes with an area of 1451 km2 (54% of the total area) store ∼212 km3, which accounts for 76% of the total modelled volume.
Glaciers in the area range 0.1–0.5 km2 are numerous (43% of the total number) and, with an area of 306 km2, contribute significantly to regional glacier coverage. According to the model results, glaciers smaller than 0.5 (0.1) km2 have a volume of 10.2 (1.0) km3. About 400 polygons with a total area of 24 km2 classified as ‘possible snowfield’, and without assigned glacier ID, were excluded from the glacier inventory and thus not interpolated or modelled. Most of them are <0.1 km2. If we assume a mean thickness of 5 (10) m for these ice patches, they contribute a volume of 0.12 (0.24) km3 to the regional estimate, which is much smaller than the uncertainties in the volume estimates for large glaciers.
The calculated volume for all glaciers not covered by the interpolated ice thickness maps amounts to 137 ± 16 km3. Adding this volume to the measured and interpolated volume gives a total volume estimate for Norway of 271 ± 28 km3, slightly less than the 280 km3 using the modelled values for all, but well within the uncertainties in both estimates.
4.3. Volume–area scaling relationships
From the dataset of 79 glaciers we obtained a scaling constant c = 0.0511 and an exponent γ = 1.4492 (Eqn (5); Table 2; Fig. 7b). Using these coefficients resulted in a total ice volume estimate of 300 km3. Note that the dataset reveals a high correlation coefficient (coefficient of determination) of 0.75 (0.57) between thickness and area of these glaciers (Fig. 7a). In comparison, if using a subsample of 32 of the 79 glaciers considered to have the densest ice thickness data, values of c = 0.0486 and γ = 1.4862 were found, resulting in a slightly larger volume of 309 km3. Fitting a V-A scaling relation to the distributed model for all 3143 glaciers yields c = 0.0484 and γ = 1.4033, and a total ice volume of 257 km3 (Table 2).
The scaling laws and related estimates will vary depending on what is included or excluded. They are particularly sensitive to the mean thickness interpolation of the largest glaciers, and to some extent to how glacier complexes were divided into units in the inventory. A potential error source in scaling estimates is that too large an exponent leads to a positive bias in the total volume if it is applied to glaciers that are much larger than those in the calibration dataset (Reference GrinstedGrinsted, 2013). Then the V-A relationship will show a more rapid decrease at the largest glacier sizes than the power law suggests (Reference Bahr and MeierBahr and Meier, 2000). However, in our case, four of the five largest glaciers are included in the sample of 79 glaciers used for V-A calibration.
The total ice volume for Norway calculated from selected published scaling laws from the literature results in a wide range of values (Table 2; Fig. 8). When using these published scaling laws applied to glaciers divided into units, the volume estimates range from 137 km3 (Reference Chen and OhmuraChen and Ohmura, 1990) to 184 km3 (Reference GrinstedGrinsted, 2013). On the other hand using separate laws for ice caps and glaciers (e.g. following Reference Radić and HockRadić and Hock, 2010) gives a calculated ice volume of 359 km3 (336 and 23 km3, respectively, for ice caps and glaciers), which is nearly double that using their scaling law for glaciers applied to all 3143 individual glacier flow units (183 km3).

Fig. 8. Volume estimates of glaciers in Norway calculated by different methods. Simple size class scaling, interpolated from the thickness observations, results from distributed model, V-A scaling relationships calibrated to the thickness observations and to the distributed model results and obtained from selected laws from the literature. See Table 2 for V-A scaling relationships. All calculations of V shown here use the area of glaciers divided into units. Error bars are 12% for distributed model and 30% for V-A scaling.
5. Discussion
5.1. Total volume
The total ice volume calculated for glaciers in Norway substantially varies among the applied approaches (Fig. 8). The volume estimates calibrated with the ice thickness data (interpolated from measurements, distributed modelling and calibrated scaling) range from 257 to 300 km3 and are therefore within the uncertainty ranges of these individual approaches (Fig. 8). The size scaling estimate of Reference Østrem, Haakensen and MelanderØstrem and others (1973) is slightly smaller, 237 km3, whereas scaling laws from the literature give significantly smaller volumes when applying them for individual glaciers (137–188 km3). Just from the parts covered by measurements, an ice volume of 134 ± 23 km3 was interpolated, and applying the simple extrapolation assuming a mean thickness of 70 m of all others gave a volume of 262 ± 68 km3. This estimate is similar to the total estimate of 280 ± 34 km3 from the distributed model. A ‘best guess’ of total volume might be obtained by combining the volume interpolated from the measurements and using the modelled volume for the remaining parts, which results in a total volume estimate for Norway of 271 ± 28 km3.
Our scaling parameters derived for glaciers were higher than those of most other studies (Table 2; Reference GrinstedGrinsted, 2013). Our glacier sample used for fitting scaling parameters was a combination of a few single glaciers and many outlet glaciers from ice caps. Although the glaciers that comprise ice caps are considered as individual flow units, they differ from classical valley glaciers by having greater thicknesses in the upper accumulation area, due to the high mass turnover of Norwegian ice caps. Results point to the need for local calibration of scaling laws to obtain better results in a given region. The mismatch between scaling laws from the literature and those obtained by calibration of local ice thickness measurements in our study may be similar for other maritime glacier regions (e.g. Patagonia and New Zealand).
In order to assess the effect of how the glaciers are divided into flow units or complexes on calculated total volume, we recalculated ice thickness with the distributed model. For this experiment the glacier complex outlines were used (no ice divides). The glacier complexes contribute 75% of the total area. The distributed model is expected to yield smaller accuracy for glacier complexes, as it is based on ice flow considerations. Total ice volume given by the model increased by 15% (from 280 km2 to 323 km2; the glacier complexes contribute 295 km2 and the single glaciers 28 km2). This indicates that the distributed model is sensitive to how the glaciers are divided and needs to be specifically calibrated to account for this. If total glacier volume is evaluated using the V-A scaling relations for glacier complexes + single glaciers (V c+s) instead of glacier flow units (V units), results may differ substantially (Table 2). This indicates that the subdivision of glaciers into individual catchments is a major source of uncertainty in ice volume estimates, especially when they rely on scaling.
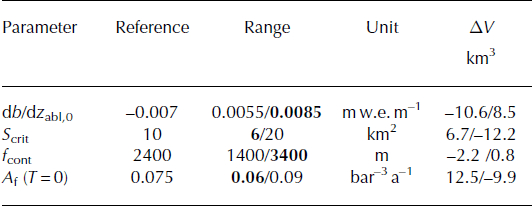
The distributed ice thickness model has a number of parameters that can be altered to achieve a better fit with observations. All parameters, however, refer to physical processes, are not freely variable and can be plausibility-checked against independent field observations. For example, the calibrated optimal value of ![]() is consistent with measured mass-balance gradients on Norwegian glaciers (Reference Rasmussen and AndreassenRasmussen and Andreassen, 2005), and good agreement was found. In order to analyse the sensitivity of the final volume result to the four most important model parameters, we performed a series of experiments and reran the model by individually varying these parameters within physically reasonable bounds (Table 3). The volume compared to the reference run was altered by up to ±12 km3, or ±4%, for an individual parameter (Table 3). The results were almost insensitive to changing f
cont and more sensitive to the assumed parameter values of S
crit,
is consistent with measured mass-balance gradients on Norwegian glaciers (Reference Rasmussen and AndreassenRasmussen and Andreassen, 2005), and good agreement was found. In order to analyse the sensitivity of the final volume result to the four most important model parameters, we performed a series of experiments and reran the model by individually varying these parameters within physically reasonable bounds (Table 3). The volume compared to the reference run was altered by up to ±12 km3, or ±4%, for an individual parameter (Table 3). The results were almost insensitive to changing f
cont and more sensitive to the assumed parameter values of S
crit, ![]() and A
f.
and A
f.
Table 3. Sensitivity of total ice volume to variations in selected model parameters used in the distributed model. The parameter value resulting in a higher volume is marked in bold
As the measured ice thickness data were obtained over several decades and the surface topography and the inventory data refer to different years, it is debatable whether our ice thickness and volume estimates are representative for today. Over the acquisition time interval of most ice thickness measurements (mid-1980s to 2013) Norwegian glaciers experienced transient mass surpluses, resulting in readvances of the glacier snouts for some glaciers but, at the same time, also mass deficit and frontal retreat (Reference Andreassen, Elvehøy, Kjøllmoen, Engeset and HaakensenAndreassen and others, 2005). Since ∼2000, most glaciers have been in a state of retreat. Over the past few decades, mass-balance observations show the largest thinning for Langfjordjøkelen (Reference Andreassen, Kjøllmoen, Rasmussen, Melvold and NordliAndreassen and others, 2012a) and glaciers in Jotunheimen (Kjøllmoen and others, 2011). For these glaciers the thickness data were collected in recent years (2005–12). Most ice thickness data from Jostedalsbreen, Svartisen and Blåmannsisen were collected in the late 1980s. For these cases, however, ice thickness data are mainly based on bed topography maps, and the ice volume was evaluated from the most recent DTM, i.e. after 2000. Thus, although some data were acquired several decades ago, we estimate that our volume calculations refer to the mid-2000s, so they are assumed to be representative for current conditions.
Dense RES measurements with good spatial coverage are required to make accurate ice thickness maps of entire glaciers. However, ice thickness measurements are problematic in inaccessible areas such as crevassed icefalls, and interpretation of RES data can be difficult due to ambiguous reflections when approaching mountain walls (e.g. Reference FischerFischer, 2009). While additional measurements on more glaciers are always desirable to cover all kinds of glacier types and area classes, the acquisition of RES data is time-consuming and expensive. The best recourse is to combine RES measurements with models.
Both the distributed model and V-A scaling are sensitive to the chosen parameter values or the scaling coefficients. V-A scaling is straightforward to apply, easy to calibrate and quickly yields a regional volume estimate. While the distributed model has the advantage of providing ice thickness based on physical relations and gives a more detailed output, it also requires more input data and is fairly time-consuming to implement. However, the distributed model can also be calibrated with relatively few measurements, a benefit over the V-A method given that RES coverage of entire glaciers is difficult to achieve and that volume calculated directly from sparse data has a larger uncertainty due to interpolation.
Applying different approaches, we derived a variety of estimates for total glacier volume in Norway (Fig. 8). Results vary over a wide range, from 137 to 359 km3, illustrating the considerable uncertainties in determination of regional ice volume. Although we do not know which of the inferred numbers is closest to reality, a clear pattern emerges from the methods used, giving at least some indication of the most plausible results. The four literature-based V-A scaling relations do not contain any region-specific adjustment, and predict an average volume of only 166 km3. Volume estimates based on the direct observations of ice thickness, which cover only one-third of the Norwegian glacier area, are consistently higher and lie within a relatively narrow range (Fig. 8). The average overall volume from the extrapolated direct measurements, the calibrated ice thickness model and calibrated V-A scaling relationships is 281 km3, 69% higher than the uncalibrated scaling. Clearly, Norway is a region with a relatively large ice volume, given its glacier coverage; this might be attributed to its mostly maritime conditions, with high mass turnover and the gentle surface slopes in the accumulation area of ice caps.
6. Conclusions
We estimated the ice volume of glaciers in Norway by combining direct ice thickness observations with different modelling approaches and estimation methods. The extensive ice thickness measurements in Norway are geographically well distributed, covering about one-third of the entire glacier area, and include both small glaciers and the largest ice caps, making Norway one of the most densely surveyed regions worldwide. Except for some early investigations, starting in the 1950s, most measurements were conducted from the 1980s onwards with RES. Measured and interpolated ice thickness values reveal relatively large and consistent ice thicknesses in the accumulation area of the largest ice caps; mean thickness varies insignificantly with their areas. The total volume of the area covered with RES data is 134 ± 23 km3; simple extrapolation of the direct measurements gives a total volume of 262 ± 68 km3. Applying a distributed ice thickness model, calibrated with the observations, yields a volume of 280 ± 34 km3. The model results generally agreed with the measured values and interpolated ice volumes, but significant deviations in thickness were found for some outlet glaciers. The method has the advantage of providing grid-based ice thickness and bedrock topography maps, which are useful for other applications, such as the assessment of future glacier change or for hydrological studies. However, results must be interpreted with care for individual glaciers, since the precision is not considered high enough for detailed analyses (i.e. flow modelling).
Ice volumes obtained using volume–area scaling parameters from the literature have a higher range (137–359 km3), and are generally lower than those derived from region-specific scaling relationships calibrated using ice thickness measurements and distributed model results (257–309 km3). For glaciers in Norway, with their high mass turnover, previously published scaling relationships for glaciers underestimate ice volume; local calibration is needed to obtain reasonable results. We consider an estimate of 271 ± 28 km3, derived from interpolated volume for the surveyed glaciers and the distributed model for the remaining glaciers, as the most reliable result for ice volume in Norway around the mid-2000s.
Acknowledgements
Jack Kohler and an anonymous reviewer provided constructive and helpful comments that improved the manuscript. We thank all those who contributed with ice thickness data. Galina Ragulina digitized bedrock maps of Jostedalsbreen and prepared the data for Trollbergdalsbreen. Ingvild Sørdal, Erlend Førre and Rune Ødegård provided data for Gråsubreen, Nordre Folgefonna and Juvfonne respectively. Trond Laumann digitized the bed map of Spørteggbreen. This is publication No. 69 of SVALI.













