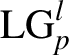1 Introduction
With the rapid development of ultra-short ultra-intense laser technology, the laser intensity can be increased up to 1022 W/cm2 in petawatt laser facilities[Reference Strickland and Mourou1–Reference Lureau, Matras, Chalus, Derycke, Morbieu, Radier, Casagrande, Laux, Ricaud, Rey, Pellegrina, Richard, Boudjemaa, Simon-Boisson, Baleanu, Banici, Gradinariu, Caldararu, Boisdeffre, Ghenuche, Naziru, Kolliopoulos, Neagu, Dabu, Dancus and Ursescu4]. Such laser pulses can be used to apply extremely high electromagnetic fields to accelerate electron beams to gigaelectronvolt levels[Reference Turner, Adli, Ahuja, Apsimon, Apsimon, Bachmann, Marin, Barrientos, Batsch, Batkiewicz, Bauche, Olsen, Bernardini, Biskup, Boccardi, Bogey, Bohl, Bracco, Braunmüller, Burger, Burt, Bustamante, Buttenschön, Caldwell, Cascella, Chappell, Chevallay, Chung, Cooke, Damerau, Deacon, Deubner, Dexter, Doebert, Farmer, Fedosseev, Fior, Fiorito, Fonseca, Friebel, Garolfi, Gessner, Gorgisyan, Gorn, Granados, Grulke, Gschwendtner, Guerrero, Hansen, Helm, Henderson, Hessler, Hofle, Hüther, Ibison, Jensen, Jolly, Keeble, Kim, Kraus, Lefevre, LeGodec, Li, Liu, Lopes, Lotov, Brun, Martyanov, Mazzoni, Godoy, Minakov, Mitchell, Molendijk, Mompo, Moody, Moreira, Muggli, Öz, Ozturk, Mutin, Pasquino, Pardons, Peña Asmus, Pepitone, Perera, Petrenko, Pitman, Plyushchev, Pukhov, Rey, Rieger, Ruhl, Schmidt, Shalimova, Shaposhnikova, Sherwood, Silva, Soby, Sosedkin, Speroni, Spitsyn, Tuev, Velotti, Verra, Verzilov, Vieira, Vincke, Welsch, Williamson, Wing, Woolley and Xia5, Reference Ren, Maurer, Katrik, Lang, Golubev, Mintsev, Zhao and Hoffmann6]. Thus far, two main accelerating mechanisms have been proposed: direct laser acceleration (DLA)Reference Thévenet, Leblanc, Kahaly, Vincenti, Vernier, Quéré and Faure[7] and indirect laser acceleration (ILA)[Reference Joshi, Mori, Katsouleas, Dawson, Kindel and Forslund8–Reference Geddes, Toth, Van Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans11]. In the ILA mechanism, electron accelerations are typically driven in a plasma environment, such as in the laser wakefield acceleration (LWFA) regime, where the accelerating gradients are larger than 100 GV/m[Reference Esarey, Schroeder and Leemans12]. Electrons can be captured and accelerated to several gigaelectronvolts with less energy spread and a charge of ∼0.1 nC in the LWFA regime[Reference Wang, Zgadzaj, Fazel, Li, Yi, Zhang, Henderson, Chang, Korzekwa, Tsai, Pai, Quevedo, Dyer, Gaul, Martinez, Bernstein, Borger, Spinks, Donovan, Khudik, Shvets, Ditmire and Downer13–Reference Gonsalves, Nakamura, Daniels, Benedetti, Pieronek, de Raadt, Steinke, Bin, Bulanov, van Tilborg, Geddes, Schroeder, Tóth, Esarey, Swanson, Fan-Chiang, Bagdasarov, Bobrova, Gasilov, Korn, Sasorov and Leemans15]. In the DLA mechanism, electrons are directly accelerated by the laser field itself, with the accelerating gradients reaching an order of 10 TV/m. Compared with the ILA mechanism (such as LWFA), the DLA mechanism yields a more compact gradient because it has a limited dependence on the plasma environment. As such, this method has attracted considerable attention[Reference Hartemann, Fochs, Le Sage, Luhmann, Woodworth, Perry, Chen and Kerman16–Reference Salamin and Keitel21].
However, the DLA mechanism has a limitation in that it cannot stably accelerate a large number of electrons for a long time. This is because the electrons are typically accelerated by the ponderomotive force 
${F}_{\mathrm{p}}=-{e}^2\nabla {E}^2/4{m}_{\mathrm{e}}{\omega}_{\mathrm{L}}^2$ in the linear limit (
$E\ll {m}_{\mathrm{e}}{c}^2/e$) and by 
${F}_{\mathrm{pN}}=-{m}_{\mathrm{e}}{c}^2\nabla \gamma$ in the nonlinear regime[Reference Downer, Zgadzaj, Debus, Schramm and Kaluza22], where e is the charge of the electron, E is the electric field amplitude, m e is the mass of the electron, 
${\omega}_{\mathrm{L}}$ is the laser frequency, c is the speed of light in vacuum, and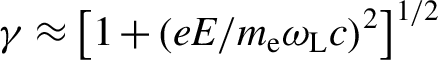 
$\gamma \approx {\left[1+{\left( eE/{m}_{\mathrm{e}}{\omega}_{\mathrm{L}}c\right)}^2\right]}^{1/2}$ is the relativistic factor associated with the quiver motion of electrons. An approximate Gaussian distribution of F p or F pN driven by a conventional Gaussian laser pulse will push the electrons to both sides of the laser beam axis, resulting in a scenario where fewer electrons are locked in the accelerating phase until they finally disappear. This is much different from that observed in the LWFA mechanism, where electrons are accelerated in ionized ‘bubble-like’ plasma channels driven by an ultra-intense Gaussian laser pulse. Gigaelectronvolt-level electron beams can be realized by accelerating the electrons in the longitudinal charge-separation field and constraining them via the transverse electric field in the bubble. For a more efficient electron acceleration in the DLA regime, the transverse confining effects should also be considered.
Fortunately, Laguerre–Gaussian (LG) lasers can provide a confining force to manipulate matter, such as proton[Reference Schreiber, Bolton and Parodi23–Reference Wang, Jiang, Dong, Lu, Li, Xu, Sun, Yu, Guo, Liang, Leng, Li and Xu26], electron[Reference Zhang, Shen, Zhang, Xu, Wang, Wang, Yi and Shi27–Reference Hu, Yu, Lu, Zhang, Zou, Zhang, Ge, Yin and Shao32], and positron[Reference Vieira and Mendonça33], in the transverse direction. Previously, optical tweezers or optical wrenches driven by LG lasers have been applied to concentrate and rotate micrometer matter in the nonrelativistic regime[Reference He, Friese, Heckenberg and Rubinsztein-Dunlop34, Reference Allen, Beijersbergen, Spreeuw and Woerdman35]. With the development of advanced laser facilities[Reference Leng2, Reference Zamfir36], an LG laser has the potential to be extended to the relativistic regime[Reference Shi, Shen, Zhang, Zhang, Wang and Xu37–Reference Vieira, Trines, Alves, Fonseca, Mendonca, Bingham, Norreys and Silva41]. Now the highest intensity of the LG laser can reach up to 6.3 × 1019 W/cm2 by using the reflected phase plate on the petawatt laser facility in experiments[Reference Wang, Jiang, Dong, Lu, Li, Xu, Sun, Yu, Guo, Liang, Leng, Li and Xu26]. The relativistic LG laser is expected to open new doors for particle manipulation in the DLA regime, because the hollow intensity distribution of the LG laser may result in the formation of a transverse potential well about the beam axis, similar to the charge-separated field structure in the bubble regime of LWFA[Reference Haddadi, Bouzid, Fromager, Hasnaoui, Harfouche, Cagniot, Forbes and Aït-Ameur42–Reference Jeong, Bulanov, Yan, Weber and Korn45]. It is believed that electrons can be accelerated in a concentrated manner in a new type of ‘bubble’ regime, to overcome some of the drawbacks of Gaussian-laser-driven DLA to a certain extent[Reference Hu, Yu, Sheng, Vieira, Zou, Yin, McKenna and Shao29, Reference Ju, Zhou, Jiang, Huang, Zhang, Cai, Cao, Qiao and Ruan31, Reference Wang, Jiang, Shen, Yuan, Gan, Zhang, Zhai and Xu46–Reference Li, Shen, Zhang, Bu and Gong48].
In this article, we report an annular electron slice obtained for the first time using a near-infrared circularly polarized (CP)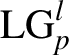 
${\mathrm{LG}}_p^l$ (p = 0, l = 1, σz = −1) laser in three-dimensional (3D) particle-in-cell (PIC) simulations. We found that a 2-μm infrared LG laser can provide a stable accelerating phase in the longitudinal direction and a concentrating force in the transverse direction, forming a ‘bubble’, similar to the case observed in the LWFA mechanism. Finally, a single attosecond electron slice was successfully accelerated up to hundreds of megaelectronvolts in the DLA regime, which is explained using a single-particle theoretical model. More importantly, the electron slice structure can be changed from a disk to an annular shape by accurately tuning the carrier-envelope phases (CEPs) of the LG laser. The novel annular attosecond electron slice captured in a ‘bubble’ is compact and is expected to have potential applications such as in the collimation of energetic particles like antiprotons in conventional linear accelerators[Reference Stancari, Valishev, Annala, Kuznetsov, Shiltsev, Still and Vorobiev49], edge-enhancement electron imaging[Reference Zhang, Hua, Wan, Pai, Guo, Zhang, Ma, Li, Wu, Chu, Gu, Xu, Mori, Joshi, Wang and Lu50], structured x-ray generation[Reference Zhao, Behm, Dong, Davoine, Kalmykov, Petrov, Chvykov, Cummings, Hou, Maksimchuk, Nees, Yanovsky, Thomas and Krushelnick51], and analysis and manipulation of nanomaterials[Reference Mousley, Thirunavukkarasu, Babiker and Yuan52].
2 Simulation results
Three-dimensional PIC simulations were carried out to investigate the formation and evolution of an annular electron slice driven by an intense near-infrared LG laser pulse. The 3D PIC simulations in this work were actualized with the code EPOCH[Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers53]. Each simulation used about 6.5 × 103 core hours on a parallel machine based on CentOS7 system. We employed the CP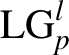 
${\mathrm{LG}}_p^l$ (p = 0, l = 1, σz = −1) laser mode, which can be expressed as follows:
$$\begin{align}&{\boldsymbol{E}}_{\boldsymbol{\perp}}={E}_0\sqrt{\frac{2p!}{\pi \left(p+l\right)!}}\frac{1}{w(x)}{\left[\frac{r\sqrt{2}}{w(x)}\right]}^l\exp \left[\frac{-{r}^2}{w^2(x)}\right]{L}_p^l\left[\frac{2{r}^2}{w^2(x)}\right]\notag\\&\qquad\times\exp \left( il\phi \right) \mathsf{\exp}\left[\frac{{{i}}{{{k}}}_{\mathsf{0}}{{{r}}}^{2}x}{2\left({\mathit{{x}}}^{2}+{\mathit{{x}}}_{{\rm R}}^{2}\right)}\right]\notag\\&\qquad\times\mathsf{\exp}\left[-\mathit{{i}}\left(2\mathit{{p}}+\mathit{{l}}+\mathsf{1}\right){\mathrm{arctan}}\left(\frac{\mathit{{x}}}{{\mathit{{x}}}_{{\rm R}}}\right)+\mathit{\mathsf{\psi}}\right]\notag\\&\qquad\times\left[{\boldsymbol{e}}_{{{y}}}+\mathsf{\exp}\left(\frac{\mathit{{i}}{\mathit{\mathsf{\pi \sigma}}}_{\mathit{z}}}{2}\right){\boldsymbol{e}}_{{\textit{z}}}\right],\end{align}$$where 
${E}_0={a}_0{m}_{\mathrm{e}}{\omega}_{\mathrm{L}}c/e$ is the peak amplitude of the electric field, a 0 = 25 is the normalization amplitude of the laser pulse (corresponding to a laser intensity I ∼ 2 × 1020 W/cm2), m e is the mass of the electron, 
${\omega}_{\mathrm{L}}$ is the laser frequency, c is the speed of light in vacuum, and e is the charge of the electron; l is the number of azimuthal phase cycles, and p + 1 denotes the number of radial nodes;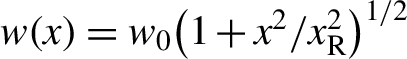 
$w(x)={w}_0{\left(1+{x}^2/{x}_{\mathrm{R}}^2\right)}^{1/2}$ is the beam waist with 
${w}_0$ ∼ 20 μm (full-width at half-maximum, FWHM) being the diameter of the focus spot, 
${x}_{\mathrm{R}}=\pi {w}_0^2/\lambda$ is the Rayleigh length, 
${L}_p^l$ is the generalized Laguerre polynomial, 
$\phi$ is the azimuthal angle, and 
$\left(l+2p+1\right)\mathrm{arctan}\left(x/{x}_{\rm R}\right)$ is the Gouy phase of the mode. The laser wavelength is λ = 2 μm, and the laser duration is 10 fs (FWHM). The foil thickness is 100 nm, corresponding to regions of 20 μm < x < 20.1 μm, −27 μm < y < 27 μm, and −27 μm < z < 27 μm. The foil density is n e = 0.5n c, where 
${n}_{\rm c}={\varepsilon}_0{\omega}_{\mathrm{L}}^2{m}_{\mathrm{e}}/{e}^2$ (
${\varepsilon}_0$ is the dielectric constant). Such ultrathin target foil may be available by using the few-nanometer carbon foil[Reference Henig, Steinke, Schnurer, Sokollik, Horlein, Kiefer, Jung, Schreiber, Hegelich, Yan, Meyer-ter-Vehn, Tajima, Nickles, Sandner and Habs54, Reference Bin, Ma, Wang, Streeter, Kreuzer, Kiefer, Yeung, Cousens, Foster, Dromey, Yan, Ramis, Meyer-ter-Vehn, Zepf and Schreiber55]. The foil is assumed to be ionized to protons and electrons before the laser reaches the target. The size of the simulation box is 30 μm (x) × 60 μm (y) × 60 μm (z) with 1200 × 1000 × 1000 cells, and a total of 1.2 × 109 electrons and 1.2 × 109 protons are uniformly distributed in foil in the initial time. The initial temperature of plasma was zero for cold target in our case. The simulation uses a moving window which starts at t = 8T with light speed, where T = λ/c is the laser cycle.
In the simulation, the near-infrared CP LG laser pulse is incident on the target from the left (see Figure 1(a)). The laser beam arrives at the front surface of the target at t = 11T. The electrons are quickly pushed away from the target area because the ponderomotive force is much greater than the charge-separated field force between the electrons and protons in this case[Reference Wang, Shen and Xu56–Reference Wang, Jiang, Li, Dong, Shen, Leng, Li and Xu59]. The electrons are then continuously accelerated through the DLA mechanism, as shown in Figure 1(b). On the one hand, the electrons are completely locked and accelerated up to 210 MeV at t = 88T in the accelerating phase of the longitudinal electric field (see Figure 1(c)). On the other hand, an electron slice can be concentrated within approximately 2° (see Figure 1(d)) in the transverse direction because of the formation of a transverse potential well about the beam axis (x axis), thus concentrating the electron toward the center to a certain extent (see Figure 1(e)). The field structure formed in the transverse and longitudinal directions in our case is similar to the formation of plasma bubbles in LWFA[Reference Haddadi, Bouzid, Fromager, Hasnaoui, Harfouche, Cagniot, Forbes and Aït-Ameur42, Reference Zhan60]. The only difference is that the accelerating phase is ahead of the decelerating phase in the ‘bubble’, and the size is determined by the wavelength of the LG laser in our case.
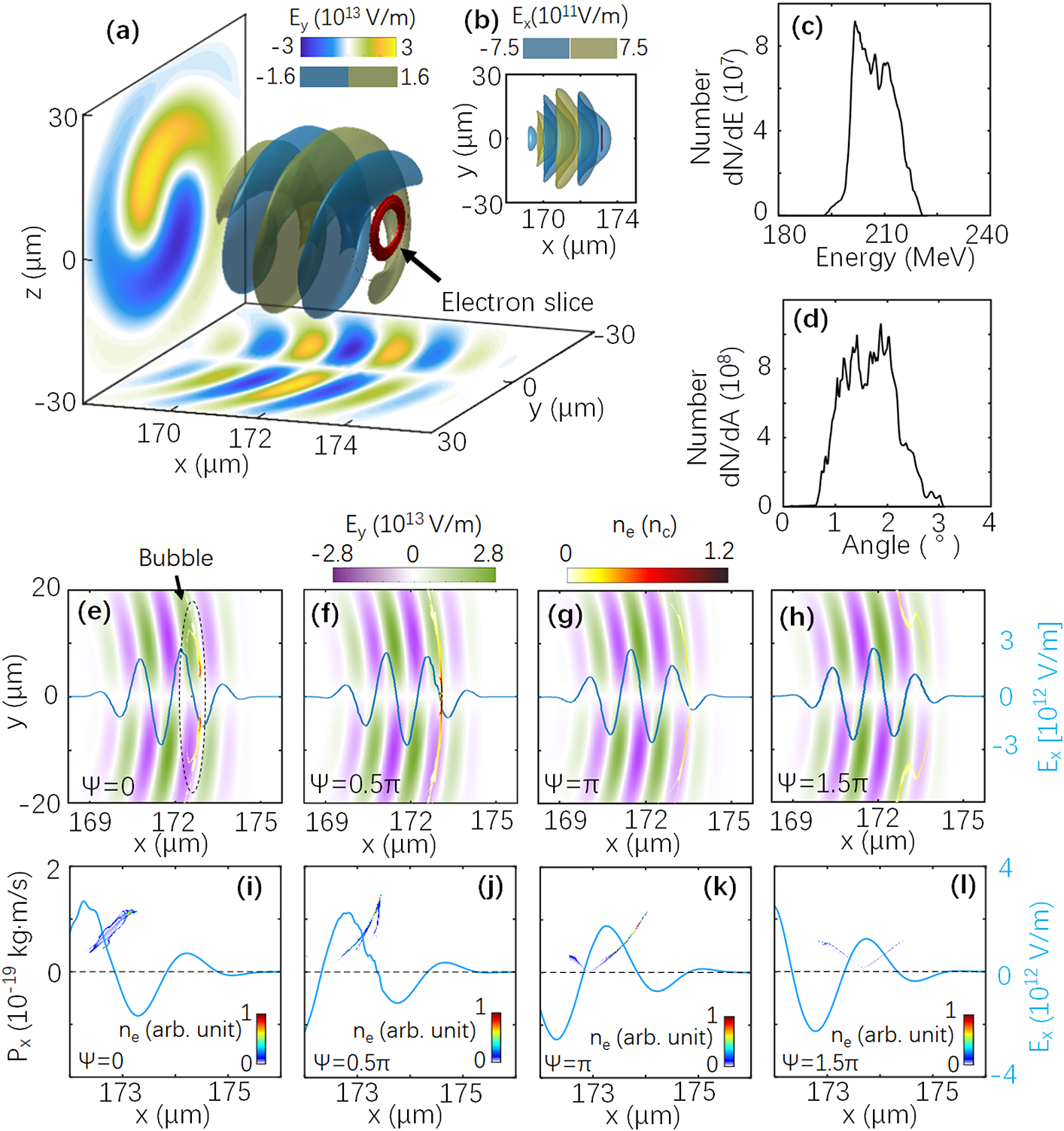
Fig. 1 Electron slice and LG laser field in PIC simulation. (a) Sketch of an electron slice driven by an LG laser. The red donut indicates the isosurface of the electron slice with n e = 0.3n c for the carrier-envelope Ψ = 0. The blue and yellow translucence isosurfaces indicate the distributions of the LG laser field Ey. (b) Distributions of the laser electric field Ex and electron slice in the x–y plane. (c), (d) Energetic spectra and angular distribution for the electrons in the regions of 173 μm < x < 183 μm, 0 < r < 8 μm at t = 88T. Density distributions of the electron slice for different CEPs (e) Ψ = 0, (f) 0.5π, (g) π and (h) 1.5π at 88T. Corresponding phase-space distributions of the electrons and amplitude of Ex (blue line) on the x-axis at t = 88T are plotted for (i) Ψ = 0, (j) 0.5π, (k) π and (l) 1.5π.
Figures 1(e)–1(h) show that the density distribution shapes of the electron slices at t = 88T can be changed from disk to annulus by varying the CEP of the LG laser. For Ψ = 0, the density distribution of the electrons is modulated to an annular shape with an inner diameter of approximately 10 μm, as shown in Figures 1(a), 1(b), and 1(e). This annular electron slice can be accelerated up to 220 MeV with a slice thickness of 0.2 μm (corresponding to approximately 670 attoseconds) at t = 88T, as shown in Figure 1(e). The total charge of such an annular electron slice can reach up to approximately 0.19 nC. By contrast, an electron disk is generated at the beam center when Ψ = 0.5π, as shown in Figure 1(f). In the other two cases shown in Figures 1(g) and 1(h), the electron slice is dispersed. The electron motion seems to have a close relationship with the phase structure in the laser field.
To explain the effects of CEP on the formation of the annular electron slice (see Figures 1(a) and 1(e)), both the transverse (Figures 2(a)–2(d)) and longitudinal electric fields (Figure 2(e)) in one laser cycle are discussed. It should be noted that most electrons travel along the direction of the laser and the transverse electron field 
$\left|{E}_{\perp}\right|$ is larger than 
$\left|{v}_x\times {B}_{\perp}\right|$ in simulations for our cases. Thus, we approximately consider that the electric field plays the main roles for the formation of electron bunch. The decelerating phase and accelerating phase for longitudinal electric field Ex are marked in Figure 2(e). When the LG laser pulse is incident on the target, the electrons are first concentrated by the dispersing electric field similar to point i (see Figure 2(a)) and subsequently rotated by the clockwise field similar to point ii (see Figure 2(b)), indicating that the electrons can be continuously concentrated in the transverse direction at the beginning of the interaction (from point i to point ii). Such a process can be clearly shown in the evolution of electron slice from t = 11T to t =25T (see Figures 2(f) and 2(g)). The electrons are then dispersed by the concentrating electric field similar to point iii (see Figure 2(c)) corresponding to t ∼ 35T (see Figure 2(h)). It can be found that the electron slice is shortly manipulated by a dispersing force (around t ∼ 5T), forming an annular structured slice. The longitudinal field increases up to Ex ∼ 1.67 × 1012 V/m at point iv, where most of the electrons can be locked in such a wide accelerating phase. The electron slice is further manipulated by the rotated electric field force and the weak inward electric field force in the accelerating region for a longer time (see Figures 1(e) and 1(i)), resulting in a stable annular slice, as shown in Figure 1(a). Compared with the case Ψ = 0 in Figure 2(e), the laser field Ex is much lower in the decelerating region (from point i to point iii) in the case of Ψ = 0.5π (see Figure 1(j)). Thus, the process of dispersing by the concentrating electric field (see Figure 2(c)) and decelerating by Ex is shorter than the case of Ψ = 0, resulting in a higher density distribution in the case of the disk structure on the beam axis (x axis).
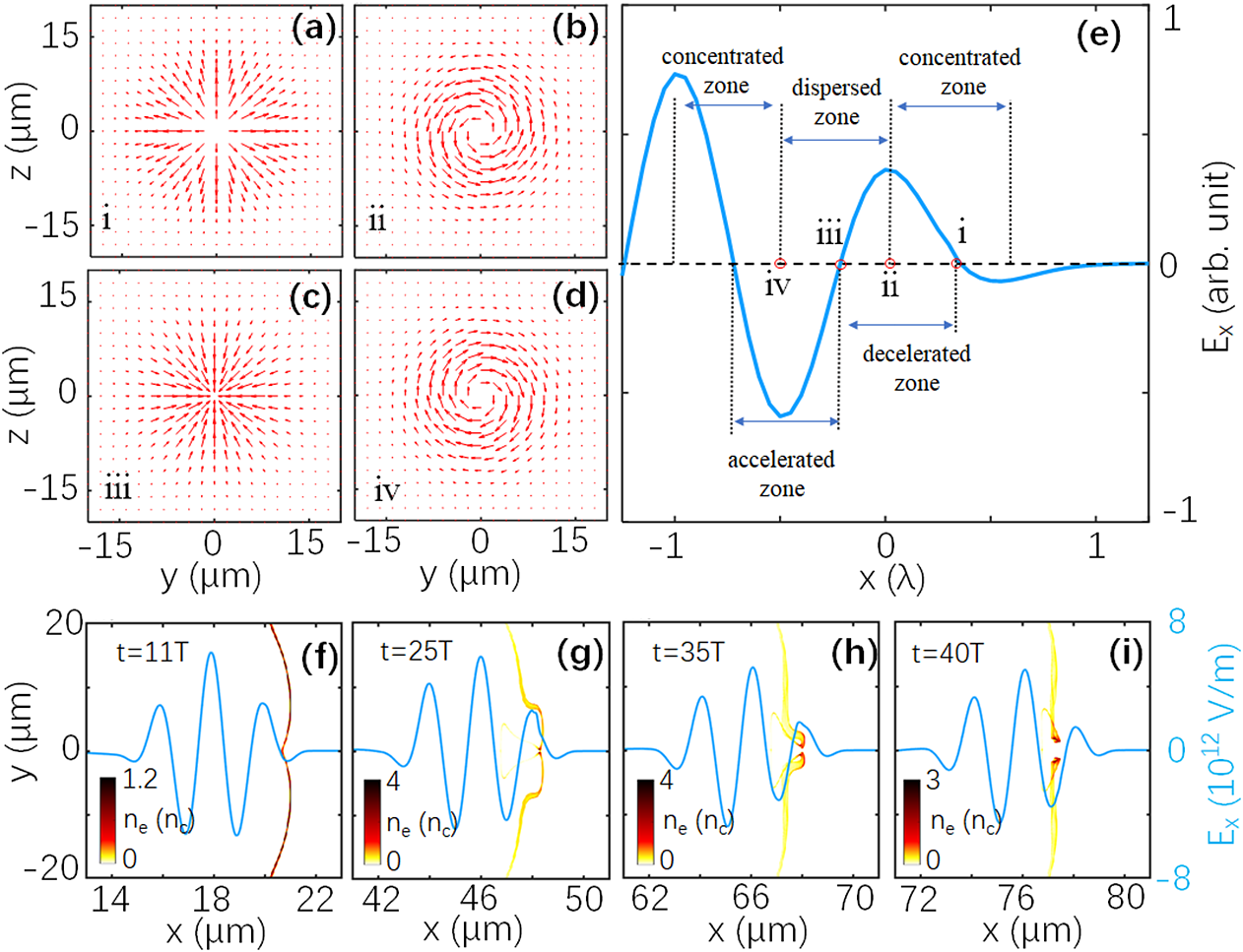
Fig. 2 Structure of electric fields of CP LG laser and phase-space distribution of electrons. Normalized vector plots of the transverse electric fields in one laser cycle for (a) point i, (b) point ii, (c) point iii, and (d) point iv marked in (e). (e) Normalized amplitude of Ex (blue line) on the x-axis for Ψ = 0. Density distributions of electron slice and amplitude of Ex (blue solid) for Ψ = 0 at (f) t = 11T, (g) t = 25T, (h) t = 35T, and (i) t = 40T are plotted.
In the other two cases shown in Figures 1(k) and 1(l), the electrons are first dispersed by the transverse fields. Although they lie in the accelerating phase at the beginning of the interaction, the amplitude of Ex is much lower than in the cases shown in Figures 1(i) and 1(j). Therefore, these electrons will easily slide into the decelerating phase and undergo considerable dispersion in the longitudinal direction. Finally, fewer electrons are formed about the beam axis, much different from the cases shown in Figures 1(i) and 1(j). This indicates that the formation of a concentrated electron slice with high energy requires two conditions in our case. On the one hand, the transverse electric fields should be concentrated on the electrons at the beginning of the interaction. On the other hand, the electrons should move into the large and stable accelerating phase as soon as possible, so that they can remain in a concentrated state in the ensuing acceleration process. If the transverse rotating fields just lie in the accelerating phase, the annular electron slice can be successfully maintained, as shown in Figures 1(a) and 1(i).
3 Theoretical analysis
To explain the simulation results, a single-particle model is employed to show the dynamic motion of a single electron in the LG laser field. The fundamental motion of the electrons can be described by the equation 
${\rm d}{p}/ {\rm d}t=e\left({E}+{v}\times {B}\right)$, where 
${p}={m}_e\gamma {v}$ is the particle momentum, E is the electric field intensity, and B is the magnetic intensity. As the azimuthal electromagnetic fields exist for a CP LG laser pulse, it becomes challenging to find an analytical solution for the single-particle motion. A feasible method is solving the equations numerically. Here 
${\boldsymbol{E}}_{\boldsymbol{\perp}}={E}_y{\boldsymbol{e}}_{\boldsymbol{y}}+{E}_z{\boldsymbol{e}}_{\boldsymbol{z}}$ is described in Equation (1), where Ey and Ez displace with 
$\pi /2$ at the propagation phase. Here, the longitudinal electric field is obtained from the Poisson’s equation, 
${E}_x=-\left(i/k\right)\nabla {\boldsymbol{E}}_{\boldsymbol{\perp}}$:
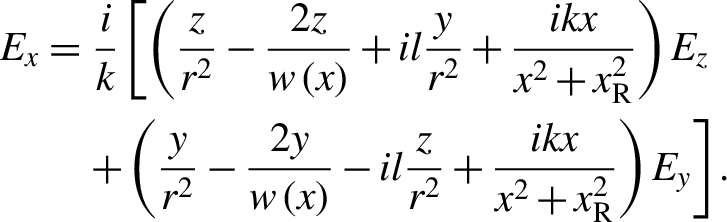$$\begin{align}{\mathit{{E}}}_{\mathit{{x}}}&=\frac{\mathit{{i}}}{\mathit{{k}}}\left[\left(\frac{\mathit{{z}}}{{\mathit{{r}}}^{2}}-\frac{2\mathit{{z}}}{\mathit{{w}}\left(\mathit{{x}}\right)}+\mathit{{i}{l}}\frac{\mathit{{y}}}{{\mathit{{r}}}^{2}}+\frac{\mathit{{i}{kx}}}{{\mathit{{x}}}^{2}+{\mathit{{x}}}_{{\rm R}}^{2}}\right){\mathit{{E}}}_{\mathit{{z}}}\right.\notag\\&\quad\left.+\left(\frac{\mathit{{y}}}{{\mathit{{r}}}^{2}}-\frac{2\mathit{{y}}}{\mathit{{w}}\left(\mathit{{x}}\right)}-\mathit{{i}{l}}\frac{\mathit{{z}}}{{\mathit{{r}}}^{2}}+\frac{\mathit{{i}{kx}}}{{\mathit{{x}}}^{2}+{\mathit{{x}}}_{{\rm R}}^{2}}\right){\mathit{{E}}}_{\mathit{{y}}}\right].\end{align}$$ For the mode of CP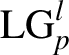 
${\mathrm{LG}}_p^l$ (p = 0, l = 1, σz = −1), there is a longitudinal electric field Ex at the beam center. The maximum value of Ex is ∼6 TV for a 0 = 25 in our case. The magnetic fields derive from the electric fields based on Maxwell’s equation
$\ \boldsymbol{B}=\left(i/ ck\right)\nabla \times \boldsymbol{E}$.
To understand the phase-locked movement of the electron slice in the PIC simulations, the single-particle model was applied for four typical electrons at x = 3.8 μm, y = ±1 μm, and z = ±1 μm, where the location of the simulation phase-locked region, shown in Figure 1(a), is considered. According to the angular distribution of electrons, the transverse velocity vr is much lower than vx (vr/vx < 3% for most electrons). The value vr = 0 is used for simplicity. The initial longitudinal velocity of the electrons is set to 0.999c, because the energy of most of the electrons that just enter the accelerating phase is approximately 11 MeV when vx = 0.999c at t = 42T in the simulations. The parameters of the electromagnetic field are the same as when Ψ = 0, as shown in Figure 1(e), in the PIC simulation. The 3D trajectories of the electrons show that they could remain in the acceleration phase of the CP LG laser for a distance more than 60 μm, as shown in Figure 3(a). It should be noted that the electron slice gains hundreds of megaelectronvolts of energy from such a phase-locked acceleration in the PIC simulation. In addition, the electrons undergo a right-handed rotation about the x axis (see Figure 3(c)), consistent with the vector distributions of the transverse electric fields in the accelerating phase (see Figure 2(d)). In PIC simulation, the direction of rotated transverse electric field does not change in the accelerating phase, so that the angular momentum (AM) of electrons can continually increase from negative to positive after t = 40T, just as shown in Figure 3(b). However, the initial AM of the electron is zero in the single-particle model. Thus, the total AM of the four electrons can only increase from zero to positive in accelerating phase, and the rotation directions of electrons do not change in Figure 3(c). We assume that the electrons can be rotated by these transverse electric fields (see Figure 2(b)), as evidenced by the evolution of their AM shown in Figure 3(b). Therein, the resonance of the AM corresponds to the different rotations (right-handed or left-handed) of the transverse electric fields (see Figures 2(b) and 2(d)).
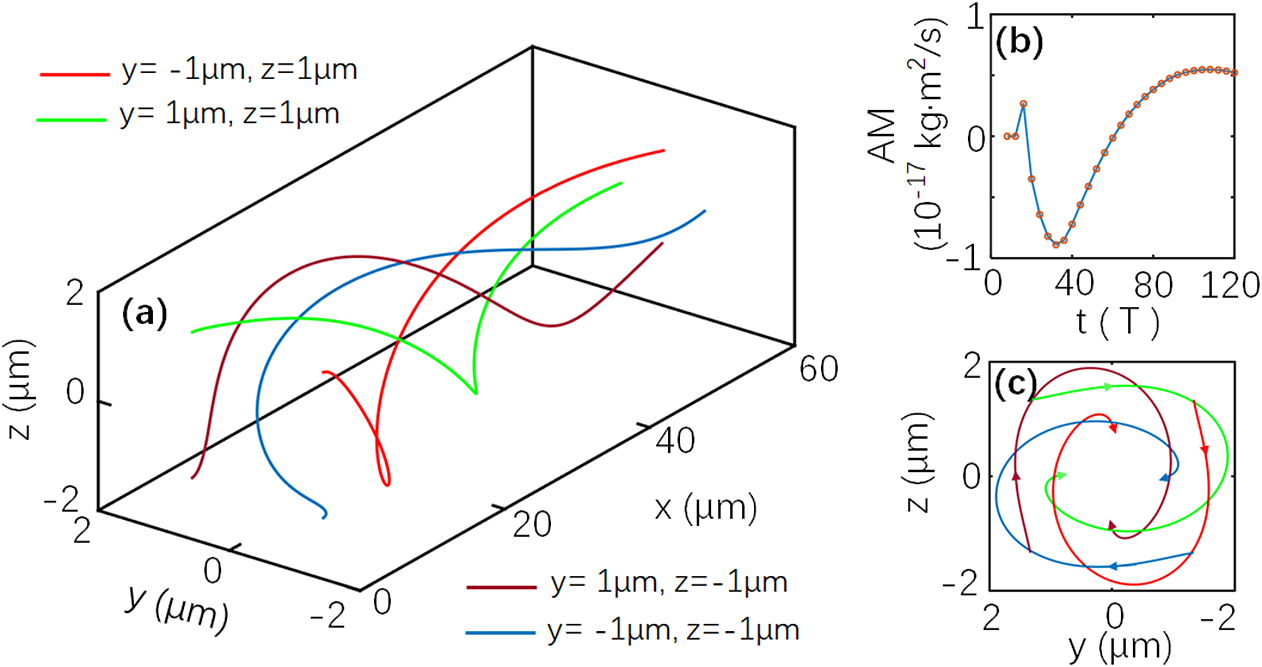
Fig. 3 Trajectories of electrons in a single-particle model and AM in PIC simulation. (a) 3D trajectories of electrons at different initial positions of x = 3.8 μm [accelerated phase corresponding to point iv in Figure 2(e)], y = ±1 μm, and z = ±1 μm. Here, the electrons have an initial velocity of vx = 0.999c. (b) AM for the electrons in the regions of 0 μm < x < 400 μm, −10 μm < y < 10 μm, and −10 μm < z < 10 μm in PIC simulation with Ψ = 0. (c) View of 3D trajectories in the forward direction.
4 Discussion
From the analyses described here, we find that a near-infrared LG laser can successfully provide a stable and efficient accelerating phase to generate a single annular attosecond electron slice in the DLA regime. The main reason is that the near-infrared LG laser (λ = 2 μm) can provide a longer accelerating field to stably maintain the annular structure of the electrons up to 853 fs (see Figure 4(a)). It should be noted that a small part of the electron beam is dragged into the next accelerating field, and can be concentrated by the transverse electric field forming a small dot around the beam axis (x axis), just as shown in Figure 4(a). A clearer annular electron slice may be obtained if we set a solid target to stop the further acceleration of the LG laser in the earlier interacting progress. From Figure 4(a), the corresponding energy of the electron slice can be further accelerated from ∼210 MeV at 88T (see Fig. 1(c)) to ∼280 MeV at t = 128T (853 fs) (see Figure 4(d)). By contrast, the electron slices are considerably dispersed at 853 fs when the laser wavelength is shorter (λ = 800 nm), as shown in Figure 4(b), and the electrons can only be accelerated up to ∼80 MeV due to the easier dephasing effect for the LG laser with a shorter wavelength (see Figure 4(e)). More importantly, the angular divergence remains at ∼2° (see Figure 4(g)) over 88T, meaning that an electron slice can be well concentrated in the ‘bubble’, thus overcoming the dispersion problem in the DLA regime when driven by a conventional Gaussian laser pulse (see Figures 4(c) and 4(i)). Although, the maximum energy can also be accelerated up to ∼150 MeV at 853 fs when using a Gaussian laser with λ = 2 μm, the energetic spread is as high as ∼30% (see Figure 4(f)). In addition, the divergence of the electron slice is 0°–7° in the case of the LG laser with λ = 800 nm (see Figure 4(h)) and 3°–6° in the case of the Gaussian laser with λ = 2 μm (see Figure 4(i)), which is greater than that (∼2°) in the case of the near-infrared LG laser with λ = 2 μm (see Figure 4(g)). All these comparisons indicate that the near-infrared LG laser discussed in this article helps accelerate the electron slice to a higher energy (hundreds of megaelectronvolts) with attosecond duration and concentrate it in a smaller divergence angle (∼2°). Such high quality of the annular electron slice may have various applications, such as antiprotons in conventional linear accelerators[Reference Stancari, Valishev, Annala, Kuznetsov, Shiltsev, Still and Vorobiev49], edge-enhancement electron imaging[Reference Zhang, Hua, Wan, Pai, Guo, Zhang, Ma, Li, Wu, Chu, Gu, Xu, Mori, Joshi, Wang and Lu50], structured X-ray generation[Reference Zhao, Behm, Dong, Davoine, Kalmykov, Petrov, Chvykov, Cummings, Hou, Maksimchuk, Nees, Yanovsky, Thomas and Krushelnick51], and analysis and manipulation of nanomaterials[Reference Mousley, Thirunavukkarasu, Babiker and Yuan52].
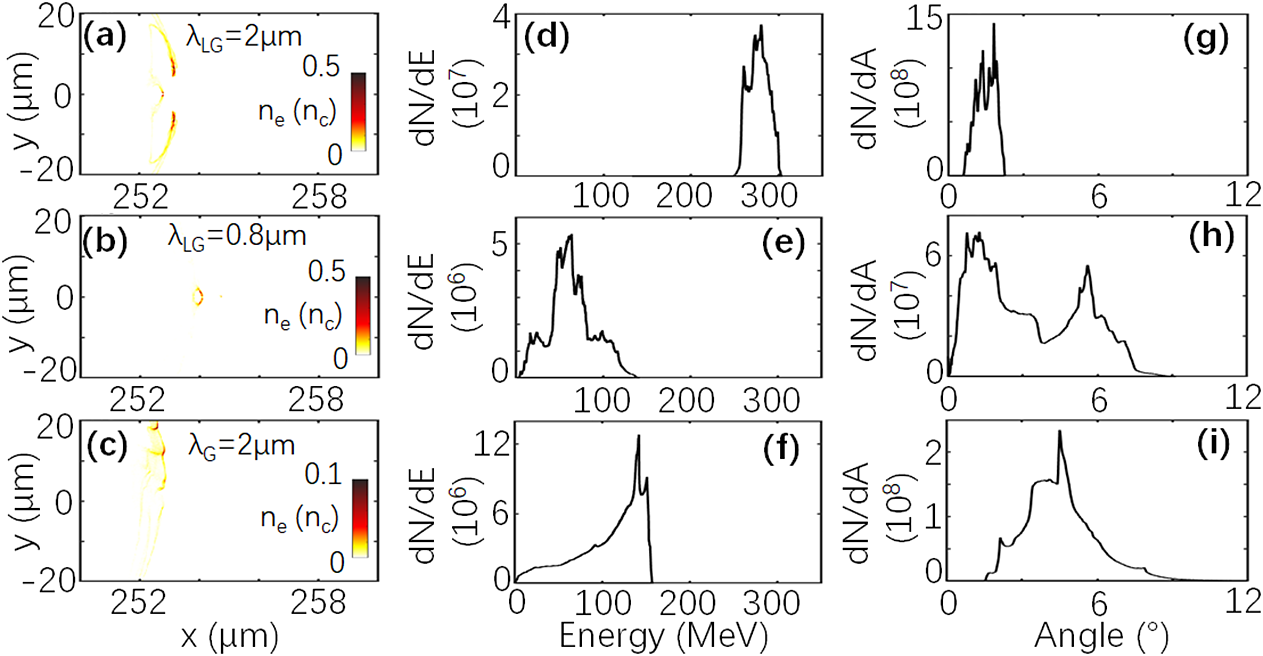
Fig. 4 Comparisons between the cases driven by LG laser and Gaussian laser. Density distributions of electrons at t = 853 fs for (a) LG laser with λ = 2 μm, (b) LG laser with λ = 0.8 μm, and (c) Gaussian laser with λ = 2 μm. (d)–(f) Energetic spectra and (g)–(i) angular distribution of the electrons in (a)–(c), respectively. The electrons in in the regions of 252.8 μm < x < 260 μm, 0 < r < 10 μm are considered for the cases in (d) and (g) and the electrons in the regions of 250 μm < x < 260 μm, 0 < r < 20 μm are considered for the cases in (e), (f), (h), and (i).
It should be noted that the longitudinal electric field (Ex) of the LG laser plays an important role in accelerating the electron slice to a high energy in the ‘bubble’ mechanism in this paper, where the charge-separation field between the electron and ion slice is not considered. It is reasonable because the normalized amplitude of the charge-separation field 
${a}_{\mathrm{cs}}=\pi {n}_{\mathrm{e}}{l}_0$ ∼ 0.08 for the initial foil thickness l 0 = 0.05λ and density n e = 0.5n c[Reference Wang, Shen and Xu56–Reference Wang, Jiang, Li, Dong, Shen, Leng, Li and Xu59] is much lower than the longitudinal amplitude ax = 1.03 (corresponding to 1.67 
$\times {10}^{12}$ V/m) for the LG laser used in our case. In this way, the dynamics of the electrons only driven by the LG laser field can be considered in Equation (2). Thus, the applicable condition of Eq. (2) is ax >> 
$\pi {n}_{\mathrm{e}}{l}_0$. Such lower area density of the foil (
${n}_{\mathrm{e}}{l}_0$) can be obtained by extending the nano carbon foil in the realistic experiments. An extending target with initial density distribution of n e(x) = n 0(x – 20 μm)/L (20 μm < x < 20.1 μm) and n e(x) = n 0(20 μm − x)/L (20.1 μm < x < 20.2 μm) is researched for an LG laser with Ψ = 0 in the PIC simulations, where n 0 = 0.5n c is the maximum electron density of target and L = 0.1 μm. The similar annular electron slice can be obtained at t = 88T. We assume that the electron slices can be better formed if the laser ponderomotive force is much larger than charge-separation field 
${a}_{\mathrm{cs}}=\pi {n}_{\mathrm{e}}{l}_0$, which is determined by the area density of the foil 
${n}_{\mathrm{e}}{l}_0$. The preplasma may have some effects on the mina structures of the electron slice, but these are not crucial effects. It is assumed that a thinner foil can work better for the mechanism proposed in this paper, because the smaller charge-separation field can be generated for the thinner foil. However, we should further increase the cell number per laser wavelength to increase the accuracy of the simulation for the thinner foil, which is limited to our present computer source and will be considered in the future. The charge-separation field should be considered in a more complex manner with the increasing of the foil thickness l 0 or density n e.
5 Summary
In conclusion, a novel annular electron slice driven by a few-cycle near-infrared LG laser has been investigated for the first time through 3D PIC simulations. We have found that a near-infrared LG laser can provide a ‘bubble’ region, characterized by a longer longitudinal electric field that can stably accelerate the electron slice up to hundreds of megaelectronvolts with attosecond duration. The longitudinal field mainly accelerates or decelerates the electrons in the forward direction in our case. The disk or annular formation of the electron slice can be tuned by the transverse fields in LG laser. A stable formation of the annular electron slice needs a proper combination of the longitudinal and transverse fields with different amplitudes, which are just determined by the CEP of the LG laser. The annular attosecond electron slice is compact and may have potential applications in the collimation of energetic particles such as antiprotons in conventional linear accelerators, edge-enhancement electron imaging, structured X-ray generation, and analysis and manipulation of nanomaterials. It should be noted that Nie et al. recently presented a new method to obtain relativistic few-cycle-tunable infrared pulses from a tailored plasma density structure[Reference Nie, Pai, Hua, Zhang, Wu, Wan, Li, Zhang, Cheng, Su, Liu, Ma, Ning, He, Lu, Chu, Wang, Mori and Joshi61]. We believe that the relativistic near-infrared LG laser discussed in this article can also be implemented as a similar technology to ultimately generate annular attosecond electron slices in experiments in the future.
Acknowledgments
This study was supported by the National Natural Science Foundation of China (grant number 12075306), Strategic Priority Research Program of the Chinese Academy of Sciences (grant number XDB16010600), Key Research Programs in Frontier Science (grant number ZDBSLY-SLH006), and Shanghai special science and technology innovation supported project (grant number 2019-jmrh1-kj1). Advanced research using high-intensity laser-produced photons and particles (ADONIS; grant number CZ.02.1.01/0.0/0.0/16 019/0000789) and High Field Initiative (HiFI; grant number CZ.02.1.01/0.0/0.0/15 003/0000449), both from European Regional Development Fund. The results of the Project LQ1606 were obtained with the financial support of the Ministry of Education, Youth and Sports as part of targeted support from the National Programme of Sustainability II.
Open access
