Hostname: page-component-6587cd75c8-gglxz Total loading time: 0.001 Render date: 2025-04-24T01:57:07.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-torsion algebraic cycles on the Jacobians of Fermat quotients

Part of: Curves Cycles and subschemes (Co)homology theory

Published online by Cambridge University Press:  22 November 2024

Yusuke Nemoto Open the ORCID record for Yusuke Nemoto [Opens in a new window]
Yusuke Nemoto*
Affiliation:
Department of Mathematics and Informatics, Graduate School of Science, Chiba University, Yayoicho 1-33, Inage, Chiba, 263-8522, Japan.
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the Abel-Jacobi image of the Ceresa cycle $W_{k, e}-W_{k, e}^-$, where $W_{k, e}$ is the image of the k-th symmetric product of a curve X with a base point e on its Jacobian variety. For certain Fermat quotient curves of genus g, we prove that for any choice of the base point and 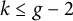$k \leq g-2$, the Abel-Jacobi image of the Ceresa cycle is non-torsion. In particular, these cycles are non-torsion modulo rational equivalence.

Keywords

Abel-Jacobi mapCeresa cycleFermat quotient

MSC classification

Primary: 14C25: Algebraic cycles 14F35: Homotopy theory; fundamental groups 14H40: Jacobians, Prym varieties
Type
Article
Information
Canadian Mathematical Bulletin , Volume 68 , Issue 1 , March 2025 , pp. 60 - 72
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Beauville, A., A non-hyperelliptic curve with torsion Ceresa class . C. R. Math. Acad. Sci. Paris 359(2021), 871–872.CrossRefGoogle Scholar
Bloch, S., Algebraic cycles and values of $L$ -functions. J. Reine Angew. Math. 350(1984), 94–108.Google Scholar
Carlson, J. A., Extensions of mixed Hodge structures . In Journées de Géometrie Algébrique d’Angers, Juillet 1979/Algebraic Geometry, Angers, 1979, Sijthoff and Noordhoff, Alphen aan den Rijn–Germantown, MD, 1980, 107–127.Google Scholar
Ceresa, G., $C$ is not algebraically equivalent to ${C}^{-}$ in its Jacobian. Ann. of Math. (2) 117(1983), no. 2, 285–291.CrossRefGoogle Scholar
Darmon, H., Rotger, V. and Sols, I., Iterated integrals, diagonal cycles and rational points on elliptic curves . In Publ. Math. Besancon Algèbre Théorie Nr., 2012/2[Mathematical Publications of Besancon, Algebra and Number Theory] Presses Universitaires de Franche-Comté, Besancon, 2012, 19–46.Google Scholar
Eskandari, P. and Murty, V. K., On the harmonic volume of Fermat curves . Proc. Amer. Math. Soc. 149(2021), no. 5, 1919–1928.CrossRefGoogle Scholar
Eskandari, P. and Murty, V. K., On Ceresa cycles of Fermat curves . J. Ramanujan Math. Soc. 36(2021), no. 4, 363–382.Google Scholar
Gross, B. H. and Rohrlich, D. E., Some results on the Mordell-Weil group of the Jacobian of the Fermat curve . Invent. Math. 44(1978), no. 3, 201–224.CrossRefGoogle Scholar
Hain, R. M., The geometry of the mixed Hodge structure on the fundamental group . In Algebraic geometry, Bowdoin, 1985 (Brunswick, Maine, 1985), Proc. Sympos. Pure Math., Vol. 46, Amer. Math. Soc., Providence, RI, 1987, 247–282.Google Scholar
Harris, B., Harmonic volumes . Acta Math. 150(1983), no. 1–2, 91–123 CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry , Grad. Texts in Math., No. 52, Springer-Verlag, New York-Heidelberg, 1977.Google Scholar
Irokawa, S. and Sasaki, R., On a family of quotients of Fermat curves . Tsukuba J. Math. 19(1995), no. 1, 121–139.CrossRefGoogle Scholar
Kaenders, R. H., The mixed Hodge structure on the fundamental group of a punctured Riemann surface . Proc. Amer. Math. Soc. 129(2001), no. 5, 1271–1281.CrossRefGoogle Scholar
Kimura, K., On modified diagonal cycles in the triple products of Fermat quotients . Math. Z. 235(2000), no. 4, 727–746.CrossRefGoogle Scholar
Lilienfeldt, D. T.-B. G. and Shnidman, A., Experiments with Ceresa classes of cyclic Fermat quotients . Proc. Amer. Math. Soc. 151(2023), no. 3, 931–947.CrossRefGoogle Scholar
Otsubo, N., On the Abel-Jacobi maps of Fermat Jacobians . Math. Z. 270(2012), no. 1–2, 423–444,CrossRefGoogle Scholar
Pulte, M. J., The fundamental group of a Riemann surface: mixed Hodge structures and algebraic cycles . Duke Math. J. 57(1988), no. 3, 721–760.CrossRefGoogle Scholar
Tadokoro, Y., A nontrivial algebraic cycle in the Jacobian variety of the Klein quartic . Math. Z. 260(2008), no. 2, 265–275.CrossRefGoogle Scholar
Tadokoro, Y., A nontrivial algebraic cycle in the Jacobian variety of the Fermat sextic . Tsukuba J. Math. 33(2009), no. 1, 29–38.CrossRefGoogle Scholar
Tadokoro, Y., Nontrivial algebraic cycles in the Jacobian varieties of some quotients of Fermat curves . Internat. J. Math. 27(2016), no. 3, 1650027, 10 pp.CrossRefGoogle Scholar