Hostname: page-component-f554764f5-fnl2l Total loading time: 0 Render date: 2025-04-20T14:37:09.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Dual-narrowband bandpass filter with exact equations of scattering parameters

Published online by Cambridge University Press:  29 April 2024

Masoud Najafi  and
Ali Reza Hazeri Open the ORCID record for Ali Reza Hazeri [Opens in a new window]
Masoud Najafi
Affiliation:
Department of Electrical Engineering, College of Engineering, Kermanshah Branch, Islamic Azad University, Kermanshah, Iran
Ali Reza Hazeri*
Affiliation:
Department of Electrical Engineering, College of Engineering, Kermanshah Branch, Islamic Azad University, Kermanshah, Iran
*
Corresponding author: Ali Reza Hazeri; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, a new microstrip dual-narrowband bandpass filter employing parallel-coupled transmission lines and open stubs is presented, investigated, and fabricated. The proposed dual-narrowband bandpass filter is analyzed and its exact scattering parameters are calculated, simulated, and measured. So, calculated scattering parameters offer a deep inside view of the performance of the proposed filter. To analyze the proposed filter, the even- and odd-mode excitation are utilized. The input impedance under even- and odd-mode excitation are achieved by transmission line theory and inserted in the scattering parameter equations. Finally, the accurate scattering parameters are derived and compared with simulation results. Simulation results prove the theoretical results. Then, an optimized proposed filter is fabricated and matched with simulation results. The center frequency bands are 4.5 and 6.8 GHz. The optimized filter occupies 0.12 $ \times $ 0.096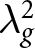$\lambda _g^2$, which is small. Its fractional bandwidth of the first and second passband are 1.5 and 2.5%, respectively. Furthermore, wide and strong rejection levels in the stopbands are offered. The structure of the proposed filter provides many freedoms to design. There is an agreement between experimental and simulation results.

Keywords

analytical resultsbandpass filterdual-band filtermicrostrip filternarrowband filterscattering parameters
Type
Research Paper
Information
International Journal of Microwave and Wireless Technologies , Volume 16 , Issue 7 , September 2024 , pp. 1089 - 1095
Check for updates
Copyright
© Kermanshah branch, Islamic azad university, 2024. Published by Cambridge University Press in association with The European Microwave Association.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abasi, H and Hazeri, AR (2018) Compact microstrip dual-narrowband bandpass filter with wider rejection band. Electromagnetics 38(6), 390–401.CrossRefGoogle Scholar
Faraji, T and Hazeri, AR (2012) Microstrip dual‐band bandstop filter to suppress DGS, DMB, GPS, UTMTS, WCDMA, WIBRO, and WLAN bands. Microwave and Optical Technology Letters 54(4), 854–856.CrossRefGoogle Scholar
Najafi, M and Hazeri, AR (2021) Microstrip dual-narrowband bandpass filter with independent passbands. Wireless Personal Communications 119, 3503–3516.CrossRefGoogle Scholar
Chen, J-X, Li, J and Shi, J (2018) Miniaturized dual-band differential filter using dual-mode dielectric resonator. IEEE Microwave and Wireless Components Letters 28(8), 657–659.CrossRefGoogle Scholar
Tan, Z, Lu, Q-Y and Chen, J-X (2019) Differential dual-band filter using ground bar-loaded dielectric strip resonators. IEEE Microwave and Wireless Components Letters 30(2), 148–151.CrossRefGoogle Scholar
Chen, R-S, Zhu, L, Lin, JY, Wong, SW, Li, Y, Yang, Y and He, Y (2020) Miniaturized full-metal dual-band filter using dual-mode circular spiral resonators. IEEE Microwave and Wireless Components Letters 30(6), 573–576.CrossRefGoogle Scholar
Chang, H, Sheng, W, Cui, J and Lu, J (2020) Multilayer dual-band bandpass filter with multiple transmission zeros using discriminating coupling. IEEE Microwave and Wireless Components Letters 30(7), 645–648.CrossRefGoogle Scholar
Tang, D, Han, C, Deng, Z, Qian, HJ and Luo, X (2020) Substrate-integrated defected ground structure for single-and dual-band bandpass filters with wide stopband and low radiation loss. IEEE Transactions on Microwave Theory & Techniques 69(1), 659–670.CrossRefGoogle Scholar
Xu, W, Ma, K and Du, C (2020) Design and loss reduction of multiple-zeros dual-band bandpass filter using SISL. IEEE Transactions on Circuits and Systems II: Express Briefs 68(4), 1168–1172.Google Scholar
Zhang, Q, Chen, C, Chen, W, Ding, J and Zhang, H (2021) Novel cross-coupled dual-band bandpass filters with compact size based on dual-mode isosceles right-angled triangular resonators. IEEE Transactions on Microwave Theory & Techniques 69(6), 3037–3047.CrossRefGoogle Scholar
Wei, Y, Wu, Y, Wang, W, Pan, L, Yang, Y and Liu, Y (2020) Double-sided spoof surface plasmon polaritons-line bandpass filter with excellent dual-band filtering and wide upper band suppressions. IEEE Transactions on Plasma Science 48(12), 4134–4143.CrossRefGoogle Scholar
Sekiya, N and Tsuruoka, T (2019) Improvement of filter properties of independently tunable superconducting dual-band bandpass filter. IEEE Transactions on Applied Superconductivity 29(5), 1–4.Google Scholar
Tang, J, Liu, H and Yang, Y (2020) Balanced dual-band superconducting filter using stepped-impedance resonators with high band-to-band isolation and wide stopband. IEEE Transactions on Circuits and Systems II: Express Briefs 68(1), 131–135.Google Scholar
Ren, B, Ma, Z, Liu, H, Guan, X, Wang, X, Wen, P and Ohira, M (2018) Differential dual-band superconducting bandpass filter using multimode square ring loaded resonators with controllable bandwidths. IEEE Transactions on Microwave Theory & Techniques 67(2), 726–737.CrossRefGoogle Scholar
Zhang, S, Rao, J-Y, Hong, J-S and Liu, F-L (2018) A novel dual-band controllable bandpass filter based on fan-shaped substrate integrated waveguide. IEEE Microwave and Wireless Components Letters 28(4), 308–310.CrossRefGoogle Scholar
Zhang, H, Kang, W and Wu, W (2018) Miniaturized dual-band SIW filters using E-shaped slotlines with controllable center frequencies. IEEE Microwave and Wireless Components Letters 28(4), 311–313.CrossRefGoogle Scholar
Azad, AR and Mohan, A (2018) Substrate integrated waveguide dual-band and wide-stopband bandpass filters. IEEE Microwave and Wireless Components Letters 28(8), 660–662.CrossRefGoogle Scholar
Zhang, H, Kang, W and Wu, W (2018) Miniaturized dual-band differential filter based on CSRR-loaded dual-mode SIW cavity. IEEE Microwave and Wireless Components Letters 28(10), 897–899.CrossRefGoogle Scholar
Liu, B-G, Lyu, Y-P, Zhu, L and Cheng, C-H (2020) Compact single- and dual-band filters on hexa-modes half-mode substrate integrated waveguide resonator with loaded H-shaped slot. IEEE Microwave and Wireless Components Letters 30(12), 1129–1132.CrossRefGoogle Scholar
Deng, J-Y, Li, M-J, Sun, D, Guo, L-X and Ma, X-H (2020) Compact dual-band inverted-microstrip ridge gap waveguide bandpass filter. IEEE Transactions on Microwave Theory & Techniques 68(7), 2625–2632.CrossRefGoogle Scholar
Basit, A, Khattak, MI, Al-Hasan, M, Nebhen, J and Jan, A (2022) Design and analysis of a compact GSM/GPS dual-band bandpass filter using a T-shaped resonator. Journal of Electromagnetic Engineering and Science 22(2), 138–145.CrossRefGoogle Scholar
Dong, G, Wang, W, Wu, Y, Li, W, Liu, Y and Tentzeris, MM (2020) Dual-band balanced bandpass filter using slotlines loaded patch resonators with independently controllable bandwidths. IEEE Microwave and Wireless Components Letters 30(7), 653–656.CrossRefGoogle Scholar
Lu, J and Zhang, F (2021) Compact fourth/third order dual‐band bandpass filter with independently controllable passbands. Microwave and Optical Technology Letters 63(12), 2921–2926.CrossRefGoogle Scholar
Ren, B, Liu, H, Ma, Z, Ohira, M, Wen, P, Wang, X and Guan, X (2018) Compact dual-band differential bandpass filter using quadruple-mode stepped-impedance square ring loaded resonators. IEEE Access 6, 21850–21858.CrossRefGoogle Scholar
Tang, J, Liu, H and Yang, Y (2020) Compact wide-stopband dual-band balanced filter using an electromagnetically coupled SIR pair with controllable transmission zeros and bandwidths. IEEE Transactions on Circuits and Systems II: Express Briefs 67(11), 2357–2361.Google Scholar
Bandyopadhyay, A, Sarkar, P, Mondal, T and Ghatak, R (2020) A dual function reconfigurable bandpass filter for wideband and tri-band operations. IEEE Transactions on Circuits and Systems II: Express Briefs 68(6), 1892–1896.Google Scholar
Ma, M, You, F, Qian, T, Shen, C, Qin, R, Wu, T and He, S (2022) A wide stopband dual-band bandpass filter based on asymmetrical parallel-coupled transmission line resonator. IEEE Transactions on Microwave Theory & Techniques 70(6), 3213–3223.CrossRefGoogle Scholar
Dong, J, Xu, K and Shi, J (2020) A voltage-controlled tunable differential dual-band bandpass filter with compact size and wide tuning range. IEEE Transactions on Industrial Electronics 68(10), 9952–9962.CrossRefGoogle Scholar
Xu, S, Ma, K, Meng, F and Yeo, KS (2015) Novel defected ground structure and two-side loading scheme for miniaturized dual-band SIW bandpass filter designs. IEEE Microwave and Wireless Components Letters 25(4), 217–219.CrossRefGoogle Scholar
Duan, Q, Song, K, Chen, F and Fan, Y (2015) Compact dual‐band bandpass filter using simply hybrid structures. Electronics Letters 51(16), 1265–1266.CrossRefGoogle Scholar
Danaeian, M, Zarezadeh, E and Ghayoumi-Zadeh, H (2018) A compact and high performance dual-band bandpass filter based on unbalanced composite right/left-handed transmission lines for WLANs applications. Analog Integrated Circuits and Signal Processing 94(3), 469–479.CrossRefGoogle Scholar
Ghaderi, A, Golestanifar, A and Shama, F (2017) Design of a compact microstrip tunable dual-band bandpass filter. AEU-International Journal of Electronics and Communications 82, 391–396.Google Scholar
Firmansyah, T, Praptodiyono, S, Rifai, A, Alam, S and Paramayudha, K (2023) Dual-band via-less band-pass filter based on cascaded closed ring resonator. Journal Elektronika Dan Telekomunikasi 23(1), 9–15.CrossRefGoogle Scholar
Yan, J-M, Kang, B-J, Yang, Y and Cao, L (2023) Single-and dual-band bandpass filters based on a novel microstrip loop-type resonators loaded with shorted stubs. Progress in Electromagnetics Research Letters 113, 61–67.CrossRefGoogle Scholar