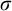1 Introduction
Computable analysis provides a way to perform computations on mathematical objects, by representing them using infinite sequences of bits or natural numbers. A class of objects can be represented in several ways, and the choice of the representation has a direct impact on the computation power of the Turing machine. In particular, each representation induces its own class of computable objects. In this article, we are interested in understanding when two representations on a set induce different subsets of computable points. This problem being too general to be analyzed, we restrict our attention to standard representations of countably based topological spaces. It is a widespread class of representations capturing most natural cases, and it enables us to develop a topological understanding of the problem.
With this restriction, the problem can be stated as follows: given two countably based topologies on the same set, when do they induce different sets of computable points?
Our main goals are to clarify the relationship between topology and computability, and to obtain general results that can be applied in concrete cases to separate computability notions. Indeed, such separation results can be challenging in practice, which means that a theoretical development of this problem is needed. Moreover, understanding when a separation result is possible is at least more informative as the separation result itself. We give an application which would be tedious to obtain directly, which is to build a copy of a given compact set which is semicomputable but not computable.
In order to study the problem of separating the notions of computable points associated with two topologies, we first relativize it, yielding a purely topological problem: whether two topologies are
$\sigma $
-homeomorphic, i.e., whether the space can be decomposed into a countable union of subsets such that the two topologies agree on each subset. The relationship between the computability-theoretic content of points and the
$\sigma $
-homeomorphism class of the space was thoroughly investigated by Kihara, Pauly, and Ng [Reference Kihara and Pauly17, Reference Kihara, Ng and Pauly18].
In this article, we use Baire category to study the problem of comparing two topologies and their computable contents, so we need one of the two topologies to be Polish, or that the space can also be endowed with a third topology which is Polish.
Given a set with a Polish topology
$\tau $
and a weaker topology
$\tau '$
, we give a characterization of the case when
$\tau $
and
$\tau '$
are not
$\sigma $
-homeomorphic. We then use this characterization to propose an effective version, implying that the two topologies induce different sets of computable points. We also extend the results to the case when
$\tau $
is not Polish, but a third Polish topology is available.
The constructions underlying the separation results are based on the priority method with finite injury. We recast the construction into a more general result of independent interest. It is an effective version of the Baire category theorem, in which simple topological conditions are identified that make the construction possible.
1.1 Content
Let
$(X,\tau )$
be a Polish space and
$\tau '$
a countably based topology on X that is weaker than
$\tau $
, i.e., such that every
$\tau '$
-open set is also
$\tau $
-open. For the effective results, we will also assume that these topologies are effective in some sense.
In Section 2, we start with an effective version of the Baire category theorem that builds
$\tau '$
-computable points in a set that is co-meager w.r.t.
$\tau $
(Theorem 2.1). This result captures the building technique that is needed for the rest of the paper, and is based on the priority method. This theorem is of independent interest and can hopefully be applied in other contexts.
In Section 3, we introduce a definition expressing that
$\tau '$
is “significantly weaker” than
$\tau $
in the sense that when
$\tau '$
and
$\tau $
coincide on a set, that set must be small in the sense of Baire category. We then say that
$\tau '$
is generically weaker than
$\tau $
(Definition 3.3). This notion immediately implies that
$\tau '$
is not
$\sigma $
-homeomorphic to
$\tau $
. We then prove that when
$\tau '$
is generically weaker than
$\tau $
in an effective way, there exist
$\tau '$
-computable points that are not
$\tau $
-computable (Theorem 3.1). This construction is obtained by applying the effective Baire category theorem from Section 2. In Section 3.3, we investigate the difficulty of
${\mathrm {id}}:(X,\tau ')\to (X,\tau )$
in terms of Weihrauch reducibility. In Section 3.4, we generalize the results to a case when the two topologies to be compared are not Polish, but a third topology is available, which is Polish.
We end in Section 4 with an application, which is a complete proof of a result announced in [Reference Amir, Hoyrup, Bojanczyk, Merelli and Woodruff1] about sets with computable type (Theorem 4.2).
1.2 Background
We assume familiarity with basic notions from computability theory: computably enumerable (c.e.) subset of
${\mathbb {N}}$
, computable function from
${\mathbb {N}}$
to
${\mathbb {N}}$
or from the Baire space
${\mathcal {N}}={\mathbb {N}}^{\mathbb {N}}$
to itself. We now recall a few classical notions from computable analysis, that can be found in [Reference Weihrauch27] or [Reference Schröder, Brattka and Hertling24].
An effective countably based space is a topological space
$(X,\tau )$
coming with a numbered basis
$(B_i)_{i\in {\mathbb {N}}}$
and a c.e. set
$E\subseteq {\mathbb {N}}^3$
such that
$B_i\cap B_j=\bigcup _{(i,j,k)\in E}B_k$
. A set
$U\subseteq X$
is an effective open set if
$U=\bigcup _{\sigma \in W}B_i$
for some c.e. set
$W\subseteq {\mathbb {N}}$
.
The Baire space
${\mathcal {N}}={\mathbb {N}}^{\mathbb {N}}$
endowed with the product of the discrete topology is naturally an effective countable-based
$T_0$
-space. Basic open sets are given by the cylinders: if
$\sigma \in {\mathbb {N}}^*$
is any finite sequence of natural numbers, then the cylinder
$[\sigma ]$
is the set of infinite extensions of
$\sigma $
.
A representation of a set X is a surjective partial map
$\delta _X:\subseteq {\mathcal {N}}\to X$
. A
$\delta _X$
-name of
$x\in X$
is any
$p\in {\mathrm {dom}}(\delta _X)$
such that
$\delta _X(p)=x$
. A point
$x\in X$
is computable if it has a computable name.
A function
$f:X\to Y$
between represented spaces is computable if there exists a computable partial function
$F:\subseteq {\mathcal {N}}\to {\mathcal {N}}$
such that
$f\circ \delta _X=\delta _Y\circ F$
. F is called a realizer of f.
An effective countably based
$T_0$
-space X can be equipped with its standard representation
$\delta _X$
encoding a point by any enumeration of its basic neighborhoods, and defined as follows: a
$\delta _X$
-name of x is any
$p\in {\mathcal {N}}$
such that for all
$i\in {\mathbb {N}}$
,
$x\in B_i\iff \exists n\in {\mathbb {N}}, p(n)=i+1$
. We will say that a point
$x\in X$
is
$\tau $
-computable if x is computable w.r.t. the standard representation associated with the topology
$\tau $
. A function
$f:X\to Y$
between effective countable-based
$T_0$
-spaces is computable if and only if the preimages of basic open sets
$f^{-1}(B^Y_i)$
are effectively open, uniformly in i.
A computable metric space is a metric space
$(X,d)$
coming with a dense sequence
$(s_i)_{i\in {\mathbb {N}}}$
such that the function
$(i,j)\mapsto d(s_i,s_j)$
is computable. It is an effective countably based space, by taking the basis of metric balls
$B(s_i,r)$
for positive rational r.
A computable Polish space is a computable metric space whose metric is complete. For every computable Polish space, there exists a computable surjective function
$f:{\mathcal {N}}\to X$
which is effectively open, i.e., such that the images of cylinders
$f([\sigma ])$
are effectively open, uniformly in
$\sigma $
(see, for instance, [Reference Selivanov, Beckmann, Mitrana and Soskova25]).
On a set X endowed with two effective countably based topologies
$\tau _1,\tau _2$
, we say that
$\tau _1$
is effectively weaker than
$\tau _2$
if the basic
$\tau _1$
-open sets are effective
$\tau _2$
-open sets, uniformly.
2 A computable Baire category theorem
In this section, we prove an effective version of the Baire category theorem. In a computable Polish space, it allows to build points in a co-meager set, that are computable w.r.t. another topology. It will be applied in the next sections to build points with specific properties.
The Baire category theorem is known to help proving existence results. First, it has many classical applications in mathematics, some of which can be found in the survey [Reference Jones15] by Jones. Computable versions of the Baire category theorem have been developed. The simplest one allows to build computable points, and was studied by Brattka [Reference Brattka, Sgall, Pultr and Kolman3], Brattka, Hendtlass, and Kreutzer [Reference Brattka, Hendtlass and Kreuzer4], Kalantari [Reference Kalantari, Brattka, Schröder, Weihrauch and Zhong16], and Yasugi, Mori, and Tusjii [Reference Yasugi, Mori and Tsujii28]. Jockush [Reference Jockush, Drake and Wainer14] introduced
$1$
-genericity as an effective version of Baire category that enables one to build
${\boldsymbol {0}'}$
-computable points. A notion of genericity that enables one to build points that are computable w.r.t. a given topology was proposed by Hoyrup in [Reference Hoyrup12]. A complexity-theoretic version of Baire category was introduced by Breutzmann, Juedes, and Lutz [Reference Breutzmann, Juedes and Lutz8] in order to build polynomial-time computable points.
We work in a computable Polish space
$(X,\tau )$
, coming with an effectively weaker countably based topology
$\tau '$
. We identify a condition for a sequence of subsets
$A_n$
of X which implies the existence of a
$\tau '$
-computable point in
$\bigcap _n A_n$
.
Let
$(X,\tau )$
be a computable Polish space and
$\tau '$
be an additional countably based topology on X which is effectively weaker than
$\tau $
, i.e., which has a basis
$(V_i)_{i\in {\mathbb {N}}}$
consisting of uniformly effective
$\tau $
-open sets.
Definition 2.1. A set
$A\subseteq X$
is effectively dense w.r.t.
$(\tau ,\tau ')$
if there is a computable procedure that given a non-empty basic
$\tau $
-open set B, outputs a sequence of non-empty effective
$\tau $
-open sets
$U_s\subseteq B$
satisfying:
-
•
$U_s$
is eventually constant, with limit
$U_\infty \subseteq B\cap A$
. -
•
$U_{s}$
is contained in
${\mathrm {cl}_{\tau '}({U_{s+1}})}$
.
The procedure actually outputs indices of effective open sets, and the sequence of indices is eventually constant.
Example 2.1. Here is the simplest example of an effectively dense set. If
$A\subseteq X$
is an effective
$\tau $
-open set that is dense w.r.t.
$\tau $
, then A is effectively dense w.r.t.
$(\tau ,\tau ')$
, whatever
$\tau '$
is.
Indeed, given B, one can directly compute
$U=B\cap A$
with no mind-change. In other words, we define
$U_s=U_\infty =B\cap A$
for all s.
We now state the main result of this section.
Theorem 2.1 (An effective Baire category theorem).
Let
$(X,\tau )$
be a computable Polish space and
$\tau '$
a countably based topology that is effectively weaker than
$\tau $
. If
$A_n\subseteq X$
are uniformly effectively dense w.r.t.
$(\tau ,\tau ')$
, then
$\bigcap _n A_n$
contains a
$\tau '$
-computable point.
The proof is an application of the priority method with finite injury. We first prove the result on the Baire space, because it is simpler to work with: points of the Baire space are more concrete, and the Baire space has a basis of clopen sets.
Proof on the Baire space
Let
$(X,\tau )$
be the Baire space with the usual product topology, and
$\tau '$
be a countably based topology, effectively weaker than
$\tau $
.
A basic
$\tau $
-open set B has the form
$[\sigma ]$
for some finite sequence
$\sigma \in {\mathbb {N}}^{<{\mathbb {N}}}$
. We then denote by
$U^n_s(\sigma )$
and
$U^n_\infty (\sigma )$
the open sets witnessing the effective density of
$A_n$
and associated with B.
We can assume w.l.o.g. that the strings defining the open sets
$U^n_s(\sigma )$
are proper extensions of
$\sigma $
, which can be achieved by appending a
$0$
at the end of each string if needed. We recall that the basic
$\tau '$
-open sets
$V_i$
are uniformly effective
$\tau $
-open sets. Let
$V_i[s]$
be the finite union of cylinders obtained at stage s in the computable enumeration of
$V_i$
.
We build a
$\tau '$
-computable point as a limit
$x=\lim _s\lim _n\sigma _n[s]$
of a computable double-sequence of finite strings
$\sigma _n[s]$
. We will build this double-sequence with the following properties:
-
(i) The string
$\sigma _{n+1}[s]$
extends some string defining
$U^n_s(\sigma _n[s])$
. Therefore,
$\sigma _{n+1}[s]$
properly extends
$\sigma _n[s]$
and these strings converge to some
$x[s]=\lim _n\sigma _n[s]$
. -
(ii) For each n, if s is sufficiently large then
$\sigma _n[s]$
is constant w.r.t. s and
$[\sigma _n[s]]\subseteq A_n$
, so
$x[s]$
converge to some
$x\in \bigcap _n A_n$
. -
(iii) For
$i\leq r\leq s$
, if
$x[r]\in V_i[r]$
, then
$x[s]\in V_i$
and
$x\in V_i$
.
Claim 1. Condition (iii) implies that x is
$\tau '$
-computable.
Proof of the claim
It implies that for each i, one has
$$ \begin{align} x\in V_i\iff\exists s\geq i\text{ such that }x[s]\in V_i[s]. \end{align} $$
The backward direction is immediate, using
$r=s$
. The forward direction is also easy: if
$x\in V_i$
then
$x\in V_i[r]$
for some
$r\geq i$
, so
$x[s]\in V_i[r]$
for some
$s\geq r$
as
$x[s]$
converges to x and
$V_i[r]$
is open. As
$V_i[r]\subseteq V_i[s]$
, one has
$x[s]\in V_i[s]$
and moreover
$s\geq r\geq i$
.
As the right-hand side of (1) is c.e., the set
$\{i:x\in V_i\}$
is c.e. so x is
$\tau '$
-computable.
Therefore, conditions (i)–(iii) imply the result. It might be helpful to have in mind that in addition to condition (i), for each s,
$\sigma _{n+1}[s]$
will be exactly one of the strings defining
$U^n_s(\sigma _n[s])$
for almost all n.
We now build the double-sequence
$\sigma _n[s]$
, by induction on s. We first consider the case
$s=0$
: let
$\sigma _0[0]$
be the empty string, and inductively let
$\sigma _{n+1}[0]$
be the first (or any) string defining
$U^n_0(\sigma _n[0])$
.
Let
$s\in {\mathbb {N}}$
and assume that
$\sigma _n[r]$
has been defined for all
$r\leq s$
and all n and satisfy conditions (i) and (iii). Start with
$n=0$
, and as long as
$U^n_{s+1}(\sigma _n[s])=U^n_s(\sigma _n[s])$
, define
$\sigma _n[s+1]=\sigma _n[s]$
and increment n. If equality holds for all n, then we are done, otherwise let n be minimal such that
$U^n_{s+1}(\sigma _n[s])\neq U^n_s(\sigma _n[s])$
.
We now define
$\sigma _n[s+1]$
. To lighten the notations, let
$C=U^n_s(\sigma _n[s])$
and
$D=U^n_{s+1}(\sigma _n[s])$
. By assumption, C is contained in the
$\tau '$
-closure of D. Let V be the finite intersection of the
$V_i$
’s such that there exists r satisfying
$i\leq r\leq s$
and
$x[r]\in V_i[r]$
. It is a
$\tau '$
-open set.
Claim 2. V intersects C.
Proof of the claim
Both V and C contain
$x[s]$
. Indeed, if
$i\leq r\leq s$
and
$x[r]\in V_i[r]$
, then
$x[s]\in V_i$
by induction hypothesis (iii), so
$x[s]\in V$
. Moreover,
$x[s]$
extends
$\sigma _{n+1}[s]$
which extends a string defining
$U^n_s(\sigma _n[s])=C$
by (i), so
$x[s]\in C$
.
As C is contained in the
$\tau '$
-closure of D, V must intersect D. As a result, one can effectively find a string
$\sigma $
such that
$[\sigma ]\subseteq D\cap V$
. We then define
$\sigma _{n}[s+1]=\sigma $
, and inductively for
$m\geq n$
,
$$ \begin{align*} \sigma_{m+1}[s+1]\text{ is the first string defining }U^m_{s+1}(\sigma_{m}[s+1]). \end{align*} $$
Conditions (i) and (iii) are satisfied by construction. Condition (ii) holds by induction on n: if
$\sigma _n[s]$
is constantly equal to a string
$\sigma $
for sufficiently large s, then
$U^n_s(\sigma _n[s])$
is constantly equal to
$U^n_\infty (\sigma )\subseteq A_n$
for large s, so
$\sigma _{n+1}[s+1]=\sigma _{n+1}[s]$
for large s. As a result,
$\sigma _{n+1}[s]$
is eventually constant when s grows, and eventually contained in
$A_n$
.
We now show how the result on the Baire space can be transferred to an arbitrary computable Polish space X.
Proof on any computable Polish space
Let
$(X,\tau )$
be a computable Polish space and
$\tau '$
and
$A_n$
satisfy the assumptions of the theorem. There exits a computable effectively open surjective map
$f:{\mathcal {N}}\to X$
. Using f, we can work in the Baire space, by considering the sets
$f^{-1}(A_n)$
and the topology
$\tau ^{\prime }_f:=f^{-1}(\tau ')$
. It suffices to show that these sets are effectively dense w.r.t.
$(\tau _{\mathcal {N}},\tau ^{\prime }_f)$
, and that a point
$x\in {\mathcal {N}}$
is
$\tau ^{\prime }_f$
-computable if and only if
$f(x)$
is
$\tau '$
-computable.
For the first fact, we need to compute
$U^{\prime }_s$
associated with
$f^{-1}(A_n)$
. Given a finite string
$\sigma $
, compute a basic
$\tau $
-open set
$B\subseteq f([\sigma ])$
, then compute
$U_s$
and let
$U^{\prime }_s=[\sigma ]\cap f^{-1}(U_s)$
. One easily shows that they satisfy the conditions to make
$f^{-1}(A_n)$
effectively dense.
Finally, the basic
$\tau ^{\prime }_f$
-neighborhoods of
$x\in {\mathcal {N}}$
are precisely the preimages of the basic
$\tau '$
-neighborhoods of
$f(x)$
, so x is
$\tau ^{\prime }_f$
-computable iff
$f(x)$
is
$\tau '$
-computable.
In the sequel, we will see applications of this technique. As the classical Baire category theorem, Theorem 2.1 is very modular: if one can build a
$\tau '$
-computable point satisfying properties
$A_n$
and a
$\tau '$
-computable point satisfying properties
$B_n$
, both using Theorem 2.1, then one can build a
$\tau '$
-computable point satisfying
$A_n$
and
$B_n$
at the same time. We state a direct consequence which is particularly useful in practice. Say that
$P\subseteq X$
is a
$\Pi ^0_2(\tau )$
-set if P is the intersection of a sequence of uniformly effective
$\tau $
-open sets. Under the same assumptions as Theorem 2.1, we obtain:
Corollary 2.1. Let
$A_n\subseteq X$
be uniformly effective dense w.r.t.
$(\tau ,\tau ')$
and
$P\subseteq X$
be a
$\Pi ^0_2(\tau )$
-set that is dense w.r.t.
$\tau $
. The set
$P\cap \bigcap _n A_n$
contains a
$\tau '$
-computable point.
3 Generically weaker topology
We now come to the main topic of this article. Let X be a set endowed with two countably based topologies
$\tau ,\tau '$
where
$\tau '$
is weaker than
$\tau $
. We want to understand when these two topologies induce different sets of computable points.
If C is a subset of X, then a topology on X induces a topology on C, obtained by intersecting the open sets with C. We say that
$\tau $
and
$\tau '$
agree on C if they induce the same topology on C.
Definition 3.1. Let
$\tau '$
be weaker than
$\tau $
. We say that
$\tau '$
is generically weaker than
$\tau $
if every
$C\subseteq X$
on which
$\tau $
and
$\tau '$
agree is meager in
$(X,\tau )$
.
This definition has a first immediate consequence.
Proposition 3.1. If
$\tau '$
is generically weaker than
$\tau $
then there exists
$x\in X$
such that no Turing machine translates its
$\tau '$
-names into
$\tau $
-names.
Proof Indeed, for every Turing machine
$M_n$
, if
$C_n$
is the set of points x such that
$M_n$
translates
$\tau '$
-names of x into
$\tau $
-names of x, then
$\tau $
and
$\tau '$
agree on
$C_n$
, so
$C_n$
is meager. As there are countably many Turing machines, the sets
$C_n$
cannot cover X by the Baire category theorem.
The notion of a generically weaker topology is a sufficient condition to ensure the existence of such points. However, we will see with Theorem 3.3 that it is almost necessary, if we allow the Turing machines to have access to any oracle.
In Section 3.2 we will be interested in building such a point x effectively, i.e., in making it
$\tau '$
-computable but not
$\tau $
-computable. Before, we need to briefly investigate our notion of generically weaker topology.
3.1 Characterization
Checking that
$\tau '$
is generically weaker than
$\tau $
may be difficult, using the raw definition. We give a characterization that is easier to check in practice, and which will lead to an effective version.
The following notions witness that some
$\tau $
-open sets are far from being
$\tau '$
-open.
Definition 3.2 (Witness).
Let B be a non-empty
$\tau $
-open set. A B-witness is a non-empty
$\tau $
-open set
$U\subseteq B$
that does not contain any non-empty
$V\cap B$
where V is
$\tau '$
-open.
Remark 3.1. It is helpful to have a formulation in terms of converging sequences: a non-empty open set
$U\subseteq B$
is a B-witness if and only if every
$x\in U$
is a limit, in the topology
$\tau '$
, of a sequence
$(x_n)_{n\in {\mathbb {N}}}$
in
$B\setminus U$
.
We now state and prove the main result of this section, which is a characterization of generically weaker topologies.
Proposition 3.2 (A characterization of generically weaker topologies).
Let
$(X,\tau )$
be a Polish space and
$\tau '$
be a weaker countably based topology on X. The following statements are equivalent
$:$
-
•
$\tau '$
is generically weaker than
$\tau $
. -
• Every non-empty
$\tau $
-open set B has a B-witness.
This result usually makes it easy to check that
$\tau '$
is generically weaker than
$\tau $
. In practice, one should start showing the existence of an X-witness, and then adapting the proof to any subspace
$B\in \tau $
in order to obtain a B-witness. Moreover, this characterization will naturally lead to an effective version (Definition 3.3).
Proof of Proposition 3.2
Assume that some non-empty
$B\in \tau $
has no B-witness. We first show that for every non-empty
$\tau $
-open set
$U\subseteq B$
, there exists
$V\in \tau '$
such that
$B\cap {\mathrm {cl}_{\tau }({V})}=B\cap {\mathrm {cl}_{\tau }({U})}$
. We express U as the union of all the
$\tau $
-basic open sets
$U_i\subseteq U$
. Each
$U_i$
is not a B-witness, so there exists
$V_i\in \tau '$
such that
$\emptyset \neq B\cap V_i\subseteq U_i$
. Let
$V=\bigcup _i V_i$
. One has
$B\cap V\subseteq U$
, and
$B\cap U\subseteq {\mathrm {cl}_{\tau }({V})}$
as V intersects each
$B\cap U_i$
. As a result,
$B\cap {\mathrm {cl}_{\tau }({V})}=B\cap {\mathrm {cl}_{\tau }({U})}$
.
Let
$(U_n)_{n\in {\mathbb {N}}}$
be an enumeration of the basic
$\tau $
-open sets contained in B and let
$(V_n)_{n\in {\mathbb {N}}}$
be
$\tau '$
-open sets such that
$B\cap {\mathrm {cl}_{\tau }({V_n})}=B\cap {\mathrm {cl}_{\tau }({U_n})}$
. Let
$C=\bigcap _n (U_n\triangle V_n)^c$
. By definition of C,
$\tau '$
and
$\tau $
agree on C, because
$U_n\cap C=V_n\cap C$
for all n. We show that C is
$\tau $
-co-meager in B. It is sufficient to show that each
$U_n\triangle V_n$
is nowhere
$\tau $
-dense in B, and indeed
$$ \begin{align*} B\cap {\mathrm{cl}_{\tau}({U_n\triangle V_n})}\subseteq B\cap(\partial_\tau V_n\cup \partial_\tau U_n). \end{align*} $$
The sets
$\partial _\tau {V_n}$
and
$\partial _\tau {U_n}$
are
$\tau $
-boundaries of
$\tau $
-open sets, so they are nowhere
$\tau $
-dense. Therefore,
$\tau '$
is not generically weaker than
$\tau $
.
Conversely, assume that each non-empty
$B\in \tau $
has a B-witness. Let
$C\subseteq X$
be such that
$\tau '$
and
$\tau $
agree on C, and let us show that C is nowhere dense. Given a non-empty
$\tau $
-open set B, we need to find a non-empty
$\tau $
-open set
$W\subseteq B$
disjoint from C. Let U be a B-witness and
$B'$
be a non-empty
$\tau $
-open set such that
${\mathrm {cl}_{\tau }({B'})}\subseteq U$
. If
$B'$
is disjoint from C then take
$W=B'$
. If
$B'$
intersects C, then let
$V\in \tau '$
be such that
$B'\cap C=V\cap C$
. V intersects U so V intersects
$B\setminus U$
hence
$B\setminus {\mathrm {cl}_{\tau }({B'})}$
. Therefore
$W=V\cap B\setminus {\mathrm {cl}_{\tau }({B'})}$
is non-empty and disjoint from C.
Remark 3.2. The proof of this result also implies that in Definition 3.1, one can replace the condition that C is “meager” by the apparently stronger condition that C is “nowhere dense” in
$(X,\tau )$
, giving the same notion.
The next example illustrates how Proposition 3.2 makes it easy to show that a topology is generically weaker than another one.
Example 3.1 (Cantor vs. Scott).
Let
$(X,\tau )$
be the Cantor space with the Cantor topology generated by the cylinders, and
$\tau '$
be the Scott topology generated by the sets
$\{x\in X:x_n=1\}$
, where
$n\in {\mathbb {N}}$
and
$x_n$
is the bit of x at position n. It is easy to see that
$\tau '$
is generically weaker than
$\tau $
.
First, the cylinder
$[0]$
contains no non-empty Scott open set so it is an X-witness. More generally, for any cylinder
$[u]$
, the cylinder
$[u0]$
contains no Scott open set intersected with
$[u]$
, so
$[u0]$
is a
$[u]$
-witness.
3.2 Effective version
We now effectivize the notion of a generically weaker topology, using Proposition 3.2, in order to prove the existence of
$\tau '$
-computable points that are not
$\tau $
-computable.
Definition 3.3. Say that
$\tau '$
is effectively generically weaker than
$\tau $
if there is a computable function sending each basic
$\tau $
-open set B to a B-witness
$U_B$
.
Note that
$U_B$
can be assumed to be a basic
$\tau $
-open set (because a non-empty subset of a B-witness is also a B-witness), and the computation takes an index of B as input and outputs an index of
$U_B$
. Example 3.1 is effective.
We now state the main result of this article, giving relatively simple conditions implying that
$\tau $
and
$\tau '$
do not induce the same computable points.
Theorem 3.1. Let
$(X,\tau )$
be a computable Polish space and
$\tau '$
an effectively weaker countably based topology. If
$\tau '$
is effectively generically weaker than
$\tau $
then there exists a
$\tau '$
-computable point that is not
$\tau $
-computable. Moreover, such a point can be found in any dense
$\Pi ^0_2(\tau )$
-set.
The proof is an application of the priority method with finite injury, but our effective Baire category theorem (Theorem 2.1) drastically simplifies the proof: we essentially have to give the strategy to defeat one Turing machine attempting to
$\tau $
-compute x, and the effective Baire category theorem takes charge of the intertwining between the strategies.
Proof We apply our effective Baire category theorem (Theorem 2.1). Let
$A_n$
be the set of points x whose set of indices of basic
$\tau $
-neighborhoods is not
$W_n$
, the nth c.e. subset of
${\mathbb {N}}$
. We show that
$A_n$
is effectively dense w.r.t. (
$\tau ,\tau ')$
(Definition 2.1), uniformly in n.
First, we can assume that for each basic
$\tau $
-open set B, the B-witness
$U_B$
satisfies:
$U_B$
is contained in the
$\tau '$
-closure of
$B\setminus {\mathrm {cl}_{\tau }({U_B})}$
. Indeed, it can be achieved by replacing
$U_B$
, which is a metric ball
$B(s,r)$
by the ball
$B(s,r/2)$
.
Let us now show that
$A_n$
is effectively dense w.r.t.
$(\tau ,\tau ')$
. Given a basic
$\tau $
-open ball B, we output
$U_B$
as long as the index of
$U_B$
does not appear in
$W_n$
, and then switch to
$B\setminus {\mathrm {cl}_{\tau }({U_B})}$
if it appears. More precisely, let
$$ \begin{align*} U_s=\begin{cases} U_B,&\text{if } W_n[s] \text{ does not contain the index of } U_B,\\ B\setminus {\mathrm{cl}_{\tau}({U_B}),}&\text{otherwise.} \end{cases} \end{align*} $$
We check the three conditions in Definition 2.1. First,
$U_s\subseteq B$
by definition. Condition 1: there is at most one mind-change, if the index of
$U_B$
appears in
$W_n$
at stage s. Condition 2: the limit set is
$U_\infty =B\setminus {\mathrm {cl}_{\tau }({U_B})}$
if the index of
$U_B$
belongs to
$W_n$
, and
$U_B$
if it does not. In any case,
$W_n$
is not the set of basic
$\tau $
-neighborhoods of any point in
$U_\infty $
, so
$U_\infty $
is contained in
$A_n$
. Condition 3:
$U_B$
is contained in the
$\tau '$
-closure of
$B\setminus {\mathrm {cl}_{\tau }({U_B})}$
, so
$U_s$
is always contained in the
$\tau '$
-closure of
$U_{s+1}$
.
We can apply Theorem 2.1, which produces a
$\tau '$
-computable point that belongs to
$\bigcap _n A_n$
, i.e., that is not
$\tau $
-computable.
Moreover, one can build such a point in
$\bigcap _n O_n$
, where
$O_n$
are dense uniformly effective open sets, because
$O_n$
are uniformly effectively dense in the sense of Definition 2.1.
The next example shows that when the topologies are induced by norms on a vector space, if a topology is strictly weaker then it is generically weaker, and there is no intermediate case. This phenomenon is at the core of Pour-El and Richards’ first main theorem [Reference Pour-El and Richards23].
Example 3.2 (Norms).
Let X be a computable vector space and
${\left \Vert {.} \right \Vert }_1$
and
${\left \Vert {.} \right \Vert }_2$
be computable norms (see [Reference Pour-El and Richards23] for definitions). If
${\left \Vert {.} \right \Vert }_2$
is strictly weaker than
${\left \Vert {.} \right \Vert }_1$
, then the topology induced by
${\left \Vert {.} \right \Vert }_2$
is effectively generically weaker than the topology induced by
${\left \Vert {.} \right \Vert }_1$
.
Indeed, let
$(x_n)_{n\in {\mathbb {N}}}$
be a sequence satisfying
${\left \Vert {x_n} \right \Vert }_1=1$
and
${\left \Vert {x_n} \right \Vert }_2\to 0$
. The ball
$B_1(x,r/3)$
is a
$B_1(x,r)$
-witness because any
$y\in B_1(x,r/3)$
is the limit in the
${\left \Vert {.} \right \Vert }_2$
norm of
$y+(2r/3)x_n\in B_1(x,r)\setminus B_1(x,r/3)$
.
Therefore, Theorem 3.1 implies the existence of a point x that is computable in the norm
${\left \Vert {.} \right \Vert }_2$
but not in the norm
${\left \Vert {.} \right \Vert }_1$
. It is a particular case of Pour-El and Richards’ first main theorem [Reference Pour-El and Richards23].
Example 3.3 (Ergodic decomposition).
This example is taken from [Reference Hoyrup, Mayr and Portier11, Reference Hoyrup12]. Theorem 3.4.1 in [Reference Hoyrup12] states the existence of two non-computable shift-invariant ergodic measures
$\mu _1,\mu _2$
whose average
$\frac {\mu _1+\mu _2}{2}$
is computable. Theorem 3.1 can be applied to prove this result.
Let X be the space of pairs of shift-invariant measures. Let
$\tau $
be the product of the weak* topology. Consider the average operator
$f:X\to {\mathcal {M}}(2^{\mathbb {N}})$
sending
$(\mu _1,\mu _2)$
to
$\frac {\mu _1+\mu _2}{2}$
, and let
$\tau '$
be the initial topology of f. Theorem 3.4.2 in [Reference Hoyrup12] implies that
$\tau '$
is effectively generically weaker than
$\tau $
, although it is not expressed in the same way. The idea is that if
$(\mu _1,\mu _2)$
is a pair such that
$\mu _1\neq \mu _2$
, then for
$\lambda \in [0,1]$
, the pairs
$$ \begin{align*} ((1-\lambda)\mu_1+ \lambda\mu_2,(1-\lambda)\mu_2+\lambda\mu_1) \end{align*} $$
have the same
$\tau '$
-neighborhoods as
$(\mu _1,\mu _2)$
and their proximity to
$(\mu _1,\mu _2)$
in the topology
$\tau $
can be freely controlled by the choice of
$\lambda $
.
In
$(X,\tau )$
, the set of pairs of ergodic measures is a dense
$\Pi ^0_2$
-set. Therefore, Theorem 3.1 implies the existence of a pair
$(\mu _1,\mu _2)$
of ergodic measures which is
$\tau '$
-computable but not
$\tau $
-computable; in other words,
$\mu _1$
and
$\mu _2$
are not computable but their average is.
3.3 Weihrauch reducibility
If x is a point provided by Theorem 3.1, then
$\tau $
-names of x contain strictly more information than
$\tau '$
-names of x. The proof of Theorem 3.1 can be adapted to show that computing
$\tau $
-names from
$\tau '$
-names is at least as hard as computing a limit, or equivalently the Turing jump.
Formally, it is expressed using Weihrauch reducibility. Let us recall the appropriate definitions, more details can be found in [Reference Brattka, Gherardi, Pauly, Brattka and Hertling5].
Definition 3.4. Let
$f:X\to Y$
and
$g:Z\to W$
be functions between represented spaces.
Say that f is Weihrauch reducible to g, written
$f\leq _W g$
, if there exist computable functions
$H,K:\subseteq {\mathcal {N}}\to {\mathcal {N}}$
such that for any realizer
$G:\subseteq {\mathcal {N}}\to {\mathcal {N}}$
of g, the function
$p\mapsto H(G(K(p)),p)$
is a realizer of f.
Say that f is strongly Weihrauch reducible to g, written
$f\leq _{sW} g$
, if there exist computable functions
$H,K:\subseteq {\mathcal {N}}\to {\mathcal {N}}$
such that for any realizer
$G:\subseteq {\mathcal {N}}\to {\mathcal {N}}$
of g, the function
$p\mapsto H(G(K(p)))$
is a realizer of f.
Definition 3.5. The function
$\lim $
sends a converging sequence of elements of the Baire space to its limit.
Theorem 3.2 (Weihrauch reduction of
$\lim $
is necessary).
If
$\tau '$
is effectively generically weaker than
$\tau $
, then
$\lim $
is Weihrauch reducible to
${\mathrm {id}}:(X,\tau ')\to (X,\tau )$
.
Proof idea
The function
$\lim $
is strongly Weihrauch equivalent to the function
$\mathrm {im}:{\mathcal {N}}\to 2^{\mathbb {N}}$
sending
$p\in {\mathcal {N}}$
to the set
${\mathrm {im}({p})}=\{p(n):n\in {\mathbb {N}}\}$
, so we show how to reduce
$\mathrm {im}$
to
${\mathrm {id}}$
.
Let
$p\in {\mathcal {N}}$
, be given as oracle. We apply the construction of the proof of Theorem 2.1. The sets
$A_n$
are implicitly defined by their density functions approximations as follows: given B, let
$$ \begin{align*} U_s=\begin{cases} U_B,&\text{if }n\notin \{p(0),\ldots,p(s)\},\\ B\setminus {\mathrm{cl}_{\tau}({U_B}),}&\text{if }n\in\{p(0),\ldots,p(s)\}. \end{cases} \end{align*} $$
The construction builds a point
$x_p$
that is
$\tau '$
-computable (relative to p). If one is given
$x_p$
in the topology
$\tau $
, together with p, then it is possible to inductively find for each n whether
$n\in {\mathrm {im}({p})}$
. The idea is that if we are given
$x_p$
in the topology
$\tau $
, then we can decide whether
$x_p\in U_B$
or
$x_p\in B\setminus {\mathrm {cl}_{\tau }({U_B})}$
, from which we can deduce whether
$n\in {\mathrm {im}({p})}$
.
We do not know whether a strong Weihrauch reduction can be obtained and leave it as an open question. However, it is always possible to obtain a strong Weihrauch reduction, relative to some oracle. Moreover, the notion of a generically weaker topology is necessary and sufficient for the topologies
$\tau ,\tau '$
to fail to be
$\sigma $
-homeomorphic, up to restriction to a subspace.
Theorem 3.3. Let
$(X,\tau )$
be Polish,
$\tau '\subseteq \tau $
be countably based
$T_0$
and let
$\iota ={\mathrm {id}}:(X,\tau ')\to (X,\tau )$
. The following conditions are equivalent:
-
1.
$\iota $
is not
$\sigma $
-continuous. -
2. There exists
$Y\subseteq X$
such that
$\tau _Y$
is Polish and
$\tau ^{\prime }_Y$
is generically weaker than
$\tau _Y$
. -
3.
$\lim $
is Weihrauch reducible to
$\iota $
relative to an oracle. -
4.
$\lim $
is strongly Weihrauch reducible to
$\iota $
relative to an oracle.
In that case
$(Y,\tau _Y)$
is even homeomorphic to the Baire space
${\mathcal {N}}$
. The proof uses a strong result from Descriptive Set Theory, Pawlikowski–Sabok’s theorem [Reference Pawlikowski and Sabok21, Reference Pawlikowski and Sabok22]. This theorem says that every sufficiently definable (bianalytic) map between metric spaces is either
$\sigma $
-continuous, or contains one particular function P, which is not
$\sigma $
-continuous. Let us precisely state this result.
A subset A of a topological space X is analytic if it is the image of a continuous function
$f:{\mathcal {N}}\to X$
. A set
$A\subseteq X$
is bianalytic if both A and
$X\setminus A$
are analytic. A topological space is analytic if it embeds as an analytic subset of a Polish space. A function
$f:X\to Y$
between analytic spaces is bianalytic if the preimage of every bianalytic set is bianalytic.
The Baire space
${\mathcal {N}}={\mathbb {N}}^{\mathbb {N}}$
is endowed with two different topologies, both obtained as the product topology of some topology on
${\mathbb {N}}$
. The first one is the usual topology obtained
$\tau _{\mathcal {N}}$
from the discrete topology on
${\mathbb {N}}$
. The second one,
$\tau ^{\prime }_{\mathcal {N}}$
, is obtained by identifying
${\mathbb {N}}$
with
$\{0\}\cup \{2^{-n}:n\in {\mathbb {N}}\}\subseteq {\mathcal {R}}$
, via
$0\mapsto 0$
and
$n\mapsto 2^{-n+1}$
for
$n\geq 1$
. It makes
$({\mathcal {N}},\tau ^{\prime }_{\mathcal {N}})$
homeomorphic to the Cantor space.
Definition 3.6. Pawlikowski’s function is defined as
$$ \begin{align*} P={\mathrm{id}}:({\mathcal{N}},\tau^{\prime}_{\mathcal{N}})\to ({\mathcal{N}},\tau_{\mathcal{N}}). \end{align*} $$
Theorem 3.4 (Pawlikowski–Sabok [Reference Pawlikowski and Sabok21, Reference Pawlikowski and Sabok22]).
Let
$X,Y$
be analytic spaces and
$f:X\to Y$
be bianalytic. Either f is
$\sigma $
-continuous or f contains P in the following sense
$:$
there exist two topological embeddings
$\varphi :({\mathcal {N}},\tau ^{\prime }_{\mathcal {N}})\to X$
and
$\psi :({\mathcal {N}},\tau _{\mathcal {N}})\to Y$
such that
$f\circ \varphi =\psi \circ P$
.
This result was first proved by Solecki for Baire class 1 functions in [Reference Solecki26], and then improved in this form by Pawlikowski and Sabok. We also mention an effective version of the result by Debs [Reference Debs10]. It was observed by Carroy (personal communication) and Lutz [Reference Lutz19] that Solecki’s and Pwlikowski-Sabok’s results have a direct consequence in terms of Weihrauch reducibility: if P embeds in f as in the statement, then P is strongly Weihrauch reducible to f relative to an oracle. A proof that P is strongly Weihrauch equivalent to
$\lim $
can be found in [Reference Lutz19].
We use the result in our setting, showing at the same time that some version of the result holds when X is not metrizable but still countably based.
We first observe that
$\tau ^{\prime }_{\mathcal {N}}$
, compared to
$\tau _{\mathcal {N}}$
, is another example of a generically weaker topology.
Proposition 3.3. On
${\mathcal {N}}$
, the topology
$\tau ^{\prime }_{\mathcal {N}}$
is generically weaker than
$\tau _{\mathcal {N}}$
.
Proof Given a finite string
$u\in {\mathbb {N}}^*$
, a
$[u]$
-witness is given by
$[u0]$
. Indeed, every
$p\in [u0]$
is the limit, in the topology
$\tau ^{\prime }_{\mathcal {N}}$
, of the sequence
$p_n$
obtained by replacing
$0$
by n in p at position
$|u|$
. One has
$p_n\in [u]\setminus [u0]$
, which shows that
$[u0]$
is a
$[u]$
-witness (see Remark 3.1).
We start by reducing countably based spaces to metrizable spaces. It is possible because the standard representation of countably based spaces has very good properties, already exploited in [Reference de Brecht6, Reference de Brecht, Yamamoto, Bauer, Hertling and Ko7, Reference Callard, Hoyrup, Paul and Bläser9], that allow to reduce Descriptive Set Theory on countably based spaces to Descriptive Set Theory on subspaces of the Baire space. We give another manifestation of this phenomenon, which is proved using similar techniques.
Say that a function
$f:X\to Y$
between represented spaces is
$\sigma $
-computable if there exist countably many sets
$X_n\subseteq X$
such that
$X=\bigcup _{n\in {\mathbb {N}}} X_n$
and such that the restriction of f to each
$X_n$
is computable.
Lemma 3.1 (
$\sigma $
-computable vs.
$\sigma $
-computable realizer).
Let
$X,Y$
be (effective) countably based
$T_0$
-spaces with their standard representations. A function
$f:X\to Y$
is
$\sigma $
-continuous (
$\sigma $
-computable) iff it has a
$\sigma $
-continuous (
$\sigma $
-computable) realizer.
Proof We prove the effective version, the non-effective version being obtained by relativization to any oracle.
One implication is straightforward. Assume that f is
$\sigma $
-computable, i.e.,
$X=\bigcup _{n\in {\mathbb {N}}}X_n$
and each
$f{_{|{X_n}}}$
is computable. We can assume that the sets
$X_n$
are pairwise disjoint, replacing
$X_n$
with
$X_n\setminus (X_0\cup \dots \cup X_{n-1})$
if needed. Each
$f{_{|{X_n}}}$
has a computable realizer
$F_n:\delta _X^{-1}(X_n)\to {\mathcal {N}}$
. The combination of all
$F_n$
’s is a
$\sigma $
-computable realizer of f.
We now prove the other implication. Assume that f has a
$\sigma $
-computable realizer
$F:{\mathrm {dom}}(\delta _X)\to {\mathcal {N}}$
, with
${\mathrm {dom}}(\delta _X)=\bigcup _{n\in {\mathbb {N}}} A_n$
and each
$F{_{|{A_n}}}$
is computable. For each
$n\in {\mathbb {N}}$
and
$\sigma \in {\mathbb {N}}^*$
, let
$$ \begin{align*} X_{n,\sigma}=\{x\in \delta_X([\sigma]):A_n\text{ is dense in }\delta_X^{-1}(x)\cap[\sigma]\}, \end{align*} $$
where a set A is dense in a set B if B is contained in the closure of
$A\cap B$
.
Let us show that the restriction
$f{_{|{X_{n,\sigma }}}}$
is computable. Let
$B_i\subseteq Y$
be a basic open set. We want to show that the preimage of
$B_i$
under this restriction is an effective open subset of
$X_{n,\sigma }$
, uniformly in i. As
$\delta _Y\circ F$
is computable on
$A_n$
, there exists an effective open set
$U_i\subseteq {\mathcal {N}}$
, that can be computed uniformly in i, such that
$$ \begin{align} U_i\cap A_n=(\delta_Y\circ F)^{-1}(B_i)\cap A_n=(f\circ \delta_X)^{-1}(B_i)\cap A_n. \end{align} $$
Claim 3. One has
$$ \begin{align*} f^{-1}(B_i)\cap X_{n,\sigma}=\delta_X([\sigma]\cap U_i)\cap X_{n,\sigma}. \end{align*} $$
Proof of the claim
If
$x\in X_{n,\sigma }$
, then x has a
$\delta _X$
-name
$p\in [\sigma ]\cap A_n$
. If
$x\in f^{-1}(B_i)$
then
$p\in (f\circ \delta _X)^{-1}(B_i)$
so by (2),
$p\in U_i$
, which implies that
$x\in \delta _X([\sigma ]\cap U_i)$
.
Conversely, if
$x\in X_{n,\sigma }$
has a name
$p\in [\sigma ]\cap U_i$
, then it has a name
$q\in [\sigma ]\cap U_i\cap A_n$
because
$A_n$
is dense in
$[\sigma ]\cap \delta _X^{-1}(x)$
and
$U_i$
is open. Again by (2),
$q\in (f\circ \delta _X)^{-1}(B_i)$
so
$x\in f^{-1}(B_i)$
.
The set
$\delta _X([\sigma ]\cap U_i)$
is an effective open set, uniformly in i, so
$f{_{|{X_{n,\sigma }}}}$
is computable.
It remains to show that
$X=\bigcup _{n,\sigma } X_{n,\sigma }$
. For
$x\in X$
,
$\delta _X^{-1}(x)$
is Polish and is covered by
$\bigcup _{n\in {\mathbb {N}}} A_n$
, so some
$A_n$
must be somewhere dense in
$\delta _X^{-1}(x)$
. In other words, there must exist some
$n\in {\mathbb {N}}$
and some
$\sigma \in {\mathbb {N}}^*$
such that
$A_n$
is dense in
$\delta _X^{-1}(x)\cap [\sigma ]$
, therefore
$x\in X_{n,\sigma }$
.
We will also need the following simple result.
Lemma 3.2. Let X be countably based and
$T_0$
, and
$\delta $
its standard representation. For
$A\subseteq X$
, A is analytic
$\iff \ \delta ^{-1}(A)$
is analytic.
Proof If
$\delta ^{-1}(A)$
is analytic, then
$\delta ^{-1}(A)$
is the image of a continuous function
$f:{\mathcal {N}}\to {\mathcal {N}}$
, so A is the image of the continuous function
$\delta \circ f$
, hence A is analytic.
For the converse implication, we use the following fact: X embeds in
${{\mathcal {P}}({\mathbb {N}})}$
, which has a total admissible representation
${\delta _{\mathcal {P}}}$
, and
$\delta $
is the restriction of
${\delta _{\mathcal {P}}}$
to
${\delta _{\mathcal {P}}^{-1}}(X)$
. Therefore, we can simply assume that X is
${{\mathcal {P}}({\mathbb {N}})}$
. Let
$A\subseteq {{\mathcal {P}}({\mathbb {N}})}$
be analytic. A is the image of a continuous function
$f:{\mathcal {N}}\to {{\mathcal {P}}({\mathbb {N}})}$
. Let
$F:{\mathcal {N}}\to {\mathcal {N}}$
be a continuous realizer of f, i.e., satisfy
$f={\delta _{\mathcal {P}}}\circ F$
. Let
$R=\{(p,q)\in {\mathcal {N}}\times {\mathcal {N}}:{\delta _{\mathcal {P}}}(p)={\delta _{\mathcal {P}}}\circ F\}$
is easily
and its first projection is
${\delta _{\mathcal {P}}^{-1}}(A)$
, which is therefore analytic.
Proof of Theorem 3.3
Of course, each one of conditions
$2-4$
implies
$1$
.
We show that
$1$
implies
$2-4.$
Let
$\delta $
be a total open representation of
$(X,\tau )$
, which exists as
$\tau $
is Polish. Let
$\delta '$
be the standard representation of
$(X,\tau ')$
, which is the restriction of the representation
${\delta _{\mathcal {P}}}$
of
${{\mathcal {P}}({\mathbb {N}})}$
, after embedding
$(X,\tau ')$
in
${{\mathcal {P}}({\mathbb {N}})}$
. Assume that
$\iota ={\mathrm {id}}:(X,\tau ')\to (X,\tau )$
is not
$\sigma $
-continuous. We apply Theorem 3.4 to
$f:=\iota \circ \delta ':{\mathrm {dom}}(\delta ')\to (X,\tau )$
. We need to check that f satisfies the conditions of this theorem.
Claim 4.
${\mathrm {dom}}(\delta ')$
is analytic and f is bianalytic.
Proof of the claim
As a subset of
${{\mathcal {P}}({\mathbb {N}})}$
, X is the image of the continuous function
$i_X:(X,\tau )\to {{\mathcal {P}}({\mathbb {N}})}$
, so it is analytic as
$(X,\tau )$
is Polish. Therefore,
${\mathrm {dom}}(\delta ')={\delta _{\mathcal {P}}^{-1}}(X)$
is analytic by Lemma 3.2.
Let
$A\subseteq (X,\tau )$
be analytic. It is the image of a continuous function
$h:{\mathcal {N}}\to (X,\tau )$
. The function h is also continuous from
${\mathcal {N}}$
to
$(X,\tau ')$
, so A is analytic in
$(X,\tau ')$
. Its preimage by
$\delta '$
is therefore analytic by Lemma 3.2. Applying the same argument to the complement of A,
$f^{-1}(A)$
is bianalytic.
Now, f is not
$\sigma $
-continuous. Indeed,
$f=\iota \circ \delta '$
has the same realizers as
$\iota $
. Applying Lemma 3.1 in one direction to
$\iota $
and in the other direction to f, we have:
$\iota $
is not
$\sigma $
-continuous, so it has no
$\sigma $
-continuous realizer; neither does f, so f is not
$\sigma $
-continuous.
Therefore
$f:({\mathcal {N}},\tau _{\mathcal {N}})\to (X,\tau )$
satisfies the assumptions of Theorem 3.4, which provides topological embeddings
$$ \begin{align*} \psi&:({\mathcal{N}},\tau_{\mathcal{N}})\to (X,\tau),\\ \varphi&:({\mathcal{N}},\tau^{\prime}_{\mathcal{N}})\to ({\mathcal{N}},\tau_{\mathcal{N}}), \end{align*} $$
satisfying
$f\circ \varphi =\psi \circ P$
, i.e.,
$\iota \circ \delta '\circ \varphi =\psi \circ P$
. As observed by Carroy (personal communication), and Lutz [Reference Lutz19], it implies that
$P\equiv _{sW}\lim $
is strongly Weihrauch reducible to
$\iota $
relative to an oracle computing
$\varphi $
and
$\psi $
. We have proved condition
$4$
, which also implies condition
$3.$
Let us prove condition
$2.$
Both
$\iota $
and P are the identity functions, with different topologies on their input and output spaces. Therefore, the condition
$\iota \circ \delta '\circ \varphi =\psi \circ P$
can be rewritten as
$\delta '\circ \varphi =\psi $
. As a result, we have:
-
1.
$\psi :({\mathcal {N}},\tau _{\mathcal {N}})\to (X,\tau )$
is a topological embedding. -
2.
$\psi =\delta '\circ \varphi :({\mathcal {N}},\tau ^{\prime }_{\mathcal {N}})\to (X,\tau ')$
is continuous.
Let
$Y={\mathrm {im}({\psi })}$
,
$\tau _Y$
be the topology on Y induced by
$\tau $
,
$\tau ^{\prime }_Y$
the topology on Y induced by
$\tau '$
and
$\tau ^{\prime \prime }_{\mathcal {N}}$
be the preimage of the topology
$\tau ^{\prime }_Y$
by
$\psi $
(
$\tau ^{\prime \prime }_{\mathcal {N}}=\psi ^{-1}(\tau ^{\prime }_Y)$
is usually called the initial topology of
$\psi $
). Both functions
$$ \begin{align*} \psi&:({\mathcal{N}},\tau_{\mathcal{N}})\to (Y,\tau_Y),\\ \psi&:({\mathcal{N}},\tau^{\prime\prime}_{\mathcal{N}})\to (Y,\tau^{\prime}_Y) \end{align*} $$
are homeomorphisms. The first one comes from
$1$
above. The second one comes from the fact that
$\psi $
is a bijection, is continuous and open, so it is a homeomorphism.
We now need to prove that
$\tau ^{\prime \prime }_{\mathcal {N}}$
is generically weaker than
$\tau _{\mathcal {N}}$
, which will conclude the proof. By 2,
$\tau ^{\prime \prime }_{\mathcal {N}}$
is weaker than
$\tau ^{\prime }_{\mathcal {N}}$
which is generically weaker than
$\tau _{\mathcal {N}}$
(Proposition 3.3), so
$\tau ^{\prime \prime }_{\mathcal {N}}$
is also generically weaker than
$\tau _{\mathcal {N}}$
. As a result,
$\tau ^{\prime }_Y$
is generically weaker than
$\tau _Y$
. Note that
$\tau _Y$
is Polish because
$(Y,\tau _Y)$
is homeomorphic to
$({\mathcal {N}},\tau _{\mathcal {N}})$
.
3.4 Three topologies
When comparing two topologies on a single space, the results obtained so far cannot be applied if the stronger topology is not Polish. In this section, we show a way of extending the results when one can find a third topology which is Polish.
Let
$(X,\tau )$
be a computable Polish space and
$\tau _1,\tau _2$
be effective countably based topologies such that
$\tau _1$
is effectively weaker than
$\tau _2$
and
$\tau _2$
is effectively weaker than
$\tau $
. We want to build a
$\tau _1$
-computable point that is not
$\tau _2$
-computable. The notion of generically weaker topology can be extended as follows.
Definition 3.7. We say that
$\tau _1$
is
$\tau $
-generically weaker than
$\tau _2$
if every set
$C\subseteq X$
on which
$\tau _1$
and
$\tau _2$
agree is
$\tau $
-meager.
Again, “meager” can be equivalently replaced by “nowhere dense,” with the same argument as in Remark 3.2. This notion is a generalization of Definition 3.1, which can be obtained by taking
$\tau _1=\tau '$
and
$\tau _2=\tau $
.
We introduce an effective version of being generically
$\tau $
-weaker, which will lead to Theorem 3.5.
Definition 3.8. Say that
$\tau _1$
is effectively
$\tau $
-generically weaker than
$\tau _2$
if given
$B\in \tau $
, one can compute non-empty
$B',B"\in \tau $
, and
$U\in \tau _2$
such that:
-
•
$B'\subseteq B\cap U$
, -
•
$B"\subseteq B\setminus U$
, -
•
$B'\subseteq {\mathrm {cl}_{\tau _1}({B"})}$
, i.e., every
$\tau _1$
-open set intersecting
$B'$
intersects
$B"$
.
Here,
$B,B'$
, and U are basic open sets represented by indices, but
$B"$
may be a general effective open set. By a similar argument as in Proposition 3.2, it can be shown that it is an effective version of Definition 3.7, i.e., that
$\tau _1$
is
$\tau $
-generically weaker that
$\tau _2$
if and only if it is effectively so, relative to some oracle. We now state the main result of this section. Again, it is easily proved thanks to our effective Baire category theorem 2.1.
Theorem 3.5 (
$\tau _1$
-computable but not
$\tau _2$
-computable).
If
$\tau _1$
is effectively
$\tau $
-generically weaker than
$\tau _2$
, then there exists
$x\in X$
that is
$\tau _1$
-computable but not
$\tau _2$
-computable. Moreover, such a point can be found in any
$\tau $
-dense
$\Pi ^0_2(\tau )$
-set.
Proof As in the proof of Theorem 3.1, let
$A_n$
be the set of points x whose set of
$\tau "$
-neighborhoods is not
$W_n$
. The sets
$A_n$
are uniformly effectively dense. Indeed, given B, output
$U_s=B'$
as long as
$W_n[s]$
does not contain the index of U, and then
$U_s=B"$
if
$W_n[s]$
contains that index.
4 An application
In this section, we give an application of Theorem 3.5 to give a clear and complete proof of a result that was stated in [Reference Amir, Hoyrup, Bojanczyk, Merelli and Woodruff1], just with a proof idea. A complete proof appears in the unpublished preprint [Reference Amir and Hoyrup2] but is very technical and difficult to read. Our effective Baire category theorem enables us to give a simpler proof, as it captures most of the technicality of the construction.
Let us first introduce the relevant notions.
4.1 Background on computable type
A compact pair is a pair
$(X,A)$
where X is a compact Polish space and
$A\subseteq X$
is a compact subset. The Hilbert cube is the computable Polish space
$Q=[0,1]^{\mathbb {N}}$
endowed with the metric
$$ \begin{align*} d_Q(x,y)=\sum_{i\in{\mathbb{N}}}2^{-i}|x_i-y_i|. \end{align*} $$
If X is a compact space and
$f,g:X\to Q$
are continuous functions, we define their distance
$d_X(f,g)=\max _{x\in X}d_Q(f(x),g(x))$
.
Definition 4.1. A compact set
$X\subseteq Q$
is semicomputable if the set
$Q\setminus X$
is an effective open set. A compact set
$X\subseteq Q$
is computable if it is semicomputable and contains a dense computable sequence.
A compact pair
$(X,A)$
has computable type if for every pair
$(Y,B)$
in Q that is homeomorphic to
$(X,A)$
, if Y and B are semicomputable then Y is computable.
A compact space X has computable type if the pair
$(X,\emptyset )$
has computable type.
Miller [Reference Miller20] proved that each sphere
${\mathbb {S}}_n$
and each pair
$({\mathbb {B}}_{n+1},{\mathbb {S}}_n)$
have computable type. Iljazović and Sušić [Reference Iljazović and Sušić13] proved that for each compact manifold M and each compact manifold with boundary
$(M,\partial M)$
have computable type.
In [Reference Amir, Hoyrup, Bojanczyk, Merelli and Woodruff1] we studied this property for simplicial pairs, i.e., compact pairs
$(X,A)$
consisting of a finite simplicial complex X and a subcomplex A. We gave a purely topological characterization of the simplicial pairs having computable type.
Definition 4.2. Let
$\epsilon>0$
. A compact pair
$(X,A)\subseteq Q$
has the
$\epsilon $
-surjection property if every continuous function
$f:X\to X$
satisfying
$f(A)\subseteq A$
and
$d_X(f,{\mathrm {id}}_X)<\epsilon $
is surjective.
Theorem 4.1 [Reference Amir, Hoyrup, Bojanczyk, Merelli and Woodruff1].
A simplicial pair
$(X,A)$
has computable type if and only if it has the
$\epsilon $
-surjection property for some
$\epsilon>0$
.
One implication of this theorem is that if
$(X,A)$
fails to have the
$\epsilon $
-surjection property for every
$\epsilon>0$
in an effective way (Definition 4.3), then
$(X,A)$
does not have computable type, i.e., has a copy
$(Y,B)$
in Q consisting of semicomputable sets, such that Y is not computable.
In order to formulate the definition, we recall the definition of the Hausdorff distance between non-empty compact sets
$A,B\subseteq Q$
:
$$ \begin{align*} d_H(A,B)=\max\left(\max_{a\in A}\min_{b\in B}d_Q(a,b),\max_{b\in B}\min_{a\in A}d_Q(a,b)\right). \end{align*} $$
Definition 4.3. Let
$(X,A)$
be a computable compact pair in Q. For
$\epsilon>0$
, say that
$\delta>0$
is an
$\epsilon $
-witness if there exists a continuous function
$f:X\to X$
satisfying
$f(A)\subseteq A$
and
$d_X(f,{\mathrm {id}}_X)<\epsilon $
, such that
$d_H(X,f(X))>\delta $
.
Say that
$(X,A)$
has computable witnesses if there exists a computable function sending each rational
$\epsilon>0$
to a rational
$\epsilon $
-witness
$\delta>0$
.
4.2 An application
We now state the result from [Reference Amir, Hoyrup, Bojanczyk, Merelli and Woodruff1], and give a proof by applying Theorem 3.5 and therefore using our effective Baire category theorem, Theorem 2.1.
Theorem 4.2. Let
$(X,A)\subseteq Q$
be a pair of semicomputable sets. If it has computable witnesses, then
$(X,A)$
does not have computable type, i.e., there exists a semicomputable copy of
$(X,A)$
such that X is not computable.
Remark 4.1. The statement given here is slightly stronger than the statement appearing in [Reference Amir, Hoyrup, Bojanczyk, Merelli and Woodruff1]. Indeed, in [Reference Amir, Hoyrup, Bojanczyk, Merelli and Woodruff1] the pair
$(X,A)$
is assumed to be computable. Moreover, the notion of witness defined above is weaker than in [Reference Amir, Hoyrup, Bojanczyk, Merelli and Woodruff1] (where f should be the identity on A). We have realized that this stronger result holds because the proof presented here is simpler and identifies more clearly the needed assumptions.
We now present the proof of this result.
We assume that
$(X,A)$
is embedded as a semicomputable pair in Q which has computable witnesses. First, if X is not computable then
$(X,A)$
does not have computable type and the result is proved. Therefore, we can assume for the rest of the proof that X is computable (however, A may not be computable). Consider the space
${\mathcal {C}}(X,Q)$
of continuous functions from X to Q. It is endowed with a complete computable metric
$d(f,g)=\max _{x\in Q}d_Q(f(x),g(x))$
, inducing a topology
$\tau $
. The subspace
${\mathcal {I}}(X,Q)$
of injective continuous functions from X to Q is a dense
$\Pi ^0_2$
-subset, in particular, it contains a dense computable sequence. We consider two weaker topologies
$\tau _1$
and
$\tau _2$
on
${\mathcal {C}}(X,Q)$
.
For each pair
$(U,V)$
of finite unions of basic open subsets of Q, let
$$ \begin{align*} {\mathcal{V}}_{U,V}=\{f\in{\mathcal{C}}(X,Q):f(X)\subseteq U,f(A)\subseteq V\}, \end{align*} $$
and let
$\tau _1$
be the topology generated by the sets
${\mathcal {V}}_{U,V}$
as a subbasis.
For each basic open subset B of Q, let
$$ \begin{align*} {\mathcal{U}}_B=\{f\in{\mathcal{C}}(X,Q):f(X)\cap B\neq \emptyset\}, \end{align*} $$
and let
$\tau _2$
be the topology generated by the sets
${\mathcal {U}}_B$
and
${\mathcal {V}}_{U,V}$
as a subbasis.
Our goal is to build an injective continuous function
$f\in {\mathcal {C}}(X,Q)$
such that
$f(X)$
and
$f(A)$
are semicomputable but
$f(X)$
is not computable; in other words, we want f to be
$\tau _1$
-computable but not
$\tau _2$
-computable.
We will apply Theorem 3.5, so we need to show that
$\tau _1$
is
$\tau $
-generically weaker than
$\tau _2$
.
Lemma 4.1. Let
$X\subseteq Q$
be computable and
$A\subseteq X$
be semicomputable. If the pair
$(X,A)$
has computable witnesses, then the topology
$\tau _1$
is effectively generically
$\tau $
-weaker than
$\tau _2$
.
Proof We can assume that the centers of the basic metric balls in
$({\mathcal {C}}(X,Q),d)$
are injective functions. Given a metric ball
$B=B_d(g_0,\epsilon )$
in
${\mathcal {C}}(X,Q)$
(where
$g_0$
and
$\epsilon $
are computable and
$g_0$
is injective), we need to compute
$B',B",U$
as in Definition 3.8. We are going to compute some suitable positive
$\epsilon '<\epsilon $
and define:
-
•
$B'=B_d(g_0,\epsilon ')$
. -
•
$B"=\{g\in {\mathcal {C}}(X,Q):d(g,g_0)<\epsilon \text { and }d_H(g(X),g_0(X))>\epsilon '\}$
. -
•
$U=\{g\in {\mathcal {C}}(X,Q):d_H(g(X),g_0(X))<\epsilon '\}$
.
These sets are clearly effective open sets in the respective topologies. Note that
$B'\subseteq B\cap U$
and
$B"\subseteq B\setminus U$
. We now explain how to choose
$\epsilon '$
so that
$B'$
is contained in
${\mathrm {cl}_{\tau _1}({B"})}$
.
Compute
$\delta <\epsilon /2$
such that
$d_Q(x,y)<\delta $
implies
$d_Q(g_0(x),g_0(y))<\epsilon /2$
. It implies that for all continuous functions
$g,h:Q\to Q$
,
$$ \begin{align} \text{If }d(h,g_0)<\delta \text{ and }d(g,{\mathrm{id}}_X)<\delta,\text{ then }d(h\circ g,g_0)<\epsilon. \end{align} $$
Indeed,
$d(h\circ g,g_0)\leq d(h\circ g,g_0\circ g)+d(g_0\circ g,g_0)<\delta +\epsilon /2\leq \epsilon $
.
Compute
$\beta $
, a
$\delta $
-witness for
$(X,A)$
. Compute
$\epsilon '\leq \delta $
such that for all
$x,y\in X$
,
$d_Q(g_0(x),g_0(y))\leq 2\epsilon '$
implies
$d_Q(x,y)\leq \beta $
. It implies that for all non-empty compact sets
$Y,Z\subseteq X$
,
$$ \begin{align} \text{If }d_H(Y,Z)>\beta, \text{ then }d_H(g_0(Y),g_0(Z))>2\epsilon'. \end{align} $$
We now check that
$B'$
is contained in
${\mathrm {cl}_{\tau _1}({B"})}$
. Let
$h\in B'=B_d(g_0,\epsilon ')$
. As
$\beta $
is an
$\delta $
-witness, there exists
$g:X\to X$
such that
$g(A)\subseteq A$
,
$d(g,{\mathrm {id}}_X)<\delta $
and
$d_H(X,g(X))>\beta $
. We define
$g_1=h\circ g$
and show that
$g_1\in B"$
. One has
$d(g_1,g_0)<\epsilon $
by (3), and
$$ \begin{align*} d_H(g_1(X),g_0(X))&\geq d_H(g_0(X),g_0\circ g(X))-d_H(g_0\circ g(X),h\circ g(X))\\ &>2\epsilon'-d(g_0,h)>\epsilon'\quad\text{ by (4)}, \end{align*} $$
so
$g_1\in B"$
. Moreover,
$g_1(X)=h(g(X))$
is contained in
$h(X)$
and
$g_1(A)=h(g(A))\subseteq h(A)$
, so h belongs to
${\mathrm {cl}_{\tau _1}({\{g_1\}})}\subseteq {\mathrm {cl}_{\tau _1}({B"})}$
. We have proved that
$B'\subseteq {\mathrm {cl}_{\tau _1}({B"})}$
.
Proof of Theorem 4.2
The subset of injective continuous functions from X to Q is a
$\tau $
-dense
$\Pi ^0_2(\tau )$
-subset of
${\mathcal {C}}(X,Q)$
. Therefore, applying Theorem 3.5, there exists an injective continuous function
$f:X\to Q$
that is
$\tau _1$
-computable but not
$\tau _2$
-computable. In other words, the pair
$(f(X),f(A))$
is semicomputable, but
$f(X)$
is not computable.
It may seem that using Theorems 2.1 and 3.5 is a rather convoluted path to proving Theorem 4.2. A more direct proof is indeed possible (see [Reference Amir and Hoyrup2]), but at the cost of readability, because there are many ingredients to take care of and to put together. Our abstract results isolate the appropriate concepts that make the construction possible, separating the specific properties of the application (Lemma 4.1) from the general construction (Theorems 2.1 and 3.5), and can hopefully be applied in other contexts.
Let us finish by illustrating the result of the construction obtained by applying Theorem 4.2 to a concrete pair
$(X,A)$
. The set X is shown in Figure 1 and consists of a disk attached to a pinched hollow torus, and the set A is empty. The results in [Reference Amir, Hoyrup, Bojanczyk, Merelli and Woodruff1] imply that X does not have the
$\epsilon $
-surjection property for any
$\epsilon>0$
, and that it has computable witnesses (Definition 4.3), so Theorem 4.2 implies that X does not have computable type. A semicomputable copy of X which is not computable is illustrated in Figure 2. It could be obtained more directly by encoding the halting set: if
$(n_i)_{i\in {\mathbb {N}}}$
is a computable one-to-one enumeration of the halting set, then the holes appearing in the disk have sizes
$2^{-n_0}, 2^{-n_1},\ldots $
.
Figure 1 A space that does not have computable type.
Figure 2 A semicomputable copy which is not computable.
