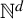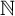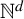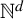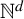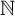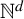1 Introduction
In this article, we would like to study the following two related topics, namely, the Hausdorff dimension of multidimensional multiplicative subshifts and the multifractal analysis of the multiple ergodic average. Before presenting our main results, we give the motivation of this study. Let
![]() $(X,T)$
be a topological dynamical system, where
$(X,T)$
be a topological dynamical system, where
![]() $T: X\rightarrow X$
is a continuous map on a compact metric space X, and
$T: X\rightarrow X$
is a continuous map on a compact metric space X, and
![]() $\mathbb {F}=(f_1,\ldots , f_d)$
be a d-tuple of functions, where
$\mathbb {F}=(f_1,\ldots , f_d)$
be a d-tuple of functions, where
![]() $f_{i}:X\rightarrow \mathbb {R}$
is continuous for
$f_{i}:X\rightarrow \mathbb {R}$
is continuous for
![]() $1\leq i\leq d$
. The multiple ergodic theory is to study the asymptotic behavior of the multiple ergodic average
$1\leq i\leq d$
. The multiple ergodic theory is to study the asymptotic behavior of the multiple ergodic average
 $$ \begin{align} A_{n}\mathbb{F}(x)= \frac{1}{n}\sum_{k=0}^{n-1}f_{1}(T_{1}^{k}(x))f_{2}(T_{2}^{k}(x)) \cdots f_{d}(T_{d}^{k}(x))\text{.} \end{align} $$
$$ \begin{align} A_{n}\mathbb{F}(x)= \frac{1}{n}\sum_{k=0}^{n-1}f_{1}(T_{1}^{k}(x))f_{2}(T_{2}^{k}(x)) \cdots f_{d}(T_{d}^{k}(x))\text{.} \end{align} $$
Such a problem was initiated by Furstenberg, Katznelson, and Ornstein [Reference Furstenberg, Katznelson and Ornstein13] in his proof of the Szemerédi’s theorem. The
![]() $L^{2}$
-convergence of equation (1) was first considered by Conze and Lesigne [Reference Conze and Lesigne7], then generalized by Host and Kra [Reference Host and Kra15] when
$L^{2}$
-convergence of equation (1) was first considered by Conze and Lesigne [Reference Conze and Lesigne7], then generalized by Host and Kra [Reference Host and Kra15] when
![]() $ T_{j}=T^{j}$
(
$ T_{j}=T^{j}$
(
![]() $T^j(x)$
means the jth iteration of x under T). Bourgain [Reference Bourgain5] proved the almost everywhere convergence when
$T^j(x)$
means the jth iteration of x under T). Bourgain [Reference Bourgain5] proved the almost everywhere convergence when
![]() $d=2$
and
$d=2$
and
![]() $f_{j}\in L^{\infty }(\mu )$
(
$f_{j}\in L^{\infty }(\mu )$
(
![]() $\mu $
is probability measure on X). Gutman et al [Reference Gutman, Huang, Shao and Ye14] obtained the almost surely convergence when the system is weakly mixing pairwise independently determined. The reader is referred to [Reference Fan, Feng and Lau9, Reference Frantzikinakis12] for an up-to-date investigation into this subject.
$\mu $
is probability measure on X). Gutman et al [Reference Gutman, Huang, Shao and Ye14] obtained the almost surely convergence when the system is weakly mixing pairwise independently determined. The reader is referred to [Reference Fan, Feng and Lau9, Reference Frantzikinakis12] for an up-to-date investigation into this subject.
Let
![]() $\Sigma _{m}=\{0,\ldots ,m-1\}$
and
$\Sigma _{m}=\{0,\ldots ,m-1\}$
and
![]() $\Omega \subseteq \Sigma _{m}^{\mathbb {N}}$
be a subshift which is a closed and shift
$\Omega \subseteq \Sigma _{m}^{\mathbb {N}}$
be a subshift which is a closed and shift
![]() $\sigma $
-invariant subset of
$\sigma $
-invariant subset of
![]() $\Sigma _{m}^{\mathbb {N}}$
with the shift action
$\Sigma _{m}^{\mathbb {N}}$
with the shift action
![]() $\sigma (x_i)=x_{i+1}$
for all
$\sigma (x_i)=x_{i+1}$
for all
![]() $i\in \mathbb {N}$
. Suppose S is the semigroup generated by primes
$i\in \mathbb {N}$
. Suppose S is the semigroup generated by primes
![]() $p_{1},\ldots ,p_{k}$
. Set
$p_{1},\ldots ,p_{k}$
. Set
where
![]() $\gcd (i,S)=1$
means that
$\gcd (i,S)=1$
means that
![]() $\gcd (i,s)=1\ \text { for all } s\in S$
. The authors of [Reference Kenyon, Peres and Solomyak16] call
$\gcd (i,s)=1\ \text { for all } s\in S$
. The authors of [Reference Kenyon, Peres and Solomyak16] call
![]() $X_{\Omega }^{(S)}$
‘multiplicative subshifts’, since it is invariant under the multiplicative action. That is,
$X_{\Omega }^{(S)}$
‘multiplicative subshifts’, since it is invariant under the multiplicative action. That is,
It is worth noting that the investigation of
![]() $X_{\Omega }^{(S)}$
was initiated by the study of the set
$X_{\Omega }^{(S)}$
was initiated by the study of the set
![]() $X^{p_{1},p_{2},\ldots ,p_{k}}$
defined below. Namely, if
$X^{p_{1},p_{2},\ldots ,p_{k}}$
defined below. Namely, if
![]() $p_{1},\ldots ,p_{k}$
are primes, define
$p_{1},\ldots ,p_{k}$
are primes, define
and it is clear that
![]() $X^{p_{1},p_{2},\ldots ,p_{k}}$
is a special case of
$X^{p_{1},p_{2},\ldots ,p_{k}}$
is a special case of
![]() $X_{\Omega }^{(S)}$
with
$X_{\Omega }^{(S)}$
with
![]() $\Omega $
being the subshift of finite type with forbidden set
$\Omega $
being the subshift of finite type with forbidden set
![]() $\mathcal {F}=\{1,\ldots ,m-1\}^{k+1}$
. The dimensional theory of the multiplicative subshifts and the multifractal analysis of the multiple ergodic average attract more attention and have become popular research topics in recent years (cf. [Reference Ban, Hu and Lai1, Reference Ban, Hu and Lin3, Reference Brunet6, Reference Fan, Liao and Ma10, Reference Fan, Schmeling and Wu11, Reference Kenyon, Peres and Solomyak16–Reference Pollicott19]). Fan, Liao, and Ma [Reference Fan, Liao and Ma10] obtained the Hausdorff dimension of the level set of equation (1) with
$\mathcal {F}=\{1,\ldots ,m-1\}^{k+1}$
. The dimensional theory of the multiplicative subshifts and the multifractal analysis of the multiple ergodic average attract more attention and have become popular research topics in recent years (cf. [Reference Ban, Hu and Lai1, Reference Ban, Hu and Lin3, Reference Brunet6, Reference Fan, Liao and Ma10, Reference Fan, Schmeling and Wu11, Reference Kenyon, Peres and Solomyak16–Reference Pollicott19]). Fan, Liao, and Ma [Reference Fan, Liao and Ma10] obtained the Hausdorff dimension of the level set of equation (1) with
![]() $f_i(x)=x_1, T_i=T^{i}$
for all
$f_i(x)=x_1, T_i=T^{i}$
for all
![]() $1\leq i\leq \ell $
. More precisely, fix
$1\leq i\leq \ell $
. More precisely, fix
![]() $\theta \in [-1,1]$
and
$\theta \in [-1,1]$
and
![]() $\ell \geq 1$
,
$\ell \geq 1$
,
 $$ \begin{align} \dim_H(B_{\theta})=1-\frac{1}{\ell}+\frac{1}{\ell}H\bigg( \frac{1+\theta}{2} \bigg), \end{align} $$
$$ \begin{align} \dim_H(B_{\theta})=1-\frac{1}{\ell}+\frac{1}{\ell}H\bigg( \frac{1+\theta}{2} \bigg), \end{align} $$
where
 $$ \begin{align} B_{\theta}:=\bigg\{ (x_k)_{k=1}^{\infty}\in \{ -1, 1\}^{\mathbb{N}} : \lim_{n \rightarrow \infty} \frac{1}{n} \sum_{k=1}^n x_k x_{2k} \cdots x_{\ell k} =\theta \bigg\} \end{align} $$
$$ \begin{align} B_{\theta}:=\bigg\{ (x_k)_{k=1}^{\infty}\in \{ -1, 1\}^{\mathbb{N}} : \lim_{n \rightarrow \infty} \frac{1}{n} \sum_{k=1}^n x_k x_{2k} \cdots x_{\ell k} =\theta \bigg\} \end{align} $$
and
![]() $H(t)=-t \log _2 t - (1-t)\log _2 (1-t)$
. In the same work of [Reference Fan, Liao and Ma10], the authors prove that the Minkowski dimension of
$H(t)=-t \log _2 t - (1-t)\log _2 (1-t)$
. In the same work of [Reference Fan, Liao and Ma10], the authors prove that the Minkowski dimension of
![]() $X^2$
(equation (3) with
$X^2$
(equation (3) with
![]() $m=2$
and
$m=2$
and
![]() $p_1=2$
) equals
$p_1=2$
) equals
 $$ \begin{align} \dim_M (X^2)=\sum_{n=1}^{\infty} \frac{\log_2 F_n}{2^{n+1}}, \end{align} $$
$$ \begin{align} \dim_M (X^2)=\sum_{n=1}^{\infty} \frac{\log_2 F_n}{2^{n+1}}, \end{align} $$
where
![]() $\{ F_n \}$
is the Fibonacci sequence with
$\{ F_n \}$
is the Fibonacci sequence with
![]() $F_1{\kern-1pt}={\kern-1pt}2$
,
$F_1{\kern-1pt}={\kern-1pt}2$
,
![]() $F_2{\kern-1pt}={\kern-1pt}3$
, and
$F_2{\kern-1pt}={\kern-1pt}3$
, and
![]() $F_{n+2}{\kern-1pt}={\kern-1pt}F_{n+1}+F_n(n{\kern-1pt}\geq{\kern-1pt} 1)$
.
$F_{n+2}{\kern-1pt}={\kern-1pt}F_{n+1}+F_n(n{\kern-1pt}\geq{\kern-1pt} 1)$
.
Later, Kenyon, Peres, and Solomyak [Reference Kenyon, Peres and Solomyak16] generalized the work of Fan, Ma, and Liao [Reference Fan, Liao and Ma10] to investigate the dimension formula of
![]() $X_A^q$
. Namely, for an integer
$X_A^q$
. Namely, for an integer
![]() $q\geq 2$
,
$q\geq 2$
,
where
![]() $A\in M_m(\{ 0,1\})$
, and
$A\in M_m(\{ 0,1\})$
, and
![]() $M_m(\{ 0,1\})$
is the space of all
$M_m(\{ 0,1\})$
is the space of all
![]() $m\times m$
0-1 matrices with entries being
$m\times m$
0-1 matrices with entries being
![]() $0$
or
$0$
or
![]() $1$
.
$1$
.
Theorem 1.1. [Reference Kenyon, Peres and Solomyak16, Theorem 1.3]
-
(1) Let A be a primitive
 $0$
-
$0$
-
 $1$
matrix. Then, (8)where
$1$
matrix. Then, (8)where $$ \begin{align} \dim_H (X_A^q)= \frac{q-1}{q} \log_m \sum_{i=0}^{m-1} t_i , \end{align} $$
$$ \begin{align} \dim_H (X_A^q)= \frac{q-1}{q} \log_m \sum_{i=0}^{m-1} t_i , \end{align} $$
 $(t_i)_{i=0}^{m-1}$
is a unique positive vector satisfying
$(t_i)_{i=0}^{m-1}$
is a unique positive vector satisfying  $$ \begin{align*} t_i^q=\sum_{j=0}^{m-1} A(i,j)t_j. \end{align*} $$
$$ \begin{align*} t_i^q=\sum_{j=0}^{m-1} A(i,j)t_j. \end{align*} $$
-
(2) The Minkowski dimension of
 $X_A^q$
exists and equals (9)where
$X_A^q$
exists and equals (9)where $$ \begin{align} \dim_M (X_A^q)=(q-1)^2 \sum_{k=1}^{\infty} \frac{\log_m | A^{k-1}|}{q^{k+1}}, \end{align} $$
$$ \begin{align} \dim_M (X_A^q)=(q-1)^2 \sum_{k=1}^{\infty} \frac{\log_m | A^{k-1}|}{q^{k+1}}, \end{align} $$
 $|A|$
is the sum of all entries of the matrix A.
$|A|$
is the sum of all entries of the matrix A.
Peres et al [Reference Peres, Schmeling, Seuret and Solomyak17] obtained the Hausdorff dimension and Minkowski dimension of
![]() $X^{2,3}$
(equation (3) with
$X^{2,3}$
(equation (3) with
![]() $p_1=2,p_2=3$
and
$p_1=2,p_2=3$
and
![]() $m=2$
). One objective of this paper is to extend Theorem 1.1 from
$m=2$
). One objective of this paper is to extend Theorem 1.1 from
![]() $\mathbb {N}$
to
$\mathbb {N}$
to
![]() $\mathbb {N}^d$
(Theorem 1.3).
$\mathbb {N}^d$
(Theorem 1.3).
The multifractal analysis of general multiple ergodic averages was pioneered by Fan, Schmeling, and Wu [Reference Fan, Schmeling and Wu11]. Specifically, they take into account the broader form of the multiple ergodic average as denoted below. Define the multiple ergodic average
 $$ \begin{align} A_n \varphi (x)= \frac{1}{n}\sum_{k=1}^n \varphi (x_k, x_{kq} ,\ldots, x_{kq^{\ell-1}} ), \end{align} $$
$$ \begin{align} A_n \varphi (x)= \frac{1}{n}\sum_{k=1}^n \varphi (x_k, x_{kq} ,\ldots, x_{kq^{\ell-1}} ), \end{align} $$
where
![]() $\varphi : S^{\ell }=\{ 0,1,\ldots , m-1\}^{\ell } \rightarrow \mathbb {R}$
is a continuous function with respect to the discrete topology and
$\varphi : S^{\ell }=\{ 0,1,\ldots , m-1\}^{\ell } \rightarrow \mathbb {R}$
is a continuous function with respect to the discrete topology and
![]() $\ell \geq 1 , q\geq 2$
. The level set with respect to the multiple ergodic average in equation (10) is defined by
$\ell \geq 1 , q\geq 2$
. The level set with respect to the multiple ergodic average in equation (10) is defined by
Let
![]() $s\in \mathbb {R}$
, and let
$s\in \mathbb {R}$
, and let
![]() $\mathcal {F}(S^{\ell -1},\mathbb {R}^+)$
denote the cone of non-negative real functions on
$\mathcal {F}(S^{\ell -1},\mathbb {R}^+)$
denote the cone of non-negative real functions on
![]() $S^{\ell -1}$
. The nonlinear operator
$S^{\ell -1}$
. The nonlinear operator
![]() $\mathcal {N}_s:\mathcal {F}(S^{\ell -1},\mathbb {R}^+)\rightarrow \mathcal {F}(S^{\ell -1},\mathbb {R}^+)$
is defined by
$\mathcal {N}_s:\mathcal {F}(S^{\ell -1},\mathbb {R}^+)\rightarrow \mathcal {F}(S^{\ell -1},\mathbb {R}^+)$
is defined by
 $$ \begin{align} \mathcal{N}_sy(a_1,a_2,\ldots,a_{\ell-1})=\bigg( \sum_{j\in S} e^{s\varphi(a_1,a_2,\ldots,a_{\ell-1},j)}y(a_2,\ldots,a_{\ell-1},j) \bigg)^{{1}/{q}}. \end{align} $$
$$ \begin{align} \mathcal{N}_sy(a_1,a_2,\ldots,a_{\ell-1})=\bigg( \sum_{j\in S} e^{s\varphi(a_1,a_2,\ldots,a_{\ell-1},j)}y(a_2,\ldots,a_{\ell-1},j) \bigg)^{{1}/{q}}. \end{align} $$
Define the pressure function by
 $$ \begin{align} P_{\varphi}(s)=(q-1)q^{\ell-2}\log \sum_{j\in S}\psi_s(j), \end{align} $$
$$ \begin{align} P_{\varphi}(s)=(q-1)q^{\ell-2}\log \sum_{j\in S}\psi_s(j), \end{align} $$
where
![]() $\psi _s$
is a unique strictly positive fixed point of
$\psi _s$
is a unique strictly positive fixed point of
![]() $\mathcal {N}_s$
. The function
$\mathcal {N}_s$
. The function
![]() $\psi _s$
is defined on
$\psi _s$
is defined on
![]() $S^{\ell -1}$
and it can be extended on
$S^{\ell -1}$
and it can be extended on
![]() $S^k$
for all
$S^k$
for all
![]() $1\leq k\leq \ell -2$
by induction. That is, for
$1\leq k\leq \ell -2$
by induction. That is, for
![]() $a\in S^k$
,
$a\in S^k$
,
 $$ \begin{align} \psi^{(k)}_s(a)=\bigg( \sum_{j\in S}\psi^{(k+1)}_s(a,j) \bigg)^{{1}/{q}}. \end{align} $$
$$ \begin{align} \psi^{(k)}_s(a)=\bigg( \sum_{j\in S}\psi^{(k+1)}_s(a,j) \bigg)^{{1}/{q}}. \end{align} $$
The Legendre transform of
![]() $P_{\varphi }$
is defined as
$P_{\varphi }$
is defined as
Denote by
![]() $L_{\varphi }$
the set of
$L_{\varphi }$
the set of
![]() $\alpha \in \mathbb {R}$
such that
$\alpha \in \mathbb {R}$
such that
![]() $E(\alpha )\neq \emptyset $
. The following theorem is obtained by Fan, Schmeling, and Wu [Reference Fan, Schmeling and Wu11] and Wu [Reference Wu20] for the one-dimensional case.
$E(\alpha )\neq \emptyset $
. The following theorem is obtained by Fan, Schmeling, and Wu [Reference Fan, Schmeling and Wu11] and Wu [Reference Wu20] for the one-dimensional case.
Theorem 1.2. ([Reference Fan, Schmeling and Wu11, Theorem 1.1], [Reference Wu20, Theorem 3.1])
-
(1)
 $L_{\varphi }= [ P^{\prime }_{\varphi }(-\infty ), P^{\prime }_{\varphi }(+\infty ) ]$
, where
$L_{\varphi }= [ P^{\prime }_{\varphi }(-\infty ), P^{\prime }_{\varphi }(+\infty ) ]$
, where
 $P^{\prime }_{\varphi }(\pm \infty )=\lim _{s\rightarrow \pm \infty }P^{\prime }_{\varphi }(s)$
.
$P^{\prime }_{\varphi }(\pm \infty )=\lim _{s\rightarrow \pm \infty }P^{\prime }_{\varphi }(s)$
. -
(2) If
 $\alpha =P^{\prime }_{\varphi }(s_{\alpha })$
for some
$\alpha =P^{\prime }_{\varphi }(s_{\alpha })$
for some
 $s_{\alpha } \in \mathbb {R}\cup \{ \pm \infty \}$
, then
$s_{\alpha } \in \mathbb {R}\cup \{ \pm \infty \}$
, then
 $E(\alpha )\neq \emptyset $
, and the Hausdorff dimension of
$E(\alpha )\neq \emptyset $
, and the Hausdorff dimension of
 $E(\alpha )$
is equal to
$E(\alpha )$
is equal to  $$ \begin{align*} \dim_H E(\alpha)=\frac{-P^{\prime}_{\varphi}(s_{\alpha})s_{\alpha}+P_{\varphi}(s_{\alpha})}{q^{\ell-1}\log m}=\frac{P^*_{\varphi}(\alpha)}{q^{\ell-1}\log m}. \end{align*} $$
$$ \begin{align*} \dim_H E(\alpha)=\frac{-P^{\prime}_{\varphi}(s_{\alpha})s_{\alpha}+P_{\varphi}(s_{\alpha})}{q^{\ell-1}\log m}=\frac{P^*_{\varphi}(\alpha)}{q^{\ell-1}\log m}. \end{align*} $$
The other objective of this paper is to extend Theorem 1.2 from
![]() $\mathbb {N}$
to
$\mathbb {N}$
to
![]() $\mathbb {N}^d$
(Theorem 1.5). The connection between Theorems 1.1 and 1.2 is that if
$\mathbb {N}^d$
(Theorem 1.5). The connection between Theorems 1.1 and 1.2 is that if
![]() $\ell =2$
(respectively
$\ell =2$
(respectively
![]() $\ell =3$
) and
$\ell =3$
) and
![]() $\varphi (x_k,x_{2k})= x_k x_{2k}$
(respectively
$\varphi (x_k,x_{2k})= x_k x_{2k}$
(respectively
![]() $\varphi (x_k,x_{2k},x_{3k})= x_k x_{2k} x_{3k}$
) in equation (10), it is mentioned in [Reference Peres and Solomyak18] (respectively [Reference Peres, Schmeling, Seuret and Solomyak17]) that
$\varphi (x_k,x_{2k},x_{3k})= x_k x_{2k} x_{3k}$
) in equation (10), it is mentioned in [Reference Peres and Solomyak18] (respectively [Reference Peres, Schmeling, Seuret and Solomyak17]) that
![]() $\dim _H E(0)=\dim _H(X^2)$
(respectively
$\dim _H E(0)=\dim _H(X^2)$
(respectively
![]() $\dim _H E(0)=\dim _H(X^{2,3})$
). The study of Hausdorff dimension of multiplicative subshifts can therefore be seen as a multifractal analysis of the multiple ergodic averages. From this vantage point, this investigation aims to provide some multifractal analysis results of the multiple ergodic averages in
$\dim _H E(0)=\dim _H(X^{2,3})$
). The study of Hausdorff dimension of multiplicative subshifts can therefore be seen as a multifractal analysis of the multiple ergodic averages. From this vantage point, this investigation aims to provide some multifractal analysis results of the multiple ergodic averages in
![]() $\mathbb {N}^d$
.
$\mathbb {N}^d$
.
To state the main results, we first introduce the multidimensional multiplicative subshift below. For
![]() $k\geq 1$
, let
$k\geq 1$
, let
![]() $\mathbf {p}_{1},\ldots ,\mathbf {p}_{k}\in \mathbb {N}^{d}$
, the multidimensional version of equation (3) is defined as
$\mathbf {p}_{1},\ldots ,\mathbf {p}_{k}\in \mathbb {N}^{d}$
, the multidimensional version of equation (3) is defined as
where
![]() $\mathbf {i\cdot j}$
denotes the coordinate-wise product vector of
$\mathbf {i\cdot j}$
denotes the coordinate-wise product vector of
![]() $\mathbf {i}$
and
$\mathbf {i}$
and
![]() $\mathbf {j}$
, that is,
$\mathbf {j}$
, that is,
![]() $\mathbf {i\cdot j}=(i_1j_1,\ldots ,i_dj_d)$
for
$\mathbf {i\cdot j}=(i_1j_1,\ldots ,i_dj_d)$
for
![]() $ \mathbf {i}=(i_{l})_{l=1}^{d}$
,
$ \mathbf {i}=(i_{l})_{l=1}^{d}$
,
![]() $\mathbf {j}=(j_{l})_{l=1}^{d}\in \mathbb {N} ^{d}$
. It is obvious that
$\mathbf {j}=(j_{l})_{l=1}^{d}\in \mathbb {N} ^{d}$
. It is obvious that
![]() $X^{\mathbf {p}_{1},\mathbf {p}_{2},\ldots ,\mathbf {p }_{k}}$
is the
$X^{\mathbf {p}_{1},\mathbf {p}_{2},\ldots ,\mathbf {p }_{k}}$
is the
![]() $\mathbb {N}^{d}$
version of
$\mathbb {N}^{d}$
version of
![]() $X^{p_{1},p_{2},\ldots ,p_{k}}$
. Recently, Ban, Hu, and Lai [Reference Ban, Hu and Lai1] established the Minkowski dimension of the set defined by equation (16). Precisely, let
$X^{p_{1},p_{2},\ldots ,p_{k}}$
. Recently, Ban, Hu, and Lai [Reference Ban, Hu and Lai1] established the Minkowski dimension of the set defined by equation (16). Precisely, let
![]() $\mathbf { p}_i=(p_{i,1},p_{i,2},\ldots ,p_{i,d})\in \mathbb {N}_{\geq 2}^d$
for all
$\mathbf { p}_i=(p_{i,1},p_{i,2},\ldots ,p_{i,d})\in \mathbb {N}_{\geq 2}^d$
for all
![]() $1\leq i\leq k$
, where
$1\leq i\leq k$
, where
![]() $\mathbb {N}_{\geq 2}^d=(\mathbb {N} \setminus \{ 1\})^d$
is the set of d-dimensional vectors that are component-wise greater than or equal to 2. Suppose
$\mathbb {N}_{\geq 2}^d=(\mathbb {N} \setminus \{ 1\})^d$
is the set of d-dimensional vectors that are component-wise greater than or equal to 2. Suppose
![]() $\gcd (p_{i,\ell },p_{j,\ell })=1$
for all
$\gcd (p_{i,\ell },p_{j,\ell })=1$
for all
![]() $1\leq i<j\leq k$
and
$1\leq i<j\leq k$
and
![]() $1\leq \ell \leq d$
. The formula for the Minkowski dimension of
$1\leq \ell \leq d$
. The formula for the Minkowski dimension of
![]() $X^{\mathbf {p}_{1},\mathbf {p}_{2},\ldots ,\mathbf {p}_{k}}$
is obtained as
$X^{\mathbf {p}_{1},\mathbf {p}_{2},\ldots ,\mathbf {p}_{k}}$
is obtained as
 $$ \begin{align} \begin{aligned} \dim_M(X^{\mathbf{p}_{1},\mathbf{p}_{2},\ldots ,\mathbf{p}_{k}})=\ &\bigg[\underset{i=1}{\overset{k}{\prod}}\bigg(1-\frac{1}{p_{i,1}p_{i,2}\cdots p_{i,d}}\bigg)\bigg] \\ &\times\sum_{M_1,M_2,\ldots,M_d=1}^{\infty}\bigg[ \prod_{i=1}^{d}\bigg(\frac{1}{r_{M_i}^{(i)}}-\frac{1}{r_{M_i+1}^{(i)}}\bigg)\bigg] \log_m b_{M_1,M_2,\ldots,M_d}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \dim_M(X^{\mathbf{p}_{1},\mathbf{p}_{2},\ldots ,\mathbf{p}_{k}})=\ &\bigg[\underset{i=1}{\overset{k}{\prod}}\bigg(1-\frac{1}{p_{i,1}p_{i,2}\cdots p_{i,d}}\bigg)\bigg] \\ &\times\sum_{M_1,M_2,\ldots,M_d=1}^{\infty}\bigg[ \prod_{i=1}^{d}\bigg(\frac{1}{r_{M_i}^{(i)}}-\frac{1}{r_{M_i+1}^{(i)}}\bigg)\bigg] \log_m b_{M_1,M_2,\ldots,M_d}, \end{aligned} \end{align} $$
where
![]() $b_{M_1,M_2,\ldots ,M_d}$
is the number of admissible patterns on the lattice
$b_{M_1,M_2,\ldots ,M_d}$
is the number of admissible patterns on the lattice
![]() $\mathbb {L}_{M_1,M_2,\ldots ,M_d}$
in
$\mathbb {L}_{M_1,M_2,\ldots ,M_d}$
in
![]() $\mathbb {N}_0^{k}=\{0,1,\ldots \}^{k}$
with forbidden set
$\mathbb {N}_0^{k}=\{0,1,\ldots \}^{k}$
with forbidden set
![]() $\mathcal {F}=\{ x_{\vec {0}}=x_{\vec {e}_1}=x_{\vec {e}_2}=\cdots =x_{\vec {e}_{k}}=1 \}$
(see [Reference Ban, Hu and Lai1, Definition 2.6] for definitions of
$\mathcal {F}=\{ x_{\vec {0}}=x_{\vec {e}_1}=x_{\vec {e}_2}=\cdots =x_{\vec {e}_{k}}=1 \}$
(see [Reference Ban, Hu and Lai1, Definition 2.6] for definitions of
![]() $\mathbb {L}_{M_1,M_2,\ldots ,M_d}$
and
$\mathbb {L}_{M_1,M_2,\ldots ,M_d}$
and
![]() $r_{M_i+1}^{(i)}$
).
$r_{M_i+1}^{(i)}$
).
To the best of our knowledge, the dimension results of the multidimensional multiplicative subshifts and the multifractal analysis of the multiple average in multidimensional lattices have rarely been reported. Brunet [Reference Brunet6] considers the self-affine sponges under the multiplicative action, and establishes the associated Ledrappier–Young formula, Hausdorff dimensions, and Minkowski dimension formula of such sponges. Ban, Hu, and Lai obtained the large deviation principle for multiple average in
![]() $\mathbb {N}^d$
[Reference Ban, Hu and Lai2].
$\mathbb {N}^d$
[Reference Ban, Hu and Lai2].
It is also emphasized that the problems of multifractal analysis and dimension formula of multiple average on ‘multidimensional lattices’ are new and challenging. The difficulty is that it is not easy to decompose the multidimensional lattices into the independent sublattices according to the given ‘multiple constraints’, e.g., the
![]() $\mathbf {p}_{i}$
in equation (16), and calculate its density among the entire lattice. Fortunately, the technique developed in [Reference Ban, Hu and Lai1] is useful and leads us to investigate the Hausdorff dimension of the multidimensional multiplicative subshifts and the multifractal analysis of multiple averages on
$\mathbf {p}_{i}$
in equation (16), and calculate its density among the entire lattice. Fortunately, the technique developed in [Reference Ban, Hu and Lai1] is useful and leads us to investigate the Hausdorff dimension of the multidimensional multiplicative subshifts and the multifractal analysis of multiple averages on
![]() $\mathbb {N}^d$
.
$\mathbb {N}^d$
.
The first result of this paper is presented below, and it extends Theorem 1.1 from
![]() $\mathbb {N}$
to
$\mathbb {N}$
to
![]() $\mathbb {N}^d$
.
$\mathbb {N}^d$
.
Theorem 1.3. Let
![]() $A\in M_m(\{0,1\})$
. For
$A\in M_m(\{0,1\})$
. For
![]() $d\geq 1$
and
$d\geq 1$
and
![]() $\mathbf {p}=(p_1,p_2,\ldots , p_d)\in \mathbb {N}_{\geq 2}^d$
, the Hausdorff dimension of the set
$\mathbf {p}=(p_1,p_2,\ldots , p_d)\in \mathbb {N}_{\geq 2}^d$
, the Hausdorff dimension of the set
is
 $$ \begin{align*} \begin{aligned} \dim_H(X^{\mathbf{p}}_A)=\frac{p_1\cdots p_d-1}{p_1\cdots p_d}\log_m\sum_{i=0}^{m-1}t_{i}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \dim_H(X^{\mathbf{p}}_A)=\frac{p_1\cdots p_d-1}{p_1\cdots p_d}\log_m\sum_{i=0}^{m-1}t_{i}, \end{aligned} \end{align*} $$
where
![]() $(t_i)_{i=0}^{m-1}$
is a unique positive vector satisfying
$(t_i)_{i=0}^{m-1}$
is a unique positive vector satisfying
 $$ \begin{align} t_i^{p_1\cdots p_d}=\sum_{j=0}^{m-1} A(i,j)t_j. \end{align} $$
$$ \begin{align} t_i^{p_1\cdots p_d}=\sum_{j=0}^{m-1} A(i,j)t_j. \end{align} $$
Theorem 1.3 is applied to show that the Hausdorff dimension of
![]() $X^{\mathbf {p}}_A$
is strictly less than its Minkowski dimension (Example 1.4).
$X^{\mathbf {p}}_A$
is strictly less than its Minkowski dimension (Example 1.4).
Example 1.4. When
![]() $m=2$
,
$m=2$
,
![]() $\mathbf {p}=(2,3)$
and
$\mathbf {p}=(2,3)$
and
![]() $A=[ \begin {smallmatrix} 1&1\\ 1&0 \end {smallmatrix}]$
, we have
$A=[ \begin {smallmatrix} 1&1\\ 1&0 \end {smallmatrix}]$
, we have
 $$ \begin{align*} \begin{aligned} p_{00}=\frac{t_0}{t_0^6},\quad p_{01}=\frac{t_1}{t_0^6},\quad p_{10}=\frac{t_0}{t_1^6},\quad p_{00}+p_{01}=1,\quad p_{10}=1, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} p_{00}=\frac{t_0}{t_0^6},\quad p_{01}=\frac{t_1}{t_0^6},\quad p_{10}=\frac{t_0}{t_1^6},\quad p_{00}+p_{01}=1,\quad p_{10}=1, \end{aligned} \end{align*} $$
then
which implies
Then the unique positive vector of equation (19) is
![]() $(t_0,t_1)\approx (1.0216,1.1368)$
. Thus,
$(t_0,t_1)\approx (1.0216,1.1368)$
. Thus,
 $$ \begin{align*} \begin{aligned} \dim_H(X_{A}^{\mathbf{p}})&=\frac{(6-1)}{6}\log_2(t_{0}+t_1)\\ &\approx\frac{5}{6\log2}\log(1.0216+1.1368)\\ &\approx 0.9251\\ &<0.9348\approx\dim_M(X_{A}^{\mathbf{p}}), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \dim_H(X_{A}^{\mathbf{p}})&=\frac{(6-1)}{6}\log_2(t_{0}+t_1)\\ &\approx\frac{5}{6\log2}\log(1.0216+1.1368)\\ &\approx 0.9251\\ &<0.9348\approx\dim_M(X_{A}^{\mathbf{p}}), \end{aligned} \end{align*} $$
where the last estimate for the Minkowski dimension is obtained by the dimension formula established in [Reference Ban, Hu and Lai1] (cf. equation (17)). Generally, the equality
![]() $\dim _H(X_{A}^{\mathbf {p}})= \dim _M(X_{A}^{\mathbf {p}})$
holds only when the row sums of A are equal. The proof is similar to [Reference Kenyon, Peres and Solomyak16, Theorem 1.3].
$\dim _H(X_{A}^{\mathbf {p}})= \dim _M(X_{A}^{\mathbf {p}})$
holds only when the row sums of A are equal. The proof is similar to [Reference Kenyon, Peres and Solomyak16, Theorem 1.3].
For
![]() $n\in \mathbb {N}$
, let [[
$n\in \mathbb {N}$
, let [[
![]() $1,n$
]] be the interval of integers
$1,n$
]] be the interval of integers
![]() $\{1,2,\ldots ,n\}$
. For
$\{1,2,\ldots ,n\}$
. For
![]() $\mathbf {N}=(N_1,N_2,\ldots , N_d)\in \mathbb {N}^d$
, denote [[
$\mathbf {N}=(N_1,N_2,\ldots , N_d)\in \mathbb {N}^d$
, denote [[
![]() $1,\mathbf { N}$
]] by [[
$1,\mathbf { N}$
]] by [[
![]() $1,N_1$
]]
$1,N_1$
]]
![]() $\times $
[[
$\times $
[[
![]() $1,N_2$
]]
$1,N_2$
]]
![]() $\times \cdots \times $
[[
$\times \cdots \times $
[[
![]() $1,N_d$
]]. The notion
$1,N_d$
]]. The notion
![]() $\mathbf {N}\rightarrow \infty $
means
$\mathbf {N}\rightarrow \infty $
means
![]() $N_i\to \infty $
for all
$N_i\to \infty $
for all
![]() $1\leq i\leq d$
. The multidimensional multiple ergodic average in
$1\leq i\leq d$
. The multidimensional multiple ergodic average in
![]() $\mathbb {N}^d$
is defined by
$\mathbb {N}^d$
is defined by
 $$ \begin{align} A_{\mathbf{N}} \varphi (x)=\frac{1}{N_1\cdots N_d} \sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}}) \end{align} $$
$$ \begin{align} A_{\mathbf{N}} \varphi (x)=\frac{1}{N_1\cdots N_d} \sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}}) \end{align} $$
and its level set is
 $$ \begin{align} E(\alpha)=\bigg\{ (x_{\mathbf{i}})_{\mathbf{i}\in \mathbb{N}^d}\in \Sigma_m^{\mathbb{N}^d} : \lim_{\mathbf{N}\rightarrow\infty} \frac{1}{N_1 \cdots N_d} \sum_{\mathbf{j}\in[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})=\alpha \bigg\}. \end{align} $$
$$ \begin{align} E(\alpha)=\bigg\{ (x_{\mathbf{i}})_{\mathbf{i}\in \mathbb{N}^d}\in \Sigma_m^{\mathbb{N}^d} : \lim_{\mathbf{N}\rightarrow\infty} \frac{1}{N_1 \cdots N_d} \sum_{\mathbf{j}\in[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})=\alpha \bigg\}. \end{align} $$
The following result is an
![]() $\mathbb {N}^d$
version of Theorem 1.2. By abuse of notation, we continue to write
$\mathbb {N}^d$
version of Theorem 1.2. By abuse of notation, we continue to write
![]() $P_{\varphi }$
for the
$P_{\varphi }$
for the
![]() $\mathbb {N}^d$
version pressure function, and it is defined in equation (34).
$\mathbb {N}^d$
version pressure function, and it is defined in equation (34).
Theorem 1.5
-
(1)
 $L_{\varphi }= [ P^{\prime }_{\varphi }(-\infty ), P^{\prime }_{\varphi }(+\infty ) ]$
, where
$L_{\varphi }= [ P^{\prime }_{\varphi }(-\infty ), P^{\prime }_{\varphi }(+\infty ) ]$
, where
 $P^{\prime }_{\varphi }(\pm \infty )=\lim _{s\rightarrow \pm \infty }P^{\prime }_{\varphi }(s)$
and
$P^{\prime }_{\varphi }(\pm \infty )=\lim _{s\rightarrow \pm \infty }P^{\prime }_{\varphi }(s)$
and
 $P_{\varphi }(s)$
is defined by equation (34).
$P_{\varphi }(s)$
is defined by equation (34). -
(2) If
 $\alpha =P^{\prime }_{\varphi }(s_{\alpha })$
for some
$\alpha =P^{\prime }_{\varphi }(s_{\alpha })$
for some
 $s_{\alpha } \in \mathbb {R}\cup \{ \pm \infty \}$
, then
$s_{\alpha } \in \mathbb {R}\cup \{ \pm \infty \}$
, then
 $E(\alpha )\neq \emptyset $
and the Hausdorff dimension of
$E(\alpha )\neq \emptyset $
and the Hausdorff dimension of
 $E(\alpha )$
is equal to
$E(\alpha )$
is equal to  $$ \begin{align*} \dim_H E(\alpha)=\frac{-P^{\prime}_{\varphi}(s_{\alpha})s_{\alpha}+P_{\varphi}(s_{\alpha})}{(p_1\cdots p_d)^{\ell-1}\log m}=\frac{P^*_{\varphi}(\alpha)}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
$$ \begin{align*} \dim_H E(\alpha)=\frac{-P^{\prime}_{\varphi}(s_{\alpha})s_{\alpha}+P_{\varphi}(s_{\alpha})}{(p_1\cdots p_d)^{\ell-1}\log m}=\frac{P^*_{\varphi}(\alpha)}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
Example 1.6. Let
![]() $p_1{\kern-1pt}={\kern-1pt}2,p_2{\kern-1pt}={\kern-1pt}3,m{\kern-1pt}={\kern-1pt}2,\ell {\kern-1pt}={\kern-1pt}2$
, and
$p_1{\kern-1pt}={\kern-1pt}2,p_2{\kern-1pt}={\kern-1pt}3,m{\kern-1pt}={\kern-1pt}2,\ell {\kern-1pt}={\kern-1pt}2$
, and
![]() $\varphi $
be the potential given by
$\varphi $
be the potential given by
![]() $\varphi (x,y)= x_{\mathbf {1}}y_{\mathbf {1}}$
with
$\varphi (x,y)= x_{\mathbf {1}}y_{\mathbf {1}}$
with
![]() $x=(x_{\mathbf { i}})_{\mathbf {i}\in \mathbb {N}^2},y=(y_{\mathbf {i}})_{\mathbf {i}\in \mathbb {N}^2}\in \Sigma _2^{\mathbb {N}^2}$
. (Here,
$x=(x_{\mathbf { i}})_{\mathbf {i}\in \mathbb {N}^2},y=(y_{\mathbf {i}})_{\mathbf {i}\in \mathbb {N}^2}\in \Sigma _2^{\mathbb {N}^2}$
. (Here,
![]() $\mathbf {1}$
denotes the d-dimensional vector with all components being 1.) So
$\mathbf {1}$
denotes the d-dimensional vector with all components being 1.) So
 $$ \begin{align*}[\varphi([i],[j])]_{(i,j)\in \{0,1\}^2}=\left[\begin{matrix} 0&0\\ 0&1 \end{matrix}\right]\!, \end{align*} $$
$$ \begin{align*}[\varphi([i],[j])]_{(i,j)\in \{0,1\}^2}=\left[\begin{matrix} 0&0\\ 0&1 \end{matrix}\right]\!, \end{align*} $$
where
![]() $[i]=\{x=(x_{\mathbf {i}})_{\mathbf {i}\in \mathbb {N}^2}: x_{\mathbf {1}}=i\}$
.
$[i]=\{x=(x_{\mathbf {i}})_{\mathbf {i}\in \mathbb {N}^2}: x_{\mathbf {1}}=i\}$
.
Then the nonlinear equation (33) becomes
 $$ \begin{align*} \begin{aligned} \psi_s(0)^6&=\psi_s(0)+\psi_s(1),\\ \psi_s(1)^6&=\psi_s(0)+e^s\psi_s(1). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \psi_s(0)^6&=\psi_s(0)+\psi_s(1),\\ \psi_s(1)^6&=\psi_s(0)+e^s\psi_s(1). \end{aligned} \end{align*} $$
Since
![]() $(0)^{\infty }\in \Sigma _2^{\mathbb {N}}$
, then by Theorem 4.18, we have
$(0)^{\infty }\in \Sigma _2^{\mathbb {N}}$
, then by Theorem 4.18, we have
![]() $0=P^{\prime }_{\varphi }(-\infty )$
. Taking
$0=P^{\prime }_{\varphi }(-\infty )$
. Taking
![]() $s=-\infty $
, we obtain
$s=-\infty $
, we obtain
 $$ \begin{align*} \begin{aligned} \psi_{-\infty}(0)^6&=\psi_{-\infty}(0)+\psi_{-\infty}(1),\\ \psi_{-\infty}(1)^6&=\psi_{-\infty}(0). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \psi_{-\infty}(0)^6&=\psi_{-\infty}(0)+\psi_{-\infty}(1),\\ \psi_{-\infty}(1)^6&=\psi_{-\infty}(0). \end{aligned} \end{align*} $$
Then,
It is worth pointing out that the set
![]() $X_A^{\mathbf {p}}$
in Example 1.4 is a subset of
$X_A^{\mathbf {p}}$
in Example 1.4 is a subset of
![]() $E(0)$
in Example 1.6, but
$E(0)$
in Example 1.6, but
![]() $\dim _H (X_A^{\mathbf {p}})=\dim _H E(0)$
. This phenomenon appears in the previous paragraph for the one-dimensional version [Reference Peres, Schmeling, Seuret and Solomyak17], and the
$\dim _H (X_A^{\mathbf {p}})=\dim _H E(0)$
. This phenomenon appears in the previous paragraph for the one-dimensional version [Reference Peres, Schmeling, Seuret and Solomyak17], and the
![]() $\mathbb {N}^d$
version of this equality is confirmed in Examples 1.4 and 1.6 as well. Moreover, the spectrum
$\mathbb {N}^d$
version of this equality is confirmed in Examples 1.4 and 1.6 as well. Moreover, the spectrum
![]() $\alpha \mapsto \dim _H E(\alpha )$
is presented in Figure 1.
$\alpha \mapsto \dim _H E(\alpha )$
is presented in Figure 1.

Figure 1 The spectrum
![]() $\alpha\mapsto \dim_H(E(\alpha))$
.
$\alpha\mapsto \dim_H(E(\alpha))$
.
The remainder of this paper is organized as follows. In §2, we give a partition of
![]() $\mathbb {N}^d$
(Lemma 2.1) and then compute the limit of density (Lemma 2.2). In §§3 and 4, we prove the Theorems 1.3 and 1.5 respectively.
$\mathbb {N}^d$
(Lemma 2.1) and then compute the limit of density (Lemma 2.2). In §§3 and 4, we prove the Theorems 1.3 and 1.5 respectively.
2 Preliminaries
Given integers
![]() $d\geq 1$
and
$d\geq 1$
and
![]() $p_1,p_2,\ldots ,p_d\geq 2$
, we let
$p_1,p_2,\ldots ,p_d\geq 2$
, we let
![]() $\mathcal {M}_{\mathbf {p}}=\{ (p_1^m,p_2^m,\ldots ,p_d^m) :m\geq 0\}$
be the subset of
$\mathcal {M}_{\mathbf {p}}=\{ (p_1^m,p_2^m,\ldots ,p_d^m) :m\geq 0\}$
be the subset of
![]() $\mathbb {N}^d$
, called a lacunary lattice. For
$\mathbb {N}^d$
, called a lacunary lattice. For
![]() $\mathbf {i}\in \mathbb {N}^d$
, denote by
$\mathbf {i}\in \mathbb {N}^d$
, denote by
![]() $\mathcal {M}_{\mathbf {p}}(\mathbf {i})=\mathbf { i}\cdot \mathcal {M}_{\mathbf {p}}$
the lattice obtained by pushing
$\mathcal {M}_{\mathbf {p}}(\mathbf {i})=\mathbf { i}\cdot \mathcal {M}_{\mathbf {p}}$
the lattice obtained by pushing
![]() $\mathcal {M}_{\mathbf {p}}$
by
$\mathcal {M}_{\mathbf {p}}$
by
![]() $\mathbf {i}$
. Finally, we define
$\mathbf {i}$
. Finally, we define
![]() $\mathcal {I}_{\mathbf {p}}=\{ \mathbf {i}\in \mathbb {N}^d : p_j\nmid i_j\mbox { for some }1\leq j \leq d \}$
as an index set of
$\mathcal {I}_{\mathbf {p}}=\{ \mathbf {i}\in \mathbb {N}^d : p_j\nmid i_j\mbox { for some }1\leq j \leq d \}$
as an index set of
![]() $\mathbb {N}^d$
such that for any
$\mathbb {N}^d$
such that for any
![]() $\mathbf {i}\neq \mathbf {j}\in \mathcal {I}_{\mathbf {p}},\mathcal {M}_{\mathbf {p}}(\mathbf { i})\cap \mathcal {M}_{\mathbf {p}}(\mathbf {j})=\emptyset $
. The following lemmas give the disjoint decomposition of
$\mathbf {i}\neq \mathbf {j}\in \mathcal {I}_{\mathbf {p}},\mathcal {M}_{\mathbf {p}}(\mathbf { i})\cap \mathcal {M}_{\mathbf {p}}(\mathbf {j})=\emptyset $
. The following lemmas give the disjoint decomposition of
![]() $\mathbb {N}^d$
which is the
$\mathbb {N}^d$
which is the
![]() $\mathbb {N}^d$
version of [Reference Ban, Hu and Lai1, Lemma 2.1].
$\mathbb {N}^d$
version of [Reference Ban, Hu and Lai1, Lemma 2.1].
Lemma 2.1. For
![]() $p_1,p_2,\ldots ,p_d\geq 2$
,
$p_1,p_2,\ldots ,p_d\geq 2$
,
 $$ \begin{align*} \mathbb{N}^d=\displaystyle\bigsqcup\limits_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}}\mathcal{M}_{\mathbf{p}}(\mathbf{i}). \end{align*} $$
$$ \begin{align*} \mathbb{N}^d=\displaystyle\bigsqcup\limits_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}}\mathcal{M}_{\mathbf{p}}(\mathbf{i}). \end{align*} $$
More notation is needed to characterize the partition of
![]() $[\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
for
$[\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
for
![]() $\mathbf {N}=(N_1,\ldots ,N_d) \in \mathbb {N}^d$
. We define
$\mathbf {N}=(N_1,\ldots ,N_d) \in \mathbb {N}^d$
. We define
![]() $\mathcal {J}_{\mathbf {N};\ell }= \!\{ \mathbf {i}\in [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt] : |\mathcal {M}_{\mathbf { p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]|=\ell \}$
, where
$\mathcal {J}_{\mathbf {N};\ell }= \!\{ \mathbf {i}\in [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt] : |\mathcal {M}_{\mathbf { p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]|=\ell \}$
, where
![]() $| \cdot |$
denotes cardinality. The following lemma gives the limit of the density of
$| \cdot |$
denotes cardinality. The following lemma gives the limit of the density of
![]() $\mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}}$
which is the
$\mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}}$
which is the
![]() $\mathbb {N}^d$
version of [Reference Ban, Hu and Lai1, Lemma 2.2].
$\mathbb {N}^d$
version of [Reference Ban, Hu and Lai1, Lemma 2.2].
Lemma 2.2. For
![]() $N_1, N_2,\ldots ,N_d$
, and
$N_1, N_2,\ldots ,N_d$
, and
![]() $\ell \geq 1$
, we have the following assertions.
$\ell \geq 1$
, we have the following assertions.
-
(1)
 $ |\mathcal {J}_{\mathbf {N};\ell }| = \prod _{k=1}^{d}\lfloor {N_k}/{p_k^{\ell -1}}\rfloor -\prod _{k=1}^{d}\lfloor {N_k}/{p_k^\ell }\rfloor .$
$ |\mathcal {J}_{\mathbf {N};\ell }| = \prod _{k=1}^{d}\lfloor {N_k}/{p_k^{\ell -1}}\rfloor -\prod _{k=1}^{d}\lfloor {N_k}/{p_k^\ell }\rfloor .$
-
(2)
 $ \lim _{\mathbf {N}\to \infty }{| \mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}} | }/{ | \mathcal {J}_{\mathbf { N};\ell }| }=1-{1}/{p_1\cdots p_d}.$
$ \lim _{\mathbf {N}\to \infty }{| \mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}} | }/{ | \mathcal {J}_{\mathbf { N};\ell }| }=1-{1}/{p_1\cdots p_d}.$
-
(3)
 $ \lim _{\mathbf {N}\to \infty }{| \mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}} | }/{ N_1\cdots N_d }={(p_1\cdots p_d-1)^2}/{(p_1\cdots p_d)^{\ell +1}}.$
$ \lim _{\mathbf {N}\to \infty }{| \mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}} | }/{ N_1\cdots N_d }={(p_1\cdots p_d-1)^2}/{(p_1\cdots p_d)^{\ell +1}}.$
-
(4)
 $\lim _{\mathbf {N}\to \infty }{1}/({N_1\cdots N_d})\sum _{\ell =1}^{N_1\cdots N_d}|\mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}}|\log F_{\ell } =\sum _{\ell =1}^{\infty }{\lim _{\mathbf {N}\to \infty }}{|\mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}}|}/N_1 \cdots N_d\log F_{\ell }.$
$\lim _{\mathbf {N}\to \infty }{1}/({N_1\cdots N_d})\sum _{\ell =1}^{N_1\cdots N_d}|\mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}}|\log F_{\ell } =\sum _{\ell =1}^{\infty }{\lim _{\mathbf {N}\to \infty }}{|\mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}}|}/N_1 \cdots N_d\log F_{\ell }.$
We decompose
![]() $\Sigma _m^{\mathbb {N}^d}$
as follows:
$\Sigma _m^{\mathbb {N}^d}$
as follows:
 $$ \begin{align*} \Sigma_m^{\mathbb{N}^d}=\bigsqcup_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}}S^{\mathcal{M}_{\mathbf{p}}(\mathbf{i})}, \end{align*} $$
$$ \begin{align*} \Sigma_m^{\mathbb{N}^d}=\bigsqcup_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}}S^{\mathcal{M}_{\mathbf{p}}(\mathbf{i})}, \end{align*} $$
where
![]() $S=\{0,1,\ldots ,m-1\}$
.
$S=\{0,1,\ldots ,m-1\}$
.
Let
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $\Sigma _m$
. We consider
$\Sigma _m$
. We consider
![]() $\mu $
as a measure on
$\mu $
as a measure on
![]() $S^{\mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
, which is identified with
$S^{\mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
, which is identified with
![]() $\Sigma _m$
, for every
$\Sigma _m$
, for every
![]() $\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
. Then we define the infinite product measure
$\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
. Then we define the infinite product measure
![]() $\mathbb {P}_\mu $
on
$\mathbb {P}_\mu $
on
![]() $\bigsqcup _{\mathbf {i} \in \mathcal {I}_{\mathbf {p}}}S^{\mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
of copies of
$\bigsqcup _{\mathbf {i} \in \mathcal {I}_{\mathbf {p}}}S^{\mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
of copies of
![]() $\mu $
. More precisely, for any word u of size
$\mu $
. More precisely, for any word u of size
![]() $[\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
, we define
$[\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
, we define
 $$ \begin{align} \mathbb{P}_\mu([u])=\prod_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mu([u|_{\mathcal{M}_{\mathbf{ p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]), \end{align} $$
$$ \begin{align} \mathbb{P}_\mu([u])=\prod_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mu([u|_{\mathcal{M}_{\mathbf{ p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]), \end{align} $$
where
![]() $[u]$
denotes the cylinder of all words starting with u.
$[u]$
denotes the cylinder of all words starting with u.
3 Proof of Theorem 1.3
Before embarking on the proof of Theorem 1.3, we sketch out the flow of the proof for readers’ convenience. We first decompose the
![]() $\mathbb {N}^d$
lattice into disjoint one-dimensional sublattices, then define the probability measure
$\mathbb {N}^d$
lattice into disjoint one-dimensional sublattices, then define the probability measure
![]() $\mathbb {P}_\mu $
on
$\mathbb {P}_\mu $
on
![]() $X_{A}^{\mathbf {p}}$
. Subsequently, we calculate the pointwise dimension (cf. equation (23)) at
$X_{A}^{\mathbf {p}}$
. Subsequently, we calculate the pointwise dimension (cf. equation (23)) at
![]() $u\in \Sigma _{m}^{\mathbb {N}^d}$
,
$u\in \Sigma _{m}^{\mathbb {N}^d}$
,
and the Hausdorff dimension of
![]() $\mathbb {P}_\mu $
(cf. equation (24), also see [Reference Fan8] for dimension of a measure),
$\mathbb {P}_\mu $
(cf. equation (24), also see [Reference Fan8] for dimension of a measure),
to obtain the lower bound of
![]() $\dim _H(X_{A}^{\mathbf {p}})$
(Lemma 3.1). Finally, we maximize the measure dimension
$\dim _H(X_{A}^{\mathbf {p}})$
(Lemma 3.1). Finally, we maximize the measure dimension
![]() $\dim _H(\mathbb {P}_\mu )$
(Lemma 3.2), and find an upper bound of
$\dim _H(\mathbb {P}_\mu )$
(Lemma 3.2), and find an upper bound of
![]() $\dim _H(X_{A}^{\mathbf {p}})$
(Lemma 3.3) to obtain the Hausdorff dimension of
$\dim _H(X_{A}^{\mathbf {p}})$
(Lemma 3.3) to obtain the Hausdorff dimension of
![]() $X_{A}^{\mathbf {p}}$
.
$X_{A}^{\mathbf {p}}$
.
Lemma 3.1. (
 $\mathbb {N}^d$
version of [Reference Kenyon, Peres and Solomyak16, Proposition 2.3])
$\mathbb {N}^d$
version of [Reference Kenyon, Peres and Solomyak16, Proposition 2.3])
Let
![]() $\Omega =\Sigma _A$
be a shift of finite type on
$\Omega =\Sigma _A$
be a shift of finite type on
![]() $\Sigma _m^{\mathbb {N}}$
and
$\Sigma _m^{\mathbb {N}}$
and
![]() $\mu $
be a probability measure on
$\mu $
be a probability measure on
![]() $\Omega $
. Then,
$\Omega $
. Then,
where
 $$ \begin{align} s(\Omega,\mu):=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}} \end{align} $$
$$ \begin{align} s(\Omega,\mu):=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}} \end{align} $$
with
![]() $\beta _k$
is the partition of
$\beta _k$
is the partition of
![]() $\Omega $
into cylinders of length k and
$\Omega $
into cylinders of length k and
 $$ \begin{align*} H_m^{\mu}(\beta_k)=-\sum_{\alpha\in\beta_k}\mu(\alpha)\log_m \mu(\alpha). \end{align*} $$
$$ \begin{align*} H_m^{\mu}(\beta_k)=-\sum_{\alpha\in\beta_k}\mu(\alpha)\log_m \mu(\alpha). \end{align*} $$
Therefore,
![]() $\dim _H(\mathbb {P}_{\mu })=s(\Omega ,\mu )$
, and
$\dim _H(\mathbb {P}_{\mu })=s(\Omega ,\mu )$
, and
![]() $\dim _H(X_{A}^{\mathbf {p}})\geq s(\Omega , \mu )$
.
$\dim _H(X_{A}^{\mathbf {p}})\geq s(\Omega , \mu )$
.
Proof. To obtain
![]() $\dim _{\mathrm {loc}}(\mathbb {P}_\mu ,u)=s(\Omega ,\mu )$
for
$\dim _{\mathrm {loc}}(\mathbb {P}_\mu ,u)=s(\Omega ,\mu )$
for
![]() $\mathbb {P}_\mu $
-a.e. u. We prove that for every
$\mathbb {P}_\mu $
-a.e. u. We prove that for every
![]() $\ell _1, \ell _2,\ldots , \ell _d\in \mathbb {N}$
and
$\ell _1, \ell _2,\ldots , \ell _d\in \mathbb {N}$
and
![]() $\ell =\min _{1\leq i \leq d} \ell _i$
,
$\ell =\min _{1\leq i \leq d} \ell _i$
,
 $$ \begin{align*} \begin{aligned} &(1)~\liminf_{\mathbf{N}\rightarrow\infty}\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{N_1 \cdots N_d}\geq (p_1\cdots p_d-1)^2\sum_{k=1}^{\ell}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}} \quad\mbox{for } \mathbb{P}_\mu\mbox{-a.e. } u,\\ &\mbox{and}\\ &(2)~\limsup_{\mathbf{N}\rightarrow\infty}\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{N_1 \cdots N_d}\\&\quad\qquad\leq (p_1\cdots p_d-1)^2\sum_{k=1}^{\ell}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}}+\frac{(\ell+1)\log_m(2m)}{(p_1\cdots p_d)^{\ell}}\quad\mbox{for } \mathbb{P}_\mu\mbox{-a.e. } u. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &(1)~\liminf_{\mathbf{N}\rightarrow\infty}\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{N_1 \cdots N_d}\geq (p_1\cdots p_d-1)^2\sum_{k=1}^{\ell}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}} \quad\mbox{for } \mathbb{P}_\mu\mbox{-a.e. } u,\\ &\mbox{and}\\ &(2)~\limsup_{\mathbf{N}\rightarrow\infty}\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{N_1 \cdots N_d}\\&\quad\qquad\leq (p_1\cdots p_d-1)^2\sum_{k=1}^{\ell}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}}+\frac{(\ell+1)\log_m(2m)}{(p_1\cdots p_d)^{\ell}}\quad\mbox{for } \mathbb{P}_\mu\mbox{-a.e. } u. \end{aligned} \end{align*} $$
Fixing
![]() $\ell _1,\ldots ,\ell _d\in \mathbb {N}$
, we can restrict to
$\ell _1,\ldots ,\ell _d\in \mathbb {N}$
, we can restrict to
![]() $N_i=p_i^{\ell _i}r_i$
and
$N_i=p_i^{\ell _i}r_i$
and
![]() $r_i\in \mathbb {N}$
for all
$r_i\in \mathbb {N}$
for all
![]() $1\leq i\leq d$
. Since for
$1\leq i\leq d$
. Since for
![]() $p_i^{\ell _i}r_i\leq N_i <p_i^{\ell _i}(r_i+1)$
,
$p_i^{\ell _i}r_i\leq N_i <p_i^{\ell _i}(r_i+1)$
,
![]() $1\leq i \leq d$
, we have
$1\leq i \leq d$
, we have
 $$ \begin{align*} \begin{aligned} \frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{N_1 \cdots N_d}&\geq\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,{(p_1^{\ell_1}r_1,\ldots, p_d^{\ell_d}r_d)}]\kern-1.2pt]}]}{p_1^{\ell_1}(r_1+1)\cdots p_d^{\ell_d}(r_d+1)}\\ &= \frac{r_1\cdots r_d}{(r_1+1)\cdots (r_d+1)} \frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,{(p_1^{\ell_1}r_1,\ldots, p_d^{\ell_d}r_d)}]\kern-1.2pt]}]}{p_1^{\ell_1}r_1\cdots p_d^{\ell_d}r_d}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{N_1 \cdots N_d}&\geq\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,{(p_1^{\ell_1}r_1,\ldots, p_d^{\ell_d}r_d)}]\kern-1.2pt]}]}{p_1^{\ell_1}(r_1+1)\cdots p_d^{\ell_d}(r_d+1)}\\ &= \frac{r_1\cdots r_d}{(r_1+1)\cdots (r_d+1)} \frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,{(p_1^{\ell_1}r_1,\ldots, p_d^{\ell_d}r_d)}]\kern-1.2pt]}]}{p_1^{\ell_1}r_1\cdots p_d^{\ell_d}r_d}, \end{aligned} \end{align*} $$
which implies that
 $$ \begin{align*} \begin{aligned} \liminf_{\mathbf{N}\rightarrow\infty}\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{N_1 \cdots N_d}= \liminf_{r_1,\ldots,r_d\rightarrow\infty}\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,{(p_1^{\ell_1}r_1,\ldots, p_d^{\ell_d}r_d)}]\kern-1.2pt]}]}{p_1^{\ell_1}r_1\cdots p_d^{\ell_d}r_d}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \liminf_{\mathbf{N}\rightarrow\infty}\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{N_1 \cdots N_d}= \liminf_{r_1,\ldots,r_d\rightarrow\infty}\frac{-\log\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,{(p_1^{\ell_1}r_1,\ldots, p_d^{\ell_d}r_d)}]\kern-1.2pt]}]}{p_1^{\ell_1}r_1\cdots p_d^{\ell_d}r_d}. \end{aligned} \end{align*} $$
The lim sup is dealt with similarly.
Recall
The method below estimates the main part
![]() $\mathcal {G}$
and remainder
$\mathcal {G}$
and remainder
![]() $\mathcal {H}$
, which is similar to that of Kenyon et al [Reference Kenyon, Peres and Solomyak16]. Let
$\mathcal {H}$
, which is similar to that of Kenyon et al [Reference Kenyon, Peres and Solomyak16]. Let
 $$ \begin{align*} \mathcal{G}_{\mathbf{N}}:=\bigcup_{k=1}^{\ell}\bigcup_{\mathbf{i}\in \mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}}(\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]) \end{align*} $$
$$ \begin{align*} \mathcal{G}_{\mathbf{N}}:=\bigcup_{k=1}^{\ell}\bigcup_{\mathbf{i}\in \mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}}(\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]) \end{align*} $$
and
Then by the definition of the measure
![]() $\mathbb {P}_\mu $
, we have
$\mathbb {P}_\mu $
, we have
Claim 1. We have
 $$ \begin{align*} \begin{aligned} \mathbb{P}_\mu[u|_{\mathcal{G}_{\mathbf{N}}}]&=\prod_{k=1}^{\ell}\prod_{\mathbf{i}\in \mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}}\mathbb{P}_\mu[u|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]\\ &=\prod_{k=1}^{\ell}\prod_{\mathbf{i}\in \mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}}\mu[u|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathbb{P}_\mu[u|_{\mathcal{G}_{\mathbf{N}}}]&=\prod_{k=1}^{\ell}\prod_{\mathbf{i}\in \mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}}\mathbb{P}_\mu[u|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]\\ &=\prod_{k=1}^{\ell}\prod_{\mathbf{i}\in \mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}}\mu[u|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]. \end{aligned} \end{align*} $$
Proof of Claim 1
The proof comes directly from the definition of
![]() $\mathbb {P}_\mu $
and it is omitted.
$\mathbb {P}_\mu $
and it is omitted.
Claim 2. For all
![]() $k\leq \ell $
,
$k\leq \ell $
,
 $$ \begin{align*} \begin{aligned} \sum_{\mathbf{i}\in\mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}} \frac{-\log_m \mu[u|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{(p_1\cdots p_d-1)^2(N_1 \cdots N_d/(p_1\cdots p_d)^{k+1})} \rightarrow H_m^{\mu}(\beta_k), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{\mathbf{i}\in\mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}} \frac{-\log_m \mu[u|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{(p_1\cdots p_d-1)^2(N_1 \cdots N_d/(p_1\cdots p_d)^{k+1})} \rightarrow H_m^{\mu}(\beta_k), \end{aligned} \end{align*} $$
as
![]() $N_i=p_i^{\ell _i} r_i\rightarrow \infty $
for
$N_i=p_i^{\ell _i} r_i\rightarrow \infty $
for
![]() $1\leq i \leq d$
and
$1\leq i \leq d$
and
![]() $\mathbb {P}_\mu $
-a.e. u.
$\mathbb {P}_\mu $
-a.e. u.
Proof of Claim 2
Since the
![]() $u\mapsto -\log _m\mu [u|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]}]$
are independent and identically distributed (i.i.d.) for
$u\mapsto -\log _m\mu [u|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]}]$
are independent and identically distributed (i.i.d.) for
![]() $\mathbf {i}\in \mathcal {J}_{\mathbf {N};k}\cap \mathcal {I}_{\mathbf {p}}$
, their expectation equals
$\mathbf {i}\in \mathcal {J}_{\mathbf {N};k}\cap \mathcal {I}_{\mathbf {p}}$
, their expectation equals
![]() $H_m^{\mu }(\beta _k)$
. Note that
$H_m^{\mu }(\beta _k)$
. Note that
 $$ \begin{align*} |\mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}|=\frac{(p_1\cdots p_d-1)^2 N_1 \cdots N_d}{(p_1\cdots p_d)^{k+1}}. \end{align*} $$
$$ \begin{align*} |\mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}|=\frac{(p_1\cdots p_d-1)^2 N_1 \cdots N_d}{(p_1\cdots p_d)^{k+1}}. \end{align*} $$
Fixing
![]() $k\leq \min _{1\leq i\leq d}{\ell _i}$
and taking
$k\leq \min _{1\leq i\leq d}{\ell _i}$
and taking
![]() $N_i=p_i^{\ell _i} r_i, r_i\rightarrow \infty $
for all
$N_i=p_i^{\ell _i} r_i, r_i\rightarrow \infty $
for all
![]() $1\leq i \leq d$
, we get infinite i.i.d. random variables. The proof is completed by the law of large numbers (LLN).
$1\leq i \leq d$
, we get infinite i.i.d. random variables. The proof is completed by the law of large numbers (LLN).
Then item (1) is followed by
 $$ \begin{align*} \begin{aligned} (3)~&\frac{-\log_m \mathbb{P}_\mu[u|_{\mathcal{G}_{\mathbf{N}}}]}{N_1 \cdots N_d}\\ &=\sum_{k=1}^{\ell}\frac{(p_1\cdots p_d-1)^2}{(p_1\cdots p_d)^{k+1}} \sum_{\mathbf{i}\in\mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}} \frac{-\log_m \mu[u|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{(p_1\cdots p_d-1)^2(N_1 \cdots N_d/(p_1\cdots p_d)^{k+1})}\\ &\longrightarrow \sum_{k=1}^{\ell}\frac{(p_1\cdots p_d-1)^2H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}},\\ \mbox{and}&\\ (4)~&\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]\leq \mathbb{P}_\mu[u|_{\mathcal{G}_{\mathbf{N}}}]. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} (3)~&\frac{-\log_m \mathbb{P}_\mu[u|_{\mathcal{G}_{\mathbf{N}}}]}{N_1 \cdots N_d}\\ &=\sum_{k=1}^{\ell}\frac{(p_1\cdots p_d-1)^2}{(p_1\cdots p_d)^{k+1}} \sum_{\mathbf{i}\in\mathcal{J}_{\mathbf{N};k}\cap \mathcal{I}_{\mathbf{p}}} \frac{-\log_m \mu[u|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]}{(p_1\cdots p_d-1)^2(N_1 \cdots N_d/(p_1\cdots p_d)^{k+1})}\\ &\longrightarrow \sum_{k=1}^{\ell}\frac{(p_1\cdots p_d-1)^2H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}},\\ \mbox{and}&\\ (4)~&\mathbb{P}_\mu[u|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]\leq \mathbb{P}_\mu[u|_{\mathcal{G}_{\mathbf{N}}}]. \end{aligned} \end{align*} $$
To prove item (2), we work with
![]() $\mathbb {P}_\mu [u|_{\mathcal {H}_{\mathbf {N}}}]$
. Since
$\mathbb {P}_\mu [u|_{\mathcal {H}_{\mathbf {N}}}]$
. Since
 $$ \begin{align*}|\mathcal{H}_{\mathbf{N}}|&=N_1 \cdots N_d-\sum_{k=1}^{\ell}(p_1\cdots p_d-1)^2\frac{N_1 \cdots N_dk}{(p_1\cdots p_d)^{k+1}}\\&=\frac{N_1 \cdots N_d}{(p_1\cdots p_d)^{\ell}}\bigg[(\ell+1)-\frac{\ell}{p_1\cdots p_d} \bigg]\\&=(\ell+1)\prod_{i=1}^dp_i^{\ell_i-\ell}r_i-\frac{\ell }{p_1\cdots p_d}\prod_{i=1}^dp_i^{\ell_i-\ell}r_i\\&<(\ell+1)\prod_{i=1}^dp_i^{\ell_i-\ell}r_i, \end{align*} $$
$$ \begin{align*}|\mathcal{H}_{\mathbf{N}}|&=N_1 \cdots N_d-\sum_{k=1}^{\ell}(p_1\cdots p_d-1)^2\frac{N_1 \cdots N_dk}{(p_1\cdots p_d)^{k+1}}\\&=\frac{N_1 \cdots N_d}{(p_1\cdots p_d)^{\ell}}\bigg[(\ell+1)-\frac{\ell}{p_1\cdots p_d} \bigg]\\&=(\ell+1)\prod_{i=1}^dp_i^{\ell_i-\ell}r_i-\frac{\ell }{p_1\cdots p_d}\prod_{i=1}^dp_i^{\ell_i-\ell}r_i\\&<(\ell+1)\prod_{i=1}^dp_i^{\ell_i-\ell}r_i, \end{align*} $$
then
 $$ \begin{align*} \begin{aligned} \sum_{r_1,\ldots,r_d=1}^{\infty} 2^{-|\mathcal{H}_{\mathbf{N}} |}=\sum_{r_1,\ldots,r_d=1}^{\infty} 2^{-Cr_1\cdots r_d}<\infty, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{r_1,\ldots,r_d=1}^{\infty} 2^{-|\mathcal{H}_{\mathbf{N}} |}=\sum_{r_1,\ldots,r_d=1}^{\infty} 2^{-Cr_1\cdots r_d}<\infty, \end{aligned} \end{align*} $$
where
![]() $C=[(\ell +1)-{\ell }/{p_1\cdots p_d} ]\prod _{i=1}^dp_i^{\ell _i-\ell }>0$
.
$C=[(\ell +1)-{\ell }/{p_1\cdots p_d} ]\prod _{i=1}^dp_i^{\ell _i-\ell }>0$
.
Define
Since there are at most
![]() $m^{|\mathcal {H}_{\mathbf {N}}|}$
cylinder sets
$m^{|\mathcal {H}_{\mathbf {N}}|}$
cylinder sets
![]() $[u|_{\mathcal {H}_{\mathbf {N}}}]$
, we have
$[u|_{\mathcal {H}_{\mathbf {N}}}]$
, we have
This implies
 $$ \begin{align*} \sum_{r_1,\ldots,r_d=1}^{\infty}\mathbb{P}_\mu(\mathcal{S}(\mathcal{H}_{\mathbf{N}})) \leq \sum_{r_1,\ldots,r_d=1}^{\infty} 2^{-|\mathcal{H}_{\mathbf{N}}|}<\infty. \end{align*} $$
$$ \begin{align*} \sum_{r_1,\ldots,r_d=1}^{\infty}\mathbb{P}_\mu(\mathcal{S}(\mathcal{H}_{\mathbf{N}})) \leq \sum_{r_1,\ldots,r_d=1}^{\infty} 2^{-|\mathcal{H}_{\mathbf{N}}|}<\infty. \end{align*} $$
Thus,
 $$ \begin{align*} \lim_{\mathbf{N\to\infty}}\sum_{r_1=N_1,\ldots,r_d=N_d}^{\infty}\mathbb{P}_\mu(\mathcal{S}(\mathcal{H}_{\mathbf{N}}))=0. \end{align*} $$
$$ \begin{align*} \lim_{\mathbf{N\to\infty}}\sum_{r_1=N_1,\ldots,r_d=N_d}^{\infty}\mathbb{P}_\mu(\mathcal{S}(\mathcal{H}_{\mathbf{N}}))=0. \end{align*} $$
That is,
 $$ \begin{align*} \begin{aligned} \mathbb{P}_\mu\bigg(\bigcap_{N_1,\ldots,N_d\geq 1}\bigcup_{r_1=N_1,\ldots,r_d=N_d}^{\infty} \mathcal{S}(\mathcal{H}_{\mathbf{N}})\bigg)=0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \mathbb{P}_\mu\bigg(\bigcap_{N_1,\ldots,N_d\geq 1}\bigcup_{r_1=N_1,\ldots,r_d=N_d}^{\infty} \mathcal{S}(\mathcal{H}_{\mathbf{N}})\bigg)=0. \end{aligned} \end{align*} $$
Hence for
![]() $\mathbb {P}_\mu $
-a.e.
$\mathbb {P}_\mu $
-a.e.
![]() $u\in X_{A}^{\mathbf {p}}$
, there exists
$u\in X_{A}^{\mathbf {p}}$
, there exists
![]() $M_1(u),\ldots ,M_d(u)\in \mathbb {N}$
such that
$M_1(u),\ldots ,M_d(u)\in \mathbb {N}$
such that
![]() $u\notin \mathcal {S}(\mathcal {H}_{\mathbf {N}})$
for all
$u\notin \mathcal {S}(\mathcal {H}_{\mathbf {N}})$
for all
![]() $N_1=p_1^{\ell _1} r_1\geq M_1(u),\ldots ,N_d=p_d^{\ell _d} r_d\geq M_d(u)$
. For such u and
$N_1=p_1^{\ell _1} r_1\geq M_1(u),\ldots ,N_d=p_d^{\ell _d} r_d\geq M_d(u)$
. For such u and
![]() $N_i\geq M_i(u)$
for all
$N_i\geq M_i(u)$
for all
![]() $1\leq i \leq d$
, we have
$1\leq i \leq d$
, we have
 $$ \begin{align*} \begin{aligned} \frac{-\log_m \mathbb{P}_\mu[u|_{\mathcal{H}_{\mathbf{N}}}]}{N_1 \cdots N_d}<\frac{|\mathcal{H}_{\mathbf{N}}|\log_m(2m)}{N_1 \cdots N_d}<\frac{(\ell+1)\log_m(2m)}{(p_1\cdots p_d)^{\ell}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{-\log_m \mathbb{P}_\mu[u|_{\mathcal{H}_{\mathbf{N}}}]}{N_1 \cdots N_d}<\frac{|\mathcal{H}_{\mathbf{N}}|\log_m(2m)}{N_1 \cdots N_d}<\frac{(\ell+1)\log_m(2m)}{(p_1\cdots p_d)^{\ell}}. \end{aligned} \end{align*} $$
The proof is complete.
Lemma 3.2. (
 $\mathbb {N}^d$
version of [Reference Kenyon, Peres and Solomyak16, Corollary 2.6])
$\mathbb {N}^d$
version of [Reference Kenyon, Peres and Solomyak16, Corollary 2.6])
Let A be a primitive
![]() $m\times m \ 0$
-
$m\times m \ 0$
-
![]() $1$
matrix and
$1$
matrix and
![]() $\Omega =\Sigma _A$
be the corresponding subshift of finite type. Let
$\Omega =\Sigma _A$
be the corresponding subshift of finite type. Let
![]() $\bar {t}=(t_i)_{i=0}^{m-1}$
be the solution of equation (18). Then the unique optimal measure on
$\bar {t}=(t_i)_{i=0}^{m-1}$
be the solution of equation (18). Then the unique optimal measure on
![]() $\Sigma _A$
is Markov, with the vector of initial probabilities
$\Sigma _A$
is Markov, with the vector of initial probabilities
![]() $\mathbf {P}=(P_i)_{i=0}^{m-1}=(\sum _{i=0}^{m-1}t_i)^{-1} \bar {t}$
and the matrix of transition probabilities
$\mathbf {P}=(P_i)_{i=0}^{m-1}=(\sum _{i=0}^{m-1}t_i)^{-1} \bar {t}$
and the matrix of transition probabilities
 $$ \begin{align} (p_{ij})_{i,j=0}^{m-1}\quad\mbox{where } p_{ij}=\frac{t_j}{t_i^{p_1\cdots p_d}}\quad \mbox{if } A(i,j)=1. \end{align} $$
$$ \begin{align} (p_{ij})_{i,j=0}^{m-1}\quad\mbox{where } p_{ij}=\frac{t_j}{t_i^{p_1\cdots p_d}}\quad \mbox{if } A(i,j)=1. \end{align} $$
Moreover,
![]() $s(\Omega , \mu )=(p_1\cdots p_d-1)\log _mt_{\phi }$
, where
$s(\Omega , \mu )=(p_1\cdots p_d-1)\log _mt_{\phi }$
, where
![]() $t_\phi ^{p_1\cdots p_d}=\sum _{i=0}^{m-1} t_i$
.
$t_\phi ^{p_1\cdots p_d}=\sum _{i=0}^{m-1} t_i$
.
Proof. Since
 $$ \begin{align*} \sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}}=\bigg[\sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_{1})}{(p_1\cdots p_d)^{k+1}}+\frac{1}{p_1\cdots p_d}\sum_{i=0}^{m-1}P_i\sum_{k=1}^{\infty} \frac{H_m^{\mu_{i}}(\beta_{k}(\Omega_i))}{(p_1\cdots p_d)^{k+1}}\bigg] \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}}=\bigg[\sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_{1})}{(p_1\cdots p_d)^{k+1}}+\frac{1}{p_1\cdots p_d}\sum_{i=0}^{m-1}P_i\sum_{k=1}^{\infty} \frac{H_m^{\mu_{i}}(\beta_{k}(\Omega_i))}{(p_1\cdots p_d)^{k+1}}\bigg] \end{align*} $$
and
 $$ \begin{align*} \sum_{k=1}^\infty \frac{1}{(p_1\cdots p_d)^k}=\frac{1}{p_1\cdots p_d-1}, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^\infty \frac{1}{(p_1\cdots p_d)^k}=\frac{1}{p_1\cdots p_d-1}, \end{align*} $$
we have
 $$ \begin{align*} s(\Omega,\mathbb{P}_\mu)=\frac{p_1\cdots p_d-1}{p_1\cdots p_d}\bigg[H_m^{\mu}(\beta_{1})+\frac{1}{p_1\cdots p_d-1}\sum_{i=0}^{m-1}P_is(\Omega_i,\mu_{i})\bigg], \end{align*} $$
$$ \begin{align*} s(\Omega,\mathbb{P}_\mu)=\frac{p_1\cdots p_d-1}{p_1\cdots p_d}\bigg[H_m^{\mu}(\beta_{1})+\frac{1}{p_1\cdots p_d-1}\sum_{i=0}^{m-1}P_is(\Omega_i,\mu_{i})\bigg], \end{align*} $$
where
![]() $P_i=\mu [i]$
and
$P_i=\mu [i]$
and
![]() $\mu _{i}$
is the conditional measures of
$\mu _{i}$
is the conditional measures of
![]() $\mu $
on
$\mu $
on
![]() $\Omega _i$
.
$\Omega _i$
.
Since the measure
![]() $\mathbb {P}_\mu $
is completely determined by the probability vector
$\mathbb {P}_\mu $
is completely determined by the probability vector
![]() $\mathbf {P}=(P_i)_{i=0}^{m-1}$
and the measures
$\mathbf {P}=(P_i)_{i=0}^{m-1}$
and the measures
![]() $\mu _{i}$
on
$\mu _{i}$
on
![]() $\Omega _i$
, the optimizations on
$\Omega _i$
, the optimizations on
![]() $\Omega _i$
are independent for all
$\Omega _i$
are independent for all
![]() $0\leq i \leq m-1$
. Thus, if
$0\leq i \leq m-1$
. Thus, if
![]() $\mathbb {P}_\mu $
is optimal for
$\mathbb {P}_\mu $
is optimal for
![]() $\Omega $
, then
$\Omega $
, then
![]() $\mu _{i}$
is optimal for
$\mu _{i}$
is optimal for
![]() $\Omega _i$
,
$\Omega _i$
,
![]() $0\leq i\leq m-1$
. Since
$0\leq i\leq m-1$
. Since
 $$ \begin{align*} &\max_{\mathbf{{p}}}\bigg[H_m^{\mu}(\beta_{1})+\frac{1}{p_1\cdots p_d-1}\sum_{i=0}^{m-1}P_is(\Omega_i)\bigg]\\ &\quad=\max_{\mathbf{{p}}}\bigg[-\sum_{i=0}^{m-1}P_i\log_mP_i+\frac{1}{p_1\cdots p_d-1}\sum_{i=0}^{m-1}P_is(\Omega_i)\bigg]\\ &\quad=\max_{\mathbf{{p}}}\bigg[\sum_{i=0}^{m-1}P_i(a_i-\log_mP_i)\bigg], \end{align*} $$
$$ \begin{align*} &\max_{\mathbf{{p}}}\bigg[H_m^{\mu}(\beta_{1})+\frac{1}{p_1\cdots p_d-1}\sum_{i=0}^{m-1}P_is(\Omega_i)\bigg]\\ &\quad=\max_{\mathbf{{p}}}\bigg[-\sum_{i=0}^{m-1}P_i\log_mP_i+\frac{1}{p_1\cdots p_d-1}\sum_{i=0}^{m-1}P_is(\Omega_i)\bigg]\\ &\quad=\max_{\mathbf{{p}}}\bigg[\sum_{i=0}^{m-1}P_i(a_i-\log_mP_i)\bigg], \end{align*} $$
we have
 $$ \begin{align*} s(\Omega):&=\max\{s(\Omega,\mathbb{P}_\mu): \mu \mbox{ is a probability measure on }\Omega\}\\ &=\max_{\mathbf{{p}}}\frac{p_1\cdots p_d-1}{p_1\cdots p_d}\bigg[\sum_{i=0}^{m-1}P_i(a_i-\log_mP_i)\bigg], \end{align*} $$
$$ \begin{align*} s(\Omega):&=\max\{s(\Omega,\mathbb{P}_\mu): \mu \mbox{ is a probability measure on }\Omega\}\\ &=\max_{\mathbf{{p}}}\frac{p_1\cdots p_d-1}{p_1\cdots p_d}\bigg[\sum_{i=0}^{m-1}P_i(a_i-\log_mP_i)\bigg], \end{align*} $$
where
![]() $a_i={s(\Omega _i)}/{p_1\cdots p_d-1}$
.
$a_i={s(\Omega _i)}/{p_1\cdots p_d-1}$
.
Then we obtain the optimal probability vector
 $$ \begin{gather*} \mathbf{P}=(P_i)_{i=0}^{m-1},\quad P_i=\frac{m^{a_i}}{\sum_{j=0}^{m-1}m^{a_j}}=\frac{t_i}{t_{\phi}^{p_1\cdots p_d}},\\[5pt] t_\phi=m^{{s(\Omega)}/{p_1\cdots p_d-1}},\quad t_i=m^{{s(\Omega_i)}/{p_1\cdots p_d-1}},\quad i\leq m-1, \end{gather*} $$
$$ \begin{gather*} \mathbf{P}=(P_i)_{i=0}^{m-1},\quad P_i=\frac{m^{a_i}}{\sum_{j=0}^{m-1}m^{a_j}}=\frac{t_i}{t_{\phi}^{p_1\cdots p_d}},\\[5pt] t_\phi=m^{{s(\Omega)}/{p_1\cdots p_d-1}},\quad t_i=m^{{s(\Omega_i)}/{p_1\cdots p_d-1}},\quad i\leq m-1, \end{gather*} $$
and
 $$ \begin{align*} \begin{aligned} t_\phi^{p_1\cdots p_d}=\sum_{i=0}^{m-1}t_i. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} t_\phi^{p_1\cdots p_d}=\sum_{i=0}^{m-1}t_i. \end{aligned} \end{align*} $$
Due to the conditional entropy, we have
where for two partitions
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
,
$\beta $
,
 $$ \begin{align*} H_m^{\mu}(\alpha|\beta)=\sum_{B\in\beta}\bigg(-\sum_{A\in\alpha}\mu(A|B)\log_m \mu(A|B) \bigg)\mu(B). \end{align*} $$
$$ \begin{align*} H_m^{\mu}(\alpha|\beta)=\sum_{B\in\beta}\bigg(-\sum_{A\in\alpha}\mu(A|B)\log_m \mu(A|B) \bigg)\mu(B). \end{align*} $$
Then,
 $$ \begin{align*} s(\Omega,\mathbb{P}_\mu)&=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}}\\&= \bigg( \frac{p_1\cdots p_d-1}{p_1\cdots p_d} \bigg)\bigg[ H_m^{\mu}(\beta_1)+\sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_{k+1}|\beta_{k})}{(p_1\cdots p_d)^{k}}\bigg]. \end{align*} $$
$$ \begin{align*} s(\Omega,\mathbb{P}_\mu)&=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_k)}{(p_1\cdots p_d)^{k+1}}\\&= \bigg( \frac{p_1\cdots p_d-1}{p_1\cdots p_d} \bigg)\bigg[ H_m^{\mu}(\beta_1)+\sum_{k=1}^{\infty}\frac{H_m^{\mu}(\beta_{k+1}|\beta_{k})}{(p_1\cdots p_d)^{k}}\bigg]. \end{align*} $$
Observe that
 $$ \begin{align*} H_m^{\mu}(\beta_1)&=-\sum_{i=0}^{m-1}\frac{t_i}{t_{\phi}^{p_1\cdots p_d}}\log_m(\frac{t_i}{t_{\phi}^{p_1\cdots p_d}})\nonumber\\ &=p_1\cdots p_d\log_mt_{\phi}-\sum_{i=0}^{m-1}\frac{t_i}{t_{\phi}^{p_1\cdots p_d}}\log_mt_i\nonumber\\ &=p_1\cdots p_d\log_mt_{\phi}-\sum_{i=0}^{m-1}\mu[i]\log_mt_i \end{align*} $$
$$ \begin{align*} H_m^{\mu}(\beta_1)&=-\sum_{i=0}^{m-1}\frac{t_i}{t_{\phi}^{p_1\cdots p_d}}\log_m(\frac{t_i}{t_{\phi}^{p_1\cdots p_d}})\nonumber\\ &=p_1\cdots p_d\log_mt_{\phi}-\sum_{i=0}^{m-1}\frac{t_i}{t_{\phi}^{p_1\cdots p_d}}\log_mt_i\nonumber\\ &=p_1\cdots p_d\log_mt_{\phi}-\sum_{i=0}^{m-1}\mu[i]\log_mt_i \end{align*} $$
and
 $$ \begin{align*} H_m^{\mu}(\beta_{k+1}|\beta_{k})&=\sum_{[u]\in \beta_k}\mu[u]\bigg(-\sum_{w:[uw]\in \beta_{k+1}}\frac{t_{uw}}{t_{u}^{p_1\cdots p_d}}\log_m\bigg(\frac{t_{uw}}{t_{u}^{p_1\cdots p_d}}\bigg) \bigg)\\ &=\sum_{[u]\in \beta_k}\mu[u]\bigg(p_1\cdots p_d\log_mt_u-\sum_{w:[uw]\in \beta_{k+1}}\frac{t_{uw}}{t_{u}^{p_1\cdots p_d}}\log_mt_{uw} \bigg)\\ &=p_1\cdots p_d\sum_{[u]\in \beta_k}\mu[u]\log_mt_u-\sum_{[v]\in \beta_{k+1}}\mu[v]\log_mt_v,\\ \end{align*} $$
$$ \begin{align*} H_m^{\mu}(\beta_{k+1}|\beta_{k})&=\sum_{[u]\in \beta_k}\mu[u]\bigg(-\sum_{w:[uw]\in \beta_{k+1}}\frac{t_{uw}}{t_{u}^{p_1\cdots p_d}}\log_m\bigg(\frac{t_{uw}}{t_{u}^{p_1\cdots p_d}}\bigg) \bigg)\\ &=\sum_{[u]\in \beta_k}\mu[u]\bigg(p_1\cdots p_d\log_mt_u-\sum_{w:[uw]\in \beta_{k+1}}\frac{t_{uw}}{t_{u}^{p_1\cdots p_d}}\log_mt_{uw} \bigg)\\ &=p_1\cdots p_d\sum_{[u]\in \beta_k}\mu[u]\log_mt_u-\sum_{[v]\in \beta_{k+1}}\mu[v]\log_mt_v,\\ \end{align*} $$
where
![]() $\mu [uw]=\mu [u]{t_{uw}}/{t_u^{p_1\cdots p_d}}$
. Then we have
$\mu [uw]=\mu [u]{t_{uw}}/{t_u^{p_1\cdots p_d}}$
. Then we have
The proof is complete.
Lemma 3.3. (
 $\mathbb {N}^d$
version of [Reference Kenyon, Peres and Solomyak16, Lemma 5.2])
$\mathbb {N}^d$
version of [Reference Kenyon, Peres and Solomyak16, Lemma 5.2])
Let
![]() $\mu $
be a Markov measure on
$\mu $
be a Markov measure on
![]() $\Omega $
, with the vector of initial probabilities
$\Omega $
, with the vector of initial probabilities
![]() $\mathbf {P}=(\sum _{i=0}^{m-1}t_i)^{-1} \bar {t}$
and the matrix of transition probabilities
$\mathbf {P}=(\sum _{i=0}^{m-1}t_i)^{-1} \bar {t}$
and the matrix of transition probabilities
 $$ \begin{align} (p_{ij})_{i,j=0}^{m-1}\quad\mbox{where}\ p_{ij}=\frac{t_j}{t_i^{p_1\cdots p_d}}\quad \mbox{if } A(i,j)=1. \end{align} $$
$$ \begin{align} (p_{ij})_{i,j=0}^{m-1}\quad\mbox{where}\ p_{ij}=\frac{t_j}{t_i^{p_1\cdots p_d}}\quad \mbox{if } A(i,j)=1. \end{align} $$
Then,
for all
![]() $x\in X_{A}^{\mathbf {p}}$
.
$x\in X_{A}^{\mathbf {p}}$
.
Proof. The proof is similar to that of Lemma 4.9 when
![]() $\varphi $
is a zero function.
$\varphi $
is a zero function.
Lemma 3.4. (
 $\mathbb {N}^d$
version of [Reference Kenyon, Peres and Solomyak16, Proposition 2.4])
$\mathbb {N}^d$
version of [Reference Kenyon, Peres and Solomyak16, Proposition 2.4])
Let
![]() $\Omega =\Sigma _A$
be a shift of finite type on
$\Omega =\Sigma _A$
be a shift of finite type on
![]() $\Sigma _m^{\mathbb {N}}$
. Then,
$\Sigma _m^{\mathbb {N}}$
. Then,
where the supremum is over the Borel probability measures on
![]() $\Omega $
.
$\Omega $
.
4 Proof of Theorem 1.5
The stages of the proof of Theorem 1.5 follow Fan, Schmeling, and Wu [Reference Fan, Schmeling and Wu11]. First, we establish the LLN in our setting (Lemma 4.4), then use the unique positive solution of nonlinear operator
![]() $\mathcal {N}_s$
to construct a family of telescopic product measures
$\mathcal {N}_s$
to construct a family of telescopic product measures
![]() $\mathbb {P}_{\mu _s}$
in equations (35) and (36). Then the convexity of such solution, LLN, and Billingsley lemma (Lemma 4.11) give the upper and lower bound of Hausdorff dimension of
$\mathbb {P}_{\mu _s}$
in equations (35) and (36). Then the convexity of such solution, LLN, and Billingsley lemma (Lemma 4.11) give the upper and lower bound of Hausdorff dimension of
![]() $E(\alpha )$
(Lemma 4.12 and Lemma 4.16 respectively), and we establish Theorem 4.1 in §4.1. To complete the proof of Theorem 1.5, we prove the case when s tends to
$E(\alpha )$
(Lemma 4.12 and Lemma 4.16 respectively), and we establish Theorem 4.1 in §4.1. To complete the proof of Theorem 1.5, we prove the case when s tends to
![]() $\pm \infty $
in §4.2 (Theorems 4.18 and 4.19).
$\pm \infty $
in §4.2 (Theorems 4.18 and 4.19).
4.1 The case when
 $s_{\alpha }$
is finite
$s_{\alpha }$
is finite
Theorem 4.1
-
(1) If
 $\alpha =P^{\prime }_{\varphi }(s_{\alpha })$
for some
$\alpha =P^{\prime }_{\varphi }(s_{\alpha })$
for some
 $s_{\alpha } \in \mathbb {R}$
, then
$s_{\alpha } \in \mathbb {R}$
, then  $$ \begin{align*} \dim_H E(\alpha)=\frac{-P^{\prime}_{\varphi}(s_{\alpha})s_{\alpha}+P_{\varphi}(s_{\alpha})}{(p_1\cdots p_d)^{\ell-1}\log m}=\frac{P^*_{\varphi}(\alpha)}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
$$ \begin{align*} \dim_H E(\alpha)=\frac{-P^{\prime}_{\varphi}(s_{\alpha})s_{\alpha}+P_{\varphi}(s_{\alpha})}{(p_1\cdots p_d)^{\ell-1}\log m}=\frac{P^*_{\varphi}(\alpha)}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
-
(2) For
 $\alpha \in (P^{\prime }_{\varphi }(-\infty ),P^{\prime }_{\varphi }(0)]$
,
$\alpha \in (P^{\prime }_{\varphi }(-\infty ),P^{\prime }_{\varphi }(0)]$
,
 $\dim _H E^+(\alpha )=\dim _H E(\alpha )$
.
$\dim _H E^+(\alpha )=\dim _H E(\alpha )$
. -
(3) For
 $\alpha \in [P^{\prime }_{\varphi }(0),P^{\prime }_{\varphi }(+\infty ))$
,
$\alpha \in [P^{\prime }_{\varphi }(0),P^{\prime }_{\varphi }(+\infty ))$
,
 $\dim _H E^-(\alpha )=\dim _H E(\alpha )$
.
$\dim _H E^-(\alpha )=\dim _H E(\alpha )$
.
Consider a probability space
![]() $(\Sigma _m^{\mathbb {N}^d},\mathbb {P}_\mu )$
. Let
$(\Sigma _m^{\mathbb {N}^d},\mathbb {P}_\mu )$
. Let
![]() $X_{\mathbf {j}}(x)=x_{\mathbf {j}}$
be the
$X_{\mathbf {j}}(x)=x_{\mathbf {j}}$
be the
![]() $\mathbf {j}$
th coordinate projection. For
$\mathbf {j}$
th coordinate projection. For
![]() $\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
, consider the process
$\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
, consider the process
![]() $Y^{(\textbf i)}=(X_{\mathbf {j}})_{\mathbf { j}\in \mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
. Then, by the definition of
$Y^{(\textbf i)}=(X_{\mathbf {j}})_{\mathbf { j}\in \mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
. Then, by the definition of
![]() $\mathbb {P}_\mu $
, the following fact is obvious.
$\mathbb {P}_\mu $
, the following fact is obvious.
Lemma 4.2. The processes
![]() $Y^{(\textbf i)}=(X_{\mathbf {j}})_{\mathbf {j}\in \mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
for
$Y^{(\textbf i)}=(X_{\mathbf {j}})_{\mathbf {j}\in \mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
for
![]() $\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
are
$\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
are
![]() $\mathbb {P}_\mu $
-independent and identically distributed with
$\mathbb {P}_\mu $
-independent and identically distributed with
![]() $\mu $
as the common probability law.
$\mu $
as the common probability law.
Now we consider
![]() $(\bigsqcup _{\mathbf {i} \in \mathcal {I}_{\mathbf {p}}}S^{\mathcal {M}_{\mathbf {p}}(\mathbf {i})},\mathbb {P}_\mu )$
as a probability space
$(\bigsqcup _{\mathbf {i} \in \mathcal {I}_{\mathbf {p}}}S^{\mathcal {M}_{\mathbf {p}}(\mathbf {i})},\mathbb {P}_\mu )$
as a probability space
![]() $(\Omega ,\mathbb {P}_\mu )$
. Let
$(\Omega ,\mathbb {P}_\mu )$
. Let
![]() $(F_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}$
be functions defined on
$(F_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}$
be functions defined on
![]() $\Sigma _m$
. For each
$\Sigma _m$
. For each
![]() $\mathbf {j}$
, there exists a unique
$\mathbf {j}$
, there exists a unique
![]() $\mathbf {i}(\mathbf {j})\in \mathcal {I}_{\mathbf {p}}$
such that
$\mathbf {i}(\mathbf {j})\in \mathcal {I}_{\mathbf {p}}$
such that
![]() $\mathbf {j}\in \mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j}))$
. Then,
$\mathbf {j}\in \mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j}))$
. Then,
![]() $x\mapsto F_{\mathbf {j}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j}))})$
defines a random variable on
$x\mapsto F_{\mathbf {j}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j}))})$
defines a random variable on
![]() $\Omega $
. Later, we will study the LLN for variables
$\Omega $
. Later, we will study the LLN for variables
![]() $\{ F_{\mathbf {j}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf { i}(\mathbf {j}))}) \}_{\mathbf {j}\in \mathbb {N}^d}$
. Notice that if
$\{ F_{\mathbf {j}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf { i}(\mathbf {j}))}) \}_{\mathbf {j}\in \mathbb {N}^d}$
. Notice that if
![]() $\mathbf {i(j)}\neq \mathbf {i(j')}$
, then the two variables
$\mathbf {i(j)}\neq \mathbf {i(j')}$
, then the two variables
![]() $F_{\mathbf {j}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j}))})$
and
$F_{\mathbf {j}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j}))})$
and
![]() $F_{\mathbf {j'}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j'}))})$
are independent. However, if
$F_{\mathbf {j'}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j'}))})$
are independent. However, if
![]() $\mathbf {i(j)}= \mathbf {i(j')}$
, they are not independent in general. To prove the LLN, we will need the following technical lemma which allows us to compute the expectation of the product of
$\mathbf {i(j)}= \mathbf {i(j')}$
, they are not independent in general. To prove the LLN, we will need the following technical lemma which allows us to compute the expectation of the product of
![]() $F_{\mathbf {j}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j}))})$
.
$F_{\mathbf {j}}(x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i}(\mathbf {j}))})$
.
Lemma 4.3. Let
![]() $(F_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}$
be functions defined on
$(F_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}$
be functions defined on
![]() $\Sigma _m$
. Then for any
$\Sigma _m$
. Then for any
![]() $N_1,N_2,\ldots ,N_d\geq 1$
, we have
$N_1,N_2,\ldots ,N_d\geq 1$
, we have
 $$ \begin{align*} \mathbb{E}_{\mathbb{P}_\mu}\bigg( \prod_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt] } F_{\mathbf{j}}(x|_{\mathcal{M}_{\mathbf{ p}}(\mathbf{i(j)})}) \bigg)=\prod_{\ell=1}^{N_1\cdots N_d} \prod_{\mathbf{i} \in\mathcal{J}_{\mathbf{N};\ell}\cap \mathcal{I}_{\mathbf{p}}} \mathbb{E}_\mu \bigg( \prod_{\mathbf{y}\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{ N}]\kern-1.2pt] } F_{\mathbf{y}}(y) \bigg). \end{align*} $$
$$ \begin{align*} \mathbb{E}_{\mathbb{P}_\mu}\bigg( \prod_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt] } F_{\mathbf{j}}(x|_{\mathcal{M}_{\mathbf{ p}}(\mathbf{i(j)})}) \bigg)=\prod_{\ell=1}^{N_1\cdots N_d} \prod_{\mathbf{i} \in\mathcal{J}_{\mathbf{N};\ell}\cap \mathcal{I}_{\mathbf{p}}} \mathbb{E}_\mu \bigg( \prod_{\mathbf{y}\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{ N}]\kern-1.2pt] } F_{\mathbf{y}}(y) \bigg). \end{align*} $$
In particular, for any function G defined on
![]() $\Sigma _m$
, for any
$\Sigma _m$
, for any
![]() $\mathbf {i}\in \mathbb {N}^d$
,
$\mathbf {i}\in \mathbb {N}^d$
,
Proof. Let
 $$ \begin{align*} Q_{\mathbf{N}}(x)= \prod_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} F_{\mathbf{j}}(x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i(j)})}) \end{align*} $$
$$ \begin{align*} Q_{\mathbf{N}}(x)= \prod_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} F_{\mathbf{j}}(x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i(j)})}) \end{align*} $$
and
 $$ \begin{align*} Q_{\mathbf{N, i}}(x)=\prod_{\mathbf{y}\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} F_{\mathbf{y}}(x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})}). \end{align*} $$
$$ \begin{align*} Q_{\mathbf{N, i}}(x)=\prod_{\mathbf{y}\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} F_{\mathbf{y}}(x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})}). \end{align*} $$
Since the variables
![]() $x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
for
$x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
for
![]() $\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
are independent under
$\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
are independent under
![]() $\mathbb {P}_\mu $
(by Lemma 4.2), we have
$\mathbb {P}_\mu $
(by Lemma 4.2), we have
 $$ \begin{align} \mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N}}=\prod_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N, i}}. \end{align} $$
$$ \begin{align} \mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N}}=\prod_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N, i}}. \end{align} $$
Then by the definition of
![]() $\mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}}$
, we can rewrite equation (30) to get
$\mathcal {J}_{\mathbf {N};\ell }\cap \mathcal {I}_{\mathbf {p}}$
, we can rewrite equation (30) to get
 $$ \begin{align*} \mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N}}=\prod_{\ell=1}^{N_1\cdots N_d} \prod_{\mathbf{i} \in\mathcal{J}_{\mathbf{N};\ell}\cap \mathcal{I}_{\mathbf{p}}}\mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N, i}}. \end{align*} $$
$$ \begin{align*} \mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N}}=\prod_{\ell=1}^{N_1\cdots N_d} \prod_{\mathbf{i} \in\mathcal{J}_{\mathbf{N};\ell}\cap \mathcal{I}_{\mathbf{p}}}\mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N, i}}. \end{align*} $$
However, the marginal measures on
![]() $S^{\mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
of
$S^{\mathcal {M}_{\mathbf {p}}(\mathbf {i})}$
of
![]() $\mathbb {P}_\mu $
are equal to
$\mathbb {P}_\mu $
are equal to
![]() $\mu $
. So,
$\mu $
. So,
 $$ \begin{align*} \mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N, i}}=\mathbb{E}_\mu \bigg( \prod_{\mathbf{y}\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} F_{\mathbf{y}}(y) \bigg). \end{align*} $$
$$ \begin{align*} \mathbb{E}_{\mathbb{P}_\mu} Q_{\mathbf{N, i}}=\mathbb{E}_\mu \bigg( \prod_{\mathbf{y}\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} F_{\mathbf{y}}(y) \bigg). \end{align*} $$
Now, for any function G defined on
![]() $\Sigma _m$
and any
$\Sigma _m$
and any
![]() $\mathbf {j}\in \mathbb {N}^d$
, if we set
$\mathbf {j}\in \mathbb {N}^d$
, if we set
![]() $F_{\mathbf {j}}=G$
and
$F_{\mathbf {j}}=G$
and
![]() $F_{\mathbf {j'}}=1$
for
$F_{\mathbf {j'}}=1$
for
![]() $\mathbf {j'}\neq \mathbf {j}$
, we have
$\mathbf {j'}\neq \mathbf {j}$
, we have
The proof is thus completed.
To prove the LLN, we need the following result. Recall that the covariance of two bounded functions
![]() $f,g$
with respect to
$f,g$
with respect to
![]() $\mu $
is defined by
$\mu $
is defined by
When the functions
![]() $(F_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}$
are all the same function F, we have the following LLN.
$(F_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}$
are all the same function F, we have the following LLN.
Lemma 4.4. Let F be a function defined on
![]() $\Sigma _m$
. Suppose that there exist
$\Sigma _m$
. Suppose that there exist
![]() $C>0$
and
$C>0$
and
![]() $0<\eta <p_1\cdots p_d$
such that for any
$0<\eta <p_1\cdots p_d$
such that for any
![]() $\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
and any
$\mathbf {i} \in \mathcal {I}_{\mathbf {p}}$
and any
![]() $\ell _1,\ell _2\in \mathbb {N}\cup \{ 0\}$
,
$\ell _1,\ell _2\in \mathbb {N}\cup \{ 0\}$
,
(
![]() $\mathbf {p}^{\ell }=(p_1^\ell ,p_2^\ell ,\ldots ,p_d^\ell ).$
) Then for
$\mathbf {p}^{\ell }=(p_1^\ell ,p_2^\ell ,\ldots ,p_d^\ell ).$
) Then for
![]() $\mathbb {P}_\mu $
-a.e.
$\mathbb {P}_\mu $
-a.e.
![]() $x\in \Sigma _m^{\mathbb {N}^d}$
,
$x\in \Sigma _m^{\mathbb {N}^d}$
,
 $$ \begin{align*} \lim_{\mathbf{N} \rightarrow \infty} \frac{1}{N_1\cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt] }( F (x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i(j)})})-\mathbb{E}_{\mu}F )=0. \end{align*} $$
$$ \begin{align*} \lim_{\mathbf{N} \rightarrow \infty} \frac{1}{N_1\cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt] }( F (x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i(j)})})-\mathbb{E}_{\mu}F )=0. \end{align*} $$
Proof. Without loss of generality, we may assume
![]() $\mathbb {E}_{\mathbb {P}_\mu } F (x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i(j)})})=0$
for all
$\mathbb {E}_{\mathbb {P}_\mu } F (x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i(j)})})=0$
for all
![]() $\mathbf {j}\in \mathbb {N}^d$
. Our goal is to prove
$\mathbf {j}\in \mathbb {N}^d$
. Our goal is to prove
![]() $\lim _{\mathbf {N} \rightarrow \infty } Y_{\mathbf {N}}=0 \ \mathbb {P}_\mu $
-almost everywhere, where
$\lim _{\mathbf {N} \rightarrow \infty } Y_{\mathbf {N}}=0 \ \mathbb {P}_\mu $
-almost everywhere, where
 $$ \begin{align*} Y_{\mathbf{N}}=\frac{1}{N_1\cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}X_{\mathbf{j}} \quad\mbox{with } X_{\mathbf{j}}=F (x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i(j)})}). \end{align*} $$
$$ \begin{align*} Y_{\mathbf{N}}=\frac{1}{N_1\cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}X_{\mathbf{j}} \quad\mbox{with } X_{\mathbf{j}}=F (x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i(j)})}). \end{align*} $$
It is enough to show
 $$ \begin{align*} \sum_{ N_1,N_2,\ldots,N_d=1}^{\infty}\mathbb{E}_{\mathbb{P}_\mu} Y_{\mathbf{N}}^2 <+\infty. \end{align*} $$
$$ \begin{align*} \sum_{ N_1,N_2,\ldots,N_d=1}^{\infty}\mathbb{E}_{\mathbb{P}_\mu} Y_{\mathbf{N}}^2 <+\infty. \end{align*} $$
Notice that
 $$ \begin{align} \mathbb{E}_{\mathbb{P}_\mu} Y_{\mathbf{N}}^2=\frac{1}{(N_1\cdots N_d)^2}\sum_{\mathbf{j}_1,\mathbf{j}_2\in[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}. \end{align} $$
$$ \begin{align} \mathbb{E}_{\mathbb{P}_\mu} Y_{\mathbf{N}}^2=\frac{1}{(N_1\cdots N_d)^2}\sum_{\mathbf{j}_1,\mathbf{j}_2\in[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}. \end{align} $$
By Lemma 4.2, we have
![]() $\mathbb {E}_{\mathbb {P}_\mu }X_{\mathbf {j}_1} X_{\mathbf {j}_2}\neq 0$
only if
$\mathbb {E}_{\mathbb {P}_\mu }X_{\mathbf {j}_1} X_{\mathbf {j}_2}\neq 0$
only if
![]() $\mathbf {i}(\mathbf { j}_1)=\mathbf {i}(\mathbf {j}_2)$
. So,
$\mathbf {i}(\mathbf { j}_1)=\mathbf {i}(\mathbf {j}_2)$
. So,
 $$ \begin{align*} \sum_{\mathbf{j}_1,\mathbf{j}_2\in[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}= \sum_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \sum_{\mathbf{j}_1,\mathbf{j}_2\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}. \end{align*} $$
$$ \begin{align*} \sum_{\mathbf{j}_1,\mathbf{j}_2\in[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}= \sum_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \sum_{\mathbf{j}_1,\mathbf{j}_2\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}. \end{align*} $$
By Lemma 2.2, we can rewrite the above sum as
 $$ \begin{align} \sum_{\ell=1}^{N_1\cdots N_d} \sum_{\mathbf{i} \in\mathcal{J}_{\mathbf{N};\ell}\cap \mathcal{I}_{\mathbf{p}}} \sum_{\mathbf{j}_1,\mathbf{ j}_2\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}. \end{align} $$
$$ \begin{align} \sum_{\ell=1}^{N_1\cdots N_d} \sum_{\mathbf{i} \in\mathcal{J}_{\mathbf{N};\ell}\cap \mathcal{I}_{\mathbf{p}}} \sum_{\mathbf{j}_1,\mathbf{ j}_2\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}. \end{align} $$
Recall that
![]() $\mathbb {E}_{\mathbb {P}_\mu }X_{\mathbf {j}}=\mathbb {E}_{\mu }F$
for all
$\mathbb {E}_{\mathbb {P}_\mu }X_{\mathbf {j}}=\mathbb {E}_{\mu }F$
for all
![]() $\mathbf {j}\in \mathbb {N}^d$
(Lemma 4.3). For
$\mathbf {j}\in \mathbb {N}^d$
(Lemma 4.3). For
![]() $\mathbf {j}_1,\mathbf {j}_2\in \mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
, we write
$\mathbf {j}_1,\mathbf {j}_2\in \mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
, we write
![]() $\mathbf {j}_1=\mathbf {i}\cdot \mathbf {p}^{\ell _1}$
and
$\mathbf {j}_1=\mathbf {i}\cdot \mathbf {p}^{\ell _1}$
and
![]() $\mathbf {j}_2=\mathbf {i}\cdot \mathbf {p}^{\ell _2}$
with
$\mathbf {j}_2=\mathbf {i}\cdot \mathbf {p}^{\ell _2}$
with
![]() $0\leq \ell _1,\ell _2 \leq |\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]|$
. By the Cauchy–Schwarz inequality and hypothesis, we obtain
$0\leq \ell _1,\ell _2 \leq |\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]|$
. By the Cauchy–Schwarz inequality and hypothesis, we obtain
So,
 $$ \begin{align*} \sum_{\mathbf{j}_1,\mathbf{j}_2\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} | \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2} | \leq C |\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|^2 \eta^{| \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|}. \end{align*} $$
$$ \begin{align*} \sum_{\mathbf{j}_1,\mathbf{j}_2\in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} | \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2} | \leq C |\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|^2 \eta^{| \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|}. \end{align*} $$
Substituting this estimate into equation (32) and using Lemma 2.2, we get
 $$ \begin{align*} \begin{aligned} \bigg|\sum_{\mathbf{j}_1,\mathbf{j}_2\in[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}\bigg| &\leq \sum_{\ell=1}^{N_1\cdots N_d} \sum_{\mathbf{i} \in\mathcal{J}_{\mathbf{N};\ell}\cap \mathcal{I}_{\mathbf{p}}}\ell^2 \eta^\ell\\ &=\sum_{\ell=1}^{\min_i\{\lfloor \log_{p_i}N_i \rfloor \}} \bigg( \prod_{k=1}^{d}\bigg\lfloor\frac{N_k}{p_k^{\ell-1}}\bigg\rfloor-\prod_{k=1}^{d}\bigg\lfloor\frac{N_k}{p_k^\ell}\bigg\rfloor \bigg) \ell^2 \eta^\ell\\ &\leq\sum_{\ell=1}^{\lfloor \log_{p_1\cdots p_d}N_1\cdots N_d \rfloor } \bigg( \prod_{k=1}^{d}\bigg\lfloor\frac{N_k}{p_k^{\ell-1}}\bigg\rfloor-\prod_{k=1}^{d}\bigg\lfloor\frac{N_k}{p_k^\ell}\bigg\rfloor \bigg) \ell^2 \eta^\ell. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \bigg|\sum_{\mathbf{j}_1,\mathbf{j}_2\in[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \mathbb{E}_{\mathbb{P}_\mu}X_{\mathbf{j}_1} X_{\mathbf{j}_2}\bigg| &\leq \sum_{\ell=1}^{N_1\cdots N_d} \sum_{\mathbf{i} \in\mathcal{J}_{\mathbf{N};\ell}\cap \mathcal{I}_{\mathbf{p}}}\ell^2 \eta^\ell\\ &=\sum_{\ell=1}^{\min_i\{\lfloor \log_{p_i}N_i \rfloor \}} \bigg( \prod_{k=1}^{d}\bigg\lfloor\frac{N_k}{p_k^{\ell-1}}\bigg\rfloor-\prod_{k=1}^{d}\bigg\lfloor\frac{N_k}{p_k^\ell}\bigg\rfloor \bigg) \ell^2 \eta^\ell\\ &\leq\sum_{\ell=1}^{\lfloor \log_{p_1\cdots p_d}N_1\cdots N_d \rfloor } \bigg( \prod_{k=1}^{d}\bigg\lfloor\frac{N_k}{p_k^{\ell-1}}\bigg\rfloor-\prod_{k=1}^{d}\bigg\lfloor\frac{N_k}{p_k^\ell}\bigg\rfloor \bigg) \ell^2 \eta^\ell. \end{aligned} \end{align*} $$
Then, applying Lemma 2.2, the last sum is bounded by
 $$ \begin{align*} \begin{aligned} &(N_1\cdots N_d)(p_1\cdots p_d-1)^2\sum_{\ell=1}^{\lfloor \log_{p_1\cdots p_d}N_1\cdots N_d \rfloor } \frac{\ell^2\eta^\ell}{(p_1\cdots p_d)^{\ell+1}}\\ &\quad=O\bigg( N_1\cdots N_d\bigg( \frac{\eta}{p_1\cdots p_d} \bigg)^{{\lfloor \log_{p_1\cdots p_d}N_1\cdots N_d \rfloor } } \bigg)\\ &\quad=O( (N_1\cdots N_d)^{1-\epsilon} ) \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &(N_1\cdots N_d)(p_1\cdots p_d-1)^2\sum_{\ell=1}^{\lfloor \log_{p_1\cdots p_d}N_1\cdots N_d \rfloor } \frac{\ell^2\eta^\ell}{(p_1\cdots p_d)^{\ell+1}}\\ &\quad=O\bigg( N_1\cdots N_d\bigg( \frac{\eta}{p_1\cdots p_d} \bigg)^{{\lfloor \log_{p_1\cdots p_d}N_1\cdots N_d \rfloor } } \bigg)\\ &\quad=O( (N_1\cdots N_d)^{1-\epsilon} ) \end{aligned} \end{align*} $$
for some
![]() $\epsilon>0$
, which gives the convergence of the series preceding equation (31). The proof is complete.
$\epsilon>0$
, which gives the convergence of the series preceding equation (31). The proof is complete.
Lemma 4.5. Let
![]() $\mu $
be any probability measure on
$\mu $
be any probability measure on
![]() $\Sigma _m$
and let
$\Sigma _m$
and let
![]() $F\in \mathcal {F}(S^\ell )$
. For
$F\in \mathcal {F}(S^\ell )$
. For
![]() $\mathbb {P}_\mu $
-a.e.
$\mathbb {P}_\mu $
-a.e.
![]() $x\in \Sigma _m^{\mathbb {N}^d}$
, we have
$x\in \Sigma _m^{\mathbb {N}^d}$
, we have
 $$ \begin{align*} \begin{aligned} &\lim_{\mathbf{N} \rightarrow \infty} \frac{1}{N_1\cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt] } F (x_{\mathbf{ j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}}) \\ &\quad =(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}}\sum_{j=0}^{k-1}\mathbb{E}_{\mu}F(y_j,\ldots, y_{j+\ell-1}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\lim_{\mathbf{N} \rightarrow \infty} \frac{1}{N_1\cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt] } F (x_{\mathbf{ j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}}) \\ &\quad =(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}}\sum_{j=0}^{k-1}\mathbb{E}_{\mu}F(y_j,\ldots, y_{j+\ell-1}). \end{aligned} \end{align*} $$
Proof. For each
![]() $\mathbf {j}\in [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
, take
$\mathbf {j}\in [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
, take
Lemma 4.6. For
![]() $\mathbb {P}_\mu $
-a.e.
$\mathbb {P}_\mu $
-a.e.
![]() $x\in \Sigma _m^{\mathbb {N}^d}$
, we have
$x\in \Sigma _m^{\mathbb {N}^d}$
, we have
 $$ \begin{align*} D(\mathbb{P}_\mu,x)=\frac{(p_1\cdots p_d-1)^2}{\log m}\sum_{\ell=1}^{\infty}\frac{H_{\ell}(\mu)}{(p_1\cdots p_d)^{\ell+1}}, \end{align*} $$
$$ \begin{align*} D(\mathbb{P}_\mu,x)=\frac{(p_1\cdots p_d-1)^2}{\log m}\sum_{\ell=1}^{\infty}\frac{H_{\ell}(\mu)}{(p_1\cdots p_d)^{\ell+1}}, \end{align*} $$
where
![]() $H_{\ell }(\mu )=-\sum _{a_1\cdots a_\ell }\mu ([a_1\cdots a_\ell ])\log \mu ([a_1\cdots a_\ell ])$
.
$H_{\ell }(\mu )=-\sum _{a_1\cdots a_\ell }\mu ([a_1\cdots a_\ell ])\log \mu ([a_1\cdots a_\ell ])$
.
Proof. The proof is similar to the proof of [Reference Fan, Schmeling and Wu11, Theorem 1.3] combined with Lemmas 2.1, 2.2, and 4.5.
Let
![]() $\mathcal {F}(S^{\ell -1},\mathbb {R}^+)$
denote the cone of non-negative real functions on
$\mathcal {F}(S^{\ell -1},\mathbb {R}^+)$
denote the cone of non-negative real functions on
![]() $S^{\ell -1}$
and
$S^{\ell -1}$
and
![]() $s\in \mathbb {R}$
. The nonlinear operator
$s\in \mathbb {R}$
. The nonlinear operator
![]() $\mathcal {N}_s:\mathcal {F}(S^{\ell -1},\mathbb {R}^+)\rightarrow \mathcal {F}(S^{\ell -1},\mathbb {R}^+)$
is defined by
$\mathcal {N}_s:\mathcal {F}(S^{\ell -1},\mathbb {R}^+)\rightarrow \mathcal {F}(S^{\ell -1},\mathbb {R}^+)$
is defined by
 $$ \begin{align} \mathcal{N}_sy(a_1,a_2,\ldots,a_{\ell-1})=\bigg( \sum_{j\in S} e^{s\varphi(a_1,a_2,\ldots,a_{\ell-1},j)}y(a_2,\ldots,a_{\ell-1},j) \bigg)^{{1}/{p_1\cdots p_d}}. \end{align} $$
$$ \begin{align} \mathcal{N}_sy(a_1,a_2,\ldots,a_{\ell-1})=\bigg( \sum_{j\in S} e^{s\varphi(a_1,a_2,\ldots,a_{\ell-1},j)}y(a_2,\ldots,a_{\ell-1},j) \bigg)^{{1}/{p_1\cdots p_d}}. \end{align} $$
Define the pressure function by
 $$ \begin{align} P_{\varphi}(s)=(p_1\cdots p_d-1)(p_1\cdots p_d)^{\ell-2}\log \sum_{j\in S}\psi_s(j), \end{align} $$
$$ \begin{align} P_{\varphi}(s)=(p_1\cdots p_d-1)(p_1\cdots p_d)^{\ell-2}\log \sum_{j\in S}\psi_s(j), \end{align} $$
where
![]() $\psi _s$
is the unique strictly positive fixed point of
$\psi _s$
is the unique strictly positive fixed point of
![]() $\mathcal {N}_s$
. The function
$\mathcal {N}_s$
. The function
![]() $\psi _s$
is defined on
$\psi _s$
is defined on
![]() $S^{\ell -1}$
and it can be extended on
$S^{\ell -1}$
and it can be extended on
![]() $S^k$
for all
$S^k$
for all
![]() $1\leq k\leq \ell -2$
by induction: for
$1\leq k\leq \ell -2$
by induction: for
![]() $a\in S^k$
,
$a\in S^k$
,
 $$ \begin{align*} \psi^{(k)}_s(a)=\bigg( \sum_{j\in S}\psi^{(k+1)}_s(a,j) \bigg)^{{1}/{p_1\cdots p_d}}. \end{align*} $$
$$ \begin{align*} \psi^{(k)}_s(a)=\bigg( \sum_{j\in S}\psi^{(k+1)}_s(a,j) \bigg)^{{1}/{p_1\cdots p_d}}. \end{align*} $$
Then we defined
![]() $(\ell -1)$
-step Markov measure
$(\ell -1)$
-step Markov measure
![]() $\mu _s$
on
$\mu _s$
on
![]() $\Sigma _m$
with the initial law
$\Sigma _m$
with the initial law
 $$ \begin{align} \pi_s([a_1,\ldots,a_{\ell-1}])=\prod_{j=1}^{\ell-1}\frac{\psi_s(a_1,\ldots,a_j)}{\psi^{p_1\ldots p_d}_s(a_1,\ldots,a_{j-1})} \end{align} $$
$$ \begin{align} \pi_s([a_1,\ldots,a_{\ell-1}])=\prod_{j=1}^{\ell-1}\frac{\psi_s(a_1,\ldots,a_j)}{\psi^{p_1\ldots p_d}_s(a_1,\ldots,a_{j-1})} \end{align} $$
and the transition probability
In the following, we are going to establish a relation between the mass
![]() $\mathbb {P}_{\mu _s}([x_{\mathbf {1}}^{N_1,\ldots ,N_d}])$
and the multiple ergodic sum
$\mathbb {P}_{\mu _s}([x_{\mathbf {1}}^{N_1,\ldots ,N_d}])$
and the multiple ergodic sum
![]() $\sum _{\mathbf {j}\in [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]} \varphi (x_{\mathbf {j}},\ldots ,x_{\mathbf {j}\cdot \mathbf { p}^{\ell -1}})$
. This can be regarded as the Gibbs property of the measure
$\sum _{\mathbf {j}\in [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]} \varphi (x_{\mathbf {j}},\ldots ,x_{\mathbf {j}\cdot \mathbf { p}^{\ell -1}})$
. This can be regarded as the Gibbs property of the measure
![]() $\mathbb {P}_{\mu _s}$
.
$\mathbb {P}_{\mu _s}$
.
Recall that for any
![]() $\mathbf {j}\in \mathbb {N}^d$
, there is a unique
$\mathbf {j}\in \mathbb {N}^d$
, there is a unique
![]() $\mathbf {i(j)}\in \mathcal {I}_{\mathbf {p}}$
such that
$\mathbf {i(j)}\in \mathcal {I}_{\mathbf {p}}$
such that
![]() $\mathbf {j}=\mathbf { i(j)}\cdot \mathbf {p}^j$
,
$\mathbf {j}=\mathbf { i(j)}\cdot \mathbf {p}^j$
,
![]() $j \geq 0$
.
$j \geq 0$
.
Define
 $$ \begin{align*} \unicode{x3bb}_{\mathbf{j}}:=\left\{ \begin{aligned} &\{ \mathbf{i(j)}, \mathbf{i(j)}\cdot \mathbf{p},\ldots, \mathbf{i(j)}\cdot \mathbf{p}^j\} &\mbox{if } j<\ell-1,\\ &\{ \mathbf{i(j)}\cdot \mathbf{p}^{j-(\ell-1)},\ldots, \mathbf{i(j)}\cdot \mathbf{p}^j\} &\mbox{if } j \geq \ell-1. \end{aligned} \right. \end{align*} $$
$$ \begin{align*} \unicode{x3bb}_{\mathbf{j}}:=\left\{ \begin{aligned} &\{ \mathbf{i(j)}, \mathbf{i(j)}\cdot \mathbf{p},\ldots, \mathbf{i(j)}\cdot \mathbf{p}^j\} &\mbox{if } j<\ell-1,\\ &\{ \mathbf{i(j)}\cdot \mathbf{p}^{j-(\ell-1)},\ldots, \mathbf{i(j)}\cdot \mathbf{p}^j\} &\mbox{if } j \geq \ell-1. \end{aligned} \right. \end{align*} $$
For
![]() $x= (x_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}\in \Sigma _m^{\mathbb {N}^d}$
, we define
$x= (x_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}\in \Sigma _m^{\mathbb {N}^d}$
, we define
 $$ \begin{align*} B_{\mathbf{N}}(x):=\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s (x|_{\unicode{x3bb}_{\mathbf{j}}}). \end{align*} $$
$$ \begin{align*} B_{\mathbf{N}}(x):=\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s (x|_{\unicode{x3bb}_{\mathbf{j}}}). \end{align*} $$
The following formula is a consequence of the definitions of
![]() $\mu _s$
and
$\mu _s$
and
![]() $\mathbb {P}_{\mu _s}$
.
$\mathbb {P}_{\mu _s}$
.
Lemma 4.7. We have
 $$ \begin{align*} \begin{aligned} \log \mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])&= s\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad-\bigg(N_1\cdots N_d-\bigg\lfloor \frac{N_1\cdots N_d}{p_1\cdots p_d} \bigg\rfloor \bigg)p_1\cdots p_d \log\psi_s(\emptyset)\\ &\quad-p_1\cdots p_d B_{\mathbf{\lfloor N/p \rfloor}}(x)+B_{\mathbf{N}}(x). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \log \mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])&= s\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad-\bigg(N_1\cdots N_d-\bigg\lfloor \frac{N_1\cdots N_d}{p_1\cdots p_d} \bigg\rfloor \bigg)p_1\cdots p_d \log\psi_s(\emptyset)\\ &\quad-p_1\cdots p_d B_{\mathbf{\lfloor N/p \rfloor}}(x)+B_{\mathbf{N}}(x). \end{aligned} \end{align*} $$
(For
![]() $\ell \geq 1$
,
$\ell \geq 1$
,
![]() ${ \lfloor \mathbf {N}/\mathbf {p}^\ell \rfloor }=( \lfloor {N_1}/{p_1^\ell } \rfloor ,\ldots , \lfloor {N_d}/{p_d^\ell } \rfloor )$
.)
${ \lfloor \mathbf {N}/\mathbf {p}^\ell \rfloor }=( \lfloor {N_1}/{p_1^\ell } \rfloor ,\ldots , \lfloor {N_d}/{p_d^\ell } \rfloor )$
.)
Proof. By the definition of
![]() $\mathbb {P}_{\mu _s}$
, we have
$\mathbb {P}_{\mu _s}$
, we have
 $$ \begin{align} \log\mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])= \sum_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \mu_s([x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]). \end{align} $$
$$ \begin{align} \log\mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])= \sum_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \mu_s([x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]). \end{align} $$
However, by the definition of
![]() $\mu _s$
, if
$\mu _s$
, if
![]() $|\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]| \leq \ell -1$
, we have
$|\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]| \leq \ell -1$
, we have
 $$ \begin{align} \begin{aligned} \log \mu_s([x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]) &=\sum_{j=0}^{| \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|-1} \log \frac{\psi_s(x_{\mathbf{i}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})}{\psi_s^{p_1\cdots p_d}(x_{\mathbf{i}},\ldots,x_{\mathbf{ i}\cdot\mathbf{p}^{j-1}})}\\ &=\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \log \mu_s([x|_{\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}]) &=\sum_{j=0}^{| \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|-1} \log \frac{\psi_s(x_{\mathbf{i}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})}{\psi_s^{p_1\cdots p_d}(x_{\mathbf{i}},\ldots,x_{\mathbf{ i}\cdot\mathbf{p}^{j-1}})}\\ &=\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})}. \end{aligned} \end{align} $$
If
![]() $|\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]| \geq \ell $
,
$|\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]| \geq \ell $
,
![]() $\log \mu _s([x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]}])$
is equal to
$\log \mu _s([x|_{\mathcal {M}_{\mathbf {p}}(\mathbf {i})\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]}])$
is equal to
 $$ \begin{align} &\sum_{j=0}^{\ell-2} \log \frac{\psi_s(x_{\mathbf{i}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})}{\psi_s^{p_1\cdots p_d}(x_{\mathbf{i}},\ldots,x_{\mathbf{ i}\cdot\mathbf{p}^{j-1}})}\nonumber\\ &\qquad+\sum_{j=\ell-1}^{|\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|-1} \log \frac{\psi_s(x_{\mathbf{i}\cdot \mathbf{p}^{j-\ell+2}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})e^{s\varphi(x_{\mathbf{i}\cdot \mathbf{p}^{j-\ell+1}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})}}{\psi_s^{p_1\cdots p_d}(x_{\mathbf{i}\cdot \mathbf{ p}^{j-\ell+1}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j-1}})}\nonumber\\ &\quad= \sum_{j=0}^{| \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|-1} \log \frac{\psi_s(x_{\mathbf{i}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})}{\psi_s^{p_1\cdots p_d}(x_{\mathbf{i}},\ldots,x_{\mathbf{ i}\cdot\mathbf{p}^{j-1}})} +s\sum_{j=\ell-1}^{|\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|-1} \varphi(x_{\mathbf{i}\cdot \mathbf{p}^{j-\ell+1}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})\nonumber\\ &\quad=\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})} +\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt],\mathbf{k \leq N}}\varphi(x|_{\unicode{x3bb}_{\mathbf{k}}}), \end{align} $$
$$ \begin{align} &\sum_{j=0}^{\ell-2} \log \frac{\psi_s(x_{\mathbf{i}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})}{\psi_s^{p_1\cdots p_d}(x_{\mathbf{i}},\ldots,x_{\mathbf{ i}\cdot\mathbf{p}^{j-1}})}\nonumber\\ &\qquad+\sum_{j=\ell-1}^{|\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|-1} \log \frac{\psi_s(x_{\mathbf{i}\cdot \mathbf{p}^{j-\ell+2}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})e^{s\varphi(x_{\mathbf{i}\cdot \mathbf{p}^{j-\ell+1}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})}}{\psi_s^{p_1\cdots p_d}(x_{\mathbf{i}\cdot \mathbf{ p}^{j-\ell+1}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j-1}})}\nonumber\\ &\quad= \sum_{j=0}^{| \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|-1} \log \frac{\psi_s(x_{\mathbf{i}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})}{\psi_s^{p_1\cdots p_d}(x_{\mathbf{i}},\ldots,x_{\mathbf{ i}\cdot\mathbf{p}^{j-1}})} +s\sum_{j=\ell-1}^{|\mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]|-1} \varphi(x_{\mathbf{i}\cdot \mathbf{p}^{j-\ell+1}},\ldots,x_{\mathbf{i}\cdot\mathbf{p}^{j}})\nonumber\\ &\quad=\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})} +\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt],\mathbf{k \leq N}}\varphi(x|_{\unicode{x3bb}_{\mathbf{k}}}), \end{align} $$
where
![]() $\mathbf {k}\leq \mathbf {N}$
means
$\mathbf {k}\leq \mathbf {N}$
means
![]() $k_i\leq N_i$
for all
$k_i\leq N_i$
for all
![]() $1\leq i \leq d$
.
$1\leq i \leq d$
.
Substituting equations (38) and (39) into equation (37), we get
where
 $$ \begin{align*} \begin{aligned} &S_{\mathbf{N}}'=\sum_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})}\\ &S_{\mathbf{N}}"=\sum_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt],\mathbf{k \leq N}}\varphi(x|_{\unicode{x3bb}_{\mathbf{k}}}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &S_{\mathbf{N}}'=\sum_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})}\\ &S_{\mathbf{N}}"=\sum_{\mathbf{i} \in \mathcal{I}_{\mathbf{p}}\cap[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt],\mathbf{k \leq N}}\varphi(x|_{\unicode{x3bb}_{\mathbf{k}}}). \end{aligned} \end{align*} $$
For any fixed
![]() $\mathbf {i} \in \mathcal {I}_{\mathbf {p}}\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
, we write
$\mathbf {i} \in \mathcal {I}_{\mathbf {p}}\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
, we write
 $$ \begin{align*} \begin{aligned} \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})}=& \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}}) \\ &-p_1\cdots p_d\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})}=& \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}}) \\ &-p_1\cdots p_d\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}}). \end{aligned} \end{align*} $$
Recall that if
then we denote
and when
![]() $\mathbf {k}=\mathbf {i}$
, we have
$\mathbf {k}=\mathbf {i}$
, we have
![]() $x|_{\unicode{x3bb} _{\mathbf {k/p}}}=\emptyset $
.
$x|_{\unicode{x3bb} _{\mathbf {k/p}}}=\emptyset $
.
Then we can write
 $$ \begin{align*} \begin{aligned} \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})}&= (1-p_1\cdots p_d)\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\lfloor\mathbf{N/p} \rfloor]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}}) \\ &\quad-p_1\cdots p_d \log \psi_s(\emptyset)\\ &\quad+\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt],\mathbf{k\cdot p} \notin \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \frac{\psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})}{\psi_s^{p_1\cdots p_d}(x|_{\unicode{x3bb}_{\mathbf{\lfloor k/p \rfloor}}})}&= (1-p_1\cdots p_d)\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\lfloor\mathbf{N/p} \rfloor]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}}) \\ &\quad-p_1\cdots p_d \log \psi_s(\emptyset)\\ &\quad+\sum_{\mathbf{k} \in \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt],\mathbf{k\cdot p} \notin \mathcal{M}_{\mathbf{p}}(\mathbf{i})\cap [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}}). \end{aligned} \end{align*} $$
Now we take the sum over
![]() $\mathbf {i} \in \mathcal {I}_{\mathbf {p}}\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
to get
$\mathbf {i} \in \mathcal {I}_{\mathbf {p}}\cap [\kern-1.3pt[ 1,\mathbf {N}]\kern-1.2pt]$
to get
 $$ \begin{align*} \begin{aligned} S_{\mathbf{N}}'&=(1-p_1\cdots p_d)\sum_{\mathbf{k \leq\lfloor\mathbf{N/p} \rfloor}}\log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})\\ &\quad-p_1\cdots p_d \bigg( N_1\cdots N_d- \bigg\lfloor \frac{N_1\cdots N_d}{p_1\cdots p_d} \bigg\rfloor \bigg)\log \psi_s(\emptyset)\\ &\quad+\sum_{\mathbf{k\leq N}, \mathbf{k\cdot p} \notin [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}}). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} S_{\mathbf{N}}'&=(1-p_1\cdots p_d)\sum_{\mathbf{k \leq\lfloor\mathbf{N/p} \rfloor}}\log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})\\ &\quad-p_1\cdots p_d \bigg( N_1\cdots N_d- \bigg\lfloor \frac{N_1\cdots N_d}{p_1\cdots p_d} \bigg\rfloor \bigg)\log \psi_s(\emptyset)\\ &\quad+\sum_{\mathbf{k\leq N}, \mathbf{k\cdot p} \notin [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}}). \end{aligned} \end{align*} $$
We can rewrite
 $$ \begin{align*} &(1-p_1\cdots p_d)\sum_{\mathbf{k \leq \lfloor\mathbf{N/p} \rfloor}}\log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})+\sum_{\mathbf{k\leq N}, \mathbf{ k\cdot p} \notin [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}\log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})\\&\quad=-p_1\cdots p_d B_{\lfloor\mathbf{ N/p} \rfloor}(x)+B_{\mathbf{N}}(x). \end{align*} $$
$$ \begin{align*} &(1-p_1\cdots p_d)\sum_{\mathbf{k \leq \lfloor\mathbf{N/p} \rfloor}}\log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})+\sum_{\mathbf{k\leq N}, \mathbf{ k\cdot p} \notin [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}\log \psi_s(x|_{\unicode{x3bb}_{\mathbf{k}}})\\&\quad=-p_1\cdots p_d B_{\lfloor\mathbf{ N/p} \rfloor}(x)+B_{\mathbf{N}}(x). \end{align*} $$
Thus,
 $$ \begin{align*} S_{\mathbf{N}}'=-p_1\cdots p_d \bigg( N_1\cdots N_d- \bigg\lfloor \frac{N_1\cdots N_d}{p_1\cdots p_d} \bigg\rfloor \bigg)\log \psi_s(\emptyset) -p_1\cdots p_d B_{\lfloor\mathbf{N/p} \rfloor}(x)+B_{\mathbf{N}}(x). \end{align*} $$
$$ \begin{align*} S_{\mathbf{N}}'=-p_1\cdots p_d \bigg( N_1\cdots N_d- \bigg\lfloor \frac{N_1\cdots N_d}{p_1\cdots p_d} \bigg\rfloor \bigg)\log \psi_s(\emptyset) -p_1\cdots p_d B_{\lfloor\mathbf{N/p} \rfloor}(x)+B_{\mathbf{N}}(x). \end{align*} $$
However, we have
 $$ \begin{align*} S_{\mathbf{N}}"=\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}}). \end{align*} $$
$$ \begin{align*} S_{\mathbf{N}}"=\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}}). \end{align*} $$
Substituting these expressions of
![]() $S_{\mathbf {N}}'$
and
$S_{\mathbf {N}}'$
and
![]() $S_{\mathbf {N}}"$
into equation (40), we get the desired result.
$S_{\mathbf {N}}"$
into equation (40), we get the desired result.
4.1.1 Upper bound for the Hausdorff dimension
The purpose of this subsection is to provide a few lemmas needed to prove Lemma 4.12. The following results will be useful for estimation of the pointwise dimensions of
![]() $\mathbb {P}_{\mu _s}$
.
$\mathbb {P}_{\mu _s}$
.
Lemma 4.8. [Reference Fan, Schmeling and Wu11, Lemma 7.1]
Let
![]() $(a_n)_{n\geq 1}$
be a bounded sequence of non-negative real numbers. Then,
$(a_n)_{n\geq 1}$
be a bounded sequence of non-negative real numbers. Then,
We define
 $$ \begin{align*} E^+(\alpha):=\bigg\{ (x_{\mathbf{j}})_{\mathbf{j}\in \mathbb{N}^d} \in \Sigma_m^{\mathbb{N}^d} : \limsup_{\mathbf{N}\rightarrow\infty} \frac{1}{\mathbf{N}} \sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\leq \alpha \bigg\} \end{align*} $$
$$ \begin{align*} E^+(\alpha):=\bigg\{ (x_{\mathbf{j}})_{\mathbf{j}\in \mathbb{N}^d} \in \Sigma_m^{\mathbb{N}^d} : \limsup_{\mathbf{N}\rightarrow\infty} \frac{1}{\mathbf{N}} \sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\leq \alpha \bigg\} \end{align*} $$
and
 $$ \begin{align*} E^-(\alpha):=\bigg\{ (x_{\mathbf{j}})_{\mathbf{j}\in \mathbb{N}^d}\in \Sigma_m^{\mathbb{N}^d} : \liminf_{\mathbf{ N}\rightarrow\infty} \frac{1}{\mathbf{N}} \sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\geq \alpha \bigg\}. \end{align*} $$
$$ \begin{align*} E^-(\alpha):=\bigg\{ (x_{\mathbf{j}})_{\mathbf{j}\in \mathbb{N}^d}\in \Sigma_m^{\mathbb{N}^d} : \liminf_{\mathbf{ N}\rightarrow\infty} \frac{1}{\mathbf{N}} \sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\geq \alpha \bigg\}. \end{align*} $$
It is clear that
The upper bound of pointwise dimensions are obtained.
Lemma 4.9. For every
![]() $x\in E^+(\alpha )$
, we have
$x\in E^+(\alpha )$
, we have
For every
![]() $x\in E^-(\alpha )$
, we have
$x\in E^-(\alpha )$
, we have
Consequently, for every
![]() $x\in E(\alpha )$
, we have
$x\in E(\alpha )$
, we have
Proof. The proof is based on Lemma 4.7, which implies that for any
![]() $x\in \Sigma _m^{\mathbb {N}^d}$
and
$x\in \Sigma _m^{\mathbb {N}^d}$
and
![]() $N_1,\ldots , N_d\geq 1$
, we have
$N_1,\ldots , N_d\geq 1$
, we have
 $$ \begin{align*} \begin{aligned} \underline{D}(\mathbb{P}_{\mu_s},x):&=-\frac{ \log \mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])}{N_1 \cdots N_d}\\ &=-\frac{s}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad+\frac{(N_1\cdots N_d-\lfloor {N_1\cdots N_d}/{p_1\cdots p_d} \rfloor )}{N_1 \cdots N_d}p_1\cdots p_d \log\psi_s(\emptyset)\\ &\quad+ \frac{B_{\mathbf{\lfloor N/p \rfloor}}(x)}{{N_1 \cdots N_d}/{p_1\cdots p_d}}-\frac{B_{\mathbf{N}}(x)}{N_1 \cdots N_d}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \underline{D}(\mathbb{P}_{\mu_s},x):&=-\frac{ \log \mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])}{N_1 \cdots N_d}\\ &=-\frac{s}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad+\frac{(N_1\cdots N_d-\lfloor {N_1\cdots N_d}/{p_1\cdots p_d} \rfloor )}{N_1 \cdots N_d}p_1\cdots p_d \log\psi_s(\emptyset)\\ &\quad+ \frac{B_{\mathbf{\lfloor N/p \rfloor}}(x)}{{N_1 \cdots N_d}/{p_1\cdots p_d}}-\frac{B_{\mathbf{N}}(x)}{N_1 \cdots N_d}. \end{aligned} \end{align*} $$
Since the function
![]() $\psi _s$
is bounded, so is the sequence
$\psi _s$
is bounded, so is the sequence
![]() $({B_{\mathbf {k}\cdot \mathbf {p}^{i} }(x)}/{k_1p_1^i \cdots k_dp_d^i} )_{i=0}^{\infty }$
. Then by Lemma 4.8 with
$({B_{\mathbf {k}\cdot \mathbf {p}^{i} }(x)}/{k_1p_1^i \cdots k_dp_d^i} )_{i=0}^{\infty }$
. Then by Lemma 4.8 with
![]() $n=k_1p_1^i \cdots k_dp_d^i$
and
$n=k_1p_1^i \cdots k_dp_d^i$
and
![]() $q=p_1\cdots p_d$
, we have
$q=p_1\cdots p_d$
, we have
 $$ \begin{align*} &\liminf_{\mathbf{N}\rightarrow\infty}\frac{B_{\mathbf{\lfloor N/p \rfloor}}(x)}{{N_1 \cdots N_d}/{p_1\cdots p_d}}-\frac{B_{\mathbf{N}}(x)}{N_1 \cdots N_d}\\ &\quad\leq \liminf_{i\rightarrow\infty} \frac{B_{\mathbf{k}\cdot \mathbf{p}^{i-1} }(x)}{k_1p_1^{i-1} \cdots k_dp_d^{i-1}} -\frac{B_{\mathbf{k}\cdot \mathbf{p}^{i} }(x)}{k_1p_1^{i} \cdots k_dp_d^{i}} \leq 0. \end{align*} $$
$$ \begin{align*} &\liminf_{\mathbf{N}\rightarrow\infty}\frac{B_{\mathbf{\lfloor N/p \rfloor}}(x)}{{N_1 \cdots N_d}/{p_1\cdots p_d}}-\frac{B_{\mathbf{N}}(x)}{N_1 \cdots N_d}\\ &\quad\leq \liminf_{i\rightarrow\infty} \frac{B_{\mathbf{k}\cdot \mathbf{p}^{i-1} }(x)}{k_1p_1^{i-1} \cdots k_dp_d^{i-1}} -\frac{B_{\mathbf{k}\cdot \mathbf{p}^{i} }(x)}{k_1p_1^{i} \cdots k_dp_d^{i}} \leq 0. \end{align*} $$
Therefore,
 $$ \begin{align*} \begin{aligned} \underline{D}(\mathbb{P}_{\mu_s},x)\leq& \liminf_{\mathbf{N}\rightarrow\infty}-\frac{s}{N_1 \cdots N_d \log m}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &+(p_1\cdots p_d-1) \log_m\psi_s(\emptyset). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \underline{D}(\mathbb{P}_{\mu_s},x)\leq& \liminf_{\mathbf{N}\rightarrow\infty}-\frac{s}{N_1 \cdots N_d \log m}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &+(p_1\cdots p_d-1) \log_m\psi_s(\emptyset). \end{aligned} \end{align*} $$
Now suppose that
![]() $x\in E^+(\alpha )$
and
$x\in E^+(\alpha )$
and
![]() $s \leq 0$
. Since
$s \leq 0$
. Since
 $$ \begin{align*} \begin{aligned} &\liminf_{\mathbf{N}\rightarrow\infty}\frac{1}{N_1 \cdots N_d }\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad\leq\limsup_{\mathbf{N}\rightarrow\infty}\frac{1}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad\leq\frac{\alpha}{(p_1\cdots p_d)^{\ell-1}}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\liminf_{\mathbf{N}\rightarrow\infty}\frac{1}{N_1 \cdots N_d }\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad\leq\limsup_{\mathbf{N}\rightarrow\infty}\frac{1}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad\leq\frac{\alpha}{(p_1\cdots p_d)^{\ell-1}}, \end{aligned} \end{align*} $$
we have
 $$ \begin{align*} \begin{aligned} &\liminf_{\mathbf{N}\rightarrow\infty}-\frac{s}{N_1 \cdots N_d }\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad\leq-s\liminf_{\mathbf{N}\rightarrow\infty}\frac{1}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad\leq\frac{-s\alpha}{(p_1\cdots p_d)^{\ell-1}}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\liminf_{\mathbf{N}\rightarrow\infty}-\frac{s}{N_1 \cdots N_d }\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad\leq-s\liminf_{\mathbf{N}\rightarrow\infty}\frac{1}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &\quad\leq\frac{-s\alpha}{(p_1\cdots p_d)^{\ell-1}}, \end{aligned} \end{align*} $$
so that
 $$ \begin{align*} \underline{D}(\mathbb{P}_{\mu_s},x)&\leq\frac{-s\alpha}{(p_1\cdots p_d)^{\ell-1}\log m}+(p_1\cdots p_d-1) \log_m\psi_s(\emptyset)\\&=\frac{P_{\varphi}(s)-\alpha s}{(p_1\cdots p_d)^{\ell-1}\log m}, \end{align*} $$
$$ \begin{align*} \underline{D}(\mathbb{P}_{\mu_s},x)&\leq\frac{-s\alpha}{(p_1\cdots p_d)^{\ell-1}\log m}+(p_1\cdots p_d-1) \log_m\psi_s(\emptyset)\\&=\frac{P_{\varphi}(s)-\alpha s}{(p_1\cdots p_d)^{\ell-1}\log m}, \end{align*} $$
where the last equation follows from
 $$ \begin{align*} \begin{aligned} P_{\varphi}(s)&=(p_1\cdots p_d-1)(p_1\cdots p_d)^{\ell-2}\log \sum_{j\in S}\psi_s(j)\\ &=(p_1\cdots p_d-1)(p_1\cdots p_d)^{\ell-1}\log \psi(\emptyset). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} P_{\varphi}(s)&=(p_1\cdots p_d-1)(p_1\cdots p_d)^{\ell-2}\log \sum_{j\in S}\psi_s(j)\\ &=(p_1\cdots p_d-1)(p_1\cdots p_d)^{\ell-1}\log \psi(\emptyset). \end{aligned} \end{align*} $$
By an analogous argument, we can prove the same result for
![]() $x\in E^-(\alpha )$
and
$x\in E^-(\alpha )$
and
![]() $s\geq 0$
. The proof is complete.
$s\geq 0$
. The proof is complete.
Recall that
![]() $L_{\varphi }$
is the set of
$L_{\varphi }$
is the set of
![]() $\alpha $
such that
$\alpha $
such that
![]() $E(\alpha )\neq \emptyset $
. The following lemma gives the range of
$E(\alpha )\neq \emptyset $
. The following lemma gives the range of
![]() $L_{\varphi }$
.
$L_{\varphi }$
.
Lemma 4.10. We have
![]() $L_{\varphi }\subset [ P^{\prime }_{\varphi }(-\infty ),P^{\prime }_{\varphi }(+\infty ) ]$
.
$L_{\varphi }\subset [ P^{\prime }_{\varphi }(-\infty ),P^{\prime }_{\varphi }(+\infty ) ]$
.
Proof. We prove it by contradiction. Suppose that
![]() $E(\alpha )\neq \emptyset $
for some
$E(\alpha )\neq \emptyset $
for some
![]() $\alpha <P^{\prime }_{\varphi }(-\infty )$
. Let
$\alpha <P^{\prime }_{\varphi }(-\infty )$
. Let
![]() $x\in E(\alpha )$
. Then by Lemma 4.9, we have
$x\in E(\alpha )$
. Then by Lemma 4.9, we have
However, by mean value theorem, we have
for some real number
![]() $\eta _s$
between
$\eta _s$
between
![]() $0$
and s. Since
$0$
and s. Since
![]() $P_{\varphi }$
is convex,
$P_{\varphi }$
is convex,
![]() $P^{\prime }_{\varphi }$
is increasing on
$P^{\prime }_{\varphi }$
is increasing on
![]() $\mathbb {R}$
. Assume
$\mathbb {R}$
. Assume
![]() $s<0$
, we have
$s<0$
, we have
Since
![]() $P^{\prime }_{\varphi }(-\infty )-\alpha>0$
, we deduce from equations (42) and (43) that for s close to
$P^{\prime }_{\varphi }(-\infty )-\alpha>0$
, we deduce from equations (42) and (43) that for s close to
![]() $-\infty $
, we have
$-\infty $
, we have
![]() $P_{\varphi }(s)-\alpha s<0$
. Then by equation (41), for s small enough, we obtain
$P_{\varphi }(s)-\alpha s<0$
. Then by equation (41), for s small enough, we obtain
which implies
![]() $\mathbb {P}_{\mu _s}([x|_{[\kern-1.3pt[ 1,(N_{1,i},\ldots ,N_{d,i})]\kern-1.2pt]}])>1$
with
$\mathbb {P}_{\mu _s}([x|_{[\kern-1.3pt[ 1,(N_{1,i},\ldots ,N_{d,i})]\kern-1.2pt]}])>1$
with
![]() $\min _{1\leq j \leq d}N_{j,i} \to \infty $
as
$\min _{1\leq j \leq d}N_{j,i} \to \infty $
as
![]() $i\rightarrow \infty $
. This contradicts the fact that
$i\rightarrow \infty $
. This contradicts the fact that
![]() $\mathbb {P}_{\mu _s}$
is a probability measure on
$\mathbb {P}_{\mu _s}$
is a probability measure on
![]() $\Sigma _m^{\mathbb {N}^d}$
. Thus, we have proved that for
$\Sigma _m^{\mathbb {N}^d}$
. Thus, we have proved that for
![]() $\alpha $
such that
$\alpha $
such that
![]() $E(\alpha )\neq \emptyset $
, we have
$E(\alpha )\neq \emptyset $
, we have
![]() $\alpha \geq P^{\prime }_{\varphi }(-\infty )$
. By a similar argument, we have
$\alpha \geq P^{\prime }_{\varphi }(-\infty )$
. By a similar argument, we have
![]() $\alpha \leq P^{\prime }_{\varphi }(+\infty )$
.
$\alpha \leq P^{\prime }_{\varphi }(+\infty )$
.
Lemma 4.11. (Billingsley’s lemma [Reference Billingsley4])
Let E be a Borel set in
![]() $\Sigma _m^{\mathbb {N}^d}$
and let
$\Sigma _m^{\mathbb {N}^d}$
and let
![]() $\nu $
be a finite Borel measure on
$\nu $
be a finite Borel measure on
![]() $\Sigma _m^{\mathbb {N}^d}$
.
$\Sigma _m^{\mathbb {N}^d}$
.
-
(1) We have
 $\dim _H(E)\geq c$
if
$\dim _H(E)\geq c$
if
 $\nu (E)>0$
and
$\nu (E)>0$
and
 $\underline {D}(\nu ,x)\geq c$
for
$\underline {D}(\nu ,x)\geq c$
for
 $\nu $
-a.e. x.
$\nu $
-a.e. x. -
(2) We have
 $\dim _H(E)\leq c$
if
$\dim _H(E)\leq c$
if
 $\underline {D}(\nu ,x) \leq c$
for all
$\underline {D}(\nu ,x) \leq c$
for all
 $x\in E$
.
$x\in E$
.
Recall that
An upper bound of the Hausdorff dimensions of level sets is a direct consequence of Lemmas 4.9 and 4.11.
Lemma 4.12. For any
![]() $\alpha \in (P^{\prime }_{\varphi }(-\infty ),P^{\prime }_{\varphi }(0))$
, we have
$\alpha \in (P^{\prime }_{\varphi }(-\infty ),P^{\prime }_{\varphi }(0))$
, we have
For any
![]() $\alpha \in (P^{\prime }_{\varphi }(0),P^{\prime }_{\varphi }(+\infty ))$
, we have
$\alpha \in (P^{\prime }_{\varphi }(0),P^{\prime }_{\varphi }(+\infty ))$
, we have
In particular, we have
 $$ \begin{align*} \dim_H E(\alpha)\leq \frac{P^*_{\varphi}(\alpha)}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
$$ \begin{align*} \dim_H E(\alpha)\leq \frac{P^*_{\varphi}(\alpha)}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
4.1.2 Lower bound for the Hausdorff dimension
This subsection is intended to establish Lemma 4.16. First, we need to do some preparations for proving the Ruelle-type formula below. We deduce some identities concerning the functions
![]() $\psi _s$
.
$\psi _s$
.
Recall that
![]() $\psi _s(a)$
are defined for
$\psi _s(a)$
are defined for
![]() $a\in \bigcup _{1\leq k \leq \ell -1}S^k$
. For
$a\in \bigcup _{1\leq k \leq \ell -1}S^k$
. For
![]() $a\in S^{\ell -1}$
, we have
$a\in S^{\ell -1}$
, we have
and for
![]() $a\in S^k, 1\leq k \leq \ell -2$
, we have
$a\in S^k, 1\leq k \leq \ell -2$
, we have
Differentiating the two sides of each of the above two equations with respect to s, we get for all
![]() $s\in S^{\ell -1}$
,
$s\in S^{\ell -1}$
,
and for all
![]() $a\in \bigcup _{1\leq k \leq \ell -2}S^k$
,
$a\in \bigcup _{1\leq k \leq \ell -2}S^k$
,
Dividing these equations by
![]() $\psi _s^{p_1\cdots p_d}(a)$
(for different a), we get the following lemma.
$\psi _s^{p_1\cdots p_d}(a)$
(for different a), we get the following lemma.
Lemma 4.13. For any
![]() $a\in S^{\ell -1}$
, we have
$a\in S^{\ell -1}$
, we have
 $$ \begin{align} p_1\cdots p_d \frac{\psi^{\prime}_s(a)}{\psi_s(a) }=\sum_{b\in S} \frac{e^{s\varphi(a,b)}\varphi(a,b) \psi_s(Ta,b)}{\psi_s^{p_1\cdots p_d}(a)}+\sum_{b\in S} \frac{e^{s\varphi(a,b)} \psi^{\prime}_s(Ta,b)}{\psi_s^{p_1\cdots p_d}(a)} \end{align} $$
$$ \begin{align} p_1\cdots p_d \frac{\psi^{\prime}_s(a)}{\psi_s(a) }=\sum_{b\in S} \frac{e^{s\varphi(a,b)}\varphi(a,b) \psi_s(Ta,b)}{\psi_s^{p_1\cdots p_d}(a)}+\sum_{b\in S} \frac{e^{s\varphi(a,b)} \psi^{\prime}_s(Ta,b)}{\psi_s^{p_1\cdots p_d}(a)} \end{align} $$
and for any
![]() $a\in \bigcup _{1\leq k \leq \ell -2}S^k$
,
$a\in \bigcup _{1\leq k \leq \ell -2}S^k$
,
 $$ \begin{align} p_1\cdots p_d \frac{ \psi^{\prime}_s(a)}{\psi_s(a)}=\sum_{b\in S} \frac{\psi^{\prime}_s(a,b)}{\psi_s^{p_1\cdots p_d}(a)}. \end{align} $$
$$ \begin{align} p_1\cdots p_d \frac{ \psi^{\prime}_s(a)}{\psi_s(a)}=\sum_{b\in S} \frac{\psi^{\prime}_s(a,b)}{\psi_s^{p_1\cdots p_d}(a)}. \end{align} $$
We denote
 $$ \begin{align*} w(a)=\frac{\psi^{\prime}_s(a)}{\psi^{\prime}_s(a)}, ~ v(a)=\sum_{b\in S}\frac{e^{s\varphi (a,b)}\psi^{\prime}_s(Ta,b)}{\psi_s^{p_1\cdots p_d}(a)}\quad (\text{for all } a\in S^{\ell-1}). \end{align*} $$
$$ \begin{align*} w(a)=\frac{\psi^{\prime}_s(a)}{\psi^{\prime}_s(a)}, ~ v(a)=\sum_{b\in S}\frac{e^{s\varphi (a,b)}\psi^{\prime}_s(Ta,b)}{\psi_s^{p_1\cdots p_d}(a)}\quad (\text{for all } a\in S^{\ell-1}). \end{align*} $$
Then we have the following identities.
Lemma 4.14. (
 $\mathbb {N}^d$
version of [Reference Fan, Schmeling and Wu11, Lemma 7.7 and Theorem 5.1])
$\mathbb {N}^d$
version of [Reference Fan, Schmeling and Wu11, Lemma 7.7 and Theorem 5.1])
For any
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
 $$ \begin{align} \mathbb{E}_{\mu_s} w(y_0^{\ell-2})=\frac{P^{\prime}_{\varphi}(s)}{p_1\cdots p_d (p_1\cdots p_d-1)}, \end{align} $$
$$ \begin{align} \mathbb{E}_{\mu_s} w(y_0^{\ell-2})=\frac{P^{\prime}_{\varphi}(s)}{p_1\cdots p_d (p_1\cdots p_d-1)}, \end{align} $$
and
 $$ \begin{align} (p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}} \sum_{j=0}^{k-1}\mathbb{E}_{\mu_s}\varphi(y_j,\ldots, y_{j+\ell-1}) =P^{\prime}_{\varphi}(s). \end{align} $$
$$ \begin{align} (p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}} \sum_{j=0}^{k-1}\mathbb{E}_{\mu_s}\varphi(y_j,\ldots, y_{j+\ell-1}) =P^{\prime}_{\varphi}(s). \end{align} $$
Proof. Using a similar argument from Lemma 4.5, the proof is almost identical to the proof of of [Reference Fan, Schmeling and Wu11, Lemma 7.7 and Theorem 5.1] by changing q to
![]() $p_1\cdots p_d$
.
$p_1\cdots p_d$
.
As an application of Lemma 4.14, we get the following formula for
![]() $\dim _H \mathbb {P}_{\mu _s}$
.
$\dim _H \mathbb {P}_{\mu _s}$
.
Lemma 4.15. For any
![]() $s\in \mathbb {R}$
, we have
$s\in \mathbb {R}$
, we have
 $$ \begin{align*} \dim_H \mathbb{P}_{\mu_s}=\frac{-s P^{\prime}_{\varphi}(s)+P_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}}. \end{align*} $$
$$ \begin{align*} \dim_H \mathbb{P}_{\mu_s}=\frac{-s P^{\prime}_{\varphi}(s)+P_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}}. \end{align*} $$
Proof. By Lemma 4.7, we have
 $$ \begin{align*} \begin{aligned} -\frac{ \log \mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])}{N_1 \cdots N_d} =&-\frac{s}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &+\frac{(N_1\cdots N_d-\lfloor {N_1\cdots N_d}/{p_1\cdots p_d} \rfloor )}{N_1 \cdots N_d}p_1\cdots p_d \log\psi_s(\emptyset)\\ &+ \frac{B_{\mathbf{\lfloor N/p \rfloor}}(x)}{{N_1 \cdots N_d}/{p_1\cdots p_d}}-\frac{B_{\mathbf{N}}(x)}{N_1 \cdots N_d}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} -\frac{ \log \mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])}{N_1 \cdots N_d} =&-\frac{s}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\ &+\frac{(N_1\cdots N_d-\lfloor {N_1\cdots N_d}/{p_1\cdots p_d} \rfloor )}{N_1 \cdots N_d}p_1\cdots p_d \log\psi_s(\emptyset)\\ &+ \frac{B_{\mathbf{\lfloor N/p \rfloor}}(x)}{{N_1 \cdots N_d}/{p_1\cdots p_d}}-\frac{B_{\mathbf{N}}(x)}{N_1 \cdots N_d}. \end{aligned} \end{align*} $$
Applying the LLN to the function
![]() $\psi _s$
, we get the
$\psi _s$
, we get the
![]() $\mathbb {P}_{\mu _s}$
-almost everywhere existence of the limit
$\mathbb {P}_{\mu _s}$
-almost everywhere existence of the limit
![]() $\lim _{\mathbf { N}\rightarrow \infty } {B_{\mathbf {N}}(x)}/{N_1\cdots N_d}$
. So,
$\lim _{\mathbf { N}\rightarrow \infty } {B_{\mathbf {N}}(x)}/{N_1\cdots N_d}$
. So,
However, by the Lemmas 4.14 and 4.5, we have
 $$ \begin{align*} &\lim_{\mathbf{N} \rightarrow \infty}\frac{1}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\&\quad=\frac{P^{\prime}_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}},\quad \mathbb{P}_{\mu_s}\mbox{-almost everywhere}. \end{align*} $$
$$ \begin{align*} &\lim_{\mathbf{N} \rightarrow \infty}\frac{1}{N_1 \cdots N_d}\sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\lfloor\mathbf{N}/\mathbf{ p}^{\ell-1}\rfloor]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})\\&\quad=\frac{P^{\prime}_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}},\quad \mathbb{P}_{\mu_s}\mbox{-almost everywhere}. \end{align*} $$
So we obtain that for
![]() $ \mathbb {P}_{\mu _s}$
-a.e.
$ \mathbb {P}_{\mu _s}$
-a.e.
![]() $x\in \Sigma _m^{\mathbb {N}^d}$
,
$x\in \Sigma _m^{\mathbb {N}^d}$
,
 $$ \begin{align*} \lim_{\mathbf{N} \rightarrow \infty} -\frac{ \log \mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])}{N_1 \cdots N_d} =\frac{-s P^{\prime}_{\varphi}(s)+P_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}}. \end{align*} $$
$$ \begin{align*} \lim_{\mathbf{N} \rightarrow \infty} -\frac{ \log \mathbb{P}_{\mu_s}([x|_{[\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]}])}{N_1 \cdots N_d} =\frac{-s P^{\prime}_{\varphi}(s)+P_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}}. \end{align*} $$
The proof is complete.
By Lemmas 4.14, 4.15, and Billingsley’s lemma, we get the following lower bound for
![]() $\dim _H E(P^{\prime }_{\varphi }(s))$
.
$\dim _H E(P^{\prime }_{\varphi }(s))$
.
Lemma 4.16. For any
![]() $s\in \mathbb {R}$
, we have
$s\in \mathbb {R}$
, we have
 $$ \begin{align*} \dim_H E(P^{\prime}_{\varphi}(s))\geq \frac{-s P^{\prime}_{\varphi}(s)+P_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
$$ \begin{align*} \dim_H E(P^{\prime}_{\varphi}(s))\geq \frac{-s P^{\prime}_{\varphi}(s)+P_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
4.2 The case when
 $s_{\alpha }$
tends to
$s_{\alpha }$
tends to
 $\pm \infty $
$\pm \infty $
Lemma 4.17. [Reference Fan, Schmeling and Wu11, Theorem 5.6]
Suppose that
![]() $\alpha _{\min }< \alpha _{\max }$
. Then:
$\alpha _{\min }< \alpha _{\max }$
. Then:
-
(1)
 $P^{\prime }_{\varphi }(s)$
is strictly increasing on
$P^{\prime }_{\varphi }(s)$
is strictly increasing on
 $\mathbb {R}$
;
$\mathbb {R}$
; -
(2)
 $\alpha _{\min }\leq P^{\prime }_{\varphi }(-\infty ) < P^{\prime }_{\varphi }(+\infty ) \leq \alpha _{\max }$
.
$\alpha _{\min }\leq P^{\prime }_{\varphi }(-\infty ) < P^{\prime }_{\varphi }(+\infty ) \leq \alpha _{\max }$
.
Proof. The proof is similar to [Reference Fan, Schmeling and Wu11, Theorem 5.6]. Thus, we omit it.
Theorem 4.18
-
(1) We have the equality
 $$ \begin{align*} \alpha_{\min}= P^{\prime}_{\varphi}(-\infty) \end{align*} $$
$$ \begin{align*} \alpha_{\min}= P^{\prime}_{\varphi}(-\infty) \end{align*} $$
if and only if there exists a sequence
 $(y_i)_{i=1}^{\infty }\in \Sigma _m$
such that
$(y_i)_{i=1}^{\infty }\in \Sigma _m$
such that  $$ \begin{align*} \varphi(y_k, y_{k+1},\ldots, y_{k+\ell-1})=\alpha_{\min} \quad\text{for all } k\geq 1. \end{align*} $$
$$ \begin{align*} \varphi(y_k, y_{k+1},\ldots, y_{k+\ell-1})=\alpha_{\min} \quad\text{for all } k\geq 1. \end{align*} $$
-
(2) We have the equality
 $$ \begin{align*} \alpha_{\max}= P^{\prime}_{\varphi}(+\infty) \end{align*} $$
$$ \begin{align*} \alpha_{\max}= P^{\prime}_{\varphi}(+\infty) \end{align*} $$
if and only if there exists a sequence
 $(x_i)_{i=1}^{\infty }\in \Sigma _m$
such that
$(x_i)_{i=1}^{\infty }\in \Sigma _m$
such that  $$ \begin{align*} \varphi(x_k, x_{k+1},\ldots, x_{k+\ell-1})=\alpha_{\max} \quad\text{for all } k\geq 1. \end{align*} $$
$$ \begin{align*} \varphi(x_k, x_{k+1},\ldots, x_{k+\ell-1})=\alpha_{\max} \quad\text{for all } k\geq 1. \end{align*} $$
Proof. We give the proof of the criterion for
![]() $\alpha _{\min }= P^{\prime }_{\varphi }(-\infty )$
. That for
$\alpha _{\min }= P^{\prime }_{\varphi }(-\infty )$
. That for
![]() $P^{\prime }_{\varphi }(+\infty ) =\alpha _{\max }$
is similar.
$P^{\prime }_{\varphi }(+\infty ) =\alpha _{\max }$
is similar.
Sufficient condition. Suppose that there exists a sequence
![]() $(z_i)_{j=0}^{\infty }\in \Sigma _m$
such that
$(z_i)_{j=0}^{\infty }\in \Sigma _m$
such that
We are going to prove that
![]() $\alpha _{\min }= P^{\prime }_{\varphi }(-\infty )$
. By Lemma 4.17, we have
$\alpha _{\min }= P^{\prime }_{\varphi }(-\infty )$
. By Lemma 4.17, we have
![]() $\alpha _{\min }\leq P^{\prime }_{\varphi }(-\infty )$
, thus we only need to show that
$\alpha _{\min }\leq P^{\prime }_{\varphi }(-\infty )$
, thus we only need to show that
![]() $\alpha _{\min }\geq P^{\prime }_{\varphi }(-\infty )$
. To see this, we need to find an
$\alpha _{\min }\geq P^{\prime }_{\varphi }(-\infty )$
. To see this, we need to find an
![]() $x\in \Sigma _m^{\mathbb {N}^d}$
such that
$x\in \Sigma _m^{\mathbb {N}^d}$
such that
 $$ \begin{align*} \lim_{\mathbf{N}\rightarrow\infty} \frac{1}{\mathbf{N}} \sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})=\alpha_{\min}. \end{align*} $$
$$ \begin{align*} \lim_{\mathbf{N}\rightarrow\infty} \frac{1}{\mathbf{N}} \sum_{\mathbf{j}\in [\kern-1.3pt[ 1,\mathbf{N}]\kern-1.2pt]} \varphi (x_{\mathbf{j}},\ldots,x_{\mathbf{j}\cdot\mathbf{p}^{\ell-1}})=\alpha_{\min}. \end{align*} $$
Then by Lemma 4.10,
![]() $\alpha _{\min }\in [P^{\prime }_{\varphi }(-\infty ), P^{\prime }_{\varphi }(+\infty ) ]$
, so
$\alpha _{\min }\in [P^{\prime }_{\varphi }(-\infty ), P^{\prime }_{\varphi }(+\infty ) ]$
, so
![]() $\alpha _{\min }\geq P^{\prime }_{\varphi }(-\infty )$
. We can do this by choosing
$\alpha _{\min }\geq P^{\prime }_{\varphi }(-\infty )$
. We can do this by choosing
![]() $x=(x_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}=\prod _{\mathbf {i}\in \mathcal {I}_{\mathbf {p}}} (x_{\mathbf {i} \cdot \mathbf {p}^{j}})_{j=0}^{\infty }$
with
$x=(x_{\mathbf {j}})_{\mathbf {j}\in \mathbb {N}^d}=\prod _{\mathbf {i}\in \mathcal {I}_{\mathbf {p}}} (x_{\mathbf {i} \cdot \mathbf {p}^{j}})_{j=0}^{\infty }$
with
Necessary condition. Suppose that there is no
![]() $(z_j)_{j=0}^{\infty }\in \Sigma _m$
such that
$(z_j)_{j=0}^{\infty }\in \Sigma _m$
such that
We show that there exists an
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
which will imply that
![]() $P^{\prime }_{\varphi }(-\infty )\geq \alpha _{\min }$
.
$P^{\prime }_{\varphi }(-\infty )\geq \alpha _{\min }$
.
From the hypothesis, we deduce that there are no words
![]() $z_0^{n+\ell -1}$
with
$z_0^{n+\ell -1}$
with
![]() $n\geq m^{\ell }$
such that
$n\geq m^{\ell }$
such that
Indeed, since
![]() $z_j^{j+\ell -1}\in S^{\ell }$
for all
$z_j^{j+\ell -1}\in S^{\ell }$
for all
![]() $0\leq j \leq n$
, there are at most
$0\leq j \leq n$
, there are at most
![]() $m^\ell $
choices for
$m^\ell $
choices for
![]() $z_j^{j+\ell -1}$
. So for any word with
$z_j^{j+\ell -1}$
. So for any word with
![]() $n\geq m^{\ell }$
, there exist at least two
$n\geq m^{\ell }$
, there exist at least two
![]() $j_1<j_2\in \{0,\ldots , n \}$
such that
$j_1<j_2\in \{0,\ldots , n \}$
such that
Then if the word
![]() $z_0^{n+\ell -1}$
satisfies equation (50), the infinite sequence
$z_0^{n+\ell -1}$
satisfies equation (50), the infinite sequence
would verify that
This contradicts the hypothesis. We conclude that for any word
![]() $z_0^{m^\ell +\ell -1}\in S^{m^\ell +\ell -1}$
, there exists at least one
$z_0^{m^\ell +\ell -1}\in S^{m^\ell +\ell -1}$
, there exists at least one
![]() $0\leq j \leq m^\ell $
such that
$0\leq j \leq m^\ell $
such that
where
![]() $\alpha ^{\prime }_{\min }$
is the second smallest value of
$\alpha ^{\prime }_{\min }$
is the second smallest value of
![]() $\varphi $
over
$\varphi $
over
![]() $S^\ell $
.
$S^\ell $
.
We deduce from the above discussions that for any
![]() $(z_j)_{j=0}^{\infty }\in \Sigma _m$
and
$(z_j)_{j=0}^{\infty }\in \Sigma _m$
and
![]() $k \geq 0$
, we have
$k \geq 0$
, we have
 $$ \begin{align*} \sum_{j=k}^{k+m^\ell} \varphi(z_j, z_{j+1},\ldots, z_{j+\ell-1}) \geq m^\ell \alpha_{\min} + \alpha^{\prime}_{\min}=(m^\ell +1)\alpha_{\min}+ \delta, \end{align*} $$
$$ \begin{align*} \sum_{j=k}^{k+m^\ell} \varphi(z_j, z_{j+1},\ldots, z_{j+\ell-1}) \geq m^\ell \alpha_{\min} + \alpha^{\prime}_{\min}=(m^\ell +1)\alpha_{\min}+ \delta, \end{align*} $$
where
![]() $\delta =\alpha ^{\prime }_{\min }-\alpha _{\min }>0$
. This implies that for any
$\delta =\alpha ^{\prime }_{\min }-\alpha _{\min }>0$
. This implies that for any
![]() $(z_j)_{j=0}^{\infty }\in \Sigma _m$
and
$(z_j)_{j=0}^{\infty }\in \Sigma _m$
and
![]() $n \geq 1$
, we have
$n \geq 1$
, we have
 $$ \begin{align} \sum_{j=0}^{n-1} \varphi(z_j, z_{j+1},\ldots, z_{j+\ell-1}) \geq n\alpha_{\min} + \bigg\lfloor \frac{n}{m^\ell+1} \bigg\rfloor \delta. \end{align} $$
$$ \begin{align} \sum_{j=0}^{n-1} \varphi(z_j, z_{j+1},\ldots, z_{j+\ell-1}) \geq n\alpha_{\min} + \bigg\lfloor \frac{n}{m^\ell+1} \bigg\rfloor \delta. \end{align} $$
By Lemma 4.14, we have
 $$ \begin{align} P^{\prime}_{\varphi}(s)&=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}} \sum_{j=0}^{k-1}\mathbb{E}_{\mu_s}\varphi(y_j,\ldots, y_{j+\ell-1})\nonumber\\ &=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}} \mathbb{E}_{\mu_s} \sum_{j=0}^{k-1}\varphi(y_j,\ldots, y_{j+\ell-1}). \end{align} $$
$$ \begin{align} P^{\prime}_{\varphi}(s)&=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}} \sum_{j=0}^{k-1}\mathbb{E}_{\mu_s}\varphi(y_j,\ldots, y_{j+\ell-1})\nonumber\\ &=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}} \mathbb{E}_{\mu_s} \sum_{j=0}^{k-1}\varphi(y_j,\ldots, y_{j+\ell-1}). \end{align} $$
By equations (51) and (52), we get
 $$ \begin{align*} \begin{aligned} P^{\prime}_{\varphi}(s)&=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}} \bigg(k\alpha_{\min} + \bigg\lfloor \frac{k}{m^\ell+1} \bigg\rfloor \delta\bigg)\\ &=\alpha_{\min}+\delta (p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{\lfloor {k}/({m^\ell+1}) \rfloor}{(p_1\cdots p_d)^{k+1}}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} P^{\prime}_{\varphi}(s)&=(p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{1}{(p_1\cdots p_d)^{k+1}} \bigg(k\alpha_{\min} + \bigg\lfloor \frac{k}{m^\ell+1} \bigg\rfloor \delta\bigg)\\ &=\alpha_{\min}+\delta (p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{\lfloor {k}/({m^\ell+1}) \rfloor}{(p_1\cdots p_d)^{k+1}}. \end{aligned} \end{align*} $$
Since
 $$ \begin{align*} \delta (p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{\lfloor {k}/({m^\ell+1}) \rfloor}{(p_1\cdots p_d)^{k+1}}>0, \end{align*} $$
$$ \begin{align*} \delta (p_1\cdots p_d-1)^2\sum_{k=1}^{\infty}\frac{\lfloor {k}/({m^\ell+1}) \rfloor}{(p_1\cdots p_d)^{k+1}}>0, \end{align*} $$
we have proved that there exists an
![]() $\epsilon>0$
such that
$\epsilon>0$
such that
![]() $P^{\prime }_{\varphi }(s)\geq \alpha _{\min }+\epsilon , \text { for all } s\in \mathbb {R}$
.
$P^{\prime }_{\varphi }(s)\geq \alpha _{\min }+\epsilon , \text { for all } s\in \mathbb {R}$
.
So far, we have calculated
![]() $\dim _H E(\alpha )$
for
$\dim _H E(\alpha )$
for
![]() $\alpha \in (P^{\prime }_{\varphi }(-\infty ),P^{\prime }_{\varphi }(+\infty ))$
. Now we turn to the case when
$\alpha \in (P^{\prime }_{\varphi }(-\infty ),P^{\prime }_{\varphi }(+\infty ))$
. Now we turn to the case when
![]() $\alpha =P^{\prime }_{\varphi }(-\infty )$
or
$\alpha =P^{\prime }_{\varphi }(-\infty )$
or
![]() $P^{\prime }_{\varphi }(+\infty )$
.
$P^{\prime }_{\varphi }(+\infty )$
.
Theorem 4.19. [Reference Fan, Schmeling and Wu11, Theorem 7.11]
If
![]() $\alpha =P^{\prime }_{\varphi }(\pm \infty )$
, then
$\alpha =P^{\prime }_{\varphi }(\pm \infty )$
, then
![]() $E(\alpha )\neq \emptyset $
and
$E(\alpha )\neq \emptyset $
and
 $$ \begin{align*} \dim_H E(P^{\prime}_{\varphi}(\pm\infty))=\frac{P^*_{\varphi}(P^{\prime}_{\varphi}(\pm\infty))}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
$$ \begin{align*} \dim_H E(P^{\prime}_{\varphi}(\pm\infty))=\frac{P^*_{\varphi}(P^{\prime}_{\varphi}(\pm\infty))}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
Proof. The proof of Theorem 4.19 follows from the following three lemmas established by Fan, Schmeling, and Wu [Reference Fan, Schmeling and Wu11].
The same argument of Lemma 4.14 is applied for obtaining the lemmas below.
Lemma 4.20. [Reference Fan, Schmeling and Wu11, Proposition 7.12]
We have
In particular,
![]() $E(P^{\prime }_{\varphi }(-\infty ))\neq \emptyset $
.
$E(P^{\prime }_{\varphi }(-\infty ))\neq \emptyset $
.
Lemma 4.21. [Reference Fan, Schmeling and Wu11, Proposition 7.13]
We have
 $$ \begin{align*} \dim_H \mathbb{P}_{\mu_{-\infty}} = \lim_{s\rightarrow -\infty} \frac{-P^{\prime}_{\varphi}(s)s_{\alpha}+P_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}\log m}=\frac{P^*_{\varphi}(P^{\prime}_{\varphi}(-\infty))}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
$$ \begin{align*} \dim_H \mathbb{P}_{\mu_{-\infty}} = \lim_{s\rightarrow -\infty} \frac{-P^{\prime}_{\varphi}(s)s_{\alpha}+P_{\varphi}(s)}{(p_1\cdots p_d)^{\ell-1}\log m}=\frac{P^*_{\varphi}(P^{\prime}_{\varphi}(-\infty))}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
Lemma 4.22. [Reference Fan, Schmeling and Wu11, Proposition 7.14]
 $$ \begin{align*} \dim_H E(P^{\prime}_{\varphi}(-\infty))=\frac{P^*_{\varphi}(P^{\prime}_{\varphi}(-\infty))}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
$$ \begin{align*} \dim_H E(P^{\prime}_{\varphi}(-\infty))=\frac{P^*_{\varphi}(P^{\prime}_{\varphi}(-\infty))}{(p_1\cdots p_d)^{\ell-1}\log m}. \end{align*} $$
Acknowledgements
We would like to sincerely thank the anonymous referee for providing inspiring comments and helpful suggestions for the first draft of this article. These significantly improved the readability and solidified the validity of theorems in the paper. J.-C.B. is partially supported by the National Science and Technology Council, ROC (Contract No NSTC 111-2115-M-004-005-MY3) and National Center for Theoretical Sciences. W.-G.H. is partially supported by the National Natural Science Foundation of China (Grant No.12271381). G.-Y.L. is partially supported by the National Science and Technology Council, ROC (Contract NSTC 111-2811-M-004-002-MY2).