Introduction
Friction anisotropy has been observed in non-metallic solids such as diamond and sapphire and in metals (e.g. copper). In these materials, track widths caused by a sliding indenter have been shown to be related to friction coefficients; wide track widths and high friction coefficients were observed for the non-metallic solids (Bowden and Brooks, 1966), whereas narrow tracks were observed for copper (Dyer, 1961; Barquins and others, 1968).
In their explanation of frictional anisotropy Bowden and Brooks related low friction with narrow track width. Barquins and others examined the anisotropies in work-hardened materials and the development of a bulge in front of the friction slider. Since these studies of anisotropy were restricted to qualitative analysis only, they failed to give a clear interpretation of the anisotropy mechanisms.
Two problems are found in the anisotropy literature. First, the track width caused by the friction was not measured accurately; secondly, the ploughing term of the adhesion theory (Bowden and Tabor, 1950) was not seen as a cause of the anisotropy, although the radii of the sliders used were always very small.
If frictional heating is ignored, the resistance friction is considered to be composed of two parts: the interfacial shear resistance between the frictional surface and slider, and the resistance due to ploughing of the slider. Therefore, mechanical properties such as hardness, yield, and shearing strength must be very important in any interpretation of the mechanism of friction between solids. In particular, anisotropies in these properties should be taken into account in dealing with the friction made on the crystalline solid surfaces. The present author has attempted to examine the anisotropy of the friction coefficient as a function of orientation and temperature on a single crystal of ice. He used tungsten carbide balls as sliders and also measured the width of tracks through a microscope.
Apparatus and Experimental Method
The apparatus used here has been reported in previous work (Tusima, 1977). An ice sample was cut from a large single crystal of glacier ice; its surface lay parallel to a desired crystallographic plane. The specimen surface was carefully machined to a smooth finish, and then the samples were annealed for two hours in a cold room kept at —3°C. After this time, the ice was moved to the cold room and mounted on the experimental apparatus. Frictional experiments were never begun less than five hours after completion of this sample preparation.
In order to measure the friction coefficient as a function of sliding direction on a fresh surface for each test, the slider was moved radially 5 or 10° between tests. The sliders used were tungsten carbide spheres made by Ultra-Spheric Co., U.S.A., which had diameters of 2.34 or 6.4 mm (although some tests were carried out with different diameter sliders). The surface roughness of the spheres was less than 10 μm.
Experimental Results
(1) Anisotropies in friction and track width on prism planes (0110) and (1120)
Friction was measured every 10° on a prism plane (0110). No abrasive fragmentation occurred along the track, thus, friction tracks formed only by plastic deformation of ice.
Figure 1 shows the variations in the coefficient of kinetic friction μk and the track width φ as a function of the angle θ from the [1120] direction. Other parameters of the test were: temperature, —21°C; sliding velocity, 6.0 × 10–5 m/s; applied load, 6.9 N; diameter of the slider, 2.34 mm. The friction coefficient μk reached its maximum in the [1120] direction and a minimum along [0001]. The value of μk ranged from 0.115 to 0.155, the ratio maximum/minimum being 1.35. In contrast to the friction coefficient, the maximum track width was observed in the direction [0001] and the minimum width along [1120]. These widths were, respectively, 0.46 and 0.31 mm, their ratio being 1.48.
The inverse relationship between the friction coefficient and the track width reversed when the experiment was repeated at temperatures of — 10°C and above. Figure 2 shows the friction coefficient and the track width plotted against θ measured from [1120]. For this experiment, the temperature was —10°C, the sliding velocity was 6.0 × 10-5 m/s, the load was 14.4 N, and the slider diameter was 6.4 mm. The maxima of the friction coefficient and the track width were observed to be in the same direction, which contrasts with the results obtained at temperatures of —21°C and below.

Fig. 1. Anisotropies in the kinerc friction coefficient μk and the track width on (0110). Temperature: — 21°C; load: 6.9 N; velocity: 6.0 × 10-5 m/s; slider: 2.34 mm diameter.
A series of experiments were carried out on a prism plane (1120). Similar results were obtained to those observed on the prism plane (0110). Inversion of the frictional anisotropy at a particular temperature was also observed when the sliders were the same size for all tests, though the friction curves showed different maximum/minimum ratios.
(2) Friction on basal plane (0001)
A series of friction experiments were carried out on the basal plane (0001). A fairly strong variation in the friction force was observed along whichever sliding direction was chosen. This was in strong contrast to results observed for the prism planes where large fluctuations were never observed during sliding. The mean frictional force for each run was calculated, but no marked friction anisotropy was observed on this plane.
(3) Anisotropy in friction on inclined surfaces to (0001)
As shown in Figures 1 and 2, a significant amount of anisotropy in the μk value was found on the prismatic surface where the orientation of the basal planes in ice are normal to the test surface, but on the basal surface itself no such anisotropy was observed. This may suggest that the μk value measured on a given surface of ice depends on the relationship between the sliding direction and the orientation of the basal planes in ice. Figure 3 shows anisotropies in the μk value and the track width measured on a surface of ice cut diagonally against the basal plane. In this sample the (0001) plane was inclined at approximately 30° to the test surface. The abscissa is the angle of revolution of the test surface against the slider. When the angle of the test surface was fixed at 0°, the slider moved parallel to the basal plane on the surface. As shown in Figure 3, two maxima in μk appeared at 0° and 180° (where the slider moved in parallel with the basal plane), but two minima appeared at about 120° and 260° (where the slider moved nearly perpendicular to the basal plane). Although values of changed significantly with sliding direction, a slight variation in track width was observed.

Fig. 2. Anisotropies in friction μk and track width φ on (0110). Temperature: –10°C; load: 14.4 N; velocity: 6.0 × 10-5 m/s; slider: 6.4 mm in diameter.

Fig. 3. Anisotropies in friction and track width on pyramidal plane. Temperature: — 19°C; load: 6.9 N; velocity: 7.4 × 10-5 m/s; slider: 2.34 mm in diameter.
(4) Microscope observation of frictional track
As seen above, μk values on the prismatic plane in diagonally cut surfaces depended on sliding direction. In order to interpret the observed anisotropy, the friction tracks produced on the specimen surfaces were observed using optical microscopy. According to our observation, recrystallization, cleavage fissures, microcracks, slip lines, and small-angle boundaries were found to have formed along a friction track.
Figure 4 shows photographs of the terminal areas of friction tracks produced by a slider on the prismatic surface at —21°C. The deformed regions (broken lines) are extended beyond the sides of the track revealing mainly horizontal slip lines and microscopic cracks oriented normally to the slip lines. The symbol Φ indicates the width of frictional track produced by the slider (2.34 mm in diameter). Figure 4(b) shows a deformed bulge that moved in front of the slider parallel to the basal plane. Note that many cracks which are oriented normal to the basal planes propagate ahead of the slider, but that no significant deformation areas were found at the sides of track. The deformed area which formed near the terminus when the slider was moved diagonally to the basal plane (Fig. 4(c)) showed an intermediate pattern between those of Figure 4(a) and (b). Note that many cracks were created normal to slip lines oriented in the [1120] direction.
From inspection of these photographs, we may conclude that when the slider is moved parallel to the basal plane (Fig. 4(b)), comparatively higher values of μk may be obtained because of bulge formation in front of the slider.

Fig 4. Traces in track ends of friction on (0110). Sliding directions: (a) [0001]; (b) [1120]; (c) 30° from [0001]. Note that the basal slit) lines extend parallel to [1120] and there is a dark line normal to the slip lilies.
Discussion
Since the velocity of the slider was roughly 10-5 m/s in our experiments, frictional heat created at the interface between the slider and ice can be ignored. The coefficient of kinetic friction μk may be explained solely in terms of the plastic deformation of ice. According to the adhesion theory, μk is given by
where s is the interfacial shear strength between ice and slider, p the ploughing strength of ice, R the diameter of slider, W the applied load on the slider, φ the width of track produced by friction, k and k′ the shape factors (for the sake of convenience, we shall assume that k = 0.8 and that k′ = 1 (Tusima, 1977)).
As seen in Equation (1), μk is composed of two terms, the first term of the right-hand side of this equation represents the friction due to interfacial shear and the second term represents friction associated with the ploughing effect of the slider.
Figure 5 shows μk, measured on the prism surface, as a function of temperature and reciprocal slider diameter. The velocity of the slider and value of applied load are indicated on the figure. μk is inversely proportional to the diameter of the slider , suggesting that Equation (1) can be used in the interpretation of our results. According to Equation (1), the effect of slider ploughing disappears if the slider can be considered to have an infinite diameter. The largest slider diameter used in our experiments was 12.5 mm. If we assume that the ploughing term is negligible in values of μk measured with this slider, then we can plot the shear strength of ice calculated by the shear term in Equation (1) as a function of temperature (Fig. 6).
From Equation (1), the ploughing strength p of ice is expressed as
Since the s is known from Figure 6, if we substitute numerical values for μk and φ measured in the various sliding directions into Equation (2), we can estimate italic>p as a function of direction. Figure 7 shows the p anisotropy measured on the prism surface (0010), p is one of the indices used to express ice surface hardness.
Butkovich (1954) and Offenbacher and Roselman (1971) measured the hardness anisotropy of ice single crystals. Offenbacher and Roselman found that, on the prism plane, Knoop hardness measured in the direction normal to the basal plane was smaller than the value obtained parallel to the basal plane. The p anisotropy obtained by the present author seems to agree roughly with the Knoop-hardness values obtained by Offenbacher and Roselman.

Fig. 5. The size effect of a slider on the friction. Friction coefficients on (0110) are plotted against the inverse diameters of sliders and the temperature. Velocity: 7.4 × 10-5 m/s;. load: 4·7 N.

Fig. 6. Interfacial shear strength plotted against temperature, for planes (0110) and (0001).

Fig. 7. Ploughing strength on (0110) calculated from friction coefficients and track width. (a) Temperature: -10°C; load: 14.4 N; velocity: 6.0 × 10 -5 m/s; slider: 6.4 mm in diameter. (b) Temperature: - 21°C; load: 6.9 N; velocity: 6.0 × 10-5 m/s; slider: 2.34 mm. (c) Temperature: - 30°C; load: 6.9 N; velocity 7.4 × 10-5 m/s; slider: 2.34 mm.
The appearance of a maximum in the value of p along [1120] may be understood by the bulge formed a head of the slider (Fig. 4 (b)). The anisotropy in the coefficient of kinetic friction on the prism surface of ice can be explained in terms of the anisotropy in p and φ. Therefore, the anisotropy in μk depends on pφ
3. The values of p and φ showed maxima or minima in the sliding directions [1120] and [0001] . Thus, the frictional anisotropy μk [1120 [0001] may be proportional to ![]() . These values are summarized for various temperatures in Table I. When the ratio of
. These values are summarized for various temperatures in Table I. When the ratio of ![]() becomes smaller than 1, frictional anisotropy is dominated by the track-width anisotropy. When the ratio is larger than 1, frictional anisotropy is dominated by ploughing-strength anisotropy. Both results agree with the experimental observations. The anisotropy in friction can be well explained by the anisotropies in ploughing strength and track width.
becomes smaller than 1, frictional anisotropy is dominated by the track-width anisotropy. When the ratio is larger than 1, frictional anisotropy is dominated by ploughing-strength anisotropy. Both results agree with the experimental observations. The anisotropy in friction can be well explained by the anisotropies in ploughing strength and track width.
Table I. THE RATIO OF TRACK WIDTH, PLOUGHING STRENGTH, AND FRICTION COEFFICIENT BETWEEN [DIRECTIONS OF [1120] AND [0001] FOR DIFFERENT TEMPERATURES ON PRISM PLANE (0110)

Conclusion
Friction anisotropy on the basal (0001), prism (0110) and (1120), and pyramidal planes of ice was measured as a function of track width, the amount of plastic deformation caused by frictional sliding, and so on. It was found that, for the prism planes, friction reaches a maximum in the [1120] sliding direction on the (0110) planes and in the [0110] direction on the (1120) planes: Friction is a t a minimum in the [0001] direction for both planes at temperatures below –19°C. At temperatures of –10°C and above, the maximum friction was observed in the [0001] direction and the minimum in the [1120] direction for (0110) planes, and in the [1010] direction for (1120). A remarkable friction anisotropy was observed in pyramidal planes, although track-width anisotropy was very small. No marked anisotropy in friction was observed on the basal plane.
The width of the frictional track also varied with the sliding direction on the prism plane; that is, it was at a maximum along [0001] and reached minima along [1120] for the (0110) plane and along [0110] for the (1120) plane, independent of temperature. The anisotropy was closely correlated with the volume of distortion caused by plastic deformation of ice in and around the friction track.
Acknowledgements
The author wishes to express his deepest appreciation to Professor G. Wakahama and Professor D. Kuroiwa for their kind discussion and comments while he was conducting this study.
Discussion
W. B. KAMB: Can you explain why a maximum in friction corresponds to a mll11mum in track width at one temperature and to a maximum at another?
K. TUSIMA: In this experiment, friction is mainly composed of ploughing resistance. The values of track width φ and ploughing strength p were inverse as regards the position of maxima and minima. These tendencies do not change with temperature. Anisotropy of φ increased with increasing temperature and anisotropy of p increased with decreasing temperature. So the tendency of friction is mainly dependent on the behaviour of φ at higher temperatures and p at lower temperatures. Taking all this into account, friction changes from maximum to minimum at a particular temperature.
D. TABOR: The results are very pretty. However the sliding of a hard sphere over the ice measures the sum of the adhesion and ploughing term. I wonder if the author would consider measuring each of these terms separately: first, by sliding an ice slider on a hard substrate (adhesion without ploughing); secondly, by rolling a hard sphere over ice (ploughing with negligible adhesion)?
TUSIMA: I think so. I am now carrying out friction experiments with a hemispherical single crystal of ice on a metal plate to obtain the shearing term. I want to do experiments on rolling friction to find the ploughing term according to your suggestion.


 . A remarkable frictional anisotropy was also observed on the surface inclined to the basal plane at 30°; the maximum friction coefficient was twice the minimum, whereas the maximum track width was only 1.3 times the minimum.
. A remarkable frictional anisotropy was also observed on the surface inclined to the basal plane at 30°; the maximum friction coefficient was twice the minimum, whereas the maximum track width was only 1.3 times the minimum.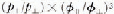 Une anisotropie notable est aussi observée sur une surface inclinée de 30° sur le plan basal; le coefficient de frottement maximal est deux fois plus élevé que la valeur minimale alors que la largeur de trace maximale est seulement 1,3 fois la valour minimale.
Une anisotropie notable est aussi observée sur une surface inclinée de 30° sur le plan basal; le coefficient de frottement maximal est deux fois plus élevé que la valeur minimale alors que la largeur de trace maximale est seulement 1,3 fois la valour minimale.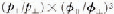 beinflusst wurde. Eine bemerkungswerte Reibungsanisotropie wurde auch auf der urn 30° zur Basisebene geneigten Fläche beobachtet; der grösste Reibungskoeffizient war doppelt so gross wie der kleinstc, wohingegen die grösste Spurbreite nur das 1,3-fache der kleinsten betrug.
beinflusst wurde. Eine bemerkungswerte Reibungsanisotropie wurde auch auf der urn 30° zur Basisebene geneigten Fläche beobachtet; der grösste Reibungskoeffizient war doppelt so gross wie der kleinstc, wohingegen die grösste Spurbreite nur das 1,3-fache der kleinsten betrug.







