Introduction
In rock and soil mechanics, multiaxial yield criteria have been used for several decades. Mames like Tresca, Coulomb and von Mises are most common in this field. An important stimulus for improving Doth the theory of yield under multiaxial stress states and the methods of multiaxial testing came from the necessarily high safety requirements at nuclear power plants.
In the field of glaciology several problems can be sensibly treated by means of the multiaxial yield theory, e.g. plastic flow analysis of glaciers, estimation of ice loads on marine structures or evaluation of the bearing capacity of an ice cover. It is mainly the lack of data on multiaxial ice strength which has prevented, up to now, the application of these advanced methods to glaciological and ice-engineering problems. One of the first attempts in this direction was made by Ralston and Reinicke (e.g. Reference RalstonRalston 1977, Reinicke and Reference RalstonRalston 1977). They used ice-strength data reported by Carter and Michel (1971), Reference FrederkingFrederking (1977) and Jones (197B) to determine yield functions valid for freshwater ice, and applied them to plastic limit analyses. Ef problems of sea ice are to be examined, e.g. the theoretical estimation of ice loads on a marine structure in the Arctic, it is necessary to know the properties of saline ice. Recently-published data on the multiaxial compressive strength of saline ice (Hausier 193Z) combined with results from uniaxial tests in compression and tension on sea ice (Reference PeytonPeyton 1966, Weeks and Assur 1969) now make it possible to determine yield functions, even for saline ice. This was one of the objectives of this study. The other was to clarify whether or not it is necessary to use the rather complex Smith yield function for saline ice. As an alternative, the simpler Pariseau yield function was studied.
Yield Functions
A yield function f is used to characterize the elastic-plastic behaviour of a solid material. It describes that part of the stress space, which contains all possible stress states of a special material. The surface of this partial stress space, i.e. where f - 0, characterizes all stress states at which the material ceases to behave elastically and begins to behave plastically. At all stress states inside the partial stress space, i.e. where f < 0, the material behaves elastically. Generally a yield function can be written as
where a-jj is the stress tensor and e-jj the plastic strain tensor. If the material has never undergone any plastic strains, f is the initial yield function and depends only on the stresses °ij:
In this study only the initial yield function was studied.
Many different yield functions have been public-shed in the past. Since ice that is naturally grown in an ice cover is anisotropic, all yield functions describing isotropic materials must lead to more or less imperfect results if applied to this type of ice. In this study two of the more general yield functions describing anisotropic materials have been chosen: the Pariseau and the Smith yield functions (Reference Pariseau and K EPariseau 1972, Smith unpublished). Using Smith's notation the Pariseau yield function can be written as
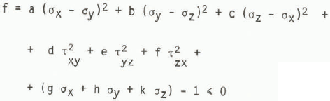
and describes an orthotropic material with a linear dependency on the normal stresses. If a quadratic term of the normal stresses is added to Equation (3) the Smith yield function is obtained:

which is able to describe a material which compacts under plastic deformation and which shows a finite hydrostatic strength.
Since ice very often exhibits isotropic proper-ties in the plane of the ice cover, both yield functions can be reduced to transverse isotropy for the purpose of this study. The Pari seau yield function for transversely isotropic materials can be written as

The Smith yield function for transversely isotropic materials can be written as

The orientation of the axes was chosen so that the x and y axes were in plane with, and the z axis was normal to, the surface of the ice cover.
COEFFICIENTS OF THE YIELD FUNCTIONS The coefficients of the Pariseau yield function of ice can be determined if five stress states are known at which ice fails, i.e. where f = 0. The failure stress states that were used in this study (compression positive) are T z: uniaxial tensile strength parallel to the growth direction (normal to the ice cover), Cz: uniaxial compressive strength parallel to the growth direction, Tx: uniaxial tensile strength in plane with the ice cover, Cx: uniaxial compressive strength in plane with the ice cover, and Cz4s: uniaxial compressive strength under an angle of 45 to the growth direction.
With these five strength values the coefficients of the Pariseau yield function (Equation (5)) (compare with Reference RalstonRalston (1977)are

In the case of the Smith yield function two addi-tional strength values are necessary. These are Bxy: biaxial compressive strength with e x = ay and az = 0 (no stresses normal to the ice cover) and Bxy: biaxial compressive strength with ax = oz and ay = 0 (no stresses in one of the two directions in plane with the ice cover). With
and
the coefficients of the Smith yield function (Equa-tion (6)) can be evaluated as follows:
and

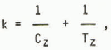
Values of Cx, Cz, Bxy and Bxz uniaxial and biaxial compress i ve strength have been obtained from tests on saline ice having a salinity of 10.6% NaCl at the moment of sampling. After testing, the salinity of the meltwater was 7.0 ± 0.9% NaCl, and showed no effects due to duration of storage. This ice was prepared under simulated natural conditions at the ice laboratory of the Hamburgische Schiffbau-Versuchsanstalt (HSVA). All samples were taken from the same ice cover. Before testing, they were stored for 7 to 13 weeks at -30°C. Preparation of samples was conducted within this period at -22°C (Reference HäuslerHäusler 1982). The tests were performed on a triaxial closed-loop controlled loading frame with brush-type loadinn platens at a temperature TI of -10°C The strain-rate in the x-direction (for Czε in z-direction) was ε= 2.0 × 10-4 s 1 and the relation between the three stresses σ xσ yσ zwas kept constant durino each test (see Table I). The shear strength was acquired from uniaxial compressive strength tests where the load direction was at an angle” of 45° to the growth direction C z45 (Häusler unpublished). The two tensile strengths T xand T zare related to the corresponding compressive strengths
and
This was necessary because the brush-type loading platens used by Reference HäuslerHäusler (1982) did not allow tests of tensile strength. The ratios in Equations (10.1) and (10.2) have been estimated graphically from a plot showing the uniaxial compressive and tensile strengths versus sample orientation as determined by Reference PeytonPeyton (1966) and Weeks and Assur (1969).
Table 1. Multiaxial Strengths Of Saline Ice With Salinity Of 10.6% Nacl At The Moment Of Sampling At Itf Temperature T, = -10 °C And Strain-Rate ?= 2.0 × 10-4 S-L. Measured Values (HÄUsler 1981) And Calculated Values From Smith And Pariseau Yield Criterions

It would have been possible to take other values of the multiaxial compressive strength that were determined in the same study (compare with Table I) instead of T x and T z for example, the ice strength where the ratio between the three stresses was a x:oy:(i z = 3:1:1. But if only strength values of the pure compression octant of the principal stress space are used to determine the coefficients of the yield function, the resulting tensile strengths would be too high compared with the values obtained by Reference PeytonPeyton (1966) and Weeks and Assur (1969).
Another possibility would have been to apply curve-fitting methods to the entire data set of uni-axial and multiaxial compressive strengths (compare with Table I) completed with the tensile strengths from Equations 10.1 and 10.2 and the uniaxial com-pressive strength under 45° to the growth direction C z a45- In the case of the Smith yield function, curve-fitting methods might give reasonable results, but not if applied to the Pari seau yield function, because the latter cannot describe a finite hydro-static compressive strength if a reasonable tensile strength description is required.
The coefficients of both yield functions calcul-ated by means of five and seven strength values mentioned above are listed in Table II. It is import-ant to note that the coefficients 1 and n in the Smith yield function have been found to be imaginary.
Table 2. Coefficients Of Smith And Pariseau Yield Functions Reduced For Transversely Isotropic Saline Ice (S = 10.6% Nacl At The Moment Of Sampling, T

Comparison Of Results
The coefficients listed in Table I have been used to evaluate four curves on both of the two yield sur-faces in the principal stress space. At each of the four curves the ratio between the principal stresses
MPa 2 HPa −2 MPa 2 MPa 1 MPa 1 MPa 1 MPa −1 σ x and σ z was kept constant with σ z = (0, 1/3, 2/3, 1) σ x. The projections of the four curves onto the σ x- σ y-plane are shown in Figure 1. Because of the symmetry of the x-y plane only one half of each set of curves was drawn: the curves belonging to the Pariseau yield surface are shown in the lower right half, while those belonging to the Smith yield surface are reflected at the σ x σ y line and are shown in the upper left half. In addition to the theoretical curves the measured strengths are shown. Here the points with a constant σ x- σ z ratio are connected by thin dashed lines. All the measured strengths are listed in Table I together with the corresponding yield stresses calculated by means of the two yield functions studied here.
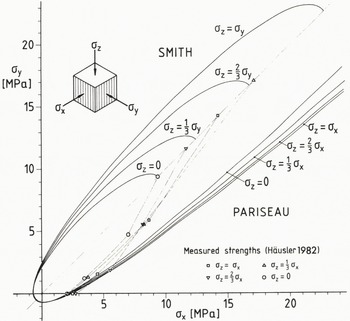
Fig. 1. Projections of the Smith and Pariseau yield surfaces of saline ice (S = 10.6% NaCl at the moment of sampling, T I = -10 °C ,?= 2.0 × 10-4 s-1) and of corresponding measured ice strengths onto the σ x- σ y-plane of the principal stress space.
It is obvious that in all octants of the principal stress space where tension stresses occur, both yield functions (Pariseau and Smith) give nearly the same results. In the pure compression octant of the prince-pal stress space only the Smith yield function describes the measured strengths sufficiently well. The Pariseau yield function only gives satisfactory results in the vicinity of the uniaxial strengths, i.e. up to stresses not exceeding twice the uniaxial compressive strengths.
Conclusions
It is possible to d saline ice by means of seven parameters suffic between strengths compu and measured values is stress space. If intere states on a rather low the Pariseau yield func be applied to saline ic escribe the yield behaviour of the Smith yield function using iently well. The agreement ted with this yield function rather good over the whole st is restricted to stress hydrostatic stress level even tion using five parameters can e with sufficient accuracy.
Nearly the same results are obtained with both fun-ctions, particularly in the octants of the principal stress space where tension stresses exist.
The yield functions determined in this study do not represent the best fit to all measured strengths. For practical applications it may be more appropri-ate to determine the coefficients of the yield func-tions by means of curve-fitting methods applied to a certain range of interest than to choose whether the Pariseau or the Smith yield function should be used.
Acknowledgments
The author acknowledges the financial support of the Bundesministerium für Forschung und Technologie which made this study possible and is grateful to the colleagues at HSVA who contributed to this work.





