2.1. Governing equations

We consider a rectangular cavity of height $h$ along $x$ and length $l$ along $y$ (aspect ratio $A_y=l/h$) filled with a homogeneous Newtonian fluid and subject to a vertical temperature gradient and to the effect of ultrasound waves (see figure 1). The vertical temperature gradient is due to differentially heated horizontal walls. The waves are generated by an ultrasound source, of size $h_b$ ($h_b< h$), located in the middle of the left endwall of the cavity. The right endwall is assumed to be absorbing for sound waves so that reflection is avoided and the waves propagate in the horizontal $y$ direction, towards the right. The physical model is the one already used by Ben Hadid et al. (Reference Ben Hadid, Dridi, Botton, Moudjed and Henry2012). The previous study, however, considered a cavity with an infinite length and focused on the stability thresholds.

Figure 1. Sketch of the studied configuration. The rectangular cavity has an aspect ratio $A_y=10$. The horizontal walls are isothermal: the bottom wall (in red) is at a hot temperature $T_h$, whereas the top wall (in blue) is at a colder temperature $T_c$. The lateral walls (in black) are adiabatic. All the boundaries are rigid walls with no-slip conditions. An acoustic wave is emitted by a transducer on the left wall and absorbed by an absorber at the right wall. It generates streaming taken into account through a body force $F$ considered as a gate function on the beam width (dashed lines).

The attenuation of the wave inside the fluid generates a body force. As shown by Nyborg (Reference Nyborg1998), this force is equal to the spatial variation of the Reynolds stress and can be written as $F= -\rho \langle (u' \boldsymbol {\cdot } \boldsymbol {\nabla })u' +u' (\boldsymbol {\nabla } \boldsymbol {\cdot } u') \rangle$, where $\rho$ is the constant equilibrium density, $u'$ is the fluctuating velocity in the sound wave and $\langle \,\rangle$ means a time average over a large number of cycles. For a plane wave propagating in the $y$ direction, this body force is oriented in the $y$ direction and its intensity is given by $F= \rho \gamma V_a^2 \, {\rm e}^{- 2 \gamma y}$, where $\gamma$ is the sound wave spatial attenuation coefficient and $V_a$ is the sound wave velocity amplitude. Note that this expression of $F$ can also be derived from the more general expression $F=2 \gamma I_a/c$, where $I_a$ is the acoustic intensity, assuming a plane wave and c is the sound velocity (Nyborg Reference Nyborg1998; Moudjed et al. Reference Moudjed, Botton, Henry, Ben Hadid and Garandet2014, Reference Moudjed, Botton, Henry, Millet, Garandet and Ben Hadid2015). The real wave initiated by a transducer is more complex: it induces a pressure field with an amplitude which presents a complex structure in the near field, a maximum at the Fresnel length and a further decrease in the far field, where a cardinal-Bessel shape is obtained in the beam cross-section. However, provided the divergence of the beam is weak (Dridi et al. Reference Dridi, Henry and Ben Hadid2008a) and the attenuation of the wave is sufficiently small, the body force can be considered as constant ($F= \rho \gamma V_a^2$) in the acoustic beam of characteristic width $h_b$ and zero outside. It is a rather crude approximation, but it reflects well the effect of the force induced by the acoustic beam on the fluid in many situations. For example, for decimetric experiments in water using ultrasound at $2$ MHz as in Moudjed et al. (Reference Moudjed, Botton, Henry, Millet, Garandet and Ben Hadid2015) ($l=0.1$ m, $\gamma =0.1$), the attenuation along the length of the cavity, controlled by $2 \gamma l = 0.02 \ll 1$, remains very weak. Note that such an approximation was proposed by Eckart (Reference Eckart1948) and later used by Rudenko & Sukhorukov (Reference Rudenko and Sukhorukov1998), Dridi, Henry & Ben Hadid (Reference Dridi, Henry and Ben Hadid2008b), Dridi et al. (Reference Dridi, Henry and Ben Hadid2008a, Reference Dridi, Henry and Ben Hadid2010), Ben Hadid et al. (Reference Ben Hadid, Dridi, Botton, Moudjed and Henry2012) and Charrier-Mojtabi et al. (Reference Charrier-Mojtabi, Fontaine and Mojtabi2012, Reference Charrier-Mojtabi, Jacob, Dochy and Mojtabi2019).

The top and bottom horizontal walls are perfectly conducting and held at different temperatures, respectively $T_c$ and $T_h$ with $T_h > T_c$, whereas the vertical walls are adiabatic. All the boundaries are rigid walls with no-slip conditions. We assume that the physical properties of the fluid are constant (kinematic viscosity $\nu$, thermal diffusivity $\kappa$, density $\rho$) except for the fluid density in the buoyancy term, which obeys the Boussinesq approximation, $\rho =\rho _0 (1-\beta (\bar {T} - T_m))$, where $\beta$ is the thermal expansion coefficient and $T_m=(T_c+T_h)/2$ is a reference temperature. Using $h$, $h^2/\nu$, $\nu /h$ and $(T_h - T_c)$ as scales for length, time, velocity and temperature, respectively, the governing equations, which are the Navier–Stokes equations coupled to the energy equation, can be written in a dimensionless form as

(2.1)$$\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{V} = 0, \end{gather}$$

(2.2)$$\begin{gather}\frac{\partial{\boldsymbol{V}}}{\partial t} + ({\bbox V}\boldsymbol{\cdot}{\bbox \nabla}){\bbox V} ={-}{\bbox \nabla} P + {\nabla}^2 {\bbox V} + \frac{{\textit{Ra}}}{{\textit{Pr}}} \, T {\bbox{e_x}} + f(x)\, {\bbox {e_y}}, \end{gather}$$

(2.3)$$\begin{gather}\frac{\partial T}{\partial t} + ({\bbox V}\boldsymbol{\cdot}{\bbox \nabla} T ) = \frac{1}{{\textit{Pr}}} \, {\nabla}^2 T, \end{gather}$$

where the dimensionless variables are the velocity vector $[{\bbox V}=(u,v)]$ ($u$ along the vertical and $v$ along the horizontal), the pressure $P$ and the temperature $T$ defined by $T=(\bar {T}-T_m)/(T_h-T_c)$. Here, $f(x)= A \delta _b$ is the dimensionless force inducing the acoustic streaming (deduced from $F$), and $\delta _b$ is a function of the vertical $x$ coordinate; its value is 1 inside the acoustic beam and 0 outside, corresponding to a gate function on the beam width. In these equations, ${\textit {Ra}}=\beta g (T_h-T_c) h^3/(\kappa \nu )$ is the Rayleigh number with g the gravitational acceleration, $ {\textit {Pr}}=\nu /\kappa$ is the Prandtl number and $A= \gamma V_a^2 h^3/\nu ^2$ is the acoustic streaming parameter. The dimensionless beam width is given by $H_b=h_b/h$.

The study is focused on the flow in a fluid with a Prandtl number $ {\textit {Pr}}=1$, inside a two-dimensional (2-D) cavity heated from below, with aspect ratio $A_y=10$. The streaming is induced by an acoustic beam with a dimensionless width $H_b=0.338$.

2.2. Kinetic energy budgets

In order to better understand the stabilizing or destabilizing mechanisms which will affect the Rayleigh–Bénard situation when acoustic streaming is applied, we can perform kinetic energy analyses based on the critical eigenvectors at threshold. The steady solution at threshold $[u_i,T](x_i)$ (generally referred as the basic solution or basic flow) and the critical eigenvector $[u_{p,i}, T_p](x_i)$ both enter the equation of the energy budget giving the rate of change of the fluctuating kinetic energy defined as $e_k=Re(u_{p,i} \, \bar {u}_{p,i} /2)$ ($Re$ and the overbar denote the real part and the complex conjugate, respectively). In these expressions, $x_1$ ($u_1$) and $x_2$ ($u_2$) are assumed to be $x$ ($u$) and $y$ ($v$), respectively. After integration on the volume of the cavity, an equation for the rate of change of the total fluctuating kinetic energy ($E_k= \int _{\varOmega } e_k \, {\rm d}\varOmega$) can be obtained

(2.4)\begin{equation} \frac{\partial E_k}{\partial t} = E_{s} + E_{b} + E_{v}, \end{equation}

where

(2.5)\begin{equation} \left.\begin{gathered} E_{s}= Re \left (- \int_{\varOmega} u_{p,j} \, \frac{\partial u_i}{\partial x_j} \, \bar{u}_{p,i} \, {\rm d}\varOmega \right ),\\ E_{b}= Re \left ( \frac{{\textit{Ra}}}{{\textit{Pr}}} \, \int_{\varOmega} T_p \, \bar{u}_{p,i} \delta_{i1} \, {\rm d}\varOmega \right ),\\ E_{v}= Re \left (- \int_{\varOmega} \frac{\partial u_{p,i}}{\partial x_j}\,\frac{\partial \bar{u}_{p,i}}{\partial x_j} \, {\rm d}\varOmega \right ). \end{gathered}\right\} \end{equation}

Since no acoustic force term appears in the perturbation equations, the rate of change of the total fluctuating kinetic energy has 3 contributions: $E_{s}$ represents the production of fluctuating kinetic energy by shear of the basic flow (inertia term), $E_{b}$ the production of fluctuating kinetic energy by buoyancy and $E_{v}$ the viscous dissipation of fluctuating kinetic energy. At threshold, the critical eigenvector is associated with an eigenvalue with zero real part. This implies that ${\partial E_k / \partial t}$ is equal to zero at marginal stability. Finally, we normalize (2.4) by $-E_{v}=|E_{v}|$, which is always positive, to get an equation involving normalized energy terms $E'=E/|E_{v}|$ at threshold

(2.6)\begin{equation} E'_{s} + E'_{b} =1. \end{equation}

Finally, the critical Rayleigh number can also be expressed as a function of energetic contributions. For that, we use the fact that the expression of $E'_{b}$ linearly depends on ${\textit {Ra}}$. At the threshold, we can write $E'_{b} = {\textit {Ra}}_c E''_{b}$. And from (2.6), we get ${\textit {Ra}}_c E''_{b} = 1- E'_{s}$ which, for $A=0$, i.e. in the pure buoyancy case, gives ${\textit {Ra}}_0 E''_{b,0} = 1$, where the subscript 0 refers to the case $A=0$ and ${\textit {Ra}}_0={\textit {Ra}}_c(A=0)$. Finally, the ratio of these two equations gives

(2.7)\begin{equation} \frac{{\textit{Ra}}_c}{{\textit{Ra}}_0} = \frac{ \overbrace{(1- E'_{s})}^{{R_{s}}}}{ \underbrace{ \left ( { E''_{b} / E''_{b_0} } \right ) }_{{R_{b}}} } , \end{equation}

which indicates that the variation of ${\textit {Ra}}_c$ with $A$ can be expressed through the ratio of the two quantities $R_{s}$ and $R_{b}$, the first quantity being connected to the shear of the basic flow due to acoustic streaming and the second quantity to buoyancy. For $A=0$, $R_{s}$ and $R_{b}$ are equal to 1 and ${\textit {Ra}}_c={\textit {Ra}}_0$.

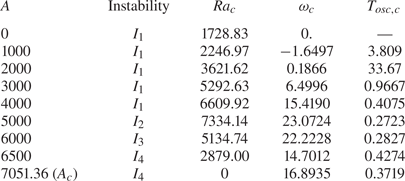
6.1. Forward waves for the instability $I_1$ at $A=1000$

In our 2-D cavity, for small values of $A$, the steady perturbation of the Rayleigh–Bénard situation ($A=0$) will become oscillatory and progress away from the transducer, in the direction of the beam propagation, giving what we have called a forward wave. Such forward wave is illustrated in figure 13 for $A=1000$ and ${\textit {Ra}}=2400$ by the plots of the vertical velocity contours at different times during the period. The perturbation, initiated at the left endwall, is still not much deformed by the streaming flow. It is more intense in the right half of the cavity, but remains visible in the whole cavity. The bifurcation diagram and phase diagram for $A=1000$ are also given in figure 14. We see that the bifurcation is supercritical and that the cycle amplitude at $u_1$ increases with ${\textit {Ra}}$ above the threshold. The period, which is $T_{osc,c}=3.809$ at threshold, first decreases down to approximately $3.68$ at ${\textit {Ra}}=2450$ and then increases (see figure 15).

Figure 13. Vertical velocity contour plots during a cycle at $A=1000$ and for ${\textit {Ra}}=2400$ (the oscillatory instability threshold is at ${\textit {Ra}}_c=2246.97$ and corresponds to the instability $I_1$, see table 3). The period of this cycle is $T_{osc}=3.6790$ and 5 plots are given, each $T_{osc}/4$ from 0 to $T_{osc}$ (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

Figure 14. Bifurcation diagram (a) and phase diagram (b) giving the periodic orbits above the oscillatory instability threshold (${\textit {Ra}}_c=2246.97$, red open circle) for $A=1000$ in a 2-D cavity with aspect ratio $A_y=10$ ($H_b=0.338$, $ {\textit {Pr}}=1$). The cycle presented in figure 13 is given in red.

Figure 15. Variation of the period beyond the oscillatory instability threshold (given as a red open circle) for different values of the acoustic streaming parameter $A$. The characteristics at the critical thresholds, type of instability, critical Rayleigh number ${\textit {Ra}}_c$ and critical period $T_{osc,c}$ are given in table 3 (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

6.2. Backward waves for the instability $I_1$ at $A=4000$

For larger values of $A$ ($A \geq 2000$), backward waves, i.e. waves travelling in the direction opposite to the beam propagation, are expected. Such backward wave is illustrated in figure 16 for $A=4000$ and ${\textit {Ra}}=6800$ by the plots of the velocity vectors fields at different times during the period. This case is on the same branch of instability (instability $I_1$) as the previous case at $A=1000$, but the instability has evolved with the stronger influence of the streaming on both its shape and its localization in the cavity (figure 5e). For ${\textit {Ra}}=6800$, i.e. not far from the oscillatory instability threshold at ${\textit {Ra}}_c=6609.92$, the instability has already well developed, giving a wavy shape to the streaming jet, with eddies alternately arranged on its both sides. The isotherms, given in figure 16(e), are also well deformed, with a wavy shape following that of the jet. The bifurcation diagram and phase diagram for $A=4000$ are given in figure 17. Here also, the bifurcation is supercritical and the cycle amplitude at $u_1$ increases with ${\textit {Ra}}$ above the threshold, very slowly close to the threshold, quickly around $A=6800$, and then more slowly beyond $A=7100$. The period, which is $T_{osc,c}=0.4075$ at threshold, regularly increases, reaching the value $0.5806$ at ${\textit {Ra}}=7600$ and $0.7862$ at ${\textit {Ra}}=8540.7$ (figure 15).

Figure 16. Velocity vectors plots during a cycle at $A=4000$ and for ${\textit {Ra}}=6800$ (the oscillatory instability threshold is at ${\textit {Ra}}_c=6609.92$ and corresponds to the instability $I_1$, see table 3). The period of this cycle is $T_{osc}=0.4419$ and 5 plots are given, each $T_{osc}/4$ from 0 to $T_{osc}$. For $t=T_{osc}$ (last plot e), the isotherms are also given (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

Figure 17. Bifurcation diagram (a) and phase diagram (b) giving the periodic orbits above the oscillatory instability threshold (${\textit {Ra}}_c=6609.92$, red open circle) for $A=4000$ in a 2-D cavity with aspect ratio $A_y=10$ ($H_b=0.338, {\textit {Pr}}=1$). The cycle presented in figure 16 is given in red.

6.3. Backward waves for the other instabilities $I_2$, $I_3$ and $I_4$

We have seen that the critical curve (figure 8) involves other instabilities than $I_1$ when the acoustic streaming parameter $A$ is increased. The waves connected with the instability $I_4$ have been illustrated in figure 7 for $A=A_c$. We now show the waves corresponding to the instability $I_2$ for $A=5000$ and ${\textit {Ra}}=7500$ and the instability $I_3$ for $A=6000$ and ${\textit {Ra}}=5400$ in figures 18 and 19, respectively. For these two instabilities, the waves are backward waves, which look similar to those obtained for the instability $I_4$ at $A=A_c$, with an even stronger localization near the right endwall. The velocity vectors plots used to depict the waves for $A=6000$ show that, for ${\textit {Ra}}=5400$, the perturbation of the streaming jet remains moderate and is only visible through a slight undulation of the jet close to the right endwall. Comparing these results with those shown in figure 16, we thus observe a strong variation between the waves of the instability $I_1$ at $A=4000$ and those of the instability $I_2$ at $A=5000$ and the instability $I_3$ at $A=6000$. Concerning the period of these cycles, for the three instabilities $I_2$, $I_3$ and $I_4$, the periods are rather short ($T_{osc}<0.5$). They regularly increase above the thresholds when ${\textit {Ra}}$ is increased, but in a rather moderate way (figure 15).

Figure 18. Vertical velocity contour plots during a cycle at $A=5000$ and for ${\textit {Ra}}=7500$ (the oscillatory instability threshold is at ${\textit {Ra}}_c=7334.14$ and corresponds to the instability $I_2$, see table 3). The period of this cycle is $T_{osc}=0.27645$ and 5 plots are given, each $T_{osc}/4$ from 0 to $T_{osc}$ (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

Figure 19. Velocity vectors plots during a cycle at $A=6000$ and for ${\textit {Ra}}=5400$ (the oscillatory instability threshold is at ${\textit {Ra}}_c=5134.74$ and corresponds to the instability $I_3$, see table 3). The period of this cycle is $T_{osc}=0.28639$ and 5 plots are given, each $T_{osc}/4$ from 0 to $T_{osc}$ (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

7.1. Specific dynamics for $A=2000$

The bifurcation diagram for $A=2000$ and its associated phase diagram are presented in figure 21. For $A=2000$, it is possible to obtain the backward wave predicted at the threshold ${\textit {Ra}}_c=3621.62$ only in a small ${\textit {Ra}}$ range above the threshold and then with a weak amplitude (cycles coloured in blue in figure 21). Such a backward wave is presented in figure 22 at different times during the period for ${\textit {Ra}}=3630$. The wave has a weak intensity and a long period. In contrast with the previous cases, its travel inside the cavity does not seem regular during the period (figure 22). Moreover, the calculated period at ${\textit {Ra}}=3630$ is $T_{osc}=41.711$, a value already much stronger than the critical value at the very close threshold, $T_{osc,c}=33.67$. Such cycles are obtained up to ${\textit {Ra}}=3640$, but not for ${\textit {Ra}}=3650$ where steady solutions are finally reached. Following these steady solutions by continuation, it was found that they belong to a closed curve extending between saddle-node points at ${\textit {Ra}}_c=3642.27$ and ${\textit {Ra}}_c=3711.24$. Those steady solutions, however, are stable only along the upper and lower parts of the closed curve in figure 21(a), where we can find the blue solid circles corresponding to the two stable solutions at ${\textit {Ra}}=3650$. The steady flow corresponding to one of these stable solutions is given in figure 23 where we see the steady wavy shape of the jet, the other stable steady solution being obtained by up–down symmetry. Finally, for values of ${\textit {Ra}}$ above the steady solutions range (${\textit {Ra}} \geq 3720$), it was again possible to get cycles (solid green curves in figure 21), but they now correspond to forward waves and appear with an already large amplitude, which then increases with ${\textit {Ra}}$. In fact, we observe a kind of continuity between the amplitude increase of the backward waves, the stable steady solutions and the forward waves. As an example of forward wave, we give the cycle obtained at ${\textit {Ra}}=3800$ in figure 24. This cycle is characterized by a rather moderate period $T_{osc}=15.233$ and a seemingly regular travel of the wave.

Figure 21. Bifurcation diagram (a) and phase diagram (b) giving the solutions above the oscillatory instability threshold (${\textit {Ra}}_c=3621.62$, red open circle) for $A=2000$ in a 2-D cavity with aspect ratio $A_y=10$ ($H_b=0.338, {\textit {Pr}}=1$). The cycles in blue correspond to backward waves, whereas those in green correspond to forward waves. Among these cycles, those presented in figures 22 and 24 are given in red. The dashed left green curve in (a) (inner green curve in (b)) corresponds to the cycle at ${\textit {Ra}}=3710$ and its evolution with time is shown in figure 25(b). The black arrows in (b) indicate the direction of the evolution along the cycles, clockwise and counterclockwise for the cycles associated with backward and forward waves, respectively. The steady solutions are found along the solid black curve, but they are stable only along the upper and lower parts of this curve in (a), where we can find the blue solid circles corresponding to ${\textit {Ra}}=3650$.

Figure 22. Vertical velocity contour plots during a cycle at $A=2000$ and for ${\textit {Ra}}=3630$ (the oscillatory instability threshold is at ${\textit {Ra}}_c=3621.62$, see table 3). The period of this cycle is $T_{osc}=41.711$ and 5 plots are given, each $T_{osc}/4$ from 0 to $T_{osc}$ (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

Figure 23. Velocity vectors plot for the steady flow obtained for $A=2000$ at ${\textit {Ra}}=3650$ (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

Figure 24. Vertical velocity contour plots during a cycle at $A=2000$ and for ${\textit {Ra}}=3800$ (the oscillatory instability threshold is at ${\textit {Ra}}_c=3621.62$, see table 3). The period of this cycle is $T_{osc}=15.233$ and 5 plots are given, each $T_{osc}/4$ from 0 to $T_{osc}$ (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

Some interesting information can be obtained from the change of the cycles and their periods when ${\textit {Ra}}$ is increased. For that, the time evolution of $u_1$ along a period for some of the cycles at $A=2000$ is shown in figure 25 and the variation of their period is given in table 4 and plotted in figure 26. When ${\textit {Ra}}$ is increased, we first see the strong increase of the period for the backward waves from the value at the threshold $T_{osc,c}=33.67$ to $T_{osc}=88.374$ at ${\textit {Ra}}=3640$. Beyond the steady solutions range, we then observe a strong decrease of the period for the forward waves, from $T_{osc}=56.538$ at ${\textit {Ra}} \approx 3718$ to the minimum $T_{osc} \approx 5.85$ at ${\textit {Ra}} \approx 4680$, before a further increase (figure 26). The shape of the cycles also strongly changes in the ${\textit {Ra}}$ range of increasing period for the backward waves and of decreasing period for the forward waves (figure 25). The cycles no longer have a classical temporal sine shape, but present alternatively time periods with strong evolution and time periods with weak evolution. The ultimate (asymptotic) shape at very large period can correspond to what is obtained at ${\textit {Ra}}=3710$ by time stepping, the period $T_{osc} \approx 864.9$ being too long to use the cycle continuation method in this case. The time evolution of $u_1$ for this case of forward wave is shown in figure 25(b) and its plot in the bifurcation and phase diagrams in figure 21 is given as dashed green curves. In figure 25(b), we see that the cycle remains a long time ($t \approx 400$) at an almost constant negative value of $u_1$, in the neighbourhood of the steady solutions with negative $u_1$ values (see figure 21), then evolves rapidly towards the opposite positive value of $u_1$, now in the neighbourhood of the other steady solutions with positive $u_1$ values, where it remains a long time, before returning rapidly close to the former steady solutions. Such an evolution is typical of a heteroclinic cycle. A similar, however, less marked, evolution can be found for the cycle associated with backward waves at ${\textit {Ra}}=3640$. As seen in figure 21, this cycle (right blue curve in (a) and outer blue curve in (b)) visits the neighbourhood of the steady solutions, which induces a longer time spent close to these steady solutions (figure 25a). We can then think that the cycles corresponding to backward waves (forward waves) will evolve towards long period heteroclinic cycles as they get closer to the steady solutions when ${\textit {Ra}}$ is increased (decreased). In both cases, the cycles are expected to disappear at heteroclinic bifurcations.

Figure 25. Time evolution of $u_1$ for periodic solutions obtained at different values of ${\textit {Ra}}$ above the Hopf threshold (${\textit {Ra}}_c=3621.62$) for $A=2000$ in a 2-D cavity with aspect ratio $A_y=10$ ($H_b=0.338$, $ {\textit {Pr}}=1$). In (a), the evolution is given during a period for the cycles at ${\textit {Ra}}=3630$ and 3640 corresponding to backward waves (blue solid curves) and the cycles at ${\textit {Ra}}=3720$, 3740 and 3800 corresponding to forward waves (green solid curves). In (b), the evolution corresponds to the very long period oscillatory solution obtained at ${\textit {Ra}}=3710$ (forward wave). The solution remains a long time close to the steady solutions with negative $u_1$ values, then evolves rapidly towards the other steady solutions with positive $u_1$ values where it remains for a long time, before returning rapidly close to the former steady solutions (see the cycle in the phase space in figure 21b).

Table 4. Period $T_{osc}$ of the oscillatory solutions obtained at $A=2000$ for increasing values of ${\textit {Ra}}$ above ${\textit {Ra}}_c=3621.62$ for which the critical period is $T_{osc,c}=33.67$.

Figure 26. Variation of the period beyond the oscillatory instability thresholds (given as open circles) for two values of the acoustic streaming parameter, $A=1000$ and 2000 (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

7.2. Dynamics in the neighbourhood of $\omega _c$ sign change

The study for $A=2000$ has shown the existence of steady solutions in a certain ${\textit {Ra}}$ range, on a closed curve. The change of this curve when $A$ is decreased is shown in figure 27. For $A=1970$, the curve has evolved, but with a similar shape, and it appears in a lower ${\textit {Ra}}$ range. In contrast, for $A=1953.14$, there is a clear change of shape of the steady solutions curve, which accompanies the lowering of the ${\textit {Ra}}$ range. The change seems to be connected with the collision between two previous saddle-node points, which gives two new steady bifurcation points. If we now fix ${\textit {Ra}}$, the steady solutions also belong to a closed curve, which is now limited in a $A$ range, as it is illustrated in figure 27 for ${\textit {Ra}}=3650$ with the green curve.

Figure 27. Loci in the parameter space (a) and in the phase space (b) for the intermediate steady solutions at fixed values of $A$ ($A=1953.14$, 1970 and 2000, red curves) or fixed value of ${\textit {Ra}}$ (${\textit {Ra}}=3650$, green curve) in a 2-D cavity with aspect ratio $A_y=10$ ($H_b=0.338, {\textit {Pr}}=1$).

To better characterize the changes that affect the steady solutions range, we have followed the characteristic points of the closed curves by continuation, more precisely the upper and lower saddle-node points obtained for example for $A=2000$ and 1970 and the steady bifurcation points appearing after collision for $A=1953.14$. The stability diagram thus obtained for $1910 \leq {\textit {Ra}} \leq 2010$ is shown in figure 28. On this diagram, the oscillatory instability threshold (corresponding to the curve given in figure 8) is plotted as a dashed line, the saddle-node points appear along the solid, almost straight, lines $SN_L$ and $SN_{U_1}$, and the two bifurcation points belong to the solid ellipse. The loci of the steady solutions presented in figure 27 are also given as coloured lines. We first see that the critical curve of the oscillatory instability thresholds is not continuous with $A$, but is interrupted in the interval $1941.25 \leq A \leq 1961.62$ by steady thresholds. At both extremities $A_{c_1}$ and $A_{c_2}$ of this interval, the critical complex conjugate eigenvalues collide on the real axis and give two real eigenvalues, which will split and give two different steady thresholds. At the lower threshold (lower part of the ellipse) corresponding to a first primary pitchfork bifurcation on the basic solution branch, two branches of stable steady solutions are created (see the curve for $A=1953.14$ in figure 27a). These branches reverse direction and become unstable at saddle-node points belonging to the solid line $SN_{U_1}$ above the ellipse, and finally meet at a second primary pitchfork bifurcation point (upper part of the ellipse). These saddle-node points $SN_{U_1}$ are secondary points which have appeared at the first collision point at $A_{c_1}=1941.25$. At the second collision point ($A_{c_2}=1961.62$), the two primary bifurcation points merge and give birth to saddle-node points $SN_{L}$ (belonging to the lower solid straight line in figure 28), which are now the lower bounds of the steady solutions curve, now disconnected from the basic solution branch (see the curves for $A=1970$ and 2000 in figure 27a). Beyond this second collision point, the steady solutions then exist between the two solid straight lines $SN_{L}$ and $SN_{U_1}$ which feature the lower and upper saddle-node points on the steady solutions curve.

Figure 28. Stability diagram giving the critical Rayleigh number ${\textit {Ra}}_c$ for the oscillatory instability threshold (black dashed line) and the steady instability thresholds (black solid lines) for values of the acoustic streaming parameter $A$ close to the change of wave travelling direction (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$). The steady thresholds include pitchfork bifurcation points (points on the ellipse) and saddle-node points $SN_L$ and $SN_{U_1}$ (points on the two other solid curves) which delimit the domain of the intermediate steady solutions. The coloured curves give the loci of the steady solutions obtained at constant $A$ (red curves) or ${\textit {Ra}}$ (green curve) and shown in figure 27.

7.3. Global dynamics description

Figure 28 only shows the dynamics in the close neighbourhood of the sign change of $\omega _c$. To obtain the global dynamics shown in figure 20 in large ranges of $A$ and ${\textit {Ra}}$, we have first followed the lower and upper saddle-node points in figure 28 by continuation. The variation of the corresponding critical Rayleigh numbers with $A$ is shown as black solid lines in figure 20, together with the oscillatory instability threshold given as a dashed line. In this larger range of $A$ from 0 to 5000, the steady bifurcation points along the ellipse observed in figure 28 are almost not visible. We see that the lower saddle-node points $SN_{L}$ can be followed over a large range of values of $A$, at least up to $A=5000$, and that their threshold increases almost linearly with $A$ up to $A=3000$ and then with a slowly increasing slope, in any case more quickly than the oscillatory instability thresholds. In contrast, the thresholds for the upper saddle-node points $SN_{U_1}$ strongly increase, with an increasing slope which even becomes very large for $A \approx 2296$ with ${\textit {Ra}}_c \approx 5721$. In fact, additional calculations showed us that this point, denoted as $P_{SN}$, is a limit point for the upper saddle-node curve, which can then be followed back for decreasing $A$ by continuation. The curve, now denoted as $SN_{U_2}$, then first increases for decreasing $A$, reaches a maximum at ${\textit {Ra}} \approx 8515$ for $A \approx 1520$, and then decreases down to ${\textit {Ra}}=2630.63$ for $A=0$.

From figures 28 and 20, we can infer different conclusions. Backward waves are observed for $A > A_{c_2}$, but in a limited ${\textit {Ra}}$ range between the Hopf bifurcation curve and the lower saddle-node curve $SN_{L}$. This range, however, increases in size with the increase of $A$. Steady solutions as the one shown in figure 23 (belonging to the loci shown in figure 27a) are observed for $A > A_{c_1}$, and they appear for ${\textit {Ra}}$ values above the lower saddle-node curve $SN_{L}$, i.e. after the backward waves when ${\textit {Ra}}$ is increased. The corresponding ${\textit {Ra}}$ range increases with the increase of $A$, and seems to have no upper limit when $A > 2296$. To clarify this point, we have computed the loci of the steady solutions for $A=2320$ and they are presented in figure 29(a). We see that the steady solutions belong to curves with complex shapes exhibiting new saddle-node points depicted, for some of them, with blue and green solid circles. For ${\textit {Ra}}$ values above the lower limit at ${\textit {Ra}}_c=4551.70$, two stable steady solutions related by the up–down symmetry can be found, and even four for ${\textit {Ra}}$ values between the values associated with the green saddle points. These stable solutions exist in a very large ${\textit {Ra}}$ range, as they are still found beyond ${\textit {Ra}}=30000$, where we stopped following them. The corresponding flow structures are shown in figure 30 for three values of ${\textit {Ra}}$. For ${\textit {Ra}}=4700$, the flow has evolved with respect to what was obtained for $A=2000$ and ${\textit {Ra}}=3650$ in figure 23: the wavy shape of the jet is more pronounced on the whole cavity length and is connected with the presence of 10 main cells along its sides. The wavy shape is still increased for larger ${\textit {Ra}}$, but it is connected with 9 cells for ${\textit {Ra}}=6000$ and 8 cells for ${\textit {Ra}}=10\,000$. For ${\textit {Ra}}=10\,000$, the roll structure is more visible than the jet, which rather sinuates between the rolls. For larger values of $A$ as $A=3000$ and 5000, we have verified that the loci of the steady solutions begin at the lower saddle-node curve $SN_{L}$ given in figure 20 and that they extend up to very large values of ${\textit {Ra}}$. These loci are still more complex and are not studied in detail here.

Figure 29. Loci in the parameter space for the steady solutions at $A=2320$ (a) and $A=2280$ (b) in a 2-D cavity with aspect ratio $A_y=10$ ($H_b=0.338, {\textit {Pr}}=1$). The solid circles along the curves (black in (a), red or black in (b)) indicate the stable parts of these curves, delimited either by two saddle nodes or by a saddle node and the upper limit of the curve. The saddle nodes indicated by blue or green solid circles in (a) (which also exist in (b)) are those followed in figure 20.

Figure 30. Velocity vectors plots for the stable steady flows obtained for $A=2320$ at ${\textit {Ra}}=4700$ (a), 6000 (b) and 10 000 (c). These stable solutions belong to the loci presented in figure 29(a), as well as the stable solutions obtained by up–down symmetry from these ones (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

To understand what occurs at the limit point $P_{SN}$ at $A \approx 2296$ (figure 20), we have calculated the loci of the steady solutions just before this limit point, for $A=2280$. In figure 29(b), we can see that the steady solutions belong to two different loci corresponding to different ranges of ${\textit {Ra}}$. These loci appear to result from the splitting of the steady solutions curves obtained for $A=2320$ (figure 29a), with the creation of saddle-node points (in fact $SN_{U_1}$ and $SN_{U_2}$), which appear at the limit point $P_{SN}$ and now limit these loci. We first find a closed curve, which extends between the lower saddle-node curve $SN_{L}$ and the upper saddle-node curve $SN_{U_1}$ (figure 20). This closed curve is the continuation of the closed curves found for $A=1970$ and 2000 (figure 21), but it extends on a larger ${\textit {Ra}}$ range (approximately 1000) and has a very sharp evolution at the upper saddle nodes, due to the proximity to the splitting. The second set of steady solutions exists above the saddle-node curve $SN_{U_2}$ and extends over a very large ${\textit {Ra}}$ range. Finally, in between these two sets of steady solutions (i.e. between $SN_{U_1}$ and $SN_{U_2}$), is the domain of the forward waves (figure 20).

The study of the steady solutions initiated at $SN_{U_2}$ for smaller values of $A$ necessitates catching the evolution of the green and blue saddle-node points mentioned in figure 29(a). These points have been followed as a function of $A$ and the corresponding variations of their thresholds are given in figure 20. The loci of the steady solutions initiated at $SN_{U_2}$ have also been determined for different values of $A$, and the results obtained for $A=2280$, 2200, 2000 and 1000 are plotted in figure 31. Note that, as we have two loci corresponding to solutions related by up–down symmetry, we only focus on one of them. The lower blue and green saddle-node points first collapse together with the saddle-node curve $SN_{U_2}$ at $A \approx 2220$ (figure 20). As shown in figure 31 for $A=2200$, two different loci appear beyond this collapse. One of them (in red) is a closed curve limited by two new lower saddle-node points initiated at the collapse and by the former upper blue and green saddle-node points. The other locus is the main curve initiated at $SN_{U_2}$ and extending towards large ${\textit {Ra}}$. Both loci contain stable parts mentioned by a solid circle on the plot. The thresholds for the new saddle-node points on the red curve are very close to that of $SN_{U_2}$ and are then not plotted in figure 20. When $A$ is further decreased, the red closed curve shrinks and finally disappears at $A \approx 2170$, when the upper blue and green saddle-node points collapse together with the new lower saddle-node points (figure 20). As a consequence, for $A < 2170$, only the main curve initiated at $SN_{U_2}$ exists, as shown in figure 31 for $A=2000$ and 1000.

Figure 31. Loci in the parameter space for the upper steady solutions (above $SN_{U_2}$) at $A=1000$ (magenta), 2000 (blue), 2200 (green and red) and 2280 (black). For each value of $A$, as we have two loci corresponding to solutions related by up–down symmetry, we here focus on the lower locus, as can be seen in figure 29 for $A=2280$. The solid circles along the curves indicate the stable parts of these curves, delimited either by two saddle nodes or by a saddle node and the upper limit of the curve (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

Examples of flow structures on the stable part of the steady solutions curves initiated at $SN_{U_2}$ are shown in figure 32 for three values of $A$. For $A=2000$ and ${\textit {Ra}}=9000$ (${\textit {Ra}}_c=7639$ at $SN_{U_2}$), the flow structure looks similar to that presented for $A=2320$ and ${\textit {Ra}}=10\,000$ in figure 30 with the streaming flow sinuating between 8 quite regular rolls. The isotherms, also given in figure 32 for this case, appear to be strongly deformed by the rolls. For $A=1000$ and ${\textit {Ra}}=9000$ (${\textit {Ra}}_c=7721$ at $SN_{U_2}$), the streaming is still less visible. The 8 rolls are also not regular with a size decreasing from the left endwall to the right endwall. Finally for $A=0$ and ${\textit {Ra}}=4000$ (${\textit {Ra}}_c=2631$ at $SN_{U_2}$), there is no more streaming and the rolls are regular. Such 8 rolls solution of the Rayleigh–Bénard problem ($A=0$) appears at a saddle-node point and is then not directly connected to a primary bifurcation, in contrast with the 10 rolls solution that appears at the first primary bifurcation point (${\textit {Ra}}_c=1728.83$).

Figure 32. Velocity vector plots for the stable steady flows initiated at the upper saddle-nodes curve $SN_{U_2}$ in figure 20 for $A=2000$ and ${\textit {Ra}}=9000$ (a), $A=1000$ and ${\textit {Ra}}=9000$ (b), $A=0$ and ${\textit {Ra}}=4000$ (c). For $A=2000$ (a), the isotherms are also given. The steady flows obtained by up–down symmetry from these ones are also stable solutions (2-D cavity with $A_y=10$, $H_b=0.338$, $ {\textit {Pr}}=1$).

It is interesting to come back to the oscillatory solutions. As already mentioned, the backward waves (denoted as BW in figure 20) are observed for $A > A_{c_2}$, between their initiation thresholds at the Hopf bifurcation curve and the saddle-node curve $SN_L$. Their domain of existence is very thin close to $A_{c_2}$ but increases in size with the increase of $A$. If a very strong increase of the period is found for these waves for $A=2000$ at the approach of $SN_L$ (figure 26), this increase becomes more and more limited when $A$ is increased (figure 15). Moreover, before reaching $SN_L$, bifurcation of cycles can sometimes be found. For example, for $A=3000$, a steady bifurcation of cycle occurs at ${\textit {Ra}} \approx 5850$, leading to a new periodic cycle, whereas for $A=5000$, a Naimark–Sacker bifurcation occurs at ${\textit {Ra}} \approx 7600$, leading to a quasi-periodic solution. In contrast, the forward waves (denoted as FW in figure 20) are observed for $0 < A < 2296$, in a domain limited by the Hopf bifurcation curve and the saddle-node curves $SN_{U_1}$ and $SN_{U_2}$. As shown for $A=1000$ and 2000 in figure 26, there is a very strong increase of the periods for the cycles in this domain at the approach of $SN_{U_1}$ and $SN_{U_2}$, indicating the presence of heteroclinic bifurcations. We can note that there is a domain of $A$ where both backward and forward waves can be observed. This domain extends between $A_{c_2}$ and $P_{SN}$, i.e. for $1961.62 < A < 2296$. In this domain, as observed for $A=2000$, we get successively forward waves, steady solutions on closed curves, backward waves and steady solutions again, when increasing the Rayleigh number.

Finally, while looking for the closed curve at $A=2280$ (red curve in figure 29b), we found another set of steady solutions along closed curves, which evolves with $A$ similarly to the set shown in figure 27(a). This new set of solutions, shown in figure 33, is now associated with the second Hopf bifurcation, which has its critical thresholds ${\textit {Ra}}_c$ slightly above those shown in figure 8 for the first Hopf bifurcation. The closed curve for $A=2100$ (which needs a zoom to be seen clearly) includes two primary pitchfork bifurcations, which are found in the domain of $A$ where the angular frequency sign change occurs for this second Hopf bifurcation (as the ellipse domain shown in figure 28 for the first Hopf bifurcation). The other closed curves give solutions for values of $A$ close above this domain. The shape of the curves is modified when $A$ is increased, in particular at the upper saddle node, where it is a sign of further changes in the dynamics, such as those shown in figure 29. In any case, all these steady solutions are unstable as they all have at least an unstable complex conjugate pair of eigenvalues, which is due to the previously occurred first Hopf transition.

Figure 33. Loci in the parameter space for a set of unstable steady solutions found for fixed values of $A$ ($A=2100$, 2150, 2220, 2280, 2350 and 2500, from left to right) in a 2-D cavity with aspect ratio $A_y=10$ ($H_b=0.338, {\textit {Pr}}=1$). These unstable steady solutions are associated with the second Hopf bifurcation, as those in figure 27(a) were associated with the first Hopf bifurcation.