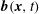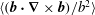1. Introduction
The process of magnetic relaxation in a low-resistivity plasma was envisaged by Woltjer (Reference Woltjer1958), who showed that, under certain circumstances, minimisation of energy subject to the single constraint of invariance of total magnetic helicity leads to a force-free equilibrium, in which current
![]() $\boldsymbol{j}$
and magnetic field
$\boldsymbol{j}$
and magnetic field
![]() $\boldsymbol{B}$
satisfy the Beltrami relationFootnote
1
$\boldsymbol{B}$
satisfy the Beltrami relationFootnote
1
where
![]() ${\it\alpha}_{0}$
is a constant. It was subsequently recognised (Moffatt Reference Moffatt1969) that there is a whole family of helicity invariants
${\it\alpha}_{0}$
is a constant. It was subsequently recognised (Moffatt Reference Moffatt1969) that there is a whole family of helicity invariants
where
![]() ${\mathcal{D}}$
is any Lagrangian subdomain of fluid on whose surface the normal component of
${\mathcal{D}}$
is any Lagrangian subdomain of fluid on whose surface the normal component of
![]() $\boldsymbol{B}$
vanishes. If due account is taken of the invariance of these ‘sub-helicities’, then the field still relaxes to a force-free equilibrium, but now with
$\boldsymbol{B}$
vanishes. If due account is taken of the invariance of these ‘sub-helicities’, then the field still relaxes to a force-free equilibrium, but now with
i.e. with
![]() ${\it\alpha}$
merely constant on magnetic lines of force (‘
${\it\alpha}$
merely constant on magnetic lines of force (‘
![]() $\boldsymbol{B}$
-lines’).
$\boldsymbol{B}$
-lines’).
It was conjectured by Taylor (Reference Taylor1974) that, in a turbulent low-density plasma, only the global invariant
![]() ${\mathcal{H}}_{V}$
survives, where
${\mathcal{H}}_{V}$
survives, where
![]() ${\mathcal{D}}=V$
is the whole plasma volume. This evidently leads to Beltrami fields of the form (1.1), a conclusion that provided a plausible explanation for the observed field structures in ‘reversed-field-pinch’ (RFP) experiments of that period. This conjecture, together with associated theory and further extensive experimental evidence, was reviewed by Taylor (Reference Taylor1986), and has become part of the ‘received knowledge’ concerning turbulent relaxation processes in plasma physics. Escande (Reference Escande, Diamond, Garbet, Ghendrih and Sarazin2015) provides a recent review of relaxation in the RFP context, and of variants of the Taylor conjecture. An excellent review of the role of magnetic helicity in laboratory and astrophysical plasma dynamics has been provided by Berger (Reference Berger1999).
${\mathcal{D}}=V$
is the whole plasma volume. This evidently leads to Beltrami fields of the form (1.1), a conclusion that provided a plausible explanation for the observed field structures in ‘reversed-field-pinch’ (RFP) experiments of that period. This conjecture, together with associated theory and further extensive experimental evidence, was reviewed by Taylor (Reference Taylor1986), and has become part of the ‘received knowledge’ concerning turbulent relaxation processes in plasma physics. Escande (Reference Escande, Diamond, Garbet, Ghendrih and Sarazin2015) provides a recent review of relaxation in the RFP context, and of variants of the Taylor conjecture. An excellent review of the role of magnetic helicity in laboratory and astrophysical plasma dynamics has been provided by Berger (Reference Berger1999).
Despite the appeal of the Taylor conjecture, there is as yet no rigorous justification for it, although various heuristic arguments have been advanced. Counter-arguments can however be advanced with equal force. For example, if an untwisted flux tube in the form of a figure of eight, and of cross-section small compared with its length, reconnects by a purely diffusive process to form two unlinked flux tubes, then, according to the theory of Kimura & Moffatt (Reference Kimura and Moffatt2014), the initial ‘writhe’ helicity can be destroyed without any compensating generation of ‘twist’, whereas the magnetic energy is reduced by a relatively small amount. This suggests that there are circumstances in which helicity is destroyed more rapidly than energy, rather than more slowly as required by the Taylor scenario.
Examples of relaxation of initially braided magnetic fields have been considered by Pontin et al. (Reference Pontin, Wilmot-Smith, Hornig and Galsgaard2011), and more recently by Russell et al. (Reference Russell, Yeates, Hornig and Wilmot-Smith2015), which further reveal that the invariance of global helicity is in itself insufficient to determine the end state of a relaxation process. These authors define a ‘field-line helicity’ loosely related to the ‘sub-helicities’ defined above, which can evidently play an important role in the process.
In fact, as pointed out by Qin et al. (Reference Qin, Liu, Li and Squire2012), ‘there is no conclusive experimental or numerical evidence in support of Taylor’s conjecture’. These authors have considered alternative mechanisms that may lead to equilibrium states described by (1.1), without invoking this conjecture. However, they make a significant assumption in relation to the relaxation process, namely that ‘the variation of magnetic energy due to the Lorentz force is small compared with that due to the resistivity’. The Lorentz force generates kinetic energy that may indeed be small compared with the magnetic energy, but, as we shall find, the rate of dissipation of energy by viscosity via this route can, during the primary phase of relaxation of a non-equilibrium field, be much larger than the direct rate of dissipation of magnetic energy by resistivity.
We propose here to analyse the relaxation process for a simple one-dimensional model, for which the evolution of magnetic, velocity and density fields, as well as of energy density, helicity density, total energy and total helicity, can be followed in detail. In adopting a one-dimensional model, we follow the precedent of Cowley et al. (Reference Cowley, Cowley, Henneberg and Wilson2015), who provide a similar one-dimensional model for explosive instabilities in a magnetised plasma. The great advantage of one-dimensional models is their simplicity and the physical insight that they can thereby provide. It is hoped that the model presented in this paper retains enough of the essential physics of the fully three-dimensional situation as to be not wholly without relevance for the general problem of turbulent relaxation.
A closely related paper, in which many useful references can be found, has appeared very recently (Smiet et al. Reference Smiet, Candelaresi, Thompson, Swearngin, Dalhuisen and Bouwmeester2015). The authors present a brilliant set of fully three-dimensional computations of relaxation in an isothermal plasma, the end state being a slowly decaying magnetostatic (rather than force-free) equilibrium. This is consistent with the scenario developed by Moffatt (Reference Moffatt1985), but with the incorporation of weak magnetic diffusion effects that are responsible for changes in the magnetic field topology and ultimate slow decay.
For general background concerning plasma physics in relation to tokamak reactor design, we may refer to the recent article by Freidberg, Mangiarotti & Minervini (Reference Freidberg, Mangiarotti and Minervini2015), where some outstanding challenges are presented.
2. One-dimensional relaxation in a pressureless plasma
Suppose that a low-resistivity, low-density plasma is contained between two perfectly conducting planes
![]() $x=\pm {\rm\pi}L$
. Suppose that, at time
$x=\pm {\rm\pi}L$
. Suppose that, at time
![]() $t=0$
, the plasma has uniform density
$t=0$
, the plasma has uniform density
![]() ${\it\rho}_{0}$
, and is at rest and permeated by a two-component magnetic field,
${\it\rho}_{0}$
, and is at rest and permeated by a two-component magnetic field,
where
![]() $B_{0}$
is a representative value of
$B_{0}$
is a representative value of
![]() $|\boldsymbol{B}(x,0)|$
. The
$|\boldsymbol{B}(x,0)|$
. The
![]() $\boldsymbol{B}$
-lines are rectilinear and lie in planes
$\boldsymbol{B}$
-lines are rectilinear and lie in planes
![]() $x=\text{const.}$
, the magnitude and direction of
$x=\text{const.}$
, the magnitude and direction of
![]() $\boldsymbol{B}$
being dependent on
$\boldsymbol{B}$
being dependent on
![]() $x$
. The associated current is
$x$
. The associated current is
and the Lorentz force is
where
![]() $p_{M0}(x)=\boldsymbol{B}^{2}/2$
is the magnetic pressure distribution. The electric field is
$p_{M0}(x)=\boldsymbol{B}^{2}/2$
is the magnetic pressure distribution. The electric field is
![]() $\boldsymbol{E}={\it\eta}\,\boldsymbol{j}$
, where
$\boldsymbol{E}={\it\eta}\,\boldsymbol{j}$
, where
![]() ${\it\eta}$
is the magnetic resistivity of the plasma, assumed small; and since
${\it\eta}$
is the magnetic resistivity of the plasma, assumed small; and since
![]() $E_{y}$
and
$E_{y}$
and
![]() $E_{z}$
must be zero at the perfectly conducting boundaries, it follows that
$E_{z}$
must be zero at the perfectly conducting boundaries, it follows that
conditions that we shall assume to persist for all
![]() $t>0$
.
$t>0$
.
We further assume that the density of the plasma is so low that its pressure is negligible compared with the magnetic pressure (the ‘low-
![]() ${\it\beta}$
’ approximation). For
${\it\beta}$
’ approximation). For
![]() $t>0$
, the plasma flows in response to the magnetic pressure with velocity
$t>0$
, the plasma flows in response to the magnetic pressure with velocity
The electric field
![]() $\boldsymbol{E}(x,t)$
in the plasma is then given by Ohm’s law,
$\boldsymbol{E}(x,t)$
in the plasma is then given by Ohm’s law,
and the magnetic field
![]() $\boldsymbol{B}(x,t)$
with components
$\boldsymbol{B}(x,t)$
with components
![]() $[0,b_{y}(x,t),b_{z}(x,t)]$
evolves for
$[0,b_{y}(x,t),b_{z}(x,t)]$
evolves for
![]() $t>0$
according to the induction equation
$t>0$
according to the induction equation
with components
We note that, together with the boundary conditions (2.4) and (2.5), these equations imply that
i.e. the flux vector
![]() $(0,{\it\Phi}_{y},{\it\Phi}_{z})$
is constant, being trapped between the perfectly conducting boundaries. We may choose the axes
$(0,{\it\Phi}_{y},{\it\Phi}_{z})$
is constant, being trapped between the perfectly conducting boundaries. We may choose the axes
![]() $Oyz$
so that
$Oyz$
so that
![]() ${\it\Phi}_{y}=0$
. Flux conservation then implies that, whatever the initial field
${\it\Phi}_{y}=0$
. Flux conservation then implies that, whatever the initial field
![]() $\boldsymbol{b}_{0}$
may be, the long-term asymptotic state is just the uniform field
$\boldsymbol{b}_{0}$
may be, the long-term asymptotic state is just the uniform field
Following Bajer & Moffatt (Reference Bajer and Moffatt2013), we adopt a viscous model for the relaxation process, with an effective viscosity
![]() ${\it\mu}$
; then
${\it\mu}$
; then
![]() $u$
and
$u$
and
![]() ${\it\rho}$
evolve according to the one-dimensional equations
${\it\rho}$
evolve according to the one-dimensional equations
where
![]() $p_{M}=B_{0}^{2}(b_{y}^{2}+b_{z}^{2})/2$
. We note that, for this geometry, (2.7) and (2.11b
) may be combined to give
$p_{M}=B_{0}^{2}(b_{y}^{2}+b_{z}^{2})/2$
. We note that, for this geometry, (2.7) and (2.11b
) may be combined to give
where
![]() $\text{D}/\text{D}t$
is the Lagrangian derivative following a material element of fluid.
$\text{D}/\text{D}t$
is the Lagrangian derivative following a material element of fluid.
As explained in the introduction, a primary aim of this paper is to explore the extent to which the Taylor conjecture is valid for the model under consideration. That is, is the global helicity the only relevant invariant during relaxation to a minimum energy state? And does the field relax to a ‘Taylor state’ in which the Beltrami condition (1.1) is satisfied? For this purpose we need to introduce a vector potential
![]() $\boldsymbol{A}=[0,a_{y}(x,t),a_{z}(x,t)]$
with
$\boldsymbol{A}=[0,a_{y}(x,t),a_{z}(x,t)]$
with
It is evident that any vector potential of this kind satisfies
![]() $\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{A}=0$
. We may further pin down the gauge of
$\boldsymbol{{\rm\nabla}}\boldsymbol{\cdot }\boldsymbol{A}=0$
. We may further pin down the gauge of
![]() $\boldsymbol{A}$
so that
$\boldsymbol{A}$
so that
![]() $a_{y}(0,t)=a_{z}(0,t)=0$
. Since from (2.6),
$a_{y}(0,t)=a_{z}(0,t)=0$
. Since from (2.6),
![]() $\boldsymbol{E}$
has no
$\boldsymbol{E}$
has no
![]() $x$
component, we may assume that
$x$
component, we may assume that
![]() $\boldsymbol{E}=-\partial \boldsymbol{A}/\partial t$
, so that
$\boldsymbol{E}=-\partial \boldsymbol{A}/\partial t$
, so that
![]() $\boldsymbol{A}$
then satisfies the equation
$\boldsymbol{A}$
then satisfies the equation
With
![]() $\boldsymbol{u}\times \boldsymbol{B}=(0,-ub_{z},ub_{y})$
, we then have
$\boldsymbol{u}\times \boldsymbol{B}=(0,-ub_{z},ub_{y})$
, we then have
or equivalently
The helicity density is given by
and it is evident from (2.12) and (2.16) that, when
![]() ${\it\eta}=0$
,
${\it\eta}=0$
,
i.e.
![]() ${\mathcal{H}}/{\it\rho}$
is a Lagrangian invariant. Thus, a fortiori, the ‘global’ helicity per unit area of the
${\mathcal{H}}/{\it\rho}$
is a Lagrangian invariant. Thus, a fortiori, the ‘global’ helicity per unit area of the
![]() $(y,z)$
plane, given byFootnote
2
$(y,z)$
plane, given byFootnote
2
is invariant when
![]() ${\it\eta}=0$
. When
${\it\eta}=0$
. When
![]() ${\it\eta}\neq 0$
, standard manipulations give
${\it\eta}\neq 0$
, standard manipulations give
The vector potential
![]() $\boldsymbol{A}$
is of course generally not unique: under the gauge transformation
$\boldsymbol{A}$
is of course generally not unique: under the gauge transformation
![]() $\boldsymbol{A}\rightarrow \boldsymbol{A}^{\ast }=\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\phi}$
, the helicity density becomes
$\boldsymbol{A}\rightarrow \boldsymbol{A}^{\ast }=\boldsymbol{A}+\boldsymbol{{\rm\nabla}}{\it\phi}$
, the helicity density becomes
![]() ${\mathcal{H}}^{\ast }(x,t)={\mathcal{H}}+\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\phi}$
. If we insist that
${\mathcal{H}}^{\ast }(x,t)={\mathcal{H}}+\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}{\it\phi}$
. If we insist that
![]() $\boldsymbol{A}$
as well as
$\boldsymbol{A}$
as well as
![]() $\boldsymbol{B}$
be one-dimensional, then
$\boldsymbol{B}$
be one-dimensional, then
![]() $\boldsymbol{{\rm\nabla}}{\it\phi}=(\partial {\it\psi}/\partial x,c_{1},c_{2})$
, where
$\boldsymbol{{\rm\nabla}}{\it\phi}=(\partial {\it\psi}/\partial x,c_{1},c_{2})$
, where
![]() ${\it\psi}(x,t)$
is arbitrary and
${\it\psi}(x,t)$
is arbitrary and
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
are at most functions of time. Hence
$c_{2}$
are at most functions of time. Hence
Here
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
, with dimensions of magnetic flux, are actually fluxes that may be imposed (in the
$c_{2}$
, with dimensions of magnetic flux, are actually fluxes that may be imposed (in the
![]() $z$
and
$z$
and
![]() $y$
directions, respectively!) external to the slab
$y$
directions, respectively!) external to the slab
![]() $|x|<{\rm\pi}L$
in which the plasma is located. We shall suppose that these external fluxes are zero for all
$|x|<{\rm\pi}L$
in which the plasma is located. We shall suppose that these external fluxes are zero for all
![]() $t$
, i.e.
$t$
, i.e.
![]() $c_{1}=c_{2}=0$
. They cannot therefore contribute to gauge transformation. With this understanding, the helicity density, like the total helicity, is in fact gauge-invariant.
$c_{1}=c_{2}=0$
. They cannot therefore contribute to gauge transformation. With this understanding, the helicity density, like the total helicity, is in fact gauge-invariant.
It will be convenient to use non-dimensional variables. Defining
equations (2.11) and (2.8) become (dropping the hats)
where the dimensionless parameters
![]() ${\it\epsilon}$
and
${\it\epsilon}$
and
![]() ${\it\kappa}$
(both assumed small) are given by
${\it\kappa}$
(both assumed small) are given by
Here,
![]() ${\it\epsilon}$
is like a Reynolds number based on the velocity scale
${\it\epsilon}$
is like a Reynolds number based on the velocity scale
![]() $B_{0}^{2}L/{\it\mu}$
, and is small by virtue of the smallness of
$B_{0}^{2}L/{\it\mu}$
, and is small by virtue of the smallness of
![]() ${\it\rho}_{0}$
; and
${\it\rho}_{0}$
; and
![]() ${\it\kappa}$
is small by virtue of the smallness of
${\it\kappa}$
is small by virtue of the smallness of
![]() ${\it\eta}$
. For this combination of reasons, we must suppose that the magnetic Prandtl number
${\it\eta}$
. For this combination of reasons, we must suppose that the magnetic Prandtl number
![]() ${\it\mu}/{\it\rho}_{0}{\it\eta}=({\it\epsilon}{\it\kappa})^{-1}$
is large, not unreasonable in a very low-density, high-conductivity plasma.
${\it\mu}/{\it\rho}_{0}{\it\eta}=({\it\epsilon}{\it\kappa})^{-1}$
is large, not unreasonable in a very low-density, high-conductivity plasma.
3. Two-stage process
We may ensure that the initial helicity is non-zero by adopting initial conditions of the form
The coefficients
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() ${\it\gamma}$
are arbitrary; the only important thing is that they are unequal, and, for the sake of illustration, we shall adopt values
${\it\gamma}$
are arbitrary; the only important thing is that they are unequal, and, for the sake of illustration, we shall adopt values
![]() ${\it\beta}=2,~{\it\gamma}=3$
. The variable wavenumber
${\it\beta}=2,~{\it\gamma}=3$
. The variable wavenumber
![]() $m(x)$
must be chosen in such a way that the conditions
$m(x)$
must be chosen in such a way that the conditions
![]() $b_{y0}^{\prime }(\pm {\rm\pi})=b_{z0}^{\prime }(\pm {\rm\pi})=0$
are satisfied. A simple choice is
$b_{y0}^{\prime }(\pm {\rm\pi})=b_{z0}^{\prime }(\pm {\rm\pi})=0$
are satisfied. A simple choice is
where
![]() $k$
is constant. The field (3.1) provides an initial non-uniform magnetic pressure distribution,
$k$
is constant. The field (3.1) provides an initial non-uniform magnetic pressure distribution,
It is the gradient of this magnetic pressure that drives the subsequent flow. Note that
![]() $p_{M0}(x)$
nowhere vanishes, i.e. there are no null points of
$p_{M0}(x)$
nowhere vanishes, i.e. there are no null points of
![]() $\boldsymbol{B}$
. In this respect, the situation differs from that considered by Bajer & Moffatt (Reference Bajer and Moffatt2013), wherein the null points played a crucial role.
$\boldsymbol{B}$
. In this respect, the situation differs from that considered by Bajer & Moffatt (Reference Bajer and Moffatt2013), wherein the null points played a crucial role.
Obviously
![]() $b_{y0}(-x)=-b_{y0}(x)$
and
$b_{y0}(-x)=-b_{y0}(x)$
and
![]() $b_{z0}(-x)=b_{z0}(x)$
, and, with the further initial conditions
$b_{z0}(-x)=b_{z0}(x)$
, and, with the further initial conditions
and boundary conditions
these symmetries are respected for
![]() $t>0$
, as are the symmetries
$t>0$
, as are the symmetries
With the choice
![]() $k=0.1$
(again arbitrary), the initial field components
$k=0.1$
(again arbitrary), the initial field components
![]() $b_{y0}(x)$
and
$b_{y0}(x)$
and
![]() $b_{z0}(x)$
are as shown in figure 1. The corresponding fluxes are then
$b_{z0}(x)$
are as shown in figure 1. The corresponding fluxes are then
and these values are conserved. Adopting the suitably small parameter values
![]() ${\it\epsilon}=0.001$
and
${\it\epsilon}=0.001$
and
![]() ${\it\kappa}=0.001$
, (2.23) and (2.24) may be integrated numericallyFootnote
3
. Figure 2 shows the manner in which the initial magnetic energy distribution
${\it\kappa}=0.001$
, (2.23) and (2.24) may be integrated numericallyFootnote
3
. Figure 2 shows the manner in which the initial magnetic energy distribution
![]() $M(x,t)~(=p_{M}(x,t))$
relaxes to a near-uniform (i.e. nearly force-free) state. Figure 2(a) shows that, by time
$M(x,t)~(=p_{M}(x,t))$
relaxes to a near-uniform (i.e. nearly force-free) state. Figure 2(a) shows that, by time
![]() $t=1$
, the energy density (and so the magnetic pressure) is nearly uniform in
$t=1$
, the energy density (and so the magnetic pressure) is nearly uniform in
![]() $x$
, and remains so for later times. It does not however become exactly uniform, as indicated by figure 2(b), which shows
$x$
, and remains so for later times. It does not however become exactly uniform, as indicated by figure 2(b), which shows
![]() $M(x,50)$
expanded in the vertical by a factor of about
$M(x,50)$
expanded in the vertical by a factor of about
![]() $100$
. Figure 3 shows the relatively rapid initial decay of the mean magnetic energy
$100$
. Figure 3 shows the relatively rapid initial decay of the mean magnetic energy
![]() $M(t)$
up to about
$M(t)$
up to about
![]() $t=0.2$
(with
$t=0.2$
(with
![]() $M(0)=3.396$
), and the subsequent relatively slow decay driven by magnetic resistivity (which forces a continuing weak
$M(0)=3.396$
), and the subsequent relatively slow decay driven by magnetic resistivity (which forces a continuing weak
![]() $x$
dependence of magnetic energy density and pressure).
$x$
dependence of magnetic energy density and pressure).

Figure 2. (a) Magnetic energy
![]() $M(x,t)~(=p_{M}(x,t))$
for
$M(x,t)~(=p_{M}(x,t))$
for
![]() $t=0,0.2,1$
and 50. (b) Expanded view of
$t=0,0.2,1$
and 50. (b) Expanded view of
![]() $M(x,t)$
at time
$M(x,t)$
at time
![]() $t=50$
; the ordinate here runs just from 1.86 to 1.89.
$t=50$
; the ordinate here runs just from 1.86 to 1.89.

Figure 3. Relaxation of the mean magnetic energy
![]() $M(t)$
for
$M(t)$
for
![]() $0<t<1$
;
$0<t<1$
;
![]() $M(0)=3.396$
. Note the initial rapid relaxation followed by relatively slow decay for
$M(0)=3.396$
. Note the initial rapid relaxation followed by relatively slow decay for
![]() $t\gtrsim 0.2$
.
$t\gtrsim 0.2$
.
As previously noted, the lines of force are rectilinear and lie in planes
![]() $x=\text{const}$
. At time
$x=\text{const}$
. At time
![]() $t$
, as
$t$
, as
![]() $x$
increases from
$x$
increases from
![]() $-{\rm\pi}$
to
$-{\rm\pi}$
to
![]() ${\rm\pi}$
, the line of force through the point
${\rm\pi}$
, the line of force through the point
![]() $(x,0,0)$
sweeps out a ruled surface
$(x,0,0)$
sweeps out a ruled surface
![]() $S[t]$
with parametric representation
$S[t]$
with parametric representation
![]() $[x,sb_{y}(x,t),sb_{z}(x,t)]$
. This surface is shown in figure 4 for the range
$[x,sb_{y}(x,t),sb_{z}(x,t)]$
. This surface is shown in figure 4 for the range
![]() $\{-{\rm\pi}<x<{\rm\pi},-1<s<1\}$
at the initial instant
$\{-{\rm\pi}<x<{\rm\pi},-1<s<1\}$
at the initial instant
![]() $t=0$
and at time
$t=0$
and at time
![]() $t=50$
when the field is well relaxed; the helical character of the field structure is very evident from this representation.
$t=50$
when the field is well relaxed; the helical character of the field structure is very evident from this representation.

Figure 4. Ruled surface
![]() $S\;[t]$
containing the
$S\;[t]$
containing the
![]() $\boldsymbol{B}$
-lines through the points
$\boldsymbol{B}$
-lines through the points
![]() $(x,0,0)$
for
$(x,0,0)$
for
![]() $-{\rm\pi}<x<{\rm\pi}$
: (a) non-equilibrium initial field; (b) nearly force-free relaxed field at time
$-{\rm\pi}<x<{\rm\pi}$
: (a) non-equilibrium initial field; (b) nearly force-free relaxed field at time
![]() $t=50$
.
$t=50$
.
Our interest is primarily focused on the behaviour of the helicity during the relaxation process. The helicity density is shown in figure 5(a) for times
![]() $t=0,~0.5$
and
$t=0,~0.5$
and
![]() $10$
. Up to about time
$10$
. Up to about time
![]() $t=0.5$
, there is merely a redistribution of lines of force, with conservation of mean helicity
$t=0.5$
, there is merely a redistribution of lines of force, with conservation of mean helicity
![]() ${\mathcal{H}}(t)={\mathcal{H}}_{V}(t)/2{\rm\pi}$
(actually about a 1 % decrease due to diffusive decay). For greater values of
${\mathcal{H}}(t)={\mathcal{H}}_{V}(t)/2{\rm\pi}$
(actually about a 1 % decrease due to diffusive decay). For greater values of
![]() $t$
, this diffusive decay continues (figure 5
b), with no sign of any change of behaviour as
$t$
, this diffusive decay continues (figure 5
b), with no sign of any change of behaviour as
![]() $t$
increases through values
$t$
increases through values
![]() $O(1)$
. This is entirely consistent with conservation of global helicity in the non-diffusive limit
$O(1)$
. This is entirely consistent with conservation of global helicity in the non-diffusive limit
![]() ${\it\kappa}=0$
. However, the non-uniformity of
${\it\kappa}=0$
. However, the non-uniformity of
![]() ${\mathcal{H}}(x,t)$
remains marked throughout, as expected given that, as shown above,
${\mathcal{H}}(x,t)$
remains marked throughout, as expected given that, as shown above,
![]() ${\mathcal{H}}(x,t)/{\it\rho}$
is a Lagrangian invariant when
${\mathcal{H}}(x,t)/{\it\rho}$
is a Lagrangian invariant when
![]() ${\it\kappa}=0$
. The contrasting behaviour of
${\it\kappa}=0$
. The contrasting behaviour of
![]() $M(t)/M(0)$
(figure 3) and
$M(t)/M(0)$
(figure 3) and
![]() ${\mathcal{H}}(t)/{\mathcal{H}}(0)$
(figure 5
b) is to be noted.
${\mathcal{H}}(t)/{\mathcal{H}}(0)$
(figure 5
b) is to be noted.

Figure 5. (a) Helicity density
![]() ${\mathcal{H}}(x,t)$
at times
${\mathcal{H}}(x,t)$
at times
![]() $t=0$
(solid),
$t=0$
(solid),
![]() $0.5$
(dashed) and
$0.5$
(dashed) and
![]() $10$
(dotted). (b) Mean helicity
$10$
(dotted). (b) Mean helicity
![]() ${\mathcal{H}}(t)~(={\mathcal{H}}_{V}(t)/2{\rm\pi})$
for
${\mathcal{H}}(t)~(={\mathcal{H}}_{V}(t)/2{\rm\pi})$
for
![]() $0<t<1$
;
$0<t<1$
;
![]() ${\mathcal{H}}(0)=2.367$
. The ordinate runs from 0.95 to 1.005, as in figure 3. There is a redistribution of helicity density but mean helicity is almost constant.
${\mathcal{H}}(0)=2.367$
. The ordinate runs from 0.95 to 1.005, as in figure 3. There is a redistribution of helicity density but mean helicity is almost constant.

Figure 6. The
![]() $x$
dependence of
$x$
dependence of
![]() $j_{y}/b_{y}$
(solid) and
$j_{y}/b_{y}$
(solid) and
![]() $j_{z}/b_{z}$
(dashed) at times
$j_{z}/b_{z}$
(dashed) at times
![]() $t=0$
, 0.1 and 1. (The vertical segments on these curves appear at points where the ratios are not well defined other than by continuity.) By time
$t=0$
, 0.1 and 1. (The vertical segments on these curves appear at points where the ratios are not well defined other than by continuity.) By time
![]() $t=1$
, the two curves are almost indistinguishable, as implied by (3.8).
$t=1$
, the two curves are almost indistinguishable, as implied by (3.8).
We may view this differently in terms of an
![]() ${\it\alpha}$
-effect. After the early stage of relaxation when the magnetic pressure has become approximately uniform, the field is nearly force-free, so that at leading order
${\it\alpha}$
-effect. After the early stage of relaxation when the magnetic pressure has become approximately uniform, the field is nearly force-free, so that at leading order
![]() $\boldsymbol{j}={\it\alpha}(x,t)\boldsymbol{B}$
, i.e.
$\boldsymbol{j}={\it\alpha}(x,t)\boldsymbol{B}$
, i.e.
Figure 6 shows curves for
![]() $j_{y}/b_{y}$
and
$j_{y}/b_{y}$
and
![]() $j_{z}/b_{z}$
for
$j_{z}/b_{z}$
for
![]() $t=0,~0.1$
and
$t=0,~0.1$
and
![]() $1$
. There is indeed a convergence of the two curves as
$1$
. There is indeed a convergence of the two curves as
![]() $t$
increases, and by time
$t$
increases, and by time
![]() $t=1$
they are almost indistinguishable. From this point on, the single curve evidently gives an excellent approximation for the function
$t=1$
they are almost indistinguishable. From this point on, the single curve evidently gives an excellent approximation for the function
![]() ${\it\alpha}(x,t)$
. This is obviously non-uniform in
${\it\alpha}(x,t)$
. This is obviously non-uniform in
![]() $x$
, providing a clear signal that the Taylor state (1.1) is not attained, and therefore that global helicity is certainly not the only relevant invariant during the initial rapid relaxation process.
$x$
, providing a clear signal that the Taylor state (1.1) is not attained, and therefore that global helicity is certainly not the only relevant invariant during the initial rapid relaxation process.
During this initial phase, there is a transfer of energy from the magnetic field to the velocity field, i.e. to kinetic energy
![]() $K(t)$
defined by
$K(t)$
defined by
Figure 7(a) shows this kinetic energy for
![]() $0<t<0.5$
. It rises initially very rapidly to a maximum,
$0<t<0.5$
. It rises initially very rapidly to a maximum,
![]() $u$
being subsequently determined in quasi-static manner. The kinetic energy
$u$
being subsequently determined in quasi-static manner. The kinetic energy
![]() $K(t)$
falls to a low value (
$K(t)$
falls to a low value (
![]() $K\lesssim 10^{-3}$
for
$K\lesssim 10^{-3}$
for
![]() $t>0.5$
), a further indication of the nearly force-free state. Figure 7(b) shows
$t>0.5$
), a further indication of the nearly force-free state. Figure 7(b) shows
![]() $K(t)$
for
$K(t)$
for
![]() $0<t<0.01$
, showing how this kinetic energy grows initially on an
$0<t<0.01$
, showing how this kinetic energy grows initially on an
![]() $O({\it\epsilon})$
time scale.
$O({\it\epsilon})$
time scale.

Figure 7. Kinetic energy
![]() $K(t)$
in (3.9): (a) for
$K(t)$
in (3.9): (a) for
![]() $0<t<0.5$
,
$0<t<0.5$
,
![]() $K(t)$
rises rapidly from zero to a maximum of 0.393 at
$K(t)$
rises rapidly from zero to a maximum of 0.393 at
![]() $t=0.004$
, and then decays monotonically; (b) for
$t=0.004$
, and then decays monotonically; (b) for
![]() $0<t<0.01$
, showing the initial rise on an
$0<t<0.01$
, showing the initial rise on an
![]() $O({\it\epsilon})$
time scale.
$O({\it\epsilon})$
time scale.
We may note that, if
![]() ${\it\epsilon}=0$
, then the development is truly quasi-static as far as the velocity is concerned. In this situation, a single integration of (2.23) using the boundary conditions (3.5) gives
${\it\epsilon}=0$
, then the development is truly quasi-static as far as the velocity is concerned. In this situation, a single integration of (2.23) using the boundary conditions (3.5) gives
where
![]() $b^{2}=b_{y}^{2}+b_{y}^{2}$
, and the angular brackets indicate an average over the range
$b^{2}=b_{y}^{2}+b_{y}^{2}$
, and the angular brackets indicate an average over the range
![]() $(-{\rm\pi},{\rm\pi})$
. This gives an initial kinetic energy (with
$(-{\rm\pi},{\rm\pi})$
. This gives an initial kinetic energy (with
![]() ${\it\rho}_{0}=1$
)
${\it\rho}_{0}=1$
)
which may be evaluated numerically using (3.3). The result is
![]() $K(0)=0.416$
, marginally greater than the maximum of
$K(0)=0.416$
, marginally greater than the maximum of
![]() $K(t)$
shown in figure 7 (actually, with
$K(t)$
shown in figure 7 (actually, with
![]() ${\it\epsilon}=0.001$
,
${\it\epsilon}=0.001$
,
![]() $K_{max}(t)=0.393$
at
$K_{max}(t)=0.393$
at
![]() $t=0.004$
). This is consistent with the establishment of quasi-static evolution in a time
$t=0.004$
). This is consistent with the establishment of quasi-static evolution in a time
![]() $t=O({\it\epsilon})$
.
$t=O({\it\epsilon})$
.
Note that if we return to dimensional variables via (2.22), the dimensional magnetic and kinetic energies are
so that
and this ratio is certainly small. Nevertheless, the initial drop in
![]() $M(t)$
evident in figure 2(c) is due to conversion
$M(t)$
evident in figure 2(c) is due to conversion
![]() $M(t)\rightarrow K(t)$
and immediate dissipation by viscosity.
$M(t)\rightarrow K(t)$
and immediate dissipation by viscosity.
Finally, we may consider the evolution of the density field
![]() ${\it\rho}(x,t)$
, bearing in mind that, in the zero-resistivity limit (
${\it\rho}(x,t)$
, bearing in mind that, in the zero-resistivity limit (
![]() ${\it\kappa}=0$
),
${\it\kappa}=0$
),
![]() $b_{y}/{\it\rho}$
and
$b_{y}/{\it\rho}$
and
![]() $b_{z}/{\it\rho}$
are both Lagrangian invariants so that evolution of
$b_{z}/{\it\rho}$
are both Lagrangian invariants so that evolution of
![]() $b_{y}$
and
$b_{y}$
and
![]() $b_{z}$
is necessarily accompanied by corresponding evolution of
$b_{z}$
is necessarily accompanied by corresponding evolution of
![]() ${\it\rho}$
. This correspondence is of course broken when
${\it\rho}$
. This correspondence is of course broken when
![]() ${\it\kappa}\neq 0$
. Figure 8 shows the density field at times
${\it\kappa}\neq 0$
. Figure 8 shows the density field at times
![]() $t=0,~1$
and
$t=0,~1$
and
![]() $50$
. During the early relaxation phase, the density field, initially uniform, is significantly perturbed, as expected. The evolution continues during the subsequent slow diffusive phase, due to the cumulative effect of the non-vanishing velocity field (as similarly found by Bajer & Moffatt (Reference Bajer and Moffatt2013)), and persistent convergence towards the four minima of magnetic pressure (see figure 2
a) causes these maxima of density to become increasingly pronounced while the magnetic field slowly decays.
$50$
. During the early relaxation phase, the density field, initially uniform, is significantly perturbed, as expected. The evolution continues during the subsequent slow diffusive phase, due to the cumulative effect of the non-vanishing velocity field (as similarly found by Bajer & Moffatt (Reference Bajer and Moffatt2013)), and persistent convergence towards the four minima of magnetic pressure (see figure 2
a) causes these maxima of density to become increasingly pronounced while the magnetic field slowly decays.

Figure 8. Density field
![]() ${\it\rho}(x,t)$
at times
${\it\rho}(x,t)$
at times
![]() $t=0$
(solid),
$t=0$
(solid),
![]() $t=1$
(dashed) and
$t=1$
(dashed) and
![]() $t=50$
(dotted). Note the development of increasingly sharp maxima as
$t=50$
(dotted). Note the development of increasingly sharp maxima as
![]() $t$
increases.
$t$
increases.
In a fully three-dimensional situation,
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() ${\it\rho}$
are still strongly coupled in the non-diffusive limit through the equation
${\it\rho}$
are still strongly coupled in the non-diffusive limit through the equation
![]() $\text{D}(\boldsymbol{B}/{\it\rho})/\text{D}t=(\boldsymbol{B}/{\it\rho})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}$
, so a similar development of density variations is to be expected, although perhaps not with such strong peaks. Previous computations have mainly focused on the evolution of the magnetic field, ignoring the associated evolution of the density field that must clearly be significant in any low-
$\text{D}(\boldsymbol{B}/{\it\rho})/\text{D}t=(\boldsymbol{B}/{\it\rho})\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\boldsymbol{u}$
, so a similar development of density variations is to be expected, although perhaps not with such strong peaks. Previous computations have mainly focused on the evolution of the magnetic field, ignoring the associated evolution of the density field that must clearly be significant in any low-
![]() ${\it\beta}$
plasma.
${\it\beta}$
plasma.

Figure 9. Plots of
![]() $\langle {\it\alpha}^{2}\rangle$
and
$\langle {\it\alpha}^{2}\rangle$
and
![]() $\langle {\it\alpha}\rangle$
as functions of time for
$\langle {\it\alpha}\rangle$
as functions of time for
![]() $0<t<30$
.
$0<t<30$
.
4. Energy and helicity decay during the slow diffusion stage
During the slow diffusion stage, although
![]() $b_{y}$
and
$b_{y}$
and
![]() $b_{z}$
are still strongly non-uniform in
$b_{z}$
are still strongly non-uniform in
![]() $x$
,
$x$
,
![]() $b^{2}=b_{y}^{2}+b_{z}^{2}$
is approximately uniform, and
$b^{2}=b_{y}^{2}+b_{z}^{2}$
is approximately uniform, and
![]() $\boldsymbol{j}\approx {\it\alpha}(x,t)\boldsymbol{B}$
. The exact equation for
$\boldsymbol{j}\approx {\it\alpha}(x,t)\boldsymbol{B}$
. The exact equation for
![]() $b^{2}$
may be readily found from (2.24) in the form
$b^{2}$
may be readily found from (2.24) in the form
Here,
![]() $\partial u/\partial x$
is now given by the quasi-static relation (3.10), and it is the first term on the right that is responsible for keeping
$\partial u/\partial x$
is now given by the quasi-static relation (3.10), and it is the first term on the right that is responsible for keeping
![]() $b^{2}$
approximately uniform. (Note that
$b^{2}$
approximately uniform. (Note that
![]() $b^{2}$
would not remain uniform under purely diffusive decay, without the all-important smoothing effect of magnetic pressure.) Here, using
$b^{2}$
would not remain uniform under purely diffusive decay, without the all-important smoothing effect of magnetic pressure.) Here, using
![]() $\boldsymbol{j}={\it\alpha}(x,t)\boldsymbol{B}$
, the diffusive term becomes, at leading order,
$\boldsymbol{j}={\it\alpha}(x,t)\boldsymbol{B}$
, the diffusive term becomes, at leading order,
Now, we may average (4.1) over the range
![]() $(-{\rm\pi},{\rm\pi})$
using
$(-{\rm\pi},{\rm\pi})$
using
![]() $u(\pm {\rm\pi},t)=0$
, giving, again at leading order using the approximate uniformity of
$u(\pm {\rm\pi},t)=0$
, giving, again at leading order using the approximate uniformity of
![]() $b^{2}$
,
$b^{2}$
,
where
![]() $b_{0}^{2}$
is the value of
$b_{0}^{2}$
is the value of
![]() $\langle b^{2}\rangle$
at some nominal instant
$\langle b^{2}\rangle$
at some nominal instant
![]() $t=t_{d}\sim 1$
by which time the slow diffusive stage may be deemed to be established. The function
$t=t_{d}\sim 1$
by which time the slow diffusive stage may be deemed to be established. The function
![]() $\langle {\it\alpha}^{2}\rangle (t)=\langle (\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{b}/b^{2})^{2}\rangle$
is shown in figure 9. It varies by only
$\langle {\it\alpha}^{2}\rangle (t)=\langle (\,\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{b}/b^{2})^{2}\rangle$
is shown in figure 9. It varies by only
![]() $\pm 1\,\%$
from the value 5.7 over the (diffusive) range
$\pm 1\,\%$
from the value 5.7 over the (diffusive) range
![]() $t_{d}<t<30$
, so that (4.3) indicates mild exponential decrease of energy over this range:
$t_{d}<t<30$
, so that (4.3) indicates mild exponential decrease of energy over this range:
The decay of mean helicity
![]() ${\mathcal{H}}(t)~(=(2{\rm\pi})^{-1}{\mathcal{H}}_{V}(t))$
may be calculated to the same modest degree of accuracy. We have
${\mathcal{H}}(t)~(=(2{\rm\pi})^{-1}{\mathcal{H}}_{V}(t))$
may be calculated to the same modest degree of accuracy. We have
exploiting again the near-uniformity of
![]() $b^{2}$
. The function
$b^{2}$
. The function
![]() $\langle {\it\alpha}\rangle$
is also shown in figure 9; it is remarkably constant near the value 1.98, over the whole range
$\langle {\it\alpha}\rangle$
is also shown in figure 9; it is remarkably constant near the value 1.98, over the whole range
![]() $0<t<30$
. Adopting this value, and noting that
$0<t<30$
. Adopting this value, and noting that
![]() ${\mathcal{H}}(t)$
must tend to zero as
${\mathcal{H}}(t)$
must tend to zero as
![]() $t\rightarrow \infty$
, (4.5) integrates to give
$t\rightarrow \infty$
, (4.5) integrates to give
at least for
![]() $t_{d}\lesssim t\lesssim 30$
. What is important here is that both energy and helicity decrease at the same rate, the characteristic decay time for both being
$t_{d}\lesssim t\lesssim 30$
. What is important here is that both energy and helicity decrease at the same rate, the characteristic decay time for both being
![]() $t_{d}\sim (2{\it\kappa}\langle {\it\alpha}^{2}\rangle )^{-1}$
. Clearly, the ratio
$t_{d}\sim (2{\it\kappa}\langle {\it\alpha}^{2}\rangle )^{-1}$
. Clearly, the ratio
![]() ${\mathcal{H}}(t)/\langle b^{2}\rangle$
remains constant throughout the diffusive stage.
${\mathcal{H}}(t)/\langle b^{2}\rangle$
remains constant throughout the diffusive stage.
We note however that this behaviour cannot continue for ever, since ultimately
![]() $b_{y}(x,t)$
must decay to zero, whereas
$b_{y}(x,t)$
must decay to zero, whereas
![]() $b_{z}(x,t)$
must level off at the level
$b_{z}(x,t)$
must level off at the level
![]() ${\it\Phi}_{z}/2{\rm\pi}\approx 0.5491$
determined by the conserved flux. This levelling off occurs when
${\it\Phi}_{z}/2{\rm\pi}\approx 0.5491$
determined by the conserved flux. This levelling off occurs when
![]() $M(t)$
has fallen to such a low level that the nonlinear convection terms of (2.24) become negligible compared with the diffusion terms. For the parameter values chosen here, this occurs when
$M(t)$
has fallen to such a low level that the nonlinear convection terms of (2.24) become negligible compared with the diffusion terms. For the parameter values chosen here, this occurs when
![]() $t\sim 250$
, well beyond the range shown in figures 3 and 5(b). For
$t\sim 250$
, well beyond the range shown in figures 3 and 5(b). For
![]() $t\gtrsim 250$
, the field gradient is so weak that the continuing decay is due to ohmic diffusion alone.
$t\gtrsim 250$
, the field gradient is so weak that the continuing decay is due to ohmic diffusion alone.
5. Lagrangian invariance of
 $\langle {\it\alpha}\rangle$
$\langle {\it\alpha}\rangle$
The near-constancy of
![]() $\langle {\it\alpha}\rangle$
evident in figure 9 contrasts with the behaviour of
$\langle {\it\alpha}\rangle$
evident in figure 9 contrasts with the behaviour of
![]() $\langle {\it\alpha}^{2}\rangle$
and calls for explanation. First, whether the force-free equation
$\langle {\it\alpha}^{2}\rangle$
and calls for explanation. First, whether the force-free equation
![]() $\boldsymbol{j}={\it\alpha}(x,t)\boldsymbol{b}$
is satisfied or not, we may define
$\boldsymbol{j}={\it\alpha}(x,t)\boldsymbol{b}$
is satisfied or not, we may define
![]() ${\it\alpha}(x,t)$
(a measure of the rate of rotation of the field vector with increasing
${\it\alpha}(x,t)$
(a measure of the rate of rotation of the field vector with increasing
![]() $x$
, as shown in figure 4) by the equation
$x$
, as shown in figure 4) by the equation
Then we have the following theorem.
Theorem. If
![]() $\boldsymbol{b}=(0,b_{y}(x,t),b_{z}(x,t))$
and
$\boldsymbol{b}=(0,b_{y}(x,t),b_{z}(x,t))$
and
![]() $\boldsymbol{u}=(u(x,t),0,0)$
with
$\boldsymbol{u}=(u(x,t),0,0)$
with
![]() $u(\pm {\rm\pi},t)=0$
, and if
$u(\pm {\rm\pi},t)=0$
, and if
![]() $\{\boldsymbol{b}(x,0),u(x,0),{\it\rho}(x,0)\}$
are arbitrary
$\{\boldsymbol{b}(x,0),u(x,0),{\it\rho}(x,0)\}$
are arbitrary
![]() $\mathbb{C}^{2}$
fields subject only to
$\mathbb{C}^{2}$
fields subject only to
![]() $u(\pm {\rm\pi},0)=0$
, then
$u(\pm {\rm\pi},0)=0$
, then
![]() $\langle (\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{b})/b^{2}\rangle$
is an invariant of the zero-resistivity equations
$\langle (\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{b})/b^{2}\rangle$
is an invariant of the zero-resistivity equations
where the angular brackets represent an average over the range
![]() $(-{\rm\pi},{\rm\pi})$
.
$(-{\rm\pi},{\rm\pi})$
.
Proof. Writing
![]() $\langle {\it\alpha}\rangle$
in the form
$\langle {\it\alpha}\rangle$
in the form
and using the standard Lagrangian results
![]() $(\text{D}/\text{D}t)(\boldsymbol{b}/{\it\rho})=0$
and
$(\text{D}/\text{D}t)(\boldsymbol{b}/{\it\rho})=0$
and
![]() $(\text{D}/\text{D}t)({\it\rho}\,\text{d}x)=0$
, we have immediately that
$(\text{D}/\text{D}t)({\it\rho}\,\text{d}x)=0$
, we have immediately that
Now from (5.2), we may readily derive the equations
Hence we have
and so
It follows immediately from (5.4) that
(Actually, it is clear from the above argument that
![]() $\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{b}/{\it\rho}b^{2}$
is a Lagrangian invariant, so the integral (5.3) is in fact constant if taken over any Lagrangian (co-moving) sub-interval of
$\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{b}/{\it\rho}b^{2}$
is a Lagrangian invariant, so the integral (5.3) is in fact constant if taken over any Lagrangian (co-moving) sub-interval of
![]() $({\rm\pi},{\rm\pi})$
.)
$({\rm\pi},{\rm\pi})$
.)
6. An example with concentrated initial field near the boundaries
We now briefly consider what happens if the initial field is more concentrated near the boundaries
![]() $x=\pm {\rm\pi}$
. We adopt initial conditions (again somewhat arbitrarily)
$x=\pm {\rm\pi}$
. We adopt initial conditions (again somewhat arbitrarily)
These field components are shown in figure 10(a). Again, in this case, by symmetry
![]() ${\it\Phi}_{y}=0$
, and the conserved flux in the
${\it\Phi}_{y}=0$
, and the conserved flux in the
![]() $z$
direction is
$z$
direction is
![]() ${\it\Phi}_{z}=9.0881$
. The initial magnetic pressure distribution is shown by the solid curve of figure 10(b). Note how this distribution is quite concentrated near the boundaries; there are two minima at
${\it\Phi}_{z}=9.0881$
. The initial magnetic pressure distribution is shown by the solid curve of figure 10(b). Note how this distribution is quite concentrated near the boundaries; there are two minima at
![]() $x=\pm 1.5$
, and a very flat weak maximum (not visible in this plot) at
$x=\pm 1.5$
, and a very flat weak maximum (not visible in this plot) at
![]() $x=0$
. The pressure maxima near the boundaries push in towards the centre, as evidenced by the dashed curve (for time
$x=0$
. The pressure maxima near the boundaries push in towards the centre, as evidenced by the dashed curve (for time
![]() $t=0.01$
). By time
$t=0.01$
). By time
![]() $t=0.2$
(dotted curve), the magnetic pressure is close to its ultimate uniform value (indicated by the thin red line). Figure 10(c,d) shows the ruled surface representation of the field; just as in figure 4, the field lines are the intersections of these surfaces with planes
$t=0.2$
(dotted curve), the magnetic pressure is close to its ultimate uniform value (indicated by the thin red line). Figure 10(c,d) shows the ruled surface representation of the field; just as in figure 4, the field lines are the intersections of these surfaces with planes
![]() $x=\text{const}$
.
$x=\text{const}$
.

Figure 10. (a) Initial field components
![]() $b_{y0}$
(solid) and
$b_{y0}$
(solid) and
![]() $b_{z0}$
(dashed), as defined by (6.1). (b) Associated magnetic pressure distribution at times
$b_{z0}$
(dashed), as defined by (6.1). (b) Associated magnetic pressure distribution at times
![]() $t=0$
(solid), 0.01 (dashed), 0.2 (dotted) and 0.6 (faint). (c) Three-dimensional representation of field at
$t=0$
(solid), 0.01 (dashed), 0.2 (dotted) and 0.6 (faint). (c) Three-dimensional representation of field at
![]() $t=0$
, as in figure 4. (d) Same as (c) at
$t=0$
, as in figure 4. (d) Same as (c) at
![]() $t=5$
. (e) Density
$t=5$
. (e) Density
![]() ${\it\rho}(x,t)$
and (f) helicity density
${\it\rho}(x,t)$
and (f) helicity density
![]() ${\mathcal{H}}(x,t)$
at times
${\mathcal{H}}(x,t)$
at times
![]() $t=0$
(solid), 0.2 (dashed) and 3 (dotted). (g) Mean magnetic energy
$t=0$
(solid), 0.2 (dashed) and 3 (dotted). (g) Mean magnetic energy
![]() $M(t)$
and mean helicity
$M(t)$
and mean helicity
![]() ${\mathcal{H}}(t)$
, both relative to their initial values, for
${\mathcal{H}}(t)$
, both relative to their initial values, for
![]() $0<t<0.6$
. (h) Plots of
$0<t<0.6$
. (h) Plots of
![]() $10\langle {\it\alpha}(t)\rangle$
and
$10\langle {\it\alpha}(t)\rangle$
and
![]() $\langle {\it\alpha}^{2}(t)\rangle$
for
$\langle {\it\alpha}^{2}(t)\rangle$
for
![]() $0<t<5$
.
$0<t<5$
.
Figure 10(e,f) shows the density and helicity fields at times
![]() $t=0$
(solid),
$t=0$
(solid),
![]() $t=0.2$
(dashed) and
$t=0.2$
(dashed) and
![]() $t=3$
(dotted). Peaks of density form near
$t=3$
(dotted). Peaks of density form near
![]() $x=\pm 0.4$
, and there is also a build-up of density at the boundaries due to the local magnetic pressure gradient. As regards the helicity density, there is a corresponding redistribution (as implied by (2.18)), but it remains distinctly non-uniform after the initial relaxation is complete. This initial relaxation is evident in the lower curve of figure 10(g), which shows that the mean magnetic energy has in fact relaxed by time
$x=\pm 0.4$
, and there is also a build-up of density at the boundaries due to the local magnetic pressure gradient. As regards the helicity density, there is a corresponding redistribution (as implied by (2.18)), but it remains distinctly non-uniform after the initial relaxation is complete. This initial relaxation is evident in the lower curve of figure 10(g), which shows that the mean magnetic energy has in fact relaxed by time
![]() $t\approx 0.2$
. Here,
$t\approx 0.2$
. Here,
![]() $M(0)=11.943$
and we may note that the asymptotic mean magnetic energy as
$M(0)=11.943$
and we may note that the asymptotic mean magnetic energy as
![]() $t\rightarrow \infty$
is
$t\rightarrow \infty$
is
![]() $M(\infty )=1.0461$
, so that
$M(\infty )=1.0461$
, so that
![]() $M(\infty )/M(0)=0.0876$
. The upper curve of figure 10(g) indicates the very nearly constant value of mean helicity right through the initial relaxation phase and well beyond. This behaviour is much the same as found in the previous sections (figures 3 and 5
b).
$M(\infty )/M(0)=0.0876$
. The upper curve of figure 10(g) indicates the very nearly constant value of mean helicity right through the initial relaxation phase and well beyond. This behaviour is much the same as found in the previous sections (figures 3 and 5
b).
Finally, figure 10(h) shows the time dependence of
![]() $10\langle {\it\alpha}\rangle$
and
$10\langle {\it\alpha}\rangle$
and
![]() $\langle {\it\alpha}^{2}\rangle$
, where
$\langle {\it\alpha}^{2}\rangle$
, where
![]() ${\it\alpha}$
is again defined as
${\it\alpha}$
is again defined as
![]() $\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{b}/b^{2}$
. Here, the anomalous behaviour of
$\boldsymbol{j}\boldsymbol{\cdot }\boldsymbol{b}/b^{2}$
. Here, the anomalous behaviour of
![]() $\langle {\it\alpha}\rangle$
for
$\langle {\it\alpha}\rangle$
for
![]() $t\lesssim 0.1$
must be attributed to diffusion near the boundaries where
$t\lesssim 0.1$
must be attributed to diffusion near the boundaries where
![]() $\text{d}^{2}b_{y0}/\text{d}x^{2}$
is largeFootnote
4
. This curvature actually has a maximum value of approximately
$\text{d}^{2}b_{y0}/\text{d}x^{2}$
is largeFootnote
4
. This curvature actually has a maximum value of approximately
![]() $496$
at
$496$
at
![]() $x={\rm\pi}$
, so that diffusion is immediately (and permanently) significant in this neighbourhood, and similarly near
$x={\rm\pi}$
, so that diffusion is immediately (and permanently) significant in this neighbourhood, and similarly near
![]() $x=-{\rm\pi}$
.
$x=-{\rm\pi}$
.
All in all, although the initial condition (6.1) is very different in this example from that in § 3 (3.1), the gross features of the behaviour are very similar: magnetic pressure drives a flow that tends to make this pressure uniform, thus establishing a nearly force-free state, energy being dissipated indirectly by viscosity; helicity density is redistributed, the mean helicity being approximately constant; and density peaks develop near minima of magnetic pressure, a process that persists during the slow diffusive stage.
7. Discussion
We have presented a one-dimensional model of magnetic relaxation having the following properties:
-
(i) The initial two-component magnetic field has non-zero helicity, and is not force-free, i.e.
 $\boldsymbol{j}\times \boldsymbol{B}\neq 0$
at time
$\boldsymbol{j}\times \boldsymbol{B}\neq 0$
at time
 $t=0$
.
$t=0$
. -
(ii) The plasma pressure is assumed negligible compared with the magnetic pressure, and flow is driven by the gradient of this magnetic pressure.
-
(iii) The flow is governed by the Navier–Stokes equation with effective viscosity
 ${\it\mu}$
. The plasma is initially at rest, with uniform density. (What is important here is that some mechanism that dissipates kinetic energy without compromising the ‘frozen-in’ character of the magnetic field during the initial relaxation phase should be operative; Newtonian viscosity is the simplest such mechanism.)
${\it\mu}$
. The plasma is initially at rest, with uniform density. (What is important here is that some mechanism that dissipates kinetic energy without compromising the ‘frozen-in’ character of the magnetic field during the initial relaxation phase should be operative; Newtonian viscosity is the simplest such mechanism.) -
(iv) When non-dimensionalised, the system involves two dimensionless parameters,
 ${\it\epsilon}={\it\rho}_{0}B_{0}^{2}L^{2}/{\it\mu}^{2}$
and
${\it\epsilon}={\it\rho}_{0}B_{0}^{2}L^{2}/{\it\mu}^{2}$
and
 ${\it\kappa}={\it\eta}{\it\mu}/B_{0}^{2}L^{2}$
, both assumed small. If
${\it\kappa}={\it\eta}{\it\mu}/B_{0}^{2}L^{2}$
, both assumed small. If
 ${\it\epsilon}=0$
, the response of the plasma to the magnetic field is quasi-static.
${\it\epsilon}=0$
, the response of the plasma to the magnetic field is quasi-static. -
(v) The relaxation proceeds in two stages: an initial relatively rapid stage in which approximate uniformity of magnetic pressure is established; and a subsequent slow-diffusion stage.
-
(vi) During the initial stage, magnetic energy decreases, and total magnetic helicity is relatively constant; however, the helicity density, although redistributed, remains strongly non-uniform. The current
 $\boldsymbol{j}$
becomes nearly aligned with
$\boldsymbol{j}$
becomes nearly aligned with
 $\boldsymbol{B}$
, i.e.
$\boldsymbol{B}$
, i.e.
 $\boldsymbol{j}\approx {\it\alpha}(x,t)\boldsymbol{B}$
, but
$\boldsymbol{j}\approx {\it\alpha}(x,t)\boldsymbol{B}$
, but
 ${\it\alpha}$
also remains strongly non-uniform, i.e. a ‘Taylor state’ is not established. This is essentially because
${\it\alpha}$
also remains strongly non-uniform, i.e. a ‘Taylor state’ is not established. This is essentially because
 ${\mathcal{H}}/{\it\rho}$
is a Lagrangian invariant, a constraint on the relaxation process.
${\mathcal{H}}/{\it\rho}$
is a Lagrangian invariant, a constraint on the relaxation process. -
(vii) During the subsequent diffusive stage, quasi-static conditions persist, with magnetic pressure remaining approximately (but never exactly) uniform. Magnetic energy and helicity both decay exponentially with the same decay rate proportional to
 ${\it\kappa}\langle {\it\alpha}^{2}\rangle$
.
${\it\kappa}\langle {\it\alpha}^{2}\rangle$
. -
(viii) A non-uniform density field develops, initially in step with the relaxing magnetic field. This field continues to develop during the diffusive stage, with maxima becoming more pronounced near to the (slowly moving) minima of magnetic energy, as a result of cumulative transport by the velocity field.
As a by-product of the investigation, we have proved in § 5 that
![]() $\langle (\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{b})/b^{2}\rangle$
is an invariant of the zero-resistivity one-dimensional induction equation governing the model.
$\langle (\boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{{\rm\nabla}}\times \boldsymbol{b})/b^{2}\rangle$
is an invariant of the zero-resistivity one-dimensional induction equation governing the model.
The behaviour has interesting points of comparison with the fully three-dimensional relaxation situation studied by Smiet et al. (Reference Smiet, Candelaresi, Thompson, Swearngin, Dalhuisen and Bouwmeester2015): in particular, the two-stage character of the relaxation process, and the fact that a Taylor state does not emerge from it. The one-dimensional model presented here is of course computationally far more economical, and the details are easier to visualise. However, in three dimensions, magnetic tension (hoop stress) as well as magnetic pressure drives the flow. Moreover, an initially chaotic magnetic field has no magnetic surfaces and only one helicity invariant for each chaotic subdomain. For these reasons, the details of the evolution are inevitably very different in this much more complex situation.
For the sake of illustration, we have adopted particular values of the parameters
![]() ${\it\epsilon}$
and
${\it\epsilon}$
and
![]() ${\it\kappa}$
. The choice is to some extent arbitrary, but it seems likely that the above conclusions are reasonably robust provided only that these parameters are both small. Adaptation to a cylindrical or toroidal domain, for which magnetic tension as well as magnetic pressure gradient must play a part, should be reasonably straightforward. This will be the subject of a future communication.
${\it\kappa}$
. The choice is to some extent arbitrary, but it seems likely that the above conclusions are reasonably robust provided only that these parameters are both small. Adaptation to a cylindrical or toroidal domain, for which magnetic tension as well as magnetic pressure gradient must play a part, should be reasonably straightforward. This will be the subject of a future communication.
Acknowledgements
This paper is dedicated to the memory of K. Bajer (1956–2014), close friend and colleague, with whom I enjoyed spirited scientific discussions on topics such as this. The paper has evolved from the Rosenbluth lecture presented at the July 2015 Festival de Théorie, Aix-en-Provence, and has greatly benefited from discussions that this lecture provoked. I am particularly grateful to Y. Sarazin and P. Diamond for their invitation to participate in this stimulating gathering. The comments from three referees have been particularly helpful.