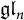1 Introduction
Weight systems and chord diagrams are central objects in the study of finite-type invariants, and Chern–Simons theory, in different contexts. Universal Vassiliev-type invariants typically take values in a space of diagrams (e.g., Jacobi and chord) and weight systems are used to recover specific invariants from the universal ones. General references for these topics are, for instance, [Reference Chmutov, Duzhin and Mostovoy2, Reference Jackson and Moffatt5, Reference Ohtsuki8].
To study finite-type invariant for braids, rather than links, a relevant space of diagrams is the space of horizontal chord diagrams. Recently, horizontal chord diagrams appeared as natural objects in the study of a mathematical framework for quantum physics of branes [Reference Corfield, Sati and Schreiber3, Reference Sati and Schreiber9]. Roughly speaking, an horizontal chord diagram on N-strands is given by N lines oriented upward (strands or Wilson lines), and a number (possibly none) of horizontal segments (chords) joining pairs of strands (cf. Figure 1a). One advantage of horizontal chord diagrams with respect to multicircle chord diagrams is that they can be endowed with a natural algebraic structure. The algebra of horizontal chord diagrams
![]() $\mathscr {A}^{\mathrm {h}}$
is defined as the algebra generated by (formal) complex linear combinations of horizontal chord diagrams, where the multiplication is given by stacking two diagrams one on top of the other (cf. Figure 1b), modulo the infinitesimal pure braid relations (see Figure 2). Furthermore, we have an anti-linear involution
$\mathscr {A}^{\mathrm {h}}$
is defined as the algebra generated by (formal) complex linear combinations of horizontal chord diagrams, where the multiplication is given by stacking two diagrams one on top of the other (cf. Figure 1b), modulo the infinitesimal pure braid relations (see Figure 2). Furthermore, we have an anti-linear involution
![]() $\star $
on
$\star $
on
![]() $\mathscr {A}^{\mathrm {h}}$
which acts on each horizontal chord diagram by reversing the direction of the strands, and reflecting the page along an horizontal axis. This involution endows
$\mathscr {A}^{\mathrm {h}}$
which acts on each horizontal chord diagram by reversing the direction of the strands, and reflecting the page along an horizontal axis. This involution endows
![]() $\mathscr {A}^{\mathrm {h}}$
with the structure of complex
$\mathscr {A}^{\mathrm {h}}$
with the structure of complex
![]() $\star $
-algebra (Definition 2.1). In [Reference Sati and Schreiber9] (see also [Reference Corfield, Sati and Schreiber3, Section 4]), the
$\star $
-algebra (Definition 2.1). In [Reference Sati and Schreiber9] (see also [Reference Corfield, Sati and Schreiber3, Section 4]), the
![]() $\star $
-algebra of horizontal chord diagrams
$\star $
-algebra of horizontal chord diagrams
![]() $\mathscr {A}^{\mathrm {h}}$
was interpreted as “higher observables” on certain brane moduli. This interpretation is coherent with some expected effects in the quantum theory of branes.
$\mathscr {A}^{\mathrm {h}}$
was interpreted as “higher observables” on certain brane moduli. This interpretation is coherent with some expected effects in the quantum theory of branes.

Figure 1 (a) An horizontal chord diagram on five strands, and (b) the vertical composition of two horizontal chord diagrams with the same number of strands.

Figure 2 The pictorial representation of the generators of
![]() $I\subset \mathscr {A}^{\mathrm {h}}$
.
$I\subset \mathscr {A}^{\mathrm {h}}$
.
Given a
![]() $\star $
-algebra of observables
$\star $
-algebra of observables
![]() $\mathscr {O}$
, a quantum state (or, simply, state) is linear map
$\mathscr {O}$
, a quantum state (or, simply, state) is linear map
![]() $\varphi :\mathscr {O} \to \mathbb {C}$
such that
$\varphi :\mathscr {O} \to \mathbb {C}$
such that
![]() $\varphi (x\cdot x^\star ) \geq 0$
, for all
$\varphi (x\cdot x^\star ) \geq 0$
, for all
![]() $x\in \mathscr {O}$
, and
$x\in \mathscr {O}$
, and
![]() $\varphi (1_{\mathscr {O}})>0$
. A weight system on horizontal chord diagrams is, by definition, a (complex) linear function from
$\varphi (1_{\mathscr {O}})>0$
. A weight system on horizontal chord diagrams is, by definition, a (complex) linear function from
![]() $\mathscr {A}^{\mathrm {h}}$
to
$\mathscr {A}^{\mathrm {h}}$
to
![]() $\mathbb {C}$
. Since horizontal chord diagrams can be interpreted as observables, it is natural to ask the following question [Reference Corfield, Sati and Schreiber3, Question 1.1].
$\mathbb {C}$
. Since horizontal chord diagrams can be interpreted as observables, it is natural to ask the following question [Reference Corfield, Sati and Schreiber3, Question 1.1].
Question Which weight systems on horizontal chord diagrams are quantum states?
Lie algebra weight systems are weight systems associated with a labeling of the Wilson lines by (finite-dimensional) irreducible representations of a (fixed) Lie algebra. These weight systems are used to recover quantum invariants of links, knots, and braids form the Kontsevich integral. In [Reference Corfield, Sati and Schreiber3], it was shown that the
![]() $\mathfrak {gl}_{n}$
-weight systems associated with the defining representation of
$\mathfrak {gl}_{n}$
-weight systems associated with the defining representation of
![]() $\mathfrak {gl}_{n}$
, which are generators of sorts for all weight systems on
$\mathfrak {gl}_{n}$
, which are generators of sorts for all weight systems on
![]() $\mathscr {A}^{\mathrm {h}}$
, are indeed quantum states. The proof of [Reference Corfield, Sati and Schreiber3, Theorem 1.2] is conceptually simple and exploits an interesting relation between these weight systems and certain distance kernels on Cayley graphs. The aim of this note is to extend the main result of [Reference Corfield, Sati and Schreiber3] to
$\mathscr {A}^{\mathrm {h}}$
, are indeed quantum states. The proof of [Reference Corfield, Sati and Schreiber3, Theorem 1.2] is conceptually simple and exploits an interesting relation between these weight systems and certain distance kernels on Cayley graphs. The aim of this note is to extend the main result of [Reference Corfield, Sati and Schreiber3] to
![]() $\mathfrak {gl}_{n}$
-weight systems associated with a more general labeling. Recall that an irreducible
$\mathfrak {gl}_{n}$
-weight systems associated with a more general labeling. Recall that an irreducible
![]() $\mathfrak {gl}_{n}$
-representation is identified by a Young diagram and a complex number. In this paper, we are only concerned with the case when this complex number is
$\mathfrak {gl}_{n}$
-representation is identified by a Young diagram and a complex number. In this paper, we are only concerned with the case when this complex number is
![]() $1$
. We call these representations Young diagram representations.
$1$
. We call these representations Young diagram representations.
Theorem 1.1 All
![]() $\mathfrak {gl}_{n}$
-weight systems associated with labeling by symmetric and/or exterior powers of the standard representation are quantum states.
$\mathfrak {gl}_{n}$
-weight systems associated with labeling by symmetric and/or exterior powers of the standard representation are quantum states.
It is well known that the symmetric powers of the standard representation are all the irreducible Young diagram representations of
![]() $\mathfrak {gl}_2$
.
$\mathfrak {gl}_2$
.
Corollary 1.2 All
![]() $\mathfrak {gl}_2$
-weight systems corresponding to irreducible Young diagram representations are quantum states.
$\mathfrak {gl}_2$
-weight systems corresponding to irreducible Young diagram representations are quantum states.
The fundamental representations of
![]() $\mathfrak {gl}_n$
are the given by exterior powers of the standard representation, which gives the next corollary.
$\mathfrak {gl}_n$
are the given by exterior powers of the standard representation, which gives the next corollary.
Corollary 1.3 All
![]() $\mathfrak {gl}_n$
-weight systems corresponding to any labeling given by fundamental representations are quantum states.
$\mathfrak {gl}_n$
-weight systems corresponding to any labeling given by fundamental representations are quantum states.
The paper is organised as follows: in Section 2, we recall some basic definitions and properties of
![]() $\star $
-algebras, horizontal chord diagrams, representations of
$\star $
-algebras, horizontal chord diagrams, representations of
![]() $\mathfrak {gl}_{n}$
, and Young symmetrizers. In Section 3, we prove our main result.
$\mathfrak {gl}_{n}$
, and Young symmetrizers. In Section 3, we prove our main result.
2 Background material
In this section, we collect some background material concerning
![]() $\star $
-algebras, representation theory and Lie algebra weight systems.
$\star $
-algebras, representation theory and Lie algebra weight systems.
2.1 The
 $\star $
-algebra of horizontal chord diagrams
$\star $
-algebra of horizontal chord diagrams
We start with a definition.
Definition 2.1 Given a commutative ring C endowed with a ring involution
![]() $\overline {\cdot }:C\to C$
. A
$\overline {\cdot }:C\to C$
. A
![]() $\star $
-algebra, or involutive algebra, over C is a unital associative C-algebra
$\star $
-algebra, or involutive algebra, over C is a unital associative C-algebra
![]() $\mathscr {O}$
together with an involution
$\mathscr {O}$
together with an involution
![]() $\star :\mathscr {O} \to \mathscr {O}$
, such that:
$\star :\mathscr {O} \to \mathscr {O}$
, such that:
-
(A1)
 $(1_{\mathscr {O}})^\star = 1_{\mathscr {O}}$
.
$(1_{\mathscr {O}})^\star = 1_{\mathscr {O}}$
. -
(A2)
 $(z\cdot a+ w\cdot b)^\star = \overline {z} \cdot a^\star + \overline {w}\cdot b^\star $
, for all
$(z\cdot a+ w\cdot b)^\star = \overline {z} \cdot a^\star + \overline {w}\cdot b^\star $
, for all
 $z,w\in C$
and
$z,w\in C$
and
 $a,b\in \mathscr {O}$
.
$a,b\in \mathscr {O}$
. -
(A3)
 $(ab)^\star = b^\star a^\star $
, for all
$(ab)^\star = b^\star a^\star $
, for all
 $a,b\in \mathscr {O}$
.
$a,b\in \mathscr {O}$
.
A morphism of
![]() $\star $
-algebras is a morphism of algebras which commutes with the involution.
$\star $
-algebras is a morphism of algebras which commutes with the involution.
A first class of examples of
![]() $\star $
-algebras is given by group rings.
$\star $
-algebras is given by group rings.
Example 2.1 Given a group G, the group ring
![]() $\mathbb {C}[G]$
has a natural structure of
$\mathbb {C}[G]$
has a natural structure of
![]() $\star $
-algebra given by setting
$\star $
-algebra given by setting
 $$\begin{align*}\left(\sum_{i=1}^{k} z_i \cdot g_i\right)^\star = \sum_{i=1}^{k}\overline{z}_i\cdot g_i^{-1}, \end{align*}$$
$$\begin{align*}\left(\sum_{i=1}^{k} z_i \cdot g_i\right)^\star = \sum_{i=1}^{k}\overline{z}_i\cdot g_i^{-1}, \end{align*}$$
for all
![]() $z_1,\ldots ,z_k\in \mathbb {C}$
and
$z_1,\ldots ,z_k\in \mathbb {C}$
and
![]() $g_1,\ldots ,g_k\in G$
.
$g_1,\ldots ,g_k\in G$
.
In the next example, we present a formal definition of the
![]() $\star $
-algebra of horizontal chord diagrams
$\star $
-algebra of horizontal chord diagrams
![]() $\mathscr {A}^{\mathrm {h}}$
. While the reader can keep in mind the pictorial definition given in the introduction, it is useful to have an explicit definition.
$\mathscr {A}^{\mathrm {h}}$
. While the reader can keep in mind the pictorial definition given in the introduction, it is useful to have an explicit definition.
Example 2.2 An horizontal chord diagram on N strands is an element of the free monoid
![]() $(\mathscr {D}^{\mathrm {h}}_N, \circ )$
generated by the pairs
$(\mathscr {D}^{\mathrm {h}}_N, \circ )$
generated by the pairs
![]() $(i,j)$
, with
$(i,j)$
, with
![]() $1\leq i < j \leq N$
, called chords, with neutral element the chord-less diagram
$1\leq i < j \leq N$
, called chords, with neutral element the chord-less diagram
![]() $\uparrow _N$
. We also consider the empty chord diagram
$\uparrow _N$
. We also consider the empty chord diagram
![]() $\uparrow _0 = \emptyset $
, defined as the diagram with neither chords nor strands, and set
$\uparrow _0 = \emptyset $
, defined as the diagram with neither chords nor strands, and set
![]() ${\mathscr {D}^{\mathrm {h}}_0 = \{ \uparrow _0 \}}$
. This monoid has a natural involution
${\mathscr {D}^{\mathrm {h}}_0 = \{ \uparrow _0 \}}$
. This monoid has a natural involution
![]() $^\star $
given by “reading the chord diagram backward,” that is,
$^\star $
given by “reading the chord diagram backward,” that is,
The algebra of horizontal chord diagrams on N strands is given by the quotient algebra
where
![]() $I\subseteq \mathbb {C}[\mathscr {D}^{\mathrm {h}}_N]$
is the ideal generated by elements of the form
$I\subseteq \mathbb {C}[\mathscr {D}^{\mathrm {h}}_N]$
is the ideal generated by elements of the form
for
![]() $ i, j, k, l$
such that the two closed intervals
$ i, j, k, l$
such that the two closed intervals
![]() $[i,j],\ [k,l]\subset \mathbb {R}$
are either disjoint or one contains the other, and also elements of the form
$[i,j],\ [k,l]\subset \mathbb {R}$
are either disjoint or one contains the other, and also elements of the form
(see Figure 2 for a pictorial representation). Finally, define the algebra of horizontal chord diagrams as
![]() $\mathscr {A}^{\mathrm {h}} = \bigoplus _{N\geq 0} \mathscr {A}^{\mathrm {h}}_N$
. Extending
$\mathscr {A}^{\mathrm {h}} = \bigoplus _{N\geq 0} \mathscr {A}^{\mathrm {h}}_N$
. Extending
![]() $^\star $
by anti-linearity, since
$^\star $
by anti-linearity, since
![]() $I^\star = I$
, the algebra of horizontal chord diagrams acquires the structure of complex
$I^\star = I$
, the algebra of horizontal chord diagrams acquires the structure of complex
![]() $\star $
-algebra. This involution has actually a deeper and more abstract interpretation as the antipode of an Hopf algebra associated with the homology of some loop spaces (cf. [Reference Corfield, Sati and Schreiber3, Section 4]).
$\star $
-algebra. This involution has actually a deeper and more abstract interpretation as the antipode of an Hopf algebra associated with the homology of some loop spaces (cf. [Reference Corfield, Sati and Schreiber3, Section 4]).
For small values of N, we can explicitly identify
![]() $\mathscr {A}^{\mathrm {h}}_N$
; we have the following isomorphisms of
$\mathscr {A}^{\mathrm {h}}_N$
; we have the following isomorphisms of
![]() $\star $
-algebras:
$\star $
-algebras:
![]() $\mathscr {A}^{\mathrm {h}}_1 \cong \mathscr {A}^{\mathrm {h}}_0 \cong \mathbb {C}$
and
$\mathscr {A}^{\mathrm {h}}_1 \cong \mathscr {A}^{\mathrm {h}}_0 \cong \mathbb {C}$
and
![]() $\mathscr {A}^{\mathrm {h}}_2 \cong \mathbb {C}[x]$
, where the involution on the latter algebra is defined by setting
$\mathscr {A}^{\mathrm {h}}_2 \cong \mathbb {C}[x]$
, where the involution on the latter algebra is defined by setting
![]() $x^\star = x$
. For
$x^\star = x$
. For
![]() $N\geq 3$
, the algebra
$N\geq 3$
, the algebra
![]() $\mathscr {A}^{\mathrm {h}}_N$
is noncommutative. In fact, we have a natural embedding
$\mathscr {A}^{\mathrm {h}}_N$
is noncommutative. In fact, we have a natural embedding
![]() $\mathscr {A}^{\mathrm {h}}_{N-1}\subseteq \mathscr {A}^{\mathrm {h}}_{N}$
and
$\mathscr {A}^{\mathrm {h}}_{N-1}\subseteq \mathscr {A}^{\mathrm {h}}_{N}$
and
![]() $\mathscr {A}^{\mathrm {h}}_3$
is noncommutative; it is a direct product of the free algebra on two generators
$\mathscr {A}^{\mathrm {h}}_3$
is noncommutative; it is a direct product of the free algebra on two generators
![]() $\mathbb {C}\langle x,y\rangle $
and
$\mathbb {C}\langle x,y\rangle $
and
![]() $\mathbb {C}[u]$
(see [Reference Chmutov, Duzhin and Mostovoy2, Proposition 5.11.1]).
$\mathbb {C}[u]$
(see [Reference Chmutov, Duzhin and Mostovoy2, Proposition 5.11.1]).
2.2 Horizontal chord diagrams, permutations, and standard weight systems
To each horizontal chord diagram
![]() $C = (i_r,j_r) \circ \cdots \circ (i_1,j_1) \in \mathscr {A}^{\mathrm {h}}_N$
, there is a naturally associated permutation:
$C = (i_r,j_r) \circ \cdots \circ (i_1,j_1) \in \mathscr {A}^{\mathrm {h}}_N$
, there is a naturally associated permutation:
where
![]() $\tau _{i,j}$
denotes the transposition of i and j. Recall, from Example 2.1, that the group ring
$\tau _{i,j}$
denotes the transposition of i and j. Recall, from Example 2.1, that the group ring
![]() $\mathbb {C}[\mathfrak {S}_N]$
has a natural structure of
$\mathbb {C}[\mathfrak {S}_N]$
has a natural structure of
![]() $\star $
-algebra. Indeed, we have the following proposition.
$\star $
-algebra. Indeed, we have the following proposition.
Proposition 2.3 The map
![]() $\sigma : \mathscr {A}^{\mathrm {h}}_N \to \mathbb {C}[\mathfrak {S}_N]: C\mapsto \sigma (C)$
is a morphism of
$\sigma : \mathscr {A}^{\mathrm {h}}_N \to \mathbb {C}[\mathfrak {S}_N]: C\mapsto \sigma (C)$
is a morphism of
![]() $\star $
-algebras.
$\star $
-algebras.
Proof We have to prove that
![]() $\sigma $
is a well-defined ring homomorphism. That is, we have to show that the images of elements in equations (2T) and (4T) are trivial. This is immediate for the elements in equation (2T). On the other hand, a direct computation shows that
$\sigma $
is a well-defined ring homomorphism. That is, we have to show that the images of elements in equations (2T) and (4T) are trivial. This is immediate for the elements in equation (2T). On the other hand, a direct computation shows that
and that
Since
![]() $\sigma $
commutes with
$\sigma $
commutes with
![]() $\star $
, this concludes the proof.
$\star $
, this concludes the proof.
Following [Reference Bar-Natan1, Section 2.2], the
![]() $\mathfrak {gl}_{n}$
weight system associated with the defining representation, here called standard
$\mathfrak {gl}_{n}$
weight system associated with the defining representation, here called standard
![]() $\mathfrak {gl}_{n}$
weight system, is the map
$\mathfrak {gl}_{n}$
weight system, is the map
![]() $ W_{\mathtt {st}} : \mathscr {A}^{\mathrm {h}} \to \mathbb {C} $
which assigns to each chord diagram
$ W_{\mathtt {st}} : \mathscr {A}^{\mathrm {h}} \to \mathbb {C} $
which assigns to each chord diagram
![]() $C\in \mathscr {A}^{\mathrm {h}}_N$
, the integer
$C\in \mathscr {A}^{\mathrm {h}}_N$
, the integer
extended by
![]() $\mathbb {C}$
-linearity. We remark that here the number of cycles in a permutation also includes the trivial cycles (i.e., the fixed points).
$\mathbb {C}$
-linearity. We remark that here the number of cycles in a permutation also includes the trivial cycles (i.e., the fixed points).
2.3 Tensor splitting
Another important operation on
![]() $\mathscr {A}^{\mathrm {h}}$
is what we call tensor splitting. Intuitively, the
$\mathscr {A}^{\mathrm {h}}$
is what we call tensor splitting. Intuitively, the
![]() $\underline {i}$
-tensor splitting, with
$\underline {i}$
-tensor splitting, with
![]() $\underline {i} = (i_1 ,\ldots , i_N)\in \mathbb {N}^N$
, is obtained by replacing the rth strand with
$\underline {i} = (i_1 ,\ldots , i_N)\in \mathbb {N}^N$
, is obtained by replacing the rth strand with
![]() $i_r$
parallel strands, and replacing each chord with the sum of all possible “liftings” of said chord in the new horizontal chord diagram. More formally, we have the following definition.
$i_r$
parallel strands, and replacing each chord with the sum of all possible “liftings” of said chord in the new horizontal chord diagram. More formally, we have the following definition.
Definition 2.2 ([Reference Bar-Natan1, Definition 2.2])
Let
![]() $\underline {i} = (i_1 ,\ldots , i_N)$
be an N-tuple of positive integers. The
$\underline {i} = (i_1 ,\ldots , i_N)$
be an N-tuple of positive integers. The
![]() $\underline {i}$
-tensor splitting is the ring homomorphism
$\underline {i}$
-tensor splitting is the ring homomorphism
 $$\begin{align*}\Delta^{\underline{i}}:\: \mathscr{A}^{\mathrm{h}}_{N} \to \mathscr{A}^{\mathrm{h}}_{\ell_{N+1}(\underline{i})}:\: (j,k) \mapsto \sum_{r=\ell_{j}(\underline{i}) + 1}^{\ell_{j+1}(\underline{i}) }\sum_{s=\ell_{k}(\underline{i}) + 1}^{\ell_{k+1}(\underline{i}) } (r,s),\end{align*}$$
$$\begin{align*}\Delta^{\underline{i}}:\: \mathscr{A}^{\mathrm{h}}_{N} \to \mathscr{A}^{\mathrm{h}}_{\ell_{N+1}(\underline{i})}:\: (j,k) \mapsto \sum_{r=\ell_{j}(\underline{i}) + 1}^{\ell_{j+1}(\underline{i}) }\sum_{s=\ell_{k}(\underline{i}) + 1}^{\ell_{k+1}(\underline{i}) } (r,s),\end{align*}$$
where
![]() $\ell _{1}(\underline {i}) = 0$
and
$\ell _{1}(\underline {i}) = 0$
and
![]() $\ell _{r}(\underline {i} ) = i_1 + \cdots +i_{r-1}$
, for
$\ell _{r}(\underline {i} ) = i_1 + \cdots +i_{r-1}$
, for
![]() $0 < r \leq N +1$
.
$0 < r \leq N +1$
.
Let us see in an example the effect of the tensor splitting.
Example 2.4 Denote
![]() $C = (2,3) \circ (1,3)\in \mathscr {A}^{\mathrm {h}}_3$
, we explicitly compute some tensor splittings in this case; for instance, we have that
$C = (2,3) \circ (1,3)\in \mathscr {A}^{\mathrm {h}}_3$
, we explicitly compute some tensor splittings in this case; for instance, we have that
and also that
Note that
![]() $\Delta ^{\underline {1}}$
, where
$\Delta ^{\underline {1}}$
, where
![]() $\underline {1} = (1,\ldots ,1)$
, is just the identity map. We conclude this subsection with the following, useful, observation.
$\underline {1} = (1,\ldots ,1)$
, is just the identity map. We conclude this subsection with the following, useful, observation.
Remark 2.5 The tensor splitting
![]() $\Delta ^{\underline {i}}:\mathscr {A}^{\mathrm {h}}_N\to \mathscr {A}^{\mathrm {h}}_{\ell _{N+1}(\underline {i})}$
is a morphism of
$\Delta ^{\underline {i}}:\mathscr {A}^{\mathrm {h}}_N\to \mathscr {A}^{\mathrm {h}}_{\ell _{N+1}(\underline {i})}$
is a morphism of
![]() $\star $
-algebras.
$\star $
-algebras.
2.4 Young symmetrizers
A partition of
![]() $n\in \mathbb {N}$
is a (nonempty) ordered collection of positive integers
$n\in \mathbb {N}$
is a (nonempty) ordered collection of positive integers
![]() ${\lambda = (n_1,\ldots , n_k)}$
, with
${\lambda = (n_1,\ldots , n_k)}$
, with
![]() $n_1 \geq n_2 \geq \dots \geq n_k> 0$
, which add up to n. If
$n_1 \geq n_2 \geq \dots \geq n_k> 0$
, which add up to n. If
![]() $\lambda $
is a partition of n, we shall write
$\lambda $
is a partition of n, we shall write
![]() $\lambda \vdash n$
or, if it is understood that
$\lambda \vdash n$
or, if it is understood that
![]() $\lambda $
is a partition,
$\lambda $
is a partition,
![]() $|\lambda | = n$
. The (positive) integers
$|\lambda | = n$
. The (positive) integers
![]() $n_1,\ldots , n_k$
are called parts, and the number of parts, which is k in the case at hand, is called the length of the partition.
$n_1,\ldots , n_k$
are called parts, and the number of parts, which is k in the case at hand, is called the length of the partition.
The Young diagram associated with a partition
![]() $\lambda = (n_1,\ldots , n_k)$
is a finite collection of boxes arranged in k (left-justified) rows of length (from top to bottom)
$\lambda = (n_1,\ldots , n_k)$
is a finite collection of boxes arranged in k (left-justified) rows of length (from top to bottom)
![]() $n_1,\ldots , n_k$
, respectively. Conversely, to each Young diagram, we can associate a partition whose parts are the length of its rows. We denote both a partition and its associated Young diagram by the same symbol.
$n_1,\ldots , n_k$
, respectively. Conversely, to each Young diagram, we can associate a partition whose parts are the length of its rows. We denote both a partition and its associated Young diagram by the same symbol.
Example 2.6 The partition
![]() $\lambda = (5,3,1,1)$
is a partition of
$\lambda = (5,3,1,1)$
is a partition of
![]() $10$
whose length is
$10$
whose length is
![]() $4$
. The corresponding Young diagram
$4$
. The corresponding Young diagram
![]() $\lambda $
is the following.
$\lambda $
is the following.

An essential tool for building irreducible representations of
![]() $\mathfrak {sl}_n$
, and thus of
$\mathfrak {sl}_n$
, and thus of
![]() $\mathfrak {gl}_{n}$
, are Young symmetrizers (cf. [Reference Fulton and Harris4, pp. 45–46]).
$\mathfrak {gl}_{n}$
, are Young symmetrizers (cf. [Reference Fulton and Harris4, pp. 45–46]).
Definition 2.3 Given
![]() $\lambda \vdash n$
, a Young tableau of shape
$\lambda \vdash n$
, a Young tableau of shape
![]() $\lambda $
is a filling of the Young diagram
$\lambda $
is a filling of the Young diagram
![]() $\lambda $
with the numbers
$\lambda $
with the numbers
![]() $1,\ldots ,n$
. A tableau is standard if the number (label) on each box is strictly increasing along both rows and columns, and there are no repeated labels.
$1,\ldots ,n$
. A tableau is standard if the number (label) on each box is strictly increasing along both rows and columns, and there are no repeated labels.
Given a Young diagram of shape
![]() $\lambda = (n_1, n_2,\ldots , n_k)$
, there is a canonical (standard) Young tableau associated with it, which is the following tableau.
$\lambda = (n_1, n_2,\ldots , n_k)$
, there is a canonical (standard) Young tableau associated with it, which is the following tableau.

To get hold of how the canonical tableau is defined, we give a concrete example.
Example 2.7 The canonical Young tableau of shape
![]() $\lambda = (5,3,1,1)$
is the following.
$\lambda = (5,3,1,1)$
is the following.

Let
![]() $T^\lambda $
be the set of all tableaux of shape
$T^\lambda $
be the set of all tableaux of shape
![]() $\lambda =(n_1,\ldots ,n_k)$
. A permutation
$\lambda =(n_1,\ldots ,n_k)$
. A permutation
![]() $\sigma \in \mathfrak {S}_{|\lambda |}$
acts on each tableau
$\sigma \in \mathfrak {S}_{|\lambda |}$
acts on each tableau
![]() $t^\lambda \in T^\lambda $
by permuting the labels, denote by
$t^\lambda \in T^\lambda $
by permuting the labels, denote by
![]() $\sigma .t^\lambda $
the resulting tableau. Fixed a tableau
$\sigma .t^\lambda $
the resulting tableau. Fixed a tableau
![]() $t^\lambda $
, we can define two subgroups of
$t^\lambda $
, we can define two subgroups of
![]() $\mathfrak {S}_{|\lambda |}$
; that is, the row stabilizer
$\mathfrak {S}_{|\lambda |}$
; that is, the row stabilizer
 $$\begin{align*}\mathfrak{R}_{t^{\lambda}} = \left\{\ \sigma \in \mathfrak{S}_{|\lambda|}\ \left\vert\ \begin{array}{c}\text{the set of labels on corresponding} \\ \text{rows of } \sigma.t^\lambda \text{ and } t^\lambda \text{ are the same}\end{array} \right.\right\}, \end{align*}$$
$$\begin{align*}\mathfrak{R}_{t^{\lambda}} = \left\{\ \sigma \in \mathfrak{S}_{|\lambda|}\ \left\vert\ \begin{array}{c}\text{the set of labels on corresponding} \\ \text{rows of } \sigma.t^\lambda \text{ and } t^\lambda \text{ are the same}\end{array} \right.\right\}, \end{align*}$$
and the column stabilizer
 $$\begin{align*}\mathfrak{C}_{t^{\lambda}} = \left\{\ \sigma \in \mathfrak{S}_{|\lambda|}\ \left\vert\ \begin{array}{c}\text{the set of labels on corresponding} \\ \text{columns of } \sigma.t^\lambda \text{ and } t^\lambda \text{ are the same}\end{array} \right.\right\}. \end{align*}$$
$$\begin{align*}\mathfrak{C}_{t^{\lambda}} = \left\{\ \sigma \in \mathfrak{S}_{|\lambda|}\ \left\vert\ \begin{array}{c}\text{the set of labels on corresponding} \\ \text{columns of } \sigma.t^\lambda \text{ and } t^\lambda \text{ are the same}\end{array} \right.\right\}. \end{align*}$$
Using these subgroups, we can associate with each tableau its Young symmetrizer.
Definition 2.4 The unnormalized Young symmetrizer
![]() $\tilde {c}_{t^{\lambda }}\in \mathbb {C}[\mathfrak {S}_{|\lambda |}]$
associated with the tableau
$\tilde {c}_{t^{\lambda }}\in \mathbb {C}[\mathfrak {S}_{|\lambda |}]$
associated with the tableau
![]() $t^\lambda $
is defined as
$t^\lambda $
is defined as
![]() $\tilde {c}_{t^{\lambda }} := a_{t^{\lambda }} b_{t^{\lambda }}$
, where
$\tilde {c}_{t^{\lambda }} := a_{t^{\lambda }} b_{t^{\lambda }}$
, where
The Young symmetrizer
![]() $ c_{t^{\lambda }}\in \mathbb {C}[\mathfrak {S}_{|\lambda |}]$
is a rescaling of
$ c_{t^{\lambda }}\in \mathbb {C}[\mathfrak {S}_{|\lambda |}]$
is a rescaling of
![]() $\tilde {c}_{t^{\lambda }}$
by a positive rational number, in such a way that
$\tilde {c}_{t^{\lambda }}$
by a positive rational number, in such a way that
![]() ${c}_{t^{\lambda }} {c}_{t^{\lambda }} = {c}_{t^{\lambda }}$
(cf. [Reference Fulton and Harris4, Lemma 4.6]).
${c}_{t^{\lambda }} {c}_{t^{\lambda }} = {c}_{t^{\lambda }}$
(cf. [Reference Fulton and Harris4, Lemma 4.6]).
Notation 2.8 The Young symmetrizer associated with a partition
![]() $\lambda $
, and not to a tableau
$\lambda $
, and not to a tableau
![]() $t^{\lambda }$
, is the symmetrizer associated with the canonical tableau, and we write
$t^{\lambda }$
, is the symmetrizer associated with the canonical tableau, and we write
![]() $c_\lambda $
en lieu of
$c_\lambda $
en lieu of
![]() $c_{t^{\lambda }}$
.
$c_{t^{\lambda }}$
.
Remark 2.9 Note that if
![]() $\sigma $
appears in
$\sigma $
appears in
![]() $a_\lambda $
(or
$a_\lambda $
(or
![]() $b_\lambda $
) then also
$b_\lambda $
) then also
![]() $\sigma ^{-1}$
does, and they appear with the same (real) coefficients. The same does not hold for
$\sigma ^{-1}$
does, and they appear with the same (real) coefficients. The same does not hold for
![]() $c_\lambda $
(see the example below). Nonetheless, if
$c_\lambda $
(see the example below). Nonetheless, if
![]() $\lambda $
is either of the form
$\lambda $
is either of the form
![]() $(n)$
or
$(n)$
or
![]() $(1,\ldots ,1)$
, then
$(1,\ldots ,1)$
, then
![]() $c_\lambda = c_\lambda ^\star $
as elements of
$c_\lambda = c_\lambda ^\star $
as elements of
![]() $\mathbb {C}[\mathfrak {S}_{\vert \lambda \vert }]$
.
$\mathbb {C}[\mathfrak {S}_{\vert \lambda \vert }]$
.
Example 2.10 Consider the partition
![]() $\lambda \vdash 3$
given by
$\lambda \vdash 3$
given by
![]() $(2,1)$
, the corresponding Young diagram
$(2,1)$
, the corresponding Young diagram
![]() $\lambda $
is the following.
$\lambda $
is the following.

Two examples of Young tableau of shape
![]() $\lambda $
are the following.
$\lambda $
are the following.

Observe that
![]() $s^\lambda $
is standard (actually, it is the canonical tableau), whereas
$s^\lambda $
is standard (actually, it is the canonical tableau), whereas
![]() $t^\lambda $
is not. In these cases, we have
$t^\lambda $
is not. In these cases, we have
and
respectively. It follows that
and
The next subsection is dedicated to the description of irreducible
![]() $\mathfrak {gl}_{n}$
-representations in terms of partitions. Our main scope there is to set some notation, for the general theory, the reader may refer to [Reference Fulton and Harris4, Chapter 15].
$\mathfrak {gl}_{n}$
-representations in terms of partitions. Our main scope there is to set some notation, for the general theory, the reader may refer to [Reference Fulton and Harris4, Chapter 15].
2.5 Representations of
 $\mathfrak {gl}_{n}$
$\mathfrak {gl}_{n}$
Denote by
![]() $\rho _{\mathtt {st}}$
the defining representation of
$\rho _{\mathtt {st}}$
the defining representation of
![]() $\mathfrak {gl}_{n}$
, that is the natural action of
$\mathfrak {gl}_{n}$
, that is the natural action of
![]() ${\mathfrak {gl}_{n} = \mathrm { End}(\mathbb {C}^n)}$
on
${\mathfrak {gl}_{n} = \mathrm { End}(\mathbb {C}^n)}$
on
![]() $\mathbb {C}^n$
, and denote by
$\mathbb {C}^n$
, and denote by
![]() $\rho ^{\mathfrak {sl}}_{\mathtt {st}}$
the defining representation of
$\rho ^{\mathfrak {sl}}_{\mathtt {st}}$
the defining representation of
![]() $\mathfrak {sl}_n$
, which is the restriction of
$\mathfrak {sl}_n$
, which is the restriction of
![]() $\rho _{\mathtt {st}}$
to
$\rho _{\mathtt {st}}$
to
![]() $\mathfrak {sl}_n$
.
$\mathfrak {sl}_n$
.
It is well known that (finite-dimensional) irreducible representation of
![]() $\mathfrak {sl}_n$
are associated with a partition of length at most n [Reference Fulton and Harris4, Section 15.3]. The representation corresponding to a partition
$\mathfrak {sl}_n$
are associated with a partition of length at most n [Reference Fulton and Harris4, Section 15.3]. The representation corresponding to a partition
![]() $\lambda $
can be described explicitly. Consider the natural action (by permutation of the tensor factors) of the symmetric group
$\lambda $
can be described explicitly. Consider the natural action (by permutation of the tensor factors) of the symmetric group
![]() $\mathfrak {S}_k$
on the tensor product of k copies of
$\mathfrak {S}_k$
on the tensor product of k copies of
![]() $\mathbb {C}^n$
. This action commutes with the action of
$\mathbb {C}^n$
. This action commutes with the action of
![]() $\mathfrak {sl}_n$
, given by
$\mathfrak {sl}_n$
, given by
![]() $(\rho _{\mathtt {st}}^{\mathfrak {sl}})^{\otimes k}$
. In particular, we can consider the images of the action of a Young symmetrizer
$(\rho _{\mathtt {st}}^{\mathfrak {sl}})^{\otimes k}$
. In particular, we can consider the images of the action of a Young symmetrizer
![]() $c_{t^{\lambda }}\in \mathbb {C}[\mathfrak {S}_k]$
(with
$c_{t^{\lambda }}\in \mathbb {C}[\mathfrak {S}_k]$
(with
![]() $|\lambda | = k$
) in
$|\lambda | = k$
) in
![]() $\mathbb {C}^{n} \otimes \dots \otimes \mathbb {C}^{n}$
.
$\mathbb {C}^{n} \otimes \dots \otimes \mathbb {C}^{n}$
.
Definition 2.5 Let
![]() $\lambda \vdash k$
, and
$\lambda \vdash k$
, and
![]() $n\geq k$
. The image of the action of
$n\geq k$
. The image of the action of
![]() $c_\lambda $
on
$c_\lambda $
on
![]() $(\mathbb {C}^{n})^{\otimes k}$
is called the Weyl module corresponding to
$(\mathbb {C}^{n})^{\otimes k}$
is called the Weyl module corresponding to
![]() $\lambda $
, and is denoted by
$\lambda $
, and is denoted by
![]() $\mathbb {S}_\lambda (\mathbb {C}^n)$
.
$\mathbb {S}_\lambda (\mathbb {C}^n)$
.
The restriction of
![]() $(\rho _{\mathtt {st}}^{\mathfrak {sl}})^{\otimes k}$
to the Weyl module
$(\rho _{\mathtt {st}}^{\mathfrak {sl}})^{\otimes k}$
to the Weyl module
![]() $\mathbb {S}_\lambda (\mathbb {C}^n)$
associated with
$\mathbb {S}_\lambda (\mathbb {C}^n)$
associated with
![]() $\lambda \vdash k$
is isomorphic to the irreducible representation of
$\lambda \vdash k$
is isomorphic to the irreducible representation of
![]() $\mathfrak {sl}_n$
with highest weight
$\mathfrak {sl}_n$
with highest weight
![]() $w_{\lambda }$
, denoted by
$w_{\lambda }$
, denoted by
![]() $\rho ^{\mathfrak {sl}}_\lambda $
. We can extend
$\rho ^{\mathfrak {sl}}_\lambda $
. We can extend
![]() $\rho ^{\mathfrak {sl}}_\lambda $
to a representation of
$\rho ^{\mathfrak {sl}}_\lambda $
to a representation of
![]() $\mathfrak {gl}_{n} =\mathfrak {sl}_n\oplus \mathbb {C}\langle \mathrm { Id}_{\mathbb {C}} \rangle $
by making
$\mathfrak {gl}_{n} =\mathfrak {sl}_n\oplus \mathbb {C}\langle \mathrm { Id}_{\mathbb {C}} \rangle $
by making
![]() $ \mathrm {I}_n$
act trivially on
$ \mathrm {I}_n$
act trivially on
![]() $V_\lambda $
. For
$V_\lambda $
. For
![]() $z\in \mathbb {C}$
, consider the representation
$z\in \mathbb {C}$
, consider the representation
![]() $\rho _{z}:\mathfrak {gl}_{n} \to \mathrm {End}(\mathbb {C})$
defined by
$\rho _{z}:\mathfrak {gl}_{n} \to \mathrm {End}(\mathbb {C})$
defined by
Each irreducible representation of
![]() $\mathfrak {sl}_n\oplus \mathbb {C}\langle \mathrm {Id}_{\mathbb {C}} \rangle = \mathfrak {gl}_n$
is isomorphic to a tensor product of the form
$\mathfrak {sl}_n\oplus \mathbb {C}\langle \mathrm {Id}_{\mathbb {C}} \rangle = \mathfrak {gl}_n$
is isomorphic to a tensor product of the form
![]() $\rho _\lambda \otimes \rho _{z}$
(see [Reference Fulton and Harris4, Section 15.5]), where the tensor product of two representations, say
$\rho _\lambda \otimes \rho _{z}$
(see [Reference Fulton and Harris4, Section 15.5]), where the tensor product of two representations, say
![]() $\rho $
and
$\rho $
and
![]() $\rho '$
, is given by
$\rho '$
, is given by
We refer to the Young diagram representation
![]() $\rho _\lambda \otimes \rho _1$
simply as
$\rho _\lambda \otimes \rho _1$
simply as
![]() $\lambda $
. The symmetric and exterior power of the defining representation are associated with the partitions of the form
$\lambda $
. The symmetric and exterior power of the defining representation are associated with the partitions of the form
![]() $(k)$
and
$(k)$
and
![]() $(1,\ldots ,1)$
, respectively.
$(1,\ldots ,1)$
, respectively.
2.6 General Lie algebra weight systems
In this subsection, we recall the general construction of Lie algebra weight system, and then we specialize this construction to the case at hand (see [Reference Bar-Natan1, Section 2], [Reference Chmutov, Duzhin and Mostovoy2, Chapter 6], [Reference Jackson and Moffatt5, Chapter 14], and the references therein for a comprehensive overview).
The main ingredients in the definitions of Lie algebra weight system on
![]() $\mathscr {A}^{\mathrm {h}}_N$
are:
$\mathscr {A}^{\mathrm {h}}_N$
are:
-
(1) a (finite-dimensional complex) Lie algebra
 $\mathfrak {g}$
;
$\mathfrak {g}$
; -
(2) an
 $\mathrm {ad}$
-invariant nondegenerate bi-linear form
$\mathrm {ad}$
-invariant nondegenerate bi-linear form
 $\langle \cdot , \cdot \rangle $
on
$\langle \cdot , \cdot \rangle $
on
 $\mathfrak {g}$
; and
$\mathfrak {g}$
; and -
(3) an ordered collection of finite-dimensional
 $\mathfrak {g}$
-representations
$\mathfrak {g}$
-representations
 $\underline {\rho } = (\rho _1, \ldots , \rho _N)$
, called labeling where
$\underline {\rho } = (\rho _1, \ldots , \rho _N)$
, called labeling where
 $\rho _i:\mathfrak {g} \to \mathrm {End}(V_i)$
for each
$\rho _i:\mathfrak {g} \to \mathrm {End}(V_i)$
for each
 $i=1,\ldots ,N$
.
$i=1,\ldots ,N$
.
The basic idea is to associate with each horizontal chord diagram
![]() $C\in \mathscr {A}^{\mathrm {h}}_N$
an element in
$C\in \mathscr {A}^{\mathrm {h}}_N$
an element in
![]() $\mathrm {End}(V_1 \otimes \cdots \otimes V_N)$
, and then take the trace to obtain a complex number.
$\mathrm {End}(V_1 \otimes \cdots \otimes V_N)$
, and then take the trace to obtain a complex number.
First, fix an orthonormal basis (with respect to
![]() $\langle \cdot , \cdot \rangle $
) for
$\langle \cdot , \cdot \rangle $
) for
![]() $\mathfrak {g}$
, say
$\mathfrak {g}$
, say
![]() $e_1,\ldots ,e_d$
. This choice, and the fact that
$e_1,\ldots ,e_d$
. This choice, and the fact that
![]() $\langle \cdot , \cdot \rangle $
is nondegenerate, allow us to identify the aforementioned bilinear form with the element
$\langle \cdot , \cdot \rangle $
is nondegenerate, allow us to identify the aforementioned bilinear form with the element
 $$ \begin{align*}\sum_{i=1}^{\mathrm{dim}(\mathfrak{g})} e_i \otimes e_i \in \mathfrak{g} \otimes \mathfrak{g} .\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{\mathrm{dim}(\mathfrak{g})} e_i \otimes e_i \in \mathfrak{g} \otimes \mathfrak{g} .\end{align*} $$
We can decompose, by creating a unique minima on each chord, each horizontal chord diagram in local pieces like the ones shown in Figure 3, which correspond to the illustrated maps. Interpreting horizontal juxtaposition as tensor product, and vertical composition as the usual composition, we obtain the desired map. (Crossings between chords and Wilson lines have no meaning.) More explicitly, to each chord
![]() $C_{i,j}^{N} = [(i,j)]\in \mathscr {A}^{\mathrm {h}}_N$
, we are associating the element
$C_{i,j}^{N} = [(i,j)]\in \mathscr {A}^{\mathrm {h}}_N$
, we are associating the element
 $$\begin{align*}\widetilde{W}_{\underline{\rho}}(C_{i,j}^{N}) = \sum_{r=1}^{\mathrm{dim}(\mathfrak{g})} \mathrm{Id}_{V_1}\otimes \cdots \otimes \overset{i\text{th pos.}}{\rho_i(e_r)} \otimes \cdots \otimes \overset{j\text{th pos.}}{\rho_j(e_r)}\otimes \cdots \otimes \mathrm{Id}_{V_N}\, .\end{align*}$$
$$\begin{align*}\widetilde{W}_{\underline{\rho}}(C_{i,j}^{N}) = \sum_{r=1}^{\mathrm{dim}(\mathfrak{g})} \mathrm{Id}_{V_1}\otimes \cdots \otimes \overset{i\text{th pos.}}{\rho_i(e_r)} \otimes \cdots \otimes \overset{j\text{th pos.}}{\rho_j(e_r)}\otimes \cdots \otimes \mathrm{Id}_{V_N}\, .\end{align*}$$

Figure 3 Dictionary between graphical and abstract construction of Lie algebra weight systems.
It can be shown that
![]() $\widetilde {W}_{{\underline {\rho }}}$
induces a well-defined morphism of
$\widetilde {W}_{{\underline {\rho }}}$
induces a well-defined morphism of
![]() $\star $
-algebras between
$\star $
-algebras between
![]() $\mathscr {A}^{\mathrm {h}}_N$
and
$\mathscr {A}^{\mathrm {h}}_N$
and
![]() $\mathrm {End}(V^{\otimes N})$
(cf. [Reference Bar-Natan1, Section 2.1], [Reference Jackson and Moffatt5, Sections 14.2 and 14.3]). We can now give the definition of Lie algebra weight system.
$\mathrm {End}(V^{\otimes N})$
(cf. [Reference Bar-Natan1, Section 2.1], [Reference Jackson and Moffatt5, Sections 14.2 and 14.3]). We can now give the definition of Lie algebra weight system.
Definition 2.6 Given a metrized Lie algebra
![]() $(\mathfrak {g},\langle \cdot , \cdot \rangle )$
and an ordered collection
$(\mathfrak {g},\langle \cdot , \cdot \rangle )$
and an ordered collection
![]() ${\underline {\rho } = (\rho _1, \ldots , \rho _N)}$
of
${\underline {\rho } = (\rho _1, \ldots , \rho _N)}$
of
![]() $\mathfrak {g}$
-representations, the corresponding Lie algebra weight system is given by
$\mathfrak {g}$
-representations, the corresponding Lie algebra weight system is given by
for each
![]() $C\in \mathscr {A}^{\mathrm {h}}_N$
.
$C\in \mathscr {A}^{\mathrm {h}}_N$
.
Remark 2.11 For each
![]() $\mathfrak {g}$
-weight system
$\mathfrak {g}$
-weight system
![]() $W_{\underline {\rho }}(\uparrow _{N}) = \mathrm {Tr} (\mathrm {Id}_{V_1 \otimes \cdots \otimes V_N})= \prod _i \mathrm {dim}(V_i)> 0$
.
$W_{\underline {\rho }}(\uparrow _{N}) = \mathrm {Tr} (\mathrm {Id}_{V_1 \otimes \cdots \otimes V_N})= \prod _i \mathrm {dim}(V_i)> 0$
.
The
![]() $\mathfrak {gl}_{n}$
-weight system
$\mathfrak {gl}_{n}$
-weight system
![]() $W_{\mathtt {st}}$
, associated with the bilinear form
$W_{\mathtt {st}}$
, associated with the bilinear form
![]() $\langle A , B \rangle = \mathrm {Tr}( AB)$
and to the defining representation, admits a simple combinatorial description in terms of permutations, as recalled in equation (2.2) (cf. [Reference Bar-Natan1]). There exists a similar description for more general
$\langle A , B \rangle = \mathrm {Tr}( AB)$
and to the defining representation, admits a simple combinatorial description in terms of permutations, as recalled in equation (2.2) (cf. [Reference Bar-Natan1]). There exists a similar description for more general
![]() $\mathfrak {gl}_{n}$
-weight system—compare with [Reference Nagasato6].
$\mathfrak {gl}_{n}$
-weight system—compare with [Reference Nagasato6].
Definition 2.7 Let
![]() $i_{0}\in \{1,\ldots ,N\}$
,
$i_{0}\in \{1,\ldots ,N\}$
,
![]() $0\leq k \leq N-i_0$
, and
$0\leq k \leq N-i_0$
, and
![]() $\lambda $
be a partition of k. The small Young symmetrizer
$\lambda $
be a partition of k. The small Young symmetrizer
![]() $c_{(N,i_0,\lambda )}\in \mathbb {C}[\mathfrak {S}_N]$
is the image of the Young symmetrizer
$c_{(N,i_0,\lambda )}\in \mathbb {C}[\mathfrak {S}_N]$
is the image of the Young symmetrizer
![]() $c_\lambda \in \mathbb {C} [\mathfrak {S}_k]$
via the inclusion
$c_\lambda \in \mathbb {C} [\mathfrak {S}_k]$
via the inclusion
Given a vector of
![]() $\mathfrak {gl}_{n}$
-representations
$\mathfrak {gl}_{n}$
-representations
![]() $\underline {\rho } = (\lambda ^1,\ldots ,\lambda ^N)$
, we can define the Young symmetrizer associated with
$\underline {\rho } = (\lambda ^1,\ldots ,\lambda ^N)$
, we can define the Young symmetrizer associated with
![]() $\underline {\rho }$
as the product
$\underline {\rho }$
as the product

The weight system
![]() $W_{\underline {\rho }}$
can be also defined as the following composition:
$W_{\underline {\rho }}$
can be also defined as the following composition:
where
![]() —cf. [Reference Nagasato6, Reference Nagasato and Takamuki7]. Roughly speaking, we are writing each
—cf. [Reference Nagasato6, Reference Nagasato and Takamuki7]. Roughly speaking, we are writing each
![]() $\lambda ^i$
as the composition of the representation
$\lambda ^i$
as the composition of the representation
![]() $\rho _{\mathtt {st}}^{\otimes \vert \lambda ^i\vert }$
—encoded by
$\rho _{\mathtt {st}}^{\otimes \vert \lambda ^i\vert }$
—encoded by
![]() $\Delta ^{(\vert \lambda ^1\vert ,\ldots , \vert \lambda ^N\vert )}$
, cf. [Reference Bar-Natan1, Definition 2.2]—and the projection onto
$\Delta ^{(\vert \lambda ^1\vert ,\ldots , \vert \lambda ^N\vert )}$
, cf. [Reference Bar-Natan1, Definition 2.2]—and the projection onto
![]() $\mathbb {S}_{\lambda }(\mathbb {C})$
—encoded by the multiplication by
$\mathbb {S}_{\lambda }(\mathbb {C})$
—encoded by the multiplication by
![]() $c_{\underline {\rho }}$
—and taking the trace by applying
$c_{\underline {\rho }}$
—and taking the trace by applying
![]() $w_{\mathtt { st}}$
.
$w_{\mathtt { st}}$
.
3 Proof of the main result
In [Reference Corfield, Sati and Schreiber3], it was proven that the standard
![]() $\mathfrak {gl}_{n}$
-weight system is a quantum state. The proof goes as follows: first, one observes that
$\mathfrak {gl}_{n}$
-weight system is a quantum state. The proof goes as follows: first, one observes that
![]() $W_{\mathtt {st}}$
factors as
$W_{\mathtt {st}}$
factors as

where
![]() $\sigma $
is the morphism of
$\sigma $
is the morphism of
![]() $\star $
-algebras defined in Section 2.2. The key observation made in [Reference Corfield, Sati and Schreiber3] is that
$\star $
-algebras defined in Section 2.2. The key observation made in [Reference Corfield, Sati and Schreiber3] is that
![]() $w_{\mathtt {st}}$
is the kernel of the Cayley distance function, which is a class functions (i.e., it is constant on conjugacy classes). Eigenvalues and eigenvectors of class functions on the symmetric group are known— cf. [Reference Corfield, Sati and Schreiber3, Section 3] and references therein. So one concludes by observing that these eigenvalues are nonnegative for all possible n. This proves that
$w_{\mathtt {st}}$
is the kernel of the Cayley distance function, which is a class functions (i.e., it is constant on conjugacy classes). Eigenvalues and eigenvectors of class functions on the symmetric group are known— cf. [Reference Corfield, Sati and Schreiber3, Section 3] and references therein. So one concludes by observing that these eigenvalues are nonnegative for all possible n. This proves that
![]() $w_{\mathtt {st}}$
is a quantum state, and the main result of [Reference Corfield, Sati and Schreiber3] is now a consequence of the following easy lemma.
$w_{\mathtt {st}}$
is a quantum state, and the main result of [Reference Corfield, Sati and Schreiber3] is now a consequence of the following easy lemma.
Lemma 3.1 Let
![]() $\mathscr {O}$
and
$\mathscr {O}$
and
![]() $\mathscr {O}'$
be
$\mathscr {O}'$
be
![]() $\star $
-algebras. If
$\star $
-algebras. If
![]() $\phi : \mathscr {O}' \to \mathbb {C}$
is a state, and
$\phi : \mathscr {O}' \to \mathbb {C}$
is a state, and
![]() $f: \mathscr {O} \to \mathscr {O}'$
is a morphism of
$f: \mathscr {O} \to \mathscr {O}'$
is a morphism of
![]() $\star $
-algebras, then
$\star $
-algebras, then
![]() $\phi \circ f$
is a state.
$\phi \circ f$
is a state.
We want to use a similar reasoning to prove our main result. We know that
![]() $W_{\underline {\rho }}$
factors as the following composition:
$W_{\underline {\rho }}$
factors as the following composition:
While the map
![]() $\sigma \circ \Delta _{\vert \underline {\rho }\vert }$
is a morphism of
$\sigma \circ \Delta _{\vert \underline {\rho }\vert }$
is a morphism of
![]() $\star $
-algebras, the map
$\star $
-algebras, the map
![]() $c_{\underline {\rho }}$
is not—for any choice of
$c_{\underline {\rho }}$
is not—for any choice of
![]() ${\underline {\rho }}$
which is not
${\underline {\rho }}$
which is not
![]() $\mathtt {st}$
. Therefore, we cannot conclude using Lemma 3.1. Nonetheless, we can show that the composition
$\mathtt {st}$
. Therefore, we cannot conclude using Lemma 3.1. Nonetheless, we can show that the composition
![]() $w_{\mathtt {st}} \circ c_{{\underline {\rho }}}$
is a state for suitable choices of
$w_{\mathtt {st}} \circ c_{{\underline {\rho }}}$
is a state for suitable choices of
![]() ${\underline {\rho }}$
, proving our main result.
${\underline {\rho }}$
, proving our main result.
Definition 3.1 Let
![]() $\mathscr {O}$
be a
$\mathscr {O}$
be a
![]() $\star $
-algebra, and
$\star $
-algebra, and
![]() $x\in \mathscr {O}$
. A linear function
$x\in \mathscr {O}$
. A linear function
![]() $\phi : \mathscr {O} \to \mathbb {C}$
is class-like with respect to x if
$\phi : \mathscr {O} \to \mathbb {C}$
is class-like with respect to x if
![]() $\phi (xy) = \phi (y x)$
, for each
$\phi (xy) = \phi (y x)$
, for each
![]() $y\in \mathscr {O}$
.
$y\in \mathscr {O}$
.
Linear functions arising from class functions are class-like functions
Example 3.2 If
![]() $f: \mathfrak {S}_m \to \mathbb {C}$
is a class function (i.e., it is constant in each conjugacy class), then
$f: \mathfrak {S}_m \to \mathbb {C}$
is a class function (i.e., it is constant in each conjugacy class), then

is class-like for all c. In fact, given
![]() $c = \sum _{j} x_j \eta _j $
and
$c = \sum _{j} x_j \eta _j $
and
![]() $x = \sum _{i} z_i \sigma _i$
, we have
$x = \sum _{i} z_i \sigma _i$
, we have
States which are class-like with respect to special elements can be used to produce new states, as shown in the following lemma.
Lemma 3.3 Let
![]() $c \in \mathscr {O}$
be such that
$c \in \mathscr {O}$
be such that
![]() $c^2 = \alpha c$
,
$c^2 = \alpha c$
,
![]() $\alpha \in \mathbb {R}_{> 0}$
, and
$\alpha \in \mathbb {R}_{> 0}$
, and
![]() $c^\star = c$
. If a state
$c^\star = c$
. If a state
![]() $\phi : \mathscr {O} \to \mathbb {C}$
is class-like with respect to c, then
$\phi : \mathscr {O} \to \mathbb {C}$
is class-like with respect to c, then
![]() $\psi = \phi \circ (c \cdot )$
is also a state.
$\psi = \phi \circ (c \cdot )$
is also a state.
Proof Let
![]() $a \in \mathscr {O}$
, then
$a \in \mathscr {O}$
, then
We remark that the hypothesis
![]() $c = c^\star $
plays a key role in the above lemma. Now, we are ready to prove the main theorem.
$c = c^\star $
plays a key role in the above lemma. Now, we are ready to prove the main theorem.
Proof of Theorem 1.1
Let
![]() ${\underline {\rho }}= ( \lambda ^1 ,\ldots , \lambda ^N)$
be a labeling such that each
${\underline {\rho }}= ( \lambda ^1 ,\ldots , \lambda ^N)$
be a labeling such that each
![]() $\lambda _i$
is either a symmetric or an exterior power of the standard representation. Since
$\lambda _i$
is either a symmetric or an exterior power of the standard representation. Since
![]() $W_{\underline {\rho }}(\uparrow _N)>0$
(see Remark 2.5), we only have to prove that
$W_{\underline {\rho }}(\uparrow _N)>0$
(see Remark 2.5), we only have to prove that
![]() $W_{\underline {\rho }}(CC^\star )\geq 0$
, for each
$W_{\underline {\rho }}(CC^\star )\geq 0$
, for each
![]() $C\in \mathscr {A}^{\mathrm {h}}_N$
. We recall that the following triangle
$C\in \mathscr {A}^{\mathrm {h}}_N$
. We recall that the following triangle

is commutative. From Proposition 2.3, it follows that
![]() $\sigma \circ \Delta _{\rho }$
is a morphism of
$\sigma \circ \Delta _{\rho }$
is a morphism of
![]() $\star $
-algebras. Thence, by Lemma 3.1, in order to show that
$\star $
-algebras. Thence, by Lemma 3.1, in order to show that
![]() $W_{\underline {\rho }}$
is a state it is sufficient to prove that
$W_{\underline {\rho }}$
is a state it is sufficient to prove that
![]() $w_{\mathtt {st}}\circ (c_{\underline {\rho }}\cdot )$
is a state. Note that
$w_{\mathtt {st}}\circ (c_{\underline {\rho }}\cdot )$
is a state. Note that
![]() $c_{\underline {\rho }}$
is idempotent since small Young symmetrizers are idempotent and their actions commute (as they have disjoint support). Furthermore, since each
$c_{\underline {\rho }}$
is idempotent since small Young symmetrizers are idempotent and their actions commute (as they have disjoint support). Furthermore, since each
![]() $\lambda ^i$
is either a symmetric or exterior power of the defining representation, the commutativity of the small Young symmetrizer and Remark 2.9, ensure that
$\lambda ^i$
is either a symmetric or exterior power of the defining representation, the commutativity of the small Young symmetrizer and Remark 2.9, ensure that
![]() $c_{\underline {\rho }} = c_{\underline {\rho }}^\star $
. Since
$c_{\underline {\rho }} = c_{\underline {\rho }}^\star $
. Since
![]() $w_{\mathtt {st}}$
is state-like with respect to
$w_{\mathtt {st}}$
is state-like with respect to
![]() $c_{\underline {\rho }}$
(cf. Example 3.2), the statement follows directly from Lemma 3.3.
$c_{\underline {\rho }}$
(cf. Example 3.2), the statement follows directly from Lemma 3.3.
Acknowledgment
The author thanks Luigi Caputi, Roberto Castorrini, Sabino Di Trani, Hisham Sati, and Urs Schreiber for the helpful comments and the interesting conversations. Many thanks are due to the anonymous referees for their valuable comments. This project started when the author was a post-doc at NYU Abu Dhabi.