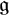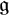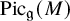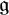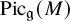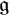1 Introduction
1.1 Background on relative invariants
Consider a manifold M together with a Lie group G acting on M. Let
![]() $\mathcal{F}(M)$
be the algebra of functions on M and
$\mathcal{F}(M)$
be the algebra of functions on M and
![]() $\mathcal {F}(M)^\times $
the multiplicative subgroup of nonvanishing functions. The action of
$\mathcal {F}(M)^\times $
the multiplicative subgroup of nonvanishing functions. The action of
![]() $g \in G$
on M induces the pullback (right) action
$g \in G$
on M induces the pullback (right) action
![]() $g^*$
on
$g^*$
on
![]() $\mathcal {F}(M)$
. A (scalar) relative invariant is a function
$\mathcal {F}(M)$
. A (scalar) relative invariant is a function
![]() $R \in \mathcal {F}(M)$
satisfying
$R \in \mathcal {F}(M)$
satisfying
for some map
![]() $\Lambda \colon G \to \mathcal {F}(M)^\times $
, called the multiplier, or weight, of R. If
$\Lambda \colon G \to \mathcal {F}(M)^\times $
, called the multiplier, or weight, of R. If
![]() ${\mathfrak g} \subset \mathcal {D}(M)$
denotes the Lie algebra of vector fields on M corresponding to the Lie group action, then R also satisfies
${\mathfrak g} \subset \mathcal {D}(M)$
denotes the Lie algebra of vector fields on M corresponding to the Lie group action, then R also satisfies
for some (infinitesimal) multiplier
![]() $\lambda \in {\mathfrak g}^* \otimes \mathcal {F}(M)$
, or weight, of R. It follows from the definition that the locus
$\lambda \in {\mathfrak g}^* \otimes \mathcal {F}(M)$
, or weight, of R. It follows from the definition that the locus
![]() $\{R=0\} \subset M$
is G-invariant (resp.
$\{R=0\} \subset M$
is G-invariant (resp.
![]() ${\mathfrak g}$
-invariant).
${\mathfrak g}$
-invariant).
In the case
![]() $\Lambda =1$
(resp.
$\Lambda =1$
(resp.
![]() $\lambda =0$
), the function R is called an absolute invariant, and each level set
$\lambda =0$
), the function R is called an absolute invariant, and each level set
![]() $\{R=\mathrm {const}\} \subset M$
is invariant, so that we get an invariant foliation of M. Absolute invariants are well understood in several different settings; see [Reference Weyl30, Reference Mumford22, Reference Olver24, Reference Ferrer Santos and Rittatore28] for the classical invariant theory and [Reference Olver23, Reference Kruglikov and Lychagin18] for its differential counterpart.
$\{R=\mathrm {const}\} \subset M$
is invariant, so that we get an invariant foliation of M. Absolute invariants are well understood in several different settings; see [Reference Weyl30, Reference Mumford22, Reference Olver24, Reference Ferrer Santos and Rittatore28] for the classical invariant theory and [Reference Olver23, Reference Kruglikov and Lychagin18] for its differential counterpart.
For example, in the case of a regular smooth Lie group action on a smooth manifold, locally by the Frobenius theorem, the number of functionally independent absolute invariants is equal to the codimension of an orbit, and orbits are locally separated by that many invariants (see, for example, Chapter 2 of [Reference Olver23]). In the case of an algebraic group action on an algebraic variety, globally by the Rosenlicht theorem, orbits in general position are separated by rational absolute invariants, and the number of algebraically independent rational absolute invariants is equal to the codimension of a generic orbit (see, for example, Chapter 13 of [Reference Ferrer Santos and Rittatore28]).
Relative invariants with nontrivial weight are less understood, although they appear in many important applications (we refer to the introduction to [Reference Fels and Olver7] and also to the more recent [Reference Olver25]). In particular, they are often used to describe
![]() ${\mathfrak g}$
-invariant hypersurfaces containing singular orbits. An infinitesimal multiplier
${\mathfrak g}$
-invariant hypersurfaces containing singular orbits. An infinitesimal multiplier
![]() $\lambda $
is a 1-cocycle of the Chevalley-Eilenberg complex of
$\lambda $
is a 1-cocycle of the Chevalley-Eilenberg complex of
![]() ${\mathfrak g}$
with coefficients in
${\mathfrak g}$
with coefficients in
![]() $\mathcal {F}(M)$
. Relationships between the weights of relative (differential) invariants and the Chevalley-Eilenberg cohomology was discussed in [Reference Cariñena, del Olmo and Winternitz4, Reference Olver23]. The question of realizability of a given cocycle as the weight of some relative invariant was answered locally in the case of a regular smooth G-action and
$\mathcal {F}(M)$
. Relationships between the weights of relative (differential) invariants and the Chevalley-Eilenberg cohomology was discussed in [Reference Cariñena, del Olmo and Winternitz4, Reference Olver23]. The question of realizability of a given cocycle as the weight of some relative invariant was answered locally in the case of a regular smooth G-action and
![]() $\mathcal {F}(M)=C^\infty (M)$
by M. Fels and P. Olver ([Reference Fels and Olver7] and [Reference Olver23, Th. 3.36]), also in the context of vector-valued relative invariants. In the general case, the answer is not known.
$\mathcal {F}(M)=C^\infty (M)$
by M. Fels and P. Olver ([Reference Fels and Olver7] and [Reference Olver23, Th. 3.36]), also in the context of vector-valued relative invariants. In the general case, the answer is not known.
Note that rescaling of R by a nonzero function
![]() $e^f$
,
$e^f$
,
![]() $f\in \mathcal {F}(M)$
, changes
$f\in \mathcal {F}(M)$
, changes
![]() $\lambda $
by a coboundary
$\lambda $
by a coboundary
![]() $df$
, which naturally associates the Chevalley-Eilenberg cohomology class
$df$
, which naturally associates the Chevalley-Eilenberg cohomology class
![]() $[\lambda ]\in {\mathrm {H}}^1({\mathfrak g},\mathcal {F}(M))$
to the (equivalence class of the) relative invariant R. A proper version of this cohomology will be central in our work.
$[\lambda ]\in {\mathrm {H}}^1({\mathfrak g},\mathcal {F}(M))$
to the (equivalence class of the) relative invariant R. A proper version of this cohomology will be central in our work.
1.2 A setup for global invariants
In general, the description of invariant hypersurfaces (analytic subvarieties of codimension 1) by relative invariants works only locally: there exist invariant hypersurfaces that cannot be described globally as the zero locus of a relative invariant. In this paper, we restrict to holomorphic actions on complex manifolds, where this problem can be solved using the language of divisors. Some results extend to real analytic and algebraic situations, but smooth versions of our global results in general are not available. Thus, we specialize our algebra of functions
![]() $\mathcal {F}(M)$
to consist of holomorphic functions, and we will work with the sheaf
$\mathcal {F}(M)$
to consist of holomorphic functions, and we will work with the sheaf
![]() $\mathcal {O}=\mathcal {O}_M$
of such functions on a complex manifold M.
$\mathcal {O}=\mathcal {O}_M$
of such functions on a complex manifold M.
In most of the paper, we will concentrate on the infinitesimal (Lie algebra) picture as it is conceptually simpler and lends itself well to computations. Moreover, it is more general, as a Lie group action always gives rise to a Lie algebra of (complete) vector fields, but not every Lie algebra action can be integrated (the manifold M is not assumed compact; the Lie algebra may be infinite-dimensional). It should be noted that for algebraic groups G (as well as for compact Lie groups), the equivariant line bundles have been well studied; see [Reference Mumford22, Ch. 1.3] and [Reference Brion3, §4.2] for the definition and properties of the G-equivariant Picard group
![]() $\mathrm {Pic}_G(M)$
in the context of algebraic geometry. Our setup is more general, and we present the corresponding theory for Lie groups in Section 2.5. The main object of study, however, will be the Picard group
$\mathrm {Pic}_G(M)$
in the context of algebraic geometry. Our setup is more general, and we present the corresponding theory for Lie groups in Section 2.5. The main object of study, however, will be the Picard group
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
of
$\mathrm {Pic}_{\mathfrak g}(M)$
of
![]() ${\mathfrak g}$
-equivariant line bundles defined for any Lie algebra
${\mathfrak g}$
-equivariant line bundles defined for any Lie algebra
![]() ${\mathfrak g}$
of holomorphic vector fields on M.
${\mathfrak g}$
of holomorphic vector fields on M.
A divisor D on M is given by a collection of meromorphic functions
![]() $f_\alpha $
defined on each chart in an open cover
$f_\alpha $
defined on each chart in an open cover
![]() $\{U_\alpha \}$
of M (if the functions
$\{U_\alpha \}$
of M (if the functions
![]() $f_\alpha $
are holomorphic, then D is called effective). The functions
$f_\alpha $
are holomorphic, then D is called effective). The functions
![]() $f_\alpha $
are required to be consistent, in the sense that the zeros and poles of
$f_\alpha $
are required to be consistent, in the sense that the zeros and poles of
![]() $f_\alpha $
and
$f_\alpha $
and
![]() $f_\beta $
agree on
$f_\beta $
agree on
![]() $U_\alpha \cap U_\beta $
, which is equivalent to
$U_\alpha \cap U_\beta $
, which is equivalent to
![]() $f_\alpha /f_\beta $
being a nonvanishing holomorphic function on
$f_\alpha /f_\beta $
being a nonvanishing holomorphic function on
![]() $U_\alpha \cap U_\beta $
. (Our D correspond to Cartier divisors, which are equivalent to Weyl divisors for the nonsingular analytic varieties we consider.) Analytic hypersurfaces of a complex manifold M are given locally by the vanishing of a holomorphic function and globally by an effective divisor.
$U_\alpha \cap U_\beta $
. (Our D correspond to Cartier divisors, which are equivalent to Weyl divisors for the nonsingular analytic varieties we consider.) Analytic hypersurfaces of a complex manifold M are given locally by the vanishing of a holomorphic function and globally by an effective divisor.
If
![]() ${\mathfrak g}$
is a Lie algebra of vector fields on M and
${\mathfrak g}$
is a Lie algebra of vector fields on M and
![]() $N \subset M$
is a
$N \subset M$
is a
![]() ${\mathfrak g}$
-invariant hypersurface defined by the divisor
${\mathfrak g}$
-invariant hypersurface defined by the divisor
![]() $D= \{f_\alpha \}$
, then each vector field of
$D= \{f_\alpha \}$
, then each vector field of
![]() ${\mathfrak g}$
is tangent to N, implying that for each
${\mathfrak g}$
is tangent to N, implying that for each
![]() $\alpha $
,
$\alpha $
,
for some weight
![]() $\lambda _\alpha \in {\mathfrak g}^* \otimes \mathcal {O}(U_\alpha )$
, which is a 1-cocycle in the Chevalley-Eilenberg complex of
$\lambda _\alpha \in {\mathfrak g}^* \otimes \mathcal {O}(U_\alpha )$
, which is a 1-cocycle in the Chevalley-Eilenberg complex of
![]() ${\mathfrak g}$
with coefficients in the
${\mathfrak g}$
with coefficients in the
![]() ${\mathfrak g}$
-module
${\mathfrak g}$
-module
![]() $\mathcal {O}(U_\alpha )$
of holomorphic functions on
$\mathcal {O}(U_\alpha )$
of holomorphic functions on
![]() $U_\alpha \subset M$
. Such a divisor is called
$U_\alpha \subset M$
. Such a divisor is called
![]() ${\mathfrak g}$
-invariant. Multiplying each
${\mathfrak g}$
-invariant. Multiplying each
![]() $f_\alpha $
by nonvanishing holomorphic functions gives a different representative of the same divisor, and the weight
$f_\alpha $
by nonvanishing holomorphic functions gives a different representative of the same divisor, and the weight
![]() $\lambda _\alpha $
is in this case changed by a coboundary, so the weights can be identified with elements in the Chevalley-Eilenberg cohomology
$\lambda _\alpha $
is in this case changed by a coboundary, so the weights can be identified with elements in the Chevalley-Eilenberg cohomology
![]() ${\mathrm {H}}^1({\mathfrak g},\mathcal {O}(U_\alpha ))$
or, more precisely, a slightly modified version thereof. A collection of such weights, or multipliers, for each element of the cover
${\mathrm {H}}^1({\mathfrak g},\mathcal {O}(U_\alpha ))$
or, more precisely, a slightly modified version thereof. A collection of such weights, or multipliers, for each element of the cover
![]() $\{U_\alpha \}$
, that are compatible on overlaps, yields a multiplier group that we will denote
$\{U_\alpha \}$
, that are compatible on overlaps, yields a multiplier group that we will denote
![]() $\mathfrak {M}_{\mathfrak g}(M)$
. Below, we will define it in terms of a certain double complex.
$\mathfrak {M}_{\mathfrak g}(M)$
. Below, we will define it in terms of a certain double complex.
As is well known, any divisor D on M gives rise to a line bundle
![]() $[D] \to M$
, with transition functions
$[D] \to M$
, with transition functions
![]() $g_{\alpha \beta } = f_\alpha / f_\beta $
, on which
$g_{\alpha \beta } = f_\alpha / f_\beta $
, on which
![]() $f_\alpha $
are local defining functions of a particular section (and, geometrically, D is the locus of this section). When D is
$f_\alpha $
are local defining functions of a particular section (and, geometrically, D is the locus of this section). When D is
![]() ${\mathfrak g}$
-invariant, then there exists a lift of the Lie algebra
${\mathfrak g}$
-invariant, then there exists a lift of the Lie algebra
![]() ${\mathfrak g} \subset \mathcal {D}(M)$
to a Lie algebra
${\mathfrak g} \subset \mathcal {D}(M)$
to a Lie algebra
![]() ${\mathfrak g}^\lambda \subset \mathcal {D}([D])$
defined locally in terms of the weights
${\mathfrak g}^\lambda \subset \mathcal {D}([D])$
defined locally in terms of the weights
![]() $\lambda = \{ \lambda _\alpha \}$
of D, meaning that
$\lambda = \{ \lambda _\alpha \}$
of D, meaning that
![]() $([D],{\mathfrak g}^\lambda )$
is a
$([D],{\mathfrak g}^\lambda )$
is a
![]() ${\mathfrak g}$
-equivariant line bundle. Properly localized, the obstruction for such a lift, and thus for the existence of invariant divisors, belongs in general to the equivariant Picard group
${\mathfrak g}$
-equivariant line bundle. Properly localized, the obstruction for such a lift, and thus for the existence of invariant divisors, belongs in general to the equivariant Picard group
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
.
$\mathrm {Pic}_{\mathfrak g}(M)$
.
1.3 Overview of the novel results
Due to a close relationship between
![]() ${\mathfrak g}$
-invariant divisors and
${\mathfrak g}$
-invariant divisors and
![]() ${\mathfrak g}$
-equivariant line bundles, Section 2.1 starts with an investigation of prerequisites for the latter. The Picard group
${\mathfrak g}$
-equivariant line bundles, Section 2.1 starts with an investigation of prerequisites for the latter. The Picard group
![]() $\mathrm {Pic}(M)$
, consisting of holomorphic line bundles over M up to equivalence, is isomorphic to the Čech cohomology group
$\mathrm {Pic}(M)$
, consisting of holomorphic line bundles over M up to equivalence, is isomorphic to the Čech cohomology group
![]() ${\check {\mathrm {H}}}^1(M,\mathcal {O}^\times )$
.
${\check {\mathrm {H}}}^1(M,\mathcal {O}^\times )$
.
In order to describe the group
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
of
$\mathrm {Pic}_{\mathfrak g}(M)$
of
![]() ${\mathfrak g}$
-equivariant line bundles, we unite the Čech complex with the Chevalley-Eilenberg complex into a double complex
${\mathfrak g}$
-equivariant line bundles, we unite the Čech complex with the Chevalley-Eilenberg complex into a double complex
![]() $C^{\bullet ,\bullet }$
. The direct limit of the first total cohomology of this complex (also called hypercohomology; cf. [Reference Grothendieck12]) is exactly the desired group:
$C^{\bullet ,\bullet }$
. The direct limit of the first total cohomology of this complex (also called hypercohomology; cf. [Reference Grothendieck12]) is exactly the desired group:
![]() $\mathrm {Pic}_{\mathfrak g}(M):=\varinjlim {\mathrm {H}}^1(\mathrm {Tot}^\bullet (C))$
.
$\mathrm {Pic}_{\mathfrak g}(M):=\varinjlim {\mathrm {H}}^1(\mathrm {Tot}^\bullet (C))$
.
There exist natural homomorphisms
![]() $\Phi _1\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathrm {Pic}(M)$
and
$\Phi _1\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathrm {Pic}(M)$
and
![]() $\Phi _2\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathfrak {M}_{\mathfrak g}(M)$
. The image of
$\Phi _2\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathfrak {M}_{\mathfrak g}(M)$
. The image of
![]() $\varpi := \Phi _1\times \Phi _2$
in
$\varpi := \Phi _1\times \Phi _2$
in
![]() $\mathrm {Pic}(M)\times \mathfrak {M}_{\mathfrak g}(M)$
defines the reduced Picard group
$\mathrm {Pic}(M)\times \mathfrak {M}_{\mathfrak g}(M)$
defines the reduced Picard group
whence a double homomorphism
![]() $(\Psi _1,\Psi _2)$
such that
$(\Psi _1,\Psi _2)$
such that
![]() $\Psi _i\circ \varpi =\Phi _i$
and
$\Psi _i\circ \varpi =\Phi _i$
and
![]() $\ker \Psi _1\cap \ker \Psi _2=0$
:
$\ker \Psi _1\cap \ker \Psi _2=0$
:

Theorem 1.1. The group
![]() $T_{\mathfrak g}(M):=\ker (\varpi )$
of equivariant line bundles with trivial reduction is defined by (2.7) and consists of the global lifts of
$T_{\mathfrak g}(M):=\ker (\varpi )$
of equivariant line bundles with trivial reduction is defined by (2.7) and consists of the global lifts of
![]() ${\mathfrak g}$
to the trivial line bundle over M that are locally trivial, modulo globally trivial lifts.
${\mathfrak g}$
to the trivial line bundle over M that are locally trivial, modulo globally trivial lifts.
When
![]() $T_{\mathfrak g}(M)=0$
,
$T_{\mathfrak g}(M)=0$
,
![]() $\Phi _1\times \Phi _2$
embeds
$\Phi _1\times \Phi _2$
embeds
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
in
$\mathrm {Pic}_{\mathfrak g}(M)$
in
![]() $\mathrm {Pic}(M)\times \mathfrak {M}_{\mathfrak g}(M)$
(Corollary 2.11 gives two sufficient conditions for this); generally the same is true for
$\mathrm {Pic}(M)\times \mathfrak {M}_{\mathfrak g}(M)$
(Corollary 2.11 gives two sufficient conditions for this); generally the same is true for
![]() $\mathrm {Pic}_{\mathfrak g}(M)/T_{\mathfrak g}(M)$
.
$\mathrm {Pic}_{\mathfrak g}(M)/T_{\mathfrak g}(M)$
.
The homomorphisms
![]() $\Psi _1,\Psi _2$
(and likewise
$\Psi _1,\Psi _2$
(and likewise
![]() $\Phi _1,\Phi _2$
) are neither injective nor surjective, in general. We will describe
$\Phi _1,\Phi _2$
) are neither injective nor surjective, in general. We will describe
![]() $\ker (\Psi _i)$
and
$\ker (\Psi _i)$
and
![]() $\mathrm {im}(\Psi _i)$
in terms of the iterated cohomology of the double complex
$\mathrm {im}(\Psi _i)$
in terms of the iterated cohomology of the double complex
![]() $C^{\bullet ,\bullet }$
. In particular, we will show that under certain topological conditions, if the isotropy algebra
$C^{\bullet ,\bullet }$
. In particular, we will show that under certain topological conditions, if the isotropy algebra
![]() ${\mathfrak g}_p$
of a generic point
${\mathfrak g}_p$
of a generic point
![]() $p\in M$
is perfect, then
$p\in M$
is perfect, then
![]() $\ker (\Psi _1)=0$
and
$\ker (\Psi _1)=0$
and
![]() $\mathrm {Pic}_{\mathfrak g}(M)\subset \mathrm {Pic}(M)$
. This is an infinitesimal version of Proposition 1.4 from [Reference Mumford22], which gives sufficient conditions for an algebraic group G to admit at most one linearization on any line bundle. The following statements elaborate on the cases considered in [Reference Mumford22] and [Reference Fels and Olver7], respectively.
$\mathrm {Pic}_{\mathfrak g}(M)\subset \mathrm {Pic}(M)$
. This is an infinitesimal version of Proposition 1.4 from [Reference Mumford22], which gives sufficient conditions for an algebraic group G to admit at most one linearization on any line bundle. The following statements elaborate on the cases considered in [Reference Mumford22] and [Reference Fels and Olver7], respectively.
Corollary 1.2.
-
(i) If
 $\mathfrak {M}_{\mathfrak g}(M)=0$
and
$\mathfrak {M}_{\mathfrak g}(M)=0$
and
 $T_{\mathfrak g}(M)=0$
, then
$T_{\mathfrak g}(M)=0$
, then
 $\Phi _1\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathrm {Pic}(M)$
is injective.
$\Phi _1\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathrm {Pic}(M)$
is injective. -
(ii) Likewise, if
 $\mathrm {Pic}(M)=0$
and
$\mathrm {Pic}(M)=0$
and
 $T_{\mathfrak g}(M)=0$
, then
$T_{\mathfrak g}(M)=0$
, then
 $\Phi _2\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathfrak {M}_{\mathfrak g}(M)$
is injective.
$\Phi _2\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathfrak {M}_{\mathfrak g}(M)$
is injective.
In Section 2.4, we consider the homomorphism
mapping a
![]() ${\mathfrak g}$
-invariant divisor D with weight
${\mathfrak g}$
-invariant divisor D with weight
![]() $\lambda $
to the
$\lambda $
to the
![]() ${\mathfrak g}$
-equivariant line bundle
${\mathfrak g}$
-equivariant line bundle
![]() $([D],{\mathfrak g}^\lambda )$
. The canonical morphism
$([D],{\mathfrak g}^\lambda )$
. The canonical morphism
![]() $j\colon \mathrm {Div}(M)\to \mathrm {Pic}(M)$
, which takes D to
$j\colon \mathrm {Div}(M)\to \mathrm {Pic}(M)$
, which takes D to
![]() $[D]$
, is well understood: its kernel and cokernel are given by exact sequence (2.10); for smooth projective varieties, j is epimorphic and
$[D]$
, is well understood: its kernel and cokernel are given by exact sequence (2.10); for smooth projective varieties, j is epimorphic and
![]() $\mathrm {Pic}(M)$
corresponds to the class group
$\mathrm {Pic}(M)$
corresponds to the class group
![]() $\mathrm {Cl}(M)$
of equivalent divisors ( cf. [Reference Griffiths and Harris11]). In contrast, even in the smooth projective case, the map
$\mathrm {Cl}(M)$
of equivalent divisors ( cf. [Reference Griffiths and Harris11]). In contrast, even in the smooth projective case, the map
![]() $j_{\mathfrak g}$
is generally neither injective nor surjective.
$j_{\mathfrak g}$
is generally neither injective nor surjective.
We will give a necessary criterion for a
![]() ${\mathfrak g}$
-equivariant line bundle
${\mathfrak g}$
-equivariant line bundle
![]() $(L \to M, \hat {\mathfrak g})$
, where
$(L \to M, \hat {\mathfrak g})$
, where
![]() $\hat {\mathfrak g}$
is a lift of
$\hat {\mathfrak g}$
is a lift of
![]() ${\mathfrak g}$
to L, to be the image of a
${\mathfrak g}$
to L, to be the image of a
![]() ${\mathfrak g}$
-invariant divisor – namely, that generic
${\mathfrak g}$
-invariant divisor – namely, that generic
![]() $\hat {\mathfrak g}$
-orbits on L project bijectively (in our setup: biholomorphic) to
$\hat {\mathfrak g}$
-orbits on L project bijectively (in our setup: biholomorphic) to
![]() ${\mathfrak g}$
-orbits on M (projection may be non-injective on singular orbits). We call such Lie algebras transversal, borrowing the terminology from [Reference Anderson and Fels1], although their notion of transversality was a slightly stronger requirement.
${\mathfrak g}$
-orbits on M (projection may be non-injective on singular orbits). We call such Lie algebras transversal, borrowing the terminology from [Reference Anderson and Fels1], although their notion of transversality was a slightly stronger requirement.
Theorem 1.3. If
![]() $D=\{f_\alpha \}$
is a
$D=\{f_\alpha \}$
is a
![]() ${\mathfrak g}$
-invariant divisor and
${\mathfrak g}$
-invariant divisor and
![]() $\lambda =\{\lambda _\alpha \}$
is the corresponding weight, then the lift
$\lambda =\{\lambda _\alpha \}$
is the corresponding weight, then the lift
![]() ${\mathfrak g}^\lambda \subset \mathcal {D}([D])$
defined by
${\mathfrak g}^\lambda \subset \mathcal {D}([D])$
defined by
![]() $\lambda $
is transversal.
$\lambda $
is transversal.
Thus, if
![]() $\hat {\mathfrak g}\subset \mathcal {D}(L)$
is not transversal, then the
$\hat {\mathfrak g}\subset \mathcal {D}(L)$
is not transversal, then the
![]() ${\mathfrak g}$
-equivariant line bundle
${\mathfrak g}$
-equivariant line bundle
![]() $(L\to M,\hat {\mathfrak g})$
is not in
$(L\to M,\hat {\mathfrak g})$
is not in
![]() $\mathrm {im}(j_{\mathfrak g})$
. The condition
$\mathrm {im}(j_{\mathfrak g})$
. The condition
![]() $(L,\hat {\mathfrak g})\in \mathrm {im}(j_{\mathfrak g})$
restricts not only
$(L,\hat {\mathfrak g})\in \mathrm {im}(j_{\mathfrak g})$
restricts not only
![]() $\hat {\mathfrak g}$
, but also L via
$\hat {\mathfrak g}$
, but also L via
![]() $\mathrm {im}(\Psi _1\circ j_{\mathfrak g})\subset \mathrm {im}(j)$
.
$\mathrm {im}(\Psi _1\circ j_{\mathfrak g})\subset \mathrm {im}(j)$
.
The proof of Theorem 1.3 is based on a local argument and is similar to that of [Reference Olver23, Th. 3.36] and [Reference Fels and Olver7, Th. 5.4], where lifts of
![]() ${\mathfrak g}$
to the trivial bundle are considered. It is important to note that in our general setting, contrary to the local regular settings of [Reference Fels and Olver7, Reference Olver23], this criterion is only necessary but not sufficient, which will be illustrated in examples. Yet, in an algebraic context the converse statement holds true, up to an integer factor for the degree (see Theorem 2.33).
${\mathfrak g}$
to the trivial bundle are considered. It is important to note that in our general setting, contrary to the local regular settings of [Reference Fels and Olver7, Reference Olver23], this criterion is only necessary but not sufficient, which will be illustrated in examples. Yet, in an algebraic context the converse statement holds true, up to an integer factor for the degree (see Theorem 2.33).
In Section 2.5, we show that the group of G-equivariant line bundles can be described by a certain Lie group cohomology with coefficients in the sheaf
![]() $\mathcal {O}^\times $
, which combines the Čech cohomology of
$\mathcal {O}^\times $
, which combines the Čech cohomology of
![]() $\mathcal {O}^\times $
and the continuous Lie group cohomology with coefficients in the G-module
$\mathcal {O}^\times $
and the continuous Lie group cohomology with coefficients in the G-module
![]() $\mathcal {O}^\times (M)$
. This in turn is related to the equivariant Picard group
$\mathcal {O}^\times (M)$
. This in turn is related to the equivariant Picard group
![]() $\mathrm {Pic}_G(M)$
, studied before in particular situations when G is algebraic or compact. We also discuss its relation to
$\mathrm {Pic}_G(M)$
, studied before in particular situations when G is algebraic or compact. We also discuss its relation to
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
.
$\mathrm {Pic}_{\mathfrak g}(M)$
.
Several examples of computation are spread throughout Section 2, demonstrating global constraints in the theory of
![]() ${\mathfrak g}$
-invariant divisors and
${\mathfrak g}$
-invariant divisors and
![]() ${\mathfrak g}$
-equivariant line bundles. For instance, when
${\mathfrak g}$
-equivariant line bundles. For instance, when
![]() $M=\mathbb CP^1$
with the standard coordinate charts
$M=\mathbb CP^1$
with the standard coordinate charts
![]() $U_0, U_\infty \subset \mathbb CP^1$
, and
$U_0, U_\infty \subset \mathbb CP^1$
, and
![]() ${\mathfrak g}=\mathfrak {aff}(1,\mathbb C)$
is the 2-dimensional Lie subalgebra of
${\mathfrak g}=\mathfrak {aff}(1,\mathbb C)$
is the 2-dimensional Lie subalgebra of
![]() $\mathfrak {sl}(2,\mathbb C) \subset \mathcal {D}(M)$
, then
$\mathfrak {sl}(2,\mathbb C) \subset \mathcal {D}(M)$
, then
The isomorphism between the group of
![]() ${\mathfrak g}$
-equivariant line bundles and the Chevalley-Eilenberg cohomology group follows from the fact that all line bundles over
${\mathfrak g}$
-equivariant line bundles and the Chevalley-Eilenberg cohomology group follows from the fact that all line bundles over
![]() $\mathbb C$
are trivial. On
$\mathbb C$
are trivial. On
![]() $\mathbb CP^1$
, however, there are only countably many line bundles – namely,
$\mathbb CP^1$
, however, there are only countably many line bundles – namely,
![]() $\mathcal {O}_{\mathbb CP^1}(k)$
for
$\mathcal {O}_{\mathbb CP^1}(k)$
for
![]() $k \in \mathbb Z$
. In this case,
$k \in \mathbb Z$
. In this case,
![]() $\mathrm {Pic}_{\mathfrak g}(\mathbb CP^1) =\mathbb C \times \mathbb Z$
, where
$\mathrm {Pic}_{\mathfrak g}(\mathbb CP^1) =\mathbb C \times \mathbb Z$
, where
![]() $\mathbb Z=\mathrm {Pic}(\mathbb CP^1)$
. However, not all
$\mathbb Z=\mathrm {Pic}(\mathbb CP^1)$
. However, not all
![]() ${\mathfrak g}$
-equivariant line bundles are of the form
${\mathfrak g}$
-equivariant line bundles are of the form
![]() $[D]$
for some
$[D]$
for some
![]() ${\mathfrak g}$
-invariant divisor D. Instead, as a consequence of the necessary criterion of Theorem 1.3, we have
${\mathfrak g}$
-invariant divisor D. Instead, as a consequence of the necessary criterion of Theorem 1.3, we have
![]() $\mathrm {Div}_{\mathfrak g}(\mathbb CP^1) = \mathbb Z$
. For more details, see Example 2.27.
$\mathrm {Div}_{\mathfrak g}(\mathbb CP^1) = \mathbb Z$
. For more details, see Example 2.27.
In Section 3, we focus on the important cases of projectable Lie algebras of vector fields on affine bundles and on jet bundles. In these situations, one can consider divisors whose restriction to fibers are polynomial. Let
![]() $\hat {\mathfrak g}$
be a projectable Lie algebra of vector fields on the total space of an affine bundle
$\hat {\mathfrak g}$
be a projectable Lie algebra of vector fields on the total space of an affine bundle
![]() $\pi \colon E\to M$
that preserves the affine structure on E, and let
$\pi \colon E\to M$
that preserves the affine structure on E, and let
![]() ${\mathfrak g}=d\pi (\hat {\mathfrak g})\subset \mathcal {D}(M)$
.
${\mathfrak g}=d\pi (\hat {\mathfrak g})\subset \mathcal {D}(M)$
.
Theorem 1.4. If D is a
![]() $\hat {\mathfrak g}$
-invariant polynomial divisor on the affine bundle E, then
$\hat {\mathfrak g}$
-invariant polynomial divisor on the affine bundle E, then
![]() $[D] = \pi ^*L$
for some
$[D] = \pi ^*L$
for some
![]() ${\mathfrak g}$
-equivariant line bundle
${\mathfrak g}$
-equivariant line bundle
![]() $L\in \Phi _1(\mathrm {Pic}_{\mathfrak g}(M))$
.
$L\in \Phi _1(\mathrm {Pic}_{\mathfrak g}(M))$
.
In other words, the
![]() $\hat {\mathfrak g}$
-equivariant line bundle over E corresponding to a
$\hat {\mathfrak g}$
-equivariant line bundle over E corresponding to a
![]() $\hat {\mathfrak g}$
-invariant polynomial divisor is the pullback of a
$\hat {\mathfrak g}$
-invariant polynomial divisor is the pullback of a
![]() ${\mathfrak g}$
-equivariant line bundle over M. The same idea works for jet bundles because the bundle
${\mathfrak g}$
-equivariant line bundle over M. The same idea works for jet bundles because the bundle
![]() $\pi _{k+1,k}\colon \mathbf {J}^{k+1}\to \mathbf {J}^k$
for
$\pi _{k+1,k}\colon \mathbf {J}^{k+1}\to \mathbf {J}^k$
for
![]() $k\geq 1$
has a natural affine structure in fibers. (For jet spaces of sections of line bundles with the contact transformation algebra, the natural affine structure in fibers starts at
$k\geq 1$
has a natural affine structure in fibers. (For jet spaces of sections of line bundles with the contact transformation algebra, the natural affine structure in fibers starts at
![]() $k=2$
, with the corresponding modification of the claim.)
$k=2$
, with the corresponding modification of the claim.)
Theorem 1.5. Let
![]() ${\mathfrak g}^{(k)} \subset \mathcal {D}(\mathbf {J}^k)$
be the prolongation of a Lie algebra
${\mathfrak g}^{(k)} \subset \mathcal {D}(\mathbf {J}^k)$
be the prolongation of a Lie algebra
![]() ${\mathfrak g}$
of point transformations on
${\mathfrak g}$
of point transformations on
![]() $\mathbf {J}^0$
,
$\mathbf {J}^0$
,
![]() $0<k\leq \infty $
. If D is a
$0<k\leq \infty $
. If D is a
![]() ${\mathfrak g}^{(k)}$
-invariant divisor that is polynomial in fibers of
${\mathfrak g}^{(k)}$
-invariant divisor that is polynomial in fibers of
![]() $\pi _{k,1}\colon \mathbf {J}^k \to \mathbf {J}^1$
, then
$\pi _{k,1}\colon \mathbf {J}^k \to \mathbf {J}^1$
, then
![]() $[D] = \pi _{k,1}^*L$
for some
$[D] = \pi _{k,1}^*L$
for some
![]() ${\mathfrak g}^{(1)}$
-equivariant line bundle
${\mathfrak g}^{(1)}$
-equivariant line bundle
![]() $L \in \Phi _1(\mathrm {Pic}_{{\mathfrak g}^{(1)}}(\mathbf {J}^1))$
.
$L \in \Phi _1(\mathrm {Pic}_{{\mathfrak g}^{(1)}}(\mathbf {J}^1))$
.
This result provides our main application for classification of global relative invariants of the prolonged
![]() ${\mathfrak g}$
-action on
${\mathfrak g}$
-action on
![]() $\mathbf {J}^\infty $
, which is an essential step in the classification of all invariant differential equations (see [Reference Kruglikov and Schneider20] for a series of examples of this technique). We note that while the Gelfand-Fuks type cohomology
$\mathbf {J}^\infty $
, which is an essential step in the classification of all invariant differential equations (see [Reference Kruglikov and Schneider20] for a series of examples of this technique). We note that while the Gelfand-Fuks type cohomology
![]() $H^1({\mathfrak g}^{(\infty )},\mathcal {F}(\mathbf {J}^\infty ))$
may be large and hard to compute, the theorem reduces the problem to finite dimensions. To illustrate this, we will show how this allows to effectively treat relative differential invariants of curves in
$H^1({\mathfrak g}^{(\infty )},\mathcal {F}(\mathbf {J}^\infty ))$
may be large and hard to compute, the theorem reduces the problem to finite dimensions. To illustrate this, we will show how this allows to effectively treat relative differential invariants of curves in
![]() $\mathbb CP^2$
under the action of the Möbius algebra of projective transformations as well as relative differential invariants of second-order ODEs under the infinite-dimensional Lie algebra of point transformations.
$\mathbb CP^2$
under the action of the Möbius algebra of projective transformations as well as relative differential invariants of second-order ODEs under the infinite-dimensional Lie algebra of point transformations.
The main results are proved and expanded in the following sections. To be precise, Theorem 1.1 corresponds to Propositions 2.10 and 2.13, Theorem 1.3 to Propositions 2.22 and 2.25, and Theorem 1.4 to Propositions 3.2 and 3.3. Theorem 1.5 is an instance of results summarized in Propositions 3.6, 3.7 and 3.8. Other results are presented in the main text – in particular, Theorem 2.33 which is a partial converse to Theorem 1.3 in the case of algebraic group actions. We end with examples that illustrate computations of global relative differential invariants using our formalism.
In this paper, we concentrate on the complex analytic and complex algebraic situation, using notation
![]() ${\mathbb C} P^n$
instead of
${\mathbb C} P^n$
instead of
![]() $\mathbb P^n$
to stress that a part of our results extend to the real analytic and real algebraic case, with examples like real projective spaces
$\mathbb P^n$
to stress that a part of our results extend to the real analytic and real algebraic case, with examples like real projective spaces
![]() ${\mathbb R} P^n$
, real jet spaces
${\mathbb R} P^n$
, real jet spaces
![]() $\mathbf {J}^\infty $
, etc. In particular, examples A–C may be treated in the real context.
$\mathbf {J}^\infty $
, etc. In particular, examples A–C may be treated in the real context.
2 Analytic invariant divisors and equivariant line bundles
Let
![]() ${\mathfrak g} \subset \mathcal {D}(M)$
denote a Lie algebra of holomorphic vector fields on the complex manifold M. For
${\mathfrak g} \subset \mathcal {D}(M)$
denote a Lie algebra of holomorphic vector fields on the complex manifold M. For
![]() $M= \mathbb C^n$
, it is well known that lifts of a Lie algebra
$M= \mathbb C^n$
, it is well known that lifts of a Lie algebra
![]() ${\mathfrak g}$
to the trivial line bundle
${\mathfrak g}$
to the trivial line bundle
![]() $M \times \mathbb C$
are parametrized by the Chevalley-Eilenberg cohomology
$M \times \mathbb C$
are parametrized by the Chevalley-Eilenberg cohomology
![]() ${\mathrm {H}}^1(\mathfrak g, \mathcal {O}(M))$
. This is also the space where weights of relative
${\mathrm {H}}^1(\mathfrak g, \mathcal {O}(M))$
. This is also the space where weights of relative
![]() ${\mathfrak g}$
-invariants take values. We refer to [Reference Chevalley and Eilenberg6, Reference Fuks9] for the general Lie algebra cohomology theory to [Reference Cariñena, del Olmo and Winternitz4] for its relation to relative (differential) invariants and to [Reference Fels and Olver7, Reference Schneider27] for a relation to lifts.
${\mathfrak g}$
-invariants take values. We refer to [Reference Chevalley and Eilenberg6, Reference Fuks9] for the general Lie algebra cohomology theory to [Reference Cariñena, del Olmo and Winternitz4] for its relation to relative (differential) invariants and to [Reference Fels and Olver7, Reference Schneider27] for a relation to lifts.
The goal of this section is to generalize these results to arbitrary holomorphic line bundles over complex manifolds and replace the notion of relative
![]() ${\mathfrak g}$
-invariant functions with
${\mathfrak g}$
-invariant functions with
![]() ${\mathfrak g}$
-invariant divisors on M.
${\mathfrak g}$
-invariant divisors on M.
2.1 Picard group and multipliers
Let us start with a quick overview of holomorphic line bundles, sufficient for our purpose (see [Reference Griffiths and Harris11, Reference Huybrechts15]). For an open subset
![]() $U \subset M$
, denote by
$U \subset M$
, denote by
![]() $\mathcal {O}(U)$
the space of holomorphic functions on U, and by
$\mathcal {O}(U)$
the space of holomorphic functions on U, and by
![]() $\mathcal {O}^\times (U)$
the subspace of nonvanishing functions. The corresponding sheaves on M are denoted by
$\mathcal {O}^\times (U)$
the subspace of nonvanishing functions. The corresponding sheaves on M are denoted by
![]() $\mathcal {O}$
and
$\mathcal {O}$
and
![]() $\mathcal {O}^\times $
, respectively. Let
$\mathcal {O}^\times $
, respectively. Let
![]() $\pi \colon L \to M$
be a line bundle and consider an open cover
$\pi \colon L \to M$
be a line bundle and consider an open cover
![]() $\mathcal {U} = \{U_\alpha \}$
of M that trivializes
$\mathcal {U} = \{U_\alpha \}$
of M that trivializes
![]() $\pi $
(i.e.,
$\pi $
(i.e.,
![]() $\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C$
). The line bundle is uniquely determined by its transition functions
$\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C$
). The line bundle is uniquely determined by its transition functions
![]() $g_{\alpha \beta } \in \mathcal {O}^\times (U_\alpha \cap U_\beta )$
, which satisfy
$g_{\alpha \beta } \in \mathcal {O}^\times (U_\alpha \cap U_\beta )$
, which satisfy
![]() $ g_{\alpha \beta } g_{\beta \gamma } = g_{\alpha \gamma }$
. Two collections of transition functions
$ g_{\alpha \beta } g_{\beta \gamma } = g_{\alpha \gamma }$
. Two collections of transition functions
![]() $\{g_{\alpha \beta }\}$
,
$\{g_{\alpha \beta }\}$
,
![]() $\{\tilde g_{\alpha \beta }\}$
define the same bundle if and only if
$\{\tilde g_{\alpha \beta }\}$
define the same bundle if and only if
![]() $\tilde g_{\alpha \beta } = \frac {f_\alpha }{f_\beta } g_{\alpha \beta }$
for some functions
$\tilde g_{\alpha \beta } = \frac {f_\alpha }{f_\beta } g_{\alpha \beta }$
for some functions
![]() $f_\alpha \in \mathcal {O}^\times (U_\alpha )$
.
$f_\alpha \in \mathcal {O}^\times (U_\alpha )$
.
This leads to a description of line bundles in terms of Čech cohomology. Define the complex
 $$\begin{align*}0 \xrightarrow{} \prod_{\alpha} \mathcal{O}^\times (U_\alpha) \xrightarrow{\delta^0} \prod_{\alpha \neq \beta} \mathcal{O}^\times(U_\alpha \cap U_\beta) \xrightarrow{\delta^1} \prod_{\alpha \neq \beta \neq \gamma \neq \alpha}\mathcal{O}^\times(U_\alpha \cap U_\beta \cap U_\gamma) \xrightarrow{} \cdots, \end{align*}$$
$$\begin{align*}0 \xrightarrow{} \prod_{\alpha} \mathcal{O}^\times (U_\alpha) \xrightarrow{\delta^0} \prod_{\alpha \neq \beta} \mathcal{O}^\times(U_\alpha \cap U_\beta) \xrightarrow{\delta^1} \prod_{\alpha \neq \beta \neq \gamma \neq \alpha}\mathcal{O}^\times(U_\alpha \cap U_\beta \cap U_\gamma) \xrightarrow{} \cdots, \end{align*}$$
with differentials given by
 $$ \begin{align*} (\delta^q \mu)_{\alpha_0 \cdots \alpha_{q+1}} = \prod_{i=0}^{q+1} \mu^{(-1)^{i+1}}_{\alpha_0 \cdots \hat \alpha_i \cdots \alpha_{q+1}} \Big|_{U_{\alpha_0} \cap \cdots \cap U_{\alpha_{q+1}}}, \qquad \mu = \{\mu_{\alpha_0 \cdots \alpha_q}\} \in \prod_{\alpha_0,\dots, \alpha_q} \mathcal{O}^\times(U_{\alpha_0} \cap \cdots \cap U_{\alpha_q}). \end{align*} $$
$$ \begin{align*} (\delta^q \mu)_{\alpha_0 \cdots \alpha_{q+1}} = \prod_{i=0}^{q+1} \mu^{(-1)^{i+1}}_{\alpha_0 \cdots \hat \alpha_i \cdots \alpha_{q+1}} \Big|_{U_{\alpha_0} \cap \cdots \cap U_{\alpha_{q+1}}}, \qquad \mu = \{\mu_{\alpha_0 \cdots \alpha_q}\} \in \prod_{\alpha_0,\dots, \alpha_q} \mathcal{O}^\times(U_{\alpha_0} \cap \cdots \cap U_{\alpha_q}). \end{align*} $$
In particular,
![]() $\delta ^0$
and
$\delta ^0$
and
![]() $\delta ^1$
are defined in the following way:
$\delta ^1$
are defined in the following way:
 $$ \begin{align*} (\delta^0\mu)_{\alpha \beta} &= \mu_{\alpha}/\mu_{\beta}, \qquad && \mu = \{\mu_\alpha\} \in \prod_{\alpha} \mathcal{O}^\times (U_\alpha),\\ (\delta^1\nu)_{\alpha \beta \gamma} &=\frac{ \nu_{\alpha \gamma}}{ \nu_{\alpha \beta} \nu_{\beta \gamma}} , \qquad && \nu = \{\nu_{\alpha \beta}\} \in \prod_{\alpha \neq \beta} \mathcal{O}^\times(U_\alpha \cap U_\beta). \end{align*} $$
$$ \begin{align*} (\delta^0\mu)_{\alpha \beta} &= \mu_{\alpha}/\mu_{\beta}, \qquad && \mu = \{\mu_\alpha\} \in \prod_{\alpha} \mathcal{O}^\times (U_\alpha),\\ (\delta^1\nu)_{\alpha \beta \gamma} &=\frac{ \nu_{\alpha \gamma}}{ \nu_{\alpha \beta} \nu_{\beta \gamma}} , \qquad && \nu = \{\nu_{\alpha \beta}\} \in \prod_{\alpha \neq \beta} \mathcal{O}^\times(U_\alpha \cap U_\beta). \end{align*} $$
The first Čech-cohomology with respect to the fixed open cover
![]() $\mathcal {U}$
, defined by
$\mathcal {U}$
, defined by
![]() ${\check {\mathrm {H}}}^1(\mathcal {U}, \mathcal {O}^\times ) = \ker (\delta ^1)/\mathrm {im}(\delta ^0)$
, is the group of transition functions on
${\check {\mathrm {H}}}^1(\mathcal {U}, \mathcal {O}^\times ) = \ker (\delta ^1)/\mathrm {im}(\delta ^0)$
, is the group of transition functions on
![]() $\mathcal {U}$
modulo the above equivalence relation.
$\mathcal {U}$
modulo the above equivalence relation.
The Picard group
![]() $\mathrm {Pic}(M)$
of equivalence classes of holomorphic line bundles over M can be described in terms of this cohomology group as follows:
$\mathrm {Pic}(M)$
of equivalence classes of holomorphic line bundles over M can be described in terms of this cohomology group as follows:
-
• If all line bundles are trivializable on the open charts in
 $\mathcal {U}$
(for instance, each
$\mathcal {U}$
(for instance, each
 $U_\alpha $
is biholomorphic to a polydisc with a possible factor
$U_\alpha $
is biholomorphic to a polydisc with a possible factor
 $\mathbb C^\times $
), then
$\mathbb C^\times $
), then
 $\mathrm {Pic}(M) \simeq {\check {\mathrm {H}}}^1(\mathcal {U},\mathcal {O}^\times )$
.
$\mathrm {Pic}(M) \simeq {\check {\mathrm {H}}}^1(\mathcal {U},\mathcal {O}^\times )$
. -
• In general,
 $\mathrm {Pic}(M) \simeq {\check {\mathrm {H}}}^1(M,\mathcal {O}^\times ):= \varinjlim {\check {\mathrm {H}}}^1(\mathcal {U}, \mathcal {O}^\times )$
is the direct limit as
$\mathrm {Pic}(M) \simeq {\check {\mathrm {H}}}^1(M,\mathcal {O}^\times ):= \varinjlim {\check {\mathrm {H}}}^1(\mathcal {U}, \mathcal {O}^\times )$
is the direct limit as
 $\mathcal {U}$
becomes finer.
$\mathcal {U}$
becomes finer.
In both cases, the identification is a group isomorphism. In particular, if the conditions of Leray’s theorem hold, the first description is applicable (see [Reference Griffiths and Harris11, p.40] or the simpler Theorem 12.8 of [Reference Forster8], which will usually be sufficient for us).
Definition 2.1. A lift of
![]() $\mathfrak g \subset \mathcal {D}(M)$
to the line bundle
$\mathfrak g \subset \mathcal {D}(M)$
to the line bundle
![]() $\pi \colon L \to M$
is a Lie algebra
$\pi \colon L \to M$
is a Lie algebra
![]() $\hat {\mathfrak g} \subset \mathcal {D}_{\text {proj}}(L)$
of projectable vector fields, such that
$\hat {\mathfrak g} \subset \mathcal {D}_{\text {proj}}(L)$
of projectable vector fields, such that
![]() $d\pi \colon \hat {\mathfrak g}\to \mathfrak g$
is a Lie algebra isomorphism and
$d\pi \colon \hat {\mathfrak g}\to \mathfrak g$
is a Lie algebra isomorphism and
![]() $\hat {{\mathfrak g}}$
commutes with the natural vertical vector field
$\hat {{\mathfrak g}}$
commutes with the natural vertical vector field
![]() $u \partial _u$
(u is a linear fiber coordinate). The pair
$u \partial _u$
(u is a linear fiber coordinate). The pair
![]() $(\pi , \hat {\mathfrak g})$
is called a
$(\pi , \hat {\mathfrak g})$
is called a
![]() ${\mathfrak g}$
-equivariant line bundle. (We also refer to
${\mathfrak g}$
-equivariant line bundle. (We also refer to
![]() $\pi $
or L as a
$\pi $
or L as a
![]() ${\mathfrak g}$
-equivariant bundle when a lift exists.)
${\mathfrak g}$
-equivariant bundle when a lift exists.)
For instance, the canonical line bundle
![]() $K_M = \Lambda ^{\dim M} T^*M$
(see [Reference Huybrechts15, Ch. 2.2]) always admits a canonical lift of
$K_M = \Lambda ^{\dim M} T^*M$
(see [Reference Huybrechts15, Ch. 2.2]) always admits a canonical lift of
![]() ${\mathfrak g} \subset \mathcal {D}(M)$
. Thus, it is an (often nontrivial)
${\mathfrak g} \subset \mathcal {D}(M)$
. Thus, it is an (often nontrivial)
![]() ${\mathfrak g}$
-equivariant line bundle.
${\mathfrak g}$
-equivariant line bundle.
In general, the lift of a vector field
![]() $X\in {\mathfrak g}$
can be defined on
$X\in {\mathfrak g}$
can be defined on
![]() $\pi ^{-1}(U_\alpha )\simeq U_\alpha \times {\mathbb C}$
by
$\pi ^{-1}(U_\alpha )\simeq U_\alpha \times {\mathbb C}$
by
similar to formula (4.1) in [Reference Fels and Olver7]. To simplify notation, we will write X instead of
![]() $X|_{U_\alpha }$
when there is no room for confusion. The condition
$X|_{U_\alpha }$
when there is no room for confusion. The condition
![]() $[\hat X, \hat Y] = \widehat {[X,Y]}$
for each
$[\hat X, \hat Y] = \widehat {[X,Y]}$
for each
![]() $X,Y\in {\mathfrak g}$
implies that
$X,Y\in {\mathfrak g}$
implies that
![]() $\lambda _\alpha $
satisfies
$\lambda _\alpha $
satisfies
Changing the coordinate function on the fiber,
![]() $v=e^{\mu _\alpha }u$
for some function
$v=e^{\mu _\alpha }u$
for some function
![]() $\mu _\alpha \in \mathcal {O}(U_\alpha )$
gives
$\mu _\alpha \in \mathcal {O}(U_\alpha )$
gives
In this sense, two lifts
![]() $\lambda _\alpha , \tilde \lambda _\alpha $
on
$\lambda _\alpha , \tilde \lambda _\alpha $
on
![]() $U_\alpha $
are equivalent if and only if there exists a
$U_\alpha $
are equivalent if and only if there exists a
![]() $\mu _\alpha $
satisfying
$\mu _\alpha $
satisfying
The conditions (2.1) and (2.2) can be interpreted in terms of Lie algebra cohomology of
![]() $\mathfrak g$
with coefficients in the
$\mathfrak g$
with coefficients in the
![]() $\mathfrak g$
-module
$\mathfrak g$
-module
![]() $\mathcal {O}(U_\alpha )$
. Consider the Chevalley-Eilenberg complex
$\mathcal {O}(U_\alpha )$
. Consider the Chevalley-Eilenberg complex
where the maps
![]() $d^0$
and
$d^0$
and
![]() $d^1$
are given by
$d^1$
are given by
 $$\begin{align*} (d^0 \mu_\alpha)(X) &= X(\mu_\alpha), \qquad &&\mu_\alpha \in \mathcal{O}(U_\alpha), \\ (d^1 \lambda_\alpha)(X,Y) &= X(\lambda_\alpha(Y))-Y(\lambda_\alpha(X))-\lambda_\alpha([X,Y]), \qquad &&\lambda_\alpha \in {\mathfrak g}^* \otimes \mathcal{O}(U_\alpha), \end{align*}$$
$$\begin{align*} (d^0 \mu_\alpha)(X) &= X(\mu_\alpha), \qquad &&\mu_\alpha \in \mathcal{O}(U_\alpha), \\ (d^1 \lambda_\alpha)(X,Y) &= X(\lambda_\alpha(Y))-Y(\lambda_\alpha(X))-\lambda_\alpha([X,Y]), \qquad &&\lambda_\alpha \in {\mathfrak g}^* \otimes \mathcal{O}(U_\alpha), \end{align*}$$
for
![]() $X,Y \in {\mathfrak g}$
(see [Reference Chevalley and Eilenberg6]). Notice that
$X,Y \in {\mathfrak g}$
(see [Reference Chevalley and Eilenberg6]). Notice that
![]() $\mathrm {Hom}({\mathfrak g},F)={\mathfrak g}^* \otimes F$
when one of the factors is finite-dimensional. If both factors are infinte-dimensional, a completion of the tensor product is required. We omit this from the notation, understanding by default that
$\mathrm {Hom}({\mathfrak g},F)={\mathfrak g}^* \otimes F$
when one of the factors is finite-dimensional. If both factors are infinte-dimensional, a completion of the tensor product is required. We omit this from the notation, understanding by default that
![]() $\Lambda ^i {\mathfrak g}^*\otimes F$
may stand for
$\Lambda ^i {\mathfrak g}^*\otimes F$
may stand for
![]() $\mathrm {Hom}(\Lambda ^i {\mathfrak g}^*,F)$
here and below.
$\mathrm {Hom}(\Lambda ^i {\mathfrak g}^*,F)$
here and below.
Define the cohomology groups
It is clear that
![]() $\lambda _\alpha \in \mathfrak g^* \otimes \mathcal {O}(U_\alpha )$
defines a lift of
$\lambda _\alpha \in \mathfrak g^* \otimes \mathcal {O}(U_\alpha )$
defines a lift of
![]() $\mathfrak g$
to
$\mathfrak g$
to
![]() $U_\alpha \times \mathbb C$
if and only if
$U_\alpha \times \mathbb C$
if and only if
![]() $d^1 \lambda _\alpha =0$
. Furthermore, two cocycles
$d^1 \lambda _\alpha =0$
. Furthermore, two cocycles
![]() $\lambda _\alpha , \tilde \lambda _\alpha $
define equivalent lifts if and only if
$\lambda _\alpha , \tilde \lambda _\alpha $
define equivalent lifts if and only if
![]() $\tilde \lambda _\alpha = \lambda _\alpha + d^0 \mu _\alpha $
for some
$\tilde \lambda _\alpha = \lambda _\alpha + d^0 \mu _\alpha $
for some
![]() $\mu _\alpha \in \mathcal {O}(U_\alpha )$
. Thus, equivalence classes of lifts of
$\mu _\alpha \in \mathcal {O}(U_\alpha )$
. Thus, equivalence classes of lifts of
![]() $\mathfrak g|_{U_\alpha }$
to
$\mathfrak g|_{U_\alpha }$
to
![]() $U_\alpha \times \mathbb C$
are in one-to-one correspondence with elements in
$U_\alpha \times \mathbb C$
are in one-to-one correspondence with elements in
![]() ${\mathrm {H}}^1(\mathfrak g, \mathcal {O}(U_\alpha ))$
. (Note also that
${\mathrm {H}}^1(\mathfrak g, \mathcal {O}(U_\alpha ))$
. (Note also that
![]() ${\mathrm {H}}^0({\mathfrak g}, \mathcal {O}(U_\alpha ))=\mathcal {O}(U_\alpha )^{\mathfrak g}$
consists of
${\mathrm {H}}^0({\mathfrak g}, \mathcal {O}(U_\alpha ))=\mathcal {O}(U_\alpha )^{\mathfrak g}$
consists of
![]() ${\mathfrak g}$
-invariants.)
${\mathfrak g}$
-invariants.)
Remark 2.2. If
![]() $U_\alpha $
is a polydisc for each
$U_\alpha $
is a polydisc for each
![]() $\alpha $
, then any function in
$\alpha $
, then any function in
![]() $\mathcal {O}^\times (U_\alpha )$
is of the form
$\mathcal {O}^\times (U_\alpha )$
is of the form
![]() $e^\mu $
, and the argument above works. If
$e^\mu $
, and the argument above works. If
![]() $U_\alpha $
is a general open set, one replaces
$U_\alpha $
is a general open set, one replaces
![]() $e^{\mu _\alpha } f_\alpha $
with
$e^{\mu _\alpha } f_\alpha $
with
![]() $\mu _\alpha f_\alpha $
, where
$\mu _\alpha f_\alpha $
, where
![]() $\mu _\alpha \in \mathcal {O}^\times (U_\alpha )$
. Then the local lifts are in one-to-one correspondence with elements in the cohomology group of the complex
$\mu _\alpha \in \mathcal {O}^\times (U_\alpha )$
. Then the local lifts are in one-to-one correspondence with elements in the cohomology group of the complex
We will use this slightly modified complex below with the notation
 $$\begin{align*}{\tilde{\mathrm{H}}}^1({\mathfrak g},\mathcal{O}(U_\alpha)) = \frac{\ker(d^1)}{\mathrm{im}(d^0 \log)}. \end{align*}$$
$$\begin{align*}{\tilde{\mathrm{H}}}^1({\mathfrak g},\mathcal{O}(U_\alpha)) = \frac{\ker(d^1)}{\mathrm{im}(d^0 \log)}. \end{align*}$$
Elements in
![]() ${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(U_\alpha ))$
yield local lifts of
${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(U_\alpha ))$
yield local lifts of
![]() ${\mathfrak g}$
to
${\mathfrak g}$
to
![]() $\pi ^{-1}(U_\alpha )$
that may not glue together to a global lift on L. On
$\pi ^{-1}(U_\alpha )$
that may not glue together to a global lift on L. On
![]() $U_\alpha \cap U_\beta $
, a lift is given by both
$U_\alpha \cap U_\beta $
, a lift is given by both
![]() $X+\lambda _\alpha (X)\,u_\alpha \partial _{u_\alpha }$
and
$X+\lambda _\alpha (X)\,u_\alpha \partial _{u_\alpha }$
and
![]() $X+\lambda _\beta (X)\,u_\beta \partial _{u_\beta }$
. The fiber coordinates relate on overlaps by
$X+\lambda _\beta (X)\,u_\beta \partial _{u_\beta }$
. The fiber coordinates relate on overlaps by
![]() $u_\alpha = g_{\alpha \beta } u_\beta $
, where the transition functions
$u_\alpha = g_{\alpha \beta } u_\beta $
, where the transition functions
![]() $\{g_{\alpha \beta }\}$
represent an element of
$\{g_{\alpha \beta }\}$
represent an element of
![]() ${\check {\mathrm {H}}}^1(\mathcal {U},\mathcal {O}^\times (M))$
. Thus,
${\check {\mathrm {H}}}^1(\mathcal {U},\mathcal {O}^\times (M))$
. Thus,
![]() $X+\lambda _\alpha (X)\,u_\alpha \partial _{u_\alpha }$
becomes
$X+\lambda _\alpha (X)\,u_\alpha \partial _{u_\alpha }$
becomes
![]() $X+(\lambda _\alpha (X)-X(g_{\alpha \beta })/g_{\alpha \beta })\,u_\beta \partial _{u_\beta }$
, resulting in the following compatibility condition on
$X+(\lambda _\alpha (X)-X(g_{\alpha \beta })/g_{\alpha \beta })\,u_\beta \partial _{u_\beta }$
, resulting in the following compatibility condition on
![]() $U_\alpha \cap U_\beta $
:
$U_\alpha \cap U_\beta $
:
 $$ \begin{align} \lambda_\alpha(X)-\lambda_\beta(X)=\frac{X(g_{\alpha \beta})}{g_{\alpha \beta}} = X(\log g_{\alpha \beta}), \qquad \forall X \in \mathfrak g. \end{align} $$
$$ \begin{align} \lambda_\alpha(X)-\lambda_\beta(X)=\frac{X(g_{\alpha \beta})}{g_{\alpha \beta}} = X(\log g_{\alpha \beta}), \qquad \forall X \in \mathfrak g. \end{align} $$
2.2 A double complex
To better understand the compatibility condition, consider the double complex

where
![]() $C^{p,q}$
are given by
$C^{p,q}$
are given by
 $$ \begin{align*} C^{0,q} &= \prod_{\alpha_0, \cdots, \alpha_q} \mathcal{O}^\times (U_{\alpha_0} \cap \cdots\cap U_{\alpha_q}),\\ C^{p,q} &= \prod_{\alpha_0, \cdots, \alpha_q} \Lambda^p \mathfrak g^* \otimes \mathcal{O}(U_{\alpha_0} \cap \cdots\cap U_{\alpha_q}), \quad p \geq 1, \end{align*} $$
$$ \begin{align*} C^{0,q} &= \prod_{\alpha_0, \cdots, \alpha_q} \mathcal{O}^\times (U_{\alpha_0} \cap \cdots\cap U_{\alpha_q}),\\ C^{p,q} &= \prod_{\alpha_0, \cdots, \alpha_q} \Lambda^p \mathfrak g^* \otimes \mathcal{O}(U_{\alpha_0} \cap \cdots\cap U_{\alpha_q}), \quad p \geq 1, \end{align*} $$
and the differentials
![]() $\delta ^{p,q} \colon C^{p,q} \to C^{p,q+1}$
and
$\delta ^{p,q} \colon C^{p,q} \to C^{p,q+1}$
and
![]() $d^{p,q} \colon C^{p,q} \to C^{p+1,q}$
are defined for
$d^{p,q} \colon C^{p,q} \to C^{p+1,q}$
are defined for
![]() $p=0$
by
$p=0$
by
 $$ \begin{align*} (\delta^{0,q} \mu)_{\alpha_0 \cdots \alpha_{q+1}} &= \prod_{i=0}^{q+1} \mu_{\alpha_0 \cdots \hat \alpha_i \cdots \alpha_{q+1}}^{(-1)^{i+1}} \Big|_{U_{\alpha_0} \cap \cdots \cap U_{\alpha_{q+1}}}, \\ (d^{0,q}\mu_{\alpha_0 \cdots \alpha_q})(X) &= X(\log \mu_{\alpha_0 \cdots \alpha_q}) = \frac{X(\mu_{\alpha_0 \cdots \alpha_q})}{\mu_{\alpha_0 \cdots \alpha_q}}, \end{align*} $$
$$ \begin{align*} (\delta^{0,q} \mu)_{\alpha_0 \cdots \alpha_{q+1}} &= \prod_{i=0}^{q+1} \mu_{\alpha_0 \cdots \hat \alpha_i \cdots \alpha_{q+1}}^{(-1)^{i+1}} \Big|_{U_{\alpha_0} \cap \cdots \cap U_{\alpha_{q+1}}}, \\ (d^{0,q}\mu_{\alpha_0 \cdots \alpha_q})(X) &= X(\log \mu_{\alpha_0 \cdots \alpha_q}) = \frac{X(\mu_{\alpha_0 \cdots \alpha_q})}{\mu_{\alpha_0 \cdots \alpha_q}}, \end{align*} $$
and for
![]() $p> 0$
by
$p> 0$
by
 $$ \begin{align*} (\delta^{p,q} \mu)_{\alpha_0 \cdots \alpha_{q+1}} &= \sum_{i=0}^{q+1} (-1)^{i+1} \mu_{\alpha_0 \cdots \hat \alpha_i \cdots \alpha_{q+1}} \Big|_{U_{\alpha_0} \cap \cdots \cap U_{\alpha_{q+1}}}, \\ (d^{p,q}\mu_{\alpha_0 \cdots \alpha_q})(X_0, \dots, X_p) &=\sum_{i=0}^{p} (-1)^i X_i(\mu_{\alpha_0 \cdots \alpha_q}(X_0,\dots, X_{i-1}, X_{i+1}, \dots, X_p))\\ +\sum_{i<j}(-1)^{i+j}&(\mu_{\alpha_0 \cdots \alpha_q}([X_i,X_j],X_0,\dots, X_{i-1}, X_{i+1}, \dots, X_{j-1}, X_{j+1}, \dots, X_p)). \end{align*} $$
$$ \begin{align*} (\delta^{p,q} \mu)_{\alpha_0 \cdots \alpha_{q+1}} &= \sum_{i=0}^{q+1} (-1)^{i+1} \mu_{\alpha_0 \cdots \hat \alpha_i \cdots \alpha_{q+1}} \Big|_{U_{\alpha_0} \cap \cdots \cap U_{\alpha_{q+1}}}, \\ (d^{p,q}\mu_{\alpha_0 \cdots \alpha_q})(X_0, \dots, X_p) &=\sum_{i=0}^{p} (-1)^i X_i(\mu_{\alpha_0 \cdots \alpha_q}(X_0,\dots, X_{i-1}, X_{i+1}, \dots, X_p))\\ +\sum_{i<j}(-1)^{i+j}&(\mu_{\alpha_0 \cdots \alpha_q}([X_i,X_j],X_0,\dots, X_{i-1}, X_{i+1}, \dots, X_{j-1}, X_{j+1}, \dots, X_p)). \end{align*} $$
We will sometimes write
![]() $C^{p,q}({\mathfrak g},\ \mathcal {U})$
for precision when there would otherwise be ambiguity. The horizontal lines (q fixed) are nearly Chevalley-Eilenberg complexes of
$C^{p,q}({\mathfrak g},\ \mathcal {U})$
for precision when there would otherwise be ambiguity. The horizontal lines (q fixed) are nearly Chevalley-Eilenberg complexes of
![]() $\mathfrak g$
with coefficients in the
$\mathfrak g$
with coefficients in the
![]() $\mathfrak g$
-modules
$\mathfrak g$
-modules
![]() $\mathcal {O}(U_\alpha ), \mathcal {O}(U_{\alpha } \cap U_{\beta })$
, etc; however,
$\mathcal {O}(U_\alpha ), \mathcal {O}(U_{\alpha } \cap U_{\beta })$
, etc; however,
![]() $(C^{0,q},d^{0,q})$
are adjusted in accordance with Remark 2.2. The vertical lines (p fixed) are Čech complexes with respect to the open cover
$(C^{0,q},d^{0,q})$
are adjusted in accordance with Remark 2.2. The vertical lines (p fixed) are Čech complexes with respect to the open cover
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Remark 2.3. For
![]() $C^{0,q}$
, it is natural to use multiplicative notation (with identity element
$C^{0,q}$
, it is natural to use multiplicative notation (with identity element
![]() $1$
), while for
$1$
), while for
![]() $C^{p,q}$
for
$C^{p,q}$
for
![]() $p \geq 1$
, it is better to use additive notation (with identity element
$p \geq 1$
, it is better to use additive notation (with identity element
![]() $0$
). Using these notations consistently becomes difficult when we are dealing with this double complex, and even more so when we work with the total complex defined below. We will therefore use
$0$
). Using these notations consistently becomes difficult when we are dealing with this double complex, and even more so when we work with the total complex defined below. We will therefore use
![]() $0$
to denote the identity element in these groups and in the corresponding cohomology groups.
$0$
to denote the identity element in these groups and in the corresponding cohomology groups.
The total complex corresponding to the double complex
![]() $C^{\bullet , \bullet }$
is defined as follows:
$C^{\bullet , \bullet }$
is defined as follows:
The identity
![]() $\partial ^{i+1} \circ \partial ^i =0$
expresses the fact that the double complex is a commutative diagram. The cohomology groups of the total complex are defined in the usual way:
$\partial ^{i+1} \circ \partial ^i =0$
expresses the fact that the double complex is a commutative diagram. The cohomology groups of the total complex are defined in the usual way:
 $$\begin{align*}{\mathrm{H}}^0(\mathrm{Tot}^\bullet(C))= \ker(\partial^0), \qquad {\mathrm{H}}^i(\mathrm{Tot}^\bullet(C))= \frac{\ker(\partial^i)}{\mathrm{im}(\partial^{i-1})}.\end{align*}$$
$$\begin{align*}{\mathrm{H}}^0(\mathrm{Tot}^\bullet(C))= \ker(\partial^0), \qquad {\mathrm{H}}^i(\mathrm{Tot}^\bullet(C))= \frac{\ker(\partial^i)}{\mathrm{im}(\partial^{i-1})}.\end{align*}$$
The double complex also gives us several complexes of cohomology groups. The cohomology groups with respect to
![]() $d^{i,j}$
(with j fixed) make up the following complexes:
$d^{i,j}$
(with j fixed) make up the following complexes:

Simultaneously, the cohomology groups with respect to
![]() $\delta ^{i,j}$
(with i fixed) also give complexes:
$\delta ^{i,j}$
(with i fixed) also give complexes:

Thus, we get the induced cohomology groups
 $$\begin{align*}{\mathrm{H}}_\delta^i({\mathrm{H}}_d^j(C^{\bullet, \bullet})) = \frac{\ker(\delta^{j,i}_*)}{\mathrm{im}(\delta^{j,i-1}_*)}, \qquad {\mathrm{H}}_d^i({\mathrm{H}}_\delta^j(C^{\bullet,\bullet})) = \frac{\ker(d^{i,j}_*)}{\mathrm{im}(d^{i-1,j}_*)}, \end{align*}$$
$$\begin{align*}{\mathrm{H}}_\delta^i({\mathrm{H}}_d^j(C^{\bullet, \bullet})) = \frac{\ker(\delta^{j,i}_*)}{\mathrm{im}(\delta^{j,i-1}_*)}, \qquad {\mathrm{H}}_d^i({\mathrm{H}}_\delta^j(C^{\bullet,\bullet})) = \frac{\ker(d^{i,j}_*)}{\mathrm{im}(d^{i-1,j}_*)}, \end{align*}$$
for
![]() $i \geq 1$
and
$i \geq 1$
and
In the general setting of the total complex, we have the two projections (homomorphisms)

defined by
where
![]() $[(g,\lambda )]$
denotes the equivalence class of
$[(g,\lambda )]$
denotes the equivalence class of
![]() $(g,\lambda ) \in \ker (\partial ^1)$
. We use the notation
$(g,\lambda ) \in \ker (\partial ^1)$
. We use the notation
![]() $g = \{g_{\alpha \beta }\}$
for an element in
$g = \{g_{\alpha \beta }\}$
for an element in
![]() $C^{0,1}$
and
$C^{0,1}$
and
![]() $\lambda =\{\lambda _\alpha \}$
for an element in
$\lambda =\{\lambda _\alpha \}$
for an element in
![]() $C^{1,0}$
, and note that
$C^{1,0}$
, and note that
Lemma 2.4. The maps
![]() $\Phi _1, \Phi _2$
have the following kernels:
$\Phi _1, \Phi _2$
have the following kernels:
Proof. The arguments for the two isomorphisms are similar to each other, so we prove the statement only for
![]() $\ker (\Phi _2)$
. If
$\ker (\Phi _2)$
. If
![]() $[(g,\lambda )] \in \ker (\Phi _2)$
, then there exists an element
$[(g,\lambda )] \in \ker (\Phi _2)$
, then there exists an element
![]() $\tilde g \in \ker (\delta ^{0,1})$
such that
$\tilde g \in \ker (\delta ^{0,1})$
such that
![]() $[(\tilde g,0)] = [(g,\lambda )]$
. We have
$[(\tilde g,0)] = [(g,\lambda )]$
. We have
![]() $d^{0,1}\tilde g = \delta ^{1,0} 0=0$
, so that
$d^{0,1}\tilde g = \delta ^{1,0} 0=0$
, so that
![]() $\tilde g\in \ker (d^{0,1})$
. Furthermore, since
$\tilde g\in \ker (d^{0,1})$
. Furthermore, since
![]() $(\tilde g,0) + \partial ^0(\mu ) = (\tilde g \cdot \delta ^{0,0} \mu , d^{0,0}\mu )$
, the freedom in choice of representative
$(\tilde g,0) + \partial ^0(\mu ) = (\tilde g \cdot \delta ^{0,0} \mu , d^{0,0}\mu )$
, the freedom in choice of representative
![]() $\tilde g$
is exactly
$\tilde g$
is exactly
![]() $\delta ^{0,0}(\ker (d^{0,0}))$
. Thus,
$\delta ^{0,0}(\ker (d^{0,0}))$
. Thus,
![]() $\ker (\Phi _2)={\mathrm {H}}_\delta ^1({\mathrm {H}}_d^0(C^{\bullet ,\bullet }))$
.
$\ker (\Phi _2)={\mathrm {H}}_\delta ^1({\mathrm {H}}_d^0(C^{\bullet ,\bullet }))$
.
Lemma 2.4 is equivalent to exactness of the two sequences
and furthermore, we have
where
![]() $(\mathcal {O}^\times )^{\mathfrak g} \subset \mathcal {O}^\times $
is the subsheaf of
$(\mathcal {O}^\times )^{\mathfrak g} \subset \mathcal {O}^\times $
is the subsheaf of
![]() ${\mathfrak g}$
-invariants.
${\mathfrak g}$
-invariants.
Corollary 2.5.
-
(i) If
 ${\mathrm {H}}_\delta ^1(C^{0,\bullet }) = 0$
, then
${\mathrm {H}}_\delta ^1(C^{0,\bullet }) = 0$
, then
 ${\mathrm {H}}^1(\mathrm {Tot}^\bullet (C)) \simeq {\mathrm {H}}_d^1({\mathrm {H}}_\delta ^0(C^{\bullet , \bullet }))$
.
${\mathrm {H}}^1(\mathrm {Tot}^\bullet (C)) \simeq {\mathrm {H}}_d^1({\mathrm {H}}_\delta ^0(C^{\bullet , \bullet }))$
. -
(ii) Likewise, if
 ${\mathrm {H}}_d^1(C^{\bullet ,0})=0$
, then
${\mathrm {H}}_d^1(C^{\bullet ,0})=0$
, then
 ${\mathrm {H}}^1(\mathrm {Tot}^\bullet (C)) \simeq {\mathrm {H}}_\delta ^1({\mathrm {H}}_d^0(C^{\bullet ,\bullet }))$
.
${\mathrm {H}}^1(\mathrm {Tot}^\bullet (C)) \simeq {\mathrm {H}}_\delta ^1({\mathrm {H}}_d^0(C^{\bullet ,\bullet }))$
.
Lemma 2.6. The images of
![]() $\Phi _1,\Phi _2$
are given by the following exact sequences:
$\Phi _1,\Phi _2$
are given by the following exact sequences:
 $$ \begin{align*} 0 \longrightarrow \mathrm{im}(\Phi_1) \longrightarrow {\mathrm{H}}_d^0({\mathrm{H}}_\delta^1(C^{\bullet, \bullet})) \longrightarrow {\mathrm{H}}_d^2({\mathrm{H}}_\delta^0(C^{\bullet,\bullet})), \\ 0 \longrightarrow \mathrm{im}(\Phi_2) \longrightarrow {\mathrm{H}}_\delta^0({\mathrm{H}}_d^1(C^{\bullet,\bullet})) \longrightarrow {\mathrm{H}}_\delta^2({\mathrm{H}}_d^0(C^{\bullet,\bullet})). \end{align*} $$
$$ \begin{align*} 0 \longrightarrow \mathrm{im}(\Phi_1) \longrightarrow {\mathrm{H}}_d^0({\mathrm{H}}_\delta^1(C^{\bullet, \bullet})) \longrightarrow {\mathrm{H}}_d^2({\mathrm{H}}_\delta^0(C^{\bullet,\bullet})), \\ 0 \longrightarrow \mathrm{im}(\Phi_2) \longrightarrow {\mathrm{H}}_\delta^0({\mathrm{H}}_d^1(C^{\bullet,\bullet})) \longrightarrow {\mathrm{H}}_\delta^2({\mathrm{H}}_d^0(C^{\bullet,\bullet})). \end{align*} $$
Proof. We give the proof for the first exact sequence. The proof for the second one is similar. Consider an element
![]() $[g] \in \mathrm {im}(\Phi _1) \subset {\mathrm {H}}_\delta ^1(C^{0,\bullet })$
. Since it lies in the image of
$[g] \in \mathrm {im}(\Phi _1) \subset {\mathrm {H}}_\delta ^1(C^{0,\bullet })$
. Since it lies in the image of
![]() $\Phi _1$
, there exists an element
$\Phi _1$
, there exists an element
![]() $\lambda \in C^{1,0}$
satisfying
$\lambda \in C^{1,0}$
satisfying
![]() $\delta ^{1,0} \lambda = d^{0,1} g$
. This implies that
$\delta ^{1,0} \lambda = d^{0,1} g$
. This implies that
![]() $d_*^{0,1}[g] = [d^{0,1} g] = [\delta ^{1,0} \lambda ]=0$
, and thus,
$d_*^{0,1}[g] = [d^{0,1} g] = [\delta ^{1,0} \lambda ]=0$
, and thus,
![]() $[g] \in {\mathrm {H}}_d^0({\mathrm {H}}_\delta ^1(C^{\bullet ,\bullet }))$
. The map
$[g] \in {\mathrm {H}}_d^0({\mathrm {H}}_\delta ^1(C^{\bullet ,\bullet }))$
. The map
![]() ${\mathrm {H}}_\delta ^1(C^{0,\bullet }) \supset \mathrm {im}(\Phi _1) \to {\mathrm {H}}_d^0({\mathrm {H}}_\delta ^1(C^{\bullet ,\bullet }))$
is obviously injective.
${\mathrm {H}}_\delta ^1(C^{0,\bullet }) \supset \mathrm {im}(\Phi _1) \to {\mathrm {H}}_d^0({\mathrm {H}}_\delta ^1(C^{\bullet ,\bullet }))$
is obviously injective.
Now, consider an element
![]() $[g] \in {\mathrm {H}}_d^0({\mathrm {H}}_\delta ^1(C^{\bullet ,\bullet }))$
. Since
$[g] \in {\mathrm {H}}_d^0({\mathrm {H}}_\delta ^1(C^{\bullet ,\bullet }))$
. Since
![]() $d_*^{0,1}[g]=0$
, there exists an element
$d_*^{0,1}[g]=0$
, there exists an element
![]() $\lambda \in C^{1,0}$
satisfying
$\lambda \in C^{1,0}$
satisfying
![]() $\delta ^{1,0} \lambda = d^{0,1} g$
. If
$\delta ^{1,0} \lambda = d^{0,1} g$
. If
![]() $\tilde \lambda \in C^{1,0}$
is another such element, then
$\tilde \lambda \in C^{1,0}$
is another such element, then
![]() $\tilde \lambda - \lambda =\lambda _0 \in {\mathrm {H}}_\delta ^0(C^{1,\bullet })$
. The element
$\tilde \lambda - \lambda =\lambda _0 \in {\mathrm {H}}_\delta ^0(C^{1,\bullet })$
. The element
![]() $d^{1,0}(\lambda + \lambda _0) \in C^{2,0}$
is
$d^{1,0}(\lambda + \lambda _0) \in C^{2,0}$
is
![]() $\delta ^{2,0}$
-closed since
$\delta ^{2,0}$
-closed since
![]() $\delta ^{2,0} \circ d^{1,0} = d^{1,1} \circ \delta ^{1,0}$
and
$\delta ^{2,0} \circ d^{1,0} = d^{1,1} \circ \delta ^{1,0}$
and
![]() $\delta ^{1,0} \lambda =d^{0,1} g$
. Thus,
$\delta ^{1,0} \lambda =d^{0,1} g$
. Thus,
![]() $d^{1,0}(\lambda + \lambda _0) \in {\mathrm {H}}_\delta ^0(C^{2,\bullet })$
. Since the freedom in representative
$d^{1,0}(\lambda + \lambda _0) \in {\mathrm {H}}_\delta ^0(C^{2,\bullet })$
. Since the freedom in representative
![]() $\lambda + \lambda _0$
is exactly
$\lambda + \lambda _0$
is exactly
![]() ${\mathrm {H}}_\delta ^0(C^{1,\bullet })$
, we obtain a unique element
${\mathrm {H}}_\delta ^0(C^{1,\bullet })$
, we obtain a unique element
![]() $[d^{1,0} \lambda ] \in {\mathrm {H}}^2_d({\mathrm {H}}_\delta ^0(C^{\bullet ,\bullet }))$
. We have
$[d^{1,0} \lambda ] \in {\mathrm {H}}^2_d({\mathrm {H}}_\delta ^0(C^{\bullet ,\bullet }))$
. We have
![]() $[d^{1,0} \lambda ]=0$
, or equivalently,
$[d^{1,0} \lambda ]=0$
, or equivalently,
![]() $d^{1,0} \lambda \in d_*^{1,0}({\mathrm {H}}_\delta ^0(C^{1,\bullet }))$
, if and only if
$d^{1,0} \lambda \in d_*^{1,0}({\mathrm {H}}_\delta ^0(C^{1,\bullet }))$
, if and only if
![]() $[g] \in \mathrm {im}(\Phi _1)$
.
$[g] \in \mathrm {im}(\Phi _1)$
.
While
![]() $\mathrm {Pic}(M) = \varinjlim {\mathrm {H}}_\delta ^1(C^{0,\bullet })$
plays an important role, the group
$\mathrm {Pic}(M) = \varinjlim {\mathrm {H}}_\delta ^1(C^{0,\bullet })$
plays an important role, the group
![]() ${\mathrm {H}}_d^1(C^{\bullet ,0})$
will in general grow without bound as the cover
${\mathrm {H}}_d^1(C^{\bullet ,0})$
will in general grow without bound as the cover
![]() $\mathcal {U}$
becomes finer. Therefore, as a counterpart to
$\mathcal {U}$
becomes finer. Therefore, as a counterpart to
![]() ${\check {\mathrm {H}}}^1(\mathcal {U},\mathcal {O}^\times )= {\mathrm {H}}_\delta ^1(C^{0,\bullet })$
, we define
${\check {\mathrm {H}}}^1(\mathcal {U},\mathcal {O}^\times )= {\mathrm {H}}_\delta ^1(C^{0,\bullet })$
, we define
![]() $\mathfrak {M}_{\mathfrak g}(\mathcal {U}) := {\mathrm {H}}_\delta ^0({\mathrm {H}}_d^1(C^{\bullet , \bullet }))$
which can be interpreted as the collection of local (infinitesimal) multipliers of
$\mathfrak {M}_{\mathfrak g}(\mathcal {U}) := {\mathrm {H}}_\delta ^0({\mathrm {H}}_d^1(C^{\bullet , \bullet }))$
which can be interpreted as the collection of local (infinitesimal) multipliers of
![]() ${\mathfrak g}$
with respect to the cover
${\mathfrak g}$
with respect to the cover
![]() $\mathcal {U}$
that are equivalent on overlaps. Note that this is also a reasonable definition in this context due to Lemma 2.6.
$\mathcal {U}$
that are equivalent on overlaps. Note that this is also a reasonable definition in this context due to Lemma 2.6.
Definition 2.7. The group of multipliers of
![]() ${\mathfrak g}$
on M is the direct limit
${\mathfrak g}$
on M is the direct limit
![]() $\mathfrak {M}_{\mathfrak g}(M) := \varinjlim \mathfrak {M}_{\mathfrak g}(\mathcal {U})$
.
$\mathfrak {M}_{\mathfrak g}(M) := \varinjlim \mathfrak {M}_{\mathfrak g}(\mathcal {U})$
.
The group
![]() $\mathfrak {M}_{\mathfrak g}(M)$
should not be confused with the group of global multipliers
$\mathfrak {M}_{\mathfrak g}(M)$
should not be confused with the group of global multipliers
![]() ${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))$
, which is often trivial as the algebra of global functions
${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))$
, which is often trivial as the algebra of global functions
![]() $\mathcal {O}(M)$
may be small (for instance,
$\mathcal {O}(M)$
may be small (for instance,
![]() ${\mathbb C}$
for compact M). To see the difference, consider an element
${\mathbb C}$
for compact M). To see the difference, consider an element
![]() $\lambda = \{\lambda _\alpha \} \in \ker (d^{1,0})$
. We have
$\lambda = \{\lambda _\alpha \} \in \ker (d^{1,0})$
. We have
![]() $[\lambda ] \in {\mathrm {H}}_d^1({\mathrm {H}}_\delta ^0(C^{\bullet ,\bullet }))$
if and only if
$[\lambda ] \in {\mathrm {H}}_d^1({\mathrm {H}}_\delta ^0(C^{\bullet ,\bullet }))$
if and only if
![]() $\lambda _\alpha = \lambda _\beta $
on
$\lambda _\alpha = \lambda _\beta $
on
![]() $U_\alpha \cap U_\beta $
, and
$U_\alpha \cap U_\beta $
, and
![]() $[\lambda ] \in \mathfrak {M}_{\mathfrak g}(\{U_\alpha \})={\mathrm {H}}_\delta ^0({\mathrm {H}}_d^1(C^{\bullet ,\bullet }))$
if and only if
$[\lambda ] \in \mathfrak {M}_{\mathfrak g}(\{U_\alpha \})={\mathrm {H}}_\delta ^0({\mathrm {H}}_d^1(C^{\bullet ,\bullet }))$
if and only if
![]() $\lambda _\alpha = \lambda _\beta + d \log \mu _{\alpha \beta }$
for some
$\lambda _\alpha = \lambda _\beta + d \log \mu _{\alpha \beta }$
for some
![]() $\mu =\{\mu _{\alpha \beta }\} \in \mathcal {O}^\times (U_\alpha \times U_\beta )$
.
$\mu =\{\mu _{\alpha \beta }\} \in \mathcal {O}^\times (U_\alpha \times U_\beta )$
.
2.3 The equivariant Picard group
From the description of lifts at the end of Section 2.1, we see that the pair
![]() $(g,\lambda )\in C^{0,1}\times C^{1,0}$
defines a
$(g,\lambda )\in C^{0,1}\times C^{1,0}$
defines a
![]() ${\mathfrak g}$
-equivariant line bundle if and only if
${\mathfrak g}$
-equivariant line bundle if and only if
The three conditions correspond to the cocycle condition for transition functions, the cocycle condition for the local lift (2.1) and the compatibility condition (2.4), respectively. Rescaling the fiber coordinates
![]() $u_\alpha $
in the line bundle corresponds exactly to changing the cocycle
$u_\alpha $
in the line bundle corresponds exactly to changing the cocycle
![]() $(g,\lambda )$
by a coboundary in
$(g,\lambda )$
by a coboundary in
![]() $\mathrm {im}(\partial ^0)$
.
$\mathrm {im}(\partial ^0)$
.
Definition 2.8. The group of equivalence classes of
![]() ${\mathfrak g}$
-equivariant line bundles is called the
${\mathfrak g}$
-equivariant line bundles is called the
![]() ${\mathfrak g}$
-equivariant Picard group and denoted by
${\mathfrak g}$
-equivariant Picard group and denoted by
![]() $\mathrm {Pic}_{\mathfrak g}(M):=\varinjlim {\mathrm {H}}^1(\mathrm {Tot}^\bullet (C))$
, where we exploit the direct limit by refinements (or use a fine cover
$\mathrm {Pic}_{\mathfrak g}(M):=\varinjlim {\mathrm {H}}^1(\mathrm {Tot}^\bullet (C))$
, where we exploit the direct limit by refinements (or use a fine cover
![]() $\mathcal {U}$
) as before.
$\mathcal {U}$
) as before.
Denoting by
![]() $\mathfrak {C}_{\mathfrak g}$
the modified Chevalley-Eilenberg sheaf complex (2.3),
$\mathfrak {C}_{\mathfrak g}$
the modified Chevalley-Eilenberg sheaf complex (2.3),
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
may be identified with the first hypercohomology
$\mathrm {Pic}_{\mathfrak g}(M)$
may be identified with the first hypercohomology
![]() $\mathbb {H}^1(M,\mathfrak {C}_{\mathfrak g})$
, cf. [Reference Griffiths and Harris11, Ch. 3.5] for a discussion of hypercohomology
$\mathbb {H}^1(M,\mathfrak {C}_{\mathfrak g})$
, cf. [Reference Griffiths and Harris11, Ch. 3.5] for a discussion of hypercohomology
![]() $\mathbb {H}^q$
.
$\mathbb {H}^q$
.
The maps
![]() $\Phi _1 \colon {\mathrm {H}}^1(\mathrm {Tot}^\bullet (C)) \to {\mathrm {H}}_\delta ^1(C^{0,\bullet })$
and
$\Phi _1 \colon {\mathrm {H}}^1(\mathrm {Tot}^\bullet (C)) \to {\mathrm {H}}_\delta ^1(C^{0,\bullet })$
and
![]() $\Phi _2 \colon {\mathrm {H}}^1(\mathrm {Tot}^\bullet (C)) \to {\mathrm {H}}_d^1(C^{\bullet ,0})$
induce maps
$\Phi _2 \colon {\mathrm {H}}^1(\mathrm {Tot}^\bullet (C)) \to {\mathrm {H}}_d^1(C^{\bullet ,0})$
induce maps
denoted by the same letters (Lemma 2.6 justifies the choice of codomain for the second map). We define
![]() $\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M):=\mathrm {im}(\Phi _1\times \Phi _2)\subset \mathrm {Pic}(M)\times \mathfrak {M}_{\mathfrak g}(M)$
, which we call the reduced
$\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M):=\mathrm {im}(\Phi _1\times \Phi _2)\subset \mathrm {Pic}(M)\times \mathfrak {M}_{\mathfrak g}(M)$
, which we call the reduced
![]() ${\mathfrak g}$
-equivariant Picard group, and denote by
${\mathfrak g}$
-equivariant Picard group, and denote by
![]() $\Psi _1,\Psi _2$
the projections
$\Psi _1,\Psi _2$
the projections
Then
![]() $\varpi :=\Phi _1\times \Phi _2$
epimorphically maps
$\varpi :=\Phi _1\times \Phi _2$
epimorphically maps
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
to
$\mathrm {Pic}_{\mathfrak g}(M)$
to
![]() $\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)$
.
$\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)$
.
Proposition 2.9.
![]() $\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M) \simeq \ker (\partial ^1)/\sim $
, where the equivalence relation is defined by
$\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M) \simeq \ker (\partial ^1)/\sim $
, where the equivalence relation is defined by
![]() $(g,\lambda )\sim (\tilde g, \tilde \lambda )$
if
$(g,\lambda )\sim (\tilde g, \tilde \lambda )$
if
![]() $\tilde g=g \cdot \delta ^{0,0} \nu $
and
$\tilde g=g \cdot \delta ^{0,0} \nu $
and
![]() $\tilde \lambda = \lambda + d^{0,0} \mu $
, where
$\tilde \lambda = \lambda + d^{0,0} \mu $
, where
![]() $\mu ,\nu \in C^{0,0}$
satisfy
$\mu ,\nu \in C^{0,0}$
satisfy
Proof. The reduced equivalence relation is weaker, as the coboundaries for g and
![]() $\lambda $
can be chosen independently. Thus, if
$\lambda $
can be chosen independently. Thus, if
![]() $(g,\lambda )\in \ker (\partial ^1)$
and
$(g,\lambda )\in \ker (\partial ^1)$
and
![]() $(g\cdot \delta ^{0,0} \nu , \lambda +d^{0,0} \mu ) \in C^{0,1} \times C^{1,0}$
is an equivalent cocycle, then it automatically satisfies the first two conditions:
$(g\cdot \delta ^{0,0} \nu , \lambda +d^{0,0} \mu ) \in C^{0,1} \times C^{1,0}$
is an equivalent cocycle, then it automatically satisfies the first two conditions:
![]() $\delta ^{0,1}(g\cdot \delta ^{0,0}\nu )=0$
and
$\delta ^{0,1}(g\cdot \delta ^{0,0}\nu )=0$
and
![]() $d^{1,0}(\lambda +d^{0,0}\mu )=0$
. However, the third condition applied to the new pair is
$d^{1,0}(\lambda +d^{0,0}\mu )=0$
. However, the third condition applied to the new pair is
![]() $d^{0,1}(g\cdot \delta ^{0,0}\nu )=\delta ^{1,0} (\lambda +d^{0,0}\mu )$
, which is equivalent to
$d^{0,1}(g\cdot \delta ^{0,0}\nu )=\delta ^{1,0} (\lambda +d^{0,0}\mu )$
, which is equivalent to
![]() $\mu /\nu \in \ker (d^{0,1}\circ \delta ^{0,0})=\ker (\delta ^{1,0}\circ d^{0,0})$
.
$\mu /\nu \in \ker (d^{0,1}\circ \delta ^{0,0})=\ker (\delta ^{1,0}\circ d^{0,0})$
.
Let us investigate the relationship between
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
and
$\mathrm {Pic}_{\mathfrak g}(M)$
and
![]() $\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)$
. By Proposition 2.9, the admissible pair
$\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)$
. By Proposition 2.9, the admissible pair
![]() $(\nu ,\mu )\in C^{0,0}\times C^{0,0}$
characterizing the freedom in choice of representatives
$(\nu ,\mu )\in C^{0,0}\times C^{0,0}$
characterizing the freedom in choice of representatives
![]() $(g,\lambda ) \in \ker (\partial ^1)$
for the reduced group can be rewritten as
$(g,\lambda ) \in \ker (\partial ^1)$
for the reduced group can be rewritten as
![]() $(\nu ,\mu )=(\nu /\mu ,1)\cdot (\mu ,\mu )\simeq (\nu /\mu ,\mu ) \in \ker (d^{0,1}\circ \delta ^{0,0})\times C^{0,0}$
. It follows that (for a good cover)
$(\nu ,\mu )=(\nu /\mu ,1)\cdot (\mu ,\mu )\simeq (\nu /\mu ,\mu ) \in \ker (d^{0,1}\circ \delta ^{0,0})\times C^{0,0}$
. It follows that (for a good cover)
![]() $\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)$
is equal to
$\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)$
is equal to
 $$\begin{align*}\frac{\ker(\partial^1)}{\mathrm{im}(\tilde\partial)\cdot\mathrm{im}(\partial^0)} = \frac{\ker(\partial^1)}{\frac{\mathrm{im}(\tilde \partial)}{\mathrm{im}(\tilde \partial)\cap\mathrm{im}(\partial^0)} \cdot\mathrm{im}(\partial^0)}= \frac{{\mathrm{H}}^1(\mathrm{Tot}^\bullet (C))}{\frac{\mathrm{im}(\tilde \partial)}{\mathrm{im}(\tilde \partial) \cap \mathrm{im}(\partial^0)}}, \end{align*}$$
$$\begin{align*}\frac{\ker(\partial^1)}{\mathrm{im}(\tilde\partial)\cdot\mathrm{im}(\partial^0)} = \frac{\ker(\partial^1)}{\frac{\mathrm{im}(\tilde \partial)}{\mathrm{im}(\tilde \partial)\cap\mathrm{im}(\partial^0)} \cdot\mathrm{im}(\partial^0)}= \frac{{\mathrm{H}}^1(\mathrm{Tot}^\bullet (C))}{\frac{\mathrm{im}(\tilde \partial)}{\mathrm{im}(\tilde \partial) \cap \mathrm{im}(\partial^0)}}, \end{align*}$$
where the map
![]() $\tilde \partial \colon \ker (d^{0,1}\circ \delta ^{0,0})\to C^{0,1}\times C^{1,0}$
is defined as
$\tilde \partial \colon \ker (d^{0,1}\circ \delta ^{0,0})\to C^{0,1}\times C^{1,0}$
is defined as
![]() $\delta ^{0,0}\times 0$
. We have
$\delta ^{0,0}\times 0$
. We have
 $$ \begin{align*} \mathrm{im}(\partial^0) &= \{(\delta^{0,0} \mu, d^{0,0} \mu)\in C^{0,1}\times C^{1,0} \mid\mu\in C^{0,0}\}, \\ \mathrm{im}(\tilde \partial) &= \{(\delta^{0,0} \kappa, 0) \in C^{0,1} \times C^{1,0} \mid \kappa \in \ker(d^{0,1} \circ \delta^{0,0})\} \simeq \ker(d^{0,1} \circ \delta^{0,0}) /\ker(\delta^{0,0}). \end{align*} $$
$$ \begin{align*} \mathrm{im}(\partial^0) &= \{(\delta^{0,0} \mu, d^{0,0} \mu)\in C^{0,1}\times C^{1,0} \mid\mu\in C^{0,0}\}, \\ \mathrm{im}(\tilde \partial) &= \{(\delta^{0,0} \kappa, 0) \in C^{0,1} \times C^{1,0} \mid \kappa \in \ker(d^{0,1} \circ \delta^{0,0})\} \simeq \ker(d^{0,1} \circ \delta^{0,0}) /\ker(\delta^{0,0}). \end{align*} $$
If
![]() $d^{0,0} \mu =0$
, then
$d^{0,0} \mu =0$
, then
![]() $\mu \in \ker (\delta ^{1,0} \circ d^{0,0}) = \ker (d^{0,1} \circ \delta ^{0,0})$
, and therefore,
$\mu \in \ker (\delta ^{1,0} \circ d^{0,0}) = \ker (d^{0,1} \circ \delta ^{0,0})$
, and therefore,
 $$ \begin{align*} \mathrm{im}(\tilde\partial)\cap\mathrm{im}(\partial^0) &= \{(\delta^{0,0} \mu,0) \in C^{0,1} \times C^{1,0} \mid \mu \in \ker (d^{0,0}) \} \\ &= \delta^{0,0}(\ker(d^{0,0})) \simeq \ker(d^{0,0})/(\ker(\delta^{0,0}) \cap \ker(d^{0,0})). \end{align*} $$
$$ \begin{align*} \mathrm{im}(\tilde\partial)\cap\mathrm{im}(\partial^0) &= \{(\delta^{0,0} \mu,0) \in C^{0,1} \times C^{1,0} \mid \mu \in \ker (d^{0,0}) \} \\ &= \delta^{0,0}(\ker(d^{0,0})) \simeq \ker(d^{0,0})/(\ker(\delta^{0,0}) \cap \ker(d^{0,0})). \end{align*} $$
It follows that
 $$ \begin{align*} \frac{\mathrm{im}(\tilde \partial)}{\mathrm{im}(\tilde \partial) \cap \mathrm{im}(\partial^0)} = \frac{\ker(d^{0,1} \circ \delta^{0,0})}{\ker(\delta^{0,0}) \cdot \ker(d^{0,0})}. \end{align*} $$
$$ \begin{align*} \frac{\mathrm{im}(\tilde \partial)}{\mathrm{im}(\tilde \partial) \cap \mathrm{im}(\partial^0)} = \frac{\ker(d^{0,1} \circ \delta^{0,0})}{\ker(\delta^{0,0}) \cdot \ker(d^{0,0})}. \end{align*} $$
Defining
 $$ \begin{align} T_{\mathfrak g}(\mathcal{U}) :=\frac{\ker(d^{0,1} \circ \delta^{0,0})}{\ker(\delta^{0,0}) \cdot \ker(d^{0,0})}, \qquad T_{\mathfrak g}(M) := \varinjlim T_{\mathfrak g}(\mathcal{U}) \end{align} $$
$$ \begin{align} T_{\mathfrak g}(\mathcal{U}) :=\frac{\ker(d^{0,1} \circ \delta^{0,0})}{\ker(\delta^{0,0}) \cdot \ker(d^{0,0})}, \qquad T_{\mathfrak g}(M) := \varinjlim T_{\mathfrak g}(\mathcal{U}) \end{align} $$
gives us the relation between
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
and
$\mathrm {Pic}_{\mathfrak g}(M)$
and
![]() $\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)$
:
$\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)$
:
Proposition 2.10. The following sequence is exact:
The commutative diagram in Figure 1 gives relations between the groups we have considered, leading to vanishing conditions for
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
and various isomorphisms.
$\mathrm {Pic}_{\mathfrak g}(M)$
and various isomorphisms.

Figure 1 Commutative diagram: The dotted and dashed long sequences as well as three straight line sequences are exact.
The diagram contains the short exact sequence (2.8), the (direct limit of) short exact sequences (2.5)–(2.6), and also two longer exact sequences. For instance, exactness at
![]() $\delta ^{0,0}_*$
and
$\delta ^{0,0}_*$
and
![]() $d^{0,0}_*$
can be seen as follows. If
$d^{0,0}_*$
can be seen as follows. If
![]() $\mu \in \ker (d^{0,1} \circ \delta ^{0,0})$
, then
$\mu \in \ker (d^{0,1} \circ \delta ^{0,0})$
, then
![]() $\delta ^{0,0} \mu \in \ker (d^{0,1}) \cap \ker (\delta ^{0,1})$
and
$\delta ^{0,0} \mu \in \ker (d^{0,1}) \cap \ker (\delta ^{0,1})$
and
![]() $d^{0,0} \mu \in \ker (\delta ^{1,0}) \cap \ker (d^{1,0})$
, whence
$d^{0,0} \mu \in \ker (\delta ^{1,0}) \cap \ker (d^{1,0})$
, whence
![]() $[\delta ^{0,0} \mu ] \in {\mathrm {H}}_\delta ^1({\mathrm {H}}_d^0(C^{\bullet ,\bullet }))$
and
$[\delta ^{0,0} \mu ] \in {\mathrm {H}}_\delta ^1({\mathrm {H}}_d^0(C^{\bullet ,\bullet }))$
and
![]() $[d^{0,0} \mu ] \in {\mathrm {H}}_d^1({\mathrm {H}}_\delta ^0(C^{\bullet ,\bullet }))$
. We have
$[d^{0,0} \mu ] \in {\mathrm {H}}_d^1({\mathrm {H}}_\delta ^0(C^{\bullet ,\bullet }))$
. We have
![]() $[\delta ^{0,0} \mu ]=0$
if and only if there exists an element
$[\delta ^{0,0} \mu ]=0$
if and only if there exists an element
![]() $\mu _0 \in \ker (d^{0,0})$
such that
$\mu _0 \in \ker (d^{0,0})$
such that
![]() $\delta ^{0,0} \mu = \delta ^{0,0} \mu _0$
. This happens if and only if
$\delta ^{0,0} \mu = \delta ^{0,0} \mu _0$
. This happens if and only if
![]() $\mu =\frac {\mu }{\mu _0} \mu _0 \in \ker (\delta ^{0,0}) \cdot \ker (d^{0,0})$
. By a similar argument,
$\mu =\frac {\mu }{\mu _0} \mu _0 \in \ker (\delta ^{0,0}) \cdot \ker (d^{0,0})$
. By a similar argument,
![]() $[d^{0,0} \mu ] = 0$
if and only if
$[d^{0,0} \mu ] = 0$
if and only if
![]() $\mu \in \ker (\delta ^{0,0}) \cdot \ker (d^{0,0})$
.
$\mu \in \ker (\delta ^{0,0}) \cdot \ker (d^{0,0})$
.
Note that the maps
![]() ${\check {\mathrm {H}}}^1(M,(\mathcal {O}^\times )^{\mathfrak g}) \to \mathrm {Pic}_{\mathfrak g}(M)$
and
${\check {\mathrm {H}}}^1(M,(\mathcal {O}^\times )^{\mathfrak g}) \to \mathrm {Pic}_{\mathfrak g}(M)$
and
![]() ${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M)) \to \mathrm {Pic}_{\mathfrak g}(M)$
in the commutative diagram are defined by
${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M)) \to \mathrm {Pic}_{\mathfrak g}(M)$
in the commutative diagram are defined by
![]() $[g] \mapsto [(g,0)]$
and
$[g] \mapsto [(g,0)]$
and
![]() $[\lambda ] \mapsto [(1,-\lambda )]$
, respectively.
$[\lambda ] \mapsto [(1,-\lambda )]$
, respectively.
Corollary 2.11. If
![]() ${\check {\mathrm {H}}}^1(M, (\mathcal {O}^\times )^{\mathfrak g})=0$
or
${\check {\mathrm {H}}}^1(M, (\mathcal {O}^\times )^{\mathfrak g})=0$
or
![]() ${\tilde {\mathrm {H}}}^1({\mathfrak g}, \mathcal {O}(M))=0$
, then
${\tilde {\mathrm {H}}}^1({\mathfrak g}, \mathcal {O}(M))=0$
, then
![]() $\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)\simeq \mathrm {Pic}_{\mathfrak g}(M)$
.
$\mathrm {Pic}^{\mathrm {red}}_{\mathfrak g}(M)\simeq \mathrm {Pic}_{\mathfrak g}(M)$
.
Corollary 2.12.
-
(i) We have
 ${\tilde {\mathrm {H}}}^1({\mathfrak g}, \mathcal {O}(M))=0$
if and only if
${\tilde {\mathrm {H}}}^1({\mathfrak g}, \mathcal {O}(M))=0$
if and only if
 $\Phi _1\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathrm {Pic}(M)$
is injective.
$\Phi _1\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathrm {Pic}(M)$
is injective. -
(ii) Likewise,
 $\check {\mathrm {H}}^1(M,(\mathcal {O}^\times )^{\mathfrak g})=0$
if and only if
$\check {\mathrm {H}}^1(M,(\mathcal {O}^\times )^{\mathfrak g})=0$
if and only if
 $\Phi _2\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathfrak {M}_{\mathfrak g}(M)$
is injective.
$\Phi _2\colon \mathrm {Pic}_{\mathfrak g}(M)\to \mathfrak {M}_{\mathfrak g}(M)$
is injective.
Notice
![]() $\mathrm {im}(\Psi _1)= \mathrm {im}(\Phi _1)$
and
$\mathrm {im}(\Psi _1)= \mathrm {im}(\Phi _1)$
and
![]() $\mathrm {im}(\Psi _2)= \mathrm {im}(\Phi _2)$
, which are described by Lemmata 2.4 and 2.6.
$\mathrm {im}(\Psi _2)= \mathrm {im}(\Phi _2)$
, which are described by Lemmata 2.4 and 2.6.
Proposition 2.13. The group
![]() $T_{\mathfrak g}(M)$
of equivariant line bundles with trivial reduction corresponds to global locally trivial lifts of
$T_{\mathfrak g}(M)$
of equivariant line bundles with trivial reduction corresponds to global locally trivial lifts of
![]() ${\mathfrak g}$
to the trivial line bundle over M modulo globally trivial lifts.
${\mathfrak g}$
to the trivial line bundle over M modulo globally trivial lifts.
Proof. First, note that an element
![]() $[(g,\lambda )]\in \mathrm {Pic}_{\mathfrak g}(M)$
in the kernel of
$[(g,\lambda )]\in \mathrm {Pic}_{\mathfrak g}(M)$
in the kernel of
![]() $\varpi $
also belongs to the kernel of
$\varpi $
also belongs to the kernel of
![]() $\Phi _1=\Psi _1\circ \varpi $
, so g determines a trivial line bundle. Similarly, using
$\Phi _1=\Psi _1\circ \varpi $
, so g determines a trivial line bundle. Similarly, using
![]() $\Phi _2=\Psi _2\circ \varpi $
, we conclude that
$\Phi _2=\Psi _2\circ \varpi $
, we conclude that
![]() $\lambda $
yields a locally trivial lift (the multiplier is cohomologous to zero on open sets
$\lambda $
yields a locally trivial lift (the multiplier is cohomologous to zero on open sets
![]() $U_\alpha $
).
$U_\alpha $
).
Next, applying
![]() $d^{0,0}$
to both the numerator and the denominator of the right-hand side of (2.3), we get
$d^{0,0}$
to both the numerator and the denominator of the right-hand side of (2.3), we get
![]() $T_{\mathfrak g}(M)\simeq \ker \big (\delta ^{1,0}|_{\mathrm {im} d^{0,0}}\big )/d^{0,0}(\ker \delta ^{0,0})$
, whence the required interpretation.
$T_{\mathfrak g}(M)\simeq \ker \big (\delta ^{1,0}|_{\mathrm {im} d^{0,0}}\big )/d^{0,0}(\ker \delta ^{0,0})$
, whence the required interpretation.
Finally, by applying
![]() $\delta ^{0,0}$
to (2.3), we conclude
$\delta ^{0,0}$
to (2.3), we conclude
![]() $T_{\mathfrak g}(M)\simeq \ker \big (d^{0,1}|_{\mathrm {im}\delta ^{0,0}}\big )/\delta ^{0,0}(\ker d^{0,0})$
, which corresponds to line bundles with
$T_{\mathfrak g}(M)\simeq \ker \big (d^{0,1}|_{\mathrm {im}\delta ^{0,0}}\big )/\delta ^{0,0}(\ker d^{0,0})$
, which corresponds to line bundles with
![]() ${\mathfrak g}$
-invariant transition functions modulo global
${\mathfrak g}$
-invariant transition functions modulo global
![]() ${\mathfrak g}$
-invariants.
${\mathfrak g}$
-invariants.
Propositions 2.10 and 2.13 combine into Theorem 1.1.
Example 2.14 (Rational curve).
Consider the projective space
![]() $\mathbb CP^1$
with charts
$\mathbb CP^1$
with charts
![]() $U_0\simeq \mathbb C^1(x)$
and
$U_0\simeq \mathbb C^1(x)$
and
![]() $U_\infty \simeq \mathbb C^1(y)$
, with coordinates related by
$U_\infty \simeq \mathbb C^1(y)$
, with coordinates related by
![]() $y=1/x$
on
$y=1/x$
on
![]() $U_0 \cap U_\infty $
. The Lie algebra
$U_0 \cap U_\infty $
. The Lie algebra
![]() $\mathfrak {sl}(2,\mathbb C)$
acts naturally on this space with the basis
$\mathfrak {sl}(2,\mathbb C)$
acts naturally on this space with the basis
![]() $X,Y,Z$
given in local coordinates:
$X,Y,Z$
given in local coordinates:
Let
![]() $\lambda _i$
be a representative of an element in
$\lambda _i$
be a representative of an element in
![]() $H^1(\mathfrak {sl}(2,\mathbb C),\mathcal {O}(U_i))$
for
$H^1(\mathfrak {sl}(2,\mathbb C),\mathcal {O}(U_i))$
for
![]() $i=0,\infty $
.
$i=0,\infty $
.
Taking
![]() $\mu _0= e^{\int \lambda _0(X_0) dx}$
(the integral sign denotes the anti-derivative on
$\mu _0= e^{\int \lambda _0(X_0) dx}$
(the integral sign denotes the anti-derivative on
![]() $\mathbb C$
) gives
$\mathbb C$
) gives
so we can without loss of generality assume that
![]() $\lambda _0(X)=0$
. The values
$\lambda _0(X)=0$
. The values
![]() $\lambda _0(Y)$
and
$\lambda _0(Y)$
and
![]() $\lambda _0(Z)$
are now determined by the cocycle conditions
$\lambda _0(Z)$
are now determined by the cocycle conditions
 $$ \begin{align*} X(\lambda_0(Y))-Y(\lambda_0(X))&=\lambda_0 ([X,Y]) = \lambda_0(X) = 0, \\ X(\lambda_0(Z))-Z(\lambda_0(X))&=\lambda_0 ([X,Z]) = 2 \lambda_0(Y), \\ Y(\lambda_0(Z))-Z(\lambda_0(Y))&=\lambda_0 ([Y,Z]) = \lambda_0(Z). \end{align*} $$
$$ \begin{align*} X(\lambda_0(Y))-Y(\lambda_0(X))&=\lambda_0 ([X,Y]) = \lambda_0(X) = 0, \\ X(\lambda_0(Z))-Z(\lambda_0(X))&=\lambda_0 ([X,Z]) = 2 \lambda_0(Y), \\ Y(\lambda_0(Z))-Z(\lambda_0(Y))&=\lambda_0 ([Y,Z]) = \lambda_0(Z). \end{align*} $$
This leads to
Analogous computations on
![]() $U_\infty $
give
$U_\infty $
give
Next, we require that
![]() $d^{0,1} g_{0 \infty } = (\delta ^{1,0} \lambda )_{0 \infty }$
for some
$d^{0,1} g_{0 \infty } = (\delta ^{1,0} \lambda )_{0 \infty }$
for some
![]() $\delta ^{0,1}$
-cocycle
$\delta ^{0,1}$
-cocycle
![]() $g_{0 \infty } \in \mathcal {O}^\times (U_0 \cap U_\infty )$
. Evaluating this on X, Y and Z leads to the following overdetermined system of ODEs:
$g_{0 \infty } \in \mathcal {O}^\times (U_0 \cap U_\infty )$
. Evaluating this on X, Y and Z leads to the following overdetermined system of ODEs:
 $$\begin{align*}\frac{\partial_x (g_{0 \infty})}{g_{0 \infty}} = -\frac{B}{x}, \qquad \frac{x\partial_x (g_{0 \infty})}{g_{0 \infty}} = \frac{A-B}2 , \qquad \frac{x^2\partial_x (g_{0 \infty})}{g_{0 \infty}} = Ax. \end{align*}$$
$$\begin{align*}\frac{\partial_x (g_{0 \infty})}{g_{0 \infty}} = -\frac{B}{x}, \qquad \frac{x\partial_x (g_{0 \infty})}{g_{0 \infty}} = \frac{A-B}2 , \qquad \frac{x^2\partial_x (g_{0 \infty})}{g_{0 \infty}} = Ax. \end{align*}$$
The system has a solution if and only if
![]() $A=-B$
, in which case,
$A=-B$
, in which case,
![]() $g_{0 \infty } = C x^A$
. This solution is holomorphic on
$g_{0 \infty } = C x^A$
. This solution is holomorphic on
![]() $U_0 \cap U_\infty $
if and only if
$U_0 \cap U_\infty $
if and only if
![]() $A \in \mathbb Z$
. The constant C can be set equal to
$A \in \mathbb Z$
. The constant C can be set equal to
![]() $1$
by multiplying
$1$
by multiplying
![]() $g_{0 \infty }$
with
$g_{0 \infty }$
with
![]() $(\delta ^{0,0} \mu )_{0 \infty }$
for
$(\delta ^{0,0} \mu )_{0 \infty }$
for
![]() $\mu = \{\mu _0=1, \mu _\infty =C\} \in \ker (d^{0,0})$
. Thus, the global lifts are given by
$\mu = \{\mu _0=1, \mu _\infty =C\} \in \ker (d^{0,0})$
. Thus, the global lifts are given by
![]() $(\lambda _0, \lambda _\infty )$
with
$(\lambda _0, \lambda _\infty )$
with
![]() $A=-B \in \mathbb Z$
, and the corresponding
$A=-B \in \mathbb Z$
, and the corresponding
![]() $\mathfrak {sl}(2,\mathbb C)$
-equivariant line bundle has transition function
$\mathfrak {sl}(2,\mathbb C)$
-equivariant line bundle has transition function
![]() $g_{0 \infty } = x^{A}$
. To sum up, the cover
$g_{0 \infty } = x^{A}$
. To sum up, the cover
![]() $\mathcal {U}=\{U_0,U_\infty \}$
is nice and we get
$\mathcal {U}=\{U_0,U_\infty \}$
is nice and we get
The first isomorphism is a consequence of
![]() ${\check {\mathrm {H}}}^1(M, (\mathcal {O}^\times )^{\mathfrak g}) \simeq {\mathrm {H}}_\delta ^1({\mathrm {H}}_d^0(C^{\bullet ,\bullet })) =0$
and Corollary 2.11. Since
${\check {\mathrm {H}}}^1(M, (\mathcal {O}^\times )^{\mathfrak g}) \simeq {\mathrm {H}}_\delta ^1({\mathrm {H}}_d^0(C^{\bullet ,\bullet })) =0$
and Corollary 2.11. Since
![]() $\mathbb CP^1$
is covered by two open charts, we have
$\mathbb CP^1$
is covered by two open charts, we have
![]() $C^{0,2}=0$
, implying
$C^{0,2}=0$
, implying
![]() ${\mathrm {H}}_d^0(C^{\bullet ,2})=0$
and
${\mathrm {H}}_d^0(C^{\bullet ,2})=0$
and
![]() ${\mathrm {H}}_\delta ^2({\mathrm {H}}_d^0(C^{\bullet ,\bullet }))=0$
. By Lemma 2.6,
${\mathrm {H}}_\delta ^2({\mathrm {H}}_d^0(C^{\bullet ,\bullet }))=0$
. By Lemma 2.6,
![]() $\mathrm {im}(\Psi _2) \simeq {\mathrm {H}}_\delta ^0({\mathrm {H}}_d^1(C^{\bullet ,\bullet })) = \mathfrak {M}_{\mathfrak g}(\{U_0,U_\infty \})$
, which for this cover is isomorphic to
$\mathrm {im}(\Psi _2) \simeq {\mathrm {H}}_\delta ^0({\mathrm {H}}_d^1(C^{\bullet ,\bullet })) = \mathfrak {M}_{\mathfrak g}(\{U_0,U_\infty \})$
, which for this cover is isomorphic to
![]() $\mathbb Z$
.
$\mathbb Z$
.
A straightforward generalization of this computation gives
![]() $T_{\mathfrak g}({\mathbb C} P^n)=0$
,
$T_{\mathfrak g}({\mathbb C} P^n)=0$
,
![]() $\mathfrak {M}_{\mathfrak g}({\mathbb C} P^n)={\mathbb C}$
(for
$\mathfrak {M}_{\mathfrak g}({\mathbb C} P^n)={\mathbb C}$
(for
![]() $n=1$
this is parametrized by the above
$n=1$
this is parametrized by the above
![]() $A=-B$
, but with a finer cover
$A=-B$
, but with a finer cover
![]() $\mathcal {U}$
it is unconstrained:
$\mathcal {U}$
it is unconstrained:
![]() $A\in {\mathbb C}$
) and
$A\in {\mathbb C}$
) and
![]() $\mathrm {Pic}_{\mathfrak g}({\mathbb C} P^n)=\mathbb Z$
for
$\mathrm {Pic}_{\mathfrak g}({\mathbb C} P^n)=\mathbb Z$
for
![]() ${\mathfrak g}=\mathfrak {sl}(n+1,{\mathbb C})$
.
${\mathfrak g}=\mathfrak {sl}(n+1,{\mathbb C})$
.
Remark 2.15. Recall that
![]() $\mathrm {Pic}({\mathbb C} P^n) = \{\mathcal {O}_{{\mathbb C} P^n}(k)\}_{k\in \mathbb Z}\simeq \mathbb Z$
, where
$\mathrm {Pic}({\mathbb C} P^n) = \{\mathcal {O}_{{\mathbb C} P^n}(k)\}_{k\in \mathbb Z}\simeq \mathbb Z$
, where
![]() $\mathcal {O}_{\mathbb CP^n}(0)$
is the trivial line bundle and
$\mathcal {O}_{\mathbb CP^n}(0)$
is the trivial line bundle and
![]() $\mathcal {O}_{\mathbb CP^n}(-1)$
is the tautological line bundle and for
$\mathcal {O}_{\mathbb CP^n}(-1)$
is the tautological line bundle and for
![]() $k>0$
:
$k>0$
:
The canonical line bundle is
![]() $K_{\mathbb CP^n}=\Lambda ^n T^* \mathbb CP^n= \mathcal {O}_{\mathbb CP^n}(-n-1)$
, cf. [Reference Huybrechts15, Ch. 2.2].
$K_{\mathbb CP^n}=\Lambda ^n T^* \mathbb CP^n= \mathcal {O}_{\mathbb CP^n}(-n-1)$
, cf. [Reference Huybrechts15, Ch. 2.2].
We will see later that
![]() $\Psi _1$
and
$\Psi _1$
and
![]() $\Phi _1$
may be non-injective. The following shows it for
$\Phi _1$
may be non-injective. The following shows it for
![]() $\Psi _2$
and
$\Psi _2$
and
![]() $\Phi _2$
.
$\Phi _2$
.
Example 2.16 (Elliptic curve).
Consider
![]() $\mathbb C^2$
with coordinates
$\mathbb C^2$
with coordinates
![]() $(x,u)$
and two commuting maps
$(x,u)$
and two commuting maps
where
![]() $\omega _1\in {\mathbb C}\setminus {\mathbb R}$
,
$\omega _1\in {\mathbb C}\setminus {\mathbb R}$
,
![]() $\omega _2\neq 0$
. Both of these maps respect the projection
$\omega _2\neq 0$
. Both of these maps respect the projection
![]() $\mathbb C^2 \to \mathbb C$
given by
$\mathbb C^2 \to \mathbb C$
given by
![]() $(x,u)\mapsto x$
, and the vector field
$(x,u)\mapsto x$
, and the vector field
![]() $\partial _x$
. Thus, in the quotient by the
$\partial _x$
. Thus, in the quotient by the
![]() $\mathbb Z^2$
action generated by
$\mathbb Z^2$
action generated by
![]() $h_1,h_2$
, we get that the vector field
$h_1,h_2$
, we get that the vector field
![]() $\partial _x$
on the elliptic curve
$\partial _x$
on the elliptic curve
![]() $\Gamma = \mathbb C/\mathbb Z^2$
lifts to the vector field
$\Gamma = \mathbb C/\mathbb Z^2$
lifts to the vector field
![]() $\partial _x$
on the line bundle
$\partial _x$
on the line bundle
![]() $\mathbb C^2/\mathbb Z^2$
over the elliptic curve. This line bundle
$\mathbb C^2/\mathbb Z^2$
over the elliptic curve. This line bundle
![]() $L_\omega $
is topologically trivial but holomorphically nontrivial for
$L_\omega $
is topologically trivial but holomorphically nontrivial for
![]() $\omega _2 \neq e^{2 \pi i \omega _1}$
, and all line bundles of this form lie in
$\omega _2 \neq e^{2 \pi i \omega _1}$
, and all line bundles of this form lie in
![]() $\ker (\Psi _2)$
; see Section 27 of [Reference Arnold2] for details. The general lift of
$\ker (\Psi _2)$
; see Section 27 of [Reference Arnold2] for details. The general lift of
![]() ${\mathfrak g}$
is given by
${\mathfrak g}$
is given by
![]() $\partial _x+c\,u\partial _u$
,
$\partial _x+c\,u\partial _u$
,
![]() $c\in {\mathbb C}$
.
$c\in {\mathbb C}$
.
For holomorphic curves, we have a short exact sequence (where
![]() $c_1$
is the first Chern class)
$c_1$
is the first Chern class)
and for elliptic curves
![]() $\mathrm {Pic}^0(\Gamma )=\mathrm {Div}^0(\Gamma )\simeq \Gamma $
,
$\mathrm {Pic}^0(\Gamma )=\mathrm {Div}^0(\Gamma )\simeq \Gamma $
,
![]() $x\mapsto x-x_0$
, whence
$x\mapsto x-x_0$
, whence
![]() $\mathrm {Pic}(\Gamma )\simeq \Gamma \oplus \mathbb Z$
.
$\mathrm {Pic}(\Gamma )\simeq \Gamma \oplus \mathbb Z$
.
The summand
![]() $\mathbb Z$
in
$\mathbb Z$
in
![]() $\mathrm {Pic}(\Gamma )$
corresponds to divisors
$\mathrm {Pic}(\Gamma )$
corresponds to divisors
![]() $m\cdot x_0$
,
$m\cdot x_0$
,
![]() $m\in \mathbb Z$
,
$m\in \mathbb Z$
,
![]() $x_0\in \Gamma $
. However, for topologically nontrivial line bundles,
$x_0\in \Gamma $
. However, for topologically nontrivial line bundles,
![]() $m=c_1(L)\neq 0$
, the algebra
$m=c_1(L)\neq 0$
, the algebra
![]() ${\mathfrak g}$
does not possess a lift to L. Indeed, such a lift would define a flat connection, at which point we can use the formula
${\mathfrak g}$
does not possess a lift to L. Indeed, such a lift would define a flat connection, at which point we can use the formula
![]() $c_1(L)=\Big [\frac {-1}{2\pi i}\mathrm {tr} R_\nabla \Big ]$
. Alternatively, denoting by
$c_1(L)=\Big [\frac {-1}{2\pi i}\mathrm {tr} R_\nabla \Big ]$
. Alternatively, denoting by
![]() $\pi :{\mathbb C}\to \Gamma $
the quotient-projection by the lattice
$\pi :{\mathbb C}\to \Gamma $
the quotient-projection by the lattice
![]() $\langle 1,\omega _1\rangle $
, the pullback
$\langle 1,\omega _1\rangle $
, the pullback
![]() $\pi ^*L$
is trivial and can be identified with
$\pi ^*L$
is trivial and can be identified with
![]() ${\mathbb C}^2(x,u)$
, on which
${\mathbb C}^2(x,u)$
, on which
![]() $\mathbb Z^2$
acts through the above
$\mathbb Z^2$
acts through the above
![]() $h_1,h_2$
. Invariance of the lift
$h_1,h_2$
. Invariance of the lift
![]() $\partial _x+f(x)\,u\partial _u$
gives periodicity
$\partial _x+f(x)\,u\partial _u$
gives periodicity
![]() $f(x+1)=f(x)$
and the constraint
$f(x+1)=f(x)$
and the constraint
![]() $f(x+\omega _1)-f(x)=2\pi im$
, which are incompatible unless
$f(x+\omega _1)-f(x)=2\pi im$
, which are incompatible unless
![]() $m=0$
.
$m=0$
.
It is easy to see that
![]() $\mathfrak {M}_{\mathfrak g}(\Gamma )=0$
. Moreover,
$\mathfrak {M}_{\mathfrak g}(\Gamma )=0$
. Moreover,
![]() $T_{\mathfrak g}(\Gamma )={\mathbb C}$
as it corresponds to 0-cochains
$T_{\mathfrak g}(\Gamma )={\mathbb C}$
as it corresponds to 0-cochains
![]() $c_\alpha e^{sx}\in \mathcal {O}(U_\alpha )$
modulo local constants
$c_\alpha e^{sx}\in \mathcal {O}(U_\alpha )$
modulo local constants
![]() $\{c_\alpha \}$
(so the quotient coordinate is s). This can be also identified with
$\{c_\alpha \}$
(so the quotient coordinate is s). This can be also identified with
![]() ${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))={\mathbb C}$
generated by global 1-form
${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))={\mathbb C}$
generated by global 1-form
![]() $dx$
on
$dx$
on
![]() $\Gamma $
.
$\Gamma $
.
We conclude:
Note that the equivariant Picard group can be identified with
![]() ${\check {\mathrm {H}}}^1(M,(\mathcal {O}^\times )^{\mathfrak g}) =({\mathbb C}^\times )^2$
, but simultaneously, it corresponds to trivial one-dimensional bundle, with fibers
${\check {\mathrm {H}}}^1(M,(\mathcal {O}^\times )^{\mathfrak g}) =({\mathbb C}^\times )^2$
, but simultaneously, it corresponds to trivial one-dimensional bundle, with fibers
![]() ${\mathbb C}(c)$
, over
${\mathbb C}(c)$
, over
![]() $\Gamma $
. This fits well the commutative diagram of Figure 1.
$\Gamma $
. This fits well the commutative diagram of Figure 1.
Corollary 2.12 gives a sufficient condition for
![]() $\Phi _1$
to be injective. For a connected algebraic group G, Mumford’s Proposition 1.4 in [Reference Mumford22] gives a sufficient condition for the map
$\Phi _1$
to be injective. For a connected algebraic group G, Mumford’s Proposition 1.4 in [Reference Mumford22] gives a sufficient condition for the map
![]() $\mathrm {Pic}_G(M)\to \mathrm {Pic(M)}$
to be injective, in terms of nonexistence of a homomorphism
$\mathrm {Pic}_G(M)\to \mathrm {Pic(M)}$
to be injective, in terms of nonexistence of a homomorphism
![]() $G \to GL(1,\mathbb C)$
. (The group of G-equivariant line bundles will be discussed in Section 2.5.) This does not straightforwardly adapt to the infinitesimal analytic setting, yet below we obtain a result inspired by that of Mumford.
$G \to GL(1,\mathbb C)$
. (The group of G-equivariant line bundles will be discussed in Section 2.5.) This does not straightforwardly adapt to the infinitesimal analytic setting, yet below we obtain a result inspired by that of Mumford.
Let
![]() ${\mathfrak g}_p\subset {\mathfrak g}$
denote the isotropy algebra of the point
${\mathfrak g}_p\subset {\mathfrak g}$
denote the isotropy algebra of the point
![]() $p\in M$
:
$p\in M$
:
Let
![]() ${\mathrm {H}}^k_{dR}(M)$
denote the holomorphic de Rham cohomology of M. It is known that in the affine case (for Stein manifolds) as well as for the compact Kähler case, this coincides with the singular cohomology
${\mathrm {H}}^k_{dR}(M)$
denote the holomorphic de Rham cohomology of M. It is known that in the affine case (for Stein manifolds) as well as for the compact Kähler case, this coincides with the singular cohomology
![]() ${\mathrm {H}}^k(M,{\mathbb C})$
, see [Reference Grothendieck12, Reference Griffiths and Harris11]. In general, the holomorphic de Rham cohomology
${\mathrm {H}}^k(M,{\mathbb C})$
, see [Reference Grothendieck12, Reference Griffiths and Harris11]. In general, the holomorphic de Rham cohomology
![]() ${\mathrm {H}}^k_{dR}(M)$
is equal to the hypercohomology
${\mathrm {H}}^k_{dR}(M)$
is equal to the hypercohomology
![]() $\mathbb {H}^k(M,\Omega ^\bullet _M)$
of the sheaf of holomorphic forms on M.
$\mathbb {H}^k(M,\Omega ^\bullet _M)$
of the sheaf of holomorphic forms on M.
Lemma 2.17. Let
![]() ${\mathfrak g}$
be a transitive Lie algebra of vector fields on a manifold M. Define
${\mathfrak g}$
be a transitive Lie algebra of vector fields on a manifold M. Define
![]() $Z=\{[\lambda ]\in {\tilde {\mathrm {H}}}^1({\mathfrak g}, \mathcal {O}(M)) \mid \lambda (Y)_p=0\,\forall Y \in {\mathfrak g}_p,\forall p\in M\}$
(the defining property is representative-independent). Then we have a natural embedding
$Z=\{[\lambda ]\in {\tilde {\mathrm {H}}}^1({\mathfrak g}, \mathcal {O}(M)) \mid \lambda (Y)_p=0\,\forall Y \in {\mathfrak g}_p,\forall p\in M\}$
(the defining property is representative-independent). Then we have a natural embedding
![]() $Z\hookrightarrow {\mathrm {H}}^1_{dR}(M)$
.
$Z\hookrightarrow {\mathrm {H}}^1_{dR}(M)$
.
In particular, if
![]() ${\mathrm {H}}^1_{dR}(M)=0$
, then every
${\mathrm {H}}^1_{dR}(M)=0$
, then every
![]() $[\lambda ]\in Z$
is exact:
$[\lambda ]\in Z$
is exact:
![]() $\lambda =d^{0,0}\mu $
for some
$\lambda =d^{0,0}\mu $
for some
![]() $\mu \in \ker (\delta ^{0,0})$
.
$\mu \in \ker (\delta ^{0,0})$
.
Proof. Consider
![]() $[\lambda ] \in Z$
. Since its representative
$[\lambda ] \in Z$
. Since its representative
![]() $\lambda $
is defined globally on M, the value
$\lambda $
is defined globally on M, the value
![]() $\lambda (X)_p \in \mathbb C$
is well defined for any
$\lambda (X)_p \in \mathbb C$
is well defined for any
![]() $p \in M$
and any
$p \in M$
and any
![]() $X \in {\mathfrak g}$
. Transitivity of
$X \in {\mathfrak g}$
. Transitivity of
![]() ${\mathfrak g}$
implies that for every
${\mathfrak g}$
implies that for every
![]() $v \in T_p M$
, there exists
$v \in T_p M$
, there exists
![]() $X\in {\mathfrak g}$
satisfying
$X\in {\mathfrak g}$
satisfying
![]() $X_p=v$
, which means that the following linear function on
$X_p=v$
, which means that the following linear function on
![]() $T_p M$
is well defined:
$T_p M$
is well defined:
This gives a well-defined 1-form
![]() $\alpha $
on M. Choosing
$\alpha $
on M. Choosing
![]() $X_i\in {\mathfrak g}$
for
$X_i\in {\mathfrak g}$
for
![]() $v_i\in T_pM$
such that
$v_i\in T_pM$
such that
![]() $v_i=(X_i)_p$
, we get for every
$v_i=(X_i)_p$
, we get for every
![]() $p\in M$
,
$p\in M$
,
Thus,
![]() $d\alpha =0$
, so the closed 1-forms in two cohomologies correspond; the same clearly concerns exact 1-forms. This yields the embedding
$d\alpha =0$
, so the closed 1-forms in two cohomologies correspond; the same clearly concerns exact 1-forms. This yields the embedding
![]() $[\lambda ]\mapsto [\alpha ]$
.
$[\lambda ]\mapsto [\alpha ]$
.
If
![]() ${\mathrm {H}}^1_{dR}(M)=0$
, then
${\mathrm {H}}^1_{dR}(M)=0$
, then
![]() $\alpha =d\log \mu $
for some
$\alpha =d\log \mu $
for some
![]() $\mu \in \mathcal {O}^\times (M)$
, and therefore,
$\mu \in \mathcal {O}^\times (M)$
, and therefore,
![]() $\lambda =d^{0,0}\mu $
.
$\lambda =d^{0,0}\mu $
.
Proposition 2.18. Let
![]() ${\mathfrak g}$
be a transitive Lie algebra of vector fields on a manifold M such that
${\mathfrak g}$
be a transitive Lie algebra of vector fields on a manifold M such that
![]() $ \dim {\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))>\dim {\mathrm {H}}^1_{dR}(M)$
. This holds, for instance, when
$ \dim {\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))>\dim {\mathrm {H}}^1_{dR}(M)$
. This holds, for instance, when
![]() $ {\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))\neq 0$
and
$ {\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))\neq 0$
and
![]() ${\mathrm {H}}^1_{dR}(M)=0$
. Then for all
${\mathrm {H}}^1_{dR}(M)=0$
. Then for all
![]() $p\in M$
, there exists a surjective Lie algebra homomorphism
$p\in M$
, there exists a surjective Lie algebra homomorphism
![]() ${\mathfrak g}_p\to \mathfrak {gl}(1,\mathbb C)$
.
${\mathfrak g}_p\to \mathfrak {gl}(1,\mathbb C)$
.
Proof. Consider an element
![]() $[\lambda ]\in {\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M)) \setminus Z$
(by our assumption and Lemma 2.17, this set is nonempty). Since
$[\lambda ]\in {\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M)) \setminus Z$
(by our assumption and Lemma 2.17, this set is nonempty). Since
![]() $\delta ^{1,0} \lambda =0$
,
$\delta ^{1,0} \lambda =0$
,
![]() $\lambda $
defines a global lift of
$\lambda $
defines a global lift of
![]() ${\mathfrak g}$
to the trivial bundle
${\mathfrak g}$
to the trivial bundle
![]() $M \times \mathbb C$
,
$M \times \mathbb C$
,
For any point
![]() $p \in M$
, all vector fields of the Lie subalgebra
$p \in M$
, all vector fields of the Lie subalgebra
are tangent to the fiber
![]() $\pi ^{-1}(p)$
. Therefore, the restriction to the fiber results in a Lie algebra homomorphism:
$\pi ^{-1}(p)$
. Therefore, the restriction to the fiber results in a Lie algebra homomorphism:
By definition of Z,
![]() $\lambda (Y)_p\not \equiv 0$
for a generic point p. Thus, at this point, (2.9) is surjective. Since, for a transitive
$\lambda (Y)_p\not \equiv 0$
for a generic point p. Thus, at this point, (2.9) is surjective. Since, for a transitive
![]() ${\mathfrak g}$
, the isotropies
${\mathfrak g}$
, the isotropies
![]() ${\mathfrak g}_p$
at different points p are conjugate, the claim follows.
${\mathfrak g}_p$
at different points p are conjugate, the claim follows.
The existence of a surjective Lie algebra homomorphism to
![]() $\mathfrak {gl}(1,\mathbb C)$
implies that
$\mathfrak {gl}(1,\mathbb C)$
implies that
![]() ${\mathfrak g}_p$
has an ideal of codimension 1, the kernel of (2.9). Corollary 2.12 then leads to the following statement.
${\mathfrak g}_p$
has an ideal of codimension 1, the kernel of (2.9). Corollary 2.12 then leads to the following statement.
Corollary 2.19. Let
![]() ${\mathfrak g}$
be a transitive Lie algebra of vector fields on a manifold M with
${\mathfrak g}$
be a transitive Lie algebra of vector fields on a manifold M with
![]() ${\mathrm {H}}^1_{dR}(M)=0$
. If
${\mathrm {H}}^1_{dR}(M)=0$
. If
![]() ${\mathfrak g}_p$
does not have an ideal of codimension 1, then
${\mathfrak g}_p$
does not have an ideal of codimension 1, then
![]() $\mathrm {Pic}_{\mathfrak g}(M) \to \mathrm {Pic}(M)$
is injective.
$\mathrm {Pic}_{\mathfrak g}(M) \to \mathrm {Pic}(M)$
is injective.
As a consequence,
![]() $\Phi _1$
is injective if
$\Phi _1$
is injective if
![]() ${\mathfrak g}_p$
is perfect
${\mathfrak g}_p$
is perfect
![]() $[{\mathfrak g}_p,{\mathfrak g}_p]={\mathfrak g}_p$
(this also applies to infinite-dimensional Lie algebras
$[{\mathfrak g}_p,{\mathfrak g}_p]={\mathfrak g}_p$
(this also applies to infinite-dimensional Lie algebras
![]() ${\mathfrak g}$
) and, in particular, if
${\mathfrak g}$
) and, in particular, if
![]() ${\mathfrak g}_p$
is semisimple (for finite-dimensional
${\mathfrak g}_p$
is semisimple (for finite-dimensional
![]() ${\mathfrak g}$
).
${\mathfrak g}$
).
Example 2.20 (Special affine algebra on the plane).
Consider the Lie algebra
The Lie algebra is transitive with simple isotropy
![]() ${\mathfrak g}_p$
. By Proposition 2.18, we have
${\mathfrak g}_p$
. By Proposition 2.18, we have
![]() ${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))=0$
, implying that
${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(M))=0$
, implying that
![]() $\mathrm {Pic}_{\mathfrak g}(\mathbb C^2)\to \mathrm {Pic}(\mathbb C^2)$
is injective by Corollary 2.12. Since
$\mathrm {Pic}_{\mathfrak g}(\mathbb C^2)\to \mathrm {Pic}(\mathbb C^2)$
is injective by Corollary 2.12. Since
![]() $\mathrm {Pic}(\mathbb C^2) =0$
, it follows that
$\mathrm {Pic}(\mathbb C^2) =0$
, it follows that
![]() $\mathrm {Pic}_{\mathfrak g}(\mathbb C^2) = 0$
.
$\mathrm {Pic}_{\mathfrak g}(\mathbb C^2) = 0$
.
Next, for the Lie algebra
the isotropy of the point
![]() $p=0$
$p=0$
is 4-dimensional and solvable, and it has a 3-dimensional ideal. In this case,
![]() $\mathrm {Pic}_{\mathfrak {h}}({\mathbb C}^2)={\mathbb C}$
.
$\mathrm {Pic}_{\mathfrak {h}}({\mathbb C}^2)={\mathbb C}$
.
Note that
![]() ${\mathfrak g}$
and
${\mathfrak g}$
and
![]() $\mathfrak {h}$
can be viewed as the same Lie subalgebra
$\mathfrak {h}$
can be viewed as the same Lie subalgebra
![]() $\mathfrak {sl}(2,{\mathbb C})\ltimes {\mathbb C}^2\subset \mathfrak {sl}(3,{\mathbb C})\subset \mathcal {D}(\mathbb CP^2)$
restricted to two different open charts of
$\mathfrak {sl}(2,{\mathbb C})\ltimes {\mathbb C}^2\subset \mathfrak {sl}(3,{\mathbb C})\subset \mathcal {D}(\mathbb CP^2)$
restricted to two different open charts of
![]() $\mathbb CP^2$
.
$\mathbb CP^2$
.
2.4 Line bundles admitting a transversal lift
We start by recalling some basic information about divisors; cf. [Reference Griffiths and Harris11, Reference Huybrechts15]. Let
![]() $\mathcal {O}^\times $
denote the multiplicative sheaf of nonvanishing holomorphic functions on a complex manifold M, and
$\mathcal {O}^\times $
denote the multiplicative sheaf of nonvanishing holomorphic functions on a complex manifold M, and
![]() $\mathcal {M}^\times $
the sheaf of meromorphic functions that are not identically zero on M. A divisor D is a global section of
$\mathcal {M}^\times $
the sheaf of meromorphic functions that are not identically zero on M. A divisor D is a global section of
![]() $\mathcal {M}^\times /\mathcal {O}^\times $
. It is defined by a collection of functions
$\mathcal {M}^\times /\mathcal {O}^\times $
. It is defined by a collection of functions
![]() $f_\alpha \in \mathcal {M}^\times (U_\alpha )$
for an open cover
$f_\alpha \in \mathcal {M}^\times (U_\alpha )$
for an open cover
![]() $\{U_\alpha \}$
of M, such that
$\{U_\alpha \}$
of M, such that
![]() $f_\alpha /f_\beta \in \mathcal {O}^\times (U_\alpha \cap U_\beta )$
. Any divisor D gives rise to a line bundle, denoted by
$f_\alpha /f_\beta \in \mathcal {O}^\times (U_\alpha \cap U_\beta )$
. Any divisor D gives rise to a line bundle, denoted by
![]() $[D]$
, whose transition functions are given by
$[D]$
, whose transition functions are given by
![]() $g_{\alpha \beta } = f_\alpha /f_\beta \in \mathcal {O}^\times (U_\alpha \cap U_\beta )$
, and the long exact sequence (see [Reference Griffiths and Harris11]) relates the group of divisors
$g_{\alpha \beta } = f_\alpha /f_\beta \in \mathcal {O}^\times (U_\alpha \cap U_\beta )$
, and the long exact sequence (see [Reference Griffiths and Harris11]) relates the group of divisors
![]() $\mathrm {Div}(M) := {\check {\mathrm {H}}}^0 (M,\mathcal {M}^\times /\mathcal {O}^\times )$
to the Picard group on M:
$\mathrm {Div}(M) := {\check {\mathrm {H}}}^0 (M,\mathcal {M}^\times /\mathcal {O}^\times )$
to the Picard group on M:
Here,
![]() ${\check {\mathrm {H}}}^0(M, \mathcal {M}^\times )$
is the group of global meromorphic functions on M, and
${\check {\mathrm {H}}}^0(M, \mathcal {M}^\times )$
is the group of global meromorphic functions on M, and
![]() $\mathrm {Div}(M)/{\check {\mathrm {H}}}^0(M,\mathcal {M}^\times )$
is the group of equivalence classes of divisors (equivalent divisors give equivalent line bundles).
$\mathrm {Div}(M)/{\check {\mathrm {H}}}^0(M,\mathcal {M}^\times )$
is the group of equivalence classes of divisors (equivalent divisors give equivalent line bundles).
Definition 2.21. Let
![]() $\mathfrak g \subset \mathcal {D}(M)$
be a Lie algebra of vector fields on M. The divisor
$\mathfrak g \subset \mathcal {D}(M)$
be a Lie algebra of vector fields on M. The divisor
![]() $D=\{f_\alpha \}$
defined on the open cover
$D=\{f_\alpha \}$
defined on the open cover
![]() $\{U_\alpha \}$
of M is a
$\{U_\alpha \}$
of M is a
![]() ${\mathfrak g}$
-invariant divisor if for each
${\mathfrak g}$
-invariant divisor if for each
![]() $\alpha $
$\alpha $
where
![]() $\lambda _\alpha \in {\mathfrak g}^* \otimes \mathcal O(U_\alpha )$
. The group of
$\lambda _\alpha \in {\mathfrak g}^* \otimes \mathcal O(U_\alpha )$
. The group of
![]() ${\mathfrak g}$
-invariant divisors is denoted by
${\mathfrak g}$
-invariant divisors is denoted by
![]() $\mathrm {Div}_{\mathfrak g}(M)$
. The collection
$\mathrm {Div}_{\mathfrak g}(M)$
. The collection
![]() $\lambda =\{\lambda _\alpha \}$
is called the weight of D.
$\lambda =\{\lambda _\alpha \}$
is called the weight of D.
It follows that
![]() $\mathfrak g$
is tangent to the set of zeros of D, and also to the set of poles. In this way, D defines a (possibly reducible) invariant hypersurface in M.
$\mathfrak g$
is tangent to the set of zeros of D, and also to the set of poles. In this way, D defines a (possibly reducible) invariant hypersurface in M.
Proposition 2.22. Let
![]() ${\mathfrak g} \subset \mathcal {D}(M)$
be a Lie algebra of vector fields on M, and let
${\mathfrak g} \subset \mathcal {D}(M)$
be a Lie algebra of vector fields on M, and let
![]() $D=\{f_\alpha \}$
be a
$D=\{f_\alpha \}$
be a
![]() ${\mathfrak g}$
-invariant divisor with weight
${\mathfrak g}$
-invariant divisor with weight
![]() $\lambda =\{\lambda _\alpha \}$
. Set
$\lambda =\{\lambda _\alpha \}$
. Set
![]() $g_{\alpha \beta } = f_\alpha /f_\beta $
and define
$g_{\alpha \beta } = f_\alpha /f_\beta $
and define
![]() $g=\{g_{\alpha \beta }\}$
. Then the pair
$g=\{g_{\alpha \beta }\}$
. Then the pair
![]() $(g, \lambda )$
defines a
$(g, \lambda )$
defines a
![]() ${\mathfrak g}$
-equivariant line bundle
${\mathfrak g}$
-equivariant line bundle
![]() $L=[D]$
, which is independent of the choice of representative functions
$L=[D]$
, which is independent of the choice of representative functions
![]() $f_\alpha $
.
$f_\alpha $
.
Proof. To show that the pair defines a
![]() ${\mathfrak g}$
-equivariant line bundle, we must verify that
${\mathfrak g}$
-equivariant line bundle, we must verify that
![]() $\partial ^1(g,\lambda )=0$
. It is clear that
$\partial ^1(g,\lambda )=0$
. It is clear that
![]() $\delta ^{0,1} g=0$
since
$\delta ^{0,1} g=0$
since
![]() $g_{\alpha \beta }$
are transition functions of
$g_{\alpha \beta }$
are transition functions of
![]() $[D]$
. Next, the condition
$[D]$
. Next, the condition
![]() $d^{1,0} \lambda _\alpha =0$
holds for each
$d^{1,0} \lambda _\alpha =0$
holds for each
![]() $\alpha $
since
$\alpha $
since
![]() $f_\alpha \not \equiv 0$
, and for arbitrary vector fields
$f_\alpha \not \equiv 0$
, and for arbitrary vector fields
![]() $X,Y\in {\mathfrak g}$
, we have
$X,Y\in {\mathfrak g}$
, we have
What remains is to verify that the weights
![]() $\lambda _\alpha $
are compatible with the transition functions
$\lambda _\alpha $
are compatible with the transition functions
![]() $g_{\alpha \beta }= f_\alpha /f_\beta $
. On
$g_{\alpha \beta }= f_\alpha /f_\beta $
. On
![]() $U_\alpha \cap U_\beta $
, we have
$U_\alpha \cap U_\beta $
, we have
 $$\begin{align*}\lambda_\alpha(X) f_\alpha = X(f_\alpha) = X(g_{\alpha \beta} f_\beta) = X(g_{\alpha \beta}) f_\beta + g_{\alpha \beta} X(f_\beta) = \left(\frac{X(g_{\alpha \beta})}{g_{\alpha \beta}}+\lambda_\beta(X)\right) f_\alpha, \end{align*}$$
$$\begin{align*}\lambda_\alpha(X) f_\alpha = X(f_\alpha) = X(g_{\alpha \beta} f_\beta) = X(g_{\alpha \beta}) f_\beta + g_{\alpha \beta} X(f_\beta) = \left(\frac{X(g_{\alpha \beta})}{g_{\alpha \beta}}+\lambda_\beta(X)\right) f_\alpha, \end{align*}$$
which is equivalent to
![]() $\delta ^{1,0}\lambda = d^{0,1} g$
.
$\delta ^{1,0}\lambda = d^{0,1} g$
.
Next, to show that the
![]() ${\mathfrak g}$
-equivariant bundle is independent of representative functions
${\mathfrak g}$
-equivariant bundle is independent of representative functions
![]() $f_\alpha $
of D, take another representative
$f_\alpha $
of D, take another representative
![]() $\tilde f_\alpha = \mu _\alpha f_\alpha $
with
$\tilde f_\alpha = \mu _\alpha f_\alpha $
with
![]() $\mu _\alpha \in \mathcal {O}^\times (U_\alpha )$
. This results in an equivalent
$\mu _\alpha \in \mathcal {O}^\times (U_\alpha )$
. This results in an equivalent
![]() ${\mathfrak g}$
-equivariant line bundle
${\mathfrak g}$
-equivariant line bundle
![]() $(\{\tilde g_{\alpha \beta }\}, \{\tilde \lambda _\alpha \})$
:
$(\{\tilde g_{\alpha \beta }\}, \{\tilde \lambda _\alpha \})$
:
![]() $\tilde g_{\alpha \beta } = g_{\alpha \beta } \mu _\alpha /\mu _\beta $
and
$\tilde g_{\alpha \beta } = g_{\alpha \beta } \mu _\alpha /\mu _\beta $
and
![]() $\tilde \lambda _\alpha (X) = \lambda _\alpha (X) + X(\mu _\alpha )/\mu _\alpha $
for all
$\tilde \lambda _\alpha (X) = \lambda _\alpha (X) + X(\mu _\alpha )/\mu _\alpha $
for all
![]() $X \in {\mathfrak g}$
.
$X \in {\mathfrak g}$
.
The lifted Lie algebra
![]() ${\mathfrak g}^{\lambda } \subset \mathcal {D}([D])$
is given locally on
${\mathfrak g}^{\lambda } \subset \mathcal {D}([D])$
is given locally on
![]() $\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C$
by
$\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C$
by
The lift
![]() ${\mathfrak g}^\lambda $
has exactly the same form as the lifts in Section 2.1, the only difference being that
${\mathfrak g}^\lambda $
has exactly the same form as the lifts in Section 2.1, the only difference being that
![]() $\lambda $
is now specifically determined by a
$\lambda $
is now specifically determined by a
![]() ${\mathfrak g}$
-invariant divisor. Thus, we have a map
${\mathfrak g}$
-invariant divisor. Thus, we have a map
In general, this map is neither injective nor surjective. For instance, the kernel of this map contains all global
![]() ${\mathfrak g}$
-invariant functions in
${\mathfrak g}$
-invariant functions in
![]() $\mathcal {M}^\times (M)$
. If
$\mathcal {M}^\times (M)$
. If
![]() ${\mathfrak g}$
is transitive, then
${\mathfrak g}$
is transitive, then
![]() $\mathrm {Div}_{\mathfrak g}(M)=0$
, but
$\mathrm {Div}_{\mathfrak g}(M)=0$
, but
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
may be nontrivial as in Example 2.14. The next example exhibits nontrivial
$\mathrm {Pic}_{\mathfrak g}(M)$
may be nontrivial as in Example 2.14. The next example exhibits nontrivial
![]() $\mathrm {Div}_{\mathfrak g}(M)$
.
$\mathrm {Div}_{\mathfrak g}(M)$
.
Example 2.23 (
 $\mathfrak {sl}(2,\mathbb C) \subset \mathcal {D}(\mathbb CP^2)$
).
$\mathfrak {sl}(2,\mathbb C) \subset \mathcal {D}(\mathbb CP^2)$
).
The manifold
![]() $\mathbb CP^2$
is covered by the three charts
$\mathbb CP^2$
is covered by the three charts
 $$ \begin{align*} U_3 &= \{[x:y:z] \in \mathbb CP^2 \mid z \neq 0\}, \\ U_2 &= \{[x:y:z] \in \mathbb CP^2 \mid y \neq 0\} , \\ U_1 &= \{[x:y:z] \in \mathbb CP^2 \mid x \neq 0\}, \end{align*} $$
$$ \begin{align*} U_3 &= \{[x:y:z] \in \mathbb CP^2 \mid z \neq 0\}, \\ U_2 &= \{[x:y:z] \in \mathbb CP^2 \mid y \neq 0\} , \\ U_1 &= \{[x:y:z] \in \mathbb CP^2 \mid x \neq 0\}, \end{align*} $$
on which coordinates are given respectively by
Consider the Lie algebra
![]() $\mathfrak {sl}(2,\mathbb C) \subset \mathfrak {sl}(3,\mathbb C)$
given in the respective charts by
$\mathfrak {sl}(2,\mathbb C) \subset \mathfrak {sl}(3,\mathbb C)$
given in the respective charts by
 $$ \begin{gather*} \langle x_2\partial_{x_1}, x_1\partial_{x_2}, x_1\partial_{x_1}-x_2\partial_{x_2} \rangle, \\ \langle\partial_{y_1}, -y_1^2\partial_{y_1}-y_1 y_3\partial_{y_3}, 2y_1\partial_{y_1}+y_3\partial_{y_3} \rangle, \\ \langle -z_2^2\partial_{z_2}-z_2 z_3\partial_{z_3},\partial_{z_2}, -2z_2\partial_{z_2}-z_3\partial_{z_3} \rangle. \end{gather*} $$
$$ \begin{gather*} \langle x_2\partial_{x_1}, x_1\partial_{x_2}, x_1\partial_{x_1}-x_2\partial_{x_2} \rangle, \\ \langle\partial_{y_1}, -y_1^2\partial_{y_1}-y_1 y_3\partial_{y_3}, 2y_1\partial_{y_1}+y_3\partial_{y_3} \rangle, \\ \langle -z_2^2\partial_{z_2}-z_2 z_3\partial_{z_3},\partial_{z_2}, -2z_2\partial_{z_2}-z_3\partial_{z_3} \rangle. \end{gather*} $$
A computation shows that the Chevalley-Eilenberg cohomology groups are
with representative cocycles
The holomorphic transition functions, compatible via overdetermined system (2.4), exist only for
![]() $B_2=C_2=0$
,
$B_2=C_2=0$
,
![]() $C_1=B_1=b$
and are given by formulae
$C_1=B_1=b$
and are given by formulae
Requiring
![]() $g_{\alpha \beta }$
to be holomorphic gives the further restriction
$g_{\alpha \beta }$
to be holomorphic gives the further restriction
![]() $b\in \mathbb Z$
. The constants
$b\in \mathbb Z$
. The constants
![]() $A_1, A_2, A_3$
can be set equal to
$A_1, A_2, A_3$
can be set equal to
![]() $1$
by multiplying with an
$1$
by multiplying with an
![]() $\mathfrak {sl}(2,\mathbb C)$
-invariant
$\mathfrak {sl}(2,\mathbb C)$
-invariant
![]() $\delta ^{0,0}$
-coboundary. We conclude:
$\delta ^{0,0}$
-coboundary. We conclude:
In this case,
![]() $\mathrm {Div}_{\mathfrak {sl}(2,{\mathbb C})}({\mathbb C} P^2)\simeq \mathrm {Pic}_{\mathfrak {sl}(2,{\mathbb C})} ({\mathbb C} P^2)$
. The unique divisor
$\mathrm {Div}_{\mathfrak {sl}(2,{\mathbb C})}({\mathbb C} P^2)\simeq \mathrm {Pic}_{\mathfrak {sl}(2,{\mathbb C})} ({\mathbb C} P^2)$
. The unique divisor
![]() $D=\{f_1,f_2,f_3\}$
corresponding to
$D=\{f_1,f_2,f_3\}$
corresponding to
![]() $b\in \mathbb Z$
is given by
$b\in \mathbb Z$
is given by
We will now describe an obstruction for the existence of invariant divisors, elaborating upon [Reference Fels and Olver7]. The following definition is adapted from [Reference Anderson and Fels1] where it was used for group actions.
Definition 2.24. For a Lie algebra
![]() ${\mathfrak g}\subset \mathcal {D}(M)$
and a holomorphic line bundle
${\mathfrak g}\subset \mathcal {D}(M)$
and a holomorphic line bundle
![]() $\pi \colon L \to M$
, a lift
$\pi \colon L \to M$
, a lift
![]() $\hat {\mathfrak g}\subset \mathcal {D}(L)$
is called transversal if generic
$\hat {\mathfrak g}\subset \mathcal {D}(L)$
is called transversal if generic
![]() $\hat {\mathfrak g}$
-orbits on L
$\hat {\mathfrak g}$
-orbits on L
![]() $\pi $
-project biholomorphically.
$\pi $
-project biholomorphically.
Note that singular orbits of
![]() $\hat {\mathfrak g}$
may project non-injectively (but indeed surjectively) to
$\hat {\mathfrak g}$
may project non-injectively (but indeed surjectively) to
![]() ${\mathfrak g}$
-orbits on M (see Example 2.27 below). The following is a reformulation of Theorem 1.3.
${\mathfrak g}$
-orbits on M (see Example 2.27 below). The following is a reformulation of Theorem 1.3.
Proposition 2.25. Let
![]() $(L,\hat {\mathfrak g})$
be a
$(L,\hat {\mathfrak g})$
be a
![]() ${\mathfrak g}$
-equivariant line bundle over M. Suppose
${\mathfrak g}$
-equivariant line bundle over M. Suppose
![]() $L\in \mathrm {im}(\Psi _1\circ j_{\mathfrak g})$
(i.e.,
$L\in \mathrm {im}(\Psi _1\circ j_{\mathfrak g})$
(i.e.,
![]() $L=[D]$
for some
$L=[D]$
for some
![]() ${\mathfrak g}$
-invariant divisor D with weight
${\mathfrak g}$
-invariant divisor D with weight
![]() $\lambda $
and
$\lambda $
and
![]() $\hat {\mathfrak g} = {\mathfrak g}^\lambda $
). Then
$\hat {\mathfrak g} = {\mathfrak g}^\lambda $
). Then
![]() $\hat {\mathfrak g}$
is transversal.
$\hat {\mathfrak g}$
is transversal.
Proof. Let
![]() $D=\{f_\alpha \}$
be a
$D=\{f_\alpha \}$
be a
![]() $\mathfrak g$
-invariant divisor with weight
$\mathfrak g$
-invariant divisor with weight
![]() $\lambda =\{\lambda _\alpha \}$
, and
$\lambda =\{\lambda _\alpha \}$
, and
![]() $[D]$
the corresponding line bundle defined by transition functions
$[D]$
the corresponding line bundle defined by transition functions
![]() $g_{\alpha \beta } = f_\alpha /f_\beta $
. Any element
$g_{\alpha \beta } = f_\alpha /f_\beta $
. Any element
![]() $\hat X \in {\mathfrak g}^\lambda $
takes on
$\hat X \in {\mathfrak g}^\lambda $
takes on
![]() $U_\alpha $
the form
$U_\alpha $
the form
![]() $\hat X|_{U_\alpha } = X|_{U_\alpha } + \lambda _\alpha (X) u \partial _u$
for some
$\hat X|_{U_\alpha } = X|_{U_\alpha } + \lambda _\alpha (X) u \partial _u$
for some
![]() $X \in {\mathfrak g}$
. A straightforward computation shows that
$X \in {\mathfrak g}$
. A straightforward computation shows that
 $$\begin{align*}\hat X(u/f_\alpha) = \frac{\hat{X}(u) f_\alpha - u \hat{X}(f_\alpha)}{f_\alpha^2} = \frac{u \lambda_\alpha(X) f_\alpha-u X(f_\alpha)}{f_\alpha^2} =0. \end{align*}$$
$$\begin{align*}\hat X(u/f_\alpha) = \frac{\hat{X}(u) f_\alpha - u \hat{X}(f_\alpha)}{f_\alpha^2} = \frac{u \lambda_\alpha(X) f_\alpha-u X(f_\alpha)}{f_\alpha^2} =0. \end{align*}$$
Thus, the function
![]() $u/f_\alpha $
on
$u/f_\alpha $
on
![]() $U_\alpha \times \mathbb C$
is a meromorphic absolute invariant (constant on
$U_\alpha \times \mathbb C$
is a meromorphic absolute invariant (constant on
![]() ${\mathfrak g}^\lambda $
-orbits). It follows that the dimension of generic
${\mathfrak g}^\lambda $
-orbits). It follows that the dimension of generic
![]() $\mathfrak g$
-orbits on
$\mathfrak g$
-orbits on
![]() $U_\alpha $
is equal to the dimension of generic
$U_\alpha $
is equal to the dimension of generic
![]() ${\mathfrak g}^\lambda $
-orbits on
${\mathfrak g}^\lambda $
-orbits on
![]() $U_\alpha \times \mathbb C$
. This holds simultaneously on each
$U_\alpha \times \mathbb C$
. This holds simultaneously on each
![]() $U_\alpha $
, and therefore globally on M.
$U_\alpha $
, and therefore globally on M.
Remark 2.26. Local absolute invariants
![]() $u/f_\alpha $
define a collection of local sections tangent to
$u/f_\alpha $
define a collection of local sections tangent to
![]() ${\mathfrak g}^\lambda $
, which are given by
${\mathfrak g}^\lambda $
, which are given by
![]() $u=C f_\alpha $
with C being an absolute
$u=C f_\alpha $
with C being an absolute
![]() ${\mathfrak g}$
-invariant. Choosing C to be a global invariant on M gives a global
${\mathfrak g}$
-invariant. Choosing C to be a global invariant on M gives a global
![]() ${\mathfrak g}^\lambda $
-invariant section of
${\mathfrak g}^\lambda $
-invariant section of
![]() $[D]$
.
$[D]$
.
Returning to Example 2.14 on
![]() $\mathfrak {sl}(2,{\mathbb C})\subset \mathcal {D}({\mathbb C} P^1)$
, we observe that generic orbits of any nontrivial lift are 2-dimensional. Thus, there are no nontrivial invariant divisors, which also follows from the fact that
$\mathfrak {sl}(2,{\mathbb C})\subset \mathcal {D}({\mathbb C} P^1)$
, we observe that generic orbits of any nontrivial lift are 2-dimensional. Thus, there are no nontrivial invariant divisors, which also follows from the fact that
![]() $\mathfrak {sl}(2,\mathbb C)$
is transitive on
$\mathfrak {sl}(2,\mathbb C)$
is transitive on
![]() $\mathbb CP^1$
. Here is another demonstration of Proposition 2.25.
$\mathbb CP^1$
. Here is another demonstration of Proposition 2.25.
Example 2.27 (
 $\mathfrak {aff}(1,\mathbb C) \subset \mathcal {D}(\mathbb CP^1)$
).
$\mathfrak {aff}(1,\mathbb C) \subset \mathcal {D}(\mathbb CP^1)$
).
Consider again coordinate charts
![]() $U_0 \simeq \mathbb C^1(x)$
and
$U_0 \simeq \mathbb C^1(x)$
and
![]() $U_\infty \simeq \mathbb C^1(y)$
of
$U_\infty \simeq \mathbb C^1(y)$
of
![]() $\mathbb CP^1$
, with the Lie subalgebra
$\mathbb CP^1$
, with the Lie subalgebra
![]() ${\mathfrak g}=\mathfrak {aff}(1,{\mathbb C})=\langle X,Y\rangle \subset \mathfrak {sl}(2,{\mathbb C})$
given by
${\mathfrak g}=\mathfrak {aff}(1,{\mathbb C})=\langle X,Y\rangle \subset \mathfrak {sl}(2,{\mathbb C})$
given by
General representatives
![]() $\lambda _s$
of elements in
$\lambda _s$
of elements in
![]() ${\mathrm {H}}^1(\mathfrak {aff}(1,{\mathbb C}),\mathcal {O}(U_s))$
, for
${\mathrm {H}}^1(\mathfrak {aff}(1,{\mathbb C}),\mathcal {O}(U_s))$
, for
![]() $s=0,\infty $
, in basis
$s=0,\infty $
, in basis
![]() $(X,Y)$
are given by
$(X,Y)$
are given by
A general compatible transition function exists only when
![]() $A=B_1-B_2$
, in which case it is cohomologous to
$A=B_1-B_2$
, in which case it is cohomologous to
![]() $g_{0 \infty }=y^{B_2}=x^{-B_2}$
. Requiring
$g_{0 \infty }=y^{B_2}=x^{-B_2}$
. Requiring
![]() $g_{0 \infty }$
to be holomorphic results in
$g_{0 \infty }$
to be holomorphic results in
![]() $B_2\in \mathbb Z$
. The local lifts corresponding to
$B_2\in \mathbb Z$
. The local lifts corresponding to
![]() $\lambda _0$
and
$\lambda _0$
and
![]() $\lambda _\infty $
are given by
$\lambda _\infty $
are given by
It is clear that the generic orbit dimension is 1 if and only if
![]() $B_2=B_1$
. In this case, we get the invariant divisor D given by
$B_2=B_1$
. In this case, we get the invariant divisor D given by
![]() $f_0=1$
and
$f_0=1$
and
![]() $f_\infty =y^{-B_1}$
. Thus,
$f_\infty =y^{-B_1}$
. Thus,
Note that the map
![]() $\Psi _1\colon \mathrm {Pic}_{\mathfrak g}({\mathbb C} P^1)\to \mathrm {Pic}({\mathbb C} P^1)$
is not injective:
$\Psi _1\colon \mathrm {Pic}_{\mathfrak g}({\mathbb C} P^1)\to \mathrm {Pic}({\mathbb C} P^1)$
is not injective:
![]() $\ker (\Psi _1) \simeq {\mathrm {H}}_d^1({\mathrm {H}}_\delta ^0(C^{\bullet ,\bullet }))={\mathbb C}$
. Similar to Example 2.14, we have
$\ker (\Psi _1) \simeq {\mathrm {H}}_d^1({\mathrm {H}}_\delta ^0(C^{\bullet ,\bullet }))={\mathbb C}$
. Similar to Example 2.14, we have
![]() $\mathfrak {M}_{\mathfrak g}(M) = \mathbb C$
even though
$\mathfrak {M}_{\mathfrak g}(M) = \mathbb C$
even though
![]() $\mathfrak {M}_{\mathfrak g}(\{U_0, U_\infty \}) = \mathbb Z$
.
$\mathfrak {M}_{\mathfrak g}(\{U_0, U_\infty \}) = \mathbb Z$
.
Proposition 2.25 can be viewed as a global version of [Reference Fels and Olver7, Th. 5.4]. According to it, locally, in smooth regular case, the statement allows a converse, giving a criterion for the (local) existence of relative invariants. Globally, in general analytic context, there is no converse to Proposition 2.25, due to other reasons for nonexistence of meromorphic invariant divisors/relative invariants. This is shown in the following simple example and also in a more complicated example of Section 3.4. Yet, in the following section, we will give a converse statement in the algebraic context.
Example 2.28. Consider the Lie algebra
![]() ${\mathfrak g}=\langle x^2\partial _x\rangle \subset \mathcal {D}({\mathbb C})$
. All line bundles over
${\mathfrak g}=\langle x^2\partial _x\rangle \subset \mathcal {D}({\mathbb C})$
. All line bundles over
![]() ${\mathbb C}$
are trivial,
${\mathbb C}$
are trivial,
![]() $\mathrm {Pic}_{\mathfrak g}({\mathbb C})=0$
, while we have
$\mathrm {Pic}_{\mathfrak g}({\mathbb C})=0$
, while we have
![]() $\mathrm {Pic}_{\mathfrak g}({\mathbb C})={\mathbb C}^2$
. A general representative cocycle of
$\mathrm {Pic}_{\mathfrak g}({\mathbb C})={\mathbb C}^2$
. A general representative cocycle of
![]() ${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(\mathbb C))$
has the form
${\tilde {\mathrm {H}}}^1({\mathfrak g},\mathcal {O}(\mathbb C))$
has the form
![]() $\lambda (x^2\partial _x)=A+Bx$
with
$\lambda (x^2\partial _x)=A+Bx$
with
![]() $A,B\in {\mathbb C}$
, and the corresponding lifted Lie algebra is
$A,B\in {\mathbb C}$
, and the corresponding lifted Lie algebra is
Generic orbits of both
![]() ${\mathfrak g}$
and
${\mathfrak g}$
and
![]() ${\mathfrak g}^\lambda $
are 1-dimensional for any choice of A and B; thus,
${\mathfrak g}^\lambda $
are 1-dimensional for any choice of A and B; thus,
![]() ${\mathfrak g}^\lambda $
is transversal. However, the general solution of the system
${\mathfrak g}^\lambda $
is transversal. However, the general solution of the system
![]() $x^2\partial _x(f(x)) = (A+Bx) f(x)$
is
$x^2\partial _x(f(x)) = (A+Bx) f(x)$
is
This is a (meromorphic)
![]() ${\mathfrak g}$
-invariant divisor on
${\mathfrak g}$
-invariant divisor on
![]() $\mathbb C$
only when
$\mathbb C$
only when
![]() $A=0$
and
$A=0$
and
![]() $B \in \mathbb Z$
(i.e.,
$B \in \mathbb Z$
(i.e.,
![]() $\mathrm {Div}_{\mathfrak g}({\mathbb C} P^1)=\mathbb {Z}$
and not all equivariant line bundles come from invariant divisors).
$\mathrm {Div}_{\mathfrak g}({\mathbb C} P^1)=\mathbb {Z}$
and not all equivariant line bundles come from invariant divisors).
2.5 Lie group vs Lie algebra approach
Let G be a Lie group acting on M. We consider the group
![]() $\mathrm {Pic}_G(M)$
of G-equivariant line bundles over M. In the setting of algebraic schemes, it was studied in [Reference Mumford22, Ch. 1.3]. Here, we give a different description of
$\mathrm {Pic}_G(M)$
of G-equivariant line bundles over M. In the setting of algebraic schemes, it was studied in [Reference Mumford22, Ch. 1.3]. Here, we give a different description of
![]() $\mathrm {Pic}_G(M)$
, emphasizing its relation to
$\mathrm {Pic}_G(M)$
, emphasizing its relation to
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
when
$\mathrm {Pic}_{\mathfrak g}(M)$
when
![]() ${\mathfrak g}$
is the Lie algebra of vector fields corresponding to the Lie group action, but demonstrate that, in general,
${\mathfrak g}$
is the Lie algebra of vector fields corresponding to the Lie group action, but demonstrate that, in general,
![]() $\mathrm {Pic}_G(M)$
is not isomorphic to
$\mathrm {Pic}_G(M)$
is not isomorphic to
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
.
$\mathrm {Pic}_{\mathfrak g}(M)$
.
Definition 2.29. A lift
![]() $\hat \rho $
of a group action
$\hat \rho $
of a group action
![]() $\rho \colon G \times M \to M$
to a line bundle
$\rho \colon G \times M \to M$
to a line bundle
![]() $\pi \colon L \to M$
is a map
$\pi \colon L \to M$
is a map
![]() $\hat \rho \colon G \times L \to L$
such that
$\hat \rho \colon G \times L \to L$
such that
![]() $\rho _g \colon L \to L$
is a vector bundle automorphism for each
$\rho _g \colon L \to L$
is a vector bundle automorphism for each
![]() $g \in G$
, and the following diagram commutes:
$g \in G$
, and the following diagram commutes:

The pair
![]() $(\pi \colon L\to M,\hat \rho )$
is called a G-equivariant line bundle. The space of such bundles, modulo the natural equivalences, has the group structure with the operation of tensor product. The group of G-equivariant line bundles
$(\pi \colon L\to M,\hat \rho )$
is called a G-equivariant line bundle. The space of such bundles, modulo the natural equivalences, has the group structure with the operation of tensor product. The group of G-equivariant line bundles
![]() $\mathrm {Pic}_G(M)$
is called the G-equivariant Picard group.
$\mathrm {Pic}_G(M)$
is called the G-equivariant Picard group.
We assume G acts by biholomorphisms on M. The general description of G-equivariant line bundles over M can be done in terms of a cohomology theory that generalizes both the Čech cohomology and the Lie group cohomology with coefficients in the G-module
![]() $\mathcal {O}^\times (M)$
.
$\mathcal {O}^\times (M)$
.
Let
![]() $\pi \colon L \to M$
be a line bundle. Assume there exists a lift of the group action to L (i.e. for each
$\pi \colon L \to M$
be a line bundle. Assume there exists a lift of the group action to L (i.e. for each
![]() $\varphi \in G$
, there exists a (holomorphic) vector bundle automorphism
$\varphi \in G$
, there exists a (holomorphic) vector bundle automorphism
![]() $\hat \varphi $
on L, satisfying
$\hat \varphi $
on L, satisfying
![]() $\pi (\hat \varphi (p)) = \varphi (\pi (p))$
for each
$\pi (\hat \varphi (p)) = \varphi (\pi (p))$
for each
![]() $p \in L$
(to simplify formulas, we use the notation
$p \in L$
(to simplify formulas, we use the notation
![]() $\varphi = \rho _g$
and
$\varphi = \rho _g$
and
![]() $\hat \varphi = \hat \rho _g$
). Let
$\hat \varphi = \hat \rho _g$
). Let
![]() $\mathcal {U}=\{U_\alpha \}$
be a trivializing chart for L, and
$\mathcal {U}=\{U_\alpha \}$
be a trivializing chart for L, and
![]() $u_\alpha $
be a (linear) fiber coordinate on
$u_\alpha $
be a (linear) fiber coordinate on
![]() $\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C$
. Then
$\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C$
. Then
![]() $\hat \varphi $
acts on
$\hat \varphi $
acts on
![]() $u_\alpha $
in the following way:
$u_\alpha $
in the following way:
Composing with a second element in the Lie group gives
on
![]() $U_\gamma \cap \psi ^{-1}(U_\beta \cap \varphi ^{-1}(U_\alpha ))$
. Simultaneously, on
$U_\gamma \cap \psi ^{-1}(U_\beta \cap \varphi ^{-1}(U_\alpha ))$
. Simultaneously, on
![]() $U_\gamma \cap \psi ^{-1}(\varphi ^{-1}(U_\alpha ))$
, we have
$U_\gamma \cap \psi ^{-1}(\varphi ^{-1}(U_\alpha ))$
, we have
Thus, on
![]() $U_\gamma \cap \psi ^{-1}(U_\beta ) \cap \psi ^{-1}(\varphi ^{-1}(U_\alpha ))$
we get
$U_\gamma \cap \psi ^{-1}(U_\beta ) \cap \psi ^{-1}(\varphi ^{-1}(U_\alpha ))$
we get
When
![]() $\varphi $
is equal to the identity transformation on M, equation (2.11) gives
$\varphi $
is equal to the identity transformation on M, equation (2.11) gives
![]() $\Lambda _{\alpha \beta }(\mathrm {id}) = g_{\alpha \beta }$
, where
$\Lambda _{\alpha \beta }(\mathrm {id}) = g_{\alpha \beta }$
, where
![]() $g_{\alpha \beta }$
is the transition function of
$g_{\alpha \beta }$
is the transition function of
![]() $\pi $
on
$\pi $
on
![]() $U_\alpha \cap U_\beta $
. Setting
$U_\alpha \cap U_\beta $
. Setting
![]() $\varphi =\mathrm {id}$
in (2.12) gives
$\varphi =\mathrm {id}$
in (2.12) gives
while setting
![]() $\psi =\mathrm {id}$
leads to
$\psi =\mathrm {id}$
leads to
The last equality shows that if the transition functions are given, then
![]() $\Lambda _{\alpha \beta }(\varphi )$
on
$\Lambda _{\alpha \beta }(\varphi )$
on
![]() $U_\beta \cap U_\alpha \cap \varphi ^{-1}(U_\alpha )$
is uniquely determined by
$U_\beta \cap U_\alpha \cap \varphi ^{-1}(U_\alpha )$
is uniquely determined by
![]() $\Lambda _{\alpha \alpha }(\varphi )$
.
$\Lambda _{\alpha \alpha }(\varphi )$
.
Next, changing the fiber coordinates
![]() $v_\alpha = \mu _\alpha u_\alpha $
for
$v_\alpha = \mu _\alpha u_\alpha $
for
![]() $\mu _\alpha \in \mathcal {O}^\times (U_\alpha )$
,
$\mu _\alpha \in \mathcal {O}^\times (U_\alpha )$
,
results in the equivalence relation
 $$\begin{align*}\Lambda_{\alpha \beta}(\varphi) \sim \frac{\varphi^*(\mu_\alpha)}{\mu_\beta} \Lambda_{\alpha \beta}(\varphi). \end{align*}$$
$$\begin{align*}\Lambda_{\alpha \beta}(\varphi) \sim \frac{\varphi^*(\mu_\alpha)}{\mu_\beta} \Lambda_{\alpha \beta}(\varphi). \end{align*}$$
Introducing the differentials
 $$ \begin{align*} (D^0 \mu (\varphi))_{\alpha \beta} &= \frac{\varphi^*(\mu_\alpha)}{\mu_\beta}, \\ (D^1 \Lambda(\varphi, \psi))_{\alpha \beta \gamma} &= \frac{\Lambda_{\alpha \gamma}(\varphi \circ \psi)}{\psi^*(\Lambda_{\alpha \beta}(\varphi)) \Lambda_{\beta \gamma} (\psi)}, \end{align*} $$
$$ \begin{align*} (D^0 \mu (\varphi))_{\alpha \beta} &= \frac{\varphi^*(\mu_\alpha)}{\mu_\beta}, \\ (D^1 \Lambda(\varphi, \psi))_{\alpha \beta \gamma} &= \frac{\Lambda_{\alpha \gamma}(\varphi \circ \psi)}{\psi^*(\Lambda_{\alpha \beta}(\varphi)) \Lambda_{\beta \gamma} (\psi)}, \end{align*} $$
we see that
![]() $\Lambda =\{\Lambda _{\alpha \beta }\}$
defines a G-equivariant line bundle over M if and only if
$\Lambda =\{\Lambda _{\alpha \beta }\}$
defines a G-equivariant line bundle over M if and only if
![]() $D^1 \Lambda =0$
. Moreover, the G-equivariant line bundles defined by
$D^1 \Lambda =0$
. Moreover, the G-equivariant line bundles defined by
![]() $\Lambda $
and
$\Lambda $
and
![]() $\tilde \Lambda $
are equivalent if and only if
$\tilde \Lambda $
are equivalent if and only if
![]() $\tilde \Lambda = \Lambda \cdot D^0 \mu $
for some
$\tilde \Lambda = \Lambda \cdot D^0 \mu $
for some
![]() $\mu $
. We define the action group cohomology for a given cover
$\mu $
. We define the action group cohomology for a given cover
![]() $\mathcal {U}$
$\mathcal {U}$
 $$\begin{align*}{\mathrm{H}}^1_{\mathcal{U}}(G,\mathcal{O}^\times)= \frac{\ker(D^1)}{\mathrm{im}(D^0)}, \end{align*}$$
$$\begin{align*}{\mathrm{H}}^1_{\mathcal{U}}(G,\mathcal{O}^\times)= \frac{\ker(D^1)}{\mathrm{im}(D^0)}, \end{align*}$$
and in general, we use the direct limit of this cohomology,
![]() ${\mathrm {H}}^1(G,\mathcal {O}^\times ):=\varinjlim {\mathrm {H}}^1_{\mathcal {U}}(G,\mathcal {O}^\times )$
.
${\mathrm {H}}^1(G,\mathcal {O}^\times ):=\varinjlim {\mathrm {H}}^1_{\mathcal {U}}(G,\mathcal {O}^\times )$
.
Proposition 2.30. The group
![]() $\mathrm {Pic}_G(M)$
of G-equivariant line bundles is isomorphic to
$\mathrm {Pic}_G(M)$
of G-equivariant line bundles is isomorphic to
![]() $H^1(G,\mathcal {O}^\times )$
.
$H^1(G,\mathcal {O}^\times )$
.
Let us note that we consider not abstract but rather continuous (van Est) group cohomology; cf. [Reference Fuks9]. In fact, the above specifies cochains to be holomorphic.
Remark 2.31. For a trivial line bundle, we get the Lie group cohomology
![]() ${\mathrm {H}}^1(G,\mathcal {O}^\times (M))$
of the Lie group G with the values in the module
${\mathrm {H}}^1(G,\mathcal {O}^\times (M))$
of the Lie group G with the values in the module
![]() $\mathcal {O}^\times (M)$
. However, with
$\mathcal {O}^\times (M)$
. However, with
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
being
$\psi $
being
![]() $\mathrm {id}_M$
, the above definition gives the Čech cohomology
$\mathrm {id}_M$
, the above definition gives the Čech cohomology
![]() ${\check {\mathrm {H}}}^1(M,\mathcal {O}^\times )$
of M with the values in the sheaf
${\check {\mathrm {H}}}^1(M,\mathcal {O}^\times )$
of M with the values in the sheaf
![]() $\mathcal {O}^\times $
. Thus,
$\mathcal {O}^\times $
. Thus,
![]() $\mathrm {Pic}_G(M)$
interpolates between the two cohomologies.
$\mathrm {Pic}_G(M)$
interpolates between the two cohomologies.
Any Lie group action gives rise to a Lie algebra
![]() $\mathfrak g$
of vector fields. Consider a one-parameter group
$\mathfrak g$
of vector fields. Consider a one-parameter group
![]() $\varphi _t \subset G$
and the corresponding vector field X. Denote the vector field on L corresponding to
$\varphi _t \subset G$
and the corresponding vector field X. Denote the vector field on L corresponding to
![]() $\hat \varphi _t$
by
$\hat \varphi _t$
by
![]() $\hat X$
. For small t, the set
$\hat X$
. For small t, the set
![]() $U_\alpha \cap \varphi _t^{-1}(U_\alpha )$
is nonempty, and on this set, we have
$U_\alpha \cap \varphi _t^{-1}(U_\alpha )$
is nonempty, and on this set, we have
When t approaches
![]() $0$
,
$0$
,
![]() $U_\alpha \cap \varphi _t^{-1}(U_\alpha )$
approaches
$U_\alpha \cap \varphi _t^{-1}(U_\alpha )$
approaches
![]() $U_\alpha $
, and the Lie derivative of
$U_\alpha $
, and the Lie derivative of
![]() $u_\alpha $
with respect to
$u_\alpha $
with respect to
![]() $\hat X$
on
$\hat X$
on
![]() $U_\alpha $
is given by
$U_\alpha $
is given by
Comparing this to the lifts
![]() $\hat X=X +\lambda _{\alpha }(X) u_\alpha \partial _{u_\alpha }$
discussed in Section 2.1 results in the relation
$\hat X=X +\lambda _{\alpha }(X) u_\alpha \partial _{u_\alpha }$
discussed in Section 2.1 results in the relation
Thus, a G-equivariant line bundle on M yields a
![]() ${\mathfrak g}$
-equivariant line bundle for
${\mathfrak g}$
-equivariant line bundle for
![]() ${\mathfrak g}=\mathrm {Lie}(G)$
. However, the map
${\mathfrak g}=\mathrm {Lie}(G)$
. However, the map
in general is neither injective nor surjective. Non-injectivity is illustrated by an action of a discrete group, like
![]() $\mathbb Z_m:z\mapsto z^m$
on
$\mathbb Z_m:z\mapsto z^m$
on
![]() ${\mathbb C} P^1$
. Non-surjectivity is demonstrated as follows.
${\mathbb C} P^1$
. Non-surjectivity is demonstrated as follows.
Example 2.32 (Projective action revisited).
The Lie groups
![]() $SL(2,{\mathbb C})$
and
$SL(2,{\mathbb C})$
and
![]() $PGL(2,{\mathbb C})$
act on
$PGL(2,{\mathbb C})$
act on
![]() ${\mathbb C} P^1$
by Möbius transformations. In the open cover given by charts
${\mathbb C} P^1$
by Möbius transformations. In the open cover given by charts
![]() $U_0\simeq {\mathbb C}(x)$
and
$U_0\simeq {\mathbb C}(x)$
and
![]() $U_\infty \simeq {\mathbb C}(y)$
, the action is
$U_\infty \simeq {\mathbb C}(y)$
, the action is
 $$\begin{align*}\varphi=\left(\begin{matrix} a & b \\ c & d \end{matrix}\right):\quad \varphi^*(x) = \frac{ax+b}{cx+d}, \qquad \varphi^*(y) = \frac{dy+c}{by+a}. \end{align*}$$
$$\begin{align*}\varphi=\left(\begin{matrix} a & b \\ c & d \end{matrix}\right):\quad \varphi^*(x) = \frac{ax+b}{cx+d}, \qquad \varphi^*(y) = \frac{dy+c}{by+a}. \end{align*}$$
For
![]() $SL(2,\mathbb C)$
, the lifts are given by
$SL(2,\mathbb C)$
, the lifts are given by
where
![]() $A\in \mathbb Z$
, as in Example 2.14. However, for
$A\in \mathbb Z$
, as in Example 2.14. However, for
![]() $PGL(2,\mathbb C)$
, the lifts are given by
$PGL(2,\mathbb C)$
, the lifts are given by
 $$\begin{align*}\hat\varphi^*(u_0)=\frac{(ad-bc)^{A/2} u_0}{(cx+d)^A}, \qquad \hat\varphi^*(u_\infty) = \frac{(ad-bc)^{A/2} u_\infty}{(by+a)^A}, \end{align*}$$
$$\begin{align*}\hat\varphi^*(u_0)=\frac{(ad-bc)^{A/2} u_0}{(cx+d)^A}, \qquad \hat\varphi^*(u_\infty) = \frac{(ad-bc)^{A/2} u_\infty}{(by+a)^A}, \end{align*}$$
which is well defined if and only if
![]() $A=2m\in 2\mathbb Z$
. In other words, the line bundle
$A=2m\in 2\mathbb Z$
. In other words, the line bundle
![]() $\mathcal {O}_{\mathbb CP^1}(1)$
is not
$\mathcal {O}_{\mathbb CP^1}(1)$
is not
![]() $PGL(2,\mathbb C)$
-equivariant, but
$PGL(2,\mathbb C)$
-equivariant, but
![]() $\mathcal {O}_{\mathbb CP^1}(2)$
is.
$\mathcal {O}_{\mathbb CP^1}(2)$
is.
This example, borrowed from [Reference Mumford22, Ch. 1.3], works in any dimension n: the line bundle
![]() $\mathcal {O}_{{\mathbb C} P^n}(k)$
is
$\mathcal {O}_{{\mathbb C} P^n}(k)$
is
![]() $PGL(n+1,{\mathbb C})$
-equivariant iff
$PGL(n+1,{\mathbb C})$
-equivariant iff
![]() $k\in (n+1)\mathbb Z$
(i.e., this group lifts only to the powers of the canonical bundle
$k\in (n+1)\mathbb Z$
(i.e., this group lifts only to the powers of the canonical bundle
![]() $K_{{\mathbb C} P^n}$
). However, all bundles
$K_{{\mathbb C} P^n}$
). However, all bundles
![]() $\mathcal {O}_{{\mathbb C} P^n}(k)$
are
$\mathcal {O}_{{\mathbb C} P^n}(k)$
are
![]() $SL(n+1,{\mathbb C})$
-equivariant. (Note that the center of
$SL(n+1,{\mathbb C})$
-equivariant. (Note that the center of
![]() $SL(n+1,{\mathbb C})$
is
$SL(n+1,{\mathbb C})$
is
![]() $\mathbb Z_{n+1}$
and
$\mathbb Z_{n+1}$
and
![]() $PGL(n+1,{\mathbb C})=SL(n+1,{\mathbb C})/\mathbb Z_{n+1}$
.) This difference cannot be seen at the Lie algebra level, since the two Lie group actions give rise to the same Lie algebra of vector fields. Summarizing, we have
$PGL(n+1,{\mathbb C})=SL(n+1,{\mathbb C})/\mathbb Z_{n+1}$
.) This difference cannot be seen at the Lie algebra level, since the two Lie group actions give rise to the same Lie algebra of vector fields. Summarizing, we have
Note that in this example, both groups
![]() $PGL(n+1,{\mathbb C})$
and
$PGL(n+1,{\mathbb C})$
and
![]() $SL(n+1,{\mathbb C})$
are algebraic, so this example illustrates a general result in [Reference Mumford22, Cor. 1.6] on G-linearization of high powers
$SL(n+1,{\mathbb C})$
are algebraic, so this example illustrates a general result in [Reference Mumford22, Cor. 1.6] on G-linearization of high powers
![]() $L^m$
of an algebraic line bundle L. Next, we discuss a similar effect for invariant divisors.
$L^m$
of an algebraic line bundle L. Next, we discuss a similar effect for invariant divisors.
Recall that an algebraic Lie algebra is
![]() ${\mathfrak g}=\mathrm {Lie}(G)$
for an algebraic Lie group G. If M is an algebraic variety, we call a Lie algebra
${\mathfrak g}=\mathrm {Lie}(G)$
for an algebraic Lie group G. If M is an algebraic variety, we call a Lie algebra
![]() ${\mathfrak g} \subset \mathcal {D}(M)$
algebraic if it is the Lie algebra of an algebraic action by an algebraic Lie group on M. The following is a converse to Proposition 2.25 in the algebraic context (there is a version of this statement for
${\mathfrak g} \subset \mathcal {D}(M)$
algebraic if it is the Lie algebra of an algebraic action by an algebraic Lie group on M. The following is a converse to Proposition 2.25 in the algebraic context (there is a version of this statement for
![]() $\mathrm {Pic}_G(M)$
).
$\mathrm {Pic}_G(M)$
).
Theorem 2.33. Let
![]() $(L,\hat {\mathfrak g}) \in \mathrm {Pic}_{\mathfrak g}(M)$
be a
$(L,\hat {\mathfrak g}) \in \mathrm {Pic}_{\mathfrak g}(M)$
be a
![]() ${\mathfrak g}$
-equivariant line bundle over an algebraic variety M for an algebraic Lie algebra
${\mathfrak g}$
-equivariant line bundle over an algebraic variety M for an algebraic Lie algebra
![]() ${\mathfrak g}$
of vector fields. Assume that the lift
${\mathfrak g}$
of vector fields. Assume that the lift
![]() $\hat {\mathfrak g}$
is algebraic and transversal. Then there exists an integer
$\hat {\mathfrak g}$
is algebraic and transversal. Then there exists an integer
![]() $m\in \mathbb Z_+$
such that
$m\in \mathbb Z_+$
such that
![]() $L^m\in \mathrm {im}(\Phi _1\circ j_{\mathfrak g})$
(i.e.,
$L^m\in \mathrm {im}(\Phi _1\circ j_{\mathfrak g})$
(i.e.,
![]() $L^m=[D]$
for some invariant divisor D with weight
$L^m=[D]$
for some invariant divisor D with weight
![]() $\lambda $
, and
$\lambda $
, and
![]() $\hat {\mathfrak g}={\mathfrak g}^{\lambda /m}$
).
$\hat {\mathfrak g}={\mathfrak g}^{\lambda /m}$
).
Proof. Since
![]() ${\mathfrak g}$
is transversal, it admits on L an absolute invariant
${\mathfrak g}$
is transversal, it admits on L an absolute invariant
![]() $I=I(x,u)$
, with x coordinate on M and u a fiber coordinate on L, such that
$I=I(x,u)$
, with x coordinate on M and u a fiber coordinate on L, such that
![]() $\partial _u(I)\not \equiv 0$
. This complements absolute invariants
$\partial _u(I)\not \equiv 0$
. This complements absolute invariants
![]() $J=J(x)$
obtained by pullback from M. By Rosenlicht’s theorem [Reference Rosenlicht26] the algebraicity of the action implies that the invariant I can be chosen rational in proper (local) variables
$J=J(x)$
obtained by pullback from M. By Rosenlicht’s theorem [Reference Rosenlicht26] the algebraicity of the action implies that the invariant I can be chosen rational in proper (local) variables
![]() $x,u$
(on
$x,u$
(on
![]() $U_\alpha $
with algebraic overlaps). Decompose I into its Laurent series by the fiber variable u
$U_\alpha $
with algebraic overlaps). Decompose I into its Laurent series by the fiber variable u
 $$ \begin{align} I=\sum_{k=-N}^\infty h_k(x)u^k. \end{align} $$
$$ \begin{align} I=\sum_{k=-N}^\infty h_k(x)u^k. \end{align} $$
Since
![]() $[u\partial _u,\hat {\mathfrak g}]=0$
, we get that
$[u\partial _u,\hat {\mathfrak g}]=0$
, we get that
![]() $(u\partial _u)^r(I)$
is an absolute invariant for every r. The spectrum of the operator
$(u\partial _u)^r(I)$
is an absolute invariant for every r. The spectrum of the operator
![]() $u\partial _u$
on generators
$u\partial _u$
on generators
![]() $u^k$
is simple, and due to rationality, the coefficients of I are determined by a finite number of base functions
$u^k$
is simple, and due to rationality, the coefficients of I are determined by a finite number of base functions
![]() $h(x)$
. Thus, every term in the series (2.13) is an absolute invariant. Choose such invariant of the lowest (in absolute value) degree by u. This degree m does not depend on local coordinate chart
$h(x)$
. Thus, every term in the series (2.13) is an absolute invariant. Choose such invariant of the lowest (in absolute value) degree by u. This degree m does not depend on local coordinate chart
![]() $U_\alpha ,\alpha \in A$
, we are using, and we get
$U_\alpha ,\alpha \in A$
, we are using, and we get
 $$\begin{align*}I_\alpha=\frac{u_\alpha^m}{f_\alpha(x)}\quad\ \Longrightarrow\ \quad 1=\frac{I_\alpha}{I_\beta}=\frac{u_\alpha^m/f_\alpha(x)}{u_\beta^m/f_\beta(x)} =g^m_{\alpha\beta}\frac{f_\beta}{f_\alpha}\quad\text{ on }\quad U_\alpha\cap U_\beta. \end{align*}$$
$$\begin{align*}I_\alpha=\frac{u_\alpha^m}{f_\alpha(x)}\quad\ \Longrightarrow\ \quad 1=\frac{I_\alpha}{I_\beta}=\frac{u_\alpha^m/f_\alpha(x)}{u_\beta^m/f_\beta(x)} =g^m_{\alpha\beta}\frac{f_\beta}{f_\alpha}\quad\text{ on }\quad U_\alpha\cap U_\beta. \end{align*}$$
The collection of functions
![]() $\{f_\alpha \in \mathcal {O}(U_\alpha ):\alpha \in A\}$
defines a
$\{f_\alpha \in \mathcal {O}(U_\alpha ):\alpha \in A\}$
defines a
![]() ${\mathfrak g}$
-invariant divisor D with weight
${\mathfrak g}$
-invariant divisor D with weight
![]() $\lambda _\alpha (X)=X(\log f_\alpha )$
,
$\lambda _\alpha (X)=X(\log f_\alpha )$
,
![]() $X\in {\mathfrak g}$
, and the corresponding line bundle
$X\in {\mathfrak g}$
, and the corresponding line bundle
![]() $[D]$
has transition functions
$[D]$
has transition functions
Thus,
![]() $[D]=L^m$
, and the claim follows.
$[D]=L^m$
, and the claim follows.
Example 2.34. Consider the Lie algebra
![]() ${\mathfrak g}=\langle x\partial _x\rangle $
on
${\mathfrak g}=\langle x\partial _x\rangle $
on
![]() ${\mathbb C}$
and its lift
${\mathbb C}$
and its lift
![]() $\hat {\mathfrak g}=\langle x\partial _x+C u\partial _u\rangle $
on the trivial line bundle
$\hat {\mathfrak g}=\langle x\partial _x+C u\partial _u\rangle $
on the trivial line bundle
![]() ${\mathbb C}\times {\mathbb C}$
. It is algebraic if
${\mathbb C}\times {\mathbb C}$
. It is algebraic if
![]() $C=\frac {p}{q}\in \mathbb Q$
with absolute invariant
$C=\frac {p}{q}\in \mathbb Q$
with absolute invariant
![]() $I=\frac {u^m}{x^{Cm}}$
being algebraic for minimal
$I=\frac {u^m}{x^{Cm}}$
being algebraic for minimal
![]() $m=q$
(i.e.,
$m=q$
(i.e.,
![]() $I=\frac {u^q}{x^p}$
). Such a situation occurs for differential invariants of curves in Euclidean plane with respect to the motion group – namely, for the ‘square of the curvature’; see the end of Introduction in [Reference Kruglikov and Lychagin18]. The
$I=\frac {u^q}{x^p}$
). Such a situation occurs for differential invariants of curves in Euclidean plane with respect to the motion group – namely, for the ‘square of the curvature’; see the end of Introduction in [Reference Kruglikov and Lychagin18]. The
![]() ${\mathfrak g}$
-equivariant line bundle
${\mathfrak g}$
-equivariant line bundle
![]() $(\mathbb C \times \mathbb C, \hat {\mathfrak g})$
is in
$(\mathbb C \times \mathbb C, \hat {\mathfrak g})$
is in
![]() $\mathrm {im}(j_{\mathfrak g})$
if and only if
$\mathrm {im}(j_{\mathfrak g})$
if and only if
![]() $C \in \mathbb Z$
.
$C \in \mathbb Z$
.
3 Invariant polynomial divisors on algebraic bundles
In this section, we will consider Lie algebras of vector fields on bundles that have additional structure on the fibers, and where it makes sense to consider divisors that are polynomial in the fiber coordinates. More precisely, we will focus on affine bundles in Section 3.1 and on jet bundles in Section 3.2. In the remaining three subsections, we will apply the obtained results to examples involving Lie algebras of vector fields on jet spaces.
3.1 Lie algebra action on affine bundles
Let
![]() $\pi \colon E \to M$
be an affine bundle (of rank
$\pi \colon E \to M$
be an affine bundle (of rank
![]() $r\ge 1$
), and let
$r\ge 1$
), and let
![]() $\hat {\mathfrak g} \subset \mathcal {D}_{\mathrm {proj}}(E)$
be a Lie algebra of projectable vector fields on E that preserves the affine structure in the fibers. In this section, we will focus on
$\hat {\mathfrak g} \subset \mathcal {D}_{\mathrm {proj}}(E)$
be a Lie algebra of projectable vector fields on E that preserves the affine structure in the fibers. In this section, we will focus on
![]() $\hat {\mathfrak g}$
-invariant divisors whose restriction to fibers are polynomials. We define for
$\hat {\mathfrak g}$
-invariant divisors whose restriction to fibers are polynomials. We define for
![]() $U \subset M$
$U \subset M$
where polynomiality is checked in affine coordinates on E. This space of functions is preserved by automorphisms: If
![]() $\varphi \colon E \to E$
is an automorphism of affine bundles and
$\varphi \colon E \to E$
is an automorphism of affine bundles and
![]() $f \in \mathfrak {P}(U)$
, then
$f \in \mathfrak {P}(U)$
, then
![]() $\varphi ^*f \in \mathfrak {P}(\varphi ^{-1}(U))$
.
$\varphi ^*f \in \mathfrak {P}(\varphi ^{-1}(U))$
.
Assume that
![]() $\mathcal {U}=\{U_\alpha \}$
is an open cover for M such that
$\mathcal {U}=\{U_\alpha \}$
is an open cover for M such that
![]() $\pi ^{-1}(U_\alpha )\simeq U_\alpha \times {\mathbb C}^r$
for any affine bundle
$\pi ^{-1}(U_\alpha )\simeq U_\alpha \times {\mathbb C}^r$
for any affine bundle
![]() $\pi $
. Then
$\pi $
. Then
![]() $\{\pi ^{-1}(U_\alpha )\}$
is open cover for the total space E.
$\{\pi ^{-1}(U_\alpha )\}$
is open cover for the total space E.
Definition 3.1. A divisor
![]() $D=\{f_\alpha \}$
on an affine bundle
$D=\{f_\alpha \}$
on an affine bundle
![]() $\pi \colon E \to M $
is called polynomial if its defining functions
$\pi \colon E \to M $
is called polynomial if its defining functions
![]() $f_\alpha \in \mathcal {O}( \pi ^{-1}(U_\alpha ))$
can be chosen to be in
$f_\alpha \in \mathcal {O}( \pi ^{-1}(U_\alpha ))$
can be chosen to be in
![]() $\mathfrak {P}(U_\alpha )$
.
$\mathfrak {P}(U_\alpha )$
.
In local coordinates
![]() $x^i, u^j$
on
$x^i, u^j$
on
![]() $\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C^r$
,
$\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C^r$
,
![]() $f_\alpha $
takes the form
$f_\alpha $
takes the form
Here,
![]() $u^\sigma =\prod (u^i)^{m_i}$
for the multi-index
$u^\sigma =\prod (u^i)^{m_i}$
for the multi-index
![]() $\sigma =(m_1\dots m_r)$
. The defining functions of a polynomial divisor D satisfy
$\sigma =(m_1\dots m_r)$
. The defining functions of a polynomial divisor D satisfy
![]() $g_{\alpha \beta } = f_\alpha /f_\beta \in \mathcal {O}^\times (\pi ^{-1}(U_\alpha ) \cap \pi ^{-1}(U_\beta ))$
, where both the numerator and denominator are polynomials in
$g_{\alpha \beta } = f_\alpha /f_\beta \in \mathcal {O}^\times (\pi ^{-1}(U_\alpha ) \cap \pi ^{-1}(U_\beta ))$
, where both the numerator and denominator are polynomials in
![]() $u^1, \dots , u^r$
. It follows that the polynomials must cancel each other out, which implies that the transition functions
$u^1, \dots , u^r$
. It follows that the polynomials must cancel each other out, which implies that the transition functions
![]() $g_{\alpha \beta } = f_\alpha /f_\beta $
are the pullback of functions
$g_{\alpha \beta } = f_\alpha /f_\beta $
are the pullback of functions
![]() $\tilde g_{\alpha \beta }\in \mathcal {O}^\times (U_\alpha \cap U_\beta )$
. Thus, we obtain the following proposition.
$\tilde g_{\alpha \beta }\in \mathcal {O}^\times (U_\alpha \cap U_\beta )$
. Thus, we obtain the following proposition.
Proposition 3.2. Let
![]() $D=\{f_\alpha \}$
be a polynomial divisor on the affine bundle
$D=\{f_\alpha \}$
be a polynomial divisor on the affine bundle
![]() $\pi \colon E \to M$
. Then
$\pi \colon E \to M$
. Then
![]() $[D] = \pi ^*L$
for some line bundle
$[D] = \pi ^*L$
for some line bundle
![]() $L \to M$
.
$L \to M$
.
In the above argument, it is clear that the degree s can be taken to be the same for each
![]() $\alpha $
. We call the smallest such s the degree of the polynomial divisor D.
$\alpha $
. We call the smallest such s the degree of the polynomial divisor D.
Next, we let
![]() $\hat {\mathfrak g} \subset \mathcal {D}_{\mathrm {proj}}(E)$
be a projectable Lie algebra of vector fields on E preserving the affine structure on fibers, and consider
$\hat {\mathfrak g} \subset \mathcal {D}_{\mathrm {proj}}(E)$
be a projectable Lie algebra of vector fields on E preserving the affine structure on fibers, and consider
![]() $\hat {\mathfrak g}$
-invariant polynomial divisors.
$\hat {\mathfrak g}$
-invariant polynomial divisors.
Proposition 3.3. Let
![]() $\pi: E\to M$
be an affine bundle and let
$\pi: E\to M$
be an affine bundle and let
![]() $\hat {\mathfrak g} \subset \mathcal {D}_{\mathrm {proj}}(E)$
be a projectable Lie algebra of vector fields on E preserving the affine structure on fibers;
$\hat {\mathfrak g} \subset \mathcal {D}_{\mathrm {proj}}(E)$
be a projectable Lie algebra of vector fields on E preserving the affine structure on fibers;
![]() ${\mathfrak g}=d\pi (\hat {\mathfrak g})$
. If D is a
${\mathfrak g}=d\pi (\hat {\mathfrak g})$
. If D is a
![]() $\hat {\mathfrak g}$
-invariant polynomial divisor on E, then
$\hat {\mathfrak g}$
-invariant polynomial divisor on E, then
![]() $[D]=\pi ^* L$
for some
$[D]=\pi ^* L$
for some
![]() ${\mathfrak g}$
-equivariant line bundle
${\mathfrak g}$
-equivariant line bundle
![]() $L \to M$
.
$L \to M$
.
Proof. What remains to be proven is that the bundle
![]() $\pi \colon L \to M$
with transition functions
$\pi \colon L \to M$
with transition functions
![]() $\tilde g_{\alpha \beta }$
admits a
$\tilde g_{\alpha \beta }$
admits a
![]() ${\mathfrak g}$
-lift. In local coordinates
${\mathfrak g}$
-lift. In local coordinates
![]() $x^i, u^j$
on
$x^i, u^j$
on
![]() $\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C^r$
, each
$\pi ^{-1}(U_\alpha ) \simeq U_\alpha \times \mathbb C^r$
, each
![]() $X \in \hat {\mathfrak g}$
takes the form
$X \in \hat {\mathfrak g}$
takes the form
![]() $X = a^i(x) \partial _{x^i} + (b_0^j(x)+b_l^j(x) u^l) \partial _{u^j}$
. Consider an invariant divisor D given by
$X = a^i(x) \partial _{x^i} + (b_0^j(x)+b_l^j(x) u^l) \partial _{u^j}$
. Consider an invariant divisor D given by
![]() $f_\alpha = \sum _{|\sigma | \leq s} F_{\sigma }(x) u^\sigma $
, a polynomial in
$f_\alpha = \sum _{|\sigma | \leq s} F_{\sigma }(x) u^\sigma $
, a polynomial in
![]() $u^1, \dots , u^r$
of degree s. We have
$u^1, \dots , u^r$
of degree s. We have
Looking at the coordinate form of X, it is clear that
![]() $X(f_\alpha )$
is a polynomial in
$X(f_\alpha )$
is a polynomial in
![]() $u^1, \dots , u^r$
and, furthermore, that its degree is
$u^1, \dots , u^r$
and, furthermore, that its degree is
![]() $\leq s$
. Thus,
$\leq s$
. Thus,
![]() $\lambda _\alpha (X)=X(f_\alpha )/f_\alpha $
is a rational function in
$\lambda _\alpha (X)=X(f_\alpha )/f_\alpha $
is a rational function in
![]() $u^1, \dots , u^r$
, and it is defined everywhere on
$u^1, \dots , u^r$
, and it is defined everywhere on
![]() $U_\alpha \times \mathbb C^r$
only if
$U_\alpha \times \mathbb C^r$
only if
![]() $\lambda _\alpha (X)$
is the pullback of a function
$\lambda _\alpha (X)$
is the pullback of a function
![]() $ \tilde \lambda _\alpha (X) \in \mathcal {O}(U_\alpha )$
. Thus, the
$ \tilde \lambda _\alpha (X) \in \mathcal {O}(U_\alpha )$
. Thus, the
![]() $\hat {\mathfrak g}$
-equivariant line bundle over E defined by
$\hat {\mathfrak g}$
-equivariant line bundle over E defined by
![]() $(\{g_{\alpha \beta }\}, \{\lambda _\alpha \})$
is the pullback of the
$(\{g_{\alpha \beta }\}, \{\lambda _\alpha \})$
is the pullback of the
![]() ${\mathfrak g}$
-equivariant line bundle over M defined by
${\mathfrak g}$
-equivariant line bundle over M defined by
![]() $(\{\tilde g_{\alpha \beta }\}, \{\tilde \lambda _\alpha \})$
.
$(\{\tilde g_{\alpha \beta }\}, \{\tilde \lambda _\alpha \})$
.
Proposition 3.3 (which was reformulated in Theorem 1.4) is relevant, for instance, for investigation of relative invariants of tensor fields (and other geometric objects like affine connections) on a manifold M under the action of some Lie algebra
![]() ${\mathfrak g} \subset \mathcal {D}(M)$
.
${\mathfrak g} \subset \mathcal {D}(M)$
.
Example 3.4. Consider the bundle
![]() $E=S^2 T^* M \to M$
whose sections are symmetric 2-forms on M, and let
$E=S^2 T^* M \to M$
whose sections are symmetric 2-forms on M, and let
![]() ${\mathfrak g}$
be the Lie algebra of holomorphic vector fields on M. There is a canonical lift
${\mathfrak g}$
be the Lie algebra of holomorphic vector fields on M. There is a canonical lift
![]() $\hat {\mathfrak g} \subset \mathcal {D}(E)$
of
$\hat {\mathfrak g} \subset \mathcal {D}(E)$
of
![]() ${\mathfrak g}$
. Let
${\mathfrak g}$
. Let
![]() $x^1, \dots , x^n$
be coordinates on M and
$x^1, \dots , x^n$
be coordinates on M and
![]() $u_{11}, u_{12}, \dots , u_{nn}$
be the additional induced coordinates on E. The function
$u_{11}, u_{12}, \dots , u_{nn}$
be the additional induced coordinates on E. The function
![]() $\det ([u_{ij}])$
, with
$\det ([u_{ij}])$
, with
![]() $u_{ji}=u_{ij}$
for
$u_{ji}=u_{ij}$
for
![]() $i<j$
, is the local expression for a
$i<j$
, is the local expression for a
![]() ${\mathfrak g}$
-invariant divisor, and its (local) weight is
${\mathfrak g}$
-invariant divisor, and its (local) weight is
![]() $-2 \mathrm {div}_{dx^1 \wedge \cdots \wedge dx^n}$
. Globally, the line bundle given by this
$-2 \mathrm {div}_{dx^1 \wedge \cdots \wedge dx^n}$
. Globally, the line bundle given by this
![]() ${\mathfrak g}$
-invariant divisor is the pullback of the line bundle
${\mathfrak g}$
-invariant divisor is the pullback of the line bundle
![]() $(\Lambda ^n T^*M)^{\otimes 2} = (K_M)^{\otimes 2}$
over M.
$(\Lambda ^n T^*M)^{\otimes 2} = (K_M)^{\otimes 2}$
over M.
Let us make a brief remark about invariant rational divisors. Each such is a ratio of two invariant polynomial divisors. The weights of invariant rational divisors form a lattice generated by weights of invariant polynomial divisors. In other words, we have the following relation:
3.2 Lie algebra action on jet bundles
Now we consider polynomial divisors on jet bundles. Most of the arguments here closely resemble those in Section 3.1, but some additional care must be taken. Our introduction to jets will be very brief, and we refer to [Reference Kruglikov, Lychagin, Krupka and Saunders19, Reference Vinogradov and Krasil’shchik21, Reference Olver23] for a more comprehensive treatment.
Let
![]() $J^k(E,m)$
denote the space of k-jets of codimension-m submanifolds of E, and
$J^k(E,m)$
denote the space of k-jets of codimension-m submanifolds of E, and
![]() $J^k \pi $
the space of k-jets of sections of the fiber bundle
$J^k \pi $
the space of k-jets of sections of the fiber bundle
![]() $\pi $
. In statements that are true for both
$\pi $
. In statements that are true for both
![]() $J^k(E,m)$
and
$J^k(E,m)$
and
![]() $J^k \pi $
, we will use the notation
$J^k \pi $
, we will use the notation
![]() $\mathbf {J}^k$
which can always be replaced with either of the two (an exception to this convention occurs only in Section 3.5). There are natural bundle structures
$\mathbf {J}^k$
which can always be replaced with either of the two (an exception to this convention occurs only in Section 3.5). There are natural bundle structures
![]() $\pi _{k,l}\colon \mathbf {J}^k \to \mathbf {J}^l$
for
$\pi _{k,l}\colon \mathbf {J}^k \to \mathbf {J}^l$
for
![]() $0 \leq l \leq k$
, and
$0 \leq l \leq k$
, and
![]() $\pi _k\colon J^k \pi \to M$
.
$\pi _k\colon J^k \pi \to M$
.
Coordinates on
![]() $J^k \pi $
and
$J^k \pi $
and
![]() $J^k(E,m)$
are induced from coordinates on the total space of
$J^k(E,m)$
are induced from coordinates on the total space of
![]() $\pi $
or E, respectively. Given a bundle
$\pi $
or E, respectively. Given a bundle
![]() $\pi \colon E \to M$
, and an open cover
$\pi \colon E \to M$
, and an open cover
![]() $\{U_\alpha \}$
of coordinate charts of E, the collection
$\{U_\alpha \}$
of coordinate charts of E, the collection
![]() $\{\pi _{k,0}^{-1}(U_\alpha )\}$
is an open cover of
$\{\pi _{k,0}^{-1}(U_\alpha )\}$
is an open cover of
![]() $J^k \pi $
. The split coordinates
$J^k \pi $
. The split coordinates
![]() $x^1,\dots x^n, u^1, \dots , u^m$
on
$x^1,\dots x^n, u^1, \dots , u^m$
on
![]() $U_\alpha $
induce additional canonical coordinates
$U_\alpha $
induce additional canonical coordinates
![]() $u_\sigma ^j$
,
$u_\sigma ^j$
,
![]() $|\sigma |\leq k$
where
$|\sigma |\leq k$
where
![]() $\sigma $
is a multi-index, on
$\sigma $
is a multi-index, on
![]() $\pi _{k,0}^{-1}(U_\alpha )$
.
$\pi _{k,0}^{-1}(U_\alpha )$
.
To get an open cover of
![]() $J^k(E,m)$
, we let
$J^k(E,m)$
, we let
![]() $\{U_\alpha \}$
be an open cover of coordinate charts of E that trivializes the bundle
$\{U_\alpha \}$
be an open cover of coordinate charts of E that trivializes the bundle
![]() $J^1(E,m) \to E$
. On each
$J^1(E,m) \to E$
. On each
![]() $U_\alpha $
, for a given set of
$U_\alpha $
, for a given set of
![]() $m+n$
coordinates, we choose a splitting
$m+n$
coordinates, we choose a splitting
![]() $x^1,\dots , x^n, u^1, \dots , u^m$
, and we denote the corresponding coordinate chart on
$x^1,\dots , x^n, u^1, \dots , u^m$
, and we denote the corresponding coordinate chart on
![]() $J^1(E,m)$
by
$J^1(E,m)$
by
![]() $U_\alpha ^{i_1 \cdots i_m}$
with
$U_\alpha ^{i_1 \cdots i_m}$
with
![]() $1 \leq i_1 < \cdots < i_m \leq \dim E$
. For each way of splitting, there is one chart. The split coordinates on
$1 \leq i_1 < \cdots < i_m \leq \dim E$
. For each way of splitting, there is one chart. The split coordinates on
![]() $U_\alpha $
induce additional canonical coordinates
$U_\alpha $
induce additional canonical coordinates
![]() $u_\sigma ^i$
(
$u_\sigma ^i$
(
![]() $|\sigma |\leq k$
) on
$|\sigma |\leq k$
) on
![]() $\pi _{k,1}^{-1}(U_\alpha ^{i_1 \cdots i_m})$
for
$\pi _{k,1}^{-1}(U_\alpha ^{i_1 \cdots i_m})$
for
![]() $k \geq 1$
. The collection
$k \geq 1$
. The collection
![]() $\{\pi _{k,1}^{-1}(U_\alpha ^{i_1 \cdots i_m})\}$
is an open cover of
$\{\pi _{k,1}^{-1}(U_\alpha ^{i_1 \cdots i_m})\}$
is an open cover of
![]() $J^k(E,m)$
. We define for
$J^k(E,m)$
. We define for
![]() $U \subset \mathbf {J}^i$
$U \subset \mathbf {J}^i$
Polynomiality is defined with respect to the canonical coordinates described above. For example, in the case of
![]() $J^k(E,m)$
, then
$J^k(E,m)$
, then
![]() $f \in \mathfrak {P}_j(U)$
if and only if we have, for each
$f \in \mathfrak {P}_j(U)$
if and only if we have, for each
![]() $\alpha $
,
$\alpha $
,
 $$\begin{align*}f\Big|_{\pi_{\infty,j}^{-1}\left(U \right) \cap \pi_{\infty,1}^{-1}\left(U_\alpha^{i_1 \cdots im}\right)} = \sum_{j \leq |\sigma|\leq k, |\tau| \leq r} F^\sigma_\tau u_\sigma^\tau \end{align*}$$
$$\begin{align*}f\Big|_{\pi_{\infty,j}^{-1}\left(U \right) \cap \pi_{\infty,1}^{-1}\left(U_\alpha^{i_1 \cdots im}\right)} = \sum_{j \leq |\sigma|\leq k, |\tau| \leq r} F^\sigma_\tau u_\sigma^\tau \end{align*}$$
for some
![]() $k,r \in \mathbb Z_{\geq 0}$
and a collection
$k,r \in \mathbb Z_{\geq 0}$
and a collection
![]() $\{F^\sigma _\tau \}$
of functions on
$\{F^\sigma _\tau \}$
of functions on
![]() $J^j(E,m)$
.
$J^j(E,m)$
.
If
![]() $\varphi \colon E \to E$
is a point transformation and
$\varphi \colon E \to E$
is a point transformation and
![]() $f \in \mathfrak {P}_i(U)$
, then
$f \in \mathfrak {P}_i(U)$
, then
![]() $(\varphi ^{(\infty )})^* f \in \mathfrak {P}_i(\varphi ^{-1}(U))$
for
$(\varphi ^{(\infty )})^* f \in \mathfrak {P}_i(\varphi ^{-1}(U))$
for
![]() $i \geq 1$
. Similarly, if
$i \geq 1$
. Similarly, if
![]() $\pi \colon E \to M$
is a fiber bundle,
$\pi \colon E \to M$
is a fiber bundle,
![]() $\varphi \colon E \to E$
is a fiber-preserving biholomorphism, and
$\varphi \colon E \to E$
is a fiber-preserving biholomorphism, and
![]() $f \in \mathfrak {P}_i(U)$
, then
$f \in \mathfrak {P}_i(U)$
, then
![]() $(\varphi ^{(\infty )})^* f \in \mathfrak {P}_i(\varphi ^{-1}(U))$
for
$(\varphi ^{(\infty )})^* f \in \mathfrak {P}_i(\varphi ^{-1}(U))$
for
![]() $i \geq 0$
. In particular, point transformations preserve
$i \geq 0$
. In particular, point transformations preserve
![]() $\mathfrak {P}_1$
, while fiber-preserving transformations do the same for
$\mathfrak {P}_1$
, while fiber-preserving transformations do the same for
![]() $\mathfrak {P}_0$
. Based on this, we introduce the following notion.
$\mathfrak {P}_0$
. Based on this, we introduce the following notion.
Definition 3.5. A divisor on
![]() $J^k(E,m)$
is called polynomial if its defining functions
$J^k(E,m)$
is called polynomial if its defining functions
![]() $f_\alpha ^{i_1 \cdots i_m} \in \mathcal {O}(\pi ^{-1}_{k,1} (U_\alpha ^{i_1 \cdots i_m}))$
can be chosen to be in
$f_\alpha ^{i_1 \cdots i_m} \in \mathcal {O}(\pi ^{-1}_{k,1} (U_\alpha ^{i_1 \cdots i_m}))$
can be chosen to be in
![]() $\mathfrak {P}_1(U_\alpha ^{i_1 \cdots i_m})$
. If
$\mathfrak {P}_1(U_\alpha ^{i_1 \cdots i_m})$
. If
![]() $\pi \colon E \to M$
is a fiber bundle, a divisor on
$\pi \colon E \to M$
is a fiber bundle, a divisor on
![]() $J^k \pi $
is called polynomial if its defining functions
$J^k \pi $
is called polynomial if its defining functions
![]() $f_\alpha \in \mathcal {O}(\pi ^{-1}_{k,0}(U_\alpha ))$
can be chosen to be in
$f_\alpha \in \mathcal {O}(\pi ^{-1}_{k,0}(U_\alpha ))$
can be chosen to be in
![]() $\mathfrak {P}_0(U_\alpha )$
.
$\mathfrak {P}_0(U_\alpha )$
.
Proposition 3.6.
-
(1) Let
 $\pi \colon E \to M$
be a fiber bundle, and let
$\pi \colon E \to M$
be a fiber bundle, and let
 $D=\{f_\alpha \}$
be a polynomial divisor on
$D=\{f_\alpha \}$
be a polynomial divisor on
 $J^k \pi $
. Then
$J^k \pi $
. Then
 $[D] = \pi _{k,0}^*L$
for some line bundle
$[D] = \pi _{k,0}^*L$
for some line bundle
 $L \to E=J^0 \pi $
.
$L \to E=J^0 \pi $
. -
(2) Let E be a manifold and
 $D = \{ f_{\alpha }^{i_1 \cdots i_m} \}$
be a polynomial divisor on
$D = \{ f_{\alpha }^{i_1 \cdots i_m} \}$
be a polynomial divisor on
 $J^k(E,m)$
. Then
$J^k(E,m)$
. Then
 $[D] = \pi _{k,1}^* L$
for some line bundle
$[D] = \pi _{k,1}^* L$
for some line bundle
 $L \to J^1(E,m)$
.
$L \to J^1(E,m)$
.
Proof. The proofs of (1) and (2) are very similar, so we prove only (2). Since
![]() $f_\alpha ^{i_1 \cdots i_m}/f_\beta ^{j_1 \cdots j_m}$
are elements in
$f_\alpha ^{i_1 \cdots i_m}/f_\beta ^{j_1 \cdots j_m}$
are elements in
![]() $\mathcal {O}^\times (\pi _{k,1}^{-1} (U_\alpha ^{i_1 \cdots i_m} \cap U_\beta ^{j_1 \cdots j_m}))$
, the polynomial parts are required to cancel. Thus, the transition functions
$\mathcal {O}^\times (\pi _{k,1}^{-1} (U_\alpha ^{i_1 \cdots i_m} \cap U_\beta ^{j_1 \cdots j_m}))$
, the polynomial parts are required to cancel. Thus, the transition functions
![]() $f_\alpha ^{i_1 \cdots i_m}/f_\beta ^{j_1 \cdots j_m}$
are the pullback of elements in
$f_\alpha ^{i_1 \cdots i_m}/f_\beta ^{j_1 \cdots j_m}$
are the pullback of elements in
![]() $\mathcal {O}^\times (U_\alpha ^{i_1 \cdots i_m} \cap U_\beta ^{j_1 \cdots j_m})$
, which are the transition functions of a line bundle over
$\mathcal {O}^\times (U_\alpha ^{i_1 \cdots i_m} \cap U_\beta ^{j_1 \cdots j_m})$
, which are the transition functions of a line bundle over
![]() $J^1(E,m)$
.
$J^1(E,m)$
.
From the proof, it follows that the order and degree of the polynomials
![]() $f_\alpha ^{i_1 \cdots i_m}$
and
$f_\alpha ^{i_1 \cdots i_m}$
and
![]() $f_\beta ^{j_1 \cdots j_m}$
agree. Therefore, the order and degree are also well-defined notions for
$f_\beta ^{j_1 \cdots j_m}$
agree. Therefore, the order and degree are also well-defined notions for
![]() $D = \{f_\alpha ^{i_1 \cdots i_m}\}$
, and this is true also for divisors on
$D = \{f_\alpha ^{i_1 \cdots i_m}\}$
, and this is true also for divisors on
![]() $J^k \pi $
. We define the weighted degree of the monomial
$J^k \pi $
. We define the weighted degree of the monomial
![]() $c(x,y,y_i) y_{\sigma _1}^{j_1} \cdots y_{\sigma _s}^{j_s} \in \mathfrak {P}_1(U_\alpha ^{i_1 \cdots i_m})$
(with
$c(x,y,y_i) y_{\sigma _1}^{j_1} \cdots y_{\sigma _s}^{j_s} \in \mathfrak {P}_1(U_\alpha ^{i_1 \cdots i_m})$
(with
![]() $|\sigma _l| \geq 2$
for each l) to be
$|\sigma _l| \geq 2$
for each l) to be
![]() $\sum _{l=1}^s |\sigma _l|$
, and the weighted degree of a sum of such to be the maximal weighted degree of its monomial parts. The weighted degree can be defined for a divisor in the same way that order and degree were defined above. (In the case when E is a bundle, the weighted degree also counts the first-order jet variables
$\sum _{l=1}^s |\sigma _l|$
, and the weighted degree of a sum of such to be the maximal weighted degree of its monomial parts. The weighted degree can be defined for a divisor in the same way that order and degree were defined above. (In the case when E is a bundle, the weighted degree also counts the first-order jet variables
![]() $y_i^j$
.)
$y_i^j$
.)
Next, consider a Lie algebra of vector fields
![]() ${\mathfrak g}\subset \mathcal {D}(\mathbf {J}^0)$
; in the case
${\mathfrak g}\subset \mathcal {D}(\mathbf {J}^0)$
; in the case
![]() $\mathbf {J}^0=J^0\pi $
, assume also that
$\mathbf {J}^0=J^0\pi $
, assume also that
![]() ${\mathfrak g}$
is
${\mathfrak g}$
is
![]() $\pi $
-projectable. The Lie algebra prolongs to a unique Lie algebra
$\pi $
-projectable. The Lie algebra prolongs to a unique Lie algebra
![]() ${\mathfrak g}^{(k)} \subset \mathcal {D}(\mathbf {J}^k)$
; see, for instance, [Reference Kruglikov, Lychagin, Krupka and Saunders19, Sec. 1.5]. We are interested in polynomial
${\mathfrak g}^{(k)} \subset \mathcal {D}(\mathbf {J}^k)$
; see, for instance, [Reference Kruglikov, Lychagin, Krupka and Saunders19, Sec. 1.5]. We are interested in polynomial
![]() ${\mathfrak g}^{(k)}$
-invariant divisors on
${\mathfrak g}^{(k)}$
-invariant divisors on
![]() $\mathbf {J}^k$
.
$\mathbf {J}^k$
.
Proposition 3.7.
-
(1) Let
 ${\mathfrak g}$
be a Lie algebra of projectable vector fields on a fiber bundle
${\mathfrak g}$
be a Lie algebra of projectable vector fields on a fiber bundle
 $\pi \! : E\to M$
and let D be a
$\pi \! : E\to M$
and let D be a
 ${\mathfrak g}^{(k)}$
-invariant polynomial divisor on
${\mathfrak g}^{(k)}$
-invariant polynomial divisor on
 $J^k \pi $
. Then
$J^k \pi $
. Then
 $[D]=\pi _{k,0}^*L$
for some
$[D]=\pi _{k,0}^*L$
for some
 ${\mathfrak g}$
-equivariant line bundle
${\mathfrak g}$
-equivariant line bundle
 $L\to E$
.
$L\to E$
. -
(2) Let
 ${\mathfrak g}$
be a Lie algebra of point vector fields on
${\mathfrak g}$
be a Lie algebra of point vector fields on
 $J^0(E,m)$
and D a
$J^0(E,m)$
and D a
 ${\mathfrak g}^{(k)}$
-invariant polynomial divisor on
${\mathfrak g}^{(k)}$
-invariant polynomial divisor on
 $J^k(E,m)$
. Then
$J^k(E,m)$
. Then
 $[D]=\pi _{k,1}^*L$
for some
$[D]=\pi _{k,1}^*L$
for some
 ${\mathfrak g}^{(1)}$
-equivariant line bundle
${\mathfrak g}^{(1)}$
-equivariant line bundle
 $L\to J^1(E,m)$
.
$L\to J^1(E,m)$
.
Proof. On
![]() $J^k(E,m)$
we will use the split coordinate charts
$J^k(E,m)$
we will use the split coordinate charts
![]() $\pi _{k,1}^{-1}(U_\alpha ^{i_1 \cdots i_m})$
. If
$\pi _{k,1}^{-1}(U_\alpha ^{i_1 \cdots i_m})$
. If
![]() $\pi \colon E\to M$
is a bundle, then the splitting is canonical, and we use the charts
$\pi \colon E\to M$
is a bundle, then the splitting is canonical, and we use the charts
![]() $\pi ^{-1}_{k,0}(U_\alpha )$
on
$\pi ^{-1}_{k,0}(U_\alpha )$
on
![]() $J^k \pi $
.
$J^k \pi $
.
The prolongation of a vector field
![]() $X=a^i \partial _{x^i} + b^j \partial _{y^j} \in \mathfrak g \subset \mathcal {D}(E)$
is given by
$X=a^i \partial _{x^i} + b^j \partial _{y^j} \in \mathfrak g \subset \mathcal {D}(E)$
is given by
where
![]() $b_{\sigma }^j$
are given recursively by (see [Reference Vinogradov and Krasil’shchik21, Th. 3.4])
$b_{\sigma }^j$
are given recursively by (see [Reference Vinogradov and Krasil’shchik21, Th. 3.4])
When
![]() $|\sigma |=d$
, it is clear that
$|\sigma |=d$
, it is clear that
![]() $b^j_{\sigma }$
is a sum of monomials of the form
$b^j_{\sigma }$
is a sum of monomials of the form
![]() $c(x,y) y^{j_1}_{\sigma _1} \cdots y^{j_s}_{\sigma _s}$
with
$c(x,y) y^{j_1}_{\sigma _1} \cdots y^{j_s}_{\sigma _s}$
with
![]() $|\sigma _l| \leq d$
for each l and
$|\sigma _l| \leq d$
for each l and
![]() $|\sigma _1|+\cdots + |\sigma _s| \leq d+1$
. Thus, the weighted degree of
$|\sigma _1|+\cdots + |\sigma _s| \leq d+1$
. Thus, the weighted degree of
![]() $b_\sigma ^j$
is
$b_\sigma ^j$
is
![]() $\leq d+1$
.
$\leq d+1$
.
If
![]() $D=\{f_\alpha ^{i_1 \cdots i_m}\}$
is a polynomial invariant divisor on
$D=\{f_\alpha ^{i_1 \cdots i_m}\}$
is a polynomial invariant divisor on
![]() $J^k(E,m)$
of weighted degree d, then for any
$J^k(E,m)$
of weighted degree d, then for any
![]() $X \in {\mathfrak g}$
, the function
$X \in {\mathfrak g}$
, the function
![]() $X^{(k)}(f_\alpha ^{i_1 \cdots i_m})$
has weighted degree
$X^{(k)}(f_\alpha ^{i_1 \cdots i_m})$
has weighted degree
![]() $\leq d+1$
. The equality
$\leq d+1$
. The equality
![]() $X^{(k)}(f_\alpha ^{i_1 \cdots i_m}) = \lambda _\alpha ^{i_1 \cdots i_m}(X) f_\alpha ^{i_1 \cdots i_m}$
implies that
$X^{(k)}(f_\alpha ^{i_1 \cdots i_m}) = \lambda _\alpha ^{i_1 \cdots i_m}(X) f_\alpha ^{i_1 \cdots i_m}$
implies that
![]() $\lambda _\alpha ^{i_1 \cdots i_m}(X) = X^{(k)}(f_\alpha ^{i_1 \cdots i_m})/f_\alpha ^{i_1 \cdots i_m}$
is holomorphic on
$\lambda _\alpha ^{i_1 \cdots i_m}(X) = X^{(k)}(f_\alpha ^{i_1 \cdots i_m})/f_\alpha ^{i_1 \cdots i_m}$
is holomorphic on
![]() $\pi _{k,1}^{-1}(U_\alpha ^{i_1 \cdots i_m})$
if and only if the polynomial parts of the denominator is canceled out by the numerator. In this case,
$\pi _{k,1}^{-1}(U_\alpha ^{i_1 \cdots i_m})$
if and only if the polynomial parts of the denominator is canceled out by the numerator. In this case,
![]() $\lambda _\alpha ^{i_1 \cdots i_m}(X)$
is polynomial of weighted degree
$\lambda _\alpha ^{i_1 \cdots i_m}(X)$
is polynomial of weighted degree
![]() $\leq 1$
, meaning that it is the pullback of a function
$\leq 1$
, meaning that it is the pullback of a function
![]() $\tilde {\lambda }_\alpha ^{i_1 \cdots i_m}(X) \in \mathcal {O}(U_\alpha ^{i_1 \cdots i_m})$
. Thus, we see that the
$\tilde {\lambda }_\alpha ^{i_1 \cdots i_m}(X) \in \mathcal {O}(U_\alpha ^{i_1 \cdots i_m})$
. Thus, we see that the
![]() ${\mathfrak g}^{(k)}$
-equivariant line bundle over
${\mathfrak g}^{(k)}$
-equivariant line bundle over
![]() $J^k(E,m)$
defined by the pair
$J^k(E,m)$
defined by the pair
![]() $(\{f_\alpha ^{i_1 \cdots i_m}/f_\beta ^{j_1 \cdots j_m}\}, \{\lambda _\alpha ^{i_1 \cdots i_m}\})$
is the pullback of a
$(\{f_\alpha ^{i_1 \cdots i_m}/f_\beta ^{j_1 \cdots j_m}\}, \{\lambda _\alpha ^{i_1 \cdots i_m}\})$
is the pullback of a
![]() ${\mathfrak g}^{(1)}$
-equivariant line bundle over
${\mathfrak g}^{(1)}$
-equivariant line bundle over
![]() $J^1(E,m)$
.
$J^1(E,m)$
.
If
![]() $E \to M$
is a fiber bundle, then we get a similar argument, but now
$E \to M$
is a fiber bundle, then we get a similar argument, but now
![]() $\lambda _\alpha (X)$
has weighted degree
$\lambda _\alpha (X)$
has weighted degree
![]() $0$
and is therefore the pullback of a function in
$0$
and is therefore the pullback of a function in
![]() $\mathcal {O}(U_\alpha )$
.
$\mathcal {O}(U_\alpha )$
.
This proposition, whose second part was reformulated in Theorem 1.5, tells us that invariant polynomial divisors on
![]() $\mathbf {J}^k$
are sections of pullbacks of equivariant line bundles over
$\mathbf {J}^k$
are sections of pullbacks of equivariant line bundles over
![]() $\mathbf {J}^1$
or
$\mathbf {J}^1$
or
![]() $\mathbf {J}^0$
. In particular, they are controlled by
$\mathbf {J}^0$
. In particular, they are controlled by
![]() ${\mathrm {H}}^1(\mathrm {Tot}^\bullet (C))$
, where
${\mathrm {H}}^1(\mathrm {Tot}^\bullet (C))$
, where
![]() $C^{p,q}=C^{p,q}({\mathfrak g}^{(1)},\{U_\alpha ^{i_1\cdots i_m}\})$
or
$C^{p,q}=C^{p,q}({\mathfrak g}^{(1)},\{U_\alpha ^{i_1\cdots i_m}\})$
or
![]() $C^{p,q}=C^{p,q}({\mathfrak g},\{U_\alpha \})$
or, more precisely, by
$C^{p,q}=C^{p,q}({\mathfrak g},\{U_\alpha \})$
or, more precisely, by
![]() $\mathrm {Pic}_{{\mathfrak g}^{(r)}}(\mathbf {J}^r)$
for
$\mathrm {Pic}_{{\mathfrak g}^{(r)}}(\mathbf {J}^r)$
for
![]() $r=1,0$
, respectively. It is remarkable that this fact is independent of the order k (one should compare to the statement of the Lie-Bäcklund theorem [Reference Vinogradov and Krasil’shchik21, Reference Olver23], although the proofs are different).
$r=1,0$
, respectively. It is remarkable that this fact is independent of the order k (one should compare to the statement of the Lie-Bäcklund theorem [Reference Vinogradov and Krasil’shchik21, Reference Olver23], although the proofs are different).
If the bundle
![]() $\pi $
has, in addition, an affine structure, then we can consider divisors with local defining functions
$\pi $
has, in addition, an affine structure, then we can consider divisors with local defining functions
![]() $f_\alpha $
in
$f_\alpha $
in
(i.e., divisors that are polynomial on fibers of
![]() $\pi _k \colon J^k \pi \to M$
). These are preserved under (
$\pi _k \colon J^k \pi \to M$
). These are preserved under (
![]() $k^{\text {th}}$
-prolongation of) morphisms of affine bundles, and we will refer to them as ‘polynomial divisors’ in this context. For such a divisor D, we have
$k^{\text {th}}$
-prolongation of) morphisms of affine bundles, and we will refer to them as ‘polynomial divisors’ in this context. For such a divisor D, we have
![]() $[D]=\pi _k^* L$
for some line bundle
$[D]=\pi _k^* L$
for some line bundle
![]() $L \to M$
. We can apply the same ideas as above to obtain the following result, which we leave without proof.
$L \to M$
. We can apply the same ideas as above to obtain the following result, which we leave without proof.
Proposition 3.8. Let
![]() ${\mathfrak g}$
be a Lie algebra of projectable vector fields on an affine bundle
${\mathfrak g}$
be a Lie algebra of projectable vector fields on an affine bundle
![]() $\pi \colon E \to M$
that preserves the affine structure, and D be a
$\pi \colon E \to M$
that preserves the affine structure, and D be a
![]() ${\mathfrak g}^{(k)}$
-invariant polynomial divisor on
${\mathfrak g}^{(k)}$
-invariant polynomial divisor on
![]() $J^k \pi $
. Then
$J^k \pi $
. Then
![]() $[D]=\pi _k^*L$
for some
$[D]=\pi _k^*L$
for some
![]() $d\pi ({\mathfrak g})$
-equivariant line bundle
$d\pi ({\mathfrak g})$
-equivariant line bundle
![]() $L \to M$
.
$L \to M$
.
Example 3.9 (Riemannian geometry).
Let
![]() $\pi \colon S^2_+T^*M\to M$
denote the bundle of nondegenerate symmetric 2-forms on M and
$\pi \colon S^2_+T^*M\to M$
denote the bundle of nondegenerate symmetric 2-forms on M and
![]() ${\mathfrak g}$
the Lie algebra of holomorphic vector fields on M, which induces a Lie algebra
${\mathfrak g}$
the Lie algebra of holomorphic vector fields on M, which induces a Lie algebra
![]() ${\mathfrak g}^{(k)}$
of vector fields on
${\mathfrak g}^{(k)}$
of vector fields on
![]() $J^k \pi $
for
$J^k \pi $
for
![]() $k=0,1,\dots $
. If D a polynomial
$k=0,1,\dots $
. If D a polynomial
![]() ${\mathfrak g}^{(k)}$
-invariant divisor on
${\mathfrak g}^{(k)}$
-invariant divisor on
![]() $J^k \pi $
, then
$J^k \pi $
, then
![]() $[D]$
is the pullback of a line bundle
$[D]$
is the pullback of a line bundle
![]() $L\to M$
. For example, if D is the divisor on
$L\to M$
. For example, if D is the divisor on
![]() $J^2 \pi $
that is given locally by the numerator of the scalar curvature of the metric, then
$J^2 \pi $
that is given locally by the numerator of the scalar curvature of the metric, then
![]() $[D]=\pi _{2}^*(\Lambda ^nT^*M)^{\otimes 4}$
.
$[D]=\pi _{2}^*(\Lambda ^nT^*M)^{\otimes 4}$
.
Computations of invariants in jets often result in rational relative differential invariants, which are related to polynomial differential invariants via a jet analogue of formula (3.1). This will be demonstrated in the following examples.
3.3 Example A: Three-dimensional Heisenberg algebra on the plane
Consider the following Lie algebra of vector fields on the plane:
It has the structure relations of the Heisenberg algebra and it prolongs naturally to the Lie algebra
![]() ${\mathfrak g}^{(1)}$
of vector fields on
${\mathfrak g}^{(1)}$
of vector fields on
![]() $J^1(\mathbb C^2,1)$
. Choosing y as the dependent variable gives
$J^1(\mathbb C^2,1)$
. Choosing y as the dependent variable gives
where
![]() $U_1 \subset J^1(\mathbb C^2,1)$
denotes the open chart determined by our choice of dependent variable on
$U_1 \subset J^1(\mathbb C^2,1)$
denotes the open chart determined by our choice of dependent variable on
![]() $\mathbb C^2$
. Taking instead x as the dependent variable results in a different chart
$\mathbb C^2$
. Taking instead x as the dependent variable results in a different chart
![]() $U_2 \subset J^1(\mathbb C^2,1)$
, where the prolongation of
$U_2 \subset J^1(\mathbb C^2,1)$
, where the prolongation of
![]() $\mathfrak g$
takes the form
$\mathfrak g$
takes the form
These two charts cover
![]() $J^1(\mathbb C^2,1)=U_1 \cup U_2$
. On overlap
$J^1(\mathbb C^2,1)=U_1 \cup U_2$
. On overlap
![]() $U_1 \cap U_2$
we get
$U_1 \cap U_2$
we get
![]() $(x,y,y_1)\equiv (x,y,1/x_1)$
. In each of the two charts, we compute the Chevalley-Eilenberg cohomology:
$(x,y,y_1)\equiv (x,y,1/x_1)$
. In each of the two charts, we compute the Chevalley-Eilenberg cohomology:
A representative
![]() $\lambda _1$
of a general element in
$\lambda _1$
of a general element in
![]() ${\mathrm {H}}^1({\mathfrak g}^{(1)},\mathcal {O}(U_1))$
takes the form
${\mathrm {H}}^1({\mathfrak g}^{(1)},\mathcal {O}(U_1))$
takes the form
The compatibility condition
![]() $\lambda _1(X) - \lambda _2(X) = X(g_{12})/g_{12}$
,
$\lambda _1(X) - \lambda _2(X) = X(g_{12})/g_{12}$
,
![]() $\forall X \in {\mathfrak g}^{(1)}$
gives the general transition function
$\forall X \in {\mathfrak g}^{(1)}$
gives the general transition function
![]() $g_{12} = C y_1^{-B} e^{A/y_1}$
. This function is holomorphic on
$g_{12} = C y_1^{-B} e^{A/y_1}$
. This function is holomorphic on
![]() $U_1 \cap U_2$
if and only if
$U_1 \cap U_2$
if and only if
![]() $B \in \mathbb Z$
. Changing the representative
$B \in \mathbb Z$
. Changing the representative
![]() $(g,\lambda )\in C^{0,1}\times C^{1,0}$
by the coboundary
$(g,\lambda )\in C^{0,1}\times C^{1,0}$
by the coboundary
![]() $\partial ^0\mu $
where
$\partial ^0\mu $
where
![]() $\mu _1=1, \mu _2=C e^{A x_1}$
, we get
$\mu _1=1, \mu _2=C e^{A x_1}$
, we get
![]() $g_{12} = y_1^{-B}$
and
$g_{12} = y_1^{-B}$
and
Thus,
![]() $\mathrm {Pic}_{{\mathfrak g}^{(1)}}(\mathbf {J}^1)={\mathbb C}\times \mathbb Z\to \mathrm {Pic}(\mathbf {J}^1)=\mathbb Z$
is epimorphic.
$\mathrm {Pic}_{{\mathfrak g}^{(1)}}(\mathbf {J}^1)={\mathbb C}\times \mathbb Z\to \mathrm {Pic}(\mathbf {J}^1)=\mathbb Z$
is epimorphic.
We identify a generating set
![]() $(I,\nabla )$
of absolute differential invariants in charts as follows:
$(I,\nabla )$
of absolute differential invariants in charts as follows:
 $$\begin{align*}\Big(-\frac{y_2}{y_1^3},\frac{1}{y_1}D_x\Big)\ \text{ on }\ U_1\quad\longleftrightarrow\quad \big(x_2,D_y\big)\ \text{ on }\ U_2. \end{align*}$$
$$\begin{align*}\Big(-\frac{y_2}{y_1^3},\frac{1}{y_1}D_x\Big)\ \text{ on }\ U_1\quad\longleftrightarrow\quad \big(x_2,D_y\big)\ \text{ on }\ U_2. \end{align*}$$
The invariant divisors on
![]() $J^1(\mathbb C^2,1)$
are generated by
$J^1(\mathbb C^2,1)$
are generated by
![]() $f_1=y_1, f_2=1$
of weight
$f_1=y_1, f_2=1$
of weight
![]() $(A,B)=(0,-1)$
. Note that the invariant ODE
$(A,B)=(0,-1)$
. Note that the invariant ODE
![]() $y_1=0$
is not visible from the local computations on
$y_1=0$
is not visible from the local computations on
![]() $U_2$
. Indeed, its solutions are
$U_2$
. Indeed, its solutions are
![]() $y=\mathrm {const}$
for the independent variable y, which are not graphs
$y=\mathrm {const}$
for the independent variable y, which are not graphs
![]() $x=h(y)$
.
$x=h(y)$
.
General
![]() ${\mathfrak g}^{(2)}$
-invariant divisors on
${\mathfrak g}^{(2)}$
-invariant divisors on
![]() $J^2(\mathbb C^2,1)$
are generated by
$J^2(\mathbb C^2,1)$
are generated by
![]() $f=\{f_1,f_2\}$
and the absolute invariant I. In particular, the irreducible invariant submanifolds of codimension 1 in
$f=\{f_1,f_2\}$
and the absolute invariant I. In particular, the irreducible invariant submanifolds of codimension 1 in
![]() $\mathbf {J}^2$
are given by the divisors
$\mathbf {J}^2$
are given by the divisors
![]() $\tilde f=\{\tilde {f}_1,\tilde {f}_2\}=\{y_2-C y_1^3,x_2+C\}$
of weight
$\tilde f=\{\tilde {f}_1,\tilde {f}_2\}=\{y_2-C y_1^3,x_2+C\}$
of weight
![]() $(A,B)=(0,-3)$
, parametrized by
$(A,B)=(0,-3)$
, parametrized by
![]() $C \in \mathbb C$
.
$C \in \mathbb C$
.
Note that the nonzero parameter A above is not realizable by an invariant divisor (on
![]() $\mathbf {J}^1$
such are
$\mathbf {J}^1$
such are
![]() $y_1^{-B}$
). Higher prolongations give no new weights of polynomial divisors, and we conclude, with the help of Proposition 3.7,
$y_1^{-B}$
). Higher prolongations give no new weights of polynomial divisors, and we conclude, with the help of Proposition 3.7,
3.4 Example B: Invariant divisors of curves in the projective plane
Consider the Lie algebra
![]() $\mathfrak {sl}(3,{\mathbb C})\subset \mathcal {D}({\mathbb C} P^2)$
of projective vector fields. Differential invariants of curves in the projective plane were studied already in 1878 by Halphen in his PhD thesis [Reference Huybrechts15] (see also the recent treatment [Reference Konovenko and Lychagin16] in the real case). In this section, we demonstrate how the framework developed in this paper sheds new light on those classical invariants.
$\mathfrak {sl}(3,{\mathbb C})\subset \mathcal {D}({\mathbb C} P^2)$
of projective vector fields. Differential invariants of curves in the projective plane were studied already in 1878 by Halphen in his PhD thesis [Reference Huybrechts15] (see also the recent treatment [Reference Konovenko and Lychagin16] in the real case). In this section, we demonstrate how the framework developed in this paper sheds new light on those classical invariants.
The manifold
![]() $\mathbb CP^2$
is covered by the three charts
$\mathbb CP^2$
is covered by the three charts
![]() $U_i=\mathbb CP^2 \setminus \{z_i =0\}$
,
$U_i=\mathbb CP^2 \setminus \{z_i =0\}$
,
![]() $i=1,2,3$
, where
$i=1,2,3$
, where
![]() $[z_1:z_2:z_3]$
are homogeneous coordinates. Let us start by focusing on
$[z_1:z_2:z_3]$
are homogeneous coordinates. Let us start by focusing on
![]() $U_3$
with coordinates
$U_3$
with coordinates
![]() $x=z_1/z_3, y=z_2/z_3$
. In these local coordinates, we have
$x=z_1/z_3, y=z_2/z_3$
. In these local coordinates, we have
3.4.1 Equivariant line bundles
The cohomology group
![]() ${\mathrm {H}}^1(\mathfrak {sl}(3,{\mathbb C}),\mathcal {O}(U_3))={\mathbb C}$
was computed in [Reference González-López, Kamran and Olver10, Table 3], and also in [Reference Schneider27]. Our global approach shows that
${\mathrm {H}}^1(\mathfrak {sl}(3,{\mathbb C}),\mathcal {O}(U_3))={\mathbb C}$
was computed in [Reference González-López, Kamran and Olver10, Table 3], and also in [Reference Schneider27]. Our global approach shows that
Skipping the details of this computation, we instead focus on the corresponding computation in
![]() $J^1({\mathbb C} P^2,1)$
. Choosing y as the ‘dependent’ variable, we get an open coordinate chart
$J^1({\mathbb C} P^2,1)$
. Choosing y as the ‘dependent’ variable, we get an open coordinate chart
![]() $U_{3}^y \subset J^1(U_3,1)$
in which the prolonged vector fields take the form
$U_{3}^y \subset J^1(U_3,1)$
in which the prolonged vector fields take the form
 $$ \begin{align}\begin{gathered} \hskip-7pt X_1=\partial_x, \ \ X_2=\partial_y, \ \ X_3=y \partial_x-y_1^2 \partial_{y_1}, \ \ X_4 = x \partial_y+\partial_{y_1}, \ \ X_5 = x \partial_x-y\partial_y-2 y_1 \partial_{y_1}, \hskip-8pt \\ \hskip-7pt X_6 = x \partial_x+y\partial_y, \ \ X_7 = x^2 \partial_x+xy \partial_y+(y-xy_1)\partial_{y_1}, \ \ X_8 = xy\partial_x+y^2 \partial_y+(y-xy_1)y_1 \partial_{y_1}. \hskip-7pt \end{gathered}\end{align} $$
$$ \begin{align}\begin{gathered} \hskip-7pt X_1=\partial_x, \ \ X_2=\partial_y, \ \ X_3=y \partial_x-y_1^2 \partial_{y_1}, \ \ X_4 = x \partial_y+\partial_{y_1}, \ \ X_5 = x \partial_x-y\partial_y-2 y_1 \partial_{y_1}, \hskip-8pt \\ \hskip-7pt X_6 = x \partial_x+y\partial_y, \ \ X_7 = x^2 \partial_x+xy \partial_y+(y-xy_1)\partial_{y_1}, \ \ X_8 = xy\partial_x+y^2 \partial_y+(y-xy_1)y_1 \partial_{y_1}. \hskip-7pt \end{gathered}\end{align} $$
Let us start by computing
![]() ${\mathrm {H}}^1(\mathfrak {sl}(3,{\mathbb C})^{(1)},\mathcal {O} (U_3^y))$
. For a general cocycle
${\mathrm {H}}^1(\mathfrak {sl}(3,{\mathbb C})^{(1)},\mathcal {O} (U_3^y))$
. For a general cocycle
![]() $\lambda _3^y$
, we define
$\lambda _3^y$
, we define
By subtracting a coboundary, we can set
![]() $a_1= 0$
. The cocycle condition involving
$a_1= 0$
. The cocycle condition involving
![]() $X_1$
and
$X_1$
and
![]() $X_2$
implies that
$X_2$
implies that
![]() $\partial _x(a_2)=0$
, and by subtracting a coboundary (now x-independent), we set
$\partial _x(a_2)=0$
, and by subtracting a coboundary (now x-independent), we set
![]() $a_2 = 0$
. The eight cocycle conditions
$a_2 = 0$
. The eight cocycle conditions
reduce to
![]() $X_i(a_j)=0$
and imply that
$X_i(a_j)=0$
and imply that
![]() $a_3, a_4, a_5, a_6$
are independent of x and y.
$a_3, a_4, a_5, a_6$
are independent of x and y.
By subtracting a coboundary (independent of x and y), we set
![]() $a_4(y_1) = 0$
. Then for the PDE system defined by the remaining cocycle conditions, we get the general holomorphic solution:
$a_4(y_1) = 0$
. Then for the PDE system defined by the remaining cocycle conditions, we get the general holomorphic solution:
 $$ \begin{gather*} a_1 = 0, \quad a_2 = 0, \quad a_3= A_2 y_1, \quad a_4= 0, \quad a_5=A_2, \quad a_6=A_1, \\ a_7 = \frac{3A_1+A_2}{2} x, \quad a_8 = A_2 x y_1+\frac{3A_1-A_2}{2} y, \end{gather*} $$
$$ \begin{gather*} a_1 = 0, \quad a_2 = 0, \quad a_3= A_2 y_1, \quad a_4= 0, \quad a_5=A_2, \quad a_6=A_1, \\ a_7 = \frac{3A_1+A_2}{2} x, \quad a_8 = A_2 x y_1+\frac{3A_1-A_2}{2} y, \end{gather*} $$
from which we see that
![]() ${\mathrm {H}}^1(\mathfrak {sl}_3^{(1)}, \mathcal {O}(U_3^y))=\mathbb C^2$
.
${\mathrm {H}}^1(\mathfrak {sl}_3^{(1)}, \mathcal {O}(U_3^y))=\mathbb C^2$
.
A similar computation can be done in the open coordinate chart
![]() $U_3^x \subset J^1(U_3,1)$
, where x is the dependent variable. In these coordinates, related to the previous by
$U_3^x \subset J^1(U_3,1)$
, where x is the dependent variable. In these coordinates, related to the previous by
![]() $x_1=1/y_1$
on overlap
$x_1=1/y_1$
on overlap
![]() $U_3^y \cap U_3^x$
, the prolonged vector fields take the form
$U_3^y \cap U_3^x$
, the prolonged vector fields take the form
 $$ \begin{gather*} X_1=\partial_x, \quad X_2=\partial_y, \quad X_3=y \partial_x+ \partial_{x_1}, \quad X_4 = x \partial_y-x_2^2\partial_{x_1}, \quad X_5 = x \partial_x-y\partial_y+2 x_1 \partial_{x_1}, \\ X_6 = x \partial_x+y\partial_y, \quad \tilde X_7 = x^2 \partial_x+xy \partial_y+(x-yx_1)x_1 \partial_{x_1}, \quad X_8 = xy\partial_x+y^2 \partial_y+(x-yx_1)\partial_{x_1}. \end{gather*} $$
$$ \begin{gather*} X_1=\partial_x, \quad X_2=\partial_y, \quad X_3=y \partial_x+ \partial_{x_1}, \quad X_4 = x \partial_y-x_2^2\partial_{x_1}, \quad X_5 = x \partial_x-y\partial_y+2 x_1 \partial_{x_1}, \\ X_6 = x \partial_x+y\partial_y, \quad \tilde X_7 = x^2 \partial_x+xy \partial_y+(x-yx_1)x_1 \partial_{x_1}, \quad X_8 = xy\partial_x+y^2 \partial_y+(x-yx_1)\partial_{x_1}. \end{gather*} $$
Defining
![]() $b_i(y,x,x_1):= \lambda _3^x(X_i) \in \mathcal {O}(U_3^x)$
, and repeating the computations above, a general representative of an element in
$b_i(y,x,x_1):= \lambda _3^x(X_i) \in \mathcal {O}(U_3^x)$
, and repeating the computations above, a general representative of an element in
![]() ${\mathrm {H}}^1(\mathfrak {sl}_3^{(1)},\mathcal {O}(U_3^x))$
is given by
${\mathrm {H}}^1(\mathfrak {sl}_3^{(1)},\mathcal {O}(U_3^x))$
is given by
 $$ \begin{gather*} b_1 = 0, \quad b_2 = 0, \quad b_3=0, \quad b_4=\tilde A_2 x_1, \quad b_5=-\tilde A_2, \quad b_6=\tilde A_1, \\ b_7 = \tilde A_2 y x_1+\frac{3\tilde A_1-\tilde A_2}{2} x, \quad b_8 = \frac{3 \tilde A_1+\tilde A_2}{2} y, \end{gather*} $$
$$ \begin{gather*} b_1 = 0, \quad b_2 = 0, \quad b_3=0, \quad b_4=\tilde A_2 x_1, \quad b_5=-\tilde A_2, \quad b_6=\tilde A_1, \\ b_7 = \tilde A_2 y x_1+\frac{3\tilde A_1-\tilde A_2}{2} x, \quad b_8 = \frac{3 \tilde A_1+\tilde A_2}{2} y, \end{gather*} $$
implying
![]() ${\mathrm {H}}^1(\mathfrak {sl}(3,\mathbb C)^{(1)}, \mathcal {O}(U_3^x))=\mathbb C^2$
.
${\mathrm {H}}^1(\mathfrak {sl}(3,\mathbb C)^{(1)}, \mathcal {O}(U_3^x))=\mathbb C^2$
.
The compatibility condition
![]() $\lambda _3^y(X)-\lambda _3^x(X)= X(g_{33}^{yx})/g_{33}^{yx}$
implies that
$\lambda _3^y(X)-\lambda _3^x(X)= X(g_{33}^{yx})/g_{33}^{yx}$
implies that
![]() $\tilde A_1=A_1$
and
$\tilde A_1=A_1$
and
![]() $\tilde A_2=A_2$
. In this case, the transition function has the form
$\tilde A_2=A_2$
. In this case, the transition function has the form
![]() $g_{33}^{yx} = Cy_1^{-A_2}$
, and it is holomorphic if and only if
$g_{33}^{yx} = Cy_1^{-A_2}$
, and it is holomorphic if and only if
![]() $A_2 \in \mathbb Z$
. The constant C can be set equal to
$A_2 \in \mathbb Z$
. The constant C can be set equal to
![]() $1$
via a suitable
$1$
via a suitable
![]() $\mathfrak {sl}(3,\mathbb C)^{(1)}$
-invariant
$\mathfrak {sl}(3,\mathbb C)^{(1)}$
-invariant
![]() $\delta ^{0,0}$
-coboundary. Thus, we conclude
$\delta ^{0,0}$
-coboundary. Thus, we conclude
![]() $\mathrm {Pic}_{\mathfrak {sl}(3,{\mathbb C})^{(1)}}(J^1(U_3,1))={\mathbb C}\times \mathbb Z$
.
$\mathrm {Pic}_{\mathfrak {sl}(3,{\mathbb C})^{(1)}}(J^1(U_3,1))={\mathbb C}\times \mathbb Z$
.
Next, we perform similar computations on the remaining charts
![]() $U_1^x, U_1^y, U_2^x, U_2^y$
of
$U_1^x, U_1^y, U_2^x, U_2^y$
of
![]() $J^1({\mathbb C} P^2,1)$
. In
$J^1({\mathbb C} P^2,1)$
. In
![]() $U_2\subset {\mathbb C} P^2$
, we have coordinates
$U_2\subset {\mathbb C} P^2$
, we have coordinates
![]() $(\tilde x, \tilde y)=(z_1/z_2, z_3/z_2)$
. Choosing
$(\tilde x, \tilde y)=(z_1/z_2, z_3/z_2)$
. Choosing
![]() $\tilde y$
as dependent variable results in coordinates
$\tilde y$
as dependent variable results in coordinates
![]() $(\tilde x,\tilde y,\tilde y_1)$
on
$(\tilde x,\tilde y,\tilde y_1)$
on
![]() $U_2^y\subset J^1({\mathbb C} P^2,1)$
. On
$U_2^y\subset J^1({\mathbb C} P^2,1)$
. On
![]() $U_3^y \cap U_{2}^y$
, we have
$U_3^y \cap U_{2}^y$
, we have
![]() $x=\tilde x/\tilde y$
,
$x=\tilde x/\tilde y$
,
![]() $y=1/\tilde y$
and
$y=1/\tilde y$
and
![]() $y_1=\tilde y_1/(\tilde x\tilde y_1-\tilde y)$
. In these coordinates, the generators of
$y_1=\tilde y_1/(\tilde x\tilde y_1-\tilde y)$
. In these coordinates, the generators of
![]() $\mathfrak {sl}(3,\mathbb C)^{(1)}$
are
$\mathfrak {sl}(3,\mathbb C)^{(1)}$
are
 $$ \begin{gather*} X_1 = \tilde y \partial_{\tilde x} - \tilde y_1^2 \partial_{\tilde y_1}, \quad X_2 = - \tilde x \tilde y \partial_{\tilde x} - \tilde y^2 \partial_{\tilde y} + (\tilde x \tilde y_1-\tilde y) \tilde y_1 \partial_{\tilde y_1}, \quad X_3 = \partial_{\tilde x}, \\ X_4 = - \tilde x^2 \partial_{\tilde x} - \tilde x \tilde y \partial_{\tilde y}+ (\tilde x \tilde y_1 - \tilde y) \partial_{\tilde y_1}, \quad X_5= 2 \tilde x \partial_{\tilde x}+\tilde y \partial_{\tilde y}-\tilde y_1 \partial_{\tilde y_1}, \\ X_6 = - \tilde y \partial_{\tilde y} - \tilde y_1 \partial_{\tilde y_1}, \quad X_7 = -\tilde x \partial_{\tilde y} - \partial_{\tilde y_1}, \quad X_8 = - \partial_{\tilde y}. \end{gather*} $$
$$ \begin{gather*} X_1 = \tilde y \partial_{\tilde x} - \tilde y_1^2 \partial_{\tilde y_1}, \quad X_2 = - \tilde x \tilde y \partial_{\tilde x} - \tilde y^2 \partial_{\tilde y} + (\tilde x \tilde y_1-\tilde y) \tilde y_1 \partial_{\tilde y_1}, \quad X_3 = \partial_{\tilde x}, \\ X_4 = - \tilde x^2 \partial_{\tilde x} - \tilde x \tilde y \partial_{\tilde y}+ (\tilde x \tilde y_1 - \tilde y) \partial_{\tilde y_1}, \quad X_5= 2 \tilde x \partial_{\tilde x}+\tilde y \partial_{\tilde y}-\tilde y_1 \partial_{\tilde y_1}, \\ X_6 = - \tilde y \partial_{\tilde y} - \tilde y_1 \partial_{\tilde y_1}, \quad X_7 = -\tilde x \partial_{\tilde y} - \partial_{\tilde y_1}, \quad X_8 = - \partial_{\tilde y}. \end{gather*} $$
Defining
![]() $c_i(\tilde x, \tilde y, \tilde y_1) := \lambda _{2}^y(X_i) \in \mathcal {O}(U_{2}^y)$
yields a general element in
$c_i(\tilde x, \tilde y, \tilde y_1) := \lambda _{2}^y(X_i) \in \mathcal {O}(U_{2}^y)$
yields a general element in
![]() ${\mathrm {H}}^1(\mathfrak {sl}(3,\mathbb C)^{(1)}, \mathcal {O}(U_{2}^y))$
:
${\mathrm {H}}^1(\mathfrak {sl}(3,\mathbb C)^{(1)}, \mathcal {O}(U_{2}^y))$
:
 $$ \begin{gather*} c_1 = \frac{3 B_1 + B_2}{2} \tilde y_1,\quad c_2 = - \frac{3 B_1+B_2}{2} \tilde x \tilde y_1 + \frac{3 B_1-B_2}{2} \tilde y, \quad c_3= 0, \\ c_4= -B_2 \tilde x, \quad c_5= B_2, \quad c_6= B_1, \quad c_7= 0, \quad c_8= 0. \end{gather*} $$
$$ \begin{gather*} c_1 = \frac{3 B_1 + B_2}{2} \tilde y_1,\quad c_2 = - \frac{3 B_1+B_2}{2} \tilde x \tilde y_1 + \frac{3 B_1-B_2}{2} \tilde y, \quad c_3= 0, \\ c_4= -B_2 \tilde x, \quad c_5= B_2, \quad c_6= B_1, \quad c_7= 0, \quad c_8= 0. \end{gather*} $$
The compatibility condition
![]() $\lambda _{3}^y(X) - \lambda _{2}^y(X) = X(g_{32}^{yy})/g_{32}^{yy}$
implies that
$\lambda _{3}^y(X) - \lambda _{2}^y(X) = X(g_{32}^{yy})/g_{32}^{yy}$
implies that
![]() $B_1=(A_2-A_1)/2$
and
$B_1=(A_2-A_1)/2$
and
![]() $B_2=(3A_1+A_2)/2$
. The transition function on
$B_2=(3A_1+A_2)/2$
. The transition function on
![]() $U_3^y \cap U_{2}^y$
is given by
$U_3^y \cap U_{2}^y$
is given by
![]() $g_{32}^{yy} = \tilde C \tilde y^{-B_2} (\tilde x \tilde y_1 - \tilde y)^{A_2}$
. It is holomorphic if and only if
$g_{32}^{yy} = \tilde C \tilde y^{-B_2} (\tilde x \tilde y_1 - \tilde y)^{A_2}$
. It is holomorphic if and only if
![]() $A_2,B_2 \in \mathbb Z$
. To sum up, we have
$A_2,B_2 \in \mathbb Z$
. To sum up, we have
By doing a similar analysis on the intersection of the remaining charts, one gets
Furthermore, the map
![]() $\mathrm {Pic}_{\mathfrak {sl}(3,{\mathbb C})^{(1)}} (J^1({\mathbb C} P^2,1))\to \mathrm {Pic}(J^1({\mathbb C} P^2,1))$
is injective since we have
$\mathrm {Pic}_{\mathfrak {sl}(3,{\mathbb C})^{(1)}} (J^1({\mathbb C} P^2,1))\to \mathrm {Pic}(J^1({\mathbb C} P^2,1))$
is injective since we have
![]() ${\tilde {\mathrm {H}}}^1(\mathfrak {sl}(3,{\mathbb C})^{(1)},J^1({\mathbb C} P^2,1))=0$
.
${\tilde {\mathrm {H}}}^1(\mathfrak {sl}(3,{\mathbb C})^{(1)},J^1({\mathbb C} P^2,1))=0$
.
Let us compare this to known bundles over
![]() $J^1(\mathbb CP^2,1)$
, starting with canonical bundles. The line bundle
$J^1(\mathbb CP^2,1)$
, starting with canonical bundles. The line bundle
![]() $\Lambda ^3 T^* J^1(\mathbb CP^2,1) \to J^1( \mathbb CP^2,1)$
corresponds to
$\Lambda ^3 T^* J^1(\mathbb CP^2,1) \to J^1( \mathbb CP^2,1)$
corresponds to
![]() $(A_1,A_2)=(-2,2)$
, while the pullback of the line bundle
$(A_1,A_2)=(-2,2)$
, while the pullback of the line bundle
![]() $\Lambda ^2T^*{\mathbb C} P^2\to {\mathbb C} P^2$
via
$\Lambda ^2T^*{\mathbb C} P^2\to {\mathbb C} P^2$
via
![]() $\pi _{1,0}\colon J^1({\mathbb C} P^2,1)\to {\mathbb C} P^2$
corresponds to
$\pi _{1,0}\colon J^1({\mathbb C} P^2,1)\to {\mathbb C} P^2$
corresponds to
![]() $(A_1,A_2)=(-2,0)$
. This is easy to check by computing divergences of
$(A_1,A_2)=(-2,0)$
. This is easy to check by computing divergences of
![]() $X_1,\dots ,X_8$
with respect to the volume forms
$X_1,\dots ,X_8$
with respect to the volume forms
![]() $\Omega _0= dx \wedge dy$
and
$\Omega _0= dx \wedge dy$
and
![]() $\Omega _1 = dx \wedge dy \wedge dy_1$
on
$\Omega _1 = dx \wedge dy \wedge dy_1$
on
![]() $U_3 \subset \mathbb CP^2$
and
$U_3 \subset \mathbb CP^2$
and
![]() $U_3^y \subset J^1(\mathbb CP^2,1)$
, respectively:
$U_3^y \subset J^1(\mathbb CP^2,1)$
, respectively:
![]() $\mathrm {div}_{\Omega _0}$
corresponds to
$\mathrm {div}_{\Omega _0}$
corresponds to
![]() $(A_1,A_2)=(2,0)$
and
$(A_1,A_2)=(2,0)$
and
![]() $\mathrm {div}_{\Omega _1}$
corresponds to
$\mathrm {div}_{\Omega _1}$
corresponds to
![]() $(A_1,A_2)=(2,-2)$
. (Note that divergences with respect to different volume forms differ (locally) by a coboundary in the modified Chevalley-Eilenberg complex.)
$(A_1,A_2)=(2,-2)$
. (Note that divergences with respect to different volume forms differ (locally) by a coboundary in the modified Chevalley-Eilenberg complex.)
Furthermore, the pullback of the line bundle
![]() $\mathcal {O}_{\mathbb CP^2}(1) \to \mathbb CP^2$
corresponds to
$\mathcal {O}_{\mathbb CP^2}(1) \to \mathbb CP^2$
corresponds to
![]() $(A_1,A_2)=(2/3,0)$
because of the relation between the canonical and tautological bundles over
$(A_1,A_2)=(2/3,0)$
because of the relation between the canonical and tautological bundles over
![]() ${\mathbb C} P^2$
(see Remark 2.15). The vertical bundle
${\mathbb C} P^2$
(see Remark 2.15). The vertical bundle
![]() $VJ^1({\mathbb C} P^2,1) \subset TJ^1({\mathbb C} P^2,1)$
corresponds to
$VJ^1({\mathbb C} P^2,1) \subset TJ^1({\mathbb C} P^2,1)$
corresponds to
![]() $(A_1,A_2)=(0,-2)$
, while the subbundle
$(A_1,A_2)=(0,-2)$
, while the subbundle
![]() $\langle \omega \rangle \subset T^*J^1({\mathbb C} P^2,1)$
defined by the contact form
$\langle \omega \rangle \subset T^*J^1({\mathbb C} P^2,1)$
defined by the contact form
![]() $\omega \in \Gamma (T^*J^1({\mathbb C} P^2,1))$
corresponds to
$\omega \in \Gamma (T^*J^1({\mathbb C} P^2,1))$
corresponds to
![]() $(A_1,A_2)=(-1,1)$
. The subset
$(A_1,A_2)=(-1,1)$
. The subset
![]() $(A_1,A_2)\subset {\mathbb C}^2$
satisfying (3.4) is generated by the elements
$(A_1,A_2)\subset {\mathbb C}^2$
satisfying (3.4) is generated by the elements
![]() $(2/3,0)$
and
$(2/3,0)$
and
![]() $(-1,1)$
. This leads to the following concrete description:
$(-1,1)$
. This leads to the following concrete description:
Proposition 3.10. Consider the standard realization of
![]() $\mathfrak {sl}(3,{\mathbb C})\subset \mathcal {D}({\mathbb C} P^2)$
and its prolongation
$\mathfrak {sl}(3,{\mathbb C})\subset \mathcal {D}({\mathbb C} P^2)$
and its prolongation
![]() $\mathfrak {sl}(3,{\mathbb C})^{(1)}\subset \mathcal {D}(J^1({\mathbb C} P^2,1))$
. The equivariant Picard group (3.5) is
$\mathfrak {sl}(3,{\mathbb C})^{(1)}\subset \mathcal {D}(J^1({\mathbb C} P^2,1))$
. The equivariant Picard group (3.5) is
The integer parameters are related to the above weights like this:
![]() $A_1=-k_1+\frac 23k_0, A_2=k_1$
.
$A_1=-k_1+\frac 23k_0, A_2=k_1$
.
3.4.2 Invariant divisors and absolute differential invariants
Generators for the absolute differential invariants are well known; see, for example, [Reference Olver23, Table 5]. The field of rational absolute differential invariants is generated by
 $$\begin{align*}\Big( I_7=\frac{R_7^3}{R_5^8}, \nabla=\frac{R_2 R_7}{R_5^3} D_x\Big), \end{align*}$$
$$\begin{align*}\Big( I_7=\frac{R_7^3}{R_5^8}, \nabla=\frac{R_2 R_7}{R_5^3} D_x\Big), \end{align*}$$
where
![]() $R_2, R_5, R_7$
are expressed in the following way on
$R_2, R_5, R_7$
are expressed in the following way on
![]() $\pi _{7,1}^{-1}(U_3^y)$
:
$\pi _{7,1}^{-1}(U_3^y)$
:
 $$ \begin{align*} R_2 &= y_2, \\ R_5 &= 9y_2^2y_5-45y_2 y_3 y_4+40 y_3^3, \\ R_7 &= 18 y_2^4 (9 y_2^2 y_5 - 45 y_2 y_3 y_4 + 40 y_3^3) y_7 - 189 y_2^6 y_6^2 + 126 y_2^4 (9 y_2 y_3 y_5 + 15 y_2 y_4^2 - 25 y_3^2 y_4) y_6\\ & - 189 y_2^4 (15 y_2 y_4 + 4 y_3^2) y_5^2 + 210 y_2^2 y_3 (63 y_2^2 y_4^2 - 60 y_2 y_3^2 y_4+32 y_3^4) y_5 - 4725 y_2^4 y_4^4 \\ & - 7875 y_2^3 y_3^2 y_4^3 + 31500 y_2^2 y_3^4 y_4^2 - 33600 y_2 y_3^6 y_4 + 11200 y_3^8. \end{align*} $$
$$ \begin{align*} R_2 &= y_2, \\ R_5 &= 9y_2^2y_5-45y_2 y_3 y_4+40 y_3^3, \\ R_7 &= 18 y_2^4 (9 y_2^2 y_5 - 45 y_2 y_3 y_4 + 40 y_3^3) y_7 - 189 y_2^6 y_6^2 + 126 y_2^4 (9 y_2 y_3 y_5 + 15 y_2 y_4^2 - 25 y_3^2 y_4) y_6\\ & - 189 y_2^4 (15 y_2 y_4 + 4 y_3^2) y_5^2 + 210 y_2^2 y_3 (63 y_2^2 y_4^2 - 60 y_2 y_3^2 y_4+32 y_3^4) y_5 - 4725 y_2^4 y_4^4 \\ & - 7875 y_2^3 y_3^2 y_4^3 + 31500 y_2^2 y_3^4 y_4^2 - 33600 y_2 y_3^6 y_4 + 11200 y_3^8. \end{align*} $$
We use a different set of generators than [Reference Olver23] in order to obtain rational invariants, which by [Reference Kruglikov and Lychagin18] are sufficient to separate orbits in general position. Table 5 in [Reference Olver23] also contains the Lie determinant
![]() $R_2 R_5^2$
on the locus of which the orbit dimension drops. The Lie algebra
$R_2 R_5^2$
on the locus of which the orbit dimension drops. The Lie algebra
![]() $\mathfrak {sl}(3,\mathbb C)^{(6)}$
acts simply transitively on the complement of
$\mathfrak {sl}(3,\mathbb C)^{(6)}$
acts simply transitively on the complement of
![]() $\{R_2 R_5=0\} \subset \pi _{6,1}^{-1}(U_3^y)$
; note that
$\{R_2 R_5=0\} \subset \pi _{6,1}^{-1}(U_3^y)$
; note that
![]() $\dim J^6({\mathbb C} P^2,1)=\dim \mathfrak {sl}(3,\mathbb C)$
. A complete description of the orbit structure (over
$\dim J^6({\mathbb C} P^2,1)=\dim \mathfrak {sl}(3,\mathbb C)$
. A complete description of the orbit structure (over
![]() $\mathbb R$
) can be found in [Reference Konovenko and Lychagin16].
$\mathbb R$
) can be found in [Reference Konovenko and Lychagin16].
Remark 3.11. Proposition 2.25 gains the following insight. Computing orbit dimensions of
![]() ${\mathfrak g}=\mathfrak {sl}(3,{\mathbb C})$
in
${\mathfrak g}=\mathfrak {sl}(3,{\mathbb C})$
in
![]() $J^4({\mathbb C} P^2,1)$
shows that an invariant divisor exist only if
$J^4({\mathbb C} P^2,1)$
shows that an invariant divisor exist only if
![]() $A_2 = 3 A_1$
, in which case it is
$A_2 = 3 A_1$
, in which case it is
![]() $y_2^{-A_1}$
, but this is meromorphic only if
$y_2^{-A_1}$
, but this is meromorphic only if
![]() $A_1\in \mathbb Z$
. For
$A_1\in \mathbb Z$
. For
![]() $k\geq 5$
, the generic orbit dimension of
$k\geq 5$
, the generic orbit dimension of
![]() ${\mathfrak g}^{(k)}$
on
${\mathfrak g}^{(k)}$
on
![]() $J^k({\mathbb C} P^2,1)$
is the same as that of
$J^k({\mathbb C} P^2,1)$
is the same as that of
![]() $({\mathfrak g}^{(k)})^{\lambda }$
, independently of
$({\mathfrak g}^{(k)})^{\lambda }$
, independently of
![]() $\lambda $
. The general invariant divisor is given by
$\lambda $
. The general invariant divisor is given by
![]() $R_2^{2A_1-A_2} R_5^{(A_2-3 A_1)/6}$
; however, this function is meromorphic if and only if
$R_2^{2A_1-A_2} R_5^{(A_2-3 A_1)/6}$
; however, this function is meromorphic if and only if
![]() $(2A_1-A_2), (A_2-3A_1)/6 \in \mathbb Z$
. Together with (3.4), this implies that weights
$(2A_1-A_2), (A_2-3A_1)/6 \in \mathbb Z$
. Together with (3.4), this implies that weights
![]() $(A_1,A_2)$
belong to the lattice generated by
$(A_1,A_2)$
belong to the lattice generated by
![]() $(3,-3)$
and
$(3,-3)$
and
![]() $(2,0)$
.
$(2,0)$
.
The polynomials
![]() $R_2, R_5, R_7$
are local expressions, defined on
$R_2, R_5, R_7$
are local expressions, defined on
![]() $\pi _{7,1}^{-1}(U_3^y)$
, for invariant polynomial divisors. But they extend uniquely to polynomial divisors on
$\pi _{7,1}^{-1}(U_3^y)$
, for invariant polynomial divisors. But they extend uniquely to polynomial divisors on
![]() $J^7(\mathbb CP^2,1)$
. For
$J^7(\mathbb CP^2,1)$
. For
![]() $R_2$
,
$R_2$
,
![]() $R_5$
and
$R_5$
and
![]() $R_7$
, the weight
$R_7$
, the weight
![]() $\lambda _3^y$
is given by
$\lambda _3^y$
is given by
![]() $(A_1,A_2)=(-1,-3)$
,
$(A_1,A_2)=(-1,-3)$
,
![]() $(A_1,A_2)=(-6,-12)$
and
$(A_1,A_2)=(-6,-12)$
and
![]() $(A_1,A_2)=(-16,-32)$
, respectively. In particular,
$(A_1,A_2)=(-16,-32)$
, respectively. In particular,
![]() $R_2$
and
$R_2$
and
![]() $R_5$
do not combine to a rational absolute differential invariant (weight
$R_5$
do not combine to a rational absolute differential invariant (weight
![]() $0$
), which is consistent with the fact that
$0$
), which is consistent with the fact that
![]() ${\mathfrak g}^{(6)}$
has an open orbit on
${\mathfrak g}^{(6)}$
has an open orbit on
![]() $J^6(\mathbb CP^2,1)$
. It is also clear that
$J^6(\mathbb CP^2,1)$
. It is also clear that
![]() $R_2$
and
$R_2$
and
![]() $R_5$
are local generators for polynomial invariant divisors on
$R_5$
are local generators for polynomial invariant divisors on
![]() $J^6(\mathbb CP^2,1)$
since they generate a 2-dimensional space of weights.
$J^6(\mathbb CP^2,1)$
since they generate a 2-dimensional space of weights.
Combining weights of the invariant divisors, we obtain the above absolute invariant
![]() $I_7$
together with the following invariant meromorphic tensor fields:
$I_7$
together with the following invariant meromorphic tensor fields:
 $$\begin{align*}\alpha_5 = \frac{R_5}{R_2^4} dx \wedge dy \in \Gamma(\pi_{5,0}^*\Lambda^2 T^* \mathbb CP^2), \qquad \alpha_7=\frac{R_7}{R_2^3 R_5^2} (dy-y_1 dx) \in \Gamma(\pi_{7,1}^{*}\langle \omega \rangle). \end{align*}$$
$$\begin{align*}\alpha_5 = \frac{R_5}{R_2^4} dx \wedge dy \in \Gamma(\pi_{5,0}^*\Lambda^2 T^* \mathbb CP^2), \qquad \alpha_7=\frac{R_7}{R_2^3 R_5^2} (dy-y_1 dx) \in \Gamma(\pi_{7,1}^{*}\langle \omega \rangle). \end{align*}$$
The inverse bivector
![]() $\alpha _5^{-1}=\frac {R_2^4}{R_5}D_x \wedge \partial _y$
contracted with
$\alpha _5^{-1}=\frac {R_2^4}{R_5}D_x \wedge \partial _y$
contracted with
![]() $\alpha _7$
gives the invariant derivation
$\alpha _7$
gives the invariant derivation
![]() $\nabla $
above.
$\nabla $
above.
Remark 3.12. These tensor fields can be compared to those of Theorem 5.1 of [Reference Konovenko and Lychagin16]. Their
![]() $R_2^{-3} R_5^{2/3} (dy-y_1 dx)$
is multi-valued over
$R_2^{-3} R_5^{2/3} (dy-y_1 dx)$
is multi-valued over
![]() ${\mathbb C}$
, but its cube is the rational invariant tensor
${\mathbb C}$
, but its cube is the rational invariant tensor
![]() $I_7^{-1}\alpha _7^3$
.
$I_7^{-1}\alpha _7^3$
.
Note that, in general, polynomial divisors
![]() $\mathrm {Div}^{\text {pol}}_{\mathfrak g}(M)$
determine a weight sub-monoid in
$\mathrm {Div}^{\text {pol}}_{\mathfrak g}(M)$
determine a weight sub-monoid in
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
, while rational divisors
$\mathrm {Pic}_{\mathfrak g}(M)$
, while rational divisors
![]() $\mathrm {Div}^{\text {rat}}_{\mathfrak g}(M)$
, obtained as ratios of the former, determine a lattice.
$\mathrm {Div}^{\text {rat}}_{\mathfrak g}(M)$
, obtained as ratios of the former, determine a lattice.
Theorem 3.13. The lattice generated by polynomial divisors for
![]() ${\mathfrak g}=\mathfrak {sl}(3,{\mathbb C})$
acting on
${\mathfrak g}=\mathfrak {sl}(3,{\mathbb C})$
acting on
![]() $J^\infty ({\mathbb C} P^2,1)$
is a sublattice of order 3 in the equivariant Picard group on 1-jets:
$J^\infty ({\mathbb C} P^2,1)$
is a sublattice of order 3 in the equivariant Picard group on 1-jets:
This is basically a summary of the computations. Indeed, from the tensor fields
![]() $\alpha _5$
,
$\alpha _5$
,
![]() $\alpha _7$
we see that (pullbacks of) line bundles in
$\alpha _7$
we see that (pullbacks of) line bundles in
![]() $\mathrm {Pic}_{\mathfrak {sl}(3,{\mathbb C})^{(1)}}(J^1({\mathbb C} P^2,1))$
are realized as
$\mathrm {Pic}_{\mathfrak {sl}(3,{\mathbb C})^{(1)}}(J^1({\mathbb C} P^2,1))$
are realized as
![]() $[D]$
for some rational
$[D]$
for some rational
![]() $\mathfrak {sl}(3,\mathbb C)^{(7)}$
-invariant divisor D on
$\mathfrak {sl}(3,\mathbb C)^{(7)}$
-invariant divisor D on
![]() $J^7(\mathbb CP^2,1)$
when
$J^7(\mathbb CP^2,1)$
when
![]() $k_0/3,k_1 \in \mathbb Z$
, where
$k_0/3,k_1 \in \mathbb Z$
, where
![]() $k_0$
and
$k_0$
and
![]() $k_1$
are the parameters used in Proposition 3.10. To understand why
$k_1$
are the parameters used in Proposition 3.10. To understand why
![]() $\mathcal {O}_{\mathbb CP^2}(1)$
is not realized in this way, one must consider which Lie group is acting here. The Lie algebra
$\mathcal {O}_{\mathbb CP^2}(1)$
is not realized in this way, one must consider which Lie group is acting here. The Lie algebra
![]() ${\mathfrak g}=\mathfrak {sl}(3,{\mathbb C})$
on
${\mathfrak g}=\mathfrak {sl}(3,{\mathbb C})$
on
![]() ${\mathbb C} P^2$
integrates to the Lie group
${\mathbb C} P^2$
integrates to the Lie group
![]() $G=PGL(3,{\mathbb C})$
and then results from Example 2.32 apply.
$G=PGL(3,{\mathbb C})$
and then results from Example 2.32 apply.
Remark 3.14. Nondegenerate curves in
![]() ${\mathbb C} P^n$
up to projective transformations
${\mathbb C} P^n$
up to projective transformations
![]() ${\mathfrak g}=\mathfrak {sl}(n+1,{\mathbb C})$
were studied by Wilczynski [Reference Wilczynski31]. He computed fundamental differential invariants via the correspondence with linear ordinary differential equations of order
${\mathfrak g}=\mathfrak {sl}(n+1,{\mathbb C})$
were studied by Wilczynski [Reference Wilczynski31]. He computed fundamental differential invariants via the correspondence with linear ordinary differential equations of order
![]() $n+1$
. Our results generalize to give two-dimensional lattice
$n+1$
. Our results generalize to give two-dimensional lattice
![]() $\mathrm {Pic}_{{\mathfrak g}^{(1)}}\big (J^1({\mathbb C} P^n,1)\big )$
, which constrains the weights of relative differential invariants.
$\mathrm {Pic}_{{\mathfrak g}^{(1)}}\big (J^1({\mathbb C} P^n,1)\big )$
, which constrains the weights of relative differential invariants.
3.5 Example C: Second-order ODEs modulo point transformations revisited
Finally, for
![]() $h\in \mathcal {O}(U)$
,
$h\in \mathcal {O}(U)$
,
![]() $U\subset J^1(\mathbb C P^2,1)$
, we consider scalar second-order ODEs
$U\subset J^1(\mathbb C P^2,1)$
, we consider scalar second-order ODEs
together with the Lie algebra sheaf
![]() ${\mathfrak g}=\mathcal {D}(\mathbf {J}^0)$
of germs of holomorphic vector fields on
${\mathfrak g}=\mathcal {D}(\mathbf {J}^0)$
of germs of holomorphic vector fields on
![]() $\mathbf {J}^0={\mathbb C} P^2$
. Here and throughout this section, we use the notation
$\mathbf {J}^0={\mathbb C} P^2$
. Here and throughout this section, we use the notation
![]() $\mathbf {J}^s=J^s(\mathbb C P^2,1)$
, while
$\mathbf {J}^s=J^s(\mathbb C P^2,1)$
, while
![]() $J^k(\mathbf {J}^1)$
consists of k-jets of functions h on
$J^k(\mathbf {J}^1)$
consists of k-jets of functions h on
![]() $\mathbf {J}^1$
. Our goal is to find generators for the invariant divisors on
$\mathbf {J}^1$
. Our goal is to find generators for the invariant divisors on
![]() $J^4(\mathbf {J}^1)$
.
$J^4(\mathbf {J}^1)$
.
Relative invariants were first found by A. Tresse in [Reference Tresse29] via Lie theory and then by E. Cartan via his theory of moving frames [Reference Cartan5]. We apply our global framework to justify the (two-dimensional) weight lattice introduced in [Reference Kruglikov17] and generate relative invariants for this classical problem in a novel and conceptually transparent manner.
Any vector field on
![]() $\mathbf {J}^0$
prolongs uniquely to a vector field on
$\mathbf {J}^0$
prolongs uniquely to a vector field on
![]() $\mathbf {J}^2$
. This action induces an (infinitesimal) transformation on the space of second-order ODEs. Choose local coordinates
$\mathbf {J}^2$
. This action induces an (infinitesimal) transformation on the space of second-order ODEs. Choose local coordinates
![]() $x,y$
on
$x,y$
on
![]() ${\mathbb C} P^2$
and denote
${\mathbb C} P^2$
and denote
![]() $p=y_1,u=y_2$
the induced coordinates on
$p=y_1,u=y_2$
the induced coordinates on
![]() $\mathbf {J}^2$
; then an ODE is a hypersurface
$\mathbf {J}^2$
; then an ODE is a hypersurface
![]() $u=h(x,y,p)$
in
$u=h(x,y,p)$
in
![]() $J^0(\mathbf {J}^1)=\mathbf {J}^2$
. Redefining
$J^0(\mathbf {J}^1)=\mathbf {J}^2$
. Redefining
![]() ${\mathfrak g}$
to be the image (prolongation) of
${\mathfrak g}$
to be the image (prolongation) of
![]() $\mathcal {D}(\mathbf {J}^0)$
in
$\mathcal {D}(\mathbf {J}^0)$
in
![]() $\mathbf {J}^2$
, its further prolongation, the Lie algebra
$\mathbf {J}^2$
, its further prolongation, the Lie algebra
![]() $\mathfrak g^{(k)} \subset \mathcal {D}(J^k(\mathbf {J}^1))$
, is spanned by the vector fields of the form
$\mathfrak g^{(k)} \subset \mathcal {D}(J^k(\mathbf {J}^1))$
, is spanned by the vector fields of the form
where
![]() $a,b$
are functions of
$a,b$
are functions of
![]() $x,y$
,
$x,y$
,
![]() $c=(\partial _x+p\partial _y)\varphi $
for
$c=(\partial _x+p\partial _y)\varphi $
for
![]() $\varphi = b-pa$
,
$\varphi = b-pa$
,
![]() $D_x$
is the operator of total derivative by x and similar for
$D_x$
is the operator of total derivative by x and similar for
![]() $D_y,D_p$
, while
$D_y,D_p$
, while
![]() $D_\sigma $
is their composition for multi-indices of variables (see [Reference Kruglikov17]), and the function
$D_\sigma $
is their composition for multi-indices of variables (see [Reference Kruglikov17]), and the function
![]() $\psi $
is given by
$\psi $
is given by
The Lie algebra
![]() $\mathfrak g^{(0)}={\mathfrak g}$
preserves the fibers of the affine bundle
$\mathfrak g^{(0)}={\mathfrak g}$
preserves the fibers of the affine bundle
![]() $J^0(\mathbf {J}^1)\to \mathbf {J}^1$
(and their affine structure). Thus, in order to compute invariant divisors that are polynomial on fibers of
$J^0(\mathbf {J}^1)\to \mathbf {J}^1$
(and their affine structure). Thus, in order to compute invariant divisors that are polynomial on fibers of
![]() $J^k(\mathbf {J}^1)\to \mathbf {J}^1$
, we exploit Proposition 3.8 and start with classification of
$J^k(\mathbf {J}^1)\to \mathbf {J}^1$
, we exploit Proposition 3.8 and start with classification of
![]() ${\mathfrak g}$
-equivariant line bundles on
${\mathfrak g}$
-equivariant line bundles on
![]() $\mathbf {J}^1$
.
$\mathbf {J}^1$
.
3.5.1
 ${\mathfrak g}$
-equivariant line bundles
${\mathfrak g}$
-equivariant line bundles
In Example B, we saw that the
![]() $\mathfrak {sl}(3,{\mathbb C})^{(1)}$
-equivariant line bundles on
$\mathfrak {sl}(3,{\mathbb C})^{(1)}$
-equivariant line bundles on
![]() $\mathbf {J}^1$
were generated by the line bundles
$\mathbf {J}^1$
were generated by the line bundles
![]() $\pi _{1,0}^*\mathcal {O}_{\mathbb CP^2}(1)$
and
$\pi _{1,0}^*\mathcal {O}_{\mathbb CP^2}(1)$
and
![]() $\langle \omega \rangle \subset T^*\mathbf {J}^1$
. Since
$\langle \omega \rangle \subset T^*\mathbf {J}^1$
. Since
![]() $\mathfrak {sl}(3,{\mathbb C})^{(1)}\subset {\mathfrak g}$
, we have a natural homomorphism
$\mathfrak {sl}(3,{\mathbb C})^{(1)}\subset {\mathfrak g}$
, we have a natural homomorphism
Proposition 3.15. Homomorphism (3.8) is an isomorphism.
Proof. We first prove that (3.8) is surjective. Clearly, the bundle
![]() $\mathcal {O}_{\mathbb CP^2}(-3) \simeq \pi _{1,0}^* \Lambda ^2 T^* \mathbb CP^2$
admits a
$\mathcal {O}_{\mathbb CP^2}(-3) \simeq \pi _{1,0}^* \Lambda ^2 T^* \mathbb CP^2$
admits a
![]() ${\mathfrak g}$
-lift, due to naturality of the cotangent bundle. The bundle
${\mathfrak g}$
-lift, due to naturality of the cotangent bundle. The bundle
![]() $\langle \omega \rangle \subset T^*\mathbf {J}^1$
admits a
$\langle \omega \rangle \subset T^*\mathbf {J}^1$
admits a
![]() ${\mathfrak g}$
-lift since the prolongation preserves the Cartan distribution
${\mathfrak g}$
-lift since the prolongation preserves the Cartan distribution
![]() $\mathrm {Ann}(\omega )\subset T \mathbf {J}^1$
. What remains to be seen is that
$\mathrm {Ann}(\omega )\subset T \mathbf {J}^1$
. What remains to be seen is that
![]() $\mathcal {O}_{{\mathbb C} P^2}(1)$
admits a
$\mathcal {O}_{{\mathbb C} P^2}(1)$
admits a
![]() ${\mathfrak g}$
-lift. On
${\mathfrak g}$
-lift. On
![]() $\mathcal {O}_{{\mathbb C} P^2}(1)$
, the local weight
$\mathcal {O}_{{\mathbb C} P^2}(1)$
, the local weight
![]() $\lambda _3$
of a general vector field
$\lambda _3$
of a general vector field
![]() $X=a(x,y) \partial _x+b(x,y)\partial _y$
on
$X=a(x,y) \partial _x+b(x,y)\partial _y$
on
![]() $U_3$
(for example) is
$U_3$
(for example) is
![]() $\lambda _3(X)=(a_x + b_y)/3$
, and it is not difficult to check that this extends to a compatible weight for each
$\lambda _3(X)=(a_x + b_y)/3$
, and it is not difficult to check that this extends to a compatible weight for each
![]() $X \in {\mathfrak g}$
.
$X \in {\mathfrak g}$
.
Now we prove injectivity. Let
![]() $[(g,\lambda )]\in \mathrm {Pic}_{\mathfrak g}(\mathbf {J}^1)$
be in the kernel of (3.8). Then
$[(g,\lambda )]\in \mathrm {Pic}_{\mathfrak g}(\mathbf {J}^1)$
be in the kernel of (3.8). Then
![]() $[g]=0\in \mathrm {Pic}(\mathbf {J}^1)$
, and there exists a representative for
$[g]=0\in \mathrm {Pic}(\mathbf {J}^1)$
, and there exists a representative for
![]() $[\lambda ]$
such that
$[\lambda ]$
such that
![]() $\lambda |_{\mathfrak {sl}(3,{\mathbb C})^{(1)}} =0$
.
$\lambda |_{\mathfrak {sl}(3,{\mathbb C})^{(1)}} =0$
.
Take an arbitrary point in
![]() $\mathbf {J}^1$
and choose a chart with coordinates centered at this point (origin). Due to transitivity of
$\mathbf {J}^1$
and choose a chart with coordinates centered at this point (origin). Due to transitivity of
![]() $\mathfrak {sl}(3,{\mathbb C})^{(1)}$
on
$\mathfrak {sl}(3,{\mathbb C})^{(1)}$
on
![]() $\mathbf {J}^1$
, we can assume, without loss of generality, that the coordinate chart is
$\mathbf {J}^1$
, we can assume, without loss of generality, that the coordinate chart is
![]() $U_3^y$
from Section 3.4. We will compute
$U_3^y$
from Section 3.4. We will compute
![]() $\lambda |_{U_3^y}$
. It is clear that if
$\lambda |_{U_3^y}$
. It is clear that if
![]() $\lambda (X) \neq 0$
for some
$\lambda (X) \neq 0$
for some
![]() $X\in {\mathfrak g}$
, then
$X\in {\mathfrak g}$
, then
![]() $\lambda (X)|_{U_3^y}\neq 0$
since
$\lambda (X)|_{U_3^y}\neq 0$
since
![]() $U_3^y\subset \mathbf {J}^1$
is a dense subset.
$U_3^y\subset \mathbf {J}^1$
is a dense subset.
We continue with the notation from Section 3.4, so that
![]() $\mathfrak {sl}(3,{\mathbb C})^{(1)}|_{U_3^y} = \langle X_1, \cdots , X_8 \rangle $
with
$\mathfrak {sl}(3,{\mathbb C})^{(1)}|_{U_3^y} = \langle X_1, \cdots , X_8 \rangle $
with
![]() $X_i$
given by (3.3). We have
$X_i$
given by (3.3). We have
![]() $\lambda (X_1)=\cdots =\lambda (X_8)=0$
. Next, consider the vector fields
$\lambda (X_1)=\cdots =\lambda (X_8)=0$
. Next, consider the vector fields
 $$ \begin{gather*} Y_1 = x^2 \partial_y+2x\partial_{y_1} , \quad Y_2 = x^2\partial_x-2xy \partial_y - (4xy_1+2y)\partial_{y_1}, \\ Y_3 = y^2 \partial_y -2xy \partial_x+(2xy_1^2+4yy_1)\partial_{y_1}, \quad Y_4=y^2 \partial_x-2yy_1^2 \partial_{y_1}. \end{gather*} $$
$$ \begin{gather*} Y_1 = x^2 \partial_y+2x\partial_{y_1} , \quad Y_2 = x^2\partial_x-2xy \partial_y - (4xy_1+2y)\partial_{y_1}, \\ Y_3 = y^2 \partial_y -2xy \partial_x+(2xy_1^2+4yy_1)\partial_{y_1}, \quad Y_4=y^2 \partial_x-2yy_1^2 \partial_{y_1}. \end{gather*} $$
The commutation relations
 $$ \begin{gather*} [X_1,Y_1]= 2 X_4, \quad [X_2,Y_1]=0, \quad [X_4,Y_1]=0, \\ [X_1,Y_2]= 2 X_5, \quad [X_2,Y_2]=-2X_4, \quad [X_4,Y_2]=-3 Y_1, \\ [X_1,Y_3]= -2 X_3, \quad [X_2,Y_3]=-2X_5, \quad [X_4,Y_3]=-2 Y_2, \\ [X_1,Y_4]=0, \quad [X_2,Y_4]=2 X_3, \quad [X_4, Y_4]=-Y_3, \\ [X_6, Y_i]=Y_i, \qquad i=1,2,3,4 \end{gather*} $$
$$ \begin{gather*} [X_1,Y_1]= 2 X_4, \quad [X_2,Y_1]=0, \quad [X_4,Y_1]=0, \\ [X_1,Y_2]= 2 X_5, \quad [X_2,Y_2]=-2X_4, \quad [X_4,Y_2]=-3 Y_1, \\ [X_1,Y_3]= -2 X_3, \quad [X_2,Y_3]=-2X_5, \quad [X_4,Y_3]=-2 Y_2, \\ [X_1,Y_4]=0, \quad [X_2,Y_4]=2 X_3, \quad [X_4, Y_4]=-Y_3, \\ [X_6, Y_i]=Y_i, \qquad i=1,2,3,4 \end{gather*} $$
give four differential equations on each function
![]() $\lambda (Y_i)$
, implying
$\lambda (Y_i)$
, implying
![]() $\lambda (Y_1)=\cdots =\lambda (Y_4)=0$
.
$\lambda (Y_1)=\cdots =\lambda (Y_4)=0$
.
Furthermore, all polynomial vector fields are generated by
![]() $X_1,\dots , X_8$
and
$X_1,\dots , X_8$
and
![]() $Y_1, \dots , Y_4$
. Indeed, for
$Y_1, \dots , Y_4$
. Indeed, for
![]() $j \geq 3$
, we have
$j \geq 3$
, we have
 $$ \begin{align*} x^i y^{j-i} \partial_x &= \frac{1}{i-3} [x^2 \partial_x,x^{i-1} y^{j-i} \partial_x], \qquad i \neq 0,3, \\ y^{j} \partial_x &= \frac{1}{j-1} [y^2 \partial_y, y^{j-1} \partial_x],\\ x^3 y^{j-3} \partial_x &= \frac{1}{j-2} \left([x^2 \partial_y,xy^{j-2} \partial_x] +2x^2 y^{j-2} \partial_y\right), \end{align*} $$
$$ \begin{align*} x^i y^{j-i} \partial_x &= \frac{1}{i-3} [x^2 \partial_x,x^{i-1} y^{j-i} \partial_x], \qquad i \neq 0,3, \\ y^{j} \partial_x &= \frac{1}{j-1} [y^2 \partial_y, y^{j-1} \partial_x],\\ x^3 y^{j-3} \partial_x &= \frac{1}{j-2} \left([x^2 \partial_y,xy^{j-2} \partial_x] +2x^2 y^{j-2} \partial_y\right), \end{align*} $$
and by swapping x and y, we also generate
![]() $x^i y^{j-i} \partial _y$
for
$x^i y^{j-i} \partial _y$
for
![]() $i=0,\dots ,j$
. Thus, all vector fields with polynomial coefficients of degree
$i=0,\dots ,j$
. Thus, all vector fields with polynomial coefficients of degree
![]() $\geq 3$
are of the form
$\geq 3$
are of the form
![]() $[Z,Y]$
, where the coefficients of Y have degree
$[Z,Y]$
, where the coefficients of Y have degree
![]() $2$
and the coefficients of Z have degree strictly lower than those of
$2$
and the coefficients of Z have degree strictly lower than those of
![]() $[Z,Y]$
. Then the general cocycle condition
$[Z,Y]$
. Then the general cocycle condition
implies that
![]() $\lambda (X)=0$
for any polynomial vector field X on
$\lambda (X)=0$
for any polynomial vector field X on
![]() $U_3^y$
.
$U_3^y$
.
On any compact subset
![]() $K\subset U_3^y$
, the subspace of vector fields in
$K\subset U_3^y$
, the subspace of vector fields in
![]() $\mathcal {D}(K)$
with polynomial coefficients is dense in
$\mathcal {D}(K)$
with polynomial coefficients is dense in
![]() $\mathcal {D}(K)$
. It follows that
$\mathcal {D}(K)$
. It follows that
![]() $\lambda (X)|_K = 0$
for every
$\lambda (X)|_K = 0$
for every
![]() $X \in {\mathfrak g}$
for any K, and hence that
$X \in {\mathfrak g}$
for any K, and hence that
![]() $\lambda (X)|_{U_3^y}=0$
for every
$\lambda (X)|_{U_3^y}=0$
for every
![]() $X \in {\mathfrak g}$
. Thus
$X \in {\mathfrak g}$
. Thus
![]() $\lambda =0$
.
$\lambda =0$
.
3.5.2 Invariant divisors
Now we compute the
![]() ${\mathfrak g}^{(4)}$
-invariant divisors on
${\mathfrak g}^{(4)}$
-invariant divisors on
![]() $J^4(\mathbf {J}^1)$
. Let us work in the coordinate chart
$J^4(\mathbf {J}^1)$
. Let us work in the coordinate chart
![]() $\tau _{4}^{-1}(U_3^y)$
, where
$\tau _{4}^{-1}(U_3^y)$
, where
![]() $\tau _4$
denotes the projection
$\tau _4$
denotes the projection
![]() $\tau _{4}\colon J^4(\mathbf {J}^1)\to \mathbf {J}^1$
. From Proposition 3.15, we know that
$\tau _{4}\colon J^4(\mathbf {J}^1)\to \mathbf {J}^1$
. From Proposition 3.15, we know that
![]() $[\lambda ]\in H^1({\mathfrak g},\mathcal {O}(U_3^y))$
has a representative of the form
$[\lambda ]\in H^1({\mathfrak g},\mathcal {O}(U_3^y))$
has a representative of the form
where
![]() $(C_0,C_1)$
is related to
$(C_0,C_1)$
is related to
![]() $(A_1,A_2)$
by
$(A_1,A_2)$
by
![]() $A_1=2(C_0+C_1)$
and
$A_1=2(C_0+C_1)$
and
![]() $A_2=-2C_1$
. Condition (3.4) is equivalent to
$A_2=-2C_1$
. Condition (3.4) is equivalent to
![]() $3 C_0 ,2 C_1 \in \mathbb Z$
. If f is a general polynomial of some fixed degree, then the system
$3 C_0 ,2 C_1 \in \mathbb Z$
. If f is a general polynomial of some fixed degree, then the system
reduces to a linear system on the coefficients of f for each choice of
![]() $(C_0,C_1)$
. By sequentially setting
$(C_0,C_1)$
. By sequentially setting
![]() $C_0=0, \pm 1/3, \pm 2/3, \dots $
and
$C_0=0, \pm 1/3, \pm 2/3, \dots $
and
![]() $C_1=0, \pm 1/2, \pm 1, \dots $
and letting f be a general polynomial of degree 3 with undetermined coefficients, we get a series of linear systems determining the coefficients of the polynomial. In this way, we obtain the solutions
$C_1=0, \pm 1/2, \pm 1, \dots $
and letting f be a general polynomial of degree 3 with undetermined coefficients, we get a series of linear systems determining the coefficients of the polynomial. In this way, we obtain the solutions
 $$ \begin{align*} f_1 &= u_{pppp}, \\ f_2 &=u_{xxpp} + 2 p u_{xypp} + 2 u u_{xppp} + p^2 u_{yypp} + 2 p u u_{yppp} + u^2 u_{pppp} + (u_x+p u_{y}) u_{ppp} \\ &-u_{p} u_{xpp} - 4 u_{xyp} - 4 pu_{yyp} - (p u_{p} + 3 u ) u_{ypp} + 6 u_{yy}+ 4u_{p} u_{yp} - 3 u_{y} u_{pp} , \end{align*} $$
$$ \begin{align*} f_1 &= u_{pppp}, \\ f_2 &=u_{xxpp} + 2 p u_{xypp} + 2 u u_{xppp} + p^2 u_{yypp} + 2 p u u_{yppp} + u^2 u_{pppp} + (u_x+p u_{y}) u_{ppp} \\ &-u_{p} u_{xpp} - 4 u_{xyp} - 4 pu_{yyp} - (p u_{p} + 3 u ) u_{ypp} + 6 u_{yy}+ 4u_{p} u_{yp} - 3 u_{y} u_{pp} , \end{align*} $$
which have weights
![]() $(C_0, C_1)= (2,-5/2)$
and
$(C_0, C_1)= (2,-5/2)$
and
![]() $(-2,1/2)$
, respectively. Computing the rank of prolonged vector fields at generic point, we conclude that the action of
$(-2,1/2)$
, respectively. Computing the rank of prolonged vector fields at generic point, we conclude that the action of
![]() ${\mathfrak g}^{(4)}$
has an open orbit in
${\mathfrak g}^{(4)}$
has an open orbit in
![]() $J^4(\mathbf {J}^1)$
. Thus, there are no (nonconstant) absolute invariants on
$J^4(\mathbf {J}^1)$
. Thus, there are no (nonconstant) absolute invariants on
![]() $\mathbf {J}^4$
. Now, if
$\mathbf {J}^4$
. Now, if
![]() $f_3$
was another invariant divisor of general weight
$f_3$
was another invariant divisor of general weight
![]() $(C_0,C_1)=(2A-2B,(B-5A)/2)$
with rational
$(C_0,C_1)=(2A-2B,(B-5A)/2)$
with rational
![]() $A,B$
, then for some integer m, the ratio
$A,B$
, then for some integer m, the ratio
 $$\begin{align*}\frac{f_3^m}{f_1^{Am} f_2^{Bm}} \end{align*}$$
$$\begin{align*}\frac{f_3^m}{f_1^{Am} f_2^{Bm}} \end{align*}$$
is a rational function with weight
![]() $(0,0)$
and hence is an absolute differential invariant, and therefore constant. Hence,
$(0,0)$
and hence is an absolute differential invariant, and therefore constant. Hence,
![]() $f_3^m$
is proportional to
$f_3^m$
is proportional to
![]() $f_1^{Am} f_2^{Bm}$
.
$f_1^{Am} f_2^{Bm}$
.
Taking into account Proposition 3.8, we conclude the following.
Theorem 3.16. The lattice generated by polynomial divisors for the Lie algebra
![]() ${\mathfrak g}=\mathcal {D}(\mathbf {J}^0)$
acting on
${\mathfrak g}=\mathcal {D}(\mathbf {J}^0)$
acting on
![]() $J^\infty (\mathbf {J}^1)$
is a sublattice in the equivariant Picard group on 1-jets:
$J^\infty (\mathbf {J}^1)$
is a sublattice in the equivariant Picard group on 1-jets:
Let us note that cohomology of line bundles was explored in [Reference Hurtubise and Kamran14] to compute Cartan invariants of projective connections, which correspond to a particular class of ODEs of the form (3.6) with h cubic in
![]() $y_1$
; our methods though are quite distinct.
$y_1$
; our methods though are quite distinct.
4 Outlook
In this work, we proposed a theory of global scalar relative differential invariants, based on familiar notions of divisors and line bundles. While G-equivariant line bundles were known for algebraic and compact groups, the more general notions of equivariant Picard group
![]() $\mathrm {Pic}_{\mathfrak g}(M)$
and invariant divisor group
$\mathrm {Pic}_{\mathfrak g}(M)$
and invariant divisor group
![]() $\mathrm {Div}_{\mathfrak g}(M)$
for a Lie algebra
$\mathrm {Div}_{\mathfrak g}(M)$
for a Lie algebra
![]() ${\mathfrak g}$
appear to be new and have certain subtleties. (These notions even extend to Lie algebra sheaves, as seen in Example C.)
${\mathfrak g}$
appear to be new and have certain subtleties. (These notions even extend to Lie algebra sheaves, as seen in Example C.)
The basic setup is analytic, but we also consider polynomial divisors in affine bundles. Such bundles arise in successive jet-prolongation, and polynomial relative differential invariants are natural and sufficient in the equivalence problem of invariant hypersurfaces. We thus explore polynomial divisors in jet spaces. While
![]() $j\big (\mathrm {Div}(\mathbf {J}^\infty )\big )=j\big (\mathrm {Div}(\mathbf {J}^1)\big )$
in
$j\big (\mathrm {Div}(\mathbf {J}^\infty )\big )=j\big (\mathrm {Div}(\mathbf {J}^1)\big )$
in
![]() $\mathrm {Pic}(\mathbf {J}^\infty )=\mathrm { Pic}(\mathbf {J}^1)$
(in the case of fiber/affine bundle
$\mathrm {Pic}(\mathbf {J}^\infty )=\mathrm { Pic}(\mathbf {J}^1)$
(in the case of fiber/affine bundle
![]() $\pi $
, this can be pushed down to
$\pi $
, this can be pushed down to
![]() $\mathbf {J}^0$
, resp. M), the
$\mathbf {J}^0$
, resp. M), the
![]() ${\mathfrak g}$
-equivariant counterpart is more complicated. In general,
${\mathfrak g}$
-equivariant counterpart is more complicated. In general,
![]() $\mathrm {Pic}_{{\mathfrak g}^{(\infty )}}(\mathbf {J}^\infty )\neq \mathrm {Pic}_{{\mathfrak g}^{(1)}}(\mathbf {J}^1)$
, and similarly for invariant divisors. However, weights of invariant polynomial divisors are 1-jet determined, as Propositions 3.7 and 3.8 state. This gives an effective bound on multipliers for relative invariants and, in many cases, an algorithmic approach to compute them.
$\mathrm {Pic}_{{\mathfrak g}^{(\infty )}}(\mathbf {J}^\infty )\neq \mathrm {Pic}_{{\mathfrak g}^{(1)}}(\mathbf {J}^1)$
, and similarly for invariant divisors. However, weights of invariant polynomial divisors are 1-jet determined, as Propositions 3.7 and 3.8 state. This gives an effective bound on multipliers for relative invariants and, in many cases, an algorithmic approach to compute them.
Invariant submanifolds of higher codimensions are related, in the same manner, to higher rank equivariant vector bundles. While there are no general tools that classify analytic/algebraic vector bundles of higher rank, some part of the theory generalizes. Weights of vector-valued relative invariants are matrix-valued cocycles, leading to a more general cohomology theory.
Lastly, there is a differential algebra aspect to the theory of invariant divisors on jet bundles. The structure theory of these global relative differential invariants will be discussed elsewhere.
Competing interest
The authors have no competing interests to declare.
Funding statement
The research leading to our results has received funding from the Norwegian Financial Mechanism 2014-2021 (GRIEG project SCREAM, registration number 2019/34/H/ST1/00636) and the Tromsø Research Foundation (project ‘Pure Mathematics in Norway’), as well as UiT Aurora project MASCOT. The research of E.S. was partially funded by COST Action CaLISTA CA21109 supported by COST (European Cooperation in Science and Technology).
Data availability statement
All necessary data are provided in the paper.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Author contributions
Both authors contributed to all parts of this research.