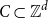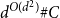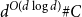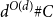1. Introduction
A classical theorem of John [Reference John2] shows that for any centrally symmetric convex set
![]() $K\subset \mathbb{R}^d$
, there exists an ellipsoid
$K\subset \mathbb{R}^d$
, there exists an ellipsoid
![]() $E$
centred at the origin so that
$E$
centred at the origin so that
![]() $E\subset K\subset \sqrt{d}E$
. This immediately implies that there exists a parallelotope
$E\subset K\subset \sqrt{d}E$
. This immediately implies that there exists a parallelotope
![]() $P$
so that
$P$
so that
![]() $P\subset E\subset K\subset \sqrt{d}E\subset dP$
. In the discrete setting, quantitative covering results are of great interest in Additive Combinatorics, a prominent example being the Polynomial Freiman–Ruzsa Conjecture, which asks for effective bounds on covering sets of small doubling by convex progressions. In this context, a natural analogue of John’s theorem in
$P\subset E\subset K\subset \sqrt{d}E\subset dP$
. In the discrete setting, quantitative covering results are of great interest in Additive Combinatorics, a prominent example being the Polynomial Freiman–Ruzsa Conjecture, which asks for effective bounds on covering sets of small doubling by convex progressions. In this context, a natural analogue of John’s theorem in
![]() $\mathbb{Z}^d$
would be covering centrally symmetric convex progressions by generalised arithmetic progressions. Here, a
$\mathbb{Z}^d$
would be covering centrally symmetric convex progressions by generalised arithmetic progressions. Here, a
![]() $d$
-dimensional convex progression is a set of the form
$d$
-dimensional convex progression is a set of the form
![]() $K\cap \mathbb{Z}^d$
, where
$K\cap \mathbb{Z}^d$
, where
![]() $K\subset \mathbb{R}^d$
is convex and a
$K\subset \mathbb{R}^d$
is convex and a
![]() $d$
-dimensional generalised arithmetic progression (
$d$
-dimensional generalised arithmetic progression (
![]() $d$
-GAP) is a translate of a set of the form
$d$
-GAP) is a translate of a set of the form
![]() $\left \{\sum _{i=1}^d m_ia_i\,:\, 1\leq m_i\leq n_i\right \}$
for some
$\left \{\sum _{i=1}^d m_ia_i\,:\, 1\leq m_i\leq n_i\right \}$
for some
![]() $n_i\in \mathbb{N}$
and
$n_i\in \mathbb{N}$
and
![]() $a_i\in \mathbb{Z}^d$
.
$a_i\in \mathbb{Z}^d$
.
Tao and Vu [Reference Tao and Vu4, Reference Tao and Van5] obtained such a discrete version of John’s theorem, showing that for any origin-symmetric
![]() $d$
-dimensional convex progression
$d$
-dimensional convex progression
![]() $C\subset \mathbb{Z}^d$
there exists a
$C\subset \mathbb{Z}^d$
there exists a
![]() $d$
-GAP
$d$
-GAP
![]() $P$
so that
$P$
so that
![]() $P\subset C\subset O(d)^{3d/2}\cdot P$
, where
$P\subset C\subset O(d)^{3d/2}\cdot P$
, where
![]() $m\cdot P\,:\!=\,\left \{\sum _{i=1}^m p_i\,:\, p_i\in P\right \}$
denotes the iterated sumset. Berg and Henk [Reference Berg and Henk1] improved this to
$m\cdot P\,:\!=\,\left \{\sum _{i=1}^m p_i\,:\, p_i\in P\right \}$
denotes the iterated sumset. Berg and Henk [Reference Berg and Henk1] improved this to
![]() $P\subset C\subset d^{O(\log (d))}\cdot P$
. Our focus will be on the covering aspect of these results, that is, minimising the ratio
$P\subset C\subset d^{O(\log (d))}\cdot P$
. Our focus will be on the covering aspect of these results, that is, minimising the ratio
![]() $\# P^{\prime}/ \# C$
, where
$\# P^{\prime}/ \# C$
, where
![]() $P^{\prime}$
is a
$P^{\prime}$
is a
![]() $d$
-GAP covering
$d$
-GAP covering
![]() $C$
. This ratio is bounded by
$C$
. This ratio is bounded by
![]() $d^{O(d^2)}$
by Tao and Vu and by
$d^{O(d^2)}$
by Tao and Vu and by
![]() $d^{O(d\log d)}$
by Berg and Henk. We obtain the bound
$d^{O(d\log d)}$
by Berg and Henk. We obtain the bound
![]() $d^{O(d)}$
, which is optimal.
$d^{O(d)}$
, which is optimal.
Theorem 1.1.
For any origin-symmetric convex progression
![]() $C\subset \mathbb{Z}^d$
, there exists a
$C\subset \mathbb{Z}^d$
, there exists a
![]() $d$
-GAP
$d$
-GAP
![]() $P$
containing
$P$
containing
![]() $C$
with
$C$
with
![]() $\# P\leq O(d)^{3d} \# C$
.
$\# P\leq O(d)^{3d} \# C$
.
Corollary 1.2.
For any origin-symmetric convex progression
![]() $C\subset \mathbb{Z}^d$
and linear map
$C\subset \mathbb{Z}^d$
and linear map
![]() $\phi \,:\,\mathbb{R}^d\to \mathbb{R}$
, there exists a
$\phi \,:\,\mathbb{R}^d\to \mathbb{R}$
, there exists a
![]() $d$
-GAP
$d$
-GAP
![]() $P$
containing
$P$
containing
![]() $C$
with
$C$
with
![]() $\# \phi (P)\leq O(d)^{3d} \# \phi (C)$
.
$\# \phi (P)\leq O(d)^{3d} \# \phi (C)$
.
The optimality of Theorem 1.1 is demonstrated by the intersection of a ball
![]() $B$
with a lattice
$B$
with a lattice
![]() $L$
. Moreover, Lovett and Regev [Reference Lovett and Regev3] obtained a more emphatic negative result, disproving the GAP analogue of the Polynomial Freiman–Ruzsa Conjecture, by showing that by considering a random lattice
$L$
. Moreover, Lovett and Regev [Reference Lovett and Regev3] obtained a more emphatic negative result, disproving the GAP analogue of the Polynomial Freiman–Ruzsa Conjecture, by showing that by considering a random lattice
![]() $L$
one can find a convex
$L$
one can find a convex
![]() $d$
-progression
$d$
-progression
![]() $C = B \cap L$
such that any
$C = B \cap L$
such that any
![]() $O(d)$
-GAP
$O(d)$
-GAP
![]() $P$
with
$P$
with
![]() $\# P \le \# C$
has
$\# P \le \# C$
has
![]() $\# (P \cap C) \lt d^{-\Omega (d)} \# C$
. Our result can be viewed as the positive counterpart that settles this line of enquiry, showing that indeed
$\# (P \cap C) \lt d^{-\Omega (d)} \# C$
. Our result can be viewed as the positive counterpart that settles this line of enquiry, showing that indeed
![]() $d^{\Theta (d)}$
is the optimal ratio for covering convex progressions by GAPs.
$d^{\Theta (d)}$
is the optimal ratio for covering convex progressions by GAPs.
2. Proof
We start by recording two simple observations and a proposition on a particular basis of a lattice, known as the Mahler Lattice Basis.
Observation 2.1.
Given an origin-symmetric convex set
![]() $K\subset \mathbb{R}^d$
, there exists a origin-symmetric parallelotope
$K\subset \mathbb{R}^d$
, there exists a origin-symmetric parallelotope
![]() $Q$
and an origin-symmetric ellipsoid
$Q$
and an origin-symmetric ellipsoid
![]() $E$
so that
$E$
so that
![]() $\frac 1d Q\subset E\subset K\subset \sqrt{d}E\subset Q$
, so in particular
$\frac 1d Q\subset E\subset K\subset \sqrt{d}E\subset Q$
, so in particular
![]() $|Q|\leq d^{d}|K|$
.
$|Q|\leq d^{d}|K|$
.
This is a simple consequence of John’s theorem.
Observation 2.2.
Let
![]() $X,X^{\prime}\in \mathbb{R}^{d\times d}$
be so that the rows of
$X,X^{\prime}\in \mathbb{R}^{d\times d}$
be so that the rows of
![]() $X$
and
$X$
and
![]() $X^{\prime}$
generate the same lattice of full rank in
$X^{\prime}$
generate the same lattice of full rank in
![]() $\mathbb{R}^d$
. Then
$\mathbb{R}^d$
. Then
![]() $\exists T\in GL_n(\mathbb{Z})$
so that
$\exists T\in GL_n(\mathbb{Z})$
so that
![]() $TX=X^{\prime}$
.
$TX=X^{\prime}$
.
This can be seen by considering the Smith Normal Form of the matrices
![]() $X$
and
$X$
and
![]() $X^{\prime}$
.
$X^{\prime}$
.
Proposition 2.3 (Corollary 3.35 from [Reference Tao and Vu4]). Given a lattice
![]() $\Lambda \subset \mathbb{R}^d$
of full rank, there exists a lattice basis
$\Lambda \subset \mathbb{R}^d$
of full rank, there exists a lattice basis
![]() $v_1,\dots, v_d$
of
$v_1,\dots, v_d$
of
![]() $\Lambda$
so that
$\Lambda$
so that
![]() $\prod _{i=1}^{d} \|v_i\|_2 \leq O(d^{3d/2})\det\! (v_1,\dots, v_d)$
.
$\prod _{i=1}^{d} \|v_i\|_2 \leq O(d^{3d/2})\det\! (v_1,\dots, v_d)$
.
With these three results in mind, we prove the theorem.
Proof of Theorem
1.1. By passing to a subspace if necessary, we may assume that
![]() $C$
is full-dimensional. Write
$C$
is full-dimensional. Write
![]() $C = K \cap \mathbb{Z}^d$
where
$C = K \cap \mathbb{Z}^d$
where
![]() $K\subset \mathbb{R}^d$
is origin-symmetric and convex. Use Observation 2.1 to find a parallelotope
$K\subset \mathbb{R}^d$
is origin-symmetric and convex. Use Observation 2.1 to find a parallelotope
![]() $Q\supset K$
so that
$Q\supset K$
so that
![]() $|Q|\leq d^d |K|$
. Let the defining vectors of
$|Q|\leq d^d |K|$
. Let the defining vectors of
![]() $Q$
be
$Q$
be
![]() $u_1,\dots,u_d$
, that is,
$u_1,\dots,u_d$
, that is,
![]() $Q=\big\{\!\sum_i \lambda _i u_i\,:\, \lambda _i\in [{-}1,1]\big\}$
. Write
$Q=\big\{\!\sum_i \lambda _i u_i\,:\, \lambda _i\in [{-}1,1]\big\}$
. Write
![]() $u_i^j$
for the
$u_i^j$
for the
![]() $j$
-th coordinate of
$j$
-th coordinate of
![]() $u_i$
and write
$u_i$
and write
![]() $U$
for the matrix
$U$
for the matrix
![]() $\big(u_i^j\big)$
with rows
$\big(u_i^j\big)$
with rows
![]() $u^j$
and columns
$u^j$
and columns
![]() $u_i$
.
$u_i$
.
Consider the lattice
![]() $\Lambda$
generated by the vectors
$\Lambda$
generated by the vectors
![]() $u^j$
(these are the vectors formed by the
$u^j$
(these are the vectors formed by the
![]() $j$
-th coordinates of the vectors
$j$
-th coordinates of the vectors
![]() $u_i$
). Using Proposition 2.3 find a basis
$u_i$
). Using Proposition 2.3 find a basis
![]() $v^1,\dots,v^d$
of
$v^1,\dots,v^d$
of
![]() $\Lambda$
so that
$\Lambda$
so that
![]() $\prod _{j=1}^{d} ||v^j||_2\leq O\big(d^{3d/2}\big)\det\! \big(v^1,\dots, v^d\big)$
. Write
$\prod _{j=1}^{d} ||v^j||_2\leq O\big(d^{3d/2}\big)\det\! \big(v^1,\dots, v^d\big)$
. Write
![]() $v^j_i$
for the
$v^j_i$
for the
![]() $i$
-th coordinate of
$i$
-th coordinate of
![]() $v^j$
and write
$v^j$
and write
![]() $V\,:\!=\,\big(v_i^j\big)$
. By Observation 2.2, we can find
$V\,:\!=\,\big(v_i^j\big)$
. By Observation 2.2, we can find
![]() $T\in GL_n(\mathbb{Z})$
so that
$T\in GL_n(\mathbb{Z})$
so that
![]() $TU=V$
, so that
$TU=V$
, so that
![]() $T u_i = v_i$
for
$T u_i = v_i$
for
![]() $1 \le i \le d$
and
$1 \le i \le d$
and
![]() $T(\mathbb{Z}^d)=\mathbb{Z}^d$
.
$T(\mathbb{Z}^d)=\mathbb{Z}^d$
.
Write
![]() $Q^{\prime}\,:\!=\,T(Q)=\big\{\!\sum_i \lambda _i v_i\,:\, \lambda _i\in [{-}1,1]\big\}$
and consider the smallest axis aligned box
$Q^{\prime}\,:\!=\,T(Q)=\big\{\!\sum_i \lambda _i v_i\,:\, \lambda _i\in [{-}1,1]\big\}$
and consider the smallest axis aligned box
![]() $B\,:\!=\,\prod_{i} [{-}a_i,a_i]$
containing
$B\,:\!=\,\prod_{i} [{-}a_i,a_i]$
containing
![]() $Q^{\prime}$
. Note that
$Q^{\prime}$
. Note that
![]() $a_j\leq \sum _{i} |v_i^j|=||v^{j}||_1\leq \sqrt{d}||v^{j}||_2$
. Hence, we find
$a_j\leq \sum _{i} |v_i^j|=||v^{j}||_1\leq \sqrt{d}||v^{j}||_2$
. Hence, we find
 \begin{align*} |B|&=2^d\prod _{i=1}^d a_i\leq 2^d\prod _{j=1}^d \sqrt{d}||v^j||_2\leq O(d)^{2d} \det\! \big(v^1,\dots,v^d\big)= O(d)^{2d} \det\! (v_1,\dots,v_d)=O(d)^{2d} |Q^{\prime}|. \end{align*}
\begin{align*} |B|&=2^d\prod _{i=1}^d a_i\leq 2^d\prod _{j=1}^d \sqrt{d}||v^j||_2\leq O(d)^{2d} \det\! \big(v^1,\dots,v^d\big)= O(d)^{2d} \det\! (v_1,\dots,v_d)=O(d)^{2d} |Q^{\prime}|. \end{align*}
Now we cover
![]() $C$
by a
$C$
by a
![]() $d$
-GAP
$d$
-GAP
![]() $P$
, constructed by the following sequence:
$P$
, constructed by the following sequence:
It remains to bound
![]() $\# P$
. As
$\# P$
. As
![]() $C$
is full-dimensional each
$C$
is full-dimensional each
![]() $a_i \ge 1$
, so
$a_i \ge 1$
, so
where the last inequality follows from Minkowski’s First Theorem (see for instance equation (3.14) in [Reference Tao and Vu4]).
Proof of Corollary
1.2. Let
![]() $m\,:\!=\,\max _{x\in \mathbb{Z}}\#(\phi ^{-1}(x)\cap C)$
and note that
$m\,:\!=\,\max _{x\in \mathbb{Z}}\#(\phi ^{-1}(x)\cap C)$
and note that
![]() $\# \phi (C)\geq \# C/ m$
. Analogously, let
$\# \phi (C)\geq \# C/ m$
. Analogously, let
![]() $m^{\prime}\,:\!=\,\max _{x\in \mathbb{Z}}\#(\phi ^{-1}(x)\cap P)$
so that
$m^{\prime}\,:\!=\,\max _{x\in \mathbb{Z}}\#(\phi ^{-1}(x)\cap P)$
so that
![]() $m^{\prime}\geq m$
. By translation, we may assume that
$m^{\prime}\geq m$
. By translation, we may assume that
![]() $m^{\prime}$
is achieved at
$m^{\prime}$
is achieved at
![]() $x=0$
. Note that for any
$x=0$
. Note that for any
![]() $x = \phi (p)$
with
$x = \phi (p)$
with
![]() $p \in P$
and
$p \in P$
and
![]() $p^{\prime} \in P \cap \phi ^{-1}(0)$
we have
$p^{\prime} \in P \cap \phi ^{-1}(0)$
we have
![]() $p+p^{\prime} \in P+P$
with
$p+p^{\prime} \in P+P$
with
![]() $\phi (p+p^{\prime})=x$
, so
$\phi (p+p^{\prime})=x$
, so
![]() $\#\big(\phi ^{-1}(x)\cap (P+P)\big)\geq m^{\prime}$
. We conclude that
$\#\big(\phi ^{-1}(x)\cap (P+P)\big)\geq m^{\prime}$
. We conclude that