1 Introduction
Among the most important operator space modules over C*-algebras are the Hilbert C*-modules, the operator modules and the matrix normed modules. The first class became prominent through the work of Paschke and Rieffel and was intensively studied by Blecher, among others, see, e.g., [Reference Blecher5, Reference Blecher and Le Merdy6]. The main difference between the second and the third class lies in the kind of complete boundedness which is required of the bilinear mappings that give the module action. For operator modules (we will follow the terminology of [Reference Blecher and Le Merdy6] in this paper), one demands (multiplicatively) completely bounded bilinear mappings, and the associated tensor product is the Haagerup module tensor product
![]() ${{}}\otimes _{{h{A}}}\mkern 2mu{{}}$
over the C*-algebra A. Jointly completely bounded bilinear mappings and the module operator space projective tensor product
${{}}\otimes _{{h{A}}}\mkern 2mu{{}}$
over the C*-algebra A. Jointly completely bounded bilinear mappings and the module operator space projective tensor product
![]() govern the class of matrix normed modules; for details, we refer to [Reference Blecher and Le Merdy6, Chapter 3]. Both these classes have been put to good use and found a range of interesting applications; we only mention the recent papers [Reference Bearden and Crann4, Reference Crann10–Reference Crisp and Higson12] as samples.
govern the class of matrix normed modules; for details, we refer to [Reference Blecher and Le Merdy6, Chapter 3]. Both these classes have been put to good use and found a range of interesting applications; we only mention the recent papers [Reference Bearden and Crann4, Reference Crann10–Reference Crisp and Higson12] as samples.
For historical reasons the terminology is (still) not uniform; we will follow the convention in [Reference Blecher and Le Merdy6], see also [Reference Rosbotham28, Appendix A]. Suffice it to say at this point that operator modules form a full subcategory of the matrix normed modules (over any operator algebra). These categories are not abelian and therefore the usual homological algebra does not apply directly. Nevertheless, homological methods have been successfully developed in this framework, for example by Helemskii and his school. In [Reference Helemskii15, Theorem III.5.17 and Corollary IV.4.12] Helemskii proved that a C*-algebra A is classically semisimple (i.e., finite dimensional) if and only if all objects in the category
![]() of Banach A-modules are projective with respect to the class of epimorphisms that split as morphisms in
of Banach A-modules are projective with respect to the class of epimorphisms that split as morphisms in
![]() . See also [Reference Aristov2, Reference Aristov3, Reference Helemskii16].
. See also [Reference Aristov2, Reference Aristov3, Reference Helemskii16].
For an operator algebra A (on a Hilbert space) it is pertinent to use operator modules to build a cohomology theory (for the definitions, see Section 2.2); of the numerous contributions, we only mention [Reference Blecher, Muhly and Paulsen7, Reference Helemskii16, Reference Paulsen24, Reference Volosova32, Reference Wood34] here. In this paper, we focus on an appropriate definition of cohomological dimension and, in particular, answer a question raised by Helemskii [Reference Helemskii16] whether quantized global dimension zero is equivalent to the algebra being classically semisimple; see Theorem 5.3. In contrast to the situation in ring theory, it appears necessary to limit ourselves to a relative cohomology theory since, otherwise, there exist too many monomorphisms (equivalently, epimorphisms) and the concepts of injectivity (respectively, projectivity) become too restrictive. For example, the canonically defined injective global dimension of any C*-algebra with regard to the category of its operator modules always is at least
![]() $2$
, as shown in [Reference Rosbotham28]. Paulsen discussed relative cohomology in [Reference Paulsen24] and related it to completely bounded Hochschild cohomology. His notions of relative injectivity and projectivity coincide with ours (defined in Section 4) and Helemskii’s approach is also compatible.
$2$
, as shown in [Reference Rosbotham28]. Paulsen discussed relative cohomology in [Reference Paulsen24] and related it to completely bounded Hochschild cohomology. His notions of relative injectivity and projectivity coincide with ours (defined in Section 4) and Helemskii’s approach is also compatible.
The main novelty in this paper is the systematic use of exact categories enabling us to bring category theory to the foreground in order to take advantage of its unifying strength. Typically, categories that appear in analysis are not abelian which has hindered the full application of homological algebra methods. Exact structures in the sense of Quillen [Reference Quillen27] (to be defined in Section 4) on additive categories like
![]() were employed by Bühler in [Reference Bühler9], see also [Reference Bühler8] for a very nice introduction. The use of exact structures for categories of operator modules, and indeed sheaves of operator modules over C*-ringed spaces, was initiated in [Reference Ara and Mathieu1], see also the survey articles [Reference Mathieu19, Reference Mathieu and Rosbotham20], and further studied in [Reference Rosbotham28]. Exact categories are ideally suited for the important tools of homological algebra such as (short) exact sequences, diagram lemmas, and derived functors.
were employed by Bühler in [Reference Bühler9], see also [Reference Bühler8] for a very nice introduction. The use of exact structures for categories of operator modules, and indeed sheaves of operator modules over C*-ringed spaces, was initiated in [Reference Ara and Mathieu1], see also the survey articles [Reference Mathieu19, Reference Mathieu and Rosbotham20], and further studied in [Reference Rosbotham28]. Exact categories are ideally suited for the important tools of homological algebra such as (short) exact sequences, diagram lemmas, and derived functors.
Not assuming an in-depth knowledge of category theory (as this article is written for functional analysts), we have included the main categorical concepts deployed throughout this paper in Section 2.1. In Section 2.2, our assumptions on operator spaces, operator algebras. and the type of operator space modules we work with are stated.
In Section 3, we show how the categorical notions of kernels and cokernels can be expressed, using language and concepts of operator space theory, in the additive category
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
of nondegenerate right operator A-modules over an operator algebra A. This prepares Section 4 in which we explore the concept of exact categories and some techniques for working in this setting. We show that there is a canonical exact structure that can be placed on our main category
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
of nondegenerate right operator A-modules over an operator algebra A. This prepares Section 4 in which we explore the concept of exact categories and some techniques for working in this setting. We show that there is a canonical exact structure that can be placed on our main category
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
(Theorem 4.4) and discuss how a global dimension arises in exact categories with enough injectives.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
(Theorem 4.4) and discuss how a global dimension arises in exact categories with enough injectives.
Section 5 deals with another exact structure that can be placed on
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. This structure is related to the study of “relative homological algebra” for operator modules as it is done in [Reference Aristov3, Reference Helemskii16, Reference Paulsen24], for example. Our main Theorem 5.3 states that, for a unital operator algebra A, the global dimension of this exact category is zero if and only if A is classically semisimple, hence a finite direct sum of full matrix algebras over the complex numbers. We also discuss similarities and differences between our preferred category,
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. This structure is related to the study of “relative homological algebra” for operator modules as it is done in [Reference Aristov3, Reference Helemskii16, Reference Paulsen24], for example. Our main Theorem 5.3 states that, for a unital operator algebra A, the global dimension of this exact category is zero if and only if A is classically semisimple, hence a finite direct sum of full matrix algebras over the complex numbers. We also discuss similarities and differences between our preferred category,
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
, and
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
, and
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
, the category of matrix normed modules over an operator algebra A in this section.
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
, the category of matrix normed modules over an operator algebra A in this section.
2 Terminology, notation, and conventions
2.1 Category theory
Let
![]() $\mathcal {A}$
be a category. To indicate that E belongs to the class of objects in
$\mathcal {A}$
be a category. To indicate that E belongs to the class of objects in
![]() $\mathcal {A}$
, we write
$\mathcal {A}$
, we write
![]() $E\in \mathcal {A}$
. The set of morphisms from
$E\in \mathcal {A}$
. The set of morphisms from
![]() $E\in \mathcal {A}$
to
$E\in \mathcal {A}$
to
![]() $F\in \mathcal {A}$
is denoted
$F\in \mathcal {A}$
is denoted
![]() $\mathrm {Mor}_{\mathcal {A}}{({E},{F})}$
, with the
$\mathrm {Mor}_{\mathcal {A}}{({E},{F})}$
, with the
![]() $\mathcal {A}$
sometimes dropped if the category we are working in is obvious. If
$\mathcal {A}$
sometimes dropped if the category we are working in is obvious. If
![]() $\mathcal {M}$
is a class of morphisms in
$\mathcal {M}$
is a class of morphisms in
![]() $\mathcal {A}$
, we denote the subset of
$\mathcal {A}$
, we denote the subset of
![]() $\mathrm {Mor}_{\mathcal {A}}{({E},{F})}$
that consists only of the morphisms in
$\mathrm {Mor}_{\mathcal {A}}{({E},{F})}$
that consists only of the morphisms in
![]() $\mathcal {M}$
by
$\mathcal {M}$
by
![]() ${\mathcal {M}}{({E},\,{F})}$
. Two of the most important classes of morphisms in a category are the classes of monomorphisms and of epimorphisms. Recall that a morphism f in
${\mathcal {M}}{({E},\,{F})}$
. Two of the most important classes of morphisms in a category are the classes of monomorphisms and of epimorphisms. Recall that a morphism f in
![]() $\mathcal {A}$
is a monomorphism if it is “left cancellable,” that is, if
$\mathcal {A}$
is a monomorphism if it is “left cancellable,” that is, if
![]() $g,h$
are morphisms in
$g,h$
are morphisms in
![]() $\mathcal {A}$
, composable with f, such that
$\mathcal {A}$
, composable with f, such that
![]() $fg=fh$
, then we must have
$fg=fh$
, then we must have
![]() $g=h$
. The “right cancellable” morphisms in a category are epimorphisms. An important class of epimorphisms are the retractions. A morphism
$g=h$
. The “right cancellable” morphisms in a category are epimorphisms. An important class of epimorphisms are the retractions. A morphism
![]() $r\in \mathrm {Mor}_{\mathcal {A}}{({E},{F})}$
is a retraction if there exists a morphism
$r\in \mathrm {Mor}_{\mathcal {A}}{({E},{F})}$
is a retraction if there exists a morphism
![]() $s\in \mathrm {Mor}_{\mathcal {A}}{({F},{E})}$
such that
$s\in \mathrm {Mor}_{\mathcal {A}}{({F},{E})}$
such that
![]() $rs=\mathrm {id}_{F}$
, the identity morphism of F. In this case, we say s is a section of r and F is a retract of E.
$rs=\mathrm {id}_{F}$
, the identity morphism of F. In this case, we say s is a section of r and F is a retract of E.
The categories we work in will contain a zero object and, therefore, zero morphisms. Thus, we can talk about kernels and cokernels.
Definition 2.1 Let
![]() $\mathcal {A}$
be a category with a zero object. Suppose
$\mathcal {A}$
be a category with a zero object. Suppose
![]() $E,F\in \mathcal {A}$
and
$E,F\in \mathcal {A}$
and
![]() $f\in \mathrm {Mor}{({E},{F})}$
.
$f\in \mathrm {Mor}{({E},{F})}$
.
A kernel of f is a pair
![]() $(K,\mu )$
, where
$(K,\mu )$
, where
![]() $K\in \mathcal {A}$
and
$K\in \mathcal {A}$
and
![]() $\mu \in \mathrm {Mor}{({K},{E})}$
with
$\mu \in \mathrm {Mor}{({K},{E})}$
with
![]() $f\mu =0$
such that, when
$f\mu =0$
such that, when
![]() $G\in \mathcal {A}$
and
$G\in \mathcal {A}$
and
![]() $g\in \mathrm {Mor}{({G},{E})}$
satisfies
$g\in \mathrm {Mor}{({G},{E})}$
satisfies
![]() $fg=0$
, there exists a unique morphism
$fg=0$
, there exists a unique morphism
![]() $\overline {g}\in \mathrm {Mor}{({G},{K})}$
making the following diagram commutative
$\overline {g}\in \mathrm {Mor}{({G},{K})}$
making the following diagram commutative

A cokernel of f is a pair
![]() $(C,\pi )$
, where
$(C,\pi )$
, where
![]() $C\in \mathcal {A}$
and
$C\in \mathcal {A}$
and
![]() $\pi \in \mathrm {Mor}{({F},{C})}$
such that
$\pi \in \mathrm {Mor}{({F},{C})}$
such that
![]() $\pi {}f=0$
and, whenever
$\pi {}f=0$
and, whenever
![]() $G\in \mathcal {A}$
and
$G\in \mathcal {A}$
and
![]() $g\in \mathrm {Mor}{({F},{G})}$
satisfy
$g\in \mathrm {Mor}{({F},{G})}$
satisfy
![]() $gf=0$
, there exists a unique morphism
$gf=0$
, there exists a unique morphism
![]() $\overline {g}\in \mathrm {Mor}{({C},{G})}$
making the following diagram commutative
$\overline {g}\in \mathrm {Mor}{({C},{G})}$
making the following diagram commutative
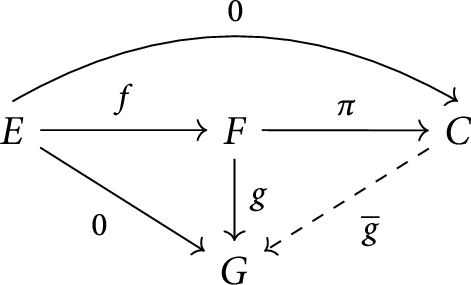
Remark 2.1 It is easy to see that kernel morphisms must be monomorphisms. We also note that the property of being a kernel of a morphism is universal. That is, in Diagram 2.1,
![]() $(G,g)$
is a kernel for f if and only if
$(G,g)$
is a kernel for f if and only if
![]() $\overline {g}$
is an isomorphism. Similarly, cokernel morphisms are epimorphisms and cokernel objects are unique up to isomorphism.
$\overline {g}$
is an isomorphism. Similarly, cokernel morphisms are epimorphisms and cokernel objects are unique up to isomorphism.
It is not difficult to show that, in a category
![]() $\mathcal {A}$
where every morphism has a kernel and a cokernel, a morphism is a kernel if and only if it is the kernel of its cokernel and is a cokernel if and only if it is the cokernel of its kernel. Moreover, let the following diagram in
$\mathcal {A}$
where every morphism has a kernel and a cokernel, a morphism is a kernel if and only if it is the kernel of its cokernel and is a cokernel if and only if it is the cokernel of its kernel. Moreover, let the following diagram in
![]() $\mathcal {A}$
be commutative.
$\mathcal {A}$
be commutative.

Suppose
![]() $\mu $
is a kernel of
$\mu $
is a kernel of
![]() $\pi $
and
$\pi $
and
![]() $\pi $
is a cokernel of
$\pi $
is a cokernel of
![]() $\mu $
and that all of the vertical arrows are isomorphisms. Then, by the universal properties of kernels and cokernels, f is a kernel of g and g is a cokernel of f.
$\mu $
and that all of the vertical arrows are isomorphisms. Then, by the universal properties of kernels and cokernels, f is a kernel of g and g is a cokernel of f.
Definition 2.2 Let
![]() $\mathcal {A}$
be a category.
$\mathcal {A}$
be a category.
Suppose
![]() $\mathcal {M}$
is a class of monomorphisms in
$\mathcal {M}$
is a class of monomorphisms in
![]() $\mathcal {A}$
, closed under composition and such that every isomorphism in
$\mathcal {A}$
, closed under composition and such that every isomorphism in
![]() $\mathcal {A}$
is in
$\mathcal {A}$
is in
![]() $\mathcal {M}$
. An object
$\mathcal {M}$
. An object
![]() $I\in \mathcal {A}$
is
$I\in \mathcal {A}$
is
![]() $\mathcal {M}$
-injective if, when given
$\mathcal {M}$
-injective if, when given
![]() ${\mu }\in {\mathcal {M}}{({E},\,{F})}$
and
${\mu }\in {\mathcal {M}}{({E},\,{F})}$
and
![]() $f\in \mathrm {Mor}_{\mathcal {A}}{({E},{I})}$
, for objects
$f\in \mathrm {Mor}_{\mathcal {A}}{({E},{I})}$
, for objects
![]() $E,F\in \mathcal {A}$
, there exists a morphism
$E,F\in \mathcal {A}$
, there exists a morphism
![]() ${g}\in \mathrm {Mor}_{\mathcal {A}}{({F},{I})}$
making the following diagram commutative
${g}\in \mathrm {Mor}_{\mathcal {A}}{({F},{I})}$
making the following diagram commutative
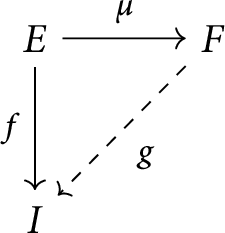
Suppose
![]() $\mathcal {P}$
is a class of epimorphisms in
$\mathcal {P}$
is a class of epimorphisms in
![]() $\mathcal {A}$
, closed under composition and such that every isomorphism in
$\mathcal {A}$
, closed under composition and such that every isomorphism in
![]() $\mathcal {A}$
is in
$\mathcal {A}$
is in
![]() $\mathcal {P}$
. An object
$\mathcal {P}$
. An object
![]() $P\in \mathcal {A}$
is
$P\in \mathcal {A}$
is
![]() $\mathcal {P}$
-projective if, when given
$\mathcal {P}$
-projective if, when given
![]() ${\pi }\in {\mathcal {P}}{({E},\,{F})}$
and
${\pi }\in {\mathcal {P}}{({E},\,{F})}$
and
![]() $f\in \mathrm {Mor}_{\mathcal {A}}{({P},{F})}$
, for objects
$f\in \mathrm {Mor}_{\mathcal {A}}{({P},{F})}$
, for objects
![]() $E,F\in \mathcal {A}$
, there exists a morphism
$E,F\in \mathcal {A}$
, there exists a morphism
![]() ${g}\in \mathrm {Mor}_{\mathcal {A}}{({P},{E})}$
making the following diagram commutative
${g}\in \mathrm {Mor}_{\mathcal {A}}{({P},{E})}$
making the following diagram commutative

We say
![]() $\mathcal {A}$
has enough
$\mathcal {A}$
has enough
![]() $\mathcal {M}$
-injectives (respectively, enough
$\mathcal {M}$
-injectives (respectively, enough
![]() $\mathcal {P}$
-projectives) if, for every
$\mathcal {P}$
-projectives) if, for every
![]() $E\in \mathcal {A}$
, there exists an
$E\in \mathcal {A}$
, there exists an
![]() $\mathcal {M}$
-injective object I (respectively,
$\mathcal {M}$
-injective object I (respectively,
![]() $\mathcal {P}$
-projective object P) such that
$\mathcal {P}$
-projective object P) such that
![]() ${\mathcal {M}}{({E},\,{I})}\neq \emptyset $
(respectively,
${\mathcal {M}}{({E},\,{I})}\neq \emptyset $
(respectively,
![]() ${\mathcal {\mathcal {P}}}{({P},\,{E})}\neq \emptyset $
).
${\mathcal {\mathcal {P}}}{({P},\,{E})}\neq \emptyset $
).
Remark 2.2 Fix a category
![]() $\mathcal {A}$
and classes
$\mathcal {A}$
and classes
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {P}$
of morphisms. It is easy to see that any retract of an
$\mathcal {P}$
of morphisms. It is easy to see that any retract of an
![]() $\mathcal {M}$
-injective object must be
$\mathcal {M}$
-injective object must be
![]() $\mathcal {M}$
-injective and every retract of a
$\mathcal {M}$
-injective and every retract of a
![]() $\mathcal {P}$
-projective object must be
$\mathcal {P}$
-projective object must be
![]() $\mathcal {P}$
-projective. Moreover, if I is
$\mathcal {P}$
-projective. Moreover, if I is
![]() $\mathcal {M}$
-injective and there exists a morphism
$\mathcal {M}$
-injective and there exists a morphism
![]() $\mu \in {\mathcal {M}}{({I},\,{E})}$
, then
$\mu \in {\mathcal {M}}{({I},\,{E})}$
, then
![]() $\mu $
must be a section of some retraction
$\mu $
must be a section of some retraction
![]() $r\in \mathrm {Mor}_{\mathcal {A}}{({E},{I})}$
. If P is
$r\in \mathrm {Mor}_{\mathcal {A}}{({E},{I})}$
. If P is
![]() $\mathcal {P}$
-projective and
$\mathcal {P}$
-projective and
![]() $\pi \in {\mathcal {P}}{({E},\,{P})}$
, then
$\pi \in {\mathcal {P}}{({E},\,{P})}$
, then
![]() $\pi $
must be a retraction.
$\pi $
must be a retraction.
We will need the notion of kernels and cokernels when we talk about exact categories and the notion of injectives and projectives when we discuss their global dimensions in Section 4.
2.2 Operator spaces
In the background, we will be using Ruan’s Representation Theorem [Reference Effros and Ruan13, Theorem 2.3.5]. Hence, we will not distinguish between spaces arising as subspaces of
![]() $B(H)$
, the bounded operators on a Hilbert space H, and matrix normed spaces satisfying Ruan’s axioms (see, for example, [Reference Blecher and Le Merdy6, 1.2.12]). However, when we refer to operator spaces, we will mean spaces of this type that we also assume to be complete. If E is an operator space we will write
$B(H)$
, the bounded operators on a Hilbert space H, and matrix normed spaces satisfying Ruan’s axioms (see, for example, [Reference Blecher and Le Merdy6, 1.2.12]). However, when we refer to operator spaces, we will mean spaces of this type that we also assume to be complete. If E is an operator space we will write
![]() $x=[x_{i j}]\in M_n(E)$
to say that x is an
$x=[x_{i j}]\in M_n(E)$
to say that x is an
![]() $n\times n$
matrix with entries
$n\times n$
matrix with entries
![]() $x_{i j}$
,
$x_{i j}$
,
![]() $i,j\in \{1,\ldots , n\}$
in E, and
$i,j\in \{1,\ldots , n\}$
in E, and
![]() $\lVert x\rVert _n$
is the norm of x in the Banach space
$\lVert x\rVert _n$
is the norm of x in the Banach space
![]() $M_n(E)$
, whose norm is inherited by the matrix norm of E.
$M_n(E)$
, whose norm is inherited by the matrix norm of E.
When
![]() $E,F$
are operator spaces, we will denote the operator space consisting of all completely bounded linear maps from E to
$E,F$
are operator spaces, we will denote the operator space consisting of all completely bounded linear maps from E to
![]() ${F}$
by
${F}$
by
![]() $C\!B({E},\,{F})$
. The completely bounded norm of an element
$C\!B({E},\,{F})$
. The completely bounded norm of an element
![]() $\phi \in C\!B({E},\,{F})$
is
$\phi \in C\!B({E},\,{F})$
is
![]() $\lVert \phi \rVert _{\mathrm {cb}}$
.
$\lVert \phi \rVert _{\mathrm {cb}}$
.
By A being an operator algebra we will mean A is a closed subalgebra of
![]() $B(H)$
of some Hilbert space H such that A contains a contractive approximate identity. By the Blecher–Ruan–Sinclair Theorem [Reference Blecher and Le Merdy6, Theorem 2.3.2], we need not distinguish between A being an operator algebra and A being an operator space which is also a Banach algebra with a contractive approximate identity such that the map
$B(H)$
of some Hilbert space H such that A contains a contractive approximate identity. By the Blecher–Ruan–Sinclair Theorem [Reference Blecher and Le Merdy6, Theorem 2.3.2], we need not distinguish between A being an operator algebra and A being an operator space which is also a Banach algebra with a contractive approximate identity such that the map
![]() ${{A}}\otimes _{{h}}\mkern 2mu{{A}}\rightarrow {A}$
from the Haagerup tensor product of A with itself to A induced by the multiplication on A is completely contractive.
${{A}}\otimes _{{h}}\mkern 2mu{{A}}\rightarrow {A}$
from the Haagerup tensor product of A with itself to A induced by the multiplication on A is completely contractive.
A complex algebra is said to be classically semisimple if it is a direct sum of minimal right ideals and if it is finitely generated, finitely many minimal right ideals suffice. Hence, combining the Artin–Wedderburn theorem with the Gelfand–Mazur theorem it follows that a unital complex Banach algebra is classically semisimple if and only if it is the direct sum of finitely many full matrix algebras over the complex numbers; in particular, it is finite dimensional.
Definition 2.3 Let A be an operator algebra. We say that a right A-module E that is also an operator space is a right operator A-module if the map
![]() ${{E}}\otimes _{{h}}\mkern 2mu{{A}}\rightarrow {E}$
, induced by the module action, is completely contractive.
${{E}}\otimes _{{h}}\mkern 2mu{{A}}\rightarrow {E}$
, induced by the module action, is completely contractive.
It follows from the associativity of the Haagerup tensor product that, for any operator space E,
![]() ${{E}}\otimes _{{h}}\mkern 2mu{{A}}$
is a right operator A-module; this works analogous to [Reference Blecher and Le Merdy6, 3.1.5 (3)].
${{E}}\otimes _{{h}}\mkern 2mu{{A}}$
is a right operator A-module; this works analogous to [Reference Blecher and Le Merdy6, 3.1.5 (3)].
Definition 2.4 Let E be a right Banach A-module. If the linear span of elements of the form
![]() $x\cdot {a}$
, where
$x\cdot {a}$
, where
![]() $x\in E, a\in A$
, is dense in E then we say E is nondegenerate. By Cohen’s Factorization Theorem [Reference Blecher and Le Merdy6, Theorem A.6.2], this happens if and only if, for each
$x\in E, a\in A$
, is dense in E then we say E is nondegenerate. By Cohen’s Factorization Theorem [Reference Blecher and Le Merdy6, Theorem A.6.2], this happens if and only if, for each
![]() $x\in E$
, there exist
$x\in E$
, there exist
![]() $x'\in E, a\in A$
such that
$x'\in E, a\in A$
such that
![]() $x=x'\cdot {a}$
.
$x=x'\cdot {a}$
.
We will always restrict ourselves to categories of nondegenerate operator modules, and unital modules if the algebra is unital. If E is an nondegenerate right operator A-module and F is a closed submodule of E then F and
![]() $E/F$
become nondegenerate right operator A-modules when equipped with the standard induced operator space structures and module actions [Reference Blecher and Le Merdy6, Section 3.1].
$E/F$
become nondegenerate right operator A-modules when equipped with the standard induced operator space structures and module actions [Reference Blecher and Le Merdy6, Section 3.1].
For a Banach space E and some
![]() $\gamma>0$
, we will denote
$\gamma>0$
, we will denote
![]() $\left \{{x\in E}\,|\,{\lVert x\rVert <\gamma } \right \}$
by
$\left \{{x\in E}\,|\,{\lVert x\rVert <\gamma } \right \}$
by
![]() $E_{\lVert \cdot \rVert <\gamma }$
. Recall that a linear map
$E_{\lVert \cdot \rVert <\gamma }$
. Recall that a linear map
![]() ${f}\colon {E}\rightarrow {F}$
between Banach spaces is an open map if and only there exists
${f}\colon {E}\rightarrow {F}$
between Banach spaces is an open map if and only there exists
![]() $\gamma>0$
such that
$\gamma>0$
such that
![]() $f(E_{\lVert \cdot \rVert <1})\supseteq F_{\lVert \cdot \rVert <\gamma }$
. If E and F are, moreover, operator spaces we say that f is completely open if there exists some common
$f(E_{\lVert \cdot \rVert <1})\supseteq F_{\lVert \cdot \rVert <\gamma }$
. If E and F are, moreover, operator spaces we say that f is completely open if there exists some common
![]() $\gamma $
such that each amplification
$\gamma $
such that each amplification
![]() $f_n$
is open and for each
$f_n$
is open and for each
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
 $f_n\bigl (M_n(E)_{\lVert \cdot \rVert <1}\bigr )\supseteq M_n(F)_{\lVert \cdot \rVert <\gamma }$
. These maps can be characterized in the following way.
$f_n\bigl (M_n(E)_{\lVert \cdot \rVert <1}\bigr )\supseteq M_n(F)_{\lVert \cdot \rVert <\gamma }$
. These maps can be characterized in the following way.
Proposition 2.3 Let E and F be operator spaces. Then
![]() $f\in C\!B({E},\,{F})$
is completely open if and only if there exists
$f\in C\!B({E},\,{F})$
is completely open if and only if there exists
![]() $\lambda>1$
such that, for each
$\lambda>1$
such that, for each
![]() $n\in \mathbb {N}$
, every
$n\in \mathbb {N}$
, every
![]() $y\in M_n(F)$
is equal to
$y\in M_n(F)$
is equal to
![]() $f_n(x)$
for some
$f_n(x)$
for some
![]() $x\in M_n(E)$
with
$x\in M_n(E)$
with
![]() $\lVert x\rVert _n\leq \lambda \lVert y\rVert _n$
.
$\lVert x\rVert _n\leq \lambda \lVert y\rVert _n$
.
For a completely open map f, we will refer to
![]() $\lambda $
as in Proposition 2.3 as an openness constant for f.
$\lambda $
as in Proposition 2.3 as an openness constant for f.
Example 2.4 When E is an operator space and F is a closed subspace, then the canonical projection
![]() $\pi \in C\!B({E},\,{E/F})$
is a completely open map and any
$\pi \in C\!B({E},\,{E/F})$
is a completely open map and any
![]() $\lambda>{1}$
is an openness constant.
$\lambda>{1}$
is an openness constant.
Injectivity and self-duality of the Haagerup tensor product provide us with the following useful result.
Lemma 2.5 Let E and F be operator spaces and let
![]() $u\in {{E}}\otimes _{{h}}\mkern 2mu{{F}}$
be nonzero. There exist bounded linear functionals
$u\in {{E}}\otimes _{{h}}\mkern 2mu{{F}}$
be nonzero. There exist bounded linear functionals
![]() $\alpha \in E^*$
,
$\alpha \in E^*$
,
![]() $\beta \in F^*$
such that
$\beta \in F^*$
such that
![]() $(\alpha \otimes \beta )(u)\neq 0$
.
$(\alpha \otimes \beta )(u)\neq 0$
.
This follows immediately from the completely isometric embeddings
given by
![]() $(x\otimes y)(\alpha \otimes \beta )=\alpha (x)\beta (y)$
for
$(x\otimes y)(\alpha \otimes \beta )=\alpha (x)\beta (y)$
for
![]() $x\in E$
,
$x\in E$
,
![]() $y\in F$
,
$y\in F$
,
![]() $\alpha \in E^*$
and
$\alpha \in E^*$
and
![]() $\beta \in F^*$
, see [Reference Effros and Ruan13, Proposition 9.2.5 and Theorem 9.4.7].
$\beta \in F^*$
, see [Reference Effros and Ruan13, Proposition 9.2.5 and Theorem 9.4.7].
3 The additive category of operator modules
It is well known how the notion of the global dimension for module categories extends to the setting of abelian categories with enough injectives (or enough projectives). See, e.g., [Reference Hilton and Stammbach18, Reference Mitchell22] or [Reference Osborne23]. In this section, we will see to what extent the canonical additive category of nondegenerate (right) operator A-modules over an operator algebra A fails to be abelian. In order to remedy this by introducing an exact structure in the next section, we need to study the kernels and cokernels in this category in detail.
We first recall the definition of an additive category.
Definition 3.1 A category
![]() $\mathcal {A}$
is additive if
$\mathcal {A}$
is additive if
![]() $\mathcal {A}$
has a zero object; morphism sets have the structure of abelian groups; composition is distributive with respect to this abelian group structure; and a product exists for each pair of objects.
$\mathcal {A}$
has a zero object; morphism sets have the structure of abelian groups; composition is distributive with respect to this abelian group structure; and a product exists for each pair of objects.
For
![]() $E,F\in \mathcal {A}$
, where
$E,F\in \mathcal {A}$
, where
![]() $\mathcal {A}$
is additive, we denote by
$\mathcal {A}$
is additive, we denote by
![]() $\mathrm {Hom}_{\mathcal {A}}{({E},{F})}$
the morphism set equipped with the abelian group structure. A functor
$\mathrm {Hom}_{\mathcal {A}}{({E},{F})}$
the morphism set equipped with the abelian group structure. A functor
![]() ${{\mathsf {F}}}\colon {\mathcal {A}}\rightarrow {\mathcal {B}}$
is additive if, when
${{\mathsf {F}}}\colon {\mathcal {A}}\rightarrow {\mathcal {B}}$
is additive if, when
![]() $E,F\in \mathcal {A}$
,
$E,F\in \mathcal {A}$
,
![]() ${\mathsf {F}}(f+g)={\mathsf {F}}(f)+{\mathsf {F}}(g)$
for all morphisms
${\mathsf {F}}(f+g)={\mathsf {F}}(f)+{\mathsf {F}}(g)$
for all morphisms
![]() $f,g\in \mathrm {Hom}_{\mathcal {A}}{({E},{F})}$
. Note that, in an additive category,
$f,g\in \mathrm {Hom}_{\mathcal {A}}{({E},{F})}$
. Note that, in an additive category,
![]() $E,F\in \mathcal {A}$
have a product
$E,F\in \mathcal {A}$
have a product
![]() $G\in \mathcal {A}$
if and only if G is also their coproduct. Moreover, this happens precisely when G is a direct sum of E and F, that is, there exists a quintuplet
$G\in \mathcal {A}$
if and only if G is also their coproduct. Moreover, this happens precisely when G is a direct sum of E and F, that is, there exists a quintuplet
![]() $(G,\iota _E,\iota _F,\pi _E,\pi _F)$
, where
$(G,\iota _E,\iota _F,\pi _E,\pi _F)$
, where
![]() $\iota _E\in \mathrm {Hom}{({E},{G})}, \iota _F\in \mathrm {Hom}{({F},{G})}$
, and
$\iota _E\in \mathrm {Hom}{({E},{G})}, \iota _F\in \mathrm {Hom}{({F},{G})}$
, and
![]() $\pi _E\in \mathrm {Hom}{({G},{E})}, \pi _F\in \mathrm {Hom}{({G},{F})}$
, such that
$\pi _E\in \mathrm {Hom}{({G},{E})}, \pi _F\in \mathrm {Hom}{({G},{F})}$
, such that
![]() $\pi _E\iota _E=\mathrm {id}_{E}$
,
$\pi _E\iota _E=\mathrm {id}_{E}$
,
![]() $\pi _F\iota _F=\mathrm {id}_{F}$
and
$\pi _F\iota _F=\mathrm {id}_{F}$
and
![]() $\iota _E\pi _E+\iota _F\pi _F=\mathrm {id}_{G}$
.
$\iota _E\pi _E+\iota _F\pi _F=\mathrm {id}_{G}$
.
For the remainder of this section, we fix an operator algebra A. We will use
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
to denote the category whose objects are the nondegenerate right operator A-modules and whose morphisms are the completely bounded A-module maps. Instead of
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
to denote the category whose objects are the nondegenerate right operator A-modules and whose morphisms are the completely bounded A-module maps. Instead of
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!{\mathbb {C}}}}}}$
, we write
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!{\mathbb {C}}}}}}$
, we write
![]() . For
. For
![]() $E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
, we denote the set
$E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
, we denote the set
![]() $\mathrm {Mor}_{{{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}}{({E},{F})}$
by
$\mathrm {Mor}_{{{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}}{({E},{F})}$
by
![]() $C\!B_{A}({E},\,{F})$
, and by
$C\!B_{A}({E},\,{F})$
, and by
![]() $C\!B({E},\,{F})$
if
$C\!B({E},\,{F})$
if
![]() $A={\mathbb {C}}$
. It is clear that this is an abelian group.
$A={\mathbb {C}}$
. It is clear that this is an abelian group.
Proposition 3.1 Let A be an operator algebra. The category
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is additive.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is additive.
The only part of Proposition 3.1 that is perhaps not immediately apparent is the existence of a product for each pair of objects in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. For any operator spaces
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. For any operator spaces
![]() $E_1, E_2,$
let
$E_1, E_2,$
let
![]() $E_1\oplus E_2$
be the vector space direct sum equipped with the norm
$E_1\oplus E_2$
be the vector space direct sum equipped with the norm
![]() $\lVert (x,y)\rVert =\lVert x\rVert +\lVert y\rVert $
for each
$\lVert (x,y)\rVert =\lVert x\rVert +\lVert y\rVert $
for each
![]() $x\in E_1, y\in E_2$
. For each
$x\in E_1, y\in E_2$
. For each
![]() $n\in \mathbb {N}$
, the obvious identifications
$n\in \mathbb {N}$
, the obvious identifications
![]() $M_n(E_1\oplus E_2)\cong M_n(E_1)\oplus M_n(E_2)$
yield an operator space structure on
$M_n(E_1\oplus E_2)\cong M_n(E_1)\oplus M_n(E_2)$
yield an operator space structure on
![]() $E_1\oplus E_2$
. Moreover, if
$E_1\oplus E_2$
. Moreover, if
![]() $E_1, E_2\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},$
then we equip
$E_1, E_2\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},$
then we equip
![]() $E_1\oplus E_2$
with the module action
$E_1\oplus E_2$
with the module action
![]() $(x,y)\cdot {a}:= (x\cdot {a},y\cdot {a})$
for all
$(x,y)\cdot {a}:= (x\cdot {a},y\cdot {a})$
for all
![]() $x\in E_1, y\in E_2, a\in A$
. With this, we have
$x\in E_1, y\in E_2, a\in A$
. With this, we have
![]() $E_1\oplus E_2\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and the quintuplet
$E_1\oplus E_2\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and the quintuplet
![]() $(E_1\oplus E_2,\iota _{1},\iota _{2},\pi _{1},\pi _{2})$
, where for each
$(E_1\oplus E_2,\iota _{1},\iota _{2},\pi _{1},\pi _{2})$
, where for each
![]() $i\in \{1,2\}$
,
$i\in \{1,2\}$
,
![]() ${\iota _{i}}\colon {E_i}\rightarrow {E_1\oplus E_2}$
denotes the inclusion and
${\iota _{i}}\colon {E_i}\rightarrow {E_1\oplus E_2}$
denotes the inclusion and
![]() ${\pi _{i}}\colon {E_1\oplus E_2}\rightarrow {E_i}$
is the projection, makes
${\pi _{i}}\colon {E_1\oplus E_2}\rightarrow {E_i}$
is the projection, makes
![]() $E_1\oplus E_2$
a direct sum of
$E_1\oplus E_2$
a direct sum of
![]() $E_1$
and
$E_1$
and
![]() $E_2$
.
$E_2$
.
The next result is elementary.
Proposition 3.2 Let
![]() $E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. For every
$E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. For every
![]() $f\in C\!B_{A}({E},\,{F})$
, we have
$f\in C\!B_{A}({E},\,{F})$
, we have
-
(i) f is a monomorphism in
 ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
if and only if it is injective.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
if and only if it is injective. -
(ii) f is an epimorphism in
 ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
if and only if it has dense range.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
if and only if it has dense range.
Kernels and cokernels are fundamental tools in our approach.
Proposition 3.3 Let A be an operator algebra. Suppose
![]() $E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
$E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
![]() $f\in C\!B_{A}({E},\,{F})$
. Then f has a kernel and a cokernel.
$f\in C\!B_{A}({E},\,{F})$
. Then f has a kernel and a cokernel.
Proof We first deal with the kernel of f. Let K be
![]() $\ker {f}=f^{-1}(0)$
; this is clearly an object in
$\ker {f}=f^{-1}(0)$
; this is clearly an object in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Let
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Let
![]() ${\mu }\colon {K}\rightarrow {E}$
be the inclusion. Then
${\mu }\colon {K}\rightarrow {E}$
be the inclusion. Then
![]() $\mu \in C\!B_{A}({E},\,{F})$
and
$\mu \in C\!B_{A}({E},\,{F})$
and
![]() $f\mu =0$
. Suppose
$f\mu =0$
. Suppose
![]() $G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and there exists
$G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and there exists
![]() $g\in C\!B_{A}({G},\,{E})$
with
$g\in C\!B_{A}({G},\,{E})$
with
![]() $fg=0$
. Then
$fg=0$
. Then
![]() $g(G)\subseteq {K},$
so we let
$g(G)\subseteq {K},$
so we let
![]() $\overline {g}\in C\!B_{A}({G},\,{K})$
just be the A-module map g. As morphisms we have
$\overline {g}\in C\!B_{A}({G},\,{K})$
just be the A-module map g. As morphisms we have
![]() $g=\mu \overline {g}$
. That this is the only such morphism making Diagram (2.1) commutative, follows from the fact that
$g=\mu \overline {g}$
. That this is the only such morphism making Diagram (2.1) commutative, follows from the fact that
![]() $\mu $
is a monomorphism.
$\mu $
is a monomorphism.
To prove that f has a cokernel, we let
 $C=F/{\overline {f(E)}}$
and
$C=F/{\overline {f(E)}}$
and
![]() $\pi \in C\!B_{A}({F},\,{C})$
be the canonical projection. Obviously,
$\pi \in C\!B_{A}({F},\,{C})$
be the canonical projection. Obviously,
![]() $\pi {}f=0$
. Suppose there exist
$\pi {}f=0$
. Suppose there exist
![]() $G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
$G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
![]() $g\in C\!B_{A}({F},\,{G})$
such that
$g\in C\!B_{A}({F},\,{G})$
such that
![]() $gf=0$
. For each
$gf=0$
. For each
![]() $y\in F,$
let
$y\in F,$
let
![]() $\overline {g}(\pi (y))=g(y)$
. If
$\overline {g}(\pi (y))=g(y)$
. If
![]() $\pi (y)=0$
then
$\pi (y)=0$
then
 $y\in \overline {F(E)}$
and, by continuity,
$y\in \overline {F(E)}$
and, by continuity,
![]() $g(y)=0$
. Hence
$g(y)=0$
. Hence
![]() ${\overline {g}}\colon {C}\rightarrow {G}$
is a well-defined map and is clearly an A-module map. In fact, it is completely open with openness constant
${\overline {g}}\colon {C}\rightarrow {G}$
is a well-defined map and is clearly an A-module map. In fact, it is completely open with openness constant
![]() $\lambda>1$
since
$\lambda>1$
since
![]() $M_n(C)\cong M_n(F)/M_n(\overline {F(E)})$
[Reference Blecher and Le Merdy6, 1.2.14]. For each
$M_n(C)\cong M_n(F)/M_n(\overline {F(E)})$
[Reference Blecher and Le Merdy6, 1.2.14]. For each
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $c\in M_n(C)$
choose
$c\in M_n(C)$
choose
![]() $y\in M_n(F)$
such that
$y\in M_n(F)$
such that
![]() $\pi _{n}(y)=c$
and
$\pi _{n}(y)=c$
and
![]() $\lVert y\rVert _n\leq \lambda \lVert c\rVert _n$
. Then
$\lVert y\rVert _n\leq \lambda \lVert c\rVert _n$
. Then
![]() $\lVert \overline {g}(c)\rVert _n=\lVert g(y)\rVert _n\leq \lVert g\rVert _{\mathrm {cb}}\lambda \lVert c\rVert _n$
. Hence
$\lVert \overline {g}(c)\rVert _n=\lVert g(y)\rVert _n\leq \lVert g\rVert _{\mathrm {cb}}\lambda \lVert c\rVert _n$
. Hence
![]() $\overline {g}$
is completely bounded, i.e.,
$\overline {g}$
is completely bounded, i.e.,
![]() $\overline {g}\in C\!B_{A}({C},\,{G})$
such that
$\overline {g}\in C\!B_{A}({C},\,{G})$
such that
![]() $\overline {g}\pi =g$
. Lastly, we note since
$\overline {g}\pi =g$
. Lastly, we note since
![]() $\pi $
is an epimorphism,
$\pi $
is an epimorphism,
![]() $\overline {g}$
is the only morphism
$\overline {g}$
is the only morphism
![]() $C\rightarrow {G}$
making Diagram (2.2) commutative. ▪
$C\rightarrow {G}$
making Diagram (2.2) commutative. ▪
Proposition 3.4 Let A be an operator algebra. Let
![]() $E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
$E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
![]() $\mu \in C\!B_{A}({E},\,{F})$
. Then
$\mu \in C\!B_{A}({E},\,{F})$
. Then
![]() $\mu $
is the kernel of some morphism
$\mu $
is the kernel of some morphism
![]() $\pi \in C\!B_{A}({F},\,{G})$
,
$\pi \in C\!B_{A}({F},\,{G})$
,
![]() $G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
if and only if
$G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
if and only if
![]() $\mu $
has closed range and is an isomorphism in
$\mu $
has closed range and is an isomorphism in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
(that is, a completely bounded bijective A-module map, with completely bounded inverse) when viewed as a map onto its range.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
(that is, a completely bounded bijective A-module map, with completely bounded inverse) when viewed as a map onto its range.
Proof By Remark 2.1 and Proposition 3.3, we need only consider the case where
 $G=F/\overline {\mu (E)}$
and
$G=F/\overline {\mu (E)}$
and
![]() $\pi $
is the canonical quotient mapping. Let
$\pi $
is the canonical quotient mapping. Let
![]() $K=\ker {\pi }$
and
$K=\ker {\pi }$
and
![]() $\iota \in C\!B_{A}({K},\,{F})$
be the inclusion map. Then
$\iota \in C\!B_{A}({K},\,{F})$
be the inclusion map. Then
![]() $\mu $
is a kernel of
$\mu $
is a kernel of
![]() $\pi $
if and only if there exists an isomorphism
$\pi $
if and only if there exists an isomorphism
![]() $\phi \in C\!B_{A}({K},\,{E})$
making the following diagram commutative.
$\phi \in C\!B_{A}({K},\,{E})$
making the following diagram commutative.
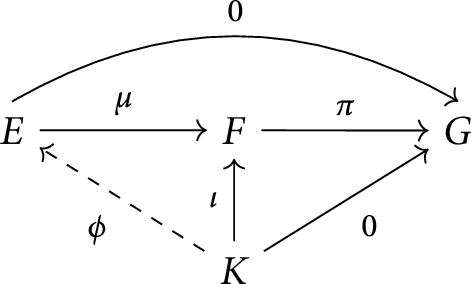
Note that
 $\overline {\mu (E)}=\iota (K)$
. Suppose
$\overline {\mu (E)}=\iota (K)$
. Suppose
![]() $\mu $
has closed range and is an isomorphism in
$\mu $
has closed range and is an isomorphism in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
when considered as a map onto its range. Then
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
when considered as a map onto its range. Then
![]() $\mu (E)=\iota (K)$
and we simply let
$\mu (E)=\iota (K)$
and we simply let
![]() $\phi $
be the completely bounded inverse
$\phi $
be the completely bounded inverse
![]() $\mu (E)\rightarrow {E}$
composed with
$\mu (E)\rightarrow {E}$
composed with
![]() $\iota $
. So
$\iota $
. So
![]() $\mu $
is a kernel.
$\mu $
is a kernel.
On the other hand, if
![]() $\mu $
is the kernel of
$\mu $
is the kernel of
![]() $\pi $
then
$\pi $
then
![]() $\phi $
exists. Since
$\phi $
exists. Since
![]() $\mu =\iota \circ \phi ^{-1}$
and
$\mu =\iota \circ \phi ^{-1}$
and
![]() $\iota $
is an isometry,
$\iota $
is an isometry,
![]() $\mu (E)$
is closed and we are done.▪
$\mu (E)$
is closed and we are done.▪
Proposition 3.5 Let A be an operator algebra. Let
![]() $E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
$E,F\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
![]() $\pi \in C\!B_{A}({E},\,{F})$
. Then
$\pi \in C\!B_{A}({E},\,{F})$
. Then
![]() $\pi $
is the cokernel of some morphism
$\pi $
is the cokernel of some morphism
![]() $\mu \in C\!B_{A}({G},\,{E})$
,
$\mu \in C\!B_{A}({G},\,{E})$
,
![]() $G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
if and only if
$G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
if and only if
![]() $\pi $
is completely open.
$\pi $
is completely open.
Proof By Remark 2.1 and Proposition 3.3, we need only look at the case where
![]() $G=\ker {\pi }$
and
$G=\ker {\pi }$
and
![]() $\mu $
is the inclusion mapping. Let
$\mu $
is the inclusion mapping. Let
![]() $C=E/{\mu (G)}$
and
$C=E/{\mu (G)}$
and
![]() $g\in C\!B_{A}({E},\,{C})$
be the quotient map. Then
$g\in C\!B_{A}({E},\,{C})$
be the quotient map. Then
![]() $\pi $
is cokernel for
$\pi $
is cokernel for
![]() $\mu $
if and only if there exists an isomorphism
$\mu $
if and only if there exists an isomorphism
![]() ${\phi }\colon {F}\rightarrow {C}$
making the following diagram commutative.
${\phi }\colon {F}\rightarrow {C}$
making the following diagram commutative.
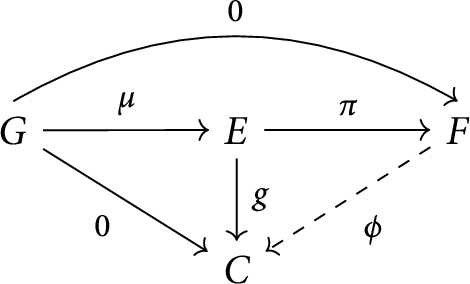
Suppose that
![]() $\pi $
is completely open and hence surjective. Note that, if
$\pi $
is completely open and hence surjective. Note that, if
![]() $x\in E$
is such that
$x\in E$
is such that
![]() $\pi (x)=0$
, then
$\pi (x)=0$
, then
![]() $x\in \mu (G)$
and
$x\in \mu (G)$
and
![]() $g(\mu (x))=0$
, so the map
$g(\mu (x))=0$
, so the map
![]() ${\phi }\colon {F}\rightarrow {C}$
,
${\phi }\colon {F}\rightarrow {C}$
,
![]() $\pi (x)\mapsto g(x)$
is well defined. As
$\pi (x)\mapsto g(x)$
is well defined. As
![]() $\pi , g$
are A-module maps so is
$\pi , g$
are A-module maps so is
![]() $\phi $
. For any
$\phi $
. For any
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $y\in M_n(F)$
, we have by Proposition 2.3 that
$y\in M_n(F)$
, we have by Proposition 2.3 that
![]() $\lVert \phi _n(y)\rVert _n=\lVert g_n(x)\rVert _n\leq \lambda \lVert g\rVert _{\mathrm {cb}}\lVert y\rVert _n$
for some
$\lVert \phi _n(y)\rVert _n=\lVert g_n(x)\rVert _n\leq \lambda \lVert g\rVert _{\mathrm {cb}}\lVert y\rVert _n$
for some
![]() $x\in E$
and openness constant
$x\in E$
and openness constant
![]() $\lambda>1$
. So
$\lambda>1$
. So
![]() $\phi \in C\!B_{A}({F},\,{C})$
. A similar argument (using the fact that g is completely open) gives that there is a morphism
$\phi \in C\!B_{A}({F},\,{C})$
. A similar argument (using the fact that g is completely open) gives that there is a morphism
![]() $\psi \in C\!B_{A}({C},\,{F})$
defined by setting
$\psi \in C\!B_{A}({C},\,{F})$
defined by setting
![]() $\psi (g(x))=\pi (x)$
for any
$\psi (g(x))=\pi (x)$
for any
![]() $x\in E$
. By definition,
$x\in E$
. By definition,
![]() $\phi \pi =g$
and it is clear that
$\phi \pi =g$
and it is clear that
![]() $\psi $
is the inverse of
$\psi $
is the inverse of
![]() $\phi $
, thus
$\phi $
, thus
![]() $\phi $
is an isomorphism. It follows that
$\phi $
is an isomorphism. It follows that
![]() $\pi $
is a cokernel of
$\pi $
is a cokernel of
![]() $\mu $
.
$\mu $
.
Conversely, suppose there exists an isomorphism
![]() $\phi $
making Diagram (3.2) commutative. Let
$\phi $
making Diagram (3.2) commutative. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $y\in M_n(F)$
. By Proposition 2.3, there exists
$y\in M_n(F)$
. By Proposition 2.3, there exists
![]() $x\in M_n(E)$
such that
$x\in M_n(E)$
such that
![]() $g_n(x)=\phi _n(y)$
and
$g_n(x)=\phi _n(y)$
and
![]() $\lVert x\rVert _n\leq \lambda \lVert \phi _n(y)\rVert _n\leq \lambda \lVert \phi \rVert _{\mathrm {cb}}\lVert y\rVert _n$
, where
$\lVert x\rVert _n\leq \lambda \lVert \phi _n(y)\rVert _n\leq \lambda \lVert \phi \rVert _{\mathrm {cb}}\lVert y\rVert _n$
, where
![]() $\lambda $
is an openness constant for g. Moreover, the commutativity of Diagram (3.2) gives that
$\lambda $
is an openness constant for g. Moreover, the commutativity of Diagram (3.2) gives that
![]() $\pi _n(x)=\phi _n^{-1}g_n(x)=\phi _n^{-1}\phi ^{}_n(y)=y$
and by Proposition 2.3,
$\pi _n(x)=\phi _n^{-1}g_n(x)=\phi _n^{-1}\phi ^{}_n(y)=y$
and by Proposition 2.3,
![]() $\pi $
is completely open.▪
$\pi $
is completely open.▪
An additive category
![]() $\mathcal {A}$
is called abelian if every morphism in
$\mathcal {A}$
is called abelian if every morphism in
![]() $\mathcal {A}$
has both a kernel and a cokernel; every monomorphism in
$\mathcal {A}$
has both a kernel and a cokernel; every monomorphism in
![]() $\mathcal {A}$
is the kernel of its cokernel; and every epimorphism in
$\mathcal {A}$
is the kernel of its cokernel; and every epimorphism in
![]() $\mathcal {A}$
is the cokernel of its kernel. Comparing the descriptions above of the kernels and cokernels in
$\mathcal {A}$
is the cokernel of its kernel. Comparing the descriptions above of the kernels and cokernels in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
with the monomorphisms and epimorphisms in that category, it is perhaps obvious that
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
with the monomorphisms and epimorphisms in that category, it is perhaps obvious that
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
fails to be abelian. Here is the probably simplest example for
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
fails to be abelian. Here is the probably simplest example for
![]() $A={\mathbb {C}}$
. Let E be an infinite-dimensional Banach space. Recall that the identity map on E is completely contractive when considered as a map
$A={\mathbb {C}}$
. Let E be an infinite-dimensional Banach space. Recall that the identity map on E is completely contractive when considered as a map
![]() ${f}\colon {\mathrm {Max}(E)}\rightarrow {\mathrm {Min}(E)}$
, where
${f}\colon {\mathrm {Max}(E)}\rightarrow {\mathrm {Min}(E)}$
, where
![]() ${\mathrm {Max}(E)}$
is E equipped with its maximal quantization and
${\mathrm {Max}(E)}$
is E equipped with its maximal quantization and
![]() ${\mathrm {Min}(E)}$
is its minimal quantization. Then
${\mathrm {Min}(E)}$
is its minimal quantization. Then
![]() $f\in C\!B_{\mathbb {C}}({\mathrm {Max}(E)},\,{\mathrm {Min}(E)})$
is surjective and hence an epimorphism in
$f\in C\!B_{\mathbb {C}}({\mathrm {Max}(E)},\,{\mathrm {Min}(E)})$
is surjective and hence an epimorphism in
![]() ${\mathcal {O\!M\!o\!d}^{\infty }_{{\mathbb {C}}}}$
. However, it cannot be completely open, that is, an isomorphism as E is infinite dimensional (see, e.g., [Reference Pisier26, Corollary 3.9]).
${\mathcal {O\!M\!o\!d}^{\infty }_{{\mathbb {C}}}}$
. However, it cannot be completely open, that is, an isomorphism as E is infinite dimensional (see, e.g., [Reference Pisier26, Corollary 3.9]).
As a result, the homological algebra which is highly developed in abelian categories is not directly available in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. In the next section, we show how we can get around this issue by introducing exact categories. The following two results will be essential.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. In the next section, we show how we can get around this issue by introducing exact categories. The following two results will be essential.
Proposition 3.6 Let
![]() $E,F,G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
with
$E,F,G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
with
![]() $f_E\in C\!B_{A}({E},\,{G})$
and
$f_E\in C\!B_{A}({E},\,{G})$
and
![]() $f_F\in C\!B_{A}({F},\,{G})$
.
$f_F\in C\!B_{A}({F},\,{G})$
.
-
(i) There exist
 $L\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
$L\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
 $\ell _E\in C\!B_{A}({L},\,{E})$
,
$\ell _E\in C\!B_{A}({L},\,{E})$
,
 $\ell _F\in C\!B_{A}({L},\,{F})$
making the following diagram a pullback square. (3.3)
$\ell _F\in C\!B_{A}({L},\,{F})$
making the following diagram a pullback square. (3.3)
-
(ii) For any such pullback square, if
 $f_E$
is a cokernel map, then so is
$f_E$
is a cokernel map, then so is
 $\ell _F$
.
$\ell _F$
.
Proof (i) Let
![]() $L=\left \{{(x,y)\in E\oplus F}\,|\,{f_E(x)=f_F(y)} \right \}$
. Then L is a closed submodule of
$L=\left \{{(x,y)\in E\oplus F}\,|\,{f_E(x)=f_F(y)} \right \}$
. Then L is a closed submodule of
![]() $E\oplus F$
so inherits the operator A-module structure of
$E\oplus F$
so inherits the operator A-module structure of
![]() $E\oplus F$
. Let
$E\oplus F$
. Let
![]() $\ell _F$
and
$\ell _F$
and
![]() $\ell _E$
be the restrictions to L of the canonical projections
$\ell _E$
be the restrictions to L of the canonical projections
![]() ${\pi _F}\colon {E\oplus {F}}\rightarrow {F}$
and
${\pi _F}\colon {E\oplus {F}}\rightarrow {F}$
and
![]() ${\pi _E}\colon {E\oplus {F}}\rightarrow {E}$
, respectively. By definition of L, Diagram (3.3) is commutative.
${\pi _E}\colon {E\oplus {F}}\rightarrow {E}$
, respectively. By definition of L, Diagram (3.3) is commutative.
If there exist
![]() $L'\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
$L'\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
![]() $\ell ^{\prime }_E\in C\!B_{A}({L'},\,{E})$
,
$\ell ^{\prime }_E\in C\!B_{A}({L'},\,{E})$
,
![]() $\ell ^{\prime }_F\in C\!B_{A}({L'},\,{F})$
such that
$\ell ^{\prime }_F\in C\!B_{A}({L'},\,{F})$
such that
![]() $f_F\ell ^{\prime }_F=f_E\ell ^{\prime }_E$
, then, by the universal property of products, there exists a unique
$f_F\ell ^{\prime }_F=f_E\ell ^{\prime }_E$
, then, by the universal property of products, there exists a unique
![]() $\phi \in C\!B_{A}({L'},\,{L})$
such that
$\phi \in C\!B_{A}({L'},\,{L})$
such that
![]() $\ell ^{\prime }_E=\pi _{E}\phi $
and
$\ell ^{\prime }_E=\pi _{E}\phi $
and
![]() $\ell ^{\prime }_F=\pi _{F}\phi $
and it is clear that
$\ell ^{\prime }_F=\pi _{F}\phi $
and it is clear that
![]() $\phi (L')\subseteq {L}$
; hence L must make Diagram (3.3) a pullback square.
$\phi (L')\subseteq {L}$
; hence L must make Diagram (3.3) a pullback square.
(ii) By Remark 2.1 and the universal property of pullbacks, the result holds if and only if it holds for the pullback square defined in (i). Suppose that
![]() $f_E$
is a cokernel map. Proposition 3.5 tells us that
$f_E$
is a cokernel map. Proposition 3.5 tells us that
![]() $f_E$
is completely open and we are done if
$f_E$
is completely open and we are done if
![]() $\ell _F$
is completely open.
$\ell _F$
is completely open.
Let
![]() $\lambda $
be an openness constant for
$\lambda $
be an openness constant for
![]() $f_{E}$
and set
$f_{E}$
and set
![]() $\lambda '=\max {\{\lambda \lVert f_F\rVert _{\mathrm {cb}}, 1\}}$
. For
$\lambda '=\max {\{\lambda \lVert f_F\rVert _{\mathrm {cb}}, 1\}}$
. For
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $y\in M_n(F)$
, we have
$y\in M_n(F)$
, we have
![]() $(f_F)_n(y)\in M_n(G)$
and, by Proposition 2.3, there exists
$(f_F)_n(y)\in M_n(G)$
and, by Proposition 2.3, there exists
![]() $x\in M_n(E)$
such that
$x\in M_n(E)$
such that
![]() $(f_E)_n(x)=(f_F)_n(y)$
(hence
$(f_E)_n(x)=(f_F)_n(y)$
(hence
![]() $(x, y)\in L$
) with
$(x, y)\in L$
) with
![]() $\lVert x\rVert _n\leq \lambda \lVert (f_F)_n(y)\rVert _n\leq \lambda '\lVert y\rVert _n$
. We note that
$\lVert x\rVert _n\leq \lambda \lVert (f_F)_n(y)\rVert _n\leq \lambda '\lVert y\rVert _n$
. We note that
![]() $(\ell _F)_n(x,y)=y$
with
$(\ell _F)_n(x,y)=y$
with
![]() $\lVert (x,y)\rVert _n\leq 2\lambda '\lVert y\rVert _n$
. Proposition 2.3 tells us
$\lVert (x,y)\rVert _n\leq 2\lambda '\lVert y\rVert _n$
. Proposition 2.3 tells us
![]() $\ell _F$
is completely open.▪
$\ell _F$
is completely open.▪
Proposition 3.7 Let
![]() $E,F,G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
with
$E,F,G\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
with
![]() $f_E\in C\!B_{A}({G},\,{E})$
and
$f_E\in C\!B_{A}({G},\,{E})$
and
![]() $f_F\in C\!B_{A}({G},\,{F})$
.
$f_F\in C\!B_{A}({G},\,{F})$
.
-
(i) There exist
 $C\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
$C\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
 $h_E\in C\!B_{A}({E},\,{C}), h_F\in C\!B_{A}({F},\,{C})$
making the following diagram a pushout square. (3.4)
$h_E\in C\!B_{A}({E},\,{C}), h_F\in C\!B_{A}({F},\,{C})$
making the following diagram a pushout square. (3.4)
-
(ii) For any such pushout square, if
 $f_E$
is a kernel map, then so is
$f_E$
is a kernel map, then so is
 $h_F$
.
$h_F$
.
Proof (i) Let
![]() $H=\left \{{(f_E(z),-f_F(z))}\,|\,{z\in G} \right \}$
and
$H=\left \{{(f_E(z),-f_F(z))}\,|\,{z\in G} \right \}$
and
![]() $C= {E\oplus {F}}/\overline {H}$
. Let
$C= {E\oplus {F}}/\overline {H}$
. Let
![]() $h_E$
be the composition of the embedding
$h_E$
be the composition of the embedding
![]() ${\iota _E}\colon {E}\rightarrow {E\oplus {F}}$
with the canonical projection
${\iota _E}\colon {E}\rightarrow {E\oplus {F}}$
with the canonical projection
![]() ${\pi }\colon {E\oplus {F}}\rightarrow {C}$
and
${\pi }\colon {E\oplus {F}}\rightarrow {C}$
and
![]() $h_F=\pi \iota _F$
, where
$h_F=\pi \iota _F$
, where
![]() $\iota _F$
is the embedding
$\iota _F$
is the embedding
![]() ${F}\rightarrow {E\oplus {F}}$
. Clearly
${F}\rightarrow {E\oplus {F}}$
. Clearly
![]() $h_E\in C\!B_{A}({E},\,{C})$
and
$h_E\in C\!B_{A}({E},\,{C})$
and
![]() $h_F\in C\!B_{A}({F},\,{C}).$
For any
$h_F\in C\!B_{A}({F},\,{C}).$
For any
![]() $z\in G$
,
$z\in G$
,
![]() $(f_E(z),0) - (0, f_F(z))=(f_E(z), -f_F(z))\in H$
; this means that Diagram (3.4) is commutative.
$(f_E(z),0) - (0, f_F(z))=(f_E(z), -f_F(z))\in H$
; this means that Diagram (3.4) is commutative.
Suppose there exists
![]() $C'\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
$C'\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
![]() $h^{\prime }_E\in C\!B_{A}({E},\,{C'})$
and
$h^{\prime }_E\in C\!B_{A}({E},\,{C'})$
and
![]() $h^{\prime }_F\in C\!B_{A}({F},\,{C'})$
with
$h^{\prime }_F\in C\!B_{A}({F},\,{C'})$
with
![]() $ h^{\prime }_Ef_E=h^{\prime }_Ff_F$
. By the universal property of coproducts, there exists
$ h^{\prime }_Ef_E=h^{\prime }_Ff_F$
. By the universal property of coproducts, there exists
![]() $\phi \in C\!B_{A}({E\oplus {F}},\,{C'})$
such that
$\phi \in C\!B_{A}({E\oplus {F}},\,{C'})$
such that
![]() $\phi \iota _E=h^{\prime }_E$
and
$\phi \iota _E=h^{\prime }_E$
and
![]() $\phi \iota _F=h^{\prime }_F$
. For Diagram (3.4) to be a pushout square it remains to show that there exists
$\phi \iota _F=h^{\prime }_F$
. For Diagram (3.4) to be a pushout square it remains to show that there exists
![]() $\tau \in C\!B_{A}({C},\,{C'})$
such that
$\tau \in C\!B_{A}({C},\,{C'})$
such that
![]() $\tau {}h_E=h_E'$
and
$\tau {}h_E=h_E'$
and
![]() $\tau {}h_F=h_F'$
. Suppose
$\tau {}h_F=h_F'$
. Suppose
![]() $(x,y)\in H$
, then there exists
$(x,y)\in H$
, then there exists
![]() $z\in G$
such that
$z\in G$
such that
![]() $x=f_E(z)$
and
$x=f_E(z)$
and
![]() $y=-f_F(z)$
. Therefore,
$y=-f_F(z)$
. Therefore,
That is, the A-module map
![]() ${\tau }\colon {C}\rightarrow {C'},\, \pi (x,y)\mapsto \phi (x,y)$
is well defined. Let
${\tau }\colon {C}\rightarrow {C'},\, \pi (x,y)\mapsto \phi (x,y)$
is well defined. Let
![]() $c\in M_n(C)$
and
$c\in M_n(C)$
and
![]() $\lambda>1$
. As in Example 2.4,
$\lambda>1$
. As in Example 2.4,
![]() $\pi $
is completely open and
$\pi $
is completely open and
![]() $\lambda $
is an openness constant for
$\lambda $
is an openness constant for
![]() $\pi $
. Therefore, there exists
$\pi $
. Therefore, there exists
![]() $(x,y)\in M_n(E\oplus {F})$
such that
$(x,y)\in M_n(E\oplus {F})$
such that
![]() $c=\pi _n(x,y)$
with
$c=\pi _n(x,y)$
with
![]() $\lVert \tau {(c)}\rVert _n=\lVert \phi (x,y)\rVert _n\leq \lVert \phi \rVert _{\mathrm {cb}}\lVert (x,y)\rVert _n\leq \lambda \lVert \phi \rVert _{\mathrm {cb}}\lVert c\rVert _n$
. Hence
$\lVert \tau {(c)}\rVert _n=\lVert \phi (x,y)\rVert _n\leq \lVert \phi \rVert _{\mathrm {cb}}\lVert (x,y)\rVert _n\leq \lambda \lVert \phi \rVert _{\mathrm {cb}}\lVert c\rVert _n$
. Hence
![]() $\tau $
is completely bounded.
$\tau $
is completely bounded.
(ii) By Remark 2.1 and the universal property of pushouts, the result holds if and only if it holds for the pushout square defined in (i). Suppose that
![]() $f_E$
is a kernel map in
$f_E$
is a kernel map in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. That is,
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. That is,
![]() $f_E(G)$
is closed in E and there exists
$f_E(G)$
is closed in E and there exists
![]() $g\in C\!B_{A}({f_E(G)},\,{G})$
such that
$g\in C\!B_{A}({f_E(G)},\,{G})$
such that
![]() $gf_E=\mathrm {id}_{G}$
and
$gf_E=\mathrm {id}_{G}$
and
![]() $f_Eg=\mathrm {id}_{f_E(G)}$
. We will show that
$f_Eg=\mathrm {id}_{f_E(G)}$
. We will show that
![]() $h_F$
is a kernel map too.
$h_F$
is a kernel map too.
Suppose, we have a sequence
![]() $(f_E(z_n), -f_F(z_n))_{n\in \mathbb {N}}$
in H with limit
$(f_E(z_n), -f_F(z_n))_{n\in \mathbb {N}}$
in H with limit
![]() $(x,y)\in E\oplus F$
. By continuity,
$(x,y)\in E\oplus F$
. By continuity,
![]() $g(x)$
is the limit of
$g(x)$
is the limit of
![]() $(z_n)_{n\in \mathbb {N}}=(gf_E(z_n))_{n\in \mathbb {N}}$
and
$(z_n)_{n\in \mathbb {N}}=(gf_E(z_n))_{n\in \mathbb {N}}$
and
![]() $y=-f_F(g(x))$
. That is,
$y=-f_F(g(x))$
. That is,
![]() $(x,y)=(f_E(g(x)), -f_F(g(x)))\in H$
. Therefore, H is closed and
$(x,y)=(f_E(g(x)), -f_F(g(x)))\in H$
. Therefore, H is closed and
![]() $C=E\oplus {F}/H$
.
$C=E\oplus {F}/H$
.
For
![]() $h_F$
to be a kernel map, we need that
$h_F$
to be a kernel map, we need that
![]() $h_F(F)$
is closed in C. Let
$h_F(F)$
is closed in C. Let
![]() $(h_F(y_n))_{n\in \mathbb {N}}\subseteq C$
and
$(h_F(y_n))_{n\in \mathbb {N}}\subseteq C$
and
![]() $c\in C$
be such that
$c\in C$
be such that
![]() $\lVert h_F(y_n)-c\rVert \to {0}$
. There exist
$\lVert h_F(y_n)-c\rVert \to {0}$
. There exist
![]() $x\in E$
,
$x\in E$
,
![]() $y\in F$
with
$y\in F$
with
![]() $c=\pi (x,y)$
is the limit of
$c=\pi (x,y)$
is the limit of
![]() $(\pi (0,y_n))_{n\in \mathbb {N}}$
; that is,
$(\pi (0,y_n))_{n\in \mathbb {N}}$
; that is,
![]() $\lVert \pi (-x, y_{n}-y)-\pi (0,y_n)\rVert \to 0$
. Because H is closed in
$\lVert \pi (-x, y_{n}-y)-\pi (0,y_n)\rVert \to 0$
. Because H is closed in
![]() $E\oplus {F}$
there must exist a sequence
$E\oplus {F}$
there must exist a sequence
![]() $(z_n)\in G$
such that
$(z_n)\in G$
such that
![]() $(f_E(z_n),-f_F(z_n))\in H$
with
$(f_E(z_n),-f_F(z_n))\in H$
with
![]() $\lVert (-x-f_E(z_n), y_n-y+f_F(z_n))\rVert \to 0$
. In particular,
$\lVert (-x-f_E(z_n), y_n-y+f_F(z_n))\rVert \to 0$
. In particular,
![]() $\lVert -x-f_E(z_n)\rVert \to 0$
and, as
$\lVert -x-f_E(z_n)\rVert \to 0$
and, as
![]() $f_E(G)$
is closed in E, there exists some
$f_E(G)$
is closed in E, there exists some
![]() $z\in G$
with
$z\in G$
with
![]() $f_E(z)=-x$
. By continuity,
$f_E(z)=-x$
. By continuity,
![]() $z_n=g(f_E(z_n))\to z$
and
$z_n=g(f_E(z_n))\to z$
and
![]() $f_F(z_n)\to f_F(z)$
. Set
$f_F(z_n)\to f_F(z)$
. Set
![]() $y'=y-f_F(z)$
, then
$y'=y-f_F(z)$
, then
![]() $\lVert y_n-y'\rVert \to 0$
. Therefore,
$\lVert y_n-y'\rVert \to 0$
. Therefore,
and hence,
![]() $\pi (x,y)\in h_F(F)$
.
$\pi (x,y)\in h_F(F)$
.
Note that
![]() $h_F$
is injective. Indeed, if
$h_F$
is injective. Indeed, if
![]() $h_F(y)=0,$
then there exists
$h_F(y)=0,$
then there exists
![]() $z\in G$
such that
$z\in G$
such that
![]() $(0,y)=(f_E(z),-f_F(z))$
but
$(0,y)=(f_E(z),-f_F(z))$
but
![]() $f_E$
is injective so
$f_E$
is injective so
![]() $z=0$
and therefore
$z=0$
and therefore
![]() $y=0$
. So, we certainly have an A-module map
$y=0$
. So, we certainly have an A-module map
![]() ${\ell }\colon {h_F(F)}\rightarrow {F}$
defined by
${\ell }\colon {h_F(F)}\rightarrow {F}$
defined by
![]() $\ell (h_F(y))=y$
. We are done if
$\ell (h_F(y))=y$
. We are done if
![]() $\ell $
is completely bounded.
$\ell $
is completely bounded.
Note that, for each
![]() $z\in M_n(G),$
we have
$z\in M_n(G),$
we have
If
![]() $f_F=0$
, the result is obvious, so we can suppose otherwise. Then equation (3.5) tells us that
$f_F=0$
, the result is obvious, so we can suppose otherwise. Then equation (3.5) tells us that
![]() $\lVert f_E(z)\rVert _n\geq K{\lVert f_F(z)\rVert _n}$
where
$\lVert f_E(z)\rVert _n\geq K{\lVert f_F(z)\rVert _n}$
where
![]() $K=\min {\{(\lVert f_F\rVert _{\mathrm {cb}}\,\lVert g\rVert _{\mathrm {cb}})^{-1}, 1\}}$
. Recall that for each
$K=\min {\{(\lVert f_F\rVert _{\mathrm {cb}}\,\lVert g\rVert _{\mathrm {cb}})^{-1}, 1\}}$
. Recall that for each
![]() $y\in M_n(F)$
,
$y\in M_n(F)$
,
![]() $\lVert (h_F)_n(y)\rVert _n=\inf \lVert (0,y)+((f_E)_n(z), -(f_F)_n(z))\rVert _n$
, where the infimum is over all
$\lVert (h_F)_n(y)\rVert _n=\inf \lVert (0,y)+((f_E)_n(z), -(f_F)_n(z))\rVert _n$
, where the infimum is over all
![]() $z\in M_n(G)$
. Then, for each
$z\in M_n(G)$
. Then, for each
![]() $n\in \mathbb {N}$
, there exists
$n\in \mathbb {N}$
, there exists
![]() $z\in M_n(G)$
such that
$z\in M_n(G)$
such that
 $$ \begin{align*} \lVert(h_F)_n(y)\rVert_n &\geq\frac{1}{2}\lVert(0,y)+((f_E)_n(z),-(f_F)_n(z))\rVert_n \\ &=\frac{1}{2}\lVert((f_E)_n(z),y-(f_F)_n(z))\rVert_n \\ &=\frac{1}{2}\bigl(\lVert(f_E)_n(z)\rVert_n+\lVert y-(f_F)_n(z)\rVert_n\bigr) \\ &\geq\frac{K}{2}\bigl(\lVert(f_F)_n(z)\rVert_n+\lVert y-(f_F)_n(z)\rVert_n\bigr)\geq\frac{K}{2}\lVert y\rVert_n. \end{align*} $$
$$ \begin{align*} \lVert(h_F)_n(y)\rVert_n &\geq\frac{1}{2}\lVert(0,y)+((f_E)_n(z),-(f_F)_n(z))\rVert_n \\ &=\frac{1}{2}\lVert((f_E)_n(z),y-(f_F)_n(z))\rVert_n \\ &=\frac{1}{2}\bigl(\lVert(f_E)_n(z)\rVert_n+\lVert y-(f_F)_n(z)\rVert_n\bigr) \\ &\geq\frac{K}{2}\bigl(\lVert(f_F)_n(z)\rVert_n+\lVert y-(f_F)_n(z)\rVert_n\bigr)\geq\frac{K}{2}\lVert y\rVert_n. \end{align*} $$
Therefore,
 $\lVert \ell _n((h_F)_n(y))\rVert _n=\lVert y\rVert _n\leq \frac {2}{K}\lVert (h_F)_n(y)\rVert _n$
for all n and
$\lVert \ell _n((h_F)_n(y))\rVert _n=\lVert y\rVert _n\leq \frac {2}{K}\lVert (h_F)_n(y)\rVert _n$
for all n and
![]() $\ell $
is completely bounded.▪
$\ell $
is completely bounded.▪
We are now ready to embark on setting up the new framework for homological algebra.
4 Exact categories and global dimension
Exact categories are additive categories equipped with a class of kernel-cokernel pairs that satisfy certain axioms (see Definition 4.2). In this section, we show how exact categories provide a framework to arrive at a more general version of the notion of a global dimension for an abelian category. Our main source for exact categories is the survey article of Bühler [Reference Bühler8]. We show that for a general operator algebra A,
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
has a canonical exact structure.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
has a canonical exact structure.
Definition 4.1 Suppose, we have a pair of composable morphisms

in an additive category
![]() $\mathcal {A}$
, where
$\mathcal {A}$
, where
![]() $\mu _K$
is a kernel of
$\mu _K$
is a kernel of
![]() $\pi _C$
and
$\pi _C$
and
![]() $\pi _C$
is a cokernel of
$\pi _C$
is a cokernel of
![]() $\mu _K$
. Then we say that
$\mu _K$
. Then we say that
![]() $(\mu _K, \pi _C)$
is a kernel-cokernel pair. Suppose
$(\mu _K, \pi _C)$
is a kernel-cokernel pair. Suppose
![]() $\mathcal {E}$
is a fixed class of kernel-cokernel pairs in
$\mathcal {E}$
is a fixed class of kernel-cokernel pairs in
![]() $\mathcal {A}$
. Then a morphism
$\mathcal {A}$
. Then a morphism
![]() $\mu $
is called an admissible monomorphism if there exists a morphism
$\mu $
is called an admissible monomorphism if there exists a morphism
![]() $\pi $
such that
$\pi $
such that
![]() $(\mu ,\pi )\in \mathcal {E}$
. A morphism
$(\mu ,\pi )\in \mathcal {E}$
. A morphism
![]() $\pi $
is called an admissible epimorphism if there exists a morphism
$\pi $
is called an admissible epimorphism if there exists a morphism
![]() $\mu $
such that
$\mu $
such that
![]() $(\mu ,\pi )\in \mathcal {E}$
. In diagrams admissible monomorphisms (respectively, epimorphisms) will be depicted by
$(\mu ,\pi )\in \mathcal {E}$
. In diagrams admissible monomorphisms (respectively, epimorphisms) will be depicted by
![]() $\rightarrowtail $
(respectively,
$\rightarrowtail $
(respectively,
![]() $\twoheadrightarrow $
).
$\twoheadrightarrow $
).
We define exact categories using the axioms of an exact structure given in [Reference Bühler8]. In Section 2 of that paper, Bühler shows these axioms are equivalent to Quillen’s axioms [Reference Quillen27].
Definition 4.2 An exact structure on
![]() $\mathcal {A}$
is a class
$\mathcal {A}$
is a class
![]() ${\mathcal {E\!x}}$
of kernel-cokernel pairs which is closed under isomorphisms and satisfies the following axioms:
${\mathcal {E\!x}}$
of kernel-cokernel pairs which is closed under isomorphisms and satisfies the following axioms:
-
[E0]
 $\forall \ E\in \mathcal {A}\colon \mathrm {id}_{E}$
is an admissible monomorphism;
$\forall \ E\in \mathcal {A}\colon \mathrm {id}_{E}$
is an admissible monomorphism; -
[E0 op ]
 $\forall \ E\in \mathcal {A}\colon \mathrm {id}_{E}$
is an admissible epimorphism;
$\forall \ E\in \mathcal {A}\colon \mathrm {id}_{E}$
is an admissible epimorphism; -
[E1] the class of admissible monomorphisms is closed under composition;
-
[E1 op ] the class of admissible epimorphisms is closed under composition;
[E2] the pushout of an admissible monomorphism along an arbitrary morphism exists and yields an admissible monomorphism;
-
[E2 op ] the pullback of an admissible epimorphism along an arbitrary morphism exists and yields an admissible epimorphism.
An exact category is a pair (
![]() $\mathcal {A}, {\mathcal {E\!x}}$
) consisting of an additive category
$\mathcal {A}, {\mathcal {E\!x}}$
) consisting of an additive category
![]() $\mathcal {A}$
and an exact structure
$\mathcal {A}$
and an exact structure
![]() ${\mathcal {E\!x}}$
on
${\mathcal {E\!x}}$
on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Definition 4.3 For an additive category
![]() $\mathcal {A}$
, a kernel-cokernel pair
$\mathcal {A}$
, a kernel-cokernel pair

is split if there exist morphisms
![]() $\mu _C\in \mathrm {Hom}{({C},{E})}$
and
$\mu _C\in \mathrm {Hom}{({C},{E})}$
and
![]() $\pi _K\in \mathrm {Hom}{({E},{K})}$
such that the quintuplet
$\pi _K\in \mathrm {Hom}{({E},{K})}$
such that the quintuplet
![]() $(E,\mu _K,\mu _C,\pi _K,\pi _C)$
makes E a direct sum.
$(E,\mu _K,\mu _C,\pi _K,\pi _C)$
makes E a direct sum.
Example 4.1 The class of all split kernel-cokernel pairs forms an exact structure on any additive category. We denote this class
![]() ${{\mathcal {E\!x}}_{min}}$
and note that
${{\mathcal {E\!x}}_{min}}$
and note that
![]() ${{\mathcal {E\!x}}_{min}}$
will be a substructure of any other exact structure placed on
${{\mathcal {E\!x}}_{min}}$
will be a substructure of any other exact structure placed on
![]() $\mathcal {A}$
. This is trivial to show, but has useful consequences (see Section 5).
$\mathcal {A}$
. This is trivial to show, but has useful consequences (see Section 5).
Example 4.2 The class of all kernel-cokernel pairs in an additive category
![]() $\mathcal {A}$
is denoted
$\mathcal {A}$
is denoted
![]() ${{\mathcal {E\!x}}_{max}}$
. If
${{\mathcal {E\!x}}_{max}}$
. If
![]() $\mathcal {A}$
is an abelian category then
$\mathcal {A}$
is an abelian category then
![]() $(\mathcal {A},{{\mathcal {E\!x}}_{max}})$
is an exact category and
$(\mathcal {A},{{\mathcal {E\!x}}_{max}})$
is an exact category and
![]() ${{\mathcal {E\!x}}_{max}}$
is the class of all short exact sequences in
${{\mathcal {E\!x}}_{max}}$
is the class of all short exact sequences in
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
For a general additive category
![]() $\mathcal {A}$
, the class
$\mathcal {A}$
, the class
![]() ${{\mathcal {E\!x}}_{max}}$
is closed under isomorphisms (Remark 2.1) and satisfies [E
${{\mathcal {E\!x}}_{max}}$
is closed under isomorphisms (Remark 2.1) and satisfies [E
![]() $0$
] and [E
$0$
] and [E
![]() $0^{\mathrm {op}}$
]. We introduce some conditions that ensure that this class forms an exact structure on
$0^{\mathrm {op}}$
]. We introduce some conditions that ensure that this class forms an exact structure on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Definition 4.4 Let
![]() $\mathcal {A}$
be an additive category. We say
$\mathcal {A}$
be an additive category. We say
![]() $\mathcal {A}$
is a quasi-abelian category if:
$\mathcal {A}$
is a quasi-abelian category if:
-
(i) each morphism in
 $\mathcal {A}$
has a kernel and a cokernel and
$\mathcal {A}$
has a kernel and a cokernel and -
(ii) the class
 ${{\mathcal {E\!x}}_{max}}$
of all kernel-cokernel pairs satisfies conditions [E2] and [E
${{\mathcal {E\!x}}_{max}}$
of all kernel-cokernel pairs satisfies conditions [E2] and [E
 $2^{\mathrm {op}}$
] from Definition 4.2.
$2^{\mathrm {op}}$
] from Definition 4.2.
The following can be proven by diagram chasing, from the definitions of kernels, cokernels, pushouts, and pullbacks. (See [Reference Bühler8, Proposition 4.4].)
Proposition 4.3 [Reference Schneiders30, Proposition 1.1.7]
Let
![]() $\mathcal {A}$
be a quasi-abelian category. Then
$\mathcal {A}$
be a quasi-abelian category. Then
![]() ${{\mathcal {E\!x}}_{max}}$
, the class of all kernel-cokernel pairs, satisfies conditions [E1] and [E
${{\mathcal {E\!x}}_{max}}$
, the class of all kernel-cokernel pairs, satisfies conditions [E1] and [E
![]() $1^{\mathrm {op}}$
] from Definition 4.2 and thus forms an exact structure.
$1^{\mathrm {op}}$
] from Definition 4.2 and thus forms an exact structure.
Theorem 4.4 Let A be an operator algebra. The class of all kernel-cokernel pairs in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
forms an exact structure on
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
forms an exact structure on
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
.
Proof By Propositions 3.3, 3.6, and 3.7,
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is quasi-abelian. The result then follows from Proposition 4.3. Alternatively, one can check [E1] and [E
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is quasi-abelian. The result then follows from Proposition 4.3. Alternatively, one can check [E1] and [E
![]() $1^{\mathrm {op}}$
] “by hand” [Reference Rosbotham28, Section 3.4].▪
$1^{\mathrm {op}}$
] “by hand” [Reference Rosbotham28, Section 3.4].▪
In an abelian category, the short exact sequences are the smallest building blocks for homological algebra which then emerges from long exact sequences and so-called diagram lemmas. The kernel-cokernel pairs take the role of short exact sequences, and the axioms of an exact category entail enough of the diagram lemmas to build a viable theory. This is demonstrated in detail in [Reference Bühler8] and successfully applied to a functional analytic setting in [Reference Bühler9].
Another fundamental tool is the concept of an exact functor.
Definition 4.5 An additive functor
![]() ${{\mathsf {F}}}\colon {(\mathcal {A},{\mathcal {E\!x}}_{1})}\rightarrow {(\mathcal {B}, {\mathcal {E\!x}}_{2})}$
between two exact categories is exact if
${{\mathsf {F}}}\colon {(\mathcal {A},{\mathcal {E\!x}}_{1})}\rightarrow {(\mathcal {B}, {\mathcal {E\!x}}_{2})}$
between two exact categories is exact if
![]() ${\mathsf {F}}(\mathcal {{\mathcal {E\!x}}_{1}})\subseteq {{\mathcal {E\!x}}_{2}}$
.
${\mathsf {F}}(\mathcal {{\mathcal {E\!x}}_{1}})\subseteq {{\mathcal {E\!x}}_{2}}$
.
We will note for later (see Section 5) how exact functors are useful for inducing alternate exact structures on an exact category.
Proposition 4.5 Let
![]() ${{\mathsf {F}}}\colon {(\mathcal {A},{\mathcal {E\!x}}_{1})}\rightarrow {(\mathcal {B}, {\mathcal {E\!x}}_{2})}$
be an exact functor between exact categories. Suppose there is another exact structure
${{\mathsf {F}}}\colon {(\mathcal {A},{\mathcal {E\!x}}_{1})}\rightarrow {(\mathcal {B}, {\mathcal {E\!x}}_{2})}$
be an exact functor between exact categories. Suppose there is another exact structure
![]() ${\mathcal {E\!x}}^{\prime }_{2}$
on
${\mathcal {E\!x}}^{\prime }_{2}$
on
![]() $\mathcal {B}$
. Then
$\mathcal {B}$
. Then
 $$\begin{align*}{\mathcal{E\!x}}^{\prime}_{1} = \left\{{(\mu,\pi)\in{\mathcal{E\!x}}_{1}}\,|\,{\mathcal{({\mathsf{F}}\mu,{\mathsf{F}}\pi) \in{\mathcal{E\!x}}^{\prime}_{2}}} \right\} \end{align*}$$
$$\begin{align*}{\mathcal{E\!x}}^{\prime}_{1} = \left\{{(\mu,\pi)\in{\mathcal{E\!x}}_{1}}\,|\,{\mathcal{({\mathsf{F}}\mu,{\mathsf{F}}\pi) \in{\mathcal{E\!x}}^{\prime}_{2}}} \right\} \end{align*}$$
forms an exact structure on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proposition 4.5 is [Reference Heller17, Proposition 7.3]; the proof also follows easily from [Reference Bühler8, Proposition 5.2]. We will call the exact structure
![]() ${\mathcal {E\!x}}^{\prime }_{1}$
appearing in this way a relative exact structure as it involves constraints relative to another exact structure.
${\mathcal {E\!x}}^{\prime }_{1}$
appearing in this way a relative exact structure as it involves constraints relative to another exact structure.
Injectivity and projectivity can be described using the notion of exact functors. For any object E in an additive category
![]() $\mathcal {A}$
we have the following contravariant functor
$\mathcal {A}$
we have the following contravariant functor
 $$ \begin{align*} \mathrm{Hom}{({-},{E})}\colon{\mathcal{A}}&\xrightarrow{\hphantom{fgl}}{\mathcal{A\!b}}\\ F&\longmapsto\mathrm{Hom}_{\mathcal{A}}{({F},{E})}\\ \mathrm{Hom}_{\mathcal{A}}{({F},{G})}\ni{f}&\longmapsto f^*=\mathrm{Hom}{({f},{E})}, \end{align*} $$
$$ \begin{align*} \mathrm{Hom}{({-},{E})}\colon{\mathcal{A}}&\xrightarrow{\hphantom{fgl}}{\mathcal{A\!b}}\\ F&\longmapsto\mathrm{Hom}_{\mathcal{A}}{({F},{E})}\\ \mathrm{Hom}_{\mathcal{A}}{({F},{G})}\ni{f}&\longmapsto f^*=\mathrm{Hom}{({f},{E})}, \end{align*} $$
where
![]() $f^*(g)=gf$
for
$f^*(g)=gf$
for
![]() $g\in \mathrm {Hom}_{\mathcal {A}}{({G},{E})}$
and
$g\in \mathrm {Hom}_{\mathcal {A}}{({G},{E})}$
and
![]() ${\mathcal {A\!b}}$
is the category of abelian groups. There is also the similarly defined covariant functor
${\mathcal {A\!b}}$
is the category of abelian groups. There is also the similarly defined covariant functor
![]() $\mathrm {Hom}{({E},{-})}$
, where
$\mathrm {Hom}{({E},{-})}$
, where
![]() $f_*=\mathrm {Hom}{({E},{f})}$
is given by postcomposition of f. We call these
$f_*=\mathrm {Hom}{({E},{f})}$
is given by postcomposition of f. We call these
![]() $\mathrm {Hom}$
-functors.
$\mathrm {Hom}$
-functors.
Let
![]() $\mathcal {M}$
be the class of admissible monomorphisms in an exact category (
$\mathcal {M}$
be the class of admissible monomorphisms in an exact category (
![]() $\mathcal {A}, {\mathcal {E\!x}}$
) and
$\mathcal {A}, {\mathcal {E\!x}}$
) and
![]() $\mathcal {P}$
be the class of admissible epimorphisms in this category. We shall write
$\mathcal {P}$
be the class of admissible epimorphisms in this category. We shall write
![]() ${\mathcal {E\!x}}=(\mathcal {M},\mathcal {P})$
for brevity. Then an object
${\mathcal {E\!x}}=(\mathcal {M},\mathcal {P})$
for brevity. Then an object
![]() $I\in \mathcal {A}$
is
$I\in \mathcal {A}$
is
![]() $\mathcal {M}$
-injective precisely when
$\mathcal {M}$
-injective precisely when
![]() $\mathrm {Hom}{({-},{I})}$
is exact as a functor to
$\mathrm {Hom}{({-},{I})}$
is exact as a functor to
![]() $({\mathcal {A\!b}}, {{\mathcal {E\!x}}_{max}})$
and
$({\mathcal {A\!b}}, {{\mathcal {E\!x}}_{max}})$
and
![]() $P\in \mathcal {A}$
is
$P\in \mathcal {A}$
is
![]() $\mathcal {P}$
-projective precisely when
$\mathcal {P}$
-projective precisely when
![]() $\mathrm {Hom}{({P},{-})}$
is exact.
$\mathrm {Hom}{({P},{-})}$
is exact.
In an abelian category with enough injectives there is a standard notion of injective dimension of an object. This is defined using injective resolutions. In order for these methods to transfer to the setting of exact categories we need to take extra care in our set up. To this end, we work with resolutions built from particular types of morphisms.
Definition 4.6 Let
![]() $(\mathcal {A},{\mathcal {E\!x}})$
be an exact category and
$(\mathcal {A},{\mathcal {E\!x}})$
be an exact category and
![]() ${\mathcal {E\!x}}=(\mathcal {M},\mathcal {P})$
. A morphism
${\mathcal {E\!x}}=(\mathcal {M},\mathcal {P})$
. A morphism
![]() $f\in \mathrm {Hom}{({E},{F})}$
is called admissible if there exist an object
$f\in \mathrm {Hom}{({E},{F})}$
is called admissible if there exist an object
![]() $G\in \mathcal {A}$
and morphisms
$G\in \mathcal {A}$
and morphisms
![]() $\pi _f\in {\mathcal {P}}{({E},\,{G})}$
and
$\pi _f\in {\mathcal {P}}{({E},\,{G})}$
and
![]() $\mu _f\in {\mathcal {M}}{({G},\,{E})}$
such that
$\mu _f\in {\mathcal {M}}{({G},\,{E})}$
such that
![]() $f=\mu _f\pi _f$
. (Such decomposition is unique up to unique isomorphism.)
$f=\mu _f\pi _f$
. (Such decomposition is unique up to unique isomorphism.)
A sequence of admissible morphisms

is called exact if, for each
![]() $n\in \mathbb {Z}$
,
$n\in \mathbb {Z}$
,
![]() $(\iota _{n},\pi _{n+1})$
is in
$(\iota _{n},\pi _{n+1})$
is in
![]() ${\mathcal {E\!x}}$
.
${\mathcal {E\!x}}$
.
An exact sequence of admissible morphisms of the form

where each
![]() $I^n$
is
$I^n$
is
![]() $\mathcal {M}$
-injective is called an
$\mathcal {M}$
-injective is called an
![]() $\mathcal {M}$
-injective resolution of E.
$\mathcal {M}$
-injective resolution of E.
It is easy to see that, if
![]() $\mathcal {M}$
is the class of admissible monomorphisms in an exact category
$\mathcal {M}$
is the class of admissible monomorphisms in an exact category
![]() $(\mathcal {A},{\mathcal {E\!x}})$
and
$(\mathcal {A},{\mathcal {E\!x}})$
and
![]() $\mathcal {A}$
has enough
$\mathcal {A}$
has enough
![]() $\mathcal {M}$
-injectives, then an injective resolution exists for every object in
$\mathcal {M}$
-injectives, then an injective resolution exists for every object in
![]() $\mathcal {A}$
. In the same situation, a little more work gives the following analogue of the injective dimension theorem for modules over rings.
$\mathcal {A}$
. In the same situation, a little more work gives the following analogue of the injective dimension theorem for modules over rings.
Theorem 4.6 Let
![]() $\mathcal {M}$
be the class of admissible monomorphisms in an exact category
$\mathcal {M}$
be the class of admissible monomorphisms in an exact category
![]() $(\mathcal {A},{\mathcal {E\!x}})$
. Suppose
$(\mathcal {A},{\mathcal {E\!x}})$
. Suppose
![]() $\mathcal {A}$
has enough
$\mathcal {A}$
has enough
![]() $\mathcal {M}$
-injectives. The following are equivalent for
$\mathcal {M}$
-injectives. The following are equivalent for
![]() $n\geq {1}$
and every
$n\geq {1}$
and every
![]() $E\in \mathcal {A}$
.
$E\in \mathcal {A}$
.
-
(i) If there is an exact sequence of admissible morphisms
(4.1)with each
 $I^{m}$
,
$I^{m}$
,
 $0\leq m\leq n-1$
injective, then F must be injective.
$0\leq m\leq n-1$
injective, then F must be injective.
-
(ii) There is an exact sequence of admissible morphisms
(4.2)with each
 $I^{m}$
,
$I^{m}$
,
 $0\leq m\leq n$
injective.
$0\leq m\leq n$
injective.
Remark 4.7 That (i) implies (ii) in Theorem 4.6 follows easily from the fact that every object in such a category
![]() $\mathcal {A}$
has an
$\mathcal {A}$
has an
![]() $\mathcal {M}$
-injective resolution and by the definition of an exact sequence of admissible morphisms. To get (ii) implies (i), one can follow the method of the same result for general abelian categories, or indeed module categories, making slight adjustments when necessary. That is, one goes via the route of Ext groups. These are defined using derived functors arising from Hom-functors. A nice explanation of derived functors from exact categories can be found in [Reference Bühler8, Section 12]. The module category versions of the injective dimension theorem can be found in various places, see, for example, [Reference Weibel33, Lemma 4.1.8] or [Reference Osborne23, Proposition 4.8]. An explicit proof of Theorem 4.6 is given in [Reference Rosbotham28].
$\mathcal {M}$
-injective resolution and by the definition of an exact sequence of admissible morphisms. To get (ii) implies (i), one can follow the method of the same result for general abelian categories, or indeed module categories, making slight adjustments when necessary. That is, one goes via the route of Ext groups. These are defined using derived functors arising from Hom-functors. A nice explanation of derived functors from exact categories can be found in [Reference Bühler8, Section 12]. The module category versions of the injective dimension theorem can be found in various places, see, for example, [Reference Weibel33, Lemma 4.1.8] or [Reference Osborne23, Proposition 4.8]. An explicit proof of Theorem 4.6 is given in [Reference Rosbotham28].
Theorem 4.6 can also be seen as a consequence of an injective version of Schanuel’s lemma for exact categories; for details see [Reference Mathieu and Rosbotham21]. This approach is useful if one wants to avoid the use of Ext groups.
We now introduce the homological dimension we are after.
Definition 4.7 Let
![]() $E\in \mathcal {A}$
and
$E\in \mathcal {A}$
and
![]() $\mathcal {M}$
be the class of admissible monomorphisms in an exact category
$\mathcal {M}$
be the class of admissible monomorphisms in an exact category
![]() $(\mathcal {A},{\mathcal {E\!x}})$
. We say E has finite
$(\mathcal {A},{\mathcal {E\!x}})$
. We say E has finite
![]() $\mathcal {M}$
-injective dimension if there exists an exact sequence of admissible morphisms as in Diagram (4.2) with all
$\mathcal {M}$
-injective dimension if there exists an exact sequence of admissible morphisms as in Diagram (4.2) with all
![]() $I^m \ \mathcal {M}$
-injective. If E is of finite
$I^m \ \mathcal {M}$
-injective. If E is of finite
![]() $\mathcal {M}$
-injective dimension we write
$\mathcal {M}$
-injective dimension we write
![]() $\mathrm {Inj}_{\mathcal {M}}\mathrm {-dim}\,{(E)}=0$
if E is
$\mathrm {Inj}_{\mathcal {M}}\mathrm {-dim}\,{(E)}=0$
if E is
![]() $\mathcal {M}$
-injective and
$\mathcal {M}$
-injective and
![]() $\mathrm {Inj}_{\mathcal {M}}\mathrm {-dim}\,{(E)}=n$
if E is not
$\mathrm {Inj}_{\mathcal {M}}\mathrm {-dim}\,{(E)}=n$
if E is not
![]() $\mathcal {M}$
-injective and n is the smallest natural number such that there exists an exact sequence of admissible morphisms as in Diagram (4.2) with all
$\mathcal {M}$
-injective and n is the smallest natural number such that there exists an exact sequence of admissible morphisms as in Diagram (4.2) with all
![]() $I^m \ \mathcal {M}$
-injective. If E is not of finite
$I^m \ \mathcal {M}$
-injective. If E is not of finite
![]() $\mathcal {M}$
-injective dimension, we write
$\mathcal {M}$
-injective dimension, we write
![]() $\mathrm {Inj}_{\mathcal {M}}\mathrm {-dim}\,{(E)}=\infty $
.
$\mathrm {Inj}_{\mathcal {M}}\mathrm {-dim}\,{(E)}=\infty $
.
The global dimension of the exact category
![]() $(\mathcal {A},{\mathcal {E\!x}})$
is
$(\mathcal {A},{\mathcal {E\!x}})$
is
 $$\begin{align*}\sup\left\{{\mathrm{Inj}_{\mathcal{M}}\mathrm{-dim}\,{(E)}}\,|\,{E\in\mathcal{A}} \right\}\in{\mathbb{N}}_0\cup\{\infty\}. \end{align*}$$
$$\begin{align*}\sup\left\{{\mathrm{Inj}_{\mathcal{M}}\mathrm{-dim}\,{(E)}}\,|\,{E\in\mathcal{A}} \right\}\in{\mathbb{N}}_0\cup\{\infty\}. \end{align*}$$
Remark 4.8 It is easy to observe, that the
![]() $\mathcal {M}$
-injective dimension of an object E in an exact category
$\mathcal {M}$
-injective dimension of an object E in an exact category
![]() $(\mathcal {A},{\mathcal {E\!x}})$
is independent of any choice of injective resolutions. Indeed, suppose
$(\mathcal {A},{\mathcal {E\!x}})$
is independent of any choice of injective resolutions. Indeed, suppose

is an
![]() $\mathcal {M}$
-injective resolution of E. Terminate this exact sequence by replacing
$\mathcal {M}$
-injective resolution of E. Terminate this exact sequence by replacing
![]() $d^{n-1}$
and
$d^{n-1}$
and
![]() $I^n$
by the cokernel of
$I^n$
by the cokernel of
![]() $d^{n-2}$
to get a sequence as in Diagram (4.1). Then, by Theorem 4.6,
$d^{n-2}$
to get a sequence as in Diagram (4.1). Then, by Theorem 4.6,
![]() $\mathrm {Inj}_{\mathcal {M}}\mathrm {-dim}\,{(E)}\leq {n}$
if and only if the cokernel object of
$\mathrm {Inj}_{\mathcal {M}}\mathrm {-dim}\,{(E)}\leq {n}$
if and only if the cokernel object of
![]() $d^{n-2}$
is
$d^{n-2}$
is
![]() $\mathcal {M}$
-injective.
$\mathcal {M}$
-injective.
If
![]() $\mathcal {P}$
is the class of admissible epimorphisms then the dual procedure to the above yields the notion of projective resolutions and projective dimension for an object. There is a dual result to Theorem 4.6 which leads to the notion of the projective dimension of an object. An object will have projective dimension
$\mathcal {P}$
is the class of admissible epimorphisms then the dual procedure to the above yields the notion of projective resolutions and projective dimension for an object. There is a dual result to Theorem 4.6 which leads to the notion of the projective dimension of an object. An object will have projective dimension
![]() $0$
if and only if it is
$0$
if and only if it is
![]() $\mathcal {P}$
-projective. We are able to characterize global dimension
$\mathcal {P}$
-projective. We are able to characterize global dimension
![]() $0$
using projectives by Corollary 4.11.
$0$
using projectives by Corollary 4.11.
Remark 4.9 Let
![]() $\mathcal {M}$
be the class of admissible monomorphisms and
$\mathcal {M}$
be the class of admissible monomorphisms and
![]() $\mathcal {P}$
be the class of admissible epimorphisms in an exact category. If there are enough
$\mathcal {P}$
be the class of admissible epimorphisms in an exact category. If there are enough
![]() $\mathcal {P}$
-projectives and enough
$\mathcal {P}$
-projectives and enough
![]() $\mathcal {M}$
-injectives, the supremum of all the
$\mathcal {M}$
-injectives, the supremum of all the
![]() $\mathcal {P}$
-projective dimensions will coincide with the supremum of all the
$\mathcal {P}$
-projective dimensions will coincide with the supremum of all the
![]() $\mathcal {M}$
-injective dimensions. So we are always able to define the global dimension using only
$\mathcal {M}$
-injective dimensions. So we are always able to define the global dimension using only
![]() $\mathcal {P}$
-projectives provided there are enough of them.
$\mathcal {P}$
-projectives provided there are enough of them.
The following proposition is a classical result known as the “Splitting Lemma.”
Proposition 4.10 (Splitting Lemma)
Let
![]() $\mathcal {A}$
be an additive category with kernels and cokernels and suppose
$\mathcal {A}$
be an additive category with kernels and cokernels and suppose

is a kernel-cokernel pair in
![]() $\mathcal {A}$
. Then the following are equivalent:
$\mathcal {A}$
. Then the following are equivalent:
-
(i) the kernel-cokernel pair is split;
-
(ii) there exists
 $\pi _E\in \mathrm {Hom}_{\mathcal {A}}{({F},{E})}$
such that
$\pi _E\in \mathrm {Hom}_{\mathcal {A}}{({F},{E})}$
such that
 $\pi _E\mu =\mathrm {id}_{E}$
; and
$\pi _E\mu =\mathrm {id}_{E}$
; and -
(iii) there exists
 $\mu _F\in \mathrm {Hom}_{\mathcal {A}}{({G},{F})}$
such that
$\mu _F\in \mathrm {Hom}_{\mathcal {A}}{({G},{F})}$
such that
 $\pi \mu _F=\mathrm {id}_{G}$
.
$\pi \mu _F=\mathrm {id}_{G}$
.
Corollary 4.11 Let
![]() $(\mathcal {A},{\mathcal {E\!x}})$
be an exact category and
$(\mathcal {A},{\mathcal {E\!x}})$
be an exact category and
![]() ${\mathcal {E\!x}}=(\mathcal {M},\mathcal {P})$
. Every object in
${\mathcal {E\!x}}=(\mathcal {M},\mathcal {P})$
. Every object in
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\mathcal {M}$
-injective if and only if every object is
$\mathcal {M}$
-injective if and only if every object is
![]() $\mathcal {P}$
-projective.
$\mathcal {P}$
-projective.
Proof This follows from the Splitting Lemma and Remark 2.2.▪
5 Operator algebras with global dimension zero
When A is a unital operator algebra and
![]() $\mathcal {M}$
is the class of admissible monomorphisms in the exact category
$\mathcal {M}$
is the class of admissible monomorphisms in the exact category
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
, it is unclear whether there are enough
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
, it is unclear whether there are enough
![]() $\mathcal {M}$
-injectives. The canonical object
$\mathcal {M}$
-injectives. The canonical object
![]() $C\!B({A},\,{I})$
, where I is injective in
$C\!B({A},\,{I})$
, where I is injective in
![]() , which is the analogue of the canonical injective object in algebraic module categories, lies in the larger category of matrix normed modules [Reference Crann10]. We will discuss this issue at the end of the present section. However, there is a different exact structure we can place on
, which is the analogue of the canonical injective object in algebraic module categories, lies in the larger category of matrix normed modules [Reference Crann10]. We will discuss this issue at the end of the present section. However, there is a different exact structure we can place on
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
that has enough projectives. In this section, we discuss this structure and give a characterization of when the global dimension associated to this exact category is zero.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
that has enough projectives. In this section, we discuss this structure and give a characterization of when the global dimension associated to this exact category is zero.
Let
![]() ${{\mathcal {E\!x}}_{rel}}$
be the class of kernel-cokernel pairs in
${{\mathcal {E\!x}}_{rel}}$
be the class of kernel-cokernel pairs in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
that split in
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
that split in
![]() .
.
Proposition 5.1 Let A be an operator algebra. Then
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
is an exact category.
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
is an exact category.
Proof By Theorem 4.4,
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
is an exact category. In particular, this holds for
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
is an exact category. In particular, this holds for
![]() . The forgetful functor
. The forgetful functor
![]() is exact and as in Example 4.1, we know that
is exact and as in Example 4.1, we know that
![]() ${{\mathcal {E\!x}}_{min}}$
forms an exact structure on
${{\mathcal {E\!x}}_{min}}$
forms an exact structure on
![]() . The result follows from Proposition 4.5.▪
. The result follows from Proposition 4.5.▪
We next show that
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
has enough projectives.
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
has enough projectives.
Proposition 5.2 Let A be a unital operator algebra. For every
![]() , the Haagerup tensor product
, the Haagerup tensor product
![]() ${{E}}\otimes _{{h}}\mkern 2mu{{A}}$
is
${{E}}\otimes _{{h}}\mkern 2mu{{A}}$
is
![]() ${\mathcal {P}_{rel}}$
-projective. In particular,
${\mathcal {P}_{rel}}$
-projective. In particular,
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
has enough
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
has enough
![]() ${\mathcal {P}_{rel}}$
-projectives.
${\mathcal {P}_{rel}}$
-projectives.
Proof Suppose, we have the following diagram of morphisms in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
,
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
,

with
![]() $\pi \in {\mathcal {P}_{rel}}$
and that
$\pi \in {\mathcal {P}_{rel}}$
and that
![]() $\widetilde \pi \in C\!B({G},\,{F})$
satisfies
$\widetilde \pi \in C\!B({G},\,{F})$
satisfies
![]() $\pi \widetilde \pi =\mathrm {id}_{G}$
. Let
$\pi \widetilde \pi =\mathrm {id}_{G}$
. Let
![]() ${g'}\colon {{{E}}\otimes _{{h}}\mkern 2mu{{A}}}\rightarrow {F}$
be the map defined on elementary tensors by
${g'}\colon {{{E}}\otimes _{{h}}\mkern 2mu{{A}}}\rightarrow {F}$
be the map defined on elementary tensors by
![]() $g'(x\otimes {a})=(\widetilde {\pi }f(x\otimes {1}))\cdot {a}$
for
$g'(x\otimes {a})=(\widetilde {\pi }f(x\otimes {1}))\cdot {a}$
for
![]() $x\in E, a\in A$
. Since
$x\in E, a\in A$
. Since
![]() $g'$
is the composition of
$g'$
is the composition of

where
![]() $\iota \colon E\to {{E}}\otimes _{{h}}\mkern 2mu{{A}}$
is
$\iota \colon E\to {{E}}\otimes _{{h}}\mkern 2mu{{A}}$
is
![]() $x\mapsto x\otimes 1$
and m is the completely contractive linearization of the module action of A on F, it is a well-defined completely bounded A-module map. As
$x\mapsto x\otimes 1$
and m is the completely contractive linearization of the module action of A on F, it is a well-defined completely bounded A-module map. As
we have
![]() $\pi g'=f$
.
$\pi g'=f$
.
Now let
![]() $E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Let
$E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Let
![]() ${P}\colon {{{E}}\otimes _{{h}}\mkern 2mu{{A}}}\rightarrow {E}$
be the canonical complete contraction given by
${P}\colon {{{E}}\otimes _{{h}}\mkern 2mu{{A}}}\rightarrow {E}$
be the canonical complete contraction given by
![]() $P(x\otimes {a})=x\cdot {a}$
. As each
$P(x\otimes {a})=x\cdot {a}$
. As each
![]() $x=[x_{i j}]\in M_n(E)$
is of the form
$x=[x_{i j}]\in M_n(E)$
is of the form
![]() $P_{n}([x_{i j}\otimes {1}])$
and
$P_{n}([x_{i j}\otimes {1}])$
and
![]() $\lVert [x_{i j}\otimes {1}]\rVert _{n}\leq \lVert [x_{ij}]\rVert _n$
, P is completely open. For each
$\lVert [x_{i j}\otimes {1}]\rVert _{n}\leq \lVert [x_{ij}]\rVert _n$
, P is completely open. For each
![]() $x\otimes {a}$
in
$x\otimes {a}$
in
![]() ${{E}}\otimes _{{h}}\mkern 2mu{{A}}$
and
${{E}}\otimes _{{h}}\mkern 2mu{{A}}$
and
![]() $a_0\in {A}$
, we have
$a_0\in {A}$
, we have
that is, P is an A-module map. Define
![]() $\widetilde {P}\in C\!B({E},\,{{{E}}\otimes _{{h}}\mkern 2mu{{A}}})$
by
$\widetilde {P}\in C\!B({E},\,{{{E}}\otimes _{{h}}\mkern 2mu{{A}}})$
by
![]() ${\widetilde {P}(x)}=x\otimes {1}$
. Then
${\widetilde {P}(x)}=x\otimes {1}$
. Then
![]() $P\widetilde {P}=\mathrm {id}_{E}$
, hence
$P\widetilde {P}=\mathrm {id}_{E}$
, hence
![]() $P\in {\mathcal {P}_{rel}}$
as required.▪
$P\in {\mathcal {P}_{rel}}$
as required.▪
Here comes the main result of the paper.
Theorem 5.3 Let A be a unital operator algebra. The following are equivalent:
-
(i) The global dimension of
 $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}, {{\mathcal {E\!x}}_{rel}})$
is zero.
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}, {{\mathcal {E\!x}}_{rel}})$
is zero. -
(ii) Every object in
 ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
 $\mathcal {M}_{rel}$
-injective, where
$\mathcal {M}_{rel}$
-injective, where
 $\mathcal {M}_{rel}$
is the class of admissible monomorphisms in
$\mathcal {M}_{rel}$
is the class of admissible monomorphisms in
 ${{\mathcal {E\!x}}_{rel}}$
.
${{\mathcal {E\!x}}_{rel}}$
. -
(iii) Every object in
 ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
 $\mathcal {P}_{rel}$
-projective, where
$\mathcal {P}_{rel}$
-projective, where
 $\mathcal {P}_{rel}$
is the class of admissible epimorphisms in
$\mathcal {P}_{rel}$
is the class of admissible epimorphisms in
 ${{\mathcal {E\!x}}_{rel}}$
.
${{\mathcal {E\!x}}_{rel}}$
. -
(iv) A is classically semisimple.
In keeping with traditional notation we shall write
![]() ${\mathrm {dg}_{cb}\,{A}}$
for the global dimension of
${\mathrm {dg}_{cb}\,{A}}$
for the global dimension of
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}, {{\mathcal {E\!x}}_{rel}})$
and call it the completely bounded global dimension of the operator algebra A.
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}, {{\mathcal {E\!x}}_{rel}})$
and call it the completely bounded global dimension of the operator algebra A.
Corollary 5.4 For every unital operator algebra A, its completely bounded global dimension
![]() ${\mathrm {dg}_{cb}\,{A}}$
is zero if and only if A is a finite direct sum of full matrix algebras.
${\mathrm {dg}_{cb}\,{A}}$
is zero if and only if A is a finite direct sum of full matrix algebras.
The equivalence of (i) and (ii) in Theorem 5.3 follows from Definition 4.7 and (ii)
![]() ${}\iff {}$
(iii) is a consequence of the splitting lemma (Corollary 4.11).
${}\iff {}$
(iii) is a consequence of the splitting lemma (Corollary 4.11).
The argument for the implication (iv)
![]() ${}\Rightarrow {}$
(iii) follows closely the proof of [Reference Helemskii15, Theorem 3.5.17]; for the details see [Reference Rosbotham28], Section 5.3. A direct argument of (iv)
${}\Rightarrow {}$
(iii) follows closely the proof of [Reference Helemskii15, Theorem 3.5.17]; for the details see [Reference Rosbotham28], Section 5.3. A direct argument of (iv)
![]() ${}\Rightarrow {}$
(ii) is provided by Proposition 5.11. The final implication (iii)
${}\Rightarrow {}$
(ii) is provided by Proposition 5.11. The final implication (iii)
![]() ${}\Rightarrow {}$
(iv) needs some preparation.
${}\Rightarrow {}$
(iv) needs some preparation.
Our approach is based on the following well-known characterization; see, e.g., [Reference Osborne23, Theorem 4.40].
Proposition 5.5 A unital algebra is classically semisimple if and only if each of its maximal submodules is a direct summand.
In other words, to show that a unital algebra A is classically semisimple, we have to show that, for every maximal right ideal I of A, the exact sequence of right A-modules

splits. As
![]() $A/I$
is a simple right A-module, this is evidently equivalent to the existence of an A-module map
$A/I$
is a simple right A-module, this is evidently equivalent to the existence of an A-module map
![]() $f\colon A/I\to A$
such that
$f\colon A/I\to A$
such that
![]() $f(A/I)\nsubseteq I$
(cf. Lemma 4.10).
$f(A/I)\nsubseteq I$
(cf. Lemma 4.10).
Let A be a unital operator algebra; as every maximal right ideal I of A is closed, we can consider the sequence (5.1) above within
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. The next auxiliary result will enable us to complete the final step in the proof of Theorem 5.3.
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. The next auxiliary result will enable us to complete the final step in the proof of Theorem 5.3.
Lemma 5.6 Let I be a closed right ideal in the unital operator algebra A. Set
 $$ \begin{align*} S_1 &=\left\{{f(x)}\,|\,{x\in A/I, {f}\colon {A/I}\rightarrow {A} \text{ is an }A\text{-module map} } \right\},\\ S_2 &=\left\{{ab}\,|\,{a,b\in A,\ ay=0 \text{ for all } y\in I} \right\}. \end{align*} $$
$$ \begin{align*} S_1 &=\left\{{f(x)}\,|\,{x\in A/I, {f}\colon {A/I}\rightarrow {A} \text{ is an }A\text{-module map} } \right\},\\ S_2 &=\left\{{ab}\,|\,{a,b\in A,\ ay=0 \text{ for all } y\in I} \right\}. \end{align*} $$
Then
![]() $S_1=S_2$
and its linear span S is a two-sided ideal.
$S_1=S_2$
and its linear span S is a two-sided ideal.
Proof That the linear span of
![]() $S_2$
is a two-sided ideal is obvious. Let
$S_2$
is a two-sided ideal is obvious. Let
![]() ${\pi }\colon {A}\rightarrow {A/I}$
be the canonical quotient map. Let
${\pi }\colon {A}\rightarrow {A/I}$
be the canonical quotient map. Let
![]() $a\in A$
. We claim that there exists an A-module map
$a\in A$
. We claim that there exists an A-module map
![]() ${f}\colon {A/I}\rightarrow {A}$
such that
${f}\colon {A/I}\rightarrow {A}$
such that
![]() $f(\pi (1_A))=a$
if and only if
$f(\pi (1_A))=a$
if and only if
![]() $ay=0$
for all
$ay=0$
for all
![]() $y\in I$
.
$y\in I$
.
Suppose, there exists such an f. Take
![]() $y\in I$
. Then
$y\in I$
. Then
![]() $ay=f(\pi (1_A))y=f(\pi (y))=f(0)=0$
. Now suppose
$ay=f(\pi (1_A))y=f(\pi (y))=f(0)=0$
. Now suppose
![]() $ay=0$
for all
$ay=0$
for all
![]() $y\in I$
. Define
$y\in I$
. Define
![]() ${f}\colon {A/I}\rightarrow {A}$
by
${f}\colon {A/I}\rightarrow {A}$
by
![]() $f(x)=ab$
, where
$f(x)=ab$
, where
![]() $\pi (b)=x$
. Clearly, this is well defined and
$\pi (b)=x$
. Clearly, this is well defined and
![]() $f(\pi (1_A))=a$
. So the claim is true. The result then follows as an element is of the form
$f(\pi (1_A))=a$
. So the claim is true. The result then follows as an element is of the form
![]() $f(x)$
if and only if it is of the form
$f(x)$
if and only if it is of the form
![]() $f(\pi (1_A)){b}$
for
$f(\pi (1_A)){b}$
for
![]() $b\in A$
such that
$b\in A$
such that
![]() $\pi (b)=x$
.▪
$\pi (b)=x$
.▪
The proof of the next result mirrors [Reference Helemskii15, Proposition IV.4.4.].
Proposition 5.7 Let
![]() ${\phi }\colon {A}\rightarrow {B}$
be a unital completely contractive homomorphism between unital operator algebras and let
${\phi }\colon {A}\rightarrow {B}$
be a unital completely contractive homomorphism between unital operator algebras and let
![]() $E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
be
$E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
be
![]() $\mathcal {P}_{rel}$
-projective. Suppose
$\mathcal {P}_{rel}$
-projective. Suppose
![]() $F\in {\mathcal {O\!M\!o\!d}^{\infty }_{{B}}}$
and
$F\in {\mathcal {O\!M\!o\!d}^{\infty }_{{B}}}$
and
![]() ${f}\colon {E}\rightarrow {F}$
is a completely bounded A-module map, where we consider F as an A-module by the restriction of scalars via
${f}\colon {E}\rightarrow {F}$
is a completely bounded A-module map, where we consider F as an A-module by the restriction of scalars via
![]() $\phi $
. For any
$\phi $
. For any
![]() $x\in E$
with
$x\in E$
with
![]() $f(x)\neq 0$
, there exists a completely bounded A-module map
$f(x)\neq 0$
, there exists a completely bounded A-module map
![]() ${g}\colon {E}\rightarrow {A}$
such that
${g}\colon {E}\rightarrow {A}$
such that
![]() $\phi {g}(x)\neq 0$
.
$\phi {g}(x)\neq 0$
.
Proof In the following proof, for any
![]() $G\in {\mathcal {O\!M\!o\!d}^{\infty }_{{C}}}$
, where C is an operator algebra, we will denote by
$G\in {\mathcal {O\!M\!o\!d}^{\infty }_{{C}}}$
, where C is an operator algebra, we will denote by
![]() $P_{G,C}$
the completely contractive C-module map
$P_{G,C}$
the completely contractive C-module map
![]() ${{G}}\otimes _{{h}}\mkern 2mu{{C}}\rightarrow {G}$
defined on elementary tensors by
${{G}}\otimes _{{h}}\mkern 2mu{{C}}\rightarrow {G}$
defined on elementary tensors by
![]() $P_{G,C}(z\otimes {c})=z\cdot {c}$
(where
$P_{G,C}(z\otimes {c})=z\cdot {c}$
(where
![]() $z\in G, c\in C$
). If G is a left operator C-module, we denote the similarly defined completely contractive C-module map by
$z\in G, c\in C$
). If G is a left operator C-module, we denote the similarly defined completely contractive C-module map by
![]() ${{}_{C,G}P}\colon {{{C}}\otimes _{{h}}\mkern 2mu{{G}}}\rightarrow {G}$
.
${{}_{C,G}P}\colon {{{C}}\otimes _{{h}}\mkern 2mu{{G}}}\rightarrow {G}$
.
By our assumptions, we have the following commutative diagram of completely bounded linear maps.

As in the proof of Proposition 5.2, we have
![]() $P_{E,A}\in \mathcal {P}_{rel}$
. Hence, there exists a completely bounded A-module map
$P_{E,A}\in \mathcal {P}_{rel}$
. Hence, there exists a completely bounded A-module map
![]() ${\iota }\colon {E}\rightarrow {{{E}}\otimes _{{h}}\mkern 2mu{{A}}}$
such that
${\iota }\colon {E}\rightarrow {{{E}}\otimes _{{h}}\mkern 2mu{{A}}}$
such that
![]() $P_{E,A}\,\iota =\mathrm {id}_{E}$
. Then it is clear that the above diagram stays commutative if we replace
$P_{E,A}\,\iota =\mathrm {id}_{E}$
. Then it is clear that the above diagram stays commutative if we replace
![]() $P_{E,A}$
with
$P_{E,A}$
with
![]() $\iota $
. Moreover, for any (completely) bounded linear functional
$\iota $
. Moreover, for any (completely) bounded linear functional
![]() ${\alpha }\colon {F}\rightarrow {\mathbb {C}}$
it is easy to see the following diagram of completely bounded linear maps is commutative:
${\alpha }\colon {F}\rightarrow {\mathbb {C}}$
it is easy to see the following diagram of completely bounded linear maps is commutative:

Let
![]() $a\in A$
and
$a\in A$
and
![]() $x\otimes {a'}$
be an elementary tensor in
$x\otimes {a'}$
be an elementary tensor in
![]() ${{E}}\otimes _{{h}}\mkern 2mu{{A}}$
and
${{E}}\otimes _{{h}}\mkern 2mu{{A}}$
and
![]() $\lambda \otimes {a''}$
be an elementary tensor in
$\lambda \otimes {a''}$
be an elementary tensor in
![]() ${{\mathbb {C}}}\otimes _{{h}}\mkern 2mu{{A}}$
. Then
${{\mathbb {C}}}\otimes _{{h}}\mkern 2mu{{A}}$
. Then
and
![]() $_{\mathbb {C}, A}P(\lambda \otimes {a''})\cdot {a}=\lambda {a''a}= {}_{\mathbb {C}, A}P((\lambda \otimes {a''})\cdot {a})$
. By continuity and linearity,
$_{\mathbb {C}, A}P(\lambda \otimes {a''})\cdot {a}=\lambda {a''a}= {}_{\mathbb {C}, A}P((\lambda \otimes {a''})\cdot {a})$
. By continuity and linearity,
![]() $\alpha f\otimes \mathrm {id}_{A}$
and
$\alpha f\otimes \mathrm {id}_{A}$
and
![]() ${}_{\mathbb {C}, A}P$
are A-module maps. So, for any linear functional
${}_{\mathbb {C}, A}P$
are A-module maps. So, for any linear functional
![]() $\alpha $
, we have that
$\alpha $
, we have that
![]() ${{}_{\mathbb {C}, A}P(\alpha f\otimes \mathrm {id}_{A})\iota }\colon {E}\rightarrow {A}$
is a completely bounded A-module map. We now show that there exists an
${{}_{\mathbb {C}, A}P(\alpha f\otimes \mathrm {id}_{A})\iota }\colon {E}\rightarrow {A}$
is a completely bounded A-module map. We now show that there exists an
![]() $\alpha $
that makes this the desired A-module map.
$\alpha $
that makes this the desired A-module map.
Let
![]() $x\in E$
such that
$x\in E$
such that
![]() $f(x)\neq 0$
. Then
$f(x)\neq 0$
. Then
![]() $P_{F,B}(f\otimes \phi )\iota (x)\neq 0$
; in particular
$P_{F,B}(f\otimes \phi )\iota (x)\neq 0$
; in particular
![]() $u=(f\otimes \phi )\iota (x)\in {{F}}\otimes _{{h}}\mkern 2mu{{B}}$
is nonzero. By Lemma 2.5, there exist
$u=(f\otimes \phi )\iota (x)\in {{F}}\otimes _{{h}}\mkern 2mu{{B}}$
is nonzero. By Lemma 2.5, there exist
![]() $\alpha \in F^*$
,
$\alpha \in F^*$
,
![]() $\beta \in B^*$
such that
$\beta \in B^*$
such that
![]() $(\alpha \otimes \beta )(u)\neq 0$
. As
$(\alpha \otimes \beta )(u)\neq 0$
. As
![]() $\alpha \otimes \beta $
is the composition
$\alpha \otimes \beta $
is the composition
![]() $(\mathrm {id}_{E}\otimes \beta )(\alpha \otimes \mathrm {id}_{B})$
we obtain that
$(\mathrm {id}_{E}\otimes \beta )(\alpha \otimes \mathrm {id}_{B})$
we obtain that
![]() $(\alpha \otimes \mathrm {id}_{B})u\neq 0$
and therefore
$(\alpha \otimes \mathrm {id}_{B})u\neq 0$
and therefore
![]() ${}_{\mathbb {C}, B}P(\alpha \otimes \mathrm {id}_{B})u\neq 0$
.
${}_{\mathbb {C}, B}P(\alpha \otimes \mathrm {id}_{B})u\neq 0$
.
Let
![]() $g={}_{\mathbb {C}, A}P(\alpha (f)\otimes \mathrm {id}_{A})\iota $
. Commutativity of the diagram gives then that
$g={}_{\mathbb {C}, A}P(\alpha (f)\otimes \mathrm {id}_{A})\iota $
. Commutativity of the diagram gives then that
![]() $\phi {g}(x)\neq 0$
as required.▪
$\phi {g}(x)\neq 0$
as required.▪
We can now complete the Proof of Theorem 5.3 (iii)
![]() ${}\Rightarrow {}$
(iv):
${}\Rightarrow {}$
(iv):
Let I be a maximal right ideal of A. Suppose that the image of every A-module map
![]() $A/I\rightarrow {A}$
is a subset of I; then, with notation as in Lemma 5.6,
$A/I\rightarrow {A}$
is a subset of I; then, with notation as in Lemma 5.6,
![]() $S_1\subseteq {I}$
, and hence
$S_1\subseteq {I}$
, and hence
![]() $S\subseteq {I}$
. Put
$S\subseteq {I}$
. Put
![]() $E=A/I$
and
$E=A/I$
and
![]() $P=\left \{{a\in A}\,|\,{x\cdot {a}=0, \forall x\in E} \right \},$
the right annihilator of E. Then P is a closed two-sided ideal in A. Moreover,
$P=\left \{{a\in A}\,|\,{x\cdot {a}=0, \forall x\in E} \right \},$
the right annihilator of E. Then P is a closed two-sided ideal in A. Moreover,
![]() $S\subseteq P$
. Indeed, suppose
$S\subseteq P$
. Indeed, suppose
![]() $a\in S$
and
$a\in S$
and
![]() $x\in E$
is of the form
$x\in E$
is of the form
![]() $\pi (b)$
for some
$\pi (b)$
for some
![]() $b\in A$
, where
$b\in A$
, where
![]() ${\pi }\colon {A}\rightarrow {E}$
is the canonical epimorphism. Then
${\pi }\colon {A}\rightarrow {E}$
is the canonical epimorphism. Then
![]() $x\cdot {a}=\pi (b)\cdot {a}=\pi (ba)=0$
because S is a left ideal contained in I.
$x\cdot {a}=\pi (b)\cdot {a}=\pi (ba)=0$
because S is a left ideal contained in I.
Put
![]() $B=A/P$
and let
$B=A/P$
and let
![]() ${\phi }\colon {A}\rightarrow {B}$
be the canonical epimorphism of unital operator algebras. Then E is a right B-module with action defined in the following way: for
${\phi }\colon {A}\rightarrow {B}$
be the canonical epimorphism of unital operator algebras. Then E is a right B-module with action defined in the following way: for
![]() $x\in E$
and
$x\in E$
and
![]() $b\in B$
,
$b\in B$
,
![]() $x\cdot {b}=\pi (aa')$
where
$x\cdot {b}=\pi (aa')$
where
![]() $x=\pi (a)$
,
$x=\pi (a)$
,
![]() $b=\phi (a')$
. This is well defined by the definition of P. Then
$b=\phi (a')$
. This is well defined by the definition of P. Then
![]() $x\cdot {b}=x\cdot {a'}$
. In fact,
$x\cdot {b}=x\cdot {a'}$
. In fact,
![]() $E\in {\mathcal {O\!M\!o\!d}^{\infty }_{{B}}}$
; suppose
$E\in {\mathcal {O\!M\!o\!d}^{\infty }_{{B}}}$
; suppose
![]() $x\in M_n(E)$
,
$x\in M_n(E)$
,
![]() $b\in M_n(B)$
. For every
$b\in M_n(B)$
. For every
![]() $a'\in M_n(A)$
with
$a'\in M_n(A)$
with
![]() $b=\phi _n(a')$
,
$b=\phi _n(a')$
,
![]() $\lVert x\cdot {b}\rVert _n=\lVert x\cdot {a'}\rVert _n\leq \lVert x\rVert _n\lVert a'\rVert _n,$
so
$\lVert x\cdot {b}\rVert _n=\lVert x\cdot {a'}\rVert _n\leq \lVert x\rVert _n\lVert a'\rVert _n,$
so
![]() $\lVert x\cdot {b}\rVert _n\leq \lVert x\rVert _n\lVert b\rVert _n$
. Let
$\lVert x\cdot {b}\rVert _n\leq \lVert x\rVert _n\lVert b\rVert _n$
. Let
![]() $F=E$
and
$F=E$
and
![]() $f=\mathrm {id}_{E}$
; then obviously we have that
$f=\mathrm {id}_{E}$
; then obviously we have that
![]() $f(\pi (1_A))\neq 0$
. If E is
$f(\pi (1_A))\neq 0$
. If E is
![]() $\mathcal {P}_{rel}$
-projective, by Proposition 5.7, for each
$\mathcal {P}_{rel}$
-projective, by Proposition 5.7, for each
![]() $x\notin I$
, there exists an A-module map
$x\notin I$
, there exists an A-module map
![]() ${g}\colon {E}\rightarrow {A}$
such that
${g}\colon {E}\rightarrow {A}$
such that
![]() $\phi (g(\pi (x)))\neq 0$
, so
$\phi (g(\pi (x)))\neq 0$
, so
![]() $g(\pi (x))\notin {P}$
.
$g(\pi (x))\notin {P}$
.
Since, by (the proof of) Lemma 5.6,
![]() $g(\pi (x))\in S\subseteq P$
it follows that E cannot be
$g(\pi (x))\in S\subseteq P$
it follows that E cannot be
![]() $\mathcal {P}_{rel}$
-projective. Consequently, if A is not classically semisimple, using Proposition 5.5, we conclude that not all modules in
$\mathcal {P}_{rel}$
-projective. Consequently, if A is not classically semisimple, using Proposition 5.5, we conclude that not all modules in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
can be
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
can be
![]() $\mathcal {P}_{rel}$
-projective. That is, if (iv) does not hold, then (iii) cannot hold either.
$\mathcal {P}_{rel}$
-projective. That is, if (iv) does not hold, then (iii) cannot hold either.
Remark 5.8 Implication (iii)
![]() ${}\Rightarrow {}$
(iv) in Theorem 5.3 answers Helemskii’s question, for operator algebras, in [Reference Helemskii16, Section 7] in the positive since it is easy to see that his relative structure is equivalent to ours. Relative homological algebra is common in the ring theory setting, cf., e.g., [Reference Hilton and Stammbach18, Chapter IX] or [Reference Mitchell22, Section V.7]. Paulsen undertook a systematic study in the setting of operator modules in [Reference Paulsen24], see also [Reference Frank and Paulsen14]. He discovered an intimate interrelation between the cohomology groups that arise in this relative theory (which is equivalently described here by our relative exact structure) and the completely bounded Hochschild cohomology groups. See in particular Propositions 5.5 and 6.4 in [Reference Paulsen24]. Specialising to bimodules it then follows that all operator A-bimodules over a unital C*-algebra A are relatively projective if and only if A is finite dimensional which in turn is equivalent to A possessing a diagonal [Reference Paulsen24, Theorem 6.13 and Corollary 6.14]. For an extension of the latter to unital operator algebras, see [Reference Paulsen and Smith25].
${}\Rightarrow {}$
(iv) in Theorem 5.3 answers Helemskii’s question, for operator algebras, in [Reference Helemskii16, Section 7] in the positive since it is easy to see that his relative structure is equivalent to ours. Relative homological algebra is common in the ring theory setting, cf., e.g., [Reference Hilton and Stammbach18, Chapter IX] or [Reference Mitchell22, Section V.7]. Paulsen undertook a systematic study in the setting of operator modules in [Reference Paulsen24], see also [Reference Frank and Paulsen14]. He discovered an intimate interrelation between the cohomology groups that arise in this relative theory (which is equivalently described here by our relative exact structure) and the completely bounded Hochschild cohomology groups. See in particular Propositions 5.5 and 6.4 in [Reference Paulsen24]. Specialising to bimodules it then follows that all operator A-bimodules over a unital C*-algebra A are relatively projective if and only if A is finite dimensional which in turn is equivalent to A possessing a diagonal [Reference Paulsen24, Theorem 6.13 and Corollary 6.14]. For an extension of the latter to unital operator algebras, see [Reference Paulsen and Smith25].
In the remainder of this section, we shall discuss the interrelations between the various types of injectivity within
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
, but also in comparison to the larger category
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
, but also in comparison to the larger category
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. It will become clear that injectivity is not determined by the category but rather the exact structure which one puts on the category. For a discussion of injectivity in general terms, we refer to [Reference Mathieu and Rosbotham20].
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. It will become clear that injectivity is not determined by the category but rather the exact structure which one puts on the category. For a discussion of injectivity in general terms, we refer to [Reference Mathieu and Rosbotham20].
Let
![]() ${\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}$
be any additive category whose objects are operator spaces which are right A-modules and whose morphisms are the completely bounded A-module maps between these objects, where A is a unital operator algebra (in the sense of [Reference Blecher and Le Merdy6, Section 2.1]). Suppose
${\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}$
be any additive category whose objects are operator spaces which are right A-modules and whose morphisms are the completely bounded A-module maps between these objects, where A is a unital operator algebra (in the sense of [Reference Blecher and Le Merdy6, Section 2.1]). Suppose
![]() ${\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}$
is closed under direct sums, closed submodules and quotients. Then the kernels (respectively, cokernels) in
${\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}$
is closed under direct sums, closed submodules and quotients. Then the kernels (respectively, cokernels) in
![]() ${\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}$
are as described in Proposition 3.4 (respectively, Proposition 3.5). Moreover, the proofs of Propositions 3.7 and 3.6 still work for
${\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}$
are as described in Proposition 3.4 (respectively, Proposition 3.5). Moreover, the proofs of Propositions 3.7 and 3.6 still work for
![]() ${\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}$
and therefore,
${\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}$
and therefore,
![]() $({\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}, {{\mathcal {E\!x}}_{max}})$
and
$({\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}, {{\mathcal {E\!x}}_{max}})$
and
![]() $({\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}, {{\mathcal {E\!x}}_{rel}})$
are exact categories, where
$({\mathcal {X\!M\!o\!d}^{\infty }_{{A}}}, {{\mathcal {E\!x}}_{rel}})$
are exact categories, where
![]() ${{\mathcal {E\!x}}_{rel}}$
again denotes the kernel-cokernel pairs that split in
${{\mathcal {E\!x}}_{rel}}$
again denotes the kernel-cokernel pairs that split in
![]() (Proposition 5.1).
(Proposition 5.1).
In particular, this holds for the category
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
, whose objects are the nondegenerate matrix normed A-modules. An operator space E that is also a right A-module is known as a matrix normed A-module if the A-module action induces a completely contractive linear mapping
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
, whose objects are the nondegenerate matrix normed A-modules. An operator space E that is also a right A-module is known as a matrix normed A-module if the A-module action induces a completely contractive linear mapping
![]() , where
, where
![]() denotes the operator space projective tensor product. Comparing
denotes the operator space projective tensor product. Comparing
![]() with
with
![]() $\otimes _h$
immediately tells us that
$\otimes _h$
immediately tells us that
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is a full subcategory of
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is a full subcategory of
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}.$
(see [Reference Blecher and Le Merdy6, Example 3.1.5]). The category
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}.$
(see [Reference Blecher and Le Merdy6, Example 3.1.5]). The category
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
is, e.g., used in [Reference Aristov3, Reference Crann10, Reference Rosbotham29].
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
is, e.g., used in [Reference Aristov3, Reference Crann10, Reference Rosbotham29].
For each
![]() , on
, on
![]() $C\!B({A},\,{E})$
we define the right A-module action by
$C\!B({A},\,{E})$
we define the right A-module action by
![]() $(T\cdot {a})(b)=T(ab)$
, for all
$(T\cdot {a})(b)=T(ab)$
, for all
![]() $T\in C\!B({A},\,{E})$
and
$T\in C\!B({A},\,{E})$
and
![]() $a,b\in A$
. Then
$a,b\in A$
. Then
![]() $C\!B({A},\,{E})$
is an object in
$C\!B({A},\,{E})$
is an object in
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
which is just a specific case of [Reference Blecher and Le Merdy6, 3.5.2].
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
which is just a specific case of [Reference Blecher and Le Merdy6, 3.5.2].
Proposition 5.9 Let A be a unital operator algebra and let
![]() ${\mathcal {N}_{rel}}$
be the class of admissible monomorphisms in
${\mathcal {N}_{rel}}$
be the class of admissible monomorphisms in
![]() $({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}}).$
For any
$({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}}).$
For any
![]() , the matrix normed module
, the matrix normed module
![]() $C\!B({A},\,{G})$
is
$C\!B({A},\,{G})$
is
![]() ${\mathcal {N}_{rel}}$
-injective in
${\mathcal {N}_{rel}}$
-injective in
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Moreover,
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Moreover,
![]() $E\in {{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
$E\in {{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
![]() ${\mathcal {N}_{rel}}$
-injective if and only if it is a retract of some
${\mathcal {N}_{rel}}$
-injective if and only if it is a retract of some
![]() $C\!B({A},\,{G})$
.
$C\!B({A},\,{G})$
.
Proof Suppose
![]() . Let
. Let
![]() $\mu \in {{{\mathcal {N}_{rel}}}}{({E},\,{F})}$
and
$\mu \in {{{\mathcal {N}_{rel}}}}{({E},\,{F})}$
and
![]() $f\in C\!B_{A}({E},\,{C\!B({A},\,{G})})$
. We show that
$f\in C\!B_{A}({E},\,{C\!B({A},\,{G})})$
. We show that
![]() $C\!B({A},\,{G})$
is
$C\!B({A},\,{G})$
is
![]() ${\mathcal {N}_{rel}}$
-injective by finding a morphism
${\mathcal {N}_{rel}}$
-injective by finding a morphism
![]() $g\in C\!B_{A}({F},\,{C\!B({A},\,{G})})$
such that
$g\in C\!B_{A}({F},\,{C\!B({A},\,{G})})$
such that
![]() $f=g\mu $
.
$f=g\mu $
.
As
![]() $\mu \in {\mathcal {N}_{rel}}$
, there exists
$\mu \in {\mathcal {N}_{rel}}$
, there exists
![]() $\widetilde {\mu }\in C\!B({F},\,{E})$
such that
$\widetilde {\mu }\in C\!B({F},\,{E})$
such that
![]() ${\widetilde {\mu }}\mu =\mathrm {id}_{E}$
. For
${\widetilde {\mu }}\mu =\mathrm {id}_{E}$
. For
![]() $y\in F$
write
$y\in F$
write
![]() $f(\widetilde {\mu }(y\cdot {a}))(1_A)$
as
$f(\widetilde {\mu }(y\cdot {a}))(1_A)$
as
![]() $g(y)(a)$
, for each
$g(y)(a)$
, for each
![]() $a\in A$
. This defines a completely bounded linear map
$a\in A$
. This defines a completely bounded linear map
![]() $g(y)\in C\!B({A},\,{G})$
.
$g(y)\in C\!B({A},\,{G})$
.
It is routine to verify that, in fact, this yields a morphism
![]() $g\in C\!B_{A}({F},\,{C\!B({A},\,{G})})$
and moreover, for all
$g\in C\!B_{A}({F},\,{C\!B({A},\,{G})})$
and moreover, for all
![]() $x\in E, a\in A$
$x\in E, a\in A$
 $$ \begin{align*} g(\mu(x))(a)=f(\widetilde{\mu}(\mu(x)\cdot{a}))(1)= f(\widetilde{\mu}(\mu(x\cdot{a}))(1) &=f(x\cdot{a})(1)\\ &=(f(x)\cdot{a})(1)=f(x)(a). \end{align*} $$
$$ \begin{align*} g(\mu(x))(a)=f(\widetilde{\mu}(\mu(x)\cdot{a}))(1)= f(\widetilde{\mu}(\mu(x\cdot{a}))(1) &=f(x\cdot{a})(1)\\ &=(f(x)\cdot{a})(1)=f(x)(a). \end{align*} $$
So
![]() $g\mu =f$
as required.
$g\mu =f$
as required.
Now suppose that
![]() $E\in {{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
and define
$E\in {{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
and define
![]() ${\iota }\colon {E}\rightarrow {C\!B({A},\,{E})}$
by
${\iota }\colon {E}\rightarrow {C\!B({A},\,{E})}$
by
![]() $\iota (x)(a)=x\cdot {a}$
for each
$\iota (x)(a)=x\cdot {a}$
for each
![]() $x\in E, a\in A$
. Clearly,
$x\in E, a\in A$
. Clearly,
![]() $\iota $
is a completely isometric A-module map and thus a kernel map in
$\iota $
is a completely isometric A-module map and thus a kernel map in
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Define
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Define
![]() ${\widetilde {\iota }}\colon {C\!B({A},\,{E})}\rightarrow {E}$
by
${\widetilde {\iota }}\colon {C\!B({A},\,{E})}\rightarrow {E}$
by
![]() $\widetilde {\iota }(T)= T(1_A)$
for all
$\widetilde {\iota }(T)= T(1_A)$
for all
![]() $T\in C\!B({A},\,{E})$
. Then
$T\in C\!B({A},\,{E})$
. Then
![]() $\widetilde {\iota }$
is a completely bounded linear map such that
$\widetilde {\iota }$
is a completely bounded linear map such that
![]() ${\widetilde {\iota }}\iota =\mathrm {id}_{E}$
. That is,
${\widetilde {\iota }}\iota =\mathrm {id}_{E}$
. That is,
![]() $\iota \in {\mathcal {N}_{rel}}$
. The result follows by Remark 2.2.▪
$\iota \in {\mathcal {N}_{rel}}$
. The result follows by Remark 2.2.▪
The above proposition is obtained in [Reference Crann10, Section 2] in a similar way but without making the categorical setting explicit. Since we shall compare injectivity in different categories, we need to make sure our arguments fit the correct situation.
Remark 5.10 Let
![]() ${\mathcal {M}_{rel}}$
denote the class of admissible monomorphisms in
${\mathcal {M}_{rel}}$
denote the class of admissible monomorphisms in
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}, {{\mathcal {E\!x}}_{rel}})$
and
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}, {{\mathcal {E\!x}}_{rel}})$
and
![]() ${\mathcal {N}_{rel}}$
be the admissible monomorphisms in
${\mathcal {N}_{rel}}$
be the admissible monomorphisms in
![]() $({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
. If
$({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
. If
![]() $E,F,I\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
, then
$E,F,I\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
, then
![]() ${{{\mathcal {M}_{rel}}}}{({E},\,{F})}={{{\mathcal {N}_{rel}}}}{({E},\,{F})}$
and
${{{\mathcal {M}_{rel}}}}{({E},\,{F})}={{{\mathcal {N}_{rel}}}}{({E},\,{F})}$
and
Hence, if I is
![]() ${\mathcal {N}_{rel}}$
-injective it must also be
${\mathcal {N}_{rel}}$
-injective it must also be
![]() ${\mathcal {M}_{rel}}$
-injective. Therefore, if
${\mathcal {M}_{rel}}$
-injective. Therefore, if
![]() $E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and E is a retract (in
$E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and E is a retract (in
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
) of
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
) of
![]() $C\!B({A},\,{E})$
, then E will be
$C\!B({A},\,{E})$
, then E will be
![]() ${\mathcal {M}_{rel}}$
-injective.
${\mathcal {M}_{rel}}$
-injective.
The next result shows that “completely bounded global dimension zero” does not depend on which of the two categories one chooses.
Proposition 5.11 Suppose A is a classically semisimple unital operator algebra. Then every object in
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
![]() ${\mathcal {M}_{rel}}$
-injective and every object in
${\mathcal {M}_{rel}}$
-injective and every object in
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
is
![]() ${\mathcal {N}_{rel}}$
-injective.
${\mathcal {N}_{rel}}$
-injective.
Proof By Proposition 5.9 and Remark 5.10, it suffices to show that for every
![]() $E\in {{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},$
there exist
$E\in {{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},$
there exist
![]() $r\in C\!B_{A}({C\!B({A},\,{E})},\,{E})$
and
$r\in C\!B_{A}({C\!B({A},\,{E})},\,{E})$
and
![]() $s\in C\!B_{A}({E},\,{C\!B({A},\,{E})})$
such that
$s\in C\!B_{A}({E},\,{C\!B({A},\,{E})})$
such that
![]() $rs=\mathrm {id}_{E}.$
First we will fix some notation:
$rs=\mathrm {id}_{E}.$
First we will fix some notation:
There exists
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $A=M_{m_1}(\mathbb {\mathbb {C}})\oplus M_{m_2}(\mathbb {\mathbb {C}})\oplus \cdots \oplus M_{m_n}(\mathbb {\mathbb {C}})$
. For each
$A=M_{m_1}(\mathbb {\mathbb {C}})\oplus M_{m_2}(\mathbb {\mathbb {C}})\oplus \cdots \oplus M_{m_n}(\mathbb {\mathbb {C}})$
. For each
![]() $k\in \{1,\ldots , n\}$
and
$k\in \{1,\ldots , n\}$
and
![]() $i,j\in \{1,\ldots , m_k\}$
, let
$i,j\in \{1,\ldots , m_k\}$
, let
![]() $e^k_{ij}$
denote the n-tuple in A with all zero entries apart from the kth entry which is a matrix in
$e^k_{ij}$
denote the n-tuple in A with all zero entries apart from the kth entry which is a matrix in
![]() $M_{m_k}(\mathbb {C})$
with
$M_{m_k}(\mathbb {C})$
with
![]() $1$
for the
$1$
for the
![]() $ij$
th entry and
$ij$
th entry and
![]() $0$
everywhere else.
$0$
everywhere else.
Note that A is the linear span of the elements
![]() $e^k_{ij}$
. Moreover,
$e^k_{ij}$
. Moreover,
 $\lVert e^k_{ij}\rVert =1$
and
$\lVert e^k_{ij}\rVert =1$
and
 $e^k_{ij}e^{\ell }_{pq}=0$
unless
$e^k_{ij}e^{\ell }_{pq}=0$
unless
![]() $j=p,$
and
$j=p,$
and
![]() $k={\ell }$
in which case
$k={\ell }$
in which case
 $e^k_{ij}e^{\ell }_{pq}=e^k_{iq}$
. Then
$e^k_{ij}e^{\ell }_{pq}=e^k_{iq}$
. Then
 $1_A=\sum _{k=1}^{n}\sum _{i=1}^{m_{k}}e^k_{ii}$
and for any
$1_A=\sum _{k=1}^{n}\sum _{i=1}^{m_{k}}e^k_{ii}$
and for any
![]() $x\in E$
we have
$x\in E$
we have
 $x=\sum _{k=1}^{n}\sum _{i=1}^{m_{k}}x\cdot {e^k_{ii}}$
.
$x=\sum _{k=1}^{n}\sum _{i=1}^{m_{k}}x\cdot {e^k_{ii}}$
.
Let
![]() ${s}\colon {E}\rightarrow {C\!B({A},\,{E})}$
be the completely bounded A-module map defined by
${s}\colon {E}\rightarrow {C\!B({A},\,{E})}$
be the completely bounded A-module map defined by
![]() $s(x)(a)=x\cdot {a}$
for all
$s(x)(a)=x\cdot {a}$
for all
![]() $x\in E$
,
$x\in E$
,
![]() $a\in A$
. For each
$a\in A$
. For each
![]() $T\in C\!B({A},\,{E})$
, let
$T\in C\!B({A},\,{E})$
, let
 $$\begin{align*}r(T)= \sum_{k=1}^{n}\sum_{i=1}^{m_{k}}T(e^k_{i1})\cdot e^k_{1i}. \end{align*}$$
$$\begin{align*}r(T)= \sum_{k=1}^{n}\sum_{i=1}^{m_{k}}T(e^k_{i1})\cdot e^k_{1i}. \end{align*}$$
It is clear that this defines a linear mapping
![]() ${r}\colon {C\!B({A},\,{E})}\rightarrow {E}$
and so will be an A-module map if for each
${r}\colon {C\!B({A},\,{E})}\rightarrow {E}$
and so will be an A-module map if for each
![]() $T\in C\!B({A},\,{E})$
we have
$T\in C\!B({A},\,{E})$
we have
 $r(T)\cdot {e^{\ell }_{pq}}=r(T\cdot {e^{\ell }_{pq}})$
for arbitrary
$r(T)\cdot {e^{\ell }_{pq}}=r(T\cdot {e^{\ell }_{pq}})$
for arbitrary
![]() $t\in \{1,\ldots , n \}$
and
$t\in \{1,\ldots , n \}$
and
![]() $p,q\in \{1,\ldots , m_k\}$
.
$p,q\in \{1,\ldots , m_k\}$
.
We compute the two terms in question:
 $$ \begin{align} r(T\cdot{e^{\ell}_{pq}})=\sum_{k=1}^{n}\sum_{i=1}^{m_{k}}T(e^{\ell}_{pq}e^k_{i1})\cdot e^k_{1i}=T(e^{\ell}_{pq}e^{\ell}_{q1})\cdot{e}^{\ell}_{1q}=T(e^{\ell}_{p1})\cdot {e}^{\ell}_{1q}, \end{align} $$
$$ \begin{align} r(T\cdot{e^{\ell}_{pq}})=\sum_{k=1}^{n}\sum_{i=1}^{m_{k}}T(e^{\ell}_{pq}e^k_{i1})\cdot e^k_{1i}=T(e^{\ell}_{pq}e^{\ell}_{q1})\cdot{e}^{\ell}_{1q}=T(e^{\ell}_{p1})\cdot {e}^{\ell}_{1q}, \end{align} $$
as every other term is zero. Similarly, as
 $e^k_{1i}e^{\ell }_{pq}=0$
unless
$e^k_{1i}e^{\ell }_{pq}=0$
unless
![]() $k={\ell }$
and
$k={\ell }$
and
![]() $i=p,$
we have
$i=p,$
we have
 $$ \begin{align} r(T)\cdot{e^{\ell}_{pq}}=\sum_{k=1}^{n}\sum_{i=1}^{m_{k}}T(e^k_{i1})\cdot e^k_{1i}e^{\ell}_{pq}= T(e^{\ell}_{p1}) \cdot (e^{\ell}_{1p}e^{\ell}_{pq}) =T(e^{\ell}_{p1})\cdot {e}^{\ell}_{1q}. \end{align} $$
$$ \begin{align} r(T)\cdot{e^{\ell}_{pq}}=\sum_{k=1}^{n}\sum_{i=1}^{m_{k}}T(e^k_{i1})\cdot e^k_{1i}e^{\ell}_{pq}= T(e^{\ell}_{p1}) \cdot (e^{\ell}_{1p}e^{\ell}_{pq}) =T(e^{\ell}_{p1})\cdot {e}^{\ell}_{1q}. \end{align} $$
Comparing equations (5.2) and (5.3) gives us that r is an A-module map.
Let
![]() $x\in E$
. Then
$x\in E$
. Then
 $$\begin{align*}rs(x)= \sum_{k=1}^{n}\sum_{i=1}^{m_{k}}s(x)(e^k_{i1})\cdot e^k_{1i}=\sum_{k=1}^{n}\sum_{i=1}^{m_{k}}(x\cdot e^k_{i1})\cdot e^k_{1i} =\sum_{k=1}^{n}\sum_{i=1}^{m_{k}}x\cdot{e^k_{ii}} =x, \end{align*}$$
$$\begin{align*}rs(x)= \sum_{k=1}^{n}\sum_{i=1}^{m_{k}}s(x)(e^k_{i1})\cdot e^k_{1i}=\sum_{k=1}^{n}\sum_{i=1}^{m_{k}}(x\cdot e^k_{i1})\cdot e^k_{1i} =\sum_{k=1}^{n}\sum_{i=1}^{m_{k}}x\cdot{e^k_{ii}} =x, \end{align*}$$
so
![]() $rs=\mathrm {id}_{E}$
and all that remains is to show r is completely bounded.
$rs=\mathrm {id}_{E}$
and all that remains is to show r is completely bounded.
Note that for
![]() $T\in C\!B({A},\,{E}),$
$T\in C\!B({A},\,{E}),$
 $$\begin{align*}r(T)=\sum_{k=1}^{n}\sum_{i=1}^{m_{k}} r^k_{i}(T), \end{align*}$$
$$\begin{align*}r(T)=\sum_{k=1}^{n}\sum_{i=1}^{m_{k}} r^k_{i}(T), \end{align*}$$
where
![]() $r^k_{i}(T)$
is defined to be
$r^k_{i}(T)$
is defined to be
![]() $T(e^k_{i1})\cdot e^k_{1i}$
. Each
$T(e^k_{i1})\cdot e^k_{1i}$
. Each
![]() ${r^k_{i}}\colon {C\!B({A},\,{E})}\rightarrow {E}$
is a linear map. Hence, it suffices that each
${r^k_{i}}\colon {C\!B({A},\,{E})}\rightarrow {E}$
is a linear map. Hence, it suffices that each
![]() $r^k_{i}$
is completely bounded.
$r^k_{i}$
is completely bounded.
Let
![]() $k\in \{1,\ldots , n \}$
and
$k\in \{1,\ldots , n \}$
and
![]() $i\in \{1,\ldots , m_k\}$
. For each
$i\in \{1,\ldots , m_k\}$
. For each
![]() $N\in \mathbb {N}$
, let
$N\in \mathbb {N}$
, let
![]() $e_N\in M_N(A)$
be the matrix with
$e_N\in M_N(A)$
be the matrix with
![]() $e^k_{1i}$
as every entry in the leading diagonal and zero everywhere else. Note
$e^k_{1i}$
as every entry in the leading diagonal and zero everywhere else. Note
![]() $\lVert e_N\rVert _N=\lVert e^k_{1i}\rVert =1$
. For each
$\lVert e_N\rVert _N=\lVert e^k_{1i}\rVert =1$
. For each
![]() $T=[T_{vw}]\in M_N(C\!B({A},\,{E}))$
we have
$T=[T_{vw}]\in M_N(C\!B({A},\,{E}))$
we have
 $$\begin{align*}\bigl\lVert[(r^k_i)_N(T_{vw})]\bigr\rVert_N=\bigl\lVert[T_{vw}(e^k_{i1})\cdot e^k_{1i}]\bigr\rVert_N\leq\bigl\lVert[T_{vw}(e^k_{i1})]\bigr\rVert_N\,\lVert e_N\rVert_N \leq \lVert T\rVert_N\leq\lVert T\rVert_{\mathrm{cb}}. \end{align*}$$
$$\begin{align*}\bigl\lVert[(r^k_i)_N(T_{vw})]\bigr\rVert_N=\bigl\lVert[T_{vw}(e^k_{i1})\cdot e^k_{1i}]\bigr\rVert_N\leq\bigl\lVert[T_{vw}(e^k_{i1})]\bigr\rVert_N\,\lVert e_N\rVert_N \leq \lVert T\rVert_N\leq\lVert T\rVert_{\mathrm{cb}}. \end{align*}$$
So
![]() $r^k_i$
is completely contractive and r is completely bounded as required.▪
$r^k_i$
is completely contractive and r is completely bounded as required.▪
Corollary 5.12 Let A be a unital operator algebra. The following are equivalent.
-
(i)
 ${\mathrm {dg}_{cb}\,{A}}=0$
.
${\mathrm {dg}_{cb}\,{A}}=0$
. -
(ii) A is classically semisimple.
-
(iii) The global dimension of
 $({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}, {{\mathcal {E\!x}}_{rel}})$
is zero.
$({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}, {{\mathcal {E\!x}}_{rel}})$
is zero.
It is interesting to compare the relation between “global injectivity,” that is, injectivity with respect to the maximal exact structure and relative injectivity. To this end, we record the following general result which is part of the “injective version” of [Reference Bühler8, Proposition 11.3] where it is obtained for projective objects.
Lemma 5.13 Let
![]() $\mathcal {(A,{\mathcal {E\!x}})}$
be an exact category and
$\mathcal {(A,{\mathcal {E\!x}})}$
be an exact category and
![]() $\mathcal {M}$
be the class of admissible monomorphisms. Then
$\mathcal {M}$
be the class of admissible monomorphisms. Then
![]() $I\in \mathcal {A}$
is
$I\in \mathcal {A}$
is
![]() $\mathcal {M}$
-injective if and only if it is an absolute
$\mathcal {M}$
-injective if and only if it is an absolute
![]() $\mathcal {M}$
-retract, that is, for every
$\mathcal {M}$
-retract, that is, for every
![]() $\mu \in {\mathcal {M}}{({I},\,{F})}$
with
$\mu \in {\mathcal {M}}{({I},\,{F})}$
with
![]() $F\in \mathcal {A}$
there exists
$F\in \mathcal {A}$
there exists
![]() ${\nu }\in \mathrm {Mor}{({F},{I})}$
such that
${\nu }\in \mathrm {Mor}{({F},{I})}$
such that
![]() $\nu \mu =\mathrm {id}_{I}$
.
$\nu \mu =\mathrm {id}_{I}$
.
Proof That every
![]() $\mathcal {M}$
-injective is an absolute retract is immediate from the definition. Suppose
$\mathcal {M}$
-injective is an absolute retract is immediate from the definition. Suppose
![]() $I\in \mathcal {A}$
is an absolute
$I\in \mathcal {A}$
is an absolute
![]() $\mathcal {M}$
-retract and that
$\mathcal {M}$
-retract and that
![]() $E,F\in \mathcal {A}$
with morphisms
$E,F\in \mathcal {A}$
with morphisms
![]() $\mu \in {\mathcal {M}}{({E},\,{F})}$
and
$\mu \in {\mathcal {M}}{({E},\,{F})}$
and
![]() $f\in \mathrm {Mor}{({E},{I})}$
are given. By axiom [E2] of Definition 4.2, there exists a (commutative) pushout square:
$f\in \mathrm {Mor}{({E},{I})}$
are given. By axiom [E2] of Definition 4.2, there exists a (commutative) pushout square:

such that
![]() $\mu '\in {\mathcal {M}}{({I},\,{C})}.$
As I is an absolute
$\mu '\in {\mathcal {M}}{({I},\,{C})}.$
As I is an absolute
![]() $\mathcal {M}$
-retract, there exists
$\mathcal {M}$
-retract, there exists
![]() $\nu \in \mathrm {Mor}{({C},{I})}$
such that
$\nu \in \mathrm {Mor}{({C},{I})}$
such that
![]() $\nu \mu '=\mathrm {id}_{I}$
. Then
$\nu \mu '=\mathrm {id}_{I}$
. Then
![]() $\nu {g}\in \mathrm {Mor}{({F},{I})}$
with
$\nu {g}\in \mathrm {Mor}{({F},{I})}$
with
![]() $(\nu {g})\mu = \nu \mu 'f=f$
as required.▪
$(\nu {g})\mu = \nu \mu 'f=f$
as required.▪
The next result can also be obtained in the general setting; however, this would require to fix two categories and four exact structures. In order to avoid such unnecessary generality, we restrict our attention to the two categories of operator space modules,
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. We will suppress the formal forgetful functor from either of these categories to
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. We will suppress the formal forgetful functor from either of these categories to
![]() and simply consider the modules as operator spaces when needed. But it is essential to note that the morphisms in
and simply consider the modules as operator spaces when needed. But it is essential to note that the morphisms in
![]() are the completely bounded linear mappings and not the complete contractions. Therefore,
are the completely bounded linear mappings and not the complete contractions. Therefore,
![]() -injectivity is not what one usually calls “injective operator space.”
-injectivity is not what one usually calls “injective operator space.”
Let
![]() $\mathcal {A}$
denote either
$\mathcal {A}$
denote either
![]() ${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
or
${{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
or
![]() ${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
, for a unital operator algebra A. Since the morphisms, the (global) admissible monomorphisms, and the admissible monomorphisms in the relative structure are the same in both categories, we can simply talk about “injective object” and “relatively injective object” in
${{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
, for a unital operator algebra A. Since the morphisms, the (global) admissible monomorphisms, and the admissible monomorphisms in the relative structure are the same in both categories, we can simply talk about “injective object” and “relatively injective object” in
![]() $\mathcal {A}$
below.
$\mathcal {A}$
below.
Proposition 5.14 Let
![]() $E\in \mathcal {A}$
. Suppose E is relatively injective and
$E\in \mathcal {A}$
. Suppose E is relatively injective and
![]() -injective. Then E is injective.
-injective. Then E is injective.
Proof Take
![]() $\mu \in {\mathcal {M}}{({E},\,{F})}$
for some
$\mu \in {\mathcal {M}}{({E},\,{F})}$
for some
![]() $F\in \mathcal {A}$
. By the lemma above, we are done if there exists
$F\in \mathcal {A}$
. By the lemma above, we are done if there exists
![]() $\nu \in C\!B_{A}({F},\,{E})$
such that
$\nu \in C\!B_{A}({F},\,{E})$
such that
![]() $\nu \mu =\mathrm {id}_{E}$
. As
$\nu \mu =\mathrm {id}_{E}$
. As
![]() $\mu $
is an admissible monomorphism there exists a kernel-cokernel pair in
$\mu $
is an admissible monomorphism there exists a kernel-cokernel pair in
![]() ${{\mathcal {E\!x}}_{max}}$
:
${{\mathcal {E\!x}}_{max}}$
:

which gives a kernel-cokernel pair in
![]()

Since E is
![]() -injective, E is an absolute retract in
-injective, E is an absolute retract in
![]() (Lemma 5.13); hence there exists
(Lemma 5.13); hence there exists
![]() $\theta \in C\!B({F},\,{E})$
such that
$\theta \in C\!B({F},\,{E})$
such that
![]() $\theta \mu =\mathrm {id}_{E}$
. By the Splitting Lemma (Lemma 4.10),
$\theta \mu =\mathrm {id}_{E}$
. By the Splitting Lemma (Lemma 4.10),
![]() $(\mu ,\pi )\in {{\mathcal {E\!x}}_{min}}$
in
$(\mu ,\pi )\in {{\mathcal {E\!x}}_{min}}$
in
![]() , in (5.5) and therefore
, in (5.5) and therefore
![]() $(\mu ,\pi )\in {\mathcal {E\!x}}_{rel}$
in (5.4). In particular,
$(\mu ,\pi )\in {\mathcal {E\!x}}_{rel}$
in (5.4). In particular,
![]() $\mu \in {\mathcal {M}_{rel}}$
. As E is relatively injective, by the other implication in Lemma 5.13, there exists
$\mu \in {\mathcal {M}_{rel}}$
. As E is relatively injective, by the other implication in Lemma 5.13, there exists
![]() $\nu \in C\!B_{A}({F},\,{E})$
such that
$\nu \in C\!B_{A}({F},\,{E})$
such that
![]() $\nu \mu =\mathrm {id}_{E}$
as required so that E is injective in
$\nu \mu =\mathrm {id}_{E}$
as required so that E is injective in
![]() $\mathcal {A}$
.▪
$\mathcal {A}$
.▪
With the same caveats as above, we obtain a converse under an additional assumption.
Proposition 5.15 Suppose that, for every
![]() $E\in \mathcal {A}$
, there exists
$E\in \mathcal {A}$
, there exists
![]() $\mu \in C\!B_{A}({E},\,{J_E})$
for some
$\mu \in C\!B_{A}({E},\,{J_E})$
for some
![]() $J_E\in \mathcal {A}$
such that
$J_E\in \mathcal {A}$
such that
![]() $J_E$
is
$J_E$
is
![]() -injective. If
-injective. If
![]() $I\in \mathcal {A}$
is injective then I is relatively injective as well as
$I\in \mathcal {A}$
is injective then I is relatively injective as well as
![]() -injective.
-injective.
Proof Let
![]() $I\in \mathcal {A}$
be injective in
$I\in \mathcal {A}$
be injective in
![]() $\mathcal {A}$
; then it is clearly relatively injective. By assumption, there exist
$\mathcal {A}$
; then it is clearly relatively injective. By assumption, there exist
![]() $J_I\in \mathcal {A}$
which is
$J_I\in \mathcal {A}$
which is
-injective and a kernel cokernel pair in
![]() ${{\mathcal {E\!x}}_{max}}$
:
${{\mathcal {E\!x}}_{max}}$
:

By Lemma 5.13, there exists
![]() ${\nu }\in C\!B_{A}({J_I},\,{I})$
such that
${\nu }\in C\!B_{A}({J_I},\,{I})$
such that
![]() $\nu \mu =\mathrm {id}_{I}$
. This identity persists in
$\nu \mu =\mathrm {id}_{I}$
. This identity persists in
so that I is a retract of the
-injective operator space
![]() $J_I$
. Hence I is injective in
$J_I$
. Hence I is injective in
too.▪
For clarity, we formulate the individual statements for the two categories involved separately.
Corollary 5.16 Let A be a unital operator algebra and
![]() $E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Then E is
$E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Then E is
![]() ${{\mathcal {E\!x}}_{max}}$
-injective in
${{\mathcal {E\!x}}_{max}}$
-injective in
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
if and only if E is
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
if and only if E is
![]() ${{\mathcal {E\!x}}_{max}}$
-injective in
${{\mathcal {E\!x}}_{max}}$
-injective in
![]() and
and
![]() ${{\mathcal {E\!x}}_{rel}}$
-injective in
${{\mathcal {E\!x}}_{rel}}$
-injective in
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
.
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
.
The “if”-part follows directly from Proposition 5.14 and the “only if”-part follows from Proposition 5.15 together with the CES theorem [Reference Blecher and Le Merdy6, Theorem 3.3.1]: for every
![]() $E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
there exists a Hilbert space H such that
$E\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
there exists a Hilbert space H such that
![]() $B(H)\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and E is a closed submodule of
$B(H)\in {{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}}$
and E is a closed submodule of
![]() $B(H)$
. The fact that
$B(H)$
. The fact that
![]() $B(H)$
is the prototypical injective operator space finished the argument.
$B(H)$
is the prototypical injective operator space finished the argument.
This result was obtained for C*-algebras in [Reference Rosbotham28, Proposition 5.11]. For
![]() $E=A$
a unital C*-algebra, the “if”-part is also given by [Reference Frank and Paulsen14, Theorem 3.5].
$E=A$
a unital C*-algebra, the “if”-part is also given by [Reference Frank and Paulsen14, Theorem 3.5].
The next result implies [Reference Crann10, Proposition 2.3], without the estimate on the constants which are irrelevant in the completely bounded category. It follows straight from Proposition 5.14.
Corollary 5.17 Let A be a unital operator algebra and
![]() $E\in {{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Then E is
$E\in {{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}}$
. Then E is
![]() ${{\mathcal {E\!x}}_{max}}$
-injective in
${{\mathcal {E\!x}}_{max}}$
-injective in
![]() $({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
if E is
$({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
if E is
![]() ${{\mathcal {E\!x}}_{max}}$
-injective in
${{\mathcal {E\!x}}_{max}}$
-injective in
![]() and
and
![]() ${{\mathcal {E\!x}}_{rel}}$
-injective in
${{\mathcal {E\!x}}_{rel}}$
-injective in
![]() $({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
.
$({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{rel}})$
.
The converse direction, however, fails in general: by the operator algebra version of [Reference Rosbotham29, Corollary 4.11],
![]() $C\!B({A},\,{G})$
is always
$C\!B({A},\,{G})$
is always
![]() ${{\mathcal {E\!x}}_{max}}$
-injective for an injective operator space G and thus automatically
${{\mathcal {E\!x}}_{max}}$
-injective for an injective operator space G and thus automatically
![]() ${{\mathcal {E\!x}}_{rel}}$
-injective. So we can choose for A a C*-algebra whose dual
${{\mathcal {E\!x}}_{rel}}$
-injective. So we can choose for A a C*-algebra whose dual
![]() $A^*=C\!B({A},\,{{\mathbb {C}}})$
is not injective in
$A^*=C\!B({A},\,{{\mathbb {C}}})$
is not injective in
![]() . An example using the (completely contractive) Fourier–Stieltjes algebra
. An example using the (completely contractive) Fourier–Stieltjes algebra
![]() $B(\Gamma )$
for a non-amenable discrete group
$B(\Gamma )$
for a non-amenable discrete group
![]() $\Gamma $
is discussed in [Reference Crann10, p. 1068]; there,
$\Gamma $
is discussed in [Reference Crann10, p. 1068]; there,
![]() $E=C^*(\Gamma )^{**}=C\!B({B(\Gamma )},\,{{\mathbb {C}}})$
.
$E=C^*(\Gamma )^{**}=C\!B({B(\Gamma )},\,{{\mathbb {C}}})$
.
Considered as a
![]() $C^*(\Gamma )$
-module on the other hand,
$C^*(\Gamma )$
-module on the other hand,
![]() $C^*(\Gamma )^{**}$
is not injective in
$C^*(\Gamma )^{**}$
is not injective in
 ${\mathcal {O\!M\!o\!d}^{\infty }_{{C^*(\Gamma )}}}$
by [Reference Frank and Paulsen14, Theorem 3.4]. This reveals a subtle difference between the two operator space module categories.
${\mathcal {O\!M\!o\!d}^{\infty }_{{C^*(\Gamma )}}}$
by [Reference Frank and Paulsen14, Theorem 3.4]. This reveals a subtle difference between the two operator space module categories.
The above results help to understand the issue of the existence of enough injectives in our module categories; that is, for each
![]() $E\in \mathcal {A}$
, do there exist
$E\in \mathcal {A}$
, do there exist
![]() $I\in \mathcal {A}$
injective and
$I\in \mathcal {A}$
injective and
![]() $\mu \in {\mathcal {M}}(E,I)$
? When A is a C*-algebra,
$\mu \in {\mathcal {M}}(E,I)$
? When A is a C*-algebra,
![]() $B(H)$
supplies
$B(H)$
supplies
![]() $({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
with enough injectives, however it loses its role when A is a general operator algebra [Reference Smith31, Example 3.5] and in fact, the question seems to be open. For C*-algebras, [Reference Rosbotham29, Proposition 4.13] answers the question affirmatively for
$({{\mathcal {O\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
with enough injectives, however it loses its role when A is a general operator algebra [Reference Smith31, Example 3.5] and in fact, the question seems to be open. For C*-algebras, [Reference Rosbotham29, Proposition 4.13] answers the question affirmatively for
![]() $({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
, and the argument extends to general (unital) operator algebras. The question remains unresolved for either of the two categories with the relative structure
$({{\mathcal {m\!n\!M\!o\!d}^{\infty }_{{\!A}}}},{{\mathcal {E\!x}}_{max}})$
, and the argument extends to general (unital) operator algebras. The question remains unresolved for either of the two categories with the relative structure
![]() ${{\mathcal {E\!x}}_{rel}}$
. The expectation seems to be that it fails, compare [Reference Aristov2] and [Reference Aristov3], for example. By the above corollaries, a module which is not injective in
${{\mathcal {E\!x}}_{rel}}$
. The expectation seems to be that it fails, compare [Reference Aristov2] and [Reference Aristov3], for example. By the above corollaries, a module which is not injective in
![]() cannot be embedded into a module which is injective in
cannot be embedded into a module which is injective in
![]() ${{\mathcal {E\!x}}_{max}}$
which restricts the possible choices to modules which are only
${{\mathcal {E\!x}}_{max}}$
which restricts the possible choices to modules which are only
![]() ${{\mathcal {E\!x}}_{rel}}$
-injective and not injective in
${{\mathcal {E\!x}}_{rel}}$
-injective and not injective in
![]() ${{\mathcal {E\!x}}_{max}}$
nor in
${{\mathcal {E\!x}}_{max}}$
nor in
![]() .
.
Acknowledgment
The authors thank the anonymous referee for carefully reading our manuscript and some useful comments which improved the exposition of the paper.





