1. Introduction
Mountain glaciers play an important role in local hydrological processes, so it is worth knowing how mass balance varies with changes in parameters such as surface conditions and climate. Many hydroelectric stations have been established or are planned in the Himalayan region, where the main source of water is glacier meltwater and snowmelt runoff from glacierized basins; the former is closely related to summer mass balance. In order to predict possible changes in mass balance, and to assess the long-term availability of water, it is necessary to study the sensitivity of glacier mass balance to climatic parameters.
There have been a number of studies on the relationship between mass balance and climate. Reference Ageta, Ohata, Tanaka, lkegami and HiguchiAgeta and others (1980), in a study of summer mass balance in the Nepalese Himalaya, established an empirical relation between ablation and air temperature. Reference Kuhn and OerlemansKuhn (1989) expanded the number of variables, formulating mass balance in terms of seasonal values of accumulation, radiation balance, air temperature and humidity. Reference Oerlemans and HoogendoornOerlemans and Hoogendoorn (1989) developed an altitude-dependent mass-balance model which was based on the energy balance of the ice or snow surface; precipitation was included in a parameterized form, and the slope and exposure of the ice or snow surface were taken into account. Reference Braithwaite and OlesenBraithwaite and Olesen (1990) calculated ablation on two outlet glaciers from the Greenland ice sheet by a simple energy-balance model which used climate data. Reference OerlemansOerlemans (1993) presented a model for the mass balance of glaciers in the Alps based on the energy balance at the surface; the various fluxes were parameterized in such a way that altitudinal dependence was taken into account. Reference MunroMunro (1991) used a surface energy-exchange model of glacier melt and net mass balance to simulate ablation and net mass balance on Peyto Glacier, Canada. Reference Arnold, Willis, Sharp, Richards and LawsonArnold and others (1996) developed and tested a surface energy-balance model to calculate rates of surface melting on a glacier in Switzerland, using a digital elevation model of the glacier surface and surrounding topography together with meteorological data from a site in front of the glacier. They determined hourly or daily energy-balance components and calculated melting over the entire glacier surface with a spatial resolution of 20 m. Models such as these, which use surface energy-balance concepts to calculate ablation, have not been applied to Himalayan glaciers previously.
Climatic conditions in the Himalaya are different from those of other regions. Himalayan glaciers are located in a monsoon area, and most annual accumulation occurs in summer. Reference Ageta and HiguchiAgeta and Higuchi (1984) referred to them as "the summer-accumulation type". Variations in air temperature and relative humidity are high at the beginning and at the end of the summer monsoon season, and incoming solar radiation is quite high throughout the season, despite the extensive cloud cover.
Radiation is the dominant component of the heat balance in the Himalaya (Reference Ohata and HiguchiOhata and Higuchi, 1980). Therefore, special attention must be given to the parameters and processes which influence radiation. For example:
-
(1) Glaciers in the Himalaya have a wide range of surface albedo due to the presence of dirt on the surface.
-
(2) When new snow falls, the albedo of the underlying surface affects the surface albedo if the layer of new snow is thin. Usually, the effective albedo of thin new-snow layers is less than that of the thicker snow layers (Reference Ohata and HiguchiOhata and others, 1980).
-
(3) Mountain walls have an appreciable screening effect on shortwave radiation owing to the high relief of Himalayan topography. The intensity of downward longwave radiation, from both the atmosphere and mountain walls, also depends on the surrounding topography.
-
(4) Shortwave radiation is reflected between the glacier surface and clouds; thus on small glaciers, whose size is comparable to the cloud height, global radiation depends on the size of the glacier (Reference OhataOhata, 1991).
The main objective of this paper is to formulate a mass-balance model to study the characteristics of a small glacier in the Himalaya. First, an energy-balance model is used to calculate ablation, using meteorological parameters to drive the model. A unique aspect of the model is the classification of snow into three types - new, old and dirty to specify the condition, and hence albedo, of the glacier surface. In addition, processes (2) to (4) described above are considered in the model. Second, the sensitivity of glacier mass balance to input parameters and to the various processes is tested. Third, the sensitivity of the mass balance to climatic parameters (driving parameters) is also tested.
Although the lower parts of large glaciers in the Himalaya are typically covered with thick debris layers, the present model does not include the effect of this debris. The model is applied to Glacier AX010 (Fig. 1), a small glacier where detailed glaciological and meteorological observations were carried out in 1978. As a typical debris-free glacier in the eastern Nepalese Himalaya, this glacier has been chosen for long-term study.

Fig. 1. Glacier AXO1O, Shorong Himal, Nepal. SH is the location of the Shorong area.
2. A Model for Glacier Mass Balance
The structure of the model to calculate the specific surface mass balance is shown in Figure 2.

Fig. 2. Structure of the model.
The energy available for melting is calculated using the energy-balance concept and measured or observed meteorological parameters and surface conditions. It is assumed that all rain and meltwater runs off, as significant amounts of superimposed ice were not observed on the glacier to which the model is applied (Reference Ageta, Ohata, Tanaka, lkegami and HiguchiAgeta and others, 1980). This is because ice temperatures are not cold enough to freeze percolating water. The effect of percolation on snow density and on albedo is not calculated in the model, but the effect is incorporated by parameterizing the surface conditions, as described later.
2.1. Surface energy balance
The basic energy-balance equation employed is:
where QM is the energy used for melting snow and ice, K* is the net shortwave-radiation flux, L* is the net longwave-radiation flux Qs is the sensible-heat flux, QL is the latent-heat flux and Q G is the heat conduction at the glacier surface. Heat transport by precipitation is assumed to be negligible. Incoming energy is taken as positive, and outgoing as negative.
(a) Shortware-radiation flux
The net shortwave-radiation flux, K*, is calculated as:
where G is the global radiation (W m-2 ) and α is the surface albedo.
Field observations at Glacier AX010 have shown that the presence of even a thin snow layer during the ablation season has an important effect on albedo. This was taken into account using a relationship similar to that used by Reference Ohata and HiguchiOhata and others (1980) relating the depth of new snow to the albedo of the underlying surface:

where α(d) is the surface albedo when the thickness of new snow is d in meters, αs is the albedo of new snow, and αb is the observed albedo of the underlying surface before the snowfall. Based on measurements, the albedo of new snow is assumed to be 0.69 when the thickness exceeds 0.02 m. Since the effect of such thin snow layers is most pronounced on the lower part of the glacier, and most new snow melts within a few days, the change from new snow into old snow is not considered.
In the presence of clouds, high-albedo snow and ice surfaces intensify the effect of multiple reflections between the surface and the clouds. This leads to higher values of K* than would be predicted solely from the fraction of shortwave solar radiation penetrating the cloud cover and the surface albedo. Because meteorological parameters are frequently observed close to the ground near the glacier, where measurements can be monitored easily, it is necessary to consider the effect of such multiple reflections when calculating the solar-radiation input to the glacier surface. According to Reference OhataOhata (1991), the global radiation, GR , observed at a reference point on the ground can be converted to global radiation, Gp, at a point on the glacier, taking into consideration the multiple-reflection effect and assuming the same cloud parameters at both points, by the following relation:

where γ is the reflectance of the clouds, c is the decimal cloud cover, and αP and αR are the areal albedo of the point on the glacier and of the reference point, respectively. In the simulation, the height of the cloud base is assumed to be 200 m due to the high elevation of the glacier surface. Similarly, the area influenced by the cloud reflectance is taken to be an area whose diameter is twice the height of the cloud base (400 m). The reflectance of the clouds is taken as 0.62, based on an average value for cumulonimbus and cirrus clouds (Reference Reynolds, vonder Haar and CoxReynolds and others, 1975).
(b) Longwave-radiation flux
The longwave radiation emitted from the snow surface, L↑, can be calculated from the Stefan-Boltzmann law:
where σs is the Stefan-Boltzmann constant (5.67 x 10-8 W m-2K-4), Ts is the surface temperature (K), and εs is surface emissivity, which was assumed to be unity.
The downward longwave radiation under clear skies, L↓0 is calculated from:
(Reference Kuz'min.Kuz'min, 1961) where Ta is the air temperature (K) and ea is the vapor pressure of the air (Pa).
In a valley, radiation from the atmosphere is reduced wherever part of the sky is obscured by the valley walls. However, the valley floor will receive longwave radiation from the valley walls in an amount governed by a form of Equation (5). Reference Marks, Colbeck and RayMarks (1979) considered this effect by using a thermal-view factor, Vf . The fraction of the hemisphere which is obscured by the valley walls is determined from elevations of the surrounding terrain. The un -obscured part is termed the thermal-view factor, and is expressed as a number between 0 and 1, thus:
(Reference LeeLee, 1962) where H is the average horizon angle measured from the zenith.
Thus, in mountainous areas the longwave radiation incident at a point under clear skies, including the topographic effect, L↓, is given by:
The second term on the right side of Equation (8) is the contribution from the valley sides in which the temperature of the valley sides is assumed to be the same as the air temperature.
Clouds have a strong influence on longwave-radiation exchange because they are almost perfect radiators. The most common approach to estimating the effect of clouds upon the net longwave radiation is to modify the cloudless-sky value by a non-linear cloud term. Thus, the net longwave radiation under cloudy skies, L* is given by:
where C is the decimal cloud cover assuming a fog-type cloud (Reference OkeOke, 1987).
(c) Sensible-heat flux
Sensible-heat flux,Qs, is determined from:
where ρa is the density of air, C p is the specific heat of air at constant pressure, and Ds, is the turbulent-transfer coefficient under stable conditions (assumed here to be the same for transfer of either heat or water vapor).
The turbulent-transfer coefficient under stable conditions over snow is obtained by converting the turbulent-transfer coefficient for neutral-stability conditions to that for stable conditions using the bulk Richardson number, Ri. For neutral-stability conditions (in which buoyancy effects are absent) in the boundary layer, the turbulent-transfer coefficient, Du , is given by:

where k is the von Kármán constant (0.41), u is the wind speed (m s-1), z is the measurement level above the snow or ice surface, and zo is the aerodynamic-roughness length. Ds is then calculated from:
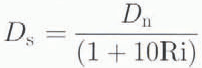
(Reference BraunBraun,1985) where the Ri is calculated from:

where g is the acceleration due to gravity (9.8 m s-2).
(d) Latent-heat flux
The latent-heat flux QL is determined using:
where L is the latent heat of evaporation (2.5 x 106J kg-1), qa is the specific humidity of air at measurement level z, and qs is the specific humidity at the snow surface. The term (Q>a -Qs) is given by:
where p is atmospheric pressure, e a is vapor pressure of the air, and es is the saturation vapor pressure at the snow surface (all in 103Pa).
ea is calculated from the saturation vapor pressure over a plane surface of pure water using the Goff—Gratch formulation (Reference ListList, 1971) and the prevailing relative humidity. es is assumed to be the same as the saturation vapor pressure over a plane surface of pure water at surface temperature Ts .
(e) Heat conduction
Assuming no meltwater percolation, heat conduction into the glacier from the surface, QG is calculated from:
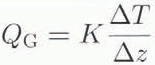
where K* is the thermal conductivity of snow (Wm-1 K-1) and ΔT/Δz is the temperature gradient. The temperature profile from the surface to ten different points (0.02 m, 0.04 m, 0.08 m, 0,16 m... 10.24 m) vertically below the surface is calculated with the thermodynamic energy equation:

where ρ is the density of snow or ice (kg m-3 ), t is time and cp is the specific heat capacity of ice (2009 J kg-1 K-1). Equation (17) is integrated numerically. The change in surface temperature is assumed to be due only to heal conduction (through the snow or ice normal to the surface).
The thermal conductivity, K, is calculated from:
2.2. Mass balance
Based on the algebraic sum of the individual surface energy-balance components and solid precipitation, Ps , the mass balance, MB, is calculated from:
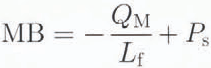
where Lf is the latent heat of fusion (3.34 x 105 J kg-1 ).
2.3. Calculation procedure
The model calculates the energy available for melting snow or ice, QM , every hour from Equation (1) using an iteration method. The energy-balance calculations are performed using hourly meteorological data with initial surface conditions (Fig. 3), and the initial surface snow temperature (269.5 K) based on observations and measurements on 25 May 1978. Because heat conduction is effective only near the glacier surface, it is calculated between the snow or ice surface and 0.02 m below the surface every 5 min, and summed up every hour. The model calculates the surface temperature, which balances the right hand side of Equation (1): if the surface temperature is below 0°C, QM is taken as zero. If the surface temperature rises above 0°C, the excess heat calculated by fixing the surface temperature at 0°C is taken as QM . This QM is used to calculate the amount of ablation. At the end of a 1 hour calculation, the resulting surface-snow or ice temperature is used to begin the next iteration.

Fig. 3. Initial snow and ice conditions at various points on Glacier AX010 on 25 May 1978. The altitude and the area represented by each point are shown.
If the calculated mass balance indicates that all snow has melted and ice has appeared, the values of the surface albedo, density and roughness length are altered to reflect those of ice (Table 1). If more than 0.02 m of new snow is added to the surface, the values assigned to these parameters are those of new snow, and the calculation for the next hour begins with these new values together with the appropriate meteorological and surface parameters. As mentioned above, intermediate values are assigned if the depth of new snow is less than 0.02 m. This process of calculation continues for all hours of the day every day.

Table 1. Values of density and thermodynamic parameters for the various snow and ice types used in the simulation (the values are based on observations)
3. Application of the Model
3.1. Description of the glacier
As noted, the model has been applied to Glacier AX010 (Fig. 1), a small mountain glacier of the summer-accumulation type in Shorong Himal, east Nepal, using meteorological and other observations from the Japan-Nepal Joint Glaciological Expedition in Nepal during the 1978 summer monsoon season. The highest and lowest elevations on the glacier in 1978 were 5360 and 4950 m a.s.l., respectively, the centerline length was 1.7 km and the area was 0.57 km2. The glacier ends at a pond. The altitude of the meteorological station near the base camp, BC (beside the pond), was 4958 m a.s.l. Seven points on the glacier were considered for the model test, namely L10, L30, L50, L70, L100, U10 and U30 (Fig. 1), as stake observation data and initial snow-depths were known for these points. The altitude and area represented by each point are shown in Figure 3, along with the initial snow and ice conditions.
The average air temperature, relative humidity and wind speed were 2.3°C, 88% and 1.5 ms -1, respectively, and total precipitation was 1453 mm during the observation period, which lasted from 25 May to 25 September 1978.
3.2. Input data
3.2.1. Meteorological data
The hourly air temperature, Ta. observed at the meteorological station, is used in the simulation. A lapse rate of 0.6 °C/ 100 m ( Reference Ageta, Ohata, Tanaka, lkegami and HiguchiAgeta and others, 1980) is used for estimating temperatures at higher altitudes.
Global radiation, GL50, was measured from 14 to 29 June 1978 near L50 for a heat-balance study (Reference Ohata, Ikegami and HiguchiOhata and others, 1980). Since GL50 is more representative of the glacier as a whole, it is compared with global radiation measured at the meteorological station, GMS, collected from 25 May to 25 September 1978, in order to adjust for areal variations in global radiation due to the surrounding topography. By comparing these two datasets, the following relation is obtained for 14-29 June:
The estimate of global radiation obtained is used for positions up to L50 for the whole observation period. Because global radiation at higher elevations may increase due to high areal albedo, GL50 is substituted for GR in Equation (4) to estimate GP for points higher than L50.
Precipitation at high altitudes occurs both in solid (snow, snow flakes, snow-grains, snow pellets and ice pellets) and liquid (rain, drizzle) phases, and mixtures. The type of precipitation observed hourly is used to obtain a relationship between air temperature and relative humidity so as to distinguish snow from liquid precipitation. From the relation used in the model, it was found, for example, that at an air temperature of 2°G and 90% relative humidity, 62% of the precipitation was snow.
Hourly values of relative humidity, wind speed, precipitation and cloud cover, interpolated from observed data obtained at 3 and 4 hour intervals at the meteorological station, are used in the model. As the basin is small, it is assumed that relative humidity and wind speed do not vary across the basin. As shown by Reference Ageta, Ohata, Tanaka, lkegami and HiguchiAgeta and others (1980), there-was almost no variation in precipitation with altitude, and hence precipitation for the whole glacier is well represented by values from the meteorological station.
3.2.2. Surface conditions
The initial surface conditions (Fig. 3), as defined by the relative amounts of new snow, old snow, dirty snow, and ice, changed as a result of continuing accumulation and ablation. Snow that existed on the glacier surface at the beginning of the model calculation is classed as old snow. The observed surface composition at L10 changed to ice after 16 July, following the melting of all old and dirty snow layers, and at L50 after 1 June following the melting of a layer of old snow. Thereafter until 10 September, the ice at L10 and L50 was frequently covered by new snow which, however, melted quickly. The surface was covered by new snow continuously after 10 September. At U30, the observed surface composition was dirty snow from 29 May, except for frequent periods of new snow, and was new snow continuously after 15 August. Surface parameters for different snow and ice types used in the simulation are shown In Table 1. These parameters were measured at or near the seven points on the glacier. The density of ice was assumed to be 850 kg m-3. (Reference Kadota, Fujita, Scko, Kayastha and AgetaKadota and others, 1997). Roughness length and albedo were based on the values used in Reference Ohata and HiguchiOhata and Higuchi (1980) and Reference Ohata, Ikegami and HiguchiOhata and others (1980), respectively.
4. Results
The model was run from 25 May to 25 September 1978, as meteorological data are available for this period. A comparison with observed mass balance was done from 10 June to 24 September 1978, the dates on which field measurements were made. Calculated values of the energy-balance components are shown in Table 2, and calculated energy fluxes at L10, L50 and U30 are shown in Figure 4. From Table 2, it is clear that net radiation is the main energy source for melting. The contribution of sensible heat and latent heat is small in comparison. The latent-heat flux at U30 is negative because evaporation exceeded condensation at the beginning of the calculation period. This is a result of low precipitation and high air temperature.

Fig. 4. Variation in calculated energy fluxes at U30, L50 and L1O on Glacier AXO10, 25 May-25 September 1978.

Table 2. Calculated total values (Wm-2) of energy-balance components at three points on Glacier AX010, 25 May-25 September 1978 (124 days). Values in parentheses show the percentage of each component in the total energy income
A heat-balance study was carried out on the glacier near L50 from 14 to 29 June 1978 by Reference Ohata and HiguchiOhata and Higuchi (1980), Excluding the values on 21 and 24 June due to insufficient data, their results indicate that the total melt calculated from the model during this period is more than twice the actual amount. The main cause for this discrepancy is that the surface albedo calculated by the model is low compared with albedo measured between 14 and 29 June 1978.
Because surface-elevation data at L10, L50 and U30 are available for the entire observation period, observed and calculated surface-elevation changes at these three points were compared (Fig. 5). At U30, the calculated surface elevation is considerably lower than that observed during the first 2 months. It then becomes higher during most of the second 2 months. The changes in the surface elevation at L10 and L50 also show this trend, but not as noticeably. The overestimate of the energy balance by the model due to the low surface albedo during the first half of the season and the lower input of shortwave radiation, especially at U30 and L50 compared to L10, in the second half (Fig. 4) presumably contributed to these results.

Fig. 5. Observed and calculated surface-elevation changes at U30, L50 and L10 on Glacier AX010 in 1978.
Values of mean daily calculated and observed (Reference Ageta, Ohata, Tanaka, lkegami and HiguchiAgeta and others, 1980) mass balance, averaged over periods of 15 days, are plotted in Figure 6. There is some scatter, but the overall correlation coefficient is 0.77. The différence (df= b-b*) between observed (b) and calculated (b*) mass balance is calculated, as statistics involving df are a useful check on the accuracy of the model. The mean error is found to be -0.1 x 10-3 m w.e.d-1 with a standard deviation of 5.1 x 10-3 m w.e. d-1. The most likely sources of error are: (a) errors in the relation used to separate snow and rain during precipitation events; (b) neglect of the small variations with altitude of precipitation that do exist, and the variations with altitude of meltwater percolation and heat transfer due to rainfall; (c) generalization of values of surface parameters averaged from an inadequate number of samples; and (d) extrapolation of meteorological data observed at the base camp to distant sites (note in Figure 5 that errors increase from L10 to U30). However, the overall result of the model is good. The above errors, for example, are smaller than those found by Reference Braithwaite and OlesenBraithwaite and Olesen (1990) for ablation on two outlet glaciers of the Greenland ice sheet, Qamanarssup sermia (21 months) and Nordbogletscher (14 months), errors -1.3x10-3 and 1.1x10-3 m w.e. d-l, respectively. However, the above standard deviation is higher than at Nordbogletscher (±3 x 10-3 m w.e. d-1) but lower than at Qamanarssup sermia (±7.0x10-3m w.e. d-1 ). Such differences are probably a consequence, at least in part, of differences in. sample size and duration.

Fig. 6. Observed and calculated mean daily mass balance at L10, L50 and U30 for each half-month from 10 June-24 September 1978.
The area-averaged mass balance of the whole glacier from 10 June to 24 September 1978 was derived from observations at 32 stakes (Reference Ageta, Ohata, Tanaka, lkegami and HiguchiAgeta and others, 1980). This value was compared with that calculated by the model at the seven points mentioned over the same time-span. The calculated and the observed values were in good agreement, namely -0.44 and 0.46 m w.e., respectively.
5. Sensitivity Tests of Input Parameters and Processes
Tests of the sensitivity of the glacier mass balance to the input parameters were performed by changing values of the thermodynamic parameters through a range of 10% of the difference between the maximum and minimum observed values, except for roughness length, which was changed 25%. In the case of global radiation, in one test the value measured at the meteorological observation site was used directly rather than adjusted it for elevation. Other meteorological parameters were the same as in the model run described above. In one test, the multiple-reflection effect was circumvented by setting α p =αR in order to study the importance of this effect. The test run with a cloud reflectance of 0.66 represents a condition with developed cumulus cloud rather than the combination of cumulonimbus and cirrus clouds used in the standard model. Test runs without the screening and thin-snow effects were also carried out.
In all of these sensitivity tests, it was found that, intuitively, the dependence is reasonable; no unusual model behavior was detected. Some important results are listed in Table 3.

Table 3. Results of sensitivity analyses of the model. The mass balance was calculated from 25 May to 25 September 1978 as an area-average for the Whole glacier
The mass balance is more sensitive to changes in the amount of dirty snow and in albedo than to changes in the amount of old snow, in density, and in roughness length. This is because surface albedo has a strong effect on net radiation, which is the most important contributor to melting. Density and roughness length do not affect the mass balance appreciably because their effect appears only in the heat conduction, and sensible- and latent-heat fluxes, respectively. These heat fluxes make relatively small contributions to the total energy available for melting, compared with the net radiation (Table 2).
The processes which affect or depend upon the surface albedo—thin layers of snow over the ice, multiple reflection, and screening of the mountain walls—play a significant role in the mass-balance sensitivity. Screening by mountain walls has a stronger influence on the receipt of shortwave than longwave radiation. Therefore, the strong influence of global radiation on mass balance is due to the areal variation of the screening effect and to the multiple-reflection effect. Screening of longwave radiation and variations in cloud types, and hence reflectance, have less influence on the mass balance.
6. Sensitivity Tests of Climatic Parameters
Tests of the sensitivity of the mass balance to changes in air temperature, precipitation and relative humidity from 1978 conditions were also performed. The standard deviations (σ) from 20-25 years' climatic data, collected in Kathmandu (1336 m a.s.1.) about 120 km west of the study area, are used to constrain the range of reasonable variations, as long-term data from glacier areas are lacking. Summer mean (June-September) air temperature and summer total precipitation in Kathmandu for 25 years (1962-86) were found to be 23.4°C and 1068 mm, respectively. Similarly, the 20 year (1967—86) mean summer relative humidity in Kathmandu was 82%.The average air temperature and relative humidity in Kathmandu in 1978 were 23.4°C and 81 %, respectively, and the summer total precipitation was 1175 mm. Thus, summer mean temperature and relative humidity in 1978 are very similar to the long-term mean values, but total precipitation was about 100 mm higher than the long-term mean. The standard deviations of the long-term air-temperature, precipitation and relative humidity values are 0.4°C, 13% and 2%, respectively. Sensitivity tests were carried out for ± 1σ and ± 2σ from the values observed in 1978. The results are plotted in Figure 7.

Fig. 7. Response of glacier mass balance to changes in air temperature, precipitation and relative humidity on Glacier AX010, from conditions during summer 1978 (25 May—25 September).
A 0.8°C increase in summer air temperature decreases the mass balance by 0.80m w.e. compared to 1978, and a decrease in summer air temperature by 0.8° C increases the mass balance by 0.60 m w.e. Similarly, the mass balance increases by 0.40 m w.e. when precipitation increases by 26%, and decreases by 0.51 m w.e. when the precipitation decreases by 26%. The glacier mass balance is more sensitive to air temperature because temperature has a strong influence on glacier melting and also controls the phase of precipitation (snow or rain). Thus, an increase in temperature decreases accumulation due to the decrease in snowfall during a precipitation event, and also intensities ablation by lowering albedo due to the decrease in the quantity of new snow. The mass balance is also sensitive to precipitation through its effect on albedo as well as on accumulation. Relative humidity affects the longwave radiation and phase of precipitation, but the sensitivity is low in comparison with that of air temperature and precipitation.
Reference KuhnKuhn's (1981) perturbation theory can be applied to this glacier, and the results compared with those of the model. The calculations are carried out with altitudinal gradients of net radiation -0.08 Wm2 m-1 and heat-transfer coefficient 2.1 Wm -2° C-1, and without any precipitation gradient from 25 May to 25 September 1978 (124 days). The values at L10, L50 and U30 were used to calculate the net-radiation gradient and heat-transfer coefficient. The results show that the equilibrium line rises by 100 m if the radiation balance increases by 9.3 W m -2, the accumulation decreases by 300 mm or the air temperature increases by 4.5°C .For comparison, Kuhn's model predicts a similar increase in equilibrium-line altitude if the radiation balance increases by 15.4 W m-2, the annual accumulation decreases by 400 mm, or the free air temperature increases by 0.8°C. The largest discrepancies between these results arc in the values for radiation balance and air temperature. This is probably due to the negative net-radiation gradient and low heat-transfer coefficient on this glacier. Although the radiation receipt at lower altitudes is lower than at higher altitudes due to topographic effects, the negative net-radiation gradient is due to the strong absorption of shortwave radiation on the low-albedo ice surfaces at lower altitudes. Another reason may be that several years of data are used in Kuhn's study, but only data from one season are available in the present one. The probability of the occurrence of such fluctuations can be assessed by comparing their magnitude to the long-term variance of seasonal means. Based on the data from Kathmandu, it seems that such fluctuations are unlikely.
7. Conclusions
We have formulated a mass-balance model based on a surface energy balance to calculate spatial and temporal variations of energy-balance components, and hence ablation, over a glacier and successfully applied the model to a small glacier in the Nepalese Himalaya. The model treats shortwave as well as longwave radiation in detail. Surface albedo is calculated internally by programming the model to take into account the effect of thin snow layers on the effective albedo of ice and dirty snow. The screening effect of surrounding mountain walls on the shortwave as well as longwave radiation, and the effect of multiple reflection are also accounted for in the model. A relationship between air temperature and relative humidity is used to distinguish snow from liquid precipitation during precipitation events.
Modelled and observed surface-elevation changes at different altitudes on Glacier AX010 agree well, as does the summer 1978 specific mass balance for the entire ablation season. Discrepancies are largest at the beginning of the season (June) when thin snow layers frequently covered the ice or dirty snow. Heat-balance modelling for this period needs to be improved.
The mass balance is found to be most sensitive to the areal variation of global radiation, multiple-reflection effects, snow or ice albedo and the thin-snow effect. The areal variation in the multiple-reflection and the thin-snow effect is due to processes related to surface albedo. In other words, mass balance is most sensitive to global radiation and surface albedo (cf. Reference Arnold, Willis, Sharp, Richards and LawsonArnold and others, 1996). This is because both have a strong influence on radiation, which dominates the ablation energy. Consideration of effects of thin snow-layers and screening of surrounding mountain walls improved the model output significantly. The results of tests of sensitivity to climatic parameters show that the mass balance is quite sensitive to air temperature and precipitation, but only weakly sensitive to relative humidity.
The model, based on well-established physical laws, can be used to study the sensitivity of the glacier mass balance to climatic perturbations. Such studies will elucidate similarities and differences between the glaciers in the Himalaya and other regions. Such a model can also be a tool for studying degree-day models and other empirical relations used to calculate ablation on the Himalayan glaciers. The model described in this paper does not take into account altitudinal variations in precipitation and formation of superimposed ice due to refreezing of percolated meltwater. These processes might need to be included when applying the model to other glaciers. It would also be good to have several years of observational data to validate the results of such a model. This might allow development of a simpler, but still reasonably accurate, model for calculating ablation on Himalayan glaciers.
Acknowledgements
We are grateful to R. LeB. Hooke, M. Kuhn, P. Cutler and M. Nakawo for their valuable comments and suggestions on the first draft of this paper.












