Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-20T18:18:13.970Z Has data issue: false hasContentIssue false
  • English
  • Français

On bifurcation of statistical properties of partially hyperbolic endomorphisms

Part of: Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  18 April 2023

MASATO TSUJII Open the ORCID record for MASATO TSUJII [Opens in a new window]  and
ZHIYUAN ZHANG
MASATO TSUJII
Affiliation:
Department of Mathematics, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan
ZHIYUAN ZHANG
Affiliation:
CNRS, Institut Galilée, Université Paris 13, 99 avenue Jean-Baptiste Clément, 93430 Villetaneuse, France
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an example of a path-wise connected open set of 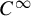$C^{\infty }$ partially hyperbolic endomorphisms on the 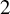$2$-torus, on which the (unique) Sinai–Ruelle–Bowen (SRB) measure exists for each system and varies smoothly depending on the system, while the sign of its central Lyapunov exponent changes.

Keywords

Sinai–Bowen–Ruelle measurepartially hyperbolic endomorphismLyapunov exponent

MSC classification

Primary: 37C30: Zeta functions, (Ruelle-Frobenius) transfer operators, and other functional analytic techniques in dynamical systems
Secondary: 37C40: Smooth ergodic theory, invariant measures 37D30: Partially hyperbolic systems and dominated splittings
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 3 , March 2024 , pp. 933 - 944
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alves, J. F., Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140(2) (2000), 351–398.Google Scholar
Arnold, L.. Random Dynamical Systems (Springer Monographs in Mathematics). Springer-Verlag, Berlin, 1998.Google Scholar
Barreira, L. and Pesin, Y.. Introduction to Smooth Ergodic Theory (Graduate Studies in Mathematics, 148). American Mathematical Society, Providence, RI, 2013.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.Google Scholar
Brin, M. I. and Pesin, J. B.. Partially hyperbolic dynamical systems. Izv. Akad. Nauk SSSR Ser. Mat. 38 (1974), 170–212.Google Scholar
Carrasco, P. D., Rodriguez-Hertz, F., Rodriguez-Hertz, J. and Ures, R.. Partially hyperbolic dynamics in dimension three. Ergod. Th. & Dynam. Sys. 38(8) (2018), 2801–2837.Google Scholar
Crauel, H. and Flandoli, F.. Attractors for random dynamical systems. Probab. Theory Related Fields 100(3) (1994), 365–393.Google Scholar
Crauel, H. and Flandoli, F.. Additive noise destroys a pitchfork bifurcation. J. Dynam. Differential Equations 10(2) (1998), 259–274.Google Scholar
Gouëzel, S. and Liverani, C.. Banach spaces adapted to Anosov systems. Ergod. Th. & Dynam. Sys. 26(1) (2006), 189–217.Google Scholar
Grayson, M., Pugh, C. and Shub, M.. Stably ergodic diffeomorphisms. Ann. of Math. (2) 140(2) (1994), 295–329.Google Scholar
Hall, L. and Hammerlindl, A.. Classification of partially hyperbolic surface endomorphisms. Geom. Dedicata 216(3) (2022), article no. 29.Google Scholar
Ikeda, T. and Morita, T.. Central limit theorem of mixed type for transformations with quasi-compact Perron–Frobenius operators. Kyushu J. Math. 71(1) (2017), 31–64.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54). Cambridge University Press, Cambridge, 1995; with a supplementary chapter by A. Katok and L. Mendoza.CrossRefGoogle Scholar
Kifer, Y.. Random Perturbations of Dynamical Systems (Progress in Probability and Statistics, 16). Birkhäuser Boston, Inc., Boston, MA, 1988.Google Scholar
Mi, Z. and Cao, Y.. Statistical stability for diffeomorphisms with mostly expanding and mostly contracting centers. Math. Z. 299(3–4) (2021), 2519–2560.Google Scholar
Pollicott, M.. Lectures on Ergodic Theory and Pesin Theory on Compact Manifolds (London Mathematical Society Lecture Note Series, 180). Cambridge University Press, Cambridge, 1993.Google Scholar
Tsujii, M.. Physical measures for partially hyperbolic surface endomorphisms. Acta Math. 194(1) (2005), 37–132.Google Scholar
Tsujii, M.. Virtually expanding dynamics. Kyushu J. Math. 77(2) (2023), to appear.Google Scholar
Wilkinson, A.. Conservative partially hyperbolic dynamics. Proceedings of the International Congress of Mathematicians. Volume III. Eds. R. Bhatia, A. Pal, G. Rangarajan, V. Srinivas and M. Vanninathan. Hindustan Book Agency, New Delhi, 2010, pp. 1816–1836.Google Scholar
Zhang, Z.. On the smooth dependence of SRB measures for partially hyperbolic systems. Comm. Math. Phys. 358(1) (2018), 45–79.Google Scholar