Introduction
The snow cover on sea ice plays a key role in the climate system because it strongly modifies energy and freshwater fluxes between atmosphere, ice and ocean. snow cover and thickness have a large seasonal cycle. however, the seasonal cycle of snow thickness is generally very different on arctic and antarctic sea ice. in the arctic, snow usually melts completely during summer, and then melting of the upper ice layers begins, and the ice surface becomes extensively covered by melt ponds (e.g. Reference Willmes, Bareiss, Haas and NicolausMaykut, 1986). on perennial antarctic sea ice extensive melt ponding is not observed, and an intact or highly metamorphosed snow cover persists throughout the summer (Reference Stroeve, Markus, Meier and MillerMassom and others, 2001). however, there is widespread internal snowmelt on antarctic sea ice, too, often leading to the formation of ice layers and superimposed ice due to the refreezing of meltwater in lower and colder layers or at the snow/ice interface (e.g. Reference Kawamura, Ohshima, Takizawa and UshioKawamura and others, 1997, Reference Kawamura, Jeffries, Tison and Krouse2004; haas and others, 2001). in the arctic, superimposed ice formation is mostly a transient process only before snow and upper ice layers disappear, as surface ice melt is generally so strong (Reference Willmes, Bareiss, Haas and NicolausMaykut, 1986; nicolaus and others, 2003; Reference Eicken, Grenfell, Perovich, Richter-Menge and FreyEicken and others, 2004).
The arctic–antarctic contrast is even more remarkable given the higher latitudinal coverage of sea ice in the arctic compared to the southern ocean, where snow survives the summer (e.g. at 68˚ s in the weddell sea). Reference Andreas and AckleyAndreas and ackley (1982) proposed that the survival of snow on antarctic sea ice is due to cold and dry katabatic winds blowing off the antarctic continent. this leads to an increase in turbulent fluxes of sensible and latent heat, with associated cooling of the snow surface and thus reduced melt rates.
The numerical, one-dimensional snow model sntherm (Reference JordanJordan, 1991) was used to further investigate the differences of snowmelt on arctic and antarctic sea ice. first, the model is validated against field observations from two arctic and one antarctic measurement campaigns. then, the model is used for regional studies along seven meridional transects across the arctic and southern ocean to simulate the different characteristics of snow thinning. our focus is on examining the fundamental differences between snowmelt in the arctic and antarctic. complicated interactions between the snow, sea ice and ocean (e.g. flooding and snow-ice formation) are not treated by the model.
It should be noted that snow thinning is composed of many different processes including melting, evaporation, sublimation and compaction, which can be distinguished with the aid of sntherm. during summer these processes are enhanced because snow temperature profiles are close to or at the melting point of 0˚c. here, we focus on the role of melting and evaporation in snow thinning.
We define snowmelt onset as the instance when the first meltwater reaches the snow/ice interface in the sntherm model. this is the transition from the pendular to the funicular regime (Reference ColbeckColbeck, 1982) when, due to stronger internal snowmelt, liquid water occupies paths through the pore space and can percolate downwards. however, even after melt onset, snowmelt is not necessarily the dominant process for snow thinning, as compaction and evaporation can be at least as important. snowmelt-season duration is the time between snowmelt onset and the disappearance of snow. it should be noted that surface ablation often continues after all the snow has melted.
Methods and Database
The snow model Sntherm
Sntherm is a one-dimensional energy- and mass-balance model. it simulates snow properties and physical processes in a layered control volume scheme with a moving mesh, which allows the treatment of natural stratigraphic units within the snow. each layer distinguishes ice, liquid water, water vapor and dry air, which is essential for phase-change and water-flow simulations, two important aspects during melt seasons. other main processes are heat conduction, (subsurface) solar absorption, surface energy exchange, densification, evaporation and grain growth. simulated evaporation includes sublimation and is computed as the product of water vapor in air, fractional humidity, water-vapor pressure at the surface and latent-heat flux, divided by the latent heat of sublimation. detailed model descriptions are given by Reference JordanJordan (1991) and Reference Andreas, Jordan and MakshtasAndreas and others (2004).
For our studies, we used the public version sntherm. 89ver4 (http://snobear.colorado.edu/markw/snowhydro/modeling/sntherm.html). this version was designed for simulations of snow on frozen ground (Reference JordanJordan, 1991) and does not include modifications as they have successfully been applied to arctic (Reference Jordan, Andreas and MakshtasJordan and others, 1999) and antarctic (Reference Andreas, Jordan and MakshtasAndreas and others, 2004) sea ice. because heat capacity and heat conduction of saline sea ice differ from those of freshwater ice and snow, all simulations were performed on top of sea ice with constant thickness (0.60 m, 20 layers), bulk salinity (4.0) and bottom temperature (–1.8˚c). as sntherm is only a snow model and not capable of simulating ice bottom melt, we neglect the ocean heat flux and treat the sea ice as a lower boundary determining the temperature at the snow/ice interface. similarly, a realistic computation of freeboard is not performed by the model, and therefore flooding and snow-ice formation are not treated. in our model the sea ice persists until all snow has disappeared.
For our studies, we used the public version sntherm. 89ver4 (http://snobear.colorado.edu/markw/snowhydro/modeling/sntherm.html). this version was designed for simulations of snow on frozen ground (Reference JordanJordan, 1991) and does not include modifications as they have successfully been applied to arctic (Reference Jordan, Andreas and MakshtasJordan and others, 1999) and antarctic (Reference Andreas, Jordan and MakshtasAndreas and others, 2004) sea ice. because heat capacity and heat conduction of saline sea ice differ from those of freshwater ice and snow, all simulations were performed on top of sea ice with constant thickness (0.60 m, 20 layers), bulk salinity (4.0) and bottom temperature (–1.8˚c). as sntherm is only a snow model and not capable of simulating ice bottom melt, we neglect the ocean heat flux and treat the sea ice as a lower boundary determining the temperature at the snow/ice interface. similarly, a realistic computation of freeboard is not performed by the model, and therefore flooding and snow-ice formation are not treated. in our model the sea ice persists until all snow has disappeared.
The thickness of superimposed ice is a prognostic variable. it is calculated by summing up the thickness of a basal ice layer composed of compacted snow and refrozen meltwater with a density larger than 850 kgm–3, and an additional amount of meltwater, which passes the ice/snow interface, because saturation and ponding cannot be modeled in sntherm.
Meteorological forcing consists of air temperature (T air), relative humidity (rh), wind velocity (v), incoming (S↓, L↓) as well as outgoing (S↑, L↑) short- and longwave radiation.
Field measurements
Three field campaigns were performed to study snow thinning and superimposed ice formation on arctic and antarctic sea ice. they were carried out on first-year fast ice in kongsfjorden, svalbard, (80˚ n) and on first-year pack ice in the western weddell sea (68˚ s) (fig. 1). sebisup02 and 03 (surface energy budget and its impact on super-imposed ice formation; nicolaus and others, 2003) took place at svalbard during 22 may–3 june 2002 and 16 may–3june 2003, respectively. ispol (ice station polarstern) was carried out on antarctic sea ice from 29 november 2004 to 2 january 2005 (Reference Hellmer, Dieckmann, Haas and SchröderHellmer and others, 2006). all observation periods included melt onset, but had different meteorological conditions leading to essential differences in the temporal evolution of the snow cover.
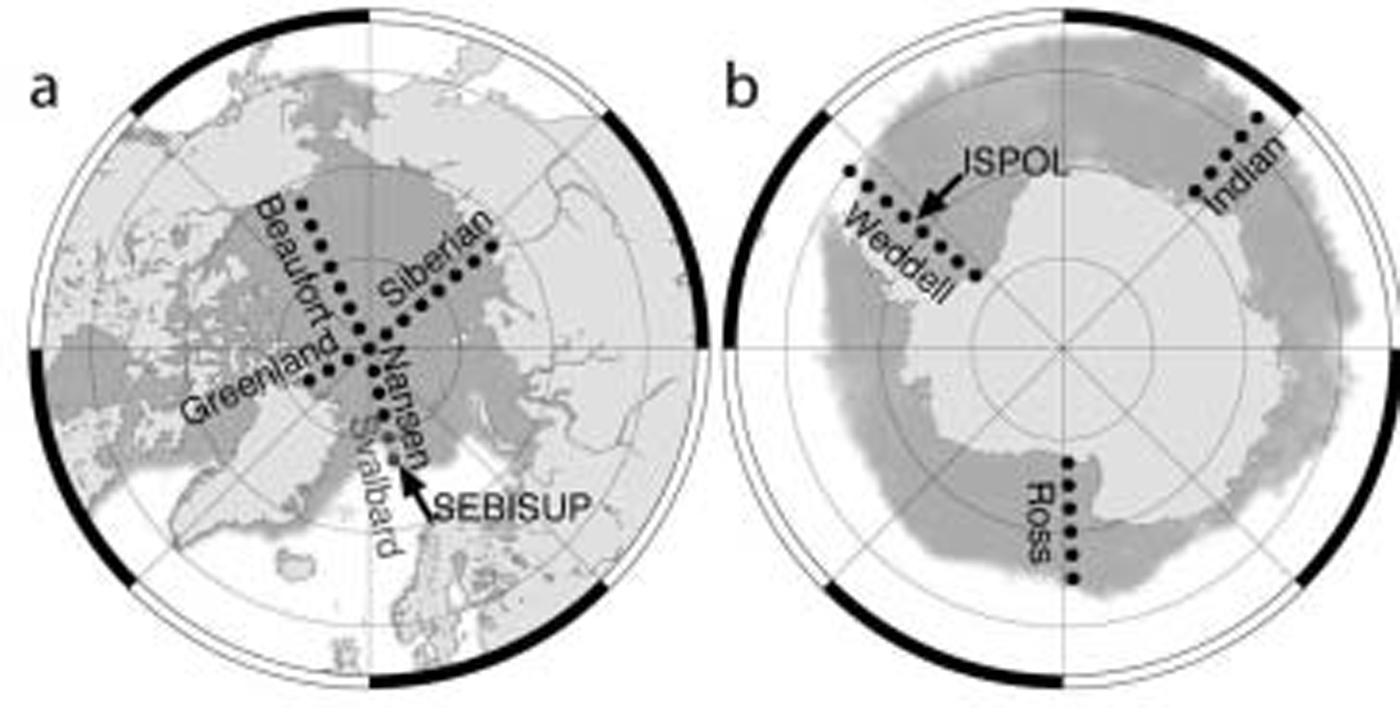
Fig. 1. Map of the model study sites on (a) Arctic and (b) Antarctic sea ice. Locations of field measurements are indicated by black arrows, and the profiles for simulation are named as used in the text. The gray shaded area shows sea-ice extent on 1 March 2002 (Arctic) and 1 September 2002 (Antarctic), as derived from satellite passive microwave data.
Standard meteorological parameters (T air, rh, v) and radiation budget data (S↓, L↓, S↑, L↑) were collected by an automatic weather station (nicolaus and others, 2003). from these, turbulent fluxes (q turb) were derived using bulk formulas as proposed by Reference Launiainen and ChengLauniainen and cheng (1995). net short- and longwave fluxes (sw, lw) were used to compute the net atmospheric fluxes as Q = sw+ lw+ q turb. all fluxes into the snow cover are defined to be positive. snow properties such as thickness (z s), and vertical profiles of temperature, density, stratigraphy and wetness were measured along 50m long profiles several times per day (nicolaus and others, 2003; Reference C., Nicolaus, Willmes and BatzkeHaas and others, in press).
The measured meteorological variables and snow properties were used to force and validate the model. initial snow properties in the model were taken from observed density, temperature and grain-size profiles, interpolated to layers of 0.01 m thickness. similarly, the initial sea-ice temperature profile was determined from observations. meteorological forcing consisted of station measurements in 5 min intervals.
Regional studies
figure 1 shows the 42 locations where the model has been applied. they are arranged in five arctic (nansen including north pole, greenland, beaufort, siberian and svalbard) and three antarctic (weddell, ross, indian) meridional profiles from lower latitudes to the north pole and to the antarctic continent, respectively (table 1). the profiles cover all important sea-ice regions and include locations in which snow and sea-ice studies have been performed by others in the past. the meridional distance between two adjacent points is 2.5˚ latitude, the same as the spatial resolution of the european centre for medium-range weather forecasts (ecmwf) data. the two svalbard locations are included because they represent the sebisup field measurement site. the term central arctic excludes the svalbard profile.
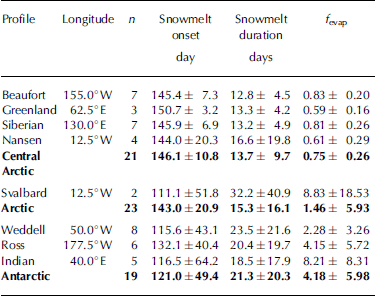
Table 1. Snowmelt-season variables for each profile of the regional simulations and means for all Arctic and Antarctic profiles (Fig. 1). The number of locations along the profile is indicated by n. For better comparison, days of Antarctic profiles are given relative to 1 July; to calculate the actual Antarctic day of year, add 181. The fraction of evaporation vs melt is indicated by f evap
For the regional studies, initial snow thickness and density are set to 0.30 m and 300 kgm–3, respectively, in all regions, representing mean values for snow on first- and multi-year arctic and first-year antarctic sea ice (e.g. warren and others, 1999; Reference Stroeve, Markus, Meier and MillerMassom and others, 2001). this uniform snow mass at all locations is important to simplify comparison of different years and regions; hence, snowfall and precipitation are excluded, too. an initial snow temperature of –3.0˚c and grain size of 0.5 mm are assumed. thickness and properties of sea ice are the same as for the field simulations.
For the regional studies, initial snow thickness and density are set to 0.30 m and 300 kgm–3, respectively, in all regions, representing mean values for snow on first- and multi-year arctic and first-year antarctic sea ice (e.g. warren and others, 1999; Reference Stroeve, Markus, Meier and MillerMassom and others, 2001). this uniform snow mass at all locations is important to simplify comparison of different years and regions; hence, snowfall and precipitation are excluded, too. an initial snow temperature of –3.0˚c and grain size of 0.5 mm are assumed. thickness and properties of sea ice are the same as for the field simulations.
Meteorological forcing data of the snow model include four-times-daily parameters obtained from the ecmwf. the selected ecmwf re-analysis data (era-40) cover the period from 1 july 1992 to 30 june 2002, comprising ten melt seasons in the sea-ice region. model runs begin on 1 january for arctic and on 1 july (day of year 182) for antarctic profiles and end when snow thickness z s = 0. for easier comparison, all antarctic days of year are given relative to 1 july. sw is computed as (1–α)s↓, and albedo (α) is based on snow grain size following a parameterization of the snow model Crocus (Reference Brun, David, Sudul and BrunotBrun and others, 1992). the original data were linearly interpolated to 15 min values to reduce the computational efforts of the snow model. to reduce the influence of interannual variations and to obtain more general results, the discussion only focuses on the 10 year means.
The results of the regional studies describe differences in snow ablation seasons on arctic and antarctic sea ice. the analyses focus on snow thickness decrease and the differentiation of the dominant processes, melt and evaporation. snowmelt is defined as the mass of liquid water reaching the ice/snow interface, and evaporation is defined as the loss of mass to the atmosphere. we define f evap as the ratio
Results
Model validation
Measurements of snow and superimposed ice thickness during the three field experiments and a comparison with model results are summarized in figure 2. figure 2a–c show that all three field measurements occurred under different meteorological boundary conditions.

Fig. 2. Meteorological conditions and the comparison of field measurements with model results shown as time series for SEBISUP02 (left column), SEBISUP03 (middle column) and ISPOL (right column). (a–c) Daily means of net atmospheric fluxes (Q), their single components (SW, LW, q turb) and albedo (α); (d–f) measured daily means of snow and superimposed ice thickness; and (g–i) model results of snow and superimposed ice thickness and depth of T = –0.05˚C isotherm as a measure of the melting point. All snow thicknesses exclude superimposed ice layers. Missing data during ISPOL are due to floe break-up and were interpolated for model forcing. Error bars denote one standard deviation. z s = 0 refers to the snow/ice (sea ice, or superimposed ice, if present) interface. Note that all ISPOL plots (c, f, i) have different x-axis scale.
Sebisup02 was characterized by a strong increase of lw after 27 may, leading to an extremely positive total energy balance from this day onwards (fig. 2a). as a consequence, snow thickness decreased from 0.23m to 0.00m within 5 days (fig. 2d). turbulent heat fluxes were below ±6.4wm–2, which was due to very low wind velocities with an overall mean of 0.56ms–1. the strong albedo decrease (minimum: 0.38) represents the deteriorated superimposed- and sea-ice surface at the end of the observation period (nicolaus and others, 2003).
The mean (over the whole observation period) surface energy balance during sebisup03 was the lowest (7.47wm–2) of all three campaigns, mainly resulting from only 47wm–2 sw compared to 62 and 77wm–2 during sebisup02 and ispol, respectively. compared to sebisup02, when melt onset was clearly defined, meteorological conditions during sebisup03 did not show two distinct phases. as a consequence, snow thickness decreased only very slowly from initially 0.15 m. therefore, at the end of observations on 4 june, 0.02 m of snow remained (fig. 2e). this snow then melted the following week (personal communication from s. gerland, 2003). but the snow cover of sebisup03 was already more metamorphosed than that of the previous year at the beginning of the field measurements, due to episodes of warm weather in late winter (Reference Gerland, Haas, Nicolaus and WintherGerland and others, 2004). accordingly, mean snow density was 367 kgm–3, slightly higher than the 345 kgm–3 in 2002.
The daily mean surface energy balance and albedo during ispol were intermediate between the two svalbard cases (fig. 2c). due to the highest v of 3.8ms–1, turbulent heat fluxes contributed strongly to the surface energy balance. fluctuations in albedo and the non-monotonic character of snow-thickness decrease were due to snowfall events on 1 and 26 december. the ispol snow cover was the thickest (0.32 m) and had the lowest density (302 kgm–3) at the beginning of the observation period. it decreased to 0.14m over the course of 35 days (fig. 2f). although the ispol ice floe consisted predominantly of perennial sea ice with thick snow cover, here we only discuss first-year ice.
As a result of snowmelt, superimposed ice formed during all field studies (fig. 2d–f). maximum thicknesses were 0.03–0.07 mm at the end of observations. at the end of sebisup02 the high surface energy balance (>50wm–2) led to a deterioration of superimposed ice after all snow had disappeared. note that extremely high net shortwave fluxes after 31 may caused energy-balance values above 100wm–2. these measurements should not be considered further since they are strongly biased by a station tilt, resulting from strong melting at the station poles.
Results of the numerical simulations are shown in figure 2g–i. mean differences between measured and simulated snow thickness are 13.1 mm (sebisup02), 17.8mm (sebisup03) and 27.1 mm (ispol, until snowfall on 26 december). the model tends to slightly overestimate snow thinning. sntherm reproduces superimposed ice formation during each spring and its deterioration as observed during sebisup02. mean differences between measured and simulated superimposed ice thickness range from 20.5 to 43.9 mm.
As a qualitative measure of snowmelt, the –0.05˚c isotherm is also included in figure 2g–i (sntherm does not allow snow temperatures of 0˚c). it can be seen that the total snow cover became permanently isothermal during sebisup02, whereas distinct diurnal melt–freeze cycles are modeled during the course of both other field studies. low snow temperatures during sebisup03 explain and underline the observed small thinning rates.
Regional studies
figure 3 compares the temporal development of snow thickness on arctic and antarctic sea ice. at all central arctic sites, snow thickness decreases uniformly and in a narrow band. snow thinning is dominated by compaction, and the mean thinning rate is 0.09cm d–1 until melt onset on day 146.1±10.8 (26 may). after melt onset, the mean thinning rate increases to 1.50cmd–1, indicating that rapid snowmelt is the dominant process. in contrast, in the antarctic, melt onset occurs on day 121.0±49.4 (29 october), about 25 days earlier than in the arctic, and it shows higher variability. thinning rates are 0.25 and 1.05 cmd–1 before and after melt onset, respectively, i.e., thinning rates before and after melt onset are higher and lower, respectively, than those observed in the arctic. snow thinning on svalbard differs significantly from other arctic locations and is more similar to antarctic ablation seasons (see discussion below).

Fig. 3. Modeled snow thickness for each location in Figure 1 in (a) central Arctic (solid lines) and Svalbard (dashed lines) and (b) Antarctica. Lines show 10 year medians, with day 1 representing 1 January and 1 July for Arctic and Antarctic, respectively. Gray dots indicate melt onset as defined in the text. z s = 0 refers to the snow/ice (sea ice, or superimposed ice, if present) interface.
Snowmelt onset and snowmelt-season duration are shown in figure 4. figure 4a clearly shows that melt onset occurs later with increasing latitude on all antarctic profiles, ranging from day 17.8 (17 july north on the indian profile) to day 157.2 (27 january south on the ross profile). in the arctic, melt onset is almost simultaneous at different latitudes, and ranges only from day 131.9 (11 may) to day 150.9 (30 may). again, the two svalbard locations are an exception. results of every year of the simulation show that interannual variation of melt-onset dates is much stronger in the antarctic than in the arctic (fig. 4a).

Fig. 4. (a) Snowmelt onset and (b) snowmelt-season duration for locations in Figure 1. Black symbols (Arctic: open symbols; Antarctic: filled circles) show 10 year means. Symbols correspond to different profiles as in Figure 5. Small grey circles represent values for every year for Arctic (open circles) and Antarctic (filled circles) locations. For better comparison, southern latitudes are signed positive, and days of Antarctic profiles are given relative to 1 July; to obtain actual Antarctic day of year, add 181.
Snowmelt-season duration is 21.3±20.3 days in the antarctic and 13.7±9.7 days in the arctic on average. however, this difference is due to longer melt-season durations at four antarctic locations at lower latitudes. melt-season duration for all other antarctic locations is very similar to the arctic (fig. 4b).
The ratio f evap provides insight into the dominant processes responsible for the thinning of snow (fig. 5). in the central arctic, snow thinning is dominated by melting (f evap = 0.75±0.26), and only svalbard locations are dominated by evaporation (8.83±18.53). the highest melt fractions are found along the greenland and nansen profiles. as for all other melt-season parameters, the snow covers in the central arctic behave very uniformly. in contrast, evaporation is predominant on antarctic sea ice, where only 20% of the snow-cover thickness decrease is due to melting (f evap = 4.18±5.98) and pronounced regional differences become clear. the highest evaporation fractions of 8.22±8.31 occur on the indian profile, and all other 10 year means are also above 1.0. the indian profiles also show another phenomenon: all snow evaporates (melt = 0) at some locations in a few ablation seasons. the latter are not included in the 10 year mean.

Fig. 5. Modeled 10 year mean fraction f evap of evaporated to melted snow for Arctic and Antarctic locations (Fig. 1). Note that y-axis scaling is different in the upper part. Southern latitudes are signed positive for better comparison.
According to the high f evap, mean evaporation rates in the antarctic are nearly twice as high (0.0268 kg h–1; maximum: 0.15 kg h–1) as in the central arctic (0.0144 kg h–1; maximum: 0.12 kg h–1). compared to evaporation, snowmelt is the more efficient ablation process and melt rates may reach up to 1.0 kg h–1 in both hemispheres, usually at the end of the ablation season. as indicated by snow-thinning patterns (fig. 3), if they occur over long time periods, high evaporation rates may remove large snow masses.
Discussion
Simulations of snowmelt and superimposed ice formation on sea ice with sntherm agree well with observations under different meteorological conditions, showing that even the simplified implementation of sea ice performs well in prescribing snow/ice interface temperatures. however, model results are sensitive to initial snow mass, which is derived from measurements of thickness and density. inaccuracies of those observations, which are used for model initialization, can easily exceed 10% and thus explain the underestimation of simulated snow thickness, even after a few time-steps of model integration.
For a most accurate simulation of snow and sea-ice conditions, variable ocean heat flux and saturation of snow and ice layers should also be included. this would allow the explicit treatment of sea-ice thinning due to bottom ablation or even the complete disappearance of sea ice prior to complete snow ablation, as frequently observed on antarctic sea ice (Reference MassomLytle and ackley, 2001). but sea-ice mass balance is of minor importance here, because this study is designed to show differences in snow thinning, especially melting and evaporation, and these differences are dominated by atmospheric conditions. an increase of total snow mass (through initialization or precipitation) would also cause longer snowmelt-season durations, but melt-onset dates and fractional evaporation values would change only little. other uncertainties result from the parameterization of albedo, which has a strong effect on thinning rates at the end of the thinning season (fig. 1) due to the snow–albedo feedback mechanism.
A comparison of simulated melt-onset dates (table 1) with melt-onset dates observed by means of passive satellite microwave data shows no systematic deviation. in the arctic, our melt-onset dates agree reasonably well with those derived by Reference Willmes, Bareiss, Haas and NicolausStroeve and others (2006); our melt onset is 3 days later for the beaufort and siberian profile and 1 week later for the central arctic (day 139.7, 19 may, between 1979 and 2005). on the other hand, our melt-onset dates are 24 days earlier than those derived by Reference Anderson and S.D.Anderson and drobot (2001) in coincident regions (day 163, 12 june, between 1993 and 2002). we cannot explain the large difference between those satellite-derived melt-onset dates. in the weddell sea, between 1992 and 1999 melt onset was observed by satellite on day 130.3 (7 november) on average (Reference HaasHaas, 2001), 16 days later than in this study.
Model deficiencies as outlined above can partly explain this disagreement. however, there are also differences in the definition of melt onset. in the satellite data, a prominent and permanent change of microwave properties due to a high liquid-water fraction in the snow is taken as melt onset. in contrast, here we have defined it as the first occurrence of liquid water at the snow/ice interface, which can be a temporary event and can occur significantly before the snow becomes saturated with meltwater.
The intention of the regional study was to outline general differences between snowmelt on arctic and antarctic sea ice, and not to simulate regional processes to the highest accuracy. therefore, representative values of snow thickness (0.30 m) and snow density (300 kgm–3) on arctic and first-year antarctic sea ice were chosen for the initial snow cover (e.g. warren and others, 1999; Reference Stroeve, Markus, Meier and MillerMassom and others, 2001). on perennial antarctic sea ice, snow thickness ranges between 0.10 and 1.65 m, however (Reference Haas, Thomas and BareissHaas and others, 2001; Reference Stroeve, Markus, Meier and MillerMassom and others, 2001). therefore, the snow will not disappear during one summer season at the thinning rates computed here, and with the inclusion of new snow accumulation, and true duration of the melt season will be much longer than derived here (table 1). on the other hand, in most regions with thin first-year ice, bottom melt caused by strong ocean heat flux will actually be much more important than snowmelt (e.g. Reference Nicolaus, Haas and BareissLytle and ackley, 2001). therefore, the ice will disappear earlier than the dates derived here for the completion of the snowmelt season, and the snow will dissolve in the ocean (table 1), as visible in satellite-derived maps of ice extent.
Our results show that the fraction of evaporated to melted snow mass is much higher in the antarctic than in the arctic. this is probably due to the special climatic conditions around antarctica, with a low relative humidity and dry and relatively strong winds off the antarctic continent, as discussed by Reference Andreas and AckleyAndreas and ackley (1982). therefore, turbulent fluxes of heat are predominantly upwards, with associated cooling of the snow surface and hence reduced melt rates. evaporation can still be strong even when the contribution of melting to overall thinning is only small. this can explain the more constant and slower thinning rates on most antarctic transects. in contrast, in the arctic, melting contributes to wetting and a more rapid thinning of the snow (fig. 3). the lower albedo of wet snow triggers the snow–albedo feedback and accelerates snowmelting.
Because evaporation plays a greater role than melting in thinning of antarctic snow, the saturations of the snow with water and the occurrence of melt ponds is less likely. however, there is enough moisture in the snowpack to enable the formation of superimposed ice. this also explains the different microwave signatures during summer in the arctic (Reference HaasHaas, 2001; willmes and others, 2006).
The strong contrast between the arctic and antarctic modelling results agrees with observations, and also demonstrates the quality of the ecmwf forcing data with respect to their representation of arctic vs antarctic meteorological conditions and parameterization of the different components of the energy balance. in addition, the deviation of the results for the svalbard locations (figs 3–5; table 1) might be explained by the inclusion of the particular topography and climate of the mountainous and glaciated archipelago, which could make the forcing data of these particular gridcells more similar to antarctic than to arctic conditions.
Conclusions
The one-dimensional snow model sntherm has been used to simulate snow thinning and superimposed ice formation on arctic and antarctic sea ice. there is good agreement between model results and observations from three field studies. in regional studies, 10 years of snow thinning at 42 locations on arctic and antarctic sea ice have been simulated with ecmwf forcing. these showed large differences in the temporal behavior of the snow cover in different regions. considering hemispherical means, snow-melt onset is almost simultaneous all over the arctic ocean, but is earlier and strongly dependent on latitude in the antarctic. this might be explained by the different contributions of melt, evaporation and compaction to snow thinning. before melt onset, compaction dominates snow thinning in the arctic, which is indicated by relatively low thinning rates. in contrast, on antarctic sea ice, evaporation is the dominant process and causes more rapid thinning and higher total mass loss than in the arctic before melt onset. once snowmelt has begun, it dominates arctic snow thinning with high melt rates. in the antarctic, snowmelt also occurs, but evaporation is still an important factor, causing more uniform thinning rates. summarized over the whole spring and summer season, evaporation dominates snow thinning in the antarctic, and snowmelt is predominant on arctic sea ice.
We plan to perform a similar study using a large-scale dynamic–thermodynamic sea-ice model to study its ability to simulate snowmelting compared with the more detailed sntherm model. this will also enable more specific regional investigations, and will allow an assessment of the role of bottom ice melt due to variable ocean heat flux, and the role of snowmelt. the advantage of using a model is that it integrates over the different components of the surface energy budget, which can reveal regional differences more clearly than an investigation of meteorological conditions alone.
Acknowledgements
We thank g. könig-langlo and b. loose for advice on field measurements, and the koldewey station, ny-ålesund, svalbard, and rv Polarstern (cruise xxii/2) for logistical support. sntherm was kindly provided by r. jordan of the us army cold regions research and engineering laboratory. forcing data were obtained from the european centre for medium-range weather forecasts, reading, uk. careful reviews by m. jeffries, t. kawamura and b. cheng significantly improved the manuscript. the work was partially financed by the german research council (dfg, project ha2724/3).








