Introduction

Ice thicknesses in the polar regions are commonly measured by radio echo-sounding using half-wave dipole aerials. Several investigators (e.g. Reference JiracekJiracek, 1967; Reference Bogorodskiy, Bogorodskiy, Trepov, Federov and GudmandsenBogorodskiy and others, 1970; Reference Kluga, Kluga, Trepov, Federov and KhokhlovKluga and others, 1973; Clough, unpublished) have noticed that the linearly polarized waves transmitted from such aerials are depolarized in the received echo, and have therefore suggested that naturally occurring ice might be birefringent at radio frequencies. Reference HargreavesHargreaves (1977) has used returns from reflecting layers within the Greenland ice sheet to put a lower limit on the anisotropy of the radio-frequency dielectric constant of polycrystalline ice of 0.028%. He also shows (Reference HargreavesHargreaves, 1978) that the orientation fabric of ice crystals controls the overall birefringence of the ice sheet and that his quoted value is therefore an absolute minimum for the single crystal of ice Ih.

Because the orientation fabric depends on the strain history of the ice (Reference BuddBudd, 1972), the birefringence of the ice sheet and therefore the depolarization should be a function of position on the surface. In general there is also depolarization on reflection from a boundary where there is a change in the electrical properties of the media (see e.g. Reference McPetrieMcPetrie, 1938; Reference Von HippelVon Hippel, 1954), and which is rough (Reference Beckmann and SpizzichinoBeckmann and Spizzichino, 1963). Measured at the surface, the polarization of the echo returned from the glacier bed is due to a combination of these three effects.

This paper discusses the results of an experiment into the polarization behaviour of radio echoes from the bed of both ice shelf and land ice in the Antarctic. At normal and near-normal incidence, the birefringence of the ice would appear to be the dominant factor in determining any polarization changes. The effect of tidal strain on crystal orientation and therefore birefringence may allow floating and grounded ice to be distinguished.

The experiment

Our measurements were carried out on Alexander Island in the Antarctic Peninsula. Five sites were chosen along a 10 km line running from the summit of a snow dome out onto the Bach Ice Shelf. The line was along part of a stake scheme which had been set up and surveyed in the previous season. Re-surveying the stakes after approximately one year gave the ice movements over the scheme, as shown in Figure I.

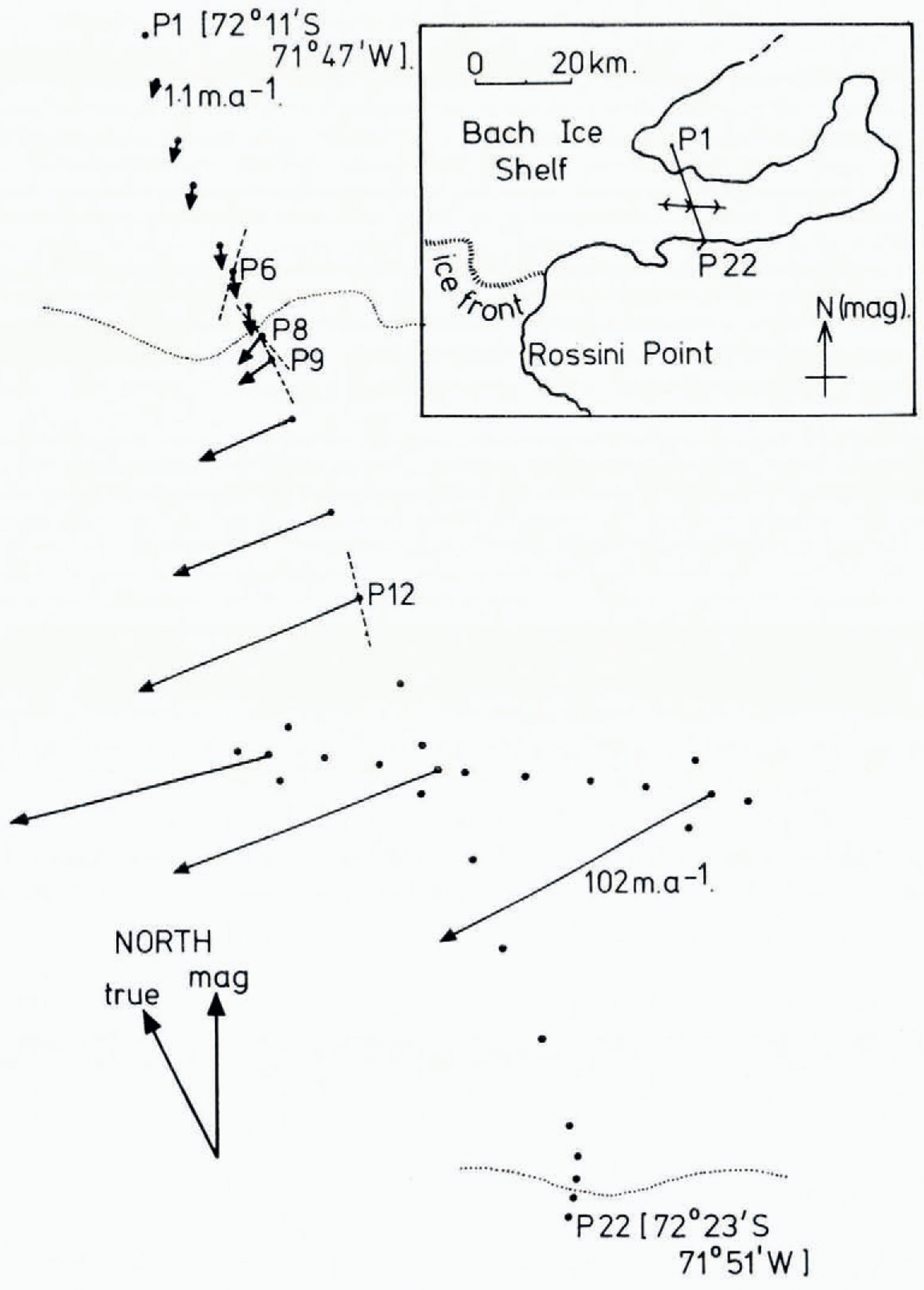
Fig. 1. The stake scheme P on the Bach Ice Shelf showing movement vectors after 1 year, polarization sites, and optic-axis orientations (except for a 90° ambiguity) where present.

• ...... Ice-shelf grounding line.

• ----- Optic-axis orientation.

• → Velocity vectors for scheme stakes.

A modified Scott Polar Research Institute Mk 4 radio echo-sounder was operated at a frequency of 60 MHz. Initially an intensity-modulated profile of the whole scheme was obtained for ice thickness, and to ensure that there were no anomalous features such as large-scale bottom crevassing near the sites proposed for detailed polarization studies. The record showed the fading expected from small-scale bottom irregularities. The fading was spatially more rapid over the land ice than the ice shelf indicating a smaller horizontal roughness scale over the bedrock. The ice thickness varied gradually from (351±6) m at P1 to (269±5) m at P8 and then increased to (293±5) m at P12 (Fig. 1).

For the polarization experiment separate transmitting and receiving half-wave dipole aerials were used. They were separated by several wavelengths and kept at least a quarter wavelength above the snow surface: these were empirical criteria that were found to produce no detectable antenna loading (to ±0.5 dB or better) in several control experiments covering both wet and hard-frozen surfaces. The positioning of the cables relative to the aerials was also found to be of great importance. However, providing that the feeds were from vertically above the aerial centres and no horizontal cables came within half a wavelength of the aerial, there was no detectable anisotropy in the system.

At each site, for a given orientation of the transmitting aerial, the receiving aerial was rotated horizontally through 360° and the echo strength was continuously recorded. The transmitting aerial was then rotated 15° and the receiving aerial again rotated through 360°. This procedure was continued, at each site, until the transmitting aerial had been turned through 195°. The echo strength was, as anticipated, symmetric about 180° and it was therefore unnecessary to turn the transmitting aerial the full 360°. The full rotation in the case of the receiving aerial was to check for any experimental anisotropy and also to increase measurement accuracy. In this way horizontal polar patterns of received power (to ±1 dB) were recorded as a function of receiving-aerial orientation θ for each transmitting-aerial orientation α. Calibration pips were put on the θ axis of the recording film at intervals of 5°, θ and α were measured with respect to the same arbitrary magnetic reference axis at each site.

Polarization results

At each site the measured angular distribution of returned power for any one value of α took the form of a dumbbell, from which the parameters of the polarization ellipse can be obtained (see e.g. Reference Stavis, Dorne and ReichStavis and Dorne, 1947; Reference KrausKraus, 1950). The difference between the powers along the major and minor axis of the dumbbell ranged from 6 to 20 dB. This ratio, varying with α and site, was less than would be expected from perfectly isotropic propagation and reflection: the cross-polarized component transmitted or received from a dipole is typically some 30 dB down on the principal radiated component (Reference HargreavesHargreaves, 1977). However, it is the orientation of the echo maximum θ _m, i.e. the major axis of the dumbbell, with respect to the reference axis and its variation with α at the various sites which is of interest here. Figure 2 shows that the results could be split into two distinct groups according to the direction of rotation of θ _m. When operating on grounded ice the orientation of the echo maximum rotated in the same sense as the rotation of the transmitting aerial, while on the ice shelf the echo maximum rotated in the opposite direction. At only one site, P6 on the steepest-sloping grounded ice, was there a significant departure from a linear-relationship between θ _m and α.

Fig. 2. Dependence of the orientation θ_m of maximum returned signal on the transmitted orientation α from measurements at: + typical ice-shelf site (P₉ ), × snow-dome side-slope site (P₆ ), O snow-dome summit (P₁ ). The solid lines are the curves of Equation (4) for (a) r = 1, δ = 0°, (b) r = 1, δ = 180°, (c) r = 1.8, δ = 20°.

The measured power patterns are related to the polarization of the returned wave. However, because the dipole radiation field is asymmetric, it might be expected that the angular distribution of the returned power will also depend on the relative orientation of the transmitting and receiving aerials, even when all polarization effects are neglected. From a consideration of the area of the zone at the bed of the ice sheet from which each pulse is returned we can put upper limits on this anisotropy. Under our experimental conditions such a reflection zone will closely approximate to a circle which is small compared with the dipole beam-width. Allowing for the electric field parallel to a half-wavelength dipole to be smaller than the field normal to the dipole by a factor (Reference KrausKraus, 1950)

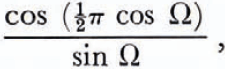
where Ω is the angle measured from the horizontal to a point in the reflection zone, it can be shown that the maximum difference in power as the receiving dipole rotates through 360° is less than 0.5±0.2 dB. Such small differences would scarcely have been detected with our measurement accuracy of ± 1 dB and are therefore ignored. We conclude that within the experimental error, the measured power distribution was due to polarization effects alone.

In the most general case the power distributions include an unpolarized component which will give an isotropic power increase when added to the purely polarized component. Therefore the polarization ellipse obtained by the method described above may be a broadened version of the true polarization ellipse but the orientation of the axes will be unchanged. Hence the measurement of θ _m, the orientation of the major axis of the dumbbell, gives the orientation of the major axis of the polarization ellipse and is independent of any unpolarized component. It is the behaviour of this parameter that we will now try to explain, leaving the information which can be derived from the ellipticity for further analysis.

Discussion of results

The electric vector of an elliptically polarized wave describes an ellipse, given by the equation (see e.g. Reference Clarke and GraingerClarke and Grainger, 1971)

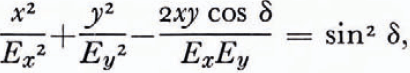
where E_x and E_y are the amplitudes of the electric vector in the x, y directions of an arbitrary cartesian frame, the wave propagation is in the z direction, and δ is the phase difference between E_x and E_y . The ellipse is in general orientated so that its major axis makes an angle ∊ to the x axis, where

(1)

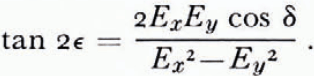
If then the x axis is chosen to be the experimental reference axis, ∊ = θ _m, and by defining tan β = E_y /E_x we get

This is the equation we shall use to explain the observed orientation behaviour of the polarization ellipse.

Assuming that naturally occurring polycrystalline ice is a uniaxial birefringent material (Reference JiracekJiracek, 1967; Reference HargreavesHargreaves, 1977), the direction of the effective optic axis is taken to define the yz plane of the coordinate system and is one of the unknowns to be found in any experiment. We assume that this direction is constant with depth at any particular site, although this may not be true in a complex flow pattern. Our linearly-polarized transmitting aerial is taken to be at an angle α to the x axis. Thus, for the transmitted wave

(2)

Now if A_x and A_y are the overall attenuation coefficients of the ordinary and extraordinary waves respectively due to absorption by the ice, attenuation on reflection, and geometrical attenuation, then the returned wave will have components A_xE_x and A_yE_y in the x, y directions, which by Equation (1) implies that the orientation of the received ellipse will be given by:

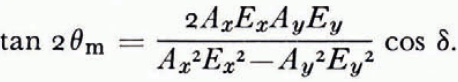
By defining

(3)

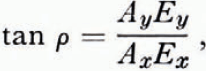
then

(4)

where the phase shift δ is that introduced by propagation through the ice and reflection at the bottom surface, and the angle ρ is related to the orientation of the transmitting aerial (α) through Equations (2) and (3) giving

where r = A_y/A_x . Thus Equation (4) gives the relationship between the orientation of the maximum received signal and the orientation of the transmitting aerial, in terms of the phase shift δ, the ratio r, and the azimuth of the optic axis.

In our experiment all angles were measured at each site with respect to an arbitrary magnetic bearing. The effective optic axis is determined, except for a 90° uncertainty, by the directions where α and θ _m are equal. Transforming the results to a coordinate system defined by the optic axis gives the points shown in Figure 2, where θ _m is plotted against α. The solid lines in Figure 2 are curves representing Equation (4) for different values of the parameters δ and r which have been chosen to fit the experimental points to within the experimental error (Table I). The curves clearly show that the opposite sense of rotation of the received ellipse on the ice-shelf sites can be explained by an additional phase shift of 180° compared with the land-based sites. Only at one site, P6, does δ deviate appreciably from 0 or 180°, or r from unity.

Table I. Values required in Equation (4) to numerically fit measured points to within experimental error

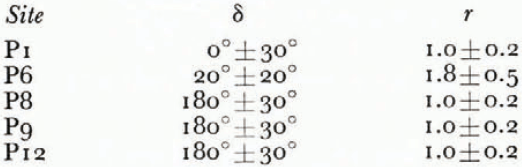
Before discussing how reflection at the bottom surface or transmission through the ice could cause a phase shift, we shall briefly examine whether the experimental arrangement could provide an explanation of the observed behaviour. Because separate transmitting and receiving aerials were used, usually about 1 m above the snow surface, there is the possibility that capacitative coupling between them may allow the transmitted and received power levels to depend on the relative orientation of the aerials (personal communication from W. R. Piggott). If for example the amount of coupling depended on surface conditions which varied from dry-snow facies on the land-based sites to wet snow on the ice shelf, then a difference in behaviour of θ _m with α might be expected. However one of the control experiments performed at each site was the rotation of a single transmitting and receiving aerial through 360°. In so doing large variations in signal received of the order 12 dB were still generally present and there were two major and two minor maxima in the full circle, each being separated by 90° (similar to the results of Reference HargreavesHargreaves, 1977). The orientation of the major maxima was the same, to within ±5° experimental error, as one of the orientations at which θ _m equalled α in the two aerial experiment. (This fact was used to resolve the 90° ambiguity in the direction of the optic axis.) Capacitative linking of the separate aerials therefore, if present, must have had an effect below the experimental measurement error of ±5°.

In general, the amplitude and phase of a reflected wave depend on the electrical properties of the transmitting and reflecting medium, the angle of incidence (i), and the polarization of the incident wave. Reference McPetrieMcPetrie (1938) gives the complex reflection coefficient as a function of these parameters both for polarization in the plane of incidence and perpendicular to it, components into which any polarization may be resolved. McPetrie’s curves may be extended for relative permittivities of less than one to cover all possible subglacial materials (e.g. see Reference JiracekJiracek, 1967, p. 41), taking the mean relative permittivity for ice as 3.2 (Reference Glen and ParenGlen and Paren, 1975). It can be then seen that for normal or near-normal incidence (i < c. 20°) a good conductor, such as sea-water at our frequencies, gives an equal phase change in both polarizations of very nearly 180°, while poor conductors such as frozen bedrock may give an equal phase change in both polarizations of anything from 0 to 180°. For wider angles of incidence the phase change in both polarizations for a good conductor is very similar until i is large, but for a poor conductor the relative phase change can reach 180° at smaller angles. Hence the small departure from normal incidence in our experiment of separating the two aerials (up to 4° for the shallower sites) could not account for any significant change in the relative phase of the wave resolved into these two polarizations, irrespective of the electrical characteristics of the reflecting surface.

However this argument has assumed that the reflecting surface is smooth and electrically isotropic. Reference Beckmann and SpizzichinoBeckmann and Spizzichino (1963) state that for a rough surface with irregularities large in comparison to the wavelength, the field scattered into any one direction would be depolarized in the same way as a field reflected by a smooth plane of the same electrical properties inclined in such a way that it reflected the incident field into that direction. Such a plane we have already seen is unable to explain the observed results. For irregularities of the order of a wavelength or less, even a physically simple surface of, for example, parallel corrugations with varying conductivity between them, could affect the reflected polarization in a complicated way. But without further evidence of how to describe the reflecting surface, we shall instead examine in detail how varying levels of birefringence in the ice can account for the different phase shifts. An anisotropic reflection coefficient is assumed to account for the value of r at the P6 site.

Birefringence And Ice Movement

Reference HargreavesHargreaves (1978) relates levels of birefringence to different common ice fabrics. Because the fabric at any particular site depends on the integrated strain history of the ice (Reference BuddBudd, 1972), different ice fabrics and thus different values of the birefringence are expected at our various sites. On this basis the phase shift for the ice-shelf sites is just coincidentally 180° and there is no fundamental reason for this value. The variation in ice-shelf thickness was unfortunately too small to check whether the phase shift was proportional to thickness, which would imply a constant level of birefringence per unit thickness of ice, or whether the phase shift of 180° was independent of thickness and therefore possibly due to the reflecting surface. Taking the results as suggesting a uniform birefringence, a phase change of 180° in an ice shelf only 270 m thick requires the mean anisotropy in the permittivity to be (0.52±0.08)%. Most of this phase shift occurs in the 1.2 km separation between sites P6 and P8.

The question then arises as to how such levels of birefringence could be caused. Figure 1 shows the polarization data against the background of the flow regime in the area. From consideration of particle paths there is no evidence up-stream from the scheme of any features capable of creating strains large enough to produce the change in the observed levels of birefringence between P6 and P8, except for the abrupt and continuously changing strain at the hinge zone.

A very well-formed fabric is required to produce a 180° phase shift in the 270 m thick ice shelf if there is an upper limit on the anisotropy in the radio-frequency permittivity of the single crystal of 1% (Reference Johari and CharetteJohari and Charette, 1975). However, with a value for the single crystal slightly below this figure, several different fabrics could explain our result. In particular Reference RigsbyRigsby (1960) reports that a strong two-pole fabric, with the poles perpendicular to the planes of maximum shear, is produced in laboratory experiments on initially isotropic polycrystalline ice when a sample is subject, over a period of about two months, to repeated simple shear six of seven times in each direction at a shear strain-rate of some 10^–7s^–1. This situation is not unlike the repeated tidal shear in the hinge zone of an ice shelf. For the Bach Ice Shelf, theodolite readings of stakes up to 3 km out on the ice shelf gave a tidal range of 1.5 m, a fairly typical value for the Antarctic. These results give a mean shear strain-rate over the entire hinge zone of 1 × 10^–8 s^–1, with a maximum strain-rate in the central region of shear of 2 × 10^–7 for a few hours each day. Moreover from knowledge of the surface velocities, it can be shown that an elemental volume of the sheet will be subject to such a continuous stress field for at least 20 years.

From the work of Reference BuddBudd (1972) and knowledge of the movements we can expect a weak, roughly annular, fabric at the dome summit (P1). This would show no birefringent effects to vertically travelling radio waves. A single-pole fabric would be gradually superimposed on the annular fabric as the flow increases down the slope, but due to the low slopes and strains involved this should only be weakly developed by the time the ice, accumulating at the rate of some 0.6 m water equivalent per year on the side slope, reaches the hinge zone. This would then explain a certain degree of birefringence (δ = 20°±20°) at P6. However, we suggest that it is the tidal flexure of the ice sheet in the hinge zone that is responsible for the greater part of the birefringence observed on the ice shelf (δ = 180°±30°) through a well-formed two-pole fabric superimposed on the existing one. An effective optic axis to the ice sheet is defined by the plane containing these two poles. At the hinge zone the optic axis will be created perpendicular to the principal shear direction, i.e. it will lie in the vertical plane containing the normal to the hinge line. After leaving the zone of highest stress, the existing fabric will be largely frozen into the ice shelf. The optic axes at P8, P9 and P12 rotated clockwise by 13°±5° between each site as we moved further out onto the ice shelf (see Fig. 1). By backward extrapolation of the particle paths from these sites to the hinge zone, the optic axis orientations appear to coincide with the normals to the hinge line to within experimental error. We do not know if there is any significance in the nearly constant angle that the velocity vector makes with the optic axis at these sites.

Conclusions

1. 1. The general level of radio-frequency birefringence in ice sheets, and especially in ice shelves, can be high. Our results show that even when a single half-wave dipole aerial is used to transmit and receive, azimuth changes cause variations in received power of up to 12 dB purely as a result of polarization effects. Aerial azimuths and the strain history of the ice must therefore be carefully considered in any conclusions drawn from comparative returned power in radio echo-sounding.

2. 2. From our data for the ice shelf sites we are able to give a new higher value of (0.52±0.8)% to the minimum anisotropy in the radio-frequency permittivity of ice. This shows that the anisotropy at 60 MHz is larger than the figure for sodium light of 0.22% (Reference HobbsHobbs, 1974). Because we do not expect an ice shelf to have a perfectly aligned fabric, a true figure for the anisotropy of between 0.5% and Johari and Charette’s figure of 1% is expected.

3. 3. Because much of the ice in many Antarctic ice shelves has crossed a hinge zone and has thus been subject to high levels of tidal flexure, strong fabrics and therefore generally increased levels of birefringence should be expected. However, as fabric generation is temperature as well as strain dependent (Reference BuddBudd, 1972), the Bach Ice Shelf with a 10 m temperature of only —9.8°C might have a stronger fabric than the large colder ice shelves. Nevertheless, even with simple rotating aerials for detecting the polarization changes, a marked change in the birefringence should be generally detectable across the hinge zone, and if found would be a confirmation that the ice was at least partially afloat on tidal ocean water.

4. 4. This work is relevant to the possible future use of the polarization of radio waves to help in the identification of subglacial bedrock. By increasing the level of the minimum radio-frequency anisotropy of ice by nearly twenty times the minimum level set by Reference HargreavesHargreaves (1977), we are underlining the importance of the fabric in an ice sheet and its distribution with depth in determining the polarization of a radio echo signal. The strain history is therefore crucial, especially in ice of greater depth than we have discussed here, where a phase change of more than 360° could easily occur. However, from the proportion of the unpolarized component in the first returns it is possible that vertical roughness of different subglacial beds might be characterized. Moreover if an independent determination of the fabric profile were possible, from wide-angle polarization work with separated aerials, the permittivities and conductivities of subglacial bedrocks might be determined from their complex reflection coefficients.