1. Introduction
In their now classic work on viscous fingering, Saffman & Taylor (Reference Saffman and Taylor1958) consider the situation of a single finger of air – or an otherwise less viscous substance – steadily penetrating a Hele-Shaw cell filled with a viscous fluid. A key quantity of interest is the proportion of the channel occupied by the width of the finger, denoted ![]() $\lambda \in (0,1)$. Experimentally, Saffman and Taylor observed that
$\lambda \in (0,1)$. Experimentally, Saffman and Taylor observed that ![]() $\lambda \approx 1/2$. However, their asymptotic analysis, valid at small values of the non-dimensional surface-tension parameter
$\lambda \approx 1/2$. However, their asymptotic analysis, valid at small values of the non-dimensional surface-tension parameter ![]() $\epsilon \to 0$, did not seem to restrict the value of
$\epsilon \to 0$, did not seem to restrict the value of ![]() $\lambda$. Today, it is known that for a fixed
$\lambda$. Today, it is known that for a fixed ![]() $\epsilon$ there exists a countably infinite number of possible values of
$\epsilon$ there exists a countably infinite number of possible values of ![]() $\lambda = \lambda _i$ with the property that
$\lambda = \lambda _i$ with the property that
In the limit ![]() $\epsilon \to 0$, every element in the family converges to 1/2 (see e.g. Vanden-Broeck Reference Vanden-Broeck2010). The resultant plot of the eigenvalue,
$\epsilon \to 0$, every element in the family converges to 1/2 (see e.g. Vanden-Broeck Reference Vanden-Broeck2010). The resultant plot of the eigenvalue, ![]() $\lambda$, vs the surface-tension parameter,
$\lambda$, vs the surface-tension parameter, ![]() $\epsilon$, is shown in figure 1(a). The resolution of the Saffman–Taylor problem, including the asymptotic derivation of (1.1), is obtained using exponential asymptotics; today, it is a prototypical example of such beyond-all-orders asymptotics (see e.g. works by McLean & Saffman Reference McLean and Saffman1981; Combescot et al. Reference Combescot, Dombre, Hakim, Pomeau and Pumir1986, Reference Combescot, Hakim, Dombre, Pomeau and Pumir1988; Hong & Langer Reference Hong and Langer1986; Tanveer Reference Tanveer1987, Reference Tanveer2000; Chapman Reference Chapman1999; Pullin & Meiron Reference Pullin and Meiron2013).
$\epsilon$, is shown in figure 1(a). The resolution of the Saffman–Taylor problem, including the asymptotic derivation of (1.1), is obtained using exponential asymptotics; today, it is a prototypical example of such beyond-all-orders asymptotics (see e.g. works by McLean & Saffman Reference McLean and Saffman1981; Combescot et al. Reference Combescot, Dombre, Hakim, Pomeau and Pumir1986, Reference Combescot, Hakim, Dombre, Pomeau and Pumir1988; Hong & Langer Reference Hong and Langer1986; Tanveer Reference Tanveer1987, Reference Tanveer2000; Chapman Reference Chapman1999; Pullin & Meiron Reference Pullin and Meiron2013).

Figure 1. (a) The bifurcation diagram for the classic Saffman–Taylor problem in a channel showing the first 10 branches of selected ![]() $\lambda$ values against the surface-tension parameter
$\lambda$ values against the surface-tension parameter ![]() $\epsilon ^2$. Labels are shown for the first four branches:
$\epsilon ^2$. Labels are shown for the first four branches: ![]() $\lambda _1$,
$\lambda _1$, ![]() $\lambda _2$,
$\lambda _2$, ![]() $\lambda _3$,
$\lambda _3$, ![]() $\lambda _4.$ This is equivalent to the results of Chapman (Reference Chapman1999). (b) The solid lines show the bifurcation diagram which we calculate using exponential asymptotics for wedge angle
$\lambda _4.$ This is equivalent to the results of Chapman (Reference Chapman1999). (b) The solid lines show the bifurcation diagram which we calculate using exponential asymptotics for wedge angle ![]() $\theta _0 = 20^\circ$. This shows the permitted
$\theta _0 = 20^\circ$. This shows the permitted ![]() $\lambda (\epsilon )$ values that are selected by the selection mechanism. Details of the derivation of this selection mechanism follow in the rest of the paper. The circles show the numerically calculated values extracted from Ben Amar (Reference Ben Amar1991b). Notice that
$\lambda (\epsilon )$ values that are selected by the selection mechanism. Details of the derivation of this selection mechanism follow in the rest of the paper. The circles show the numerically calculated values extracted from Ben Amar (Reference Ben Amar1991b). Notice that ![]() $\lambda _1$ and
$\lambda _1$ and ![]() $\lambda _2$ merge at
$\lambda _2$ merge at ![]() $\epsilon \approx 0.3$ and
$\epsilon \approx 0.3$ and ![]() $\lambda _3$ and
$\lambda _3$ and ![]() $\lambda _4$ merge at
$\lambda _4$ merge at ![]() $\epsilon \approx 0.07$.
$\epsilon \approx 0.07$.
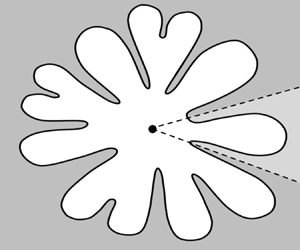
In this paper, we are interested in deriving a similar selection law to (1.1) but for an analogue problem where fluid is injected at the corner of a Hele-Shaw cell limited by side walls consisting of a wedge of specified angle. Although this wedge scenario is interesting in its own right, it gains further importance as a partial model for the fingering seen where fluid is injected into a Hele-Shaw cell from a central source. As the injected fluid moves outwards, the interface destabilises and fingering occurs in the manner illustrated in figure 2. Thus, the limited wedge configuration considered in this work serves as a model for each sector of the full source problem.

Figure 2. Sketch of the free surface for viscous fingering in the full circular geometry, where a central source injects fluids outwards in all directions. Assuming axisymmetry, a single finger from this free surface can be considered as arising due to injecting fluid in the corner of the Hele-Shaw cell limited by sidewalls consisting of a wedge of angle ![]() $\theta _0$.
$\theta _0$.
Consider the wedge problem characterised by a wedge angle, ![]() $\theta _0$, measured at the corner. The key parameter,
$\theta _0$, measured at the corner. The key parameter, ![]() $\lambda$, now describes the angular proportion,
$\lambda$, now describes the angular proportion, ![]() $\lambda \theta _0$, of the cell occupied by the finger. In comparison with the previous figure 1(a) for classic Saffman–Taylor viscous fingering, in figure 1(b) we plot the bifurcation diagram for the case of a wedge of angle
$\lambda \theta _0$, of the cell occupied by the finger. In comparison with the previous figure 1(a) for classic Saffman–Taylor viscous fingering, in figure 1(b) we plot the bifurcation diagram for the case of a wedge of angle ![]() $\theta _0 = 20^\circ$. The solid lines correspond to the new asymptotic predictions developed in this work, while the circles correspond to the previous numerical results of Ben Amar (Reference Ben Amar1991b). The figure shows the existence of distinct solution families,
$\theta _0 = 20^\circ$. The solid lines correspond to the new asymptotic predictions developed in this work, while the circles correspond to the previous numerical results of Ben Amar (Reference Ben Amar1991b). The figure shows the existence of distinct solution families, ![]() $\lambda = \lambda _i(\epsilon, \theta _0)$.
$\lambda = \lambda _i(\epsilon, \theta _0)$.
In addition to the expected solution families, ![]() $\lambda _i$, there is now an additional phenomenon for the wedge-limited configurations. As seen in figure 1(b), there exist certain critical values of the surface-tension parameter,
$\lambda _i$, there is now an additional phenomenon for the wedge-limited configurations. As seen in figure 1(b), there exist certain critical values of the surface-tension parameter, ![]() $\epsilon$, where each solution family,
$\epsilon$, where each solution family, ![]() $\lambda _i$, reaches a turning point connected to the adjacent family, i.e.
$\lambda _i$, reaches a turning point connected to the adjacent family, i.e. ![]() $\lambda _i = \lambda _{i+1}$. In this work, we will explain how this merging of eigenvalues can be understood from the perspective of the exponential asymptotics. As noted by Ben Amar (Reference Ben Amar1991b), the merging of eigenvalue pairs causes a loss of existence of the solutions for sufficiently small
$\lambda _i = \lambda _{i+1}$. In this work, we will explain how this merging of eigenvalues can be understood from the perspective of the exponential asymptotics. As noted by Ben Amar (Reference Ben Amar1991b), the merging of eigenvalue pairs causes a loss of existence of the solutions for sufficiently small ![]() $\epsilon$. Physically, in connection with the full geometry in figure 2, this results in the finger splitting into two through a tip-splitting instability. One should then consider two wedges of half the angle to continue to follow the finger profiles. It is then interesting to consider the consequences of the exponential asymptotic analysis towards the more complicated problem of time-dependent tip-splitting instabilities in the unrestricted planar domain. This will be further discussed in § 10.
$\epsilon$. Physically, in connection with the full geometry in figure 2, this results in the finger splitting into two through a tip-splitting instability. One should then consider two wedges of half the angle to continue to follow the finger profiles. It is then interesting to consider the consequences of the exponential asymptotic analysis towards the more complicated problem of time-dependent tip-splitting instabilities in the unrestricted planar domain. This will be further discussed in § 10.
1.1. Background and open challenges of the wedge problem
The literature on Hele-Shaw flows and viscous fingering problems is extensive; here, we provide a review of selected papers, primarily focused on wedge configurations or closed bubbles in channels.
Experimental observations and initial analysis for the wedge geometry can be found in the works of Paterson (Reference Paterson1981) and Thomé et al. (Reference Thomé, Rabaud, Hakim and Couder1989). Then, in the early 1990s, a number of works appeared on the beyond-all-orders aspects of the wedge configuration (Brener et al. Reference Brener, Kessler, Levine and Rappel1990; Ben Amar Reference Ben Amar1991a,Reference Ben Amarb; Tu Reference Tu1991; Combescot Reference Combescot1992; Levine & Tu Reference Levine and Tu1992). Combescot (Reference Combescot1992) identified the singularities in the complex plane that are responsible for the selection mechanism. The solvability condition was found exactly by Brener et al. (Reference Brener, Kessler, Levine and Rappel1990) for the case with a ![]() $90^{\circ }$ separation angle, where the solution reduces to a closed analytic form. Both Combescot (Reference Combescot1992) and Tu (Reference Tu1991) used WKBJ (Wentzel-Kramers-Brillouin-Jeffreys or Liouville–Green) methods to make analytical progress on the problem with a general wedge angle whilst numerical results were obtained by Ben Amar (Reference Ben Amar1991b). More recently, there has been additional experimental works, showing clear photographs, of the tip-splitting instabilities in the wedge problem by Lajeunesse & Couder (Reference Lajeunesse and Couder2000).
$90^{\circ }$ separation angle, where the solution reduces to a closed analytic form. Both Combescot (Reference Combescot1992) and Tu (Reference Tu1991) used WKBJ (Wentzel-Kramers-Brillouin-Jeffreys or Liouville–Green) methods to make analytical progress on the problem with a general wedge angle whilst numerical results were obtained by Ben Amar (Reference Ben Amar1991b). More recently, there has been additional experimental works, showing clear photographs, of the tip-splitting instabilities in the wedge problem by Lajeunesse & Couder (Reference Lajeunesse and Couder2000).
This paper is most strongly motivated by the work of Tu (Reference Tu1991) and Ben Amar (Reference Ben Amar1991b). Tu (Reference Tu1991) had linearised the free-surface problem with a general wedge angle to obtain a model differential equation. For this new equation, a WKBJ approximation was used to derive a solvability condition that can predict the theoretical zero-surface-tension limit for ![]() $\lambda$, as well as a condition that finds the point in the bifurcation diagram where branch merging occurs.
$\lambda$, as well as a condition that finds the point in the bifurcation diagram where branch merging occurs.
Ben Amar (Reference Ben Amar1991b) produced accurate numerical results for parts of the bifurcation diagram. However, on account of the challenges in numerical computations of the eigenvalue problem, Ben Amar (Reference Ben Amar1991b) noted that:
Our predictions concerning levels [branches] higher than the first two require confirmation by a very careful WKB analysis, which is the most suitable treatment at extremely low surface tension. Probably, the results of analytic solutions without surface tension will make this analysis possible.
At this point (and until the present) we do not believe any group has managed to derive the exact selection mechanism (i.e. the missing analysis referenced above).
Modern techniques of exponential asymptotics allow us to study the wedge problem in the small-surface-tension limit without the need to linearise in the same fashion as previous practitioners (Chapman, King & Adams Reference Chapman, King and Adams1998). In this paper, we will use these techniques to address the open problem identified by Ben Amar (Reference Ben Amar1991b) and obtain an analytic solvability condition for the selected eigenvalues.
Because the approach presented here combines a hybrid asymptotic–numerical insight, it is likely that the methods can be extended to much more general flow configurations. More recently, further work has been done on closely related problems in Hele-Shaw channels. There is particular interest in Hele-Shaw channels with a central raised rail, which can change the stability of the finger (Thompson, Juel & Hazel Reference Thompson, Juel and Hazel2014; Franco-Gómez, Thompson & Hazel Reference Franco-Gómez, Thompson and Hazel2016). Further, there have been many recent experimental (Franco-Gómez et al. Reference Franco-Gómez, Thompson, Hazel and Juel2017; Gaillard et al. Reference Gaillard, Keeler, Le Lay, Lemoult, Thompson, Hazel and Juel2021; Lawless et al. Reference Lawless, Keeler, Hazel and Juel2023), numerical (Franco-Gómez et al. Reference Franco-Gómez, Thompson, Hazel and Juel2017; Keeler et al. Reference Keeler, Thompson, Lemoult, Juel and Hazel2019; Thompson Reference Thompson2021) and analytical (Keeler et al. Reference Keeler, Thompson, Lemoult, Juel and Hazel2019; Booth, Griffiths & Howell Reference Booth, Griffiths and Howell2023) developments concerning closed bubbles propagating along Hele-Shaw channels. We will return at the end of the paper to discuss the connection of our work with these newer problems.
2. Mathematical formulation
A traditional Hele-Shaw cell consists of two parallel plates separated by a small distance, ![]() $b$, and filled with viscous fluid with viscosity,
$b$, and filled with viscous fluid with viscosity, ![]() $\mu$. For the case of a circular geometry, like that depicted in figure 2, an inviscid fluid is injected at a point, and this drives an outwards-expanding interface between viscous and inviscid fluids.
$\mu$. For the case of a circular geometry, like that depicted in figure 2, an inviscid fluid is injected at a point, and this drives an outwards-expanding interface between viscous and inviscid fluids.
We now consider the related wedge-shaped geometry, as shown in figure 3(a). Here, the inviscid fluid is injected at the wedge corner at some prescribed flow rate. The viscous fluid is constrained to lie between the wedge walls separated by an internal angle ![]() $\theta _0$. As can be observed experimentally (Thomé et al. Reference Thomé, Rabaud, Hakim and Couder1989), a self-similar shape is reached eventually, where the inviscid fluid occupies an angle
$\theta _0$. As can be observed experimentally (Thomé et al. Reference Thomé, Rabaud, Hakim and Couder1989), a self-similar shape is reached eventually, where the inviscid fluid occupies an angle ![]() $\lambda \theta _0$, with
$\lambda \theta _0$, with ![]() $0<\lambda <1$. This set-up is referred to as divergent flow in Ben Amar (Reference Ben Amar1991a). For the case of zero-surface-tension, a prototypical solution is shown in figure 3(a), and we observe the petal-shaped interface between viscous fluid and inviscid fluid.
$0<\lambda <1$. This set-up is referred to as divergent flow in Ben Amar (Reference Ben Amar1991a). For the case of zero-surface-tension, a prototypical solution is shown in figure 3(a), and we observe the petal-shaped interface between viscous fluid and inviscid fluid.

Figure 3. (a) A numerical plot of the top-down view of the self-similar physical profile in the ![]() $\hat {z}$-plane is shown for the zero-surface-tension case, with parameter values
$\hat {z}$-plane is shown for the zero-surface-tension case, with parameter values ![]() $\theta _0 = 20^{\circ }$ and
$\theta _0 = 20^{\circ }$ and ![]() $\lambda = 0.6$. The free surface was computed using (3.7). The Hele-Shaw cell is bounded by the thick black lines and is filled with a viscous fluid, shown in grey. An inviscid fluid is injected from the corner of the wedge and forms a finger with angle
$\lambda = 0.6$. The free surface was computed using (3.7). The Hele-Shaw cell is bounded by the thick black lines and is filled with a viscous fluid, shown in grey. An inviscid fluid is injected from the corner of the wedge and forms a finger with angle ![]() $\lambda \theta _0$. The corner of the wedge lies at
$\lambda \theta _0$. The corner of the wedge lies at ![]() $\hat z = 0$ (
$\hat z = 0$ (![]() $BF$) and the tip of the finger lies at
$BF$) and the tip of the finger lies at ![]() $\hat {z}=1$ (
$\hat {z}=1$ (![]() $CE$). (b) A sketch of the
$CE$). (b) A sketch of the ![]() $z$-plane, computed via the conformal map
$z$-plane, computed via the conformal map ![]() $z=(2/\theta _0)\log \hat {z}$. This configuration is analogous to the traditional Saffman–Taylor finger (McLean & Saffman Reference McLean and Saffman1981).
$z=(2/\theta _0)\log \hat {z}$. This configuration is analogous to the traditional Saffman–Taylor finger (McLean & Saffman Reference McLean and Saffman1981).
The classic problem of Saffman–Taylor viscous fingering in a channel is typically studied in a travelling frame corresponding to a steady-state finger. In the wedge geometry, the analogue of a travelling wave frame of reference is a self-similar solution. In Appendix A, we demonstrate how the original equations of potential flow for a Hele-Shaw cell, with boundary conditions on the channel walls and free boundary, and an injection condition can be reposed in the self-similar framework. The key idea relates to a transformation of the original dimensional lengths, ![]() $\bar {x}$ and
$\bar {x}$ and ![]() $\bar {y}$, which are scaled via
$\bar {y}$, which are scaled via
where ![]() $R_0$ is a length scale (chosen to be the distance between the corner of the wedge and the tip of the finger at
$R_0$ is a length scale (chosen to be the distance between the corner of the wedge and the tip of the finger at ![]() $t=0$) and
$t=0$) and ![]() ${A}(t)$ is a dimensionless scaling factor that depends on dimensionless time,
${A}(t)$ is a dimensionless scaling factor that depends on dimensionless time, ![]() $t$. As shown in Appendix A, two possible choices of
$t$. As shown in Appendix A, two possible choices of ![]() ${A}(t)$ result in effectively the same self-similar problem, given by (A6), in dimensionless variables with a time-independent effective surface-tension parameter
${A}(t)$ result in effectively the same self-similar problem, given by (A6), in dimensionless variables with a time-independent effective surface-tension parameter ![]() $\sigma$. This
$\sigma$. This ![]() $\sigma$, when rescaled, then gives us our small parameter
$\sigma$, when rescaled, then gives us our small parameter ![]() $\epsilon$, defined below in (2.10); see Ben Amar (Reference Ben Amar1991b) for further details.
$\epsilon$, defined below in (2.10); see Ben Amar (Reference Ben Amar1991b) for further details.
We thus have the governing set of potential-flow equations in (A6) corresponding to a scaled velocity potential, ![]() $\hat {\phi }$, and self-similar physical-plane coordinates, written in complex form as
$\hat {\phi }$, and self-similar physical-plane coordinates, written in complex form as ![]() $\hat {z} = \hat {x} + \mathrm {i} \hat {y}$ (figure 3a). Note that the free surface is now stationary. We introduce the complex potential,
$\hat {z} = \hat {x} + \mathrm {i} \hat {y}$ (figure 3a). Note that the free surface is now stationary. We introduce the complex potential, ![]() $\hat {f}=\hat {\phi }+\mathrm {i}\hat {\psi }$, with harmonic conjugate given by the streamfunction
$\hat {f}=\hat {\phi }+\mathrm {i}\hat {\psi }$, with harmonic conjugate given by the streamfunction ![]() $\hat{\psi}$. Within the
$\hat{\psi}$. Within the ![]() $\hat {f}$-plane, fluid is located in the infinite strip bounded by
$\hat {f}$-plane, fluid is located in the infinite strip bounded by ![]() $\hat {\psi } \in [-1,1]$.
$\hat {\psi } \in [-1,1]$.
Finally, the flow domain is mapped to a channel geometry via
so that the walls ![]() $BA$ and
$BA$ and ![]() $FG$ lie on
$FG$ lie on ![]() $\operatorname {Im} z=\pm 1$, respectively, and the tip
$\operatorname {Im} z=\pm 1$, respectively, and the tip ![]() $CE$ is fixed to the origin
$CE$ is fixed to the origin ![]() $z=0$. This is shown in figure 3(b).
$z=0$. This is shown in figure 3(b).
Following § 3B of Ben Amar (Reference Ben Amar1991b), we review the procedure for developing a set of boundary-integral equations for the potential-flow problem. First, the velocity potential is shifted as
Above, ![]() $2Q_0$ is the dimensionless flux of fluid across the wedge at infinity in the self-similar frame (cf. later (2.8)). The function
$2Q_0$ is the dimensionless flux of fluid across the wedge at infinity in the self-similar frame (cf. later (2.8)). The function ![]() $H(z)$ is implicitly defined so that the free surface lies on
$H(z)$ is implicitly defined so that the free surface lies on ![]() $\psi ^*=$ constant (cf. (3.10) of Ben Amar Reference Ben Amar1991b). For the case of the classic Saffman–Taylor viscous fingering problem in a parallel channel,
$\psi ^*=$ constant (cf. (3.10) of Ben Amar Reference Ben Amar1991b). For the case of the classic Saffman–Taylor viscous fingering problem in a parallel channel, ![]() $H(z) = z$, as shown by McLean & Saffman (Reference McLean and Saffman1981).
$H(z) = z$, as shown by McLean & Saffman (Reference McLean and Saffman1981).
As in Chapman (Reference Chapman1999), it is convenient for later analysis to map the fluid region to the upper-half-![]() $\zeta$-plane via
$\zeta$-plane via
The mapped fluid domain for the configuration in figure 3 is shown in figure 4. Thus we see that, under the map (2.4), the free surface (![]() $BCEF$) lies on the real
$BCEF$) lies on the real ![]() $\zeta$-axis while the tip of the finger (
$\zeta$-axis while the tip of the finger (![]() $CE$) is at
$CE$) is at ![]() $\zeta = 0$.
$\zeta = 0$.

Figure 4. The fluid region (grey) is mapped to the upper-half-![]() $\zeta$-plane. The key points from figure 3 are labelled here. Within the
$\zeta$-plane. The key points from figure 3 are labelled here. Within the ![]() $\zeta$-plane, there is a branch cut from the point
$\zeta$-plane, there is a branch cut from the point ![]() $D$ (
$D$ (![]() $\zeta = \mathrm {i}$). Here, the branch cut is taken vertically up the imaginary axis from
$\zeta = \mathrm {i}$). Here, the branch cut is taken vertically up the imaginary axis from ![]() $\zeta = \mathrm {i}$.
$\zeta = \mathrm {i}$.
In the governing equations to follow, we shall seek to solve for the unknown free-surface location and fluid velocities along the interface, ![]() $\zeta = \xi \in \mathbb {R}$. It is convenient to introduce quantities
$\zeta = \xi \in \mathbb {R}$. It is convenient to introduce quantities ![]() $q$ and
$q$ and ![]() $\tau$ via
$\tau$ via
which are analogues of speed and streamline angle, respectively (and reduce to the actual fluid speed and streamline angle in the limit ![]() $\theta _0\rightarrow 0$). Therefore, we require a set of governing equations for the unknowns
$\theta _0\rightarrow 0$). Therefore, we require a set of governing equations for the unknowns ![]() $(x(\xi ), y(\xi ), q(\xi ), \tau (\xi ))$.
$(x(\xi ), y(\xi ), q(\xi ), \tau (\xi ))$.
With the various conformal maps now established, at this point, we may follow the same procedures as found in § 3B of Ben Amar (Reference Ben Amar1991b). We find on the free surface, where ![]() $\zeta = \xi$ is real, that continuity of pressure yields Bernoulli's equation
$\zeta = \xi$ is real, that continuity of pressure yields Bernoulli's equation
 \begin{align} &\epsilon^2
\frac{P(\xi)}{4} \frac{\partial}{\partial \xi}\left(r(x)
\left[{-}P(\xi) q(\xi)\frac{\partial \tau}{\partial \xi} +
\frac{\ell}{2}\sin\tau(\xi)\right]\right) \nonumber\\
&\quad\quad = \frac{Q_0}{1-\lambda} -
\frac{2}{\rm \pi}(1+\xi^2){\int\hskip -1,05em -\,}_{-\infty}^0
\frac{K(\tilde{\xi})\operatorname{d}{}{\tilde{\xi}}}{P(\tilde{\xi})(\xi^2-
\tilde{\xi}^2)},
\end{align}
\begin{align} &\epsilon^2
\frac{P(\xi)}{4} \frac{\partial}{\partial \xi}\left(r(x)
\left[{-}P(\xi) q(\xi)\frac{\partial \tau}{\partial \xi} +
\frac{\ell}{2}\sin\tau(\xi)\right]\right) \nonumber\\
&\quad\quad = \frac{Q_0}{1-\lambda} -
\frac{2}{\rm \pi}(1+\xi^2){\int\hskip -1,05em -\,}_{-\infty}^0
\frac{K(\tilde{\xi})\operatorname{d}{}{\tilde{\xi}}}{P(\tilde{\xi})(\xi^2-
\tilde{\xi}^2)},
\end{align}which can be compared with (3.10) of Ben Amar (Reference Ben Amar1991b). In (2.6), we have defined a number of functions for convenience. Firstly, we have written
Note that ![]() $r$ is a function of
$r$ is a function of ![]() $x$ which, in turn, depends on
$x$ which, in turn, depends on ![]() $\xi$. In (2.6), we have defined
$\xi$. In (2.6), we have defined ![]() $Q_0$ to be
$Q_0$ to be
 \begin{equation} Q_0 = \frac{2(1-\lambda)}{\rm \pi} \int_{-\infty}^0 \frac{K(\tilde{\xi})}{P(\tilde{\xi})}\,{\rm d}{\tilde{\xi}}, \end{equation}
\begin{equation} Q_0 = \frac{2(1-\lambda)}{\rm \pi} \int_{-\infty}^0 \frac{K(\tilde{\xi})}{P(\tilde{\xi})}\,{\rm d}{\tilde{\xi}}, \end{equation}
which, as mentioned above, represents a dimensionless constant describing the fluid flux. It is also convenient to define a scaled value for the interior wedge angle ![]() $\theta _0$
$\theta _0$
where ![]() $\lambda$ is the proportional finger angle parameter. Finally, we have introduced the key non-dimensional parameter,
$\lambda$ is the proportional finger angle parameter. Finally, we have introduced the key non-dimensional parameter, ![]() $\epsilon$, by
$\epsilon$, by
where ![]() $\hat {\sigma }$ is the modified surface-tension parameter presented in (A9a–c) in Appendix A. We consider
$\hat {\sigma }$ is the modified surface-tension parameter presented in (A9a–c) in Appendix A. We consider ![]() $\epsilon ^2$ to be a small parameter, corresponding to the small-surface-tension regime, and we will therefore study the problem in the asymptotic limit
$\epsilon ^2$ to be a small parameter, corresponding to the small-surface-tension regime, and we will therefore study the problem in the asymptotic limit ![]() $\epsilon \rightarrow 0$.
$\epsilon \rightarrow 0$.
Analyticity of ![]() $q\mathrm {e}^{-\mathrm {i} \tau }$ in the upper-half-
$q\mathrm {e}^{-\mathrm {i} \tau }$ in the upper-half-![]() $\zeta$-plane gives, by the Hilbert transform,
$\zeta$-plane gives, by the Hilbert transform,
 \begin{equation} \log q(\xi) = \mathcal{H}[\tau](\xi) \quad \text{where} \ \mathcal{H}[\tau](\xi) = \frac{2}{\rm \pi}{\int\hskip -1,05em -\,}_{-\infty}^0 \frac{\tau(\tilde{\xi}) \, \tilde{\xi}}{\xi^2 - \tilde{\xi}^2} \, {\rm d}{\tilde{\xi}}, \end{equation}
\begin{equation} \log q(\xi) = \mathcal{H}[\tau](\xi) \quad \text{where} \ \mathcal{H}[\tau](\xi) = \frac{2}{\rm \pi}{\int\hskip -1,05em -\,}_{-\infty}^0 \frac{\tau(\tilde{\xi}) \, \tilde{\xi}}{\xi^2 - \tilde{\xi}^2} \, {\rm d}{\tilde{\xi}}, \end{equation}
where we have defined the operator, ![]() $\mathcal {H}$. Finally, we close the system by integrating the free-surface velocity relationships (2.5). This yields
$\mathcal {H}$. Finally, we close the system by integrating the free-surface velocity relationships (2.5). This yields
 \begin{equation} x(\xi) +\mathrm{i} y(\xi) = \frac{2(1-\lambda)}{\rm \pi}\int_\xi^0 \frac{\mathrm{e}^{\mathrm{i}\tau(\tilde{\xi})}}{q(\tilde{\xi}) P(\tilde{\xi})} \, {\rm d}{\tilde{\xi}}. \end{equation}
\begin{equation} x(\xi) +\mathrm{i} y(\xi) = \frac{2(1-\lambda)}{\rm \pi}\int_\xi^0 \frac{\mathrm{e}^{\mathrm{i}\tau(\tilde{\xi})}}{q(\tilde{\xi}) P(\tilde{\xi})} \, {\rm d}{\tilde{\xi}}. \end{equation} Thus, the full system consists of (2.6), (2.11) and (2.12) for the unknowns ![]() $(x, y, q, \tau )$ in addition to the boundary conditions
$(x, y, q, \tau )$ in addition to the boundary conditions
Above, the first set of boundary conditions corresponds to imposing the geometrical constraints while the second set corresponds to the velocity and streamline angle constraints. In total, the equations and boundary conditions are equivalent to those of Ben Amar (Reference Ben Amar1991a). In the next section, we shall examine the zero-surface-tension solutions of these equations.
3. Zero-surface-tension solutions
We first discuss the zero-surface-tension solutions, ![]() $(x_0(\xi ), y_0(\xi ), q_0(\xi ), \tau _0(\xi ))$, which correspond to setting
$(x_0(\xi ), y_0(\xi ), q_0(\xi ), \tau _0(\xi ))$, which correspond to setting ![]() $\epsilon = 0$ in the governing equations (2.6), (2.11) and (2.12). We thus approximate
$\epsilon = 0$ in the governing equations (2.6), (2.11) and (2.12). We thus approximate ![]() $x \sim x_0$,
$x \sim x_0$, ![]() $y \sim y_0$,
$y \sim y_0$, ![]() $q \sim q_0$ and
$q \sim q_0$ and ![]() $\tau \sim \tau _0$ in the limit
$\tau \sim \tau _0$ in the limit ![]() $\epsilon \to 0$. The zero-surface-tension equations are given by
$\epsilon \to 0$. The zero-surface-tension equations are given by
 $$\begin{gather} 0 =\frac{Q_0}{1-\lambda} - \frac{2}{\rm \pi} (1+\xi^2){\int\hskip -1,05em -\,}_{-\infty}^0 \frac{K_0(\tilde{\xi}) }{ P(\tilde{\xi})(\xi^2-\tilde{\xi}^2)}\,{\rm d}{\tilde{\xi}}, \end{gather}$$
$$\begin{gather} 0 =\frac{Q_0}{1-\lambda} - \frac{2}{\rm \pi} (1+\xi^2){\int\hskip -1,05em -\,}_{-\infty}^0 \frac{K_0(\tilde{\xi}) }{ P(\tilde{\xi})(\xi^2-\tilde{\xi}^2)}\,{\rm d}{\tilde{\xi}}, \end{gather}$$ $$\begin{gather}x_0(\xi) + \mathrm{i} y_0(\xi) ={-} \frac{2(1-\lambda)}{\rm \pi}\int_\zeta^0 \frac{\mathrm{e}^{\mathrm{i}\tau_0(\tilde{\xi})}} {q_0(\tilde{\xi})P(\tilde{\xi})}\,{\rm d}{\tilde{\xi}}, \end{gather}$$
$$\begin{gather}x_0(\xi) + \mathrm{i} y_0(\xi) ={-} \frac{2(1-\lambda)}{\rm \pi}\int_\zeta^0 \frac{\mathrm{e}^{\mathrm{i}\tau_0(\tilde{\xi})}} {q_0(\tilde{\xi})P(\tilde{\xi})}\,{\rm d}{\tilde{\xi}}, \end{gather}$$where
The corresponding boundary conditions are
As shown by Ben Amar (Reference Ben Amar1991a) and Tu (Reference Tu1991), the leading-order system (3.1) can be re-arranged so as to obtain a Riccati equation
with boundary conditions
where the new unknown is defined by
It was shown by Ben Amar (Reference Ben Amar1991a) and Tu (Reference Tu1991) that the leading-order (zero-surface-tension) solutions can then be written in terms of the hypergeometric function ![]() $F$ (Abramowitz & Stegun Reference Abramowitz and Stegun1972)
$F$ (Abramowitz & Stegun Reference Abramowitz and Stegun1972)
where we have also defined the constant
 \begin{equation} \tilde{A} = 2 \tan \left(\frac{\lambda \theta_0}{2}\right)\dfrac{\varGamma\left(1-\dfrac{\theta_0(2-\lambda)}{2{\rm \pi}}\right) \varGamma \left(1+ \dfrac{\lambda\theta_0}{2{\rm \pi}}\right)}{\varGamma \left(\dfrac{1}{2} - \dfrac{\theta_0 (2-\lambda)}{2{\rm \pi}}\right)\varGamma \left(\dfrac{1}{2}+\dfrac{\lambda\theta_0}{2{\rm \pi}}\right)}. \end{equation}
\begin{equation} \tilde{A} = 2 \tan \left(\frac{\lambda \theta_0}{2}\right)\dfrac{\varGamma\left(1-\dfrac{\theta_0(2-\lambda)}{2{\rm \pi}}\right) \varGamma \left(1+ \dfrac{\lambda\theta_0}{2{\rm \pi}}\right)}{\varGamma \left(\dfrac{1}{2} - \dfrac{\theta_0 (2-\lambda)}{2{\rm \pi}}\right)\varGamma \left(\dfrac{1}{2}+\dfrac{\lambda\theta_0}{2{\rm \pi}}\right)}. \end{equation}
By differentiating and rearranging (3.1c) we also obtain expressions for ![]() $q_0(\xi )$ and
$q_0(\xi )$ and ![]() $\tau _0(\xi )$
$\tau _0(\xi )$
 \begin{align} q_0 = \ell\,\frac{\xi}{1+\xi^2}\,\sqrt{\frac{x_0^2+y_0^2}{\left(\dfrac{\mathrm{d}\kern1pt x_0}{\mathrm{d}\xi}\right)^2 + \left(\dfrac{\mathrm{d}y_0}{\mathrm{d}\xi}\right)^2}}, \quad \cos\tau_0 ={-}\frac{q_0}{\ell}\,\frac{1+\xi^2}{\xi}\,\frac{x_0\dfrac{\mathrm{d}\kern1pt x_0}{\mathrm{d}\xi} + y_0 \dfrac{\mathrm{d}y_0}{\mathrm{d}\xi}}{x_0^2 + y_0^2}. \end{align}
\begin{align} q_0 = \ell\,\frac{\xi}{1+\xi^2}\,\sqrt{\frac{x_0^2+y_0^2}{\left(\dfrac{\mathrm{d}\kern1pt x_0}{\mathrm{d}\xi}\right)^2 + \left(\dfrac{\mathrm{d}y_0}{\mathrm{d}\xi}\right)^2}}, \quad \cos\tau_0 ={-}\frac{q_0}{\ell}\,\frac{1+\xi^2}{\xi}\,\frac{x_0\dfrac{\mathrm{d}\kern1pt x_0}{\mathrm{d}\xi} + y_0 \dfrac{\mathrm{d}y_0}{\mathrm{d}\xi}}{x_0^2 + y_0^2}. \end{align}
In figure 5, we plot example profiles for the leading-order solutions, ![]() $(x_0, y_0, q_0, \tau _0)$, along the free surface for parameter values
$(x_0, y_0, q_0, \tau _0)$, along the free surface for parameter values ![]() $\theta _0 = 20^\circ$ and
$\theta _0 = 20^\circ$ and ![]() $\lambda = 0.6.$ These solutions are generated using (3.7) and (3.8a,b).
$\lambda = 0.6.$ These solutions are generated using (3.7) and (3.8a,b).

Figure 5. Plots of the leading-order (zero-surface-tension) solutions for the four variables ![]() $(x_0,y_0,q_0,\tau _0)$ on the free surface,
$(x_0,y_0,q_0,\tau _0)$ on the free surface, ![]() $\zeta = \xi \in \mathbb {R}$. These plots show the solutions for parameter values
$\zeta = \xi \in \mathbb {R}$. These plots show the solutions for parameter values ![]() $\theta _0 = 20^\circ$ and
$\theta _0 = 20^\circ$ and ![]() $\lambda = 0.6$ generated using (3.7) and (3.8a,b). The tip of the finger lies at
$\lambda = 0.6$ generated using (3.7) and (3.8a,b). The tip of the finger lies at ![]() $\xi = 0.$ In figure 3 we plot this solution in the physical plane.
$\xi = 0.$ In figure 3 we plot this solution in the physical plane.
4. Analytic continuation of the free surface
The leading-order profiles, as evaluated on the physical free surface, ![]() $\zeta = \xi \in \mathbb {R}$, were shown in the previous section. The analytic continuation of these profiles to the complex plane contains square-root singularities. We shall see that such singularities form one of the key ingredients in the exponential asymptotics procedure of § 6; these points cause the asymptotic expansion to diverge, and will be crucial in determining the eventual selection mechanism. In this section, we discuss the numerical procedure for generating the analytic continuation of the leading-order solutions
$\zeta = \xi \in \mathbb {R}$, were shown in the previous section. The analytic continuation of these profiles to the complex plane contains square-root singularities. We shall see that such singularities form one of the key ingredients in the exponential asymptotics procedure of § 6; these points cause the asymptotic expansion to diverge, and will be crucial in determining the eventual selection mechanism. In this section, we discuss the numerical procedure for generating the analytic continuation of the leading-order solutions ![]() $(x_0, y_0, q_0, \tau _0)$, as well as the analytic continuation of the governing equations (2.6), (2.11) and (2.12).
$(x_0, y_0, q_0, \tau _0)$, as well as the analytic continuation of the governing equations (2.6), (2.11) and (2.12).
4.1. Analytic continuation of the leading-order solutions
In the analytic continuation, we allow the previously real-valued ![]() $\xi$ to take complex values. Keeping in mind the potential for confusion with the previously introduced
$\xi$ to take complex values. Keeping in mind the potential for confusion with the previously introduced ![]() $\zeta$, we write
$\zeta$, we write ![]() $\xi = \xi _r + \mathrm {i} \xi _c \mapsto \zeta \in \mathbb {C}$. Note that, under this notational choice,
$\xi = \xi _r + \mathrm {i} \xi _c \mapsto \zeta \in \mathbb {C}$. Note that, under this notational choice, ![]() $q(\zeta )$ is complex valued within the fluid region, and it is rather the combination
$q(\zeta )$ is complex valued within the fluid region, and it is rather the combination ![]() $\operatorname {Re}[q\mathrm {e}^{-\mathrm {i}\tau }/(1-\lambda )]$ that is identified with the fluid speed (cf. (2.5)).
$\operatorname {Re}[q\mathrm {e}^{-\mathrm {i}\tau }/(1-\lambda )]$ that is identified with the fluid speed (cf. (2.5)).
In theory, one can replace ![]() $\xi$ with
$\xi$ with ![]() $\zeta$, and evaluate the special-function solution (3.7) using standard built-in packages (e.g. Mathematica) to obtain an analytically continued leading-order solution. However, the branch structure of the solutions is complicated and standard software does not easily allow fine-tune control of the branch placement; generation of the full Riemann surface is subsequently difficult. In order to develop the results later in the paper, we must implement a scheme that allows for better control over the generation of the Riemann surface and placement of branches.
$\zeta$, and evaluate the special-function solution (3.7) using standard built-in packages (e.g. Mathematica) to obtain an analytically continued leading-order solution. However, the branch structure of the solutions is complicated and standard software does not easily allow fine-tune control of the branch placement; generation of the full Riemann surface is subsequently difficult. In order to develop the results later in the paper, we must implement a scheme that allows for better control over the generation of the Riemann surface and placement of branches.
For this analytic continuation scheme we first split the Riccati equation (3.4) into its real and imaginary parts
where
Recall that ![]() $\ell$ is the rescaled angle parameter introduced in (2.9). Here, we prefer to use
$\ell$ is the rescaled angle parameter introduced in (2.9). Here, we prefer to use ![]() $\zeta$, as we are now working with the complexified version of the Riccati equation (3.4).
$\zeta$, as we are now working with the complexified version of the Riccati equation (3.4).
We may now solve the above system along a chosen parameterised path in the complex ![]() $\zeta$-plane by using the exact solution on the free surface as an initial condition. More specifically, we first pre-solve for
$\zeta$-plane by using the exact solution on the free surface as an initial condition. More specifically, we first pre-solve for ![]() $(x_0(\zeta ), y_0(\zeta ), q_0(\zeta ), \tau _0(\zeta ))$ on the free surface using (3.7) and (3.8a,b) and setting
$(x_0(\zeta ), y_0(\zeta ), q_0(\zeta ), \tau _0(\zeta ))$ on the free surface using (3.7) and (3.8a,b) and setting ![]() $\zeta = \xi \in \mathbb {R}$. Then, we parameterise a path into the complex plane that starts on the free surface. For example
$\zeta = \xi \in \mathbb {R}$. Then, we parameterise a path into the complex plane that starts on the free surface. For example
We can then solve (4.1) along the parameterised path using any standard ordinary differential equation integrator (we use MATLAB's ode113 with absolute and relative tolerances set to ![]() $10^{-10}$) and the initial condition
$10^{-10}$) and the initial condition ![]() $\zeta _{IC}$.
$\zeta _{IC}$.
The solution consists of eight complexified components (the real and imaginary parts of each of the four variables, ![]() $(x_0,y_0,q_0,\tau _0)$). In figure 6, we show the analytically continued surface for one of these components,
$(x_0,y_0,q_0,\tau _0)$). In figure 6, we show the analytically continued surface for one of these components, ![]() $\operatorname {Re}(q_0)$. The figure shows one possible path of analytic continuation. By repeatedly solving along a mesh of different paths, the primary Riemann sheet is generated.
$\operatorname {Re}(q_0)$. The figure shows one possible path of analytic continuation. By repeatedly solving along a mesh of different paths, the primary Riemann sheet is generated.

Figure 6. Illustrations of the analytic continuation corresponding to ![]() $\theta _0 = 20^{\circ }$ and
$\theta _0 = 20^{\circ }$ and ![]() $\lambda = 0.6$ shown via (a) the
$\lambda = 0.6$ shown via (a) the ![]() $(\operatorname {Re} \zeta, \operatorname {Im} \zeta, \operatorname {Re} q_0)$-space; and (b) a top-down view of the
$(\operatorname {Re} \zeta, \operatorname {Im} \zeta, \operatorname {Re} q_0)$-space; and (b) a top-down view of the ![]() $\zeta$-plane. In both, a prototypical path of analytic continuation from the physical free surface is shown with an arrow; branch cuts are shown wavy. Singularities (white circles) lie at
$\zeta$-plane. In both, a prototypical path of analytic continuation from the physical free surface is shown with an arrow; branch cuts are shown wavy. Singularities (white circles) lie at ![]() $\zeta _1=0.59+1.32\mathrm {i}$ and
$\zeta _1=0.59+1.32\mathrm {i}$ and ![]() $\zeta _{C}=0.96\mathrm {i}$; these both correspond to square-root singularities. There is an additional square-root branch point at
$\zeta _{C}=0.96\mathrm {i}$; these both correspond to square-root singularities. There is an additional square-root branch point at ![]() $\mathrm {i}$. The leading-order solution
$\mathrm {i}$. The leading-order solution ![]() $q_0$ on the free surface lies on the real
$q_0$ on the free surface lies on the real ![]() $\zeta$ axis.
$\zeta$ axis.
Next, we find the location of the singularities in the complex plane numerically. Numerical analytic continuation along a closed loop around a branch point demonstrates that the start and end points of the solution differ. Hence, continuation around smaller and smaller loops allows the branch point location to be identified. The singularities in this problem are all square-root singularities. Their locations can be found using the method described above; the singularity strength can be further confirmed by verifying the rate of blow up of the solution as the singularity is approached.
Using this scheme, we find three pairs of complex conjugate singularities, which we denote as ![]() $\{\zeta _1, \overline {\zeta _1}\}, \{\zeta _{C}, \overline {\zeta _{C}}\}$ and
$\{\zeta _1, \overline {\zeta _1}\}, \{\zeta _{C}, \overline {\zeta _{C}}\}$ and ![]() $\{ \zeta _2,\overline {\zeta _2}\}$. The central singularities,
$\{ \zeta _2,\overline {\zeta _2}\}$. The central singularities, ![]() $\{\zeta _{C}, \, \overline {\zeta _{C}}\}$, lie on the imaginary axis and the non-central singularities
$\{\zeta _{C}, \, \overline {\zeta _{C}}\}$, lie on the imaginary axis and the non-central singularities ![]() $\{\zeta _1, \overline {\zeta _1}\}$ and
$\{\zeta _1, \overline {\zeta _1}\}$ and ![]() $\{\zeta _2, \overline {\zeta _2}\}$ lie equidistant from the imaginary axis. The conformal map introduces branch points at
$\{\zeta _2, \overline {\zeta _2}\}$ lie equidistant from the imaginary axis. The conformal map introduces branch points at ![]() $\pm \mathrm {i}$ in the
$\pm \mathrm {i}$ in the ![]() $\zeta$-plane. Consequently, the
$\zeta$-plane. Consequently, the ![]() $\{\zeta _1, \overline {\zeta _1}\}$ singularities do not lie on the same Riemann sheet of the complex
$\{\zeta _1, \overline {\zeta _1}\}$ singularities do not lie on the same Riemann sheet of the complex ![]() $\zeta$-plane as the
$\zeta$-plane as the ![]() $\{ \zeta _2, \overline {\zeta _2}\}$ singularities. The three groupings of singularity locations are shown in figure 7 panels (a–c) for the specific case of
$\{ \zeta _2, \overline {\zeta _2}\}$ singularities. The three groupings of singularity locations are shown in figure 7 panels (a–c) for the specific case of ![]() $\theta _0 = 20^\circ$ and
$\theta _0 = 20^\circ$ and ![]() $\lambda =0.6$.
$\lambda =0.6$.

Figure 7. Plots of the locations of the three complex conjugate pairs of singularities in the ![]() $\zeta$-plane: (a)
$\zeta$-plane: (a) ![]() $\{\zeta _1, \overline {\zeta _1}\}$, (b)
$\{\zeta _1, \overline {\zeta _1}\}$, (b) ![]() $\{\zeta _{C}, \overline {\zeta _{C}}\}$, (c)
$\{\zeta _{C}, \overline {\zeta _{C}}\}$, (c) ![]() $\{\zeta _2, \overline {\zeta _2}\}$. These plots are for parameter values
$\{\zeta _2, \overline {\zeta _2}\}$. These plots are for parameter values ![]() $\theta _0 = 20^\circ$ and
$\theta _0 = 20^\circ$ and ![]() $\lambda = 0.6.$ The branch cuts at
$\lambda = 0.6.$ The branch cuts at ![]() $\pm \mathrm {i}$ are chosen to show the relevant branches of the Riemann surface which the singularities lie on. The free surface lies on the real
$\pm \mathrm {i}$ are chosen to show the relevant branches of the Riemann surface which the singularities lie on. The free surface lies on the real ![]() $\zeta$ axis,
$\zeta$ axis, ![]() $\zeta = \xi \in \mathbb {R}.$
$\zeta = \xi \in \mathbb {R}.$
We can track the locations of the singularities as we vary the parameters ![]() $\theta _0$ (the wedge angle) and
$\theta _0$ (the wedge angle) and ![]() $\lambda$ (the proportion of the wedge angle occupied by the finger). If
$\lambda$ (the proportion of the wedge angle occupied by the finger). If ![]() $\theta _0>0$ and
$\theta _0>0$ and ![]() $\lambda >0.5$, the non-central singularities
$\lambda >0.5$, the non-central singularities ![]() $\{\zeta _1, \overline {\zeta _1}, \zeta _2, \overline {\zeta _2}\}$ lie off the imaginary axis. In the limit
$\{\zeta _1, \overline {\zeta _1}, \zeta _2, \overline {\zeta _2}\}$ lie off the imaginary axis. In the limit ![]() $\theta _0 \rightarrow 0$ the two singularities
$\theta _0 \rightarrow 0$ the two singularities ![]() $\zeta _1$ and
$\zeta _1$ and ![]() $\zeta _2$ converge to the same point on the imaginary axis, but one will be directly above the other on a separate sheet. A reflection of this behaviour occurs for singularities
$\zeta _2$ converge to the same point on the imaginary axis, but one will be directly above the other on a separate sheet. A reflection of this behaviour occurs for singularities ![]() $\overline {\zeta _1}$ and
$\overline {\zeta _1}$ and ![]() $\overline {\zeta _2}$ in the lower-half-
$\overline {\zeta _2}$ in the lower-half-![]() $\zeta$-plane. The singularity locations in the limit
$\zeta$-plane. The singularity locations in the limit ![]() $\theta _0 \to 0$ agree with those found by Chapman (Reference Chapman1999) in the classic Saffman–Taylor problem with parallel channel walls. A summary of the locations of these non-central singularities, for varying values of
$\theta _0 \to 0$ agree with those found by Chapman (Reference Chapman1999) in the classic Saffman–Taylor problem with parallel channel walls. A summary of the locations of these non-central singularities, for varying values of ![]() $\theta _0$ and
$\theta _0$ and ![]() $\lambda$, is shown in figure 8.
$\lambda$, is shown in figure 8.

Figure 8. Complex ![]() $\zeta$-plane showing how the location of the non-central singularities
$\zeta$-plane showing how the location of the non-central singularities ![]() $\{\zeta _1, \overline {\zeta _1} \}, \{\zeta _2, \overline {\zeta _2} \}$ vary with the parameters
$\{\zeta _1, \overline {\zeta _1} \}, \{\zeta _2, \overline {\zeta _2} \}$ vary with the parameters ![]() $\theta _0$ and
$\theta _0$ and ![]() $\lambda$. The
$\lambda$. The ![]() $\zeta _1$ singularity is shown in the top right quadrant with corresponding
$\zeta _1$ singularity is shown in the top right quadrant with corresponding ![]() $\theta _0$ and
$\theta _0$ and ![]() $\lambda$ values. The locations of the
$\lambda$ values. The locations of the ![]() $\zeta _2,$
$\zeta _2,$ ![]() $\overline {\zeta _2}$ and
$\overline {\zeta _2}$ and ![]() $\overline {\zeta _1}$ singularities are shown in the top left, bottom left and bottom right quadrants, respectively.
$\overline {\zeta _1}$ singularities are shown in the top left, bottom left and bottom right quadrants, respectively.
Finally, the central singularity, ![]() $\zeta _{C}$, remains on the imaginary axis between the origin and
$\zeta _{C}$, remains on the imaginary axis between the origin and ![]() $\mathrm {i}$ for all parameter values. It moves closer to
$\mathrm {i}$ for all parameter values. It moves closer to ![]() $\mathrm {i}$ as either
$\mathrm {i}$ as either ![]() $\lambda$ decreases towards 0.5, or as
$\lambda$ decreases towards 0.5, or as ![]() $\theta _0$ decreases towards zero. A reflection of this behaviour occurs for
$\theta _0$ decreases towards zero. A reflection of this behaviour occurs for ![]() $\overline {\zeta _{C}}$ in the lower-half-plane. Example locations of the singularity
$\overline {\zeta _{C}}$ in the lower-half-plane. Example locations of the singularity ![]() $\zeta _{C}$ as
$\zeta _{C}$ as ![]() $\theta _0$ and
$\theta _0$ and ![]() $\lambda$ are varied are listed in table 1.
$\lambda$ are varied are listed in table 1.
Table 1. The locations of the central singularity, ![]() $\zeta _{C}$ (to 4 significant figures) for different values of
$\zeta _{C}$ (to 4 significant figures) for different values of ![]() $\theta _0$ and
$\theta _0$ and ![]() $\lambda$.
$\lambda$.

4.2. Analytic continuation for the full problem
If the variable ![]() $\zeta$ is analytically continued into the upper-half-
$\zeta$ is analytically continued into the upper-half-![]() $\zeta$-plane, the Bernoulli equation (2.6) becomes
$\zeta$-plane, the Bernoulli equation (2.6) becomes
 \begin{equation} \epsilon^2 \frac{P(\zeta)}{4} \frac{\partial}{\partial\zeta} \left(r(x) \left[P(\zeta) q(\zeta) \frac{\partial\tau}{\partial\zeta} - \ell \sin\tau(\zeta)\right]\right) = \frac{2}{\rm \pi} \int_{-\infty}^0 \frac{K(\tilde{\zeta}) \,\tilde{\zeta}}{\zeta^2-\tilde{\zeta}^2}\,{\rm d}{\tilde{\zeta}} + \mathrm{i} K(\zeta). \end{equation}
\begin{equation} \epsilon^2 \frac{P(\zeta)}{4} \frac{\partial}{\partial\zeta} \left(r(x) \left[P(\zeta) q(\zeta) \frac{\partial\tau}{\partial\zeta} - \ell \sin\tau(\zeta)\right]\right) = \frac{2}{\rm \pi} \int_{-\infty}^0 \frac{K(\tilde{\zeta}) \,\tilde{\zeta}}{\zeta^2-\tilde{\zeta}^2}\,{\rm d}{\tilde{\zeta}} + \mathrm{i} K(\zeta). \end{equation} Here, the principal-value integral becomes a normal integral and can then be combined with the ![]() $Q_0$ term in (2.6) to simplify the right-hand side. Recall that
$Q_0$ term in (2.6) to simplify the right-hand side. Recall that ![]() $P(\zeta ), r(x(\zeta )),\ell, K(\zeta )$ were introduced in (2.7a–c) for convenience.
$P(\zeta ), r(x(\zeta )),\ell, K(\zeta )$ were introduced in (2.7a–c) for convenience.
To analytically continue the boundary-integral equation (2.11) we must consider the complexification of the Hilbert transform
where ![]() $\hat {\mathcal {H}}[\tau ]$ is the complex-valued Hilbert transform
$\hat {\mathcal {H}}[\tau ]$ is the complex-valued Hilbert transform
 \begin{equation} \hat{\mathcal{H}}[\tau](\xi) = \frac{2}{\rm \pi}\int_{-\infty}^0 \frac{\tau(\tilde{\xi}) \, \tilde{\xi}}{\xi^2 - \tilde{\xi}^2} \, {\rm d}{\tilde{\xi}}. \end{equation}
\begin{equation} \hat{\mathcal{H}}[\tau](\xi) = \frac{2}{\rm \pi}\int_{-\infty}^0 \frac{\tau(\tilde{\xi}) \, \tilde{\xi}}{\xi^2 - \tilde{\xi}^2} \, {\rm d}{\tilde{\xi}}. \end{equation}The boundary-integral equation (2.11) then becomes
and hence the integrated equation for the surface position (2.12) becomes
 \begin{equation} x(\zeta)+\mathrm{i} y(\zeta) = \frac{2(1-\lambda)}{\rm \pi}\int_\zeta^0 \frac{\exp\left(-\hat{\mathcal{H}}[\tau](\tilde{\zeta})\right)}{P(\tilde{\zeta})}\,{\rm d}{\tilde{\zeta}}. \end{equation}
\begin{equation} x(\zeta)+\mathrm{i} y(\zeta) = \frac{2(1-\lambda)}{\rm \pi}\int_\zeta^0 \frac{\exp\left(-\hat{\mathcal{H}}[\tau](\tilde{\zeta})\right)}{P(\tilde{\zeta})}\,{\rm d}{\tilde{\zeta}}. \end{equation}
This results in a set of analytically continued governing equations (4.3) that hold in the upper-half-![]() $\zeta$-plane.
$\zeta$-plane.
5. Exponential asymptotics
Our procedure for the exponential asymptotic analysis follows similar work by Tanveer (Reference Tanveer1987) and Chapman (Reference Chapman1999), using the methodology established in Chapman et al. (Reference Chapman, King and Adams1998). In essence, the goal is to derive the behaviour of the late terms in the asymptotic series. After, in § 6, these late terms are used to study the exponentially small terms via the Stokes-line switching.
As ![]() $\epsilon \rightarrow 0$, we expand the dependent variables as
$\epsilon \rightarrow 0$, we expand the dependent variables as
 \begin{equation} \begin{gathered}
x(\zeta) \sim \sum_{n=0}^\infty \epsilon^{2n}x_n(\zeta),
\quad y(\zeta) \sim \sum_{n=0}^\infty
\epsilon^{2n}y_n(\zeta), \\ q(\zeta) \sim \sum_{n=0}^\infty
\epsilon^{2n}q_n(\zeta), \quad \tau(\zeta) \sim
\sum_{n=0}^\infty \epsilon^{2n}\tau_n(\zeta). \end{gathered}\end{equation}
\begin{equation} \begin{gathered}
x(\zeta) \sim \sum_{n=0}^\infty \epsilon^{2n}x_n(\zeta),
\quad y(\zeta) \sim \sum_{n=0}^\infty
\epsilon^{2n}y_n(\zeta), \\ q(\zeta) \sim \sum_{n=0}^\infty
\epsilon^{2n}q_n(\zeta), \quad \tau(\zeta) \sim
\sum_{n=0}^\infty \epsilon^{2n}\tau_n(\zeta). \end{gathered}\end{equation}
We substitute the above into the analytically continued governing equations (4.3) and this yields, at ![]() ${O}(\epsilon ^{2n})$ for Bernoulli's equation (4.3a),
${O}(\epsilon ^{2n})$ for Bernoulli's equation (4.3a),
 \begin{align}
&\frac{P}{4}\frac{\partial}{\partial
\zeta}\left(r(x_0)\left[Pq_{n-1} \frac{\partial
\tau_0}{\partial \zeta} + Pq_0 \frac{\partial
\tau_{n-1}}{\partial \zeta} - \ell
\tau_{n-1}\cos\tau_0\right.\right.\nonumber\\ &\qquad \qquad \qquad \
\left.\left.-\frac{\theta_0 x_{n-1}}{2} \left(Pq_0
\frac{\partial \tau_0}{\partial \zeta} - \ell \sin\tau_0
\right) + \ldots \right] \right) \nonumber\\ &\qquad\qquad\qquad\qquad \qquad =
\ldots +
\frac{\mathrm{i}}{r^2(x_0)\,q_0}\left(\tau_n\cos\tau_0 -
\frac{q_n}{q_0}\sin\tau_0 +\ldots\right),
\end{align}
\begin{align}
&\frac{P}{4}\frac{\partial}{\partial
\zeta}\left(r(x_0)\left[Pq_{n-1} \frac{\partial
\tau_0}{\partial \zeta} + Pq_0 \frac{\partial
\tau_{n-1}}{\partial \zeta} - \ell
\tau_{n-1}\cos\tau_0\right.\right.\nonumber\\ &\qquad \qquad \qquad \
\left.\left.-\frac{\theta_0 x_{n-1}}{2} \left(Pq_0
\frac{\partial \tau_0}{\partial \zeta} - \ell \sin\tau_0
\right) + \ldots \right] \right) \nonumber\\ &\qquad\qquad\qquad\qquad \qquad =
\ldots +
\frac{\mathrm{i}}{r^2(x_0)\,q_0}\left(\tau_n\cos\tau_0 -
\frac{q_n}{q_0}\sin\tau_0 +\ldots\right),
\end{align}while for (4.3d) and (4.3e) we have
 $$\begin{gather}x_n + \mathrm{i} y_n = \frac{2(1-\lambda)}{\rm \pi}\int_\zeta^0 \frac{\exp(-\hat{\mathcal{H}}[\tau_0]) \hat{\mathcal{H}}[\tau_n] + \ldots}{P}\,{\rm d}{\tilde{\zeta}}. \end{gather}$$
$$\begin{gather}x_n + \mathrm{i} y_n = \frac{2(1-\lambda)}{\rm \pi}\int_\zeta^0 \frac{\exp(-\hat{\mathcal{H}}[\tau_0]) \hat{\mathcal{H}}[\tau_n] + \ldots}{P}\,{\rm d}{\tilde{\zeta}}. \end{gather}$$
At these later orders we see that the ![]() $n$th terms in the power series for
$n$th terms in the power series for ![]() $q$ and
$q$ and ![]() $\tau$ are obtained by differentiating the
$\tau$ are obtained by differentiating the ![]() $(n-1)$th terms twice. Any singularities in the leading-order solution will grow in strength with each successive differentiation. This means that later terms in the power series will have singularities at the same locations as earlier terms, but with increasing strength. We therefore follow the method of Chapman et al. (Reference Chapman, King and Adams1998) and predict a factorial-over-power form for the late-order terms
$(n-1)$th terms twice. Any singularities in the leading-order solution will grow in strength with each successive differentiation. This means that later terms in the power series will have singularities at the same locations as earlier terms, but with increasing strength. We therefore follow the method of Chapman et al. (Reference Chapman, King and Adams1998) and predict a factorial-over-power form for the late-order terms
where ![]() $Q$ and
$Q$ and ![]() $\varTheta$ are prefactors and
$\varTheta$ are prefactors and ![]() $\chi$ is a singulant function, which is zero at the singularity. The singulant ensures that each series term has singularities with the correct locations and
$\chi$ is a singulant function, which is zero at the singularity. The singulant ensures that each series term has singularities with the correct locations and ![]() $\gamma$ ensures they have the correct strengths. The gamma function (Abramowitz & Stegun Reference Abramowitz and Stegun1972) is a consequence of the factorial behaviour caused by repeated differentiation. The late-order terms are a sum of such factorial-over-power terms – one associated with each distinct complex singularity. Note that the prototypical factorial-over-power divergence of singular asymptotic expansions is a consequence of Darboux's theorem (cf. p. 4 of Dingle Reference Dingle1973; Crew & Trinh Reference Crew and Trinh2023).
$\gamma$ ensures they have the correct strengths. The gamma function (Abramowitz & Stegun Reference Abramowitz and Stegun1972) is a consequence of the factorial behaviour caused by repeated differentiation. The late-order terms are a sum of such factorial-over-power terms – one associated with each distinct complex singularity. Note that the prototypical factorial-over-power divergence of singular asymptotic expansions is a consequence of Darboux's theorem (cf. p. 4 of Dingle Reference Dingle1973; Crew & Trinh Reference Crew and Trinh2023).
In the limit ![]() $n\to \infty$, the behaviour of the asymptotic expansion will be dictated by the divergence caused by the singularities driving (5.3) (Chapman et al. Reference Chapman, King and Adams1998). From § 4 we know that the singularities lie in the complex plane away from the free surface. The complex Hilbert transform,
$n\to \infty$, the behaviour of the asymptotic expansion will be dictated by the divergence caused by the singularities driving (5.3) (Chapman et al. Reference Chapman, King and Adams1998). From § 4 we know that the singularities lie in the complex plane away from the free surface. The complex Hilbert transform, ![]() $\hat {\mathcal {H}}[\tau _n]$, involves the integrand evaluated along the free surface. Once the ansatzes for
$\hat {\mathcal {H}}[\tau _n]$, involves the integrand evaluated along the free surface. Once the ansatzes for ![]() $q_n$ and
$q_n$ and ![]() $\tau _n$ via (5.3) are substituted into the Hilbert transform, we may observe that the contribution of
$\tau _n$ via (5.3) are substituted into the Hilbert transform, we may observe that the contribution of ![]() $\hat {\mathcal {H}}[\tau _n]$ will be subdominant in the limit that
$\hat {\mathcal {H}}[\tau _n]$ will be subdominant in the limit that ![]() $n \rightarrow \infty$, compared with
$n \rightarrow \infty$, compared with ![]() $q_n$ and
$q_n$ and ![]() $\tau _n$. This follows from the increasing nature of
$\tau _n$. This follows from the increasing nature of ![]() $|\chi |$ along Stokes lines, as explained on p. 526 of Chapman (Reference Chapman1999). The combination of
$|\chi |$ along Stokes lines, as explained on p. 526 of Chapman (Reference Chapman1999). The combination of ![]() $x_n+\mathrm {i} y_n$ will also be subdominant in this limit, although the individual components may still diverge. We will assume in this analysis that the individual components do not diverge, and this assumption will be validated a posteriori, as is done in similar asymptotic analyses of boundary-integral problems (Shelton & Trinh Reference Shelton and Trinh2022).
$x_n+\mathrm {i} y_n$ will also be subdominant in this limit, although the individual components may still diverge. We will assume in this analysis that the individual components do not diverge, and this assumption will be validated a posteriori, as is done in similar asymptotic analyses of boundary-integral problems (Shelton & Trinh Reference Shelton and Trinh2022).
Using these assumptions gives the dominant behaviour from the boundary-integral equation (5.2b)
The Bernoulli equation (5.2a) can then be simplified to
Here, and for the rest of the paper, we use primes (![]() $'$) to denote differentiation with respect to
$'$) to denote differentiation with respect to ![]() $\zeta$. Substitution of the factorial-over-power ansatz (5.3) and matching terms in the limit that
$\zeta$. Substitution of the factorial-over-power ansatz (5.3) and matching terms in the limit that ![]() $n \rightarrow \infty$ gives at leading order an equation for the singulant,
$n \rightarrow \infty$ gives at leading order an equation for the singulant, ![]() $\chi$,
$\chi$,
which can be solved to obtain
 \begin{equation} \chi ={-}\int_{\zeta_*}^\zeta \frac{2\sqrt{\sin\tau_0 + \mathrm{i}\cos\tau_0}}{P\,q_0\,r(x_0)^{{3}/{2}}} \,{\rm d}{\tilde{\zeta}}. \end{equation}
\begin{equation} \chi ={-}\int_{\zeta_*}^\zeta \frac{2\sqrt{\sin\tau_0 + \mathrm{i}\cos\tau_0}}{P\,q_0\,r(x_0)^{{3}/{2}}} \,{\rm d}{\tilde{\zeta}}. \end{equation}
In this expression, ![]() $\zeta _*$ is the singularity location and the integration limits are chosen so that
$\zeta _*$ is the singularity location and the integration limits are chosen so that ![]() $\chi (\zeta _*) = 0$. There will be a singulant function
$\chi (\zeta _*) = 0$. There will be a singulant function ![]() $\chi$ for each complex singularity. The negative sign is selected when taking the square root so that the Stokes line intersects the free surface, which lies on the real
$\chi$ for each complex singularity. The negative sign is selected when taking the square root so that the Stokes line intersects the free surface, which lies on the real ![]() $\zeta$ axis.
$\zeta$ axis.
Matching terms in (5.5) at the next order as ![]() $n \rightarrow \infty$ shows that
$n \rightarrow \infty$ shows that ![]() $\gamma$ is constant, and at the following order we obtain
$\gamma$ is constant, and at the following order we obtain
which can be solved to give an expression for the prefactor
 \begin{equation} Q = \varLambda \mathrm{i} \left(\frac{q_0\, \mathrm{e}^{-\mathrm{i}\tau_0} \exp \left[\displaystyle\int\nolimits_0^\zeta \ell \dfrac{\cos\tau_0}{Pq_0} {\rm d}{\tilde{\zeta}}\right]}{\chi' r(x_0)P}\right)^{{1}/{2}}, \end{equation}
\begin{equation} Q = \varLambda \mathrm{i} \left(\frac{q_0\, \mathrm{e}^{-\mathrm{i}\tau_0} \exp \left[\displaystyle\int\nolimits_0^\zeta \ell \dfrac{\cos\tau_0}{Pq_0} {\rm d}{\tilde{\zeta}}\right]}{\chi' r(x_0)P}\right)^{{1}/{2}}, \end{equation}
where ![]() $\varLambda$ is a constant that remains to be determined. From the boundary-integral equation (5.4) we find
$\varLambda$ is a constant that remains to be determined. From the boundary-integral equation (5.4) we find
By definition, ![]() $\ell \rightarrow 0$ (see (2.9)) and
$\ell \rightarrow 0$ (see (2.9)) and ![]() $r(x_0) \rightarrow 1$ (see (2.7a–c)) in the limit
$r(x_0) \rightarrow 1$ (see (2.7a–c)) in the limit ![]() $\theta _0 \rightarrow 0$. This means that these results are consistent with those found by Chapman (Reference Chapman1999) for the Saffman–Taylor problem in a channel geometry.
$\theta _0 \rightarrow 0$. This means that these results are consistent with those found by Chapman (Reference Chapman1999) for the Saffman–Taylor problem in a channel geometry.
The late-order series terms in the divergent power series solution for ![]() $q(\zeta )$ therefore have the form
$q(\zeta )$ therefore have the form
 \begin{equation} q_n \sim \varLambda \mathrm{i} \left(\frac{q_0 \mathrm{e}^{-\mathrm{i}\tau_0} \exp \left[\displaystyle\int\nolimits_0^\zeta \ell \dfrac{\cos\tau_0}{Pq_0} {\rm d}{\tilde{\zeta}}\right]}{\chi' r(x_0)P}\right)^{{1}/{2}} \frac{\varGamma(2n+ \gamma)}{\chi^{2n+\gamma}}, \quad \text{as} \ n\rightarrow \infty. \end{equation}
\begin{equation} q_n \sim \varLambda \mathrm{i} \left(\frac{q_0 \mathrm{e}^{-\mathrm{i}\tau_0} \exp \left[\displaystyle\int\nolimits_0^\zeta \ell \dfrac{\cos\tau_0}{Pq_0} {\rm d}{\tilde{\zeta}}\right]}{\chi' r(x_0)P}\right)^{{1}/{2}} \frac{\varGamma(2n+ \gamma)}{\chi^{2n+\gamma}}, \quad \text{as} \ n\rightarrow \infty. \end{equation}6. Optimal truncation and Stokes lines
In the previous section, we noted that complex singularities cause the power series to become divergent and so they will need to be truncated. We will truncate the divergent power series at some to be determined optimal point ![]() $N$, and introduce the remainder terms
$N$, and introduce the remainder terms
 $$\begin{gather} x = \sum_{n=0}^{N-1} \epsilon^{2n} x_n + R_x, \quad y = \sum_{n=0}^{N-1} \epsilon^{2n}y_n + R_y, \end{gather}$$
$$\begin{gather} x = \sum_{n=0}^{N-1} \epsilon^{2n} x_n + R_x, \quad y = \sum_{n=0}^{N-1} \epsilon^{2n}y_n + R_y, \end{gather}$$ $$\begin{gather}q = \sum_{n=0}^{N-1} \epsilon^{2n} q_n + R_q, \quad \tau = \sum_{n=0}^{N-1} \epsilon^{2n} \tau_n + R_\tau. \end{gather}$$
$$\begin{gather}q = \sum_{n=0}^{N-1} \epsilon^{2n} q_n + R_q, \quad \tau = \sum_{n=0}^{N-1} \epsilon^{2n} \tau_n + R_\tau. \end{gather}$$
We can substitute these into the governing equations (4.3). Given that the first ![]() $N$ orders must exactly satisfy the relationships in (5.2), we derive leading-order relationships between the remainder terms.
$N$ orders must exactly satisfy the relationships in (5.2), we derive leading-order relationships between the remainder terms.
From the boundary-integral equation (5.4), we derive at leading order as ![]() $\epsilon \rightarrow 0$ that
$\epsilon \rightarrow 0$ that
Using this in the ![]() $x+\mathrm {i} y$ equation (5.2c) we see that
$x+\mathrm {i} y$ equation (5.2c) we see that ![]() $R_x$ and
$R_x$ and ![]() $R_y$ are subdominant compared with the leading orders of
$R_y$ are subdominant compared with the leading orders of ![]() $R_q$ and
$R_q$ and ![]() $R_\tau$ in the limit
$R_\tau$ in the limit ![]() $\epsilon \rightarrow 0$.
$\epsilon \rightarrow 0$.
We substitute these relationships into the Bernoulli equation (4.3a) and derive a single ordinary differential equation for ![]() $R_q$, which we now rename as
$R_q$, which we now rename as ![]() $R_N$ for consistency with other works, including Chapman (Reference Chapman1999). This ordinary differential equation, known as the remainder equation, reduces to
$R_N$ for consistency with other works, including Chapman (Reference Chapman1999). This ordinary differential equation, known as the remainder equation, reduces to
as ![]() $\epsilon \rightarrow 0$, where the terms that do not appear at the leading or second order in this limit have been omitted. Changing the independent variable to
$\epsilon \rightarrow 0$, where the terms that do not appear at the leading or second order in this limit have been omitted. Changing the independent variable to ![]() $\chi$ (primes will continue to denote differentiation with respect to
$\chi$ (primes will continue to denote differentiation with respect to ![]() $\zeta$) gives
$\zeta$) gives
Using the definition for the prefactor (5.9), this can be simplified to
To solve (6.5) we pose a Liouville–Green or WKBJ-style ansatz for the form of the remainder given by
Then equating the coefficients at different powers of ![]() $\epsilon$ for the homogeneous version of the remainder equation (6.5), we find that
$\epsilon$ for the homogeneous version of the remainder equation (6.5), we find that ![]() $b = \pm \chi + \textrm {const.}$ and
$b = \pm \chi + \textrm {const.}$ and ![]() $B\sim Q.$ The arbitrary constant in
$B\sim Q.$ The arbitrary constant in ![]() $b$ is equivalent to multiplying the entire expression (6.6) by an arbitrary constant that is not determined by the WKBJ analysis.
$b$ is equivalent to multiplying the entire expression (6.6) by an arbitrary constant that is not determined by the WKBJ analysis.
To solve the full inhomogeneous remainder equation (6.5) we apply the method of variation of parameters and permit the arbitrary constant to vary in ![]() $\zeta$. This quantity is known as the Stokes multiplier, and we denote it by
$\zeta$. This quantity is known as the Stokes multiplier, and we denote it by ![]() $A(\chi )$. The remainder becomes
$A(\chi )$. The remainder becomes
where the negative sign in the exponent ensures the remainder is exponentially small. The inhomogeneous equation (6.5) gives
where we have substituted in the late-order expression for ![]() $q_N$ from (5.3).
$q_N$ from (5.3).
The next step involves truncating the series at an optimal point. We define this optimal truncation point, ![]() $N$, to be where successive terms in the divergent series are approximately equal in magnitude, so
$N$, to be where successive terms in the divergent series are approximately equal in magnitude, so
This condition gives ![]() $N \approx {|\chi |}/{2\epsilon }$. As
$N \approx {|\chi |}/{2\epsilon }$. As ![]() $N$ must be an integer we let
$N$ must be an integer we let ![]() $N = {|\chi |}/{2\epsilon } +\beta$, where
$N = {|\chi |}/{2\epsilon } +\beta$, where ![]() $\beta$ is bounded as
$\beta$ is bounded as ![]() $\epsilon \rightarrow 0.$ This form motivates the transformation to polar coordinates, so we define
$\epsilon \rightarrow 0.$ This form motivates the transformation to polar coordinates, so we define ![]() $\chi = |\chi |\mathrm {e}^{\mathrm {i}\eta }.$
$\chi = |\chi |\mathrm {e}^{\mathrm {i}\eta }.$
By the chain rule we have
We substitute the optimal value of ![]() $N$ into (6.8) and note that
$N$ into (6.8) and note that ![]() $N$ is large, which allows us to use Stirling's formula (Abramowitz & Stegun Reference Abramowitz and Stegun1972) to approximate
$N$ is large, which allows us to use Stirling's formula (Abramowitz & Stegun Reference Abramowitz and Stegun1972) to approximate ![]() $N!$ in the large
$N!$ in the large ![]() $N$ limit. Then using (6.10) we obtain
$N$ limit. Then using (6.10) we obtain
 \begin{equation} \frac{\mathrm{d}A}{\mathrm{d}\eta} \sim \frac{\mathrm{i} \epsilon^{2N-1}}{2}\frac{\exp\left(\dfrac{|\chi|}{\epsilon}\mathrm{e}^{\mathrm{i}\eta}\right) \sqrt{2{\rm \pi}} \left(2N+\gamma\right)^{2N+\gamma-{1}/{2}}}{\mathrm{e}^{2N+\gamma}|\chi|^{2N+\gamma-1}\mathrm{e}^{\mathrm{i}\eta(2N+\gamma-1)}}. \end{equation}
\begin{equation} \frac{\mathrm{d}A}{\mathrm{d}\eta} \sim \frac{\mathrm{i} \epsilon^{2N-1}}{2}\frac{\exp\left(\dfrac{|\chi|}{\epsilon}\mathrm{e}^{\mathrm{i}\eta}\right) \sqrt{2{\rm \pi}} \left(2N+\gamma\right)^{2N+\gamma-{1}/{2}}}{\mathrm{e}^{2N+\gamma}|\chi|^{2N+\gamma-1}\mathrm{e}^{\mathrm{i}\eta(2N+\gamma-1)}}. \end{equation}
We substitute in the optimal value of ![]() $N$ to give
$N$ to give
 \begin{align} \frac{\mathrm{d}A}{\mathrm{d}\eta} \sim \frac{\mathrm{i}\sqrt{\rm \pi}}{\sqrt{2}c}\frac{|\chi|^{{1}/{2}}}{\epsilon^{\gamma+{1}/{2}}}\frac{\mathrm{e}^{2\beta+\gamma}}{ \exp\left(\mathrm{i}\eta\left( \dfrac{|\chi|}{\epsilon}+2\beta+\gamma\right)\right)}\frac{\exp\left(\dfrac{|\chi|}{\epsilon} \mathrm{e}^{\mathrm{i}\eta}\right)}{\exp\left(\dfrac{|\chi|}{\epsilon} + 2\beta+\gamma\right)} \quad \text{as} \ \epsilon \rightarrow 0. \end{align}
\begin{align} \frac{\mathrm{d}A}{\mathrm{d}\eta} \sim \frac{\mathrm{i}\sqrt{\rm \pi}}{\sqrt{2}c}\frac{|\chi|^{{1}/{2}}}{\epsilon^{\gamma+{1}/{2}}}\frac{\mathrm{e}^{2\beta+\gamma}}{ \exp\left(\mathrm{i}\eta\left( \dfrac{|\chi|}{\epsilon}+2\beta+\gamma\right)\right)}\frac{\exp\left(\dfrac{|\chi|}{\epsilon} \mathrm{e}^{\mathrm{i}\eta}\right)}{\exp\left(\dfrac{|\chi|}{\epsilon} + 2\beta+\gamma\right)} \quad \text{as} \ \epsilon \rightarrow 0. \end{align}
The right-hand side of (6.12) is exponentially small in ![]() $\epsilon$ unless
$\epsilon$ unless ![]() $\eta = 2{\rm \pi} k,$
$\eta = 2{\rm \pi} k,$ ![]() $k \in \mathbb {Z},$ in which case it will be algebraic in the limit that
$k \in \mathbb {Z},$ in which case it will be algebraic in the limit that ![]() $\epsilon \rightarrow 0.$ Therefore, the greatest change in the Stokes multiplier
$\epsilon \rightarrow 0.$ Therefore, the greatest change in the Stokes multiplier ![]() $A$ will occur across curves, or Stokes lines, on which
$A$ will occur across curves, or Stokes lines, on which ![]() $\eta = 2{\rm \pi} k$, and so
$\eta = 2{\rm \pi} k$, and so
This recovers the classic result of Dingle (Reference Dingle1973). We compute the Stokes lines numerically, with the results shown in figure 9.

Figure 9. Complex ![]() $\zeta$-plane showing the Stokes lines emanating from the singularities (circles) and intersecting the free surface (real axis). In this figure, the wedge angle is
$\zeta$-plane showing the Stokes lines emanating from the singularities (circles) and intersecting the free surface (real axis). In this figure, the wedge angle is ![]() $\theta _0 = 20^\circ$ and
$\theta _0 = 20^\circ$ and ![]() $\lambda = 0.6$. Branch cuts (shown wavy) lie up and down the imaginary axis from
$\lambda = 0.6$. Branch cuts (shown wavy) lie up and down the imaginary axis from ![]() $\pm \mathrm {i}$. Stokes lines are shown with dashed when they lie on a different Riemann sheet to the free surface. The three points where the Stokes lines intersect the real axis are labelled
$\pm \mathrm {i}$. Stokes lines are shown with dashed when they lie on a different Riemann sheet to the free surface. The three points where the Stokes lines intersect the real axis are labelled ![]() $S_1,$
$S_1,$ ![]() $S_{C}$ and
$S_{C}$ and ![]() $S_2$.
$S_2$.
When Stokes lines intersect the free surface (the real axis in the ![]() $\zeta$-plane) then an exponentially small term will be smoothly switched on across this intersection point in the solution. We can see from figure 9 that there are three points on the free surface where such exponentially small terms will be switched on.
$\zeta$-plane) then an exponentially small term will be smoothly switched on across this intersection point in the solution. We can see from figure 9 that there are three points on the free surface where such exponentially small terms will be switched on.
To find the jump in solution behaviour across a Stokes line, we rescale ![]() $\eta$ and
$\eta$ and ![]() $A$ and consider the behaviour in the neighbourhood of the Stokes line. We apply the rescaling
$A$ and consider the behaviour in the neighbourhood of the Stokes line. We apply the rescaling
We let ![]() $k = 0$ and then (6.12) becomes
$k = 0$ and then (6.12) becomes
Integrating this gives
 \begin{equation} \tilde{A} = \text{const.} + \mathrm{i}\sqrt{\rm \pi} \int_{-\infty}^{\tilde{\eta}\sqrt{{|\chi|}/{2}}} \mathrm{e}^{-\tilde{\xi}^2}\,{\rm d}{\tilde{\xi}}, \end{equation}
\begin{equation} \tilde{A} = \text{const.} + \mathrm{i}\sqrt{\rm \pi} \int_{-\infty}^{\tilde{\eta}\sqrt{{|\chi|}/{2}}} \mathrm{e}^{-\tilde{\xi}^2}\,{\rm d}{\tilde{\xi}}, \end{equation}and hence the jump in the Stokes multiplier across the Stokes line is
That is, upon crossing a Stokes line at its intersection with the real axis, a contribution in the ![]() $q$ variable is switched on. This has the form
$q$ variable is switched on. This has the form
where c.c. represents the complex conjugate expression, which arises from the singularity located at the complex conjugate location in the complex plane (figure 9). Similarly, by (5.10), the contribution that is switched on in the ![]() $\tau$ variable has the form
$\tau$ variable has the form
In the next section, we show how these terms switched on across Stokes lines will determine the selection mechanism.
7. Selection mechanism
In figure 9 we see that there are three points on the free surface (![]() $\zeta = \xi \in \mathbb {R}$) that are intersected by Stokes lines. We will continue the notation from the singularities (introduced in § 4.1) and use the subscripts ‘
$\zeta = \xi \in \mathbb {R}$) that are intersected by Stokes lines. We will continue the notation from the singularities (introduced in § 4.1) and use the subscripts ‘![]() $1$’, ‘
$1$’, ‘![]() ${C}$’ and ‘
${C}$’ and ‘![]() $2$’ to label the Stokes lines, i.e. each subscript matches the respective label of the associated Stokes-line singularity. We denote the three intersection points as
$2$’ to label the Stokes lines, i.e. each subscript matches the respective label of the associated Stokes-line singularity. We denote the three intersection points as ![]() $S_1$,
$S_1$, ![]() $S_{C}$ and
$S_{C}$ and ![]() $S_2$. Each Stokes line will have different corresponding values for
$S_2$. Each Stokes line will have different corresponding values for ![]() $\varLambda,$
$\varLambda,$ ![]() $\gamma$ and
$\gamma$ and ![]() $\chi$, which will also be labelled with the same subscripts.
$\chi$, which will also be labelled with the same subscripts.
At each intersection point an exponentially small asymptotic contribution of the form (6.19) will be switched on or off. The far-field conditions ![]() $\tau (-\infty ) = 0$ and
$\tau (-\infty ) = 0$ and ![]() $\tau ( \infty ) = -{\rm \pi}$ imply there are no exponentially small contributions present on the free surface as
$\tau ( \infty ) = -{\rm \pi}$ imply there are no exponentially small contributions present on the free surface as ![]() $\tau \to \pm \infty$, so the exponential terms must only be present in the region of the free surface between the Stokes-line intersection points; that is, in the range
$\tau \to \pm \infty$, so the exponential terms must only be present in the region of the free surface between the Stokes-line intersection points; that is, in the range ![]() $\zeta =\xi \in (S_1, S_2)$.
$\zeta =\xi \in (S_1, S_2)$.
To check for existence of a solution, we can check that the conditions in both far fields are satisfied. However, due to the symmetry of the problem, it is equivalent to consider half the domain and impose symmetry conditions at the origin: ![]() $q(0) = 0,$
$q(0) = 0,$ ![]() $\tau (0) = -{\rm \pi} /2$. A similar symmetry condition is used in Chapman et al. (Reference Chapman, Dallaston, Kalliadasis, Trinh and Witelski2023). Enforcing the condition on
$\tau (0) = -{\rm \pi} /2$. A similar symmetry condition is used in Chapman et al. (Reference Chapman, Dallaston, Kalliadasis, Trinh and Witelski2023). Enforcing the condition on ![]() $\tau$ implies
$\tau$ implies
Requiring that the solution satisfies the far field conditions as ![]() $\xi \to -\infty$ and the conditions at the origin from (7.1) will result in a selection condition that must be satisfied for solutions to exist.
$\xi \to -\infty$ and the conditions at the origin from (7.1) will result in a selection condition that must be satisfied for solutions to exist.
At the point ![]() $S_1$, a contribution of the form (6.19) is switched on as the Stokes line is crossed from left to right. And then to reach the origin we switch on half of another contribution of the form (6.19) (as we have only crossed half the boundary layer about the ‘
$S_1$, a contribution of the form (6.19) is switched on as the Stokes line is crossed from left to right. And then to reach the origin we switch on half of another contribution of the form (6.19) (as we have only crossed half the boundary layer about the ‘![]() ${C}$’ Stokes line). That is, the integral in (6.16) will only range from
${C}$’ Stokes line). That is, the integral in (6.16) will only range from ![]() $-\infty$ to
$-\infty$ to ![]() $\tilde {\eta } = 0.$ The symmetry condition from (7.1) says that the sum of these contributions must be zero at the origin. This means
$\tilde {\eta } = 0.$ The symmetry condition from (7.1) says that the sum of these contributions must be zero at the origin. This means
 \begin{align} &{\rm \pi}
\epsilon^{-\gamma_1-1}\frac{\varLambda_1}{\sqrt{2}}
\mathrm{e}^{-\mathrm{i}{\tau_0}/{4}}I(\zeta)r(x_0)^{{1}/{4}}\mathrm{e}^{3\mathrm{i}{\rm \pi}/{8}}
\exp\left(-\frac{\chi_1}{\epsilon}\right) + \mathrm{c.
c.}\nonumber\\ &\qquad +\left.\frac{1}{2}{\rm \pi}
\epsilon^{-\gamma_{\text{C}}-1}\frac{\varLambda_C}{\sqrt{2}}
\mathrm{e}^{-\mathrm{i}{\tau_0}/{4}}I(\zeta)r(x_0)^{{1}/{4}}\mathrm{e}^{3\mathrm{i}{\rm \pi}/{8}}
\exp\left(-\frac{\chi_{\text{C}}}{\epsilon}\right) +
\mathrm{c.c.}\right|_{\zeta=0} = 0,
\end{align}
\begin{align} &{\rm \pi}
\epsilon^{-\gamma_1-1}\frac{\varLambda_1}{\sqrt{2}}
\mathrm{e}^{-\mathrm{i}{\tau_0}/{4}}I(\zeta)r(x_0)^{{1}/{4}}\mathrm{e}^{3\mathrm{i}{\rm \pi}/{8}}
\exp\left(-\frac{\chi_1}{\epsilon}\right) + \mathrm{c.
c.}\nonumber\\ &\qquad +\left.\frac{1}{2}{\rm \pi}
\epsilon^{-\gamma_{\text{C}}-1}\frac{\varLambda_C}{\sqrt{2}}
\mathrm{e}^{-\mathrm{i}{\tau_0}/{4}}I(\zeta)r(x_0)^{{1}/{4}}\mathrm{e}^{3\mathrm{i}{\rm \pi}/{8}}
\exp\left(-\frac{\chi_{\text{C}}}{\epsilon}\right) +
\mathrm{c.c.}\right|_{\zeta=0} = 0,
\end{align}
where ![]() $I(\zeta ) := \exp [\int _0^\zeta \ell ({\cos \tau _0}/{2Pq_0})\,\textrm {d}{\tilde {\zeta }}].$ We simplify this expression using the conditions at the origin,
$I(\zeta ) := \exp [\int _0^\zeta \ell ({\cos \tau _0}/{2Pq_0})\,\textrm {d}{\tilde {\zeta }}].$ We simplify this expression using the conditions at the origin, ![]() $\tau _0(0) = -{{\rm \pi} }/{2}$ and
$\tau _0(0) = -{{\rm \pi} }/{2}$ and ![]() $x_0(0) = 0$. Noting that the origin lies on the ‘
$x_0(0) = 0$. Noting that the origin lies on the ‘![]() ${C}$’ Stokes line, we use the definition for a Stokes line obtained in (6.13a,b), i.e.
${C}$’ Stokes line, we use the definition for a Stokes line obtained in (6.13a,b), i.e. ![]() $\mathrm {Im}(\chi _{C}(0)) = 0$. Then
$\mathrm {Im}(\chi _{C}(0)) = 0$. Then
 \begin{align}
&\frac{|\varLambda_1|}{|\varLambda_{C}|}
\epsilon^{-\gamma_1+\gamma_{C}}e^{{-\mathrm{Re}(\chi_1(0))/\epsilon+\mathrm{Re}(\chi_{C}(0))/\epsilon}}
\cos\left(\arg(\varLambda_1) + \frac{\rm \pi}{2} -
\frac{\mathrm{Im}(\chi_1(0))}{\epsilon}\right)\nonumber\\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad + \frac{1}{2}\cos\left(\arg(\varLambda_{C}) +
\frac{\rm \pi}{2}\right) = 0.
\end{align}
\begin{align}
&\frac{|\varLambda_1|}{|\varLambda_{C}|}
\epsilon^{-\gamma_1+\gamma_{C}}e^{{-\mathrm{Re}(\chi_1(0))/\epsilon+\mathrm{Re}(\chi_{C}(0))/\epsilon}}
\cos\left(\arg(\varLambda_1) + \frac{\rm \pi}{2} -
\frac{\mathrm{Im}(\chi_1(0))}{\epsilon}\right)\nonumber\\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad + \frac{1}{2}\cos\left(\arg(\varLambda_{C}) +
\frac{\rm \pi}{2}\right) = 0.
\end{align}
By the symmetry of the problem, this condition could also be obtained by calculating the values that appear across the ‘![]() $2$’ and ‘
$2$’ and ‘![]() ${C}$’ Stokes lines. Note that, for this problem, we always have symmetry of
${C}$’ Stokes lines. Note that, for this problem, we always have symmetry of ![]() $q_0$ at the origin and so
$q_0$ at the origin and so ![]() $q_0(0) = q_0'(0) = 0$. This means that the possible selection condition,
$q_0(0) = q_0'(0) = 0$. This means that the possible selection condition, ![]() $q'(0) = 0$, is automatically satisfied. We therefore use the
$q'(0) = 0$, is automatically satisfied. We therefore use the ![]() $\tau$ variable to derive the selection mechanism.
$\tau$ variable to derive the selection mechanism.
The constants ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _{C}$ are derived by an inner matching of the local singularity strengths at lower orders in the asymptotic series. The details of the derivation can be found in Appendix B. We find that
$\gamma _{C}$ are derived by an inner matching of the local singularity strengths at lower orders in the asymptotic series. The details of the derivation can be found in Appendix B. We find that ![]() $\gamma _1 = \gamma _{C} = {1}/{14}$ and thus we can simplify the selection condition to
$\gamma _1 = \gamma _{C} = {1}/{14}$ and thus we can simplify the selection condition to
 \begin{align}
&\frac{|\varLambda_1|}{|\varLambda_{C}|}
{\rm e}^{-\mathrm{Re}(\chi_1(0))/\epsilon+\mathrm{Re}(\chi_{C}(0))/\epsilon}
\cos\left(\arg(\varLambda_1) + \frac{\rm \pi}{2} -
\frac{\mathrm{Im}(\chi_1(0))}{\epsilon}\right)\nonumber\\
&\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad \ + \frac{1}{2}\cos\left(\arg(\varLambda_{C}) +
\frac{\rm \pi}{2}\right) = 0.
\end{align}
\begin{align}
&\frac{|\varLambda_1|}{|\varLambda_{C}|}
{\rm e}^{-\mathrm{Re}(\chi_1(0))/\epsilon+\mathrm{Re}(\chi_{C}(0))/\epsilon}
\cos\left(\arg(\varLambda_1) + \frac{\rm \pi}{2} -
\frac{\mathrm{Im}(\chi_1(0))}{\epsilon}\right)\nonumber\\
&\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad\qquad \ + \frac{1}{2}\cos\left(\arg(\varLambda_{C}) +
\frac{\rm \pi}{2}\right) = 0.
\end{align}
Above, the constants ![]() $\varLambda _1$ and
$\varLambda _1$ and ![]() $\varLambda _{C}$ are derived in Appendix C by using an asymptotic matching process to connect the late-order term behaviour (5.3) with a local expansion of the solution in a neighbourhood of the relevant singularity. We perform this matching numerically, and find that the values of
$\varLambda _{C}$ are derived in Appendix C by using an asymptotic matching process to connect the late-order term behaviour (5.3) with a local expansion of the solution in a neighbourhood of the relevant singularity. We perform this matching numerically, and find that the values of ![]() $\varLambda _1$ and
$\varLambda _1$ and ![]() $\varLambda _{C}$ depend on both the parameters
$\varLambda _{C}$ depend on both the parameters ![]() $\theta _0$ and
$\theta _0$ and ![]() $\lambda$. For example, when
$\lambda$. For example, when ![]() $\theta _0 = 20^\circ$ and
$\theta _0 = 20^\circ$ and ![]() $\lambda = 0.6$ then
$\lambda = 0.6$ then ![]() $\varLambda _1 \approx -0.48-0.15\mathrm {i}$ and
$\varLambda _1 \approx -0.48-0.15\mathrm {i}$ and ![]() $\varLambda _{C} \approx -0.49-0.24\mathrm {i}$.
$\varLambda _{C} \approx -0.49-0.24\mathrm {i}$.
8. Results
For each ![]() $\epsilon$ value we now use a numerical root finding scheme to find the corresponding family of
$\epsilon$ value we now use a numerical root finding scheme to find the corresponding family of ![]() $\lambda$ values that satisfy the selection condition (7.4). The dependence on
$\lambda$ values that satisfy the selection condition (7.4). The dependence on ![]() $\lambda$ in the selection condition (7.4) appears through the constants
$\lambda$ in the selection condition (7.4) appears through the constants ![]() $\varLambda _1$ and
$\varLambda _1$ and ![]() $\varLambda _{C}$, as shown in Appendix C, and also through
$\varLambda _{C}$, as shown in Appendix C, and also through ![]() $\chi _1(0)$ and
$\chi _1(0)$ and ![]() $\chi _{C}(0)$, as given in (5.7). The selected solution families, for different values of
$\chi _{C}(0)$, as given in (5.7). The selected solution families, for different values of ![]() $\theta _0$, are shown in figures 10(a)–10(d).
$\theta _0$, are shown in figures 10(a)–10(d).

Figure 10. Bifurcation diagrams produced using (7.4). The first ten selected values of ![]() $\lambda$ as functions of
$\lambda$ as functions of ![]() $\epsilon$ are shown. Panel (a) shows the bifurcation diagram for the channel geometry. The other panels (b–d) show the bifurcation diagram for different values of the wedge angle
$\epsilon$ are shown. Panel (a) shows the bifurcation diagram for the channel geometry. The other panels (b–d) show the bifurcation diagram for different values of the wedge angle ![]() $\theta _0$.
$\theta _0$.
The figure shows that the bifurcation diagram differs qualitatively between the channel geometry with ![]() $\theta _0 = 0^\circ$ and the general wedge geometry with
$\theta _0 = 0^\circ$ and the general wedge geometry with ![]() $\theta _0>0$. For the channel geometry, each branch,
$\theta _0>0$. For the channel geometry, each branch, ![]() $\lambda _n(\epsilon )$, continues to exist as
$\lambda _n(\epsilon )$, continues to exist as ![]() $\epsilon \rightarrow 0$. However, for the wedge geometry, we see that the branches merge and disappear in pairs and no solutions will exist when
$\epsilon \rightarrow 0$. However, for the wedge geometry, we see that the branches merge and disappear in pairs and no solutions will exist when ![]() $\epsilon =0$. The lowest two branches,
$\epsilon =0$. The lowest two branches, ![]() $\lambda _1(\epsilon )$ and
$\lambda _1(\epsilon )$ and ![]() $\lambda _2(\epsilon )$, merge at the greatest value of
$\lambda _2(\epsilon )$, merge at the greatest value of ![]() $\epsilon$ and then merging continues to happen between higher branches as
$\epsilon$ and then merging continues to happen between higher branches as ![]() $\epsilon \rightarrow 0.$ Each time such a merge happens, the solutions corresponding to those two branches will cease to exist. In practice, we hypothesise that the existence of the self-similar solution is lost due to a tip-splitting instability which occurs when the flow rate or surface tension reaches a critical value. In figure 10 we see that, for smaller wedge angles, the tip-splitting will occur at a smaller value of the effective surface tension
$\epsilon \rightarrow 0.$ Each time such a merge happens, the solutions corresponding to those two branches will cease to exist. In practice, we hypothesise that the existence of the self-similar solution is lost due to a tip-splitting instability which occurs when the flow rate or surface tension reaches a critical value. In figure 10 we see that, for smaller wedge angles, the tip-splitting will occur at a smaller value of the effective surface tension ![]() $\epsilon$. In the limit
$\epsilon$. In the limit ![]() $\theta _0 \rightarrow 0$, the surface-tension value at which the branch merging occurs approaches zero.
$\theta _0 \rightarrow 0$, the surface-tension value at which the branch merging occurs approaches zero.
As noted in e.g. Ben Amar (Reference Ben Amar1991b), it is expected that, as is the case in the channel geometry, only the ![]() $\lambda _1$ branch is stable. Then the merging of the
$\lambda _1$ branch is stable. Then the merging of the ![]() $\lambda _1$ and
$\lambda _1$ and ![]() $\lambda _2$ branches as
$\lambda _2$ branches as ![]() $\epsilon \to 0$ is associated with a loss of stable solutions, resulting in a tip-splitting instability.
$\epsilon \to 0$ is associated with a loss of stable solutions, resulting in a tip-splitting instability.
The key observation is that the relative size of the terms in the selection condition (7.4) provides an approximate criterion for the existence of solutions. We recall that, as ![]() $\epsilon \to 0$, the classic Saffman–Taylor fingering in a channel involves
$\epsilon \to 0$, the classic Saffman–Taylor fingering in a channel involves ![]() $\lambda = \lambda _i \to \lambda _{lim} = 0.5$ for all indices
$\lambda = \lambda _i \to \lambda _{lim} = 0.5$ for all indices ![]() $i$. It can be asked whether a similar limiting value of
$i$. It can be asked whether a similar limiting value of ![]() $\lambda$ is reached as
$\lambda$ is reached as ![]() $\epsilon \to 0$ and
$\epsilon \to 0$ and ![]() $i \to \infty$ for general
$i \to \infty$ for general ![]() $\theta _0$.
$\theta _0$.
In figure 11 we plot the real parts of ![]() $\chi _1(0)$ and
$\chi _1(0)$ and ![]() $\chi _{C}(0)$ for the
$\chi _{C}(0)$ for the ![]() $\theta _0 = 20^\circ$ case. As indicated in the figure, for
$\theta _0 = 20^\circ$ case. As indicated in the figure, for ![]() $\lambda > \lambda _{lim}$, then
$\lambda > \lambda _{lim}$, then ![]() $0 < \operatorname {Re}\chi _1(0) < \operatorname {Re}\chi _{C}(0)$. Therefore, from the selection condition, the contribution from the central Stokes line is exponentially dominated by the contribution from the ‘1’ Stokes line(s).
$0 < \operatorname {Re}\chi _1(0) < \operatorname {Re}\chi _{C}(0)$. Therefore, from the selection condition, the contribution from the central Stokes line is exponentially dominated by the contribution from the ‘1’ Stokes line(s).

Figure 11. (a) Relative sizes of the real parts of ![]() $\chi _1(0)$ and
$\chi _1(0)$ and ![]() $\chi _{C}(0)$ for different values of
$\chi _{C}(0)$ for different values of ![]() $\lambda$ in the
$\lambda$ in the ![]() $\theta _0 = 20^\circ$ case. The
$\theta _0 = 20^\circ$ case. The ![]() $\lambda$ value where
$\lambda$ value where ![]() $\mathrm {Re}(\chi _{C}(0)) =\mathrm {Re}(\chi _1(0))$ is denoted
$\mathrm {Re}(\chi _{C}(0)) =\mathrm {Re}(\chi _1(0))$ is denoted ![]() $\lambda _{lim}$. Above this value the selection condition (7.4) can be satisfied. (b) The limiting
$\lambda _{lim}$. Above this value the selection condition (7.4) can be satisfied. (b) The limiting ![]() $\lambda$ value,
$\lambda$ value, ![]() $\lambda _{lim}$, in the small-surface-tension limit as a function of the wedge angle.
$\lambda _{lim}$, in the small-surface-tension limit as a function of the wedge angle.
When ![]() $\mathrm {Re}(\chi )$ is smaller, the corresponding
$\mathrm {Re}(\chi )$ is smaller, the corresponding ![]() $\exp ({-\mathrm {Re}(\chi )/\epsilon })$ term dominates in the selection condition. As figure 11 shows, in the small
$\exp ({-\mathrm {Re}(\chi )/\epsilon })$ term dominates in the selection condition. As figure 11 shows, in the small ![]() $\epsilon$ limit, for smaller
$\epsilon$ limit, for smaller ![]() $\lambda$ values, the contribution from the ‘
$\lambda$ values, the contribution from the ‘![]() $C$’ Stokes line dominates; while for larger
$C$’ Stokes line dominates; while for larger ![]() $\lambda$ values, the contribution from the ‘
$\lambda$ values, the contribution from the ‘![]() $1$’ Stokes line dominates. When the contribution from the ‘1’ Stokes line dominates, then the exponentially small oscillations can be switched off by the symmetric ‘2’ Stokes line and solutions will exist, similarly to the channel case. However, when the ‘C’ Stokes line dominates, then in the small
$1$’ Stokes line dominates. When the contribution from the ‘1’ Stokes line dominates, then the exponentially small oscillations can be switched off by the symmetric ‘2’ Stokes line and solutions will exist, similarly to the channel case. However, when the ‘C’ Stokes line dominates, then in the small ![]() $\epsilon$ limit it becomes impossible to satisfy the selection condition and no solutions will exist. The
$\epsilon$ limit it becomes impossible to satisfy the selection condition and no solutions will exist. The ![]() $\lambda$ value at which
$\lambda$ value at which ![]() $\mathrm {Re}(\chi _1(0)) = \mathrm {Re}(\chi _{C}(0))$ gives the limiting
$\mathrm {Re}(\chi _1(0)) = \mathrm {Re}(\chi _{C}(0))$ gives the limiting ![]() $\lambda$ value,
$\lambda$ value, ![]() $\lambda _{lim}$. The
$\lambda _{lim}$. The ![]() $\lambda _{lim}$ values as a function of
$\lambda _{lim}$ values as a function of ![]() $\theta _0$ are shown in figure 11.
$\theta _0$ are shown in figure 11.
9. Conclusion
We have used exponential asymptotics to derive the selection mechanism in the small-surface-tension limit for the divergent Saffman–Taylor fingers in a wedge of an arbitrary angle. The selection mechanism is based on the requirement for the exponentially small contributions, which are switched on at Stokes lines, to satisfy the far-field boundary conditions. This Stokes-line structure in the complex plane relies on an understanding of the singularities in the analytic continuation of the leading-order solution. Here, we must obtain this using a numerical scheme for the analytic continuation. We find the countable family of ![]() $\lambda (\epsilon )$ values and associated selected solutions that satisfy the selection condition. The bifurcation diagrams are plotted in figure 10 and show the merging of branches of
$\lambda (\epsilon )$ values and associated selected solutions that satisfy the selection condition. The bifurcation diagrams are plotted in figure 10 and show the merging of branches of ![]() $\lambda$ values as the surface-tension parameter,
$\lambda$ values as the surface-tension parameter, ![]() $\epsilon$, is decreased. We hypothesise that the loss of existence of solutions through this branch merging relates to the tip-splitting instability observed in the time-dependent flows in a circular geometry.
$\epsilon$, is decreased. We hypothesise that the loss of existence of solutions through this branch merging relates to the tip-splitting instability observed in the time-dependent flows in a circular geometry.
10. Discussion
There are a number of interesting extensions to the work in this paper in the fields of exponential asymptotics and Hele-Shaw problems.
In order to verify the correctness of the asymptotic predictions, we have used some of the early numerical work of Ben Amar (Reference Ben Amar1991b). As it turns out, there are a few aspects of numerical computations of the governing equations (2.6), (2.11) and (2.12) that render it more challenging. In a forthcoming work, we will present a specialised scheme that solves for the free-surface profile of the fingers.
One of the main difficulties with the analysis in this paper arises from the form of the leading-order solutions. Traditionally, in problems considered with exponential asymptotics, the leading-order solution will have a simple closed form; then, locations and strengths of the singularities in the complex plane are easily identified. For this problem, the leading-order solution is written in terms of special functions (cf. (3.7) and (3.8a,b)); however, the singularities of these expressions are not so easily obtained. In practice, we use a numerical scheme to analytically continue the leading-order solutions into the complex ![]() $\zeta$-plane and search for singularities. This numerical scheme could equally be used to analytically continue a fully numerical leading-order solution into the complex plane. Similar numerical analytic continuation schemes can be found in Chandler & Trinh (Reference Chandler and Trinh2018) and Crew & Trinh (Reference Crew and Trinh2016). With the advancement of such schemes, in the field of exponential asymptotics we are no longer restricted only to problems with a simple analytic leading-order solution.
$\zeta$-plane and search for singularities. This numerical scheme could equally be used to analytically continue a fully numerical leading-order solution into the complex plane. Similar numerical analytic continuation schemes can be found in Chandler & Trinh (Reference Chandler and Trinh2018) and Crew & Trinh (Reference Crew and Trinh2016). With the advancement of such schemes, in the field of exponential asymptotics we are no longer restricted only to problems with a simple analytic leading-order solution.
To complete the understanding of the tip-splitting behaviour in the circular geometry it will be necessary to check the stability of the branches plotted in the bifurcation diagram (figure 10). For the Saffman–Taylor problem in the channel geometry, Tanveer (Reference Tanveer1987) showed that only the lowest branch, ![]() $\lambda _1$, is linearly stable. We conjecture that the same will be true for the wedge geometry and so the merging of branches
$\lambda _1$, is linearly stable. We conjecture that the same will be true for the wedge geometry and so the merging of branches ![]() $\lambda _1$ and
$\lambda _1$ and ![]() $\lambda _2$ will correspond to the loss of existence of any solutions which could be observed physically. We have written a time-dependent code for the circular geometry based on the numerical method described in Dallaston & McCue (Reference Dallaston and McCue2014) and we hope that this will provide an insight into the stability of the branches observed in the bifurcation diagram for the wedge problem.
$\lambda _2$ will correspond to the loss of existence of any solutions which could be observed physically. We have written a time-dependent code for the circular geometry based on the numerical method described in Dallaston & McCue (Reference Dallaston and McCue2014) and we hope that this will provide an insight into the stability of the branches observed in the bifurcation diagram for the wedge problem.
Finally, there are many recent experimental and numerical results for different Hele-Shaw problems, some of which appear to have similar selected branches of permitted solutions (Gaillard et al. Reference Gaillard, Keeler, Le Lay, Lemoult, Thompson, Hazel and Juel2021; Keeler et al. Reference Keeler, Gaillard, Lawless, Thompson, Juel and Hazel2022). We expect that the techniques used here can also be applied to these problems to derive selection conditions, governed by exponentially small components of the solutions. In particular, the ability to do exponential asymptotics without a simple analytic leading-order solution will be necessary to make progress in these problems.
Acknowledgements
We especially thank J. Chapman (Oxford) for helping us navigate the formulation of this problem and getting us started on the analysis. His time and effort is very much appreciated. Further, we thank J. Shelton (Bath) and J. King (Nottingham) for many stimulating and helpful discussions. We would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programmes ‘Complex Analysis: Techniques, Applications and Computations’ and ‘Applicable Resurgent Asymptotics: Towards a Universal Theory’, where some work on this paper was undertaken (EPSRC grant no. [EP/R014604/1]). Some work on this paper was also conducted while visiting the Okinawa Institute of Science and Technology (OIST) through the Theoretical Sciences Visiting Program (TSVP). C.A. and P.H.T. gratefully acknowledge support by the Engineering and Physical Sciences Research Council (EPSRC) [EP/V012479/1]. C.J.L. gratefully acknowledges support by Australian Research Council Discovery Project DP190101190.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Further details on governing equations
In this section, we briefly present the details for deriving the governing equations. The fluid within the Hele-Shaw cell is governed by Stokes flow, and we consider the setup as shown in figure 3(a). We shall use bars for dimensional quantities, including Cartesian coordinates ![]() $(\bar {x},\bar {y})$ and polar coordinates
$(\bar {x},\bar {y})$ and polar coordinates ![]() $(\bar {r},\theta )$. Let
$(\bar {r},\theta )$. Let ![]() ${\bar {\boldsymbol {q}}}$ be the dimensional velocity averaged over the gap. The fluid pressure,
${\bar {\boldsymbol {q}}}$ be the dimensional velocity averaged over the gap. The fluid pressure, ![]() $\bar {p}$, is given by Darcy flow,
$\bar {p}$, is given by Darcy flow, ![]() ${\bar {\boldsymbol {q}}}=-(b^2/12\mu )\bar {\boldsymbol {\nabla }} \bar {p}$, where
${\bar {\boldsymbol {q}}}=-(b^2/12\mu )\bar {\boldsymbol {\nabla }} \bar {p}$, where ![]() $b$ is the Hele-Shaw cell gap thickness and
$b$ is the Hele-Shaw cell gap thickness and ![]() $\mu$ is the viscosity. We introduce a potential via
$\mu$ is the viscosity. We introduce a potential via ![]() $\bar {\phi }=-(b^2/12\mu )p$. Then, following the standard derivation via Stokes flow (Ockendon & Ockendon Reference Ockendon and Ockendon1995), we see the viscous fluid within the Hele-Shaw cell is governed by Laplace's equation,
$\bar {\phi }=-(b^2/12\mu )p$. Then, following the standard derivation via Stokes flow (Ockendon & Ockendon Reference Ockendon and Ockendon1995), we see the viscous fluid within the Hele-Shaw cell is governed by Laplace's equation, ![]() $\nabla ^2\bar \phi =0$, for a velocity potential with
$\nabla ^2\bar \phi =0$, for a velocity potential with ![]() ${\bar {\boldsymbol {q}}}=\bar {\boldsymbol {\nabla }}\bar {\phi }$.
${\bar {\boldsymbol {q}}}=\bar {\boldsymbol {\nabla }}\bar {\phi }$.
Inviscid fluid is injected at the origin and the interface between viscous and inviscid fluids is given by ![]() $\bar {r}=\bar {R}(\theta,\bar {t})$. The full set of governing equations, including interfacial and flux conditions are
$\bar {r}=\bar {R}(\theta,\bar {t})$. The full set of governing equations, including interfacial and flux conditions are
where ![]() $\sigma$ is the dimensional surface tension,
$\sigma$ is the dimensional surface tension, ![]() $\bar {v}_n$ is the velocity normal to the interface,
$\bar {v}_n$ is the velocity normal to the interface, ![]() $\bar {\kappa }$ is the curvature of the interface and
$\bar {\kappa }$ is the curvature of the interface and ![]() $\bar {\phi }_0$ an arbitrary shift of the potential. Equations (A1b) and (A1d) correspond to kinematic conditions on the interface and wall, respectively, (A1c) to the dynamic boundary condition on the interface and (A1e) the fluid injection condition for a dimensional source strength
$\bar {\phi }_0$ an arbitrary shift of the potential. Equations (A1b) and (A1d) correspond to kinematic conditions on the interface and wall, respectively, (A1c) to the dynamic boundary condition on the interface and (A1e) the fluid injection condition for a dimensional source strength ![]() $\bar {Q}$.
$\bar {Q}$.
A.1. Temporal scaling and non-dimensionalisation
We scale time by a yet-to-be-specified time scale, ![]() $T$, so that dimensionless time is
$T$, so that dimensionless time is ![]() $t=\bar {t}/T$ and introduce a length scale,
$t=\bar {t}/T$ and introduce a length scale, ![]() $R_0$, which is the initial distance (
$R_0$, which is the initial distance (![]() $t = 0$) between the tip of the bubble and the apex. We shall apply a time-dependent stretching of the domain via
$t = 0$) between the tip of the bubble and the apex. We shall apply a time-dependent stretching of the domain via
where ![]() $A(t)$ is to be specified. Our dimensionless variables are now denoted without the overbar and we write
$A(t)$ is to be specified. Our dimensionless variables are now denoted without the overbar and we write
and so forth. The governing equations are now
We review two ways to further reduce the above set of equations via the choice of ![]() $\textit {A}$. The first is to define
$\textit {A}$. The first is to define ![]() $\hat {\phi }={A}(t)(\phi -\phi _0)$ and
$\hat {\phi }={A}(t)(\phi -\phi _0)$ and
Then, the governing equations (A4) become
In this way, our domain stretching function and time scale become
our surface-tension parameter ![]() $\hat {\sigma }$ is a constant and the flow rate must be
$\hat {\sigma }$ is a constant and the flow rate must be
This way of reducing the equations has the attraction of keeping the surface tension constant (which is what happens in reality), while also requiring a non-constant flow rate with a ![]() $t^{1/3}$ scaling. Such a flow rate is perfectly realisable in practice (Li et al. Reference Li, Lowengrub, Fontana and Palffy-Muhoray2009).
$t^{1/3}$ scaling. Such a flow rate is perfectly realisable in practice (Li et al. Reference Li, Lowengrub, Fontana and Palffy-Muhoray2009).
The other way of reducing the equations is to set ![]() $\hat {\phi }=\phi -\phi _0$ and define
$\hat {\phi }=\phi -\phi _0$ and define
so the governing equations (A4) are the same as above (A6). This time, we have
This approach has the advantage of keeping the flow rate, ![]() $\bar {Q}$, constant; this is the most common realisation in an experimental set-up, but has the consequence of requiring the consideration of a time-dependent surface-tension parameter
$\bar {Q}$, constant; this is the most common realisation in an experimental set-up, but has the consequence of requiring the consideration of a time-dependent surface-tension parameter ![]() $\hat {\sigma }$ – conceptually, we may consider
$\hat {\sigma }$ – conceptually, we may consider ![]() $\sigma$ as slowly varying, and even treated as constant within the context of a simulation (see further discussion in Ben Amar Reference Ben Amar1991b).
$\sigma$ as slowly varying, and even treated as constant within the context of a simulation (see further discussion in Ben Amar Reference Ben Amar1991b).
Appendix B. Deriving the power  $\gamma$
$\gamma$
In this section we derive the constants ![]() $\gamma _1$ and
$\gamma _1$ and ![]() $\gamma _{C}$, which arise in (7.4), by matching the strengths of the singularities in the inner region. Firstly, we introduce a new variable,
$\gamma _{C}$, which arise in (7.4), by matching the strengths of the singularities in the inner region. Firstly, we introduce a new variable, ![]() $Y = \zeta - \zeta _*$, where
$Y = \zeta - \zeta _*$, where ![]() $\zeta _*$ is one of the singularities,
$\zeta _*$ is one of the singularities, ![]() $\zeta _1$ or
$\zeta _1$ or ![]() $\zeta _{C}$.
$\zeta _{C}$.
It can be verified, either through dominant balance or via the numerical continuation of § 4, that all the complex plane singularities of the leading-order speed, ![]() $q_0$, are square-root singularities. Hence,
$q_0$, are square-root singularities. Hence, ![]() $q_0 \sim Y^{-{1}/{2}}$ as
$q_0 \sim Y^{-{1}/{2}}$ as ![]() $Y \rightarrow 0$. Close to the singularity, the Hilbert transform in the boundary-integral equation will be subdominant and so we can use
$Y \rightarrow 0$. Close to the singularity, the Hilbert transform in the boundary-integral equation will be subdominant and so we can use ![]() $q_0 - \textrm {i}\tau _0 = \mathcal {H}[\tau _0]$ and the behaviour of
$q_0 - \textrm {i}\tau _0 = \mathcal {H}[\tau _0]$ and the behaviour of ![]() $q_0$ to derive the local
$q_0$ to derive the local ![]() $\tau _0$ behaviour
$\tau _0$ behaviour
and hence ![]() $\mathrm {e}^{\mathrm {i}\tau _0} \sim Y^{-1/2}$ in this limit. The asymptotic singular behaviour for other key variables is given as
$\mathrm {e}^{\mathrm {i}\tau _0} \sim Y^{-1/2}$ in this limit. The asymptotic singular behaviour for other key variables is given as ![]() $Y \to 0$ by
$Y \to 0$ by
The local expression for the singulant equation (5.6) is given by
Integrating this expression gives ![]() $\chi = {O}(Y^{7/4})$ as
$\chi = {O}(Y^{7/4})$ as ![]() $Y \to 0$. The factorial-over-power ansatz (5.3) then gives the strength of the singularity in the later-order terms
$Y \to 0$. The factorial-over-power ansatz (5.3) then gives the strength of the singularity in the later-order terms
Now we take ![]() $n=0$ and choose
$n=0$ and choose ![]() $\gamma$ so that the correct predicted singularity strength is given for
$\gamma$ so that the correct predicted singularity strength is given for ![]() $q_0.$ Although the factorial-over-power ansatz was posed for the limit
$q_0.$ Although the factorial-over-power ansatz was posed for the limit ![]() $n \rightarrow \infty,$ the singularity strength at lower orders still needs to match for the two expressions to be consistent. The
$n \rightarrow \infty,$ the singularity strength at lower orders still needs to match for the two expressions to be consistent. The ![]() $\gamma$ that satisfies this condition is
$\gamma$ that satisfies this condition is
This analysis is valid for each singularity, so ![]() $\gamma _1 = \gamma _{C} = 1/14$, irrespective of the wedge angle
$\gamma _1 = \gamma _{C} = 1/14$, irrespective of the wedge angle ![]() $\theta _0$.
$\theta _0$.
Appendix C. Deriving the pre-factor  $\varLambda$
$\varLambda$
To find ![]() $\varLambda$, which appears in the late-order expression (5.11) and also the exponential switching (7.4) we consider the solution in an inner region near the singularity at
$\varLambda$, which appears in the late-order expression (5.11) and also the exponential switching (7.4) we consider the solution in an inner region near the singularity at ![]() $\zeta = \zeta ^*$. We define a new inner variable
$\zeta = \zeta ^*$. We define a new inner variable ![]() $\nu$ such that
$\nu$ such that ![]() $\zeta - \zeta _* = \epsilon ^\alpha \nu$. The value of
$\zeta - \zeta _* = \epsilon ^\alpha \nu$. The value of ![]() $\alpha$ determines the width of the inner region. From (B4) with
$\alpha$ determines the width of the inner region. From (B4) with ![]() $\gamma = 1/14$, the local behaviour of the late terms near the singularity is given by
$\gamma = 1/14$, the local behaviour of the late terms near the singularity is given by
We locate the inner region by identifying where terms in the power series (5.1) reorder, and the power series expansion is therefore no longer valid. This occurs when ![]() $\epsilon ^{2n}q_n$ is approximately
$\epsilon ^{2n}q_n$ is approximately ![]() ${O}(q_0)$ as
${O}(q_0)$ as ![]() $n \rightarrow \infty$. That is
$n \rightarrow \infty$. That is
which gives ![]() $\alpha = {4}/{7}$. The correct scaling for the inner region is thus
$\alpha = {4}/{7}$. The correct scaling for the inner region is thus
which is identical to the scaling for the channel geometry (Chapman Reference Chapman1999).
We also require the local behaviour of the dependent variables near the singularities. This is done numerically using the analytic continuation scheme of § 4. Beginning from the free surface, we solve for the analytic continuation along a path that approaches the singularity, ![]() $\zeta _*$. Once done, the local behaviour of the dependent variables can be determined by numerical fitting to log–log plots. In particular, we find
$\zeta _*$. Once done, the local behaviour of the dependent variables can be determined by numerical fitting to log–log plots. In particular, we find
Here, the coefficients ![]() $b_{1*}, b_{2*}, c_{1*}, c_{2*}, d_{1*}, d_{2*}$ are constant with respect to the independent variables, but they depend on the parameters
$b_{1*}, b_{2*}, c_{1*}, c_{2*}, d_{1*}, d_{2*}$ are constant with respect to the independent variables, but they depend on the parameters ![]() $\theta _0$ and
$\theta _0$ and ![]() $\lambda$ and also vary between the different singularities. We indicate the choice of singularity using the
$\lambda$ and also vary between the different singularities. We indicate the choice of singularity using the ![]() $*$ subscript. The constants are typically complex. Selected values of the constants as
$*$ subscript. The constants are typically complex. Selected values of the constants as ![]() $\theta _0$ and
$\theta _0$ and ![]() $\lambda$ vary are tabulated in figure 12 and table 2 for the ‘1’ and ‘
$\lambda$ vary are tabulated in figure 12 and table 2 for the ‘1’ and ‘![]() ${C}$’ singularities, respectively.
${C}$’ singularities, respectively.

Figure 12. Locations of the ‘1’ singularity for different values of ![]() $\lambda$ and
$\lambda$ and ![]() $\theta _0$. At each singularity we have included the corresponding triplet of complex constants for the leading-order inner behaviour around the ‘1’ singularity,
$\theta _0$. At each singularity we have included the corresponding triplet of complex constants for the leading-order inner behaviour around the ‘1’ singularity, ![]() $(b_1, c_1, d_1).$
$(b_1, c_1, d_1).$
Table 2. The triplet of complex constants for the leading-order inner behaviours in the inner region about the ‘C’ singularity for different values of ![]() $\theta _0$ and
$\theta _0$ and ![]() $\lambda$.
$\lambda$.

From the expansions given above it follows that ![]() $\tau$ can be written in terms of
$\tau$ can be written in terms of ![]() $q$
$q$
 \begin{align} \log q - \mathrm{i}\tau &= \hat{\mathcal{H}}[\tau_0] + O(\epsilon^2) = \log q_0 - \mathrm{i}\tau_0 + O(\epsilon^2) \nonumber\\ &= \log \left(\frac{c_{1*}}{d_{1*}}\right) + \left(\frac{c_{2*}}{c_{1*}} - \frac{d_{2*}}{d_{1*}}\right)\epsilon^{4/7}\nu + O\left(\epsilon^{8/7}\right), \end{align}
\begin{align} \log q - \mathrm{i}\tau &= \hat{\mathcal{H}}[\tau_0] + O(\epsilon^2) = \log q_0 - \mathrm{i}\tau_0 + O(\epsilon^2) \nonumber\\ &= \log \left(\frac{c_{1*}}{d_{1*}}\right) + \left(\frac{c_{2*}}{c_{1*}} - \frac{d_{2*}}{d_{1*}}\right)\epsilon^{4/7}\nu + O\left(\epsilon^{8/7}\right), \end{align}
and ![]() $r$ can be expanded
$r$ can be expanded
Next, we will derive the inner equation from the Bernoulli equation in terms of the inner variable for ![]() $q$, which is defined as
$q$, which is defined as
The analytically continued Bernoulli equation (4.3a) is
 \begin{equation} \epsilon^2 \frac{P}{4}\frac{\partial}{\partial \zeta}\left(r(x)\left[Pq\frac{\partial \tau}{\partial \zeta} - \ell \sin\tau\right]\right) = \frac{2}{\rm \pi}\int_{-\infty}^0 \frac{K(\tilde{\zeta}) \tilde{\zeta}}{\zeta^2 - \tilde{\zeta}^2}\,{\rm d}{\tilde{\zeta}} + \mathrm{i} K(\zeta), \end{equation}
\begin{equation} \epsilon^2 \frac{P}{4}\frac{\partial}{\partial \zeta}\left(r(x)\left[Pq\frac{\partial \tau}{\partial \zeta} - \ell \sin\tau\right]\right) = \frac{2}{\rm \pi}\int_{-\infty}^0 \frac{K(\tilde{\zeta}) \tilde{\zeta}}{\zeta^2 - \tilde{\zeta}^2}\,{\rm d}{\tilde{\zeta}} + \mathrm{i} K(\zeta), \end{equation}
where ![]() $P,r(x), \ell, K(\zeta )$ are as defined in (2.7a–c) and (2.9). The left-hand side and second term on the right-hand side can be straightforwardly expanded using the expressions above. The integral term on the right-hand side needs to be treated more carefully. Firstly, we expand using the asymptotic series
$P,r(x), \ell, K(\zeta )$ are as defined in (2.7a–c) and (2.9). The left-hand side and second term on the right-hand side can be straightforwardly expanded using the expressions above. The integral term on the right-hand side needs to be treated more carefully. Firstly, we expand using the asymptotic series
 \begin{equation} \frac{2}{\rm \pi}\int_{-\infty}^0 \frac{K(\tilde{\zeta}) \tilde{\zeta}}{\zeta^2 - \tilde{\zeta}^2}\,{\rm d}\tilde{\zeta} = \frac{2}{\rm \pi}\int_{-\infty}^0 \frac{K_0(\tilde{\zeta}) \tilde{\zeta}}{\zeta^2 - \tilde{\zeta}^2}\,{\rm d}{\tilde{\zeta}}+ O(\epsilon^2), \end{equation}
\begin{equation} \frac{2}{\rm \pi}\int_{-\infty}^0 \frac{K(\tilde{\zeta}) \tilde{\zeta}}{\zeta^2 - \tilde{\zeta}^2}\,{\rm d}\tilde{\zeta} = \frac{2}{\rm \pi}\int_{-\infty}^0 \frac{K_0(\tilde{\zeta}) \tilde{\zeta}}{\zeta^2 - \tilde{\zeta}^2}\,{\rm d}{\tilde{\zeta}}+ O(\epsilon^2), \end{equation}
where ![]() $K_0(\zeta )$ is the leading-order part of
$K_0(\zeta )$ is the leading-order part of ![]() $K$ as defined in (3.2). Then we apply the residue theorem to the leading-order contribution by deforming the contour to a semicircular contour in the upper-half-
$K$ as defined in (3.2). Then we apply the residue theorem to the leading-order contribution by deforming the contour to a semicircular contour in the upper-half-![]() $\zeta$-plane and noting the symmetry between the negative and positive real axes. At the first two orders the contribution from the integral cancels with the contribution from the second term on the right-hand side of Bernoulli's equation (4.3a). The leading-order inner equation therefore becomes
$\zeta$-plane and noting the symmetry between the negative and positive real axes. At the first two orders the contribution from the integral cancels with the contribution from the second term on the right-hand side of Bernoulli's equation (4.3a). The leading-order inner equation therefore becomes
It is natural to change variables
 \begin{equation} \nu = A_*^{2/7} \nu_{in} = \left(-\frac{\mathrm{i} P^2(\zeta_*)r^3(b_{1*})c_{1*}^2d_{1*}}{2}\right)^{2/7} \nu_{in}, \end{equation}
\begin{equation} \nu = A_*^{2/7} \nu_{in} = \left(-\frac{\mathrm{i} P^2(\zeta_*)r^3(b_{1*})c_{1*}^2d_{1*}}{2}\right)^{2/7} \nu_{in}, \end{equation}so then the inner equation becomes
which is the same as the inner equation for the classic Saffman–Taylor problem in a channel (Chapman Reference Chapman1999). In the outer limit (as ![]() $\tilde {\nu } \rightarrow \infty$) we thus derive the same relation as in the channel
$\tilde {\nu } \rightarrow \infty$) we thus derive the same relation as in the channel
 \begin{equation} q_{in} = \sum_{n=0}^\infty A_n \nu_{in}^{{-}7n/2}, \end{equation}
\begin{equation} q_{in} = \sum_{n=0}^\infty A_n \nu_{in}^{{-}7n/2}, \end{equation}
where the constants ![]() $A_n$ satisfy the recurrence relation
$A_n$ satisfy the recurrence relation
 $$\begin{gather} \sum_{m=1}^n \left(\frac{7m}{2}-3\right)\left(\frac{7m}{2}-2\right)A_{m-1} \sum_{k=0}^{n-m}A_{n-m-k}A_k = \sum_{m=0}^n A_{n-m}A_m, \quad n\geqslant 1, \end{gather}$$
$$\begin{gather} \sum_{m=1}^n \left(\frac{7m}{2}-3\right)\left(\frac{7m}{2}-2\right)A_{m-1} \sum_{k=0}^{n-m}A_{n-m-k}A_k = \sum_{m=0}^n A_{n-m}A_m, \quad n\geqslant 1, \end{gather}$$Then the inner expansion gives
 \begin{equation} q = c_{1*}\epsilon^{{-}2/7}\nu^{{-}1/2}\sum_{n=0}^\infty A_n \nu^{{-}7n/2}A_*^{n}, \end{equation}
\begin{equation} q = c_{1*}\epsilon^{{-}2/7}\nu^{{-}1/2}\sum_{n=0}^\infty A_n \nu^{{-}7n/2}A_*^{n}, \end{equation}
which means the ![]() $n{\textrm {th}}$ term is
$n{\textrm {th}}$ term is
Now, writing the outer expansion (5.7) in terms of the inner variable, we find
 \begin{align} \chi &={-}\int_{\zeta_*}^\zeta \frac{2\mathrm{e}^{\mathrm{i}{\rm \pi}/4}\mathrm{e}^{-\mathrm{i}\tau_0/2}}{Pq_0r(x_0)^{3/2}}\,{\rm d}{\tilde{\zeta}} \nonumber\\ &\sim{-}\int_0^\nu \frac{2\mathrm{e}^{\mathrm{i}{\rm \pi}/4}d_{1*}^{{-}1/2}\epsilon^{1/7}\tilde{\nu}^{1/4}}{P(\zeta_*)r(b_{1*})^{3/2} c_{1*}\epsilon^{{-}2/7}\tilde{\nu}^{{-}1/2}}\epsilon^{4/7}\,{\rm d}{\tilde{\nu}} \nonumber\\ &= \frac{8}{7} \frac{\mathrm{e}^{{-}3\mathrm{i}{\rm \pi}/4}d_{1*}^{{-}1/2}}{c_{1*}P(\zeta_*)r(b_{1*})^{3/2}}\epsilon \nu^{7/4}, \end{align}
\begin{align} \chi &={-}\int_{\zeta_*}^\zeta \frac{2\mathrm{e}^{\mathrm{i}{\rm \pi}/4}\mathrm{e}^{-\mathrm{i}\tau_0/2}}{Pq_0r(x_0)^{3/2}}\,{\rm d}{\tilde{\zeta}} \nonumber\\ &\sim{-}\int_0^\nu \frac{2\mathrm{e}^{\mathrm{i}{\rm \pi}/4}d_{1*}^{{-}1/2}\epsilon^{1/7}\tilde{\nu}^{1/4}}{P(\zeta_*)r(b_{1*})^{3/2} c_{1*}\epsilon^{{-}2/7}\tilde{\nu}^{{-}1/2}}\epsilon^{4/7}\,{\rm d}{\tilde{\nu}} \nonumber\\ &= \frac{8}{7} \frac{\mathrm{e}^{{-}3\mathrm{i}{\rm \pi}/4}d_{1*}^{{-}1/2}}{c_{1*}P(\zeta_*)r(b_{1*})^{3/2}}\epsilon \nu^{7/4}, \end{align}and so from the factorial over power ansatz (5.3)
 \begin{align} \epsilon^{2n}q_n &\sim \varLambda_* \left(\frac{64}{49} \frac{\mathrm{i}}{d_{1*}c_{1*}^2 P^2(\zeta_*) r^3(b_{1*})}\right)^{{-}n} \nu^{{-}7n/2} \left(\frac{8\mathrm{e}^{{-}3\mathrm{i}{\rm \pi}/4}d_{1*}^{{-}1/2}\epsilon}{7c_{1*}P(\zeta_*)r(b_{1*})^{3/2}}\right)^{{-}1/14} \nonumber\\ &\quad \times \nu^{{-}1/8} \mathrm{e}^{7\mathrm{i}{\rm \pi}/8}2^{{-}1/2}d_{1*}^{{-}1/4}\epsilon^{{-}3/14} \nu^{{-}3/8} c_{1*}r(b_{1*})^{1/4}\varGamma(2n+\gamma), \end{align}
\begin{align} \epsilon^{2n}q_n &\sim \varLambda_* \left(\frac{64}{49} \frac{\mathrm{i}}{d_{1*}c_{1*}^2 P^2(\zeta_*) r^3(b_{1*})}\right)^{{-}n} \nu^{{-}7n/2} \left(\frac{8\mathrm{e}^{{-}3\mathrm{i}{\rm \pi}/4}d_{1*}^{{-}1/2}\epsilon}{7c_{1*}P(\zeta_*)r(b_{1*})^{3/2}}\right)^{{-}1/14} \nonumber\\ &\quad \times \nu^{{-}1/8} \mathrm{e}^{7\mathrm{i}{\rm \pi}/8}2^{{-}1/2}d_{1*}^{{-}1/4}\epsilon^{{-}3/14} \nu^{{-}3/8} c_{1*}r(b_{1*})^{1/4}\varGamma(2n+\gamma), \end{align}
where the ![]() $*$ subscript on the
$*$ subscript on the ![]() $\varLambda$ labels the corresponding singularity. Then equating the inner and outer expansions gives
$\varLambda$ labels the corresponding singularity. Then equating the inner and outer expansions gives
Using the large ![]() $n$ solution to the recurrence relation from Chapman (Reference Chapman1999) we obtain a final expression for the constant
$n$ solution to the recurrence relation from Chapman (Reference Chapman1999) we obtain a final expression for the constant
 \begin{equation} \varLambda_* \approx 0.46048 \times 2^{{-}1/7}\exp({-13\mathrm{i}{\rm \pi}/14})\left(\frac{d_{1*}^3}{c_{1*}P(\zeta_*)r(b_{1*})^5}\right)^{1/14} . \end{equation}
\begin{equation} \varLambda_* \approx 0.46048 \times 2^{{-}1/7}\exp({-13\mathrm{i}{\rm \pi}/14})\left(\frac{d_{1*}^3}{c_{1*}P(\zeta_*)r(b_{1*})^5}\right)^{1/14} . \end{equation}