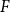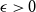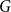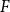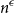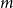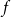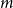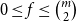1. Introduction
For an integer
![]() $r\geq 2$
, an
$r\geq 2$
, an
![]() $r$
-graph or
$r$
-graph or
![]() $r$
-uniform hypergraph is a pair
$r$
-uniform hypergraph is a pair
![]() $H=(V, E)$
, where
$H=(V, E)$
, where
![]() $V=V(H)$
is the set of vertices and
$V=V(H)$
is the set of vertices and
![]() $E=E(H) \subseteq \binom{V}{r}$
is the set of edges. A
$E=E(H) \subseteq \binom{V}{r}$
is the set of edges. A
![]() $2$
-graph is simply a graph. A homogeneous set is a set of vertices that is either a clique or a coclique (independent set). For an
$2$
-graph is simply a graph. A homogeneous set is a set of vertices that is either a clique or a coclique (independent set). For an
![]() $r$
-graph
$r$
-graph
![]() $H$
, let
$H$
, let
![]() $h(H)$
be the size of a largest homogeneous set. Given
$h(H)$
be the size of a largest homogeneous set. Given
![]() $r$
-graphs
$r$
-graphs
![]() $F, H$
, say that
$F, H$
, say that
![]() $H$
is
$H$
is
![]() $F$
-free if
$F$
-free if
![]() $H$
contains no isomorphic copy of
$H$
contains no isomorphic copy of
![]() $F$
as an induced subgraph. We say that an
$F$
as an induced subgraph. We say that an
![]() $r$
-graph
$r$
-graph
![]() $F$
has the Erdős-Hajnal-property or simply EH property if there is a constant
$F$
has the Erdős-Hajnal-property or simply EH property if there is a constant
![]() $\epsilon =\epsilon _F\gt 0$
such that every
$\epsilon =\epsilon _F\gt 0$
such that every
![]() $n$
-vertex
$n$
-vertex
![]() $F$
-free
$F$
-free
![]() $r$
-graph
$r$
-graph
![]() $H$
satisfies
$H$
satisfies
![]() $h(H) \geq n^{\epsilon }$
. A conjecture of Erdős and Hajnal [Reference Erdős and Hajnal13] states that any
$h(H) \geq n^{\epsilon }$
. A conjecture of Erdős and Hajnal [Reference Erdős and Hajnal13] states that any
![]() $2$
-graph has the EH property. The conjecture remains open, see for example a survey by Chudnovsky [Reference Chudnovsky8], as well as [Reference Alon, Pach and Solymosi1, Reference Bousquet, Lagoutte and Thomassé5, Reference Fox, Pach and Suk17], to name a few central results on the topic. When
$2$
-graph has the EH property. The conjecture remains open, see for example a survey by Chudnovsky [Reference Chudnovsky8], as well as [Reference Alon, Pach and Solymosi1, Reference Bousquet, Lagoutte and Thomassé5, Reference Fox, Pach and Suk17], to name a few central results on the topic. When
![]() $F$
is a fixed graph and
$F$
is a fixed graph and
![]() $G$
is an
$G$
is an
![]() $F$
-free
$F$
-free
![]() $n$
-vertex graph, Erdős and Hajnal proved that
$n$
-vertex graph, Erdős and Hajnal proved that
![]() $h(G) \ge 2^{c\sqrt{\log n}}$
. This was recently improved to
$h(G) \ge 2^{c\sqrt{\log n}}$
. This was recently improved to
![]() $h(G) \ge 2^{c\sqrt{\log n\log \log n}}$
by Bucić, Nguyen, Scott, and Seymour [Reference Bucić, Nguyen, Scott and Seymour7].
$h(G) \ge 2^{c\sqrt{\log n\log \log n}}$
by Bucić, Nguyen, Scott, and Seymour [Reference Bucić, Nguyen, Scott and Seymour7].
The Erdős-Hajnal conjecture fails for
![]() $r$
-graphs,
$r$
-graphs,
![]() $r\geq 3$
, already when
$r\geq 3$
, already when
![]() $F$
is a clique of size
$F$
is a clique of size
![]() $r+1$
. Indeed, well-known results on off-diagonal hypergraph Ramsey numbers show that there are
$r+1$
. Indeed, well-known results on off-diagonal hypergraph Ramsey numbers show that there are
![]() $n$
-vertex
$n$
-vertex
![]() $r$
-graphs that do not have a clique on
$r$
-graphs that do not have a clique on
![]() $r+1$
vertices and do not have cocliques on
$r+1$
vertices and do not have cocliques on
![]() $f_r(n)$
vertices, where
$f_r(n)$
vertices, where
![]() $f_r$
is an iterated logarithmic function (see [Reference Mubayi and Suk25] for the best known results). Moreover, the following result (Claim 1.3 in [Reference Gishboliner and Tomon19]) tells us exactly which
$f_r$
is an iterated logarithmic function (see [Reference Mubayi and Suk25] for the best known results). Moreover, the following result (Claim 1.3 in [Reference Gishboliner and Tomon19]) tells us exactly which
![]() $r$
-graphs,
$r$
-graphs,
![]() $r\geq 3$
, have the EH property. Here
$r\geq 3$
, have the EH property. Here
![]() $D_2$
is the unique
$D_2$
is the unique
![]() $3$
-graph on
$3$
-graph on
![]() $4$
vertices with exactly
$4$
vertices with exactly
![]() $2$
edges.
$2$
edges.
Theorem 1.1 (Gishboliner and Tomon [Reference Gishboliner and Tomon19]). Let
![]() $r\geq 3$
. If
$r\geq 3$
. If
![]() $F$
is an
$F$
is an
![]() $r$
-graph on at least
$r$
-graph on at least
![]() $r+1$
vertices and
$r+1$
vertices and
![]() $F\neq D_2$
, then there is an
$F\neq D_2$
, then there is an
![]() $F$
-free
$F$
-free
![]() $r$
-graph
$r$
-graph
![]() $H$
on
$H$
on
![]() $n$
vertices such that
$n$
vertices such that
![]() $h(H) = O(\log n)$
. On the other hand, there is a constant
$h(H) = O(\log n)$
. On the other hand, there is a constant
![]() $c \gt 0$
such that if
$c \gt 0$
such that if
![]() $H$
is an
$H$
is an
![]() $D_2$
-free
$D_2$
-free
![]() $n$
-vertex
$n$
-vertex
![]() $3$
-graph, then
$3$
-graph, then
![]() $h(H) \geq n^c$
.
$h(H) \geq n^c$
.
It is natural to consider the EH property for families of
![]() $r$
-graphs instead of a single
$r$
-graphs instead of a single
![]() $r$
-graph. In this paper, we consider families determined by a given set of orders and sizes. Several special cases of this have been extensively studied over the years (see, e.g. [Reference Erdős and Hajnal12]). For
$r$
-graph. In this paper, we consider families determined by a given set of orders and sizes. Several special cases of this have been extensively studied over the years (see, e.g. [Reference Erdős and Hajnal12]). For
![]() $0\leq f \leq \binom{m}{r}$
, we call an
$0\leq f \leq \binom{m}{r}$
, we call an
![]() $r$
-graph
$r$
-graph
![]() $F$
on
$F$
on
![]() $m$
vertices and
$m$
vertices and
![]() $f$
edges an
$f$
edges an
![]() $(m,f)$
-graph and we call the pair
$(m,f)$
-graph and we call the pair
![]() $(m,f)$
the order-size pair for
$(m,f)$
the order-size pair for
![]() $F$
. Say that
$F$
. Say that
![]() $H$
is
$H$
is
![]() $(m,f)$
-free if it contains no induced copy of an
$(m,f)$
-free if it contains no induced copy of an
![]() $(m,f)$
-graph. If
$(m,f)$
-graph. If
![]() $Q=\{(m_1, f_1), \ldots, (m_t, f_t)\}$
, say that
$Q=\{(m_1, f_1), \ldots, (m_t, f_t)\}$
, say that
![]() $H$
is
$H$
is
![]() $Q$
-free if
$Q$
-free if
![]() $H$
is
$H$
is
![]() $(m_i,f_i)$
-free for all
$(m_i,f_i)$
-free for all
![]() $i=1, \ldots, t$
.
$i=1, \ldots, t$
.
Definition 1.2. Given
![]() $r \ge 2$
and
$r \ge 2$
and
![]() $Q=\{(m_1, f_1), \ldots, (m_t, f_t)\}$
, let
$Q=\{(m_1, f_1), \ldots, (m_t, f_t)\}$
, let
![]() $h(n,Q)=h_r(n,Q)$
be the minimum of
$h(n,Q)=h_r(n,Q)$
be the minimum of
![]() $h(H)$
, taken over all
$h(H)$
, taken over all
![]() $n$
-vertex
$n$
-vertex
![]() $Q$
-free
$Q$
-free
![]() $r$
-graphs
$r$
-graphs
![]() $H$
. Say that
$H$
. Say that
![]() $Q$
has the EH property if there exists
$Q$
has the EH property if there exists
![]() $\epsilon =\epsilon _Q\gt 0$
such that
$\epsilon =\epsilon _Q\gt 0$
such that
![]() $h(n, Q) \gt n^{\epsilon }$
.
$h(n, Q) \gt n^{\epsilon }$
.
For example
![]() $h_3(n, \{(4,0), (4,2)\}) = k$
means that every
$h_3(n, \{(4,0), (4,2)\}) = k$
means that every
![]() $n$
-vertex
$n$
-vertex
![]() $3$
-graph in which any
$3$
-graph in which any
![]() $4$
vertices induce
$4$
vertices induce
![]() $1$
,
$1$
,
![]() $3$
, or
$3$
, or
![]() $4$
edges has a homogenous set of size
$4$
edges has a homogenous set of size
![]() $k$
, and there is a
$k$
, and there is a
![]() $3$
-graph
$3$
-graph
![]() $H$
as above with
$H$
as above with
![]() $h(H) = k$
. We may omit the subscript
$h(H) = k$
. We may omit the subscript
![]() $r$
in the notation
$r$
in the notation
![]() $h_r(n, Q)$
if it is obvious from context. When
$h_r(n, Q)$
if it is obvious from context. When
![]() $Q=\{(m,f)\}$
we use the simpler notation
$Q=\{(m,f)\}$
we use the simpler notation
![]() $h(n,m,f)$
instead of
$h(n,m,f)$
instead of
![]() $h(n, \{(m,f)\})$
. Let us make two simple observations:
$h(n, \{(m,f)\})$
. Let us make two simple observations:
Our first result concerns 2-graphs, where we show that forbidding a single order-size pair already guarantees large homogeneous sets.
Proposition 1.3.
For any integers
![]() $m,f$
with
$m,f$
with
![]() $m\geq 2$
and
$m\geq 2$
and
![]() $0\leq f\leq \binom{m}{2}$
there exists
$0\leq f\leq \binom{m}{2}$
there exists
![]() $c\gt 0$
such that
$c\gt 0$
such that
![]() $h_2(n, m, f) \geq c \, n^{1/(m-1)}$
.
$h_2(n, m, f) \geq c \, n^{1/(m-1)}$
.
Proposition 1.3 is proved in Section 2. It seems a challenging problem to give good upper bounds on
![]() $h_2(n, m, f)$
. For example, determining
$h_2(n, m, f)$
. For example, determining
![]() $h_2(n,m,\left(\substack{m\\2}\right))$
is equivalent to determining off-diagonal Ramsey numbers.
$h_2(n,m,\left(\substack{m\\2}\right))$
is equivalent to determining off-diagonal Ramsey numbers.
Our second main result concerns the case
![]() $r=3$
and
$r=3$
and
![]() $m=4$
. We shall consider sets
$m=4$
. We shall consider sets
![]() $Q$
consisting of pairs
$Q$
consisting of pairs
![]() $(4,i)$
for
$(4,i)$
for
![]() $i\in \{0, 1, 2, 3, 4\}$
. The cases where
$i\in \{0, 1, 2, 3, 4\}$
. The cases where
![]() $Q$
contains both
$Q$
contains both
![]() $(4,0)$
and
$(4,0)$
and
![]() $(4,4)$
are trivial, because Ramsey’s theorem guarantees that for sufficiently large
$(4,4)$
are trivial, because Ramsey’s theorem guarantees that for sufficiently large
![]() $n$
we cannot avoid both
$n$
we cannot avoid both
![]() $(4,0)$
and
$(4,0)$
and
![]() $(4,4)$
. In all remaining cases, the following theorem determines whether
$(4,4)$
. In all remaining cases, the following theorem determines whether
![]() $h_3(n,Q)$
is polynomial or polylogarithmic in
$h_3(n,Q)$
is polynomial or polylogarithmic in
![]() $n$
.
$n$
.
Theorem 1.4.
Let
![]() $\emptyset \neq S \subseteq \{0,1,2,3,4\}$
and suppose that
$\emptyset \neq S \subseteq \{0,1,2,3,4\}$
and suppose that
![]() $\{0,4\} \not \subseteq S$
. Set
$\{0,4\} \not \subseteq S$
. Set
![]() $Q = \{(4,i) \;:\; i \in S\}$
.
$Q = \{(4,i) \;:\; i \in S\}$
.
-
1. If
 $S = \{0\},\{1\},\{0,1\},\{1,3\}$
or
$S = \{0\},\{1\},\{0,1\},\{1,3\}$
or
 $\overline S \;:\!=\; \{4-i \;:\; i \in S\}$
is one of these four sets, then there are constants
$\overline S \;:\!=\; \{4-i \;:\; i \in S\}$
is one of these four sets, then there are constants
 $c_1,c_2 \gt 0$
such that
$c_1,c_2 \gt 0$
such that
 $\log ^{c_1}(n) \leq h_3(n,Q) \leq \log ^{c_2}(n)$
.
$\log ^{c_1}(n) \leq h_3(n,Q) \leq \log ^{c_2}(n)$
. -
2. In all other cases, there is a constant
 $c \gt 0$
such that
$c \gt 0$
such that
 $h_3(n,Q) \geq n^{c}$
.
$h_3(n,Q) \geq n^{c}$
.
We will prove Theorem 1.4 by considering separately each of the cases (up to complementation, see (2)). Some cases follow from known results, and these are surveyed in Section 1.1. Many cases are new results, and these are presented in Section 1.2.
1.1. Prior work
In this section we review the cases of Theorem 1.4 that follow from prior work. The problem of estimating
![]() $h(n,4,0)$
(or, equivalently, of
$h(n,4,0)$
(or, equivalently, of
![]() $h(n,4,4)$
) is equivalent to estimating the Ramsey number
$h(n,4,4)$
) is equivalent to estimating the Ramsey number
![]() $R_3(4,t)$
. Recall that
$R_3(4,t)$
. Recall that
![]() $R_r(s,t)$
is the minimum
$R_r(s,t)$
is the minimum
![]() $n$
such that every
$n$
such that every
![]() $n$
-vertex
$n$
-vertex
![]() $r$
-graph contains a clique of size
$r$
-graph contains a clique of size
![]() $s$
or an independent set of size
$s$
or an independent set of size
![]() $t$
. It is known [Reference Conlon, Fox and Sudakov9] that
$t$
. It is known [Reference Conlon, Fox and Sudakov9] that
![]() $2^{c_1 t\log t} \leq R_3 (4, t) \leq 2^{c_2 t^2 \log t}$
. This yields positive constants
$2^{c_1 t\log t} \leq R_3 (4, t) \leq 2^{c_2 t^2 \log t}$
. This yields positive constants
![]() $c_1$
and
$c_1$
and
![]() $c_2$
such that
$c_2$
such that
Similarly, the case
![]() $Q = \{(4,0),(4,1)\}$
is equivalent (due to complementation (2)) to estimating the minimum possible independence number of an
$Q = \{(4,0),(4,1)\}$
is equivalent (due to complementation (2)) to estimating the minimum possible independence number of an
![]() $n$
-vertex
$n$
-vertex
![]() $3$
-graph where no
$3$
-graph where no
![]() $4$
vertices span at least
$4$
vertices span at least
![]() $3$
edges. This is a well-studied problem in hypergraph Ramsey theory, and an old result of Erdős and Hajnal [Reference Erdős and Hajnal12] gives the bound
$3$
edges. This is a well-studied problem in hypergraph Ramsey theory, and an old result of Erdős and Hajnal [Reference Erdős and Hajnal12] gives the bound
![]() $h_3(n,\{(4,0),(4,1)\}) \geq c_1 \frac{\log n}{\log \log n}$
for some constant
$h_3(n,\{(4,0),(4,1)\}) \geq c_1 \frac{\log n}{\log \log n}$
for some constant
![]() $c_1 \gt 0$
. Recently, Fox and He [Reference Fox and He16] proved a corresponding upper bound, showing that
$c_1 \gt 0$
. Recently, Fox and He [Reference Fox and He16] proved a corresponding upper bound, showing that
for a suitable constant
![]() $c_2$
. It is worth mentioning that the case
$c_2$
. It is worth mentioning that the case
![]() $Q = \{(4,3),(4,4)\}$
(which is equivalent to
$Q = \{(4,3),(4,4)\}$
(which is equivalent to
![]() $\{(4,0),(4,1)\}$
) is the first instance of a (different) conjecture of Erdős and Hajnal [Reference Erdős and Hajnal12] about the growth rate of generalized hypergraph Ramsey numbers that correspond to our setting of
$\{(4,0),(4,1)\}$
) is the first instance of a (different) conjecture of Erdős and Hajnal [Reference Erdős and Hajnal12] about the growth rate of generalized hypergraph Ramsey numbers that correspond to our setting of
![]() $h(n, Q)$
, where
$h(n, Q)$
, where
![]() $Q = \{ (m, f), (m, f+1), \ldots, (m, \binom{m}{r}) \}$
. Recent results of Mubayi and Razborov [Reference Mubayi and Razborov24] on this problem determine, for each
$Q = \{ (m, f), (m, f+1), \ldots, (m, \binom{m}{r}) \}$
. Recent results of Mubayi and Razborov [Reference Mubayi and Razborov24] on this problem determine, for each
![]() $m\gt r \ge 4$
, the minimum
$m\gt r \ge 4$
, the minimum
![]() $f$
such that
$f$
such that
![]() $h_r(n, Q) \lt c \log ^an$
for some
$h_r(n, Q) \lt c \log ^an$
for some
![]() $a$
and
$a$
and
![]() $Q=\{(m,f), \ldots, (m, \binom{m}{r})\}$
. When
$Q=\{(m,f), \ldots, (m, \binom{m}{r})\}$
. When
![]() $r=3$
, the minimum
$r=3$
, the minimum
![]() $f$
was determined by Conlon, Fox, and Sudakov [Reference Conlon, Fox and Sudakov9] for
$f$
was determined by Conlon, Fox, and Sudakov [Reference Conlon, Fox and Sudakov9] for
![]() $m$
being a power of
$m$
being a power of
![]() $3$
and for growing
$3$
and for growing
![]() $m$
, as well as some other values.
$m$
, as well as some other values.
For the case
![]() $Q = \{(4,2)\}$
, we have
$Q = \{(4,2)\}$
, we have
![]() $h(n,4,2) \geq n^c$
for a suitable constant
$h(n,4,2) \geq n^c$
for a suitable constant
![]() $c \gt 0$
, by Theorem 1.1.
$c \gt 0$
, by Theorem 1.1.
Finally, we discuss two known cases with
![]() $|Q| = 3$
. If
$|Q| = 3$
. If
![]() $Q=\{(4,0), (4,1), (4,2)\}$
, then a
$Q=\{(4,0), (4,1), (4,2)\}$
, then a
![]() $\overline Q$
-free 3-graph is the same as a partial Steiner system (STS), and it is well-known [Reference de Brandes, Phelps and Rödl6, Reference Erdős, Hajnal and Rothschild14, Reference Phelps and Rödl26] that the minimum independence number of an
$\overline Q$
-free 3-graph is the same as a partial Steiner system (STS), and it is well-known [Reference de Brandes, Phelps and Rödl6, Reference Erdős, Hajnal and Rothschild14, Reference Phelps and Rödl26] that the minimum independence number of an
![]() $n$
-vertex partial STS has order of magnitude
$n$
-vertex partial STS has order of magnitude
![]() $\sqrt{n \log n}$
. Thus
$\sqrt{n \log n}$
. Thus
![]() $h_3(n, Q)$
has order of magnitude
$h_3(n, Q)$
has order of magnitude
![]() $\sqrt{n \log n}$
.
$\sqrt{n \log n}$
.
If
![]() $Q=\{(4,1),(4,2), (4,3)\}$
and
$Q=\{(4,1),(4,2), (4,3)\}$
and
![]() $n \ge 4$
, then it is a simple exercise to show that any
$n \ge 4$
, then it is a simple exercise to show that any
![]() $Q$
-free 4-graph on at least four vertices is a clique or coclique and therefore
$Q$
-free 4-graph on at least four vertices is a clique or coclique and therefore
![]() $h_3(n, Q)=n$
for
$h_3(n, Q)=n$
for
![]() $n \ge 4$
.
$n \ge 4$
.
1.2. New results
In this section we state our new results for the cases not covered in Section 1.1. The results of this section and Section 1.1 immediately imply Theorem 2. Up to complementation, the missing cases correspond to the following sets
![]() $Q$
of order-size pairs:
$Q$
of order-size pairs:
-
•
 $\{(4,1)\}$
;
$\{(4,1)\}$
; -
•
 $ \{ (4,0), (4,2) \}$
,
$ \{ (4,0), (4,2) \}$
,
 $ \{ (4,0), (4,3) \}$
,
$ \{ (4,0), (4,3) \}$
,
 $ \{ (4,1), (4,2) \}$
,
$ \{ (4,1), (4,2) \}$
,
 $ \{ (4,1), (4,3) \}$
; and
$ \{ (4,1), (4,3) \}$
; and -
•
 $\{ (4,0), (4,1), (4,3) \}$
,
$\{ (4,0), (4,1), (4,3) \}$
,
 $\{ (4,0), (4,2), (4,3) \}$
.
$\{ (4,0), (4,2), (4,3) \}$
.
For
![]() $|Q|=1,2$
, we summarize our results in the following table. Here,
$|Q|=1,2$
, we summarize our results in the following table. Here,
![]() $c_1,c_2$
always denote suitable positive constants. The table also indicates the section where each result is proved. Note that for
$c_1,c_2$
always denote suitable positive constants. The table also indicates the section where each result is proved. Note that for
![]() $Q = \{(4,1)\}$
, the lower bound is proved in Section 3.1 and the upper bound follows from (3).
$Q = \{(4,1)\}$
, the lower bound is proved in Section 3.1 and the upper bound follows from (3).
For the two remaining cases with
![]() $|Q| = 3$
, we obtain exact results:
$|Q| = 3$
, we obtain exact results:
Theorem 1.5.
Let
![]() $n \ge 4$
. Then
$n \ge 4$
. Then
![]() $h_3(n, \{(4,0),(4,2), (4,3)\}) =n-1$
and
$h_3(n, \{(4,0),(4,2), (4,3)\}) =n-1$
and
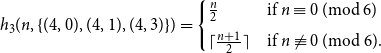 \begin{equation*} h_3(n, \{(4,0), (4,1), (4,3)\}) =\begin{cases} \frac{n}{2} &\text{if $n \equiv 0$ (mod 6)} \\[5pt] \lceil \frac{n+1}{2}\rceil & \text{if $n \not \equiv 0$ (mod 6).} \end{cases} \end{equation*}
\begin{equation*} h_3(n, \{(4,0), (4,1), (4,3)\}) =\begin{cases} \frac{n}{2} &\text{if $n \equiv 0$ (mod 6)} \\[5pt] \lceil \frac{n+1}{2}\rceil & \text{if $n \not \equiv 0$ (mod 6).} \end{cases} \end{equation*}
Theorem 1.5 is proved in Section 7.
Notation:
Throughout the paper, for a hypergraph
![]() $H$
, let
$H$
, let
![]() $\omega (H)$
and
$\omega (H)$
and
![]() $\alpha (H)$
denote the size of a largest clique and independent set in
$\alpha (H)$
denote the size of a largest clique and independent set in
![]() $H$
, respectively. Recall that
$H$
, respectively. Recall that
![]() $h(H) = \max \{\omega (H),\alpha (H)\}$
. For a
$h(H) = \max \{\omega (H),\alpha (H)\}$
. For a
![]() $3$
-graph
$3$
-graph
![]() $H$
and one of its vertices
$H$
and one of its vertices
![]() $v$
, we define the link graph of
$v$
, we define the link graph of
![]() $v$
to be the graph
$v$
to be the graph
![]() $L(v)$
whose vertex set is
$L(v)$
whose vertex set is
![]() $V(H)\setminus \{v\}$
and whose edge set is
$V(H)\setminus \{v\}$
and whose edge set is
![]() $\{e \subseteq V(H)\setminus \{v\}\;:\; e \cup \{v\} \in E(H)\}$
. Moreover, for
$\{e \subseteq V(H)\setminus \{v\}\;:\; e \cup \{v\} \in E(H)\}$
. Moreover, for
![]() $S \subseteq V(H) \setminus \{v\}$
, we use
$S \subseteq V(H) \setminus \{v\}$
, we use
![]() $L_S(v)$
to denote the subgraph of
$L_S(v)$
to denote the subgraph of
![]() $L(v)$
induced by
$L(v)$
induced by
![]() $S$
. A clique on
$S$
. A clique on
![]() $s$
vertices is denoted
$s$
vertices is denoted
![]() $K_s$
. When denoting edges in
$K_s$
. When denoting edges in
![]() $3$
-graphs, we shall often omit parentheses and commas; for example, instead of writing
$3$
-graphs, we shall often omit parentheses and commas; for example, instead of writing
![]() $\{x,y,z\}$
, we shall simply write
$\{x,y,z\}$
, we shall simply write
![]() $xyz$
. A star is a hypergraph consisting of a set
$xyz$
. A star is a hypergraph consisting of a set
![]() $S$
and a vertex
$S$
and a vertex
![]() $v \notin S$
with edge set
$v \notin S$
with edge set
![]() $\{vxy \;:\; x,y \in S, x \neq y\}$
. We will denote this star by
$\{vxy \;:\; x,y \in S, x \neq y\}$
. We will denote this star by
![]() $(v,S)$
. As usual, we write
$(v,S)$
. As usual, we write
![]() $f(n) = O(g(n))$
if there is a constant
$f(n) = O(g(n))$
if there is a constant
![]() $C \gt 0$
such that
$C \gt 0$
such that
![]() $f(n) \leq C g(n)$
for all
$f(n) \leq C g(n)$
for all
![]() $n$
, and we write
$n$
, and we write
![]() $f(n) = \Omega (g(n))$
to mean that
$f(n) = \Omega (g(n))$
to mean that
![]() $g(n) = O(f(n))$
.
$g(n) = O(f(n))$
.
2. Graphs: Proof of Proposition 1.3
Proof of Proposition
1.3
. We show that
![]() $c = 2/\sqrt{5}$
suffices. We shall use induction on
$c = 2/\sqrt{5}$
suffices. We shall use induction on
![]() $m$
with basis
$m$
with basis
![]() $m=2$
. In this case
$m=2$
. In this case
![]() $f\in \{0,1\}$
. Note that
$f\in \{0,1\}$
. Note that
![]() $h(n, 2, 0) =h(n, 2, 1) =n = n^1 = n^{1/(m-1)}$
, since forbidden graphs are either a non-edge or an edge. Consider an
$h(n, 2, 0) =h(n, 2, 1) =n = n^1 = n^{1/(m-1)}$
, since forbidden graphs are either a non-edge or an edge. Consider an
![]() $(m, f)$
-free graph
$(m, f)$
-free graph
![]() $G$
on
$G$
on
![]() $n$
vertices,
$n$
vertices,
![]() $m\geq 3$
, and assume that the statement of the proposition holds for smaller values of
$m\geq 3$
, and assume that the statement of the proposition holds for smaller values of
![]() $m$
. We can also assume that
$m$
. We can also assume that
![]() $G$
is not a complete graph or an empty graph. Suppose first that
$G$
is not a complete graph or an empty graph. Suppose first that
![]() $G$
is an odd cycle or a complement of an odd cycle. Then
$G$
is an odd cycle or a complement of an odd cycle. Then
![]() $\alpha (G)$
or
$\alpha (G)$
or
![]() $\omega (G)$
is at least
$\omega (G)$
is at least
![]() $\frac{n-1}{2}$
, so it suffices to check that
$\frac{n-1}{2}$
, so it suffices to check that
![]() $\frac{n-1}{2} \geq cn^{1/2}$
, as
$\frac{n-1}{2} \geq cn^{1/2}$
, as
![]() $n^{1/2} \geq n^{1/(m-1)}$
. And indeed, by squaring, we get the inequality
$n^{1/2} \geq n^{1/(m-1)}$
. And indeed, by squaring, we get the inequality
![]() $(n-1)^2 \geq 4c^2 n = \frac{16}{5}n$
, and after rearranging we get
$(n-1)^2 \geq 4c^2 n = \frac{16}{5}n$
, and after rearranging we get
![]() $n^2 - \frac{26n}{5} + 1 \geq 0$
, which holds for every
$n^2 - \frac{26n}{5} + 1 \geq 0$
, which holds for every
![]() $n\geq 5$
.
$n\geq 5$
.
So from now on, suppose that
![]() $G$
is neither an odd cycle nor the complement of an odd cycle. Let
$G$
is neither an odd cycle nor the complement of an odd cycle. Let
![]() $\Delta$
and
$\Delta$
and
![]() $\overline{\Delta }$
be the maximum degree of
$\overline{\Delta }$
be the maximum degree of
![]() $G$
and of the complement
$G$
and of the complement
![]() $\overline{G}$
of
$\overline{G}$
of
![]() $G$
, respectively. Using Brooks’ theorem, the chromatic number of
$G$
, respectively. Using Brooks’ theorem, the chromatic number of
![]() $G$
and of
$G$
and of
![]() $\overline{G}$
is at most
$\overline{G}$
is at most
![]() $\Delta$
and
$\Delta$
and
![]() $\overline{\Delta }$
, respectively. Thus,
$\overline{\Delta }$
, respectively. Thus,
![]() $\alpha (G)\geq n/\Delta$
and
$\alpha (G)\geq n/\Delta$
and
![]() $\omega (G)\geq n/\overline{\Delta }$
. Therefore, we can assume that
$\omega (G)\geq n/\overline{\Delta }$
. Therefore, we can assume that
![]() $\Delta \geq n^{(m-2)/(m-1)}$
and
$\Delta \geq n^{(m-2)/(m-1)}$
and
![]() $\overline{\Delta }\geq n^{(m-2)/(m-1)}$
, otherwise we are done. Thus, there is a vertex with at least
$\overline{\Delta }\geq n^{(m-2)/(m-1)}$
, otherwise we are done. Thus, there is a vertex with at least
![]() $n^{(m-2)/(m-1)}$
edges incident to it and there is a vertex with at least
$n^{(m-2)/(m-1)}$
edges incident to it and there is a vertex with at least
![]() $n^{(m-2)/(m-1)}$
non-edges incident to it.
$n^{(m-2)/(m-1)}$
non-edges incident to it.
Assume first that
![]() $f\leq m-2$
. Then
$f\leq m-2$
. Then
![]() $f \leq \binom{m-1}{2}$
. Take
$f \leq \binom{m-1}{2}$
. Take
![]() $v \in V(G)$
with at least
$v \in V(G)$
with at least
![]() $n^{(m-2)/(m-1)}$
non-edges incident to it, i.e. with a set
$n^{(m-2)/(m-1)}$
non-edges incident to it, i.e. with a set
![]() $X$
of vertices each non-adjacent to
$X$
of vertices each non-adjacent to
![]() $v$
,
$v$
,
![]() $|X|\geq n^{(m-2)/(m-1)}$
. Since
$|X|\geq n^{(m-2)/(m-1)}$
. Since
![]() $G$
is
$G$
is
![]() $(m,f)$
-free,
$(m,f)$
-free,
![]() $G[X]$
is
$G[X]$
is
![]() $(m-1, f)$
-free. Thus, by induction,
$(m-1, f)$
-free. Thus, by induction,
![]() $h(G) \geq h(G[X]) \geq c|X|^{1/(m-2)}\geq cn^{1/(m-1)}.$
$h(G) \geq h(G[X]) \geq c|X|^{1/(m-2)}\geq cn^{1/(m-1)}.$
Now assume that
![]() $f\geq m-1$
. Consider a vertex
$f\geq m-1$
. Consider a vertex
![]() $v$
with at least
$v$
with at least
![]() $n^{(m-2)/(m-1)}$
edges incident to it, i.e. with a set
$n^{(m-2)/(m-1)}$
edges incident to it, i.e. with a set
![]() $X$
of vertices each adjacent to
$X$
of vertices each adjacent to
![]() $v$
,
$v$
,
![]() $|X|\geq n^{(m-2)/(m-1)}$
. Since
$|X|\geq n^{(m-2)/(m-1)}$
. Since
![]() $G$
is
$G$
is
![]() $(m,f)$
-free,
$(m,f)$
-free,
![]() $G[X]$
is
$G[X]$
is
![]() $(m-1, f-(m-1))$
-free. Thus, by induction,
$(m-1, f-(m-1))$
-free. Thus, by induction,
![]() $h(G) \geq h(G[X]) \geq c|X|^{1/(m-2)}\geq cn^{1/(m-1)}.$
$h(G) \geq h(G[X]) \geq c|X|^{1/(m-2)}\geq cn^{1/(m-1)}.$
3. Two short proofs
3.1.
 $Q = \{(4,1)\}$
$Q = \{(4,1)\}$
To prove the lower bound on
![]() $h(n, 4, 1)$
from Table 1, we shall consider the complementary setting and an arbitrary
$h(n, 4, 1)$
from Table 1, we shall consider the complementary setting and an arbitrary
![]() $n$
-vertex
$n$
-vertex
![]() $(4,3)$
-free
$(4,3)$
-free
![]() $3$
-graph
$3$
-graph
![]() $H$
. We need the following theorem of Fox and He [Reference Fox and He16].
$H$
. We need the following theorem of Fox and He [Reference Fox and He16].
Table 1 Bounds for
![]() $h_3(n,Q)$
$h_3(n,Q)$

Theorem 3.1 (Fox and He [Reference Fox and He16], Thm. 1.4). For all
![]() $t, s\geq 3$
, any
$t, s\geq 3$
, any
![]() $3$
-graph on more than
$3$
-graph on more than
![]() $(2t)^{st}$
vertices contains either a coclique on
$(2t)^{st}$
vertices contains either a coclique on
![]() $t$
vertices or a star
$t$
vertices or a star
![]() $(v,S)$
with
$(v,S)$
with
![]() $|S| = s$
.
$|S| = s$
.
Proposition 3.2.
![]() $h(n,4,3) \geq c \left ( \frac{\log n}{\log \log n} \right )^{1/2}$
for a constant
$h(n,4,3) \geq c \left ( \frac{\log n}{\log \log n} \right )^{1/2}$
for a constant
![]() $c \gt 0$
.
$c \gt 0$
.
Proof. We shall apply Theorem 3.1 with the largest possible
![]() $t=s$
such that
$t=s$
such that
![]() $ (2t)^{st}\lt n$
. In this case
$ (2t)^{st}\lt n$
. In this case
![]() $t=s \geq c(\log n/ \log \log n)^{1/2}$
. If
$t=s \geq c(\log n/ \log \log n)^{1/2}$
. If
![]() $H$
has a coclique of size
$H$
has a coclique of size
![]() $t$
, then
$t$
, then
![]() $h(H) \geq t$
and we are done. Otherwise
$h(H) \geq t$
and we are done. Otherwise
![]() $H$
contains a star
$H$
contains a star
![]() $(v,S)$
with
$(v,S)$
with
![]() $|S| = s$
. Note that
$|S| = s$
. Note that
![]() $S$
induces a clique in
$S$
induces a clique in
![]() $H$
, because otherwise
$H$
, because otherwise
![]() $v$
and three vertices of
$v$
and three vertices of
![]() $S$
not inducing an edge give a
$S$
not inducing an edge give a
![]() $(4,3)$
-subgraph. Thus,
$(4,3)$
-subgraph. Thus,
![]() $h(H) \geq s$
. In each case
$h(H) \geq s$
. In each case
![]() $h(H) \geq c(\log n/ \log \log n)^{1/2}$
.
$h(H) \geq c(\log n/ \log \log n)^{1/2}$
.
3.2.
 $Q = \{(4,0),(4,3)\}$
$Q = \{(4,0),(4,3)\}$
Let us restate our result from Table 1:
Proposition 3.3.
![]() $\Omega (n) \leq h_3(n,\{(4,0),(4,3)\}) \leq \left \lceil{\frac{n}{3}}\right \rceil + 1$
.
$\Omega (n) \leq h_3(n,\{(4,0),(4,3)\}) \leq \left \lceil{\frac{n}{3}}\right \rceil + 1$
.
Proof. Let
![]() $H$
be a
$H$
be a
![]() $\{(4,0),(4,3)\}$
-free
$\{(4,0),(4,3)\}$
-free
![]() $3$
-graph. We may assume that
$3$
-graph. We may assume that
![]() $e(H) = \Omega (n^3)$
, else
$e(H) = \Omega (n^3)$
, else
![]() $H$
is not
$H$
is not
![]() $(4,0)$
-free. (Indeed, if
$(4,0)$
-free. (Indeed, if
![]() $e(H) = o(n^3)$
, then the probability that a random set of
$e(H) = o(n^3)$
, then the probability that a random set of
![]() $4$
vertices contains an edge is
$4$
vertices contains an edge is
![]() $o(1)$
, so
$o(1)$
, so
![]() $H$
contains a
$H$
contains a
![]() $(4,0)$
-subgraph.) Fix
$(4,0)$
-subgraph.) Fix
![]() $v \in V(H)$
with
$v \in V(H)$
with
![]() $e(L(v)) = \Omega (n^2)$
. Note that
$e(L(v)) = \Omega (n^2)$
. Note that
![]() $L(v)$
is induced
$L(v)$
is induced
![]() $C_4$
-free. Indeed, if
$C_4$
-free. Indeed, if
![]() $C$
is an induced
$C$
is an induced
![]() $C_4$
in
$C_4$
in
![]() $L(v)$
, then for each
$L(v)$
, then for each
![]() $A \subseteq V(C)$
,
$A \subseteq V(C)$
,
![]() $|A| = 3$
, it holds that
$|A| = 3$
, it holds that
![]() $A \notin E(H)$
, because else
$A \notin E(H)$
, because else
![]() $A \cup \{v\}$
spans exactly
$A \cup \{v\}$
spans exactly
![]() $3$
edges. This means that
$3$
edges. This means that
![]() $V(C)$
spans
$V(C)$
spans
![]() $0$
edges, a contradiction. By a result of Gyárfás, Hubenko and Solymosi [Reference Gyárfás, Hubenko and Solymosi21], an
$0$
edges, a contradiction. By a result of Gyárfás, Hubenko and Solymosi [Reference Gyárfás, Hubenko and Solymosi21], an
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $\Omega (n^2)$
edges and no induced
$\Omega (n^2)$
edges and no induced
![]() $C_4$
contains a clique of size
$C_4$
contains a clique of size
![]() $\Omega (n)$
. So
$\Omega (n)$
. So
![]() $L(v)$
contains a clique
$L(v)$
contains a clique
![]() $X$
of size
$X$
of size
![]() $\Omega (n)$
. For each
$\Omega (n)$
. For each
![]() $A \subseteq X$
,
$A \subseteq X$
,
![]() $|A| = 3$
, we have
$|A| = 3$
, we have
![]() $A \in E(H)$
because else
$A \in E(H)$
because else
![]() $A \cup \{v\}$
spans exactly
$A \cup \{v\}$
spans exactly
![]() $3$
edges. So
$3$
edges. So
![]() $X$
is a clique in
$X$
is a clique in
![]() $H$
, implying
$H$
, implying
![]() $\omega (H) = \Omega (n)$
. This proves the lower bound in the proposition.
$\omega (H) = \Omega (n)$
. This proves the lower bound in the proposition.
For the upper bound, let
![]() $H$
be a
$H$
be a
![]() $3$
-graph on
$3$
-graph on
![]() $n$
vertices with vertex set
$n$
vertices with vertex set
![]() $A\cup B\cup C$
, where
$A\cup B\cup C$
, where
![]() $A, B,$
and
$A, B,$
and
![]() $C$
are pairwise disjoint sets of almost equal sizes. Let
$C$
are pairwise disjoint sets of almost equal sizes. Let
![]() $E(H)=\{abc\;:\; a\in A, \;b\in B, c\in C\} \cup \{abb' \;:\; a\in A,\; b, b' \in B\} \cup \{bcc'\;:\; b\in B, \;c, c'\in C\} \cup \{caa'\;:\; c\in C, \;a, a' \in A\}$
. We see that
$E(H)=\{abc\;:\; a\in A, \;b\in B, c\in C\} \cup \{abb' \;:\; a\in A,\; b, b' \in B\} \cup \{bcc'\;:\; b\in B, \;c, c'\in C\} \cup \{caa'\;:\; c\in C, \;a, a' \in A\}$
. We see that
![]() $H$
is
$H$
is
![]() $\{(4,1), (4,4)\}$
-free,
$\{(4,1), (4,4)\}$
-free,
![]() $\alpha (H) \leq \lceil n/3 \rceil +1$
, and
$\alpha (H) \leq \lceil n/3 \rceil +1$
, and
![]() $\omega (H) =3$
. Using complementation gives the required upper bound.
$\omega (H) =3$
. Using complementation gives the required upper bound.
4.
 $Q = \{(4,0),(4,2)\}$
$Q = \{(4,0),(4,2)\}$
It will be convenient to consider
![]() $Q = \{(4,2),(4,4)\}$
(which is equivalent to
$Q = \{(4,2),(4,4)\}$
(which is equivalent to
![]() $\{(4,0),(4,2)\}$
via complementation). Let us restate our result from Table 1:
$\{(4,0),(4,2)\}$
via complementation). Let us restate our result from Table 1:
Theorem 4.1.
![]() $\Omega (\sqrt{n}) \leq h_3(n,\{(4,2),(4,4)\}) \leq O(\sqrt{n\log n})$
.
$\Omega (\sqrt{n}) \leq h_3(n,\{(4,2),(4,4)\}) \leq O(\sqrt{n\log n})$
.
To lower bound
![]() $h_3(n,\{(4,2),(4,4)\})$
, we prove the following characterization of
$h_3(n,\{(4,2),(4,4)\})$
, we prove the following characterization of
![]() $\{(4,2),(4,4)\}$
-free
$\{(4,2),(4,4)\}$
-free
![]() $3$
-graphs. A tight component is a maximal (with respect to inclusion) set of edges
$3$
-graphs. A tight component is a maximal (with respect to inclusion) set of edges
![]() $C$
such that for any distinct
$C$
such that for any distinct
![]() $e_1,e_2 \in C$
, there is a tight walk from
$e_1,e_2 \in C$
, there is a tight walk from
![]() $e_1$
to
$e_1$
to
![]() $e_2$
, i.e. a sequence of edges
$e_2$
, i.e. a sequence of edges
![]() $e_1 = f_1,\dots,f_k = e_2$
with
$e_1 = f_1,\dots,f_k = e_2$
with
![]() $|f_i \cap f_{i+1}| = 2$
. We call a tight component a star if it is an edge set of a star.
$|f_i \cap f_{i+1}| = 2$
. We call a tight component a star if it is an edge set of a star.
Theorem 4.2.
A
![]() $3$
-graph
$3$
-graph
![]() $H$
is
$H$
is
![]() $\{(4,2),(4,4)\}$
-free if and only if every tight component is a star.
$\{(4,2),(4,4)\}$
-free if and only if every tight component is a star.
Proof. Suppose first that every tight component of
![]() $H$
is a star. If
$H$
is a star. If
![]() $H$
contains
$H$
contains
![]() $4$
vertices spanning exactly
$4$
vertices spanning exactly
![]() $2$
or
$2$
or
![]() $4$
edges, then the edges on these vertices are in the same tight component, but a star does not contain
$4$
edges, then the edges on these vertices are in the same tight component, but a star does not contain
![]() $4$
vertices spanning exactly
$4$
vertices spanning exactly
![]() $2$
or
$2$
or
![]() $4$
edges, a contradiction. So
$4$
edges, a contradiction. So
![]() $H$
is
$H$
is
![]() $\{(4,2),(4,4)\}$
-free.
$\{(4,2),(4,4)\}$
-free.
We now prove the other direction. Let
![]() $H$
be a
$H$
be a
![]() $\{(4,2),(4,4)\}$
-free
$\{(4,2),(4,4)\}$
-free
![]() $3$
-graph. Observe that for every star
$3$
-graph. Observe that for every star
![]() $(v,S)$
in
$(v,S)$
in
![]() $H$
, the set
$H$
, the set
![]() $S$
is independent, because otherwise
$S$
is independent, because otherwise
![]() $H$
would not be
$H$
would not be
![]() $(4,4)$
-free.
$(4,4)$
-free.
Claim 4.3.
Let
![]() $(v,S)$
be a star in
$(v,S)$
be a star in
![]() $H$
with
$H$
with
![]() $|S| \geq 3$
. There is no edge in
$|S| \geq 3$
. There is no edge in
![]() $H$
of the form
$H$
of the form
![]() $uxy$
with
$uxy$
with
![]() $u \notin \{v\} \cup S$
and
$u \notin \{v\} \cup S$
and
![]() $x,y \in S$
.
$x,y \in S$
.
Proof. Suppose otherwise. The vertices
![]() $\{v,u,x,y\}$
must span exactly
$\{v,u,x,y\}$
must span exactly
![]() $3$
edges, because
$3$
edges, because
![]() $vxy,uxy \in E(H)$
but
$vxy,uxy \in E(H)$
but
![]() $\{v,u,x,y\}$
cannot span
$\{v,u,x,y\}$
cannot span
![]() $2$
or
$2$
or
![]() $4$
edges. Without loss of generality, suppose that
$4$
edges. Without loss of generality, suppose that
![]() $vux \in E(H)$
,
$vux \in E(H)$
,
![]() $vuy \notin E(H)$
. Let
$vuy \notin E(H)$
. Let
![]() $z \in S \setminus \{x,y\}$
. Suppose first that
$z \in S \setminus \{x,y\}$
. Suppose first that
![]() $vuz \in E(H)$
. Then
$vuz \in E(H)$
. Then
![]() $uyz \in E(H)$
because otherwise
$uyz \in E(H)$
because otherwise
![]() $\{v,u,y,z\}$
spans
$\{v,u,y,z\}$
spans
![]() $2$
edges. This implies that
$2$
edges. This implies that
![]() $uxz \in E(H)$
, because else
$uxz \in E(H)$
, because else
![]() $\{u,x,y,z\}$
spans
$\{u,x,y,z\}$
spans
![]() $2$
edges. Now
$2$
edges. Now
![]() $\{v,u,x,z\}$
spans
$\{v,u,x,z\}$
spans
![]() $4$
edges, contradiction. Similarly, suppose that
$4$
edges, contradiction. Similarly, suppose that
![]() $vuz \notin E(H)$
. Then
$vuz \notin E(H)$
. Then
![]() $uyz \notin E(H)$
because else
$uyz \notin E(H)$
because else
![]() $\{v,u,y,z\}$
spans
$\{v,u,y,z\}$
spans
![]() $2$
edges. This implies that
$2$
edges. This implies that
![]() $uxz \notin E(H)$
, because else
$uxz \notin E(H)$
, because else
![]() $\{u,x,y,z\}$
spans
$\{u,x,y,z\}$
spans
![]() $2$
edges. Now,
$2$
edges. Now,
![]() $\{v,u,x,z\}$
spans
$\{v,u,x,z\}$
spans
![]() $2$
edges, contradiction.
$2$
edges, contradiction.
Now we complete the proof of the theorem. Let
![]() $C$
be a tight component of
$C$
be a tight component of
![]() $H$
, and let us show that
$H$
, and let us show that
![]() $C$
is a star. If
$C$
is a star. If
![]() $|C|=1$
(i.e.
$|C|=1$
(i.e.
![]() $C$
contains only one edge) then this is immediate, so suppose that
$C$
contains only one edge) then this is immediate, so suppose that
![]() $C$
contains at least
$C$
contains at least
![]() $2$
edges. Let
$2$
edges. Let
![]() $e,f \in C$
with
$e,f \in C$
with
![]() $|e \cap f| = 2$
. Write
$|e \cap f| = 2$
. Write
![]() $e = uvx, f = uvy$
. Then exactly one of the triples
$e = uvx, f = uvy$
. Then exactly one of the triples
![]() $vxy, uxy$
is an edge, say
$vxy, uxy$
is an edge, say
![]() $vxy \in E(H)$
. So
$vxy \in E(H)$
. So
![]() $C$
contains the edges of the star
$C$
contains the edges of the star
![]() $(v,\{u,x,y\})$
. Let
$(v,\{u,x,y\})$
. Let
![]() $S$
be a maximal subset of
$S$
be a maximal subset of
![]() $V(H) \setminus \{v\}$
such that
$V(H) \setminus \{v\}$
such that
![]() $C$
contains the edges of the star
$C$
contains the edges of the star
![]() $(v,S)$
, so
$(v,S)$
, so
![]() $|S| \geq 3$
. We claim that
$|S| \geq 3$
. We claim that
![]() $C$
contains no other edges. Suppose otherwise. Recall that
$C$
contains no other edges. Suppose otherwise. Recall that
![]() $S$
induces no edges. So there must be an edge
$S$
induces no edges. So there must be an edge
![]() $e \in C$
which contains one vertex
$e \in C$
which contains one vertex
![]() $w$
outside
$w$
outside
![]() $\{v\} \cup S$
and two vertices
$\{v\} \cup S$
and two vertices
![]() $s,t$
in
$s,t$
in
![]() $\{v\} \cup S$
. By Claim 4.3, it is impossible that
$\{v\} \cup S$
. By Claim 4.3, it is impossible that
![]() $s,t \in S$
. So suppose that
$s,t \in S$
. So suppose that
![]() $s = v, t \in S$
. Fix an arbitrary
$s = v, t \in S$
. Fix an arbitrary
![]() $z \in S \setminus \{t\}$
. We have
$z \in S \setminus \{t\}$
. We have
![]() $vzt \in E(H)$
. Also,
$vzt \in E(H)$
. Also,
![]() $vwt \in E(H)$
(because
$vwt \in E(H)$
(because
![]() $s = v$
). By Claim 4.3,
$s = v$
). By Claim 4.3,
![]() $wzt \notin E(H)$
, which implies that
$wzt \notin E(H)$
, which implies that
![]() $vwz \in E(H)$
as otherwise
$vwz \in E(H)$
as otherwise
![]() $\{ v, w, t, z\}$
spans exactly two edges. As this holds for every
$\{ v, w, t, z\}$
spans exactly two edges. As this holds for every
![]() $z \in S$
, we get that
$z \in S$
, we get that
![]() $(v,S \cup \{w\})$
is a star contained in
$(v,S \cup \{w\})$
is a star contained in
![]() $C$
, contradicting the maximality of
$C$
, contradicting the maximality of
![]() $S$
.
$S$
.
In what follows, for a tight component
![]() $C$
that is a star, we denote by
$C$
that is a star, we denote by
![]() $V(C)$
the vertex set of the respective graph and
$V(C)$
the vertex set of the respective graph and
![]() $e(C)=|C|$
, the number of edges in
$e(C)=|C|$
, the number of edges in
![]() $C$
.
$C$
.
Lemma 4.4.
Let
![]() $C_1,C_2$
be distinct tight components of a
$C_1,C_2$
be distinct tight components of a
![]() $\{(4,2),(4,4)\}$
-free
$\{(4,2),(4,4)\}$
-free
![]() $3$
-graph. Then
$3$
-graph. Then
![]() $|V(C_1) \cap V(C_2)| \leq 1$
.
$|V(C_1) \cap V(C_2)| \leq 1$
.
Proof. Suppose by contradiction that there are distinct
![]() $x,y \in V(C_1) \cap V(C_2)$
. Note that in a star, every pair of vertices is contained in some edge of the star. Let
$x,y \in V(C_1) \cap V(C_2)$
. Note that in a star, every pair of vertices is contained in some edge of the star. Let
![]() $e_i$
be an edge of
$e_i$
be an edge of
![]() $C_i$
containing
$C_i$
containing
![]() $x,y$
,
$x,y$
,
![]() $i=1,2$
. Then there is a tight walk between every edge of
$i=1,2$
. Then there is a tight walk between every edge of
![]() $C_1$
and every edge of
$C_1$
and every edge of
![]() $C_2$
by using the connection
$C_2$
by using the connection
![]() $e_1,e_2$
. It follows that
$e_1,e_2$
. It follows that
![]() $C_1,C_2$
are in the same tight component, a contradiction.
$C_1,C_2$
are in the same tight component, a contradiction.
Next, we prove a tight bound for the number of edges in a
![]() $\{(4,2),(4,4)\}$
-free
$\{(4,2),(4,4)\}$
-free
![]() $3$
-graph. The extremal case is when
$3$
-graph. The extremal case is when
![]() $H$
is a star.
$H$
is a star.
Proposition 4.5.
For a
![]() $\{(4,2),(4,4)\}$
-free
$\{(4,2),(4,4)\}$
-free
![]() $n$
-vertex
$n$
-vertex
![]() $3$
-graph
$3$
-graph
![]() $H$
, it holds that
$H$
, it holds that
![]() $e(H) \leq \binom{n-1}{2}$
.
$e(H) \leq \binom{n-1}{2}$
.
Proof. Let
![]() $C_1,\dots,C_m$
be the tight connected components of
$C_1,\dots,C_m$
be the tight connected components of
![]() $H$
. Each edge is contained in a unique
$H$
. Each edge is contained in a unique
![]() $C_i$
, and
$C_i$
, and
![]() $e(C_i) = \binom{|V(C_i)|-1}{2}$
because
$e(C_i) = \binom{|V(C_i)|-1}{2}$
because
![]() $C_i$
is a star. Therefore,
$C_i$
is a star. Therefore,
![]() $e(H) = \sum _{i=1}^m \binom{|V(C_i)|-1}{2}$
. Also,
$e(H) = \sum _{i=1}^m \binom{|V(C_i)|-1}{2}$
. Also,
![]() $\sum _{i=1}^m\binom{|V(C_i)|}{2} \leq \binom{n}{2},$
because each pair of vertices is contained in at most one
$\sum _{i=1}^m\binom{|V(C_i)|}{2} \leq \binom{n}{2},$
because each pair of vertices is contained in at most one
![]() $V(C_i)$
, by Lemma 4.4. Let
$V(C_i)$
, by Lemma 4.4. Let
![]() $f$
be the function
$f$
be the function
![]() $f(x) = x - \frac{1}{2}\sqrt{8x+1}+\frac{1}{2}$
, so that
$f(x) = x - \frac{1}{2}\sqrt{8x+1}+\frac{1}{2}$
, so that
![]() $f(\binom{k}{2}) = \binom{k-1}{2}$
. Put
$f(\binom{k}{2}) = \binom{k-1}{2}$
. Put
![]() $x_i = \binom{|V(C_i)|}{2}$
, so that
$x_i = \binom{|V(C_i)|}{2}$
, so that
![]() $f(x_i) = \binom{|V(C_i)|-1}{2}$
. We have
$f(x_i) = \binom{|V(C_i)|-1}{2}$
. We have
![]() $\sum _{i=1}^m x_i \leq \binom{n}{2}$
. The function
$\sum _{i=1}^m x_i \leq \binom{n}{2}$
. The function
![]() $f$
is convex on
$f$
is convex on
![]() $[0,\infty )$
, so
$[0,\infty )$
, so
![]() $\sum _{i=1}^m f(x_i)$
is maximized when exactly one of the
$\sum _{i=1}^m f(x_i)$
is maximized when exactly one of the
![]() $x_i$
’s, say
$x_i$
’s, say
![]() $x_1$
, is non-zero. As
$x_1$
, is non-zero. As
![]() $x_1 \leq \binom{n}{2}$
, we have
$x_1 \leq \binom{n}{2}$
, we have
![]() $e(H) = \sum _{i=1}^m f(x_i) \leq f(\binom{n}{2}) = \binom{n-1}{2}$
.
$e(H) = \sum _{i=1}^m f(x_i) \leq f(\binom{n}{2}) = \binom{n-1}{2}$
.
Proof of Theorem
4.1
. The upper bound in the theorem follows from the fact that every linear
![]() $3$
-graph is
$3$
-graph is
![]() $\{(4,2),(4,4)\}$
-free (this follows, e.g. from Theorem 4.2, because every tight component of a linear hypergraph has size
$\{(4,2),(4,4)\}$
-free (this follows, e.g. from Theorem 4.2, because every tight component of a linear hypergraph has size
![]() $1$
), and the well-known result that there exist linear
$1$
), and the well-known result that there exist linear
![]() $3$
-graphs with independence number
$3$
-graphs with independence number
![]() $O(\sqrt{n \log n})$
(which is tight), see [Reference de Brandes, Phelps and Rödl6, Reference Erdős, Hajnal and Rothschild14, Reference Phelps and Rödl26].
$O(\sqrt{n \log n})$
(which is tight), see [Reference de Brandes, Phelps and Rödl6, Reference Erdős, Hajnal and Rothschild14, Reference Phelps and Rödl26].
The lower bound in the theorem follows from Proposition 4.5 and the known fact that every
![]() $n$
-vertex
$n$
-vertex
![]() $3$
-graph
$3$
-graph
![]() $H$
has an independent set of size
$H$
has an independent set of size
![]() $\min \left \{ \frac{n}{2}, \frac{c n^{3/2}}{e(H)^{1/2}}\right \}$
. (To see this, take a random subset
$\min \left \{ \frac{n}{2}, \frac{c n^{3/2}}{e(H)^{1/2}}\right \}$
. (To see this, take a random subset
![]() $X \subseteq V(H)$
by keeping each vertex with probability
$X \subseteq V(H)$
by keeping each vertex with probability
![]() $p = \frac{cn^{1/2}}{e(H)^{1/2}}$
, and delete one vertex from each edge inside
$p = \frac{cn^{1/2}}{e(H)^{1/2}}$
, and delete one vertex from each edge inside
![]() $X$
.)
$X$
.)
5.
 $Q = \{(4,1),(4,2)\}$
$Q = \{(4,1),(4,2)\}$
Here we consider
![]() $Q = \{(4,1),(4,2)\}$
. By complementation, we may equivalently consider
$Q = \{(4,1),(4,2)\}$
. By complementation, we may equivalently consider
![]() $Q = \{(4,2),(4,3)\}$
. Let us restate our result from Table 1.
$Q = \{(4,2),(4,3)\}$
. Let us restate our result from Table 1.
Theorem 5.1.
![]() $\Omega (n^{1/3}\log ^{1/3}n) \leq h_3(n,\{(4,2),(4,3)\}) \leq O(n^{1/3}\log ^{4/3})$
.
$\Omega (n^{1/3}\log ^{1/3}n) \leq h_3(n,\{(4,2),(4,3)\}) \leq O(n^{1/3}\log ^{4/3})$
.
For the lower bound in Theorem 5.1, we need the following result of Kostochka, Mubayi, and Verstraëte [Reference Kostochka, Mubayi and Verstraëte23] on independent sets in sparse hypergraphs.
Theorem 5.2 (Kostochka, Mubayi, and Verstraëte [Reference Kostochka, Mubayi and Verstraëte23]). Suppose that
![]() $H$
is an
$H$
is an
![]() $n$
-vertex 3-graph in which every pair of vertices lies in at most
$n$
-vertex 3-graph in which every pair of vertices lies in at most
![]() $d$
edges, where
$d$
edges, where
![]() $0\lt d\lt n/(\log n)^{27}$
. Then
$0\lt d\lt n/(\log n)^{27}$
. Then
![]() $H$
has an independent set of size at least
$H$
has an independent set of size at least
![]() $c \sqrt{(n/d)\log (n/d)}$
where
$c \sqrt{(n/d)\log (n/d)}$
where
![]() $c$
is an absolute constant.
$c$
is an absolute constant.
Proof of the lower bound in Theorem
5.1
. Let
![]() $H$
be an
$H$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $\{(4,2), (4,3)\}$
-free
$\{(4,2), (4,3)\}$
-free
![]() $3$
-graph, where
$3$
-graph, where
![]() $n$
is sufficiently large. Let
$n$
is sufficiently large. Let
![]() $u,v$
be a pair of vertices in
$u,v$
be a pair of vertices in
![]() $H$
whose common neighbourhood
$H$
whose common neighbourhood
![]() $S$
has maximum size
$S$
has maximum size
![]() $d\gt 0$
. Given vertices
$d\gt 0$
. Given vertices
![]() $x,y\in S$
, the edges
$x,y\in S$
, the edges
![]() $xyu$
and
$xyu$
and
![]() $xyv$
are both in
$xyv$
are both in
![]() $H$
, else
$H$
, else
![]() $\{u,v,x,y\}$
induces a
$\{u,v,x,y\}$
induces a
![]() $(4,2)$
- or
$(4,2)$
- or
![]() $(4,3)$
-graph. Next, any three vertices
$(4,3)$
-graph. Next, any three vertices
![]() $x,y,z \in S$
must form an edge of
$x,y,z \in S$
must form an edge of
![]() $H$
, otherwise
$H$
, otherwise
![]() $\{u,x,y,z\}$
induces a
$\{u,x,y,z\}$
induces a
![]() $(4,3)$
-graph. Therefore
$(4,3)$
-graph. Therefore
![]() $S$
induces a clique in
$S$
induces a clique in
![]() $H$
of size
$H$
of size
![]() $d$
. If
$d$
. If
![]() $d\gt n^{0.4}$
, say, then we are done as
$d\gt n^{0.4}$
, say, then we are done as
![]() $h(H)\ge d$
. Recalling that
$h(H)\ge d$
. Recalling that
![]() $n$
is large enough, we may assume that
$n$
is large enough, we may assume that
![]() $d \le n^{0.4} \lt n/(\log n)^{27}$
. Now Theorem 5.2 yields a coclique in
$d \le n^{0.4} \lt n/(\log n)^{27}$
. Now Theorem 5.2 yields a coclique in
![]() $H$
of size at least
$H$
of size at least
![]() $c \sqrt{(n/d)\log n}$
for some positive constant
$c \sqrt{(n/d)\log n}$
for some positive constant
![]() $c$
. Consequently, there is a constant
$c$
. Consequently, there is a constant
![]() $c'$
such that
$c'$
such that
Replacing
![]() $c'$
by a possibly smaller constant
$c'$
by a possibly smaller constant
![]() $c_1$
yields the result for all
$c_1$
yields the result for all
![]() $n\gt 4$
.
$n\gt 4$
.
In the rest of this section, we prove the upper bound in Theorem 5.1. We begin with the following two lemmas, giving a structural characterization of
![]() $\{(4,2),(4,3)\}$
-free
$\{(4,2),(4,3)\}$
-free
![]() $3$
-graphs and rephrasing the problem of estimating
$3$
-graphs and rephrasing the problem of estimating
![]() $h_3(n,\{(4,2),(4,3)\})$
in terms of a certain extremal problem for (non-uniform) linear hypergraphs.
$h_3(n,\{(4,2),(4,3)\})$
in terms of a certain extremal problem for (non-uniform) linear hypergraphs.
Lemma 5.3.
Let
![]() $H$
be a
$H$
be a
![]() $\{(4,2),(4,3)\}$
-free
$\{(4,2),(4,3)\}$
-free
![]() $3$
-graph. Then every two maximal cliques in
$3$
-graph. Then every two maximal cliques in
![]() $H$
intersect in at most one vertex.
$H$
intersect in at most one vertex.
Proof. Let
![]() $X,Y$
be maximal cliques and suppose that
$X,Y$
be maximal cliques and suppose that
![]() $|X \cap Y| \geq 2$
. Fix
$|X \cap Y| \geq 2$
. Fix
![]() $u,v \in X \cap Y$
and
$u,v \in X \cap Y$
and
![]() $y \in Y \setminus X$
. Note that
$y \in Y \setminus X$
. Note that
![]() $uvy \in E(H)$
. For every
$uvy \in E(H)$
. For every
![]() $x \in X \setminus \{u,v\}$
, we have
$x \in X \setminus \{u,v\}$
, we have
![]() $uvx \in E(H)$
, so we must have
$uvx \in E(H)$
, so we must have
![]() $uxy,vxy \in E(H)$
, because else
$uxy,vxy \in E(H)$
, because else
![]() $\{u,v,x,y\}$
spans
$\{u,v,x,y\}$
spans
![]() $2$
or
$2$
or
![]() $3$
edges. Next, for every
$3$
edges. Next, for every
![]() $x_1,x_2 \in X \setminus \{u\}$
, we have
$x_1,x_2 \in X \setminus \{u\}$
, we have
![]() $ux_1y, ux_2y \in E(H)$
, so we must also have
$ux_1y, ux_2y \in E(H)$
, so we must also have
![]() $x_1x_2y \in E(H)$
. It follows that
$x_1x_2y \in E(H)$
. It follows that
![]() $X \cup \{y\}$
is a clique, in contradiction to the maximality of
$X \cup \{y\}$
is a clique, in contradiction to the maximality of
![]() $X$
.
$X$
.
For a (not necessarily uniform) hypergraph
![]() $\mathcal{H}$
, let
$\mathcal{H}$
, let
![]() $\alpha _2(\mathcal{H})$
be the maximum size of a set
$\alpha _2(\mathcal{H})$
be the maximum size of a set
![]() $I \subseteq V(\mathcal{H})$
such that
$I \subseteq V(\mathcal{H})$
such that
![]() $|I \cap e| \leq 2$
for every
$|I \cap e| \leq 2$
for every
![]() $e \in E(\mathcal{H})$
. Denote
$e \in E(\mathcal{H})$
. Denote
![]() $g(\mathcal{H}) = \max \left ( \max _{e \in E(\mathcal{H})}|e|, \alpha _2(\mathcal{H}) \right )$
. Denote by
$g(\mathcal{H}) = \max \left ( \max _{e \in E(\mathcal{H})}|e|, \alpha _2(\mathcal{H}) \right )$
. Denote by
![]() $g(n)$
the minimum of
$g(n)$
the minimum of
![]() $g(\mathcal{H})$
over all linear (not necessarily uniform) hypergraphs with
$g(\mathcal{H})$
over all linear (not necessarily uniform) hypergraphs with
![]() $n$
vertices.
$n$
vertices.
Lemma 5.4.
![]() $h_3(n,\{(4,2),(4,3)\}) = g(n)$
.
$h_3(n,\{(4,2),(4,3)\}) = g(n)$
.
Proof. Let
![]() $H$
be an
$H$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $Q$
-free
$Q$
-free
![]() $3$
-graph with
$3$
-graph with
![]() $h(H) = h(n,Q)$
, where
$h(H) = h(n,Q)$
, where
![]() $Q = \{(4,2),(4,3)\}$
. Let
$Q = \{(4,2),(4,3)\}$
. Let
![]() $\mathcal{H}$
be the hypergraph on
$\mathcal{H}$
be the hypergraph on
![]() $V(H)$
whose edges are the maximal cliques of
$V(H)$
whose edges are the maximal cliques of
![]() $H$
. Then
$H$
. Then
![]() $\mathcal{H}$
is linear by the previous lemma. Also,
$\mathcal{H}$
is linear by the previous lemma. Also,
![]() $\max _{e \in E(\mathcal{H})} |e| = \omega (H)$
, and
$\max _{e \in E(\mathcal{H})} |e| = \omega (H)$
, and
![]() $\alpha _2(\mathcal{H}) = \alpha (H)$
, so
$\alpha _2(\mathcal{H}) = \alpha (H)$
, so
![]() $h(H) = g(\mathcal{H})$
.
$h(H) = g(\mathcal{H})$
.
In the other direction, let
![]() $\mathcal{H}$
be an
$\mathcal{H}$
be an
![]() $n$
-vertex linear hypergraph with
$n$
-vertex linear hypergraph with
![]() $g(\mathcal{H}) = g(n)$
. Let
$g(\mathcal{H}) = g(n)$
. Let
![]() $H$
be the
$H$
be the
![]() $3$
-graph obtained by making each
$3$
-graph obtained by making each
![]() $e \in E(\mathcal{H})$
a clique. Then
$e \in E(\mathcal{H})$
a clique. Then
![]() $h(H) = g(\mathcal{H})$
, and it is easy to check that
$h(H) = g(\mathcal{H})$
, and it is easy to check that
![]() $H$
is
$H$
is
![]() $\{(4,2),(4,3)\}$
-free.
$\{(4,2),(4,3)\}$
-free.
From now on, our goal is to upper bound
![]() $g(n)$
. As we will shortly show, the problem can be translated to a problem about
$g(n)$
. As we will shortly show, the problem can be translated to a problem about
![]() $C_4$
-free bipartite graphs. We prove the following.
$C_4$
-free bipartite graphs. We prove the following.
Theorem 5.5.
For some positive constant
![]() $C$
and every large
$C$
and every large
![]() $m$
, there is a
$m$
, there is a
![]() $C_4$
-free bipartite graph
$C_4$
-free bipartite graph
![]() $G = (X, Y, E)$
with
$G = (X, Y, E)$
with
![]() $|X| \ge \frac{1}{2} m^{3/4} \log ^2 m$
and
$|X| \ge \frac{1}{2} m^{3/4} \log ^2 m$
and
![]() $|Y| = (1+o(1)) m$
, such that the following holds:
$|Y| = (1+o(1)) m$
, such that the following holds:
-
1.
 $d(y) \leq 2m^{1/4}\log ^2 m$
for every
$d(y) \leq 2m^{1/4}\log ^2 m$
for every
 $y \in Y$
.
$y \in Y$
. -
2. For every set
 $X' \subseteq X$
of size at least
$X' \subseteq X$
of size at least
 $Cm^{1/4} \log ^2 m,$
there is
$Cm^{1/4} \log ^2 m,$
there is
 $y \in Y$
with
$y \in Y$
with
 $|N(y) \cap X'| \ge 3.$
$|N(y) \cap X'| \ge 3.$
Proof of the upper bound in Theorem
5.1
. By Lemma 5.4, it is enough to show that
![]() $g(n) = O(n^{1/3}\log ^{4/3} n)$
. Let
$g(n) = O(n^{1/3}\log ^{4/3} n)$
. Let
![]() $G = (X,Y,E)$
be the graph given by Theorem 5.5. Put
$G = (X,Y,E)$
be the graph given by Theorem 5.5. Put
![]() $n = |X| = \Omega (m^{3/4}\log ^2m)$
. Let
$n = |X| = \Omega (m^{3/4}\log ^2m)$
. Let
![]() $\mathcal{H}$
be the hypergraph whose edges are the sets
$\mathcal{H}$
be the hypergraph whose edges are the sets
![]() $N_G(y) \subseteq X$
,
$N_G(y) \subseteq X$
,
![]() $y \in Y$
. Then
$y \in Y$
. Then
![]() $\mathcal{H}$
is linear because
$\mathcal{H}$
is linear because
![]() $G$
is
$G$
is
![]() $C_4$
-free. Also
$C_4$
-free. Also
![]() $\max _{e \in E(\mathcal{H})}|e| = O(m^{1/4}\log ^2m) = O(n^{1/3}\log ^{4/3}n)$
by Item 1 of Theorem 5.5. Finally,
$\max _{e \in E(\mathcal{H})}|e| = O(m^{1/4}\log ^2m) = O(n^{1/3}\log ^{4/3}n)$
by Item 1 of Theorem 5.5. Finally,
![]() $\alpha _2(\mathcal{H}) = O(m^{1/4}\log ^2m) = O(n^{1/3}\log ^{4/3}n)$
by Item 2 of Theorem 5.5.
$\alpha _2(\mathcal{H}) = O(m^{1/4}\log ^2m) = O(n^{1/3}\log ^{4/3}n)$
by Item 2 of Theorem 5.5.
5.1. Proof of Theorem 5.5
Let
![]() $H$
be the incidence graph of a finite projective plane with
$H$
be the incidence graph of a finite projective plane with
![]() $n = (1 + o(1))m$
points and lines; that is,
$n = (1 + o(1))m$
points and lines; that is,
![]() $H$
is a bipartite
$H$
is a bipartite
![]() $C_4$
-free graph with sides
$C_4$
-free graph with sides
![]() $X_0, Y$
of size
$X_0, Y$
of size
![]() $n$
, and every pair of vertices in
$n$
, and every pair of vertices in
![]() $X_0$
have exactly one common neighbour in
$X_0$
have exactly one common neighbour in
![]() $Y.$
Let
$Y.$
Let
![]() $X$
be a random subset of
$X$
be a random subset of
![]() $X_0$
obtained by including every vertex independently with probability
$X_0$
obtained by including every vertex independently with probability
![]() $p = n^{-1/4} \log ^2 n.$
Let
$p = n^{-1/4} \log ^2 n.$
Let
![]() $G = H[X, Y].$
Clearly, with high probability
$G = H[X, Y].$
Clearly, with high probability
![]() $|X| \ge \frac{3}{4}pn \geq \frac{1}{2}pm \geq \frac{1}{2} m^{3/4}\log ^2 m.$
Also, we have
$|X| \ge \frac{3}{4}pn \geq \frac{1}{2}pm \geq \frac{1}{2} m^{3/4}\log ^2 m.$
Also, we have
![]() $d_H(y) = (1+o(1))\sqrt{n}$
for every
$d_H(y) = (1+o(1))\sqrt{n}$
for every
![]() $y \in Y$
, and it is easy to show, using the Chernoff bound, that w.h.p.
$y \in Y$
, and it is easy to show, using the Chernoff bound, that w.h.p.
![]() $d(y) \leq 2\sqrt{n}p = 2n^{1/4}\log ^2 n$
for every
$d(y) \leq 2\sqrt{n}p = 2n^{1/4}\log ^2 n$
for every
![]() $y \in Y$
. So it remains to show that w.h.p.,
$y \in Y$
. So it remains to show that w.h.p.,
![]() $G$
satisfies Item 2. To this end, we use the container method. Let
$G$
satisfies Item 2. To this end, we use the container method. Let
![]() $\mathcal{I}$
be the set of all subsets
$\mathcal{I}$
be the set of all subsets
![]() $I \subseteq X_0$
of size
$I \subseteq X_0$
of size
![]() $Cn^{1/4} \log ^2 n$
such that
$Cn^{1/4} \log ^2 n$
such that
![]() $|N(y) \cap I| \le 2$
for every
$|N(y) \cap I| \le 2$
for every
![]() $y \in Y.$
We want to show that with high probability
$y \in Y.$
We want to show that with high probability
![]() $X$
contains no set in
$X$
contains no set in
![]() $\mathcal{I}.$
We will prove the following claim.
$\mathcal{I}.$
We will prove the following claim.
Claim 5.6.
There is a positive constant
![]() $C_0,$
a set
$C_0,$
a set
![]() $\mathcal{S} \subseteq \binom{X_0}{C_0 n^{1/4} \log n}$
and a function
$\mathcal{S} \subseteq \binom{X_0}{C_0 n^{1/4} \log n}$
and a function
![]() $f \colon \mathcal{S} \rightarrow \binom{X_0}{\le C_0 \sqrt{n}}$
such that for every
$f \colon \mathcal{S} \rightarrow \binom{X_0}{\le C_0 \sqrt{n}}$
such that for every
![]() $I \in \mathcal{I},$
there exists
$I \in \mathcal{I},$
there exists
![]() $S = S(I) \in \mathcal{S}$
satisfying
$S = S(I) \in \mathcal{S}$
satisfying
![]() $S \subseteq I \subseteq f(S).$
$S \subseteq I \subseteq f(S).$
Let us first complete the proof given Claim 5.6. Fix an arbitrary
![]() $S \in \mathcal{S}.$
Note that
$S \in \mathcal{S}.$
Note that
![]() $|X \cap f(S)|$
is distributed as
$|X \cap f(S)|$
is distributed as
![]() $\mathrm{Bin}(|f(S)|,p)$
. We have
$\mathrm{Bin}(|f(S)|,p)$
. We have
![]() $\mathbb{P}[\mathrm{Bin}(N,p) \geq k] \leq \binom{N}{k}p^k \leq (\frac{eNp}{k})^k$
. So for
$\mathbb{P}[\mathrm{Bin}(N,p) \geq k] \leq \binom{N}{k}p^k \leq (\frac{eNp}{k})^k$
. So for
![]() $k = Cn^{1/4} \log ^2 n \geq \frac{C}{C_0} \cdot p|f(S)|$
, we have (assuming
$k = Cn^{1/4} \log ^2 n \geq \frac{C}{C_0} \cdot p|f(S)|$
, we have (assuming
![]() $C \gg C_0$
),
$C \gg C_0$
),
Taking the union bound over all
![]() $S \in \mathcal{S},$
of which there are at most
$S \in \mathcal{S},$
of which there are at most
![]() $\binom{n}{C_0 n^{1/4} \log n} \le \exp\!(2C_0 n^{1/4} \log ^2 n),$
it follows that with high probability,
$\binom{n}{C_0 n^{1/4} \log n} \le \exp\!(2C_0 n^{1/4} \log ^2 n),$
it follows that with high probability,
![]() $|X \cap f(S)| \lt Cn^{1/4} \log ^{2} n$
holds for every
$|X \cap f(S)| \lt Cn^{1/4} \log ^{2} n$
holds for every
![]() $S \in \mathcal{S}.$
Recall that for every
$S \in \mathcal{S}.$
Recall that for every
![]() $I \in \mathcal{I}$
there is
$I \in \mathcal{I}$
there is
![]() $S \in \mathcal{S}$
such that
$S \in \mathcal{S}$
such that
![]() $I \subseteq f(S(I))$
. Hence, for every
$I \subseteq f(S(I))$
. Hence, for every
![]() $I \in \mathcal{I},$
we have
$I \in \mathcal{I},$
we have
![]() $|I \cap X| \lt Cn^{1/4} \log ^2 n \leq |I|,$
which implies
$|I \cap X| \lt Cn^{1/4} \log ^2 n \leq |I|,$
which implies
![]() $I \not \subseteq X,$
as required.
$I \not \subseteq X,$
as required.
Proof of Claim
5.6
. We present an algorithm which, given
![]() $I,$
produces sets
$I,$
produces sets
![]() $S(I) \subseteq I$
and
$S(I) \subseteq I$
and
![]() $f(S) \supseteq I.$
The algorithm maintains sets
$f(S) \supseteq I.$
The algorithm maintains sets
![]() $A^t,S^t$
. Initially, we set
$A^t,S^t$
. Initially, we set
![]() $A^0 = X_0, S^0 = \emptyset$
. The algorithm runs for
$A^0 = X_0, S^0 = \emptyset$
. The algorithm runs for
![]() $q = C_0 n^{1/4} \log n$
steps
$q = C_0 n^{1/4} \log n$
steps
![]() $t=0, \dots, q-1$
and in step
$t=0, \dots, q-1$
and in step
![]() $t$
, obtains an index
$t$
, obtains an index
![]() $i^t,$
to be defined later, and new sets
$i^t,$
to be defined later, and new sets
![]() $A^{t+1}, S^{t+1}.$
Recall that for any
$A^{t+1}, S^{t+1}.$
Recall that for any
![]() $I \in \mathcal{I},$
we have
$I \in \mathcal{I},$
we have
![]() $|I| = Cn^{1/4} \log ^2n \gt q.$
Throughout the algorithm we will have
$|I| = Cn^{1/4} \log ^2n \gt q.$
Throughout the algorithm we will have
![]() $|S^t| = t, S^t \subseteq I \subseteq S^t \cup A^t$
and
$|S^t| = t, S^t \subseteq I \subseteq S^t \cup A^t$
and
![]() $S^t \cap A^t = \emptyset .$
Now, suppose we are at step
$S^t \cap A^t = \emptyset .$
Now, suppose we are at step
![]() $t$
. We define a graph
$t$
. We define a graph
![]() $F^t$
with
$F^t$
with
![]() $V(F^t) = A^t$
and where
$V(F^t) = A^t$
and where
![]() $aa' \in E(F^t)$
if and only if there exist
$aa' \in E(F^t)$
if and only if there exist
![]() $s \in S^t$
and
$s \in S^t$
and
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $a, a', s \in N(y).$
Note that
$a, a', s \in N(y).$
Note that
![]() $F^t$
only depends on
$F^t$
only depends on
![]() $A^t, S^t,$
but not on
$A^t, S^t,$
but not on
![]() $I.$
Let
$I.$
Let
![]() $a^t_1, a^t_2, \dots, a^t_{|A_t|}$
be an ordering of
$a^t_1, a^t_2, \dots, a^t_{|A_t|}$
be an ordering of
![]() $A_t$
such that for all
$A_t$
such that for all
![]() $i,$
$i,$
![]() $a^t_i$
is a vertex of maximum degree in
$a^t_i$
is a vertex of maximum degree in
![]() $F^t[\{a^t_i, a^t_{i+1}, \dots, a^t_{|A_t|}\}],$
with ties broken according to some fixed ordering of
$F^t[\{a^t_i, a^t_{i+1}, \dots, a^t_{|A_t|}\}],$
with ties broken according to some fixed ordering of
![]() $X_0.$
Let
$X_0.$
Let
![]() $i^t$
be the minimum index
$i^t$
be the minimum index
![]() $i$
such that
$i$
such that
![]() $a^t_i \in I.$
We let
$a^t_i \in I.$
We let
![]() $S^{t+1} = S^t \cup \{a^t_{i^t}\}$
and
$S^{t+1} = S^t \cup \{a^t_{i^t}\}$
and
![]() $A^{t+1} = A^t \setminus ( \{a^t_1, \dots, a^t_{i^t}\} \cup N_{F^t}(a_{i^t})).$
Note that
$A^{t+1} = A^t \setminus ( \{a^t_1, \dots, a^t_{i^t}\} \cup N_{F^t}(a_{i^t})).$
Note that
![]() $i^t$
is well-defined since we have
$i^t$
is well-defined since we have
![]() $|S^t| \lt q \lt |I|$
and
$|S^t| \lt q \lt |I|$
and
![]() $I \subseteq S^t \cup A^t$
(which we will soon prove). After
$I \subseteq S^t \cup A^t$
(which we will soon prove). After
![]() $q$
steps, we let
$q$
steps, we let
![]() $S(I) = S_q$
and
$S(I) = S_q$
and
![]() $f(S_q) = S_q \cup A_q.$
We denote
$f(S_q) = S_q \cup A_q.$
We denote
![]() $\mathcal{S} = \{ S(I) \, \vert \, I \in \mathcal{I} \}.$
$\mathcal{S} = \{ S(I) \, \vert \, I \in \mathcal{I} \}.$
Clearly, we have
![]() $S^t \subseteq I, S^t \cap A^t = \emptyset$
for any
$S^t \subseteq I, S^t \cap A^t = \emptyset$
for any
![]() $t \in \{0, \dots q\}$
and
$t \in \{0, \dots q\}$
and
![]() $S^{t+1} \cup A^{t+1} \subseteq S^t \cup A^t$
for any
$S^{t+1} \cup A^{t+1} \subseteq S^t \cup A^t$
for any
![]() $t \in \{0, \dots, q-1\}.$
Let us also verify that
$t \in \{0, \dots, q-1\}.$
Let us also verify that
![]() $I \subseteq S^t \cup A^t$
throughout, which clearly implies that
$I \subseteq S^t \cup A^t$
throughout, which clearly implies that
![]() $I \subseteq f(S(I))$
. Indeed, suppose that
$I \subseteq f(S(I))$
. Indeed, suppose that
![]() $I \subseteq S^t \cup A^t$
at some step of the algorithm, let
$I \subseteq S^t \cup A^t$
at some step of the algorithm, let
![]() $a^t_1, \dots, a^t_{|A_t|}$
be the ordering of
$a^t_1, \dots, a^t_{|A_t|}$
be the ordering of
![]() $A^t$
as described in the algorithm, and let
$A^t$
as described in the algorithm, and let
![]() $i = i^t$
be the index chosen in the algorithm, i.e. such that
$i = i^t$
be the index chosen in the algorithm, i.e. such that
![]() $a^t_i \in I$
and
$a^t_i \in I$
and
![]() $a^t_1,\dots,a^t_{i-1} \notin I$
. Consider a neighbour
$a^t_1,\dots,a^t_{i-1} \notin I$
. Consider a neighbour
![]() $v$
of
$v$
of
![]() $a^t_i$
in
$a^t_i$
in
![]() $F^t.$
By definition, there exist
$F^t.$
By definition, there exist
![]() $s \in S^t \subseteq I$
and
$s \in S^t \subseteq I$
and
![]() $y \in Y$
such that
$y \in Y$
such that
![]() $s, a^t_i, v \in N(y).$
Then, since
$s, a^t_i, v \in N(y).$
Then, since
![]() $I \in \mathcal{I}$
and
$I \in \mathcal{I}$
and
![]() $s, a^t_i \in I,$
it follows that
$s, a^t_i \in I,$
it follows that
![]() $v \not \in I.$
Hence,
$v \not \in I.$
Hence,
![]() $I \subseteq A^{t+1} \cup S^{t+1}$
.
$I \subseteq A^{t+1} \cup S^{t+1}$
.
Let us now prove that
![]() $f(S)$
is indeed uniquely determined by
$f(S)$
is indeed uniquely determined by
![]() $S.$
In the following, we will denote by
$S.$
In the following, we will denote by
![]() $S^t(I), A^t(I)$
the relevant
$S^t(I), A^t(I)$
the relevant
![]() $S^t, A^t$
when the input of the algorithm is
$S^t, A^t$
when the input of the algorithm is
![]() $I$
, and similarly denote by
$I$
, and similarly denote by
![]() $i^t(I)$
the relevant index
$i^t(I)$
the relevant index
![]() $i^t$
. Fix
$i^t$
. Fix
![]() $I,I' \in \mathcal{I}$
such that
$I,I' \in \mathcal{I}$
such that
![]() $S(I) = S(I')$
. We show that
$S(I) = S(I')$
. We show that
![]() $S^t(I) = S^t(I')$
and
$S^t(I) = S^t(I')$
and
![]() $A^t(I) = A^t(I')$
for all
$A^t(I) = A^t(I')$
for all
![]() $t \in \{0, \dots, q\}.$
This clearly holds for
$t \in \{0, \dots, q\}.$
This clearly holds for
![]() $t = 0$
. Suppose that this holds for some
$t = 0$
. Suppose that this holds for some
![]() $t$
, and let us prove this for
$t$
, and let us prove this for
![]() $t+1$
. Denote
$t+1$
. Denote
![]() $S^t = S^t(I) = S^t(I'), A^t = A^t(I) = A^t(I')$
and
$S^t = S^t(I) = S^t(I'), A^t = A^t(I) = A^t(I')$
and
![]() $F^t = F^t(I) = F^t(I'),$
where the last equality holds since
$F^t = F^t(I) = F^t(I'),$
where the last equality holds since
![]() $F^t(J)$
is uniquely determined by
$F^t(J)$
is uniquely determined by
![]() $S^t(J)$
and
$S^t(J)$
and
![]() $A^t(J).$
Let
$A^t(J).$
Let
![]() $a^t_1, \dots, a^t_{|A^t|}$
be the ordering of
$a^t_1, \dots, a^t_{|A^t|}$
be the ordering of
![]() $A^t = V(F^t)$
as above. Denote
$A^t = V(F^t)$
as above. Denote
![]() $i = i^t(I)$
and
$i = i^t(I)$
and
![]() $i' = i^t(I').$
If
$i' = i^t(I').$
If
![]() $i = i',$
then it follows that
$i = i',$
then it follows that
![]() $S^{t+1}(I) = S^{t+1}(I')$
and from the definition of the algorithm, also
$S^{t+1}(I) = S^{t+1}(I')$
and from the definition of the algorithm, also
![]() $A^{t+1}(I) = A^{t+1}(I'),$
as required. So let us assume without loss of generality that
$A^{t+1}(I) = A^{t+1}(I'),$
as required. So let us assume without loss of generality that
![]() $i \lt i'.$
Then,
$i \lt i'.$
Then,
![]() $a^t_i \in S^{t+1}(I) \subseteq S(I).$
On the other hand, by definition of
$a^t_i \in S^{t+1}(I) \subseteq S(I).$
On the other hand, by definition of
![]() $i',$
we have
$i',$
we have
![]() $a^t_i \not \in I'$
which, using that
$a^t_i \not \in I'$
which, using that
![]() $S(I') \subseteq I',$
implies
$S(I') \subseteq I',$
implies
![]() $a^t_i \not \in S(I').$
Hence,
$a^t_i \not \in S(I').$
Hence,
![]() $S(I) \neq S(I'),$
contradicting our assumption.
$S(I) \neq S(I'),$
contradicting our assumption.
Finally, we need to show that
![]() $|f(S)| \le C_0 \sqrt{n}$
for every
$|f(S)| \le C_0 \sqrt{n}$
for every
![]() $S \in \mathcal{S}$
. We will prove the following claim.
$S \in \mathcal{S}$
. We will prove the following claim.
Claim 5.7.
Suppose that
![]() $t \ge 2n^{1/4}$
and
$t \ge 2n^{1/4}$
and
![]() $|A^t| \ge 10 \sqrt{n}.$
Then
$|A^t| \ge 10 \sqrt{n}.$
Then
![]() $|A^{t+1}| \le (1-n^{-1/4}) |A^t|$
.
$|A^{t+1}| \le (1-n^{-1/4}) |A^t|$
.
Let us finish the proof given Claim 5.7. Fix any
![]() $I \in \mathcal{I}$
and
$I \in \mathcal{I}$
and
![]() $S = S(I)$
, and suppose for the sake of contradiction that
$S = S(I)$
, and suppose for the sake of contradiction that
![]() $|f(S)| = |S \cup A^q(I)| \geq 11 \sqrt{n}.$
As
$|f(S)| = |S \cup A^q(I)| \geq 11 \sqrt{n}.$
As
![]() $|S| = q \ll \sqrt{n}$
, we must have
$|S| = q \ll \sqrt{n}$
, we must have
![]() $|A^q(I)| \geq 10\sqrt{n}$
. Then, by Claim 5.7, for any
$|A^q(I)| \geq 10\sqrt{n}$
. Then, by Claim 5.7, for any
![]() $t \in [2n^{1/4}, q-1],$
we have
$t \in [2n^{1/4}, q-1],$
we have
![]() $|A^{t+1}| \le (1-n^{-1/4}) |A^t|,$
which implies
$|A^{t+1}| \le (1-n^{-1/4}) |A^t|,$
which implies
a contradiction.
Proof of Claim
5.7
. Let
![]() $S^t, A^t, F^t, a^t_1, \dots, a^t_{|A^t|}$
and
$S^t, A^t, F^t, a^t_1, \dots, a^t_{|A^t|}$
and
![]() $i^t$
be as given in the algorithm. For
$i^t$
be as given in the algorithm. For
![]() $1 \le j \le |A^t|,$
denote
$1 \le j \le |A^t|,$
denote
![]() $F_j = F^t[\{a^t_{j}, \dots, a^t_{|A^t|}\}]$
. It is enough to prove that
$F_j = F^t[\{a^t_{j}, \dots, a^t_{|A^t|}\}]$
. It is enough to prove that
![]() $\Delta (F_j) \ge |V(F_j)|/n^{1/4}$
for every
$\Delta (F_j) \ge |V(F_j)|/n^{1/4}$
for every
![]() $j \le |A^t|/ 2.$
Indeed, then if
$j \le |A^t|/ 2.$
Indeed, then if
![]() $i^t \le |A^t|/ 2,$
we obtain
$i^t \le |A^t|/ 2,$
we obtain
![]() $|A^{t+1}| \le |A^t| - i^t - \Delta (F_{i^t}) \le |A^t| - i^t - |V(F_{i^t})|/n^{1/4} = |A^t| - i^t - (|A^t| - i^t + 1)/n^{1/4} \le (1 - n^{-1/4}) |A^t|$
, and if
$|A^{t+1}| \le |A^t| - i^t - \Delta (F_{i^t}) \le |A^t| - i^t - |V(F_{i^t})|/n^{1/4} = |A^t| - i^t - (|A^t| - i^t + 1)/n^{1/4} \le (1 - n^{-1/4}) |A^t|$
, and if
![]() $i^t \ge |A^t|/ 2,$
then
$i^t \ge |A^t|/ 2,$
then
![]() $|A^{t+1}| \le |A^t|/ 2.$
$|A^{t+1}| \le |A^t|/ 2.$
Consider a fixed
![]() $1 \leq j \leq |A^t|/2.$
Denote
$1 \leq j \leq |A^t|/2.$
Denote
![]() $A' = \{a_j, \dots, a_{|A^t|}\} = V(F_j).$
We need to show that
$A' = \{a_j, \dots, a_{|A^t|}\} = V(F_j).$
We need to show that
![]() $\Delta (F_j) \geq |A'|/n^{1/4}$
. Fix any
$\Delta (F_j) \geq |A'|/n^{1/4}$
. Fix any
![]() $s \in S^t.$
Then, for every
$s \in S^t.$
Then, for every
![]() $y \in N_H(s)$
and distinct
$y \in N_H(s)$
and distinct
![]() $a, a' \in A' \cap N_H(y),$
we have
$a, a' \in A' \cap N_H(y),$
we have
![]() $aa' \in E(F_j)$
. Note that the sets
$aa' \in E(F_j)$
. Note that the sets
![]() $(N_H(y) \setminus \{s\})_{y \in N_H(S^t)}$
partition
$(N_H(y) \setminus \{s\})_{y \in N_H(S^t)}$
partition
![]() $X_0 \setminus \{s\}$
, since every two vertices in
$X_0 \setminus \{s\}$
, since every two vertices in
![]() $X_0$
have exactly one common neighbour in
$X_0$
have exactly one common neighbour in
![]() $H$
. The number of pairs
$H$
. The number of pairs
![]() $(y, \{a, a'\})$
with
$(y, \{a, a'\})$
with
![]() $a, a' \in A'$
and
$a, a' \in A'$
and
![]() $a, a', s \in N_H(y)$
is
$a, a', s \in N_H(y)$
is
 \begin{equation*} \sum _{y \in N_H(s)} \binom { |A' \cap N_H(y)|}{2} \ge |N_H(s)| \cdot \binom {|A'|/ |N_H(s)|}{2} \ge \frac {|A'|^2}{4 \sqrt {n}}, \end{equation*}
\begin{equation*} \sum _{y \in N_H(s)} \binom { |A' \cap N_H(y)|}{2} \ge |N_H(s)| \cdot \binom {|A'|/ |N_H(s)|}{2} \ge \frac {|A'|^2}{4 \sqrt {n}}, \end{equation*}
where we used Jensen’s inequality for the convex function
![]() $\binom{x}{2}$
, the fact that
$\binom{x}{2}$
, the fact that
![]() $N_H(s) = (1 + o(1)) \sqrt{n}$
, and the assumption that
$N_H(s) = (1 + o(1)) \sqrt{n}$
, and the assumption that
![]() $|A'| \geq |A^t|/2 \geq 5\sqrt{n}$
. Hence, every
$|A'| \geq |A^t|/2 \geq 5\sqrt{n}$
. Hence, every
![]() $s \in S^t$
contributes at least
$s \in S^t$
contributes at least
![]() $\frac{|A'|^2}{4 \sqrt{n}}$
edges to
$\frac{|A'|^2}{4 \sqrt{n}}$
edges to
![]() $F_j$
. Finally, we prove that for every
$F_j$
. Finally, we prove that for every
![]() $aa' \in E(F_j),$
there are unique
$aa' \in E(F_j),$
there are unique
![]() $s \in S^t, y \in Y$
such that
$s \in S^t, y \in Y$
such that
![]() $s, a, a' \in N_H(y)$
. Indeed, recall that every pair of vertices in
$s, a, a' \in N_H(y)$
. Indeed, recall that every pair of vertices in
![]() $X_0$
have a unique common neighbour in
$X_0$
have a unique common neighbour in
![]() $Y.$
Hence, given
$Y.$
Hence, given
![]() $a, a',$
the vertex
$a, a',$
the vertex
![]() $y \in Y$
is uniquely determined. But then, the vertex
$y \in Y$
is uniquely determined. But then, the vertex
![]() $s \in S^t \cap N_H(y)$
is also uniquely determined. Indeed, suppose there are two distinct
$s \in S^t \cap N_H(y)$
is also uniquely determined. Indeed, suppose there are two distinct
![]() $s, s' \in S^t \cap N_H(y).$
Without loss of generality, there is an index
$s, s' \in S^t \cap N_H(y).$
Without loss of generality, there is an index
![]() $t_0$
such that
$t_0$
such that
![]() $\{s\} = S^{t_0} \setminus S^{t_0-1}$
and
$\{s\} = S^{t_0} \setminus S^{t_0-1}$
and
![]() $s' \in S^{t_0-1}.$
Then, by definition,
$s' \in S^{t_0-1}.$
Then, by definition,
![]() $sa \in E(F^{t_0-1}),$
so
$sa \in E(F^{t_0-1}),$
so
![]() $a \not \in S^{t_0} \cup A^{t_0} \supseteq A^t,$
a contradiction.
$a \not \in S^{t_0} \cup A^{t_0} \supseteq A^t,$
a contradiction.
Therefore, we have
![]() $e(F_j) \ge |S^t| \cdot \frac{|A'|^2}{4 \sqrt{n}} \ge \frac{|A'|^2}{2 n^{1/4}},$
which implies that
$e(F_j) \ge |S^t| \cdot \frac{|A'|^2}{4 \sqrt{n}} \ge \frac{|A'|^2}{2 n^{1/4}},$
which implies that
![]() $\Delta (F_j) \ge |A'|/ n^{1/4}$
as required.
$\Delta (F_j) \ge |A'|/ n^{1/4}$
as required.
This concludes the proof of Claim 5.6 and hence the theorem.
6.
 $Q = \{(4,1),(4,3)\}$
$Q = \{(4,1),(4,3)\}$
Here we prove that
![]() $h_3(n,\{(4,1),(4,3)\}) = \Theta (\log n)$
. We note that
$h_3(n,\{(4,1),(4,3)\}) = \Theta (\log n)$
. We note that
![]() $\{(4,1),(4,3)\}$
-free
$\{(4,1),(4,3)\}$
-free
![]() $3$
-graphs are also known as two graphs (not to be confused with 2-graphs, which are just graphs), and have been thoroughly studied in algebraic combinatorics due to their connection to sets of equiangular lines, see e.g. [Reference Godsil and Royle22, Chapter 11]. Every two-graph
$3$
-graphs are also known as two graphs (not to be confused with 2-graphs, which are just graphs), and have been thoroughly studied in algebraic combinatorics due to their connection to sets of equiangular lines, see e.g. [Reference Godsil and Royle22, Chapter 11]. Every two-graph
![]() $H$
arises from some graph
$H$
arises from some graph
![]() $G$
by taking
$G$
by taking
![]() $x,y,z \in V(G)$
to be an edge of
$x,y,z \in V(G)$
to be an edge of
![]() $H$
if and only if
$H$
if and only if
![]() $\{x,y,z\}$
induces an odd number of edges in
$\{x,y,z\}$
induces an odd number of edges in
![]() $G$
. This will be used in the proof. We start with the following lemma.
$G$
. This will be used in the proof. We start with the following lemma.
Lemma 6.1.
There is a constant
![]() $C \gt 0$
such that for every
$C \gt 0$
such that for every
![]() $n$
, there is an
$n$
, there is an
![]() $n$
-vertex graph in which every set of size
$n$
-vertex graph in which every set of size
![]() $C\log n$
contains a triangle and a coclique of size
$C\log n$
contains a triangle and a coclique of size
![]() $3$
.
$3$
.
Proof. Take
![]() $G \sim G(n,1/2)$
. Fix any
$G \sim G(n,1/2)$
. Fix any
![]() $U \subseteq V(G)$
,
$U \subseteq V(G)$
,
![]() $|U| = k \;:\!=\; C\log n$
. It is well-known that there is a partial Steiner system on
$|U| = k \;:\!=\; C\log n$
. It is well-known that there is a partial Steiner system on
![]() $U$
with
$U$
with
![]() $m = (\frac{1}{6}-o(1))k^2 \geq k^2/7$
triples,
$m = (\frac{1}{6}-o(1))k^2 \geq k^2/7$
triples,
![]() $T_1,\dots,T_m$
. The probability that no
$T_1,\dots,T_m$
. The probability that no
![]() $T_i$
is a triangle in
$T_i$
is a triangle in
![]() $G$
is
$G$
is
![]() $(7/8)^{m} \leq (7/8)^{k^2/7} = (7/8)^{\frac{1}{7} C^2 \log^2 n}$
. Taking the union bound over all
$(7/8)^{m} \leq (7/8)^{k^2/7} = (7/8)^{\frac{1}{7} C^2 \log^2 n}$
. Taking the union bound over all
![]() $\binom{n}{C\log n} \leq e^{C\log ^2 n}$
choices for
$\binom{n}{C\log n} \leq e^{C\log ^2 n}$
choices for
![]() $U$
, and assuming that
$U$
, and assuming that
![]() $C$
is large enough, we get that with high probability, every set of size
$C$
is large enough, we get that with high probability, every set of size
![]() $C\log n$
contains a triangle. By the same argument, w.h.p. every such set contains a coclique of size
$C\log n$
contains a triangle. By the same argument, w.h.p. every such set contains a coclique of size
![]() $3$
.
$3$
.
Theorem 6.2.
![]() $h_3(n,\{(4,1),(4,3)\}) = \Theta (\log n)$
.
$h_3(n,\{(4,1),(4,3)\}) = \Theta (\log n)$
.
Proof. For the lower bound, let
![]() $H$
be an
$H$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $\{(4,1),(4,3)\}$
-free
$\{(4,1),(4,3)\}$
-free
![]() $3$
-graph. Pick a vertex
$3$
-graph. Pick a vertex
![]() $v$
in
$v$
in
![]() $H$
and consider its link graph
$H$
and consider its link graph
![]() $L(v)$
. Since
$L(v)$
. Since
![]() $R_2(t,t) \lt 4^{t-1}$
(see Erdős and Szekeres [Reference Erdős and Szekeres15]), we see that
$R_2(t,t) \lt 4^{t-1}$
(see Erdős and Szekeres [Reference Erdős and Szekeres15]), we see that
![]() $L(v)$
has a clique or coclique
$L(v)$
has a clique or coclique
![]() $K$
of size at least
$K$
of size at least
![]() $\frac{1}{2} \log n$
. In the first case,
$\frac{1}{2} \log n$
. In the first case,
![]() $K$
is a clique in
$K$
is a clique in
![]() $H$
, else we find a
$H$
, else we find a
![]() $(4,3)$
-subgraph in
$(4,3)$
-subgraph in
![]() $H$
; and in the second case,
$H$
; and in the second case,
![]() $K$
is a coclique in
$K$
is a coclique in
![]() $H$
, else we find a
$H$
, else we find a
![]() $(4,1)$
-subgraph in
$(4,1)$
-subgraph in
![]() $H$
.
$H$
.
For the upper bound, let
![]() $G$
be the graph from Lemma 6.1. Let
$G$
be the graph from Lemma 6.1. Let
![]() $H$
be the
$H$
be the
![]() $3$
-graph on vertex set
$3$
-graph on vertex set
![]() $V(G)$
whose edge set consists of all triples of vertices
$V(G)$
whose edge set consists of all triples of vertices
![]() $x,y,z$
which induce an odd number of edges in
$x,y,z$
which induce an odd number of edges in
![]() $G$
. Lemma 6.1 guarantees that every set of
$G$
. Lemma 6.1 guarantees that every set of
![]() $C\log n$
vertices contains both an edge and a non-edge of
$C\log n$
vertices contains both an edge and a non-edge of
![]() $H$
. Hence,
$H$
. Hence,
![]() $h(H) \leq C\log n$
. Let us show that
$h(H) \leq C\log n$
. Let us show that
![]() $H$
is
$H$
is
![]() $Q$
-free,
$Q$
-free,
![]() $Q = \{(4,1),(4,3)\}$
. Fix any
$Q = \{(4,1),(4,3)\}$
. Fix any
![]() $X \subseteq V(G) = V(H)$
,
$X \subseteq V(G) = V(H)$
,
![]() $|X|=4$
. For each
$|X|=4$
. For each
![]() $A \subseteq X$
,
$A \subseteq X$
,
![]() $|A| = 3$
, we have
$|A| = 3$
, we have
![]() $A \in E(H)$
if and only if
$A \in E(H)$
if and only if
![]() $e_G(A)$
is odd, where
$e_G(A)$
is odd, where
![]() $e_G(A)$
is the number of edges spanned by
$e_G(A)$
is the number of edges spanned by
![]() $A$
in
$A$
in
![]() $G$
. Note that each edge of
$G$
. Note that each edge of
![]() $G[X]$
is contained in exactly two sets
$G[X]$
is contained in exactly two sets
![]() $A \subseteq X$
,
$A \subseteq X$
,
![]() $|A| = 3$
. Hence,
$|A| = 3$
. Hence,
![]() $ \sum _{A \subseteq X, |A|=3}e_G(A) = 2e_G(X).$
The right-hand side is even, so there is an even number of
$ \sum _{A \subseteq X, |A|=3}e_G(A) = 2e_G(X).$
The right-hand side is even, so there is an even number of
![]() $A$
with
$A$
with
![]() $e_G(A)$
odd. It follows that every four vertices in
$e_G(A)$
odd. It follows that every four vertices in
![]() $H$
induce an even number of edges. So
$H$
induce an even number of edges. So
![]() $H$
is
$H$
is
![]() $Q$
-free.
$Q$
-free.
7. Forbidden sets of size
 $3$
: Proof of Theorem 1.5
$3$
: Proof of Theorem 1.5
We will need the following structural characterization of
![]() $Q$
-free
$Q$
-free
![]() $3$
-graphs for
$3$
-graphs for
![]() $Q= \{ (4,1), (4,3), (4,4) \}$
.
$Q= \{ (4,1), (4,3), (4,4) \}$
.
Theorem 7.1 (Frankl and Füredi [Reference Frankl and Füredi18]). Let
![]() $H$
be an
$H$
be an
![]() $\{ (4,1), (4,3), (4,4) \})$
-free
$\{ (4,1), (4,3), (4,4) \})$
-free
![]() $3$
-graph. Then
$3$
-graph. Then
![]() $H$
is isomorphic to one of the following
$H$
is isomorphic to one of the following
![]() $3$
-graphs:
$3$
-graphs:
-
1. A blow-up of the
 $6$
vertex
$6$
vertex
 $3$
-graph
$3$
-graph
 $H'$
with vertex set
$H'$
with vertex set
 $V(H') = [6]$
and edge set
$V(H') = [6]$
and edge set
 $E(H') = \{123, 124, 345, 346, 561, 562, 135, 146, 236, 245\}$
. Here for the blow-up we replace every vertex of
$E(H') = \{123, 124, 345, 346, 561, 562, 135, 146, 236, 245\}$
. Here for the blow-up we replace every vertex of
 $H'$
by an independent set, and whenever we have
$H'$
by an independent set, and whenever we have
 $3$
vertices from three distinct of those sets, they induce an edge if and only if the corresponding vertices in
$3$
vertices from three distinct of those sets, they induce an edge if and only if the corresponding vertices in
 $H'$
do.
$H'$
do.
-
2. The
 $3$
-graph whose vertices are the points of a regular
$3$
-graph whose vertices are the points of a regular
 $n$
-gon where
$n$
-gon where
 $3$
vertices span an edge if and only if the corresponding points span a triangle whose interior contains the centre of the
$3$
vertices span an edge if and only if the corresponding points span a triangle whose interior contains the centre of the
 $n$
-gon.
$n$
-gon.
Proof of Theorem 1.5 .
Case
![]() $Q = \{ (4,1), (4,3), (4,4) \}$
.
$Q = \{ (4,1), (4,3), (4,4) \}$
.
We are to prove that
 \begin{equation*} h(n, \{(4,0), (4,1), (4,3)\})= h(n, Q) =\begin {cases} \frac {n}{2} &\text {if}\, n \equiv 0 \,\text {(mod 6)} \\[5pt] \lceil \frac {n+1}{2}\rceil & \text {if}\ n \not \equiv 0 \text {(mod 6)}. \end {cases} \end{equation*}
\begin{equation*} h(n, \{(4,0), (4,1), (4,3)\})= h(n, Q) =\begin {cases} \frac {n}{2} &\text {if}\, n \equiv 0 \,\text {(mod 6)} \\[5pt] \lceil \frac {n+1}{2}\rceil & \text {if}\ n \not \equiv 0 \text {(mod 6)}. \end {cases} \end{equation*}
First, let us prove that the second 3-graph
![]() $H$
in Theorem 7.1 has independence number exactly
$H$
in Theorem 7.1 has independence number exactly
![]() $\lceil{(n+1)/2)}\rceil$
. Assume the vertex set is
$\lceil{(n+1)/2)}\rceil$
. Assume the vertex set is
![]() $[n]$
and the vertices are labelled by consecutive integers in clockwise orientation. The lower bound is by taking
$[n]$
and the vertices are labelled by consecutive integers in clockwise orientation. The lower bound is by taking
![]() $\lceil{(n+1)/2)}\rceil$
consecutive vertices on the
$\lceil{(n+1)/2)}\rceil$
consecutive vertices on the
![]() $n$
-gon and noting that no three of them contain the centre in their interior. For the upper bound, let us see how many vertices can lie in an independent set containing
$n$
-gon and noting that no three of them contain the centre in their interior. For the upper bound, let us see how many vertices can lie in an independent set containing
![]() $1$
. When
$1$
. When
![]() $n$
is odd, the triangle formed by
$n$
is odd, the triangle formed by
![]() $\{1, i, (n-1)/2+i\}$
contains the centre and hence is an edge. Therefore we may pair the elements of
$\{1, i, (n-1)/2+i\}$
contains the centre and hence is an edge. Therefore we may pair the elements of
![]() $[n]\setminus \{1\}$
as
$[n]\setminus \{1\}$
as
![]() $(2, (n+3)/2), (3, (n+5)/2), \ldots, ((n+1)/2, n)$
and note that each pair can have at most one vertex in an independent set containing 1. Hence the maximum size of an independent set containing 1 is at most
$(2, (n+3)/2), (3, (n+5)/2), \ldots, ((n+1)/2, n)$
and note that each pair can have at most one vertex in an independent set containing 1. Hence the maximum size of an independent set containing 1 is at most
![]() $(n+1)/2$
and by vertex transitivity of
$(n+1)/2$
and by vertex transitivity of
![]() $H$
, the independence number of
$H$
, the independence number of
![]() $H$
is at most
$H$
is at most
![]() $(n+1)/2$
. For
$(n+1)/2$
. For
![]() $n$
even we consider the
$n$
even we consider the
![]() $n/2-1$
pairs
$n/2-1$
pairs
![]() $(2, n/2+1), (3, n/2+2), \ldots, (n/2, n-1)$
and add the vertex
$(2, n/2+1), (3, n/2+2), \ldots, (n/2, n-1)$
and add the vertex
![]() $n$
to get an upper bound
$n$
to get an upper bound
![]() $n/2+1=\lceil{(n+1)/2)}\rceil$
.
$n/2+1=\lceil{(n+1)/2)}\rceil$
.
Next we observe that the
![]() $6$
-vertex 3-graph
$6$
-vertex 3-graph
![]() $H'$
in Theorem 7.1 has independence number exactly
$H'$
in Theorem 7.1 has independence number exactly
![]() $3$
(we omit the short case analysis needed for the proof). Hence if we blow-up each vertex of
$3$
(we omit the short case analysis needed for the proof). Hence if we blow-up each vertex of
![]() $H'$
into sets of the same size, then we obtain
$H'$
into sets of the same size, then we obtain
![]() $n$
-vertex
$n$
-vertex
![]() $3$
-graphs with independence number exactly
$3$
-graphs with independence number exactly
![]() $n/2$
whenever
$n/2$
whenever
![]() $n \equiv 0$
(mod 6). This concludes the proof of the upper bound.
$n \equiv 0$
(mod 6). This concludes the proof of the upper bound.
For the lower bound, let
![]() $H$
be
$H$
be
![]() $Q$
-free. Then by Theorem 7.1,
$Q$
-free. Then by Theorem 7.1,
![]() $H$
is isomorphic to one of the two graphs described in Theorem 7.1. If
$H$
is isomorphic to one of the two graphs described in Theorem 7.1. If
![]() $H$
is isomorphic to the second graph, then we have already shown that its independence number is at least
$H$
is isomorphic to the second graph, then we have already shown that its independence number is at least
![]() $(n+1)/2$
, so assume that
$(n+1)/2$
, so assume that
![]() $H$
is isomorphic to the blow-up of the
$H$
is isomorphic to the blow-up of the
![]() $6$
-vertex
$6$
-vertex
![]() $10$
-edge
$10$
-edge
![]() $3$
-graph
$3$
-graph
![]() $H'$
. There are
$H'$
. There are
![]() $10$
non-edges in
$10$
non-edges in
![]() $H'$
. Let
$H'$
. Let
![]() $V_1, \ldots, V_6$
be the blown up vertex sets. Since every vertex
$V_1, \ldots, V_6$
be the blown up vertex sets. Since every vertex
![]() $i \in [6]$
in
$i \in [6]$
in
![]() $H'$
is contained in exactly
$H'$
is contained in exactly
![]() $5$
non-edges, we obtain
$5$
non-edges, we obtain
By the pigeonhole principle, there is a non-edge
![]() $i_1i_2i_3$
, such that
$i_1i_2i_3$
, such that
![]() $ |V_{i_1}| + |V_{i_2}| + |V_{i_3}|\geq n/2$
. Our bound follows by observing that for any non-edge
$ |V_{i_1}| + |V_{i_2}| + |V_{i_3}|\geq n/2$
. Our bound follows by observing that for any non-edge
![]() $i_1i_2i_3$
in the original
$i_1i_2i_3$
in the original
![]() $3$
-graph
$3$
-graph
![]() $H'$
the set
$H'$
the set
![]() $V_{i_1} \cup V_{i_2} \cup V_{i_3}$
is an independent set. This gives an independent set of size at least
$V_{i_1} \cup V_{i_2} \cup V_{i_3}$
is an independent set. This gives an independent set of size at least
![]() $n/2$
, and if
$n/2$
, and if
![]() $n \not \equiv 0$
(mod 6), then equality cannot hold throughout (a short case analysis, which we omit, is needed to prove this) and we obtain an independent set of size strictly greater than
$n \not \equiv 0$
(mod 6), then equality cannot hold throughout (a short case analysis, which we omit, is needed to prove this) and we obtain an independent set of size strictly greater than
![]() $n/2$
as required.
$n/2$
as required.
Case
![]() $Q = \{ (4,0), (4,2), (4,3) \}$
.
$Q = \{ (4,0), (4,2), (4,3) \}$
.
We now prove
![]() $h(n, \{ (4,0), (4,2), (4,3) \} ) = n-1,$
for
$h(n, \{ (4,0), (4,2), (4,3) \} ) = n-1,$
for
![]() $n\geq 4$
. Let
$n\geq 4$
. Let
![]() $H$
be a
$H$
be a
![]() $3$
-graph that is a clique on
$3$
-graph that is a clique on
![]() $n-1$
vertices and a single isolated vertex, then
$n-1$
vertices and a single isolated vertex, then
![]() $H$
is
$H$
is
![]() $Q$
-free, giving us the upper bound.
$Q$
-free, giving us the upper bound.
For the lower bound, let
![]() $H$
be a
$H$
be a
![]() $Q$
-free
$Q$
-free
![]() $3$
-graph on
$3$
-graph on
![]() $n$
vertices,
$n$
vertices,
![]() $n\geq 4$
. Assume that
$n\geq 4$
. Assume that
![]() $H$
is not a clique. We shall show that
$H$
is not a clique. We shall show that
![]() $H$
is a clique and a single isolated vertex. Consider a maximal clique
$H$
is a clique and a single isolated vertex. Consider a maximal clique
![]() $S$
in
$S$
in
![]() $H$
. Since
$H$
. Since
![]() $|S|\lt n$
, there is a vertex
$|S|\lt n$
, there is a vertex
![]() $v\in V(H)\setminus S$
. From the maximality of
$v\in V(H)\setminus S$
. From the maximality of
![]() $S$
,
$S$
,
![]() $L_S(v)$
is not a clique. If
$L_S(v)$
is not a clique. If
![]() $L_S(v)$
contains an edge, then we have that for some vertices
$L_S(v)$
contains an edge, then we have that for some vertices
![]() $x, y, y'$
,
$x, y, y'$
,
![]() $xy\in E(L_S(v))$
and
$xy\in E(L_S(v))$
and
![]() $xy'\not \in E(L_S(v))$
. But then
$xy'\not \in E(L_S(v))$
. But then
![]() $\{v, x, y, y'\}$
induces a
$\{v, x, y, y'\}$
induces a
![]() $(4,2)$
or a
$(4,2)$
or a
![]() $(4,3)$
-graph, a contradiction. Thus,
$(4,3)$
-graph, a contradiction. Thus,
![]() $L_S(v)$
is an empty graph, i.e. there is no edge in
$L_S(v)$
is an empty graph, i.e. there is no edge in
![]() $H$
containing
$H$
containing
![]() $v$
and two vertices of
$v$
and two vertices of
![]() $S$
. Now assume there exists a second vertex
$S$
. Now assume there exists a second vertex
![]() $v' \in V(H)\setminus (S \cup \{v\})$
. Then by the same argument as above,
$v' \in V(H)\setminus (S \cup \{v\})$
. Then by the same argument as above,
![]() $v'$
is also not contained in any edge with two vertices from
$v'$
is also not contained in any edge with two vertices from
![]() $S$
. Consider triples
$S$
. Consider triples
![]() $vv'x$
,
$vv'x$
,
![]() $x\in S$
. Since
$x\in S$
. Since
![]() $|S|\ge 3$
, by the pigeonhole principle there are two vertices
$|S|\ge 3$
, by the pigeonhole principle there are two vertices
![]() $x,x'\in S$
such that either
$x,x'\in S$
such that either
![]() $vv'x, vv'x'\in E(H)$
or
$vv'x, vv'x'\in E(H)$
or
![]() $vv'x, vv'x'\not \in E(H)$
. Then
$vv'x, vv'x'\not \in E(H)$
. Then
![]() $\{v,v', x, x'\}$
induces
$\{v,v', x, x'\}$
induces
![]() $2$
or
$2$
or
![]() $0$
edges respectively, a contradiction. Thus,
$0$
edges respectively, a contradiction. Thus,
![]() $|S|=n-1$
and
$|S|=n-1$
and
![]() $v$
is an isolated vertex.
$v$
is an isolated vertex.
8. Concluding remarks
-
• In Section 3.1, we showed that
 $h_3(n,4,1) \geq c_1\!\left(\frac{\log n}{\log \log n}\right)^{1/2}$
, and from (3) we have
$h_3(n,4,1) \geq c_1\!\left(\frac{\log n}{\log \log n}\right)^{1/2}$
, and from (3) we have
 $h_3(n,4,1) \leq c_2 \frac{\log n}{\log \log n}$
(for constants
$h_3(n,4,1) \leq c_2 \frac{\log n}{\log \log n}$
(for constants
 $c_1,c_2$
). It is unclear if either of these bounds represents the correct order of magnitude, but the lower bound certainly seems far off.
$c_1,c_2$
). It is unclear if either of these bounds represents the correct order of magnitude, but the lower bound certainly seems far off.Problem 8.1. Improve the exponent
 $1/2$
in the lower bound on
$1/2$
in the lower bound on
 $h_3(n,4,1)$
.
$h_3(n,4,1)$
. -
• In the cases
 $Q = \{(4,0),(4,2)\}$
and
$Q = \{(4,0),(4,2)\}$
and
 $Q = \{(4,1),(4,2)\}$
, there is a polylogarithmic gap between our lower and upper bounds in Table 1, and it would be interesting to close the gap. In particular, it would be interesting to decide whether
$Q = \{(4,1),(4,2)\}$
, there is a polylogarithmic gap between our lower and upper bounds in Table 1, and it would be interesting to close the gap. In particular, it would be interesting to decide whether
 $h(n,\{(4,2),(4,4)\}) = \Theta (\sqrt{n\log n})$
(this is equivalent to
$h(n,\{(4,2),(4,4)\}) = \Theta (\sqrt{n\log n})$
(this is equivalent to
 $Q = \{(4,0),(4,2)\}$
by complementation). Recall that in a
$Q = \{(4,0),(4,2)\}$
by complementation). Recall that in a
 $(\{(4,2),(4,4)\})$
-free
$(\{(4,2),(4,4)\})$
-free
 $3$
-graph, every tight component is a star (Theorem 4.2). One example of such
$3$
-graph, every tight component is a star (Theorem 4.2). One example of such
 $3$
-graphs is linear
$3$
-graphs is linear
 $3$
-graphs, and it is well-known that every
$3$
-graphs, and it is well-known that every
 $n$
-vertex linear
$n$
-vertex linear
 $3$
-graph has an independent set of size
$3$
-graph has an independent set of size
 $\Omega (\sqrt{n\log n})$
, and that this is tight. Another example is to take a projective plane and put a star on each line (so that each star has roughly
$\Omega (\sqrt{n\log n})$
, and that this is tight. Another example is to take a projective plane and put a star on each line (so that each star has roughly
 $\sqrt{n}$
vertices). It would be interesting to estimate the smallest possible independence number of such a hypergraph.
$\sqrt{n}$
vertices). It would be interesting to estimate the smallest possible independence number of such a hypergraph. -
• Fix integers
 $m\gt r$
. Recall that a set
$m\gt r$
. Recall that a set
 $Q$
of order-size pairs
$Q$
of order-size pairs
 $\{(m, f_1), \ldots, (m,f_t)\}$
has the Erdős-Hajnal (EH) property if there exists
$\{(m, f_1), \ldots, (m,f_t)\}$
has the Erdős-Hajnal (EH) property if there exists
 $\epsilon =\epsilon _Q$
such that
$\epsilon =\epsilon _Q$
such that
 $h_r(n, Q)\gt n^{\epsilon }$
. As
$h_r(n, Q)\gt n^{\epsilon }$
. As
 $|Q|$
grows, the collection of
$|Q|$
grows, the collection of
 $Q$
-free
$Q$
-free
 $r$
-graphs is more restrictive, and hence
$r$
-graphs is more restrictive, and hence
 $h_r(n, Q)$
grows (assuming that large
$h_r(n, Q)$
grows (assuming that large
 $Q$
-free
$Q$
-free
 $r$
-graphs are not forbidden to exist by Ramsey’s theorem). The case when
$r$
-graphs are not forbidden to exist by Ramsey’s theorem). The case when
 $h_r(n, Q) = \Omega (n)$
was treated by the first author and Balogh [Reference Axenovich and Balogh3] when
$h_r(n, Q) = \Omega (n)$
was treated by the first author and Balogh [Reference Axenovich and Balogh3] when
 $r=2$
. A natural question then is to ask what is the smallest
$r=2$
. A natural question then is to ask what is the smallest
 $t$
such that every
$t$
such that every
 $Q$
of size
$Q$
of size
 $t$
has the EH property. Call this minimum value
$t$
has the EH property. Call this minimum value
 $EH_r(m)$
. Our results for
$EH_r(m)$
. Our results for
 $r=3$
show that for
$r=3$
show that for
 $m=4$
, all
$m=4$
, all
 $Q$
of size 3 have the EH property, but there are
$Q$
of size 3 have the EH property, but there are
 $Q$
of size 2 which do not. Consequently,
$Q$
of size 2 which do not. Consequently,
 $EH_3(4) = 3$
.
$EH_3(4) = 3$
.In order to further study
 $EH_r(m)$
, we need another definition. Given integers
$EH_r(m)$
, we need another definition. Given integers
 $m\ge r\ge 3$
, let
$m\ge r\ge 3$
, let
 $g_r(m)$
be the number of edges in an
$g_r(m)$
be the number of edges in an
 $r$
-graph on
$r$
-graph on
 $m$
vertices obtained by first taking a partition of the
$m$
vertices obtained by first taking a partition of the
 $m$
vertices into almost equal parts, then taking all edges that intersect each part, and then recursing this construction within each part. For example,
$m$
vertices into almost equal parts, then taking all edges that intersect each part, and then recursing this construction within each part. For example,
 $g_3(7)= 13$
since we start with a complete 3-partite 3-graph with part sizes
$g_3(7)= 13$
since we start with a complete 3-partite 3-graph with part sizes
 $2,2,3$
and then add one edge within the part of size 3. It is known (see, e.g. [Reference Mubayi and Razborov24]) that as
$2,2,3$
and then add one edge within the part of size 3. It is known (see, e.g. [Reference Mubayi and Razborov24]) that as
 $r$
grows we haveNote that
$r$
grows we haveNote that \begin{equation*}g_r(m) = (1+o(1))\frac {r!}{r^r-r} \left(\substack{m\\r}\right).\end{equation*}
\begin{equation*}g_r(m) = (1+o(1))\frac {r!}{r^r-r} \left(\substack{m\\r}\right).\end{equation*}
 $\frac{r!}{r^r-r}$
approaches 0 as
$\frac{r!}{r^r-r}$
approaches 0 as
 $r$
grows. The second author and Razborov [Reference Mubayi and Razborov24] proved that for all fixed
$r$
grows. The second author and Razborov [Reference Mubayi and Razborov24] proved that for all fixed
 $m\gt r\gt 3$
, there are
$m\gt r\gt 3$
, there are
 $n$
-vertex
$n$
-vertex
 $r$
-graphs which are
$r$
-graphs which are
 $Q$
-free,
$Q$
-free,
 $Q=\{(m, i)\;:\; g_r(m)\lt i\le\left(\substack{m\\r}\right)\}$
, with
$Q=\{(m, i)\;:\; g_r(m)\lt i\le\left(\substack{m\\r}\right)\}$
, with
 $h(G)= O(\log n)$
. In other words, there exists
$h(G)= O(\log n)$
. In other words, there exists
 $Q$
of size
$Q$
of size
 $\left(\substack{m\\r}\right) - g_r(m)$
which does not have the EH property. This proves that
$\left(\substack{m\\r}\right) - g_r(m)$
which does not have the EH property. This proves that
 $EH_r(m) \ge\left(\substack{m\\r}\right) - g_r(m)+1$
.
$EH_r(m) \ge\left(\substack{m\\r}\right) - g_r(m)+1$
.
Erdős and Hajnal [Reference Erdős and Hajnal12] proved that for all
 $m \gt r \ge 3$
, the set
$m \gt r \ge 3$
, the set
 $Q=\{(m, i)\;:\; g_r(m) \le i \le\left(\substack{m\\r}\right)\}$
has the EH property. In other words, they proved that every
$Q=\{(m, i)\;:\; g_r(m) \le i \le\left(\substack{m\\r}\right)\}$
has the EH property. In other words, they proved that every
 $n$
-vertex
$n$
-vertex
 $r$
-graph in which every set of
$r$
-graph in which every set of
 $m$
vertices spans less than
$m$
vertices spans less than
 $g_r(m)$
edges has an independent set of size at least
$g_r(m)$
edges has an independent set of size at least
 $n^{\epsilon }$
, where
$n^{\epsilon }$
, where
 $\epsilon$
depends only on
$\epsilon$
depends only on
 $r$
and
$r$
and
 $m$
. This is a particular set
$m$
. This is a particular set
 $Q$
of size
$Q$
of size
 $\left(\substack{m\\r}\right) - g_r(m) +1$
that has the EH property, and we speculate that every other set
$\left(\substack{m\\r}\right) - g_r(m) +1$
that has the EH property, and we speculate that every other set
 $Q$
of this size also has the EH property.
$Q$
of this size also has the EH property.Problem 8.2. Prove or disprove that for all
 $m\gt r\gt 2$
,
$m\gt r\gt 2$
, \begin{equation*}EH_r(m) = \left(\substack{m\\r}\right) - g_r(m) +1.\end{equation*}
\begin{equation*}EH_r(m) = \left(\substack{m\\r}\right) - g_r(m) +1.\end{equation*}
We end by noting that
 $EH_3(4) = 3 =\left(\substack{4\\3}\right) - g_3(4) +1$
.
$EH_3(4) = 3 =\left(\substack{4\\3}\right) - g_3(4) +1$
.
Acknowledgments
The authors wish to thank the anonymous referee for a careful reading of the paper and useful suggestions which improved the presentation. The second and third authors also thank Benny Sudakov for useful discussions.