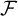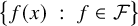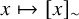1 Introduction
In the early 1960s, John Wetzel posed the following problem.
Wetzel’s Problem: If
![]() $\mathcal {F}$
is a family of analytic functions (on some common domain) such that
$\mathcal {F}$
is a family of analytic functions (on some common domain) such that
![]() $\{ f(x) \ : \ f \in \mathcal {F} \}$
is countable for every x, must
$\{ f(x) \ : \ f \in \mathcal {F} \}$
is countable for every x, must
![]() $\mathcal {F}$
be a countable family?
$\mathcal {F}$
be a countable family?
A few years later, Erdős proved that an affirmative answer to Wetzel’s Problem is equivalent to the negation of Cantor’s Continuum Hypothesis (CH). Combined with Paul Cohen’s proof of the independence of CH, this showed that Wetzel’s Problem is independent of the standard axioms of mathematics (ZFC). Upon learning of Erdős’ theorem, Wetzel remarked to his dissertation advisor (Halsey Royden) that ‘…once again a natural analysis question has grown horns!’ This quote, and other interesting history surrounding Wetzel’s Problem, appears in Garcia-Shoemaker [Reference Garcia and Shoemaker10]. Erdős’ proof even made it into Aigner-Ziegler’s ‘Proofs from the Book’ ([Reference Aigner and Ziegler1]). It will be more convenient for us to state and refer to Erdős’ equivalence in the negated form.
Theorem 1 (Erdős [Reference Erdős7])
The following are equivalent:
-
(1) CH;
-
(2) There exists an uncountable family
 $\mathcal {F}$
of analytic functions on some fixed open domain D of either
$\mathcal {F}$
of analytic functions on some fixed open domain D of either
 $\mathbb {R}$
or
$\mathbb {R}$
or
 $\mathbb {C}$
, such that for every
$\mathbb {C}$
, such that for every
 $x \in D$
, is countable.
$x \in D$
, is countable. $$\begin{align*}\big\{ f(x) \ : \ f \in \mathcal{F} \big\} \end{align*}$$
$$\begin{align*}\big\{ f(x) \ : \ f \in \mathcal{F} \big\} \end{align*}$$
Motivated by connections to work of Hardin-Taylor ([Reference Hardin and Taylor11], [Reference Hardin and Taylor12]) and Bajpai-Velleman [Reference Bajpai and Velleman2] described below, we strengthen Theorem 1 as follows. If
![]() $P \in \mathbb {R}^2$
, we denote the first coordinate of P by
$P \in \mathbb {R}^2$
, we denote the first coordinate of P by
![]() $x_P$
and the second coordinate by
$x_P$
and the second coordinate by
![]() $y_P$
. Define a sparse (real) analytic system to mean a collection
$y_P$
. Define a sparse (real) analytic system to mean a collection
such that:
-
(1) for all
 $P \in \mathbb {R}^2$
,
$P \in \mathbb {R}^2$
,
 $f_P$
is an increasing, analytic bijection from
$f_P$
is an increasing, analytic bijection from
 $\mathbb {R} \to \mathbb {R}$
that passes through the point P; and
$\mathbb {R} \to \mathbb {R}$
that passes through the point P; and -
(2) For all
 $z \in \mathbb {R}$
, the sets and
$z \in \mathbb {R}$
, the sets and $$\begin{align*}\big\{ f_P(z) \ : \ P \in \mathbb{R}^2 \text{ and } z \ne x_P \big\} \end{align*}$$
are both countable.
$$\begin{align*}\big\{ f_P(z) \ : \ P \in \mathbb{R}^2 \text{ and } z \ne x_P \big\} \end{align*}$$
are both countable. $$\begin{align*}\big\{ f^{-1}_P(z) \ : \ P \in \mathbb{R}^2 \text{ and } z \ne y_P \big\} \end{align*}$$
$$\begin{align*}\big\{ f^{-1}_P(z) \ : \ P \in \mathbb{R}^2 \text{ and } z \ne y_P \big\} \end{align*}$$
We prove the following strengthening of Erdős’ Theorem 1.
Theorem 2. The following are equivalent:
-
(1) CH
-
(2) There exists a sparse real analytic system.
We use Theorem 2 to answer a question of Bajpai and Velleman, assuming CH. Given a nonempty set S, let
![]() $\boldsymbol {{}^{\mathbb {R}} S}$
denote the collection of total functions from
$\boldsymbol {{}^{\mathbb {R}} S}$
denote the collection of total functions from
![]() $\mathbb {R}$
to S, and let
$\mathbb {R}$
to S, and let
![]() $\boldsymbol {{}^{\underset {\smile }{\mathbb {R}}} S}$
denote the collection of all S-valued functions f such that
$\boldsymbol {{}^{\underset {\smile }{\mathbb {R}}} S}$
denote the collection of all S-valued functions f such that
![]() $\text {dom}(f)=(-\infty ,t_f)$
for some
$\text {dom}(f)=(-\infty ,t_f)$
for some
![]() $t_f \in \mathbb {R}$
. An
$t_f \in \mathbb {R}$
. An
![]() $\boldsymbol {S}$
-predictor will refer to any function
$\boldsymbol {S}$
-predictor will refer to any function
![]() $\mathcal {P}$
with domain and codomain as follows:
$\mathcal {P}$
with domain and codomain as follows:
An S-predictor
![]() $\mathcal {P}$
will be called good if for all
$\mathcal {P}$
will be called good if for all
![]() $F \in {}^{\mathbb {R}} S$
, the set
$F \in {}^{\mathbb {R}} S$
, the set
has full measure in
![]() $\mathbb {R}$
. So
$\mathbb {R}$
. So
![]() $\mathcal {P}$
is good if for any total
$\mathcal {P}$
is good if for any total
![]() $F:\mathbb {R} \to S$
,
$F:\mathbb {R} \to S$
,
![]() $\mathcal {P}$
‘almost always’ correctly predicts
$\mathcal {P}$
‘almost always’ correctly predicts
![]() $F(t)$
based only on
$F(t)$
based only on
![]() $F \restriction (-\infty ,t)$
.Footnote 1 Hardin-Taylor [Reference Hardin and Taylor11] proved that for any set S, there exists a good S-predictor, and in [Reference Hardin and Taylor12], they raised the question of whether these good predictors could also be arranged to be ‘
$F \restriction (-\infty ,t)$
.Footnote 1 Hardin-Taylor [Reference Hardin and Taylor11] proved that for any set S, there exists a good S-predictor, and in [Reference Hardin and Taylor12], they raised the question of whether these good predictors could also be arranged to be ‘
![]() $\Gamma $
-anonymous’ with respect to certain classes
$\Gamma $
-anonymous’ with respect to certain classes
![]() $\Gamma \subseteq \text {Homeo}^+(\mathbb {R})$
;Footnote 2 an S-predictor
$\Gamma \subseteq \text {Homeo}^+(\mathbb {R})$
;Footnote 2 an S-predictor
![]() $\mathcal {P}$
is
$\mathcal {P}$
is
![]() $\Gamma $
-anonymous if for every
$\Gamma $
-anonymous if for every
![]() $\varphi \in \Gamma $
and every
$\varphi \in \Gamma $
and every
![]() $f \in {}^{\underset {\smile }{\mathbb {R}}} S$
,
$f \in {}^{\underset {\smile }{\mathbb {R}}} S$
,
where
![]() $f \circ \varphi $
is the member of
$f \circ \varphi $
is the member of
![]() ${}^{\underset {\smile }{\mathbb {R}}} S$
whose domain is understood to be
${}^{\underset {\smile }{\mathbb {R}}} S$
whose domain is understood to be
![]() $\big (-\infty , \varphi ^{-1}(t_f) \big )$
. Bajpai and Velleman [Reference Bajpai and Velleman2] gave a positive and a negative result:
$\big (-\infty , \varphi ^{-1}(t_f) \big )$
. Bajpai and Velleman [Reference Bajpai and Velleman2] gave a positive and a negative result:
-
• For every set S, there exists a good S-predictor that is anonymous with respect to the class of affine functions on the reals. This strengthened a previous theorem of Hardin-Taylor [Reference Hardin and Taylor12], who had gotten the same result for the smaller class of affine functions of slope 1 (i.e, shifts).
-
• There is an equivalence relation
 $\sim $
on
$\sim $
on
 $\mathbb {R}$
such that, letting
$\mathbb {R}$
such that, letting
 $S:=\mathbb {R}/\sim $
, there is no good S-predictor that is anonymous with respect to the class of increasing
$S:=\mathbb {R}/\sim $
, there is no good S-predictor that is anonymous with respect to the class of increasing
 $C^\infty $
bijections on
$C^\infty $
bijections on
 $\mathbb {R}$
.
$\mathbb {R}$
.
They asked about classes intermediate between the affine functions and the
![]() $C^\infty $
functions.
$C^\infty $
functions.
Question 3 (Bajpai-Velleman [Reference Bajpai and Velleman2], page 788)
Does there exist (for every set S) a good S-predictor that is anonymous with respect to the analytic members of
![]() $\text {Homeo}^+(\mathbb {R})$
?
$\text {Homeo}^+(\mathbb {R})$
?
We use Theorem 2, together with an argument from Bajpai-Velleman [Reference Bajpai and Velleman2], to prove:
Theorem 4. Assuming CH, the answer to Question 3 is negative.
Section 2 provides an interpolation theorem that will be used in the proof of Theorem 2, Section 3 proves Theorem 2, Section 4 proves Theorem 4, and Section 5 has concluding remarks and open questions.
2 An interpolation theorem
A key part of the proof of Theorem 2 is the (ZFC) Theorem 5 below. One of the referees pointed out that Theorem 5 follows from known results; in particular, it follows from the much more powerful Theorem 3.2 of Burke [Reference Burke4] or, with modifications in the proofs, either Theorem 2 of Barth-Schneider [Reference Barth and Schneider3] or Corollary 1.9 of Burke [Reference Burke5]. Since deriving Theorem 5 from those more powerful theorems is not trivial, we choose to present our original direct proof of Theorem 5.
Recall that Cantor proved that any two countable dense subsets of
![]() $\mathbb {R}$
are order-isomorphic and that this order-isomorphism easily extends uniquely to a homeomorphism of
$\mathbb {R}$
are order-isomorphic and that this order-isomorphism easily extends uniquely to a homeomorphism of
![]() $\mathbb {R}$
. Franklin [Reference Franklin9] considered the question of how nice this homeomorphism could be arranged to be, and showed that if D and E are countable dense subsets of
$\mathbb {R}$
. Franklin [Reference Franklin9] considered the question of how nice this homeomorphism could be arranged to be, and showed that if D and E are countable dense subsets of
![]() $\mathbb {R}$
, then there is an order-isomorphism of D with E that extends to a real analytic function. A series of papers improved this result, culminating in Barth-Schneider [Reference Barth and Schneider3], who proved that there is an order-isomorphism of D with E that extends to an entire function
$\mathbb {R}$
, then there is an order-isomorphism of D with E that extends to a real analytic function. A series of papers improved this result, culminating in Barth-Schneider [Reference Barth and Schneider3], who proved that there is an order-isomorphism of D with E that extends to an entire function
![]() $f: \mathbb {C} \to \mathbb {C}$
, answering (one interpretation of) Question 24 of Erdős [Reference Erdős8].Footnote 3 Subsequent work of Burke, mentioned above, further strengthened those results. The variant we will need for the proof of Theorem 2 follows.
$f: \mathbb {C} \to \mathbb {C}$
, answering (one interpretation of) Question 24 of Erdős [Reference Erdős8].Footnote 3 Subsequent work of Burke, mentioned above, further strengthened those results. The variant we will need for the proof of Theorem 2 follows.
Theorem 5. Suppose
![]() $\mathcal {D}$
is a partition of
$\mathcal {D}$
is a partition of
![]() $\mathbb {R}$
into dense subsets of
$\mathbb {R}$
into dense subsets of
![]() $\mathbb {R}$
; for each
$\mathbb {R}$
; for each
![]() $z \in \mathbb {R}$
, let
$z \in \mathbb {R}$
, let
![]() $D_z$
denote the unique
$D_z$
denote the unique
![]() $D \in \mathcal {D}$
such that
$D \in \mathcal {D}$
such that
![]() $z \in D$
.
$z \in D$
.
Then for any
![]() $P=(x_P,y_P) \in \mathbb {R}^2$
and any countable set W of reals, there is an entire function
$P=(x_P,y_P) \in \mathbb {R}^2$
and any countable set W of reals, there is an entire function
![]() $f: \mathbb {C} \to \mathbb {C}$
such that:
$f: \mathbb {C} \to \mathbb {C}$
such that:
-
(1)
 $f \restriction \mathbb {R}$
is real-valued (hence analytic, since
$f \restriction \mathbb {R}$
is real-valued (hence analytic, since
 $f:\mathbb {C} \to \mathbb {C}$
is entire);
$f:\mathbb {C} \to \mathbb {C}$
is entire); -
(2)
 $f \restriction \mathbb {R}$
is a bijection with strictly positive derivative;
$f \restriction \mathbb {R}$
is a bijection with strictly positive derivative; -
(3)
 $f(x_P)=y_P$
; and
$f(x_P)=y_P$
; and -
(4) for each
 $w \in W$
,
$w \in W$
,-
(a) if
 $w \ne x_P$
, then
$w \ne x_P$
, then
 $f(w) \in D_w$
;
$f(w) \in D_w$
; -
(b) if
 $w \ne y_P$
, then
$w \ne y_P$
, then
 $f^{-1}(w) \in D_w$
.
$f^{-1}(w) \in D_w$
.
-
Let us give a brief outline of the following proof of Theorem 5, which is inspired by the proof of Nienhuys-Thiemann [Reference Nienhuys and Thiemann14]. We will inductively define a sequence of functions
![]() $\langle f_n : n\in \mathbb {N}\rangle $
whose limit will be the desired function f. Each function
$\langle f_n : n\in \mathbb {N}\rangle $
whose limit will be the desired function f. Each function
![]() $f_n$
will satisfy a version of Theorem 5(4) for finitely many points in W. When we define the next function
$f_n$
will satisfy a version of Theorem 5(4) for finitely many points in W. When we define the next function
![]() $f_{n+1}$
, we will want it to be equal to
$f_{n+1}$
, we will want it to be equal to
![]() $f_n$
on these finitely many points in W that have already been taken care of, and we will want
$f_n$
on these finitely many points in W that have already been taken care of, and we will want
![]() $f_{n+1}$
to satisfy Theorem 5(4a) or Theorem 5(4b), depending on whether n is even or odd, for an additional point in W. We will write
$f_{n+1}$
to satisfy Theorem 5(4a) or Theorem 5(4b), depending on whether n is even or odd, for an additional point in W. We will write
![]() $A_n$
to denote the set of finitely many points of W that have already been taken care of at stage n with regard to Theorem 5(4a), and we will write
$A_n$
to denote the set of finitely many points of W that have already been taken care of at stage n with regard to Theorem 5(4a), and we will write
![]() $B_n$
to denote the set of finitely many points of W that have been taken care of in regard to Theorem 5(4b).
$B_n$
to denote the set of finitely many points of W that have been taken care of in regard to Theorem 5(4b).
Suppose
![]() $\mathcal {D}$
is a partition of
$\mathcal {D}$
is a partition of
![]() $\mathbb {R}$
into dense sets, W is a countable set of real numbers, and
$\mathbb {R}$
into dense sets, W is a countable set of real numbers, and
![]() $P=(x_P,y_P)$
is a point in
$P=(x_P,y_P)$
is a point in
![]() $\mathbb {R}^2$
. Fix a 1-1 enumeration
$\mathbb {R}^2$
. Fix a 1-1 enumeration
![]() $\{ w_n \ : \ n \in \mathbb {N} \}$
of W, and for each n, let
$\{ w_n \ : \ n \in \mathbb {N} \}$
of W, and for each n, let
![]() $D_n$
be the unique member of
$D_n$
be the unique member of
![]() $\mathcal {D}$
containing
$\mathcal {D}$
containing
![]() $w_n$
. Since
$w_n$
. Since
![]() $\mathcal {D}$
is a partition, we have
$\mathcal {D}$
is a partition, we have
Suppose
![]() $p:{\mathbb {R}}\to {\mathbb {R}}$
is a continuous positive function such that
$p:{\mathbb {R}}\to {\mathbb {R}}$
is a continuous positive function such that
We will inductively define sequences
![]() $\langle f_n : n\in \mathbb {N}\rangle $
,
$\langle f_n : n\in \mathbb {N}\rangle $
,
![]() $\langle A_n : n\in \mathbb {N}\rangle $
and
$\langle A_n : n\in \mathbb {N}\rangle $
and
![]() $\langle B_n : n\in \mathbb {N}\rangle $
such that
$\langle B_n : n\in \mathbb {N}\rangle $
such that
![]() $A_0=\emptyset $
and
$A_0=\emptyset $
and
![]() $B_0=\emptyset $
and for all
$B_0=\emptyset $
and for all
![]() $n\in \mathbb {N}$
, we have
$n\in \mathbb {N}$
, we have
-
(I) n
 $f_n:{\mathbb {C}}\to {\mathbb {C}}$
is entire and
$f_n:{\mathbb {C}}\to {\mathbb {C}}$
is entire and
 $f_n\upharpoonright {\mathbb {R}}$
is real-valued;
$f_n\upharpoonright {\mathbb {R}}$
is real-valued; -
(II) n
 $f_n(x_P)=y_P$
;
$f_n(x_P)=y_P$
; -
(III) n
 $\forall x\in {\mathbb {R}} \ f_n'(x)\geq \frac {1}{2}+\frac {1}{2^n}$
, and thus
$\forall x\in {\mathbb {R}} \ f_n'(x)\geq \frac {1}{2}+\frac {1}{2^n}$
, and thus
 $f_n\upharpoonright {\mathbb {R}}$
is a bijection;
$f_n\upharpoonright {\mathbb {R}}$
is a bijection; -
(IV) n if
 $n>0$
, then
$n>0$
, then
 $\forall z\in {\mathbb {C}}\ |f_n(z)-f_{n-1}(z)|<\frac {1}{2^n}p(|z|)$
;
$\forall z\in {\mathbb {C}}\ |f_n(z)-f_{n-1}(z)|<\frac {1}{2^n}p(|z|)$
; -
(V) n if
 $n=2k+1$
is odd, then
$n=2k+1$
is odd, then
 $A_n=A_{n-1}\cup \{w_k\}$
,
$A_n=A_{n-1}\cup \{w_k\}$
,
 $B_n=B_{n-1}$
and we have
$B_n=B_{n-1}$
and we have
 $w_k\neq x_P \ \implies \ f_n(w_k)\in D_k$
;
$w_k\neq x_P \ \implies \ f_n(w_k)\in D_k$
; -
(VI) n if
 $n=2k+2$
is even, then
$n=2k+2$
is even, then
 $A_n=A_{n-1}$
,
$A_n=A_{n-1}$
,
 $B_n=B_{n-1}\cup \{w_k\}$
and we have
$B_n=B_{n-1}\cup \{w_k\}$
and we have
 $w_k\neq y_P \ \implies \ f_n^{-1}(w_k)\in D_k$
; and
$w_k\neq y_P \ \implies \ f_n^{-1}(w_k)\in D_k$
; and -
(VII) n if
 $n>0$
, then
$n>0$
, then
 $f_n\upharpoonright A_{n-1}=f_{n-1}\upharpoonright A_{n-1}$
and
$f_n\upharpoonright A_{n-1}=f_{n-1}\upharpoonright A_{n-1}$
and
 $f_n^{-1}\upharpoonright B_{n-1}=f_{n-1}^{-1}\upharpoonright B_{n-1}$
.
$f_n^{-1}\upharpoonright B_{n-1}=f_{n-1}^{-1}\upharpoonright B_{n-1}$
.
First, let us show that, assuming we have sequences
![]() $\langle f_n : n\in \mathbb {N}\rangle $
and
$\langle f_n : n\in \mathbb {N}\rangle $
and
![]() $\langle A_n : n\in \mathbb {N}\rangle $
and
$\langle A_n : n\in \mathbb {N}\rangle $
and
![]() $\langle B_n : n\in \mathbb {N}\rangle $
satisfying (I)
$\langle B_n : n\in \mathbb {N}\rangle $
satisfying (I)
![]() $_n$
-(VII)
$_n$
-(VII)
![]() $_n$
for all n, the pointwise limit defined by
$_n$
for all n, the pointwise limit defined by
![]() $f(z)=\lim _{n\to \infty }f_n(z)$
has all of the desired properties. Suppose D is any compact subset of
$f(z)=\lim _{n\to \infty }f_n(z)$
has all of the desired properties. Suppose D is any compact subset of
![]() ${\mathbb {C}}$
. Since
${\mathbb {C}}$
. Since
![]() $\sum _{n=1}^\infty \frac {1}{2^n}$
converges and since
$\sum _{n=1}^\infty \frac {1}{2^n}$
converges and since
![]() $p(|z|)$
is bounded on D, the fact that (IV)
$p(|z|)$
is bounded on D, the fact that (IV)
![]() $_n$
holds for all n ensures that the sequence
$_n$
holds for all n ensures that the sequence
![]() $\langle f_n : n\in \mathbb {N}\rangle $
is uniformly Cauchy on D. Hence, we can define a function
$\langle f_n : n\in \mathbb {N}\rangle $
is uniformly Cauchy on D. Hence, we can define a function
![]() $f:{\mathbb {C}}\to {\mathbb {C}}$
by letting
$f:{\mathbb {C}}\to {\mathbb {C}}$
by letting
![]() $f(z)=\lim _{n\to \infty }f_n(z)$
. Since the sequence
$f(z)=\lim _{n\to \infty }f_n(z)$
. Since the sequence
![]() $\langle f_n : n\in \mathbb {N}\rangle $
is uniformly Cauchy on any compact set, it follows that the convergence of
$\langle f_n : n\in \mathbb {N}\rangle $
is uniformly Cauchy on any compact set, it follows that the convergence of
![]() $\langle f_n : n\in \mathbb {N}\rangle $
to f is uniform on any compact set, and hence, f is an entire function.
$\langle f_n : n\in \mathbb {N}\rangle $
to f is uniform on any compact set, and hence, f is an entire function.
Now let us verify that Theorem 5(1)–(4) hold for f. By (I)
![]() $_n$
and closure of
$_n$
and closure of
![]() ${\mathbb {R}}$
in
${\mathbb {R}}$
in
![]() ${\mathbb {C}}$
, we see that
${\mathbb {C}}$
, we see that
![]() $f\upharpoonright {\mathbb {R}}$
is real valued, and since (III)
$f\upharpoonright {\mathbb {R}}$
is real valued, and since (III)
![]() $_n$
holds for all n, we have
$_n$
holds for all n, we have
![]() $f'(x)\geq \frac {1}{2}$
for all
$f'(x)\geq \frac {1}{2}$
for all
![]() $x\in {\mathbb {R}}$
. Thus, Theorem 5(1) and Theorem 5(2) hold. Theorem 5(3) holds since the sequence
$x\in {\mathbb {R}}$
. Thus, Theorem 5(1) and Theorem 5(2) hold. Theorem 5(3) holds since the sequence
![]() $\langle f_n(x_P) : n\in \mathbb {N}\rangle $
is constantly equal to
$\langle f_n(x_P) : n\in \mathbb {N}\rangle $
is constantly equal to
![]() $y_P$
. To show that Theorem 5(4) holds, let us prove that for all
$y_P$
. To show that Theorem 5(4) holds, let us prove that for all
![]() $i\in \mathbb {N}$
, if
$i\in \mathbb {N}$
, if
![]() $w_i\neq x_P$
, then
$w_i\neq x_P$
, then
![]() $f(w_i)\in D_i$
, and if
$f(w_i)\in D_i$
, and if
![]() $w_i\neq y_P$
, then
$w_i\neq y_P$
, then
![]() $f^{-1}(w_i)\in D_i$
. Fix
$f^{-1}(w_i)\in D_i$
. Fix
![]() $i\in \mathbb {N}$
. We have
$i\in \mathbb {N}$
. We have
![]() $w_i\in A_{2i+1}$
and
$w_i\in A_{2i+1}$
and
![]() $w_i\in B_{2i+2}$
, and furthermore, by (V)
$w_i\in B_{2i+2}$
, and furthermore, by (V)
![]() $_{2i+1}$
and (VI)
$_{2i+1}$
and (VI)
![]() $_{2i+2}$
,
$_{2i+2}$
,
![]() $w_i\neq x_P$
implies
$w_i\neq x_P$
implies
![]() $f_{2i+1}(w_i)\in D_i$
and
$f_{2i+1}(w_i)\in D_i$
and
![]() $w_i\neq y_P$
implies
$w_i\neq y_P$
implies
![]() $f_{2i+2}^{-1}(w_i)\in D_i$
. Since (VII)
$f_{2i+2}^{-1}(w_i)\in D_i$
. Since (VII)
![]() $_n$
holds for all n, we see that both of the sequences
$_n$
holds for all n, we see that both of the sequences
![]() $\langle f_n(w_i) : n\in \mathbb {N}\rangle $
and
$\langle f_n(w_i) : n\in \mathbb {N}\rangle $
and
![]() $\langle f_n^{-1}(w_i) : n\in \mathbb {N}\rangle $
are eventually constant, and indeed, for
$\langle f_n^{-1}(w_i) : n\in \mathbb {N}\rangle $
are eventually constant, and indeed, for
![]() $n\geq 2i+2$
, we have
$n\geq 2i+2$
, we have
![]() $f_n(w_i)=f_{2i+1}(w_i)$
and
$f_n(w_i)=f_{2i+1}(w_i)$
and
![]() $f_n^{-1}(w_i)=f_{2i+2}^{-1}(w_i)$
. Therefore,
$f_n^{-1}(w_i)=f_{2i+2}^{-1}(w_i)$
. Therefore,
![]() $f(w_i)=f_{2i+1}(w_i)$
and
$f(w_i)=f_{2i+1}(w_i)$
and
![]() $f^{-1}(w_i)=f_{2i+2}^{-1}(w_i)$
, so (4) holds.
$f^{-1}(w_i)=f_{2i+2}^{-1}(w_i)$
, so (4) holds.
It remains to show that we can inductively define sequences
![]() $\langle f_n : n\in \mathbb {N}\rangle $
,
$\langle f_n : n\in \mathbb {N}\rangle $
,
![]() $\langle A_n : n\in \mathbb {N}\rangle $
and
$\langle A_n : n\in \mathbb {N}\rangle $
and
![]() $\langle B_n : n\in \mathbb {N}\rangle $
that satisfy (I)
$\langle B_n : n\in \mathbb {N}\rangle $
that satisfy (I)
![]() $_n$
–(VII)
$_n$
–(VII)
![]() $_n$
for all
$_n$
for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Let
![]() $f_0:{\mathbb {C}}\to {\mathbb {C}}$
be
$f_0:{\mathbb {C}}\to {\mathbb {C}}$
be
![]() $f_0(z)=\frac {3}{2}(z-x_P)+y_P$
,
$f_0(z)=\frac {3}{2}(z-x_P)+y_P$
,
![]() $A_0=\emptyset $
and
$A_0=\emptyset $
and
![]() $B_0=\emptyset $
. One may easily verify that (I)
$B_0=\emptyset $
. One may easily verify that (I)
![]() $_0$
–(VII)
$_0$
–(VII)
![]() $_0$
hold. For
$_0$
hold. For
![]() $n> 0$
, Section 2.1 shows how
$n> 0$
, Section 2.1 shows how
![]() $f_n$
is constructed when n is odd, and Section 2.2 shows how
$f_n$
is constructed when n is odd, and Section 2.2 shows how
![]() $f_n$
is constructed when n is even.
$f_n$
is constructed when n is even.
2.1 When n is odd
Suppose
![]() $n=2k+1>0$
is odd and that
$n=2k+1>0$
is odd and that
![]() $f_i$
,
$f_i$
,
![]() $A_i$
and
$A_i$
and
![]() $B_i$
satisfying (I)
$B_i$
satisfying (I)
![]() $_i$
–(VII)
$_i$
–(VII)
![]() $_i$
have already been defined for
$_i$
have already been defined for
![]() $i\leq 2k$
. If
$i\leq 2k$
. If
![]() $k=0$
, we have
$k=0$
, we have
![]() $A_0=\emptyset $
and
$A_0=\emptyset $
and
![]() $B_0=\emptyset $
, whereas if
$B_0=\emptyset $
, whereas if
![]() $k>0$
, we have
$k>0$
, we have
and
In any case, we let
![]() $A_{n}=A_{n-1}\cup \{w_k\}$
and
$A_{n}=A_{n-1}\cup \{w_k\}$
and
![]() $B_{n}=B_{n-1}$
. We define
$B_{n}=B_{n-1}$
. We define
![]() $f_{n} = f_{2k+1}$
in two cases as follows.
$f_{n} = f_{2k+1}$
in two cases as follows.
Case 2.1. A:
![]() $\boldsymbol {w_k\notin \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})}$
. Let us argue that there is an entire function
$\boldsymbol {w_k\notin \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})}$
. Let us argue that there is an entire function
![]() $g_{n}$
such that
$g_{n}$
such that
-
(i)
 $(\forall z\in {\mathbb {C}}) \ g_{n}(z)=0 \ \iff \ z\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
,
$(\forall z\in {\mathbb {C}}) \ g_{n}(z)=0 \ \iff \ z\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
, -
(ii)
 $(\forall z\in {\mathbb {C}}) \ |g_{n}(z)|\leq \frac {1}{2^{n}}p(|z|)$
and
$(\forall z\in {\mathbb {C}}) \ |g_{n}(z)|\leq \frac {1}{2^{n}}p(|z|)$
and -
(iii)
 $(\forall x\in {\mathbb {R}}) \ g_{n}'(x)\geq -\frac {1}{2^{n}}$
.
$(\forall x\in {\mathbb {R}}) \ g_{n}'(x)\geq -\frac {1}{2^{n}}$
.
Take
where
![]() $\beta _n\in \{1,2\}$
is such that the degree of
$\beta _n\in \{1,2\}$
is such that the degree of
![]() $h_n$
is odd. We will show that for small enough positive
$h_n$
is odd. We will show that for small enough positive
![]() $\alpha _n\in {\mathbb {R}}$
, the function
$\alpha _n\in {\mathbb {R}}$
, the function
![]() $g_n(z)=\alpha _nh_n(z)$
satisfies (i)–(iii). Clearly,
$g_n(z)=\alpha _nh_n(z)$
satisfies (i)–(iii). Clearly,
![]() $h_n$
satisfies (i), so any such function
$h_n$
satisfies (i), so any such function
![]() $g_n(z)$
satisfies (i). For (ii), choose
$g_n(z)$
satisfies (i). For (ii), choose
![]() $m\in \mathbb {N}$
and some positive
$m\in \mathbb {N}$
and some positive
![]() $c\in {\mathbb {R}}$
such that
$c\in {\mathbb {R}}$
such that
![]() $|h_n(z)|\leq |z|^m+c$
for all
$|h_n(z)|\leq |z|^m+c$
for all
![]() $z\in {\mathbb {C}}$
. By our assumption on p, we have
$z\in {\mathbb {C}}$
. By our assumption on p, we have
![]() $\lim _{|z|\rightarrow \infty }\frac {p(|z|)}{|z|^m+c}=\infty $
, and thus we can let
$\lim _{|z|\rightarrow \infty }\frac {p(|z|)}{|z|^m+c}=\infty $
, and thus we can let
![]() $D\subseteq {\mathbb {C}}$
be a large enough closed disk centered at the origin such that
$D\subseteq {\mathbb {C}}$
be a large enough closed disk centered at the origin such that
![]() $z\in {\mathbb {C}}\setminus D$
implies
$z\in {\mathbb {C}}\setminus D$
implies
![]() $1\leq \frac {p(|z|)}{|z|^m+c}$
. Since p is a continuous positive function, we can choose a positive
$1\leq \frac {p(|z|)}{|z|^m+c}$
. Since p is a continuous positive function, we can choose a positive
![]() $\alpha _n\in {\mathbb {R}}$
such that
$\alpha _n\in {\mathbb {R}}$
such that
![]() $\alpha _n\leq \frac {1}{2^n}$
and
$\alpha _n\leq \frac {1}{2^n}$
and
![]() $\alpha _n\leq \frac {p(|z|)}{2^n(|z|^m+c)}$
for all
$\alpha _n\leq \frac {p(|z|)}{2^n(|z|^m+c)}$
for all
![]() $z\in D$
. Then it follows that for every
$z\in D$
. Then it follows that for every
![]() $z\in {\mathbb {C}}$
, we have
$z\in {\mathbb {C}}$
, we have
Let us verify that (iii) holds for small enough
![]() $\alpha _n$
. Since
$\alpha _n$
. Since
![]() $h_n$
is odd and has a positive leading coefficient, the derivative of
$h_n$
is odd and has a positive leading coefficient, the derivative of
![]() $h_n\upharpoonright {\mathbb {R}}$
is bounded below. So we may let
$h_n\upharpoonright {\mathbb {R}}$
is bounded below. So we may let
![]() $d=\inf \{h_n'(x) : x\in {\mathbb {R}}\}\in {\mathbb {R}}$
. Thus, we may choose a small enough positive
$d=\inf \{h_n'(x) : x\in {\mathbb {R}}\}\in {\mathbb {R}}$
. Thus, we may choose a small enough positive
![]() $\alpha _n\in {\mathbb {R}}$
such that
$\alpha _n\in {\mathbb {R}}$
such that
![]() $\alpha _nd\geq -\frac {1}{2^n}$
, and then it follows that for all
$\alpha _nd\geq -\frac {1}{2^n}$
, and then it follows that for all
![]() $x\in {\mathbb {R}}$
, we have
$x\in {\mathbb {R}}$
, we have
![]() $\alpha _nh_n'(x)\geq \alpha _n d\geq -\frac {1}{2^n}$
.
$\alpha _nh_n'(x)\geq \alpha _n d\geq -\frac {1}{2^n}$
.
Using the case assumption that
![]() $w_k\notin \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
, we see that
$w_k\notin \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
, we see that
![]() $g_n(w_k)\neq 0$
, and hence it follows that the set
$g_n(w_k)\neq 0$
, and hence it follows that the set
is a nontrivial interval of real numbers. Thus, since
![]() $D_k$
is dense in
$D_k$
is dense in
![]() ${\mathbb {R}}$
, it follows that there is some
${\mathbb {R}}$
, it follows that there is some
![]() $M_{n}\in [0,1]$
such that
$M_{n}\in [0,1]$
such that
![]() $f_{n-1}(w_k)+M_{n}g_{n}(w_k)\in D_k$
. We define
$f_{n-1}(w_k)+M_{n}g_{n}(w_k)\in D_k$
. We define
Let us show that (I)
![]() $_n$
–(VII)
$_n$
–(VII)
![]() $_n$
hold. It is trivial to see that (I)
$_n$
hold. It is trivial to see that (I)
![]() $_n$
and (II)
$_n$
and (II)
![]() $_n$
are true. For (III)
$_n$
are true. For (III)
![]() $_n$
, notice that because
$_n$
, notice that because
![]() $M_n\in [0,1]$
, and since (iii) and (III)
$M_n\in [0,1]$
, and since (iii) and (III)
![]() $_{n-1}$
both hold, we have for all
$_{n-1}$
both hold, we have for all
![]() $x\in {\mathbb {R}}$
,
$x\in {\mathbb {R}}$
,
and thus
![]() $f_n:{\mathbb {R}}\to {\mathbb {R}}$
is a bijection. For (IV)
$f_n:{\mathbb {R}}\to {\mathbb {R}}$
is a bijection. For (IV)
![]() $_n$
, we have for all
$_n$
, we have for all
![]() $z\in {\mathbb {C}}$
,
$z\in {\mathbb {C}}$
,
where the last inequality follows since
![]() $M_n\in [0,1]$
and (ii) holds. Let us verify that (V)
$M_n\in [0,1]$
and (ii) holds. Let us verify that (V)
![]() $_n$
holds. From the definition of
$_n$
holds. From the definition of
![]() $f_n=f_{2k+1}$
and the way we chose
$f_n=f_{2k+1}$
and the way we chose
![]() $M_{n}$
, it follows that
$M_{n}$
, it follows that
![]() $f_n(w_k)\in D_k$
(notice that
$f_n(w_k)\in D_k$
(notice that
![]() $w_k \neq x_P$
by our case assumption). Thus, (V)
$w_k \neq x_P$
by our case assumption). Thus, (V)
![]() $_n$
holds. (VI)
$_n$
holds. (VI)
![]() $_n$
holds trivially since n is odd. To see that (VII)
$_n$
holds trivially since n is odd. To see that (VII)
![]() $_n$
holds, note that since
$_n$
holds, note that since
![]() $g_{n}(z)=0$
if
$g_{n}(z)=0$
if
![]() $z\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
, it follows directly from the definition of
$z\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
, it follows directly from the definition of
![]() $f_n$
that
$f_n$
that
![]() $f_n\upharpoonright A_{n-1}=f_n\upharpoonright A_{n-1}$
and
$f_n\upharpoonright A_{n-1}=f_n\upharpoonright A_{n-1}$
and
![]() $f_n^{-1}\upharpoonright B_n=f_{n-1}^{-1}\upharpoonright B_{n-1}$
.
$f_n^{-1}\upharpoonright B_n=f_{n-1}^{-1}\upharpoonright B_{n-1}$
.
Case 2.1. B:
![]() $\boldsymbol {w_k\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})}$
. Then we let
$\boldsymbol {w_k\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})}$
. Then we let
![]() $f_n=f_{n-1}$
,
$f_n=f_{n-1}$
,
![]() $A_n=A_{n-1}\cup \{w_k\}$
and
$A_n=A_{n-1}\cup \{w_k\}$
and
![]() $B_n=B_{n-1}$
. Let us argue that this definition of
$B_n=B_{n-1}$
. Let us argue that this definition of
![]() $f_n$
satisfies (V)
$f_n$
satisfies (V)
![]() $_n$
; the rest of (I)
$_n$
; the rest of (I)
![]() $_n$
–(VII)
$_n$
–(VII)
![]() $_n$
are easily seen to hold by the inductive hypothesis. Suppose
$_n$
are easily seen to hold by the inductive hypothesis. Suppose
![]() $w_k\neq x_P$
. Since the enumeration of W is one-to-one, we have
$w_k\neq x_P$
. Since the enumeration of W is one-to-one, we have
![]() $w_k\neq w_j$
for all
$w_k\neq w_j$
for all
![]() $j\leq k-1$
. Thus, for some
$j\leq k-1$
. Thus, for some
![]() $j\leq k-1$
, we have
$j\leq k-1$
, we have
![]() $w_k=f_{n-1}^{-1}(w_j)$
, and because
$w_k=f_{n-1}^{-1}(w_j)$
, and because
![]() $f_{n-1}(x_P)=y_P$
,
$f_{n-1}(x_P)=y_P$
,
![]() $f_{n-1}$
is injective and
$f_{n-1}$
is injective and
![]() $w_k\neq x_P$
, it follows that
$w_k\neq x_P$
, it follows that
![]() $w_j\neq y_P$
. Since
$w_j\neq y_P$
. Since
![]() $2j+2\leq n-1$
and since it follows by our inductive assumptions (VII)
$2j+2\leq n-1$
and since it follows by our inductive assumptions (VII)
![]() $_{\ell }$
for
$_{\ell }$
for
![]() $\ell \leq n-1$
, that
$\ell \leq n-1$
, that
![]() $f_{n-1}\upharpoonright A_{2j+2}=f_{2j+2}\upharpoonright A_{2j+2}$
, we see that
$f_{n-1}\upharpoonright A_{2j+2}=f_{2j+2}\upharpoonright A_{2j+2}$
, we see that
![]() $w_k=f_{n-1}^{-1}(w_j)=f_{2j+2}^{-1}(w_j)\in D_j$
. Then
$w_k=f_{n-1}^{-1}(w_j)=f_{2j+2}^{-1}(w_j)\in D_j$
. Then
![]() $D_j = D_k$
by (*) from page 4. So,
$D_j = D_k$
by (*) from page 4. So,
![]() $f_n(w_k)=f_{n-1}(w_k)=w_j\in D_j=D_k$
, and hence, (V)
$f_n(w_k)=f_{n-1}(w_k)=w_j\in D_j=D_k$
, and hence, (V)
![]() $_n$
holds.
$_n$
holds.
2.2 When n is even
Now suppose
![]() $n=2k+2$
is even, where
$n=2k+2$
is even, where
![]() $k>0$
, and that
$k>0$
, and that
![]() $f_i$
,
$f_i$
,
![]() $A_i$
and
$A_i$
and
![]() $B_i$
satisfying (I)
$B_i$
satisfying (I)
![]() $_i$
–(VI)
$_i$
–(VI)
![]() $_i$
have already been defined for
$_i$
have already been defined for
![]() $i\leq 2k+1$
. We have
$i\leq 2k+1$
. We have
and
We will define
![]() $f_n$
,
$f_n$
,
![]() $A_n$
and
$A_n$
and
![]() $B_n$
in two cases as follows.
$B_n$
in two cases as follows.
Case 2.2. A:
![]() $\boldsymbol {f_{n-1}^{-1}(w_k)\notin \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})}$
. Then we let
$\boldsymbol {f_{n-1}^{-1}(w_k)\notin \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})}$
. Then we let
![]() $g_{n}$
be an entire function such that
$g_{n}$
be an entire function such that
-
(i)
 $(\forall z\in {\mathbb {C}}) \ g_{n}(z)=0 \ \iff \ z\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
,
$(\forall z\in {\mathbb {C}}) \ g_{n}(z)=0 \ \iff \ z\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
, -
(ii)
 $(\forall z\in {\mathbb {C}}) \ |g_{n}(z)|\leq \frac {1}{2^{n}}p(|z|)$
and
$(\forall z\in {\mathbb {C}}) \ |g_{n}(z)|\leq \frac {1}{2^{n}}p(|z|)$
and -
(iii)
 $(\forall x\in {\mathbb {R}})\ g_{n}'(x)\geq -\frac {1}{2^{n}}$
.
$(\forall x\in {\mathbb {R}})\ g_{n}'(x)\geq -\frac {1}{2^{n}}$
.
For example, as in the case above where n was odd, we could take
satisfying (i)–(iii) by choosing
![]() $\alpha _n$
small enough and
$\alpha _n$
small enough and
![]() $\beta _n\in \{1,2\}$
so that the degree of
$\beta _n\in \{1,2\}$
so that the degree of
![]() $g_n$
is odd. By our inductive assumption about
$g_n$
is odd. By our inductive assumption about
![]() $f_{n-1}$
and by (iii), it follows that for any
$f_{n-1}$
and by (iii), it follows that for any
![]() $M\in [0,1]$
and any
$M\in [0,1]$
and any
![]() $x\in {\mathbb {R}}$
, we have
$x\in {\mathbb {R}}$
, we have
Thus, the function
![]() $f_{n-1}+Mg_{n}:{\mathbb {R}}\to {\mathbb {R}}$
is a bijection. Let us argue that the set
$f_{n-1}+Mg_{n}:{\mathbb {R}}\to {\mathbb {R}}$
is a bijection. Let us argue that the set
is a nontrivial interval of real numbers. It will suffice to show that
![]() $(f_{n-1}+g_n)^{-1}(w_k)\neq f^{-1}_{n-1}(w_k)$
. Suppose
$(f_{n-1}+g_n)^{-1}(w_k)\neq f^{-1}_{n-1}(w_k)$
. Suppose
![]() $(f_{n-1}+g_n)^{-1}(w_k)= f_{n-1}^{-1}(w_k)$
. Then
$(f_{n-1}+g_n)^{-1}(w_k)= f_{n-1}^{-1}(w_k)$
. Then
![]() $f_{n-1}(f_{n-1}^{-1}(w_k))=w_k$
and
$f_{n-1}(f_{n-1}^{-1}(w_k))=w_k$
and
![]() $(f_{n-1}+g_n)(f^{-1}_{n-1}(w_k))=w_k$
. This implies that the functions
$(f_{n-1}+g_n)(f^{-1}_{n-1}(w_k))=w_k$
. This implies that the functions
![]() $f_{n-1}$
and
$f_{n-1}$
and
![]() $f_{n-1}+g_n$
are equal at the point
$f_{n-1}+g_n$
are equal at the point
![]() $f_{n-1}^{-1}(w_k)$
, and hence,
$f_{n-1}^{-1}(w_k)$
, and hence,
![]() $g_n(f_{n-1}^{-1}(w_k))=0$
, which contradicts (i) by our case assumption that
$g_n(f_{n-1}^{-1}(w_k))=0$
, which contradicts (i) by our case assumption that
![]() $f_{n-1}^{-1}(w_k) \notin \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
.
$f_{n-1}^{-1}(w_k) \notin \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})$
.
Thus, since
![]() $D_k$
is dense in
$D_k$
is dense in
![]() ${\mathbb {R}}$
, it follows that there is some
${\mathbb {R}}$
, it follows that there is some
![]() $M_{n}\in [0,1]$
such that
$M_{n}\in [0,1]$
such that
![]() $(f_{n-1}+M_{n}g_{n})^{-1}(w_k)\in D_k$
. We fix such an
$(f_{n-1}+M_{n}g_{n})^{-1}(w_k)\in D_k$
. We fix such an
![]() $M_{n}$
and define
$M_{n}$
and define
We also let
![]() $A_n=A_{n-1}$
and
$A_n=A_{n-1}$
and
![]() $B_n=B_{n-1}\cup \{w_k\}$
. The verification that (I)
$B_n=B_{n-1}\cup \{w_k\}$
. The verification that (I)
![]() $_n$
–(VII)
$_n$
–(VII)
![]() $_n$
hold is straightforward and similar to the above; it is therefore left to the reader.
$_n$
hold is straightforward and similar to the above; it is therefore left to the reader.
Case 2.2. B:
![]() $\boldsymbol {f_{n-1}^{-1}(w_k)\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})}$
, or equivalently,
$\boldsymbol {f_{n-1}^{-1}(w_k)\in \{x_P\}\cup A_{n-1}\cup f_{n-1}^{-1}(B_{n-1})}$
, or equivalently,
![]() $w_k\in \{y_P\}\cup f_{n-1}(A_{n-1})\cup B_{n-1}$
. Then we define
$w_k\in \{y_P\}\cup f_{n-1}(A_{n-1})\cup B_{n-1}$
. Then we define
![]() $f_n=f_{n-1}$
. As in the odd case above, this definition of
$f_n=f_{n-1}$
. As in the odd case above, this definition of
![]() $f_n$
is easily seen to satisfy (I)
$f_n$
is easily seen to satisfy (I)
![]() $_n$
–(V)
$_n$
–(V)
![]() $_n$
and (VII)
$_n$
and (VII)
![]() $_n$
. Let us check (VI)
$_n$
. Let us check (VI)
![]() $_n$
. Suppose
$_n$
. Suppose
![]() $w_k\neq y_P$
. Since the enumeration of W is one-to-one, we have
$w_k\neq y_P$
. Since the enumeration of W is one-to-one, we have
![]() $w_k\neq w_j$
for all
$w_k\neq w_j$
for all
![]() $j\leq k-1$
, and hence,
$j\leq k-1$
, and hence,
![]() $w_k=f_{n-1}(w_j)$
for some
$w_k=f_{n-1}(w_j)$
for some
![]() $j\leq k$
, where
$j\leq k$
, where
![]() $w_j\neq x_P$
. Since
$w_j\neq x_P$
. Since
![]() $2j+1\leq n-1$
, it follows by our inductive assumptions (V)
$2j+1\leq n-1$
, it follows by our inductive assumptions (V)
![]() $_{\ell }$
for
$_{\ell }$
for
![]() $\ell \leq n-1$
that
$\ell \leq n-1$
that
![]() $f_{n-1}\upharpoonright A_{2j+1}=f_{2j+1}\upharpoonright A_{2j+1}$
and
$f_{n-1}\upharpoonright A_{2j+1}=f_{2j+1}\upharpoonright A_{2j+1}$
and
![]() $w_k=f_{n-1}(w_j)=f_{2j+1}(w_j)\in D_j$
. Then by (*) from page 4,
$w_k=f_{n-1}(w_j)=f_{2j+1}(w_j)\in D_j$
. Then by (*) from page 4,
![]() $D_j = D_k$
. So
$D_j = D_k$
. So
![]() $f_n^{-1}(w_k) = f_{n-1}^{-1}(w_k) = w_j \in D_j = D_k$
.
$f_n^{-1}(w_k) = f_{n-1}^{-1}(w_k) = w_j \in D_j = D_k$
.
This concludes the proof of Theorem 5.
3 Proof of Theorem 2
To prove the
![]() $\Leftarrow $
direction of Theorem 2, assume that
$\Leftarrow $
direction of Theorem 2, assume that
![]() $\big \{ f_P \ : \ P \in \mathbb {R}^2 \big \}$
is a sparse analytic system and consider the subcollection
$\big \{ f_P \ : \ P \in \mathbb {R}^2 \big \}$
is a sparse analytic system and consider the subcollection
![]() $\big \{ f_{(0,y)} \ : \ y \in \mathbb {R} \big \}$
. Since
$\big \{ f_{(0,y)} \ : \ y \in \mathbb {R} \big \}$
. Since
![]() $f_{(0,y)}$
passes through the point
$f_{(0,y)}$
passes through the point
![]() $(0,y)$
and each
$(0,y)$
and each
![]() $f_{(0,y)}$
is analytic, and hence continuous, it follows that for
$f_{(0,y)}$
is analytic, and hence continuous, it follows that for
![]() $y \ne y'$
,
$y \ne y'$
,
![]() $f_{(0,y)} \restriction (-\infty ,0) \ne f_{(0,y')} \restriction (-\infty ,0)$
. So
$f_{(0,y)} \restriction (-\infty ,0) \ne f_{(0,y')} \restriction (-\infty ,0)$
. So
is a continuum-sized collection of analytic functions on the common domain
![]() $D:=(-\infty ,0)$
. Furthermore, given any
$D:=(-\infty ,0)$
. Furthermore, given any
![]() $z \in D$
, since
$z \in D$
, since
![]() $z \ne 0$
and the
$z \ne 0$
and the
![]() $f_P$
’s formed a sparse analytic system, it follows that
$f_P$
’s formed a sparse analytic system, it follows that
is countable. So
![]() $\mathcal {F}$
is a collection of analytic functions as in clause (2) of Erdős’ Theorem 1. So by that theorem, CH must hold.
$\mathcal {F}$
is a collection of analytic functions as in clause (2) of Erdős’ Theorem 1. So by that theorem, CH must hold.
To prove the
![]() $\Rightarrow $
direction of Theorem 2 – which is heavily inspired by Erdős’ proof of Theorem 1 – assume CH and fix an enumeration
$\Rightarrow $
direction of Theorem 2 – which is heavily inspired by Erdős’ proof of Theorem 1 – assume CH and fix an enumeration
![]() $\langle w_\alpha \ : \ \alpha < \omega _1 \rangle $
of
$\langle w_\alpha \ : \ \alpha < \omega _1 \rangle $
of
![]() $\mathbb {R}$
. Fix any partition
$\mathbb {R}$
. Fix any partition
![]() $\mathcal {D}$
of the reals into countable dense subsets of
$\mathcal {D}$
of the reals into countable dense subsets of
![]() $\mathbb {R}$
.Footnote 4 For each
$\mathbb {R}$
.Footnote 4 For each
![]() $\alpha < \omega _1$
, let
$\alpha < \omega _1$
, let
![]() $D_\alpha $
be the unique member of
$D_\alpha $
be the unique member of
![]() $\mathcal {D}$
containing
$\mathcal {D}$
containing
![]() $w_\alpha $
. Also fix an
$w_\alpha $
. Also fix an
![]() $\omega _1$
-enumeration
$\omega _1$
-enumeration
![]() $\langle P_\alpha =(a_\alpha ,b_\alpha ) \ : \ \alpha < \omega _1 \rangle $
of
$\langle P_\alpha =(a_\alpha ,b_\alpha ) \ : \ \alpha < \omega _1 \rangle $
of
![]() $\mathbb {R}^2$
.
$\mathbb {R}^2$
.
Fix an
![]() $\alpha < \omega _1$
. By Theorem 5, there exists an entire
$\alpha < \omega _1$
. By Theorem 5, there exists an entire
![]() $f_\alpha : \mathbb {C} \to \mathbb {C}$
such that:
$f_\alpha : \mathbb {C} \to \mathbb {C}$
such that:
-
(1)
 $f_\alpha \restriction \mathbb {R}$
is a real analytic bijection with strictly positive derivative;
$f_\alpha \restriction \mathbb {R}$
is a real analytic bijection with strictly positive derivative; -
(2)
 $f_\alpha (a_\alpha ) = b_\alpha $
(i.e.,
$f_\alpha (a_\alpha ) = b_\alpha $
(i.e.,
 $f_\alpha \restriction \mathbb {R}$
passes through the point
$f_\alpha \restriction \mathbb {R}$
passes through the point
 $P_\alpha $
);
$P_\alpha $
); -
(3) For each
 $w_\xi $
in the countable set
$w_\xi $
in the countable set
 $W_\alpha :=\{ w_\xi \ : \ \xi < \alpha \}$
,
$W_\alpha :=\{ w_\xi \ : \ \xi < \alpha \}$
,-
(a) if
 $w_\xi \ne a_\alpha $
, then
$w_\xi \ne a_\alpha $
, then
 $f_\alpha (w_\xi ) \in D_\xi $
; and
$f_\alpha (w_\xi ) \in D_\xi $
; and -
(b) if
 $w_\xi \ne b_\alpha $
, then
$w_\xi \ne b_\alpha $
, then
 $f_\alpha ^{-1}(w_\xi ) \in D_\xi $
.
$f_\alpha ^{-1}(w_\xi ) \in D_\xi $
.
-
We claim that
![]() $\{ f_\alpha \restriction \mathbb {R} \ : \ \alpha < \omega _1 \}$
is a sparse analytic system, and the only nontrivial requirement to verify is that if
$\{ f_\alpha \restriction \mathbb {R} \ : \ \alpha < \omega _1 \}$
is a sparse analytic system, and the only nontrivial requirement to verify is that if
![]() $w \in \mathbb {R}$
, then both
$w \in \mathbb {R}$
, then both
and
are countable. Say
![]() $w = w_\xi $
; then,
$w = w_\xi $
; then,
 $$ \begin{align*} A_w = A_{w_\xi} & \subseteq \underbrace{\{ f_\alpha(w_\xi) \ : \ \xi < \alpha < \omega_1 \text{ and } w_\xi \ne a_\alpha \}}_{\subseteq D_\xi \text{, by 3a}} \cup \underbrace{\{ f_\alpha(w_\xi) \ : \ \alpha \le \xi \}}_{\text{countable because } \xi < \omega_1}, \end{align*} $$
$$ \begin{align*} A_w = A_{w_\xi} & \subseteq \underbrace{\{ f_\alpha(w_\xi) \ : \ \xi < \alpha < \omega_1 \text{ and } w_\xi \ne a_\alpha \}}_{\subseteq D_\xi \text{, by 3a}} \cup \underbrace{\{ f_\alpha(w_\xi) \ : \ \alpha \le \xi \}}_{\text{countable because } \xi < \omega_1}, \end{align*} $$
and hence,
![]() $A_w$
is countable. Similarly,
$A_w$
is countable. Similarly,
 $$ \begin{align*} B_w =B_{w_\xi} & \subseteq \underbrace{\{ f^{-1}_\alpha(w_\xi) \ : \ \xi < \alpha < \omega_1 \text{ and } w_\xi \ne b_\alpha \}}_{\subseteq D_\xi\text{, by 3b}} \cup \underbrace{\{ f^{-1}_\alpha(w_\xi) \ : \ \alpha \le \xi \}}_{\text{countable because } \xi < \omega_1}, \end{align*} $$
$$ \begin{align*} B_w =B_{w_\xi} & \subseteq \underbrace{\{ f^{-1}_\alpha(w_\xi) \ : \ \xi < \alpha < \omega_1 \text{ and } w_\xi \ne b_\alpha \}}_{\subseteq D_\xi\text{, by 3b}} \cup \underbrace{\{ f^{-1}_\alpha(w_\xi) \ : \ \alpha \le \xi \}}_{\text{countable because } \xi < \omega_1}, \end{align*} $$
and hence,
![]() $B_w$
is countable.
$B_w$
is countable.
4 Proof of Theorem 4
The next lemma is the key connection between sparse analytic systems and predictors.
Lemma 6. Suppose
![]() $\mathcal {F}=\langle f_P \ : \ P \in \mathbb {R}^2 \rangle $
is a sparse analytic system. Let
$\mathcal {F}=\langle f_P \ : \ P \in \mathbb {R}^2 \rangle $
is a sparse analytic system. Let
![]() $\sim $
be the equivalence relation on
$\sim $
be the equivalence relation on
![]() $\mathbb {R}$
generated by the set
$\mathbb {R}$
generated by the set
Then,
-
(1) Each
 $\sim $
-equivalence class is countable.
$\sim $
-equivalence class is countable. -
(2) For every
 $P=(x_P,y_P) \in \mathbb {R}^2$
and every
$P=(x_P,y_P) \in \mathbb {R}^2$
and every
 $z \in \mathbb {R}$
: if
$z \in \mathbb {R}$
: if
 $z \ne x_P$
, then
$z \ne x_P$
, then
 $z \sim f_P(z)$
.
$z \sim f_P(z)$
.
Before proving Lemma 6, we say how the proof of Theorem 4 is finished: assuming CH, Theorem 2 yields the existence of a sparse analytic system. Let
![]() $\sim $
be the equivalence relation on
$\sim $
be the equivalence relation on
![]() $\mathbb {R}$
induced by the sparse analytic system via Lemma 6. The properties of
$\mathbb {R}$
induced by the sparse analytic system via Lemma 6. The properties of
![]() $\sim $
listed in the conclusion of Lemma 6 satisfy the assumptions of Lemma 20 of Cox-Elpers [Reference Cox and Elpers6], and that lemma tells us that if
$\sim $
listed in the conclusion of Lemma 6 satisfy the assumptions of Lemma 20 of Cox-Elpers [Reference Cox and Elpers6], and that lemma tells us that if
![]() $S:=\mathbb {R}/\sim $
and
$S:=\mathbb {R}/\sim $
and
is any analytic-anonymous S-predictor,Footnote 5 then
![]() $\mathcal {P}$
fails to predict the function
$\mathcal {P}$
fails to predict the function
![]() $x \mapsto [x]_\sim $
for almost every
$x \mapsto [x]_\sim $
for almost every
![]() $x \in \mathbb {R}$
.Footnote 6 In particular, there is no good analytic-anonymous S-predictor.
$x \in \mathbb {R}$
.Footnote 6 In particular, there is no good analytic-anonymous S-predictor.
(Proof of Lemma 6)
Part (2) holds because, by the definition of sparse analytic system,
![]() $f_P$
is injective and
$f_P$
is injective and
![]() $f_P(x_P)=y_P$
. So if
$f_P(x_P)=y_P$
. So if
![]() $z \ne x_P$
, then
$z \ne x_P$
, then
![]() $f_P(z) \ne y_P$
; so not only is
$f_P(z) \ne y_P$
; so not only is
![]() $z \sim f_P(z)$
, but the pair
$z \sim f_P(z)$
, but the pair
![]() $\big (z,f_P(z)\big )$
is an element of X.
$\big (z,f_P(z)\big )$
is an element of X.
To prove part (1), since X generates
![]() $\sim $
, it suffices to prove that for every
$\sim $
, it suffices to prove that for every
![]() $z \in \mathbb {R}$
, both
$z \in \mathbb {R}$
, both
and
are countable. But
and
which are both countable by definition of sparse analytic system.
5 Concluding Remarks
The notion of a sparse analytic system obviously generalizes to a sparse
![]() $\Gamma $
-system for any
$\Gamma $
-system for any
![]() $\Gamma \subseteq \text {Homeo}^+(\mathbb {R})$
, and Lemma 6 easily generalizes to such systems. In fact, Section 4 of Bajpai-Velleman [Reference Bajpai and Velleman2] and Section 5 of Cox-Elpers [Reference Cox and Elpers6] can both be viewed as constructions, in ZFC alone, of sparse
$\Gamma \subseteq \text {Homeo}^+(\mathbb {R})$
, and Lemma 6 easily generalizes to such systems. In fact, Section 4 of Bajpai-Velleman [Reference Bajpai and Velleman2] and Section 5 of Cox-Elpers [Reference Cox and Elpers6] can both be viewed as constructions, in ZFC alone, of sparse
![]() $\Gamma $
-systems (with
$\Gamma $
-systems (with
![]() $\Gamma =$
‘increasing
$\Gamma =$
‘increasing
![]() $C^\infty $
bijections’ in [Reference Bajpai and Velleman2] and
$C^\infty $
bijections’ in [Reference Bajpai and Velleman2] and
![]() $\Gamma =$
‘increasing smooth diffeomorphisms’ in [Reference Cox and Elpers6]).
$\Gamma =$
‘increasing smooth diffeomorphisms’ in [Reference Cox and Elpers6]).
We have shown that CH implies a negative answer to Bajpai-Velleman’s Question 3, but it is open whether ZFC alone implies a negative solution.