Definition 1. Consider an Artin group $A_S$ with $|S| \geq 2$ , and a simplex K of dimension $|S| - 1$ . We define a simplex of groups over K as follows. The simplex K is given a trivial local group. There is a one-to-one correspondance between the elements $s_i \in S$ and the codimension 1 faces of K, and we denote by $\Delta_{ s_i }$ these codimension 1 faces. In particular, $\Delta_{ s_i }$ is given the local group $\langle s_i \rangle$ . Changing the codimension, there is a bijection between the strict subsets of S and the faces of K. Every face of K of codimension k can be written uniquely as the intersection

\begin{equation*}\Delta_{S^{\prime}} \;:\!=\; \bigcap\limits_{s_i \in S'} \Delta_{ s_i } \text{ for some } S' \subsetneq S \text{ with } |S'| = k.\end{equation*}

The face $\Delta_{S^{\prime}}$ is then given the local group $A_{S^{\prime}}$ .

The morphism associated to an inclusion of faces $K_{S^{\prime\prime}} \subset K_{S^{\prime}}$ is the natural inclusion $\psi_{S'S''} \;:\; A_{S^{\prime\prime}} \hookrightarrow A_{S^{\prime}}$ . Let $\mathcal{P}$ be the poset of standard parabolic subgroups of $A_S$ ordered with natural inclusion. As each $A_{S^{\prime}}$ is itself an Artin group [ Reference Van der Lek23 ], there is a simple morphism, $\varphi\;:\; G(\mathcal{P}) \hookrightarrow A_S$ , given by inclusion, from the complex of groups to the Artin group. The complex $X_S := D_{K}(\mathcal{P},\varphi)$ obtained by development of $\mathcal{P}$ over K along $\varphi$ is called the Artin complex associated to $A_S$ (see [ Reference Bridson and Haefliger3 , theorem II·12·18] for the definition of development, see also the remark below).

Note that the action of $A_S$ on $X_S$ is without inversions and cocompact, with strict fundamental domain a single simplex which is isomorphic to K. To avoid any confusion, we will from now on denote by $\overline{K}$ the quotient space and by $\overline{\Delta}_{S^{\prime}}$ its faces, and we will denote by K a chosen fundamental domain of $X_S$ and by $\Delta_{S^{\prime}}$ its faces. For every simplex $\Delta$ of $X_S$ , there is a unique subset $S' \subsetneq S$ such that $\Delta$ is the same orbit as $\Delta_{S^{\prime}}$ . We say that such a simplex is of type $\boldsymbol{S'}$ .

Proof. This is a direct consequence of [ Reference Bridson and Haefliger3 , chapter II·12, proposition 12·20]. $X_S$ is connected because the Artin group $A_S$ is generated by its standard parabolic subgroups. Moreover, if $|S| \geq 3$ , then $A_S$ is the colimit of its standard parabolic subgroups, by [ Reference Van der Lek23 ], and thus $X_S= D_\Delta(\mathcal{P}, \varphi)$ is the universal cover of the complex of groups $G(\mathcal{P})$ , hence is simply-connected.

Definition 5. Let Y be a simplex in a simplicial complex X. The link of Y in X is the simpicial complex $Lk_X(Y)$ consisting of the simplices of X that are disjoint from Y and which together with Y span a simplex of X.

Proof. By [ Reference Bridson and Haefliger3 , chapter II·12, construction 12·24], it is possible to describe the link of a simplex in the development of a complex of groups as the development of an appropriate subcomplex of groups. We explain below how this applies to $X_S$ .

The link of $\overline{\Delta}_{S^{\prime}}$ in $\overline{K}$ is a simplex of dimension $|S'|-1$ , whose poset of faces is isomorphic to the poset of proper subsets of S ^′ ordered with the inclusion. The complex of groups $G(\overline{K})$ induces a complex of groups on the link $Lk_{\overline{K}}\big(\overline{\Delta}_{S^{\prime}}\big)$ . Moreover, there is a simple morphism $\varphi_{S^{\prime}} \;:\; G(Lk_{\overline{K}}\big(\overline{\Delta}_{S^{\prime}}\big)) \rightarrow A_{S^{\prime}}$ given by the family of homomorphisms

\begin{equation*}(\varphi_{S^{\prime}})_{S^{\prime\prime}}\;:\; A_{S^{\prime\prime}} \underset{\psi_{S^{\prime}S^{\prime\prime}}}{\longrightarrow} A_{S^{\prime}}.\end{equation*}

It follows from the construction described in [ Reference Bridson and Haefliger3 , chapter II·12, construction 12·24] that the link of $Lk_{X_S}(\Delta_{S^{\prime}})$ is isomorphic to the development $D(Lk_{\overline{K}}\big(\overline{\Delta}_{S^{\prime}}\big),\varphi_{S^{\prime}})$ . Note that the induced complex of groups on $Lk_{\overline{K}}\big(\overline{\Delta}_{S^{\prime}}\big)$ is naturally isomorphic to the complex of groups associated to $A_{S^{\prime}}$ in Definition 1. Moreover, the simple morphism $\varphi_{S^{\prime}}$ coincides with the simple morphism used in Definition 1 to define the Artin complex $X_{S^{\prime}}$ . Putting everything together, it now follows that the link $Lk_{X_S}(\Delta_{S^{\prime}})$ is isomorphic to $X_{S^{\prime}}$ .

This argument generalises in a straightforward way to any simplex $g\Delta_{S^{\prime}}$ of $X_S$ of type S ^′.

Definition 7. The systole of a simplicial complex X is

\begin{equation*}\operatorname{sys}\!(X) := \min \{ |\gamma| \ | \ \gamma \text{ is an embedded full cycle of } X \} \in \{3,4,\ldots, \infty\}.\end{equation*}

For $k \in \{3, \ldots, \infty\}$ , we say that X is locally k-large if $\operatorname{sys}\!(Lk_X(Y)) \geq k$ for all simplices $Y \subseteq X$ . We say that X is k-large if it is locally k-large and $\operatorname{sys}(X) \geq k$ . X is k-systolic if it is connected, simply-connected and locally k-large. Finally, X is called systolic if it is 6-systolic.

Proof. If $m_{ab}=\infty$ , it follows directly from the definition of the Artin complex that $X_S$ is the Bass–Serre tree associated to the splitting $\langle a \rangle * \langle b \rangle$ . The result is then immediate.

Let us now assume that $m_{ab} < \infty$ . Let e be the edge in X whose vertices x, y correspond to the cosets $\langle a \rangle$ and $\langle b \rangle$ . Let $\gamma$ be a non-backtracking loop in $X_S$ . Since $X_S$ is a bipartite graph coloured by the cosets of $\langle a \rangle$ and $\langle b \rangle$ respectively, the length of $\gamma$ is even. Denote by $e_0 , e_1, \ldots, e_k$ the edges of $\gamma$ . Since the action of $A_S$ on $X_S$ is transitive on edges, let us assume that $e_0 = e$ .

Note that the action of $\langle a \rangle$ is transitive on the set of edges around x, and so is the action of $\langle b \rangle$ on the edges around y. Assume without loss of generality that $\gamma$ first goes through x, i.e. $e_1$ and $e_0$ share the vertex x. Then $e_1$ must be of the form $a^{r_1} e$ , for some $r_1 \in \textbf{Z} \backslash \{0\}$ . Note that the edges $e_1$ and $e_2$ then share the vertex $a^{r_1}y$ . The action of $a^{r_1} \langle b \rangle a^{-r_1}$ is transitive on the set of edges around $a^{r_1}y$ , thus $e_2$ must of the form $a^{r_1} b^{r_2} e$ , for some $r_2 \in \textbf{Z} \backslash \{0\}$ . We continue this process by induction until $\gamma$ stops. In particular, the final edge $e_k$ is of the form

\begin{equation*}a^{r_1} b^{r_2} \cdots a^{r_{k-1}} b^{r_k}\end{equation*}

for non-zero integers $r_1, \ldots, r_k$ . But since $e_k = e$ as $\gamma$ is a loop, we get $a^{r_1} b^{r_2} \cdots a^{r_{k-1}} b^{r_k} e = e$ . Since $\operatorname{Stab}\!(e) = \{1\}$ , it follows that $a^{r_1} b^{r_2} \cdots a^{r_{k-1}} b^{r_k}$ must be trivial in $A_S$ . But it is also a non-trivial word, as $\gamma$ is not homotopically trivial. By [ Reference Appel and Schupp1 , lemma 6], we must have $k \geq 2m_{ab}$ . Hence, the combinatorial length of $\gamma$ is $|\gamma| = k \geq 2 m_{ab}$ .

Proof of Theorem 8. We will prove by induction on the number $|S|$ of generators of the Artin groups $A_S$ that their associated Artin complexes $X_S$ are 2k-systolic.

If $|S| = 3$ , we know from Lemma 4 that $X_S$ is connected and simply connected. It only remains to show that for all $g \in A_S$ , for all $S' \subsetneq S$ , the simplex $g \cdot \Delta_{S^{\prime}}$ is such that $Lk_{X_S}(g \cdot \Delta_{S^{\prime}})$ is 2k-large. If $|S'| = 2$ , then the link $Lk_{X_S}(g \cdot \Delta_{S^{\prime}})$ is isomorphic to the Artin complex $X_{S^{\prime}}$ associated to the Artin group $A_{S^{\prime}}$ (Lemma 6), and the latter is 2k-large by Lemma 9. The cases $|S'| = 0$ or 1 are trivial.

Let us now assume that $|S| > 3$ and that every Artin complex $A_{S^{\prime}}$ with $S' \subsetneq S$ is 2k-systolic. Again, we know from Lemma 4 that $X_S$ is connected and simply connected, so it only remains to show that for all $g \in A_S$ , for all $S' \subsetneq S$ , the simplex $g \cdot \Delta_{S^{\prime}}$ is such that $Lk_{X_S}(g \cdot \Delta_{S^{\prime}})$ is 2k-large. If $|S'| \geq 2$ , then $Lk(g \cdot \Delta_{S^{\prime}},X_S)$ is isomorphic to the Artin complex $X_{S^{\prime}}$ associated to the Artin group $A_{S^{\prime}}$ (Lemma 6). The latter is 2k-systolic by the induction hypothesis, hence is 2k-large as well [ Reference Januszkiewicz and Światkowski16 , proposition 1·4]. Once again, the cases $|S'| = 0$ or 1 are trivial.

Definition 10. Let $P_1$ and $P_2$ be two parabolic subgroups of an Artin group $A_S$ such that $P_1\subseteq P_2$ . We say that $P_1$ is a parabolic subgroup of $P_2$ if $P_1\subseteq P_2$ is conjugate to an inclusion of standard parabolic subgroups $A_{S^{\prime\prime}}\subseteq A_{S^{\prime}}$ , $S''\subseteq S'$ .

Proof. By construction, every standard parabolic subgroup $A_{S^{\prime}}$ is precisely the stabiliser of some simplex $\Delta_{S^{\prime}}$ lying on the fundamental domain K of $X_S$ , and viceversa. Moreover, any parabolic subgroup of the form $g A_{S^{\prime}} g^{-1}$ is the stabiliser of the simplex $g\cdot \Delta_{S^{\prime}}$ , $g\in A$ . To prove the first claim, notice that any simplex of $X_S$ can be expressed as $g' \cdot \Delta'$ , where $\Delta'$ is in K and $g'\in A$ .

Let us now prove the second claim. On the one hand, let P be a parabolic subgroup of ${\rm Stab}_{X_S}(\Delta)$ . Up to conjugation, we can suppose that $\Delta$ lies in K of $X_S$ , and that P is the stabiliser of a simplex $\Delta'$ that also lies in K. Now notice that, by construction of the fundamental domain, this implies that $\Delta'$ contains $\Delta$ , as we desired. On the other hand, note that if $\Delta''$ is a simplex that contains $\Delta$ , then we can find an element $g\in A_S$ such that $g\cdot \Delta''$ belongs to K. Hence $g'{\rm Stab}_{X_S}(\Delta'')g'^{-1}\subseteq g'{\rm Stab}_{X_S}(\Delta)g'^{-1}$ is an inclusion of standard parabolic subgroups, as we wanted to prove.

Proof. We prove the result by induction on the combinatorial distance between v and v ^′. If $d(v,v')=1$ , the result is immediate, as there is unique edge between v and v ^′. Suppose by induction that the result is true for vertices at distance at most $n \geq 1$ , and let v, v ^′ be two vertices of Y at distance $n+1$ . Since Y is systolic, it follows from [ Reference Januszkiewicz and Światkowski16 , corollary 7·5] that the combinatorial ball of radius n around v ^′, denoted B(v ^′, n), is a convex subset of Y in the sense of [ Reference Januszkiewicz and Światkowski16 , definition 7·1]. Moreover, by [ Reference Januszkiewicz and Światkowski16 , lemma 7·7], this combinatorial ball intersects the combinatorial ball B(v,1) along a single simplex. This implies that there exists a simplex $\Delta$ of Y containing v, and such that every combinatorial geodesic from v to v ^′ starts with an edge of $\Delta$ . In particular, we define $\Delta'$ as the simplex of Y spanned by the first edges of all the combinatorial geodesics from v to v ^′. Since H fixes v and v ^′, H preserves the set of combinatorial geodesics from v to v ^′, and in particular H stabilises $\Delta'$ . Since G acts on Y without inversion, it follows that H fixes $\Delta'$ pointwise.

Let $\gamma$ be a combinatorial geodesic from v to v ^′. By the above, H fixes the first edge e of $\gamma$ . Let $v_1$ be the vertex of e distinct from v. We have that H fixes $v_1$ and v ^′, and these two vertices are at combinatorial distance n. By the induction hypothesis, H fixes pointwise the portion of $\gamma$ between $v_1$ and v ^′, and it now follows that H fixes pointwise all of $\gamma$ . This concludes the induction.

Proof of Theorem 11. We will prove the theorem by induction on the number n of generators of $A_S$ . If $n=2$ , $A_S$ is an Artin group on two generators a, b and there are two cases to consider. If $m_{ab}<\infty$ , then $A_S$ is a spherical Artin group, so item follows from [ Reference María Cumplido, González-Meneses and Wiest9 , theorem 9·5] and item follows from [ Reference Godelle11 , theorem 0·2]. If $m_{ab}=\infty$ , then $A_S$ is a free group on two generators a, b. Moreover, the proper parabolic subgroups are either trivial or infinite cyclic. Since the action of $A_S$ on the Bass–Serre tree associated to the splitting $\langle a \rangle * \langle b \rangle$ has trivial edge stabilisers, it follows that two distinct proper parabolic subgroups intersect trivially. Thus, item and item follow immediately.

Let us now assume that the result is known for Artin groups of large type on at most n generators with $n\geq 2$ , and let $A_S$ be an Artin group of large type on $n + 1$ generators. Let $X_S$ be its associated Artin complex.

Claim 1. Let $e_1,\dots, e_k$ be a combinatorial path p in $X_S$ . Then there exists a simplex $\Delta$ of $X_S$ containing the edge $e_k$ such that

\begin{equation*}\bigcap_{1\leq i \leq k} {\rm Stab}_{X_S}(e_i) = {\rm Stab}_{X_S} (\Delta).\end{equation*}

Proof of Claim 1. We will prove the claim by induction on k. If $k=1$ , p is just the edge $e_1$ and the proof is trivial. Now suppose that the claim is true for k and let us prove it for $k+1$ . By applying the induction hypothesis to the subpath $e_1, \ldots, e_k$ , we will then have

\begin{equation*}\bigcap_{1\leq i \leq k+1} {\rm Stab}_{X_S}(e_i) = {\rm Stab}_{X_S} (\Delta') \cap {\rm Stab}_{X_S}(e_{k+1}),\end{equation*}

where $\Delta'$ is a simplex containing the edge $e_k$ . Let v be a vertex contained in both $e_k$ and $e_{k+1}$ . By Lemma 12, this means that both ${\rm Stab}_{X_S}(\Delta')$ and ${\rm Stab}_{X_S}(e_{k+1})$ are parabolic subgroups of ${\rm Stab}_{X_S}(v)$ . Also, up to conjugacy, ${\rm Stab}(v)$ is an Artin group on n generators. Therefore, by the induction hypothesis on n, ${\rm Stab}_{X_S} (\Delta') \cap {\rm Stab}_{X_S}(e_{k+1})$ is a parabolic subgroup of ${\rm Stab}(v)$ contained in ${\rm Stab}_{X_S}(e_{k+1})$ , so it is a parabolic subgroup of ${\rm Stab}_{X_S}(e_{k+1})$ . Geometrically, ${\rm Stab}_{X_S} (\Delta') \cap {\rm Stab}_{X_S}(e_{k+1})$ is the stabiliser of some simplex containing $e_{k+1}$ . This completes the proof of Claim 1.

Claim 2. Let $\Delta_1$ and $\Delta_2$ be two simplices of $X_S$ . Then there exists a simplex $\Delta$ of $X_S$ containing $\Delta_2$ such that ${\rm Stab}_{X_S}(\Delta_1) \cap {\rm Stab}_{X_S}(\Delta_2) = {\rm Stab}_{X_S} (\Delta).$

Proof of Claim 2. Let $\Delta'$ be any simplex of $X_S$ and let $V_{\Delta'}$ be the set of vertices of $\Delta'$ . As the action of $A_S$ on $X_S$ is without inversions, we have that ${\rm Stab}_{X_S}(\Delta')= \cap_{w\in V_{\Delta^{\prime}}} {\rm Stab}(w)$ . Define a combinatorial path p that is the concatenation of the three following paths: a combinatorial path $p_1$ that travels along every vertex in $ V_{\Delta_1}$ ; a combinatorial geodesic $p_2$ between the endpoint of $p_1$ and $ V_{\Delta_2}$ ; and a combinatorial path that starts in the endpoint of $p_2$ and travels along every vertex in $ V_{\Delta_2}$ . Denote the endpoint of p by v and let $E_p$ be the set of edges of p. Then, by Claim 1 and Lemma 14,

\begin{equation*}{\rm Stab}_{X_S}(\Delta_1) \cap {\rm Stab}_{X_S}(\Delta_2)= \bigcap_{w\in {V_{\Delta_1} \cup V_{\Delta_2}} } {\rm Stab}_{X_S}(w)= \bigcap_{e\in E_p} {\rm Stab}_{X_S}(e)= {\rm Stab}_{X_S}(\Delta),\end{equation*}

for some simplex $\Delta$ containing v. Now we need to show that $\Delta$ contains also $\Delta_2$ . Notice that ${\rm Stab}_{X_S}(\Delta_2)$ contains ${\rm Stab}_{X_S}(\Delta)$ and both ${\rm Stab}_{X_S}(\Delta_2)$ and ${\rm Stab}_{X_S}(\Delta)$ are parabolic subgroups of ${\rm Stab}_{X_S}(v)$ . This group is, up to conjugacy, an Artin group on n generators. So by using the induction hypothesis on n, ${\rm Stab}_{X_S}(\Delta)$ is a parabolic subgroup of ${\rm Stab}_{X_S}(\Delta_2)$ , which means that we can choose $\Delta$ to contain $\Delta_2$ . This finishes the proof of Claim 2.

Claim 3. For every pair of simplices $\Delta_1$ and $\Delta_2$ of $X_S$ such that ${\rm Stab}_{X_S}(\Delta_1)\subseteq {\rm Stab}_{X_S}(\Delta_2)$ , there exists a simplex $\Delta$ of $X_S$ containing $\Delta_2$ such that ${\rm Stab}_{X_S}(\Delta_1) = {\rm Stab}_{X_S} (\Delta).$

Proof of Claim 3. Just notice that ${\rm Stab}_{X_S}(\Delta_1)= {\rm Stab}_{X_S}(\Delta_1) \cap {\rm Stab}_{X_S}(\Delta_2)$ , so by Claim 2 there is a simplex $\Delta$ containing $\Delta_2$ such that ${\rm Stab}_{X_S}(\Delta_1)={\rm Stab}_{X_S}(\Delta)$ . This completes the proof of the claim.

Proof. Let $\mathcal{P}$ be an arbitrary set of parabolic subgroups of $A_S$ and let $Q= \cap_{P\in\mathcal{P}} P$ . Q is contained in every parabolic subgroup in $\mathcal{P}$ , so by Theorem 11, we just need to prove that Q is equal to a finite intersection of parabolic subgroups. Notice that every parabolic subgroup is expressed as the conjugate of some standard parabolic subgroup. Since $A_S$ is a countable group and there are only finitely many standard parabolic subgroups of $A_S$ , the set of parabolic subgroups of $A_S$ is countable. In particular, $\mathcal{P}$ is countable. Enumerate the elements in $\mathcal{P}=\{P_1, P_2, P_3,\dots\}$ and let

\begin{equation*}Q_m = \bigcap_{1\leq i\leq m} P_i.\end{equation*}

By Theorem 11, all $Q_m$ ’s belong to $\mathcal{P}$ . As $Q=\cap_{i\in \mathbb{N}} Q_m$ , we need to show that the set $\{Q_m\, | \, m\in \mathbb{N} \}$ is finite.

Proof. $(\!\subseteq\!)$ Let $g \in N(P)$ , that is, $g P = P g$ , and let $v \in {\rm Fix}(P)$ . Then

\begin{equation*}P \cdot (g \cdot v) = g \cdot (P \cdot v) = g \cdot v.\end{equation*}

In particular, $g \cdot v \in {\rm Fix}(P)$ and thus $g \in {\rm Stab}({\rm Fix}(P))$ .

Proof. We have $Lk_{{\rm Fix}(P)}(\sigma) = {\rm Fix}(P)\cap Lk_{X_S}(\sigma)$ . Since $Lk_{X_S}(\sigma)$ is equivariantly isomorphic to $X_{S^{\prime\prime}}$ by Lemma 6, the previous intersection is thus isomorphic to ${\rm Fix}_{X_{S^{\prime\prime}}}(P)$ .

Proof. We will be using the following claim:

Proof. By Lemma 17 we know that $N(P) = {\rm Stab}({\rm Fix}(P))$ . Moreover, we know from Lemma 20 that there is a simplex $\Delta$ in $X_S$ such that ${\rm Fix}(P) = \Delta$ and ${\rm Stab}(\Delta)=P$ . In particular,

\begin{equation*}N(P) = {\rm Stab}({\rm Fix}(P)) = {\rm Stab}(\Delta) {=} P.\end{equation*}

Definition 23. A subcomplex Y of a simplicial complex X is 3-convex if it is full and every combinatorial geodesic of length 2 with endpoints in Y is contained in Y. It is locally 3-convex if for every simplex $\sigma$ of Y, the link $Lk_Y(\sigma)$ is 3-convex in $Lk_X(\sigma)$ .

Proof of Lemma 22. By Lemma 14, ${\rm Fix}(P)$ contains every geodesic between two vertices of ${\rm Fix}(P)$ . In particular, it is connected and 3-convex, hence locally 3-convex by [ Reference Januszkiewicz and Światkowski16 , fact 3·3·1]. By [ Reference Januszkiewicz and Światkowski16 , lemma 7·2], ${\rm Fix}(P)$ is thus contractible.

Definition 24. The dual graph $T_P$ of ${\rm Fix}(P)$ is defined as follows:

Proof. Since the star $\mathrm{Star}_X(v)$ is isomorphic to a cone over ${Lk}_X(v)$ , we first notice that X is obtained from $X-v$ by coning-off the contractible link ${Lk}_X(v)$ . Recall that for a simplicial complex Y and a contractible subcomplex Z, the quotient map $Y \rightarrow Y/Z$ obtained by collapsing Z to a point is a homotopy equivalence, see [ Reference Hatcher14 , proposition 0·17]. We thus have the following commutative diagram:

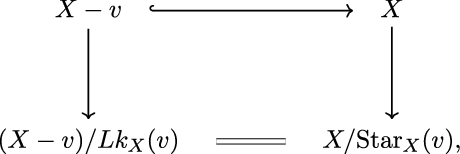
where both vertical arrows are homotopy equivalences since ${Lk}_X(v)$ and its cone $\mathrm{Star}_X(v)$ are contractible. Thus, the inclusion $X-v \hookrightarrow X$ is a homotopy equivalence, and it follows from [ Reference Hatcher14 , corollary 0·20] that the subcomplex spanned by $X-v$ is a deformation retract of X.

Proof of Lemma 25. Consider the barycentric subdivision ${\rm Fix}(P)'$ of ${\rm Fix}(P)$ . A vertex v of ${\rm Fix}(P)'$ corresponds to a simplex of ${\rm Fix}(P)$ ; We will call the dimension of the corresponding simplex the height of v. For every $0 \leq k \leq |S|-2$ , we define the subcomplex $X_k$ of ${\rm Fix}(P)'$ spanned by the vertices of height at least k. In particular, $X_0 = {\rm Fix}(P)'$ and $X_{|S|-2}$ is a subgraph of ${\rm Fix}(P)'$ containing $T_P$ .

We now show that for every $0\leq k \leq |S|-3$ , $X_{k+1}$ is a deformation retract of $X_k$ . Notice that $X_k$ is obtained from $X_{k+1}$ by adding for every vertex v of height k the star $ \mathrm{Star}_{X_{k}}(v)$ , which is isomorphic to a simplicial cone over the link ${Lk}_{X_k}(v)$ . Let v be a vertex of height $0 \leq k \leq |S|-3$ . This vertex corresponds to a simplex $\Delta$ of ${\rm Fix}(P)$ of type S ^′ for some subset $S'\subsetneq S$ with $|S'|\geq 3$ . Note that a vertex of $X_k$ adjacent to v must have height greater than k by construction, hence the link ${Lk}_{X_{k}}(v)$ is isomorphic to the first barycentric subdivision of ${Lk}_{{\rm Fix}(P)}(\Delta)$ . In particular, ${Lk}_{X_{k}}(v)$ is isomorphic to the first barycentric subdivision of ${\rm Fix}_{X_{S^{\prime}}}(P)$ by Lemma 19, and hence is contractible by Lemma 22. It thus follows from Lemma 26 that $X_{k+1}$ is a deformation retract of $X_{k+1} \cup \mathrm{Star}_{X_{k}}(v)$ . Since for two distinct vertices v, v ^′ of height k, the subcomplexes $X_{k+1} \cup \mathrm{Star}_{X_{k}}(v)$ and $X_{k+1} \cup \mathrm{Star}_{X_{k}}(v')$ intersect along $X_{k+1}$ , we can glue the various deformation retractions into a deformation retraction of

\begin{equation*}X_{k} = X_{k+1} \cup \bigcup_{\mathrm{height}(v)=k} \mathrm{Star}_{X_{k}}(v)\end{equation*}

onto $X_{k+1}$ . Thus, for every $0\leq k \leq |S|-3$ , $X_{k+1}$ is a deformation retract of $X_k$ . Thus, the graph $X_{|S|-2}$ is a deformation retract of $X_0 = {\rm Fix}(P)'$ . Since the latter complex is contractible by Lemma 22, so is the graph $X_{|S|-2}$ , and it follows that $X_{|S|-2}$ is a tree. Finally, $T_P$ is obtained from $X_{|S|-2}$ by removing the type 2 vertices that have valence 1. Thus, $T_P$ is a deformation retract of $X_{|S|-2}$ , hence $T_P$ is a tree.

Note that since $N(P) = {\rm Stab}({\rm Fix}(P))$ by Lemma 17, N(P) acts on ${\rm Fix}(P)$ , hence on the dual tree $T_P$ . We will use this action to prove the following:

Proof of Lemma 29. A type 1 vertex v of $T_P$ corresponds to a maximal simplex of ${\rm Fix}(P)$ . Such a simplex has stabiliser P by construction, hence ${\rm Stab}_{N(P)/P}(v)$ is trivial.

Let v be a type 2 vertex of $T_P$ of type $\{c, d\}$ . This vertex corresponds to a simplex with associated coset $gA_{cd}$ for some $g \in A_\Gamma$ . It follows from [ Reference Martin and Przytycki18 , lemma 4·5] and Lemma 30 that we have:

1. (i) if $m_{cd}$ is even, then

   \begin{equation*}{\rm Stab}_{N(P)/P}(v) = gZ(A_{cd})g^{-1} = \langle g\delta_{cd}g^{-1} \rangle; \end{equation*}

2. (ii) if $m_{cd}$ is odd, then

   \begin{equation*}{\rm Stab}_{N(P)/P}(v) = gZ(A_{cd})g^{-1} = \langle g\delta_{cd}^2g^{-1} \rangle,\end{equation*}

We are now ready to prove Lemma 27.

Proof of Lemma 27. Since two type 1 vertices of $T_P$ corresponding to cosets of the same standard parabolic subgroup are in the same N(P)-orbit, hence in the same $N(P)/P$ orbit, it follows that the action of $N(P)/P$ on $T_P$ is cocompact.

Thus, N(P) acts cocompactly and without inversion on a simplicial tree. By Lemma 29 the stabilisers of type 1 vertices are trivial (hence so are the stabilisers of edges) and the stabilisers of type 2 vertices are infinite cyclic. It thus follows from Bass–Serre theory that $N(P)/P$ is a finitely-generated free group, and thus N(P) splits as a semi-direct product $P\rtimes F$ , where F is a finitely generated free group. To see that this product is a direct product, it is enough to show that P is central in N(P). Let $a^k$ (with $k \in \mathbb{Z}$ ) be an element of $P = \langle a \rangle$ and let $h \in N(P)$ . Since h normalises P, there exists an integer $\ell \in \mathbb{Z}$ such that $ha^kh^{-1} = a^\ell$ . By applying to this equality the homomorphism $A_S \rightarrow \mathbb{Z}$ that sends every generator to 1, it follows that $k = \ell$ , hence $a^k$ is central in N(P). This concludes the proof.

An explicit basis of the normaliser. Finding an explicit basis for the free subgroup appearing in Theorem E is now a standard application of Bass–Serre theory, which was stated as a remark without further justification in [ Reference Martin and Przytycki18 , remark 4·6]. We first start by describing a fundamental domain for the action, as well as the quotient space $T_P/N(P)$ .

Definition 31. Let $\Gamma'$ be the first barycentric subdivision of the Coxeter graph $\Gamma_S$ . A vertex of $\Gamma'$ corresponding to a generator a of $A_S$ will be denoted $v_a$ and will be said to be of type 1, while a vertex of $\Gamma'$ corresponding to an edge of $\Gamma$ between generators a and b will be denoted $v_{ab}$ and will be said to be of type 2.

Let a be a generator of $A_S$ and let $P = \langle a \rangle$ be the corresponding standard parabolic subgroup. Let $\Gamma_{a, \mathrm{odd}}$ denote the maximal connected subgraph of $\Gamma$ that contains the vertex a and only odd-labelled edges. Let $\Gamma_P$ be the graph obtained from the disjoint union of all the edges of $\Gamma'$ that contain a vertex of $\Gamma_{a, \mathrm{odd}}$ , by the following identification: if such an edge e (e ^′ respectively) of $\Gamma'$ contains a vertex v (v ^′ respectively) such that v, v ^′ correspond to the same vertex of $\Gamma_{a, \mathrm{odd}}$ , then v and v ^′ are identified and define the same vertex of $\Gamma_P$ .

Some examples of the graph $\Gamma_P$ are given in Figure 1, when the underlying Coxeter graph is a triangle.

Definition 32. Let e be an edge of $\Gamma_P$ between a type 1 vertex $v_c$ and a type 2 vertex $v_{cd}$ , for c,d spanning an edge of $\Gamma$ . We denote by $\widetilde{e}$ the edge of $T_P$ between the vertex $A_c$ and the vertex $A_{cd}$ . Choose an orientation of each edge of $\Gamma$ . For each oriented path of $\Gamma_P$ based at $v_a$ , we denote by $e_1, \ldots, e_n$ the oriented sequences of edges of $\Gamma$ crossed by $\gamma$ , and we define

\begin{equation*}g_\gamma := \delta_{e_1}^{\pm1}\cdots \delta_{e_n}^{\pm1},\end{equation*}

where the sign for each Garside element $\delta_{e_i}$ depends on whether $\gamma$ follows the orientation of $e_i$ .

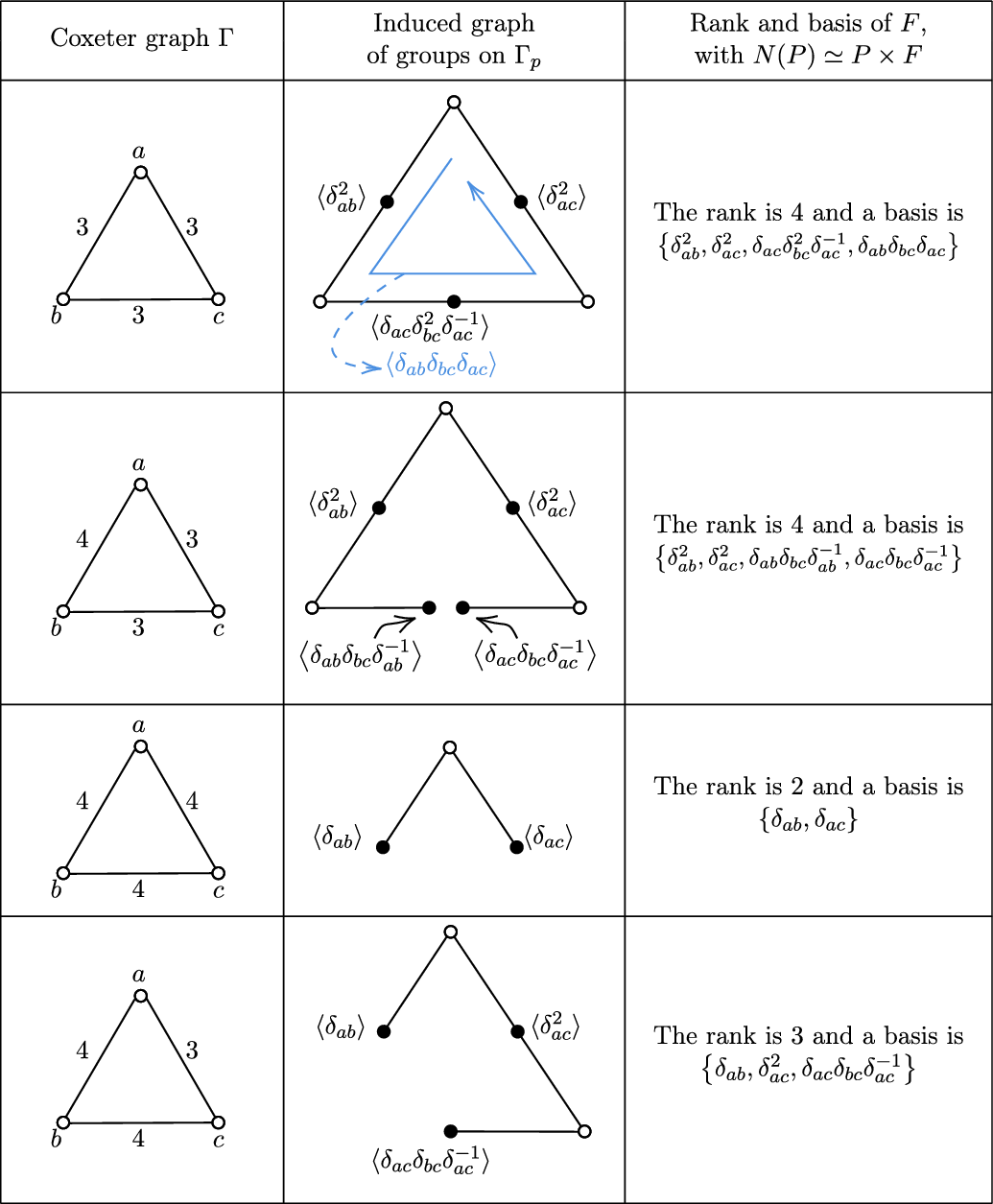
Fig. 1. Examples of computations of normalisers of the parabolic subgroup $P=\langle a \rangle$ , for various large-type triangular Artin groups. Type 2 vertices of $\Gamma_P$ are indicated in bold in the second column and come with their infinite cyclic stabilisers. The group element in blue corresponds to the element of a basis of F coming from the fundamental group of $\Gamma_P$ . Note that the structure of the normaliser for large-type triangular Artin groups depends only on the parity of the labels and not on the labels themselves, so the above cases cover all possible cases.

We now choose a spanning tree $\tau$ of $\Gamma_P$ , which we think of as being based at $v_a$ . For a vertex v of $\Gamma_P$ , we denote $\gamma_v$ the oriented geodesic of $\tau$ from $v_a$ to v. Let e be an edge of $\Gamma_P$ . If e is contained in $\tau$ , let v be the vertex of e closest to $v_a$ in $\tau$ . If e is not contained in $\tau$ , let v be the vertex of e closest to $v_a$ in $\Gamma_P$ (as $\Gamma_P$ is bipartite). We denote $g_v := g_{\gamma_v}$ , and we set

\begin{equation*}Y_P := \bigcup_{e \subset \Gamma_P} g_{v}\widetilde{e}.\end{equation*}

This defines a connected subtree of $T_P$ . To see that $Y_P$ is connected, note that if e, e ^′ are two adjacent edges of $\Gamma_P$ contained in $\tau$ , then by construction of the various elements $g_\gamma$ , we have that $g_v\widetilde{e}$ and $g_{v^{\prime}}\widetilde{e}'$ are adjacent in $Y_P$ . Moreover, if e is an edge of $\Gamma_P$ not contained in $\tau$ and if e ^′ is an edge of $\tau$ meeting e at the vertex of e closest to $v_a$ in $\Gamma_P$ , then $g_v\widetilde{e}$ and $g_{v'}\widetilde{e}'$ are adjacent in $Y_P$ .

Proof. An edge of $T_P$ corresponds to a pair consisting of a maximal simplex of $T_P$ (of type c for some $c\in V(\Gamma)$ ) and one of its codimension 1 faces (of type cd for some $d\in V(\Gamma)$ adjacent to c). We thus mention the following useful fact, which is an immediate consequence of Lemma 17:

Definition 35. Let $g \in A_S$ . The minimal parabolic subgroup $P_g$ containing g is called the parabolic closure of g.

Proof. It is obvious that $\alpha^{-1} P_g \alpha$ contains $\alpha^{-1} g \alpha$ . We need to prove that this parabolic subgroup is the minimal one containing $\alpha^{-1} g \alpha$ . Let Q be any parabolic subgroup containing $\alpha^{-1} g \alpha$ . As $\alpha Q \alpha^{-1}$ contains g, $P_g \subseteq \alpha Q \alpha^{-1}$ . Therefore, $ \alpha^{-1} P_g \alpha \subseteq Q$ .

Proof of Theorem C. Let g and g ^′ be two elements of $A_X$ that are conjugated by an element $\alpha\in A_S$ . As $P_g, P_{g'}\subset A_X$ , by Theorem 11 there must be $Y,Y'\in X$ and $\beta,\beta'\in A_X$ such that $P_g=\beta^{-1}A_Y\beta$ and $P_g=\beta'^{-1}A_{Y'}\beta'$ . Since $P_g$ and $P_g'$ are conjugate by Lemma 36, $A_Y$ and $A_{Y'}$ have to be conjugate. At the beginning of this section, we have seen that if $|Y|>1$ , then $Y=Y'$ . Also, if $|Y|=1$ , then either $Y=Y'$ , or Y and Y ^′ are single generators connected by an odd-labelled path in $\Gamma_S$ . Thus, there are two possibilities:

Proof. The statement of [ Reference Chepoi and Osajda8 , theorem 7·3] is given for a finite group G. However, their proof only uses the finiteness of G to obtain a finite G-orbit, out of which they construct an invariant simplex. In particular, their proof generalises without any change to the case of an infinite group G with a finite G-orbit.

Proof of Proposition 37. We show by induction on $|S|$ that $P_g = P_{g^n}$ . If $|S| = 2$ , $A_S$ is a dihedral Artin group. In particular, it is spherical, and the result follows from [ Reference María Cumplido, González-Meneses and Wiest9 , corollary 8·3]. Let now $|S| \geq 3$ , and suppose that $P_g \neq P_{g^n}$ . We have that $P_{g^n} \subseteq P_g$ , and then there is a chain of inclusions of the form

\begin{equation*}P_{g^n} \subsetneq P_g \subseteq A_S.\end{equation*}