No CrossRef data available.
Article contents
Shrinking parallelepiped targets for 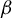 $\beta $-dynamical systems
$\beta $-dynamical systems
Published online by Cambridge University Press: 19 November 2024
Abstract
For 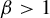 $ \beta>1 $, let
$ \beta>1 $, let 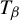 $ T_\beta $ be the
$ T_\beta $ be the 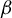 $\beta $-transformation on
$\beta $-transformation on 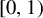 $ [0,1) $. Let
$ [0,1) $. Let 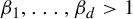 $ \beta _1,\ldots ,\beta _d>1 $ and let
$ \beta _1,\ldots ,\beta _d>1 $ and let 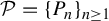 $ \mathcal P=\{P_n\}_{n\ge 1} $ be a sequence of parallelepipeds in
$ \mathcal P=\{P_n\}_{n\ge 1} $ be a sequence of parallelepipeds in 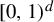 $ [0,1)^d $. Define
$ [0,1)^d $. Define 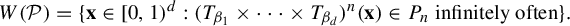 $$ \begin{align*}W(\mathcal P)=\{\mathbf{x}\in[0,1)^d:(T_{\beta_1}\times\cdots \times T_{\beta_d})^n(\mathbf{x})\in P_n\text{ infinitely often}\}.\end{align*} $$
$$ \begin{align*}W(\mathcal P)=\{\mathbf{x}\in[0,1)^d:(T_{\beta_1}\times\cdots \times T_{\beta_d})^n(\mathbf{x})\in P_n\text{ infinitely often}\}.\end{align*} $$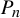 $ P_n $ is a hyperrectangle with sides parallel to the axes, the ‘rectangle to rectangle’ mass transference principle by Wang and Wu [Mass transference principle from rectangles to rectangles in Diophantine approximation. Math. Ann. 381 (2021) 243–317] is usually employed to derive the lower bound for
$ P_n $ is a hyperrectangle with sides parallel to the axes, the ‘rectangle to rectangle’ mass transference principle by Wang and Wu [Mass transference principle from rectangles to rectangles in Diophantine approximation. Math. Ann. 381 (2021) 243–317] is usually employed to derive the lower bound for 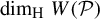 $\dim _{\mathrm {H}} W(\mathcal P)$, where
$\dim _{\mathrm {H}} W(\mathcal P)$, where 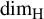 $\dim _{\mathrm {H}}$ denotes the Hausdorff dimension. However, in the case where
$\dim _{\mathrm {H}}$ denotes the Hausdorff dimension. However, in the case where 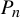 $ P_n $ is still a hyperrectangle but with rotation, this principle, while still applicable, often fails to yield the desired lower bound. In this paper, we determine the optimal cover of parallelepipeds, thereby obtaining
$ P_n $ is still a hyperrectangle but with rotation, this principle, while still applicable, often fails to yield the desired lower bound. In this paper, we determine the optimal cover of parallelepipeds, thereby obtaining 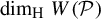 $\dim _{\mathrm {H}} W(\mathcal P)$. We also provide several examples to illustrate how the rotations of hyperrectangles affect
$\dim _{\mathrm {H}} W(\mathcal P)$. We also provide several examples to illustrate how the rotations of hyperrectangles affect 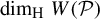 $\dim _{\mathrm {H}} W(\mathcal P)$.
$\dim _{\mathrm {H}} W(\mathcal P)$.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press



