1. Introduction
Reference HughesHughes (1981) suggested a high potential of collapse of the West Antarctic ice sheet in the sector drained by Thwaites and Pine Island Glaciers. While the detection of a collapse in this area has eluded observations for many years (Reference Vaughan, Alley and BindschadlerVaughan and others, 2001), there is now mounting evidence that this sector of West Antarctica is undergoing substantial change. In particular, satellite radar interferometry observations revealed a rapid retreat of the grounding line of Pine Island Glacier between 1992 and 1996 (Reference RignotRignot, 1998) and an increase in ice velocity of 2.2% a−1 between 1992 and 2000 (Reference Rignot, Vaughan, Schmeltz, Dupont and MacAyealRignot and others, 2002), and satellite radar altimetry revealed coastal thinning concentrated in the areas of fast flow (Reference Shepherd, Wingham, Mansley and CorrShepherd and others, 2001).
The objectives of this study are to model ice flow in the lower reaches of Pine Island Glacier and on its floating ice shelf and use the model to study the sensitivity of glacier flow to small perturbations. In many respects, this study is a first attempt at obtaining a realistic description of ice flow in Pine Island Bay. First, there are only a few quality glaciological data on this glacier (ice thickness, bed topography, ice temperature profile, etc.), so modeling is incompletely constrained by observations. Second, the flow of Pine Island Glacier is unlike that of either an ice stream or a glacier, but is somewhere in between the two flow regimes (Reference Vaughan, Alley and BindschadlerVaughan and others, 2001). There is no general model available at present which is exactly adapted to this situation, though approximations or preliminary attempts exist (e. g. A. J. Payne and others, http://igloo.gsfc.nasa.gov/wais/abstracts01/Payne.html).
The model used in this study is from Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995), and is described more completely in Reference MacAyealMacAyeal (1989). It is a coupled ice-shelf/ice-stream model which assumes no vertical shear on grounded ice, a so-called “shelfy ice-stream” model (Reference Hindmarsh and PeltierHindmarsh, 1993). As discussed later in the paper, this model should be a good approximation of the exact problem and is relatively well adapted to the case of ice flow of Pine Island Glacier. It should therefore provide us with relevant information about ice-flow controls and sensitivity of ice-flow perturbations, and we should not expect major revisions of the conclusions from the use of a more general ice-flow model.
Our first objective is to replicate the flow velocity measured with interferometric synthetic aperture radar (InSAR) data. This is achieved using a forward model approach, via the tuning of relevant model parameters. These model parameters are: (1) a softening coefficient of ice along the side margins; and (2) a coefficient of basal friction which determines the distribution of basal shear on grounded ice. Our second objective is to employ this model configuration to test the sensitivity of the glacier velocity to ice-shelf and bed perturbations. These perturbations include a reduction in ice-shelf area, basal shear stress, and softening of the ice along the side margins. Only one glacier parameter (ice-shelf area, ice softening at the margins, or basal friction coefficient) is varied at a time for each experiment. Based on the results, we make some comments on the relative importance of these parameters in controlling the flow of Pine Island Glacier into Pine Island Bay.
2. Pine Island Bay Area
Pine Island Glacier has the largest discharge of ice in West Antarctica, 76 ± 2 km3 a−1 of ice in 1996 (Reference RignotRignot, 1998). It flows rapidly into the Amundsen Sea, at > 2.5 km a−1 (Reference Lucchitta, Rosanova and MullinsLucchitta and others, 1995), through an ice shelf about 50 km long by 30 km wide (Fig. 1). The ice front is subject to periodic, large calving events which remove sizable icebergs several to 10 km in size (e.g. Reference Jenkins, Vaughan, Jacobs, Hellmer and KeysJenkins and others, 1997). The driving stress is low on the upstream part of the glacier (<50 kPa), reaches a peak value (150 kPa) along the main trunk, and subsequently decreases downstream to low values in the ice-plain area (50 kPa), and lower values on the ice shelf (Reference BentleyBentley, 1987; Reference Corr, Doake, Jenkins and VaughanCorr and others, 2001; Reference Vaughan, Alley and BindschadlerVaughan and others, 2001). Pine Island Glacier is relatively thick, 1200 m at the grounding line, and hence more similar to East Antarctic glaciers than to the Siple Coast ice streams (Reference BentleyBentley, 1987). The aforementioned region of relatively high driving stress is small in spatial extent, about one glacier width, and about 30 km upstream of the grounding line.

Fig. 1. (a) Tidal interferogram of Pine Island Glacier in 1996 (©European Space Agency 1996). The approximate outline of the reference finite-element mesh is indicated by the heavy line. The grounding line is indicated by the thin line. The two medium-weight black lines indicate the location of the margins of the glacier in our mesh. (b) Outline of the domain over a SAR image of Pine Island Glacier, with margins (red), ice front (blue) grounding line (green) and the four different zones for the value of α (yellow); parts l and 2 are the different parts removed, A-A′ is the longitudinal section along the flow center line and t1–t3 are the three transects along which the velocities are compared.
3. Model Description and Validation
This section describes the model and the parameter selection process. The overall approach is to use forward modeling, where relevant model parameters are tuned iteratively until a reasonable and physically acceptable fit is obtained between simulated and observed velocity. In particular, we make no attempt at inferring unknown parameters using a control method approach, as described in Reference MacAyealMacAyeal (1992) and Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995), which requires a more extensive description of the physical characteristics of the glacier (especially thickness) than available at present.
3.1. Model
The model is a two-dimensional ice-stream/ice-shelf flow coupled model described in Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995). The model assumes horizontal velocity independent of the vertical component z, no vertical shear and incompressibility. This requires that the characteristic vertical distance scale of the glacier be much smaller than the characteristic horizontal distance scale, and that the driving stress, τ b, be much smaller than 1000 kPa (see Reference MacAyeal, Bindschadler and ScambosMacAyeal and others, 1995, equation (8), using the characteristic scales of Pine Island Glacier: [L] = 10 km, [B] = 108 Pa s1/3, [U] = 10−5 m s−1 and [H] = 1 km). These two requirements are met for Pine Island Glacier: the characteristic vertical scale of 1 km is much smaller than the characteristic horizontal scale of 10 km; and the maximum driving stress of 150 kPa is much smaller than the model limit of 1000 kPa.
The model solves the following well-known stress balance equations:
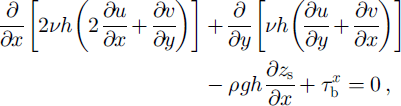
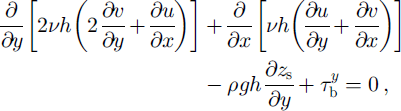
where u and v are the horizontal velocities in the x and y horizontal directions, respectively, h is the thickness, ρ = 917 kg m−3 is the density of ice, g = 9.81 m s−2 is the acceleration of gravity, z s is the surface elevation measured along the z vertical axis, τ b is the basal drag and v is the effective viscosity, defined by Glen’s flow law:

where ![]() is the flow-law rate constant averaged over the depth z and n is the flow-law exponent. Here, we choose n = 3.
is the flow-law rate constant averaged over the depth z and n is the flow-law exponent. Here, we choose n = 3.
Equations (1) and (2) are valid on both the ice-stream and the ice-shelf parts of the glacier, with ![]() on the ice-shelf part because there is no basal friction there.
on the ice-shelf part because there is no basal friction there.
3.2. Input parameters
The inputs required by the model are the geometric, physical and dynamic characteristics of the glacier. The geometric characteristics include:
-
(1) the grounding-line position, to separate the model domain between grounded ice (non-zero basal shear stress) and floating ice (zero basal shear stress),
-
(2) the location of ice rises on the ice shelf, to determine the zones of ice-flow resistance other than the side margins,
-
(3) the position and width of the glacier margins, to mark the transition between fast-moving and slow-moving ice, and identify the glacier sectors experiencing ice softening.
Characteristics (1) and (2) are taken from InSAR observations of tidal deformation of the ice shelf (Fig. 1a). The color bar indicates the vertical displacement, and a full color cycle corresponds to a 6 cm vertical displacement. The location and width of the margins are estimated from a map of the shear strain rates calculated from InSAR velocities, and based on prior work done on ice softening along the side margins of Whillans Ice Stream (formerly known as Ice Stream B) (Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others, 1994; Reference Whillans and van der VeenWhillans and van der Veen, 1997). The shear strain is extremal in marginal zones about 4–4.5 km wide (comparable to the estimate in Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others, 1994). The resulting zones are shown in red in Figure 1b.
The required physical characteristics of the glacier are: (1) ice thickness, (2) bed elevation, (3) surface elevation, (4) the flow-law constant of ice, and (5) softening of the ice along the side margins. On grounded ice, ice thickness is taken from BEDMAP (Reference Lythe and VaughanLythe and others, 2001). On the ice shelf, ice thickness is taken as equal to a multiple (7.9) of the surface elevation from Reference Bamber and BindschadlerBamber and Bindschadler’s (1997) digital elevetaion model (DEM) of Antarctica, referenced to mean sea level using the OSU91A geoid. This multiplicative factor was selected to best match the ice thickness measured by the British Antarctic Survey (BAS) along two profiles in 1998 (Reference Corr, Doake, Jenkins and VaughanCorr and others, 2001). To make the thickness map smooth and continuous at the grounding line, which is the transition boundary between the two sources of thickness information, we interpolated the thickness map in a narrow band (8–12 km) in between using a triangle-based cubic interpolation from Matlab. Along the two BAS transects (displayed in Fig. 2b), ice thickness decreases from about 1900 m upstream to 1100 m at the grounding line and 500 m at the ice front. The inferred thickness agrees with the BAS data with a standard deviation of about 60 m. The thickness gradient along these transects is about −3% (almost a linear decrease from 1600 m to 500 m over 30 km), and the surface slope is about −1%. The surface elevation is from Reference Bamber and BindschadlerBamber and Bindschadler’s (1997) DEM.

Fig. 2. Pine Island Glacier inputs for the model: surface elevation (a), thickness (b), velocity from InSAR (c).
The flow-law rate constant ![]() depends on the ice temperature profile, which is unknown on Pine Island Glacier. We choose an initial value of
depends on the ice temperature profile, which is unknown on Pine Island Glacier. We choose an initial value of ![]() (equivalent to 633 kPa a1/3), which is slightly higher than average values quoted in the literature for similarly cold Antarctic glaciers: Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others (1994) used 1.5 × 108 Pa s1/3 for Whillans Ice Stream, based on a measured temperature profile, and Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995) derived values of 1.5–2 × 108 Pa s1/3 using a control method on Ice Stream E. In section 5.3, we will discuss how the model results vary as a function of
(equivalent to 633 kPa a1/3), which is slightly higher than average values quoted in the literature for similarly cold Antarctic glaciers: Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others (1994) used 1.5 × 108 Pa s1/3 for Whillans Ice Stream, based on a measured temperature profile, and Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995) derived values of 1.5–2 × 108 Pa s1/3 using a control method on Ice Stream E. In section 5.3, we will discuss how the model results vary as a function of ![]() , varying ±10% around the chosen value.
, varying ±10% around the chosen value.
Along the side margins, we allow the flow-rate constant to vary due to ice softening. We introduce a softening coefficient, γ, to multiply the effective flow-rate constant by (1 – γ), with 0 ≤ γ < 1. A value of γ > 0 means that the ice is softened by strain heating, which results in a reduction of the flow-law parameter (Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others, 1994). The value of γ to be adopted in our model is not known a priori and is a parameter which needs to be adjusted.
Finally, we need the following dynamic characteristics: (1) the ice velocity at the surface; and (2) the intensity of the shear stress at the base of the glacier. Ice velocity is taken from InSAR observations collected in 1996 (Reference Rignot, Vaughan, Schmeltz, Dupont and MacAyealRignot and others, 2002). Figure 2 displays the known physical and dynamic characteristics of Pine Island Glacier, surface elevation, thickness, and velocity from InSAR.
The basal shear stress is modeled following the notations in Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995). We introduce a basal friction coefficient β 2, such that
where |U| is the glacier velocity at the bed. The coefficient, β 2 (in Pa s m−1), represents the sticky/slick area of the bed, i.e. the ability of the bed to resist ice flow. The basal friction is zero on the ice shelf because the water is so inviscid compared with the ice that its resistance to the flow is tiny, except on a few grounded spots like ice rises. On grounded ice, β 2 is a free parameter, which we need to adjust.
Here, we do not use a control method to invert the InSAR velocity to find unknown flow parameters. Instead, we simply proceed by trial and error in a forward approach by adjusting the two unknown variables, β 2 and γ.
3.3. Boundary conditions
Equations (1–3) are valid on the interior of the ice-stream/ice-shelf system. Two sets of boundary conditions are imposed on the model. First, the kinematic boundary conditions: velocity is specified on “land boundaries”, i.e. on all the boundaries of the model domain, except along the ice front. Velocity is here prescribed according to the InSAR velocity estimate. We set it to zero where velocity data are missing. Note here that this means that our study does not allow us to detect changes in glacier velocity at the model boundary since those velocities are prescribed in the model, hence should be unchanged in the model output. We selected those boundaries as far away as permitted by our velocity mapping of Pine Island Glacier to limit boundary effects in our model simulations.
Second, a dynamic boundary condition is specified at the ice front, where ice-shelf flow is resisted by sea-water pressure. We apply a vertical integral of force as discussed in Reference MacAyealMacAyeal (1989).
3.4. Parameter selection
The estimation of the basal friction parameter, β 2, is critical to the model and yet not unique. We have no information on the basal velocities, nor the level of basal shear stress. On the other hand, we have information on the surface velocities from InSAR and on the driving stress from the glacier elevation and thickness. The basal velocities should be closely related to the surface velocities because the glacier experiences rapid sliding in this region (the velocity due to internal deformation of the ice is negligible compared to the observed glacier velocity); and at first order, the basal shear stress follows the variations in driving stress. In effect, we parameterize the distribution of shear stress using

where α is the new variable to adjust, τ d is the driving stress, and U sar is the InSAR velocity.
The driving stress, τ d, is calculated from surface slope and ice thickness. From Equations (4) and (5), within the misfit between the modeled and the observed velocities, we have
The parameter α then measures the ratio between the driving stress and the basal shear stress, which is not known a priori, but takes values between 0 (no basal shear stress) and 1 (driving stress perfectly balanced by basal shear stress). The balance of forces on the glacier dictates that the driving stress is balanced by a combination of basal drag, lateral drag and longitudinal drag. We assume α to roughly vary where the driving stress and the velocity vary a lot, and thus expect to have different values for α upstream and in the main trunk. So we divide the grounded part of the glacier into three zones (see Fig. 1b), each corresponding to a fixed value of α. In zone 1, outside the main flow for U sar < 800 m a−1, we assume that the driving stress is completely compensated by the basal shear stress, i.e. α is equal to one. This is reasonable because the flow velocity is low and it may be assumed that ice is frozen to the bed. In zone 2 upstream, α is taken equal to a low value of 0.1. In zone 3, where the driving stress and the velocity are somewhat higher, we use a value of α = 0.68. On the ice shelf, α is effectively zero, except on ice rises for which we set β2 = 1040 Pa s m–1 as in Reference Schmeltz, Rignot and MacAyealSchmeltz and others (2001).
In the case of Ice Stream E, Reference MacAyeal, Bindschadler and ScambosMacAyeal and others (1995) inferred high values of α = 0.6 on sticky spots, and low values of 0.3 elsewhere. This suggests that our selection of α is not totally unrealistic compared with values obtained from prior studies.
The flow enhancement factor used by Reference Echelmeyer, Harrison, Larsen and MitchellEchelmeyer and others (1994) in their study of Whillans Ice Stream varied from 3 to 12.5 in the shear margin zones, which correponds to a softening coefficient γ of 30–57%. Reference MacAyeal, Rignot and HulbeMacAyeal and others (1998) found that a lower value of 20% was necessary to obtain a good fit between InSAR data and model predictions around Hemmen Ice Rise, near the front of the Filchner–Ronne Ice Shelf. In our model study, we therefore expect values of γ to range between 10% and 50%.
4. Results of Model Fitting
A good fit was obtained between predicted velocities and observed velocities using the different zones of α mentioned in subsection 3.2 and a softening coefficient of 12% along the northern margin and 28% along the southern margin. The asymmetry in the softening coefficient reflects the fact that the ice flow is asymmetric: ice velocity tends to be slightly higher along the southern margin, and the maximum glacier velocity is displaced slightly to the south of the geometric center line of the glacier. The values adopted for the softening coefficient are within the expected range.
This parameter selection is not unique. A modification of α could be compensated with a different selection of γ and still yield a good model fit. However, we find that the range of possible values of these parameters remains relatively narrow. First, we find that dividing the glacier domain into more zones according to the SAR velocity, with different values of α, does not significantly improve the model fit. Second, model fitting is not significantly improved if γ varies spatially (e.g. along flow). Third, as discussed later in more detail, a lower value for ![]() would yield values of γ outside the expected range (too low).
would yield values of γ outside the expected range (too low).
Figure 3 shows a comparison between model and observed velocity. The root-mean-square error is around 30% for low velocities (<1000 m a−1), decreasing to <10% for high velocities (>1700 m a−1), which is fairly reasonable. We may, however, notice a few differences. For instance, the model velocity increases near the ice front, whereas the observations show no increase. This could be due to errors in ice thickness (the satellite radar altimetry data used to calculate the thickness are not reliable near the front), in the definition of side margins near the ice rises (e.g. due to the presence of lines of weakness), or in the selection of model parameters (e.g. the softening on this area). In another area, below the grounding line, along the northern margin, the model predicts a higher velocity than observed. We attribute this discrepancy to errors in ice thickness. This region is close to the grounding line, close to an area of slow-moving ice that includes nunataks and volcanoes, which is not well constrained by direct observations of ice thickness (e.g. the BAS transects), and where ice thickness had to be extrapolated.

Fig. 3. Modeled velocity (a) and InSAR velocity (b) for Pine Island Glacier. Contours begin at 2600 m a−1, and contour intervals are 150 m a−1 from 2600 to 2000, and 250 m a−1 thereafter. Margins and grounding line are also displayed for better comparison.
The most significant discrepancy between the model and the observations is that we could never completely reproduce the flow asymmetry in the wake of the grounding line, and especially on the ice shelf. The model tends to predict a more symmetric flow than observed. This could be explained by two factors: one is that the map of ice thickness is not sufficiently reliable to represent the asymmetry in ice thickness across the glacier; a second factor is that the southern margin may be experiencing a different change in flow speed from the rest of the glacier. In our examination of flow changes between 1996 and 2000, we find a more rapid increase in ice velocity along the southern margin of the glacier than along the northern margin.
5. Influence of the Ice Shelf on Flow Speed
We initially simulate the calving of an unconfined piece of ice by removing a small part of the ice shelf between the margins. The model predicts no change in ice flow, as expected, which means that an unconfined ice shelf or an ice tongue would not have a significant influence on the flow if they were to be removed. This is in agreement with experiments done by Reference RommelaereRommelaere (1997) on an ideal rectangular ice shelf, where he shows that the calving of an iceberg in the unconfined part of the ice shelf has almost no influence on the flow.
We then investigate the three following scenarios of ice-shelf removal. First, we remove a small part of the ice shelf (5.5% of the initial ice-shelf area), denoted part 1 in Figure 1b, that includes part of the side margins, below the ice rise outside the northern margin. Second, we remove a larger chunk of ice shelf (13% of initial ice-shelf area), denoted part 2 in Figure 1b, that includes the northern margin up to the grounding line, where numerous rifts are present in recent imagery. Third, we remove the entire ice shelf, so that the grounding line becomes the new ice front. Thickness, bed elevation and surface elevation are kept the same in all these experiments. We also keep the same values of β 2 and γ and the same boundary conditions.
The model velocity for the different tests is compared along both a longitudinal profile (section A–A′ along the center line; Fig. 1b) and three cross-glacier transects (see Fig. 1b): transect t1 is on the ice shelf, t2 is right above the grounding line, and t3 is further upstream.
The results for the different simulations are displayed in Figure 4. The removal of part 1 increases the velocity by 9% on the ice shelf (see the floating part of the section A–A′ and transect t1; Fig. 4a and b), 3.5% at the grounding line (section A–A′ at the grounding-line position) and 2% above the grounding line (transect t2). The perturbation decreases to zero toward the boundary of our model domain, as expected since the velocity is held constant along the boundary. The removal of part 2 increases the velocity by 20% on the ice shelf, decreasing to 10% at the grounding line (Fig. 4a along section A–A′). Above the grounding line, the velocity increase is 6% at t2, decreasing to <1% upstream along t3. The removal of the whole ice shelf increases the velocity by 72% at the grounding line (section A–A′) and 35% at t2. Upstream, Figure 4d shows an increase in velocity of 2.5% at t3.

Fig. 4. Velocities of the different tests (a) along the section A–A′, (b) along the transect t1, (c) along the transect t2, and (d) along the transect t3. SAR velocity (crosses), model velocity for the reference test (blue line), model velocity after removing the small iceberg-like part (green line) model velocity after removing part 2 (red line) and model velocity after removing the whole ice shelf (cyan line). The vertical lines in (a) indicate the center position of t1, t2 and t3.
The removal of the ice shelf, or even part of it, thus has a significant influence on the flow. The effect is felt far inland, up to 50 km upstream of the grounding line. The increase in ice velocity at the grounding line is high, and implies that the glacier mass balance would be substantially affected by the flow perturbation. Since the flow acceleration decreases inland to zero, the overall effect of the glacier speed up on the lower reaches of the glacier would be to thin it at a very high rate.
The removal of parts 1 and 2 is of special interest. These are possible scenarios and show that the sides of the glacier are the parts that restrain the flow the most. Such decoupling of ice-shelf grounded ice is not unrealistic given the current evolution of rifts and cracks on Pine Island Glacier ice shelf (Reference RignotRignot, 2002).
6. Sensitivity of the Model Results to Basal Conditions
To estimate how the basal shear stress controls the ice flow, we performed different simulations where the basal friction coefficient, β 2, was decreased everywhere on grounded ice, by 5%, 10% and 15%, respectively, keeping all other parameters unchanged. The velocity at the grounding line is predicted to increase by 3.7%, 7.8% and 12.4%, respectively. The increase in velocity is therefore not directly proportional to the reduction in basal friction coefficient, but strongly correlated. The changes in basal shear stress corresponding to these changes in the basal friction coefficient are 1.5%, 2.9% and 4.5%, respectively.
These results suggest that the basal shear stress is also a parameter that exerts an important control on ice velocity, in addition to lateral shear along the ice shelf.
7. Sensitivity of the Model to the Flow-Rate Constant
First, we examine the effect of the softening coefficient γ. If γ is increased by 50% along both margins compared to its initial value (i.e. γ = 18% on the northern margin and γ = 42% on the southern margin), the predicted velocity increases by 5.3% at the grounding line. If we add 15% softening on both margins (i.e. γ = 27% on the northern margin and γ = 43% on the southern margin), the predicted velocity increases by 7.7%. Thus we need to increase γ quite significantly to observe a large change in velocity (>10%).
Second, we examine the relevance of our initial selection of the flow-rate parameter. With a higher value of ![]() , a good fit is easily achieved by increasing softening at the margins to 26% on the northern margin and 40% on the southern margin and decreasing α to 0.66 in zone 2. With a lower value
, a good fit is easily achieved by increasing softening at the margins to 26% on the northern margin and 40% on the southern margin and decreasing α to 0.66 in zone 2. With a lower value ![]() , a reasonable fit is found with no softening along the northern margin and 5% along the southern margin, and increasing α to 0.71 in zone 2. However, the model fit is reduced on floating ice. As explained in Reference MacAyeal and ThomasMacAyeal and Thomas (1986), the higher the basal melting rate, the higher
, a reasonable fit is found with no softening along the northern margin and 5% along the southern margin, and increasing α to 0.71 in zone 2. However, the model fit is reduced on floating ice. As explained in Reference MacAyeal and ThomasMacAyeal and Thomas (1986), the higher the basal melting rate, the higher ![]() should be because it stiffens the ice, and their computed values on the Ross Ice Shelf range between 1.8 and 2.6 × 108. In the case of Pine Island Glacier, the basal melting is high (Reference Jenkins, Vaughan, Jacobs, Hellmer and KeysJenkins and others, 1997; Reference RignotRignot, 1998). This might explain why
should be because it stiffens the ice, and their computed values on the Ross Ice Shelf range between 1.8 and 2.6 × 108. In the case of Pine Island Glacier, the basal melting is high (Reference Jenkins, Vaughan, Jacobs, Hellmer and KeysJenkins and others, 1997; Reference RignotRignot, 1998). This might explain why ![]() is probably not much lower than 2 × 108. Overall, our selection of
is probably not much lower than 2 × 108. Overall, our selection of ![]() is reasonable enough for the purpose of our simulations.
is reasonable enough for the purpose of our simulations.
8. Discussion
Despite the limitations of our input data, especially ice thickness and the rheology of the ice, and given the possible limitations of the model, we are still able to obtain a reasonable fit to the observations. Although the parameter selection is not unique, the range of possible values of γ, ![]() and α is rather narrow. Thus we obtain relatively robust predictions of the sensitivity of the ice velocity to perturbations in ice-shelf area and shear stress.
and α is rather narrow. Thus we obtain relatively robust predictions of the sensitivity of the ice velocity to perturbations in ice-shelf area and shear stress.
One main result is that ice-shelf changes are predicted to have a profound effect on the flow of Pine Island Glacier, and in particular could increase flow speed at the grounding line by 70% ± 20% if the entire ice shelf were to be abruptly removed. This result means that the evolution of the ice shelf in front of Pine Island Glacier ought to be carefully examined in any analysis of ice-flow changes on the ice shelf or detected inland of the grounding line. Even a modest reduction in ice-shelf area is shown to have important consequences for ice flow. Moreover, those changes propagate well above the grounding line, into the ice-stream portions of the glacier. This finding is in contrast with the situation of other glaciers (e.g. Reference Huybrechts and de WoldeHuybrechts and de Wolde, 1999) for which the region of influence of the ice shelf is at most a few kilometers. But it is qualitatively consistent with the observed flow acceleration of Pine Island Glacier between 1992 and 2000, detected from InSAR (Reference Rignot, Vaughan, Schmeltz, Dupont and MacAyealRignot and others, 2002), as well as its pattern of inland thinning (Reference Shepherd, Wingham, Mansley and CorrShepherd and others, 2001).
The relevance and significance of a change in basal shear stress as a possible explanation for the observed flow acceleration of Pine Island Glacier is less clear and requires further investigations beyond the objectives of the present paper. Our simulation does suggest that only a small change in basal friction coefficient would be necessary to yield a flow acceleration similar to that detected on Pine Island Glacier, yet the cause for a reduction in basal friction is more difficult to elucidate in the absence of observation of the bed/till physical characteristics. A lower basal friction means enhanced basal lubrication, hence higher basal water pressure or higher availability of liquid water at the glacier base. The detailed physical mechanisms which could lead to such a change in basal friction ought to be considered in the future.
9. Conclusion
Using an ice-stream/ice-shelf flow model, we are able to obtain a reasonable fit between model predictions and InSAR observations. Residual differences are mostly caused by uncertainties in ice thickness, rheology of the ice, and possible limitations of the ice-flow model. A series of experiments done with this model suggests that the glacier velocity is highly sensitive to the ice-shelf area (and hence the ice-shelf buttressing force on the glacier), and to the basal shear stress on grounded ice, but less critically sensitive to ice softening along the glacier margins. This would suggest at least two possible mechanisms of flow change on this glacier: one is a reduction in ice-shelf area following a reduction in lateral resistance caused by the formation of rifts along the side margins; the other is a change in basal conditions, which is a complete unknown at present but would invoke a change in basal water presence. Resolving these issues into more details is critical to improve our understanding of the ice-sheet evolution in this sector of the West Antarctic ice sheet.
Acknowledgements
This work was performed at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the NASA Cryospheric Sciences Program. We thank the European Space Agency VECTRA project and NASA’s Alaska SAR Facility for providing the European Remote-sensing Satellite data employed in this study. We thank A. Humbert, R. Greve and an anonymous reviewer for their insightful comments. We also thank numerous colleagues for useful discussions and interactions during the course of this research. Support for T.K.D. was provided by U.S. National Science Foundation award ATM-9870886.






