Introduction
The ice-divide region of large ice sheets is a zone of special interest. It is regarded an optimal site for ice-core drilling, since the ice stratigraphy is minimally disturbed by the flow (Johnsen and others, 1992). Furthermore, the ice-divide region provides a simple flow regime, which is useful for testing flow laws of ice. Several models have been used to analyse the conditions close to the divide in large, plane-flow ice sheets (e.g. Raymond, 1983; Hutter and others, 1986; Paterson and Waddington, 1986; Dahl-Jensen, 1989a, b; Hindmarsh and others, 1989; Szidarovszky and others, 1989; Firestone and others, 1990). Modelling the ice divide is found to be complicated for several reasons: the longitudinal stress deviators cannot be disregarded compared to the shear stresses, which is often done to simplify the equations (see, for example, discussion by Hutter (1993)); the thermodynamics and the stress-equilibrium equations are coupled; generally, the flow pattern is three-dimensional.
In this paper, a new model is presented, which solves the general thermomechanically coupled ice-flow (coupled ice and heat flow) problem with a free surface for cold steady-state ice sheets using a finite-element technique. The model is capable of treating a general plane-flow ice sheet or an axisymmetric ice sheet. The finite-element method has been used previously for modelling ice flow (e.g. Hooke and others, 1979; Raymond, 1983; Paterson and Waddington, 1984; Hodge, 1985; Hanson, 1990, 1995; Schøtt and others, 1992) but none of these models has considered the coupled thermomechanical ice-flow problem. Axisymmetric ice sheets have been examined previously (Johnson, 1981; Hutter and others, 1987) but without special emphasis on the divide zone. Here, the equations are solved by decoupling the heat-flow equation from the other equations, as suggested by Hutter (1983). Furthermore, the surface mass-balance condition is decoupled and the surface calculation is formulated as a time evolution. The capability of the model is demonstrated by some initial model experiments, which compare the steady-State flow and temperature fields of a symmetric, plane-flow ice divide and an axisymmetric ice dome.
The flow model
The model considers the slow, incompressible thermo-mechanical flow of a large, steady-state ice sheet.
Governing equations
Plane ice flow
The model uses a Cartesian coordinate system (x, y, z) (Fig. 1). x and y are the horizontal coordinates with the x-axis in the direction of the flow and z is the vertical coordinate. The corresponding velocity components are denoted (u, v, w) where v = 0. When restricted to plane flow, the governing equations are as follows. The stress-equilihrium equations are

and

where σ i are the normal .stress components, τ ij are the shear-stress components, g = 9.81 m s−2 is the gravity and ρ = 917 kg m−3 is the ice density, which is assumed constant. The strain-rate components are

where ![]() are the normal strain-rate components,
are the normal strain-rate components, ![]() are the shear-stress components. The local mass balance is expressed by the incompressibility equation
are the shear-stress components. The local mass balance is expressed by the incompressibility equation
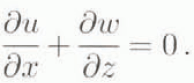
The ice is assumed to deform as described by Glen’s (1955) generalized flow law
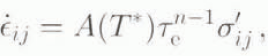
where σ′ ij are the deviatoric stress components, defined by

where σ′ x is an abbreviation of σ′ xx , etc., and the pressure p = −½ (σ x + σ z ) is the mean compressive stress, τ e. is the effective stress where

The flow-law exponent n is set to 3 (Paterson, 1994), the flow-law rate factor A(T*) is a function of temperature T* = T – T melt measured relative to the pressure-melting point Τ melt, and T is temperature. Following Dahl-Jensen (1989a), A(T*) is set to

with T* in units of °C. Equation (7) is a fit to the Arrhenius relation recommended by Paterson (1994).

Fig. 1. The coordinate system seen from the side. Notation is explained hi the text. In the model experiments of this paper, only the flow close to the divide is considered (indicated by the shaded areas).
The steady-state heat-flow equation may be written (Dahl-Jensen, 1989a) as

where the thermal-heat conductivity K and the specific-heat capacity c of ice are temperature dependent (Firestone and others, 1990):

Equations (1)–(6) and (8) are the governing equations for the fields of velocity, stress, pressure and temperature of steady-state, plane ice flow.
Axisymmetric ice flow
The model uses a cylindrical coordinate system (x, θ, Ζ) (Fig, 1). x and θ are the horizontal coordinates, where x is the radial coordinate, and z is the vertical coordinate. The corresponding velocity components are (u, v, w), where v = 0. All physical variables are independent of θ and the shear stresses along the θ direction are zero. When restricted to axisymmetric flow, the governing equations are as follows with notations and definitions as above. The stress-equilibrium equations are

and

where R = x. The strain rate components are

The local mass balance is expressed by the incompressibility equation

The ice is assumed to deform as described by Glen’s generalized flow law (Equation (4)), with the deviatoric-stress components defined by

where the pressure is p = −⅓ |(σ x + σ θ + σ z ), and the effective stress is

The steady-state heat-flow equation is here

Equations (4) and (10)–(15) are the governing equations for the fields of velocity, stress, pressure and temperature of steady-state axisymmetric ice flow. The parameter 1/R controls the effects from the three-dimensional stresses. It may be interpretated as the radius of curvature of surface contour lines of an axisymmetric ice sheet centred at x = 0. At the limit of 1/R → 0, which corresponds to plane flow, Equations (10)–(15) reduce to those for plane flow.
Boundary conditions
A kinematic condition at the surface is expressed as

where S = S(t, x) is the ice surface, t is time and a = a(x) is the accumulation rate. Equation (16) determines the evolution of the surface topography. The ice-flow boundary conditions at the free surface are

which expresses that no stresses are imposed at the surface, i.e. the atmospheric pressure is neglected compared to the stresses in the ice. At the surface, the temperature T s is assumed to be a function of surface elevation and
If the bedrock temperature is below the melting point T melt , the heat-flow boundary condition at the base B = B(x) is

where Q geo is the geothermal heat flux. In this case, the ice-flow boundary conditions at the base are assumed to be
If the basal temperatures exceed a temperature of a few-degrees below T melt , this no-slip condition is too Strict, as sliding may occur at sub-freezing temperatures. No existing theory yet describes this sliding realistically (see discussion in Paterson (1994)). Here, basal sliding is neglected, as the basal temperatures of the model studies presented below were several degrees below Τ melt,. Boundary conditions for T > T melt are not of present interest in the model studies presented in this paper.
In this paper, only the flow close to an ice-sheet divide is examined. Therefore, boundary conditions must be specified at the vertical boundaries of the solution domain (Fig. 1). The following approach is applied (Waddington and others, 1986): simple flow conditions are assumed at the vertical boundaries. The error introduced by the difference between these profiles and the real flow conditions will propagate several ice thicknesses back into the solution domain. The solution domain is therefore extended. Once the flow has been modelled, only the flow in the original not the extended region can he considered. The horizontal ice-flow boundary condition is

where u m (x) is the depth-averaged horizontal velocity at the boundary obtained from a global mass-balance calculation, and n is the flow law exponent. The vertical ice flow boundary condition is

The shapes of Equations (21) and (22) correspond to those of “laminar flow” of isothermal ice (Paterson, 1994). Following Firestone and others (1990), the applied heal flux is assumed to be zero at the vertical boundaries, i.e. the horizontal temperature gradient is neglected. How far the effect from the boundary conditions can propagate back into the grid depends on the quality of these. With the boundary conditions in Equations (21) and (22), and coupled ice and heat flow, it is necessary to extend the grid 10–15 ice thicknesses (Hvidberg, 1993).
Numerical solution technique
The problem is formulated in terms of the velocity, pressure and temperature fields, together with an unknown surface topography. The finite-element model is based on the Galerkin method (Zienkiewicz and Taylor, 1989) and it consists of three sub-models: a surface-evolution sub-model, an ice-flow sub-model and a heat-flow sub-model. The model uses nine-node, two-dimensional, quadrilateral elements with a curved, isoparametric mapping. The temperature and velocity vary biquadratically within each element. The pressure varies bilinearly within each element. The ice-flow submodel uses 4 × 4 Gaussian quadrature and a standard Galerkin weighting. The heat-flow sub-model uses 3 × 3 Gaussian quadrature and optimized Petrov–Galerkin weighting.
The flow solution is found by an iterative procedure, which is formulated as a time evolution. At each time step, the surface is developed one time step and the corresponding ice-flow pattern is calculated, while the corresponding steady-state temperature field is calculated at longer time intervals. The iteration is continued until
Table 1.1 Table with parameters used in the model studies. The parameters reflect central Greenland conditions

the surface and flow solution have converged into a steady state. Initial fields are set up a priori from simple analytic profiles in order to speed up the iteration towards steady state. The initial surface is a Vialov profile (Paterson, 1994). Initial horizontal velocities are set up from Equation (21). The initial vertical velocities are derived from Equation (21) through the incompressibility equation. The emerging matrix equations are symmetric in plane flow but the required processing time is yet relatively high.
Symmetrical ice divides
Four symmetric ice divides have been modelled: a plane-flow ice divide and an axisymmetric ice dome, both under isothermal conditions and coupled thermomechanical conditions. The purpose of these experiments is to examine the thermomechanical conditions in the vicinity of the ice divide and to obtain insight into the effect of a third dimension. The isothermal models are included for comparison with previous ice-divide models. The models assume a horizontal bedrock topography, B(x) = 0, a constant geothermal heat flux and a uniform accumulation rate. Table 1 contains the model input. The profiles are symmetric and extend to about 20 ice thicknesses (70 km) to both sides of the divide, The models used 28 × 7 elements with a horizontal dimension from 100 m at the divide to 10 km at the sides. The solution can be used only within about ten ice thicknesses to each side of the divide. Closer to the vertical boundaries, the solution is influenced by the simple shape of the boundary conditions, as mentioned above.
The surface slopes (Fig. 2a) drop sharply at the divide, as the rounding appears within one ice thickness form the divide. This was also observed by Dahl-Jensen (1989b) and Szidarovsky and others (1989). The problem of the sharp drop of the slope has been recognized previously (e.g. Morland and Johnson, 1980; Raymond. 1983; Hutter and others, 1986; Hindmarsh and others, 1989) and is due to the use of Glen’s flow law (see discussion in Hutter (1993)). The plane-flow ice divide is steeper and narrower than the axisymmetric ice dome. The isothermal models have a sharper divide than the corresponding thermomechanical models due to the lower temperature in the basal layers. Basal temperatures are shown in figure 2b. In agreement with previous models, a basal “hot spot” is seen at the divide (Dahl-Jensen 1989a, b; Paterson and Waddington, 1986; Firestone and others, 1990), which is due to the rapid change of the vertical advection close to the divide (see Figure 4 below). The width of the zone with increased temperatures is two to three ice thicknesses, widest in the axisymmetric model. The three-dimensional effects do not influence the bottom temperature at the divide, only at downstream positions. The bottom shear stresses decrease rapidly close to the divide (Fig. 2c). The decrease occurs over two to three ice thicknesses, which is a wider divide zone than that of the surface slope. The surface longitudinal-stress deviator rises at the divide (Fig. 2d).

Fig. 2. Longitudinal variations of model results: Surface slope (a), basal temperatures (b), basal shear stress (c) and surface longitudinal-stress deviator (d). Dashed lines (A) are for the thermomechanical plane-flow model. Dotted lines (B) are for the thermomechanical axisymmetric flow model. Long-dashed lines (C) are for the isothermal plane-flow model. Chain-dashed lines (D) are for the isothermal axisymmetric flow model.
Normalized depth profiles at several locations of shear stress τ xz and longitudinal deviatoric stress σ′ x . (Fig. 3) and of velocity (Fig. 4) are shown for some of the models in order to see flow the shape of the profiles changes with distance from the divide. The plane-flow results are consistent with previous results for isothermal flow (Raymond, 1983; Reeh. 1988; for the divide) and for thermomechanical flow (Dahl-Jensen, 1989a; Szidarovsky and others, 1989). Generally, the shape of the profiles changes fast close to the divide but, as above, the zone with divide conditions is wider in axisymmetric flow than in plane flow. The profiles of vertical velocity display the greatest difference: in plane flow the zone with divide conditions is about one ice thickness wide, while in axisymmetric flow it is more than four ice thicknesses wide. The profiles of shear stress are different from the usual lineal variation, which is due to the rapid change of the longitudinal stress deviator near the divide. It is most pronounced in the thermomechanical model, due to the relatively warmer temperatures in the lower parts of the ice. The normalized shear stress approaches zero at the divide, contrary to the results of Dahl-Jensen (1989a).

Fig. 3. Depth profites of shear-stress and longitudinal-stress deviator for the plane isothermal flow model (a) and the plane thermomechanical flaw model (b). The profiles are shown for seven locations: 0, one-quarter, one-half, one, two, four and ten ice thicknesses from the divide. The profiles at the divide are for the limit of x → 0. The stresses are normalized, the shear stress with – ρg(S – B)∂S/∂x, and the longitudinal-stress deviator by the surface longitudinal-stress deviator σ′xS.

Fig. 4. Depth profiles of horizontal and vertical velocity components fir the isothermal axisymmetric flow model (a), the isothermal plane-flow model (b) and for the thermomechanical plane-flow model (c), at seven locations: 0, one-quarter, one-half, one, two, four and ten ice thicknesses from the divide. The profiles at the divide are for the limit of .e → 0. The profiles are normalized by the surface velocities.
Age–depth relations at the divide are identical for plane flow and axisymmetric flow (Fig. 5). The three-dimensional stresses do not alien the vertical velocity pattern at the divide, not even when downstream conditions of temperature and velocity are different. Away from the divide, the three-dimensional effects influence the flow pattern and the surface topography, implying that the course of the isochrones are different for plane flow and axisymmetric flow (Fig. 6a). The isochrones rise at the divide as found by Dahl-Jensen (1989b), the rise being sharpest in the plane-flow model. At the divide, the isochrones coincide and away from the divide the isochrones of the plane-flow model are found at depths greater than the corresponding isochrones of the axisymmetric flow model. The largest differences occur at about one to two ice thicknesses from the divide as a result of a wider zone with divide conditions in the axisymmetric model. To test the influence from a non-uniform accumulation rate, two models were set up with linearly varying accumulation rate between 0.2 m a−1 at the divide and 1.0 m a−1 at distances of 70 km from the divide and all other parameters as before. The resulting isochrones for these models are shown at figure 6b. Again, the isochrones coincide at the divide, downstream the isochrones differ and it is seen that divergent-flow conditions increase the effect from the accumulation-rate variation, which was also pointed out by Reeh (1989).

Fig. 5. Age–depth relations at the divide for the isothermal plane flow and axisymmetric models (both dotted lines) and the thermomechanical plane-flow and axisymmetric models (both full lines).

Fig. 6. The depth of eight selected isochrones (1, 2, 5, 10, 20, 50, 100 and 200 kyear) for the thermomechanical plane-flow model (full lines) and for the thermomechanical axisymmetric flow model (dotted lines). The models assume a uniform accumulation rate at 0.2 m a−1. (b) Same isochrones as in (a) for a thermomechanical plane-flow model (full lines) and a thermomechanical axisymmetric flow model (dotted lines). The models assume a linear varying accumultion rate between 0.2 m a−1 at the divide and 1.0 m a−1 at distances of 70 km from the divide. Other model parameters are as in (a).
Conclusion and discussion
A coupled ice- and heat-flow model is described, which models the flow of steady-state, plane and axisymmetric ice sheets. The model treats the general set of equations describing the coupled flow of ice and heal flow with a free surface by using a finite-element technique. The problem is formulated in terms of the fields of velocity, pressure and temperature, and an ice surface in balance with the unknown fields. The set of equations is decoupled, allowing three sub-models to be formed: an ice-flow model, a heat-flow model and a surface-evolution model. The solution is found by an iterative procedure between the sub-models, which is formulated as a time evolution.
The ice-divide region has been examined for domes displaying various degrees of divergence: a symmetric, plane-flow ice divide and an axisymmetric ice dome. Within a few ice thicknesses from the divide, the flow pattern and thermal conditions differ qualitatively from the conditions further downstream: the longitudinal strain rate is high, especially in the upper layers; the horizontal velocity and the shear stresses vanish; the vertical velocity is smaller than compared to the sides; due to the decreased downward transport of ice, the isochrones rise at the divide, and a “hot spot” is formed below the divide with temperatures several degrees warmer than at the sides. These results are all known from previous plane-flow models. Other results are:
Divergent-flow conditions only influence the conditions at downstream positions not at the divide. Divergent-flow conditions widen die ice-divide zone; with respect to the vertical velocity, it is about one ice thickness for plane flow but about 5 to 10 ice thicknesses for axisymmetric flow.
The age–depth relationship at the divide is independent of the three-dimensional stresses. The isochrones rise at the divide, most sharply with plane flow. With a uniform accumulation rate, the isochrones of the plane-flow model are found at greater depths than those of the axisymmetric model, with the largest differences at one to two ice thicknesses from the divide, Divergent-flow conditions increase the effect of upstream variations of the accumulation rate.
The model in its present form does not consider the three-dimensional set of equations, mainly because the required CPU time is yet relatively high and it would increase considerably. Furthermore, the model is a steady-state model. When realistic ice sheets are modelled, the three-dimensional structure of the bedrock, the accumulation rate pattern, etc. may be of great importance and transient effects must he considered. The climate conditions, expressed by temperature, precipitation, dust, etc. change with time and determine the transient variation of the ice thickness, flow pattern and temperature field. The historic variations of the climate conditions have an important effect on the present conditions in the large ice sheets, as expressed by, for example, the age–depth relation (Dahl-Jensen and Others, 1993) or the temperature field (Dahl-Jensen and Johnsen, 1986; Ritz, 1989). The model is partly capable of treating time-dependent conditions; the calculation of the free surface is formulated as a time evolution, while the thermal inertia of the underlying rock still needs to be included in the heat-flow part.
Acknowledgements
This work was funded by the Danish Natural Science Research Council. During the development of the model, I visited the University of Washington with support from the Danish Research Academy and the Glaciology Section, University of Copenhagen, I wish to thank the University of Washington Geophysics Program for hospitality during my visit and E. D. Waddington and C. F. Raymond for stimulating discussions. Special thanks are due to D. Dahl-Jensen for discussions and comments on the manuscript.









