No CrossRef data available.
Article contents
On the critical regularity of nilpotent groups acting on the interval: the metabelian case
Part of:
Low-dimensional dynamical systems
Smooth dynamical systems: general theory
Special aspects of infinite or finite groups
Published online by Cambridge University Press: 24 September 2024
Abstract
Let G be a torsion-free, finitely generated, nilpotent and metabelian group. In this work, we show that G embeds into the group of orientation-preserving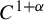 
$C^{1+\alpha }$-diffeomorphisms of the compact interval for all 
$\alpha < 1/k$, where k is the torsion-free rank of 
$G/A$ and A is a maximal abelian subgroup. We show that, in many situations, the corresponding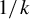 
$1/k$ is critical in the sense that there is no embedding of G with higher regularity. A particularly nice family where this happens is the family of 
$(2n+1)$-dimensional Heisenberg groups, for which we can show that the critical regularity is equal to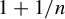 
$1+1/n$.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Bass, H.. The degree of polynomial growth of finitely generated nilpotent groups. Proc. Lond. Math. Soc. (3) 25 (1972), 603–614.CrossRefGoogle Scholar
Bergman, G.. Right-orderable groups that are not locally indicable. Pacific J. Math. 147 (1991), 243–248.CrossRefGoogle Scholar
Bonatti, C., Monteverde, I., Navas, A. and Rivas, C.. Rigidity for
${C}^1$
actions on the interval arising from hyperbolicity I: solvable groups. Math. Z. 286 (2017), 919–949.CrossRefGoogle Scholar
${C}^1$
actions on the interval arising from hyperbolicity I: solvable groups. Math. Z. 286 (2017), 919–949.CrossRefGoogle ScholarBrum, J., Matte Bon, N., Rivas, C. and Triestino, M.. Locally moving groups and laminar actions on the line. Preprint, 2024, arXiv:2104.14678.CrossRefGoogle Scholar
Calegari, D.. Nonsmoothable, locally indicable group actions on the interval. Algebr. Geom. Topol. 8 (2008), 609–613.CrossRefGoogle Scholar
Castro, G., Jorquera, E. and Navas, A.. Sharp regularity for certain nilpotent group actions on the interval. Math. Ann. 359(1–2) (2014), 101–152.CrossRefGoogle Scholar
Deroin, B., Klepstyn, V., Navas, A. and Parwani, K.. Symmetric random walks on
${\mathrm{Homeo}}_{+}\left(\mathbb{R}\right)$
. Ann. Probab. 41 (2013), 2066–2089.CrossRefGoogle Scholar
${\mathrm{Homeo}}_{+}\left(\mathbb{R}\right)$
. Ann. Probab. 41 (2013), 2066–2089.CrossRefGoogle ScholarDeroin, B., Kleptsyn, V. and Navas, A.. Sur la dynamique unidimensionnelle en régularité intermédiaire. Acta Math. 199(2) (2007), 199–262.CrossRefGoogle Scholar
Deroin, B., Navas, A. and Rivas, C.. Groups, orders, and dynamics. Preprint, 2016, arXiv:1408.5805.Google Scholar
Farb, B. and Franks, J.. Groups of homeomorphisms of one-manifolds III: Nilpotent subgroups. Ergod. Th. & Dynam. Sys. 23 (2003), 1467–1484.CrossRefGoogle Scholar
Guivarc’h, Y.. Croissance polynomiale et périodes des fonctions harmoniques. Bull. Soc. Math. France 101 (1973), 333–379.CrossRefGoogle Scholar
Jorquera, E.. A universal nilpotent group of
${C}^1$
diffeomorphisms of the interval. Topology Appl. 159 (2012), 2115–2126.CrossRefGoogle Scholar
${C}^1$
diffeomorphisms of the interval. Topology Appl. 159 (2012), 2115–2126.CrossRefGoogle ScholarJorquera, E., Navas, A. and Rivas, C.. On the sharp regularity for arbitrary actions of nilpotent groups on the interval: the case of
${N}_4$
. Ergod. Th. & Dynam. Sys. 38 (2018), 180–194.CrossRefGoogle Scholar
${N}_4$
. Ergod. Th. & Dynam. Sys. 38 (2018), 180–194.CrossRefGoogle ScholarKim, S. H. and Koberda, T.. Diffeomorphism groups of critical regularity. Invent. Math. 221(2) (2020), 421–501.CrossRefGoogle Scholar
Kim, S. H. and Koberda, T.. Structure and Regularity of Group Actions on One-Manifolds (Springer Monographs in Mathematics). Springer, Cham, 2021.CrossRefGoogle Scholar
Kim, S. H., Koberda, T. and Rivas, C.. Direct products, overlapping actions and critical regularity. J. Mod. Dyn. 17 (2021), 285–304.CrossRefGoogle Scholar
Kopell, N.. Commuting diffeomorphisms. Global Analysis (Berkeley, CA, 1968) (Proceedings of Symposia in Pure Mathematics, XIV). Ed. Chern, S.-s. and Smale, S.. American Mathematical Society, Providence, RI, 1970, pp. 165–184.Google Scholar
Mann, K. and Wolff, M.. Reconstructing maps out of groups. Ann. Sci. Éc. Norm. Supér. (4) 56(4) (2023), 1135–1154.Google Scholar
Navas, A.. A finitely generated, locally indicable group with no faithful action by
${C}^1$
diffeomorphisms of the interval. Geom. Topol. 14 (2010), 573–584.CrossRefGoogle Scholar
${C}^1$
diffeomorphisms of the interval. Geom. Topol. 14 (2010), 573–584.CrossRefGoogle ScholarNavas, A.. Groups of Circle Diffeomorphisms (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 2011.CrossRefGoogle Scholar
Parkhe, K.. Nilpotent dynamics in dimension one: structure and smoothness. Ergod. Th. & Dynam. Sys. 36 (2016), 2258–2272.CrossRefGoogle Scholar
Pixton, D.. Nonsmoothable, unstable group actions. Trans. Amer. Math. Soc. 229 (1977), 259–268.CrossRefGoogle Scholar
Plante, J. and Thurston, W.. Polynomial growth in holonomy groups of foliations. Comment. Math. Helv. 51 (1976), 567–584.CrossRefGoogle Scholar
Rivas, C. and Triestino, M.. One dimensional actions of Higman’s group. Discrete Anal. (2019), Paper No. 20.Google Scholar
Robinson, D. J. S.. A Course in the Theory of Groups (Graduate Texts in Mathematics, 80), 2nd edn. Springer-Verlag, New York, 1996.CrossRefGoogle Scholar
Thurston, W.. A generalization of the Reeb stability theorem. Topology 13 (1974), 347–352.CrossRefGoogle Scholar
Tsuboi, T.. Homological and dynamical study on certain groups of Lipschitz homeomorphisms of the circle. J. Math. Soc. Japan 47 (1995), 1–30.CrossRefGoogle Scholar