Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-11T01:33:10.184Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear and unbalanced urn models with two types of strategies: a stochastic approximation point of view

Published online by Cambridge University Press:  20 May 2022

Soumaya Idriss Open the ORCID record for Soumaya Idriss [Opens in a new window]
Soumaya Idriss*
Affiliation:
University of Monastir, Monastir, Tunisia. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we treat a nonlinear and unbalanced 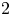$2$-color urn scheme, subjected to two different nonlinear drawing rules, depending on the color withdrawn. We prove a central limit theorem as well as a law of large numbers for the urn composition. We also give an estimate of the mean and variance of both types of balls.

Keywords

Discrete-time martingalesLimit theoremsReinforced processesStochastic approximation theoryUrn models
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 37 , Issue 3 , July 2023 , pp. 711 - 729
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aguech, R. & Selmi, O. (2019). Unbalanced multi-drawing urn with random addition matrix. Arab Journal of Mathematical Sciences 26(1/2): 57–74.CrossRefGoogle Scholar
Aguech, R., Lasmar, N., & Selmi, O. (2019). A generalized urn with multiple drawing and random addition. Annals of the Institute of Statistical Mathematics 71: 389–408.Google Scholar
Bagchi, A. & Pal, A.K. (1985). Asymptotic normality in the generalized Pólya-Eggenberger urn model, with an application to computer data structures. Siam Journal on Algebraic and Discrete Methods 6(3): 394–405.10.1137/0606041CrossRefGoogle Scholar
Bai, Z.-D. & Hu, F. (1999). Asymptotic theorems for urn models with nonhomogeneous generating matrices. Stochastic Processes and their Applications 80(1): 87–101.10.1016/S0304-4149(98)00094-5CrossRefGoogle Scholar
Bai, Z.-D., Hu, F., & Shen, L. (2002). An adaptive design for multi-arm clinical trials. Journal of Multivariate Analysis 81(1): 1–18.10.1006/jmva.2001.1987CrossRefGoogle Scholar
Chauvin, B., Mailler, C., & Pouyanne, N. (2015). Smoothing equations for large Pólya urns. Journal of Theoretical Probability 28(3): 923–957.CrossRefGoogle Scholar
Chen, M.R. & Kuba, M. (2013). On generalized Pólya urn models. Journal of Applied Probability Theory 50(4): 1169–1186.CrossRefGoogle Scholar
Chen, M.R. & Wei, C.Z. (2005). A new urn model. Journal of Applied Probability 42(4): 964–976.CrossRefGoogle Scholar
Eggenberger, F. & Pólya, G. (1923). Uber die Statistik verketer Vorgiinge. Journal of Applied Mathematics and Mechanics 3(1): 279–289.Google Scholar
Friedman, B. (1949). A simple urn model. Communications on Pure and Applied Mathematics 2(1): 59–70.10.1002/cpa.3160020103CrossRefGoogle Scholar
González-Navarrete, M. & Lambert, R. (2019). Urn models with two types of strategies. Preprint arXiv:1708.06430.Google Scholar
Idriss, S. (2021). Nonlinear unbalanced urn models via stochastic approximation. Methodology and Computing in Applied Probability: 1573–7713, doi:10.1007/s11009-021-09858-6Google Scholar
Janson, S. (2006). Limit theorems for triangular urn schemes. Probability Theory and Related Fields 134(3): 417–452.10.1007/s00440-005-0442-7CrossRefGoogle Scholar
Janson, S. (2020). Mean and variance of balanced Pólya urns. Advances in Applied Probability 52(4): 1224–1248.10.1017/apr.2020.38CrossRefGoogle Scholar
Janson, S. (2021). Functional limit theorem for multitype branching processes and generalized Pólya urns. Stochastic Processes and their Applications 110: 177–245.CrossRefGoogle Scholar
Kuba, M. & Mahmoud, H. (2017). Two-color balanced affine urn models with multiple drawings. Advances in Applied Mathematics 90: 1–26, doi:10.1016/j.aam.2017.04.004CrossRefGoogle Scholar
Laruelle, S. & Pagès, G. (2013). Randomized urn models revisited using stochastic approximation. The Annals of Applied Probability 23(4): 1409–1436.CrossRefGoogle Scholar
Laruelle, S. & Pagès, G. (2019). Nonlinear randomized urn models: a stochastic approximation viewpoint. Electronic Journal of Probabiity 24: 1–47.Google Scholar
Lasmar, N., Mailler, C., & Selmi, O. (2018). Multiple drawing multi-colour urns by stochastic approximation. Journal of Applied Probability 55(1): 254–281.CrossRefGoogle Scholar
Mahmoud, H. (2008). Pólya urn models. Orlando: Chapman-Hall.10.1201/9781420059847CrossRefGoogle Scholar
Mahmoud, H. (2021). Covariances in Pólya urn schemes. Probability in the Engineering and Informational Sciences: 1–12. doi:10.1017/S0269964821000450Google Scholar
Renlund, H. (2010). Generalized Pólya urns via stochastic approximation. Preprint arXiv:1002.3716v1.Google Scholar
Renlund, H. (2011). Limit theorem for stochastic approximation algorithm. Preprint arXiv:1102.4741v1.Google Scholar
Robbins, H. & Monro, S. (1951). A stochastic approximation method. Annals of Mathematical Statistics 22: 400–407.10.1214/aoms/1177729586CrossRefGoogle Scholar
Smythe, R. (1996). Central limit theorems for urn models. Stochastic Processes and Their Applications 65: 115–137.CrossRefGoogle Scholar